Panel Surface Area Maximization for Increasing PV Performance

1. Introduction To Solar Panel Technology

Solar energy is a form of renewable energy derived from sunlight. Since there are no greenhouse gases produced throughout the process and fewer materials that could cause pollution are used, it is therefore considered the cleanest type of renewable energy. Research and technological advancements are also driving growth in the renewable energy sector. Solar energy can be considered a basic human need that can be processed into secondary forms such as heat, light, and electricity. Solar panels are a medium for converting solar energy into electricity using photovoltaic materials. This system is widely used in many fields, such as for home use [1], in the space-based fused deposition modelling (FDM) 3D printer powered by solar photovoltaics [2], in solar-powered vehicles [3], etc. This is generally because it is easily engineered, ecologically friendly, and can reduce consumer dependence on state power companies. Despite advancements in technology, the most significant problem in the solar energy system is the rate at which sunlight is absorbed by the solar panel. The amount of sunshine that the solar panel absorbs determines the amount of electricity that it can generate.

The relationship between sunlight energy and solar panel design needs to be studied in order to increase the absorption rate of sunlight energy into the solar panel. The simplest example of ensuring that a solar panel absorbs sunlight is by considering the angle of installation [4,5], the best angle for solar panel installation is important to consider for maximum energy production. Other than the angle, solar panel design also covers the types and sizes of solar panels and solar panel components. Different types of solar panels work perfectly in the same or different aspects. Solar panel components mainly determine the lifespan of the panels. Proper solar panel components can increase the absorption of sunlight's energy and the longevity of the solar panels. For the installation, after studying the relationship of solar panel design to sunlight energy absorption, the angle will be chosen by considering the environmental aspect and electricity requirements.

Many high-quality solutions are providing high solar yields in places such as shadow areas or non-optimal spatial conditions. Currently, the standard installation angle of solar panel is placed completely perpendicular to the ground, but at low latitudes, such as the equator, this stereotype is sometimes not correct.

Visa et al. [6] designed an optimum solar thermal absorber for facade integration. The collector's isosceles trapeze design allows for a multi-coloured absorption panel.They investigated inside in steady-state settings which revealed an approximate performance of 62.38%, whereas outdoor initial examination yielded a collector performance of 62%.

Cox et al. [7] investigate many potentially beneficial characteristics in the conceptualization of photovoltaic/thermal (PV/T) devices to establish their efficacy and interaction. Their research centred on air-type collectors with single-crystalline silicon photovoltaic cells. That focuses on two major areas: improving solar absorptance and decreasing infrared emittance. The simulation results were then stated as follows. When combined with a gridded-back cell, a selective absorber affects thermal efficiency for PV cells that cover more than about 65% of the total collector area. The low emissivity coating required an infrared radiation emissivity of below 0.25 and a solar the transmissivity of at least 0.85. The best combination for airborne PV/T was determined to be gridded-back PV cells, a nonselective tertiary absorber, and a high-trans-emissivity/low-emissivity covering across the photovoltaic cells.

A computational model aiming at optimising the layout of polymer solar collectors with flat plates by Do Ango et al [8] revealed that solar energy absorbers are often constructed of copper or aluminium, and while they provide excellent efficiency, they are also expensive. In contrast, utilising polymer can increase the financial viability of solar collectors. They presented a numerical assessment of an innovative solar power collector construction to determine how the design variables (air gap thickness, collector length) and operational variables (mass flow rate, incident solar energy, inlet temperature) affect efficiency. Their research showed the major trends in the key parameters that influence the efficiency of polymer flat plate solar collectors.

Solar energy is one of the most important renewable energy sources for many settings, such as households, solar-powered vehicles, power grid support, offshore solar energy, etc. However, the amount of solar energy produced is directly proportional to the surface area of the solar panel exposed to the sun rays, and so the challenges arise for the space required to install solar panels in order to get maximum area coverage of sun radiation energy absorption in constricted spaces such as vehicles powered by solar or small residential apartments, etc. The challenges with solar energy are that once a plate is installed, the space under it or above it cannot be used for another solar panel installation. This is due to the fact that the shadow cast by the above solar panel or structure prevents sun rays from reaching the below solar panel. The introduction of flexible solar panels that can take on any shape has given us the opportunity to explore the possibility of maximising solar plate surface area using surface manifold techniques. In this optimisation study, the constraint is that we have a space with fixed dimensions (length, width, and height), and the objective is to maximise the top surface area of the panel within the given dimensions to maximise solar panel surface for sun energy absorption.

2. Surface Manifold Hypothesis

In this, the use of surface topology optimisation to maximise the surface area of solar PV panel is proposed. This is possible due to the introduction of thin fabric printable and foldable solar panels such as the one that was recently developed by MIT researcher “Paper-thin solar cells can turn any surface into a power source” [9]. See figure 1 below of the sample thin solar cells, which can be folded to take up a surface manifold, hence maximising the size of the solar panel surface for maximum energy absorption area coverage.

Figure 1. Shows Thin Fabric printable solar cells which can be folded in any shape

Figure 1. Shows Thin Fabric printable solar cells which can be folded in any shape

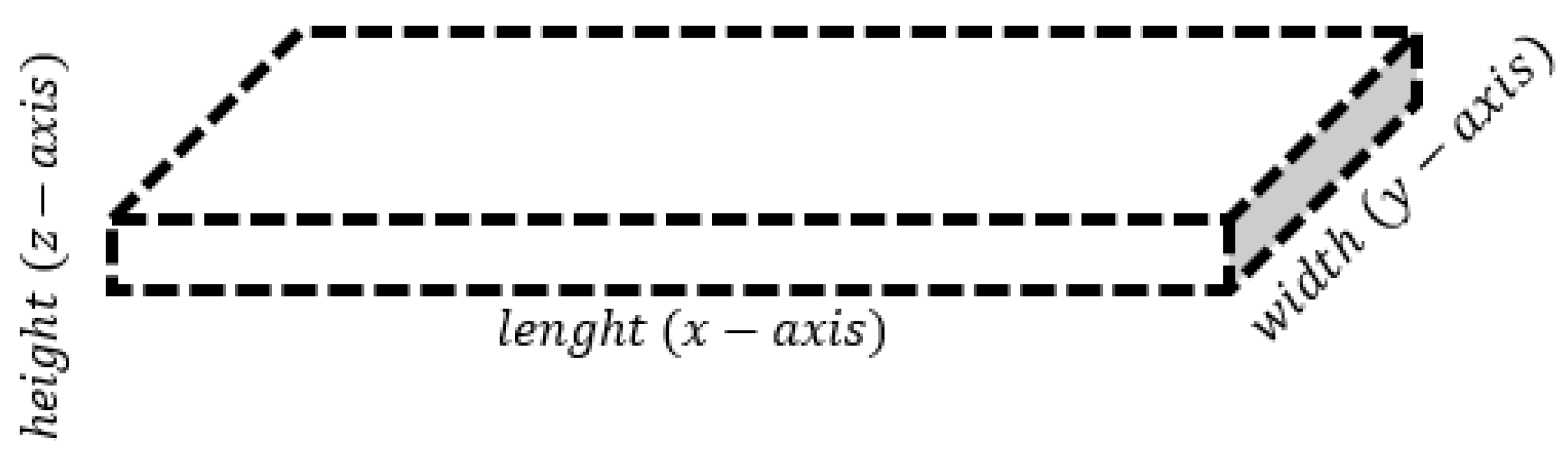
Problem Definition: Given a constricted space (frame) shown below figure 2 whose length, width, and height are fixed, design a panel that can fit in such a space with maximum top surface area:

Figure 2. Dimension of flat PV Panel before performing surface manifold

Figure 2. Dimension of flat PV Panel before performing surface manifold

From article [10], it is known that the formulae for calculating power output of solar panel is given as (1) below:

$$P=\eta V_m\left(t\right)I_m\left(t\right)$$

(1)

Where $P$ is the maximum power produced by solar panel having $\eta$ number of solar modules, and maximum voltage $V_m$ and maximum current $I_m$ over time $t$.

If we maximise the surface area of the panel, more modules can fit in the same panel, and that means more power can be produced by the same solar panel occupying the same space with the given fixed dimensions.

2.1. Curving Surface (along x-axis)

In this type of surface manifold, one side of the plate i.e. $x-axis$ is curved using either wavy (2) or zigzag (3) curve see figure 3. However, $y-axis$ is left straight (uncurved). $\lambda$ is the wave length, $\delta$ is the wave amplitude, this is an extension of zigzag and wavy line in article [11] but this is in 3D surface.

$$f\left(x\right)=\frac{\delta }{4}\cos \left(\frac{2\pi x}{\lambda }\right)$$

(2)

$$f\left(x\right)=\frac{\delta }{2\pi }{\cos }^{-1}\left(\cos \left(\frac{2\pi x}{\lambda }\right)\right)$$

(3)

To find the surface area of the above (2) and (3), see (4).

$$S=\left(y_2-y_1\right){\int }_{x_1}^{x_2}\sqrt{1+{\left(\frac{df\left(x\right)}{dx}\right)}^2} dx$$

(4)

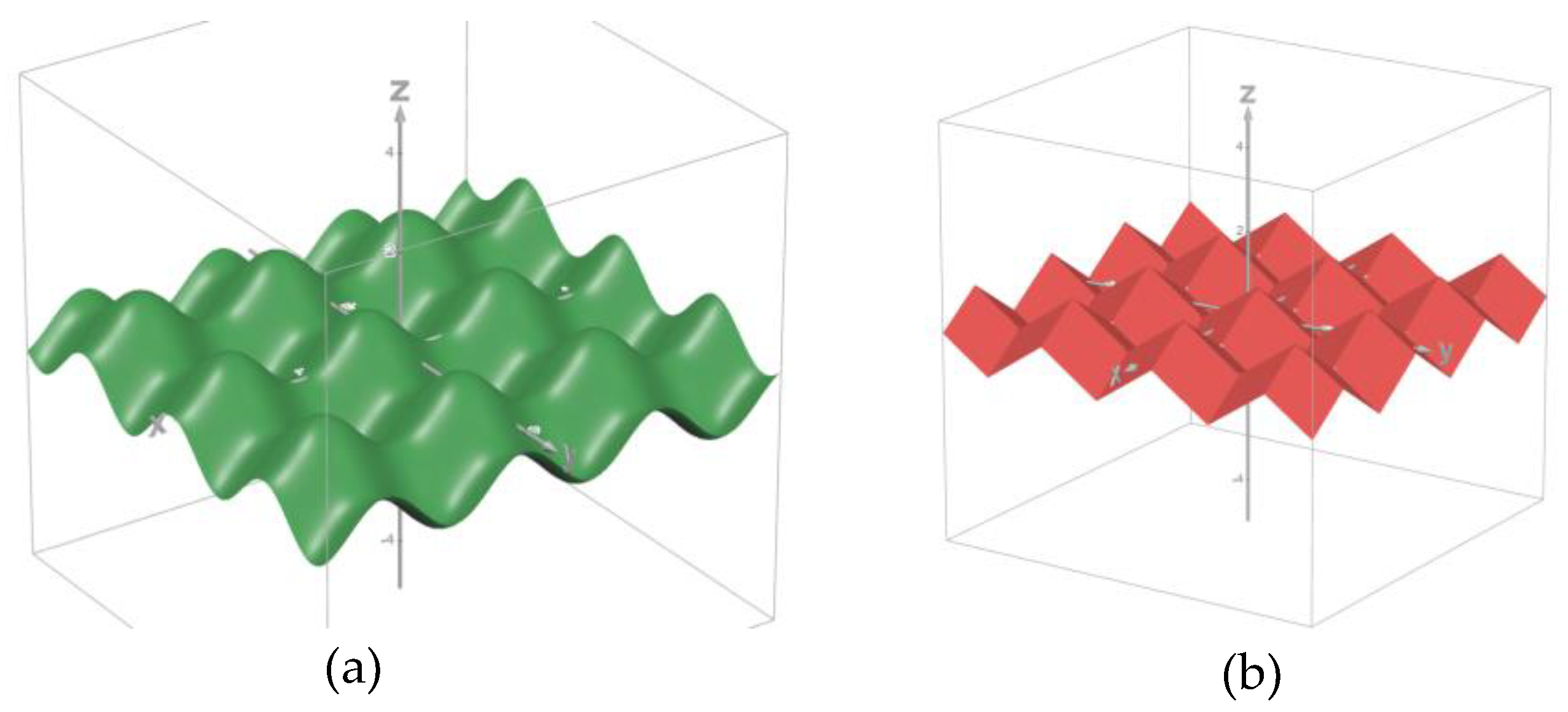
Figure 3. Folded surface along x-axis (a) is Zigzag surface from (3) and (b) is wavy surface from (2).

Figure 3. Folded surface along x-axis (a) is Zigzag surface from (3) and (b) is wavy surface from (2).

2.2. Curving Surface (along x-axis, and y-axis)

Another approach is to extend the above curve surface from the x-axis only to both x-axis and y-axis. See equations (5) and (6).

$$f\left(x,y\right)=\frac{\delta }{4}\left(\sin \left(\frac{2\pi }{\lambda }x\right)+\sin \left(\frac{2\pi }{\lambda }y\right)\right)$$

(5)

$$f\left(x,y\right)=\frac{\delta }{2\pi }\left({\sin }^{-1}\left(\sin \left(\frac{2\pi }{\lambda }x\right)\right)+{\cos }^{-1}\left(\cos \left(\frac{2\pi }{\lambda }y\right)\right)\right)$$

(6)

Figure 4. (a) Wavy Surface using equation (5) and (b) Zigzag Surface using equation (6)

Figure 4. (a) Wavy Surface using equation (5) and (b) Zigzag Surface using equation (6)

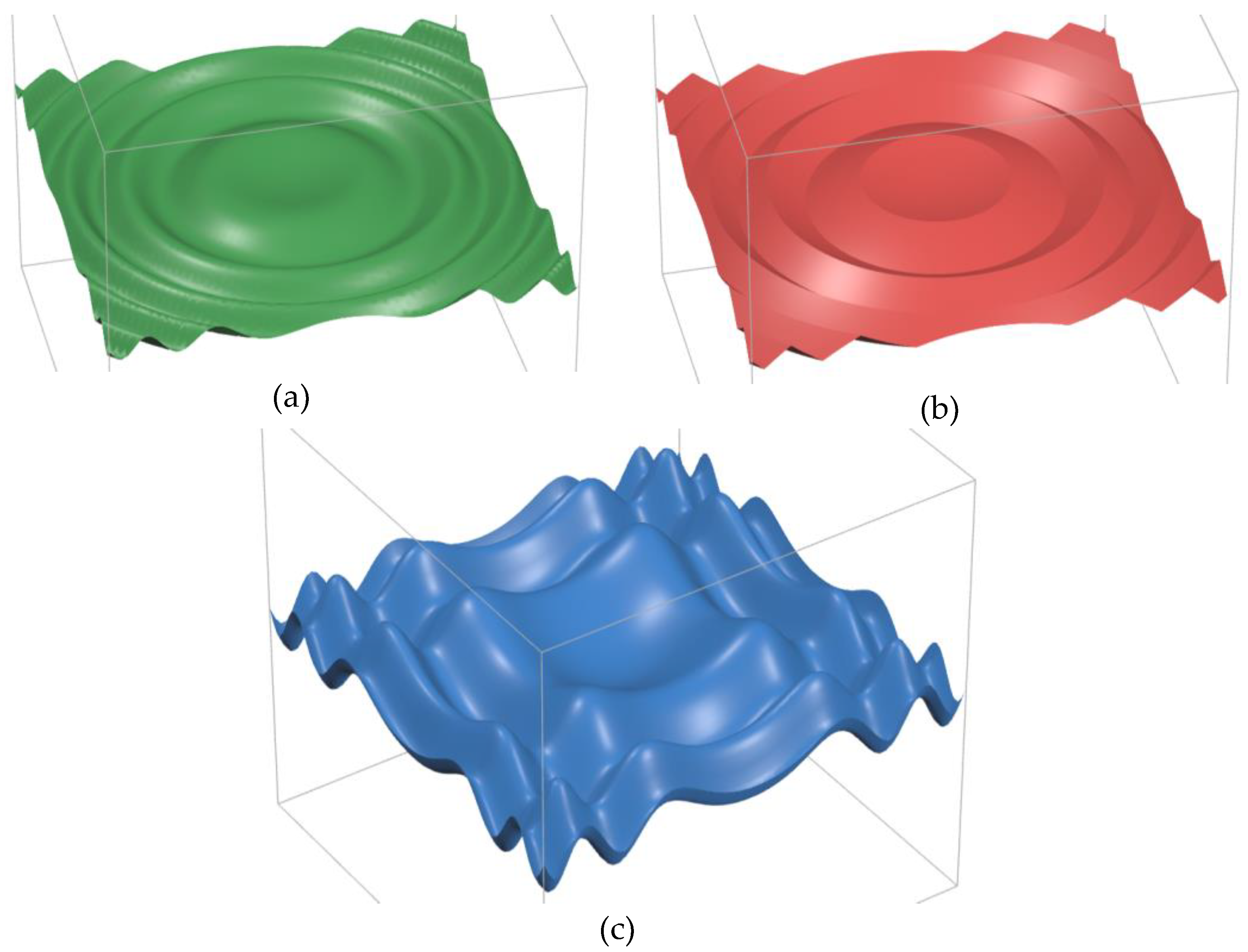
Furthermore, we can use the ripple concept to generate a circular wave (7), a circular zigzag (8), or a rectangular wavy surface like in (9) to produce another surface manifold. $p$ is a constant value for modifying the surface in equation (9).

$$f\left(x,y\right)=\frac{\delta }{4}\left[\sin \left(\frac{2\pi }{\lambda }\left[x^2+y^2\right]\right)+\sin \left(\frac{2\pi }{\lambda }\left[x^2+y^2\right]\right)\right]$$

(7)

$$f\left(x,y\right)=\frac{\delta }{2\pi }\left[{\sin }^{-1}\left(\sin \left(\frac{2\pi }{\lambda }\left[x^2+y^2\right]\right)\right)+{\sin }^{-1}\left(\sin \left(\frac{2\pi }{\lambda }\left[x^2+y^2\right]\right)\right)\right]$$

(8)

$$f\left(x,y\right)=\frac{\delta }{4}\left[\cos \left(\frac{2\pi }{\lambda }[x^2+p]\right)+\cos \left(\frac{2\pi }{\lambda }{[y}^2+p]\right)\right]$$

(9)

Figure 5. (a) Circular Wavy Ripple Plate from Equation (7); (b) Circular Zigzag Ripple Plate from Equation (8); and (c) Rectangular Wavy Ripple from Equation (9).

Figure 5. (a) Circular Wavy Ripple Plate from Equation (7); (b) Circular Zigzag Ripple Plate from Equation (8); and (c) Rectangular Wavy Ripple from Equation (9).

The surface area of the above surface manifold produced by curving along the x and y- axes can be obtained by using the below equation (10). This solution can be obtained numerically using MATLAB or any other numerical solver.

$$S={\int }_{x_1}^{x_2}{\int }_{y_1}^{y_2}\sqrt{1+{\left(\frac{d}{dx}f\left(x,y\right)\right)}^2+{\left(\frac{d}{dy}f\left(x,y\right)\right)}^2}dxdy$$

(10)

Since we have defined our equation using sin(x) and cos(x), to determine which of these produces longer length either sin(x) or cos(x) function, let’s find the length of curves produced by the two functions using equation (11). Given that $x_1=0, x_2=3$ so for $f\left(x\right)=\mathrm{s}\mathrm{i}\mathrm{n}\left(x\right)$ and $f\left(x\right)=\mathrm{c}\mathrm{o}\mathrm{s}\left(x\right)$.

$$l={\int }_{x_0}^{x_2}\sqrt{1+{\left(\frac{d}{dx}f\left(x\right)\right)}^2}dx$$

(11)

Solving the equation (11), the result shows that the length for sin(x) is 3.6203 and for cos(x) is 3.6781.

The following conclusion is made: cos(x) provides more curve surface than its counterpart sin(x). So, throughout this text, cos(x) can be used instead of sin(x) for an optimal surface manifold where those functions are applied.

2.3. Protruding Shapes on the Panel Surface

a) Cone Shape:

Given that the surface area of a cone is given as $S=\pi r\sqrt{r^2+h^2}$, and the supposed total number of cones that can fit inside a given plate surface is $n$, therefore the total surface area of the panel plus the protruding cones is given as: -

$$S=\left(\left(x_2-x_1\right)\left(y_2-y_1\right)-n\pi r\left[r-\sqrt{r^2+h^2} \right]\right)$$

(12)

b) Pyramidal shape:

In this way, the surface of the panel can be protruded with many pyramidal shapes, as shown in Figure 6 below.

$$S=2a\sqrt{{\left(\frac{a}{2}\right)}^2+h^2}$$

(13)

Figure 6. Square base Pyramidal Shape

Figure 6. Square base Pyramidal Shape

For comparison of the pyramidal surface area with cone shape and hemisphere shape, the pyramidal with a square base whose side length “a” is obtained from circle base of the cone and hemisphere whose radius is $r$, so side of the square base of the pyramid is $a=r\sqrt{\pi }$. This ensure that all have same base area occupied.

Total surface area of the panel’s top part surface with $n$ given number of pyramidal shapes is.

$$S=\left(\left(x_2-x_1\right)\left(y_2-y_1\right)-na\left[a-2\sqrt{{\left(\frac{a}{2}\right)}^2+h^2} \right]\right)$$

(14)

c) Hemisphere:

Curve Surface area of a hemisphere without base area is given as $2\pi r^2$. Therefore, the surface area of the panel with $n$ given number of hemispheres protruding out of its surface is given as.

$$S=\left(x_2-x_1\right)\left(y_2-y_1\right)+n\pi r^2$$

(15)

3. Geometry Surface Area Analysis.

Given that the panel dimensions coordinates are $x_1=0, x_2=30$ and $y_1=0, y_2=30$ and height $\delta =2$. For the surface area for circular plate in figure 7 (a) and (b), the radius $r=30$ and same height.

Table 1. Shows Comparison of some selected shape surface area having same base area.

Radius(m)	Height(m)	Base (S)	Pyramidal (S)	Hemisphere (S)	Cone (S)
4	4	50.26548	75.78660	100.53096	71.08612
2	4	12.56637	31.01872	25.13274	28.09925
4	2	50.26548	57.71365	100.53096	56.19851
1	1	3.14159	4.73666	6.28318	4.44288
2	2	12.56637	18.94665	25.13274	17.77153
3	3	28.27433	42.62996	56.54866	39.98594
4	4	50.26548	75.78660	100.53096	71.08612
5	5	78.53981	118.41657	157.07963	111.07207
6	6	113.09733	170.51986	226.19467	159.94378

Table 1. Shows Comparison of some selected shape surface area having same base area.

Radius(m)	Height(m)	Base (S)	Pyramidal (S)	Hemisphere (S)	Cone (S)
4	4	50.26548	75.78660	100.53096	71.08612
2	4	12.56637	31.01872	25.13274	28.09925
4	2	50.26548	57.71365	100.53096	56.19851
1	1	3.14159	4.73666	6.28318	4.44288
2	2	12.56637	18.94665	25.13274	17.77153
3	3	28.27433	42.62996	56.54866	39.98594
4	4	50.26548	75.78660	100.53096	71.08612
5	5	78.53981	118.41657	157.07963	111.07207
6	6	113.09733	170.51986	226.19467	159.94378

To determine the surface area of the sample geometry discussed above, sample geometry design was performed in ANSYS SpaceClaim and Design modular as shown in figure 7 below, and by using the available function to find the surface area of each geometry as shown in table 2. This helps overcome the troublesome process of solving equation (9) to find the surface area of the given equations, some of which have complex parts.

Figure 7. shows, from (a) to (g), different surface manifolds for increasing the surface area of the given Plate designed using ANSYS Space-Claim and Design Modular

Figure 7. shows, from (a) to (g), different surface manifolds for increasing the surface area of the given Plate designed using ANSYS Space-Claim and Design Modular

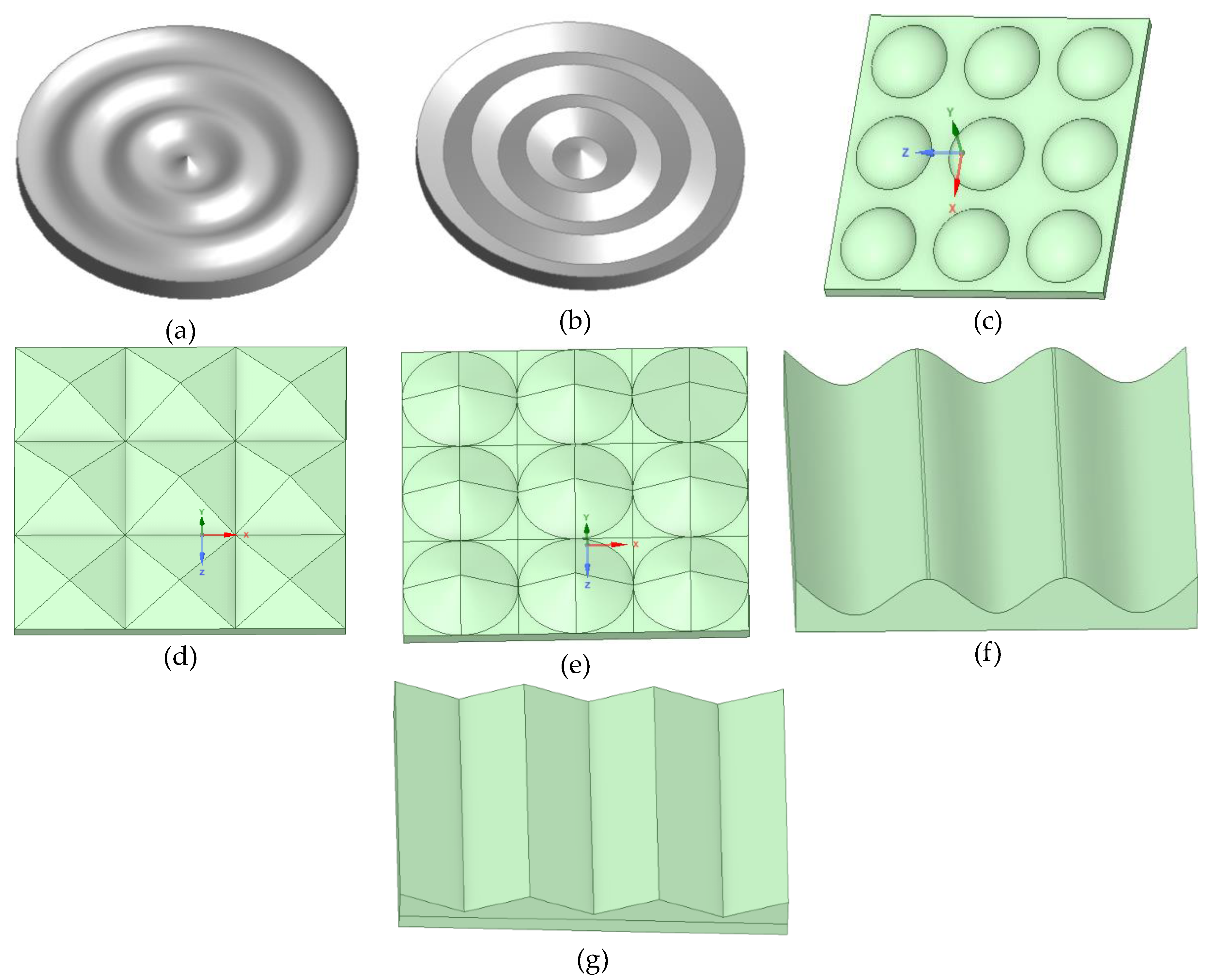
Table 2. shows the sample curve and protruding surface of a panel and their surface area, plus the percentage increase in surface area from Figure 7.

Shape	Base Area	Folded Area	Surface increase	Percentage
Circular wavy (a)	2827.43339	3402.1	574.666	20.33%
Circular zigzag (b)	2827.43339	3046.2	218.7666	7.74%
Square x-axis wavy (f)	900	984.6933	84.6933	9.41%
Square x-axis Zigzag (g)	900	969.3297	39.6276	7.7%
2/5 of Hemisphere (c)	900	1013.0973	134.3032	12.57%
Pyramidal (d)	900	969.7251	69.7251	7.75%
Cone (e)	900	954.4514	54.4514	6.05%

Table 2. shows the sample curve and protruding surface of a panel and their surface area, plus the percentage increase in surface area from Figure 7.

Shape	Base Area	Folded Area	Surface increase	Percentage
Circular wavy (a)	2827.43339	3402.1	574.666	20.33%
Circular zigzag (b)	2827.43339	3046.2	218.7666	7.74%
Square x-axis wavy (f)	900	984.6933	84.6933	9.41%
Square x-axis Zigzag (g)	900	969.3297	39.6276	7.7%
2/5 of Hemisphere (c)	900	1013.0973	134.3032	12.57%
Pyramidal (d)	900	969.7251	69.7251	7.75%
Cone (e)	900	954.4514	54.4514	6.05%

4. Discussion

Although having a curved surface increases the surface area of a given plate and maximises solar energy output, it should be noted that the solar plate angle of inclination to the source of solar energy (the sun) for maximum energy output varies, but mostly solar rays from the sun should be perpendicular to the plate surface, i.e., 90^o.

This presents a problem with the proposed method in that, due to the curving surface, some parts of the curved surface, even if the entire solar plate is set facing the sun directly, some part of the curved surface will be at a tilted angle to the sun rays, which may cause reflection and cast shadows on the neighbouring curve surface parts, which reduces energy absorption. This, however, needs to be tested practically.

A protruding surface with a sharp pointing surface may not be good because it can be prone to breakage when hit, for instance, cone, pyramidal, or zigzag curve surface manifold. So, a gentle, curved protruding surface is a better choice, such as a hemisphere, wavy curves, etc.

5. Conclusion

A solar panel with a surface manifold can have an increased surface area of up to more than 20% of its original flat surface area, depending on the chosen curvation method and setting. This increases its surface area of coverage for absorbing sunlight energy, resulting in an increase in overall solar panel performance.

However, this work does not cover how this surface manifold affects solar energy absorption with respect to the angle of solar panel inclination to sun radiation, as it is known that a panel with a surface manifold, even if it faces the sun directly, the protruding parts on the surface may be inclined to the sun rays even if the whole panel is tilted facing the sun directly. Future work extensions will cover this anticipated drawback plus experimental details to verify the concept in detail.

6. Future Extension

In this article, the only focus is to find a way to increase the surface area of a solar panel using surface manifold techniques. However, further extensive studies, specifically experimental ones, need to be performed to examine the effect of different surface manifolds (the degree of curving of the solar panel surface) on the power output performance of a solar panel. The angle of inclination of the surface, the overall solar panel, and many more.

Note:

This work should not be regarded as finished because it is only a notion that has been suggested and has not been tested (via simulation or experimentation).