An $E_8 \otimes E_8$ Unification of the Standard Model with Pre-Gravitation, on an Exceptional Lie algebra - Valued Space

1. Underlying Motivation for the Present Approach to Unification

Quantum field theory, and the standard model of particle physics, are usually formulated on a classical background spacetime which obeys the laws of classical general relativity. The presence of a classical spacetime in quantum theory should be treated as an approximation, even at energy scales much lower than Planck energy scale, such as the scales accessible to present day accelerators. This is because the presence of a classical spacetime requires that the universe must be dominated by classical material bodies such as stars and galaxies. In the absence of such bodies, only microscopic quantum systems will be present, and then it is a consequence of the Einstein hole argument that the underlying spacetime manifold (with its point structure) cannot be operationally defined. This is because operational distinguishability of spacetime points requires that the spacetime be overlaid by a classical metric. But such a classical metric cannot in general be produced by quantum matter sources, because the latter obey the quantum superposition principle and are delocalised, unlike classical material bodies.

It can therefore be convincingly argued that the assumption of a classical spacetime pre-assumes the dominant existence of classical systems in the universe. This statement is independent of the energy scale under consideration. Now, classical material bodies are a limiting case of quantum systems, which obey the laws of quantum field theory. Therefore the current formulation of quantum field theory and of the standard model of particle physics on a classical spacetime background is an approximation. There must exist a reformulation of quantum field theory, even at low energies, which does not depend on classical spacetime. Our attempt to arrive at such a reformulation also turns out to be a guide to a quantum theory of gravity, and to a unification of the standard model with gravitation.

In the search for such a reformulation, three new aspects must be necessarily addressed. Firstly, there should be a dynamics more general than quantum field theory, which can potentially be made free of classical spacetime. The theory of trace dynamics [1,2] developed by Stephen Adler and collaborators is a possible candidate for such a dynamics. This is a matrix valued Lagrangian dynamics on classical Minkowski spacetime, which possesses a novel conserved charge known as the Adler-Millard charge, which makes it a precursor of quantum field theory. Trace dynamics is assumed to hold at time scales of the order of Planck time, and the statistical thermodynamics of this theory leads to emergence of quantum field theory at time scales much larger than Planck time.

Secondly, there should be a means to incorporate gravitation in trace dynamics, in a manner independent of spacetime and its accompanying metric. In this we have been guided by the noncommutative geometry programme of Connes and collaborators, and the attendant spectral action principle [3]. The spectral action principle casts the action for general relativity and Yang-Mills gauge fields in terms of the eigenvalues of the Dirac operator, and these eigenvalues play the role of dynamical variables, as an alternative to the metric and to the gauge field vector potentials. In order to incorporate gravitation into trace dynamics, these eigenvalues are raised to the status of operators, one operator per eigenvalue. A Lagrangian is constructed from the trace of these operators, and incorporates pre-gravitation, Yang-Mills gauge degrees of freedom, and chiral fermions in a unified manner. The Lagrangian defines an ‘atom of space-time-matter’ (an STM atom) and the fundamental universe is made of enormously many copies of such STM atoms. Subsequent to the big bang event, a quantum-to-classical transition precipitates a symmetry breaking that gives rise to our present symmetry broken universe.

Thirdly, one must give up on the classical spacetime manifold and its point structure, and replace it by a more fundamental physical space from which spacetime emerges. In this search we have been guided by the role of the Dirac operator as a dynamical variable, and by the fact that this operator is closely related to a Clifford algebra and to the quaternions. Also, it is known that there are only four normed division algebras, the reals $\mathbb{R}$, the complex numbers $\mathbb{C}$, the quaternions $\mathbb{H}$ and the octonions $\mathbb{O}$. Why should nature use only real numbers in the construction of spacetime? We are proposing that in quantum theory, prior to the said symmetry breaking, physical space is labeled by quaternions / octonions. Elementary particle states are described not by complex numbers, but by complex quaternions and complex octonions. The associated symmetry groups are those which are directly associated with the octonions, starting with the smallest exceptional Lie group $G_2$ which is the automorphism group of the octonions. The other four exceptional groups $F_4,E_6,E_7,E_8$ have their corresponding Lie algebras arising as composition Lie algebras over $\mathbb{R}\otimes \mathbb{O},\mathbb{C}\otimes \mathbb{O},\mathbb{H}\otimes \mathbb{O}$ and $\mathbb{O}\otimes \mathbb{O}$, respectively [4]. Furthermore, the division algebras relate to the Lorentz group in higher dimensional spacetimes, as follows: $SL(2,\mathbb{R})\cong SO(1,2),SL(2,\mathbb{C})\cong SO(1,3),SL(2,\mathbb{H})\cong SO(1,5),SL(2,\mathbb{O})\cong SO(1,9)$. There hence arises the possibly that 6D spacetime and 10D spacetime are of importance to the unified theory.

There then remains to specify the symmetry group of the unified theory, and its branching pattern upon symmetry breaking. We are proposing that the symmetry group is $E_8\otimes E_8$, and the pattern of symmetry breaking presented in this paper is strongly motivated by the Freudenthal-Tits magic square which selects certain Lie algebras as composition Lie algebras made from tensor products of normed division algebras. Moreover, the transition from octonions (related to exceptional Lie algebras) to quaternions (related to symplectic Lie algebra) to complex numbers (related to $\mathfrak{su}\left(n\right))$ favours inclusions involving a smaller Lie group plus an $SU\left(3\right)$. Thus the following inclusions are in a way special:

$$E_8\supset E_6\otimes SU\left(3\right),E_6\supset SU\left(3\right)\otimes SU\left(3\right)\otimes SU\left(3\right),F_4\supset SU\left(3\right)\otimes SU\left(3\right)$$

(1)

This claim is also supported by the Jordan pairs and Jordan triple systems construction of exceptional algebras, in the work of Truini and collaborators [5], using the so-called magic star.

The eventual picture of the emergent universe that we seek to confirm is shown in Figure 1 below. The $E_8\otimes E_8$ symmetry breaking is the electroweak symmetry breaking which branches a 6D spacetime $SO(3,3)$ into a 4D spacetime $(-,+,+,+)$ and a 4D anti-spacetime with flipped signature $(-,-,-,+)$. The geometry of the first 4D spacetime

is governed by a broken $SU{\left(2\right)}_R\otimes U{\left(1\right)}_{Yg}\to U{\left(1\right)}_{grav}$ symmetry, and the geometry of the second, flipped, spacetime is governed by the broken electroweak $SU{\left(2\right)}_L\otimes U{\left(1\right)}_Y\to U\left(1\right)\mathrm{em}$ symmetry. The weak interaction is presented as the ‘gravity’ of the second spacetime, although from the perspective of our spacetime it appears as a broken internal symmetry. Left chiral fermions reside on the flipped 4D spacetime, and right chiral fermions on our 4D spacetime, and two Higgs bosons couple the fermions of these two spacetimes. QCD color is present as a part of the fibre bundle on the flipped spacetime with the unbroken internal gauge symmetry $SU{\left(3\right)}_{\mathrm{color}}\otimes U{\left(1\right)}_{\mathrm{em}}$. The corresponding fibre bundle on our spacetime is the unbroken internal symmetry $SU{\left(3\right)}_{\mathrm{grav}}\otimes U{\left(1\right)}_{\mathrm{grav}}$, these being the two newly predicted theories in addition to the four already known ones. Spacetime is described by quaternions, more precisely by split biquaternions. Octonions arise only while describing the internal symmetries $SU{\left(3\right)}_{\mathrm{color}}$ and $SU{\left(3\right)}_{\mathrm{grav}}$ over the bundle. This overall scenario is currently under development and a small part of it is the content of the present paper.

It is proposed that $SU{\left(2\right)}_R\otimes U{\left(1\right)}_{Yg}\to U{\left(1\right)}_{\mathrm{grav}}$ is the precursor of general relativity which arises after symmetry breaking of the $SU{\left(2\right)}_R$. The unbroken $U{\left(1\right)}_{\mathrm{grav}}$ has recently been suggested as a possible fifth force which might explain the phenomenology of Milgrom’s MOND (Modified Newtonion Dynamics) [6]. There is evidence in the literature, for instance in the works of Ashtekar [7], and of Woit [8,9], that general relativity can be treated as a Yang-Mills gauge theory of $SU{\left(2\right)}_R$ symmetry. Our ongoing investigations attempt to put general relativity and the weak interaction on the same footing, except that they have opposite parity.

2. Introduction to the Model

In this paper we present the 248 dimensional fundamental representation (rep) of $E_8$ branched into our proposed subgroups for understanding a unified theory with gravitation on an octonionic background. The motivation for using this group is based on our previous work on unification using octonions [10,11]. We describe our space mapped by the octonions to be a prespacetime manifold on which all the fermions, bosons (including gravity) are present and follow trace dynamics (a collapse theory). The octonions are related with the Exceptional Lie groups intrinsically, therefore subgroups like $SU\left(3\right)$, $SU\left(2\right)$ used in the standard model naturally arise in the prespacetime manifold. What we call internal symmetry in spacetime manifold is geometrical dynamics on this prespacetime octonionic manifold. An important aspect of $E_8$ is that the adjoint representation is the fundamental representation, therefore we are able to write the fermions and the bosons using the same rep, something that is desired in our pre-spacetime trace dynamics theory [12].

There are works of other researchers as well who have been looking at $E_8$ and $E_8\otimes E_8$ for a unified theory. One of the earliest attempts was in string theory, which proposed an $E_8\otimes E_8$ based heterotic string theory in $D=9+1$ spacetime [13,14]. There have been some recent attempts using the octonions from Manogue, Dray, and Wilson [15]. Pavsic also discusses about the physical origins of $E_8$ [16]. Pavsic talks about SO(8,8) unification and the fact that the generators of SO(8,8) (total 120) and the spinors of $\mathbb{C}l\left(14\right)$ (total 128) sum up to 248 which is the adjoint/fundamental rep of $E_8$ - this is an important sign.

In the next section we present the maths of branching $E_8$ into our desired maximal subgroup of $E_8$. In the sections following that we will propose the physical interpretation and the reasons for choosing the desired gauge-group.

3. Branching of $E_8\otimes E_8$

$E_8\otimes E_8$ unification not only gives us all the fundamental particles including fermions and bosons but also a spacetime on which post-symmetry-breaking fields could be defined and an internal space where three generations of fermions exist as triplets. The left-right symmetric gauge group arising in our theory is given as $SU{\left(3\right)}_C\otimes SU{\left(3\right)}_{grav}\otimes SU{\left(2\right)}_L\otimes SU{\left(2\right)}_R\otimes U{\left(1\right)}_{{\gamma }_1}\otimes U{\left(1\right)}_{{\gamma }_2}$ where this gauge group involves all the interactions prescribed by the octonionic theory. The $E_8\otimes E_8$ rep is written as $(248,1)\oplus (1,248)$ broken into the two separate $E_8$. Each $E_8$ gets branched into a SU(3) $\otimes E_6$ by the following rule [17]

$$248=(8,1)\oplus (1,78)\oplus (3,27)\oplus (\overline{3},\overline{27})$$

(2)

Figure 2. Left-Right fermions [18].

Figure 2. Left-Right fermions [18].

Our corresponding E₆ will then branch into SU(3) ⊗ SU(3) ⊗ SU(3). One SU(3) (call it $SU{\left(3\right)}_{gen}$) gives the interpretation of an internal space for three generations, the second SU(3) gives strong interaction. The remaining SU(3) branches into $SU{\left(2\right)}_L\otimes U{\left(1\right)}_{{\gamma }_1}$ giving us three generations of fermions following $SU{\left(3\right)}_C\otimes SU{\left(2\right)}_L\otimes U{\left(1\right)}_{{\gamma }_1}$. From the other $E_8$ we get three generations of fermions that obey the pre-gravitational gauge group $SU{\left(3\right)}_{grav}\otimes SU{\left(2\right)}_R\otimes U{\left(1\right)}_{{\gamma }_2}$. The motivation for having a right-handed chiral gravitation under this gauge group is given in section III and the explanation for using $SU{\left(3\right)}_{gen}$ is given in section IV. The Higgs couples the left and the right sector post SSB, giving us the Dirac fermions (with the exception of neutrino) with appropriate electric charge and mass.

The $SU\left(3\right)$ in $SU\left(3\right)\otimes E_6$ branching of $E_8$ is to be interpreted as the group causing rotations on the octonionic coordinates, the subgroup of this is $SU\left(2\right)$ which causes rotations in quaternions (to be interpreted as rotations in 3-D space). We will call it $SU{\left(3\right)}_{spacetime}$, this is explained in more detail in section III.

Branching rule for 27, $\overline{27}$, 78 representations of E₆ into SU(3) ⊗ SU(3) ⊗ SU(3) is given as,

$$27=(\overline{3},3,1)\oplus (3,1,3)\oplus (1,\overline{3},\overline{3})$$

(3)

$$\overline{27}=(3,\overline{3},1)\oplus (\overline{3},1,\overline{3})\oplus (1,3,3)$$

(4)

$$78=(8,1,1)\oplus (1,8,1)\oplus (1,1,8)\oplus (3,3,\overline{3})\oplus (\overline{3},\overline{3},3)$$

(5)

The last SU(3) further branches into SU(2) ⊗ U(1), with its 3, $\overline{3}$ and 8 breaking as,

$$3=2\left(1\right)+1(-2)$$

(6)

$$\overline{3}=2(-1)+1\left(2\right)$$

(7)

$$8=1\left(0\right)\oplus 2(-3)\oplus 2\left(3\right)\oplus 3\left(0\right)$$

(8)

Substituting the above three equations in the branching of E₆,

$$E_6\to SU{\left(3\right)}_{genL}\otimes SU{\left(3\right)}_C\otimes SU{\left(2\right)}_L\otimes U{\left(1\right)}_{{\gamma }_1}$$

$$\begin{array}{c}\hfill 27=(\overline{3},3,1)\left(0\right)\oplus (3,1,2)\left(1\right)\oplus (3,1,1)(-2)\oplus (1,\overline{3},2)(-1)\oplus (1,\overline{3},1)\left(2\right)\end{array}$$

(9)

$$\begin{array}{c}\hfill \overline{27}=(3,\overline{3},1)\left(0\right)\oplus (\overline{3},1,2)(-1)\oplus (\overline{3},1,1)\left(2\right)\oplus (1,3,2)\left(1\right)\oplus (1,3,1)(-2)\end{array}$$

(10)

$$\begin{array}{c}78=(8,1,1)\left(0\right)\oplus (1,8,1)\left(0\right)\oplus (1,1,1)\left(0\right)\oplus \hfill \\ \hfill (1,1,2)(-3)\oplus (1,1,2)\left(3\right)\oplus (1,1,3)\left(0\right)\oplus (3,3,2)(-1)\hfill \\ \hfill \oplus (3,3,1)\left(2\right)\oplus (\overline{3},\overline{3},2)\left(1\right)\oplus (\overline{3},\overline{3},1)(-2)\end{array}$$

(11)

These three representations of $E_6$ contain all left chiral fermions and their right chiral anti-particles including all three generations, all gauge bosons, and Higgs doublet with antiparticles as this symmetry breaking is prior to spontaneous symmetry breaking of $SU\left(2\right)\otimes U\left(1\right)\to U{\left(1\right)}_{em}$. Similarly we can do the branching of the other $E_8$ whose $E_6$ will contain all right chiral fermions and their left chiral anti-particles also including all three generations. In this section we try to recognise all the fermions we got in E₆ branching and in next section we will talk about internal geometry we get from $SU{\left(3\right)}_{gen}$ and spacetime geometry from remaining $SU{\left(3\right)}_{spacetime}$ of $E_8$. Let us start by interpreting the states in

$$E_{8L}\to SU{\left(3\right)}_{spacetime1}\times E_{6L}\to SU{\left(3\right)}_{spacetime1}\times SU{\left(3\right)}_{genL}\times SU{\left(3\right)}_c\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y$$

(12)

We note that for getting correct hypercharges we define $U{\left(1\right)}_Y=U{\left(1\right)}_{{\gamma }_1}/2N$ where $N=3$ for an $SU{\left(3\right)}_c$ triplet, and $N=1$ for an $SU{\left(3\right)}_c$ singlet. Also, in the following the rep $(a,b,c)\left(d\right)$ stands for $(SU{\left(3\right)}_{genL},SU{\left(3\right)}_c,SU{\left(2\right)}_L)\left(U{\left(1\right)}_Y\right)$.

${\left(\begin{array}{c}u\\ d\end{array}\right)}_L$ : these particles can be recognised as ($\overline{3},\overline{3}$, 2)(1) state found in the branching of 78 representation of $E_6$. This state shows that these quarks are triplets for $SU{\left(3\right)}_{genL}$(as we have three generations), triplet for $SU{\left(3\right)}_C$ (showing strong interaction), doublet for $SU{\left(2\right)}_L$ (weak interaction) and 1/6 as weak hypercharge. If we calculate electric charge for each quark, we get

$$q_u=1/6+1/2=2/3$$

$$q_d=1/6-1/2=-1/3$$

The electric charge is given by $q=Y+T_3/2$ where the weak isospin $T_3$ is determined by the $SU{\left(2\right)}_L$.

Their anti-particle state

${\left(\begin{array}{c}\overline{u}\\ \overline{d}\end{array}\right)}_R$ : is also present as (3, 3, 2)(-1) following same symmetry but with -1/6 weak-hyper charge giving -2/3 and 1/3 as electric charges respectively. So in all we get 36 left chiral quarks including all three generations and anti-particles.

Next we go to the leptons

${\left(\begin{array}{c}{\nu }_e\\ e^{-}\end{array}\right)}_L$ : these particles can be recognised as ($\overline{3}$, 1, 2)(-1) state found in $\overline{27}$ representation of $E_6$. This state shows that left chiral leptons are triplet for $SU{\left(3\right)}_{genL}$, singlet for $SU{\left(3\right)}_C$ (does not show strong interaction), doublet for $SU{\left(2\right)}_L$ and with -1/2 as weak hypercharge.

$$q_{\nu }=-1/2+1/2=0$$

$$q_e=-1/2-1/2=-1$$

We can also find their anti-particle state

${\left(\begin{array}{c}\overline{{\nu }_e}\\ \overline{e^{-}}\end{array}\right)}_R$ : as (3, 1, 2)(1) following same symmetry but with opposite weak-hyper charge which leads to 0 and 1 electric charges. This makes the count for left chiral leptons as 12 including all three generations and anti-particles.

We also find all the adjoint representations of our symmetry group in adjoint representation of E₆ which leads to the bosons. (1, 8, 1)(0) includes adjoint representation of SU(3)_C which are all 8 gluons that mediate strong interaction. (1, 1, 3)(0) is the adjoint rep of SU(2)_L which leads to weak bosons and (1, 1, 1)(0) is $U{\left(1\right)}_Y$ boson. After spontaneous symmetry breaking of $SU{\left(2\right)}_L\otimes U\left(1\right)\to U{\left(1\right)}_{em}$, we get three massive Weak bosons (W⁺, W⁻, Z⁰) and one massless photon. We can also see a state (1, 1, 2) which is a doublet of SU(2)_L with its anti-particle (1, 1, 2) (opposite U(1) charge) that can be recognized as the Higgs, as we are prior to spontaneous symmetry breaking. Post symmetry breaking the weak bosons and fermions gain masses and Higgs becomes a singlet. So in total we have 16 bosons for the left chiral part.

Now we try to induce spacetime using the remaining $SU{\left(3\right)}_{spacetime1}$ which we have in E₈ using Eqn. (2) and see how all fermions and bosons are present in it. We will use all the equations from Eqn. (3) to Eqn. (11) in order to further branch E₈.

$$E_8\to SU{\left(3\right)}_{spacetime1}\otimes SU{\left(3\right)}_{gen}\otimes SU{\left(3\right)}_C\otimes SU{\left(2\right)}_L\otimes U{\left(1\right)}_Y$$

$$\begin{array}{c}248=(8,1,1,1)\left(0\right)\oplus (1,8,1,1)\left(0\right)\oplus (1,1,8,1)\left(0\right)\oplus \hfill \\ (1,1,1,1)\left(0\right)\oplus (1,1,1,2)(-3)\oplus (1,1,1,2)\left(3\right)\oplus \\ (1,1,1,3)\left(0\right)\oplus (1,3,3,2)(-1)\oplus (1,3,3,1)\left(2\right)\oplus \\ (1,\overline{3},\overline{3},2)\left(1\right)\oplus (1,\overline{3},\overline{3},1)(-2)\oplus (3,\overline{3},3,1)\left(0\right)\oplus \\ (3,3,1,2)\left(1\right)\oplus (3,3,1,1)(-2)\oplus (3,1,\overline{3},2)(-1)\oplus \\ (3,1,\overline{3},1)\left(2\right)\oplus (\overline{3},3,\overline{3},1)\left(0\right)\oplus (\overline{3},\overline{3},1,2)(-1)\oplus \\ \hfill (\overline{3},\overline{3},1,1)\left(2\right)\oplus (\overline{3},1,3,2)\left(1\right)\oplus (\overline{3},1,3,1)(-2)\end{array}$$

(13)

This big branching of 248 rep of E₈ contains all the left chiral fermions, their anti-particles and all gauge bosons responsible for interaction among them. After this breaking, we can see that all the left chiral quarks represented as (1, 3, 3, 2) are coming as singlet of the SU(3)_spacetime while all leptons represented as (3, 3, 1, 2) as a triplet. We have a total of 36 quarks and 12 leptons. After invoking SU(3)_spacetime1 degree of freedom we get 36 quarks and 36 leptons. Like quarks all bosons are also singlet of SU(3)_spacetime with their total number as 16.

Out of 248 degrees of freedom, we have 8 d.o.f. for spacetime, 8 d.o.f. for internal space corresponding to 3 generations, 16 bosons, and 72 fermions which means that out of 232 particles we can identify 88 left chiral particles.

Next, we analyze the Right Chiral part of the (extended) Standard Model which comes from the other ${\mathrm{E}}_{8R}$ branching to $SU{\left(3\right)}_{spacetime2}\otimes$ E_6R. Branching rules follow a similar calculation from Eqn. (1) to Eqn. (10) but with a different interpretation of all the gauge groups.

$$E_{6R}\to SU{\left(3\right)}_{genR}\otimes SU{\left(3\right)}_{grav}\otimes SU{\left(2\right)}_R\otimes U{\left(1\right)}_{{\gamma }_2}$$

We give a brief description of this gauge group here but a more detailed description is given in section III and also in [18,19]. [To obtain correct hypercharges, we here define $U{\left(1\right)}_{Yg}=U{\left(1\right)}_{{\gamma }_2}/2N$ where $N=3$ for a color triplet, and $N=1$ for a color singlet. We thank David Chester for pointing this out to us]. Here SU(3)_genR gives all three generations by creating an internal space. SU(3)_grav gives a Gravi-Strong interaction [18] where, just as $u_L$ and d_L quarks are triplets of SU(3)_c, the u_R and ${\mathrm{e}}_R^{-}$ becomes triplets of SU(3)_grav. This interaction is mediated by eight “gravi-gluons" that are represented by the adjoint representation of SU(3)_grav and acquires a state (1, 8, 1)(0). The SU(2)_R⊗ U(1)_γ2 gives us four massless gauge bosons similar to SU(2)_L⊗ U(1)^γ1 represented as (1, 1, 3)(0) and (1, 1, 1)(0). After spontaneous symmetry breaking of this gauge group into U(1)_grav, we get a pre-gravitation interaction mediated by three “Weak-Lorentz" bosons and one photon-type boson which we call “Dark Photon". This symmetry breaking is induced by the Higgs doublet (1, 1, 2) with its anti-particle also present in branching of E_6R. So in total we have 16 bosons similar to what we have for left chiral part.

There is a difference in the Spontaneous Symmetry breaking of our left chiral gauge group and right chiral gauge group. In the former, fermions acquire square-root masses which can only be done by coupling with U(1)_grav gauge field while right chiral fermions acquire electric charges which can only be done by coupling with U(1)_em gauge field. So our two Higgs doublets, each one for different chirality are taking part in a certain mechanism where post SSB, they are coupling left chiral fermions with U(1)_grav field in such a way that left chiral fermions can acquire square-root masses while they are coupling right chiral fermions with U(1)_em so that they could acquire electric charges (see Figure 1). Similarly, the right-handed up-quark and down quark will become triplets of SU(3)_c and the left-handed up quark will become a triplet of SU(3)_grav. Therefore post Spontaneous Symmetry breaking each fermion with both chiralities acquires mass, electric charge, and QCD colour that is in agreement with the standard model. However, SU(2)_L and SU(2)_R remain to be parity violating and this has been shown before by Furey [20] and by us [19]. A preliminary analysis of the Lagrangian of the theory, relating it to three generations, has been carried out in [11]. The bosonic part of the Lagrangian has been discussed in detail in [21], where the weak mixing angle is also derived from first principles. For discussion of the Lagrangian see Section 6.2 below.

We can also find all the Right fermions and their anti-particles in this branching.

${\left(\begin{array}{c}u\\ e^{-}\end{array}\right)}_R$ : these particles can be recognized as ($\overline{3}$, $\overline{3}$, 2)(1) present in the 78 dimensional representation of E₆ Eqn. (10). Triplet for SU(3)_gen (three generations), triplet for $SU{\left(3\right)}_{grav}$ (“gravi-color") and doublet for $SU{\left(2\right)}_R$ (pre-gravitation interaction) with 1/6 as “Weak-Lorentz" charge. Instead of electric charge, we have $\sqrt{mass}$ for right chiral fermions that obeys the relation:

$$\sqrt{mass}=\gamma +{\tau }_3/2$$

here $\gamma$ is “Weak-Lorentz” charge and ${\tau }_3$ is iso-spin z component.

From this equation, we see that ${\mathrm{e}}_R^{-}$ has -1/3 $\sqrt{mass}$, u_R has 2/3 $\sqrt{mass}$, and d_R has −1 $\sqrt{mass}$. This is experimentally correct. This is one of the main motivations for coming up with a pre-gravitation gauge group defined in this manner. More on it in the next section. We can also find their anti-particle state ${\left(\begin{array}{c}\overline{u}\\ e^{+}\end{array}\right)}_L$ : represented as (3, 3, 2)(−1) following same symmetry with −2/3 and 1/3 $\sqrt{mass}$ respectively.

Next we have ${\left(\begin{array}{c}{\nu }_d\\ d\end{array}\right)}_R$ : represented by the state ($\overline{3}$, 1, 2)(-1) found in 27 representation of E₆ Eqn. (9). Triplet for SU(3)_genR, singlet for SU(3)_grav and doublet for SU(2)_R with -1/2 as “Weak-Lorentz” hyper-charge.

$${\sqrt{mass}}_{\nu }=-1/2+1/2=0$$

$${\sqrt{mass}}_d=-1/2-1/2=-1$$

Their anti-particles

${\left(\begin{array}{c}\overline{{\nu }_d}\\ \overline{d}\end{array}\right)}_L$ : are present in 27 representation of E₆ in Eqn.(8) as (3, 1, 2)(1) with 1/2 as “Weak-Lorentz" hyper charge and 0, 1 as $\sqrt{mass}$ respectively.

In total we have 9 up quarks, 9 electrons, 3 neutrinos and 3 down quarks and their equal anti-particles so we have 24 quarks and 24 leptons.

In the same manner, as for left chiral fermions, we can introduce spacetime for this E_6R as well; then the branching of this $E_8$ would be similar to Eqn. (11) but here spacetime representations are a bit different for leptons and quarks than in the left chiral part. We have

${\left(\begin{array}{c}u\\ e^{-}\end{array}\right)}_R$ represented as (1, $\overline{3}$, $\overline{3}$, 2)(-1), so up quark and e⁻ both are singlet for SU(3)_spacetime2 and ${\left(\begin{array}{c}{\nu }_d\\ d\end{array}\right)}_R$ is represented as ($\overline{3}$, $\overline{3}$, 1, 2)(-1) behaving as triplet for SU(3)_spacetime2. After involving spacetime degree of freedom, we get 18 + 18 quarks (18 up and 18 down) and 18 + 18 leptons, including all three generations and anti-particles. All 16 gauge bosons for right chiral part are also a singlet for SU(3)_spacetime2.

Hence we can identify 36 quarks + 36 leptons + 16 bosons = 88 particles out 232 degree of freedom.

We can therefore represent everything in a single unified representation of E₈⊗ E₈ as (248, 1)_L⊕ (1, 248)_R. So in total, we can identify 144 degrees of freedom as fermions, 32 degrees of freedom as bosons, and 32 degrees of freedom creating spacetime and internal generation space, out of a total of 496 degrees of freedom. This leaves 288 unaccounted for degrees of freedom; we return to address them in the Discussion section.

4. Octonionic Space, $E_6$ Fermions and Gauge Fields, Including Pre-Gravitation

We propose an 8-D non-commutative space mapped by the octonions coordinates $(1,e_i),i=1,..,7$ [10]. The automorphism group of the octonions is $G_2$ with the maximal subgroup $SU\left(3\right)$. The eight-dimensional real representation of $SU{\left(3\right)}_{spacetime}$ in the $SU\left(3\right)\otimes E_6$ branching of $E_8$ is to be interpreted as the source for the 8 octonionic directions in our prespacetime manifold. The $SU{\left(3\right)}_{spacetime}$ has the subgroup $SU\left(2\right)$ that causes rotations in 3-D and is the automorphism group of quaternions that map the 4-D spacetime $(1,e_i),i=1,2,3$. Another important aspect is that we have $SU\left(3\right)\otimes E_6$ branching of both the $E_8$, therefore we talk of a complexified space with octonionic coordinates. Another important aspect to notice here is that the neutrinos are the only triplets of $SU{\left(3\right)}_{spacetime}$ irrespective of parity, therefore this rotation in the internal space might be related to neutrino oscillations, further research needs to be done to say more. In Section 7 below, we explain in some detail as to how the $SU{\left(3\right)}_{spacetime1}\otimes SU{\left(3\right)}_{spacetime2}$ part of $E_8\times E_8$ branching gives rise to a 6D space-time and to a $U\left(1\right)$ symmetry which could be the possible origin of Connes time.

We now give a short justification for the pre-gravitaion gauge group $SU{\left(3\right)}_{grav}\otimes SU{\left(2\right)}_R\otimes U{\left(1\right)}_{{\gamma }_2}$ which has been proposed earlier in [18]. The electric charge ratio of the down quark, up quark, and electron is 1:2:3, surprisingly enough the square root mass ratio of the electron, up quark, down quark is 1:2:3. We do no take this to be a mere coincidence. In [19], we showed the left-right symmetric representation of fermions, the proposal is that just like we have $U{\left(1\right)}_{em}$ for the left-handed fermions that gives electric charge to the fermions, we have a $U{\left(1\right)}_{grav}$ for the right-sector that gives square-root mass to the fermions. In the right-sector, the electrons are triplets and have a square-root mass 1/3, whereas the down quark is a singlet and has a square-root mass 1. The right-handed down quark with square-root mass 1 is coupled to the left-handed down quark triplet with electric charge 1/3 and we get a Dirac quark with square-root mass 1 and electric charge 1/3. Similarly when the right-handed electron triplet with square-root mass 1/3 couples with a left-handed electron with electric charge 1 we get a Dirac electron with square-root mass 1/3 and electric charge 1. This can be represented via Figure 1 as shown.

The $SU{\left(3\right)}_{grav}$ is to be interpreted as gravi-color and results in a gravitational interaction of the electron and up quark triplets. This interaction is confined to small length scales and is therefore not manifested in large scale gravity but we suggest that the effects of $SU{\left(3\right)}_{grav}$ will be important for understanding the gravitational effects of subatomic particles like the electron. We propose that the $SU{\left(2\right)}_R\otimes U{\left(1\right)}_{\gamma 2}$ will break into $U{\left(1\right)}_{grav}$ that corresponds to dark photon, whereas general relativity is emergent from the $SU\left(2\right)$ pre-gravitation. Theories have been proposed with the dark photon as a contender to explain dark matter [22] and testable experiments have also been proposed for the same [23]. We are also providing the emergence of the $U{\left(1\right)}_{grav}$ dark matter from $SU{\left(2\right)}_R\otimes U{\left(1\right)}_{\gamma 2}$ symmetry breaking where $SU{\left(2\right)}_R$ is giving us the ”Lorentz bosons" as mediators for chiral gravity. $SU\left(2\right)$ chiral gravity has been used in Loop quantum gravity as the gauge group for Ashtekar variables [7] that are cannonical variables in spatial hypersrufaces in the ADM formalism of gravity [24].

The understanding of gravity is very intrinsically related to the problem of mass. Why the stress-energy tensor bends spacetime? The problem of mass is also related to the problem of three generations, why the three generations are exactly similar apart from their mass? In the next section we try to answer this and our internal space (not internal in a pre-spacetime octonionic space) of SU(3) generation.

5. Triality, Jordan Matrices, Spin(9), and Three Generations

In the above analysis, we have invoked an $SU\left(3\right)$ for three generations. The existence of three generations can be motivated from the triality of $SO\left(8\right)$, its relation to the octonions, and their associated exceptional Lie groups. Triality is also crucial in explaining the observed mass ratios for the three generations [18].

There have been some recent attempts to understand the three generations of fermions through the language of octonions. Gillard and Gresnigt talk about the three generations of fermions through the algebra of Sedenions and $\mathbb{C}l\left(8\right)$ [25,26]. The broader purview of the community is shifting towards the view that the triality of SO(8) is related to the three generations. We have oursleves related the three generations using the $3\times 3$ Hermitian Jordan matrices with octonionic entries [11,18] and obeying the exceptional Jordan algebra whose automorphism group is $F_4$. The automorphism group of the complexified exceptional Jordan algebra is $E_6$; this group is also the symmetry group of the Dirac equation in 10D space-time. There have been attempts before to interpret one of the $SU\left(3\right)$ from the $SU\left(3\right)\otimes SU\left(3\right)\otimes SU\left(3\right)$ maximal subgroup of $E_6$ to represent the rotation group for 3 generations [27,28].

We have $\mathbb{C}l\left(8\right)\cong \mathbb{C}l{\left(9\right)}^0$, therefore the three generations of fermions discussed in [25] are related to spinors that we will now create from $\mathbb{C}l\left(9\right)$. Another interesting thing to note is that $\mathbb{C}l\left(9\right)$ spinors will be $2\times 2$ matrices with octonionic entries, therefore we will show shortly how our previous work on three generations from $J_3\left(\mathbb{O}\right)$ and Gresnigt’s construction [25] are related to three generations via triality.

Consider the following matrices:

$$i{e}_i{\sigma }_x,{\sigma }_y,{\sigma }_z$$

Here $e_i$ are the octonions, and ${\sigma }_i$ are the Pauli matrices, therefore the algebra is $\mathbb{H}\otimes \mathbb{O}$. These 9 matrices square to -1, and anti-commute with each other, therefore these can be used to make the generators of $\mathbb{C}l\left(9\right)$. Let’s call the generators as ${\gamma }_i$, i = 1,.., 9.

The fermionic creation and annihilation operators satisfying

$$\{{\alpha }_i,{\alpha }_j\}=0\forall i,j\mathrm{form}\mathrm{the}\mathrm{MTIS}$$

(14)

and are given as:

$$\begin{array}{c}\hfill {\alpha }_1=({\gamma }_1+i{\gamma }_9)/2=\left[\begin{array}{cc}i& i{e}_1\\ i{e}_1& -i\end{array}\right]\end{array}$$

(15)

$$\begin{array}{c}\hfill {\alpha }_2=({\gamma }_2+i{\gamma }_8)/2=\left[\begin{array}{cc}0& i{e}_2-1\\ i{e}_2+1& 0\end{array}\right]\end{array}$$

(16)

$$\begin{array}{c}\hfill {\alpha }_3=({\gamma }_3+i{\gamma }_7)/2=\left[\begin{array}{cc}0& i{e}_3-e_7\\ i{e}_3-e_7& 0\end{array}\right]\end{array}$$

(17)

$$\begin{array}{c}\hfill {\alpha }_4=({\gamma }_4+i{\gamma }_6)/2=\left[\begin{array}{cc}0& i{e}_4-e_6\\ i{e}_4-e_6& 0\end{array}\right]\end{array}$$

(18)

These are the annihilation operators and correspondingly we will have the creation operators ${\alpha }_i^{†}$s. The idempotent V is given as:

$$V={\alpha }_1{\alpha }_2{\alpha }_3{\alpha }_4{\alpha }_4^{†}{\alpha }_3^{†}{\alpha }_2^{†}{\alpha }_1^{†}$$

(19)

The total 16 spinors created (following Furey and Dixon [29,30,31,32]) by acting the creation operator on the idempotent are given by:

$$V$$

(20)

$${\alpha }_1^{†}V,{\alpha }_2^{†}V,{\alpha }_3^{†}V,{\alpha }_4^{†}V$$

(21)

$${\alpha }_2^{†}{\alpha }_1^{†}V,{\alpha }_3^{†}{\alpha }_2^{†}V,{\alpha }_4^{†}{\alpha }_3^{†}V,{\alpha }_1^{†}{\alpha }_4^{†}V,{\alpha }_4^{†}{\alpha }_3^{†}V,{\alpha }_4^{†}V{\alpha }_2^{†}V$$

(22)

$${\alpha }_3^{†}{\alpha }_2^{†}{\alpha }_1^{†}V,{\alpha }_4^{†}{\alpha }_3^{†}{\alpha }_2^{†}V,{\alpha }_1^{†}{\alpha }_4^{†}{\alpha }_3^{†}V,{\alpha }_1^{†}V{\alpha }_1^{†}V{\alpha }_1^{†}V$$

(23)

$${\alpha }_4^{†}{\alpha }_3^{†}{\alpha }_2^{†}{\alpha }_1^{†}V$$

(24)

It is interesting to note that the spinors created this way are $2\times 2$ matrices with octonionic entries. The 2x2 exceptional Jordan matrices are spinors of spin(10). It has been shown by Dray and Manogue [33] that $SU(2,\mathbb{O})\cong Spin\left(9\right)$, $Sl(2,\mathbb{O})\cong Spin(1,9)$. Therefore, the 16 spinors form the subalgebra of $J_2\left(\mathbb{O}\right)$. Also, the 16 spinors from $\mathbb{C}l\left(9\right)$ obtained here are related to the 16 spinors created by Gresnigt from $Cl\left(8\right)$ to understand three generations via $Cl{\left(9\right)}^0$. This relates the three generations created by Gresnigt to our work in $J_3\left(\mathbb{O}\right)$ via triality in the following manner:

Triality of octonions is a map from $\mathbb{O}\otimes \mathbb{O}\otimes \mathbb{O}\to \mathbb{R}$ that is achieved via the group SO(8) [34]. The octonionic spinors of $\mathbb{C}l\left(6\right)$ that are to be interpreted as particles under $SU{\left(3\right)}_c\otimes U{\left(1\right)}_{em}$ [29,31,32] can be mapped to an element of $J_2\left(\mathbb{O}\right)$ via the following map:

$$\mathbb{O}\to \left(\begin{array}{cc}charge\left(\mathbb{O}\right)& \mathbb{O}\\ {\mathbb{O}}^{*}& charge\left(\mathbb{O}\right)\end{array}\right)$$

(25)

Here $charge\left(\mathbb{O}\right)$ depicts the $U{\left(1\right)}_{em}$ charge corresponding to that octonion. And three elements of $J_2\left(\mathbb{O}\right)$ with same diagonal entries a, b, c and octonionic entries x, y, z respectively can be mapped to an element of $J_3\left(\mathbb{O}\right)$ as follows

$$J_2\left(\mathbb{O}\right)\otimes J_2\left(\mathbb{O}\right)\otimes J_2\left(\mathbb{O}\right)\to \left(\begin{array}{ccc}(b+c)/2& y^{*}& z\\ y& (a+b)/2& x^{*}\\ z^{*}& x& (c+a)/2\end{array}\right)$$

(26)

We can now calculate the eigen-values of these matrices to obtain real numbers [35]. It has been shown in [18] that the eigen-values are related to the mass-ratios of charged fermions. Therefore while going from $\mathbb{O}\otimes \mathbb{O}\otimes \mathbb{O}$ all the way to $J_3\left(\mathbb{O}\right)$ and then to its eigen-values, we are invoking the triality that is related to the three generations. The problem of the three generations is also the problem of the mass ratios!

$G_2$ is the automorphism group of the Octonions and has the maximal subgroup $SU\left(3\right)$ responsible for the colour of particles written in octonionic representation. $F_4$ is the automorphism group of $J_3\left(\mathbb{O}\right)$ and has the maximal subgroup $SU\left(3\right)\otimes SU\left(3\right)$ where the other $SU\left(3\right)$ comes for generation [27]. All the three generations follow same spinorial dynamics, the only difference is between the mass, and it is a standard procedure in QFTs to write the three generations field $\psi$ as a $3\times 1$ column vector under $U\left(3\right)$. Post symmetry breaking of $SU\left(2\right)\otimes U\left(1\right)$, the three generations obtain different mass and hence different Yukawa potentials, they can no longer be written as 3⊗1 column vector and the $U\left(3\right)$ group breaks. However, the triality of the Octonions seems to suggest that there is some non-trivial relation between the three generations, therefore prior to Higgs mechanism, the group $SU\left(3\right)$ that comes from the maximal subgroup of $F_4$ is being used instead of $U\left(3\right)$.

6. Discussion

6.1. The Unaccounted for Degrees of Freedom

Our unified group $E_8\otimes E_8$ contains every fundamental structure including spacetime, all chiral fermions, and their three generations, and all bosons. However this comes with some additional degrees of freedom whose states cannot be identified with our usual standard model particles. In this section, we attempt to give certain explanations for these unaccounted degrees of freedom. Each E₈ will give us ten unaccounted states, with five being conjugate (anti-particle) to the other five. We list the five independent unaccounted states from Eqn. (13):

$$(1,3,3,1)\left(2\right)(3,\overline{3},3.1)\left(0\right)(\overline{3},\overline{3},1,1)\left(2\right)$$

$$(\overline{3},1,3,2)\left(1\right)(3,1,\overline{3},1)\left(2\right)$$

Post symmetry breaking the electric charges corresponding to the above states in that order are 2/3, 0, 2, (2/3 and 1/3 doublet), and 2/3 respectively.

There are a total of 144 unaccounted fermions from each $E_8$, the total from both sides is 288. The total number of physical fermions from our theory are also 144, so there is a 1:2 ratio of accounted and unaccounted fermions. In the subsection below, we argue that the 288 d.o.f. go into the making of two composite Higgs, 144 each. Such a composite Higgs should be looked for at the LHC.

6.2. Overview of the Octonionic Theory

Our theory is a matrix-valued Lagrangian dynamics on an octonionic space, motivated as a pre-quantum, pre-spacetime theory, i.e. a reformulation of quantum field theory which does not depend on an external classical time [36,37]. It is a generalisation of Adler’s theory of trace dynamics, so as to include pre-gravitation. Quantum field theory and classical space-time and gravitation are emergent from this dynamics under suitable approximations. The fundamental universe is a collection of ‘atoms of space-time-matter’, an atom being a 2-brane described by matrix-valued dynamical variables on octonionic space and having the action principle (of the unified interactions)

$$\frac{S}{\hslash }=\int d\tau \mathcal{L};\mathcal{L}=\frac{1}{2}Tr\left[{\displaystyle \frac{L_p^2}{L^2}}{\dot{\tilde{Q}}}_1^{†}{\dot{\tilde{Q}}}_2\right]$$

(27)

This action defines a 2-brane residing on a split-bioctonionic space. This means that each of the two matrices ${\tilde{Q}}_1$ and ${\tilde{Q}}_2$ have sixteen components, one component per coordinate direction of the split bioctonion. This 16-dim space has $E_8\otimes E_8$ symmetry. We separate the two dynamical variables into bosonic and fermionic parts, each of which again has sixteen coordinate components:

$${\dot{\tilde{Q}}}_1^{†}={\dot{\tilde{Q}}}_B^{†}+{\displaystyle \frac{L_p^2}{L^2}}{\beta }_1{\dot{\tilde{Q}}}_F^{†};{\dot{\tilde{Q}}}_2={\dot{\tilde{Q}}}_B+{\displaystyle \frac{L_p^2}{L^2}}{\beta }_2{\dot{\tilde{Q}}}_F$$

(28)

Left-Right symmetry breaking separates the bosonic dynamical variable into its left-chiral part $q_B$ defined over 8D octonionic space and the right chiral part ${\dot{q}}_B$ defined over the 8D splt octonionic space. Similarly the fermionic dynamical variable separates into its left chiral part $q_F$ defined over 8D octonionic space and its right chiral part ${\dot{q}}_F$ defined over the split octonionic space.

$${\dot{\tilde{Q}}}_B=\frac{1}{L}(i\alpha q_B+L{\dot{q}}_B);{\dot{\tilde{Q}}}_F=\frac{1}{L}(i\alpha q_F+L{\dot{q}}_F)$$

(29)

The Yang-Mills coupling constant $\alpha$ arises as a consequence of the symmetry breaking, prior to which the theory is scale invariant, having only an associated length scale L but no other free parameter. The symmetries of the bioctonionic space are spacetime symmetries with the full symmetry being $E_8\otimes E_8$ and with symmetry breaking introducing branching as discussed earlier in the paper, and also introducing interactions and coupling constants.

By defining new variables

$$q_1^{†}=q_B^{†}+\frac{L_P^2}{L^2}{\beta }_1{q}_F^{†};q_2=q_B+\frac{L_P^2}{L^2}{\beta }_2{q}_F$$

(30)

we can also express the Lagrangian as

$$\begin{array}{cc}\hfill \mathcal{L}& =\frac{L_P^2}{2L^2}Tr\left[\left({\dot{q}}_1^{†}+\frac{i\alpha }{L}{q}_1^{†}\right)\times \left({\dot{q}}_2+\frac{i\alpha }{L}{q}_2\right)\right]\hfill \\ \hfill & =\frac{L_P^2}{2L^2}Tr\left[{\dot{q}}_1^{†}{\dot{q}}_2-\frac{{\alpha }^2}{L^2}{q}_1^{†}{q}_2+\frac{i\alpha }{L}{q}_1^{†}{\dot{q}}_2+\frac{i\alpha }{L}{\dot{q}}_1^{†}{q}_2\right]\hfill \end{array}$$

(31)

We can next expand each of these four terms inside of the trace Lagrangian as explored thoroughly in the paper [21], using the definitions of $q_1$ and $q_2$ given above:

$$\begin{array}{cc}\hfill {\dot{q}}_1^{†}{\dot{q}}_2& ={\dot{q}}_B^{†}{\dot{q}}_B+\frac{L_P^2}{L^2}{\dot{q}}_B^{†}{\beta }_2{\dot{q}}_F+\frac{L_P^2}{L^2}{\beta }_1{\dot{q}}_F^{†}{\dot{q}}_B+\frac{L_P^4}{L^4}{\beta }_1{\dot{q}}_F^{†}{\beta }_2{\dot{q}}_F\hfill \\ \hfill q_1^{†}{q}_2& =q_B^{†}{q}_B+\frac{L_P^2}{L^2}{q}_B^{†}{\beta }_2{q}_F+\frac{L_P^2}{L^2}{\beta }_1{q}_F^{†}{q}_B+\frac{L_P^4}{L^4}{\beta }_1{q}_F^{†}{\beta }_2{q}_F\hfill \\ \hfill q_1^{†}{\dot{q}}_2& =q_B^{†}{\dot{q}}_B+\frac{L_P^2}{L^2}{q}_B^{†}{\beta }_2{\dot{q}}_F+\frac{L_P^2}{L^2}{\beta }_1{q}_F^{†}{\dot{q}}_B+\frac{L_P^4}{L^4}{\beta }_1{q}_F^{†}{\beta }_2{\dot{q}}_F\hfill \\ \hfill {\dot{q}}_1^{†}{q}_2& ={\dot{q}}_B^{†}{q}_B+\frac{L_P^2}{L^2}{\dot{q}}_B^{†}{\beta }_2{q}_F+\frac{L_P^2}{L^2}{\beta }_1{\dot{q}}_F^{†}{q}_B+\frac{L_P^4}{L^4}{\beta }_1{\dot{q}}_F^{†}{\beta }_2{q}_F\hfill \end{array}$$

(32)

This form of the Lagrangian displays terms for the bosonic variables (gauge fields), the fermionic part of the action (leading to the Dirac equations upon variation), and terms bilinear in fermionic varaibles (related to the Higgs). A preliminary analysis of this Lagrangian, relating it to three generations, has been carried out in [11]. The bosonic part of the Lagrangian has been discussed in detail in [21], where the weak mixing angle is also derived from first principles. In future work we hope to report as to how the Lagrangian relates to the fermions and bosons reported in the present paper, including the unaccounted for terms discussed in the previous subsection. We note that the (8x3=24) fermions of the three generations contribute 24 x 24 = 576 = 288 x 2 terms to the Lagrangian, which are bilinear in $q_F$ and ${\dot{q}}_F$. It is striking that this is twice the number 288 of unaccounted degrees of freedom. Recall also that there are 144 physical fermions as demonstrated earlier in the paper.The terms bilinear in the $q_F$ and ${\dot{q}}_F$ possibly describe the two Higgs doublets of the theory, and hence it could be that the 288 unaccounted d.o.f. go into constituting two composite Higgs (144 for each Higgs) and hence that there are no new predicted fermions. Such a possibility is currently under investigation. We also note that there are (208-144=64=32x2) non-fermionic d.o.f. and these account for the 32 bosons corresponding to the (2x16=32) space-time d.o.f. (8+8 = 16 dimensional split bioctonioc space and the factor 2 because this space is complexified).

Such a pre-spacetime, pre-quantum dynamics is in principle essential at all energy scales, not just at the Planck energy scale [11]. Whenever a physical system has only quantum sources, the coordinate geometry of spacetime is non-commutative; and when that is an octonionic geometry, the spacetime symmetries result in the standard model and its unification with pre-gravitation, as we have seen in the present paper. Fermionic states are spinors (left minimal ideals) of the Clifford algebra $Cl\left(6\right)$ made from octonionic chains. Following the earlier work of other researchers, we constructed such $Cl\left(6\right)$ states for three generations of left chiral and right chiral quarks and leptons [18,19], and their associated bosons. We argued in these papers that pre-gravitation is the right-handed counterpart of the standard model with the associated symmetry group being $E_6\otimes E_6$. This is confirmed by the reps found in the present paper; furthermore the $E_8\otimes E_8$ symmetry unifies the spacetime with the matter and gauge degrees of freedom living on this spacetime, into a common unified description. Doing so has also introduced new so-called unaccounted fermions which are truly beyond the standard model, and whose physical significance and experimental consequences remain to be understood.

The Dirac equation resulting from this Lagrangian dynamics has an $E_6$ symmetry, and its real eigenvalues are determined by the characteristic equation of the exceptional Jordan algebra $J_3\left(8\right)$, whose automorphism group is $F_4$. These eigenvalues can be found for three generations of Dirac quarks and Dirac leptons, and also for three generations of left chiral fermions or right chiral fermions. Since the left chiral fermions are charge eigenstates, and right chiral fermions are square-root mass eigenstates, these eigenvalues help explain the strange mass ratios of quarks and leptons [18,38]. This is because experimental measurements invariably employ charge eigenstates, which are distinct from mass eigenstates.

The octonionic theory has similarities with string theory, but also differs from it in crucial ways. Our theory is also for extended objects, but in 6D = 3 + 3 spacetime and has an $E_8\otimes E_8$ symmetry. However, we build the Fock space of states for particles, not on a 10D Minkowski spacetime vacuum, but on the octonion-valued space, which is a spinor spacetime, as if a ‘square-root’ of the 10D Minkowski spacetime. The non-commutative octonion geometry has to be an essential feature of quantum theory even at low energy scales, not just at the Planck scale. Only then can the standard model be understood. The extra dimensions are complex and not to be compactified - these are the dimensions along which the internal symmetries lie. Finally, the Hamiltonian of the theory is in general not self-adjoint; thus enabling the quantum-to-classical transition, and otherwise becoming self-adjoint in the approximation in which quantum field theory is recovered from trace dynamics. Further evidence for trace dynamics comes from the result that the theory admits supra-quantum nonlocal correlations predicted by the Popescu-Rohrlich bound in the CHSH inequality, but disallowed by quantum mechanics. This constitutes strong evidence that quantum theory is approximate, and emergent from trace dynamics in a coarse-grained approximation [39,40]

The non-associativity of the octonions does bring its own challenges when they are employed in field theory. There is evidence that the challenges are eased when one uses split octonions. See e.g. the work of Gogberashvili [41] where rotations in the space of split octonions have been considered. It was shown therein that Lorentz transformations satisfy associativity when split octonions are employed. In the Freudenthal-Tits magic square as well, the space-time Lorentz algebras arise when one of the two composite algebras under consideration is split. In our own research programme, we employ split bioctonions to construct emergent spacetime. Furthermore, the work of Boyle and Farnsworth [42] extends the Connes noncommutative geometry programme to the non-associative case, rendering it plausible that Connes time is admissible in our octonionic theory.

We also note the Coleman-Mandula theorem: a no-go theorem which states that the space-time symmetry (Lorentz invariance) and internal symmetry of the S-matrix can only be combined in a trivial way, i.e. as a direct product. However, this does not prevent the $E_8\otimes E_8$ unification of gravitation and the standard model, on which the present paper is based. This is because the theorem applies only to the spontaneously broken phase, in which the Minkowski metric is present. The unified phase does not have a metric, and hence not the Minkowski metric either, and hence the Coleman-Mandula theorem does not apply to the unified symmetry.

The octonionic theory employs the octonions to define a non-commutative coordinate geometry. The symmetries of the geometry dictate the existence of standard model chiral fermions, gauge bosons, and pre-gravitation. Clifford algebras made from octonionic chains define spinorial states for the fermions, and the exceptional Jordan algebra determines values of the standard model parameters. The matrix-valued Lagrangian dynamics determines evolution of these particles. Classical general relativity emerges from pre-gravitation as a result of a quantum-to-classical spontaneous localisation which confines classical systems to our familiar 4D spacetime. However, quantum systems always live in the octonionic space, which has complex extra dimensions which are never compactified. Further work is in progress so as to attempt taking this unification program to completion.

6.3. Recovering the Standard Model and General Relativity

The fundamental action (25) is as it is written in the generalised theory of trace dynamics - a pre-spacetime pre-quantum theory. The dynamical variables are matrix-valued, with Grassmann numbers as matrix entries. Matrices which are even-grade Grassmann are called bosonic, and describe bosons. Matrices which are odd-grade Grassmann are called fermionic, and describe fermions. The variables $q_1$ and $q_2$ in the previous section are a sum of a bosonic part and a fermionic part, as shown in Eqn. 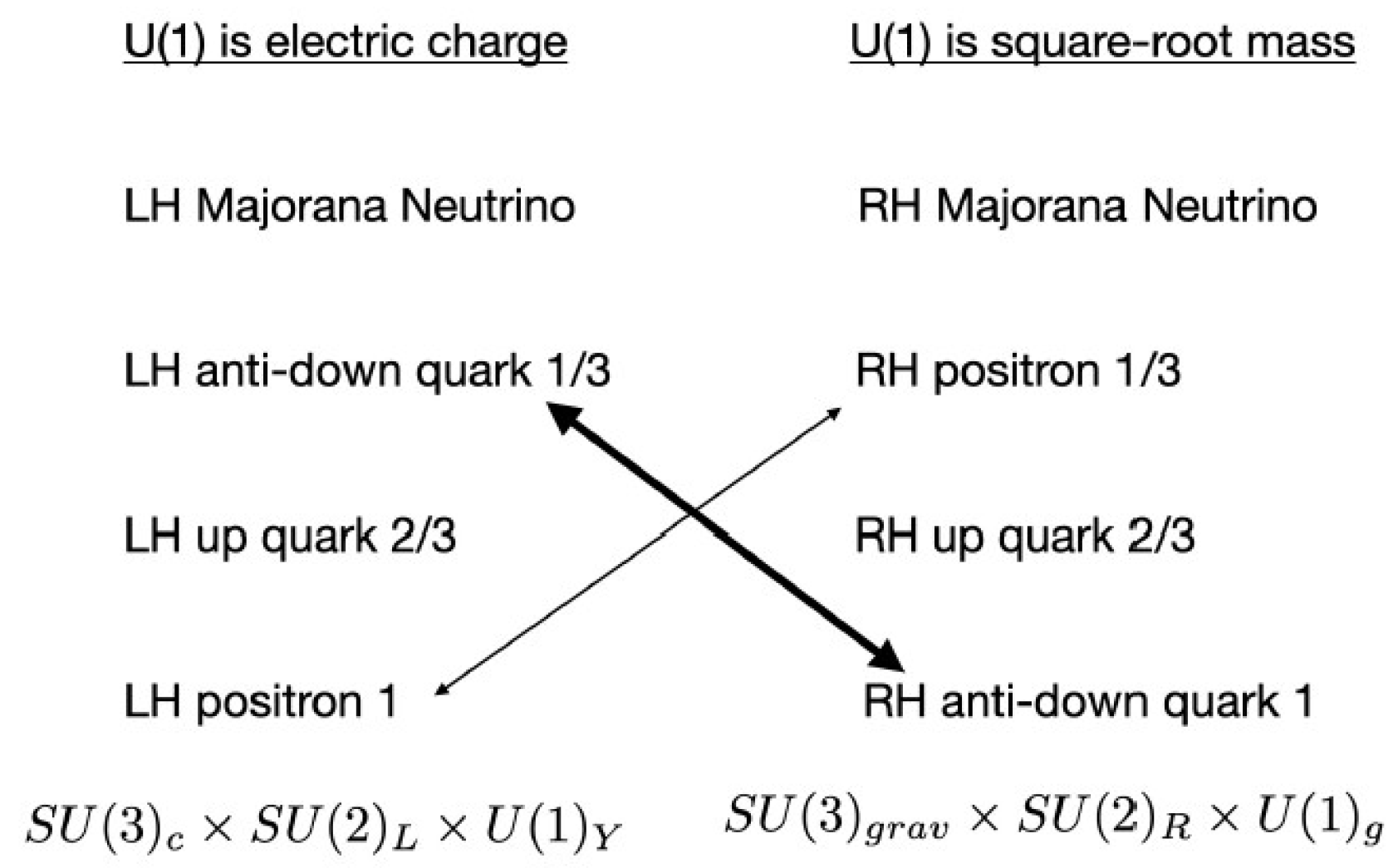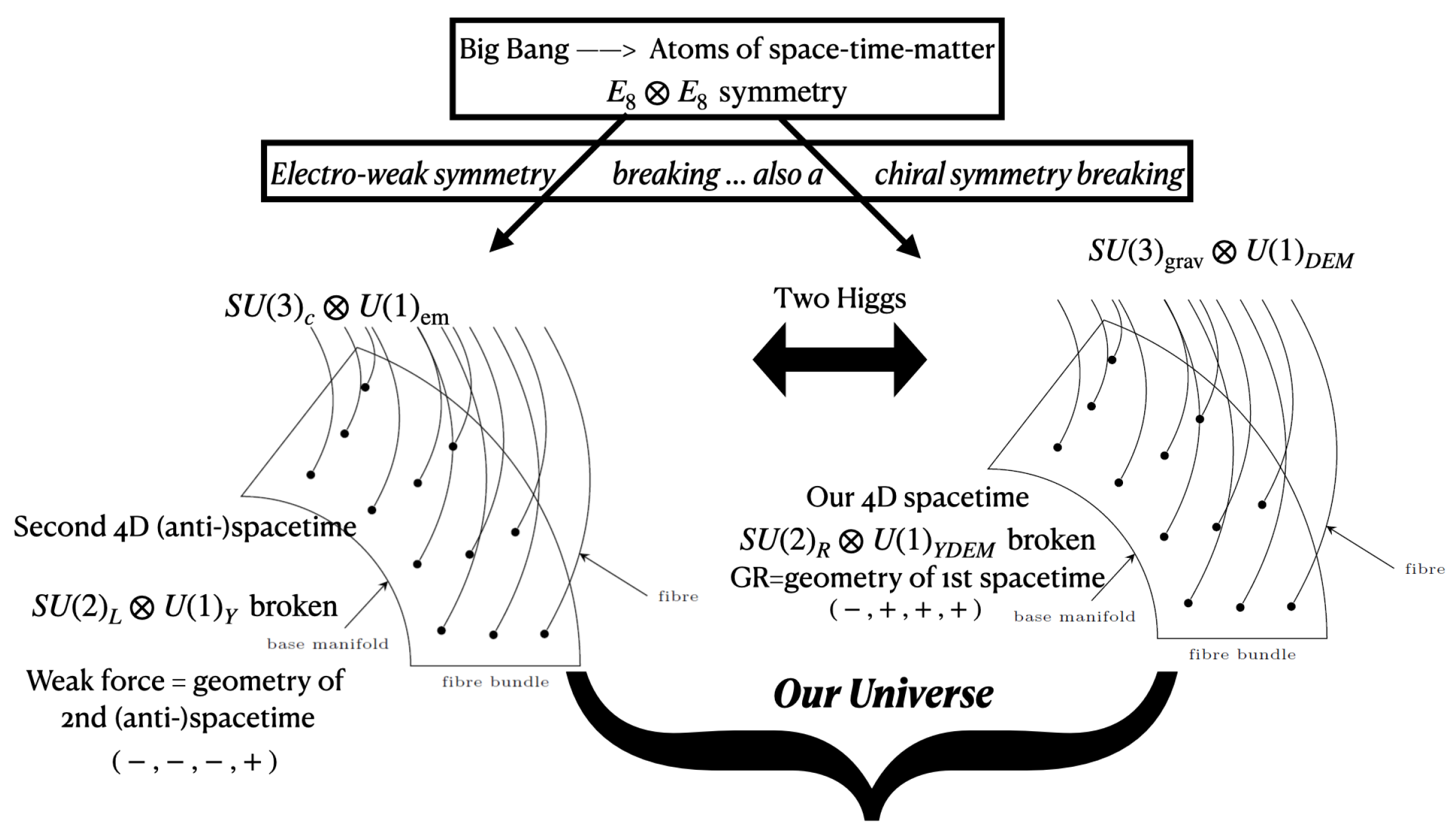(28). Thus the fundamental action describes what we call an ‘atom’ of space-time-matter (STM atom) which by definition is an elementary particle such as an electron (a fermion) along with all the (bosonic) fields it produces. Every particle gives rise to both a gravitational field and the weak force field, whereas only electrically charged particles give rise to electromagnetism, and only electrically charged particles with color give rise to the strong force field. The weak force is the spacetime symmetry of the flipped 4D spacetime $SO(1,3)$, having arisen from the breaking of the electroweak symmetry. General relativity has as its precursor the $SU{\left(2\right)}_R$ gauge symmetry, which is the spacetime symmetry of our 4D spacetime, having arisen from the breaking $SU{\left(2\right)}_R\times U{\left(1\right)}_{Yg}\to U{\left(1\right)}_{grav}$. We say more about this in Section 7.1. On the flipped 4D spacetime, a vector bundle represents the unbroken $SU{\left(3\right)}_c\times U{\left(1\right)}_{em}$ as an internal symmetry, and on our 4D spacetime another vector bundle represents the unbroken $SU{\left(3\right)}_{grav}\times U{\left(1\right)}_{grav}$ as an internal symmetry. The two 4D spacetimes have one common timelike and one common spacelike dimension. Thus overall, our universe has two extra (timelike) dimensions. These appear as internal symmetry directions from the vantage point of our 4D spacetime, whereas in reality they are part of the flipped 4D spacetime.

For every STM atom, the accompanying spacetime is labeled by non-commuting numbers - quaternions and/or octonions. Quaternions are adequate for describing the two 4D spacetimes, whereas octonions are essential for describing the internal symmetries $SU{\left(3\right)}_c$ and $SU{\left(3\right)}_{grav}$. Each STM atom, described by the action (25), is a universe unto itself - a mini-universe, say. The collection of enormously many STM atoms, $N\sim {10}^{80}$ constitutes the observed universe. Entanglement amongst subsets of the enormous collection leads to a quantum-to-classical transition resulting in the formation of classical objects such as stars and galaxies, and this transition is accompanied by the emergence of classical spacetime. Only when such a spacetime is available, the conventional formulation of quantum field theory (QFT) is possible. In principle, even at currently accessible low energies, such critical entanglement need not have taken place, and classical spacetime could be absent even at low energies. Conventional QFT would then not exist; but the trace dynamics (TD) formulation based on Eqn. (25) and on non-commuting coordinates will still exist. That is why the TD formulation is more fundamental, and it is the precise way to describe the standard model, which contains more information than the QFT based description of the standard model, even at energies accessed by the LHC. Thus the TD based description, being more precise, carries an explanation for those properties of the standard model (e.g. origin of the observed gauge symmetries and of values of dimensionless fundamental constants) which cannot be explained by the QFT based description. We now justify how the QFT based standard model can be recovered from the fundamental action, in the limit that dominantly many degrees of freedom in the universe become classical.

Variation of this trace action with respect to the matrix-valued degrees of freedom $q_1$ and $q_2$ gives rise to the Lagrange equations of motion:

$${\ddot{q}}_1=-\frac{{\alpha }^2}{L^2}{q}_1;{\ddot{q}}_2=-\frac{{\alpha }^2}{L^2}{q}_2$$

(33)

For reference, we mention two other useful and equivalent ways of writing the fundamental action:

$$\frac{S}{\hslash }=\int \frac{d\tau }{{\tau }_{Pl}}Tr\left\{\frac{L_P^2}{L^2}\left[{\dot{q}}_B^{†}+\frac{L_P^2}{L^2}{\beta }_1{\dot{q}}_F^{†}\right]\times \left[{\dot{q}}_B+\frac{L_P^2}{L^2}{\beta }_2{\dot{q}}_F\right]\right\}$$

(34)

and

$$\frac{S}{\hslash }=\int \frac{d\tau }{{\tau }_{Pl}}Tr\left\{\frac{L_P^2}{L^2}\left[\left({\dot{q}}_B^{†}+i\frac{\alpha }{L}{q}_B^{†}\right)+\frac{L_P^2}{L^2}{\beta }_1\left({\dot{q}}_F^{†}+i\frac{\alpha }{L}{q}_F^{†}\right)\right]\times \left[\left({\dot{q}}_B+i\frac{\alpha }{L}{q}_B^{†}\right)+\frac{L_P^2}{L^2}{\beta }_2\left({\dot{q}}_F+i\frac{\alpha }{L}{q}_F\right)\right]\right\}$$

(35)

This matrix-valued Lagrangian dynamics, or its equivalent Hamiltonian dynamics, is not to be quantized. It is already pre-quantum. This is because, as a result of a global unitary invariance of the trace Lagrangian, the theory possesses a novel conserved charge, denoted $\tilde{C}$ and known as the Adler-Millard charge, and not present in classical nor quantum dynamics:

$$\tilde{C}=\sum _i[{\mathbf{q}}_B,{\mathbf{p}}_B]-\left\{{\mathbf{q}}_F,{\mathbf{p}}_F\right\}$$

(36)

The commutator is over the bosonic matrices, and anti-commutator is over the fermionic matrices. We can also motivate trace dynamics with the following simple example of a collection of non-relativistic particles in classical mechanics:

$$S=\sum _i\int d\tau \frac{1}{2}{m}_i{\left(\frac{d{q}_i}{d\tau }\right)}^2$$

(37)

in which we propose to raise the real-number valued $q_i$ to matrices ${\mathbf{q}}_i$ and arrive at the trace Lagrangian:

$$S=\sum _i\int d\tau Tr\left[\frac{1}{2}\frac{L_p^2}{L^2}{\left(\frac{d{\mathbf{q}}_i}{d\tau }\right)}^2\right]$$

(38)

The variation of the trace Lagrangian gives the matrix-valued equations of motion ${\ddot{\mathbf{q}}}_i=0$ and the theory possesses the novel conserved charge mentioned above. The matrix ${\mathbf{q}}_i$ is that matrix of which the corresponding classical variable $q_i$ is an eigenvalue, to be realised in the classical limit of TD. In this sense classical dynamics is recovered from trace dynamics, and in this same sense the Lagrangian for the standard model is recovered from the fundamental trace Lagrangian in (25).

It is assumed that trace dynamics holds at some time scale resolution not accessed by current laboratory experiments, say Planck time ${\tau }_p$. We then ask what is the emergent coarse-grained dynamics, if the system is observed not at Planck time resolution, but at some lower resolution $\tau \gg {\tau }_p$? The standard techniques of statistical thermodynamics are employed to construct a phase space density distribution of the trace dynamical system, whose emergent coarse-grained dynamics is determined by maximising the Boltzmann entropy subject to constraints representing conserved quantities. It is shown that at thermodynamic equilibrium the Adler-Millard charge is equipartitioned over all degrees of freedom so that the canonical average of each commutator $[q_B,p_B]$ and each anti-commutator $\{q_F,p_F\}$ is assumed to be equal to $i\hslash$. This is how the quantum commutation relations emerge from the underlying trace dynamics. Also, in this emergent thermodynamic equilibrium, the canonically averaged Hamilton’s equations of motion become Heisenberg’s equations of motion of quantum theory. Identification of canonical averages of functions of dynamical variables (in their ground state) with Wightman functions in relativistic quantum mechanics enables the transition from trace dynamics to quantum field theory. Quantum field theory is thus shown to be an emergent (equilibrium) thermodynamic phenomenon.

At equilibrium, the Adler-Millard charge is anti-self-adjoint, and the Hamiltonian of the theory is self-adjoint. Statistical fluctuations in this charge, when significant, can drive the quantum system away from equilibrium (the charge is no longer equipartitioned). If these fluctuations are themselves dominantly self-adjoint, the Hamiltonian of the theory picks up an anti-self-adjoint component, which gets amplified if a large number of degrees of freedom are entangled with each other. This drives the system to classicality, via a Ghirardi-Rimini-Weber type of spontaneous collapse process. Thus, macroscopic classical systems, including classical fields, are far from equilibrium emergent states in trace dynamics.

The basis for the fundamental action (25) is the Chamseddine-Connes spectral action principle. Let us first recall the principle and its present application for the case of Einstein-Hilbert action of general relativity. After that we will include Yang-Mills fields. According to this principle, the Einstein-Hilbert action can be expressed in terms of the eigenvalues of the Dirac operator D on a Riemannian geometry, via a truncated heat kernel expansion in powers of $L_p^{-2}$:

$$Tr\left[L_P^2{D}^2\right]\sim L_p^{-2}\int d^{4}x\sqrt{g}R+\mathcal{O}\left(L_P^0\right)=\sum _i{L}_p^2{\lambda }_i^2$$

(39)

It has also been shown that these Dirac eigenvalues can be the dynamical observables of general relativity, in place of the metric. In the spirit of trace dynamics, every eigenvalue ${\lambda }_i$ is raised to the status of a bosonic matrix/operator ${\widehat{\lambda }}_i\equiv {\dot{q}}_{Bi}$, this being the very Dirac operator D of which it is an eigenvalue. Thus in generalised trace dynamics (a pre-quantum, pre-spacetime theory) we have a collection of ‘atoms of space-time’, as many atoms as there were Dirac eigenvalues, each atom being associated with a copy of the Dirac operator: ${\dot{q}}_{Bi}\equiv LD$, where L is a newly introduced length parameter which characterises a space-time atom. The Einstein-Hilbert action ${\sum }_i{L}_p^2{\lambda }_i^2$ transits to ${\sum }_{i}Tr(L_p^2/L^2)\left[{\dot{q}}_{Bi}^2\right]$. Since the Dirac eigenvalues have been made operators, space-time is lost, and this is simultaneously a transition to trace dynamics and to non-commutative geometry, hence showing the deep connection between the new geometry and the new dynamics. However, note that what was earlier the (dimensionless) action is now the dimensionless (trace) Lagrangian; the integral over time, which will make it into a trace dynamics action, is missing. Here, Connes time parameter $\tau$, a unique feature of non-commutative geometry, comes into play. The trace dynamics action for atoms of space-time matter, scaled with respect to Planck’s constant ℏ, is given by

$$\frac{S}{\hslash }=\int \frac{d\tau }{{\tau }_p}\sum _{i}Tr(L_p^2/L^2)\left[{\dot{q}}_{Bi}^2\right]$$

(40)

The recovery of classical general relativity is the reverse of the above : quantum-to-classical transition sends each Dirac operator back to one its eigenvalues; a different eigenvalue for every STM atom, and from the sum total of the squares of eigenvalues, the Einstein-Hilbert action is recovered.

$$\int d\tau Tr\left[D_1^2+D_2^2+D_3^2+...\right]⟶\int d\tau \left[{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2+...\right]=\int d\tau Tr\left[D^2\right]\propto \int d\tau \int d^{4}x\sqrt{-g}R$$

(41)

The Chamseddine-Connes spectral action principle continues to hold when Yang-Mills gauge fields are included. To get there, we first recall how gauge fields are treated as inner automorphisms of a non-commutative algebra. The seventh axiom of commutative geometry in Connes’ programme states that there exists an antilinear isometry $J:\mathcal{H}\to \mathcal{H}$ such that $Ja{J}^{-1}=a^{*}\forall a\in \mathcal{A}$ and $J^2=ϵ,JD={ϵ}^{\prime }DJ$ and $J\gamma ={ϵ}^{″}\gamma J$ where $ϵ,{ϵ}^{\prime },{ϵ}^{″}\in \{-1,+1\}$.

In the theory of operator algebras there is a result of great significance due to Tomita. The theorem states that given a weakly closed * algebra of operators M in Hilbert space $\mathcal{H}$ which admits a cyclic and separating vector, there exists a canonical antilinear isometric involution J from $\mathcal{H}$ to $\mathcal{H}$ such that $JM{J}^{-1}=M^{\prime }$. Here, $M^{\prime }=\{T;Ta=aT\forall a\in M\}$ is the commutant of M. Consequently, M is antiisomorphic to its commutant, where the antiisomorphism is given by the following $\mathbb{C}$-linear map: $a\in M\to J{a}^{*}{J}^{-1}\in M^{\prime }$.

As noted above, axiom 7 of commutative geometry already involves an antilinear isometry J in $\mathcal{H}$, this being complex conjugation. Since $\mathcal{A}$ was assumed commutative, the equality $J{a}^{*}{J}^{-1}=a$ is consistent with the antiisomorphism in Tomita’s theorem. In going over to the non-commutative case the requirement $J{a}^{*}{J}^{-1}=a\forall a\in \mathcal{A}$ is replaced by the condition: $[a,b^0]=0\forall a,b\in \mathcal{A}$ where $b^0=J{b}^{*}{J}^{-1}$. This converts the Hilbert space $\mathcal{H}$ into a module over the algebra $\mathcal{A}\otimes {\mathcal{A}}^0$ this being the tensor product of $\mathcal{A}$ with its opposite algebra ${\mathcal{A}}^0$. And,

$$(a\otimes b^0)\xi =aJ{b}^{*}{J}^{-1}\xi \forall a,b\in \mathcal{A}$$

(42)

We now illustrate the non-commutative case for the algebra $\mathcal{A}=C^{\infty }(M,M_k\left(\mathbb{C}\right))$ of $k\times k$ matrix-valued functions on a smooth compact Riemannian spin manifold M. A metric g is given on M and $\mathcal{H}=L^2(M,S\otimes M_k\left(\mathbb{C}\right))$ is the Hilbert space of $L^2$ sections of the tensor product $S\otimes M_k\left(\mathbb{C}\right)$ of the spinor bundle S with $M_k\left(\mathbb{C}\right)$. The algebra $\mathcal{A}$ acts on $\mathcal{H}$ by left multiplication: $\left(a\xi \right)\left(x\right)=a\left(x\right)\xi \left(x\right),\forall x\in M$. The real structure J is given as $J=C\otimes *$ where C is the charge conjugation operator, and * stands for adjoint of a matrix: $T\to T^{*}$. The adjoint operation converts left multiplication operation $\xi \to a\xi$ to right multiplication $\xi \to \xi a^{*}$ and the axiom $[a,b^0]=0$ is satisfied, where $b^0=J{b}^{*}{J}^{-1}$.

The operator D is taken as $D={\gamma }^{\mu }{\partial }_{\mu }\otimes I$ which is the tensor product of the Dirac operator on M by the identity on $M_k\left(\mathbb{C}\right)$. This gives a non-commutative geometry and conveys important properties of non-commutative geometries in general. The group $\mathrm{Aut}\left(\mathcal{A}\right)$ of * automorphisms of the algebra $\mathcal{A}$ is also the diffeomorphism group $\mathrm{Diff}\left(M\right)$ of diffeomorphisms of the manifold M. It has a natural normal subgroup $\mathrm{Int}\left(M\right)\subset \mathrm{Aut}\left(M\right)$ of inner automorphisms, these being automorphisms of the form ${\alpha }_u\left(x\right)=ux{u}^{*}\forall x\in \mathcal{A}$. Here, u is an arbitrary element of the unitary group

$$\mathcal{U}=\{u\in \mathcal{A};u{u}^{*}=u^{*}u=I\}$$

(43)

The action of this group of internal diffeomorphisms on the geometry can be expressed by replacing the Dirac operator D with

$$\tilde{D}=D+A+JA{J}^{-1}$$

(44)

where the A are Yang-Mills gauge potentials. This generalisation of the Dirac operator is a special case of $A=A^{*}$ with $A={\sum }_i{a}_i[D,b_i]$. In the commutative case this generalisation vanishes because $A=A^{*}$ implies that $A+JAJ{A}^{-1}=0$. In the non-commutative case the generalisation is non-trivial. In the present example, $\mathrm{Int}\left(M\right)=C^{\infty }(M,SU\left(k\right))$ is the group of local gauge transformations for an $SU\left(k\right)$ gauge theory on M. The internal perturbations of the metric are parametrised by $SU\left(k\right)$ gauge potentials.

It is striking to observe the parallels between non-commutative geometry and trace dynamics. In both cases, making the algebra non-commutative brings in significant new features (which are not there in the commutative case) which influence applications of the theory. For NCG, it is the inner automorphisms (responsible for standard model gauge fields arising naturally), and also the concept of Tomita-Takesaki-Connes time. For trace dynamics it is the Adler-Millard charge, which is responsible for trace dynamics being a pre-quantum theory. We have therefore suggested a merger of trace dynamics and non-commutative geometry, wherein eigenvalues of the Dirac operator will themselves be raised to the status of operators, thus generalising trace dynamics to a pre-quantum, pre-spacetime theory. This theory will then have a conserved Adler-Millard charge which incorporates pre-gravitational degrees of freedom, and it will have Connes time.

We can now return to the spectral action principle which incorporates Yang-Mills gauge fields using Dirac eigenvalues. We recall that a canonical triple $(\mathcal{A},\mathcal{H},D)$ over a manifold is defined as follows. $\mathcal{A}=C^{\infty }\left(M\right)$ is the algebra of complex-valued smooth functions on M. $\mathcal{H}=L^2(M,S)$ is the Hilbert space of square-integrable sections of the irreducible spinor bundle over M. And D is the Dirac operator of a Clifford connection. Assuming it to be an even spectral triple, a real structure (a generalised charge conjugation) is introduced through the antilinear isometry J on $\mathcal{H}$ and is crucial in deriving the spectral action for Yang-Mills fields. Thus,

$$J^{*}=J^{-1}=-J,J^2=-1,JD=DJ,Jϵ=ϵJ$$

(45)

$$[a,b^0]=0,b^0=J{b}^{*}{J}^{*}\forall a,b\in \mathcal{A},[[D,a],b^0]=0$$

(46)

We also need to define the product of two real spectral triples $({\mathcal{A}}_1,{\mathcal{H}}_1,D_1,J_1)$ and $({\mathcal{A}}_2,{\mathcal{H}}_2,D_2,J_2)$. The product triple $(\mathcal{A},\mathcal{H},D,J)$ is given by

$$\mathcal{A}={\mathcal{A}}_1\otimes {\mathcal{A}}_2,\mathcal{H}={\mathcal{H}}_1\otimes {\mathcal{H}}_2,D=D_1\otimes 1+{ϵ}_1\otimes D_2,J=J_1\otimes J_2$$

(47)

In the celebrated Chamseddine-Connes toy model for describing the bosonic sector of the standard model (at tree level) coupled to gravity, they proposed the purely geometric action

$$S_B\left(D_A\right)={\mathrm{Tr}}_{\mathcal{H}}\left(\chi \left(\frac{D_A^2}{{\Lambda }^2}\right)\right)$$

(48)

Here, $D_A=D+A+JA{J}^{*}$ and A is the gauge potential $A={\sum }_j{a}_j[D,b_j]$. ${\mathrm{Tr}}_{\mathcal{H}}$ is the usual trace in Hilbert space (this will be our point of contact with trace dynamics), $\Lambda$ is a cutoff parameter, and the function $\chi$ cuts off all eigenvalues of $D_A^2$ larger than ${\Lambda }^2$. The action is exclusively in terms of the spectrum of the self-adjoint operator $D_A$ and is motivated by the above-discussed interpretation that the inner automorphisms of $\mathcal{A}$ are the gauge degrees of freedom. As noted above, $\mathrm{Diff}\left(M\right)$ is isomorphic to $\mathrm{Aut}\left(C^{\infty }\left(M\right)\right)$ and we define $\mathrm{Out}\left(\mathcal{A}\right)=\mathrm{Aut}\left(\mathcal{A}\right)/\mathrm{Int}\left(\mathcal{A}\right)$. Then we have the following short exact sequence of groups:

$$1_{\mathrm{Aut}(\mathcal{A}})\to \mathrm{Int}\left(\mathcal{A}\right)\to \mathrm{Aut}\left(\mathcal{A}\right)\to \mathrm{Out}\left(\mathcal{A}\right)\to 1_{\mathrm{Aut}\left(\mathcal{A}\right)}$$

(49)

In comparison, for gauge theories over commutative algebras, we construct connections on a principal fibre bundle P having as structure group a Lie group G. The gauge fields are then sections of the associated vector bundle with fibres in $\mathcal{H}$. The diffeomorphisms on P form the automorphism group $\mathrm{Aut}\left(P\right)$ on P, and one has the following short exact sequence

$$1\to GA\left(P\right)\to \mathrm{Aut}\left(P\right)\to \mathrm{Diff}\left(\mathrm{M}\right)\to 1$$

(50)

where $GA\left(P\right)$ is the gauge group. The striking similarity of this sequence with the one in (47) suggests that the spectral action for a gauge theory should be constructed as follows. First, one looks for an algebra $\mathcal{A}$ such that $\mathrm{Int}\left(\mathcal{A}\right)=GA\left(P\right)$. Then, a suitable spectral triple is constructed over $\mathcal{A}$ in particular by specifying the Dirac operator. Finally, one computes the spectral action given in (46). What this yields in the end is a gauge theory of the group G with space-time gravitation induced by the diffeomorphism group $\mathrm{Out}\left(\mathcal{A}\right)=\mathrm{Aut}\left(\mathcal{A}\right)/\mathrm{Int}\left(\mathcal{A}\right)$.

A straightforward non-commutative modification of a manifold M consists of a product of the canonical spectral triple with the N-dimensional matrix algebra $M_N\left(\mathbb{C}\right)$. The spectral triple in this case is given by

$$\begin{array}{c}\hfill \mathcal{A}=C^{\infty }\left(M\right)\otimes M_N\left(\mathbb{C}\right),\mathcal{H}=L^2(S,M)\otimes M_N\left(\mathbb{C}\right),\\ \hfill D_A={\gamma }^{\mu }\left({\nabla }_{\mu }\otimes 1_N-\frac{i{g}_0}{2}{1}_4\otimes A_{\mu }^i{T}^i\right)\end{array}$$

(51)

Here, $A\in M_N\left(\mathbb{C}\right)$ is a Hermitian matrix and $T^i$ are the anti-Hermitian generators of the Lie algebra associated with the elements of a matrix group in $M_N\left(\mathbb{C}\right)$. One would like to compute the spectral action (46) using a method of operator integration similar to the one used earlier in the case of general relativity. The goal is to show that this action yields gravitation coupled to Yang-Mills fields. A detailed analysis leads to the following final result:

$$\begin{array}{c}\hfill \frac{48{\pi }^2}{N}{S}_B(D,A)=6{\Lambda }^4{\int }_M{d}^{4}x\sqrt{g}+{\Lambda }^2{\int }_M{d}^{4}x\sqrt{g}R\\ \hfill +\int d^{4}x\sqrt{g}\left(-\frac{3}{20}{C}_{\mu \nu \sigma \rho }{C}^{\mu \nu \sigma \rho }+\frac{1}{10}{R}_{;\mu }^{;\mu }\right)+\\ \hfill \frac{11}{120}{\int }_M{d}^{4}x\sqrt{g}\left(\frac{1}{2}{ϵ}^{\mu \nu \rho \sigma }{R}_{\mu \nu }^{\alpha \beta }\right)\left(\frac{1}{2}{ϵ}_{\alpha \beta \lambda \tau }{R}_{\rho \sigma }^{\lambda \tau }\right)\\ \hfill +\frac{g_0^2}{N}{\int }_M{d}^{4}x\sqrt{g}{g}^{\mu \sigma }{g}^{\nu \rho }{\partial }_{\mu }{A}_{\nu }^i{\partial }_{\sigma }{A}_{\rho }^i\end{array}$$

(52)

Here, $C_{\mu \nu \sigma \rho }$ is the Weyl tensor. The term contributing at order ${\Lambda }^4$ is the cosmological constant term; the Einstein-Hilbert action as expected is at order ${\Lambda }^2$; and the Yang-Mills action is at order ${\Lambda }^0$ along with additional gravitational terms. The term quadratic in the Weyl tensor is conformal gravity, and apart from the Gauss-Bonnet term there is a term in higher order gravity.

We set aside for now the Weyl tensor term, Gauss-Bonnet term and cosmological constant term, and focus on the Einstein-Hilbert action and Yang-Mills action. Since the action can be written as sum of squared eigenvalues of the generalised Dirac operator $D_A$, analogous to the GR case, each eigenvalue is raised to the status of a matrix/operator. The eigenvalues of the gauge potential are thereby also raised to the status of matrices, and these matrices are identified with the configuration variables $q_{Bi}$ of the corresponding original Dirac operators ${\dot{q}}_{Bi}$. That is, the dynamical variable ${\dot{Q}}_B=\frac{1}{L}(i\alpha q_B+L{\dot{q}}_B)$ defined in Eqn. (27) is the net bosonic field, incorporating gravitation as well as Yang-Mills gauge fields. Using this, the bosonic part of the fundamental action (25) can be written down for every STM atom, and hence also for the collection of STM atoms. Furthermore, analogous to the GR case in Eqn. (39) the quantum-to-classical transition leads to the recovery of the Einstein-Hilbert action plus Yang-Mills action. The Lie group of the gauge symmetry for the recovered Yang-Mils action is $SU\left(3\right)\times U\left(1\right)$ because that symmetry is the one present in the underlying fundamental action. The gauge symmetries of the bosonic part of the fundamental action have ben analysed in detail in [21]. In the classical limit, the internal symmetry $SU{\left(3\right)}_c\times U{\left(1\right)}_{em}$ is recovered on the flipped 4D spacetime, the geometry of this spacetime is the gravity equivalent of the weak force, resulting from breaking of $SU{\left(2\right)}_L\times U{\left(1\right)}_Y$. On the other hand, the internal symmetry $SU{\left(3\right)}_{grav}\times U{\left(1\right)}_{grav}$ is recovered on our 4D spacetime, the geometry of our spacetime is given by GR, resulting from breaking of $SU{\left(2\right)}_L\times U{\left(1\right)}_Y$. The trace dynamics action for gravity and Yang-Mills fields was first derived by us in [43] where the Dirac equation is also derived from the fundamental action.

Various researchers have also studied the more complete case where fermions of the standard model (quarks and leptons) are also included [44]. The analysis involves studying the action

$$\mathrm{Tr}\left[\chi \left(\frac{D_A^2}{{\Lambda }^2}\right)\right]+(\psi ,D\psi )$$

(53)

where the second term is for fermions. To convert this into a spectral action we recall the work of Landi and Rovelli, on writing general relativity in terms of Dirac eigenvalues as observables. One would like to reformulate Euclidean general relativity using eigenvalues ${\lambda }_n$ of the Dirac operator as dynamical variables. This was achieved by Landi and Rovelli in their (1996) work [45,46]. The eigenvalues ${\lambda }_n$ are an infinite sequence of real numbers, and form a diffeomorphism invariant set of physical observables for general relativity. The ${\lambda }_n$ are the eigenvalues of the Dirac operator D defined on the Riemannian space-time geometry described by $g_{\mu \nu }\left(x\right)$. In going over to the (generalised) trace dynamics we will raise each eigenvalue to the status of an operator, this being the very Dirac operator of which it is an eigenvalue. This is an act of (pre-)quantisation, and takes us to a (pre-)quantum theory of gravity. This being a pre-quantum theory, the Heisenberg quantum commutation relations will not be imposed a priori, but will be emergent, just like in trace dynamics. Space-time coordinates will be generalised too; each classical space-time point will be replaced by a quaternion. The Dirac operator will have quaternionic components and will be identified with the dynamical variable in trace dynamics.

Let us consider Euclidean general relativity on a compact 4D Riemannian spin manifold M without boundary. Given the tetrad fields $e_{\mu }^A$, the metric is $g_{\mu \nu }\left(x\right)=e_{\mu }^A\left(x\right)e_{A\nu }\left(x\right)$. The spin connection is given by ${\partial }_{[\mu }{E}_{\nu ]}^A={\omega }_{[\mu B}^A{e}_{\nu ]}^B$. The Dirac operator

$$D=i{\gamma }^A{e}_A^{\mu }\left({\partial }_{\mu }+{\omega }_{\mu BC}{\gamma }^B{\gamma }^C\right)$$

(54)

being self-adjoint, admits a complete set of real eigenvalues ${\lambda }_n$ and eigenspinors ${\psi }_n$ with a discrete spectrum (because M is compact)

$$D{\psi }_n={\lambda }_n{\psi }_n$$

(55)

We are interested in knowing how an eigenvalue varies when the tetrad field is varied. For this it helps to recall that a self-adjoint operator $D\left(v\right)$ having non-degenerate eigenvalues ${\lambda }_n\left(v\right)$ satisfies

$$\frac{d{\lambda }_n\left(v\right)}{dv}=\langle {\psi }_n\left(v\right)|\left(\frac{d}{dv}D\left(v\right)\right)|{\psi }_n\left(v\right)\rangle$$

(56)

We use this result to find the variation of ${\lambda }_n\left(e\right)$ for a small variation in the tetrad field $e_{\mu }^A\left(x\right)$. Consider a one parameter family of tetrad fields $e_{v\mu }^A\left(x\right)$ labeled by a real parameter v

$$e_{v\mu }^A\left(x\right)=e_{\mu }^A\left(x\right)+v{\widehat{e}}_{\mu }^A\left(x\right)$$

(57)

where ${\widehat{e}}_{\mu }^A\left(x\right)$ is an arbitrary chosen tetrad field. The variation $\delta {\lambda }_n\left[e\right]/\delta e_{\mu }^A\left(x\right)$ is given by the following distribution

$$\int d^{4}x\frac{\delta {\lambda }_n\left[e\right]}{\delta e_{\mu }^A\left(x\right)}{\widehat{e}}_{\mu }^A\left(x\right)={\left.\frac{d{\lambda }_n\left[e_v\right]}{dv}\right|}_{v=0}$$

(58)

Using (54), after some intermediate steps one gets the result

$${\left.\frac{d{\lambda }_n\left[e_v\right]}{dv}\right|}_{v=0}={\left.\frac{d}{dv}\right|}_{v=0}\int d^{4}y\sqrt{g\left[e_v\right]}\left({\overline{\psi }}_{n}D\left[e_v\right]{\psi }_n-{\lambda }_n{\overline{\psi }}_n{\psi }_n\right)$$

(59)

The expression under the integral is what one would get by varying the action for a Dirac spinor (with mass $\lambda$ ) with respect to the tetrad. And we know that to be nothing other than the energy-momentum tensor $T_A^{\mu }\left(x\right)$

$$T_A^{\mu }\left(x\right)\equiv \frac{\delta }{\delta e_{\mu }^A\left(x\right)}{S}_{\mathrm{Dirac}}$$

(60)

of a spinor of mass $\lambda$, where the Dirac action is given by $S_{\mathrm{Dirac}}=\int \sqrt{g}(\overline{\psi }D\psi -\lambda \overline{\psi }\psi )$. We hence conclude that

$$\frac{\delta {\lambda }_n\left[e\right]}{\delta e_{\mu }^A\left(x\right)}=T_{nA}^{\mu }\left(x\right)$$

(61)

where the subscript n on the right hand side is for denoteing the energy-momentum tensor of the eigenspinor ${\psi }_n$. This gives the desired variation of the eigenvalues, resulting from a variation of the tetrad.

One can now derive the Einstein equations by varying the action for general relativity written in terms of Dirac eigenvalues:

$$S_{GR}\left(D\right)=\mathrm{Tr}\left(\chi \left(\frac{D^2}{{\Lambda }^2}\right)\right)\Rightarrow S_{GR}\left[\lambda \right]=\kappa \sum _n\chi \left({\lambda }_n^2{\Lambda }^2\right)$$

(62)

Thus we can write the variation, and minimise the action (on the surface $\lambda \left(ϵ\right)$ of allowed Einstein geometries, not on $R^{\infty }$)

$$0=\frac{\delta S_{GR}}{\delta E_{\mu }^A\left(x\right)}=\sum _n\frac{\partial S_{GR}}{\partial {\lambda }_n}\frac{\delta {\lambda }_n}{\delta E_{\mu }^A\left(x\right)}=\sum _n\frac{d\chi \left({\Lambda }^{-2}{\lambda }_n^2\right)}{d{\lambda }_n}{T}_{nA}^{\mu }\left(x\right)$$

(63)

Hence the Einstein equations with Dirac eigenvalues as observables are

$$\sum _{n}f\left({\Lambda }^{-2}{\lambda }_n^2\right){\lambda }_n{T}_{nA}^{\mu }\left(x\right)=0$$

(64)

where $f\left(u\right)\equiv \frac{d}{du}\chi \left(u\right)$.

One can include a source term for a fermionic field, whose energy-momentum tensor will then appear on the right hand side of Einstein equations. For this, we add to the GR action the Dirac action $S_{\mathrm{Dirac}}[\psi ,e]$ for a fermionic field $\psi$

$$S_{\mathrm{Dirac}}[\psi ,e]=\int \left(\overline{\psi }D\psi -m\overline{\psi }\psi \right)\sqrt{g}{d}^{4}x=\langle \psi [D-m]\psi \rangle$$

(65)

Thus the full action is

$$S[D,\psi ]=S_{GR}\left[D\right]+S_{\mathrm{Dirac}}[D,\psi ]=\kappa \mathrm{Tr}\left[\chi \left({\Lambda }^{-2}{D}^2\right)\right]+\langle \psi [D-m]\psi \rangle$$

(66)

(In the octonionic theory that we are developing, we propose a fully trace-class action in which the second term in the above action, i.e. the fermionic part, is also inside the trace).

In order to proceed further, we expand the fermionic field $\psi$ in the basis formed by the eigenspinors ${\psi }_n$

$$\psi \left(x\right)=\sum _n{a}_n{\psi }_n\left(x\right)$$

(67)

Therefore, gravity is described by the ${\lambda }_n$ and the fermion by the components $a_n$. The action now becomes

$$S[{\lambda }_n,a_n]=\sum _n\left[\kappa \chi \left({\Lambda }^{-2}{\lambda }_n^2\right)+({\lambda }_n-m){\left|a_n\right|}^2\right]$$

(68)

The equations of motion therefore are

$$\sum _n\left[2\kappa {\Lambda }^{-2}f\left({\Lambda }^{-2}{\lambda }_n^2\right)+\left({\lambda }_n-m\right){\left|a_n\right|}^2\right]T_{nA}^{\mu }\left(x\right)=0$$

(69)

$$({\lambda }_n-m)a_n=0$$

(70)

The first equation is Einstein equation with a source term, and the second one is the Dirac equation on a curved spacetime. This second equation, being algebraic, is straightforward to solve. A solution will exist if there exists an $\widehat{n}$ such that ${\lambda }_{\widehat{n}}=m$, in which case $a_n=0\forall n\ne \widehat{n}$, and $a_{\widehat{n}}=a$, an arbitrary constant. The interpretation is that on a space-time geometry characterised by the Dirac eigenvalues ${\lambda }_n$, a fermion field of mass m is given by the eigenspinor ${\psi }_{\widehat{n}}$ corresponding to the eigenvalue m.

Once one has a spectral expansion for the fermionic term in the action, we can once again apply the trace dynamics principle and raise each eigenvalue to the status of a matrix / operator. This leads us to introduce the fermionic dynamical variables $q_F$ and ${\dot{q}}_F$ (as shown in (32) and (33)): these respectively represent left-chiral and right-chiral fermions. This results in cross-terms of the form $q_B{q}_F$, $q_B{\dot{q}}_F$, ${\dot{q}}_B{q}_F,{\dot{q}}_B{\dot{q}}_F$ as shown in Eqn. (30). These respectively have the interpretation of Yang-Mills fields action on left and right handed fermions, and spacetime acting on left and right handed fermions. $SU{\left(3\right)}_{genL}$ and $SU{\left(3\right)}_{genR}$ symmetries act on the left and right handed fermionic terms, respectively. In the quantum-to-classical transition these terms give rise to the fermionic terms in the standard model Lagrangian. The terms in (30) which are quadratic in the fermionic variables represent the two Higgs in this theory, and in the classical limit these are replaced by the Lagrangian for the Higgs in the standard model.

In this section we have summarised the relation between the action of the $E_8\times E_8$ theory and GR and standard model. A more detailed analysis of the recovery of general relativity and the standard model from the fundamental action (25) will be presented elsewhere.

So far, we have a matrix-valued Lagrangian dynamics, which is a generalisation of classical real-number valued dynamics. We have also made a transition from Riemannian geometry to Connes’ non-commutative geometry. What remains is to transit from the real-number valued coordinate system which labels the 4D space-time manifold, and to instead work with the non-commuting numbers known as quaternions and octonions. The dynamical matrices (which replace vectors) have matrix-valued ‘coordinate’ components over the field of quaternions/octonions, instead of over the field of real numbers. We then have a pre-quantum, pre-spacetime dynamics in higher dimensions, which we employ to describe the standard model as well as gravitation, because the (broken) symmetries of bi-octonionic space coincide with the ones observed in nature.

6.4. Octonions as Coordinate Systems: A Non-Commutative Manifold

The algebra automorphisms of the octonions unify space-time diffeomorphisms and standard model gauge field transformations into one common symmetry ($E_8\times E_8$). The octonionic coordinate space is defined separately for every atom of space-time-matter, one coordinate copy per atom.

There are only four division algebras: reals, complex numbers, quaternions and octonions, denoted $\mathbf{R},\mathbf{C},\mathbf{H},\mathbf{O}$. A quaternion $\mathbf{H}$

$$\mathbf{H}=a_0+a_1\widehat{i}+a_2\widehat{j}+a_3\widehat{k};{\widehat{i}}^2={\widehat{j}}^2={\widehat{k}}^2=-1;\widehat{i}\widehat{j}=\widehat{k}=-\widehat{j}\widehat{i};\widehat{j}\widehat{k}=\widehat{i}=-\widehat{k}\widehat{j};\widehat{k}\widehat{i}=\widehat{j}=-\widehat{i}\widehat{k}$$

(71)

can be used to define a vector and its rotations in 3D space. A split biquaternion is defined as

$$\mathbf{H}\oplus \omega \tilde{\mathbf{H}}=(a_0+a_1\widehat{i}+a_2\widehat{j}+a_3\widehat{k})\oplus \omega (a_0-a_1\widehat{i}-a_2\widehat{j}-a_3\widehat{k})$$

(72)

Here $\omega$ is the split complex number (i.e. ${\omega }^{*}=-\omega ,{\omega }^2=1$) made from the imaginary directions of a quaternion. Complexified split biquaternions are key to defining chiral leptons in this theory. Furthermore, the Dirac operator is nothing but the gradient operator on quaternionic space - the gamma matrices present in the Dirac operator when defined on Minkowski spacetime mimic the true nature of spacetime, which is quaternionic and non-commutative. The Lagrangian we have constructed in (33) is essentially the square of the Dirac operator (squared momentum / kinetic energy) of a free particle.

An octonion is defined as [34]

$$\mathbf{O}=a_0+a_1{\mathbf{e}}_1+a_2{\mathbf{e}}_2+a_3{\mathbf{e}}_3+a_4{\mathbf{e}}_4+a_5{\mathbf{e}}_5+a_6{\mathbf{e}}_6+a_7{\mathbf{e}}_7$$

(73)

The seven imaginary directions anti-commute, each of them squares to $-1$, and octonionic multiplication obeys the Fano plane rules. A split bioctonion is defined as

$$\begin{array}{cc}\hfill \mathbf{O}+\omega \tilde{\mathbf{O}}=& (a_0+a_1{\mathbf{e}}_1+a_2{\mathbf{e}}_2+a_3{\mathbf{e}}_3+a_4{\mathbf{e}}_4+a_5{\mathbf{e}}_5+a_6{\mathbf{e}}_6+a_7{\mathbf{e}}_7)+\hfill \\ \hfill & \omega (a_0-a_1{\mathbf{e}}_1-a_2{\mathbf{e}}_2-a_3{\mathbf{e}}_3-a_4{\mathbf{e}}_4-a_5{\mathbf{e}}_5-a_6{\mathbf{e}}_6-a_7{\mathbf{e}}_7)\hfill \end{array}$$

(74)

This time the split complex number $\omega$ is made from the imaginary directions of the octonion. Complexified split bioctonions are central to defining chiral quarks and leptons. Whereas split biquaternions are adequate for chiral leptons, the extension to split bioctonions is essential for bringing in chiral quarks: QCD is the geometry of extra spatial dimensions (there being four such extra dimensions).

For arriving at this 16D split bioctonionic space, we have mapped $SU{\left(3\right)}_{spacetime1}\times SU{\left(3\right)}_{spacetime2}$ to this space. This is how spacetime will emerge, from squaring of the bioctonionic space. Bosonic and fermionic fields described by $E_6\times E_6$ symmetry reside on this space.

Bosons and fermions are defined on split bioctonionic space; for instance

$$Q_B=Q_0+Q_1{\mathbf{e}}_1+Q_2{\mathbf{e}}_2+Q_3{\mathbf{e}}_3+Q_4{\mathbf{e}}_4+Q_5{\mathbf{e}}_5+Q_6{\mathbf{e}}_6+Q_7{\mathbf{e}}_7$$

(75)

shows the matrix-valued components $Q_i$ of a bosonic matrix $Q_B$ over octonionic space. In the action (33) the undotted matrices are defined over octonionic space and dotted matrices over the split part of the bioctonionic space. Keeping this in mind, consider the modulus square of the split bioctonion:

$$\begin{array}{cc}\hfill |O+\omega \tilde{O}{|}^2& =(\tilde{O}\ominus \omega O)\times (O\oplus \omega \tilde{O})=\tilde{O}O\oplus \omega \tilde{O}\tilde{O}\ominus \omega OO\ominus O\tilde{O}\hfill \\ \hfill & =(a_0^2+a_1^2+a_2^2+a_3^2+a_4^2+a_5^2+a_6^2+a_7^2)\oplus \hfill \\ \hfill & \omega (a_0^2-a_1^2-a_2^2-a_3^2-a_4^2-a_5^2-a_6^2-a_7^2+Im1)\ominus \hfill \\ \hfill & \omega (a_0^2-a_1^2-a_2^2-a_3^2-a_4^2-a_5^2-a_6^2-a_7^2+Im2)\ominus \hfill \\ \hfill & (a_0^2+a_1^2+a_2^2+a_3^2+a_4^2+a_5^2+a_6^2+a_7^2)\hfill \end{array}$$

(76)

The four expressions in the four lines after the second equality demonstrate the unified presence of the vector bundle (lines one and four, Euclidean line-element) and space-time (lines two and three, Lorentzian line element, with imaginary corrections). Inspecting the bosonic part of the Lagrangian (33) we see that the two Euclidean elements are for the dotted quadratic term ${\dot{q}}_B^{†}{\dot{q}}_B$ and the undotted term $q_B^{†}{q}_B$ respectively. As has been analysed in [47], and supported by the results in [48], the undotted term represents an interaction with $SU\left(3\right)$ symmetry that is identified with $SU{\left(3\right)}_{color}$, whereas the dotted term is a new $SU\left(3\right)$ symmetry interpreted as $SU{\left(3\right)}_{grav}$. The Lorentzian elements in lines two and three in the above equation are for the mixed terms ${\dot{q}}_B^{†}{q}_B$ and $q_B^{†}{\dot{q}}_B$. They represent an $SU{\left(2\right)}_L$ symmetry and an $SU{\left(2\right)}_R$ symmetry - the former, along with a contribution from the undotted quadratic term, represent the electroweak symmetry [47,48]. The latter, along with a contribution from the dotted quadratic term, represents a $SU{\left(2\right)}_R\times U{\left(1\right)}_{grav}$ symmetry which is the precursor of general relativity modified by a $U{\left(1\right)}_{grav}$. This symmetry is the right-handed counterpart of electroweak and is possibly a renormalisable theory - this might help us understand why general relativity is not renormalisable (it being a broken symmetry like the weak force), whereas the $U{\left(1\right)}_{grav}$ is possibly the theoretical origin of MOND.

The imaginary corrections arise from multiplying an octonion onto itself; when they are significant, they might help understand why in the macroscopic limit space-time becomes classical. Because these corrections contribute an anti-self-adjoint part to the trace Hamiltonian. Whereas the Euclidean sector has no imaginary terms, is responsible for the strong force and for the newly proposed $SU{\left(3\right)}_{grav}$; it remains quantum and moreover does not take part in the cosmological expansion of space-time. Also, it is evident that the weak force is a space-time symmetry, not an internal symmetry, unlike the strong force. Together, gravitation and the weak force are broken symmetries in a 6D space-time, related to $SU{\left(2\right)}_L\times U{\left(1\right)}_Y\times SU{\left(2\right)}_R\times U{\left(1\right)}_{grav}$, and stemming from the group-theoretic relation $SL(2,H)\sim SO(1,5)$. The 6D spacetime in itself emerges from breaking of $SU{\left(3\right)}_{spacetime1}\otimes SU{\left(3\right)}_{spacetime2}$ as we now argue.

6.5. Non-Associative and Lorentzian Non-Commutative Geometry

In all the discussion of NCG thus far, it has been assumed that space-time is Euclidean, and also that the algebra of interest is associative. The assumption of Euclidean space-time enables a compact Dirac operator to be considered, which then has a discrete spectrum. Of course one would like to have the NCG analysis generalised to realistic 4D spacetime with Lorentz signature. This is a challenging task, which remains a topic of ongoing research, despite serious effort having been reported to this problem. Here we briefly recall some of the works devoted to this topic; in the development of the aikyon theory we have made the assumption that the results of NCG hold in the Lorentzian case.

A Lorentzian version of the NCG of the standard model was suggested by Barrett in (2007) [47]. Strohmaeir (2002) [48] proposes the notion of a semi-Riemannian spectral triple. Moretti (2003) [49] generalised Connes’ distance formula to the Lorentzian case, using the so-called Lorentzian distance, the d’Alembert operator and the causal functions of a globally hyperbolic spacetime. An algebraic formulation of causality for noncommutative geometry was given by Franco and Eckstein (2013) [50]. It is known that whereas the spinors on a Riemannian manifold lead to a Hilbert space, the spinors on a pseudo-Riemannian manifold naturally give rise to the so-called Krein space instead. Thus, to obtain a physical description of spinor fields on spacetime, it is more natural to work with Krein spaces instead of Hilbert spaces. Building upon previous works, van den Dungen [51] (2016) proposed a definition of Krein spectral triples, which offered a natural extension of the notion of spectral triples from Hilbert spaces to Krein spaces. Using this definition, they described a Lorentzian generalisation of the fermionic action of non-commutative geometry, and called it the Krein action. Bochniak and Sitarz (2018) [52] proposed pseudo-Riemannian generalisations of real spectral triples to describe the geometries with indefinite metric over finite-dimensional algebras. Besnard and Brouder (2021) [53] studied a generalisation of the Connes-Lott version of noncommutative geometry in Lorentzian signature (the noncommutative Standard Model and its $B-L$ extension.

Devastato et al. (2017) [54] showed how ‘twisting’ the spectral triple of the standard model yields the Krein space associated with the Lorentzian signature of spacetime. They analysed the associated spectral action, both for fermions and bosons and demonstrated a close link between twists and Wick rotation. In an important work (2023), Filaci and Martinetti [55] reviewed the applications of twisted spectral triples to the standard model. The initial motivation for the twist was to generate a scalar field, required to stabilise the electroweak vacuum and fit the Higgs mass. However, they showed that the significance of the twist lies in an unexpected new field of 1-forms, which is related to the transition from Euclidean to Lorentzian signature. Boyle and Farnsworth (2014, 2015, 2018) [56,57,58] suggested a reformulation of Connes’ NCG so that several of its axioms are unified into a single axiom. And, very significantly, the reformulation generalises NCG from a non-commutative geometry to a non-associative geometry. Applying their reformulation to the traditional NCG used to describe the standard model they found instead, an extension of the standard model by an extra $U{\left(1\right)}_{B-L}$ gauge symmetry. This was accompanied with a single extra complex scalar field which is a singlet under the standard model symmetries $SU{\left(3\right)}_C\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y$, but having $B-L=2$. This scalar field offered a new solution to the discrepancy between the observed Higgs mass and the NCG prediction. The extension of the standard model which we find in the aikyon theory resonates with the findings of Boyle and Farnsworth. In another very elegant paper, Boyle and Farnsworth (2020) [59] suggested that the commutative and associative algebra of spacetime coordinates should be replaced not by a noncommutative algebra (as in noncommutative geometry), but by a Jordan algebra and a Jordan geometry. They presented a Jordan algebra for the standard model and proposed a natural extension of their construction, which describes the left-right symmetric Pati-Salam model $SU\left(4\right)\times SU{\left(2\right)}_L\times SU{\left(2\right)}_R$. The geometry associated with a Jordan algebra describing standard model internal symmetries has been discussed by Farnsworth [60].

7. Dirac Operator, and the Origin of 6D Spacetime $SO(3,3)$

We propose that the $SU{\left(3\right)}_{spacetime1}\otimes SU{\left(3\right)}_{spacetime2}$, in its $(1,8)\oplus (8,1)$ decomposition, gives rise to the 15 dimensional $SO(3,3)$ symmetry of a 6D spacetime with three time coordinates and three space coordinates. The 16th degree of freedom could offer a possible explanation of Connes time through a $U\left(1\right)$ which accompanies this decomposition. Thus what we have in mind is that each of the two $SU{\left(3\right)}_{spacetime}$ undergoes an $SU\left(2\right)\otimes U\left(1\right)$ branching, with the two emerging $SU\left(2\right)$s having opposite parity, and together they are mapped to the six imaginary directions of a split biquaternion. A 6D Dirac operator is defined as a gradient operator on this 6D space formed by the imaginary directions of the split biquaternion, and its square gives rise to the Klein-Gordon operator on 6D spacetime with signature $(3,3)$. The $U\left(1\right)$ that originates along with, could be a possible explanation for Connes time. We now explain this construction in some detail, making the Dirac operator the key focus of the discussion.

The reason we have a $D=3+3$ theory is because each of the two $SU{\left(3\right)}_{s}pacetime$ undergoes a symmetry breaking to $SU\left(2\right)\times U\left(1\right)$. The two $SU\left(2\right)$s respectively represent the isometry of the three imaginary directions each, in split biquaternions, as explained below. Together, the two $SU\left(2\right)$s give rise to the 6D spacetime.

This brings up the valid concern as to how compact groups such as $SU(3$)s can give rise to the non-compact $SO(3,3)$ spacetime? This can be explained as follows. Each of the two $SU\left(3\right)$s is mapped to an eight-dimensional octonionic space, and we label the two octonionic spaces as $O_1$ and $O_2$. By itself the square modulus of each octonion is positive definite and has Euclidean signature. However, we combine the two octonions through the split complex number $\omega$, as $O_1+\omega O_2$ into a split bioctonion. The square modulus $|O_1+\omega O_2{|}^2$ has a Euclidean component as well as a Lorentzian component, as was demonstrated in Eqn. (74) of Section 6.4. In an analogous way, after each of these two $SU\left(3\right)$s undergo symmetry breaking to $SU\left(2\right)\times U\left(1\right)$, the resulting symmetry groups can be mapped to the complex split-biquaternion $\mathbb{C}\otimes (\mathbb{H}+\omega \mathbb{H})$, which has a Lorentzian squared modulus as will be shown later in this section. Therefore the origin of the non-compact group structure lies in the presence of the split complex number. The split complex number in turn ensures the existence of chiral fermions.

The geometry of the 6D spacetime is described by the electroweak symmetry and by the darkelectro-grav symmetry. The strong interaction $SU{\left(3\right)}_{color}$ and the newly predicted $SU{\left(3\right)}_{grav}$ arise as internal symmetries on this 6D spacetime, as depicted in Figure 1. This requires four internal dimensions to be added on and described by the four imaginary octonionic directions beyond the three imaginary directions already used up in the quaternion describing spacetime. So the number of dimensions (spacetime + internal symmetry) does add up to 6+4 = 10 but spacetime is not by itself 10D. This is one of the several important differences from $E8\times E8$ heterotic string theory which favours $D=9+1$ spacetime because of anomaly cancellation. In our theory spacetime does have (two) extra dimensions, but these are timelike, not spacelike. Quaternions are adequate for describing gravitation and the weak force. Octonions are needed only when the strong force has to be described.

We now return to the Dirac operator’s role in motivating a 6D spacetime with (3,3) signature. Dirac (1928) was looking for a linearised version of the Klein-Gordon equation

$${\hslash }^2\left(-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}+\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}\right)\psi =m^2{c}^2\psi$$

(77)

The sought for linear equation is written as

$$D\psi \equiv i\hslash \left({\gamma }_0\frac{1}{c}\frac{\partial }{\partial t}+{\gamma }_1\frac{\partial }{\partial x_1}+{\gamma }_2\frac{\partial }{\partial x_2}+{\gamma }_3\frac{\partial }{\partial x_3}\right)\psi =mc\psi$$

(78)

The self-adjoint operator D on the left hand side of this equation is the Dirac operator, and one demands that acting D twice on $\psi$ yields the Klein-Gordon equation, i.e. $D^2\psi =m^2{c}^2\psi$. The operator $D^2$ must equal the Klein-Gordon operator which appears on the left side of Eqn. (75). For this to be possible, the symbols ${\gamma }_{\mu }$ must satisfy the following relations, as is easily verified

$$\begin{array}{c}\hfill {\gamma }_0^2=I,{\gamma }_1^2={\gamma }_2^2={\gamma }_3^2=-I,{\gamma }_{\mu }{\gamma }_{\nu }=-{\gamma }_{\nu }{\gamma }_{\mu }\mathrm{for}\mu \ne \nu \end{array}$$

(79)

Because the ${\gamma }_{\mu }$ anti-commute with each other they cannot be numbers. But they can be matrices. Dirac found a set of $4\times 4$ matrices which satisfy these relations, and are now known as Dirac matrices:

$$\begin{array}{cc}& {\gamma }_0=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& -1\end{array}\right),\\ & {\gamma }_1=\left(\begin{array}{cccc}0& 0& 0& -1\\ 0& 0& -1& 0\\ 0& 1& 0& 0\\ 1& 0& 0& 0\end{array}\right),{\gamma }_2=\left(\begin{array}{cccc}0& 0& 0& i\\ 0& 0& -i& 0\\ 0& -i& 0& 0\\ i& 0& 0& 0\end{array}\right),{\gamma }_3=\left(\begin{array}{cccc}0& 0& -1& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\\ 0& -1& 0& 0\end{array}\right)\end{array}$$

(80)

The Dirac matrices ${\gamma }_{\mu }$ can be expressed in terms of the $2\times 2$ Pauli spin matrices as follows

$${\gamma }_0={\gamma }^0=\left(\begin{array}{cc}I& 0\\ 0& -I\end{array}\right),{\gamma }_k=-{\gamma }^k=\left(\begin{array}{cc}0& -{\sigma }_k\\ {\sigma }_k& 0\end{array}\right)$$

(81)

This is known as the Pauli-Dirac representation. Eqn. (76) is the celebrated Dirac equation and it can also be written in the following compact notation

$$D\psi \equiv i\hslash {\gamma }^{\mu }{\partial }_{\mu }\psi =mc\psi$$

(82)

where we have set $x_0=ct$ and ${\partial }_{\mu }=\frac{\partial }{\partial x^{\mu }}$. If an electromagnetic field $F^{\mu \nu }$ defined in terms of the four-vector potential $A^{\mu }$ is present, then we must replace the derivative operator as $i\hslash {\partial }^{\mu }\to i\hslash {\partial }^{\mu }-e{A}^{\mu }$ so that the Dirac equation now becomes

$${\gamma }_{\mu }\left(i\hslash {\partial }^{\mu }-e{A}^{\mu }\right)\psi =mc\psi$$

(83)

Here, ${\gamma }_{\mu }{\partial }^{\mu }={\gamma }^{\mu }{\partial }_{\mu }$ and ${\partial }^{\mu }=\frac{\partial }{\partial x_{\mu }}$. The wave function is a four component column spinor

$$\psi =\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\\ {\psi }_4\end{array}\right)$$

(84)

where each of the four entries ${\psi }_{\alpha }$ is a complex number which satisfies the Klein-Gordon equation. The $\gamma$ matrices form a Clifford algebra: i.e. the elements of the algebra anti-commute, and each element squares to I or to $-I$. This particular Clifford algebra is $Cl(1,3)$. Clifford algebras are closely related to the quaternions and that leads us to ask what the Dirac equation, and in particular the Dirac operator, has to do with the quaternions.

In one of his lectures Michael Atiyah [61] notes that the Dirac operator was first discovered, not by Dirac, but by Hamilton, when the latter discovered the quaternions. This is a deep remark with far-reaching implications. What Atiyah means is that if we take the three imaginary directions $\widehat{i},\widehat{j},\widehat{k}$ of the quaternion and define the 3D Dirac operator $D_3$ in physical space as the gradient operator

$$D_3=\widehat{i}\frac{\partial }{\partial x_1}+\widehat{j}\frac{\partial }{\partial x_2}+\widehat{k}\frac{\partial }{\partial x_3}$$

(85)

then its square is minus the Laplacian: $D_3^2=-{\nabla }^2$. Recall that a quaternion q is defined as

$$\begin{array}{cc}& q=a_0+a_1\widehat{i}+a_2\widehat{j}+a_3\widehat{k},{\widehat{i}}^2={\widehat{j}}^2={\widehat{k}}^2=-1,\widehat{i}\widehat{j}\widehat{k}=-1\\ & \widehat{i}\widehat{j}=-\widehat{j}\widehat{i}=\widehat{k},\widehat{j}\widehat{k}=-\widehat{k}\widehat{j}=\widehat{i},\widehat{k}\widehat{i}=-\widehat{i}\widehat{k}=\widehat{j}\end{array}$$

(86)

where the four $a_i$ are real numbers, and the set of quaternions is denoted $\mathbb{H}$. If the coefficients are complex numbers $c_i$ then we have a complex quaternion $q=c_0+c_1\widehat{i}+c_2\widehat{j}+c_3\widehat{k}$ , also called a biquaternion, and the algebra is now $\mathbb{C}\times \mathbb{H}$. The Clifford algebra associated with quaternions is $Cl(0,2)$ and with biquaternions it is $Cl\left(2\right)$. The automorphism group of the quaternions is $SU\left(2\right)$ (automorphisms are transformations that preserve the quaternionic multiplication rule), and quaternions generate rotations in 3D space. Biquaternions generate the Lorentz algebra $SL(2,\mathbb{C})$ and we recall that $SL(2,\mathbb{C})$ is the double cover of the Lorentz group $SO(1,3)$ on 4D Minkowski spacetime. (Interestingly, $SL(2,\mathbb{H})$ is the double cover of $SO(1,5)$. More on this below). If we define the conjugate $\tilde{q}$ of a quaternion as $\tilde{q}=a_0-a_1\widehat{i}-a_2\widehat{j}-a_3\widehat{k}$ then $q\tilde{q}=a_0^2+a_1^2+a_2^2+a_3^2$, and if $a_0=0$ then a 3D rotation belonging to the group $SO\left(3\right)$ leaves the quadratic form $a_1^2+a_2^2+a_3^2$ invariant. This is why a 3D vector can also be represented using a quaternion, as $a_1\widehat{i}+a_2\widehat{j}+a_3\widehat{k}$. In fact given a quaternion $q^{\prime }=b_0+b_1\widehat{i}+b_2\widehat{j}+b_3\widehat{k}$ the product $q{q}^{\prime }$ is given by, after writing $q\equiv a_0+\mathbf{a}$, $q^{\prime }\equiv b_0+\mathbf{b}$,

$$q{q}^{\prime }=(a_0+\mathbf{a})(b_0+\mathbf{b})=a_0{b}_0+a_0\mathbf{b}+b_0\mathbf{a}-\mathbf{a}.\mathbf{b}+\mathbf{a}\times \mathbf{b}$$

(87)

where $\mathbf{a}.\mathbf{b}$ and $\mathbf{a}\times \mathbf{b}$ are respectively the standard scalar product and cross product of vectors in 3D space. Thus the rules of vector multiplication are already contained in the algebra of quaternions, and in fact quaternions were invented prior to vector analysis in 3D. The two are equivalent but vectors became popular and successful, whereas quaternions were mostly forgotten in theoretical physics.

Let us return to Atiyah’s remark. What about four-dimensional Minkowski spacetime? If we define the 4D quaternionic gradient operator

$$D_4=i\frac{\partial }{\partial x_0}+\widehat{i}\frac{\partial }{\partial x_1}+\widehat{j}\frac{\partial }{\partial x_2}+\widehat{k}\frac{\partial }{\partial x_3}$$

(88)

then it is obvious that $D_4^2$ cannot yield the Klein-Gordon operator because we need four non-commuting quantities, but we have only three. The imaginary $i=\sqrt{-1}$ commutes with the quaternionic imaginaries. Yet there is a gradient operator which can be made using biquaternions which coincides with the Dirac operator $D_6$, but in six spacetime dimensions with signature $(3,3)$. The familiar Dirac operator D is a special case of $D_6$ as we describe below. If we insist on describing the Dirac operator as a quaternionic gradient operator (á la Atiyah) as we do, it is not possible to escape the conclusion that our universe has six spacetime dimensions, not four, and the two extra dimensions are time-like. The six dimensional spacetime, after a symmetry breaking, contains within it a 4D Minkowski spacetime and an overlapping 4D anti-Minkowski space-time with flipped signature: the two 4D spacetimes share one time and one space direction. While the Riemannian geometry of our space-time is due to the gravitational interaction, that of the anti-spacetime is due to the weak force. The weak force is not an internal symmetry but a spacetime symmetry masquerading as an internal symmetry. Prior to symmetry breaking there is a gravi-weak unification in 6D space-time. This theme will be developed in detail in subsequent investigations. The biquaternions naturally provide the Dirac operator $D_6$ as the gradient operator of the 6D spacetime and the Dirac operator D on 4D space-time is a special case of $D_6$.

The quaternions per se do not go well with 4D special relativity, because the absolute magnitude of a quaternion $q\tilde{q}=\tilde{q}q=a_0^2+a_1^2+a_2^2+a_3^2$ is positive definite. Whereas it is left invariant by 4D rotations $SO\left(4\right)$ in Euclidean space, it is not invariant under the Lorentz transformations $SO(1,3)$ which leave the spacetime interval $x_0^2-x_1^2-x_2^2-x_3^2$ invariant. Biquaternions come to the rescue on this count. Consider a Hermitian biquaternion, which is defined as having the property $\tilde{q}=q^{*}$ where $q^{*}$ is the complex conjugate of q. A Hermitian biquaternion $q_h$ has a scalar part which is real, and a vector part which is imaginary: $q_h=a_0+a_{1}i\widehat{i}+a_{2}i\widehat{j}+a_{3}i\widehat{k}$. We have for its norm: $q_h{\tilde{q}}_h={\tilde{q}}_{h}q=a_0-a_1^2-a_2^2-a_3^2$ which has the desired Lorentz invariant form. If we take the anti-Hermitian biquaternion $q_{ah}=a_{o}i+a_1\widehat{i}+a_2\widehat{j}+a_3\widehat{k}$ which satisfies ${\tilde{q}}_{ah}=-q^{*}$ then $q_{ah}{\tilde{q}}_{ah}=-a_0^2+a_1^2+a_2^2+a_3^2$ giving the Lorentz invariant quadratic form with flipped signature.

A point in 4D Minkowski spacetime is represented using a Hermitian biquaternion as

$$x=x_0+i\mathbf{x},\mathbf{x}=x_1\widehat{i}+x_2\widehat{j}+x_3\widehat{k}$$

(89)

A Lorentz transformation must preserve its norm and is represented by action of a quaternion q which sends x to $qx{\tilde{q}}^{*}$ with $q=u+iv$ where u and v are quaternions and $q\tilde{q}=1$. A rotation is given by $q^{*}=q$ and a boost by $q^{*}=\tilde{q}$. A detailed discussion of special relativity in the language of quaternions can be found in the works of Lambek [62,63,64], and elsewhere as well.

Corresponding to the Hermitian biquaternion, we define the following 4D quaternionic gradient operator $D_{4h}$

$$D_{4h}=\frac{\partial }{\partial x_0}-i\nabla \equiv \frac{\partial }{\partial x_0}-i\widehat{i}\frac{\partial }{\partial x_1}-i\widehat{j}\frac{\partial }{\partial x_2}-i\widehat{k}\frac{\partial }{\partial x_3}$$

(90)

It is also a Hermitian biquaternion, and under Lorentz transformations it transforms just like x, that is $D_{4h}\to q{D}_{4h}{\tilde{q}}^{*}$. Using the operator $D_{4h}$ Maxwell’s equations of electrodynamics can be compactly written as

$$D_{4h}F+J=0$$

(91)

Here, the field tensor F is a biquaternion defined by $F=\mathbf{B}+i\mathbf{J}$ and it transforms under Lorentz transformations as $F\to qF{\tilde{q}}^{*}$. The charge-current density J is defined by $J=\rho +i\mathbf{J}$ and also transforms as $J\to qJ{\tilde{q}}^{*}$.

The 4D quaternionic gradient operator $D_{4h}$ serves a useful purpose in special relativity and in Maxwell’s electrodynamics. Clearly though, it is inadequate for writing down the Dirac equation. To get there, we must follow a different path, which inevitably guides us to a 6D space-time.

There is a long history of researchers attempting to write the Dirac equation using a real quaternionic gradient operator (Dirac [65], Conway [66], Lambek [63], Morita [67]). The attempt eventually succeeded; here we follow the analysis of Morita (1986) [67] in their paper titled ‘A role of quaternions in the Dirac theory’. The abstract of the paper says, and we quote: “The Dirac theory is treated by noting that the Lorentz group is realised by a subset of $SL(2,\mathbb{H})$, each element being characterised by a pair of unit quaternion (rotation) and pure quaternion (boost)." Here, by Lorentz group Morita means the one for 4D spacetime, i.e. $SO(1,3)$ and by pure quaternion is meant one that has only the vector part: $\tilde{q}=-q$.

Morita considers special $2\times 2$ matrices A belonging to $SL(2,\mathbb{H})$ and having the property $A{\sigma }_1\tilde{A}=\lambda {\sigma }_1$ and $A{\sigma }_3\tilde{A}=\mu {\sigma }_3$ with $\lambda =\mu =1$. These are matrices with quaternionic entries of the form

$$A=\left(\begin{array}{cc}Q& -P\\ P& Q\end{array}\right){,\left|Q\right|}^2-{\left|P\right|}^2=1,\tilde{P}Q+\tilde{Q}P=1,R\equiv Q^{-1}P=-\tilde{R}$$

(92)

Defining the matrix $X=x^i{\Gamma }_i$ for the space-time vector x, the matrix A generates a Lorentz transformation $x\to x^{\prime }=\Lambda x$ via $X\to X^{\prime }=AX{\tilde{A}}^T$. Here the $\Gamma$ matrices are defined as

$${\Gamma }^0=\left(\begin{array}{cc}1& .\\ .& 1\end{array}\right),{\Gamma }^1=\left(\begin{array}{cc}.& -\widehat{i}\\ \widehat{i}& .\end{array}\right),{\Gamma }^2=\left(\begin{array}{cc}.& -\widehat{j}\\ \widehat{j}& .\end{array}\right),{\Gamma }^3=\left(\begin{array}{cc}.& -k\\ k& .\end{array}\right)$$

(93)

and the vector part $\Gamma$ generates boosts. Rotations are generated by the $\Lambda$ matrices where

$${\Lambda }^1=\left(\begin{array}{cc}i& .\\ .& i\end{array}\right),{\Lambda }^2=\left(\begin{array}{cc}j& .\\ .& j\end{array}\right),{\Lambda }^3=\left(\begin{array}{cc}k& .\\ .& k\end{array}\right)$$

(94)

The Lorentz matrix A is generated by a pair of pure quaternions p and q and is also specified by a pair of unit quaternion a and pure quaternion $\mu$:

$$\begin{array}{cc}& A=expB(p,q),B(q,p)=\left(\begin{array}{cc}q& -p\\ p& q\end{array}\right),\\ & A=R\left(a\right)B\left(\mu \right),\left|a\right|=1=Q/\left|Q\right|,B\left(\mu \right)=\frac{1}{\sqrt{1+{\mu }^2}}\left(\begin{array}{cc}1& \mu \\ -\mu & 1\end{array}\right)\end{array}$$

(95)

$R\left(a\right)$ defines rotations and is made from the $\Lambda$ matrices, and $B\left(\mu \right)$ describes boosts and is made from the pure $\Gamma$ matrices. Defining ${\tilde{\Gamma }}^0={\Gamma }^0$ and ${\tilde{\Gamma }}^r=-{\Gamma }^r$, the $\Gamma$ matrices obey the Clifford algebra ${\Gamma }^i{\tilde{\Gamma }}^j+{\Gamma }^j{\tilde{\Gamma }}^i=-2{\eta }^{ij}$ which corresponds to the original Clifford algebra of the Dirac matrices: ${\gamma }^i{\gamma }^j+{\gamma }^j{\gamma }^i=2{\eta }^{ij}$. Defining the two component spinor $\varphi$ with quaternionic entries, the Dirac equation can now be written as

$$\tilde{\partial }\varphi =m{\sigma }_3\varphi \widehat{k},\tilde{\partial }\equiv {\tilde{\Gamma }}^i{\partial }_i$$

(96)

which corresponds to $({\gamma }^{\mu }{\partial }_{\mu }+m)\varphi =0$ and its complex conjugate. This quaternionic form of the Dirac equation illustrates the geometric role played by quaternions in constructing the gradient operator. And yet, this form of the Dirac operator is nowhere as neat as the 3D Dirac operator (83) and we should strive to do better. Some progress has been made by Lambek. Nonetheless the quaternionic Dirac equation strongly hints at the significance of 6D spacetime, because the occurrence of ${\sigma }_3$ and $\widehat{k}$ is result of an arbitary choice. We could equally have made two other choices: $\widehat{i}$ and ${\sigma }_1$, or $\widehat{j}$ and ${\sigma }_2$.

To get to the sought for quaternionic gradient operator, consider the Clifford algebra $Cl(0,3)$, which has three generating vectors (let us denote them by the symbol e). That is, we have $e_1^2=-1,e_2^2=-1,e_3^2=-1$. The algebra has eight elements $(1,e_1,e_2,e_3,e_1{e}_2,e_2{e}_3,e_3{e}_1,e_1{e}_2{e}_3)$. These can be separated into two quaternionic parts $(1,e_1,e_2,e_1{e}_2)$ and $(e_1{e}_2{e}_3,e_2{e}_3,e_3{e}_1,e_3)$. In the second set, ${\left(e_1{e}_{2}2e_3\right)}^2=1$; defining $e_1{e}_2{e}_3\equiv \omega$ the second set can be written as $\omega (1,-e_1,-e_2,-e_1{e}_2)$. Here, $\omega$ is the analogue of the split-complex number: $\tilde{\omega }=-\omega ,{\omega }^2=1$. Hence $Cl(0,3)$ is called the algebra of split biquaternions, and denoted $(\mathbb{H}\oplus \omega \mathbb{H})$. It can also be written as ${\mathbb{C}}^{\prime }\otimes \mathbb{H}$ where ${\mathbb{C}}^{\prime }=(1,\omega )$. The complexification of $Cl(0,3)$ is the algebra $\mathbb{C}\otimes (\mathbb{H}+\omega \mathbb{H})$ and is denoted $Cl\left(3\right)$. This is the algebra we are interested in now. Between them, the two copies of $\mathbb{H}$ have six distinct imaginary units: $(e_1,e_2,e_1{e}_2)$ and $(-\omega e_1,-\omega e_2,-\omega e_3)$. Let us denote the first set as $(\widehat{i},\widehat{j},\widehat{k})$ and the second set as $(\widehat{l},\widehat{m},\widehat{n})$. Now let us consider the six-dimensional vector, which generalises the Hermitian biquaternion:

$$x_6=i{t}_1\widehat{l}+i{t}_2\widehat{m}+i{t}_3\widehat{n}+x_1\widehat{i}+x_2\widehat{j}+x_3\widehat{k}$$

(97)

where $i=\sqrt{-1}$. The magnitude of this vector is

$$|x_6{|}^2=x_6{\tilde{x}}_6={\tilde{x}}_6{x}_6=-t_1^2-t_2^2-t_3^2+x_1^2+x_2^2+x_3^2$$

(98)

and hence it describes a space-time interval in 6D spacetime with signature $(3,3)$ and having the symmetry group $SO(3,3)$. Consider next the following proposal for the Dirac operator $D_6$

$$D_6=i\widehat{l}\frac{\partial }{\partial t_1}+i\widehat{m}\frac{\partial }{\partial t_2}+i\widehat{n}\frac{\partial }{\partial t_3}+\widehat{i}\frac{\partial }{\partial x_1}+\widehat{j}\frac{\partial }{\partial x_2}+\widehat{k}\frac{\partial }{\partial x_3}$$

(99)

which is a natural generalisation of the 3D quaternionic gradient operator (83). The square of $D_6$ is

$$D_6^2=-\frac{\partial }{\partial t_1^2}-\frac{\partial }{\partial t_2^2}-\frac{\partial }{\partial t_3^2}+\frac{\partial }{\partial x_1^2}+\frac{\partial }{\partial x_2^2}+\frac{\partial }{\partial x_3^2}$$

(100)

which is the sought for Klein-Gordon operator on 6D spacetime with signature (3, 3). We see that by going to a 6D spacetime with three time-like directions we can appreciate Atiyah’s remark that the Dirac operator was first discovered by Hamilton.

We can now propose the following as the Dirac equation in 6D space-time:

$$i\hslash D_6\psi =Qc\psi$$

(101)

There is no need for gamma matrices! The Clifford algebra of the quaternions already does the job that the gamma matrices were introduced to do. Here $\psi$ is a six-component Dirac spinor with six complex numbers as its entries. We are careful to note that the source on the right hand side is not mass, but some more general source charge Q relevant to the gravi-weak unification on 6D, from which electric charge and mass are both emergent after the electroweak symmetry breaking.

One could object to the appearance of the $i=\sqrt{-1}$ in the operator $D_6$. Dirac himself was looking for a formulation of his equation using only real quaternions, and was not interested in the biquaternions. However, we defend the appearance of the i as follows: we are seeking a quantum theory without classical time, and noncommutativity in time, as in the operator $D_6$, is welcome. Furthermore, we have argued earlier that an elementary particle such as the electron does not experience spacetime as classical, or real. Therefore, the appearance of the imaginary unit i in the spacetime vector (95) and in the operator $\left(\right)$ should not be a surprise. We do get a classical spacetime description after squaring, as in (96) and in (98), and this classical spacetime is what is experienced by bosons and by classical objects. It is one of the central themes of this book that spacetime and elementary particles ought to be described by the same mathematical entity: hence the use of complex split biquaternions for describing both of them is appropriate and reassuring. The anti-Hermitian part of the complex split biquaternion is associated with an anti-matter dominated mirror copy of our universe, which got separated from our universe at the epoch of electroweak symmetry breaking.

Our four dimensional universe (and its associated flipped 4D copy, which is also a part of physical reality) emerge from the 6D universe. There is considerable literature on geometry in a 6D spacetime with (3, 3) signature. Highly relevant for us is the (1985) paper of Patty and Smalley [68] titled ‘Dirac equation in a six-dimensional spacetime’. The authors show that a (3+3) spacetime can be divided into six copies of (3+1) subspaces. 6D spaces are also of interest from the viewpoint of a superluminal extension of (3+1) special relativity, and it has been shown that a 6D spacetime is the smallest one which can accommodate a superluminal as well as a subliminal branch of (3+1) spacetime [69]. Quaternions and three temporal dimensions have been studied also by Lambek [64] who writes in the abstract of his paper: “The application of quaternions to special relativity predicts a six-dimensional universe, which uncannily resembles ours, except that it admits three dimensions of time. Yet its mathematical description with the help of quaternions gains in transparency, due to the crucial observation that every skew-symmetric four-by-four real matrix is the sum of two matrices representing multiplication by vector quaternions on the left and on the right respectively.” His two sets of vector quaternions are the same as those we use in Eqn. (95) above. The physical interpretation of three non-commuting time dimensions will also have to be discussed. One might speculate that the three times might correspond to the three fermion generations, one time per generation, and perhaps the three times might have some role to play in flavor mixing and neutrino oscillations? Six dimensional spacetimes (3+3) spacetimes were studied extensively in a series of papers by Cole [70] and also by Teli [71]. An early work on ‘quaternions and quantum mechanics’ is Conway (1948) [66]. Very relevant for us is also Kritov (2021) [72] who shows that the Clifford algebra $Cl(3,0)$ can be used to make two copies of 4D spacetime with relatively flipped signatures. Dartora and Cabrera (2009) [73] have studied ‘The Dirac equation in six-dimensional SO(3,3) symmetry group and a non-chiral ’electroweak’ theory’. An old (1950) paper by Podolanski [74] studies unified field theory in six dimensions, and in fact the abstract starts by saying ‘The geometry of the Dirac equation is actually six-dimensional’. An elegant (2020) paper by Venancio and Batista [75] analyses ‘Two-Component spinorial formalism using quaternions for six-dimensional Spacetimes’. An insightful (1993) work by Boyling and Cole [76] studies the six-dimensional (3+3) Dirac equation and shows that particles have spatial spin-1/2 and temporal spin-1/2. See also Brody and Graefe (2011) [77] and Chester et al. [78]. In the context of twistor theory, six dimensional spacetime has been suggested by Sparling [79] and analysed by Mason et al. [80]. See also the insightful works of Pavsic on 6D spacetimes [81,82].

In Eqn. (95) we have two sets of quaternionic imaginaries, which are parity reverses of each other. After symmetry breaking, each set is associated with an automorphism group $SU\left(2\right)$. It is chiral: being $SU{\left(2\right)}_L$ for one set, and being $SU{\left(2\right)}_R$ for the other set. The former gives rise to the weak interaction on the second copy of $4D$ spacetime, whereas the latter gives rise to general relativity in our 4D spacetime.

In view of these earlier works and the above discussion in this section, we believe we have a strong case for developing the weak interaction as geometry of a 4D spacetime with flipped signature, and then going on to gravi-weak unification in six dimensions (3+3). Also, now having seen the Dirac operator as a quaternionic gradient operator on (3+3) spacetime we can begin to understand why the operator relates to Einstein-Hilbert action of general relativity. It is because curvature is the square of the connection and connection is related to the space-time gradient operator. This helps us understand why the Dirac operator is so significant in geometry; in our proposal for unification of interactions, the Lagrangian is bilinear in the Dirac operator on an octonionic space, and hence the unified Lagrangian is a kind of generalised Einstein gravity in higher dimensions.

In the standard model, there is a $U{\left(1\right)}_{chiral}$ which is the symmetry of the axial vector current, in addition to the $U\left(1\right)em$ which is the symmetry of the vector current, and the projection to chiral symmetry eigenstates is performed by $(1\pm {\gamma }_5)/2$. This structure is essential for the Coleman-Mandula no-go theorem. There opens up the possibility that the additional $U\left(1\right)$ mentioned at the start of this section could be identified with $U{\left(1\right)}_{chiral}$ [one copy for our universe, and one copy for the anti-matter dominated mirror universe] and also identified with the Connes time parameter.

An extension of the work of Pavsic [16], which considers rotational actions of $SO(8,8)$ symmetry, seems promising in the context of the unbroken $E_8\otimes E_8$ symmetry. Pavsic has also shown that a 16D Clifford space contains a 6D spacetime with signature (3,3) as a subspace [83]. The work [41] considers associativity of split octonions in $SO(4,4)$ symmetric space, also possibly relevant in the unbroken phase. These aspects will be studied in future work.

7.1. Recovering General Relativity from an Underlying $SU{\left(2\right)}_R\times U{\left(1\right)}_{grav}$ Yang-Mills Gauge Theory

Prior to the breaking of electroweak symmetry, we are proposing an $SU\left(3\right)\times SU\left(3\right)$ Yang-Mills gauge theory on 6D spacetime with (3,3) signature. After symmetry breaking, one $SU\left(3\right)$ undergoes $SU\left(3\right)\to SU{\left(2\right)}_L\times U{\left(1\right)}_Y\to U{\left(1\right)}_{em}$ on the flipped 4D spacetime, and the other $SU\left(3\right)$ undergoes $SU\left(3\right)\to SU{\left(2\right)}_R\times U{\left(1\right)}_{Yg}\to U{\left(1\right)}_{grav}$ on our 4D spacetime. We are proposing that the second broken $SU\left(2\right)$ symmetry gives rise to general relativity. In support of this proposal we have already mentioned the work of Ashtekar and of Woit. In the literature there are several other significant works supporting a Yang-Mills theory such as $SU\left(2\right)$ or $SU\left(2\right)\otimes U\left(1\right)$ as the origin of gravitation. We now draw attention to these works. In a paper titled ‘Gravity as Yang-Mills gauge theory’ authors Dehnen and Ghaboussi [84] propose a Yang-Mills field theory of gravity based on a unitary phase-gauge-invariance of the Lagrangian where the gauge transformations are of the $SU\left(2\right)\times U\left(1\right)$ symmetry of the 2-spinors. Krasnov [85] has emphasised the importance of the Plebanski formulation of general relativity based on self-dual two forms. Smolin [86], investigated an extension of the Plebanski action to a larger Lie group, thereby proposing a unification of gravity with Yang-Mills. In (2014), Alexander, Marciano and Smolin [87] wrote an important paper titled ‘gravitational origin of the weak interaction’s chirality’ which is very close in spirit to our current proposal for gravi-weak unification. These authors proposed a new unification of the electroweak and gravitational interactions based on combining the weak $SU\left(2\right)$ gauge fields with the left-handed part of the space-time connection. These are unified into a single gauge field valued in the complexification of the local Lorentz group. Consequently, the weak interactions emerge as the right-handed chiral half of the space-time connection, which explains the chirality of the weak interaction. This is made possible, because, as shown by Plebanski, Ashtekar, and others, the other chiral half of the space-time connection is enough to code the dynamics of the gravitational degrees of freedom. This unification is achieved within an extension of the Plebanski action previously proposed by Smolin. The main difference we have with their proposal is that we develop the weak interaction as gravity on the flipped 4D spacetime. A detailed analysis of gravity as an $SU\left(2\right)$ gauge theory is currently being carried out by our research group [88] and will be published in a forthcoming article. In an important recent paper Percacci [89] discusses gravity as a quantum field theory. He argues that, like the electroweak interaction, gravity is a gauge theory in the Higgs phase.