Prerpints.org logo
Preprint
Article

Enhancing Predictive Maintenance in Airborne Weapon Systems through Advanced Frequency Augmentation Techniques

Altmetrics

Downloads

160

Views

32

Comments

0

Submitted:

22 May 2024

Posted:

23 May 2024

You are already at the latest version

Alerts
Abstract
This study investigates the application of frequency augmentation techniques to improve condition-based maintenance (CBM+) systems for airborne weapon systems, focusing on the predictive accuracy of velocity and acceleration parameters. Utilizing MIL-STD-1553B MUX data from 138 sorties of fixed-wing aircraft, we explored six augmentation methods, including traditional interpolations (linear, quadratic, cubic spline) and advanced machine learning models (K-Nearest Neighbor, LSTM, and Bi-LSTM). Our findings indicate that while traditional methods like linear interpolation are more effective for velocity parameters, advanced ML techniques, particularly Bi-LSTM, provide better results for acceleration parameters, which exhibit more complex and rapid variability. The study underscores the necessity of tailoring augmentation approaches to specific parameter characteristics and highlights the potential of ML models in capturing intricate patterns within time-series data. These insights are critical for advancing CBM+ systems in military avionics, enhancing reliability and operational efficiency through improved data processing strategies. Future work should explore more performant augmentation techniques, such as by integrating multi-dimensional datasets, and explore ways to develop automated tools for a more powerful predictive maintenance framework.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

Airborne weapon systems can be costly and time-consuming to source parts, and even cause loss of life when they fail. In the case of a weapon system operated by the U.S. Department of Defense, 28% of the total life cycle cost is for procurement/development, while 72% of the cost is utilized for operation, making maintenance costly [1]. Therefore, in order to efficiently maintain airborne weapon systems, reduce maintenance costs, and prevent accidents, it is necessary to develop a CBM+ (Condition Based Maintenance) based maintenance system that identifies the optimal maintenance time through accurate condition diagnosis and failure prediction.
Meanwhile, the U.S. Department of Defense is shifting its maintenance paradigm from breakdown maintenance and preventive maintenance to condition-based maintenance and predictive maintenance to reduce inefficiencies in weapon system management [2], with the ultimate goal of improving the availability of weapon systems while minimizing total life cycle costs.
Condition-based maintenance and predictive maintenance require data monitoring to identify defects that lead to failure in a predictive method. Recently, defect identification techniques utilizing ML(Machine Learning) techniques such as anomaly detection algorithms have been studied in various fields including aerospace [3]. In order to develop a CBM+ based maintenance system by applying these techniques, it is key to secure meaningful information by building quality data to be used for training.
In this study, MUX data is selected as the data that can be utilized for the development of CBM+ based maintenance system. Currently, communication and control within the avionics system of a fixed-wing aircraft is performed through the 1553B MUX Bus, which is operated through the Flight Control-Operational Flight Program (FC-OFP). During this process, the 1553B MUX Bus data is stored in a Removable Memory Module (RMM) [4]. The 1553B MUX Bus data is transmitted using TDMA (Time Division Multiplexing Access), which means that the frequency assigned to each type of packet is different. Therefore, preprocessing the data to match the same frequency is essential for AI training.
This study aims to preprocess some data of 1553B MUX Bus data used in CBM+ based maintenance system. We found that the different frequencies of each packet have a significant impact on the fault prediction in condition-based maintenance, especially the most representative parameters are the velocity and acceleration along each axis of the aircraft. This is because, unlike civilian airplanes, airborne weapon systems are subjected to frequent maneuvers with rapid changes, such as combat missions. However, the avionics of airborne weapon systems have to be compact, require high reliability, and have very little memory capacity to record data due to the rigorous airworthiness certification process. As a result, velocity and acceleration parameters are not currently available at the frequency we need for fault prediction, and data augmentation is required.
There are several frequency augmentation methods to solve this problem. For example, forward filling, which is the most common and simple method, augments the data points and then fills the data points that need to be filled with the last non-null value of the previous data points. There are also classical augmentation techniques such as linear interpolation, quadratic interpolation, and cubic spline interpolation, as well as techniques that perform well and are effective in terms of time and resources, such as K-Nearest Neighbor (KNN) filling, Support Vector Machine (SVM) filling, and regression filling.
In recent years, the number of fields requiring such data interpolation and augmentation has increased, and examples include not only aerospace engineering, but also astronomy [5], environmental science [6], and geology [7]. As a result, there is a growing effort to improve the accuracy of interpolation and augmentation by applying machine learning (ML) techniques such as artificial neural networks and long short term memory (LSTM). In [8], the authors presented an Interpolation-Prediction Architecture that applies GRU Network as a prediction model. In [9], they presented a new deep learning framework for stochastic interpolation of time series data, HTVAE (Heteroscedastic Temporal Variational Autoencoder), which improves the performance compared to previous model. The authors of [10] improved the filling accuracy of wireless sensor data, which is essential for the construction of a Structural Health Monitoring (SHM) system, by using convolutional neural network (CNN) and kriging based sequence interpolation (KSI) after cubic spline interpolation. In [11,12], the authors used a combination of LSTM and transfer learning to perform data imputation in the fields of building energy and water quality. In [13], a model combining CNN and Bi-LSTM was successfully used to effectively interpolate temperature data inside an apartment. And in [14], an improved Bi-LSTM algorithm was used to improve the filling problem of pregnancy examination data for predicting Hypertensive Disorders of Pregnancy (HDP).
However, there are no general principles for the optimal choice of data interpolation and augmentation methods. Therefore, researching whether AI technologies like ML are truly necessary for such issues, or if existing augmentation techniques are sufficient, is a very interesting topic and can greatly vary depending on the problem at hand. In fact, several researchers have compared different methods for their respective problems. In [15], four augmentation techniques were compared for two-dimensional spatial data. In [16], the authors compare traditional augmentation techniques with Support Vector Regression for interpolation of low-dimensional, large seismic data and find that Support Vector Regression is a more competitive method. In [17], they compare many interpolation techniques with ML techniques on various datasets in the field of material science. In [18], the authors compared interpolation techniques and ML techniques for datasets in the field of High Energy Physics and found that traditional interpolation techniques perform very well in low dimensions (d=3), while MLP (Multi-Layer Perceptron) performs the fastest and most accurate in high dimensions (d=5,6,9).
These findings suggest that data interpolation and augmentation requires different methods depending on the problem at hand. Our goal is to frequency augment the axis-specific velocity and acceleration parameters of the 1553B MUX Bus data. In the case of the z-axis (down axis in the NED coordinate system), the frequency augmentation accuracy is relatively low compared to the x and y axes due to the characteristics of airborne weapon systems described above, which results in a very large change rate of altitude between flights. To overcome this characteristic, we compared six methods, including three traditional augmentation techniques, KNN, and linear interpolation combined with LSTM and Bi-LSTM. The results showed that the best performing method for each parameter was different. This suggests that the preprocessing technique should be different for each parameter when developing a predictive model for CBM+, and that the preprocessing technique should be optimized after the parameters are selected through an appropriate method.

2. Materials and Methods

2.1. Data

The data used in this study is MUX data recorded from 138 sorties of actual fixed-wing aircraft flights. The MUX data follows the MIL-STD-1553B communication specification and consists of more than 400 packets. Accordingly, each packet consists of a Command Word, Data Word, and Status Word, of which up to 32 Data Words containing actual data can be included. In addition, each data word is composed of 16 bits, so the maximum amount of information that can be transmitted in a packet is 512 bits in theory.
As described earlier, we aim to augment the frequency of the velocity and acceleration along each axis of an aircraft. These velocity and acceleration parameters are measured by the Inertia Navigation System (INS) in the avionics of an airborne weapon system, and since the position of the aircraft is basically expressed in the North, East, Down (NED) coordinate system, which is advantageous for controlling the piloting and navigation system, the velocity and acceleration parameters are also expressed in the NED coordinate system. In particular, the NED coordinate system has an intuitive relation to the ground surface compared to the Cartesian coordinate system, and unlike the Body coordinate system, it is frame-consistent, which is advantageous for derivative calculations, resulting in better accuracy of velocity and acceleration measurements. In airborne weapon systems, the alignment of coordinates is typically conducted after startup with the INS position as the origin so that the x-axis is aligned with the True North direction, so that the y-axis is aligned with the East axis and the z-axis is aligned with the Down axis. These coordinates are then maintained until the aircraft is shut off, at which point the position, velocity, and acceleration are measured and recorded.
In this study, we aim to augment the frequency of six parameters: velocity x, velocity y, velocity z, acceleration x, acceleration y, and acceleration z. Due to the characteristics of airborne weapon system that are subject to rapid changes in maneuver, these velocity and acceleration data are a major factor in the structural health of the aircraft as well as the identification of defects in various avionics that measure or compute them. To select an appropriate frequency augmentation technique and to characterize the data, we analyzed the statistical metrics of the target parameters. 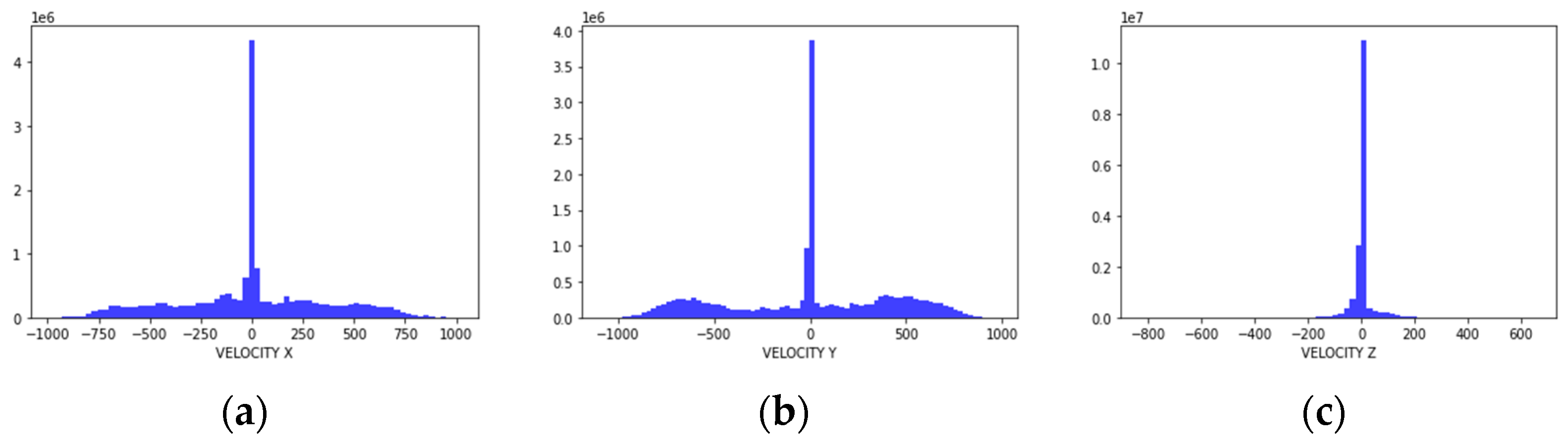Figure 1 and Table 1 show the distribution and statistical metrics of each parameter.
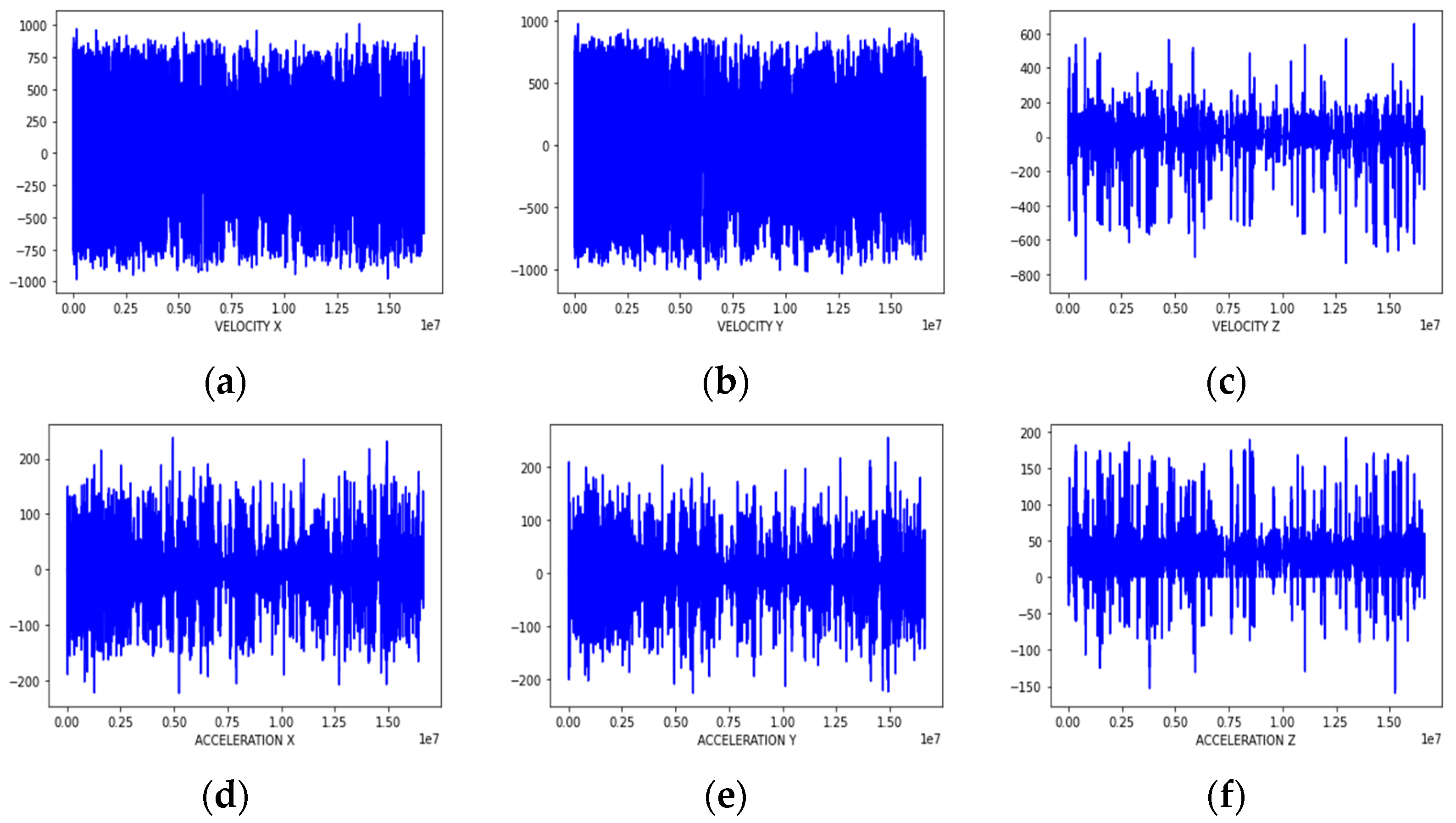
As shown in Table 1, it can be seen that acceleration has an overall lower standard deviation and higher kurtosis than velocity. In particular, acceleration z has a kurtosis of about 134, which is a parameter with many outliers. This is a result of the maneuvering characteristics of the airborne weapon system, and although the change in altitude is not large, the rate of change is very large due to rapid maneuvering. Examining the line plot results for velocity x and acceleration z, which display opposite characteristics, it can be observed that acceleration z exhibits more outliers and rapid changes compared to velocity x. Figure 2 shows the results of the line plot of parameters.

2.2. Methods

2.2.1. Data Preprocess

In order to find a frequency augmentation technique with high performance for each parameter, we first need a preprocessing for data training. We down-sampled the original data to a quarter for training and evaluation purposes. By augmenting the frequency of the down-sampled data and comparing it with the original data, we can see which augmentation technique performs the best for each parameter. We also conducted standardization to ensure ML model performance and data consistency. Standardization is not necessary when conducting only traditional augmentation techniques such as linear interpolation, but since we plan to experiment with combining ML techniques, we conducted standardization.
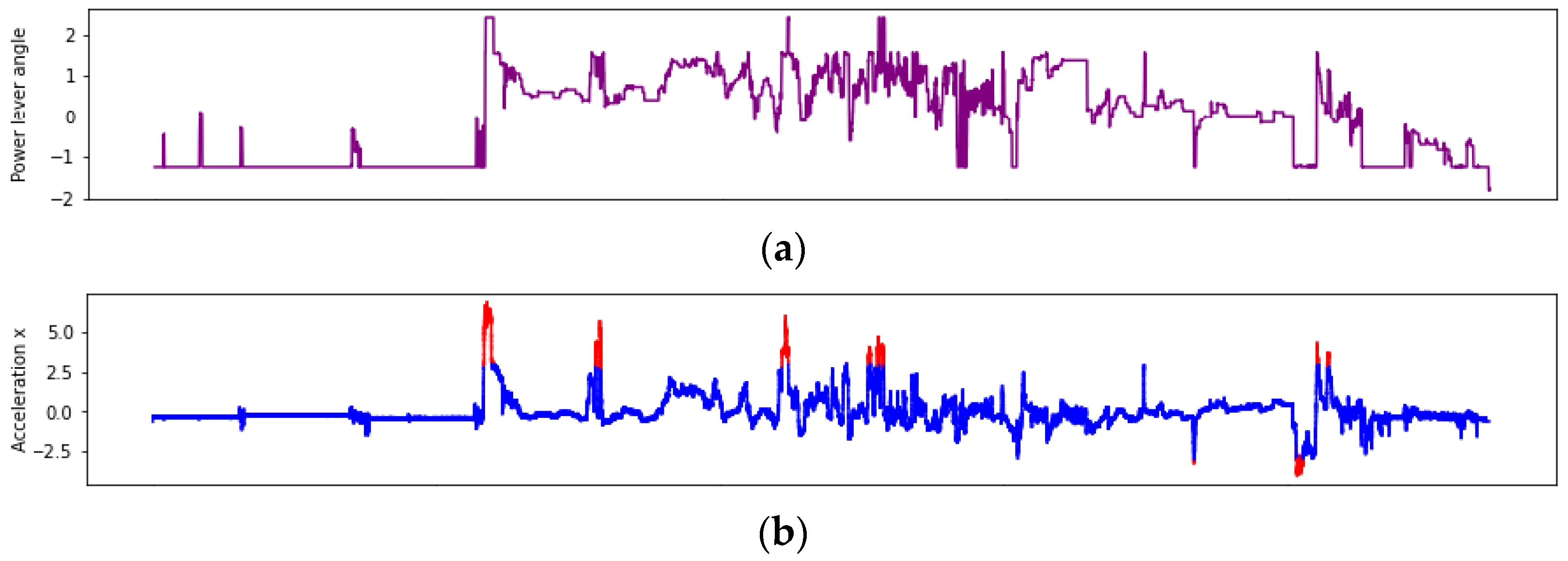
Typically, data signals are preprocessed to remove noise or outliers using various techniques. However, aircraft flight data can be characterized by rapidly changing data that can look like noise as it maneuvers, as shown in Figure 3. Figure 3 shows a line plot of power lever angle and acceleration x for one sortie. The top graph is power lever angle, which is the angle value of the lever that the pilot manipulates to increase or decrease power. The bottom graph is acceleration x, where z-scores above 3 and below -3, which are typically classified as outliers, are colored red. In these two graphs, it can be observed that the power lever angle moved in a similar fashion slightly before the spike or dip in acceleration x, which proves that this is a normal signal from the aircraft performing the maneuver as intended by the pilot. Typical data preprocessing involves identifying and removing noise or outliers using statistical methods or density-based techniques. However, such outlier removal techniques are not appropriate for aircraft flight data with frequent rapid maneuvers as described above. Therefore, we did not apply a separate outlier removal technique.

2.2.2. Methods

2.2.2.1. Linear Interpolation

The Linear Interpolation technique connects two data points with a straight line to estimate the values between them. It is simple, fast, and works well for relatively homogeneous data, but performs poorly when the data is curvilinear or non-linear.

2.2.2.2. Quadratic Interpolation

The Quadratic Interpolation technique forms a quadratic polynomial for each interval and uses it to estimate values. It produces smoother results than Linear Interpolation, but still does not achieve perfect smoothness at the points because the quadratic derivative is not continuous.

2.2.2.3. Cubic Spline Interpolation

The Cubic Spline Interpolation [19] technique extrapolates the data by forming a cubic polynomial for each interval. Unlike Linear and Quadratic Interpolation described above, the second derivative is also continuous, ensuring smooth estimates at all data points. In this study, we conducted the interpolation with the condition that the first and second segments of the curve end have the same polynomial, which is also the default condition of the Scipy.interpolate [20] library we used.

2.2.2.4. K-Nearest Neighbor

K-NN is the simplest form of training-based interpolation, where the weighted average of the values of the K nearest data points is assigned as the value of the new point. There are many ways to measure the distance, but in this study, we use Euclidean distance. Also, since K-NN is used to interpolate time series data, the closer the distance, the greater the weight. These weights are expressed as the reciprocal of the distance, as shown in Equation (1), where d X , x i k is the distance between the unknown point X and its k-th neighbor x i k .
ω k = 1 d X , x i k
The calculated weights can then be substituted into Equation (2) to calculate the predicted value, where y i k is the value of the k-th neighbor.
y ^ = ∑ k = 1 K ω k · y i k ∑ k = 1 K ω k
We relied on empirical tests to find an appropriate value of k, and found that k = 8 performed best. In this study, we used sklearn’s KNeighborRegressor to implement augmentation via K-NN.

2.2.2.5. Linear Interpolation + LSTM

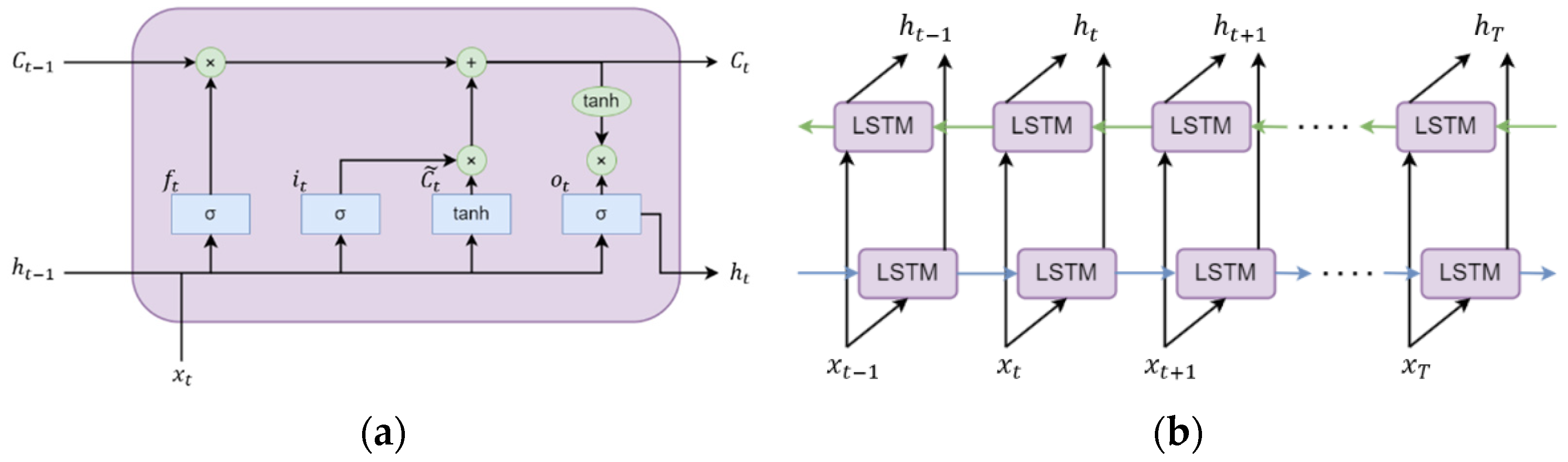
The LSTM [21] is a type of Recurrent Neural Network (RNN), which is specialized in training of long-term dependence in sequential data. Figure 4a is a structured representation of how LSTM work. LSTM can effectively train long-term dependence through an internal mechanism called cell status. Each LSTM unit utilizes three gates to regulate the flow of information through the network. Each gate in an LSTM combines the current input x and previous output h to determine how to process the information. This behavior allows LSTM to capture the temporal nature of sequences and train long-term patterns and dependencies.
The first gate, forgetting gate, is responsible for determining how long the state at a previous point in time c t − 1 will remain at the current point in time C t . The forgetting gate uses h t − 1 , the output of the previous neural cell, and x t , the input of the current cell, to calculate how much data has been recorded in the previous cell. This is calculated as a value between 0 and 1, where 0 represents complete forgetting and 1 represents complete recording. The equation for this is shown in Equation (3), where W f is the weight matrix of the forgetting gate, b f is the bias term of the forgetting gate, and σ is the sigmoid activation function.
f t = σ W f − h t − 1 , x t + b f
The second gate, input gate, is the gate that decides what and how much information to add to the current unit state and is divided into two parts. First, the input gate decides what information to update. Then, it generates a new candidate vector C ~ t through the tanh layer and adds it to the state. The current state of the unit, C t , is calculated through Equation (4) below.
i t = σ W i · h t − 1 , x t + b i
C t ~ = tanh ⁡ W C · h t − 1 , x t + b C
C t = f t ∗ C t − 1 + i t ∗ C t ~
The third gate of the LSTM, output gate, is responsible for determining which value to output from the unit based on the cell status. First, the sigmoid layer determines which part of the unit to output, and the tanh normalizes the cell state to a value between -1 and 1. Finally, it is multiplied by the sigmoid gate to determine the final output.
σ t = σ W 0 · h t − 1 , x t + b 0
h t = o t ∗ tanh ⁡ C t
In this study, we combine this LSTM model with linear interpolation. First, the data set preprocessed in Section 2.2.1 is linearly upsampled using Scipy.interpolate’s interpld. The LSTM model is then trained on the sequential information of the entire dataset to capture more sophisticated patterns and associations to model the inherent dynamic nature of the data, rather than simply making linear connections between two points.
The construction of these LSTM model was conducted using Tensorflow [22] and Keras [23]. Conducting hyperparameter optimization is computationally expensive, so we relied on empirical tests and used the optimal hyperparameters found after many tests. We use an architecture consisting of 5 LSTM layers with 64 units and one dense layer, with orthogonal weight initialization for the LSTM layers and linear activation for the dense layer. We use the Adam [24] optimizer to minimize the Mean Squared Error (MSE) loss. Equation 9 below expresses the MSE loss, where n is the batch size and y i is the true value. We train the model using NVIDIA H100 GPUs for up to 4000 epochs with an EarlyStopping callback that stops training if no improvement is achieved after 300 epochs. We also use Dropout with rate set to 0.3 as a regularization technique to prevent overfitting, and the learning rate is set to 0.001 as the default value, with a 0.85x decay every 100 epochs.
L M S E = 1 n ∑ i = 1 n ( N X i − y i ) 2

2.2.2.6. Linear Interpolation + Bidirectional-LSTM

The bidirectional-LSTM(Bi-LSTM) model consists of a forward LSTM and a reverse LSTM structure, as shown in Figure 4b. Therefore, two separate LSTM layers are used, one to process the input data in chronological order and the other to process the data in reverse chronological order. This is especially effective for interpolating time series data, which is the target data of this study. Similar to how we applied LSTM in Section 2.2.2.5, we build an architecture to train with Bi-LSTM model using Tensorflow and Keras after linear upsampling. Hyperparameters are set to be the same for accurate comparison with LSTM.

2.2.3. Cross-Validation and Evaluation Metrics

2.2.3.1. Cross-Validation

As described in Section 2.1, the target data of this study is 138 sorties data. In general, when performing tasks such as regression, the target data is divided into train, valid, and test sets. During the training process, the model adjusts its parameters to minimize the loss function using the training dataset. Concurrently, the validation dataset helps monitor the model’s performance on unseen data, allowing for early stopping if overfitting is detected. Finally, the test dataset evaluates the model’s actual performance on completely unseen data. For traditional augmentation techniques, there is no need for train and valid, so the augmentation data is just a test data set. In our target data of 138 sorties data, we set the train dataset to 100 sorties, the valid dataset to 19 sorties, and the test dataset to 19 sorties.

2.2.3.2. Evaluation Metrics

We use R 2 (coefficient of determination) and SAPE (Symmetric Absolute Percent Errors) to evaluate and compare the performance of each model we built. First, R 2 is expressed as in Equation (10), where y i ^ is the predicted value and y ¯ is the mean of true values. This results in a value less than 1, which would be 1 if all values were predicted correctly.
R 2 = ∑ i = 1 n ( y i − y i ^ ) 2 ∑ i = 1 n ( y i − y ¯ ) 2
S A P E i = y i − y i ^ ( y i + y i ^ ) / 2 · 100 %
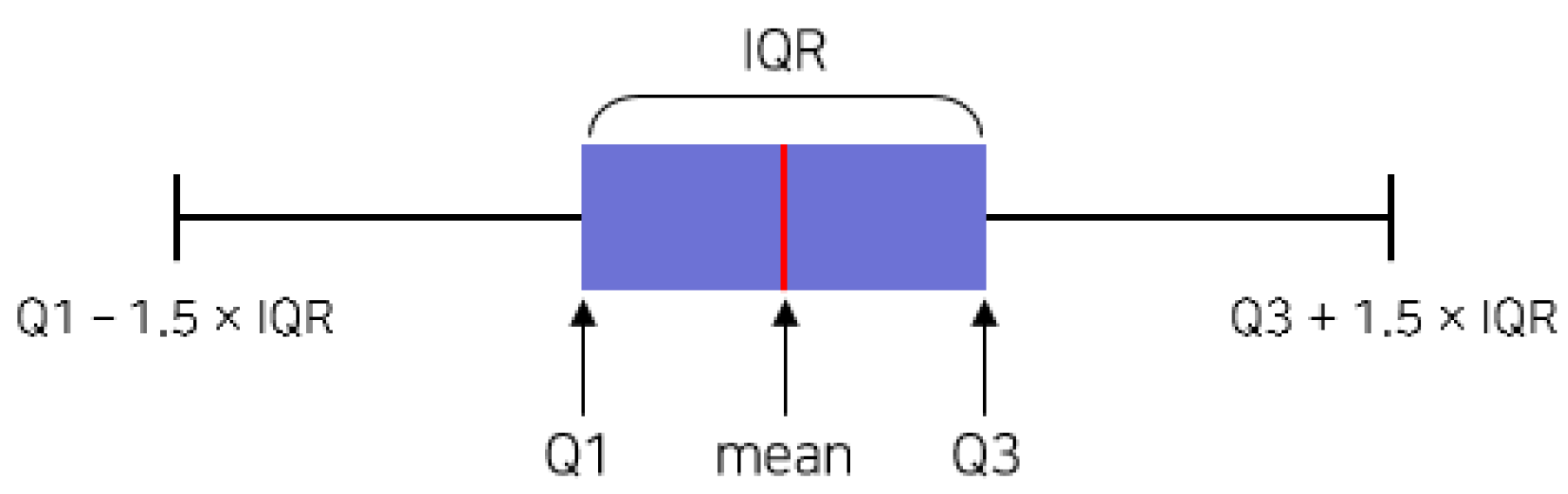
Next, SAPE is expressed as Equation (11), where the error is divided by the mean of the true and predicted values and the ratio is expressed as percent. Since it is a percentage of the error, the smaller the value, the more accurate the prediction, and the value will be between 0 and 200. Since it is calculated for all data points, it is visualized in the form of a box plot [25], as shown in Figure 5, where Q1 is the first quartile, representing 25% of the data points. Q3 is the third quartile, representing 75% of the data points. The interquartile range (IQR) is the range between Q1 and Q3. Values below Q1-1.5×IQR and above Q3+1.5×IQR are classified as outliers, but they are not displayed in this study to compare performance across models.

3. Results

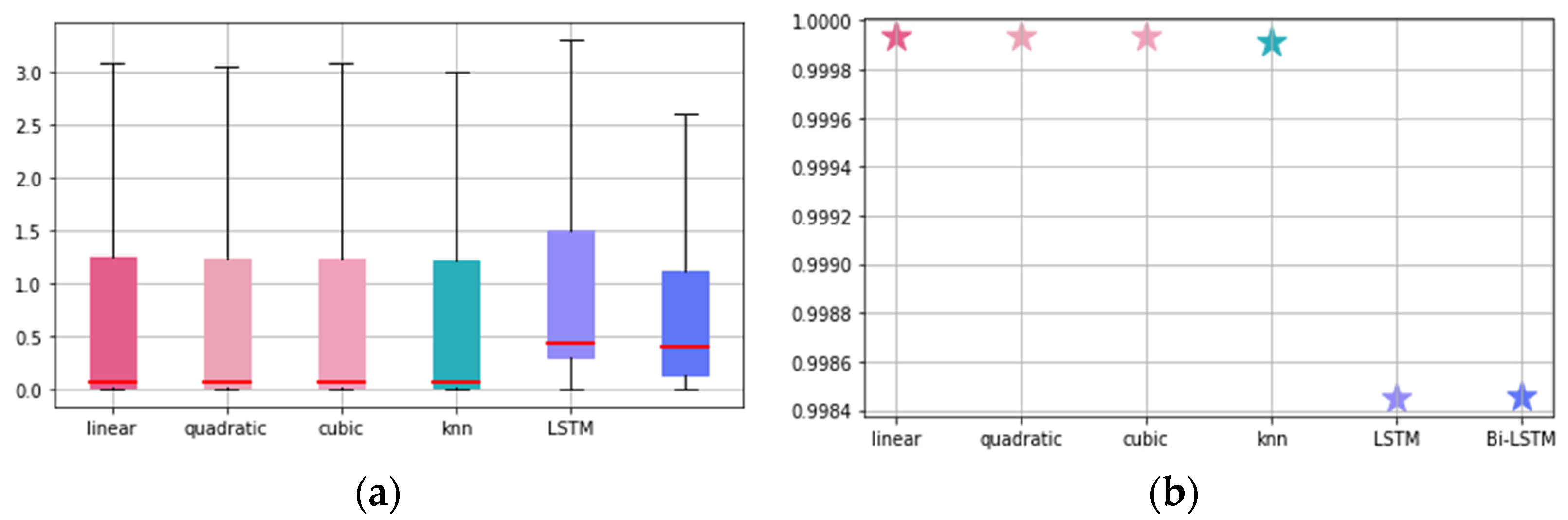
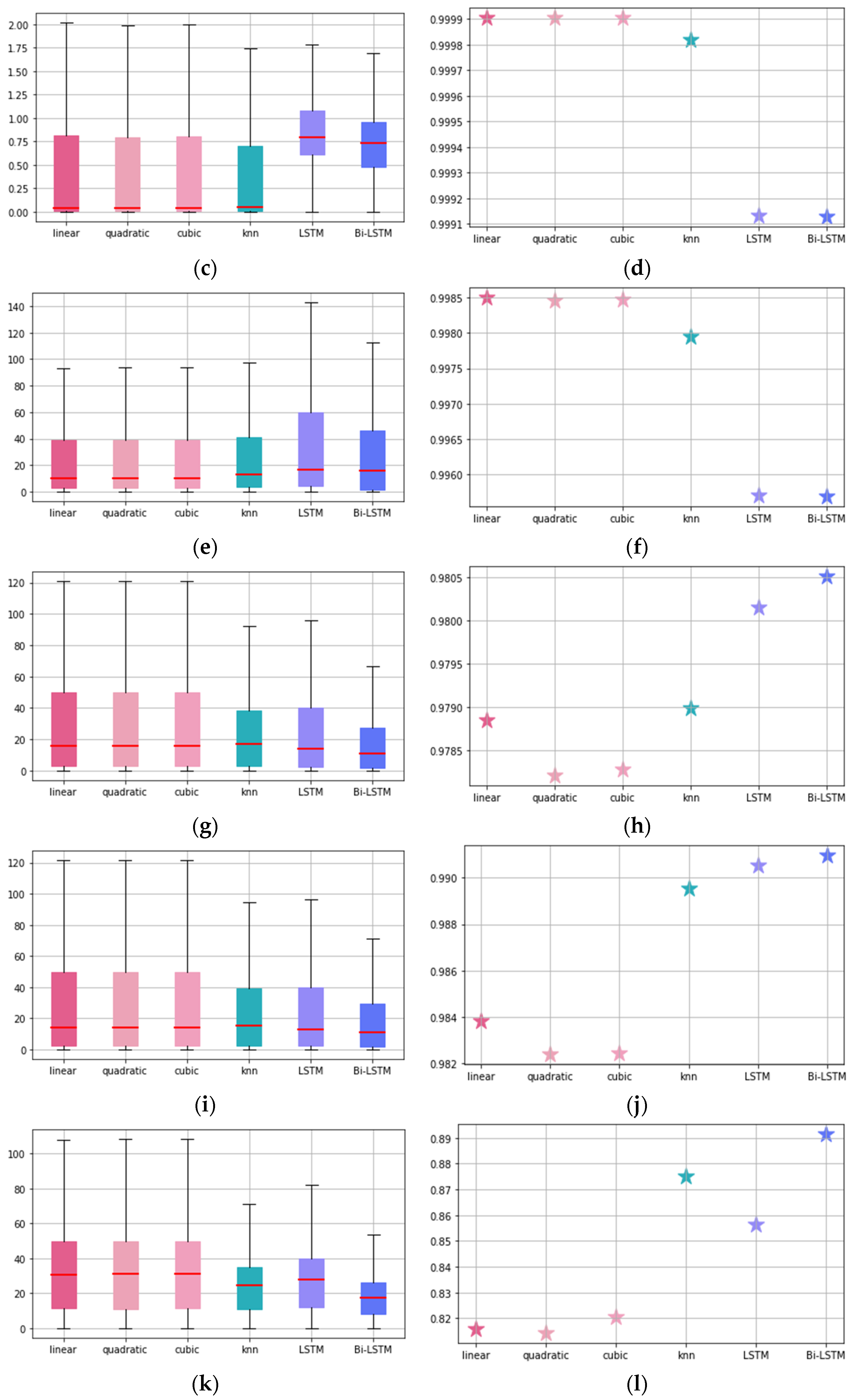
In this study, six frequency augmentation techniques were applied to six parameters of velocity and acceleration along each axis to derive the results. The R 2 and SAPE results for each parameter are shown in Figure 6 and Table 2 below. The red color represents the traditional frequency augmentation technique and the blue color represents the training-based frequency augmentation technique.

3.1. Velocity Parameters

First, we look at the results for the velocity parameters and see that overall, regardless of the frequency augmentation technique, the predictive performance is worse for the z-axis compared to the x and y-axes. It is also interesting to note that traditional augmentation techniques outperform training-based frequency augmentation techniques, with linear interpolation, the simplest technique, performing best for velocity parameters. This can be attributed to the fact that velocity is better represented by a straight line than by a complex curve, and indeed has a linear relationship.
Looking at the SAPE mean values at velocity x, linear interpolation is the best, followed by quadratic and cubic spline with no significant difference. However, the IQR is not as wide for linear as it is for quadratic. On the contrary, LSTM and Bi-LSTM have higher SAPE mean values, especially LSTM, which has a higher IQR than the other methods. R 2 also follows the same ranking as the SAPE mean values, with linear dominating. For velocity y, the ranking of the methods is the same as for velocity x, but the ML-based methods (LSTM, Bi-LSTM) perform worse than velocity x. The K-NN method is the best performer. K-NN performs well at velocity x, but at velocity y it falls slightly short of the three traditional augmentation techniques. At velocity z, not only do ML-based techniques perform worse than traditional augmentation techniques in terms of SAPE mean values, but their performance is also significantly worse, with IQRs that differ greatly from those of traditional augmentation techniques. However, it should be noted that for velocity z, traditional augmentation techniques also perform poorly compared to the x and y axes.

3.2. Acceleration Parameters

Similar to velocity parameters in Section 3.1 above, acceleration parameters also have worse predictive performance on the z-axis compared to the x- and y-axes. However, unlike with velocity, ML-based methods excel in this aspect for acceleration. Across the x, y, and z axes, ML-based methods outperform traditional augmentation techniques. Starting with acceleration x, Bi-LSTM performs the best in terms of SAPE mean value, IQR, and R 2 , followed by LSTM. Among the traditional augmentation techniques, linear has the highest R 2 . Acceleration y has almost the same ranking as x-axis, so we can see the dominance of Bi-LSTM again. Finally, acceleration z has the lowest predictive performance among the six parameters in this study. Again, the Bi-LSTM performs the best in all aspects, including SAPE mean value, IQR, and R 2 . In this situation, the K-NN technique performed better than the LSTM.

4. Discussion

In the previous section, we showed that for velocity, linear interpolation produces better fits and better results than other techniques in terms of both SAPE mean valules and R 2 for all axes. For acceleration, on the other hand, Bi-LSTM performed the best. This suggests that acceleration is data that changes relatively more rapidly as a rate of change in velocity, and that simple forms of augmentation techniques have limitations in frequency augmentation of data of this nature. To further verify the variability of the data over time, we derived the standard deviation of differences for each parameter and showed the results in Table 3. We can see that both velocity and acceleration are actually higher on the z-axis than on the x and y-axes. In addition, acceleration z has a value of 0.3143, which is very high compared to other parameters. The variability of the data is very high, which indicates that it is very difficult to ensure the accuracy of frequency augmentation. In fact, the traditional augmentation technique has a very low predictive performance, which is probably due to the fact that it only considers two points to be targeted while filling the data. Therefore, the more volatile the data is, the larger the error will be, since it is not possible to estimate the value from only two points. In this case, ML-based methods that can reflect the characteristics of time series data, such as this study, seem to be more effective. In addition, ML-based methods can adjust a large number of trainable parameters in small steps during gradient descent optimization through an efficient backpropagation algorithm, making them very flexible in finding the best model for the data. However, as described above, it was very difficult to secure excellent performance for acceleration z even with LSTM-based ML techniques. Therefore, it is necessary to further study the optimal frequency augmentation technique specialized for acceleration z.

5. Conclusions

Frequency augmentation of velocity and acceleration along each axis, which are the most important parameters in the development of CBM+ systems, is essential. But currently, due to various constraints, not enough data is recorded for system development. In this study, we experimented and analyzed six techniques for frequency augmentation of these velocity and acceleration parameters. We implemented LSTM and Bi-LSTM-based models based on the idea that since these parameters are time series data, filling the data with sequential information will be excellent for performance improvement. In this study, we first introduce in detail the velocity and acceleration parameters measured and recorded by airborne weapon system, and then propose a series of data processing strategies, including preprocessing methods. We also present a frequency augmentation method based on Bi-LSTM, and compare the results of three traditional augmentation techniques based on linear interpolation, KNN filling, and LSTM model. The results show that linear interpolation performs the best for velocity parameters and Bi-LSTM performs the best for acceleration. This paper has made some progress in data processing of velocity and acceleration parameters, especially frequency augmentation, but there are still many areas to be further researched and explored.
First, we found that Bi-LSTM is effective when the data is highly variable, such as acceleration, but it is still not satisfactory and more effective augmentation techniques are needed. Also, in this study, we only discussed techniques that augment the frequency within a single parameter. However, recently, researchers have been actively working on filling in missing data in high dimensions by utilizing MLP (Multi-Layer Perceptron), etc. and their performance is also excellent. Therefore, it would be very meaningful to build an integrated data set using parameters with higher frequencies in addition to velocity and acceleration parameters, and then augment the frequency of the target parameters. Also, since the current data preprocessing process is all done manually, it would save a lot of time and resources to standardize the processing process and build ETL (Extract - Transform - Load) tools automatically.
Continued technological advancement is essential to fully leverage the benefits of ML-based frequency augmentation techniques such as these. The development of real-time data processing tools and more sophisticated AI models could drastically improve the predictive accuracy and operational efficiency of airborne systems.

Author Contributions

Conceptualization, D.K., S.J and I.L.; methodology, D.K., S.J and I.L; software, D.K., S.J and I.L; validation, D.K., S.J, I.L., Y.L., B.S. and Y.H; formal analysis, D.K., Y.L., and Y.H; investigation S.J, Y.L. and B.S; resources, D.K., S.J, I.L., Y.L. and B.S.; data curation, D.K., I.L., Y.L. and B.S.; writing—original draft preparation, D.K.; writing—review and editing, D.K.; visualization, D.K., I.L and B.S.; supervision, B.S. and Y.H; project administration, B.S. and Y.H.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

This paper was conducted with support from KRIT (Korea Research Institute for defense Technology planning and advancement) with funding from the government (Defense Acquisition Program Administration) in 2022. (KRIT-CT-22-081, Weapon System CBM+ Research Center).

Data Availability Statement

Restrictions apply to the availability of these data. Data were obtained from the Republic of Korea Ministry of National Defense.

Acknowledgments

This paper was supported by the KRIT(Korea Research Institute for defense Technology planning and advancement) with funding from the government (Defense Acquisition Program Administration).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. United States General Accounting Office. (2016). BEST PRACTICES: F-35 SUSTAINMENT DOD Needs a Plan to Address Risks Related to Its Central Logistics System, GAO-16-439.
  2. United States of America Department of Defense. (2008). Condition Based Maintenance Plus DoD Guidebook.
  3. Park, N.S. Research Trends on Deep Learning for Anomaly Detection of Aviation Safety. Electronics and telecommunications trends, Vol.36 No.5 (May 2021); pp. 82–91.
  4. You, E.K.; Bae, C.G.; Kim, H.J.; Implementation of OFP initialization fuction in IMDC for FA-50 aircraft. Korea Society of Computer Information, Vol.24 No.2 (2019); pp. 111-118.
  5. Wong, W.K.; Gerosa, D.; Machine-learning interpolation of population-synthesis simulations to interpret gravitational-wave observations: A case study. Physical review. D, Vol.100 No.8 (2019); pp. 083015.
  6. Li, J.; Heap, A.D.; Spatial interpolation methods applied in the environmental sciences: A review. Environmental Modeling & Software, Vol.53 (2014); pp. 173 – 189.
  7. Mitasova, H.; Hofierka, J.; Interpolation by regularized spline with tension: Ⅱ. Application to terrain modeling and surface geometry analysis. Mathematical geology, Vol.25 No.6 (1993); pp. 657 – 669.
  8. Shukia, S.N.; Marlin, B.M.; Interpolation-Prediction Networks for Irregularly Sampled Time Series. arXiv 2019, arXiv:1909.07782v1.
  9. Shukia, S.N.; Marlin, B.M.; Heteroscedastic Temporal Variational Autoencoder For Irregularly Sampled Time Series. arXiv 2022, arXiv:2107.11350v1.
  10. Lin, Q.; Bao, X.; Li, C; Deep Learning based missing data recovery of non-stationary wind velocity. Journal of Wind Engineering and Industrial Aerodynamics, Vol.224 (May 2022).
  11. Ma, J.; Cheng, J.C.; Jiang, F.; Chen, W.; Wang, M.; Zhai, C. A bi-directional missing data imputation scheme based on LSTM and transfer learning for building energy data. Energy Build 2020, 216, 109941. [Google Scholar] [CrossRef]
  12. Chen, Z.; Xu, H.; Jiang, P.; Yu, S.; Lin, G.; Bychkov, I.; Hmelnov, A.; Ruzhnikov, G.; Zhu, N.; Liu, Z. A transfer Learning-Based LSTM strategy for imputing Large-Scale consecutive missing data and its application in a water quality prediction system. J.Hydrol. 2021, 602, 126573. [Google Scholar] [CrossRef]
  13. Tzoumpas, K.; Estrada, A.; Miraglio, P.; Zambelli, P.; A data filling methodology for time series based on CNN and (Bi) LSTM neural networks. arXiv 2022, arXiv:2204.09994.
  14. Lu, X.; Yuan, L.; Li, R.; Xing, Z.; Yao, N.; Yu, Y.; An Improved Bi-LSTM-Based Missing Value Imputation Approach for Pregnancy Examination Data. Algorithms 2023, 16(1), 12.
  15. Caruso, C.; Quarta, F.; Interpolation methods comparison. Computers & Mathematics with Applications. Vol.35 No.12 (1998). pp. 109-126.
  16. Jia, Y.; Ma, J.; What can machine learning do for seismic data processing? An Interpolation application. Geophysics 2017, 82(3), 163-177.
  17. Belisle, E.; Huang, Z.; Digabel, S.L.; Gheribi, A.E. Evaluation of machine learning interpolation techniques for prediction of physical properties. Computational Materials Sciences 2015, 98, 170–177. [Google Scholar] [CrossRef]
  18. Chahrour, I.; Wells, J.D. Comparing Machine Learning and Interpolation Methods for Loop-Level Calculations. arXiv 2022, arXiv:2111.14788v3. [Google Scholar] [CrossRef]
  19. McKinley, S.; Levine, M. Cubic spline Imterpolation. Coll. Redw. 1988, 45, 1049–1060. [Google Scholar]
  20. Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeay, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. et al.; SciPy 1.0: fundamental algorithms for scientific computing in Python. Nature methods 2020, 17(3), 261-272.
  21. Hochreiter, S.; Schmidhuber, J.; Long short-term memory. Neural comput. 1997, 9. 1735-1780.
  22. Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J. Devin, M.; Ghemawat, S.; Irving G.; Isard, M. et al.; Tensorflow: A system for large-scale machine learning. 12th {USENIX} symposium on operating systems design and implementation ({OSDI} 16). 2016. pp. 265-283.
  23. Chollet, F. Chollet, F. et al.; Keras. 2015. Available online: https://keras.io.
  24. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
  25. Matplotlib 3.4.3 Documentation. 2021. Available online: https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.boxplot.html.
Preprints 107198 g001aPreprints 107198 g001b
Figure 1. Distribution of each parameter: (a) velocity x; (b) velocity y; (c) velocity z; (d) acceleration x; (e) acceleration y; (f) acceleration z.
Figure 1. Distribution of each parameter: (a) velocity x; (b) velocity y; (c) velocity z; (d) acceleration x; (e) acceleration y; (f) acceleration z.
Preprints 107198 g001aPreprints 107198 g001b
Preprints 107198 g002
Figure 2. Results of the line plot of each parameter: (a) velocity x; (b) velocity y; (c) velocity z; (d) acceleration x; (e) acceleration y; (f) acceleration z.
Figure 2. Results of the line plot of each parameter: (a) velocity x; (b) velocity y; (c) velocity z; (d) acceleration x; (e) acceleration y; (f) acceleration z.
Preprints 107198 g002
Preprints 107198 g003
Figure 3. Line plot of power lever angle and acceleration x: (a) power lever angle; (b) acceleration x.
Figure 3. Line plot of power lever angle and acceleration x: (a) power lever angle; (b) acceleration x.
Preprints 107198 g003
Preprints 107198 g004
Figure 4. Structure of LSTM and bidirectional LSTM: (a) LSTM; (b) bidirectional LSTM.
Figure 4. Structure of LSTM and bidirectional LSTM: (a) LSTM; (b) bidirectional LSTM.
Preprints 107198 g004
Preprints 107198 g005
Figure 5. Box plot for SAPE comparison.
Figure 5. Box plot for SAPE comparison.
Preprints 107198 g005
Preprints 107198 g006aPreprints 107198 g006b
Figure 6. SAPE and R 2 results for each parameter: (a) SAPE results for velocity x; (b) R 2 results for velocity x; (c) SAPE results for velocity y; (d) R 2 results for velocity y; (e) SAPE results for velocity z; (f) R 2 results for velocity z; (g) SAPE results for acceleration x; (h) R 2 results for acceleration x; (i) SAPE results for acceleration y; (j) R 2 results for acceleration y; (k) SAPE results for acceleration z; (l) R 2 results for acceleration z.
Figure 6. SAPE and R 2 results for each parameter: (a) SAPE results for velocity x; (b) R 2 results for velocity x; (c) SAPE results for velocity y; (d) R 2 results for velocity y; (e) SAPE results for velocity z; (f) R 2 results for velocity z; (g) SAPE results for acceleration x; (h) R 2 results for acceleration x; (i) SAPE results for acceleration y; (j) R 2 results for acceleration y; (k) SAPE results for acceleration z; (l) R 2 results for acceleration z.
Preprints 107198 g006aPreprints 107198 g006b
Table 1. Statistical metrics of each parameter.
Table 1. Statistical metrics of each parameter.
Statistical metrics velocity
x		 velocity
y		 velocity
z		 acceleration
x		 acceleration
y		 acceleration
z
arithmetic mean -0.98 -1.37 0.11 -0.002 -0.002 32.03
standard deviation 347.75 425.05 42.04 16.19 15.76 6.25
skewness -0.04 -0.21 -2.15 -0.07 -0.02 2.10
kurtosis -0.021 -0.069 46.76 21.27 22.52 133.94
Table 2. SAPE mean values and R 2 values for each parameter: For each frequency augmentation techniques, the row above is represents SAPE mean value and the row below represents R 2 .
Table 2. SAPE mean values and R 2 values for each parameter: For each frequency augmentation techniques, the row above is represents SAPE mean value and the row below represents R 2 .
Evaluation
metrics		 velocity
x		 velocity
y		 velocity
z		 acceleration
x		 acceleration
y		 acceleration
z
linear 0.1717 0.1201 10.08 18.8736 18.0781 29.8432
0.999934 0.999904 0.998498 0.9788 0.98381 0.815943
quadratic 0.1705 0.1219 10.1059 18.8955 18.0881 29.9172
0.999933 0.999903 0.998459 0.9782 0.9824 0.814386
cubic spline 01707 0.1215 10.1752 18.9377 18.1323 29.9696
0.999933 0.999903 0.998468 0.9783 0.9845 0.820549
K-NN 0.1943 0.1264 15.4107 19.4727 19.041 22.4049
0.99991 0.999818 0.997953 0.9789 0.9895 0.875184
LSTM 0.4856 0.7785 18.785 16.9034 15.3625 25.4411
0.998451 0.999131 0.995699 0.9802 0.9905 0.856243
Bi-LSTM 0.4812 0.7451 17.8921 12.2729 12.9714 17.5193
0.998459 0.999129 0.995691 0.9805 0.9909 0.900158
Table 3. Standard deviation of differences for each parameter.
Table 3. Standard deviation of differences for each parameter.
velocity
x		 velocity
y		 velocity
z		 acceleration
x		 acceleration
y		 acceleration
z
standard
deviation		 0.0044 0.0035 0.0287 0.0713 0.0651 0.3143
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated