Prerpints.org logo
Preprint
Article

Unbreakable SU(3) Atoms of Vacuum Energy: A Solution for Cosmological Constant Problem

Altmetrics

Downloads

135

Views

516

Comments

0

This version is not peer-reviewed

Submitted:

22 May 2024

Posted:

23 May 2024

Read the latest preprint version here

Alerts
Abstract
This paper addresses the cosmological constant problem, a significant discrepancy highlighted by \cite{Weinberg:1988cp} that underlines a fundamental inconsistency between quantum field theory (QFT) and general relativity (GR). QFT examines matter dynamics within Lorentzian spacetime under standard model symmetry, while GR uses Riemannian geometry but adapts it to ensure local Lorentzian behavior in small regions. Despite the experimental successes of both theories, a major challenge exists in theoretical understanding. This letter seeks to clarify this critical misunderstanding. As the universe cools from its hot beginning, the \(SU(3) \times SU(2) \times U(1)\) standard model gauge symmetry evolves. This symmetry breaks to \(SU(3) \times U(1)\) upon cooling at the electroweak scale and ultimately to \(SU(3)\) alone as temperatures approach near-absolute zero kelvin, facilitated by the experimental Meissner effect. This suggests that \(SU(3)\) symmetry forms the foundational "atoms" of vacuum energy. Calculating the number of \(SU(3)\) vacuum atoms across the universe results in a value that perfectly aligns the theoretical predictions with the observed vacuum energy densities, thereby resolving the cosmological constant problem. Since \(SU(3)\) atoms account for the cosmological constant, they must be unbreakable. The third law of thermodynamics, which states that it is impossible to reach absolute zero Kelvin, provides the protection that prevents SU(3) atoms from breaking at zero Kelvin. This reveals the connection between the third law of thermodynamics and the quark confinement. This leads to the \(SU(3)\) atom creating a mass gap within the universe. This solution serves as a symmetric evidence of gauge-gravity duality as well as gravity-superconductor duality.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

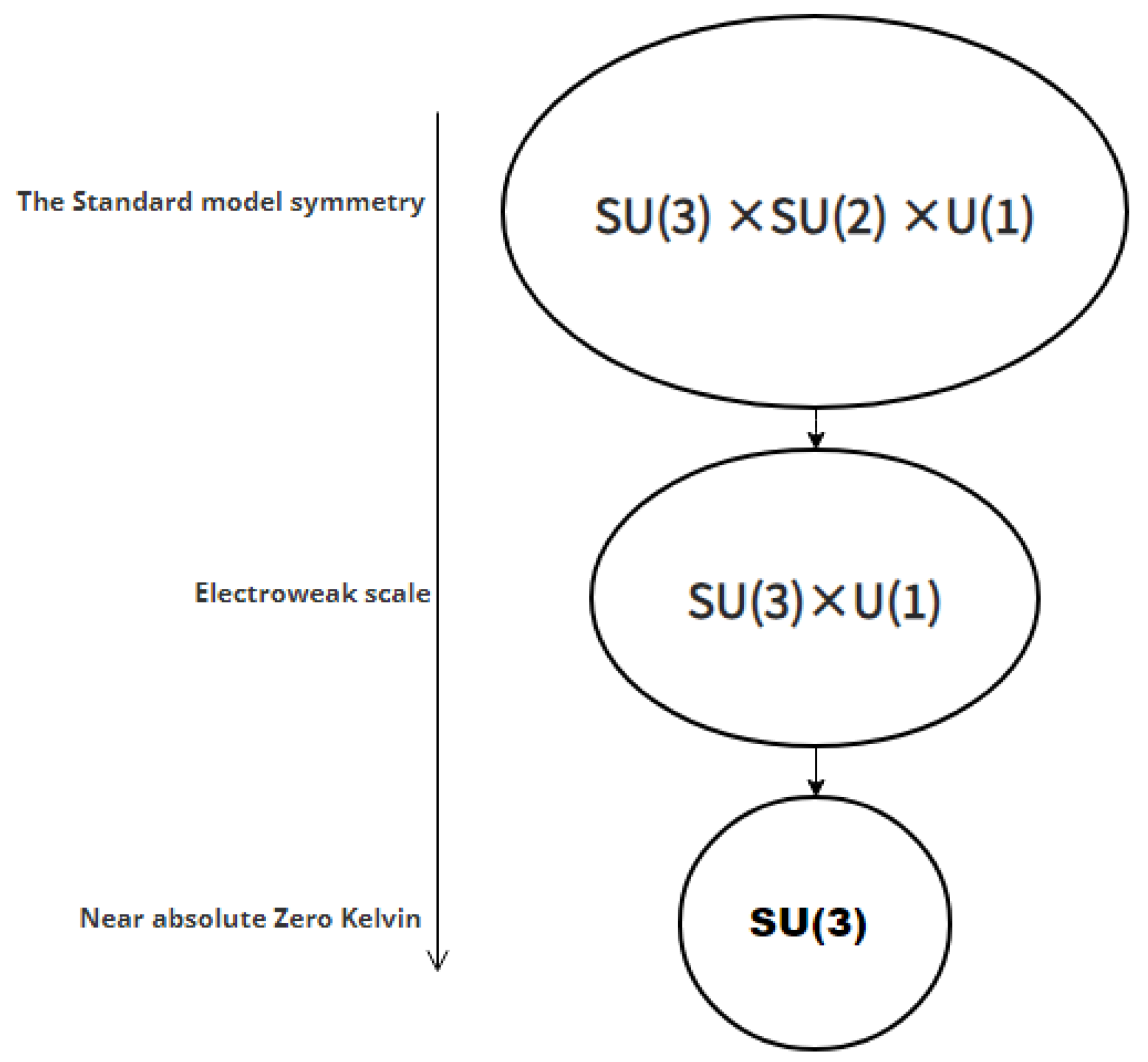
1. The remnant SU(3)

The Standard Model (SM) of particle physics is grounded in the S U ( 3 ) × S U ( 2 ) × U ( 1 ) symmetry group, highlighting the interactions among the fundamental forces and elementary particles [2,3,4]. The Higgs mechanism [5], through the vacuum expectation value of the Higgs field, facilitates the mass generation, initiating spontaneous symmetry breaking from S U ( 3 ) × S U ( 2 ) × U ( 1 ) to S U ( 3 ) × U ( 1 ) and this process has been verified experimentally [6]. This process assigns masses to most elementary particles, sparing gluons, photons, and neutrinos. However, the observation of neutrino oscillations, suggesting non-zero neutrino masses, presents a challenge to the SM’s initial assertions [7,8]. Potential mechanisms for neutrino mass include the see-saw mechanism or discrete symmetries [9,10], maintaining the S U ( 3 ) and U ( 1 ) symmetries within quantum chromodynamics [11] and quantum electrodynamics [12], respectively. Upon cooling below the critical temperature T c , a phase transition occurs, breaking U ( 1 ) symmetry and leading to superconductivity, characterized by zero electrical resistance and the expulsion of magnetic fields, known as the Meissner effect which has been verified experimentally [13]. This phase transition underlines the breaking of U ( 1 ) electromagnetic symmetry, leaving S U ( 3 ) as the sole remnant of unbroken symmetry, thereby suggesting its fundamental role in vacuum energy density at temperatures nearing absolute Zero Kelvin. Figure 1 shows the S U ( 3 ) as the remnant symmetry nearing Zero Kelvin due to the Meissner effect. It is worth mentioning that [14] models dark energy as a superconductor using a scalar-vector-tensor gravity model, unlike the standard General Relativity approach in [15], which studied the same concept, including a Meissner-like expulsion of space-time by dark energy. Taking one further step, this study elaborates on the symmetric structure of vacuum atoms with the remnant S U ( 3 ) symmetry for a better understanding of the mass gap and the cosmological constant problems.

2. SU ( 3 ) Vacuum Atoms and Third Law of Thermodynamics

At low temperatures, the Meissner effect leads to the breakdown of U ( 1 ) symmetry, while S U ( 3 ) symmetry remains intact. This phenomenon highlights a significant connection between the S U ( 3 ) symmetry group and vacuum energy, suggesting that S U ( 3 ) symmetry is a universal remnant. It manifests in structures as small as atoms, approximately 10 − 15 meters in size, equal to the size of a nucleon [16]. The presence of a critical temperature where U ( 1 ) symmetry breaks mirrors phenomena observed in superconductors. Beyond this temperature, S U ( 3 ) remains as the predominant symmetry. By combining these ideas, we aim to better understand both the mass gap problem in Yang-Mills theory [17] and the cosmological constant problem [1]. The vacuum energy of the whole universe can be realized as made of N of these S U ( 3 ) vacuum atoms, with each one showing S U ( 3 ) symmetry and being 10 − 15 meters in size. The total number of S U ( 3 ) vacuum atoms in the universe is determined by the ratio of the universe volume to the S U ( 3 ) vacuum atom volume as follows:
N = V universe V atom
Here, N is the total count of S U ( 3 ) vacuum atoms in the universe, V atom is the volume of one such atom at 10 − 15 meters across, and V universe represents the universe’s vast volume, based on a universe radius of 10 26 meters [18]. Inputting these values, we get:
N = ( 10 26 ) 3 ( 10 − 15 ) 3 = 10 123 atoms
This result perfectly matches the ratio between the predicted vacuum energy density ( ≈ E p l 4 / ( ℏ c ) 3 = 10 76 GeV 4 / ( ℏ c ) 3 ) and what we observe ( 10 − 47 GeV 4 / ( ℏ c ) 3 ), tackling the heart of the cosmological constant problem as discussed in [1] and solve it. We elaborate further on the solution in detail in the next section.
To ensure the stability of SU ( 3 ) vacuum atoms and resolve the discrepancy between observed and theoretical vacuum energy density, there must be a fundamental law operating near zero Kelvin that guarantees their unbreakability. Near absolute zero (0 Kelvin), the third law of thermodynamics states that reaching zero Kelvin—where volume and pressure theoretically disappear—is impossible due to the requirement of an infinite number of cooling steps. Consequently, SU ( 3 ) atoms of vacuum energy cannot be further subdivided or broken apart due to the third law of thermodynamics. This resilience of SU ( 3 ) symmetry, as dictated by the third law of thermodynamics, may explain the thermodynamic basis of quark confinement for the first time to our knowledge.

3. Solution of Cosmological Constant Problem

To summarize this profound problem. We start with the Einstein field equation [19]
G μ ν + Λ g μ ν = 8 π G c 4 T μ ν
where G μ ν is Einstein’s tensor, Λ is the cosmological constant and c is the speed of light. When we consider vacuum solution (i.e G μ ν = 0 and T μ ν = ρ vac c 2 g μ ν ), the cosmological constant Λ , representing the vacuum energy density ρ vac , is expressed as [1]:
ρ vac c 2 = c 4 Λ 8 π G .
Astrophysical measurements give Λ ≈ 1.1 × 10 − 52 m − 2 , resulting in an observed vacuum energy density of [16]:
ρ vac obsv c 2 = 10 − 47 GeV 4 / ( ℏ c ) 3
In Quantum Field Theory (QFT), ρ vac QFT integrates vacuum fluctuation energies across all momentum states [1],
ρ vac QFT c 2 ≈ 1 ( 2 π ℏ ) 3 ∫ 0 P P l d 3 p ℏ ω p 2 ≈ E p l 4 / ( ℏ c ) 3
≈ 10 76 GeV 4 / ( ℏ c ) 3 .
This yields a significant discrepancy between the theoretical QFT and observed values:
ρ vac QFT ρ vac obsv = 10 123 .
This significant discrepancy is recognized as the cosmological constant problem [1]. It underlines a crucial inconsistency between quantum field theory (QFT) and general relativity (GR). QFT analyzes how matter behaves at the quantum level within Lorentzian spacetime, whereas GR describes spacetime using Riemannian geometry but adapts it to be locally Lorentzian, accommodating Lorentzian behavior in small regions. Despite the experimental success of both theories, the main challenge lies in our theoretical understanding. In this letter, we address this misunderstanding. We identify a fundamental issue with Equation (7), which incorrectly assumes that the vacuum energy consists of a single unit. Through the application of standard model symmetry principles, we demonstrate in this paper that the vacuum energy comprises N = 10 123 identical units. Each of these units, or ’atoms’, exhibits S U ( 3 ) symmetry, which we refer to as S U ( 3 ) atoms of vacuum energy. Consequently, the computation of vacuum energy density in the framework of quantum field theory necessitates division by the cumulative count of vacuum atoms present in the universe (N), facilitating an outcome that aligns precisely with the observed value of vacuum energy density as follows:
1 N ρ vac QFT c 2 ≈ 1 10 123 E p l 4 ( ℏ c ) 3 ≈ 10 − 47 GeV 4 / ( ℏ c ) 3 .
Hence, using S U ( 3 ) symmetry to model vacuum energy offers an approach to solving the cosmological constant problem. It illustrates the connection between quantum mechanics and the general theory of relativity by explaining how the vacuum energy contributes to the spacetime constant in Einstein’s field equations, referred to as the cosmological constant.
According toEquation (2), one might question whether N could vary due to the universe’s increasing radius, driven by the expansion rate defined by the Hubble parameter H ( t ) . There are two possibilities: one is that the nucleon size expands at the same rate as the universe, keeping N constant and thereby ensuring that the vacuum energy density and the cosmological constant remain unchanged, thus preserving general relativity. The other possibility is that the nucleon size remains constant during the universe’s expansion. This would mean that SU ( 3 ) remains the same size, and therefore, the number of SU ( 3 ) atoms increases as the radius of the universe expands. This latter possibility implies that the dark energy, computed according toEquation (9), could be diminishing due to the expansion of the universe with an increasing number of SU ( 3 ) atoms. This might align with new experimental findings by the DESI collaboration in [20,21,22]. This possibility invites investigations beyond general relativity that could imply a changing cosmological constant [23].
Hence, using SU(3) symmetry to model vacuum energy offers an approach to solving the cosmological constant problem and provides fresh insight into the Yang-Mills theory’s mass gap [17]. SU(3) mass gap is represented by a strictly positive vacuum energy density under the protection of the third law of thermodynamics. The extensive literature on the QCD vacuum [24] addresses energy density, stability, tachyon modes, and the composition involving chromomagnetic vertices and/or monopoles, which are crucial for generating the QCD mass gap independently of external influences. This letter introduces a novel link by interpreting the vacuum energy density in QFT using SU(3) atoms, thereby establishing a direct physical connection between the QCD mass gap and the vacuum energy density that shapes the fabric of spacetime.

4. Quantum Spacetime: A Necessity

To describe these S U ( 3 ) vacuum atoms, a Lorentzian quantum spacetime framework is needed. The first Lorentzian quantum spacetime was suggested by Snyder in [25] and predicted both non-commutative geometry and the generalized uncertainty principle. The non-commutative geometry was found as limits of M/string theory as higher dimensional corrections of ordinary Yang-Mills field [26,27]. The phenomenological implications of non-commutative geometry have been extensively explored [28]. Furthermore, the generalized uncertainty principle has originated from different quantum gravity approaches such as string theory, black hole physics and quantum geometry [29,30,31,32,33], with significant investigations into its phenomenological and experimental consequences [34,35,36,37,38,39,40,41,42,43,44]. Snyder’s algebra is based on three primary generators: the position operator x μ , momentum operator p μ , and the Lorentz generators J μ ν = x μ p ν − x ν p μ . These generators fulfill the requirements of the Poincaré algebra and introduce novel commutators that encapsulate a minimal length:
[ x μ , x ν ] = i ℏ β J μ ν ,
x μ , p ν ] = i ℏ η μ ν + β p μ p ν , where μ , ν = 0 , 1 , 2 , 3
Here, β = β 0 ℓ Pl ℏ c 2 , with β 0 being a dimensionless parameter. Equation 10 illustrates the non-commutative nature of the geometry, while Equation 11 introduces a Generalized Uncertainty Principle (GUP), both preserving Lorentz symmetry [25]. In the Snyder model ( β > 0 ), space is discrete and time is continuous, whereas in the anti-Snyder model ( β < 0 ), time is discrete and space is continuous. The sub-algebra involving J μ ν and x μ is isomorphic to the de Sitter/anti-de Sitter algebra, thereby linking the momentum spaces of Snyder/anti-Snyder models geometrically to de Sitter/anti-de Sitter spacetimes [45]. Refining the Snyder model with isotropic parametrizations while maintaining Lorentz/Poincaré symmetry, lead to the same non-commutative relation and different forms of GUP as elaborated in [46,47]. In [40], it was shown that the cold atoms can be best described by GUPs forms proposed in [48,49,50]. In [51], a significant relationship between the GUP and the third law of thermodynamics was elaborated. Simultaneously, the S U ( 3 ) symmetry forms the "atoms of vacuum" constituting the quantum spacetime substrate. These studies strengthens the link we observed in this letter between quark confinement, resulting from an unbroken S U ( 3 ) symmetry, and the third law of thermodynamics.
The study [52,53] represented quantum spacetime using the charge radius as a key characteristic for a wide range of physical objects. The exploration of how mass (M) and charge radius (R) correlate across different scales—from microscopic to macroscopic, as illustrated in Figure 2—uncovers a pattern strikingly similar to the behavior seen in quark-gluon plasma (QGP) [54]. This resemblance offers experimental support that S U ( 3 ) atoms, which represent a core symmetry in the governance of quark-gluon plasma, are equally pivotal in shaping the fabric of quantum spacetime. The linkage of the mass-radius dynamic with dark matter, further explored in [55], accentuates the importance of these observations.
The findings presented in this paper establish a link between the number of SU(3) atoms and the vacuum energy density, which determines the cosmological constant of the universe. This insight highlights a correspondence between Quantum Chromodynamics (QCD) and gravity. Our symmetric analysis supporting the gauge-gravity duality [59,60,61,62]. By employing the Meissner effect, we provide symmetric proof of the gravity/superconductor duality [63].
The quanta of spacetime must be a 4-polytope. Our recent study has identified this shape as the 24-cell [64] at the electroweak scale, with its 24 vertices potentially denoting the elementary particles of the Standard Model. The permutation of these vertices, amounting to 24!= 6.2 × 10 23 , correlates with Avogadro’s number that defines the minimum number of atoms needed to create a self-replicating molecule, the molecules in a cell that can lead to multicellular life, and the cells in a sentient organism. This may point to a baseline complexity required for sentience, as suggested by Avogadro’s constant. The specificity of Avogadro’s number and its potential geometric significance warrant further investigation, given these insights. Our analysis reveals that a 24-cell can be conceptualized by selecting eight vertices from it to form a 16-cell in three distinct configurations. These eight vertices are analogous to the eight gluons, while the other sixteen vertices come together to form a tesseract, symbolizing the remaining elementary particles. Accordingly, the fundamental components of spacetime may be represented by S U ( 3 ) vacuum atoms at low temperatures, assuming the structure of a 16-cell endowed with eight vertices in the pseudo-Euclidean spacetime which agrees with the core of Riemnain geometry which is locally Lorenztian. This model proposes a geometric perspective on superconductivity that invites further investigations.

5. Conclusions

During its evolution from a hot, primordial state, the universe expands and cools, guided by the S U ( 3 ) × S U ( 2 ) × U ( 1 ) gauge symmetry foundational to the Standard Model of particle physics. This symmetry undergoes a transformation at the electroweak scale, breaking to S U ( 3 ) × U ( 1 ) , and as temperatures approach near-absolute zero, the Meissner effect leads to the further breaking of U ( 1 ) symmetry, preserving S U ( 3 ) alone. This suggests that S U ( 3 ) symmetry underpins the basic "atoms" of vacuum energy. The stability of these S U ( 3 ) "atoms" at low temperatures epitomizes the third law of thermodynamics, which declares the impossibility of reaching absolute zero in which volume and pressure vanishes. This constancy ensures that the S U ( 3 ) vacuum "atoms" are indivisible, forging a profound link between the third law of thermodynamics and quark confinement. The total number of S U ( 3 ) vacuum atoms in the universe, each roughly 10 − 15 meters in size akin to nucleons, aligns exactly with the ratio between theoretical vacuum energy and observed vacuum energy density. This alignment resolves the cosmological constant problem. It further defines dark energy using the 10 123 S U ( 3 ) vacuum atoms, offering insights into the mass gap challenge within Yang-Mills theory. It appears clearly that the mass gap in S U ( 3 ) results from a strictly positive vacuum energy density. Remarkably, this setup is reinforced by the third law of thermodynamics, which affirms the integrity of the S U ( 3 ) atom as unbreakable.

Acknowledgments

The author extends gratitude to Caroline Gorham for her assistance with the graph. Dedicated to my mother, whose love fuels my journey and wisdom lights my path. Forever grateful.

References

  1. Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
  2. Glashow, S.L. Partial Symmetries of Weak Interactions. Nucl. Phys. 1961, 22, 579–588. [Google Scholar] [CrossRef]
  3. Weinberg, S. A Model of Leptons. Phys. Rev. Lett. 1967, 19, 1264–1266. [Google Scholar] [CrossRef]
  4. Salam, A. Weak and Electromagnetic Interactions. Conf. Proc. C 1968, 680519, 367–377. [Google Scholar] [CrossRef]
  5. Higgs, P.W. Broken Symmetries and the Masses of Gauge Bosons. Phys. Rev. Lett. 1964, 13, 508–509. [Google Scholar] [CrossRef]
  6. Chatrchyan, S.; others. Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, arXiv:hep-ex/1207.7235]716, 30–61. [Google Scholar] [CrossRef]
  7. Wolfenstein, L. Neutrino Oscillations in Matter. Phys. Rev. D 1978, 17, 2369–2374. [Google Scholar] [CrossRef]
  8. Mikheyev, S.P.; Smirnov, A.Y. Resonance Amplification of Oscillations in Matter and Spectroscopy of Solar Neutrinos. Sov. J. Nucl. Phys. 1985, 42, 913–917. [Google Scholar]
  9. Mohapatra, R.N.; Senjanovic, G. Neutrino Mass and Spontaneous Parity Nonconservation. Phys. Rev. Lett. 1980, 44, 912. [Google Scholar] [CrossRef]
  10. Altarelli, G.; Feruglio, F. Discrete Flavor Symmetries and Models of Neutrino Mixing. Rev. Mod. Phys. 2010, arXiv:hep-ph/1002.0211]82, 2701–2729. [Google Scholar] [CrossRef]
  11. Gell-Mann, M. A Schematic Model of Baryons and Mesons. Phys. Lett. 1964, 8, 214–215. [Google Scholar] [CrossRef]
  12. Feynman, R.P. Mathematical formulation of the quantum theory of electromagnetic interaction. Phys. Rev. 1950, 80, 440–457. [Google Scholar] [CrossRef]
  13. Meissner, W.; Ochsenfeld, R. Ein neuer Effekt bei Eintritt der Supraleitfähigkeit. Naturwissenschaften 1933, 21, 787–788. [Google Scholar] [CrossRef]
  14. Liang, S.D.; Harko, T. Superconducting dark energy. Phys. Rev. D 2015, arXiv:gr-qc/1504.02645]91, 085042. [Google Scholar] [CrossRef]
  15. Inan, N.; Ali, A.F.; Jusufi, K.; Yasser, A. Graviton mass due to dark energy as a superconducting medium: theoretical and phenomenological aspects 2024. arXiv:gr-qc/2404.03872].
  16. Zyla, P.A.; others. Review of Particle Physics. PTEP 2020, 2020, 083C01. [Google Scholar] [CrossRef]
  17. Jaffe, A.; Witten, E. Quantum yang-mills theory. The millennium prize problems 2006, 1, 129. [Google Scholar]
  18. Ostriker, J.; Peebles, P.; Yahil, A. The size and mass of galaxies and the mass of the universe, 1974.
  19. Einstein, A. The foundation of the general theory of relativity. Annalen Phys. 1916, 49, 769–822. [Google Scholar] [CrossRef]
  20. Adame, A.G. ; others. DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations 2024. arXiv:astro-ph.CO/2404.03002].
  21. Adame, A.G. ; others. DESI 2024 III: Baryon Acoustic Oscillations from Galaxies and Quasars 2024. arXiv:astro-ph.CO/2404.03000].
  22. Adame, A.G. ; others. DESI 2024 IV: Baryon Acoustic Oscillations from the Lyman Alpha Forest 2024. arXiv:astro-ph.CO/2404.03001].
  23. Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: the equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, arXiv:gr-qc/1205.3421]342, 155–228. [Google Scholar] [CrossRef]
  24. Cloet, I.C.; Roberts, C.D. Explanation and Prediction of Observables using Continuum Strong QCD. Prog. Part. Nucl. Phys. 2014, arXiv:nucl-th/1310.2651]77, 1–69. [Google Scholar] [CrossRef]
  25. Snyder, H.S. Quantized space-time. Phys. Rev. 1947, 71, 38–41. [Google Scholar] [CrossRef]
  26. Connes, A.; Douglas, M.R.; Schwarz, A.S. Noncommutative geometry and matrix theory: Compactification on tori. JHEP 1998, 02, 003. [Google Scholar] [CrossRef]
  27. Seiberg, N.; Witten, E. String theory and noncommutative geometry. JHEP 1999, 09, 032. [Google Scholar] [CrossRef]
  28. Douglas, M.R.; Nekrasov, N.A. Noncommutative field theory. Rev. Mod. Phys. 2001, 73, 977–1029. [Google Scholar] [CrossRef]
  29. Amati, D.; Ciafaloni, M.; Veneziano, G. Can Space-Time Be Probed Below the String Size? Phys. Lett. B 1989, 216, 41–47. [Google Scholar] [CrossRef]
  30. Garay, L.J. Quantum gravity and minimum length. Int. J. Mod. Phys. A 1995, 10, 145–166. [Google Scholar] [CrossRef]
  31. Scardigli, F. Generalized uncertainty principle in quantum gravity from micro - black hole Gedanken experiment. Phys. Lett. B 1999, 452, 39–44. [Google Scholar] [CrossRef]
  32. Maggiore, M. A Generalized uncertainty principle in quantum gravity. Phys. Lett. B 1993, 304, 65–69. [Google Scholar] [CrossRef]
  33. Capozziello, S.; others. Generalized uncertainty principle from quantum geometry. Int. J. Theor. Phys. 2000, 39, 15–22. [Google Scholar] [CrossRef]
  34. Das, S.; Vagenas, E.C. Universality of Quantum Gravity Corrections. Phys. Rev. Lett. 2008, arXiv:hep-th/0810.5333]101, 221301. [Google Scholar] [CrossRef]
  35. Pikovski, I.; others. Probing Planck-scale physics with quantum optics. Nature Phys. 2012, arXiv:quant-ph/1111.1979]8, 393–397. [Google Scholar] [CrossRef]
  36. Marin, F.; others. Gravitational bar detectors set limits to Planck-scale physics on macroscopic variables. Nature Phys. 2013, 9, 71–73. [Google Scholar] [CrossRef]
  37. Petruzziello, L.; others. Quantum gravitational decoherence from fluctuating minimal length and deformation parameter at the Planck scale. Nature Commun. 2021, arXiv:gr-qc/2011.01255]12, 4449. [Google Scholar] [CrossRef]
  38. Kumar, S.P.; others. On Quantum Gravity Tests with Composite Particles. Nature Commun. 2020, arXiv:quant-ph/1908.11164]11, 3900. [Google Scholar] [CrossRef]
  39. Moradpour, H.; others. The generalized and extended uncertainty principles and their implications on the Jeans mass. Mon. Not. Roy. Astron. Soc. 2019, arXiv:gr-qc/1907.12940]488, L69–L74. [Google Scholar] [CrossRef]
  40. Gao, D.; Zhan, M. Constraining the generalized uncertainty principle with cold atoms. Phys. Rev. A 2016, arXiv:gr-qc/1607.04353]94, 013607. [Google Scholar] [CrossRef]
  41. Bawaj, M.; others. Probing deformed commutators with macroscopic harmonic oscillators. Nature Commun. 2015, arXiv:gr-qc/1411.6410]6, 7503. [Google Scholar] [CrossRef]
  42. Easther, R.; others. Imprints of short distance physics on inflationary cosmology. Phys. Rev. D 2003, 67, 063508. [Google Scholar] [CrossRef]
  43. Kober, M. Gauge Theories under Incorporation of a Generalized Uncertainty Principle. Phys. Rev. D 2010, arXiv:physics.gen-ph/1008.0154]82, 085017. [Google Scholar] [CrossRef]
  44. Hossenfelder, S. Minimal Length Scale Scenarios for Quantum Gravity. Living Rev. Rel. 2013, arXiv:gr-qc/1203.6191]16, 2. [Google Scholar] [CrossRef]
  45. Mignemi, S. Progress in Snyder model. PoS 2020, CORFU2019, 226. [Google Scholar] [CrossRef]
  46. Battisti, M.V.; Meljanac, S. Modification of Heisenberg uncertainty relations in noncommutative Snyder space-time geometry. Phys. Rev. D 2009, arXiv:hep-th/0812.3755]79, 067505. [Google Scholar] [CrossRef]
  47. Battisti, M.V.; Meljanac, S. Scalar Field Theory on Non-commutative Snyder Space-Time. Phys. Rev. D 2010, arXiv:hep-th/1003.2108]82, 024028. [Google Scholar] [CrossRef]
  48. Maggiore, M. Quantum groups, gravity and the generalized uncertainty principle. Phys. Rev. D 1994, 49, 5182–5187. [Google Scholar] [CrossRef] [PubMed]
  49. Ali, A.F.; Das, S.; Vagenas, E.C. Discreteness of Space from the Generalized Uncertainty Principle. Phys. Lett. B 2009, arXiv:hep-th/0906.5396]678, 497–499. [Google Scholar] [CrossRef]
  50. Ali, A.F.; Das, S.; Vagenas, E.C. A proposal for testing Quantum Gravity in the lab. Phys. Rev. D 2011, arXiv:hep-th/1107.3164]84, 044013. [Google Scholar] [CrossRef]
  51. Liu, T.P.; Pu, J.; Han, Y.; Jiang, Q.Q. A possible thermodynamic origin of the spacetime minimum length. Int. J. Mod. Phys. D 2020, 29, 2043022. [Google Scholar] [CrossRef]
  52. Ali, A.F.; Elmashad, I.; Mureika, J. Universality of minimal length. Phys. Lett. B 2022, arXiv:physics.gen-ph/2205.14009]831, 137182. [Google Scholar] [CrossRef]
  53. Ali, A.F.; Elmashad, I.; Mureika, J.; Vagenas, E.C. Theoretical and Observational Implications of Planck’s Constant as a Running Fine Structure Constant. submitted for publication.
  54. Bhalerao, R.S. Relativistic heavy-ion collisions. 1st Asia-Europe-Pacific School of High-Energy Physics, 2014, pp. arXiv:nucl-th/1404.3294]. [CrossRef]
  55. Ianni, A.; Mannarelli, M.; Rossi, N. A new approach to dark matter from the mass–radius diagram of the Universe. Results in Physics 2022, 38, 105544. [Google Scholar] [CrossRef]
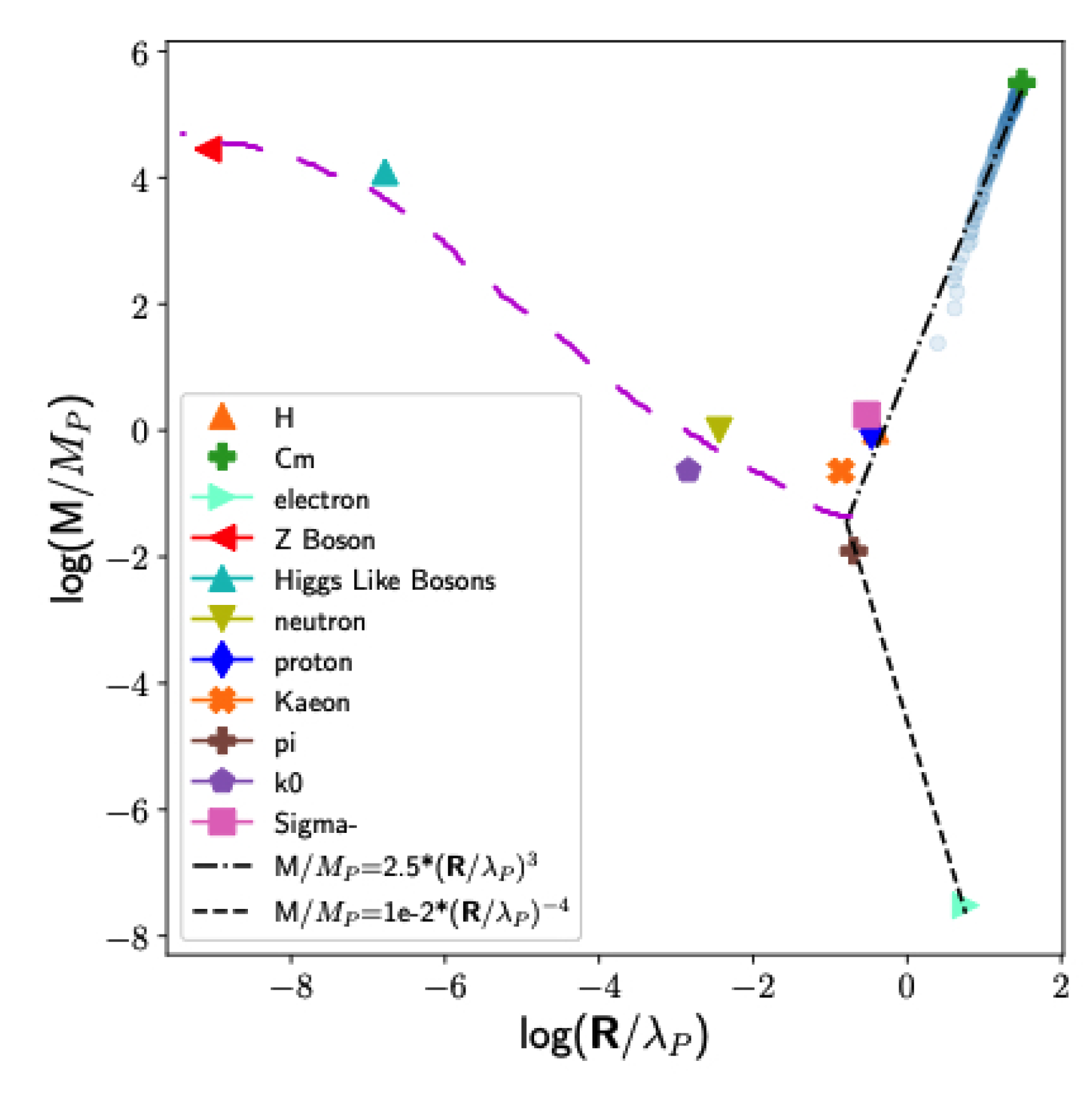
  56. Fritzsch, H. The size of the weak bosons. Physics Letters B 2012, 712, 231–232. [Google Scholar] [CrossRef]
  57. Lehnert, B. Mass-Radius Relations of Z and Higgs-Like Bosons. PROGRESS IN PHYSICS 2014, 10, 5–7. [Google Scholar] [CrossRef]
  58. Angeli, I.; Marinova, K.P. Table of experimental nuclear ground state charge radii: An update. Atomic Data and Nuclear Data Tables 2013, 99, 69–95. [Google Scholar] [CrossRef]
  59. Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
  60. Strominger, A. The dS / CFT correspondence. JHEP 2001, 10, 034. [Google Scholar] [CrossRef]
  61. Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
  62. Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from noncritical string theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef]
  63. Hartnoll, S.A.; Herzog, C.P.; Horowitz, G.T. Holographic Superconductors. JHEP 2008, arXiv:hep-th/0810.1563]12, 015. [Google Scholar] [CrossRef]
  64. Ali, A.F. The Mass Gap of the Spacetime and Its Shape. Fortsch. Phys. 2024, arXiv:hep-th/2403.02655]2024, 2200210. [Google Scholar] [CrossRef]
Preprints 107229 g001
Figure 1. S U ( 3 ) remnant at low temperature
Figure 1. S U ( 3 ) remnant at low temperature
Preprints 107229 g001
Preprints 107229 g002
Figure 2. Logarithmic plot of mass and radius for fundamental particles [16,56,57] and periodic table elements [58], normalized by the proton mass and the Compton wavelength of the proton [52]. The figure is copied from our paper [53]
Figure 2. Logarithmic plot of mass and radius for fundamental particles [16,56,57] and periodic table elements [58], normalized by the proton mass and the Compton wavelength of the proton [52]. The figure is copied from our paper [53]
Preprints 107229 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated