Prerpints.org logo
Preprint
Article

High Mechanical Property and Texture Degree of Hot-Extruded Bi0.905Sb0.095

Altmetrics

Downloads

96

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 May 2024

Posted:

24 May 2024

You are already at the latest version

Alerts
Abstract
Bi1-xSbx crystal is one of the best n-type thermoelectric materials below 200 K, but its weak mechanical strength hinders practical applications for deep refrigeration. Herein, we adopted the mechanical enhancement method of hot extrusion to investigate the comprehensive mechanical and thermoelectric properties of Bi0.905Sb0.095. It revealed that reducing the grain size of the matrix and increasing the extrusion ratio can improve the gain size uniformity and mechanical properties. While the thermoelectric performance depends on the texture, grain size, and local composition. The extruded sample prepared by ingot with the high extrusion ratio of 9:1 generated a high texture degree of (001) plane and small grain sizes between ~4-40 mm, which resulted in the high bending strength of Bi1-xSbx ~130 Mpa and a high-power factor of ~ 68 μW·cm-1·K-2@173 K, as well as the relative high figure of merit of 0.25@173K. This work highlights the importance of the uniform distribution of the grain size and the compositions for Bi1-xSbx, as well as the required universal key parameter for the hot-extrusion method.
Keywords: 
Subject: Engineering  -   Metallurgy and Metallurgical Engineering

1. Introduction

Solid-state thermoelectric cooling (TEC) technology, which can directly convert electrical and thermal energy, has the advantages of compact size, no mechanical motion, high reliability, and high precision of temperature control [1,2,3]. To date, it has become an important heat management thermal profile used for infrared detection, [4] bioanalytical devices, [5] semiconductor lasers, [6] etc. The cooling temperature difference (ΔT) of the thermoelectric cooling device depends on the figure of merit zT ( z T = S 2 σ T / κ ) of thermoelectric materials, where T is the absolute temperature, S is the Seebeck coefficient, σ is the electrical conductivity, and κ is the thermal conductivity, respectively. [7] Currently, Bi2Te3 is the best-performing thermoelectric material near room temperature. The Bi2Te3-based single-stage TEC devices can achieve a ΔTmax of about 70 K at room temperature, [8] and the four-stage cooling device can achieve a ΔTmax of 133 K at 282 K, [9] which almost reaches the cooling limit for Bi2Te3-based TEC devices, due to the quick deteriorations of the TE performance in the low-temperature range [10,11]. Therefore, there is an urgent need for thermoelectric cooling materials with high TE properties near liquid-nitrogen temperature.
The layered Bi semimetal, as one of the earliest n-type thermoelectric materials, has been considered the best thermoelectric material below 150 K [11,12]. Because electrons and holes along the two directions of [001] and [100] display strong anisotropic transports, i.e. ( σ e / σ h )∥= 9.19 and ( σ e / σ h )⊥= 2.12 (//and⊥present parallel and perpendicular to [001]-direction) at room temperature, [13] It suppresses the common deterioration of different charge carriers for the thermoelectric power in low TE materials, i.e. the Seebeck coefficient, according to the two-band mode [13]. Thus, the anisotropic transports of two different carriers result in a high Seebeck coefficient along [001]-direction, which then gives rise to the high power factor (PF, PF = S 2 σ ) of ~77 μW·cm-1·K-2 at 300 K and ~200 μW·cm-1·K-2 at 100 K, [14,15] being much higher than those of Bi2Te3 [10,16]. However, the high thermal conductivity, originating from both high electric and lattice thermal conductivity, brings about the low zT value of Bi metal (only 0.18 @ 100 K) [14]. Notably, both bismuth and antimony are semimetals and can form infinite solid solutions due to their similar crystal structures [17]. When the Sb content is between 7% and 22%, the Bi1-xSbx crystals display semiconductor band features, favoring the reduction of thermal conductivity and the improvement of the TE performance [18]. Therefore, in 1972, Yim and Amith fully investigated the temperature-dependent anisotropic thermoelectric properties of Bi1-xSbx single crystals. [14] When alloying Sb into Bi, particularly for Bi92Sb8, it can maintain the expected high power factor and effectively reduce lattice thermal conductivity, producing a high zT of about 0.6 @ 100 K along [001] direction.
Despite Bi1-xSbx single crystals exhibiting good thermoelectric properties, their poor mechanical performances have hindered their practical applications. In the past decades, powder metallurgy combined post-deformation, [19,20,21,22] extrusion, [23,24,25,26] and hot-pressing [27,28,29] have been utilized to improve mechanical strength. The reduction of grain size can effectively prevent further extension of the fracture and then improve the mechanical properties. At the same time, it also can scatter more phonons and thus reduce the thermal conductivity. However polycrystalline samples lost the most important factor of high TE performance achievement for Bi1-xSbx, namely, out-plane texture. As a result, polycrystalline Bi1-xSbx deteriorates the electrical properties and the zT value. In 2020, a single crystal grown by the Czochralski technique was used for extrusion to maintain the [001] orientation, which has successfully improved the mechanical strength and reduced the thermal conductivity [23]. When the extrusion ratio is 10, the extruded sample obtained a high bending strength of ~65 MPa at room temperature and a relatively higher peak zT of 0.45 around 140 K compared to the powder metallurgy methods. Based on this high TE performance at low temperature, the lowest cooling temperature of 140 K from 300 K has been achieved by the 6-stage TEC device consisting of n-Bi0.91Sb0.09/p-Bi2Te3 in the ultra-low temperature two-stage module and traditional n/p-Bi2Te3 materials for the other four-stage module [30].
It is known that the sample undergoes three main processes during the hot extrusion, one is the grain crack owing to the shear stress in the transition region of the die from large to small diameter, another is the grain rearrangement when passing through the transition region, and the last one is the grain growth at hot temperature [31,32,33,34]. Because of the nonuniform distribution of shear stress and temperature distribution along the radial direction, it would produce a nonuniform distribution of the grain size in the sample, which should be eliminated for the precise evaluation of materials’ TE performances and the fabrication of reliable TEC devices. Therefore, in this work, we systematically investigated the parameters affecting the grain size distribution, mechanical strength, and TE properties by using different matrices and the extrusion ratio (Ke). We discovered that reducing the grain size of the matrix and increasing the Ke can improve the uniformity of grain size.

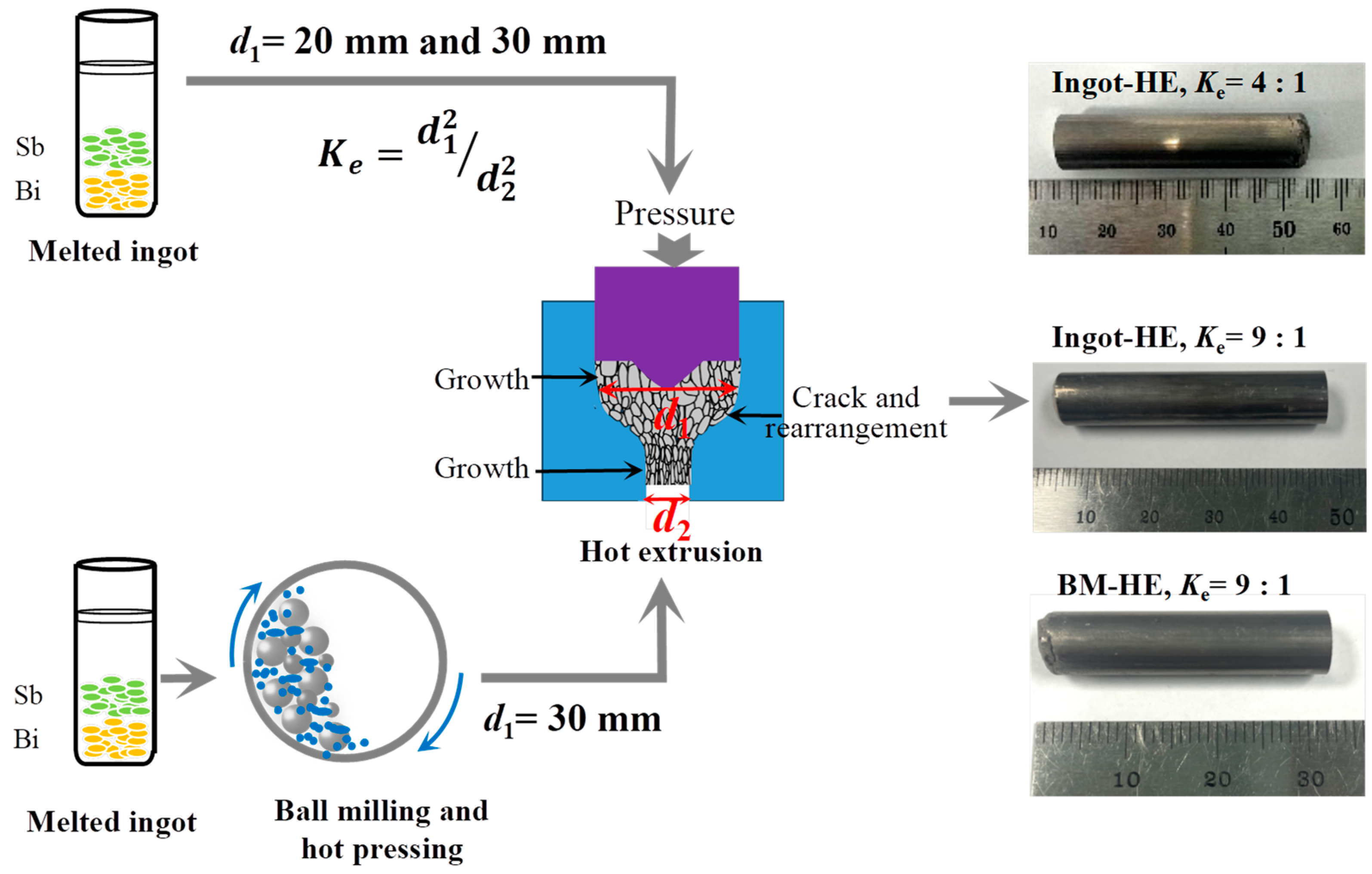
2. Materials and Methods

Synthesis: Bi0.905Sb0.095 ingot was obtained by melting the raw material (5N) at a stoichiometric ratio of Bi0.905Sb0.095 under a vacuum of 1.0 Pa at 1073 K for 3 hours and then . Two inner diameters (20 mm and 30 mm) of the quartz tubes to load the raw materials to produce the ingot with different diameters for extrusion (marked as Ingot-HE). In addition, the partial ingot was also ball milled to reduce the grain size to 1-10 μm, which was placed in the center of a larger graphite die with an inner diameter of 30 mm for hot-pressing, performing at a temperature of 473 K under a pressure of 50 MPa for 30 minutes. The hot-pressed samples with high density (> 95% of the theoretical densities) were used for extrusion (marked as MB-HE). The extrusion ratio of 4:1 and 9:1 for the ingot and 9:1 for the pressed sample at 473 K and a punch speed of ~0.2 mm/min were used for hot extrusion to investigate the main parameter affecting the grain side distribution. The middle part of the extruded sample was used for the measurement. The schematic diagram of matrices preparation and the hot extrusion, as well as the extruded samples, are shown in Figure 1.
Characterization: The phase composition of the samples was characterized using X-ray diffraction equipment (D8 Advance, Bruker, Cu Kα radiation, λ = 0.15406 nm) in the range of 2θ = 20°-70°. A scanning electron microscope (Thermo Fisher Scientific, Apreo 2) was used to observe the microstructure (SEM), determine the element distribution (EDS), and analyze texture and orientation differences (EBSD). The Seebeck coefficient and electrical conductivity were measured by LSR-1 from LINSEIS. The Seebeck coefficient was obtained by linearly fitting the potential difference at different temperature differences, and electrical conductivity was measured by the Vanderbilt method, which can accurately measure two-dimensional planar samples of arbitrary shapes. Thermal diffusion (D) was measured by the transient laser flash method (NETZSCH-LFA467, Germany). The total thermal conductivity (κtotal) was calculated by the relation of κ t o t a l = D ρ C p , where Cp is the heat capacity, ρ is the density of samples measured by Archimedes’ method. Due to the Debye temperature of Bi0.9Sb0.1 is 128.5 K, [35] the Cp within 175 K and 300 K of material was calculated by the Dulong-Petit law. The three-point bending strength of the sample was tested using a universal testing machine, with a loading speed of 0.02 mm/min.

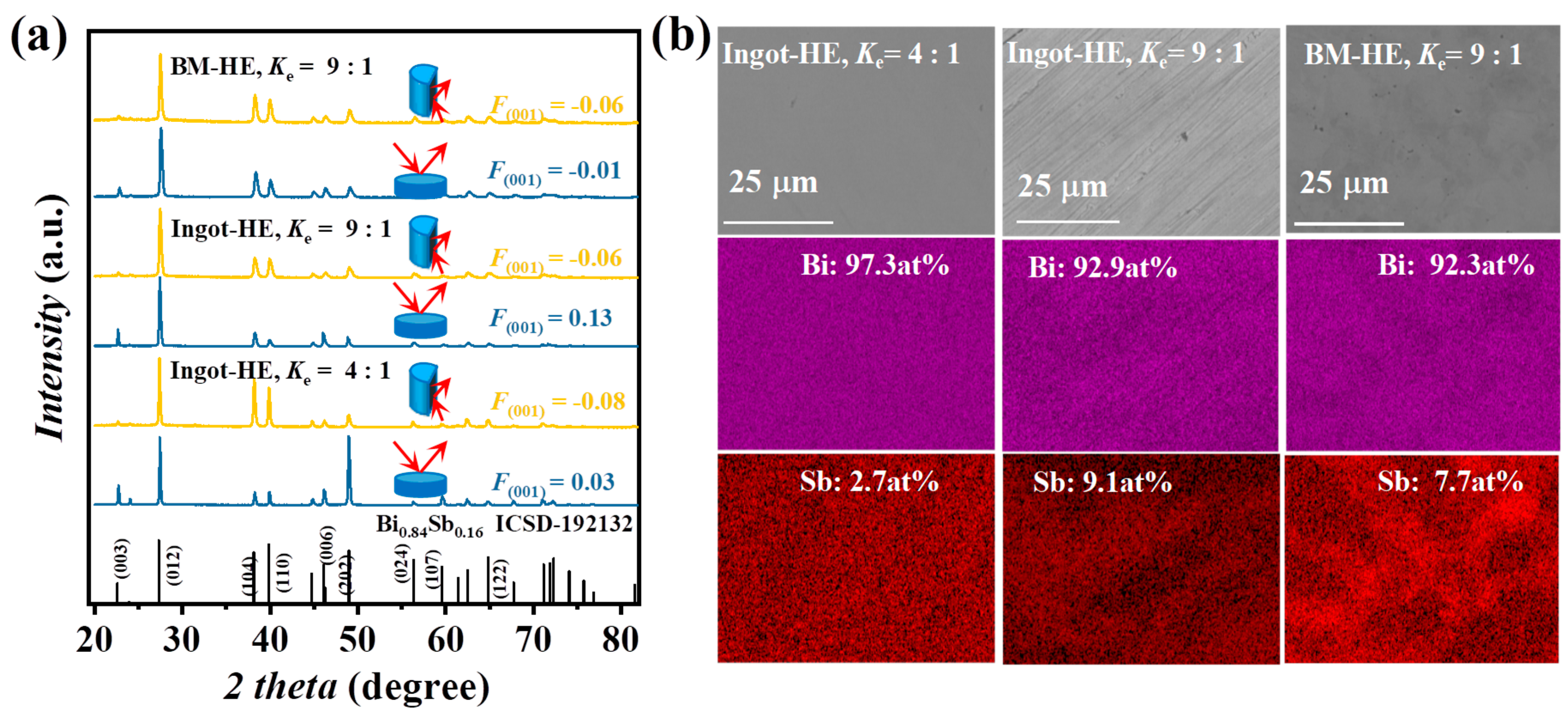
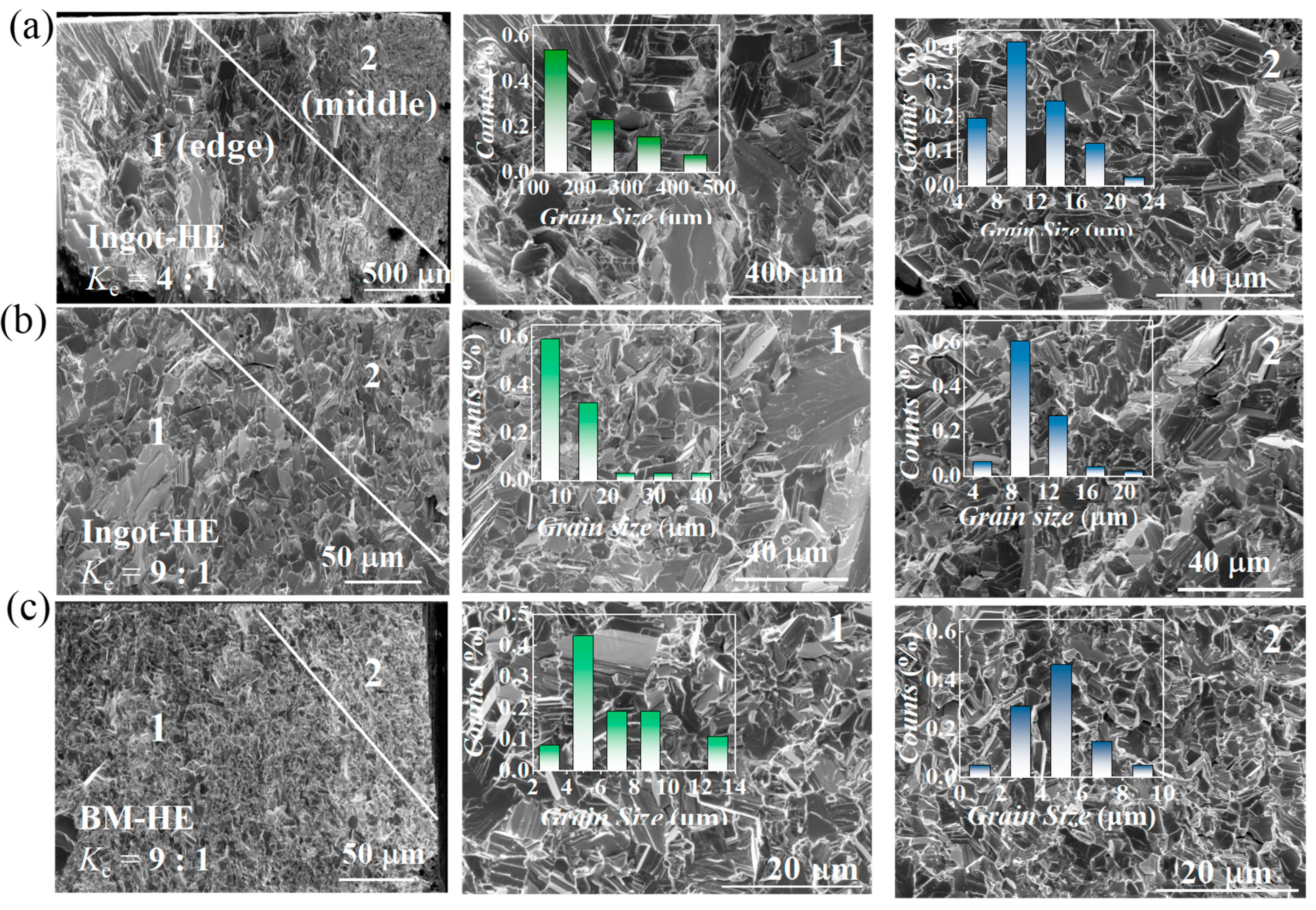
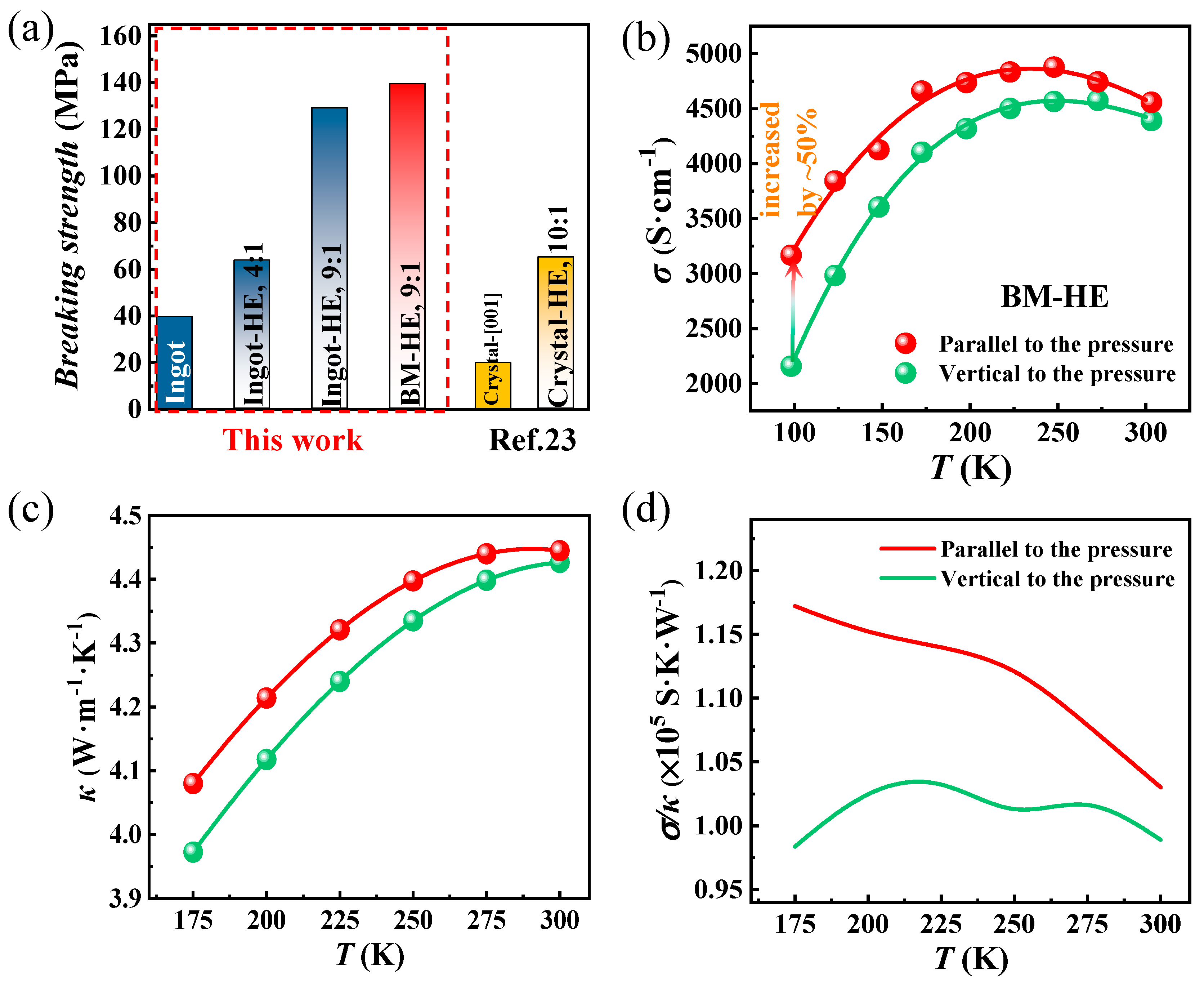
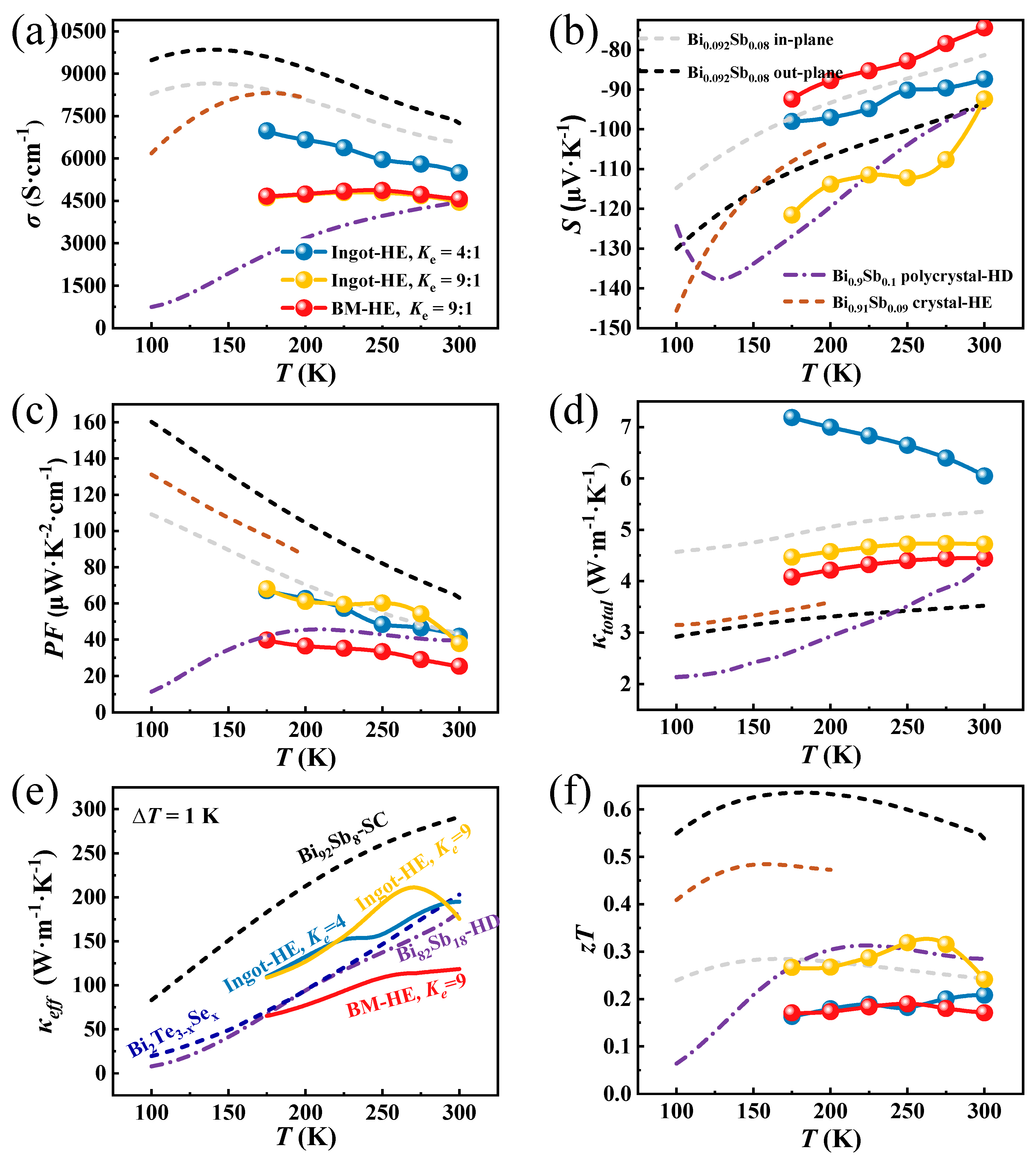
3. Results Discussion

Characterization

In order to evaluate the texture degree of the extruded sample which is significant for the high thermoelectrical properties, PXRD patterns were measured and the texture degree was calculated by the Lotgering method: F = P − P 0 1 − P 0 , P 0 = I 0 ( 00 l ) ∑ I 0 ( h k l ) , P = I ( 00 l ) ∑ I ( h k l ) , where I(hkl) and I0(hkl) are the peak integral intensities for the measured and randomly oriented samples, respectively [36]. All PXRD peaks agree with the standard peak of ICSD-192132, which can be seen from Figure 2a, indicating the high purities of the samples. In addition, due to the main slip systems of (100) [ 0 1 ¯ 1 ¯ ] and (111) [ 10 1 ¯ ] for Bi crystal, [20] all samples show a higher F(001) value vertical to the pressure direction compared to the parallel direction. Notably, this high in-plane texture of Bi1-xSbx vertical to the pressure direction is opposite to that of the commercial Bi2Te3, which is parallel to the pressure direction, despite that both Bi1-xSbx and Bi2Te3 display layered crystal structures. Nonetheless, the textures parallel to the pressure for both Bi1-xSbx and Bi2Te3 reveal their higher TE performance along this direction due to their different anisotropic transports, favoring the practical fabrication. EDS mapping results presented in Figure 2b show different ratios of Bi and Sb for the sample prepared by different method. In detail, the ingot-HE with Ke = 4:1 display a large deviation from the nominal ratio of the composition. It would be derived from the gravitational field and large difference of the element mass for Sb and Bi, which result in the segregation of the Sb along the axial direction of ingot and the ingot-HE samples [17]. In contrast, after remixing the different parts of the ingot, the BM-HE shows a closed atomic ratio of Bi0.905Sb0.095, but still with a nonuniformity in the micro range. Notwithstanding, the BM-HE can improve the element distribution in the macro range.
The grain size distribution was characterized by the SEM measurement. The Ingot-HE with Ke = 4:1 shows significantly different grain sizes around the edge (<25 μm) and the middle (>100 μm) of the sample. When Ke increased to 9:1, the difference in grain sizes reduced and the majority of grains were within the range of 10-40 μm for the edge and 4-20 μm for the middle. It is reasonable that increasing Ke is to increase the deformation extent, which could induce more proportion of the sample to experience the first two main processes, i.e. crack and rearrangement, then improve the uniformity of grain size. Furthermore, the BM-HE sample with Ke = 9:1 shows an almost uniform distribution of the grain size between 2-15 μm for the whole sample. Therefore, reducing the grain size of the matrix and increasing the Ke can improve the uniformity.
Mechanical performance is an important factor for the practical applications of TE materials. The bending strength increases as the grain size reduces and the value increases from 40 Mpa for the ingot to ~130 Mpa and 140 Mpa for the Ingot-HE and BM-HE with Ke = 9:1, which can be seen in Figure 4a. These strengths are much higher than that of the crystal-[001], and the values of HE samples in this work are also higher than that (65 Mpa) of crystal-HE with Ke = 10:1 due to their average different grain sizes [23].
Generally, contrary to the mechanical strength, the texture degree is anti-dependent on the grain size. However, despite the BM-HE sample with small grain sizes, the electrical and thermal conductivity at low temperatures show strong anisotropic transports, as shown in Figure 4b–d. The anisotropic degrees of transport weaken when the temperature increases. This phenomenon originates from the involvement of two transport features of the polycrystal and the single crystal. In detail, as the temperature increases, the electrical and the thermal conductivity of Bi1-xSbx polycrystal significantly increases, [26,37] but the electrical conductivity of the single crystal has a contrary trend while the thermal conductivity of the single crystal only increases slightly [14]. Therefore, the electrical and thermal conductivity of Bi1-xSbx around room temperature are closer compared to those at low temperatures. In addition, the parallel to the pressure direction achieves higher σ/κ than that of vertical to the pressure, therefore, the TE properties of other samples were only measured along this direction.
Figure 5a displays the comparison of the temperature-dependent electrical conductivity for the three samples in this work and the single crystal vertical and parallel to the [001] direction, crystal/polycrystal-HE, [23,26] as well as the polycrystal combined hot deformation (HD). [22] The electrical conductivity for Ingot-HE and BM-HE is located between those of single crystal and polycrystal. Interestingly, the temperature-dependent trend of electrical conductivity transformed from a single crystal to a polycrystal for the Ingot-HE as the Ke increases mainly due to the reduction of the grain size. However, the BM-HE sample with smaller gains has almost the same r σ than that of Ingot-HE with the same Ke. This is because the anisotropy of electrical conductivity is related to the element ratio of the composition (Figure 2b) and the higher texture degree of BM-HE (Figure 2a). In detail, when the ratio of Sb is smaller than 7.5%, the σ vertical to [001] direction is higher than that parallel to [001], but when the ratio is larger than 7.5 %, the anisotropy changes and the σ vertical to [001] is a smaller than that parallel to [001] [14]. Therefore, the Sb and Bi elements distribution and their ratio as well as the texture degree are significant for the electrical transport.
All samples show negative Seebeck coefficients, which are consistent with the n-type TE materials transport. According to the literature, [14] increasing the Sb ratio in the range of 0%-12% for the single crystal, the Seebeck coefficient increases below 173 K but decreases above 225 K. And the temperature-dependent trend of Seebeck coefficient also turns from increase to decrease as the ratio further increases. In comparison, the Seebeck coefficients for polycrsytal reduce as the temperature increases above 145 K. Therefore the absolute value and the temperature-dependant trend of Seebeck coefficient for Bi1-xSbx are related to the composition and the morphology, increasing the complexity of analyzing the underline mechanism. In this work, all Seebeck coefficients decreases as the temperature increases, being similar to those of single crystals. The temperature-dependent Seebeck coefficients (Figure 5b) display a similar trend of σ for different Ke, namely, increasing the Ke value promotes the transformation of S from single crystal to polycrystal for the Ingot-HE samples. Thus, the S is higher for Ke = 9:1 than that of Ke = 4:1. However, it would be for the higher texture degree, BM-HE shows the smallest S value. In addiction, the difference in S in this work reduces as the temperature increases owing to the similar value for the single crystal [14] and polycrystal around room temperature [26].
The PFs of Ingot-HE samples in this work are closed and located between those of single crystal and polycrystal with much higher peak values ~ 70 μW·cm-1·K-2 @173 K than that of the deformed polycrystal as shown in Figure 5c. However, due to the low Seebeck coefficient, BM-HE displays the lowest PF within the temperature range of 173-300K, which is even smaller than that of deformed polycrystal.
Owing to the limit of ability for LFA-467, the thermal conductivity was only measured in the temperature range of 173-300 K as shown in Figure 5d. Notably, the Ingot-HE with Ke = 4:1 displays the highest thermal conductivity in the whole temperature range, and the value is also higher than those of single crystal in-plane and out-plane. The Increase of Ke produces smaller grains which result in the reduced thermal conductivity for Ingot-HE for the increased grain boundary scattering for phonons. The thermal conductivity of Ingot-HE and BM-HE with Ke = 9:1 is located between the values of single crystal in-plane and out-plane [14] but are significantly higher than those of deformed polycrystal [22] and crystal-HE [23]. Notably, this deviation from the data in the literature would be derived from the different measurement methods and equipment. In this work, we adopted the transient laser flash method, which possesses a high precision, while indirect calculation from the zT based on the Harman method for the crystal-HE and the absolute method for the single crystal, crystal-HE, and deformed polycrystal were used in literature. Therefore, the thermal conductivity for the Bi1-xSbx prepared by different methods under the same condition is crucial for a precise comparison.
The high thermal conductivity and high power factor of the extruded samples in this work favor the achievement of effective thermal conductivity ( κ e f f ) which can be applied in heat dissipation as another main functional application of TEC [1]. It is calculated by κ e f f = κ + P F ∙ T H 2 2 ∆ T , where TH is the hot-side temperature of TEC and ΔT is the temperature difference between the two sides [38]. When the temperature difference is 1 K, κ e f f at different hot end temperatures is shown in Figure 5e, from which we can that the extruded Bi1-xSbx with higher κ e f f (62-210 W·m-1·K-1) in low-temperature and comparable value with that of the high-cost commercial Bi2Te3 when TH > 290 K for Ingot-HE with Ke = 9:1. Therefore, the low-cost extruded Bi1-xSbx is also suitable for application in heat dissipation than
The temperature-dependent zT values of all samples between 173 K and 300 K are shown in Figure 5f. Although the PFs of hot-extruded samples in this work are significantly higher than those of polycrystalline Bi1-xSbx alloys prepared by extrusion, [26] hot-deformation [22] and hot-pressing [39,40]. The high thermal conductivity measured by the transient laser flash method counteracts the high electrical properties resulting in that their zT values only lie between 0.15-0.33, which are much lower than those of the single crystals, and even lower than those of polycrystalline samples. Therefore, the evaluation of the advantage for TE performance by the extrusion method still depends on the thermal conductivity measured at the same condition for the samples prepared by different methods.

4. Conclusions

In summary, we investigated the grain size distribution and the mechanical strength and thermoelectric properties of hot-extruded Bi0.905Sb0.095 by using different matrices of ingot and ball milling combined with hot pressing as well as the extrusion ratio, discovering the inherent law of extrusion method that reducing the grain size of the matrix and increasing the extrusion ratio can improve the gain size uniformity and mechanical properties. While the thermoelectric performance depends on the texture degree, grain size, and local composition. As a result, the extruded sample prepared by ingot with high extrusion ratio achieves a high texture degree and small grains, producing a high bending strength of ~130 Mpa and a high power factor of 68 μW·cm-1·K-2@173 K, which is beneficial to the practical application. The conditions of size uniform distribution for the extrusion method in this work are universal guidance for the preparation of other materials.

Author Contributions

Investigation and writing—original draft preparation, L.H. Zhao and H.C. Zhang; Conceptualization, methodology and validation, J.H. Feng and R. H. Liu; writing—review and editing and formal analysis, J.H. Feng; supervision, D.G. Zhao, D.W. Wang, R.H. Liu; project administration and funding acquisition, R.H. Liu. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Shenzhen Science and Technology Research Funding (Nos. JCYJ202208l8102408017, JCYJ20210324115611030, and RCYX20200714114641 193). Guang Dong Basic and Applied Basic Research Foundation (No. 2022B1515020066), Youth Innovation Promotion Association of the Chinese Academy of Sciences (2019253).

Acknowledgments

The authors thank Shimadzu (China) Co., LTD. Guangzhou Branch for the mechanical strength measurement.

Competing Interest

The authors declare no conflict of interest.

References

  1. Feng, J.; Li, J.; Liu, R. Low-temperature thermoelectric materials and applications. Nano Energy 2024, 126, 109651. [Google Scholar] [CrossRef]
  2. Ling, Y.F.; Min, E.R.; Dong, G.Y.; Zhao, L.H.; Feng, J.H.; Li, J.; Zhang, P.; Liu, R.H.; Sun, R. Precise temperature control of electronic devices under ultra-high thermal shock via thermoelectric transient pulse cooling. Appl. Energ. 2023, 351, 121870. [Google Scholar] [CrossRef]
  3. Chen, W.Y.; Shi, X.L.; Zou, J.; Chen, Z.G. Thermoelectric Coolers: Progress, Challenges, and Opportunities, Small Methods 2022, 6, 2101235. 6.
  4. Rogalski, A. History of infrared detectors, Opto-Electron. Rev. 2012, 20, 279–308. [Google Scholar]
  5. Putra, N.; Sukyono, A.W.; Johansen, D.; Iskandar, F.N. The characterization of a cascade thermoelectric cooler in a cryosurgery device. Cryogenics 2010, 50, 759–764. [Google Scholar] [CrossRef]
  6. Khalatpour, A.; Paulsen, A.K.; Deimert, C.; Wasilewski, Z.R.; Hu, Q. High-power portable terahertz laser systems. Nat. Photonics 2021, 15, 16–20. [Google Scholar] [CrossRef]
  7. Rowe, D.M. THERMOELECTRICS HANDBOOK MACRO TO NANO, CRC Press Taylor & Francis Group, 2006.
  8. Zhou, J.; Feng, J.H.; Li, H.; Liu, D.; Qiu, G.J.; Qiu, F.; Li, J.; Luo, Z.Z.; Zou, Z.G.; Sun, R.; Liu, R.H. Modulation of Vacancy Defects and Texture for High Performance n-Type Bi2Te3 via High Energy Refinement. Small 2023, 19, 2300654. [Google Scholar] [CrossRef] [PubMed]
  9. Huebener, R.P.; Tsuei, C.C. Prospects for Peltier cooling of superconducting electronics. Cryogenics 1998, 38, 325–328. [Google Scholar] [CrossRef]
  10. Li, H.; Feng, J.; Zhao, L.; Min, E.; Zhang, H.; Li, A.; Li, J.; Liu, R. Hierarchical Low-Temperature n-Type Bi2Te3 with High Thermoelectric Performances. ACS Appl. Mater. Inter. 2024, 16, 22147–22154. [Google Scholar] [CrossRef] [PubMed]
  11. Mao, J.; Chen, G.; Ren, Z.F. Thermoelectric cooling materials. Nat. Mater. 2021, 20, 454–461. [Google Scholar] [CrossRef]
  12. Boydston, R.W. Thermo-electric Effect in Single-Crystal Bismuth. Phys. Rev. 1927, 30, 911–921. [Google Scholar] [CrossRef]
  13. Gallo, C.F.; Chandrasekhar, B.S.; Sutter, P.H. Transport Properties of Bismuth Single Crystals. J. Appl. Phys. 1963, 34, 144–152. [Google Scholar] [CrossRef]
  14. Yim, W.M.; Amith, A. Bi-Sb Alloys for Magneto-Thermoelectric and Thermomagnetic Cooling. Solid State Electron. 1972, 15, 1141–1165. [Google Scholar] [CrossRef]
  15. Chandrasekhar, B.S. The seebeck coefficient of bismuth single crystals. J. Phys. Chem. Solids Pergamon Press 1959, 11, 268–273. [Google Scholar] [CrossRef]
  16. Mao, J.; Zhu, H.T.; Ding, Z.W.; Liu, Z.H.; Gamage, G.A.; Chen, G.; Ren, Z.F. High thermoelectric cooling performance of n-type Mg3Bi2-based materials. Science 2019, 365, 495–498. [Google Scholar] [CrossRef] [PubMed]
  17. Schneider, G.; Herrmann, R.; Christ, B. Crystal growth and electron microprobe analysis of bismuth-antimony alloys (Bi100−xSbx). J. Cryst. Growth 1981, 52, 485–492. [Google Scholar] [CrossRef]
  18. Lenoir, B.; Dauscher, A.; Cassart, M.; Ravich, Y.I.; Scherrer, H. Effect of antimony content on the thermoelectric figure of merit of Bi1−xSbx alloys. J. Phys. Chem. Solids 1998, 59, 129–134. [Google Scholar] [CrossRef]
  19. Matsuo, T.; Suzuki, H. Phonon Scattering by Lattice-Defects in Deformed Bismuth Crystals. J. Phys. Soc. Jpn. 1977, 43, 1974–1981. [Google Scholar] [CrossRef]
  20. Matsuo, T.; Suzuki, H. Effect of Plastic-Deformation on Thermal-Conductivity of Bismuth Crystals. J. Phys. Soc. Jpn. 1976, 41, 1692–1698. [Google Scholar] [CrossRef]
  21. Tokumoto, Y.; Fujiwara, R.; Edagawa, K. High-Density Well-Aligned Dislocations Introduced by Plastic Deformation in Bi1-xSbx Topological Insulator Single Crystals. Crystals 2019, 9, 317. [Google Scholar] [CrossRef]
  22. Combe, E.; Funahashi, R.; Takeuchi, T.; Barbier, T.; Yubuta, K. Thermal deformation effects on thermoelectric properties for Bi0.82Sb0.18 alloys. J. Alloy Compd. 2017, 692, 563–568. [Google Scholar] [CrossRef]
  23. Sidorenko, N.; Parashchuk, T.; Maksymuk, M.; Dashevsky, Z. Development of cryogenic cooler based on n-type Bi-Sb thermoelectric and HTSC. Cryogenics 2020, 112, 103197. [Google Scholar] [CrossRef]
  24. Lu, T.B.; Wang, B.Y.; Li, G.D.; Yang, J.W.; Zhang, X.F.; Chen, N.; Liu, T.H.; Yang, R.G.; Niu, P.J.; Kan, Z.X.; Zhu, H.T.; Zhao, H.Z. Synergistically enhanced thermoelectric and mechanical performance of Bi2Te3 via industrial scalable hot extrusion method for cooling and power generation applications. Mater. Today Phys. 2023, 32, 101035. [Google Scholar] [CrossRef]
  25. Liu, X.S.; Xing, T.; Qiu, P.F.; Deng, T.T.; Li, P.; Li, X.W.; Li, X.Y.; Shi, X. Suppressing the donor-like effect via fast extrusion engineering for high thermoelectric performance of polycrystalline Bi2Te2.79Se0.21. J. Materiomics 2023, 9, 345–352. [Google Scholar] [CrossRef]
  26. El-Asfoury, M.S.; Nasr, M.N.A.; Nakamura, K.; Abdel-Moneim, A. Structural and Thermoelectric Properties of Bi85Sb15 Prepared by Non-equal Channel Angular Extrusion. J. Electron. Mater. 2018, 47, 242–250. [Google Scholar] [CrossRef]
  27. El-Asfoury, M.S.; Abdou, S.M.; Nassef, A. Boosting Thermoelectric-Mechanical Properties of BiSb-Based Material by SiC Nanocomposites. Jom 2021, 73, 2808–2818. [Google Scholar] [CrossRef]
  28. Norizan, M.N.; Ohishi, Y.; Kurosaki, K.; Muta, H. Fabrication and Thermoelectric Property of Bi0.88Sb0.12/InSb Eutectic Alloy by Melt Spinning and Spark Plasma Sintering. Mater. Trans. 2019, 60, 1072–1077. [Google Scholar] [CrossRef]
  29. Zhou, M.; Li, J.; Dong, G.; Gao, S.; Feng, J.; Liu, R. Enhancement of Thermoelectric Performance for InTe by Selective Substitution and Grain Size Modulation. Crystals 2023, 13, 601. [Google Scholar] [CrossRef]
  30. Parashchuk, T.; Sidorenko, N.; Ivantsov, L.; Sorokin, A.; Maksymuk, M.; Dzundza, B.; Dashevsky, Z. Development of a solid-state multi-stage thermoelectric cooler. J. Power Sources 2021, 496, 229821. [Google Scholar] [CrossRef]
  31. Zhang, Y.; Xu, G.; Nozariasbmarz, A.; Li, W.; Raman, L.; Xing, C.; Sharma, S.; Liu, N.; Ghosh, S.; Joshi, G.; Sanghadasa, M.; Shashank, P.; Poudel, B. Thermoelectric Cooling Performance Enhancement in BiSeTe Alloy by Microstructure Modulation via Hot Extrusion. Small Sci. 2024, 4, 2300245. [Google Scholar] [CrossRef]
  32. Yang, J.Y.; Chen, R.G.; Fan, X.A.; Zhu, W.; Bao, S.Q.; Duan, X.K. Microstructure control and thermoelectric properties improvement to n-type bismuth telluride based materials by hot extrusion. J. Alloy Compd. 2007, 429, 156–162. [Google Scholar] [CrossRef]
  33. Im, J.T.; Hartwig, K.T.; Sharp, J. Microstructural refinement of cast p-type Bi2Te3-Sb2Te3 by equal channel angular extrusion. Acta Mater. 2004, 52, 49–55. [Google Scholar] [CrossRef]
  34. Min, B.; Lim, S.S.; Jung, S.J.; Kim, G.; Lee, B.H.; Won, S.O.; Kim, S.K.; Rhyee, J.S.; Kim, J.S.; Baek, S.H. Texture-induced reduction in electrical resistivity of p-type (Bi,Sb)Te by a hot extrusion. J. Alloy Compd. 2018, 764, 261–266. [Google Scholar] [CrossRef]
  35. Lichnowski, A.J.; Saunders, G.A. The elastic constants of bismuth-antimony alloy single crystals. Journal of Physics C: Solid State Physics 1976, 9, 927. [Google Scholar] [CrossRef]
  36. Lotgering, F.K. Topotactical Reactions with Ferrimagnetic Oxides Having Hexagonal Crystal Structures 1. J Inorg Nucl Chem 1959, 9, 113–123. [Google Scholar] [CrossRef]
  37. Jin, H.; Heremans, J.P. Optimization of the figure of merit in Bi100-xSbx/Al2O3 nanocomposites. Phys. Rev. Mater. 2018, 2, 115401. [Google Scholar] [CrossRef]
  38. Zebarjadi, M. Electronic cooling using thermoelectric devices. Appl. Phys. Lett. 2015, 106, 203506. [Google Scholar] [CrossRef]
  39. Chen, Z.; Han, Y.M.; Zhou, M.; Song, C.M.; Huang, R.J.; Zhou, Y.; Li, L.F. Thermoelectric properties of Ge-doped Bi85Sb15 alloys at low temperatures. J. Phys. Chem. Solids 2014, 75, 523–527. [Google Scholar] [CrossRef]
  40. Lukas, K.C.; Joshi, G.; Modic, K.; Ren, Z.F.; Opeil, C.P. Thermoelectric properties of Ho-doped Bi0.88Sb0.12. J. Mater. Sci. 2012, 47. [Google Scholar] [CrossRef]
Preprints 107351 g001
Figure 1. Schematic diagram of hot extrusion, matrices preparation, and the hot extrusion. The right is the extruded samples.
Figure 1. Schematic diagram of hot extrusion, matrices preparation, and the hot extrusion. The right is the extruded samples.
Preprints 107351 g001
Preprints 107351 g002
Figure 2. (a) PXRD patterns and (b) EDS mappings of Ingot-HE and BM-HE samples.
Figure 2. (a) PXRD patterns and (b) EDS mappings of Ingot-HE and BM-HE samples.
Preprints 107351 g002
Preprints 107351 g003
Figure 3. SEM images of the fracture surface for Ingot-HE with (a) Ke = 4:1, (b) Ke = 9:1, (c) BM-HE with Ke = 9:1 around the edge and the middle of the samples.
Figure 3. SEM images of the fracture surface for Ingot-HE with (a) Ke = 4:1, (b) Ke = 9:1, (c) BM-HE with Ke = 9:1 around the edge and the middle of the samples.
Preprints 107351 g003
Preprints 107351 g004
Figure 4. (a) The bending strength of ingot and extruded Bi0.905Sb0.095 samples in comparison with the Bi0.905Sb0.095 single crystal and extrusion Bi0.9Sb0.1 sample [23]. The temperature dependence of anisotropic electrical and thermal conductivity of BM-HE with Ke = 9:1. (b) Electrical conductivity (c) thermal conductivity, (d) the ratio of the electrical and thermal conductivity.
Figure 4. (a) The bending strength of ingot and extruded Bi0.905Sb0.095 samples in comparison with the Bi0.905Sb0.095 single crystal and extrusion Bi0.9Sb0.1 sample [23]. The temperature dependence of anisotropic electrical and thermal conductivity of BM-HE with Ke = 9:1. (b) Electrical conductivity (c) thermal conductivity, (d) the ratio of the electrical and thermal conductivity.
Preprints 107351 g004
Preprints 107351 g005
Figure 5. The temperature dependence of thermoelectric properties of Ingot-HE with Ke = 4:1 and Ke = 9:1, as well BM-HE with Ke = 9:1 in comparison with the reported results of the Bi0.92Sb0.08 single crystal [14] and Bi0.82Sb0.18 hot-deformation sample, [22] extruded Bi0.91Sb0.09 (single crystal as the matrix) [23] and Bi0.85Sb0.15 (polycrystal as the matrix) [26]. (a) Electrical conductivity (b) Seebeck coefficient, (c) power factor, (d) thermal conductivity, (e) effective thermal conductivity (data of commercial Bi2Te3 provided for comparison [16]), (f) figure of merit.
Figure 5. The temperature dependence of thermoelectric properties of Ingot-HE with Ke = 4:1 and Ke = 9:1, as well BM-HE with Ke = 9:1 in comparison with the reported results of the Bi0.92Sb0.08 single crystal [14] and Bi0.82Sb0.18 hot-deformation sample, [22] extruded Bi0.91Sb0.09 (single crystal as the matrix) [23] and Bi0.85Sb0.15 (polycrystal as the matrix) [26]. (a) Electrical conductivity (b) Seebeck coefficient, (c) power factor, (d) thermal conductivity, (e) effective thermal conductivity (data of commercial Bi2Te3 provided for comparison [16]), (f) figure of merit.
Preprints 107351 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated