Prerpints.org logo
Preprint
Article

Eye Tracking Based on Event Camera and Spiking Neural Network

Altmetrics

Downloads

192

Views

85

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

24 May 2024

Posted:

24 May 2024

You are already at the latest version

Alerts
Abstract
The event camera generates an event stream based on changes in brightness, retaining only the characteristics of moving objects, addresses the high power consumption associated with using high-frame-rate cameras for high-speed eye tracking tasks. However, the asynchronous incremental nature of event camera output has not been fully utilized, and there are also issues related to missing event datasets. Combining the temporal information encoding and state-preserving properties of spiking neural network (SNN) with event camera, a near-range eye tracking algorithm is proposed as well as a novel event-based dataset for validation and evaluation. According to experimental results, the proposed solution outperforms artificial neural network (ANN) algorithms, while computational time remains only 12.5\% of that of traditional SNN algorithms. Furthermore, the proposed algorithm allows for self-adjustment of time resolution, with a maximum achievable resolution of 0.081ms, enhancing tracking stability while maintaining accuracy.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

The complex relationship between eye movements and human emotional cognition underscores the role of eye movement behavior as a potential indicator of psychological states [1,2,3]. Researchers and practitioners frequently use eye tracking technology to understand how variations in eye dynamics might reflect different emotional states, such as excitement, focused attention, or stress. Additionally, the application of eye tracking technology in Virtual Reality and Extended Reality (VR/XR) devices further bridges the gap between the virtual and real world [4,5,6]. Eye tracking typically involves gaze tracking, but it is not limited to gaze tracking alone. In fact, pure eye movement tracking which only considered the relative position of eye, can also be applied to various types of research [7,8].
High-speed eye tracking devices and low-power, low-latency algorithms are crucial. Most eye tracking devices use traditional frame-based cameras to capture images, requiring high frame rates to keep up with the rapid and subtle movements of the eye. In fact, most background information during eye movements is redundant, yet traditional cameras capture it in full, increasing bandwidth, memory consumption, and computational burden of subsequent algorithms. This prompts the consideration of novel devices and algorithms to address these issues.
As a rapidly evolving technology, event camera has gained recognition among eye tracking researchers [5,9,10,11]. Compare to traditional cameras that capture images at a fixed frame rate, event camera, also known as Dynamic Vision Sensor (DVS) or neuromorphic camera, detects brightness changes at the pixel level and output events independently. This results in low latency and microsecond-level refresh capabilities. By ignoring a large amount of redundant background data with minor brightness changes, event camera offers advantages in memory consumption and bandwidth over traditional cameras. Thus, they can adjust event density based on the speed of eye movement, utilizing camera bandwidth more effectively. The high temporal resolution, high dynamic range, and lack of motion blur of event camera are well applied in the field of eye tracking [9,10,11,12,13,14].
For example, Angelopoulos et al. [11] constructed a hybrid system for eye gaze tracking using both traditional image frames and event data, achieving an update rate exceeding 10,000 Hz. They developed an eye event data capture model and obtained a substantial amount of effective data. The model parameterized the eye’s image, fitting the pupil and eyelids with ellipses and parabolas, respectively, and refreshes these fitting parameters according to the event capture rate, achieving high frame rate eye tracking results. However, this approach relies on both traditional images and event data, resulting in higher power consumption than processing single event-form data, thus negating the low-power advantage of event cameras. Furthermore, it requires clear and undistorted pupil and eyelid images in the visual field.Stoffregen et al. [12] introduced hardware innovations by adding a ring of encodable LEDs around the event camera lens to generate Coded Differential Lighting. This retains partial specular reflections from the eye while suppressing diffuse reflection events from the surrounding scene. Their approach achieved sub-pixel precision in corneal reflection detection by encoding the flashing frequency of the LEDs. While this method adds complex lighting equipment, it still does not resolve stability issues.
Deep learning has already demonstrated its powerful capabilities in image processing, including object detection and tracking, which is also introduced to event-based eye tracking. Feng et al. [14] proposed a lightweight segmentation network that reduces the input size of the segmentation algorithm by continuously predicting regions of interest (ROIs) through event data. Chen et al. [9] introduced deep learning algorithms using a modified ConvLSTM [15] network structure for predicting the eye’s center point. This approach effectively leverages the temporal cyclic structure of LSTM, capturing the inherent spatio-temporal features in the event stream more effectively. However, both approaches were evaluated using event data generated by simulators, lacking adaptability to real datasets.
However, the asynchronous and temporal nature of event data makes it particularly suited for processing with Spiking Neural Network [16], which are adept at synchronous extraction of spatio-temporal features. SNN has emerged as a branch of deep learning in recent years, building on traditional Artificial Neural Network (ANN) to mimic the behavior of biological neurons. In an SNN, the basic computational unit is spiking neuron, which updates its membrane potential based on previous states and ongoing inputs, emitting a pulse when the potential exceeds a threshold. Unlike the activation functions in ANNs, spiking neurons communicate via binary pulses across network layers.
A key aspect of SNN is the incorporation of temporal processing. Information is encoded in the timing of spike trains, where high-frequency spike sequences can represent higher values and low-frequency spikes represent lower values. This gives SNN the capability to process both spatial and temporal information. Additionally, the retention of membrane potential after each computation grants SNN a degree of memory.These advances make SNN work well with event-based tracking tasks.
The two most common learning methods in SNN are ANN-to-SNN conversion [17] and gradient-based [18] backpropagation with surrogate gradients. In ANN-to-SNN conversion, an ANN is first trained with the ReLU activation function. Then, by replacing ReLU with spiking neurons and adding operations like weight normalization and threshold balancing, the ANN is transformed into an SNN. The backpropagation method employs a concept similar to Backpropagation Through Time (BPTT) [19], computing gradients by unfolding the network over time steps. Due to the non-differentiable nature of the threshold-based spike emission function, a surrogate gradient function is typically used during backpropagation.
SNN has been widely applied in tasks such as object tracking [20,21,22,23], optical flow estimation [24], and video reconstruction [25]. There are also several combinations of event camera and SNN [21,25,26], but exploration in the field of eye tracking is still ongoing.
Due to the nascent stage of event-based eye tracking, a lack of datasets is a significant barrier in the integration of event camera and SNN. Existing studies often use software or event data simulators [27,28,29] to generate event data from traditional images, or they only provide datasets captured with event camera without manual annotation. Both situations make it difficult to assess tracking results.
In light of these issues and challenges, the innovations and contributions are outlined below:
  • A new eye tracking dataset entirely based on real event camera footage is established and manually annotated. The dataset contains a total of 365 screened event point sequences with labels, covering various scenarios like different eyes, lighting conditions, and eye movement trajectories.
  • A novel eye tracking algorithm combining SNN with event camera is designed, better suited to handle the asynchronous incremental output of event camera than ANN, increasing stability while maintaining accuracy.
  • The proposed solution is validated on the custom dataset, achieving a maximum time resolution of approximately 0.081ms and increasing results in tracking accuracy compared to ANNs.

2. Methods

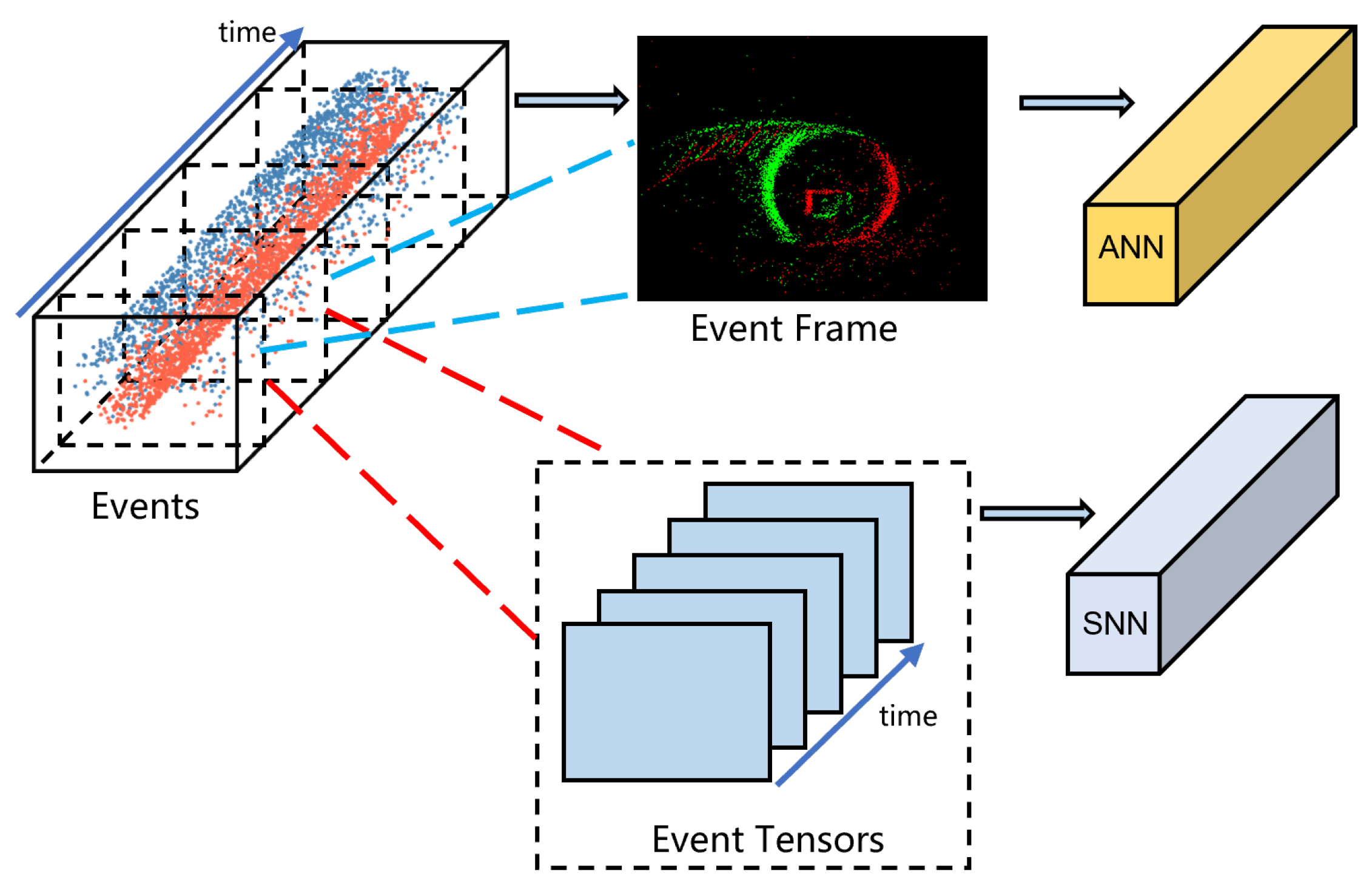
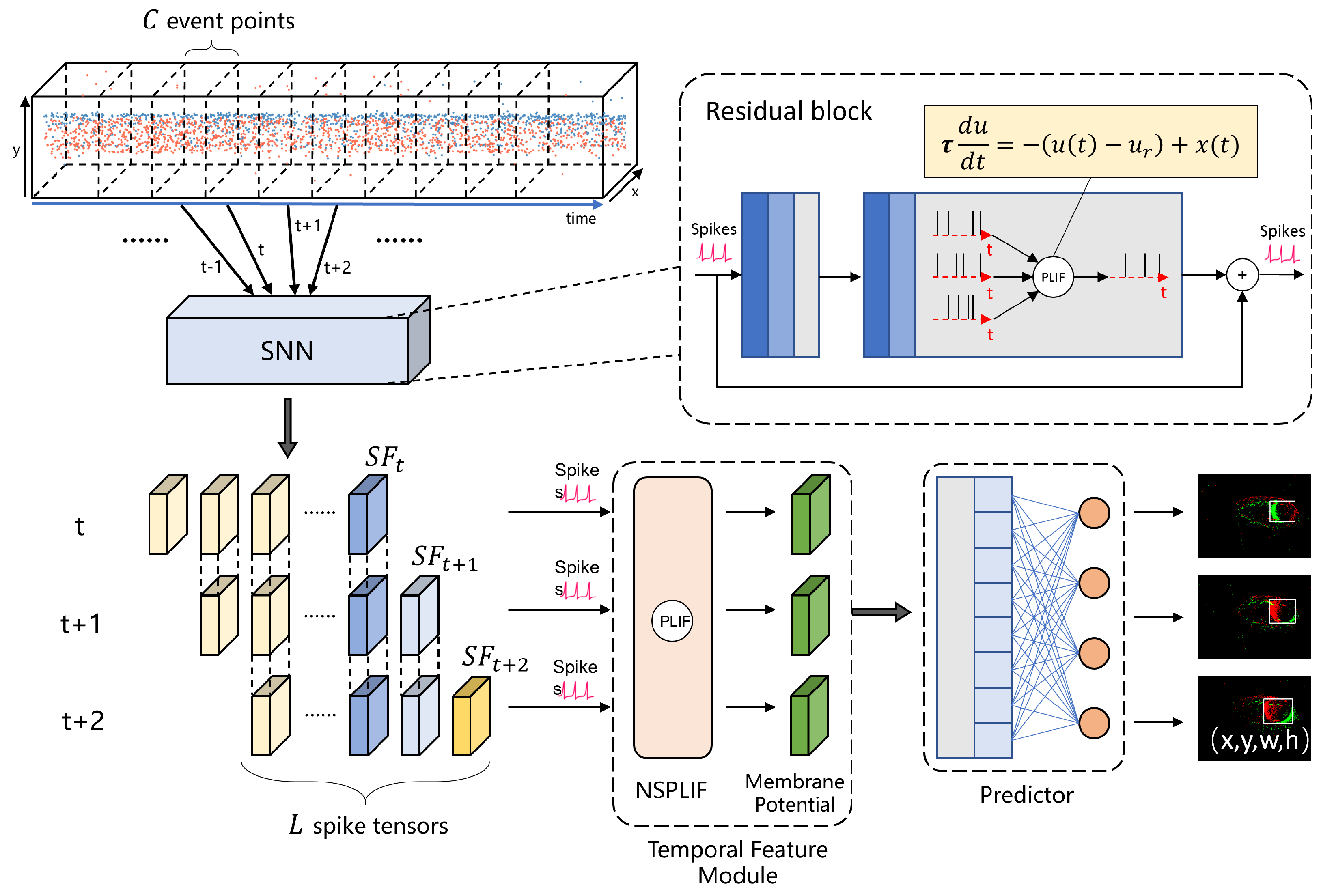
2.1. Event Data Representation

In the SNN, information is encoded in spike trains, with each spiking neuron’s firing frequency carrying certain information. To simulate asynchronous event inputs in a computer, we divide each complete set of event points in the dataset into subsets, each with a fixed number C of points, thereby introducing temporality into the input. Since feature extraction in SNN relies on convolutional layers, we need to represent event points in a tensor format recognizable by these layers. The representation of event tensors is as follows:
E = { e k } k = 1 C = { ( x k , y k , t k , p k ) } k = 1 C ,
E ± ( x , y ) = ∑ e k ∈ E ± δ x − x k , y − y k ,
E ( x , y ) = concat E + , E − ,
Each event point is represented as a quadruple e k , where ( x k , y k ) are the pixel coordinates of the event, t is the time of occurrence, and p k ∈ { − 1 , 1 } represents the polarity, determined by the direction of brightness change. E ± denotes event frames generated according to event polarity, as object motion direction can be indicated by event polarity to some extent. Thus, E ± are connected as different channels to form a 2-channel input event tensor E For each group of input event points.

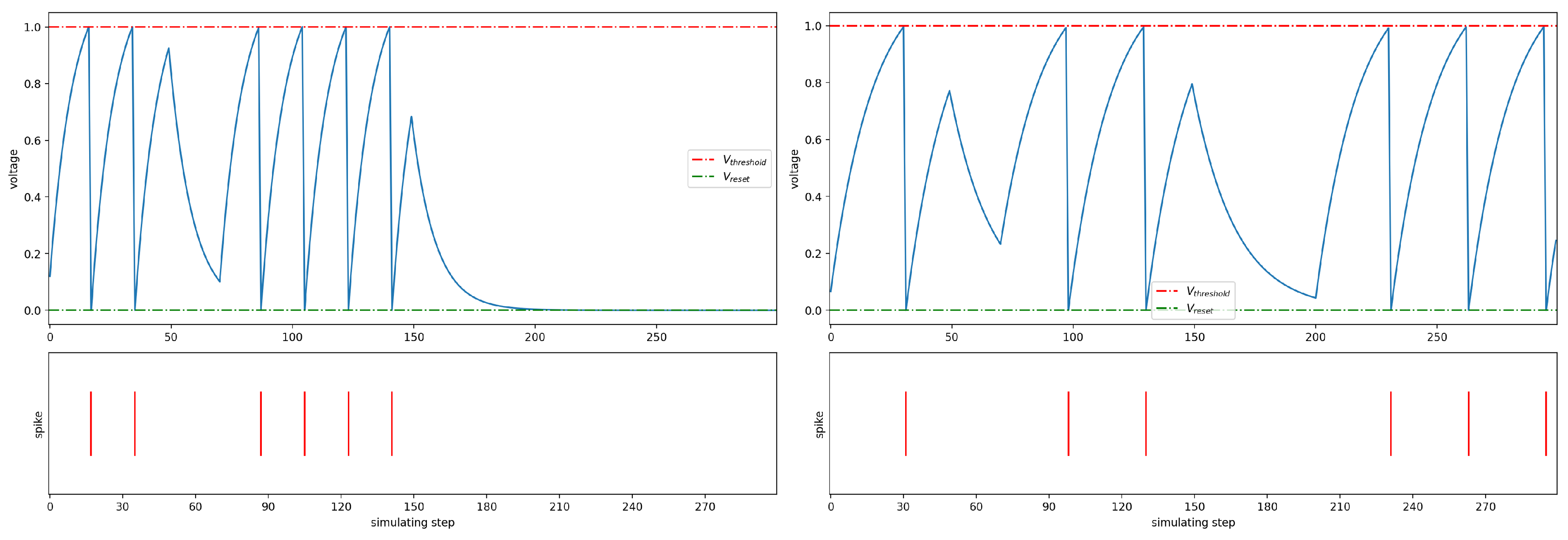
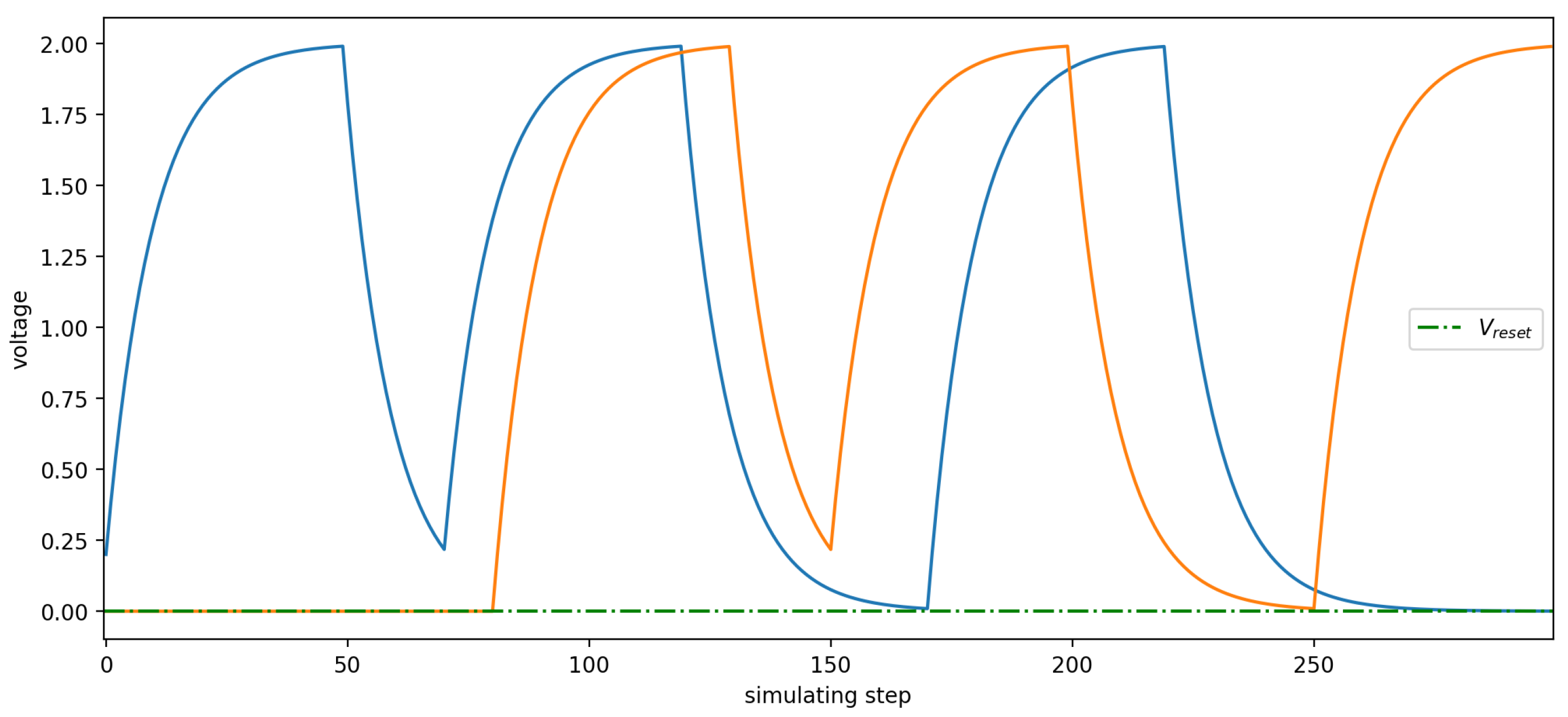
2.2. Eye Tracking Based on Spiking Neuron Network

The tracking method designed in this study consists of an SNN backbone network and a tracker. The backbone network extracts spatial features with temporal information, while the tracker generates tracking results.
SEW ResNet [30] is used as the backbone network. ResNet has shown excellent performance in various image processing fields, and SEW ResNet improves upon it by modifying the residual structure, connecting the input of the residual block to the output of the spiking layer for identity mapping:
O t = S N F S t + S t ,
where S [ t ] represents the spike input from the previous layer, F denotes convolution, pooling operations within the residual block, and SN represents the spiking layer. This adaptation makes SEW ResNet suit complex motion representation of spiking neurons.
A spiking neuron can be describe as follows:
h [ t ] = f ( u [ t − 1 ] + x [ t ] ) ,
o [ t ] = Θ ( h [ t ] − u t h ) ,
u [ t ] = h [ t ] · ( 1 − o [ t ] ) + u r · o [ t ] ,
here, x [ t ] is the input, u [ t ] is the membrane potential, u t h is the emitting threshold and u r is the reset potential. h [ t ] means the hidden state when the neuron is after charging but before emitting. f is the charging equation in which spiking neurons differs. Θ is the Heaviside function. The spiking neuron model uses the Parametric-LIF(PLIF) model [31], with a charging equation f same as the LIF model [32]:
τ d u d t = − u t − u r + x t ,
the difference between PLIF and LIF neuron is that the time constant τ of PLIF is not a preset hyper parameter but is optimized during training. Each layer of spiking neurons shares τ , while different layers have different τ values.
To obtain the firing frequency of spikes over a period, SEW ResNet or other existing SNN structures need to run for several time steps on PC to simulate the charging state of spiking neurons continuously receiving input. The spike output frequency of the neurons over these time steps is then used as the final result. As shown in Figure 1 A commonality with ANN is that the SNN still treats inputs as "frames", with each output of the SNN being independent from the others. Compared to ANNs, each output of a spiking neural network incurs several times the operational cost, which obviously contradicts the initial goal of low power consumption.
Observing the state equations of spiking neurons, one finds that the membrane potential of the spiking neurons is continuously stored internally and changes with each time step’s input. This attribute makes SNN get the ability to remember the current state. When an SNN continuously receives inputs, neurons emit spikes continuously according to the charging equation and the emission threshold, with the spike output result of each time step being related to the state of the previous time step. Therefore, in situations where the SNN continuously receives event inputs, we consider real-time recording of the spike tensor output, but the information contained in the output of a single time step is limited. Accumulating spikes over all time steps to obtain the spike firing frequency would result in the output containing information from too far back, making it difficult to differentiate the tracking target’s position. To address this, we set a record length L, with the network continuously receiving event inputs and recording the spike output S F t (spike tensor) of the backbone network at each time step. The spike feature tensor of the current and the previous L − 1 time steps is averaged over the time dimension to obtain the spike rate tensor S R t for the recent L time steps, which is considered as the feature of the current time step.
S F t x , y ∈ 0 , 1 ,
S R t = 1 L ∑ t − L t S F t ,
As shown in the Figure 2, it depicts the membrane potential changes and output spikes of two different neurons after receiving inputs.
It is evident that the inputs between these two cases differ significantly; however, the differences in the inputs did not result in any change in the output. For both inputs, there were six spikes within 300 time steps, indicating a spike firing rate of 0.02. This suggests that using spike firing rate as a feature loses the relative timing information of each spike emission. For instance, there is a distinct difference in the information contained within sequences where spikes are concentrated in a short period versus those where spikes are uniformly distributed over a longer duration.
To better extract information from spike sequences, it is necessary to consider a module capable of appropriately capturing information from different spike sequences. This module should output a higher value when continuously receiving input and also respond when input ceases. This requirement aligns well with the characteristics of the LIF neuron model. Consequently, we replaces the operation of computing the spike firing rate with a PLIF neuron as well as above. The time constant τ , which influences the neuron’s charging curve, is treated as a learnable parameter that is updated synchronously during network training. This neuron accumulates membrane potential without emitting spikes. After continuously receiving inputs for L time steps (the feature extraction window length of our model structure), the membrane potential in the neuron is extracted as a floating-point number. The final result varies based on the presence or absence of input spikes at different times. For ease of reference, such neurons are named NSPLIF (Non-Spiking PLIF).
As shown in Figure 3, the output differences exhibited by the NSPLIF under various input conditions are clearly demonstrated. By shifting the input along the time axis, the figure displays two membrane potential change curves. When the neuron continuously receives inputs, its membrane potential experiences a rapid rise followed by a gradual stabilization; when the input ceases, the membrane potential decreases gradually due to the effect of leak voltage until the arrival of the next input. This process enables the NSPLIF to effectively extract temporal information hidden at different moments from the input spikes, thereby providing a more precise basis for the final output. Additionally, it is worth mentioning that the NSPLIF model can be derived by making appropriate modifications to the PLIF model. This feature allows the entire neural network to utilize a single type of neuron model, thus ensuring structural uniformity and consistency within the network.
Eye tracking tasks can be viewed as single-object tracking, and thanks to event camera not including redundant background information in its inputs, bounding box regression is handled by a fully connected layer. S R t is passed through a pooling layer and then unrolled before being input to the fully connected layer, ultimately yielding the tracking result for the current time step.The whole structure of the algorithm is shown in Figure 4.
The algorithm network requires a warm-up period initially, as the first update result must wait for the network to run for L − 1 time steps; from the Lth time step onward, the tracking result can be updated at each time step, with each regression containing information from the previous L − 1 time steps. This enables the network to self-recover tracking when the target disappears and reappears.
In situations where there is a high similarity between successive frames in eye tracking, the memory advantage of SNN becomes evident. Common algorithms for eye tracking tasks fall into two categories: one based on object detection, independently computing each time an image frame is input, with the advantage being independent prediction, allowing for continued recognition when the target reappears after being lost; the other, OPE tracking algorithms [33,36], fundamentally rely on similarity matching between frames, which is challenging for re-tracking lost targets. The SNN-based tracking structure proposed in this study combines the advantages of both, reasonably utilizing prior information for predicting the target’s position and enabling the re-acquisition of the target without external information even after the tracking target is lost.

3. Dataset

3.1. Device Setup

To acquire near-range eye movement data, we designed a setup with a camera bracket, headrest, and an opaque black box as shown in Figure 5. The top of the black box is detachable to simulate low-light and natural lighting conditions. We also prepared a fixed light source that can be placed in different corners of the box to simulate various lighting directions. The event camera used for data collection is DAVIS346 from iniVation, with a standard resolution of 346×260 pixels. The camera is placed on the top layer of the camera bracket, about 10cm from the eye, with the ability to deploy event cameras on either side (monocular data is recorded in the dataset since eyes are symmetric). Each recording session lasted approximately 15-20 seconds. We did not instruct participants to track specific points on the screen; instead, we preferred free eye movements to collect natural data. This included saccades, consistent smooth pursuits horizontally or vertically, and transient fixations. Blink data is not excluded. Four individuals with different eye shapes participated, and conditions with or without glasses were considered. A total of 91 eye movement video sequences were recorded. Table 1 shows the number of event sequences under different conditions. Internal light source came from a lamp tube which can put in the box. Note that natural light and internal light sources may coexist.

3.2. Preprocessing

To facilitate manual annotation, the event data needs to be converted into event frames. Given the impracticality of annotating data at microsecond-level time resolutions, the event data is grouped to ensure each group has a sufficient number of event points to form a recognizable event image. Notably, we group by fixed point count rather than time intervals. Following Equations (1) and (), we generate the event tensors E ± x , y .
F ± = Θ ( E ± ) ,
here, Θ represents the Heaviside step function. F ± serve as the first two channels of the event image, with the third channel completed with zeros, giving the event image F a shape of ( 3 × 260 × 346 ) . Setting C to 4000, we compared the time span between the first and last event points in each frame with the labeled x-y coordinate trajectories in Figure 6. During smooth eye movements, the time required to produce 4000 events was consistent, averaging about 25ms (excluding overhigh values). However, when the eye changed direction, the time to produce the same number of events significantly increased, aligning with the working principle of event camera. Grouping by fixed point count ensures consistency in image distribution, aiding feature extraction by convolutional networks. It also reduces the number of frames generated in situations with reduced event rates, like when the eye moves to the corner or fixates, thus lowering subsequent computational power consumption.

3.3. Labeling

After preprocessing, the event frames underwent manual selection and annotation, with eye regions enclosed in bounding boxes. As shown in Figure 7, the blue boxes represent the annotated bounding boxes. We observed that the pupils and iris of Asians are similar in color, making it difficult to distinguish the boundaries of the pupils in low light conditions. In contrast, the boundaries of the iris are clearer. To ensure the accuracy of annotation, we chose to use bounding boxes to annotate the visible iris region. The bounding boxes contain both position and size information, which can effectively express the different shapes of the iris during movement. Our dataset, composed entirely of event data, opts for bounding box annotation, balancing accuracy and efficiency. Figure 7 shows some labeled data.
For the sake of training, the 91 original sequences in the dataset were segmented into a total of 365 shorter sequences, each containing around 100 labels, and all event points within them occur continuously.
Among the total 91 sequences and 39,572 labeled event frames, the shortest time span between frames is only 0.648ms, with a movement of approximately 8.32 pixels compared to the previous frame. The longest time span between frames is 1278ms, with a movement of about 10 pixels compared to the previous frame. Clearly, grouping events by a fixed number of points can adapt to changes in eye movement speed.

4. Experiments and Results

4.1. Training Setup

The whole experiment is based on PyTorch, while the training framework for SNN uses SpikingJelly [34], also based on PyTorch. All model training and testing were conducted on an NVIDIA GeForce RTX 3090 GPU. The dataset’s 365 sequences were divided into 296 training sequences and 69 testing sequences, with no overlap between the two.
SNN training employed the BPTT scheme, with the surrogate gradient function set to the a r c t a n function. Following the dataset processing method in section 3.2, event sets generated after dividing by the fixed point number 4000 were further divided into time steps. To align training time steps with the record length L mentioned in the method, we stipulated:
C ∗ L = 4000 ,
we used the Adam Optimizer with a learning rate of 0.005 for a total of 50 training epochs. For ANN, the comparison model was trained on the MMtracking [35] platform using the single-object tracking network siamrpn [36], also with a ResNet backbone.

4.2. Evaluation Metrics

Since our labels are in the form of bounding boxes, we base our tracking results’ evaluation metrics on the Intersection over Union (IoU) and the Precision Error (PE) between the predicted and actual bounding boxes:
I o U = P ∩ G P ∪ G ,
P E = x P − x G 2 + y P − y G 2
Here, x P , y P and ( x G , y G ) represent the center coordinates of the predicted and actual bounding boxes, respectively.
Given our dataset’s fixed interval annotations, not every prediction made by our SNN tracking algorithm corresponds to a manual label. Hence, we employ linear interpolation for unlabeled frames, as eye movements in short intervals can be approximated as uniformly linear. For ANN, inputs are adapted to overlapped frames generated from the total data of L time steps involved in each SNN operation, and evaluations are performed using such method.

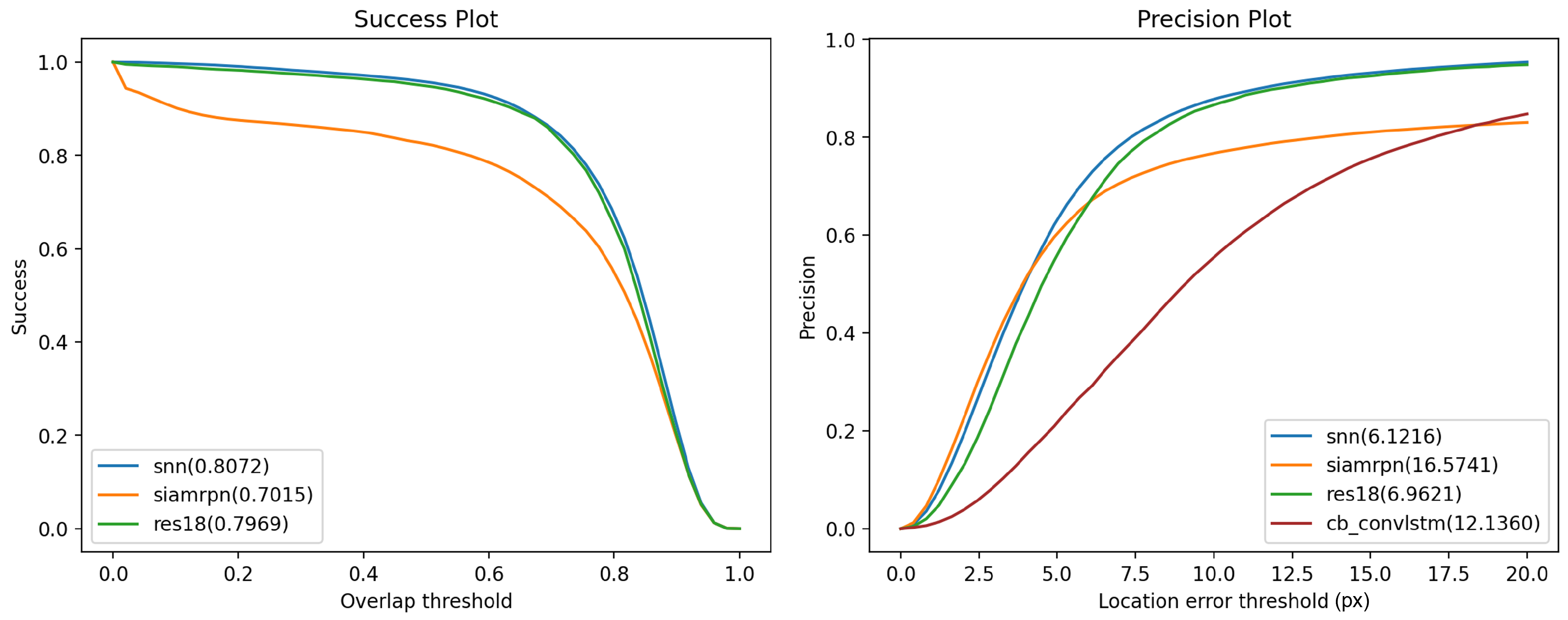
4.3. Performance

The test set comprises 69 independent eye movement data sequences. Both our proposed algorithm and the comparison ANN algorithm are applied to each sequence, calculating the average IoU and PE for each sequence. With C set to 500 and L to 8, our algorithm achieves an highest average IoU of 0.8072. As shown in Figure 8, compared to other ANN algorithms, our SNN performs better in terms of success rate and accuracy. Note that the cb-convlstm scheme directly predicts the center points of the detection boxes, so only precision error is calculated.
Table 2. Comparison Results.
Table 2. Comparison Results.
Network Average IoU↑ Average PE↓
SiamRPN 0.7015 16.5741
CB-ConvLSTM [9] - 12.1360
ResNet18 0.7969 6.9621
SNN(ours) 0.8072 6.1216
Figure 9 shows a part of the test results, where (a) represents the tracking results of the ANN algorithm, (b) represents the tracking results of our SNN algorithm, and (c) compares the IoU of the tracking results of both algorithms for this sequence. As can be seen from the figure, the ANN algorithm loses track at a certain moment, but our algorithm’s tracking results are relatively stable. After a period, our algorithm can re-acquire the target, whereas the ANN cannot continue tracking. This also proves that the proposed SNN algorithm has decent re-tracking performance.
To better verify the re-tracking performance of our algorithm, we selected 20%, 30%, and 40% of consecutive event points in each sequence and transformed them into pure 0 values to simulate situations where no events are generated at all. The algorithm’s tracking results are shown in the Table 3, including predictions with and without excluding the aforementioned 0 value outputs. Obviously, these 0 values have a minor impact on the prediction results of other event points.
Next, we analyze the performance and power consumption of our algorithm. The methodology in this paper can be divided into two parts: data acquisition with event camera and algorithmic processing with Spiking Neural Network. For high-speed eye tracking tasks, traditional cameras inevitably rely on high frame rate outputs to discern subtle movements of the eye. Taking a resolution of 346×260 as an example, a single frame of RGB color image output by a traditional camera occupies about 100KB in a computer. Assuming a frame rate of 300fps, the total data of 1500 frames over 5 seconds would occupy about 150MB. In contrast, for an event camera with the same resolution, about 742,000 event points are generated in 5 seconds in the dataset proposed in this paper. Each event point is stored as a quadruple, occupying only 9MB in total, saving about 94% compared to RGB images. For RGB images produced by traditional cameras, all pixel information is retained during data transmission, regardless of its relevance. Event camera, however, only records changes when a certain pixel brightness changes, which is clearly more resource-efficient for tracking tasks focused on the position of dynamic objects.
SNN is more energy-efficient than ANN primarily because it operates on an event-driven mechanism, meaning computations and signal transmissions only occur when a spike is received. This significantly reduces unnecessary computations and data transmissions. Additionally, SNN exhibits sparse activation, with neurons firing only when their membrane potential crosses a threshold, leading to fewer overall activations. Unlike ANN, which updates neurons at every computational cycle, SNN remains in a quiescent state without consuming energy in the absence of spikes. Moreover, neuromorphic hardware is optimized for the event-driven, sparse operations of SNN, further enhancing their energy efficiency.
Due to the inability to process asynchronous inputs on PC and graphics card hardware, the effect of SNN can only be simulated through multiple incremental inputs, using several time steps to mimic asynchronous input. Common algorithms using SNN for visual tasks treat each input as independent and subdivide time steps within each input to simulate the temporal input of SNN. This approach significantly increases the computational consumption of SNN, as each output of an SNN requires several network cycles to be obtained, equating to a time cost several times that of an ANN with the same structure. Our algorithm, however, reasonably utilizes the prior states and temporally-encoded outputs stored in the network from past time steps. A single time step’s input can produce an output, thereby saving the need for seven forward passes, significantly enhancing computational speed, reducing time loss, and only amounting to 12.5% of the previous cost (if C is set to 8).

4.4. Ablation Study

We conducted ablation experiments for different fixed point numbers C and time steps L shown in Table 4. Besides the value of 8 mentioned above, we also chose values of 2, 4, 5, 10, and 16, with corresponding partition point numbers of 2000, 1000, 800, 400, and 250, respectively.
The results demonstrate that a larger C provides more spatial information in each event image, but the short time step makes it difficult to encode enough information in spike trains. Conversely, a smaller C reduces spatial information but enhances information contained in spike trains, further improving tracking performance. Clearly, the choice of C and L plays a critical role in SNN performance. The best results in our experiment were obtained with C = 500 and L = 8 .
Indeed, the temporal resolution of the network varies with different values of L. As mentioned in section 3.2, the dataset used in this paper generates 4000 event points approximately every 25ms. When L is set to 8, the temporal resolution of the algorithm is 25/8 = 3.125ms. Although there is a slight decrease in tracking accuracy when L is at its maximum value of 16, the temporal resolution of the algorithm improves to 25/16 = 1.5625ms. However, this is not the limit of the event camera. We have statistically analyzed the event generation rate in the dataset, where the shortest time taken to generate 4000 event points is 0.648ms. This means when L = 8 , the time resolution can reach 0.648/8=0.081 ms, which exceeds 10kHz.
We also considered an extreme case of C=4000, L=1. In this scenario, the feature sequence length output by snn backbone is only 1. The average IoU in this case drops to 0.6546, indicating a decrease in tracking accuracy without temporal encoding, emphasizing the memory effect of SNN in this task.
Experiments also demonstrated the importance of NSPLIF in extracting temporal information. Compared to obtaining spike firing rates, the membrane potential from NSPLIF clearly better expresses features, leading to improved results for subsequent predictors.

5. Conclusion

This study explored a new eye tracking algorithm based on event camera and Spiking Neural Network, addressing limitations in traditional camera and algorithm. The algorithm effectively merges the strengths of both technologies, combining the temporal continuity of event data with the memory properties of SNN. Experiments demonstrate improvements in tracking accuracy, stability, and significant reductions in system power consumption and complexity. However, SNN exhibits its low-power characteristics more effectively on neuromorphic chips. Future research could focus on deployment on actual hardware, designing a fully independent eye tracking system.

Author Contributions

Conceptualization, Y.J. and L.Y.; methodology, Y.J.; software, Y.J.; validation, L.Y., W.W. and C.H.; formal analysis, Y.J.; writing—original draft preparation, Y.J; writing—review and editing, Y.J., L.Y. and C.H.; visualization, W.W.; supervision, L.Y and W.W.; funding acquisition, L.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China grant number 62271354.

Data Availability Statement

The dataset will be available later.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Poletti B, Solca F, Carelli L, et al. Association of Clinically Evident Eye Movement Abnormalities With Motor and Cognitive Features in Patients With Motor Neuron Disorders. Neurology, 2021, 97, e1835–e1846. [Google Scholar]
  2. Diao Y, Geng M, Fu Y, et al. A combination of P300 and eye movement data improves the accuracy of auxiliary diagnoses of depression. Journal of Affective Disorders, 2022, 297, 386–395. [Google Scholar] [CrossRef] [PubMed]
  3. Covers M L V, De Jongh A, Huntjens R J C, et al. Early intervention with eye movement desensitization and reprocessing (EMDR) therapy to reduce the severity of post-traumatic stress symptoms in recent rape victims: a randomized controlled trial. European Journal of Psychotraumatology, 2021, 12, 1943188. [Google Scholar] [CrossRef] [PubMed]
  4. Adhanom I B, MacNeilage P, Folmer E. Eye Tracking in Virtual Reality: a Broad Review of Applications and Challenges. Virtual Reality, 2023, 27, 1481–1505. [Google Scholar] [CrossRef] [PubMed]
  5. Li N, Bhat A, Raychowdhury A. E-Track: Eye Tracking with Event Camera for Extended Reality (XR) Applications. In Proceedings of the 2023 IEEE 5th International Conference on Artificial Intelligence Circuits and Systems (AICAS), 2023; pp. 1-5.
  6. Plopski A, Hirzle T, Norouzi N, et al. The Eye in Extended Reality: A Survey on Gaze Interaction and Eye Tracking in Head-worn Extended Reality. ACM Computing Surveys, 2022, 55, 53:1–53:39. [Google Scholar]
  7. Google Research. MediaPipe Iris: Real-time iris tracking and depth estimation. Retrieved from https://research.google/blog/mediapipe-iris-real-time-iris-tracking-depth-estimation/.
  8. Qiu H, Li Z, Yang Y, Xin C, and Bian G. Real-Time Iris Tracking Using Deep Regression Networks for Robotic Ophthalmic Surgery. IEEE Access 2020, 8, 50648–50658. [Google Scholar] [CrossRef]
  9. Chen Q, Wang Z, Liu S C, et al. 3ET: Efficient Event-based Eye Tracking using a Change-Based ConvLSTM Network. arXiv 2023. [Google Scholar]
  10. Zhao G, Yang Y, Liu J, et al. EV-Eye: Rethinking High-frequency Eye Tracking through the Lenses of Event Cameras. Advances in Neural Information Processing Systems 2023, 36, 62169–62182. [Google Scholar]
  11. Angelopoulos A N, Martel J N P, Kohli A P, et al. Event-Based Near-Eye Gaze Tracking Beyond 10,000 Hz. IEEE Transactions on Visualization and Computer Graphics, 2021, 27, 2577–2586. [Google Scholar] [CrossRef] [PubMed]
  12. Stoffregen T, Daraei H, Robinson C, et al. Event-Based Kilohertz Eye Tracking using Coded Differential Lighting. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, IEEE, 2022; pp. 3937-3945.
  13. Kagemoto T, Takemura K. Event-Based Pupil Tracking Using Bright and Dark Pupil Effect. In Proceedings of the 36th Annual ACM Symposium on User Interface Software and Technology, New York, NY, USA, Association for Computing Machinery, 2023; pp. 1-3.
  14. Feng Y, Goulding-Hotta N, Khan A, et al. Real-Time Gaze Tracking with Event-Driven Eye Segmentation. In Proceedings of the 2022 IEEE Conference on Virtual Reality and 3D User Interfaces (VR), 2022; pp. 399-408.
  15. SHI X, Chen Z, Wang H, et al. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. In Advances in Neural Information Processing Systems: Vol. 28, Curran Associates, Inc., 2015.
  16. Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Networks, 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
  17. Cao Y, Chen Y, Khosla D. Spiking Deep Convolutional Neural Networks for Energy-Efficient Object Recognition. International Journal of Computer Vision, 2015, 113, 54–66. [Google Scholar] [CrossRef]
  18. Neftci E O, Mostafa H, Zenke F. Surrogate Gradient Learning in Spiking Neural Networks: Bringing the Power of Gradient-Based Optimization to Spiking Neural Networks. IEEE Signal Processing Magazine, 2019, 36, 51–63. [Google Scholar] [CrossRef]
  19. Lee J H, Delbruck T, Pfeiffer M. Training Deep Spiking Neural Networks Using Backpropagation. Frontiers in Neuroscience, 2016, 10. [Google Scholar]
  20. Zheng Y, Yu Z, Wang S, et al. Spike-Based Motion Estimation for Object Tracking Through Bio-Inspired Unsupervised Learning. IEEE Transactions on Image Processing, 2023, 32, 335–349. [Google Scholar] [CrossRef] [PubMed]
  21. Ji M, Wang Z, Yan R, et al. SCTN: Event-based object tracking with energy-efficient deep convolutional spiking neural networks. Frontiers in Neuroscience, 2023, 17. [Google Scholar]
  22. Luo Y, Xu M, Yuan C, et al. SiamSNN: Siamese Spiking Neural Networks for Energy-Efficient Object Tracking. In Artificial Neural Networks and Machine Learning – ICANN 2021, Cham: Springer International Publishing, 2021; pp. 182-194.
  23. Yang Z, Wu Y, Wang G, et al. DashNet: A Hybrid Artificial and Spiking Neural Network for High-speed Object Tracking. arXiv 2019. [Google Scholar]
  24. Hagenaars J, Paredes-Valles F, de Croon G. Self-Supervised Learning of Event-Based Optical Flow with Spiking Neural Networks. In Advances in Neural Information Processing Systems: Vol. 34, Curran Associates, Inc., 2021; pp. 7167-7179.
  25. Zhu L, Wang X, Chang Y, et al. Event-based Video Reconstruction via Potential-assisted Spiking Neural Network. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, IEEE, 2022; pp. 3584-3594.
  26. Zhang J, Dong B, Zhang H, et al. Spiking Transformers for Event-based Single Object Tracking. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, IEEE, 2022; pp. 8791-8800.
  27. Hu Y, Liu S C, Delbruck T. v2e: From Video Frames to Realistic DVS Events. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, 2021; pp. 1312-1321.
  28. Gehrig D, Gehrig M, Hidalgo-Carrio J, et al. Video to Events: Recycling Video Datasets for Event Cameras. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, IEEE, 2020; pp. 3583-3592.
  29. Rebecq H, Gehrig D, Scaramuzza D. ESIM: an Open Event Camera Simulator. In Proceedings of The 2nd Conference on Robot Learning, PMLR, 2018; pp. 969-982.
  30. Fang W, Yu Z, Chen Y, et al. Deep Residual Learning in Spiking Neural Networks. In Advances in Neural Information Processing Systems: Vol. 34, Curran Associates, Inc., 2021; pp. 21056-21069.
  31. Fang W, Yu Z, Chen Y, et al. Incorporating Learnable Membrane Time Constant to Enhance Learning of Spiking Neural Networks. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, IEEE, 2021; pp. 2641-2651.
  32. Brunel N, Latham P E. Firing Rate of the Noisy Quadratic Integrate-and-Fire Neuron. Neural Computation, 2003, 15, 2281–2306. [Google Scholar] [CrossRef] [PubMed]
  33. Xu Y, Wang Z, Li Z, Yuan Y, and Yu G. SiamFC++: Towards Robust and Accurate Visual Tracking with Target Estimation Guidelines. In Proceedings of the AAAI Conference on Artificial Intelligence 34, no. 0707 (2020): 12549–12556.
  34. Fang W, Chen Y, Ding J, et al. SpikingJelly: An open-source machine learning infrastructure platform for spike-based intelligence. Science Advances, 2023, 9, eadi1480. [Google Scholar] [CrossRef] [PubMed]
  35. MMTracking Contributors. MMTracking: OpenMMLab video perception toolbox and benchmark. Available online: https://github.com/open-mmlab/mmtracking, 2020.
  36. Li B, Yan J, Wu W, et al. High Performance Visual Tracking with Siamese Region Proposal Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, IEEE, 2018; pp. 8971-8980.
Preprints 107361 g001
Figure 1. Comparison with ANN and SNN when processing events
Figure 1. Comparison with ANN and SNN when processing events
Preprints 107361 g001
Preprints 107361 g002
Figure 2. Membrane potential changes and output spikes of two different neurons
Figure 2. Membrane potential changes and output spikes of two different neurons
Preprints 107361 g002
Preprints 107361 g003
Figure 3. Membran potential changes of NSPLIF
Figure 3. Membran potential changes of NSPLIF
Preprints 107361 g003
Preprints 107361 g004
Figure 4. Event-SNN eye tracking model
Figure 4. Event-SNN eye tracking model
Preprints 107361 g004
Preprints 107361 g005
Figure 5. Equipment for capturing event data
Figure 5. Equipment for capturing event data
Preprints 107361 g005
Preprints 107361 g006
Figure 6. Comparison figure of time required to generate fixed event points and eye movement
Figure 6. Comparison figure of time required to generate fixed event points and eye movement
Preprints 107361 g006
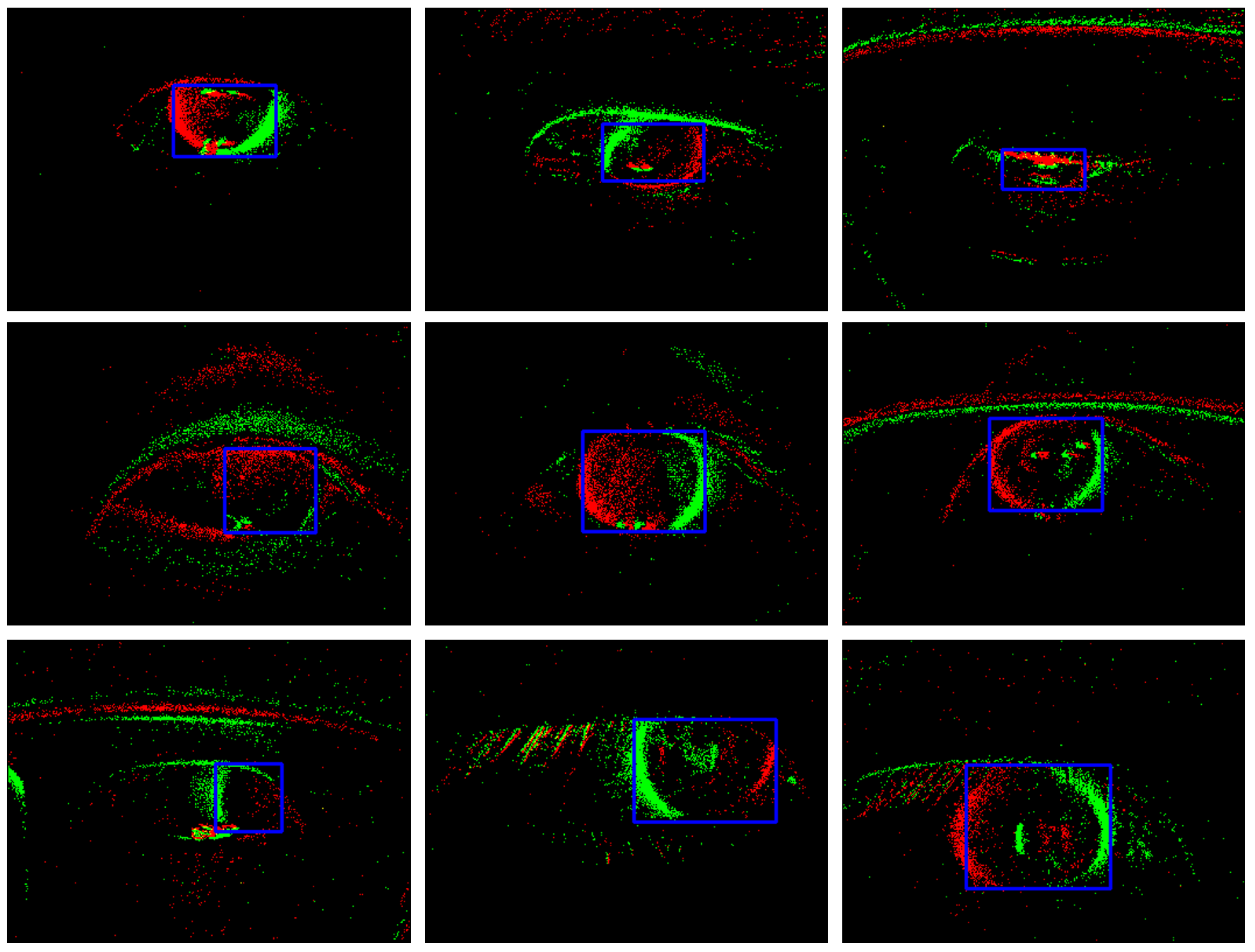
Preprints 107361 g007
Figure 7. Labeled eye data in different sequences
Figure 7. Labeled eye data in different sequences
Preprints 107361 g007
Preprints 107361 g008
Figure 8. Success Plot and Precision Plot of results
Figure 8. Success Plot and Precision Plot of results
Preprints 107361 g008
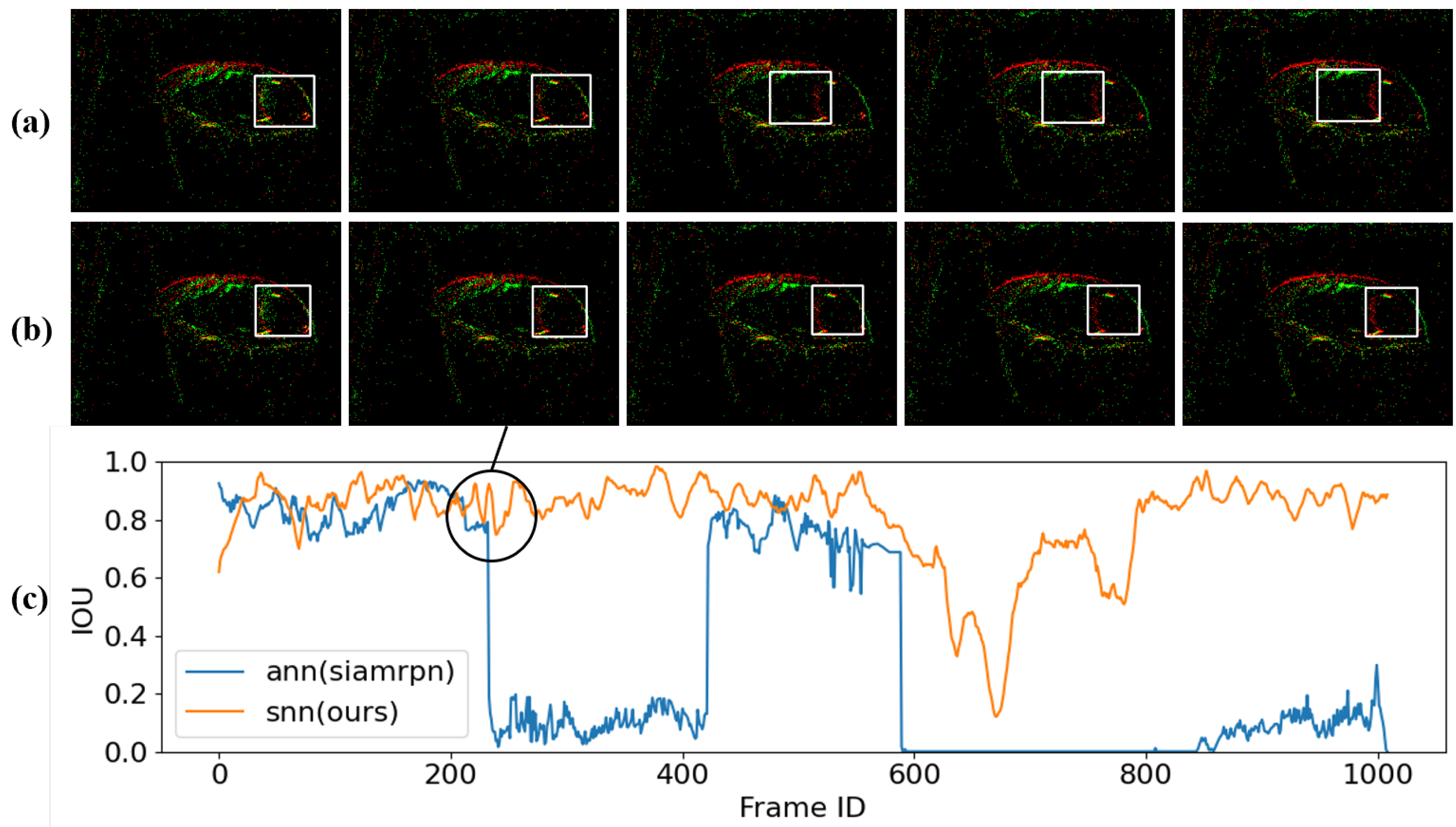
Preprints 107361 g009
Figure 9. Comparison of re-tracking performance
Figure 9. Comparison of re-tracking performance
Preprints 107361 g009
Table 1. Number of event sequences under different conditions..
Table 1. Number of event sequences under different conditions..
Condition Number
wearing glasses 22
low light 29
natural light 48
internal light 26
Table 3. Re-tracking performance.
Table 3. Re-tracking performance.
zero value percentage Average IoU (without zero value) Average IoU
20% 0.7996 0.7676
30% 0.7915 0.6838
40% 0.7892 0.6406
Table 4. Results with different C/Ls. and Temporal Feature Modules
Table 4. Results with different C/Ls. and Temporal Feature Modules
Temporal Feature Module C/L Average IoU↑ Average PE↓
NSPLIF 4000/1 0.6546 12.6459
2000/2 0.7727 7.9599
1000/4 0.7980 6.7475
800/5 0.7992 6.5223
500/8 0.8072 6.1216
400/10 0.7893 7.5871
250/16 0.7739 7.7990
Spiking Rate 4000/1 0.7095 10.7267
2000/2 0.7121 10.2529
1000/4 0.7382 9.0034
800/5 0.7197 10.1972
500/8 0.7595 8.2062
400/10 0.7512 9.1113
250/16 0.7348 9.2386
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated