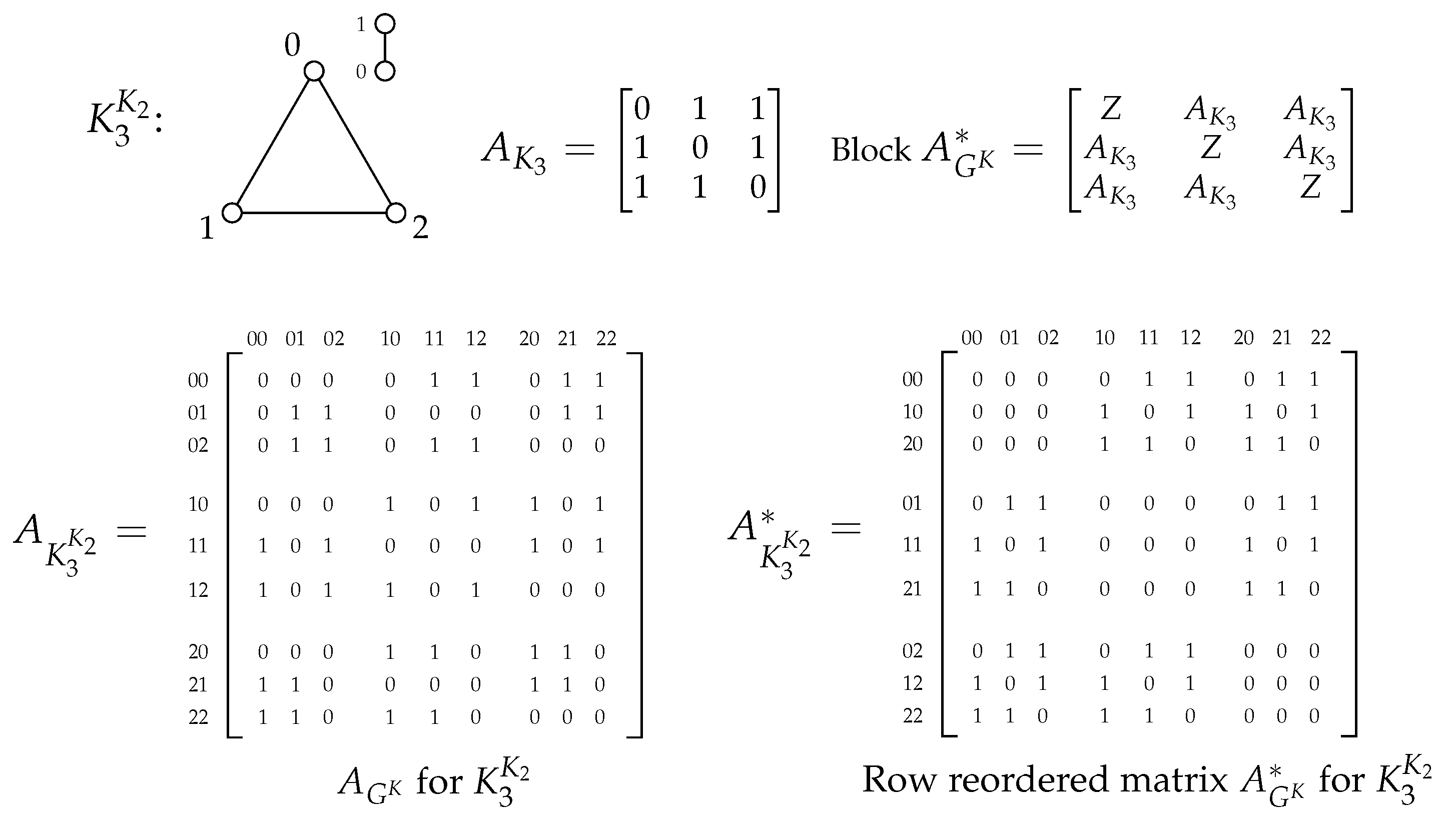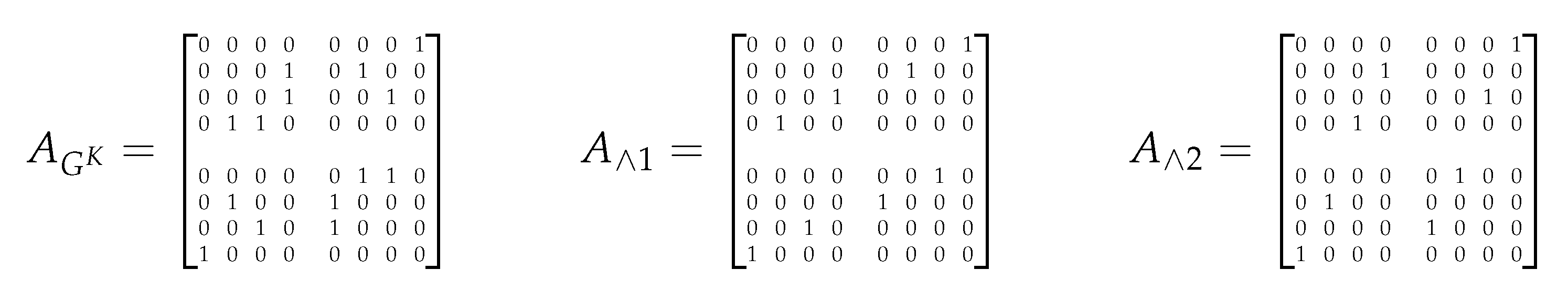Adjacency Matrix for the Graph Exponential

Preprint

Article

Adjacency Matrix for the Graph Exponential

Altmetrics

Downloads

Views

Comments

Melissa Holly^*

This version is not peer-reviewed

Submitted:

24 May 2024

Posted:

27 May 2024

You are already at the latest version

Alerts

Abstract

Introduced in 1967 by Lov\'{a}sz, graph exponentiation has received little attention over the past several decades. Since graph exponentiation produces large graphs and any graph can be constructed utilizing its adjacency matrix, we provide a four step linear construction algorithm that generates the adjacency matrix for the graph exponential.

Keywords:

Subject: Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction

As graphs are relational structures, graph exponentiation and the graph exponential

G^{K}

were introduced by Lovász in 1967 [6]. Although Lovász develops

G^{K}

based on its relationship to the direct product, he mentions that

G^{K}

is interesting in its own right and provides several properties of

G^{K}

. Over the past several decades, the

G^{K}

product has received very little attention. Any graph can be constructed using its adjacency matrix; and large graphs are generated by

G^{K}

. Proposition 4.1 states the construction of the

G^{K}

adjacency matrix when K is

K_{2}

. This proposition demonstrates the recognized connection of

G^{K}

to the direct power of G; and Proposition 4.1 is utilized in the proof of Theorem 4.3 that gives the adjacency matrix for a general K. In Figure 3 we provide a four step linear construction algorithm for the adjacency matrix of the general

G^{K}

Section 2 discusses notation plus fundamental information on the discussed matrices and on the direct product. As there exists an alternative definition of

G^{K}

, Section 3 gives detailed information concerning the form of

G^{K}

used in this note. In Section 4, we provide the construction of the adjacency matrix for

G^{K}

in the form of a construction algorithm, provide a detailed example plus give the general theorem.

2. Background

Only finite undirected graphs are considered. Basic graph theory knowledge as found in [1] is assumed. The vertex set of graph G is denoted by

V (G)

while

E (G)

indicates the edge set. It is assumed that all graphs have the same vertex labeling scheme of

{0, 1, 2, \dots, n - 1}

where n is graph order. Graph order is also indicated with

| G |

. For any vertex

v \in V (G)

N (v)

reflects the open neighborhood of v, and

N [v]

is used for the closed neighborhood. Vertex adjacency is given by

v_{1} \sim v_{2}

, two graphs being isomorphic is

G ≅ H

, and

G + H

is used for the disjoint union of G and H. For

x \in N

x G

represents x copies of G. The automorphism group of G is

Aut (G)

Complete graphs are given as

K_{n}

and complete graphs with a loop at each vertex are

K_{n}^{*}

. Notation

D_{n}

is the disjoint union of n number of

K_{1}

subgraphs and is called the empty graph. The null graph

O

has empty vertex and edge sets. Let

| S |

be the order of set S.

2.1. Matrices

In this paper, loops in an adjacency matrix are 1s along the diagonal. As will be shown, the direct product

G \times H

(or more specifically the direct power

G^{x}

) has connections to

G^{K}

as seen in the adjacency matrices of both products. Let the adjacency matrix of graph G be

A_{G}

. Denoted

A_{G \times H}

, the adjacency matrix for the direct product (

A_{G^{x}}

is the adjacency matrix for the direct power) is the Kronecker product

A_{G \times H} = A_{G} \otimes A_{H}

. The adjacency matrix for

G^{K}

is given by

A_{G^{K}}

and is discussed in Section 4. Denote the square all zero matrix as Z while J is the square matrix of all ones. Matrix multiplication is given by

A_{G} * A_{H}

2.2. Direct Product

The direct product

G \times H

has vertex set that is the Cartesian product

V (G) \times V (H)

producing ordered pair vertices

(g, h)

where

g \in V (G)

and

h \in V (H)

. An edge

(g, h) (g^{'}, h^{'})

E (G \times H)

is defined when

(g, g^{'}) \in E (G)

and

(h, h^{'}) \in E (H)

. The direct power

G^{x}

is the direct product of G to itself x number of times. Additional information on the direct product can be found in [3].

3. Graph Exponentiation Overview

As there exist multiple definitions for graph exponentiation (see [5] Figure 1 for an alternate definition), we clearly explain our interpretation of this graph product (also see [2,4,6,7]).

Graph exponentiation is a graph product operation where the vertex set of the graph exponential

G^{K}

is the set of all functions

f : V (K) \to V (G)

where two functions

f_{1}

and

f_{2}

are adjacent in

G^{K}

(f_{1} (k) f_{2} (k^{'})) \in E (G)

for all

(k, k^{'}) \in E (K)

. Thus

| V (G^{K}) |

{| G |}^{| K |}

. Since only undirected G and K are considered, all functions are symmetric and

G^{K}

is undirected as shown in [7].

Although

K_{n}

indicates a complete graph, in this paper K with no subscript exclusively refers to the graph that is the exponent in the graph exponentiation product,

G^{K}

. As shown by

K_{2}^{K_{2}}

in Figure 1, even if G and K are loopless,

G^{K}

generates two components with loops. Hence, G and K in this note are permitted to have loops thus creating a closed system.

In addition to the notation

| K |

as graph order, let

n_{K}

indicate the order of K. If

V (K) = {k_{1}, k_{2}, \dots, k_{n_{K}}}

then each function

f_{i}

can be represented by

n_{K}

-tuple

(g_{1}, g_{2}, \dots, g_{n_{K}})

where

g_{i} \in V (G)

, reflecting that

f (k_{i}) = g_{i}

Example 1. Suppose

K_{2}

is both K and G where both have vertex set

{0, 1}

as seen in Figure 1. Then

V (K_{2}^{K_{2}}) = V (K_{2}) \times V (K_{2}) = {(0, 0), (0, 1), (1, 0), (1, 1)}

and function

(g_{1}, g_{1}^{'})

is adjacent to function

(g_{2}, g_{2}^{'})

G^{K}

if and only if edges

((g_{1}, g_{2}^{'})

and

(g_{2}, g_{1}^{'}))

are in

E (G)

since K is

K_{2}

. In

G : = K_{2}

N_{G} (0) = 1

and

N_{G} (1) = 0

so exponential function/vertex

(0, 0) \sim (1, 1)

and

(0, 1) \sim (0, 1)

Denote

K_{1}^{*} + K_{1}^{*}

2 K_{1}^{*}

. Figure 1 displays

K_{2}^{K_{2}}

and

{(2 K_{1}^{*})}^{K_{2}}

. Notice that

K_{2}^{K_{2}} ≅ {(2 K_{1}^{*})}^{K_{2}}

although

K_{2} ≇ 2 K_{1}^{*}

3.1. Known Properties of $G^{K}$

K_{1}^{*}

has one function that maps vertex v to itself then

G^{K_{1}^{*}} = G

. Thus

K_{1}^{*}

is the identity for this product.

Given graphs G, H and K plus direct product

G \times H

, the following hold as proved in [6].

$G^{K_{1}^{*}} = G$ .
$G^{x (K_{1}^{*})} = G \times G \times \dots \times G$ x number of times is $G^{x}$ ,
$G^{O} = n_{G} K_{1}$
$G^{H} \times G^{K} ≅ G^{H + K}$ ,
${(G \times H)}^{K} ≅ G^{K} \times H^{K}$ ,
${(G^{H})}^{K} ≅ G^{H \times K}$ .

Any G has a neighborhood multiset

N (G)

of the open neighborhoods

N (g)

for

g \in V (G)

. For

K_{2}

with

V (K_{2}) = {0, 1}

, as

N (0) = 1

and

N (1) = 0

, then

N (K_{2}) = {{1}, {0}}

. It is not always true that if

N (G) = N (H)

then

G ≅ H

. See [2] for a couple of examples. Graph G is said to be neighborhood reconstructible if

N (G) = N (H)

implies that

G ≅ H

[2]. In [2] it is shown that G is neighborhood reconstructible if and only if

G^{K_{2}} ≅ H^{K_{2}}

implies

G ≅ H

for all H. This appears to be the only instance in which cancellation in

G^{K}

is explored.

3.2. Loops in $G^{K}$

The generation of loops in

G^{K}

happens even when both K and G are loopless. Loops in the graph exponential indicate a homomorphism between the functions of

G^{K}

as determined by the edge structure of G. In fact, f is a homomorphism if and only if

(f, f)

is a loop of

G^{K}

[7].

3.3. Acyclic versus Cyclic K

If G is loopless, then any

f_{i}

must have no fixed vertex in order to generate an edge in

G^{K}

. Ponder when K is an odd tree. For any acyclic graph, the set of all

f_{i}

form transpositions that involve an even number of vertices. Thus there is always a fixed vertex in any function set of an odd tree. Based on the definition of

G^{K}

and the fact that

V (G^{K})

is a set of

n_{K}

-tuple vertices, when K is an odd ordered acyclic graph and G is loopless,

G^{K} ≅ D_{{| G |}^{| K |}}

. However, given an even ordered acyclic K, there exist transpositions involving all of the digits in the

n_{K}

-tuple so

G^{K} ≇ D_{n}

. It also holds that when K has a cycle, then

G^{K} ≇ D_{n}

independent of whether G has a loop or not.

4. Adjacency Matrix

As any graph G can be constructed from its

A_{G}

, our goal is to find a relatively simple way to construct

A_{G^{K}}

for any G and K. We begin with the adjacency matrix for

G^{K}

when K is

K_{2}

, followed by using this construction in the proof of the general case for K.

4.1. Adjacency Matrix When $K_{2}$ is K

When K is

K_{2}

, then

V (G^{K})

is Cartesian product

V (G) \times V (G)

and function

f_{i}

is a single transposition. Thus, for the functions

(g_{1}, g_{1}^{'})

and

(g_{2}, g_{2}^{'})

V (G^{K})

(g_{1}, g_{1}^{'}) \sim (g_{2}, g_{2}^{'})

if and only if edges

(g_{1}, g_{2}^{'})

and

(g_{1}^{'}, g_{2})

are in

E (G)

Define a row reordered matrix to be a square matrix with its row indices ordered in a pattern that does not match the order of the column indices with the index ordering difference due to either a row permutation or a row labeling (or similarly for columns). For now we consider the impact of row reordering a matrix as applying only to

K : = K_{2}

. Figure 2 shows the adjacency matrix

A_{G^{K}}

for

K_{3}^{K_{2}}

along with a colexicographic row reordered matrix,

A_{G^{K}}^{*}

where the column indices of

A_{G^{K}}^{*}

differ from the row indices. As the rows of

A_{G^{K}}

are simply permuted in

A_{G^{K}}^{*}

, the row-column adjacency structure of

G^{K_{2}}

is preserved. Also shown in the top right is the block matrix of

A_{G^{K}}^{*}

. Take note that the block form of

A_{G^{K}}^{*}

reveals that

A_{G^{K}}^{*} = A_{K_{3}} \otimes A_{K_{3}}

; and note that

A_{G} \otimes A_{G}

is the adjacency matrix of the direct power

G^{2}

In Figure 2, the fact that row reordering

A_{G^{K}}

according to colexicographic order produces the matrix

A_{G} \otimes A_{G}

implies that

A_{G^{K}}

can be constructed from

A_{G} \otimes A_{G}

. Hence,

A_{G} \otimes A_{G}

A_{G^{K}}^{*}

with colexicographic row indices, followed by row permutation to lexicographic order that matches column index order, generates

A_{G^{K}}

when

K : = K_{2}

. This follows from the fact that

Aut (K_{2})

contains a single transposition.

Let P be permutation matrix

[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

that represents the transposition of

K_{2}

as K for G with order 2; and let

A A

be the matrix

A_{K_{2}} \otimes A_{K_{2}}

while

A^{'} A^{'} = A_{2 K_{1}^{*}} \otimes A_{2 K_{1}^{*}}

. Returning to Figure 1,

P * A A

gives

A_{(K_{2}^{K_{2}})}

and

P * A^{'} A^{'}

results in

A_{(2 {K_{1}^{*}}^{K_{2}})}

where

A_{(K_{2}^{K_{2}})}

and

A_{(2 {K_{1}^{*}}^{K_{2}})}

are permutation equivalent showing that

K_{2}^{(K_{2})} ≅ 2 {K_{1}^{*}}^{(K_{2})}

By choice, Proposition 4.1 is stated utilizing row labeling although a permutation matrix is a clear option.

Proposition 4.1

Let G be any graph without multiple edges and let K in

G^{K}

K_{2}

. Construct a block matrix

A_{G^{K}}^{*} = A_{G} \otimes A_{G}

using the colexicographic ordering of

V (G^{K})

as row index labels while column indices are lexicographically labeled. Matrix

A_{G^{K}}^{*}

produces

A_{G^{K}}

by row permuting to have both row and column indices in lexicographic order.

Proof.

Suppose

A_{G^{K}}

is the adjacency matrix for

G^{K_{2}}

with arbitrary

(g_{i}, g_{j}) \in V (G^{K_{2}})

and

g_{i}, g_{j} \in V (G)

where

i = j

is permitted. Since K is

K_{2}

then

(g_{1}, g_{1}^{'}) \sim (g_{2}, g_{2}^{'})

if and only if

(g_{1}, g_{2}^{'}), (g_{2}, g_{1}^{'}) \in E (G)

as reflected in the entries of

A_{G}

. Row reorder

A_{G^{K}}

via colexicographic order and call the revised matrix

A_{G^{K}}^{*}

, thus preserving the adjacency structure of

G^{K_{2}}

that is based on that of

A_{G}

A_{G^{K}}^{*}

has

n_{G} \times n_{G}

blocks where

g_{i}

(g_{i}, g_{j})

are the vertices of G in lexicographic order and all

g_{j}

are the same. Consider a block row to be the collection of rows where all

g_{j}

are the same. Let

r_{g_{j}}

be the

g_{j}

row of

A_{G}

. Then any block row reflects the adjacency structure of

g_{j}

and is equivalent to the product

r_{g_{j}} \otimes A_{G}

reflecting the

n_{G}

number of

g_{i}

(g_{i}, g_{j})

for each specific

g_{j}

of the block row. Thus,

A_{G^{K}}^{*}

A_{G} \otimes A_{G}

; and

A_{G^{K}}

is found by row permutation back to lexicographic index order.

Now suppose that we have

A_{G^{K}}^{*} = A_{G} \otimes A_{G}

which is the adjacency matrix for the direct power

G \times G = G^{2}

with vertex set

V (G) \times V (G) = V (G^{K_{2}})

. Let

(g_{i}^{*}, g_{j}^{*}) \in V (G \times G)

. In this direct power,

(g_{1}^{*}, {g_{1}^{*}}^{'}) \sim (g_{2}^{*}, {g_{2}^{*}}^{'})

if and only if

(g_{1}^{*}, g_{2}^{*}), ({g_{1}^{*}}^{'}, {g_{2}^{*}}^{'}) \in E (G)

. Each block row of

A_{G^{K}}^{*}

reflects the adjacency structure of

g_{i}^{*}

. Using

V (G^{K_{2}})

, assign a colexicographic labeling only to the rows of

A_{G^{K}}^{*}

, so that each labeled block row reflects the adjacency structure of

g_{j}^{*}

. Since

(g_{1}^{*}, {g_{1}^{*}}^{'}) \sim (g_{2}^{*}, {g_{2}^{*}}^{'})

G^{K_{2}}

if and only if

(g_{1}^{*}, {g_{2}^{*}}^{'}), (g_{2}^{*}, {g_{1}^{*}}^{'}) \in E (G)

, row reordering the colexicographic rows of

A_{G^{K}}^{*}

via lexicographic order produces

A_{G^{K}}

for

G^{K_{2}}

. □

4.2. General $A_{G^{K}}$

The adjacency matrix for the general case of

G^{K}

is now addressed. First we give some definitions.

Imagine set

{f_{1}, f_{2}, \dots, f_{k}}

n_{K}

-tuple functions where

f_{i} : V (K) \to V (G)

and k is the number of

f_{i}

that apply to G (i.e. the k number of

f_{i}

that generate edges in

G^{K}

). Let

π_{i}

be a

{| G |}^{| K |} \times {| G |}^{| K |}

permutation matrix for each

f_{i}

and

π_{i} \in Ω_{G}

. Thus, based on the structure of G,

Ω_{G}

contains only the k number of

π_{i}

where the

f_{i}

produce edges in

G^{K}

Let

A_{G \otimes}

be the Kronecker product of

A_{G}

over

| K |

where the Z blocks are maximized by having

A_{G}

as the first multiplicand:

\begin{matrix} A_{G \otimes} = \prod_{i = 1}^{n_{K} - 1} A_{G} \otimes {(A_{G})}_{i} \end{matrix}

(1)

Define

Ω_{A_{\land}}

as a collection of

| Ω_{G} |

number of

{(A_{\land})}_{i} = π_{i} * A_{G \otimes}

. Thus, each

{(A_{\land})}_{i}

is associated with a distinct member

π_{i}

Ω_{G}

. Thus each

{(A_{\land})}_{i}

member of

Ω_{A_{\land}}

is a submatrix of

A_{G^{K}}

based on a specific

π_{i}

, with set

Ω_{A_{\land}}

over all

π_{i}

Ω_{G}

Define

\sum_{Δ}

as a matrix sum of

{(A_{\land})}_{i}

such that

a_{i j}

is changed to 1 for all

a_{i j}

where

a_{i j} > 1

. This eliminates the miscounting of redundantly generated neighbors in

G^{K}

Applying

\sum_{Δ}

Ω_{A_{\land}}

generates

A_{G^{K}}

for the specific G and K. Prior to giving proof of the last statement, we provide a linear construction algorithm in Figure 3 and give Example 1 that uses the algorithm in the figure.

The use of

Ω

for sets

Ω_{G}

and

Ω_{A_{\land}}

is by design as these sets can be viewed as a single “evolving" set that begins with

Ω_{G}

Remark 4.2

Because Figure 3 provides a linear construction, the following are true. Notice that

| Ω_{A_{\land}} | = | Ω_{G} |

, and there exists a bijection between the

f_{i}

members of

Ω_{G}

, the

π_{i}

members of

Ω_{G}

and the members of

Ω_{A_{\land}}

Example 2: Imagine

K_{2}

with

V (K_{2}) = {0, 1}

and

K_{3}

with

V (G) = {v_{1}, v_{2}, v_{3}}

. Suppose exponential

K_{2}^{K_{3}}

with vertex function set of

{000, 001, 010, 011, 100, 101, 110, 111}

given in shorthand notation. Using the algorithm in Figure 3, we construct

A_{G^{K}}

for

K_{3}^{K_{2}}

as given below on the far left. Hence, this

A_{G^{K}}

is the goal of our example construction. The other two matrices displayed in Figure 4 are the two members of

Ω_{A_{\land}}

whose construction is explained following.

Figure 3. The construction algorithm of

A_{G^{K}}

Figure 3. The construction algorithm of

A_{G^{K}}

Although the set of $f_{i}$ is $Aut (K_{3})$ (the dihedral group of 3 excluding the identity: $(v_{2} v_{3} v_{1})$ , $(v_{3} v_{1} v_{2})$ , $(v_{2} v_{1} v_{3})$ , $(v_{1} v_{3} v_{2})$ , $(v_{3} v_{2} v_{1})$ ), since G is a loopless $K_{2}$ , then any function containing a fixed vertex is disregarded and the set of $f_{i}$ in $Ω_{G}$ is ${(v_{2} v_{3} v_{1}), (v_{3} v_{1} v_{2})}$ [4]. Construct two permutation matrices: $π_{1}$ for $(v_{2} v_{3} v_{1})$ and $π_{2}$ as $(v_{3} v_{1} v_{2})$ .
Given $G : = K_{2}$ and $A_{K_{2}} = [\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}]$ , using equation 1 produces $A_{G \otimes} : = A_{K_{2} \otimes}$ where $A_{K_{2} \otimes} = A_{K_{2}} \otimes A_{K_{2}} \otimes A_{K_{2}}$ ; and $A_{K_{2} \otimes}$ is a $8 \times 8$ permutation matrix of cross-diagonal 1s with indices of ${000, 001, 010, 011, 100, 101, 110, 111}$ .
Based on the $π_{i}$ members of $Ω_{G}$ and using two $A_{K_{2} \otimes}$ matrices, there are two members of $Ω_{A_{\land}}$ : $A_{\land 1} = π_{1} * A_{K_{2} \otimes}$ and $A_{\land 2} = π_{2} * A_{K_{2} \otimes}$ . Using the vertices of $A_{K_{2} \otimes}$ , the rows of $A_{K_{2} \otimes}$ are permuted by $π_{1}$ to be the ordered set $(000, 010, 100, 110, 001, 011, 101, 111)$ as shown in the center of Figure 4. Matrix $π_{2}$ permutes the rows of $A_{K_{2} \otimes}$ to be the ordered set $(000, 100, 001, 101, 010, 1101, 011, 111)$ as on the far right in Figure 4.
Utilizing $\sum_{Δ}$ , the 2s generated by the duplicate 000 and 111 entries are changed to 1s with the result being $A_{G^{K}}$ for $K_{2}^{K_{3}}$ as desired.

□

Theorem 4.3

Given

G^{K}

where G and K are graphs without multiple edges,

A_{G^{K}}

is the

\sum_{Δ}

sum of the members of

Ω_{A_{\land}}

Proof.

Consider Remark 4.2 and let

r_{g_{i}}

be the

g_{i}

indexed row of

A_{G}

where

g_{i} \in V (G)

. Although Proposition 4.1 is based on the single transposition of

K_{2}

as K, we know that for all functions

f : V (K) \to V (G)

each row of

A_{G^{K}}

is found utilizing

r_{g_{j}}

A_{G}

and the Kronecker product. Thus, keeping Proposition 4.1 in mind, consider each function/vertex of

G^{K}

with a general K. Since

A_{G^{K_{2}}}

is based on a permutation of

A_{G \otimes}

rows, then each row of

A_{G^{K}}

must be found via the rows of

A_{G}

Let

x : = (g_{1}, \dots, g_{n_{K}})

where

g_{i} \in x

with

g_{i} \in V (G)

and

r_{x}

is the row of

A_{G^{K}}

indexed by x. The neighbors of x are based on the set of neighbors of

g_{i} \in V (G)

as represented by row

r_{g_{i}}

A_{G}

. For any edge

e \in E (G^{K})

where

e : = (x, x^{'})

, each element

g_{i}

of x must be a neighbor of its corresponding element

g_{i}^{'}

x^{'}

in G based on the

f_{i}

that generate edges in

G^{K}

; so

r_{g_{i}} \otimes r_{g_{i}^{'}}

gives their joint neighborhood. As each

g_{i}

is an element of a function x, then for all

g_{i}

and all

g_{i}^{'}

for specific edge e,

r_{g_{i}} \otimes r_{g_{i}^{'}}

, (for that specific

π_{i}

Ω_{G}

), associates x with the specific

π_{i}

. Finding

r_{g_{i}} \otimes r_{g_{i}^{'}}

for all

π_{i}

Ω_{G}

gives the complete neighborhood of x in

G^{K}

; thus using

\sum_{Δ}

to sum all

r_{g_{i}} \otimes r_{g_{i}^{'}}

for a given x gives row

r_{x}

A_{G^{K}}

. Each row sum represents a basis of the vector space of

G^{K}

as the vertices are

n_{K}

-tuple functions. So the disjoint union of these rows into a matrix is

A_{G^{K}}

. □

References

Chartrand, L. Lesniak, P. Zhang (2016) Graphs & Digraphs, 6th Ed.. DCRC Press, Boca Raton, FL.
Hammack (2021) Graph exponentiation and neighborhood reconstruction. Discussiones Mathematicae Graph Theory 41. 335-339.
R. Hammack, W. Imrich, S. Klavžar (2011) Handbook of Product Graphs, 2nd Ed.. CRC Press, Boca Raton, FL.
F. Harary (1969) Graph Theory. Taylor and Francis Group, Boca Raton, FL.
B. Jónsson (1981) Arithmetic of ordered sets, in: I. Rival (Ed.), Ordered Sets (Banff Alta),, Volume 83 of NATO Advanced Study Inst. Ser. C. Math. Phys. Sci. 3â43.
L. Lovázs (1967) Operations with structures. Acta Math. Acad. Sci. Hungar. 18. 321â328. [CrossRef]
N. Sauer (2001) Hedetniemi’s conjecture - a survey. Discrete Mathematics 229. 261-292.

Figure 1. Two isomorphic graph exponentials

K_{2}^{K_{2}}

and

{(K_{1}^{*} + K_{1}^{*})}^{K_{2}}

Figure 1. Two isomorphic graph exponentials

K_{2}^{K_{2}}

and

{(K_{1}^{*} + K_{1}^{*})}^{K_{2}}

Figure 2. The graph and matrices for Example 2.

Figure 4. On the far left,

A_{G^{K}}

that is the goal for the Example 1 construction.

Figure 4. On the far left,

A_{G^{K}}

that is the goal for the Example 1 construction.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Adjacency Matrix for the Graph Exponential

Abstract

1. Introduction

2. Background

2.1. Matrices

2.2. Direct Product

3. Graph Exponentiation Overview

3.1. Known Properties of G K

3.2. Loops in G K

3.3. Acyclic versus Cyclic K

4. Adjacency Matrix

4.1. Adjacency Matrix When K 2 is K

4.2. General A G K

References

MDPI Initiatives

Important Links

Subscribe

3.1. Known Properties of $G^{K}$

3.2. Loops in $G^{K}$

4.1. Adjacency Matrix When $K_{2}$ is K

4.2. General $A_{G^{K}}$