Monogenity and Power Integral Bases: Recent Developments

Preprint

Review

Monogenity and Power Integral Bases: Recent Developments

Altmetrics

Downloads

136

Views

Comments

A peer-reviewed article of this preprint also exists.

István Gaál^*

This version is not peer-reviewed

Submitted:

27 May 2024

Posted:

27 May 2024

You are already at the latest version

Alerts

Abstract

Monogenity is a classical area of algebraic number theory that is very actively researched even today. This paper is a collection of the results obtained during the last few years in this area. Several of these results were presented at the series of online conferences "Monogenity and power integral bases".

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

1. Purpose

Let

K = Q (γ)

be an algebraic number field of degree n, generated by the algebraic integer

γ

, with ring of integers

Z_{K}

and discriminant

D_{K}

. It is a classical problem of algebraic number theory, going back to R. Dedekind [29], K. Hensel [90] and H. Hasse [89] to decide if the ring

Z_{K}

can be generated by a single element

α \in Z_{K}

, that is, if it is mono-generated,

Z_{K} = Z [α]

. In this case we say that the ring

Z_{K}

, or the field K is monogenic. In this case

{1, α, \dots α^{n - 1}}

is an integral basis, called power integral basis.

Recently this area is developing very fast. In order to create a suitable forum to present recent results on monogenity the author started a series of online meetings "Monogenity and power integral bases" 1 in 2021. The purpose was to make contacts, circulate preprints and results, support collaboration between researchers all over the world working in this area. During the time of pandemy this was the only way to contact, but later on this proved to be an easy and fast way of contacting. Therefore until March 2024 we already had nine meetings and we hope to continue.

The main purpose of this paper is to give an overview of the latest developments of monogenity theory, about the results that were presented at the online meetings and the results that appeared parallel. The paper is also a kind of extension of the book [64], appeared in 2019. Most of these results are not yet contained there.

2. Introduction

In this section in favour of the reader we collect some further concepts on monogenity.

For any primitive element

α \in Z_{K}

(that is

K = Q (α)

) the index of

α

is defined as the module index

I (α) = (Z_{K} : Z [α]) .

We obviously have

D (α) = I {(α)}^{2} D_{K},

where

D (α)

is the discriminant of

α

D (α) = \prod_{1 \leq i < j \leq n} {(α^{(i)} - α^{(j)})}^{2},

α^{(i)}

denoting the conjugates of

α

corresponding to

γ^{(i)}

(

i = 1, \dots, n

) (in the following we shall denote similarly the conjugates of any element of K). Obviously,

I (α) = 1

, if and only if

Z_{K} = Z [α]

, that is if

{1, α, \dots α^{n - 1}}

is an integral basis, or in other words

α

generates a power integral basis in K.

The field index

m (K)

of K is defined as

m (K) = gcd {I (α) | α \in Z_{K}, K = Q (α)} .

If K is monogenic, there are elements of index 1, the field index is also equal to 1. The converse is not true: the field index may happen to be 1 without the field being monogenic.

α, β

are primitive elements in

Z_{K}

and

α + β \in Z

α - β \in Z

then obviously their indices are equal. Such elements are called equivalent. It was proved by B.J. Birch and J. R. Merriman [21] and then in an effective form by K. Győry [83] that up to equivalence there are only finitely many generators of power integral bases in any number field K.

For any integral basis

(1, ω_{2}, \dots, ω_{n})

of K set

L^{(i)} (\underset{̲}{X}) = X_{1} + ω_{2}^{(i)} X_{2} + \dots + ω_{n}^{(i)} X_{n}

(

i = 1, \dots, n

). Then (see [64])

D (L (\underset{̲}{X})) = \prod_{1 \leq i < j \leq n} (L^{(i)} (\underset{̲}{X}) - L^{(j)} (\underset{̲}{X})) = I (X_{2}, \dots, X_{n}) D_{K}

where

I (X_{2}, \dots, X_{n})

is a homogeneous polynomial of degree

n (n - 1) / 2

with integer coefficients, with the property that for any primitive element

α = x_{1} + ω_{2} x_{2} + \dots ω_{n} x_{n} \in Z_{K}

we have

I (α) = | I (x_{2}, \dots, x_{n}) | .

The polynomial

I (X_{2}, \dots, X_{n})

is called the index form corresponding to the integral basis

(1, ω_{2}, \dots, ω_{n})

. Since equivalent algebraic integers have the same index, it is independent of

X_{1}

. Therefore determining elements

α \in Z_{K}

of index m is equivalent to solving the index form equation

I (x_{2}, \dots, x_{n}) = m in x_{2}, \dots, x_{n} \in Z .

A non-zero irreducible polynomial

f (x) \in Z [x]

is called monogenic if a root

α

f (x)

generates a power integral basis in the field

K = Q (α)

. Obviously, if the polynomial

f (x)

is monogenic, then K is also monogenic, but the converse is not true. The field K may happen to be monogenic without

f (x)

being monogenic. The index of

f (x)

is defined as

ind (f) = (Z_{K} : Z [α])

3. Structure of the Paper

As mentioned above, our purpose is to summarize the results obtained after 2019, the appearance of [64], with a special emphasis to the results presented at the online meetings "Monogenity and power integral bases". In the following section we collect the most important tools that were used in several works. These may be useful for further application. Then we collect the most important results and finally we try to indicate some possible perspectives of further research.

4. Tools

4.1. Dedekind’s Criterion

Let

\bar{f (x)} = \prod_{i = 1}^{r} {\bar{ϕ_{i} (x)}}^{ℓ_{i}}

modulo p be the factorization of

f (x)

modulo p into powers of monic irreducible coprime polynomials of

F_{p} [x]

For completeness we recall here a well-known theorem of Dedekind:

Theorem 1. (Chapter I, Proposition 8.3 of [145])

If p does not divide the index

I (α) = (Z_{K} : Z [α])

, then

p Z_{K} = \prod_{i = 1}^{r} p_{i}^{ℓ_{i}},

where

p_{i} = p Z_{K} + ϕ_{i} (α) Z_{K}

and the residue degree of

p_{i}

f (p_{i}) = deg (ϕ_{i})

As indicated above, it is very important to have a tool to determine prime divisors of the indices of algebraic integers. Therefore the following well known criterion of Dedekind is very frequently used:

Theorem 2. (Dedekind’s criterion [29], see also [27] Theorem 6.1.4, [147] p. 295)

Let

f (x) \in Z [x]

be a monic non-zero irreducible polynomial with a root α, let

K = Q (α)

, and let p be a prime number. Let

\bar{f (x)} = \prod_{i = 1}^{r} {\bar{ϕ_{i} (x)}}^{ℓ_{i}} mod p

be the factorization of

\bar{f (x)}

F_{p} [x]

, with monic

ϕ_{i} \in Z [x]

such that their reductions

\bar{ϕ_{i} (x)}

are irreducible and pairwise coprime over

F_{p}

. Set

M (x) = \frac{f (x) - \prod_{i = 1}^{r} {ϕ_{i}}^{ℓ_{i}} (x)}{p} .

Then

M (x) \in Z [x]

and the following statements are equivalent:

1.: p does not divide the index $I (α) = (Z_{K} : Z [α])$ .
2.: For every $i = 1, \dots, r$ , either $ℓ_{i} = 1$ or $ℓ_{i} \geq 2$ and $\bar{ϕ_{i} (x)}$ does not divide $\bar{M (x)}$ in $F_{p} [x]$ .

4.2. The Field Index

We also recall a simple but very important statement of Hensel:

Theorem 3. (K. Hensel [90] p. 280)

The prime factors of the field index are smaller than the degree of the field.

Denote by

ν_{p} (k)

the highest power of the prime p dividing the integer k.

Theorem 4. (H. T. Engström [30])

For number fields of degree

n \leq 7

ν_{p} (m (K))

is explicitly determined by the factorization of p into powers of prime ideals of

p Z_{K}

The corresponding tables of [30] are too long to include here, but they present the explicit exponents.

4.3. Newton Polygon Method

If p divides the index

I (α) = (Z_{K} : Z [α])

then Dedekind’s Theorem 1 can not be applied.

Using Newton polygons, an alternative method was given by Ore [146] to calculate

I (α) = (Z_{K} : Z [α])

D_{K}

and the prime ideal factorization of primes in

Z_{K}

. This was further developed among others by J. Montes and E. Nart [141], L. El Fadil, J. Montes and E. Nart [62], L. El Fadil [32]. This theory was extended to so called higher order Newton polygons by J. Guardia, J. Montes and E. Nart [82]. The method is also called Montes algorithm.

Here we only give a short introduction to some basic notions and statement of this very technical method, based on the explanation used in [56]. During the recent years a huge amount of papers applied this method.

For any prime p, let

ν_{p}

be the p-adic valuation of

Q

. Denote by

Q_{p}

its p-adic completion, by

Z_{p}

the ring of p-adic integers. Let

ν_{p}

be the Gauss’s extension of

ν_{p}

Q_{p} (x)

ν_{p} (P) = min (ν_{p} (a_{i}), (i = 0, \dots, n)

for any polynomial

P (x) = \sum_{i = 0}^{n} a_{i} x^{i} \in Q_{p} [x]

and extended by

ν_{p} (P / Q) = ν_{p} (P) - ν_{p} (Q)

for

0 \neq P, Q \in Q_{p} [x]

. Let

ϕ \in Z_{p} [x]

be a monic polynomial whose reduction is irreducible in

F_{p} [x]

, let

F_{ϕ}

be the field

F_{p} [x] / (\bar{ϕ})

. For any monic polynomial

f (x) \in Z_{p} [x]

, upon the Euclidean division by successive powers of

ϕ

, we expand

f (x)

as follows:

f (x) = \sum_{i = 0}^{ℓ} a_{i} (x) ϕ {(x)}^{i} .

This is called the

ϕ

-expansion of

f (x)

(

deg (a_{i} (x)) < deg (ϕ), i = 1, \dots ℓ

). The

ϕ

-Newton polygon of

f (x)

with respect to p, is the lower boundary convex envelope of the set of points

{(i, ν_{p} (a_{i} (x))), a_{i} (x) \neq 0}

in the Euclidean plane, which we denote by

N_{ϕ} f

. The

ϕ

-Newton polygon of f, is the process of joining the edges

S_{1}, \dots, S_{r}

ordered by increasing slopes, which can be expressed as

N_{ϕ} f = S_{1} + \dots + S_{r} .

For every side

S_{i}

N_{ϕ} f

, the length of

S_{i}

, denoted

ℓ (S_{i})

is the length of its projection to the x-axis. Its height, denoted by

h (S_{i})

is the length of its projection to the y-axis. Let

d (S_{i}) = gcd (ℓ (S_{i}), h (S_{i}))

be the ramification degree of S. The principal

ϕ

-Newton polygon of f, denoted

N_{ϕ}^{+} f

, is the part of the polygon

N_{ϕ} f

, which is determined by joining all sides of negative slopes. For every side S of

N_{ϕ}^{+} f

, with initial point

(s, u_{s})

and length ℓ, and for every

0 \leq i \leq ℓ

, we attach the following residue coefficient

c_{i} \in F_{ϕ}

as follows:

c_{i} = \{\begin{matrix} 0, & if (s + i, u_{s + i}) lies strictly above S, \\ (\frac{a_{s + i} (x)}{p^{u_{s + i}}}) mod (p, ϕ (x)), & if (s + i, u_{s + i}) lies on S, \end{matrix}

where

(p, ϕ (x))

is the maximal ideal of

Z_{p} [x]

generated by p and

ϕ

. Let

λ = - h / e

be the slope of S, where h and e are two positive coprime integers. Then

d = ℓ / e

is the degree of S. The points with integer coordinates lying on S are exactly

(s, u_{s}), (s + e, u_{s} - h), \dots, (s + d e, u_{s} - d h) .

Thus, if i is not a multiple of e, then

(s + i, u_{s + i})

does not lie in S, and so

c_{i} = 0

. The polynomial

f_{S} (y) = t_{d} y^{d} + t_{d - 1} y^{d - 1} + \dots + t_{1} y + t_{0} \in F_{ϕ} [y],

is called the residual polynomial of

f (x)

associated to the side S, where for every

i = 0, \dots, d

t_{i} = c_{i e}

Let

N_{ϕ}^{+} f = S_{1} + \dots + S_{r}

be the principal

ϕ

-Newton polygon of f with respect to p. We say that f is a

ϕ

-regular polynomial with respect to p, if

f_{S_{i}} (y)

is square free in

F_{ϕ} [y]

for every

i = 1, \dots, r

. The polynomial f is said to be p-regular if

\bar{f (x)} = \prod_{i = 1}^{r} {\bar{ϕ_{i} (x)}}^{ℓ_{i}}

for some monic polynomials

ϕ_{1}, \dots, ϕ_{t}

Z [x]

such that

\bar{ϕ_{1}}, \dots, \bar{ϕ_{t}}

are irreducible coprime polynomials over

F_{p}

and f is a

ϕ_{i}

-regular polynomial with respect to p for every

i = 1, \dots, t

Let

ϕ \in Z_{p} [x]

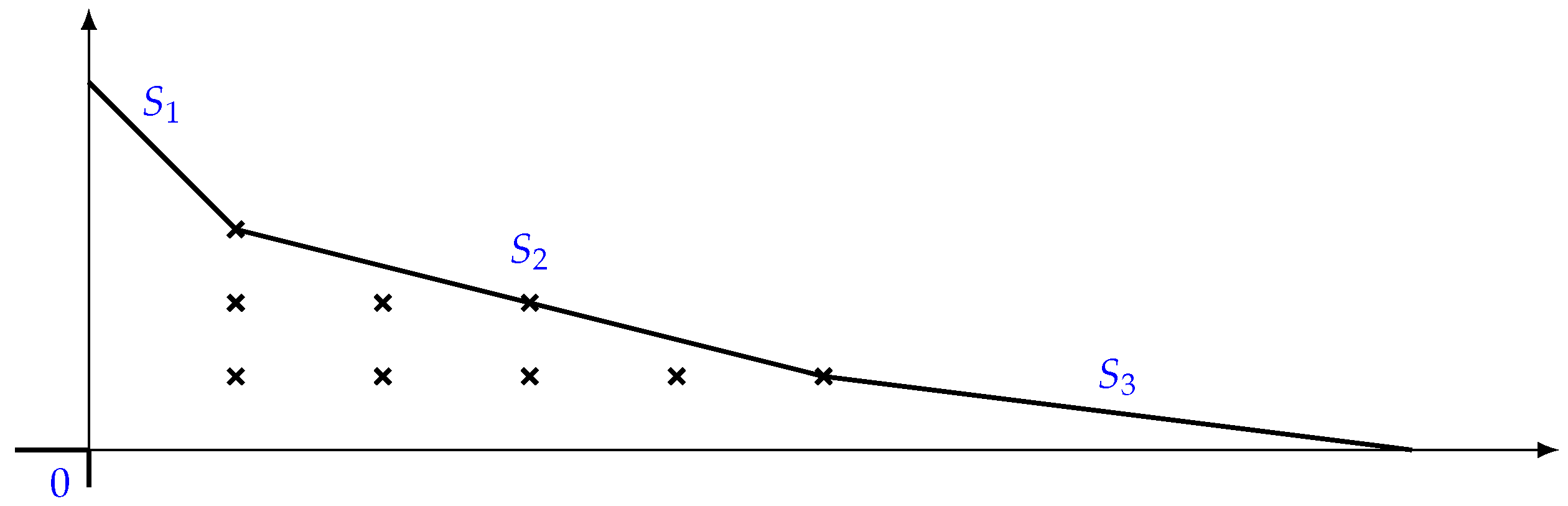
be a monic polynomial, such that

\bar{ϕ (x)}

is irreducible in

F_{p} [x]

. The

ϕ

-index of

f (x)

(cf. [62]), denoted by

{ind}_{ϕ} (f)

, is

deg (ϕ)

times the number of points with natural integer coordinates that lie below or on the polygon

N_{ϕ}^{+} f

, strictly above the horizontal axis, and strictly beyond the vertical axis (see Figure 1).

In the example of Figure 1,

i n d_{ϕ} (f) = 9 \times deg (ϕ)

Now assume that

\bar{f (x)} = \prod_{i = 1}^{r} {\bar{ϕ_{i} (x)}}^{ℓ_{i}}

is the factorization of

\bar{f (x)}

F_{p} [x]

into monic polynomials

ϕ_{i} \in Z [x]

which are irreducible and pairwise coprime in

F_{p} [x]

(

i = 1, \dots, r

For every

i = 1, \dots, r

, let

N_{ϕ_{i}}^{+} (f) = S_{i 1} + \dots + S_{i r_{i}}

be the principal

ϕ_{i}

-Newton polygon of f with respect to p. For every

j = 1, \dots, r_{i}

, let

f_{S_{i j}} (y) = \prod_{k = 1}^{s_{i j}} ψ_{i j k}^{a_{i j k}} (y)

be the factorization of

f_{S_{i j}} (y)

F_{ϕ_{i}} [y]

. Then we have the following index theorem of Ore.

Theorem 5. (Theorem of Ore, see Theorem 1.7 and Theorem 1.9 in [62], Theorem 3.9 in [32], pp. 323–325 in [141] and [146])

1.: We have

$ν_{p} (ind (f)) \geq \sum_{i = 1}^{r} {ind}_{ϕ_{i}} (f) .$

The equality holds if $f (x)$ is p-regular.
2.: If $f (x)$ is p-regular, then

$p Z_{K} = \prod_{i = 1}^{r} \prod_{j = 1}^{r_{i}} \prod_{k = 1}^{s_{i j}} p_{i j k}^{e_{i j}},$

is the factorization of $p Z_{K}$ into powers of prime ideals of $Z_{K}$ lying above p, where $e_{i j} = ℓ_{i j} / d_{i j}$ , $ℓ_{i j}$ is the length of $S_{i j}$ , $d_{i j}$ is the ramification degree of $S_{i j}$ , and $f_{i j k} = deg (ϕ_{i}) \times deg (ψ_{i j k})$ is the residue degree of the prime ideal $p_{i j k}$ over p.

4.4. Algorithmic Methods

Several of known efficient methods for the resolutions of Diophantine equations are related to Thue equations, cf. [64]. These methods are implemented e.g. in Magma [22]. Therefore the most efficient method for solving index form equations also work by reducing the index form equation to Thue equations.

In cubic fields the index form equation is a cubic Thue equation, see [64].

The below method of I. Gaál, A. Petho and M. Pohst [74,75] reduces the index form equations in quartic fields to a cubic and some corresponding quartic Thue equations. This method is quite often used even nowadays, therefore we briefly present it.

Let

K = Q (ξ)

be a quartic number field and

f (x) = x^{4} + a_{1} x^{3} + a_{2} x^{2} + a_{3} x + a_{4} \in Z [x]

the minimal polynomial of

ξ

. We represent any

α \in Z_{K}

in the form

α = \frac{a_{α} + x ξ + y ξ^{2} + z ξ^{3}}{d}

(1)

with

a_{α}, x, y, z \in Z

, and with a common denominator

d \in Z

. Consider the solutions of the equation

I (α) = m (α \in Z_{K})

(2)

for

0 < m \in Z

. We have

Theorem 6. ([74])

Let

i_{m} = d^{6} m / n

where

n = I (ξ)

. The element α of (1) is a solution of (2) if and only if there is a solution

(u, v) \in Z^{2}

of the cubic equation

F (u, v) = u^{3} - a_{2} u^{2} v + (a_{1} a_{3} - 4 a_{4}) u v^{2} + (4 a_{2} a_{4} - a_{3}^{2} - a_{1}^{2} a_{4}) v^{3} = \pm i_{m}

(3)

such that

(x, y, z)

satisfies

\begin{matrix} Q_{1} (x, y, z) & = & x^{2} - x y a_{1} + y^{2} a_{2} + x z (a_{1}^{2} - 2 a_{2}) + y z (a_{3} - a_{1} a_{2}) \\ + z^{2} (- a_{1} a_{3} + a_{2}^{2} + a_{4}) = u, \\ Q_{2} (x, y, z) & = & y^{2} - x z - a_{1} y z + z^{2} a_{2} = v . \end{matrix}

(4)

Equation (3) is either trivial to solve (when F is reducible), or it is a cubic Thue equation.

For a solution

(u, v)

of (3) we set

Q_{0} (x, y, z) = u Q_{2} (x, y, z) - v Q_{1} (x, y, z)

. If

α

in (1) is a solution of (2), then

Q_{0} (x, y, z) = 0 .

(5)

(x_{0}, y_{0}, z_{0}) \in Z^{3}

is a non-trivial solution of (5), with, say,

z_{0} \neq 0

(such a solution can be easily found, see L. J. Mordell [142]), then we can parametrize the solutions

x, y, z

in the form

x = r x_{0} + p, y = r y_{0} + q, z = r z_{0},

(6)

with rational parameters

r, p, q

. Substituting these

x, y, z

into (5) we obtain an equation of the form

r (c_{1} p + c_{2} q) = c_{3} p^{2} + c_{4} p q + c_{5} q^{2},

with integer coefficients

c_{1}, . . ., c_{5}

. Multiply the equations in (6) by

c_{1} p + c_{2} q

and replace

r (c_{1} p + c_{2} q)

c_{3} p^{2} + c_{4} p q + c_{5} q^{2}

. Further multiply the equations in (6) by the square of the common denominator of

p, q

to obtain all integer relations (cf. [75]). We divide those by

gcd {(p, q)}^{2}

and get

k x = c_{11} p^{2} + c_{12} p q + c_{13} q^{2}, k y = c_{21} p^{2} + c_{22} p q + c_{23} q^{2}, k z = c_{31} p^{2} + c_{32} p q + c_{33} q^{2},

(7)

with integer

c_{i j}

and integer parameters

p, q

. Here k is an integer parameter with the property that k divides the

det (C) / d_{0}^{2}

, where C is the 3x3 matrix with entries

c_{i j}

and

d_{0}

is the gcd of its entries (cf. [75]). Finally, substituting the

x, y, z

in (7) into (4) we obtain

F_{1} (p, q) = k^{2} u, F_{2} (p, q) = k^{2} v .

(8)

According to [75] at least one the equations (8) is a quartic Thue equation over the original number field K.

5. Results

5.1. Pure Fields, Trinomials, Quadrinomials, etc.

There is no doubt, Newton polygon method was the most powerful tool during the last couple of years. It is frequently combined with application of Dedekind’s criterion. While S. Ahmad, T. Nakahara and M. Syed [1] investigated monogenity of pure sextic fields in 2014 using its subfield structure and relative monogenity, T. A. Gassert [79] already used Montes algorithm in 2017 to describe monogenity of pure fields. Note that it is only about the monogenity of the polynomials and not the monogenity of number fields generated by a root of the polynomial (for some corrections see L. El Fadil [37]).

Together with Newton polygons (or instead of them), Dedekind’s criterion and Engström’s theorem is also often used. The following results often deal with polynomials of similar shape. It is important to add, that especially using Newton polygons, the whole calculation must be performed separately, even for polynomials of similar shape.

The first results investigated monogenity in pure fields (or radical extensions) generated by a root of an irreducible binomial of type

x^{n} - m

. Assuming that m is square-free, conditions were given for the monogenity (or non-monogenity) of such pure fields, for

n = 6, 8, 12, \dots

etc. A following step was to consider general exponents like

m = 2^{k}, 2^{k} \cdot 3^{ℓ}, \dots

etc., later on

n = p^{k}

with a prime p. For some exponents, the more complicated case of a composite m was also investigated. Here is a list of such results, for brevity indicating only the exponents considered:

Z. S. Aygin and K. D. Nguyen [8] $n = 3$
L. El Fadil [39] $n = 12$
L. El Fadil [41] $n = 18$
L. El Fadil [43] $n = 20$
L. El Fadil [33] $n = 24$
L. El Fadil [35] $n = 36$
L. El Fadil, H. Ben Yakkou and J. Didi [51] $n = 42$
L. El Fadil, H. Choulli and O. Kchit [52] $n = 60$
L. El Fadil and M. Faris [53] $n = 84$
H. Ben Yakkou and O.Kchit [18] $n = 3^{k}$
L. El Fadil [36] $n = 2 \cdot 3^{k}$
L. El Fadil [42] $n = 6, 2^{k} \cdot 3^{ℓ}$
H. Ben Yakkou, A. Chillali and L. El Fadil [15] $n = 2^{k} \cdot 5^{ℓ}$
L. El Fadil [38] $n = 3^{k} \cdot 7^{ℓ}$
L. El Fadil and A. Najim [40] $n = 2^{k} \cdot 3^{ℓ}$
L. El Fadil and O. Kchit [60] $n = 2^{k} \cdot 7^{ℓ}$
L. El Fadil [44] $n = 2^{k} \cdot 3^{ℓ} \cdot 5^{t}$
H. Ben Yakkou and L. El Fadil [16] $n = p^{k}$
L. El Fadil [34] $n = 6$ , m composite
L. El Fadil and I. Gaál [56] $n = 8$ , m composite

The exponents

n \leq 9

with a squarefree m were investigated by I. Gaál and L. Remete [77] which was extended to arbitrary m by L. El Fadil and I. Gaál [56].

A typical statement from this list is the following:

Theorem 7. (L. El Fadil and A. Najim [40])

Let α be a root of the irreducible polynomial

x^{2^{k} \cdot 3^{ℓ}} - m

with a square-free m. If

m \neg \equiv 1 (mod 4)

and

m \neg \equiv \pm 1 (mod 9)

then α generates a power integral basis in

K = Q (α)

. If

m \equiv 1 (mod 4)

m \equiv 1 (mod 9)

, or

k = 2

and

m \equiv - 1 (mod 9)

then K is not monogenic.

A next step was to consider monogenity properties of number fields generated by a root of an irreducible trinomial of type

x^{n} + a x^{m} + b

. The field index is also often determined by using Engström’s theorem. In the following list again we only indicate the type of trinomials considered:

L. El Fadil [39] $x^{4} + a x + b$
L. El Fadil and I. Gaál [54] $x^{4} + a x^{2} + b$
H. Smith [151] $x^{4} + a x + b, x^{4} + c x^{3} + d$
L. Jones [128] showed that there exist exactly three distinct monogenic trinomials of the form $x^{4} + b x^{2} + d$ with Galois $C_{4}$
A. Jakhar, S. Kaur and S. Kumar [101] $x^{5} + a x + b$
L. El Fadil [45] $x^{5} + a x^{2} + b$
L. El Fadil [47] $x^{5} + a x^{3} + b$
L. El Fadil [48] $x^{6} + a x + b$
A. Jakhar and S. Kumar [107] $x^{6} + a x + b$
L. El Fadil [46] $x^{6} + a x^{3} + b$
L. El Fadil and O. Kchit [57] $x^{6} + a x^{5} + b$
A. Jakhar and S. Kaur [102] $x^{6} + a x^{m} + b$
R. Ibarra, H. Lembeck, M. Ozaslan, H. Smith and K. E. Stange [91] $x^{n} + a x + b, x^{n} + c x^{n - 1} + d$ for $n = 5, 6$
L. El Fadil and O. Kchit [58] $x^{7} + a x^{3} + b$
H. Ben Yakkou [9] $x^{7} + a x^{5} + b$
A. Jakhar, S. Kaur and S. Kumar [105] $x^{7} + a x + b$
H. Ben Yakkou [10] $x^{8} + a x + b$
H. Ben Yakkou and B. Boudine [14] $x^{8} + a x + b$
A. Jakhar, S. Kaur and S. Kumar [104] $x^{8} + a x^{m} + b$
L. Jones [129] considered monogenic trinomials of type $x^{8} + a x^{4} + b$ with prescribed Galois group
O. Kchit [135] $x^{9} + a x + b$
H. Ben Yakkou and P. Tiebekabe [19] $x^{9} + a x + b$
L. El Fadil and O. Kchit, [59] $x^{9} + a x^{2} + b$
L. El Fadil and O. Kchit [61] $x^{12} + a x^{m} + b$
H. Ben Yakkou [11] $x^{2^{r}} + a x^{m} + b$
H. Ben Yakkou and L. El Fadil [17] $x^{n} + a x + b, n = 5, 6, 3^{k}, 2^{k} \cdot 3^{ℓ}, 2^{k} \cdot 3^{ℓ} + 1$
A. Jakhar and S. Kumar [108] gave explicit conditions for the non-monogenity of $x^{q^{s}} - a x - b$
A. Jakhar [94] $x^{p^{s}} - a x^{m} - b$
B. Jhorar and S. K. Khanduja [97] $x^{n} + a x + b$ , showed also that $f (x) = x^{n} - x - 1$ is monogenic if and only if $| D (f) | = n^{n} - {(n - 1)}^{n - 1}$ is square-free
H. Ben Yakkou [12] $x^{n} + a x^{m} + b, n = p^{k}, s \cdot p^{k}, 2^{k} \cdot 3^{ℓ}$
L. El Fadil [49] $x^{n} + a x^{m} + b, n = 2^{k} \cdot 3^{ℓ}$
A. Jakhar [93] $x^{n} - a x^{m} - b$
A. Jakhar, S. Khanduja and N. Sangwan [99] $x^{n} + a x^{m} + b$
A. Jakhar, S. Khanduja and N. Sangwan [100] gave necessary and sufficient conditions in terms of $a, b, m, n$ for a given prime p to divide $I (ϑ)$ where $ϑ$ is a root of $x^{n} + a x^{m} + b$
L. Jones [121] considered monogenic reciprocal trinomials of type $x^{2 m} + A x^{m} + 1$
L. Jones [114] showed that there are infinitely many primes p such that $x^{6} + p x^{3} + 1$ is monogenic with Galois group $D_{6}$
L. Jones [115] showed that $x^{n} + x + 1$ is monogenic, if and only if its discriminant is squarefree
L. Jones and T. Phillips [130] showed that $x^{n} + a x + b$ is monogenic infinitely often
L. Jones and D. White [131] found new infinite families of monogenic trinomials of type $x^{n} + A x^{m} + B$

A typical statement from this list is the following:

Theorem 8. (L. Jones and D. White [131])

Let

n \geq 2

be an integer, with

m \geq 1

a proper divisor of n. Let

t = n / m

and let κ denote the squarefree kernel of m. Let A and B be positive integers with

gcd (A, B) > 1

, and define

D : = \frac{t^{t} B^{t - 1} + {(1 - t)}^{t - 1} A^{t}}{gcd {(A, B)}^{t - 1}} .

If B and D are squarefree, and

gcd (A, B) = 0 (mod κ)

, then

f (x) = x^{n} + A x^{m} + B

is monogenic. Moreover,

D (f)

is not squarefree if

m \geq 2

The research was continued into the direction considering monogenity properties of of quadrinomials, quintinomials, etc., that is polynomials with four, five etc. terms and the number fields generated by a root of these polynomials:

T. A. Gassert, H. Smith and K. E. Stange [80] $x^{4} - 6 x^{2} - k x - 3$
H. Ben Yakkou [13] $x^{4} + a x^{3} + b x + c$
J. Harrington and L. Jones [88] constructed new families of quartic polynomials with various Galois groups, which are monogenic infinitely often
A. Jakhar and R. Kalwaniya [95] $x^{6} + a x^{m} + b x + c$
L. Jones [129] $x^{8} + a x^{6} + b x^{4} + a x^{2} + 1$
L. Jones [111] constructed infinitely many monogenic polynomials of degree p for every odd prime p
L. Jones [120] $x^{p} - 2 p t x^{p - 1} + p^{2} t^{2} x^{p - 2} + 1$
A. Jakhar, S. Kaur and S. Kumar [103] $x^{n} + a x^{2} + b x + c$
A. Jakhar, S. Kaur and S. Kumar [106] $x^{p^{s}} - a x^{n} - b x^{m} - c$
A. Jakhar [92] $x^{n} + a x^{n - 1} + b x^{n - 2} + c$
L. Jones [113] constructed infinite families of reciprocal monogenic polynomials with prescribed Galois group
L. Jones [116] showed that if $4 \leq n \geq m \geq 0$ and $gcd (n, m) = gcd (n, k) = 1$ then $x^{n - m} {(x + k)}^{m} + p$ is monogenic for infinitely many primes p
L. Jones [109] $x^{n} + A {(B x + 1)}^{m}$
L. Jones [110] $x^{n} + t \cdot g (x)$ with $n > deg (g)$ , when $g (x)$ is monic and $deg (g) \in {2, 3, 4}$
L. Jones [118] constructed reciprocal monogenic quintinomials of type $x^{2^{n}} + A x^{3 \cdot 2^{n - 2}} + B x^{2^{n - 1}} + A x^{2^{n - 2}} + 1$
L. Jones [119] considered infinite families of monogenic quadrinomials, quintinomials and sextinomials

5.2. The Relative Case

In addition to the absolute case (extension of

Q

) several authors considered monogenity problems in the relative case (extensions of an algebraic number field), or even similar problems in Dedekind rings. Mostly Dedekind’s criterion is used.

M. E. Charkani and A. Deajim [26] (see also A. Deajim and L. El Fadil [28]) $x^{p} - m$ over number fields
M. Sahmoudi and M. E. Charkani [148] considered relative pure cyclic extensions
A. Soullami, M. Sahmoudi and O. Boughaleb [150] $x^{3^{n}} + a x^{3^{s}} - b$ over number fields
O. Boughaleb, A. Soullami and M. Sahmoudi [23] $x^{p^{n}} + a x^{p^{s}} - b$ over number fields
H. Smith [152] relative radical extensions
S. K. Khanduja and B. Jhorar [138] give equivalent versions of Dedekind criterion in general rings
S. Arpin, S. Bozlee, L. Herr and H. Smith [5,6] study monogenity of number rings from a modul-theoretic perspective
R. Sekigawa [149] constructs an infinite number of cyclic relative extensions of prime degree that are relative monogenic

5.3. Composite Polynomials

Several authors considered monogenity of composites of polynomials, composites of binomials etc. The authors mainly use Dedekind’ criterion.

J. Harrington and L. Jones [84] gave conditions for the monogenity of ${(x^{m} - b)}^{n} - a$ the composition of $x^{n} - a$ and $x^{m} - b$
A. Jakhar, R. Kalwaniya and P. Yadav [96] consider monogenity of ${(x^{m} - b)}^{n} - a$ , the composition of $x^{n} - a$ and $x^{m} - b$ using a refined version of the Dedekind criterion
J. Harrington and L. Jones [85] considers monogenity of $Φ_{p^{a}} (Φ_{2^{b}} (x))$ , where $Φ_{N} (x)$ is the cyclotomic polynomial of index N
L. Jones [112] considers monotonically stable polynomial of type $g (f^{n} (x))$
L. Jones [117] constructs infinite collections of monic Eisenstein polynomials $f (x)$ such that $f (x^{d^{n}})$ are monogenic for all integers $n \geq 0$ and $d > 1$
L.Jones [125] considers monogenity of $S_{k} (x^{p})$ where $S_{k} (x) = x^{3} - k x^{2} - (k + 3) x - 1$ the Shanks polynomial
L. Jones [126] considers monogenity of $f (x^{p})$ where $f (x)$ is the characteristic polynomial of an Nth order linear recurrence
J. Harrington and L. Jones [86] give conditions for the monogenity of $f (x^{p^{n}})$ where $f (x) = x^{m} + a x^{m - 1} + b$
S. Kaur, S. Kumar and L. Remete [134] consider monogenity of $f (x^{k})$ where $f (x) = x^{d} + A \cdot h (x), deg h < d$

Let us recall a typical statement:

Theorem 9. (J. Harrington and L. Jones [85])

Let a and b be positive integers, and let p be a prime. Then the polynomial

Φ_{p^{a}} (Φ_{2^{b}} (x))

is monogenic, where

Φ_{N} (x)

is the cyclotomic polynomial of index N.

5.4. Connection with Primes

L. Jones [123,124,127] and J. Harrington and L. Jones [87] detected relations of monogenity of power compositional polynomials with properties of primes. We present here one of these statements.

For a recurrence sequence

U_{0} = 0, U_{1} = 1

and

U_{n} = k U_{n - 1} + U_{n - 2}

(U_{n})

is periodic modulo any integer. Denote by

π_{k} (m)

its period length modulo m. The prime p is called a k-Wall-Sun-Sun prime, if

U_{π_{k} (p)} \equiv 0 (mod p^{2}) .

Theorem 10. (L. Jones [123])

Let

D = k^{2} + 4

k \equiv 1 (mod 2)

, and

D = {(k / 2)}^{2} + 1

k \equiv 0 (mod 2)

. Suppose that

k \neg \equiv 0 (mod 4)

and that D is squarefree. Let h denote the class number of

Q (\sqrt{D})

. Let

s \geq 1

be an integer such that, for every odd prime divisor p of s, D is not a square modulo p and

gcd (p, h D) = 1

. Then

x^{2 s^{n}} - k x^{s^{n}} - 1

is monogenic for all integers

n \geq 1

if and only if no prime divisor of s is a k-Wall-Sun-Sun prime.

5.5. Number of Generators of Power Integral Bases

Some further results considered the number of non-equivalent generators of power integral bases:

M. Kang and D. Kim [132] considered the number of monogenic orders in pure cubic fields
J. H. Evertse [31] considered "rationally monogenic" orders of number fields
S. Akhtari [2] showed that a positive proportion of cubic number fields, when ordered by their discriminant, are not monogenic
L. Alpöge, M. Bhargava, A. Shnidman [4] showed that if isomorphism classes of cubic fields are ordered by absolute discriminant, then a positive proportion are not monogenic and yet have no local obstruction to being monogenic (that is, the index form equations represent $+ 1$ or $- 1$ mod p for all primes p)
M. Bhargava [20] proves that an order O in a quartic number field can have at most 2760 inequivalent generators of power integral bases (and at most 182 if $| D (O) |$ is suffciently large). The problem is reduced to counting the number solutions of cubic and quartic Thue equations, somewhat analogously like described in Section 4.4, using a refined enumeration
S. Akhtari [3] gives another proof of Bhargava’s result [20]: she uses the more direct approach of Section 4.4 and applies sharp bounds for the numbers of solutions of cubic and quartic Thue equations

5.6. Miscellaneous

In addition to the above lists, there were several further interesting statements achieved for monogenity. We try to recall them here.

H. H. Kim [139] showed that the number of monogenic dihedral quartic extensions with absolute discriminant $\leq X$ is of size $O (X^{3 / 4} {(log X)}^{3})$
N. Khan, S. Katayama, T. Nakahara and T. Uehara [137] proved that the composite of a totally real field with a cyclotomic field of odd conductor $\geq 3$ or even $\geq 8$ has no power integral basis
N. Khan, T. Nakahara and H. Sekiguchi [136] proved that there are exactly three monogenic cyclic sextic fields of prime-power conductor, namely $Q (ζ_{7}), Q (ζ_{9})$ and the maximal real subfield of $Q (ζ_{13})$
D. Gil-Mun̆oz and M. Tinková [81] considered the indices of non-monogenic simplest cubic polynomials
L. Jones [122] considered infinite families of monogenic Pisot (anti-Pisot) polynomials
A. Jakhar and S. K. Khanduja [98] gave lower bounds for the p-index of a polynomial
M. Castillo, [25] showed e.g. that $Q (α_{n}), n \geq 1$ is monogenic, where $α_{0} = 1$ and $α_{n} = \sqrt{2 + α_{n - 1}}$ for $n \geq 1$
T. Kashio and R. Sekigawa [133] showed that a monogenic normal cubic field is a simplest cubic field for some parameter
F. E. Tanoé [153] considered monogenity of biquadratic fields using a special integer basis
K. V. Kouakou and F. E. Tanoé [140,154] and F. E. Tanoé and V. Kouassi [155] considered monogenity of triquadratic fields
Aruna C. and P. Vanchinathan [7] showed that an infinite number of so called exceptional quartic fields are monogenic

5.7. Explicit Calculations, Algorithms

The powerful methods of Dedekind criterion and Newton polygons often decides about the monogenity of number fields. However, to explicitly determine all inequivalent generators of power integral bases one needs to perform calculations. These algorithms usually involve Baker type estimates, reduction method and enumeration algorithms, cf. [64]. There are efficient algorithms for low degree fields and some more complicated methods for higher degree fields. Since these procedures usually require considerable CPU time, if the number field is of high degree, or we need information about a large number of fields, then we turn to the so called "fast" algorithms for determining "small" solutions. This yields a fast method to determine solutions of the index form equation with absolute values, say

\leq 10^{100}

. These algorithms determine all solutions with a high probability but do not exclude extremely large solutions (which, however, nobody has ever met).

We collect here some recent results involving explicit determination of generators of power integral bases.

Z. Franŭsić and B. Jadrijević [63] calculated generators of relative power integral bases in a family of quartic extensions of imaginary quadratic fields
I. Gaál [65] showed that index form equations in composites of a totally real cubic field and a complex quadratic field can be reduced to absolute Thue equations
I. Gaál [68] showed that the index form equations in composites of a totally real field and a complex quadratic field can be reduced to the absolute index form equations of the totally real field
I. Gaál [66] considered generators of power integral bases in fields generated by monogenic trinomials of type $x^{6} + 3 x^{3} + 3 a$
I. Gaál [67] considered generators of power integral bases in fields generated by monogenic binomial compositions of type ${(x^{3} - b)}^{2} + 1$
I. Gaál [70] gave an efficient method to determine all generators of power integral bases of pure sextic fields
I. Gaál and L. Remete [78] considered monogenity in octic fields of type $K = Q (\sqrt[4]{a + b i})$
I. Gaál [69] determined "small" solutions of the index form equation in $K = Q (\sqrt[6]{m})$ , for $- 5000 < m < 0$ such that $x^{6} - m$ is monogenic (1521 fields) Experience: $\sqrt[6]{m}$ is the only generator of power integral bases
I. Gaál [71] determined "small" solutions of index form equations in $K = Q (\sqrt[8]{m})$ , $- 5000 < m < 0$ such that $x^{8} - m$ is monogenic (2024 fields) Experience: $\sqrt[8]{m}$ is the only generator of power integral bases, except for $m = - 1$
I. Gaál [72] extended [54] on monogenity properties of trinomials of type $x^{4} + a x^{2} + b$
I. Gaál [73] calculated generators of power integral bases in families of number fields generated by a root of monogenic quartic polynomials considered in [88]

In [72,73] the method described in Section 4.4 was used, in [63,71,78], its relative analogue, see [64,76].

Also here we recall some typical statements:

Theorem 11. (I. Gaál [68])

Let L be a totally real number field,

M = Q (\sqrt{d})

d < 0

squarefree, assume

gcd (D_{L}, D_{M}) = 1

. If α generates a power integral basis in

K = L M

, then

α = a + β \pm ω

, where

a \in Z

, β generates a power integral basis in L and

(1, ω)

is integral basis in M.

Theorem 12. (L. El Fadil and I. Gaál [54])

Assume

a > 1, b > 1

and

f (x) = x^{4} + a x^{2} + b

is irreducible and monogenic. If a, b are not of type

a = \frac{u \pm 1}{v}, b = \frac{u^{2} - 1}{4 v^{2}}

for some

u, v \in Z, v \neq 0, u \neq 1

, then up to equivalence the root α of

f (x)

is the only generator of power integral bases in

K = Q (α)

6. Further Research

The above lists of results indicate what was already done and what is still missing. It would be very interesting to somehow describe monogenity properties of quartic fields and maybe quintic fields. This would require study of quintinomials and sextinomials.

What general exponents of binomials and trinomials can still be considered? Is it possible to describe in general monogenity properties of arbitrary trinomials of degree

\leq 9

How can one extend the available algorithms to be able to calculate solutions of index form equations in higher degree fields?

All these and several other questions are to be answered. As it is seen from the above, in addition to some new ideas, often the application of old, forgotten methods may also help.

Funding

This research received no external funding.

Data Availability Statement

No data were used in this article.

Acknowledgments

The author is grateful to all participants of the online meetings "Monogenity and power integral bases". The talks encouraged the research on monogenity.

Conflicts of Interest

The author declares no conflicts of interest.

References

S. Ahmad, T. Nakahara and M. Syed, Power integral bases for certain pure sextic fields, Int. J. Number Theory 10(2014), 2257-2265.
S. Akhtari, Counting monogenic cubic orders, in: Nathanson, Melvyn B. (ed.), Combinatorial and additive number theory III. Papers based on talks given at the CANT 2017 and 2018 workshops, New York, NY, USA, May 2017 and May 2018. Cham: Springer. Springer Proc. Math. Stat. 297(2020), 13-24.
S. Akhtari, Quartic index form equations and monogenizations of quartic orders, Essent. Number Theory 1(2022), 57-72.
L. Alpöge, M. Bhargava and A. Shnidman, A positive proportion of cubic fields are not monogenic yet have no local obstruction to being so, arXiv:2011.01186 (2020).
S. Arpin, S. Bozlee, L. Herr and H. Smith, The scheme of monogenic generators I: Representability, Res. Number Theory 9(2023), Paper No. 14, 33 p.
S. Arpin, S. Bozlee, L. and H. Smith, The scheme of monogenic generators. II: Local monogenicity and twists, Res. Number Theory 9(2023), Paper No. 43, 39 p.
Aruna C. and P. Vanchinathan, Exceptional Quartics are Ubiquitous, arXiv:2306.17556 (2023).
Z. S. Aygin and K. D. Nguyen, Monogenic pure cubics, J. Number Theory 219, 356-367, corregindum J. Number Theory 242(2023), 244.
H. Ben Yakkou, The index of the septic number field defined by $x^{7} + a x^{5} + b$ , arXiv:2206.14345 (2022).
H. Ben Yakkou, On monogenity of certain number fields defined by $x^{8} + a x + b$ , Acta Math. Hung. 166(2022), 614-623.
H. Ben Yakkou, On monogenity of certain number fields defined by $x^{2^{r}} + a x^{m} + b$ , arXiv:2203.10413 (2022).
H. Ben Yakkou, On nonmonogenic number fields defined by trinomials of type $x^{n} + a x^{m} + b$ , Rocky Mt. J. Math. 53(2023), 685-699.
H. Ben Yakkou, On indices and monogenity of quartic number fields defined by quadrinomials, arXiv:2401.12782 (2024).
H. Ben Yakkou and B. Boudine, On the index of the octic number field defined by $x^{8} + a x + b$ , Acta Math. Hung. 170(2023), 585-607.
H. Ben Yakkou, A. Chillali and L. El Fadil, On power integral bases for certain pure number fields defined by $x^{2^{r} \cdot 5^{s}} - m$ , Commun. Algebra 49(2021), 2916-2926.
H. Ben Yakkou and L. El Fadil, On monogenity of certain pure number fields defined by $x^{p^{r}} - m$ , Int. J. Number Theory 17(2021), 2235-2242.
H. Ben Yakkou and L. El Fadil, On monogenity of certain number fields defined by trinomials, Funct. Approximatio, Comment. Math. 67(2022), 199-221.
H. Ben Yakkou and O.Kchit, On power integral bases of certain pure number fields defined by $x^{3^{r}} - m$ , Sao Paulo J. Math. Sci. 16(2022), 1072-1079.
H. Ben Yakkou and P. Tiebekabe, On common index divisors and monogenity of of the nonic number field defined by a trinomial $x^{9} + a x + b$ , arXiv:2212.05029 (2022).
M. Bhargava, On the number of monogenizations of a quartic order (with an appendix by Shabnam Akhtari), Publ. Math. Debr. 100(2022), 513-531.
B. J. Birch and J. R. Merriman, Finiteness theorems for binary forms with given discriminant, Proc. London Math. Soc., 24(1972), 385–394.
W. Bosma, J. Cannon and C. Playoust, The Magma Algebra System. I. The User Language. J. Symbolic Comput. 24(1997), 235-265.
O. Boughaleb, A. Soullami and M. Sahmoudi, On relative monogeneity of a family of number fields defined by $x^{p^{n}} + {a X}^{p^{s}} - b$ , Bol. Soc. Mat. Mex., III. Ser. 29(2023), Paper No. 5, 13 p.
B. W. Char, K. O. Geddes, G. H. Gonnet, M. B. Monagan, S. M. Watt (eds.), MAPLE, Reference Manual, Watcom Publications, Waterloo, Canada, 1988.
M. Castillo, A dynamical characterization for monogenity at every level of some infinite 2-towers, Canad. Math. Bull. 65(2022), 806-814.
M. E. Charkani and A. Deajim, Generating a power basis over a Dedekind ring, J. Number Theory 132(2012), 2267-2276.
H. Cohen, A Course in Computational Algebraic Number Theory, GTM 138, Springer-Verlag Berlin Heidelberg, 1993.
A. Deajim and L. El Fadil, A note on generating a power basis over a Dedekind ring, Stud. Sci. Math. Hung. 58(2021), 367-370.
R. Dedekind, Über den Zusammenhang zwischen der Theorie der Ideale und der Theorie der höheren Kongruenzen, Göttingen Abhandlungen 23 (1878) 1–23.
H. T. Engstrom, On the common index divisor of an algebraic number field, Trans. Am. Math. Soc. 32(1930), 223-237.
J. H. Evertse, Orders with few rational monogenizations, Acta Arith.(2023) 210, 307-335.
L. El Fadil, On Newton polygon techniques and factorization of polynomial over Henselian valued fields, J. Algebra and Appl 19(10), 9p. (2020), Article ID 2050188.
L. El Fadil, On power integral bases for certain pure number fields defined by $x^{24} - m$ , Stud. Sci. Math. Hung. 57(2020), 397-407.
L. El Fadil, On integral bases and monogeneity of pure sextic number fields with non-squarefree coefficients, J. Number Theory 228(2021), 375-389.
L. El Fadil, On power integral bases for certain pure number fields defined by $x^{36} - m$ , Stud. Sci. Math. Hung. 58(2021), 371-380.
L. El Fadil, On power integral bases for certain pure number fields defined by $x^{2 \cdot 3^{k}} - m$ , Acta Arith. 201(2021), 269-280.
L. El Fadil, A note on monogenity of pure number fields, arXiv:2106.00004, (2021).
L. El Fadil, On power integral bases of certain pure number fields defined by $x^{3^{r} \cdot 7^{s}} - m$ , Colloq. Math. 169(2022), 307-317.
L. El Fadil, On power integral bases for certain pure number fields, Publ. Math. Debr. 100(2022), 219-231.
L. El Fadil and A. Najim, On monogenity of certain pure number fields defined by $x^{2^{u} \cdot 3^{v}} - m$ , Acta Sci. Math. 88(2022), 581-594.
L. El Fadil, On power integral bases for certain pure number fields defined by $x^{18} - m$ , Commentat. Math. Univ. Carol. 63(2022), 11-19.
L. El Fadil, On power integral bases for certain pure sextic fields, Bol. Soc. Parana. Mat. 40(2022), Paper No. 143, 7 p.
L. El Fadil, On monogenity of certain pure number fields defined by $x^{20} - m$ , Sao Paulo J. Math. Sci. 16(2022), 1063-1071.
L. El Fadil, On monogenity of certain pure number fields defined by $x^{2^{u} \cdot 3^{v} \cdot 5^{t}} - m$ , arXiv:2204.02436 (2022).
L. El Fadil, On common index divisors and monogenity of certain number fields defined by $x^{5} + a x^{2} + b$ , Commun. Algebra 50(2022), 3102-3112.
L. El Fadil, On non monogenity of certain number fields defined by trinomials $x^{6} + a x^{3} + b$ , J. Number Theory 239(2022), 489-500.
L. El Fadil, On the index divisors and monogenity of number fields defined by $x^{5} + a x^{3} + b$ , Quaest. Math. 46(2023), 2355-2365.
L. El Fadil, On common index divisor and monogenity of certain number fields defined by trinomials $x^{6} + A X + B$ , Quaest. Math. 46(2023), 1609-1627.
L. El Fadil, On index and monogenity of certain number fields defined by trinomials. Math. Slovaca 73(2023), 861-870.
L. El Fadil, A note on indices of quartic number fields defined by trinomials $x^{4} + a x + b$ , Commun. Algebra 52(2024), 1349-1359.
L. El Fadil, H. Ben Yakkou and J. Didi, On power integral bases of certain pure number fields defined by $x^{42} - m$ , Bol. Soc. Mat. Mex., III. Ser. 27(2021), Paper No. 81, 10 p.
L. El Fadil, H. Choulli and O. Kchit, On monogenity of certain pure number fields defined by $x^{60} - m$ , Acta Math. Vietnam. 48(2023), 283-293.
L. El Fadil and M. Faris, On power integral bases of certain pure number fields defined by $x^{84} - m$ , Rev. Unión Mat. Argent. 65(2023), 197-211.
L. El Fadil and I. Gaál, On the monogenity of quartic number fields defined by $x^{4} + a x^{2} + b$ , arXiv:2204.03226 (2022).
L. El Fadil and I. Gaál, On integral bases and monogenity of pure octic number fields with non-square free parameters, arXiv:2202.04417.
L. El Fadil and I. Gaál, Integral bases and monogenity of pure number fields with non-square free parameters up to degree 9, Tatra Mt. Math. Publ. 83(2023), 61-86.
L. El Fadil and O. Kchit, On index divisors and monogenity of certain sextic number fields defined by $x^{6} + a x^{5} + b$ , arXiv:2206.05529 (2022).
L. El Fadil and O. Kchit, On index divisors and monogenity of certain septic number fields defined by $x^{7} + a x^{3} + b$ , Commun. Algebra 51(2023), 2349-2363.
L. El Fadil and O. Kchit, The index of certain nonic number fields defined by $x^{9} + a x^{2} + b$ , arXiv:2310.13509, (2023).
L. El Fadil and O. Kchit, On monogenity of certain pure number fields defined by $x^{2^{r} \cdot 7^{s}} - m$ , Bol. Soc. Parana. Mat. 41(2023), Paper No. 138, 9 p.
L. El Fadil and O. Kchit, On index divisors and monogenity of certain number fields defined by $x^{12} + a x^{m} + b$ , Ramanujan J. 63(2024), 451-482.
L. El Fadil, J. Montes and E. Nart, Newton polygons and p-integral bases of quartic number fields, J. Algebra and Appl. 11(4), 33p. (2012), Article ID 1250073.
Z. Franŭsić and B. Jadrijević, Computing relative power integral bases in a family of quartic extensions of imaginary quadratic fields Publ. Math. Debrecen 92(2018), 293ű-315.
I. Gaál, Diophantine equations and power integral bases. Theory and algorithms. 2nd edition, Birkhäuser, Boston, 2019.
I.Gaál, Monogenity in totally complex sextic fields, revisited, JP J. Algebra Number Theory Appl. 47(2020), 87-98.
I. Gaál, An experiment on the monogenity of a family of trinomials, JP J. Algebra Number Theory Appl. 51(2021), 97-111.
I. Gaál, On the monogenity of certain binomial compositions, JP J. Algebra Number Theory Appl. 57(2022), 1-16.
I. Gaál, Monogenity in totally real extensions of imaginary quadratic fields with an application to simplest quartic fields Acta Sci. Math. 89(2023), 3-12.
I. Gaál, A note on the monogenity of totally complex pure sextic fields, JP J. Algebra Number Theory Appl. 60(2023), 85-96.
I. Gaál, Calculating generators of power integral bases in pure sextic fields, Funct. Approximatio, Comment. Math. 70(2024), 85-100.
I. Gaál, On the monogenity of totally complex pure octic fields, arXiv:2402.09293 (2024).
I. Gaál. A note on the monogenity of some trinomials of type $x^{4} + a x^{2} + b$ JP J. Algebra Number Theory Appl. 63(2024), 265-279.
I. Gaál, Calculating power integral bases in some quartic fields corresponding to monogenic families of polynomials, arXiv:2405.13429 (2024).
I. Gaál, A. Petho and M. Pohst, On the resolution of index form equations in quartic number fields, J. Symbolic Comput., 16(1993), 563–584.
I. Gaál, A. Petho and M. Pohst, Simultaneous representation of integers by a pair of ternary quadratic forms – with an application to index form equations in quartic number fields, J. Number Theory, 57(1996), 90–104.
I. Gaál and M. Pohst, Computing power integral bases in quartic relative extensions, J. Number Theory 85 (2000), 201-219.
I. Gaál and L. Remete, Integral bases and monogenity of pure fields, J. Number Theory 173(2017), 129-146.
I. Gaál and L. Remete, On the monogenity of pure quartic relative extensions of Q(i), Acta Sci. Math. 89(2023), 357-371.
T.A. Gassert, A note on the monogeneity of power maps, Albanian J. of Math. 11(2017), 3-12.
T. A. Gassert, H. Smith and K. E. Stange, A family of monogenic S₄ quartic fields arising from elliptic curves, J. Number Theory 197(2019), 361-382.
D. Gil-Munoz and M. Tinková, Additive structure of non-monogenic simplest cubic fields, arXiv:2212.00364 (2022).
J. Guardia, J. Montes and E. Nart, Newton polygons of higher order in algebraic number theory, Trans. Amer. Math. Soc. 364(2012) 361–416.
K. Gyory, Sur les polynômes a coefficients entiers et de discriminant donne, III, Publ. Math. (Debrecen), 23(1976), 141–165.
J. Harrington and L. Jones, Monogenic binomial compositions, Taiwanese J. Math. 24(2020), 1073-1090.
J. Harrington and L. Jones, Monogenic cyclotomic compositions, Kodai Math. J. 44(2021), 115-125.
J. Harrington and L. Jones, The Irreducibility and Monogenicity of Power-Compositional Trinomials, arXiv:2204.07784 (2022).
J. Harrington and L. Jones, A note on generalised Wall-Sun-Sun primes, Bull. Aust. Math. Soc. 108(2023), 373-378.
J. Harrington and L. Jones, Monogenic quartic polynomials and their Galois groups, arXiv:2404.05487v2.
H. Hasse, Zahlentheorie, Akademie-Verlag, Berlin, 1963.
K. Hensel, Theorie der algebraischen Zahlen, Teubner Verlag, Leipzig, 1908.
R. Ibarra, H. Lembeck, M. Ozaslan, H. Smith and K. E. Stange, Monogenic fields arising from trinomials, Involve 15(2022), 299-317.
A. Jakhar, On primes dividing the index of a quadrinomial, Rocky Mt. J. Math. 50(2020), 2117-2125.
A. Jakhar, Nonmonogenity of number fields defined by trinomials, New York J. Math. 28(2022), 650-658.
A. Jakhar, On nonmonogenic algebraic number fields., Rocky Mt. J. Math. 53(2023), 103-110.
A. Jakhar and R. Kalwaniya, On the index divisors of certain number fields, arXiv:2303.00484 (2023).
A. Jakhar, R. Kalwaniya and P. Yadav, A study of monogenity of binomial composition, arXiv:2402.10131 (2024).
B. Jhorar and S. K. Khanduja, On power basis of a class of algebraic number fields, Int. J. Number Theory 12(2016), 2317-2321.
A. Jakhar and S. K. Khanduja, On the index of an algebraic integer and beyond, J. Pure Appl. Algebra 224(2020), Article ID 106281, 10 p.
A. Jakhar, S. K. Khanduja and N. Sangwan, On prime divisors of the index of an algebraic integer, J. Number Theory 166(2016), 47-61.
A. Jakhar, S. K. Khanduja and N. Sangwan, Characterization of primes dividing the index of a trinomial, Int. J. Number Theory 13(2017), 2505-2514.
A. Jakhar, S. Kaur and S. Kumar, Common index divisor of the number fields defined by $x^{5} + a x + b$ , Proc. Edinb. Math. Soc., II. Ser. 65(2022), 1147-1161.
A. Jakhar and S. Kaur, A note on non-monogenity of number fields arised from sextic trinomials, Quaest. Math. 46(2023), 833-840.
A. Jakhar, S. Kaur and S. Kumar, On power basis of a class of number fields, Mediterr. J. Math. 20(2023), Paper No. 315, 11 p.
A. Jakhar, S. Kaur and S. Kumar, Non-monogenity of certain octic number fields defined by trinomials, Colloq. Math. 171(2023), 145-152.
A. Jakhar, S. Kaur and S. Kumar, On common index divisor of the number fields defined by $x^{7} + a x + b$ , arXiv:2301.00365 (2023).
A. Jakhar, S. Kaur and S. Kumar, On non-monogenity of the number fields defined by certain quadrinomials, Commun. Algebra 51(2023), 2448-2459.
A. Jakhar and S. Kumar, On nonmonogenic number fields defined by $x^{6} + a x + b$ , Can. Math. Bull. 65(2022), 788-794.
A. Jakhar and S. Kumar, Non-monogenity of some number fields generated by binomials or trinomials of prime-power degree, J. Algebra Appl. 23(2024), Article ID 2450095, 8 p.
L. Jones, A brief note on some infinite families of monogenic polynomials, Bull. Aust. Math. Soc. 100(2019), 239-244.
L. Jones, Generating infinite families of monogenic polynomials using a new discriminant formula, Albanian J. Math. 14(2020), 37-45.
L. Jones, Monogenic polynomials with non-squarefree discriminant, Proc. Am. Math. Soc. 148(2020), 1527-1533.
L. Jones, Monogenically stable polynomials, Albanian J. Math. 15(2021), 85-98.
L. Jones, Infinite families of reciprocal monogenic polynomials and their Galois groups, New York J. Math. 27(2021), 1465-1493.
L. Jones, Sextic reciprocal monogenic dihedral polynomials, Ramanujan J. 56(2021), 1099-1110.
L. Jones, Infinite families of non-monogenic trinomials, Acta Sci. Math. 87(2021), 95-105.
L. Jones, Some new infinite families of monogenic polynomials with non-squarefree discriminant, Acta Arith. 197(2021), 213-219.
L. Jones, The monogenity of power-compositional Eisenstein polynomials, Ann. Math. Inform. 55(2022), 93-113.
L. Jones, Reciprocal monogenic quintinomials of degree 2ⁿ, Bull. Aust. Math. Soc. 106(2022), 437-447. .
L. Jones, Infinite families of monogenic quadrinomials, quintinomials and sextinomials, Colloq. Math. 169(2022), 1-10.
L. Jones, On necessary and sufficient conditions for the monogeneity of a certain class of polynomials, Math. Slovaca 72(2022), 591-600.
L. Jones, Monogenic reciprocal trinomials and their Galois groups, J. Algebra Appl. 21(2022), Article ID 2250026, 11 p.
L. Jones, Monogenic Pisot and anti-Pisot polynomials, Taiwanese J. Math. 26(2022), 233-250.
L. Jones, A connection between the monogenicity of certain power-compositional trinomials and k-Wall-Sun-Sun primes, arXiv:2211.14834.
L. Jones, Generalized Wall-Sun-Sun primes and monogenic power compositional trinomials, Albanian J. Math. 17(2023), 3-17.
L. Jones, On the monogenicity of power-compositional Shanks polynomials, Funct. Approximatio, Comment. Math. 69(2023), 93-103.
L. Jones, The monogenicity of power-compositional characteristic polynomials, arXiv:2311.08875 (2023).
L. Jones, A new condition for k-Wall-Sun-Sun primes, Taiwanese J. Math. 28(2024), 17-28.
L. Jones, Monogenic cyclic quartic trinomials, arXiv:2404.17869 (2024).
L. Jones, Monogenic even octic polynomials and their Galois groups, arXiv:2404.17921 (2024).
L. Jones and T. Phillips, Infinite families of monogenic trinomials and their Galois groups, Int. J. Math. 29(2018), Article ID 1850039, 11 p.
L. Jones and D. White, Monogenic trinomials with non-squarefree discriminant, Int. J. Math. 32(2021), Article ID 2150089, 21 p.
M. Kang and D. Kim, The proportion of monogenic orders of prime power indices of the pure cubic field, arXiv:2306.13295 (2023).
T. Kashio and R. Sekigawa, The characterization of cyclic cubic fields with power integral bases, Kodai Math. J. 44(2021), 290-306.
S. Kaur, S. Kumar and L. Remete, On the index of power compositional polynomials, arXiv:2404.17351 (2024).
O. Kchit, On the index divisors and monogenity of certain nonic number fields, arXiv:2307.03284.
N. Khan, T. Nakahara and H. Sekiguchi, An ideal theoretic proof on monogenity of cyclic sextic fields of prime power conductor, J. Number Theory 198(2019), 43-51.
N. Khan, S. Katayama, T. Nakahara and T. Uehara, Monogenity of totally real algebraic extension fields over a cyclotomic field, J. Number Theory 158(2016), 348-355.
S. K. Khanduja and B. Jhorar, When is $R [ϑ]$ integrally closed? J. Algebra Appl. 15(2016), Article ID 1650091, 7 p.
H. H. Kim, Monogenic dihedral quartic extensions, Ramanujan J. 50(2019), 459-464.
K. V. Kouakou and F. E. Tanoé, Chatelain’s integral bases for triquadratic number fields, Afr. Mat. 28(2017), 119-149.
J. Montes and E. Nart, On a theorem of Ore, J. Algebra, 146(2) (1992) 318–334.
L. J. Mordell, Diophantine Equations, Academic Press, New York–London, 1969.
W. Narkiewicz, Elementary and Analytic Theory of Algebraic Numbers, 3rd edn. Springer Verlag, Berlin, 2004.
E. Nart, On the index of a number field, Trans. Amer. Math. Soc., 289(1985), 171-183.
J. Neukirch, Algebraic Number Theory, Springer Verlag, Berlin (1999).
O. Ore, Newtonsche Polygone in der Theorie der algebraischen Korper, Math. Ann., 99 (1928), 84–117.
M. P. Pohst and H. Zassenhaus, Algorithmic algebraic number theory,Encyclopedia of mathematics and its applications, em Campridge University Press, 1989.
M. Sahmoudi and M. E. Charkani, On relative pure cyclic fields with power integral bases, Math. Bohem. 148(2023), 117-128.
R. Sekigawa, Rikuna’s generic cyclic polynomial and the monogenity, J. Number Theory 231(2022), 239-250 .
A. Soullami, M. Sahmoudi and O. Boughaleb, On relative power integral basis of a family of numbers fields, Rocky Mt. J. Math. 51(2021), 1443-1452.
H. Smith, Two families of monogenic S₄ quartic number fields, Acta Arith. 186(2018), 257-271.
H. Smith, The monogeneity of radical extensions, Acta Arith. 198(2021), 313-327.
F. E. Tanoé, Chatelain’s integer bases for biquadratic fields, Afr. Mat. 28(2017), 727-744.
F. E. Tanoé and K. V. Kouakou, Diophantine proof of non-monogeneity for triquadratic number fields with odd discriminant, Fundamental J. Math. and Math. Sci. 15(2021), 9-37.
F. E. Tanoé and V. Kouassi, Generators of power integral bases of $Q (ζ_{24}) = Q (\sqrt{- 3}, \sqrt{2}, \sqrt{- 1})$ , Annales Mathématiques Africaines 5(2025), 117-131.

1	https://sway.cloud.microsoft/F2kZzeZ3bmD4dFfy?ref=Link

Figure 1.

N_{ϕ}^{+} f

Figure 1.

N_{ϕ}^{+} f

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Monogenity and Power Integral Bases: Recent Developments

Abstract

1. Purpose

2. Introduction

3. Structure of the Paper

4. Tools

4.1. Dedekind’s Criterion

4.2. The Field Index

4.3. Newton Polygon Method

4.4. Algorithmic Methods

5. Results

5.1. Pure Fields, Trinomials, Quadrinomials, etc.

5.2. The Relative Case

5.3. Composite Polynomials

5.4. Connection with Primes

5.5. Number of Generators of Power Integral Bases

5.6. Miscellaneous

5.7. Explicit Calculations, Algorithms

6. Further Research

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe