Second Order Terminal Sliding Mode Control for Trajectory-Tracking of a Differential Drive Robot

Preprint

Article

Second Order Terminal Sliding Mode Control for Trajectory-Tracking of a Differential Drive Robot

Altmetrics

Downloads

136

Views

Comments

A peer-reviewed article of this preprint also exists.

Ngoc-Tuan Tran Cao,Thanh-Binh Pham,Tan-No Nguyen,

Duc-Lung Vu

Nguyen-Vu Truong^*

Ngoc-Tuan Tran Cao,Thanh-Binh Pham,Tan-No Nguyen,

Duc-Lung Vu

Nguyen-Vu Truong^*

This version is not peer-reviewed

Submitted:

27 May 2024

Posted:

27 May 2024

You are already at the latest version

Alerts

Abstract

Abstract. This paper proposes a Second Order Terminal Sliding Mode (2TSM) approach to the trajectory tracking of Differential Drive Mobile Robot (DDMR). Within this cascaded control scheme, the 2TSM dynamic controller, at the inner most loop, tracks the robot’s velocity quantities; while a kinematic controller, at the outer most loop, regulates the robot’s positions. In this manner, chattering is greatly attenuated and finite time convergence is guaranteed by the second order TSM manifold which involves higher order derivatives of the state variables, resulting in inherently robust as well as fast and better tracking precision. The simulation results demonstrate the merit of the proposed control methods.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Differential Drive Mobile Robot (DDMR) trajectory tracking has been a popular research topic in recent years [1,2,3,8,9,10,11,12,13,14,15,16,19,20,21,25]. Practical approaches [1,2,8,9,12,13,14,15,16] consider the DDMR’s dynamics in addition to its kinematics in the control loop in order to attain the tracking performance, especially in the presence of disturbances and unmodeled dynamics. These includes actuactor dynamics, systems’s instrinsic nonlinearities, changes in load, working surface/terrain, etc. which commonly encounter in many industrial applications, such as Automated Guided Vehicle (AGV), Automated Folklift Robot (AFV) and so on.

Among these methods, Sliding Mode Control [8,9,14,15,17,18,19,20,21] has emerged to be an attractive alternative due to its simplicity in implementation; and more importantly its fast dynamic response as well as strong robustness to external disturbances and parameter’s variations. Conventional linear SMC method (LSM), however, poses serious drawbacks because of its instinctive chattering phenomenon which makes it less likely efficient to be used in electro-mechanical system control scheme [4,5,6,7]. This motivates further research and development of chattering-free SMC techniques, including nonlinear terminal sliding mode (TSM), i.e. [4,5,6,7] as well as higher order sliding mode control methods, i.e.[7,22,23,24].

TSM method poccesses superior properties in both finite-time convergence, excellent tracking precision and better chattering attenuation in comparison to conventional LSM control systems. Nonetheless, in this particular application, first order TSM based controller would not be able to totally suppress chattering from the torque inputs generated by the robot’s dynamic models, making it less favourable to be employed in practical application since the forementioned “chattering” would cause severe damages to the robot’s actuacting systems.

This paper proposes a second order TSM control scheme (2TSM) for DDMR’s trajectory tracking problem. Here, by dealing with derivatives of the state variables at higher order incorporated within the nonlinear 2TSM manifold, finite-time convergence of tracking errors (i.e. velocity quantities) to zeros is guaranteed; singularities as appeared in conventional first order TSM (i.e [4]) can be avoided; and the resulted control signals (torque’s commands) are continuous, enabling the proposed method to be directly applied in practical applications. It is the original motivation of this work.

The remainder of the paper is organized as follows. Section 2 describes both the kinematic and dynamic models of DDMR system. The finite-time convergence characteristics of 2TSM manifold is discussed in Section 3. The 2TSM based controller design is presented in Section 4. The simulation results are documented in Section 5, illustrating outstanding merits of the proposed 2TSM control scheme for DDMR’s trajectory tracking in comparison to LSM and TSM methods. And finally, Section 6 concludes the paper.

2. DDMR’s Model

In order to describe the position of the Differential Drive mobile robot (DDMR), two different coordinates need to be defined.

Global coordinate system: This coordinate is used to defined exact position of DDMR in the real environment to reach desired target, it is denoted as { $X^{G}$ , $Y^{G}$ }.
Robot Coordinate system: This is local coordinate that attached to DDMR’s frame, it is denoted as { $X^{R}$ , $Y^{R}$ }.

As shown in Figure 1, point A is the origin of the Robot coordinate, also the position of DDMR respect to Global I frame, which is denoted as:

q^{G} = [\begin{matrix} x_{a} \\ y_{a} \\ θ \end{matrix}]

(1)

The position of any point on Robot can be defined in Robot coordinate or Global coordinate as follow:

X^{G} = [\begin{matrix} \cos θ & - \sin θ & 0 \\ \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}] X^{R}

(2)

where

X^{G} = [\begin{matrix} x^{G} \\ y^{G} \\ θ^{G} \end{matrix}], and X^{R} = [\begin{matrix} x^{R} \\ y^{R} \\ θ^{R} \end{matrix}]

is the coordinate of given point in the global frame and the robot frame respectively. Equation (2) is at great importance in finding position of DDMR from its linear and angular velocity, to be discussed in next section.

The motion of DDMR is characterized by two constraints, which are derived from two assumptions: no lateral slip and pure rolling. This means it is assumed that there is no slipping of the wheel along its longitudinal axis and no skidding along its orthogonal axis.

No lateral slip motion

${\dot{y}}_{a}^{r} = 0$

(3)
Pure rolling constraint

In the context of this paper, with the assumption of zero slipping, the velocity of point P, as well as the velocity of each wheel (Figure 2), is expressed by the following equations:

\{\begin{matrix} v_{p r} = v_{r} = R \dot{φ_{r}} \\ v_{p L} = v_{L} = R \dot{φ_{L}} \end{matrix}

(4)

2.1. Kinematic Model

The Kinematic model of DDMR is generalized by following equations [1]:

\{\begin{matrix} v = \frac{v_{r} + v_{L}}{2} = \frac{R (\dot{φ_{r}} + \dot{φ_{L}})}{2} \\ ω = \frac{v_{r} - v_{L}}{2 L} = \frac{R \dot{{(φ}_{r}} - \dot{φ_{L}})}{2 L} \end{matrix}

(5)

where

v

denotes the linear velocity and

ω

refers the angular velocity of DDMR in Robot frame.

The velocity of the DDMR can be expressed in terms of the velocities of the center point A (Figure 1) in the robot frame as follows:

\{\begin{array}{l} \dot{x_{a}^{r}} = \frac{R (\dot{φ_{r}} + \dot{φ_{L}})}{2} \\ \dot{y_{a}^{r}} = 0 \\ \dot{θ} = ω = \frac{R \dot{{(φ}_{r}} - \dot{φ_{L}})}{2 L} \end{array}

(6)

from (6), it gets

[\begin{matrix} \dot{x_{a}^{r}} \\ \dot{y_{a}^{r}} \\ \dot{θ} \end{matrix}] = [\begin{matrix} \frac{R}{2} & \frac{R}{2} \\ 0 & 0 \\ \frac{R}{2 L} & - \frac{R}{2 L} \end{matrix}] [\begin{matrix} \dot{φ_{r}} \\ \dot{φ_{L}} \end{matrix}]

(7)

The velocity of the DDMR in the global frame can be obtained using equations (2) and (7):

{\dot{q}}^{G} = [\begin{matrix} \dot{x_{a}^{r}} \\ \dot{y_{a}^{r}} \\ \dot{θ} \end{matrix}] = [\begin{matrix} \frac{R}{2} \cos θ & \frac{R}{2} \cos θ \\ \frac{R}{2} \sin θ & \frac{R}{2} \sin θ \\ \frac{R}{2 L} & - \frac{R}{2 L} \end{matrix}] [\begin{matrix} \dot{φ_{r}} \\ \dot{φ_{L}} \end{matrix}]

(8)

As a result,

{\dot{q}}^{G} = [\begin{matrix} \dot{x_{a}^{r}} \\ \dot{y_{a}^{r}} \\ \dot{θ} \end{matrix}] = [\begin{matrix} \cos θ & 0 \\ \sin θ & 0 \\ 0 & 1 \end{matrix}] [\begin{matrix} v \\ ω \end{matrix}]

(9)

2.2. Dynamic Model

The dynamic model of the DDMR proposed by Takanori Fukao et al. [3] is reviewed. In this model, all force components are considered. By using the Lagrange Method, a dynamic model of the DDMR is formulated as follows:

\{\begin{matrix} (m + \frac{2}{R^{2}} I_{w}) \dot{v} - m_{c} d ω^{2} = \frac{1}{R} (τ_{R} + τ_{L}) \\ (I + \frac{2 L^{2}}{R^{2}} I_{w}) \dot{ω} + m_{c} d ω v = \frac{L}{R} (τ_{R} - τ_{L}) \end{matrix}

(10)

where:

$τ_{R} {, τ}_{L}$ : The torques of right wheel actuator and the left respectively;
$L$ , R, $d$ : As shown in Figure 1;
$m$ , $m_{c}$ : The total mass of the DDMR and the mass of the DDMR without wheels and its actuators, respectively;
$I_{w}$ : The moment of inertia of each wheel;
$I$ : The total equivalent inertia.
The total equivalent inertia in (10) can be calculated as follow:

$\begin{matrix} I & = I_{C} + 2 I_{m} + 2 I_{w} \\ = m_{C} d^{2} + 2 m_{a} L^{2} + 2 m_{w} R^{2} \end{matrix}$

(11)

where
$m_{w}$ : the mass of each wheel;
$m_{a}$ : the mass of each wheel and its actuator.
The model (10) can be rearranged in the following State Space from:

$[\begin{matrix} A & 0 \\ 0 & B \end{matrix}] [\begin{matrix} \dot{v} \\ \dot{ω} \end{matrix}] = [\begin{matrix} m_{c} d ω \\ - m_{c} d ω v \end{matrix}] + [\begin{matrix} 1 / R & 1 / R \\ L / R & - L / R \end{matrix}] [\begin{matrix} τ_{R} \\ τ_{L} \end{matrix}]$

(12)

where:

$[\begin{matrix} A = m + \frac{2}{R^{2}} I_{w} \\ B = I + \frac{2 L^{2}}{R^{2}} I_{w} \end{matrix}]$

3. Finite-Time Convergence Characteristics of 2TSM Manifold

The following theorem describes the finite-time convergence of relevant state variables once 2TSM manifold is reached.

Theorem 1: The state variable

x (t)

and its derivative

\dot{x} (t)

satisfying:

\ddot{x} + γ_{1} {\dot{x}}^{α} + γ_{2} x^{β} = 0

(13)

where:

0 < α = \frac{q}{p} < 1, β = \frac{α}{2 - α} = \frac{q}{2 p - q}

p > q

are odd positive integers; while

0 < γ_{1}

a n d γ_{2} =

{γ_{1}}^{β + 1} \frac{α^{β}}{{(β + 1)}^{β}} (1 - \frac{α}{2}) > 0

Given the set of initial conditions as

x (0) = x_{0}

and

\dot{x} (0) = - {γ_{1}}^{β / α} {(\frac{α}{β + 1})}^{β / α} {x_{0}}^{1 / (2 - α)}

x (t)

and its derivative

\dot{x} (t)

converge to zeros in finite time

t_{c o n v e r g e n c e} = \frac{α}{α - β} {(\frac{γ_{1} α}{β + 1})}^{- β / α} {x_{0}}^{(α - β) / α}

Proof.

Let

y = \dot{x}

, it gets

\ddot{x} = y \frac{d y}{d x}

and equation (13) converts to the following form:

y \frac{d y}{d x} + γ_{1} y^{α} + γ_{2} x^{β} = 0

y \frac{d y}{d x} + γ_{1} y^{α} = - γ_{2} x^{β} F (y, \dot{y}) = y \frac{d y}{d x} + γ_{1} y^{α} = - γ_{2} x^{β}

(14)

Let us solve for the unforced response of (14)

F (y, \dot{y}) = 0 y \frac{d y}{d x} + γ_{1} y^{α} = 0

(15)

y = 0

is one solution of (15)

In the case of

y \neq 0

, dividing (15) by

y^{α}

gets

y^{1 - α} \frac{d y}{d x} = - γ_{1}

\begin{matrix} \frac{1}{2 - α} y^{2 - α} & = - γ_{1} x + C \\ y^{2 - α} & = - γ_{1} (2 - α) x + C (2 - α) \\ y & = {(\underset{M}{\underset{⏟}{- γ_{1} (2 - α)}} x + \underset{N}{\underset{⏟}{C (2 - α)}})}^{1 / (2 - α)} \\ y & = {(M x + N)}^{1 / (2 - α)} \end{matrix}

(16)

In the presence of a perturbation

u = - γ_{2} x^{β}

, the forced response which describes the generalised solution of

F (y, \dot{y}) = u

takes the following form:

y = {(M x + f (x))}^{1 / (2 - α)}

(17)

where

N = f (x)

is the function of x.

Substitute the following expressions:

y \frac{d y}{d x} = \frac{M + d f / d x}{2 - α} {(M x + f (x))}^{\frac{α}{2 - α}} = \frac{M + d f / d x}{2 - α} {(M x + f (x))}^{β}

γ_{1} y^{α} = {γ_{1} (M x + f (x))}^{\frac{α}{2 - α}} = {γ_{1} (M x + f (x))}^{β}

into Equation (14), it gets

F (y, \dot{y}) = (γ_{1} + \frac{M + \frac{d f}{d x}}{2 - α}) {(M x + f (x))}^{β} \equiv - γ_{2} x^{β}

(18)

This implies:

-: $M x + f (x)$ would take the form of $M x + f (x) = K x$ ; as a result, $f (x) = (K - M) x$
-: $\frac{d f}{d x} = (K - M$ )
-: The below mentioned equation is satisfied:

$(γ_{1} + \frac{M + (K - M)}{2 - α}) K^{β} = - γ_{2} (γ_{1} + \frac{K}{2 - α}) K^{β} = - γ_{2}$

(19)

Equation (19) indicates that: for $γ_{2} > 0$ , $K < 0$ ; and it is easy to show:
-: The minima of $g (K) = (γ_{1} + \frac{K}{2 - α}) K^{β} + γ_{2}$ is located at $K^{*} = - γ_{1} \frac{β (2 - α)}{β + 1} = - γ_{1} \frac{α}{β + 1}$
-: $g (K^{*} = - γ_{1} \frac{α}{β + 1}) = 0$ and $K^{*}$ is the only root of Equation (19)

As a result

y = {(K^{*} x)}^{1 / (2 - α)} = \underset{A}{\underset{⏟}{- {[γ_{1} \frac{α}{β + 1}]}^{1 / (2 - α)}}} x^{1 / (2 - α)}

Consequently, the solution would be:

y = \dot{x} = A x^{1 / (2 - α)}

(20)

Remark 1. The solution as in Equation (20) satisfies the aforementioned intial conditions

x (0) = x_{0} and \dot{x} (0) = - {γ_{1}}^{β / α} {(\frac{α}{β + 1})}^{β / α} {x_{0}}^{1 / (2 - α)}

Remark 2.

P i c a r d - L i n d e l \ddot{o} f

theorem reconfirms (20) is an unique solution of

F (y, \dot{y}) = y \frac{d y}{d x} + γ_{1} y^{α} = - γ_{2} x^{β}

for the given set of initial values.

Remark 3. With

p > q

chosen to be odd positive integers, it is easy to see that

{(- x)}^{α} = - x^{α} = {|x|}^{α} s i g n (x)

{0 < (- x)}^{α \pm 1} = x^{α \pm 1} = {|x|}^{α \pm 1}

and

{0 < (- x)}^{α \pm β} = x^{α \pm β} = {|x|}^{α \pm β}

As seen in Equation (20), it is easy to show that the convergence time of state variable

x (t)

and its derivative

\dot{x} (t)

to zeros is calculated as in the following:

t_{c o n v e r g e n c e} = \frac{2 - α}{1 - α} A^{- 1} x^{\frac{1 - α}{2 - α}} (0) = \frac{α}{α - β} {(\frac{γ_{1} α}{β + 1})}^{- β / α} {x_{0}}^{(α - β) / α}

(21)

This completes the proof.

Remark 4. With the convergence time calculated as in (21), it is observed that

t_{c o n v e r g e n c e}

is inversely proportional to

{(\frac{γ_{1} α}{β + 1})}^{β / α}

. In the practice of 2TSM based controller design to be discussed in Section 4, the selection of these relevant parameters can be accordingly selected for the delivery of efficient control performance and design criterion.

4. 2TSM Based Controller Design

4.1. Kinematic Controller

The concept (Figure 3) of trajectory tracking error involves two postures: the real robot’s posture, denoted as P = (x,y,θ), and the reference robot’s posture, denoted as P_r = (x_r,y_r,θ_r). The reference robot is an imaginary robot that ideally follows the reference trajectory, while the real robot may have some errors compared to the imaginary robot. The goal is to move the robot from its current position to a desired position, which corresponds to the reference robot’s position.

The difference between the current position and the reference position is defined as follow:

P_{e} = [\begin{matrix} x_{e} \\ y_{e} \\ θ_{e} \end{matrix}] = [\begin{matrix} x_{r} - x \\ y_{r} - y \\ θ_{r} - θ \end{matrix}]

(22)

In this section, a simple P-type only controller is used to control the velocities of the DDMR. The reference angular velocity

ω_{r e f}

, and linear velocity

v_{r e f}

which orients the DDMR to the desired position, can be designed as follows:

\begin{array}{l} ω_{r e f} = K_{w} . θ_{e} = K_{w} . (θ_{r} - θ) \\ v_{r e f} = K_{v} . d_{e} \end{array}

(23)

where:

$K_{w}$ : P gain for angular velocity controller;
$K_{v}$ : P gain for linear velocity controller;
$θ_{r}$ = ${t a n}^{- 1} (y_{e}, x_{e})$ ;
$d_{e}$ : distance between real DDMR and reference DDMR.

The

v_{r e f}

and

ω_{r e f}

represent the reference linear and angular velocities, respectively, which will be used for the dynamic controller in the next section which describes the NTSM’s dynamic controller of the DDMR’s cascaded trajectory tracking control structure as shown in Figure 4.

4.2. Dynamic Controller

In this section, a second order Terminal Sliding Mode Controller (2TSM) is designed for the DDMR to maintain tracking of the reference linear and angular velocities under unknown bounded disturbances.

The dynamic equation can be rewritten in the following form:

M \ddot{q} = V (\dot{q}) + C τ (t) + ρ (t)

(24)

where

M = [\begin{matrix} m + \frac{2}{R^{2}} I_{w} & 0 \\ 0 & I + \frac{2 L^{2}}{R^{2}} I_{w} \end{matrix}]; \dot{q} = [\begin{matrix} v \\ ω \end{matrix}]; \ddot{q} = [\begin{matrix} \dot{v} \\ \dot{ω} \end{matrix}]; V (\dot{q}) = [\begin{matrix} m_{c} d ω^{2} \\ m_{c} d v ω \end{matrix}]; C = [\begin{matrix} \frac{1}{R} & \frac{1}{R} \\ \frac{L}{R} & \frac{- L}{R} \end{matrix}]

Suppose that

q_{r}

is the desired input of DDMR, let’s define

{e (t) = q - q}_{r} = {[d_{e}, θ_{e}]}^{T}, \dot{e} (t) = \dot{q} - \dot{q_{r}} = {[v_{e}, ω_{e}]}^{T}

(25)

therefore the error dynamics can be obtained from equation (24) and (25) as follow:

\ddot{e} = M^{- 1} (V (\dot{q}) + C τ (t) + ρ (t)) - {\ddot{q}}_{r}

(26)

In order to achieve good performances, such as fast convergence, chattering free and better tracking precision, an 2TSM manifold is designed as follow:

s = \ddot{e} + {γ_{1} \dot{e}}^{α} + γ_{2} e^{β}

(27)

where

γ_{1}, γ_{2}, α, β

are as specified in Theorem 1.

In this manner, the 2TSM’s dynamic controller is designed accordingly to the following Theorem 2.

Theorem 2: The velocities’ error can converge to zero in finite time, if the 2TSM manifold is chosen as (27), and the control law is designed as follows:

u = u_{e q} + u_{n}

(28)

u_{e q} = C^{- 1} M (- M^{- 1} V + {\ddot{q}}_{r} - {γ_{1} \dot{e}}^{α} - γ_{2} e^{β})

(29)

{\dot{u}}_{n} = C^{- 1} M (s i g n (s) (k + μ))

(30)

where

k = ‖M^{- 1} \dot{ρ} (t)‖

refers the bounded disturbance and

μ

is a positive constant.

Proof: Subtituting the error dynamics (26) into the second-order TSM manifold (27) gives

s = M^{- 1} (V (\dot{q}) + C τ (t) + ρ (t)) - {\ddot{q}}_{r} + {γ_{1} \dot{e}}^{α} + γ_{2} e^{β}

Subtituting the equation (29) into the above yields

s = M^{- 1} C u_{n} + M^{- 1} ρ (t)

The following Lyapunov function candidate is considered:

V = \frac{1}{2} s^{T} s

Differentiating V with respect to time t gives

\begin{matrix} \dot{V} & = s^{T} \dot{s} \\ = s^{T} (M^{- 1} C {\dot{u}}_{n} + M^{- 1} \dot{ρ} (t)) \\ = s^{T} (- s i g n (s) k - s i g n (s) μ + M^{- 1} \dot{ρ} (t)) \end{matrix}

(31)

i.e.

\dot{V} \leq - k ‖s‖ - μ ‖s‖ + M^{- 1} \dot{ρ} (t) \leq - μ ‖s‖ = - μ \sqrt 2 V^{1 / 2} < 0 for ‖s‖ \neq 0

Therefore, according to the Lyapunov stability criterion, the second-order TSM manifold as in (27) reaches zero from

s (0) \neq 0

within a finite time

t_{r} \leq \frac{\sqrt 2 V^{1 / 2} (0)}{μ}

t_{r} \leq \frac{‖s (0)‖}{μ}

. Once the 2TSM manifold s is reaches,

e (t)

and its derivative

\dot{e} (t)

(which corresponds to the velocities’ error) converge to zeros in finite time (Theorem 1), given by

t_{e} = t_{r} + \frac{α}{α - β} {(\frac{γ_{1} α}{β + 1})}^{- β / α} x^{(α - β) / α} (t_{r})

(32)

This concludes the proof.

Remark 5. As calculated according to Theorem 2, there is no singularity existed in the 2TSM control law

u

. In the other words, the proposed approach is as well regarded as a non-singular Second order Terminal Sliding Mode (2NTSM) control scheme.

Remark 6.

u_{n}

s a t i s f y i n g {\dot{u}}_{n} = C^{- 1} M (s i g n (s) (k + μ))

is a continuous signal. This implies that the proposed 2TSM control scheme is chattering free, indicating its suitability and effectiveness to be employed in practical electro-mechanical control systems.

5. Simulation Results

In order to demonstrate the effectiveness and advantages of the proposed second-order TSM, the simulation results are compared with the TSM and the LSM. The physical parameters of DDMR are shown in Table 1. The unknown bounded disturbance is

ρ (t) = \sin (10 t) + n

, where n is random noises with the amplitudes of 0.1.

LSM controller

A LSM manifold and the control are designed as follows:

s = \dot{e} + 4 e = [\begin{matrix} {\dot{e}}_{1} \\ {\dot{e}}_{2} \end{matrix}] + [\begin{matrix} 4 & 0 \\ 0 & 4 \end{matrix}] [\begin{matrix} e_{1} \\ e_{2} \end{matrix}]

u_{e q} = C^{- 1} M (- M^{- 1} V + {\ddot{q}}_{r} - 4 e)

{u_{n} = - C}^{- 1} M (s i g n (s) (k + μ))

k = ‖M^{- 1} ρ (t)‖

TSM controller

A TSM manifold and the control are designed as follows:

s = \dot{e} + 4 e^{3 / 5} = [\begin{matrix} {\dot{e}}_{1} \\ {\dot{e}}_{2} \end{matrix}] + [\begin{matrix} 4 & 0 \\ 0 & 4 \end{matrix}] [\begin{matrix} {e_{1}}^{3 / 5} \\ {e_{2}}^{3 / 5} \end{matrix}]

u_{e q} = C^{- 1} M (- M^{- 1} V + {\ddot{q}}_{r} - 4 e^{3 / 5})

{u_{n} = - C}^{- 1} M (s i g n (s) (k + μ))

k = ‖M^{- 1} ρ (t)‖

Second-order TSM controller

A 2TSM manifold and the control are designed as follows:

s = \ddot{e} + {γ_{1} \dot{e}}^{3 / 5} + γ_{2} e^{3 / 7} = [\begin{matrix} {\ddot{e}}_{1} \\ {\ddot{e}}_{2} \end{matrix}] + γ_{1} [\begin{matrix} {\dot{e}}_{1}^{3 / 5} \\ {\dot{e}}_{2}^{3 / 5} \end{matrix}] + γ_{2} [\begin{matrix} {e_{1}}^{3 / 7} \\ {e_{2}}^{3 / 7} \end{matrix}]

γ_{1} = 4, γ_{2} = 3.49

u_{e q} = C^{- 1} M (- M^{- 1} V + {\ddot{q}}_{r} - 4 {\dot{e}}^{3 / 5} - 3.49 {\dot{e}}^{3 / 7})

{{\dot{u}}_{n} = - C}^{- 1} M (s i g n (s) (k + μ))

k = ‖M^{- 1} \dot{ρ} (t)‖

The simulation results are shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. Figure 6, Figure 7 and Figure 8 depict the output tracking errors. Figure 5 shows the control input signals of two actuators (Torque 1- left actuator, Torque 2- right actuator).

It can be seen that 2TSM controller outperforms conventional LSM and TSM counterparts in various measures, including faster response and better tracking precision as well as chattering free, non-singular control signals which make it suitable to directly apply in practical applications. Here, the finite-time convergence of 2TSM allow us to directly manipulate variety of tuning parameters as in conventional first order TSM approaches (i.e. [4,5]).

6. Conclusions

This paper proposed a second order terminal sliding mode control scheme for trajectory tracking of differential drive mobile robots. The main advantages of the presented 2TSM approach lies on faster dynamic response and better tracking precision with chattering free control signals while avoiding singularities in the control law as demonstrated. More importantly, the paper has contributed into the converging characteristics analysis and calculation of finite-time convergence of relevant state variables (velocities’ error and angular positions’ error) to zeros once 2TSM sliding manifold is reached. This facilitates the direct manipulation of various tuning parameters of 2TSM control scheme in a similar manner as of conventional well-known first order TSM control methods (i.e. [4,5]).

Acknowledgments

The authors wish to thank Vietnam Academy of Science and Technology for providing financial support via research grant number VAST01.06/20-21.

References

G. Dudek, M. Jenkin, “Computational principles of mobile robotics”, Cambridge University Press, 2rd edition, 2010.
Hatab, Rached, “Dynamic Modelling of Differential-Drive Mobile Robots using Lagrange and Newton-Euler Methodologies: A Unified Framework”, Advances in Robotics & Automation, Vol. 2, No.2, 2013. [CrossRef]
T. Fukao, H. Nakagawa, N. Adachi, “Adaptive tracking control of a nonholonomic mobile robot”, IEEE Transactions on Robotics and Automation, Vol. 16, No. 5, pp. 609-615, 2000. [CrossRef]
Y. Feng, X. Yu, F. Han, “On nonsingular terminal sliding-mode control of nonlinear systems”, Automatica, Vol. 49, Issue 6, pp. 1715-172, 2013. [CrossRef]
Y. Feng, J. Zheng, X. Yu, N. V. Truong, “Hybrid Terminal Sliding-Mode Observer Design Method for a Permanent-Magnet Synchronous Motor Control System”, IEEE Transactions on Industrial Electronics, Vol. 56, No. 9, pp. 3424-3431, 2009.
Y. Feng, X. Yu, Z. Man, “Non-singular terminal sliding mode control of rigid manipulators”, Automatica, Vol. 38, Issue 12, pp. 2159-2167, 2002. [CrossRef]
Y. Feng, X. Han , Y. Wang & X. Yu, “Second-order terminal sliding mode control of uncertain multivariable systems”, International Journal of Control, Vol. 80:6, pp. 856-862, 2007. [CrossRef]
L. Yang, S. Pan, “A Sliding mode control method for trajectory tracking control of wheeled mobile robot”, Journal of Physics: Conference Series, Vol.1074, pp. 26–28, 2018. [CrossRef]
J. K. Lee, J. B. Park, Y. H. Choi, “Tracking Control of Nonholonomic Wheeled Mobile Robot Based on New Sliding Surface with Approach Angle”, in Proc. 3rd IFAC Symposium on Telematics Applications, Vol. 46, pp. 38-43, 2013. [CrossRef]
R. L. S. Sousa, M. D. do Nascimento Forte, F. G. Nogueira, B. C. Torrico, “Trajectory tracking control of a nonholonomic mobile robot with differential drive”, in Proc. IEEE Biennial Congress of Argentina (ARGENCON), pp. 1-6, 2016.
Y. Kanayama, Y. Kimura, F. Miyazaki, T. Noguchi, “A stable tracking control method for an autonomous mobile robot”, in Proc. IEEE International Conference on Robotics and Automation, Vol.1, pp. 384-389, 1990.
S. Sun, “Designing approach on trajectory-tracking control of mobile robot”, Robotics and Computer-Integrated Manufacturing, Vol. 21, pp. 81-85, 2005. [CrossRef]
F. N. Martins, W. C. Celeste, R. Carelli, M. Silho, T. Bastos, “An adaptive dynamic controller for autonomous mobile robot trajectory tracking”, Control Engineering Practice, Vol.16, Issue 11, pp. 1354-1363, 2008. [CrossRef]
R. Solea, A. Filipescu, U. Nunes, “Sliding-mode control for trajectory-tracking of a Wheeled Mobile Robot in presence of uncertainties”, in Proc. 7th Asian Control Conference, pp. 1701-1706, Hong Kong, China, 2009.
H. Cen, B. K. Singh, “Nonholonomic Wheeled Mobile Robot Trajectory Tracking Control Based on Improved Sliding Mode Variable Structure”, Wireless Communications and Mobile Computing, 2021. [CrossRef]
J. Huang, C. Wen, W. Wang, Z. P. Jiang, “Adaptive output feedback tracking control of a nonholonomic mobile robot”, Automatica, Vol. 50, Issue 3, pp. 821-831, 2014. [CrossRef]
J. Zheng, H. Wang, Z. Man, J. Jin, M. Fu, “Robust Motion Control of a Linear Motor Positioner Using Fast Non-singular Terminal Sliding Modet”, IEEE/ASME Transactions on Mechatronics, Vol. 20, No. 4, pp. 1743-1752, 2015.
Z. Sun, H. Xie, J. Zheng, Z. Man, D. He, “Path-following control of Mecanum-wheels omnidirectional mobile robots using nonsingular terminal sliding mode”, Mechanical Systems and Signal, 2021.
J. Yang, J. Kim, “Sliding mode control for trajectory tracking of nonholonomic wheeled mobile robots”, IEEE Transactions on Robotics and Automation, Vol. 15, No. 3, pp. 578-587, 1999. [CrossRef]
D. Chwa, “Sliding-mode tracking control of nonholonomic wheeled mobile robots in polar coordinates”, IEEE Transactions on Control Systems Technology, Vol. 12, No. 4, pp. 637-644, 2004. [CrossRef]
J. Y. Zhai, Z. B. Song, “Adaptive sliding mode trajectory tracking control for wheeled mobile robots”, International Journal of Control, Vol. 92:10, pp. 2255-2262, 2019. [CrossRef]
Y. Feng, M. Zhou, X. Yu and F. Han, “Full-order sliding mode control of rigid robotics manipulators”, Asian Control Journal, Vol. 21, No. 4, pp. 1-9, 2019.
N. Nguyen, B. Pham, T. Hoang, T. Nguyen, L. Nguyen and N. Truong, “Efficient sensorless speed estimation of electrical servo drives using a full order nonsingular terminal sliding mode observer”, Mathematical Problems in Engineering, Volume 2021, Article ID 8175848, 2021.
H. Shi and Y. Feng, “ High order terminal sliding mode flux observer for induction motors”, Acta Automatica Sinica, Vol. 38, No. 2, pp. 288-294, 2012. [CrossRef]
T. Cao, B. Pham, H. Tran, L. Gia, No. Nguyen and N. Truong,” Non-singular terminal sliding mode control for trajectory tracking of a differential drive robot”, E3S Web of Conferences, Volume 496, 02005, 2024.

Figure 1. Differential Drive mobile robot (DDMR).

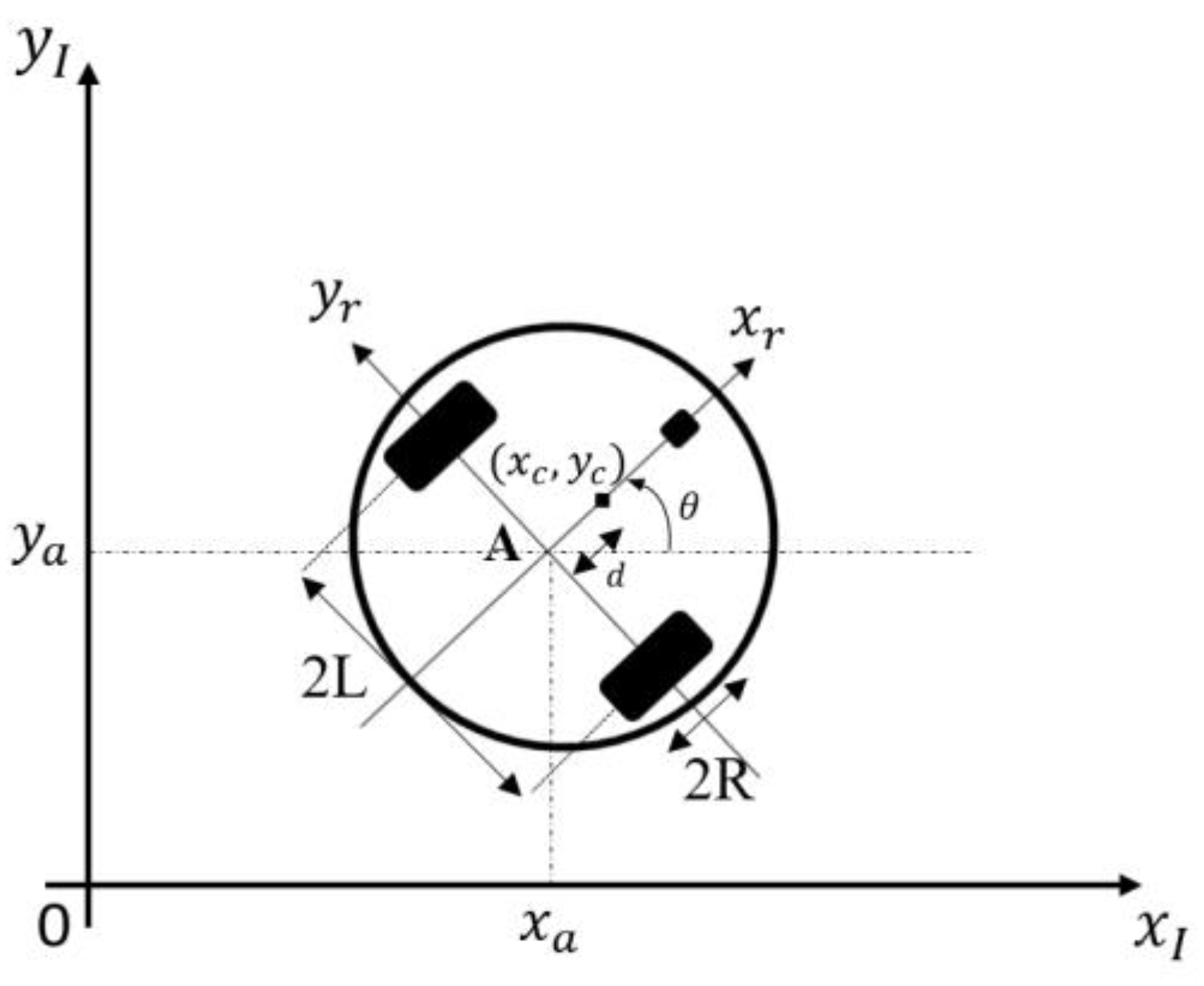
Figure 2. Right wheel of DDMR as an example to describe velocity quantities of each wheel.

Figure 3. Real robot in the trajectory tracking of reference robot.

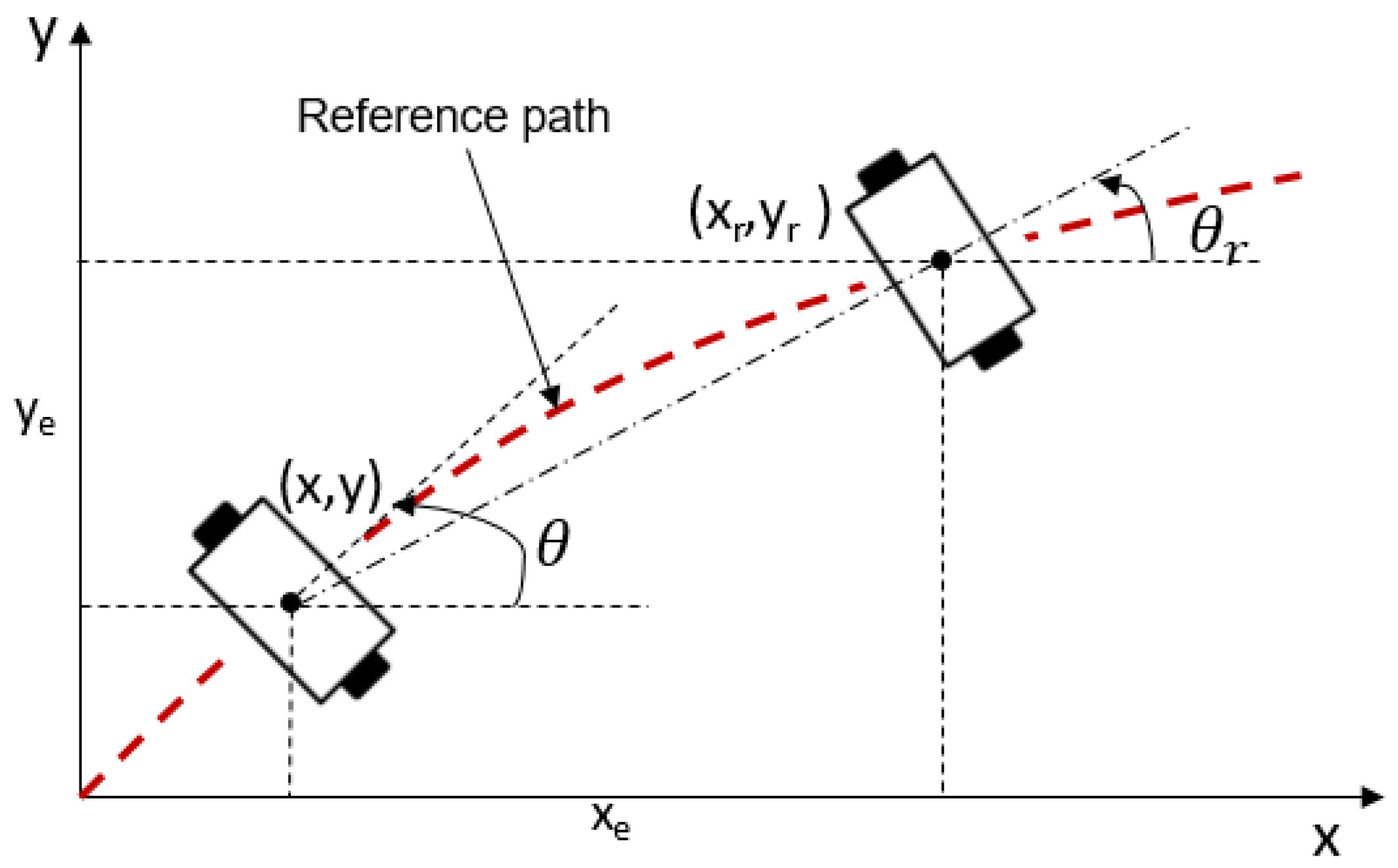
Figure 4. The cascaded controller scheme.

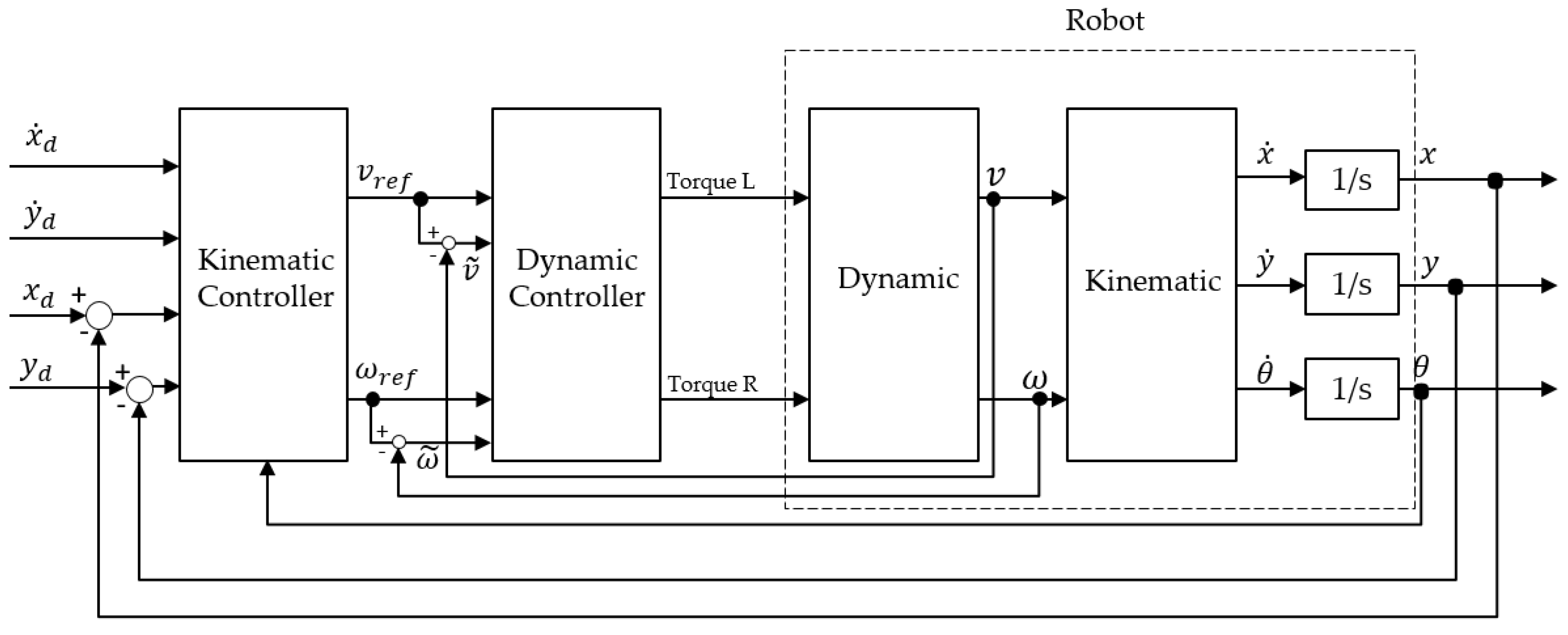
Figure 5. Control signals (Torque’s commands) of (a) LSM . (b) TSM . (c) Second-order TSM controllers.

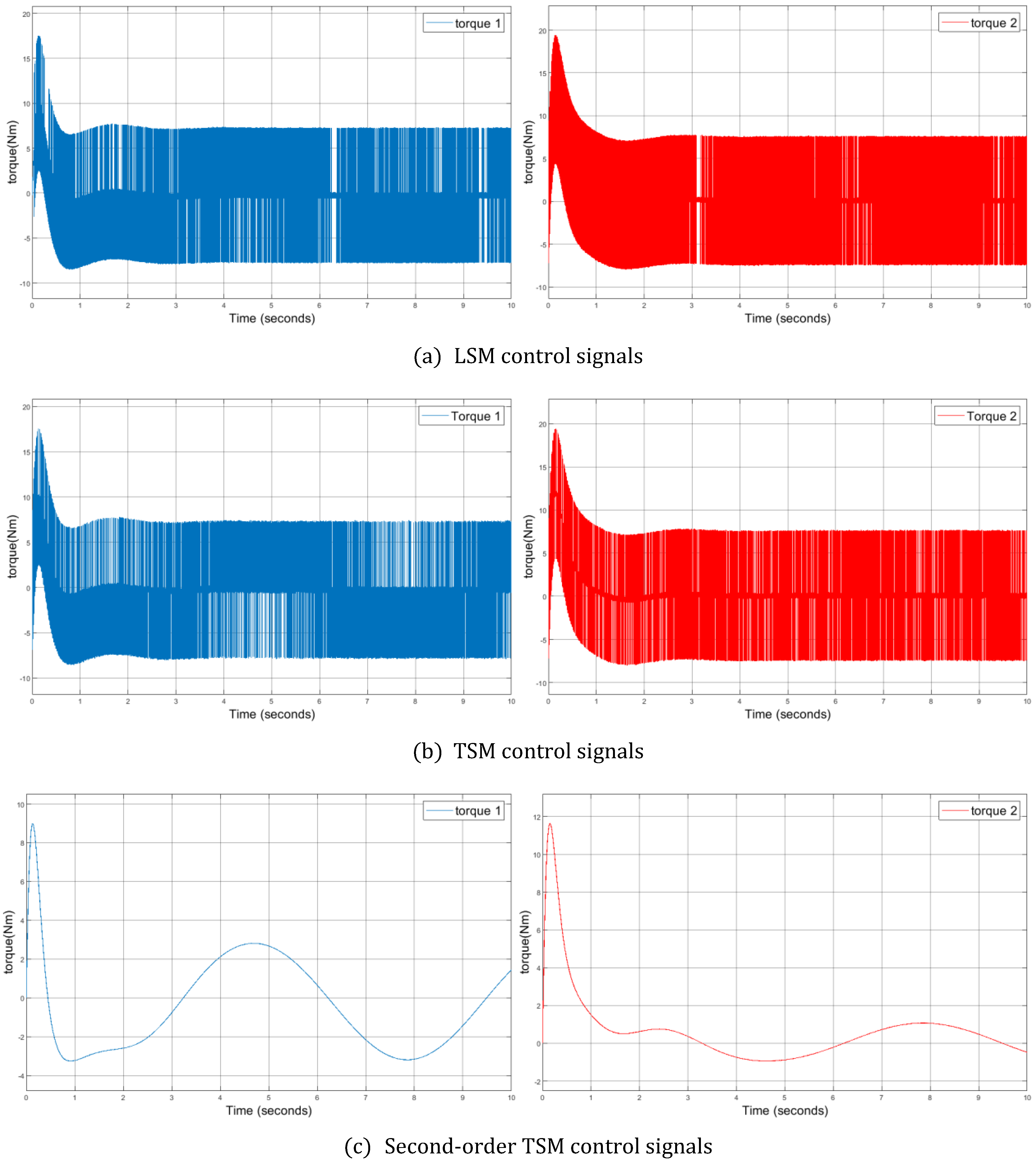
Figure 6. Angular positions’ tracking errors.

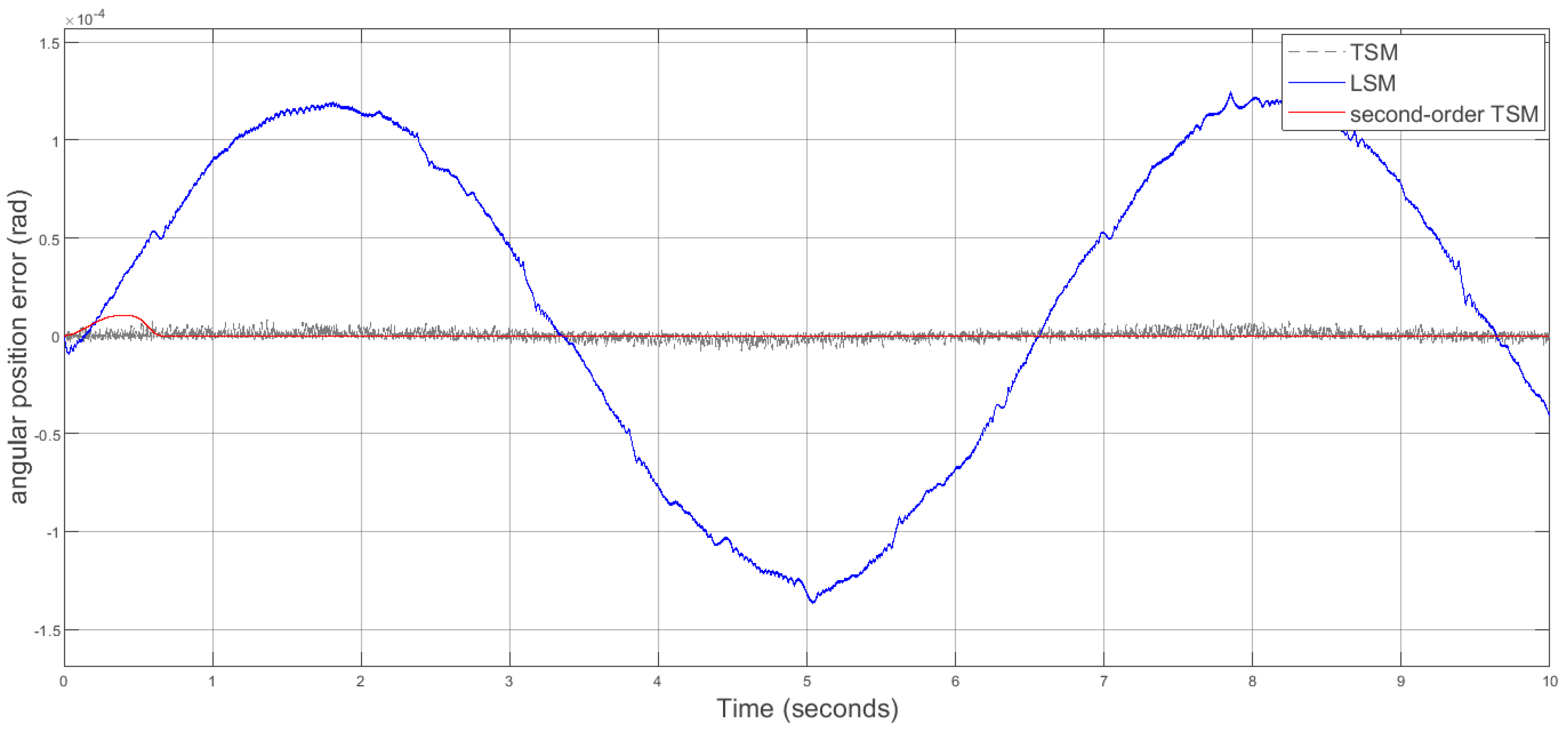
Figure 7. Tracking errors of angular velocity(rad/s).

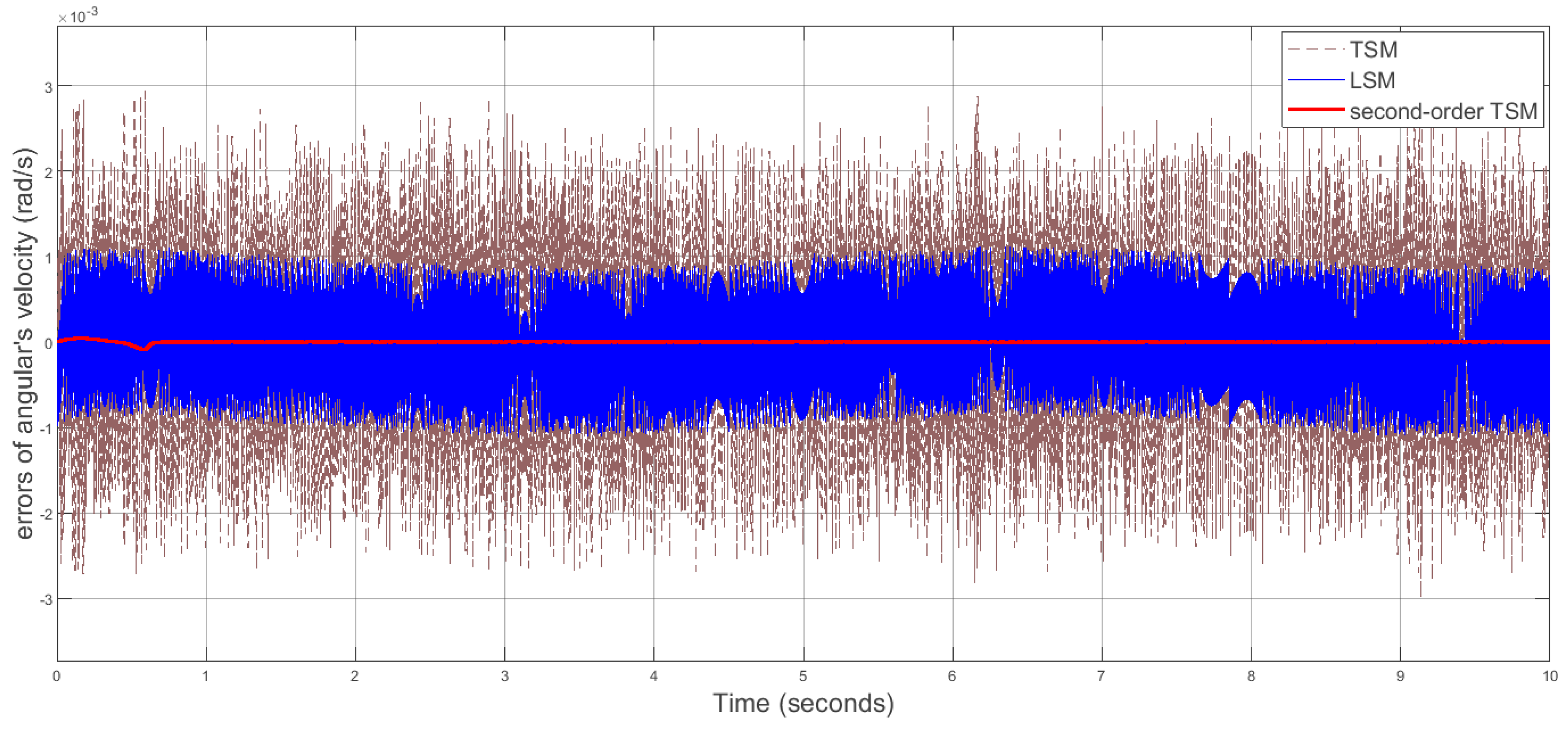
Figure 8. Tracking errors of DDMR’s trajectory (distance to reference trajectory) of LSM, TSM and 2TSM.

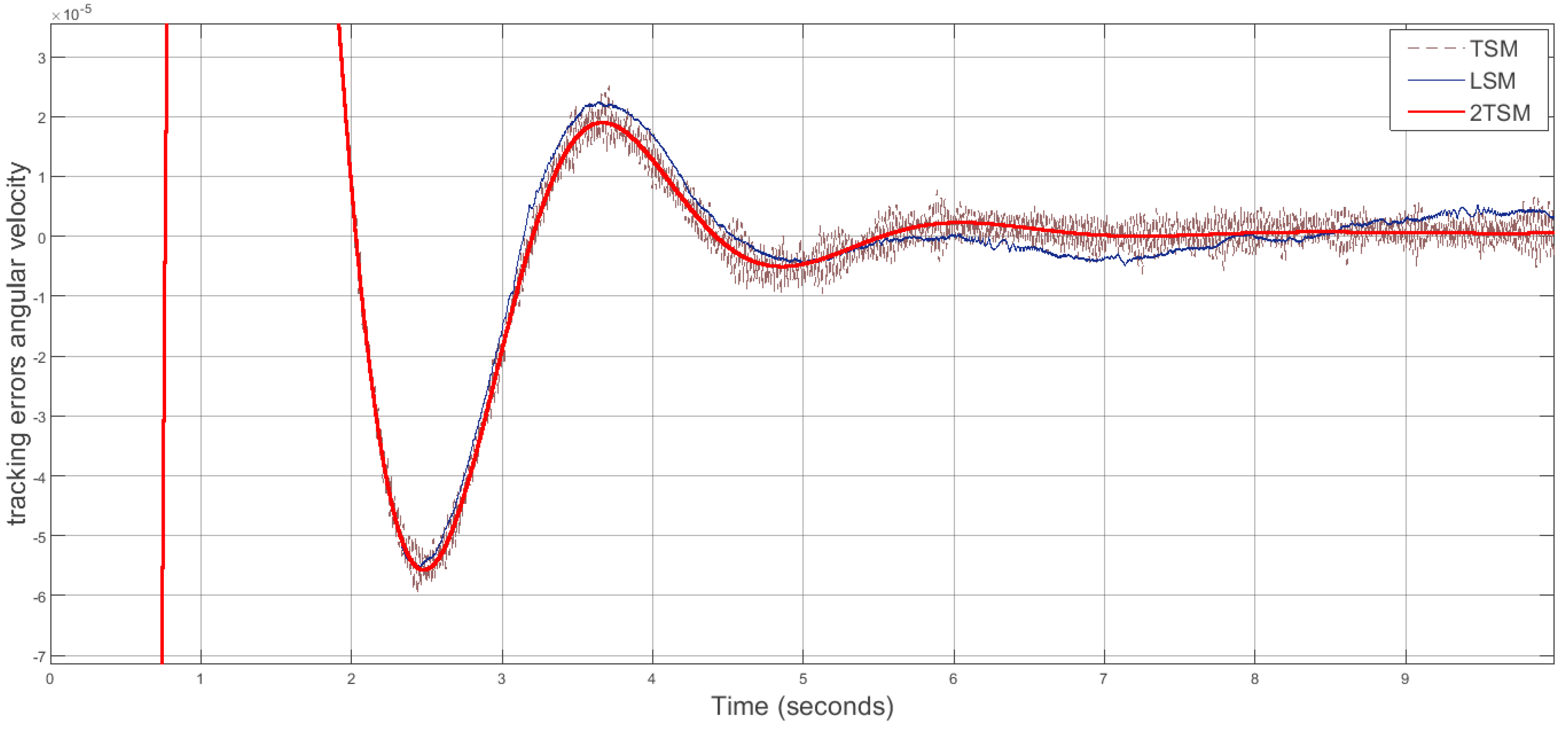
Figure 9. Tracjectory tracking performance of 2TSM based controller.

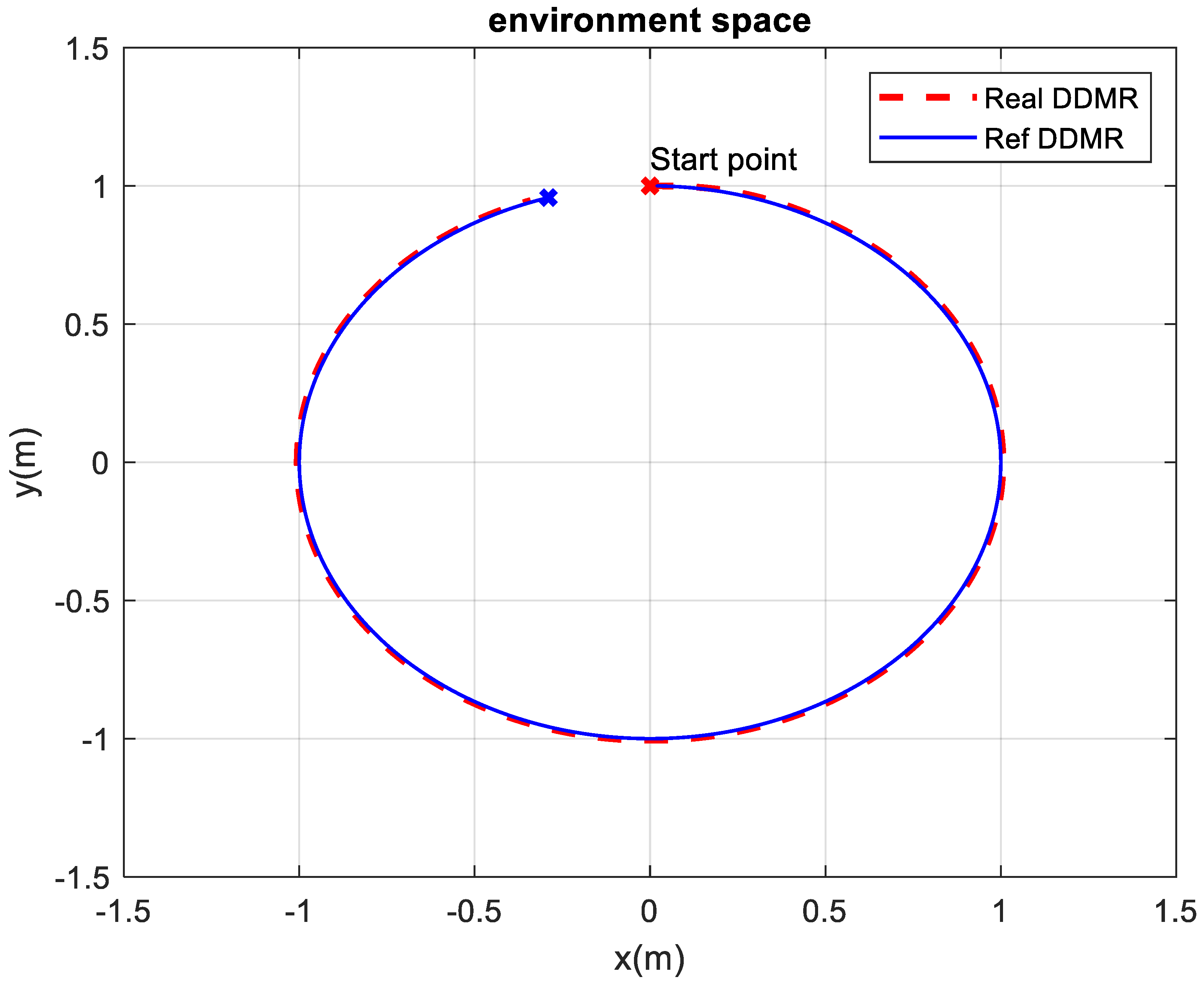
Table 1. The physical parameters of DDM used in the simulation study.

Mass of robot frame	m_c	70 kg
Mass of each robot actuator (wheel and motor)	$m_{a}$	5 kg
Radius of wheel	$r$	0.25 m
Distance from wheel to center of wheel axis	$L$	1 m
Mass of each wheel	$m_{w}$	1 kg
Distance from center of gravity to point A (Figure 1)	$d$	0.15 m

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Second Order Terminal Sliding Mode Control for Trajectory-Tracking of a Differential Drive Robot

Abstract

1. Introduction

2. DDMR’s Model

2.1. Kinematic Model

2.2. Dynamic Model

3. Finite-Time Convergence Characteristics of 2TSM Manifold

4. 2TSM Based Controller Design

4.1. Kinematic Controller

4.2. Dynamic Controller

5. Simulation Results

6. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe