Prerpints.org logo
Preprint
Article

Improvement of intrusion detection in IoT Networks using a hybrid Machine and Metaheuristic Algorithm

Altmetrics

Downloads

143

Views

50

Comments

0

Submitted:

27 May 2024

Posted:

28 May 2024

You are already at the latest version

Alerts
Abstract
In recent years, extensive research has been conducted on the IoT, one of its challenges has been the field security and penetration in these networks. security solutions it Require more planning and awareness to ensure system security and privacy protection.it has also been shown that adjusting the weights of neural networks can help improve the accuracy of detection to what extent. the challenge in the attack detection field is to increase the accuracy of attack detection by machine learning methods, in this paper, a new method is presented to adjust weights of the random neural network for attack detection. Evaluations of the proposed method show that compared to random neural network methods, nearest neighbor, and support vector machine, the accuracy of attack detection improves up to 99.49 percent, and the random neural network method has been able to improve by 99.01 percent, placing the best methods together in these experiments in the form of a multi-learning model showed that the results also had an increase in accuracy up to 99.56 percent, while the training time in the proposed model is less compared to the random neural network method.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Networks and Communications

1. Introduction

The Internet of Things (IoT) is a network composed of devices equipped with special sensors for detecting monitoring areas and transmitting collected data to end users. The IoT is widely used in many scenarios, such as COVID-19, healthcare, environmental monitoring, smart buildings, and more. Gartner reported that the global IoT market is close to 6 billion devices in 2020. McKinsey estimates that by 2025, IoT will be worth around 11 trillion dollars. Furthermore, the emergence of 6G wireless communications and mobile edge computing can help facilitate the growth and expansion of IoT devices IoT networks are highly heterogeneous networks where various types of nodes and connections multiply rapidly. The IoT framework encompasses virtual, and physical environments, as well as other developing technologies, and IoT environments often consist of four main entities such as devices, various IoT users, edge gateways, and cloud storage servers The combination of sensors and wireless interaction has paved the way for the growth of the IoT. One of the key components of IoT networks is wireless sensor nodes The distinguishing feature of IoT from WSN is that while WSN is not directly connected to the Internet, IoT devices are connected to the Internet. In these networks, sensors are connected to a central node known as a cluster head, which is then connected to the Internet IoT extends beyond smart homes and internet-connected household items. This technology also encompasses cities and is used in industries for monitoring products using interconnected sensors. The IoT, due to the independent development of its equipment and networks, is very heterogeneous and its energy and hardware resources are limited, in addition, IoT networks have experienced the development and standardization of a wide range of protocols to enable IoT applications, including wireless communication technologies such as (Zigbee, BLE, LORAWAN, Sigfox) [5].

1.1. Problem Statement

One of the key challenges in IoT networks is network efficiency and resilience against attacks. To achieve complete security in the IoT network in today's world, in addition to attack prevention equipment, systems called Intrusion Detection Systems (IDS) are required to detect intrusions if an intruder passes from security equipment and enters the network, recognize it, and think of a solution to deal with it, addressing these issues requires very scalable solutions IoT devices are resource-constrained devices that require security solutions and possess characteristics such as limited storage space, low energy consumption, and low cost. These solutions should be compatible with standard communication protocols. IoT devices generate large amounts of data during industrial operations, which can turn an industrial IoT network into a target for attackers. Due to the large volume of data, traditional data processing techniques are not suitable for IoT applications and industrial IoT. Therefore, machine learning is considered one of the most suitable computational patterns for providing insights embedded in IoT devices. One of the most common attacks in wireless networks including industrial IoT is denial of service; a type of attack whose goal is to disrupt the service integrity of a network node. Hence, proposing an efficient intrusion detection system that can inspect and eliminate malicious nodes in the network and thereby improve network performance through continuous traffic monitoring is crucially important [7].

1.2. Research Objectives

Methods such as various neural networks and other methods like Support Vector Machines have shown to be powerful classifiers in the field of intrusion detection in networks, however, precise and optimal determination of the parameters of these methods is one of the influential issues on their performance, and evolutionary methods are used for this purpose. One effective method is the Random Neural Network, which has been used for intrusion detection in Industrial IoT networks Given that the classification accuracy in this method depends on the adjustment of its architecture and weights, in this article, a model is proposed for improving the weights of this network using a combination algorithm GAO and Arithmetic Optimization algorithm, which has a high search accuracy, the main objectives of this model are as follows:
  • Increasing the accuracy of intrusion detection in IoT networks with industrial use
  • Adapting the Arithmetic Optimization and GAO combined algorithm in improving machine learning methods like neural networks
  • Introducing a new model of Random Neural Network based on the Arithmetic Optimization and GAO combined algorithm

1.3. Research Contributions

The lightweight Random Neural Network solution [8] is an appropriate approach to detecting attacks on IoT networks, and on the other hand, adjusting the weights of neural networks has a direct impact on their classification accuracy. Therefore, considering the improved performance of neural networks when their parameters are adjusted using evolutionary methods [9], in this article, for the first time, a Random Neural Network with the assistance of the GAO [10] and Arithmetic Optimization combined algorithm [11] is used to adjust the network architecture and weights, and the proposed model is employed for detecting attacks in Industrial IoT networks. The reason for the superiority of the proposed model over the standard Random Neural Network method is the fact that in the proposed model, weights are searched using a strong search mechanism related to the Arithmetic Optimization and GAO combined algorithm, achieving global optimization of weight adjustment. On the other hand, in the standard Random Neural Network method, weight adjustment occurs through the delta rule and gradient descent method, which places it in local optima and does not achieve the optimal state for network weights. In this article, a solution is proposed to enhance the Random Neural Network using the Arithmetic Optimization and GAO combined algorithm for the first time. In fact, the Arithmetic Optimization algorithm has high exploration power, and the GAO algorithm has high exploitation power, and it seems that combining these two algorithms can search the search space more accurately. The innovations of the article can be summarized as follows:
  • Improved Random Neural Network with Arithmetic Optimization and GAO algorithm in intrusion detection
  • Adjusting the weights of random neural network types with Arithmetic Optimization and GAO combined algorithms
  • Determination of architecture for various Random Neural Network types with Arithmetic Optimization and GAO combined algorithms

1.4. Paper Organization

The paper is divided into several sections to enhance its organization. Section 1 includes the introduction, problem statement, research objectives, and research innovations. In Section 2, we explain related works carried out by other researchers. Section 3 proposes the algorithm and methodology. Section 4 demonstrates the implementation and evaluation of the proposed model. Finally, in Section 5, we present the conclusion and future work.

2. Related Works

This section focuses on the research conducted in developing attack detection systems in IoT applications, which includes various machine learning methods on different datasets in this field. Intrusion detection system tools inform officials of an attack occurrence; intrusion prevention system tools go a step further and automatically block the offending agent. Intrusion detection systems and intrusion prevention systems share many characteristics. In fact, most intrusion prevention systems have an intrusion detection system at their core. The key difference between these technologies is that intrusion detection system products only detect the offending agent, while intrusion prevention systems prevent such agents from entering the network [12,13]. The efficiency of intrusion detection systems and intrusion prevention systems depends on parameters such as the technique used in the intrusion detection system, its position within the network, and its configuration. Intrusion detection and intrusion prevention techniques can be categorized into signature-based detection techniques, anomaly detection techniques, and artificial intelligence-based detection techniques. Signature-based detection aims to define a set of rules (or signatures) that can be used to decide whether a specific pattern corresponds to an attacker's behavior. As a result, signature-based systems are capable of achieving high levels of accuracy in identifying attacks. If the intrusion detection system is not properly configured, even minor changes in known attacks can affect its analysis. Therefore, signature-based detection is unable to detect unknown attacks or changes in known attacks. One of the reasons for using signature-based detection is the ease of maintaining and updating pre-configured rules. Anomaly detection involves identifying events that appear abnormal based on normal system behavior. A wide range of techniques such as data mining, statistical modeling, and hidden Markov models have been examined as different methods for addressing anomaly detection problems. An anomaly-based solution involves collecting data over a period and then using statistical tests on observed behavior to determine whether this behavior is legitimate or not. The ability of soft computing techniques to deal with uncertain data and to some extent fuzziness makes them attractive for use in intrusion detection. Numerous soft computing techniques such as artificial neural networks, fuzzy logic, association rule mining, support vector machines, and genetic algorithms exist that can be used to improve the accuracy of intrusion detection systems. In research, artificial intelligence-based intrusion detection refers to techniques such as artificial neural network-based intrusion detection systems, fuzzy logic-based intrusion detection systems, association rule mining-based intrusion detection systems, support vector machine-based intrusion detection systems, and evolutionary algorithms and their combinations. The purpose of using neural networks for intrusion detection is the ability to generalize data (from incomplete data) and classify data as normal or abnormal. Neural network-based intrusion detection systems are an effective solution for unstructured network data. The accuracy of attack detection in this solution is based on the number of hidden layers and the training phase of the neural network Fuzzy logic can be used to deal with imprecise descriptions of attacks and for reducing the training time of neural networks, fuzzy logic combined with neural networks can be used for rapid attack detection. Some attacks are based on specific attack patterns. Association rules can be used to generate new signatures. By using the newly generated signatures, various types of attacks can be immediately recognizable Support Vector Machine is used for attack detection based on limited sample data, where the data dimensions will not affect the accuracy. In intrusion detection systems in mobile wireless networks, the Support Vector Machine method provides better accuracy than neural networks, as neural networks require a large number of training samples for effective classification, while the Support Vector Machine method needs to adjust fewer parameters. However, the Support Vector Machine method is only used for binary data. Nevertheless, detection accuracy can be improved by combining the Support Vector Machine method with other techniques. If limited sample data for attack detection are specified, then using the Support Vector Machine method is an effective solution; as the data dimensions do not affect the accuracy of the Support Vector Machine-based IDS Evolutionary algorithms are used to select network features (to determine optimal parameters) that can be employed in other techniques to achieve optimization and improve IDS accuracy. This can also be used to improve the training of neural networks and adjust the parameters of Support Vector Machines In fact, guiding and efficiently controlling large-scale industrial systems in Industrial IoT is a complex and challenging task. Computational operating systems must have the ability to process and analyze data safely and in real-time for large industrial data [17,18]. Additionally, the capacity and operational power of the system must be high to transfer data with minimal delay and high reliability. Machine learning algorithms and models have significantly improved the performance of the industrial sector in terms of reliability and security. These algorithms have great potential for addressing security challenges in Industrial IoT systems [19,20]. Furthermore, have been presented some recent research works related to machine learning-based security designs for IoT and Industrial IoT. FARAHNAKIAN and Haikonen [21] presented a deep autoencoder model for identifying network attacks. The researchers used the KDD-CUP 99 dataset to evaluate their proposed design. The attack detection accuracy was 94.71%. Their experimental results proved that their model outperformed deep belief networks. Shou et al. [22] introduced a non-symmetric deep autoencoder (NDAE) that learns features in an unsupervised manner. The authors implemented their proposed model on a graphics processing unit (GPU) and evaluated the model using the NSL-KDD dataset. The attack detection accuracy was 89.22%. Ali et al. [23] presented a Fast Learning Network by combining the particle swarm optimization method. The authors ran their proposed design using the KDD 99 dataset. The attack prediction accuracy of their proposed model was 98.92%. Although their model provides satisfactory performance, its complexity is high and not suitable for devices with limited resources. MOKHAFFI et al. [24] presented a new hybrid genetic algorithm and support vector machine with a particle swarm optimization-based design for detecting DoS attacks. The researchers executed their proposed design using the KDD 99 dataset and achieved an accuracy of 96.38%. VAJAYANAND et al. [25] improved classification accuracy by proposing a Support Vector Machine (SVM)-based model. They conducted their experiments using the ADFA-LD dataset and achieved an accuracy of 94.51%. Al. KHALOUTI et al [26] successfully identified and classified IoT attacks using SVM and Bayesian algorithms. They implemented their model using the KDD CUP 99 dataset and achieved an accuracy of 91.50%. James and colleagues [27] presented a model based on deep neural networks and short-time Fourier transform for detecting data injection attacks. The researchers executed their proposed design using the IEEE 118 dataset. The attack detection accuracy of their proposed model was 91.80%. Qureshi and colleagues [28] proposed an anomaly-based intrusion detection scheme. Their approach successfully identified DoS attacks, Man-in-the-Middle attacks in IoT applications, and Industrial IoT. The researchers evaluated their proposed design using the NSL-KDD dataset, and the attack detection accuracy of their model was 91.65%. Para and colleagues [29] introduced a cloud-based deep learning framework for phishing and botnet attacks. For phishing attacks, their experimental results achieved accuracies of 94.30% and 94.80% respectively. Zeng and colleagues [30] presented an extreme learning method based on linear discriminant analysis for intrusion detection in the IoT. The researchers evaluated the performance of their proposed approach using the NSL-KDD dataset, with an accuracy of 92.35%. Singh and colleagues [31] provided a comparative analysis of existing machine learning-based techniques for IoT attack detection. IRAQUITANO et al [32] proposed an intelligent self-encoding intrusion detection scheme. The researchers evaluated their proposed design using the NSL-KDD dataset, showing better performance compared to shallow and conventional networks. Yan et al [33] proposed a novel hinge classification algorithm for detecting cyber-attacks. The researchers compared the performance of their proposed approach with decision tree algorithms and logistic regression models. Eskandari et al [34] presented an intelligent intrusion detection scheme. They presented discussions about the deployment of the plan in IoT gates. Using their proposed scheme, they successfully detected malicious traffic, port scanning, and pervasive search attacks. SAHARKHIZAN et al [35] suggested a combined IDS model for remote-to-local (R2L) and user-to-root (U2R) attacks. They successfully identified both types of attacks in IoT networks using the NSL-KDD dataset. VINAYAKUMAR et al [36] introduced a two-stage deep learning framework for phishing detection. The researchers successfully classified attacks and normal traffic using the domain generation algorithm. Their experimental results demonstrated improved performance in terms of accuracy, F1 score, and detection speed. Ravi and colleagues [37] proposed a new semi-supervised learning algorithm for DDoS attack detection. They successfully identified DDoS attacks with an accuracy of 96.28%. UYULOV et al [38] addressed the active behavior detection capabilities of intrusion detection technology in identifying abnormal behaviors in networks and its application for securing Industrial IoT networks. However, challenges exist with current intrusion detection technology for Industrial IoT, such as imbalanced class sample sizes in datasets, extraneous and meaningless features in samples, and the inability of traditional intrusion detection methods to meet the accuracy requirements in more complex Industrial IoT due to class imbalance.
In this paper, a hierarchical approach is applied, which reduces the number of majority samples using a clustering algorithm while preventing the loss of information from majority samples and addressing the issue of misidentification and misclassification of minority samples due to sample imbalance. To prevent feature redundancy and interference, this paper proposes an optimal feature selection algorithm based on a greedy approach. This algorithm can obtain optimal feature subsets for each type of data in the dataset and consequently eliminate extra and intrusive features. With the aim of addressing the insufficient detection capability of traditional detection methods, this paper suggests a deep learning-based intrusion detection model based on parallel connection. Experimental results demonstrate that the method described in this paper can enhance intrusion detection for Industrial IoT. KUJING Ju et al [39] highlighted the significant role of Industrial IoT in key infrastructure sectors and the various security threats and challenges it poses. Many existing intrusion detection approaches have limitations such as performance redundancy, excessive adaptation, and low efficiency. A combined optimization method - Lagrange coefficient - has been designed to optimize the fundamental feature screening algorithm. The optimized features are combined with random forests and selected XG-Boost features to improve the accuracy and efficiency of attack feature analysis. The proposed method has been evaluated using the UNSW-NB dataset. It has been observed that the impact degree of different features related to attack behavior can lead to an increase in binary attack detection classification to 0.93 and a reduction in attack detection time by 6.96 times. The overall accuracy of multi-class attack detection has also improved by 0.11. It is also noted that 9 key features analyzing attack behavior are essential for analyzing and detecting general attacks targeting the system, and by focusing on these features, the effectiveness and efficiency of critical industrial system security can be significantly enhanced. The CICDDOS and CICIDS datasets have been used for validation in this approach. The experimental results show that the proposed method has good generalization. Sahar Saliman et al [40] addressed the widespread deployment of the IoT in vital sectors such as industrial and manufacturing, leading to the emergence of Industrial IoT. Industrial IoT comprises sensors, actuators, and smart devices that communicate with each other to optimize production and industrial processes. While Industrial IoT offers various benefits for service providers and consumers, security and privacy preservation remain significant challenges. An intrusion detection system has been employed to mitigate cyber-attacks in such connected networks. In a study [41], the authors proposed a new semi-supervised scheme for labeled data and unlabeled data, considering the labeling challenge. In this approach, an autoencoder (AE0 is first automatically trained on each device using local or private data (unlabeled data) to learn features. Subsequently, a cloud server collects these models relative to a global autoencoder using federated learning (FL). Finally, the cloud server constructs a supervised neural network by adding fully connected layers (FCN) to the global autoencoder and trains the obtained model using labeled data, the advantages of this approach include: 1- Local private data are not exchanged. 2- Attack identification with high classification performance. 3- It works when only a few labeled data are available and also has low communication overhead. In a study [42], the authors proposed a hierarchical clustering algorithm for data sampling technology that reduces the number of majority samples in the data while resolving the issue of misidentification and misclassification of minority samples due to sample imbalance. To prevent feature redundancy and interference, this study suggests an optimal feature selection algorithm based on a greedy approach. This algorithm can obtain optimal feature subsets for each type of data in the dataset and consequently eliminate extra and intrusive features. This study proposes a deep learning-based intrusion detection model based on parallel connections under global and local subnetworks. This detection model derives a general dataset metric through deep neural network analysis.

Research Gap

Many existing solutions for intrusion detection in Industrial IoT suffer from a lack of comprehensiveness in addressing various types of network attacks, high-dimensional feature sets, models built on outdated datasets, lack of focus on the problem, and imbalance in the range of issues. To address these challenges, an intelligent intrusion detection system has been proposed for identifying Cyber Attacks in Industrial IoT networks. The proposed model utilizes the singular value decomposition technique to reduce data features and enhance detection results. The SMOTE sampling method is employed to mitigate issues of overfitting and imbalance that can lead to biased classification. Several machine learning and deep learning algorithms have been implemented for data classification in binary and multi-class settings. The performance of the proposed model in this study has been evaluated on the TON_IOT dataset. The proposed method has achieved a detection accuracy rate of 99.99% and a reduced error rate of 0.001% for classification. A review of research literature on various machine learning methods for attack detection in the IoT has revealed that different methods achieve attack detection accuracies ranging from 84% to 99% on datasets. Table 1 provides a comparative analysis of existing methods in attack detection.

3. Preliminary Concept

In this section, basic concepts such as the GAO Optimization Algorithm and the Arithmetic Optimization Algorithm are explained.
  • GAO Optimization Algorithm
One of the new evolutionary algorithms is the GAO Optimization Algorithm, inspired by the behavior of grasshoppers. Nature-inspired algorithms logically divide the search process into two parts: exploration and operation. In exploration, search agents are encouraged to make random movements, while in the operation stage, they tend to make local movements around their location. These two actions, along with the search for the target, are naturally performed by grasshoppers. Therefore, an attempt has been made to find a way to mathematically model this behavior, which is referred to in the following mathematical specifications. Formula (1) illustrates the mathematical model used to simulate the behavior of grasshoppers:
X i = S i + G i + A i
Here, Xi represents the position of the ith grasshopper, Si denotes social interaction, Gi is the gravitational force applied to the grasshopper ith, and Ai indicates the wind direction. The value of Si, meaning social interaction for grasshopper ith, is calculated according to Formula (2).
S i = ∑ j = 1 N s d i j d i j ^
where d i j represents the distance between the ith grasshopper and the jth grasshopper and is calculated using Formula (3).
d i j = x i − x j
S is a function defining the pressure of social force as shown in Formula (2), and ( d i j ^ is a unit vector from the ith grasshopper to the jth grasshopper. The function S, defining the social force, can be calculated using Formula (4).
S r = f e − r I − e − r
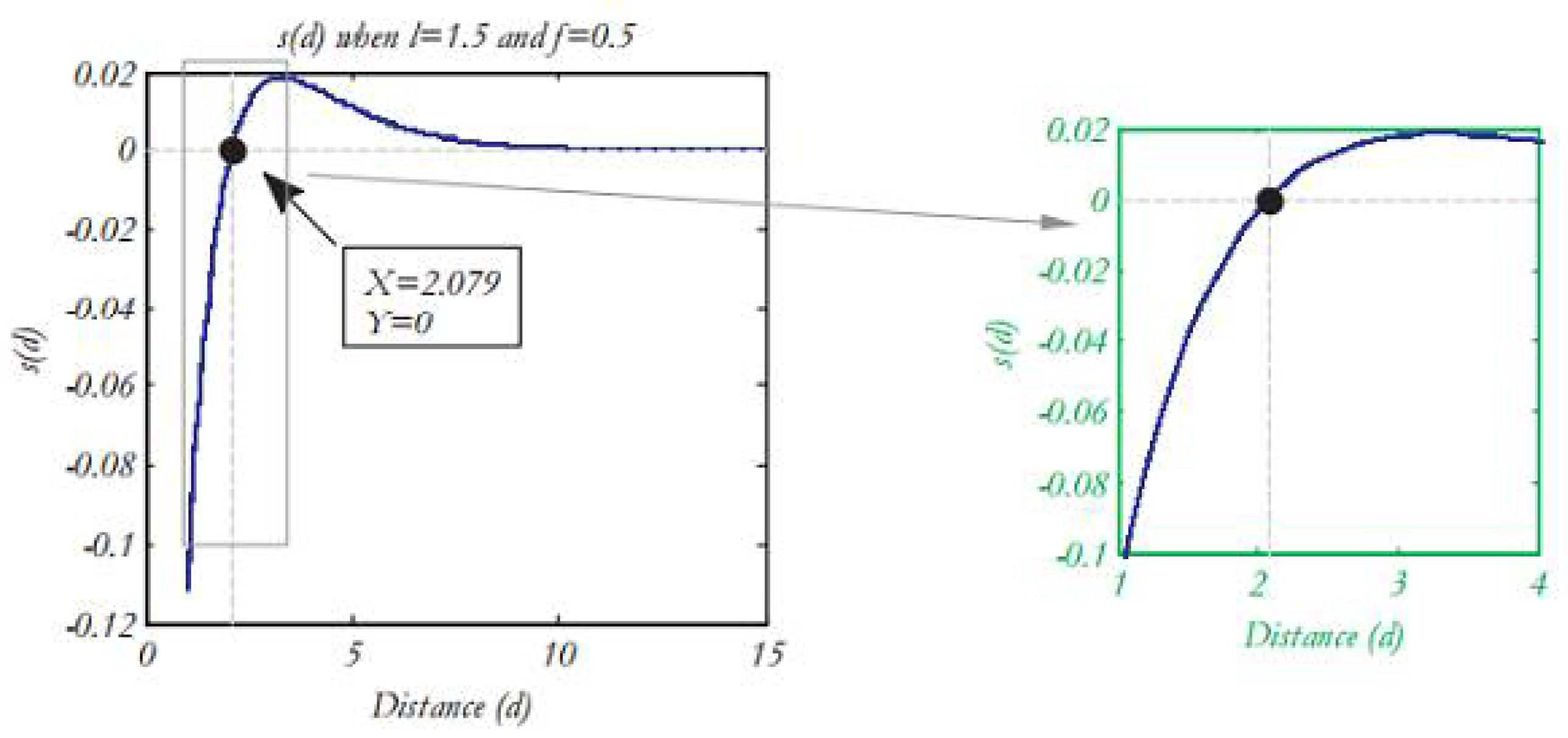
where f represents the intensity of attraction and I represent the scale length of attraction. The function S is depicted in Figure 1) to illustrate how it affects the social interaction (attraction and repulsion) among grasshoppers.
As evident from Figure 1), the distance considered ranges from 0 to 15, where repulsion occurs in the interval [0, 2.079]. When a grasshopper is at a distance of 2.079 from another grasshopper, there is neither attraction nor repulsion, which is referred to as the comfort zone or ease distance. Additionally, Figure 1) illustrates that attraction increases from a distance of 2.079 to around 4 and then gradually decreases. Changing the parameters, I and F in Formula (4) leads to different social behaviors in artificial grasshoppers. 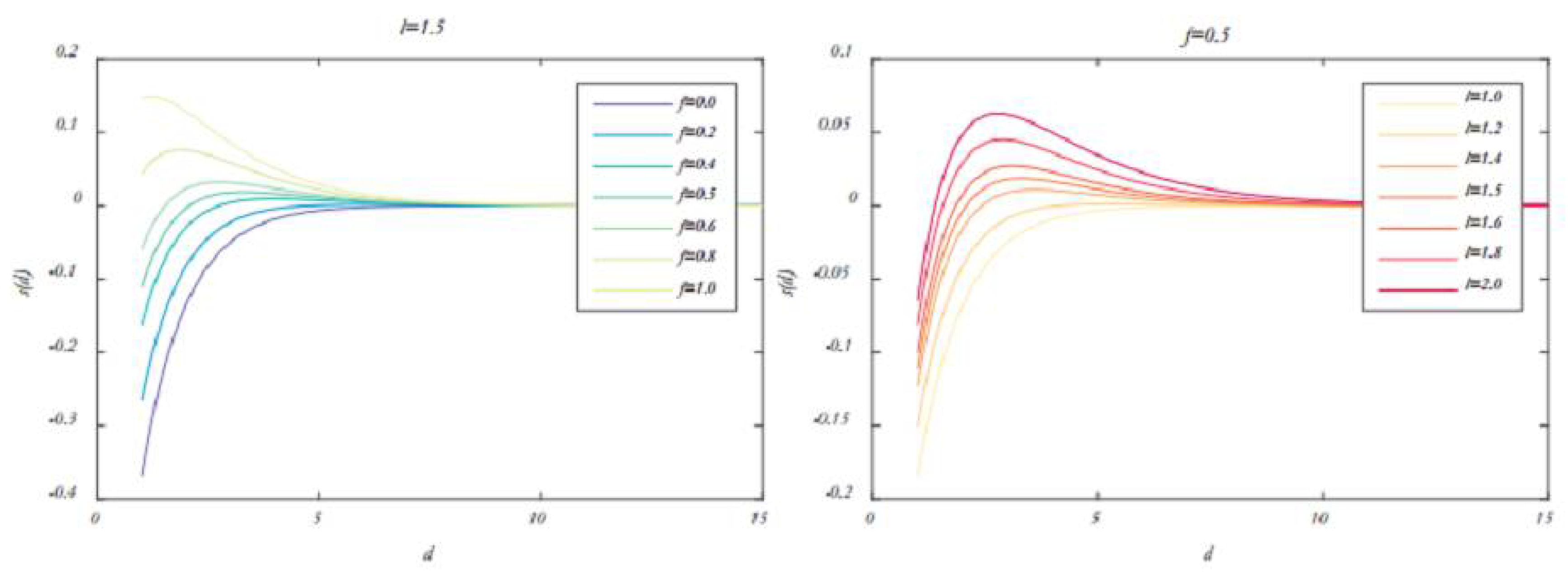To observe the impact of these two parameters, the function S in Figure 2) with different values of I and f in Formula (4) will result in various social behaviors in artificial grasshoppers.
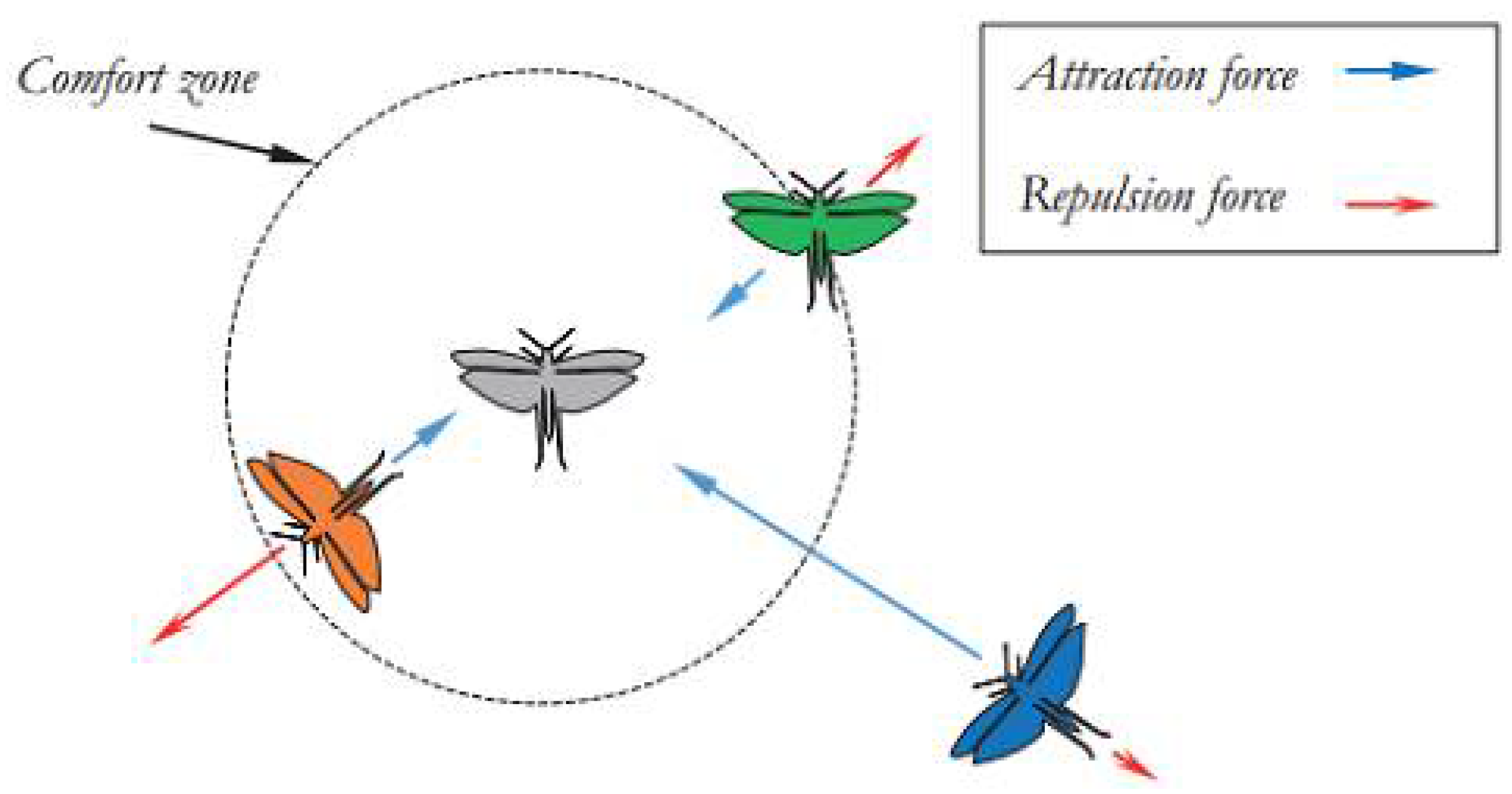
Figure 2) illustrates that the parameters I and f significantly alter the comfort, attraction, and repulsion regions. It should be noted that the attraction or repulsion regions are very small for certain values (for example, I=1 and f=1). In simulations, have been used values of I=1.5 and f=0.5. A conceptual model of interactions between grasshoppers and the comfort zone using the function S is depicted in Figure 3).
While the function S is capable of dividing the space between two grasshoppers into repulsion, attraction, and comfort regions, this function returns values close to zero for distances greater than 10, as shown in Figures (2) and (1). Therefore, this function is unable to exert strong forces between two grasshoppers that are far apart. To address this issue, the distance between two grasshoppers is mapped to the interval [1,4]. The shape of the function S in this interval is illustrated in Figure 1). Research has shown that Formula (1) cannot be used in simulations of congestion and optimization algorithms because this relationship hinders exploration and exploitation in the search space around a solution. The model has been employed for congestion in free space. Therefore, Formula (5) is utilized to simulate interactions between grasshoppers in congestion.
x i d = c ∑ j = 1 j ≠ i N c U b d − l b d 2 s x j d − x i d x j   − x i   d i j + T d ^
where U b d is the upper bound in dimension dth, l b d is the lower bound in dimension dth, T d ^ is the value in dimension dth of the target (the best solution seen so far), and c is a reduction constant for minimizing the comfort, repulsion, and attraction regions. In this equation, S is derived from Formula (4), and the parameters of gravity (G) and wind direction (A) are not considered. 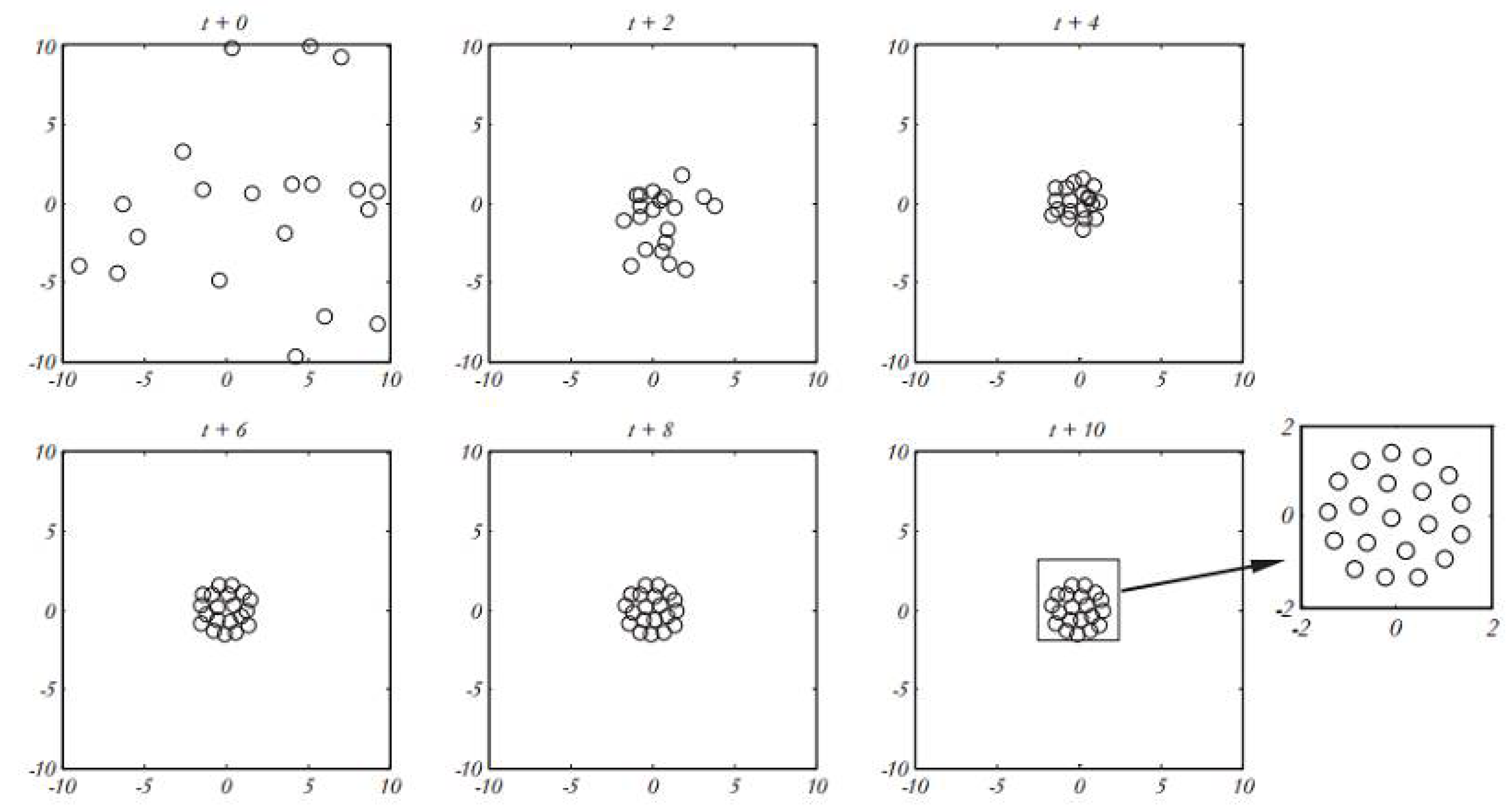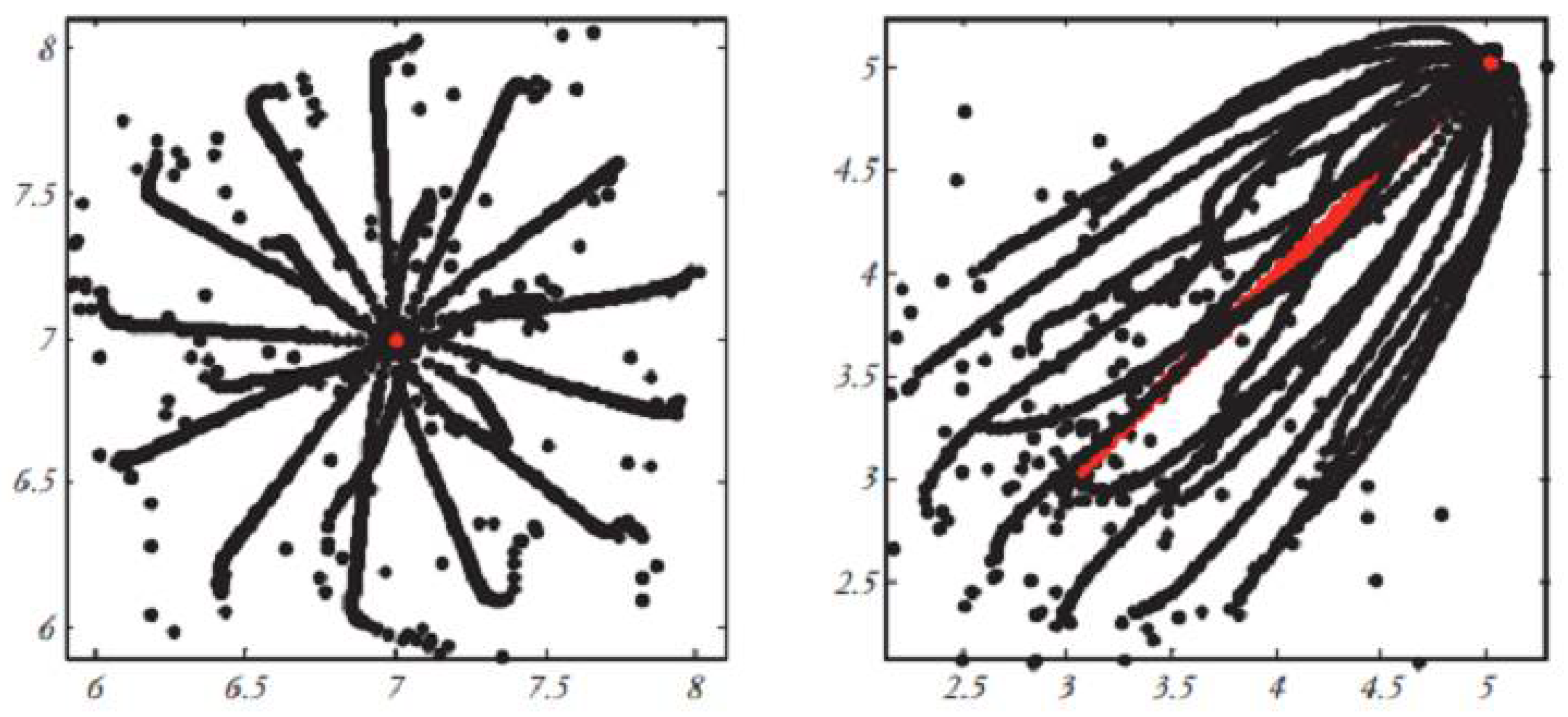The behavior of grasshoppers in a 2D space using Formula (5) is depicted in Figure 4). In Figure 4), a total of 20 artificial grasshoppers are utilized for movement within a time exceeding 10 units.
Figure 4) demonstrates how Formula (5) brings the initial random population closer together to form a unified and organized congregation. After 10-time units, all grasshoppers reach the global optimum region and cease further movement. Formula (5) defines the next position of a grasshopper based on its current position, the target position, and the positions of all other grasshoppers. Note that the first component in this relation considers the position of the current grasshopper concerning other grasshoppers. In essence, we consider the status of all grasshoppers to define the positions of search agents around the target. This is a different approach compared to the Particle Swarm Optimization (PSO) algorithm. In PSO, there are two vectors for each particle; the position vector and the velocity vector. However, in the GAO, there is only a position vector for each search agent. Another main difference between the two algorithms is that PSO updates the particle position according to the current position, personal best experience, and public best experience, but the GOA algorithm updates the position of the search agent based on its current position, the general best answer, and the positions of other locusts. It is also noteworthy that the adaptive parameter C is used twice in Formula (5) for the following reasons [9]:
  • The first c on the left is very similar to the inertia weight (W) in the PSO algorithm. It reduces the displacement of grasshoppers around the target. In other words, this parameter creates a balance between exploration and exploitation around the target.
  • The second variable c reduces the attraction, repulsion, and comfort regions between grasshoppers. Consider the component c U b d − l b d 2 s x j d − x i d in Formula (5), where U b d − l b d 2 linearly decreases the space between grasshoppers that should explore and exploit.
In Formula (5), the internal C leads to a proportional reduction in attraction/repulsion force between grasshoppers with each iteration of the algorithm, while the external c decreases the search coverage around the target with an increase in the number of algorithm iterations. In summary, the first part of Formula (5) considers the positions of other grasshoppers and simulates interactions among grasshoppers in nature, while the second part, T d ^ , simulates the tendency to move towards a food source in grasshoppers. Additionally, parameter C simulates a decrease in the speed of grasshoppers as they approach a food source and eventually consume it. To maintain a balance between exploration and operation, parameter c needs to decrease with an increase in iterations during the algorithm. The coefficient C reduces the comfort zone proportionally with the number of iterations and is calculated using Formula (6) [9].
C = C m a x − i C m a x − C m i n l
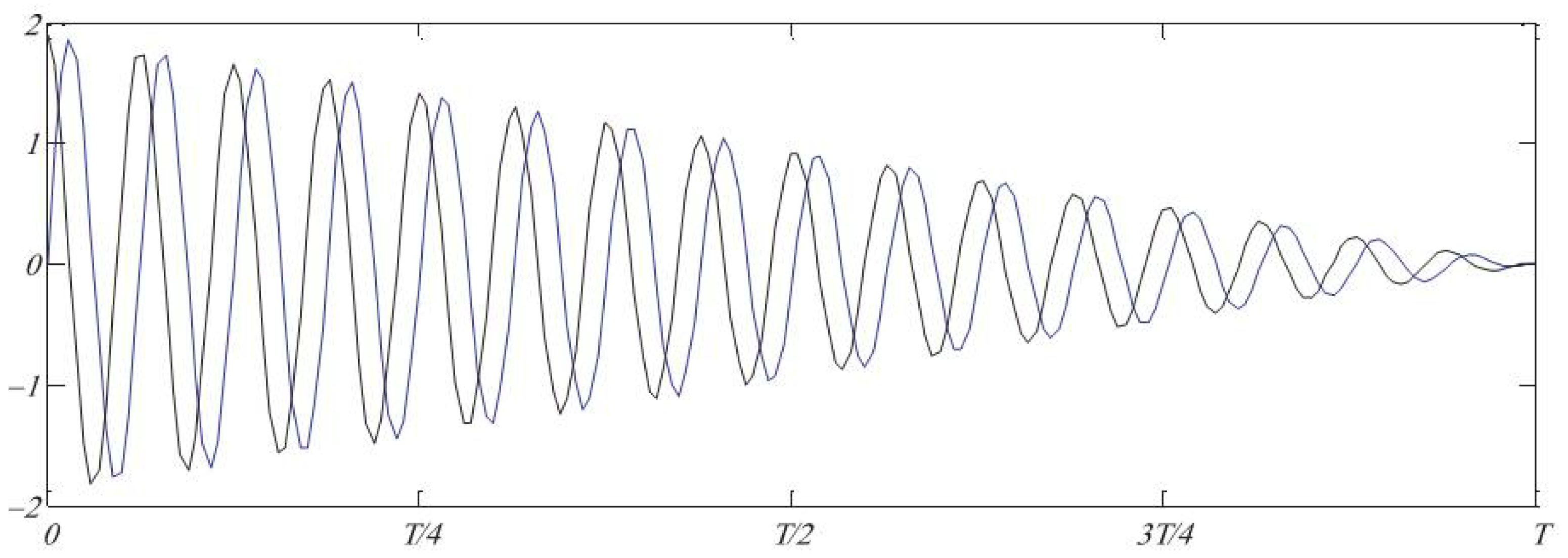
where C m a x is the maximum value, C m i n is the minimum value, i indicates the current iteration number, and L is the maximum number of algorithm iterations. In simulations, C m a x is considered as 1 and C m i n as 0.00001. The impact of this parameter on the movement and convergence of grasshoppers is illustrated in Figure 5).
Experiments have been conducted on fixed and moving targets to assess the performance of the GAO in understanding how the movement of grasshopper congregations towards the optimal solution of a problem occurs. The history of grasshopper positions over 100 iterations in Figure 5) demonstrates that the congregation gradually converges towards a fixed target in a two-dimensional space, a behavior attributed to the reduction of the comfort zone by factor C. It is also shown that the congregation effectively pursues a moving target, and this is why the last component of formula (5) is T d ^ , in which the grasshopper is pushed towards the target. These behaviors assist the GOA algorithm in avoiding rapid convergence towards a local optimum, ensuring that grasshoppers converge towards the target as much as possible, a behavior crucial during exploitation. The mathematical model presented for the GAO requires grasshoppers to gradually converge towards the target over the course of algorithm iterations. However, in real search spaces, there is no specific target because we do not know exactly where the global optimum, i.e., the main target, is located. Therefore, at each optimization stage, we will find a target for the grasshoppers. In the GAO, it is assumed that the best grasshopper during algorithm execution (the grasshopper with the best objective function value) is the target. This helps the algorithm store the most promising target in the search space at each iteration and compels grasshoppers to move toward this target. This action is performed with the hope of finding a better and more accurate target as the best approximation for the global optimum in the search space [9].
The stages of the GAO are as follows:
  • Generating a random population of grasshoppers in the search space.
  • Determining problem parameter values such as lower bound (Cmin) and upper bound (Cmax) of the comfort zone and maximum number of evolution iterations.
  • Calculating attractiveness for each grasshopper using the optimization function.
  • Identifying the best grasshopper (the grasshopper with the highest attractiveness) in variable T.
  • Until reaching the termination condition (maximum number of iterations I <):
  • Updating the comfort zone using Formula (6).
For each grasshopper:
  • Normalizing the distance between grasshoppers within the range [1,4].
  • Updating the position of each grasshopper using Formula (5).
  • Returning a grasshopper to the search space if it has moved out.
  • Updating T if a grasshopper with better attractiveness is found.
  • Incrementing the internal iteration counter (I=I+1).
Returning the best grasshopper as the final answer.
The GAO has a strong search mechanism in the sterile problem space and has shown in the optimization of high-dimensional functions, it has a high accuracy in reaching the global optimum, and due to the collective movement of the grasshoppers to a region of space where the global optimum is in that region , the optimality of the problem is found with more accuracy, which makes the convergence accuracy of this algorithm, the dependence of this algorithm on the number of search agents and the other hand the collective movement of locusts to the better area of the search space causes, some points of the search space (if there are few search agents) will not be properly explored, and this will cause premature convergence to the local optimum, and also, in this algorithm, the number of agents is fixed until the end of the algorithm iteration, which will increase the number of function evaluations. Because at the beginning of the work, the algorithm needs the right number of search factors and strong exploration, but as the end of the algorithm iterations approaches, extraction will be needed, and for optimal extraction (convergence to optimality), all search factors may not participate. Also, the important parameter of this algorithm is the comfort zone, which in this algorithm decreases linearly and according to the iterations of the algorithm, and in which the rate of convergence and the state of the locusts in the search space are not included [9].
  • Arithmetic Optimization Algorithm
The Arithmetic Optimization Algorithm is an elitist population-based method that has demonstrated high extraction power and precise convergence, leading to achieving the exact optimal point even in high-dimensional functions. This algorithm addresses both exploration and exploitation in optimization and aims to find the global optimum of the problem. In this algorithm, the best solution always represents the destination for search waves. Therefore, search waves do not deviate from the primary optimum of the problem, and also the fluctuating behavior in this algorithm allows it to search the search space around the optimum of the problem well, and have a good accuracy of obtaining the optimum [10].
The algorithm stages are as follows:
  • Generating search waves.
  • Until reaching the termination condition (maximum number of iterations I <):
  • Evaluation: Each wave is evaluated using the problem evaluation function.
  • Update: Update the best-found solution.
  • Update: r 1   و r 2   و r 3   و r 4  
  • r 1   = a − t a T
a constant variable and t the current iteration and T the final iteration
  • Update: New coordinates of waves.
  • x i t + 1 = x i t + r 1   × sin ⁡ r 2   × r 3   p i t − x i t                                   r 4   < 0.5 x i t + r 1   × c o s ⁡ ( r 2   ) × r 3   p i t − x i t                                   r 4   ≥ 0.5
Completing the final number of iterations of the algorithm and returning the best-found solution as the optimal solution of the problem.
In this algorithm, the variables include:
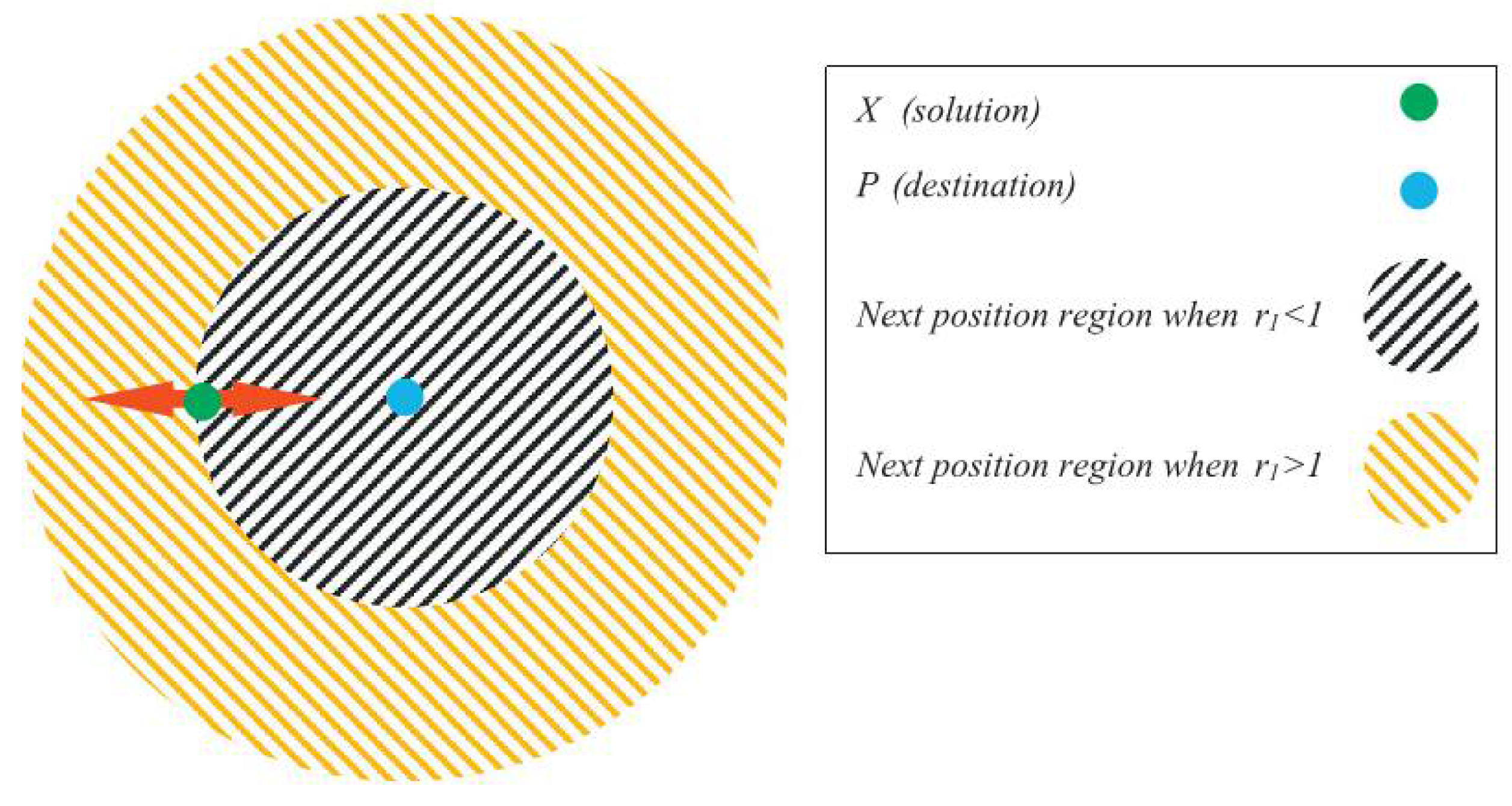
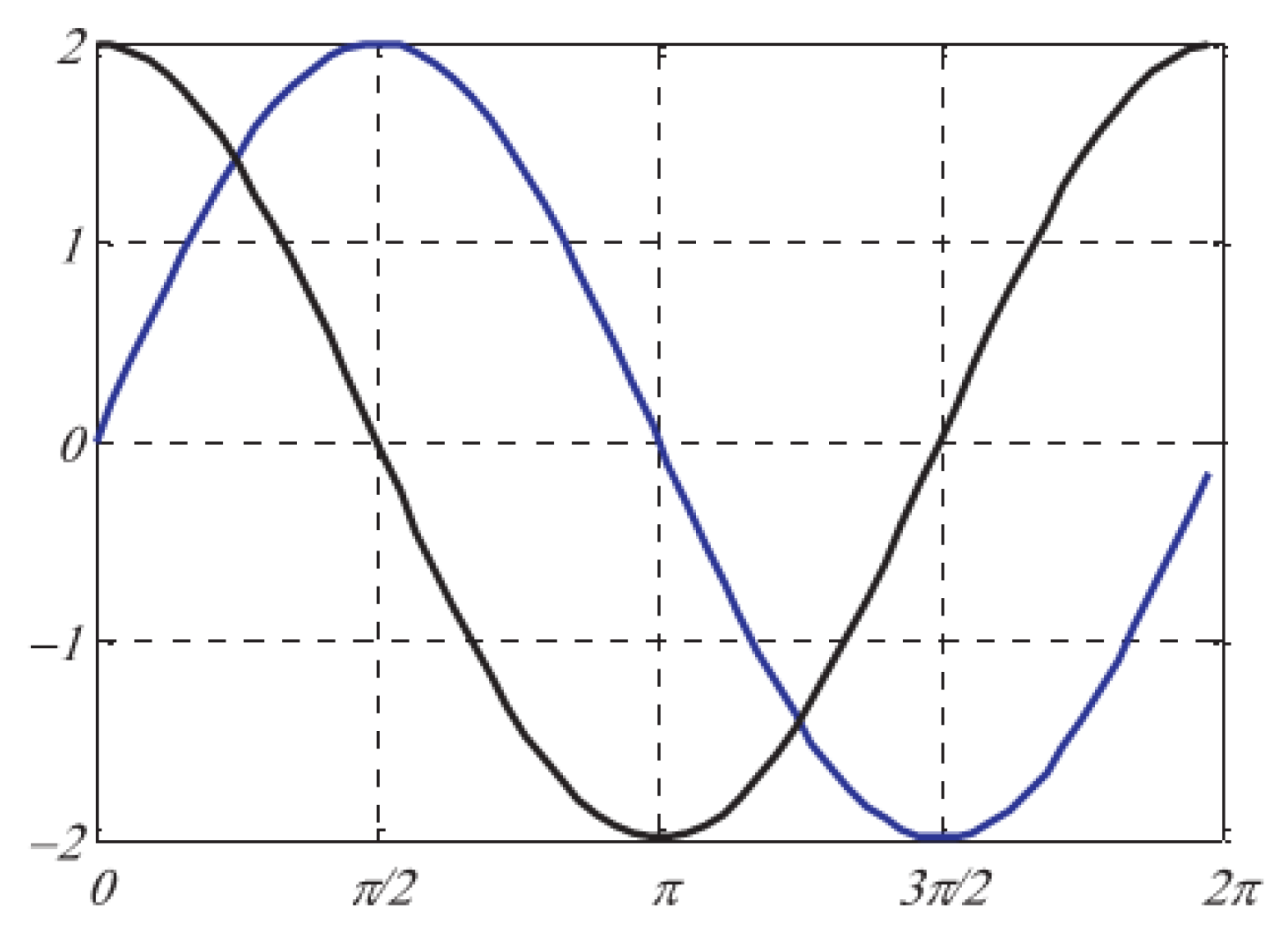
x i t + 1 the new coordinates of the search wave and x i t the previous coordinates of the search wave and p i t the coordinates of the best solution found, which is considered as the destination, and r 1   if it is less than 1, move towards the destination point, and if it is greater than 1, move away from the destination point. Figure 6) shows the effect of the r 1   parameter on the movement of waves in the sine-cosine algorithm, Figure 7) shows the effect of the r 1   parameter on the discovery and extraction of the sine-cosine algorithm.
Parameter r 2   is used to model oscillatory movement and varies between 0 and 360 degrees. Figure 8) illustrates the impact of parameter r 2   on wave movement in the Arithmetic Optimization Algorithm.
serves as a weight for the destination, where if it is considered greater than 1, a larger step towards the destination is taken, and if it is less than 1, a smaller step is taken towards the destination, and r 4     is a random variable between 0 and 1 used to switch between sine and cosine movements.

4. Proposed Method for Detecting Attacks in IoT

In this section, we present a model for detecting attacks that can be used to examine and eliminate malicious nodes in the network, thereby improving network performance through continuous intrusion detection. The proposed model enhances the random neural network method with an Arithmetic Optimization and GAO combined Algorithm for adjusting the architecture and weights of the neural network. The proposed model can be divided into several stages, including data collection and preparation, random neural network stage, and Arithmetic Optimization and GAO combined Algorithm stage for improving the neural network in two phases; architecture improvement phase and weight improvement phase. The overall stages of the proposed model are depicted in Figure 9), which include data preparation, architecture adjustment of the random neural network, and weight adjustment.
  • Stage 1: Data Collection and Preparation:
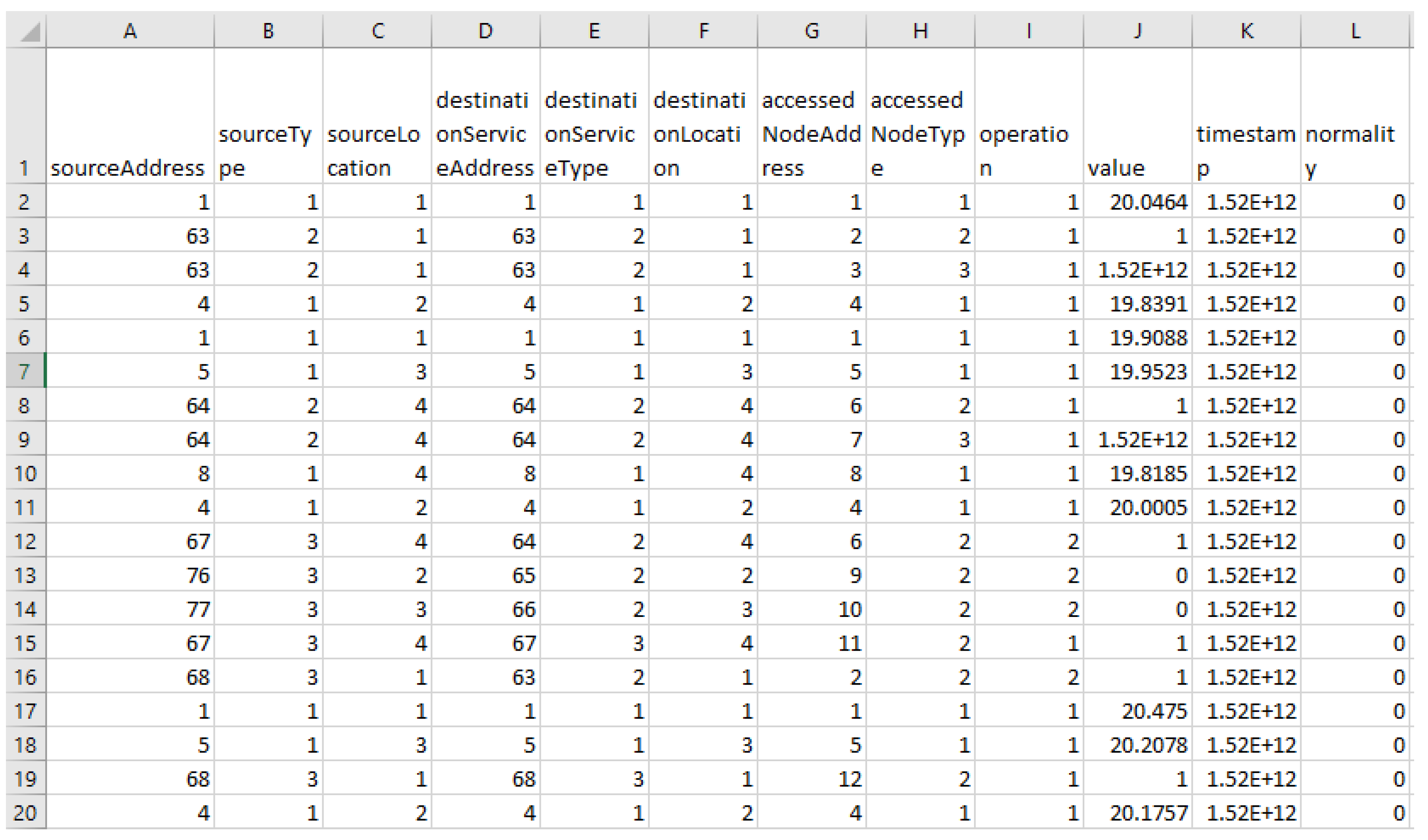
In this stage, the specified dataset in the baseline study [6], named DS2OS, is divided into 70% for training and 30% for testing the model. This dataset consists of 260,000 samples with eleven features, including the "Source Address" feature indicating the senders of messages, with 89 agents sending messages from 84 devices such as washing machines, dishwashers, etc. The "Source Type" feature refers to the type of equipment (including 8 types) such as light controllers, motion sensors, service sensors, service batteries, service door locks, environmental temperature controllers, washing services, and smartphones. The "Source Location" feature includes 21 locations such as bathrooms, dining rooms, kitchens, garages, and workrooms. Other features relate to the destination of the messages, similar to the source node, including "Destination Address," "Destination Type," and "Destination Location." Intermediate nodes are used among nodes, with three features related to these nodes including "Access Node Address" referring to the addresses of intermediate nodes, which include 170 different entries in the dataset, and "Access Node Type" similar to the source and destination types with 8 types. Finally, the operational feature includes the "Operation" feature consisting of 5 operations such as register, write, read, authenticate, and block, with the message transmission time from source to destination in the "Time" feature and the numerical value transmitted in the message in the "Value" feature [6].
  • Stage 2: Random Neural Network:
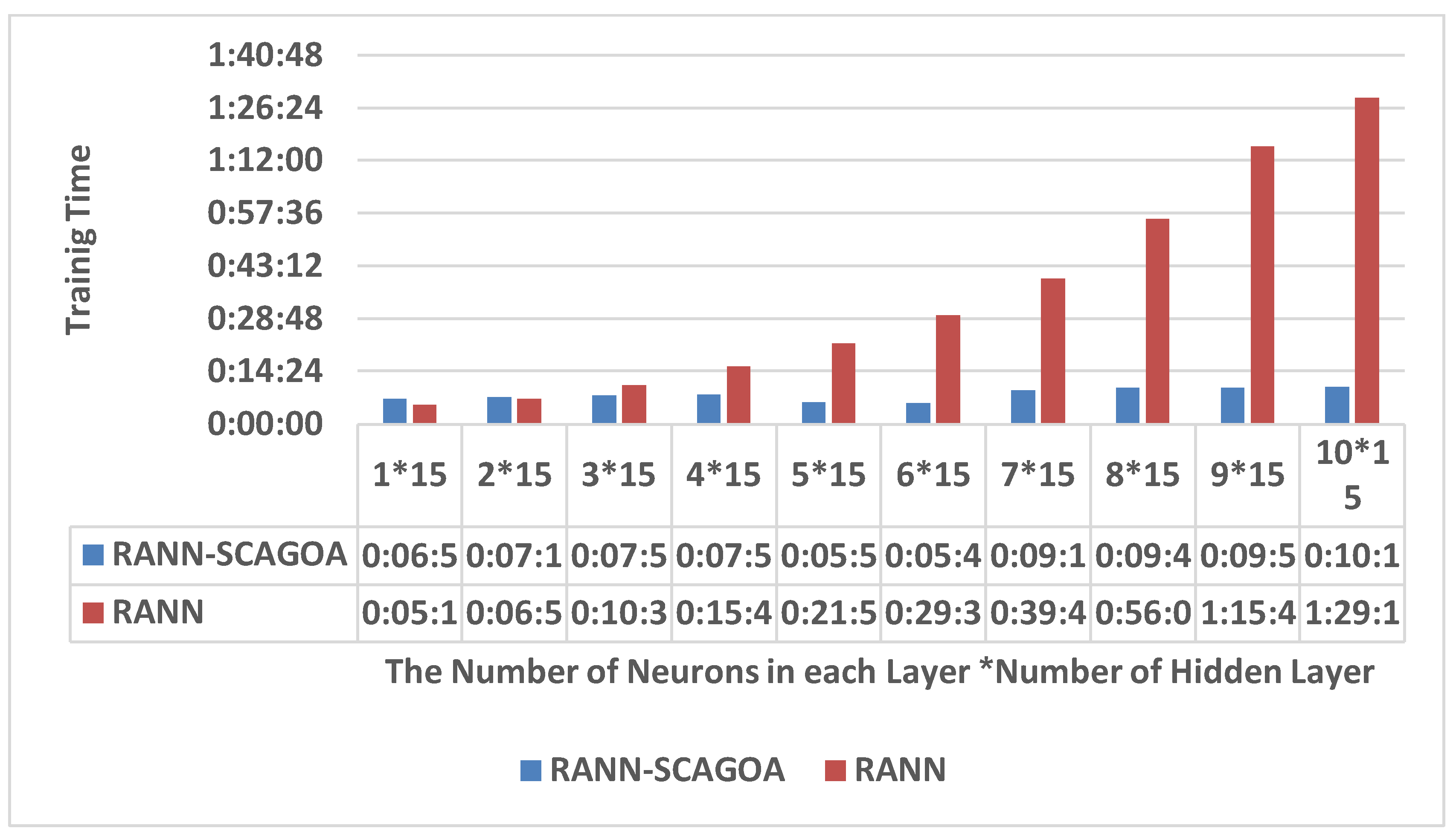
In the baseline study [6], different layers of the random neural network have been tested along with the number of neurons in each hidden layer. It has been concluded that a neural network with 8 hidden layers and 15 neurons in each layer yielded the best results. The random neural network comprises 1 input layer, 8 hidden layers, and 1 output layer. A diagram of this neural network is shown in Figure 10). As evident, the defined features in the dataset section are utilized as features for training the intrusion detection model in the neural network. The proposed model for improving the lightweight random neural network involves enhancing the neural network weights using an Arithmetic Optimization and AGO combined Algorithm. The improvement of the random neural network using an Arithmetic Optimization and AGO combined Algorithm involves assigning a random value for the weights of the neural network in each Arithmetic Optimization and AGO combined Algorithm (a possible solution). The dimensionality of each Arithmetic Optimization and AGO combined Algorithm corresponds to the number of weights in the network. For example, in a neural network with 8 hidden layers, each containing 15 neurons, there are a total of 1671 weights (88 weights connecting the input layer to hidden layers, 1575 weights in 8 hidden layers, and 8 weights connecting the hidden layer to the output layer). In standard random neural networks, gradient descent is used to adjust the network weights to obtain the least square error of the network through error backpropagation. Gradient descent is an optimization method through a derivative calculation that converges prematurely to a local minimum in optimization functions, including the error square function in random neural networks, failing to converge to the minimum point of function convergence. Therefore, Arithmetic Optimization and GAO combined evolutionary algorithms are used for convergence to the minimum point of error square function in this random neural network. The random neural network has a closer resemblance to biological neural networks and can better demonstrate the transmission of human brain signals. In these networks, neurons in different layers are connected to each other. These neurons have excitatory and inhibitory states depending on the received signal potential. If a neuron encounters a positive signal, it becomes excited and shifts to an inhibitory state for a negative signal. The state of neuron ni at time t is indicated by Si(t). Neuron ni will remain inactive until Si(t) = 0. To become excited, Si (t)> 0 must be greater than as Si(t) is considered a non-negative integer. In an excited state, a neuron transfers an impulse signal at speed hi to another neuron. Using formula (7), received signals are represented as positive or negative signals.
k ( i ) + x + ( i , j ) + p − ( i , j ) = 1 ∀ i , j = 1
In formula (7), the sent signal can be received by neuron nj as a positive signal or a negative signal with probability p+ (i, j) and p− (i, j), respectively. Additionally, this signal can exit the network with probability k (i). The weights of neurons ni and nj are updated using the following formulas:
w+ (i, j) = hip+ + (i, j) ≥ 0
w− (i, j) = hip− + (i, j) ≥ 0
In formulas (9) and (8), the parameter hi represents the transmission speed to another neuron and must have a weight value greater than 1. In the random neural network model, the signal probability is determined by a Poisson distribution.
λ + j = ∑ j = 1 n e j r j p + j . i + Λ i
λ − j = ∑ j = 1 n e j r j p − j . i + Λ i
In formulas (11) and (10), for neuron ni, positive and negative signals are represented by Poisson rates Λ (i) and λ (i), respectively. The activation function e j , which is described by formula (12), denotes the output activation function.
e i = λ + j h i + λ − j
where the transmission speed h (i) shown in formulas (9) and (8) is calculated using formula (13).
N h (i) = (1 − k (i)) − 1 X[w+ (i, j) + w− (i, j)]
j=1
where h (i) represents the firing rate during the RaNN model training period, and the positive and negative probabilities are updated, which can be described using formula (14).
N h (i) = X [w+ (i, j) + w− (i, j)]
The random neural network is trained using the gradient descent algorithm, which is used to find local minima of a function and helps reduce the overall mean square error. The error function is calculated using formula (15).
E p = 1 2 ∑ i = 1 n α i q j p − y j p . α i ≥ 0
where α ∈ (0,1) represents the state of output neuron i. The error function calculates the difference between the actual value and the predicted output value with qjp and yjp, respectively. The weights are updated using formulas (16) and (17).
w a . b + t = w a . b + t − 1 − η ∑ i = 1 n α i q j p − y j p ∂ q i ∂ w   a . b +   t − 1
w a . b − t = w a . b − t − 1 − η ∑ i = 1 n α i q j p − y j p ∂ q i ∂ w   a . b −   t − 1
where the weights are updated after training neurons a and b as w+ (a, b) and w− (a, b).
  • Step 3: Arithmetic Optimization and GAO combined algorithm in Neural Network Improvement
The Arithmetic Optimization and GAO combined algorithm has high extraction power and accurate convergence, and this leads to achieving the optimal exact point even in high-dimensional functions. In this algorithm, the best answer is always the motion indicator for search agents. Therefore, the combined chain of Arithmetic and GAO do not deviate from the original optimality of the problem, and also the various movement behaviors in this algorithm allow it to search the search space around the optimality of the problem well and have good accuracy of obtaining the optimality. In the Arithmetic Optimization and GAO combined algorithm, every possible solution (value for the W parameter) is changed using the operators of the Arithmetic Optimization and GAO combined algorithm, to finally achieve the best value of this parameter. To calculate the fitness of each person in this algorithm, is used the fitness function of the classification accuracy rate. As mentioned, the proposed model to improve the random neural network used in the basic study [6] is carried out in two stages, which include:
  • Improving the architecture of the Lightweight random neural network by using the Arithmetic Optimization and GAO combined algorithm in terms of the number of hidden layers and neurons of each layer.
  • Improving weights of Lightweight random neural network using Arithmetic Optimization and GAO combined algorithm
Figure 10) shows the improvement of the Lightweight random neural network using the Arithmetic Optimization and GAO combined algorithm in terms of the number of hidden layers and neurons in each layer.
In this stage, a search agent is an array with a specified number of cells (the number of cells in the array is equivalent to the hidden layers of the network), and the number inside each array indicates the number of neurons in that hidden layer. Figure 11) illustrates an example of a search agent.
As evident from Figure 11), the neural network consists of eight hidden layers with the number of neurons in each layer being 5-2-4-7-1-8-2-4, respectively. After improving the architecture of the lightweight random neural network, in the second stage, the proposed model adjusts the weights of the neural network.
In this stage, a search agent is an array with a specified number of cells, which corresponds to the weights of the network, and the number inside each array represents the value of each weight. For example, for a neural network with the architecture from the previous stage consisting of one input layer (eleven features of the dataset) and seven hidden layers (with the number of neurons being 5-2-4-7-8-2-4) and one output layer. The neural network has 11*5 + 5*2 + 2*4 + 4*7 + 7*8 + 8*2 + 2*4 + 4 weights, totaling 185 cells in the search agent.
  • To further clarify the discussion, several search agents in each phase are provided as examples:
For a neural network with 4 hidden layers, with the first layer having 3 neurons, the second layer having 2 neurons, the third layer having 5 neurons, and the fourth layer having 8 neurons, the search agent is specified as follows.
Preprints 107626 i001
In the following search agent, the same number of layers and hidden neurons has been specified.
Preprints 107626 i002
As evident, the number of cells in Table 21 is 21, meaning each search agent can specify up to 21 hidden layers for the neural network. For weight adjustment, the following example illustrates a neural network with 11 weights taken with values between 1 and -1.
Preprints 107626 i003
As evident, a neural network with 11 weights has been initialized. The accuracy function for both stages of adjusting the architecture and weights of the random neural network is a measure of classification accuracy, calculated according to the formula (18).
a c c u r a c y = T P + T N T P + T N + F P + F N
where TP and TN correspond to true positives and true negatives, respectively, in the fraction representing all correct and incorrect classifications. Each element of the matrix is described as follows:
  • TN: The number of records whose actual class is negative and the classification algorithm correctly identifies them as negative.
  • TP: The number of records whose actual class is positive and the classification algorithm correctly identifies them as positive.
  • FP: The number of records whose actual class is negative but the classification algorithm incorrectly identifies them as positive.
  • FN: The number of records whose actual class is positive but the classification algorithm incorrectly identifies them as negative.
The core of the intrusion detection system, which significantly impacts system performance, is the detection model that can be designed using machine learning methods or artificial neural networks. The stages of the Arithmetic Optimization and GAO combined algorithm are as follows:
  • Generating a random population of search agents (each search agent in Figure 5) represents the number of neurons in a hidden layer, and in Figure 6) represents the weights of the neural network).
  • Determining the problem parameters such as lower and upper bounds of comfort zone in the grasshopper Algorithm and the maximum number of evolution rounds.
  • As long as the number of iterations is not completed, the following steps are performed:
    -
    Calculating the suitability of each search agent using the formula (18).
    -
    Identifying the best search agent in variables T and P.
    -
    Updating the comfort zone using formula (6).
    -
    Updating parameter r 1 using formula (7).
    -
    Normalizing the distance between grasshoppers in the range [1,4].
    -
    Performing Arithmetic movements using formula (8) for all search agents.
    -
    Performing grasshopper movements using formula (5) for all search agents.
    -
    If a search agent has moved out of the search space, it should be returned to the search space.
    -
    Incrementing the internal iteration number (I = I + 1).
  • Returning the best search agent as the final answer.

5. Performance Evaluation

In this section, we conduct a comprehensive evaluation of our proposed design compared to common designs in the literature through simulation. After detailing the simulation setup, protocol comparisons, and metric evaluations, simulation results along with their analysis will be presented.

Simulation Setup

For simulation, a computer with a 5-core processor and 4 gigabytes of memory is used, along with MATLAB 2019b software. The settings of the Arithmetic Optimization and GAO combined Algorithm in Table 2 are specified, with 30 search agents set in 300 iterations. We have four scenarios for simulation. The dataset used is named DS2OS, consisting of 256012 samples and 11 features, as indicated in Table 3.
The proposed intrusion detection system is based on a random neural network method that learns from observing significant factors in network traffic changes under flood-like attacks in the training samples, labeled as: Source Address, Source Type, Source Location, Destination Address, Destination Type, Destination Location, Access Node Address, Access Node Type, Operation, Data Value, and Transmission Time. The Source and Destination Address refer to the ID of each node, and the Node Type corresponds to the type of equipment, such as whether it is a sensor or an actuator. The operation relates to the number of delivered packets, which can be inspected at the destination node and includes the number of packets delivered from the source node. The input parameter Data Value refers to the numerical value sent in the data, and the packet transmission time is another parameter in the dataset. Therefore, considering the base paper, 11 effective features for intrusion detection are listed in Table (3). An example of the dataset, transformed into numerical values for use in experiments, is specified in Figure 13).
The proposed method in this article improves the proposed model in the baseline study [6] using the Arithmetic Optimization and GAO combined algorithm. As mentioned, the Arithmetic Optimization and GAO combined algorithm helps optimize the weights of the random neural network, enabling this method to achieve better classification results in terms of accuracy.
  • Scenario 1: The results of the proposed model are evaluated using the Support Vector Machine method as a parametric method and the k-Nearest Neighbors method as a non-parametric method on the baseline dataset
  • Scenario 2: The results of the proposed model are evaluated using the random neural network with the specified architecture from the baseline study [6].
  • Scenario 3: The results of the improved random neural network method are investigated with the Arithmetic Optimization and GAO combined algorithm.
  • Scenario 4: The Support Vector Machine combined model, k-Nearest Neighbors method, and the proposed method in the ensemble learning model are evaluated on the baseline dataset [6].
Finally, based on the four simulated scenarios and the obtained results, the output of the proposed method (RaNN-SCAGOA) is compared with other methods. To evaluate the results, metrics such as false alarm rate, detection rate, and accuracy are used for comparison. The false alarm rate is calculated using equation (19) and represents the rate at which the system incorrectly detects malicious behaviors as normal behaviors. Therefore, a lower false alarm rate is desirable. The detection rate is calculated using equation (20) and represents the rate of correctly detecting attacks. A higher detection rate indicates better system performance. Accuracy is calculated using equation (21), representing how well the system has correctly identified attack detections.
f a l s e   a l a r m   r a t e = F P T P + F P
d e t e c t i o n   r a t e = T P F N + T P
a c c u r a c y = T P + T N T P + T N + F P + F N
  • Scenario 1: Simulation of the Support Vector Machine method and k-Nearest Neighbors method.
Considering that there are two classes, the number of neighbors in the k-Nearest Neighbors method should be odd. For this purpose, different numbers of neighbors including 1, 3, 5, 7, 9 have been tested. In this experiment, a 10-fold cross-validation method has been used for training. The results of the proposed model are only tested with the k-Nearest Neighbors method with one neighbor. In these results, the highest accuracy value was 0.966. Additionally, the k-Nearest Neighbors method with three neighbors was tested. In these results, the highest accuracy value was 0.964. The results are shown in Table 4. The proposed model results are only tested with the k-Nearest Neighbors method with five neighbors.
The results in Table (4) show that the highest accuracy value was 0.978. The proposed model's results were also tested using only the k-Nearest Neighbors method with seven neighbors, yielding a maximum accuracy value of 0.965. Additionally, the proposed model was tested using only the k-Nearest Neighbors method with nine neighbors, achieving a maximum accuracy value of 0.972. As evident from the average accuracy obtained in various settings of this method, the k-Nearest Neighbors method with five neighbors had the best performance with an average accuracy of 0.9732. Figure 14) illustrates the results with different neighbors.
Next, the simulation results with Support Vector Machine using different kernels are presented. The proposed model's results were tested using the Support Vector Machine method with a sigmoid kernel. In these results, the highest accuracy value was 0.984. The proposed model was also tested using only the Support Vector Machine method with a polynomial kernel, achieving a maximum accuracy value of 0.982. Furthermore, as indicated in Table 5, the proposed model's results were tested using only the Support Vector Machine method with a Gaussian kernel. In these results, the highest accuracy value was 0.988.
As evident from the average accuracy obtained in various settings of this method, the Support Vector Machine with a Gaussian kernel had the best performance with an average accuracy of 0.9862, outperforming the k-Nearest Neighbors method in terms of accuracy. Figure 15) illustrates the comparison of results from different settings of the Support Vector Machine method.
The results of the proposed model were tested using the Support Vector Machine method with a sigmoid kernel. In these results, the accuracy value was 0.985. The proposed model was also tested using only the Support Vector Machine method with a polynomial kernel, achieving an accuracy value of 0.983. Furthermore, as indicated in Figure 15), the proposed model's results were tested using only the Support Vector Machine method with a Gaussian kernel. In these results, the highest accuracy value was 0.986.
  • Scenario 2: Simulation of the Random Neural Network Method
Based on the experiments in the baseline study [6], which determined the optimal architecture with eight hidden layers and fifteen neurons in each layer in terms of the number of neurons in the hidden layer and other neural network tuning parameters. Table 6 presents the results of the Random Neural Network (RaNN) with 10-fold cross-validation.
As evident from the results of ten-fold cross-validation of the Random Neural Network method presented in the baseline study [6], the best accuracy result was 0.991, with an average detection accuracy of 0.9901.
  • Scenario 3: Simulation of the Improved Random Neural Network Method with the Arithmetic Optimization and GAO combined algorithm
Based on the optimal architecture of the Random Neural Network in the baseline study [6], which includes eight hidden layers and fifteen neurons in each layer, Table 7 presents the results of the improved Random Neural Network method with the Arithmetic Optimization and GAO combined algorithm. In this improved neural network, training is no longer performed in the usual manner, and it is the Arithmetic Optimization and GAO combined algorithm that adjusts the weights of the network. As evident from the results of ten-fold cross-validation of the improved Random Neural Network method with the Arithmetic Optimization and GAO combined algorithm, the best accuracy result was 0.996, with an average detection accuracy of 0.9949.
  • Scenario 4: Multi-Task Learning Model Simulation
In this section, the best architecture of the tested methods has been experimented in the form of multi-task learning, including the nearest neighbor method with 5 neighbors, Gaussian kernel support vector machine, and improved random neural network with the Arithmetic Optimization and GAO algorithm. As shown in Table 8, the results of the proposed model in multi-task learning show higher accuracy compared to other experiments, with the highest accuracy value being 0.997, but the average is obtained as 0.9956. Table 9 provides a comparison of the tested methods and the proposed model (RaNN-SCAGOA). Figure 18) shows a graphical comparison of the results.
Figure 16) shows that the proposed model (RaNN-SCAGOA) in the DS2OS dataset [6] has achieved higher accuracy compared to the baseline study method (RaNN) [6], and this accuracy has also been higher in the multi-task learning model (Ensemble (KNN-SVM-(RaNN-SCAGOA))). Table 10 compares training time and classification accuracy in the random neural network (RaNN) and the improved random neural network (RaNN-SCAGOA).
Figure 17): Each neural network architecture with a number of neurons in different hidden layers has been trained and tested three times, and the average training time and accuracy obtained have been recorded. In training the random neural network, the maximum number of iterations is 1000, and for the improved random neural network, the maximum number of iterations for Arithmetic Optimization and GAO combined algorithm is 1000. The default training method for the random neural network is gradient descent, while the improved model uses Arithmetic Optimization and GAO combined algorithm. When using the Arithmetic Optimization and GAO combined algorithm, an initial population of 100 Arithmetic Optimization and GAO combined algorithm is considered, with the rest of the parameters set according to the algorithm's default settings.
As seen in Table (10), in terms of training time, in the standard random neural network, as the number of neurons in the hidden layer increases, the execution time increases due to training via gradient descent. However, in the improved model, the time spent on training is related to the execution of the Arithmetic Optimization and GAO combined algorithm. In fact, increasing the number of neurons in the hidden layer of the neural network leads to an increase in the dimensions of each Arithmetic Optimization and GAO combined algorithm, and this increase in dimensions in the Arithmetic Optimization and GAO combined results in less processing time compared to training in a standard random neural network, because in the standard random neural network, it needs to reach the optimal weight values through derivation, and therefore, with an increase in the number of weights, more time is needed for training. In terms of classification accuracy, it is observed that in the standard random neural network, with changes in the number of neurons and hidden layers, the accuracy varies, and even with ten hidden layers with fifteen neurons in each hidden layer, this accuracy does not increase and the best architecture, considering the architecture introduced in the base study [6], consists of eight hidden layers with fifteen neurons in each hidden layer. In proportion to the improved random neural network's classification accuracy, better results are obtained in all cases and have achieved a classification accuracy of 99.49% in the neural network architecture with eight hidden layers and fifteen neurons in each hidden layer, while the best results of the base study [6] with the same random neural network architecture had an accuracy of 99.01%.

6. Conclusions and Future Works

In this paper, an Arithmetic Optimization and GAO combining evolutionary algorithm has been proposed for adjusting the weights of a random neural network in the field of intrusion detection in Industrial IoT networks. It has been observed that intrusion detection has been under investigation in recent studies, and researchers have tried to provide a suitable system for detecting attacks. Therefore, presenting a suitable intrusion detection system has a direct relation with selecting and the performance of the classification method, where among classifiers, neural networks are recognized as an effective method. The performance of a neural network can be improved by adjusting its parameters, including network weights. In this paper, an Arithmetic Optimization and GAO combining evolutionary algorithm has been used to adjust the weights. The results showed that in terms of training time, the standard random neural network requires more time as the number of neurons in the hidden layer increases because its training is done via gradient descent. However, less time is spent on training in the improved model because increasing the number of neurons in the hidden layer of the neural network leads to an increase in dimensions of each Arithmetic Optimization and GAO combination, and like the standard neural network, it does not require derivation and weight adjustment. Additionally, in terms of classification accuracy, the standard random neural network shows variable classification accuracy with changes in the number of neurons and hidden layers, which does not increase with an increase in the number of neurons. The results showed that the k-nearest neighbor method with 5 neighbors as a non-parametric method achieved a detection accuracy of 97.32%, and the Gaussian kernel support vector machine as a parametric method achieved an accuracy of 98.62%. This is while the baseline study method, which is a random neural network, achieved an accuracy of 99.01%, and its improved method achieved an accuracy of 99.49%. Placing the best methods together in these experiments in the form of multi-task learning showed an increase in accuracy up to 99.56%. The Arithmetic Optimization and GAO combined algorithm can help improve the architecture and weights of a random neural network to enhance its accuracy. It was observed that this accuracy has increased and can even be an effective solution for speeding up training. Furthermore, considering the assumption of improving intrusion detection accuracy, it was evident that the proposed model is effective in this area and can even increase this accuracy by combining other classification methods in multi-task learning mode. Given the performance of the proposed model and improvement in classification accuracy, it is recommended to investigate other evolutionary algorithms with higher convergence accuracy compared to Arithmetic Optimization and GAO combined algorithm for enhancing random neural networks in intrusion detection. It is also suggested to utilize the proposed model for intrusion detection in other networks such as vehicular networks.

Author Contributions

All authors contributed equally to this manuscript.

Funding

No funding was received.

Availability of data and material

'Not applicable'.

Consent to participate

'Not applicable'.

Consent for publication

'Not applicable'.

Acknowledgments

'Not applicable'.

Conflicts of interest/Competing interests

There is no conflict of interest.

Ethics approval

The paper is original, and any other publishing house is not considering it for publication. The paper reflects the author's own research and analysis in a truthful and complete manner. All sources used are properly disclosed (correct citation).

References

  1. Chao Chen, Li-Chun Wang, Chih-Min Yu (2022) D2CRP: A Novel Distributed 2-Hop Cluster Routing Protocol for Wireless Sensor Networks. IEEE INTERNET OF THINGS JOURNAL, VOL. 9, NO. 20, 15 OCTOBER 2022. [CrossRef]
  2. Lalit Kumar, Pradeep Kumar (2022) BITA-Based Secure and Energy-Efficient Multi-Hop Routing in IoT-WSN. CYBERNETICS AND SYSTEMS. [CrossRef]
  3. Sangrez Khan a, Ahmad Naseem Alvi a, Muhammad Awais Javed, Yasser D. Al-Otaibi, Ali Kashif Bashir (2021) An efficient medium access control protocol for RF energy harvesting based IoT devices. Computer Communications. [CrossRef]
  4. Mahamat M, Jaber G, Bouabdallah A (2023) Achieving efficient energy-aware security in IoT networks: a survey of recent solutions and research challenges. Wireless Networks 29(2):787–808.
  5. Aboubakar M, Kellil M, Roux P (2022) A review of IoT network management: current status and perspectives. Journal of King Saud University Computer and Information Sciences, 34(7):4163–4176.
  6. SHAHID LATIF, ZHUO ZOU. Novel Attack Detection Scheme for the Industrial Internet of Things using a Lightweight Random Neural Network. IEEE Access, 3: 391–704 ,2020. [CrossRef]
  7. N Singh, A Dumka, R Sharma. Comparative Analysis of Various Techniques of DDoS Attacks for Detection & Prevention and Their Impact in MANET. WSEAS Transactions on Communications,6: 33–43 ,2020. [CrossRef]
  8. H Liu, D Chen. Wind Power Short-Term Forecasting Based on LSTM Neural Network with Cuckoo Algorithm. Journal of Physics3: 1–6 ,2021. [CrossRef]
  9. SEYEDALI MIRJALILI. Grasshopper Optimization Algorithm: Theory and application. Advances in Engineering Software 4(14):813–818,2017. [CrossRef]
  10. MIRJALILI, S. (2016). SCA: A Sine Cosine Algorithm for solving optimization problems. Knowledge-Based Systems, 96, 120–133. [CrossRef]
  11. dash m, Balabantaray m. routing problem: manet and ant colony algorithm. int j res COMPUT COMMUN technol.954–960.2014.
  12. Ganesan Rajesh, X. MERCILIN Raajini, R. Ashoka Rajan, M. GOKULDHEV, and C. Swetha. A Multi-objective R outing Optimization Using Swarm Intelligence in IoT Networks. Intelligent Computing and Innovation on Data Science.12–a25.2020. [CrossRef]
  13. MILOUD Mihoubi, EEDIS Laboratory, Djillali LIABES University, Sidi Bel ABBES, Algeria & DAEI Laboratory, University of Ibn Khaldoun, Tiaret, Algeria. Intelligent Technique Based on Enhanced Metaheuristic for Optimization Problem in Internet of Things and Wireless Sensor Network. International Journal of Grid and High Performance Computing.51- 62.2020. [CrossRef]
  14. J Jagannath, N Polosky, A Jagannath, F Restuccia. Machine learning for wireless communications in the Internet of things: a comprehensive survey. Ad Hoc Networks.813–818.2019. [CrossRef]
  15. son t, MINH hl, sexton g, ASLAM n. a novel encounter-based metric for mobile ad-hoc networks. Ad Hoc Networks. 813–a818.2017. [CrossRef]
  16. Celestine IWENDI, PRAVEEN Kumar Reddy MADDKUNTA. A metaheuristic optimization approach for energy efficiency in the IoT networks. Software: Practice and Experience. 14-21.2020. [CrossRef]
  17. Marc-Oliver Pahl and François-Xavier Aubet. Ds2os traffic traces IoT traffic traces gathered in a the ds2os IoT environment.51- a 62.2018.
  18. Mahmudul Hasan, Md Milon Islam, Md Ishrak Islam Zarif, and MMA Hashem. Attack and anomaly detection in IoT sensors in IoT sites using machine learning approaches. Internet of Things, 1-6, 2019. [CrossRef]
  19. Olivier Brun, Yonghua Yin, and Erol GELENBE. Deep learning with dense random neural network for detecting attacks against IoT-connected home environments. Procedia computer science, 134: 458–463, 2018.
  20. R Bhuvaneswari, R Ramachandran. Denial of service attack solution in OLSR based manet by varying number of fictitious nodes. IEEE Communications Surveys and Tutorials, 5: 2046–2069,2019 A Hameed, A Al-Omary, A. Survey of Blackhole attack on MANET. IEEE Wireless Communications, 5: 85–91,2019. [CrossRef]
  21. AMUDHAVEL, J, Brindha, V, Anantharaj, B. , Karthikeyan, P. , Bhuvaneswari, B. , Vasanthi, M. , et al. A survey on intrusion detection system: State of the art review. Indian Journal of Science and Technology,1: 1–9,2016. [CrossRef]
  22. R Bhuvaneswari, R Ramachandran. Denial of service attack solution in OLSR based manet by varying number of fictitious nodes. IEEE Communications Surveys and Tutorials, 5: 2046–2069,2019. [CrossRef]
  23. Jhaveri, R. H, Patel, S. J, & JINWALA, D. C. DoS attacks in mobile ad hoc networks: A survey. In 2012 second international conference on advanced computing & communication technologies ,5: 535–541,2018.
  24. Nishani, L, Biba, M. Machine learning for intrusion detection in MANET: A state-of-theart survey. Journal of Intelligent Information Systems,3: 391–704 ,2016. [CrossRef]
  25. JIANING CHEN, Jun Wu, HAORANLIANG, SHAHIDMUMTAZ, JIANHUALI, KOSTROMITIN Konstantin, Ali Kashif Bashir, and Raheel Nawaz. Collaborative trust blockchain based unbiased control transfer mechanism for industrial automation. IEEE Transactions on Industry Applications, 5: 85–91,2019. [CrossRef]
  26. William Grant Hatcher and Wei Yu. A survey of deep learning: platforms, applications and EMERGINGRE search trends. IEEEAccess,6: 24411–24432, 2018. [CrossRef]
  27. Mehrzad LAVADANI, Stefan Forsström, Ulf JENNEHAG, and Tingting Zhang. Combining fog computing with sensor mote machine learning for industrial IoT. Sensors, 18(5): 1532, 2018. [CrossRef]
  28. Fahimeh FARAHNAKIAN and Jukka Heikkonen. A deep auto-encoder based approach for intrusion detection system. In 2018. 20th International Conference on Advanced Communication Technology (ICACT), pages 178–183. IEEE, 2018.
  29. Nathan Shone, Tran Nguyen Ngoc, Vu Dinh Phai, and Qi Shi. A deep learning approach to network intrusion detection. IEEE Transactions on Emerging Topics in Computational Intelligence, 2(1): 41–50, 2018. [CrossRef]
  30. Mohammed Hasan Ali, Bahaa Abbas Dawood Al Mohammed, Alyani Ismail, and Mohamad Fadli ZOLKIPLIA new intrusion detection system based on fast learning network and particle swarm optimization. IEEE Access, 6: a20255–20261, 2018. [CrossRef]
  31. Mehdi MOUKHAFI, Khalid El YASSINI, and Seddik Bri. A novel hybrid ga and SVM with PSO feature selection for intrusion detection system. Int. J. Adv. Sci. Res. Eng, 4: 129–134, 2018. [CrossRef]
  32. RVIJAYANAND, D Devaraj, and B KANNAPRAN. A novel intrusion detection system for wireless mesh network with hybrid feature selection technique based on ga and mi. Journal of Intelligent & Fuzzy Systems, 34(3): 1243– 1250,a2018. [CrossRef]
  33. L KHALVATI, M KESHTGARY, and N RIKHTEGAR. Intrusion detection based on a novel hybrid learning approach. Journal of AI and data mining, 6(1): 157– 162, 2018. [CrossRef]
  34. JQ James, YUNHE Hou, and Victor OK Li. Online false data injection attack detection with wavelet transform and deep neural networks. IEEE Transactions on Industrial Informatics, 14(7): 3271–3280, 2018. [CrossRef]
  35. Hadi Larijani, Abbas Javed, NHAMOJNESU Mtetwa, Jawad Ahmad, et al. Intrusion detection using swarm intelligence. In2019UK/China Emerging Technologies (UCET), pages 1–5. IEEE, a2019.
  36. Gonzalo De La Torre Parra, Paul Rad, Kim-Kwang Raymond Choo, and Nicole Beebe. Detecting internet of things attacks using distributed deep learning. Journal of Network and Computer Applications, page 102662, a2020. [CrossRef]
  37. Dehua Zheng, Zhen Hong, Ning Wang, and Ping Chen. An improved LDABA SEDELM classification for intrusion DETE CIIONALG ORITHMINIOT application. Sensors, 20(6): 1706-1712 2020. [CrossRef]
  38. TARANYEER Singh and Neeraj Kumar. Machine learning models for intrusion detection in IoT environment: A comprehensive review. Computer Communications,15-24. 2020. [CrossRef]
  39. Cosimo IERACITANO, Ahsan Adeel, Francesco Carlo Morabito, and Amir HUDAIN. A novel statistical analysis and autoencoder driven intelligent intrusion detection approach. Neurocomputing, 387: 51–62, 2020. [CrossRef]
  40. Xiaodan Yan, Yang Xu, XIOFEI Xing, BAOJIANG Cui, Zihao Guo, and TAIBJAOGUO. Trust worthy network anomaly DTE Cion based on an adaptive learning rate and momentum in INDUSTRIAL IoT. IEEE Transactions on Industrial Informatics, a31–42,2020. [CrossRef]
  41. Ons AOUEDI, KANDARAJ PIAMRAT, Guillaume Muller, Kamal Singh, Federated SEMISUPERVISED Learning for Attack Detection in Industrial Internet of Things. IEEE TRANSACTIONS ON INDUSTRIAL INFORMATICS, VOL. 19, NO. 1, JANUARY 2023. [CrossRef]
  42. YAOYAO Lu, SENCHUN Chai ∗, Yuhan Suo, FENXI Yao, Chen Zhang, Intrusion detection for Industrial Internet of Things based on deep learning, Neurocomputing, 564 (2024). [CrossRef]
Preprints 107626 g001
Figure 1. Impact of parameters f (intensity of attraction) and I (attraction scale length) on social interaction [9].
Figure 1. Impact of parameters f (intensity of attraction) and I (attraction scale length) on social interaction [9].
Preprints 107626 g001
Preprints 107626 g002
Figure 2. Impact of Parameters f (intensity of attraction) and I (attraction scale length) on Generating Various Movements [9].
Figure 2. Impact of Parameters f (intensity of attraction) and I (attraction scale length) on Generating Various Movements [9].
Preprints 107626 g002
Preprints 107626 g003
Figure 3. Conceptual Model of Interactions Between Grasshoppers and Comfort Zone [9].
Figure 3. Conceptual Model of Interactions Between Grasshoppers and Comfort Zone [9].
Preprints 107626 g003
Preprints 107626 g004
Figure 4. Behavior of grasshoppers in 2D Space [9].
Figure 4. Behavior of grasshoppers in 2D Space [9].
Preprints 107626 g004
Preprints 107626 g005
Figure 5. Impact of Parameter C on the Movement and Convergence of Grasshoppers to the Global Optimum [9].
Figure 5. Impact of Parameter C on the Movement and Convergence of Grasshoppers to the Global Optimum [9].
Preprints 107626 g005
Preprints 107626 g006
Figure 6. Impact of Parameter on r 1   Wave Movement in the Arithmetic Optimization Algorithm [10].
Figure 6. Impact of Parameter on r 1   Wave Movement in the Arithmetic Optimization Algorithm [10].
Preprints 107626 g006
Preprints 107626 g007
Figure 7. Impact of Parameter r 1   on Exploration and Exploitation in the Arithmetic Optimization Algorithm [10].
Figure 7. Impact of Parameter r 1   on Exploration and Exploitation in the Arithmetic Optimization Algorithm [10].
Preprints 107626 g007
Preprints 107626 g008
Figure 8. Impact of Parameter r 2   on Wave Movement in the Arithmetic Optimization Algorithm [10].
Figure 8. Impact of Parameter r 2   on Wave Movement in the Arithmetic Optimization Algorithm [10].
Preprints 107626 g008
Preprints 107626 g009
Figure 9. General Stages of the Proposed Model.
Figure 9. General Stages of the Proposed Model.
Preprints 107626 g009
Preprints 107626 g010
Figure 10. Structure of a Search Agent in Improving the Lightweight Random Neural Network Architecture.
Figure 10. Structure of a Search Agent in Improving the Lightweight Random Neural Network Architecture.
Preprints 107626 g010
Preprints 107626 g011
Figure 11. Sample of a Search Agent in Improving the Lightweight Random Neural Network Architecture.
Figure 11. Sample of a Search Agent in Improving the Lightweight Random Neural Network Architecture.
Preprints 107626 g011
Preprints 107626 g012
Figure 12. Structure of a Search Agent in Improving the Weights of the Lightweight Random Neural Network.
Figure 12. Structure of a Search Agent in Improving the Weights of the Lightweight Random Neural Network.
Preprints 107626 g012
Preprints 107626 g013
Figure 13. Representation of the Eleven Dataset Features.
Figure 13. Representation of the Eleven Dataset Features.
Preprints 107626 g013
Preprints 107626 g014
Figure 14. Comparison of Different Results in the k-Nearest Neighbors Method.
Figure 14. Comparison of Different Results in the k-Nearest Neighbors Method.
Preprints 107626 g014
Preprints 107626 g015
Figure 15. Comparison of Different Results in Support Vector Machine.
Figure 15. Comparison of Different Results in Support Vector Machine.
Preprints 107626 g015
Preprints 107626 g016
Figure 16. Comparison of Methods.
Figure 16. Comparison of Methods.
Preprints 107626 g016
Preprints 107626 g017
Figure 17. Comparison of RANN-SCAGOA and RANN in terms of training time.
Figure 17. Comparison of RANN-SCAGOA and RANN in terms of training time.
Preprints 107626 g017
Table 1. Comparative analysis of existing methods in attack detection.
Table 1. Comparative analysis of existing methods in attack detection.
Weakness Strength The method used Research/year Row
High run time in parsing High classification accuracy up to 94.71% Deep learning autoencoder [21]/2018 1
High training time Classification accuracy in many classes is up to 89.22% Deep learning non-symmetric autoencoder [22]/2018 2
High run time on unbalanced datasets Classification accuracy in typical datasets up to 98.92% Improved Neural Network with Particle Ensemble Algorithm [23]/2018 3
The scalability of the method has not been investigated Generalizability of the method and classification accuracy up to 96.38% Improved Support Vector Machine with Genetic Algorithm and PSO [24]/2018 4
Limited generalizability to other data sets Classification accuracy in low-sample datasets up to 94.51% Support vector machine [25]/2018 5
The scalability of the proposed method is not shown Speed is run and generalizability with 91.80% accuracy Support vector machine and Bayesian method [26]/2018 6
High training time Generalizability in different data sets with 91.80% accuracy Convolutional neural network [27] /2019 7
The scalability of the proposed method is not shown Several binary classification errors can be corrected by the code, and the classification accuracy is up to 91.65%. Anomaly method [28] /2020 8
It is not generalizable to other attacks Detection accuracy to detect DOS attacks up to 94.80% Memory Recurrent Neural Network [29]/2020 9
Generalizability to other attacks in other networks including VANET Detection accuracy to detect DOS attacks up to 92.35% Principal component analysis and machine learning [30] /2020 10
The scalability of the proposed method is not shown The speed of detecting DoS attacks with an accuracy of 84.86% Automatic encoder network [31]/2020 11
Generalizability to other attacks Attack detection accuracy with 99% accuracy Random neural network [32]/2020 12
High run time in parsing Attack detection accuracy with 98.5% accuracy Deep learning [33]/2023 13
High training time Attack detection accuracy with 97% accuracy Feature selection and random forest [34]/2024 14
High run time on unbalanced datasets Attack detection accuracy with 99.9% accuracy Sampling and deep learning [35]/2024 15
Data labeling and standardization Attack detection with high classification performance Federal Semi-Supervised Learning (FSL) 2023[41] 16
High computational overhead and execution time Removing redundant and annoying features and preventing redundancy and interference of features Hierarchical data clustering algorithm using deep neural network 2024[42] 17
Table 2. Settings of the Arithmetic Optimization and GAO combined algorithm used.
Table 2. Settings of the Arithmetic Optimization and GAO combined algorithm used.
In the GAO In the Arithmetic algorithm
Number of repetitions I f cmin cmax r   2 constant a Parameter:
300 1.5 0.5 0.00001 1 0 to 360 degrees 2 : Value
Table 3. specifications and description of the characteristics of the data set.
Table 3. specifications and description of the characteristics of the data set.
Explanation Attribute name Row
The source address refers to the sending agents and there are 89 items out of 84 equipment items. Source address 1
Resource type refers to the type of equipment, which includes 8 items. Source type 2
The source location includes 21 locations, including bathrooms, dining rooms, kitchens, garages, and work rooms. Source location 3
The destination address refers to the agent receiving the message and is the same as the source address Destination address 4
The destination type refers to the type of equipment receiving the message and is the same as the source type. Destination type 5
6 Destination location The destination location contains 21 locations, the same as the source location items.
Refers to the addresses of intermediate nodes, which include 170 different items in the dataset. Access node address 7
Like source type and destination type, it includes 8 types. Access node type 8
It includes 5 operations including register, write, read, acknowledge and block. Function 9
Contains a numerical value Value 10
Time to transfer message from source to destination Time 11
Table 4. Performance Evaluation of KNN Method with 5 Neighbors.
Table 4. Performance Evaluation of KNN Method with 5 Neighbors.
Accuracy Detection rate False alarm rate k-fold
0.974 0.972 0.021 1
0.976 0.972 0.022 2
0.973 0.971 0.028 3
0.971 0.969 0.029 4
0.974 0.973 0.024 5
0.978 0.974 0.023 6
0.973 0.972 0.021 7
0.971 0.970 0.028 8
0.973 0.971 0.024 9
0.969 0.965 0.021 10
0.9732 Average:
Table 5. Performance Evaluation of the SVM Method with a Gaussian Kernel.
Table 5. Performance Evaluation of the SVM Method with a Gaussian Kernel.
Accuracy Detection rate False alarm rate k-fold
0.986 0.985 0.013 1
0.987 0.984 0.011 2
0.988 0.984 0.014 3
0.984 0.979 0.017 4
0.986 0.983 0.013 5
0.989 0.985 0.011 6
0.984 0.982 0.012 7
0.984 0.982 0.016 8
0.987 0.984 0.014 9
0.987 0.985 0.015 10
0.9862 Average:
Table 6. Performance Evaluation of the RaNN Method with Eight Hidden Layers and Fifteen Neurons in Each Layer.
Table 6. Performance Evaluation of the RaNN Method with Eight Hidden Layers and Fifteen Neurons in Each Layer.
Accuracy Detection rate False alarm rate k-fold
0.990 0.989 0.011 1
0.989 0.987 0.012 2
0.991 0.989 0.009 3
0.990 0.979 0.012 4
0.991 0.985 0.009 5
0.989 0.987 0.013 6
0.989 0.988 0.018 7
0.990 0.989 0.012 8
0.991 0.990 0.011 9
0.991 0.987 0.009 10
0.9901 Average:
Table 7. Performance Evaluation of the RaNN-SCAGOA Method with Eight Hidden Layers and Fifteen Neurons in Each Layer.
Table 7. Performance Evaluation of the RaNN-SCAGOA Method with Eight Hidden Layers and Fifteen Neurons in Each Layer.
Accuracy Detection rate False alarm rate k-fold
0.996 0.995 0.005 1
0.995 0.993 0.006 2
0.994 0.993 0.007 3
0.994 0.993 0.007 4
0.995 0.994 0.008 5
0.995 0.993 0.006 6
0.996 0.994 0.006 7
0.995 0.994 0.008 8
0.994 0.993 0.007 9
0.995 0.994 0.008 10
0.9949 Average:
Table 8. Evaluation of the performance of the combined method with the nearest neighbor method, support vector machine, and improved random neural network.
Table 8. Evaluation of the performance of the combined method with the nearest neighbor method, support vector machine, and improved random neural network.
Accuracy Detection rate False alarm rate k-fold
0.995 0.993 0.005 1
0.996 0.895 0.006 2
0.997 0.995 0.004 3
0.995 0.994 0.006 4
0.996 0.994 0.005 5
0.995 0.994 0.007 6
0.994 0.993 0.007 7
0.995 0.993 0.006 8
0.996 0.994 0.005 9
0.997 0.995 0.004 10
0.9956 Average:
Table 9. comparison of the tested methods and the proposed model.
Table 9. comparison of the tested methods and the proposed model.
Detection rate False alarm rate Accuracy rate Sum data Methods
0.9902 0.008 99.01% DS2OS Random Neural Network (RaNN)[6]
0.9711 0.024 97.32 % DS2OS KNN
0.9849 0.014 98.62 % DS2OS SVM
0.9928 0.005 99.49 % DS2OS RaNN-SCAGOA
0.9937 0.004 99.56 % DS2OS Ensemble (KNN-SVM- (RaNN-SCAGOA))
0.9602 0.021 95.84% DS2OS FSL (FEDERATED SEMISUPERVISED LEARNING)
0.9701 0.007 98.01 DS2OS DEEP NEURAL NETWORK (DNN)
Table 10. Comparison of training time and classification accuracy in the random neural network (RaNN) and the improved random neural network (RaNN-SCAGOA).
Table 10. Comparison of training time and classification accuracy in the random neural network (RaNN) and the improved random neural network (RaNN-SCAGOA).
The number of neurons in each layer * the number of hidden layers Average training time RaNN-SCAGOA Average training time RaNN Average accuracy RaNN Average accuracy RaNN-SCAGOA
1*15 00:06:44 00:04:14 97.4105% 97.9103%
2*15 00:07:15 00:06:55 97.8506% 98.1214%
3*15 00:06:51 00:09:35 97.1084% 97.8145%
4*15 00:06:59 00:14:43 98.8895% 99.1042%
5*15 00:07:51 00:19:51 99.0147% 99.1274%
6*15 00:07:45 00:28:37 99.0159% 99.1108%
7*15 00:08:14 00:39:46 99.0101% 99.1654%
8*15 00:08:48 00:46:04 99.0199% 99.4923%
9*15 00:08:55 01:05:44 99.0174% 99.1544%
10*15 00:09:11 01:29:14 99.0151% 99.1498%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated