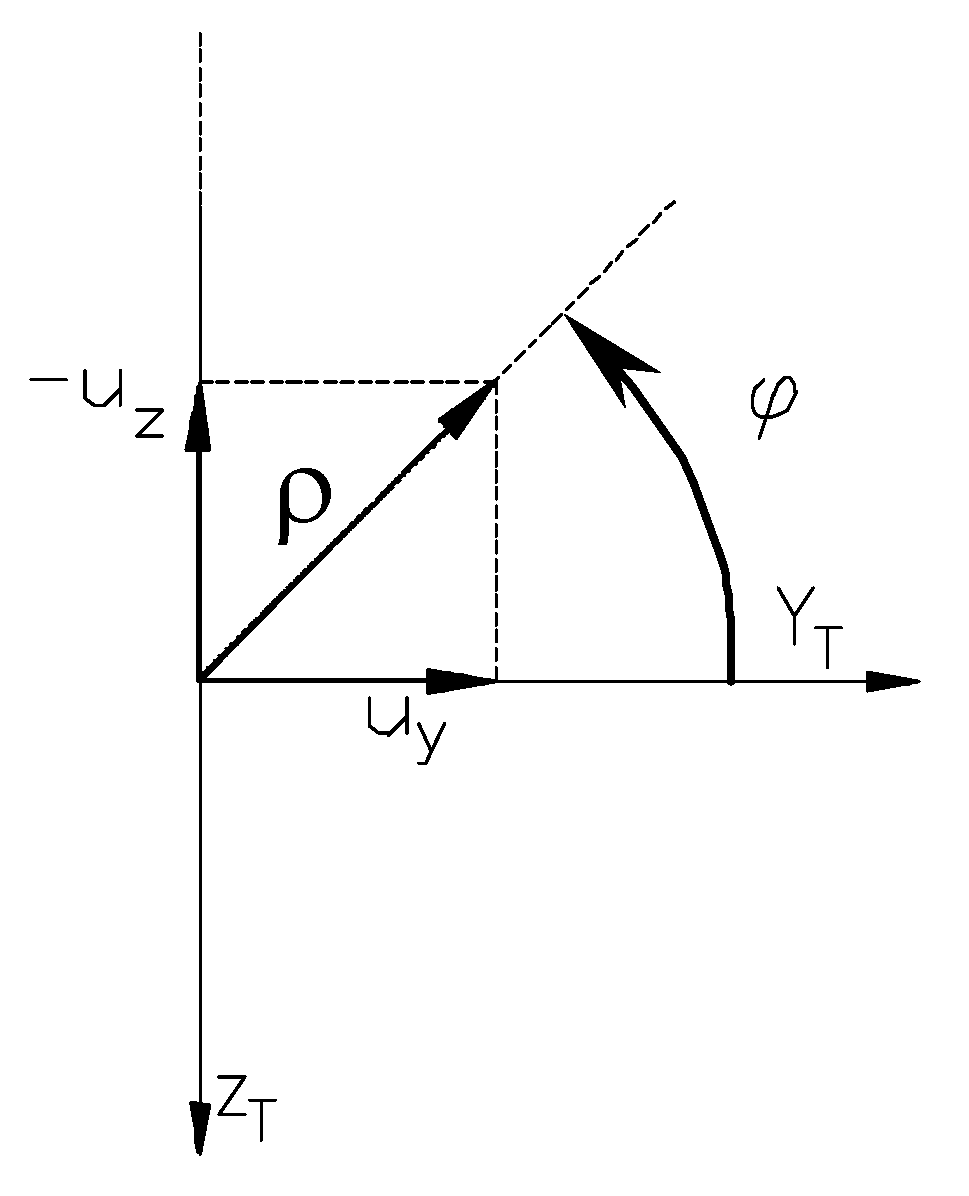Stability of Single Channel Homing Slow-Rolling Missile

Starting from the model of a slow-rolling missile with six degrees of freedom (6 DOF) in the body frame, a 6 DOF model in the Resal frame is obtained, which is used to linearize the coupled commanded motion. Based on the linearized model, we obtain the structural scheme of the commanded object and define the quality parameters. The obtained parameters have a complex representation (with real and imaginary parts) due to the coupling between longitudinal channels. Then, the kinematic guidance equations, the seeker equations and the actuator specific to the slow-rolling single-channel missile are defined using a switching function. The guidance kinematic equations, the seeker equations and the actuator model are linearized in the Resal frame, and the structural diagram of the homing missile is constructed. Starting from this, the characteristic polynomial having complex coefficients is determined and then analyzed with the Frank-Wall stability criterion. Based on the analysis, a stability range is determined for the navigation constant and a minimum and possibly a maximum limit for the time to hit the target is obtained. The stability range defined for the navigation constant on the linear model is finally validated on the nonlinear model in the body frame.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

In modern weaponry technology, slow-rolling missiles play a significant role in combating close air targets. In anti-aircraft combat, due to the high angular velocity of the target line-of-site, the missile is directly self-guided, using a proportional navigation method. This method does not ensure a direct hit of the target but achieves a sufficient reach to the proximity fuse so that the warhead destroys the target (because an aircraft does not have armor elements).

If the velocity regime is supersonic, the missiles can use aerodynamic command (canard), effectively performing the target interception maneuver. The advantage of using slow-rotating missiles lies primarily in reducing the size and, implicitly, their mass. At the same time, the rotation cancels the disturbing force and torque due to aerodynamic or gasodynamic asymmetries. Thanks to rolling rotation, the control can be carried out on a single channel, i.e., through a single pair of canards, which reduces the size of the control system and the required energy, leading to a portable missile system known as a man-portable air defense system (MANPADS). From this category, we can mention the systems: FIM 92 Stinger [1] – USA, 9K32 Strela 2 [2], 9K38 Igla [3], 9K333 Verba [4]- Russia.

The problem of rotationally guided missiles has been addressed in several stages and forms in the literature. Some of these works refer to two-channel rotation missiles [5,6,7], and others to single-channel missiles with time-modulated control [8,9,10,11]. Among the two-channel rockets, there is a group of papers dealing with double-rotational guided projectiles, in which the projectile body rotates at a very high velocity in order to ensure gyroscopic stability, and the tip of the projectile, which rotates at a lower velocity, has a cruciform canard for trajectory control and improved accuracy [12]. Regarding two-channel rotational missiles, several recent works have proposed the following: the design of an autopilot with a single feedback loop [13], double [14] or triple feedback loop [15]. At the same time, other papers aim to assess the stability of precession motion (conical) [5,6,7] under erroneous signal conditions introduced by the target tracking system [14,16]. Another category of papers aims to define sensors with which to determine the attitude, especially the roll angle of the rocket necessary to form the command signal [17,18]. Since we intend to address the case of the time-controlled single-channel missile, we will analyze in detail the results obtained in papers [8,9,10,11].

In [8], a digital controller is proposed to replace the classic analogue time-modulation controller. As shown in the paper, replacing the analogue control phase with the amplitude of the digital control can ensure the decoupling of the yaw from pitch and thereby eliminate the error introduced by the actuator's delay and noise from the sensors. The proposed solution's disadvantage lies in complicating the missile's control and implicitly increasing its cost.

In [9], the stability of the commanded motion regarding the rocket with single-channel rotation is analyzed based on the linear form of the equations of motion with the development of closed analytical solutions. A feature of the analysis is that it works with the command in the body frame, while the equations of motion are constructed in the Resal frame (which does not participate in the roll rotation). The order to command switch is built based on series development, separately analyzing the ideal case with the rectangular command and the case where the command shape contains a delay.

The paper [11] analyzes the possibility of controlling an autonomous flight rocket with roll rotation and single-channel with reactive command. The classic solution, with six reactive nozzles, ensures complete control of the attitude of the rocket, including the roll, is compared with the solution with only two reactive nozzles (RCS) that provide attitude control in pitch and yaw, leaving the roll angle free, which allows roll rotation of the rocket.

In paper [10], starting from the equations of motion written in the Resal frame, a linear model of the command motion for the slow-rotating rocket is constructed. Due to the coupling between channels given by gyroscopic and Magnus terms, the linear model is constructed with complex coefficients, highlighting both nutation and precession motion and defining the flying quality parameters in complex form. The linear development of the commanded motion ends with constructing a structural scheme of the commanded object specific to the slow-rolling missile with complex coefficients. Unlike work [9], which uses serial development, in work [10], the generation of the switch command for a single-channel missile is done considering the sign of a trigonometric expression dependent on the roll angle, as shown in [19]. Further in the paper [10] are analyzed two models of slow-rolling single-channel guided missiles, the portable anti-aircraft single-channel homing missile and the portable anti-tank single-channel wire-guided missile. Unlike work [9], which forms the command in the body frame, in work [10], starting from the duration modulated form of the command, an equivalent command is obtained in the Resal frame with which, in the end, structural diagrams of the guided missile are built for the two cases: homing missile and a wire-guided missile. Given that the structural schemes have complex coefficients, the paper was limited to determining in the case of the wire-guided rocket the location of the roots of the characteristic polynomial and the phase-frequency / amplitude frequency diagrams, highlighting the differences from the case of the non-rotating rocket.

In the present paper, we aim to develop the results obtained in paper [10] by analyzing the stability of the single-channel slow-rolling homing missile using the Frank-Wall stability criterion [20] used in paper [7] for the case of two-channel slow-rolling of the homing missile. The essential difference between the two-channel and the single-channel rockets is in how the command is formed. Thus, if in the two-channel rockets, we have a proportional deflection with both canards, in the case of the single-channel rocket, we have only one maximum deflection of one of the canards, time-modulation, by a switching function, oriented by command phase. Unlike paper [7], which develops a characteristic polynomial of order 3, we will also consider the time constant of the target tracking system (seeker), which will lead to a characteristic polynomial of order 4, which introduces an additional stability condition that will be analyzed in detail. At the same time, the influence of phase shift introduced by the delay given by the actuator and the imprecision of determining the roll angle will be analyzed. In order to facilitate the understanding of this paper, a series of essential elements introduced in the paper [10] will be resumed. For details, we recommend reading the original work [10].

In the paper, we will distinguish between slow-rolling missiles (max 30 rot/s) aerodynamically stabilized by tail and gyroscopically stabilized projectiles with fast roll rotation (minimum 300 rot/s).

The novelty of the paper is the analysis of the stability of single-channel homing missiles with slow roll using the Frank-Wall stability criterion. This analysis follows the influence of the main parameters in the missile's guidance system, and for some of them, restrictions and stability domains will be defined.

2. Equations of the General Motion in the Body Frame

First, we will build a model with six degrees of freedom (6DOF) in the body frame.

2.1. Kinematic Equations Using Attitude Angles

The orientation of the body frame

(O x y z)

related to the local (start) frame

(O_{0} X_{0} Y_{0} Z_{0})

is defined according to ISO 1151-75. We will start by constructing the rotational matrix between the local and body frames to deduce kinematic equations using Euler-type attitude angles. For this purpose, starting in the local frame

(O_{0} X_{0} Y_{0} Z_{0})

and ending in the mobile ground frame (

O x_{g} y_{g} z_{g}

), a

180 °

rotation around the

O X_{0}

axis is necessary, after which, in order to overlap the mobile ground frame (

O x_{g} y_{g} z_{g}

) over the axes of the body frame (

O x y z

) we apply successively three rotations with angular velocities

\dot{ψ}

\dot{θ}

and

\dot{ϕ}

around the axes

O z_{g}, O y^{'}

, respectively

O x

(O x_{g} y_{g} z_{g}) \frac{\dot{ψ}}{(O z_{g})} ⊳ (O x^{'} y^{'} z_{g}) \frac{\dot{θ}}{(O y^{'})} ⊳ (O x y^{'} z^{'}) \frac{\dot{ϕ}}{(O x)} ⊳ (O x y z) .

The rotational matrix from the local frame to the body frame, is:

A_{I} = [\begin{matrix} \cos θ \cos ψ & - \cos θ \sin ψ & \sin θ \\ - \cos ϕ \sin ψ + \sin ϕ \sin θ \cos ψ & - \cos ϕ \cos ψ - \sin ϕ \sin θ \sin ψ & - \sin ϕ \cos θ \\ \sin ϕ \sin ψ + \cos ϕ \sin θ \cos ψ & \sin ϕ \cos ψ - \cos ϕ \sin θ \sin ψ & - \cos ϕ \cos θ \end{matrix}] .

(1)

2.2. Dynamic Equations of Motion in the Body Frame

The main notations and symbols are consistent with the standards [21,22].

Considering the missile as a body with variable mass and applying the momentum theorem and the angular momentum theorem, the established dynamic equations of motion [23,24] written vectorially are of the form:

m \frac{d V}{d t} = F + G + T; \frac{d K}{d t} = H + U,

(9)

in which the terms due to changes in mass and moments of inertia are contained in the right member of the relations.

By explaining the absolute derivative of velocity and angular momentum vectors in the body frame, the previous relations become:

m \frac{\partial V}{\partial t} = F + T + G - m (Ω \times V); \frac{\partial K}{\partial t} = H + U - Ω \times K .

(10)

For the further development of these relations, the forces and torques applied by components according to the axes of the body frame are explained:

F = X^{A} i + Y^{A} j + Z^{A} k; T = X^{T} i + Y^{T} j + Z^{T} k; G = G_{x} i + G_{y} j + G_{z} k = m (g_{x} i + g_{y} j + g_{z} k); H = L^{A} i + M^{A} j + N^{A} k; U = L^{T} i + M^{T} j + N^{T} k

(11)

where the components of gravitational acceleration are obtained from the matrix relation:

{[\begin{matrix} g_{x} & g_{y} & g_{z} \end{matrix}]}^{T} = A_{I} {[\begin{matrix} 0 & 0 & - g \end{matrix}]}^{T},

(12)

in which the rotation matrix

A_{I}

was previously defined.

In order to bring the equation to the matrix form, the vectors of velocities and angular momentum are also explained by projections according to the axes of the body frame:

\begin{matrix} V = u i + v j + w k & Ω = p i + q j + r k & K = K_{x} i + K_{y} j + K_{z} k \end{matrix} .

(13)

The components of angular momentum can be obtained from the matrix relation:

{[\begin{matrix} K_{x} & K_{y} & K_{z} \end{matrix}]}^{T} = J {[\begin{matrix} p & q & r \end{matrix}]}^{T},

(14)

where

J

represents the matrix of moments of inertia. Developing the vector products of relations (10) and considering the components of the previously explicit terms, one obtains the matrix form of the equations of general motion in the body frame. Thus, the translation equation becomes:

\dot{V} = m^{- 1} (F + T) + A_{I} g_{o} - S_{Ω} V;

(15)

where:

g_{0} = {[\begin{matrix} 0 & 0 & - g \end{matrix}]}^{T}

, and

S_{Ω}

is the antisymmetric matrix associated with the angular velocity vector

Ω

S_{Ω} = [\begin{matrix} 0 & - r & q \\ r & 0 & - p \\ - q & p & 0 \end{matrix}],

(16)

Relations (15) can also be put in the form of:

[\begin{matrix} \dot{u} \\ \dot{v} \\ \dot{w} \end{matrix}] = m^{- 1} [\begin{matrix} X \\ Y \\ Z \end{matrix}] - S_{Ω} [\begin{matrix} u \\ v \\ w \end{matrix}]

(17)

where we defined the components of the applied forces as:

X = X^{A} + X^{T} + G_{x}

;

Y = Y^{A} + Y^{T} + G_{y}

;

Z = Z^{A} + Z^{T} + G_{z}

Similarly, the rotation Equation (10) acquires the matrix form:

\dot{Ω} = J^{- 1} (H + U) - J^{- 1} S_{Ω} J Ω .

(18)

For axially symmetrical configurations, the inverse of the matrix of moments of inertia acquires the diagonal shape:

J^{- 1} = [\begin{matrix} 1 / A & 0 & 0 \\ 0 & 1 / B & 0 \\ 0 & 0 & 1 / C \end{matrix}],

(19)

Equation (18) can be put into the form:

[\begin{matrix} \dot{p} \\ \dot{q} \\ \dot{r} \end{matrix}] = [\begin{matrix} L A^{- 1} \\ M B^{- 1} \\ N C^{- 1} \end{matrix}] - S_{Ω} [\begin{matrix} p \\ q \\ r \end{matrix}],

(20)

where the components of the applied torques are:

L = L^{A} + L^{T}

;

M = M^{A} + M^{T}

;

N = N^{A} + N^{T}

Having defined the direct rotation matrix

A_{I}

, one can write the connection between the velocity vector components in the local and the body frames:

{[\begin{matrix} u & v & w \end{matrix}]}^{T} = A_{I} {[\begin{matrix} {\dot{x}}_{0} & {\dot{y}}_{0} & {\dot{z}}_{0} \end{matrix}]}^{T}

Multiplying left by the inverse matrix

A_{I}

yields the relation necessary to express the translational velocity components from the body frame, connected to the missile, in the local frame.

{[\begin{matrix} {\dot{x}}_{0} & {\dot{y}}_{0} & {\dot{z}}_{0} \end{matrix}]}^{T} = B_{I} {[\begin{matrix} u & v & w \end{matrix}]}^{T}

(2)

where

B_{I} = A_{I}^{- 1} = A_{I}^{T}

For determining the connecting matrix between the derivatives of attitude angles and the components of rotational velocity, starting from the vector relation:

Ω = \dot{ψ} + \dot{θ} + \dot{ϕ}

(3)

Moreover, given that the rotation around its axis does not produce any effect, the relation can be written as:

[\begin{matrix} p \\ q \\ r \end{matrix}] = A_{ϕ, θ, ψ} [\begin{matrix} 0 \\ 0 \\ \dot{ψ} \end{matrix}] + A_{ϕ, θ} [\begin{matrix} 0 \\ \dot{θ} \\ 0 \end{matrix}] + A_{ϕ} [\begin{matrix} \dot{ϕ} \\ 0 \\ 0 \end{matrix}] = A_{ϕ, θ} [\begin{matrix} 0 \\ \dot{θ} \\ \dot{ψ} \end{matrix}] + [\begin{matrix} \dot{ϕ} \\ 0 \\ 0 \end{matrix}],

(4)

hence the following:

[\begin{matrix} p \\ q \\ r \end{matrix}] = [\begin{matrix} 1 & 0 & - \sin θ \\ 0 & \cos ϕ & \sin ϕ \cos θ \\ 0 & - \sin ϕ & \cos ϕ \cos θ \end{matrix}] [\begin{matrix} \dot{ϕ} \\ \dot{θ} \\ \dot{ψ} \end{matrix}]

(5)

Determining the inverse of the matrix, we finally get:

[\begin{matrix} \dot{ϕ} \\ \dot{θ} \\ \dot{ψ} \end{matrix}] = [\begin{matrix} 1 & \sin ϕ \tan θ & \cos ϕ \tan θ \\ 0 & \cos ϕ & - \sin ϕ \\ 0 & \sin ϕ \sec θ & \cos ϕ \sec θ \end{matrix}] [\begin{matrix} p \\ q \\ r \end{matrix}]

(6)

Developing the relations: (2) and (6) the systems of differential equations sought are obtained:

{\dot{x}}_{o} = u c o s θ c o s ψ + v (s i n ϕ s i n θ c o s ψ - c o s ϕ s i n ψ) + w (c o s ϕ s i n θ c o s ψ + s i n ϕ s i n ψ); {\dot{y}}_{o} = - u c o s θ s i n ψ - v (s i n ϕ s i n θ s i n ψ + c o s ϕ c o s ψ) - w (c o s ϕ s i n θ s i n ψ - s i n ϕ c o s ψ); {\dot{z}}_{o} = - u s i n θ - v s i n ϕ c o s θ - w c o s ϕ c o s θ

(7)

respectively:

\dot{ϕ} = p + q t a n θ s i n ϕ + r t a n θ c o s ϕ; \dot{θ} = q c o s ϕ - r s i n ϕ;

(8)

\dot{ψ} = q s i n ϕ s e c θ + r c o s ϕ s e c θ .

(8)

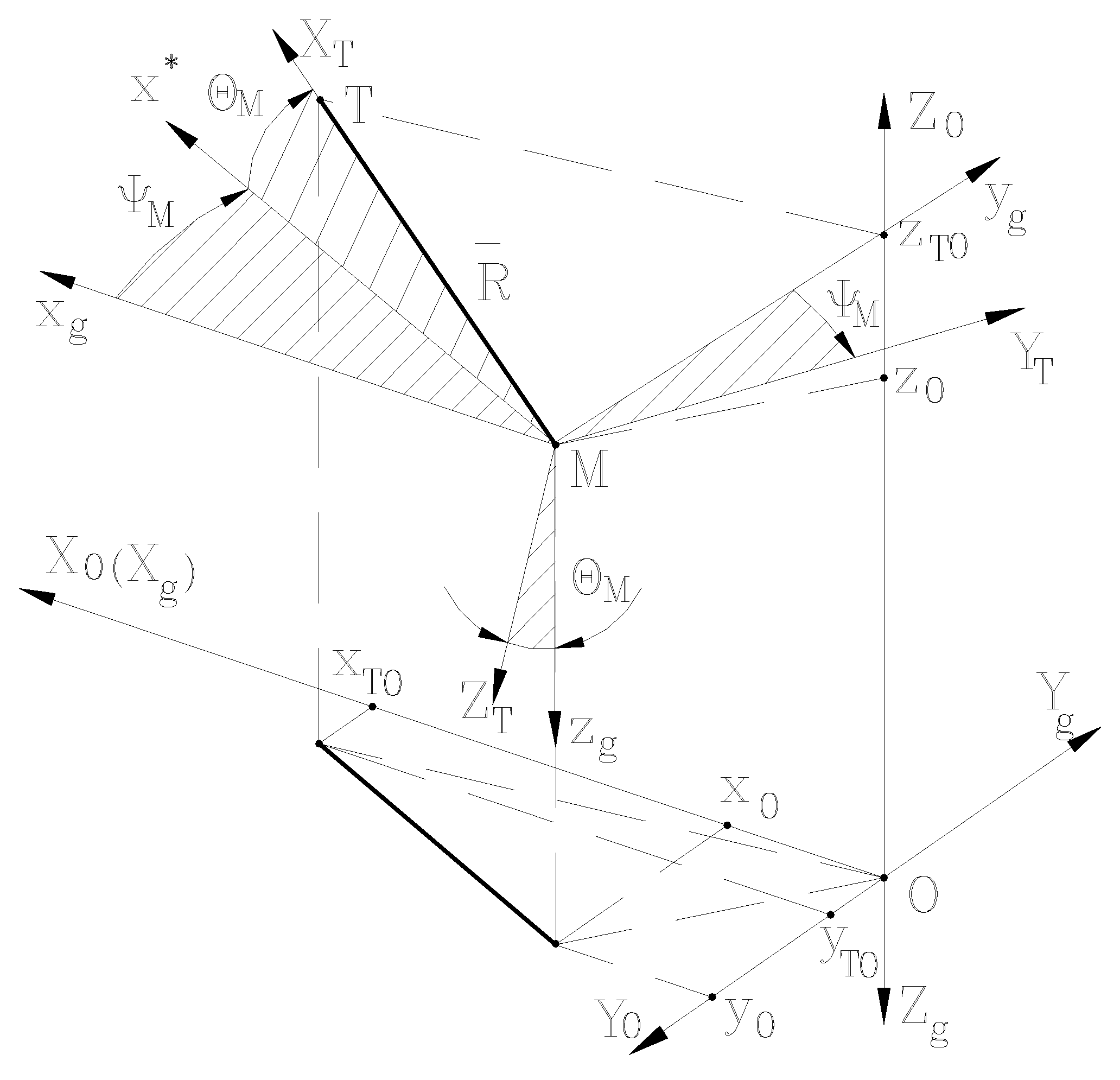
3. Equations of the General Motion in the Resal Frame

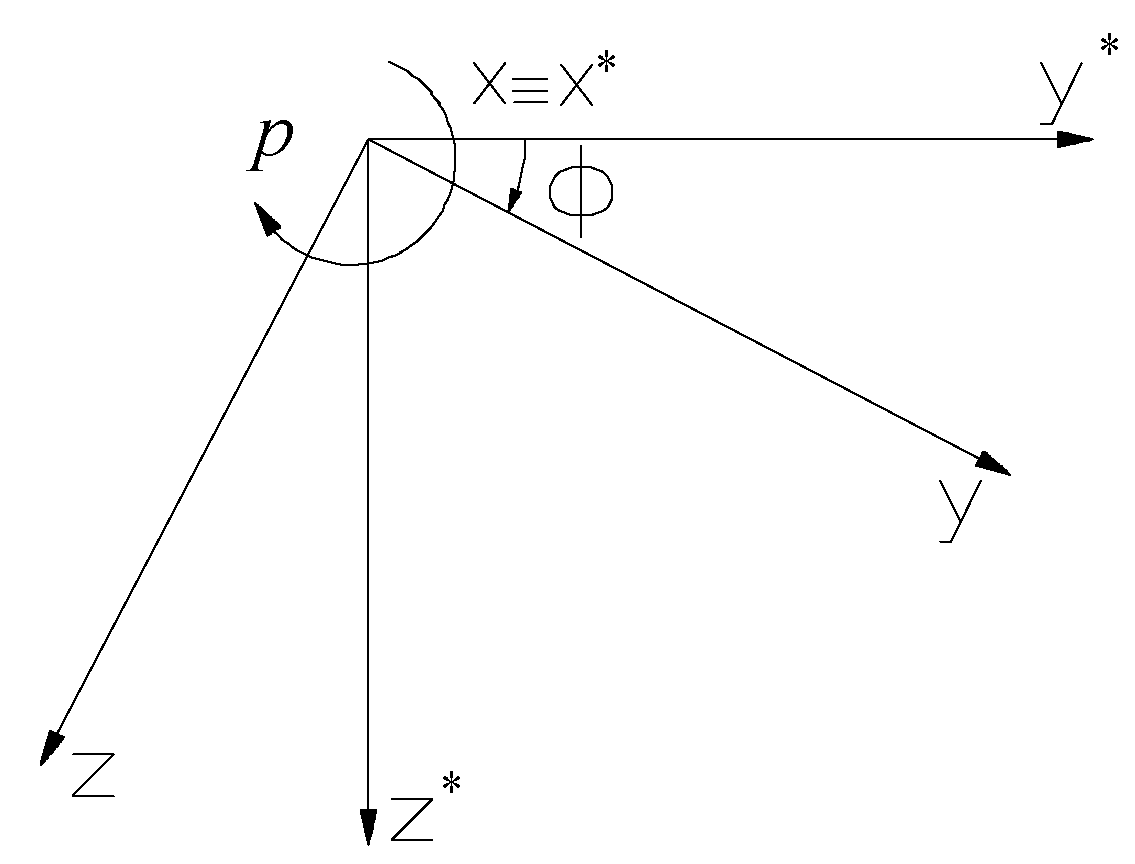
Unlike classical aircraft, with stabilized roll, in the case of rolling rocket, most authors [23,24,25], in order to obtain the equations of motion, use a quasi-linked frame, called "Resal" frame, which has the specificity that it does not participate in its roll motion (Figure 2).

The advantages of using this frame are that by isolating gyroscopic coupling terms, the equations of motion are brought to a form similar to that of the stabilized roll equations of an aircraft, allowing the use of common study methods, at least in terms of their linear form. Next, we will rewrite the equations of general motion in the body frame, but we will write them this time in the Resal frame. To reformulate the general equations, we start from the observation that the elements of motion in the body frame (

O x y z

) are obtained from the quasi-linked frame (

O x^{*} y^{*} z^{*}

) using the rotation matrix:

A_{ϕ} = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos ϕ & \sin ϕ \\ 0 & - \sin ϕ & \cos ϕ \end{matrix}]

(21)

As shown in [10,24], we can express the terms of the dynamic equations from the body frame in the quasi-linked frame. Thus, the velocity

V

components in the body frame become:

{[\begin{matrix} u & v & w \end{matrix}]}^{T} = A_{ϕ} {[\begin{matrix} u^{*} & v^{*} & w^{*} \end{matrix}]}^{T},

(22)

and their derivatives are:

[\begin{matrix} \dot{u} \\ \dot{v} \\ \dot{w} \end{matrix}] = A_{ϕ} [\begin{matrix} {\dot{u}}^{*} \\ {\dot{v}}^{*} \\ {\dot{w}}^{*} \end{matrix}] + ω_{x} \frac{\partial A_{ϕ}}{\partial ϕ} [\begin{matrix} u^{*} \\ v^{*} \\ w^{*} \end{matrix}] = A_{ϕ} [\begin{matrix} {\dot{u}}^{*} \\ {\dot{v}}^{*} + ω_{x} w^{*} \\ {\dot{w}}^{*} - ω_{x} v^{*} \end{matrix}] .

(23)

Considering that:

Ω = Ω^{*} + ω_{x}

, the components of the rotational velocity in the body frame are expressed as follows:

{[\begin{matrix} p & q & r \end{matrix}]}^{T} = A_{ϕ} {[\begin{matrix} ω_{x} + p^{*} & q^{*} & r^{*} \end{matrix}]}^{T},

(24)

and after derivation become:

[\begin{matrix} \dot{p} \\ \dot{q} \\ \dot{r} \end{matrix}] = A_{ϕ} [\begin{matrix} {\dot{ω}}_{x} + {\dot{p}}^{*} \\ {\dot{q}}^{*} \\ {\dot{r}}^{*} \end{matrix}] + ω_{x} \frac{\partial A_{ϕ}}{\partial ϕ} [\begin{matrix} ω_{x} + p^{*} \\ q^{*} \\ r^{*} \end{matrix}] = A_{ϕ} [\begin{matrix} {\dot{ω}}_{x} + {\dot{p}}^{*} \\ {\dot{q}}^{*} + ω_{x} r^{*} \\ {\dot{r}}^{*} - ω_{x} q^{*} \end{matrix}]

(25)

Expressing the forces and torques components containing the applied terms (aerodynamics, propulsion and weight) and the antisymmetric matrix attached to the angular velocity vector

Ω

in the Resal frame, as shown in [10], multiplying the relations of the dynamic equations in the body frame by the inverse of the rotation matrix:

A_{ϕ}

, yields:

[\begin{matrix} {\dot{u}}^{*} \\ {\dot{v}}^{*} \\ {\dot{w}}^{*} \end{matrix}] = m^{- 1} [\begin{matrix} X^{*} \\ Y^{*} \\ Z^{*} \end{matrix}] - S_{Ω}^{*} [\begin{matrix} u^{*} \\ v^{*} \\ w^{*} \end{matrix}]

(26)

[\begin{matrix} {\dot{p}}^{*} \\ {\dot{q}}^{*} \\ {\dot{r}}^{*} \end{matrix}] = [\begin{matrix} L^{*} A^{- 1} \\ M^{*} B^{- 1} \\ N^{*} C^{- 1} \end{matrix}] - S_{Ω}^{*} [\begin{matrix} p^{*} \\ q^{*} \\ r^{*} \end{matrix}] - [\begin{matrix} {\dot{ω}}_{x} \\ r^{*} ω_{x} A B^{- 1} \\ - q^{*} ω_{x} A C^{- 1} \end{matrix}]

(27)

where:

S_{Ω}^{*} = [\begin{matrix} 0 & - r^{*} & q^{*} \\ r^{*} & 0 & - p^{*} \\ - q^{*} & p^{*} & 0 \end{matrix}],

(28)

Comparing these equations with the relations (17) (20) obtained in the body frame, it is observable that in the momentum Equation (27), the gyroscopic coupling term appears between the longitudinal channels, which is due to the rotational motion in roll. From the first line of the matrix relation (27), in order to bring the previous relations to a more suitable form, we can write:

p = p^{*} + ω_{x}

, Euler dynamic equations taking on scalar form:

\begin{matrix} \dot{p} = \frac{L^{*}}{A}; & {\dot{q}}^{*} = \frac{M^{*}}{B} + r^{*} p^{*} - \frac{A}{B} r^{*} p; & {\dot{r}}^{*} = \frac{N^{*}}{C} - p^{*} q^{*} + \frac{A}{C} q^{*} p \end{matrix} .

(29)

Regarding kinematic equations, written with elements of the quasi-linked frame (Resal), will coincide with (7) and (8) for the particular case where the roll angle is null. Thus, from the Euler kinematic Equation (8) is obtained

\dot{θ} = q^{*}; \dot{ψ} = r^{*} \sec θ,

(30)

the equation of roll angular velocity becomes a connecting relation between quasi-linked components:

p^{*} = - r^{*} tg θ .

(31)

Finally, the other kinematic equations, corresponding to relations (7) expressing the connection between the velocity components in the local frame and the quasi-linked frame, become:

{\dot{x}}_{0} = u^{*} \cos θ \cos ψ - v^{*} \sin ψ + w^{*} \sin θ \cos ψ; {\dot{y}}_{0} = - u^{*} \cos θ \sin ψ - v^{*} \cos ψ - w^{*} \sin θ \sin ψ; {\dot{z}}_{0} = u^{*} \sin θ - w^{*} \cos θ .

(32)

4. Basic Movement and Maximum Maneuverability

Determining the basic movement is first necessary to linearize the equations of motion in the Resal frame.

4.1. Basic Movement

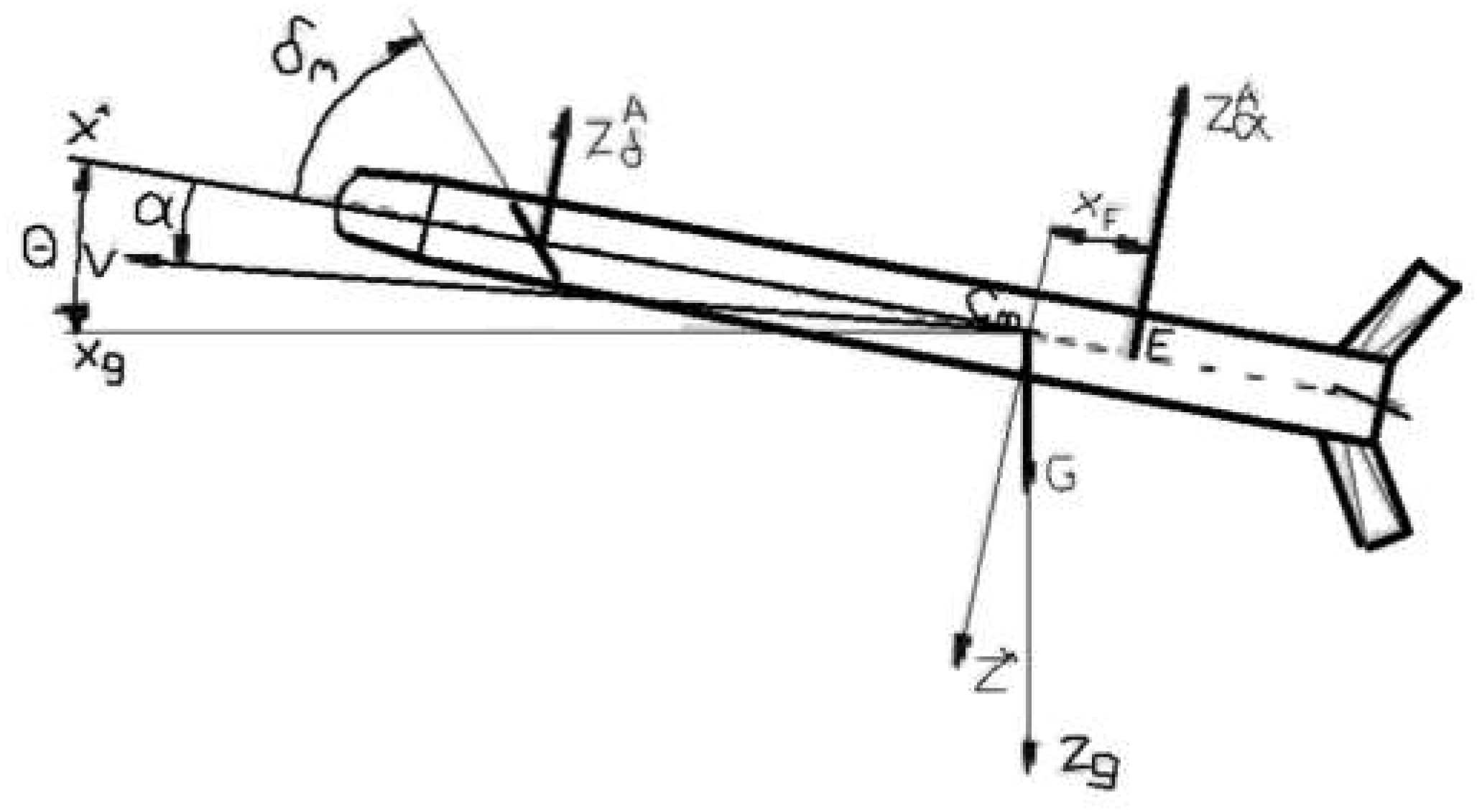
With the notations from Figure 3, equilibrium equations in the vertical plane of the Resal frame are written as follows:

\begin{matrix} a_{z}^{*} = \frac{F_{0}}{m} C_{z} + g \cos θ; & C_{m} = 0 \end{matrix}

(33)

where we denoted the lateral acceleration:

a_{z}^{*} = - q^{*} u^{*}

In this case, relations (33) becomes

\frac{F_{0}}{m} C_{z} + g \cos θ + q^{*} u^{*} = 0; C_{m} = 0 .

(34)

If a development of aerodynamic coefficients containing rotational terms is considered:

C_{z} = C_{z α} α + C_{z q} {\hat{q}}^{*} + C_{z δ m} δ_{m}^{*};

(35)

{C_{m} = C}_{m α} α + C_{m q} {\hat{q}}^{*} + C_{m δ m} δ_{m}^{*},

(35)

furthermore, this development is introduced into the system of equations defining basic motion, we will obtain:

\begin{matrix} C_{z α} α + C_{q} {\hat{q}}^{*} + C_{z δ m} δ_{m}^{*} = - \frac{G}{F_{0}} \cos θ; & C_{m α} α + C_{m q} {\hat{q}}^{*} + C_{m δ m} δ_{m}^{*} = 0 \end{matrix},

(36)

where:

C_{q} = C_{z q} + \frac{2 m}{ρ S l} \cos α .

(37)

As shown in [24], if an angular velocity

(q^{*})

and a value of the climb angle (γ) are imposed, and denote:

R_{α} = (C_{z δ m} C_{m q} - C_{m δ m} C_{q}) {\hat{q}}^{*} - \frac{G}{F_{0}} C_{m δ m} \cos θ; R_{δ} = (C_{m α} C_{q} - C_{z α} C_{m q}) {\hat{q}}^{*} + \frac{G}{F_{0}} C_{m α} \cos θ;

(38)

R = C_{z α} C_{m δ m} - C_{m α} C_{z δ m},

(38)

where:

θ = γ + α,

(39)

a system of equations is obtained and is solved iteratively for incidence and angular canard deflection:

\begin{matrix} α_{e} = R_{α} / R; & δ_{m e}^{*} = R_{δ} / R \end{matrix}

(40)

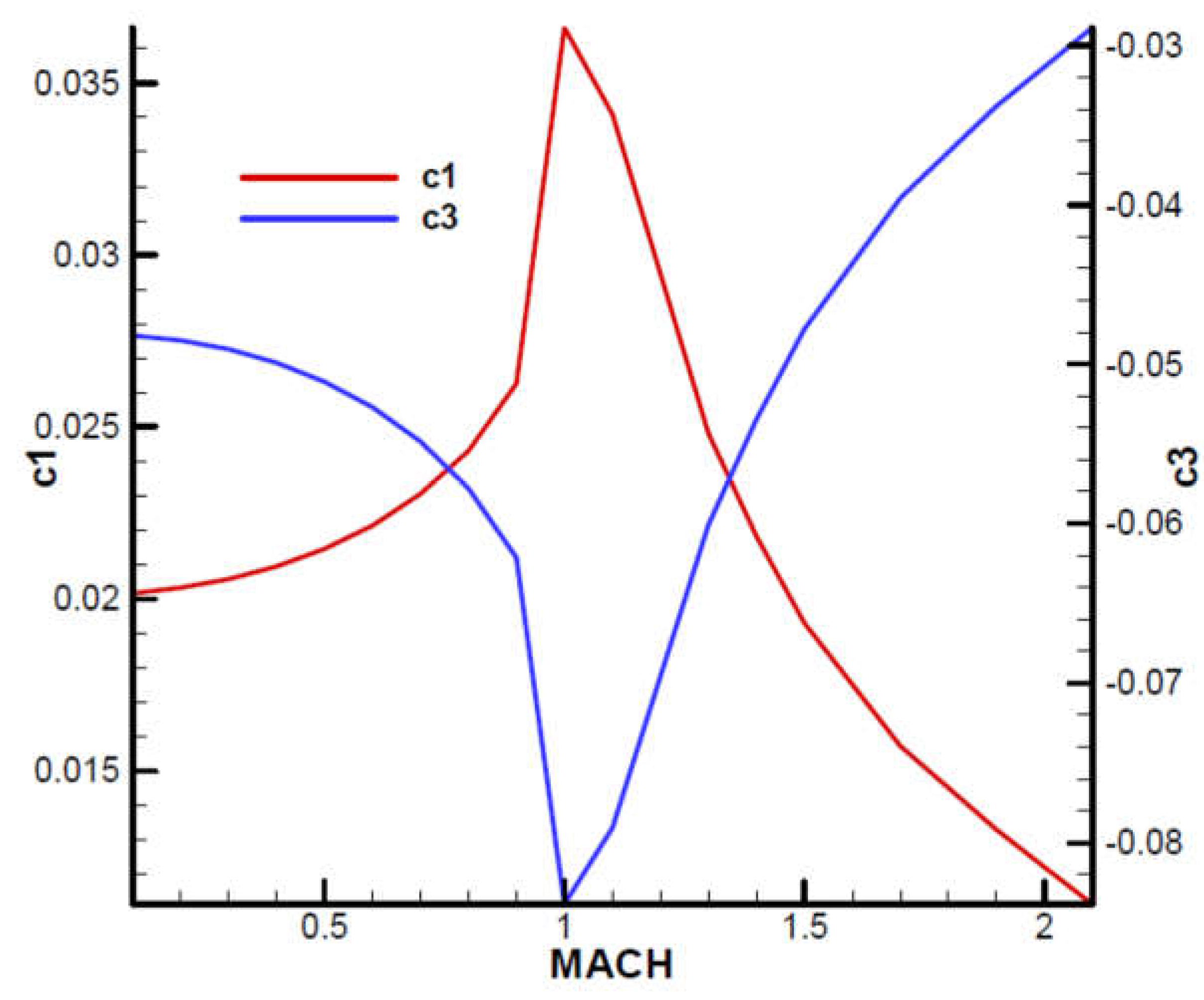
The diagrams of the equilibrium incidence and canard angular deflection according to the Mach number are presented in Figure A11 and A12 from Appendix B

4.2. Maximum Maneuverability

If the maximum equivalent deflection angle for single-channel missiles is considered known:

δ_{m a x}^{*} = \frac{2}{π} δ_{m a x}

(41)

and a value of the climb angle

γ

is imposed, the system (36) can be put in the form:

\begin{matrix} C_{z α} α + C_{q} {\hat{q}}^{*} = - \frac{G}{F_{0}} \cos θ - C_{z δ m} δ_{m a x}^{*}; & C_{m α} α + C_{m q} {\hat{q}}^{*} = - C_{m δ m} δ_{m a x}^{*} \end{matrix}

(42)

Considering:

R_{α} = (C_{m δ m} C_{q} - C_{z δ m} C_{m q}) δ_{m a x}^{*} - \frac{G}{F_{0}} C_{m q} \cos θ; R_{q} = (C_{z δ m} C_{m α} - C_{m δ m} C_{z α}) δ_{m a x}^{*} + \frac{G}{F_{0}} C_{m α} \cos θ;

(43)

R = C_{z α} C_{m q} - C_{m α} C_{q},

(43)

where:

θ = γ + α

(44)

a system of equations is obtained, which is solved iteratively for incidence and angular velocity of rotation:

\begin{matrix} α_{m a x} = R_{α} / R; & {\hat{q}}^{*} = R_{q} / R \end{matrix}

(45)

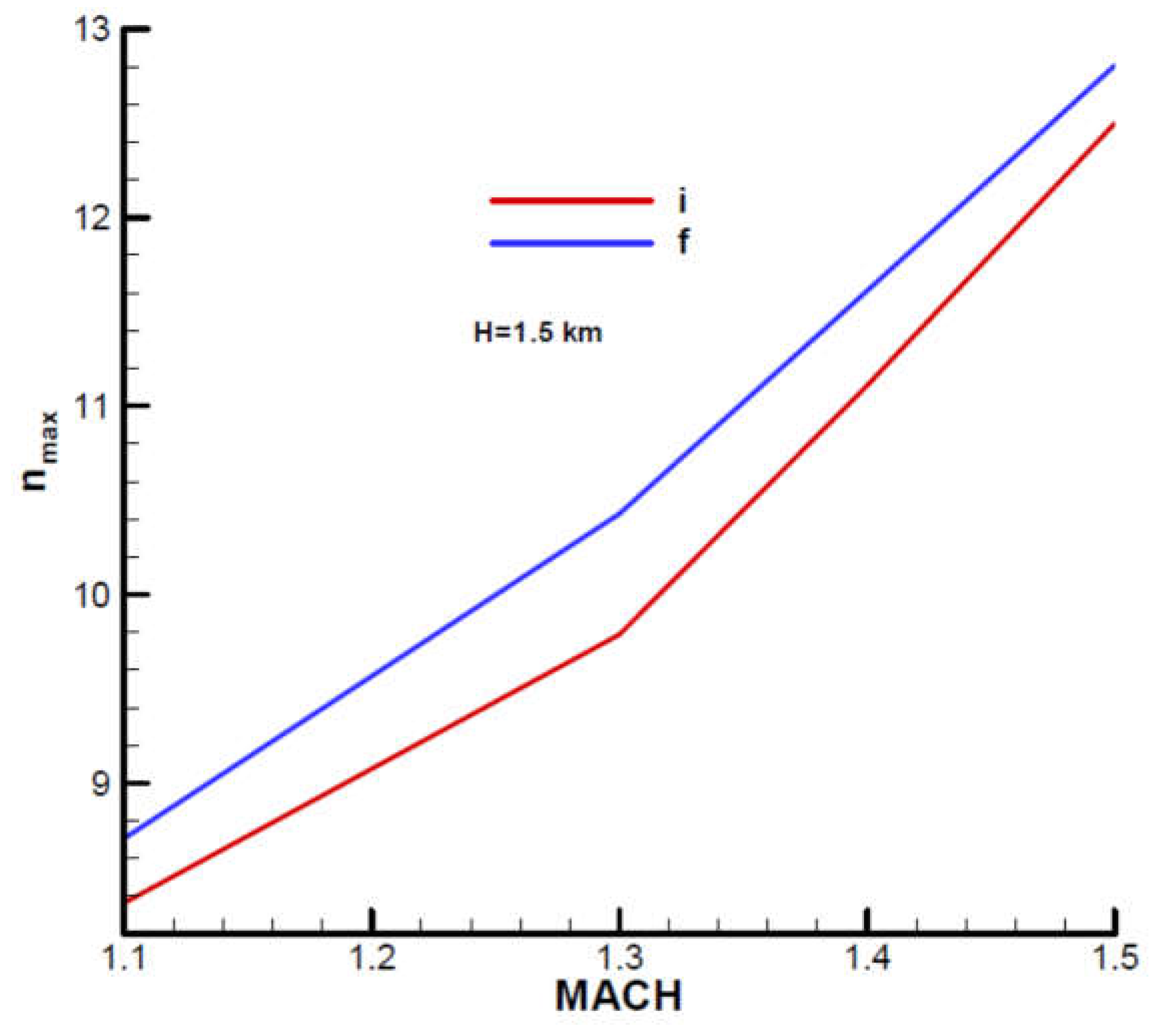
From that we get the maximum load factor (Figure A17):

n_{m a x} = {\hat{q}}^{*} / \hat{g},

(46)

where

\hat{g} = g l / V^{2}

is called reduced gravitational acceleration [26]

5. The Linear form of the Equations of Rapid Motion Around the Center of Mass

Using a quasi-linked frame (Resal) for missiles with roll rotation, the equations of rapid motion in the vertical and lateral planes can be grouped and analyzed. For this purpose, it is assumed that the elements of slow motion and roll are "frozen" at their equilibrium values, the perturbation introduced into the system developing only for rapid motion around the center of mass, which, as we will show later, cannot be analyzed separately on each channel, being, in fact, a unique spiral evolution.

To analyze this motion, we start from the symmetrisation of the dynamic translation equations by the axes

y^{*}, z^{*}

of the Resal frame. For this, it is considered that the components of the disturbing force given by aerodynamic and gasodynamic asymmetries are cancelled due to rotation. The only remaining perturbations are those due to gravitational acceleration, which by gyroscopic terms also affect the lateral plane and those due to wind1. In addition, due to rolling, the aerodynamic coefficients contain Magnus coupling terms, which appear on both channels. With these specifications, linearizing (17), we obtain:

∆ {\dot{w}}^{*} = \frac{F_{o}}{m} C_{z α} ∆ α + (\frac{F_{o} l}{m V} C_{z q} + u^{*}) ∆ q^{*} + \frac{F_{o} l}{m V} C_{z \dot{α}} ∆ \dot{α} + \frac{F_{o} l}{m V} C_{z p β} p ∆ β + \frac{F_{o} l^{2}}{m V^{2}} C_{z p r} p ∆ r^{*} + \frac{F_{o}}{m} C_{z δ m} ∆ δ_{m}^{*} - \frac{F_{o}}{m} C_{z α} ∆ α_{W} + \frac{∆ Z_{p}^{*}}{m};

(47)

∆ {\dot{v}}^{*} = \frac{F_{o}}{m} C_{y β} ∆ β + (\frac{F_{o} l}{m V} C_{y r} - u^{*}) ∆ r^{*} + \frac{F_{o} l}{m V} C_{y \dot{β}} ∆ \dot{β} + \frac{F_{o} l}{m V} C_{y p α} p ∆ \propto + \frac{F_{o} l^{2}}{m V^{2}} C_{y p q} p ∆ q^{*} + \frac{F_{o}}{m} C_{y δ n} ∆ δ_{n}^{*} - \frac{F_{o}}{m} C_{y β} ∆ β_{W} + \frac{∆ Y_{p}^{*}}{m}

(47)

where the velocity components define the incidences according to the axes of the Resal frame:

\begin{matrix} α = atan (w^{*} / u^{*}); & β = - atan (v^{*} / u^{*}) \end{matrix}

(48)

and the aerodynamic coefficients are:

C_{y} = Y^{*} / F_{0}; C_{z} = Z^{*} / F_{0}; C_{m} = M^{*} / H_{0}

(49)

; C_{n} = N^{*} / H_{0} .

(49)

Considering the basic movement, we have:

p = ω_{x} + p^{*} ≅ ω_{x}; \begin{matrix} Δ {\dot{v}}^{*} = - u^{*} Δ \dot{β} & Δ {\dot{w}}^{*} \end{matrix} = \sin α Δ \dot{V} + V \cos α Δ \dot{α}

(50)

If the incidence in the vertical plane is considered small, the previous relations take on the approximately symmetrical form:

\begin{matrix} Δ {\dot{v}}^{*} = {- u}^{*} Δ \dot{β}; & Δ {\dot{w}}^{*} \end{matrix} ≅ u^{*} Δ \dot{α}

(51)

Equation (47) can be brought to the following form:

∆ \dot{α} = \frac{F_{o}}{m u^{*}} C_{z α} ∆ α + (\frac{F_{o} l}{m V u^{*}} C_{z q} + 1) ∆ q^{*} + \frac{F_{o} l}{m V u^{*}} C_{z \dot{α}} ∆ \dot{α} + \frac{F_{o} l}{m V u^{*}} C_{z p β} p ∆ β + \frac{F_{o} l^{2}}{m u^{*} V^{2}} C_{z p r} p ∆ r^{*} + \frac{F_{o}}{m u^{*}} C_{z δ m} ∆ δ_{m}^{*} - \frac{F_{o}}{m u^{*}} C_{z α} ∆ α_{W} + \frac{1}{m u^{*}} ∆ Z_{p}^{*}

(52)

∆ \dot{β} = - \frac{F_{o}}{m u^{*}} C_{y β} ∆ β + (1 - \frac{F_{o} l}{m V u^{*}} C_{y r}) ∆ r^{*} - \frac{F_{o} l}{m V u^{*}} C_{y \dot{β}} ∆ \dot{β} - \frac{F_{o} l}{m V u^{*}} C_{y p α} p ∆ \propto - \frac{F_{o} l^{2}}{m {u^{*} V}^{2}} C_{y p q} p ∆ q^{*} - \frac{F_{o}}{m u^{*}} C_{y δ n} ∆ δ_{n}^{*} + \frac{F_{o}}{m u^{*}} C_{y β} ∆ β_{W} - \frac{1}{m u^{*}} ∆ Y_{p}^{*}

(52)

where in the components of the permanent perturbation

Δ Z_{p}^{*}, Δ Y_{p}^{*}

are found both gravitational terms and the remaining terms by the approximation made when symmetrizing the equation of the angle of incidence

α

Next, we will rewrite the dynamic equations of rotation. We will consider the gyroscopic coupling terms highlighted by the transition from the body frame to the Resal frame and consider null the components of the disturbing moment mainly from aerodynamic and gasodynamic asymmetry. In addition to the conditions imposed on the stabilized roll base motion, we will consider that the evolution in the vertical plane is translational, i.e.,

q^{*} = 0

. At the same time, as we did in the case of translation equations, in the pitch moment equation development, the terms corresponding to the slow mode

(Δ V)

will be considered null. Similarly, the yaw moment equation development will not be affected by the roll motion, which is also considered frozen. Instead, gyroscopic coupling and Magnus terms arising from rotational movement around the longitudinal axis will be highlighted. With these additional clarifications, linearizing (20), we obtain:

∆ {\dot{q}}^{*} = \frac{H_{0}}{B} C_{m α} ∆ α + \frac{H_{0} l}{B V} C_{m q} ∆ q^{*} + \frac{H_{0} l}{B V} C_{m \dot{α}} ∆ \dot{α} + \frac{H_{0} l}{B V} C_{m p β} p ∆ β + (\frac{H_{0} l^{2}}{B V^{2}} C_{m p r} - \frac{A}{B}) p ∆ r^{*} + \frac{H_{0}}{B} C_{m δ m} ∆ δ_{m}^{*} - \frac{H_{0}}{B} C_{m α} ∆ α_{W};

(53)

∆ {\dot{r}}^{*} = \frac{H_{0}}{C} C_{n β} ∆ β + \frac{H_{0} l}{C V} C_{n r} ∆ r^{*} + \frac{H_{0} l}{C V} C_{n \dot{β}} ∆ \dot{β} + \frac{H_{0} l}{C V} C_{n p α} p ∆ α + (\frac{H_{0} l^{2}}{C V^{2}} C_{n p q} + \frac{A}{C}) p ∆ q^{*} + \frac{H_{0}}{C} C_{n δ n} ∆ δ_{n}^{*} - \frac{H_{0}}{C} C_{n β} ∆ β_{W} .

(53)

If the following notations are made:

a_{γ}^{α} = \frac{F_{o}}{m u^{*}} C_{z α} = - \frac{F_{o}}{m u^{*}} C_{y β}; a_{γ}^{q} = 1 + \frac{F_{o} l}{m V u^{*}} C_{z q} = 1 - \frac{F_{o} l}{m V u^{*}} C_{y r}; a_{γ}^{\dot{α}} = \frac{F_{o} l}{m V u^{*}} C_{z \dot{α}} = - \frac{F_{o} l}{m V u^{*}} C_{y \dot{β}}; a_{γ}^{β} = \frac{F_{o} l p}{m V u^{*}} C_{z p β} = \frac{F_{o} l p}{m V u^{*}} C_{y p α}; a_{γ}^{r} = \frac{F_{o} l^{2} p}{m V^{2} u^{*}} C_{z p r} = \frac{F_{o} l^{2} p}{m V^{2} u^{*}} C_{y p q}; b_{γ}^{δ} = \frac{F_{o}}{m u^{*}} C_{z δ m} = - \frac{F_{o}}{m u^{*}} C_{y δ n}; a_{ϖ}^{α} = \frac{H_{o}}{B} C_{m α} = \frac{H}{C} C_{n β}; a_{ϖ}^{q} = \frac{H_{o} l}{B V} C_{m q} = \frac{H_{o} l}{C V} C_{n r}; a_{ϖ}^{\dot{α}} = \frac{H_{o} l}{B V} C_{m \dot{α}} = \frac{H_{o} l}{C V} C_{n \dot{β}}; a_{ϖ}^{β} = \frac{H_{o} l p}{B V} C_{m p β} = - \frac{H_{o} l p}{C V} C_{n p α}; a_{ϖ}^{r} = (\frac{H_{o} l^{2}}{B V^{2}} C_{m p r} - \frac{A}{B}) p = - (\frac{H_{o} l^{2}}{C V^{2}} C_{n p q} + \frac{A}{C}) p

(54)

; b_{ϖ}^{δ} = \frac{H_{o}}{B} C_{m δ_{m}} = \frac{H_{o}}{C} C_{n δ_{n}},

(54)

valid for the case where

α

is small, and complex quantities are defined:

\begin{matrix} γ^{*} = α - i β; & ϖ^{*} = q^{*} - i r^{*}; & δ^{*} = δ_{m}^{*} - i δ_{n}^{*}; & γ_{W}^{*} = α_{W} - {i β}_{W}; & F_{p}^{*} = Z_{p}^{*} + i Y_{p}^{*}; \end{matrix} a_{γ}^{γ} = a_{γ}^{α} + i a_{γ}^{β}; a_{γ}^{ϖ} = a_{γ}^{q} + i a_{γ}^{r}; a_{ϖ}^{γ} = a_{ϖ}^{α} + i a_{ϖ}^{β}; a_{ϖ}^{ϖ} = a_{ϖ}^{q} + i a_{ϖ}^{r}

(55)

where:

i = \sqrt{- 1}

, the system can be brought to the form:

Δ {\dot{γ}}^{*} = a_{γ}^{γ} Δ γ^{*} + a_{γ}^{ϖ} Δ ϖ^{*} + a_{γ}^{\dot{α}} Δ {\dot{γ}}^{*} + b_{γ}^{δ} Δ δ^{*} - a_{γ}^{α} Δ γ_{W}^{*} + Δ F_{p}^{*} / (m u^{*}) Δ {\dot{ϖ}}^{*} = a_{ϖ}^{γ} Δ γ^{*} + a_{ϖ}^{ϖ} Δ ϖ^{*} + a_{ϖ}^{\dot{α}} Δ {\dot{γ}}^{*} + b_{ϖ}^{δ} Δ δ^{*} - a_{ϖ}^{α} Δ γ_{W}^{*}

(56)

Its homogeneous form, after applying the Laplace transform, is:

[\begin{matrix} (1 - a_{γ}^{\dot{α}}) s - a_{γ}^{γ} & - a_{γ}^{ϖ} \\ - (a_{ϖ}^{\dot{α}} s + a_{ϖ}^{γ}) & s - a_{ϖ}^{ϖ} \end{matrix}] [\begin{matrix} Δ γ^{*} \\ Δ ϖ^{*} \end{matrix}] = [\begin{matrix} 0 \\ 0 \end{matrix}]

(57)

The characteristic polynomial becomes:

P (s) = (1 - a_{γ}^{\dot{α}}) s^{2} - (a_{γ}^{γ} + a_{ϖ}^{ϖ} + a_{ϖ}^{\dot{α}} a_{γ}^{ϖ} - a_{γ}^{\dot{α}} a_{ϖ}^{ϖ}) s + a_{γ}^{γ} a_{ϖ}^{ϖ} - a_{γ}^{ϖ} a_{ϖ}^{γ}

(58)

Alternatively, after separating complex terms:

P (s) = (1 - a_{γ}^{\dot{α}}) s^{2} - [a_{γ}^{α} + a_{ϖ}^{q} + a_{ϖ}^{\dot{α}} a_{γ}^{q} - a_{γ}^{\dot{α}} a_{ϖ}^{q} + i (a_{γ}^{β} + a_{ϖ}^{r} + a_{ϖ}^{\dot{α}} a_{γ}^{r} - a_{γ}^{\dot{α}} a_{ϖ}^{r})] s + a_{γ}^{α} a_{ϖ}^{q} - a_{γ}^{q} a_{ϖ}^{α} + a_{γ}^{r} a_{ϖ}^{β} - a_{γ}^{β} a_{ϖ}^{r} + i (a_{γ}^{α} a_{ϖ}^{r} - a_{γ}^{q} a_{ϖ}^{β} + a_{ϖ}^{q} a_{γ}^{β} - a_{ϖ}^{α} a_{γ}^{r}) .

(59)

The characteristic polynomial contains coefficients with the real part corresponding to the pitch motion and the imaginary part given by coupling with the yaw motion. However, due to the symmetry evidenced by the relations (54), the characteristic polynomial can contain coefficients with the real part corresponding to the yaw motion and the imaginary part corresponding to its coupling with the pitch motion. This observation remains valid for further motion analysis coupled with slow roll. However, for the complex form of motion, the relations obtained describe a single motion with coupling elements from the other.

For analyzing this expression and those that will be elaborated on later, evaluating the order of magnitude of the main parameters is useful, allowing for keeping only important terms in approximate relations. For this, in addition to the reference time

t^{*} = l / V

, also known as the aerodynamic second [27], which is a small parameter, in [26], the following dimensionless parameters are also defined:

\tilde{m} = m / (ρ S l)

- called the reduced mass of the aircraft or relative density;

i_{B} = \tilde{m} {(i_{y} / l)}^{2}

called reduced moment of inertia in pitch, where

i_{y}

is the radius of inertia of the aircraft for the pitch axis being given by the relation

i_{y} = \sqrt{B / m}

. In this case, the mass and pitch moment of inertia of the missile shall be expressed as follows:

m = \tilde{m} ρ S l; B = m i_{B} l^{2} / \tilde{m} = i_{B} ρ S l^{3}

(60)

As an order of magnitude, it is observed that the reference time

t^{*}

is small, while the reduced mass

\tilde{m}

and reduced moment of inertia in pitch

i_{B}

are large.

Next, we will rewrite the main coefficients of the equations of motion previously defined, which we will now include these parameters, obtaining:

a_{γ}^{α} = \frac{C_{z α}}{2 t^{*} \tilde{m}}; a_{γ}^{q} = 1 + \frac{C_{z q}}{2 \tilde{m}} ≅ 1; a_{γ}^{\dot{α}} = \frac{C_{z \dot{α}}}{2 \tilde{m}} ≅ 0; a_{γ}^{β} = \frac{\hat{p}}{2 \tilde{m} t^{*}} C_{z p β} ≅ 0; a_{γ}^{r} = \frac{\hat{p}}{2 \tilde{m}} C_{z p r}; b_{γ}^{δ} = \frac{C_{z δ m}}{2 \tilde{m} t^{*}}; a_{ϖ}^{α} = \frac{C_{m α}}{2 t^{* 2} i_{B}} a_{ϖ}^{q} = \frac{C_{m q}}{2 t^{*} i_{B}}; a_{ϖ}^{\dot{α}} = \frac{C_{m \dot{α}}}{2 t^{*} i_{B}}; a_{ϖ}^{β} = \frac{\hat{p}}{2 t^{* 2} i_{B}} C_{m p β} ≅ 0; a_{ϖ}^{r} = (\frac{C_{m p r}}{2 t^{*} i_{B}} - \frac{A}{B t^{*}}) \hat{p} ≅ - \frac{A}{B t^{*}} \hat{p}; b_{ϖ}^{δ} = \frac{C_{m δ m}}{2 t^{* 2} i_{B}}

(61)

and we can use dimensionless angular velocity in roll:

\hat{p} = p t^{*}

(62)

With the above notations, after dropping the secondary terms, the characteristic polynomial can be approximated as follows:

P (s) ≅ s^{2} + \frac{1}{t^{*}} \{\frac{1}{2 i_{B}} [η ({- C}_{m α}) + ({- C}_{m q}) + ({- C}_{m \dot{α}})] + i \frac{A}{B} \hat{p}\} s + \frac{1}{t^{* 2}} [\frac{({- C}_{m α})}{2 i_{B}} + i \frac{({- C}_{z α})}{2 \tilde{m}} \frac{A}{B} \hat{p}] .

(63)

6. Quality Parameters of the Motion with Slow-Rolling

If we are in the case of aerodynamically stabilized slow-rolling rockets, where the focus is behind the center of mass and the notations are entered:

ω_{p} = \frac{A}{2 B} p; ϕ = \frac{ω_{p}}{Ω}; η = \frac{i_{B}}{ζ \tilde{m}}; χ = 2 η {\hat{ω}}_{p}

(64)

; ζ = \frac{C_{m α}}{C_{z α}}

(64)

where

ω_{p}

represents the angular velocity of precession, with dimensionless form

{\hat{ω}}_{p} = ω_{p} t^{*}

;

ζ

represents static stability (Figure A13) the characteristic polynomial with the coefficient of the free term having the real part positive can be written in the form:

P (s) = s^{2} + 2 Ω (ξ + i ϕ) s + Ω^{2} (1 + i χ),

(65)

where its natural pulsation

Ω

and damping factor

ξ

have the same significance as a stabilized roll missile:

Ω^{2} ≅ \frac{(- C_{m α})}{2 t^{* 2} i_{B}};

- natural pulsation of nutation movement,

ξ ≅ \frac{1}{\sqrt{8 i_{B} (- C_{m α})}} [η (- C_{m α}) + (- C_{m q}) + (- C_{m \dot{α}})]

- damping factor of nutation movement.

Sometimes, instead of natural pulsation, its inverse is used:

T = 1 / Ω

- time constant of nutation movement.

The natural pulsation, damping factor and time constant according to the Mach number are presented in Figure A14, Figure A15 and Figure A16 from Appendix B

The roots of the characteristic polynomial, so the eigenvalues of the stability matrix, are given by:

s_{1,2} = - ξ Ω - i ω_{p} \pm i Ω \sqrt{{1 - ξ}^{2} + ϕ^{2} + i (χ - 2 ξ ϕ)},

(66)

Alternatively, if it is accepted that

χ ≅ 2 ξ ϕ

the roots of the characteristic polynomial can be put in simplified form:

s_{1,2} ≅ - ξ Ω - i ω_{p} \pm i Ω \sqrt{σ},

(67)

where:

σ = 1 - ξ^{2} + ϕ^{2}

Note that since the characteristic polynomial has complex coefficients, its roots are not complex conjugate, the additional complex term given by the angular rate of precession.

To define the command parameter of the rolling missile, we start from the equations of rapid motion (56) written in the non-homogeneous form:

[\begin{matrix} Δ γ^{*} \\ Δ ϖ^{*} \end{matrix}] = A^{- 1} (s) [\begin{matrix} b_{γ}^{δ} & - a_{γ}^{α} & 1 / (m u^{*}) \\ b_{ϖ}^{δ} & - a_{ϖ}^{α} & 0 \end{matrix}] {[\begin{matrix} Δ δ^{*} & Δ γ_{W}^{*} & Δ F_{p}^{*} \end{matrix}]}^{T},

(68)

the inverse matrix is given by:

A^{- 1} (s) = \frac{1}{P (s)} [\begin{matrix} s - a_{ϖ}^{ϖ} & a_{γ}^{ϖ} \\ a_{ϖ}^{\dot{α}} s + a_{ϖ}^{γ} & (1 - a_{γ}^{\dot{γ}}) s - a_{γ}^{γ} \end{matrix}],

(69)

where

P (s)

is the characteristic polynomial with complex coefficients associated with the previously analyzed homogeneous system.

In this case the main transfer functions are:

H_{γ}^{δ} (s) = \frac{b_{γ}^{δ} s + a_{γ}^{ϖ} b_{ϖ}^{δ} - a_{ϖ}^{ϖ} b_{γ}^{δ}}{P (s)}; H_{ϖ}^{δ} = \frac{(b_{ϖ}^{δ} + a_{ϖ}^{\dot{α}} b_{γ}^{δ} - a_{γ}^{\dot{α}} b_{ϖ}^{δ}) s + a_{ϖ}^{γ} b_{γ}^{δ} - a_{γ}^{γ} b_{ϖ}^{δ}}{P (s)};

(70)

system (68) may be put in the form of:

Δ γ^{*} = H_{γ}^{δ} (s) Δ δ^{*}; Δ ϖ = H_{ϖ}^{δ} (s) Δ δ^{*} .

(71)

For the construction of a global structural scheme of the commanded missile system, as was done in the papers [10,24], from the relations (71), we shall express the angular velocity of the tangent to the trajectory. For this, we start with the angular relation:

Δ ω^{*} = Δ ϖ^{*} - Δ {\dot{γ}}^{*} = Δ ϖ^{*} - s Δ γ^{*},

(72)

where:

ω^{*} = ω_{m} - i ω_{n} .

(73)

Next, we build a relation of the same type as the system (71) :

Δ ω^{*} = H_{ω}^{δ} (s) Δ δ^{*}

(74)

where:

H_{ω}^{δ} (s) = H_{ϖ}^{δ} (s) - s H_{γ}^{δ} (s);

(75)

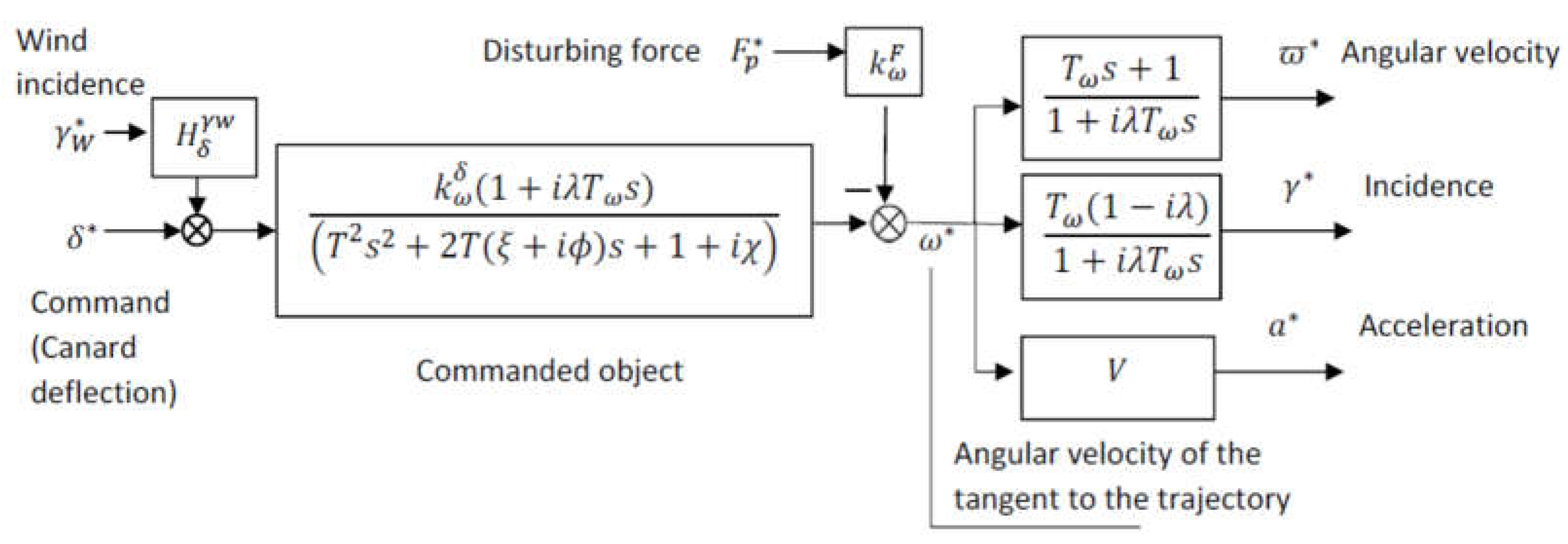
Based on the relations (61), we will seek to bring the angular velocity of the tangent to the trajectory transfer function with input in canard angular deflection to an approximate, simplified form.

Thus, we start with the form:

H_{ω}^{δ} (s) = \frac{- b_{γ}^{δ} s^{2} + [(1 - a_{γ}^{ϖ} - a_{γ}^{\dot{α}}) b_{ϖ}^{δ} + (a_{ϖ}^{ϖ} + a_{ϖ}^{\dot{α}}) b_{γ}^{δ}] s + a_{ϖ}^{γ} b_{γ}^{δ} - a_{γ}^{γ} b_{ϖ}^{δ}}{P (s)},

(76)

or, rewriting with the explicit complex terms:

H_{ω}^{δ} (s) = [- b_{γ}^{δ} s^{2} + \{[(a_{ϖ}^{q} + a_{ϖ}^{\dot{α}}) b_{γ}^{δ} - (a_{γ}^{q} + a_{γ}^{\dot{α}} - 1) b_{ϖ}^{δ}] + i (a_{ϖ}^{r} b_{γ}^{δ} - a_{γ}^{r} b_{ϖ}^{δ})\} s + (a_{ϖ}^{α} b_{γ}^{δ} - a_{γ}^{α} b_{ϖ}^{δ}) + i (a_{ϖ}^{β} b_{γ}^{δ} - a_{γ}^{β} b_{ϖ}^{δ})] / P (s),

(77)

where the characteristic polynomial is given by (65).

Next, making the notations:

k_{ω}^{δ} = \frac{a_{ϖ}^{α} b_{γ}^{δ} - a_{γ}^{α} b_{ϖ}^{δ}}{a_{ϖ}^{q} a_{γ}^{α} - a_{γ}^{q} a_{ϖ}^{α}}; λ T_{ω} = 2 ϑ {\hat{ω}}_{p} T_{ω} = \frac{a_{ϖ}^{r} b_{γ}^{δ} - a_{γ}^{r} b_{ϖ}^{δ}}{a_{ϖ}^{α} b_{γ}^{δ} - a_{γ}^{α} b_{ϖ}^{δ}}

(78)

the angular velocity of the tangent to the trajectory transfer function with the input in canard deflection can be brought to the form:

H_{ω}^{δ} (s) = \frac{k_{ω}^{δ} (1 + i λ T_{ω} s)}{T^{2} s^{2} + 2 T (ξ + i ϕ) s + 1 + i χ},

(79)

where

k_{ω}^{δ}

is called the command factor and the parameter

T_{ω}

means, as in the case of the stabilized rolling aircraft, the advance time on command or the aircraft's time constant.

Dropping the secondary terms for the aerodynamically commanded missile, the parameters defined by the notations (78) become:

k_{ω}^{δ} = \frac{C_{m δ m} (1 - ζ \frac{C_{z δ m}}{C_{m δ m}})}{2 t^{*} \tilde{m} ζ}; ϑ = ζ η \frac{(- C_{z δ m})}{C_{m δ m}}; T_{ω} ≅ \frac{2 t^{*} \tilde{m}}{(- C_{z α}) (1 - ζ \frac{C_{z δ m}}{C_{m δ m}})} .

Next, we will seek to find the connection between incidence

(γ^{*})

, angular velocity

(ϖ^{*})

, and angular velocity of the tangent to the trajectory

(ω^{*})

. To begin with, we will establish the link between incidence and angular velocity, starting from the main transfer functions that express these parameters depending on the canard deflection. Thus, from (70), one can construct the transfer function:

H_{γ}^{ϖ} (s) = H_{γ}^{δ} (s) / H_{ϖ}^{δ} (s),

(80)

which, after eliminating the secondary terms, may take the form of:

H_{γ}^{ϖ} (s) = \frac{T_{ω} (1 - i λ)}{T_{ω} s + 1},

(81)

which means that the simplified link between incidence and angular velocity has the following form:

\frac{Δ γ^{*}}{Δ ϖ^{*}} ≅ \frac{T_{ω} (1 - i λ)}{T_{ω} s + 1} .

(82)

Returning to the relation between angular velocities (72) we can write successively:

Δ ω^{*} = (1 - s \frac{Δ γ^{*}}{Δ ϖ^{*}}) Δ ϖ^{*} ≅ (1 - \frac{T_{ω} (1 - i λ) s}{T_{ω} s + 1}) Δ ϖ^{*} = \frac{1 + i λ T_{ω} s}{T_{ω} s + 1} Δ ϖ^{*},

(83)

where in order to obtain the transfer function we are interested in:

H_{ϖ}^{ω} (s) ≅ \frac{T_{ω} s + 1}{1 + i λ T_{ω} s} .

(84)

Further, for the expression of incidence, it can be written:

H_{γ}^{ω} (s) = H_{γ}^{ϖ} (s) H_{ϖ}^{ω} (s) ≅ \frac{T_{ω} (1 - i λ)}{1 + i λ T_{ω} s} .

(85)

Finally, we can also evaluate the components of the normal complex acceleration on velocity, which, if we consider the hypothesis of small incidences introduced when symmetrizing longitudinal motion, have the direction of the axes

y^{*}

and

z^{*}

of the quasi-linked frame, being given by the approximate relation:

Δ a^{*} ≅ V Δ ω^{*},

(86)

where:

a^{*} = a_{z}^{*} + i a_{y}^{*} .

(87)

Based on the resulted relations, one can construct the structural scheme of the commanded movement for missiles with slow roll rotation, shown in Figure 4.

7. The Guided Flight Model

As shown in [24], the guidance kinematic equations will be constructed into a frame linked to the target's line of sight called the guiding frame (Figure 5). The guiding frame

M X_{T} Y_{T} Z_{T}

originates at point (

M)

, which represents the position of the missile, the axis

X_{T}

pointed target

(T)

, the axis

Z_{T}

is in a vertical plane facing downwards, and axis

Y_{T}

horizontally, it follows from the condition of the right frame. The guiding frame is non-inertial.

The angles defining the orientation of the guiding frame with respect to the local frame are given by the relations:

\begin{matrix} ψ_{M} = - arctg \frac{y_{T 0} - y_{0}}{x_{T 0} - x_{0}}; & θ_{M} = arctg \frac{z_{T 0} - z_{0}}{\sqrt{{(x_{T 0} - x_{0})}^{2} + {(y_{T 0} - y_{0})}^{2}}} \end{matrix},

(88)

where

x_{0}, y_{0}

and

z_{0}

were the coordinates of the rocket in the local frame, respective

x_{T 0}

y_{T 0}

and

z_{T 0}

target coordinates in the local frame.

With the help of these two angles, the rotational matrix is formed, which makes the transition from the local frame to the guiding frame:

A_{M} = A_{θ M} A_{ψ M} A_{π} = [\begin{matrix} {cosθ}_{M} {c o s ψ}_{M} & - {cosθ}_{M} {s i n ψ}_{M} & {s i n θ}_{M} \\ - {s i n ψ}_{M} & - {c o s ψ}_{M} & 0 \\ {sinθ}_{M} {c o s ψ}_{M} & - {sinθ}_{M} {c o s ψ}_{M} & - {c o s θ}_{M} \end{matrix}]

(89)

Next, we will obtain the guidance kinematic equations in the guiding frame, which is a non-inertial.

7.1. Kinematic Guidance Equations

Figure 6 and Figure 7 show the decompositions of velocity and acceleration of the missile and target according to the axes of the guiding frame. Given the general relations of derivation, in a non-inertial frame, one can write:

[\begin{matrix} {\tilde{u}}_{T} \\ {\tilde{v}}_{T} \\ {\tilde{w}}_{T} \end{matrix}] = [\begin{matrix} \dot{R} \\ 0 \\ 0 \end{matrix}] + S_{ω} [\begin{matrix} R \\ 0 \\ 0 \end{matrix}]; [\begin{matrix} {\tilde{a}}_{x T} \\ {\tilde{a}}_{y T} \\ {\tilde{a}}_{z T} \end{matrix}] = [\begin{matrix} \ddot{R} \\ 0 \\ 0 \end{matrix}] + 2 S_{ω} [\begin{matrix} \dot{R} \\ 0 \\ 0 \end{matrix}] + R_{ω} [\begin{matrix} R \\ 0 \\ 0 \end{matrix}],

(90)

where the relative velocities and accelerations were expressed in the guiding frame:

{\tilde{u}}_{T} = u_{T} - u_{M}; {\tilde{v}}_{T} = v_{T} - v_{M}; {\tilde{w}}_{T} = w_{T} - w_{M}; {\tilde{a}}_{x T} = a_{x T} - a_{x M}; {\tilde{a}}_{y T} = a_{y T} - a_{y M}; {\tilde{a}}_{z T} = a_{z T} - a_{z M};

(91)

i.e., matrices resulting from vector products:

S_{ω} = [\begin{matrix} 0 & - ω_{z} & ω_{y} \\ ω_{z} & 0 & - ω_{x} \\ - ω_{y} & ω_{x} & 0 \end{matrix}]; R_{ω} = [\begin{matrix} - (ω_{y}^{2} + ω_{z}^{2}) & ω_{x} ω_{y} - {\dot{ω}}_{z} & ω_{z} ω_{x} + {\dot{ω}}_{y} \\ ω_{x} ω_{y} + {\dot{ω}}_{z} & - (ω_{z}^{2} + ω_{x}^{2}) & ω_{y} ω_{z} - {\dot{ω}}_{x} \\ ω_{z} ω_{x} - {\dot{ω}}_{y} & ω_{y} ω_{z} + {\dot{ω}}_{x} & - (ω_{x}^{2} + ω_{y}^{2}) \end{matrix}]

(92)

in which:

ω_{x} = - {\dot{ψ}}_{M} \sin θ; ω_{y} = {\dot{θ}}_{M}; ω_{z} = {\dot{ψ}}_{M} \cos θ {\dot{ω}}_{x} = {- \ddot{ψ}}_{M} \sin θ - {\dot{θ}}_{M} \dot{ψ}_{M} \cos θ; {\dot{ω}}_{y} = {\ddot{θ}}_{M}; {\dot{ω}}_{z} = {\ddot{ψ}}_{M} \cos θ - {\dot{θ}}_{M} \dot{ψ}_{M} \sin θ

(93)

Based on these relations, the components of relative velocity and relative acceleration in the guiding frame are:

{\tilde{u}}_{T} = \dot{R}; {\tilde{v}}_{T} = R ω_{z}; {\tilde{w}}_{T} = - R ω_{y},

(94)

respectively:

{\tilde{a}}_{x T} = \ddot{R} - (ω_{y}^{2} + ω_{z}^{2}) R; {\tilde{a}}_{y T} = 2 ω_{z} \dot{R} + R ({\dot{ω}}_{z} + ω_{x} ω_{y}); {\tilde{a}}_{z T} = - 2 ω_{y} \dot{R} - R ({\dot{ω}}_{y} - ω_{z} ω_{x})

(95)

relations from which the components of rotational velocity and acceleration of the guiding frame can be expressed, relations which represent the kinematic equations of guidance:

ω_{y} = - \frac{{\tilde{w}}_{T}}{R}; ω_{z} = \frac{{\tilde{v}}_{T}}{R},

(96)

respectively:

{\dot{ω}}_{y} = - 2 \frac{\dot{R}}{R} ω_{y} - \frac{{\tilde{a}}_{z T}}{R} + ω_{z} ω_{x}; {\dot{ω}}_{z} = - 2 \frac{\dot{R}}{R} ω_{z} + \frac{{\tilde{a}}_{y T}}{R} - ω_{x} ω_{y} .

(97)

7.2. Linear form of Kinematic Guidance Equations

The basic motion in proportional navigation is a parallel approach, which is characterized by the fact that the absolute angular velocity of the line of sight and the derivative of the absolute angular velocity of the line of sight are null:

ω_{y} = 0; ω_{z} = 0; {\dot{ω}}_{y} = 0; {\dot{ω}}_{z} = 0 .

(98)

Because in the basic movement the guidance parameters are null (

\begin{matrix} ω_{y} = 0; & ω_{z} = 0 \end{matrix}

), the guidance components for basic movement shall also be null:

\begin{matrix} u_{y} = 0; & u_{z} = 0 \end{matrix}

(99)

In order to linearize the angular velocity equations of the line of sight, one can start from the relation (96), obtaining:

[\begin{matrix} Δ {\dot{σ}}_{y} \\ Δ {\dot{σ}}_{z} \end{matrix}] = \frac{1}{R} [\begin{matrix} - Δ {\tilde{w}}_{T} \\ Δ {\tilde{v}}_{T} \end{matrix}] = \frac{1}{R} [\begin{matrix} - Δ w_{T} \\ Δ v_{T} \end{matrix}] - \frac{1}{R} [\begin{matrix} - Δ w_{M} \\ Δ v_{M} \end{matrix}] = \frac{u_{T}}{R} [\begin{matrix} Δ γ_{T} \\ Δ χ_{T} \end{matrix}] - \frac{u_{M}}{R} [\begin{matrix} Δ γ_{M} \\ Δ χ_{M} \end{matrix}] - \frac{\dot{R}}{R} [\begin{matrix} Δ σ_{y} \\ Δ σ_{z} \end{matrix}]

(100)

Denoting the input due to launch error:

[\begin{matrix} Δ f_{1 y} \\ Δ f_{1 z} \end{matrix}] = \frac{u_{T}}{u_{M}} [\begin{matrix} Δ γ_{T} \\ Δ χ_{T} \end{matrix}],

(101)

we obtain:

\frac{R}{u_{M}} [\begin{matrix} Δ {\dot{σ}}_{y} \\ Δ {\dot{σ}}_{z} \end{matrix}] + \frac{\dot{R}}{u_{M}} [\begin{matrix} Δ σ_{y} \\ Δ σ_{z} \end{matrix}] + [\begin{matrix} Δ γ_{M} \\ Δ χ_{M} \end{matrix}] = [\begin{matrix} Δ f_{1 y} \\ Δ f_{1 z} \end{matrix}]

(102)

If the complex components are introduced:

σ^{*} = σ_{y} - i σ_{z}, ϑ^{*} = γ_{M} - i χ_{M}; f_{1}^{*} = f_{1 y} - {i f}_{1 z}

(103)

the equation of the absolute angle of the line of sight in complex form is obtained:

\frac{R}{u_{M}} {Δ \dot{σ}}^{*} + \frac{\dot{R}}{u_{M}} {Δ σ}^{*} + Δ ϑ^{*} = Δ f_{1}^{*}

(104)

Next, we start from the Equation (97), which, by neglecting the product of two small terms

ω_{z} ω_{x}

, becomes:

[\begin{matrix} Δ {\dot{ω}}_{y} \\ Δ {\dot{ω}}_{z} \end{matrix}] + 2 \frac{\dot{R}}{R} [\begin{matrix} Δ ω_{y} \\ Δ ω_{z} \end{matrix}] + [\frac{\ddot{R}}{R} - (ω_{y}^{2} + ω_{z}^{2})] [\begin{matrix} Δ σ_{y} \\ Δ σ_{z} \end{matrix}] = \frac{1}{R} [\begin{matrix} - Δ {\tilde{a}}_{z T} \\ Δ {\tilde{a}}_{y T} \end{matrix}] = \frac{1}{R} [\begin{matrix} - Δ a_{z T} \\ Δ a_{y T} \end{matrix}] - \frac{1}{R} [\begin{matrix} - Δ a_{z M} \\ Δ a_{y M} \end{matrix}] = \frac{u_{T}}{R} [\begin{matrix} Δ ω_{y T} \\ Δ ω_{z T} \end{matrix}] - \frac{u_{M}}{R} [\begin{matrix} Δ ω_{y M} \\ Δ ω_{z M} \end{matrix}]

(105)

Neglecting the small terms

\frac{\ddot{R}}{R} - (ω_{y}^{2} + ω_{z}^{2})

and denoting the input function due to target maneuvers:

[\begin{matrix} Δ f_{2 y} \\ Δ f_{2 z} \end{matrix}] = \frac{u_{T}}{u_{M}} [\begin{matrix} Δ ω_{y T} \\ Δ ω_{z T} \end{matrix}]

(106)

we obtain:

\frac{R}{u_{M}} [\begin{matrix} Δ {\dot{ω}}_{y} \\ Δ {\dot{ω}}_{z} \end{matrix}] + 2 \frac{\dot{R}}{u_{M}} [\begin{matrix} Δ ω_{y} \\ Δ ω_{z} \end{matrix}] + [\begin{matrix} Δ ω_{y M} \\ Δ ω_{z M} \end{matrix}] = [\begin{matrix} Δ f_{2 y} \\ Δ f_{2 z} \end{matrix}] .

(107)

If we define complex components:

{\dot{σ}}^{*} = ν^{*} = ω_{y} - i ω_{z}; {\dot{ϑ}}^{*} = ω^{*} = ω_{y M} - i ω_{z M}; f_{2}^{*} = f_{2 y} - i f_{2 z}

(108)

the equation of the angular velocity of the line of sight in complex form is obtained:

\frac{R}{u_{M}} Δ {\dot{ν}}^{*} + 2 \frac{\dot{R}}{u_{M}} Δ ν^{*} + Δ ω^{*} = Δ f_{2}^{*}

(109)

Considering the coefficients of the guidance equation frozen at the values corresponding to the base motion and the current missile-target distance (R) changing slowly with respect to the guidance parameters, the Laplace transform can be applied to Equation (109), obtaining:

Δ σ^{*} = \frac{u_{M}}{R s + 2 \dot{R}} (Δ f^{*} - Δ ϑ^{*})

(110)

where the input function is:

Δ f^{*} = Δ f_{1}^{*} + \frac{1}{s} Δ f_{2}^{*}

(111)

Considering that distance

R

is constant and equal to the value at a given moment, the transfer function of the kinematic block becomes:

H_{C} (t_{g o}, s) = \frac{u_{M}}{(t_{g o} s - 2) u_{C}}

(112)

where

t_{g o} = - R / \dot{R}

, is considered a frozen parameter corresponding to the distance

R

to the target.

7.3. Target Tracker Equations

The equation of the target tracker (seeker) provides guidance commands in two planes is:

[\begin{matrix} {\dot{u}}_{y} \\ {\dot{u}}_{z} \end{matrix}] = - \frac{1}{τ_{c}} [\begin{matrix} u_{y} \\ u_{z} \end{matrix}] + \frac{k_{u}^{ω}}{τ_{c}} [\begin{matrix} ω_{y} \\ ω_{z} \end{matrix}],

(113)

where the control parameters are angular velocities

ω_{y}

ω_{z}

in the guiding frame defined by the line of sight.

If we linearize, considering that in basic movement the guidance signal is null, we get:

[\begin{matrix} Δ {\dot{u}}_{y} \\ Δ {\dot{u}}_{z} \end{matrix}] = - \frac{1}{τ_{c}} [\begin{matrix} {Δ u}_{y} \\ Δ u_{z} \end{matrix}] + \frac{k_{u}^{ω}}{τ_{c}} [\begin{matrix} {Δ ω}_{y} \\ Δ ω_{z} \end{matrix}],

(114)

Defining the complex component of the guidance command:

u^{*} = u_{y} - i u_{z}

(115)

the equation of the target tracking device in complex form is obtained:

Δ {\dot{u}}^{*} = - \frac{1}{τ_{c}} Δ u^{*} + \frac{k_{u}^{ω}}{τ_{c}} Δ ν^{*}

(116)

, and after application of the Laplace transformation, the transfer function of the target tracker (seeker) can be obtained:

Δ u^{*} = \frac{k_{u}^{ω} s}{1 + τ_{c} s} Δ σ^{*}

(117)

function that will be used for the guided missile system diagram.

7.4. The Command for Slow-Rolling Single-Channel Missile

In [10], two guided models were built, one for the homing missile and the other for the remote-controlled missile, but for which no detailed analysis was made. In section 3. equations of motion in the Resal frame were presented. The rapid motion around the center of mass was analyzed by linearizing these relations, and the quality parameters of the commanded longitudinal motion, specific to the slow-rolling missile, were defined. In paragraph 7.2, we built the linear form of the guided kinematic and seeker equations. Starting from these results, we will build a guided flight model for the homing missile and will do a detailed analysis of the stability. For this, we start from the expression of the two-channel command, which, considering only the guiding terms, has the following form:

[\begin{matrix} u_{m} \\ u_{n} \end{matrix}] = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] A_{I} A_{M}^{T} [\begin{matrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \end{matrix}] [\begin{matrix} u_{y} \\ u_{z} \end{matrix}]

(118)

Since in the basic uncoupled guidance equation, it is assumed that the head angle of the rocket coincides with that of the guiding frame:

ψ = ψ_{M}

θ = θ_{M}

and neglecting the angle of incidence in the vertical plane, in order to be able to achieve the symmetrisation of the two guiding planes, the command can be put in the following form:

{[\begin{matrix} u_{m} & u_{n} \end{matrix}]}^{T} = K_{ϕ} {[\begin{matrix} u_{y} & u_{z} \end{matrix}]}^{T}

(119)

where the following notation was made:

K_{ϕ} = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] A_{ϕ} [\begin{matrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \end{matrix}] = [\begin{matrix} \cos ϕ & \sin ϕ \\ - \sin ϕ & \cos ϕ \end{matrix}]

(120)

, with

A_{ϕ}

being the direct rotation matrix with roll angle.

Next, we will seek to bring matrix expressions to complex form by using a polar coordinate system that highlights the module and phase of the guidance command. Thus, if the commands are put in the complex form:

u = u_{m} - i u_{n}; u^{*} = u_{y} - i u_{z}

(121)

The relation (119) becomes:

u = u^{*} e^{i ϕ}

(122)

On the other hand, as seen in Figure 8, the guidance command can be expressed in polar coordinates:

u^{*} = ρ e^{i φ}

(123)

, where:

ρ = \sqrt{u_{y}^{2} + u_{z}^{2}}

– is the command module;

φ = arctg \frac{{- u}_{z}}{u_{y}}

– is the command phase.

In this case, the command for the two channels (pitch and yaw) in the body frame becomes:

u = ρ e^{i (φ + ϕ + ε)},

(124)

where

ε

is phase shift error:

ε = θ - τ_{δ} ω_{x} + ∆ ϕ

(125)

In this relation, we introduce:

θ

- command advance angle intended to cancel out the delay effect;

τ_{δ}

- command delay time;

∆ ϕ

-roll angle error.

The phase shift value

ε,

thus introduced, may be due both to the choice of a constant value for the delay compensation angle

θ

(which in the case of rotational velocity

ω_{x}

variation during the trajectory leads to an erroneous phase) and to the poor assessment of the roll angle

ϕ

(required to form the command, with deviation

∆ ϕ

). Since this phase shift is due to rolling angular velocity, being specific to rolling missiles, we shall eliminate it in the case of the stabilized roll missile analysis.

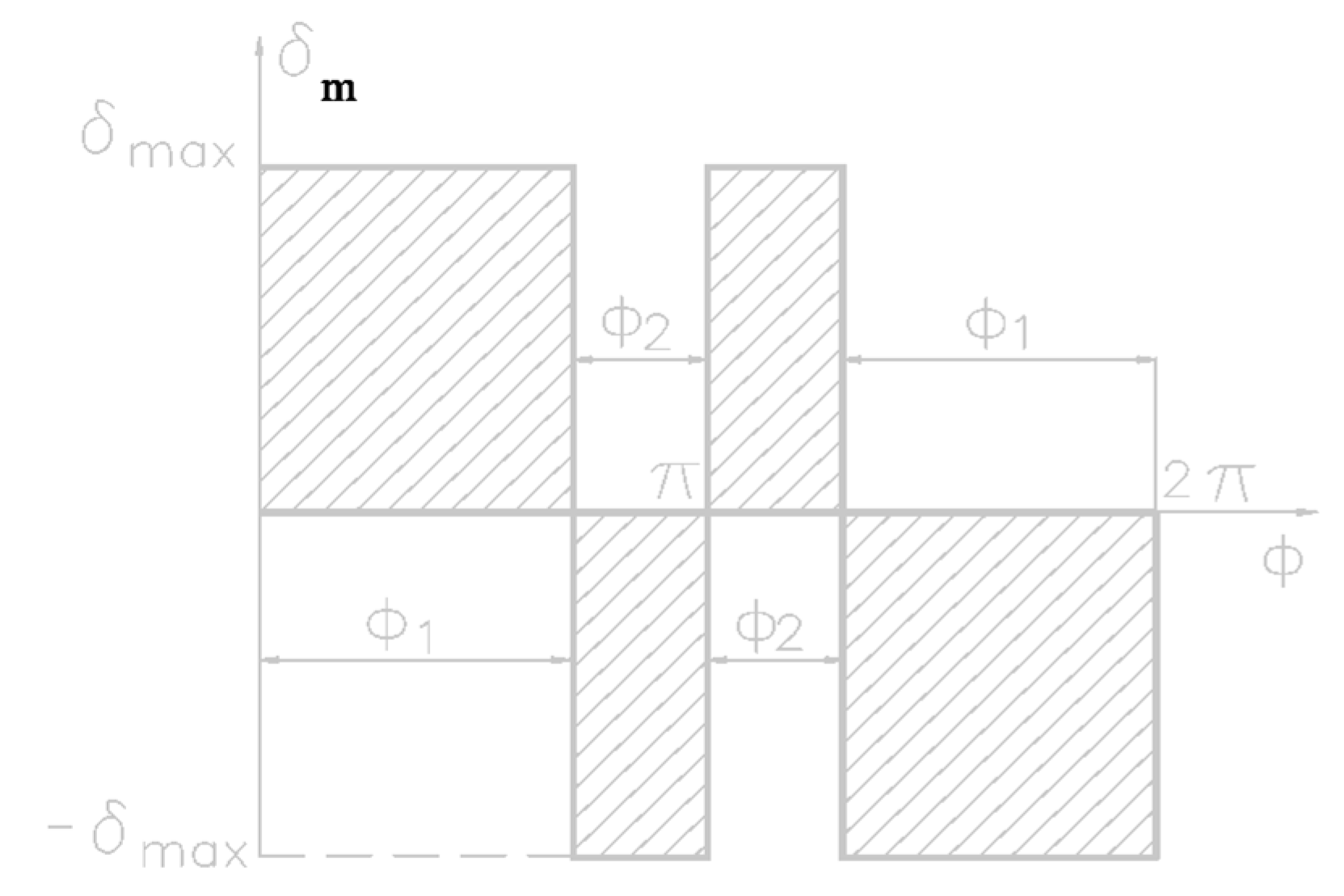
To obtain the time modulation of the command in duration, for single-channel missile, it is necessary to use a switching function of the form [19]:

f (\tilde{φ}, x) = \sin Φ (x + \cos Φ)

(126)

, where

x

, called the fill factor, is given by the relation:

x = ρ / u_{m a x}

(127)

, in which

ρ

is the command module,

u_{m a x}

is the maximum guidance command, and the argument

Φ

, called relative roll angle, is given by:

Φ = φ + ϕ + π / 2 + ε,

(128)

where

φ

represents the command phase (Figure 8),

ϕ

is the roll angle (Figure 2), and

ε

is the phase shift error.

The switching function (126) is applied instantaneously through a nonlinear element, relay-type, the pitch canard deflection angle expression being:

δ_{m} (Φ, x) = δ_{m a x} s i g n (f (Φ, x))

(129)

To check how the function

f (Φ, x)

generates a canard angular deflection correlated with roll rotation, it is necessary to determine the zeros of this function that coincide with the deflection switching points. For this, the expression (126) is put in the form of an equation:

\sin Φ (x + \cos Φ) = 0

(130)

, the solutions of which are obtained by imposing, in turn, the conditions:

\sin Φ = 0 and \cos Φ = - x

(131)

For the interval

[0,2 π]

in which

Φ

get values, we have a group of switch points due to condition

\sin Φ = 0

, which are

Φ = \begin{matrix} 0, & π, & 2 π \end{matrix}

From the condition

\cos Φ = - x

, the second group of switch points are obtained. For extreme values of the fill factor

x = 1

we obtain

Φ = \begin{matrix} π \end{matrix}

, which is the maximum command after a certain direction, and for

x = 0

, results

Φ = \begin{matrix} π / 2 \end{matrix}

3 π / 2

, which means the null command.

For better understanding, in papers [10,24], the equivalent deflection was determined for the particular case when the control phase is φ

= 0

(Figure 8), with a null phase shift error

ε

=0, which drives a positive pitch command.

Based on dynamic equations of motion in the body frame (17), (20), kinematic Equations (7) and (8) and kinematic guidance Equation (96) as well as target tracker Equation (113), switching function (126) with the relative roll angle definition relation (128) and expression of pitch canard deflection angle (129), the nonlinear model of guided flight of the single-channel, slow-rolling, homing missile is obtained. This will be used later within the paper in order to validate and verify the linear results.

Next, we obtain the expression of the single-channel command for an equivalent canard deflection in the Resal frame that will be used to define the linear form of the actuator necessary to build the structural scheme of the guided system. For this, we start from the shape of the canard deflection in one rotation period given by the relation (129).

For the single-channel case, considering only pitch deflection

δ_{m}

, we have:

δ_{m} = \tilde{δ} e^{i ϕ}

(132)

, where

\tilde{δ}

is the equivalent instant deflection in the Resal frame.

The relation can be reversed:

\tilde{δ} = δ_{m} e^{- i ϕ} = δ_{m} e^{- i (Φ - φ - ε - π / 2)} = i δ_{m} e^{- i Φ} e^{i (φ + ε)}

(133)

In this case, the average equivalent canard deflection over one rotation in the Resal frame shall be given by:

δ^{*} = \frac{1}{2 π} \int_{0}^{2 π} \tilde{δ} d Φ = \frac{i}{2 π} e^{i (φ + ε)} \int_{0}^{2 π} δ_{m} e^{- i Φ} d Φ

(134)

Considering command parity for a full rotation, the average equivalent canard deflection becomes:

δ^{*} = e^{i (φ + ε)} \frac{1}{2 π} \int_{0}^{2 π} δ_{m} \sin Φ d Φ

(135)

The integral in this relation can be calculated with the diagram from Figure 9 , obtaining successively:

\frac{1}{2 π} \int_{0}^{2 π} δ_{m} \sin Φ d Φ = = \frac{δ_{m a x}}{2 π} [\int_{0}^{Φ_{1}} \sin Φ d Φ - \int_{Φ_{1}}^{π} \sin Φ d Φ + \int_{π}^{π + Φ_{2}} \sin Φ d Φ - \int_{π + Φ_{2}}^{2 π} \sin Φ d Φ] = - \frac{δ_{m a x}}{π} [{\cos Φ}_{1} - {\cos Φ}_{2}] = - \frac{2 δ_{m a x}}{π} {\cos Φ}_{1} = \frac{2 δ_{m a x}}{π} x

(136)

Thus, having the integral determined from the relation (135) and the relation defining the fill factor (127), average equivalent deflection becomes:

δ^{*} = \frac{2 δ_{m a x}}{π} x e^{i (φ + ε)} = \frac{2 δ_{m a x}}{π u_{m a x}} e^{i ε} u^{*}

(137)

, hence the linear form of the actuator is obtained:

Δ δ^{*} = k_{δ}^{u} e^{i ε} Δ u^{*}

(138)

, where:

k_{δ}^{u} = \frac{2 δ_{m a x}}{π u_{m a x}}

(139)

OBSERVATION

Given that the average equivalent deflection

δ^{*}

is carried out in a full period of rotation, it can be considered that it follows the command signal

u^{*}

in steps, the duration of a stage corresponding to the rocket's rotation period. If the rocket's rotation frequency is high enough (over 10 Hz), the output of the actuator may be considered smooth enough to be approximated as continuous.

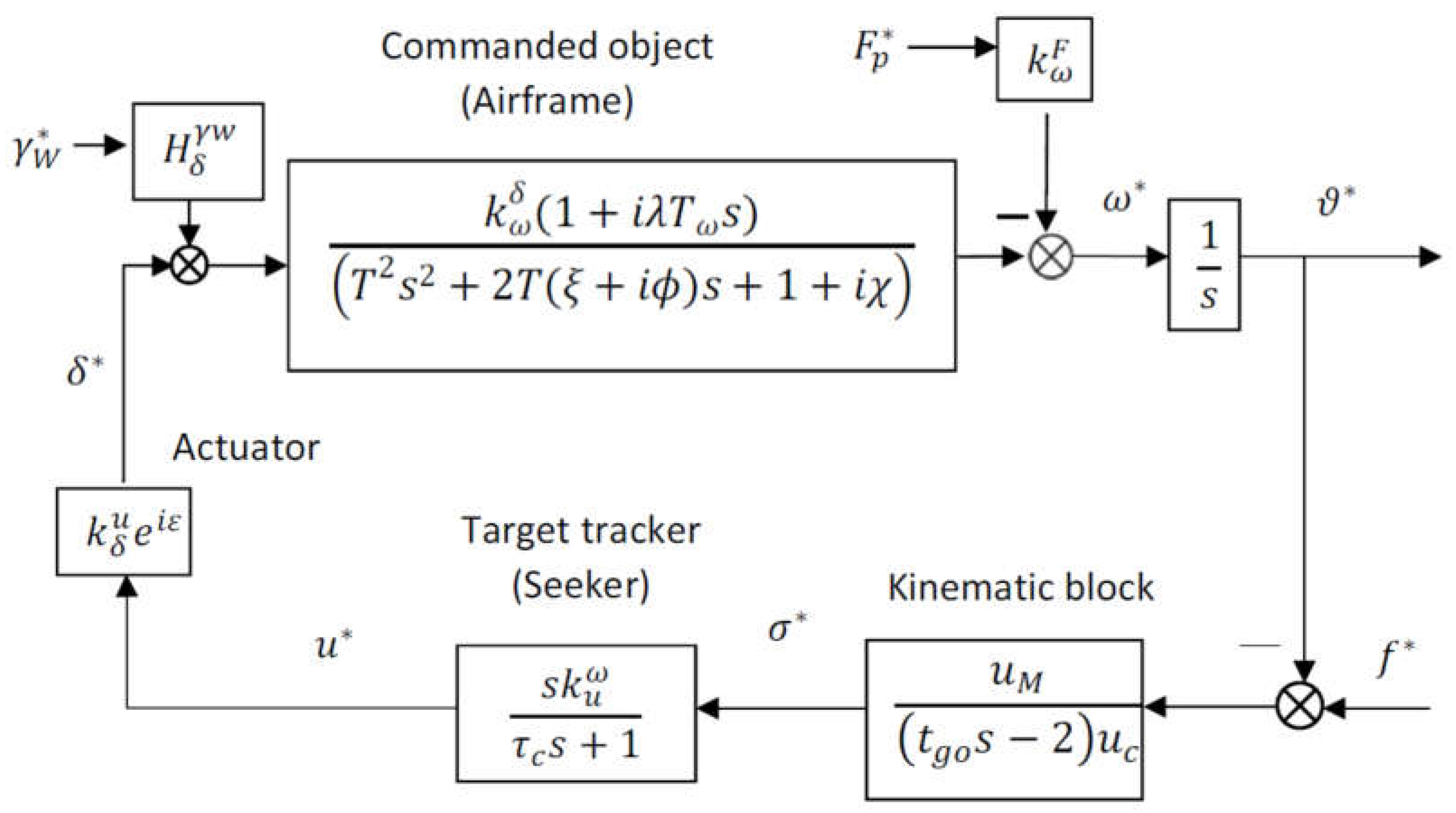
If the actuator (138) is also added to the transfer function of the kinematic block (112), the transfer function of the target tracker (117), and the commanded object (Figure 4), the structural scheme for the homing missile with a single channel and slow roll rotation can be obtained (Figure 10).

8. The Guided Flight Stability on the Linear Model

8.1. Determination of Stability Parameters

For system stability analysis, the transfer function of the open system is required:

H (s) = \frac{k (1 + i λ T_{ω} s) (c o s ε + i s i n ε)}{(t_{g o} s - 2) (τ_{c} s + 1) (T^{2} s^{2} + 2 T (ξ + i ϕ) s + 1 + i χ)};

(140)

, where we highlighted the modified navigation constant [29], which we will now call the navigation constant:

k = k_{u}^{ω} k_{δ}^{u} k_{ω}^{δ} \frac{u_{M}}{u_{c}} = K \frac{u_{M}}{u_{c}}

(141)

In this case, the transfer function of the closed system becomes:

H_{0} (s) = \frac{k Ω^{2} (1 + i λ T_{ω} s) (c o s ε + i s i n ε) / (t_{g o} τ_{c})}{(s - 2 / t_{g o}) (s + 1 / τ_{c}) [s^{2} + 2 Ω (ξ + i ϕ) s + Ω^{2} (1 + i χ)] + k Ω^{2} (1 + i λ T_{ω} s) (c o s ε + i s i n ε) / (t_{g o} τ_{c})} .

(142)

To check the stability, we develop the characteristic polynomial from the denominator of the transfer function:

P (s) = s^{4} + [2 Ω (ξ - T / t_{g o}) + 1 / τ_{c} + i 2 Ω ϕ] s^{3} + [Ω^{2} (1 - 4 ξ T / t_{g o}) + 2 Ω (ξ / τ_{c} - T / (t_{g o} τ_{c})) + i (χ Ω^{2} - 4 Ω ϕ / t_{g o} + 2 Ω ϕ / τ_{c})] s^{2} + [Ω^{2} (1 / τ_{c} - 4 ξ T / (t_{g o} τ_{c}) - k λ T_{ω} s i n ε / (t_{g o} τ_{c})) - 2 Ω^{2} / t_{g o} + i (Ω^{2} (χ / τ_{c} + k λ T_{ω} c o s ε / (t_{g o} τ_{c}) - 4 ϕ T / (t_{g o} τ_{c})) - 2 χ Ω^{2} / t_{g o})] s + Ω^{2} (k c o s ε - 2) / (t_{g o} τ_{c}) + i Ω^{2} (k s i n ε - 2 χ) / (t_{g o} τ_{c})

(143)

Next, we will proceed similarly with [7], based on the work [20], which indicates a method for establishing the conditions that the roots of the characteristic polynomial have the real side negative, which ensures the stability of the system. The method is similar to the Routh-Hurwitz stability criterion and consists of checking the sign with a number of parameters equal to the degree of the characteristic polynomial.

Thus, the characteristic polynomial is put in the form:

P (s) = s^{4} + (p_{1} + i q_{1}) s^{3} + (p_{2} + i q_{2}) s^{2} + (p_{3} + i q_{3}) s + (p_{4} + i q_{4})

(144)

where:

p_{1} = 2 (ξ - T / t_{g o}) Ω + 1 / τ_{c}; q_{1} = 2 ϕ Ω; p_{2} = (1 - 4 ξ T / t_{g o}) Ω^{2} + 2 Ω ξ / τ_{c} - 2 / (t_{g o} τ_{c}); q_{2} = (χ - 4 T ϕ / t_{g o} + 2 T ϕ / τ_{c}) Ω^{2}; p_{3} = [1 / τ_{c} - 4 ξ T / (t_{g o} τ_{c}) - k λ T_{ω} s i n ε / (t_{g o} τ_{c}) - 2 / t_{g o}] Ω^{2}; q_{3} = [(χ / τ_{c} + k λ T_{ω} c o s ε / (t_{g o} τ_{c}) - 4 ϕ T / (t_{g o} τ_{c})) - 2 χ / t_{g o}] Ω^{2};

(145)

p_{4} = Ω^{2} (k c o s ε - 2) / (t_{g o} τ_{c}); q_{4} = Ω^{2} (k s i n ε - 2 χ) / (t_{g o} τ_{c}) .

(145)

Stability conditions for systems with characteristic polynomials with complex coefficients are formulated by two theorems in the paper [20]. The first theorem shows that the n^th order polynomial with complex coefficients to have all the roots with the negative real parts, it is necessary and sufficient that the parameters

a_{1}, a_{2}; \dots; a_{n}

, be positive and that

b_{1}, \dots b_{n}

be pure complex numbers or null. The second theorem shows that the n^th order polynomial with complex coefficients has as many roots with the positive real part as many as the number of negative

a_{1}; \dots; a_{n}

, parameters.

In the same work, an algorithm for obtaining parameters

a_{1}, \dots; a_{n}

b_{1}, \dots b_{n}

is indicated, the algorithm presented in Annex D of the paper. These conditions will be referred to next as Frank-Wall (F-W) stability conditions after the authors' names.

Given the 4th order polynomial from (144), by denoting:

D = ({p_{1}^{2} p}_{2} - p_{1} p_{3} + p_{1} q_{1} q_{2} - q_{2}^{2}) ({p_{1} p}_{2} p_{3} - p_{3}^{2} + {p_{1} q}_{3} q_{2} + p_{1} q_{1} q_{4} {- p}_{4} p_{1}^{2} - 2 q_{4} q_{2}) - {({p_{1}^{2} q}_{3} - p_{1} q_{1} p_{3} + p_{3} q_{2} - p_{1} q_{4})}^{2} E = q_{4} - \frac{a_{2}^{2}}{p_{1}^{6}} ({p_{1}^{2} p}_{2} q_{2} + p_{1} q_{1} q_{2}^{2} - q_{2}^{3} + p_{1}^{2} q_{1} p_{3} - {p_{1}^{3} q}_{3} - 2 p_{1} p_{3} q_{2} + p_{1}^{2} q_{4}) ({p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4}),

(146)

F-W stability parameters are:

a_{1} = \frac{1}{p_{1}}; a_{2} = \frac{p_{1}^{3}}{{p_{1}^{2} p}_{2} - p_{1} p_{3} + p_{1} q_{1} q_{2} - q_{2}^{2}}; a_{3} = \frac{p_{1}^{6}}{a_{2}^{3}} D^{- 1} a_{4} = \frac{p_{1}}{a_{3} a_{2}} {[\frac{{p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4}}{p_{1}^{2}} + \frac{({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2}) a_{3} a_{2}}{p_{1}^{3}} E - \frac{a_{3}^{2} a_{2}}{p_{1}} E^{2}]}^{- 1},

(147)

respectively:

b_{1} = i \frac{(p_{1} q_{1} - q_{2})}{p_{1}^{2}} b_{2} = i \frac{({p_{1}^{2} p}_{2} q_{2} - p_{1} p_{3} q_{2} + p_{1} q_{1} q_{2}^{2} - q_{2}^{3} - {p_{1}^{3} q}_{3} + p_{1}^{2} q_{4} + p_{1}^{2} q_{1} p_{3} - p_{1} p_{3} q_{2}) a_{2}}{({p_{1}^{2} p}_{2} - p_{1} p_{3} + p_{1} q_{1} q_{2} - q_{2}^{2}) p_{1}} b_{3} = i \frac{[({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2}) - a_{3} p_{1}^{2} E] p_{1}^{3}}{a_{2}^{2} D} b_{4} = i \frac{E p_{1}^{3}}{({p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4}) p_{1} + ({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2}) a_{3} a_{2} E - {a_{3}^{2} a_{2} p_{1}^{2} E}^{2}}

(148)

From previous relations,

b_{1}; \dots; b_{n}

are pure complex numbers in all cases, which, depending on the values

p_{1}, p_{2}, p_{3}, p_{4},

and

q_{1}, q_{2}, q_{3}, q_{4},

can be null. The only conditions to be verified or imposed are

a_{1} > 0, a 2 > 0, a 3 > 0, a n d a_{4} > 0

, which, based on relations (147), translates into the following four conditions:

p_{1} > 0; {p_{1}^{2} p}_{2} - p_{1} p_{3} + p_{1} q_{1} q_{2} - q_{2}^{2} > 0; D > 0; ({p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4}) p_{1} + ({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2}) a_{3} a_{2} E - p_{1}^{2} a_{3}^{2} a_{2} E^{2} > 0

(149)

8.2. Non-Rotational Case Analysis

For the case of a non-rotational rocket, in which the phase shift is considered null (

ε = 0

), conditions (149) become:

p_{1} > 0; p_{1} p_{2} - p_{3} > 0; {p_{1} p}_{2} p_{3} - p_{3}^{2} {{- p}_{4} p}_{1}^{2} > 0;

(150)

p_{4} > 0;

(150)

relations that coincide with Routh–Hurwitz (R-H) conditions for polynomials with real coefficients.

Next, we are looking for analytical solutions for stability conditions in the case of non-rolling missiles, and numerical solutions in the case of rolling missiles.

The first condition (150) provides the lower bound for the remaining interception time (

t_{g o})

, i.e., the minimum distance to which the missile can approach the target:

2 (ξ - T / t_{g o}) Ω + 1 / τ_{c} > 0; t_{g o} > T / (ξ + \frac{T}{{2 τ}_{c}})

(151)

The second condition, since it does not contain the navigation constant, may introduce an additional restriction on the remaining interception duration (

t_{g o})

p_{1} p_{2} - p_{3} > 0 \Rightarrow (t_{g o} - 2 τ_{c} + 2 Ω ξ τ_{c} t_{g o}) [Ω^{2} t_{g o} τ_{c} + 2 Ω ξ (t_{g o} - 2 τ_{c}) - 2] - Ω [(t_{g o} - 2 τ_{c}) Ω - 4 ξ] (t_{g o} τ_{c}) > 0

(152)

To impose the condition, we construct a quadratic polynomial in

t_{g o}

and look for its roots:

Ω ξ {(Ω^{2} τ_{c}^{2} + 2 Ω ξ τ_{c} + 1) t}_{g o}^{2} - {(2 Ω ξ τ_{c} + 1)}^{2} t_{g o} + 2 τ_{c} (2 Ω ξ τ_{c} + 1) = 0

(153)

. we make the notations:

e_{1} = 2 τ_{c} Ω ξ + 1; e_{2} = 2 Ω ξ τ_{c} (τ_{c}^{2} Ω^{2} + e 1)

(154)

, from which the roots derive:

t_{g o 1,2} = τ_{c} \frac{e_{1}^{2} \pm \sqrt{∆}}{e_{2}}

(155)

with the discriminant:

∆ = e_{1}^{4} - 4 e_{1} e_{2}

(156)

If we develop the first root, we get an approximate solution:

t_{g o 1} = τ_{c} \frac{e_{1}^{2} - \sqrt{∆}}{e_{2}} = τ_{c} \frac{e_{1}^{2}}{e_{2}} (1 - \sqrt{1 - \frac{4 e_{1} e_{2}}{e_{1}^{4}}}) ≅ τ_{c} \frac{e_{1}^{2}}{e_{2}} (1 - 1 + \frac{2 e_{2}}{e_{1}^{3}}) = 2 \frac{τ_{c}}{e_{1}} = \frac{1}{Ω ξ + 1 / {2 τ}_{c}}

(157)

relation that represents the first condition R-H (151).

It follows that the value of interest is given by the second solution of the Equation (153) :

t_{g o 2} = τ_{c} \frac{e_{1}^{2} + \sqrt{∆}}{e_{2}}

(158)

relation, which can be interpreted as a decrease in stable guided time until

t_{g o 2}

, which means an increase in the minimum distance the missile can approach the target.

On the other hand, given the form of the polynomial (153), with the second derivative positive (the coefficient of the quadratic term is positive), if

∆ < 0

, then the roots are complex, so the second condition is fulfilled all the time. The sign of discriminant

∆

depends on the value of the time constant

τ_{c}

and, if we increase its value,

∆

becomes negative.

The third R-H condition limits the upper navigation constant

k

{p_{1} p}_{2} p_{3} - p_{3}^{2} {{- p}_{4} p}_{1}^{2} > 0 \Rightarrow p_{4} < \frac{p_{2} p_{3}}{p_{1}} - \frac{p_{3}^{2}}{p_{1}^{2}} \Rightarrow k < 2 + \frac{(t_{g o} τ_{c} - 4 T ξ τ_{c} + 2 T ξ t_{g o} - 2 T^{2}) [(t_{g o} - 2 τ_{c}) Ω^{2} - 4 Ω ξ]}{(2 Ω ξ t_{g o} τ_{c} + t_{g o} - 2 τ_{c})} - \frac{{(t_{g o} τ_{c}) [(t_{g o} - 2 τ_{c}) Ω - 4 ξ]}^{2}}{{(2 Ω ξ t_{g o} τ_{c} + t_{g o} - 2 τ_{c})}^{2}}

(159)

Finally, the fourth R-H condition sets the navigation constant

k

lower bound:

p_{4} = Ω^{2} (k - 2) / (t_{g o} τ_{c}) > 0

(160)

\Rightarrow k > 2

(160)

The first condition, the limitation of the duration of interception, since it does not depend on complex terms, also applies to the rolling missile. For the other conditions, in the case of the rolling missile, we will make a numerical analysis based on a calculation model that we present below.

9. Calculus Model

In order to obtain numerical results, we will further specify the data of the calculus model.

9.1. Aerodynamic Characteristics

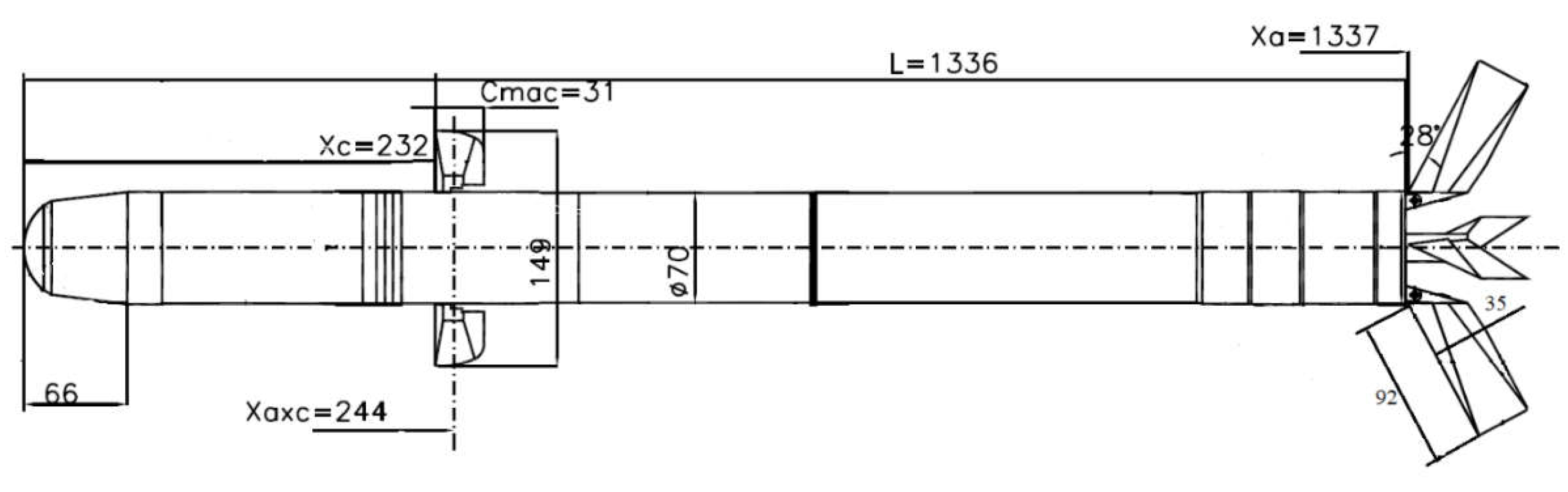
The aerodynamic characteristics were determined using the configuration from Figure 11, which is typical for the class of missiles analyzed.

In current flight dynamics applications or in the analysis and synthesis of guided systems, it is necessary to know the values of aerodynamic coefficients for certain given situations characterized by Mach numbers, incidences, rotational velocities, canard deflections, or flight altitude.

For this purpose, functions are sought to approximate the aerodynamic coefficients in relation to the system's state variables, functions that, for simplicity, can be chosen by the polynomial form [30,31]. The state variables considered will be small (incidences, angular deflections, rotational velocity), and to highlight the advantages of configuration symmetry, thus, polynomial development will be done around zero. Obviously, the coefficients of polynomial development terms remain dependent on the Mach number and possibly the Reynolds number or height.

In the following, considering the specifics of the configuration and the wide range of flight regimes, starting from the aerodynamic coefficients indicated in [30] we introduce additional terms in the development. These terms shall contain rotational and non-stationary motion and combinations with incidences and angular canard deflection.

Using the reference time:

t^{*} = l / V

, rotational velocities and non-stationary translational variables can be considered dimensionless, the notations being according to the standard [22]:

\hat{p} = p t^{*}; \hat{q} = q t^{*}; \hat{r} = r t^{*}; \hat{α} = \dot{α} t^{*}; \hat{β} = \dot{β} t^{*} .

(161)

In addition to these, this paper also uses the dimensionless height defined by the relation:

{\hat{z}}_{0} = z_{0} / l .

(162)

Thus, the development of aerodynamic coefficients in the body frame for the slow-rolling single-channel airframe from Figure 11 is given by:

C_{x} = a_{1} + a_{21} α^{2} + a_{22} β^{2} + a_{6} δ_{m}^{2} + a_{13} ({\hat{z}}_{0} - {\hat{z}}_{0 c}) C_{y} = b_{12} β + b_{22} β^{3} - b_{42} \hat{r} - b_{92} \hat{β} + b_{13} \hat{p} α + b_{14} \hat{p} \hat{q} C_{z} = b_{11} α + b_{21} α^{3} + b_{41} \hat{q} + b_{5} δ_{m} + b_{6} {(α^{2} + β^{2}) δ}_{m} {+ b}_{91} \hat{α} + b_{13} \hat{p} β + b_{14} \hat{p} \hat{r} C_{l} = c_{1} + c_{3} \hat{p} C_{m} = d_{11} α + d_{21} α^{3} + d_{41} \hat{q} + d_{5} δ_{m} + d_{6} {(α^{2} + β^{2}) δ}_{m} {+ d}_{91} \hat{α} + d_{13} \hat{p} β + d_{14} \hat{p} \hat{r}

(163)

C_{n} = d_{12} β + d_{22} β^{3} + d_{42} \hat{r} - d_{92} \hat{β} - d_{13} \hat{p} α - d_{14} \hat{p} \hat{q}

(163)

The main terms of development of aerodynamic coefficients are presented graphically against the Mach number in Appendix A.

9.2. Mechanical and Reference Characteristics

The mechanical characteristics of the model are indicated in Table 1

For the considered configuration, the reference length is

l = 1.336 m, the

reference surface is

S = 0.003848 m^{2}

, and the maximum angular canard deflection is

δ_{m a x} = 20 °

9.3. Thrust Characteristic

The thrust characteristic of the model is shown in Figure 12.

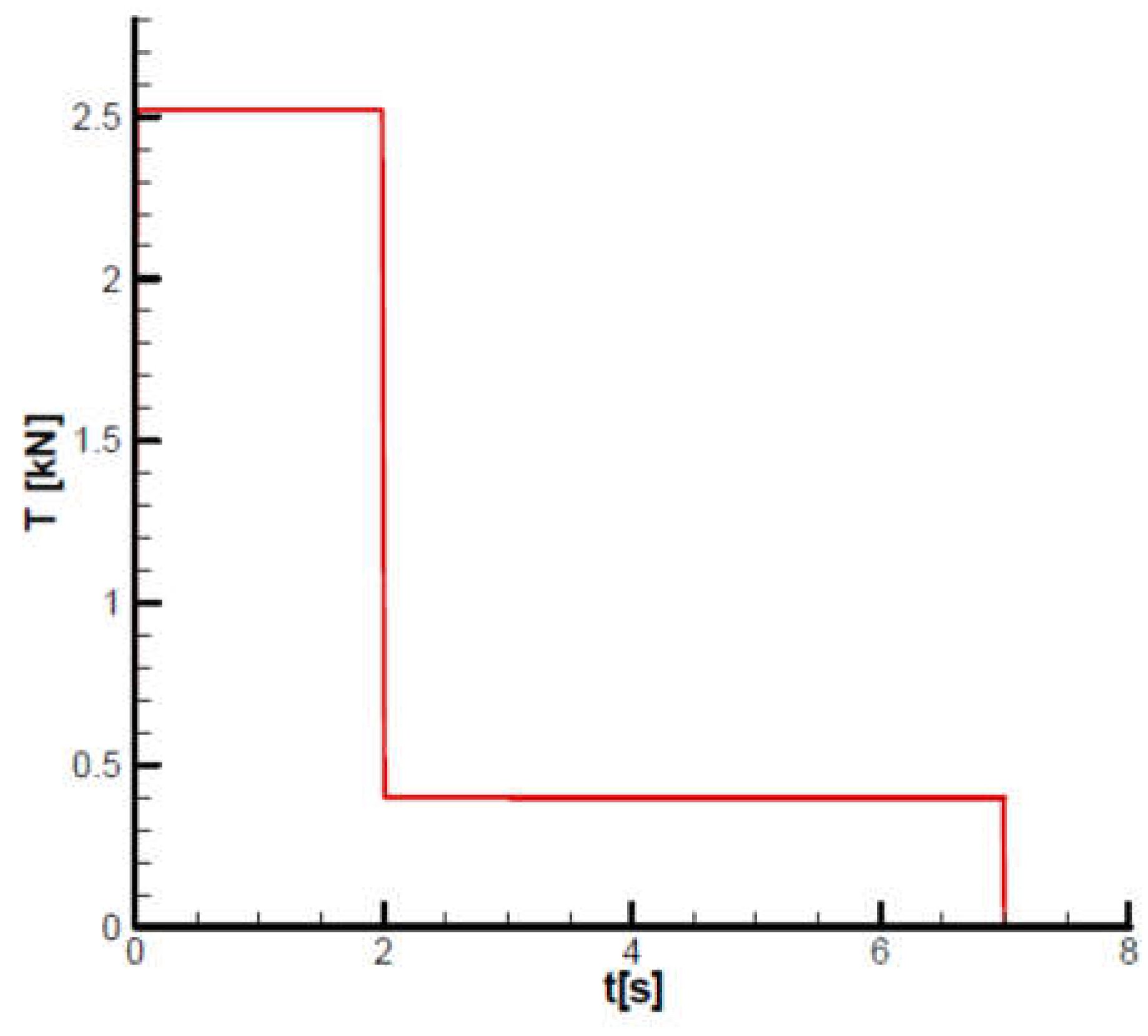
Given the thrust diagram and the table of mechanical characteristics, the missile will have two flight phases: a first phase of acceleration (boosting) and a second phase of marching flight, with approximately constant velocity, as shown in the velocity diagram Figure 31.

9.4. Time Constants and Controller Gains

As basic data for the linear model, the following parameters were considered:

Constant navigation

k = 3

indicated as the optimal value for the PN method [32]

The time constant for the target tracker

τ_{c} = 0.05 [s]

Time to reach the target starting from the second phase of flight

t_{g o} = 5 [s]

Rolling rotational velocity close to that indicated in Figure 32

p ≅ ω_{x} = 140 [\frac{r a d}{s}] ≅ 22 [\frac{r o t}{s}]

Calculation altitude

H = 1.5 [k m]

Phase shift

ε = 20 °

10. Stability Analysis of the Single Channel Homing Slow-Rolling Missile

10.1. Organization of Results

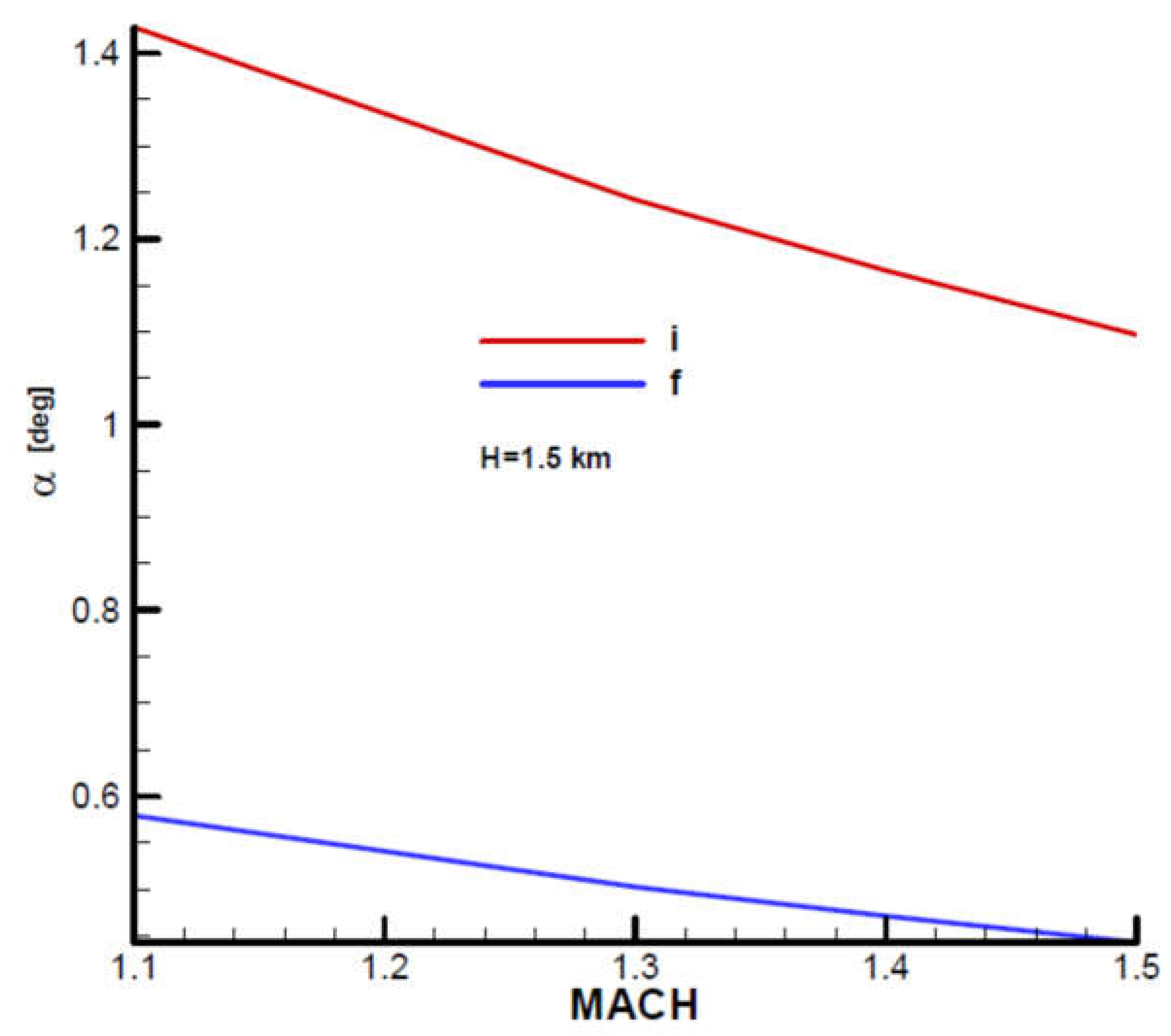
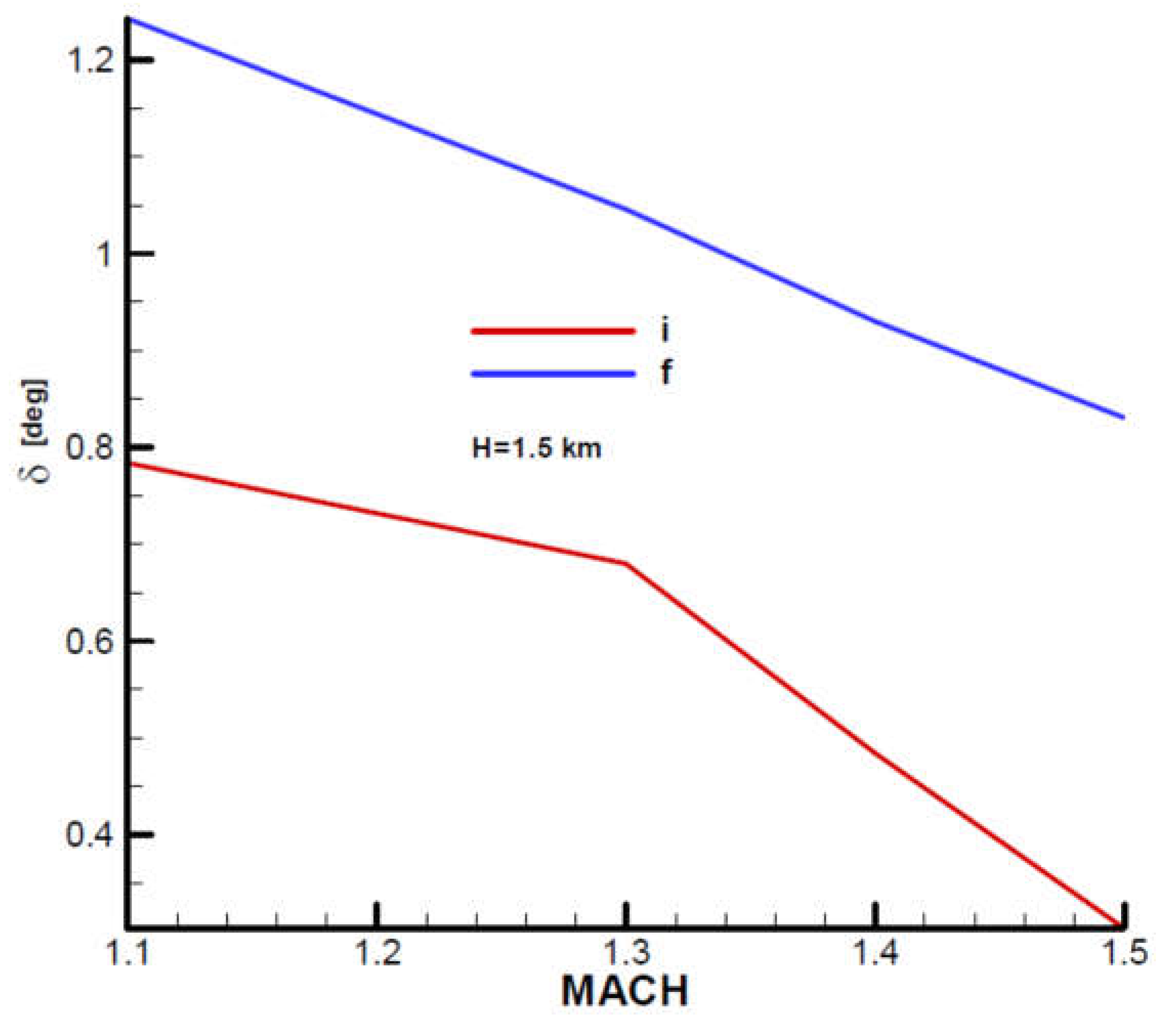
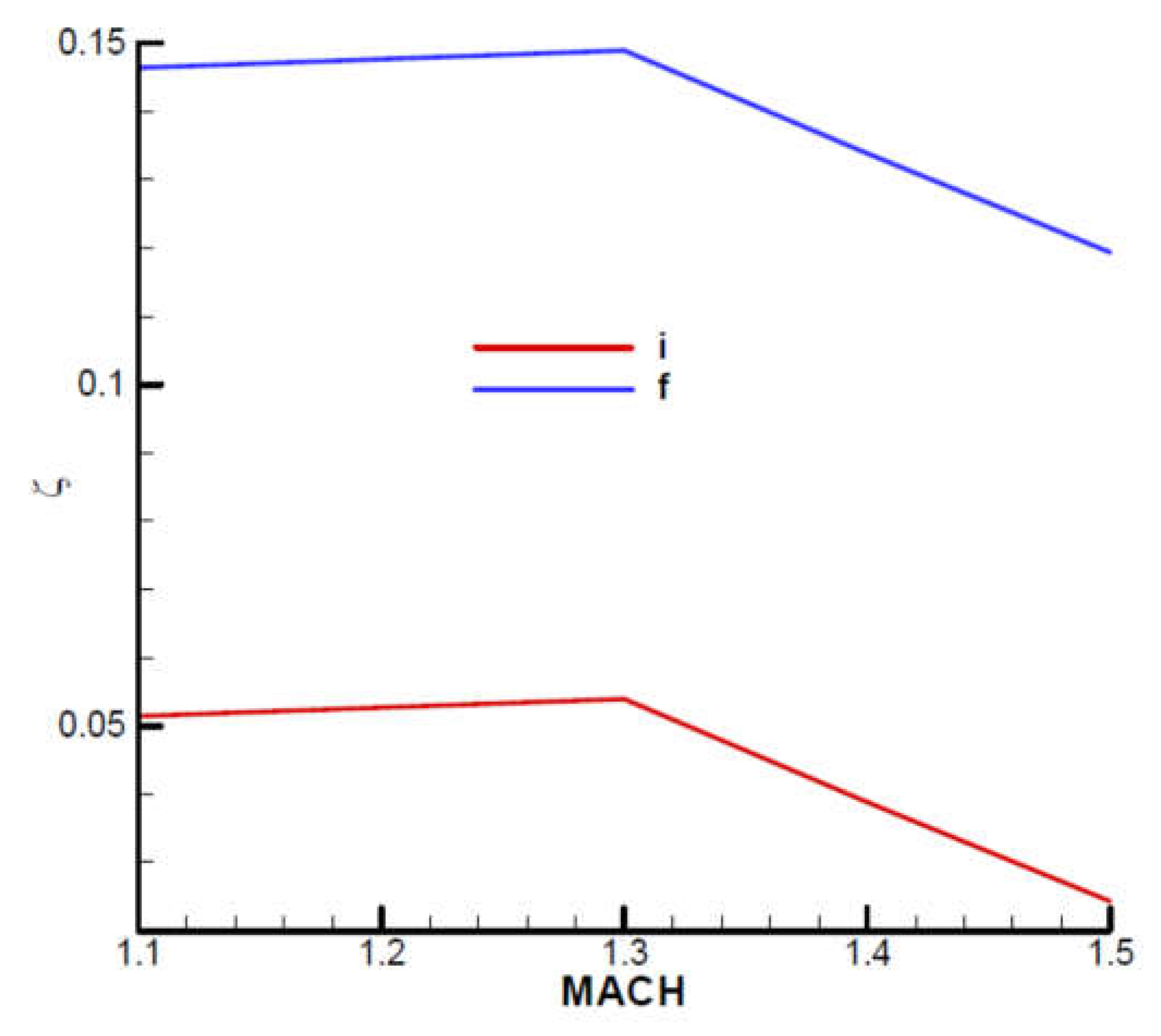
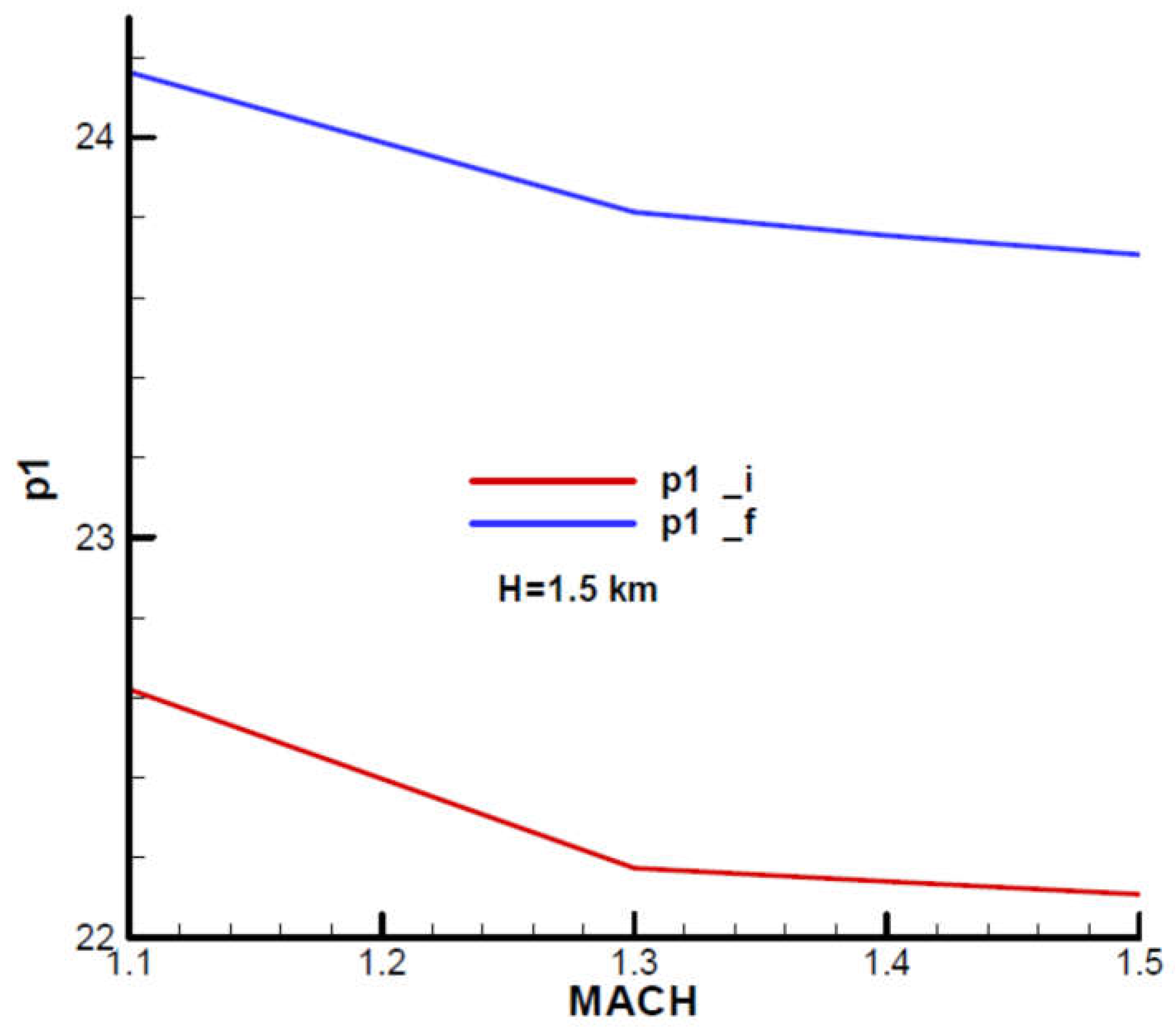
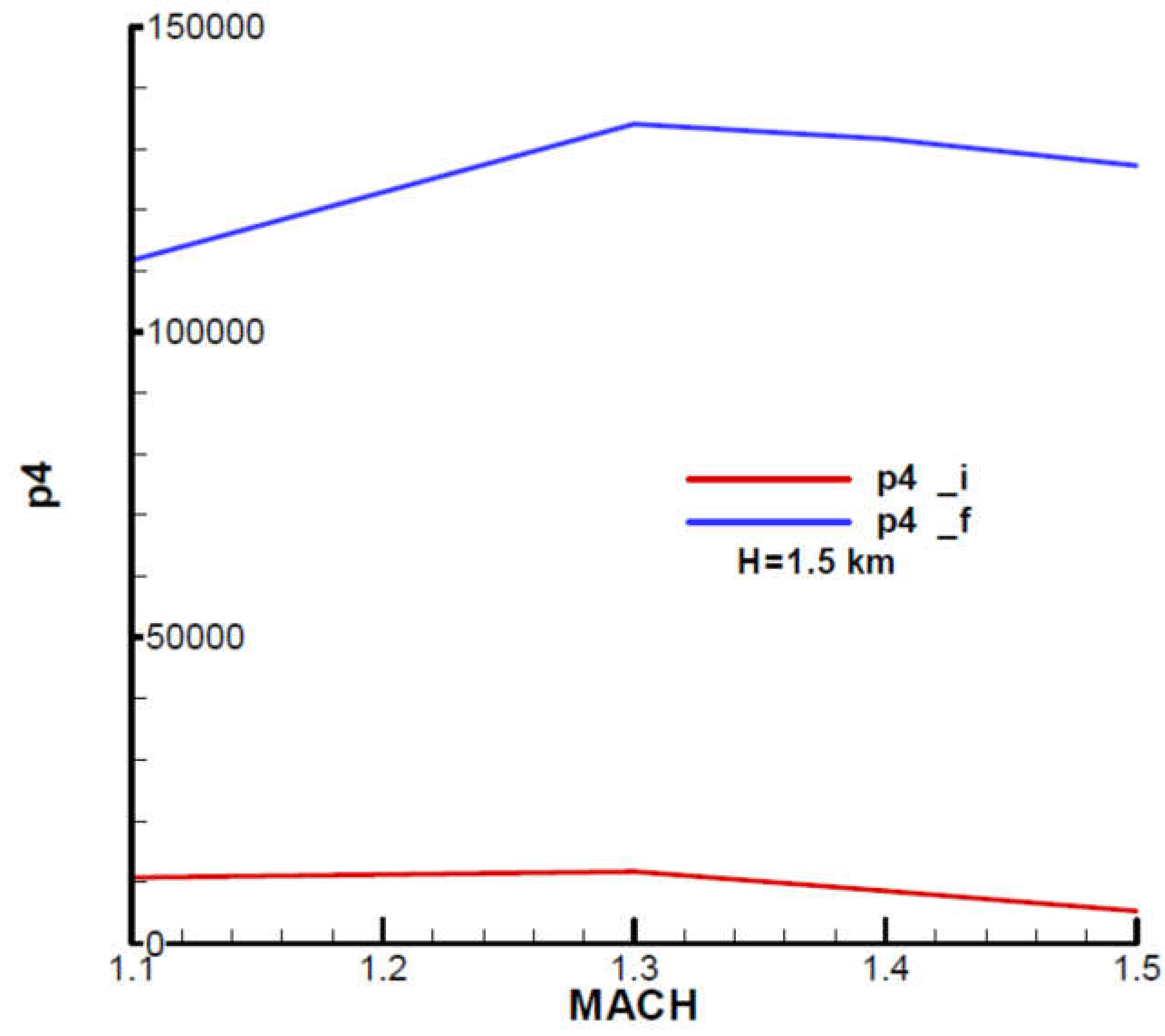
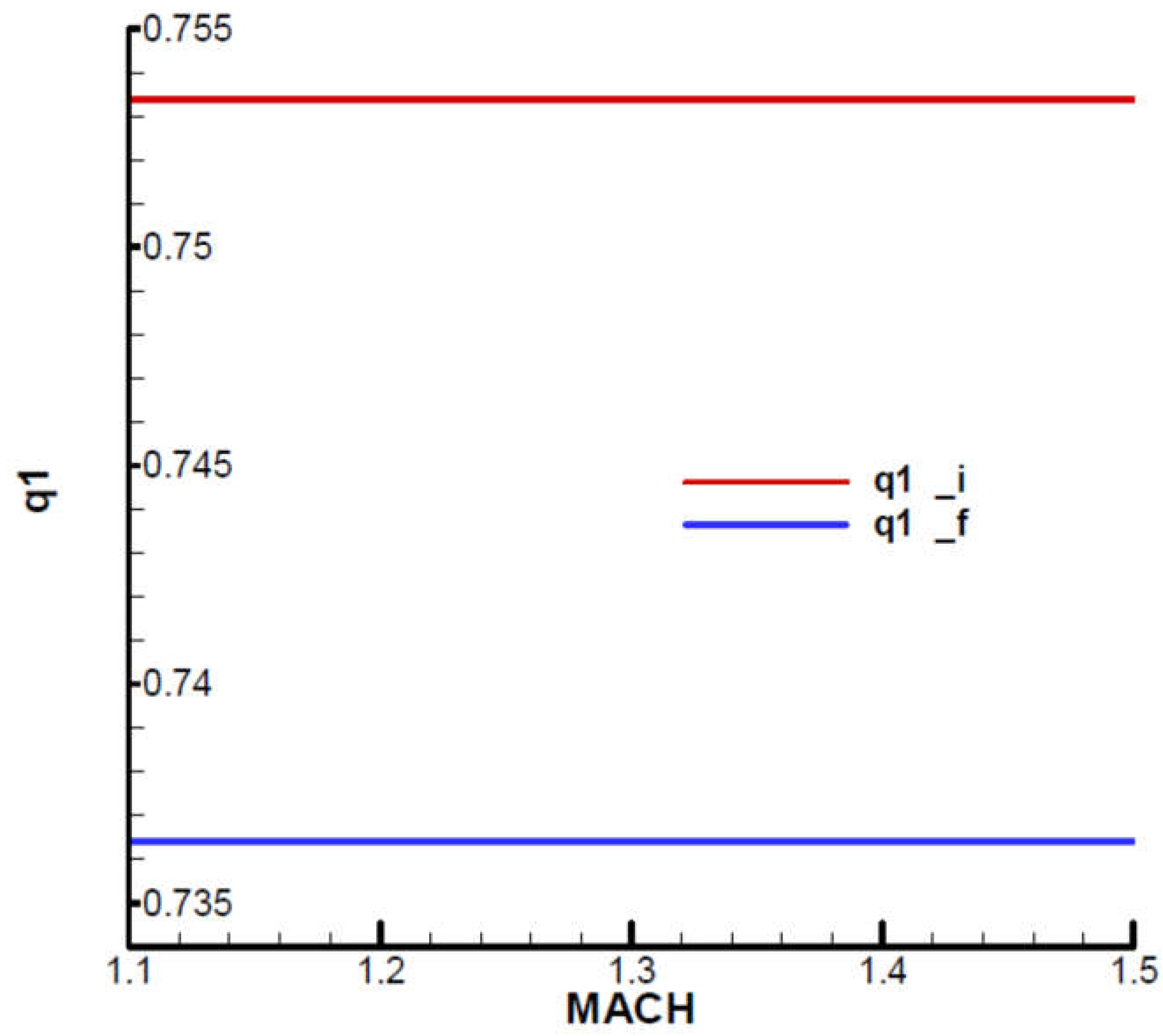
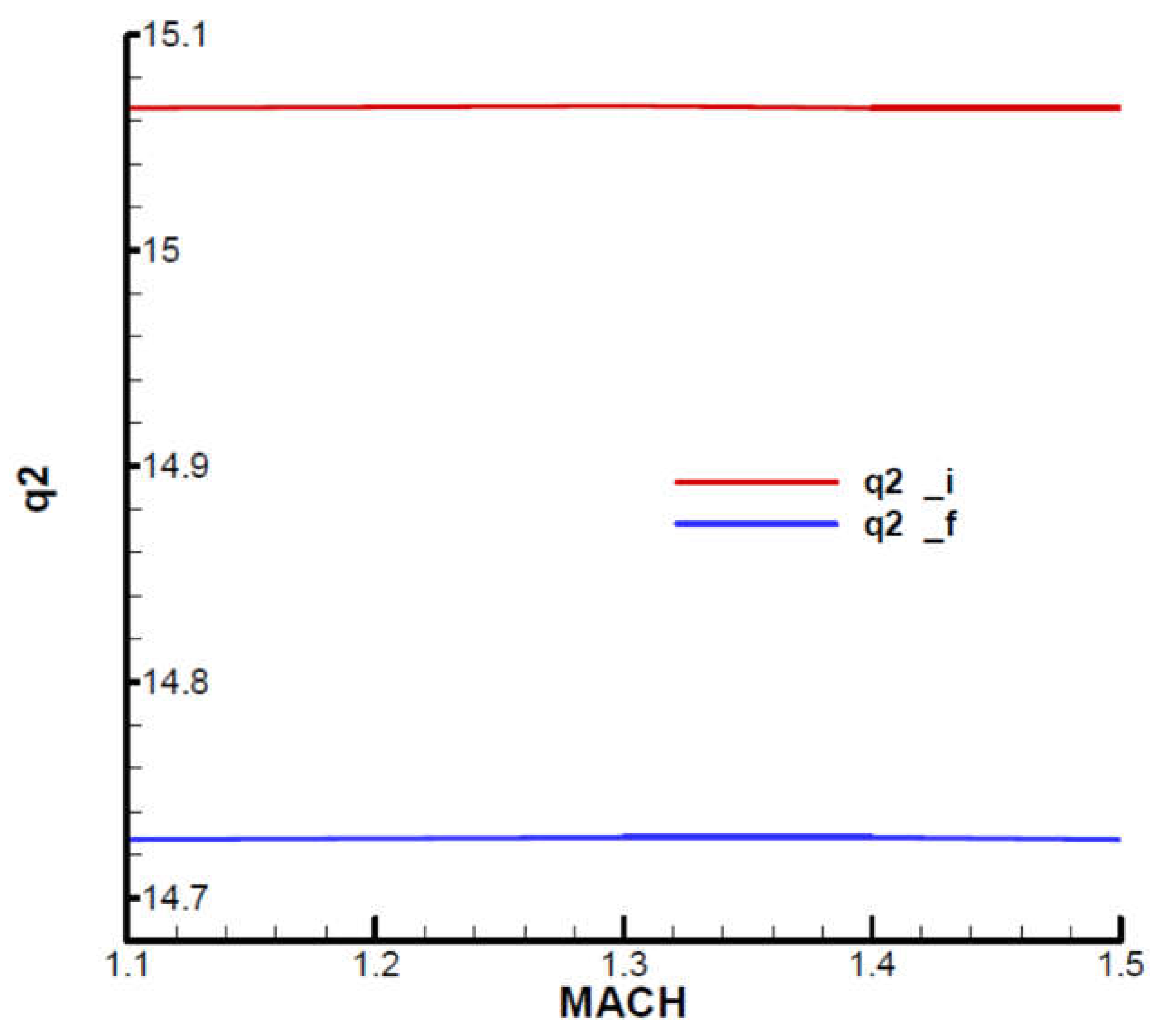
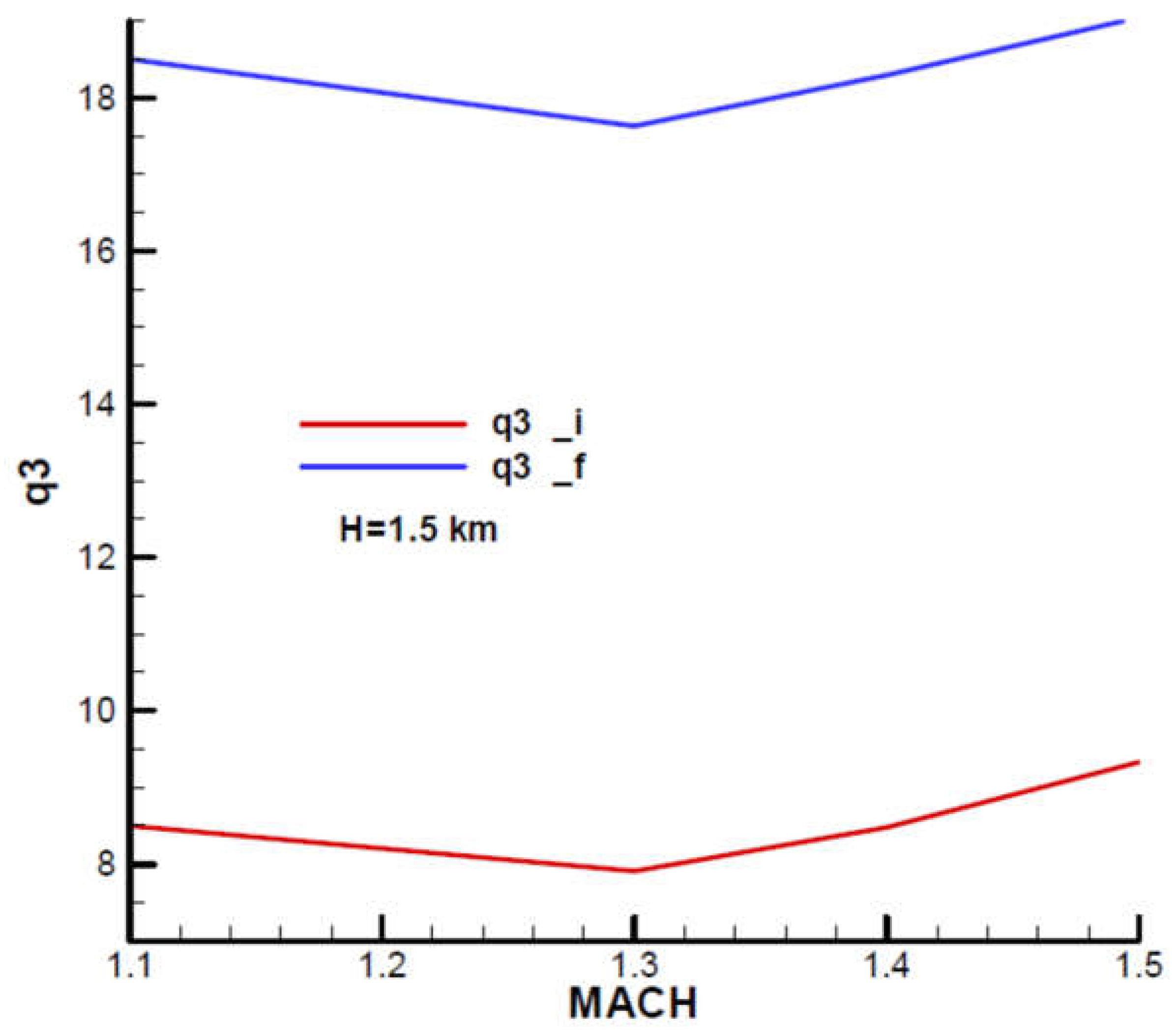
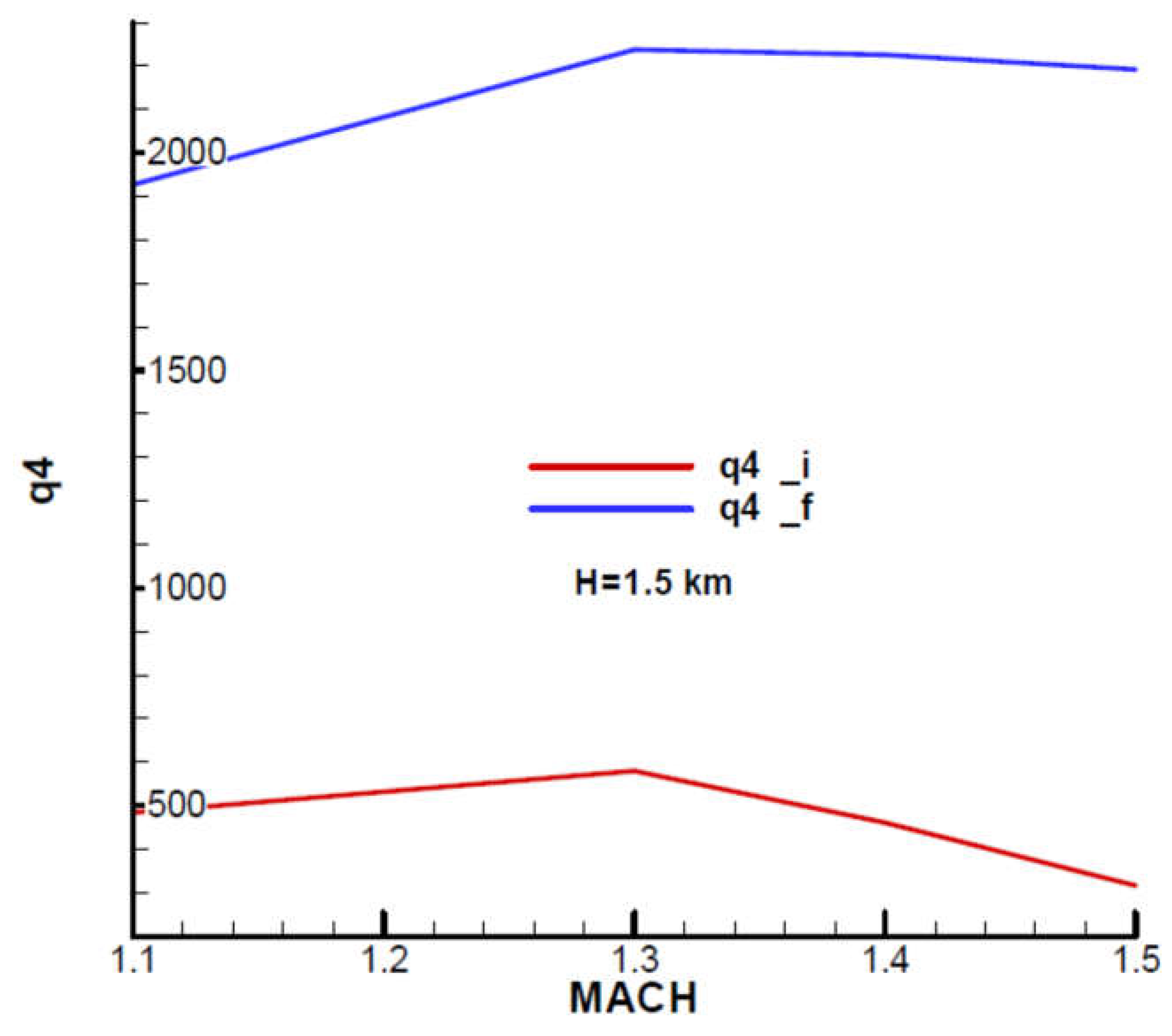
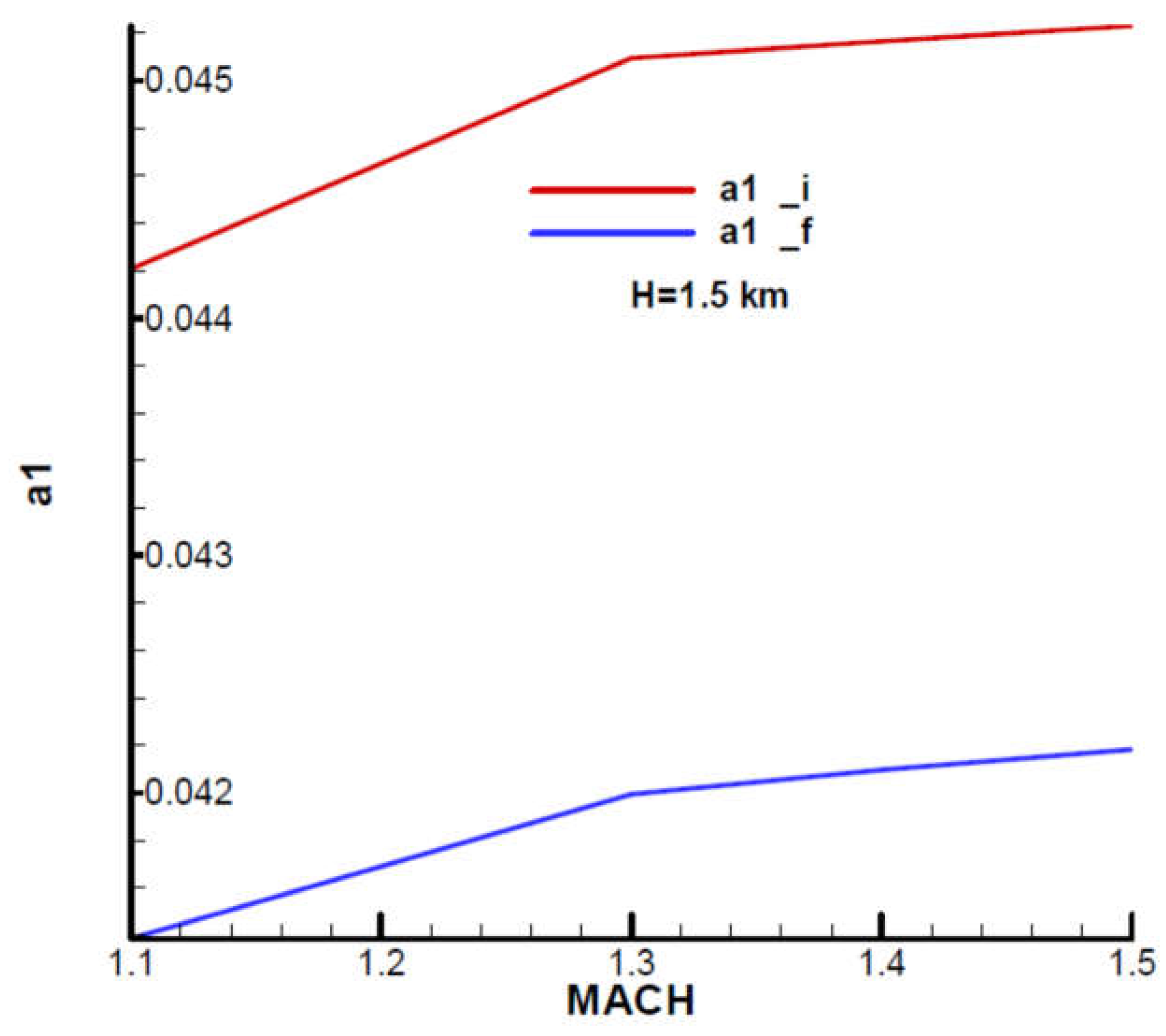
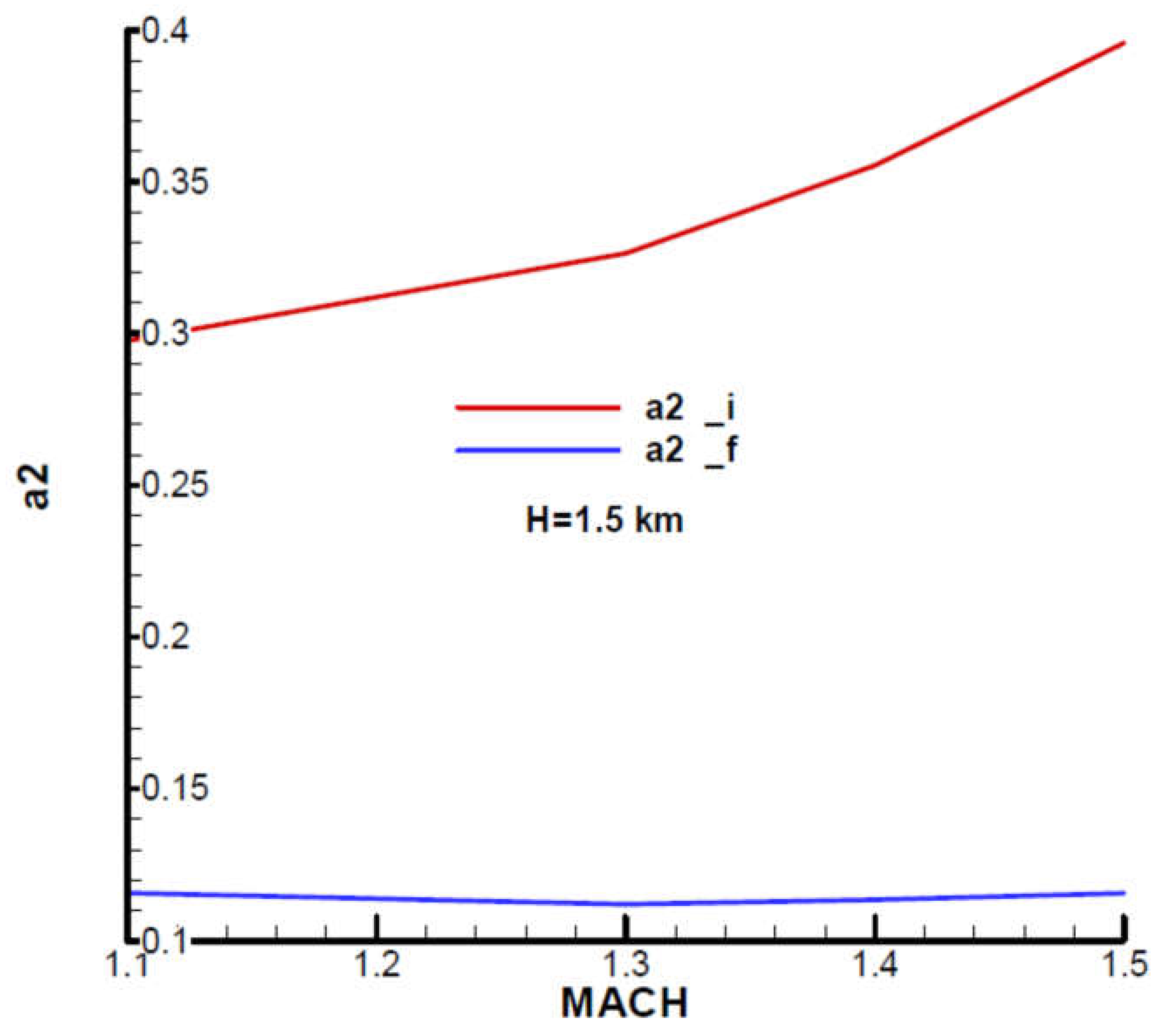
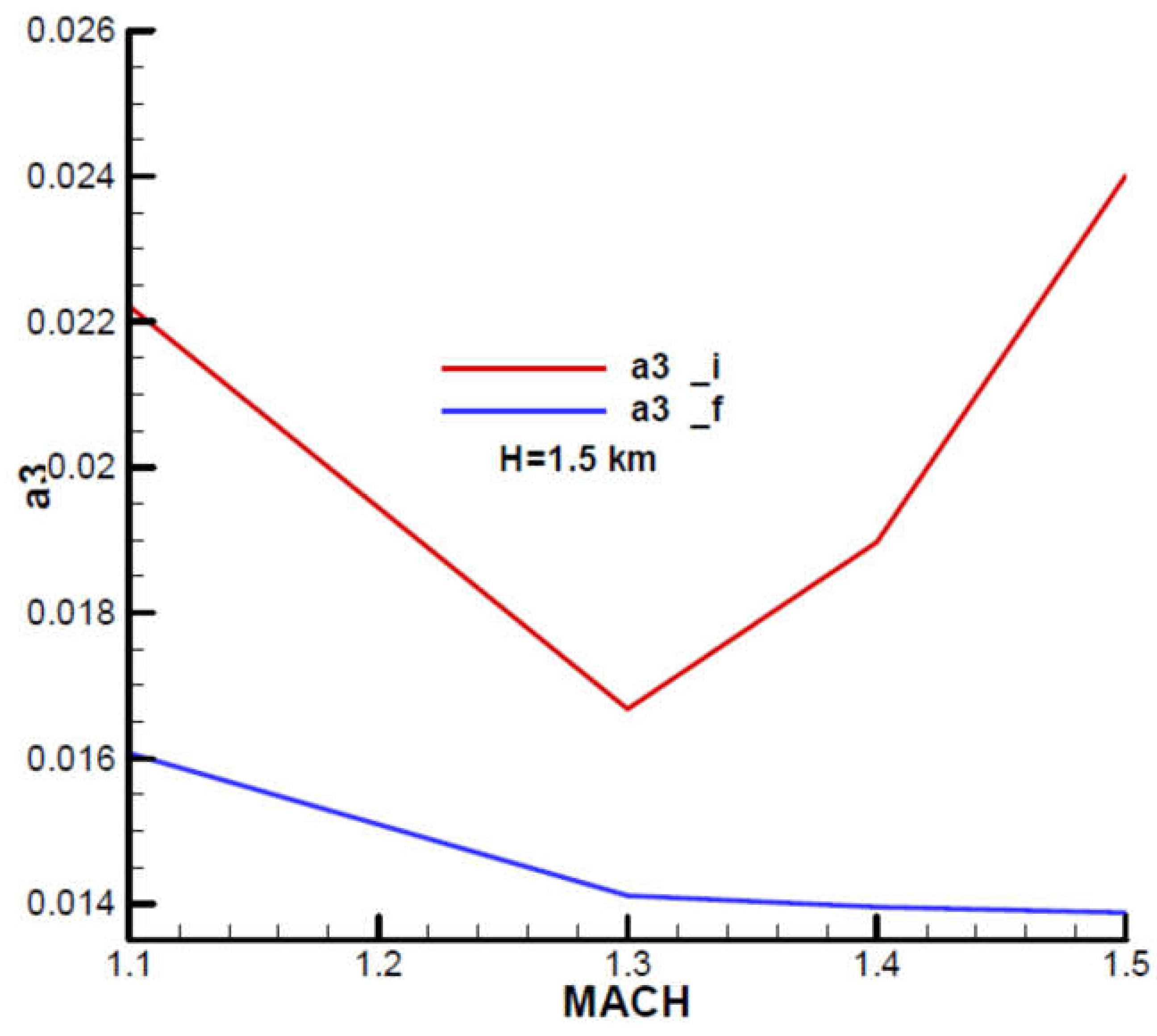
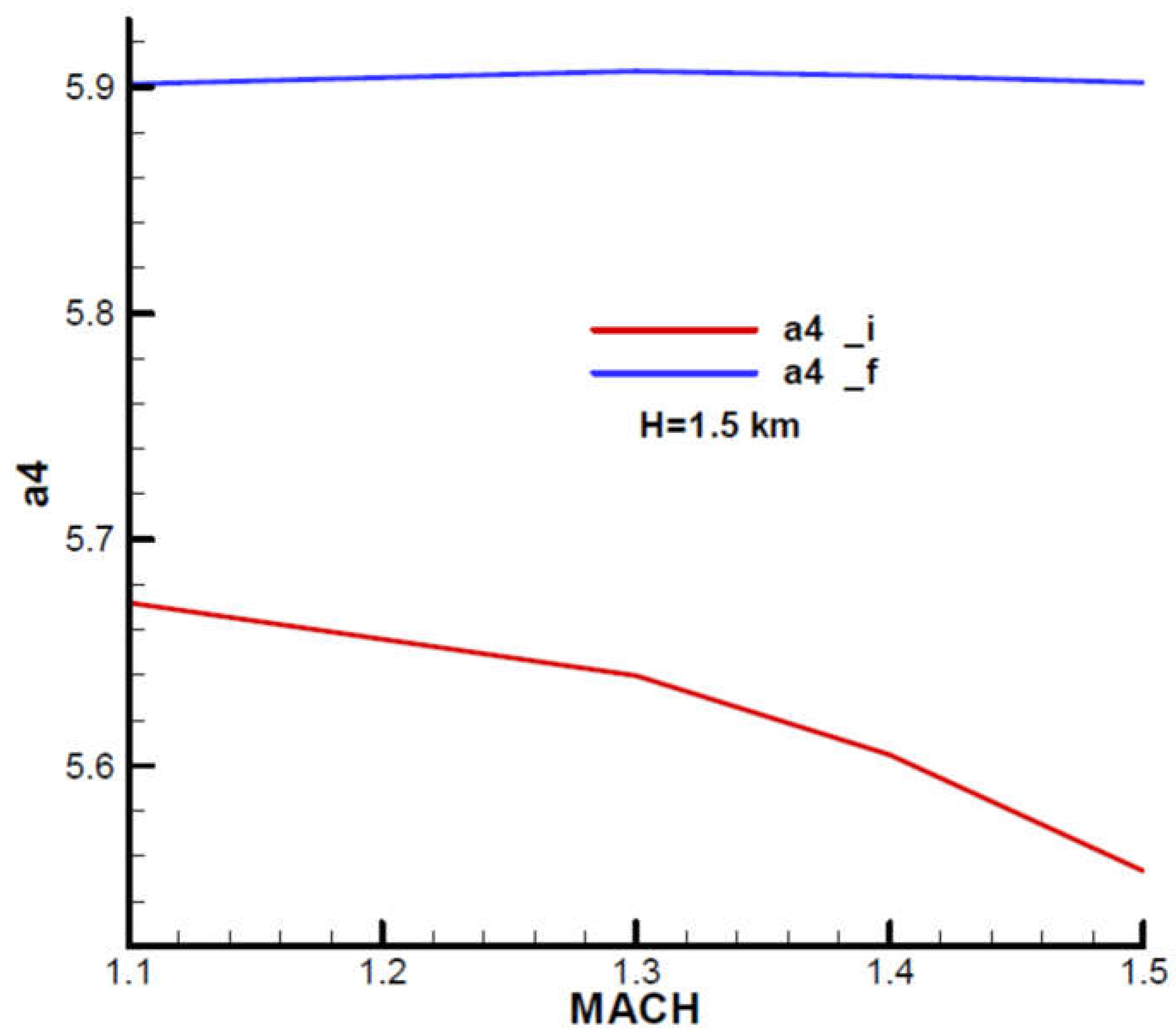
Appendix B presents the incidence and equilibrium deflection angle of the canard and the main flight quality parameters for the initial and final moment of the second phase of flight (marching mode) according to the mechanical data from Table 1. Given the velocity diagram (Figure 31), the field of analysis was chosen

M a c h = [1.1, \dots, 1.5]

, and the height

H = 1.5 k m,

corresponding to the field of altitude to this phase of flight.

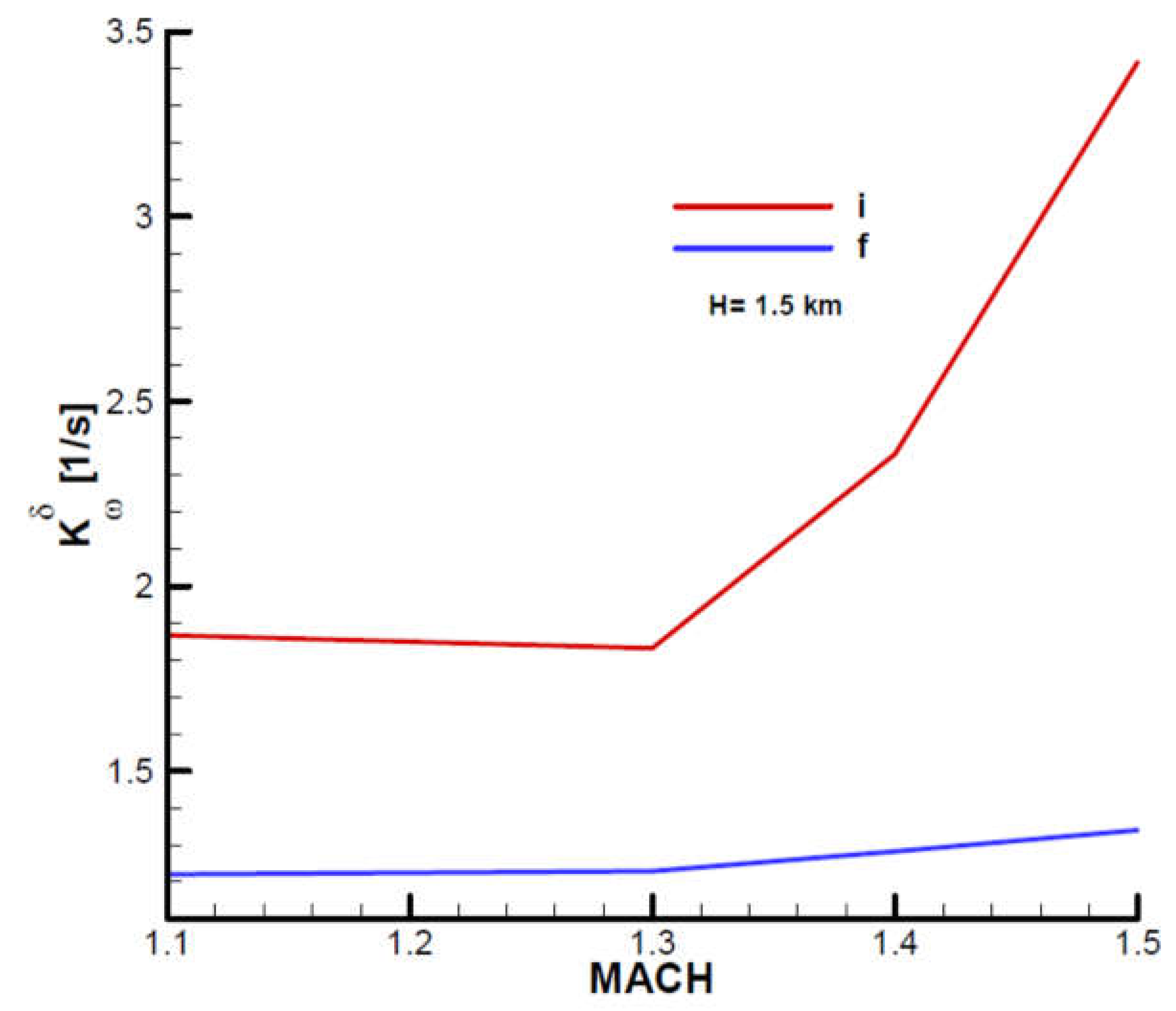
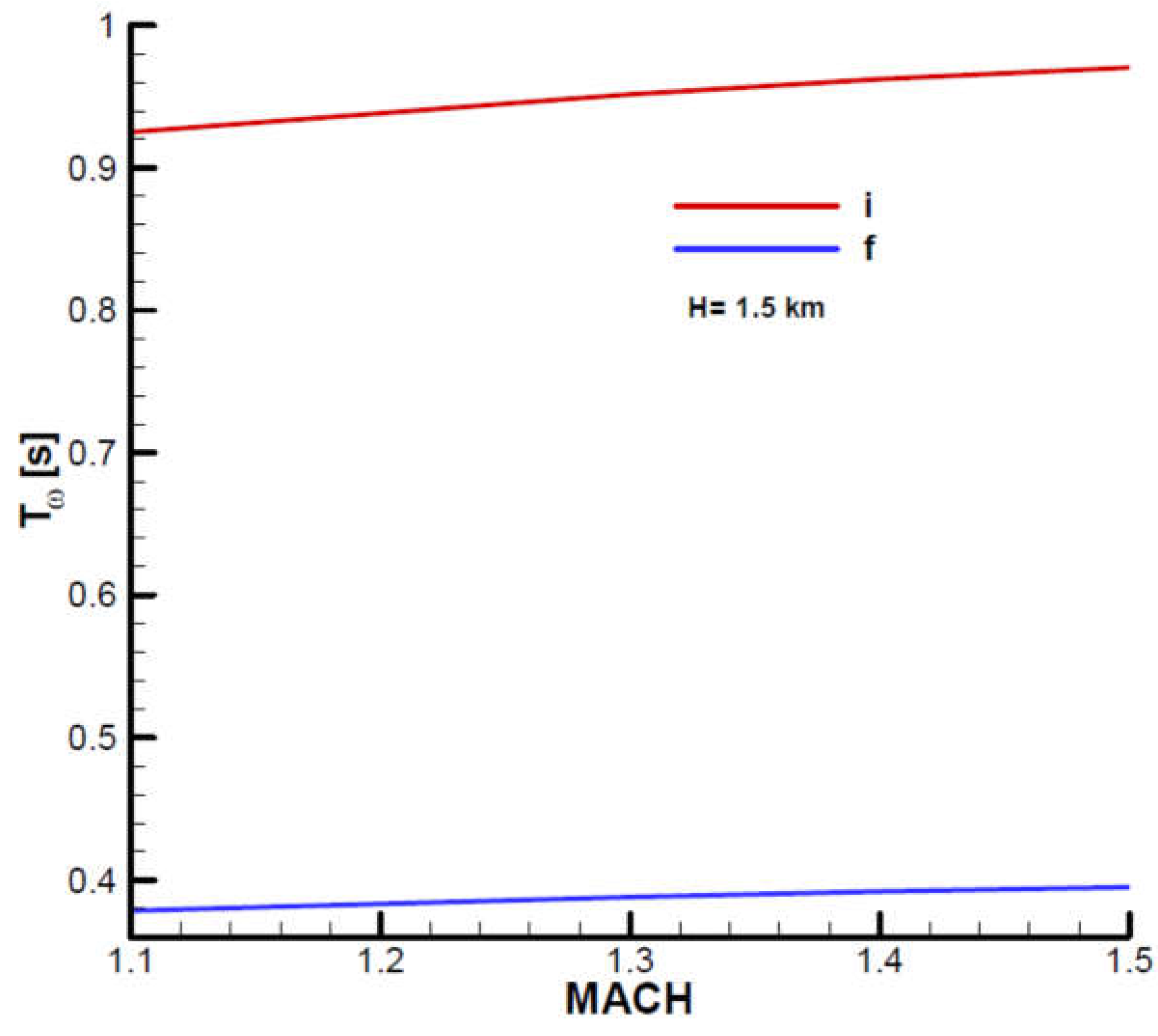
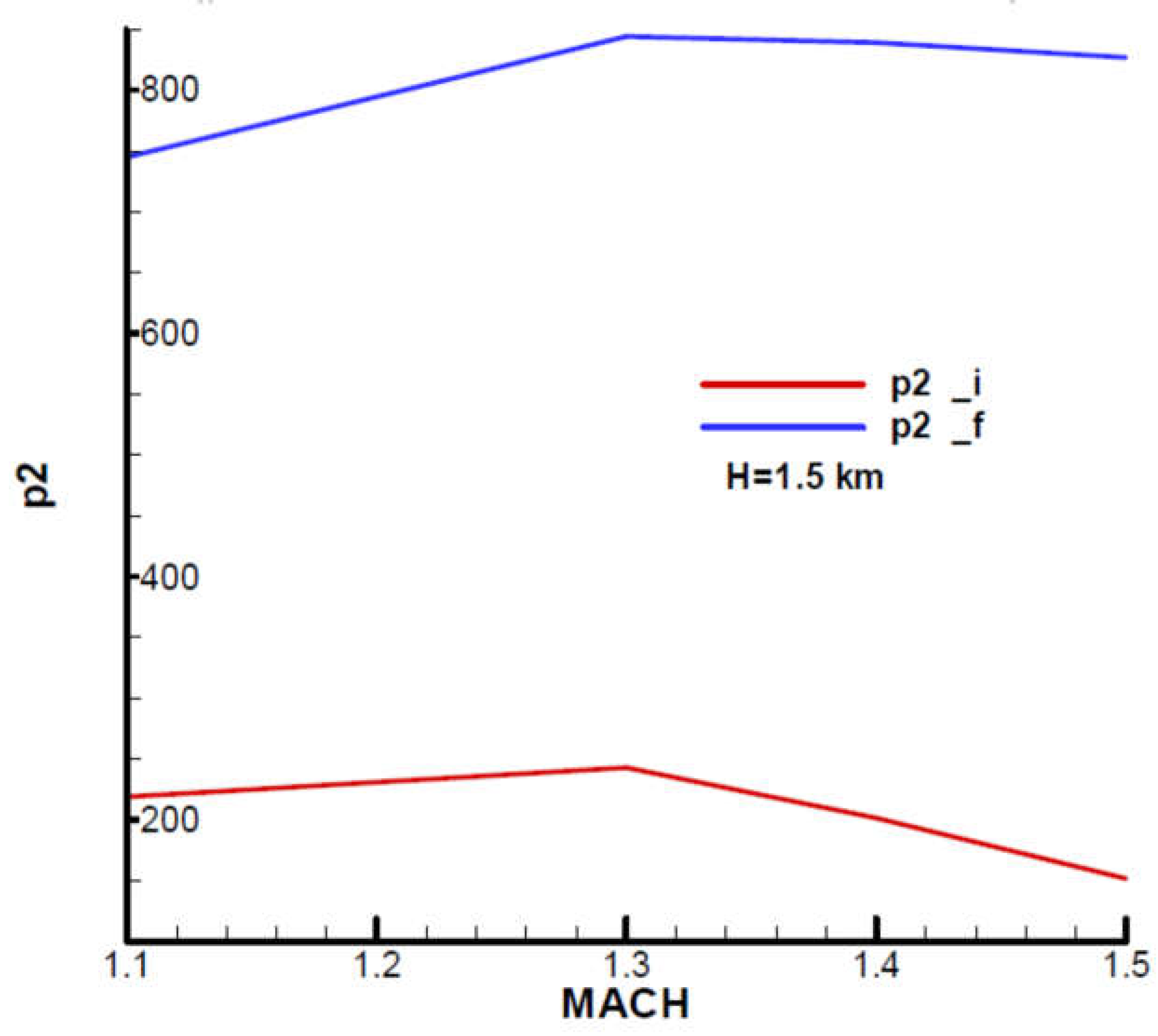
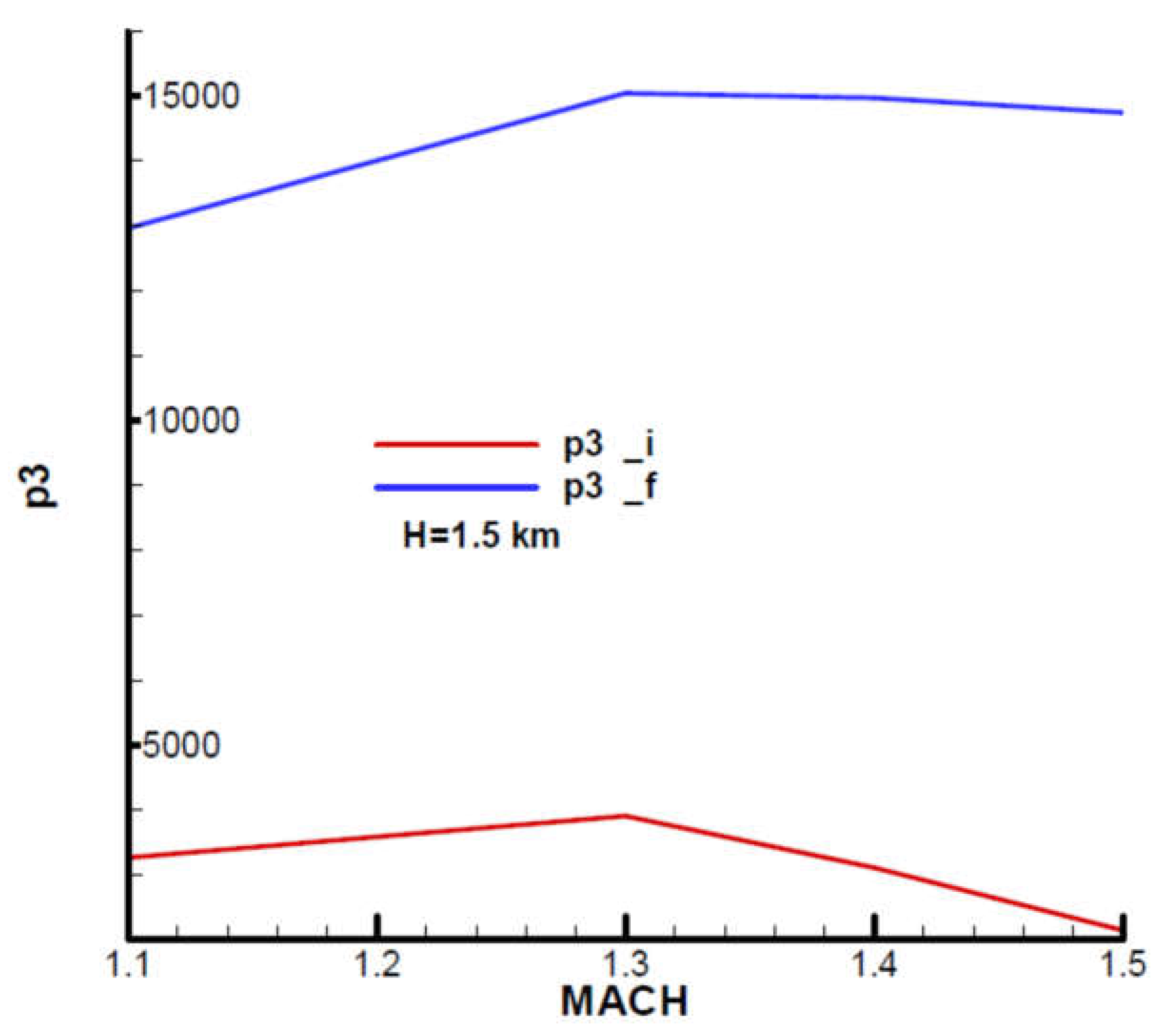
Based on the relations (145) and quality parameters from Appendix B, the characteristic polynomial coefficients were determined, which are also indicated at the beginning and end of the second phase with respect to the Mach number and altitude. The characteristic polynomial coefficients, both real and imaginary, are shown graphically in Appendix C. Based on the relations (147) and the characteristic polynomial coefficients, the Frank-Wall coefficients (

a_{1}, a_{2}, a_{3}, a_{4})

were determined and graphically shown in Appendix C. For the basic input data considered, stability criterion F-W is met:

a_{1} > 0; a_{2} > 0; a_{3} > 0; a_{4} > 0

, as we can see from Figure A26, Figure A27, Figure A28 and Figure A29.

10.2. The Root Locus

Next, we will analyze the root locus of the characteristic polynomial.

To begin, we shall consider the basic test case set out in section 9.4 for the second phase of flight at two points, at the beginning (Figure 13) and the end of the phase (Figure 14). The analysis is done on the range of Mach numbers corresponding to phase 2 (

M a c h = [1.1, \dots, 1.5]

) and height

H = 1.5 k m

. A first observation of a general nature is that the roots do not have a symmetrical distribution with respect to the real axis, as in the case of stabilized roll rockets, where the characteristic polynomial has real coefficients. There are four roots of the polynomial, thus:

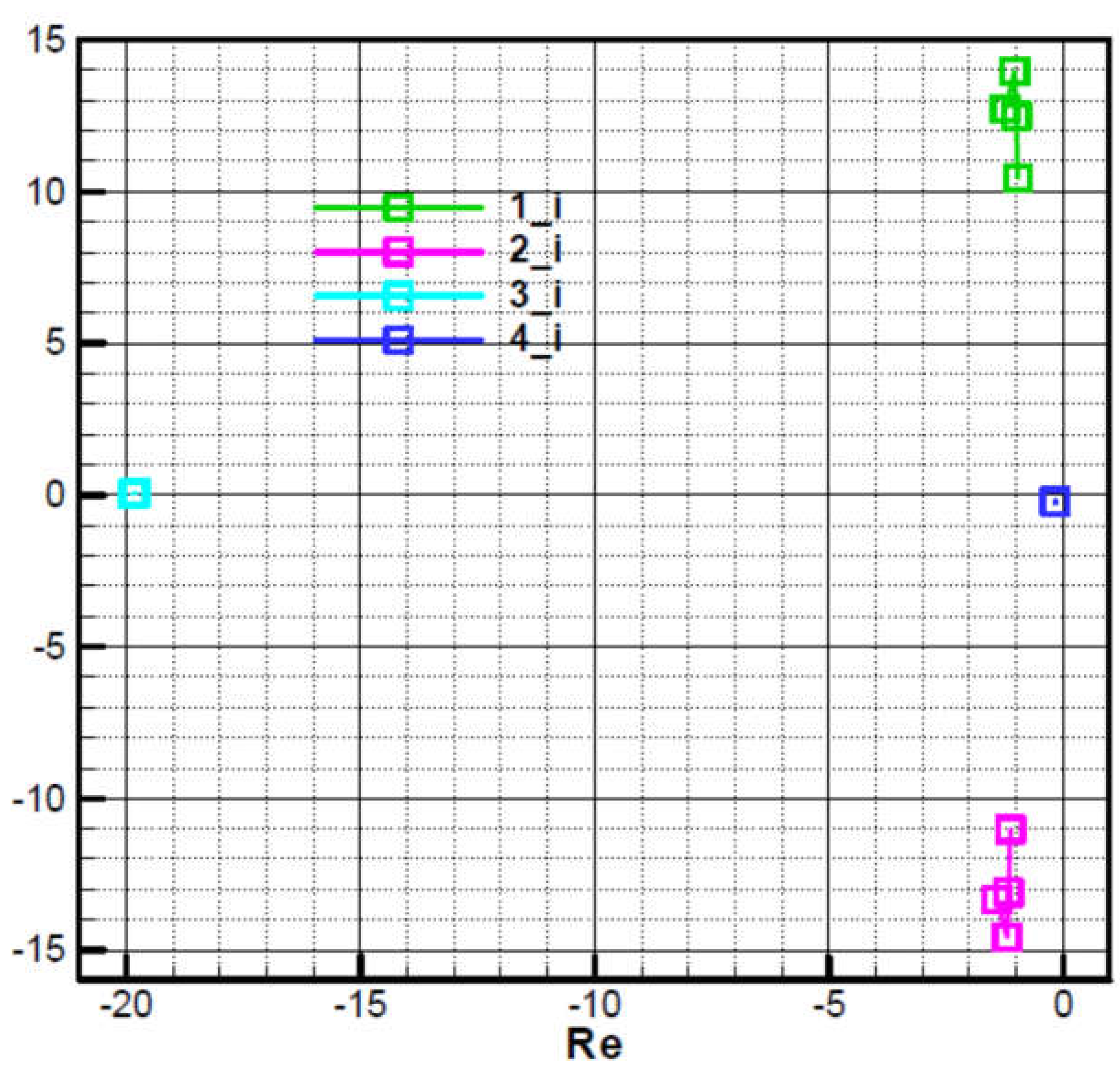
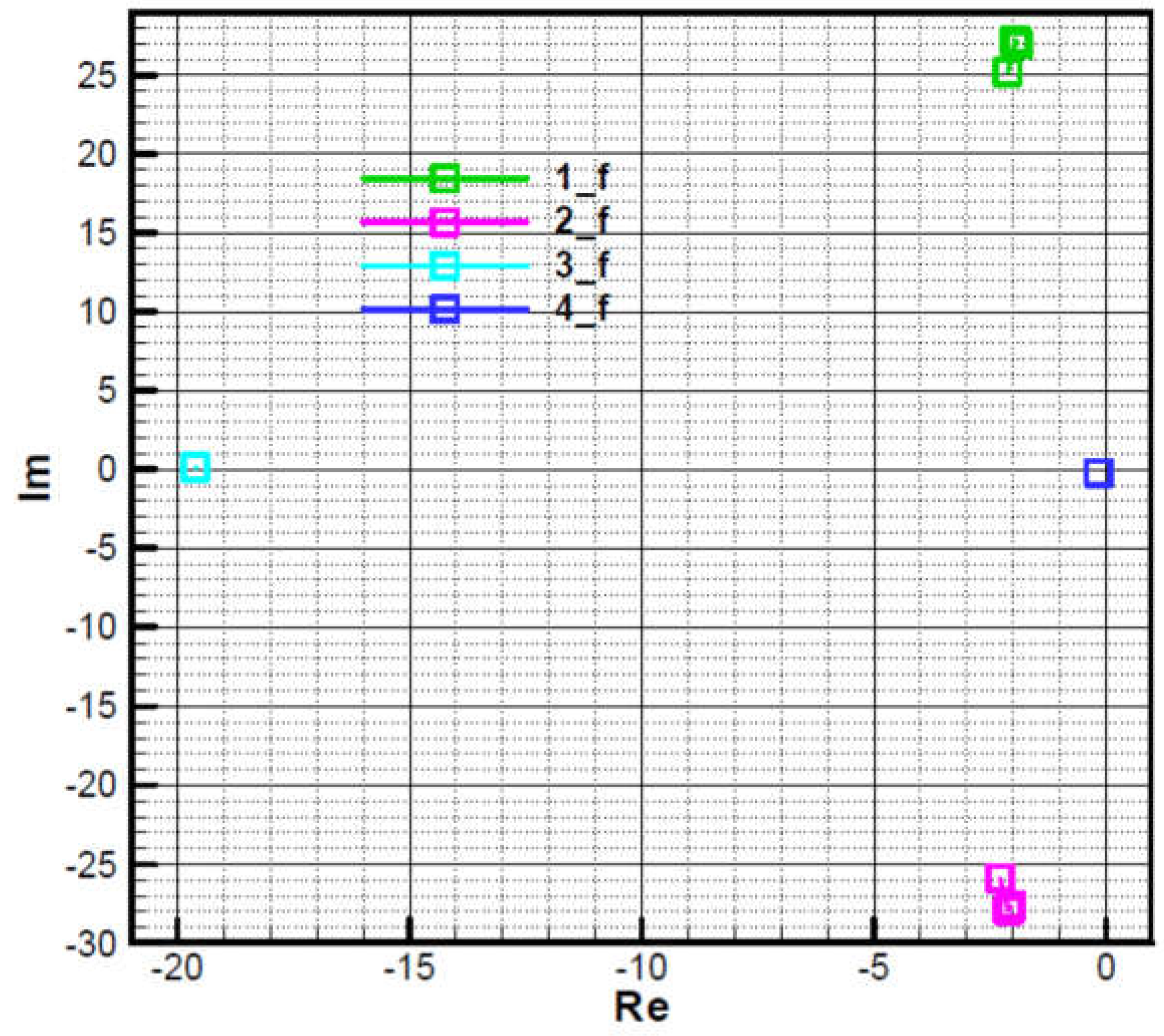
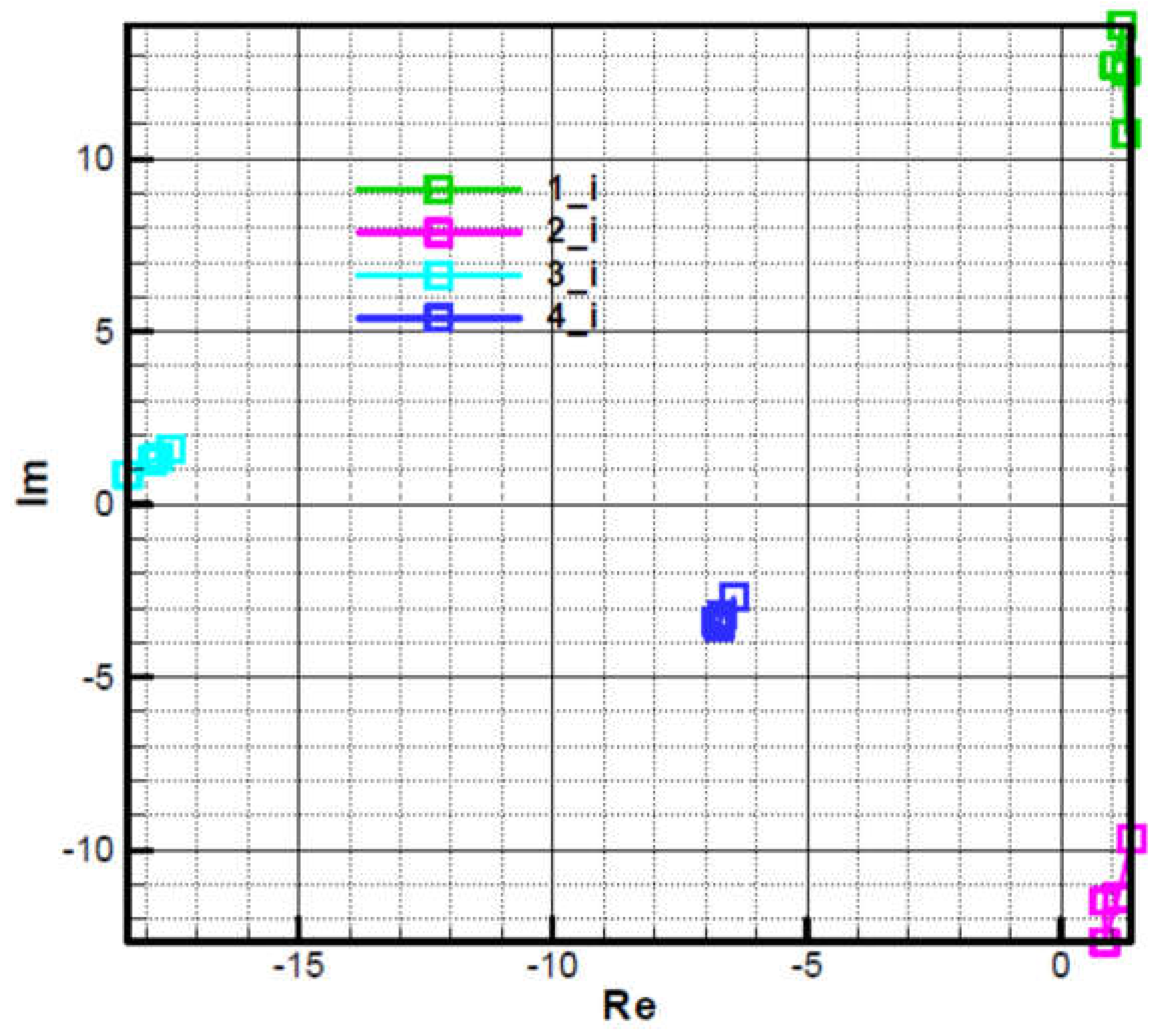
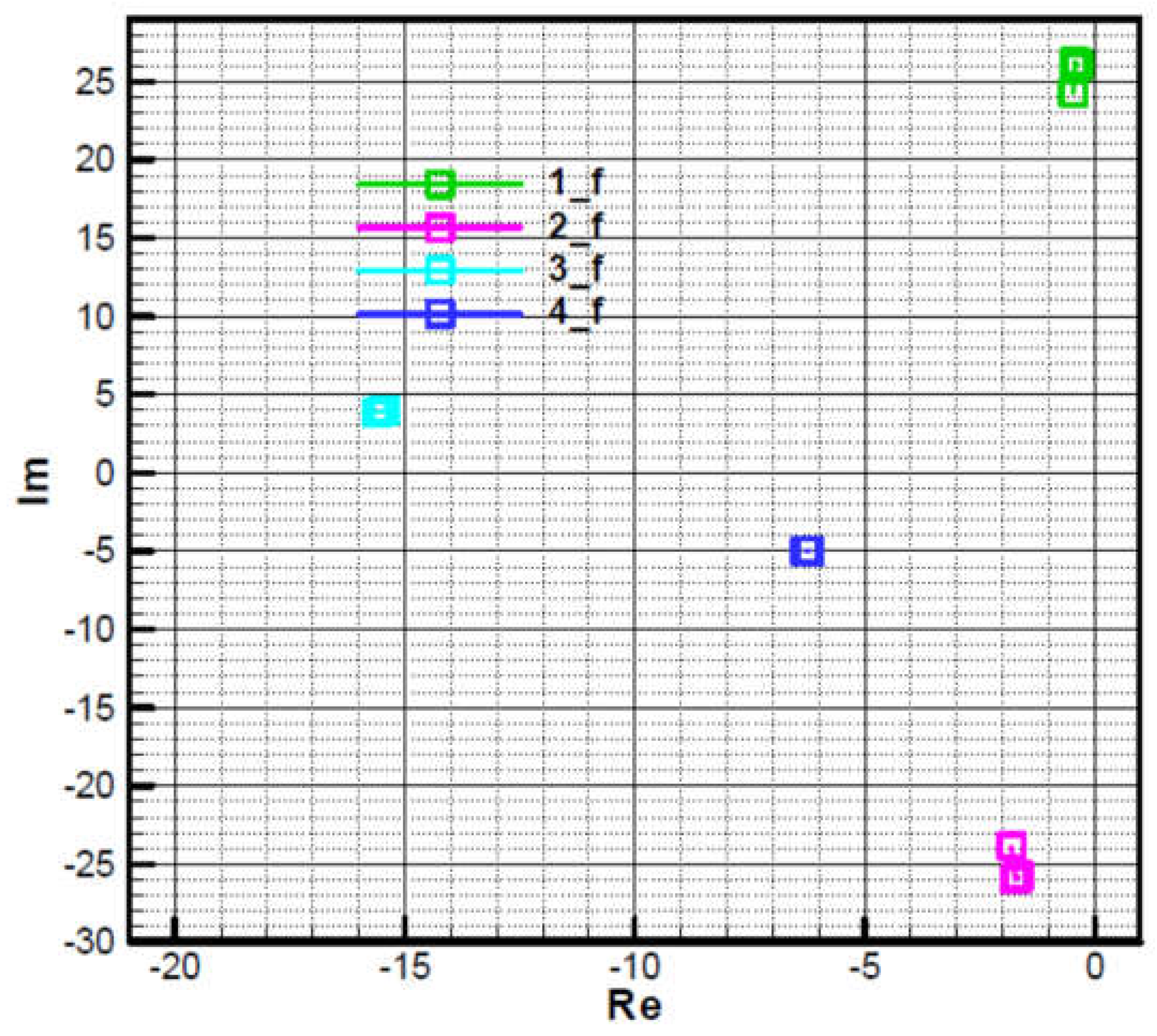
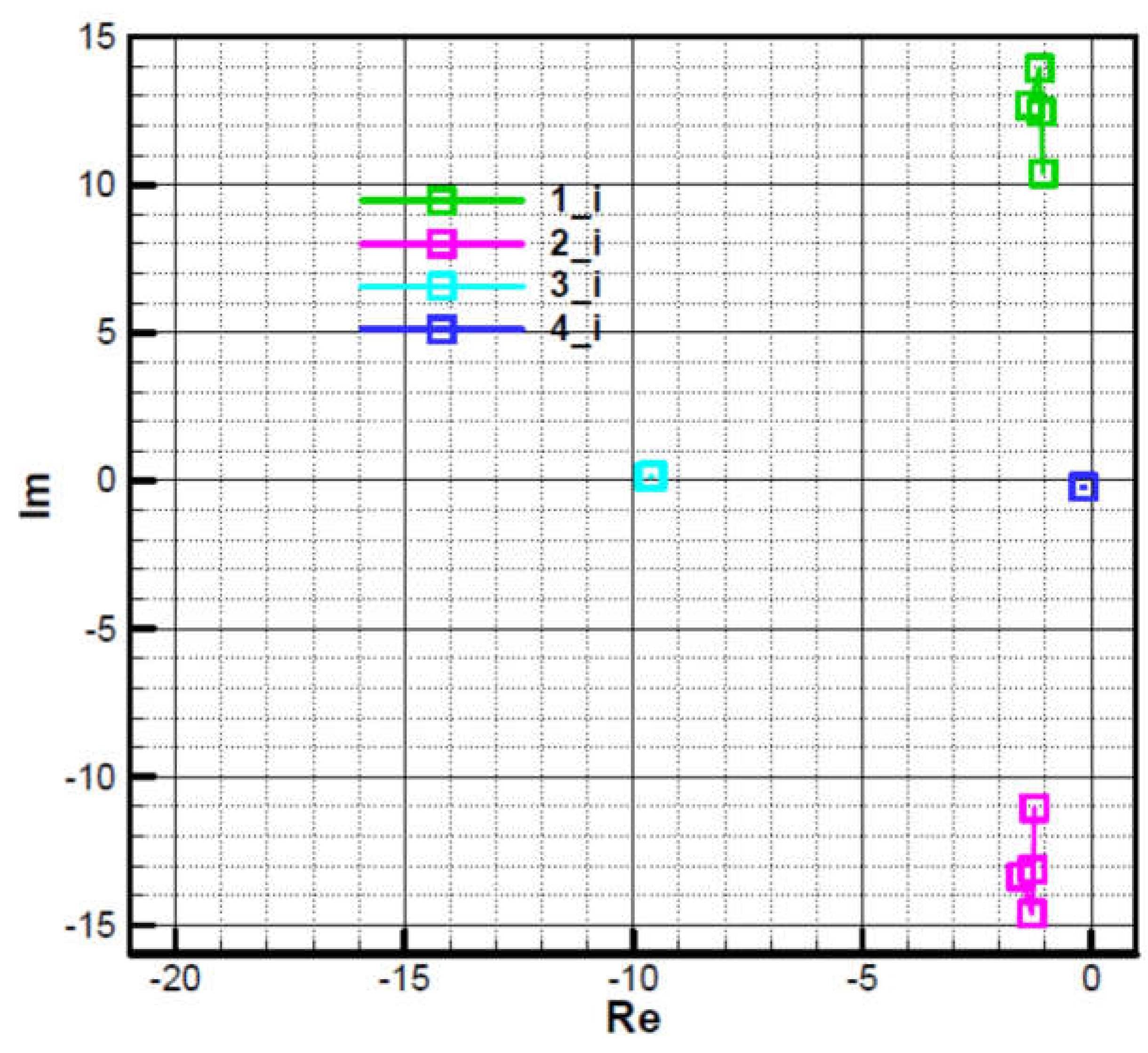
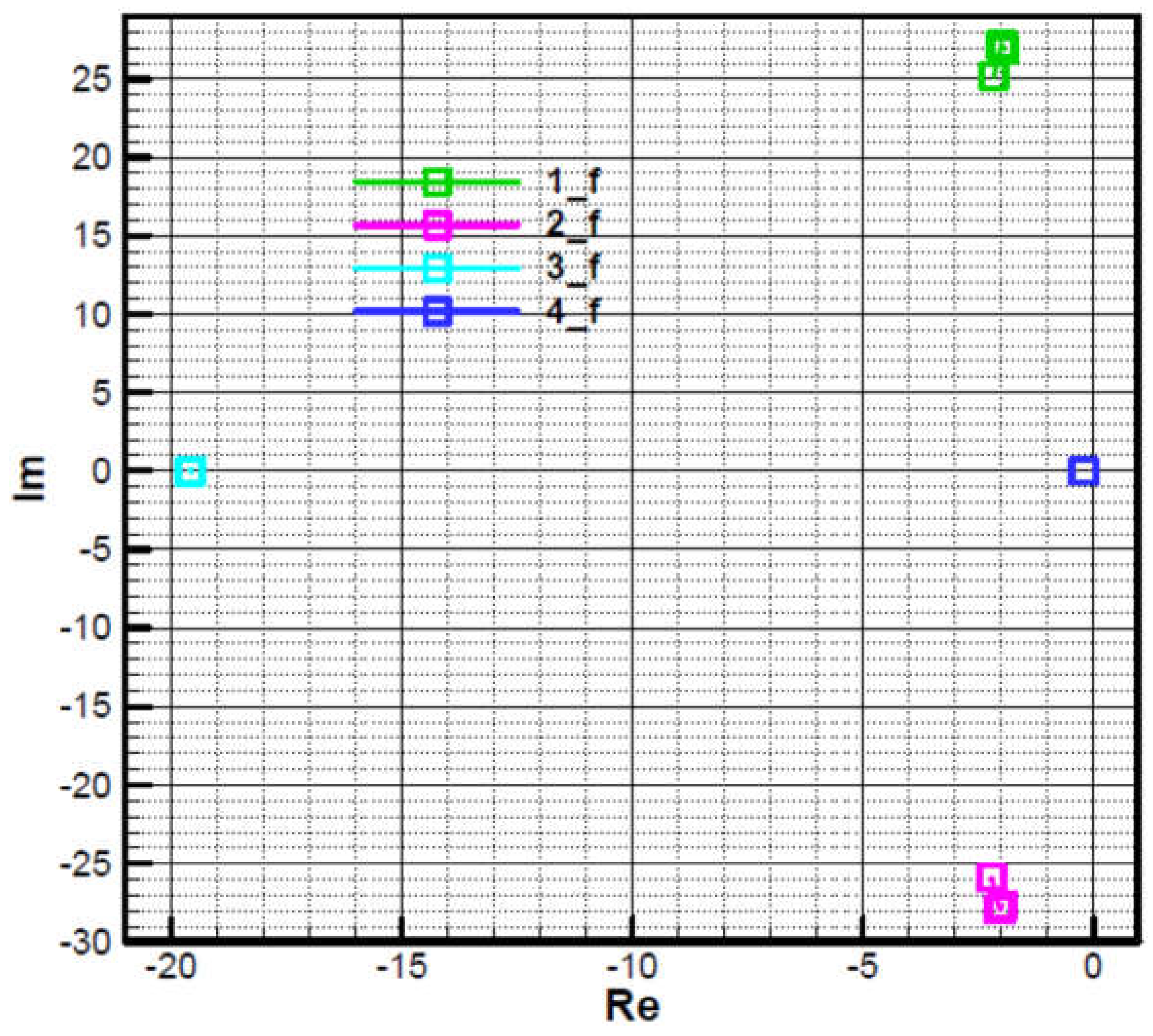
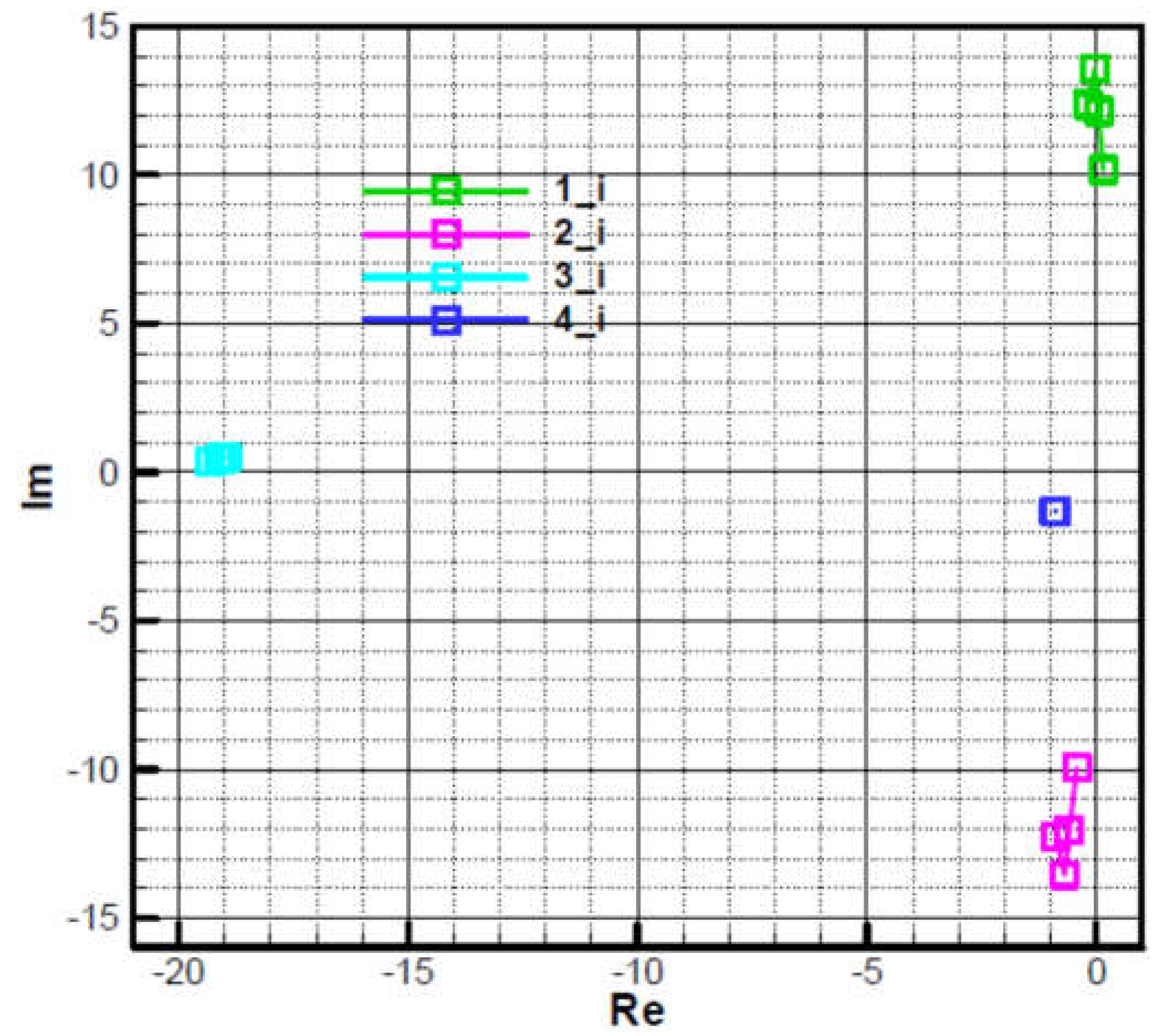
Roots 1 and 2 are close to those of the characteristic polynomial of the commanded object (66), which has a negative real part and a large complex part in modulus, almost conjugate.

- Big root 3 in the module, with a negative real part and a small complex part, due to target tracker response time.

- Root 4, small in module, with negative real part, with small complex part due to guidance loop.

In Figure 15 and Figure 16, the position of the four roots is shown when an increased navigation constant

(k = 30)

is used. There is a shift to the left of root 4, while roots 1 and 2 move to the right and may have real positive values initially but negative values in the end. It will be shown that the chosen value for the navigation constant, in this case, is greater than the permissible limit resulting from the third condition F-W for the initial moment.

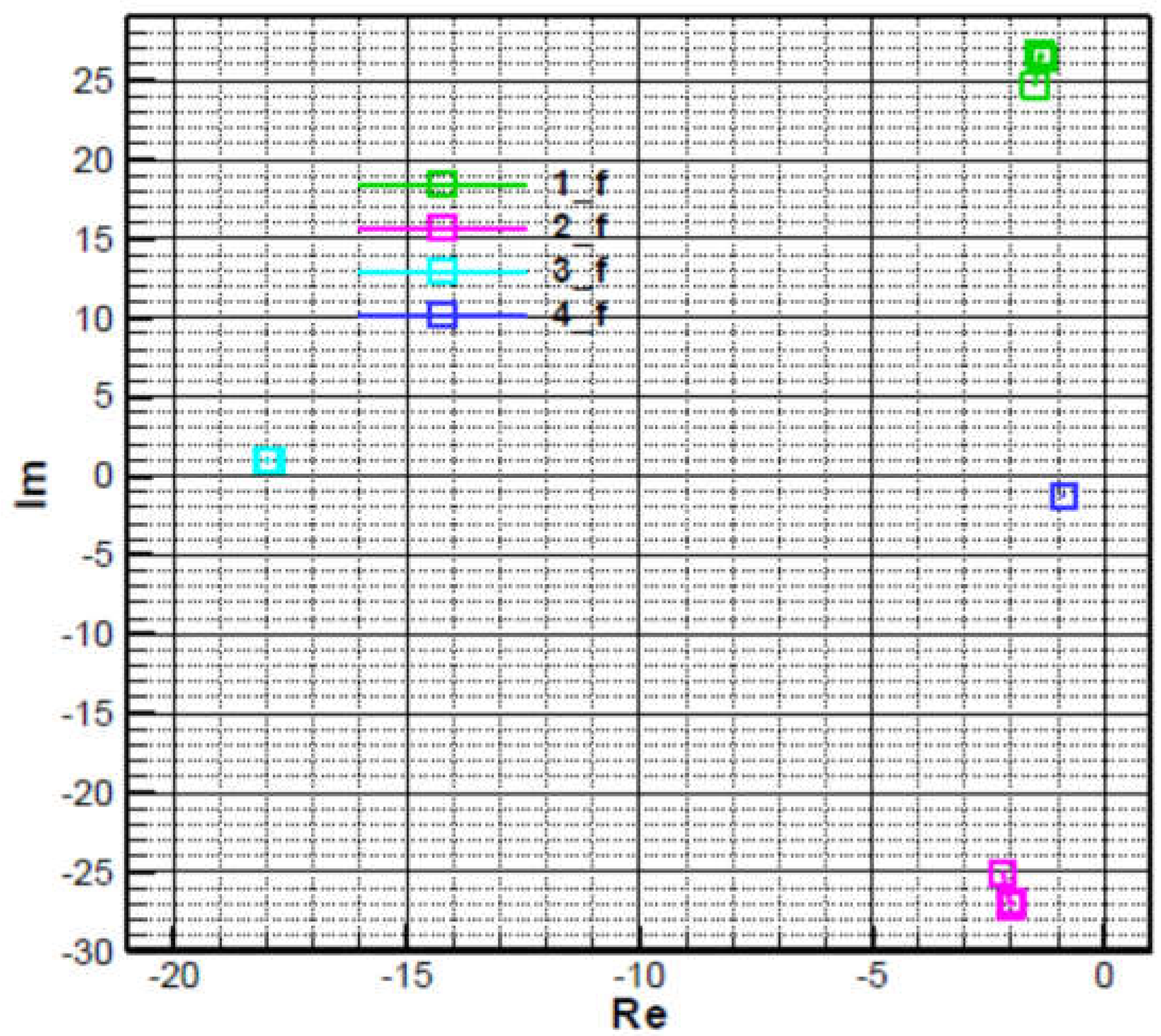
Figure 17 and Figure 18 analyses the influence of increasing the time constant of the target tracker. Thus, if the time constant value is doubled (

τ_{c} = 0.1 [s])

, displacement to the right of the third root is obtained without significantly affecting the other roots.

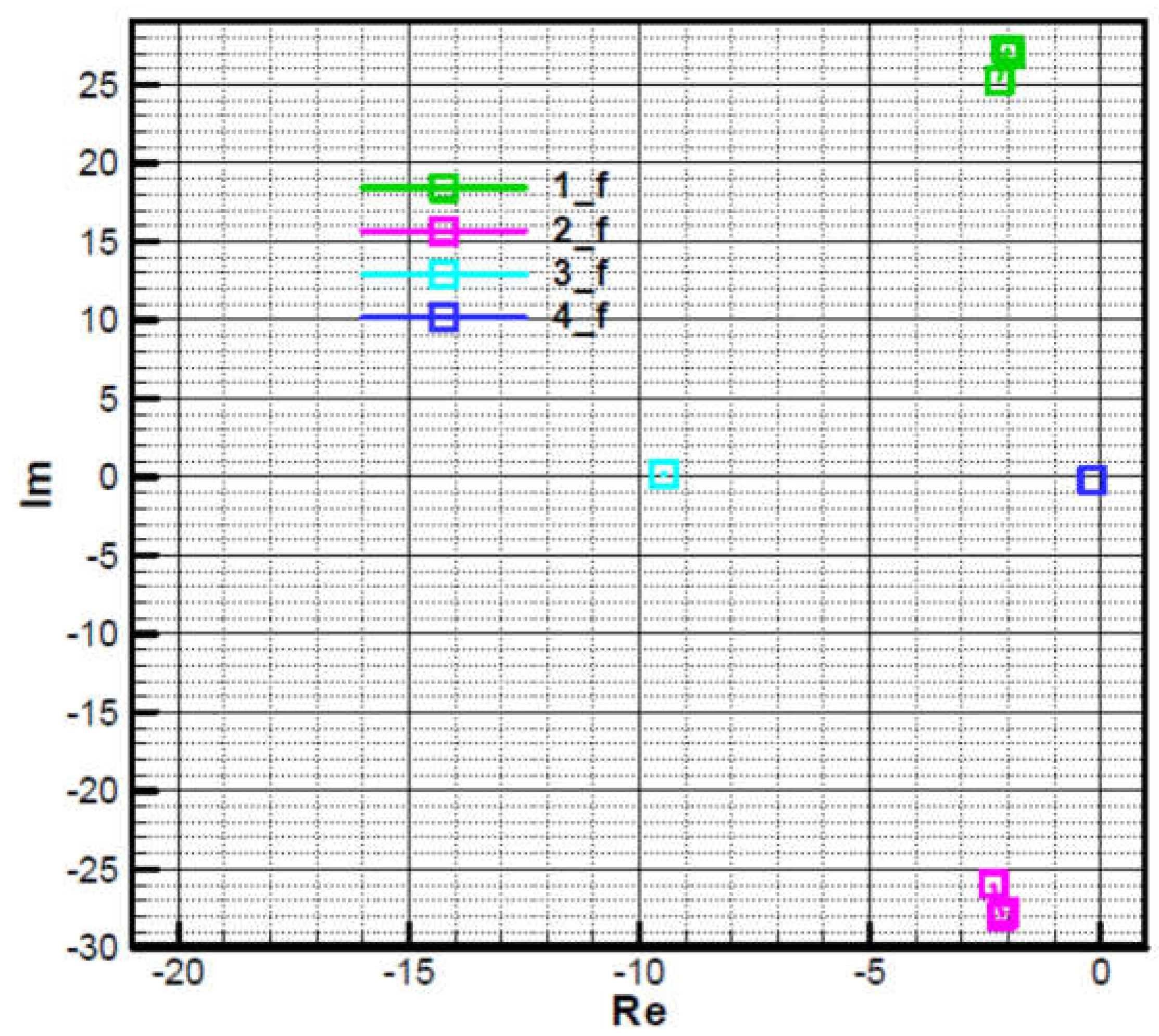
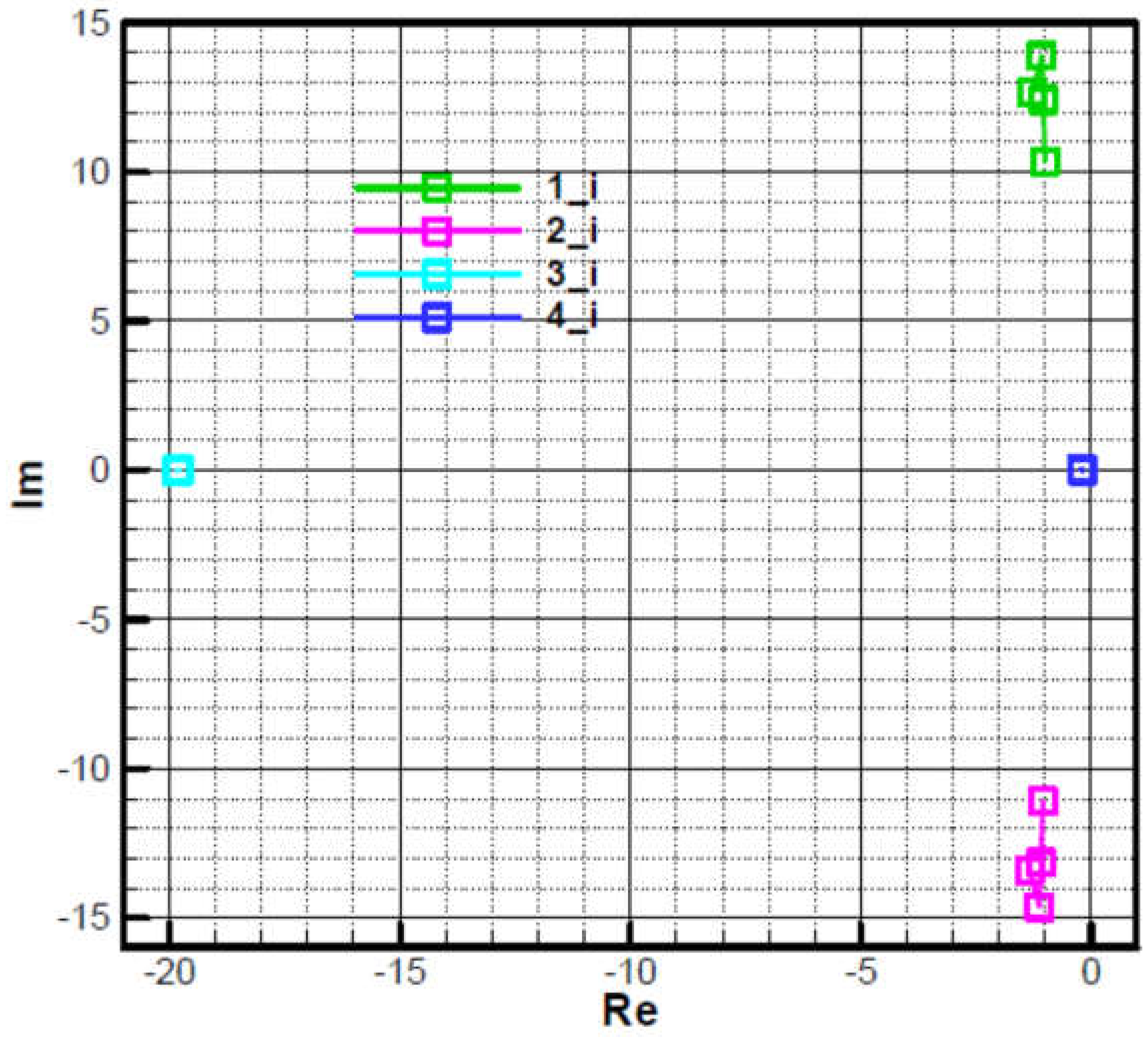
In Figure 19 and Figure 20, the influence of phase shift

(ε)

on the root location of the characteristic polynomial is analyzed. Thus, if the phase shift is cancelled

(ε = 0 °)

, a symmetrization of roots 3 and 4 is obtained, that are on the real axis (the imaginary part is null) while roots 1 and 2 remain asymmetrical with respect to the real axis due to precession, as follows from the relation (66).

In Figure 21 and Figure 22 the influence of the parameter

t_{g o}

on the location of the roots of the characteristic polynomial is analyzed. Thus, if this parameter is subtracted from

t_{g o} = 5

t_{g o} = 1

at both calculation points (initial and final), a small displacement to the left of the fourth root and to the right of the other roots is obtained. Note that initially, root one may have the real part positive (Figure 21), which leads to instability, but finally it cancels out, with root 1 having the negative real side (Figure 22).

10.3. Constraints due to Stability Conditions

Next, we will analyze the constraints on the target's time to hit (

t_{g o}

) and the navigation constant (

k

) due to the stability conditions F-W.

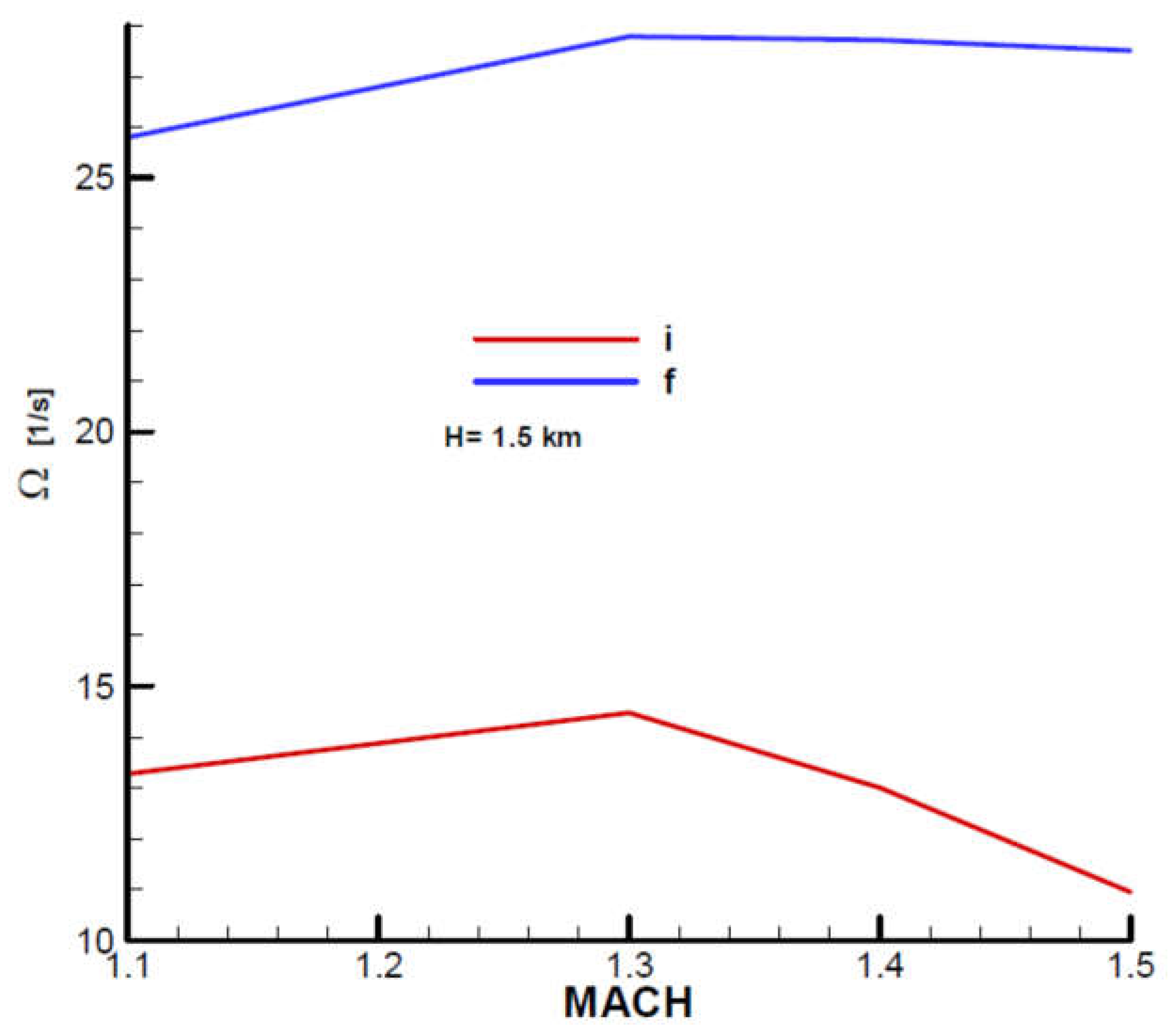
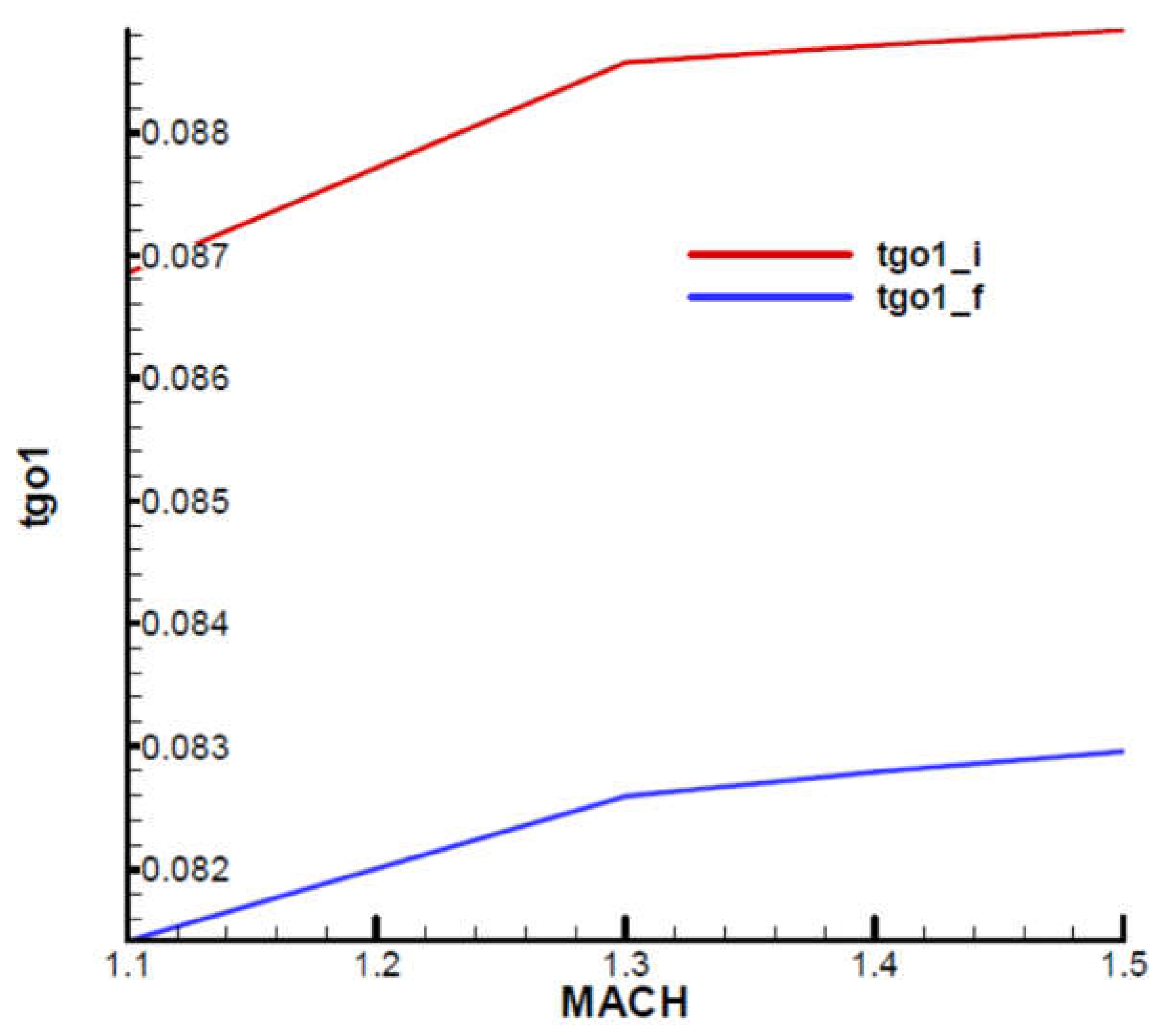
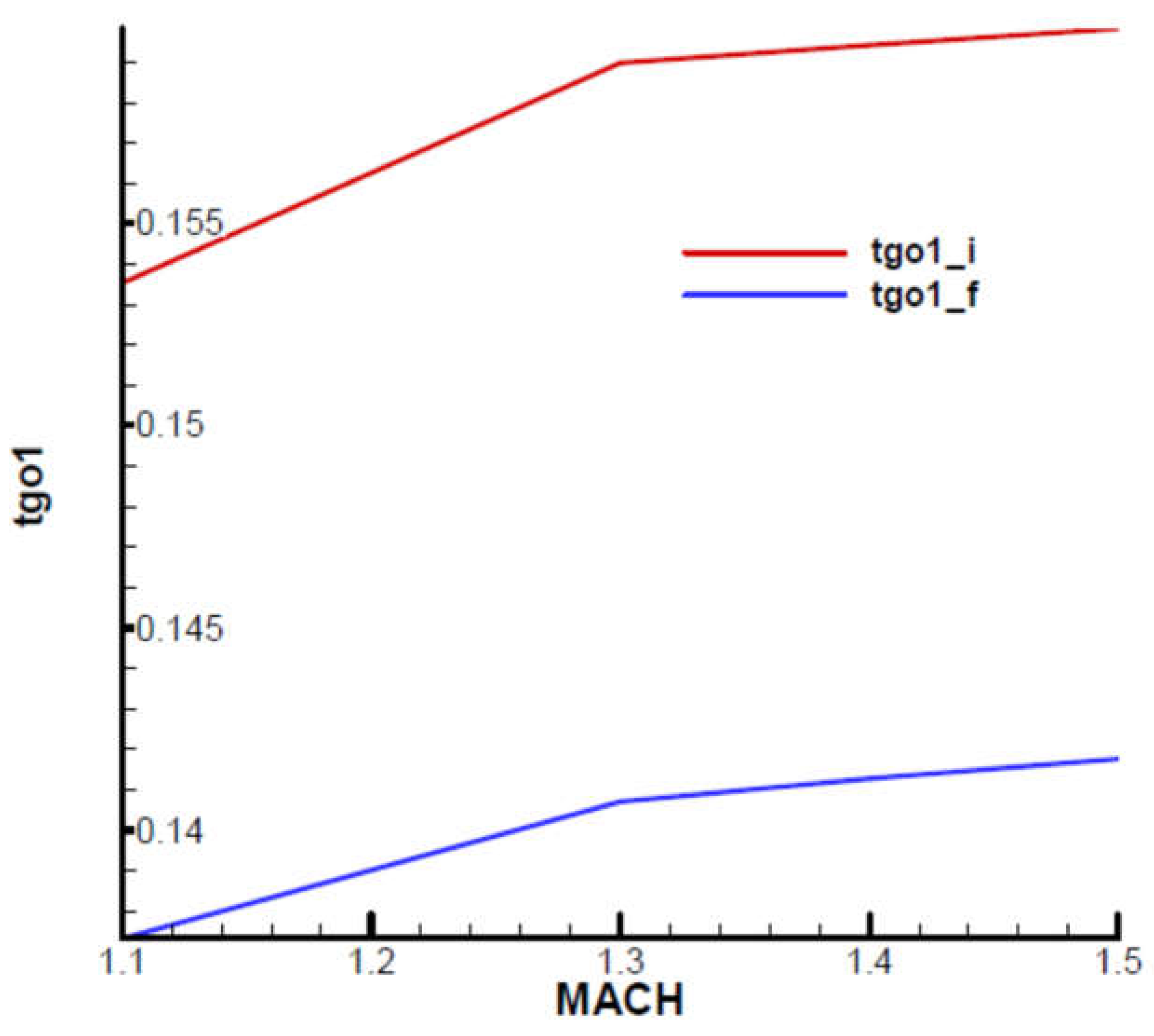
Time to hit the target

The first stability condition of F-W is identical to the first R-H condition for the non-rolling rocket and refers to the lower limit

t_{g o}

. It is found that the limit at the final moment is lower than that at the initial moment and increases with velocity.

Since the lower limit depends on

τ_{c}

, we must evaluate its influence. So, if we double the value

τ_{c} = 0.1 [s],

we get the results from Figure 24 for the lower limit

t_{g o}

. It is observed that doubling the time constant

τ_{c}

leads to approximately doubling the lower limit of

t_{g o}

As for the second condition F-W, similar to the R-H case analyzed for the non-rotating rocket, an upper limit for

t_{g o}

is obtained, which fortunately disappears at the end of the phase, as can be seen from Figure 25.

If we double the time constant

τ_{c} = 0.1 [s]

, the upper limit of

t_{g o}

disappears completely, as can be seen from Figure 26.

Synthesizing, increasing the time constant of the target tacker

τ_{c}

leads to an increase in the lower limit

t_{g o}

, which is bad because it increases the distance to which the missile can approach the target. However, it can also have a beneficial role by eliminating the upper limit of

t_{g o}

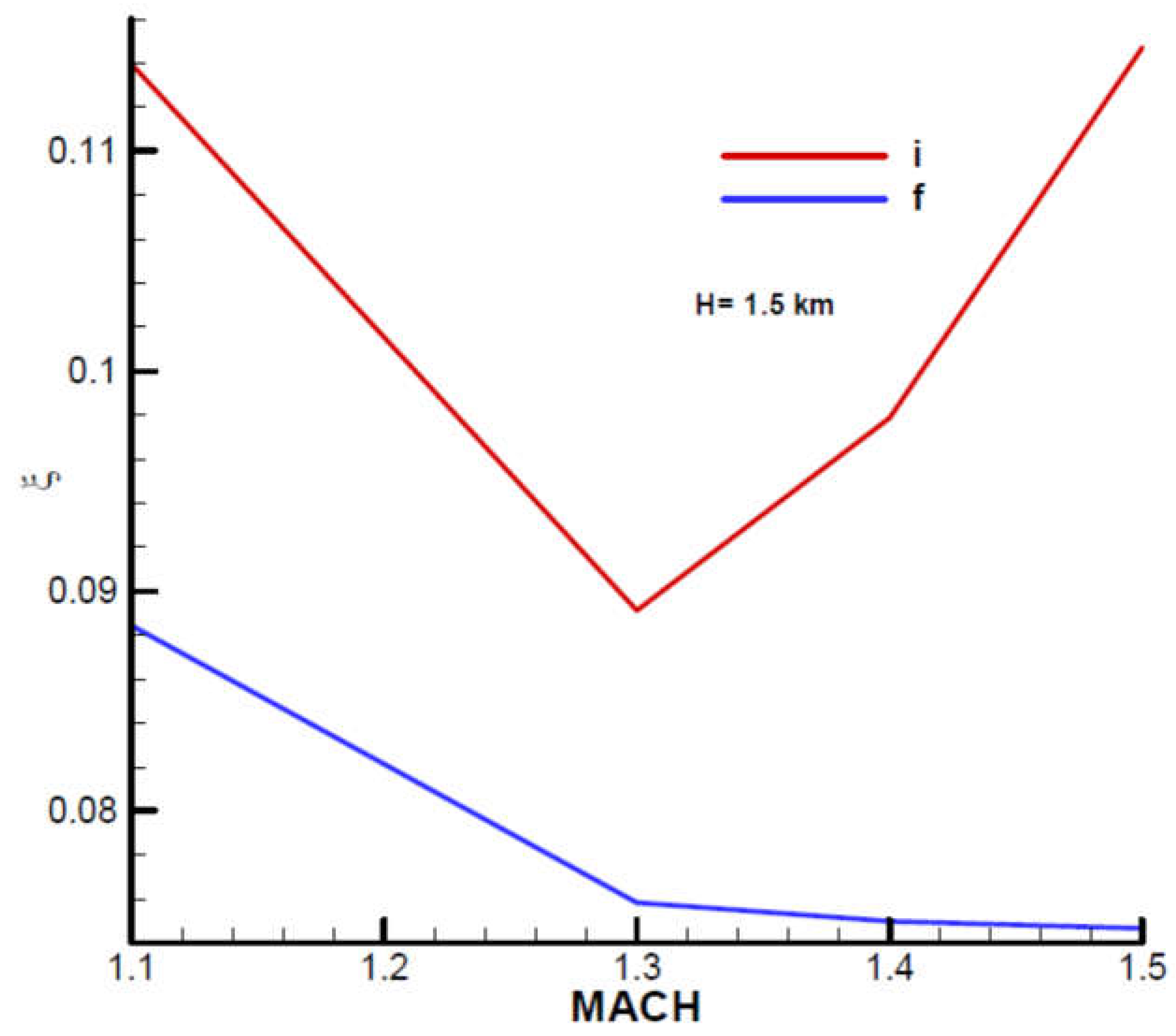
Navigation Constant

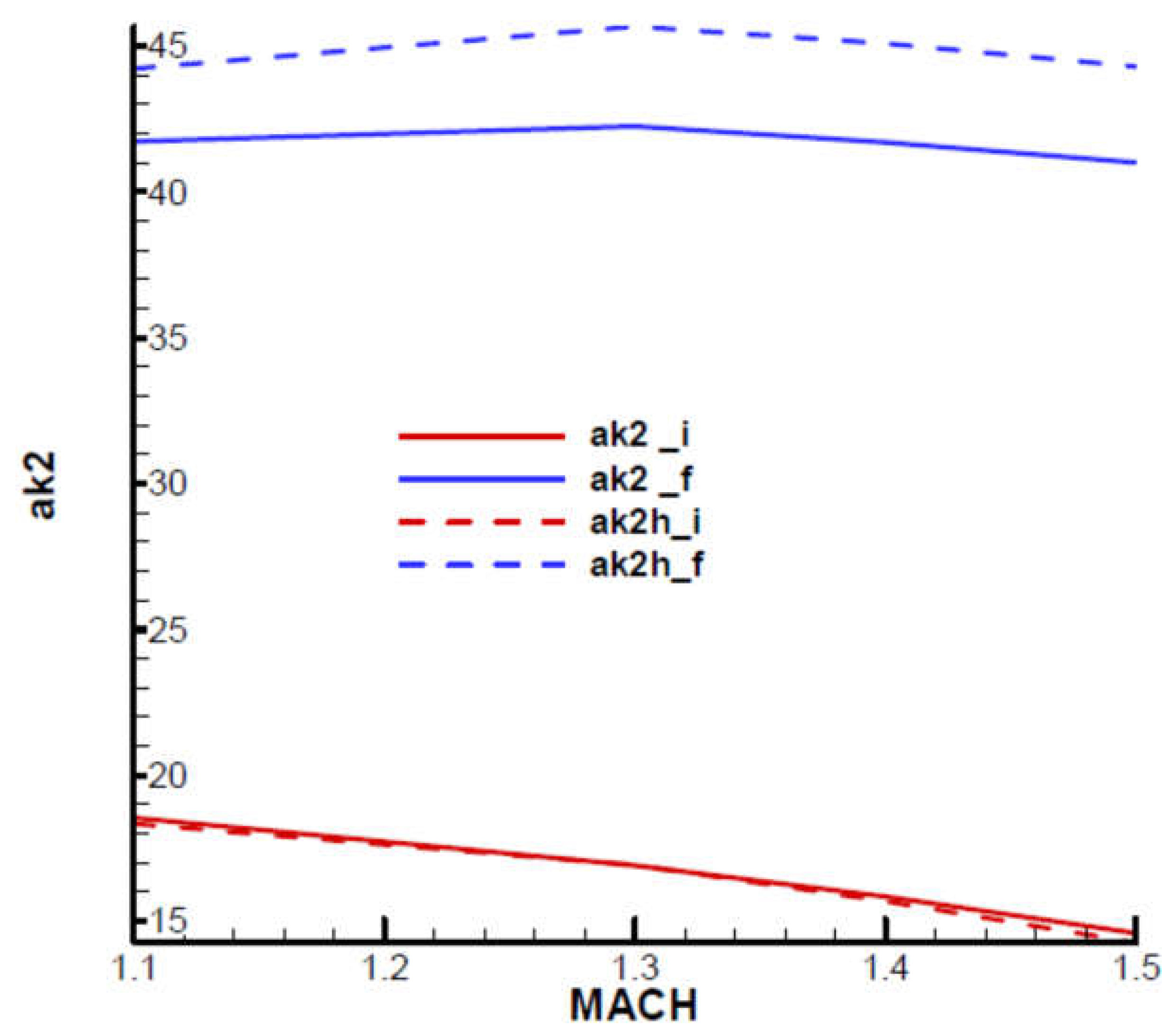
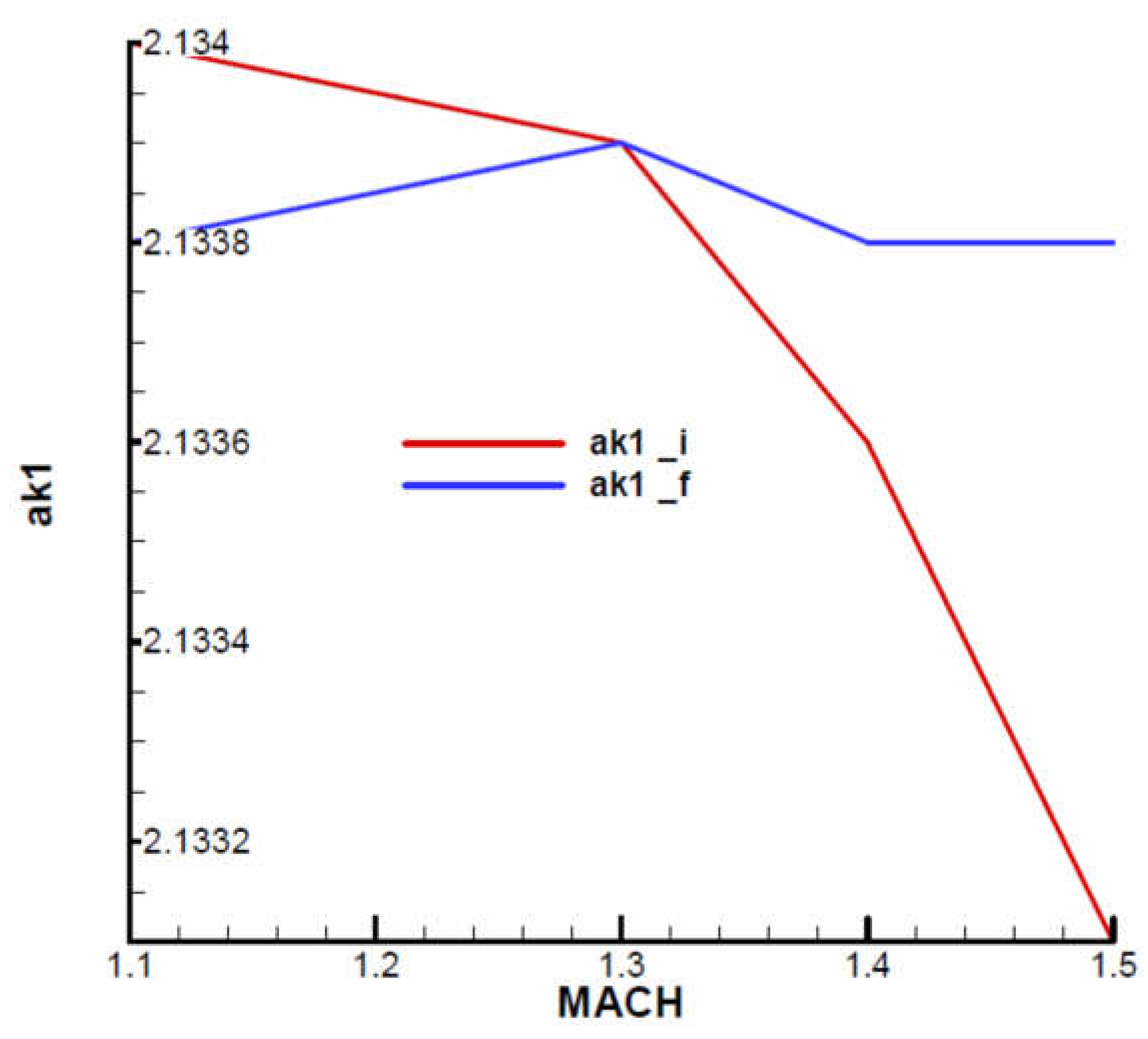
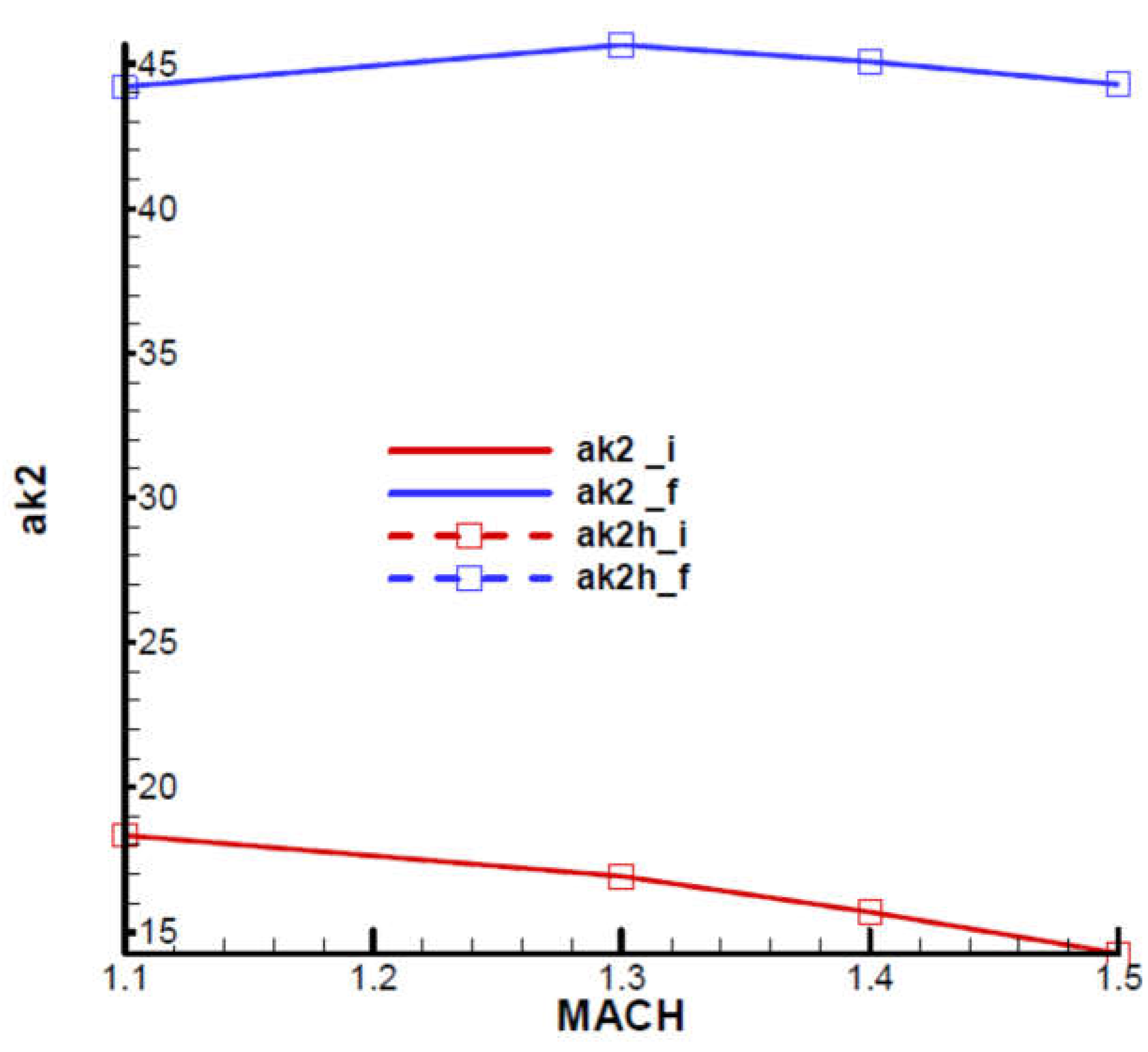
The third stability condition of F-W gives the upper limit of the navigation constant indicated in Figure 27. It is higher at the flight phase's end and slightly decreases with velocity. For comparison, they are presented in the same diagram cases without rolling, marked with ak2h_i, ak2h_f, and rolling cases marked with ak2_i, ak2_f. It can be noted that at the beginning of the flight phase, the values with rolling are very close to those without rolling, while at the end of the phase, the values without rolling are higher than those with rolling.

For the fourth stability condition of F-W, in the case of a rolling rocket, the minimum value of the navigation constant is also obtained (Figure 28). It can be seen from the diagram that in the case of rolling, the minimum value is slightly higher than in the case without rolling, in which case the minimum value is

k = 2

. It is also noted that, for the field of interest, the final value becomes higher than the initial one with increasing velocity. However, on the whole, it does not depend significantly on the velocity (Mach number).

Summarizing the last two cases, it is found that in the rolling case, the range of the navigation constant decreases both in terms of the lower limit, which is slightly higher (Figure 28) and in terms of the upper limit, which is significantly lower (Figure 27).

Note that this difference in the upper limit is mainly due to phase shifting

ε

; in its absence, the limits with rolling are almost identical to those without rolling, as can be seen in Figure 29.

10.4. Stability Analysis Based on the Nonlinear Model

The objective of the nonlinear model analysis is to verify the limits of the navigation constant (

k)

set out in the previous point, such as the lower limit of the parameter

t_{g o}

. We will consider parameters similar to linear analysis:

ε = 20 °; τ_{c} = 0.05 [s]

and a tactical situation with a fixed target placed at a distance of 2.5 km and height of 2.5 km. The choice of a fixed target was made in order to simplify the construction of the navigation gain, in which case

u_{M} / u_{c} = 1

, and the navigation constant coincides with the modified navigation constant:

k = K = k_{u}^{ω} k_{δ}^{u} k_{ω}^{δ}

(164)

From the relation (164), only the first factor

k_{u}^{ω}

can be imposed because it is related to the constructive solution of the target tracker, possibly by an additional amplification constant. At the same time, the second factor is constant

k_{δ}^{u} = 2 δ_{m a x} / (π u_{m a x})

and the third-factor

k_{ω}^{δ}

depends on the dynamics of the missile, being difficult to control. In this case, we will choose

k_{u}^{ω}

so that, when multiplied by the other two gains, a value close to the desired

k

is obtained. Given the objectives of this section of the paper, we will seek to obtain three navigation gains, the first less than 2.0, representing the defined lower limit of condition 4 F-W; the second close to 3.0, a value used in linear analysis, and the third larger than the upper limit resulting from condition 3 F-W. As previously stated, these values will be determined as a function of time simultaneously with the integration of nonlinear equations of motion that will be done in the body frame. Obviously, due to the variation of the third-factor

k_{ω}^{δ}

, the navigation gain will vary over time, as can be seen in Figure 30. The analysis is performed considering three identical missiles but with different navigation gains, the first below the lower limit, the second within the limits defined in the linear analysis, and the third above the upper limit.

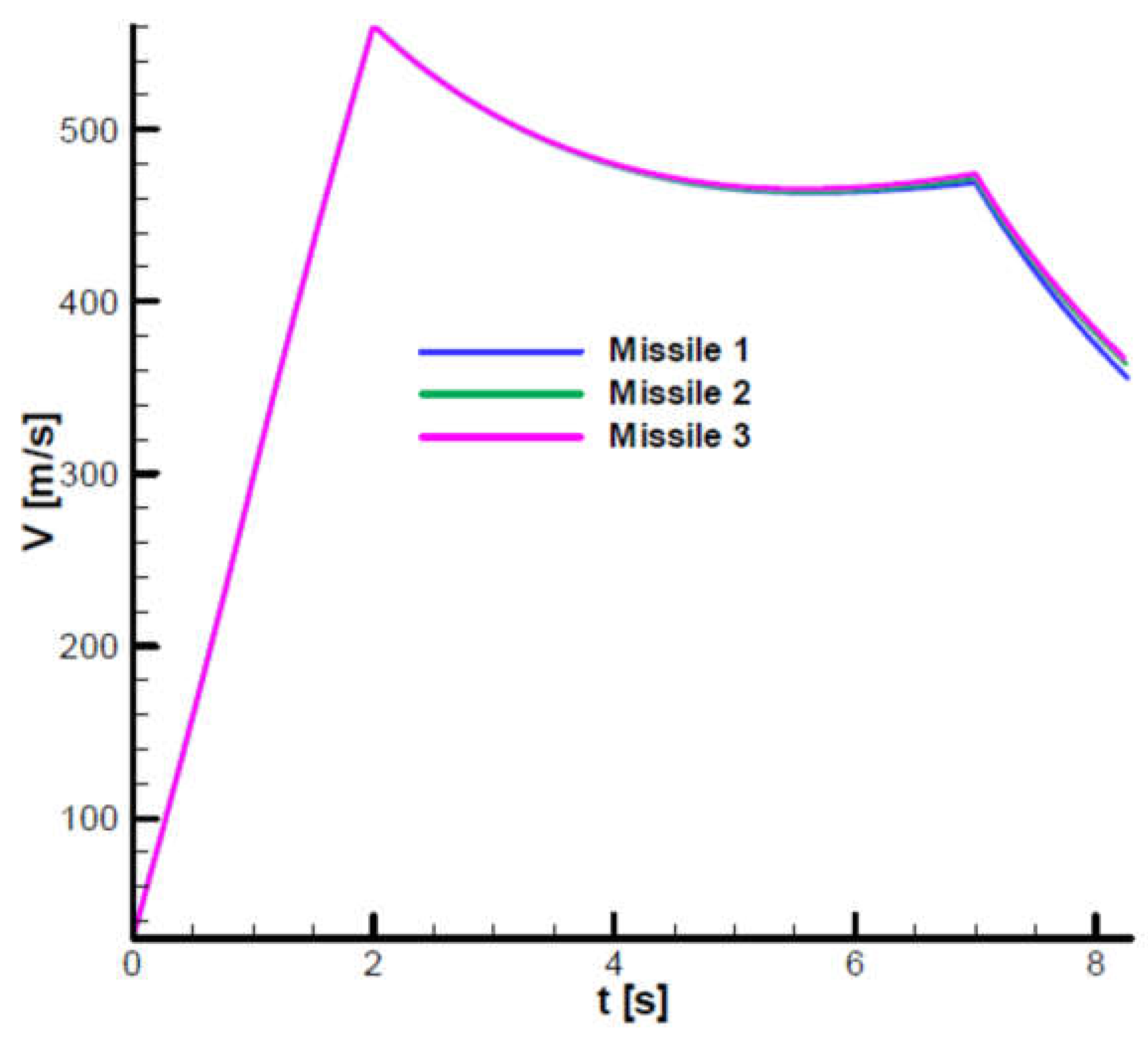
For the three rocket models defined above, Figure 31 shows the velocity diagram that was previously used to define the analysis range on the linear model

M a c h = [1.1, \dots, 1.5]

, which corresponds to the second phase of flight. There are no major differences between the three cases analyzed.

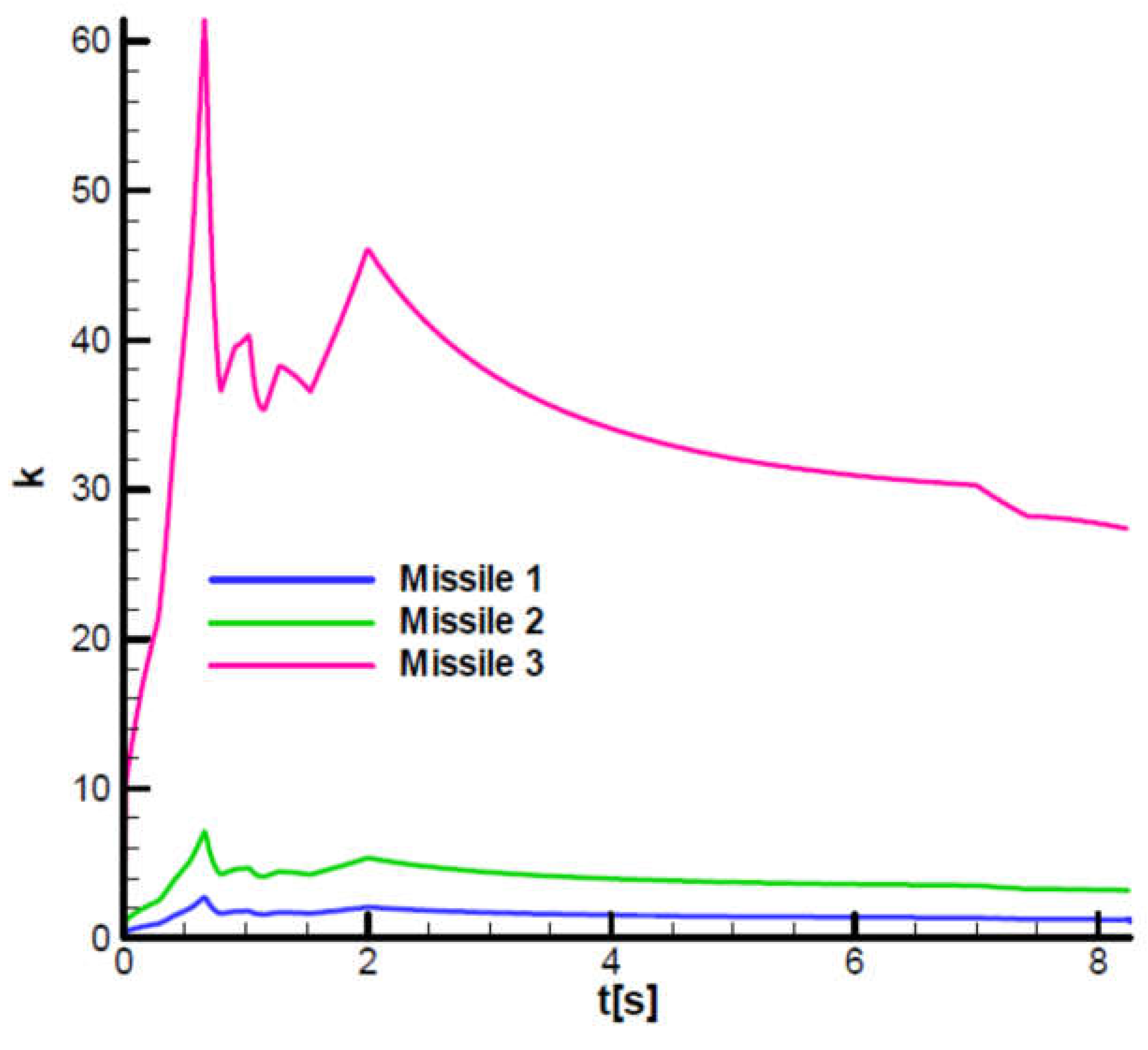
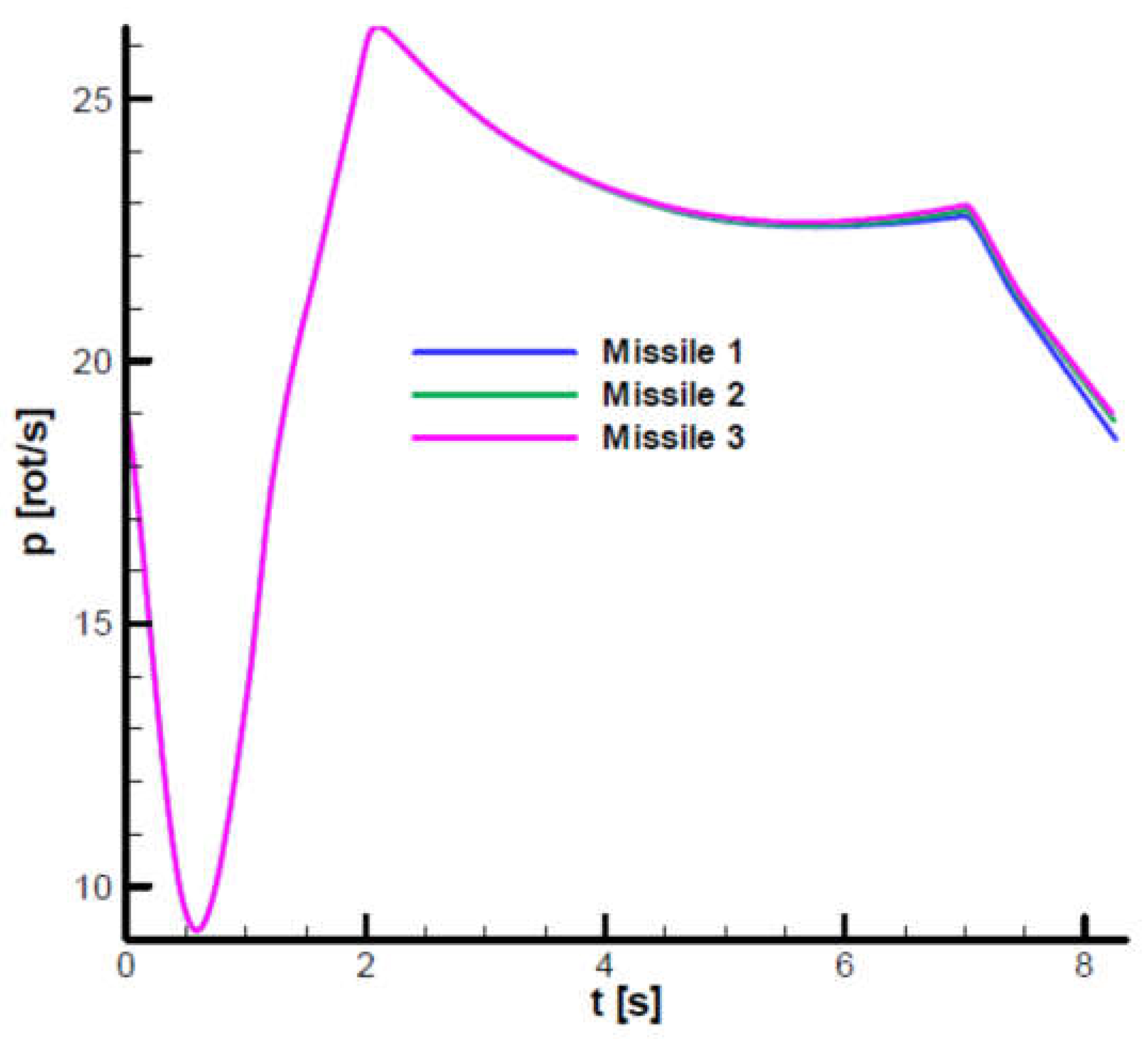
Figure 32 shows the angular roll velocity diagram based on which the rotational velocity of

p ≅ 22 [\frac{r o t}{s}]

, corresponding to the second phase of flight used in linear analysis, was chosen. It is observed that the roll velocity follows the velocity profile and does not differ substantially between the three cases.

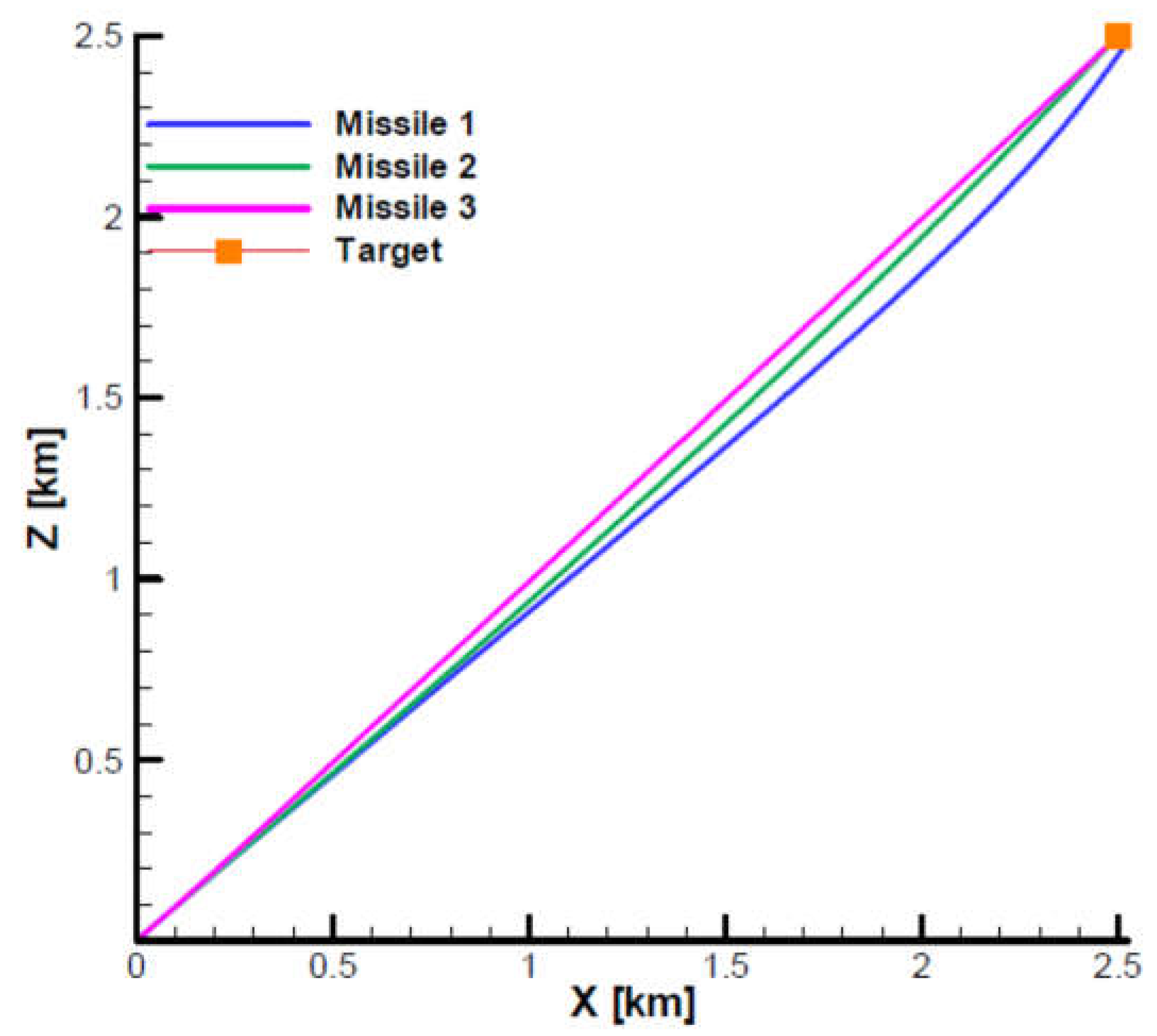
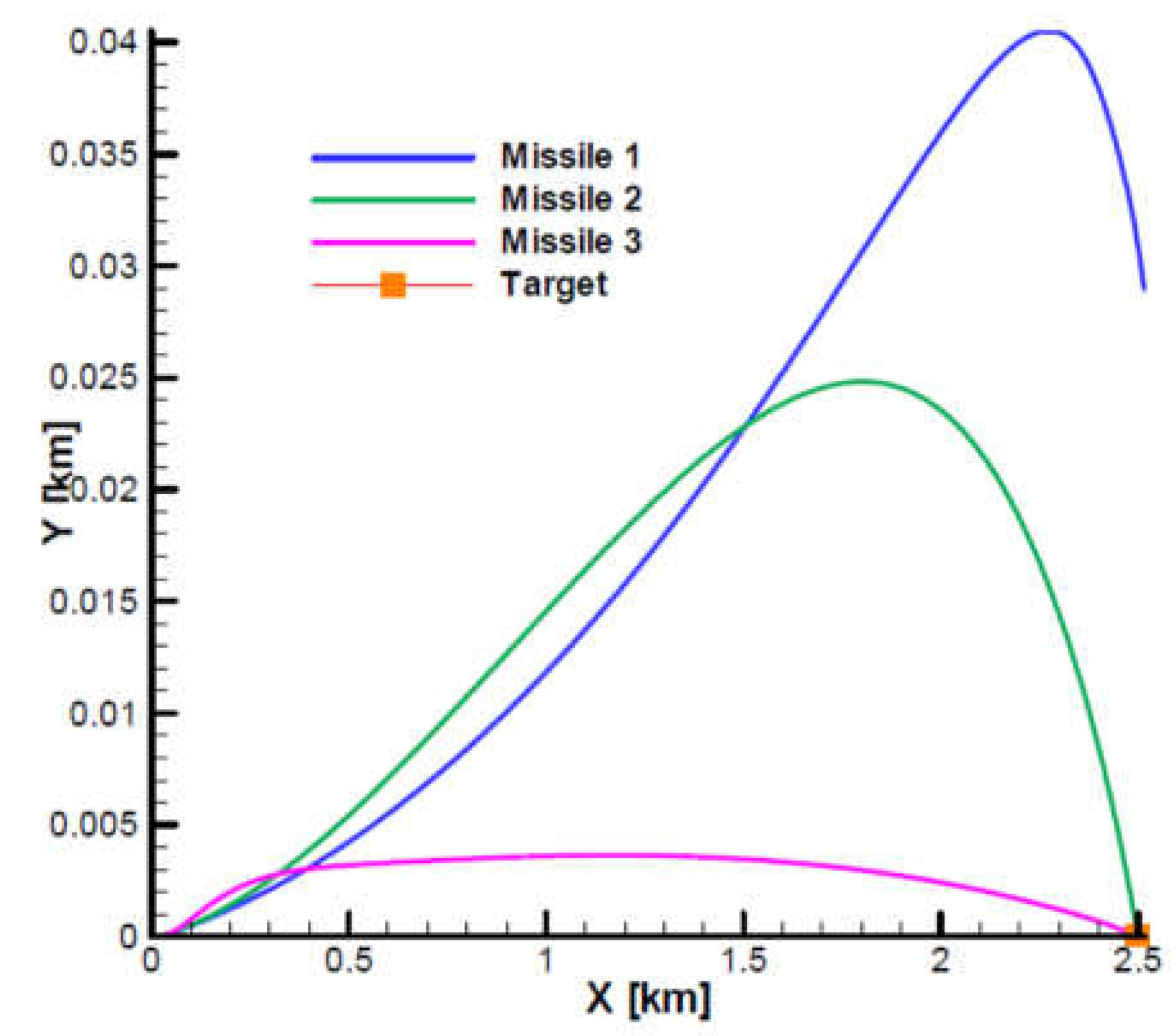
Figure 33 and Figure 34 show the vertical and horizontal projection of the trajectories for the three analyzed cases. From the horizontal projection (Figure 34), it can be seen that all trajectories have a slight deviation to the left of the shooting plane, a phenomenon specific to aerodynamically stabilized slow-rolling rockets. Note that for case 1, with the navigation gain below the limit, the trajectory is more curved than the trajectory in case 2, which is considered a reference case. In contrast, for case 3, with the navigation gain above the maximum limit, the trajectory is less curved than for case 2. From the horizontal projection it can be seen that for case 1 the trajectory of the missile does not reach the target.

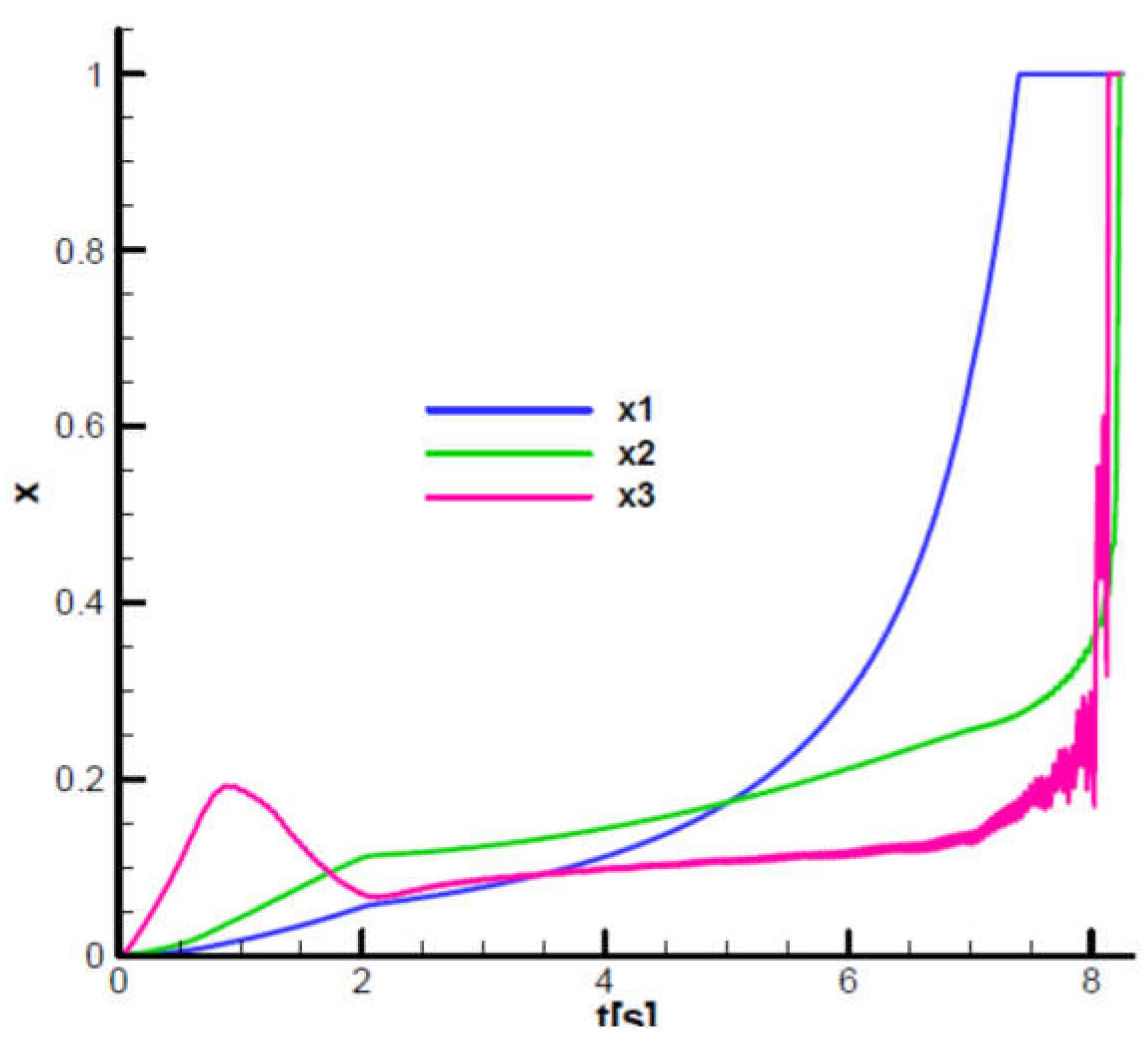
Figure 35 and Figure 36 show the command fill factor and the command phase. Figure 35 shows that for case 1 with a low navigation gain, the fill factor saturates before reaching the target, which leads to the missile's inability to continue the guidance process to the target. On the other hand, in case 3, with a large navigation gain, oscillations of the fill factor in the final phase occur, which, in the end, will also lead to the loss of the target. In contrast, in case 2, reference case, the fill factor increases progressively, reaching a unit value at the moment of reaching the target.

As for the command phase (Figure 36), it varies around 20 degrees due to the fact that the main maneuver is in the vertical plane to which a phase shift

(ε = 20 °)

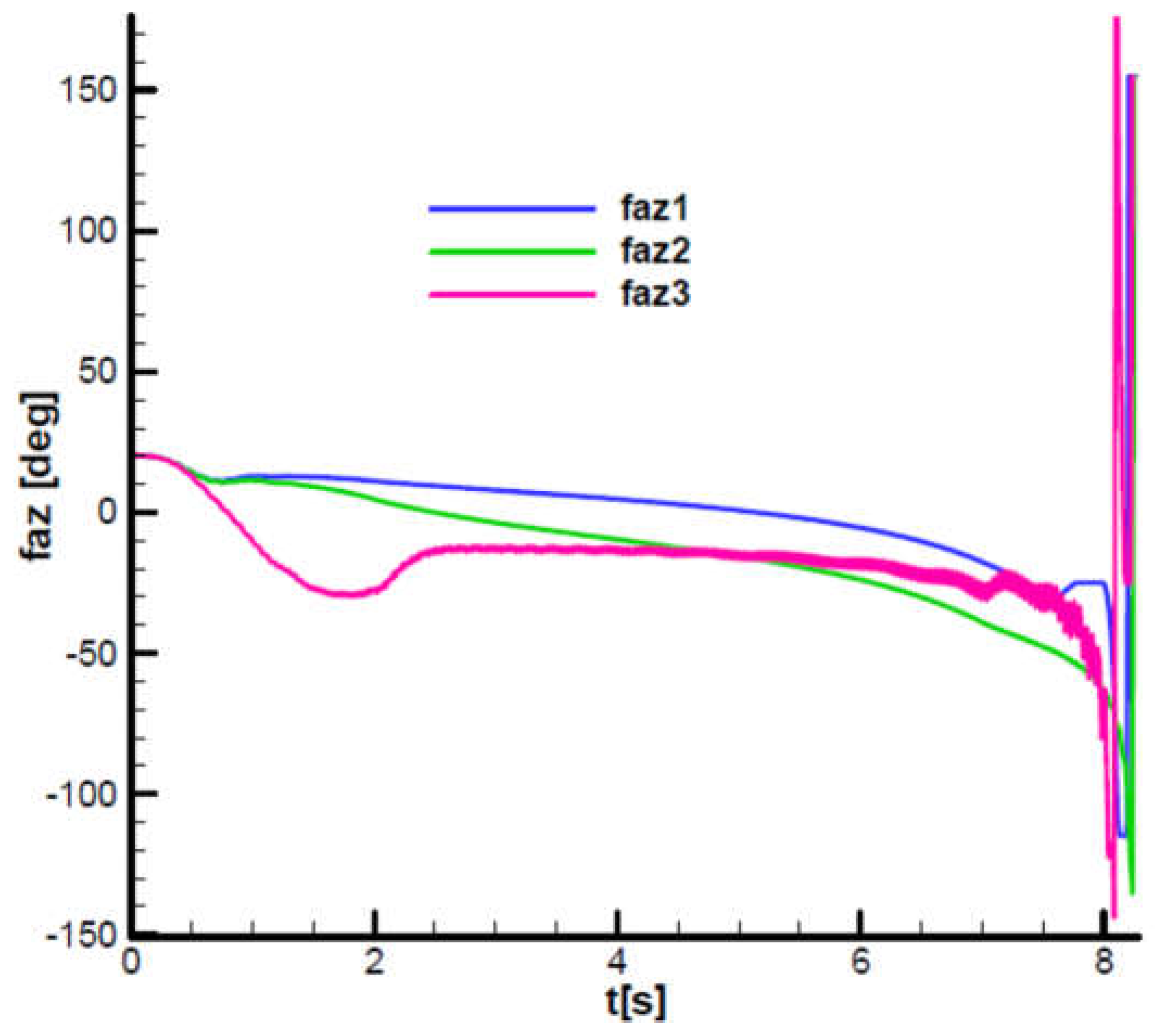
has been added. It is observed for cases 1 and 3 very large phase oscillations in the vicinity of the target, which will ultimately lead to interruption of the guidance process for the two extreme cases. In contrast, in case 2, the command phase progressively decreases until the target is hit.

Figure 37 shows the variation of the parameter

t_{g o}

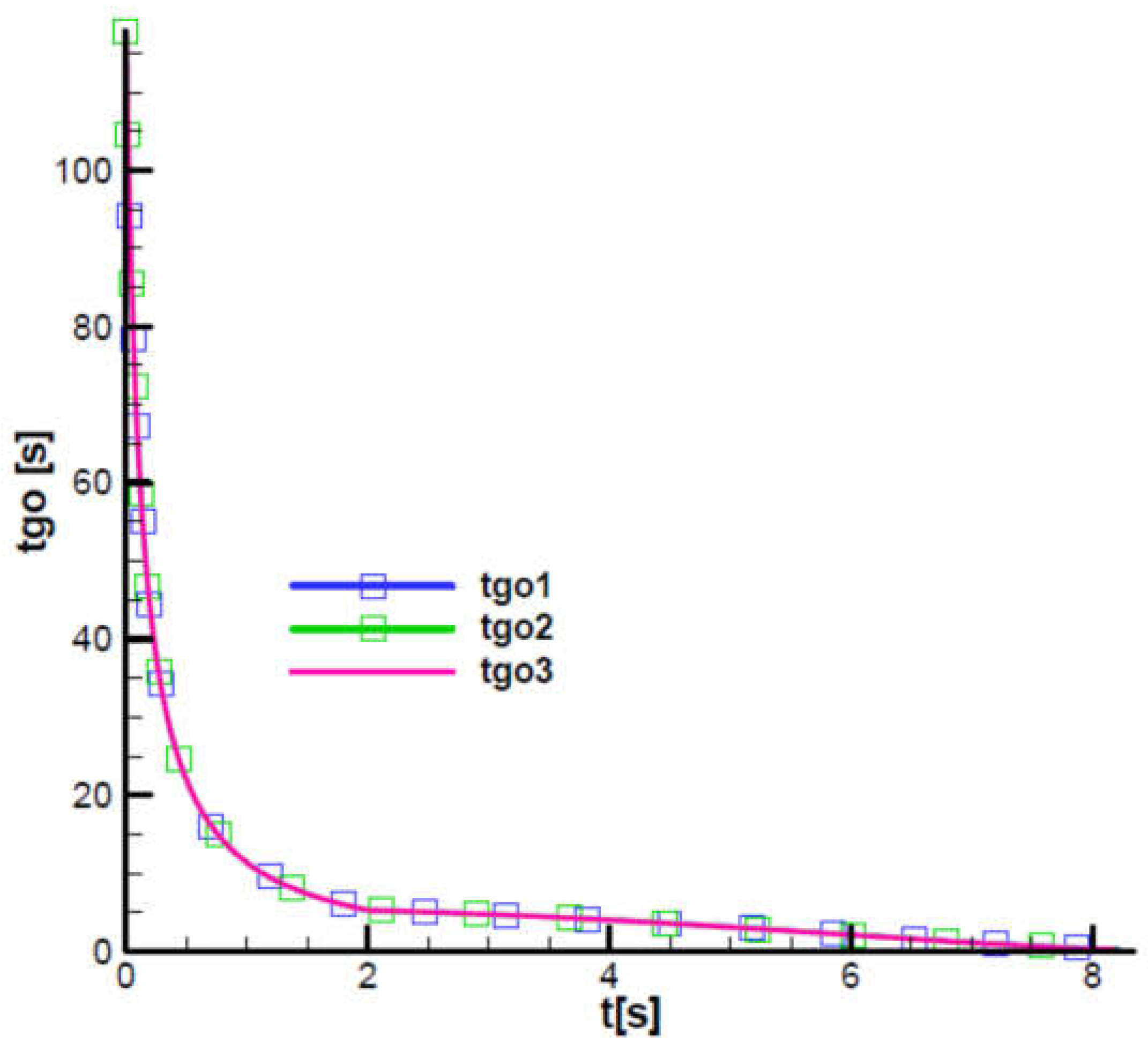
along the trajectory. It ranges from high values (100 s) in the initial phase of the trajectory when the rocket velocity is low; at the entrance to the second phase of flight (after second 2), its values decrease to 5 s, being very low at the end of the second phase, as indicated by stability criterion 1 F-W. Note that the diagram

t_{g o}

is unaffected by the navigation gain values in the three cases analyzed.

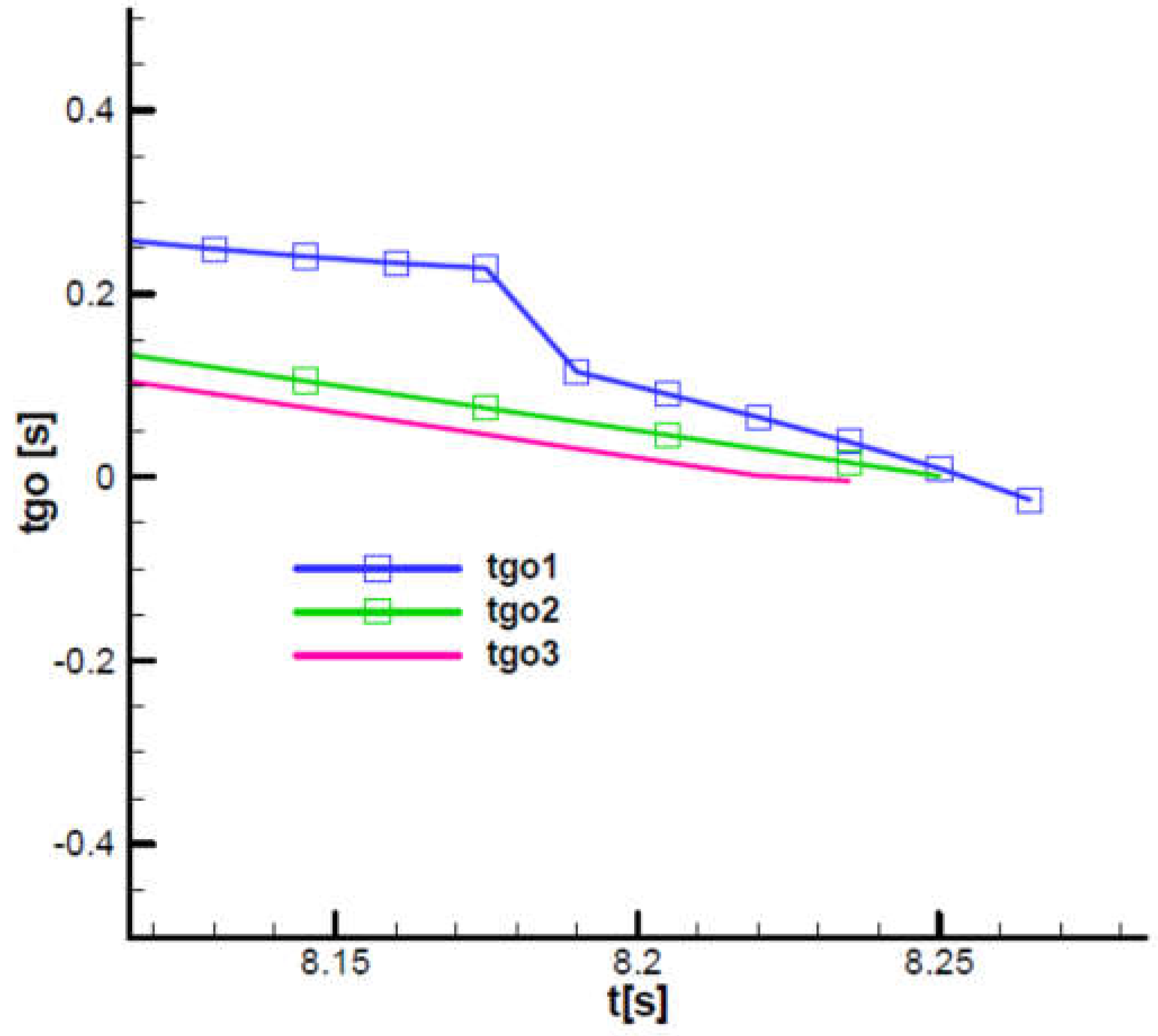
Figure 38 (detail) shows that while for nominal case 2, the evolution of the parameter

t_{g o}

is linearly decreasing towards 0 at the end, in extreme cases 1 and 3, the evolution shows jumps due to oscillations of the command parameters presented above.

11. Conclusions

Several items were covered in the analysis of the stability of the homing missile with single-channel slow-rolling. Thus, in paragraph 2, the equations of general motion were constructed in the body frame, and in section 3, the equations of general motion were obtained in the Resal frame. Paragraph 4 defined the basic motion and maximum maneuver that a single-channel slow-rolling rocket with aerodynamic command can achieve. Next, in paragraph 5, the coupled linear form of the commanded motion of the rolling missile was obtained. Based on the symmetry of the configuration, symmetrical terms were highlighted on the two channels (pitch and yaw), as well as coupling terms as complex quantities. Based on these coupled equations, in paragraph 6 the quality parameters of the motion were highlighted, obtaining the structural scheme for the commanded motion in the case of the rolling missile. Due to the coupling of the two channels, the scheme contains complex parameters specific to this type of missile. Next, in section 7, the guided flight model was built. For this, the kinematic equations of guidance and the equations of the target tracker, in nonlinear and linear form, are defined. Next, the actuator was analyzed, particularly the way the command is formed for the single-channel rolling missile, highlighting the phase and amplitude of the command, thus linking the guidance signal coming from the seeker to the commanded object by the complex form of the actuator. Given the specific mode of forming the command with time-modulated maximum deflection, the command switching function has been defined based on the relative roll angle obtained from summing the control phase and the current roll angle value. Given the possible errors in determining the roll angle and the imprecision in defining the advance angle in compensating the actuator response time to the relative roll angle, an additional phase shift was considered, and the analysis was carried out taking this angle into account. Based on this development, in section 7 the guidance equations that complete the nonlinear 6 DOF model resulted in the body frame, obtaining the model of nonlinear guided flight. On the other hand, the structural diagram of the commanded object obtained in section 5 and the transfer functions for the kinematic guidance block of both seeker and actuator were connected through the guidance loop, obtaining a closed-loop structural diagram of the homing missile. Within this scheme, two parameters are highlighted, namely the time to hit the target (

t_{g o}

) and the navigation constant

(k)

, parameters that will be the main object of analysis in the following sections. In paragraph 8 we start from the established structural diagram and build the characteristic polynomial of the transfer function associated with the closed-loop scheme. Since the scheme contains complex elements (with real and imaginary parts), the characteristic polynomial obtained will also contain complex coefficients. For this reason, the Frank-Wall (F-W) criterion, equivalent to the Routh-Hurwitz (R-H) criterion, was applied to verify the stability of the system polynomials with complex coefficients. Since the obtained characteristic polynomial is of

4^{t h}

order, the stability criterion defines four parameters whose value must be positive to guarantee stability. Because these parameters have complicated expressions and are difficult to handle analytically, rolling was neglected, obtaining the R-H parameters with much simpler expressions that were analyzed analytically. The analysis of the four R-H parameters resulted in four system limitations. Thus, from the first condition R-H resulted a lower limitation

t_{g o}

, from the second condition an eventual upper limitation

t_{g o}

, depending on the values of some parameters. The third condition resulted in an upper limitation for the navigation constant

(k)

, and the fourth condition imposed a lower limitation of the navigation constant. If analytical expressions were obtained for the R-H parameters that could be analyzed, the more complicated F-W parameters were solved using numerical solutions. For this, section 9 defined a calculation model similar to a rocket of the analyzed category for which aerodynamic, mechanical, thrust, time constants and amplification constants were provided, including a value for the time to reach the target

(t_{g o})

and for the navigation constant

(k)

. With this model data, in section 10, the four F-W parameters that checked the stability conditions were evaluated. At the same time, the influence of the main parameters

(k; τ_{c}; ε {; t}_{g o})

on the location of the roots of the characteristic polynomial was evaluated. Next, the analysis was resumed, but this time was performed numerically for the F-W stability parameters, identifying the two limits of the duration of hitting the target (

t_{g o})

and the two limits for the navigation constant

(k)

. The comparison of the results obtained with the two criteria (R-H and F-W) shows that the stability range obtained for the navigation constant is reduced for the case of the rolling rocket by comparison to the case of the no-rolling rocket, especially at the upper limit. In order to verify the results obtained on the linear model with the stability criterion F-W, a tactical situation was built on the fixed target with the nonlinear model in which the flight parameters and the guidance parameters were evaluated for three cases: the first case where the navigation constant was less than the minimum defined limit condition 4 of F-W, the second case where the navigation constant is similar to the value used in linear model analysis within the stability range, and the third case where the navigation constant is greater than the maximum permissible value in condition 3 F-W. The results of the nonlinear model confirmed the limitations obtained with the F-W criterion. In the first and last cases, with the navigation constants out of range, the missile could not hit the target, having large oscillations of the guidance parameters (phase and fill factor) near the target. Instead, in the second case, with the navigation constant in the prescribed range, the missile hit the target, the guidance parameters having an asymptotic behavior up to the vicinity of the target. In parallel with the guidance parameters, the behavior of

t_{g o}

for the three cases was analyzed, finding that in case 1 and 3, it shows jumps in the vicinity of the target. In contrast, for case 2, it is asymptotically close to 0.

Synthesizing, the paper starts from a 6 DOF model in the body frame from which a 6 DOF model in the Resal frame is obtained, which is used to linearize the coupled commanded motion for the case of the slow-rolling missile. The commanded object's structural scheme is obtained, quality parameters are defined, and the quantities obtained have a complex form (with real and imaginary parts) due to the coupling between longitudinal channels. Then, the kinematic guidance equation, the seeker equations and the actuator specific to the slow-rolling single-channel missile are defined by using a switching function. The guidance kinematic equations, the seeker equations, and the actuator relation are linearized in the Resal frame, and the structural diagram of the homing missile is constructed. Starting from this, the characteristic polynomial is determined, which, having complex coefficients, is analyzed with the F-W stability criterion. Based on the analysis, a stability range is determined for the navigation constant

(k)

, and also minimum limit and possibly maximum limit for the time to hit the target

(t_{g o})

are obtained. The stability range defined for the navigation constant on the linear model is finally verified on the nonlinear body frame model.

Starting from the results obtained, in the future paper we intend to analyze the stability of the slow-rotating single-channel remote guided missiles, used to combat armored vehicles

The paper contains four Appendixes, as follows: Appendix A presents in graphical form the main terms of development of aerodynamics coefficients; Appendix B presents in graphical form the linear model flight quality parameters used for the characteristic polynomial of the transfer function; Appendix C presents in graphical form the real and imaginary part of the characteristic polynomial coefficients as well as the four stability parameters F-W; Appendix D detailing the calculation of stability parameters F-W.

Notations

References Frames

0_{0} X_{0} Y_{0} Z_{0}

- The local frame (start frame) with the fixed origin located at sea level, where the axis

X_{0}

is in a conveniently chosen direction, and the axis

Z_{0}

is oriented vertically upwards. The local frame is considered an inertial frame.

O x_{g} y_{g} z_{g}

—The mobile ground frame, with a movable origin, is located at the missile's center of mass. Its axes are parallel to those of the local frame, but the

z_{g}

axis is oriented vertically downwards. The mobile ground frame is considered an inertial frame.

O x y z

—The body frame with the mobile origin is situated at the missile's center of mass. The axis

x

coincides with the configuration's axis of symmetry, pointing towards the missile's top. The axes

y

and

z

are in the configuration's symmetry planes. The body frame is considered a non-inertial frame.

O x^{*} y^{*} z^{*}

- The Resal frame is a quasi-linked body frame that does not participate in its roll motion;

The Equation of Movement Parameters

u, v, w

– The components of velocity

V

in the body frame.

p, q, r

– The components of rotation velocity

Ω

in the body frame.

ψ

-yaw angle;

θ

– pitch angle;

ϕ

– roll angle.

α

- Angle of incidence (attack angle) in the pitch plane;

β

- the angle of incidence (attack angle) in the yaw plane;

m

- Mass;

K

- Angular momentum;

F

- Aerodynamic force;

H

- Aerodynamic torque,

T

- Thrust;

U

- Gasodynamic torque;

G

- Weight;

g

- Gravitational acceleration.

u^{*}, v^{*}, w^{*}

- The components of velocity

V

in Resal frame;

p^{*}, q^{*}, r^{*}

- The components of rotational velocity

Ω^{*}

in Resal frame;

\dot{ϕ} = ω_{x}

- The velocity of rotation of the body frame connected to the rocket in relation to the Resal frame.

The Guidance Parameters

M T

- Line of sight (LOS);

R

- Range;

σ_{y}

σ_{z}

- Absolute angles of the line of sight;

γ_{M}, χ_{M}

– Missile climb angle and flight path azimuth angle;

γ_{T}, χ_{T}

- Target climb angle and flight path azimuth angle;

V_{M}

– Missile velocity;

V_{T}

– Target velocity;

a_{M}

- Missile acceleration;

a_{T}

- Target acceleration;

ω_{y}

ω_{z}

- Angular rate of LOS;

ω_{M}

- Missile angular rate of the velocity vector;

ω_{T}

- Target angular rate of the velocity vector.

K

- Proportional navigation constant (gain);

k

- Modified proportional navigation constant (gain);

t_{g o}

- Time to go.

Appendix A. Aerodynamics

The aerodynamic coefficients are obtained in the body frame.

The reference surface for all coefficients is the cross-section of the fuselage;

The reference length used for torque coefficients is the length of the fuselage;

The momentum coefficients were related to the final position of the rocket's center of mass without fuel.

The main terms in the development of the presented aerodynamic coefficients have been obtained according the work [33] and corrected by dedicated experimental results in the wind tunnel.

Figure A1. Term of axial force coefficient at zero incidence.

Figure A2. Terms of development of the coefficient of axial force with squares of incidences.

Figure A3. The term of development of the coefficient of axial force with the square of the canard angular deflection.

Figure A4. Terms of development of coefficients of normal forces with incidences.

Figure A5. Terms of development of coefficients of normal forces with incidence cube.

Figure A6. Terms of development of normal force coefficients with angular canard deflection.

Figure A7. Terms of development of the torque coefficients in pitch and yaw with incidences.

Figure A8. Terms of development of pitch and yaw torque coefficients with incidence cube.

Figure A9. Terms of development of the torque coefficient in pitch with angular canard deflection.

Figure A10. Terms of development of the roll torque coefficient.

Nonstationary and rotational terms, including Magnus terms, were determined using apparent mass theory from the work [30].

Appendix B

Basic Movement

Figure A11. Equilibrium incidence.

Figure A12. Equilibrium angular canard deflection.

Flight Quality Parameters

Figure A13. Static stability.

Figure A14. Natural pulsation of nutation.

Figure A15. Nutation damping factor.

Figure B39. Command factor.

Figure A16. The time constant of the missile.

Figure A17. Maximum load factor.

Appendix C

Coefficients of the Characteristic Polynomial. i - Initial; f - Final

Figure A18. Coefficient of the cubic term – the real part.

Figure A19. Coefficient of the quadratic term – the real part.

Figure A20. Coefficient of the term of the first order – the real part.

Figure A21. Free term coefficient – the real part.

Figure A22. Coefficient of the cubic term – the imaginary part.

Figure A23. The coefficient of the term square - the imaginary part.

Figure A24. Coefficient of the term of the first order - the imaginary part.

Figure A25. Free term coefficient - the imaginary part.

Stability Parameters F-W. i-Initial; f- Final

Figure A26. First parameter F-W.

Figure A27. Second parameter F-W.

Figure A28. Third parameter F-W.

Figure A29. Fourth parameter F-W.

Appendix D. Frank-Wall Stability Criterion for the 4th Order Polynomial

Let the polynomial of order 4 with complex coefficients be:

P (s) = s^{4} + (p_{1} + i q_{1}) s^{3} + (p_{2} + i q_{2}) s^{2} + (p_{3} + i q_{3}) s + (p_{4} + i q_{4}) .

(D 1)

In order to verify that the real part of the roots is negative, according to [20], an associated polynomial of the form is constructed:

Q (s) = p_{1} s^{3} + i q_{2} s^{2} + p_{3} s + i q_{4},

(D 2)

After which, the ratio of the polynomials is put in the form:

\frac{Q (s)}{P (s)} = \frac{1}{a_{1} s + b_{1} + 1 + \frac{1}{a_{2} s + b_{2} + \frac{1}{a_{3} s + b_{3} + \frac{1}{a_{4} s + b_{4}}}}}

(D 3)

The stability condition F-W is formulated by two theorems in the paper [20].

The first theorem shows that for the polynomial of order

n

(D 1), with complex coefficients, to have all its roots on the negative real side, it is necessary and sufficient that

a_{1} > 0; \dots; a_{n} > 0

and that

b_{1}, \dots b_{n}

be pure complex numbers or null.

The second theorem shows that the polynomial of order

n

, with complex coefficients, has as many roots on the positive real side as values

a_{1}; \dots; a_{n}

are negative.

In the same work, an algorithm for obtaining parameters

a_{1}, \dots; a_{n}

b_{1}, \dots b_{n}

is indicated, which will be briefly presented below.

Thus, the coefficients of the two polynomials are denoted by:

P (s) = α_{00} s^{4} + α_{01} s^{3} + α_{02} s^{2} {+ α}_{03} s {+ α}_{04}

; Q (s) = α_{11} s^{3} + α_{12} s^{2} + α_{13} s {+ α}_{14}

(D 4)

After which, for the 4th order polynomial is obtained successively:

β_{11} = α_{01} - α_{00} \frac{α_{12}}{α_{11}}; β_{12} = α_{02} - α_{00} \frac{α_{13}}{α_{11}}; β_{13} = α_{03} - α_{00} \frac{α_{14}}{α_{11}}; β_{14} = α_{04}; α_{22} = β_{12} - β_{11} \frac{α_{12}}{α_{11}}; α_{23} = β_{13} - β_{11} \frac{α_{13}}{α_{11}} α_{24} = β_{14} - β_{11} \frac{α_{14}}{α_{11}}; β_{22} = α_{12} - α_{11} \frac{α_{23}}{α_{22}}; β_{23} = α_{13} - α_{11} \frac{α_{24}}{α_{22}}; β_{24} = α_{14}; α_{33} = β_{23} - β_{22} \frac{α_{23}}{α_{22}}; α_{34} = β_{24} - β_{22} \frac{α_{24}}{α_{22}} β_{33} = α_{23} - α_{22} \frac{α_{34}}{α_{33}}; β_{34} = α_{24} α_{44} = β_{34} - β_{33} \frac{α_{34}}{α_{33}} β_{44} = α_{34}

(D 5)

Based on these intermediate parameters, the parameters of interest can be determined:

a_{1} = \frac{α_{00}}{α_{11}}; a_{2} = \frac{α_{11}}{α_{22}}; a_{3} = \frac{α_{22}}{α_{33}}; a_{4} = \frac{α_{33}}{α_{44}}

(D 6)

respectively:

b_{1} = \frac{β_{11}}{α_{11}} - 1; b_{2} = \frac{β_{22}}{α_{22}}; b_{3} = \frac{β_{33}}{α_{33}}; b_{4} = \frac{β_{44}}{α_{44}}

(D 7)

Based on the algorithm described above, for the 4th order polynomial, the following expressions were obtained:

α_{00} = 1; α_{01} = p_{1} + i q_{1}; α_{02} = p_{2} + i q_{2}; α_{03} = p_{3} + i q_{3}; α_{04} = p_{4} + i q_{4}; α_{11} = p_{1}; α_{12} = {i q}_{2}; α_{13} = p_{3}; α_{14} = {i q}_{4}; β_{11} = \frac{p_{1}^{2} + i (p_{1} q_{1} - q_{2})}{p 1}; β_{12} = \frac{{p_{1} p}_{2} - p_{3} + i q_{2} p_{1}}{p_{1}}; β_{13} = \frac{{p_{1} p}_{3} + i ({p_{1} q}_{3} - q_{4})}{p_{1}}; β_{14} = p_{4} + i q_{4}; α_{22} = \frac{{p_{1}^{2} p}_{2} - p_{1} p_{3} + p_{1} q_{1} q_{2} - q_{2}^{2}}{p_{1}^{2}}; α_{23} = i \frac{({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2})}{p_{1}^{2}}; α_{24} = \frac{({p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4})}{p_{1}^{2}} β_{22} = i ({p_{1}^{2} p}_{2} q_{2} - p_{1} p_{3} q_{2} + p_{1} q_{1} q_{2}^{2} - q_{2}^{3} - {p_{1}^{3} q}_{3} + p_{1}^{2} q_{4} + p_{1}^{2} q_{1} p_{3} - p_{1} p_{3} q_{2}) \frac{a_{2}}{p_{1}^{3}}; β_{23} = ({p_{1}^{2} p}_{2} p_{3} - p_{1} p_{3}^{2} + p_{1} q_{1} q_{2} p_{3} - q_{2}^{2} p_{3} {{- p}_{4} p}_{1}^{3} + p_{1}^{2} q_{1} q_{4} - {p_{1} q}_{2} q_{4}) \frac{a_{2}}{p_{1}^{3}}; β_{24} = {i q}_{4}; α_{33} = \frac{a_{2}^{2}}{p_{1}^{5}} D; α_{34} = i E; β_{33} = i \frac{({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2}) - a_{3} p_{1}^{2} E}{p_{1}^{2}} β_{34} = \frac{({p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4})}{p_{1}^{2}}; α_{44} = \frac{{p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4}}{p_{1}^{2}} + \frac{({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2}) a_{3} a_{2}}{p_{1}^{3}} E - \frac{a_{3}^{2} a_{2}}{p_{1}} E^{2}; β_{44} = i E;

(D 8)

where it was denoted by:

D = ({p_{1}^{2} p}_{2} - p_{1} p_{3} + p_{1} q_{1} q_{2} - q_{2}^{2}) ({p_{1} p}_{2} p_{3} - p_{3}^{2} + {p_{1} q}_{3} q_{2} + p_{1} q_{1} q_{4} {- p}_{4} p_{1}^{2} - 2 q_{4} q_{2}) - {({p_{1}^{2} q}_{3} - p_{1} q_{1} p_{3} + p_{3} q_{2} - p_{1} q_{4})}^{2} E = q_{4} - \frac{a_{2}^{2}}{p_{1}^{6}} ({p_{1}^{2} p}_{2} q_{2} + p_{1} q_{1} q_{2}^{2} - q_{2}^{3} + p_{1}^{2} q_{1} p_{3} - {p_{1}^{3} q}_{3} - 2 p_{1} p_{3} q_{2} + p_{1}^{2} q_{4}) ({p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4})

(D 9)

Hence the following:

a_{1} = \frac{1}{p_{1}}; a_{2} = \frac{p_{1}^{3}}{{p_{1}^{2} p}_{2} - p_{1} p_{3} + p_{1} q_{1} q_{2} - q_{2}^{2}} a_{3} = \frac{p_{1}^{6}}{a_{2}^{3}} D^{- 1}; a_{4} = \frac{p_{1}^{2}}{a_{3} a_{2}} {[\frac{{p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4}}{p_{1}} + \frac{({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2}) a_{3} a_{2}}{p_{1}^{2}} E - a_{3}^{2} a_{2} E^{2}]}^{- 1} b_{1} = i \frac{(p_{1} q_{1} - q_{2})}{p_{1}^{2}} b_{2} = i \frac{({p_{1}^{2} p}_{2} q_{2} - p_{1} p_{3} q_{2} + p_{1} q_{1} q_{2}^{2} - q_{2}^{3} - {p_{1}^{3} q}_{3} + p_{1}^{2} q_{4} + p_{1}^{2} q_{1} p_{3} - p_{1} p_{3} q_{2}) a_{2}}{({p_{1}^{2} p}_{2} - p_{1} p_{3} + p_{1} q_{1} q_{2} - q_{2}^{2}) p_{1}}; b_{3} = i \frac{[({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2}) - a_{3} p_{1}^{2} E] p_{1}^{3}}{a_{2}^{2} D}; b_{4} = i \frac{E p_{1}^{3}}{({p_{4} p}_{1}^{2} + p_{1} q_{1} q_{4} - q_{2} q_{4}) p_{1} + ({p_{1}^{2} q}_{3} - p_{1} q_{4} - p_{1} q_{1} p_{3} + p_{3} q_{2}) a_{3} a_{2} E - {a_{3}^{2} a_{2} p_{1}^{2} E}^{2}}

(D 10)

From the previous relation, it is observed that

b_{1}; \dots; b_{n}

are pure complex numbers in all cases, which, according to the values

p_{1}, p_{2}, p_{3}, p_{4},

and

q_{1}, q_{2}, q_{3}, q_{4},

may be null. The only conditions to be verified or imposed are that

a_{1} > 0, a 2 > 0, a 3 > 0, a n d a_{4} > 0

Check for non-rolling case.

For the case without rotation, the four parameters become.

a_{1} = \frac{1}{p_{1}}; a_{2} = \frac{p_{1}^{2}}{{p_{1} p}_{2} - p_{3}}; a_{3} = \frac{{({p_{1} p}_{2} - p_{3})}^{2}}{p_{1} ({p_{1} p}_{2} p_{3} - p_{3}^{2} {{- p}_{4} p}_{1}^{2})}; a_{4} = \frac{p_{1}}{{p_{4} a}_{3} a_{2}} = \frac{{p_{1} p}_{2} p_{3} - p_{3}^{2} {{- p}_{4} p}_{1}^{2}}{p_{4} ({p_{1} p}_{2} - p_{3})},

(D 11)

Which leads to the following stability conditions:

p_{1} > 0; {p_{1} p}_{2} - p_{3} > 0; {p_{1} p}_{2} p_{3} - p_{3}^{2} {{- p}_{4} p}_{1}^{2} > 0; p_{4} > 0 .

(D 12)

On the other hand, the Routh – Hurwitz conditions for the 4th order polynomial with real coefficients are obtained from the matrix of coefficients constructed as follows:

|\begin{matrix} p_{1} & p_{3} & 0 & 0 \\ 1 & p_{2} & p_{4} & 0 \\ 0 & p_{1} & p_{3} & 0 \\ 0 & 1 & p_{2} & p_{4} \end{matrix}|

(D 13)

The condition is that all determinants in the table are positive.

In this case, it follows:

p_{1} > 0; {p_{1} p}_{2} - p_{3} > 0; {p_{1} p}_{2} p_{3} - p_{3}^{2} {{- p}_{4} p}_{1}^{2} > 0; p_{4} > 0

(D 14)

conditions identical to conditions F-W (D 12)for the case of real coefficients.

References

xxx, "https://en.wikipedia.org/wiki/FIM-92_Stinger," [Online].
xxx, "https://en.wikipedia.org/wiki/9K32_Strela-2," [Online].
xxx, "https://en.wikipedia.org/wiki/9K38_Igla," [Online].
xxx, "https://en.wikipedia.org/wiki/9K333_Verba," [Online].
Hu, X.; Yang, S.X. Coning motion instability of spinning missiles induced by the delay of strap-down seeker. CHINESE JOURNAL OF AERONAUTICS 2021, 33, 3360–3368. [Google Scholar] [CrossRef]
Hu, Shaoyong; Wang, Jiang ;Wang, Yuchen; Tian, Song, "Stability Limits for the Velocity Orientation Autopilot of Rolling Missiles IEEE ACCESS, vol. 9, pp. 110940-110951, 2021. [CrossRef]
Hu, Xiao ; Yang, Shuxing; Xiong, Fenfen; Zhang, Guoqing, "Stability of spinning missile with homing proportional guidance law," AEROSPACE SCIENCE AND TECHNOLOGY, vol. 71, pp. 546-555, 2017.
Suiçmez, E.C.; Kutay, A.T. , "Single channel digital controller design for a high spinning rate rolling airframe missile," AERONAUTICAL JOURNAL,, vol. 126, no. 1305, pp. 1815-1833, NOV 2022. [CrossRef]
Karimi, J. A new closed form solution for dynamic stability analysis of rolling airframes having one pair on-off actuator. Aviation, Open Access 2021, 25, 92–103. [Google Scholar] [CrossRef]
Botez, RM; Chelaru, V; Parvu, P; Gheorghe, C. Calculus model for a rolling guided missile. JOURNAL OF VIBRATION AND CONTROL 2001, 7, 863–889. [Google Scholar] [CrossRef]
Chelaru, T.-V. , Constantinescu, C. In E.,, "Theoretical and experimental solutions for multistage quasi-guided rocket.," in Proceedings of the International Astronautical Congress, IAC, Washington; 2019. [Google Scholar]
Zheng, Qiushi; Zhou, Zhiming, "Flight Stability of Canard-Guided Dual-Spin Projectiles with Angular Rate Loops," INTERNATIONAL JOURNAL OF AEROSPACE ENGINEERING, 2020. [CrossRef]
Gao, Qing-Feng; Xia, Qun-Li; Fang, Shu-Zhou; Chen, Luo-Jing; Liu, Xu-Hui, Autopilot design of single channel rolling missile. Transaction of Beijing Institute of Technology 2011, 31, 670–674.
Zheng, Duo; Lin,Lin, Defu ; Wang, Jiang; Xu, Xinghua, "Dynamic stability of rolling missiles employing a two-loop autopilot with consideration for the radome aberration parasitic feedback loop. AEROSPACE SCIENCE AND TECHNOLOGY 2017, 61, 1–10. [CrossRef]
Tian, Song; Lin, Defu; Wang, Jiang; Li, Bin, "Dynamic stability of rolling missiles with angle-of-attack feedback three-loop autopilot considering parasitic effect," AEROSPACE SCIENCE AND, TECHNOLOGY, vol. 71, pp. 592-602, DEC 2017.
Zheng, Duo ; Lin, Defu; Xu, Xinghua; Tian, Song, "Dynamic stability of rolling missile with proportional navigation & PI autopilot considering parasitic radome loop," AEROSPACE SCIENCE AND TECHNOLOGY, vol. 67, pp. 41-48, AUG 2017. [CrossRef]
Qin, Sheng-jie; Zhang, Fu-xue, "A Combination of Silicon Micro-gyroscope that Application Rotary Missile Attitude Control System," in 2011 INTERNATIONAL CONFERENCE ON PHYSICS SCIENCE AND TECHNOLOGY (ICPST), Hong Kong,, 2011.
Yan, Xiaolong ; Chen, Guoguang; Tian, Xiaoli, "Two-Step Adaptive Augmented Unscented Kalman Filter for Roll Angles of Spinning Missiles Based on Magnetometer Measurements, MEASUREMENT & CONTROL," vol. 51, no. 3-4, pp. 73-82, APR-MAY 2018.
Kocetkov,V.T, Polovko,A.M., Ponomarev, B.M.,Theory of self-guided and remote-controlled missile systems, Moskva: Nauka, 1964.
E. Frank, "On the zeros of polynomials with complex coefficients. Bull. Amer. Math. Soc. 1946, 52, 144–157. [CrossRef]
xxx, " ISO 1151 -1:1988; -2: 1985-3:1989, " 1989.
xxx, "STP M 40406-99 The Commanded Missile System - Terminology and Symbols," Bucharest, 1998.
Niţă, M.M. , Andreescu, D.ŞT., Rocket flight, Bucharest: Militara, 1964.
Chelaru,T.V., Dynamics of Flight – Guided Missile, 2nd Ed Revised and Added, Bucharest: Printech, 2004, p. 434.
Kuzovkov, N.T. ,, Flight stabilization systems, ballistic missile and anti-aircraft missile, Moskva: Visaia Skola, 1976.
Belea, C. , Lungu, R., Cismaru, C., Gyroscopic systems and their applications, Craiova: Scrisul Romanesc, 1986.
Hacker, T. , Stability and control in flight theory, Bucharest: Romanian Academy, 1968.
xxx, "STP M 40455-99 The Guided Missile System - Terminology and Symbols," Bucharest, 1998.
Carpantier,R., Guidance des avions et des missiles aerodynamiques, Tom I,II,III, lit. ENSAE, 1989.
J. Nielsen, Missile Aerodynamics, New-York, Toronto, London, : McGraw-Hill Book Company, Inc., 1960.
V. Sviatoduh, Dynamics of spatial motion of guided missiles, Moskva: Masinostroenie, 1969.
Ben-Asher, J.Z. , Yaesh Isaac, Advanced in Missile Guidance Theory, Preston,Virginia, : American Institute of Aernautics and Astronautics, 1998.
Niţă, M.M. , Moraru, FL., Patraulea, R., Airplanes and missiles, design concepts, Bucharest: Militară, 1985.

1	1 Disturbance due to wind, from the point of view of the analyzed motion, can induce only additional incidences; the variation in velocity modulus, being specific to slow motion.

Figure 1. Slow-rolling single-channel homing missile.

Figure 2. The Resal frame and body frame connected to the rocket.

Figure 3. Basic motion elements in the case of the aerodynamically controlled missile.

Figure 4. Structural scheme of commanded movement for slow-rolling missile.

Figure 5. Orientation of the guiding frame with respect to the local frame [28].

Figure 6. Decomposition of velocities in the guiding frame.

Figure 7. Decomposition of accelerations in the guiding frame.

Figure 8. Expression of the guidance command in polar coordinates.

Figure 9. The shape of the canard deflection for one period of missile roll.

Figure 10. The structural scheme for the homing missile with single-channel and slow roll rotation.

Figure 11. Airframe sketch (all dimensions are in mm).

Figure 12. Thrust diagram.

Figure 13. The roots of the characteristic polynomial in phase 2-initial

(k = 3; τ_{c} = 0.05 [s]; ε = 20 °; t_{g o} = 5 [s])

Figure 13. The roots of the characteristic polynomial in phase 2-initial

(k = 3; τ_{c} = 0.05 [s]; ε = 20 °; t_{g o} = 5 [s])

Figure 14. The roots of the characteristic polynomial in phase 2 -final

(k = 3; τ_{c} = 0.05 [s]); ε = 20 °; t_{g o} = 5 [s]

Figure 14. The roots of the characteristic polynomial in phase 2 -final

(k = 3; τ_{c} = 0.05 [s]); ε = 20 °; t_{g o} = 5 [s]

Figure 15. The roots of the characteristic polynomial in phase 2 -initial (

k = 30; τ_{c} = 0.05 [s]; ε = 20 °; t_{g o} = 5 [s]

Figure 15. The roots of the characteristic polynomial in phase 2 -initial (

k = 30; τ_{c} = 0.05 [s]; ε = 20 °; t_{g o} = 5 [s]

Figure 16. The roots of the characteristic polynomial in phase 2 -final (

k = 30; τ_{c} = 0.05 [s]; ε = 20 °; t_{g o} = 5 [s])

Figure 16. The roots of the characteristic polynomial in phase 2 -final (

k = 30; τ_{c} = 0.05 [s]; ε = 20 °; t_{g o} = 5 [s])

Figure 17. The roots of the characteristic polynomial in phase 2 -initial

(k = 3; τ_{c} = 0.1 [s]; ε = 20 °; t_{g o} = 5 [s])

Figure 17. The roots of the characteristic polynomial in phase 2 -initial

(k = 3; τ_{c} = 0.1 [s]; ε = 20 °; t_{g o} = 5 [s])

Figure 18. The roots of the characteristic polynomial in phase 2 -final

(k = 3; τ_{c} = 0.1 [s]; ε = 20 °; t_{g o} = 5 [s])

Figure 18. The roots of the characteristic polynomial in phase 2 -final

(k = 3; τ_{c} = 0.1 [s]; ε = 20 °; t_{g o} = 5 [s])

Figure 19. The roots of the characteristic polynomial in phase 2 -initial

(k = 3; τ_{c} = 0.05 [s]; ε = 0 °; t_{g o} = 5 [s])

Figure 19. The roots of the characteristic polynomial in phase 2 -initial

(k = 3; τ_{c} = 0.05 [s]; ε = 0 °; t_{g o} = 5 [s])

Figure 20. The roots of the characteristic polynomial in phase 2 -final

(k = 3; τ_{c} = 0.05 [s]; ε = 0 °; t_{g o} = 5 [s])

Figure 20. The roots of the characteristic polynomial in phase 2 -final

(k = 3; τ_{c} = 0.05 [s]; ε = 0 °; t_{g o} = 5 [s])

Figure 21. The roots of the characteristic polynomial in phase 2 -initial

(k = 3; τ_{c} = 0.05 [s]; ε = 20 ° {; t}_{g o} = 1 [s])

Figure 21. The roots of the characteristic polynomial in phase 2 -initial

(k = 3; τ_{c} = 0.05 [s]; ε = 20 ° {; t}_{g o} = 1 [s])

Figure 22. The roots of the characteristic polynomial in phase 2 -final

(k = 3; τ_{c} = 0.05 [s]; ε = 20 °; t_{g o} = 1 [s])

Figure 22. The roots of the characteristic polynomial in phase 2 -final

(k = 3; τ_{c} = 0.05 [s]; ε = 20 °; t_{g o} = 1 [s])

Figure 23. The lower limit

t_{g o}

from the first condition F-W,

τ_{c} = 0.05 [s]

Figure 23. The lower limit

t_{g o}

from the first condition F-W,

τ_{c} = 0.05 [s]

Figure 24. The lower limit

t_{g o}

from the first condition F-W,

τ_{c} = 0.1 [s]

Figure 24. The lower limit

t_{g o}

from the first condition F-W,

τ_{c} = 0.1 [s]

Figure 25. The upper limit

t_{g o}

from the second condition F-W,

τ_{c} = 0.05 [s]

Figure 25. The upper limit

t_{g o}

from the second condition F-W,

τ_{c} = 0.05 [s]

Figure 26. The upper limit

t_{g o}

from the second condition F-W,

τ_{c} = 0.1 [s]

Figure 26. The upper limit

t_{g o}

from the second condition F-W,

τ_{c} = 0.1 [s]

Figure 27. The upper limit of the navigation constant

k

(

ε = 20 °)

Figure 27. The upper limit of the navigation constant

k

(

ε = 20 °)

Figure 28. Lower limit of the navigation constant

k

Figure 28. Lower limit of the navigation constant

k

Figure 29. The upper limit of the navigation constant

k

without phase shift (

ε = 0 °)

Figure 29. The upper limit of the navigation constant

k

without phase shift (

ε = 0 °)

Figure 30. Navigation gain.

Figure 31. Velocity diagram.

Figure 32. Roll velocity diagram.

Figure 33. Target interception – vertical view.

Figure 34. Target interception – horizontal view.

Figure 35. Command fill factor.

Figure 36. Command phase.

Figure 37. Time to hit the target.

Figure 38. Time to hit the target – detail.

Table 1. Mechanical characteristics.

Phase	Mass m[kg]	Center of Mass $x_{cm}$ [m]	Roll Inertial Moment A [ $kg m^{2}$ ]	Yaw/Pitch Inertial Moment B $[kg m^{2}]$	Time [s]
Initial	9.85	0.707	0.00748	1.39	0
Intermediate 1	6.72	0.615	0.00589	1.11	2
Final	5.48	0.579	0.00526	1.00	7

¹After finishing the booster.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Stability of Single Channel Homing Slow-Rolling Missile

Abstract

1. Introduction

2. Equations of the General Motion in the Body Frame

2.1. Kinematic Equations Using Attitude Angles

2.2. Dynamic Equations of Motion in the Body Frame

3. Equations of the General Motion in the Resal Frame

4. Basic Movement and Maximum Maneuverability

4.1. Basic Movement

4.2. Maximum Maneuverability

5. The Linear form of the Equations of Rapid Motion Around the Center of Mass

6. Quality Parameters of the Motion with Slow-Rolling

7. The Guided Flight Model

7.1. Kinematic Guidance Equations

7.2. Linear form of Kinematic Guidance Equations

7.3. Target Tracker Equations

7.4. The Command for Slow-Rolling Single-Channel Missile

8. The Guided Flight Stability on the Linear Model

8.1. Determination of Stability Parameters

8.2. Non-Rotational Case Analysis

9. Calculus Model

9.1. Aerodynamic Characteristics

9.2. Mechanical and Reference Characteristics

9.3. Thrust Characteristic

9.4. Time Constants and Controller Gains

10. Stability Analysis of the Single Channel Homing Slow-Rolling Missile

10.1. Organization of Results

10.2. The Root Locus

10.3. Constraints due to Stability Conditions

Navigation Constant

10.4. Stability Analysis Based on the Nonlinear Model

11. Conclusions

Notations

References Frames

The Equation of Movement Parameters

The Guidance Parameters

Appendix A. Aerodynamics

Appendix B

Basic Movement

Flight Quality Parameters

Appendix C

Coefficients of the Characteristic Polynomial. i - Initial; f - Final

Stability Parameters F-W. i-Initial; f- Final

Appendix D. Frank-Wall Stability Criterion for the 4th Order Polynomial

References

MDPI Initiatives

Important Links

Subscribe