Prerpints.org logo
Preprint
Article

Building an Analog Circuit Synapse for Deep Learning Neuromorphic Processing

Altmetrics

Downloads

160

Views

106

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 May 2024

Posted:

28 May 2024

You are already at the latest version

Alerts
Abstract
In this article, we propose a circuit to imitate the behavior of a Reward-Modulated Spike-Timing-Dependent Plasticity synapse. When two neurons in adjacent layers produce spikes, each spike modifies the thickness of the common synapse. As a result, the synapse’s ability to conduct impulses is controlled, leading to an unsupervised learning rule. By introducing a reward signal, reinforcement learning is enabled by redirecting the growth and shrinkage of synapses based on signal feedback from the environment. The proposed synapse manages the convolution of the emitted spike signals to promote either the strengthening or weakening of the synapse, which is represented as the resistance value of a memristor device. As memristors have a conductance range that may differ from the available current input range of typical CMOS neuron designs, the synapse circuit can be adjusted to regulate the spike’s amplitude current to comply with the neuron. The circuit described in this work allows for the implementation of fully interconnected layers of neuron analog circuits. This is achieved by having each synapse reconform the spike signal, thus removing the burden of providing enough power from the neurons to each memristor. The synapse circuit was tested using a CMOS analog neuron described in the literature. Additionally, the article provides insight into how to properly describe the hysteresis behavior of the memristor in Verilog-A code. The testing and learning capabilities of the synapse circuit are demonstrated in simulation using the Skywater-130nm process. The article’s main goal is to provide the basic building blocks for Deep Neural Neural Networks relying on spiking neurons and memristors as the basic processing elements to handle spike generation, propagation, and synaptic plasticity.
Keywords: 
Subject: Computer Science and Mathematics  -   Hardware and Architecture

1. Introduction

Neural networks are mathematical models that can be used to approximate functions. They work by adjusting the strengths of connections between neurons, called synaptic weights, based on the difference between the actual output and the desired output. This difference, called the error function, helps the network learn. Different learning rules are used in different contexts, such as control signals in control theory or policies in machine learning. Reinforcement learning (RL) methodologies are useful in tasks where scarcely available reward signals are provided, or well, the exact relationship between the system’s state vector s t , the current action, a t , and the reward signal is not clearly mapped into a function (i.e., a model-free system). Generative Adversarial Networks involve two neural networks that compete with each other for content generation. The goal of the first net is to generate new content (i.e., images, audio) indistinguishable from training data. The second network assesses the effectiveness of the first one by assigning a score to be maximized. DDPG, TD3, and Soft Actor-Critic neural architectures are advanced control algorithms that use two, three, and even four neural networks working together to produce the best results in control tasks. These algorithms are particularly useful when modeling the system and creating a proper policy is difficult. However, the training process can be computationally expensive, and conventional Von Neumann architectures are not optimal for this task because the storage and processing units are separated from each other, and additional circuitry is required to feed the processor with the necessary data. Spiking Neural Networks (SNN) attempt to replicate the cognitive mechanisms of biological brains by simulating the dynamics of neurons and synapses. This involves encoding and decoding information as spiking activity. Neuromorphic computing aims to create hardware that mimics this neuronal model, to achieve energy-efficient hardware with high throughput, embedded learning capabilities, and low energy consumption. The circuit implementation can be in the digital or analog domain. Digital neuromorphic computing involves developing digital hardware that can solve the differential equations of SNNs as quickly as possible. Examples of this type of hardware include Intel’s Loihi [1] and IBM’s Truenorth. This technology has already shown promising results regarding power efficiency and is a research platform compatible with current digital technologies. Digital to Analog Converters (DACs) and Analog to Digital Converters (ADCs) are used to quantify or binarize signals. However, using these converters always results in a quantization error, as larger binary words require larger DACs and ADCs. This implies that a greater number of quantization levels would lead to a smaller quantization error but larger circuit implementations without being reflected in better performance [2].
However, working entirely in the analog domain eliminates the quantization problem by treating information as circuit currents, voltages, charge, and resistance values. This approach allows for implementing neurons in analog counterparts, synapses with memristors, and additional circuitry in crossbar arrays. Using Kirchoff’s laws, values can be added instantaneously.
The conductance in each memristor enables in-memory computing and suppresses the von Neumann bottleneck. Using SNN models to assemble RL architectures can be counterproductive when executed on typical CPUs and GPUs. However, the same models can lead to high-performance and low-energy implementations if executed on neuromorphic devices, especially analog ones. However, as circuit analog design can be a challenging and iterative process, most frameworks/libraries or available tools for SNN are implemented in current digital technologies. For instance, Nest, SNN Torch, and Nengo [3,4,5] are software libraries that deploy SNN easily but are executed into current CPUs and GPUs. NengoFPGA is a Nengo extension to compile the network architecture into FPGA devices, which results in a digital neuromorphic hardware implementation. Therefore, most available tools and frameworks for SNN are currently implemented using existing technologies. Intel’s Lava is a compiler that uploads software-modeled SNN into Loihi chip. Both extensions, referred to as frameworks, result in digital neuromorphic implementations that are more efficient than running on von Neumann architectures. However, they are still digital. At [6], a population encoding framework for SNN is presented purely in the analog domain. The framework uses bandpass filters to distribute input signals into input currents for analog neurons evenly. However, storage and learning are not included in this framework. At [7], a Trainable Analog Block (TAB) is proposed that only considers encoding of signals. Information storage and obtention is left outside the scope of the study, as synapse values are computed offline and stored as binary words. To our knowledge, no end-to-end analog neuromorphic framework is available, including encoding, learning, and decoding in purely analog blocks.
This article presents a novel reward signal synapse circuit designed in the Skywater 130nm technological node to enable supervised learning into analog SNN circuits. The proposed structure enables a reward signal to switch between potentiation/depreciation of the synapse and spike reconformation to be implemented into a n × m fully interconnected neuron layers without having loss of power into the spikes, and also current decoupling, to supply the proper amount of current to the receptor neurons. Section 2 explains the modeling of SNN and the implementation of RSTDP learning rule dynamics in the synapse circuit. Section 3 describes the implementation of the memristor model in Verilog-A and the synapse circuit. Section 4 describes the neuron CMOS model used to test the synapse. A 2 × 1 neuron network structure is tested in simulation, demonstrating adequate learning capabilities. Section 5 consists of discussion, conclusions, and future work.

2. Preeliminars

Now, lets proceed by describing briefly the system dynamics of neurons, synapses and learning algorithms for SNN´s, in order to understand the resulting circuitry, down further the text.

2.1. Spiking Neural Networks

The behavior of biological brains, including the interactions between synapses and neurons, can be mathematically modeled and recreated using equivalent circuitry. One such example is the biological neuron, which has various models that range from biologically plausible but computationally expensive (such as the Hodgkin and Huxley model [8]) to simplified yet reasonably accurate models. The Leaky Integrate and Fire (LIF) neuron model simplifies neuron dynamics by approximating the neuron’s membrane as a switched low-pass filter:
τ m d v m ( t ) d t = E L − v m ( t ) + R m I e x t ( t )
v o u t = v s p k · δ ( t ) , ∀ v m = v t h 0 , ∀ v m < v t h
In Equation (1), v m ( t ) represents the membrane’s voltage, which has certain membrane’s resistance R m and capacitance C m . The temporal charging constant of the neuron τ m = R m C m imposes a charging/discharging rate as a function of an input excitation current I e x t , starting from a resting potential E L . When v m overpasses certain threshold voltage v t h , the neuron emits a spike of amplitude v s p k , being δ ( t ) the Dirac delta function. As described at [9], by solving the differential equation in the time interval it takes to the neuron to v m = v t h and considering the frequency definition, a function which relates I e x t with the output spiking frequency can be obtained as:
f s p k ( I e x t ) = 1 τ m ln v t h − E L − R m I e x t R m I e x t
The resulting graph is called tuning curve [7] and depicts the sensibility of the neurons against an excitatory signal. By varying C M , R m , different tuning curves, i.e., spike responses, can be obtained for neurons in the same layer. (See Figure 1). For instance, a larger value for C m will make the neuron take more time to charge, reducing the spike output frequency and leading to a different tuning curve. This feature can encode input signals into spiking activity by letting neurons in the same layer have different spike responses for the same input signal (i.e., Population Encoding).

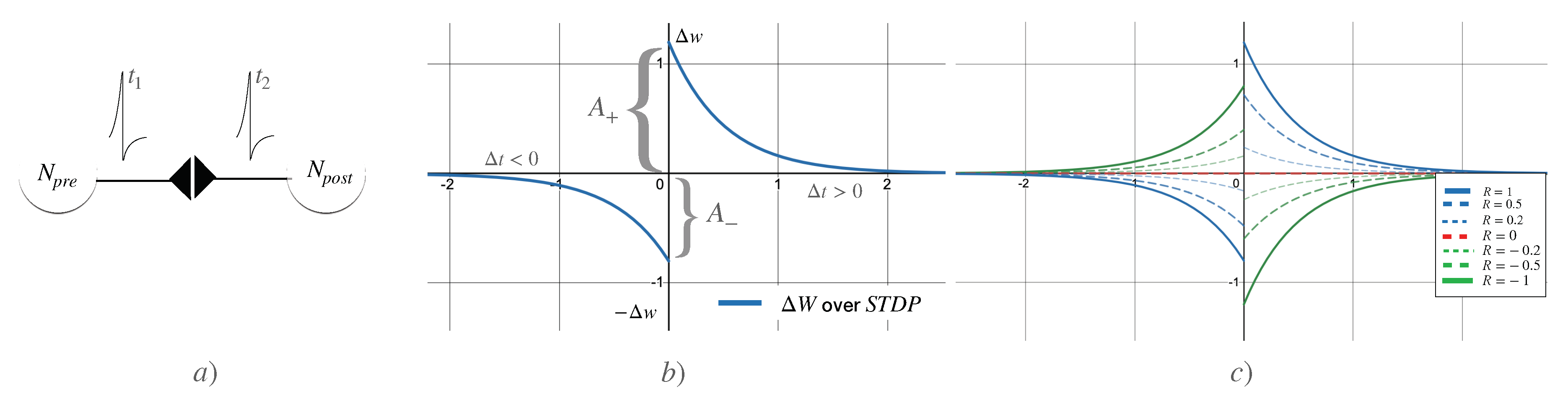
2.2. R-STDP Learning Rule

Spike-Timing-Dependent Plasticity (STDP) describes Hebbian learning as neurons that fire together, wire together. Given a couple of neurons interconnected through a synapse, the ability to conduct the spikes is controlled by a synaptic weight w ∈ [ w m i n , w m a x ] . The neuron that emits a spike at time t i is denoted as the pre-synaptic neuron N i , making the synapse increase its conductance value by a certain differential amount Δ w . A spike of current resulting from the convolution of the spike’s voltage through the synapse is produced and fed a receptor post-synaptic neuron N j . Each spike contributes to the membrane’s voltage of N j until it emits a spike at time t j , becoming then the pre-synaptic neuron, and setting Δ t = t i − t j as the time difference between spikes. Δ w is then defined as:
Δ w ( Δ t ) = A + e − Δ t τ + , ∀ Δ t ≥ 0 − A − e Δ t τ − , ∀ Δ t < 0
For each spike, the synaptic weight will be modified by a learning rate of A + , A − , multiplied by an exponential decay defined by τ + , τ − , respectively. As Δ t → 0 , the change in the synaptic weight is bigger. Figure 2b) shows the characteristic graph of STDP, showing that for presynaptic spikes ( Δ t ≤ 0 ), the synapse gets Long Term Potentiation (LTP), while for post-synaptic spikes (i.e., Δ t ≥ 0 ), the synapse suffers with Long Term Depreciation (LTD). The resulting plasticity rule models how the synaptic weight is modified, considering only the spiking activity. According to [10,11,12], a global reward signal R is introduced to model neuromodulatory signals. Setting R ∈ [ − 1 , 1 ] , Equation (4) is changed then to:
Δ w ( Δ t ) = R × A + e − Δ t τ + , ∀ Δ t ≥ 0 − R × A − e Δ t τ − , ∀ Δ t < 0
Figure 2c) shows the role of the reward signal R = − 1 , inverting the role of presynaptic and postsynaptic spikes. Presynaptic spikes now lead to LTD, while postsynaptic spikes lead to LTP. This is the opposite of STDP (i.e., R = 1 ). Notice when R = 0 , learning (modification of the synaptic weights) gets deactivated, as Δ w = 0 .

3. Materials and Methods

This section describes the necessary circuitry assembled to emulate the models for synapses, neurons, and learning rules.

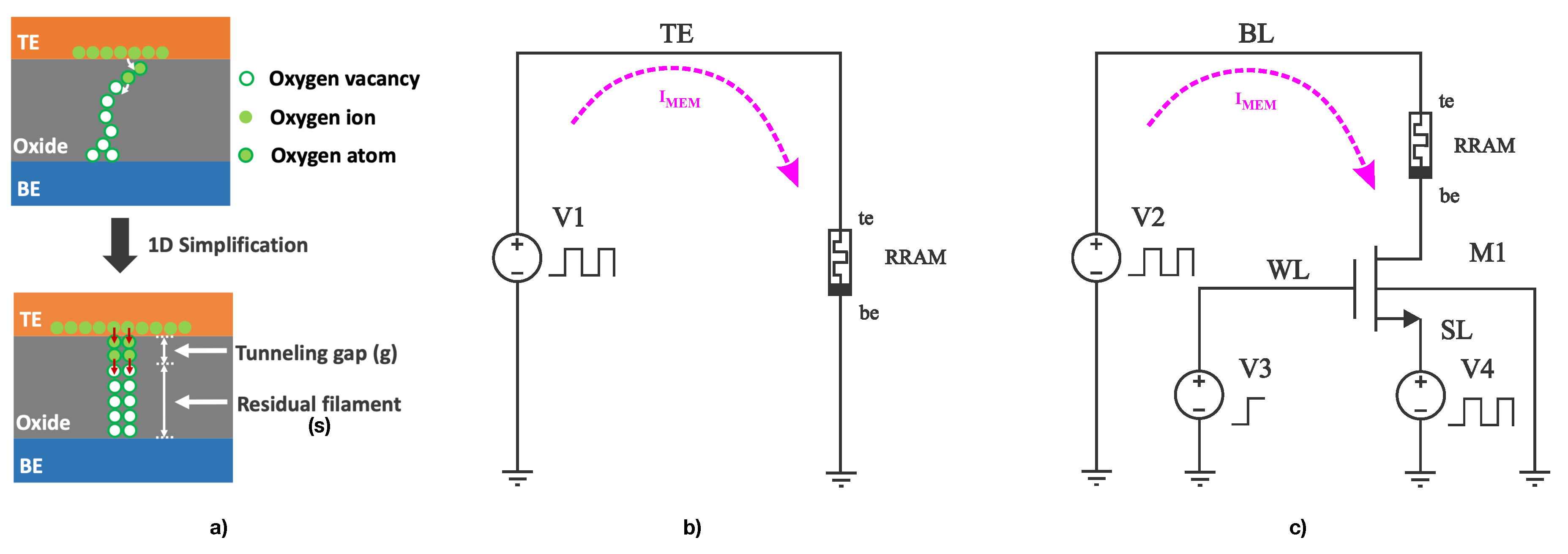
3.1. Memristor Device

A Resistive Random Access Memory (RRAM) device consists of a top and bottom metal electrodes (TE and BE, respectively), enclosing a metal-oxide switching layer, forming a metal insulator metal (MIM) structure. A conductive filament starts to be formed with oxygen vacancies when current flows through the device. The distance from the tip of the filament to the opposite bottom electrode is called gap g. Notice that the length of the filament s is complementary, as the thickness of the oxide layer t o x = g + s , as it can be seen in Figure 3a). Reverse current increases g while the device’s resistance increases, and vice-versa. Skywater’s 130nm fabrication process (see [13]), incorporates memristor cells produced between the Metal 1 and Metal 2 layers and can be made using materials that exhibit memristive behavior, such as titanium dioxide (TiO2), hafnium dioxide (HfO2), or other comparable materials based on transition metal oxides.
The RRAM can store bits of information by switching the memristor resistance value R m e m between a Low Resistance State (LRS) and a High Resistance State (HRS). However, this work’s intention is to use the whole range of resistance available to store the synaptic weights by directly representing w m i n with H R S , w m a x with L R S and any continuous value in-between. UC Berkeley’s model [14] defines the internal state of the memristor as an extra node in the tip of the formed filament. The memristor dynamics is described by the current between TE and BE electrode i T E , B E , the rate of growth of the gap g ˙ , and the local field enhancement factor γ :
i T E , B E ( t ) = I 0 · exp ( − g / g 0 ) · sinh ( v T E , B E / V 0 )
d d t g ( t ) = − ν 0 · exp ( − E a V T ) · sinh ( v T E , B E · γ · a 0 t o x V T )
γ = γ 0 − β · g 3
where v T E , B E is the voltage between TE and BE, t o x is the thickness of the oxide separating TE and BE, a 0 is the atomic distance, and I 0 , V 0 , g 0 , V T , ν 0 , γ 0 , β are fitting parameters obtained from measurements of the manufactured memristor device [15].
Then, to introduce a device model as a circuit component in a simulation environment, the user can a) use SPICE code to reflect the memristor model, or b) describe the device dynamics using Verilog-A, and then use the simulator’s compiler, being the latter option the standard. Simulation results described at [16,17,18], shows succesfull transitionary simulations, using a 1T1R (one-transitor-one-resistor) and 1C1R (one-capacitor-one-resistor) configurations, using the Verilog-A code provided at [19], compiled and simulated with Xyce/ADMS [20] software. However, over these simulations using pulse excitation signals, while they report successful decay in the memristance value, they do not report how the memristance value goes up again by applying pulses in the opposite direction. We could not reproduce the mentioned behavior to the best of our efforts.
It can be noticed on the provided code that the Euler integration method is described, alongside the model, by request to the simulator engine the absolute simulation time at each timestep with Verilog-A directives such as initial-timestep or absolute-time. While this works for .tran simulations, this model description will fail for .op, .dc simulations, where time is not involved or will lead to convergence simulation issues. These and other bad practices are described in detail by the UC Berkeley’s team article [14]. They provide insight into how to model devices with hysteresis in Verilog-A by properly:
  • Defining a couple of differential equations, f 1 ( v T E , B E , g ) (Equation (6)) to describe the current from between TE and BE terminals, and a second function f 2 ( v T E , B E , g ) ) (Equation (7)) to describe the rate of growth/shrinkage of the width of the filament.
  • Defining TE, BE and the tip of the filament (i.e., g) as electric nodes in Verilog-A. As each node in an electrical circuit possesses properties (Voltage, Currents, Magnetic Flow, and charge), the compiler knows how to compute the current from the tip of the filament to B E , by using f 2 ( v T E , B E , g ) )
  • Providing alternative functions implementations for exp(), sinh(), to limit the maximum slope these can reach between the past and the next timestep. Several simulator engines use dynamic timestep selection for faster simulation periods and convergence issues. Of course, this limits the minimum timestep a simulator can use but avoids convergence issues or extended execution periods.
  • Avoiding the usage of if-then-else statements to set the boundaries for the thickness of the filament. Instead, use a smooth, differentiable version of the unit step function.
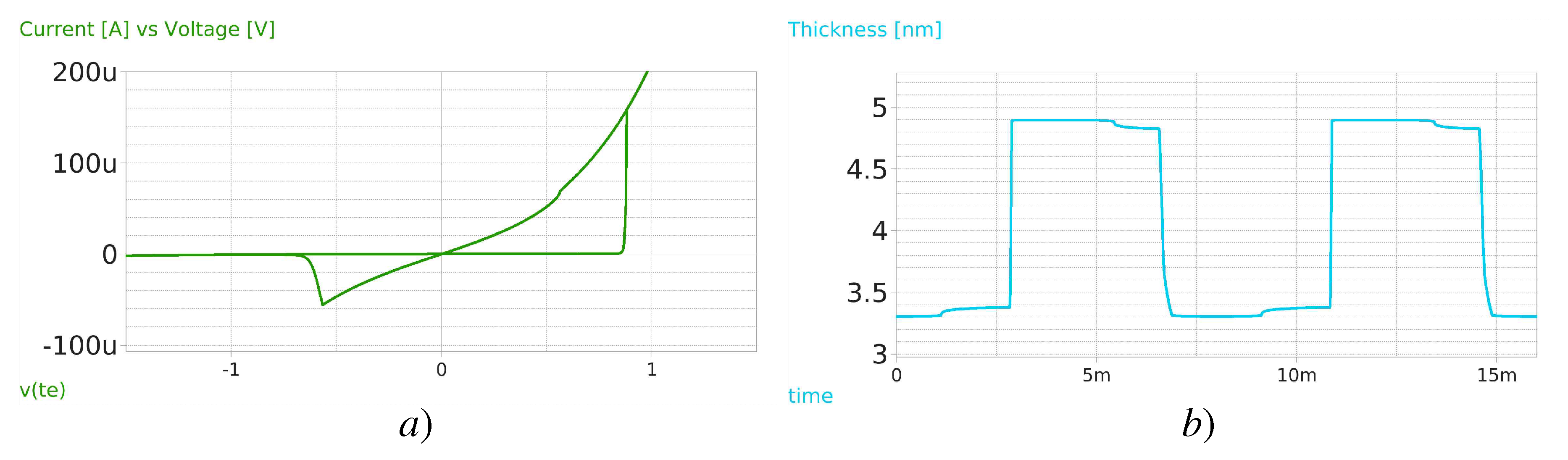
This article uses the memristor Verilog-A implementation methodology described at [14] but replaces the manufacturing parameters found at [16,17]. Figure 3a) shows a memristor testbench where a triangular signal from − 2 V to 2 V is applied, resulting in the Lissajous curve (I-V graph) (Figure 4a), with the typical hysteresis characteristics from memristors, reflecting the V o n ≈ 0.9 V and V o f f ≈ − 0.6 threshold voltages to increase/decrease the resistance in the device. Figure 4b) shows the thickness of the filament, which lies between 4.9 n m to 3.3 n m . 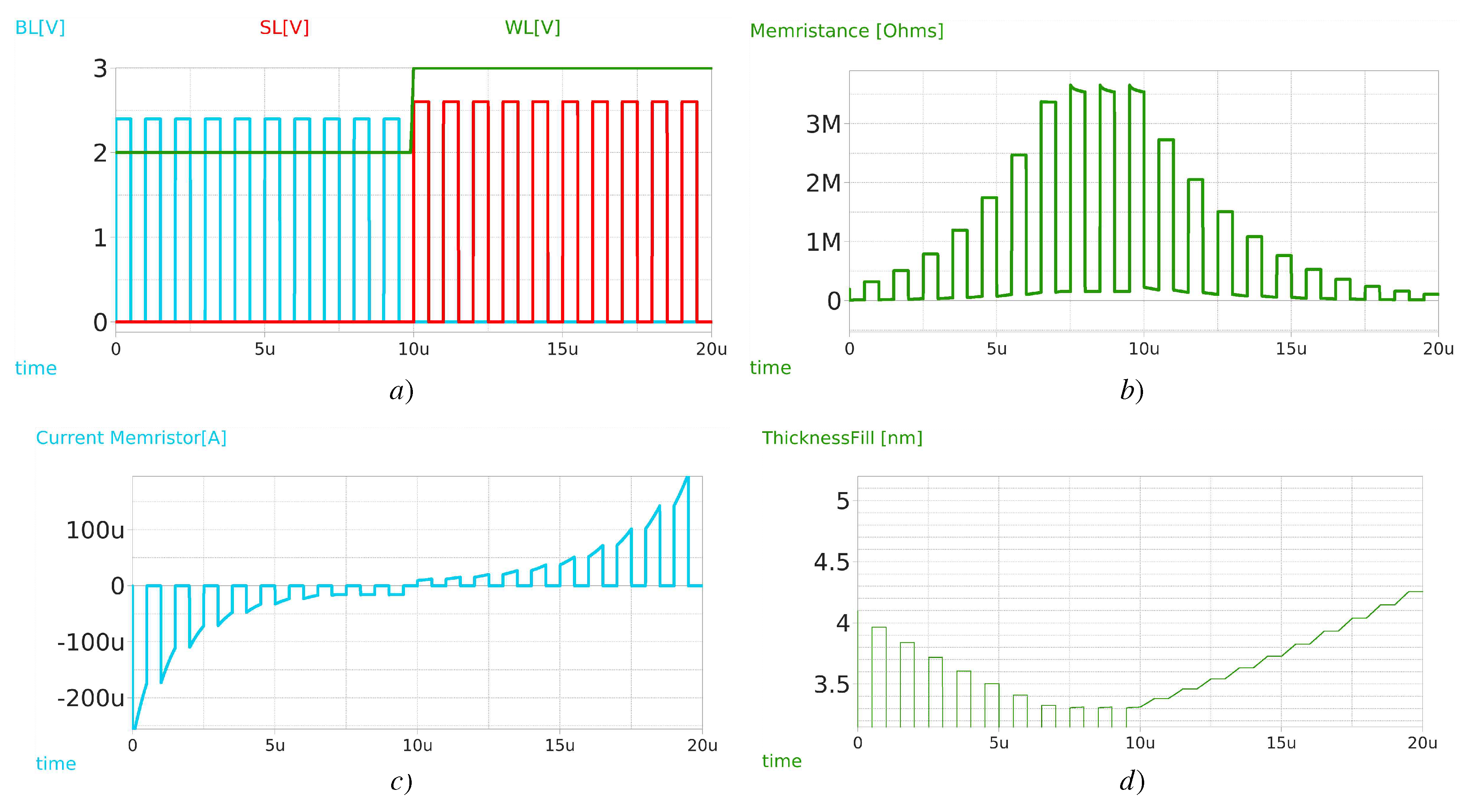On a second testbench depicted in Figure (Figure 3b), a 1T1M (one transistor-one memristor) setup where squared pulses ((Figure 4a) are applied first at B E , then at T E to foster the resistance value exploration, reflecting a proper evolution from LRS to HRS and backward, showing the appropriate previously reported memristance values of the device, this is, R m e m ∈ [ 10 k Ω , 3.3 M Ω ] (Figure 4b). The current flown through the memristor goes from − 200 μ A to 100 μ A , matching the obtained Lissajous curve in the previous testbench (Figure 4c). The resulting code is available at our Github repository [21], compiled by the OpenVAF tool [22], and simulation results were obtained using the Ngspice simulation engine [23].

3.2. R-STDP Circuit Implementation

Figure 6 shows a 4T1M (four transitors-one memristor) cell replacing the 1T1M cell to manage the current flow of the memristor. Proposed at [24], the structure pretends to invert the current flow according to a reward voltage signal V R ∈ [ 0 , 1.8 V ] . When V R = 1.8 V , transistors M 1 , M 2 are enabled, and M 3 , M 4 disabled. If V p r e > V p o s t , the current then will flow from BE of the memristor towards TE. However, when V R = 0 V , M 2 , M 3 are disabled, and M 1 , M 4 are enabled, yielding the current direction from TE to BE. The current direction determines whether the memristor´s resistance increases or decreases. On Figure 7a) testbench signals with triangular shapes are applied with a delay of 5 μ s . Two scenarios are presented: In the first scenario, V R = 0 for the entire simulation, while in the second scenario, V R flips from 0 V to 1.8 V at 100 μ s . Notice at Figure 7c), Figure 7d) the voltage difference ( V m e m = V B E − V T E ) is shown for both scenarios, overpassing the memristor threshold voltage for potentiation. However, when the reward signal is flipped, V m e m overpasses the memristor value but in the opposite direction. Notice also at Figure 7e), Figure 7f) the magnitude of the spike currents the memristor delivers, given by the M 1 − M 4 geometry W / L , which in this case, where selected to provide symmetrical pulses of current. However, these aspect ratios can be selected to foster asymmetric STDP curves.

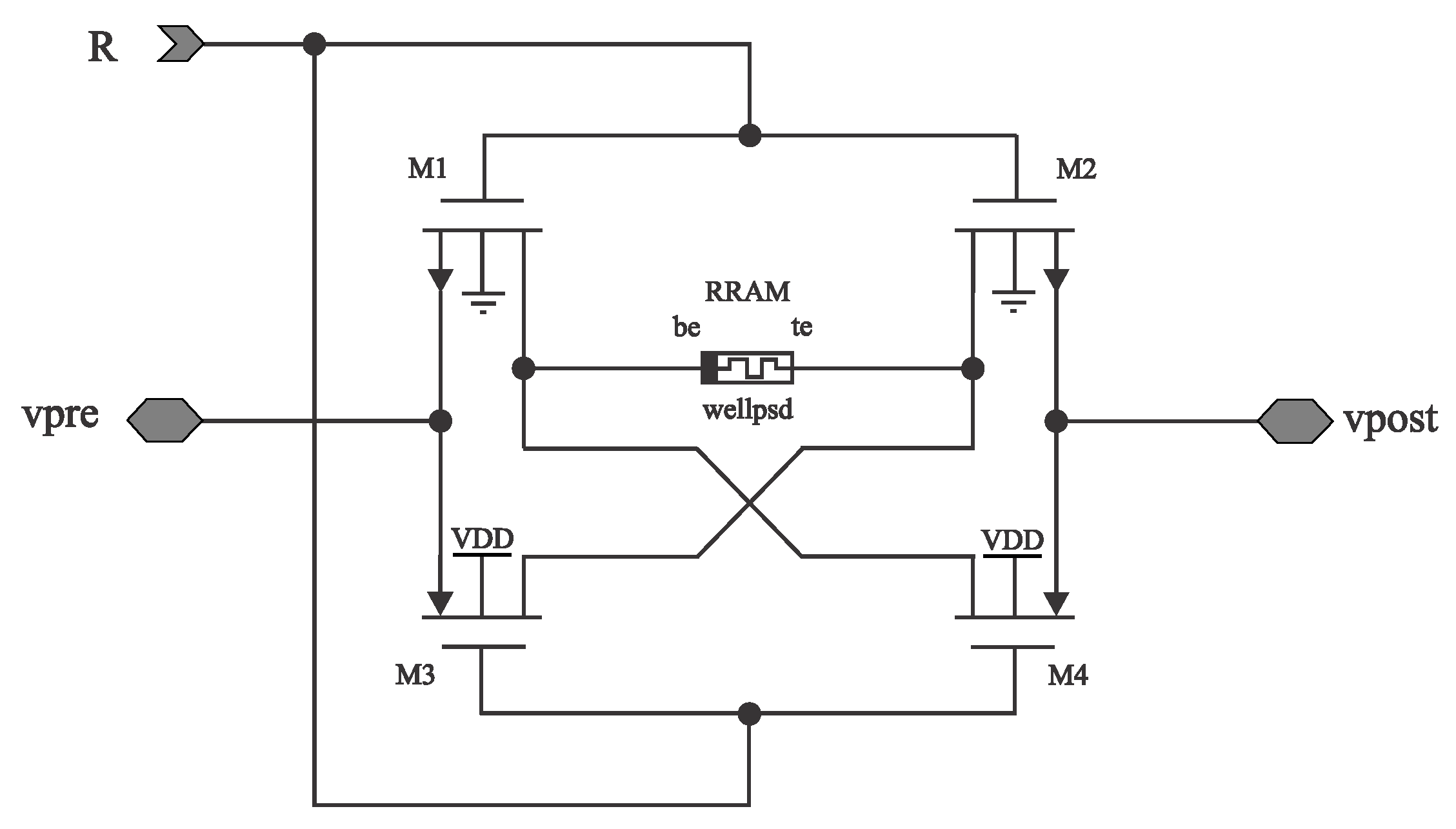
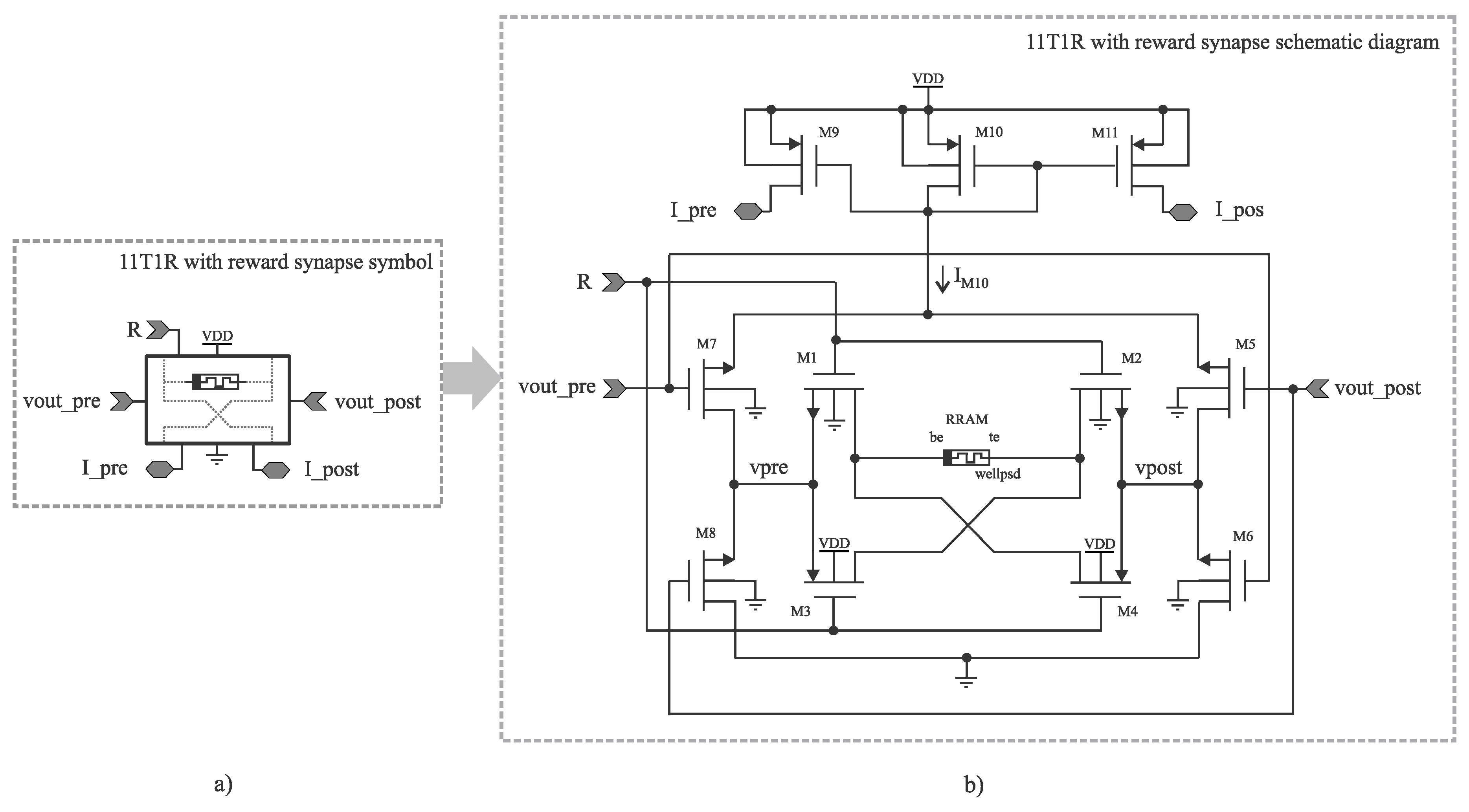
3.3. Adding Spike Reconformation and Current Decoupling to the Synapse

Now consider two fully-interconnected neuron layers, with N and M neurons needing N × M synaptic connections. When the i − t h neuron of the first layer emits a spike, it should be able to provide enough power for the M post-synaptic neurons. Moreover, when the j − t h neuron in the second layer emits a spike, it must provide enough power to the N post-synaptic neurons. Consider then the schematic in Figure 8. Notice that the 4 T 1 R R-STDP structure of the previous section is embedded inside this new 11 T 1 R structure, supporting the polarity switch according to the arrival of spikes. The port labeled as V o u t , p r e activates transistor M 6 , M 7 . making V p r e > V p o s t . On the other side, the port labeled as V o u t , p o s t enables transistors M 5 , M 8 , setting V p o s t > V p r e . 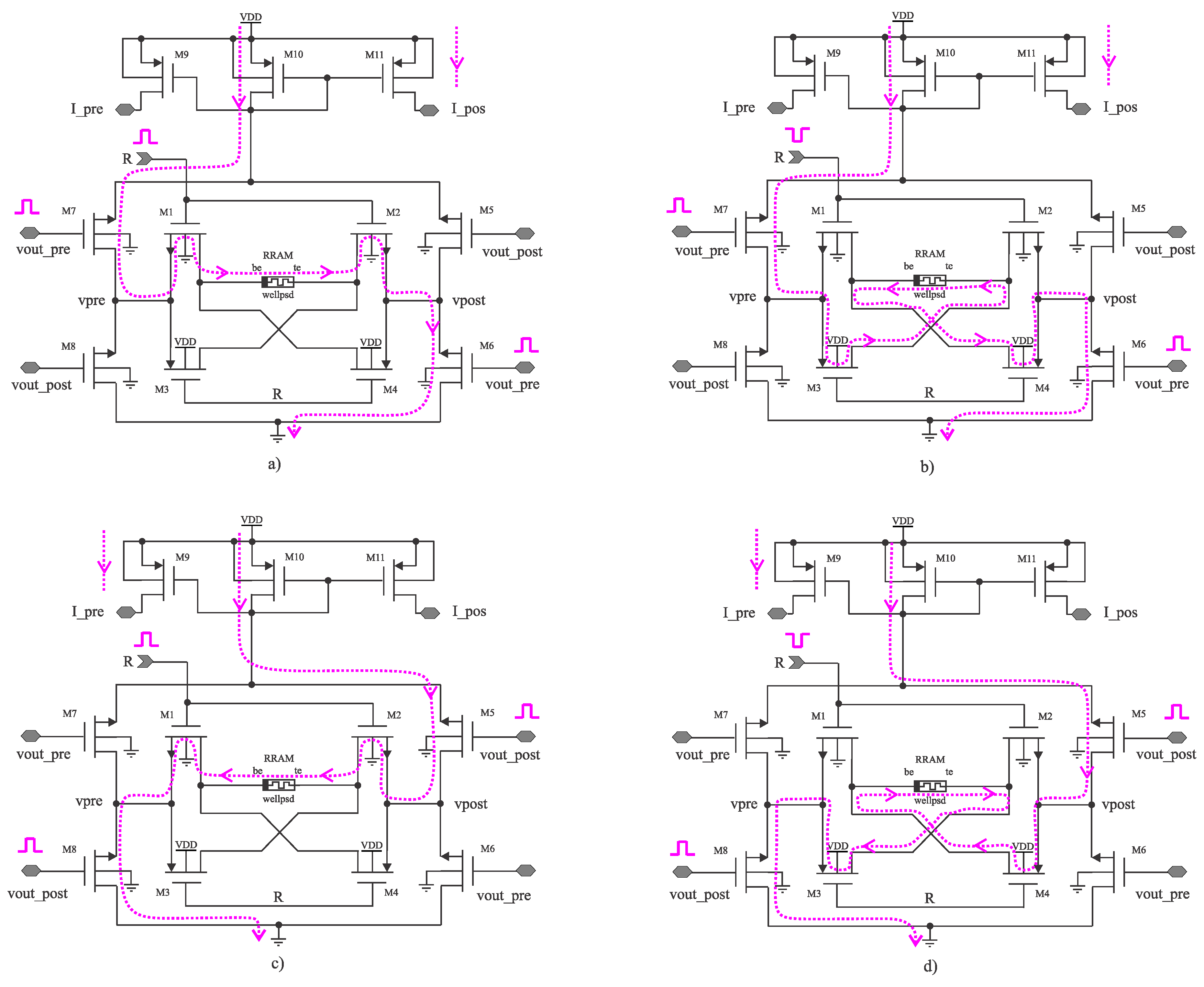Then, four scenarios, depicted at Figure 9) emerge:
  • V p r e > V p o s t R = 1.8 V . When a presynaptic spike arrives and the reward signal is on. This routes the current from BE to TE in the memristor, yielding to LTD;
  • V p r e > V p o s t R = − 1.8 V . Due to the reward signal being negative, the same spike train that should produce LTD now produces LTP, as the current flows from TE to BE;
  • V p o s t > V p r e R = 1.8 V . Postsynaptic spikes with reward signal on, the current flows from TE to BE, producing LTP;
  • V p o s t > V p r e R = − 1.8 V . Postsynaptic spikes with a reward signal off, the current flows from BE to TE, producing LTD;
As the input spikes are pointing toward the transistor’s gates, no current is provided by the neurons. Instead, each synapse only receives the trigger signal (a spike, with amplitude larger than the threshold value of the transistors), and provides enough current straight from the power source, instead of the output node v o u t of each neuron. Regarding the upper part of the circuit, it’s important to note whether the spike was presynaptic or postsynaptic; the current that flows through transistor I M 10 always travels from source to drain. Additionally, this current is the same that flows through the memristor, regardless of its polarity. Transistors M 9 , M 11 then serve as current mirrors of I M 10 . When the postsynaptic neuron fires, current is delivered to the presynaptic neuron by I p r e . Then, when a presynaptic spike arrives, I p o s t feeds the post-synaptic neuron. I p o s t and I p r e are defined as:
I p o s t = ( W / L ) 11 ( W / L ) 10 I M 10
I p r e = ( W / L ) 9 ( W / L ) 10 I M 10
As mentioned in the previous sections, the resistance range of the memristor allows it to provide at most 200 u A . However, the input current range of the neuron may differ from the input current ranges the memristor can provide for the same v d d . Therefore, Equations (9) and (10) enable regulation of the current contribution for each spike.

3.4. Neuron circuit

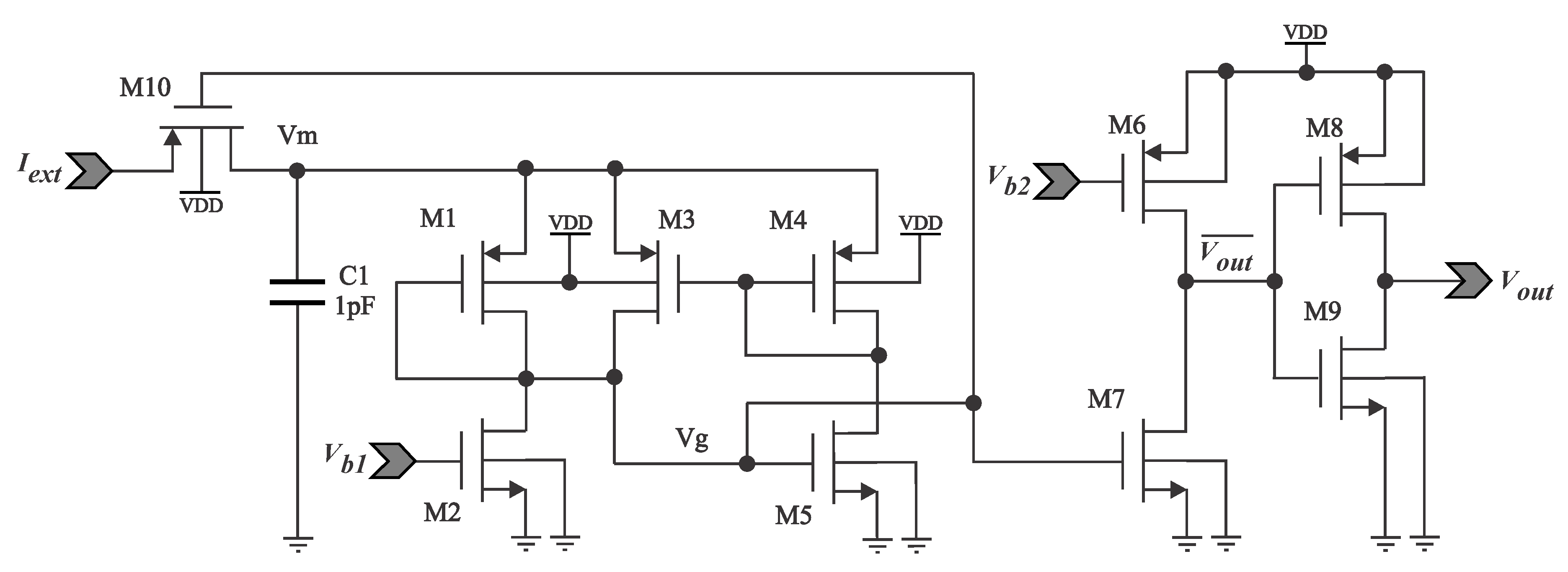
Figure 10 depicts the neuron model used in this work, based on the original design by [25], but with some modifications for the avoidance of the output spike to be fed into the same neuron, as seen as [24]. Transistors M 3 , M 4 , M 5 emulate a thyristor with hysteresis by harnessing the fact that PMOS and NMOS have different threshold voltage values (i.e., v T H N ≠ v T H P ). The circuit dynamics can be described as follows:
  • An external input current excitation I e x t arrives through M 10 (PMOS), enabled at start. M 1 is set as a diode.
  • C 1 charges for each incoming spike, increasing the voltage at node V m .
  • A leaky current I l e a k is flowing thourgh M 2 at all times. If no further incoming electrical impulses are received, the neuron will lose all of its electrical charge. V b 1 defines I l e a k .
  • When V m ≈ 1.5 V , V g ≈ 0.75 V , which is the threshold voltage for the M 5 NMOS device, enabling the C 1 charge to flow through M 4 and M 5 .
  • M 7 also turns on, enabling current to flow and making voltage at V o u t ¯ drops. At the same time, V g > 0 , turning off transistor M 10 , disabling current integration for the neuron.
  • As v ¯ o u t drops, v o u t rises, as M 8 − M 9 works as an inverter. V b 2 controls the current of the transistor M 6 , and conforming the width of the spike. The node v o u t provides the final output spike, which can be fed to subsequent synapses.
  • M 10 acts as a controlled diode, blocking any current from I e x t when the neuron is spiking.
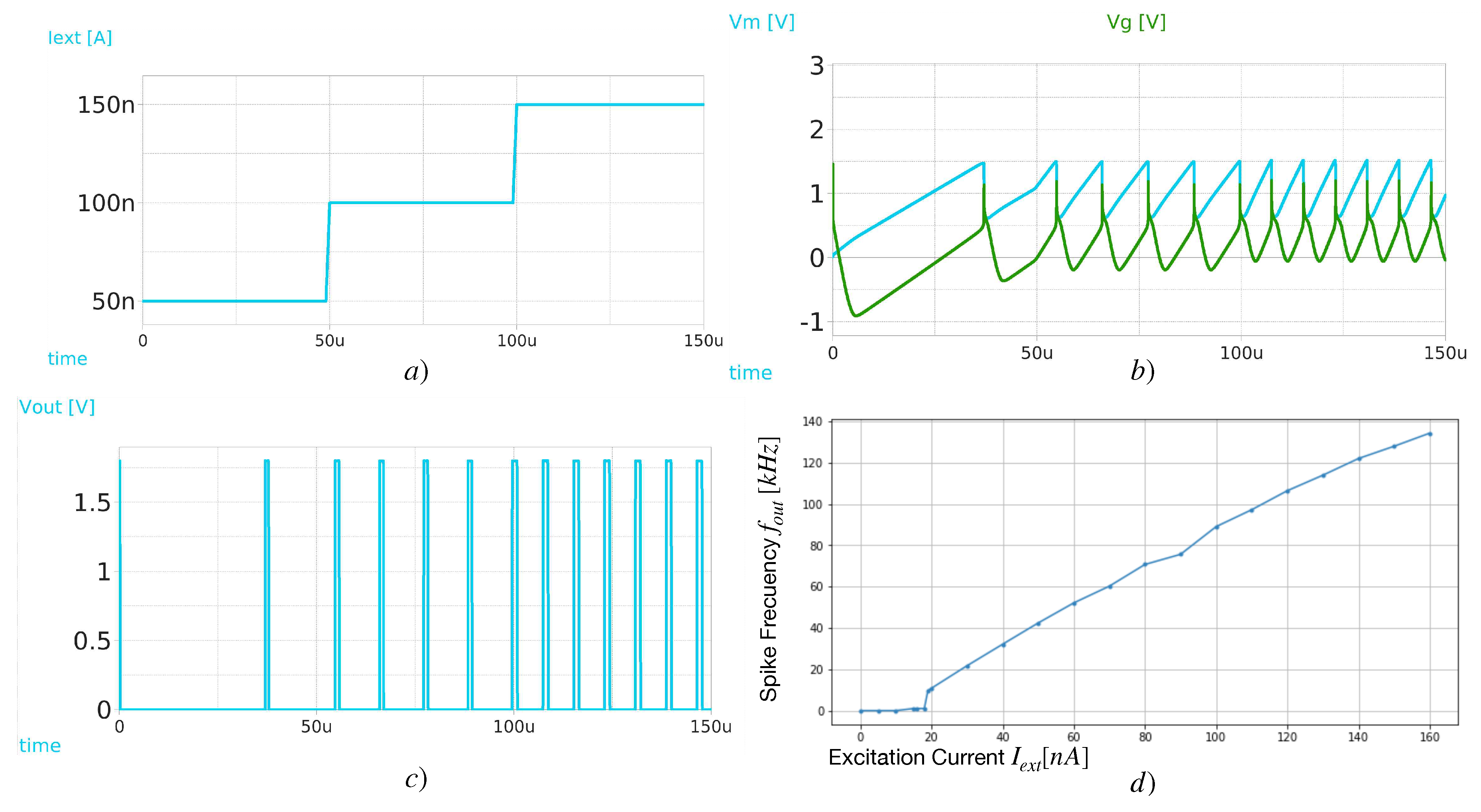
Figure 11 shows the neuron’s spiking activity for an input step signal, which rises each 50 μ s a step of 50 n A . It can be observed that the frequency increases as more current is added. The amplitude of the output spikes is set as v o u t = 1.8 V , but it can be set differently, according to the synapse needs, while the thickness of the spike is approximately 1 m s . The maximum reached spike frequency is f o u t ≈ 140 k H z , for I e x t ≈ 160 n A . The neuron output voltage v o u t remains on 1.8 V for bigger input currents. The final design then needs ten transistors. However, notice M 8 − M 9 can be removed by considering V g as the output voltage node. The geometry of M 5 can be reshaped to regulate its current, defining then the width of the output spike.

4. Results

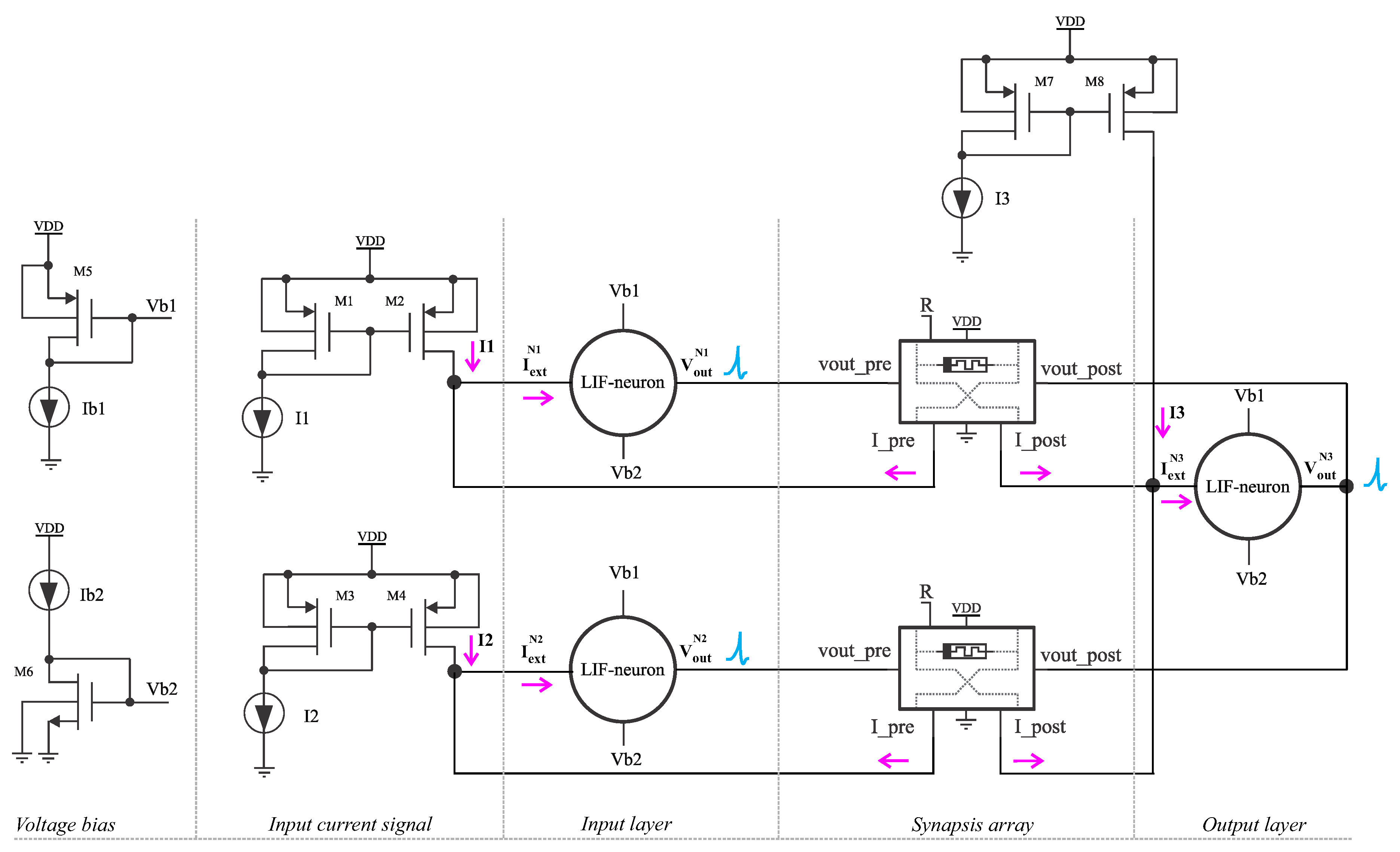
The testbench shown in Figure 12 intends to test all the capabilities of the proposed synapse by using a 2-1 neuron network array, using then two 11 T 1 R synapses to interconnect the first layer with the second. During the first half of the simulation, the neurons N1 and N2 in the input layer receive testing excitation currents for each neuron, supported by current mirrors. The neurons at the first layer spike at different rates, as I e x t , N 1 > I e x t , N 2 . 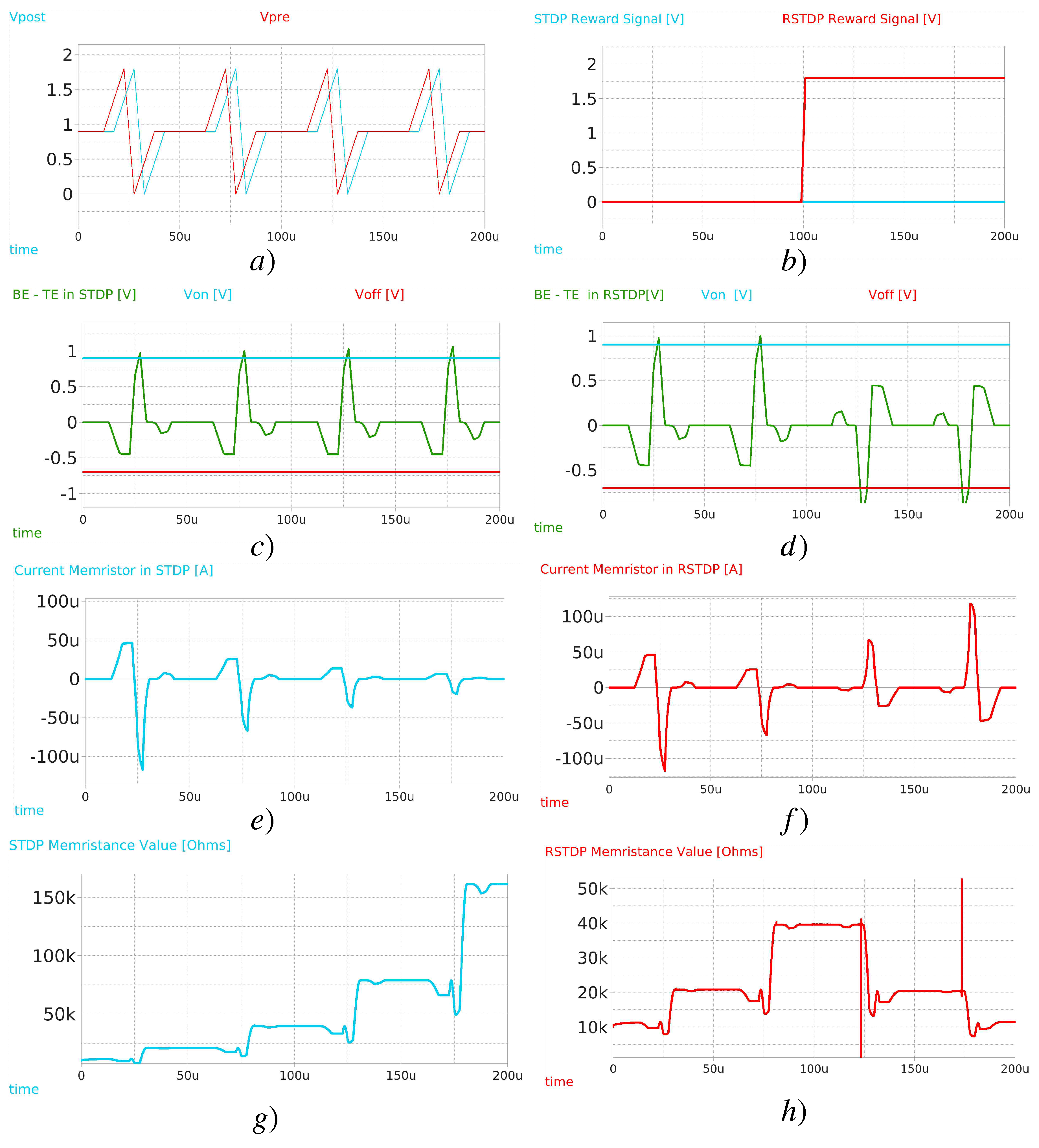In the second half of the simulation, the neuron N3 in the output layer receives an excitation current I e x t , N 3 , while the current mirrors for N1 and N2 get deactivated. This should result in Long-Term Potentiation (LTP) for the first half and Long-Term Depression (LTD) in the second half of the execution. However, the reward signal R is set to switch from 1.8V to -1.8V at each quarter of the simulation, leading to the four cases previously described.
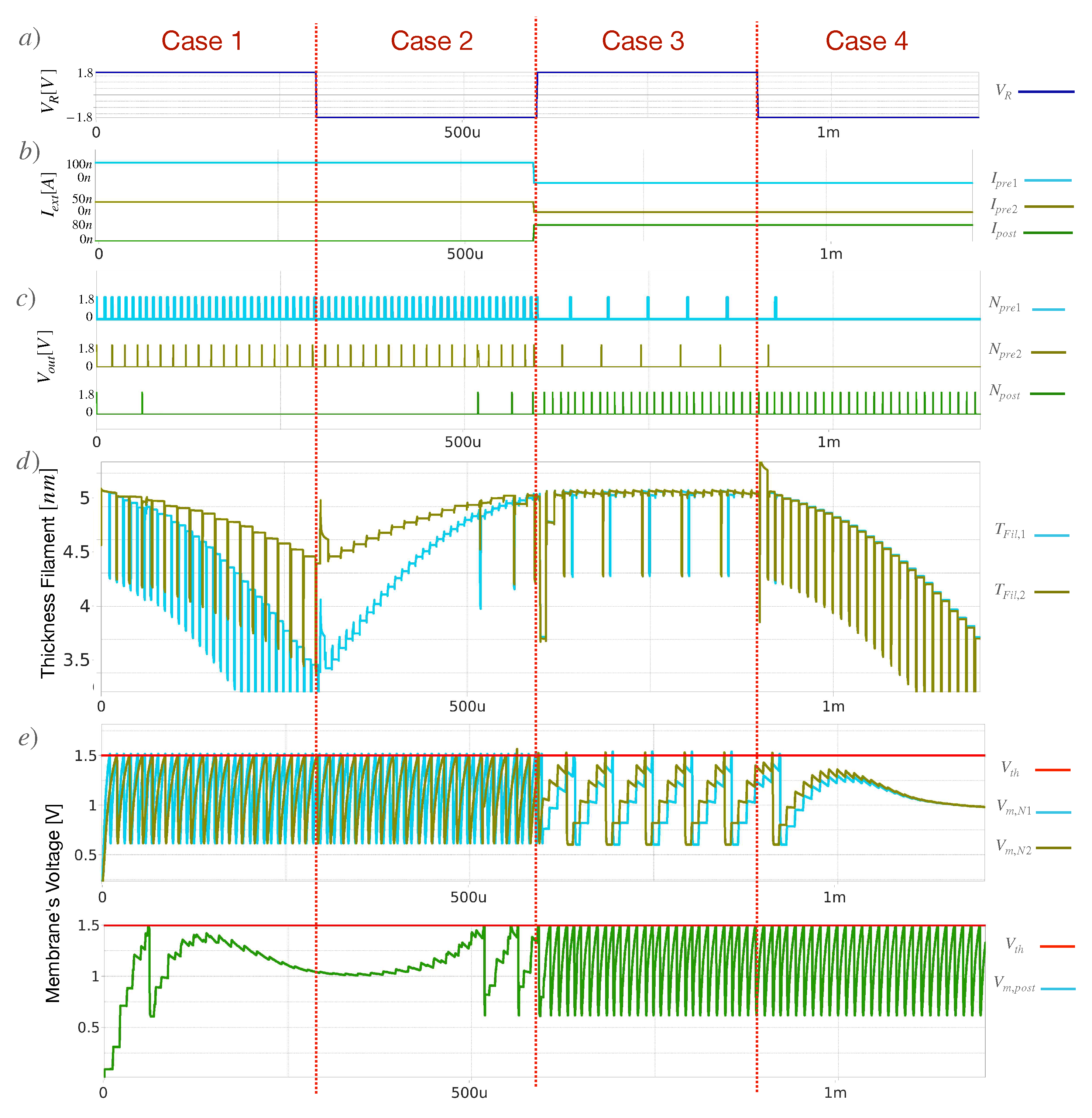
Figure 13d shows the evolution of the simulation results. In the first quarter, the first case occurs, showing how the thickness of the filament s in the memristor decreases at distinct rates. Remember, as the thickness decreases, so does the conductivity (i.e., LTP is produced). In the second quarter, the same spiking activity led to the opposite effect in the filament, as the reward signal R went from 1.8 V to − 1.8 V , leading the thickness to 4.9 n m (i.e., LTD is then produced). In the third quarter, N 3 spikes, and N 1 , N 2 ceases to receive excitation current from the current mirrors. With R = 1.8 V , the filament should increase in size; however, as its value is already at the maximum, it stays at 4.9 n m . Finally, R flips again to R = − 1.8 V , and the spikes of N 3 decrease the filament, obtaining the opposite behavior. Notice the neural activity (spikes), byproduct of current integration of incoming spikes of other neurons (See Figure 13c).
The whole circuit is implemented using Xschem and Ngspice. The geometries for each transistor used for this testbench are described in Table 1. The final list of archives is available at our Github repository [21].

5. Discussion

Next, we point towards some considerations into the obtained circuitry, how this device can be manufactured, and new opportunities of research which emerge from this work.

5.1. Regarding the synapse circutry

The simulation took around 10 s − 15 s for a timestep of Δ t = 100 n s to the implementations, without sudden crashes or singular matrix values in simulation runtime. This is thanks to the well-posed memristor Verilog-A code. This will enable the simulation of larger Deep Neural SNNs purely implemented on an integrated circuit. Also, at [24], while they do implement a GAN network, some blocks like the memristor Generic VTEAM memristor mathematical model [26] are not manufacturable. All the presented architecture has feasible manufacturing using the Skywater 130nm process node.

5.2. Future Work towards Tailor-Made Neuromorphic Computing

The presented blocks then work properly once assembled, leading to the research into how to assemble larger structures. Drawing a schematic of a bigger network with hundreds/thousands of neurons per layer may be problematic, even using the neurons and synapses as sub-blocks. Not to mention the layout. Figure 14a) shows the resulting layout of the 11 T 1 R synapse structure, comparable in size with the LIF neuron at Figure 14b), drawn in the Magic VLSI EDA software [27]. Notice that both structures have internal geometries that might be parameterizable. For instance, the length of the current mirrors for I p r e , I p o s t in the synapse, or well, the capacitance value C 1 for the neuron. As future work, the authors consider that our efforts should focus on automatizing the SPICE files (using programming libraries like PySPICE) for simulation and the GDS files (like implementing PCELLs in TCL scripting) for manufacturing. This will enable research into implement deep neural networks architecture purely in analog hardware.

6. Conclusions

In this article, a proper implementation in Verilog-A of the Skywater130 reram model is presented, enabling the simulation of the behavior reported in the characterization of the physical device while allowing simulations in shorter periods without convergence issues. Then, a 11 T 1 R synapse structure, which uses the memristor inside, is presented. This structure not only enables reward modulation for STDP but also decouples the current feeding from the neuron and successfully transfers the power duties to the synapse. The output spikes of the neuron then do not provide current for the memristor but only provide the signaling to enable the flow into one direction or the other.

Author Contributions

Conceptualization, A.J.L; Data curation, A.J.L; Formal analysis, V.P.P and E.R.E; Funding acquisition, H.S.A; Investigation, A.J.L and V.P.P; Methodology, A.J.L and E.R.E; Project administration, H.S.A and E.R.E; Resources, V.P.P; Software, O.E.S; Supervision, H.S.A; Validation, O.E.S; Visualization, O.E.S; Writing – original draft, A.J.L; Writing – review & editing, V.P.P and H.S.A. All authors have read and agreed to the published version of the manuscript.

Funding

The authors are thankful for the financial support of the projects to the Secretería de Investigación y Posgrado del Instituto Politécnico Nacional with grant numbers 20232264, 20242280, 20231622, 20240956, 20232570 and 20242742, as well as the support from Comisión de Operación y Fomento de Actividades Académicas and Consejo Nacional de Humanidades Ciencia y Tecnología (CONAHCYT).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All of the scripts used in this article are available on the following Github page: h t t p s : / / g i t h u b . c o m / A l e j a n d r o J u a r e z L o r a / S N N I P N (accessed on May 7, 2024).

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ADC Analog to Digital Converter
BE Bottom Electrode
CMOS Complementary Metal Oxide Semiconductor
CPU Central Processing Unit
DAC Digital to Analog Converter
DDPG Deep Deterministic Policy Gradient
FPGA Field Programmable Gate Array
GAN Generative Adversarial Network
GDS Graphic Database System
GPU Graphic Processing Unit
HRS High Resistance State
IBM International Business Machines
LIF Leaky Integrate and Fire
LRS Low Resistance State
LTD Long Term Depreciation
LTP Long Term Potentiation
MIM Metal Insulator Metal
NMOS Negative Metal Oxide Semiconductor
PCELL Parametric Cell
PMOS Positive Metal Oxide Semiconductor
RL Reinforcement Learning
RRAM Resistive Random Access Memory
RSTDP Reward-Modulated Spike Time Dependant Plasticity
SNN Spiking Neural Networks
SPICE Simulation Program with Integrated Circuit Emphasis
STDP Spike Time Dependant Plasticity
TAB Trainable Analog Block
TCL Tool Command Language
TD3 Twin Delayed Deep Deterministic Policy Gradient
TE Top Electrode
VTEAM Voltage Threshold Adaptive Memristor

References

  1. Akl, M.; Sandamirskaya, Y.; Walter, F.; Knoll, A. Porting Deep Spiking Q-Networks to Neuromorphic Chip Loihi. International Conference on Neuromorphic Systems 2021; Association for Computing Machinery: New York, NY, USA, 2021; ICONS 2021. [Google Scholar] [CrossRef]
  2. Matos, J.B.P.; de Lima Filho, E.B.; Bessa, I.; Manino, E.; Song, X.; Cordeiro, L.C. Counterexample Guided Neural Network Quantization Refinement. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2024, 43, 1121–1134. [Google Scholar] [CrossRef]
  3. Gewaltig, M.O.; Diesmann, M. NEST (NEural Simulation Tool). Scholarpedia 2007, 2, 1430. [Accessed 20-05-2024]. [Google Scholar] [CrossRef]
  4. Eshraghian, J.K.; Ward, M.; Neftci, E.; Wang, X.; Lenz, G.; Dwivedi, G.; Bennamoun, M.; Jeong, D.S.; Lu, W.D. Training spiking neural networks using lessons from deep learning. Proceedings of the IEEE 2023, 111, 1016–1054. [Google Scholar] [CrossRef]
  5. Bekolay, T.; Bergstra, J.; Hunsberger, E.; DeWolf, T.; Stewart, T.; Rasmussen, D.; Choo, X.; Voelker, A.; Eliasmith, C. Nengo: a Python tool for building large-scale functional brain models. Frontiers in Neuroinformatics 2014, 7, 1–13. [Accessed 20-05-2024]. [Google Scholar] [CrossRef] [PubMed]
  6. Khan, S.Q.; Ghani, A.; Khurram, M. Population coding for neuromorphic hardware. Neurocomputing 2017, 239, 153–164. [Google Scholar] [CrossRef]
  7. Thakur, C.S.; Hamilton, T.J.; Wang, R.; Tapson, J.; van Schaik, A. A neuromorphic hardware framework based on population coding. 2015 International Joint Conference on Neural Networks (IJCNN), 2015, pp. 1–8. [CrossRef]
  8. Schöfmann, C.M.; Fasli, M.; Barros, M.T. Investigating Biologically Plausible Neural Networks for Reservoir Computing Solutions. IEEE Access 2024, 12, 50698–50709. [Google Scholar] [CrossRef]
  9. Juárez-Lora, A.; García-Sebastián, L.M.; Ponce-Ponce, V.H.; Rubio-Espino, E.; Molina-Lozano, H.; Sossa, H. Implementation of Kalman Filtering with Spiking Neural Networks. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
  10. Li, X.; Sun, J.; Sun, Y.; Wang, C.; Hong, Q.; Du, S.; Zhang, J. Design of Artificial Neurons of Memristive Neuromorphic Networks Based on Biological Neural Dynamics and Structures. IEEE Transactions on Circuits and Systems I: Regular Papers 2024, 71, 2320–2333. [Google Scholar] [CrossRef]
  11. Shi, C.; Lu, J.; Wang, Y.; Li, P.; Tian, M. Exploiting Memristors for Neuromorphic Reinforcement Learning. 2021 IEEE 3rd International Conference on Artificial Intelligence Circuits and Systems (AICAS), 2021, pp. 1–4. [CrossRef]
  12. Akl, M.; Ergene, D.; Walter, F.; Knoll, A. Toward robust and scalable deep spiking reinforcement learning. Frontiers in Neurorobotics 2023, 16. [Google Scholar] [CrossRef] [PubMed]
  13. Hsieh, E.; Zheng, X.; Nelson, M.; Le, B.; Wong, H.S.; Mitra, S.; Wong, S.; Giordano, M.; Hodson, B.; Levy, A.; Osekowsky, S.; Radway, R.; Shih, Y.; Wan, W.; Wu, T.F. High-Density Multiple Bits-per-Cell 1T4R RRAM Array with Gradual SET/RESET and its Effectiveness for Deep Learning. 2019 IEEE International Electron Devices Meeting (IEDM). IEEE, 2019. [CrossRef]
  14. Wang, T.; Roychowdhury, J. Well-Posed Models of Memristive Devices 2016.
  15. Jiang, Z.; Yu, S.; Wu, Y.; Engel, J.H.; Guan, X.; Wong, H.S.P. Verilog-A compact model for oxide-based resistive random access memory (RRAM). 2014 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), 2014, pp. 41–44. [CrossRef]
  16. Alshaya, A.; Han, Q.; Papavassiliou, C. RRAM, Device, Model and Memory. 2022 International Conference on Microelectronics (ICM). IEEE, 2022. [CrossRef]
  17. Alshaya, A.; Malik, A.; Mifsud, A.; Papavassiliou, C. Comparison of 1T1R and 1C1R ReRAM Arrays. Journal of Physics: Conference Series 2023, 2613, 012010. [Google Scholar] [CrossRef]
  18. Alshaya, A.; Han, Q.; Papavassiliou, C. Passive Selectorless Memristive Structure with One Capacitor-One Memristor. 2022 International Conference on Microelectronics (ICM), 2022, pp. 121–124. [CrossRef]
  19. Skywater. User Guide 2014; SkyWater SKY130PDK 0.0.0-22-g72df095 documentation. https://sky130-fd-pr-reram.readthedocs.io/en/latest/user_guide.html, 2019. [Accessed 25-04-2024].
  20. Xyce(™) Parallel Electronic Simulator. [Computer Software] https://doi.org/10.11578/dc.20171025.1421, 2013. [CrossRef]
  21. Juarez-Lora, A. GitHub - AlejandroJuarezLora. SNN-IPN, MICROSE-IPN. https://github.com/AlejandroJuarezLora/SNN_IPN, 2024. [Accessed 25-04-2024].
  22. Kuthe, P.; Muller, M.; Schroter, M. VerilogAE: An Open Source Verilog-A Compiler for Compact Model Parameter Extraction. IEEE Journal of the Electron Devices Society 2020, 8, 1416–1423. [Google Scholar] [CrossRef]
  23. Vogt, H. Ngspice, the open source Spice circuit simulator - Intro — ngspice.sourceforge.io. https://ngspice.sourceforge.io/index.html, 2024. [Accessed 25-04-2024].
  24. Tian, M.; Lu, J.; Gao, H.; Wang, H.; Yu, J.; Shi, C. A Lightweight Spiking GAN Model for Memristor-centric Silicon Circuit with On-chip Reinforcement Adversarial Learning. 2022 IEEE International Symposium on Circuits and Systems (ISCAS), 2022, pp. 3388–3392. [CrossRef]
  25. Stoliar, P.; Akita, I.; Schneegans, O.; Hioki, M.; Rozenberg, M.J. A spiking neuron implemented in VLSI. Journal of Physics Communications 2022, 6, 021001. [Google Scholar] [CrossRef]
  26. Kvatinsky, S.; Ramadan, M.; Friedman, E.G.; Kolodny, A. VTEAM: A General Model for Voltage-Controlled Memristors. IEEE Transactions on Circuits and Systems II: Express Briefs 2015, 62, 786–790. [Google Scholar] [CrossRef]
  27. Edwards, T. Magic User Guide, 2024.
Preprints 107603 g001
Figure 1. Leaky Integrate and Fire Model. The resulting tuning curve can be modified by changing C m and R m values.
Figure 1. Leaky Integrate and Fire Model. The resulting tuning curve can be modified by changing C m and R m values.
Preprints 107603 g001
Preprints 107603 g002
Figure 2. (a)A presynaptic and a postsynaptic neuron emits spikes, producing Hebbian Learning (b) Spike Time Dependant Plasticity (STDP) graph, which models the rate of growth ( Δ w > 0 ) or shrinkage ( Δ w < 0 ) of the synaptic weight. (c) By introducing a reward signal R ∈ [ − 1 , 1 ] , the same spikes that produce potentiation LTP may produce now depreciation LTD. The response curve is shown with different values of R
Figure 2. (a)A presynaptic and a postsynaptic neuron emits spikes, producing Hebbian Learning (b) Spike Time Dependant Plasticity (STDP) graph, which models the rate of growth ( Δ w > 0 ) or shrinkage ( Δ w < 0 ) of the synaptic weight. (c) By introducing a reward signal R ∈ [ − 1 , 1 ] , the same spikes that produce potentiation LTP may produce now depreciation LTD. The response curve is shown with different values of R
Preprints 107603 g002
Preprints 107603 g003
Figure 3. (a) Lateral diagram of the memristor, where oxygen vacancies and ions form a filament of thickness s, a gap g. Extracted from [15]. (b) Testbench used for the first scenario, a triangular pulse − 2 V to 2 V signal is fed. (c) testbench used for the second scenario, where pulses are applied, using a 1T1R structure.
Figure 3. (a) Lateral diagram of the memristor, where oxygen vacancies and ions form a filament of thickness s, a gap g. Extracted from [15]. (b) Testbench used for the first scenario, a triangular pulse − 2 V to 2 V signal is fed. (c) testbench used for the second scenario, where pulses are applied, using a 1T1R structure.
Preprints 107603 g003
Preprints 107603 g004
Figure 4. Memristor simulations scenarios for the first testbench (a) Lissajous Curve (I-V) of the memristor, clearly showing hysteresis and the V o n ≈ 0.9 V and V o f f ≈ − 0.6 (b) Thickness of the filament s, showing the exponential growth/shrinkage once the memristor threshold voltage is overpassed.
Figure 4. Memristor simulations scenarios for the first testbench (a) Lissajous Curve (I-V) of the memristor, clearly showing hysteresis and the V o n ≈ 0.9 V and V o f f ≈ − 0.6 (b) Thickness of the filament s, showing the exponential growth/shrinkage once the memristor threshold voltage is overpassed.
Preprints 107603 g004
Preprints 107603 g005
Figure 5. Memristor simulations scenarios for the second testbench (a) Voltage pulses applied in the terminals alongside time 20 μ s (b) Evolution of the memristance value, going from 10 k Ω to 3.3 M Ω (c) Current flowing through the memristor, considering positive current when it flows from TE to BE (a) Evolution of the thickness of the filament s
Figure 5. Memristor simulations scenarios for the second testbench (a) Voltage pulses applied in the terminals alongside time 20 μ s (b) Evolution of the memristance value, going from 10 k Ω to 3.3 M Ω (c) Current flowing through the memristor, considering positive current when it flows from TE to BE (a) Evolution of the thickness of the filament s
Preprints 107603 g005
Preprints 107603 g006
Figure 6. R-STDP hardware implementation testbench. 1M4T structure to handle current direction.
Figure 6. R-STDP hardware implementation testbench. 1M4T structure to handle current direction.
Preprints 107603 g006
Preprints 107603 g007
Figure 7. (b) Applied triangular pulses for V p r e and V p o s t , varying from [ 0 V , 1.8 V ] . Notice that V p o s t is delayed 5 μ s from V p r e , making that Δ t > 0 . (c) Reward signal R = [ 0 V , 1.8 V ] , to deactivate/activate drain the gate voltage in the NMOS and PMOS transistors. STDP scenario, with no reward signal (Blue) and RSTDP scenario, enabling a reward signal at the second half of the simulation (d) Voltage difference between TE and BE electrodes of the memristor. Notice V o n (Blue) and V o f f (Red) are overpassed, yielding to a modification in the memristance (e) Current flowing through the memristor. (f) Obtained memristance values in the STDP scenario. (g, h, i) picture the same testbench but activating the reward signal R = 1.8 V , showing that current now flows in the opposite direction, yielding a reduction in memristance after 100 μ s
Figure 7. (b) Applied triangular pulses for V p r e and V p o s t , varying from [ 0 V , 1.8 V ] . Notice that V p o s t is delayed 5 μ s from V p r e , making that Δ t > 0 . (c) Reward signal R = [ 0 V , 1.8 V ] , to deactivate/activate drain the gate voltage in the NMOS and PMOS transistors. STDP scenario, with no reward signal (Blue) and RSTDP scenario, enabling a reward signal at the second half of the simulation (d) Voltage difference between TE and BE electrodes of the memristor. Notice V o n (Blue) and V o f f (Red) are overpassed, yielding to a modification in the memristance (e) Current flowing through the memristor. (f) Obtained memristance values in the STDP scenario. (g, h, i) picture the same testbench but activating the reward signal R = 1.8 V , showing that current now flows in the opposite direction, yielding a reduction in memristance after 100 μ s
Preprints 107603 g007
Preprints 107603 g008
Figure 8. 11 T 1 R Synapse circuit proposal, including the RSTDP subcircuit, the memristor, and current mirrors for the receiving neurons
Figure 8. 11 T 1 R Synapse circuit proposal, including the RSTDP subcircuit, the memristor, and current mirrors for the receiving neurons
Preprints 107603 g008
Preprints 107603 g009
Figure 9. Proposed synapse circuit, reflecting the four possible scenarios for the evolution of the synaptic weight: a) V p r e > V p o s t R = 1.8 V b) V p r e > V p o s t R = − 1.8 V c) V p o s t > V p r e R = 1.8 V d) V p o s t > V p r e R = − 1.8 V
Figure 9. Proposed synapse circuit, reflecting the four possible scenarios for the evolution of the synaptic weight: a) V p r e > V p o s t R = 1.8 V b) V p r e > V p o s t R = − 1.8 V c) V p o s t > V p r e R = 1.8 V d) V p o s t > V p r e R = − 1.8 V
Preprints 107603 g009
Preprints 107603 g010
Figure 10. Analog Neuron Circuit.
Figure 10. Analog Neuron Circuit.
Preprints 107603 g010
Preprints 107603 g011
Figure 11. Simulation results for the Analog Neuron Circuit (a) Testbench used to supply an step increasing current excitation I e x t , startin from 50 n A , 100 n A and 150 n A (b). When v m = 1.5 V , it can be seen in c that v g ≈ 0.75 V , turning on transistor M 5 , which acts as a charge sink for C 1 = 1 p F through M 2 . Fig (d) shows the spike frequency for each I e x t , resulting in a respective frequency of 42 k H z , 89 k H Z , a n d 128 k H z , respectively. e) Current excitation I e x t against spike frequency graph, obtained by sweeping from 0 n A to 190 n A and obtaining the corresponding spike frequency
Figure 11. Simulation results for the Analog Neuron Circuit (a) Testbench used to supply an step increasing current excitation I e x t , startin from 50 n A , 100 n A and 150 n A (b). When v m = 1.5 V , it can be seen in c that v g ≈ 0.75 V , turning on transistor M 5 , which acts as a charge sink for C 1 = 1 p F through M 2 . Fig (d) shows the spike frequency for each I e x t , resulting in a respective frequency of 42 k H z , 89 k H Z , a n d 128 k H z , respectively. e) Current excitation I e x t against spike frequency graph, obtained by sweeping from 0 n A to 190 n A and obtaining the corresponding spike frequency
Preprints 107603 g011
Preprints 107603 g012
Figure 12. Testbench to test a 2-1 neuron array, with two neurons at the input layer and one at the input layer.
Figure 12. Testbench to test a 2-1 neuron array, with two neurons at the input layer and one at the input layer.
Preprints 107603 g012
Preprints 107603 g013
Figure 13. Simulation results for the testbench shown, producing the four scenarios a) Signaling for the reward voltage V R , which flips from 1.8 V to − 1.8 V from quarter to quarter. b) Excitation current I e x t for each of the neurons in the first and second layer. The neurons at the first layer get 0 n A at the second half of the simulation c)Spiking activity for each of the 3 neurons. Notice all neurons are able to emit spikes, with enough current integration. d)Thickness of the filament s of each memristor. When decreases, so does the conductivity. e) Membrane’s voltage for neuron N1 and N2 in the first layer. Once v m overpasses a threshold voltage of the neuron, it emits a spike. Notice the difference between first and second half. The spikes at the second half are byproduct of current integration of spikes.
Figure 13. Simulation results for the testbench shown, producing the four scenarios a) Signaling for the reward voltage V R , which flips from 1.8 V to − 1.8 V from quarter to quarter. b) Excitation current I e x t for each of the neurons in the first and second layer. The neurons at the first layer get 0 n A at the second half of the simulation c)Spiking activity for each of the 3 neurons. Notice all neurons are able to emit spikes, with enough current integration. d)Thickness of the filament s of each memristor. When decreases, so does the conductivity. e) Membrane’s voltage for neuron N1 and N2 in the first layer. Once v m overpasses a threshold voltage of the neuron, it emits a spike. Notice the difference between first and second half. The spikes at the second half are byproduct of current integration of spikes.
Preprints 107603 g013
Preprints 107603 g014
Figure 14. Layout structure of the described blocks: a) 11T1R layout structure, b) LIF neuron structure without the C 1 capacitor.
Figure 14. Layout structure of the described blocks: a) 11T1R layout structure, b) LIF neuron structure without the C 1 capacitor.
Preprints 107603 g014
Table 1. Geometries for each transistor used for the testbenches described. The scale is set in micrometers 1 .
Table 1. Geometries for each transistor used for the testbenches described. The scale is set in micrometers 1 .
4T1M structure 11T1M Neuron 2 × 1 testbench
( W / L ) 1 = 7.5 / 0.15 ( W / L ) 1 , 2 = 7.5 / 0.15 ( W / L ) 1 = 1 / 10 ( W / L ) 1 , 2 = 2 / 10
( W / L ) 2 = 7.5 / 0.15 ( W / L ) 3 , 4 = 15 / 0.15 ( W / L ) 2 = 1 / 0.15 ( W / L ) 3 , 4 = 2 / 10
( W / L ) 3 = 30 / 0.15 ( W / L ) 5 − 8 = 7.5 / 0.15 ( W / L ) 3 = 1.5 / 0.15 ( W / L ) 5 = 2 / 10
( W / L ) 4 = 30 / 0.15 ( W / L ) 9 , 11 = 1 / 5 ( W / L ) 4 = 15 / 0.15 ( W / L ) 6 = 1 / 0.15
( W / L ) 1 0 = 2 / 0.15 ( W / L ) 5 = 1 / 4 ( W / L ) 7 , 8 = 2 / 10
( W / L ) 6 , 8 = 2 / 0.15
( W / L ) 7 , 9 = 1 / 0.15
1 this is 0.15 = 150 n m
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated