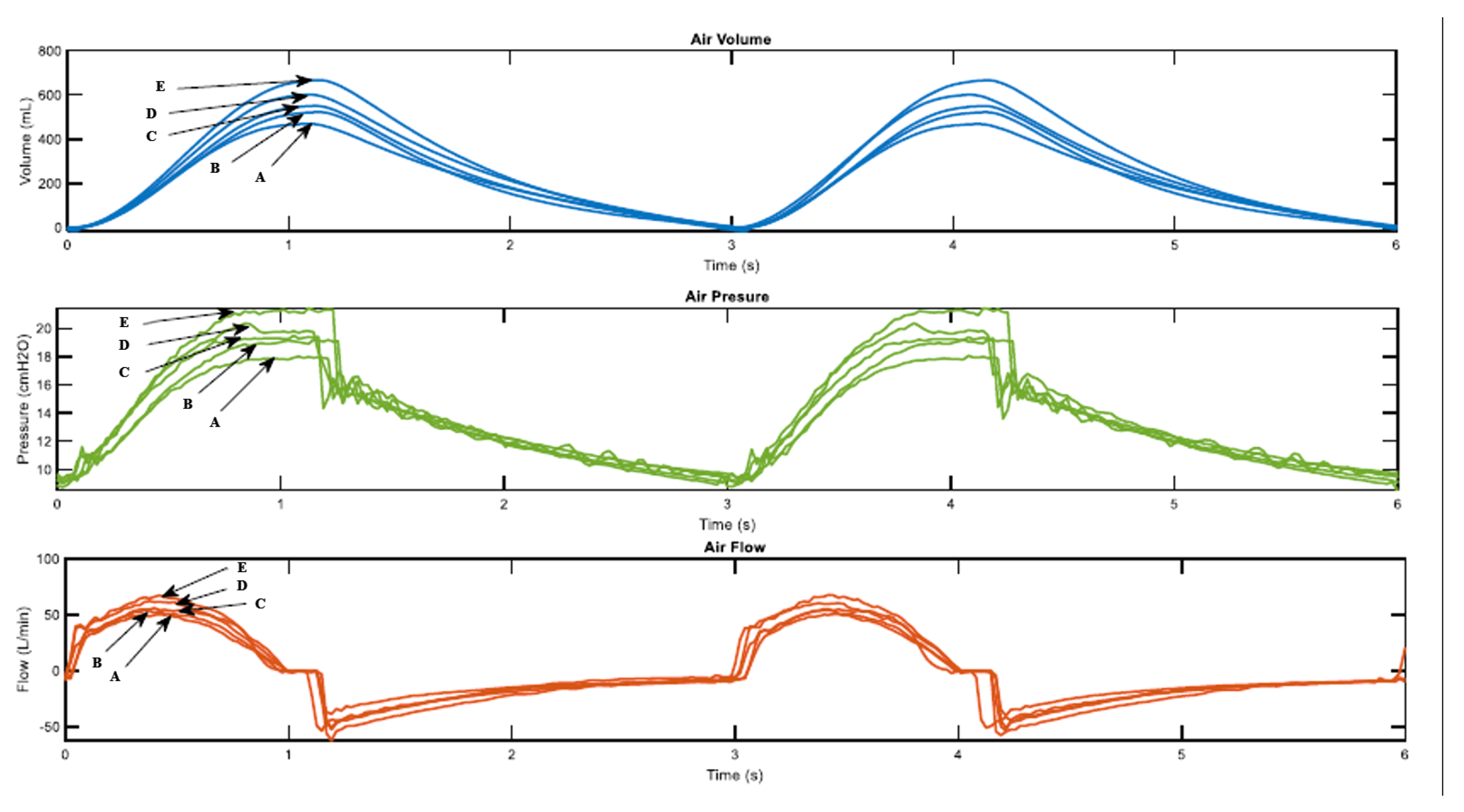
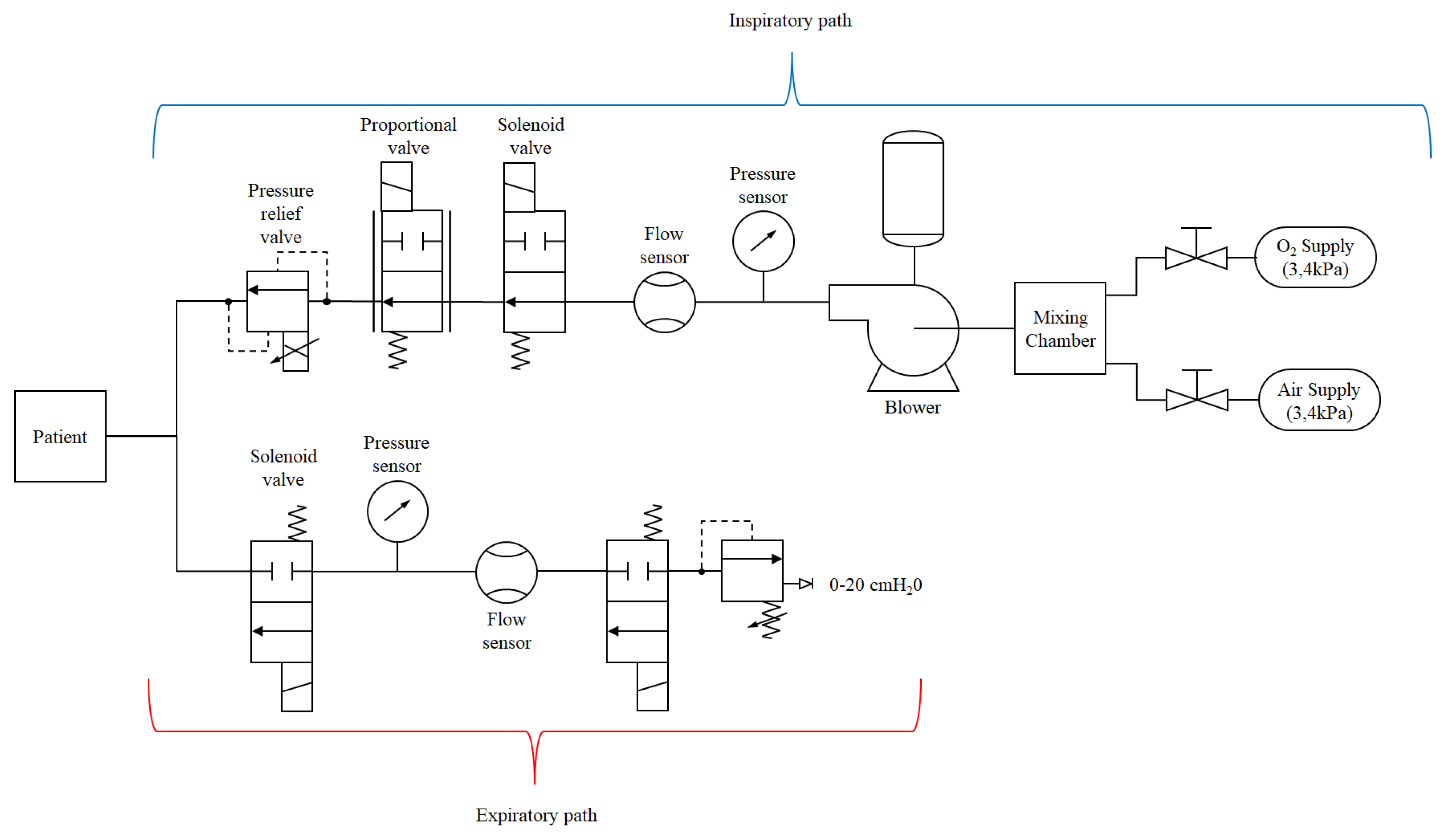
2. Related works
Tran et al, [
2], conducted research whose main goal was to design, control, model, and simulate a mechanical ventilator that is light in weight, portable, and suitable for use at home. [
2], modelled the mechanical ventilator as a voltage source. El-Hadj et al [
3], applied the fluid-structure Interaction (FSI) to a couple of computational fluid dynamics used for fluid flow with finite element analysis for the solid domain. This facilitated the investigation of fluid behaviour, structural behavior, and interactions. Two designs were proposed for the mechanical ventilator. The first design was reported to be uncontrollable and the second design considers Computational Fluid Dynamics (CDF) with a moving boundary which is applied to the piston cylinder based ventilator. Tharton et al [
4], designed and developed a ventilator prototype to be used by professionals in medical emergencies and in any other context where the regular ventilator is not available. The mechanical ventilator was modelled using the crank rocker mechanism in order to meet specific requirements for mechanical ventilator design. Pivk et al, [
5], developed an empirical model for a low-cost mechanical ventilator by observing the response of each of the ventilator subsystems. The current progress made globally in the development of affordable and effective designs is important. However, research in mechanical ventilator development lacks model development. The Port-Hamiltonian approach applied in this research work acts as a modelling template for future energy-based mechanical ventilator modelling and design. It is important to develop designs that rest on a solid understanding of a significant aspect of the design. Naggar, [
6] developed a piecewise model of a mechanical ventilator which described the artificial behaviour of a mechanical ventilator. A pressure-controlled ventilator is created and simulated. The mechanical ventilator is modelled using a periodic function with inequalities to control the beginning of inspiration and expiration periods. Shi et al, [
7] developed a mathematical model of volume-controlled mechanical ventilation. The model is viewed as a pneumatic system where the ventilator is regarded as an air compressor. The exhalation valve is considered as throttle. The compressor and the container represent the ventilator. Naggar et al, [
8] proposed an integrated mathematical model of the mechanical ventilator and the lung. Linear quadratic and exponential equations were used to model the system. The integrated model was used to simulate volume-controlled artificial ventilation. Giri et al, [
9], proposed a simplified design of a mechanical ventilator, to reduce cost and automate the mechanical ventilation process. The proposed design was simulated on the MATLAB platform. Hannon et al, [
10] presented a review on the advancement in the modelling of human anatomy, physiology and pathophysiology via mathematical modelling and computer simulation. Clinical applications in various disease states were emphasized. The research work discussed the current limitations and potential of in-silico modelling. There are currently no existing Port Hamiltonian models of mechanical ventilators intergrated with a human repiratory system. The main contribution in this research work is the development of an intergrated Port-Hamiltonian model representation of a mechanical ventilator-human respiratory system. The model consists of electromechanical and electromagnetic components modelled in the finite-dimensional representation, interconnected with fluid components in the infinite-dimensional representation. As a result, this Port-Hamiltonian model is of a mixed finite/infinite dimensional nature.
3. Materials and Method
This section presents the mathematical preliminaries of the Port Hamiltonian approach that have been followed in later sections. These definitions are standard definitions from literature and are mostly derived from the following references: [
11,
12] and [
13]
Definition 1 (Dirac Structure)
A Dirac Structure (DS) is a pair of elements,
and
, that satisfies the set:
The DS is a subset , where and represent the flows and efforts, respectively.
The DS in electric circuits can be represented as:
Proposition 1:
The subspace
is called a DS iff, there exist
such that
satisfying the condition
Definition 2 (Resistive Relation)
Any relation
is said to be resistive if
the
is satisfied.
Definition 3 (Port-Hamiltonian (pH) System).
The set , defines a pH system where:
is a DS
is a LS and
a Resistive relation.
The elements of the sets:
and are known as flows and efforts
and are known as resistive flows and efforts
and are known as external flows and efforts, respectively.
where and .
The dynamics of the pH system are given by the differential inclusion
where
,
and
Definition 4 (Interconnection of n pH Systems)
Let (
) denote the space of the
pH system in a set of
n pH systems that are to be interconnected. The space of flows is divided into an external part and a part to be linked and is given by
Similarly, the space of efforts is divided into an external part and a part to be linked and is expressed as
The interconnection of two pH systems
and
with respect to the link
results in a new interconnected pH system,
. This interconnected system is given by the expression
Definition 5 (Directed Graph).
A directed graph is a quadruple where
V is a set of vertices
E is a set of edges
maps each edge, e, to an initial vertex
maps each edge, e, to a terminal vertex
Definition 5.1 (Loop-free directed Graph).
If
G is a directed graph, then
G is said to be loop-free if for all
,
Definition 5.2 (Subgraphs).
Given the graphs and , then is said to be a subgraph of if and . Furthermore,
A subgraph is said to be an induced subgraph on if
A subgraph is said to be spanning if
A subgraph is said to be a proper subgraph if
If both V and E are finite, then is said to be finite
Definition 6 (Paths, Connectivity and Cycles).
Let be a directed finite graph.
-
An n-tuple is called a path from to , if
- (a)
are distinct
- (b)
for all
- (c)
A path from to is called a cycle.
Two vertices, and are said to be connected if there exists a path from to .
The existence of paths from vertices gives an equivalence relation on the set of vertices.
A subgraph is a component of the graph.
A graph with only one component is said to be connected.
Definition 7 (Incidence Matrix).
Let
be a directed graph that is finite and loop-free such that
and
. Then the
row and
columns of the incidence matrix,
of
is given by
If the , then the graph has components, such that k rows can be removed from resulting in matrix with same rank.
Definition 8 (Kirchhoff-Dirac Structure, Kirchhoff-Lagrange Submanifold).
The Kirchhoff-Dirac structure of
can thus be defined by the set
where
i and
u are the currents and voltages at the edges of the graph, respectively, whereas
q and
are the charges and potentials at the vertices of the graph, respectively.
Assuming that
, the Kirchhoff-Lagrange submanifold of
with respect to
S is defined as
where
is a directed graph that
If are the components of with corresponding vertices so that there exists a subset such that containing at most one vertex from each component, i.e. , then can be constructed by deleting the rows corresponding to the vertices from .
Remark. According to Proposition 1, Equations
1 and
2 indicate that
is a DS and
is a LS in the space
.
Definition 8 caters for an introduction of a pH system
with dynamics
where
.
Using the equivalence of
to
and
, we see that equation
3 holds, iff, the condition holds.
On this basis, one can define a DS
with dynamics
and an LS
with dynamics
Together, they form a the pH system defined by the set .
3.1. Dirac Structure
A key feature of a Dirac structure is the fact that the standard composition of two Dirac structures is again a Dirac structure. The implication of this statement is that any power-conserving interconnection of a Port Hamiltonian system is also a Port Hamiltonian system itself. This constitutes the foundation feature in the Port Hamiltonian approach to modelling, simulation and control of complex physical systems. The intricate Dirac structure is the guide to the algebraic constraints of the interconnected system as well as its Casimir functions [
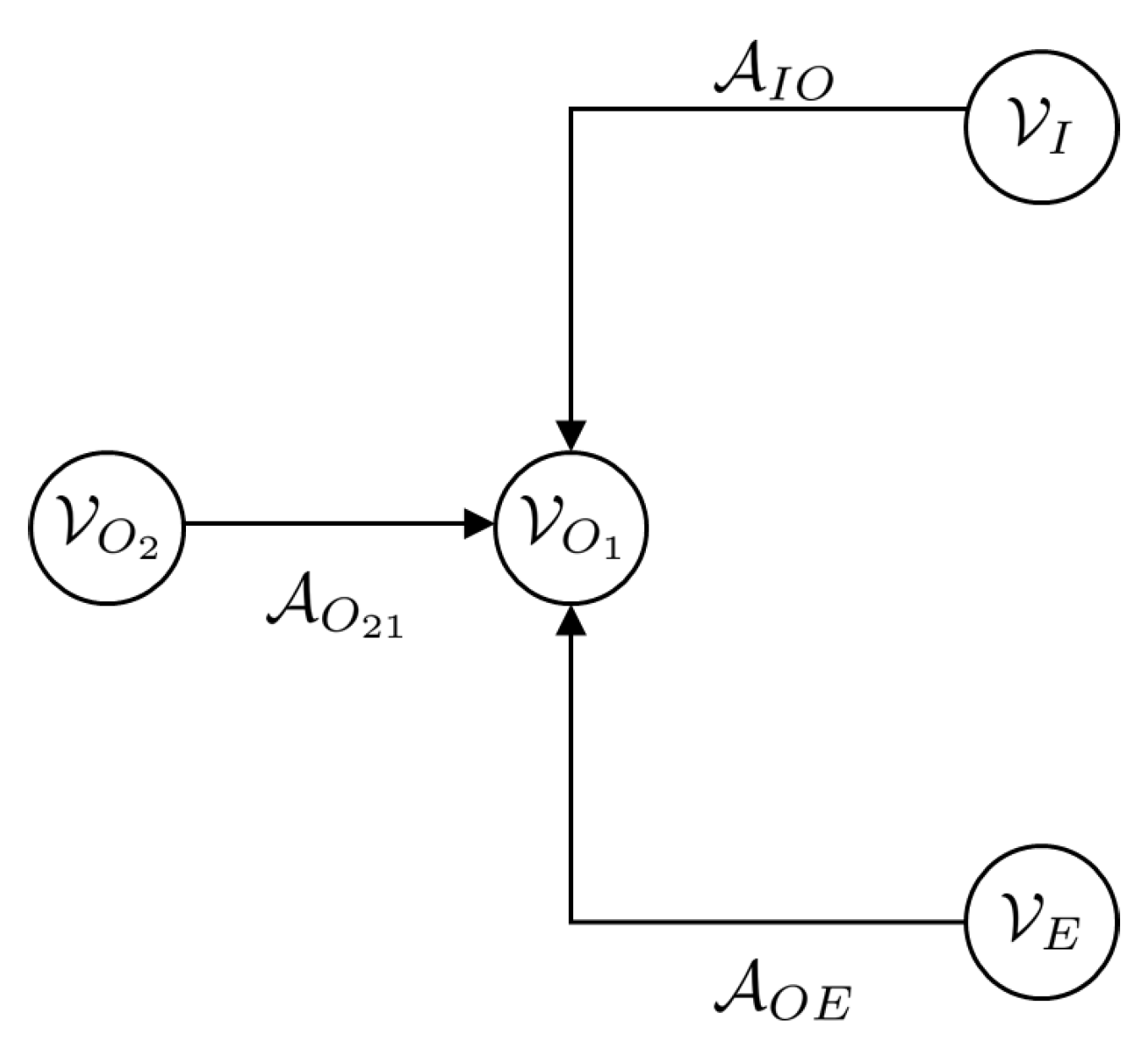
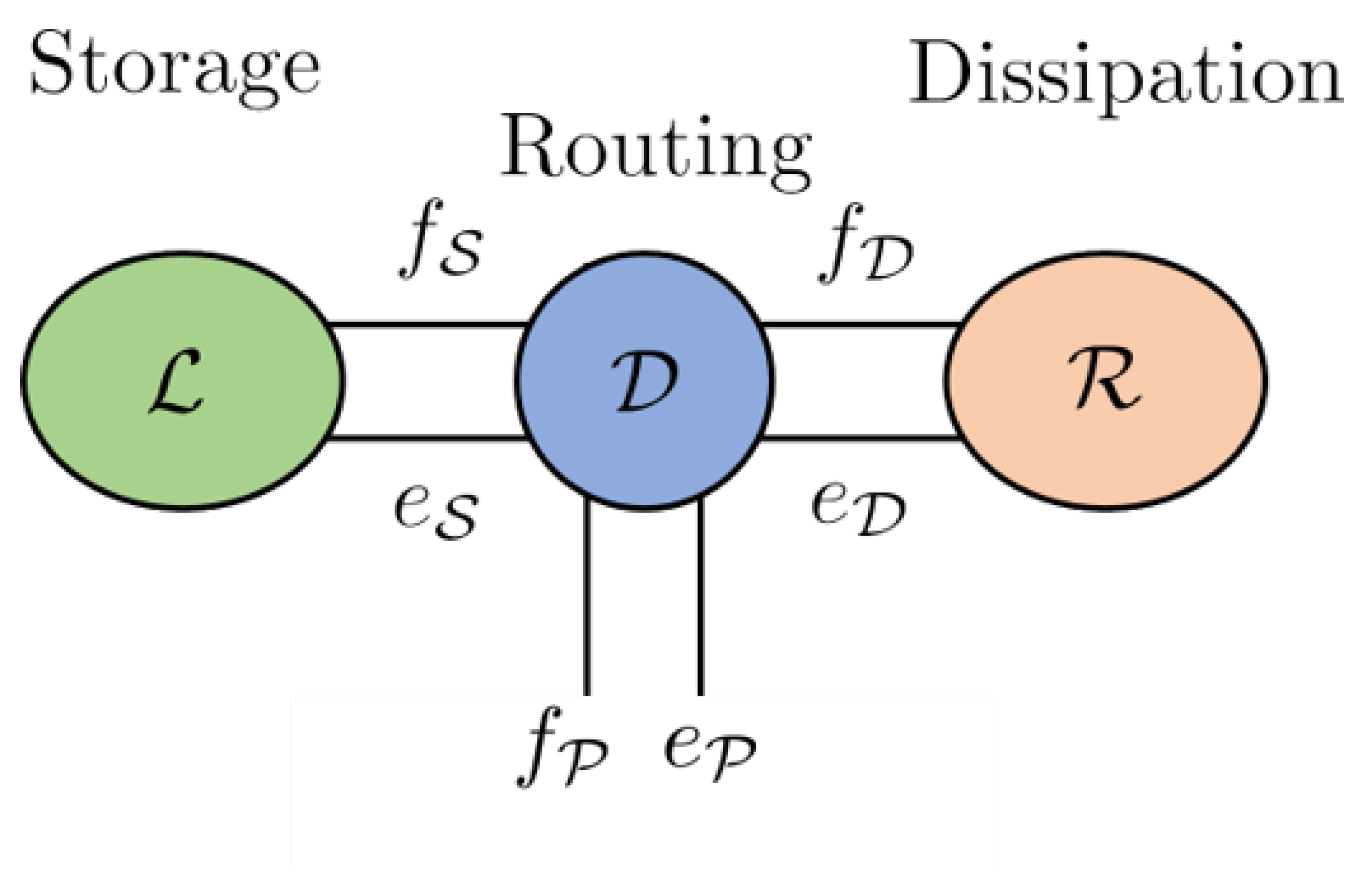
13]. The Casimir are significant in the set point regulation of Port Hamiltonian systems. The framework for the Port Hamiltonian allows for port-based modelling. Port-based modelling means that we are interconnecting many different elements through ports. Dirac structures are the tools used to connect multiple elements. These various elements are energy-storing elements, energy-dissipating elements and external elements which could be supplying energy. A diagram to demonstrate the connection structure is given in
Figure 1,
13]
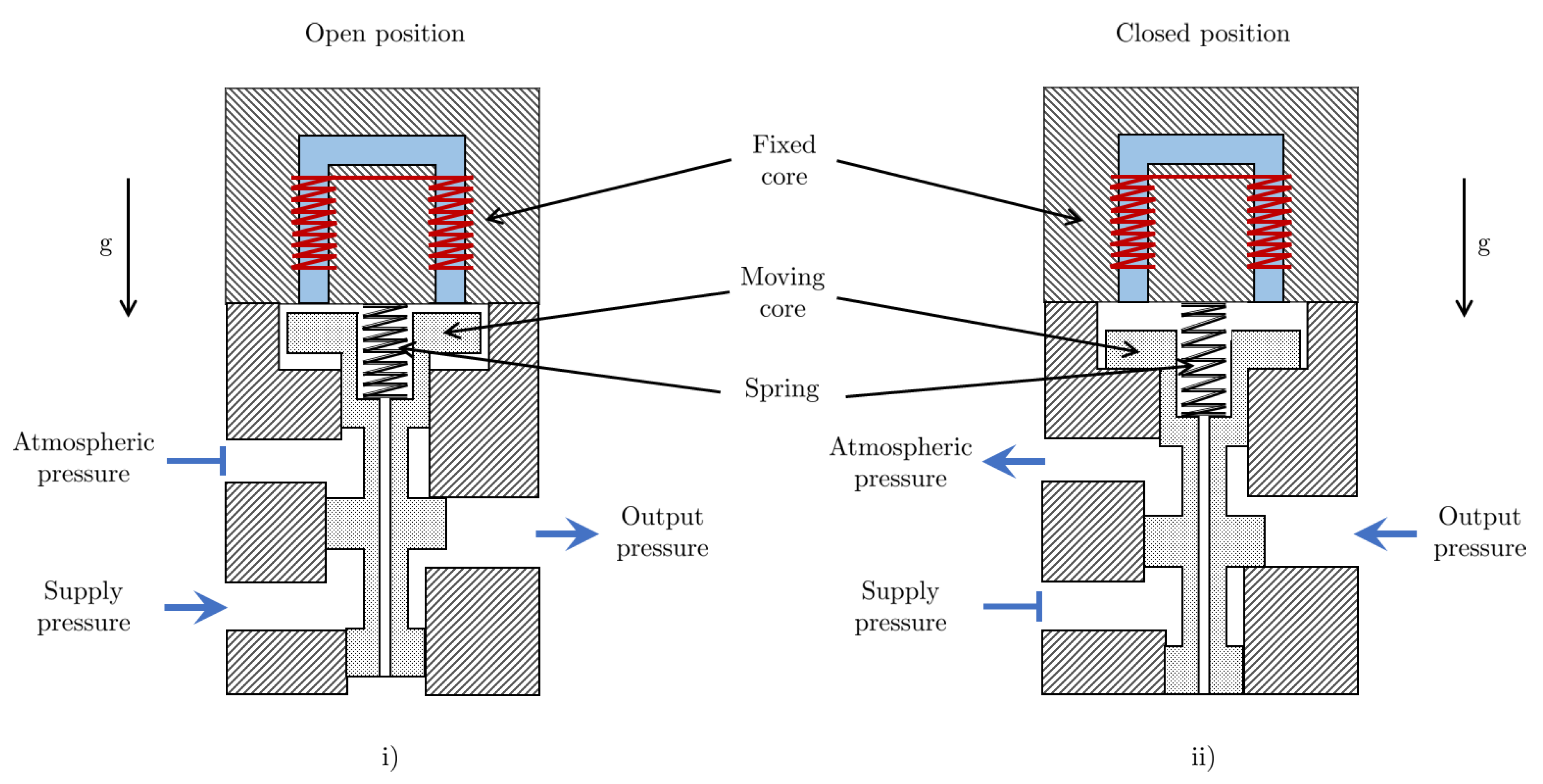
5. Solenoid Valve Subsystem
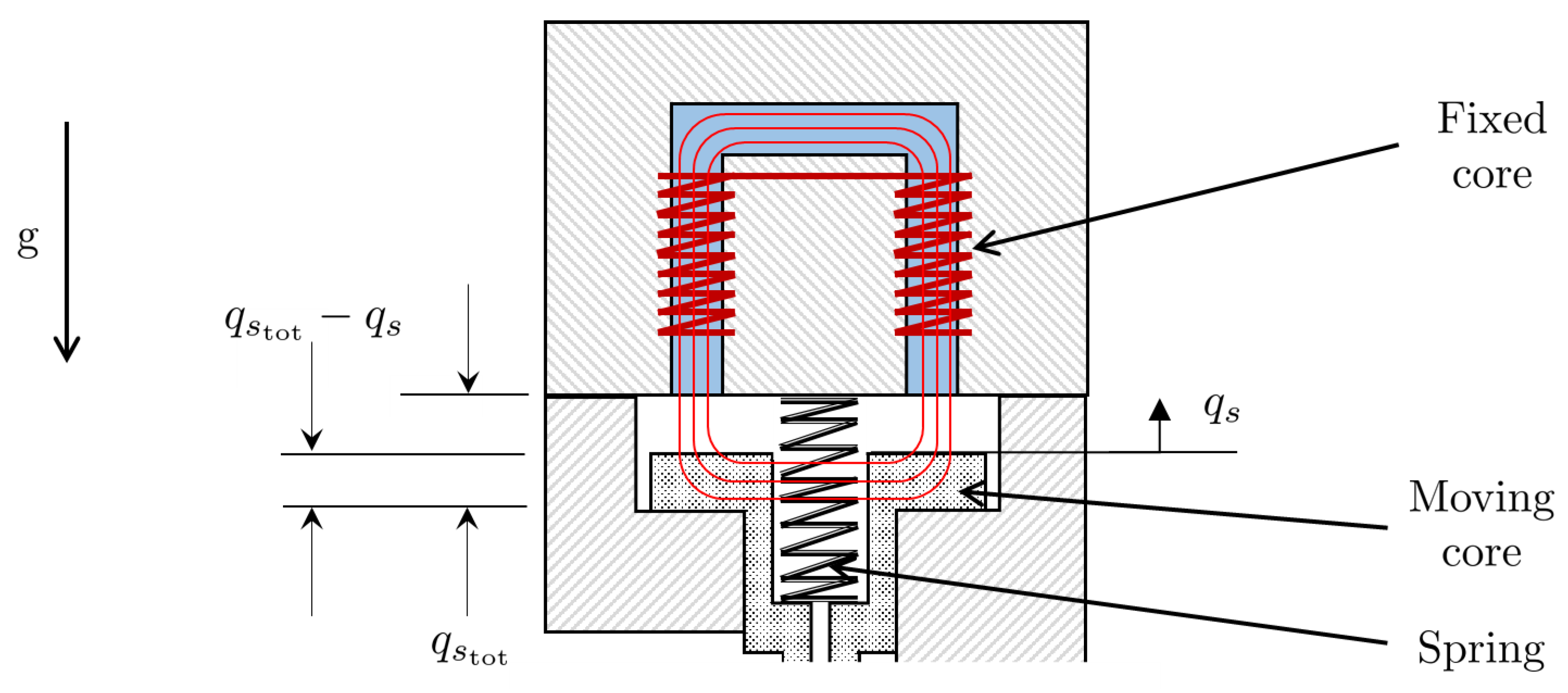
Figure 3 shows a solenoid valve in the open and closed position. It is assumed that the air gaps are sufficiently small such that the effect of fringing of the magnetic flux is negligible. Consider a solenoid in which the permeability of the core and the length of the part of the magnetic circuit inside the core are denoted by
and
, respectively. The equivalent length of the solenoid’s magnetic circuit,
is dependent on the displacement of the spool,
, and can be written as
where
are the permeability of air and
is the total air-gap. The solenoid coordinate systems is represented in
Figure 4.
Figure 4.
Solenoid coordinate system
Figure 4.
Solenoid coordinate system
Figure 3.
Diagram of a Solenoid valve in the i) open position which allows fluid flow and ii) closed position which stops fluid flow
Figure 3.
Diagram of a Solenoid valve in the i) open position which allows fluid flow and ii) closed position which stops fluid flow
Thus, the inductance of the solenoid varies with displacement of the spool and hence can be expressed by the function
given by
where
is the number of turns in the coil of the solenoid and
is the effective cross-sectional area of the path of the magnetic flux. The magnetic and mechanical subsystems in the solenoid valve are therefore coupled magnetically due to the dependence of the inductance on the displacement of the spool.
The total energy of the solenoid is given by the Hamiltonian,
, which is a function of the state vector
, expressed as the sum of the magnetic, kinetic and potential energies denoted by
,
and
, respectively. Thus
given a magnetic flux
.
Assuming that the pretension of the spring is set to
, the Hamiltonian is
where
is the momentum of the spool,
is the mass of the spool,
is the spring stiffness and
is the acceleration due to gravity.
Hence, the solenoid’s state and output dynamics are expressed in Port-Hamiltonian form in equations
13 and respectively
where
where
is the resistance of the coil,
is the viscous damping acting on the spool and
∇ is the gradient operator.
are the various cross-sectional areas of the lands of the spool and the input vector
consists of the input voltage
and the supply pressure
. It can be seen that
possesses skew-symmetry, while
is positive semi-definite.
Taking the time derivative of the Hamiltonian
This system has power and resistive ports.
5.1. Pipe Model
In this section, a port-Hamiltonian model of a single pipe segment is developed. The basis of these developments is the Navier Stokes equations for one-dimensional non-stationary flow of gas in a pipe. The following assumptions are taken for the sake of model simplification [
14,
15]:
The pipe is taken as rigid (it does not expand in cross-section as a result of fluid flow).
Frictional and gravitational effects are neglected (this will be relaxed in future works in this research area),
The model parameters of the gas remain constant along the pipe cross-section but vary in time along the pipe length. Thus they can be averaged about the cross-section and thus the gas flow is one-dimensional.
The temperatures of the pipe walls are assumed to be constant and equal to the ambient room temperature. Hence temperature effects are ignored.
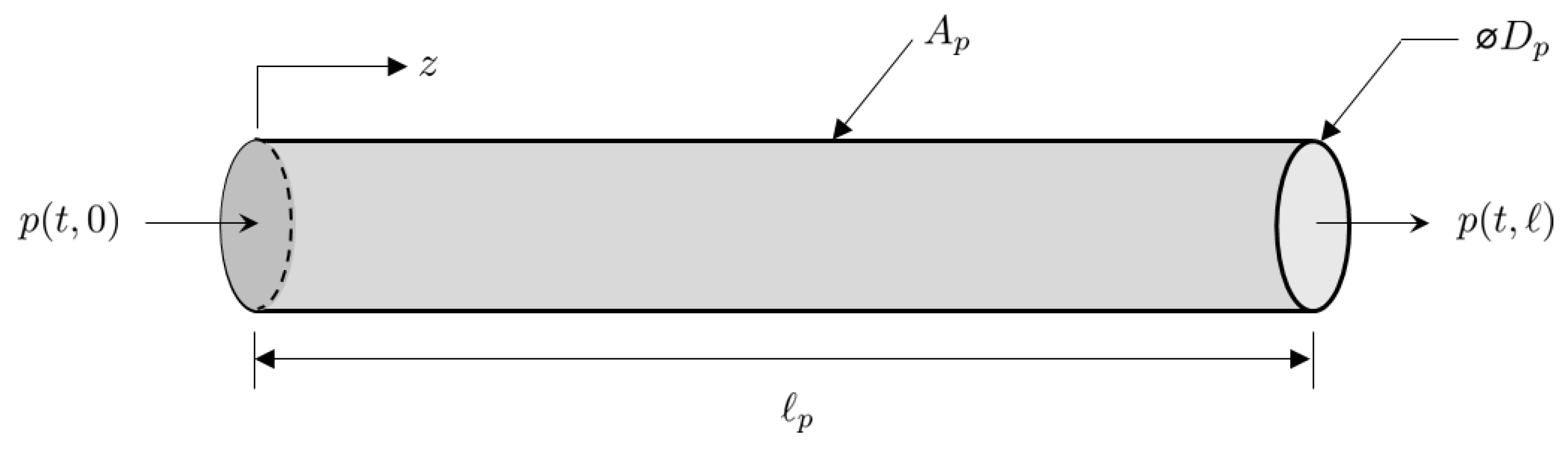
Taking into account these assumptions, the coordinate system attached to a segment of pipe is illustrated in
Figure 5.
Thus, for a given time interval
with start time
and finish time
, the length normalized one-dimensional Euler equations for gas of density
flowing at a velocity
through a pipe of length
and cross-sectional area
are given by:
where
is the pressure and
is the partial derivative with respect to the temporal and spatial variables given by the subscripts
.
5.1.1. Port-Hamiltonian Formulation of Pipe-Flow Model
The fluid dynamics can be written in terms of mass per unit length, i.e.
, as well as the fluid momentum,
. Thus equations
16a and can be expressed as
Defining the state vector of the gas flow through a pipe segment as
, the energy of the gas can be expressed in form of a Hamiltonian
given by
where
is the Hamiltonian density and
is the internal energy of the gas which in the case of an isentropic fluid, can be expressed as a function of density.
The port-Hamiltonian dynamics take the following form
where
, the formally skew-symmetric operator and
, the variational derivative of the Hamiltonian density are expressed as
where
h is the enthalpy, and
is a formally skew-symmetric operator.
The rate of change of the Hamiltonian can be found as
where
with components given by
Thus, the rate of change of the Hamiltonian is
5.2. Electric Circuit Model of the Lung
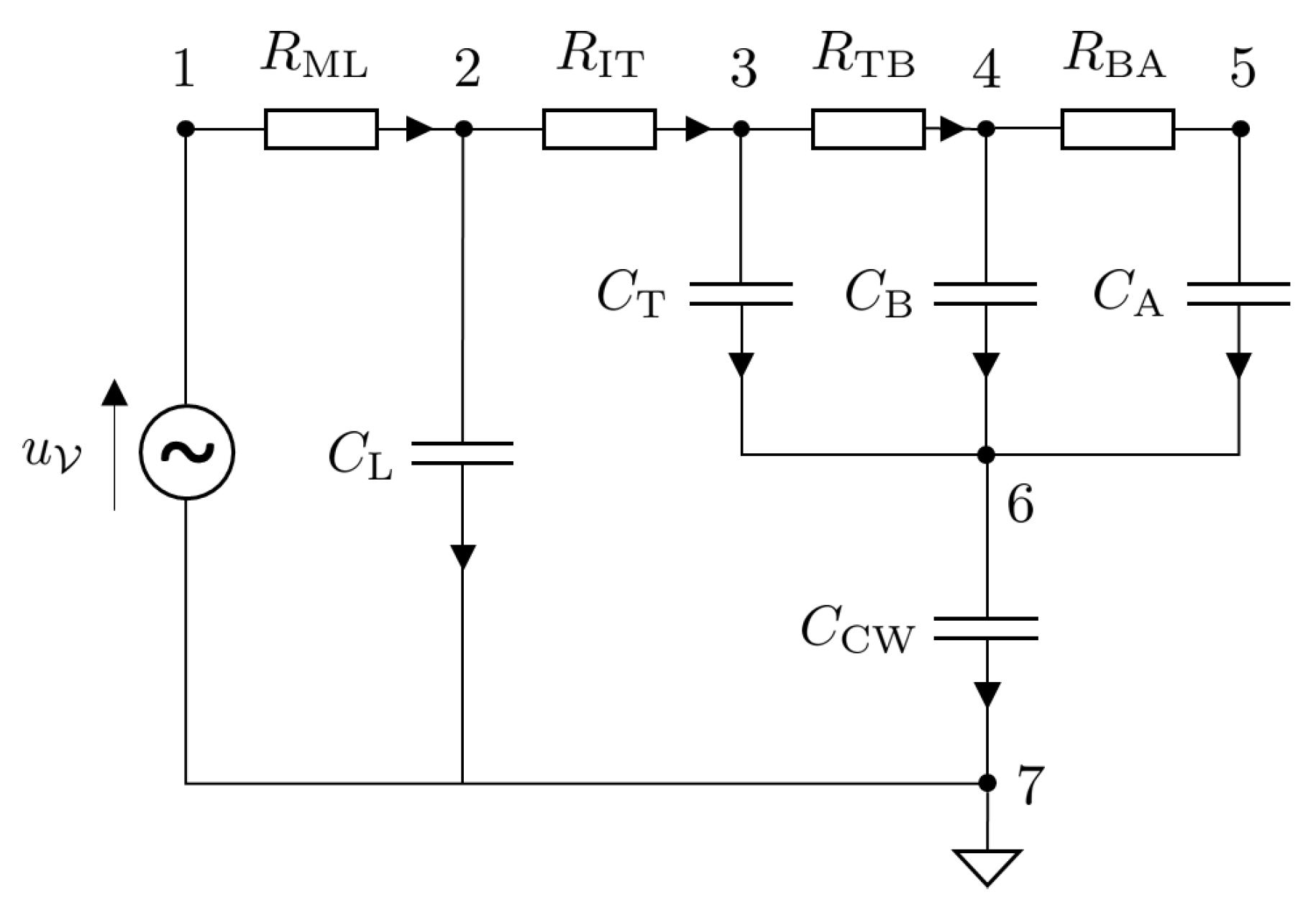
The port Hamiltonian formulation for nonlinear electric circuits is presented in this section. Since the main focus of this article is on the mechanical ventilator model, the lung model is simplified by considering an electric circuit analogy. The model under consideration is that of a fully sedated patient who relies completely on the mechanical ventilator to breathe. The circuit model is shown in
Figure 6.
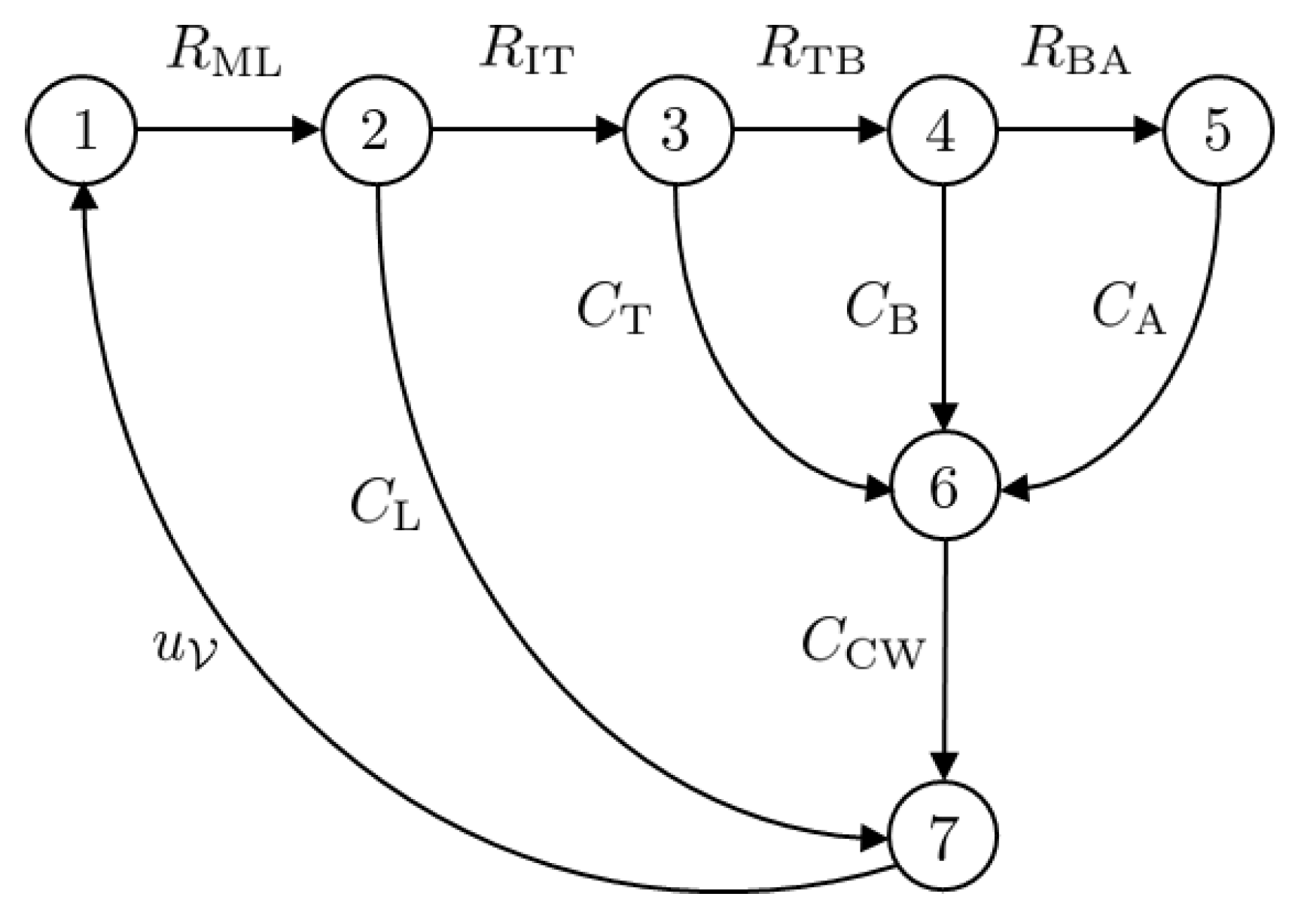
The circuit can be represented in the form of a network graph using graph theory. The graph of the circuit given in
Figure 6 is given in
Figure 7. The model has
vertices.
The complete graph of the circuit, , is
The ventilator input voltage is represented as a source . The set of sources is and the dimension source. The circuit also consists of capacitors (storage elements) that are represented as where the index is used to distinguish between the components is . Furthermore there are resistors (dissipative elements) that are represented as where the index is given by .
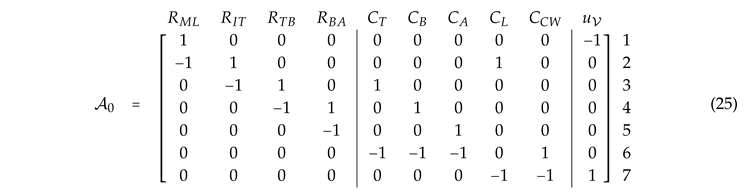
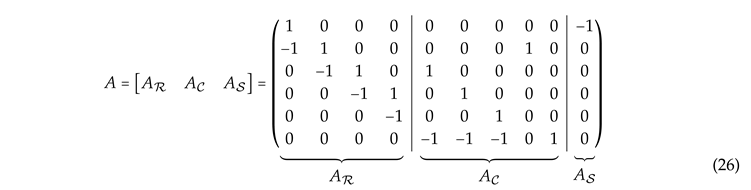
Selecting node 7 as the ground, the reduced incidence matrix, , is given by
where the dimensions of the components of are , and .
The total energy of the circuit is given by the Hamiltonian
where
is the charge of the
capacitor for
where
and
are appropriately sized identity and zero matrices, respectively and
and
is the node potential. Expanding Equation
41
The Dirac structure is given by the set where
8. Structure Preserving Discretization
The port Hamiltonian model of the pipe is a partial differential equation, continuous in space. As such it is difficult to simulate the dynamics of a pipe section. In order to do this, it is necessary to approximate the model with a discrete model, in this case, a finite difference model which is an approximation of the original system. Within the context of port Hamiltonian systems, an additional requirement is the need to ensure that the discrete approximation maintains the structural properties of the original system e.g. skew symmetry etc.
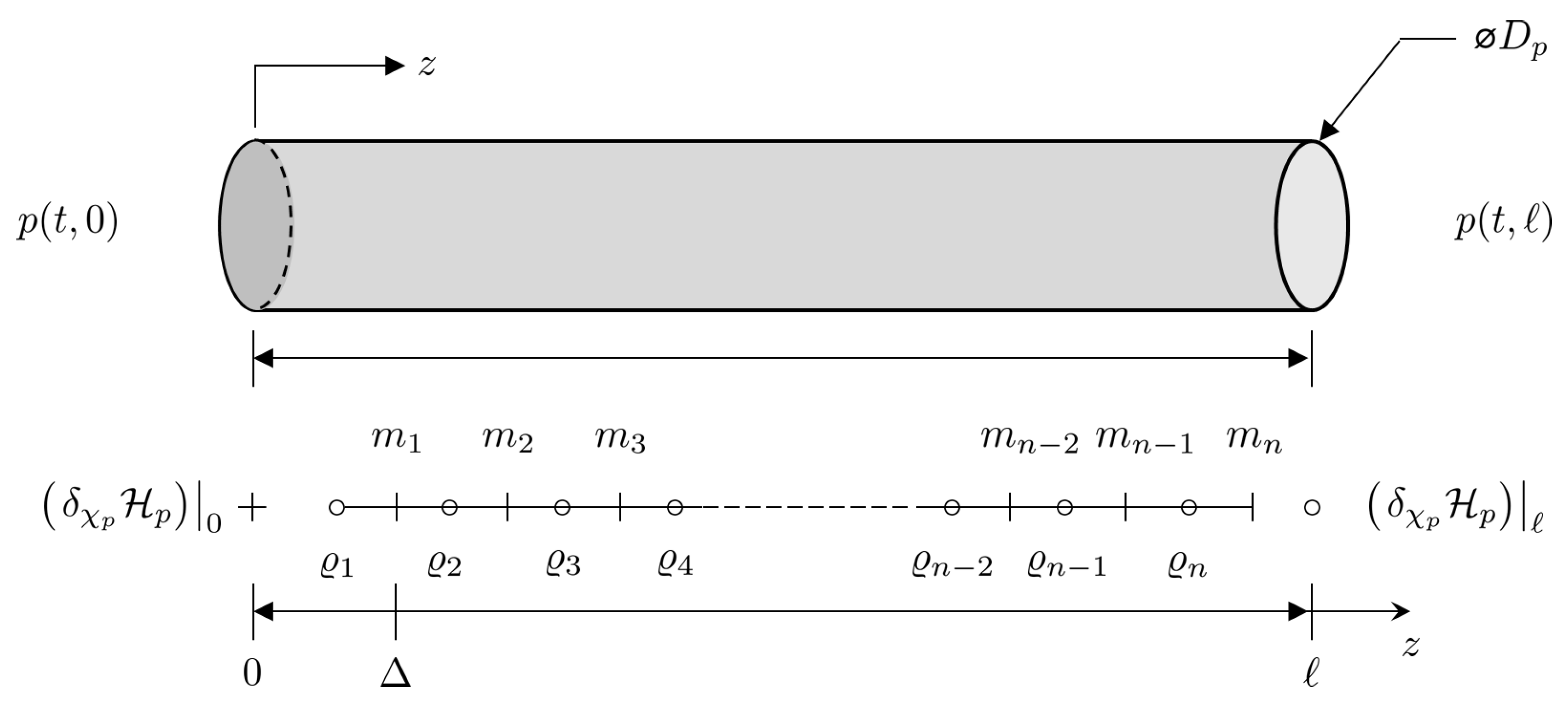
Each system state can be replaced with a discrete approximation consisting of a total on
n elements as can be seen in
Figure 10. As such,
and
. As such, state vector
can be replaced by a discrete approximation
. The
element of
is located at
, where
is the fixed discrete step size between points and
. In addition, the efforts at the boundaries are given by
and
. Thus the Hamiltonian given in Equation
18 can be approximated by a discrete approximation such that
so that the discrete system effort is now
. A finite difference approximation of the spatial derivatives at the
point is
The central difference approximation at the
point is
In matrix form this is
which can be re-written as
where
The skew-symmetric operator is clear from Equation
Section 8.
Figure 10.
Staggered grid discretization of the one dimensional port Hamiltonian pipe dynamic model
Figure 10.
Staggered grid discretization of the one dimensional port Hamiltonian pipe dynamic model