A Simulated Annealing Approach to the Scheduling of Battery-Electric Bus Charging

Preprint

Article

A Simulated Annealing Approach to the Scheduling of Battery-Electric Bus Charging

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.zip (479.35KB )

This version is not peer-reviewed

Submitted:

20 May 2024

Posted:

28 May 2024

You are already at the latest version

Alerts

Abstract

With an increasing adoption of Battery Electric Bus (BEB) fleets, developing a reliable charging schedule is vital to a successful migration from their fossil fuel counterparts. In this paper, a Simulated Annealing (SA) implementation is developed for a charge scheduling framework for a fixed-schedule fleet of BEBs that utilizes a proportional battery dynamics model, accounts for multiple charger types, allows partial charging, and further considers the total energy consumed by the schedule as well as peak power use. Two generation mechanisms are implemented for the SA algorithm denoted as the "quick" and "heuristic" implementations, respectively. The model validity is demonstrated by utilizing a set of routes sampled from the Utah Transit Authority (UTA) and comparing the results against two other models: the BPAP and the Qin-Modified. The results presented show that both SA techniques offer a means of generating operationally feasible schedules quickly while minimizing the cost of operation and considering battery health.

Keywords:

Subject: Engineering - Transportation Science and Technology

1. Introduction

With an ever-increasing interest in the electrification of vehicles in the push for green transportation, many organizations and companies have been looking to adopt a fleet of electric vehicles [1]. This transition includes battery electric buses (BEBs) [2,3]. In particular, agencies such as the Utah Transit Authority (UTA) have directed focus in replacing their fleets with BEBs. Alongside all the benefits that are associated with BEBs come new challenges that must be addressed prior to their integration into mainstream utilization. The energy storage capacity of BEBs is typically significantly less than their combustion counterparts while also having significantly longer refueling periods [2,4]. This is further complicated due to the care that must be taken in prolonging the lifespan of the battery [5,6,7]. As another complication, BEB refueling is not a fixed cost (i.e. price per gallon multiplied by tank size). Utility companies, in addition to charging for the total energy consumed over a pay period, often charge a demand cost. The demand cost is based on the peak power drawn during the pay period and can significantly impact the overall monetary cost of maintaining the BEBs. This work introduces a scheduling framework for a fleet of BEBs that minimizes charging costs while considering other constraints pertinent for operation.

A host of strategies have been proposed to solve the BEB charger scheduling problem. Strategies vary in terms of their basic formulation, many using variations of the vehicle scheduling problem [8,9,10,11,12,13] while [14] utilizes a network flow approach and [15] utilizes a rectangle packing approach referred to as the Position Allocation Problem (PAP). Some works assume that BEBs always charge to full capacity each time they connect to a charger [8,9,16,17], while others allow for partial charging using a linear battery charge model [13,18,19], and others use a higher-fidelity, non-linear battery model [8,14,20,21,22]. Some works consider only fast chargers during planing [12,18,23,24,25], while others assume that different types of chargers can exist in different locations [11,13].

When considering the utility rate schedules, two key elements must be considered: the consumption cost and the demand cost. Most approaches consider a consumption cost [9,10,16,19,20,21,22,23]. This is akin to the combustion engine fuel cost. Fewer works, however, consider the demand cost [13,19,20,21,22]. The demand cost calculation requires a fine sampling of the power usage at any given time. Approaches that assume a full charge whenever the bus connects typically employ a coarse sampling of charger time periods and may not be well-suited to demand cost calculations. Furthermore, the assumption of always using fast-chargers is adverse to battery health [6,7,16].

To accurately calculate the demand cost, an inherent tradeoff exists between the low computation of a representative linear model and the high computation of a high-fidelity nonlinear model. A linear, proportional model is used in this work as they have been shown to be accurate below an 80% threshold [2]. This is considered sufficient for this work as charging a battery nearly to capacity is detrimental to the health and can significantly reduce the total charge cycles a battery may undergo [6,7]. Thus, staying within the linear operating region is desirable for battery health.

The contributions of this work lie in the formulation of a Simulated Annealing (SA) framework that generates a charging schedule that considers 1) Different types of chargers at the same location, 2) Minimization of the consumption and demand utility costs, 3) Partial charging through a representative linear charge model. These contributions are demonstrated via simulation and comparison to two other models: an implementation of the PAP for BEBs, denoted as BPAP, and what is known as the Qin-Modified technique.

The remainder of this paper goes as follows. Section 2 provides the problem statement associated with this work. Section 3 provides a description of the input parameters and decision variables then introduces the structure of the formulation. In Section 4, the concept and theory of SA is introduced. In particular, the algorithms and methods utilized for the SA implementation for this work are discussed. Section 5 combines the previous sections to introduce the particular pseudocode for the SA PAP. In Section 6, an example problem is provided to demonstrate the capability of the work provided in this paper. The results will be presented and discussed.

2. Problem Description

Consider a fleet of BEBs scheduled to perform a set of prescribed routes on a given day. An individual BEB from said fleet begins and completes an individual route at the same station from which it also receives its charge. During each route, the BEB’s State of Charge (SOC) is depleted by a certain amount. The charge supplied during its visit must be enough to sustain the BEB’s SOC at an appropriate level so that it may complete its next route. Provided there is a set of chargers at the station, the bus may be placed in any single queue to receive its charge. Let the term “arrival” describe the time at which a BEB reaches the station. Furthermore, let the term “visit” denote a BEB having arrived, awaited its predetermined time (whether it has received a charge or not), and departed from the station. Each BEB is allowed to have multiple visits throughout the working day.

Because each bus may visit the station more than once, let the previously considered fleet contains

n_{B}

BEBs that collectively visit a station

n_{V}

times. At said station, let there exist a pool of

n_{Q}

charging queues from which a visiting BEB may be assigned. Upon arrival to the station, a bus is admitted to one of the

n_{Q}

queues for charging. Each queue represents a charger that supplies the bus with a charge at a particular rate or allows the bus to sit idle when no charging is required (i.e., a charge rate of zero). The set of possible queue indices is denoted as

Q \in {1, . . ., n_{Q}} \subset Z

, where

Z

is the set of integers. It is assumed that charger

q \in Q

has an associated charge rate, denoted as

r_{q}

. Let the set of arrivals be written as

I = {1, . . . n_{V}} \subset Z

, and let each BEB be prescribed an identification number from the set

B = {1, . . ., n_{B}} \subset Z

. As such, each visit can be represented by the tuple:

(i, b, a, e, u, d, q, η, ξ)

, in which the elements within the tuple denote the visit index,

i \in I

, BEB identification number,

b \in B

, arrival time to the station,

a \in R

, departure time from the station,

e \in R

, time at which the BEB begins charging,

u \in R

, time at which the BEB ends charging,

d \in R

, the charger queue for the BEB to be placed into,

q \in Q

, the SOC upon arrival,

η \in R

, and the index of the next visit for the currently visiting BEB,

ξ \in I \cup ⌀

. The null element, ⌀, is used to specify when a BEB has no future visits. Let the set of visits be denoted as

I

where the

i^{th}

visit is denoted is

I_{i}

. Furthermore, let a particular item from the tuple for visit i to be written as

\cdot_{i}

. For example, the arrival time for visit i is written as

a_{i}

The amount of time the BEB is allowed to charge during visit i is dictated by the scheduled arrival time and required departure time,

[a_{i}, e_{i}]

. Partial charging is allowed; however, the SOC may not exceed the BEB battery capacity,

κ_{b}

, and the SOC is desired to stay above some minimum percentage of the battery capacity,

ν_{b} \in [0, 1]

. The battery dynamics in this work is modeled as linear, which remains accurate up to about an SOC of 80% [26]. Note that excessively charging the BEBs is undesirable due to battery health concerns as at higher SOCs overshoot become a concern and may also cause the battery to undergo deep cycles may accelerate battery degradation [6,7].

Each BEB arrival, except for the last arrival for each BEB, has a paired “route” that the BEB must perform after the visit. This route, as one would expect, causes the BEB to discharge by some certain amount. Each bus route is assumed to have a fixed discharge. Let the discharge of the route for visit i be denoted as

Δ_{i} \in R

. Note that the last visit for each BEB does not have an associated route, implying that there is no discharge after these particular visits, i.e.,

Δ_{i} = 0

for all i corresponding to a final visit.

3. Optimization Problem

The objective of this work is to present a framework that optimizes the assignment of

n_{V}

BEB visits to a set of

n_{Q}

charging queues over the interval

[0, T]

provided a fleet of

n_{A}

BEBs with fixed route schedules. Particularly, the framework aims to minimize over peak power usage, energy consumption, encouraging battery health via slow charging, and maintaining the SOC of each BEB above a minimum SOC threshold.

The optimization problem outlined in this work is presented in form of an objective function with constraints. The constraints ensure that candidate solutions are operationally feasible. The variables of optimization are to be introduced in Section 3.1 followed by a discussion of the constraints in Section 3.3. The objective function is employed to allow relative comparisons between candidate solutions and is introduced in Section 3.2.

3.1. Variable Definitions

This section defines the input and decision variables used in this work. The input parameters are assumed to be fixed prior to optimizing, whereas the decision variables are the values that the SA algorithm has the freedom to manipulate. The variables definitions used in this work are summarized in Table 1.

3.1.1. Input Parameters

Parameters are used to indicate values that are assumed to be known prior to optimization. They will be presented in two sections: packing and discretization parameters then battery dynamic parameters. The spatiotemporal parameters are those that ensure no scheduling overlap in either space or time. The discretization parameters describe the parameters that discretize the time horizon, and the battery dynamic parameters are those associated with the SOC of the BEB.

Spatiotemporal and Discretization Parameters

As previously introduced,

ξ_{i}

represents the next arrival index for bus

b_{i}

. As an example of its use, suppose the ID of each BEB is recorded in order of arrival as

{2, 1, 3, 2}

. Using a starting index of 1,

ξ_{1} = 4

as that is the next visit by bus 2. Each visit is prescribed arrival and departure times,

a_{i}

and

e_{i}

, respectively. An associated cost is employed when a visit is assigned to a charging queue. Let the assignment cost be represented by

ϵ_{q}

. Lastly, the time horizon is to be discretized to assist in computing the peak demand cost, let

t_{h}

denote a discrete time step, and let

d t

denote the discrete time step

d t = t_{h} - t_{h - 1}

Battery Dynamic Parameters

It is assumed that each bus begins the working day with an initial SOC percentage of

α_{b}

. Let the set of initial visits by each BEB be denoted as

I_{0}

where

I_{0} \subset I

and the cardinality of the set is

| I_{0} | = n_{B}

. The initial SOC for bus

b_{i}

can be represented as

η_{i} = α_{b_{i}} κ_{b_{i}}; \forall i \in I_{0}

where

κ_{b_{i}}

is the battery capacity for bus

b_{i}

. After each arrival, the BEB is assigned to a charging queue. Let

r_{q}

represent the power supplied from the charger in queue

q \in Q

. Each visit, except for the final visit of each BEB, is paired with a subsequent route to be executed with a corresponding energy requirement,

Δ_{i}

. As alluded to earlier, there are no routes after the last visit for each BEB. Thus, similarly to the set of initial visits, let the set of final visits for all BEBs be denoted as

I_{f}

. The discharge for the final visit of each BEB is then defined as

Δ_{i} = 0; \forall i \in I_{f}

3.1.2. Decision Variables

Decision variables are those chosen by the optimizer. There are three direct decision variables for each visit: the initial and final charging times,

u_{i}

and

d_{i}

, respectfully, and the selected charging queue,

q_{i} \in Q

The remaining variables are slack variables, which are introduced to track the vehicle charge and queuing position based on the problem parameters and direct decision variables. Recall the initial SOC for a visit is written as

η_{i}

, where

i \in I ∖ I_{0}

. Further recall the set of initial visits,

I_{0}

, have an assumed known SOC (i.e., the initial SOC of each BEB at the beginning of the working day is considered as an input parameter). The charge for bus i’s next visit is equal to the initial charge for visit i plus the charge added to it by charger

q_{i}

over duration

s_{i} = d_{i} - u_{i}

minus the discharge accumulated after visit i,

η_{ξ_{i}} = η_{i} + r_{q_{i}} s_{i} - Δ_{i} .

(1)

The variables

σ_{i j}

and

ψ_{i j}

are used to indicate whether a visit pair

(i, j)

overlap the same space, as show in Figure 1. These spatiotemporal variables uphold the following relationships: for every visit,

σ_{i j} = 1 \Rightarrow

the start charge time of visit j is greater than the end charge time of visit i. Similarly,

ψ_{i j} = 1 \Rightarrow

the queue for visit j is of a greater index than visit i. A value of zero for either of these variables conveys no information.

The variable

C

is the set that describes the availability for all chargers. That is,

C

is a set of

n_{Q}

sets that contain available charger times for each queue

q \in Q

. Let a set of available charge times for queue q be defined as

C_{q}

3.2. Objective Function

This work aims to minimize the total “cost” of utilizing a given charge schedule. Let

J (I)

represent the objective function. The objective function for this problem has four main considerations: an assignment cost, a penalty method for visits with insufficient SOCs, consumption cost, and a demand cost. Each of which will be discussed in turn throughout the subsequent sections.

3.2.1. Assignment Cost

The assignment cost represents the cost of assigning a bus to a queue. Particularly, the cost consists of summing a prescribed weight for the selected charger,

ϵ_{q_{i}}

, multiplied by the charge rate,

r_{q}

. Formally, the cost is written as follows:

\sum_{i = 1}^{n_{V}} ϵ_{q_{i}} r_{q_{i}} .

(2)

This is effectively the cost of selecting queue

q_{i}

. While any set of weights may be selected, Section 6 uses a particular choice for the assignment cost to encourage the use of slow chargers over fast for the sake of battery health. The charger queue indices are ordered such that the first

n_{B}

queues correspond to idle queues. This allows all BEBs to simultaneously sit idle if needed. All

n_{B}

idle queues have assignment costs of zero to denote that there is no cost when not charging. The next group of chargers is assumed to be the slow chargers subsequently followed by the fast. Letting

P \in R

, then the set of slow and fast charging queues be of the form

[P, 2 P, . . ., n_{Q} P]

. Concatenating these vectors yields

ϵ = [0, 0, . . ., P, 2 P, 3 P, . . .]

, where

ϵ

describes the vector of assignment costs and the first

n_{B}

values are zero.

3.2.2. Penalty Method

A penalty method is to be implemented to provide a soft constraint on the lower bound of the charge. Due to the uncertainty of the initial SOC for each visit, a soft constraint is desired to increase the solution space while penalizing non-operationally feasible solutions. If a hard constraint were to be implemented, the constraint would restrict the set of allowable schedules to only operationally feasible schedules. Let the piecewise function that enables/disables the penalty method be of the form

ϕ (x) = \{\begin{matrix} 0 & x \geq 0 \\ x^{2} & x < 0 . \end{matrix}

(3)

Letting x be defined by the difference of the initial SOC for visit i,

η_{i}

, and the minimum charge threshold,

ν_{b_{i}} κ_{b_{i}}

, applies a penalty proportional to the difference of the SOC and the threshold squared. That is,

x = η_{i} - ν_{b_{i}} κ_{b_{i}}

. A scalar,

z_{p}

, is added which can be utilized either as a monetary conversion or a simple gain. This method is employed as a means of encouraging that the schedule has enough charge for each BEB to complete its next route. Therefore, the penalty method is written as

\sum_{i = 1}^{n_{V}} z_{p} ϕ_{i} (η_{i} - ν_{b_{i}} κ_{b_{i}}) .

(4)

3.2.3. Consumption Cost

In most cases, utility companies have a portion of the cost related to the total electricity consumed over a billing period, referred to herein as the consumption cost. The consumption cost is the summation of all the energy being used over all the active periods for each charger in the time horizon. A scaling

z_{c}

is applied as a weight on the summation (this could correspond to a monetary cost imposed by the utility). This is represented by the summation

z_{c} \sum_{i = 1}^{n_{V}} r_{q_{i}} s_{i} .

(5)

3.2.4. Demand Cost

Utility companies often charge a “demand cost” in an effort to reduce peak power use. A particular example of peak demand is the fifteen minute average energy usage employed by Rocky Mountain Power Schedule 8 [27].

A method of calculating the demand charge is done by calculating the average power consumption over a given period of time. Let the average power used over an arbitrary interval,

T_{p}

, be represented by

p_{T_{p}} (t) = \frac{1}{T_{p}} \int_{t - T_{p}}^{t} p (τ) d τ .

(6)

The largest average power usage over

T_{p}

is used as the demand cost for the billing period. Therefore, let the cost of the peak power consumption be dictated by the maximum average power:

p_{m a x} (t) = max_{τ \in [0, t]} p_{T_{p}} (τ) .

(7)

Furthermore, a fixed minimum average power is introduced that is intended to act as a base threshold before the cost begins to increase. Let this fixed threshold be defined as

p_{f i x}

, the demand cost is calculated using

p_{d} (t) = max (p_{f i x}, p_{m a x} (t)) .

(8)

For the sake of implementation, the integral in Equation 6 is discretized. Let

d t

denote the discretization time step and

p_{h}

the power for the

h^{th}

step, Equation 6 is approximated as

p_{T_{p}, h} = \frac{1}{T_{p}} \sum_{k = h - \frac{T_{p}}{d t} + 1}^{h} p_{k} d t .

(9)

The discrete demand cost is expressed as

p_{d} = max (p_{f i x}, p_{m a x}) .

(10)

Similarly to the consumption cost, a scaling

z_{d}

is applied. Again, this may be a monetary conversion or simply just a gain.

The objective function written in its entirety is

J (I) = z_{d} p_{d} + \sum_{i = 1}^{n_{V}} [ϵ_{q_{i}} r_{q_{i}} + z_{p} ϕ_{i} (η_{i} - ν_{b_{i}} κ_{b_{i}}) + z_{c} r_{q_{i}} s_{i}] .

(11)

3.3. Constraints

While the objectives are used to compare solutions, constraints are introduced to ensure that the solutions are operationally valid. Operationally validity requires that allocated BEBs do not overlap spatially or temporally. Furthermore, the SOC of a bus at a particular visit is related to the charge from its previous visit by the amount of charging and discharging that has occurred. Finally, buses must leave the charger before their scheduled departure time. These constraints are represented as follows:

u_{j} - d_{i} - (σ_{i j} - 1) T \geq 0

(12a)

q_{j} - q_{i} - 1 - (ψ_{i j} - 1) Q \geq 0

(12b)

σ_{i j} + σ_{j i} \leq 1

(12c)

ψ_{i j} + ψ_{j i} \leq 1

(12d)

σ_{i j} + σ_{j i} + ψ_{i j} + ψ_{j i} \geq 1

(12e)

s_{i} = d_{i} - u_{i}

(12f)

η_{ξ_{i}} = η_{i} + r_{q_{i}} s_{i} - Δ_{i}

(12g)

κ_{b_{i}} \geq η_{i} + r_{q_{i}} s_{i}

(12h)

a_{i} \leq u_{i} \leq d_{i} \leq e_{i} \leq T

(12i)

Equations 12a-12e are denoted as “queuing constraints”. They prevent overlap both spatially and temporally as shown in Section Figure 2. The y-axis represents the possible queues for a bus visit to be placed into, and the x-axis represents the time that can be reserved for each visit. The shaded rectangles represent time that has been scheduled in the horizontal direction, and the queue allocated for each bus visit in the vertical direction. In other words, the set of constraints Equations 12a - 12e aim to ensure that these shaded rectangles never overlap.

Constraint Equation12a states that the starting charge time for BEB

u_{j}

must begin after the previous BEB departs,

d_{i}

. A value of

σ_{i j} = 1 \Rightarrow

bus i has detached from the charger before bus j has begun charging. If

σ_{i j} = 0

, then the constraint is of the form

T + d_{i} > u_{j}

rendering the constraint “inactive”. Similarly, for Equations 12b,

ψ_{i j}

determines spacial positioning of BEB i and j relative to one another. A value of

ψ_{i j} = 1 \Rightarrow

BEB i is in a queue index that is less than BEB j. If

ψ_{i j} = 0

then the constraint is deactivated. Constraints Equations 12c - 12e enforce spatial and temporal ordering between each queue/vehicle pair. Equations 12c and 12d ensure that BEB i is not placed before and after j spatially or temporally as that is not possible. Equation 12e enforces at least one of the spatial or temporal relationships between each visit is active. This ensures there are no scheduling conflicts (i.e. either charging sessions are ordered temporally or are in different queues).

Equation 12f describes the service time of the bus. Equation 12g calculates the initial charge for the next visit for bus

b_{i}

. Equation 12h ensures that the bus is not being over-charged. Equation 12i ensures the continuity of the times (i.e. the arrival time is less than the initial charge which is less than the detach time which is less than the time the bus exits the station and all must be less than the time horizon).

4. Simulated Annealing

SA is a well-studied local search metaheuristic used to solve various optimization problems [28,29]. The algorithm is often applied to problems that contain many local solutions as it employs a stochastic approach that explores the solution space for an approximate global optimum. This model is named after its analogized process where a crystalline solid is heated then allowed to cool at a slow rate until it achieves its most regular possible crystal lattice configuration (i.e. lowest energy state) [29,30]. SA establishes a connection between the thermodynamic process and the search for global optimum in optimization problems. Within the SA process there are three key components: cooling equation, acceptance criteria, and generation mechanisms [29,31].

The cooling equation describes the speed at which the figurative temperature is decreased in a controlled manner over time. Throughout the SA process, many “candidate” solutions are generated and compared to an “active” solution. The method by which the solutions are accepted is determined by the acceptance criteria. The acceptance criteria is a function of the system temperature that makes the decision whether the system will accept an inferior solution in favor of exploring the solution space. The means by which candidate solutions are generated is via the generation mechanisms. These generators modify the solution by some singular discrete change [28]. Each of these components are elaborated in the subsequent sections.

4.1. Cooling Equation

The cooling equation models the rate at which the temperature decreases over time in the SA process. Initially, when the temperature is high, SA encourages exploration. As the process begins to “cool down” (in accordance to the cooling schedule), it begins to encourage local exploitation of the solution (rather than exploration) [30,32]. There are three common basic types of cooling equations: linear, geometric, and exponential. Geometric cooling schedules are most widely used in practice [31]. As such, it will also be employed by this work. It is defined by the difference equation

t_{m} = β t_{m - 1} .

(13)

In Equations 13,

β

controls the cooling rate. Typical values of

β

are within the range

[0.8, 0.99]

citehenderson-1989-theor-pract. Figure 3 demonstrates this principle by plotting the geometric schedule using varying values of

β

. The variable

t_{m}

represents the temperature at the

m^{th}

step of the temperature function. The total amount of steps, M, is dictated by the initial temperature and

β

4.2. Acceptance Criteria

In SA, the algorithm stores a solution that is continuously compared to newly generated solutions. Let the stored solution be referred to as the “active solution”. During each iteration, a new “candidate” solution is generated and compared to the active solution to determine if the candidate solution should replace the active solution. The method of determining whether the active solution should be replaced is defined by an acceptance criteria. In an effort to encourage exploration, inferior candidate solutions have a probability of being accepted. The probability of accepting an inferior candidate solution is determined by the objective functions of the active and candidate solutions,

J (I)

and

J (\bar{I})

, respectively, and the current temperature,

t_{m}

. Let

Δ E \equiv J (I) - J (\bar{I})

and let

f (\cdot)

be the function that describes the probability of accepting a candidate solution

\bar{I}

. The probability of accepting a candidate solution is thus of the form [31]

f (I, \bar{I}, t_{m}) = \{\begin{matrix} 1 & Δ E > 0 \\ e^{- \frac{Δ E}{t_{m}}} & otherwise \end{matrix} .

(14)

4.3. Neighbor Generators and Wrappers

Generation mechanisms are used to create a neighboring candidate solution [28]. That is, the generating function creates a solution that can be reached in a single iteration from the active solution. In response to the problem statement made in Section 2, five primitive generation mechanism are used: new visit, slide visit, new charger, wait, and new window. The purpose of each of these generators is to assign new visits to a charger, adjust a bus visits initial and final charge time within the same time frame/queue, move a BEB from one charger to another with the same charge schedule, move a bus to its idle queue. Each generator will be discussed in more detail in Section 4.3.2.

These primitive generation mechanisms will, in turn, be utilized by two wrapper functions. The charge schedule generator is to used create an initial candidate solutions for SA and the perturb schedule generator is used to take a candidate solution and alter it slightly in an attempt to step toward a global or local minimum. The wrapper functions will be discussed in Section 4.3.3. However, prior to discussing the primitives and wrapper generating functions, their respective inputs and outputs must be defined.

4.3.1. Generator Input/Output

Each generator primitive accepts a tuple

S \equiv (i, I, C)

where i is the visit index being manipulated,

I

is the set of visits, and

C

is the set that describes the availability for all chargers

q \in Q

. The output of the generating functions is the same as the input, but with changes applied to it by a generator. Let a modified variable be denoted with a bar,

\bar{\cdot}

. Thus, the modified input tuple is written as

\bar{S}

4.3.2. Generators

The mechanism by which candidate solutions are generated are now introduced. Recall that to satisfy constraints,

n_{B}

extra idle queues are added that provide no power to the BEB. Because of this, the set of queues is fully defined where Q is the ordered set of idle queues, slow queues, then fast queue. The use case for the idle queues are for when a bus is not to be placed on a charger. Rather, it will be placed in the queue,

q \in B

, which satisfies the previously defined spatial constraints while allowing the bus to be “set aside”. The charge queues are denoted by

q \in {1, . . ., n_{B}, n_{B} + 1, . . ., n_{Q}}

For the sake of ease in referring to the various variables associated with a visit, dot notation is used. For example, suppose the arrival time is desired to be extracted from visit i. Given

I

, the notation that describes extracting the initial charge time for visit i is written as

u_{i} \equiv I_{i . u}

New Visit

The new visit generator defined in Algorithm 1 describes the process of moving a BEB,

b \in B

, from a waiting queue,

q \in B

, to a charging queue,

q_{i} \in {n_{B} + 1, . . ., n_{Q}}

, within its arrival/departure time

[a_{i}, e_{i}]

. Let

U_{{\cdot}}

indicate that an element is selected randomly with a uniform distribution from the set

{\cdot}

. For example,

U_{[a_{i}, e_{i}]}

indicates that a value will be selected between a and e with a uniform distribution. Algorithm 1 begins by extracting variables. Lines 8 and 9 randomly select a charging queue and available time frame with a uniform distribution, respectively. Line 10 attempts to assign the visit to the previously select time slice, if it succeeds, the updated visit is returned. Otherwise, the null value is returned.

The function FindFreeTime is the algorithm that determines whether a visit’s time at the station

[a_{i}, e_{i}]

can be placed in the time availability of charger q. Let the available time for charger q for visit i be denoted as

C \equiv C_{i . q}

. Furthermore, let the lower and upper bound of

C

be denoted as

C_{L}

and

C_{U}

, respectively. The algorithm checks whether the BEB time at the station,

[a_{i}, e_{i}]

fits within the charger availability

[C_{L}, C_{U}]

. If it does, a random charging time frame is returned such that

a_{i} \leq u_{i} \leq d_{i} \leq e_{i}

. Otherwise the null value is returned.

Algorithm 1: New visit algorithm

Slide Visit

This primitive generator is used for visits that have already been scheduled. Because of the constraint Equation 12i, there may be some slack to manipulate

[u_{i}, d_{i}]

within the window

[a_{i}, e_{i}]

. That is, two new values,

u_{i}

and

d_{i}

are randomly selected with a uniform distribution that satisfy the constraint

a_{i} \leq u_{i} \leq d_{i} \leq e_{i}

. Algorithm 2 begins be extracting variables. Line 5 purges the visit from the charger availability schedule. The Purge function simply removes an assigned charge time from the set

C

. Without altering selected queue, the charge time randomly re-assigned with a uniform distribution. Upon success, the updated tuple is returned, otherwise the null value is returned.

Algorithm 2: Slide Visit Algorithm

New Charger

The new charger generator moves a visit

I_{i}

to a new charging queue while maintaining the same charge time,

[u_{i}, d_{i}]

. Algorithm 3 begins be extracting variables, and then purges the visit from the charger availability set, a queue is selected at random with a uniform distribution, then the new selection is checked whether the charge time

[u_{i}, d_{i}]

may be assigned to the new queue.

Algorithm 3: New Charger Algorithm

Wait

The wait generator simply removes a bus from a charger queue and places it in its idle queue,

q_{i} \in B

. Algorithm 4 begins by purging the visit from the charger availability set, the visit is then assigned to its idle queue for the duration of its time at the station.

Algorithm 4: Wait algorithm

New Window

New window, as shown in Algorithm 5, is a combination of Algorithm 1 (new visit) and Algorithm 4 (wait). By this it is meant that visit i is placed in its wait queue then added back in as if it were a new visit. This implies that the BEB may be assigned to a different queue with a new charging time frame. Upon success, the algorithm returns the updated tuple, otherwise return the null value.

Algorithm 5: New window algorithm

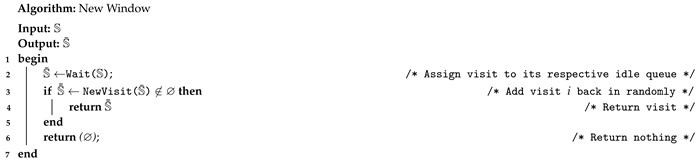4.3.3. Generator Wrappers

The generator wrappers provide the highest level of abstraction from which the SA algorithm directly interacts. These wrapper functions utilize the primitive generators previously described to either create a new charge schedule to initialize the SA algorithm, or to modify an existing schedule.

Charge Schedule Generation

The objective of Algorithm 6 is to introduce a method that provides the SA algorithm with an initial charging schedule. The schedule generation is chosen to initialize the algorithm in a greedy manner by looping through each visit and executing Algorithm 1 to place visit i at random queue with a random charge time.

Algorithm 6: Charge schedule generation algorithm

Perturb Schedule

Algorithm 7 describes the method by which the SA algorithm decides how to perturb a given charge schedule. The method that will be employed to generate neighboring solutions is as follows: pick a visit, pick a primitive generator, and execute said primitive generator once. Let

W_{[\cdot]}^{y}

denote a random selection with a distribution specified by a weight vector

y \in R

. Lines 2-12 of Algorithm 7 generate a vector of weights for the visit index selection. The weights have a default value of one. Each visit is then indexed in reverse order. If the SOC of the visit is less than

ν_{b} κ_{b}

, then the weight for the visit is calculated as shown on Line 10. The route for BEB b is then set as a “priority” on Line 9 to propagate the previously calculated weight to earlier visits of BEB b as shown on Line 5. This is done in an attempt to encourage the SA algorithm to “fix” the current or previous visits so that the SOC stays above the minimum threshold. The algorithm then selects a visit index with weighted distribution

y^{v}

and selects a primitive with a weighted distribution,

y^{p}

. Letting

n_{G}

denote the number of primitive generating functions, line 15 selects a primitive generating function with a weighted distribution,

W_{[1, n_{G}]}^{y^{v}}

. The primitive is then executed, and the results are returned.

Algorithm 7: Perturb schedule algorithm

4.4. Alternative Heuristic Implementation

As suggested by the works in [33,34], applying heuristics to the generating functions can manipulate the searched neighborhoods in a way that may assist the SA algorithm with convergence. As a test to assist in minimizing charger utilization, a simple heuristic is applied to Algorithm 1 and Algorithm 3 in the method that they select new charging queues. Rather than selecting a queue at random from

q \in Q

, the algorithms randomly select whether to place a BEB in a slow or fast charging queue with a weighted distribution favoring slow chargers. Once the charger type has been selected, the algorithm will then begin incrementally attempting to place the BEB in a queue of that type beginning from the smallest index of that charger type. For example, if a BEB has been selected to be placed in a queue with a slow charger, the algorithm begins by attempting to place the BEB in the charger queue

q = n_{B} + 1

. If it is unable to be placed in that queue, it then attempts to be placed in the next queue

q = n_{B} + 2

. This is done incrementally until all the queues have been exhausted. The objective of this alternative approach is to explore whether the added up-front computation cost by including the heuristic will positively influence the output of the results and to what degree.

5. Optimization Algorithm

This section combines the generation algorithms and the optimization problem into a single Algorithm(8). Generally, SA assumes that the generated candidate solutions are within the solution space of the problem,

S \in S

where S is the solution space. In other words, the initialization and perturbations of a schedule must be verified to ensure that the generated schedule is in the solution space. Therefore, the objective function and constraints introduced in Section 3.3 and Section 3.2, respectively, must be employed to verify that the outputs of Algorithm 6 and Algorithm 7 are in the feasible space, S.

As previously stated, the generating functions directly influence the values of the assigned charge queue, charge initialization time, and charge completion time:

q_{i}

u_{i}

, and

d_{i}

, respectively. Having generated those values, the rest of the decision variables may be derived. Beginning with the packing constraints, Equations 12a-12b are employed to enable and disable

σ_{i j}

and

ψ_{i j}

and Equations 12c-12e ensure the validity of the values. Equations 12f can be directly calculated and Equation 12i is fully defined.

Changing the focus over to the dynamic constraints, similarly to what was seen with the packing constraints, the battery dynamic constraints are also fully defined. Equation 12g is sequentially calculated after a given schedule has been created. Equation 12h is evaluated to ensure the BEB is not overcharged. The penalty method implemented in Section 3.2 is set in place to allow the SOC to go below the specified threshold,

ν_{b_{i}} κ_{b_{i}}

, but punish the solution for doing so. Thus, over time, the candidate solutions will be encouraged toward a solution that does not activate the penalty method (i.e., is solution is operationally feasible).

The implementation of the SA PAP, outlined in Algorithm 8, will now be discussed. The algorithm begins by creating a temperature schedule and creating an initial solution. The algorithm then iterates through the temperature schedule (outer loop). For each iteration of the outer loop, an inner loop is executed

n_{K}

times. During this inner loop, the solution is modified by a primitive generating function to create a candidate solution. The candidate is solution is then compared with the active solution, and updated according to the acceptance criteria. These actions are performed until the cooling equation is exhausted.

Algorithm 8: Simulated annealing approach to the position allocation problem

6. Example

An example is now provided to demonstrate the utility of the developed SA charge scheduling technique. In Section 6.1 a description of the example scenario is presented followed by a brief introduction of the BEB implementation of the PAP (BPAP) and an alternative threshold based strategy called the Qin-Modified technique. Section 6.2 presents the results for each of planning strategies. The results are then analyzed and discussed.

6.1. BEB Scenario

The test scenario was run over a time horizon of

T = 24

hours, with a total of

n_{V} = 338

visits to the station shared between

n_{B} = 35

buses. Each BEB is assumed to have a battery capacity of

κ_{b} =

388 kWh that is required to stay above an SOC of

ν_{b} =

25% (97 kWh). Each bus is assumed to begin the working day with

α =

90% charge (349.2 kWh). A total of 30 chargers are utilized where 15 of the chargers are slow charging (30 kW) and 15 are fast charging (911 kW). The gains of

z_{p} =

5000,

z_{c} = 1

, and

z_{d} =

10000 are used. As previously introduced, to encourage slow charging for battery health, the values of

ϵ

in the objective function are

\forall q \in {1, 2, . . ., n_{B}}; ϵ_{q} = 0

and

\forall q \in {n_{B} + 1, n_{B} + 2, . . ., n_{Q}}; ϵ_{q} = 10 q

. The SA algorithm utilizes the geometric cooling schedule with an initial temperature of

T_{0} =

9000 with

β = 0.997

, resulting in a total of

n_{M} =

3832 steps. Rocky Mountain Power utilizes fifteen-minute intervals to calculate the demand cost [27]. To match the method by which Rocky Mountain Power determines its demand cost, this work employed an interval of

T_{p} =

900 seconds in its demand cost calculation. A weight vector of

[0.3333, 0.3333, 0.1667, 0.1667]

is used to influence the distribution of selecting the new charger, new window, wait, and slide visit primitives, respectively. The algorithm also assumes a total of

n_{K} = 500

iterations for the local search at a constant temperature. In total, that results in 1 916 000 configurations being searched in a total runtime of 1532.8 seconds.

Section 4.4 introduced the idea of an alternative heuristic implementation for the SA algorithm. To distinguish the heuristic implementation from the method derived in Section 4.3, let this implementation be referred to as “heuristic” implementation and the previous as the “quick” implementation due to the fact that it is designed to execute more quickly. Using the same weights for randomly selecting the primitive generators, the heuristic approach further implemented a weighted distribution vector of

[0.75, 0.25]

to decide whether to select a slow or fast charger, respectively. The heuristic approach had a total runtime of 1916 seconds. The heuristic generators were expected to be slightly slower due to its iterative approach.

The Qin-Modified is a threshold-based strategy that is also employed as a means of comparison with the results of the SA BPAP. The Qin-Modified algorithm is a based on the threshold strategy of [20]. The algorithm has been modified slightly to accommodate the case of multiple charger types without a heuristic search for the best charger type. The heuristic is based on a set of rules that revolve around the initial charge of the bus at visit i. There are three different thresholds, low (60%), medium (70%), and high (90%). Buses below the low threshold are prioritized to fast chargers then are allowed to utilize slow chargers if no fast chargers are available. Buses between the low and medium threshold prioritize slow chargers first and utilize fast chargers only if no slow chargers are available. Buses above the medium threshold and below high will only be assigned to slow chargers. Buses above the high threshold will not be charged. Once a bus has been assigned to a charger, it remains on the charger for the duration of the time it is at the station, or it reaches 90% charge, whichever comes first.

Another method utilized to compare with against SA PAP is the BEB implementation of the PAP [15]. The BPAP implementation is utilized in this work as a benchmark for the other schedules as it is implemented utilizing a commercial solver. The inputs to the system are the same as those discussed above. It is of note that the BPAP does not implement the demand cost in its objective function. In an attempt to compare the solution of the BPAP with the SA output more directly, a similar solve time of 1,900 seconds is utilized. The BPAP was executed using the Gurobi MILP solver [35]. The previously described simulations were run on a machine equipped with an AMD Ryzen 9 5900X 12 - Processor (24 core) at 4.95GHz.

6.2. Results

The schedules generated by each of the methods is presented in Figure 4. For the sake of conciseness of the schedule plots, the waiting queues are excluded. Therefore, rows 0-14 represent slow charging queues and rows 15-29 represent fast charging queues. The hollow circles with an ’X’ represent the initial charge times, and the horizontal line with the vertical tick signifies the region of time the charger is active. The Qin-Modified schedule utilized two fast chargers and fourteen slow chargers as can be seen in Figure . The BPAP framework generated a schedule that utilizes three fast charges and four slow chargers as shown in Figure . The heuristic SA strategy created a schedule with nine slow charger queues and one fast charging queue as shown in Figure 4. The quick strategy for the SA algorithm created a schedule utilizing seven slow chargers and two fast chargers as is demonstrated in Figure 4. That is to say, while each schedule emphasized the utilization of slow chargers, the Qin-Modified required fast charging most frequently followed by the BPAP, quick SA, and then heuristic SA. At the expense of incorporating more slow chargers than the BPAP, the SA techniques chose to utilize fast chargers less frequently in their respective schedules showing an emphasis on battery health.

Table 2 tabulates the mean, minimum, and maximum SOC upon arrival for each visit. The BPAP requires each BEB to stay above an SOC of 25% while the quick and heuristic SA approaches heavily penalize a schedule for allowing a BEB to go below the 25% SOC threshold. The BPAP was able to successfully keep the SOC above the threshold while both SA approaches were a few kWh below the threshold. The SOC of the quick SA approach dropped to a minimum of 94.760 kWh and the heuristic had a minimum SOC of 91.265 kWh, as shown in Table 2. Due to the threshold constraint being soft, the SA objective function may find it better to allow a small deficit in the threshold penalty function in favor of another action. As a remedy to ensure the SA schedules stays above the threshold, a safety factor could be introduced to artificially increase the threshold,

S_{f} ν_{b_{i}} κ_{b_{i}}

where

S_{f} > 1; S_{f} \in R

The Qin-Modified schedule allowed the SOC for one of the BEBs to reach 0% as shown in Table 2. The Qin-Modified strategy, being a purely reactive model, does not have foresight to determine whether a set of routes has a particularly taxing route later in the time horizon. As such, and in the case of the example scenario, the BEB that reached a charge of 0% began with a sequence of short routes, much like the other BEBs. However, rather than continuing this trend, these sets of routes had one or two longer routes which the Qin-Modified algorithm was unable to account for. Interestingly, despite having a bus drop to zero charge, the Qin-Modified strategy had the highest mean SOC, followed by the quick SA, heuristic SA, and then the BPAP.

Figure 7 depicts the power utilized over the time horizon for each model. Referencing Figure 7, the Qin maintained long periods of steady slow and fast charger use. This is again a symptom of the Qin-Modified strategy placing BEBs on chargers based solely on the SOC upon arrival. The BPAP and SA techniques, having demand peaks in the first half of the time horizon, were able to effectively maintain lower demand profiles during slower moments throughout the day (the SA techniques more so than the BPAP). Figure 7 is also of interest as it shows the peak power demand over the time horizon. The peaks for each schedule shown in Table 3. Both the quick and heuristic SA techniques were able to maintain peak power use below 1,130 kW whereas the BPAP and Qin had peaks above 1,900 kW demonstrating significant demand cost reduction.

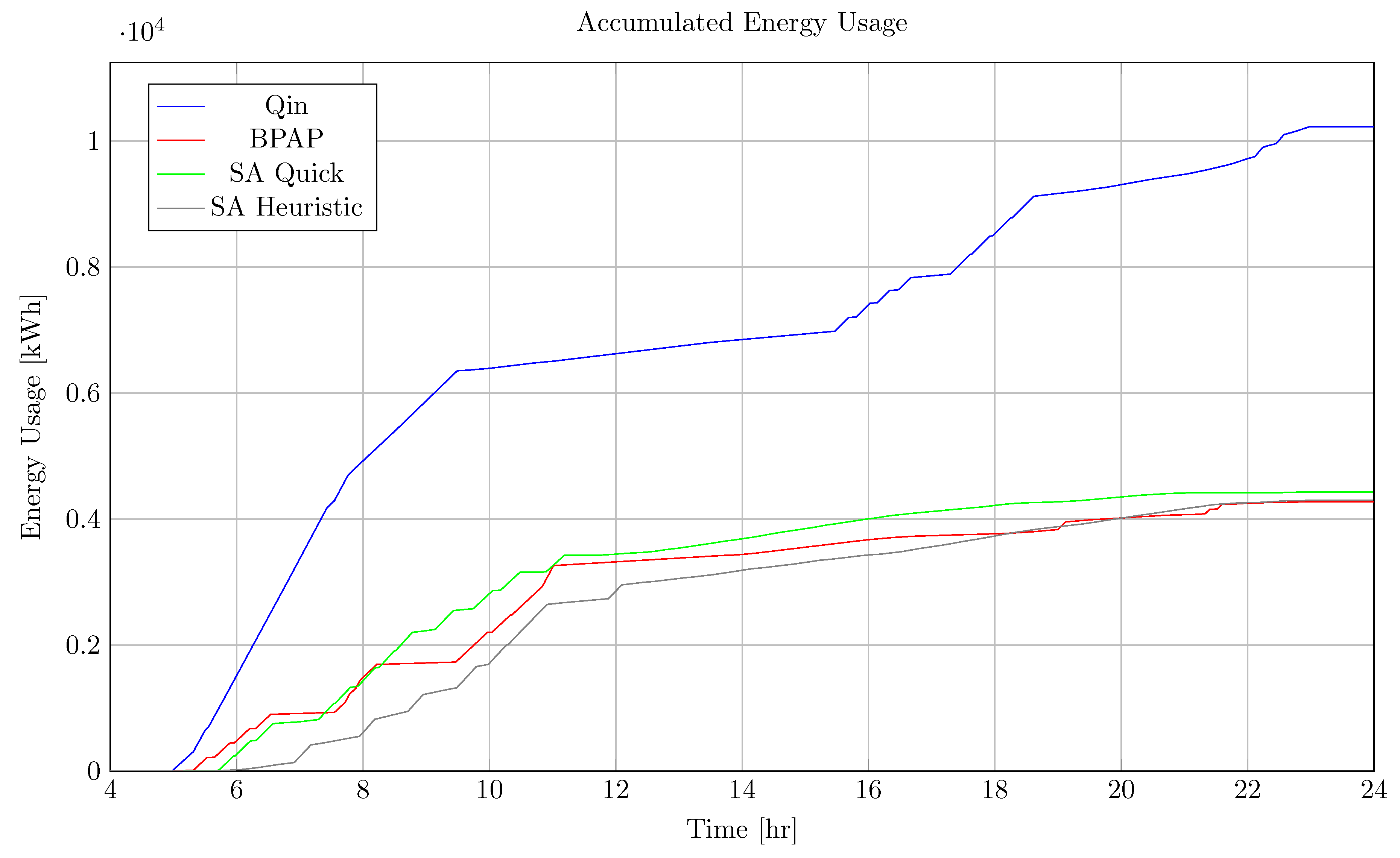
The total energy consumed by each schedule is shown in Figure 8. The ordering of most energy consumed to least is as follows: Qin-Modified, quick SA, heuristic SA, and the BPAP. The respective energy consumption for each technique is: 9,459.120 kWh, 4,428.670 kWh, 4,295.660 kWh, and 4,237.200 kWh with the heuristic SA consuming about 58.5 kWh more than the BPAP. While the quick and heuristic SA techniques were slightly above the BPAP in energy consumption, it is expected that the BPAP would have the lowest consumed energy as it only considers consumption cost. Despite considering peak demand, the SA methods had nearly the same consumption as the BPAP. Referencing Table 2 and Table 3 for the mean SOC and mean demand, respectively, the descending order of consumed energy is correlated to the descending order of the mean SOC and the descending order of the mean power demand. This makes sense as a higher mean SOC implies the chargers being active more often; similarly for the mean demand.

As a final comparison, the scores for the Qin-Modified, quick SA, BPAP, and heuristic SA are shown in Table 4. The Qin-Modified strategy naturally has the highest score as it performed the worst in each metric of the objective function. Although the BPAP was able to maintain the SOC of each BEB above the minimum charge threshold, due to large peaks in the power demand in the BPAP schedule, both SA techniques were able to achieve lower scores. In other words, although the SA techniques allowed small breaches in the minimum SOC, the objective function found the quick and heuristic SA schedule configurations to be more desirable than that of the BPAP. The quick SA was able to successfully obtain the lowest score due to its substantial reduction in the demand cost and its smaller breach of the minimum SOC threshold.

Figure 4. Various schedules generated by the different frameworks. Figure 4a is the Qin-Modified schedule, Figure 4b is the BPAP schedule, Figure 4c is the heuristic SA schedule, and Figure 4d is the quick SA schedule. The horizonontal line stemming from the nodes ending with a vertical tick indicate the charge duration for that particular visit.

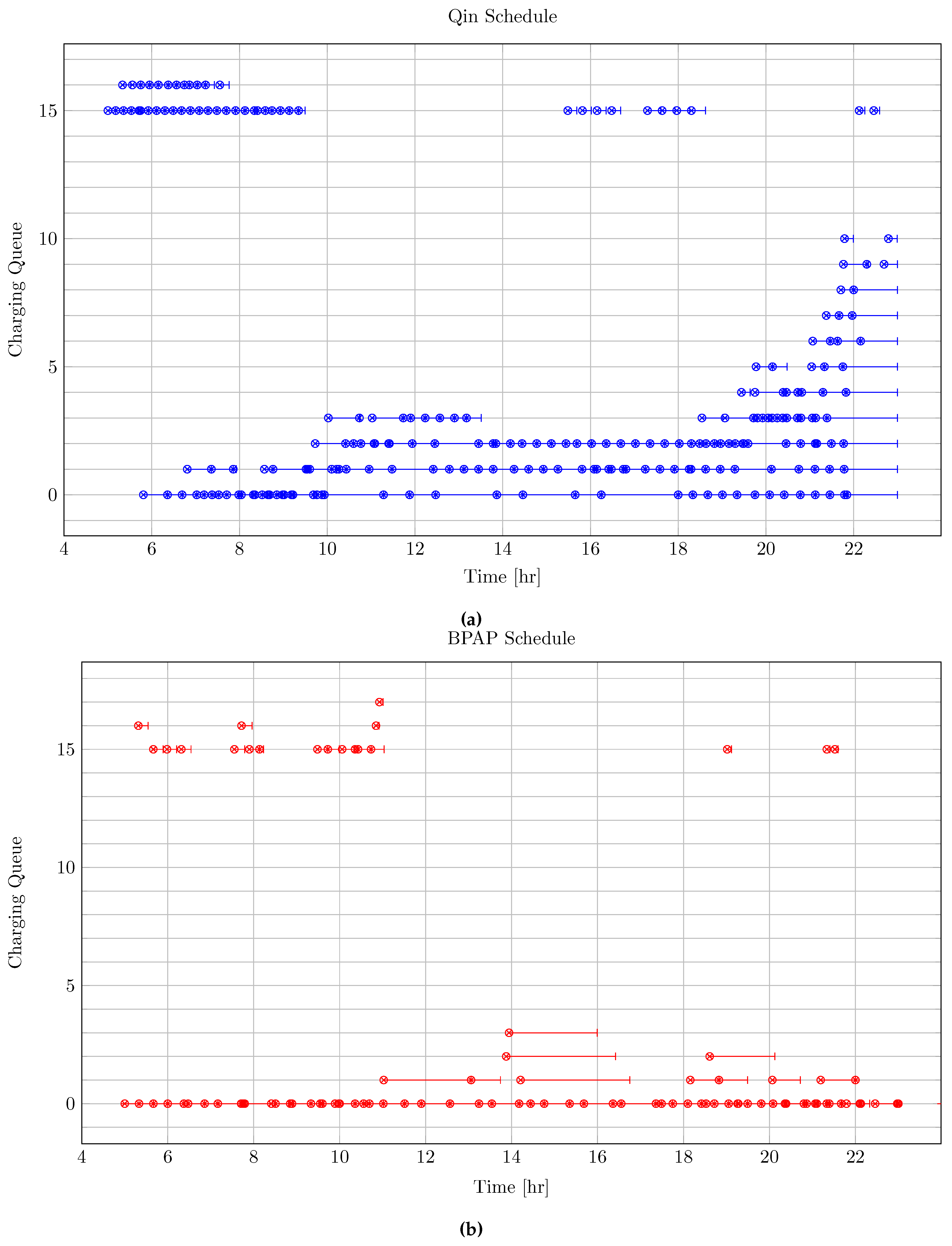
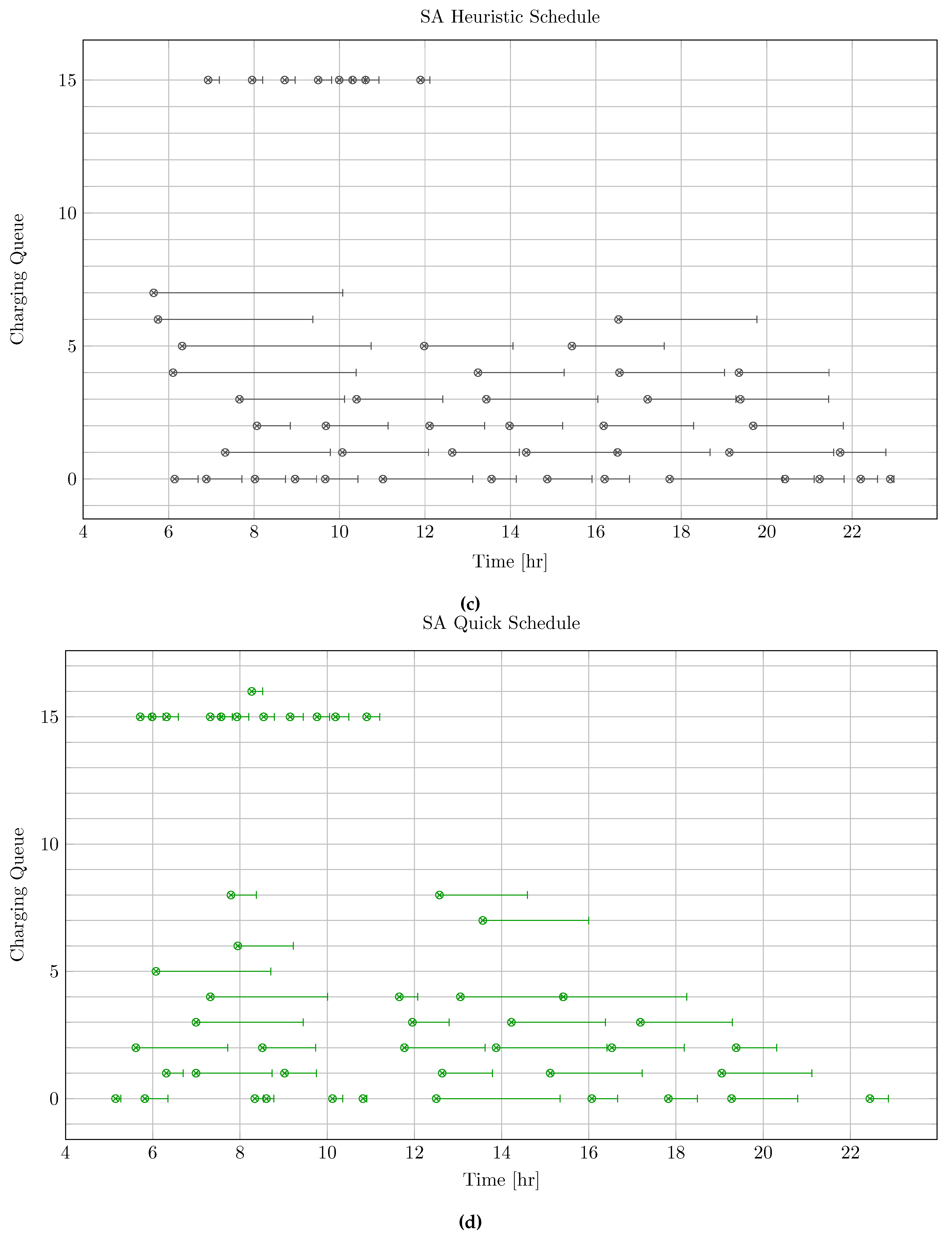
Figure 5. Number of fast chargers utilized in parallel over the time horizon. Figure 5 plots the fast charger count for the BPAP and Qin schedules and Figure 5 plots the fast charger count for the quick and heuristic SA schedules.

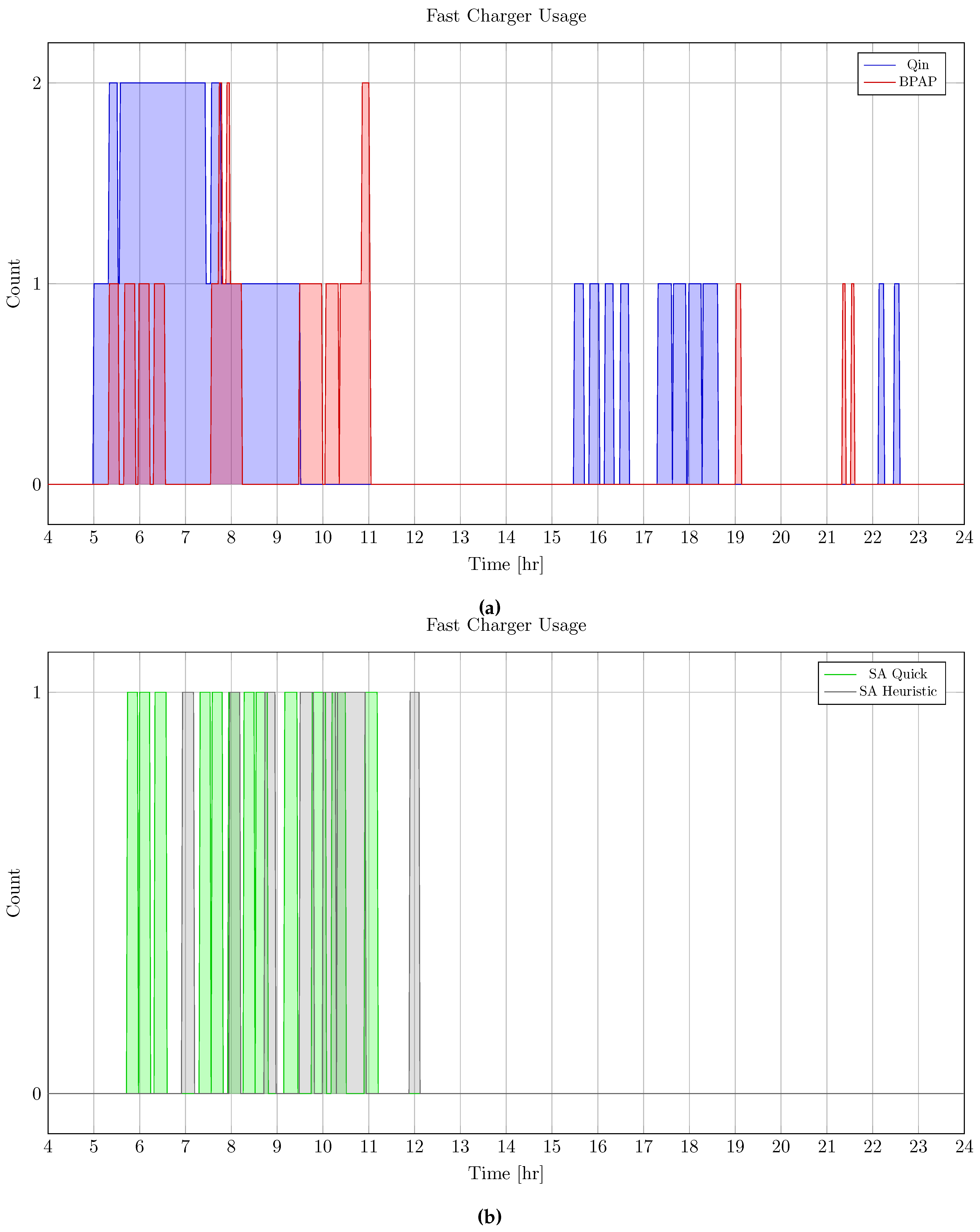
Figure 6. Number of slow chargers utilized in parallel over the time horizon. Figure 6 plots the slow charger count for the BPAP and Qin schedules and Figure 6 plots the slow charger count for the quick and heuristic SA schedules.

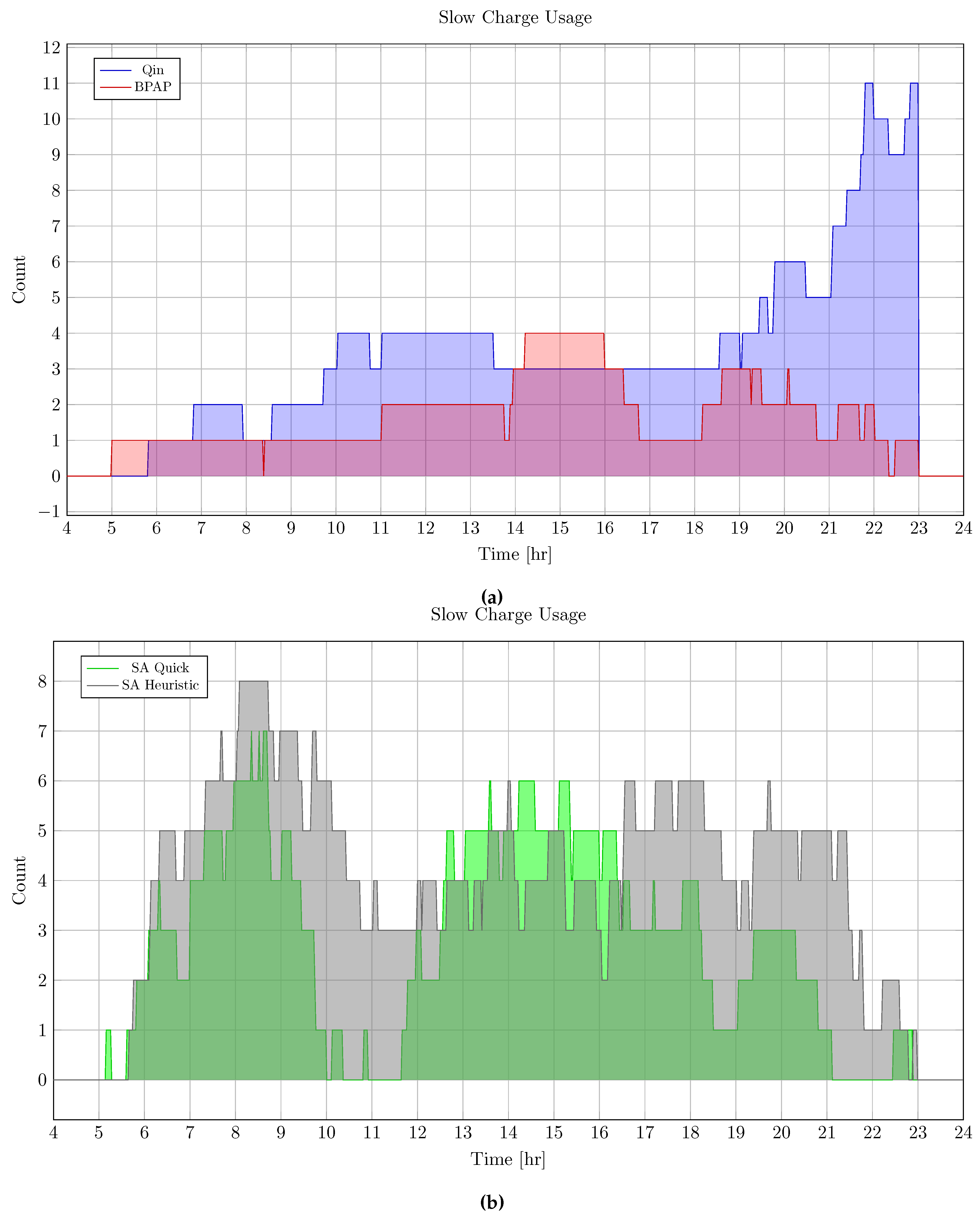
Figure 7. Power demand for each schedule over the time horizon. Figure 7 plots the power demand for the Qin and BPAP schedules and Figure 7 plots the power demand for the quick and heuristic SA schedules.

Figure 8. Total accumulated energy consumed by the Qin-Modified, BPAP, quick and heuristic SA schedules throughout the time horizon.

7. Conclusion

This work developed an SA implementation of the BEB charge scheduling problem derived from the works of the Position Allocation Problem [15]. The model is designed to encourage the use of slow chargers for battery health, minimize the peak energy consumption, and minimize the total energy consumed. The problem description was provided along with the scenario in which this model is designed for. The optimization problem was then introduced by describing the components of the objective function and outlining the constraints utilized to ensure candidate solutions are in the solution space.

An example of the SA PAP algorithm was presented and compared against the BPAP, which acted as a baseline for the other schedule. Another threshold-based strategy called the Qin-Modified technique was also introduced as a means of comparing the schedules. The SA PAP was run utilizing two different neighborhood searching techniques named the “quick” and “heuristic” techniques, respectively. The quick SA’s objective was to randomly search a wide neighborhood while the heuristic technique was designed to incrementally search a neighborhood by randomly selecting a fast or slow charging queue and then stepping through the queues one at a time. The execution time compounds as the number of iterations in the cooling function increases as shown by the respective quick and heuristic execution times: 1532.8 seconds and 1916 seconds. The Qin-Modified strategy favored the use of fast chargers due to its inability to identify when demanding routes were on the horizon, whereas the other methods used fast charges sparingly. Particularly, the SA techniques favored higher number of slow chargers with longer charge durations in comparison to the BPAP.

Both of the SA techniques were unable to keep the SOC above the 25% SOC threshold with SOC falling to 23.5% for the heuristic SA and 24.4% for the quick SA. Due to the minimum charge threshold being a soft constraint for the SA, the algorithm found another actions to be more favorable at the expense of moderately breaching the threshold. The Qin-Modified, on the other hand, had the SOC of one BEB fall to 0% SOC. The schedule that consumed the least amount of energy is the BPAP (4,237.2 kWh) followed by the heuristic SA (4,295.6 kWh). The difference between the two being about 58.4 kWh. The quick SA energy consumption came in a close third at 4,428.7 kWh. Both the quick and SA techniques were able to significantly reduce the peak power demand having peaks below 1,200 kW. The BPAP and Qin both had peak power demands above 1,800 kW. The best scoring schedule was the quick SA due to its significant reduction in demand cost, similar energy consumption as the heuristic SA and BPAP, and its small minimum SOC threshold deficit.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, A.B. and G.D..; methodology, A.B.; software, A.B.; validation, A.B., G.D.; formal analysis, A.B., G.D.; investigation, A.B. G.D.; resources, A.B., G.D.; data curation, G.D.; writing—original draft preparation, A.B.; writing—review and editing, A.B., G.D.; visualization, A.B.; supervision, G.D.; project administration, A.B., G.D.. All authors have read and agreed to the published version of the manuscript.”

Funding

This research received no external funding.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Khan, S.; Maoh, H. Investigating attitudes towards fleet electrification – An exploratory analysis approach. Transportation Research Part A: Policy and Practice 2022, 162, 188–205. [CrossRef]
Li, J.Q. Battery-Electric Transit Bus Developments and Operations: a Review. International Journal of Sustainable Transportation 2016, 10, 157–169.
Guida, U.; Abdulah, A. ZeEUS eBus Report# 2-An updated overview of electric buses in Europe. Technical Report 2, International Association of Public Transport (UITP), 2017.
Xylia, M.; Silveira, S. The Role of Charging Technologies in Upscaling the Use of Electric Buses in Public Transport: Experiences From Demonstration Projects. Transportation Research Part A: Policy and Practice 2018, 118, 399–415.
Lutsey, N.; Nicholas, M. Update on Electric Vehicle Costs in the United States Through 2030. The International Council on Clean Transportation 2019, 2.
Edge, J.S.; O’Kane, S.; Prosser, R.; Kirkaldy, N.D.; Patel, A.N.; Hales, A.; Ghosh, A.; Ai, W.; Chen, J.; Yang, J.; Li, S.; Pang, M.C.; Bravo Diaz, L.; Tomaszewska, A.; Marzook, M.W.; Radhakrishnan, K.N.; Wang, H.; Patel, Y.; Wu, B.; Offer, G.J. Lithium ion battery degradation: what you need to know. Physical Chemistry Chemical Physics 2021, 23, 8200–8221. [CrossRef]
Millner, A. Modeling Lithium Ion battery degradation in electric vehicles. 2010 IEEE Conference on Innovative Technologies for an Efficient and Reliable Electricity Supply. IEEE, 2010. [CrossRef]
Zhang, L.; Wang, S.; Qu, X. Optimal Electric Bus Fleet Scheduling Considering Battery Degradation and Non-Linear Charging Profile. Transportation Research Part E: Logistics and Transportation Review 2021, 154, 102445. [CrossRef]
Duan, M.; Qi, G.; Guan, W.; Lu, C.; Gong, C. Reforming Mixed Operation Schedule for Electric Buses and Traditional Fuel Buses By an Optimal Framework. IET Intelligent Transport Systems 2021, 15, 1287–1303. [CrossRef]
Rinaldi, M.; Picarelli, E.; D’Ariano, A.; Viti, F. Mixed-Fleet Single-Terminal Bus Scheduling Problem: Modelling, Solution Scheme and Potential Applications. Omega 2020, 96, 102070. [CrossRef]
Tang, X.; Lin, X.; He, F. Robust Scheduling Strategies of Electric Buses Under Stochastic Traffic Conditions. Transportation Research Part C: Emerging Technologies 2019, 105, 163–182. [CrossRef]
Li, J.Q. Transit Bus Scheduling With Limited Energy. Transportation Science 2014, 48, 521–539. [CrossRef]
He, Y.; Liu, Z.; Song, Z. Optimal Charging Scheduling and Management for a Fast-Charging Battery Electric Bus System. Transportation Research Part E: Logistics and Transportation Review 2020, 142, 102056. [CrossRef]
Whitaker, J.; Droge, G.; Hansen, M.; Mortensen, D.; Gunther, J. A Network Flow Approach to Battery Electric Bus Scheduling. IEEE Transactions on Intelligent Transportation Systems 2023, 24, 9098–9109. [CrossRef]
Brown, A.; Droge, G.; Gunther, J. A Position Allocation Approach to the Scheduling of Battery-Electric Bus Charging. Frontiers in Energy Research Under Revision, p. 18. Avaible for download at: https://arxiv.org/submit/5603923.
Zhou, Y.; Liu, X.C.; Wei, R.; Golub, A. Bi-Objective Optimization for Battery Electric Bus Deployment Considering Cost and Environmental Equity. IEEE Transactions on Intelligent Transportation Systems 2020, 22, 2487–2497.
Wang, X.; Yuen, C.; Hassan, N.U.; An, N.; Wu, W. Electric Vehicle Charging Station Placement for Urban Public Bus Systems. IEEE Transactions on Intelligent Transportation Systems 2017, 18, 128–139. [CrossRef]
Wei, R.; Liu, X.; Ou, Y.; Fayyaz, S.K. Optimizing the Spatio-Temporal Deployment of Battery Electric Bus System. Journal of Transport Geography 2018, 68, 160–168.
Mortensen, D.; Gunther, J.; Droge, G.; Whitaker, J. Cost Minimization for Charging Electric Bus Fleets. World Electric Vehicle Journal 2023, 14, 351. [CrossRef]
Qin, N.; Gusrialdi, A.; Paul Brooker, R.; T-Raissi, A. Numerical Analysis of Electric Bus Fast Charging Strategies for Demand Charge Reduction. Transportation Research Part A: Policy and Practice 2016, 94, 386–396. [CrossRef]
Jahic, A.; Eskander, M.; Schulz, D. Preemptive vs. non-preemptive charging schedule for large-scale electric bus depots. 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe). IEEE, 2019. [CrossRef]
Frendo, O.; Gaertner, N.; Stuckenschmidt, H. Open Source Algorithm for Smart Charging of Electric Vehicle Fleets. IEEE Transactions on Industrial Informatics 2021, 17, 6014–6022. [CrossRef]
Zhou, G.J.; Xie, D.F.; Zhao, X.M.; Lu, C. Collaborative Optimization of Vehicle and Charging Scheduling for a Bus Fleet Mixed With Electric and Traditional Buses. IEEE Access 2020, 8, 8056–8072. [CrossRef]
Wang, Y.; Huang, Y.; Xu, J.; Barclay, N. Optimal Recharging Scheduling for Urban Electric Buses: a Case Study in Davis. Transportation Research Part E: Logistics and Transportation Review 2017, 100, 115–132. [CrossRef]
Sebastiani, M.T.; Lüders, R.; Fonseca, K.V.O. Evaluating Electric Bus Operation for a Real-World Brt Public Transportation Using Simulation Optimization. IEEE Transactions on Intelligent Transportation Systems 2016, 17, 2777–2786. [CrossRef]
Liu, T.; (Avi) Ceder, A. Battery-Electric Transit Vehicle Scheduling With Optimal Number of Stationary Chargers. Transportation Research Part C: Emerging Technologies 2020, 114, 118–139. [CrossRef]
Power, R.M. Large General Service. https://www.rockymountainpower.net/content/dam/pcorp/documents/en/rockymountainpower/rates-regulation/utah/rates/008LargeGeneralService1000kWandOverDistributionVoltage.pdf , 2021. [Accessed 03-04-2024].
Gendreau, M.; Potvin, J.Y., Eds. Handbook of Metaheuristics, 3 ed.; Internationalseries in operation research & management science, Springer International Publishing, 2018. [CrossRef]
William H. Press.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C book set: Numerical Recipes in C: The Art of Scientific Computing, 2 ed.; Cambridge University Press: Cambridge, England, 1992.
Henderson, D.; Jacobson, S.H.; Johnson, A.W. The Theory and Practice of Simulated Annealing. In International Series in Operations Research and Management Science; Kluwer Academic Publishers, 1989; pp. 287–319. [CrossRef]
Keller, A.A. Multi-Objective Optimization In Theory and Practice II: Metaheuristic Algorithms; BENTHAM SCIENCE PUBLISHERS, 2019. [CrossRef]
Rutenbar, R. Simulated Annealing Algorithms: an Overview. IEEE Circuits and Devices Magazine 1989, 5, 19–26. [CrossRef]
Zhang, D.; Liu, Y.; M’Hallah, R.; Leung, S.C. A simulated annealing with a new neighborhood structure based algorithm for high school timetabling problems. European Journal of Operational Research 2010, 203, 550–558. [CrossRef]
Xinchao, Z. Simulated annealing algorithm with adaptive neighborhood. Applied Soft Computing 2011, 11, 1827–1836. [CrossRef]
Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual, 2021.

Figure 1. Examples of different methods of overlapping. Space overlap:

q_{k_{1}} > q_{i} + 1 ∴ ψ_{i k_{1}} = 1

. Time overlap

u_{k_{2}} < u_{j} + s_{j} ∴ σ_{k_{2} j} = 0

. Similarly,

σ_{k_{3} i} = 0

Figure 1. Examples of different methods of overlapping. Space overlap:

q_{k_{1}} > q_{i} + 1 ∴ ψ_{i k_{1}} = 1

. Time overlap

u_{k_{2}} < u_{j} + s_{j} ∴ σ_{k_{2} j} = 0

. Similarly,

σ_{k_{3} i} = 0

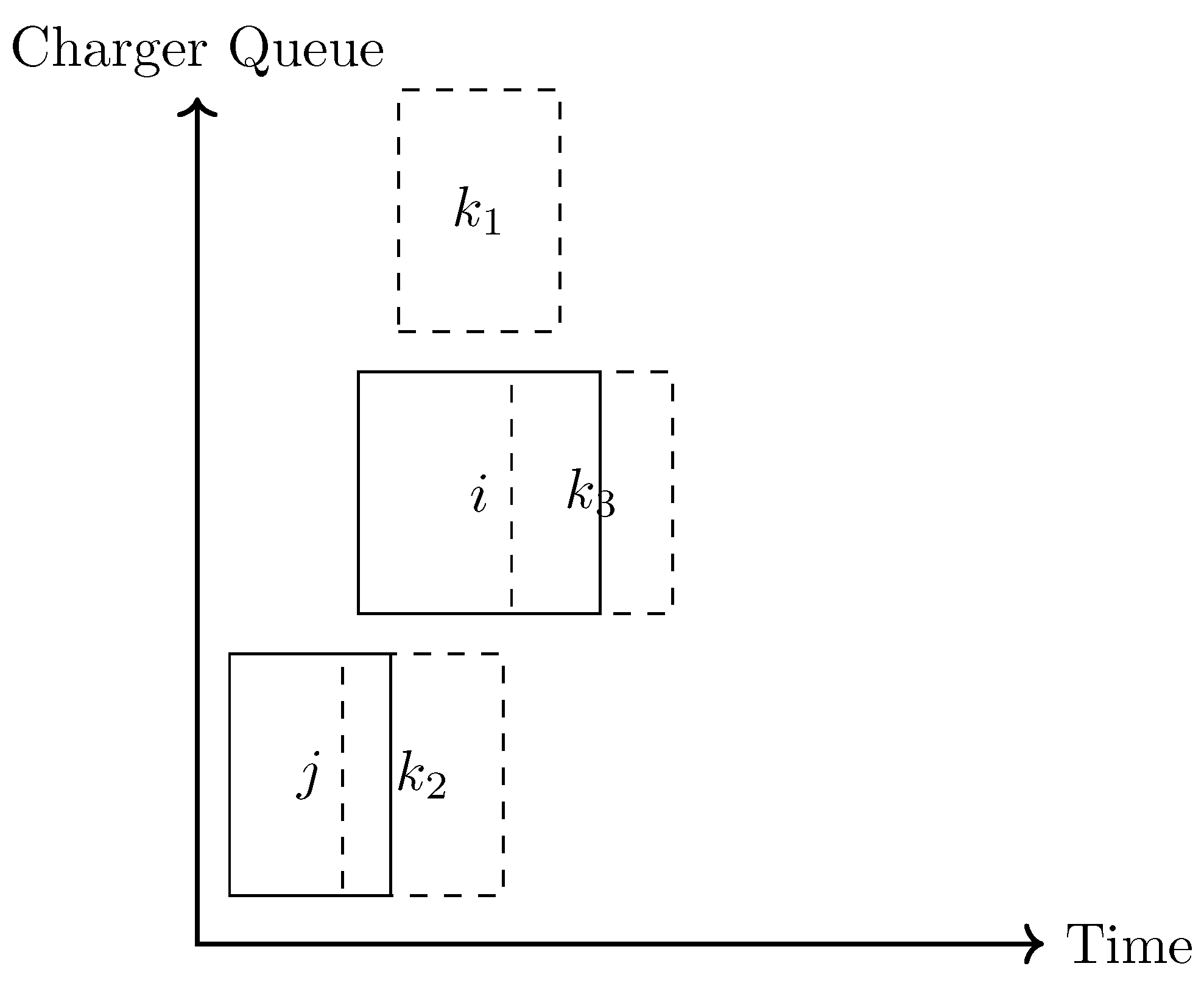
Figure 2. The representation of the queue-time space. The x and y-axis represent time and space, respectively. Along the y-axis, the dashed lines represent discrete queuing locations. The shaded rectangles represent schedules BEBs to be charged. The height of each shaded rectangle represents the space taken on the queue and the width being the time to service said BEB. The vertical dashed lines are associated with vessel D and represent the arrival time, initial charge time, charge completion time, and departure time. Note that the arrival time may be before the initial charge time and the completion time may before the departure time.

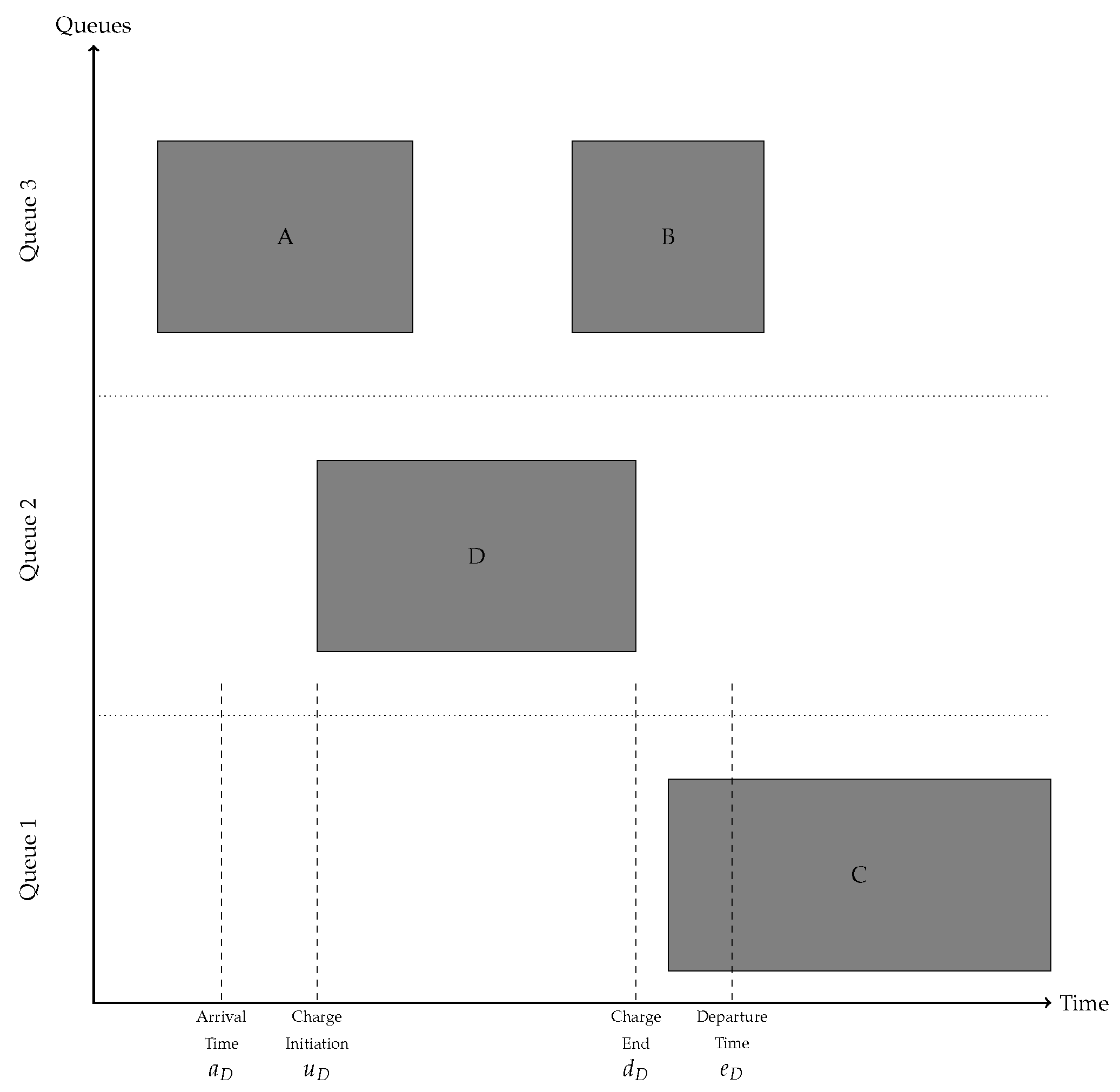
Figure 3. Geometric cooling schedule utilizing various value of

β

Figure 3. Geometric cooling schedule utilizing various value of

β

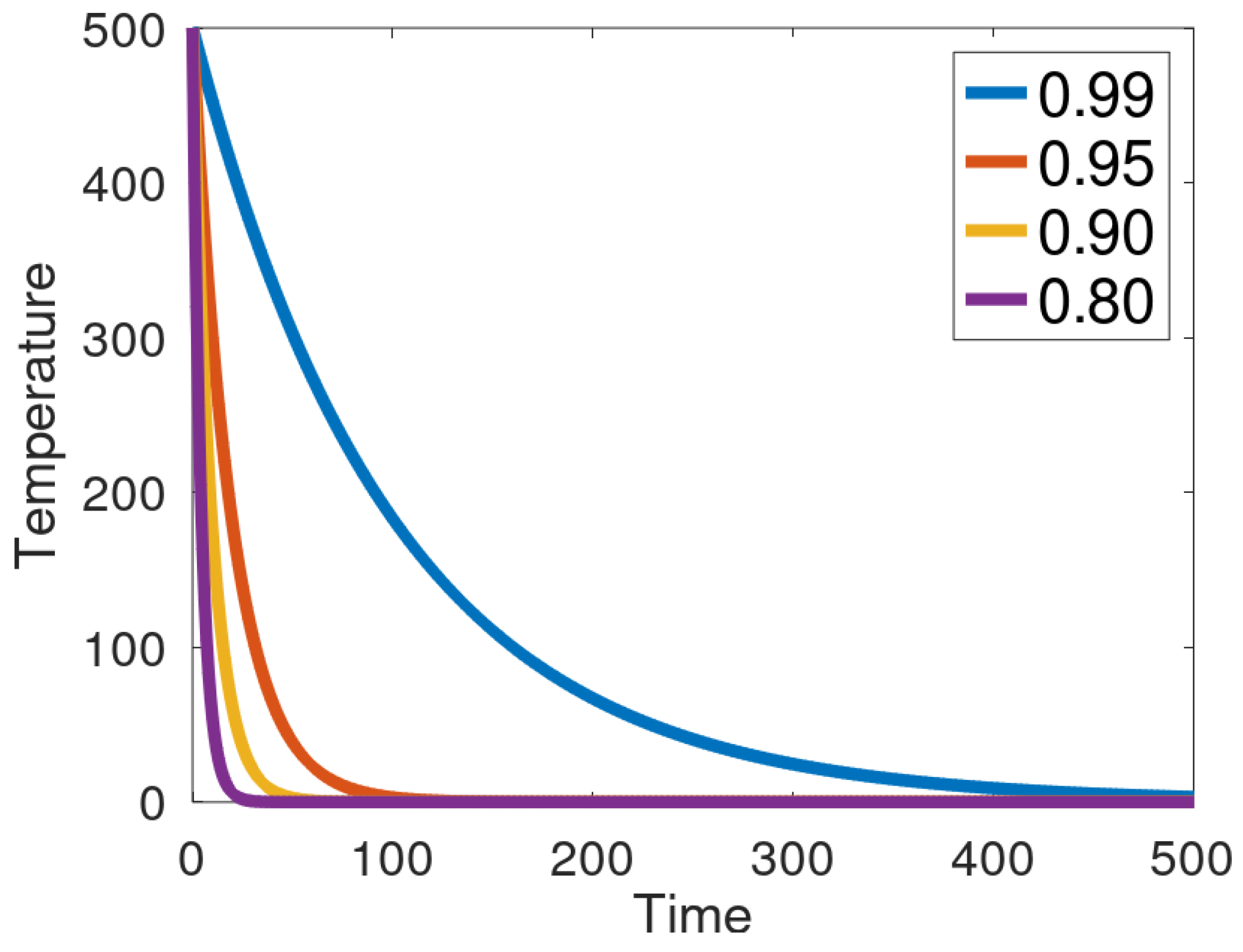
Table 1. Table of variables used in the paper.

Variable	Description	Variable	Description
Constants		Constants
$T$	Time horizon	$n_{K}$	Number of iterations in the repetition schedule
$n_{M}$	Total number of steps created by initial temperature, $T_{0}$ , and cooling schedule	$n_{Q}$	Number of chargers
$n_{V}$	Total number of visits	$n_{H}$	Number of discrete steps in time horizon
$n_{B}$	Number of buses in the fleet
Input Variables		Input Variables
$Δ_{i}$	Discharge of visit over after visit i	$α_{b}$	Initial charge percentage time for bus b
$ϵ_{q}$	Cost of using charger q	$κ_{b}$	Battery capacity for each BEB
$ξ_{i}$	The next index bus b will arrive
$a_{i}$	Arrival time of visit i	$e_{i}$	Departure time for visit i
$t_{h}$	Discrete step in time horizon	$d t$	Step size $d t_{h} = t_{h} - t_{h - 1}$
$r_{q}$	Charge rate of charger q	$t_{m}$	Element of the temperature vector created by cooling equation, $t_{m} \in t$
$ν_{b}$	Minimum charge percentage allowed for each BEB
Direct Decision Variables		Direct Decision Variables
$u_{i}$	Initial charge time for visit i	$d_{i}$	Final charge time for charger for visit i
$q_{i}$	Assigned queue for visit i
Slack Variables		Slack Variables
$η_{i}$	Charge for the bus upon arrival for visit i	$s_{i}$	Amount of time spent on charger for visit i
$σ_{i j}$	Binary variable determining temporal ordering of vehicles i and j	$ψ_{i j}$	Binary variable determining spatial ordering of vehicles i and j
$p_{d}$	Demand cost of the schedule	$ϕ_{i}$	Charge penalty for visit i
$C$	Set of available charging times

Table 2. Table of mean, min, and max SOC (kWh) for each charging schedule.

	BPAP	Qin-Modifid	Heuristic	Quick
Mean	181.327	248.864	182.004	188.327
Min	97.000	0.000	91.265	94.760
Max	382.930	349.200	387.829	388.000

Table 3. Table of mean and max power demand for each charging schedule.

	BPAP	Qin-Modified	Heuristic	Quick
Mean	176.550	394.130	180.858	186.858
Max	1,910.000	2,000.000	1,150.950	1,120.950

Table 4. Table of objective function scores for each of the schedules.

Schedule	Score
BPAP	18500000
Qin-Modified	34578526
Heuristic	11673937
Quick	11234577

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Simulated Annealing Approach to the Scheduling of Battery-Electric Bus Charging

Abstract

1. Introduction

2. Problem Description

3. Optimization Problem

3.1. Variable Definitions

3.1.1. Input Parameters

Spatiotemporal and Discretization Parameters

Battery Dynamic Parameters

3.1.2. Decision Variables

3.2. Objective Function

3.2.1. Assignment Cost

3.2.2. Penalty Method

3.2.3. Consumption Cost

3.2.4. Demand Cost

3.3. Constraints

4. Simulated Annealing

4.1. Cooling Equation

4.2. Acceptance Criteria

4.3. Neighbor Generators and Wrappers

4.3.1. Generator Input/Output

4.3.2. Generators

New Visit

Slide Visit

New Charger

Wait

New Window

4.3.3. Generator Wrappers

Charge Schedule Generation

Perturb Schedule

4.4. Alternative Heuristic Implementation

5. Optimization Algorithm

6. Example

6.1. BEB Scenario

6.2. Results

7. Conclusion

Author Contributions

Funding

Informed Consent Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe