Preprint
Article
Improved Performance of the PMSM Sensorless Control System Based on DTC Strategy and SMC Using Fractional Order and Fractal Dimension Calculus
Altmetrics
Downloads
108
Views
47
Comments
0
This version is not peer-reviewed
Submitted:
28 May 2024
Posted:
29 May 2024
You are already at the latest version
Alerts
Abstract
Starting from the fact that one of the global control strategies of the Permanent Magnet Synchronous Motor (PMSM), namely the Direct Torque Control (DTC) type control strategy, is characterised by the fact that the inner flux and torque control loop usually uses hysteresis ON-OFF type controllers and the oscillations introduced by them have to be cancelled out by the outer speed loop controller (which is usually a PI speed controller and whose performance is good around the global operating points and for relatively small variations of the external parameters and disturbances caused in particular by the load torque variation), while retaining the advantages of the DTC strategy, this paper presents the improvement of the performance of the PMSM sensorless control system using Proportional Integrator (PI), PI Equilibrium Optimizer Algorithm (EOA), Fractional Order (FO) PI, Tilt Integral Derivative (TID) and FO Lead-Lag for constant flux, and Sliding Mode Control (SMC) and FOSMC for variable flux. The performance indicators of the control system are the usual ones: response time, settling time, overshoot, steady-state error and speed ripple, plus another one given by the fractal dimension (FD) of the PMSM rotor speed signal, and the hypothesis that the FD of the controlled signal is higher when the control system provides better performance is verified. The paper also presents the basic equations of the PMSM, based on which the synthesis of integer and fractional controllers, the synthesis of an observer for estimating the PMSM rotor speed, electromagnetic torque and stator flux are presented. The comparison of the performance of the proposed control systems and the demonstration of the parametric robustness are performed by numerical simulations in Matlab/Simulink using Simscape Electrical and Fractional Order Modelling and Control (FOMCON). Real-time control based on an embedded system using a TMS320F28379D controller demonstrates the good performance of the PMSM sensorless control system based on the DTC strategy in a complete hardware-in-the-loop (HIL) implementation.
Keywords:
Subject: Engineering - Control and Systems Engineering
1. Introduction
Major applications of PMSM include: industrial applications, aerospace applications, electric drives and electric vehicles, computer peripherals and robotics. The growing interest in the widespread use of PMSMs in a very wide variety of applications can be explained both by the fact that PMSMs have a number of advantageous design features, and by the fact that PMSM control systems can be characterised by a wide range of control algorithms with increased flexibility and performance, ranging from their mathematical description to their implementation in embedded systems [1,2,3,4,5].
In terms of overall PMSM control strategies, two strategies can be distinguished, namely the Field Oriented Control (FOC) [6,7] type strategy and the DTC [8,9] type strategy. The FOC type strategy in the classical description contains two tandem control loops, the outer loop for speed and the inner loop for current, and the controllers are of the classical PI controller type. When using the DTC strategy, there are two tandem control loops, the outer one for speed control and the inner one for torque and flow control. As far as the controllers are concerned, in the classical description the speed controller is of the PI type, while the flux and torque controllers are of the hysteresis ON-OFF type. At first sight, the advantages and disadvantages of using the FOC-type strategy vs. the DTC strategy in terms of control algorithm complexity vs. control algorithm computation times are clearly antagonistic. Obviously, the use of hysteresis ON-OFF controllers, which require very short computing times, will inherently introduce small oscillations that must be cancelled out by the outer speed loop controller. Typically, the classical PI-type controller for the outer speed control loop can be an acceptable compromise between the required computation time when implemented in an embedded system and the overall performance of the control system, represented by: response time, settling time, overshoot, steady-state error and speed ripple.
In order to improve this global performance of PMSM control systems, given that PI type controllers provide good performance around global operating points even for relatively small variations of external parameters and disturbances caused in particular by load torque variations, a number of more complex controllers of the following types can be used: adaptive [10], predictive [11], robust [12], fuzzy [13] and neural [14]. Although the performance of these controllers is superior to that of classical PI-type controllers, care must be taken when implementing them in real-time in terms of the trade-off between the computing power of the embedded system and the overall cost of implementation.
A special type of controller can be obtained by using fractional elements. Thus, a number of advanced integer-order controllers can be described by fractional means, with the following control system performance improvements [15,16,17,18,19,20].
A convergent approach to that represented by the control system synthesis is the use of velocity observers to estimate the PMSM rotor speed and possibly other control system characteristic parameters, in the case of the DTC strategy, torque and flux. The use of these observers ensures the sensorless nature of the control system and also contributes to the overall reliability of the PMSM control system through the use of sensors, particularly those using mechanical elements in motion [21,22,23,24].
In addition to the performance indicators described above, an additional one can be introduced, namely the FD of the controlled signal, in this case the FD of the PMSM rotor speed signal. In the papers [25,26], a hypothesis verified by numerical simulations is introduced, namely that more efficient control systems are also characterised by a higher value of the FD [27,28] of the controlled signal.
Taking into account these elements, the paper starts from the PMSM control based on the DTC strategy and presents the improvement of the control system performance in the case of constant reference flux by using PI type fractional controllers, the optimisation of the controller parameters using a computational intelligence algorithm, namely the EOA type algorithm [29,30,31], the synthesis of a speed, torque and flux observer, and in terms of the performance of the control system, the comparison between these control systems uses both the usual performance indicators and the FD of the PMSM speed signal. In the case of a variable reference flux, the speed controller provides the reference for the torque controller, while an SMC controller [32,33] is used to provide the flux reference in both the integer-order and fractional-order FOSMC variants [34,35,36].
The main contributions of this article are as follows:
- Presentation of the PMSM control system based on the DTC strategy;
- Synthesis and implementation of a PMSM control system based on a constant flux DTC strategy and optimisation of PI speed controller parameters using an EOA type algorithm;
- Synthesis and implementation of an observer for estimating PMSM rotor speed, electromagnetic torque and stator flux;
- Synthesis and implementation of a PMSM sensorless control system based on DTC type constant flux strategy using FOMCON toolbox in Matlab for synthesis and implementation of the speed controller in fractional form: FOPI, TID and FO-Lead-Lag;
- Synthesis and implementation of a PMSM sensorless control system based on DTC strategy with variable flux by synthesis and implementation of SMC and FOSMC type controllers to provide stator flux reference;
- Calculation of PMSM speed signal FD for high-end controllers: PI, PI-EOA, FOPI, TID and FO-Lead-Lag for constant flux and SMC and FOSMC for variable flux;
- Comparison of PMSM sensorless control systems based on DTC strategy using high-end controllers: PI, PI-EOA, FOPI, TID and FO-Lead-Lag for constant flux and SMC and FOSMC for variable flux;
- Demonstration of the parametric robustness of the sensorless control system based on the DTC strategy by maintaining the control performance even in the case of a 50% increase in the J parameter, which represents the combined inertia of the PMSM rotor and load;
- Real-time HIL implementation in an embedded system of the proposed PMSM sensorless control system based on a DTC strategy in case of constant flux and variable flux using FOPI, SMC, and FOSMC type controller.
The rest of the paper is presented and structured as follows: Section 2 presents the proposed PMSM sensorless control system using the DTC strategy, while the Matlab/Simulink implementation and numerical simulations for the proposed PMSM sensorless control system using the DTC strategy are presented in Section 3. The real-time implementation and experimental setup are presented in Section 4, and some conclusions and suggestions for future research are presented in the final section.
2. Proposed PMSM Sensorless Control System Using DTC Strategy
The DTC-type control strategy together with the FOC-type control strategy are the most commonly used PMSM control strategies. Each of these control strategies has a number of advantages and disadvantages when compared directly with each other. Therefore, this section presents the DTC strategy based on the PMSM operating equations in the d–q rotating reference frame coordinate system, and Figure 1 shows the block diagram of the DTC strategy. The operating equations are given in relations (1)–(4) [8,9,24].
In the above relations, the usual notations are used for the inductance L, the stator resistance Rs, the stator flux ψ, the currents i and the voltages u in the coordinate system of the d-q rotating reference frame, plus the mechanical angular speed of the PMSM rotor denoted by ω, the flux linkage denoted by λ0, the viscous friction coefficient denoted by B, the rotor inertia combined with the load inertia denoted by J. Te is the electromagnetic torque, TL is the load torque and the number of PMSM pole pairs is given by np.
Figure 1 shows that a two-stage control system is implemented, where the outer stage implements speed control and the inner stage implements torque and flux control via two control loops based on hysteresis ON-OFF controllers. In the case of sensorless control, it is also necessary to synthesise an observer that provides the estimated value of the stator flux, the estimated value of the PMSM rotor speed and the load torque. The main characteristic of this DTC strategy is the use of fast response controllers with reduced design simplicity for the inner loops, while classical PI type controllers generally ensure good performance for the outer loop, maintaining a reduced complexity of real-time implementation.
Based on these aspects, this section presents implementations of control structures that provide improved performance without significantly burdening the hardware/software structure for real-time implementation. Therefore, these types of controllers for outer loop control are presented when the reference stator flux is constant. If the reference stator flux is variable, a separate section presents the implementation of SMC and FOSMC type control structures. The implementation of a flow, speed and torque load observer is also presented in a separate section. In order to compare the performance of the control systems presented, in addition to the classic comparison elements such as response time, settling time and PMSM speed signal ripple, the fractal dimensions (FD) of the control signals, in this case the PMSM speed signal, are also compared.
2.1. PMSM Sensorless Control Based on DTC Strategy Using Constant Flux
In this section, as shown in Figure 2, the classic PI speed controller is replaced by optimally tuned PI controllers using an EOA algorithm and FO controllers: FOPI, TID and FO-Lead-Lag speed controllers respectively. In all these cases the stator reference flux is constant. Throughout this article, the representations of the PMSM operating equations, both in the d−q rotating reference frame coordinate system and in the α−β stationary reference frame coordinate system, prove useful.
In this sense, relation (5) presents a coordinate transformation between the d−q rotating reference frame and the α−β stationary reference frame for the quantities describing the PMSM operating equations [34].
where: fα and fβ are the variables in the α−β stationary reference frame, fd and fq are the variables in the d−q rotor reference frame.
In relation (5) in the coupling matrix, the electrical angle θe is used, whose relation to the mechanical angle θ, which represents the position of the PMSM rotor, is: .
Using relation (5), the following relations, which describe the operation of the PMSM, can be written in the α−β stationary reference frame coordinate system:
The back-EMF voltages eα and eβ are defined as follows:
The time variation of the currents iα and iβ can be obtained from relation (6) in the following form:
Similarly, the time variation of the stator flux in the α−β stationary reference frame can be written as follows:
The expression of the electromagnetic torque Te in the stationary reference frame α−β is given by the relation (10).
In an obvious way, relation (11) shows the relationship between the stator flux and its projections in the α−β stationary reference frame and in the d−q rotating reference frame:
2.1.1. Equilibrium Optimizer Algorithm
For PI-type controller tuning, in addition to heuristic or classical Ziegler-Nichols tuning [37], superior control system results can be achieved by using computational intelligence algorithms, of which the EOA algorithm is presented below.
Equation (12) shows the operating equation of a PID controller, where the output is u(t) and the input is the error e(t). The tuning parameters of the PID controller are Kp, Ki, and Kd. When using a PI controller, Kd = 0.
For the PI speed control presented in this section, the tuning parameters are Kp and Ki. They are tuned using an EOA algorithm.
In summary, the operation of an EOA-type algorithm can be described by analogy with the differential equation describing the variation of the concentration C in a volume V, which is equal to the amount of mass entering the system minus the amount of mass leaving the system plus the amount of mass generated within the volume. The following equation can be written (13) [29]:
where: the rate of change of the mass in the control volume is denoted by , the volumetric flow rate into and out of the control volume by Q, the concentration at equilibrium, where there is no generation inside the control volume, by Ceq.
Given equation (13) becomes:
The integration of equation (14) gives:
Equation (15) gives:
where:
where: .
From relation (16) it can be seen that the concentration expression C, which can be considered as the position of a particle in the PSO-type algorithm [35], consists of three terms. The first term is given by the equilibrium concentration Ceq, the second term is given by the current and equilibrium concentration values and the third term is given by the generation rate. In analogy to the PSO-type algorithm, the second term can be used for the direct search part of the algorithm, while the third term can be used for the exploration part of the algorithm. By analogy with the PSO-type algorithm, a population is initialised as in the relation (18).
where: represents the initial concentration vector of the i-th particle, Cmin and Cmax represents the minimum and maximum values for the dimensions, randi is a random vector in the interval of [0,1], and n is the number of particles as the population.
Particles are evaluated to obtain a fitness function that determines equilibrium candidates. The equilibrium candidates are given by the equation (19).
The average index of indicates a particle average value formed, while the pool index of represents the current selection index.
Equation (17) is modified to equation (20).
where: a1 is a constant value that controls exploration ability. The term provides directions for exploitation and exploration.
The generation rate G is given by the relation (21) [29].
where: G0 represents the initial value and k indicates a decay constant. For k = λ the final set for G is:
where:
where: r1 and r2 represents random numbers in [0,1] and GCP is set to 0.5.
The final tuning equation of the EOA type algorithm is given by the relation (25).
In the application presented in this paper, the global optimization criterion used for the EOA type algorithm is an Integral Absolute Error (IAE) criterion:
where: , namely the difference between the reference speed and the instantaneous speed of the PMSM rotor.
As a result of implementing this algorithm, the optimal values for tuning the PI controller are obtained. This results in the proposed PI-EOA-type controller shown in Figure 2.
2.1.2. Elements and Notions of Fractional Calculus
For the implementation of the FO-type controllers proposed in Figure 2 (FOPI, TID and FO-Lead-Lag speed controllers), some notions of fractional integration and differentiation are briefly presented. Thus, the non-integer order operator for integration and differentiation is denoted by , where α is the fractional order, and the limits of the interval to which the operator is applied are denoted by a and t. The operator is shown in relation (27) [15,16,35]:
The Riemann-Liouville definition of the operator is given by the following relation:
where: ; – Euler’s gamma function.
The Grünwald-Letnikov definition of the operator is useful in practical applications of numerical representation:
where: operator [·] provides the integer part.
Please note that the application of these definitions to the system presented in this article is under initial null conditions [16,17]. Similar to the case of integer order of the operator defined in relation (27), the transfer function for signals with fractional derivative can be defined by applying the Laplace transform. If the orders of the fractional operator s are integer multiples with respect to the proportional order q (), the transfer function H(λ) is obtained, expressed by the following relation:
where: .
Based on this, the description of a system in the fractional case can be similar to the transfer function described in relation (30), and a description in the states space as in relation (31).
The stability of system (31) can be verified by the equation:
where: is the proportional order and eig(A) is the eigenvalue of the associated matrix A.
In terms of numerical implementation by simulation or in real-time, the problem is to approximate fractional FO transfer functions in a given frequency range and order N with an integer-order transfer function to obtain an integer-order difference equation that can be directly implemented in a simulation program or an embedded system. This allows Oustaloup recursive filters to be used with [15,16,35]. The form of the integer transfer function used to obtain this approximation is given by the following relation:
where: the values of , and K are expressed by equations (34).
Another variant of the Oustaloup filter that gives a more accurate conversion is given by relation (35), where the usual values are b = 10 and d = 9.
where:
2.1.3. Fractional Order Speed Controllers for the PMSM Control Using DTC Strategy
Starting from equation (12), after applying the Laplace transform in the complex domain s, we get:
Starting from relation (37), which represents the output of the controller in the complex domain s in the integer case, FO-type controllers can be further described in the fractional case using the notions of fractional computation described above.
- FO-PI Speed Controller for Sensorless PMSM Control System Using DTC Strategy
The most commonly used FO controllers are of the PIλDμ type. The description relation in the time domain is given by (38).
where: e(t) – signal error.
Applying the Laplace transform to (38) with zero initial conditions gives the following equation, which represents the FO-PI speed controller for the DTC-type sensorless PMSM control system:
where: Kp – the proportional factor; Ki – the integral factor; λ – the integrator order (positive); Kd – the differential factor; μ – the differentiator order. For λ = μ = 1, the result is an integer order PID controller.
- TID Speed Controller for Sensorless PMSM Control System Using DTC Strategy
Another fractional controller similar to the PIλDμ controller is the TID controller, which can be described by the following transfer function for PMSM sensorless control system using DTC:
unde: Kt – tilt gain; n – order of integration of the tilt term; Ki - gain of the integrator term; Kd - gain of the derivator term.
- FO-FO-Lead-Lag Speed Controller for Sensorless PMSM Control System Using DTC Strategy
The general form of the transfer function of a FO-FO-Lead-Lag controller is given by the relation (41):
where: λ – the fractional order of the FO-FO-Lead-Lag controller.
Note that for α > 0, the FO-FO-Lead-Lag controller has a lead effect, while for α < 0, the FO-FO-Lead-Lag controller has a lag effect.
In relation (41), for , it is obtained the usual form of the FO-FO-Lead-Lag speed controller:
Also, if , and x has a very large value (e.g. x > 10000), the FO-FO-Lead-Lag controller transfer function becomes the FO-PI controller transfer function.
This allows greater flexibility in using the FO-FO-Lead-Lag type controller in a control loop and the possibility of obtaining higher performance from the sensorless PMSM control system using DTC strategy.
2.1.4. Observer for the Speed, Electromagnetic Torque, and Flux Estimations
The sensorless nature of the PMSM control system based on the DTC strategy is given by the fact that an observer is used to estimate rotor speed, electromagnetic torque and flux. Starting from equation (9), the expressions for the stator flux in the α–β stationary reference frame are given in relations (43) and (44).
An observer based on equations (45) is used to estimate the stator flux in the α–β stationary reference frame [23,24].
where: and – estimated stator flux variables in the α–β stationary reference frame; and – stator current errors in the α–β stationary reference frame if given in relation (46); k1, k2 K1SMO, and K2SMO - projected factors (observer gains).
Equations (47) are used to estimate the and stator currents in the α–β stationary reference frame [23,24].
where: ; ; ; and the transformation matrix is given by the following relation:
Equation (47), explained for the components α and β, can be written as:
In relation (45), which describes a sliding mode observer (SMO), the sign function is replaced by the sigmoid function to achieve a smooth transition between +1 and –1.
The definition of the sigmoid function is given by the relation (52).
where: a = 4 and b = 0 are positive constants.
The graphical representation of the sigmoid function is shown in Figure 3.
The convergence of the observer is demonstrated by choosing a Lyapunov function of the following form:
in which . After a few calculations, we obtain , which demonstrates global asymptotic stability [23,24].
Similarly, by deriving equation (50), the PMSM rotor speed estimate is obtained as follows:
where: Ts – the sampling period, k – the current sampling step.
2.2. PMSM Sensorless Control Based on DTC Strategy Using Variable Flux
If the reference stator flux is not constant, the DTC control strategy is modified to use more complex controllers to obtain ψref. Therefore, Figure 4 shows the block diagram of the PMSM sensorless control system based on the DTC strategy using SMC and FOSMC variable flux controllers.
2.2.1. SMC-type Controller for the PMSM Sensorless Control Based on DTC Strategy Using Variable Flux
Rewriting equations (1)-(4) in the following form [35]:
to synthesise an SMC-type controller to control a PMSM, the state variables x1 and x2 are selected and described by the following relations:
unde: x1 – speed tracking error.
The sliding surface S of the zero error variation is defined in equation (59), and by deriving this equation we obtain equation (60).
where: the parameter c is positive and adjustable, and is obtained from the equations (1)–(3).
Equation (61) shows the condition of the time evolution of the surface S; this condition ensures the control of the response time of the PMSM sensorless control based on the DTC strategy.
where: the parameters ε and q are positive and the signum function is denoted by sgn().
The above sgn function is replaced by the sigmoid function defined in relation (52), and this is used in the synthesis of the SMC-type controller in order to reduce the chattering phenomenon characteristic of the structure of this type of controller.
From the above relations, according to the SMC specific methods, we obtain:
From equations (9), (10) and (11) the following custom equations can be obtained for the reference values of the electromagnetic torque, the reference current iqref and the reference value of the stator flux in the usual case where Ld = Lq:
The stability of the PMSM control system based on the DTC strategy using the control law given by equation (62) is demonstrated by selecting a Lyapunov function of the following form:
The following relation is obtained by calculating the derivative :
The stability of the system is given by the negativity of the derivative .
2.2.2. FOSMC-type Controller for PMSM Sensorless Control Based on DTC Strategy Using Variable Flux
To improve the performance of PMSM sensorless control system based on DTC strategy, the synthesis of a FOSMC type controller is proposed to obtain iqref and then flux ψref based on relations (63) and (64).
For this purpose, the sliding surface S is selected as follows:
Calculating the derivative of the surface S, we obtain:
Based on the descriptive equations of the PMSM mathematical model, the following relation can be written:
Substituting equation (69) into equation (68) gives:
According to the SMC methods for , we obtain the following relation:
Applying the operator to relation (68) to both members, we obtain the following relation:
After processing relation (69), we obtain:
By rewriting relation (70), we obtain:
The current reference iqref is obtained from equation (71) as follows:
Then, as in the case of the integer-order SMC-type controller, the reference value of the flux ψref is obtained by using equations (63) and (64).
3. Matlab/Simulink Implementation and Numerical Simulations for the Proposed PMSM Sensorless Control System Using DTC Strategy
In this section, for the values of a PMSM given in Table 1, numerical simulations are performed for the corresponding PMSM control systems according to the cases of DTC strategy controllers presented in Section 2.
3.1. Numerical Simulation for the PMSM Sensorless Control System Based on DTC Strategy Using Constant Flux
The Matlab/Simulink implementation of the PMSM sensorless control based on the constant flux DTC strategy is shown in Figure 5. Therefore, Figure 5 (a) shows the main Simulink model of the sensorless PMSM control based on the DTC strategy, where the speed controllers are: PI, PI-EOA, FOPI, TID and FO-Lead-Lag. The transfer functions obtained for the control of the PMSM, whose parameters are given in Table 1, are presented below. Figure 5 (b) also shows the detail of the Simulink subsystem implementation of the observer for the speed, torque and flux estimation.
For the PI speed controller described in equation (12), in the case of the sensorless PMSM control system based on the constant flux DTC strategy, the tuning parameters obtained by empirical methods are Kp = 0.05 and Ki = 0.91. Using an EOA-type algorithm, the tuning parameters obtained are Kp = 0.03 and Ki = 0.66.
The FOMCON toolbox in Matlab allows the tuning of an FOPI type controller described by equation (39), in the case of PMSM sensorless control based on a constant flux DTC strategy. The values obtained are: Kp = 6.2; Ki = 24; λ = 1,1; Kd = μ = 0, and the FOPI speed controller transfer function becomes:
For the closed-loop study of the system consisting of the FOPI controller given in relation (73) and the fixed part given by the PMSM using the FOMCON toolbox in Matlab, the following fractional-order transfer function is obtained:
The stability of the closed-loop system of the PMSM sensorless control system based on the constant flux DTC strategy and PI speed controller is given by satisfying the condition given by relation (32) and is shown graphically in Figure 6 using the FOMCON toolbox. The analysis of Figure 6 shows that the system is stable. Figure 7 shows the step signal response of the closed loop system when using the FOPI speed controller.
Figure 8 shows the Bode diagram plot of magnitude/frequency and phase/frequency of the closed loop system consisting of the FOPI controller given by relation (73) in the case of PMSM sensorless control system based on DTC strategy using FOPI speed controller at constant flux.
For real-time implementation in an embedded system, it is necessary to obtain the equivalent transfer function of integer order of the transfer function of the FOPI type speed controller given in equation (73) in the fractional form. The equivalent transfer function in the discrete variable z of integer order can be implemented as a recursive equation. The Oustaloup filter is used to approximate the fractional order transfer function with a continuous integer order transfer function. This is done using the FOMCON toolbox for Matlab in the frequency range ω = [10-2; 103] rad/s, which contains the common frequencies for the presented application. Figure 9 (a) shows the equivalent transfer function obtained in the s-domain. The equivalent transfer function in the z-domain is obtained using the Tustin substitution. The form of the discrete transfer function obtained is shown in Figure 9 (b).
Based on the second fractional order controller of the PMSM sensorless control system based on the constant flux DTC strategy, i.e. the TID controller described in equation (40), whose tuning parameters are Kt = 0.035, Ki = 0.31, n = 10 and Kd = 0, the following transfer function is obtained:
Similar to the case of the FOPI speed controller, using the Oustaloup zpk filter, the integer order results for the TID controller are shown in Figure 10. Therefore, the continuous form is shown in Figure 10 (a) and the discrete form is shown in Figure 10 (b).
For the FO-Lead-Lag speed controller shown in equations (41) and (42), the following transfer function is obtained for the tuning parameters k’ = 300, x = 50, λ = 1,4 și α = 0.11:
Using the Oustaloup zpk filter, the integer order results for the FO-Lead-Lag type speed controller are shown in Figure 11. Therefore, the continuous form is shown in Figure 11 (a) and the discrete form is shown in Figure 11 (b).
Based on the nominal PMSM parameters in the case of the sensorless control system based on the DTC strategy using PI, PI-EOA, FOPI, TID, and FO-Lead-Lag speed controllers at constant flux, the numerical simulations are presented below.
Graphs of the following parameters of interest are presented for each sensorless control system based on the DTC strategy using speed controllers: Reference speed and estimated PMSM rotor speed, load and electromagnetic torque, stator currents and fluxes in the α–β stationary reference frame. The load torque reference TL is of 1Nm and the speed reference signal ωref used is expressed as a sequence of steps: [400 600 900]rpm→[0 0.1 0.2]s. For the speed, electromagnetic torque and flux estimation observer presented in section 2.1.4, the tuning parameters are: k1 = 150 and k2 = 50, K1SMO = K2SMO = 0.1.
Figure 12 shows the parameter evolution of the PMSM sensorless control system using the DTC strategy with PI speed controller at constant flux. Note that the response time is tr = 12ms and the settling time is ts = 72ms.
The parameter evolution of the PMSM sensorless control system using the DTC strategy when using the PI-EOA speed controller is shown in Figure 13. In this case, the response time is tr = 9.2ms and the settling time is ts = 30ms. There is a 25% reduction in response time and a reduction in settling time of around 60%.
Using the FOPI speed controller for the PMSM sensorless control system with DTC strategy at constant flux, the evolution of the parameters is shown in Figure 14. This gives a response time tr = 7.9ms and a settling time ts = 15ms. There is a 34% reduction in response time and a 79% reduction in settling time.
Using the TID speed controller for the PMSM sensorless control system with DTC strategy at constant flux, the evolution of the parameters is shown in Figure 15. A response time tr = 5.9ms and a settling time ts = 14.5ms are obtained. There is a 50% reduction in response time and an 80% reduction in settling time.
Using the FO-Lead-Lag speed controller for the PMSM sensorless control system with DTC strategy at constant flux, the evolution of the parameters is shown in Figure 16. This gives a response time tr = 3.2ms and a settling time ts = 9.1ms. There is a 73% reduction in response time and approximately 87% reduction in settling time.
Figure 17 shows the flux space vector trajectory components in the α–β stationary reference frame for the PMSM sensorless control system based on the DTC strategy using the PI speed controller at constant flux.
A comparison of the evolution of the PMSM rotor speed for the sensorless control system based on the DTC strategy using PI, PI-EOA, FOPI, TID and FO-Lead-Lag speed controllers at constant flux is shown in Figure 18. It can be seen that the use of FO type controllers improves the performance of the control system, so the best performance in the comparison presented is obtained by FO-Lead-Lag speed controllers, followed by TID and FOPI speed controllers.
3.2. Numerical Simulation for the PMSM Sensorless Control System Based on DTC Strategy Using Variable Flux
The Matlab/Simulink implementation of the PMSM sensorless control system based on the DTC strategy using variable flux is shown in Figure 19. Therefore, Figure 19 (a) shows the main Simulink model of the PMSM sensorless control system based on the DTC strategy using SMC and FOSMC type controllers. In addition, Figure 19 (b) shows the detail of the Simulink subsystem implementation for the SMC-type controller, and Figure 19 (c) shows the detail of the Simulink subsystem implementation for the FOSMC-type controller. The Matlab/Simulink implementation presented is based on the SMC and FOSMC type controller description equations presented in Section 2.2.
For the numerical simulations performed in Matlab/Simulink using the SMC-type controller described in section 2, the parameters in Eqs. (56)–(66) are as follows: ε = 300, q = 200, and c = 100. For the FOSMC-type controller described in Section 2, equations (67)–(72), the parameters are as follows: kp = 100, kd =1, and μ = 0.55.
Using the SMC-type controller for the PMSM sensorless control system with DTC strategy at variable flux, the evolution of the parameters is shown in Figure 20. The response time is tr = 2.3ms and the settling time is ts = 2.3ms. There is an 80% reduction in response time and approximately 96% reduction in settling time compared to the original PI controller performance. In addition, using the FOSMC-type controller for the PMSM sensorless control system with DTC strategy at variable flux, the evolution of the parameters is shown in Figure 21. The response time is tr = 2.2ms and the settling time is ts = 2.2ms. There is an 82% reduction in response time and approximately 97% reduction in settling time compared to the initial performance of the PI controller.
In terms of parametric robustness, Figure 22 shows the parameter evolution of the PMSM sensorless control system using the DTC strategy with the FOSMC variable flux controller, where the J parameter increases by 50% compared to the nominal valueGood dynamic performance is also observed in this case, in the sense that the overshoot is negligible and the steady-state error is less than 0.1%, just as in the case where the J parameter is at the nominal value. Obviously, given the importance of the J parameter, which represents the combined inertia of the PMSM rotor and load, the response time increases to 4ms and the stator currents increase by approximately 20%.
The flux space vector trajectory for the PMSM sensorless control system based on the DTC strategy using the FOSMC variable flux controller is shown in Figure 23, and the evolution of the flux reference for the FOSMC-type controller is shown in Figure 24.
The comparison of the evolution of the PMSM rotor speed for the sensorless control system based on the DTC strategy using SMC and FOSMC variable flux controllers is shown in Figure 25. Note that this comparison is made between SMC and FOSMC type controllers and FO-Lead-Lag controllers, which provide the best performance of the group of controllers presented in the previous section. Thus, the best performance of the PMSM sensorless control system based on the DTC strategy is achieved using the FOSMC-type controller.
3.3. Description of the Fractal Dimension and Calculus for the Speed Signal Controled by Proposed Controllers used in PMSM Sensorless Control Based on DTC Strategy
In order to compare the performance of the PMSM sensorless control system using the DTC strategy in the case of all the controllers presented in the previous sections, the FD of the signal controlled by the control system, in this case the PMSM speed, is proposed as a performance indicator. According to [28], a FD value of the controlled signal is higher if the control system provides better performance.
One of the most widely used methods for calculating the FD of a one-dimensional signal is the box-counting method [28]. It starts with a square in which the signal can fit, and the unit of measurement used below is the side of that square. For numerical reasons, the side of the square is chosen as a power of 2. By iteratively dividing the unit of measurement by 2, the algorithm continues until a value lower than a predetermined threshold is obtained. At each iteration, the division has the expression 1/2k, where k is the current step. On the second axis, the division is in the form of , where nk is the total number of occupied domains, relative to the scale given by the initial signal. At each iteration, the coordinates of the points Mk(x,y) corresponding to the two axes are maintained, using a Cartesian system in logarithmic coordinates for the representation. The sequence of points M1, M2, ...,Mn is calculated iteratively until the stop condition, given by exceeding the selected threshold, is met. It is interesting to calculate the slope of the line closest to points M1, M2, ...,Mn, closest in the sense of least squares. The value obtained using the above algorithm represents the FD of the initial signal. The command “[n,r] = boxcount(signal,'slope')” in the Matlab environment is used to obtain the vectors of the two dimensions according to the algorithm described above. The logarithmic coordinates of the Mk points, together with the slope of the line closest to the points obtained by applying the algorithm, where the slope represents the FD of the analysed signal, are obtained by the following Matlab commands: “fd = -diff(log(n))./diff(log(r))” and “['FD = 'num2str(mean(df(1:length(df)))) '+/- 'num2str(std(df(1:length(df))))])”.
For the PMSM with the parameters given in Table 1, the graphical representation of the FD of the speed signal for the PMSM sensorless control system based on the DTC strategy is shown in Figure 26. Thus, for the constant flux case: Figure 26(a) shows the FD of the speed signal for the PI speed controller, Figure 26(b) shows the FD of the speed signal for the PI-EOA speed controller, Figure 26(c) shows the FD of the speed signal for the FOPI speed controller, Figure 26(d) shows the FD of the speed signal for the TID speed controller, and Figure 26(e) shows the FD of the speed signal for the FO-Lead-Lag speed controller. In addition, for the case of a variable flux: Figure 26(f) shows the FD of the speed signal for the SMC-type controller and Figure 26(g) shows the FD of the speed signal for the FOSMC-type controller. It can be seen that the FD of the speed signal increases according to the controllers that bring performance improvements to closed-loop PMSM systems based on the DTC strategy.
The usual performances of the PMSM sensorless control system based on the DTC strategy for the controllers presented in the previous sections are summarised in Table 2. In addition to FD, time response and settling time, the speed ripple is also shown, defined by the following relation [35]:
where: N – number of samples; ω – PMSM speed; ωref – PMSM reference speed.
Also, the usual performance indicators of a control system, namely overshoot and steady state error, have not been included in Table 2 because for all the types of controllers presented, with the exception of the classic PI speed controller, overshoot is negligible and steady state error is less than 0.1%. Improvements in the performance of the PMSM control system based on the DTC strategy are obtained when using a classical PI speed controller, when using an EOA type algorithm and when using FO type controllers, i.e. FOPI, TID, FO-Lead-Lag speed controllers at constant flux. In the case of variable flux, the SMC-type controller and the FO controller, i.e. the FOSMC-type controller, provide the best performance of the PMSM sensorless control system based on the DTC strategy.
4. Real-Time Implementation and Experimental Setup
Section 3 introduced a very important step in the development of a prototype, namely the numerical simulation step. At the numerical simulation stage, generally referred to as Software In the Loop (SIL), both the mathematical model of the controlled process and the mathematical model of the controller run on a host PC, and the execution of the closed-loop simulation program does not overlap with the so-called real-time execution, where there is a correlation between the evolution of the real signals and the speed of display in the monitoring and control software application. At this stage, the controller parameters are adjusted and the performance of the analysed control systems is compared in a safe operating environment. After this stage, there is an option to go through the Processor In the Loop (PIL) stage, where the driven process is still simulated but the controller is real, but the final stage of developing a prototype controller is the Hardware In the Loop (HIL) stage, where the driven process is real and the controller is also implemented in an embedded system [37].
The PMSM sensorless control system based on the DTC strategy presented in this article uses the Matlab/Simulink development environment, which uses the Motor Control Blockset (MCB) and Embedded Coder Support Package (ECSP) toolboxes suitable for Texas Instruments C2000 microcontrollers for its real-time implementation [38,39]. The MCB toolbox provides the ability to implement the proposed control structures in the SIL stage through specialised blocks for real-time implementation in the HIL stage. The ECSP toolbox allows the generation and execution of the corresponding code of the PMSM control algorithm based on the DTC control strategy. The generated code runs on C2000 microcontrollers, specifically the TMS320F28379D microcontroller. [40].
Real-time software blocks perform enhanced pulse width modulator (ePWM) control, serial peripheral interface (SPI) serial communication control, host PC and embedded system communication blocks, digital motor control (DMC) specific blocks, and the IQMath library for optimising code for real-time calculations through fixed-point implementation while maintaining high accuracy. Key features of the TMS320F28379D microcontroller include a 32-bit floating-point Control Law Accelerator (CLA) module that parallels mathematical calculations with the main processor on a 32-bit fixed-point architecture. We also recall that the main processor has a clock frequency of 200MHz, 1MB of flash memory, 16-bit digital-to-analogue converters (DAC), serial communication ports and a general-purpose input/output (GPIO) subsystem [40]. To interface with the TelcoMotion DT4260 PMSM, a 3-phase smart gate driver with current shunt amplifiers & SPI type BOOSTXL-DRV8305 is used, which communicates with the LAUNCHXL-F28379D development board on which the TMS320F28379D main controller is integrated (Figure 27).
Analogous to the software blocks used for the numerical simulations presented in Section 3, Figure 28 shows the main software frames implemented in Matlab/Simulink, which contain software blocks for the real-time implementation of the PMSM sensorless control system based on DTC strategy using PI controllers. Therefore, Figure 28 (a) shows the Simulink model of the main software application for the PMSM sensorless control system using functions from the MCB and ECSP toolboxes. Figure 28 (b) shows the Simulink subsystem implementation of the torque control, and Figure 28 (c) shows the Simulink subsystem implementation of the flux, position and speed of the PMSM observer. In addition, Figure 28 (d) shows the Simulink subsystem implementation of the speed control based on PI-EOA controller.
Following the real-time implementation of the PMSM sensorless control system based on DTC strategy for a series of speed reference signal variations imposed by the real-time monitoring and control software interface implemented in Simulink on the PC host and shown in Figure 29.
The following presents the real-time testing of the proposed sensorless PMSM control system based on the DTC strategy in the constant flux case and in the variable flux case as presented in Section 3, where numerical simulations were performedReal-time performance was obtained by implementing the constant flux PMSM control structure shown in Figure 2 using PI-EOA and FOPI controllers, and the variable flux PMSM control structure shown in Figure 4 using SMC and FOSMC type controllers.
Please note that the controller structures presented in the numerical simulations implemented in Matlab/Simulink are preserved in the real-time implementation, but the 1/s integrators expressed in the continuous domain are equated with integrators in the discrete domain by using a bilinear Tustin transform.
4.1. PMSM Real-Time Sensorless Control System Based on DTC Strategy Using Constant Flux
Using the Simulink model shown in Figure 29, a series of experimental tests were carried out by applying acceleration and deceleration steps to the PMSM rotor speed reference. In the following the graphs obtained for the main parameters of interest of the sensorless PMSM control system based on the DTC strategy are presented. Thus, Figure 30 presents the real-time speed evolution for PMSM sensorless control based on DTC strategy in case of constant flux. Figure 30 (a) shows the real-time speed response in case of using the PI-EOA controller, and Figure 30 (b) shows the real-time speed response in case of using the FOPI controller. It can be seen that the performance of the PMSM sensorless control system based on DTC strategy with PI-EOA controller is very good in real-time implementation. Small inherent differences with the numerical simulations are observed, but from a practical point of view we can say that the control system offers good performance even for applications where high accuracy is required, in this sense an argument is that the steady-state error is less than 0.2%. In addition, the settling time is 70ms and the overshoot is less than 2%, which is good performance for systems implemented in real-time. Improved performance is observed when using the FOPI controller, thus achieving an overshooting of 1% and a settling time of 60ms.
The real-time evolution of the stator currents ia and ib is shown in Figure 31 (a) for the case of using the PI-EOA controller, and for the case of using the FOPI controller is shown in Figure 31 (b). A reduction of the current values during the transitory regime is observed when using the FOPI controller in the PMSM control structure.
In addition, graphs of the real-time evolution of some parameters of interest of the control system are presented in the following. Thus, Figure 32 (a) presents the real-time evolutions of flux reference and flux feedback (estimated flux given by flux observer), real-time evolution of electromagnetic torque is shown in Figure 32 (b), and the detail of the real-time evolution of PMSM rotor position is shown in Figure 32 (c).
Graphical representation of the FD of the real-time speed signal for the PMSM sensorless control system based on the DTC strategy in the case of constant flux is presented in Figure 33. Thus, Figure 33(a) shows the FD of the real-time speed signal in case of using PI-EOA controller, and Figure 33(b) shows the FD of the real-time speed signal in case of using FOPI controller.
4.2. PMSM Real-time Sensorless Control System Based on DTC Strategy Using Variable Flux
Similarly to what presented in the previous subsection in this subsection we present the real-time experimental tests performed for the case of the sensorless PMSM control system based on the DTC strategy where the flow is variable and is provided by the two controllers type SMC and FOSMC. By imposing the same series of steps on the reference speed of the PMSM rotor, the graphs obtained for the parameters of interest are presented in order to highlight the control performance. Real-time speed evolution for PMSM sensorless control based on DTC strategy in case of variable flux using SMC-type controller is shown in Figure 34 (a), and using FOSMC-type controller is shown in Figure 34 (b). It is observed in this case of using integer and fractional order SMC-type controllers that the overshooting is practically zero and the settling time is 34.5ms and 33.9ms respectively.
Flux reference and estimated flux real-time evolution PMSM sensorless control system based on DTC strategy using FOSMC-type controller are presented in Figure 35.
The real-time evolution of the stator currents ia and ib is shown in Figure 36 (a) for the case of using the SMC-type controller, and for the case of using the FOSMC-type controller is shown in Figure 36 (b).
Graphical representation of the FD of the real-time speed signal for the PMSM sensorless control system based on the DTC strategy in the case of variable flux is presented in Figure 37. Thus, Figure 37 (a) shows the FD of the real-time speed signal in case of using SMC-type controller, and Figure 37 (b) shows the FD of the real-time speed signal in case of using FOSMC-type controller.
The results of the experimental tests performed in real-time are summarized in Table 3, both when using a constant flux and when using a variable flux for the sensorless PMSM control system based on the DTC strategy. The superior performance of SMC-type controllers compared to the classical PI-type controller is observed, as well as the preservation of this hierarchy when using fractional calculus. We point out that in real-time PI-type controllers have better performances in terms of response time, but not in terms of overshooting, settling time, speed signal ripple and FD of controled signal. We also point out that in real real-time the speed signal ripple is lower than in the case of numerical simulations because the number of samples is 1000 in the first case and 10000 in the second case. Regarding the FD of the speed signal, the hypothesis that a better performing controller implies a higher FD value is verified. We point out that in the case of real-time implementations, if the computational power of the embedded system is insufficient, it is possible that complex control algorithms, which in numerical simulations offer better performance than classical PI-type algorithms, may give contrary results. In the case presented in this article the development platform offers superior computational performance so that a biunivocity between the performance obtained in numerical simulations and real-time implementation was obtained. In this case FO type controllers bring improvements over integer type controllers, the best performance being provided by FOSMC-type controllers.
5. Conclusions
Using notions of fractional calculus, this paper has presented several integer-order or FO controllers that have been integrated into the structure of the PMSM sensorless control system based on the DTC strategy to improve performance. Thus, starting from PI type controllers, the performance of the control system was improved by using EOA type algorithm for optimal tuning of controller parameters and by using FO type controllers: FOPI, TID and FO-Lead-Lag speed controllers. These types of controllers, embedded in the DTC strategy, are based on a constant reference flux for the flux control loop. When the reference flux is variable, the performance of the control system is improved by using an integer-order SMC-type controller and the improved fractional FOSMC-type controller. The performance indicators of the PMSM sensorless control system based on the DTC strategy are the usual ones: response time, settling time, overshoot, steady-state error and speed ripple. In addition, a performance indicator in the form of the FD of the PMSM rotor speed signal is used and the hypothesis that the FD of the controlled signal is higher when the control system provides better performance is tested. The parametric robustness of the control system based on the DTC strategy is also demonstrated by the fact that good control performance is obtained by increasing the J parameter, which represents the combined inertia of the PMSM rotor and the load.
The real-time implementation in an embedded system (HIL stage) follows the stages presented in the controller synthesis and numerical simulations (SIL stage), and good control performance of the PMSM based on the DTC strategy is obtained for the real-time control system. Future work will build on the development of controller vendor libraries to implement specific machine learning capabilities in Simulink to design and implement control systems that deliver superior performance.
Author Contributions
Conceptualization, M.N., C.-I.N. and D.S.; Data curation, M.N., C.-I.N., D.S. and D.Ș.; Formal analysis, M.N., C.-I.N., C.I. and D.Ș.; Funding acquisition, M.N.; Investigation, M.N., C.-I.N., D.S., C.I. and D.Ș.; Methodology, M.N., C.-I.N., D.S., C.I. and D.Ș.; Project administration, M.N.; Resources, M.N.; Software, M.N. and C.-I.N.; Supervision, M.N., C.-I.N., D.S. and C.I.; Validation, M.N., C.-I.N., D.S., C.I. and D.Ș.; Visualization, M.N., C.-I.N., D.S. and D.Ș.; Writing – original draft, M.N. and C.-I.N.; Writing – review & editing, M.N. and C.-I.N. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was elaborated as part of the NUCLEU Program within the framework of the National Research, Development, and Innovation Plan for 2022-2027, developed with the support of the Ministry of Research, Innovation, and Digitization, Project No. PN 23 33 02 04 and partially funded by Installation of National Interest “System for generating, measuring and recording short circuit currents” - SPMICS.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kang, L.; Jiang, D.; Xia, C.; Xu, Y.; Sun, K. Research and Analysis of Permanent Magnet Transmission System Controls on Diesel Railway Vehicles. Electronics 2021, 10, pp. 1–18. [CrossRef]
- Avinash, N.; A, C.; W, R.; Vanishree, J.; V, J.; Tarcar, R. K. Design and Analysis of ZSI fed PMSM Drive for Pumping Applications with Field Oriented Control. In Proceedings of the 2021 Innovations in Power and Advanced Computing Technologies (i-PACT), Kuala Lumpur, Malaysia, 2021, pp. 1–7.
- Lekshmi, S.; Lal Priya, P.S. Range Extension of Electric Vehicles with Independently Driven Front and Rear PMSM Drives by Optimal Driving and Braking Torque Distribution. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE), Cochin, India, 2–4 January 2020; pp. 1–6.
- Pillai, S.; Forsyth, A.; Abdalmagid, M.; Pietrini, G.; Goykhman, M.; Emadi, A. Investigating the Effects of PWM Currents on a High-Speed PMSM for an Aerospace Application, In Proceedings of the 2023 IEEE Transportation Electrification Conference & Expo (ITEC), Detroit, MI, USA, 21–23 June 2023; pp. 1–6.
- Kovacik, M.; Rafajdus, P.; Bastovansky, R. Mechanical Analysis of Different Rotor Topologies for High Speed PMSM in Automotive Application. In Proceedings of the 2021 International Conference on Electrical Drives & Power Electronics (EDPE), Dubrovnik, Croatia, 22–24 September 2021; pp. 50–55.
- Kumar, M.; Deosarkar, P.; Inamdar S.; Mahanty, R. N. Field Oriented Control of Traction PMSM Drive Using WBG Devices for EV Application, In Proceedings of the 2023 IEEE Renewable Energy and Sustainable E-Mobility Conference (RESEM), Bhopal, India, 17–18 May 2023; pp. 1–8.
- Furmanik, M.; Gorel, L.; Konvičný, D.; Rafajdus, P. Comparative Study and Overview of Field-Oriented Control Techniques for Six-Phase PMSMs. Appl. Sci. 2021, 11, pp. 1–16. [CrossRef]
- Zhang, Y.; Zhu, J. Direct Torque Control of Permanent Magnet Synchronous Motor with Reduced Torque Ripple and Commutation Frequency. IEEE Trans. Power Electron. 2011, 26, pp. 235–248. [CrossRef]
- Vujji, A.; Dahiya, R. Design of PI Controller for Space Vector Modulation based Direct Flux and Torque Control of PMSM Drive. In Proceedings of the First IEEE International Conference on Measurement, Instrumentation, Control and Automation (ICMICA), Kurukshetra, India, 2 November 2020; pp. 1–6.
- Niu, H.; Liu, L.; Jin, D.; Liu, S. High-Tracking-Precision Sensorless Control of PMSM System Based on Fractional Order Model Reference Adaptation. Fractal Fract. 2023, 7, pp. 1–17. [CrossRef]
- Chi, C.; Cajo, R.; Zhao, S.; Liu, G.-P.; Ionescu, C.-M. Fractional Order Distributed Model Predictive Control of Fast and Strong Interacting Systems. Fractal Fract. 2022, 6, pp. 1–18. [CrossRef]
- Ullah, K.; Guzinski, J.; Mirza, A.F. Critical Review on Robust Speed Control Techniques for Permanent Magnet Synchronous Motor (PMSM) Speed Regulation. Energies 2022, 15, pp. 1–13. [CrossRef]
- Zhang, Q.; Zhang, C. Speed Control of PMSM Based on Fuzzy Active Disturbance Rejection Control under Small Disturbances. Appl. Sci. 2023, 13, pp. 1–18. [CrossRef]
- Wang, Q.; Yu, H.; Wang, M.; Qi, X. A Novel Adaptive Neuro-Control Approach for Permanent Magnet Synchronous Motor Speed Control. Energies 2018, 11, pp. 1–21. [CrossRef]
- Tepljakov, A.; Petlenkov, E.; Belikov, J.; Finajev, J. Fractional-order controller design and digital implementation using FOMCON toolbox for MATLAB. In Proceedings of the IEEE Conference on Computer Aided Control System Design (CACSD), Hyderabad, India, 28–30 August 2013; pp. 340–345.
- Agarwal, R.; Hristova, S.; O’Regan, D. Stability Concepts of Riemann-Liouville Fractional-Order Delay Nonlinear Systems. Mathematics 2021, 9, pp. 1–16. [CrossRef]
- Matignon, D. Stability result on fractional differential equations with applications to control. In Proceedings of the IMACS SMC, Lille, France, 1996; pp. 963–968.
- Mohd Tumari, M.Z.; Ahmad, M.A.; Suid, M.H.; Hao, M.R. An Improved Marine Predators Algorithm-Tuned Fractional-Order PID Controller for Automatic Voltage Regulator System. Fractal Fract. 2023, 7, pp. 1–38. [CrossRef]
- Liu, X.; Gan, H.; Luo, Y.; Chen, Y.; Gao, L. Digital-Twin-Based Real-Time Optimization for a Fractional Order Controller for Industrial Robots. Fractal Fract. 2023, 7, pp. 1–16. [CrossRef]
- Bingi, K.; Rajanarayan Prusty, B.; Pal Singh, A. A Review on Fractional-Order Modelling and Control of Robotic Manipulators. Fractal Fract. 2023, 7, pp. 1–29. [CrossRef]
- Zhu, Y.; Tao, B.; Xiao, M.; Yang, G.; Zhang, X.; Lu, K. Luenberger Position Observer Based on Deadbeat-Current Predictive Control for Sensorless PMSM. Electronics 2020, 9, pp. 1–17. [CrossRef]
- Son, D.-I.; Han, J.-S.; Park, J.-S.; Lim, H.-S.; Lee, G.-H. Performance Improvement of DTC-SVM of PMSM with Compensation for the Dead Time Effect and Power Switch Loss Based on Extended Kalman Filter. Electronics 2023, 12, pp. 1–17. [CrossRef]
- Foo, G. H. B.; Rahman, M. F. Direct Torque Control of an IPM-Synchronous Motor Drive at Very Low Speed Using a Sliding-Mode Stator Flux Observer. IEEE Trans. Power Electron. 2010, 25, pp. 933–942. [CrossRef]
- Nicola, M.; Nicola, C.-I. Improvement Performances of Sensorless Control for PMSM Based on DTC Strategy Using SMO Observer and RL-TD3 Agent. In Proceedings of the 2023 5th Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkyie, 25–27 June 2020; pp. 131–136.
- Cheng, J.; Chen, Q.; Huang, X. An Algorithm for Crack Detection, Segmentation, and Fractal Dimension Estimation in Low-Light Environments by Fusing FFT and Convolutional Neural Network. Fractal Fract. 2023, 7, pp. 1–16. [CrossRef]
- Popa, B.; Selișteanu, D.; Lorincz, A.E. Possibilities of Use for Fractal Techniques as Parameters of Graphic Analysis. Fractal Fract. 2022, 6, pp. 1–25. [CrossRef]
- Voncilă, I.; Selim, E.; Voncilă, M.-L. Use of fractal analysis for quality evaluation of control methods in induction motor drive systems. In Proceedings of the 6th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 19–21 October 2022; pp. 524–529.
- Nicola, M.; Nicola, C.-I.; Sacerdoțianu, D.; Vintilă, A. Comparative Performance of UPQC Control System Based on PI-GWO, Fractional Order Controllers, and Reinforcement Learning Agent. Electronics 2023, 12, pp. 1–22. [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowledge-Based Systems 2020, 7, pp. 1–39. [CrossRef]
- Nusair, K.; Alhmoud, L. Application of Equilibrium Optimizer Algorithm for Optimal Power Flow with High Penetration of Renewable Energy. Energies 2020, 13, pp. 1–35. [CrossRef]
- ElSayed, S.K.; Al Otaibi, S.; Ahmed, Y.; Hendawi, E.; Elkalashy, N.I.; Hoballah, A. Probabilistic Modeling and Equilibrium Optimizer Solving for Energy Management of Renewable Micro-Grids Incorporating Storage Devices. Energies 2021, 14, pp. 1–24. [CrossRef]
- Wang, Y.; Yu, H.; Che, Z.; Wang, Y.; Liu, Y. The Direct Speed Control of PMSM Based on Terminal Sliding Mode and Finite Time Observer. Processes 2019, 7, pp. 1–14. [CrossRef]
- Li, S.; Li, H.; Wang, H.; Yang, C.; Gui, J.; Fu, R. Sliding Mode Active Disturbance Rejection Control of Permanent Magnet Synchronous Motor Based on Improved Genetic Algorithm. Actuators 2023, 12, pp. 1–25. [CrossRef]
- Huang, J.; Cui, L.; Shi, X. Direct Torque Control of PMSM Based on Fractional Order Sliding Mode Variable Structure and Experiment Research. International Journal of Control and Automation 2014, 7, pp. 217–232. [CrossRef]
- Nicola, M.; Nicola, C.-I. Sensorless Fractional Order Control of PMSM Based on Synergetic and Sliding Mode Controllers. Electronics 2020, 9, pp. 1–44. [CrossRef]
- Nicola, M.; Nicola, C.-I. Improved Performance in the Control of DC-DC Three-Phase Power Electronic Converter Using Fractional-Order SMC and Synergetic Controllers and RL-TD3 Agent. Fractal Fract. 2022, 6, pp. 1–27. [CrossRef]
- Nicola, C.-I.; Nicola, M. Real Time Implementation of the PMSM Sensorless Control Based on FOC Strategy. In Proceedings of the 2023 5th Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkyie, 25–27 June 2020; pp. 179–183.
- Simscape Electrical. Available online: https://www.mathworks.com/getting-started-with-simscape-electrical.html (accessed on 4 May 2020).
- MathWorks—Motor Control Blockset. Design and implement motor control algorithms. Available online: https://www.mathworks.com/products/motor-control.html (accessed on 10 December 2021).
- LAUNCHXL-F28379D C2000 Delfino MCU F28379D LaunchPad™ Development Kit. Available online: https://www.ti.com/tool/LAUNCHXL-F28379D (accessed on 10 August 2020).
Figure 1.
Block diagram of the PMSM sensorless control system based on DTC strategy using PI speed controller. .
Figure 1.
Block diagram of the PMSM sensorless control system based on DTC strategy using PI speed controller. .
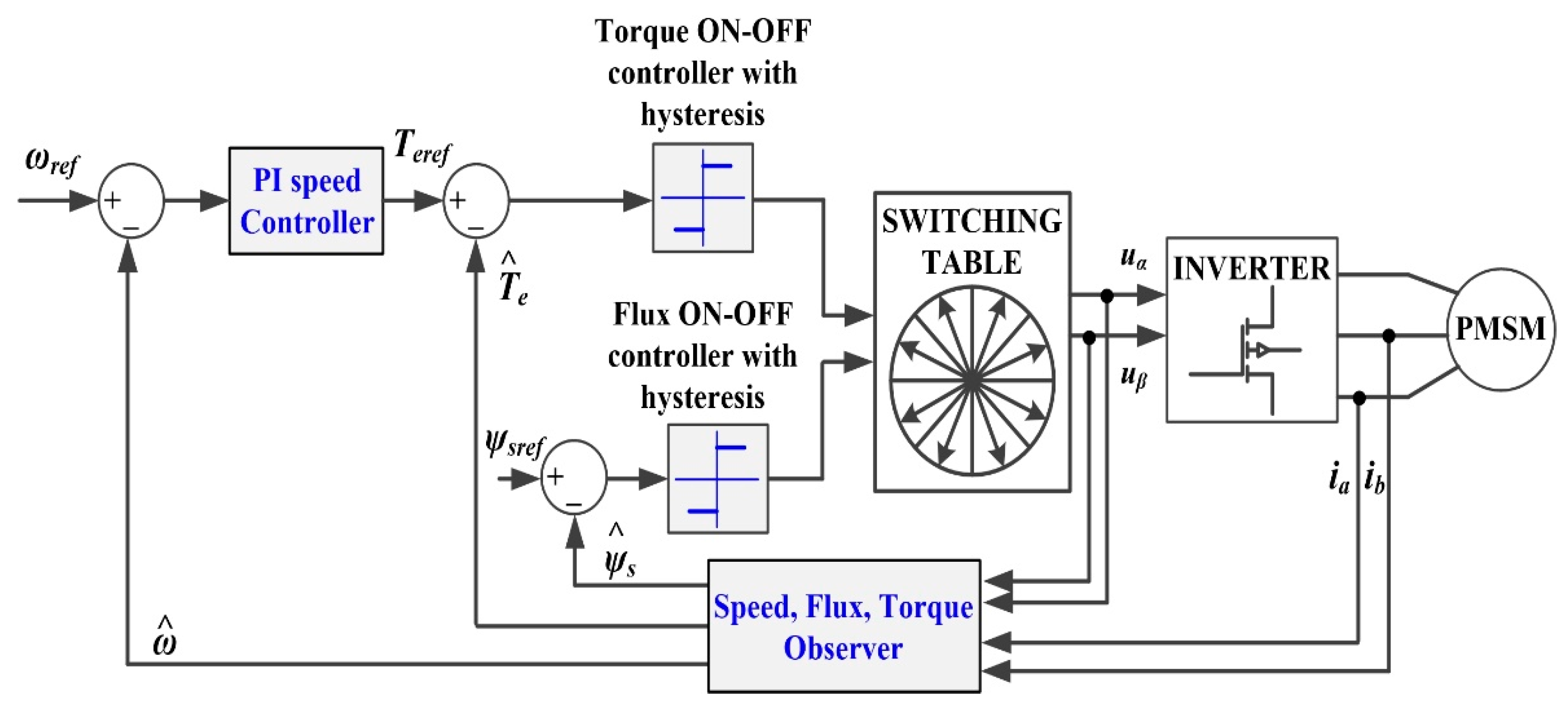
Figure 2.
Block diagram of the PMSM sensorless control system based on DTC strategy using PI-EOA, FOPI, TID, and FO-Lead-Lag speed controllers in case of constant flux.
Figure 2.
Block diagram of the PMSM sensorless control system based on DTC strategy using PI-EOA, FOPI, TID, and FO-Lead-Lag speed controllers in case of constant flux.
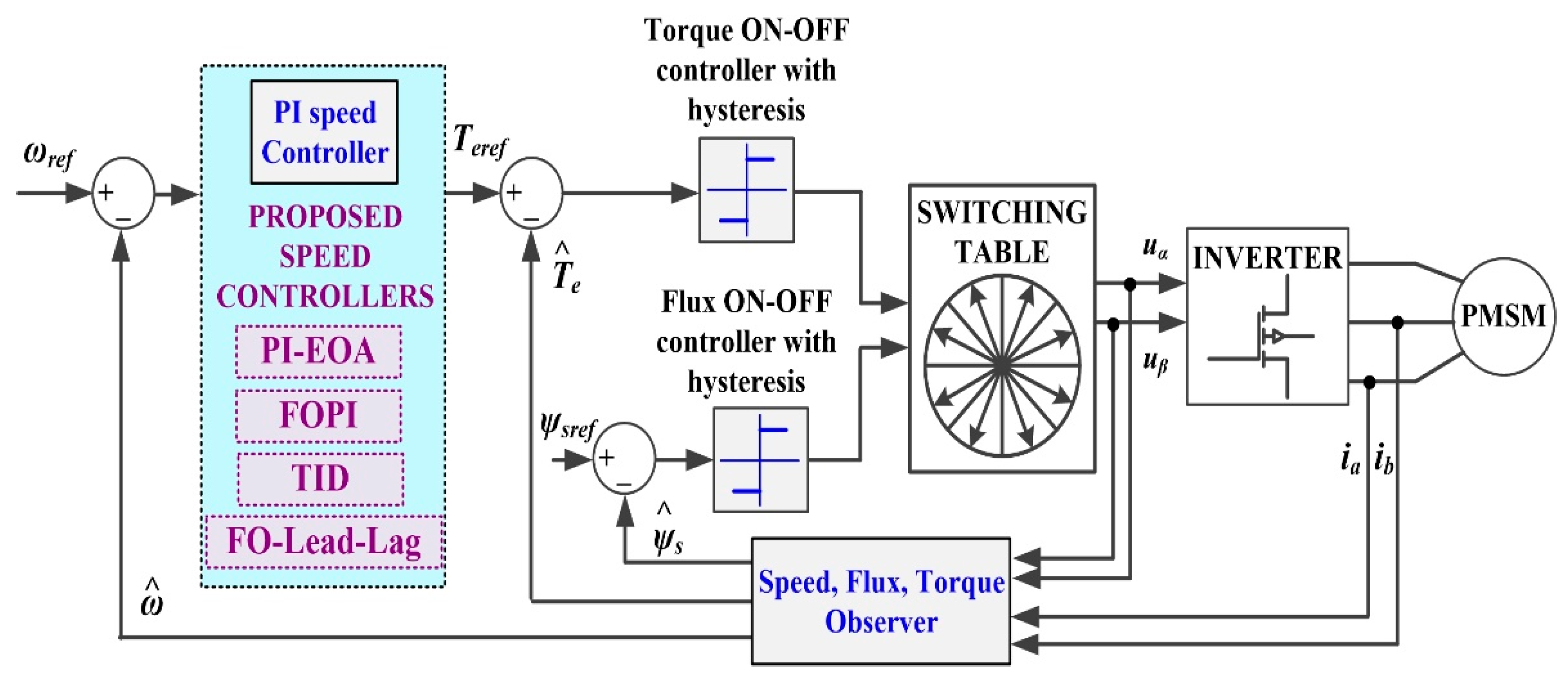
Figure 3.
Graphical representation of the sigmoid function H(x).
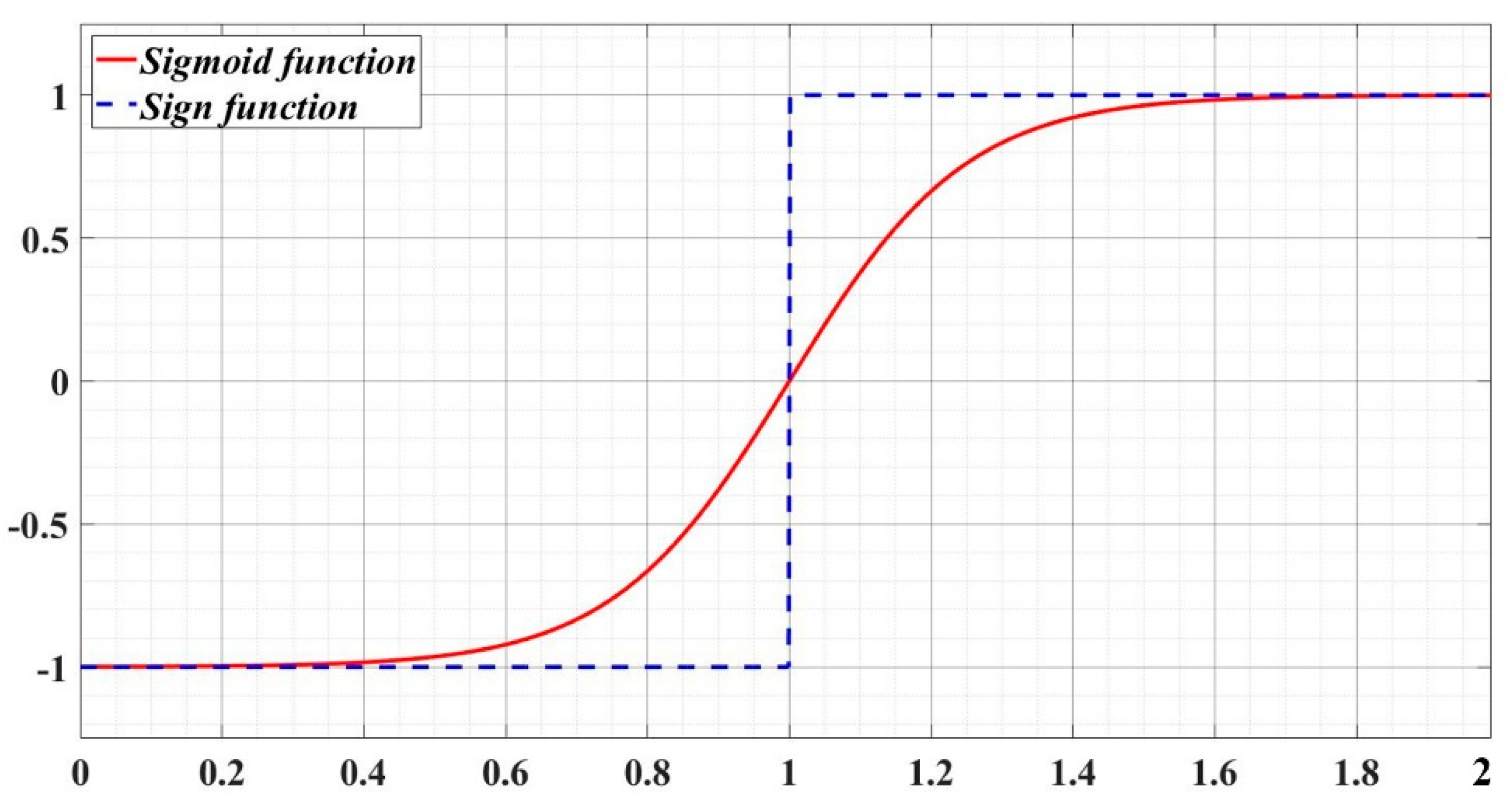
Figure 4.
Block diagram of the PMSM sensorless control system based on DTC strategy using SMC and FOSMC type controllers in case of variable flux.
Figure 4.
Block diagram of the PMSM sensorless control system based on DTC strategy using SMC and FOSMC type controllers in case of variable flux.
Figure 5.
Matlab/Simulink implementation of the PMSM sensorless control system based on DTC strategy using constant flux: (a) Main Simulink model of PMSM sensorless control based on DTC strategy using PI, PI-EOA, FOPI, TID, and FO-Lead-Lag speed controllers; (b) Simulink subsystem implementation of the observer for speed, torque, and flux estimations.
Figure 5.
Matlab/Simulink implementation of the PMSM sensorless control system based on DTC strategy using constant flux: (a) Main Simulink model of PMSM sensorless control based on DTC strategy using PI, PI-EOA, FOPI, TID, and FO-Lead-Lag speed controllers; (b) Simulink subsystem implementation of the observer for speed, torque, and flux estimations.
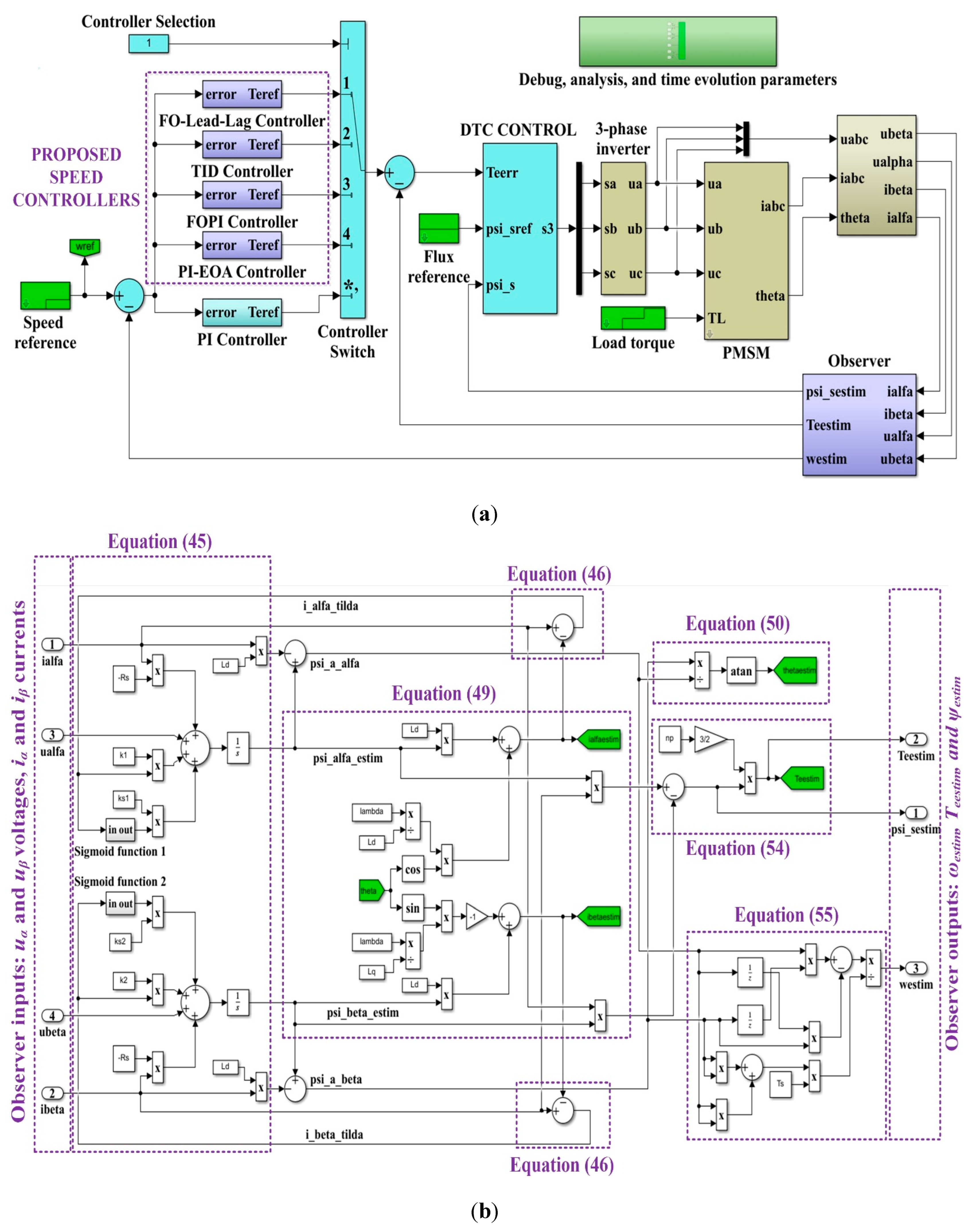
Figure 6.
Graphical representation of the closed-loop stability test for the PMSM sensorless control system based on the DTC strategy using the FOPI speed controller at constant flux.
Figure 6.
Graphical representation of the closed-loop stability test for the PMSM sensorless control system based on the DTC strategy using the FOPI speed controller at constant flux.
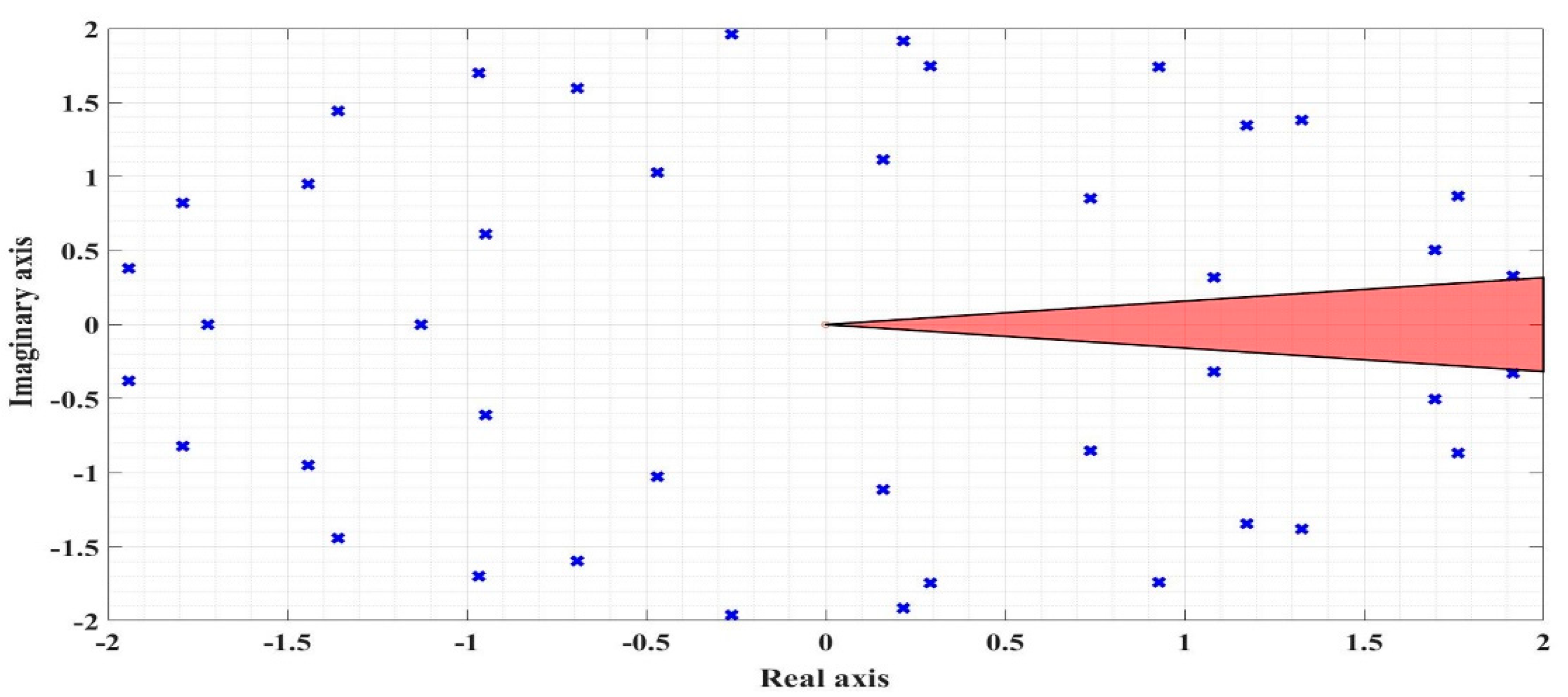
Figure 7.
Closed-loop step response for PMSM sensorless control system based on DTC strategy using FOPI speed controller at constant flux.
Figure 7.
Closed-loop step response for PMSM sensorless control system based on DTC strategy using FOPI speed controller at constant flux.
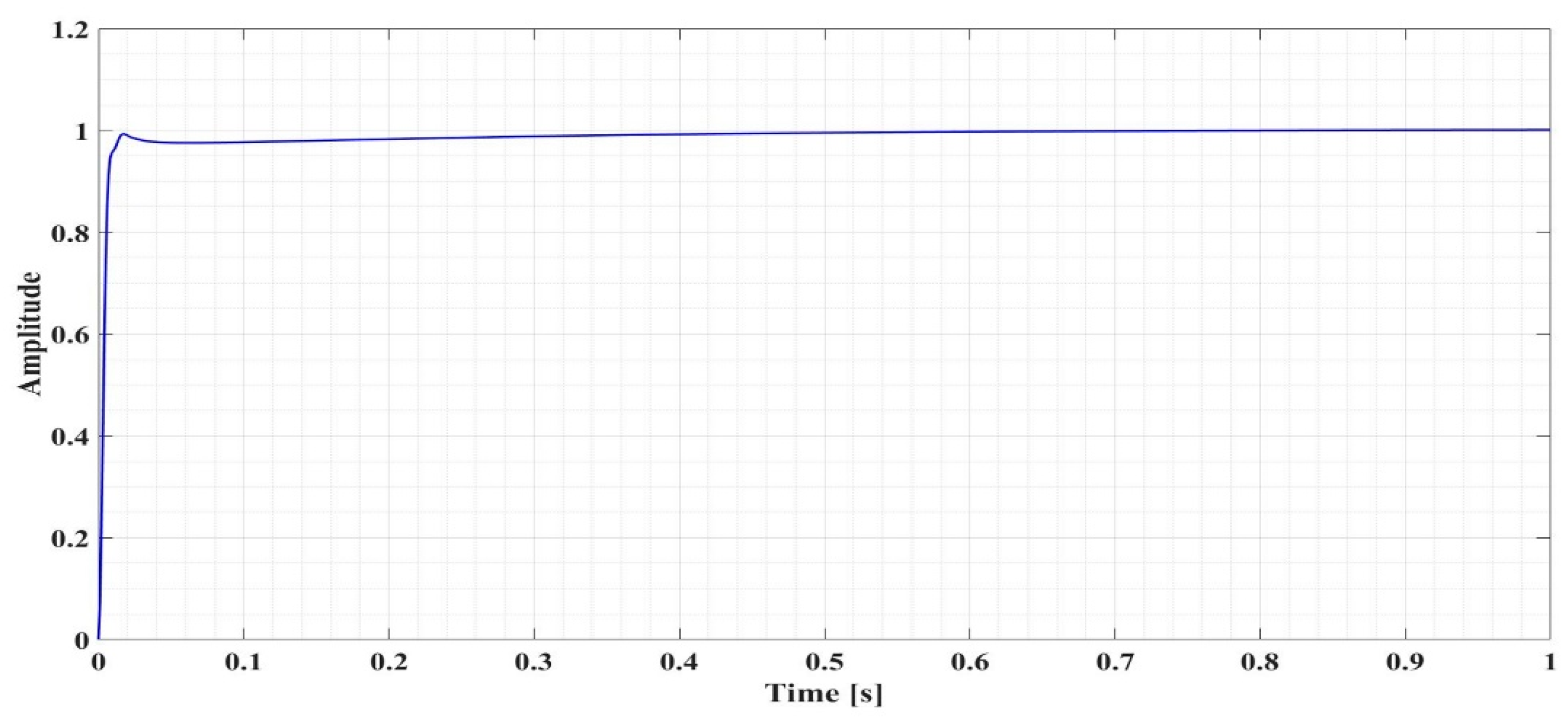
Figure 8.
Bode diagram graphical representation of closed loop system of the PMSM sensorless control system based on DTC strategy using FOPI speed controller in case of the constant flux.
Figure 8.
Bode diagram graphical representation of closed loop system of the PMSM sensorless control system based on DTC strategy using FOPI speed controller in case of the constant flux.
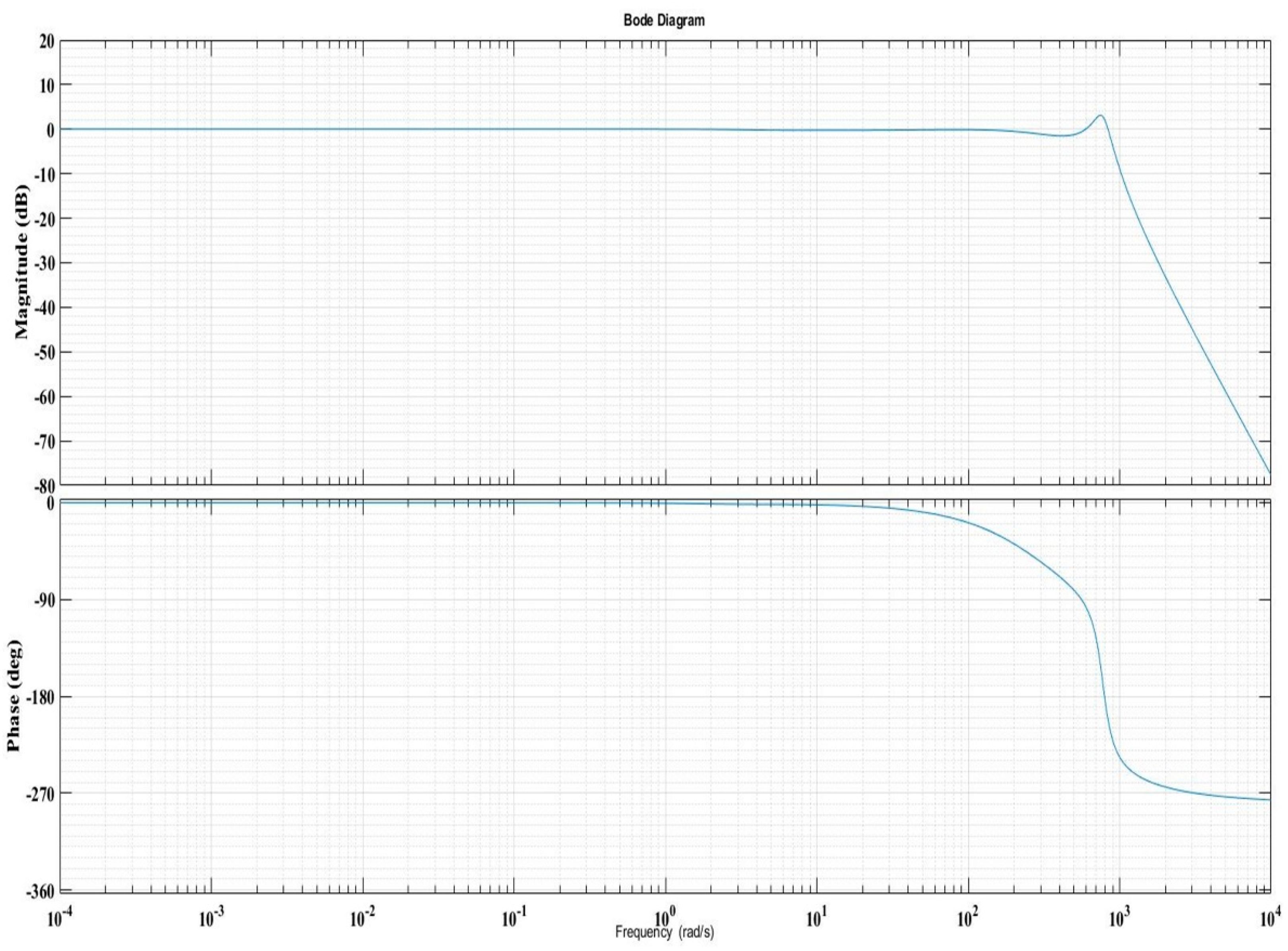
Figure 9.
Transfer functions of the FOPI speed controller for PMSM sensorless control system based on DTC strategy in case of the constant flux: (a) Continuous transfer function; (b) Discrete transfer function.
Figure 9.
Transfer functions of the FOPI speed controller for PMSM sensorless control system based on DTC strategy in case of the constant flux: (a) Continuous transfer function; (b) Discrete transfer function.

Figure 10.
Transfer functions of the TID speed controller for PMSM sensorless control system based on DTC strategy in case of the constant flux: (a) Continuous transfer function; (b) Discrete transfer function.
Figure 10.
Transfer functions of the TID speed controller for PMSM sensorless control system based on DTC strategy in case of the constant flux: (a) Continuous transfer function; (b) Discrete transfer function.

Figure 11.
Transfer functions of the FO-Lead-Lag speed controller for PMSM sensorless control system based on DTC strategy in case of the constant flux: (a) Continuous transfer function; (b) Discrete transfer function.
Figure 11.
Transfer functions of the FO-Lead-Lag speed controller for PMSM sensorless control system based on DTC strategy in case of the constant flux: (a) Continuous transfer function; (b) Discrete transfer function.

Figure 12.
Parameters evolution of the PMSM sensorless control system using DTC strategy using PI controller in case of constant flux.
Figure 12.
Parameters evolution of the PMSM sensorless control system using DTC strategy using PI controller in case of constant flux.
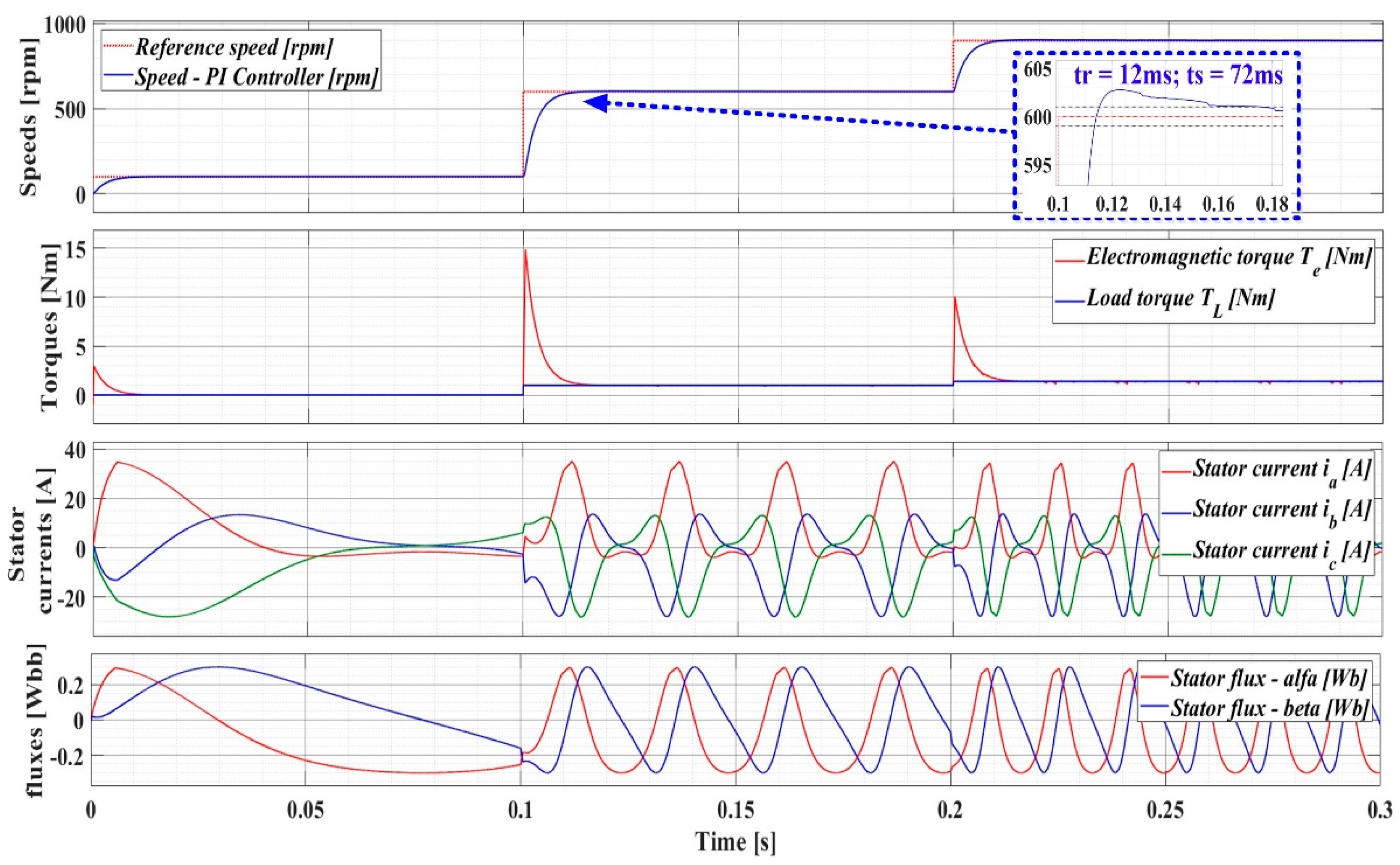
Figure 13.
Parameters evolution of the PMSM sensorless control system using DTC-type strategy using PI-EOA controller in case of constant flux.
Figure 13.
Parameters evolution of the PMSM sensorless control system using DTC-type strategy using PI-EOA controller in case of constant flux.
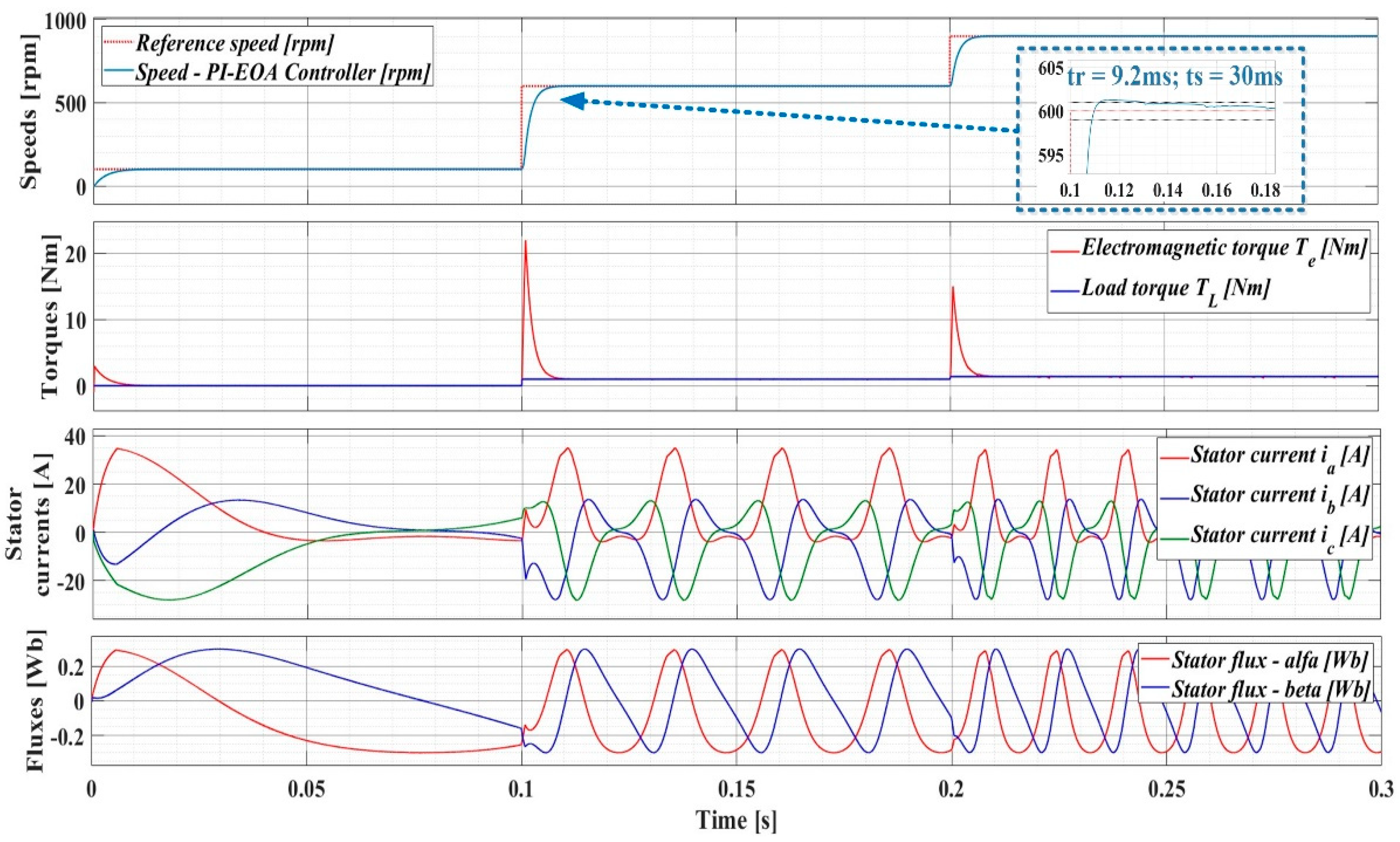
Figure 14.
Parameters evolution of the PMSM sensorless control system using DTC strategy using FOPI controller in case of constant flux.
Figure 14.
Parameters evolution of the PMSM sensorless control system using DTC strategy using FOPI controller in case of constant flux.
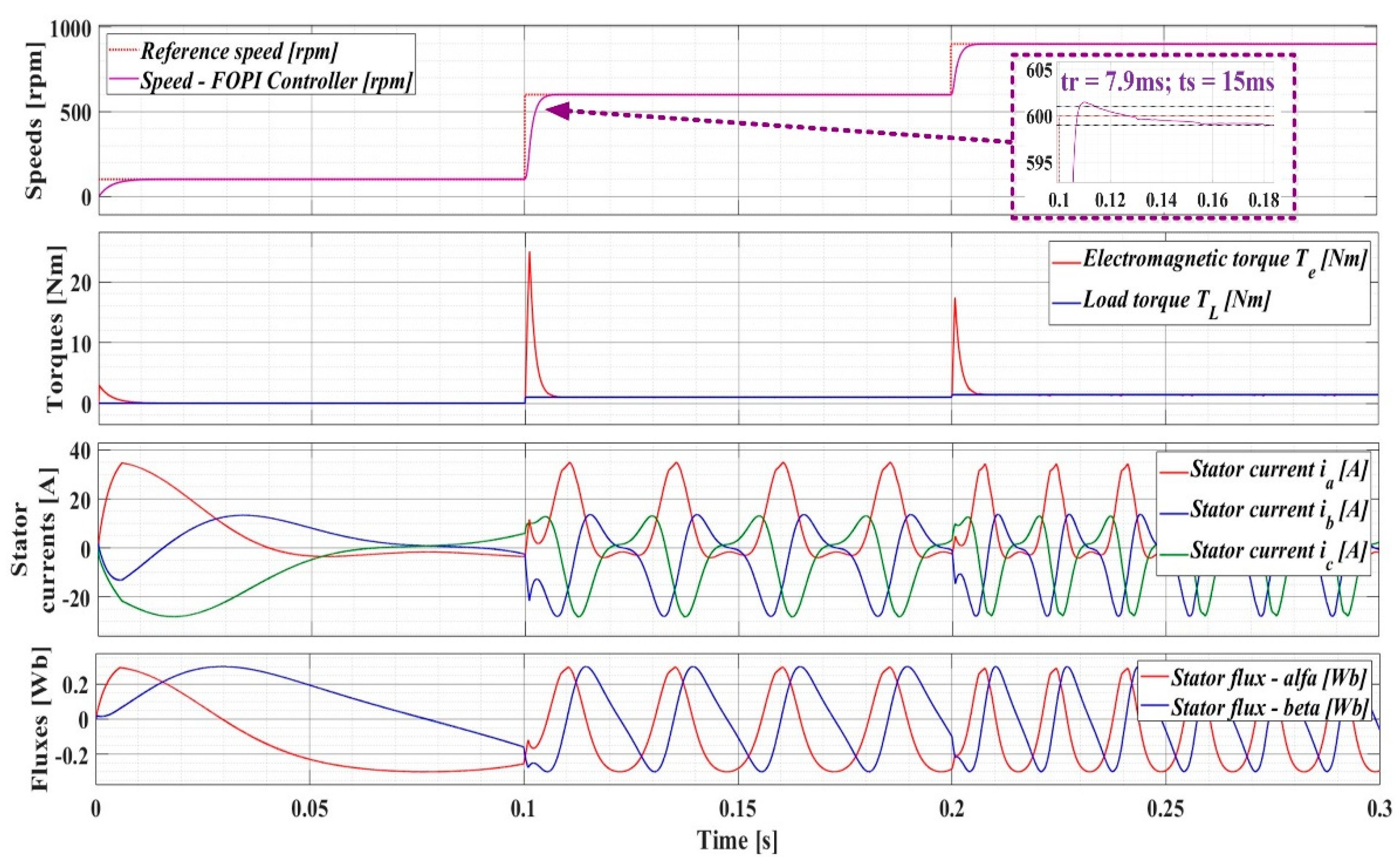
Figure 15.
Parameters evolution of the PMSM sensorless control system using DTC strategy using TID controller in case of constant flux.
Figure 15.
Parameters evolution of the PMSM sensorless control system using DTC strategy using TID controller in case of constant flux.
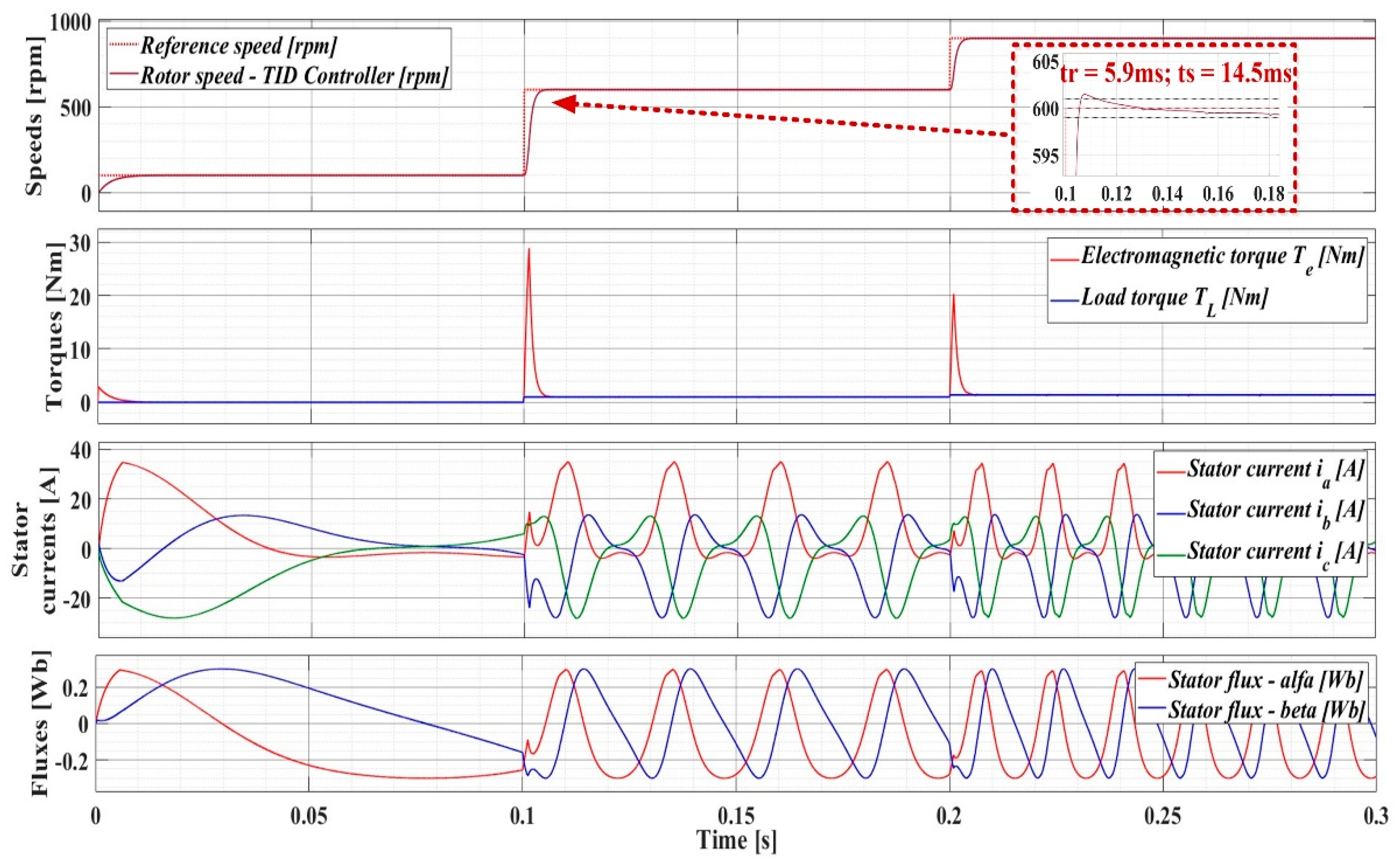
Figure 16.
Parameters evolution of the PMSM sensorless control system using DTC strategy using FO-Lead-Lag controller in case of constant flux.
Figure 16.
Parameters evolution of the PMSM sensorless control system using DTC strategy using FO-Lead-Lag controller in case of constant flux.
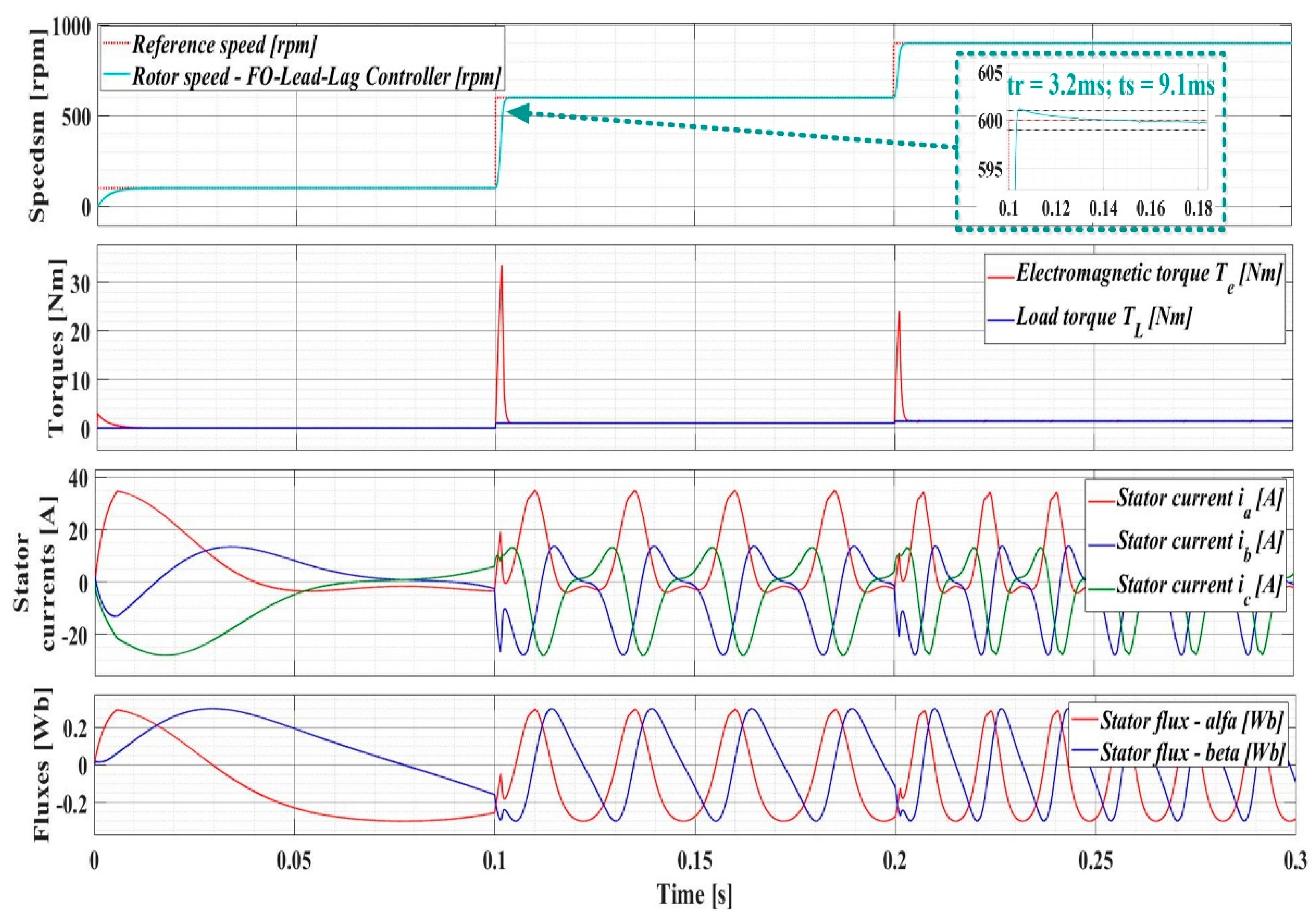
Figure 17.
Flux space vector trajectory for the PMSM sensorless control system based on DTC strategy using PI speed controller in case of constant flux.
Figure 17.
Flux space vector trajectory for the PMSM sensorless control system based on DTC strategy using PI speed controller in case of constant flux.
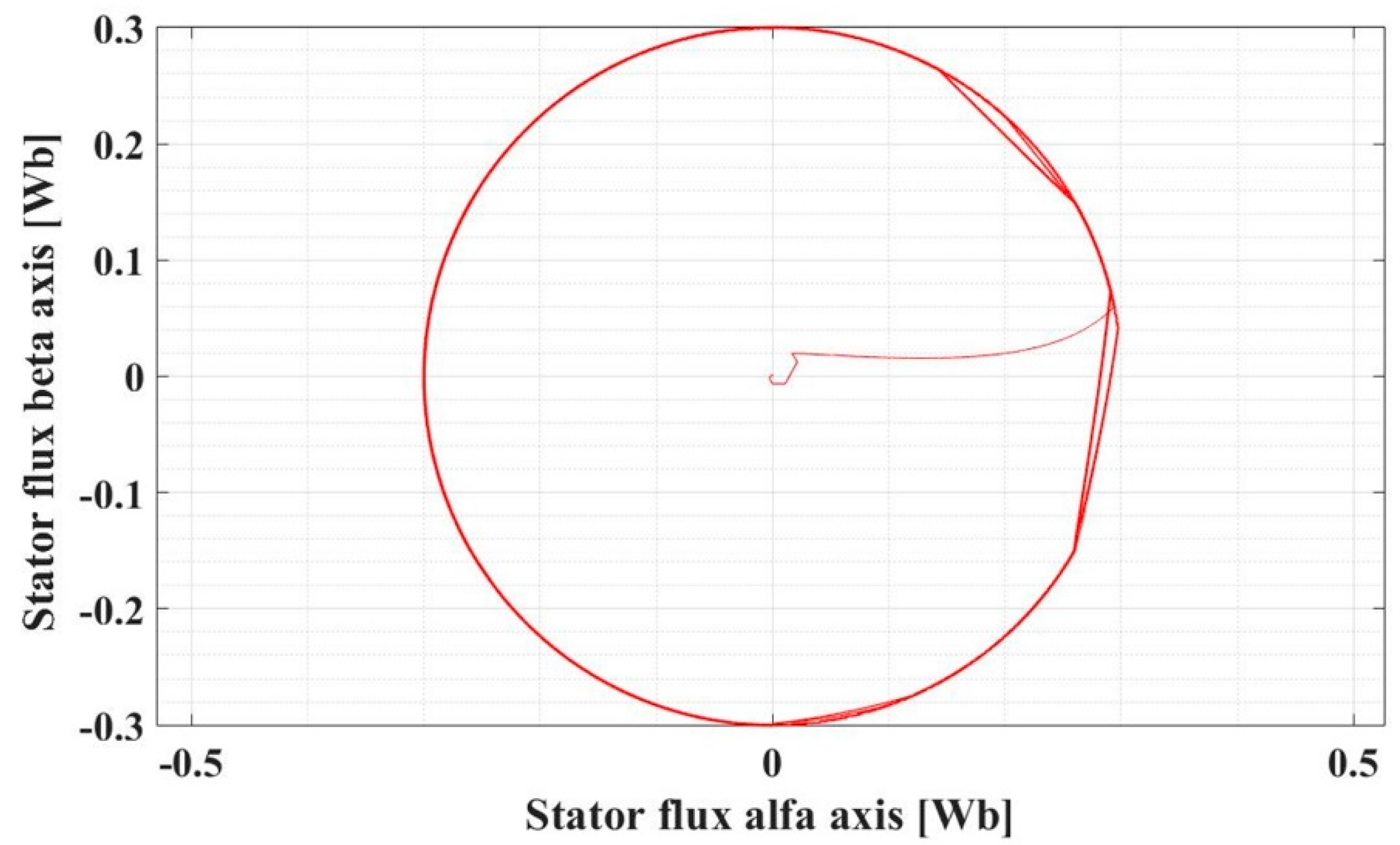
Figure 18.
Speed comparison evolution of the PMSM sensorless control system using DTC strategy using PI, PI-EOA, FOPI, TID, and FO-Lead-Lag controllers in case of constant flux.
Figure 18.
Speed comparison evolution of the PMSM sensorless control system using DTC strategy using PI, PI-EOA, FOPI, TID, and FO-Lead-Lag controllers in case of constant flux.
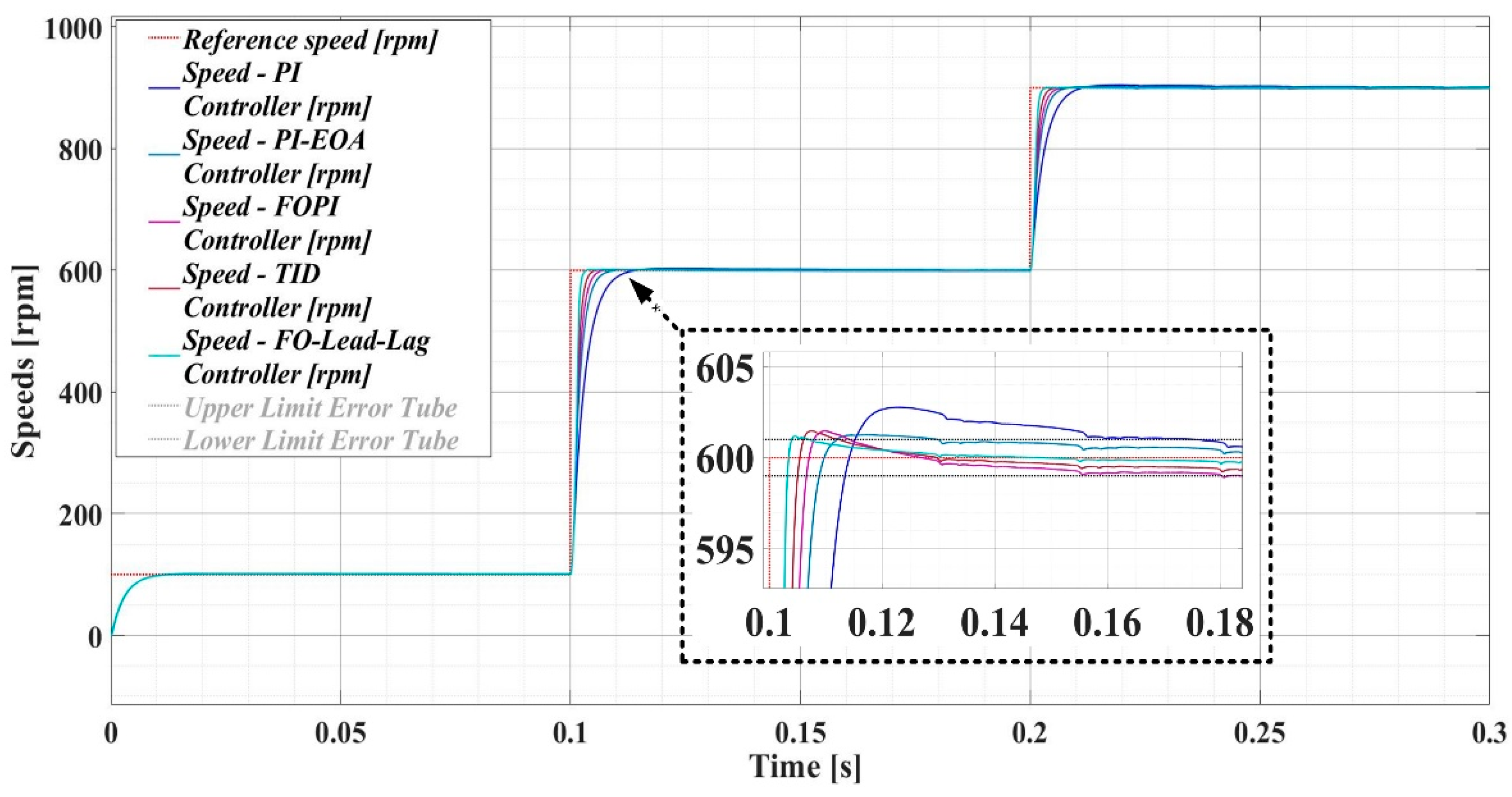
Figure 19.
Matlab/Simulink implementation of the PMSM sensorless control system based on DTC strategy using variable flux: (a) Main Simulink model of PMSM sensorless control system based on DTC strategy using SMC and FOSMC type controllers; (b) Simulink subsystem implementation of the SMC-type controller; (c) Simulink subsystem implementation of the FOSMC-type controller.
Figure 19.
Matlab/Simulink implementation of the PMSM sensorless control system based on DTC strategy using variable flux: (a) Main Simulink model of PMSM sensorless control system based on DTC strategy using SMC and FOSMC type controllers; (b) Simulink subsystem implementation of the SMC-type controller; (c) Simulink subsystem implementation of the FOSMC-type controller.
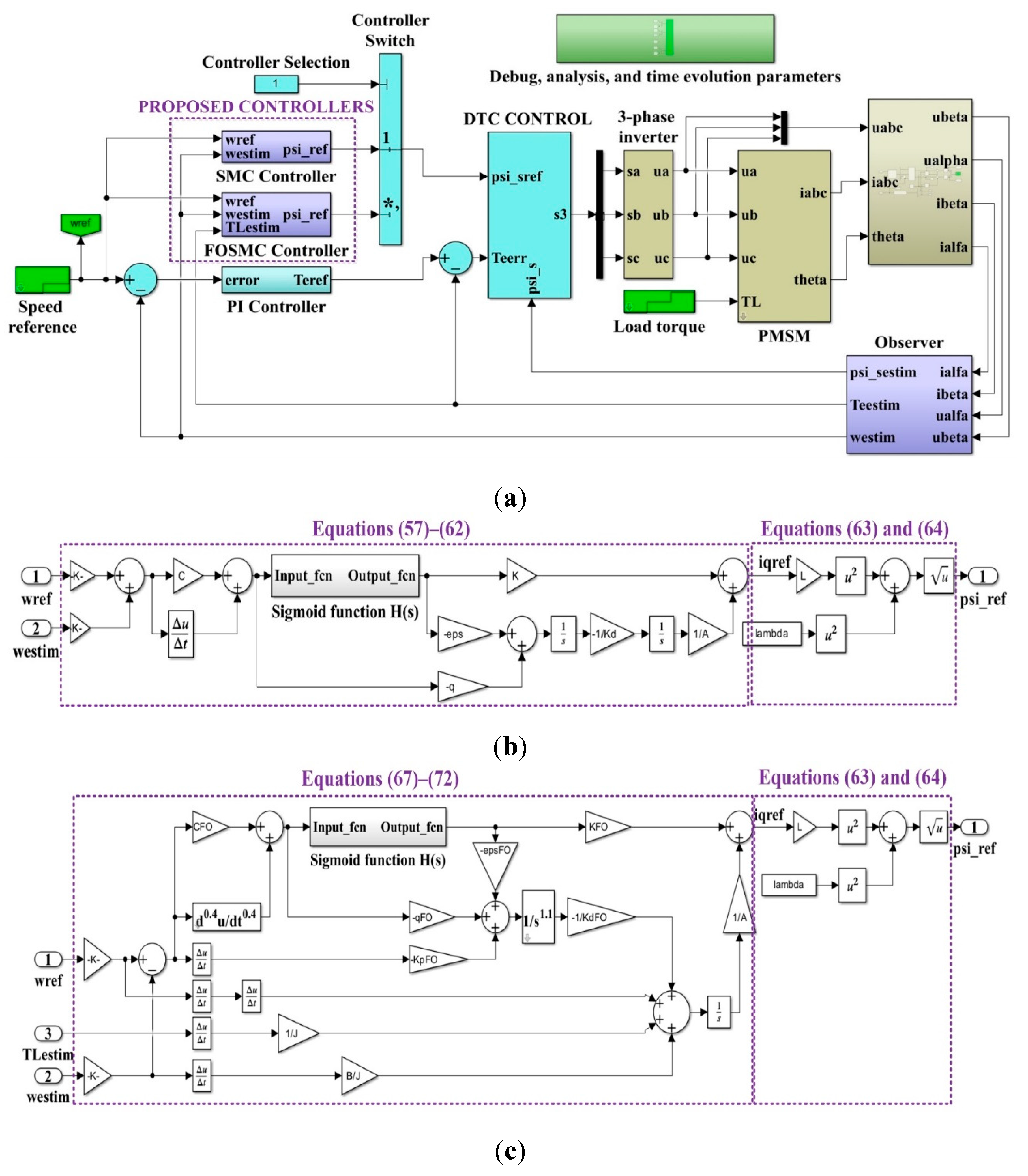
Figure 20.
Parameters evolution of the PMSM sensorless control system using DTC strategy using SMC-type controller in case of variable flux.
Figure 20.
Parameters evolution of the PMSM sensorless control system using DTC strategy using SMC-type controller in case of variable flux.
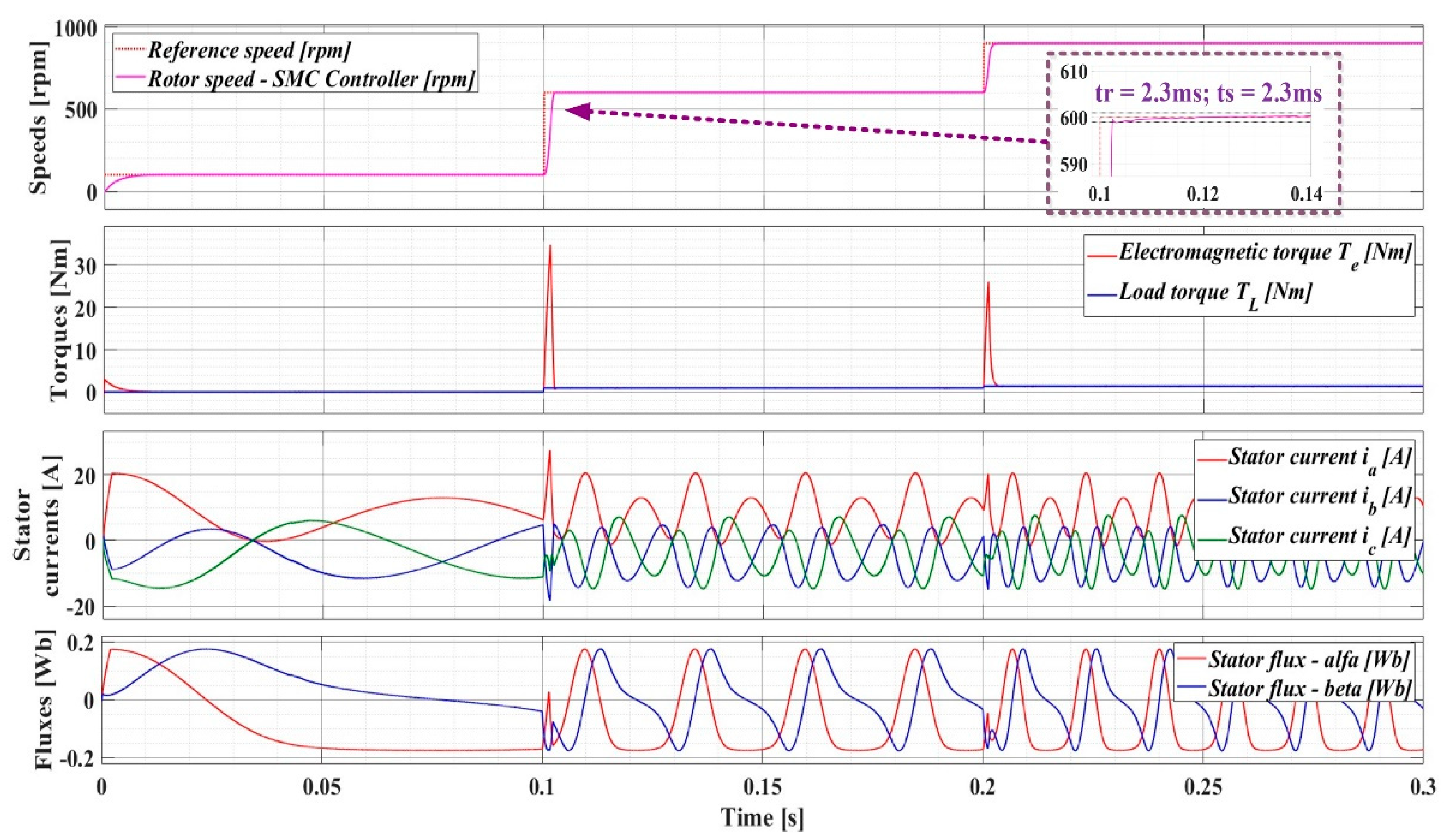
Figure 21.
Parameters evolution of the PMSM sensorless control system using DTC strategy using FOSMC-type controller in case of variable flux.
Figure 21.
Parameters evolution of the PMSM sensorless control system using DTC strategy using FOSMC-type controller in case of variable flux.
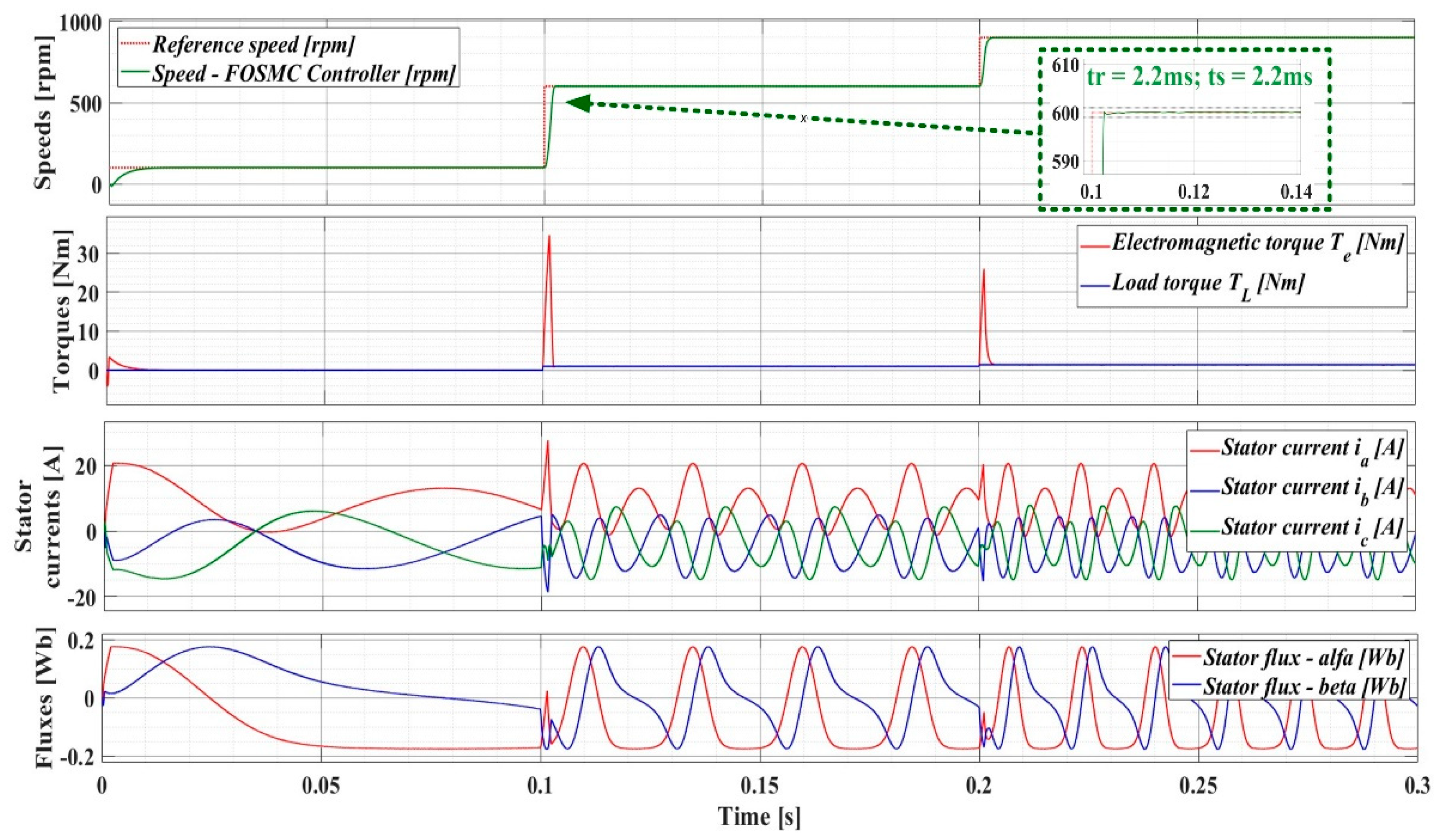
Figure 22.
Parameters evolution of the PMSM sensorless control system using DTC strategy using FOSMC-type controller in case of variable flux – J parameter increased by 50%.
Figure 22.
Parameters evolution of the PMSM sensorless control system using DTC strategy using FOSMC-type controller in case of variable flux – J parameter increased by 50%.
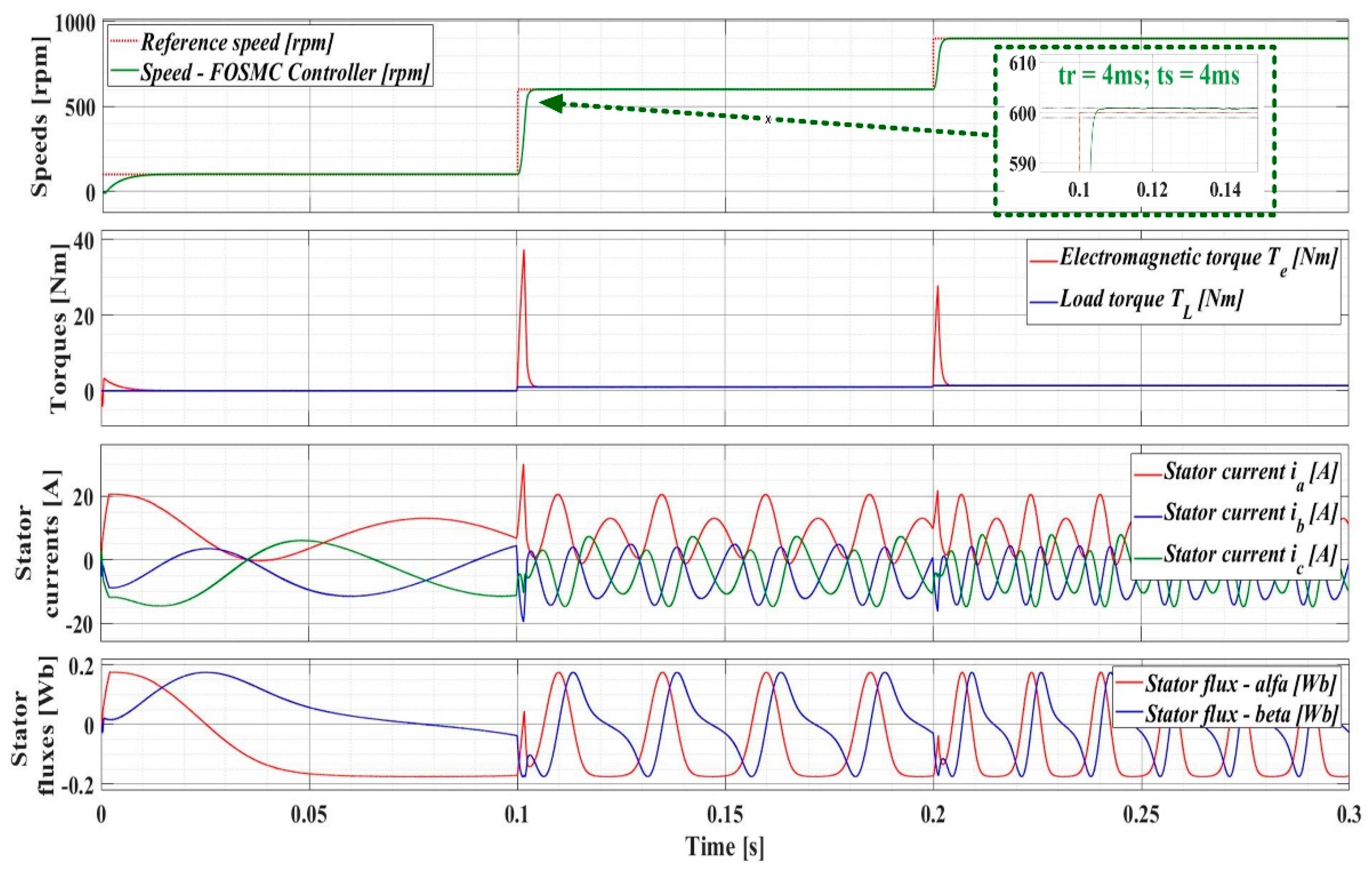
Figure 23.
Flux space vector trajectory for the PMSM sensorless control system based on DTC strategy using FOSMC-type controller in case of variable flux.
Figure 23.
Flux space vector trajectory for the PMSM sensorless control system based on DTC strategy using FOSMC-type controller in case of variable flux.
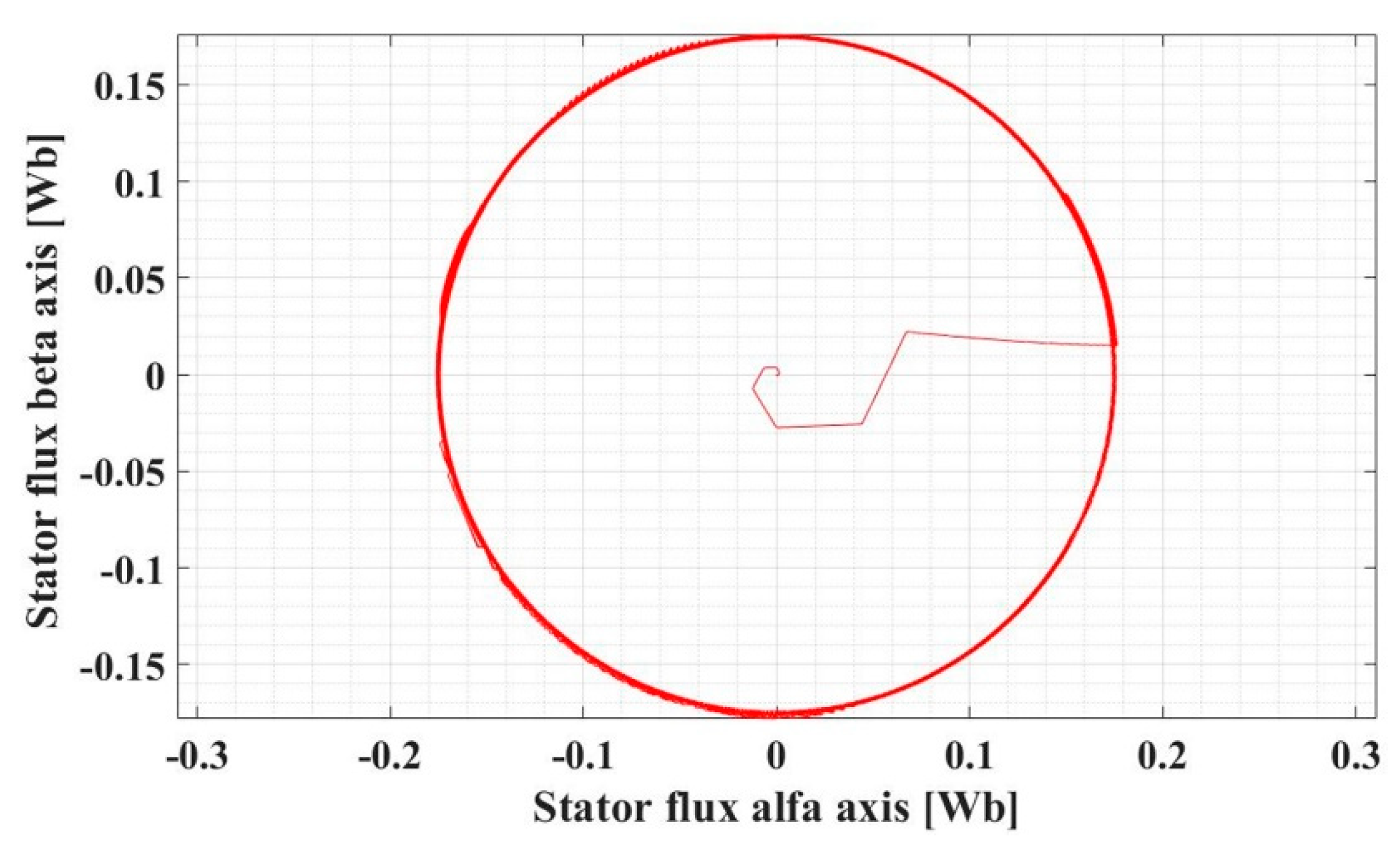
Figure 24.
Flux reference evolution for the PMSM sensorless control system based on DTC-type strategy using FOSMC-type controller in case of variable flux.
Figure 24.
Flux reference evolution for the PMSM sensorless control system based on DTC-type strategy using FOSMC-type controller in case of variable flux.
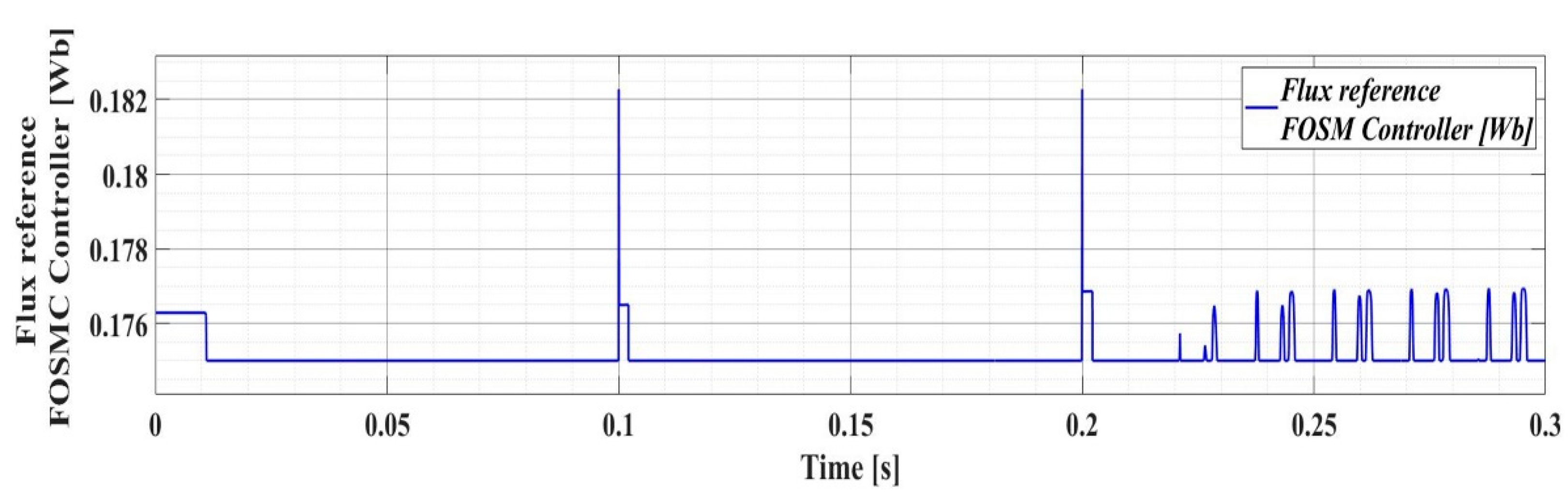
Figure 25.
Comparison of speed evolution of PMSM sensorless control system using DTC strategy using FO-Lead-Lag speed controller in case of constant flux and SMC and FOSMC type controllers in case of variable flux.
Figure 25.
Comparison of speed evolution of PMSM sensorless control system using DTC strategy using FO-Lead-Lag speed controller in case of constant flux and SMC and FOSMC type controllers in case of variable flux.
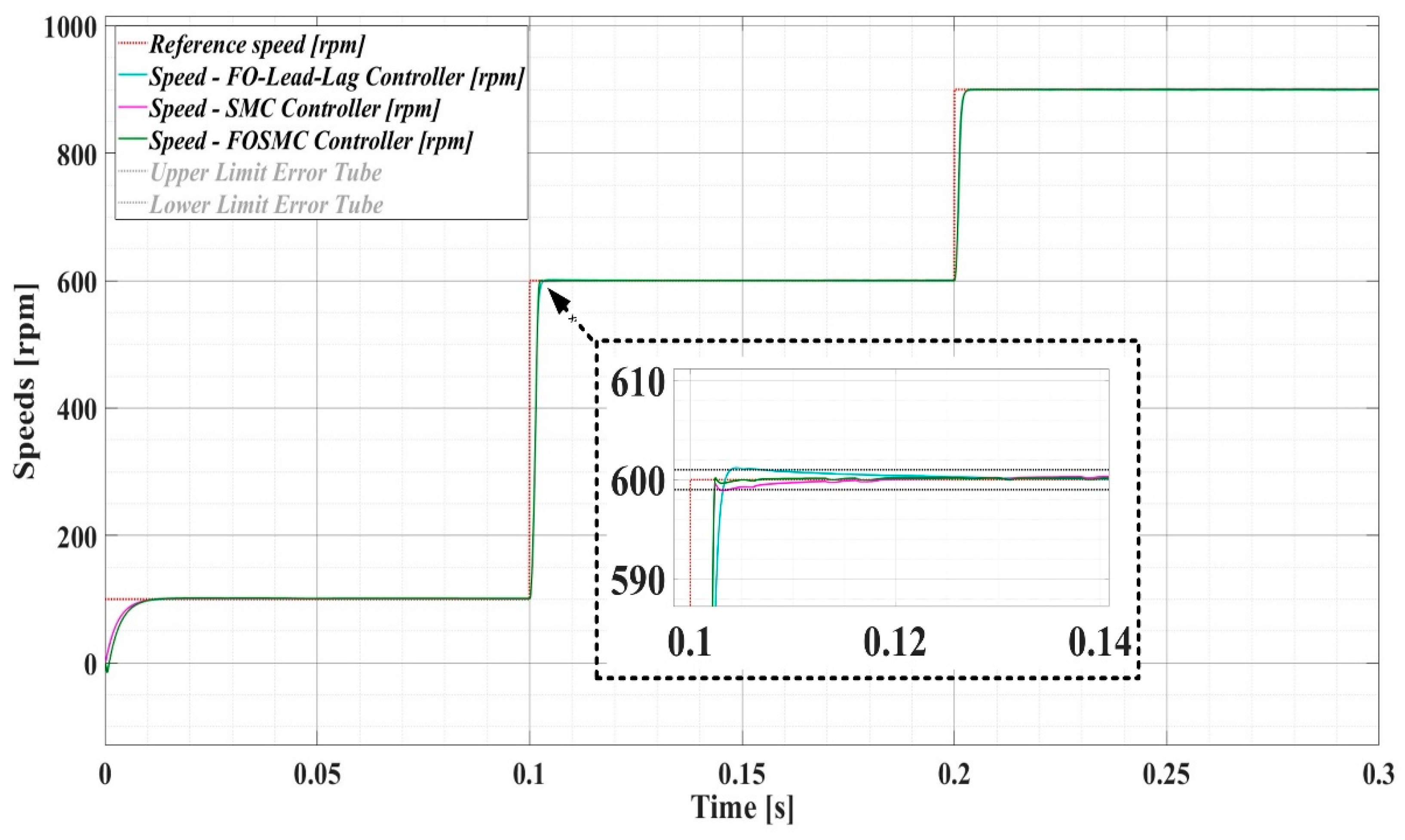
Figure 26.
Graphical representation of the FD of the speed signal for the PMSM sensorless control system based on the DTC strategy for the case of constant flux or variable flux: (a) PI controller at constant flux; (b) PI-EOA controller at constant flux; (c) FOPI controller at constant flux; (d) TID controller at constant flux; (e) FO-Lead-Lag controller at constant flux; (f) SMC-type controller at variable flux; (g) FOSMC-type controller at variable flux. .
Figure 26.
Graphical representation of the FD of the speed signal for the PMSM sensorless control system based on the DTC strategy for the case of constant flux or variable flux: (a) PI controller at constant flux; (b) PI-EOA controller at constant flux; (c) FOPI controller at constant flux; (d) TID controller at constant flux; (e) FO-Lead-Lag controller at constant flux; (f) SMC-type controller at variable flux; (g) FOSMC-type controller at variable flux. .
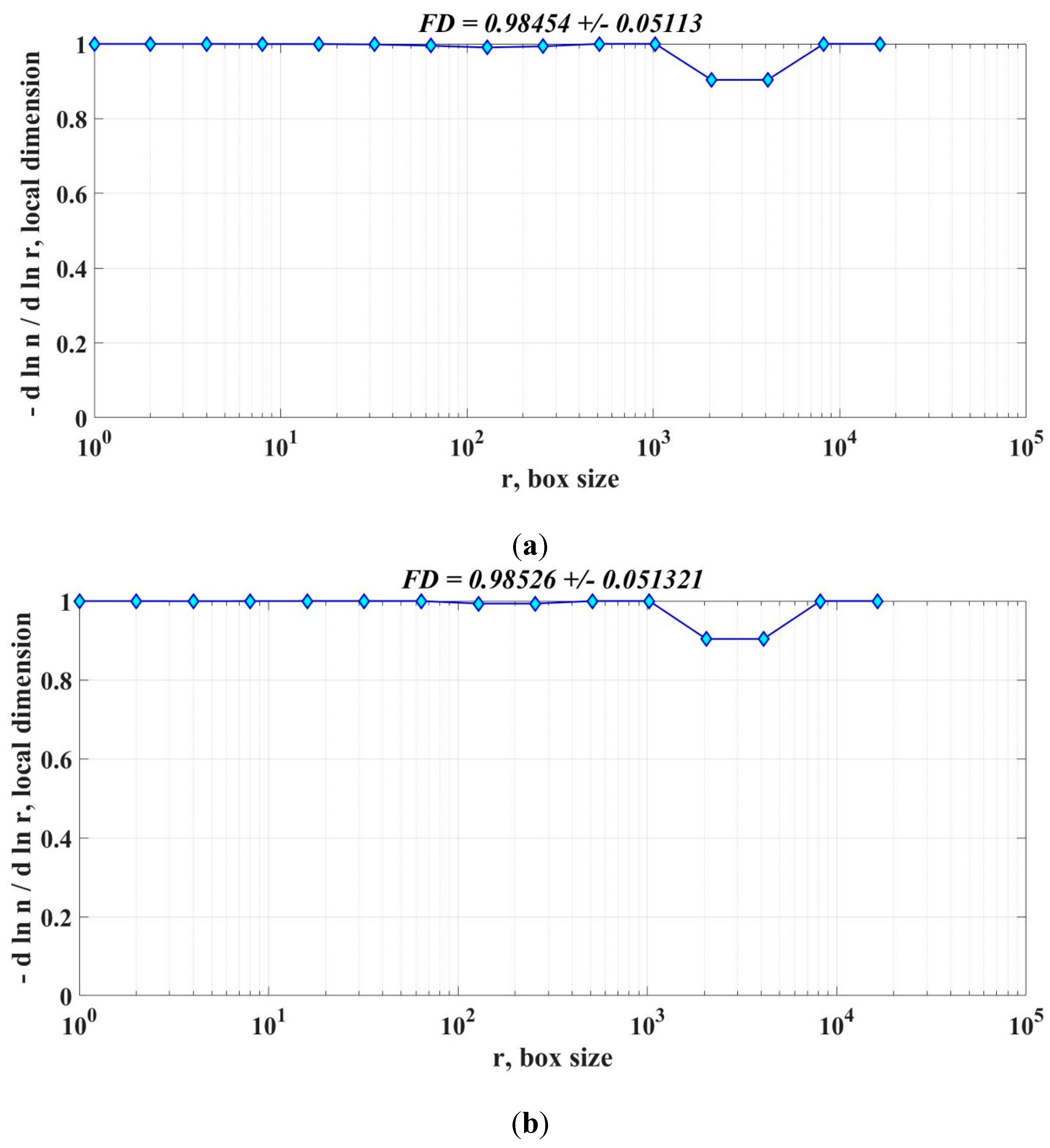
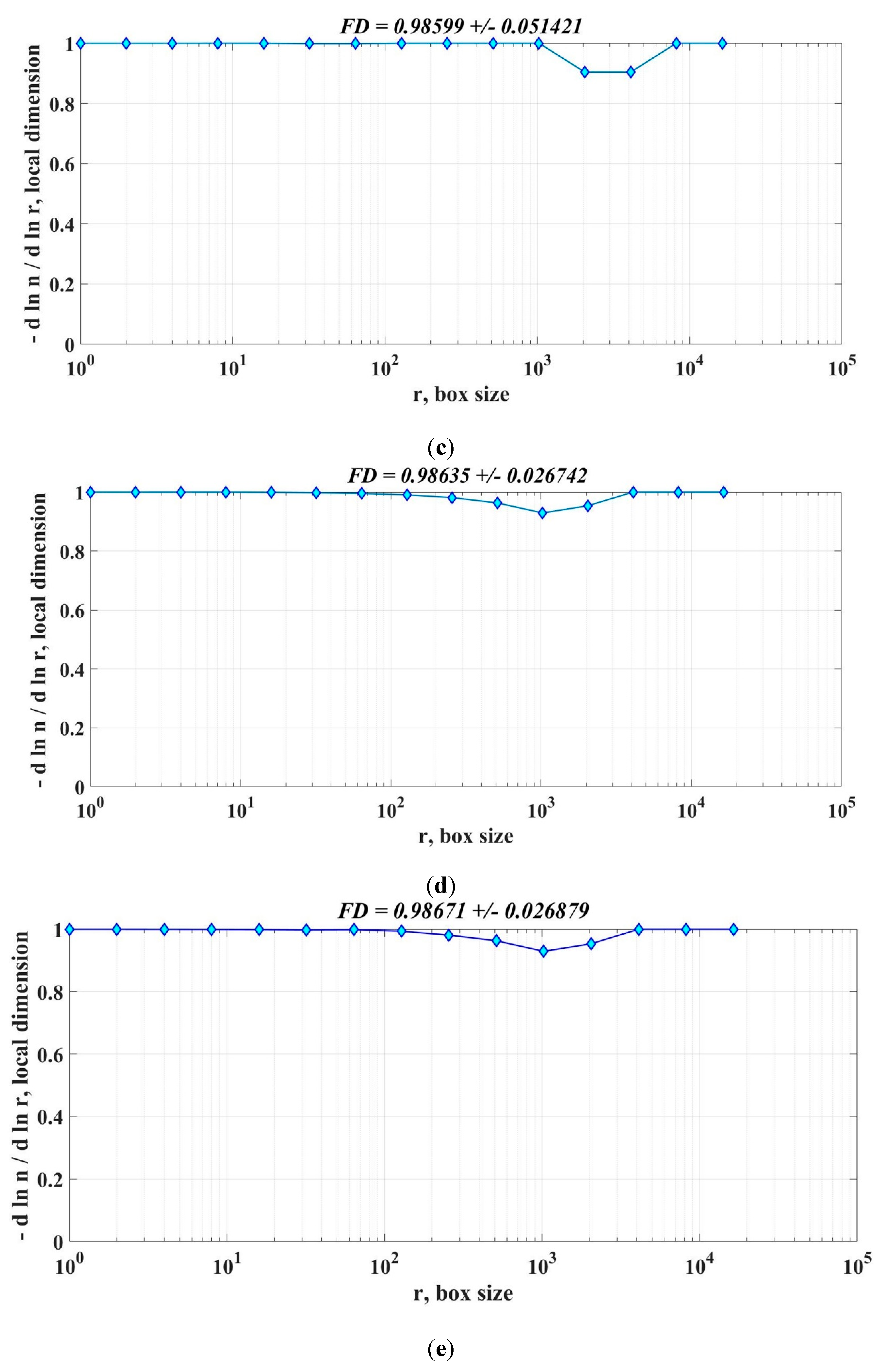
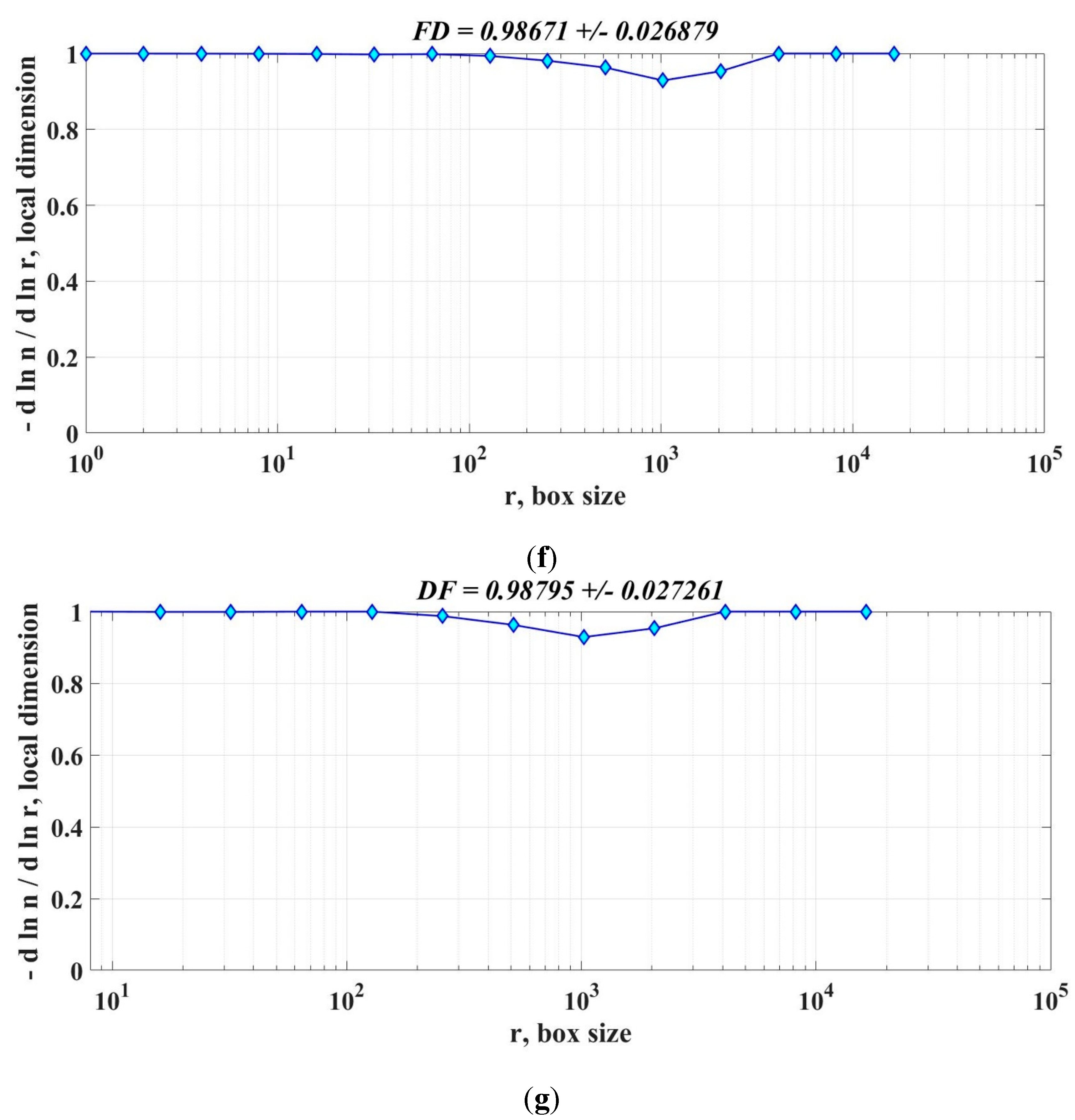
Figure 27.
Experimetal setup image for real-time implemenatation of PMSM sensorless control system based on DTC strategy.
Figure 27.
Experimetal setup image for real-time implemenatation of PMSM sensorless control system based on DTC strategy.
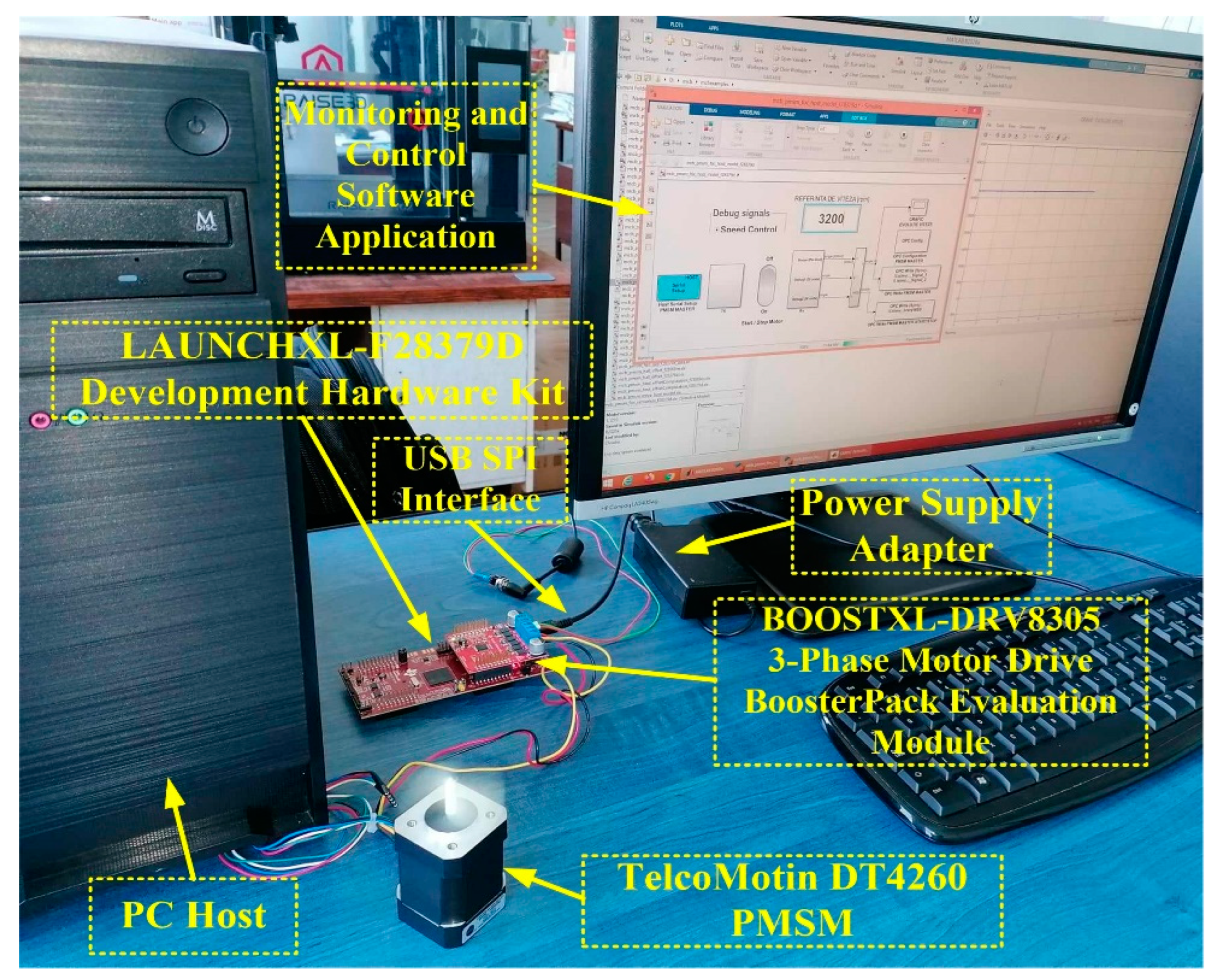
Figure 28.
Software application for real-time implementation of PMSM sensorless control system based on DTC strategy using PI-EOA controller: (a) Simulink model of the main software application for the PMSM sensorless control system using functions from the MCB and ECSP toolboxes; (b) Simulink subsystem implementation of torque control; (c) Simulink subsystem implementation of flux, position, and speed of PMSM observer; (d) Simulink subsystem implementation of speed control. .
Figure 28.
Software application for real-time implementation of PMSM sensorless control system based on DTC strategy using PI-EOA controller: (a) Simulink model of the main software application for the PMSM sensorless control system using functions from the MCB and ECSP toolboxes; (b) Simulink subsystem implementation of torque control; (c) Simulink subsystem implementation of flux, position, and speed of PMSM observer; (d) Simulink subsystem implementation of speed control. .
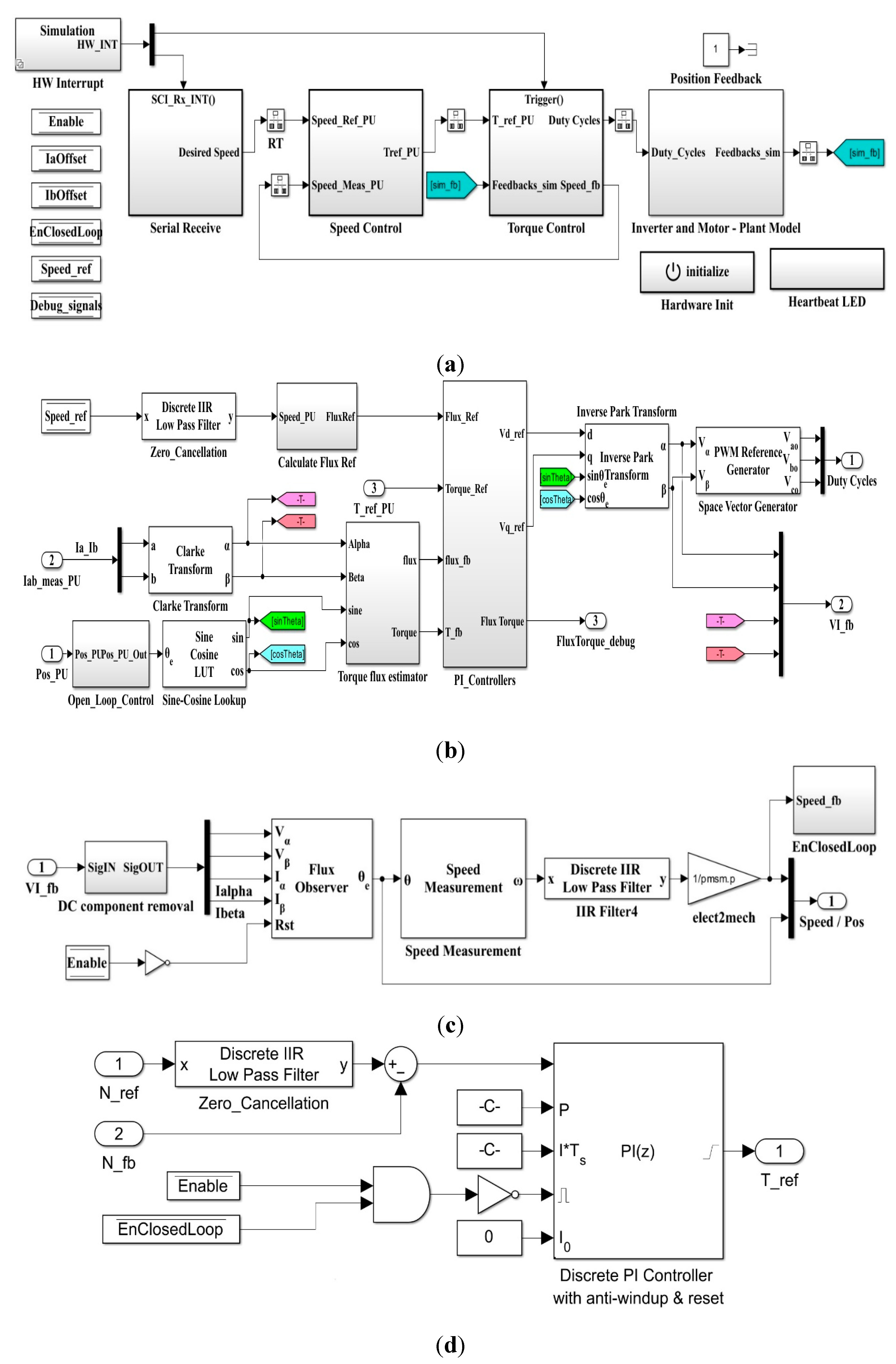
Figure 29.
Real-time monitoring and control interface implemented in Simulink.
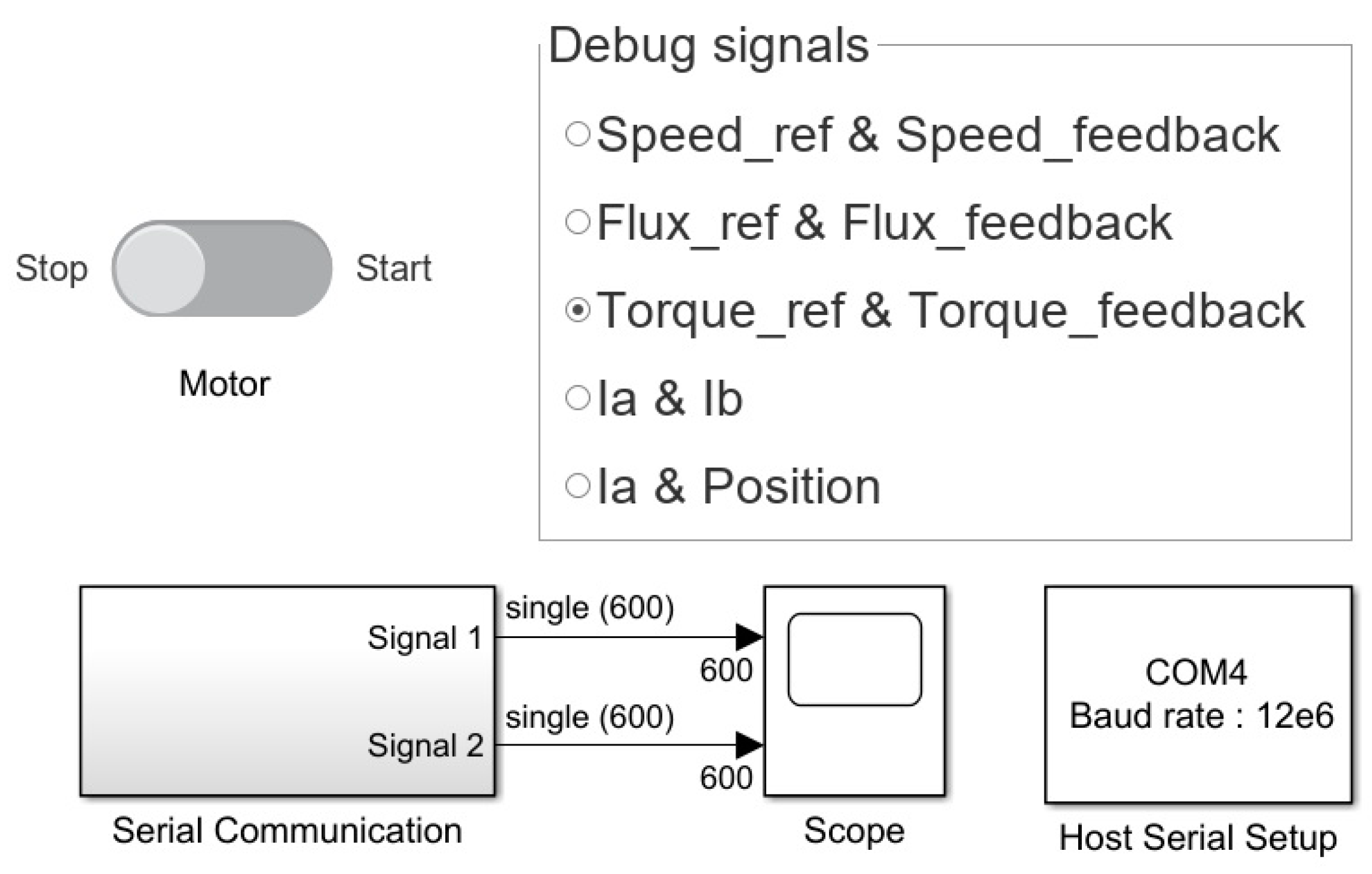
Figure 30.
Real-time speed evolution for PMSM sensorless control based on DTC strategy in case of constant flux: (a) PI-EOA controller; (b) FOPI controller.
Figure 30.
Real-time speed evolution for PMSM sensorless control based on DTC strategy in case of constant flux: (a) PI-EOA controller; (b) FOPI controller.
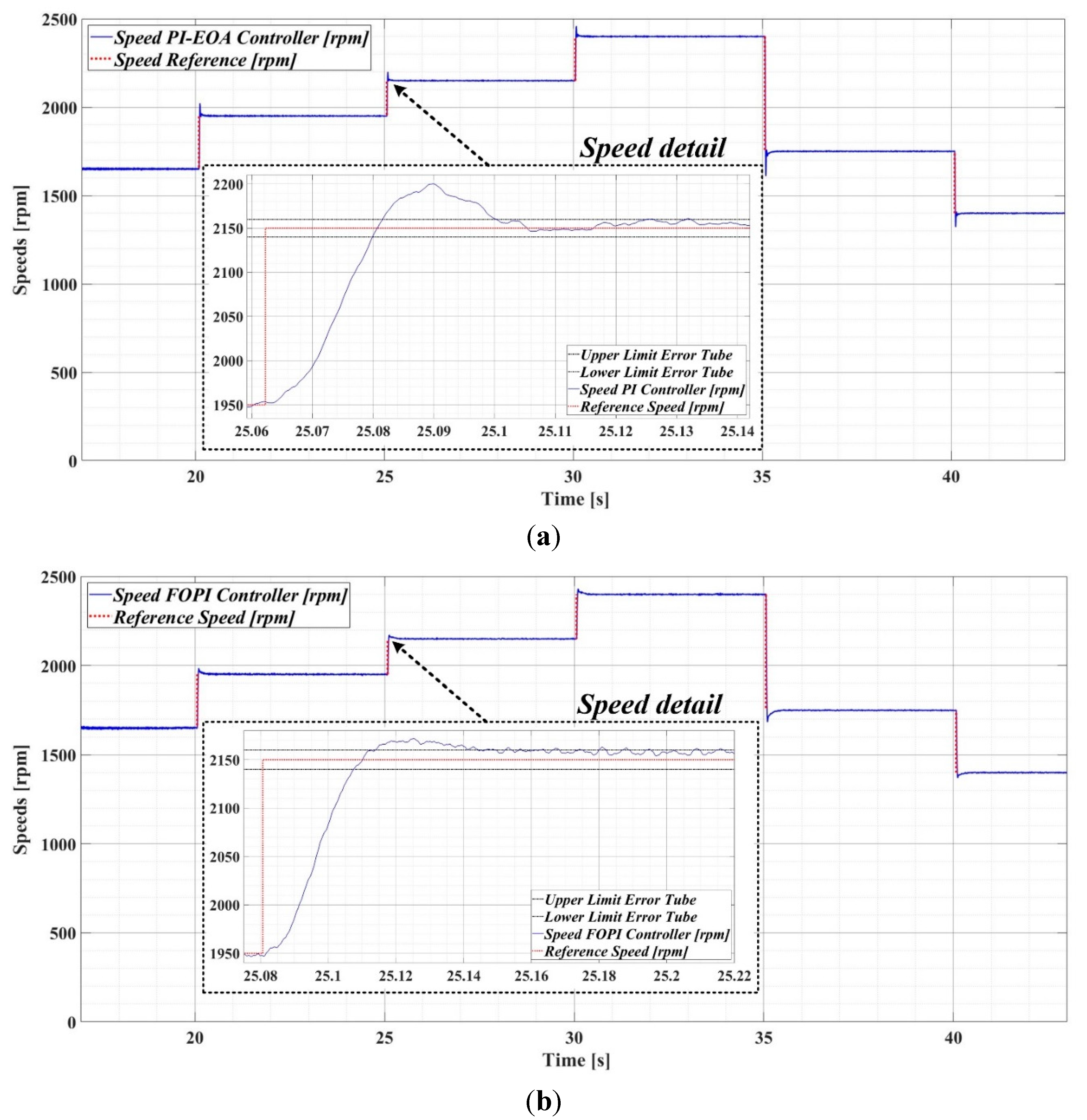
Figure 31.
Stator currents ia and ib in real-time evolution for PMSM sensorless control based on DTC strategy using variable flux: (a) SMC-type controller; (b) FOSMC-type controller. .
Figure 31.
Stator currents ia and ib in real-time evolution for PMSM sensorless control based on DTC strategy using variable flux: (a) SMC-type controller; (b) FOSMC-type controller. .
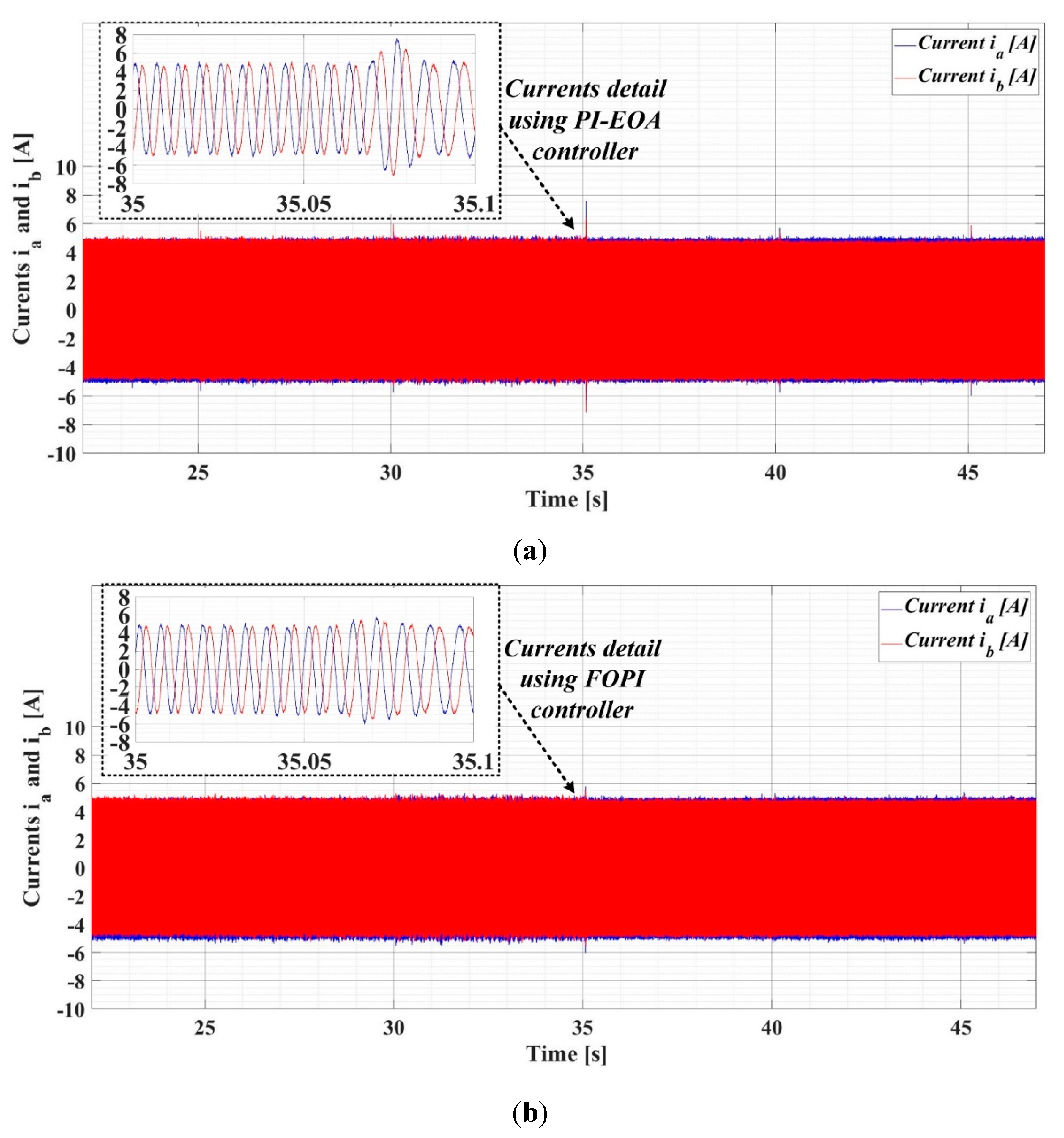
Figure 32.
Real-time parameters evolution of PMSM sensorless control based on DTC using PI-EOA controllers: (a) real-time evolution of flux; (b) real-time evolution of electromagnetic torque; (c) detail of the rotor position real-time evolution.
Figure 32.
Real-time parameters evolution of PMSM sensorless control based on DTC using PI-EOA controllers: (a) real-time evolution of flux; (b) real-time evolution of electromagnetic torque; (c) detail of the rotor position real-time evolution.
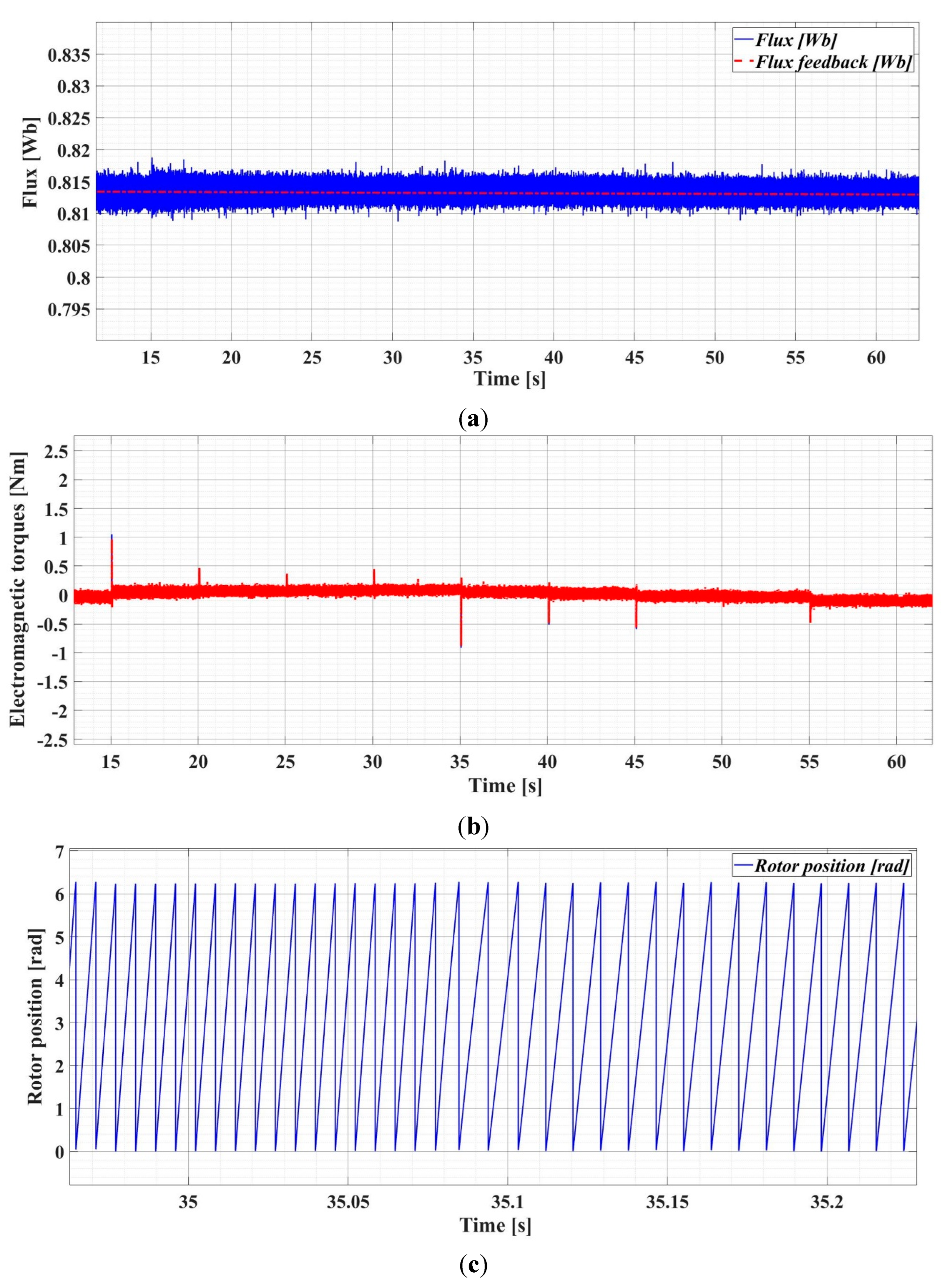
Figure 33.
Graphical representation of the FD of the real-time speed signal for the PMSM sensorless control system based on the DTC strategy for the case of constant flux: (a) PI-EOA controller; (b) FOPI controller. .
Figure 33.
Graphical representation of the FD of the real-time speed signal for the PMSM sensorless control system based on the DTC strategy for the case of constant flux: (a) PI-EOA controller; (b) FOPI controller. .
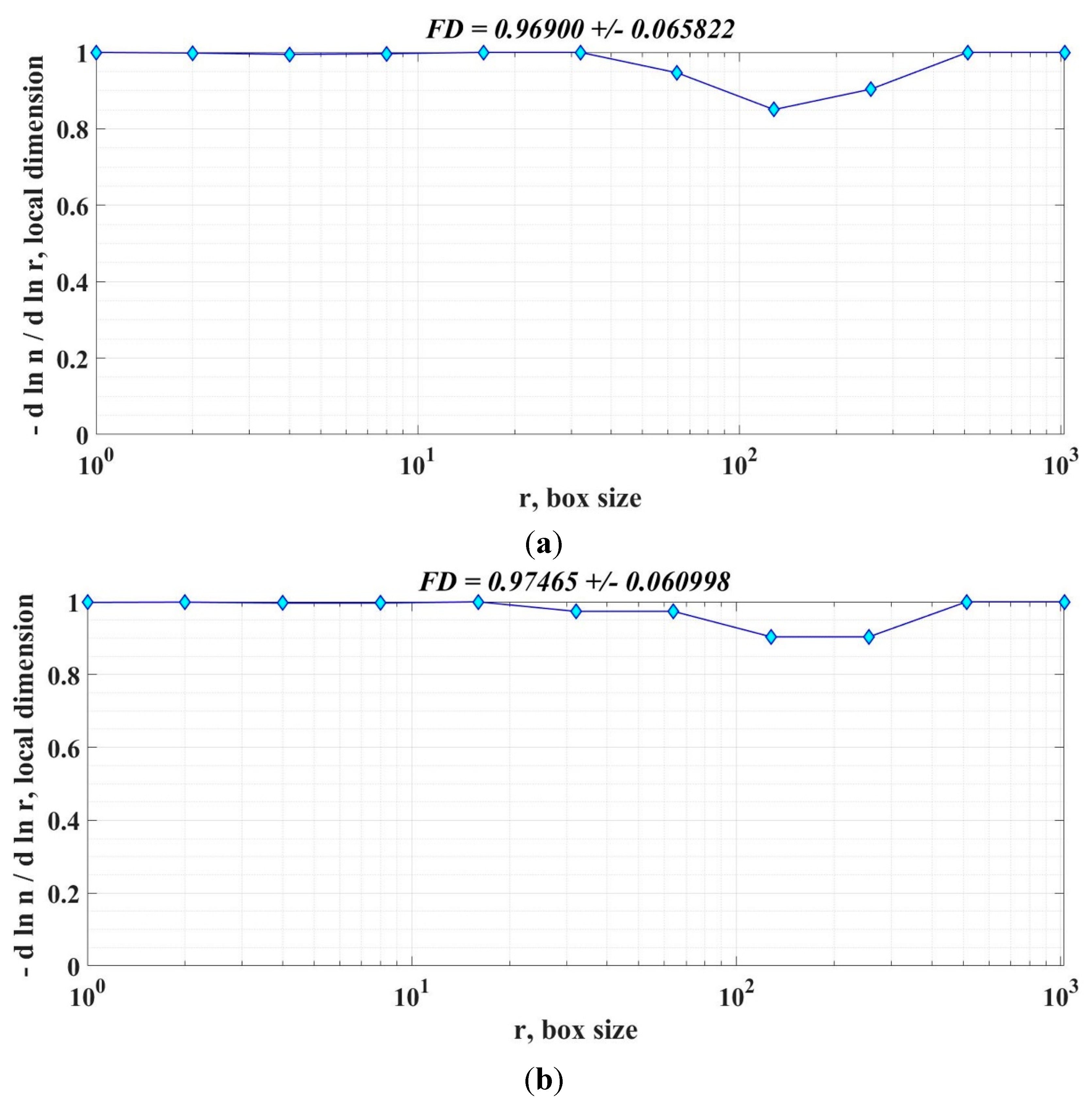
Figure 34.
Real-time speed evolution for PMSM sensorless control based on DTC strategy in case of variable flux: (a) SMC-type controller; (b) FOSMC-type controller. .
Figure 34.
Real-time speed evolution for PMSM sensorless control based on DTC strategy in case of variable flux: (a) SMC-type controller; (b) FOSMC-type controller. .
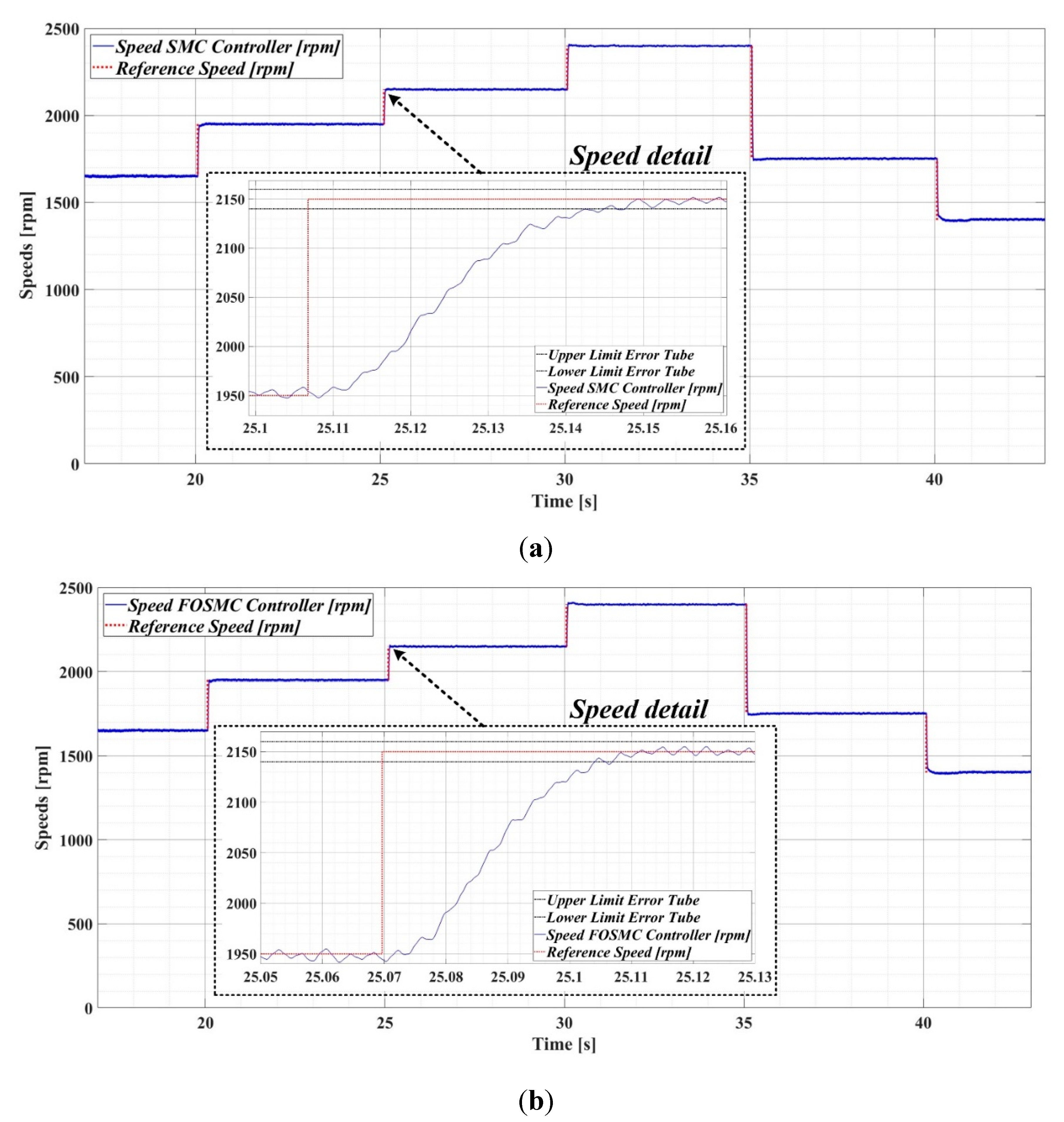
Figure 35.
Flux reference and estimated flux real-time evolution PMSM sensorless control system based on DTC strategy using FOSMC-type controller.
Figure 35.
Flux reference and estimated flux real-time evolution PMSM sensorless control system based on DTC strategy using FOSMC-type controller.
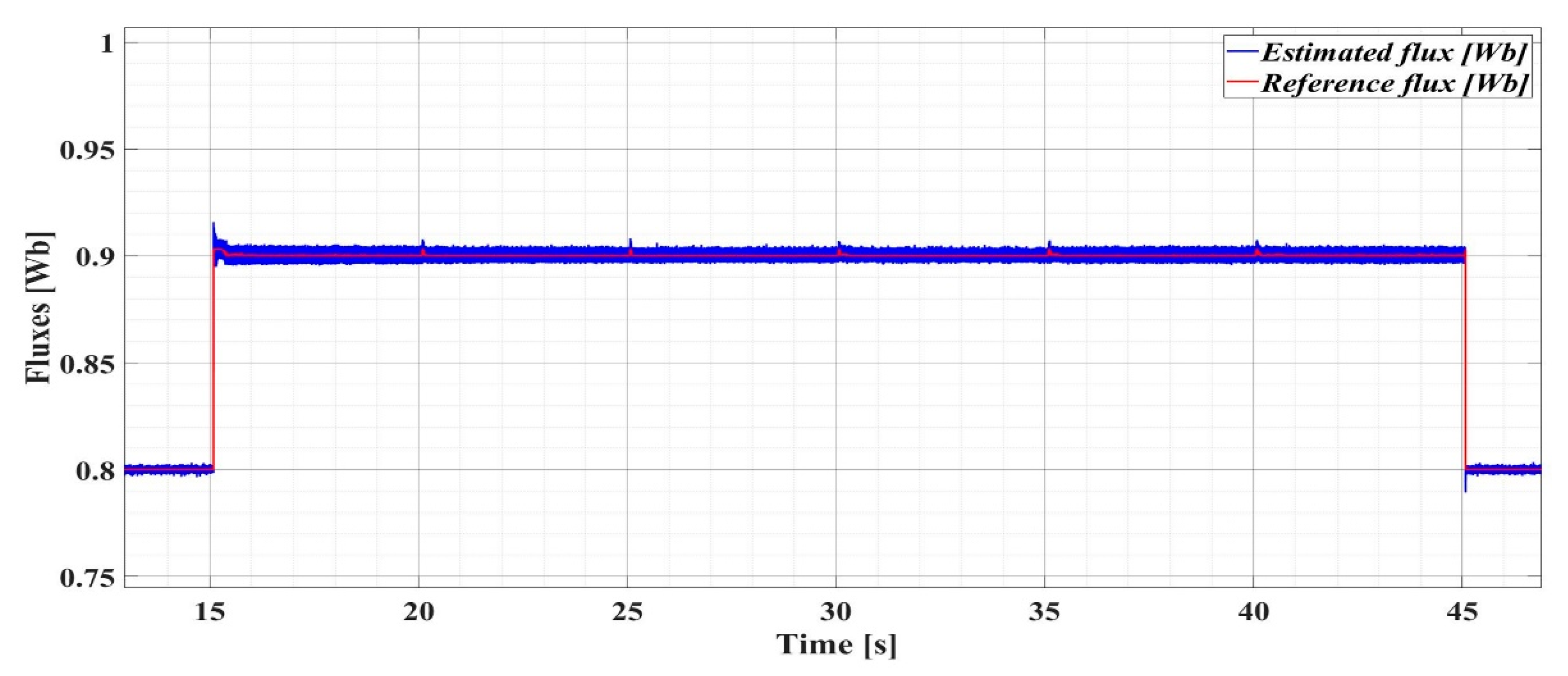
Figure 36.
Stator currents ia and ib in real-time evolution for PMSM sensorless control based on DTC strategy using variable flux: (a) SMC-type controller; (b) FOSMC-type controller. .
Figure 36.
Stator currents ia and ib in real-time evolution for PMSM sensorless control based on DTC strategy using variable flux: (a) SMC-type controller; (b) FOSMC-type controller. .
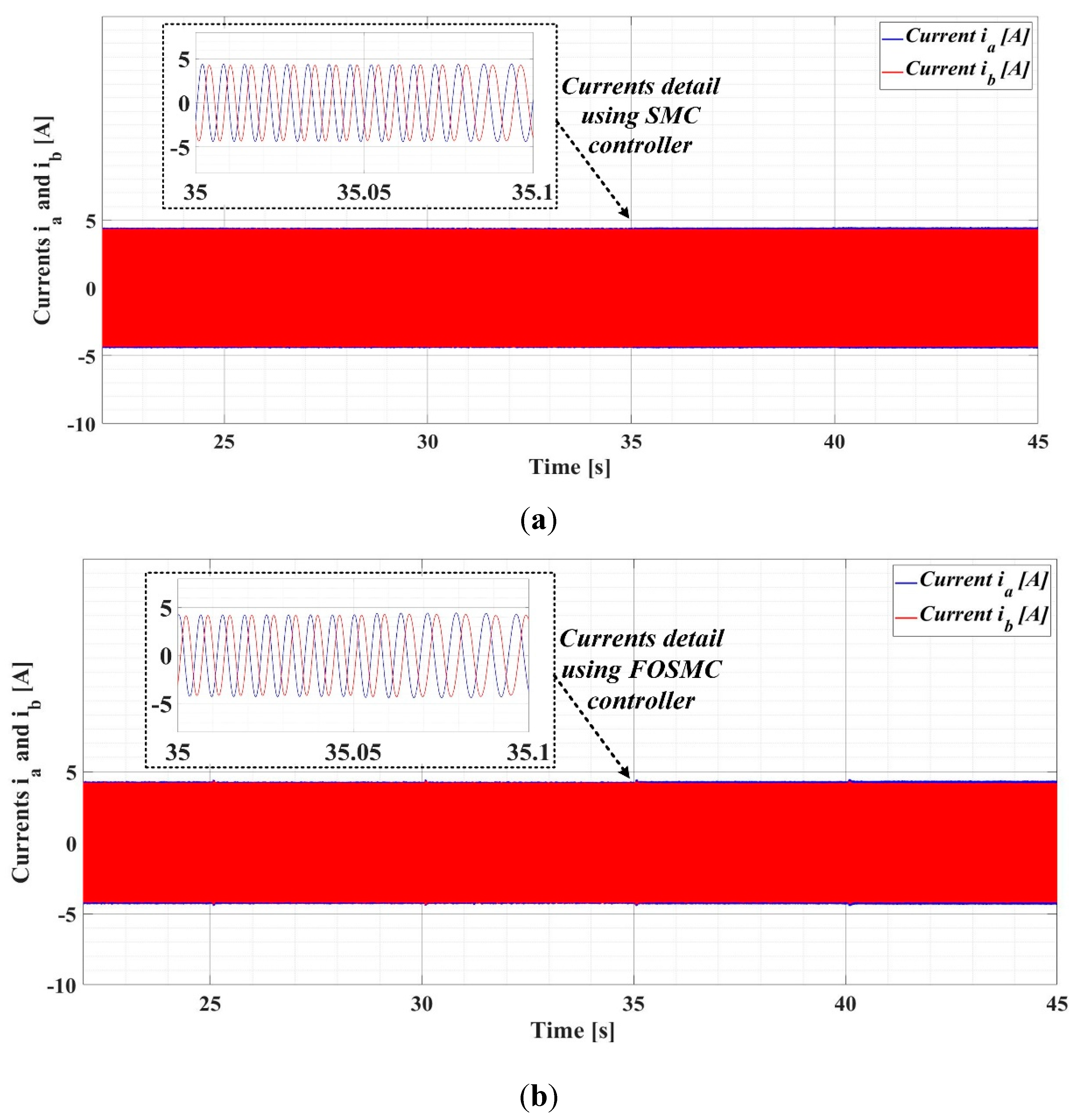
Figure 37.
Graphical representation of the FD of the real-time speed signal for the PMSM sensorless control system based on the DTC strategy for the case of variable flux: (a) SMC-type controller; (b) FOSMC-type controller.
Figure 37.
Graphical representation of the FD of the real-time speed signal for the PMSM sensorless control system based on the DTC strategy for the case of variable flux: (a) SMC-type controller; (b) FOSMC-type controller.
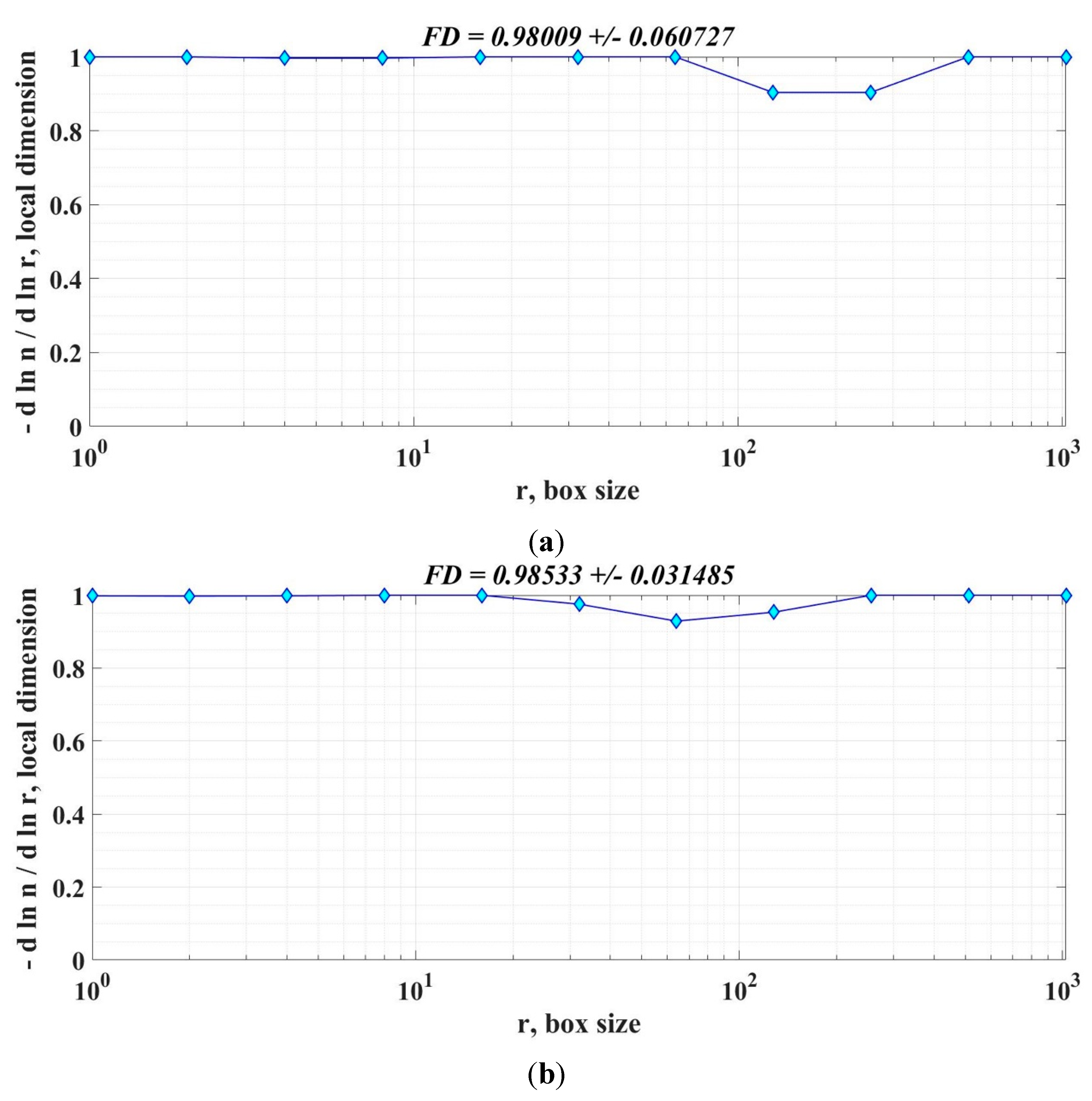
Table 1.
PMSM nominal parameters from the sensorless control system based on DTC strategy.
| Parameter | Value | Unit |
|---|---|---|
| Stator resistance—Rs | 2.875 | Ω |
| Inductances on the d-q rotating reference frame—Ld and Lq | 0.0085 | H |
| Combined inertia of rotor and load—J | 0.0008 | kg·m2 |
| Combined viscous friction of rotor and load—B | 0.005 | N·m·s/rad |
| Flux induced by the permanent magnets of the rotor in the stator phases—λ0 | 0.175 | Wb |
| PMSM pole pairs number—nP | 4 | - |
Table 2.
Performance of proposed controllers for PMSM sensorless type control systems.
| Controller Type for PMSM Sensorless Control System | Response Time [ms] | Settling Time [ms] |
Speed Ripple [rpm] |
FD of PMSM Speed Signal | |
|---|---|---|---|---|---|
| PI | constant flux | 12 | 72 | 43.36 | 0.984540 +/– 0.051130 |
| PI-EOA | 9.2 | 30 | 37.17 | 0.984526 +/– 0.051321 | |
| FOPI | 7.9 | 15 | 35.61 | 0.984599 +/– 0.051421 | |
| TID | 5.9 | 14.5 | 34.38 | 0.986350 +/– 0.026742 | |
| FO-Lead-Lag | 3.2 | 9.1 | 33.54 | 0.986710 +/– 0.026879 | |
| SMC | variable flux | 2.3 | 2.3 | 32.79 | 0.987770 +/– 0.027187 |
| FOSMC | 2.2 | 2.2 | 32.21 | 0.987950 +/– 0.027261 | |
Table 3.
Performance of proposed controllers for PMSM sensorless type control systems in real-time implementation.
Table 3.
Performance of proposed controllers for PMSM sensorless type control systems in real-time implementation.
| Controller Type for PMSM Sensorless Real-Time Control System | Response Time [ms] | Settling Time [ms] |
Speed Ripple [rpm] |
FD of PMSM Speed Signal | |
|---|---|---|---|---|---|
| PI-EOA | constant flux | 18.2 | 70 | 16.76 | 0.96900 +/– 0.065622 |
| FOPI | 25.8 | 60 | 15.83 | 0.97465 +/– 0.060998 | |
| SMC | variable flux | 34.5 | 34.5 | 14.95 | 0.98009 +/– 0.060727 |
| FOSMC | 33.9 | 33.9 | 10.61 | 0.98533 +/– 0.031485 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








