Prerpints.org logo
Preprint
Article

Algorithmic Implementation to Visually Controlled Interception: Harmonic Ratios and Stimulation Invariants

Altmetrics

Downloads

81

Views

40

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 May 2024

Posted:

29 May 2024

You are already at the latest version

Alerts
Abstract
This research presents a novel algorithmic implementation to improve the analysis of visually controlled interception and accompanying motor action through the computational application of harmonic ratios and stimulation invariants. Unlike traditional models that focus mainly on psychological aspects, our approach integrates the relevant constructs into a practical mathematical framework. This allows for dynamic prediction of interception points with improved accuracy and real-time perception-action capabilities, essential for applications in neurorehabilitation and virtual reality. Our methodology uses stimulation invariants as key parameters within a mathematical model to quantitatively predict and improve interception outcomes. The results demonstrate the superior performance of our algorithms over conventional methods, confirming their potential for ad-vancing robotic vision systems and adaptive virtual environments. By translating complex theo-ries of visual perception into algorithmic solutions, this study provides innovative ways to im-prove motion perception and interactive systems. This study aims to articulate the complex inter-play of geometry, perception, and technology in understanding and utilizing cross-ratios at infin-ity, emphasizing their practical applications in virtual and augmented reality settings.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Virtual and augmented reality (VR and AR) technologies are rapidly evolving, driven by advances in computational algorithms and the increasing accessibility of advanced hardware. These technologies, historically utilized for training in high-stakes environments such as aviation, are now penetrating broader domains, including neuropsychology, neurorehabilitation, and complex surgical procedures. At the heart of this technological shift is the growing capability to simulate intricate dynamic interactions in virtual spaces, making them increasingly relevant for both educational and therapeutic applications.
This manuscript builds upon foundational work by Reed [1] and Gibson [2], who delineated between exploratory and performative activities, proposing that both action and awareness can be scientifically studied and enhanced through virtual environments. A significant limitation, however, has been the lack of explicit mathematical foundations in the theories of motion perception, particularly those proposed by Gibson [2]. Our study addresses this gap by applying the “Theory of Screws” [3], a sophisticated mathematical model historically used to describe the dynamics of rigid bodies, to the domain of VR and AR. Application of the theory in this context provides a structured method for handling the complexities of motion and interaction in virtual environments.
A roadblock prevented Gibson’s theories of motion and self-movement from progressing further because they lacked explicit mathematical foundations despite being fundamentally geometric. By integrating Gibson’s conceptual framework with the mathematical rigor of screw theory [3], we explore how harmonic ratios and stimulation invariants can be leveraged to improve the design and functionality of VR and AR systems. Specifically, this approach allows for the modeling of visual interception behaviors that are critical in scenarios where precise coordination and motion control are necessary, such as in training simulations for sports or rehabilitative applications. Harmonic ratios and stimulation invariants serve as the backbone for developing algorithms that enhance the realism and responsiveness of virtual environments, thereby facilitating more effective training and rehabilitation protocols.
This study formulates the issues that the “Theory of Screws”, which is not a dynamical form of calculus in general, claims to resolve. We discuss a specific category of dynamical problems that arise in the development of optic flow mathematics and that can only be solved using the definition of the theorem. The screw is an ingenious and valuable element of a three-dimensional space that can be used to model the general infinitesimal displacement of a rigid body. At the same time, it can be used to model the available load exerted on a body. One body twists relative to another body in a screw, as well as a body applies a wrench to another body along a screw. The screw solves all cases of instantaneous displacement and all instances of loading under the same theory. Screws of zero pitch are lines used to model pure rotations and pure forces. Screws of infinite pitch (or zero pitch on lines at infinity) are used to model pure translations and couples. The screw theory has long been poised to unify the sciences of dynamics and statics [4].
The first kind of invariant can be demonstrated by showing that, whenever a body is moving, there is a unique axis at every instant, designated the instantaneous screw axis (ISA), about which the body twists with a specific pitch h. Note that every point on the body has a velocity vector tangential to the helix that passes through it (see Figure 1(a)). The pattern of these velocity vectors is described as a helicoidal vector field. The ISA is often referred to as the motion screw [5]. It can, thus, be argued that the body in Figure 1(b) twists at the instant about its motion screw. To describe this field, we may imagine that all helices of the same pitch as those of the ISA are drawn concentrically with the ISA. Theoretically, there must be a helix at every radius from zero to infinity, and there must be an infinite number of helices at each radius, each displaced from its neighbor at an infinitesimal distance in the axial direction [5]. The motion of objects produces a helicoidal vector field V1, V2, …, V5, which manifests perspective changes in a part of the optic array [Figure 1(b)].
The second kind of invariant, the motion perspective, may be derived from an object’s movement through the use of the moving reference frame. The motion perspective denotes the optical flow pattern in the visual field resulting from the observer’s own movement, in fact, their own locomotion, and its direction [2]. While working on visually guided airplane landings, Gibson identified a perceptual invariant that could be observed in animals. An animal in motion within its environment will create an optic flow with what Gibson termed a “perspective transformation of perspective flow structure." This structure can be conveniently described in a vector field V1, V2, …, V5, [1] (see Figure 2). The point toward which the animal is heading is the source of all optical motion vectors, and the point away from which the animal is heading is the sink for those vectors. This condition results in a pure translation parallel to the animal’s heading, with the pitch being infinite (Figure 3). The screw theory has numerous points of connection with certain geometrical researchers on the linear complex by Plücker and Klein [3].
In the analytical treatment by Descartes of the geometry of space, the point is the fundamental element of space. In contrast to Plücker and Klein, it is the line that serves as a space element. If only one condition is imposed, the lines that fulfill it are said to form the field lines [6]. Consequently, the field lines in the optic array flow are the tangents to a series of helices, with each helix being on a cylinder of radius r and an axis of the field lines (see Figure 1(a)). The axis of the field is conditioned as the ISA.
A ‘complex of lines’ was discovered independently by Gibson and Jessop: Jessop defined it as the assemblage of lines that satisfy one condition [6] while Gibson defined it as the optic flow, whose axis is the line of the displacement of the observer. The linear complex of lines represents an essential ensemble of lines in the visual perception of space. It is an axisymmetric group of lines comprising only a very few of the ∞4 of lines that are available in space. Such a shift from particle to field descriptions is clearly reflected in Gibson’s constructs, such as the optical flow field and its invariant [7]. Moreover, field descriptions afford prominence to abstract relations as the fundamental basis of causality [8].
When an observer travels on a straight path, a radial optic flow pattern is produced, with a focus on the expansion (FOE) in the current direction of locomotion or heading. Warren manipulated the optic flow by displacing the FOE from the walking direction, and measured the virtual heading error between the FOE and the goal [9]. In this case, the FOE of optic flow on the target and the central axis of the line complex are coincident. These virtual headings must be in harmony with the given kinematic constraints, and we shall assume that they are reversible, i.e., that the given constraints do not prevent actors from changing an arbitrary δ R i into − δ R i . If all the lines of a complex are subjected to a screw motion of a virtual velocity about the central axis, the complex itself remains unaltered. The optic flow of the ambient array is rarely perceived as motion; rather, it is experienced as kinesthesis or ego locomotion. The movement of the self when passing from one position to another, that is, indefinitely adjacent, is indistinguishable from the translation about an appropriately chosen line by which the same displacement could be effectuated. The line about which the actor is translating at any instant is referred to as the instantaneous translational axis. Therefore, the complex lines are tangent to a series of helices, each on a cylinder of radius r and an axis of the complex because the velocities of particles in the surfaces of the environment are covariant to the axis of the complex as the non-holonomic constraint.
Therefore, animals encounter two distinct geometrical perspective transformations: (1) as a change of coordinates from one perspective system to another, with (x, y, z) and (x´, y´, z´) being the coordinates of the same point in the two systems (and a moving point of observation ‘A’ with the fixed environment as illustrated in Figure 2); and (2) as a perspective transformation of points within one coordinate system, with (x, y, z) and (x´, y´, z´) being the coordinates of the original point and the transformed point, respectively, in the single system (and a stationary point of observation at a fixed location ‘A’ in an environment as illustrated in Figure 1). The process of maintaining different stationary links (shown as ISA in Figure 1(b)) of a kinematic chain is referred to as inversion. Since the algebra is the same in both cases, it makes no difference whether we define a perspective invariant as invariant over perspective transformations or as described in the second invariant. In either case, continuous perspective transformations can be employed as stimuli for perceiving rigid motion in the environment [10].
Moreover, our research delves into the application of these mathematical models in the diagnosis and treatment of conditions such as Parkinson’s disease within augmented environments. By simulating realistic interaction dynamics and providing controlled, adaptable settings for patients, VR and AR can significantly advance therapeutic outcomes. The visual interception tasks modeled in our study not only demonstrate the potential of virtual environments in medical interventions, but also provide a pathway for broader applications in neuropsychology.
The convergence of these historically disparate strands — Gibson’s perceptual theories and the mathematical modeling of dynamic systems — illustrates the multidisciplinary nature of contemporary VR and AR applications. Our findings underscore the importance of a robust algorithmic foundation that can adapt to the complexities of human motion and perception, thereby enhancing the capability of virtual systems to serve diverse scientific and practical needs.

2. Materials and Methods

2.1. Mathematical Solutions to Terrestrial Interception Based on the Geometrical Constraints

First, researchers have exhibited that human interception behavior is best accounted for by the constant bearing angle (CBA), which refers to the angle between the direction of the heading and the agent’s line of sight [11,12,13]. According to this model, an agent adopts a straight path to the target to keep the angle β constant, as illustrated in Figure 3(a).
It has been claimed that the agent does not need to adjust explicitly or compute the bearing angle β to null the change in β, but simply steering a straight path will result in a successful interception at a constant angle β [14]. To understand these fundamental abilities, Fajen and Warren proposed a mathematical model of β, the behavioral dynamics of locomotion, i.e., the time evolution of behavior as an agent interacts with the environment [15]. This model is consistent with the view that the decision-making process, as an integral part of goal-directed behavior, is influenced by functional constraints at the scale of the environment–performer relationship. Thus, decision-making behavior emerges from the individual’s interactions with environmental constraints over time toward specific goals [16]. We argue here that a simple perception of the approaching constant rate of change and bearing of the target informs the catcher whether they are moving at the right speed and in the right direction for the interception [17].
At this point, it is proper to recall the Chapman problem to determine β: A ballplayer (point A) is running at the right speed in the right direction to make the catch (or point B) [17]. In which direction should he set off to catch the ball? We have tried to show here that a ballplayer solves trigonometric equations to catch a ball. The first step of the solution is to construct a pair of harmonic poles C and D [18] such that their ratio is given by the ratio of the player’s speed λ1 to the ball’s speed λ2, as shown in Figure 3(b). Note that the agent has two control variables: direction and running speed. Adopting a different running speed would result in a different angle β. This is shown by computing a solution in the harmonic ratio in interceptive walking.
The first step of the solution is to construct harmonic poles C and D so that their length ratio is the ratio of the player’s speed to the ball’s speed (Figure 3):
A C B C = A D B D = 1 g ,
where g ≡ λ2/λ1 is the ratio of the speed of the target to the speed of the agent. Starting at points A and B, the next step is to construct point P as follows: Draw a circle of radius PA around A and draw a circle of radius PB around B so that the intersection P of these two circles forms the correct ratio with or without any scaling, as needed. Next, dropping the internal and external angle bisectors, a line segment dividing the angle APB into two equal parts gives the harmonic conjugates C and D. If the velocities λ1 and λ2 had opposite signs, then the point would have to divide the angle APB externally into the given ratio so that they are centered in the system. The coordinates of C and D are treated as a column vector of homogeneous coordinates by augmenting one and are given by
C = g A + B , D = − g A + B 1 − g .
At the point P, the ray from B (target) intersects a circle with a diameter CD (Figure 3). A straight line drawn to this point will intersect it. For example, the Matlab function ‘linecirc’ (MathWorks, MA, USA) can be used to find the intersection point of a circle defined by its center and radius in x-y coordinates and a line defined by its slope and y-intercept (Appendix A).
This raises a new question: How could an effective bearing angle somehow be determined by a locomoting agent [19]? Obviously, no agent ever solves synthetic trigonometric equations based on the geometries of the constraint to intercept a target [20]. Wilson calls this “physics avoidance” [21], which allows us to avoid having to know the constraint they refer to. To determine the equilibrium condition of a system, what we need to know is not the internal macroscopic mechanism of the system, but merely how the internal mechanism constrains the moving components of the system [22].
Coordinating the direction and speed of self-motion when intercepting a target moving on a parabolic trajectory while projected in parallel on the ground plane involves at least three separable yet closely related problems: How do we see the target in motion? How do we perceive a stable environment? And how do we perceive self-motion? In addition, the kinetic experience in motion stability and movement involves space perception problems [23]. Gibson’s 1954 article on visual motion is remarkable in several aspects because the three questions above define much of the motion perception field as practiced today. This approach has a crucial component of the animal-environment link and typically uses large-field animation sequences that portray changes in the optic array with locomotion [24].
Gibson argued that the visual perception of space might be better understood in the context of its biological function of guiding action, with locomotion as a paradigmatic example [25]. Thus, the question can be refined: What kind of concept is “space”? A rarely discussed answer is that space is an ecological concept [26]. Relatedly, Reed made an extension of the indissociable perception-action coupling as advanced by Gibson, by conceiving two modes of activity: exploratory and performatory. Without this distinction, action scientists will forever be separated by the objective-subjective divide [1]. Reed takes the exploration of an actual interceptive action over the infinitesimal neighborhood as an exploratory activity. This exploration must show that the interception path has a stationary value.

2.2. Canonical Base of the Reference Frame for the Interception System

The ecological approach demonstrates how human (and other animal) perceptions and actions are continuous with interactions between animate and inanimate physical systems [27,28]. However, because interactions between inanimate targets and animate agents are continuous, there is no need to identify the CBA as a separate category that can be incorporated into the larger theory. In the following section, we present a case of the more general methods of degrees-of-freedom (DOF) coordination, by which agents’ interception paths can be determined such that the chosen action implies two paths as the canonical base of the system.
The goal-directed actions emerge spontaneously from the nonlinear interaction of the system elements under the influence of specific agents, tasks, and environmental constraints. Here we discuss how an animal property, degeneracy (i.e., many coordinative structures to achieve one function), can help us understand how agents functionally adapt perception and action to interacting constraints during interceptive activities [29]. As such, Bernstein’s degrees-of-freedom (DOF) problem can be addressed through dynamics [30].
This fundamental problem was posed independently by both Nicolai Bernstein and James J. Gibson. It replaces mind-matter dualism with animal-environment duality (isomorphism) — a better-posed scientific problem because commensurability is assured [31]. Shaw proposed some features of organized control that we found promising. The core idea may be a “coordinative structure” or synergy, a complex system that acts as a unit. A coordinative structure would be a system with many degrees of freedom organized by a system of constraints that allows the whole complex to be controlled with one degree of freedom [32]. We illustrate that, if a target-agent chain is limited by a constraint (Figure 6) such that its position can be expressed by a single coordinate, then the target-agent chain is said to have one degree of freedom. Thus, its possible movements are only those that could be accomplished by heading about the instantaneous translational axis [3].
The general discussion of the quadratic system is a subject of interest for both geometrical and ecological approaches [33] since the locus of the intersection P forms a circle with a diameter CD (Figure 1(a)). We begin by introducing
U ( C P , D P ) = C P 2 + D P 2 − C D 2 = 0 ,
which is the homogeneous relation of the circle between two coordinates of CP and DP of the paths. These constitute a quadratic one-DOF system. Let CP and DP denote any rays other than AP and BP and chosen from the enclosing two-DOF system from which the rays of the quadratic one-DOF system are selected by the condition U = 0.
Then, adopting the fertile method of investigation introduced by Joachismthal [3,34], we substitute λU = 0 for CP and DP the respective values
λ 1 B P 1 + λ 2 A P 1   and   λ 1 B P 2 + λ 2 A P 2 ,
which yields
λ 1   2 U B P + λ 1 λ 2 U B P , A P + λ 2   2 U A P = 0
with
U B P , A P = A P 1 ∂ U B P ∂ B P 1 + A P 2 ∂ U B P ∂ B P 2 ,
Solving this quadratic equation for λ1/λ2, we obtain two values. If the two rays AP and BP had been selected to satisfy the condition
U B P , A P = A P 1 ∂ U B P ∂ B P 1 + A P 2 ∂ U B P ∂ B P 2 = 0
then the roots of the quadratic are equal, but with opposite signs.
If the condition UBP,AP = 0 is satisfied by the coordinates of two rays, AP and BP, which belong to the enclosing two-DOF system, then these two rays and the other two rays lying on the pencil of (AP, BP), which also belong to the quadratic one-DOF system U = 0, will be parallel to the four rays of a harmonic pencil. An inspection of equation (7) reveals that there is a linearly dependent ray along each of the CP- and DP-axes (Figure 3(a)), corresponding to λ1 – λ2 = 0 and λ1 + λ2 = 0, respectively.
Because CP and DP are centrally located in the system and have other unique properties, Ball [3] called them the principal screws (rays) of the system. It is evident that the principal rays exploring the infinitesimal neighborhood must have the same value (to the first order), which means that the virtual displacements are reversible and symmetric, i.e., the given constraints of the rays CP and DP do not prevent us from changing an arbitrary δAP into –δAP [35].

2.3. Harmonic Cross-Ratio Model with Constant Ratios and Proportions

Just as the length of a line segment is the key to metric geometry, there is a fundamental concept of projective geometry in which all the distinctive properties of projective figures can be expressed [36]. Shape constancy depends on perspective, and the visual system operates on the projective principle of perspective. For James Gibson, the equality of cross-ratios implies shape constancy [37]. Followers of James Gibson have proposed that the cross-ratio, a projective invariant for four collinear points, underlies the perception of objects in motion [38]. According to the seminal discovery of projective geometry, if we have four points A, C, B, and D on a straight line and project them onto A´, B´, C´, and D´ on another line, then there is a specific property of the four points, called the cross-ratio, which retains its value under the projection. The cross-ratio is neither a length nor the ratio of two lengths but the ratio of two such ratios. For instance, for two ratios, AC/BC and AD/BD, the cross-ratio is given by
A ,   B ;   C ,   D = A C ⋅ B D B C ⋅ A D ,
where the sign of a length is taken appropriately after fixing a specific orientation of the line. If a straight line CD is divided internally at B and externally at A in the same ratio A , B ; C , D = − 1 , then the segment CD is said to be harmonically divided at A and B, and each of the points A and B is called the harmonic conjugate of the other, with respect to the pair C and D. The harmonic division symmetry is a remarkable property. Namely, if C and D divide AB harmonically, then A and B also divide CD harmonically, reinforcing each other.
The problem of intercepting a target that moves in the horizontal plane is conceived as the cross-ratio of four coplanar (i.e., lying in a common plane) and concurrent straight lines PA, PB, PC, and PD, namely, the four points of intersection cross-ratio of these lines with another straight line lying in the same plane (Figure 4). For an arbitrary point P and a harmonic range [11], the lines PA, PB, PC, PD are said to form a harmonic pencil, a linear line space where paths are centrally placed at the point P. Line space denotes a set where linear combinations also locate lines in the set [39].
Equivalent to equation (8) is the definition
A ,   B ;   C ,   D = sin ∠ APC sin ∠ APD ⋅ sin ∠ BPD sin ∠ BPC ,
where the cross-ratio depends only on the angles subtended by the connecting segments A, B, C, and D at P. Since these angles are the same for any four points A´, B´, C´, and D´ into which A, B, C, and D can be projected from P, it follows that the cross-ratio remains invariant by projection. The problem of intercepting a target moving parallel to the ground plane is ubiquitous in animal locomotion. It involves at least three separable phenomenal motions, called transformations. The first (translation along the line of sight) is called expansion or contraction; the second is translation to the right or left; and the third is rotation about a vertical axis (indicated by arrows in Figure 4) [10]. The coordination of the self-motion direction and speed when intercepting a target moving parallel to the ground plane can be modeled as a plane pencil of screws, a typical line space (Figure 4).
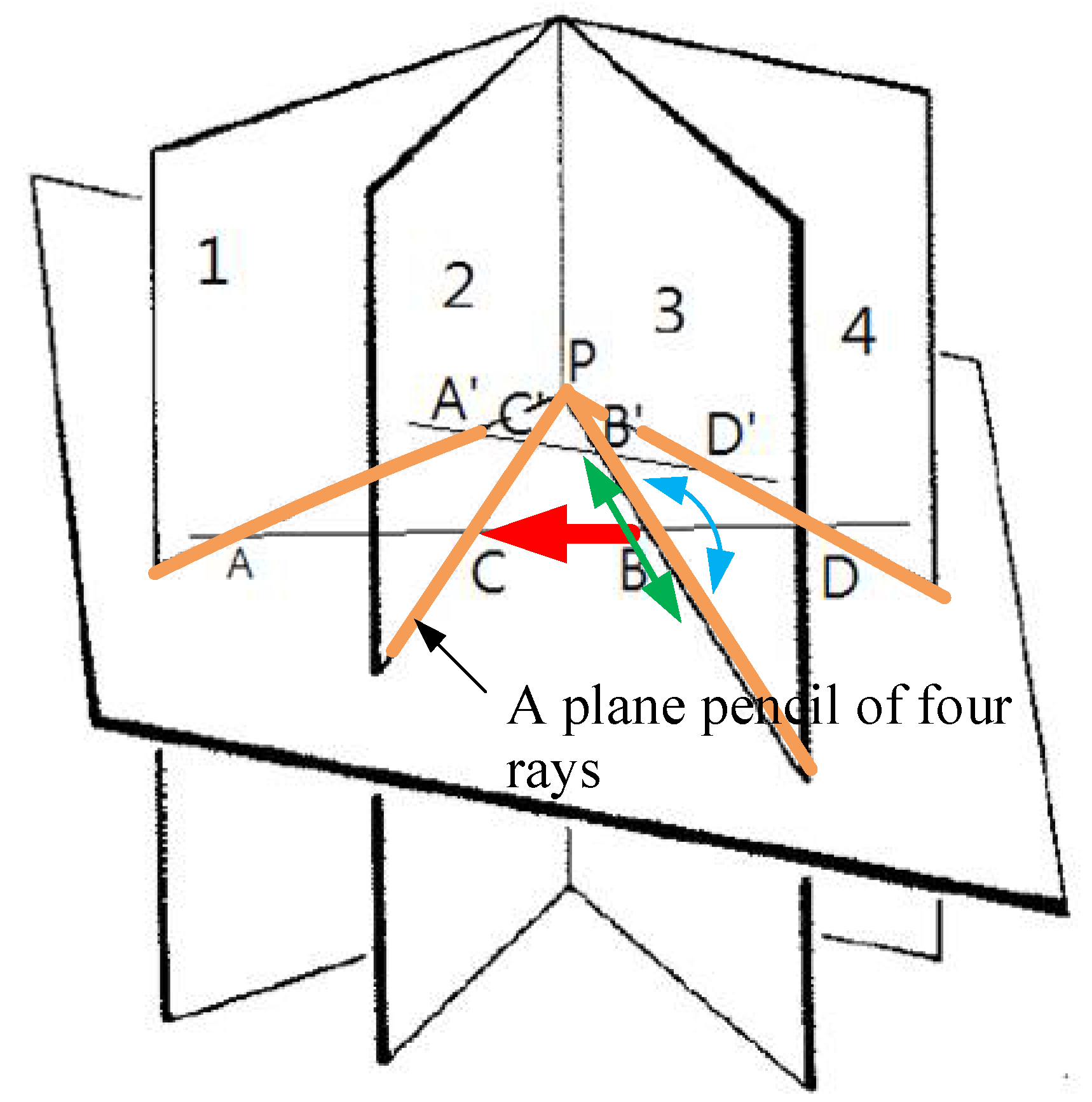
Preprints 107752 g004
Figure 4. Cross-ratio of coaxial planes for the problem of intercepting a target that moves in a horizontal plane. Patterns of optic flow by translation along the line of sight are called expansion or contraction; second, the translation right or left; and the rotation around a vertical axis. Three are indicated: translation along the line of sight (BC), translation right or left (BB´ on plane 3), and rotation around a vertical axis [40].
Figure 4. Cross-ratio of coaxial planes for the problem of intercepting a target that moves in a horizontal plane. Patterns of optic flow by translation along the line of sight are called expansion or contraction; second, the translation right or left; and the rotation around a vertical axis. Three are indicated: translation along the line of sight (BC), translation right or left (BB´ on plane 3), and rotation around a vertical axis [40].
Preprints 107752 g004

2.4. Cross-Ratios at Infinity

Cross-ratios at infinity provide a pivotal framework for understanding perspective and motion in dynamic environments. Drawing on the behavior of a dragonfly that uses a fixed visual reference to intercept prey, we explore how cross-ratios can define and enhance our understanding of motion perception in more complex settings [41]. For instance, maintaining a consistent trajectory in human navigation requires compensation for body motion, typically through visible landmarks or internal sensory feedback [14].
The concept of a motion perspective offers a sophisticated means of describing the optic array from a moving viewpoint. This perspective is crucial when analyzing objects aligned along a common visual path, where the cross-ratio — the projective invariant — becomes essential. It allows us to distinguish between different perspectives by maintaining consistent geometric relations despite changes in the observer’s position.
When we come to a figure consisting of collinear tetrads, {A,B;C,D}, we have for the first time a metric characteristic, the cross-ratio of the points, which is a projective invariant enabling us to discriminate in perspective, as shown in Figure 4. However, the motion perspective has been analyzed for an optic array at an unoccupied observation point, marked as the perception of two rays, CP and DP.
One critical method for capturing accurate motion perspectives involves utilizing the vanishing limit, an advanced technique in which all parallel lines within the optic array converge. This approach not only aids in navigation and orientation but also ensures that the perceived environment remains stable and consistent, regardless of the observer’s motion [2]. For example, eye movements or head movements do not alter this basic pattern but merely superimpose a certain amount of flow around the equator or a vanishing limit.
Therefore, cross-ratios involving elements at infinity should be considered. By perceiving geometric figures as capable of continuous variation, we can make them less sharp in the following ways. This phenomenon is illustrated in Figure 5, where the theoretical intersection disappears if line l becomes parallel to line AB, challenging our perception of space and motion. Cross-ratios involving elements at infinity are particularly valuable in scenarios where geometric elements extend beyond the visible landscape, such as in urban planning or astronomy simulations. By understanding how these ratios function, particularly in how they cause distant objects to interact perceptually, designers can create more realistic and engaging virtual environments.
In practical terms, as one line intersects another and gradually adjusts to become parallel, the intersection point recedes toward infinity, illustrating the continuous nature of space and perception [18]. Figure 5 also shows how the cross-ratio adjusts as elements reach infinity, altering our perception of distance and orientation. This has profound implications for virtual reality systems, where understanding and manipulating these ratios can significantly enhance the user’s experience by providing a more stable and coherent visual field.
We have mentioned that the point pairs (A, B) and (C, D) are harmonic if A , B ; C , D = − 1 . This means that there exists an invariant representation in which the four points have parameters 1 , − 1 ; 0 , ∞ in Figure 5. Let the symbol ∞ mark the infinity point on a straight line l. If A, B, and C are three ordinary points on l, we can assign a value to their ratio in the following way: Choose a point D on l; then A , B ; C , ∞ should be the limit approached by A , B ; C , D as D recedes to infinity along l. If A , B ; C , ∞ = − 1 , then C is the midpoint of the segment AB (Figure 5). The midpoint and the infinity point in the direction of a segment divide the segment harmonically [6].
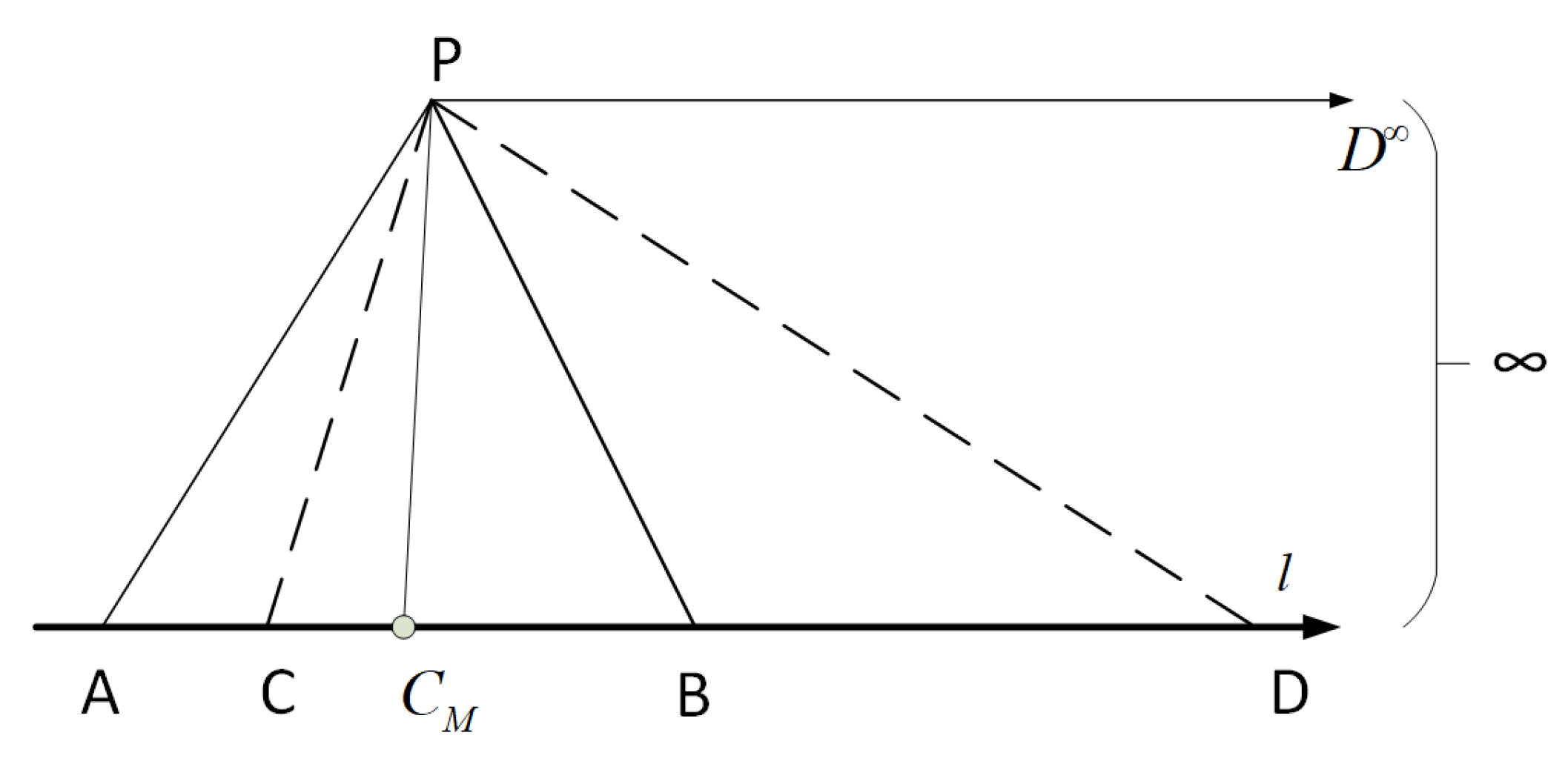
Preprints 107752 g005
Figure 5. Cross-ratio with elements at infinity, where one pole reaches infinity. The interceptor uses two sources of information: optical flow generated by taking the path A D ∞ and optical flow generated by taking the route CMP. The perception with covariation is different from either of the two information sources without covariation [42].
Figure 5. Cross-ratio with elements at infinity, where one pole reaches infinity. The interceptor uses two sources of information: optical flow generated by taking the path A D ∞ and optical flow generated by taking the route CMP. The perception with covariation is different from either of the two information sources without covariation [42].
Preprints 107752 g005
To refer to the flow pattern that informs about a stable environment, take the point at infinity as a point of the cross-ratio reference. The arrangement shown in Figure 6, where elements such as CP and the line l form the principal axes of a system, illustrates how dynamic adjustments based on cross-ratios can facilitate complex interactions within a controlled environment. These configurations allow for precise control over the movement and interaction of objects in virtual spaces, optimizing both the aesthetic and functional aspects of the environment.
In essence, the role of cross-ratios at infinity is not merely theoretical, but of substantial practical application in enhancing how we interact with and perceive virtual and augmented realities. By exploiting these projective invariants, we can create more immersive and navigable environments that closely mimic the real world or offer new ways of experiencing space that are not possible in physical settings. The interception paths are synthesized by a four-bar link connected by a slider-pin joint model. The dynamical link (equations of constraint) selectively reduces the number of independently controlled DOFs, allowing a rich set of trajectories (Kelso and Tuller 1984). The configuration allows link l to move only parallel to the agent’s line of sight, since it is equal to the line l defined in Figure 5. The configuration shows a trapezoid AA´B´B, where AB is parallel to A´B´. If C and C´ are the midpoints of AB and A´B,´ respectively, the lines AA,´ CC,´ and BB´ are all coincident at P. It is necessary to displace the agent along with the desired path CC´ without disturbing the path AB approach mapping (Figure 6). Displacements around the two rays of the principal screws achieve this. Perception with covariation is different from either source of information without covariation [42].
As noted already, CP and the line l are called the principal screws (rays). Inspection of equation (5) reveals that there is a linearly dependent screw along each of the x- and y-axes (Figure 6), corresponding respectively to
λ 2 = λ 1 λ 2 = − λ 1 .
Equation (10) shows that the corresponding velocity of the agent, along with CC´ is equal to the target. In contrast, the velocity of the agent along AB is equal and opposite to the target. Then let the axis of the optic flow used by the agent’s line of sight be considered as the central line for the flow pattern during the agent’s approach to the target object. The flow pattern is now referred to as two rays, CP and AB, of origin P, i.e., the principal screws (rays) of the system, and the four-bar linkages meet at a common point P, the interception point.
Denoting the velocity components parallel and perpendicular to the line of the sight l as V A / l and V A / n , respectively, we have the bearing angle β of the pattern given by the ratio of the two components:
V A / n V A / l = tan β
Thus, for the flow pattern, β takes the same value, called the chief parameter of the flow pattern (Figure 6). A motor action normally produces both CP and AB. Together, they have a different meaning than the simple motion of CP and AB, and the particular invariant β, the unity between them, specifies a particular external configuration of the intercept space [42].
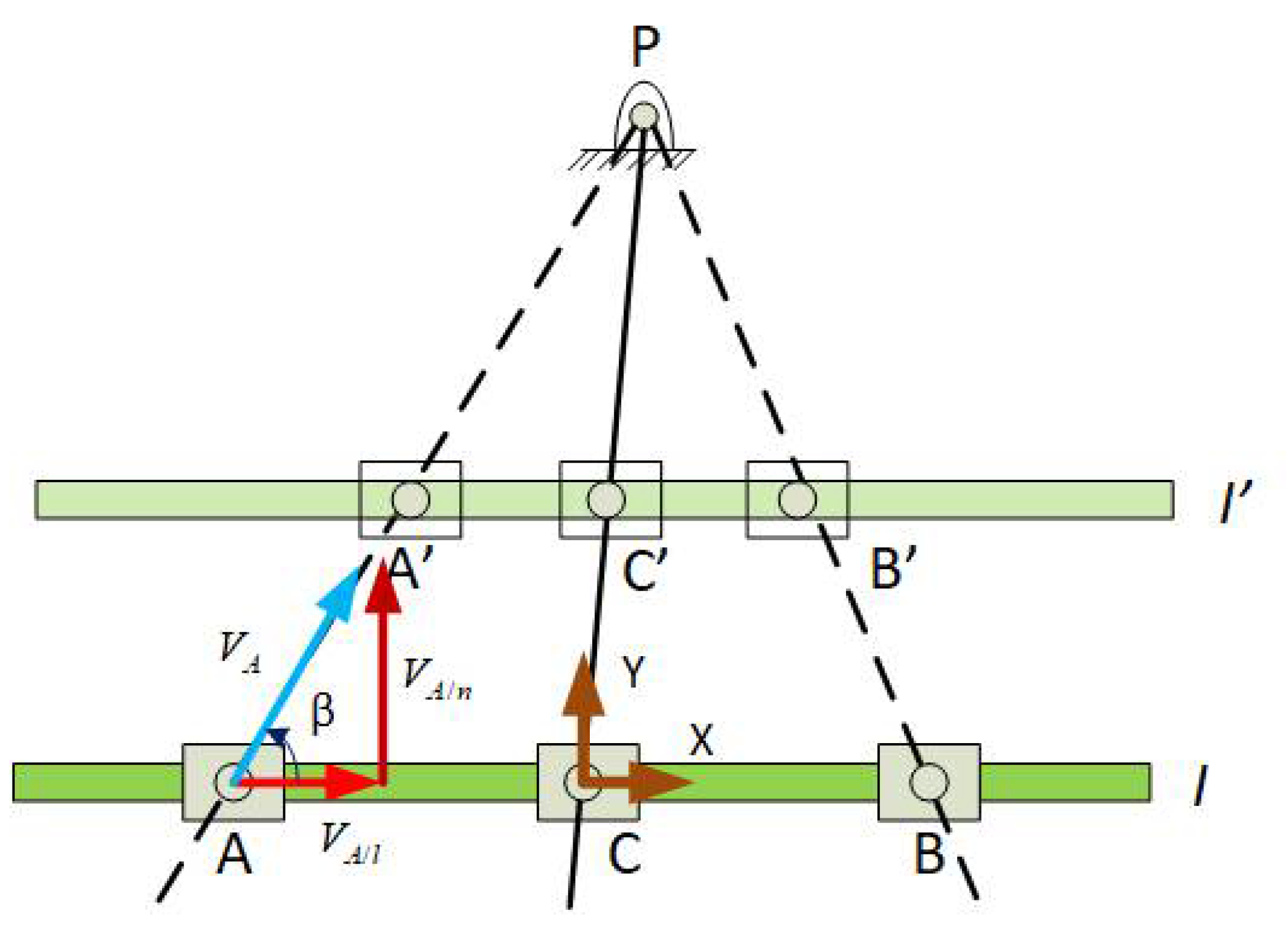
Preprints 107752 g006
Figure 6. Virtual heading chains in a four-bar linkage system. This diagram displays the configuration of virtual heading chains featuring links and a slider pin joint model, with CP and line l centrally positioned at point P. The arrangement demonstrates how dynamic motion and heading are controlled within a virtual environment. The diagram highlights the paths of rays CP and AB, representing the principal screws of the system, and shows how they meet at a common interception point, P. The paths are designed to illustrate how adjustments are made to the agent’s trajectory to maintain a constant bearing angle β, which is crucial for precise object interception in simulated environments. This setup exemplifies the practical application of cross-ratios at infinity, showing how geometric and kinematic constraints are managed to ensure stable and accurate navigational outcomes in virtual reality systems.
Figure 6. Virtual heading chains in a four-bar linkage system. This diagram displays the configuration of virtual heading chains featuring links and a slider pin joint model, with CP and line l centrally positioned at point P. The arrangement demonstrates how dynamic motion and heading are controlled within a virtual environment. The diagram highlights the paths of rays CP and AB, representing the principal screws of the system, and shows how they meet at a common interception point, P. The paths are designed to illustrate how adjustments are made to the agent’s trajectory to maintain a constant bearing angle β, which is crucial for precise object interception in simulated environments. This setup exemplifies the practical application of cross-ratios at infinity, showing how geometric and kinematic constraints are managed to ensure stable and accurate navigational outcomes in virtual reality systems.
Preprints 107752 g006

3. Results

3.1. Perception and Action Coupling in Virtual Environments

Our study validates the intricate coupling of perception and action as outlined by Gibson’s theory, within virtual environments. D’Alembert’s Principle, addressing virtual displacements within a system, played a crucial role in our analysis. This principle states that although the displacement is potential and theoretical, it effectively contributes to maintaining the equilibrium of the interception system where both pursuer and fugitive remain stationary relative to each other at any specific instant. Consequently, at such instants, the actual motion of the agent is disregarded, aligning with theoretical considerations (Lanczos 2012). [35] (see Figure 9(a) below). This foundational understanding guided our experimental validations.
We utilized previously published datasets to validate our model, which simulates the perception dynamics within a four-ray pencil during interception tasks. The experimental setup demonstrated that perception in virtual environments is inherently tied to possible actions. Experiments were conducted in the Virtual Environment Navigation Lab (VENLab) at Brown University, where participants navigated a 12 m x 12 m area within an immersive virtual environment designed by WorldViz, CA, USA. This environment was crafted to elicit nuanced postural responses and directional headings [14]. Adjustments were made to the head-mounted display (HMD) to accommodate the interocular distances of the participants, ensuring accurate data capture of the x and z positions as the participants interacted with the virtual targets, designated as room posts.

3.2. Action Shaping Perception

The actions taken by participants continuously shaped their perceptual experience within the virtual environment. As they moved, the feedback provided by the environment refined their perception of affordances. Walking paths and trajectories for two agents were meticulously recorded (see Figures 7 and 8). A quiver plot was employed to display the velocity vectors at various points, illustrating both the actual path taken by the agents and the theoretical path predicted by the model using principal screws (MathWorks MA USA).
From the initial conditions, unique bearing angles β were essential for intercepting targets directly. Alternative angles resulted in spiral paths, suggesting a dynamic interaction between the agents and their environment. This interaction was cyclic and rapid, indicative of exploratory behavior that adjusts until the optimal path is identified based on visual perception maintaining a constant bearing angle β.
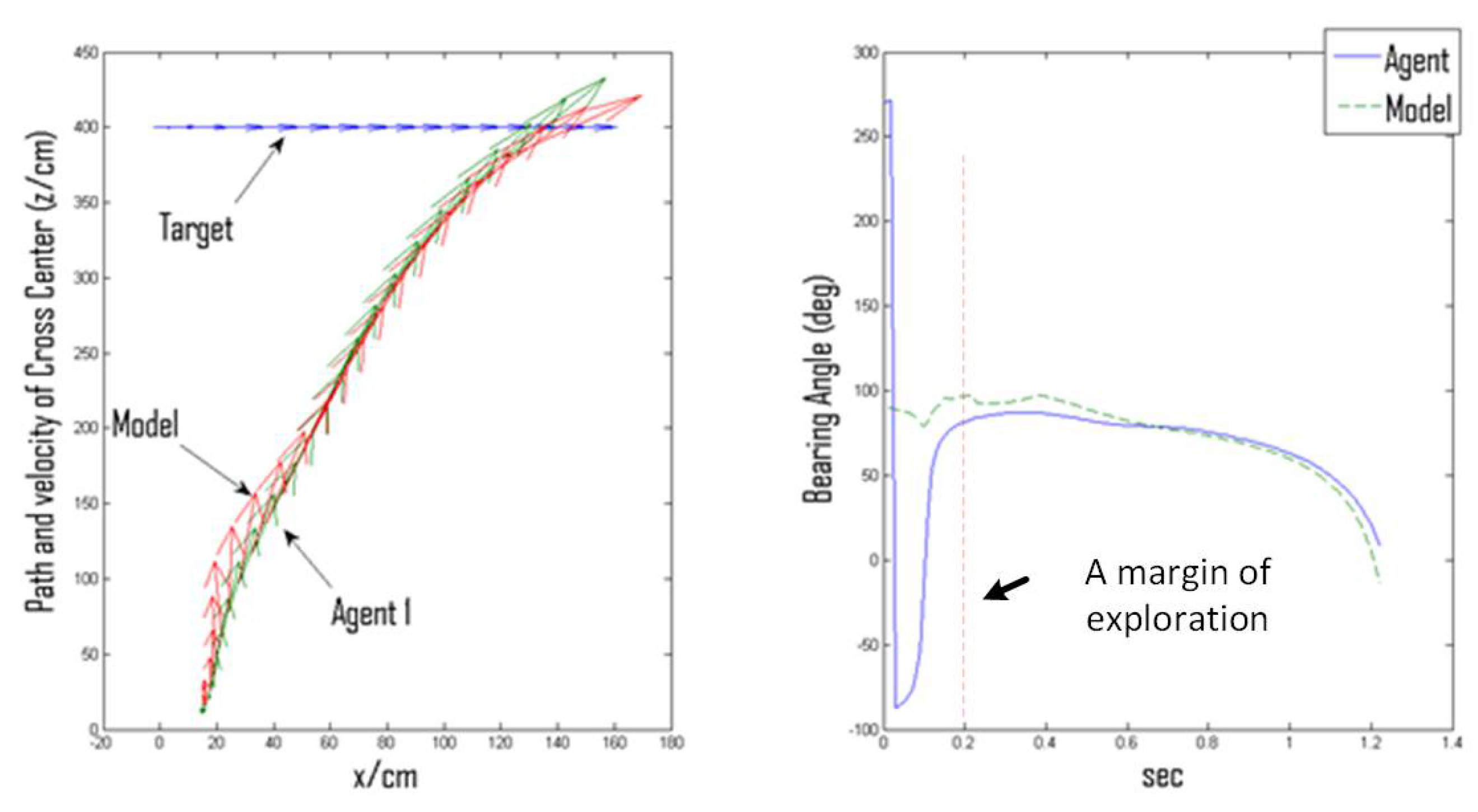
Preprints 107752 g007
Figure 7. (a) Agent 1’s walking paths and model trajectories. (b) The affordance of interception is quantified by the invariant unity of β, reflecting the effectiveness of the interception path as aligned with theoretical predictions.
Figure 7. (a) Agent 1’s walking paths and model trajectories. (b) The affordance of interception is quantified by the invariant unity of β, reflecting the effectiveness of the interception path as aligned with theoretical predictions.
Preprints 107752 g007
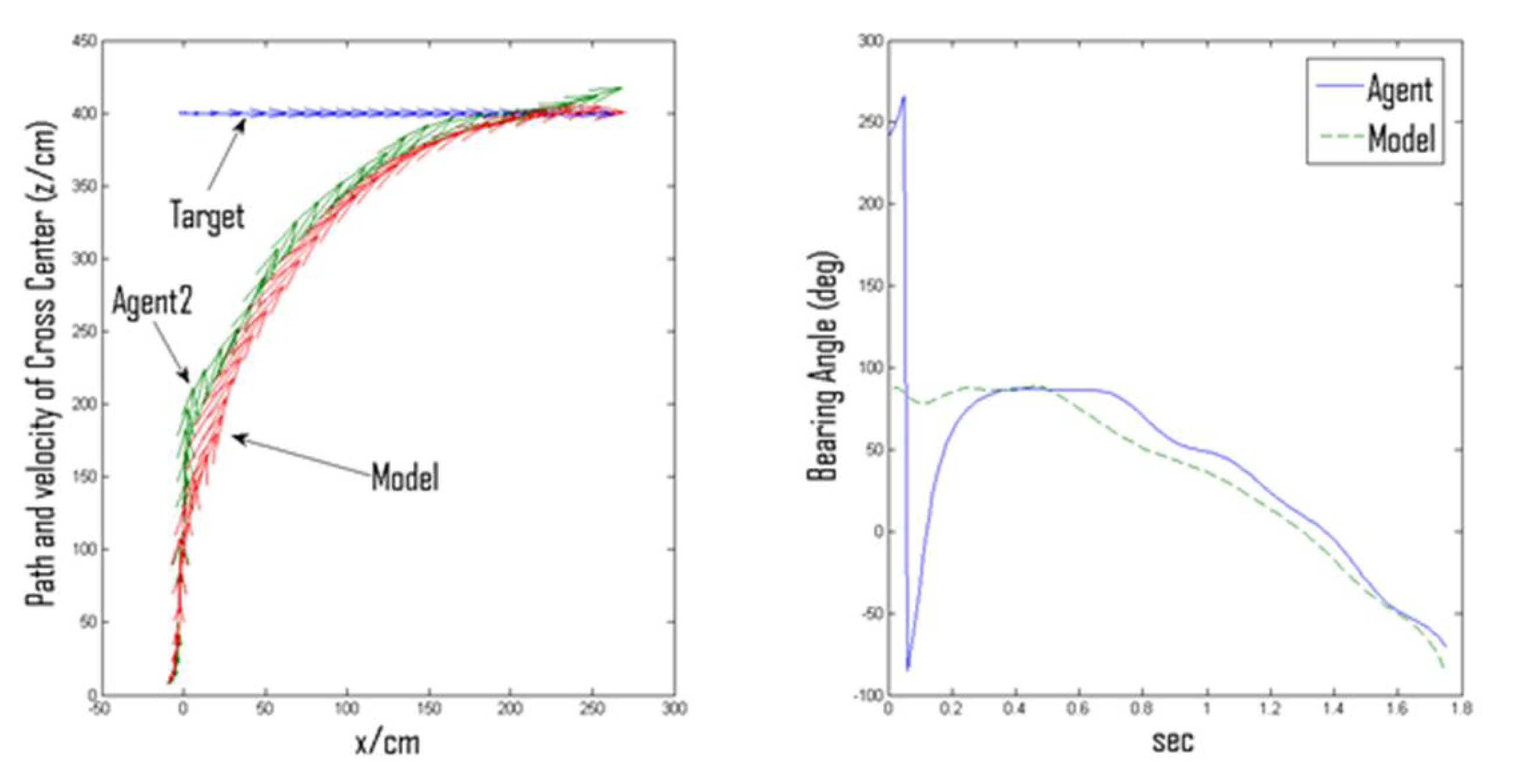
Preprints 107752 g008
Figure 8. Details for Agent 2’s results, similar to those of Agent 1, underscoring consistent findings across different study participants.
Figure 8. Details for Agent 2’s results, similar to those of Agent 1, underscoring consistent findings across different study participants.
Preprints 107752 g008
The paths and bearing angles closely matched the model predictions except for minor deviations during the initial stages of motion exploration. These deviations highlight the agents’ adjustments to perceive and align with the principal rays of the field, steering through complex paths towards optimal interception routes. This supports the idea that action shapes perception, as the continuous interaction with the environment allows the agents to refine their perceptual strategies.
This experimental setup confirmed that while agents do not always follow straight paths, their movements adjust based on the structured affordances (i.e., action possibilities or actionable properties offered by the environment to an animal, Gibson 1979) provided by the virtual environment. These affordances, defined by the coordinating screws of the system, dictate possible behaviors that emerge from the interactions within the system [2]. As theorized by Michael T. Turvey, behaviors manifest when the system’s structures allow, highlighting the interdependence of system design and agent interaction [43].
In conclusion, our results validate D’Alembert’s Principle within virtual environments, demonstrating that virtual displacements, while not physically enacted, play a crucial role in defining the dynamics of interaction and perception in immersive settings. This understanding advances our capability to design virtual environments that more accurately mimic real-world physics and affordances.

3.3. Kinematical Possibilities of Interception: Virtual vs. Actual Directional Heading

The concept of affordance is concerned with potential behavior, rather than actual realization, such as following a straight path. As noted by Lanczos, possible displacements within this context are designated as “virtual displacements” (see Figure 9(a)) [35]. These are intentional displacements that occur within the limits of kinematics and are employed in theoretical models to probe dynamical systems.
Our theoretical framework posits that an interceptor must maintain a consistent pattern within the optic array while transforming this array relative to the substrate, as described by Gibson [44]. To illustrate, consider connecting two hypothetical paths, CP and DP, with any possible trajectory. This chosen path, represented as an arbitrary continuous curve, generally does not align with the interceptor’s actual motion path. Over time, through iterative adjustments, the model path may converge towards the actual motion path, as depicted in Figure 9(b).
The distinction between virtual and actual displacements highlights the core concept of affordance, where virtual displacements represent small, theoretical shifts in position termed "variations" of the position. These variations affect the bearing angle, β, according to the function described in equation 11. Consequently, while we control the variation in position, the resultant change in the function β must be derived independently. In practice, we attempt to align tentative variations of the path, such as ray AP, with the actual displacements that occur over time dt. This alignment process, inspired by Gibson’s notion of an organism’s perceptual system resonating to invariants, involves reinforcing perceptual data to enhance system accuracy [2]. However, the initial application of these variations — applied instantaneously — assumes infinite velocity, which contrasts with the finite velocity of actual movements [35].
These exploratory adjustments facilitate the perceiver’s navigation from disequilibrium toward equilibrium, from a state of perceptual blur to clarity. Gibson characterizes this as a “self-tuning system” that actively seeks informational resonance, enhancing clarity and thus the value of the perceptual experience [42]. This process is crucial for the differentiation of invariant aspects of the environment from those that vary, thus ensuring accurate interaction within virtual settings.
This discussion integrates theoretical constructs with practical implications, elucidating how virtual environments can be meticulously designed to enhance the accuracy and realism of user interactions by leveraging the dynamics of virtual and actual displacements.
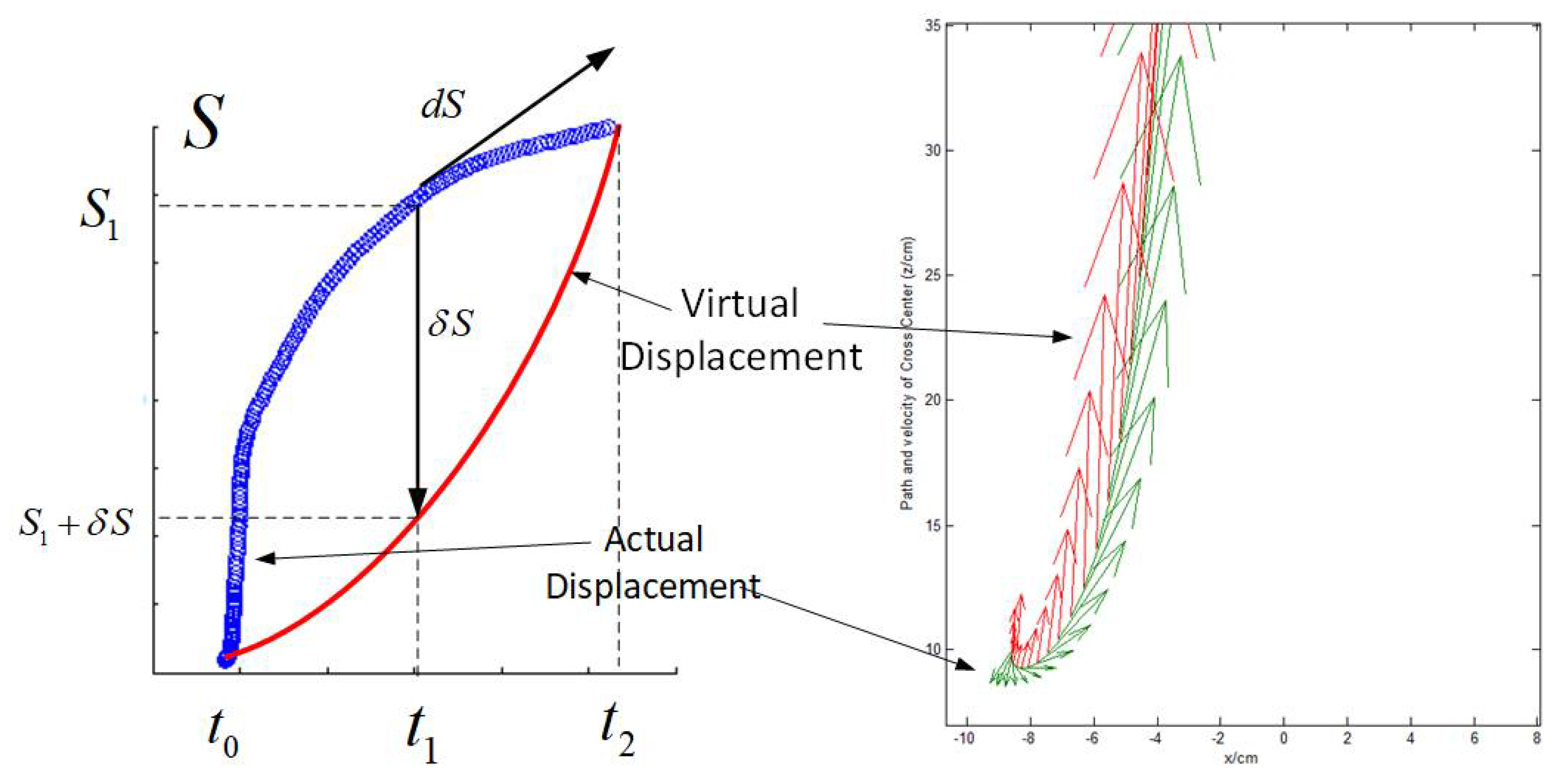
Preprints 107752 g009
Figure 9. (a) For the interception and virtual trajectory at a position S1(t) and time t1. The virtual displacement is designated as δS. The initial and final positions for both trajectories are at t1 and t2, respectively. Lagrange’s ingenious idea was to introduce a unique symbol δ for the process of variations to emphasize its virtual character [35]. The analogy to d recalls that both symbols refer to infinitesimal changes. However, dS refers to an actual change whereas δS refers to a virtual change. In problems involving the variation of definite paths, both types of change should be considered simultaneously, as the distinction between them is vital. (b) The trajectory of Figure 7(a) is extended until 0.2 seconds. The behavioral dynamics dictate that the actual displacements approach the virtual displacements during the time interval dt.
Figure 9. (a) For the interception and virtual trajectory at a position S1(t) and time t1. The virtual displacement is designated as δS. The initial and final positions for both trajectories are at t1 and t2, respectively. Lagrange’s ingenious idea was to introduce a unique symbol δ for the process of variations to emphasize its virtual character [35]. The analogy to d recalls that both symbols refer to infinitesimal changes. However, dS refers to an actual change whereas δS refers to a virtual change. In problems involving the variation of definite paths, both types of change should be considered simultaneously, as the distinction between them is vital. (b) The trajectory of Figure 7(a) is extended until 0.2 seconds. The behavioral dynamics dictate that the actual displacements approach the virtual displacements during the time interval dt.
Preprints 107752 g009

4. Discussion

The present study demonstrates that kinematic invariants, such as the screw theory, play a crucial role in understanding movement within virtual environments. At each instant of an agent’s movement, a unique axis can be identified, suggesting that the motion is characterized by a continuous twist around a screw. This concept aligns not only with the kinematic variables [35] described by Nikolai Bernstein [45], but also with ecological dynamics, which emphasizes the interaction between an agent and its environment through perception and action [16].
Bernstein defined coordination as mastering the many degrees of freedom of a particular movement by reducing the number of variables to control. His idea of reducing the degrees of freedom in movement to master complex actions has been extended in our model to include the interaction dynamics of virtual entities. Our approach models the interception of a moving target along a ground plane as the interaction of four rays within that plane, introducing a non-equilibrium state that challenges traditional physicalist perspectives. This model suggests that all elements, whether they are part of a mechanical system or a living ecosystem, possess equal reality and concreteness.
In our research, we have explored how theoretical constructs manifest in practical scenarios, particularly through understanding dynamic movements in virtual environments. By examining the movements of a baseball fielder to intercept a fly ball, we can gain insight into how environmental affordances shape and direct human actions. This observation shifts our perspective from a simple analysis of particle dynamics to a broader examination of field dynamics [8]. Such insights are invaluable in designing virtual environments that focus on facilitating action rather than merely passive perception. Moreover, our findings suggest that replacing one type of optic flow with another of appropriate speed does not alter the interception dynamics as long as the path involves only a single degree of freedom. This underpins the flexible yet controlled design of interactive virtual simulations [46], which is essential for immersive experiences.
The principle of d’Alembert, integrated with screw theory, enriches our understanding of virtual displacement, offering a valuable educational tool for students exploring the theory of affordances. This principle helps clarify how virtual environments can be designed to enhance the experiential reality by aligning with functional rather than merely visual aspects.
Our study leverages the mathematical constructs of harmonic ratios and stimulation invariants to simulate and predict visually controlled interceptions with unprecedented precision. These mathematical tools are crucial for developing algorithms that not only enhance the realism of virtual environments, but also ensure their functional utility in applications such as sports training, military simulations, and medical rehabilitation. The ecological approach further allows these environments to be more adaptable and sensitive to the perceptual and motor capabilities of individual users, promoting an effective learning and interaction system that is grounded in the ecological dynamics of the real world. This study proposes the implementation of mathematical models with algorithms to enhance the analysis of visual perception and motor action. However, it does not suggest that perception and action are inherently algorithmic in nature.
To clarify, we distinguish between Algorithmic Implementation and Algorithmic Nature:
Algorithmic Implementation: This involves the practical use of algorithms to simulate, predict, and analyze phenomena. In this context, mathematical models and algorithms serve as tools to help us understand and process data related to visual perception and motor action.
Algorithmic Nature: This implies that perception and action themselves are driven by algorithmic processes, which can be an oversimplification. Perception and action are often emergent properties of complex biological systems that involve both deterministic and stochastic elements.

5. Conclusions

The application of the anharmonic ratio in our study illustrates a methodology for synchronizing the movements of a target and an agent, analogous to integrating forces in a parallelogram of force. This approach constitutes a closed system of interception dynamics, wherein the virtual displacements of elements are in symmetrical harmony, thereby leading to the formation of a stable interaction system.
Furthermore, the cross-ratio, or double ratio, proves fundamental in maintaining the integrity of projective transformations in virtual environments. In contrast to traditional Euclidean measurements, which focus on distances and lengths, the cross-ratio provides a projective measure that remains invariant under perspective transformations. This is crucial for maintaining consistent spatial relationships in dynamic virtual scenes.
Our research confirms that the cross-ratio is not only a theoretical invariant, but also a practical tool that ensures the realism and accuracy of virtual interactions. By demonstrating that the anharmonic ratio is a fundamental geometric method capable of guiding the interception processes, we show that it is possible to achieve harmonic resonance within the system, where all inputs and outputs align perfectly with the external conditions. This understanding is of paramount importance for the advancement of the design and functionality of VR and AR systems, ensuring that they are both immersive and responsive to user actions. This study aims to elucidate the intricate interrelationship between geometry, perception, and technology in understanding and employing cross-ratios at infinity, with a particular focus on their practical applications in virtual and augmented reality settings.

Author Contributions

Conceptualization, W.K.; writing—original draft preparation, W.K.; formal analysis, W.K.; writing—review and editing, D.A.; writing—review and editing, M.C.; writing—review and editing, A.V.; writing—review and editing, E.O.; funding acquisition, E.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by PROCIENCIA under contract N° PE501080681-2022-PROCIENCIA Proyectos Especiales: Proyectos de Investigadores Visitan. In addition, the authors acknowledge the support from The MIT-Peru UTEC Seed Fund, awarding the project titled "Development of Proper Tunnel Syndrome Placement Device to Avoid Impingement" and the UTEC Fondo Semilla 2022-2, awarding "Aprendizaje Perceptivo de los Movimientos de las Piernas y Pateo de Infantes con Espina Bífida utilizando un Sistema de Entrenamiento de Realidad Virtual." In addition, DA was partly funded by Fundação para a Ciência e Tecnologia, grant number UIDB/00447/2020 attributed to CIPER–Centro Interdisciplinar para o Estudo da Performance Humana (unit 447); MYC acknowledges the support from the National Research Foundation of Korea (Grant No. 2022R1A2C1012532).

Data Availability Statement

Not aplicable.

Acknowledgments

We thank Professor Brett R Fajen of the Rensselaer Polytechnic Institute and Professor William H Warren of Brown University for making their data available (Grant No. NSF 9720327).

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Matlab script: The harmonic cross-ratio model for interceptive paths
%FILTERING PROGRM ACCORDING Ying Ning’s dynamic filtering algorithm
% produced by W Kim 05/23/2016
%and plotting rtn for quiver velocity and direction
clear all;
%Coords=xlsread(’S15C3_s.xlsx’);
%Coords=xlsread(’fajen_sub1s.xlsx’);
Coords=xlsread(’Sub31_s.xlsx’);
%Coords=xlsread(’Sub35_s.xlsx’);
[m,n]=size(Coords);
b=2;
%m=115;
%%The harmonic cross-ratio model for interceptive paths
for i=1:m
      A=[Coords(i,1);Coords(i,2)];
      AV=[Coords(i,5);Coords(i,6)];
      B=[Coords(i,3);Coords(i,4)];
      BV=[Coords(i,7);Coords(i,8)];
ratio=norm(BV)/norm(AV);
slope=BV(2)/BV(1);
intercpt=B(2)-slope*B(1);
C=norm(BV)*[A;1]+norm(AV)*[B;1];
D=-norm(BV)*[A;1]+norm(AV)*[B;1];
center=C+D;
%radius=sqrt((C(1)/C(3)-center(1)/center(3))^2 + (C(2)/C(3)-center(2)/center(3))^2);
radius=norm(center(1:2)/center(3)-C(1:2)/C(3));
[xout,yout]=linecirc(slope,intercpt,center(1)/center(3),center(2)/center(3),radius);
inter=[xout;yout];
inter1=inter-[A,A];
%inserted on 9/1 2017 for the choice
if inter1(1,1) > 0
      Coords(i,10:11)=inter1(:,1)’;
else
      Coords(i,10:11)=inter1(:,2)’;
end
CV=[Coords(i,10);Coords(i,11)]/norm([Coords(i,10);Coords(i,11)]);
CVN=norm(AV)*CV;
Coords(i,10:11)=CVN’;
end
% set m=360
B=5;
%Coord(1:m,:)=[Coords(:,1:2),Coords(:,10:11)];
%Coord(m+1:2*m,:)=[Coords(:,1:2),Coords(:,5:6)];
%Coord(m+1:2*m,:)=[Coords(:,3:4),Coords(:,7:8)];
%quiver(Coords(1:B:n,1),Coords(1:B:n,2),Coords(1:B:n,5),Coords(1:B:n,6));
figure;
%we modified to overlab two plots
subplot(1,2,1)
quiver(Coords(1:b:m,3),Coords(1:b:m,4),Coords(1:b:m,7),Coords(1:b:m,8));
hold on
quiver(Coords(1:b:m,1),Coords(1:b:m,2),Coords(1:b:m,5),Coords(1:b:m,6));
quiver(Coords(1:b:m,1),Coords(1:b:m,2),Coords(1:b:m,10),Coords(1:b:m,11));
hold off
xlabel(’x/cm’);
ylabel(’Path and velocity of Cross Center (z/cm)’);
%quiver(Coord(1:B:2*m,1),Coord(1:B:2*m,2),Coord(1:B:2*m,3),Coord(1:B:2*m,4));
%quiver(Coord(1:B:m,1),Coord(1:B:m,2),Coord(1:B:m,3),Coord(1:B:m,4),.5,’--r’);
%quiver(Coord(1:B:m,1),Coord(1:B:m,2),Coord(1:B:m,3),Coord(1:B:m,4));
%Compute bearing angle
%bearing=heading-target angle
for i=1:m
      headingA(i)=atan2(Coords(i,5),Coords(i,6));%agent haeding
      headingM(i)=atan2(Coords(i,10),Coords(i,11));%model heading
      %measure line of sight%
      acoord=[Coords(i,1) Coords(i,2)];
      tcoord=[Coords(i,3) Coords(i,4)];
      %los=(tcoord-acoord)/norm(tcoord-acoord);
      los=(tcoord-acoord);
      linesight(i)=atan2(los(2), los(1));
      CBM(1,i)=180*(headingA(i)-linesight(i))/pi;
      CBM(2,i)=180*(headingM(i)-linesight(i))/pi;
end
time=[0:0.01:m*001];
subplot(1,2,2)
plot(time(1:m),-CBM(1,:),time(1:m),-CBM(2,:),’--’);
xlabel(’sec’);
ylabel(’Bearing Angle (deg)’);
legend(’Agent’,’Model’);

References

  1. Reed, E.S., Encountering the World: Toward an Ecological Psychology. 1996: Oxford University Press.
  2. Gibson, J.J., The ecological approach to visual perception. 1979: Houghton Mifflin.
  3. Ball, R., A treatise on the theory of screws. 1900: Cambridge University Press.
  4. Ball, R.S., A Treatise on the Theory of Screws. 1998: Cambridge University Press.
  5. Phillips, J., Freedom in Machinery: Volume 1, Introducing Screw Theory. 1984: Cambridge University Press.
  6. Jessop, C.M., Treatise on the Line Complex. 1903: American Mathematical Society.
  7. Gibson, J.J. and L.E. Crooks, A theoretical field-analysis of automobile-driving. The American journal of psychology, 1938. 51(3): p. 453-471. [CrossRef]
  8. Flach, J.M. and J.G. Holden, The Reality of Experience: Gibson’s Way. Presence: Teleoperators and Virtual Environments, 1998. 7(1): p. 90-95.
  9. Warren, W.H., et al., Optic flow is used to control human walking. Nature neuroscience, 2001. 4(2): p. 213-216.
  10. Gibson, J.J. and E.J. Gibson, Continuous perspective transformations and the perception of rigid motion. Journal of Experimental Psychology, 1957. 54(2): p. 129-138. [CrossRef]
  11. Lenoir, M., et al., Intercepting Moving Objects During Self-Motion. J Mot Behav, 1999. 31(1): p. 55-67. [CrossRef]
  12. Lenoir, M., et al., Intercepting moving objects during self-motion: effects of environmental changes. Res Q Exerc Sport, 1999. 70(4): p. 349-60. [CrossRef]
  13. Diaz, G.J., F. Phillips, and B.R. Fajen, Intercepting moving targets: a little foresight helps a lot. Exp Brain Res, 2009. 195(3): p. 345-60. [CrossRef]
  14. Fajen, B.R. and W.H. Warren, Visual guidance of intercepting a moving target on foot. Perception, 2004. 33(6): p. 689-715. [CrossRef]
  15. Fajen, B.R. and W.H. Warren, Behavioral dynamics of intercepting a moving target. Experimental Brain Research, 2007. 180(2): p. 303-319. [CrossRef]
  16. Araújo, D., K. Davids, and R. Hristovski, The ecological dynamics of decision making in sport. Psychology of Sport and Exercise, 2006. 7(6): p. 653-676. [CrossRef]
  17. Chapman, S., Catching a Baseball. American Journal of Physics, 1968. 36(10): p. 868-870.
  18. Courant, R., H. Robbins, and I. Stewart, What is mathematics? : an elementary approach to ideas and methods. 2nd ed. 1996, New York: Oxford University Press. 566 p.
  19. Zhao, H. and W.H. Warren, Intercepting a moving target: On-line or model-based control? Journal of vision, 2017. 17(5): p. 12-12.
  20. Stepp, N. and M.T. Turvey, On strong anticipation. Cognitive systems research, 2010. 11(2): p. 148-164.
  21. Wilson, M., Physics Avoidance: and other essays in conceptual strategy. 2017: Oxford University Press.
  22. Lange, M., The principle of virtual work, counterfactuals, and the avoidance of physics. European Journal for Philosophy of Science, 2019. 9(3): p. 33.
  23. Gibson, J.J., The perception of the visual world. 1974, Westport, Conn.: Greenwood Press. xii, 235 p.
  24. Blake, R., Gibson’s inspired but latent prelude to visual motion perception. Psychol Rev, 1994. 101(2): p. 324-8.
  25. Warren Jr, W.H., Visually Controlled Locomotion: 40 years Later. Ecological Psychology, 1998. 10(3-4): p. 177-219.
  26. Turvey, M.T., et al., Ecological laws of perceiving and acting: in reply to Fodor and Pylyshyn (1981). Cognition, 1981. 9(3): p. 237-304.
  27. Kelso, J.A.S., Dynamic Patterns: The Self-organization of Brain and Behavior. 1995: MIT Press.
  28. Kim, W., et al., Affordance-Based Surgical Design Methods Considering Biomechanical Artifacts. Ecological Psychology, 2020: p. 1-15.
  29. Seifert, L., et al., Neurobiological degeneracy: A key property for functional adaptations of perception and action to constraints. Neuroscience & Biobehavioral Reviews, 2016. 69: p. 159-165.
  30. Thelen, E., Motor development. A new synthesis. Am Psychol, 1995. 50(2): p. 79-95.
  31. Shaw, R.E. and M. Turvey, Ecological foundations of cognition. II: Degrees of freedom and conserved quantities in animal-environment systems. Journal of Consciousness Studies, 1999. 6(11-12): p. 111-124.
  32. Shaw, R.E., J.M. Kinsella-Shaw, and W.M. Mace, Affordance types and affordance tokens: Are Gibson’s affordances trustworthy? Ecological Psychology, 2019. 31(1): p. 49-75.
  33. Henrici, O., The Theory of Screws1. Nature, 1890. 42(1075): p. 127-132.
  34. Semple, J.G. and G.T. Kneebone, Algebraic Projective Geometry. 1952: Clarendon Press.
  35. Lanczos, C., The variational principles of mechanics. 2012: Courier Corporation.
  36. Courant, R. and H. Robbins, What is Mathematics? An elementary approach to ideas and methods. 1941, London, New York etc.: Oxford university press. 3 p. l., v-xix, 521 p.
  37. Emmer, M., The visual mind II. 2005: MIT press.
  38. Simpson, W.A. The cross-ratio and the perception of motion and structure. in Proc. of the ACM SIGGRAPH/SIGART interdisciplinary workshop on Motion: representation and perception. 1986.
  39. Griffis, M. and J.M. Rico, The nut in screw theory. Journal of Robotic Systems, 2003. 20(8): p. 437-476.
  40. Gibson, J.J. and E.J. Gibson, Continuous perspective transformations and the perception of rigid motion. Journal of Experimental Psychology, 1957. 54(2): p. 129.
  41. Olberg, R.M., A.H. Worthington, and K.R. Venator, Prey pursuit and interception in dragonflies. Journal of Comparative Physiology A, 2000. 186(2): p. 155-162.
  42. Gibson, J.J., The senses considered as perceptual systems. 1966, Boston: Houghton.
  43. Turvey, M.T., Ecological foundations of cognition: Invariants of perception and action, in Cognition: Conceptual and methodological issues. 1992, American Psychological Association: Washington, DC, US. p. 85-117.
  44. Gibson, J.J., Visually controlled locomotion and visual orientation in animals. Br J Psychol, 1958. 49(3): p. 182-94.
  45. Bernstein, N.A., The co-ordination and regulation of movements. 1967: Pergamon Press.
  46. Rheingold, H., Virtual reality: exploring the brave new technologies. 1991: Simon & Schuster Adult Publishing Group.
Preprints 107752 g001
Figure 1. (a) Illustration of the helicoidal velocity field: A twist of pitch h = τ / ω about an instantaneous screw axis provides a complete description of the velocity of a rigid body. Every point of the body has its velocity vector tangential to the helix that passes through it. This velocity vector pattern is a helicoidal velocity field. (b) The helicoidal field of linear velocity for any point on a rigid body results from general motion. At any moment, the net velocity Vi (i = 1, …, 5) consists of two parts: (1) translational velocity parallel to the screw axis; and (2) tangential velocity representing the rotational body motion about the screw axis.
Figure 1. (a) Illustration of the helicoidal velocity field: A twist of pitch h = τ / ω about an instantaneous screw axis provides a complete description of the velocity of a rigid body. Every point of the body has its velocity vector tangential to the helix that passes through it. This velocity vector pattern is a helicoidal velocity field. (b) The helicoidal field of linear velocity for any point on a rigid body results from general motion. At any moment, the net velocity Vi (i = 1, …, 5) consists of two parts: (1) translational velocity parallel to the screw axis; and (2) tangential velocity representing the rotational body motion about the screw axis.
Preprints 107752 g001
Preprints 107752 g002
Figure 2. Gibson’s representation of the optic flow at moving points of observation: The center of the flow pattern during the animal’s forward movement is the field’s axis. Each vector Vi (i = 1, …, 5) represents the optical motion of the corresponding environmental element. All vectors radiate outward from a focus of expansion in relation to the animal’s virtual heading.
Figure 2. Gibson’s representation of the optic flow at moving points of observation: The center of the flow pattern during the animal’s forward movement is the field’s axis. Each vector Vi (i = 1, …, 5) represents the optical motion of the corresponding environmental element. All vectors radiate outward from a focus of expansion in relation to the animal’s virtual heading.
Preprints 107752 g002
Preprints 107752 g003
Figure 3. Based on a baseball analogy: (a) Trajectories of a catcher (agent) A attempting to intercept the ball (pop up at point B to the infield). There is a point P where the agent catches the ball (B – the interception with the target) via a straight line. This observation suggests a unique interception strategy: Run so that the bearing angle β remains constant [17]. (b) The first step is to construct harmonic poles C and D so that their ratio is given by the ratio of the agent’s speed λ1 to the target’s speed λ2. Next, dropping the new triangle’s internal and external angle bisectors gives the harmonic poles C and D.
Figure 3. Based on a baseball analogy: (a) Trajectories of a catcher (agent) A attempting to intercept the ball (pop up at point B to the infield). There is a point P where the agent catches the ball (B – the interception with the target) via a straight line. This observation suggests a unique interception strategy: Run so that the bearing angle β remains constant [17]. (b) The first step is to construct harmonic poles C and D so that their ratio is given by the ratio of the agent’s speed λ1 to the target’s speed λ2. Next, dropping the new triangle’s internal and external angle bisectors gives the harmonic poles C and D.
Preprints 107752 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated