Prerpints.org logo
Preprint
Article

Pore Structure Characterization and Fractal Characteristics of Tight Limestone Based on Low Temperature Nitrogen Adsorption and Nuclear Magnetic Resonance

Altmetrics

Downloads

76

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 May 2024

Posted:

29 May 2024

You are already at the latest version

Alerts
Abstract
Pore structure characterization and fractal analysis have great significance for understanding and evaluating tight limestone reservoirs. In this work, the pore structure of tight limestone is characterized combined with low-temperature nitrogen adsorption (LTNA) and low-field nuclear magnetic resonance (NMR), and the fractal dimension of tight limestone pore structure is discussed based on LTNA and NMR data. The results indicate that the pores of tight limestone have H3 and H4 types, the pore size distribution (PSD) of H3 type is a wave distribution ranging from 2 to 10 nm, and the PSD of H4 type is a unimodal distribution ranging from 2 to 10 nm. The transverse relaxation time (T2) spectrum of tight limestone shows single peak (DF), double peak (SF) and three peak (TF), and the T2 spectrums for micropores, mesopores and macropores range from 0.1 to 10 ms, from 10 to 100 ms, and greater than 100 ms, respectively. The LTNA fractal dimension of tight limestone (DL) ranges between 2.4446 and 2.7688, with an average of 2.5729, and the NMR fractal dimensions of micropores (DNMR1), mesopores (DNMR2) and macropores (DNMR3) are distributed between 0.3744 to 1.1293, 2.4263 to 2.9395 and 2.6582 to 2.9989, respectively. Moreover, there is no correlation between fractal dimension and permeability and porosity, a negative correlation between DL and average pore radius, a positive correlation between DL and specific surface area, and a positive correlation between DNMR2 and DNMR3 and micropore content, while DNMR2 and DNMR3 are negatively correlated with the content of mesopores and macropores.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Inspired by the economic and efficient development of North American marine tight oil, China began to explore and develop tight oil and gas resources (Hughes 2013; Wang et al. 2017; Hu et al. 2018; Zhou et al. 2019; Shen et al. 2018, 2019). In China, tight oil resources are mainly distributed in the Ordos Basin, Sichuan Basin, and Songliao Basin et al. (Sun et al. 2015; Luo et al. 2019; Guo et al. 2019; Yang et al. 2019; Pang et al. 2019). For example, the tight oil resources are abundant in the Jurassic Da’anzhai Member, Sichuan Basin, and are the typical lacustrine carbonate tight oil resource (Wang et al. 2019). In the development of tight oil, the accurate pore structure characterization of tight reservoir is not only a comprehensive understanding of oil storage space, but also the basis for its efficient development.
At present, there are many techniques for characterizing the pore structure of tight reservoirs, such as scanning electron microscopy (SEM), X-ray Computed Tomography (X-CT), high-pressure mercury injection (HPMI), constant-pressure mercury injection (CPMI), low-temperature nitrogen adsorption (LTNA), and nuclear magnetic resonance (NMR) and so on. Generally, HPMI test is prone to making micro-fractures in rocks due to high mercury entry pressure (Zhao et al. 2015; Wu et al. 2018). At the same time, CPMI test can only characterize the pore ssize distribution above 120nm (Zhao et al. 2019a, b). Tian et al. (2017) used SEM to explore the pore structure of tight limestone in Da’anzhai Member in Jurassic Ziliujing Formation, central Sichuan Basin. He believed that multi-type nano- to micro-meter micropores or microfractures develop in tight limestone. Additionally, Volery et al. (2010) used SEM to study the factors controlling the difference between microporous and tight facies in the tight limestone of the Urgonian Formation of the French Jura Mountains. Liu et al. (2018) analyzed the full-scale distribution map of tight limestone by using capillary pressure curve test data and LTNA experimental data, and compared it with NMR data. They found that the main peak of tight limestone pores in central Sichuan Basin was in the range of 10–50 nm; the average pore diameter was 27–967 nm, and the average was 235 nm. However, their study did not explain how to establish a full-scale map. Zhao et al. (2018) used CPMI test to study the pore size distribution characteristics of tight limestone and tight sandstone in central Sichuan Basin, and also discussed the fractal characteristics of these two types of rocks. He found that the fractal dimension of tight limestone was greater than the fractal dimension of tight sandstone, indicating that the pore structure of tight sandstone was simpler than that of tight limestone.
In this study, LTNA and NMR are employed to characterize the pore structure and pore size distribution of tight limestone. Furthermore, based on LTNA and NMR data, the fractal theory is used to calculate the fractal dimensions of tight limestone pores, and the fractal characteristics of tight limestone pores is discussed. These comprehensive results help to reveal the pore space characteristics of the tight limestone reservoirs.

2. Experiment and Samples

2.1. Experimental Samples

In this study, LTNA experiments and NMR experiments are carried out on the 35 cores collected from the typical tight oil areas of SW, China. In the LTNA experiment, the core porosity ranges from 0.89% to 3.47%, with an average of 1.72%. In addition, the permeability is between 0.00079-0.25×10-3μm2 with an average of 0.03276×10-3μm2. In the NMR experiment, the tight limestone core plug porosity ranges from 0.85% to 3.47%, with an average of 1.61%. The core plug permeability is between 0.00098-0.435 ×10-3μm2 with an average of 0.08009×10-3μm2. Moreover, all of these tight limestone cores come from the same research block. It can be known that these cores are typical tight limestones (Permeability<1×10-3μm2 and porosity<10%). According to the previous study, we can know that the pores of the tight limestone in the target area can be divided into three types: intragranular pores (Figure 1d), intergranular pores (Figure 1e), and microfractures (Figure 1b, f) (Wei, 2018).

2.2. LTNA Experiment

For the analysis on the distribution of micropores and mesopores, LTNA is carried out using USA autosor-6B automatic isothermal adsorption instrument of Quantachrome under 77.35 K and a relative pressure of 0.01–1. In LTNA test, the critical step is to measure the equilibrium pressure (P) and quantity adsorption (V) of nitrogen from a series of given pressures under a constant temperature (T) for generating the isothermal adsorption curve. It can be applied to obtain specific surface areas, as well as pore diameter and pore volume of tight samples by using the BET adsorption isotherm (Brunauer et al. 1938), and determine the pore size distribution curve through the BJH model (Barrett et al. 1951; Haul et al. 1969).

2.3. NMR Experiment

In the NMR experiment, a small RecCore04 low-field NMR core analyzer is used, which was independently produced by the Institute of Porous Flow and Fluid Mechanics, Chinese Academy of Sciences. The specific parameters are set up as follows, main frequency is 3.841 MHz, the echo interval time is 600 μs, the waiting time is 3000 ms, the number of echoes is 1024, the number of scans is 64, the gain is 50, and the experimental ambient temperature is 24 ℃.

3. Fractal Dimension Calculation Method

We apply the Frenkel-Halsey-Hill (FHH) model proposed by PFEIFER et al. (Naveen et al. 2018) to calculate the LTNA fractal dimension of tight limestone (DL).
ln ⁡ V V 0 = A [ l n ⁡ ( l n P 0 P ) ] + C
where, V is the volume of gas molecules adsorbed under equilibrium pressure P, cm3/g; V0 is the volume of monomolecular adsorption gas, cm3/g; P0 is the saturated vapor pressure of gas adsorption, MPa; P is equilibrium pressure, MPa; A and C are undetermined coefficients, and their values are related to the adsorption mechanism of gas molecules. Furthermore, DL is obtained by Equation (2).
D L = A + 3
In the calculations of the NMR fractal dimensions, we refer to the previous practices (Zhang et al. 2014; Wang et al. 2018; Lai et al. 2018; Zheng et al. 2018; Zhang et al. 2019; Li et al. 2019; Chen et al. 2019). Firstly, the relationship between the capillary pressure and the pore radius can be calculated according to the Washburn equation (Mandelbrot et al. 1998):
p c = 2 σ c o s θ r
where pc is the capillary pressure, MPa; σ is the surface tension, N/m; and θ is the contact angle between the water molecules and the surface of the sandstone.
The relationship between the Sv and the pc and pcmin can be calculated according to the Chen et al. equation (Chen et al. 2019).
S V = ( p c p c m i n ) D − 3
where Sv is the volume fraction of pores occupied by a wetting phase when the capillary pressure is equal to Pc, and Pcmin is the capillary pressure corresponding to the maximum diameter, MPa.
The relaxation time T2 can be expressed as follows:
1 T 2 = F s . ρ r
where T2 is relaxation time, ms; Fs is the geometry factor, and r is the pore diameter. For spherical pores, Fs = 3. For a columnar pipe, Fs = 2.
The relationship between the pc and T2 can be calculated as follows.
p c = C 1 T 2
The conversion coefficient C can be expressed as:
C = 2 σ c o s θ F s ρ
Hence:
p c m i n = C 1 T 2 m a x
where T2max is maximum relaxation time, ms.
By substituting Equation (6) and Equation (8) into Equation (4), Equation (9) is obtained:
V c = ( T 2 T 2 m a x ) 3 − D
where Vc is the percent of cumulative pore volume with a transverse relaxation time less than T2 in terms of the total pore volume.
Taking the logarithm of both sides of Equation (9), an approximate fractal geometry formula for the NMR T2 spectra can be expressed as follows:
log ⁡ V c = D − 3 log ⁡ P c − D − 3 log ⁡ P c   m i n
where, D is the fractal dimension, dimensionless; Pc min is the capillary pressure related to the largest pore radius, MPa.

4. Results and Discussion

4.1. LTNA Characterization

The LTNA experiment can quantitatively characterize the pore size distribution and calculate the specific surface area (Ap) of tight limestone. The detailed LTNA test data of the tight limestones is shown in Table 1. Among them, the specific surface area of the rock sample is between 0.11-2.06 m2/g, with an average of 0.76 m2/g. Chen et al. (2019) measured the specific surface area of shale in southwest China between 7.67 m2/g and 26.33 m2/g. It can be seen that the specific surface area of the tight limestone sample is much smaller than the specific surface area of the shale. In other words, the pore throat structure of shale is complex with respect to tight limestone. In addition, the pore radius (ra) of the tight limestone sample is between 8.71 nm and 44.89 nm, with an average of 23.99 nm. Its pore volume (Vc) is between 0.35 and 5.26 mm3/g, with an average of 2.76 mm3/g.
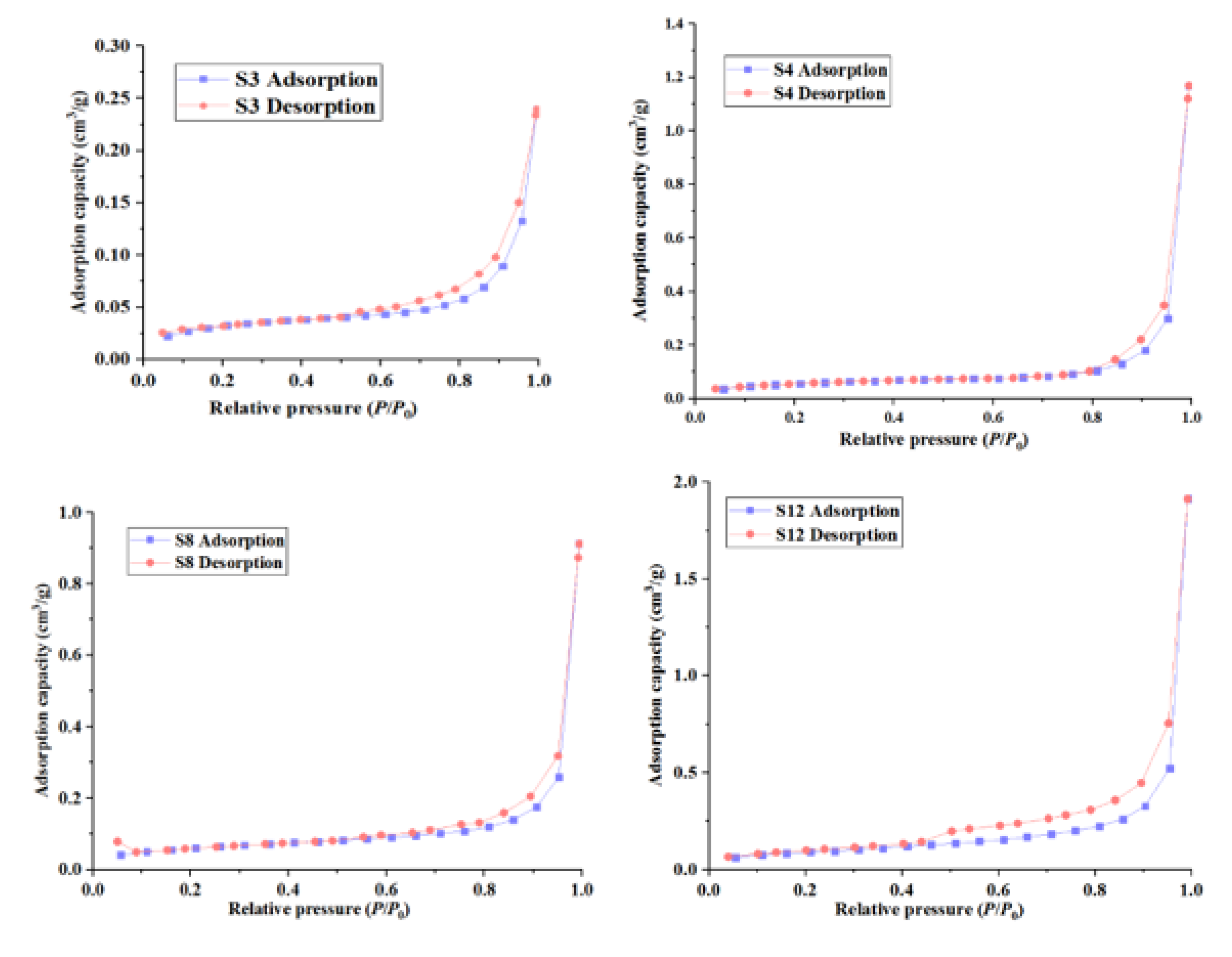
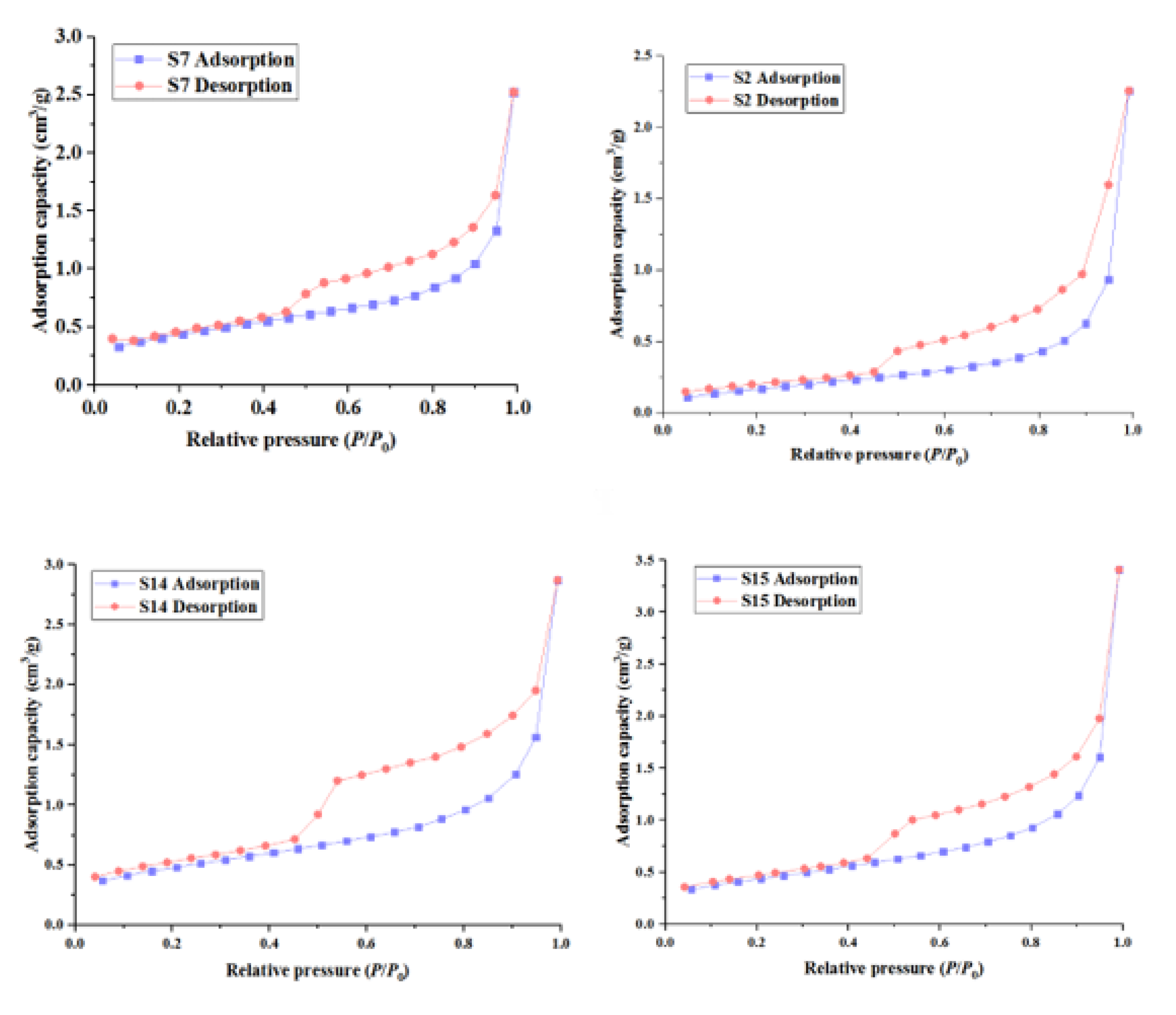
A large number of studies have shown that the shape of the adsorption and desorption curves obtained by LTNA experiments can qualitatively evaluate the pore size distribution of tight rock samples (Ojha et al. 2017; Zhao et al. 2019, 2020). At the same time, based on the IUPAC classification criteria, the isothermal adsorption curves of the tight rock samples in this study block can be divided into two categories (Figure 2) (Thommes et al. 2015). The first type is the H3 hysteresis loop, it mainly includes five rock samples of S3, S4, S8, S11 and S12. In addition, the other 10 tight reservoir rock samples belong to the H4 hysteresis loop. Due to the complexity of tight reservoirs, its pore type is diverse. 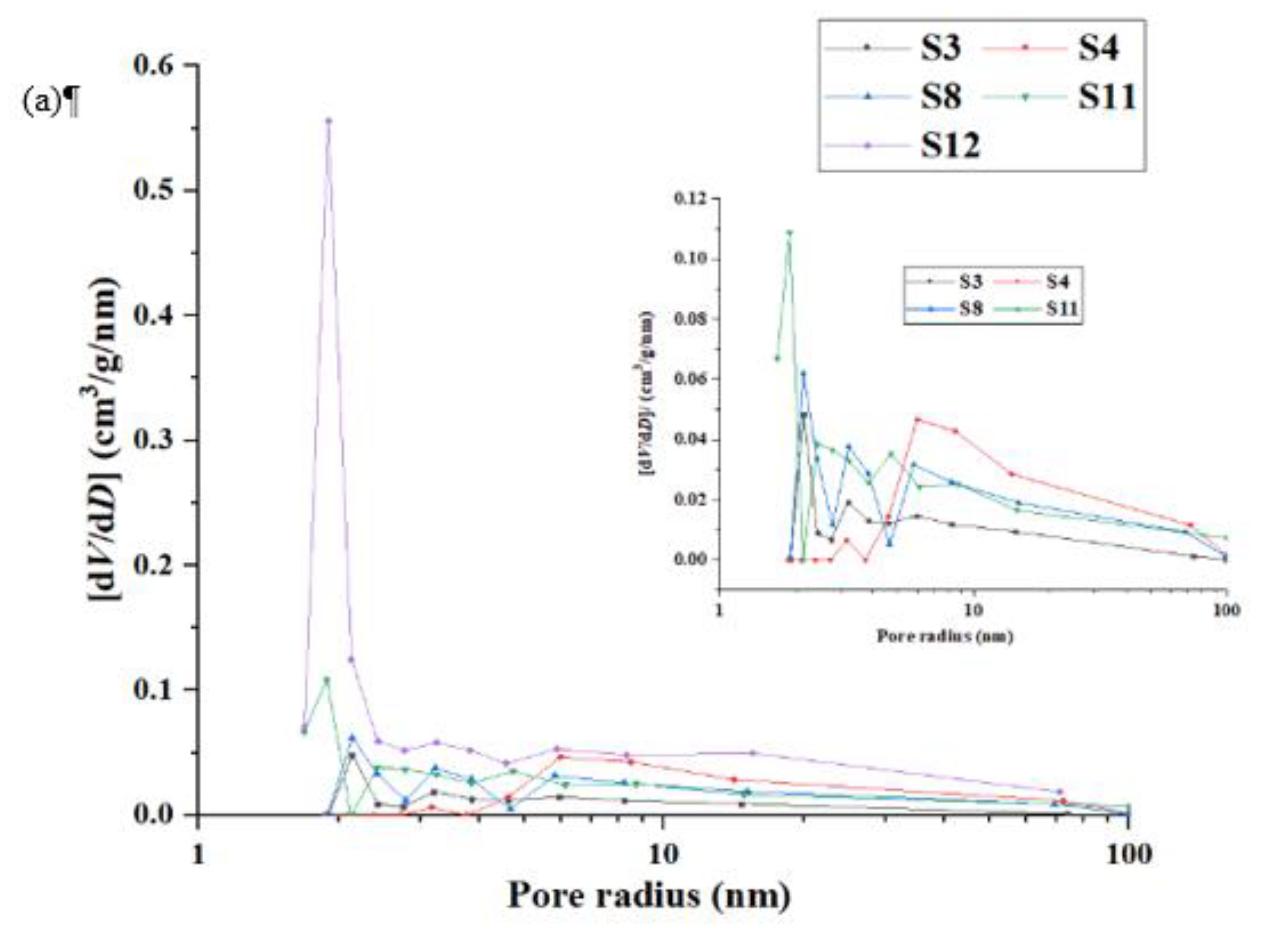It can be seen from Figure 3(a) that the H3 type pore radius distribution is mainly between 2nm and 15 nm. 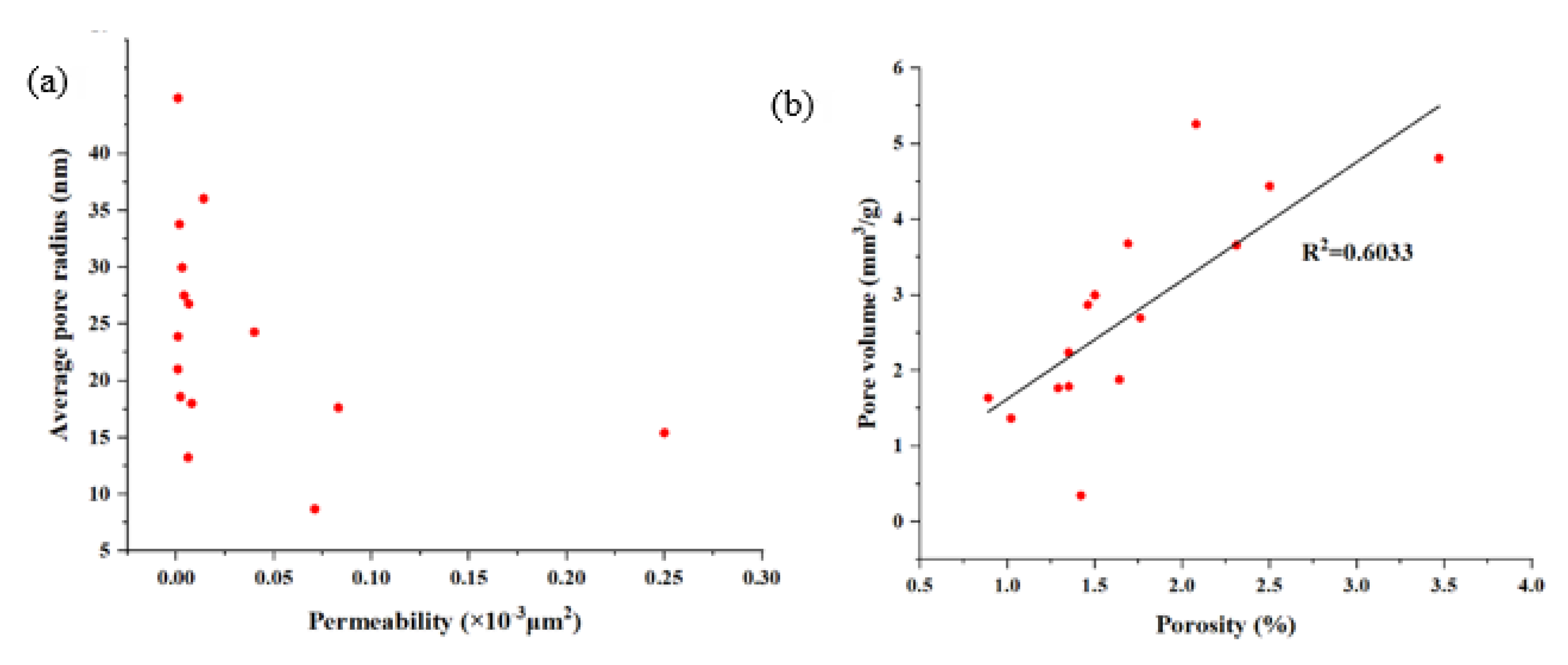The H4 type pore radius is mainly distributed between 1.7nm and 5 nm (Figure 3b). Simultaneously, H3 type samples have multiple peaks, while H4 type samples are single peaks. This indicates that there is a bimodal type of rock sample (H3) whose micropores are more developed. It is worth noting that the permeability decreases as the average pore radius increases (Figure 4a). This suggests that when the pore space of tight oil rock exists in the form of micropores, although micropores provide reservoir space, they do not contribute much to rock seepage capability. In addition, there is a positive correlation between porosity and pore volume (Figure 4b).

4.2. NMR Characterization

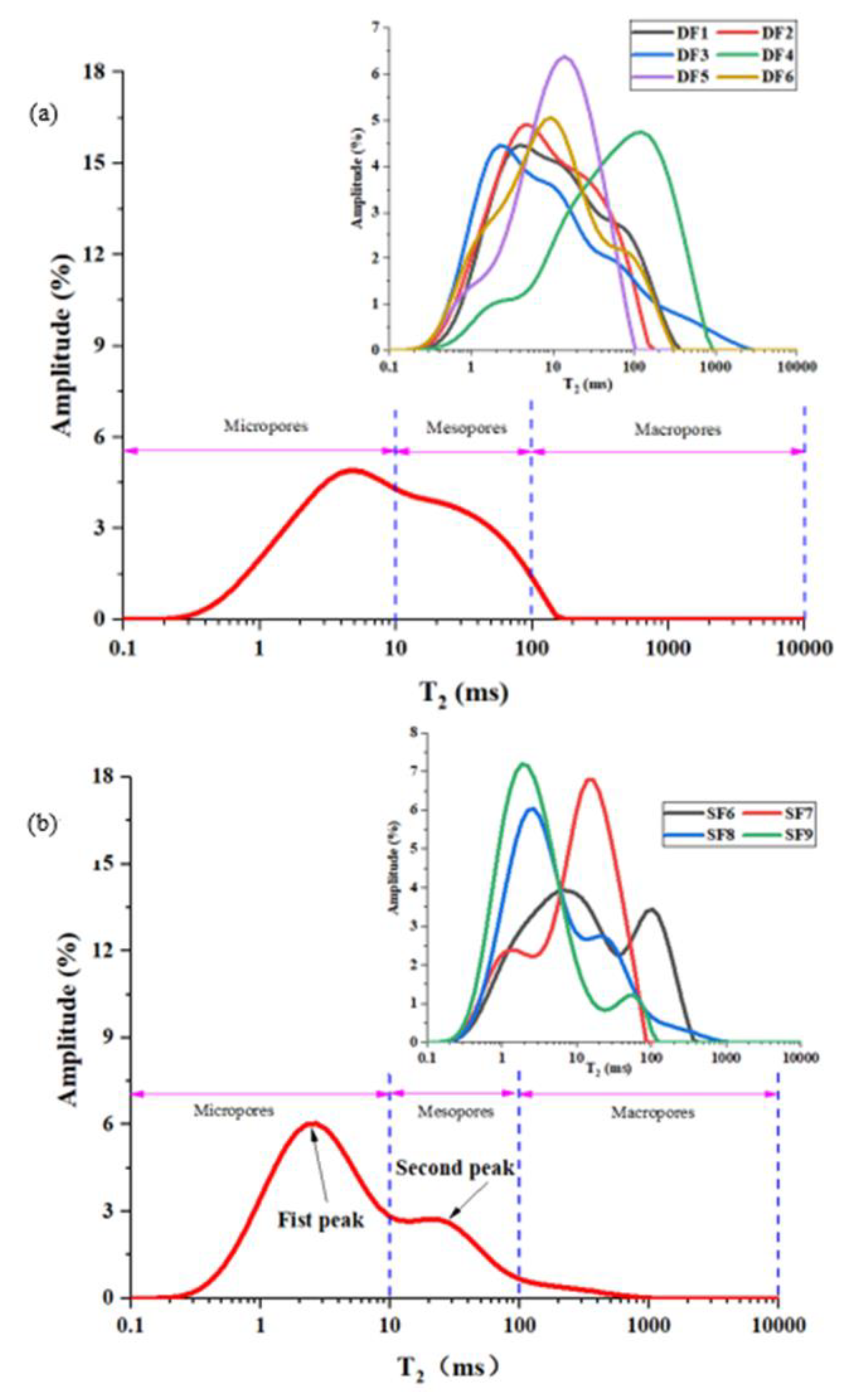
NMR technology has unique advantages in studying the pore structure of tight limestones (eg, non-destructive testing), it obtains the pore size distribution of the core by detecting the relaxation time (T2 spectrum) of the hydrogen protons in core with the 100% saturated water. In this study, NMR experiments are carried out using 20 tight reservoir cores with 100% saturated formation water. At the same time, according to the NMR test principle, the large pores have a long T2 relaxation time; in turn, the small pores have a short T2 relaxation time. Therefore, we can characterize the pores with a T2 relaxation time between 0.1ms and10ms as micropores; the pores having a T2 relaxation time between 10ms and 100 ms are characterized as mesopores. Finally, we define pores with a T2 relaxation time greater than 100 ms as macropores.
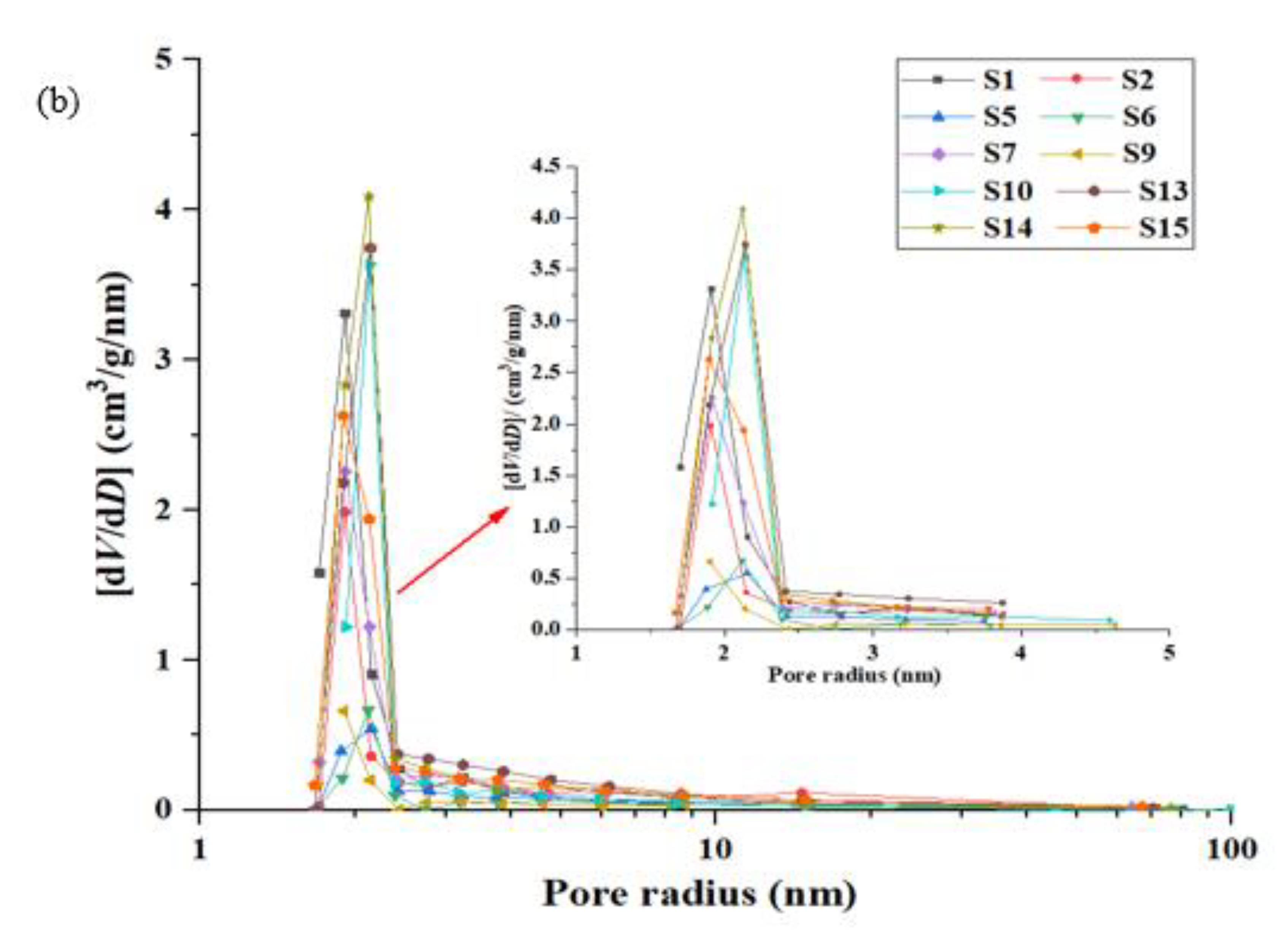
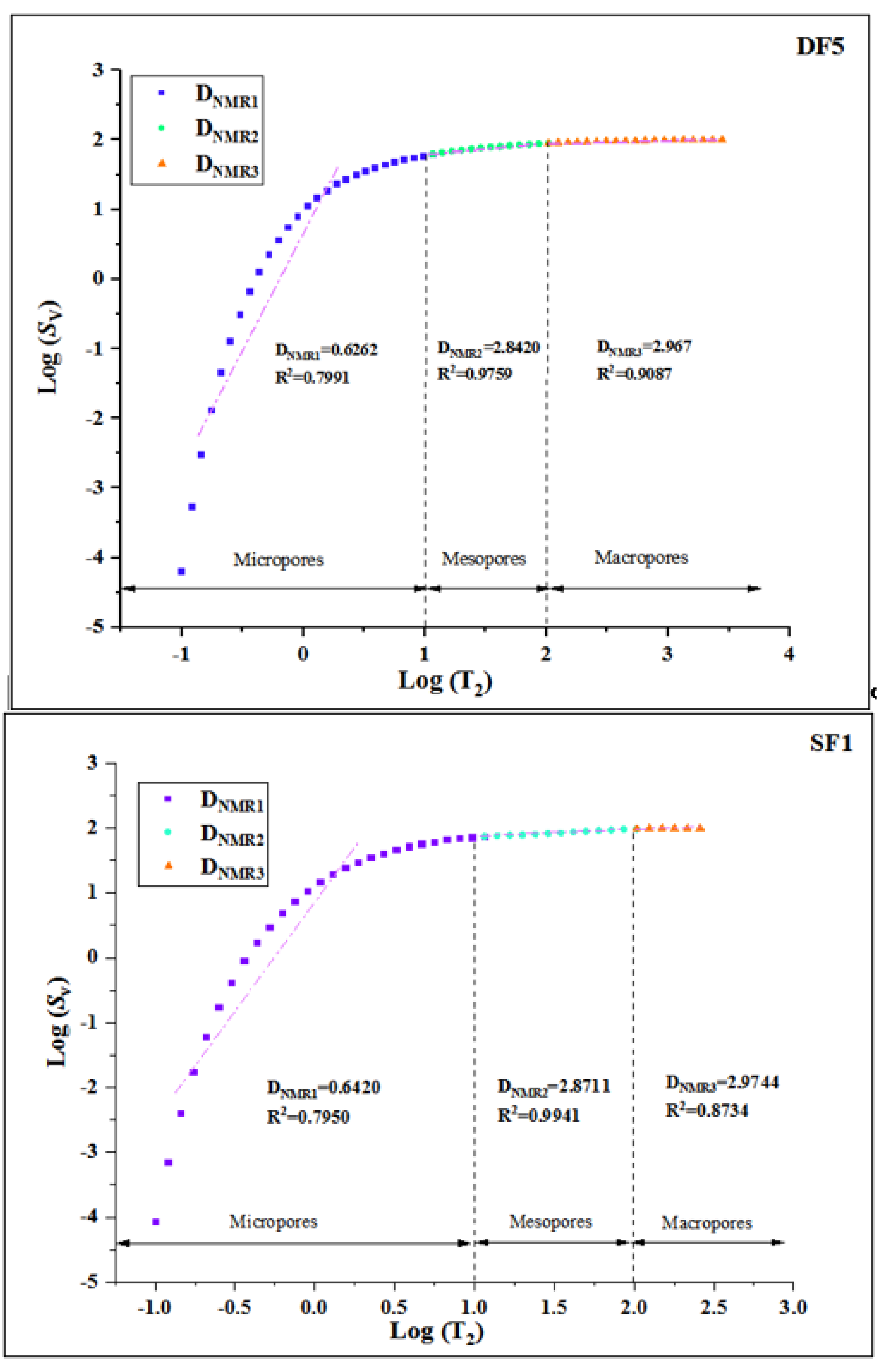
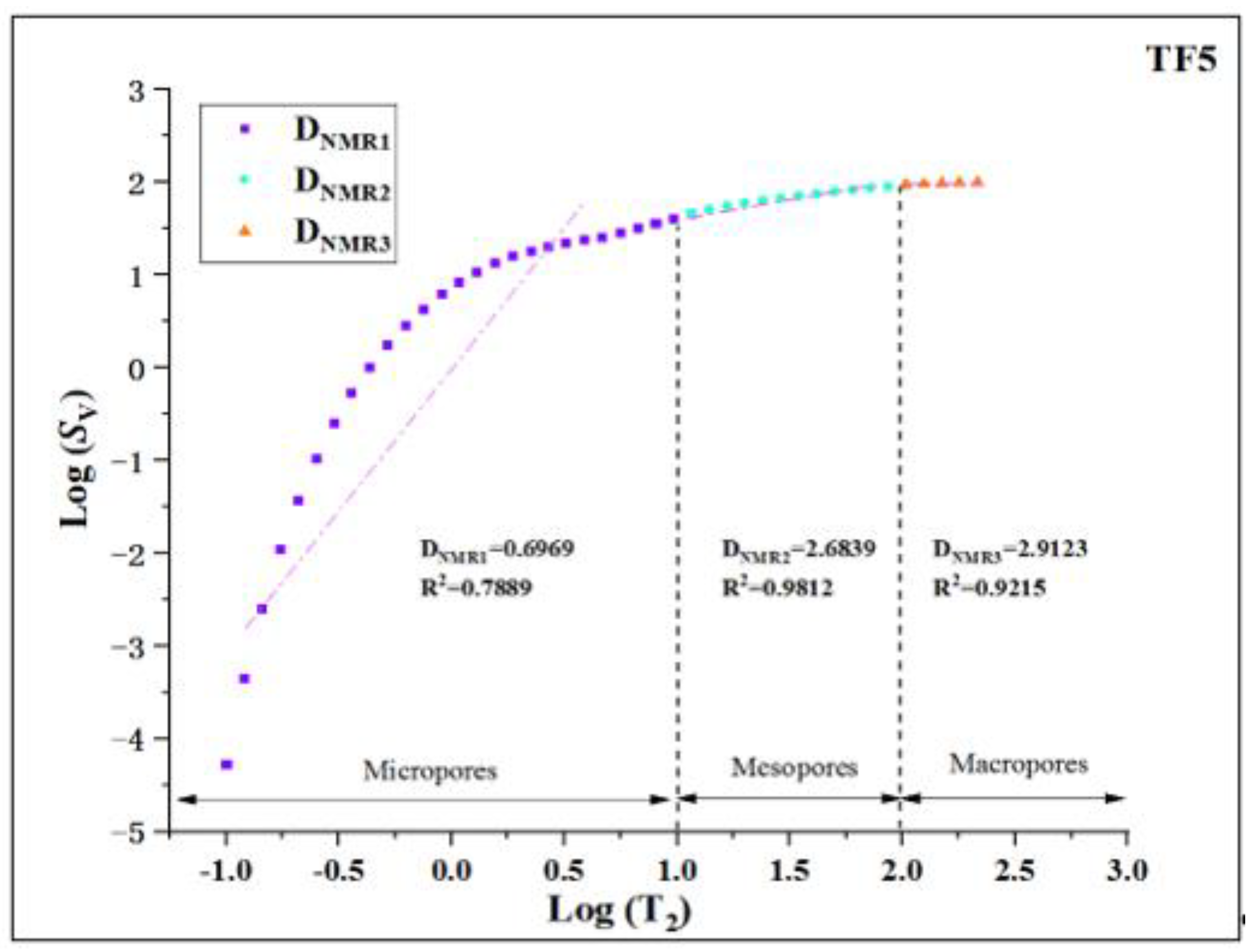
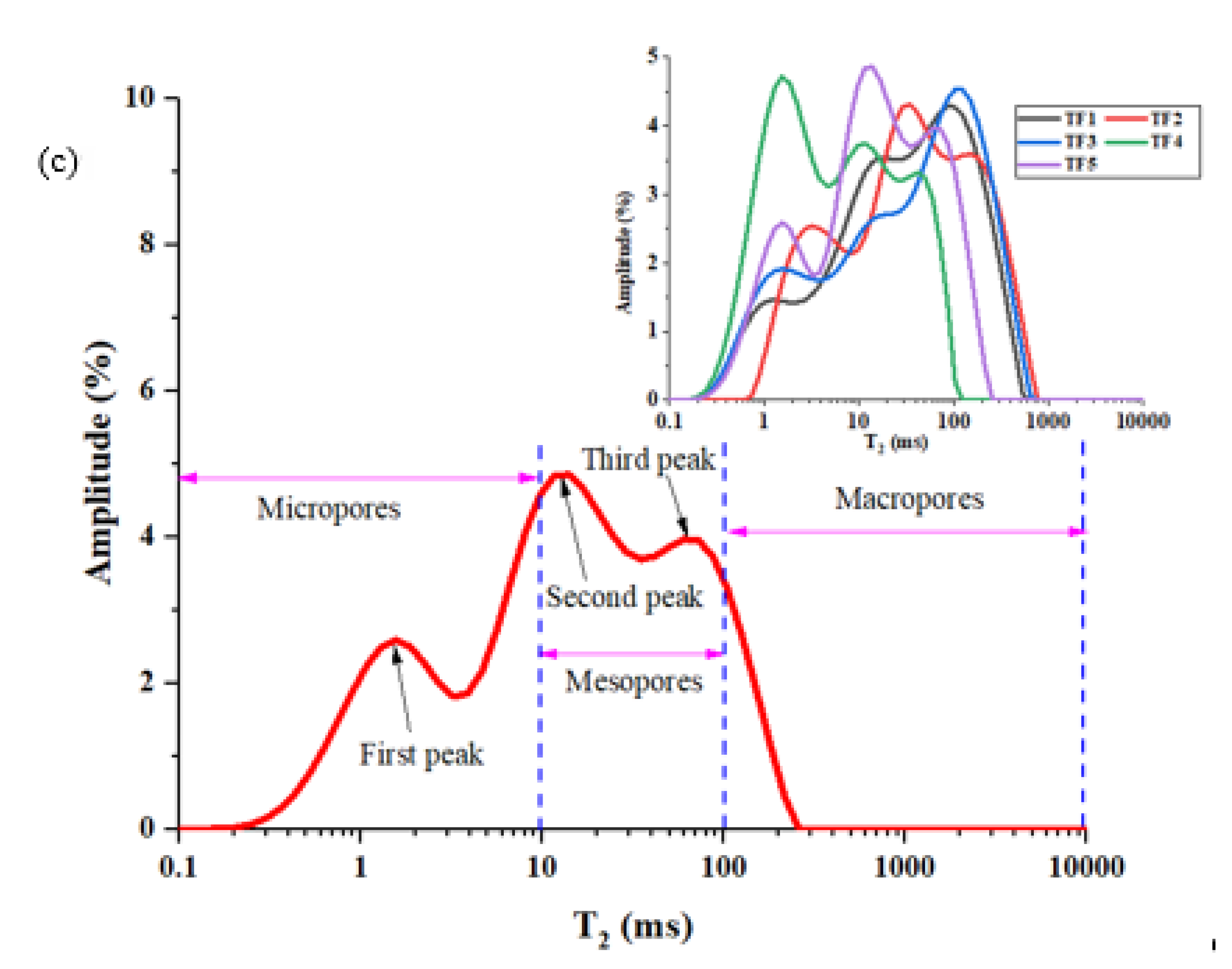
According to the experimental test results (Figure 5), the tight limestone cores are divided into three types; the first type is that there is only one peak in the core (DF); the second type is that there are two peaks in the core (SF); the third type is the presence of three peaks in the core (TF). It can be seen from Figure 5 that in the tight limestone core, these three types of cores contain micropores, mesopores and macropores, and the pore size exhibits a continuous distribution. In addition, we define three different pores (micropores, mesopores and macropores) in proportions of Ω1, Ω2 and Ω3, respectively. Among them, the calculation method of Ω1, Ω2 and Ω3 is as follows (Chen et al. 2018):
Ω 1 = ∫ T 2 , m i n T 2,10 S i d S ∫ T 2 , m i n T 2 , m a x S i d S × 100 %
Ω 2 = ∫ T 2,10 T 2,100 S i d S ∫ T 2 , m i n T 2 , m a x S i d S × 100 %
Ω 3 = ∫ T 2,100 T 2 , m a x S i d S ∫ T 2 , m i n T 2 , m a x S i d S × 100 %
where, Ω1, Ω2 and Ω3 represent the volume ratio of the micropores, mesopores and macropores, respectively, %; T2,10 and T2,100 are relaxation time 10ms, 100ms respectively; T2,min and T2,max are minimum and maximum relaxation times, respectively, ms; Si is the amplitude value corresponding to each point on the saturated water T2 curve, %.
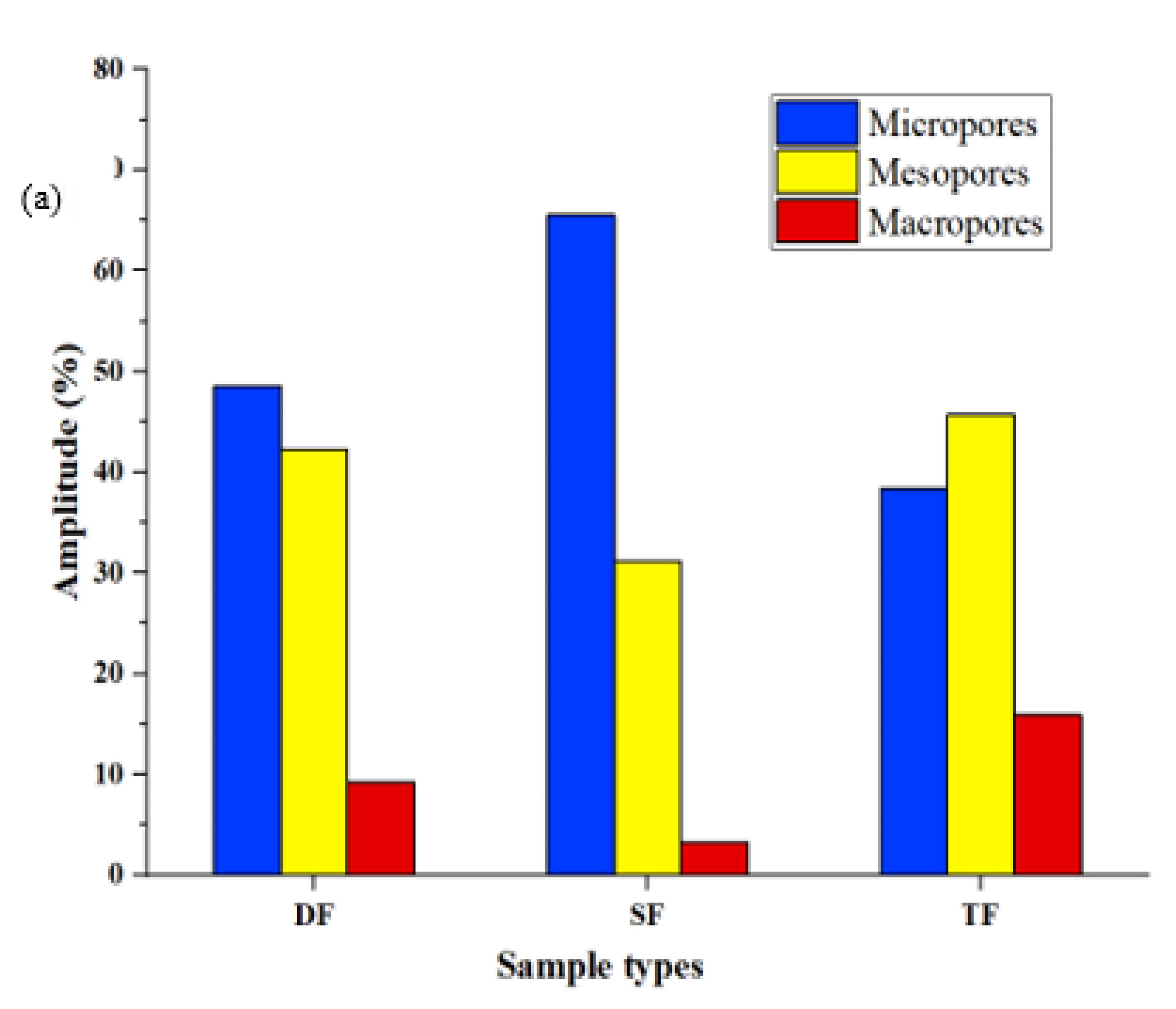
Table 1 is a calculated statistical table of the volume fraction of each tight limestone core. Figure 6 is a statistical plot of the average proportion of different pore types in three types of cores. It can be seen from Figure 5 that the average proportion of micropores of DF, SF and TF are 48.55%, 42.19% and 9.26%, respectively; the average mesopores of the three types of cores are 65.52%, 31.21% and 3.27%; the average proportion of macro holes in the three types of cores is 38.43%, 45.68% and 15.89%. It can be seen that the content of mesopores and macropores in TF type cores is more than 60%, so the TF type core pore development is better than the other two types of cores.

4.3. Fractal Characterization

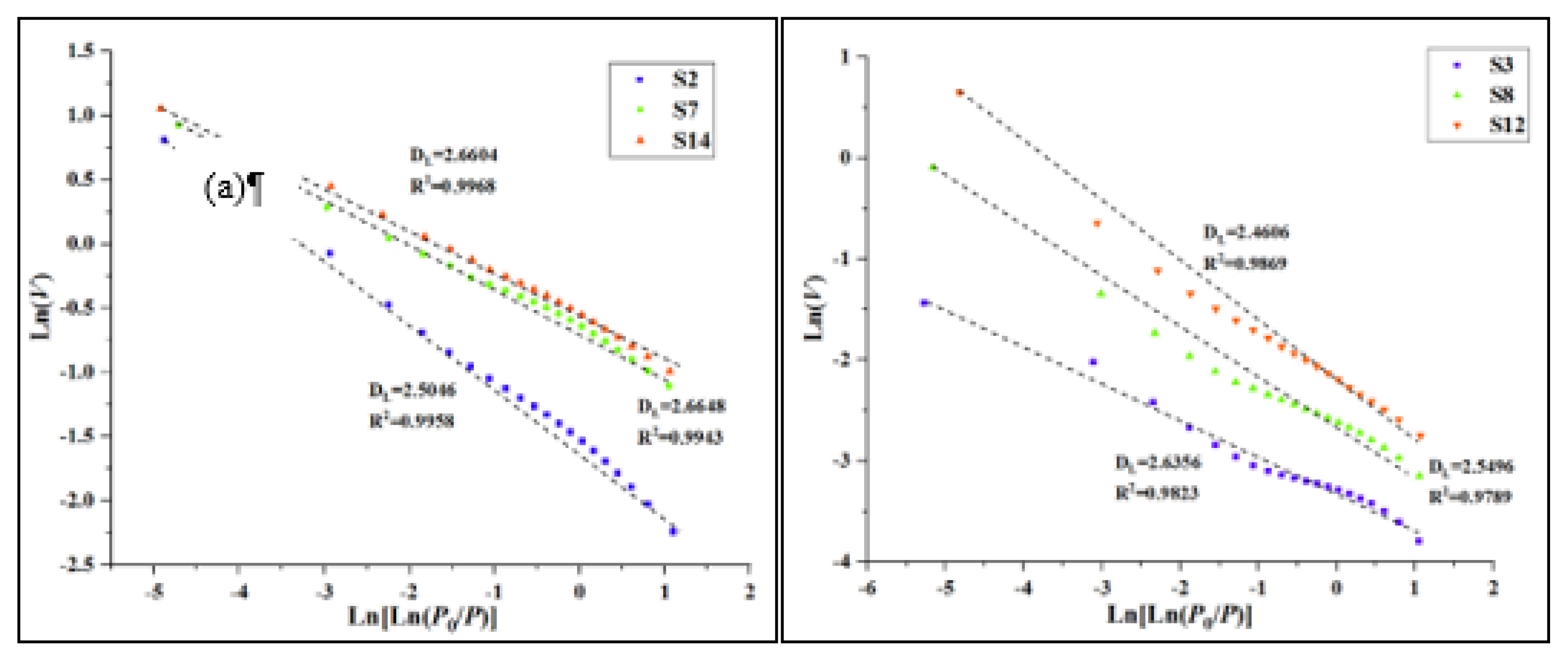
LTNA data is analyzed by the fractal theory, we linearly fit the ln V/V0 and ln[ln(P0/P)] data. It can be seen from Figure 7 that the correlation curve (R2) of the two types of cores is greater than 0.9, indicating that the tight limestone reservoir core has obvious fractal features. The fractal dimension of LTNA (DL) is between 2.4446-2.7688, with an average of 2.5729 (Table 1). At the same time, we calculate the multi-scale fractal dimension of the limestone cores by using NMR data (Table 2). The fractal dimension fitting lines of the three types of cores DF, SF and TF are shown in Figure 8. 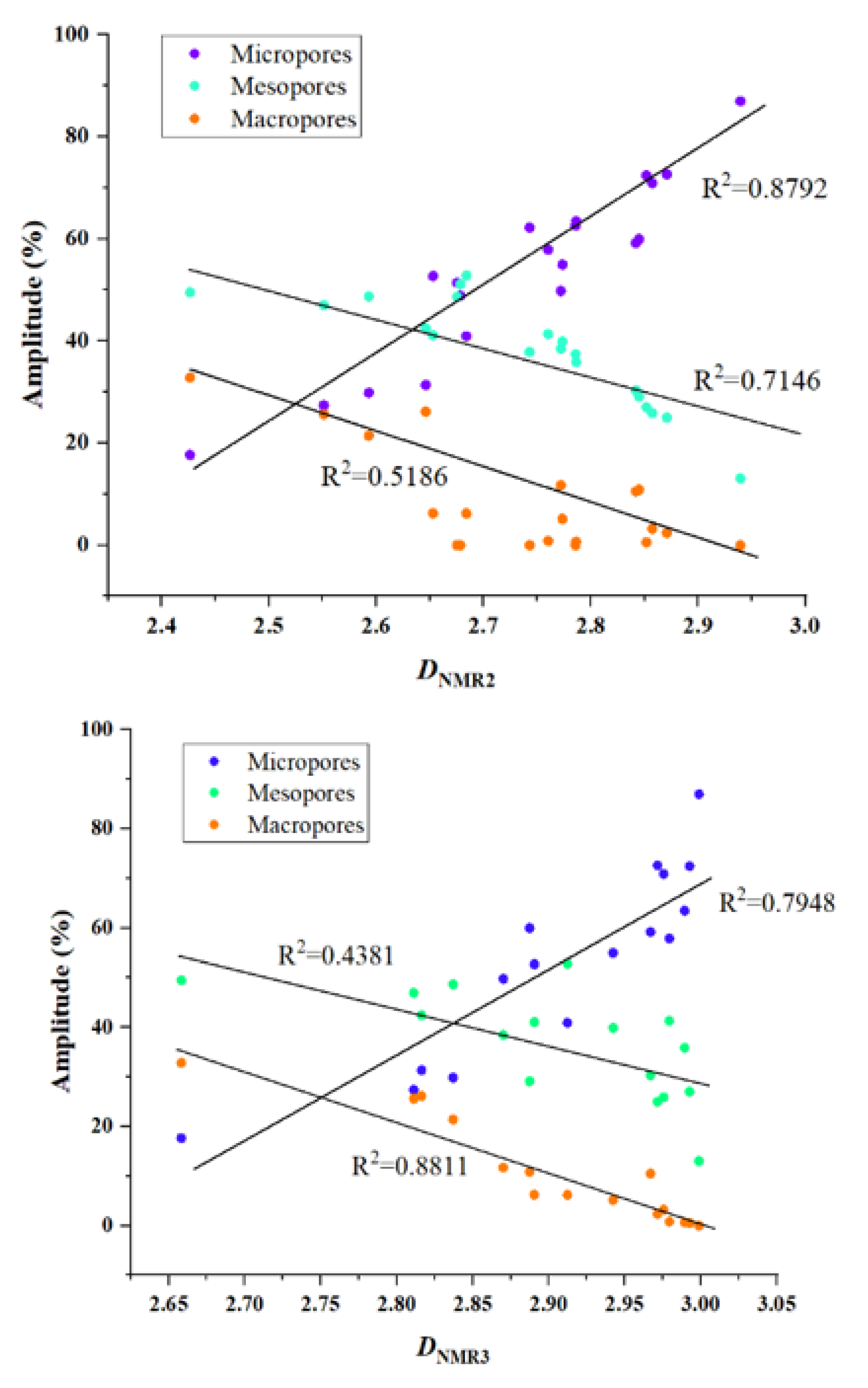Among them, the mesopores fractal dimension (DNMR2) of the DF type tight limestone core is between 2.4263 and 2.8420, with an average of 2.6889; and the macropores fractal dimension (DNMR3) is between 2.6582 and 2.9794, with an average of 2.8875. The mesopores fractal dimension of the SF type tight limestone core is between 2.6752 and 2.9395, with an average of 2.8156; the macropores fractal dimension is between 2.8701 and 2.9989, with an average of 2.9551. The mesopores fractal dimension of the TF type tight reservoir core is between 2.5509 and 2.7859, with an average of 2.6519; the macropores fractal dimension is between 2.8111 and 2.9123, with an average of 2.8442. It can be seen that the fractal dimension of macropores in the TF type core is smaller than that of the other two types of cores, so the pore structure is relatively simple and the pore surface is relatively smooth.
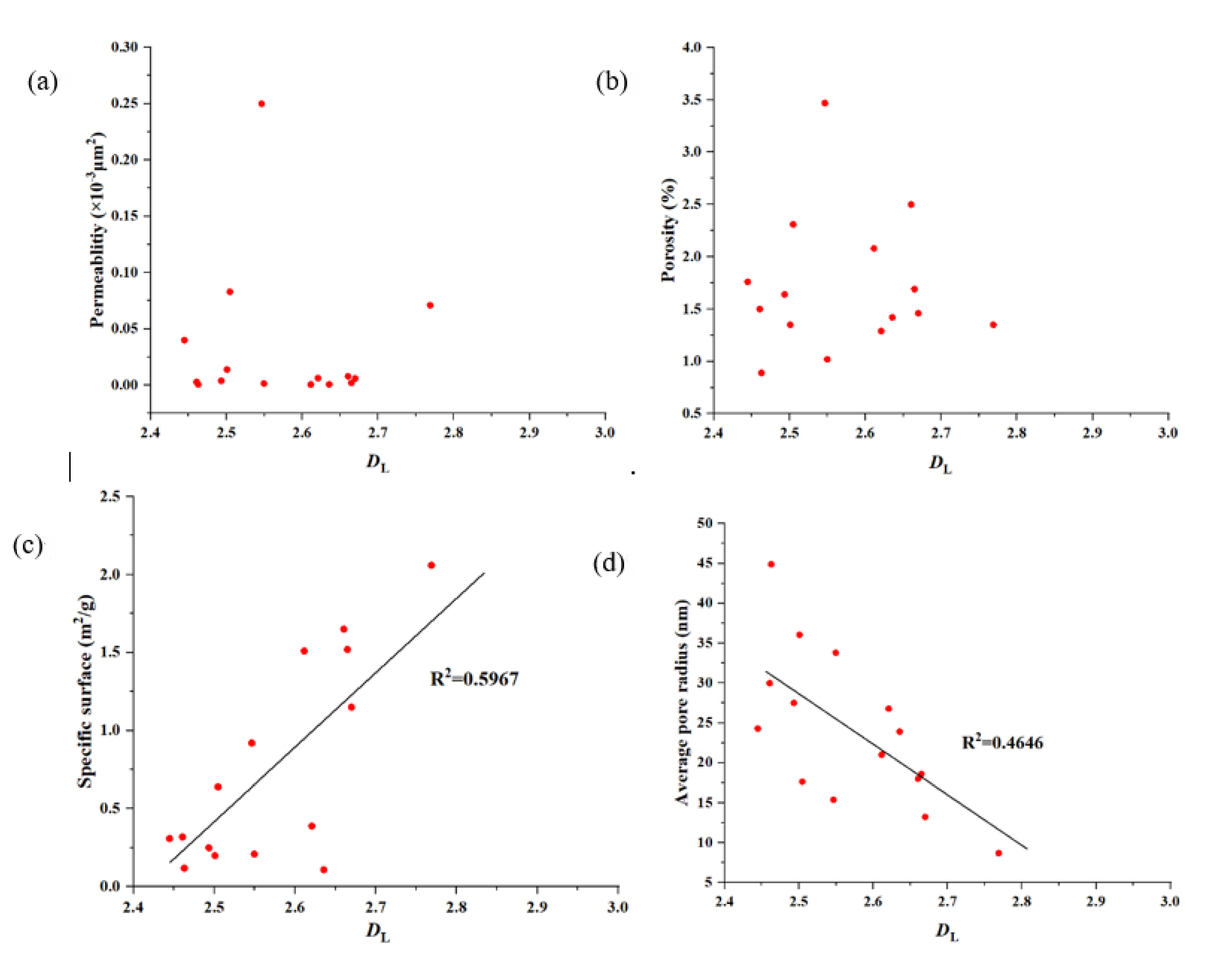
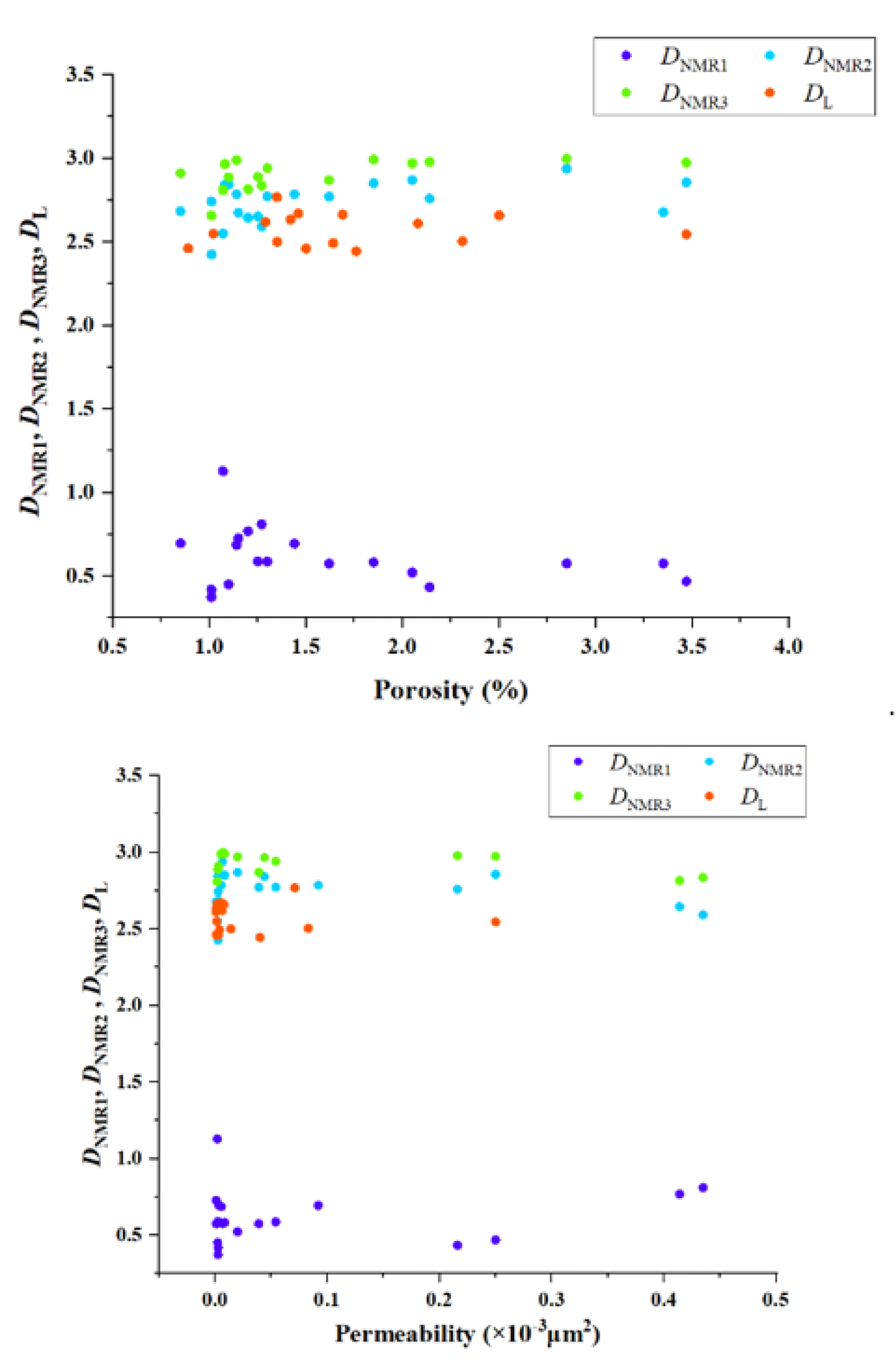
What is more, we discuss the correlation relationship between the fractal dimension and permeability, porosity etc. An obvious phenomenon is that there is no specific relationship between the fractal dimension and permeability and porosity in the tight limestone (Figure 9a, b; Figure 11), which is consistent with the results of other scholars (Sun et al. 2019; Wang et al. 2019). Besides, there is a positive correlation between the fractal dimension calculated from the LTNA data and the specific surface (Figure 8c). This indicates that as the specific surface area of tight limestone becomes larger, the complexity of its pore structure becomes higher. In addition, as the fractal dimension increases, the average pore radius of tight limestone shows a decreasing trend (Figure 8d). At the same time, by analyzing the fractal dimension calculated by the NMR data, it can be seen that DNMR2 has a positive correlation with the content of micropores in tight limestone (Figure 10a), and a negative correlation with the content of mesopores and macropores (Figure 9a). Moreover, DNMR3 also has a positive correlation with the content of micropores in tight limestone(Figure 10b) , and a negative correlation with the content of mesopores and macropores (Figure 9b). In other words, with the increase of micropore content in tight limestone, its fractal dimension tends to increase, as the content of micropores is a significant factor affecting the fractal dimension in tight limestone.

5. Conclusions

In this work, the LTNA and NMR are applied to characterize the pore structure of tight limestone, while these experimental data are used to analyze the fractal features of the tight limestone, the following conclusions can be drawn:
(1)
The tight limestones have intergranular pore, intragranular pore and microfracture, their LTNA test data indicates that the pores of tight limestone have H3 and H4 types, and the pore radius of tight limestone is between 8.71nm and 44.89 nm, with an average of 23.99 nm.
(2)
The NMR results of tight limestones show that there are three types of T2 distribution curve: DF, SF and TF, and the contents of micropores, mesopores and macropores of the three types of cores are different. Among them, the SF type tight limestone core has the most micropores content, with an average of 65.52%. In addition, the average content of macropores in TF type tight limestone is 45.68%.
(3)
The fractal dimension of LTNA (DL) is between 2.4446 and 2.7688, with an average of 2.5729. There is a good positive correlation between DL and specific surface area of tight limestone, and there is a good positive correlation between DNMR2, DNMR3 and the content of micropores in the tight limestone, which shows that with the increase of micropores content, the surface roughness of the pores in the tight limestone is more complex.

Funding

This work is funded by the National Science and Technology Major Project (2017ZX05013-001) and the CNPC Innovation Found (2022DQ02-0102).

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Conflicts of Interest

All authors declare that there is no conflict of interest in this article.

References

  1. Brunauer, S., Emmett, P. H., & Teller, E. (1938). Adsorption of Gases in Multimolecular Layers. JOURNAL OF THE AMERICAN CERAMIC SOCIETY, 60(02), 309–319.
  2. Barrett, E. P., Joyner, L. G., & Halenda, P. P. (1951). The determination of pore volume and area distributions in porous substances. I. Computations from nitrogen isotherms. JOURNAL OF THE AMERICAN CERAMIC SOCIETY, 73(01), 373–380.
  3. Chen, S., Tang, D., Tao, S., Ji, X., & Xu, H. (2019). Fractal analysis of the dynamic variation in pore-fracture systems under the action of stress using a low-field NMR relaxation method: An experimental study of coals from western Guizhou in China. Journal of Petroleum Science and Engineering, 173, 617-629.
  4. Chen, L., Jiang, Zh., Liu, Q., Jiang, S., Liu, K., Tan, J., et al. (2019). Mechanism of shale gas occurrence: Insights from comparative study on pore structures of marine and lacustrine shales. Marine and Petroleum Geology, 104, 200-216.
  5. Chen, T., Yang, Zh., Ding, Y., Luo, Y., Qi, D., Lin, W., et al. (2018). Waterflooding Huff-n-puff in Tight Oil Cores Using Online Nuclear Magnetic Resonance. Energies, 11 (6), 1524.
  6. Guo, Q., Wang, Sh., & Chen, X. (2019). Assessment on tight oil resources in major basins in China. Journal of Asian Earth Sciences, 178, 52-63.
  7. Hughes, J.D. (2013). Energy: a reality check on the shale revolution. Nature, 494, 307–308.
  8. Hu, S., Zhu, R., Wu, S., Bai, B., Yang, Zh., & Cui, J. (2018). Exploration and development of continental tight oil in China. Petroleum Exploration and Development, 45(4), 737-748.
  9. Haul, R. (1969). Adsorption, surface area and porosity. Zeitschrift Für Physikalische Chemie, 63(01–04), 220–221.
  10. Luo, Y., Wang, Y., Liu, H., Wang, Ch., & Zhao, Y. (2019). Overpressure controlling factors for tectonic fractures in near-source tight reservoirs in the southwest Ordos Basin, China. Journal of Petroleum Science and Engineering. [CrossRef]
  11. Liu, Y., Zhang, Y., Wang, Y., & Wang, L. (2018). The pore structure of tight limestone—Jurassic Ziliujing Formation, Central Sichuan Basin, China. Applied Geophysics, 15(02), 165-174.
  12. Lai, J., Wang, G., Fan, Zh., Zhou, Zh., Chen, J., & Wang, Sh. (2018). Fractal analysis of tight shaly sandstones using nuclear magnetic resonance measurements. AAPG Bulletin, 102(02), 175-193.
  13. Li, C., Liu, G., Cao, Z., Yuan, W., Wang, P., & You, Y. (2019). Analysis of Petrophysical Characteristics and Water Movability of Tight Sandstone Using Low-Field Nuclear Magnetic Resonance. Natural Resources Research. [CrossRef]
  14. Mandelbrot, B.B., Wheeler, J.A., 1998. The fractal geometry of nature. Am. J. Phys. 51 (4) 468 pp. [CrossRef]
  15. Naveen, P., Asif, M., & Ojha, K. (2018). Integrated fractal description of nanopore structure and its effect on CH4, adsorption on Jharia coals, India. Fuel, 232, 190–204.
  16. Ojha, S.P., Misra, S., Tinni, A., Sondergeld, C., & Rai, C., (2017). Pore connectivity and pore size distribution estimates for Wolfcamp and Eagle Ford shale samples from oil, gas and condensate windows using adsorption-desorption measurements. Journal of Petroleum Science and Engineering, 158, 454–468.
  17. Pang, Zh., Tao, Sh., Zhang, Q., Zhang, T., Yang, J., Fan, J., et al. (2019). Enrichment factors and sweep spot evaluation of Jurassic tight oil in central Sichuan Basin, SW China. Petroleum Research, 4(4), 334-347.
  18. Shen, W., Li, X., Lu, X., Guo, W., Zhou, S., & Wan, Y. (2018). Experimental study and isotherm models of water vapor adsorption in shale rocks. Journal of Natural Gas Science and Engineering, 52, 484-491.
  19. Shen, W., Song, F., Hu, X., Zhu, G., & Zhu, W. (2019). Experimental study on flow characteristics of gas transport in micro- and nanoscale pores. Scientific Reports, 9, 10196.
  20. Sun, Y., Deng, M., Ma, Sh., Chen, Y., Yu, L., Zhang, Y., et al. (2015). Distribution and controlling factors of tight sandstone oil in Fuyu oil layers of Da’an area, Songliao Basin, NE China. Petroleum Exploration and Development, 42(5), 646-655.
  21. Sun, W., Zuo, Y., Wu, Zh., Liu, H., Xia, Sh., Shui, Y., et al. (2019). Fractal analysis of pores and the pore structure of the Lower Cambrian Niutitang shale in northern Guizhou province: Investigations using NMR, SEM and image analyses. Marine and Petroleum Geology, 99, 416-428.
  22. Tian, Z., Song, X., Wang, Y., Ran, Q., Liu, B., Xu, Q., et al. (2017). Classification of lacustrine tight limestone considering matrix pores or fractures: A case study of Da’anzhai Member of Jurassic Ziliujing Formation in central Sichuan Basin, SW China. Petroleum Exploration and Development, 44(2), 234-246.
  23. Thommes, M., Kaneko, K., Neimark, A. V., Olivier, J. P., Francisco, R. R., Jean, R., et al. (2015). Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure and Applied Chemistry, 87(9-10), 1051-1069.
  24. Volery, C., Davaud, E., Durlet, C., Clavel, B., Charollais, B., Calined, B. (2010). Microporous and tight limestones in the Urgonian Formation (late Hauterivian to early Aptian) of the French Jura Mountains: Focus on the factors controlling the formation of microporous facies. Sedimentary Geology, 230(1-2), 21-34.
  25. Wang, Sh., Yu, Y., Guo, Q., Wang, Sh., & Wu, X. (2017). New advances in the assessment of tight oil resource in China. Petroleum Research, 2(1), 1-12.
  26. Wang, J., Tong, M., Sun, Y., Zhang, Y., & Yuan, D. (2019). Reservoir and development characteristics of the Da’anzhai tight oil in Sichuan Basin, SW China. Petroleum Research, 4, 212-226.
  27. Wu, H., Zhang, Ch., Ji, Y., Liu, R., Wu, H., Zhang, Y., et al. (2018). An Improved Method of Characterizing the Pore Structure in Tight oil Reservoirs: Integrated NMR and Constant-Rate-Controlled Porosimetry Data. Journal of Petroleum Science and Engineering, 166, 778–796.
  28. Wei, Y. (2018). Study on Tight Sandstone Reservoir Characteristics and Development in Sichuan. University of Chinese Academy of Sciences, Beijing.
  29. Wang, F., Yang, K., & Cai, J. (2018). Fractal characterization of tight oil reservoir pore structure using nuclear magnetic resonance and mercury intrusion porosimetry. Fractals, 26(2), 1840017.
  30. Wang, J., Cao, Y., Liu, K., Gao, Y., & Qin, Zh. (2019). Fractal characteristics of the pore structures of fine-grained, mixed sedimentary rocks from the Jimsar Sag, Junggar Basin: Implications for lacustrine tight oil accumulations. Journal of Petroleum Science and Engineering, 182, 106363.
  31. Yang, Zh., Zou, C., Hou, L., Wu, S., Lin, S., Luo, X., et al. (2019). Division of fine-grained rocks and selection of “sweet sections” in the oldest continental shale in China: Taking the coexisting combination of tight and shale oil in the Permian Junggar Basin. Marine and Petroleum Geology, 109, 339-348.
  32. Zhou, F., Su, H., Liang, X., Meng, L., Yuan, L., Li X., et al. (2019). Integrated hydraulic fracturing techniques to enhance oil recovery from tight rocks. Petroleum Exploration and Development, 46(5), 1007-1014.
  33. Zhao, H., Ning, Zh., Wang, Q., Zhang, R., Zhao, T., Niu, T., et al. (2015). “Petrophysical Characterization of Tight Oil Reservoirs Using Pressure-Controlled Porosimetry Combined With Rate-Controlled Porosimetry. Fuel, 154, 233–242.
  34. Zhao, X., Yang, Zh., Lin, W., Xiong, Sh., Luo, Y., Wang, Zh., et al. (2019a). Study on pore structures of tight sandstone reservoirs based on nitrogen adsorption, high-pressure mercury intrusion and rate-controlled mercury intrusion. JOURNAL OF ENERGY RESOURCES TECHNOLOGY-TRANSACTIONS OF THE ASME, 141(11), 112903-112903-11.
  35. Zhao, X., Yang, Zh., Lin, W., Xiong, Sh., Luo, Y., Liu, X., et al. (2019b). Fractal study on pore structure of tight sandstone based on full-scale map. International Journal of Oil, Gas and Coal Technology, 22(2), 123-138.
  36. Zhao, X., Yang, Zh., Lin, W., Xiong, Sh., & Wei, Y. (2018). Characteristics of microscopic pore-throat structure of tight oil reservoirs in Sichuan Basin measured by rate-controlled mercury injection. Open Physics, 16, 675–684.
  37. Zhang, Z., & Weller, A. (2014). Fractal dimension of pore-space geometry of an Eocene sandstone formation. GEOPHYSICS, 79(6), 377-387.
  38. Zhang, J., Deng, H., Deng, J., & Gao, R. (2019). Fractal analysis of pore structure development of sandstone: A nuclear magnetic resonance investigation. IEEE Access, 7, 47282-47293.
  39. Zheng, S., Yao, Y., Liu, D., Cai, Y., & Liu, Y. (2018). Characterizations of full-scale pore size distribution, porosity and permeability of coals: A novel methodology by nuclear magnetic resonance and fractal analysis theory. International Journal of Coal Geology, 196, 148-158.
  40. Zhao, P., Wang, L., Xu, Ch., Fu, J., Shi, Y., Mao, Zh., et al. (2020). Nuclear magnetic resonance surface relaxivity and its advanced application in calculating pore size distributions. Marine and Petroleum Geology, 111, 66-74.
  41. Zhao, P., Wang, X., Cai, J., Luo, M., Zhang, J., Liu, Y., et al. (2019). Multifractal analysis of pore structure of Middle Bakken formation using low temperature N2 adsorption and NMR measurements. Journal of Petroleum Science and Engineering, 176, 312-320.
Preprints 107761 g001
Figure 1. SEM and CT photographs of tight limestone in the study block (Wei 2018).
Figure 1. SEM and CT photographs of tight limestone in the study block (Wei 2018).
Preprints 107761 g001
Preprints 107761 g002aPreprints 107761 g002b
Figure 2. LTNA adsorption–desorption isotherm curve of tight limestone.
Figure 2. LTNA adsorption–desorption isotherm curve of tight limestone.
Preprints 107761 g002aPreprints 107761 g002b
Preprints 107761 g003aPreprints 107761 g003b
Figure 3. Pore volume difference curve of LTNA of tight limestone.
Figure 3. Pore volume difference curve of LTNA of tight limestone.
Preprints 107761 g003aPreprints 107761 g003b
Preprints 107761 g004
Figure 4. Relationship between permeability, porosity and average pore radius and pore volume.
Figure 4. Relationship between permeability, porosity and average pore radius and pore volume.
Preprints 107761 g004
Preprints 107761 g005aPreprints 107761 g005b
Figure 5. T2 distribution of tight limestone.
Figure 5. T2 distribution of tight limestone.
Preprints 107761 g005aPreprints 107761 g005b
Preprints 107761 g006
Figure 6. Different pore space amplitudes of three types of tight limestone.
Figure 6. Different pore space amplitudes of three types of tight limestone.
Preprints 107761 g006
Preprints 107761 g007
Figure 7. Relationship between Ln(V/V0) and Ln[Ln(P0/P)].
Figure 7. Relationship between Ln(V/V0) and Ln[Ln(P0/P)].
Preprints 107761 g007
Preprints 107761 g008aPreprints 107761 g008b
Figure 8. T2 fractal spectrum of tight limestone.
Figure 8. T2 fractal spectrum of tight limestone.
Preprints 107761 g008aPreprints 107761 g008b
Preprints 107761 g009
Figure 9. Relationship between DL and tight limestone physical parameter.
Figure 9. Relationship between DL and tight limestone physical parameter.
Preprints 107761 g009
Preprints 107761 g010
Figure 10. Relationship between fractal dimension of NMR and different pore amplitudes.
Figure 10. Relationship between fractal dimension of NMR and different pore amplitudes.
Preprints 107761 g010
Preprints 107761 g011
Figure 11. Intersecting graph of fractal dimension and porosity and permeability.
Figure 11. Intersecting graph of fractal dimension and porosity and permeability.
Preprints 107761 g011
Table 1. LTNA test data of different samples.
Table 1. LTNA test data of different samples.
Sample Depth Lithology φ K Ap Vc ra DL
S1 2514.37~2516.06 Limestone 1.46 0.00600 1.15 2.87 13.25 2.6698
S2 2517.56~2519.43 Limestone 2.31 0.08300 0.64 3.66 17.63 2.5046
S3 2577.88~2579.35 Limestone 1.42 0.00084 0.11 0.35 23.90 2.6356
S4 2579.35~2580.68 Limestone 1.35 0.01400 0.20 1.79 36.04 2.5007
S5 2825.99~2827.59 Limestone 1.76 0.04000 0.31 2.70 24.29 2.4446
S6 2841.91~2843.56 Limestone 1.64 0.00400 0.25 1.88 27.51 2.4933
S7 2666.12~2667.36 Limestone 1.69 0.00210 1.52 3.68 18.59 2.6648
S8 2672.69~2674.56 Limestone 1.02 0.00160 0.21 1.37 33.79 2.5496
S9 2679.78~2682.04 Limestone 1.29 0.00640 0.39 1.77 26.78 2.6208
S10 2857.60~2858.60 Limestone 1.35 0.07100 2.06 2.24 8.71 2.7688
S11 2874.00~2875.10 Limestone 0.89 0.00084 0.12 1.64 44.89 2.4628
S12 2878.25~2879.43 Limestone 1.50 0.00300 0.32 3.00 29.98 2.4606
S13 2151.53~2153.70 Limestone 3.47 0.25000 0.92 4.81 15.41 2.5464
S14 1723.09~1725.29 Limestone 2.50 0.00790 1.65 4.44 18.01 2.6604
S15 1725.29~1727.32 Limestone 2.08 0.00079 1.51 5.26 21.01 2.6114
Note: φ, porosity, %; K, permeability, ×10-3μm2；Ap, specific surface, m2/g; Vc, pore volume, mm3/g; ra, average pore radius, nm; DL, fractal dimension, dimensionless.
Table 2. NMR test data of different samples.
Table 2. NMR test data of different samples.
Sample Lithology φ/% K/×10-3μm2 DNMR1 DNMR2 DNMR3 Ω1/% Ω2/% Ω3/%
DF1 Limestone 1.25 0.00260 0.5897 2.6529 2.8905 52.71 41.05 6.24
DF2 Limestone 2.14 0.21600 0.4347 2.7603 2.9794 57.87 41.30 0.83
DF3 Limestone 1.08 0.04400 0.6262 2.8420 2.9670 59.18 30.31 10.51
DF4 Limestone 1.01 0.00260 0.3744 2.4263 2.6582 17.66 49.50 32.84
DF5 Limestone 3.35 0.00110 0.5769 2.6783 / 48.89 51.11 0.00
DF6 Limestone 1.30 0.05400 0.5875 2.7735 2.9423 54.96 39.89 5.15
SF1 Limestone 2.05 0.02000 0.5233 2.8709 2.9716 72.61 25.01 2.38
SF2 Limestone 1.85 0.00850 0.5829 2.8517 2.9927 72.42 27.03 0.55
SF3 Limestone 1.14 0.00540 0.6876 2.7863 2.9895 63.46 35.86 0.68
SF4 Limestone 1.10 0.00240 0.4519 2.8449 2.8874 59.97 29.14 10.89
SF5 Limestone 1.01 0.00260 0.4199 2.7429 / 62.19 37.81 0.00
SF6 Limestone 1.62 0.03900 0.5754 2.7721 2.8701 49.79 38.47 11.74
SF7 Limestone 1.15 0.00098 0.7286 2.6752 / 51.36 48.64 0.00
SF8 Limestone 3.47 0.25000 0.4694 2.8573 2.9756 70.90 25.87 3.23
SF9 Limestone 2.85 0.00670 0.5774 2.9395 2.9989 86.94 13.06 0.00
TF1 Limestone 1.27 0.43500 0.8115 2.5930 2.8371 29.86 48.70 21.44
TF2 Limestone 1.07 0.00200 1.1293 2.5509 2.8111 27.38 46.99 25.63
TF3 Limestone 1.20 0.41400 0.7702 2.6460 2.8163 31.37 42.47 26.16
TF4 Limestone 1.44 0.09200 0.6950 2.7859 / 62.61 37.39 0.00
TF5 Limestone 0.85 0.00300 0.6969 2.6839 2.9123 40.94 52.83 6.23
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated