Prerpints.org logo
Preprint
Article

A Universal Image Compression Sensing-Encryption Algorithm Based on DNA-Triploid Mutation

Altmetrics

Downloads

97

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 May 2024

Posted:

29 May 2024

You are already at the latest version

Alerts
Abstract
As the fast growth of information technology (IT), the safety of image transmission and the storing of images are increasingly concerned. Traditional image encryption algorithms have certain limitations in transmission and security, so there is an urgent need for a secure and reliable image encryption algorithm. A universal compression sensing (CS) image encryption (IE) algorithm based on DNA-triploid mutation (DTM) is presented in this paper. Firstly, by using CS algorithm an image is compressed while obtaining a range of chaotic sequences by iteration of chaotic map. Then DNA sequences are generated by encoding the image, and based on the DTM, new mutant DNA sequences are generated according to specific rules. Next, the chaotic sequences are operated at the DNA level to do confusion and diffusion operations on the image to ensure the security of the data. At last, DNA decoding is carried out to obtain the compressed-encrypted image. Both simulation experiments and performance tests fully show that a high level of security and reliability of the proposed algorithm in protecting image privacy is achieved.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

MSC:  37N99

1. Introduction

As IT develops rapidly, digital images are applied in many fields [1], such as medical images, security monitoring, digital art and so on. No matter which field it is applied to, privacy protection of digital images is always a problem that needs to be focused on. In order to protect private information, researchers have designed traditional encryption algorithms such as AES [2], RSA [3], DES [4] and so on, but due to the large amount of data contained by digital images, the effectiveness of the algorithms needs to be improved [5]. So, researchers have proposed many new encryption algorithms to improve the performance of encryption.
Recently, chaotic systems are widely exploited in IE due to excellent characteristics. And the design of systems with complex dynamics has received wide attention [6]. Chaotic sequences produced by the iteration of chaotic systems are featured with unpredictability [7], sensitivity to initial values, and randomness [8,9], and therefore are often used as keys for IE. However, classical chaotic systems have some limitations such as small key space and phase space can be easily destroyed [10]. While because many nonlinear dynamic behaviors that can be generated by neural networks [11,12], IE algorithms can be provided with randomness and security. Memristor Rulkov Neuron Network (M-RNN) [13] is utilized for the presented algorithm. High efficiency, security and reliability can be provided to the encryption algorithm by the M-RNN with those characteristics, which can better protect the transmission of private information.
Many encryption algorithms have been proposed based on chaos theory. For instance, Mohamed et al. raised a substitution matrix created by using chaotic state variables, using it as the key and the encryption algorithm itself for encryption [14]. Based on the combination of IE and chaotic systems, some researchers have combined encryption algorithms with DNA rules [15,16,17,18,19] to create a more secure and efficient encryption algorithm that provides a more reliable algorithm for privacy protection. Fan. et al. raised the algorithm on the basis of horizontal confusion and diffusion of eight-base DNA [20]. Wang. et al. employed the look-up table algorithm to quickly get the results of DNA arithmetic and save the encryption time [21]. Furthermore a nonlinear feedback shift registers and image encryption with DNA computation algorithm was utilized to provide high security to the algorithm [22]. In addition, the encryption process can be made random and unpredictable by performing mutation operations on DNA sequences, thus increasing the difficulty of cracking. And in this algorithm an effective algorithm based on triplet mutation [23] is proposed and a series of encryption operations are performed at the DNA level by using chaotic sequences. The algorithm is able to resist attack tests well and protects image information without being destroyed which improves safety of image encryption.
The quantity of data in an image is increased due to the need to convert binary data into a sequence of four bases when encrypting at the DNA level. In order to reduce the amount of data when encryption, the image can be compressed before performing the encryption algorithm. Gao et al. presented a compression technique using back propagation neural network [24], but because of the "jaggedness phenomenon" and step size selection, the training speed was slow. Liu et al. suggested an modified image compression algorithm which combined Huffman coding, integer wavelet transform and linear prediction [25], but it was low in the compression speed. While, CS [26] technique performs better in terms of compression speed and this algorithm uses CS. It utilizes the sparsity or low dimensional structure of the signal to efficiently rebuilt the original signal with few sampled data [27]. Discrete Cosine Transform (DCT) [28] algorithm is utilized in this algorithm to sparsely represent original signal by combining Hadamard matrix and the chaotic sequences to generate observation matrix. In the stage of signal reconstruction, to reconstruct the compressed signal, Orthogonal Matching Pursuit (OMP) [29] algorithm is applied. The size of the image data is significantly reduced by this algorithm, which helps to reduce transmission and storage costs.
To conclusion, a universal compression-encryption technique using DTM is presented. Key highlights from this paper:
  • The universal image is first compressed before encryption to decrease size of the image to be encrypted and increase encryption efficiency.
  • The chaotic sequences generated by M-RNN through iteration are fully utilized to provide pseudo-randomness to the encryption algorithm by combining it with the encryption algorithm.
  • Due to the high randomness in the way DNA sequences combined, confusion and diffusion operations at the DNA level provide a strong randomization.
The paper is organized as follows. Rich dynamics of M-RNN chaotic map, the process of CS and the details of DTM are shown in Section 2. Specific steps of the IE algorithm are described in Section 3. Effects of this algorithm are illustrated in Section 4. Performance tests and analysis are carried out in Section 5. What is done is summed up in final section.

2. Preliminaries

2.1. Chaotic System

2.1.1. Chaotic Map

The 2D hyperchaotic map M-RNN used is shown in Equation (1):
{ x ( i + 1 ) = − a x ( i ) + b sin ( g x ( i ) ) + y ( i ) y ( i + 1 ) = − c y ( i ) − d sin ( g x ( i ) ) ,
where activation gradients are g, a, b, c, d for the system parameters, and initial values are x0 and y0.
Phase diagrams (PD) of M-RNN are given in Figure 1 (a), (b) and (c) with parameters (b, c, d, g) = (1, 0.9, -0.8, 3.1), and y0 = 0, x0 = -0.1 are the initial values. The PD for different initial values of parameter a are shown as a = -0.4, -0.6 and -0.8. The PD show that the system has a multi-structured phenomenon as the value of a increases. This phenomenon can generate high quality random sequences. Bifurcation diagram (BD) and Lyapunov exponential spectrum (LEs) of M-RNN are shown in Figure 1 (e) and Figure 1 (d). When parameter ranges a ∈ [-0.98, 0.98], it is in the full domain hyperchaotic state. In the full domain hyperchaotic state, the state variables of the system have high randomness, which can generate more random and complex key sequences and increase the security of the IE algorithm. The complexity diagram for parameters a and d can be seen in Figure 1 (f). The complexity of the system is close to 1, which indicates that the chaotic sequences iteratived by the hyperchaotic map have high complexity.

2.1.2. Randomness Test

To prove reliability of chaotic map in IE, NIST test is performed, which represents a usual method to check the randomness of sequences with 15 different tests. Results of the tests are analyzed by standards of P-value and pass rate (PR). Sequences are considered to be random when 15 tests have all p-values equal to 0.01 or more and all PRs are greater than 96%. The results obtained after the NIST test are presented in Figure 2 and Figure 3, from which it is clear that all the tests pass the standards, and the chaotic sequences have a high degree of randomness, which makes them well suited for application in IE algorithm.

2.2. Compression Sensing Technology

The three processes of the CS are represented in Figure 4. DCT algorithm is used for representing the original signal sparsely and Hadamard matrices and chaotic sequences are combined to generate observation matrices. Sparse observations can be seen in Equation (2).
y = φ x = φ ψ x ,
where φ is observation matrix. x is a bunch of signals of length N. Ψ is the sparse matrix that transforms the signal into the frequency domain S. y is the observation and is the final sampling result.
Signal reconstruction is as presented in Equation (3). After obtaining reconstructed signal, original signal is reconstructed with transformed base values. In the signal reconstruction stage, OMP algorithm is utilized which has less complexity and closely related to the value in each iteration.
x = arg min ‖ x ‖ 0 s . t . φ x = y .

2.3. DNA-Triploid Mutation

In the nucleotide structure, four bases are included, guanine (G), cytosine (C), adenine (A) and thymine (T). Based on the Watson-Crick rule of complementarity, complementary base pairs are formed by A and T, and C and G. In binary coding of DNA, binary (11, 10, 01, 00) are assigned to bases (T, A, G, C) to generate 24 coding rules in total. However, only eight coding rules are in line with the base complementarity rules, as presented in Figure 5. Furthermore, mutation of bases may be caused by the self-replication of DNA during the transmission of genetic information.
Under the rules of the DNA triploid replication stage, a design for DNA mutation rule is performed. During triploid replication, each base is copied three times, so the presence of each base is more stable in the new DNA strand after mutation. This helps to reduce base pairing errors, improving the accuracy of DNA replication. In triploid organisms, DNA mutation is hypothesized to occur through the replication of one DNA strand into three strands, followed by the synthesis of a new mutant DNA strand based on specific rules. The synthesis rule defined by the algorithm takes binary numbers denoted by the basis and adds them together to generate a newly binary number which corresponds with the base number. In addition, eight DTM rules based on eight DNA coding rules are listed in Figure 6. The DTM provides a good algorithm for IE.

3. Designed Algorithm

For securing the image, an algorithm for encryption at the DNA level after compression is proposed. Take a color image as an example, first an image is input and then compressed in a certain compression ratio (CR). After that DNA encoding is performed on it and then triploid mutation is performed on the encoded image. Finally, perform confusion and diffusion operation at the DNA level, and then it is decoded to obtain the encrypted image. The specific algorithm is illustrated in Figure 7.

3.1. Encryption Algorithm

Step 1: Input an image and record the image S sized H × W × L.
Step 2: CS. A certain CR is set, the following is the detailed image compression process.
  • Sparse representation. Set a CR, and the sparse basis ψ is obtained by inputting the size of H into the sparse basis function DCT. Signal is transformed into the frequency domain and an expression of sparse representation presented in Equation (4). R, G, and B respectively for the sparse representation channels, with the corresponding results are denoted as R1, G1, B1.
    { R 1 = ψ R ψ ′ G 1 = ψ G ψ ′ B 1 = ψ B ψ ′ .
  • Signal observation. Input parameters and initial values of chaotic map, then perform the pre-iteration process. Observation matrices φ1, φ2, and φ3 are obtained by combining Hadamard matrices with partial pre-iterative results. These observation matrices are utilized with R1, G1 and B1 to obtain the observation results S1, S2, and S3, as shown in Equation (5).
    { S 1 = φ 1 ( φ 1 R 1 ) ′ S 2 = φ 2 ( φ 2 G 1 ) ′ S 3 = φ 3 ( φ 3 B 1 ) ′ .
  • Quantitative processing. The minimum and maximum observations mini, maxi by R, G and B groups are taken separately. According to those results, three groups of results D1, D2 and D3 are quantified and presented in Equation (6). At last, RGB images are reconstructed by quantization results, after CS the result is called SS1 with its size HH × WW × LL.
    { D 1 = round ( 255 S 1 − min R max R − min R ) D 2 = round ( 255 S 2 − min G max G − min G ) D 3 = round ( 255 S 3 − min B max B − min B ) .
Step 3: Generate the chaotic sequences. Input SS1 into hash-256 function to obtain four hash values ha, hb, hc and hd. Combine the hash values with the initial values to generate new initial values. Three new chaotic sequences chaoSeq1, chaoSeq2, chaoSeq3 are obtained by iterating through the M-RNN chaotic map. Reshaping results are Seqq1, Seqq2 and Seqq3 which are shown in Equation (7).
{ S e q q 1 = ⌊ c h a o S e q 1 + 100 ) × 10 10 ⌋ % 256 + 1 S e q q 2 = ⌊ c h a o S e q 2 + 100 ) × 10 10 ⌋ % 256 + 1 S e q q 3 = ⌊ c h a o S e q 3 + 100 ) × 10 10 ⌋ % 256 + 1 .
Step 4: Perform DNA encoding. Divide the compressed image SS1 into three channels for encoding operation respectively. The specific operation steps are as follows.
  • Convert decimal pixel values to binary.
  • Encode the binary numbers into DNA sequences, the specific encoding rules as given above.
  • Reshape them into three channels DD1, DD2, DD3 of size HH1 × WW1.
Since both the confusion and diffusion are operated at the DNA level, the chaotic sequences Seqq1, Seqq2 and Seqq3 need to be subjected to DNA encoding operations so as to obtain three chaotic sequence matrices XX, YY, ZZ of size HH1 × WW1.
Step 5: DNA mutation. DNA mutation is performed at each position in the three channels according to the eight mutation rules, which are listed above. The value DDi (i, j) of each channel after encoding and the same position of the three chaotic sequences Seqq1, Seqq2, Seqq3 are mutated based on certain mutation rules and the results are stored on D1, D2, D3.
Step 6: Confusion operation. Recombine D1, D2, D3 into NNN of size 3HH1 × 4WW1. Perform point-to-point confusion on the reorganized matrix. The confusion operation is performed by using an Arnold pseudo-random matrix. The new coordinate position vector k is calculated from the coordinates (i, j), and then the elements at coordinates (i, j) are exchanged with the elements at coordinates (k (1), k (2)) to obtain the confused matrix. Then reorganize the confused matrix into three matrices U1, U2 and U3 of size HH1 × 4WW1.
Step 7: Diffusion operation. Reshape the three matrices into XX, YY, ZZ of the same size to get SS1, SS2, SS3. Respectively perform the xor operation at the DNA level between SS1, SS2, SS3 and XX, YY, ZZ. The xor operation is performed in parity. Take SS1 as an example, set a flag i, when i is even, SS1 and XX carry out the xor operation. When i is odd, SS1 and YY carry out the xor operation. The operation is carried out a total of HH1 × 4WW1 times. Finally, the matrix after the xor operation is reorganized into three matrices SD11, SD22, SD33 of size HH1 × 4WW1.
Step 8: DNA decoding operation. Decode the three channels separately and then merge them together to get the cipher image TT1.

3.2. Decryption Algorithm

In this algorithm, decryption-decompression is shown in Figure 8. First encode the TT1. Specifically, the inverse diffusion and inverse confusion operations are first carried out. Then inverse DNA mutation is performed on it, and it is allowed to perform DNA decoding operations to obtain a decrypted image. Finally, the image is decompressed and the OMP is used for reconstruction to get the decompressed image.

4. Experimental Results and Simulation Effects

In this chapter, extensive simulation experiments are conducted to assess both efficiency and security from the presented encryption algorithm. This algorithm is realized in Windows 10 system based on MATLAB R2019b platform with computer hardware environment of Intel CPU 1.60GHz; RAM 8.00GB; Core i5-10210U.
Due to copyright problems, this experiment uses multiple images for simulation tests, and finally uses "1.1.tiff"(256 × 256 × 3), "1.2.tiff"(256 × 256 × 3), "2.1.tiff"(512 × 512 × 3), "2.2.tiff"(512 × 512 × 3), "3.1.tiff"(1024 × 1024 × 3), "3.2.tiff"(1024 × 1024 × 3) “4.1.tiff”(256 × 256) and “4.2.tiff”(256 × 256) to test the simulation of the algorithm. As shown in Figure 9, this algorithm can achieve encryption of the images with good results and restore the original images well.

5. Security Analysis

5.1. Performance of Compression

The CR is set to 0.2, 0.4, and 0.6 respectively, and three images of different sizes are compressed and reconstructed. The results of the tests for compression and reconstruction of the same image using different CRs can be seen in Figure 10. The quality of reconstruction is represented as Peak signal-to-noise ratio (PSNR) by a comparison between reconstructed and original images given in Equation (8). Results of the reconstruction as presented in Fig. 11. From this, it is clear that even with low CRs, an excellent quality of the reconstructed image can be achieved. Comparison between the algorithm and other algorithms for reconstruction quality is given in Table 1 [30,31,32], which shows the advantages of this algorithm that reconstruction quality in this algorithm compared with other algorithms is better.
{ M S E = 1 C K ∑ i = 0 C − 1 ∑ j = 0 K − 1 ‖ M ( i , j ) − R ( i , j ) ‖ 2 P S N R = 10 log 10 ( M A X I 2 M S E ) ,
where it is denoted as M and R for the before-compression image and the reconstructed image.

5.2. Analysis of Security Key

5.2.1. Key Space

Key to the algorithm is divided into three parts: chaotic system related parameters, the initial values and hash values. After a series of tests, the key space of each part and key space in total are given out, listed in Table 2. Encryption algorithm in general is considered to be resistant to brute force attacks when a larger than 2100 [33] key space is available. Comparison of key space in this algorithm with that of other algorithms presented in Table 3 [34,35,36,37] directly shows that it has a sufficiently big key space, which ensures security of the encryption algorithm.

5.2.2. Key Sensitivity

Key sensitivity test is a method for evaluating the security of an encryption algorithm. In testing key sensitivity of encryption process, a 10-15 perturbation is added to b to change the encryption process key. In the case of the encryption process, the number of pixels change rate (NPCR) is used as a measure to evaluate the key sensitivity, as shown in Equation (9). The NPCRs of different images are shown in Figure 12. Even a slight perturbation in the key during the encryption process may cause the encryption results to differ from the original results by more than 99.6094%. A 10-16 perturbation is added in the decryption process for the three sets of parameters a, c and d. It is clear from Figure 13 that images after decryption are not restored correctly. As can be seen from the figures, even though the perturbations added are very small, decryption cannot be successfully made, which indicates that the key is very sensitive.
N P C R ( S 1 , S 2 ) = 1 255 C K ∑ i = 1 C ∑ j = 1 K | S 1 ( i , j ) − S 2 ( i , j ) | × 100 % ,
where S1(i, j) and S2(i, j) are two cipher images that change only one pixel before and after the plaintext images. Cipher images are of size C × K.

5.3. Attack Resistance Test

5.3.1. Differential Attack

Information obtained by attackers through changing information in plaintext images to analyze changes in cipher images caused as differential attack. To measure ability of an algorithm to resist differential attacks, NPCR and uniform average changing intensity (UACI, Equation (10)) are utilized. IE algorithm can be successfully against differential attacks as proved by over 99.6094% of NPCR and close to 33.4635% of UACI. Test results in Table 4 show that both values are close to theoretical expectations of NPCR and UACI which indicate that a certain ability to resist differential attacks is provided by this algorithm. It is presented in Table 5 for a comparison with other algorithms for both NPCR and UACI [38,39,40,41].
U A C I ( D 1 , D 2 ) = 1 C K ∑ i = 0 C ∑ j = 0 K | D 1 ( i , j ) − D 2 ( i , j ) | 255 − 0 × 100 % .

5.3.2. Plaintext Attack

Plaintext attack is essential for encryption algorithms. In the plaintext attack tests, select both all black and white images for original images, as presented in Figure 14 (a). The results after compression-encryption and reconstruction are presented in Figure 14 (b) and Figure 14 (c). The results of decryption-decompression show visually no difference with plaintext images, indicating that it is resistant to plaintext attacks.

5.4. Statistical Characteristics Analysis

5.4.1. Histogram

In this section the distribution of image pixel points is analyzed by plotting histograms of images. For testing, two color images are chosen to observe distribution of pixels in plaintext images and decryption-decompression images presented in Figure 15. Waving patterns are displayed in histograms of original images, while encrypted images (CR = 0.6) show relatively even. This means that the encrypted images have a high degree of randomness. Information in the original images from the histogram is made extremely hard for attackers to access.

5.4.2. Correlation

The Two neighboring pixels in plaintext images are highly correlated in vertical (V), horizontal (H) and diagonal (D) directions, while in cipher images correlation between neighboring pixels is low. The formula used to calculate correlation of neighboring pixels of the image as shown in Equation (11).
{ r x y = U ( ( x − U ( x ) ) ( y − U ( y ) ) ) V ( x ) V ( y ) U ( x ) = 1 T ∑ i = 1 N x i V ( x ) = 1 T ∑ i = 1 N ( x i − U ( x ) ) 2
where variable x is denoted by U(x), V(x) represents the variance of variable x, gray scale values of x and y refer to the neighboring pixels, and samples in total are represented by T.
It is evident from Figure 16 and Figure 17 (three channels of a color image are R, G and B, grayscale image is indicated by Gr, all-black image is b, and all-white image is w) that correlation coefficients for different plaintext images as well as compressed-encrypted images are listed. Obviously, correlation coefficients in cipher images are nearly zero. Distributions of neighboring pixels for both plaintext and cipher images are illustrated in Figure 18. Cipher image has more scattered neighboring pixels in all three directions as compared to the plaintext image as can be clearly seen in Figure 18. Thus, it is observed that related information with plaintext images can be well hidden by this encryption algorithm.

5.4.3. Information Entropy

To measure randomness of information, information entropy is a theory which has a value of 8 [42]. When a measured information entropy is close to theoretical value, it indicates that the image pixels are well distributed. The values of information entropy for different images encrypted by this algorithm refer to Table 6. It is concluded that information entropy of the cipher images closely matches the theoretical one, illustrating that excellent effects of encryption is achieved.

5.5. Robustness

Noise attacks and shearing attacks are tested in this subsection to measure the robustness of this encryption algorithm.

5.5.1. Noise Attack

In the cipher images (CR = 0.6) salt and pepper noise (SPN) of 0.01 and 0.05 are added respectively, and decrypted-decompressed results are presented in Figure 19. Results after adding SPN are successfully decrypted-decompressed and are still visually recognizable. The PSNR of each image after adding noise respectively as illustrated in Figure 20. As can be seen from the figures, after suffering from different sizes of SPN after compression, the PSNR is still close to 30 dB, indicating that the algorithm can resist some levels of noise attacks.

5.5.2. Shearing Attack

Cutting 12.5% of the cipher images, the results after decrypted-decompressed are shown in Figure 21. With the CR of 0.6, even though 12.5% of the images are cut off, it is still possible to recognize major information about original images after decrypted-decompressed. The test results show that a certain extent of shearing attacks can be resisted in this algorithm.

6. Conclusion

A universal image compression-encryption algorithm based on DTM is proposed from this paper. Firstly, the image is compressed, and then chaotic sequences iterated by RNN are used to perform DTM operations. Finally, the encrypted image can be obtained by utilizing chaotic sequences in the DNA level with confusion and diffusion algorithms. In the simulation tests, images of different sizes are chosen for encryption. The simulation results not only prove the effectiveness of the algorithm, but also show that the algorithm can encrypt universal images of different sizes. As shown by performance tests, a sufficiently big key space is provided by M-RNN to withstand brute force attacks. Moreover, this algorithm has the ability to withstand statistical analysis attacks and passes robustness tests. The security and reliability of the algorithm is proved. The compression operation is performed by the algorithm before encryption, which reduces the workloads of encryption at the DNA level and improves the efficiency of the algorithm.
However, the algorithm also has certain limitation, which is that the reconstruction time after decryption is long. In the future, this problem will be addressed to improve the efficiency of decompression without affecting the security of the algorithm.

Author Contributions

Conceptualization, Y.C. and L.T.; Methodology, Y.C. and L.T.; Validation, Software L.T., Y.C., L.T., B.L. and X.X.; Formal analysis, Y.C. and L.T.; Investigation, X.X. and B.L.; Resources, Y.C., L.T., B.L. and X.X.; Data curation, L.T. and X.X.; Writing—original draft preparation, Y.C. and L.T.; Writing—review and editing, Y.C. and L.T.; Visualization, X.X. and B.L.; Supervision, Y.C.; Project Administration, B.L. and X.X.; Funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the National Natural Science Foundation of China (Grant Nos. 62061014), Technological innovation projects in the field of artificial intelligence in Liaoning province (Grant Nos. 2023JH26/10300011), Basic scientific research projects in department of education of Liaoning Province (Grant Nos. JYTZD2023021).

Data Availability Statement

No applicable.

Acknowledgments

The authors thank the referees for their detailed reading and comments that were both helpful and insightful.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Liu, C.; Xu, B. A night pavement crack detection method based on image-to-image translation. Computer-Aided Civil and Infrastructure Engineering 2022, 37, 1737–1753. [Google Scholar] [CrossRef]
  2. Sun, F.; Lv, Z. A secure image encryption based on spatial surface chaotic system and AES algorithm. Multimedia Tools and Applications 2022, 1–21. [Google Scholar] [CrossRef]
  3. Sahoo, A.; Mohanty, P.; Sethi, P.C. Image encryption using RSA algorithm. In Intelligent Systems: Proceedings of ICMIB 2021; Springer, 2022; pp. 641–652. [Google Scholar] [CrossRef]
  4. Zhang, X.; Wang, L.; Cui, G.; Niu, Y. Entropy-based block scrambling image encryption using DES structure and chaotic systems. International Journal of Optics 2019, 2019. [Google Scholar] [CrossRef]
  5. Rehman, M.U.; Shafique, A.; Khan, K.H.; Hazzazi, M.M. Efficient and secure image encryption using key substitution process with discrete wavelet transform. Journal of King Saud University-Computer and Information Sciences 2023, 35, 101613. [Google Scholar] [CrossRef]
  6. Lin, H.; Wang, C.; Sun, Y. A universal variable extension method for designing multiscroll/wing chaotic systems. IEEE Transactions on Industrial Electronics 2023. [Google Scholar] [CrossRef]
  7. Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting newly designed fractional-order 3D Lorenz chaotic system and 2D discrete polynomial hyper-chaotic map for high-performance multi-image encryption. Fractal and Fractional 2023, 7, 887. [Google Scholar] [CrossRef]
  8. Wang, C.; Tang, D.; Lin, H.; Yu, F.; Sun, Y. High-dimensional memristive neural network and its application in commercial data encryption communication. Expert Systems with Applications 2024, 242, 122513. [Google Scholar] [CrossRef]
  9. Feng, W.; Zhao, X.; Zhang, J.; Qin, Z.; Zhang, J.; He, Y. Image encryption algorithm based on plane-level image filtering and discrete logarithmic transform. Mathematics 2022, 10, 2751. [Google Scholar] [CrossRef]
  10. Zhang, B.; Liu, L. Chaos-based image encryption: Review, application, and challenges. Mathematics 2023, 11, 2585. [Google Scholar] [CrossRef]
  11. Tang, D.; Wang, C.; Lin, H.; Yu, F. Dynamics analysis and hardware implementation of multi-scroll hyperchaotic hidden attractors based on locally active memristive Hopfield neural network. Nonlinear Dynamics 2024, 112, 1511–1527. [Google Scholar] [CrossRef]
  12. Deng, Q.; Wang, C.; Lin, H. Memristive Hopfield neural network dynamics with heterogeneous activation functions and its application. Chaos, Solitons & Fractals 2024, 178, 114387. [Google Scholar] [CrossRef]
  13. Bao, B.; Wang, Z.; Hua, Z.; Chen, M.; Bao, H. Regime transition and multi-scroll hyperchaos in a discrete neuron model. Nonlinear Dynamics 2023, 111, 13499–13512. [Google Scholar] [CrossRef]
  14. Maazouz, M.; Toubal, A.; Bengherbia, B.; Houhou, O.; Batel, N. FPGA implementation of a chaos-based image encryption algorithm. Journal of King Saud University-Computer and Information Sciences 2022, 34, 9926–9941. [Google Scholar] [CrossRef]
  15. Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Optics and Lasers in Engineering 2017, 88, 197–213. [Google Scholar] [CrossRef]
  16. Enayatifar, R.; Abdullah, A.H.; Isnin, I.F. Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence. Optics and Lasers in Engineering 2014, 56, 83–93. [Google Scholar] [CrossRef]
  17. Masood, F.; Masood, J.; Zhang, L.; Jamal, S.S.; Boulila, W.; Rehman, S.U.; Khan, F.A.; Ahmad, J. A new color image encryption technique using DNA computing and Chaos-based substitution box. Soft Computing 2022, 1–17. [Google Scholar] [CrossRef]
  18. Ts'o, P.O. Basic Principles in Nucleic Acid Chemistry V2. Elsevier, 2012; Volume 2. [Google Scholar]
  19. Li, Q.; Chen, L. An image encryption algorithm based on 6-dimensional hyper chaotic system and DNA encoding. Multimedia Tools and Applications 2024, 83, 5351–5368. [Google Scholar] [CrossRef]
  20. Fan, W.; Li, T.; Wu, J.; Wu, J. Chaotic Color Image Encryption Based on Eight-Base DNA-Level Permutation and Diffusion. Entropy 2023, 25, 1268. [Google Scholar] [CrossRef] [PubMed]
  21. Wang, Q.; Zhang, X.; Zhao, X. Color image encryption algorithm based on bidirectional spiral transformation and DNA coding. Physica Scripta 2023, 98, 025211. [Google Scholar] [CrossRef]
  22. Kumari, P.; Mondal, B. Lightweight image encryption algorithm using NLFSR and CBC mode. The Journal of Supercomputing 2023, 79, 19452–19472. [Google Scholar] [CrossRef]
  23. Sha, Y.; Bo, S.; Yang, C.; Mou, J.; Jahanshahi, H. A chaotic image encryption scheme based on genetic central dogma and KMP method. International Journal of Bifurcation and Chaos 2022, 32, 2250186. [Google Scholar] [CrossRef]
  24. Gao, X.; Mou, J.; Banerjee, S.; Zhang, Y. Color-gray multi-image hybrid compression–encryption scheme based on BP neural network and knight tour. IEEE Transactions on Cybernetics 2023. [Google Scholar] [CrossRef] [PubMed]
  25. Liu, X.; An, P.; Chen, Y.; Huang, X. An improved lossless image compression algorithm based on Huffman coding. Multimedia Tools and Applications 2022, 81, 4781–4795. [Google Scholar] [CrossRef]
  26. Zhang, Z.; Cao, Y.; Jahanshahi, H.; Mou, J. Chaotic color multi-image compression-encryption/LSB data type steganography scheme for NFT transaction security. Journal of King Saud University-Computer and Information Sciences 2023, 35, 101839. [Google Scholar] [CrossRef]
  27. Bao, P.; Xia, W.; Yang, K.; Chen, W.; Chen, M.; Xi, Y.; Niu, S.; Zhou, J.; Zhang, H.; Sun, H. Convolutional sparse coding for compressed sensing CT reconstruction. IEEE Transactions on Medical Imaging 2019, 38, 2607–2619. [Google Scholar] [CrossRef] [PubMed]
  28. Ahmed, N.; Natarajan, T.; Rao, K.R. Discrete cosine transform. IEEE transactions on Computers 1974, 100, 90–93. [Google Scholar] [CrossRef]
  29. Buiakova, O.; Baker, H.; Scott, J.; Farbman, A.; Kream, R.; Grillo, M.; Franzen, L.; Richman, M.; Davis, L.; Abbondanzo, S. Olfactory marker protein (OMP) gene deletion causes altered physiological activity of olfactory sensory neurons. Proceedings of the National Academy of Sciences 1996, 93, 9858–9863. [Google Scholar] [CrossRef] [PubMed]
  30. Wang, X.; Su, Y. Image encryption based on compressed sensing and DNA encoding. Signal Processing: Image Communication 2021, 95, 116246. [Google Scholar] [CrossRef]
  31. Xu, Q.; Sun, K.; Cao, C.; Zhu, C. A fast image encryption algorithm based on compressive sensing and hyperchaotic map. Optics and Lasers in Engineering 2019, 121, 203–214. [Google Scholar] [CrossRef]
  32. Chai, X.; Zheng, X.; Gan, Z.; Han, D.; Chen, Y. An image encryption algorithm based on chaotic system and compressive sensing. Signal Processing 2018, 148, 124–144. [Google Scholar] [CrossRef]
  33. Gan, Z.; Chai, X.; Bi, J.; Chen, X. Content-adaptive image compression and encryption via optimized compressive sensing with double random phase encoding driven by chaos. Complex & Intelligent Systems 2022. [Google Scholar] [CrossRef]
  34. Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Information Sciences 2019, 480, 403–419. [Google Scholar] [CrossRef]
  35. Yang, F.; An, X. A new discrete chaotic map application in image encryption algorithm. Physica Scripta 2022, 97, 035202. [Google Scholar] [CrossRef]
  36. Xian, Y.; Wang, X. Fractal sorting matrix and its application on chaotic image encryption. Information Sciences 2021, 547, 1154–1169. [Google Scholar] [CrossRef]
  37. Zhu, L.; Song, H.; Zhang, X.; Yan, M.; Zhang, T.; Wang, X.; Xu, J. A robust meaningful image encryption scheme based on block compressive sensing and SVD embedding. Signal Processing 2020, 175, 107629. [Google Scholar] [CrossRef]
  38. Zhou, Z.; Xu, X.; Jiang, Z.; Sun, K. Multiple-Image Encryption Scheme Based on an N-Dimensional Chaotic Modular Model and Overlapping Block Permutation–Diffusion Using Newly Defined Operation. Mathematics 2023, 11, 3373. [Google Scholar] [CrossRef]
  39. Wang, X.; Liu, L.; Song, M. Remote sensing image and multi-type image joint encryption based on NCCS. Nonlinear Dynamics 2023, 111, 14537–14563. [Google Scholar] [CrossRef]
  40. Du, Y.; Long, G.; Jiang, D.; Chai, X.; Han, J. Optical image encryption algorithm based on a new four-dimensional memristive hyperchaotic system and compressed sensing. Chinese Physics B 2023, 32, 114203. [Google Scholar] [CrossRef]
  41. Zhang, X.; Liao, J. Multiple-image encryption algorithm based on 3D-LWT and dynamic stereo S-box. Multimedia Tools and Applications 2024, 83, 16337–16362. [Google Scholar] [CrossRef]
  42. Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Information Sciences 2013, 222, 323–342. [Google Scholar] [CrossRef]
Preprints 107772 g001
Figure 1. M-RNN (a) PD of M-RNN when a = -0.4 (a) PD of M-RNN when a = -0.6 (a) PD of M-RNN when a = -0.8 (d) LEs of M-RNN (e) BD of M-RNN (f) complexity of parameters a and d.
Figure 1. M-RNN (a) PD of M-RNN when a = -0.4 (a) PD of M-RNN when a = -0.6 (a) PD of M-RNN when a = -0.8 (d) LEs of M-RNN (e) BD of M-RNN (f) complexity of parameters a and d.
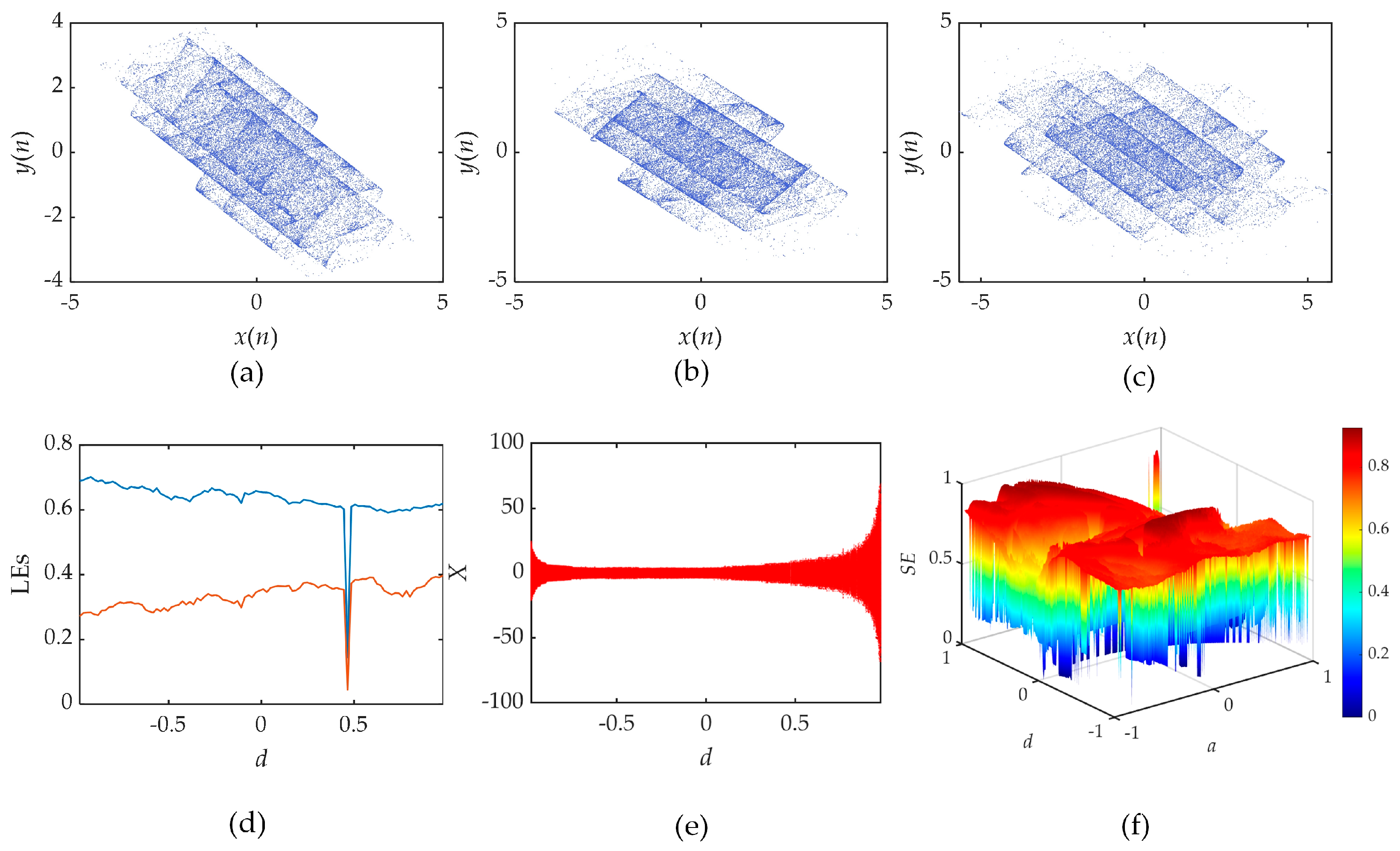
Preprints 107772 g001
Preprints 107772 g002
Figure 2. P-value tests.
Figure 2. P-value tests.
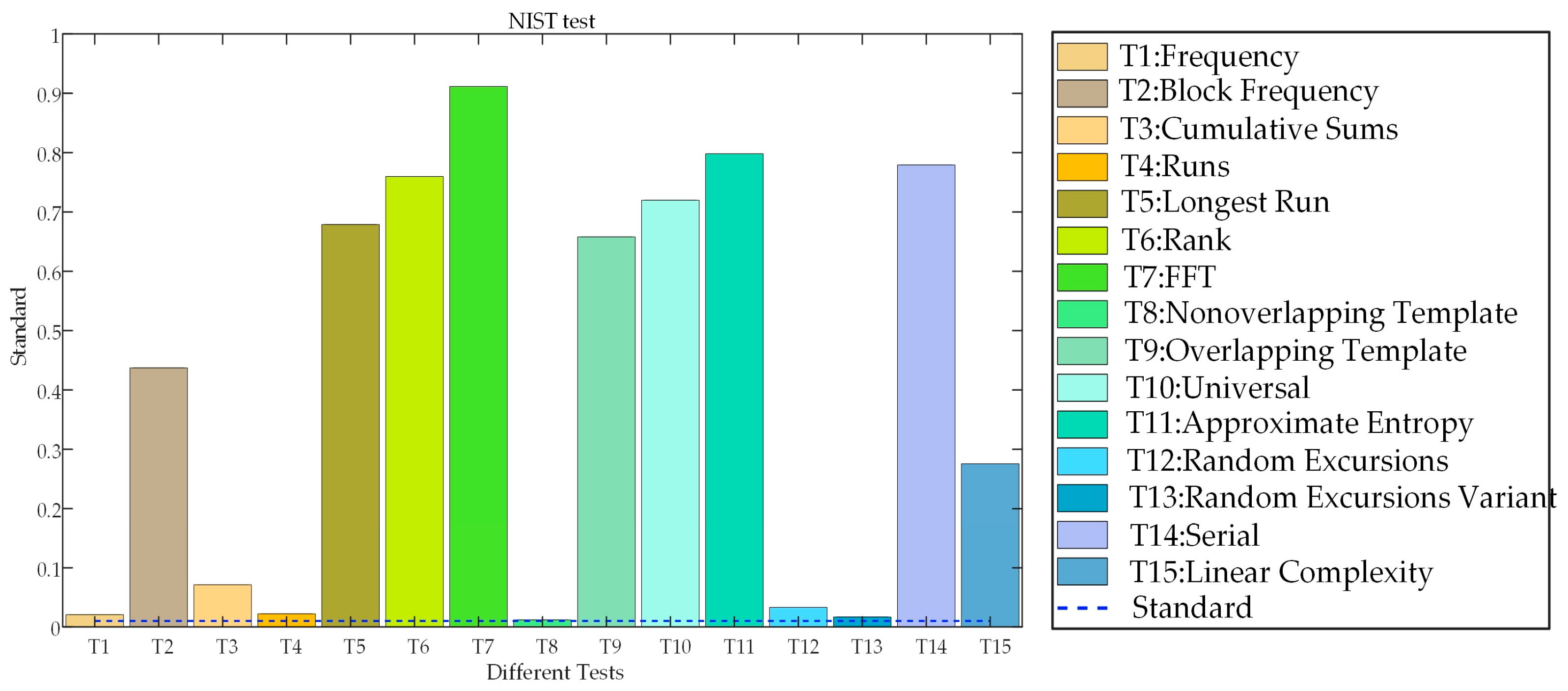
Preprints 107772 g002
Preprints 107772 g003
Figure 3. PR tests.
Figure 3. PR tests.
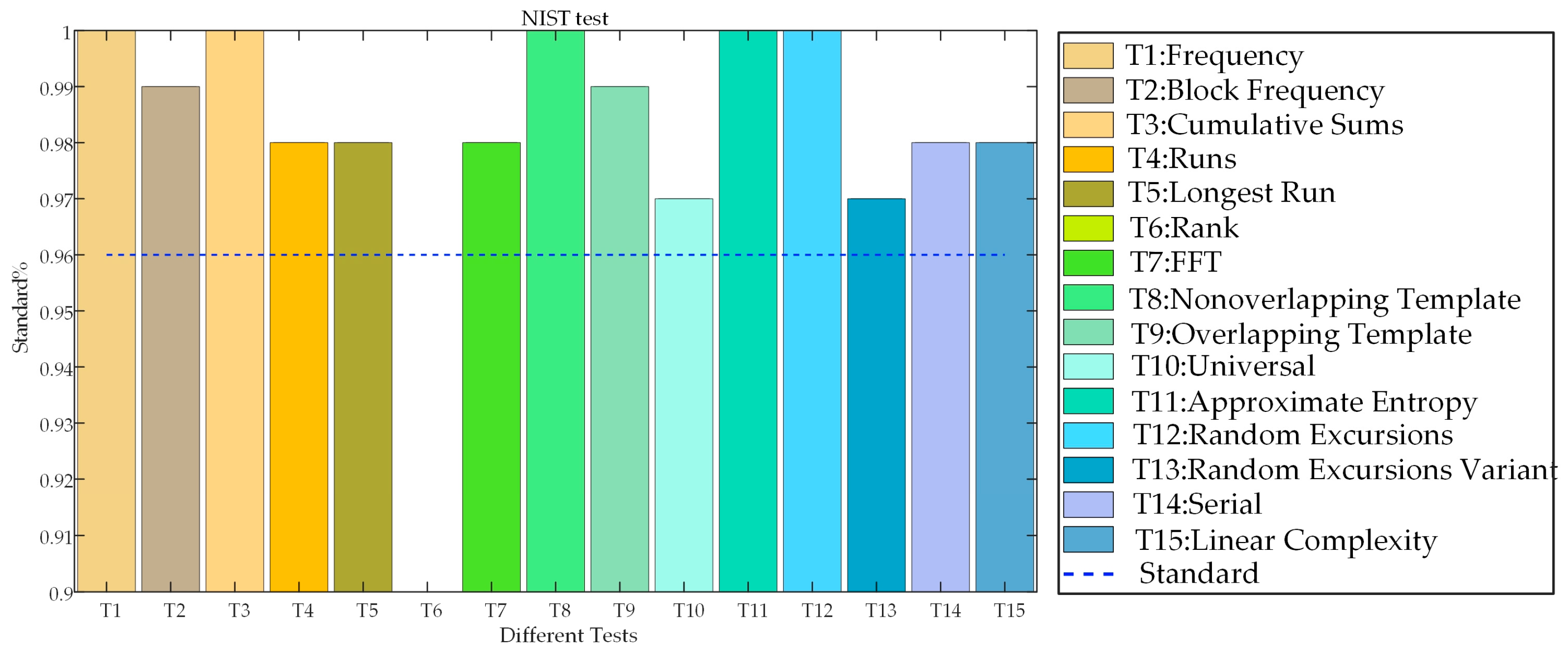
Preprints 107772 g003
Preprints 107772 g004
Figure 4. CS process.
Figure 4. CS process.
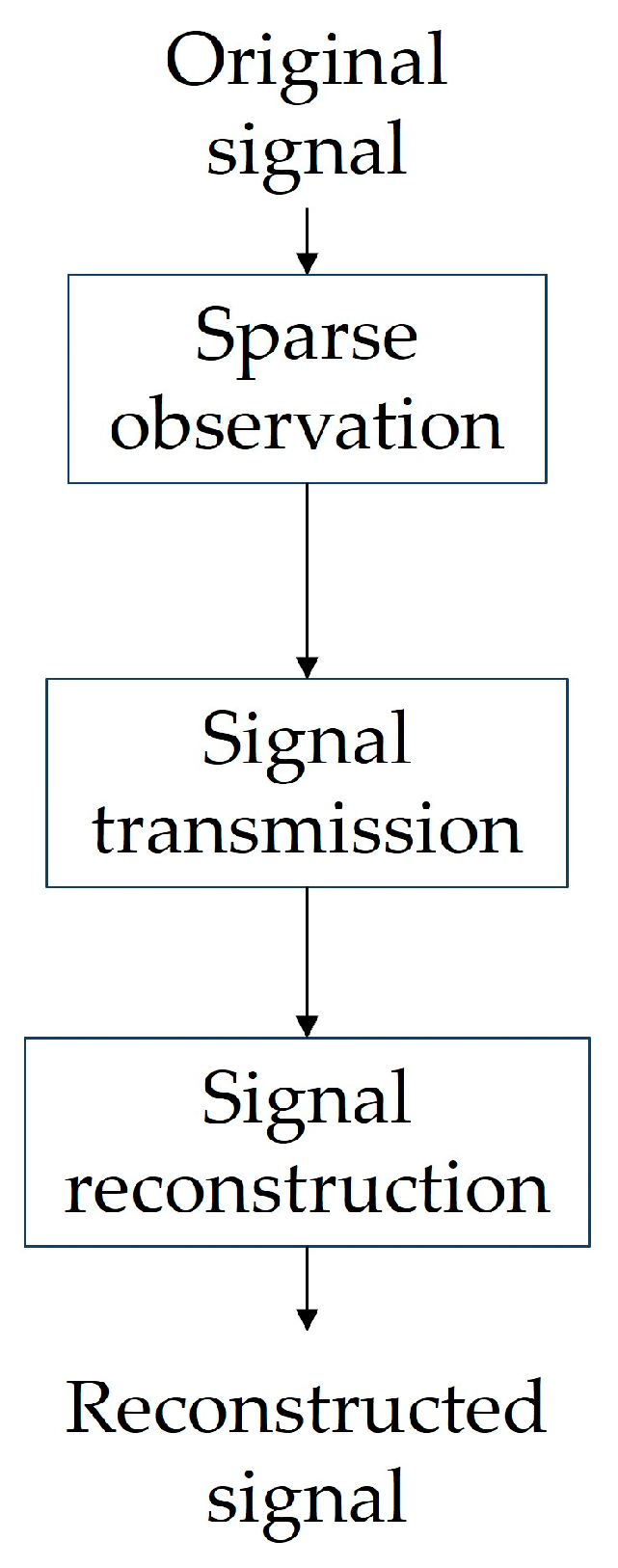
Preprints 107772 g004
Preprints 107772 g005
Figure 5. DNA rules.
Figure 5. DNA rules.
Preprints 107772 g005
Preprints 107772 g006
Figure 6. DTM.
Figure 6. DTM.
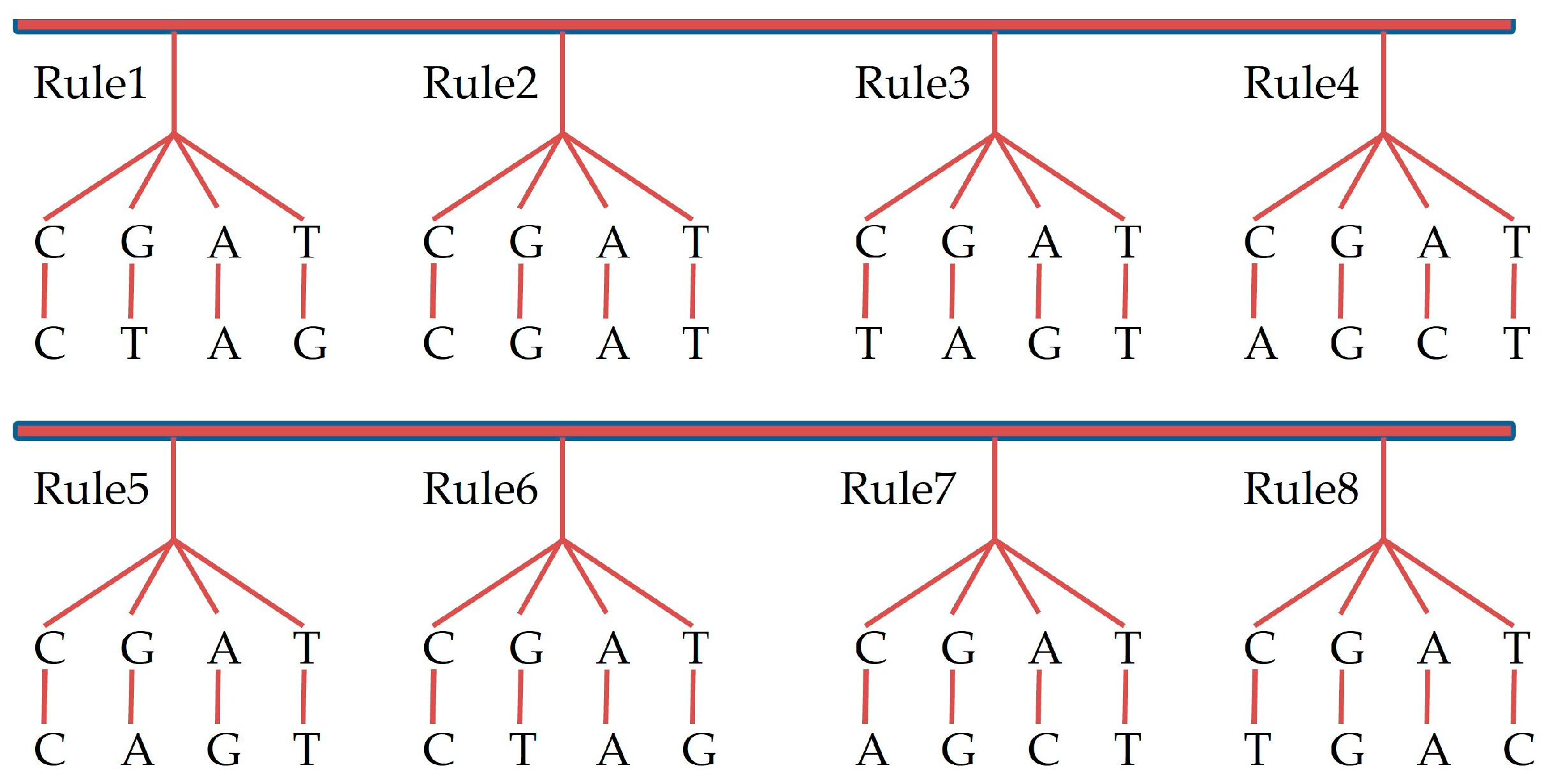
Preprints 107772 g006
Preprints 107772 g007
Figure 7. Encryption algorithm flowchart.
Figure 7. Encryption algorithm flowchart.
Preprints 107772 g007
Preprints 107772 g008
Figure 8. Decryption algorithm flowchart.
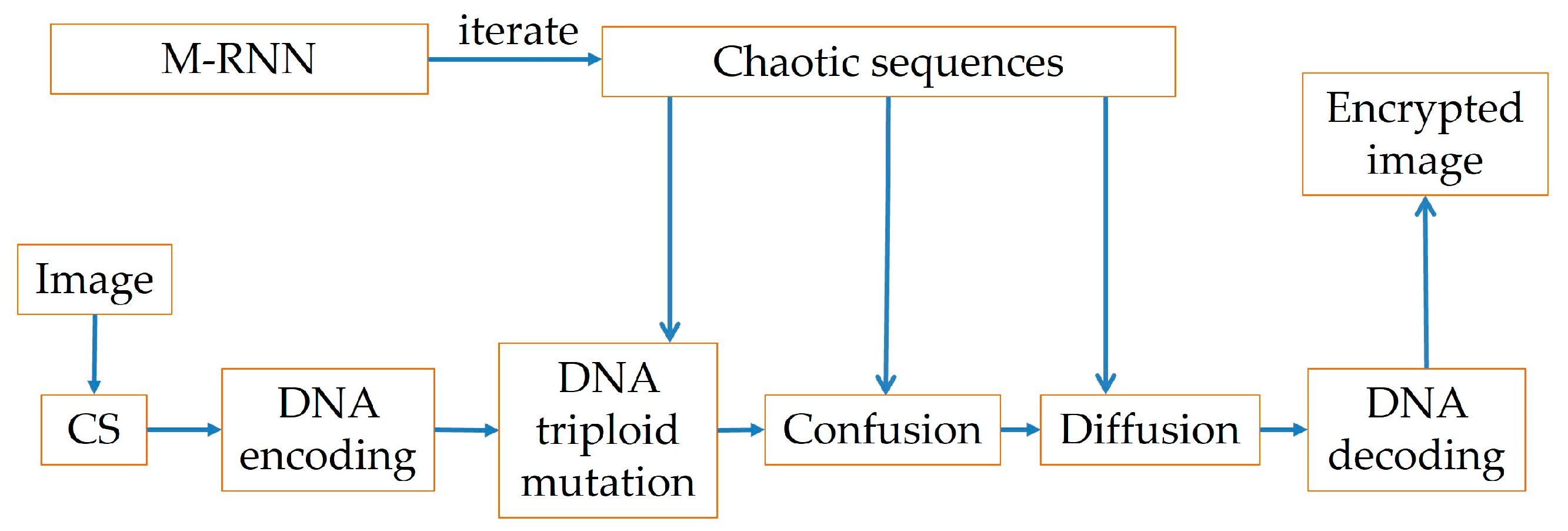
Figure 8. Decryption algorithm flowchart.
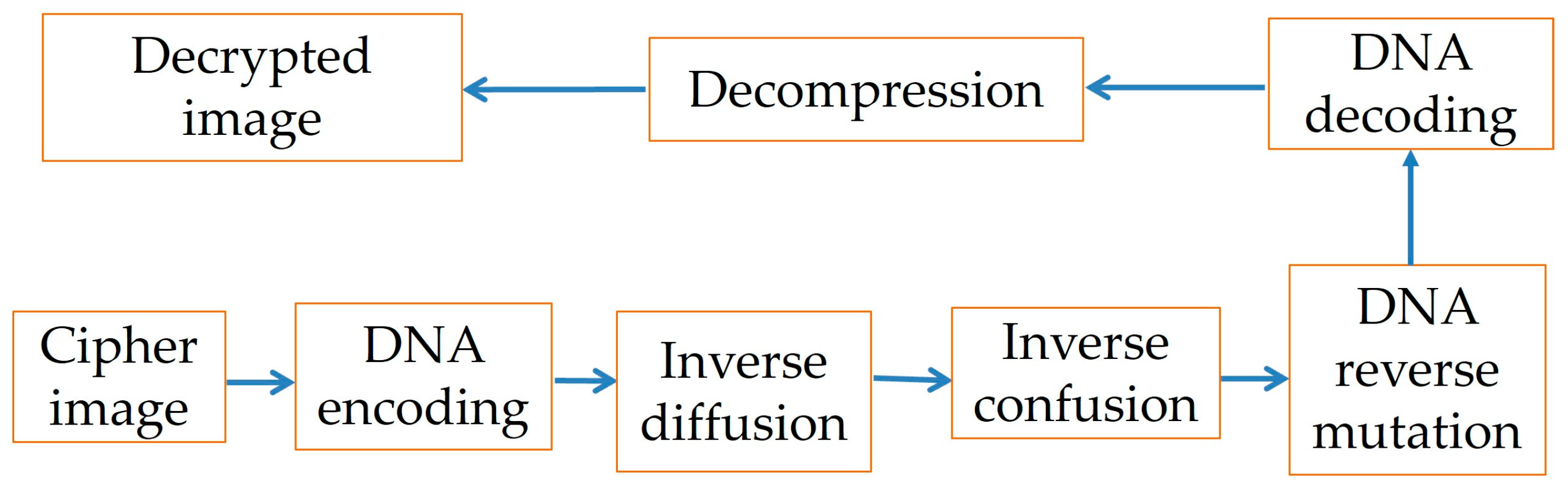
Preprints 107772 g008
Preprints 107772 g009
Figure 9. Simulation results of the images during IE (a) original (b) cipher (c) decrypted.
Figure 9. Simulation results of the images during IE (a) original (b) cipher (c) decrypted.
Preprints 107772 g009
Preprints 107772 g010
Figure 10. Compression reconstruction effects under different CRs (a) 0.2 (b) 0.4 (c) 0.6.
Figure 10. Compression reconstruction effects under different CRs (a) 0.2 (b) 0.4 (c) 0.6.
Preprints 107772 g010
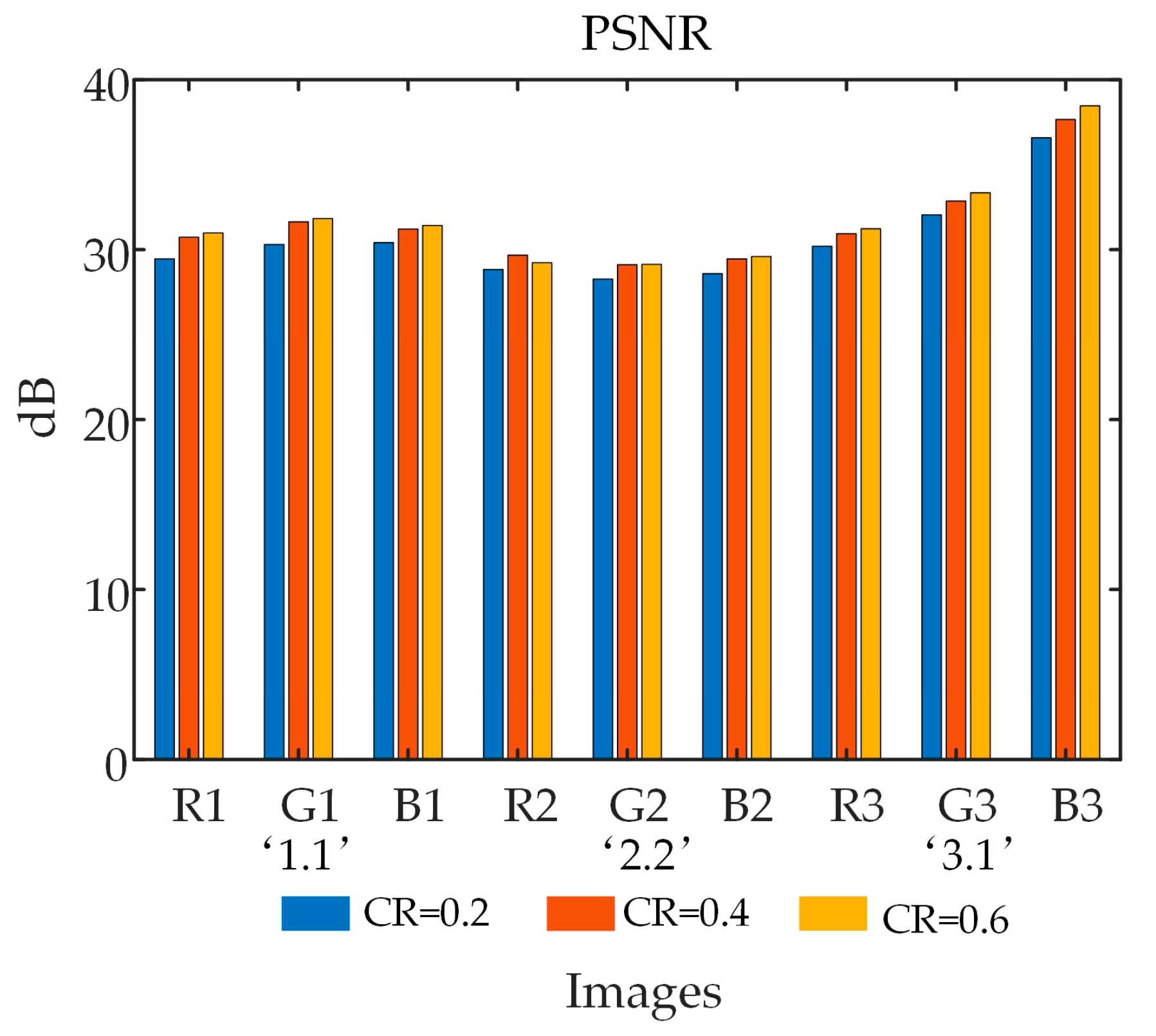
Preprints 107772 g011
Figure 11. Comparison of PSNR with different CRs for different images.
Figure 11. Comparison of PSNR with different CRs for different images.
Preprints 107772 g011
Preprints 107772 g012
Figure 12. Results of key sensitivity tests.
Figure 12. Results of key sensitivity tests.
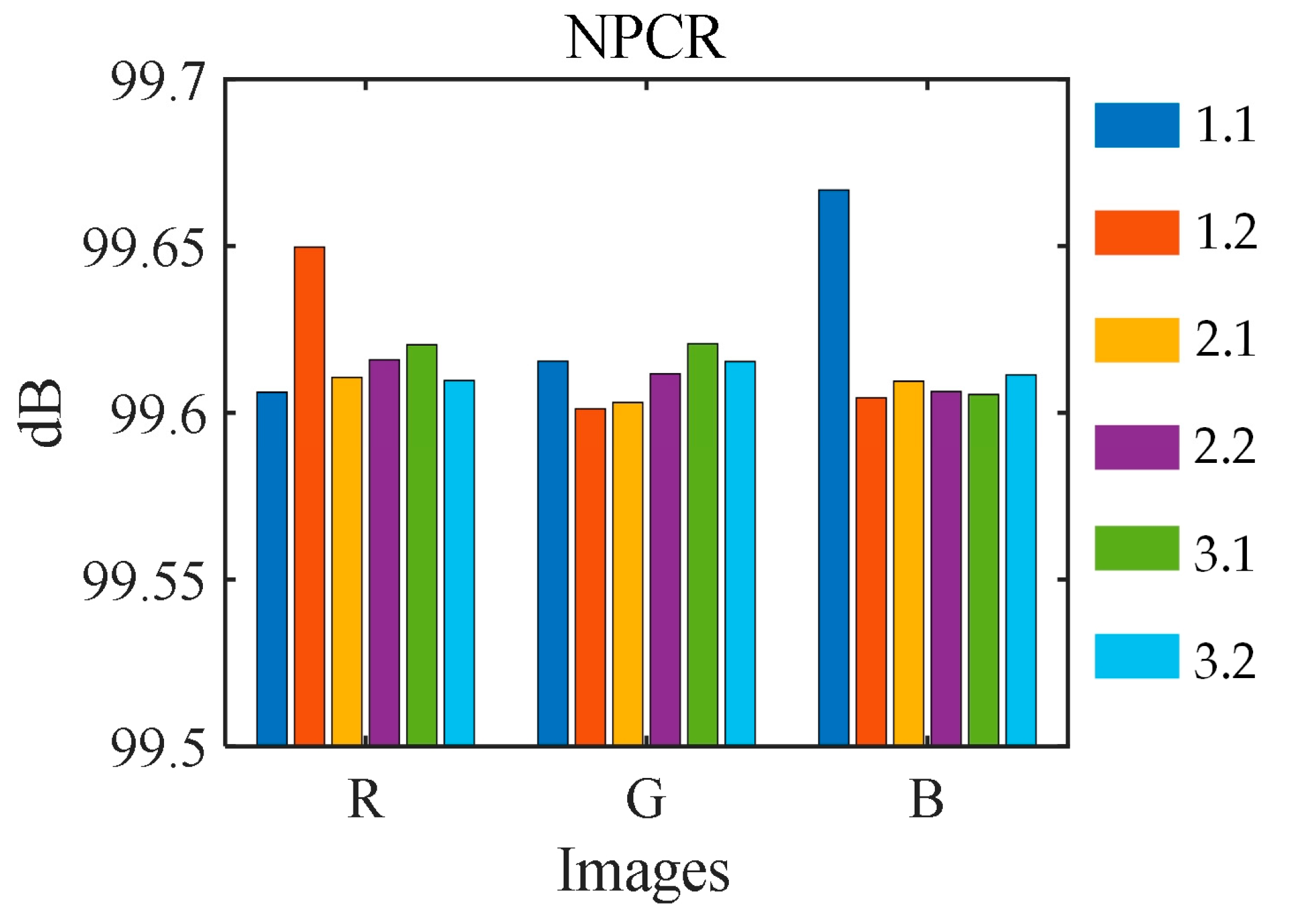
Preprints 107772 g012
Preprints 107772 g013
Figure 13. Key sensitivity of decryption process (a) parameter a = a + 10-16 (b) parameter c = c + 10-16 (c) parameter d = d + 10-16.
Figure 13. Key sensitivity of decryption process (a) parameter a = a + 10-16 (b) parameter c = c + 10-16 (c) parameter d = d + 10-16.
Preprints 107772 g013
Preprints 107772 g014
Figure 14. Result images of plaintext attacks.
Figure 14. Result images of plaintext attacks.
Preprints 107772 g014
Preprints 107772 g015
Figure 15. Histograms.
Figure 15. Histograms.
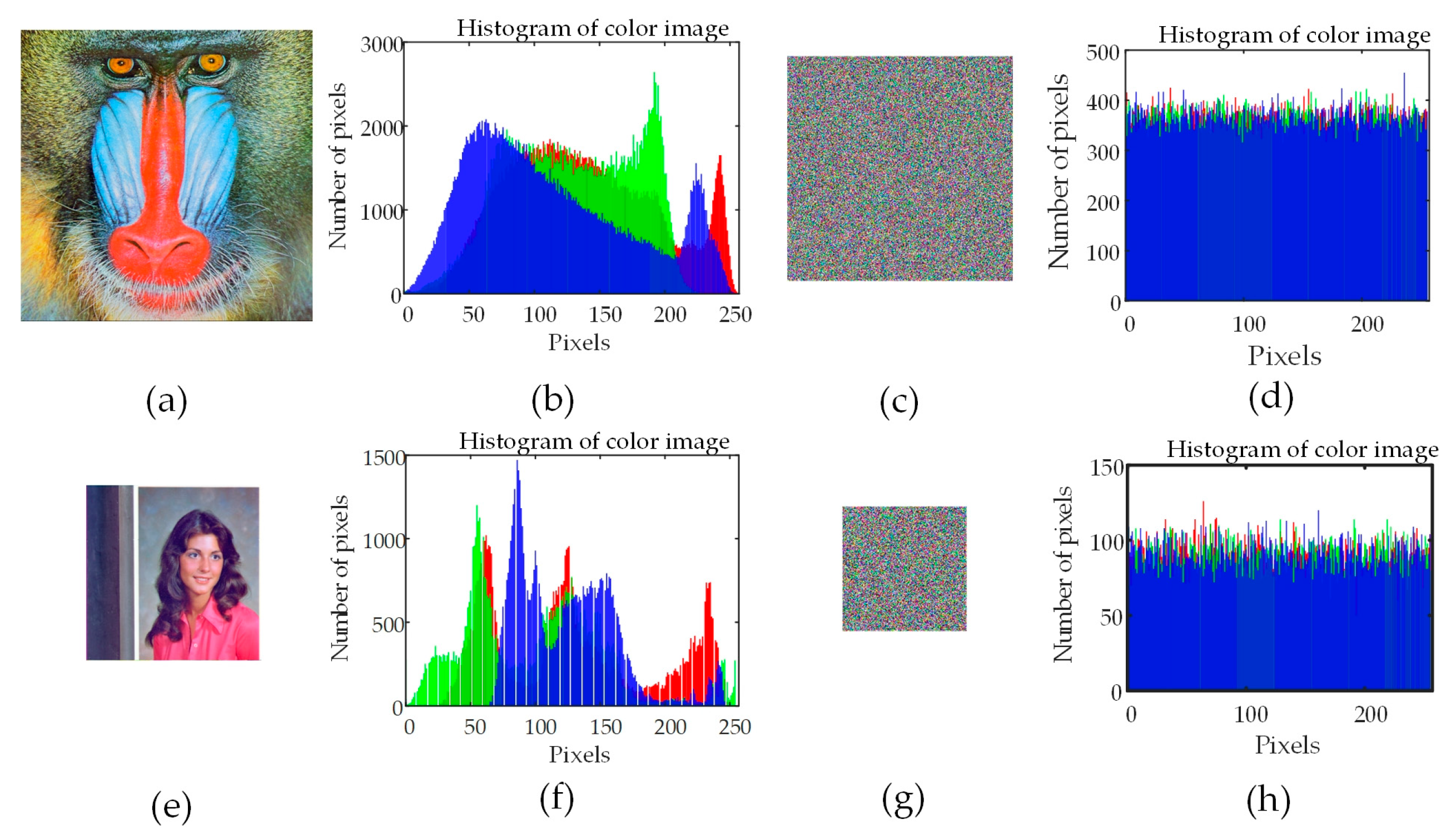
Preprints 107772 g015
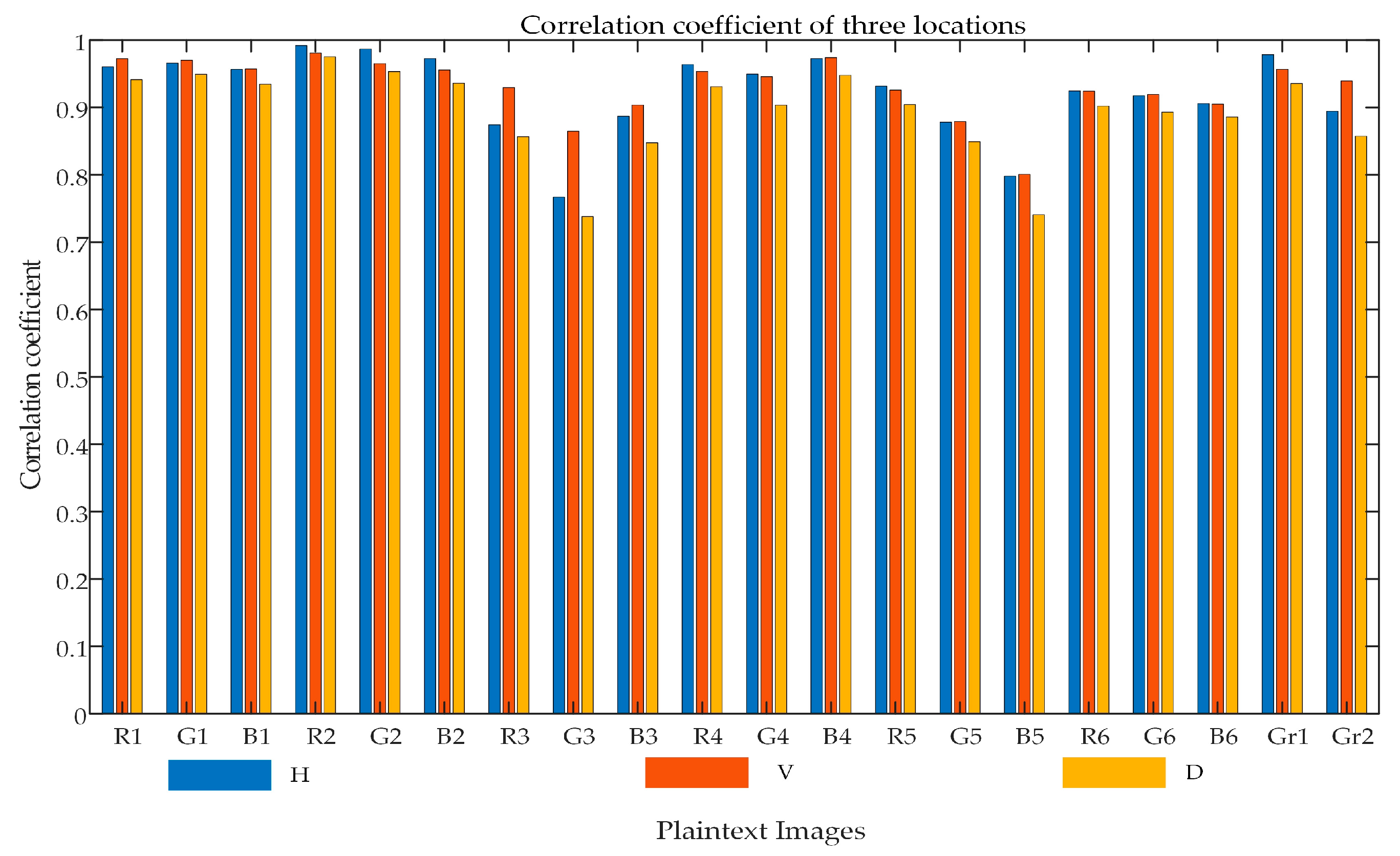
Preprints 107772 g016
Figure 16. Correlation in plaintext images.
Figure 16. Correlation in plaintext images.
Preprints 107772 g016
Preprints 107772 g017
Figure 17. Correlation in cipher images.
Figure 17. Correlation in cipher images.
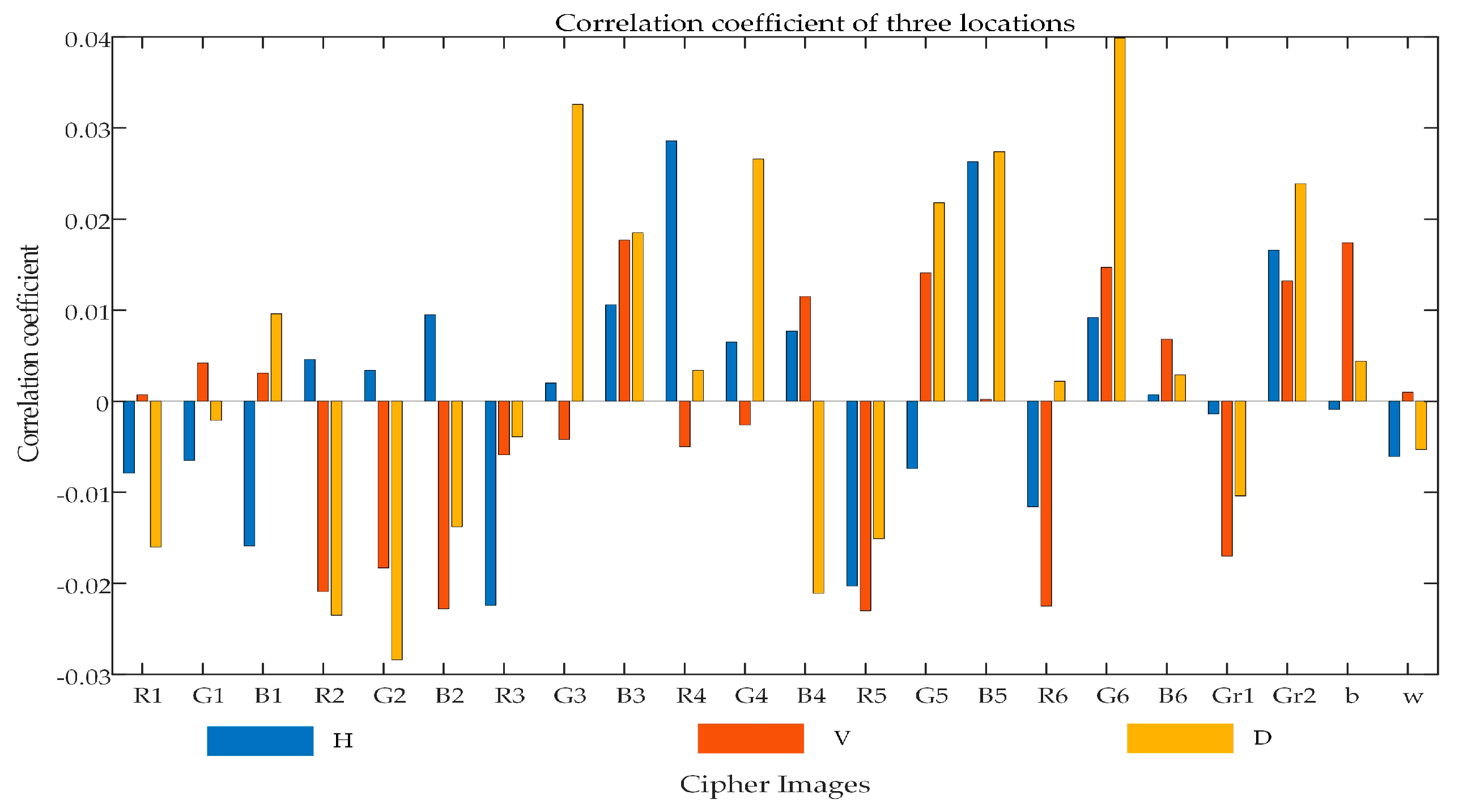
Preprints 107772 g017
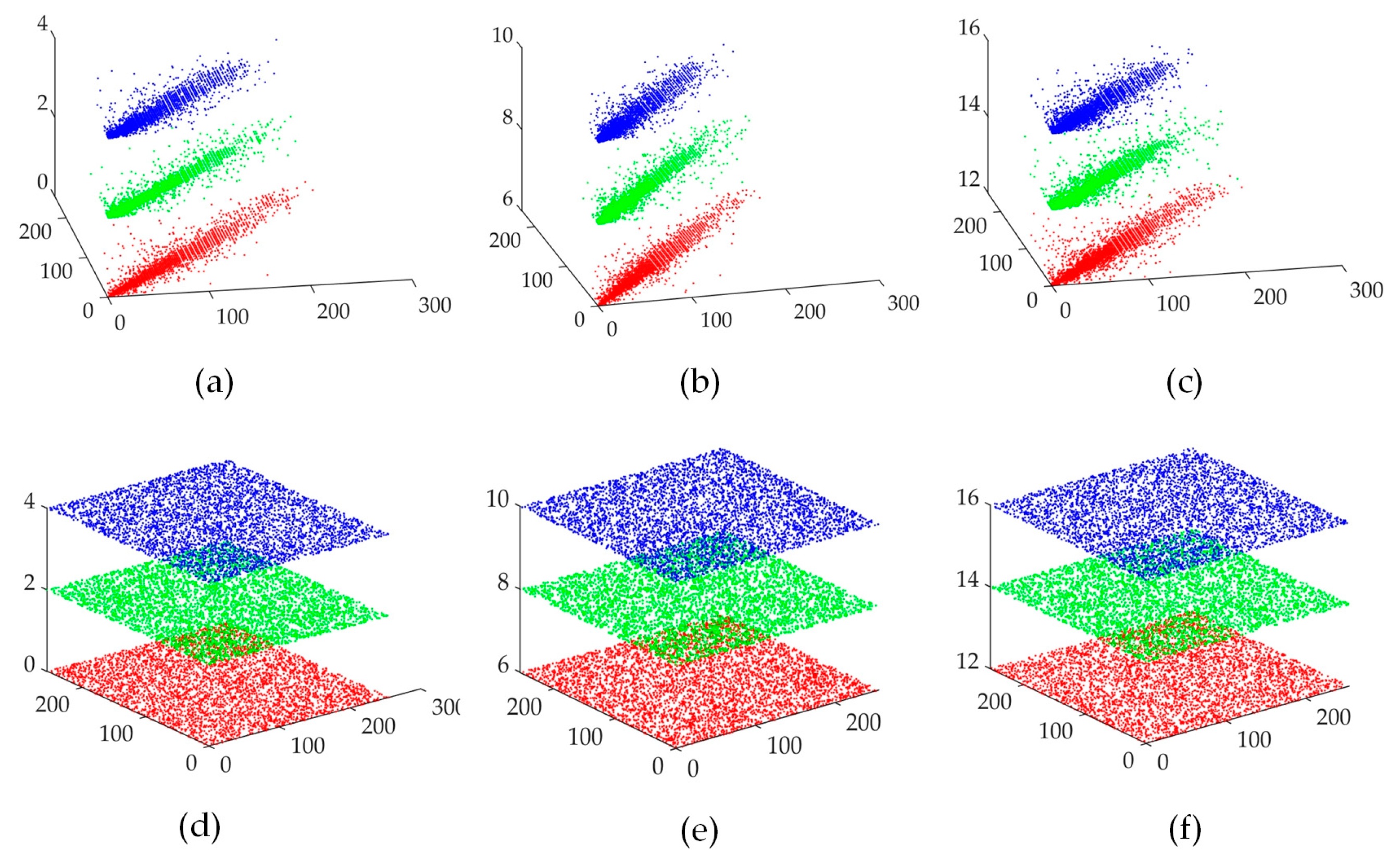
Preprints 107772 g018
Figure 18. Correlation diagram of image "1.1" in three directions of original image (a) H (b) V (c) D correlation diagram in three directions of cipher image (d) H (e) V (f) D.
Figure 18. Correlation diagram of image "1.1" in three directions of original image (a) H (b) V (c) D correlation diagram in three directions of cipher image (d) H (e) V (f) D.
Preprints 107772 g018
Preprints 107772 g019
Figure 19. Image ‘1.1’, ‘1.2’, ’2.1’, ‘2.2’ restoration results of noise attacks (a) 0.01 SPN (b) 0.05 SPN.
Figure 19. Image ‘1.1’, ‘1.2’, ’2.1’, ‘2.2’ restoration results of noise attacks (a) 0.01 SPN (b) 0.05 SPN.
Preprints 107772 g019
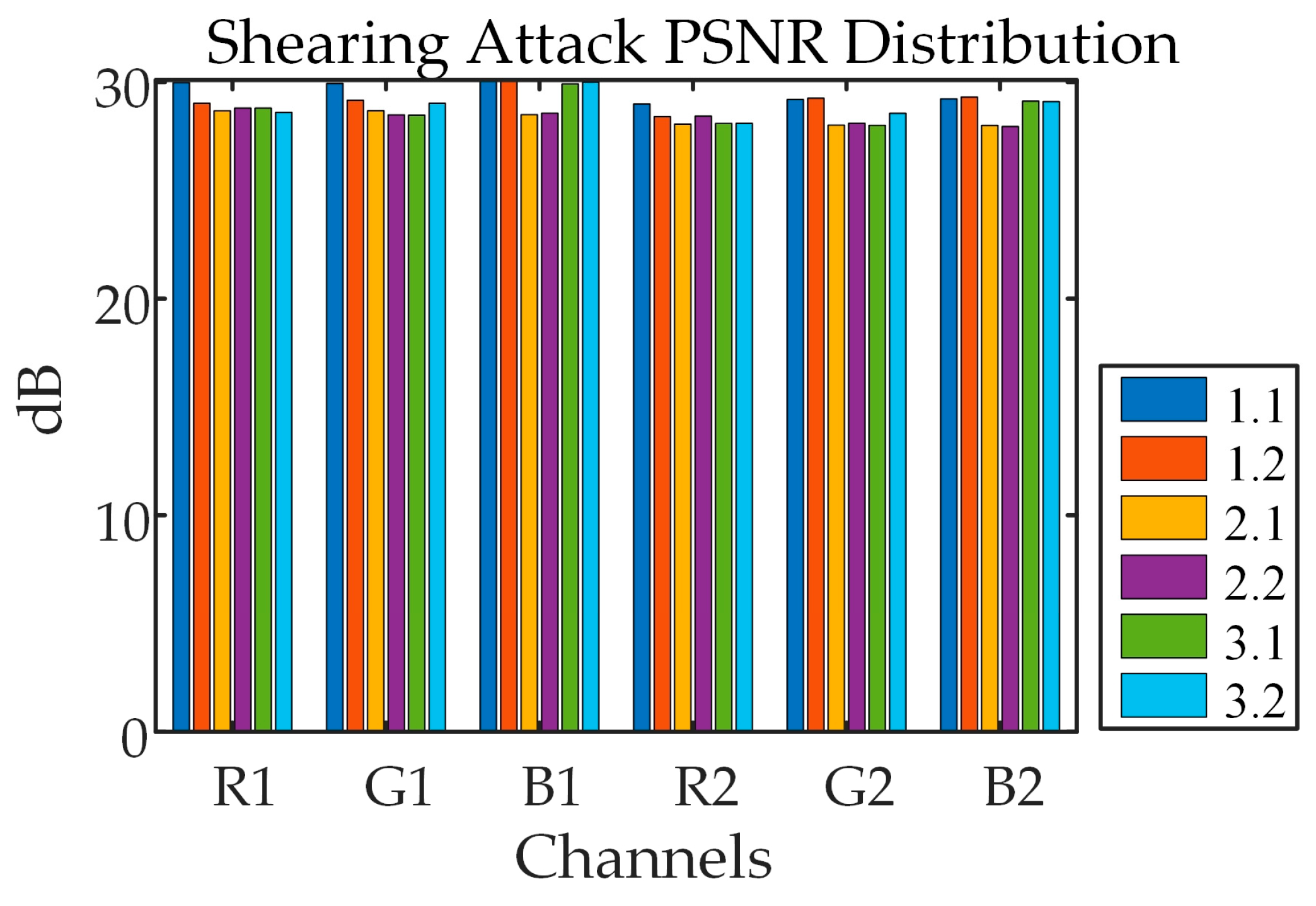
Preprints 107772 g020
Figure 20. Reconstructed image quality with different intensities of noise attacks (R1, G1, B1, SPN = 0.01; R2, G3, B3, SPN = 0.05).
Figure 20. Reconstructed image quality with different intensities of noise attacks (R1, G1, B1, SPN = 0.01; R2, G3, B3, SPN = 0.05).
Preprints 107772 g020
Preprints 107772 g021
Figure 21. Results of shearing attack images (a) size of sheared (b) decrypted-decompressed.
Figure 21. Results of shearing attack images (a) size of sheared (b) decrypted-decompressed.
Preprints 107772 g021
Table 1. Comparison of PSNR with other algorithms.
Table 1. Comparison of PSNR with other algorithms.
Algorithm Sizes CRs PSNRaver
Reference [30] 512 × 512 0.5 23.3608
Proposed1 512 × 512 0.5 34.3512
Reference [31] 256 × 256 0.5 28.0714
Proposed2 256 × 256 0.5 28.6956
Reference [32] 256 × 256 0.75 29.5600
Proposed3 256 × 256 0.75 33.5205
Table 2. Key space.
Table 2. Key space.
Parameters Key space
b, g 1015
a, c, d, y0, hc, hd
x0, ha, hb 		1016
1017
Total key space 10177 ≈ 2587
Table 3. Comparison between key space and other algorithms.
Table 3. Comparison between key space and other algorithms.
Algorithms Reference [34] Reference [35] Reference [36] Reference [37] Proposed
Key space 2256 2256 2197 2154 2587
Table 4. Differential attack test results.
Table 4. Differential attack test results.
Images Sizes Cipher Images
NPCR (%) UACI (%)
R G B R G B
1.1 256 × 256 × 3 99.6094 99.6100 99.6187 33.6512 33.5969 33.8661
1.2 256 × 256 × 3 99.6151 99.6131 99.6098 33.5268 33.4695 33.8211
2.1 512 × 512 × 3 99.6167 99.6118 99.6135 33.4630 33.4661 33.5041
2.2 512 × 512 × 3 99.6094 99.6103 99.6102 33.4661 33.4947 33.4760
3.1 1024 × 1024 × 3 99.6092 99.6098 99.6117 33.4661 33.4651 33.4602
3.2 1024 × 1024 × 3 99.6099 99.6166 99.6099 33.4833 33.4601 33.4631
4.1 256 × 256 99.6147 33.5980
4.2 256 × 256 99.6132 33.4699
Table 5. Comparison of performance in resisting differential attacks with other algorithms.
Table 5. Comparison of performance in resisting differential attacks with other algorithms.
Algorithm NPCR (%) UACI (%)
Reference [38] 99.6049 99.4838
Reference [39] 99.6089 99.4374
Reference [40] 99.5900 33.4467
Reference [41] 99.6100 33.4500
Proposed 99.6120 33.5166
Theoretical value 99.6094 33.4635
Table 6. Information entropy for different images.
Table 6. Information entropy for different images.
Image Cipher images (CR = 0.6)
R G B
1.1 7.9711 7.9812 7.9860
1.2 7.9922 7.9921 7.9923
2.1 7.9979 7.9978 7.9980
2.2 7.9981 7.9981 7.9981
3.1 7.9887 7.9840 7.9898
3.2 7.9995 7.9995 7.9995
4.1 7.9915
4.2 7.9981
All black 7.9911
All white 7.9922
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated