Prerpints.org logo
Preprint
Article

Tsallis Q-statistics Fingerprints in Precipitation Data Across Sicily

Altmetrics

Downloads

102

Views

93

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 May 2024

Posted:

29 May 2024

You are already at the latest version

Alerts
Abstract
Precipitation patterns are critical for understanding the hydrological and climatological dynamics of any region. Sicily, the largest island of the Mediterranean sea, with its diverse topography and climatic conditions, serves as an ideal case study for analyzing precipitation data to gain insights into regional water resources, agricultural productivity, and climate change impacts. This paper employs advanced statistical physics methods, particularly Tsallis q-statistics, to analyze sub-hourly precipitation data from 2002 to 2023, provided by the Sicilian Agrometeorological Informative System (SIAS). We investigate several critical variables related to rainfall events, including duration, depth, maximum record, and inter-event time. The study spans two decades (2002-2012 and 2013-2023), analyzing the distributions of relevant variables. Additionally, we examine the simple returns of these variables to identify significant temporal changes, fitting these returns with q-Gaussian distributions. Our findings reveal the scale-invariant nature of precipitation events, the presence of long-range interactions and memory effects, characteristic of complex environmental processes.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Precipitation patterns play a crucial role in understanding the hydrological and climatological dynamics of any region. In the context of Sicily, an island characterized by diverse topographical and climatic conditions, analyzing precipitation data provides valuable insights into regional water resources, agricultural productivity, and climate change impacts. Being the largest island of the Mediterranean sea and located just in the middle of it, Sicily is also of great interest for the entire Mediterranean area.
A robust statistical approach is essential to uncovering the underlying patterns and anomalies in precipitation data, thereby enabling more accurate predictions and effective water management strategies. In recent years, the application of advanced statistical physics methods has provided new insights into the analysis of complex environmental data. In particular, various studies have emphasized the importance of different probability distributions in rainfall analysis. For instance, the Poisson Hurwitz-Lerch Zeta Distribution has been used to model the frequency of interarrival times and rainfall depths [1]. Some studies assumed that the daily precipitation intensity are distributed according to a Gamma [2] or a mixed exponential [3], light-tailed or heavy tailed distributions [4,5], while other authors found a log-normal [6] or a stretched exponential [7] distribution. Probability distributions of daily rainfall extremes have been also studied to make design rainfall inferences [8] and entropy-based derivations of probability distributions have been applied to daily rainfall data [9]. Understanding the fundamental probability distribution for heavy rainfall can provide insights into extreme weather events [10] and analyzing extreme rainfall trends is crucial for evaluating depth-duration-frequency curves in climate change scenarios [11].
In this context, q-statistics offers a robust framework for analyzing the variability and distribution of complex environmental data, as it is particularly effective in capturing the non-linear and multi-scalar nature of such events. Raw data often follow power law distributions, indicating the presence of scale-invariant processes and the frequent occurrence of extreme events [12]. For instance, Yang et al. demonstrated the power-law behavior of hourly precipitation intensity and dry spell duration over the United States, highlighting the scale-invariant nature of these phenomena [13]. Additionally, studies have focused on the use of probability distributions in rainfall analysis [14] and memory in volatility return intervals and decumulative probability function, following the methodologies usually employed in the study of financial markets [15]. Decumulated data can be effectively modeled using Tsallis exponential distributions, which account for long-range interactions and memory effects typical of many natural processes. Pluchino et al. showed the applicability of Tsallis statistics in capturing long-term correlations at the edge of chaos [16]. Similarly, Ludescher et al. described the universal behavior of interoccurrence times between losses in financial markets using Tsallis statistics [17], emphasizing the presence of memory effects [18]. Furthermore, the simple returns of these events, representing changes over time, conform to q-Gaussian distributions [19], which better capture the heavy tails and non-Gaussian behavior observed in the data. Recently Tsallis statistics was also successfully applied by Greco et al. to study acoustic emissions close to the rupture point of compressed rocks of various nature [20,21]. Bogachev and Bunde (2008) discussed memory effects in the statistics of interoccurrence times between large returns in financial markets, demonstrating the relevance of q-Gaussian distributions in modeling heavy tails and non-Gaussian behaviors [22]. Yamasaki et al. also highlighted scaling and memory in volatility return intervals in financial markets, further supporting the use of q-Gaussian distributions for this kind of analysis [23].
In this paper, we present a comprehensive analysis of precipitation data through the lens of q-statistics. Specifically, we analyze sub-hourly precipitation data from 2002 to 2023, provided by the Sicilian Agrometeorological Informative System (SIAS). A preliminary analysis on the same dataset has been recently performed in [24], but at a lower (hourly) time resolution and without any reference to Tsallis statistics. The considered dataset comprises records from 107 meteorological stations, with a focus on nine key rain gauges located in Messina, Catania, Siracusa, Ragusa, Enna, Caltanissetta, Agrigento, Trapani, and Palermo. We examine several key variables related to rainfall events, including:
- Duration [minutes], the length of consecutive wet records;
- Depth [mm], the total amount of precipitation during an event;
- Maximum Record [mm/10’], the highest recorded precipitation in a 10-minute interval during an event.
To investigate the temporal evolution of these variables, we analyze their distributions over two decades (2002-2012 and 2013-2023). We also explore simple returns of these variables. In order to characterize our distributions and to identify any significant changes over time, we consider Tsallis q-statistics [17].
Our analysis aims to uncover patterns and trends in Sicilian precipitation data, providing insights into regional climate dynamics and potential impacts of climate change. This study could offer valuable information to scientists, policymakers, and stakeholders involved in environmental and water resource management in Sicily.

2. Dataset and Relevant Variables

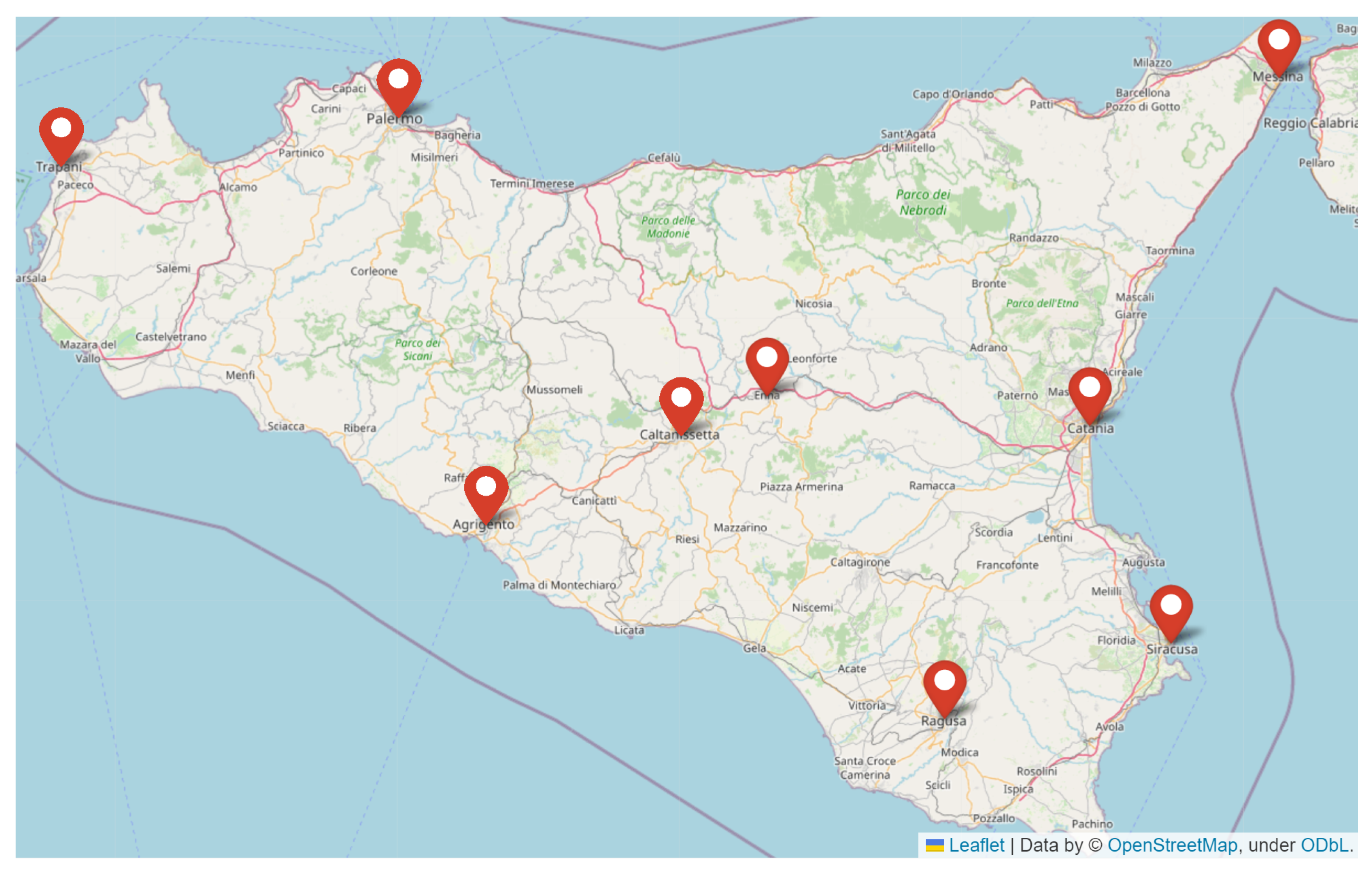
This study is based on precipitation records from 2002 to 2023 provided by a robust and extensive rain gauge network under the maintenance of the Sicilian Agrometeorological Informative System (SIAS), which comprehends 107 meteorological stations. The analysed sub hourly time series consists on 10-minutes precipitation data observed in a subset of 9 rain gauge stations located in the main Sicilian cities, namely Messina, Catania, Siracusa, Ragusa, Enna, Caltanissetta, Agrigento, Trapani and Palermo, see Figure 1. The minimum quantity observable with the SIAS’s pluviometers is 0 . 2 m m and, as we said, the time resolution is 10 minutes: we use such granular data per station and build a new timeseries based on rainfall events.
A rainfall event over a rain gauge in our dataset, is the episode of consecutive wet records, i.e the consecutive not null rows. It follows that each rainfall event can be characterized by two quantities: a duration [in minutes] and a depth [in mm]. The duration of an event is the length of consecutive wet records or, in other words, the number of consecutive not null rows. The rainfall depth relative to an event is the sum of precipitation amount over the corresponding event duration, otherwise, how much it rained during the event. Each rainfall event is formed by one or more not null records and one of those values is the maximum value recorded during the event. We focus our study on the previous relevant variables related to rainfall events: depth [mm], maximum record [mm/10’], duration [minutes]. The first two variables are related to the amount of precipitation, whilst the duration length is a temporal variable. We will group results following such criterion. In order to investigate any possible macroscopic change in these variables across time, we adopt a seasonal approach exploring the principal features of the distributions of these variables over two decades: 2002-2012 and 2013-2023.

3. Statistical Analysis of Precipitation Events

3.1. Probability Density Functions

First, we analyze the probability density function (PDF) for our relevant variables, considering both seasonal and decades variations. This approach helps in managing the complexity and volume of the data while still providing clear insights into the overall trends.
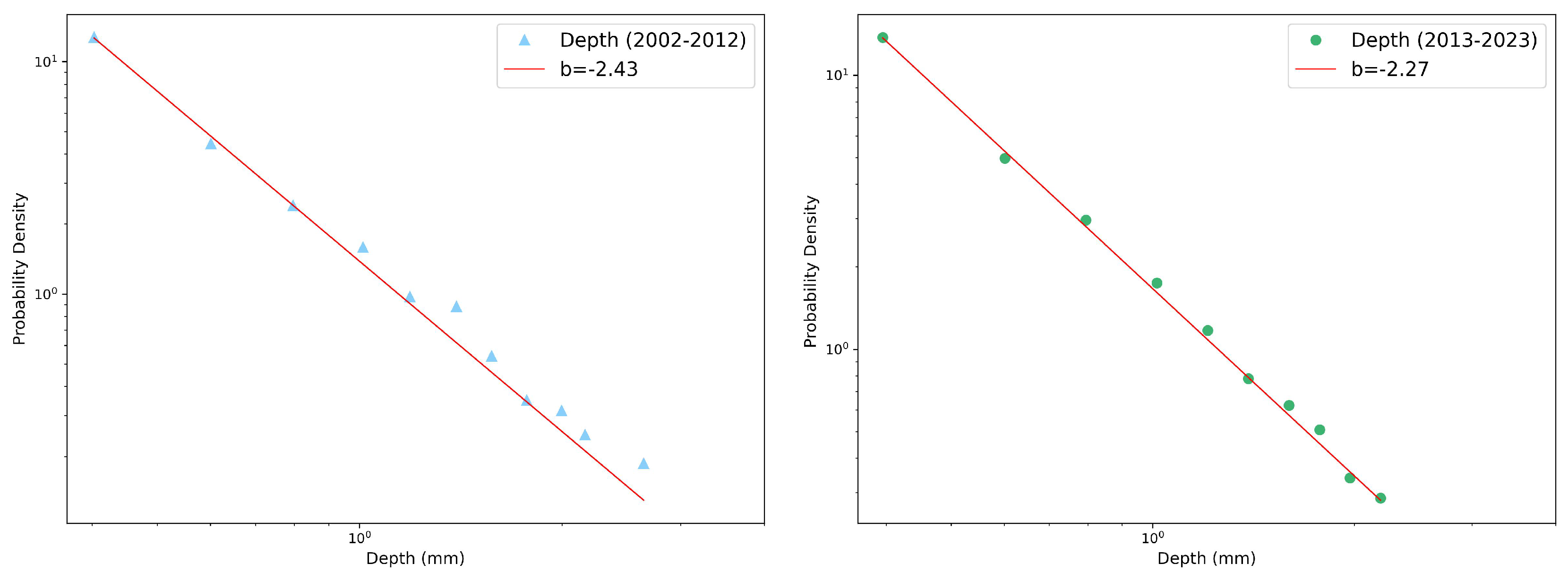
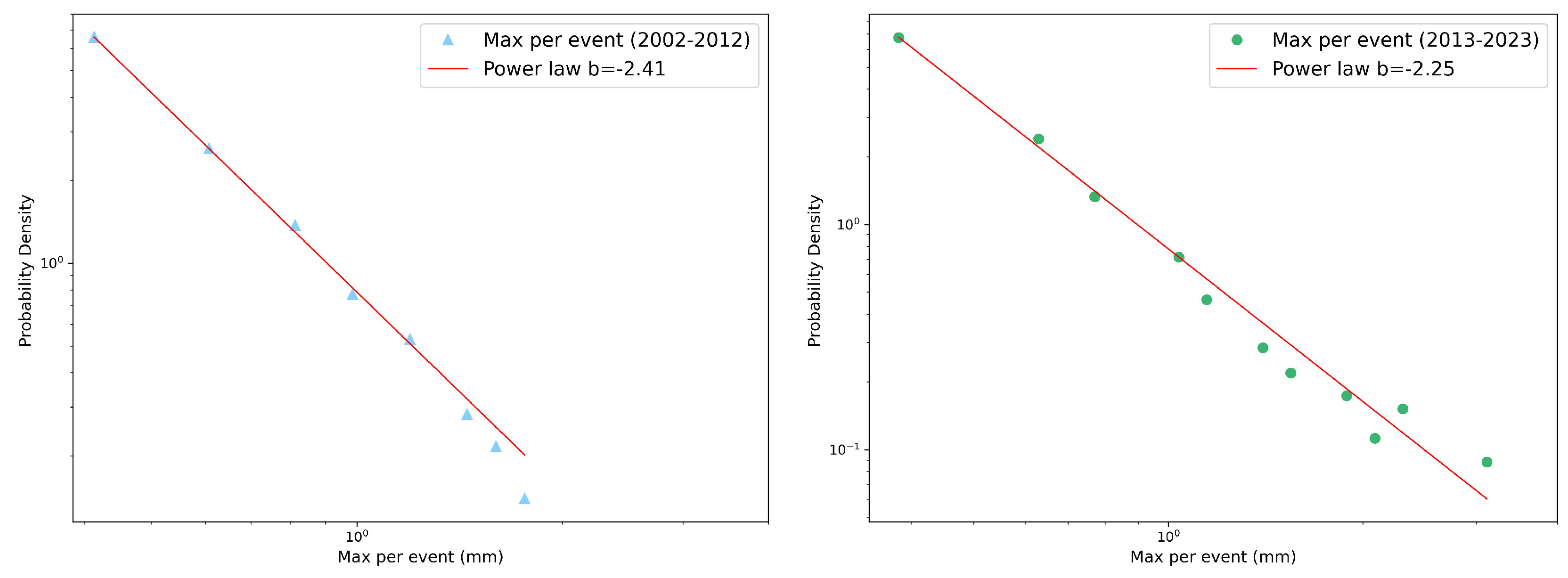
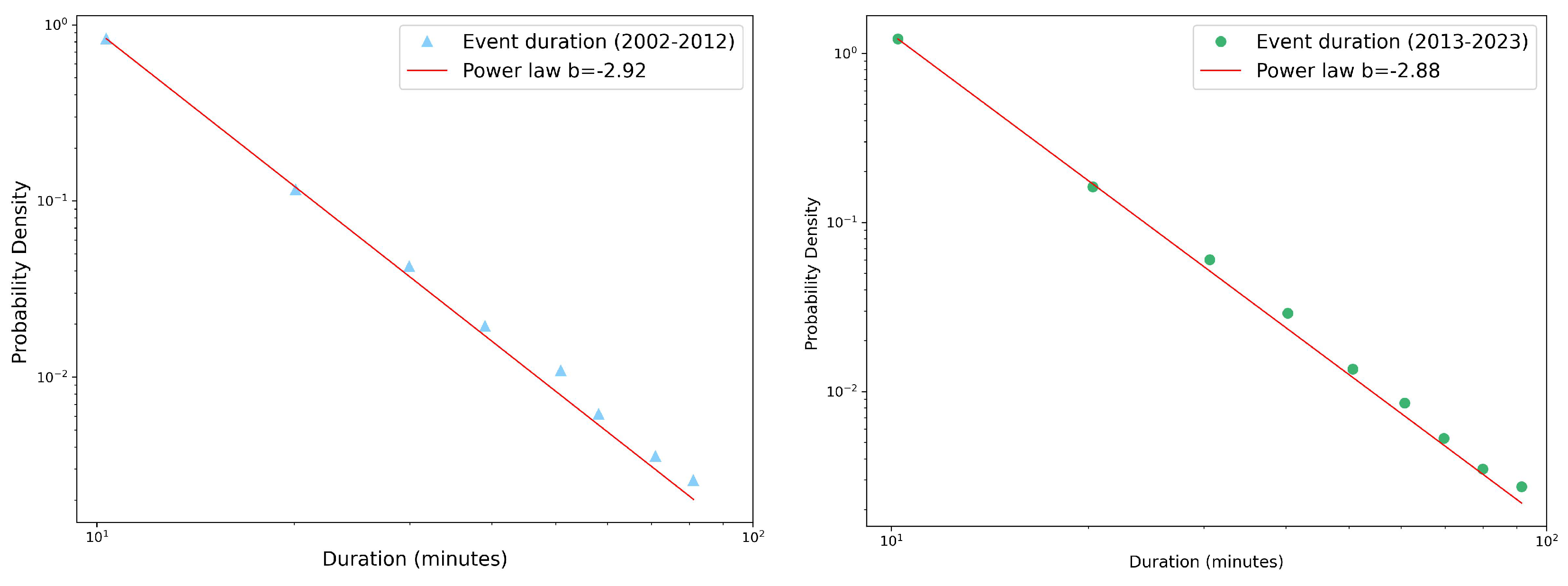
Due to the extensive number of reports generated for each season, variable, and decade, we present only a few selected plots, then we summarize all the results in a more compact way. Figure 2, Figure 3 and Figure 4 illustrates the PDFs of events’ rainfall depth, maximum record and duration, respectively, cumulated over all the gauge station for the autumn season in each of the two decades, 2002 − 2012 (left panel) and 2013 − 2023 (right panel). All the distributions can be well fitted by power-law functions y ∼ x − b , indicating the scale-invariant nature of the precipitation data, but with different slopes (reported in the legends).
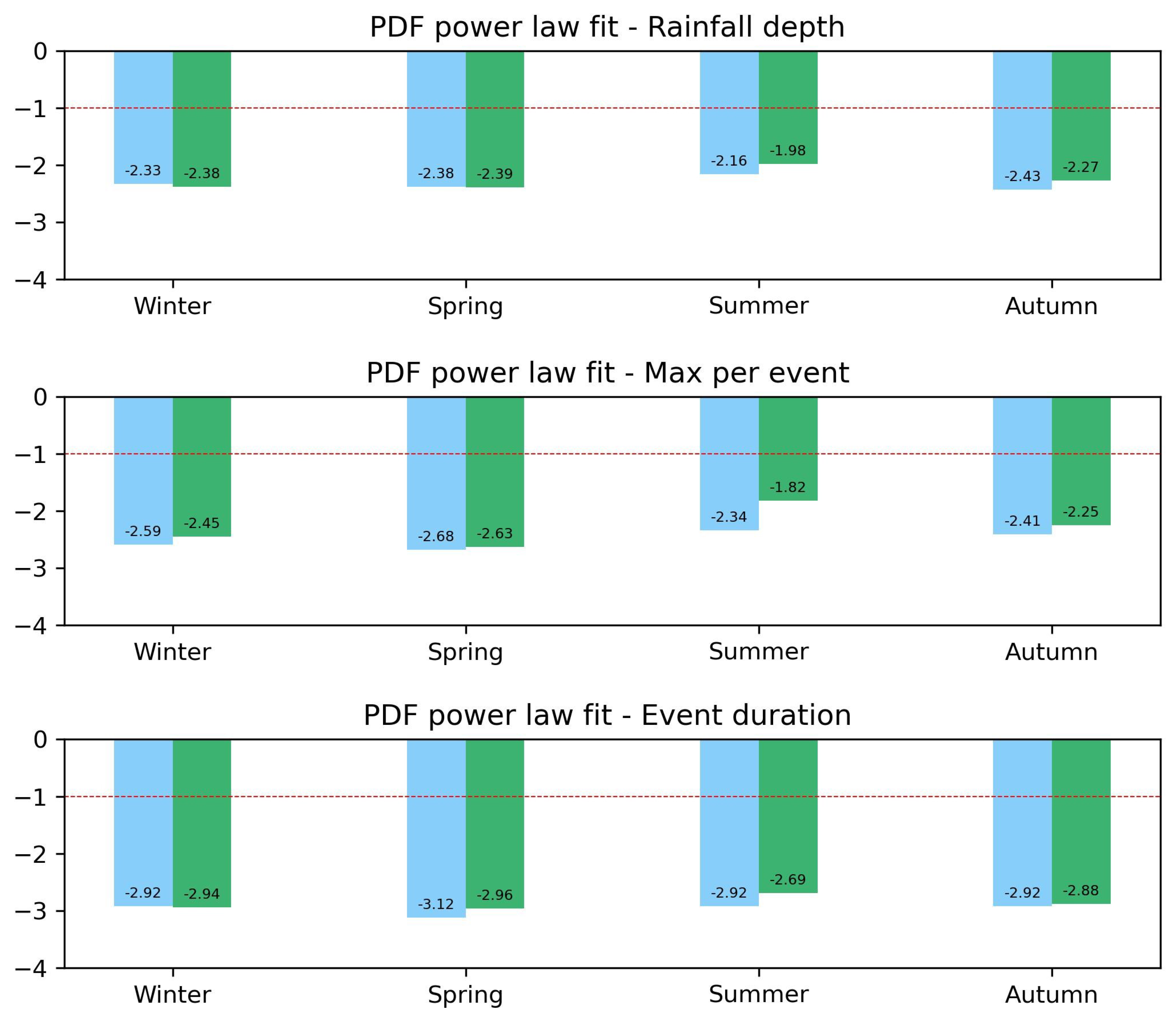
In Figure 5 we compare, as bar charts, the slopes of all the power-law fits performed on the seasonal distributions of the same three variables for the two considered decades. Bars are colored in blue for 2002 − 2012 and in green for 2013 − 2023 . The analysis of rainfall depth and maximum record (top and central panel, respectively) reveals a sensitive increase of extreme events, indicated by a lower absolute value of the slopes, only for summer and autumn of the second decade, confirming a trend already found in previous studies [24]. A slight increase in the events’ duration of the second decade can be also appreciated (bottom panel), but only for spring and summer. Winter behavior remain quite unchanged from one decade to another, even if a small decrease of rainfall depth together with a slight increase in the max intensity are visible in this season (in top and central panel, respectively).

3.2. Decumulative Probability Distributions

In this section we investigate the decumulative probability distributions for our three relevant variables in the four seasons and the two decades by means of q-statistics. For each variable, we plot the fraction of precipitation events (collected for all the gauge stations) with values above the threshold reported on the x-axis. As in the previous section, we start by presenting some selected examples of these distributions in the two decades. 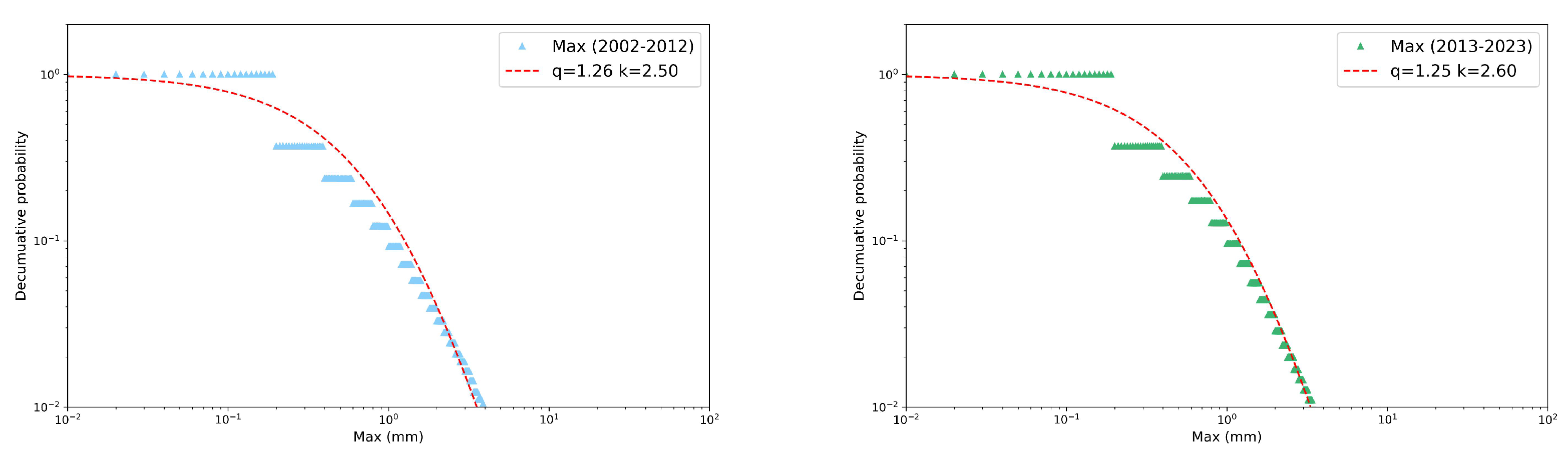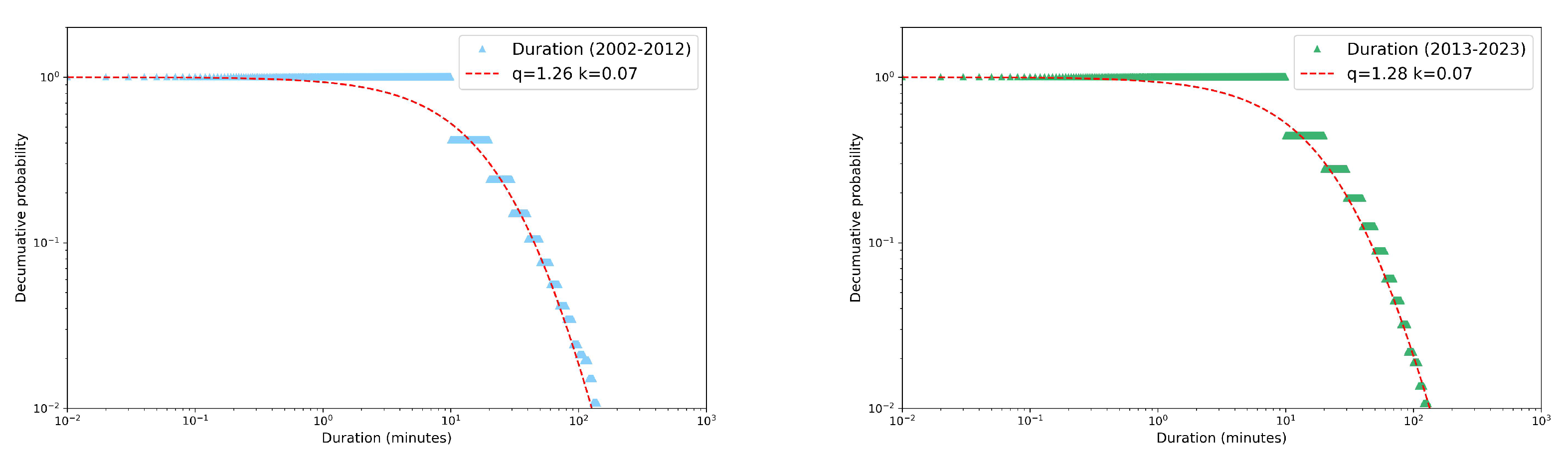In particular, in Figure 6 and Figure 7 we analyze the rainfall depth and the maximum record in winter, while in Figure 8 we focus on the event duration in summer. All the distributions result to be well fitted by Tsallis q-exponential functions in the usual form[17]:
e q ( x ) = 1 + ( 1 − q ) k x 1 1 − q ,
where q is the entropic index and k is a constant which controls the inflection point of the curve. For q = 1 the standard exponential function is recovered. Values of the entropic index grater than 1 indicate fat tailed tails and typically quantifies the degree of long-range correlations and memory effects present in the system, expressed by the entity of the deviation from unit. In these examples, the entropic index show a slight difference between the two decades only for winter rainfall depth, while winter maximum intensity and summer duration remains quite unchanged.
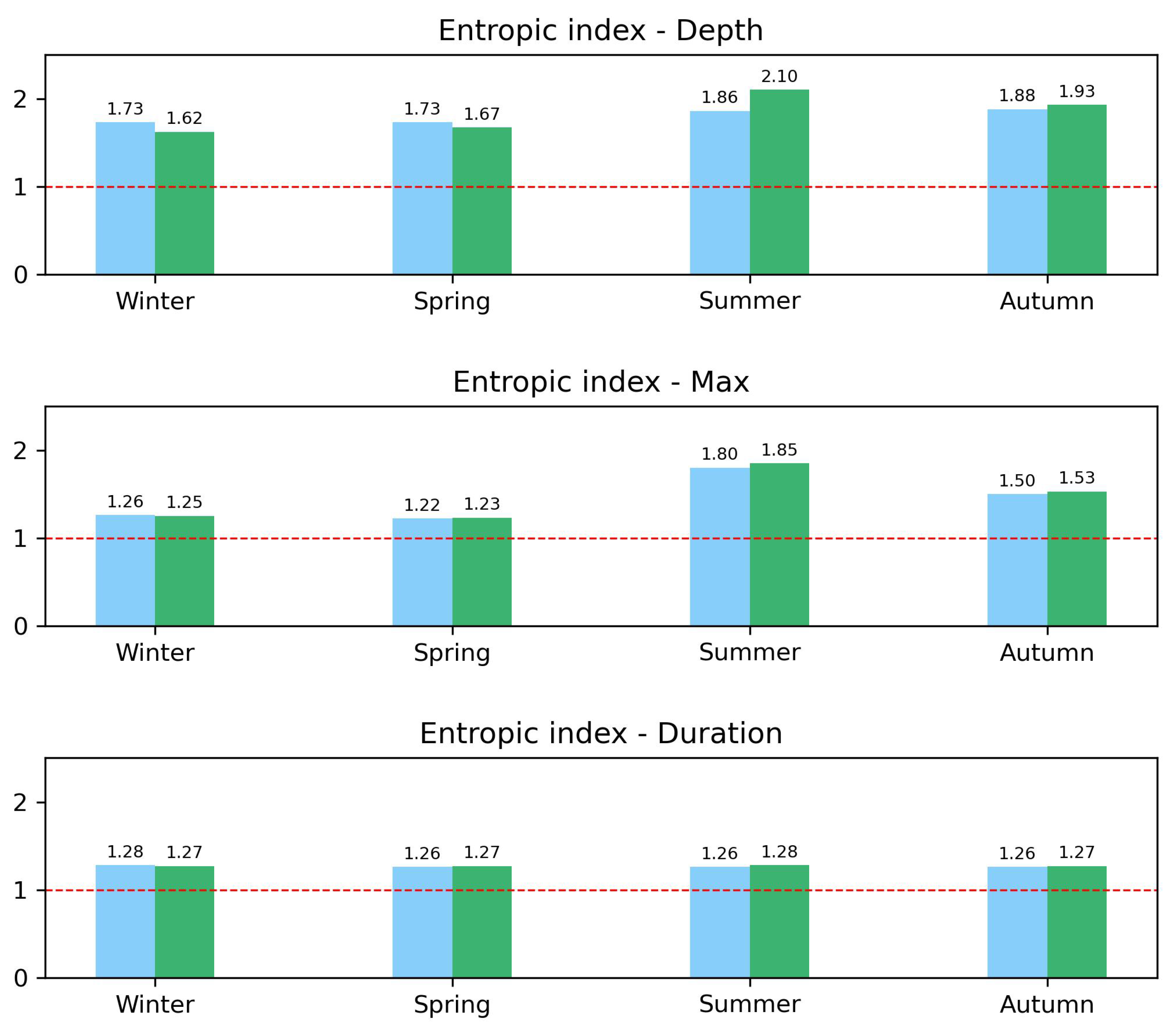
Detailed results of the values of the entropic index q for each variable and each season are reported in the three panels of Figure 9, where bar charts are again colored in blue and green for 2002 − 2012 and 2013 − 2023 respectively,
In the top panel, the comparison of entropic indexes for the events’ rainfall depth unveils an increase of correlations in the second decade for summer and autumn only, while a decrease is observed for winter and spring. A slight increase of the index q among decades can also be observed only in summer for the maximum per event intensity (central panel). All the other comparisons in both the central and bottom panels just show very similar values of the entropic index.

3.3. Returns Distribution

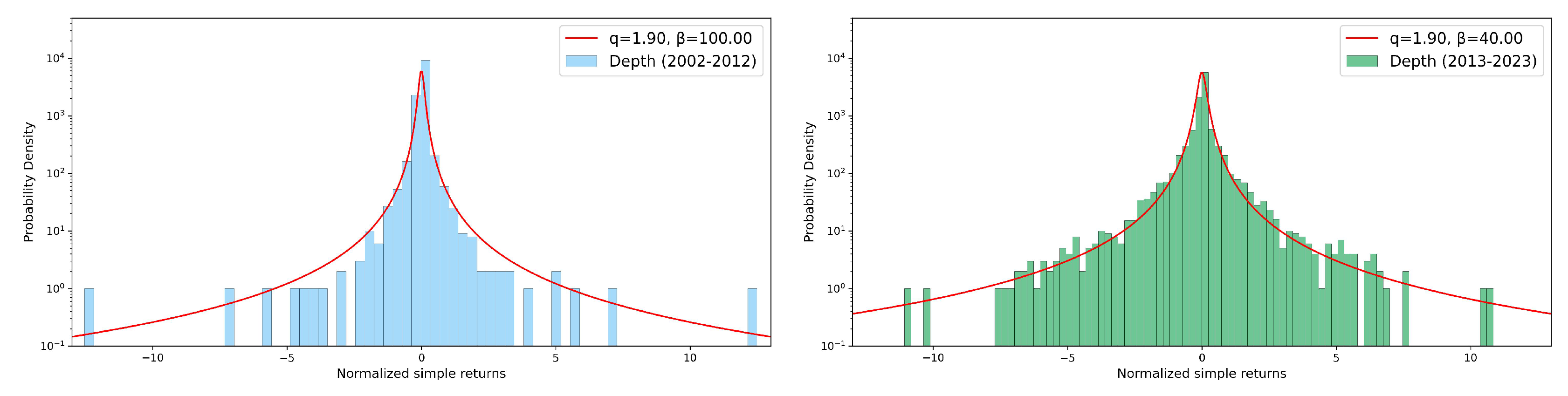
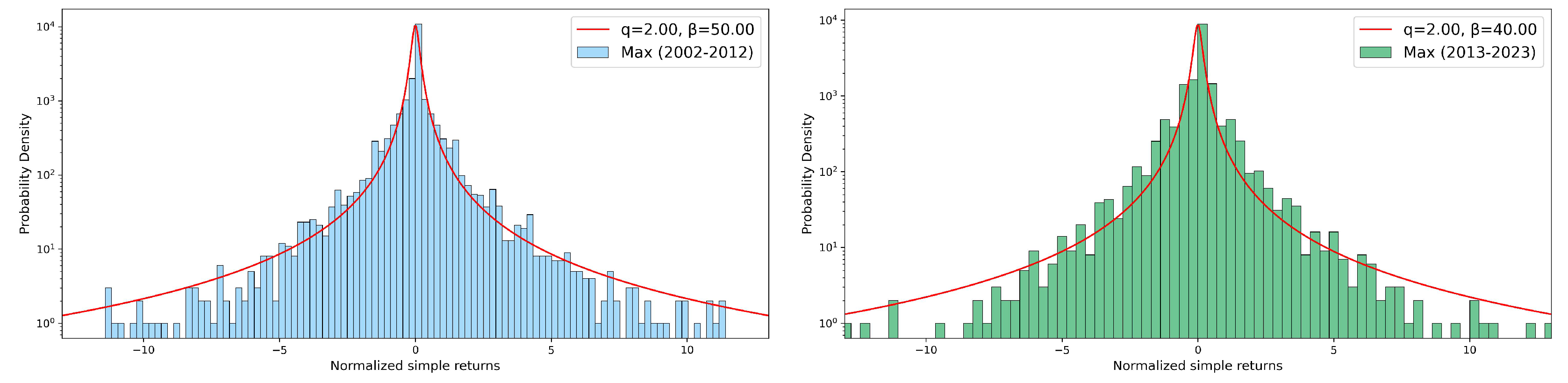
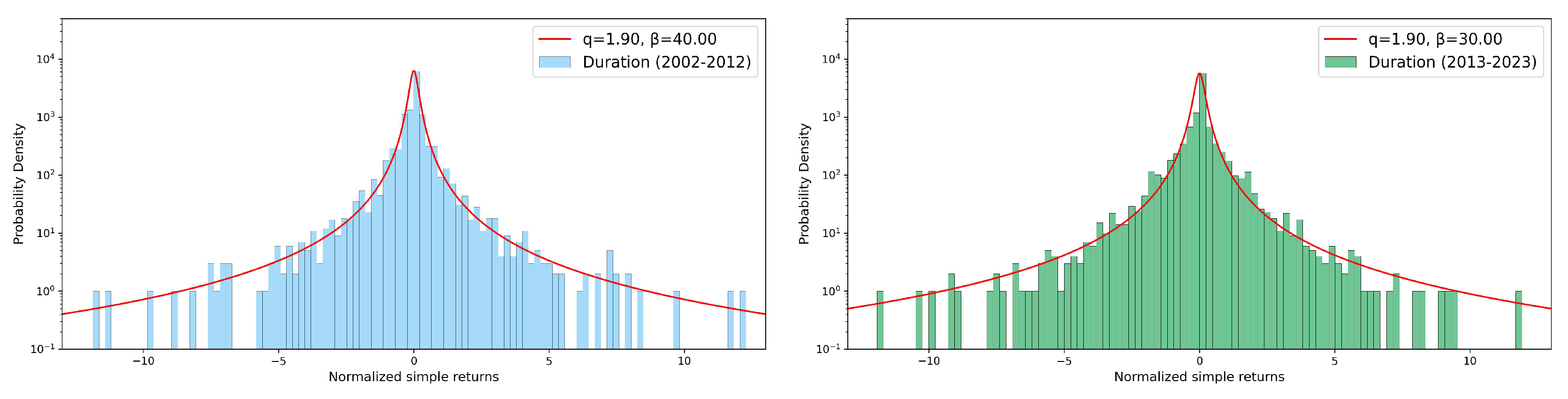
Finally, in this section we investigate the behavior of simple returns distributions for each relevant variable, for the different seasons and decades studied. We consider normalized simple returns R defined as follows:
R = ( x n + 1 − x n ) − x m e a n σ s t d . d e v .
Being the distributions of returns symmetric, they are well fitted by Tsallis q-Gaussian curves defined as [17]:
G q ( x ) = A 1 − ( 1 − q ) β x 2 1 1 − q ,
where A is a normalization parameter, q is the entropic index and β is a parameter related to the spread around the mean. Values of the entropic index greater than unit quantify the deviations from a Gaussian behavior, also indicating a violation of the standard Central Limit Theorem due to correlations present in the system. In Figure 10, Figure 11 and Figure 12 We report, as in the previous sections, some seasonal examples of distributions of simple returns for our three variables, comparing the two decades: the spring season has been chosen for both rainfall depth and duration, winter season for the maximum recorded value. No relevant differences among decades are visible in any case for the entropic index q although different values of β are obtained. 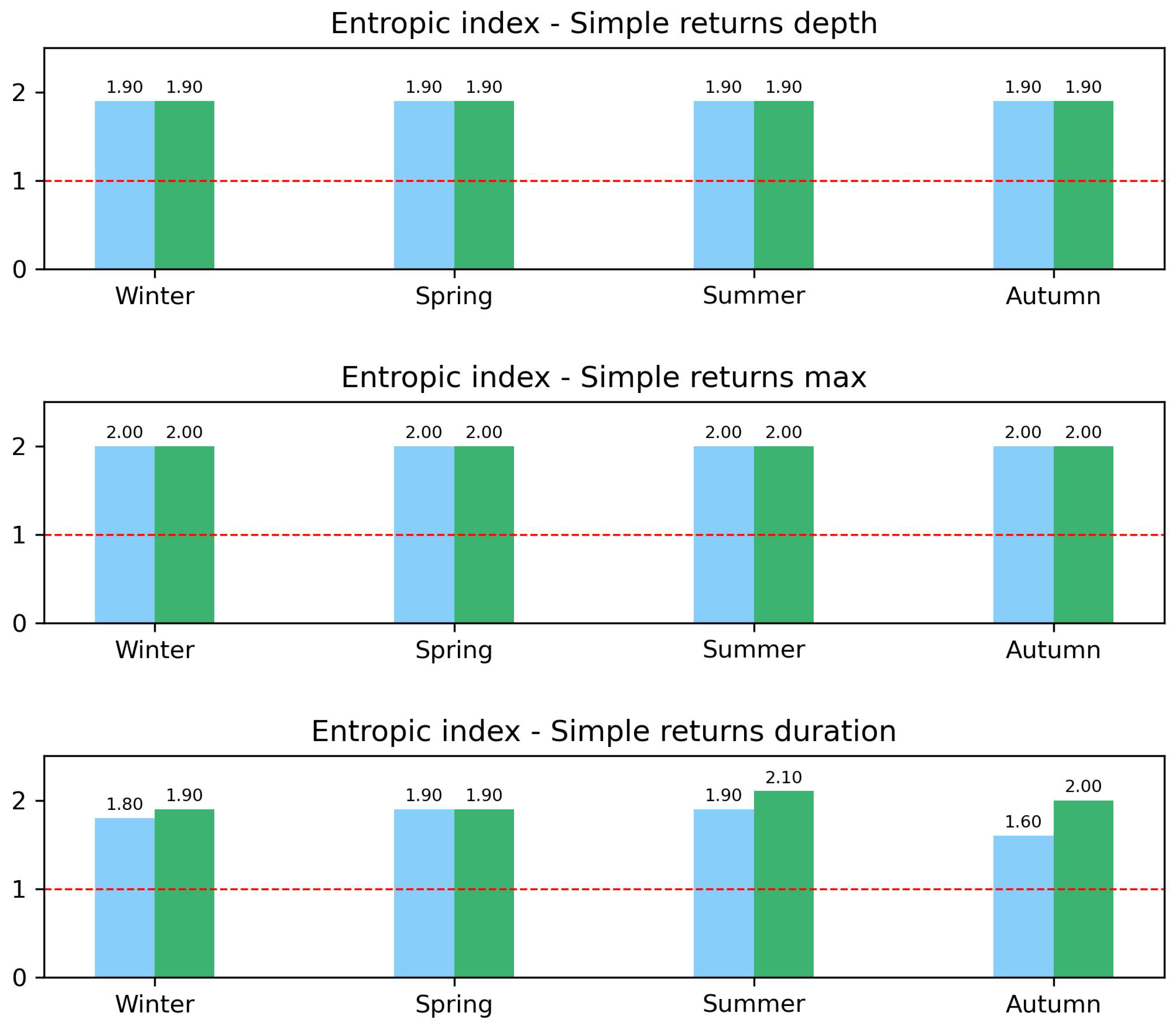Such an absence of any change in q among 2002 − 2012 and 2013 − 2023 can be also appreciated in the summary presented in Figure 13, where we report the bar charts of the entropic index values extracted from q-Gaussian fits. For both rainfall depth (top panel) and maximum intensity (central panel) the fitted entropic index does not vary significantly across decades and seasons, suggesting a consistent statistical behavior over time. However, the event duration (bottom panel) shows a substantial increase in winter and, in particular, in summer and autumn, indicating potential changes in the dynamics of rainfall events in these seasons over the considered decades.

4. Discussion and Conclusions

In this study, we analyzed sub-hourly precipitation data from nine rain gauge stations located in the main cities of Sicily over two decades, 2002 − 2012 and 2013 − 2023 . Our analysis focused on several key features of rainfall events: depth, maximum recorded value of the event and duration of the event. The aim was to understand the statistical properties of these variables and possible changes over time.
Our analysis provided for the first time a comprehensive quantitative analysis of precipitation data across Sicily using Tsallis q-statistics, revealing significant insights into the statistical properties of rainfall events. The power law distributions of the relevant variables indicate the prevalence of extreme events, while the q-exponential and q-Gaussian distributions highlight the presence of long-range correlations and memory effects in the data.
The application of Tsallis q-statistics in this context has proven to be particularly valuable. By comparing the deviation from exponential and Gaussian behavior among decades and seasons, we were able to capture the deep out-of-equilibrium nature of the precipitation data, which classical statistics often fail to describe accurately. Tsallis q-statistics, with its foundations in non-extensive entropy, provides a more flexible and encompassing framework that accounts for the complex dynamics and interactions inherent the environmental data.
Our findings indicate, in several cases, notable changes among the two decades considered, particularly during the summer and - to a lesser extent - the autumn seasons. We observe an increase of correlations, on one hand, in the decumulative distributions for rainfall depth and the maximum intensity of events and, on the other hand, in the normalized returns distributions for the event duration. These quantitative changes, if correctly interpreted, could have significant implications for water resource management and agricultural planning in Sicily, especially in the context of climate change adaptation. In fact, the investigation of the underlying mechanisms driving the observed changes in rainfall patterns could offer valuable insights for developing adaptive strategies to mitigate the impacts of climate variability and change.
Overall, this study contributes to the growing body of knowledge on precipitation variability and its impacts, offering a valuable resource for scientists, policymakers, and stakeholders involved in environmental and water resource management in Sicily. The use of Tsallis q-statistics, in particular, provides a robust tool for understanding the complexity of precipitation patterns and their broader climatic implications. Future research should focus on extending this analysis to other regions and incorporating additional climatic variables to provide a more detailed understanding of precipitation dynamics.

Author Contributions

All authors equally contributed to the work.

Funding

This study was funded by the European Union - NextGenerationEU, in the framework of the GRINS - Growing Resilient, INclusive and Sustainable project (GRINS PE00000018 – CUP E63C22002120006). The views and opinions expressed are solely those of the authors and do not necessarily reflect those of the European Union, nor can the European Union be held responsible for them.

Data Availability Statement

Data are available on request.

Acknowledgments

Authors thank L. Pasotti and C. Tsallis for useful discussions.

Conflicts of Interest

Authors declare no conflicts of interest.

References

  1. C. Agnese, G. Baiamonte, E. Di Nardo, S. Ferraris, T. Martini. Modelling the Frequency of Interarrival Times and Rainfall Depths with the Poisson Hurwitz-Lerch Zeta Distribution, Fractal and Fractional 6 (2022) 509.
  2. T. Buishand. Some remarks on the use of daily rainfall models, J. oh Hydro 295 (1978) 36.
  3. D.S. Wilks, R.L. Wilby. The weather generation game: a review of stochastic weather models, Progress in Phys. Geo. 23 (1999) 3.
  4. P.W. Mielke, E.S. Johnson. Some generalized beta distributions of the second kind having desirable application features in hydrology and meteorology, Water Res. 223 (1974) 10.
  5. S. Papalexiou, D. Koutsoyiannis, C. Makropoulos. How extreme is extreme? An assessment of daily rainfall distribution tails, Hydro. and Earth Syst. Sci. 851 (2013) 17.
  6. L.W. Swift, H.T. Schreuder. Fitting daily precipitation amounts using the SB distribution, Mon. Weather Rev. 2535(1981) 109.
  7. P. Wilson, R. Toumi. A fundamental probability distribution for heavy rainfall, Geophys. Res. Lett. 14 (2005) 32.
  8. B. Moccia, C. Mineo, E. Ridolfi, F. Russo, F. Napolitano. Probability distributions of daily rainfall extremes in Lazio and Sicily, Italy, and design rainfall inferences, J. of Hydro. 33 (2021) 100771.
  9. S. M. Papalexiou, D. Koutsoyiannis. Entropy based derivation of probability distributions: A case study to daily rainfall, Advances in Water Res. 51 (2011) 45.
  10. P. S. Wilson, R. Toumi. A fundamental probability distribution for heavy rainfall, Geophys. Research Letters 32 (2005) 14.
  11. L. Liuzzo, G. Freni. Analysis of Extreme Rainfall Trends in Sicily for the Evaluation of Depth-Duration-Frequency Curves in Climate Change Scenarios, J. of Hydrol. Eng. 20 (2015) 12.
  12. A. Bunde, J. Kropp, H.J. Schellnhuber. The science of disasters: climate disruptions, heart attacks, and market crashes, Springer (2002).
  13. L. Yang, C.L.E. Franzke, Z. Fu. Power-law behaviour of hourly precipitation intensity and dry spell duration over the United States, Royal Meteor. Soc. 2429 (2019) 40.
  14. M. Anand Sharma, J. B. Singh. Use of Probability Distribution in Rainfall Analysis, NY Science Journal 100771 (2010) 33.
  15. A. Bunde, J.F. Eichner, J.W. Kantelhardt, S. Havlin. The effects of multifractality on the statistics of return intervals, Phys. Rev. Lett. 181 (2005) 161.
  16. A. Pluchino, A. Rapisarda, C. Tsallis. Noise, synchrony and correlations at the edge of chaos, Phys. Rev. E 87 (2013) 022910.
  17. C. Tsallis. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World. 2nd Ed. Springer 2023.
  18. J. Ludescher, C. Tsallis, A. Bunde. Universal behaviour of interoccurrence times between losses in financial markets: an analytical description, Europhys. Letters 6 (2011) 95.
  19. C. Tsallis, R.S. Mendes. The role of constraints within generalized nonextensive statistics, Physica A. 534 (1998) 261.
  20. A. Greco, C. Tsallis, A. Rapisarda, A. Pluchino, G. Fichera, L. Contrafatto. The European Physical Journal Special Topics. 229 (2020) 841.
  21. S.C. Vinciguerra, A. Greco, A. Pluchino, A. Rapisarda, C. Tsallis. Acoustic emissions in rock deformation and failure: New insights from q-statistical analysis, Entropy 25 (2023) 701.
  22. M.I. Bogachev, A. Bunde. Memory effects in the statistics of interoccurrence times between large returns in financial markets, Phys. Rev. E78(2008) 036114.
  23. K. Yamasaki, L. Muchnik, S. Havlin, A. Bunde, H.E. Stanley. Scaling and memory in volatility return intervalsin financial markets.PNAS 102 (2005) 9424.
  24. V. Pecorino, T. Di Matteo, M. Milazzo, L. Pasotti, A. Pluchino, A. Rapisarda, Evidence of climate change in Sicily by means of rainfall data analysis. Preprint on Research Square. [CrossRef]
Preprints 107780 g001
Figure 1. SIAS meteorological network: location of the 9 rain gauge stations considered in this paper. See text for more details.
Figure 1. SIAS meteorological network: location of the 9 rain gauge stations considered in this paper. See text for more details.
Preprints 107780 g001
Preprints 107780 g002
Figure 2. Probability density function of autumn rainfall depth in log-log scale and its fits with a power law (red line) for the two decades considered: 2002 − 2012 (left panel) and 2013 − 2023 (right panel). The slopes of the fits are also reported, see text for more details.
Figure 2. Probability density function of autumn rainfall depth in log-log scale and its fits with a power law (red line) for the two decades considered: 2002 − 2012 (left panel) and 2013 − 2023 (right panel). The slopes of the fits are also reported, see text for more details.
Preprints 107780 g002
Preprints 107780 g003
Figure 3. Probability density function of autumn max per event in log-log scale and its fits with a power law (red line) for the two decades considered: 2002 − 2012 (left panel) and 2013 − 2023 (right panel). The slopes of the fits are also reported, see text for more details.
Figure 3. Probability density function of autumn max per event in log-log scale and its fits with a power law (red line) for the two decades considered: 2002 − 2012 (left panel) and 2013 − 2023 (right panel). The slopes of the fits are also reported, see text for more details.
Preprints 107780 g003
Preprints 107780 g004
Figure 4. Probability density function of autumn rainfall event duration in log-log scale and its fits with a power law (red line) for the two decades considered: 2002 − 2012 (left panel) and 2013 − 2023 (right panel). The slopes of the fits are also reported, see text for more details.
Figure 4. Probability density function of autumn rainfall event duration in log-log scale and its fits with a power law (red line) for the two decades considered: 2002 − 2012 (left panel) and 2013 − 2023 (right panel). The slopes of the fits are also reported, see text for more details.
Preprints 107780 g004
Preprints 107780 g005
Figure 5. We report the values of the slopes of the power-law fits for events’ rainfall depth (top panel), maximum record (central panel) and duration (bottom panel). The different colors refers to the two decades studies: blue for the period 2002 − 2012 and green for the period 2013 − 2023 . Differences between the two decades can be appreciated, in particular for summer. See text for more details.
Figure 5. We report the values of the slopes of the power-law fits for events’ rainfall depth (top panel), maximum record (central panel) and duration (bottom panel). The different colors refers to the two decades studies: blue for the period 2002 − 2012 and green for the period 2013 − 2023 . Differences between the two decades can be appreciated, in particular for summer. See text for more details.
Preprints 107780 g005
Preprints 107780 g006
Figure 6. Decumulative probability distributions in log-log scale of winter rainfall depth per event and their q-exponential fits. Comparison between decades: 2002 − 2012 (left panel) and 2013 − 2023 (right panel).
Figure 6. Decumulative probability distributions in log-log scale of winter rainfall depth per event and their q-exponential fits. Comparison between decades: 2002 − 2012 (left panel) and 2013 − 2023 (right panel).
Preprints 107780 g006
Preprints 107780 g007
Figure 7. Decumulative probability distributions in log-log scale of winter maximum per event and their q-exponential fits. Comparison between decades: 2002 − 2012 (left panel) and 2013 − 2023 (right panel).
Figure 7. Decumulative probability distributions in log-log scale of winter maximum per event and their q-exponential fits. Comparison between decades: 2002 − 2012 (left panel) and 2013 − 2023 (right panel).
Preprints 107780 g007
Preprints 107780 g008
Figure 8. Decumulative probability distributions in log-log scale of summer event duration and their q-exponential fits. Comparison between decades: 2002 − 2012 (left panel) and 2013 − 2023 (right panel).
Figure 8. Decumulative probability distributions in log-log scale of summer event duration and their q-exponential fits. Comparison between decades: 2002 − 2012 (left panel) and 2013 − 2023 (right panel).
Preprints 107780 g008
Preprints 107780 g009
Figure 9. Seasonal bar chart of the entropic index q calculated for the rainfall depth, maximun intensity per event and duration decumulative distributions. Comparison between decades: 2002 − 2012 (blue) and 2013 − 2023 (green). See text for more details.
Figure 9. Seasonal bar chart of the entropic index q calculated for the rainfall depth, maximun intensity per event and duration decumulative distributions. Comparison between decades: 2002 − 2012 (blue) and 2013 − 2023 (green). See text for more details.
Preprints 107780 g009
Preprints 107780 g010
Figure 10. Simple returns in log-lin scale: data and q-Gaussian fits of spring events’ rainfall depth. The comparison between the two considered decades, i.e. 2002 − 2012 (left panel) and 2013 − 2023 (right panel), does not show any relevant difference in the entropic index q.
Figure 10. Simple returns in log-lin scale: data and q-Gaussian fits of spring events’ rainfall depth. The comparison between the two considered decades, i.e. 2002 − 2012 (left panel) and 2013 − 2023 (right panel), does not show any relevant difference in the entropic index q.
Preprints 107780 g010
Preprints 107780 g011
Figure 11. Simple returns in log-lin scale: data and q-Gaussian fits of winter maximum per event. On the left panel we report the 2002 − 2012 decade, while right panel the 2013 − 2023 decade. See text for more details.
Figure 11. Simple returns in log-lin scale: data and q-Gaussian fits of winter maximum per event. On the left panel we report the 2002 − 2012 decade, while right panel the 2013 − 2023 decade. See text for more details.
Preprints 107780 g011
Preprints 107780 g012
Figure 12. Simple returns in log-lin scale: data and q-Gaussian fits of spring rainfall event duration. On the left panel we report the 2002 − 2012 decade, while right panel the 2013 − 2023 decade. See text for more details.
Figure 12. Simple returns in log-lin scale: data and q-Gaussian fits of spring rainfall event duration. On the left panel we report the 2002 − 2012 decade, while right panel the 2013 − 2023 decade. See text for more details.
Preprints 107780 g012
Preprints 107780 g013
Figure 13. Bar chart of entropic index q for rainfall depth (top panel), maximum intensity recorded per event (central panel) and event duration (bottom panel) are reported for decade ( 2002 − 2012 in green and 2013 − 2023 in blue) and season. See text for more details.
Figure 13. Bar chart of entropic index q for rainfall depth (top panel), maximum intensity recorded per event (central panel) and event duration (bottom panel) are reported for decade ( 2002 − 2012 in green and 2013 − 2023 in blue) and season. See text for more details.
Preprints 107780 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated