Prerpints.org logo
Preprint
Article

Comprehensive Neural Cryptanalysis on Block Ciphers Using Different Encryption Methods

Altmetrics

Downloads

132

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 May 2024

Posted:

31 May 2024

You are already at the latest version

Alerts
Abstract
In this paper, we perform the neural cryptanalysis and comprehensively analyze five block ciphers, Data Encryption Standard (DES), Simplified DES (SDES), Advanced Encryption Standard (AES), Simplified AES (SAES), and SPECK. The vulnerability of the block ciphers is investigated in three different attacks, such as Encryption Emulation (EE), Plaintext Recovery (PR), Key Recovery (KR), and Ciphertext Classification (CC) attacks. For the plaintexts, randomly generated block-sized bit arrays and texts are used. The block ciphers apply different numbers of round functions in the encryption of the block-sized bit arrays, and they are investigated by using the deep learning models trained with different numbers of data in EE, PR, and KR attacks. Moreover, the block ciphers use two different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE), to encrypt the texts in various operation modes, and they are analyzed with deep learning models in EE, PR, and CC attacks. As a result, the block ciphers can be vulnerable to deep learning-based EE and PR attacks using a large amount of train data, and STE can improve the strength of the block ciphers, unlike WTE, which shows almost the same classification accuracy as the plaintexts, especially in CC attack. Additionally, when the keys that are the same as the plaintexts are used in encryption, the block ciphers can be perfectly broken in KR attack. Moreover, especially in KR attack, the RNN-based deep learning model shows higher average Bit Accuracy Probability (BAPavg) than the fully connected-based deep learning model, which is used more often in previous works of neural cryptanalysis. Furthermore, although the transformer-based deep learning model is a state-of-the-art model in Natural Language Processing (NLP), the RNN-based deep learning model is more suitable for CC attack and shows higher classification accuracy.
Keywords: 
Subject: Computer Science and Mathematics  -   Security Systems

1. Introduction

Due to the frequent data breaches, security and privacy concerns have increased. To protect personal information in data, various cryptographic algorithms [1,2] have been utilized in data encryption. Since encrypted data differs from the original data, the sensitive information in data can be concealed and cannot be exposed to anyone who is not authorized. Thus, to ensure data confidentiality, cryptographic algorithms must be secure against attacks. Cryptanalysis can evaluate the strength of the cryptographic algorithms through legitimate attacks. The weaknesses found from the cryptanalysis can help prevent the attacks and construct new cryptographic algorithms that are more resistant to attacks. There are four types of attacks in cryptanalysis, Ciphertext Only Attack (COA), Known Plaintext Attack (KPA), Chosen Plaintext Attack (CPA), and Chosen Ciphertext Attack (CCA), which are distinguished according to information that attackers can access. The ciphertext is used in COA, the pair of plaintext and ciphertext is used in KPA, the ciphertext of the plaintext chosen by the attacker is used in CPA, and the plaintext of the ciphertext chosen by the attacker is used in CCA. Furthermore, the Brute-force attack [3] tries all possible keys to decrypt ciphertext until the plaintext is correctly recovered. Linear cryptanalysis [4,5] finds a linear equation of relation between plaintext, ciphertext, and key. Differential cryptanalysis [6] analyzes the effect of plaintext changes on ciphertext by comparing ciphertexts of slightly different plaintexts.
Recently, deep learning has been actively applied in information security [7]. It can automatically detect intrusion and malware to protect computing resources, programs, and data from attacks in cyberspace. Moreover, deep learning-based cryptanalysis can enhance the efficiency and effectiveness in finding the weaknesses of cryptographic algorithms. Neural-aided cryptanalysis, one of the deep learning-based cryptanalysis, uses deep learning models in traditional cryptanalysis, and neural cryptanalysis investigates the vulnerability of cryptographic algorithms by using only deep learning models [8]. Unlike the conventional cryptanalysis methods that require mathematical calculations and knowledge of cryptographic algorithms, neural cryptanalysis can automatically identify the vulnerability of cryptographic algorithms by recovering the keys from the pair of the plaintext and the ciphertext, recovering the plaintext from the ciphertext, generating the ciphertext from the plaintext, and analyzing the ciphertext without decryption.
In this paper, we perform neural cryptanalysis and comprehensively analyze five block ciphers, such as Data Encryption Standard (DES) [9], Simplified DES (SDES) [2], Advanced Encryption Standard (AES) [10], Simplified AES (SAES) [11], and SPECK [12]. The block ciphers are investigated on deep learning-based Encryption Emulation (EE), Plaintext Recovery (PR), Key Recovery (KR), and Ciphertext Classification (CC) attacks by using randomly generated block-sized bit arrays and texts as plaintexts. The block ciphers apply different numbers of round functions in the encryption of the block-sized bit arrays, and they are investigated by using the deep learning models trained with different numbers of data in EE, PR, and KR attacks. Moreover, the block ciphers use two different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE), to encrypt the texts in various operation modes, and they are analyzed with deep learning models in EE, PR, and CC attacks.
The main contributions of this paper are summarized as follows:
  • We perform comprehensive neural cryptanalysis to analyze the vulnerability of five block ciphers, DES, SDES, AES, SAES, and SPECK, on Encryption Emulation (EE), Plaintext Recovery (PR), Key Recovery (KR), and Ciphertext Classification (CC) attacks.
  • For the block ciphers on randomly generated block-sized bit arrays, different numbers of round functions are applied in the encryption of the block-sized bit arrays, and the deep learning models trained with different numbers of data are used for EE, PR, and KR attacks.
  • For the block ciphers on texts, two different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE), are used in various operation modes to encrypt the texts, and the deep learning models are utilized for EE, PR, and CC attacks.
  • Experimental results show that the block ciphers can be more vulnerable to deep learning-based EE and PR attacks using more data in model training, and STE can improve the strength of block ciphers compared to WTE, which has almost the same classification accuracy as the plaintexts, especially in CC attack.
  • In KR attack, the secret keys can be perfectly recovered when the randomly generated keys are the same as the plaintexts.
  • For neural cryptanalysis, the RNN-based deep learning model is more suitable than the fully connected-based and transformer-based deep learning models, especially in KR and CC attacks.

2. Related Works

Deep learning [13,14] has been applied in various fields, such as medical, financial, and other industries. Neural cryptanalysis is one of the important deep learning applications that evaluates the strength of cryptographic algorithms against deep learning-based attacks. Unlike neuro-aide cryptanalysis, which utilizes deep learning to improve the effectiveness of traditional cryptanalysis, neural cryptanalysis breaks the cryptographic algorithms only with deep learning [8].

2.1. Deep Learning-Based Cryptanalysis on Image Data

Computer vision [15] analyzes visual data with deep learning models and uses the analytic information in various tasks, such as self-driving car and medical diagnosis. It can also be utilized in cryptanalysis [16,17,18] to investigate the weaknesses of cryptographic algorithms used for image encryption. In [16], they identified the vulnerability of optical-based cryptographic algorithms, Double Random Phase Encoding (DRPE) [19] and Triple Random Phase Encoding (TRPE) [20], by recovering the encrypted image into the original image with deep learning model based on ResNet [21]. The model was trained to output original image corresponding to the encrypted image fed into the model. Moreover, they evaluated the proposed model by removing some pixel values in the encrypted image and adding noise to the encrypted image. In [17], they used both simple [22] and complex real-world [23] images and classified the encrypted images of DRPE with DRPE pre-trained deep learning model. In [18], they decrypted the encrypted images of chaos-based cryptographic algorithm [24] by using Convolutional Neural Network (CNN) [25] with encoder-decoder structure.
Although Privacy-preserving Deep Learning (PPDL) schemes [26,27] with image encryption were proposed to protect personal information in image data, they can also be evidence of the weaknesses of the cryptographic algorithms as encrypted images can be analyzed. In [28,29], they classified images encrypted with Homomorphic Encryption (HE) [30,31], which has the same result in calculation regardless of whether the encryption is performed before or after the operations. Considering the properties of HE, which only supports addition and multiplication, activation functions in deep learning models were approximated to low-degree polynomials. In [32], they encrypted images with AES [10], Twofish [33], Serpent [34], and ChaosNet [35] in different operation modes, Electronic Codebook (ECB), Cipher Block Chaining (CBC), and Enhanced Cipher Block Chaining (ECBC). The encrypted images were decrypted in the last single round and then classified with CNN-based deep learning model.

2.2. Deep Learning-Based Cryptanalysis on Text Data

Natural Language Processing (NLP) [36], which mainly manipulates human language, has been applied in many tasks, such as language translation and Chatbot. It can also be utilized in cryptanalysis [8,37,38,39,40,41,42,43,44] to investigate the vulnerability of cryptographic algorithms used for text encryption. In [38], they recovered keys with deep learning model from the ciphertexts encrypted with classical cryptographic algorithms, Caesar, Vigenère, and substitution cipher. The model was trained by using the relative frequencies of characters in the ciphertexts. Similarly, in [39], they classified the ciphertexts of Caesar, Vigenère, and substitution cipher with Recurrent Neural Network (RNN)-based deep learning model [45]. The model predicted the class of the ciphertexts fed into the model. In [40], they encrypted plaintexts with Data Encryption Standard (DES) [9], and the ciphertexts were recovered into the plaintexts by using deep learning model with Multi-Layer Perceptron (MLP) structure. The plaintexts of 64-bit block size and the keys were generated by using Pseudo Random Number Generator (PRNG) and used to train the model. In [41], they used round-reduced DES in text encryption and predicted plaintexts from the ciphertexts by using MLP-based deep learning model. In [42], they recovered plaintexts with deep learning model, which consists of only Fully-Connected layers (FC), from the ciphertexts encrypted with Advanced Encryption Standard (AES) [10] using 128-bit and 256-bit key sizes. In [43], they used randomly generated block-sized plaintexts and encrypted the plaintexts with lightweight block ciphers, Simplified DES (SDES) [2], SIMON, and SPECK [12]. The keys from the ciphertexts were recovered by using deep learning model with only FC layers. In [44], they encrypted plaintexts with SDES [2], Simplified AES (SAES) [11], and round-reduced SPECK. The model with skip connection [21] was used for key prediction. In this paper, we comprehensively analyze block ciphers on deep learning-based attacks from various perspectives and suggest ideas to improve the security of the block ciphers.

3. Material and Methods

3.1. Block Ciphers

In this section, we introduce five block ciphers, Data Encryption Standard (DES), Simplified DES (SDES), Advanced Encryption Standard (AES), Simplified AES (SAES), and SPECK32/64, evaluated in this paper.

3.1.1. Data Encryption Standard (DES)

In the 1970s, Data Encryption Standard (DES) [9], first developed by IBM, was adopted as an encryption standard by the National Institute of Standards and Technology (NIST), known as the National Bureau of Standards (NBS). DES is a block cipher of Feistel Network (FN) and uses symmetric key in encryption. It generates 64-bit ciphertext from 64-bit plaintext by using 64-bit key, including 8-bit parity bits. Initial Permutation (IP) is first applied to the plaintext P before round functions and then divided into right and left half blocks, R0 and L0, as follows:
I P P = L 0 R 0
where IP(·) represents Initial Permutation (IP). In each round function f, expansion P-Box expands 32-bit right half block Rr-1 into 48-bit block, and then XOR operation is applied to it with 48-bit key kr of the round function. After that, S-Box transforms 48-bit block into 32-bit block and straight P-Box permutes it. Finally, right output block Rr of the round function is generated by XOR operation of the straight P-Box output and the left half block Lr-1. The right half block Rr-1 is the left output block Lr as follows:
  R r = f R r − 1 ,     k r ⊕ L r − 1
L r = R r − 1
where R, L, and k represent the right block, left block, and the key in the round function of the corresponding subscript. After repeating this process 15 more times, Final Permutation (FP), the inverse process of the IP, is applied and generates 64-bit ciphertext C as follows:
C = F P R 16 L 16 = I P − 1 ( R 16 L 16 )
where FP(·) represents Final Permutation (FP). The keys for each round function are generated by shifting and compressing the block after removing 8-bit parity bits.
The simplified version of DES, Simplified DES (SDES) [2], has 16-bit plaintext, 16-bit ciphertext, and 16-bit key in 4 round functions. Straight P-Box, including IP and FP, is not used in SDES.

3.1.2. Advanced Encryption Standard (AES)

As the key space of DES is not large enough to be secure against brute-force attack, Advanced Encryption Standard (AES) [10], developed by Joan Daemen and Vincent Rijmen, was selected as the new encryption standard in 2001. AES is a block cipher of Substitution Permutation Network (SPN) and uses symmetric key in encryption. It encrypts 128-bit plaintext into 128-bit ciphertext. According to the key size, different numbers of round functions are applied, which are 10, 12, and 14 round functions for 128, 192, and 256-bit keys, respectively. There are four operations in each round function: SubBytes, ShiftRows, MixColumns, and AddRoundKey. Plaintext is arranged into 4X4 byte matrix called state. SubBytes substitutes 16 bytes in the state according to the S-BOX that has 8-bit input and 8-bit output. ShiftRows shifts second, third, and fourth rows in a state once, twice, and thrice to the left, respectively. MixColumns multiplies each column in a state with constant matrix over the finite field GF(28) as follows:
  d 1 ,     j d 2 ,     j d 3 ,     j d 4 ,     j = 02     03     01     01 01     02     03     01 01     01     02   03 03     01     01     02   ∙   c 1 ,     j c 2 ,     j c 3 ,     j c 4 ,     j
where ci,j and di,j represent byte at (i, j) in a state and result of MixColumns operation, respectively. AddRoundKey is XOR operation for each byte in the state and corresponding byte in the key of each round function. It is applied to the state of the plaintext before the round functions, and then SubBytes, ShiftRows, MixColumns, and AddRoundKey are applied in sequence for each round function. The final round function applies only three operations, except Mixcolumns, in the same order as the previous round functions. The keys for each round function are generated by key expansion.
The simplified version of AES, Simplified AES (SAES) [11], encrypts 16-bit plaintext into 16-bit ciphertext by using 16-bit key in 2 round functions. Since the block size of SAES is smaller than AES, plaintext is arranged into the 2X2 nibble matrix, not 4X4 byte matrix as AES. It also uses SubNibbles instead of SubBytes as AES in each round function.

3.1.3. SPECK

Lightweight ciphers have been actively studied for security in constrained environments like Internet of Things (IoT) devices. SPECK [12] is one of the lightweight block ciphers, which was released by the National Security Agency (NSA) in 2013. It is based on Addition-Rotation-XOR (ARX) operation and uses various sizes of blocks and keys. The block has two words of 16, 24, 32, 48, and 64-bit, and key has two, three, and four words that are the same size as the block. The number of round functions also differs according to the size of the block and key and the number of the words in the key. It can be written as SPECK2n/nm, where 2 represents the number of words in the block, n represents the size of the word in the block and key, and m represents the number of words in the key. For example, SPECK32/64 used in this paper has two 16-bit words in a block and four 16-bit words in the key, and it applies 22 round functions. Each round function r first applies right rotation to left half word Lr-1 and then adds right half word Rr-1. It then generates left output word Lr of the round function by XOR operation with key kr of the round function. The right output word Rr of the round function is the result of the XOR operation of the left rotated right half word and left output word Lr of the round function as follows:
  L r = L r − 1 ≫ r 1   ⊞ R r − 1 ⊕ k r
R r = R r − 1 ≪   r 2   ⊕ L r
where ≫ and ≪ represent right and left rotations, ⊞ represents addition modulo word size in the block and key, and ⊕ represents bitwise XOR operation, respectively. The rotated bits r1 and r2 are r1 = 7 and r2 = 2 for SPECK32/64 and r1 = 8 and r2 = 3 for the other cases. The keys for each round function are generated by the same process as the round function in encryption.

3.2. Text Encryption Methods

In this section, two different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE), are described, which are used to figure out how to improve the strength of block ciphers in text encryption.

3.2.1. Word-Based Text Encryption (WTE)

Since sentence consists of words, text can be encrypted word by word. In other words, text is divided into word units, and each word is separately encrypted. The Word-based Text Encryption (WTE) consists of five steps, which are text pre-processing, tokenization, binary encoding, padding, and encryption steps. The text pre-processing step first changes uppercase to lowercase and removes the punctuation in plaintext. The clean plaintext, pre-processed plaintext, is then divided into words in the tokenization step, and each word is encoded into bit array in the binary encoding step, according to the ASCII code. Each bit array is divided into blocks, which are the same size as the block size in the block cipher. If the length of the bit array is not multiple of the block size and cannot be divided by block size, zero-padding is applied in the padding step, and then each block is encrypted with block cipher in the encryption step. The encrypted blocks in each word are combined, and it results in one cipher word for one word. Thus, the number of cipher words CW in ciphertext CWTE encrypted with WTE is the same as the number of words PW in clean plaintext P as follows:
N C W C W T E = N P W ( P )
where NCW (CWTE) and NPW (P) represent the number of cipher words in the ciphertext encrypted with WTE and the number of words in the clean plaintext, respectively. The process of WTE is depicted in Figure 1.

3.2.2. Sentence-Based Text Encryption (STE)

Sentence can be encrypted as itself without dividing sentence into words or characters. In Sentence-based Text Encryption (STE), there are four steps, text pre-processing, binary encoding, padding, and encryption steps. After generating clean plaintext in the text pre-processing step, every character in the clean plaintext, including whitespace, is encoded into bit array B in the binary encoding steps, according to the ASCII code. The bit array is then divided into blocks of the specific size corresponding to the block size bs in the block cipher. To fit the bit array into the multiple of the block size, zero-padding Z is applied in the padding step. The blocks in the bit array with padding are then encrypted with block cipher in the encryption step. Consequently, the number of cipher words CW is the same as the number of the divided blocks in the bit array with padding as follows:
N C W C S T E = l e n B + Z b s
where NCW (CSTE) and len(B + Z) represent the number of cipher words in the ciphertext encrypted with STE and the length of bit array with padding, respectively. The process of STE is depicted in Figure 2.

3.3. Deep Learning Model Architectures

We investigate the security of five block ciphers, such as SDES [2], SAES [11], DES [9], AES-128 [10], and SPECK32/64 [12], by performing deep learning-based attacks, Encryption Emulation (EE), Plaintext Recovery (PR), Key Recovery (KR), and Ciphertext Classification (CC) attacks. The EE is an attack that tries to generate the ciphertexts from the plaintexts, and PR is the reverse process of EE, which tries to recover the plaintexts from the ciphertexts without knowledge of the key. The KR attempts to recover the keys from the pairs of plaintext and ciphertext, and CC is an attack that attempts to classify the ciphertexts without decryption. The deep learning model architectures used for attacks on block ciphers using block-sized bit arrays and texts as plaintext, respectively, are presented in this section.

3.3.1. Deep Learning Models for Encryption Emulation (EE), Plaintext Recovery (PR), and Key Recovery (KR) Attacks on Block-Sized Bit Arrays

For Encryption Emulation (EE), Plaintext Recovery (PR), and Key Recovery (KR) attacks on block-sized bit arrays, fully connected-based and RNN-based, bidirectional Long Short-Term Memory (BiLSTM) [45], deep learning models are utilized. Although fully connected-based deep learning model is the most straightforward neural network, it is still mainly used in neural cryptanalysis because it can train the global features in the data. Since all of the cryptographic algorithms have diffusion and confusion properties, the single bit in the plaintext or key can affect all of the bits in the ciphertext. Therefore, we perform EE, PR, and KR attacks on block-sized bit arrays by using fully connected-based deep learning model at first. As shown in Figure 3 (a), the model comprises four fully-connected layers, which are followed by batch normalization and ReLU, but the last layer is applied sigmoid for activation function. Each layer has 512, 1,024, and 512 nodes, respectively, and the last layer has the number of nodes that is the same as the block size.
In addition, we perform EE, PR, and KR attacks on block-sized bit arrays by using BiLSTM, one of the RNN-based deep learning models, which uses input, output, and forget gates to control the information passed, stored, and removed in each step. As shown in Figure 3 (b), the model consists of three BiLSTM with 256 hidden state sizes, and fully connected layer followed by sigmoid. Since DES and SPECK encrypt the plaintexts split into left and right blocks, the plaintexts, inputs for EE attack, and the ciphertexts, inputs for PR attack, were divided into two parts, and each part was then fed into the model in sequence. Similarly, in the KR attack, the pair of plaintext and the ciphertext was fed into the model separately. Thus, the models had sequence length of 2, and each input size was half of the block size for EE and PR attacks and the same size as the block size for KR attack.

3.3.2. Deep Learning Models for Encryption Emulation (EE) and Plaintext Recovery (PR) Attacks on Texts

For Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on texts, transformer-based deep learning model, T5-small [46], is utilized. The transformer is the model that uses only attention mechanisms without RNN-based deep learning models and performs better in capturing the long-term dependencies than Long Short-Term Memory (LSTM), Gated Recurrent Unit (GRU), and even attention mechanisms in RNN-based deep learning models. As shown in Figure 4, the model comprises stack of encoder blocks and decoder blocks. Each encoder has encoder self-attention and feed-forward layer, and each decoder has decoder self-attention, encoder-decoder attention, and feed-forward layer with ReLU. The outputs of the last decoder block are passed into the fully-connected layer with softmax. Every layer is followed by normalization layer and residual skip connection, and all the attention mechanisms use multi-head attention. The inputs for the first encoder block and decoder block are applied to the embedding process before they are fed into the first encoder block and decoder block. The embedding dimension is 512, the number of self-attention heads is 6, feed forward has 2,048 output dimensionality, and 6 encoder blocks and 6 decoder blocks are stacked.

3.3.3. Deep Learning Models for Ciphertext Classification (CC) Attack on Texts

For Ciphertext Classification (CC) attacks on texts, RNN-based, bidirectional GRU (BiGRU) [47], and transformer-base, BERT-base [48], deep learning models are utilized. Since the plaintexts are sequential data, we classify the ciphertexts by using RNN-based deep learning models that can store and use the information of the context sequences. The GRU, one of the RNN-based deep learning models, uses reset and update gates to determine how much information of the context sequences is to be removed and passed, which can solve gradient vanishing problems and learn long-term dependencies. Furthermore, BiGRU can process the sequences in the backward direction as well as forward direction. As shown in Figure 5 (a), the model consists of input embedding, three of BiGRU, and fully-connected layer followed by softmax. The embedding dimension is 256, and each BiGRU has 128 hidden state size.
Furthermore, the transformer-based model, BERT-base [48], is used in CC attack on texts. The BERT uses only the encoder part, stack of encoder blocks as shown in Figure 4, in the transformer, each encoder block has the encoder self-attention and the feed-forward, and they are followed by normalization layer and skip connection. The fully connected layer with softmax comes after the stack of the encoder blocks to classify the ciphertexts. The inputs are fed into the first encoder block after applying the input embedding and positional embedding. As shown in Figure 5 (b), embedding dimension is 768, the number of self-attention heads is 12, feed forward has 3,072 output dimensionality, 12 encoder blocks and 12 decoder blocks are stacked, and the last fully-connected layer has class number of nodes.

4. Experiments

4.1. Experimental Setup

All of the models in this paper were constructed by using Python with the PyTorch framework. A server of Intel Xeon Silver 4214 CPU and NVIDIA RTX A5000 GPU was used to train the models and generate the data.

4.2. Neural Cryptanalysis on Block-Sized Data

4.2.1. Data Generation

We generated the block-sized bit arrays and used them as plaintexts for Encryption Emulation (EE) and Plaintext Recovery (PR) attacks. The integers were randomly selected between 0 and the maximum integer of that can be generated in the block-sized bit array by using random generator function. Then, the integers were encoded into the binary arrays and then encrypted with the block ciphers.
For Key Recovery (KR) attack, we used a randomly selected block-sized bit array as a plaintext and encrypted it with keys that were randomly generated by using the same method for the plaintexts in EE and PR attacks. The sample plaintexts and the ciphertexts for EE and PR attacks on the five block ciphers using block-sized bit arrays are shown in Table 1.

4.2.2. Results on Different Numbers of Train Data and Round Functions

To investigate the impact of the data amount used in training the models for Encryption Emulation (EE) and Plaintext Recovery (PR) attacks, we trained the fully connected-based deep learning model while increasing the number of train data. Since SDES and SAES use 16-bit block size, we used only half of the data, 215 (=32,768), among the possible block-sized bit arrays, 216 (=65,536), as the train data. In the other block ciphers, DES, AES-128, and SPECK32/64, the number of train data was increased by 4 times from 216 (=65,536) and used to train the models. The model was trained with cross entropy loss function, and AdamW optimizer with 0.001 learning rate. We compared the results in different numbers of round functions by calculating the average of Bit Accuracy Possibility (BAPavg) [43,44] in 215 (=32,768) of test data as follows:
p r e d i n = 0 ,       i f     p r e d i n   ≤   0.5         1 ,       o t h e r w i s e .                       B A P i = ∑ n = 1 N X N O R r e a l i n ,     p r e d i n N
B A P a v g = ∑ i = 1 b s B A P i b s
where r e a l i n and p r e d i n  represent ith bit of the nth real and predicted outputs, respectively. BAPi is the BAP of ith bit, N is the total number of test data, BAPavg is the average of BAP in total data, and bs is the block size of the block cipher. As shown in Figure 6 and Figure 7, the more train data used in training, the higher accuracy showed in every block cipher. In SPECK32/64, 216 of train data was enough to break the single round function, and the BAPavg reached 1.0 when the train data was increased to 222 in two round functions. Furthermore, for the three round functions in SPECK32/64, BAPavg increased to 0.6 ~ 0.7 in 222 of train data. Also, DES with single and two round functions reached 1.0 and 0.8 ~ 0.9 BAPavg, respectively, on 222 of train data. However, every BAPavg of AES-128 was 0.5, even in the single round function. As a result, the possibility for EE and PR attacks on block ciphers using block-sized bit array was higher when we trained the deep learning models with as much data as possible.

4.2.3. Results on Different Deep Learning Models

To identify the impact of the deep learning model architecture in neural cryptanalysis, we additionally performed the Encryption Emulation (EE), Plaintext Recovery (PR), and Key Recovery (KR) attacks on block ciphers using block-sized bit arrays by using RNN-based deep learning model, BiLSTM [45]. The result was compared with that of the fully connected-based deep learning model. The model was trained with cross-entropy loss function and AdamW optimizer with 0.001 learning rate and used 222 (4,194,304) train data, which was the maximum number of train data in the fully connected-based deep learning model. The BAPavg in the RNN-based deep learning model was slightly increased compared to the fully connected-based deep learning model as shown in Table 2. Consequently, it was more efficient to extract the features by dividing inputs into meaningful parts with the RNN-based deep learning model, BiLSTM, rather than using them all at once with the fully connected-based deep learning model.
Interestingly, the single round function showed lower BAPavg than the two round functions in KR attacks on SDES, DES, and SPECK32/64. Since SDES and DES split the plaintexts into two blocks, left and right, and then apply the XOR operation with the key only to the right block of the input for the round function, only half of the ciphertexts for the single round function have information about the keys. Because the left block of the first round function is the same as the right block of the input for the first round function, the ciphertexts for the single round function in SDES and DES have less information of the key than the ciphertexts of two round functions. Similarly, SPECK32/64 splits the plaintexts and the keys into two blocks, respectively. However, the inputs for the first round function are applied to the operations with the right block of the keys, which are not applied to any operations in the key schedule. Therefore, the ciphertexts encrypted with the single round function in SPECK32/64 have information about the only half key, the right part of the key. In other words, the deep learning model could extract more features related to the keys from the ciphertexts of the two round functions than those of the single round function in SDES, DES, and SPECK32/64.
Furthermore, we performed the KR attack on DES using randomly generated block-sized bit arrays of 222 (=4,194,304), not only for a randomly generated single block-sized bit array, by using the RNN-based deep learning model, BiLSTM. The keys were generated for two cases, the same keys as the plaintexts and randomly generated keys. As shown in Figure 8 (c), when the keys were the same as the plaintexts, DES was vulnerable and perfectly broken. In contrast, it was difficult to recover the keys, which were randomly generated regardless of the plaintexts, and showed 0.5 BAPavg as shown in Figure 8 (d). Consequently, using the same key as the plaintexts can make the block ciphers vulnerable even if the plaintexts are randomly generated.

4.3. Neural Cryptanalysis on Text Data

4.3.1. Data Generation

We randomly generated texts and used them as plaintexts for Encryption Emulation (EE) and Plaintext Recovery (PR) attacks. Each sentence has 30 words, and the words are combinations of randomly selected lowercase of alphabets. The length of each word was randomly decided in the range from 1 to 15. The number of sentences is 50,000, and they were divided into 25,000 sentences for train data and 25,000 sentences for the test.
We used the IMDB dataset [49] as plaintexts for Ciphertext Classification (CC) attack. The texts in the dataset are the movie reviews that have two classes, positive and negative. The total number of the texts is 50,000, consisting of 25,000 positive reviews and 25,000 negative reviews. They were divided in half and used each for train and test data, respectively, which have 12,500 positive reviews and 12,500 negative reviews for total of 25,000 texts. The texts were encrypted with the block ciphers using two different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE). Sample plaintexts and the ciphertexts for CC attack on five block ciphers using texts are shown in Table 3.

4.3.2. Results on Different Text Encryption Methods

To figure out how to improve the strength of block ciphers using texts, we encrypted plaintexts with two different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE). In Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on block ciphers using texts, transformer-based deep learning model, T5-small [46], was used to generate the ciphertexts and recover the plaintexts. It tokenizes the plaintexts and the ciphertexts by using the SentencePiece [50] and considers context information of the sequences in word embedding. The model was trained with 64 batch sizes, cross-entropy loss function, and Adam optimizer with 0.005 learning rate. We used the ratio of the correctly predicted tokens over the total tokens as metrics, which can be calculated as follows:
C o r r e c t l y P r e d i c t e d T o k e n R a t i o = 100 M × ∑ n = 1 M   N p r e d t o k c o r n N p r e d t o k c o r n + N p r e d t o k i n c o r n
where M represents the total number of test data, and N p r e d t o k c o r n and N p r e d t o k i n c o r n are the number of correctly and incorrectly predicted tokens in nth test data, respectively.
The correctly predicted token ratio in WTE was higher than that in STE, as shown in Figure 9, which means STE can make the block ciphers more secure compared to the WTE in EE and PR attacks.
In Ciphertext Classification (CC) attack on block ciphers using texts, the ciphertexts for each text encryption method were classified by using the RNN-based deep learning model that consists of BiGRU [47], which utilized Word2Vec [51,52] to represent the words as embedding vectors that deep learning model can train. The model was trained with 128 batch sizes, cross-entropy loss function, and Adam optimizer with 0.001 learning rate. The result was compared using classification accuracy, which is the percentage of correctly classified ciphertexts out of the total ciphertexts as follows:
C l a s s i f i c a t i o n   A c c = N ( p r e d C c o r ) N ( p r e d C c o r ) + ( p r e d C i n c o r ) × 100 M
where N p r e d C c o r and N p r e d C i n c o r represent the number of correctly and incorrectly classified test ciphertexts, respectively, and M is the total number of test data.
The classification accuracy of the ciphertexts encrypted with STE was lower than that of ciphertexts encrypted with WTE in every block cipher as shown in Figure 10 (a). Furthermore, the accuracy of ciphertext classification on WTE was almost the same as the accuracy of plaintext classification. Therefore, ciphertexts encrypted with WTE were more vulnerable to CC attack than STE in every block cipher.

4.3.3. Results on Different Deep Learning Models

To identify the impact of the deep learning model architecture in the Ciphertext Classification (CC) attack on block ciphers using texts, we additionally classified the ciphertexts with transformer-based deep learning model, BERT-base [48], which represents the words into the embedding vectors according to the context information in the sentences. It also tokenizes the words by using subword-based tokenizer, WordPiece. The model was trained with 8 batch sizes, cross-entropy loss function, and Adam optimizer with 0.00001 learning rate. Since transformer-based deep learning model uses sub-word tokenizer, it can divide a single block in the ciphertexts into several tokens. Thus, the classification accuracy of WTE in transformer-based deep learning model was lower than that in the RNN-based deep learning model with Word2Vec as shown in Figure 10 (b). In other words, it was challenging to capture the features from the separated blocks because the block ciphers encrypt the texts as block-wise. Moreover, unlike WTE, contexts in the ciphertexts were removed in STE, transformer-based deep learning model that uses only attention mechanisms to extract context information and relations between the tokens was not proper in neural cryptanalysis on block ciphers. Thus, transformer-based deep learning model could not train the ciphertexts encrypted with STE and showed 50% classification accuracy in every block cipher. Consequently, word-based tokenization and static word embedding were more efficient in CC attack on block ciphers using texts than the subword-based tokenization and contextualized word embedding.

4.3.4. Results on Different Operation Modes

To confirm that the block cipher using WTE is more vulnerable than that using STE against Encryption Emulation (EE), Plaintext Recovery (PR), and Ciphertext Classification (CC) attacks, we also performed neural cryptanalysis on the block ciphers using texts in the other operation modes. The attacks on DES [9] and AES-128 [10] in CBC and CFB modes were compared with the attacks in ECB mode. The models and hyper-parameters for EE, PR, and CC attacks in CBC and CFB modes were the same as the model and hyper-parameters previously used in ECB mode. The correctly predicted token ratio for EE attack was higher than that in PR attack. However, both DES and AES-128 were more difficult to break when the texts were encrypted with STE than WTE as shown in Figure 11. The average correctly predicted token ratio was around 10% in STE but 15% and 25% for EE and PR attacks, respectively, in WTE. Although the classification accuracy decreased in CBC and CFB modes compared to that in ECB mode, the classification accuracy of the ciphertexts encrypted with WTE still showed over 80% as shown in Figure 12. In contrast, deep learning models could not train and classify the ciphertexts encrypted with STE, and the classification accuracy was almost 50% in every operation mode. As a result, STE could improve strength of the block ciphers against the EE, PR, and CC attacks on block ciphers using texts, and STE must be used for text encryption instead of WTE.

5. Conclusions

We comprehensively analyze five block ciphers, DES, SDES, AES, SAES, and SPECK, on deep learning-based Encryption Emulation (EE), Plaintext Recovery (PR), Key Recovery (KR), and Ciphertext Classification (CC) attacks. The block ciphers using different numbers of round functions in block-sized bit array encryption are investigated in EE, PR, and KR attacks using deep learning models trained with different numbers of data. Also, the block ciphers with two different text encryption methods, Word-based Text Encryption (WTE) and Sentence Text Encryption (STE), for text encryption are analyzed in three operation modes, ECB, CBC and CFB, on EE, PR, and CC attacks using the deep learning models. As a result, more data for training the models can increase the possibility of successful attacks, and STE can improve security, even in the CBC and CFB modes, unlike WTE, which shows almost the same classification accuracy as the plaintexts, especially in CC attack. Moreover, using the same key as the plaintext is vulnerable against KR attack, and applying the two round functions in the encryption of SDES, DES, and SPECK32/64 provides a better KR attack performance than applying the single round function. Also, the RNN-based deep learning model is more suitable in neural cryptanalysis than the fully connected-based and transformer-based deep learning models, especially in KR and CC attacks, and shows higher BAPavg and classification accuracy.

Author Contributions

Conceptualization, I.M; methodology, O.J. and E.A.; software, O.J. and E.A.; validation, O.J. and I.M.; writing—original draft preparation, O.J. and E.A; writing—review and editing, I.M.; visualization, O.J.; supervision, I.M.; funding acquisition, I.M. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No.2020-0-00126, Research on AI-based Cryptanalysis and Security Evaluation). This work was supported by Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (RS-2024-00400368, Development of Image Integrity Verification Technology for Forgery Prevention and Original Proof).

Data Availability Statement

The dataset used in this paper is public dataset, which has been referenced in the manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Paar, C.; Pelzl, J. <italic>Understanding cryptography: a textbook for students and practitioners</italic>; Springer Science & Business Media: 2009.
  2. Stamp, M. <italic>Information security: principles and practice</italic>; John Wiley & Sons: 2011.
  3. Adleman, L.M.; Rothemund, P.W.; Roweis, S.; Winfree, E. On applying molecular computation to the data encryption standard. Journal of computational biology 1999, 6, 53–63. [Google Scholar] [CrossRef]
  4. Matsui, M.; Yamagishi, A. A new method for known plaintext attack of FEAL cipher. In Proceedings of the Advances in Cryptology—EUROCRYPT’92: Workshop on the Theory and Application of Cryptographic Techniques Balatonfüred, Hungary, 1992 Proceedings 11, 1993, May 24–28; pp. 81–91.
  5. Cipher, D. Linear Cryptanalysis Method for. In Proceedings of the Advances in Cryptology–EUROCRYPT’93: Workshop on the Theory and Application of Cryptographic Techniques Lofthus, Norway, 1993 Proceedings, 2003, May 23–27; p. 386.
  6. Biham, E.; Shamir, A. <italic>Differential cryptanalysis of the data encryption standard</italic>; Springer Science & Business Media: 2012.
  7. Berman, D.S.; Buczak, A.L.; Chavis, J.S.; Corbett, C.L. A survey of deep learning methods for cyber security. Information 2019, 10, 122. [Google Scholar] [CrossRef]
  8. Baek, S.; Kim, K. Recent advances of neural attacks against block ciphers. In Proceedings of the 2020 Symposium on Cryptography and Information Security (SCIS 2020), 2020.
  9. Standard, D.E. Data encryption standard. Federal Information Processing Standards Publication 1999, 112. [Google Scholar]
  10. Rijmen, V.; Daemen, J. Advanced encryption standard. Proceedings of federal information processing standards publications, national institute of standards and technology 2001, 19, 22. [Google Scholar]
  11. Musa, M.A.; Schaefer, E.F.; Wedig, S. A simplified AES algorithm and its linear and differential cryptanalyses. Cryptologia 2003, 27, 148–177. [Google Scholar] [CrossRef]
  12. Beaulieu, R.; Shors, D.; Smith, J.; Treatman-Clark, S.; Weeks, B.; Wingers, L. The SIMON and SPECK families of lightweight block ciphers. cryptology eprint archive 2013. [Google Scholar]
  13. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
  14. Goodfellow, I.; Bengio, Y.; Courville, A. <italic>Deep learning</italic>; MIT press: 2016.
  15. Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep learning for computer vision: A brief review. Computational intelligence and neuroscience 2018, 2018. [Google Scholar] [CrossRef]
  16. Hai, H.; Pan, S.; Liao, M.; Lu, D.; He, W.; Peng, X. Cryptanalysis of random-phase-encoding-based optical cryptosystem via deep learning. Optics express 2019, 27, 21204–21213. [Google Scholar] [CrossRef]
  17. Jeong, O.; Moon, I. Adaptive transfer learning-based cryptanalysis on double random phase encoding. Optics & Laser Technology 2024, 168, 109916. [Google Scholar]
  18. He, C.; Ming, K.; Wang, Y.; Wang, Z.J. A deep learning based attack for the chaos-based image encryption. arXiv 2019, arXiv:1907.12245 2019. [Google Scholar]
  19. Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Optics letters 1995, 20, 767–769. [Google Scholar] [CrossRef] [PubMed]
  20. Ahouzi, E.; Zamrani, W.; Azami, N.; Lizana, A.; Campos, J.; Yzuel, M.J. Optical triple random-phase encryption. Optical Engineering 2017, 56, 113114–113114. [Google Scholar] [CrossRef]
  21. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2016; pp. 770–778.
  22. Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747 2017. [Google Scholar]
  23. Liu, X.; Liu, W.; Mei, T.; Ma, H. Provid: Progressive and multimodal vehicle reidentification for large-scale urban surveillance. IEEE Transactions on Multimedia 2017, 20, 645–658. [Google Scholar] [CrossRef]
  24. Guan, Z.-H.; Huang, F.; Guan, W. Chaos-based image encryption algorithm. Physics letters A 2005, 346, 153–157. [Google Scholar] [CrossRef]
  25. LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. The handbook of brain theory and neural networks 1995, 3361, 1995. [Google Scholar]
  26. Tanuwidjaja, H.C.; Choi, R.; Baek, S.; Kim, K. Privacy-preserving deep learning on machine learning as a service—a comprehensive survey. IEEE Access 2020, 8, 167425–167447. [Google Scholar] [CrossRef]
  27. Boulemtafes, A.; Derhab, A.; Challal, Y. A review of privacy-preserving techniques for deep learning. Neurocomputing 2020, 384, 21–45. [Google Scholar] [CrossRef]
  28. Gilad-Bachrach, R.; Dowlin, N.; Laine, K.; Lauter, K.; Naehrig, M.; Wernsing, J. Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy. In Proceedings of the International conference on machine learning; 2016; pp. 201–210. [Google Scholar]
  29. Hesamifard, E.; Takabi, H.; Ghasemi, M. Cryptodl: Deep neural networks over encrypted data. arXiv 2017, arXiv:1711.05189 2017. [Google Scholar]
  30. Rivest, R.L.; Adleman, L.; Dertouzos, M.L. On data banks and privacy homomorphisms. Foundations of secure computation 1978, 4, 169–180. [Google Scholar]
  31. Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the Proceedings of the forty-first annual ACM symposium on Theory of computing, 2009; pp. 169–178.
  32. Lidkea, V.M.; Muresan, R.; Al-Dweik, A. Convolutional neural network framework for encrypted image classification in cloud-based ITS. IEEE Open Journal of Intelligent Transportation Systems 2020, 1, 35–50. [Google Scholar] [CrossRef]
  33. Ferguson, N. Impossible differentials in Twofish. Counterpane Systems. October 1999, 19. [Google Scholar]
  34. Biham, E.; Dunkelman, O.; Keller, N. Linear cryptanalysis of reduced round Serpent. In Proceedings of the International Workshop on Fast Software Encryption; 2001; pp. 16–27. [Google Scholar]
  35. Thoms, G.R.; Muresan, R.; Al-Dweik, A. Chaotic encryption algorithm with key controlled neural networks for intelligent transportation systems. IEEE Access 2019, 7, 158697–158709. [Google Scholar] [CrossRef]
  36. Otter, D.W.; Medina, J.R.; Kalita, J.K. A survey of the usages of deep learning for natural language processing. IEEE transactions on neural networks and learning systems 2020, 32, 604–624. [Google Scholar] [CrossRef] [PubMed]
  37. Sikdar, S.; Kule, M. Recent Trends in Cryptanalysis Techniques: A Review. In Proceedings of the International Conference on Frontiers in Computing and Systems; 2022; pp. 209–222. [Google Scholar]
  38. Focardi, R.; Luccio, F.L. Neural Cryptanalysis of Classical Ciphers. In Proceedings of the ICTCS; 2018; pp. 104–115. [Google Scholar]
  39. Ahmadzadeh, E.; Kim, H.; Jeong, O.; Kim, N.; Moon, I. A deep bidirectional LSTM-GRU network model for automated ciphertext classification. IEEE Access 2022, 10, 3228–3237. [Google Scholar] [CrossRef]
  40. Alani, M.M. Neuro-cryptanalysis of DES and triple-DES. In Proceedings of the Neural Information Processing: 19th International Conference, ICONIP 2012, Doha, Qatar, 2012, Proceedings, Part V 19, 2012, November 12-15; pp. 637–646.
  41. Xiao, Y.; Hao, Q.; Yao, D.D. Neural cryptanalysis: metrics, methodology, and applications in CPS ciphers. In Proceedings of the 2019 IEEE conference on dependable and secure computing (DSC); 2019; pp. 1–8. [Google Scholar]
  42. Hu, X.; Zhao, Y. Research on plaintext restoration of AES based on neural network. Security and Communication Networks 2018, 2018, 1–9. [Google Scholar] [CrossRef]
  43. So, J. Deep learning-based cryptanalysis of lightweight block ciphers. Security and Communication Networks 2020, 2020, 1–11. [Google Scholar] [CrossRef]
  44. Kim, H.; Lim, S.; Kang, Y.; Kim, W.; Kim, D.; Yoon, S.; Seo, H. Deep-learning-based cryptanalysis of lightweight block ciphers revisited. Entropy 2023, 25, 986. [Google Scholar] [CrossRef]
  45. Graves, A.; Mohamed, A.-r.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE international conference on acoustics, speech and signal processing; 2013; pp. 6645–6649. [Google Scholar]
  46. Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the limits of transfer learning with a unified text-to-text transformer. Journal of machine learning research 2020, 21, 1–67. [Google Scholar]
  47. Cho, K.; Van, Merri&#xEB; nboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078 2014. [Google Scholar]
  48. Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805 2018. [Google Scholar]
  49. Maas, A.; Daly, R.E.; Pham, P.T.; Huang, D.; Ng, A.Y.; Potts, C. Learning word vectors for sentiment analysis. In Proceedings of the Proceedings of the 49th annual meeting of the association for computational linguistics: Human language technologies, 2011; pp. 142–150.
  50. Kudo, T.; Richardson, J. Sentencepiece: A simple and language independent subword tokenizer and detokenizer for neural text processing. arXiv 2018, arXiv:1808.06226 2018. [Google Scholar]
  51. Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781 2013. [Google Scholar]
  52. Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. Advances in neural information processing systems 2013, 26. [Google Scholar]
Preprints 107874 g001
Figure 1. The Word-based Text Encryption (WTE) process. There are five steps, text pre-processing, tokenization, binary encoding, padding, and WTE encryption. After cleansing the plaintext in the text pre-processing step, the clean plaintext is tokenized in words in the tokenization step. Then, each word is converted into the binary form in the binary encoding step. To fit the binary form of the words in the plaintext into the multiple of block size, zero-padding is applied in the padding step, and the block cipher encrypts each block in the encryption step.
Figure 1. The Word-based Text Encryption (WTE) process. There are five steps, text pre-processing, tokenization, binary encoding, padding, and WTE encryption. After cleansing the plaintext in the text pre-processing step, the clean plaintext is tokenized in words in the tokenization step. Then, each word is converted into the binary form in the binary encoding step. To fit the binary form of the words in the plaintext into the multiple of block size, zero-padding is applied in the padding step, and the block cipher encrypts each block in the encryption step.
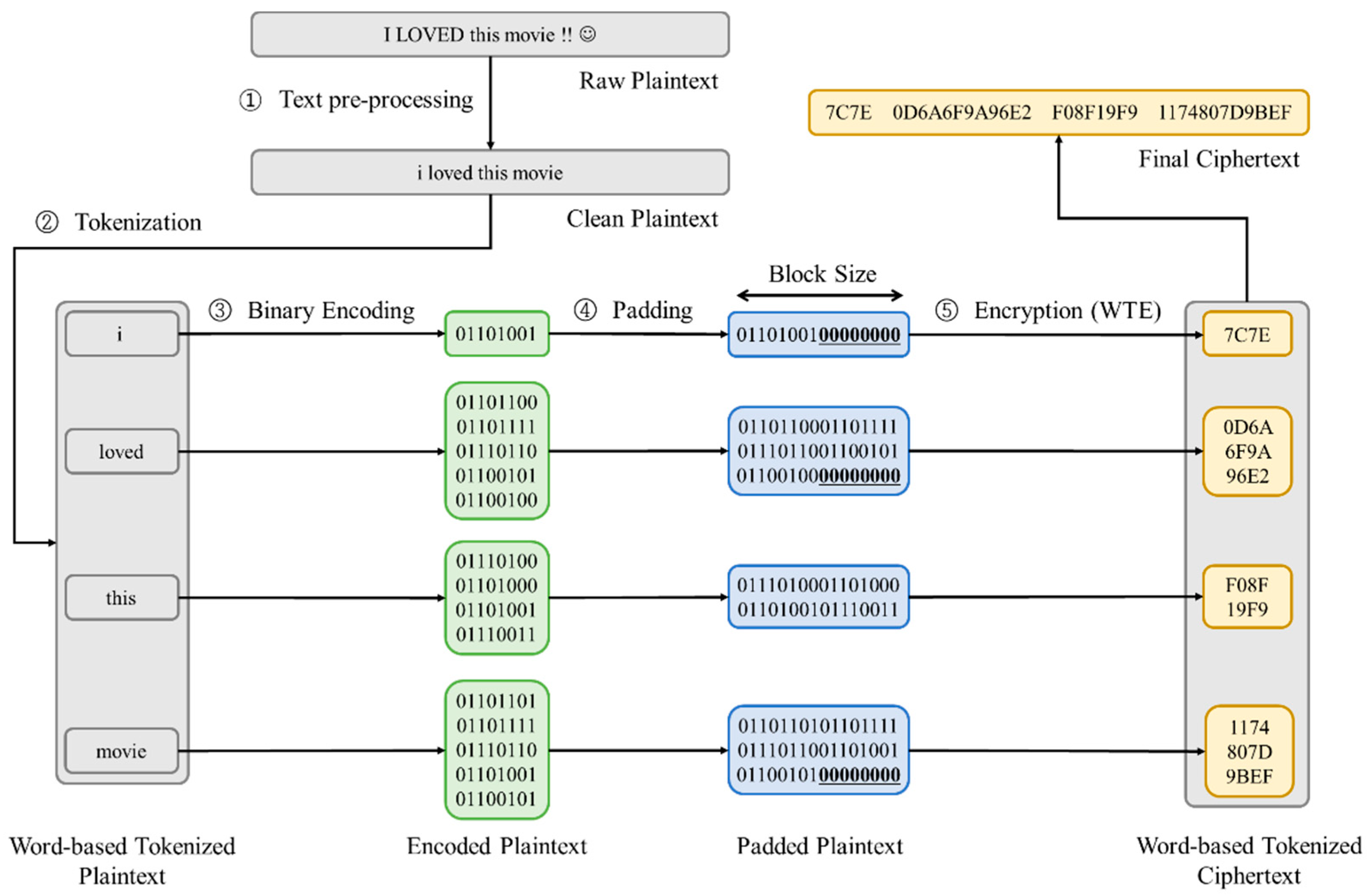
Preprints 107874 g001
Preprints 107874 g002
Figure 2. The Sentence-based Text Encryption (STE) process. There are four steps, text pre-processing, binary encoding, padding, and STE encryption. After cleansing the plaintext in the text pre-processing step, the clean plaintext is converted into the binary form in the binary encoding step. To fit the binary form of the words in the plaintext into the multiple of block size, zero-padding is applied in the padding step, and the block cipher encrypts each block in the encryption step.
Figure 2. The Sentence-based Text Encryption (STE) process. There are four steps, text pre-processing, binary encoding, padding, and STE encryption. After cleansing the plaintext in the text pre-processing step, the clean plaintext is converted into the binary form in the binary encoding step. To fit the binary form of the words in the plaintext into the multiple of block size, zero-padding is applied in the padding step, and the block cipher encrypts each block in the encryption step.
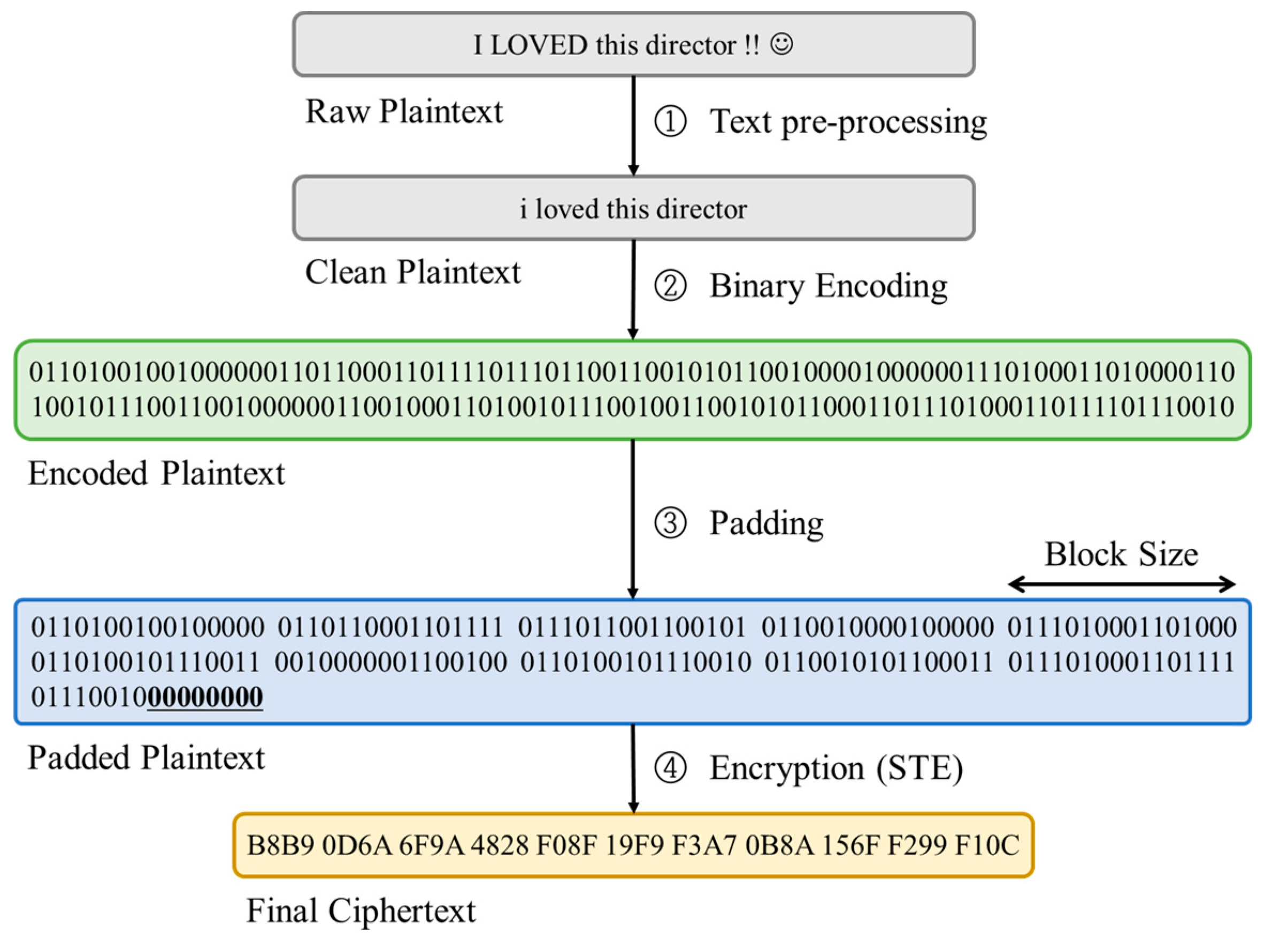
Preprints 107874 g002
Preprints 107874 g003
Figure 3. The deep learning models for Encryption Emulation (EE), Plaintext Recovery (PR), and Key Recovery (KR) attacks on block-sized bit arrays. (a) Fully connected-based deep learning model for EE, PR, KR attacks on block-sized bit arrays. The model consists of three fully-connected layers followed by batch normalization and ReLU, and the last fully connected layer has the same number of nodes as the output size. (b) RNN-based deep learning model (BiLSTM) for EE, PR, and KR attacks on block-sized bit arrays. The model consists of three BiLSTM layers with 256 hidden sizes, and the last fully connected layer has the same number of nodes as the output size.
Figure 3. The deep learning models for Encryption Emulation (EE), Plaintext Recovery (PR), and Key Recovery (KR) attacks on block-sized bit arrays. (a) Fully connected-based deep learning model for EE, PR, KR attacks on block-sized bit arrays. The model consists of three fully-connected layers followed by batch normalization and ReLU, and the last fully connected layer has the same number of nodes as the output size. (b) RNN-based deep learning model (BiLSTM) for EE, PR, and KR attacks on block-sized bit arrays. The model consists of three BiLSTM layers with 256 hidden sizes, and the last fully connected layer has the same number of nodes as the output size.
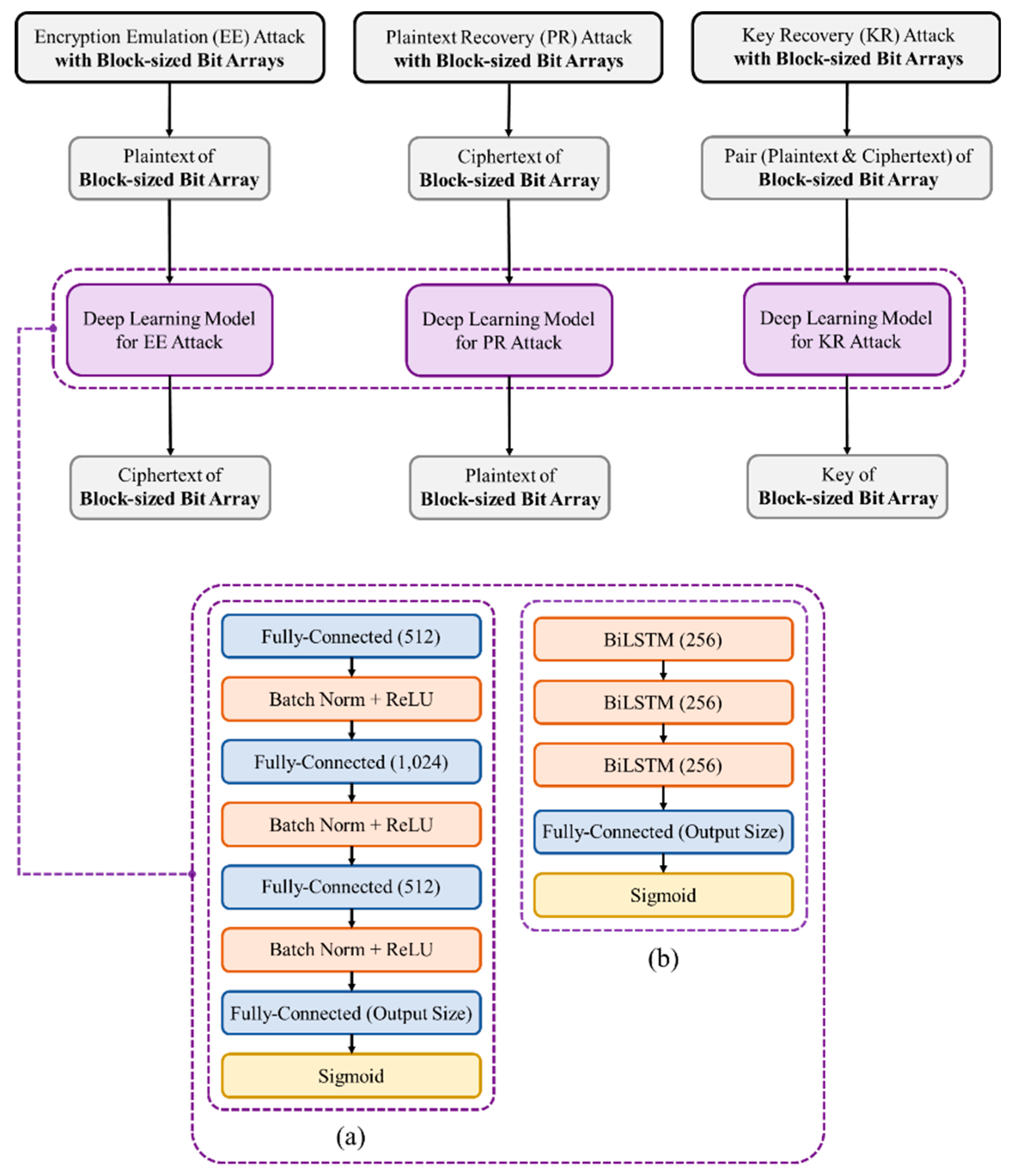
Preprints 107874 g003
Preprints 107874 g004
Figure 4. The deep learning models for Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on texts. Transformer-based deep learning model (T5-small) for EE and PR attacks on texts consists of stack of encoder blocks and decoder blocks, which has 512 dimensions, 2,048 feed-forward output dimensionality, and 6 heads in the attention.
Figure 4. The deep learning models for Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on texts. Transformer-based deep learning model (T5-small) for EE and PR attacks on texts consists of stack of encoder blocks and decoder blocks, which has 512 dimensions, 2,048 feed-forward output dimensionality, and 6 heads in the attention.
Preprints 107874 g004
Preprints 107874 g005
Figure 5. The deep learning models for Ciphertext Classification (CC) attack on texts. (a) RNN-based deep learning model (BiGRU) for CC attack on texts. The model consists of three BiGRU layers with 128 hidden sizes, and the last fully connected layer has the same number of nodes as the number of the class. The input is converted into the embedding vector with 256 dimensions. (b) Transformer-based deep learning model (BERT-base) for CC attack on texts. The model consists of stack of encoder blocks with 768 dimensions, 3,072 feed-forward output dimensionality, and 12 heads in the attention. The last fully-connected layer has the same number of nodes as class.
Figure 5. The deep learning models for Ciphertext Classification (CC) attack on texts. (a) RNN-based deep learning model (BiGRU) for CC attack on texts. The model consists of three BiGRU layers with 128 hidden sizes, and the last fully connected layer has the same number of nodes as the number of the class. The input is converted into the embedding vector with 256 dimensions. (b) Transformer-based deep learning model (BERT-base) for CC attack on texts. The model consists of stack of encoder blocks with 768 dimensions, 3,072 feed-forward output dimensionality, and 12 heads in the attention. The last fully-connected layer has the same number of nodes as class.
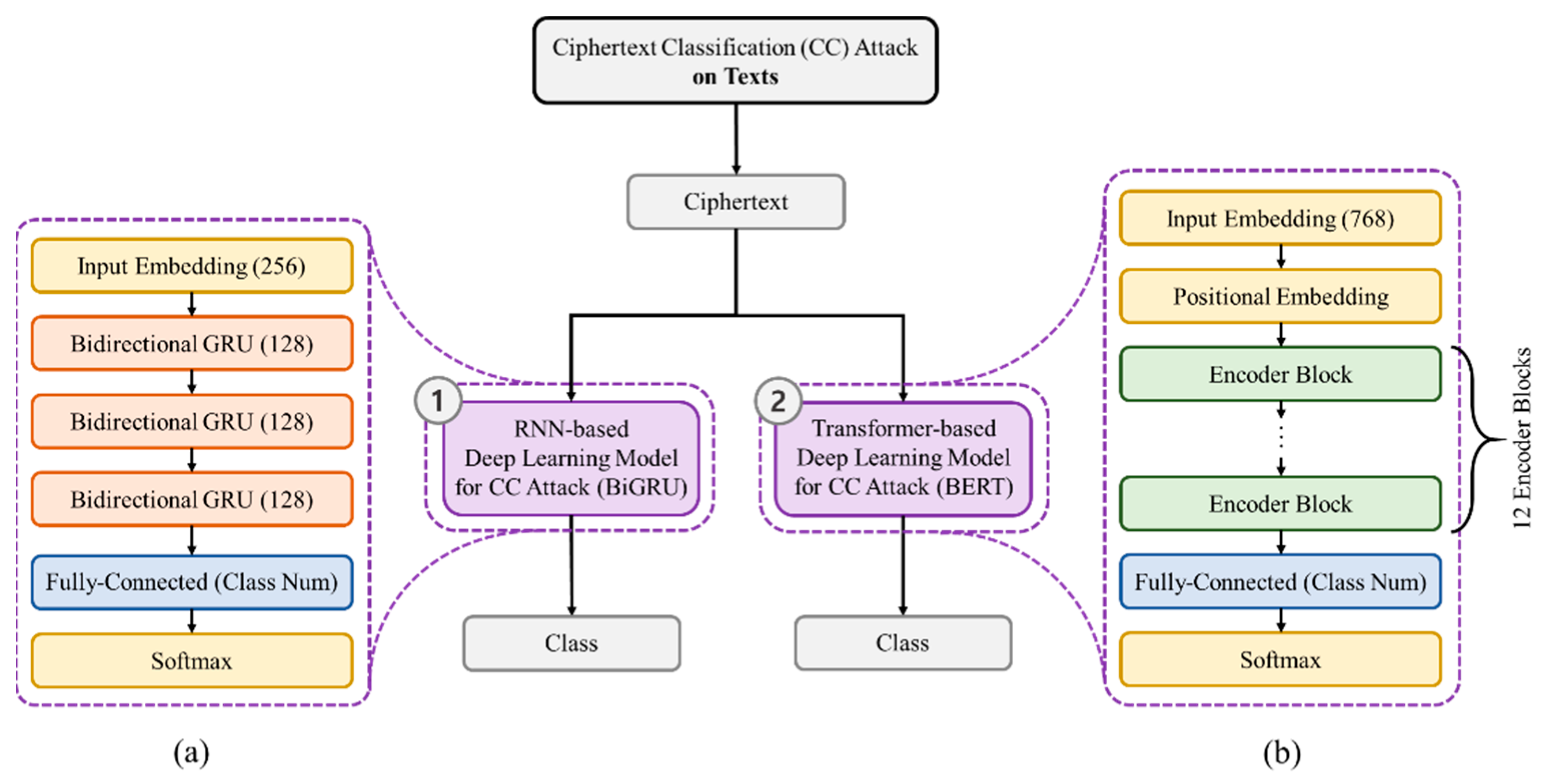
Preprints 107874 g005
Preprints 107874 g006
Figure 6. Average Bit Accuracy Probability (BAPavg) of Encryption Emulation (EE) attack with different numbers of train data on the five block ciphers using different numbers of round functions in block-sized bit arrays. (a) SDES and SAES with 215 train data. (b) DES. (c) AES-128. (d) SPECK32/64.
Figure 6. Average Bit Accuracy Probability (BAPavg) of Encryption Emulation (EE) attack with different numbers of train data on the five block ciphers using different numbers of round functions in block-sized bit arrays. (a) SDES and SAES with 215 train data. (b) DES. (c) AES-128. (d) SPECK32/64.
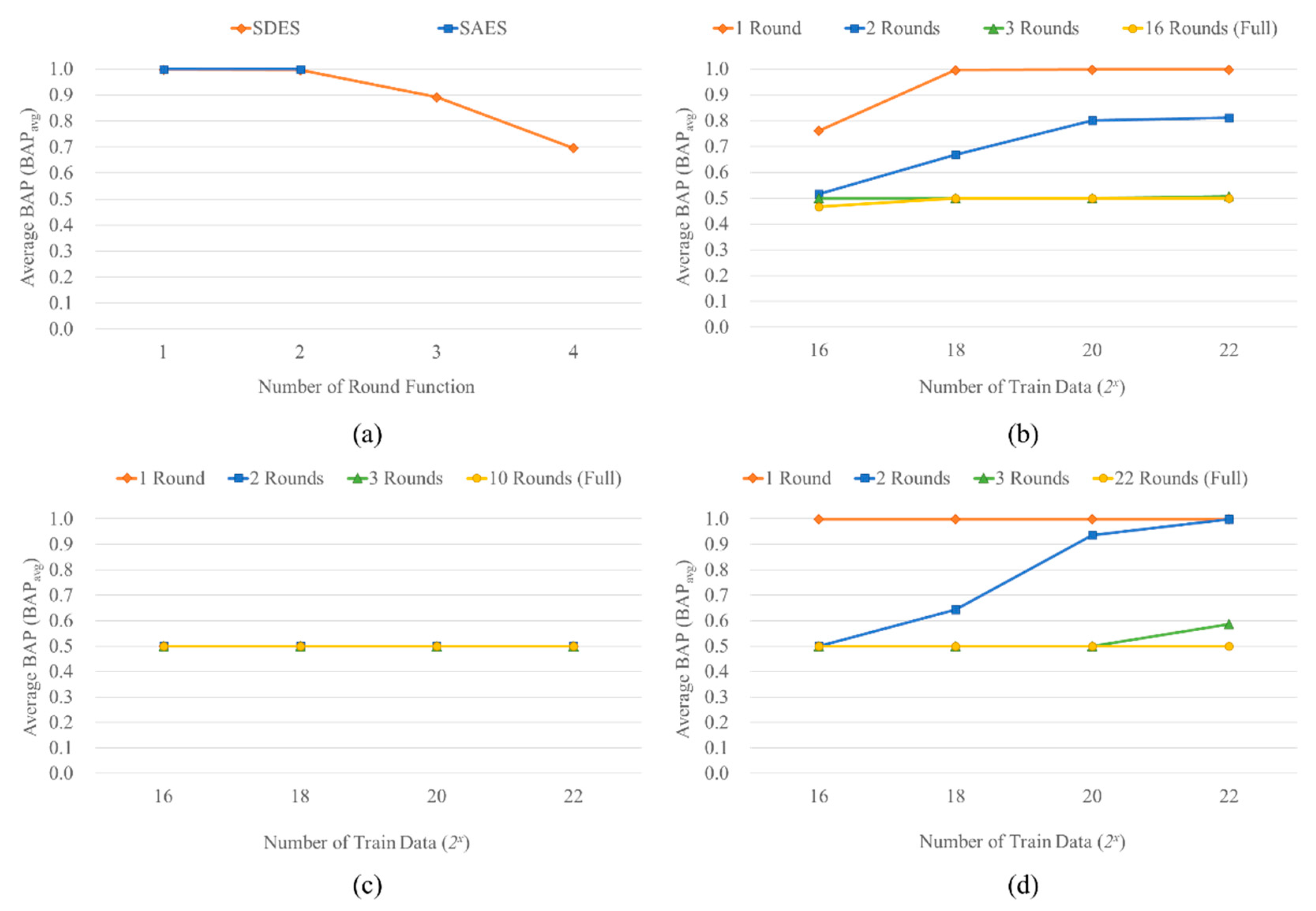
Preprints 107874 g006
Preprints 107874 g007
Figure 7. Average Bit Accuracy Probability (BAPavg) of Plaintext Recovery (PR) attack with different numbers of train data on the five block ciphers using different numbers of round functions in block-sized bit arrays. (a) SDES and SAES with 215 train data. (b) DES. (c) AES-128. (d) SPECK32/64.
Figure 7. Average Bit Accuracy Probability (BAPavg) of Plaintext Recovery (PR) attack with different numbers of train data on the five block ciphers using different numbers of round functions in block-sized bit arrays. (a) SDES and SAES with 215 train data. (b) DES. (c) AES-128. (d) SPECK32/64.
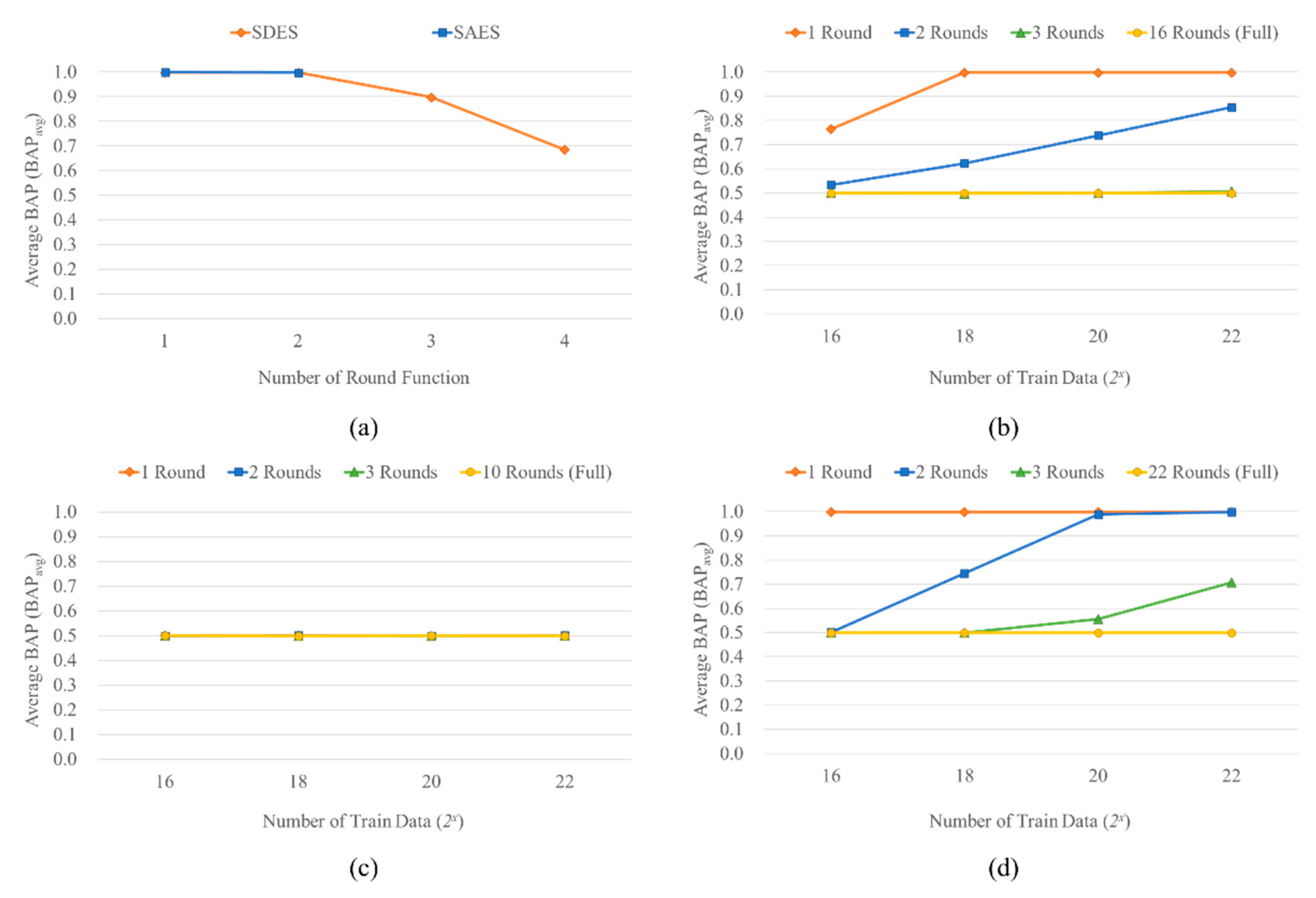
Preprints 107874 g007
Preprints 107874 g008
Figure 8. Bit Accuracy Probability (BAP) for each bit position in the key of Key Recovery (KR) attack on DES using keys generated in two different ways, the same keys as the plaintexts and keys randomly generated regardless of the plaintexts. (a) KR attack on DES using randomly generated plaintexts and the same keys as the plaintexts. (b) KR attack on DES using randomly generated plaintexts and keys randomly generated regardless of the plaintexts.
Figure 8. Bit Accuracy Probability (BAP) for each bit position in the key of Key Recovery (KR) attack on DES using keys generated in two different ways, the same keys as the plaintexts and keys randomly generated regardless of the plaintexts. (a) KR attack on DES using randomly generated plaintexts and the same keys as the plaintexts. (b) KR attack on DES using randomly generated plaintexts and keys randomly generated regardless of the plaintexts.
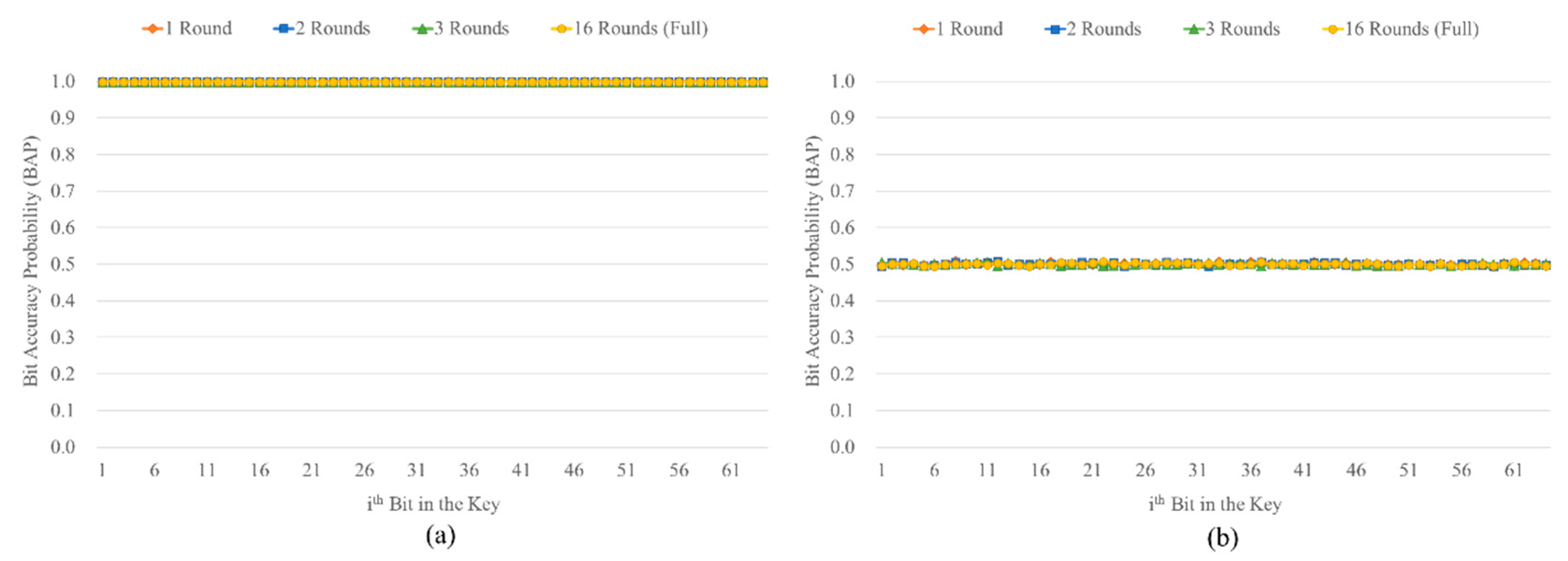
Preprints 107874 g008
Preprints 107874 g009
Figure 9. Correctly predicted token ratio of Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on the five block ciphers with different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE) Methods, in texts. (a) EE attack. (b) PR attack.
Figure 9. Correctly predicted token ratio of Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on the five block ciphers with different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE) Methods, in texts. (a) EE attack. (b) PR attack.
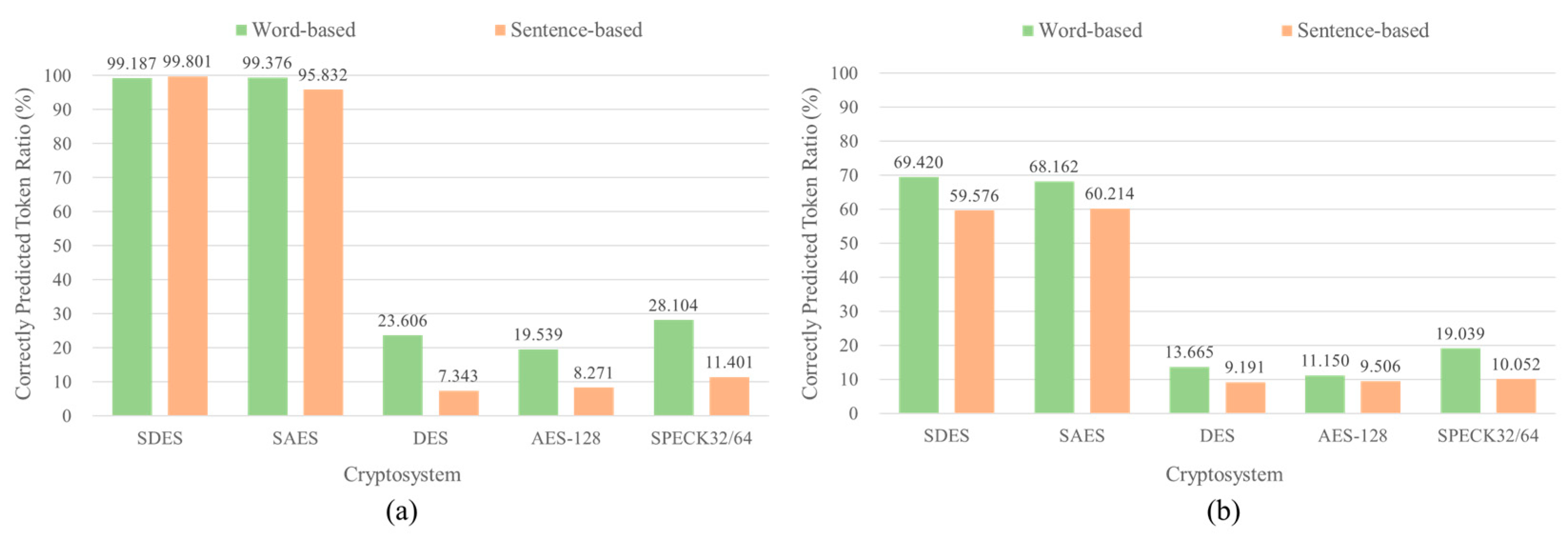
Preprints 107874 g009
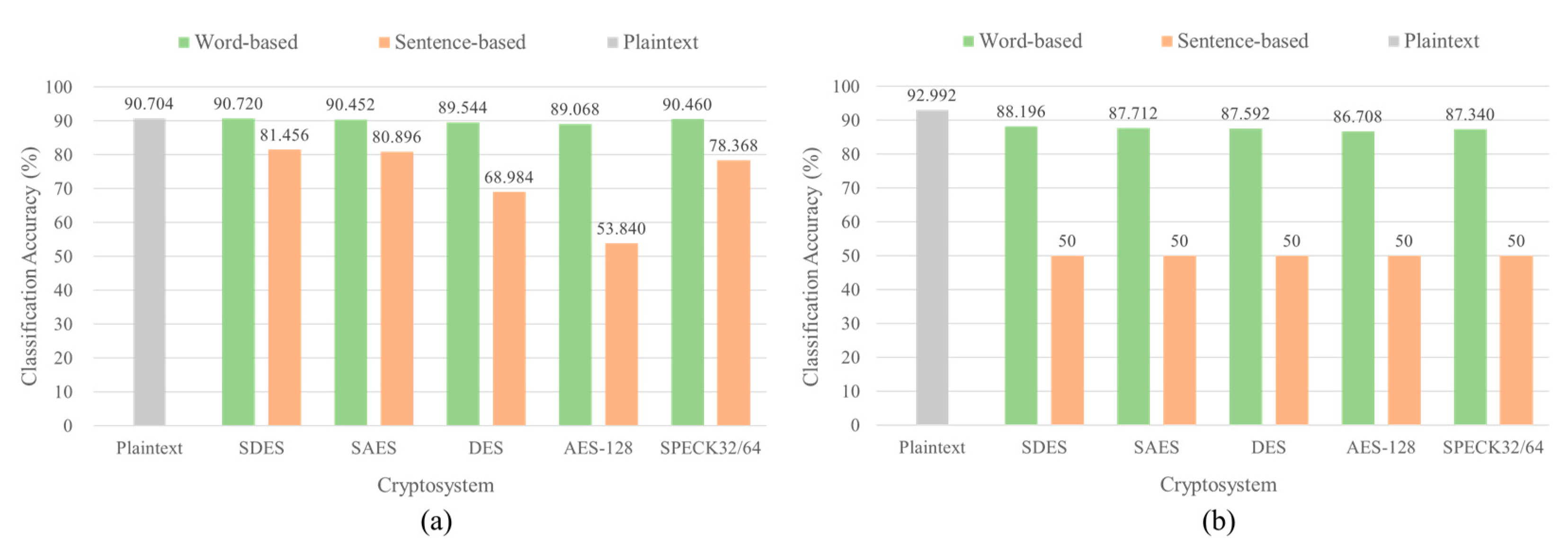
Preprints 107874 g010
Figure 10. Classification accuracy of Ciphertext Classification (CC) attack using different deep learning models on the five block ciphers with different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE) Methods, in texts. (a) RNN-based (BiGRU) CC attack. (b) Transformer-based (BERT-base) CC attack.
Figure 10. Classification accuracy of Ciphertext Classification (CC) attack using different deep learning models on the five block ciphers with different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE) Methods, in texts. (a) RNN-based (BiGRU) CC attack. (b) Transformer-based (BERT-base) CC attack.
Preprints 107874 g010
Preprints 107874 g011
Figure 11. Correctly predicted token ratio of Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on DES and AES-128 using texts in various operation modes with different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE). (a) EE attack. (b) PR attack.
Figure 11. Correctly predicted token ratio of Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on DES and AES-128 using texts in various operation modes with different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE). (a) EE attack. (b) PR attack.
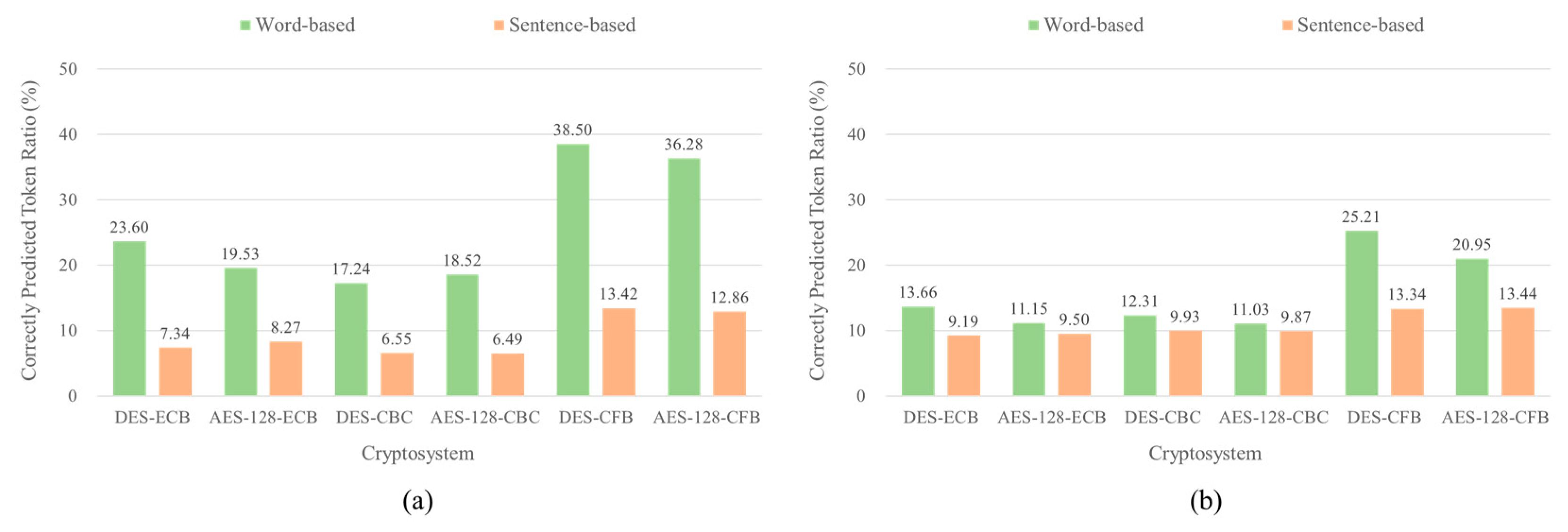
Preprints 107874 g011
Preprints 107874 g012
Figure 12. Classification accuracy of Ciphertext Classification (CC) attack on DES and AES-128 using texts in various operation modes with different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE). (a) RNN-based (BiGRU) CC attack on DES. (b) Transformer-based (BERT-base) CC attack on DES. (c) RNN-based (BiGRU) CC attack on AES-128. (d) Transformer-based (BERT-base) CC attack on AES-128.
Figure 12. Classification accuracy of Ciphertext Classification (CC) attack on DES and AES-128 using texts in various operation modes with different text encryption methods, Word-based Text Encryption (WTE) and Sentence-based Text Encryption (STE). (a) RNN-based (BiGRU) CC attack on DES. (b) Transformer-based (BERT-base) CC attack on DES. (c) RNN-based (BiGRU) CC attack on AES-128. (d) Transformer-based (BERT-base) CC attack on AES-128.
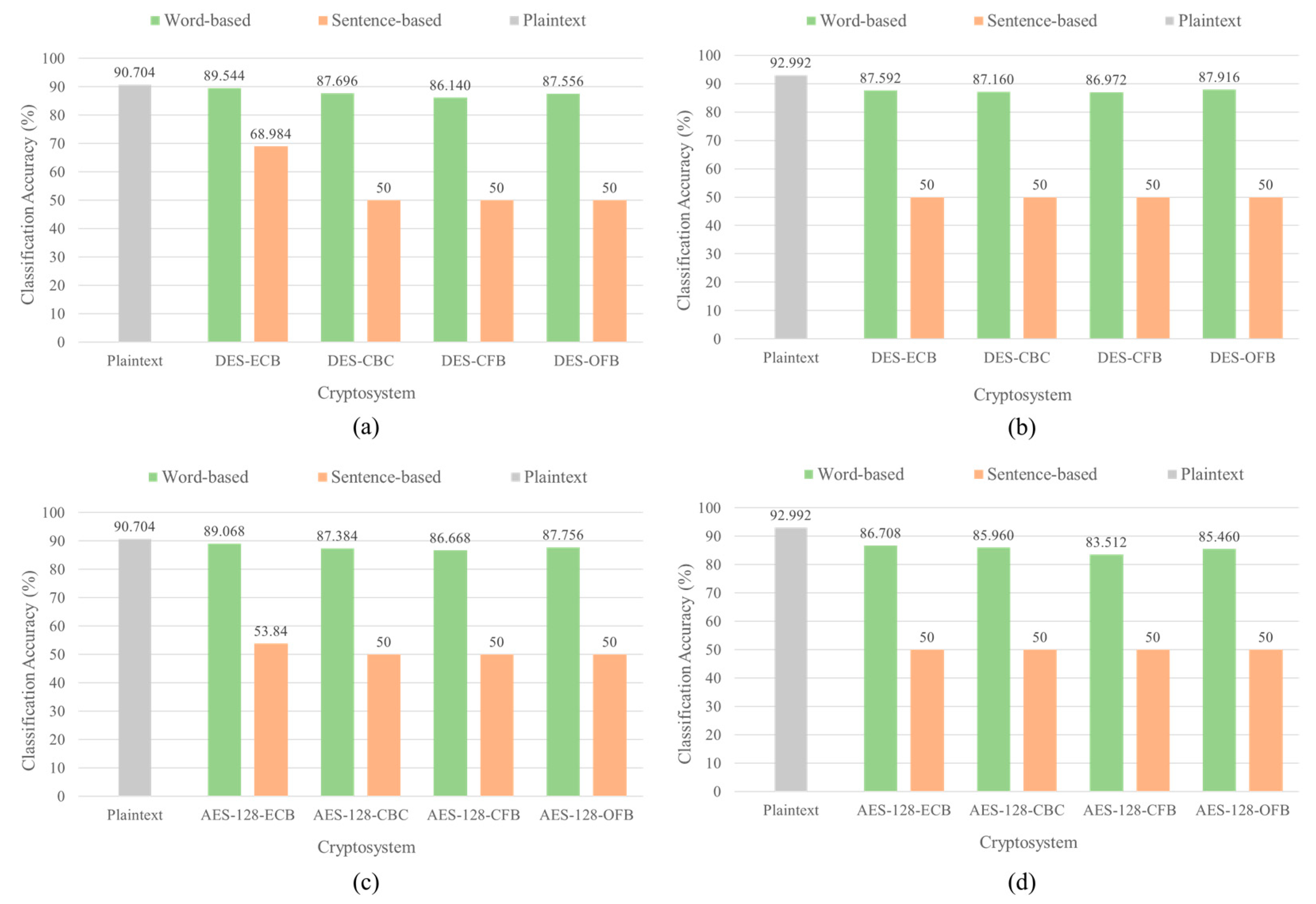
Preprints 107874 g012
Table 1. Sample plaintexts (PT) and ciphertexts (CT) for Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on the five block ciphers using block-sized bit arrays.
Table 1. Sample plaintexts (PT) and ciphertexts (CT) for Encryption Emulation (EE) and Plaintext Recovery (PR) attacks on the five block ciphers using block-sized bit arrays.
Block Cipher Block Size
SDES 16-bit PT 11000011 00110011
CT 10101110 00000011
SAES 16-bit PT 11000111 01010100
CT 10100101 11000011
DES 64-bit PT 10000010 00000001 00001100 01100010
11110101 11110101 10011011 00100010
CT 10100001 01100101 10110101 10011101
01100011 11100100 01101100 01100000
AES-128 128-bit PT 11010111 00101011 01100001 00001000
00101010 01000000 01011111 00010010
10111001 01100011 11110011 01111111
01100111 10000001 01001100 00011111
CT 10100110 01111011 00010010 11001010
00011001 01101110 01110001 11000111
00111010 01010110 10010001 10010111
01101111 11111010 00001110 01010001
SPECK32/64 32-bit PT 11100100 01100101 11100001 01010000
CT 10011011 11010000 01110000 11100101
Table 2. Average Bit Accuracy Probability (BAPavg) of Encryption Emulation (EE), Plaintext Recovery (PR), and Key Recovery (KR) attacks using different deep learning models on the five block ciphers with different numbers of round functions for block-sized bit array encryption.
Table 2. Average Bit Accuracy Probability (BAPavg) of Encryption Emulation (EE), Plaintext Recovery (PR), and Key Recovery (KR) attacks using different deep learning models on the five block ciphers with different numbers of round functions for block-sized bit array encryption.
Block
Cipher		 Round Number EE Attack PR Attack KR Attack
Fully
Connected-based		 RNN-based (BiLSTM) Fully
Connected-based		 RNN-based (BiLSTM) Fully
Connected-based		 RNN-based (BiLSTM)
SDES 1 0.998 1.0 0.998 1.0 0.601 0.601
2 0.997 1.0 0.998 0.999 0.826 0.851
3 0.892 0.817 0.898 0.828 0.593 0.651
4 (F) 0.696 0.691 0.686 0.689 0.450 0.607
SAES 1 1.0 1.0 1.0 0.998 0.573 0.621
2 (F) 0.998 0.999 1.0 0.999 0.528 0.610
DES 1 1.0 1.0 0.999 1.0 0.589 0.589
2 0.812 0.875 0.855 0.961 0.666 0.825
3 0.507 0.510 0.508 0.513 0.517 0.510
16 (F) 0.500 0.500 0.500 0.500 0.500 0.499
AES-128 1 0.500 0.499 0.500 0.499 0.500 0.500
2 0.499 0.499 0.500 0.500 0.499 0.499
3 0.500 0.500 0.499 0.500 0.500 0.499
10 (F) 0.499 0.499` 0.499 0.499 0.499 0.499
SPECK32/64 1 1.0 1.0 0.999 0.999 0.624 0.624
2 1.0 0.999 0.999 0.999 0.698 0.749
3 0.587 0.883 0.708 0.925 0.499 0.499
22 (F) 0.500 0.500 0.500 0.500 0.500 0.500
Table 3. Sample plaintexts (PT) and ciphertexts (CT) for Ciphertext Classification (CC) attack on the five block ciphers using texts.
Table 3. Sample plaintexts (PT) and ciphertexts (CT) for Ciphertext Classification (CC) attack on the five block ciphers using texts.
Block
Cipher		 Word-based Text Encryption
(WTE)		 Sentence-based Text Encryption
(STE)
Raw PT Long, boring, blasphemous. Never have I been so glad to see ending credits roll.
Clean PT <sos> long boring <unk> never have i been so glad to see ending credits roll
CT SDES F898FCF0 0D6AE0E4 E49D609FE0E4
63147C7C E8746F9AF10C E3F76F9A
7C7E 0E05778D F898
65628A18 F299 E48E9BEF
778D728CE0E4 0A687F707660FCF0 F4947585		 F898 CD2F 0D6A E0E4 13A4 E0E1
7AE0 252C 6314 B8BB E874 6F9A
3151 E3F7 6F9A 7A5B 13A4 E2E4
28A3 F898 154D 1E6D 4828 F299
E5B3 E2E4 9D5C 836B 7AE0 252C
0A68 7F70 7660 CD2F F494 7585
SAES 99C6AA77 D589FBB8 DD698D6CFBB8
BF396E2B 5BB17E13AC87 A3F47E13
60EB 5D618F36 99C6
C2AE919C 9A56 79C361FB
8F36BA52FBB8 E7D79F3C99FCAA77 9D66C58E		 99C6 ABF7 D589 FBB8 A008 E4B7
8726 6D9B BF39 63BB 5BB1 7E13
A207 A3F4 7E13 D00A A008 5F31
69EB 99C6 0007 A584 654B 9A56
2A4B 5F31 C006 9BBC 8726 6D9B
E7D7 9F3C 99FC ABF7 9D66 C58E
DES CD4566317E56A93A B08A99398DBA92F9
4EEB5E9AFEA28938 AF17B02BA5C5338C
9DFC755044A4DCBA D6C05F3006D20C3D
A7143EBC9CAE9204 769946F99C485DEE
5610353D62C49911 8D74B609B71E5152
3E45D02D673D4408 CB329810D3237036
62D20D09B363E0E8 3B3D46C16952F5E1
80DF7F1D6EDA029D		 77237D3087C01421 1C625E2ACFA91E43
1798A6F4C1728A3 441CB1F82DE88B91
D115601D4635B08B 17E83944B92A2C3
6EDEE356D92CFB57 9C307FC6A8AB315C
DA6307B428EFA210
AES-128 4E868947AE87032CB4AB3AB1259FD2CC 70F97BAD90E32C3DC2BA64F333C8FC34 79782DCA09F8F78E79D155EF275766AB 7D380847DE6926FEE197829340375F85 DB4A3E7157DCCD0DE4532E6D513CE3E3 FED33C19304B8BFAE39F312D59B8679F 7A3DBE11315B8BD7F325BA9F0A560E42 85672272B1FD784F4FCE630D87CECF45 37A8F73D65868E4D2AD78E3817611106 F2440CE66FB9A30D2F3496AAFFE8D40B EEB323DDA10073F6D56137102684D6D9 44A2565D57F17525BE9FEBE534550C61 1FECEA93FC81AE8541C24FB09BA36BAF CD66B413450473A63082B3CBCC2673B7 F5171781FD2E56C8575C778F38F16402 606DD27DB193B86D47E752D9C414C902 58965476EDC7D79BCB9F010B90913C18 CE5AFF1E3E248FBB30A80BD0850C65E0 83BBE3B98C3FA6EEDB22DF9A2FD954F0 A1CF4930A7119C65861CB17D8A1A7D40
SPECK32/64 763B3E6C 9A74EB3F F7E740D152C9C786
46D232A0 A9D02DB1A873A100 B1C1106D
59C3F40D B6D58649 28D6EEC1
A47F9C19 64625A3A 4FA8C3B4
D691084652C9C786 33CBDB0F0E5F734E 765A23F2		 994E22A7 9A74EB3F F8727415
6CA852E0 EF876AE3 A9D02DB1
15112268 8C2B4007 EF230235
73914DFB F9692D63 9663649E
53C4D879 112B4EAD 6CA852E0
33CBDB0F 61BE74EB 765A23F2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated