Prerpints.org logo
Preprint
Article

Crystal Plasticity Parameter Optimization in Cyclically Deformed Electrodeposited Copper – A Machine Learning Approach

Altmetrics

Downloads

89

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 May 2024

Posted:

30 May 2024

You are already at the latest version

Alerts
Abstract
The paper describes an application of machine learning approach for parameter optimization. The method is demonstrated for the elasto-viscoplastic model with both isotropic and kinematic hardening. It is shown that the proposed method based on long-short term memory networks enabled to obtain reasonable agreement of stress-strain curves for cyclic deformation in low-cycle fatigue regime. The main advantage of the proposed approach over traditional optimization schemes lies in the possibility to get parameters for a new material without the necessity to conduct any further optimizations. As the power and robustness of the developed method was demonstrated on the very challenging problem (cyclic deformation, crystal plasticity, self-consistent model, isotropic and kinematic hardening), it is directly applicable to other experiments and models.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Constitutive models enable to predict the behaviour of materials subjected to external loadings from small [1] to large [2] length scales. In some most straightforward problems, the constitutive models are simple and their parameters are relatively easy to establish using standard experiments. For example, establishment of the Young’s modulus of an isotropic, linearly elastic material is unambiguous using just the result of uniaxial tension test. However, in more complex situations, the constitutive models tend to use multiple non-linear equations and many parameters in order to capture the material’s behaviour. Such a situation is present e. g. in crystal plasticity, that is the topic of this paper.
The crystal plasticity (CP) theory in its most standard version accounts for dislocation glide on strictly defined crystallographic planes. Therefore, the information about orientations of crystallites in a polycrystalline microstructure of a given material has to be provided. Besides taking into account these microstructural details, the hardening equations of crystal plasticity are typically similar to conventional plasticity and typically account for isotropic and kinematic hardening. Various optimization algorithms such as gradient optimization [3], Newton-Raphson algorithm [4], Levenberg-Marquardt method [5], Bayesian optimization [6], particle swarm optimization [7] and evolutionary algorithms [8,9,10,11,12,13,14,15,16,17,18,19] are used in order to establish the correct set of material parameters (see the introduction in [19] for a thorough discussion). However, all of them share the basic disadvantage: one has to repeat the optimization in the case of having new material or new test result.
In order to overcome this limitation, Wang et al. [20] developed a neural network based methodology for parameter optimization. The idea behind the approach is performing the training of a neural network (NN) once and then building the database of predicted outputs using the trained NN. The created database is used to predict the set of optimal parameters based on the provided input. Both the neural network and the database can be stored and thus the main advantage of the proposed approach is that one does not need to perform a new optimization to get the parameters of a different material. Similar idea was presented in [21]. The main difference wrt. [20] is that machine learning was used only to establish reasonable parameter bounds and then fine-tuning was performed using a genetic algorithm.
In this article we propose to perform the optimization for the case of elasto-viscoplastic self-consistent (EVPSC) crystal plasticity model [14]. The investigated case is that of electrodeposited copper subjected to cyclic elasto-plastic deformation. We demonstrate that the proposed method is robust enough in order to provide correct predictions even in the highly complex problem as the one considered.
We build on the idea of using ML for the optimization of constitutive model parameters as described in [20]. However, there are important differences wrt. to op. cit. First of all, we study the case of a two-scale elasto-viscoplastic model, while the single-scale viscoelastic model was used in [20]. Second, we apply the LSTM approach directly to cyclic plasticity model data, while deep neural networks applied to data preprocessed using singular value decomposition technique were used in op. cit. Finally, single loading-unloading was considered in [20], while up to 50 cycles are simulated in the current paper.
The article is structured as follows. After this introductory section, we describe the methodology (Section 2). This includes the description of te EVPSC model (SubSection 2.1) that was already thoroughly described in [14,22] and machine learning (ML) methodology (SubSection 2.2). These are followed by the optimization results using two approaches for feature extraction from stress-strain curves (Section 3). Discussion (Section 4) is related to the applicability of the proposed method to other non-obvious tasks. The paper ends with conclusions (Section 5).

2. Methodology

This section contains two subsections. The first one (Section 2.1) covers the description of the constitutive model together with the corresponding micromechanical scheme, which was used to provide input data for training the machine learning framework. The second one (Section 2.2) describes the machine learning approach applied for the purpose of parameter optimization in this paper.

2.1. The EVPSC Model

The sequential elasto-visco plastic self-consistent (SEVPSC) code1 was recently developed and validated for the case of electrodeposited copper films [14] and is based on the sequential linearization scheme by [22]. The scheme coincides with the additive tangent approach [23] for the case of the Mori-Tanaka scheme. The results for the case of the self-consistent case were presented in [24] and [14]. Details of the self-consistent formulation can be found in the aforementioned papers. Nevertheless, some equations essential for the understanding of the present paper are provided in the following.
The strain rate, stress rate and stress have to fulfill the conditions stating that the average response over the polycrystal is consistent with the corresponding macroscopic values:
ε ¯ ˙ = 〈 ε ˙ g 〉 , σ ¯ ˙ = 〈 σ ˙ g 〉 , σ ¯ = 〈 σ g 〉 .
In order to account for the interaction of the grain-level and overall quantities, the additive tangent interaction law proposed by [25] or [26] is adopted:
ε ˙ g − ε ¯ ˙ = − M ¯ * e · ( σ ˙ g − σ ¯ ˙ ) − M ¯ * v · ( σ g − σ ¯ ) ,
where ε ¯ ˙ , σ ¯ ˙ and σ ¯ denote the overall strain rate, stress rate and stress. In Eq.(2), M ¯ * v and M ¯ * e are the fourth order inverse Hill tensors for a purely viscous problem and a purely elastic problem, respectively.
The parameters to be established with the proposed ML methodology concern the isotropic and kinematic hardening at the level of individual grain. In the following the formulation of the single grain (subscript g) constitutive model is provided. The total strain rate is calculated by adding elastic ε ˙ g e and viscoplastic strain rates (the current version of the model is formulated in the small-strain theory) ε ˙ g v :
ε ˙ g = ε ˙ g e + ε ˙ g v
In order to account for the elastic part, the anisotropic Hooke’s law is used:
σ ˙ g = A g e · ε ˙ g e or ε ˙ g e = M g e · σ ˙ g ,
where A g e is the fourth order elastic stiffness tensor. The associated compliance tensor is M g e = ( A g e ) − 1 .
We use rate-dependent CP formulation for a constitutive description at the single grain level. The plastic strain rate tensor at this level is calculated as a sum of shears on slip systems:
ε ˙ g v = ∑ r = 1 N γ ˙ r , g P r , g , where P r , g = 1 2 ( m r , g ⊗ n r , g + n r , g ⊗ m r , g )
where γ ˙ r , g is the slip rate, { m r , g , n r , g } are the slip direction and the slip plane unit normal respectively. Superscripts r and g denote respectively a given slip systems and grain. P r , g is the symmetric Schmid tensor. The resolved shear stress (RSS) is a projection of the Cauchy stress tensor on the given slip system:
τ r , g = P r , g : σ g .
The slip rate depends on the RSS as well as on the slip system backstress χ r , g and the critical resolved shear stress (CRSS) τ c r , g [27]:
γ ˙ r , g = γ ˙ 0 τ r , g − χ r , g τ c r , g n sign ( τ r , g − χ r , g ) .
Note that in Eq. 7 both isotropic and kinematic hardening is included. The other quantities are the reference slip rate γ ˙ 0 and the inverse of the strain rate sensitivity n. The tangent viscous compliance tensor is equal to a derivative of viscoplastic strain rate over the stress and thus equals:
M g v = n γ ˙ 0 ∑ r = 1 N τ r , g − χ r , g τ c r , g n − 1 sign ( τ r , g − χ r , g ) τ c r , g P r , g ⊗ P r , g .
Evolution of the CRSS and backstress are governed by isotropic and kinematic hardening laws, respectively. The linear-exponential isotropic hardening evolution looks as follows:
τ c r , g = τ c 0 + h 1 γ g + τ sat − τ c 0 1 − e − h b γ g ,
where τ c 0 , τ sat , h 1 , h b are material parameters of the isotropic hardening and γ g = ∫ 0 t γ ˙ g d t is the accumulated shear in the grain. The Ohno-Wang kinematic hardening law [28] reads:
χ ˙ r , g = h k γ ˙ r , g − h kb γ ˙ r , g χ r , g h kb h k h m ,
where h k , h kb and h m denote the inematic hardening parameters. We have thus 4 isotropic hardening and 3 kinematic hardening parameters which yields in total 7 hardening parameters subjected to optimization, cf. [14].

2.2. Machine Learning

Long Short-Term Memory (LSTM) networks are a type of Recurrent Neural Networks (RNN) [29]. RNNs generate output by sequentially applying the same weights to each element in the input and network’s internal state. LSTM model architecture was selected because of its proven performance in other sequential prediction tasks, such as speech recognition and low parameter count when compared to fully connected networks. Our implementation is a unidirectional LSTM as defined in Pytorch 2.0 [30] with a hidden state vector length of 2048. All three curves from the dataset are generated simultaneously by the network. Output is a tensor whose shape depends on the approach. Two ways of evaluating the fitness of a given parameter set have been tested. 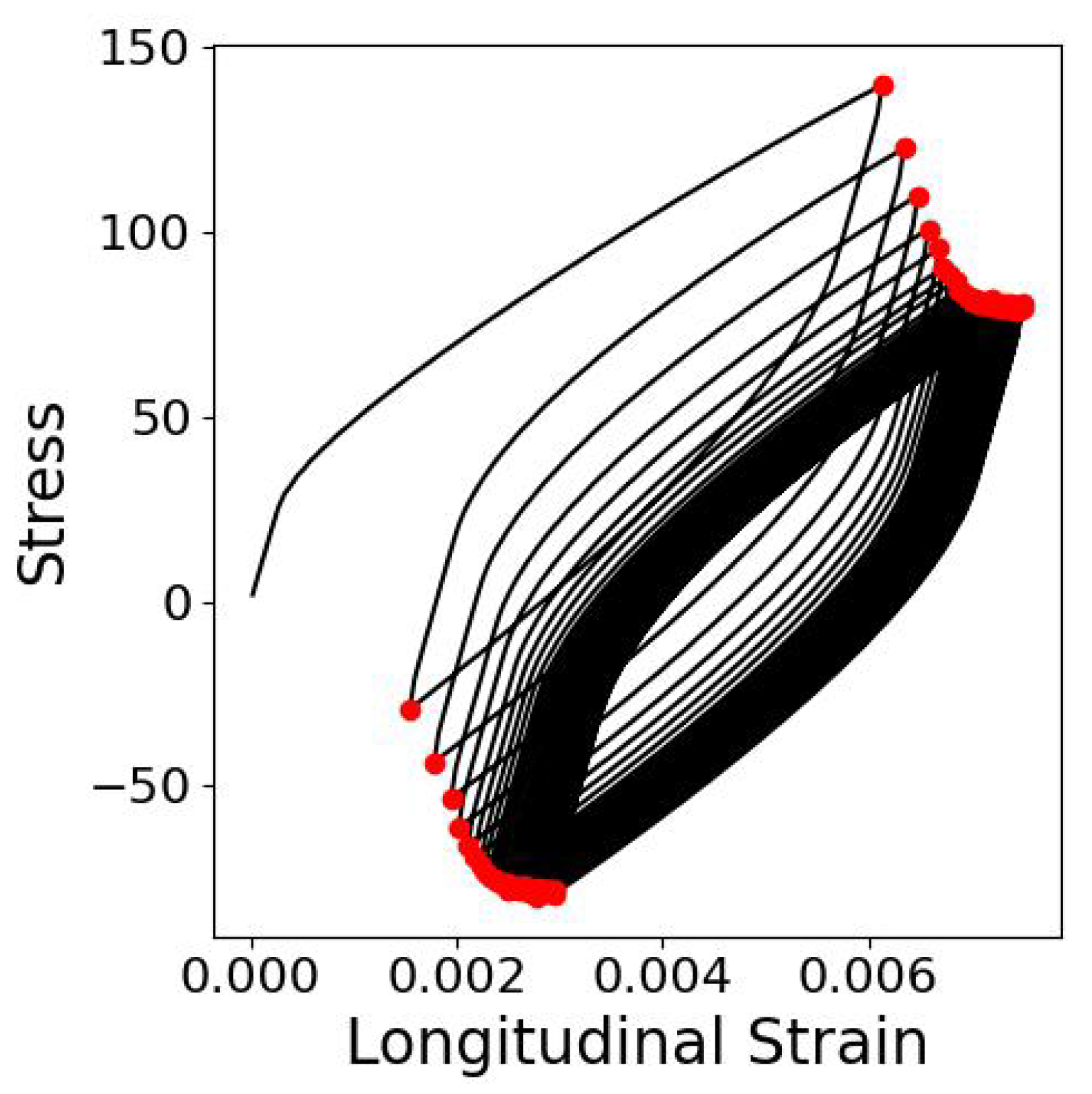The first was exactly the same as in [14], i.e., the stress values at the points where loading changes its direction were compared, cf. Figure 1. This approach will be from now on termed App1. In this case the shape of the output tensor is 2-by-100. 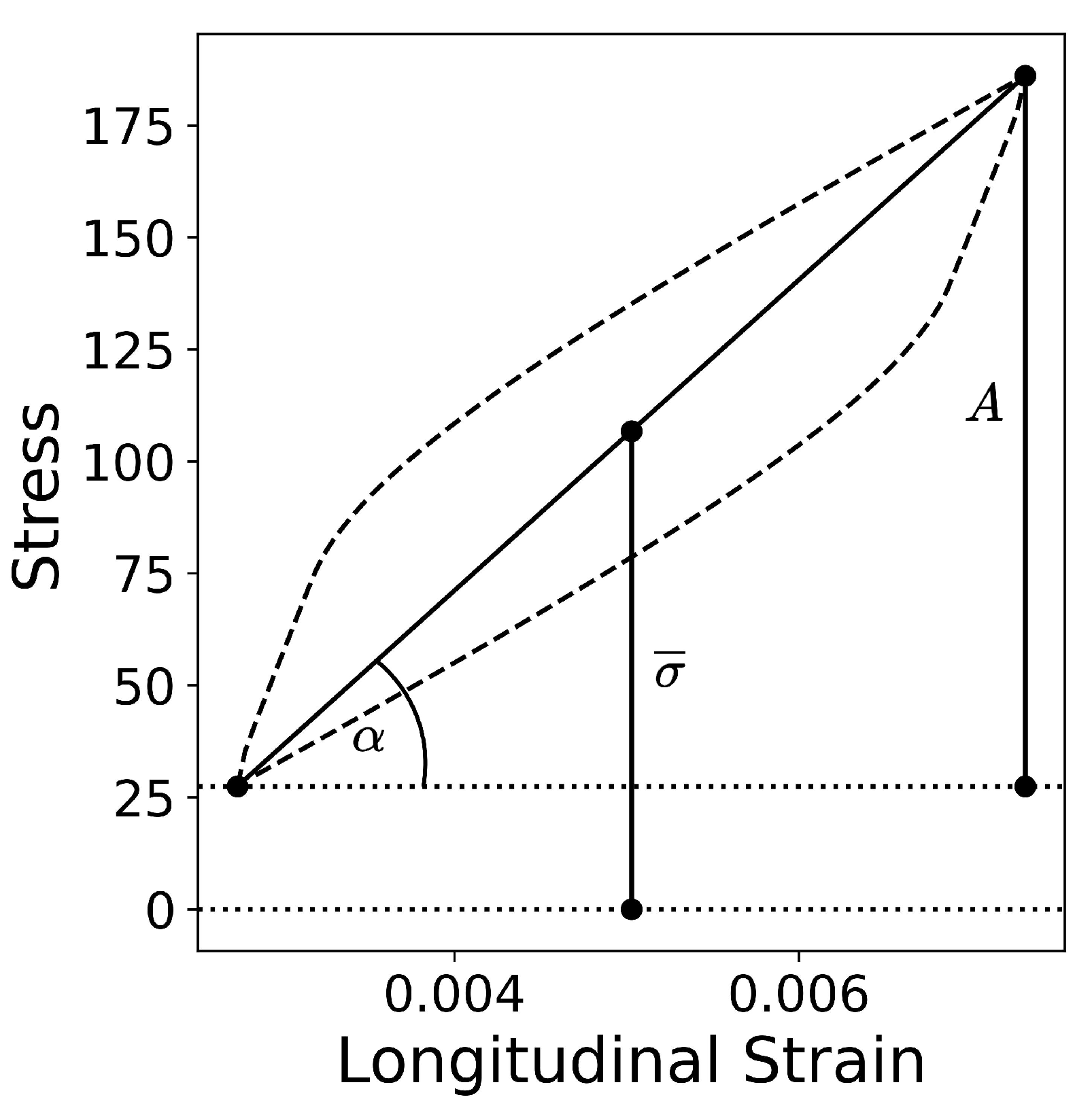In the second approach (App2), the stress-strain curves for each example were replaced with 3 simpler curves: stress amplitude A, mean stress σ ¯ , and slope of each cycle α in order to simplify the prediction task, cf. Figure 2. In this second case the shape of the output tensor is 3-by-50. Input to the network is the same vector of seven parameters repeated 100 or 50 times (depending on the approach) to match the desired output sequence length.
Both input and output data were normalized to improve training stability by eliminating large differences in the scale of data. The model was trained for 300 epochs with a batch size of 16 and an initial learning rate of 1e-3. The learning rate was decayed for each batch with cosine annealing schedule. Warm restarts were applied after the first 50 epochs and after doubling the previous learning rate decay period after that until the end of training [31]. Weight decay of 1e-5 was used for regularization. Adam optimization algorithm was applied to train the network with mean squared error as a loss function. The architecture of the network is shown in Figure 3.

3. Results

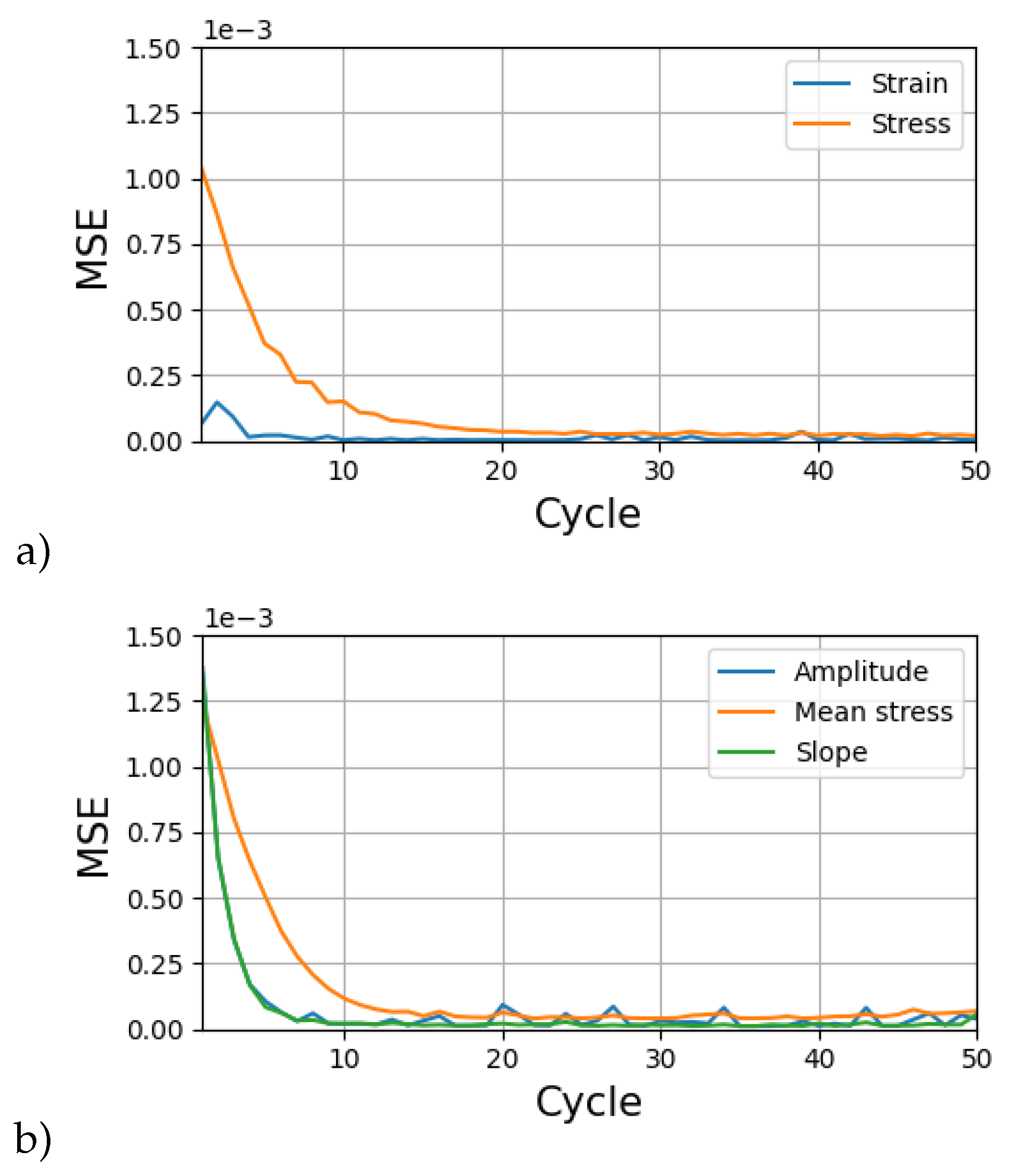
The method was applied as follows. First, the database of SEVPSC code results was created by generating 36370 loading-unloading curves. Each result was produced by running the SEVPSC code for the same loading scheme but with a different set of parameters. The parameters were generated by selecting every possible combination of parameters from a list of values. The list for each parameter was generated by selecting 5 equally spaced values from a set range (cf. Table 1). Then, part of the database was used for training the LSTM network, while the remaining part was moved to the test set (the ratio of training set size to the whole set size was equal to 60%). The MSE obtained in both approaches are shown in Figure 4.
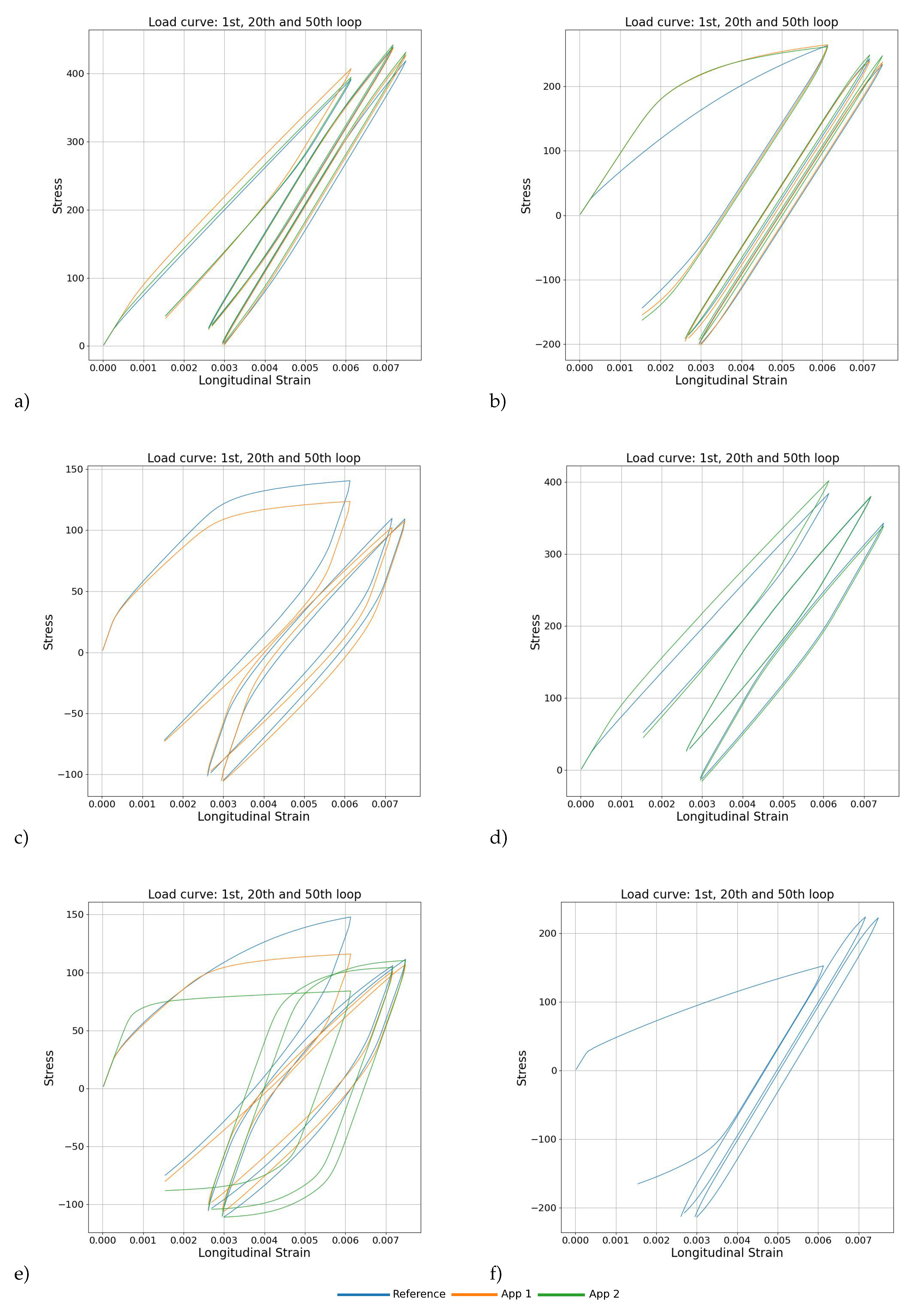
Next step was thus using the trained LSTM network for parameter optimization. The approach consists in using the trained LSTM to generate predictions in points lying in the parameter space that are more densely distributed than the set used for training. For this 35.8 million results were generated. Then, for the reference case (obtained by running the SEVPSC code with random parameters), the closest result in the LSTM-generated database is searched by calculating the mean squared error (MSE) between reference case curves and generated examples and selecting the generated example with the lowest MSE. We have tested the method for 30 different parameter sets. The 6 representative parameter sets obtained using this technique are shown in Table 2. The corresponding stress-strain curves obtained using the optimized parameters compared against the reference ones are shown in Figure 5. The entire group of parameter sets is presented in the Supplementary material. We have divided the results into 6 categories:
  • Very good or reasonable agreement of SS curves obtained using parameters optimized in both apporaches – Figure 5 a and supplementary Figure S.1,
  • Disagreement in the first cycle and reasonable agreement of SS curves obtained using parameters optimized in both apporaches – Figure 5 b and supplementary Figure S.2,
  • Reasonable agreement of SS curves obtained using parameters optimized in App 1 (lack of convergence for App 2 parameters) – Figure 5 c and supplementary Figure S.3,
  • Reasonable agreement of SS curves obtained using parameters optimized in App 2 (lack of convergence for App 1 parameters) – Figure 5 d and supplementary Figure S.4,
  • Striking disagreement or lack of convergence – Figure 5 e and supplementary Figure S.5,
  • Lack of convergence for the optimized parameters in both approaches – Figure 5 f and supplementary Figure S.6.
Out of 30 cases examined, 13 cases show very good or reasonable agreement in both approaches (category 1). 3 cases show reasonable agreement in late cycles but disagreement in the first cycle (category 2). It can be thus stated that more than half of the cases the method worked correctly in the case of both approaches. Then, in 4 cases App 1 provided correct prediction while App 2 did not converge (category 3). The reverse situation (category 4) was present in another 4 cases. Therefore, in 24 cases (80%) at least one approach provided the reasonably correct set of parameters. Concerning category 5, in 1 case, both approaches provided parameter sets leading to striking disagreement in SS curves (Figure 5e and Figure S.5.b). In 1 another case (cf. supplementary Figure S.5.a) there was striking disagreement for App 2 and lack of convergence for App 1. Finally, in 4 cases, neither approach provided a parameter set that can converge in actual SEVPSC simulation (category 6).
Let us now take a closer look on the obtained results. In terms of the approach, it seems that both of them are balanced and we cannot argue that either App1 or App2 is better. Cases where the predicted SS curve agrees with the actual one (Category 1, cf. Figure 5a and Figure S. 1.) prove the potential of the method. The fact that almost half of cases show only sligt deviations of the shape of the curve in the first cycle is actually a little bit surprising as the information about the shape of the first cycle was absent in both methods. It is thus easy to understand why 3 other cases (Category 2, cf. Figure 5b and Figure S. 2.) agree with the reference curve in the cyclic deformation regime while having some deviation in the first cycle. Morover, these 3 cases can be treated as correct prediction since the LSTM had no information about the shape of the initial loading curve. In the rest of cases (Categories 3-6) there was either agreement or lack of convergence, except for the curve shown in Figure 5e. Cases where the simulations with optimized parameters fails to converge are not useful but also harmless. Thus, only one case out of 30 led to a misleading prediction.

4. Discussion

The trained network was used for parameter identification. But it could be also used as a surrogate model enabling to obtain the same overall information in far shorter time. Such an approach was already presented in a number of papers. e.g., in [32] the surrogate ML model was trained using data from discrete dislocation dynamics. The network was able to tell what will be the stress-strain curve based on the initial dislocation configuration. On the other hand, Deshpande, Lengiewicz and Bordas [33] trained their deep learning (DL) network based on large deformation finite element method (FEM) simulations. Such an approach made it possible to predict the deformed shape based on the initial specimen geometry and applied boundary conditions.
Many surrogate models were also constructed in the framework of crystal plasticity (CP). A surrogate model for the ViscoPlastic Self-Consistent (VPSC) model was built in [34]. The researchers developed both forward and backward ML configurations. The first enabled to predict final crystallographic texture and stress-strain curve based on the initial texture and hardening parameters. The second enabled to predict initial texture and hardening parameters based on the final texture and stress-strain curve. A neural network enabling to predict stress-strain curve and texture but this time trained using the crystal plasticity finite element method (CPFEM) was presented in [35]. CPFEM trained ML architecture was used to predict cyclic stress values in low cycle fatigue experiments in [36]. An interesting contribution was presented in [37] where the ML was trained on elastic-viscoplastic fast fourier transform (EVPFFT) model and the prediction concerned spatially resolved crystallographic orientations. A novelty in [38] was application of CP-trained ML to non-monotonic strain paths. In [39] it was demonstrated that using an encoder-decoder deep learning framework it is possible to regenerate stress-strain curves for a material subjected to several loading-unloading cycles.

5. Conclusions

The paper demonstrated the possibility to use a machine learning framework based on LSTM to efficiently optimize material parameters in a highly complex situation of modelling the cyclic deformation of copper films using the elasto-viscoplastic self-consistent model with isotropic and kinematic hardening. One can conclude that the method is able to provide a reasonably accurate guess of the parameter set that in most cases provides the correct cyclic stress-strain.
The big advantage of the proposed machine learning-based method over optimization algorithms is that in the case of having a different material subjected to the same loading conditions one does not need to perform any other simulations to get the optimal parameters. One could argue that similar result could be obtained using only a large enough database. Using such a database instead of the machine learning approach has however two disadvantages. First, in order to have accuracy comparable to the one attained here, one should perform about 10 thousand times more simulations (because the number of simulations used for training was 3670 and the number of data points generated by trained ML framework was 35.8 million. Second, in order to use the database for future purposes, one would have to store the whole database of results (which would be 35.8 million times 977 kB = 35 TB), while in our case it is enough to store the trained model (which would be just 50.8MB) and when necessary regenerate the database with arbitrarily large or small number of example inputs to achieve a desired size of database.
Of course, the developed approach is not able to provide the material parameters based on different loading conditions than were used as an input. Therefore, in such a case one would have to repeat the optimization. The method was demonstrated for a highly challenging problem of cyclic deformation simulated with the micromechanical model accounting for both isotropic and kinematic hardening. It is expected that the approach is directly applicable to other cases. In particular, one can naturally apply the developed methodology to a case of studying low and high cycle fatigue with plasticity and damage models, cf. e.g., [40].

References

  1. Zhao, Y.; Chen, X.; Park, C.; Fay, C.C.; Stupkiewicz, S.; Ke, C. Mechanical deformations of boron nitride nanotubes in crossed junctions. Journal of Applied Physics 2014, 115. [Google Scholar] [CrossRef]
  2. Kacprzak, G.; Zbiciak, A.; Józefiak, K.; Nowak, P.; Frydrych, M. One-Dimensional Computational Model of Gyttja Clay for Settlement Prediction. Sustainability 2023, 15, 1759. [Google Scholar] [CrossRef]
  3. Ganesan, S.; Yaghoobi, M.; Githens, A.; Chen, Z.; Daly, S.; Allison, J.E.; Sundararaghavan, V. The effects of heat treatment on the response of WE43 Mg alloy: crystal plasticity finite element simulation and SEM-DIC experiment. Int. J. Plast. 2021, 137, 102917. [Google Scholar] [CrossRef]
  4. Guery, A.; Hild, F.; Latourte, F.; Roux, S. Identification of crystal plasticity parameters using DIC measurements and weighted FEMU. Mechanics of Materials 2016, 100, 55–71. [Google Scholar] [CrossRef]
  5. Cruzado, A.; LLorca, J.; Segurado, J. Modeling cyclic deformation of inconel 718 superalloy by means of crystal plasticity and computational homogenization. International Journal of Solids and Structures 2017, 122, 148–161. [Google Scholar] [CrossRef]
  6. Kuhn, J.; Spitz, J.; Sonnweber-Ribic, P.; Schneider, M.; Bö hlke, T. Identifying material parameters in crystal plasticity by Bayesian optimization. Optimization and Engineering 2021, 1–35. [Google Scholar] [CrossRef]
  7. Hu, L.; Jiang, S.y.; Zhang, Y.q.; Zhu, X.m.; Sun, D. Texture evolution and inhomogeneous deformation of polycrystalline Cu based on crystal plasticity finite element method and particle swarm optimization algorithm. Journal of Central South University 2017, 24, 2747–2756. [Google Scholar] [CrossRef]
  8. Skippon, T.; Mareau, C.; Daymond, M.R. On the determination of single-crystal plasticity parameters by diffraction: optimization of a polycrystalline plasticity model using a genetic algorithm. Journal of Applied Crystallography 2012, 45, 627–643. [Google Scholar] [CrossRef]
  9. Acar, P.; Ramazani, A.; Sundararaghavan, V. Crystal plasticity modeling and experimental validation with an orientation distribution function for ti-7al alloy. Metals 2017, 7, 459. [Google Scholar] [CrossRef]
  10. Cauvin, L.; Raghavan, B.; Bouvier, S.; Wang, X.; Meraghni, F. Multi-scale investigation of highly anisotropic zinc alloys using crystal plasticity and inverse analysis. Mater. Sci. Eng. A 2018, 729, 106–118. [Google Scholar] [CrossRef]
  11. Kapoor, K.; Sangid, M.D. Initializing type-2 residual stresses in crystal plasticity finite element simulations utilizing high-energy diffraction microscopy data. Materials Science and Engineering: A 2018, 729, 53–63. [Google Scholar] [CrossRef]
  12. Sedighiani, K.; Diehl, M.; Traka, K.; Roters, F.; Sietsma, J.; Raabe, D. An efficient and robust approach to determine material parameters of crystal plasticity constitutive laws from macro-scale stress–strain curves. Int. J. Plast. 2020, 134, 102779. [Google Scholar] [CrossRef]
  13. Frydrych, K.; Maj, M.; Urbański, L.; Kowalczyk-Gajewska, K. Twinning-induced anisotropy of mechanical response of AZ31B extruded rods. Mater. Sci. Eng. A 2020, 771, 1–14. [Google Scholar] [CrossRef]
  14. Girard, G.; Frydrych, K.; Kowalczyk-Gajewska, K.; Martiny, M.; Mercier, S. Cyclic response of electrodeposited copper films. Experiments versus elastic-viscoplastic mean-field approach predictions. Mech. Mater. 2021, 153, 1–17. [Google Scholar] [CrossRef]
  15. Savage, D.J.; Feng, Z.; Knezevic, M. Identification of crystal plasticity model parameters by multi-objective optimization integrating microstructural evolution and mechanical data. Computer Methods in Applied Mechanics and Engineering 2021, 379, 113747. [Google Scholar] [CrossRef]
  16. Frydrych, K.; Kowalczyk-Gajewska, K.; Libura, T.; Kowalewski, Z.; Maj, M. On the role of slip, twinning and detwinning in magnesium alloy AZ31b sheet. Mater. Sci. Eng. A 2021, 813, 141152. [Google Scholar] [CrossRef]
  17. Frydrych, K.; Jarzebska, A.; Virupakshi, S.; Kowalczyk-Gajewska, K.; Bieda, M.; Chulist, R.; Skorupska, M.; Schell, N.; Sztwiertnia, K. Texture-Based Optimization of Crystal Plasticity Parameters: Application to Zinc and Its Alloy. Metall. Mater. Trans. A 2021, 52, 3257–3273. [Google Scholar] [CrossRef]
  18. Frydrych, K. Texture evolution of magnesium alloy AZ31B subjected to severe plastic deformation. Engineering Transactions 2021, 69, 337–352. [Google Scholar]
  19. Frydrych, K.; Papanikolaou, S. Unambiguous Identification of Crystal Plasticity Parameters from Spherical Indentation. Crystals 2022, 12, 1341. [Google Scholar] [CrossRef]
  20. Wang, J.; Zhu, B.; Hui, C.Y.; Zehnder, A.T. Determination of material parameters in constitutive models using adaptive neural network machine learning. Journal of the Mechanics and Physics of Solids 2023, 177, 105324. [Google Scholar] [CrossRef]
  21. Schulte, R.; Karca, C.; Ostwald, R.; Menzel, A. Machine learning-assisted parameter identification for constitutive models based on concatenated loading path sequences. European Journal of Mechanics-A/Solids 2023, 98, 104854. [Google Scholar] [CrossRef]
  22. Kowalczyk-Gajewska, K.; Petryk, H. Sequential linearization method for viscous/elastic heterogeneous materials. Eur. J. Mech. Solids/A 2011, 30, 650–664. [Google Scholar] [CrossRef]
  23. Mercier, S.; Molinari, A. Homogenization of elastic-viscoplastic heterogeneous materials: Self-consistent and Mori-Tanaka schemes. Int. J. Plast. 2009, 25, 1024–1048. [Google Scholar] [CrossRef]
  24. Kowalczyk-Gajewska, K. Micromechanical modelling of metals and alloys of high specific strength. In IFTR Reports 1/2011; 2011; pp. 1–299. [Google Scholar]
  25. Molinari, A.; Ahzi, S.; Kouddane, R. On the self-consistent modelling of elastic-plastic behavior of polycrystals. Mech. Mater. 1997, 26, 43–62. [Google Scholar] [CrossRef]
  26. Molinari, A. Averaging Models for heterogeneous viscoplastic and elastic viscoplastic materials. J. Engng. Mat. Tech. 2002, 124, 62–70. [Google Scholar] [CrossRef]
  27. Hennessey, C.; Castelluccio, G.M.; McDowell, D.L. Sensitivity of polycrystal plasticity to slip system kinematic hardening laws for Al 7075-T6. Materials Science and Engineering: A 2017, 687, 241–248. [Google Scholar] [CrossRef]
  28. Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part I: formulation and basic features for ratchetting behavior. International Journal of Plasticity 1993, 9, 375–390. [Google Scholar] [CrossRef]
  29. Sak, H.; Senior, A.; Beaufays, F. Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition. arXiv, 2014; arXiv:1402.1128 2014. [Google Scholar]
  30. PyTorch Contributors. PyTorch LSTM Description. https://pytorch.org/docs/stable/generated/torch.nn.LSTM.html#torch.nn.LSTM. Accessed: 2023-11-06.
  31. Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv preprint arXiv:1608.03983, arXiv:1608.03983 2016.
  32. Salmenjoki, H.; Alava, M.; Laurson, L. Machine learning plastic deformation of crystals. Nature communications 2018, 9, 1–7. [Google Scholar] [CrossRef]
  33. Deshpande, S.; Lengiewicz, J.; Bordas, S.P. Probabilistic deep learning for real-time large deformation simulations. Computer Methods in Applied Mechanics and Engineering 2022, 398, 115307. [Google Scholar] [CrossRef]
  34. Yuan, M.; Paradiso, S.; Meredig, B.; Niezgoda, S. Machine learning–based reduce order crystal plasticity modeling for ICME applications. Integrating Materials and Manufacturing Innovation 2018, 7, 214–230. [Google Scholar] [CrossRef]
  35. Ali, U.; Muhammad, W.; Brahme, A.; Skiba, O.; Inal, K. Application of artificial neural networks in micromechanics for polycrystalline metals. Int. J. Plast. 2019, 120, 205–219. [Google Scholar] [CrossRef]
  36. Miyazawa, Y.; Briffod, F.; Shiraiwa, T.; Enoki, M. Prediction of cyclic stress–strain property of steels by crystal plasticity simulations and machine learning. Materials 2019, 12, 3668. [Google Scholar] [CrossRef] [PubMed]
  37. Pandey, A.; Pokharel, R. Machine learning based surrogate modeling approach for mapping crystal deformation in three dimensions. Scripta Materialia 2021, 193, 1–5. [Google Scholar] [CrossRef]
  38. Ibragimova, O.; Brahme, A.; Muhammad, W.; Levesque, J.; Inal, K. A new ANN based crystal plasticity model for FCC materials and its application to non-monotonic strain paths. International Journal of Plasticity 2021, 144, 103059. [Google Scholar] [CrossRef]
  39. Li, Q.J.; Cinbiz, M.N.; Zhang, Y.; He, Q.; Beausoleil II, G.; Li, J. Robust deep learning framework for constitutive relations modeling. Acta Materialia 2023, 254, 118959. [Google Scholar] [CrossRef]
  40. Rutecka, A.; Kowalewski, Z.; Pietrzak, K.; Dietrich, L.; Makowska, K.; Woźniak, J.; Kostecki, M.; Bochniak, W.; Olszyna, A. Damage development of Al/SiC metal matrix composite under fatigue, creep and monotonic loading conditions. Procedia Engineering 2011, 10, 1420–1425. [Google Scholar] [CrossRef]
1
The code was written in FORTRAN and will be shared upon reasonable request. Researchers willing to use the code should contact Karol Frydrych.
Preprints 107873 g001
Figure 1. Scheme showing locations of difference evaluations according to Approach 1.
Figure 1. Scheme showing locations of difference evaluations according to Approach 1.
Preprints 107873 g001
Preprints 107873 g002
Figure 2. Scheme showing difference evaluations according to Approach 2: stress amplitude A, mean stress σ ¯ , and slope of each cycle tan ( α ) were used.
Figure 2. Scheme showing difference evaluations according to Approach 2: stress amplitude A, mean stress σ ¯ , and slope of each cycle tan ( α ) were used.
Preprints 107873 g002
Preprints 107873 g003
Figure 3. Scheme showing the architecture of the network used in the present contribution. The input x is a set of 7 hardening parameters, outputs y i are data describing the shape of stress-strain curves.
Figure 3. Scheme showing the architecture of the network used in the present contribution. The input x is a set of 7 hardening parameters, outputs y i are data describing the shape of stress-strain curves.
Preprints 107873 g003
Preprints 107873 g004
Figure 4. Mean squared error as a function of cycles in a) approach 1 and b) approach 2.
Figure 4. Mean squared error as a function of cycles in a) approach 1 and b) approach 2.
Preprints 107873 g004
Preprints 107873 g005
Figure 5. The results of using neural networks for optimization: stress-strain curves obtained using the SEVPSC code for the arbitrary parameter set and its closest neighbours. Only first and last cycle are shown for the sake of clarity.
Figure 5. The results of using neural networks for optimization: stress-strain curves obtained using the SEVPSC code for the arbitrary parameter set and its closest neighbours. Only first and last cycle are shown for the sake of clarity.
Preprints 107873 g005

a) b)
c) d)
e) f)
Table 1. Ranges of the hardening parameters serving to generate the database.
Table 1. Ranges of the hardening parameters serving to generate the database.
τ c 0 τ s a t h 1 h b h k h k b h m
Min 10.0 10.0 0.0 0.0 0.0 0.0 0.0
Max 80.0 120.0 5.0 120.0 1.0 · 10 5 1000.0 10.0
Table 2. Reference parameters vs parameters that made LSTM generate closest matching curves
Table 2. Reference parameters vs parameters that made LSTM generate closest matching curves
τ c 0 τ s a t h 1 h b h k h k b h m
Category 1
Reference 1.00 · 10 1 6.50 · 10 1 4.17 4.00 · 10 1 1.00 · 10 5 5.00 · 10 2 3.33
App 1 2.91 · 10 1 9.00 · 10 1 4.09 1.09 · 10 1 1.00 · 10 5 4.55 · 10 2 2.73
App 2 1.64 · 10 1 8.00 · 10 1 1.36 2.18 · 10 1 1.00 · 10 5 4.55 · 10 2 2.73
Category 2
Reference 1.00 · 10 1 8.33 · 10 1 8.33e-01 1.20 · 10 2 3.33 · 10 4 1.00 · 10 3 0.00
App 1 6.73 · 10 1 1.00 · 10 2 5.00 1.09 · 10 1 9.09 · 10 3 5.45 · 10 2 9.09e-01
App 2 6.73 · 10 1 1.20 · 10 2 4.55e-01 1.09 · 10 1 9.09 · 10 3 8.18 · 10 2 3.64
Category 3
Reference 1.00 · 10 1 1.00 · 10 1 1.67 1.20 · 10 2 3.33 · 10 4 8.33 · 10 2 8.33
App 1 1.00 · 10 1 1.00 · 10 1 5.00 2.18 · 10 1 2.73 · 10 4 8.18 · 10 2 7.27
App 2 1.64 · 10 1 1.00 · 10 1 5.00 2.18 · 10 1 2.73 · 10 4 7.27 · 10 2 3.64
Category 4
Reference 1.00 · 10 1 2.83 · 10 1 5.00 8.00 · 10 1 1.00 · 10 5 5.00 · 10 2 3.33
App 1 4.18 · 10 1 2.00 · 10 1 1.82 2.18 · 10 1 1.00 · 10 5 4.55 · 10 2 2.73
App 2 2.91 · 10 1 1.20 · 10 2 1.36 0.00 1.00 · 10 5 4.55 · 10 2 2.73
Category 5
Reference 1.00 · 10 1 1.00 · 10 1 5.00 1.20 · 10 2 3.33 · 10 4 6.67 · 10 2 0.00
App 1 1.00 · 10 1 1.00 · 10 1 5.00 2.18 · 10 1 2.73 · 10 4 9.09 · 10 2 8.18
App 2 22.73 30.00 5.00 32.73 0.00 0.00 0.00
Category 6
Reference 10.00 83.33 1.67 60.00 0.00 1000.00 0.00
App 1 35.45 90.00 2.73 43.64 0.00 1000.00 4.55
App 2 22.73 90.00 0.91 54.55 0.00 727.27 0.00
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated