Preprint
Article
The Entropy of the Collapsing Molecular Cloud
Altmetrics
Downloads
85
Views
19
Comments
0
This version is not peer-reviewed
Submitted:
30 May 2024
Posted:
31 May 2024
You are already at the latest version
Alerts
Abstract
The study of the change in entropy during the formation of stars in collapsing molecular clouds is an important area of research in astrophysics. As the cloud decreases in size, the presence of gases leads to an increase in entropy. However, the extent of this change in entropy is influenced by the amount of space available for the gases. In this scientific investigation, I conduct a detailed analysis of entropy on a small scale within the contracting cloud, following the principles of the second law of thermodynamics. Initially, my focus is on a turbulent cloud composed of N particles with a mass of M, which collapses under the force of gravity. It becomes clear that in order for the collapse to occur, gravitational energy must overcome other pressure forces that oppose it. This process results in the rapid movement of particles within the cloud, ultimately leading to a change in entropy
Keywords:
Subject: Physical Sciences - Space Science
1. Introduction
It has been stated by[4]that the arrow of time arises from the universe being at some distance from equilibrium in a nation of low entropy. This implies the Second Law of Thermodynamics tells us that the entropy of the universe does now not minimize [9]. According to a paper by way of [9] a homogeneous universe with a outstanding fluid expands adiabatically with constant entropy. It has additionally been inferred that the rate of change of the entropy is to increase the entropy for the duration of expansion and minimize the entropy in the course of contraction [1,5,9]. As [13,18] cited that black holes are the largest accumulations of entropy due to the fact they have strongest gravity. Physically speaking, gravitational collapse leads to the greatest feasible quantity of disorder. In addition [6,8] have calculated the entropy inside the observable universe. This has been observed up by means of [6] they have introduced correct consequences and additionally comprise the entropy of the cosmological horizon. But what about the entropy of the collapsing molecular cloud throughout the formation star? How entropy of the small scale constructions can be calculated from the views of thermodynamic laws? This wants detail analysis and appreciation due to the fact the gravitation pressure of the star forming core is much less than that of black holes. Many studies have stated that the cooling time and entropy thresholds are a consequence of thermal instabilities that develop in hot gases when the ratio of crossing time to free-fall time is less than 10 [14,17,19].
The formation of massive compact (MC) structures seems to take place when the diffuse interstellar medium (ISM) undergoes significant compression due to various factors such as supernovae explosions, magnetorotational instability, or gravitational instability within the stellar and gaseous disks of galaxies [3].
Over the past ten years, there have been significant advancements in our understanding of the initial stages of low-mass star formation through observations. The utilization of sensitive receivers on large radio telescopes like the JCMT and IRAM 30m MRT has allowed us to detect young protostars during the early accretion phase, known as ’Class 0’ objects. This breakthrough has also enabled us to explore the inner density structure of pre-collapse cores, which was previously unattainable. Class 0 objects exhibit strong dust continuum emission at submillimeter wavelengths, minimal emission below 10 microns, and display powerful jet-like outflows. Furthermore, we have directly observed evidence of gravitational infall in several of these objects [2].
How gravity would possibly make the entropy increases in the early collapse phase than the late one in the process of star formation is an other problem to be understood to support the existing star formation theory. Are diffuse systems have higher entropy than that of condensed systems, or vice versa? And in fact, the entropy of the early Universe was lower than at present when I consider the whole Universe. Of course there are some diffuse systems higher in entropy than some condensed systems [20] ,and vice versa. Here ’lower’ is a relative term. Considering the attractive nature of gravity it has been claimed that a uniform state has much lower-entropy than a much more dispersed state. The early Universe seems to have had a higher entropy than the present-day Universe, which after all is not a very hot, very uniform gas. But a moment’s thought shows that this is at best not obvious[20].
Turbulence in the interstellar medium of Milky Way type galaxies can be attributed to accretion, assuming the galaxies are accumulating mass at a similar pace to their star formation. This phenomenon is especially significant in the outer disks beyond the region where stars are actively forming. However, in dwarf galaxies, the accretion rate must surpass the rate of star formation by a significant margin in order to drive turbulence, indicating that other factors are likely to play a more prominent role in these smaller galaxies [12]. Turbulence serves a dual purpose, as it not only generates areas of increased density that trigger gravitational contraction or collapse, but also counteracts the gravitational effects within these regions of higher density [15]. Compressible turbulence is a significant factor in shaping the structure of the interstellar medium within our Galaxy, and it is believed to have a crucial role in the formation of structures in the early Universe as well. The density probability distribution function (PDF) and the power spectrum of this compressible, supersonic turbulence are essential components in theories related to star formation [7].
The Second Law of Thermodynamics remains a perplexing puzzle in the field of physics. The progression of the universe involves a rise in disorder, known as entropy, which cannot be derived from our current understanding of the fundamental laws of physics, nor can it be elucidated solely through statistical reasoning. Notably, the Second Law establishes a distinction between the flow of time in the past and future [16].
Entropy fluctuations are unstable in a thermal self-gravitating cloud due to its negative heat capacity. The negative heat capacity of a star is properly understood. As a star loses complete poIr by means of radiation, the contraction will increase the thermal velocities, equivalent to an growth in temperature, to maintain equilibrium with the increase in the absolute value of the potential energy. The entropy of a star decreases in conjunction with the whole energy. More generally, if a phase of a cloud loses energy, then inside this contracting region, the temperature rises while the entropy decreases. Conversely, section of the cloud that gains energy, expands with a ensuing reduce in temperature and an expand in entropy.
It has been discussed by [9] the arrow of time arises from the universe being far from equilibrium in a state of low entropy. The Second Law of Thermodynamics requires that the entropy of the universe does not decrease.Hence the universe must initially have been in a state of very low entropy [9]. According to the past hypothesis by [1] entropy of the entire universe was very low (compared to now) roughly 15 billion years ago.
At large scale, the early Universe used to be very hot, and additionally very dense; as it expanded and cooled, it grew to be much less hot, and much less dense. Since entropy is a measure of phase-space volume. It has been suggested by [10] that one can associate an entropy with an event horizon proportional to its area [10]. In addition, [21] estimated the entropy increase in Hawking evaporation. Where as my work focus on star forming region named molecular cloud which is different from the case of compact objects. It was described by [20] that the early universe was at local thermal equilibrium and was highly uniform, but it was not at global thermal equilibrium because of the expansion of the universe. The process of becoming non-uniform is leading to increasing entropy. The conversion of gravitational energy to internal energy, and the emission of electromagnetic radiation result in the growth of entropy. However, the dominating entropy increasing processes are the formation of black holes. But this paper particularly deals about the entropy of collapsing star forming molecular cloud.
The purpose of this study is to analyze the alteration in entropy of a collapsing cloud in relation to its initial and final dimensions. While the expansion of a self-gravitating gas leads to an increase in volume and subsequently entropy, the impact of turbulence on the cloud remains a question. This research incorporates the isotropic turbulent velocity dispersion, along with the number of particles and the cloud’s size, to determine the entropy change within the system under investigation.
2. Entropy
Entropy is a thermodynamic quantity representing the unavailability of a system’s thermal energy for conversion into mechanical work, or the degree of disorder or randomness in the system. Here I take into account macroscopic systems composed of N particles, with very large N (N≫ 1), I first begin from the first law of thermodynamics given by:
It states the total change in internal energy of a system is the sum of the heat added to it and the work done on it. The second law of thermodynamics is:
It asserts that processes occur in a certain direction and that the energy has quality as quantity. Combining equations (1) and (2) I have:
Now taking the time derivative of eqn. (3) one can get:
This yields
Which leads to the way stated by [11] the energies and volume are expressed per unit mass. Thus the energy in a turbulent cloud with one dimensional velocity dispersion , is ,
and pressure in a turbulent cloud with one dimensional velocity dispersion , is given by:
Thus
where R is the radius of the cloud with mass M (from equation (8)). Now equation (8) gives:
implies
where K is the turbulent kinetic energy. The quantity ln is analogous to the thermodynamic or heat engine entropy in the equation, dQ/dt = TdS/dt, with the kinetic energy analogous to the thermal temperature, T.
3. Entropy of turbulent-gravitating molecular cloud
In this section I intend to incorporate the chemical potential () in equation (3), The chemical potential () describes effect of change in number density. The term dN has been missed from the basic equation (3). Thus I included this term and reformulate (3) as:
where N is total number of particles in the volume V of the cloud. The chemical potential of a phase rises with an increase in its internal energy, E, while simultaneously decreasing with a decrease in the phase’s entropy, S, at a specific temperature. This shows, the change in entropy reduces with increasing chemical potential (ref.(12)). This implies the difference between the initial and final entropies is getting smaller and smaller as time goes, and if the chemical potential grows. Using equation (2) in (12) taking the time derivative in both sides, and rearranging I get:
From the ideal gas equation of state P = nKT = , n = N/v, implies . Where is speed of sound, is mass of a hydrogen atom.
This leads to
The chemical potential of a phase rises with an increase in its internal energy, U, while simultaneously decreasing with a decrease in the phase’s entropy, S, at a specific temperature.
using q =
implies
Then I have
where is mass of hydrogen atom, is initial radius of the cloud, R is final radius of the cloud, initial total number of particles of the cloud, N is final total number of particles, initial turbulent velocity dispersion and and is final turbulent velocity dispersion.
Applying the virial theorem for a cloud of mass M, contracting to a radius R, the temperature to which the matter gets heated up is . Using this in Eqn.(27) I have:
where G is the gravitational constant, the Boltzmann constant, Stefan-Boltzmann constant. One can write M = then eqn. (28) becomes:
As shown in Figure 1, the entropy of the molecular cloud decreases with an increase in its radius.
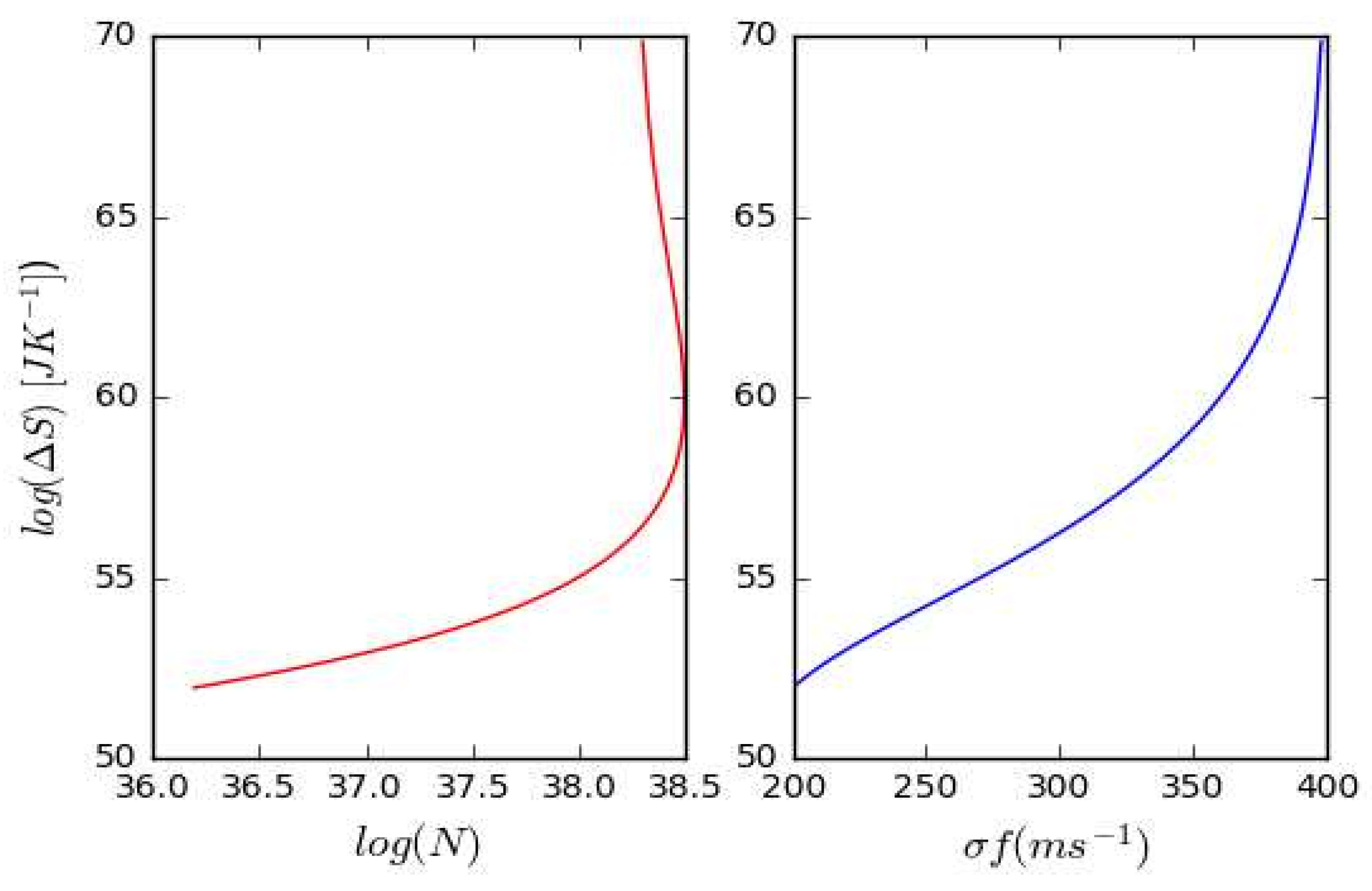
Figure 4 and Figure 5 confirm the influence of the total number of particles in the initial cloud and the final collapsed cloud. Eqn.(31) indicates the change in entropy of the collapsing molecular cloud depend on the total number of particles the cloud contains. That is: the entropy of the baryonic matter in the Universe is much lower now than it was in much earlier epochs. Namely, as matter contracted and clumped, the clumping process caused it to emit heat (despite also increasing in temperature) and that heat was emitted in the form of very-high-entropy radiation. Figure 2 shows if the total number of particles are increasing the change in entropy is reducing. Figure 3 tells that the rising velocity dispersion reduces change in entropy. The presence of turbulence leads to a rise in entropy as it amplifies the disorderly movement of particles.
4. Discussion
The concept of entropy is essential in distinguishing between the past and the future, and it also provides a sense of direction to time. By examining the value of entropy, we can determine whether a molecular cloud is actively forming a star or if it is in a state of tranquility. On a smaller scale, like in the case of a collapsing molecular cloud, entropy tends to increase during the collapse time and decrease after the free-fall time. However, it is worth noting that certain parts of the cloud gain energy and expand, leading to a decrease in temperature and an increase in entropy. This phenomenon is supported by Equation (27). The influence of gravity, the difference in dispersion velocity between the initial and final states, the total number of particles, and the size of the cloud all contribute significantly to changes in entropy during the process of star formation in a collapsing molecular cloud.
In addition, a thermally unstable molecular cloud experiences a decrease in entropy. The findings suggest that there is a disparity in the magnitude of entropy change between small and large scales. This discrepancy arises from the fact that the cloud does not continuously collapse over its entire lifespan, but rather collapses within its free-fall time. Consequently, the alteration in entropy can fluctuate depending on factors such as dispersion velocity, the gravitational energy released, and the size of the cloud in relation to the total number of particles it encompasses.
When one formulates the change in entropy of the Universe with respect to the preliminary and final size he/she obtains the increase entropy change if the final size of the Universe is larger than the preliminary universe. Since, the size of the Universe is increasing due to expansion so that the early Universe is smaller in size than the contemporary universe. Consider the early universe and the late universe we can formulate the change in entropy which can be described in terms of size. The early Universe is very small in size than the late Universe so that the change in entropy grows. For detail study, it is necessary to consider different conditions: Condition one: if the universe is expanding forever the change in entropy grows. This means, as the size of the Universe is increasing then the objects in the universe can get enough space to disperse and lose order. Condition two: if the universe is contracting the entropy reduces as the size decreases.In general, now days the Universe is expanding its size is increasing then entropy is increasing.
The relationship between turbulence velocity dispersion and entropy is demonstrated by this model. By observing Figure 1, it becomes evident that when a cloud with an initial radius R collapses to a smaller final radius R, the corresponding change in entropy decreases. This indicates that as the cloud contracts further, the disparity between the final and initial entropy of the collapsing cloud diminishes. However, the entropy continues to rise until the core achieves hydrostatic equilibrium. The same logical pattern can be observed in Figure 2 and Figure 3, similar to Figure 1. Additionally, Figure 4 illustrates how the parameters of the collapsing molecular cloud can either enhance or suppress its entropy.
5. Conclusion
In this study, I examined the relationship between entropy and the radius of a turbulent-gravitating system. The findings indicate that as a cloud with an initial radius of collapses to a much smaller radius , the change in entropy decreases. This is because the initial and final entropy of the cloud become more similar. Interestingly, it was observed that when the cloud collapses to its smallest possible size, the entropy of the core reaches its maximum point. However, after reaching this maximum value, the entropy starts to decrease and eventually reaches a state of hydrostatic equilibrium. It was demonstrated that the entropy of the cloud increases during the collapsing phase and decreases once the protostar is formed. This suggests that entropy can be reduced on a small scale for a certain period of time. Towards the end of the cloud collapse, the reduction in gravitational entropy may have occurred during the era of protostar formation, leading to an increase in thermodynamic entropy and a decrease in the overall change of entropy in the star-forming cloud. The star formation time scale determines the duration required to achieve equilibrium. Once the star formation process reaches its final stage, the cloud core attains a high density and maintains its hydrostatic equilibrium even after the completion of star formation.
There are numerous unresolved issues in the field of star formation, including the entropy of star-forming molecular clouds.In previous studies chemical potential is neglected when formulating entropy of molecular cloud. In my research, I have focused on investigating how turbulence, size,chemical potential, and particle concentration influence the entropy of collapsing molecular clouds. There are a lot of gaps to be studied in terms of other dynamic processes to have comprehensive understanding of entropy from time to time. The findings reveal that the behavior of entropy is highly intricate and influenced by various dynamic parameters of the cloud, including the time=scale of star formation. Initially, as the collapse begins, the entropy is higher, but as a central core forms, the molecules within the core become relatively more ordered compared to the collapse phase. This concept provides valuable insights into the understanding of star formation theory. However, further in-depth analysis is necessary to fully comprehend the role of entropy in both star formation and evolution.
Additional research is required to explore the dynamic factors that influence entropy. Consequently, I propose investigating the impact of entropy on the overall evolution of the universe, with a specific focus on star formation.
Acknowledgments
I would like to express my gratitude to the Space Science and Geospatial Institute (SSGI), Entoto Observatory and Research Center (EORC), Department of Astronomy and Astrophysics for their invaluable support in creating the research environment. Additionally, I would like to express my sincere gratitude and recognition to the anonymous reviewers for their constructive comments and helpful suggestions.
References
- Amarzguioui, M. ; Gr. ; Entropy of gravitationally collapsing matter in FRW universe models. Phys. Rev. D 2005, 71. [Google Scholar] [CrossRef]
- Andre, P., Ward-Thompson, D. and Barsony, M., 1999. From Pre-stellar cores to protostars: The initial conditions of star formation. arXiv preprint astro-ph/9903284.
- Ballesteros-Paredes, J., Klessen, R.S., Mac Low, M.M. and Vázquez-Semadeni, E., 2006. Molecular cloud turbulence and star formation. arXiv preprint astro-ph/0603357.
- Callender, C. ; Ernst, G., Hüttemann, A., Eds.; Cambridge University Press: Cambridge, UK, 2009; Phil. Sci. Archive 2008.Gravity. In Time, Chance and Reduction: Philosophical Aspects of Statistical Mechanics; Ernst, G., Hüttemann, A., Eds.; Cambridge University Press: Cambridge, UK, 2009; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Davies, P.C.W. The Physics of Time Symmetry. University of California Press: Los Angeles, USA, 1974.
- Egan, C.A.; LineIaver, C.H. A Larger Estimate of the Entropy of the Universe. Astrophys. J. 2010 710, 1825–1834. [CrossRef]
- Federrath, C., 2013. On the universality of supersonic turbulence. Monthly Notices of the Royal Astronomical Society, 436(2), pp.1245-1257.
- Frampton, P.H.; Hsu, D.H.; Kephart, T.W.; Reeb, D. What is the entropy of the universe? Quant. Grav. 2009, 26. [Google Scholar] [CrossRef]
- Gr ⌀n, ⌀, 2012. Entropy and gravity. Entropy, 14(12), pp.2456-2477.
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. Phys. Rev. D 1977, 15, 2738–2751. [Google Scholar] [CrossRef]
- Keto, E., Field, G.B. and Blackman, E.G., 2020. A turbulent-entropic instability and the fragmentation of star-forming clouds. Monthly Notices of the Royal Astronomical Society, 492(4), pp.5870-5877.
- Klessen, R.S. and Hennebelle, P., 2010. Accretion-driven turbulence as universal process: galaxies, molecular clouds, and protostellar disks. Astronomy & Astrophysics, 520, p.A17.
- Leubner, M.P. A measure of gravitational entropy and structure formation. 2001, ArXiv:astro-ph/0111502.
- McCourt, M., Sharma, P., Quataert, E., & Parrish, I. J. 2012, MNRAS, 419, 3319.
- McKee, C.F. and Ostriker, E.C., 2007. Theory of star formation. Annu. Rev. Astron. Astrophys., 45, pp.565-687.
- Penrose, R. , 2010. Cycles of time: an extraordinary new view of the universe. Random House.
- Sharma, P., McCourt, M., Quataert, E., & Parrish, I. J. 2012, MNRAS, 420, 3174.
- Vaas, R. ime after Time-Big Bang Cosmology and Arrows of Time. In The Arrows of Time; Mersini-Houghton, L., Vaas, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Voit, G.M. and Donahue, M., 2015. Cooling time, freefall time, and precipitation in the cores of ACCEPT galaxy clusters. The Astrophysical Journal Letters, 799(1), p.L1.
- Wallace, D., 2010. Gravity, entropy, and cosmology: In search of clarity. The British Journal for the Philosophy of Science, 61(3), pp.513-540.
- Zurek, W.H. Entropy Evaporated by a Black Hole. Phys. Rev. Lett. 1982, 49, 1683–1686. [Google Scholar] [CrossRef]
Figure 1.
versus S). = 0.001pc ; ; ; n = ; = . The decrease in entropy is observed as the radius of the molecular cloud increases.
Figure 1.
versus S). = 0.001pc ; ; ; n = ; = . The decrease in entropy is observed as the radius of the molecular cloud increases.
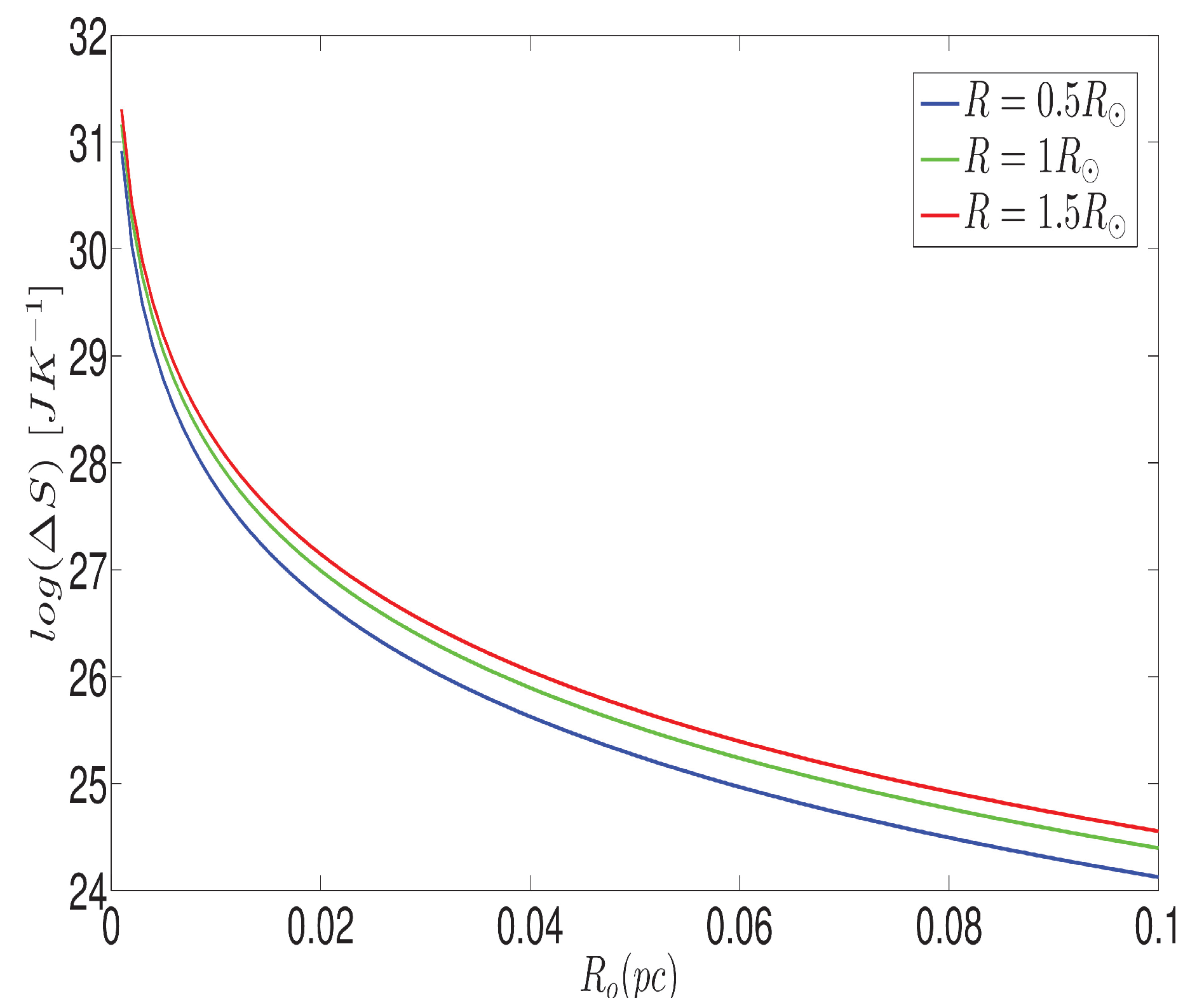
Figure 2.
versus S). = 0.001pc, , = , n = , = . The depicted illustration demonstrates that as the overall quantity of particles within the molecular cloud increases its internal energy grows leading to the entropy of the cloud decreases. This observation validates the notion that the cloud experiences a relative increase in its level of organization.
Figure 2.
versus S). = 0.001pc, , = , n = , = . The depicted illustration demonstrates that as the overall quantity of particles within the molecular cloud increases its internal energy grows leading to the entropy of the cloud decreases. This observation validates the notion that the cloud experiences a relative increase in its level of organization.
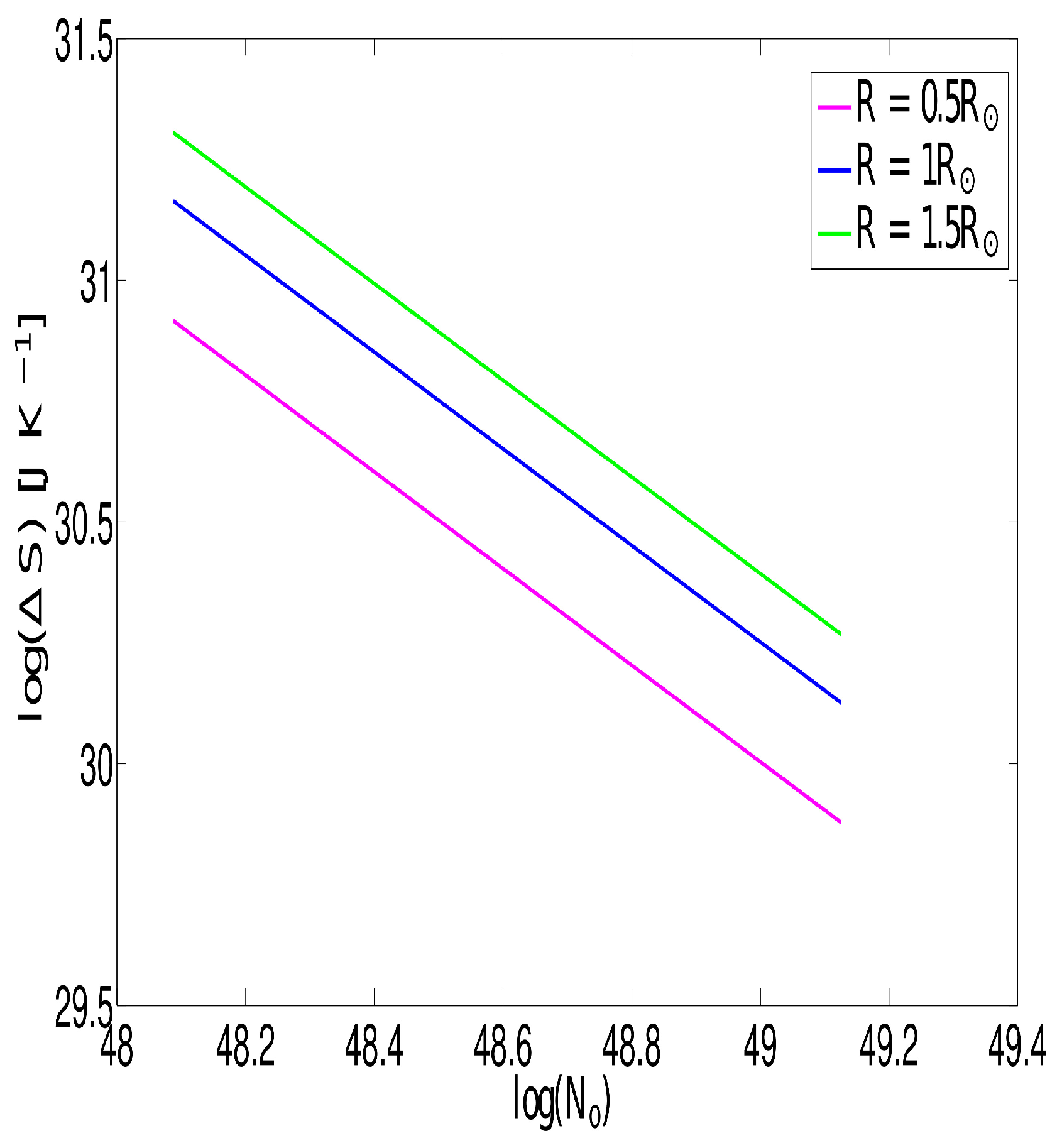
Figure 3.
Turbulent velocity dispersion versus S). = 0.001pc ; = ; n = ; = . The relationship between the radius of the cloud, turbulence, and entropy is depicted by this diagram. It illustrates that as the cloud’s size increases, entropy decreases, while an increase in turbulence leads to an increase in entropy.
Figure 3.
Turbulent velocity dispersion versus S). = 0.001pc ; = ; n = ; = . The relationship between the radius of the cloud, turbulence, and entropy is depicted by this diagram. It illustrates that as the cloud’s size increases, entropy decreases, while an increase in turbulence leads to an increase in entropy.
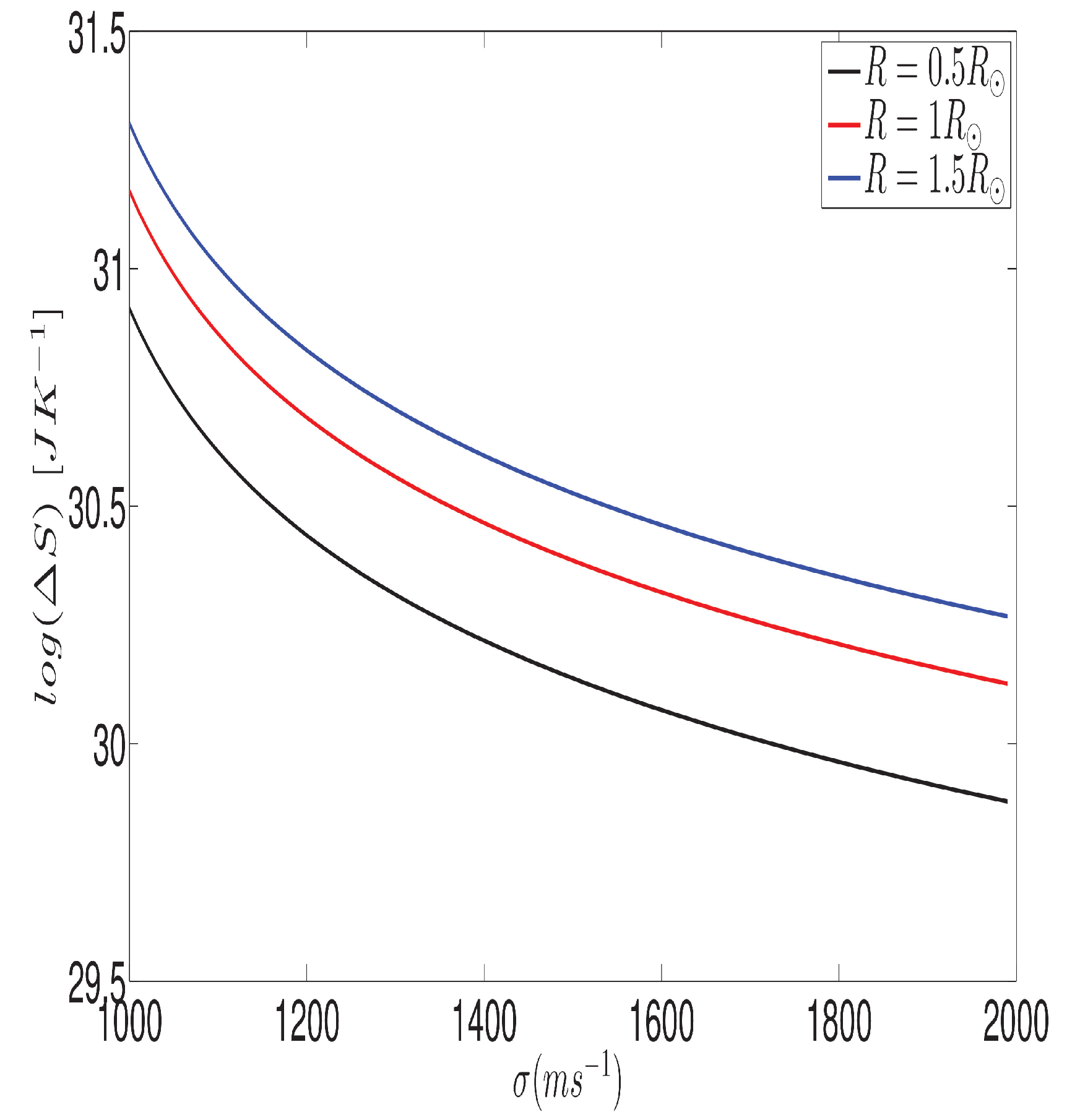
Figure 4.
S) in terms of parameters of the collapsing cloud N = , = .The diagram presented here showcases the relationship between entropy and various dynamic factors associated with molecular clouds.
Figure 4.
S) in terms of parameters of the collapsing cloud N = , = .The diagram presented here showcases the relationship between entropy and various dynamic factors associated with molecular clouds.
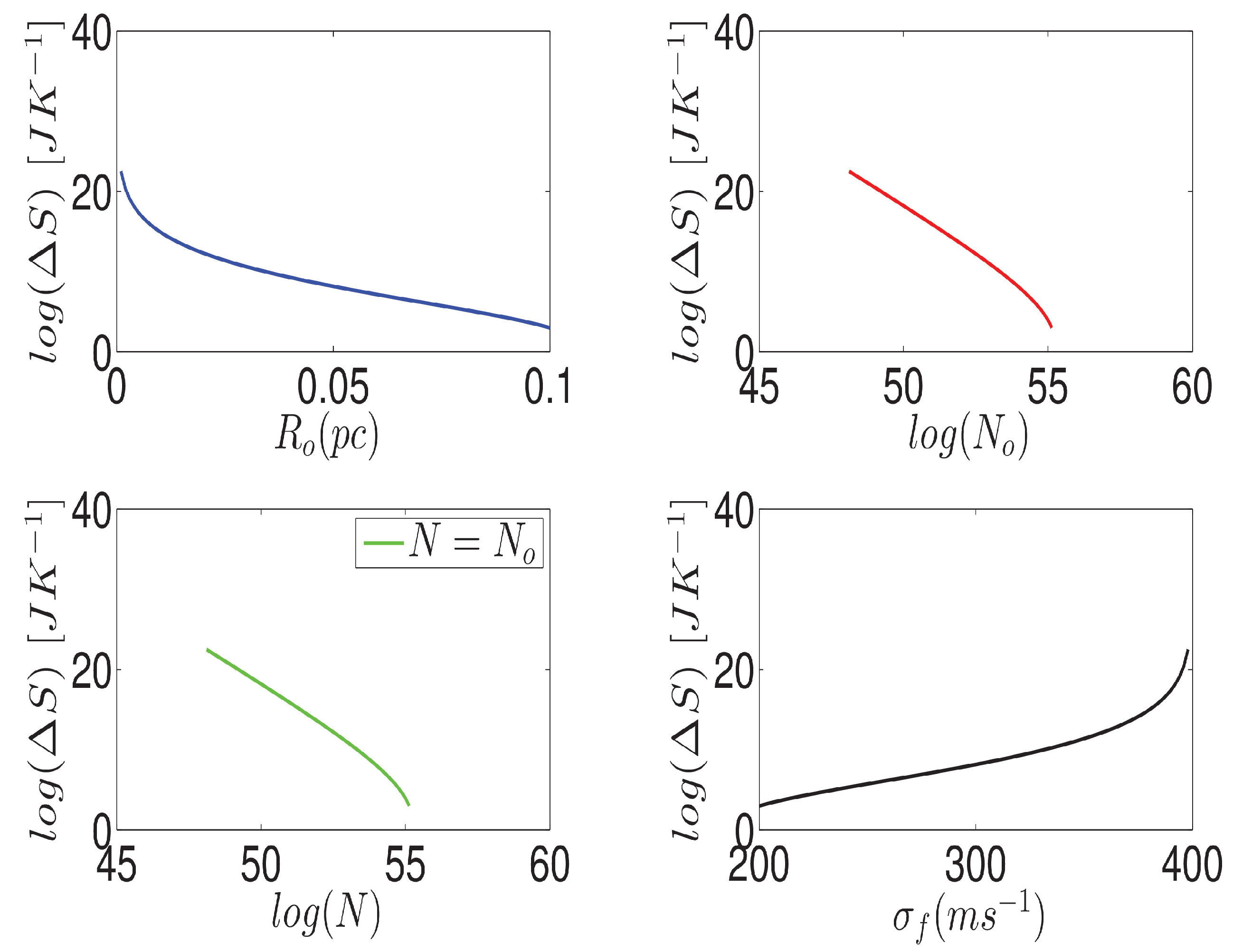
Figure 5.
S) vs N of the cloud where N ≠. The relationship between the entropy of a collapsing molecular cloud and the total number of particles it contains is illustrated in this figure.
Figure 5.
S) vs N of the cloud where N ≠. The relationship between the entropy of a collapsing molecular cloud and the total number of particles it contains is illustrated in this figure.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




