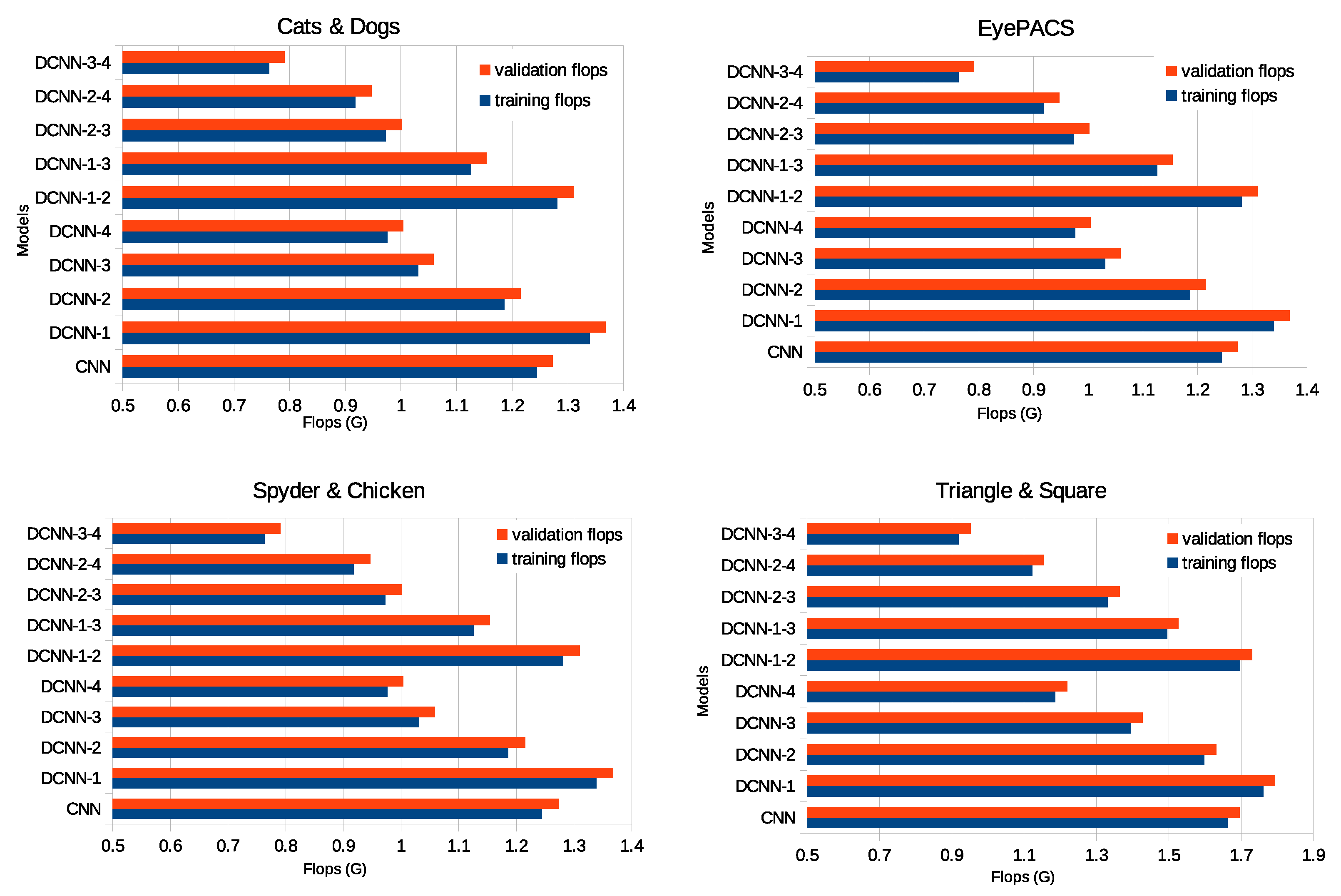Evaluation of Deformable Convolution: An Investigation In Image And Video Classification

Convolutional Neural Networks (CNNs) present drawbacks for modeling geometric transformations, such as scaling and rotation, caused by the convolution operation’s locality. Deformable convolution (DCON), a mechanism that substitutes standard convolution, increasing the receptive field to capture relevant features, is a promising approach to solve this drawback and improve the robustness of CNNs. However, the optimal way to replace the standard convolution with its deformable counterpart in a CNN model is unclear. In this study, we clarify this aseveration by conducting several experiments using deformable convolutions applied in the layers that conform a small four-layer CNN model. We also use deformable convolutions on the four-layers of several ResNet CNNs with depths 18, 34, 50, and 101. The models were tested in binary balanced classes with 2D data for image classification: Cats & Dogs, EyesPACS, Spyders & Chickens, and Shapes. After this testing, we evaluated DCON in 3D data for action recognition: UCF101 and Human2 (a dataset we compiled to control movement, clothing and background). The contribution of this research lies in a guideline to use DCON. It can be summarized as follows: if DCON is used on the first layers of the proposal of model (with simple features), the computational resources expressed as the quantity of Flops will tend to increase and produce bigger misclassification than the standard CNN. However, if the DCON is used at the end layers, the quantity of Flops used in the training and testing will decrease, and the classification accuracy will improve by up to 20% about the base model. Moreover, it gains robustness when using deformable convolutions because it can adapt to the region of interest. Also, the best kernel size of the DCON is three. It showed better results than size five. In the last case, the quantity of Flops increase quadratically, but their performance does not increase significantly. With these results, we propose a guideline to use the DCON and contribute to understanding the impact of DCON on the robustness of CNNs.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Convolutional neural networks (CNNs) have dominated the field of computer vision, achieving superior results to traditional machine learning methods [1]. Its success is due to its capacity to capture spatial features and patterns in images using a layered hierarchical architecture, where mainly convolution and pooling operations are performed [2].

The core component of CNNs is the convolution operation, which extracts features and patterns from the input image. Each convolutional layer is composed of multiple kernels [3], which, during the training phase, their weights are learned, turning them into feature extractors, identifying specific patterns, edges, and textures present in the input data [4].

Despite the astonishing results CNNs have shown, they present an inherent limitation for modeling unknown transformations, which originates mainly from the lack of internal elements to model geometric transformations [5]. As a consequence, the receptive field of the activation units remains the same in each convolutional layer, and it is limited to the kernel size.

A common technique to increase the capacity to model geometric transformations is to use data augmentation. However, this operation requires more training time, and if transformations are not appropriately modeled, the risk of overfitting increases. The approach used to expand the receptive field is to augment the kernel size, such as in [6,7]. Nevertheless, this change in kernel size increases the computational cost (due to the quadratic computational complexity).

Deformable convolution (DCON), proposed in [5], is a mechanism that replaces the standard convolution of a CNN layer with deformable convolution increasing the receptive field to capture relevant features (usually called deformable convolutional networks or DCNN). DCON is a promising approach to give a CNN the capacity to model transformations, such as scale, increasing its robustness. However, the optimal way to replace the standard convolution with its deformable counterpart is unclear.

In the state of the art, some works have been proposed that give clues on how to adequately incorporate DCON. Dai et al. [5] evaluated the effect of DCON using ResNet-101 for feature extraction, finding that accuracy improves with more DCONs included. However, the improvement gets overshaded, when three DCONs for semantic segmentation or six for object detection are used. Chen et al. [8] found better results in semantic segmentation when including from one to three DCONs in the residual block of a ResNet-101, falling the improvement as adding more convolutions. Lai et al. [9] investigated the performance of the DCON in a C3D model in different layers. Unlike us, they found that lower layers yield better results.

In this paper, we give a guideline for DCNNs by investigating the behavior of CNN models when DCON is introduced. For this purpose, several experiments to analyze DCNNs were conducted, different from previous works. We start our experiments from 2D models employing a small network composed of four stages. After that, deeper models such as ResNet-18, ResNet-34, ResNet-50, and ResNet-101 are tested. To go further in our analysis, we extend the experiments to 3D models using the 3D ResNet variants.

These models were evaluated in image classification tasks using varied datasets with controlled conditions. The models should carry on binary decisions (the presence or absence of glaucoma) and animal identification. Moreover, we applied space-time tests in the field of action recognition. DCONs perform better when placed in layers containing more complex features rather than using them in the first layers. Also, it was found that kernels with a 1x1 size learn only local features. In the case of kernels with size 5x5, the computational cost increases notably without remarkable performance benefits. Then, kernel 3x3 was left as the best option. These results are also confirmed in [6,10].

The rest of this paper is organized as follows. Section 2 gives the materials and methods involved in the study. Section 3 presents the methodology. Section 4 offers experiments and results. Section 5 and Section 6 present the discussion and conclusions of this work.

2. Materials and Methods

2.1. Standard Convolution (Used in the CNN)

The 2D convolution function works using a fixed grid R that defines both the receptive field size and dilation sizes. The receptive field is the patch of the total field of view that produces a feature [11]. For example, Equation 1 defines a grid of size 3x3:

R = (- 1, - 1), (- 1, 0), . . ., (0, 1), (1, 1)

(1)

For the sampling point

p_{0}

, the 2-D convolution equation is defined as follows:

y (p_{0}) = \sum_{p_{n} \in R} w (p_{n}) \cdot x (p_{0} + p_{n}),

(2)

where

p_{n}

enumerates the locations in R, x is the input feature map, and

w (p_{n})

is the weight at a certain position [5].

2.2. Deformable Convolutional Network (DCNN)

In deformable convolution, the regular grid is augmented with offsets

Δ p_{n} ∣ n = 1, . . . N

, where

N = ∣ R ∣

. Equation 2 becomes

y (p_{0}) = \sum_{p_{n} \in R} w_{(} p_{n}) \cdot Δ m_{n} \cdot x (p_{0} + p_{n} + Δ p_{n}),

(3)

where

Δ p_{n}

is an offset, which, since it is usually a fractional value, is implemented using a bilinear interpolation algorithm (Equation 4),

Δ m_{n}

is another trainable modulation parameter between 0 and 1 [12]. Both

Δ p_{n}

and

Δ m_{n}

are obtained via a separate convolution layer applied over the same input feature maps

Δ x

. The output is of 3K channels, where the first 2K channels correspond to the learnable offsets and the remaining K channels are further fed to a sigmoid layer to obtain a modulation of scalars. Below the equation for the bilinear interpolation function

x (p) = \sum_{q} G (q, p) \cdot x (q),

(4)

where p denotes an arbitrary (fractional) location, and q enumerates all integral spatial locations in the feature map x, and

G (\cdot, \cdot)

is the two dimensional bilinear interpolation kernel. It is separated into two one-dimensional kernels as

G (q, p) = g (q_{x}, p_{x}) \cdot g (q_{y}, p_{y}),

(5)

where

g (a, b) = m a x (0, 1 - | a - b |)

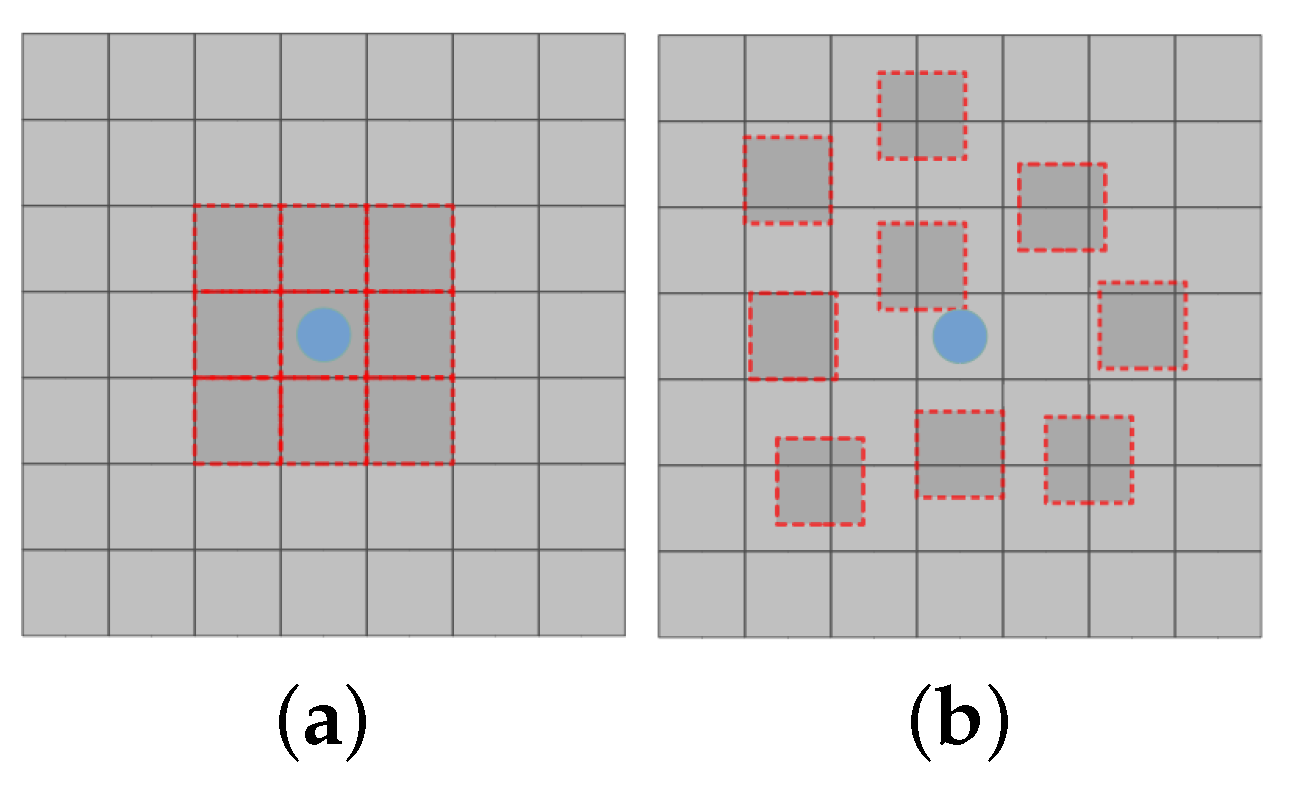
Each sampling point of the kernel learns an offset to achieve adaptation. In the process of DCON, additional convolution layers are required to extract the offset fields of the same size. Figure 1 illustrates the difference between the receptive field of standard convolution operation (Figure 1a) and the deformable convolution operation (Figure 1b), employing 3x3 kernel size. In standard convolution, the receptive field is limited to the kernel window, whereas in its deformable counterpart, the receptive field is irregular as a result of the displacement

p_{n} + Δ p_{n}

The implementations of DCONs applied in this study are listed below. These implementations can be used to replace a standard convolution layer with the deformable counterpart:

Tvdcn [14]: Torchvision-like package of the DCNN with both 1D, 2D, and 3D operators.
PyTorch-Deformable-Convolution-v2 [15]: Developed and published by Y. Kwon, this library implements a DCNN model based on the Pytorch operator deform_conv2d.

2.3. Models Tested

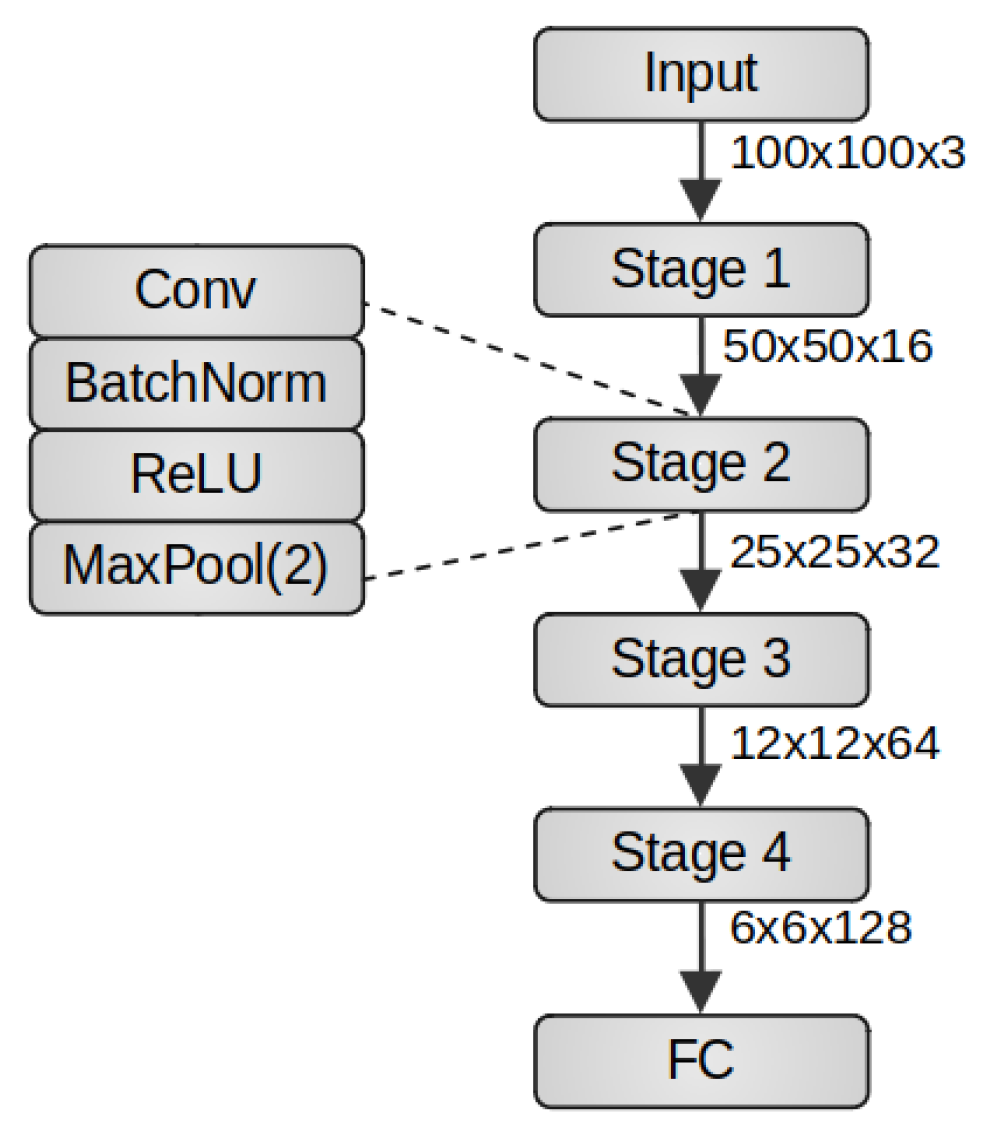
2.3.1. Small Model

The small model used in this research comprises four convolution stages and a classifier. As shown in Figure 2, each stage is composed of a convolution layer with kernel size 3x3 (except during the comparison of kernels 1x1, 3x3, and 5x5 in Section 4.1.2) and ReLU activation function, followed by a MaxPooling layer with a window size of 2x2. The classifier is a fully connected architecture with two hidden layers, composed of 6x6x128 units in the input layer, 64 and 32 units in the first and second hidden layers, respectively, with linear activation function and one neuron in the output layer, with a sigmoid activation function.

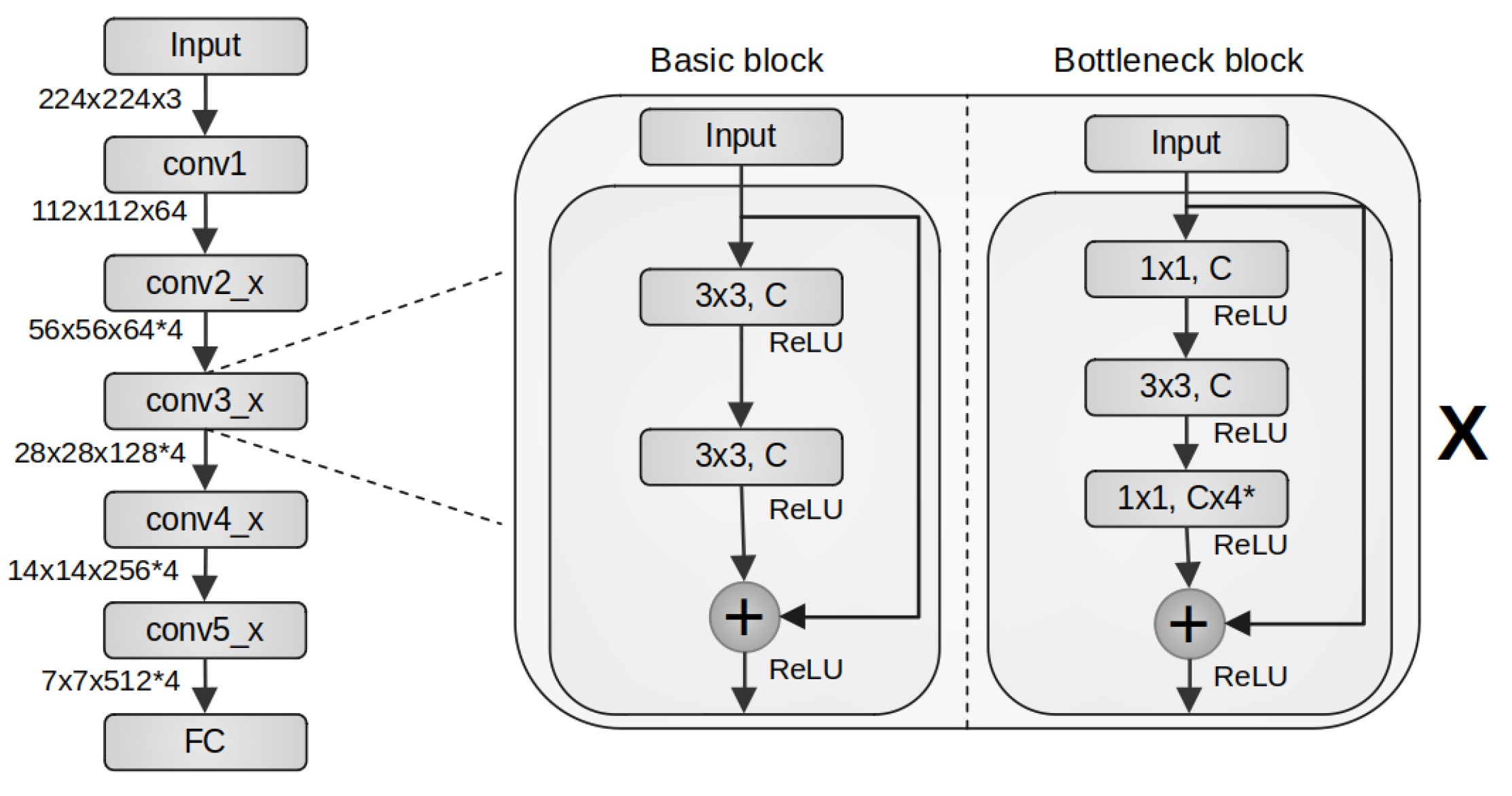
2.3.2. ResNet

The ResNet model proposed by He et al. [16] is constituted of five stages, as shown in Figure 3 (left), where the first stage, named conv1, is composed of one convolution layer with kernel 7x7, stride two, followed by a MaxPooling layer with window size three and stride two. The following, conv2_x to conv5_x stages, are composed of stacked residual blocks organized in a sequential manner, where x indicates the number of repetitions that the residual block will take in each stage.

The idea behind the residual block is to reduce the gradient vanishing, thus establishing a shortcut to avoid losing the input information. This process is done by adding the input signal to the output of the last convolutional layer of each residual block. In a residual block, the input is called residual information.

Each residual block can be replicated x times in a stage. Therefore, deeper networks can be built to preserve the input information. Common ResNet architectures are ResNet-18, ResNet-34, ResNet-50, ResNet-101, and ResNet-152. The residual block for ResNet-18 and ResNet-34 architectures is called basic block, and consists of two convolution layers with a 3x3 kernel without a MaxPooling layer. Whereas the residual block for ResNet-50 and ResNet-101 is named bottleneck block, which comprises three convolution layers, where the first and last layers use 1x1 kernel size, and the intermediate layer employs 3x3 kernel size. In addition, in case the input size does not match (spatially or in number of filters), the residual block incorporates a mechanism to project the input to the required dimensions. ResNet-18, ResNet-34, ResNet-50, and ResNet-101 architectures were considered in this research.

2.4. Metrics

The metrics used in this study are explain below.

Accuracy: In this study, we have balanced classes for all the data sets. Accuracy is defined as the sum of the number of true positives and true negatives (correct observations) divided by the total number of examples [17], it’s computed as follows.

$Accuracy = \frac{T P + F P}{T P + F P + T N + F N}$

(6)

where $T P$ is a correct observation put in class 1; $F P$ is an incorrect observation put in class 1; $T N$ is a correct observation put in class 2; $F N$ is an incorrect observation put in class 2. Then, the accuracy describes how the model performs across all classes.
Validation accuracy with transformation: A scale transformation is applied to evaluate the robustness of the model.
Flops: Denotes the number of floating point operations executed per second. Essentially, the Flops measure the processing speed of models, thereby serving as an indicative benchmark for assessing their computational cost. We used it as a measure of training and testing time in our research. It is measured through one image or per batch conformed of a group of images.
Parameters: The internal variables learned by the model from the training data.
Time execution: Amount of time that the process takes to execute.

2.5. Image Datasets

The image classification data sets are shown in Figure 4 and listed bellow.

Cats & Dogs [18]: Two classes of mammals with some characteristics in common, but at the same time, differences that are very clear to the human eye. Cats & Dogs images were collected by the Visual Geometry Group (VGG) at the University of Oxford.
EyePACS-AIROGS-light-V2 [19]: This is an improved machine-learning-ready glaucoma dataset using a balanced subset of standardized fundus images from the Rotterdam EyePACS AIROGS divided into referable glaucoma (RG) and non-referable glaucoma (NRG). A binary classification where the change between the classes is focused on the presence or absence of specific details.
Spyders & Chickens [20]: Taken from Animals10 conformed of quality animal images where two radically different animals were selected to analyze a complex spatial scenario.
Triangle & Square [21]: Geometric shapes drawn randomly on a 200 x 200 RGB image. The perimeter, the position of each shape, the rotation angle (between 0° and 360°), the background color and the filling color are selected randomly and independently for each image. Shapes is a dataset with controllable differences between each class. We expect to reflect better the deformable impact in a controllable scenario like this.

2.6. Video Datasets

The video data sets used mainly for action recognition are shown in Figure 5 and explained below.

Apply Makeup [22]: Two classes with little movement were taken from UCF101; Eye Makeup & Apply Lipstick. These classes were selected because there is no background movement, and although both activities are very close to each other, the characteristics that determine their label are based on spatial and temporal information, the spatial objects and locations in the image, and the hand movement.
Human2: We collected 15 videos per class of a human walking forward and turning to the left. The background, clothes, and light conditions are fully controlled. The speed at which the activity is performed, and the body position varies between the instances.

2.7. DCON in ResNet Models

To answer the question of where it is more suitable to use a deformable convolution layer in a deeper model, the ResNet model with architectures from ResNet-18 to ResNet-101 were tested. The switching of a standard convolution by its deformable counterpart (DCON) was conducted in the following configurations:

Stage by stage: Refers to exchanging the standard convolution layer for its counterpart only in one stage at a time, i.e., swapping the standard convolution in the blocks (basic, bottleneck) of conv2 stage for its counterpart and the other stages (conv3, conv4, conv5) remain intact.
Combining two successive stages: The same as above, but in two successive stages, i.e., swapping the standard convolution by its counterpart in conv4 and conv5, the stages conv2 and conv3 remain unchanged.
Combining all stages: Here, all stages that are composed of basic or bottleneck blocks (conv2, conv3, conv4 and conv5), include the deformable convolution instead of the standard one.

For architectures involving the basic block, the standard convolution layer was replaced by its deformable counterpart within each block. On the other hand, the standard 3x3 kernel convolution located in the middle was replaced by its deformable counterpart for the architectures involving bottleneck blocks.

In 3D ResNet, deformable convolution is applied only in convolutions with kernel size three (because with size one we already saw there was no benefit). This experiment, includes some executions with strides one or two. Stride two is present in all stages but only in the first block due to the bottleneck. On the other hand, stride one is in all the blocks that contain the stage. The stride size affects the output spatial dimension and the computation load. More importantly, a more significant stride will capture more global features but can also overlook helpful information. The choice of stride is a trade-off that needs to be carefully considered based on the specific task and dataset.

3. Methodology

This work is inspired by the studies presented by Dai et al. in [5] and Zhu et al. in [12], where they propose a mechanism to increase the receptive field of a convolution layer by deforming its kernel, referred to as DCON. These studies have reported that replacing the standard convolution layer with a deformable one improves the performance of well-known convolutional neural networks for feature extraction, such as the ResNet-50 and ResNet-101 models. However, they do not go further into the study of other architectures of the ResNet model, such as ResNet-18 and ResNet-34. Different from that research, in this work, we go further into the DCON evaluation for feature extraction, extending it to different architectures of the ResNet model, starting from ResNet-18 up to ResNet-101. In addition, to better understand the behavior of the DCNN, we incorporate a shallow convolutional network architecture called a small network. With the use of this small network, it was possible to realize several experiments.

To identify the potential of a DCON to improve a model for feature extraction, different configurations were generated to replace the standard convolution layer with its deformable counterpart according to each model type. The standard convolution layer was replaced by its deformable counterpart in the small model stage by stage. On the other hand, in the ResNet architectures, the residual blocks were replaced stage by stage by their deformable counterpart (Section 2.6). This substitution was done to identify when a deformable layer can improve the model’s performance and when it can be counterproductive.

Each configuration was trained from scratch for each dataset, and validated. A scaling transformation was applied to the test images to assess the generalization of geometric transformations when using DCON layers. Figure 6 illustrates the multiple-image scales applied during testing. The validation accuracy, time, and the quantity of Flops achieved for each configuration were evaluated.

4. Results

4.1. Small Model Analysis

The model performance using DCON was assessed by developing several configurations to incorporate DCON layers in the model. These configurations are shown in Table 1. The accuracy reflects the robustness of Triangle & Square classes.

4.1.1. Performance

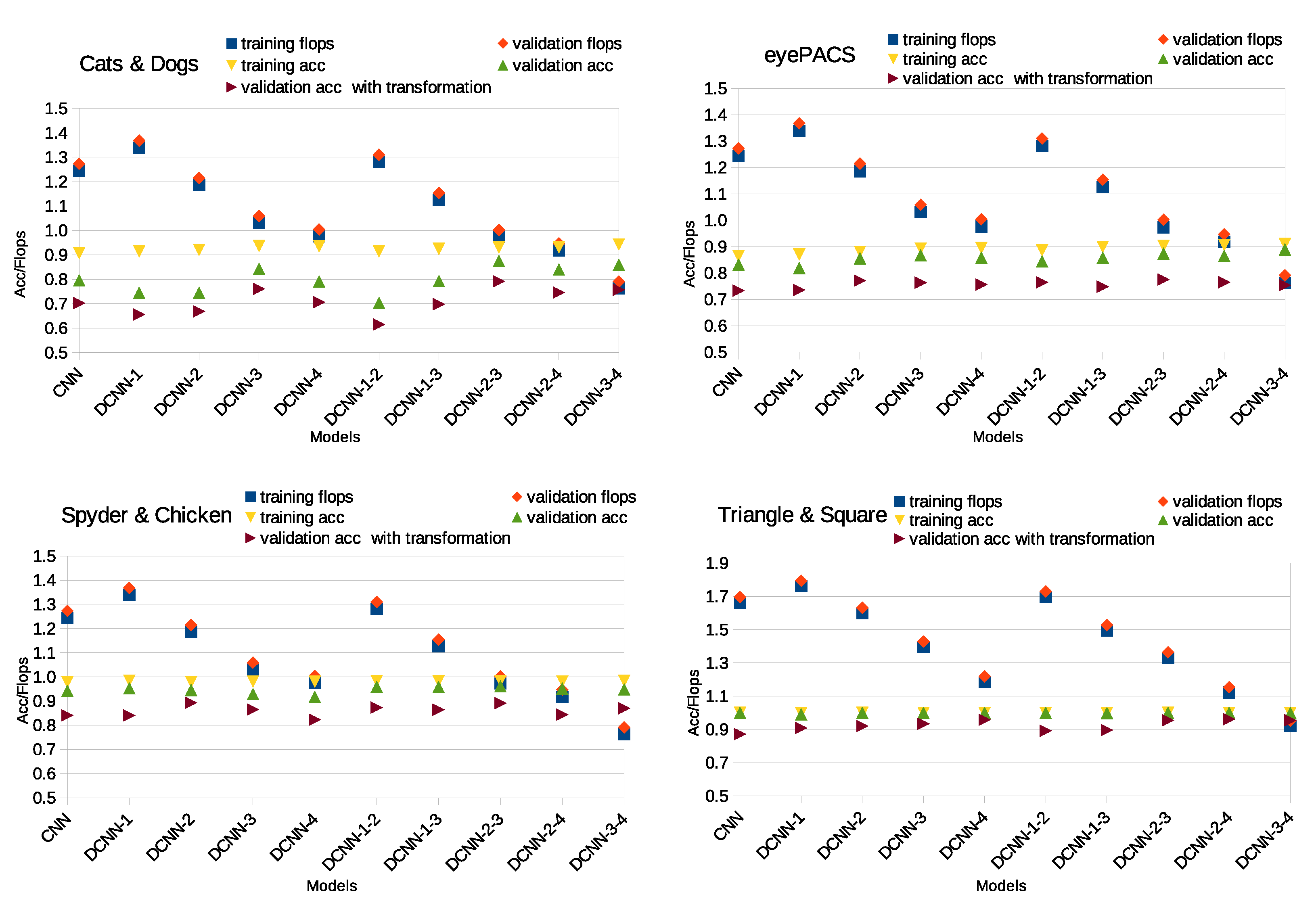
When DCON is in the first layer, the quantity of Flops and the number of parameters increment (Table 1 and Table 2, and Figure 8). Despite using DCON, accuracy often remains the same or even decreases. On the other hand, it achieves lower quantity of Flops and better performance when working with more complex features (from higher layers). In Table 1 and Table 2, it is observed that even though the number of parameters can increment (caused by the DCONs), also can be beneficial if it works with more complex features. Applying DCON will increase the number of parameters without necessarily reflecting an improvement; if applied in the first layer, the model performance will also increment, no matter the dataset analyzed. This implies that the first features obtained through convolution are still so uninformative that they confuse the deformable ones. In other words, DCONs require pre-processing before learning their parameters. The model with DCONs that achieves the best relation between accuracy and the quantity of Flops is conv3-4 (Figure 9). Nonetheless, it is also illustrated that applying DCON in the first layer is not as convenient as applying it in the latter stages where the features are more complex. It is better to work with standard convolution than a DCON in the first layer. 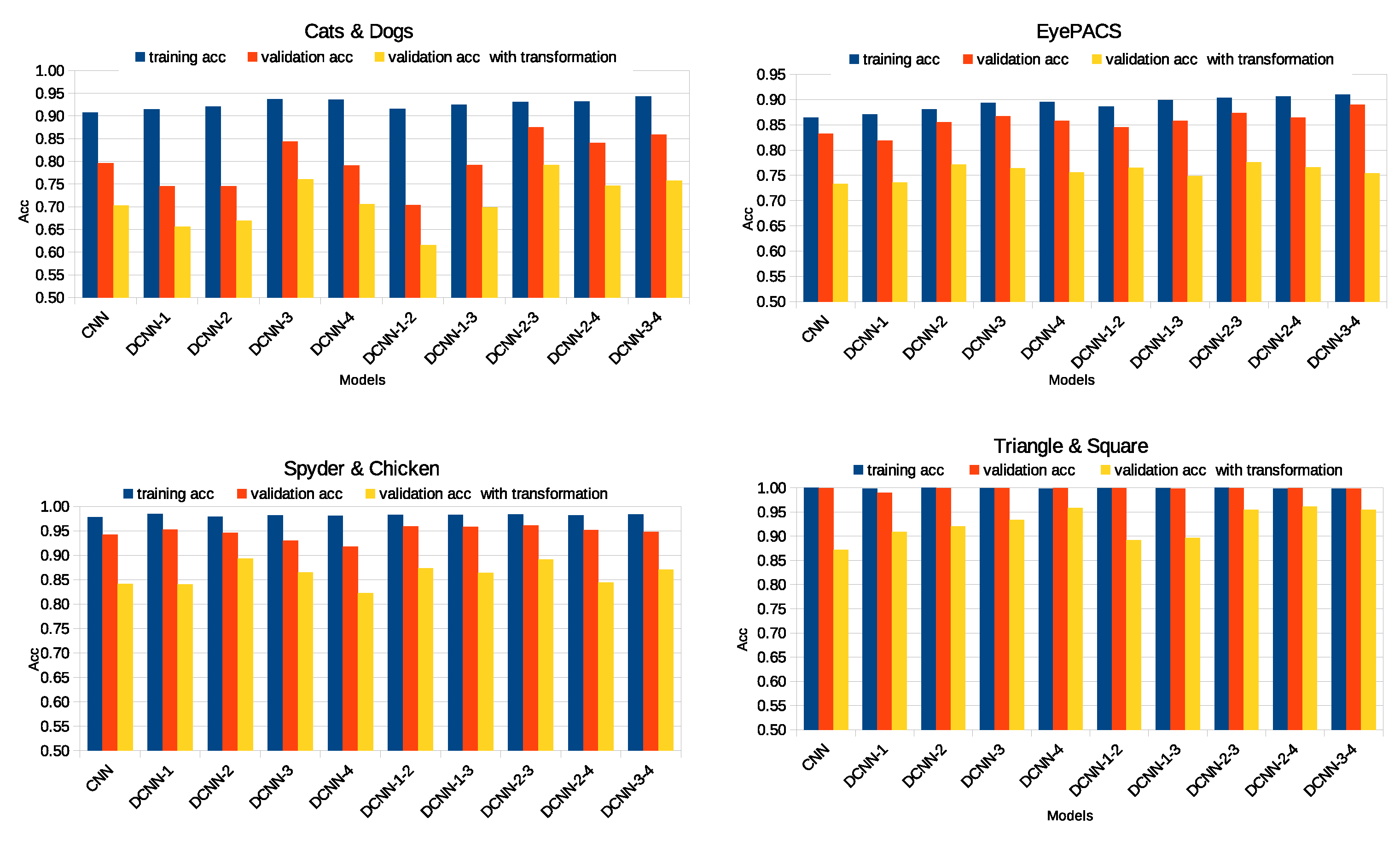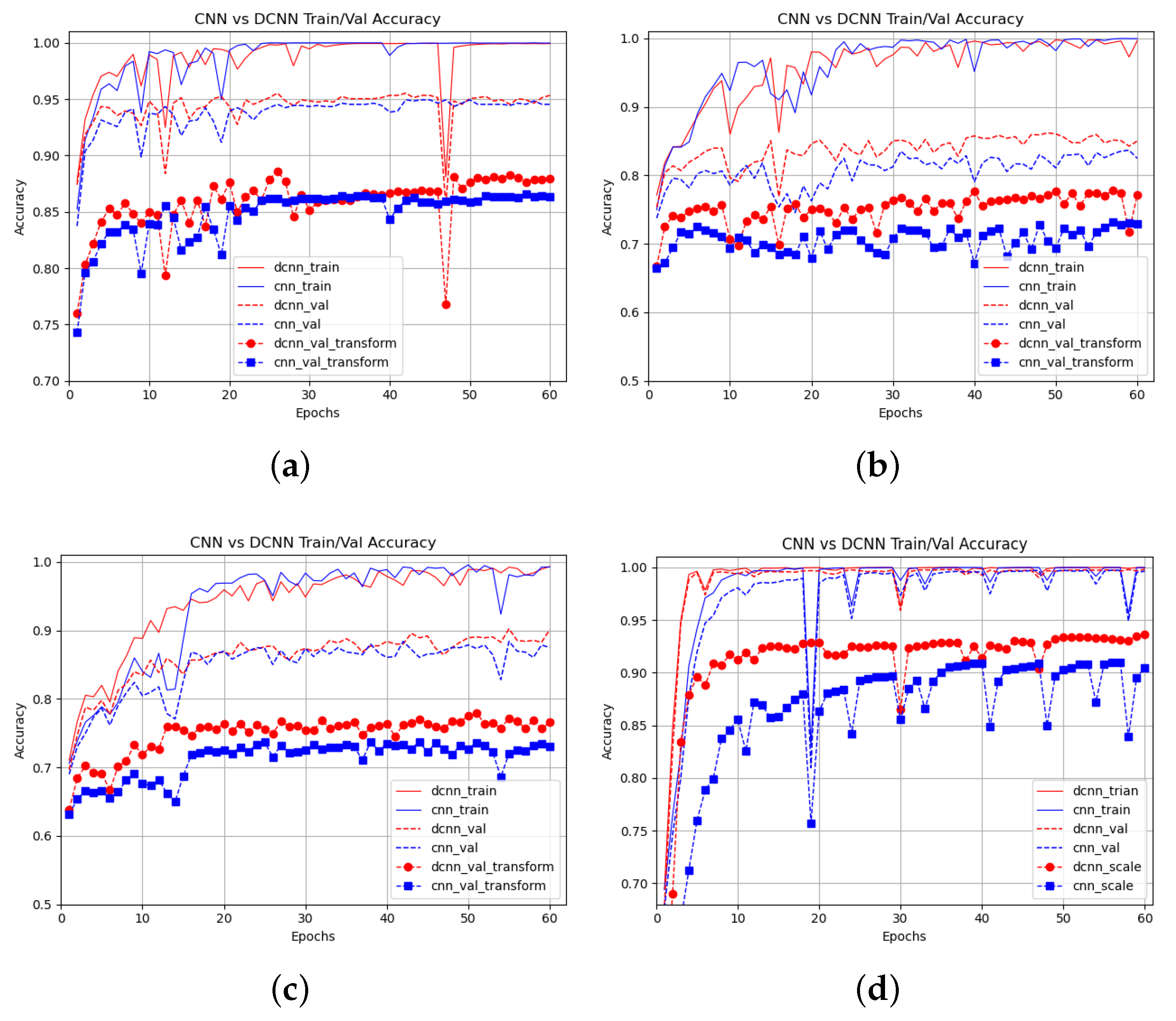Also, the validation accuracy (Figure 7) that uses scale transformation is better when the model is a DCNN, denoting gained robustness in the model. This performance improvement is due to the capability of modeling geometric transformation once the best location of DCON is found.

DCNNs show advantages because of their inherent adaptability. Nonetheless, DCONs can also become harmful or indifferent if we use them without previous knowledge acquired with standard convolution. Figure 10 compares the standard CNN (base model) and the best model with DCNNs (conv3-4). The DCNN with transformation is always over the one without deformable convolution, adding evidence that the DCNN generalizes geometric transformations. We confirm that using the DCON to calculate the most superficial features will have lower results than using complex features. The model tends to be more robust when placing the DCON in the last layers (Table 3). Although the base model reaches the best time execution, the time with DCONs increments only by 0.02 or 0.04 min. The increments are not too far. These numbers are considering the experiments with best relation between accuracy and execution time from Vanilla model (Table 4).

4.1.2. Kernels

Common choices of kernel sizes are three or five. The kernel size is related to the number of parameters and the capability of generalizing. Table 5 shows the parameters and the quantity of Flops of the best DCNN models already discussed. The increase in parameters means not necessarily decreasing the processing speed involved, probably because the added parameters are the ones that help the DCNN learn better representations. The standard convolutions require fewer parameters but higher quantity of Flops.

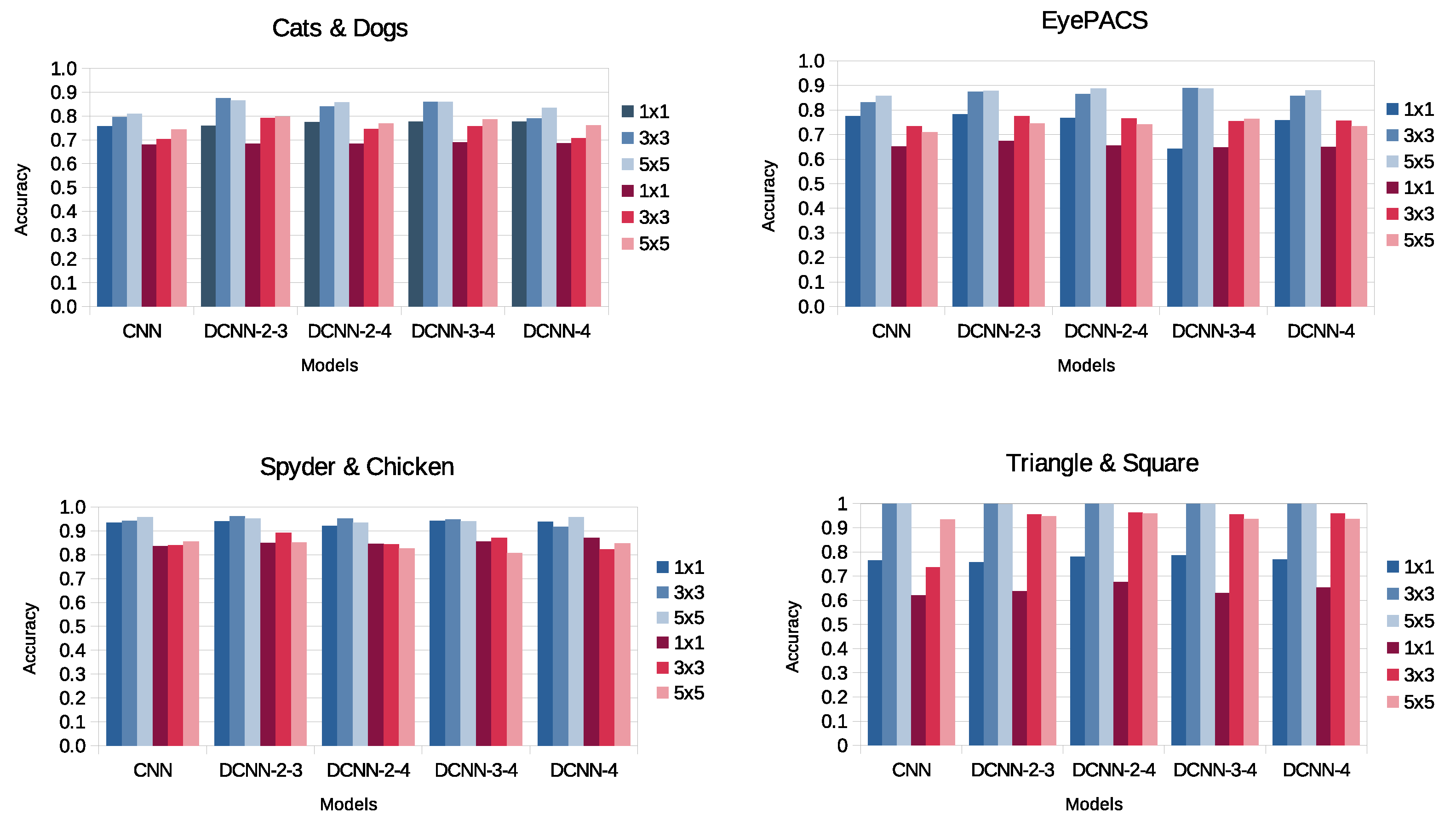
Figure 11 illustrates that kernel 5x5 has similar accuracies to the ones with kernel 3x3. But, as shown in Table 5, the quantity of Flops drastically increases with kernel 5x5. On the other hand, a kernel 1x1 always obtains less accuracy because no matter the flexibility DCONs should bring, this kernel´s size lacks context and only generates local features.

4.2. DCNN in ResNet Models for Image Classification

To further investigate the DCON performance in deeper models, we use the ResNet architectures to test the DCON, starting from ResNet-18 to ResNet-101. As in the small model, to evaluate the quality of the features, binary classification was conducted using the datasets: Cats & Dogs, EyePACS, Sypder & Chickens, and Shapes. We evaluated the accuracy achieved, the training time, and the quantity of Flops for each configuration. The results are presented in the following subsections.

4.2.1. Accuracy Test

The ResNet-18 architecture performance is shown in Table 6. In the stage-by-stage configuration, we observed that when using the deformable convolution in conv2, the poorest accuracy was achieved. The accuracy is lower even than the vanilla configuration; for all datasets except Shapes, where this configuration obtained the highest accuracy. It was found, conversely, that when applying the deformable convolution in conv4, the accuracy results are better than with the stage-by-stage configurations, except in the Shapes dataset.

Combining the subsequent stages, conv4, and conv5, the DCNN achieves higher accuracy in all datasets except EyePACS. The best accuracy was achieved in the Spyer & Chickens dataset, using this combination. Furthermore, by combining all stages, the best accuracy is achieved in the Cats & Dogs, and EyePACS datasets.

The performance of the ResNet-34 architecture is shown in Table 7. A similar behavior as the ResNet-18 architecture was observed here. The best result using the stage-by-stage configuration is obtained using conv4, reaching the highest accuracy for the Cats & Dogs dataset. Whereas combining two consecutive stages, conv4, and conv5, achieved the best accuracy on the Spyders & Chickens data set. Combining all stages achieved the best accuracy for the remaining two data sets.

Contrary to the ResNet-18 and ResNet-34 architectures, the performance of the ResNet-50 architecture exhibited better performance by replacing standard convolution for its deformable counterpart in the stage-by-stage configurations in Cats & Dogs and Shapes datasets and combining the consecutive stages conv4 and conv5 in the EyePACS dataset. Combining all stages delivers the poorest performance of all configurations, even the vanilla configuration, except for the Spyders & Chickens dataset, where this configuration presents the highest accuracy. These results are shown in Table 8.

In ResNet-101, the conv4 configuration in layer-by-layer basis exhibits the highest accuracy than the other layer-by-layer configurations. Combining the two stages conv4 and conv5, good results are achieved in the Spyders & Chickens and Shapes datasets. However, the accuracy achieved is very low in the Cats & Dogs and EyePACS datasets. In contrast to the above, combining all stages, high-accuracy results were obtained in the Spyders & Chickens and EyePACS datasets, where this configuration presented the best accuracy.

4.2.2. Training Time and the Quantity of Flops

In addition to accuracy, we also took into account the training time and computational resources needed for model execution. The aim is to determine the optimal stage and configuration for replacing the standard convolution with its deformable counterpart. For this purpose, we measure the training time and the quantity of Flops. The results obtained along these experiments are shown in Table 10 for ResNet-18, Table 11 for ResNet-34, Table 12 for ResNet-50 and Table 13 for ResNet-101.

Training time is the lowest in the vanilla model for all architectures and all datasets. In the stage-by-stage configuration, starting from conv2, the training time is higher than the vanilla model, as the deformable convolution is introduced in deeper stages, the training time decreases but is not able to be lower than the vanilla model. Conv5 configuration generally has the lowest training time of all the configurations, where the deformable convolution is applied.

When combining two consecutive stages, conv4 and conv5, the training time increases slightly, greater than the conv5 configuration of the stage-by-stage mode. When combining all stages, the training time is significantly higher than all other configurations.

Contrary to the training time, the processing speed increases as the deformable convolution is introduced in more layers. In the case of ResNet-18, using the vanilla configuration, 3.670 GFlops are reached, while in the conv5 configuration, 3.068 GFlops are achieved, and when all stages are combined, 0.794 GFlops are attained.

4.3. DCNN’s through Time Dimension

In this section, 3D ResNets with depths 18, 34, 50, and 101 were analyzed using controlled videos where the person is walking forward and turning to the left. The controlled conditions will permit the model to focus on the movement, thus allowing us to analyze the behavior of deformable convolutions over time. Also, the models were analyzed in two similar activities of applying makeup. The activities were taken from UCF101 video dataset to observe the behavior of the DCON under real-world conditions.

The improvement comes when the DCNNs are used with stride two (which are in the first block in layers 3-4-5) and when using the convolutions with stride one but in the last layers. In Table 14 and Table 15, compared with the original CNN, the parameters increment. In the cases with better accuracy, their quantity of Flops diminished during training and validation. In other words, the increase in model parameters is not equivalent to worse performance. If the DCONs help to increase the accuracy, extra parameters are used to find better representations. Also, using deformable convolutions combining stages tends to saturate the model and not give a good result.

With deeper ResNets, the accuracy showed different behavior. During Apply Makeup, the accuracy can be improved by applying the deformable convolution in layer three (only for ResNet 101) or in the layer five (for both depths) (Table 16 and Table 17). But, in Human2 the deformable convolution should be in the first layers (Table 16) or not be applied at all.

5. Discussion

Based on standard convolutions, DCNNs employ deformation to the sampling grid with learnable offsets and weights of sampling points. Standard convolution sampling position is limited to the traditional rectangular shape without adapting to the shape of an irregular object. In this study, we focused on studying how to use the DCON. First, on a small CNN model applied to image classification. After that, to a ResNet with different depths, extending the study to 3D-ResNet. From image classification to action recognition, we analyzed the feasibility of DCNNs. The implementation of DCONs applied in this study where tvdcn and Pytorch-Deformable-Convolution-v2. Bot implementations produce similar results.

In the small model, the highest accuracy was reached by replacing the last layer standard convolution with its deformable counterpart, where the Stage4, Stage2,4, and Stage3,4 configurations reached 0.96, while the vanilla model reached 0.87. During training, it was identified that when deformable convolution is employed in the last layers, the model can converge faster, as shown in Figure 10. The execution time is shorter when using the vanilla model, which reaches 0.33 min, while when combining the deformable in all stages, the execution time increases to 0.52 min. In the Stage 4 configuration, 0.35 min is consumed, which is the shortest time achieved when incorporating the deformable convolution into the small model.

When introducing the deformable convolution to the small model in the first stage, the computational cost is higher than the vanilla model, as the deformable convolution is introduced in deeper stages, the computational cost decreases. The lowest computational cost is obtained by combining stage 3,4, where 0.763 GFlops is achieved.

Based on the experiments in the small model, the validation accuracy that uses transformations is better when the model includes DCONs, denoting gained robustness in the model. Nonetheless, DCON operations are hyper-resource-thirsty; paying attention to its implementation will be a key to acquiring benefits.

The kernel with dimension 3x3 suits to be the optimal to use for deformable convolution. The accuracy decreases if the kernel size is reduced to size 1x1, because the receptive field displacement mechanism is nullified while increasing the kernel to size 5x5 does not present a significant improvement in accuracy. On the contrary, the computational cost increases.

When introducing deformable convolution in deeper models using ResNet architectures, we noticed that the behavior is similar to the small model, as the best accuracy results were generated by introducing deformable convolution in deeper stages. In ResNet-18 and ResNet-34, for all datasets, better accuracy results are achieved by combining two consecutive stages, conv4 and conv5, and by combining all stages.

Extending the research to video action recognition tasks using the 3D ResNet models, we noticed that the behavior is similar to that of their 2D counterparts but with some differences. The introduction of deformable convolution in the last layers helped to increase the accuracy. Nevertheless, the combination of consecutive stages in 3D ResNet models tends to get saturated.

The best accuracy results in all evaluated datasets were obtained in the smaller depth models, ResNet-18 and ResNet-34. Poor performance was observed in deeper models, such as ResNet-50 and ResNet-101 in both 2D and 3D, as the accuracy was lower than in smaller architectures, such as ResNet-18 and ResNet-34. We hypothesize that this drawback is caused by accumulating many deformable layers at very deep levels, where probably the bottleneck mechanism may contribute to the poor performance of these deeper architectures.

It is also observed that the depth of the network does not necessarily imply better representations (as indicated by [23]). Only a few blocks learn relevant information, while the other blocks and stages may just be confusing the network and decreasing its performance.

As deformable convolution is incorporated into the evaluated ResNet architectures, the training time increases. The highest training time using the stage-by-stage configuration is obtained when deformable convolution is incorporated in the conv1 stage; as deformable convolution is incorporated in deeper layers, the training time decreases. When incorporating deformable convolution at all stages, the training time exceeds the training time of the vanilla configuration by up to three times.

The computational cost required to execute the modified ResNet models with the deformable convolution measured in the quantity of Flops is lower than that of the vanilla models. The lowest number of Flops is achieved by combining all stages, while the worst case is when deformable convolution is incorporated in the conv2 stage, where the number of Flops is marginally lower than the vanilla configuration. DCNN helps to focus on significant information. Then, the quantity of Flops will decrease when the accuracy increases, regardless of whether the parameters increase. Therefore, their flexibility helps to focus the resources automatically.

We colected evidence that more layers of DCNNs do not necessarily lead to better results. The accumulation of deformable convolutional layers will slow down the network and may even saturate the network, preventing it from achieving any result. Then, before applying the DCNN to improve the model features maps, we suggest that the model uses a standard convolution layer.

6. Conclusions

The implementation of deformable convolution can help to improve the performance of a model, allowing the generalization of geometrical transformations such as scaling. As DCNNs alleviate geometric transformations, we encourage the readers to use DCNNs mainly if their resources are limited to work with data augmentation.

According to the obtained accuracy, training time, and the model performance results, it is optimal to introduce the deformable convolution in the last stages of the CNN since the training time and computational cost are lower than the ones obtained with vanilla models, and the accuracy is superior. When working with 3D-ResNets, the same trend can be observed. Nevertheless, we believe that the DCNN may lose its advantages with greater depth; therefore, more experiments are required.

In future work, we are seeking more experiments using DCNNs in the field of action recognition, which is a promising branch of computer vision where the application of deformable networks has not been explored as much. DCNNs improve the feature extraction capability and adapt to complex changes in the input, which is becoming a fundamental part of a recognition system. However, we propose to measure datasets quantitatively to evaluate the opportunities that deformable networks can offer for action recognition.

Author Contributions

Conceptualization, A.B.; methodology, A.B.; software, A.B. and V.R.; validation, A.B. and V.R.; formal analysis, A.B., V.R. and L.A.; investigation, A.B.;resources, A.B.; data curation, A.B.; writing—original draft preparation, A.B. and V.R.; writing—review and editing, A.B., V.R., L.A. and R.D.; visualization, A.B.; supervision, L.A.; Project administration, L.A.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by CONHACyT through a doctoral scholarship granted to Andrea Burgos Madrigal CVU 702730.

Data Availability Statement

The research data are open to Public by the authors themselves. Human2 is a dataset created by us and it is available, the reader is invited to contact the authors of this article to request it.

Acknowledgments

We are grateful for the resources provided by the supercomputer LNS "Laboratorio Nacional de Supercómputo del Sureste de México" to carry out part of this research.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:

DCNN	Deformable Convolutional Network
DCON	Deformable Convolution
Flops	Floating-type operations

References

Liu, Z.; Mao, H.; Wu, C.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2022, pp. 11966–11976.
Krichen, M. Convolutional Neural Networks: A Survey. Comput. 2023, 12, 151. [Google Scholar] [CrossRef]
Purwono, P.; Ma’arif, A.; Rahmaniar, W.; Fathurrahman, H.I.K.; Frisky, A.Z.K.; ul Haq, Q.M. Understanding of Convolutional Neural Network (CNN): A Review. International Journal of Robotics and Control Systems 2023. [CrossRef]
Younesi, A.; Ansari, M.; Fazli, M.; Ejlali, A.; Shafique, M.; Henkel, J. A Comprehensive Survey of Convolutions in Deep Learning: Applications, Challenges, and Future Trends. IEEE Access 2024, 12, 41180–41218. [Google Scholar] [CrossRef]
Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. Proceedings of the IEEE international conference on computer vision, 2017, pp. 764–773.
Ding, X.; Zhang, X.; Han, J.; Ding, G. Scaling up your kernels to 31x31: Revisiting large kernel design in cnns. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2022, pp. 11963–11975.
Wang, Z.; Bai, Y.; Zhou, Y.; Xie, C. Can CNNs Be More Robust Than Transformers? ArXiv 2022, abs/2206.03452. [Google Scholar] [CrossRef]
Chen, F.; Wu, F.; Xu, J.; Gao, G.; Ge, Q.; Jing, X.Y. Adaptive deformable convolutional network. Neurocomputing 2021, 453, 853–864. [Google Scholar]
Lai, S.C.; Tan, H.K.; Lau, P.Y. 3D deformable convolution for action classification in videos. International Workshop on Advanced Imaging Technology (IWAIT) 2021. SPIE, 2021, Vol. 11766, pp. 149–154.
Wang, W.; Dai, J.; Chen, Z.; Huang, Z.; Li, Z.; Zhu, X.; Hu, X.; Lu, T.; Lu, L.; Li, H.; others. Internimage: Exploring large-scale vision foundation models with deformable convolutions. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 14408–14419.
Araujo, A.; Norris, W.; Sim, J. Computing receptive fields of convolutional neural networks. Distill 2019, 4, e21. [Google Scholar] [CrossRef]
Zhu, X.; Hu, H.; Lin, S.; Dai, J. Deformable convnets v2: More deformable, better results. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 9308–9316.
Pominova, M.; Kondrateva, E.; Sharaev, M.; Pavlov, S.; Bernstein, A.V.; Burnaev, E. 3D Deformable Convolutions for MRI Classification. 2019 18th IEEE International Conference On Machine Learning And Applications (ICMLA) 2019, pp. 1710–1716. [CrossRef]
Hoang, T. tvdcn, 2023.
Kwon, Y. PyTorch-Deformable-Convolution-v2. https://github.com/developer0hye/PyTorch-Deformable-Convolution-v2, 2022.
He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2015, pp. 770–778.
Marsland, S.R. Machine Learning - An Algorithmic Perspective. Chapman and Hall/CRC machine learning and pattern recognition series, 2009. [CrossRef]
Cat and Dog, url = hhttps://www.kaggle.com/datasets/tongpython/cat-and-dog. Accessed: 2024-02.
Kiefer, R. Glaucoma Dataset: EyePACS-AIROGS-light-V2, 2024. [CrossRef]
Animals-10, url=https://www.kaggle.com/datasets/alessiocorrado99/animals10?rvi=1.Accessed:2024- 02.
Geometric Shapes Dataset, url= https://www.kaggle.com/datasets/dineshpiyasamara/geometric-shapes-dataset. Accessed: 2024-03.
Soomro, K.; Zamir, A.R.; Shah, M. UCF101: A dataset of 101 human actions classes from videos in the wild. arXiv preprint arXiv:1212.0402 2012. arXiv:1212.0402 2012.
Zagoruyko, S.; Komodakis, N. Wide residual networks. arXiv preprint arXiv:1605.07146. 2016; arXiv:1605.07146 2016. [Google Scholar]

Figure 1. Receptive field (represented in red). (a) Limited in standard convolution; (b) Irregular and expanded by

p_{k} + Δ p_{k}

displacement [13].

Figure 1. Receptive field (represented in red). (a) Limited in standard convolution; (b) Irregular and expanded by

p_{k} + Δ p_{k}

displacement [13].

Figure 2. Graphical description of the CNN small model implemented during the experiments of Section 4.1.

Figure 3. The ResNet model is shown on the left side. ResNet’s residual block types are the basic and bottleneck blocks, shown on the right side of the figure. C means the respective channel (derived from [16]).

Figure 4. Classes on Cats & Dogs, EyePACS, Spyders & Chickens, and Triangle & Square datasets, respectively. (a) Cat, (b) Dog; (c) NRG, (d) RG; (e) Spyder, (f) Chicken; (g)Triangle (h) Square.

Figure 5. Video class frames from UCF101 [22] and Human2, respectively: (a) Apply Eye Makeup, (b) Apply Lipstick; (c) Forward, (d) Turn left.

Figure 6. Image scale applied to validate models (from scale 1 to 1.6 in steps of 0.1). Cats & Dogs (a); Spyders & Chickens (b); EyePACS (c); Triangle & Square (d).

Figure 7. Comparison of accuracy with Vanilla (model base) and models applying the DCONs in different layers. DCONs are unsuitable for the first layer when features are still too simple. Especially if the Dataset contains complex features as Cats & Dogs, unlike Triangle & Square.

Figure 8. Comparison of the quantity of Flops (per batch) with Vanilla (base model) and applying the DCONs in different layers.

Figure 9. The figure overlaps the accuracy and the quantity of Flops to observe the best cases. We expect the accuracies to reach high values and the quantity of Flops to reach low ones.

Figure 10. DCNN vs. Vanilla during training (thin lines) and validation, without transformation (thin dotted lines), and with transformation(thick lines). (a) Spyders & Chickens (from Animal-10 dataset); (b) Cats & Dogs; (c) EyePACS; (d) Shapes.

Figure 11. Validation accuracies without transformation (blue) and with scale transformation (red) using different kernel sizes.

Table 1. The table shows the configurations that incorporate DCON into the model. Also, the number of parameters and the quantity of Flops (per batch) for each variation of DCON are listed (tvdcn implementation).

Config.	Total parameters	Training Flops	Validation Flops	Accuracy
Vanilla	394769	1.244 G	1.273 G	0.87
Stage1	395498	1.339 G	1.368 G	0.91
Stage2	398657	1.186 G	1.215 G	0.92
Stage3	402545	1.031 G	1.059 G	0.93
Stage4	410321	0.976 G	1.004 G	0.96
Stage1,2	399386	1.281 G	1.31 G	0.89
Stage1,3	403274	1.126 G	1.154 G	0.90
Stage2,3	406433	0.973 G	1.002 G	0.95
Stage2,4	414209	0.918 G	0.947 G	0.96
Stage3-4	418097	0.763 G	0.791 G	0.96

Table 2. The quantity of Flops (per image and batch) and parameters in Vanilla model and with DCNNs implemented with DCv2 and tvdcn.

	Flops per image	Flops per batch	Parameters DCv2	Parameters tvdcn
Vanilla	38.87 M	1.244 G	0.395 M	0.395 M
Stage1	41.84 M	1.339 G	0.395 M	0.395 M
Stage2	37.07 M	1.186 G	0.394 M	0.397 M
Stage3	32.21 M	1.031 G	0.384 M	0.403 M
Stage4	30.49 M	0.976 G	0.337 M	0.41 M
Stage3,4	23.83 M	0.763 G	0.326 M	0.418 M
Stage1,2,3,4	25.00 M	0.829 G	0.326 M	0.418 M

Table 3. Validation accuracies with scale transformation in the implementations DCv2 and tvdcn.

Config.	Datasets
	Cats & Dogs		EyePACS		Spyders & Chickens		Shapes
	Acc DCv2	Acc tdvcn	Acc DCv2	Acc tdvcn	Acc DCv2	Acc tdvcn	Acc DCv2	Acc tdvcn
Vanilla	0.73	0.70	0.73	0.73	0.86	0.84	0.91	0.87
Stage1	0.72	0.66	0.75	0.74	0.85	0.84	0.90	0.91
Stage2	0.74	0.67	0.76	0.77	0.86	0.89	0.91	0.92
Stage3	0.75	0.76	0.77	0.76	0.86	0.86	0.92	0.93
Stage4	0.75	0.71	0.76	0.76	0.86	0.82	0.90	0.96
Stage3,4	0.77	0.76	0.77	0.75	0.88	0.87	0.93	0.96
Stage1,2,3,4	0.77	0.80	0.77	0.67	0.87	0.87	0.93	0.78

Table 4. Time execution in image classification datasets.

Config.	Datasets
	Cats & Dogs	EyePACS	Spyders & Chickens	Shapes
	time(min)	time(min)	time(min)	time(min)
Vanilla	0.33	0.52	0.12	0.27
Stage1	0.41	0.6	0.17	0.33
Stage2	0.41	0.59	0.16	0.33
Stage3	0.37	0.55	0.15	0.31
Stage4	0.35	0.54	0.14	0.29
Stage3-4	0.39	0.58	0.15	0.32
Stage1-2-3-4	0.52	0.71	0.24	0.43

Table 5. DCNN parameters and the quantity of Flops (per batch) for the small model with different kernel sizes.

	Parameters			Training quantity of Flops			Validation quantity of Flops
	1x1	3x3	5x5	1x1	3x3	5x5	1x1	3x3	5x5
Vanilla	0.833 M	0.395 M	0.568 M	0.291 G	1.244 G	3.404 G	0.329 G	1.273 G	3.433 G
Stage2,3	0.833 M	0.406 M	0.658 M	0.181 G	0.973 G	4.956 G	0.218 G	1.002 G	4.985 G
Stage2,4	0.833 M	0.414 M	0.718 M	0.142 G	0.918 G	4.39 G	0.18 G	0.947 G	4.418 G
Stage3,4	0.833 M	0.418 M	0.748 M	0.125 G	0.763 G	3.19 G	0.162 G	0.791 G	3.218 G
Stage4	0.833 M	0.41 M	0.688 M	0.189 G	0.976 G	3.014 G	0.226 G	1.004 G	3.042 G

Table 6. Accuracy using ResNet-18 vanilla model and DCNN configurations.

Config.	Datasets
	Cats & Dogs	Spyders & Chickens	EyePACS	Shapes
Vanilla	0.756	0.907	0.772	0.936
Conv2	0.753	0.901	0.771	0.951
Conv3	0.794	0.904	0.772	0.929
Conv4	0.841	0.935	0.804	0.935
Conv5	0.785	0.931	0.773	0.949
Conv4,5	0.857	0.940	0.804	0.944
Conv2,3,4,5	0.869	0.934	0.830	0.942

Table 7. Accuracy using ResNet-34 vanilla model and DCNN configurations.

Config.	Datasets
	Cats & Dogs	Spyders & Chickens	EyePACS	Shapes
Vanilla	0.755	0.907	0.781	0.964
Conv2	0.770	0.912	0.785	0.968
Conv3	0.808	0.916	0.794	0.936
Conv4	0.852	0.932	0.836	0.934
Conv5	0.818	0.920	0.792	0.958
Conv4,5	0.842	0.935	0.817	0.967
Conv2,3,4,5	0.847	0.934	0.849	0.979

Table 8. Accuracy using ResNet-50 vanilla model and DCNN configurations.

Config.	Datasets
	Cats & Dogs	Spyders & Chickens	EyePACS	Shapes
Vanilla	0.725	0.897	0.787	0.727
Conv2	0.745	0.904	0.795	0.947
Conv3	0.769	0.916	0.808	0.949
Conv4	0.789	0.917	0.798	0.621
Conv5	0.764	0.908	0.804	0.970
Conv4,5	0.645	0.914	0.806	0.917
Conv2,3,4,5	0.688	0.932	0.666	0.513

Table 9. Accuracy using ResNet-101 vanilla model and DCNN configurations.

Config.	Datasets
	Cats & Dogs	Spyders & Chickens	EyePACS	Shapes
Vanilla	0.768	0.911	0.790	0.869
Conv2	0.768	0.919	0.795	0.871
Conv3	0.762	0.912	0.773	0.925
Conv4	0.788	0.917	0.816	0.585
Conv5	0.723	0.913	0.721	0.766
Conv4,5	0.682	0.920	0.652	0.934
Conv2,3,4,5	0.705	0.928	0.816	0.815

Table 10. Training time, Flops (per image), and parameters in ResNet-18 configurations.

Config.	Training Time in Datasets (min)
	Cats &	Spyders	EyePACS	Shapes	Flops	Parameters
	& Dogs	& Chickens
Vanilla	1.003	0.533	1.322	1.532	1.818 G	11.17 M
Conv2	1.570	0.883	1.930	2.550	1.551 G	11.23 M
Conv3	1.248	0.716	1.605	2.002	1.499 G	11.28 M
Conv4	1.122	0.644	1.467	1.754	1.456 G	11.39 M
Conv5	1.053	0.606	1.436	1.639	1.435 G	11.61 M
Conv4,5	1.197	0.701	1.532	1.931	1.073 G	11.83 M
Conv2,3,4,5	2.005	1.204	2.309	3.515	0.486 G	12.00 M

Table 11. Training time, Flops (per image), and parameters in ResNet-34 configurations.

Config.	Training Time in Datasets (min)
	Cats	Spyders	EyePACS	Shapes	Flops	Parameters
	& Dogs	& Chickens
Vanilla	1.346	0.639	1.407	1.713	3.670 G	21.28 M
Conv2	2.200	1.150	2.230	3.440	3.269 G	21.37 M
Conv3	1.873	0.982	1.974	2.854	2.986 G	21.51 M
Conv4	1.802	0.925	1.858	2.675	2.481 G	22.00 M
Conv5	1.488	0.715	1.527	2.039	3.068G	21.96 M
Conv4,5	1.885	1.035	1.986	2.954	1.879 G	22.68 M
Conv2,3,4,5	3.287	1.897	3.435	5.771	0.794 G	23.01 M

Table 12. Training time, Flops (per image), and in ResNet-50 configurations.

Config.	Training Time in Datasets (min)
	Cats	Spyders	EyePACS	Shapes	Flops	Parameters
	& Dogs	& Chickens
Vanilla	1.727	0.987	2.037	2.937	4.109 G	23.51 M
Conv2	2.120	1.26	2.500	3.780	3.908 G	23.55 M
Conv3	1.987	1.186	2.383	3.538	23.63 G	23.74 M
Conv4	1.951	1.168	2.307	3.435	3.488 G	23.88 M
Conv5	1.799	1.059	2.119	3.051	3.780 G	23.88 M
Conv4,5	2.013	1.238	2.350	3.551	3.160 G	24.25 M
Conv2,3,4,5	2.699	1.665	3.054	4.954	2.595 G	24.42 M

Table 13. Training time, Flops (per image), and parameters in ResNet-101 configurations.

Config.	Training Time in Datasets (min)
	Cats	Spyders	EyePACS	Shapes	Flops	Parameters
	& Dogs	& Chickens
Vanilla	2.462	1.399	2.586	4.188	7.831 G	42.50 M
Conv2	2.85	1.680	3.030	5.100	7.631 G	42.54 M
Conv3	2.707	1.604	2.900	4.820	7.467 G	42.62 M
Conv4	3.228	2.036	3.537	6.104	5.453 G	43.93 M
Conv5	2.496	1.426	2.629	4.302	7.503 G	42.87 M
Conv4,5	3.311	2.023	3.546	6.258	5.124 G	44.30 M
Conv2,3,4,5	4.055	2.489	4.281	7.628	4.559 G	44.47 M

Table 14. Parameters, the quantity of Flops, and Accuracy in ResNet-18. The number of parameters increases when using DCNNs but the number of Flops diminishes.

	Parameters	Training quantity	Apply Makeup	Human2
		of Flops	Accuracy	Accuracy
Vanilla	33.21 M	25.00 G	0.526	0.666
Str 1 Conv3	34.32 M	24.51 G	0.500	0.833
Str 1 Conv4	35.44 M	24.103 G	0.552	0.8333
Str 1 Conv5	37.68 M	24.20 G	0.487	1
Str 1 Conv4,5	39.92 M	23.25 G	0.395	0. 666
Str 1 Conv3,4,5	-	-	-	-
Str 1 Conv2,3,4,5	41.79 M	28.53 G	0.474	1
Str 2 Conv3,4,5	34.51 M	24.64 G	0.552	0.833

Table 15. Parameters, the quantity of Flops, and Accuracy in ResNet-34. The number of parameters increases when using DCNNs but the number of Flops diminishes.

	Parameters	Training quantity	Apply Makeup	Human2
		of Flops	Accuracy	Accuracy
Vanilla	63.52 M	38.19 G	0.368	0.833
Str 1 Conv3	66.127 M	36.992 G	0.5	0.5
Str 1 Conv4	71.726 M	34.884 G	0.4737	0.5
Str 1 Conv5	70.98 M	36.85 G	0.513	0.833
Str 1 Conv4,5	79.19 M	33.54 G	0.421	0.666
Str 1 Conv3,4,5	-	-	-	-
Str 1 Conv2,3,4,5	-	-	-	-
Str 2 Conv4,5	82.92 M	40.99 G	0.487	0.666

Table 16. Total parameters, the quantity of Flops, and Accuracy for ResNet-50. With Stride 1 the parameters and the quantity of Flops are not improving.

	Parameters	Training quantity	Apply Makeup	Human2
		of Flops	Accuracy	Accuracy
Vanilla	46.20 M	30.46 G	0.513	0.833
Str 1 Conv3	47.32 M	29.97 G	0.474	1
Str 1 Conv4	49.94 M	28.96 G	0.474	0.833
Str 1 Conv5	49.19 M	29.92 G	0.618	0.500
Str 1 Conv4,5	52.92 M	28.42 G	0.566	0.666
Str 1 Con3,4,5	-	-	-	-
Str 1 Conv2,3,4,5	54.60 M	32.22 G	0.421	0.500
Str 2 Conv3,4,5	48.82 M	29.73 G	0.500	0.333

Table 17. Parameters, the quantity of Flops, and Accuracy in ResNet-101.

	Parameters	Training quantity	Apply Makeup	Human2
		of Flops	Accuracy	Accuracy
Vanilla	85.249 M	41.962 G	0.355	0.833
Str 1 Conv3	86.37 M	41.48 G	0.697	0.666
Str 1 Conv4	102 M	35.35 G	0.421	0.5
Str 1 Conv5	88.24 M	41.43 G	0.605	0.666
Str 1 Conv4,5	-	-	-	-
Str 1 Conv3,4,5			-	-
Str 2 Conv3,4,5	87.862 M	41.231 G	0.592	0.5
Str 2 Conv4,5	87.489 M	41.394 G	0.474	0.666

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Evaluation of Deformable Convolution: An Investigation In Image And Video Classification

Abstract

1. Introduction

2. Materials and Methods

2.1. Standard Convolution (Used in the CNN)

2.2. Deformable Convolutional Network (DCNN)

2.3. Models Tested

2.3.1. Small Model

2.3.2. ResNet

2.4. Metrics

2.5. Image Datasets

2.6. Video Datasets

2.7. DCON in ResNet Models

3. Methodology

4. Results

4.1. Small Model Analysis

4.1.1. Performance

4.1.2. Kernels

4.2. DCNN in ResNet Models for Image Classification

4.2.1. Accuracy Test

4.2.2. Training Time and the Quantity of Flops

4.3. DCNN’s through Time Dimension

5. Discussion

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe