Research on Visual/Ins Integrated Navigation Technology Based on FGO

Preprint

Article

Research on Visual/Ins Integrated Navigation Technology Based on FGO

Altmetrics

Downloads

Views

Comments

Xun Cheng^*,

Yu Wang

Xun Cheng^*,

Yu Wang

This version is not peer-reviewed

Submitted:

31 May 2024

Posted:

31 May 2024

You are already at the latest version

Alerts

Abstract

In order to make full use of the complementarity of existing navigation systems to improve the navigation and positioning accuracy, this paper investigates the visual/INS integrated navigation system based on the factor graph optimization (FGO) algorithm. In the traditional visual/INS integrated navigation system, there is often the problem of image blurring due to the rapid change of light and shadow captured by the vision sensor and the attitude change of the carrier, which leads to the decrease of the positioning accuracy of the combined navigation system. Therefore, this paper firstly introduces Retinex algorithm and BID algorithm to carry out the design of image de-blurring method; then implements the visual/INS integrated navigation algorithm based on the factor graph optimization method; finally, the experimental scheme is designed, comparative experiments are carried out, and the researched method is verified by using the public dataset. The experimental results show that the combined navigation algorithm realized in this paper has high accuracy, and its positioning accuracy is improved by 40% compared with visual positioning.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Since the navigation and positioning information is the basic information to realize the functions of control, obstacle avoidance, path planning, the research on navigation and positioning system has become a research hotspot in the field of unmanned vehicle. Users' demands for navigation and positioning systems are mainly: high accuracy, high reliability, high real-time and high availability. Currently, there are three main types of navigation and positioning systems: 1) Global Navigation Satellite System (GNSS), which has high positioning accuracy, stable error, and can provide continuous real-time high-precision positioning information in the outdoor open area, but it is easily affected by the environmental impacts such as building obstruction and wall reflections; 2) Inertial Navigation System (INS), which has good anti-interference ability, high short-term accuracy, but the error accumulation is fast; 3) visual navigation and positioning system, which can provide rich environmental information and can directly estimate the position, but is easily affected by environmental interference. Because of the limitations of the above navigation systems, multi-sensor fusion localization technology came into being [1].

Multi-sensor fusion localization refers to synthesizing information from different sensors describing a certain target or environmental feature to achieve high-precision localization. This technique can overcome the limitations of using single sensor information for positioning, make full use of the complementary nature of each information source, and continuously and robustly output high-precision navigation information. The more mature data fusion algorithms can be summarized as filter-based methods and optimization-based methods [2,3]. Data fusion based on filtering commonly used Extended Kalman Filter (EKF), the method in the Jacobian matrix linearization stage, only retains the Taylor series first-order information, can not make full use of the historical information and the EKF storage and the state volume is the relationship between the square growth, is not suitable for large-scale scenarios [4] . Optimization-based methods use IMU data and image measurements to jointly minimize the residuals to obtain the optimal estimate, and jointly optimize the information of all moments of the system to make the system's position estimation more accurate. [5]. Compared with the filter-based method, this method has stronger robustness and higher positioning accuracy. It is able to improve navigation accuracy by iteratively reducing the linearization error and using all historical information for optimization.

Compared with GNSS, INS and visual sensors have the advantages of small size, light weight and low power consumption. [6] In this paper, a stereo camera is chosen as the visual sensor, and the visual/INS integrated navigation technology is investigated by using the factor graph optimization method.

2. Visual/INS Integrated Navigation Algorithmic Scheme Design

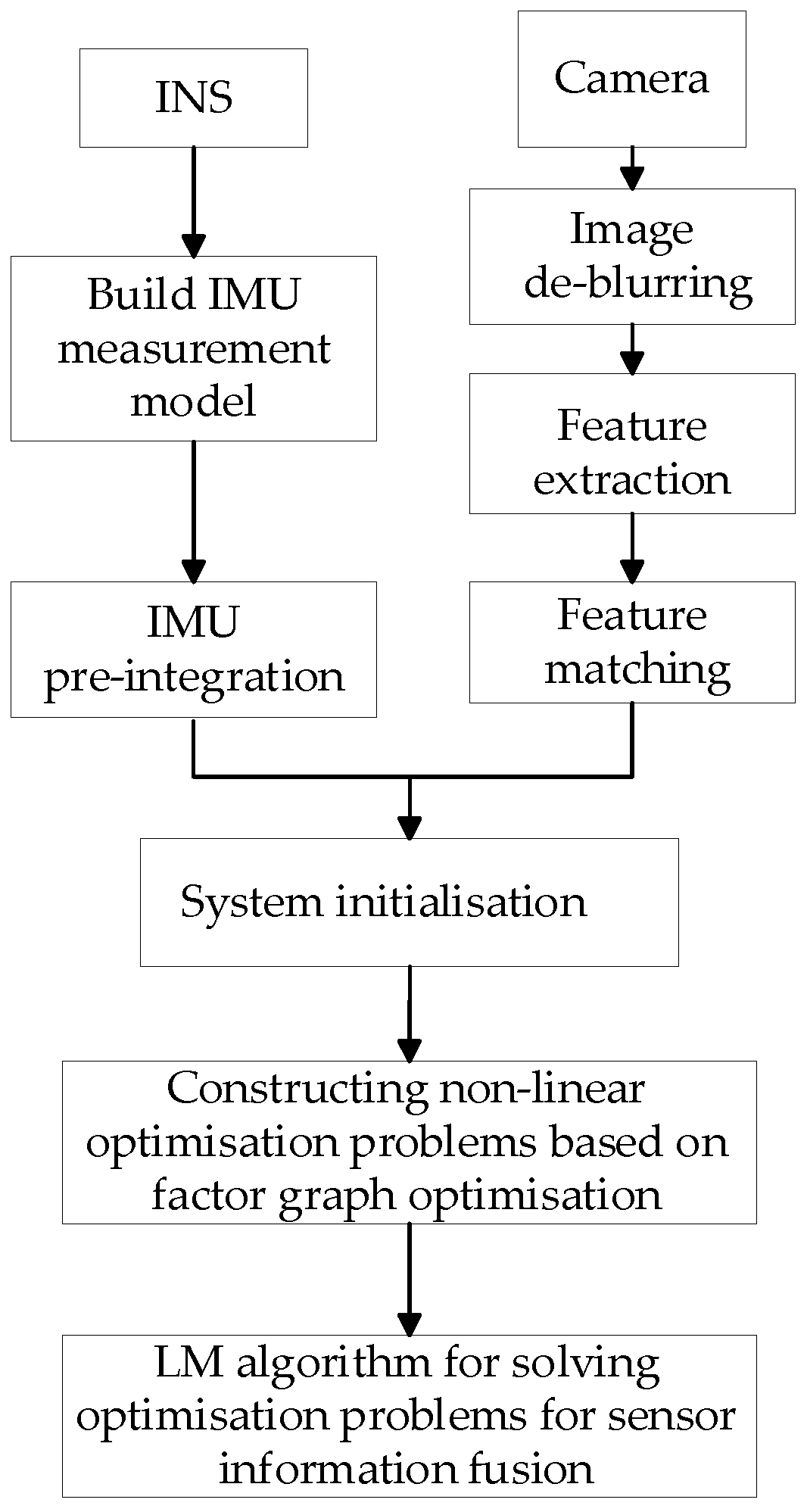
The visual/INS integrated navigation system is divided into two threads: front-end and back-end. The front-end thread focuses on camera and INS data pre-processing and initialization of the combined navigation system. The data preprocessing includes: image deblurring, feature point extraction, matching and tracking, and IMU pre-integration. The back-end thread uses graph optimization to implement camera and INS data fusion. The multi-sensor localization problem is constructed as an optimization problem, which first determines the state variables to be optimized; then constructs the objective function of the factor graph, which consists of the sum of the squares of several error terms. To obtain the optimal value of the state variables, the sum of squares of the errors must be minimized, so the nature of this optimization problem is a nonlinear least-squares problem [7] The nature of this optimization problem is therefore a nonlinear least squares problem. In this paper, the objective function is minimized by the Levenberg-Marquardt (LM) method, in which the carrier motion state with the smallest error values in a certain gradient range can be obtained, which is regarded as the accurate position information output by the visual/INS integrated navigation algorithm system. The overall scheme of this paper is shown in Figure 1.

3. Visual/INS Integrated Navigation Algorithmic Front-end Algorithm

The rapid change of the image captured by the camera and the change of the vehicle's attitude will lead to the phenomenon of blurring of the image, which makes the key information missing and thus affects the accuracy of the navigation calculations. Therefore, image de-blurring algorithms are one of the key techniques in the research of visual/INS integrated navigation. Image de-blurring algorithms can be divided into blind deconvolution (BID) and non-blind deconvolution (NBID) [8]. The NBID algorithm can only be used in the case when the blur kernel is known,since the visual image used in this paper belongs to the case where the blur kernel is unknown, the BID algorithm is used to process the blurred images. Aiming at the traditional BID algorithm has the problem of large computation, this paper proposes Retinex combined with BID image de-blurring algorithm. The Retinex algorithm is an image enhancement algorithm based on the theory of color consistency. Through Retinex [9]algorithm the original blurred image can be processed to get the image with enhanced edge information.

The motion blur is modeled as Equation (1):

R = K * L + N

(1)

Where R represents the motion blur image obtained after processing by Retinex algorithm, K denotes the motion blur kernel, L represents the clear image after deblurring, and N represents the unknown noise.

Image recovery is estimated to be:

L^{'} = \arg \min_{L} {‖ R - K * L ‖ + ρ_{L} (L)}

(2)

where

‖ R - K * L ‖

is fitted to the data using the

L_{2}

norm criterion, and for the vector

\vec{x} (x_{1}, ..., x_{n})

, the

L_{2}

norm is defined as:

‖ \vec{x} ‖ = \sqrt{x_{1}^{2} + ... + x_{n}^{2}}

;

ρ_{L}

represents the regularization term.

The recovered image is first processed by simple Gaussian deconvolution to obtain an initial estimate L of the recovered image, and then image filtering is used to recover the sharp edges of the blurred image from L and suppress the noise in the smoothed region to obtain an improved estimate of the recovered image

L^{'}

For simple deconvolution, given an estimated blur kernel K, the recovered image L can be estimated based on the input R and K. The following energy function is used:

f_{L} (L) = {\sum_{\partial_{*}} ω_{*} ‖ K * \partial_{*} L - \partial_{*} R ‖}^{2} + α {‖ \nabla L ‖}^{2}

(3)

where

ω_{*} \in {ω_{0}, ω_{1}, ω_{2}}

denotes the weight of each partial derivative

\partial_{*}

and

\partial_{*} \in {\partial_{0}, \partial_{x}, \partial_{y}, \partial_{x x}, \partial_{x y}, \partial_{y y}}

α

denotes the weight of the regularization term

{‖ \nabla L ‖}^{2}

Calculate the gradient mapping

{P_{x}^{R}, P_{y}^{R}}

of the recovered image

L^{'}

, eliminate the excess noise in the recovered image and optimize the estimation of the image blur kernel for motion blur using the gradient mapping. Minimize the energy function:

f_{K} (K) = {\sum_{(P_{*}^{R}, R_{*})} ω_{*} ‖ K * P_{*}^{R} - R_{*} ‖}^{2} + β {‖ \nabla L ‖}^{2}

(4)

where

ω_{*}

is the weight of each partial derivative,

β

is the Tikhonov regularization weight, and

(P_{*}^{R}, R_{*})

satisfies.

(P_{*}^{R}, R_{*}) \in {\begin{cases} (P_{x}^{R}, \partial_{x} R), (P_{y}^{R}, \partial_{y} R) ， \\ (\partial_{x} P_{x}^{R}, \partial_{x x} R), (\partial_{y} P_{y}^{R}, \partial_{y y} R), \\ ((\partial_{x} P_{x}^{R} + \partial_{y} P_{x}^{R}) / 2, \partial_{x y} R) \end{cases}}

(5)

The

f_{K} (K)

is converted into the form of a matrix and minimized using the conjugate gradient method, and finally the gradient formula can be obtained, and The gradient formula is then solved quickly using the Fast Fourier Transform (FFT) method to obtain an estimate of the blur kernel. If the current blur kernel estimation is the optimal estimation then the best blur kernel estimation K is utilized to perform the final deconvolution operation with the original blurred image B to obtain the final clear recovered image. Otherwise, iterative alternating optimization is used to repeat the estimation using the estimated motion blur kernel with the clear recovered image until the best blur kernel estimate is obtained.

After image deblurring, this paper selects extracting ORB feature points to complete the matching relationship between neighboring images. The feature point extraction part selects the FAST corner point [10] with high real-time performance for feature extraction. After that, the fast library for approximate nearest neighbors (FLANN) algorithm is used for feature matching [11]. And random sampling consensus (RANSAC) algorithm is used to eliminate the false matching of FLANN algorithm.

Since the sampling frequency of the IMU is much higher than that of the camera, it is necessary to integrate the IMU measurements between two consecutive image frames to calculate position, velocity and rotation. Alignment of IMU and camera sampling frequencies is realized.

The IMU pre-integration model is derived to reduce the amount of operations in the integration process and to meet the real-time requirements of the combined navigation system. The measurement errors of the IMU mainly include Gaussian white noise and bias [12]. Consider the random wandering of bias and its noise [13] the acceleration measurements

{\hat{a}}_{t}^{b}

and angular velocity measurements

{\hat{ω}}_{t}^{b}

of the IMU are modeled as follows:

{\hat{a}}_{t}^{b} = a_{t}^{b} + R_{b w} g^{w} + b_{a_{t}} + n_{a}

(6)

{\hat{ω}}_{t}^{b} = ω_{t}^{b} + b_{ω_{t}} + n_{ω}

(7)

In this paper, the East-North-Up (ENU) coordinate system is chosen as the world coordinate system. In Equation (6) and Equation(7),

R_{b w}

is the rotation matrix from the world coordinate system to the IMU coordinate system;

g^{w} = {[0, 0, g]}^{T}

is the gravity vector in the world coordinate system;

b_{a_{t}}

and

n_{a}

are the bias and noise of the acceleration;

b_{ω_{t}}

and

n_{ω}

are the bias and noise of the angular velocity, respectively. Assume that

n_{a} \sim N (0, σ_{a}^{2})

n_{ω} \sim N (0, σ_{ω}^{2})

;

b_{a_{t}}

b_{ω_{t}}

are bounded random walks and random walks, respectively [14].

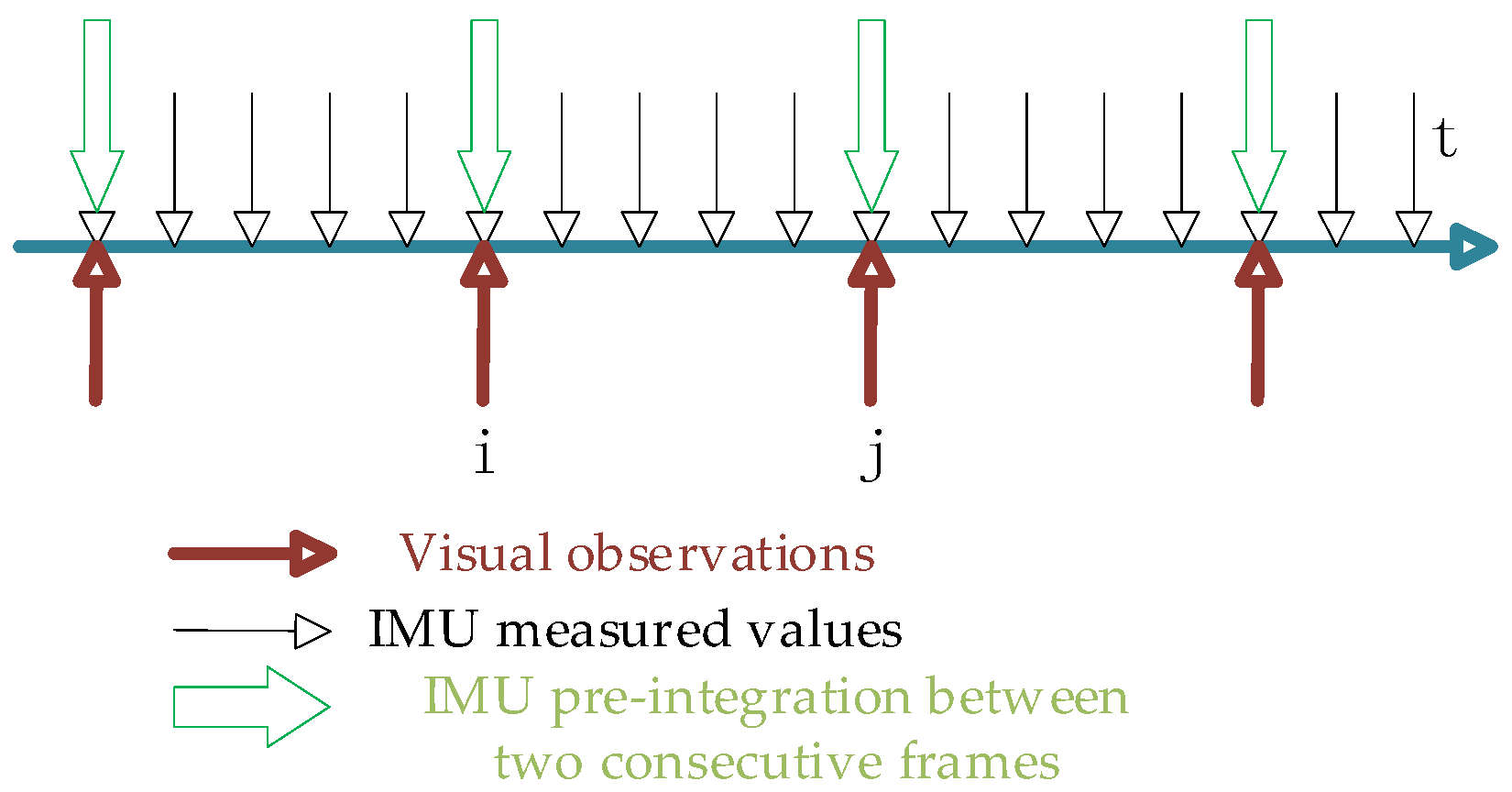
To align the sampling frequencies of the IMU and the camera, the IMU measurements between two consecutive image frames are integrated. The IMU pre-integration schematic is shown in Figure 2.

IMU pre-integration term for frame

i

and frame

i + 1

{\hat{α}}_{b_{k} b_{i + 1}} \approx {\hat{α}}_{b_{k} b_{i}} + {\hat{β}}_{b_{k} b_{i}} δ t + \frac{1}{2} a_{i} δ t^{2}

(8)

{\hat{β}}_{b_{k} b_{i + 1}} \approx {\hat{β}}_{b_{k} b_{i}} + a_{i} δ t

(9)

{\hat{γ}}_{b_{k} b_{i + 1}} \approx {\hat{γ}}_{b_{k} b_{i}} \otimes [\begin{matrix} 1 \\ \frac{1}{2} ω_{i} δ t \end{matrix}]

(10)

where

{\hat{α}}_{b_{k} b_{i + 1}}

{\hat{β}}_{b_{k} b_{i + 1}}

and

{\hat{γ}}_{b_{k} b_{i + 1}}

denote position, velocity and rotation pre-integration respectively.

δ t

is the time interval between the IMU measurements at

i

moments and

i + 1

moments, for acceleration and angular velocity in the above equation:

a_{i} = \frac{1}{2} [\begin{array}{l} R_{b_{k} b_{i}} ({\hat{a}}_{i}^{b} - b_{a_{i}} + n_{a}^{b_{i}}) + \\ R_{b_{k} b_{i + 1}} ({\hat{a}}_{i + 1}^{b} - b_{a_{i + 1}} + n_{a}^{b_{i + 1}}) \end{array}]

(11)

ω_{i} = \frac{1}{2} ({\hat{ω}}^{b_{i}} + n_{ω}^{b_{i}} + {\hat{ω}}^{b_{i + 1}} + n_{ω}^{b_{i + 1}}) - b_{ω_{i}}

(12)

Alignment of IMU and camera sampling frequencies can be accomplished by the above.

4. Visual/INS Integrated Navigation Back-end Algorithms

Based on the front-end work of visual/INS integrated navigation, this section explores the backend fusion algorithm for the visual/INS integrated navigation system. The fusion method based on factor graph optimization is adopted, framing the pose estimation problem of combined navigation as a nonlinear optimization problem. Compared with the traditional bundle adjustment (BA) and pose graph optimization methods, the factor graph optimization can improve the computational efficiency and the real-time performance of the system.

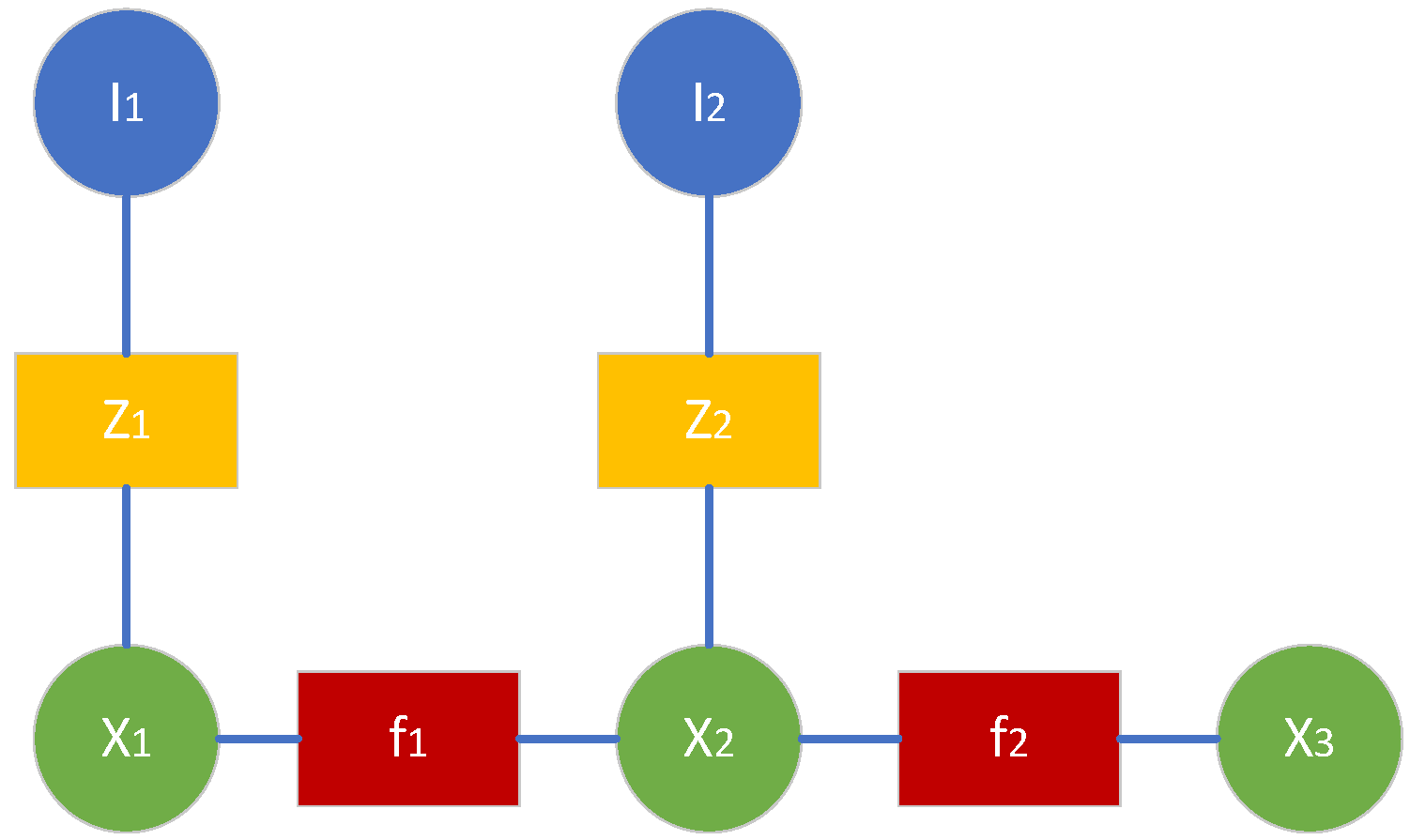
A factor graph is transformed from a Bayesian network and is an undirected graph consisting of two types of nodes: circles represent optimization variable nodes and squares represent factor nodes. The variable nodes are the parts to be optimized, including camera poses

x_{1}

x_{2}

and landmarks

l_{1}

l_{2}

.The edges of the factors represent the relationship between the variable nodes to be optimized, given based on the equations of motion and observation equations. It is shown in Figure 3.

The combined navigation equations of motion and observation equations are first constructed as in Equation (13):

{\begin{cases} x_{k} = f (x_{k - 1}, u_{k}) + ω_{k} \\ z_{k} = h (x_{k}) + v_{k, j} \end{cases}

(13)

Where,

ω_{k}

denotes the input noise of the sensor at moment k;

v_{k, j}

re denotes the observation noise when the sensor observes the corresponding landmark at time k.

ω_{k} \sim N (0, R_{k})

v_{k, j} \sim N (0, Q_{k, j})

R_{k}

and

Q_{k, j}

are the covariance matrices.

All state variables to be o ptimized at moment K are :

X = [x_{0}, x_{1}, ... x_{n}, p_{b c}, q_{b c}, P_{0}^{w}, P_{1}^{w}, ... P_{m}^{w}]

(14)

x_{k} = [p_{w b_{k}}, v_{b_{k}}^{w}, q_{w b_{k}}, b_{a}, b_{ω}]

(15)

Among them,

p_{w b_{k}}

q_{w b_{k}}

and

v_{b_{k}}^{w}

denote the position, rotational quaternion and velocity of the IMU in the world coordinate system at time k, respectively;

b_{a}

and

b_{ω}

denote the bias of the accelerometer and gyroscope of the IMU, respectively;

p_{b c}

q_{b c}

denote the translation and rotation quaternions from the camera coordinate system to the IMU coordinate system, respectively;

P_{m}^{w}

denotes the inverse depth of the waypoint.

Solving the current state distribution based on probability estimation leads to Equation (16).

P (x_{k} | x_{0}, u_{1 : k}, z_{1 : k}) \propto P (z_{k} | x_{k}) P (x_{k} | x_{0}, u_{1 : k}, z_{1 : k - 1})

(16)

where

P (z_{k} | x_{k})

denotes the likelihood and

P (x_{k} | x_{0}, u_{1 : k}, z_{1 : k - 1})

is the prior.

Optimization of the factor graph is to adjust the values of each variable to maximize the factor product, thus maximizing the overall posteriori probability. In this paper, the position of the vehicle to be estimated is taken as the nodes of the factor graph, and the observation model and the motion model are taken as the edges of the factor graph.

Record the error in the sensor observation as:

e_{k} = z_{k, j} - h (x_{k})

(17)

The observations in Equation (17)

z_{k}

are known and the objective function for factor graph optimization can be expressed as Equation (18).

\min_{x} F (x) = \sum_{k = 1}^{n} e_{k} {(x_{k})}^{T} Ω_{k} e_{k} (x_{k})

(18)

where

Ω_{k}

denotes the information matrix, representing the weight of each error. Equation (18) is equivalent to minimizing the squareed error, and the errors existing in the algorithm mainly include IMU measurement errors and camera reprojection errors. Therefore, the objective function of this paper can be expressed as Equation (19).

Z = \min [\sum {‖ E_{i m u} ‖}^{2} + \sum_{i = 1}^{N} {‖ E_{c a m} ‖}^{2}]

(19)

where

E_{i m u}

denotes the observation error of the IMU and

E_{c a m}

denotes the reprojection error of the camera. N denotes the number of feature points in the objective function.

E_{i m u} = [\begin{matrix} \bar{δ α_{b_{k} b_{k + 1}}} \\ δ β_{b_{k} b_{k + 1}} \\ δ θ_{b_{k} b_{k + 1}} \\ δ b_{a} \\ δ b_{g} \end{matrix}] = [\begin{matrix} \bar{R_{b_{k} w} (p_{w b_{k + 1}} - p_{w b_{k}} - v_{b_{k}}^{w} Δ t_{k} + \frac{1}{2} g^{w} Δ {t_{k}}^{2})} \\ R_{b_{k} w} (v_{b_{k + 1}}^{w} - v_{b_{k}}^{w} + g^{w} Δ t_{k}) \\ 2 {[q^{ω - 1} q_{b_{k + 1}}^{ω} {({\hat{γ}}_{b_{k + 1}}^{b_{k}})}^{- 1}]}_{x y z} \\ b_{a_{b_{k + 1}}} - b_{a_{b_{k}}} \\ b_{ω_{b_{k + 1}}} - b_{ω_{b_{k}}} \end{matrix}]

(20)

where

δ θ_{b_{k} b_{k + 1}}

denotes the three-dimensional error state vector of the quaternion and

{[\cdot]}_{x y z}

denotes the vector portion extracted from the quaternion to represent the error state vector.

E_{c a m} = [\begin{matrix} e_{k, i}^{l} \\ e_{k, i}^{r} \end{matrix}] = [\begin{matrix} p_{k, i}^{l} - h (R_{k, k - 1} R_{k - 1, i} + t_{k, k - 1}) \\ p_{k, i}^{r} - h (R_{k, k - 1} R_{k - 1, i} + t_{k, k - 1}) \end{matrix}]

(21)

The LM method is used to solve the factor graph optimization problem. Firstly, given an a state initial value, an increment is obtained by solving the regular equations, and the current state is continuously updated while the iteration step size of the state variable is adaptively adjusted by adding a damping factor, so that the objective function keeps getting smaller and smaller until the iteration reaches the termination condition.

The back-end fusion algorithm of the combined navigation in this paper first constructs a graph with state variables and constraints, then continuously adjusts the values of factor graph vertices to satisfy edge constraints as much as possible, thereby minimizing error terms and obtaining the optimal estimate, thus improving the accuracy of combined navigation positioning.

5. Experimental Verification

5.1 Image De-blurring Algorithm Validation

In order to verify the effectiveness of the image de-blurring algorithm proposed in this paper, three sets of images were selected from different public datasets for image de-blurring. Evaluation was conducted based on de-blurring results before and after image processing, image standard deviation, average gradient of the images, and feature point extraction and matching.

The comparison of de-blurring effect is shown in Figure 4, Figure 5 and Figure 6.

Using image standard deviation and average gradient to evaluate image quality is a common practice. Standard deviation and average gradient are commonly used indicators to verify image quality. Among them: the standard deviation reflects the degree of dispersion of the image pixel values from the mean value, the larger the standard deviation indicates the better the quality of the image; the average gradient reflects the clarity of the image and the texture changes, the larger the average gradient indicates the clearer the image is [15]. Calculate the standard deviation and average gradient of each group of image original and processed by algorithm as shown in Table 1 and Table 2.

As can be seen from Table 1, the standard deviation of the three groups of images after de-blurring is greater than the standard deviation before de-blurring, indicating that the image de-blurring algorithm proposed in this paper has a better de-blurring ability.

As can be seen from Table 2, the average gradient of the three groups of images after de-blurring is larger than the average gradient before de-blurring, indicating that the clarity of the images processed by the image de-blurring algorithm proposed in this paper has been improved.

Table 3 and table 4 give the matching and time required for extracting and matching the ORB feature points of the original images and the three groups of images processed by the proposed algorithm in this paper, and Fig. 7 shows the feature matching interface before and after de-blurring the first group of images visualized by OpenCV [16].

Figure 7. The feature matching of the first group of images before and after de-blurring(a)Image feature matching before de-blurring;(b)Image feature matching after de-blurring.From the results of feature extraction and matching, it can be observed that the logarithm of feature matching pairs and the time required for feature matching after deblurring three sets of images are smaller than before deblurring. This indicates that the image deblurring algorithm proposed in this paper can effectively improve the efficiency and accuracy of feature matching.

5.2. Validation of Visual/INS Integrated Navigation Algorithm Performance

To validate the positioning accuracy of the visual/INS integrated navigation based on factor graph optimization proposed in this paper, simulation experiments are conducted using open source datasets.

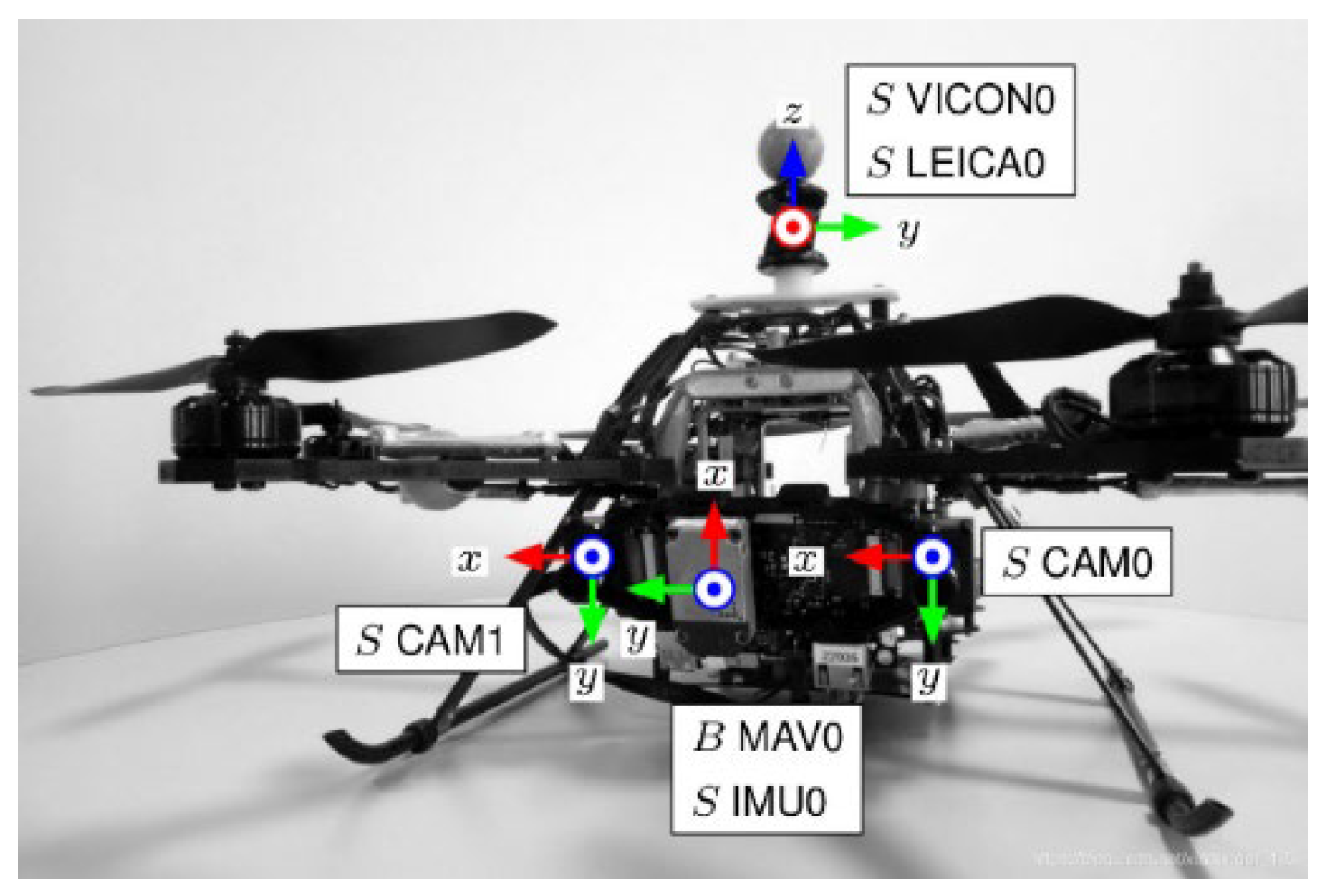
The dataset used in this paper is the EuRoC MAV dataset, which is collected from an AscTec Firefly UAV equipped with a stereo camera and an IMU. The camera model is MT9V034 with a frame rate of 20 Hz, and the IMU model is ADIS16448 with a frame rate of 200 Hz. The motion trajectory of the UAV was measured using a total station and motion capture system, with positioning accuracy at the sub-millimeter level, serving as ground truth for evaluating the positioning accuracy of the system proposed in this paper. The MH_01 dataset with rich texture was selected for validation. The physical diagram of the data collection platform is shown in Figure 8.

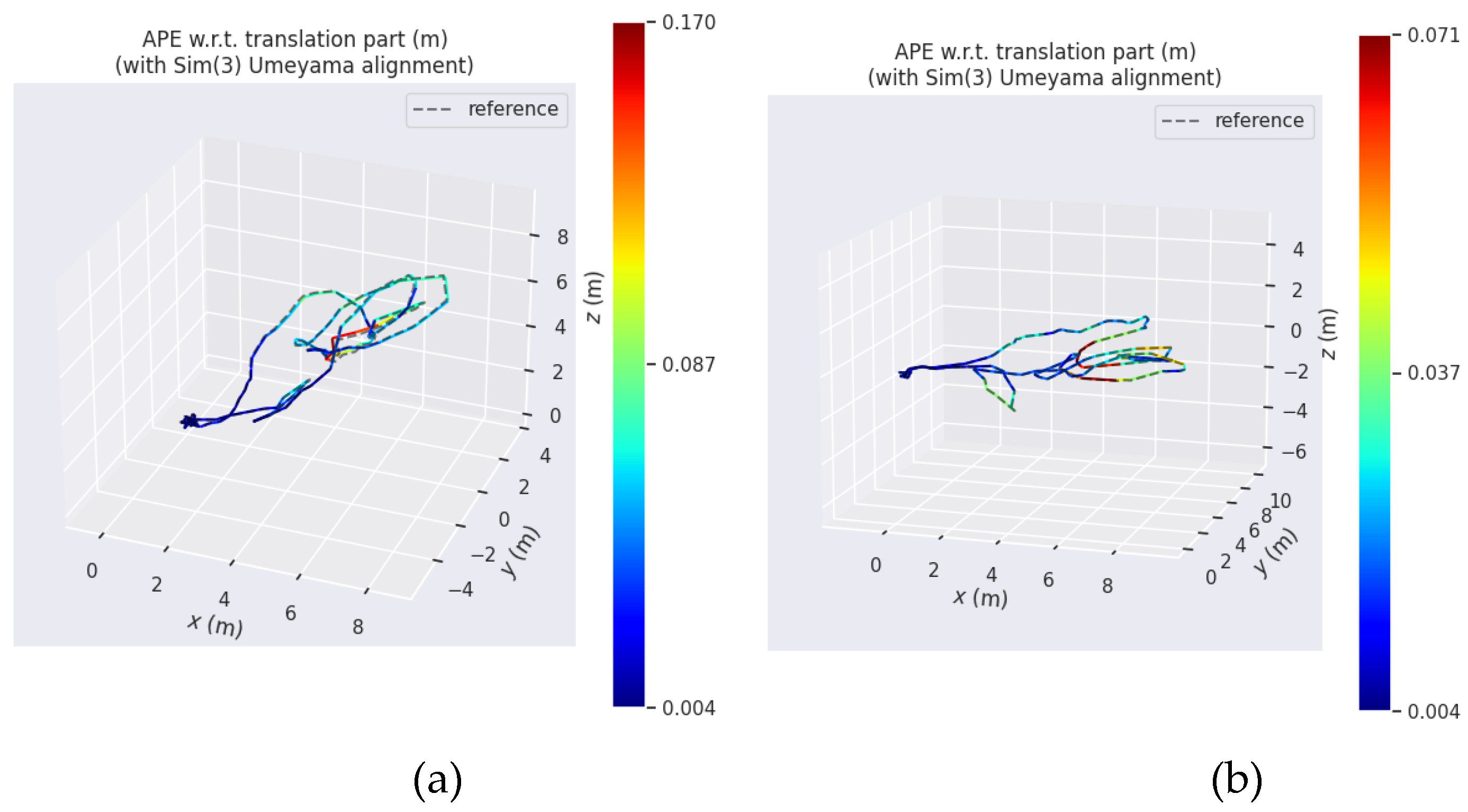
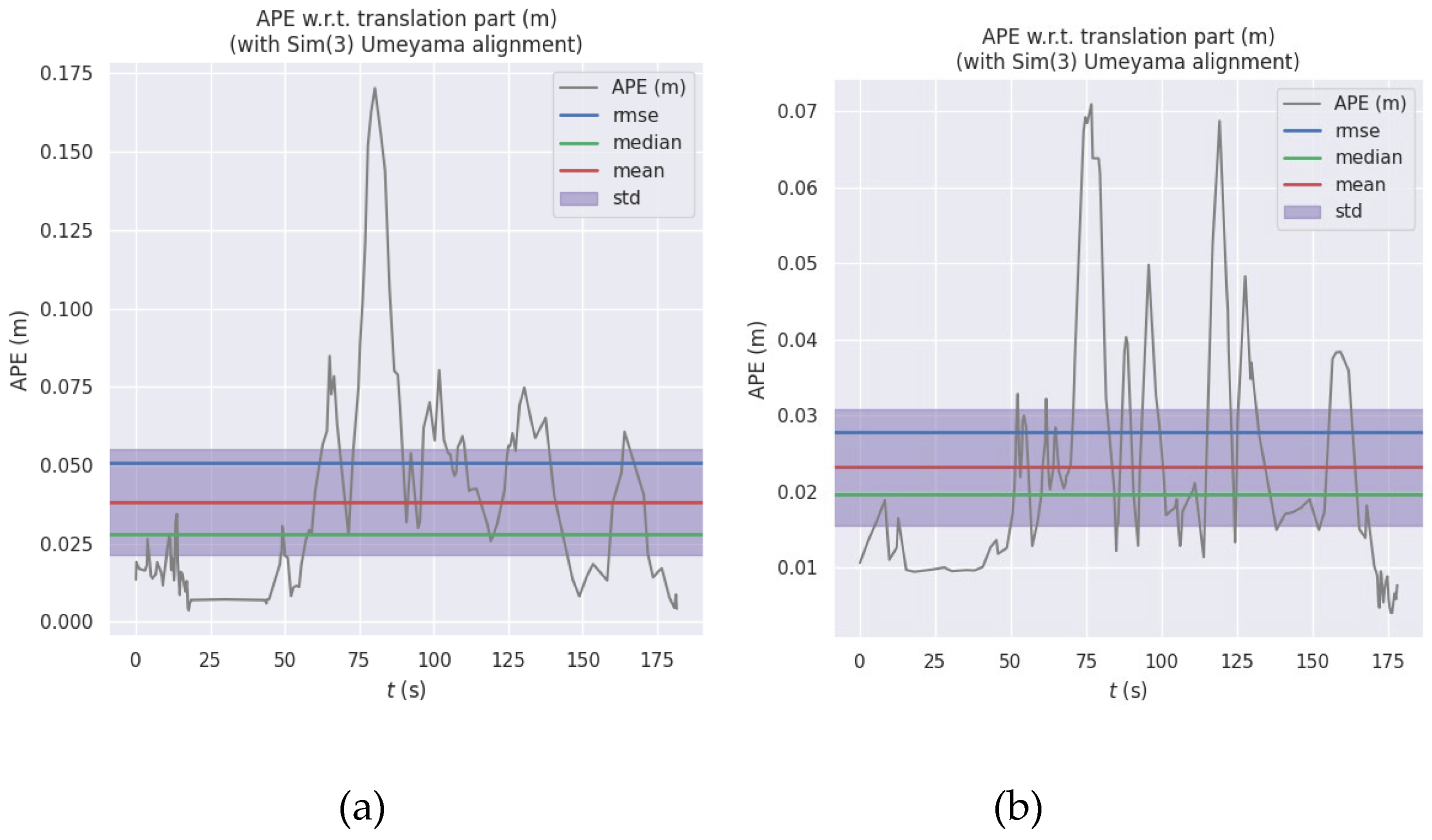
The single visual localization algorithm and the visual/INS integrated localization algorithm were run on the above data sequences to analyze the localization effect of each algorithm. The comparison graph of its localization results with the true value trajectory is shown in Figure 9.

From Figure 9 and Table 5, it can be seen that the algorithm in this paper can accurately track the estimated trajectory truth value, and its average absolute position error is about 0.02m, which is about 40% higher than that of the single visual navigation; the root mean square error is about 0.02m, which is about 45% higher than that of the single visual navigation; and the maximum error is not exceeded by 0.08m. In conclusion, the visual/INS integrated localization system designed in this paper can effectively tracking the carrier position state, and has higher positioning accuracy and higher robustness than the single vision localization system.

6. Conclusions

In order to overcome the limitations of single navigation system positioning and better meet the user's demand for positioning accuracy, this paper designs a vision/INS integrated navigation algorithm based on factor graph optimization. Firstly, to address the problem of decreased positioning accuracy of combined navigation due to image blurring in traditional visual/INS integrated navigation, the Retinex algorithm combined with the BID algorithm is used to de-blur the image; then, by deriving the objective function of the factor graph optimization, the nonlinear optimization problem is transformed into a least-squares problem and the LM algorithm is used to obtain the minimum error with multiple iterations, so as to realize the optimization of combined visual/INS navigation algorithm based on factor graph optimization, which results in the optimal navigation accuracy. of the vision/INS integrated navigation algorithm to optimize the navigation accuracy. Finally, experimental validation is carried out using public datasets, and the results show that the vision/INS integrated navigation algorithm designed in this paper improves the positioning accuracy by about 40% compared with the single vision algorithm, and has high accuracy and robustness.

Author Contributions

Conceptualization, X.C. and Y.W.; methodology, X.C.; software, X.C.; validation, X.C., Y.W.; formal analysis, X.C.; investigation, X.C.; resources, Y.W.; data curation, X.C.; writing—original draft preparation, X.C; writing—review and editing, Y.W.; visualization, X.C.; supervision, Y.W. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The data presented in this study are available on request from the

Conflicts of Interest

The authors declare no conflicts of interest.

References

Dingjie Wang.Research on dynamic initial alignment and real-time information fusion method of GNSS/MIMU combined navigation system [D]. National University of Defense Technology,2013.
QI Nai-Xin,ZHANG Sheng-Xiu,YANG Xiao-Gang,et al. Improved MSCKF algorithm based on multimode generalization of camera state equation [J]. Journal of Instrumentation,2019,40(05):89-98. [CrossRef]
PAN Linhao,TIAN Fuqing,YING Wenjian,et al. Monocular camera-IMU external parameter auto-calibration and online estimation for vision-inertial guidance SLAM [J]. Journal of Instrumentation,2019,40(06):56-67. [CrossRef]
Zhang J. Research on visual inertial localization method in dynamic environment [D]. Xi'an University of Technology,2022. [CrossRef]
Sibley G, Matthies L, Sukhatme G. A sliding window filter for incremental SLAM [J]. Springer US, 2008: 103-112. [CrossRef]
YANG Zi-Han,Lai Ji-Zhou,Lv Pin,et al. A robust visual/inertial localization method with parameterizable self-calibration [J]. Journal of Instrumentation,2021,42(07):259-267. [CrossRef]
Tao Xiaowen. Research on multi-sensor fusion positioning strategy for intelligent vehicles based on graph optimization [D]. Jilin University,2022. [CrossRef]
FANG Wenhui. Research on key technology of combined vision/inertial navigation for UAVs [D]. Southeast University, 2019. [CrossRef]
Land E H E. Lightness and retinex theory. [J]. Journal of the Optical Society of America, 1971, 61(1):1-11. [CrossRef]
Tomasi C, Manduchi R. Bilateral filtering for gray and color images [C]//In Proc. ICCV 1998, 839-846. [CrossRef]
Gao Xiang. Fourteen lectures on vision SLAM: from theory to practice [M]. Electronic Industry Press, 2017.
Forster C, Carlone L, Dellaert F, et al. IMU Preintegration on Manifold for Efficient Visual-inertial Maximum-a-Posteriori Estimation [J]. Georgia Institute of Technology, 2015, 33(2): 112-134.
Lupton T, Sukkarieh S. Visual-inertial-aided navigation for high-dynamic motion in built environments without initial conditions [J]. IEEE Transactions on Robotics, 2011, 28(1): 61-76. [CrossRef]
S. Leutenegger, S. Lynen, et al. Keyframe-Based Visual-Inertial SLAM Using Nonlinear Optimization [C]//International Journal of Robotics Research, 2015, 34(3): 314-334. [CrossRef]
QI Huan,SHEN Weihe,CHEN Xi,et al. Image quality assessment based on gradient direction distribution and its application [J]. Aerospace Control,2018,36(06):9-13+24. [CrossRef]
Bradski G. The openCV library [J]. Dr. Dobb's Journal: Software Tools for the Professional Programmer, 2000, 25(11): 120-123.

Figure 1. Overall design of the visual/INS integrated navigation programme.

Figure 2. Schematic diagram of IMU pre-integration.

Figure 3. Schematic diagram of factor graph optimization.

Figure 4. Comparison of the first set of images before and after de-blurring(a)Image before de-blurring;(b) Image after de-blurring.

Figure 5. Comparison of the second set of images before and after de-blurring(a)Image before de-blurring;( b) Image after de-blurring.

Figure 6. Comparison of the third set of images before and after de-blurring(a) Image before de-blurring;(b) Image after de-blurring.

Figure 8. Physical diagram of the data acquisition platform.

Figure 9. Trajectory Comparison Chart(a) Single visual localization trajectory map;(b) Visual/INS integrated navigation localization trajectory map

Figure 10. Trajectory Comparison Chart(a)Single visual localization APE;(b) Visual/INS integrated navigation localization APE.

Table 1. Standard deviation of the image (in pixels).

	De-blurring	De-blurred
Group I	78.8	80.3
Group II	76.3	78.1
Group III	69.6	71.1

Table 2. Image average gradient.

	De-blurring	De-blurred
Group I	2.45	4.51
Group II	3.66	5.60
Group III	2.83	5.46

Table 3. Results of ORB feature matching results (unit: pair).

	De-blurring	De-blurred
Group I	206	58
Group II	57	5
Group III	201	76

Table 4. Time required for image ORB feature matching (unit: ms).

	De-blurring	De-blurred
Group I	0.95	0.69
Group II	0.77	0.48
Group III	0.84	0.47

Table 5. Comparison of VIO and VO absolute position error (unit:m).

	VIO	VO
max	0.0709	0.170
mean	0.0232	0.0382
min	0.00407	0.00366
rmse	0.0278	0.0508
std	0.0153	0.0335

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Research on Visual/Ins Integrated Navigation Technology Based on FGO

Abstract

1. Introduction

2. Visual/INS Integrated Navigation Algorithmic Scheme Design

3. Visual/INS Integrated Navigation Algorithmic Front-end Algorithm

4. Visual/INS Integrated Navigation Back-end Algorithms

5. Experimental Verification

5.2. Validation of Visual/INS Integrated Navigation Algorithm Performance

6. Conclusions

Author Contributions

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe