Prerpints.org logo
Preprint
Article

Testing and Visualization of Associations in Three-Way Contingency Tables: A Study on Gender Gap in Patients with Type I Diabetes and Cardiovascular Complications

Altmetrics

Downloads

124

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 May 2024

Posted:

31 May 2024

You are already at the latest version

Alerts
Abstract
Using data from the Swedish National Diabetes Register, this study examines the gender disparity among patients with type I diabetes who have experienced a specific cardiovascular complication, while exploring the association between weight variability, age group, and gender. Fourteen cardiovascular complications have been considered. This analysis is conducted by using three-way correspondence analysis (CA) which allows for the partitioning and decomposition of Pearson’s three-way chi-squared statistic. The dataset comprises of information organized in a data cube, detailing how weight variability among these patients correlates with a cardiovascular complication, age group and gender. The three-way CA method presented in this paper allows for one to assess the statistical significance of the association between these variables and to visualize this association, highlighting the gender gap among these patients. It is worth noting that the association between weight variability, age group, and gender varies among different types of cardiovascular complications.
Keywords: 
Subject: Public Health and Healthcare  -   Other

1. Introduction

Patients diagnosed with type 1 diabetes (T1D) face a heightened risk of developing a range of cardiovascular complications (CVCs) compared to the general population [7,15]. It is known that women with T1D face a greater risk of all-cause mortality and experience more vascular events compared to men [2]. This study aims to assess gender differences in patients with T1D, focusing on weight variability and age in males and females who experienced a CVC, and examining the associations between these variables in different cohorts.
Utilizing data from the Swedish National Diabetes Register (NDR), this paper explores the links between weight variability, age group, and gender of patients with T1D and a CVC. The considered CVCs include: 1) stroke, 2) myocardial infarction (myo), 3) heart failure hospitalization (HFH), 4) coronary artery bypass graft (CABG), 5) percutaneous coronary intervention (PCI), 6) peripheral artery disease (PAD), 7) renal failure (RF), 8) acute renal disease (ARF), 9) chronic renal failure (CRF), 10) dialysis, 11) glomerular filtration rate of 50 mL/min/1.73 m² (GFR50), 12) macroalbuminuria (Macr), 13) retinopathy (Ret), and 14) all-cause mortality (Mort).
This population-based cohort study involved 6255 participants (3485 males and 2770 females) with T1D, ranging in age from 21 to 85, identified within the NDR. The inclusion period began on July 1st, 2003, and concluded on December 30th, 2013, during which time participants underwent at least three distinct weight measurements. Weight variability was assessed by computing the coefficient of variability (CV) for weight measurements of each patient and dividing it into quartiles. Subsequently, data concerning each of the 14 CVCs were summarized into a three-way contingency table, stratified by weight variability quartiles, age quartiles, and gender. To study the dependence relationship between the patients’ weight variability, age group and gender, we consider a three-way correspondence analysis (CA) [8,26] based on the partition and decomposition of a three-way index of association that is Pearson’s chi-squared statistic [30,31]. Pearson’s three-way chi-squared statistic will be orthogonally partitioned into two-way and three-way association terms to determine the dependence relationships between variables. Note that we use to the term "association" when analysing the dependence between variables, and the term "interaction" when analysing the dependence between the categories of the variables.
The paper is organized as follows. After introducing the notation to be used in this paper in Section 2, Section 3 and Section 4 provide a brief description of the partition of Pearson’s three-way chi-squared statistic, and of the classical three-way CA technique, respectively. Section 6 describes several illustrative examples demostrating how the association between weight variability, age group and gender varies with respect to a CVC. Section 7 provides some final remarks.

2. Materials and Methods

Before analysing the data, it is necessary to explain some of the general principles behind three-way CA.

2.1. Notation and Terminology

Define an I × J × K (three-way) contingency table by N ̲ , which contains information on the three cross-classified categorical variables observed on n individuals. This contingency table consists of I rows, J columns and K tubes, and its ( i , j , k )th element is denoted by n i j k . Let p i j k = n i j k / n be the proportion of observations in cell ( i , j , k ) , and p i • • , p • j • and p • • k are the i th row, j th column, and k th tube marginal proportions, respectively, also called expected proportions. The deviations from the three-way independence model are defined as
π i j k = p i j k p i • • p • j • p • • k − 1 .
The value π i j k will primarily be referred to as Pearson’s residual for the cell ( i , j , k ) and its square is a cell’s contribution to the chi-squared statistic X I J K 2 . We define D I to be the I × I diagonal matrix with the row marginal p i • • as its i , i th element. Similarly, D J and D K are the J × J and K × K diagonal matrices of the column and tube marginal proportions, respectively. Finally, we consider the total inertia or phi-squared statistic, Φ 2 = X I J K 2 / n which is also equal to the squared norm of the table Π ̲ = ( π i j k ) containing the Pearson residuals so that
Φ 2 = X I J K 2 n = | | Π ̲ | | 2 = ∑ i = 1 I ∑ j = 1 J ∑ k = 1 K p i • • p • j • p • • k p i j k p i • • p • j • p • • k − 1 2 .
Using Φ 2 , Carlier and Kroonenberg [8] proposed a three-way CA method employing the Tucker3 model [39], which is the most common generalization of the singular value decomposition of a matrix; see also Kroonenberg [p. 54 [21]. This model defines components for each of the three categorical variables. These components are a linear combination of the original variables, synthesizing the information from the categories of variables. It also consists of a three-way core table containing the three-way equivalent of singular values; see also Lombardo, Beh and Kroonenberg [26], Lombardo, van de Velden and Beh [27], and Beh and Lombardo [Chap. 11 [3]. The elements of the core table reflect the strengths of the links between the components of the three variables. The decomposition does not impose any restrictions on the components other than the identification constraints of orthogonality.

3. Partitioning the Chi-squared Statistic

Lombardo, Takane, and Beh [25] discuss a common method for studying the association among three categorical variables based on the orthogonal decomposition of Pearson’s chi-squared statistic, X I J K 2 , and under a variety of hypotheses about the expected proportions (hypothesized probabilities). These partitions are based on the ANOVA-like familywise partitions of Pearson’s three-way chi-squared statistic. In this paper, we focus on the most common case where these probabilities are estimated using the marginal proportions of the empirical distribution underlying the data. In some cases, however, the probabilities are prescribed by the analyst, because a priori knowledge of the phenomena suggests otherwise [23].
Under the independence assumption, Pearson’s three-way chi-squared statistic can be partitioned into four orthogonal parts, each corresponding to an association term, as detailed by, for example, Lancaster [22]. Therefore, the partition of X I J K 2 is given by
X I J K 2 = X I J 2 + X I K 2 + X J K 2 + X i n t 2 .
This can be written in more detail as
X I J K 2 = n ∑ i = 1 I ∑ j = 1 J p i • • p • j • p i j • − p i • • p • j • p i • • p • j • 2 + n ∑ i = 1 I ∑ k = 1 K p i • • p • • k p i • k − p i • • p • • k p i • • p • • k 2 + n ∑ j = 1 J ∑ k = 1 K p • j • p • • k p • j k − p • j • p • • k p • j • p • • k 2 + n ∑ i = 1 I ∑ j = 1 J ∑ k = 1 K p i • • p • j • p • • k p i j k − α p i j k p i • • p • j • p • • k 2 ,
where
  α p i j k = p i j • p • • k + p i • k p • j • + p • j k p i • • − 2 p i • • p • j • p • • k .
The first three terms of equations (3) and (4) are the two-way association terms obtained by a weighted aggregation of the total association measure across each of the variables, respectively. For example, X I J 2 is Pearson’s chi-squared statistic for the row and column variables formed by aggregating across each of the tube categories. The last term, X i n t 2 , represents the trivariate association between all three categorical variables. For further details on this partition see Carlier and Kroonenberg [p. 358 [8], Beh and Lombardo [p. 454 [3] and Lombardo, Takane and Beh [25].
The X I J K 2 , as well as the four association terms on the right-hand side of equations (3) and (4), can be tested for (asymptotic) statistical significance since all these terms are asymptotic chi-squared random variables. Specifically, under the null hypotheses that all three variables are independent, the statistical significance of X I J K 2 can be assessed using I − 1 J − 1 + I − 1 K − 1 + J − 1 K − 1 + I − 1 J − 1 K − 1 degrees of freedom. The statistical significance of the first term, X I J 2 , can be evaluated using I − 1 J − 1 degrees of freedom (df), the second term, X I K 2 , by using I − 1 K − 1 df. Similarly, the statistical significance of the third term, X J K 2 , can be assessed using J − 1 K − 1 df, and the fourth term, X I J K 2 , by using I − 1 J − 1 K − 1 df.

4. Modelling Association

When the analyst aims to not only test the statistical significance of the three-way association but also wishes to provide a graphical representation of it, a decomposition of the three-way contingency table is necessary for exploring in more detail the interactions between the categories.

4.1. The Tucker3 Decomposition

As indicated in Section 2, the most common three-way generalization of the singular value decomposition within the context of three-way CA is the Tucker3 model proposed by Tucker [39]. The general form of the decomposition is
π i j k = π ^ i j k + e i j k = ∑ p = 1 P ∑ q = 1 Q ∑ r = 1 R g p q r a i p b j q c k r + e i j k ,
where P, Q and R (with P ≤ I , Q ≤ J and R ≤ K ) represent the number of columns in the component matrices A , B and C that are associated with the rows, columns and tube categories, respectively. The sets of component vectors a p { a i p } , b q { b j q } , c r { c k r } are orthonormal with respect to D I , D J and D K , respectively. The quantities g p q r are the elements of the core table and can be interpreted as the generalized or three-way analogs, of the two-way singular values, where its magnitude indicates the strength of the relationship among the components. The magnitude of the squared core element, g p q r 2 , also indicates the contribution of the product of the P, Q, and R components to the fit of the model to the data, allowing the analyst to compute the inertia explained in a two-dimensional plot. Note that, given the orthogonality of the components, the phi-squared statistic or total inertia can be expressed as the sum of squares of the elements of the core table, so that
X I J K 2 n = ∑ p = 1 I ∑ q = 1 J ∑ r = 1 K g p q r 2 .
For more details on equation (6) see Kroonenberg [p. 226 – 227 [21].
Finally, the element e i j k in equation (5) is the error of approximation between the observed π i j k and their predicted values, π ^ i j k ; see, for example, Kroonenberg [Chap. 4 [21]. The choice of the number of row, column and tube components, P, Q and R, respectively, relies on various methodologies developed by researchers for the Tucker3 model. Literature such as Kiers [16,17], Ten Berg and Kiers [36], Timmerman and Kiers [37], Rocci [33], Kroonenberg [20], and Lombardo, van de Velden and Beh [27], illustrate this point. Here we will adopt the strategy of Lombardo, van de Velden and Beh [27] to choose P, Q, and R. This strategy uses the tunelocal() function in the R package CA3variants. The three-way CA performed in Section 6 uses the CA3variants() function of this package.

5. Biplots in Three-way Correspondence Analysis

To visualize the association structure among two or more categorical variables, we limit ourselves to the biplot, a technique first introduced by Gabriel [11]. Comprehensive discussions of the variety of biplots that can be constructed, particularly in the context of CA, are available in the works of Carlier and Kroonenberg [8], Lombardo, Carlier, and D’Ambra [24], Greenacre [14], and Beh and Lombardo [5].

5.1. Biplots for Three-Way Correspondence Analysis

To illustrate the association structure among the categorical variables of a three-way contingency table, Carlier and Kroonenberg [8,9] explored different biplot techniques. The technique of interest here employs a single component for one variable and the interactively-coded components for the other variables; this biplot is also known as a nested-mode biplot [Sect. 11.5.4 [21] or interactive biplot [p. 472 [3]. Lombardo, van de Velden, and Beh [27] discuss six variants of the interactive biplot. These variants depend on the variables chosen for the interactive representation and on the computation of the type of coordinates, i.e., standard or principal coordinates [12,13]. Firstly, we can represent the coordinates of the row categories using their A components, while the coordinates of the column and tube categories are represented interactively by the Kronecker product of their B and C components. Secondly, the coordinates of the column categories can be represented by their B components, while the coordinates of the rows and tubes are interactively represented by the Kronecker product of their A and C components. Thirdly, the coordinates of the tube categories can be represented by their C components, with the coordinates of the rows and columns being interactively represented by the Kronecker product of their A and B components.
When the coordinates are multiplied by the core elements, they are referred to as principal coordinates; otherwise, they are standard coordinates. Their features are the same as those derived for biplots in the classical approach to CA [13]; for more information, refer to Greenacre [14] and Beh and Lombardo [Chap. 11 [3]. In particular, the distances between the categories from the same variable are correctly portrayed only when using the principal coordinates.
The interactive coordinates can be expressed in either their standard or principal coordinate form. Therefore, the three previous types of variable representation lead to six types of interactive biplots; for further details, see Lombardo, van de Velden and Beh [pp. 243 – 244 [27].

6. Practical Application: Patients with T1D and CVCs

6.1. Preliminary Discussion of the NDR Data

We utilize data from the NDR to assess and visualize the association between the variables weight variability, age group, and gender among patients with T1D who experienced one of the 14 CVCs outlined in Section 1. We classify their weight variability using four quartiles: the first quartile includes patients with a CV of weight between 0 and 0.018 ( Q1: low), the second quartile includes those with a CV of weight between 0.018 and 0.028 ( Q2: moderately low), the third quartile includes those with a CV of weight between 0.028 and 0.043 ( Q3: middle-high) and the fourth quartile includes those with a CV of weight at least 0.043 ( Q4: high). The CV of weight variable is then cross-classified to create a three-way contingency table with respect to the four age group quartiles ( age1 = 21–27 years; age2 = 27–40 years; age3 = 40–52 years; age4 = 52+ years), and gender (males and females). Consequently, the data are summarized in 14 three-way contingency tables, with each table corresponding to a specific CVC.
Table 1 presents Pearson’s three-way chi-squared statistic for each of the 14 CVCs given in Section 1, as well as their p-value with respect to 24 d f . Interestingly, Pearson’s three-way chi-squared statistic does not yield statistically significant results for all 14 CVCs. Rather, it only shows that there is a statistically significant association (at the 1% level of significance) for two CVCs: macroalbuminuria and retinopathy. Therefore, among the 14 CVCs, there is no statistically significant association between weight variability, age group, and gender for any of the six cardiovascular diseases (stroke, myo, HFH, CABG, PCI, and PAD). The interested readers can find the related three-way tables in the supplementary material to this paper.
In the following sections, we discuss the partition and decomposition of Pearson’s chi-squared statistic for the CVCs macroalbuminuria and retinopathy. We focus exclusively on these two three-way contingency tables since it is only for these CVCs where there exists a statistically significant association between weight variability, age group, and gender.

6.2. Patients with TD1 and Macroalbuminuria

The main question we shall address here is:
To what extent is there an association between weight variability, age group, and gender for patients with T1D and macroalbuminuria?
Table 2 presents a cross-classification of weight variability (row variable), age group (column variable), and gender (tube variable) among patients with T1D experiencing macroalbuminuria.
To assess the nature of the association between weight variability, age group, and gender in detail, we partition Pearson’s three-way chi-squared statistic, X I J K 2 , first in accordance with equation (3) so that three bivariate terms and a trivariate term are produced. Table 3 summarizes the partition of this statistic for Table 2. This includes the partition of the phi-squared into four terms, their percentage contribution to phi-squared, the corresponding degrees of freedom (df), the p-value, and the relative size ( T e r m / d f ) of each partition term (which facilitates a comparison of the chi-squared values derived from different asymptotic chi-squared distributions). In Table 3, looking at Pearson’s three-way statistic X I J K 2 = 73.806 and its p-value that is less than 0.001 (df=24), we can conclude that there is clear evidence of a statistically significant association between the three variables of Table 2. Table 3 also shows that the most dominant source of association among the three variables is the association between weight variability and age group, denoted as T e r m − I J ; it contributes to over 75% of X I J K 2 and has a p-value that is less than 0.001. While the p-value of X I J K 2 for Table 1 shows there is a statistically significant association between the variables, Table 3 reveals that not all three bivariate terms of the partition yield a statistically significant association between the variables. Specifically, only T e r m − I J demonstrates statistical significance. Conversely, the associations between weight variability and gender ( T e r m − I K ), and between age group and gender ( T e r m − J K ), are not statistically significant, nor is the trivariate term ( T e r m − I J K ). This means that while not all sources of associations between the variables are statistically significant, at least one is. Also, while T e r m − I J K is not statistically significant we can still identify categories, and joint categories, that do provide a statistically significant contribution to the overall association between the three variables. We now turn our attention to addressing this issue for Table 2.
To identify which categories of Table 2 provide a statistically significant contribution to the total association, we calculate the p-value for each quartile of the weight variability variable. We also calculate the p-value of the interaction between the age group and gender variables. These p-values are determined using the approach described in Beh and Lombardo [4]. Their methodology constructs 100 ( 1 − α ) % confidence ellipses for points in a low-dimensional plot generated from applying a CA to the data. The methodology also included ways to calculate excellent p-value approximations for each point when assessing their contribution to the association (or lack thereof) between categorical variables. These p-values are designed to reflect the statistical significance of the distance of a category’s point from the origin, thus determining the statistical significance of the category to the association structure between the categorical variables. They are calculated taking into account the chi-squared statistic, the principal coordinates, the inertia explained by each axis, and the marginal proportions of N ̲ .
Table 4 shows that all the categories of the weight variability are statistically significant at the α = 0.01 level, except for Q2. However, only two categories of the age group for males and females shows statistical significance at the 1% level; they are "age4" for the males and "age1" for the females.
To visualize the association reflected in the p-values of Table 4, we consider a column-tube biplot with interactive coding of age group (column variable) and gender (tube variable). However since the T e r m − I J is statistically significant (see Table 3), we also portray the row-column biplot that depicts the statistically significant association that exists between weight variability and age group ( T e r m − I J ). Figure 1 shows these two biplots: on the left-side is the column-tube interactive biplot, and on the right-side is the row-column interactive biplot. The column-tube interactive biplot on the left of Figure 1 depicts the three-way association where the age group-gender interaction is depicted using principal coordinates and weight variability is depicted using standard coordinates. The row-column interactive biplot on the right of Figure 1 portrays the three-way association where the weight variability-age group interaction is depicted using principal coordinates and gender is depicted using standard coordinates. The origin of both plots represents the independence between the variables. The farther the interactive categories are from the origin, the stronger the association. The interactive principal coordinates provide an accurate depiction of their distance from the plot’s origin and from each other. Note that the distance of points that have standard coordinates cannot be appropriately evaluated. Only their angle can be considered: when this angle is acute, there is a strong positive interaction with the interactive pair of categories. When the angle is at 90 degrees, there is independence, and when the angle is obtuse, there is a strong negative interaction.
The quality of the interactive biplots in Figure 1 is very good since they visually describe about 84% (for the column-tube interactive biplot) and 83% (for the row-column interactive biplot) of the total association. Note that the farthest interactive coordinates contribute most prominently to the association. In the column-tube biplot of Figure 1, they are "age4male" which is positively related to Q1, and "age1female" which is positively related to Q4. We can also see from Figure 1 that "age1male" is negatively related to Q1, while "age4female" is negatively related to Q4. In the row-column biplot of Figure 1 we can see that "Q1age4" is positively related to males, while "Q4age1" is positively related to the females. Furthermore, "Q1age1" is negatively related to males, and "Q4age4" is negatively related to females
In summary, the biplots in Figure 1 show that males with T1D and macroalbuminuria are significantly characterized with having "low" weight variability and being in the "old" age group (aged 52 years or older). Figure 1 also shows that the females with T1D and macroalbuminuria are characterized as generally having "high" weight variability and being in the "young" age group (aged 21 – 27 years old).

6.3. Patients with TD1 and Retinopathy

The primary question we address here is:
What is the strength of the association among weight variability, age group, and gender in patients diagnosed with T1D and retinopathy?
Table 5 presents a cross-classification of weight variability (row variable), age group (column variable), and gender (tube variable) among patients experiencing retinopathy which is the most prevalent microvascular complication experienced by T1D patients, often present during adolescence [28].
Table 6 shows that Pearson’s three-way chi-squared statistic of Table 5  X I J K 2 = 168.271 (df=24), so that there is a statistically significant association between the three variables (p-value < 0.001 ). To assess the nature of the association between weight variability, age group, and gender in detail for patients with T1D and retinopathy, we examine the partition of Pearson’s three-way chi-squared statistic X I J K 2 in accordance with equation (3). This partition is summarized in Table 6 which indicates that the three indices of the bivariate association are statistically significant, albeit at different α levels. The T e r m − I J indicates a significant association between weight variability and age group since the p-value is less than 0.001.
The T e r m − I K , which represents the association between weight variability and gender, shows that there is a gender difference among patients with T1D and retinopathy at the 5% level of significance, and the T e r m − J K also shows a significant association at this level of significance between age group and gender. However, the trivariate term is not statistically significant. This implies that while not every association among the three variables is statistically significant, there is at least one that is.
To discern which categories significantly contribute to the association, we compute the approximate p-value [4] for each category within the weight variability and age group variables of the males and females; see Table 7. Table 7 shows that all the categories of weight variability have a p-value that is less than 0.001 showing that their contribution to the association that exists within Table 5 is statistically significant. Additionally, three categories among the age group for males show statistical significance: "age1Male", "age3Male", and "age4Male". However, for the females in the study, only "age1Female" is statistically significant.
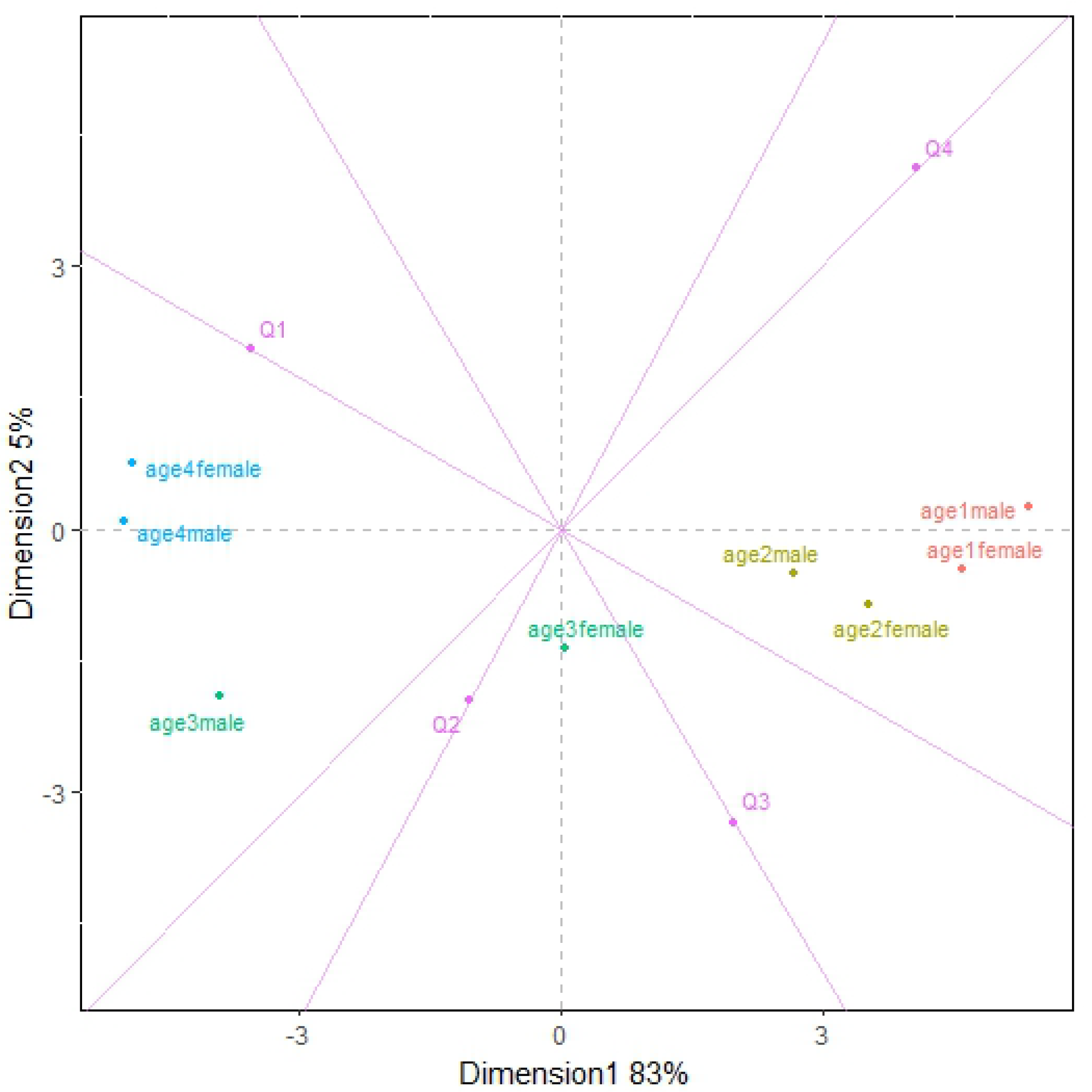
Figure 2 illustrates the three-way association. Since the association between age group and gender is statistically significant (see Term - JK in Table 6) this figure only shows the column-tube interactive biplot. Figure 2 shows that the quality of the column-tube interactive biplot is excellent since 88% of the total association is depicted. In Figure 2, our attention is directed towards the farthest age group - gender points, which are most relevant for evaluating the association. Unlike what was observed for patients with T1D and macroalbuminuria, we can say that males experiencing T1D and retinopathy are mainly characterized by having "high" weight variability and being in the "young" age group ( "age1male"). We can also see in Figure 2 that females with T1D and retinopathy are characterized as having a "low" level of weight variability and being in the "old" age group ("age4female"). This result is consistent with what Nyström et al. [28] discussed about patients with T1D and retinopathy, observing that overweight/obesity was more common in males than in females.

7. Discussion

The gender gap in patients with T1D exhibits variability across different cardiovascular complications. The analysis of the NDR data reveals that among the 14 CVCs considered, the association between weight variability, age group, and gender is statistically significant at the α = 0.01 level of significance for only two complications: macroalbuminuria and retinopathy.
Patients with T1D experiencing macroalbuminuria show distinct patterns. In particular, males are primarily characterized by a "high" level of weight variability (Q4) being in the "young" age group ("age1male"), while females are characterized by having a "low" weight variability (Q1) and being in the "old" age group ("age4female").
For those experiencing retinopathy, males are primarily characterized by having a "high" weight variability (Q4) and being of a "young" age group ("age1male"), whereas females are characterized by having "low" weight variability (Q1) and being in the "old" age group ("age4female"), confirming the findings given by Nyström et al. [28].
It is worth noting that although Pearson’s three-way chi-squared statistic is statistically significant for many of the association terms in Table 3 and Table 6, Table 4 and Table 7 show that the interaction between the categories are not all statistically significant. The computation of p-values in Table 4 and Table 7 helps to assess the significance of the categories, discerning the most relevant to the least.

Funding

This research has been funded by the following research projects of the first author: PRIN-2022 SciK-Health: Mapping Scientific Knowledge about health for decision-making (Project code: 2022825Y5E_02; CUP: B53D23009750006 Prof. M. Aria). PRIN-2022 PNRR "The value of scientific production for patient care in A. H. S. C." (Project Code: P2022RF38Y; CUP: B53D23026630001 Prof. C. Cuccurullo).

References

  1. Agresti, A. Categorical Data Analysis, 3rd ed.; Wiley: New York, US, 2013. [Google Scholar]
  2. Bak, J.C.G.; Serné, E.H.; de Valk, H.W.; Valk, N.K.; Kramer, M.H.H.; Nieuwdorp, M.; Verheugt, C.L. Gender gaps in type 1 diabetes care. Acta Diabetol. 2023, 60, 425–434. [Google Scholar] [CrossRef] [PubMed]
  3. Beh, E. J.; Lombardo, R. Correspondence Analysis: Theory, Methods and New Strategies. Wiley: Chichester, UK, 2014. [Google Scholar]
  4. Beh, E.J.; Lombardo, R. : Confidence regions and approximate p-values for classical and non symmetric correspondence analysis. Communications in Statistics - Theory and Methods 2015, 44, 95–114. [Google Scholar] [CrossRef]
  5. Beh, E.J.; Lombardo, R. Features of the polynomial biplot of ordered contingency tables. Journal of Computational and Graphical Statistics 2021, 31, 403–412. [Google Scholar] [CrossRef]
  6. Bro, R.; Kiers H. A., L. A new efficient method for determining the number of components in PARAFAC models. Journal of Chemometrics 2023, 17, 274–286. [Google Scholar] [CrossRef]
  7. Cai, X.; Li, J.; Cai, W.; Chen, C.; Ma, J.; Xie, Z.; Dong, Y.; Liu, C.; Xue, X.; Zhao, J. Meta-analysis of type 1 diabetes mellitus and risk of cardiovascular disease. Journal of Diabetes and its Complications 2021, 35, 107833. [Google Scholar] [CrossRef] [PubMed]
  8. Carlier, A.; Kroonenberg, P. M. Biplots and decompositions in two-way and three-way correspondence analysis. Psychometrika 1996, 61, 355–373. [Google Scholar] [CrossRef]
  9. Carlier, A.; Kroonenberg, P. M. The case of the French cantons: An application of three-way correspondence analysis. In Visualization of Categorical Data Blasius, J.; Greenacre, M., Ed.; Academic Press: San Diego, US, 1998; pp. 253–275. [Google Scholar]
  10. Ceulemans, E.; Kiers, H. A. L. Selecting among three-mode principal component models of different types and complexities: a numerical convex hull based method. British Journal of Mathematical & Statistical Psychology 2006, 59, 133–150. [Google Scholar]
  11. Gabriel,K. R. The biplot graphic display of matrices with application to principal component analysis. Biometrika 1971, 58, 453–467. [Google Scholar] [CrossRef]
  12. Gower, J.C.; Lubbe, S.; le Roux, N. Understanding Biplots. Wiley: Chichester, UK, 2011. [Google Scholar]
  13. Greenacre, M. J. Theory and Applications of Correspondence Analysis. Academic Press: London, UK, 1984. [Google Scholar]
  14. Greenacre, M. J. Biplots in Practice. Fundación BBVA: Barcelona, Spain, 2010. [Google Scholar]
  15. Julián, M.T.; Pérez-Montes de Oca, A.; Julve, J. et al. The double burden: type 1 diabetes and heart failure - a comprehensive review. Cardiovasc. Diabetol. 2024, 23, 65. [Google Scholar] [CrossRef] [PubMed]
  16. Kiers, H. A. L. Three-mode orthomax rotation. Psychometrika, 1997, 62, 579–598. [Google Scholar] [CrossRef]
  17. Kiers, H. A. L. Three-way SIMPLIMAX for oblique rotation of the three-mode factor analysis core to simple structure. Computational Statistics and Data Analysis, 1998, 28, 207–324. [Google Scholar] [CrossRef]
  18. Krishnan, S. , Fields, D.A., Copeland, K.C., Blackett, P.R., Anderson, M.P., Gardner, A.W.: Sex differences in cardiovascular disease risk in adolescents with type 1 diabetes. Gend Med. 2012, 9(4), 251–8. [Google Scholar] [CrossRef] [PubMed]
  19. Kroonenberg, P. M. Three Mode Principal Component Analysis. DSWO Press: Leiden, The Netherlands, 1983. [Google Scholar]
  20. Kroonenberg, P. M. Model selection procedures in three-mode component models. In New Developments in Classification and Data Analysis, Vichi, M.; Molinari, P.; Mignani, S.; Montanari, A. Eds.; Elsevier, 2005, pp. 167–172.
  21. Kroonenberg, P. M. Applied Multiway Data Analysis. Wiley: Hoboken, NJ, 2008. [Google Scholar]
  22. Lancaster, H.O. Complex contingency tables treated by the partition of the chi-square. J R Stat Soc Ser B 1951, 13, 242–249. [Google Scholar] [CrossRef]
  23. Loisel, S.; Takane, Y. : Partitions of Pearson’s chi-square statistic for frequency tables: a comprehensive account. Computational Statistics, 2016, 31, 1429–1452. [Google Scholar] [CrossRef]
  24. Lombardo, R.; Carlier, A.; D’Ambra, L. Nonsymmetric correspondence analysis for three-way contingency tables. Methodologica, 1996, 4, 59–80. [Google Scholar]
  25. Lombardo, R.; Takane, Y.; Beh, E.J. Familywise decompositions of Pearson’s chi-square statistic in the analysis of contingency tables. Advances in Data Analysis and Classification 2020, 14, 629–649. [Google Scholar] [CrossRef]
  26. Lombardo, R.; Beh, E.J.; Kroonenberg, P.M. Symmetrical and non-symmetrical variants of three-way correspondence analysis for ordered variables. Statistical Science, 2021, 36, 542–561. [Google Scholar] [CrossRef]
  27. Lombardo, R.; van de Velden, M.; Beh, E. J. Three-way correspondence analysis in R. The R Journal, 2023, 15, 237–262. [Google Scholar] [CrossRef]
  28. Nyström, T.; Andersson Franko, M.; Ludvigsson, J.; Lind, M.; Persson, M. Overweight or obesity, weight variability and the risk of retinopathy in type 1 diabetes. Diabetes Obes Metab 2024. [Google Scholar] [CrossRef] [PubMed]
  29. Östman, J.; Lönnberg, G.; Arnqvist, H.J.; Blohme, G.; Bolinder, J.; Schnell, A.E.; Eriksson, J.W.; Gudbjörnsdottir, S.; Sundkvist, G.; Nyström, L. Gender differences and temporal variability in the incidence of type 1 diabetes: Results of 8012 cases in the nationwide Diabetes Incidence Study in Sweden 1983–2002. J. Intern. Med. 2008, 263, 386–394. [Google Scholar] [CrossRef]
  30. Pearson, K. Mathematical contributions to the theory of evolution. XIII: On the theory of contingency and its relation to association and normal correlation. In Draper’s Co. Research Memoirs. Biometrie Series, no. 1.; 1904 (Reprinted 1948 in Karl Pearson’s Early Papers, ed. E. S. Pearson. Cambridge, UK: Cambridge University Press.
  31. Pearson, K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Philosophical Magazine, 1900, 50, 157–175. [Google Scholar] [CrossRef]
  32. Petria, I.; Albuquerque, S.; Varoquaux, G. et al. Body-weight variability and risk of cardiovascular outcomes in patients with type 1 diabetes: a retrospective observational analysis of data from the DCCT/EDIC population. Cardiovascular Diabetology, 2022, 21, 247. [Google Scholar] [CrossRef]
  33. Rocci, R. Core matrix rotation to natural zeros in three-mode factor analysis. In Advances in Classification and Data Analysis: Studies in Classification, Data Analysis, and Knowledge Organization, Borra, S.; Rocci, R.; Vichi, M.; Schader, M., Eds; Springer, 2001, pp. 161–168.
  34. Svensson, J. , Carstensen, B., Mortensen, H.B., Borch-Johnsen, K. Gender-associated differences in Type 1 diabetes risk factors? Diabetologia, 2003, 46, 442–443. [Google Scholar] [CrossRef] [PubMed]
  35. Tatti, P.; Pavandeep, S. Gender difference in type 1 diabetes: An underevaluated dimension of the disease. Diabetology, 2022, 3, 364–368. [Google Scholar] [CrossRef]
  36. Ten Berge, J. M. F. and Kiers, H. A. L.: Simplicity of core arrays in three-way principal component analysis and the typical rank of p. Linear Algebra and its Applications, 1999, 294, 169–179. [Google Scholar] [CrossRef]
  37. Timmerman, M. E.; Kiers, H. A. L. Three-mode principal component analysis: Choosing the numbers of components and sensitivity to local optima. British Journal of Mathematical and Statistical Psychology, 2000, 53, 1–16. [Google Scholar] [CrossRef] [PubMed]
  38. Timmerman, M. E.; Kiers, H. A. L.; Smilde, A. K. Estimating confidence intervals for principal component loadings: A comparison between the bootstrap and asymptotic results. British Journal of Mathematical and Statistical Psychology 2007, 60, 295–314. [Google Scholar] [CrossRef] [PubMed]
  39. Tucker, L. R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef] [PubMed]
Preprints 108020 g001
Figure 1. Biplots for patients with T1D and macroalbuminuria: On the left-side is the column-tube interactive biplot, on the right-side is the row-column interactive biplot.
Figure 1. Biplots for patients with T1D and macroalbuminuria: On the left-side is the column-tube interactive biplot, on the right-side is the row-column interactive biplot.
Preprints 108020 g001
Preprints 108020 g002
Figure 2. The row-column interactive biplot for patients with T1D and retinopathy from the three-way analysis of Table 5.
Figure 2. The row-column interactive biplot for patients with T1D and retinopathy from the three-way analysis of Table 5.
Preprints 108020 g002
Table 1. Test of independence between weight variability, age group, and gender for each of the 14 CVCs using Pearson’s three-way chi-squared statistic with 24 d f .
Table 1. Test of independence between weight variability, age group, and gender for each of the 14 CVCs using Pearson’s three-way chi-squared statistic with 24 d f .
CVC X IJK 2 p-value
Stroke 26.051 0.351
Myocardium 39.932 0.022
HFC 33.788 0.089
CABG 26.695 0.319
PCI 23.067 0.516
PAD 29.429 0.204
Renal failure 29.536 0.201
Acute renal failure 30.685 0.163
Chronic renal failure 28.312 0.247
Dialysis 14.212 0.942
GFR50 32.723 0.110
Macroalbuminuria 73.806 <0.001
Retinopathy 168.271 <0.001
All-cause mortality 38.280 0.032
Table 2. Patients with T1D and macroalbuminuria, cross-classification of weight variability, age group, and gender.
Table 2. Patients with T1D and macroalbuminuria, cross-classification of weight variability, age group, and gender.
Male
weight variability age1 age2 age3 age4
Q1 7 14 24 38
Q2 12 23 18 24
Q3 17 19 23 12
Q4 18 15 11 6
Female
weight variability age1 age2 age3 age4
Q1 7 10 11 20
Q2 14 12 7 10
Q3 11 15 18 8
Q4 21 10 13 5
Table 3. Partition of Pearson’s three-way association statistic for patients with T1D and macroalbuminuria of Table 2.
Table 3. Partition of Pearson’s three-way association statistic for patients with T1D and macroalbuminuria of Table 2.
Term − IJ Term − IK Term − JK Term − IJK Term − total
chi-squared 57.959 5.373 5.294 5.180 73.806
phi-squared 0.123 0.011 0.011 0.011 0.156
% of Inertia 78.528 7.281 7.173 7.018 100.000
d f 9 3 3 9 24
p-value <0.001 0.146 0.151 0.818 <0.001
Term/df 6.440 1.791 1.765 0.576 3.075
Table 4. P-values of the categories of weight variability and age group for males and females with T1D and macroalbuminuria.
Table 4. P-values of the categories of weight variability and age group for males and females with T1D and macroalbuminuria.
p-values of row principal coordinates
category p-value
Q1 0.003
Q2 0.027
Q3 0.001
Q4 0.001
p-values of column-tube principal coordinates
category p-value
age1Male 0.957
age2Male 0.998
age3Male 0.934
age4Male 0.047
age1Female 0.005
age2Female 1.000
age3Female 0.158
age4Female 0.959
Table 5. Patients with type I diabetes experiencing retinopathy, cross-classification of weight variability by age groups and gender.
Table 5. Patients with type I diabetes experiencing retinopathy, cross-classification of weight variability by age groups and gender.
Male
weight variability age1 age2 age3 age4
Q1 44 56 100 118
Q2 48 67 88 67
Q3 53 66 58 36
Q4 67 58 25 24
Female
weight variability age1 age2 age3 age4
Q1 36 32 60 97
Q2 38 49 50 66
Q3 62 49 58 40
Q4 58 44 34 35
Table 6. Partition(s) of Pearson’s three-way chi-squared statistic for patients with T1D and retinopathy of Table 5.
Table 6. Partition(s) of Pearson’s three-way chi-squared statistic for patients with T1D and retinopathy of Table 5.
Term − IJ Term − IK Term − JK Term − IJK Term − total
chi-squared 143.080 9.928 8.052 7.211 168.271
phi-squared 0.080 0.006 0.005 0.004 0.094
% of Inertia 85.029 5.900 4.785 4.286 100.000
df 9.000 3.000 3.000 9.000 24.000
p-value <0.001 0.019 0.045 0.615 <0.001
Term/df 15.898 3.309 2.684 0.801 7.011
Table 7. P-values of categories of the weight variability and age group for males and females with T1D and retinopathy.
Table 7. P-values of categories of the weight variability and age group for males and females with T1D and retinopathy.
p-values of row principal coordinates
category p-value
Q1 <0.001
Q2 <0.001
Q3 <0.001
Q4 <0.001
p-values of column-tube principal coordinates
category p-value
age1Male <0.001
age2Male 0.885
age3Male <0.001
age4Male <0.001
age1Female 0.002
age2Female 0.160
age3Female 0.192
age4Female 0.036
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated