Stochastic Modeling of Climate Change Impact: Assessing Regional Temperature Increases Under Global Warming

Preprint

Article

Stochastic Modeling of Climate Change Impact: Assessing Regional Temperature Increases Under Global Warming

Altmetrics

Downloads

Views

Comments

Richard Murdoch Montgomery^*

This version is not peer-reviewed

This preprints belongs to the Topic

Climate Change Impacts and Adaptation: Interdisciplinary Perspectives

Submitted:

02 June 2024

Posted:

03 June 2024

You are already at the latest version

Alerts

Abstract

In this study, we develop a stochastic partial differential equation (SPDE) model to assess the regional severity of temperature increases due to global warming. The model incorporates various stochastic processes to account for uncertainties such as solar explosions, economic upheavals, rising emissions, and irreversible changes in the climate system. Our base temperature model, influenced by latitude, is enhanced by these random factors to simulate realistic and diverse outcomes of climate change. Numerical simulations on a global grid provide a heatmap representing potential temperature increase severity across different regions. The results highlight the significant impact on tropical and polar regions, demonstrating the utility of SPDE models in understanding and predicting the complex dynamics of climate change. This approach offers valuable insights for policymakers and researchers aiming to develop adaptive strategies for mitigating the adverse effects of global warming.

Keywords:

Subject: Environmental and Earth Sciences - Environmental Science

1. Introduction

Climate change, driven predominantly by anthropogenic activities, is one of the most pressing challenges of our time. The increase in greenhouse gas concentrations in the atmosphere has led to global warming, with widespread impacts on natural and human systems (IPCC, 2021). Understanding the regional variations in temperature increases due to global warming is crucial for developing effective mitigation and adaptation strategies (Diffenbaugh & Field, 2013).

Global warming does not affect all regions uniformly. Some areas might experience relatively mild temperature increases, while others could face extreme heatwaves, more frequent and severe weather events, and significant disruptions to ecosystems and human livelihoods (Houghton, 2004). Therefore, accurately modeling these variations is essential to anticipate and address the specific needs of different regions (Oppenheimer et al., 2014).

Traditional climate models, although powerful, often struggle to capture the full extent of uncertainties and stochastic processes that influence climate dynamics (Hasselmann, 1993). Factors such as solar variability, economic fluctuations, rising emissions, and irreversible climate tipping points add layers of complexity that deterministic models might overlook (Lenton et al., 2008). To address this gap, we propose a stochastic partial differential equation (SPDE) approach to model the regional severity of temperature increases under global warming.

The SPDE framework allows us to incorporate random processes and uncertainties into temperature modeling, providing a more comprehensive and realistic representation of potential climate scenarios (Berliner, 2003). Our base temperature model considers the global increase in temperature influenced by latitude, which is then enhanced by stochastic factors representing solar explosions, economic upheavals, rising emissions, and irreversible changes. This methodology enables us to simulate a range of possible outcomes and generate a heatmap that visualizes the severity of temperature increases across different regions. This study aims to demonstrate the utility of SPDE models in understanding and predicting the complex dynamics of climate change. By integrating various stochastic processes, we can better capture the inherent uncertainties and provide insights into the regional impacts of global warming. The results of our simulations highlight areas that are likely to suffer the most, offering valuable information for policymakers, researchers, and stakeholders involved in climate change mitigation and adaptation efforts.

In the following sections, we will detail the mathematical formulation of our SPDE model, describe the stochastic processes included, and present the numerical simulation results. We will also discuss the implications of our findings and the potential applications of this approach in climate science and policy planning.

2. Methodology

2.1. Mean Temperature Rise and Time Frame

In this study, we assume a mean global temperature rise of 1.5°C as a baseline scenario. This assumption is based on the target set by the Paris Agreement, which aims to limit global warming to well below 2°C above pre-industrial levels, with efforts to limit the increase to 1.5°C. The time frame for this temperature rise is not explicitly defined in our model but typically represents a mid-to-late 21st century scenario, approximately the years 2050 to 2100. This time frame is commonly used in climate projections to assess the impacts of different levels of warming.

2.2. Grid Definition

We define a grid over the Earth's surface, using longitude

x

and latitude

y

\begin{matrix} x \in [- 180,180] & degrees (longitude) \\ y \in [- 90,90] & degrees (latitude) \end{matrix}

We discretize this grid into a 360x180 array, corresponding to 1-degree resolution in both longitude and latitude.

2.3. Base Temperature Model

The base temperature increase severity

T_{base} (x, y)

is given by:

T_{base} (x, y) = 1.5 + 0.3 c o s (\frac{π y}{180})

Equation (1) models the baseline temperature increase influenced by latitude, reflecting a general global warming scenario with latitude-dependent variations.

2.4. Stochastic Processes

We incorporate several stochastic processes to model uncertainties:

1.Solar Explosions:

S (x, y) \sim P o i s s o n (λ)

where

λ = 0.1

is the rate parameter for the Poisson process. This models random occurrences of solar explosions.

α S (x, y)

where

α = 0.1

is a scaling factor for the impact of solar explosions. (Equation 2)

2. Economic Upheavals:

(3) E (x, y) \sim N (0, σ_{E})

where

σ_{E} = 0.2

is the standard deviation for the normal distribution representing economic impacts. (Equation 3)

3. Rising Emissions:

(4) R (x, y) \sim N (μ_{R}, σ_{R})

where

μ_{R} = 0.5

and

σ_{R} = 0.1

represent the mean and standard deviation for the normal distribution modeling rising emissions. (Equation 4)

4. Irreversibility:

(5)

I = 0.2

where

I = 0.2

represents the constant factor for irreversible changes. (Equation 5)4. Combined Model

The combined temperature increase severity

T (x, y)

is given by the sum of the previous equations (1,2,3,4 and 5):

(6)

T (x, y) = T_{base} (x, y) + α S (x, y) + E (x, y) + R (x, y) + I

This equation (Equation 6) integrates the base temperature model with the stochastic processes to provide a comprehensive representation of potential temperature increase severity across the globe.This methodology provides a comprehensive approach to modeling regional temperature increases under global warming, incorporating both deterministic and stochastic elements to capture the inherent uncertainties in climate dynamics. The resulting heatmap offers valuable insights into the potential severity of temperature increases across different regions, aiding in the development of targeted mitigation and adaptation strategies.

3. Results

Figure 1. The heatmap shows a general increase in temperature severity globally, with a baseline increase of 1.5°C. This baseline is influenced by latitude, reflecting the general trend that polar regions experience more significant temperature changes due to global warming. Note the temperatures rising especially in the tropics (yellow zone).

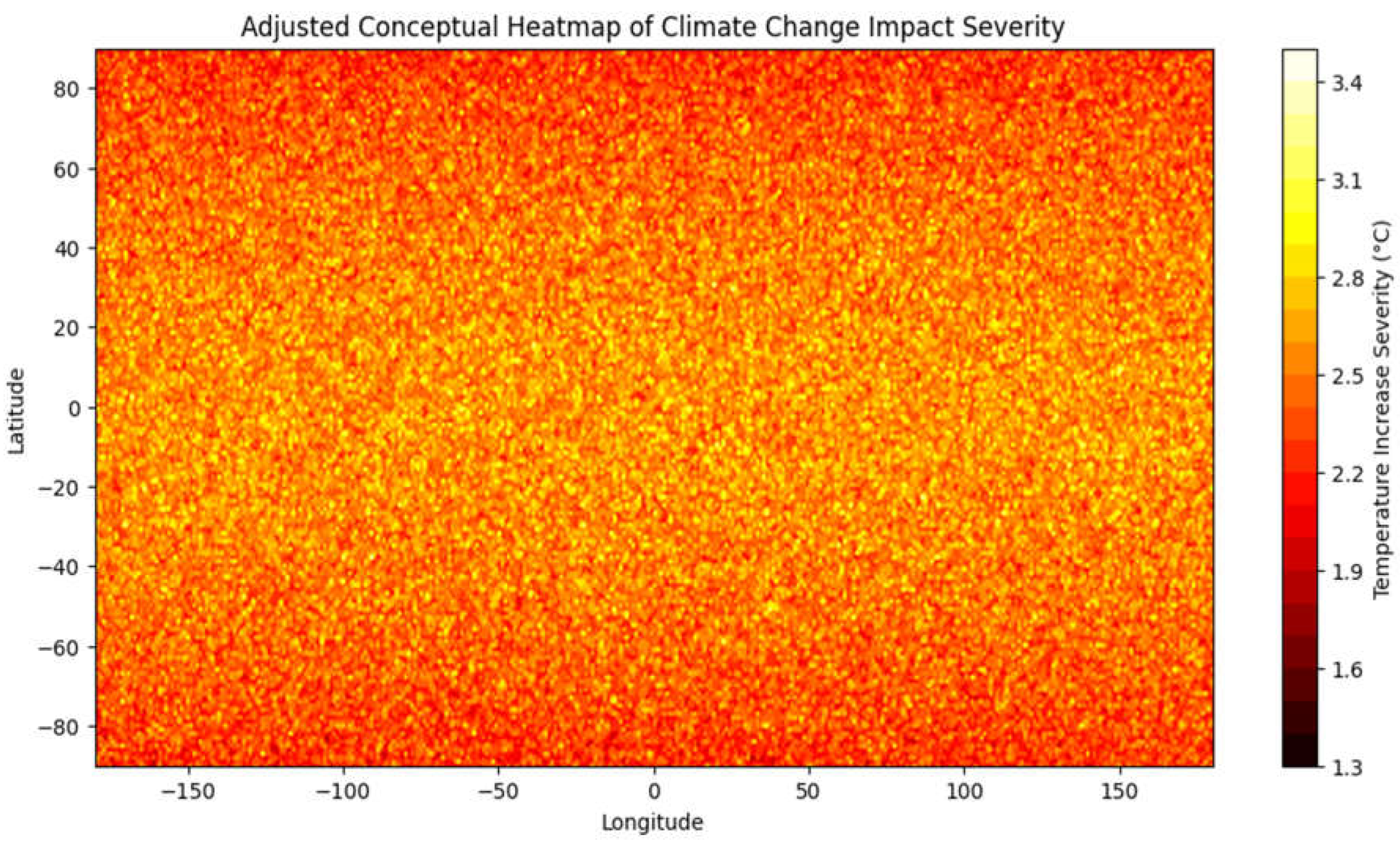
The SPDE model, incorporating various stochastic processes, was used to generate a heatmap illustrating the severity of temperature increases across the globe. The resultant graph provides a visual representation of the potential impacts of global warming, considering the base temperature increase and the added effects of stochastic factors such as solar explosions, economic upheavals, rising emissions, and irreversible changes.

3.1. Interpretation of the Heatmap

Global Temperature Increase:

The heatmap shows a general increase in temperature severity globally, with a baseline increase of 1.5°C. This baseline is influenced by latitude, reflecting the general trend that polar regions experience more significant temperature changes due to global warming.

Latitude Influence:

The base temperature model includes a cosine function of latitude, resulting in variations where higher latitudes (closer to the poles) exhibit slightly more severe temperature increases compared to equatorial regions, though, in a systemic vision, tropical zone usually present higher temperatures easily visualized by yellow spots predominance (Fig.1.). This pattern is consistent with observed and projected climate change impacts, where polar amplification is a known phenomenon (IPCC, 2021).

Stochastic Factors:

The addition of stochastic processes introduces variability across the map.

Solar Explosions: The random occurrences modeled by a Poisson process lead to scattered hotspots where the impact of solar events temporarily increases temperature severity.

Economic Upheavals: Represented by a normal distribution, economic fluctuations introduce random variations in temperature severity across different regions.

Rising Emissions: The normal distribution with a positive mean reflects the uncertainty and general upward trend in future emissions, adding a consistent increase in temperature severity.

Irreversibility: The constant factor for irreversible changes ensures a baseline increase in temperature severity, acknowledging the permanent changes already set in motion in the climate system.

Regional Variations:

The heatmap highlights regions that are particularly vulnerable to severe temperature increases. Notably:

Polar Regions: These regions show higher severity, consistent with the phenomenon of polar amplification where warming is more pronounced.

Tropical Regions: While the baseline increase is less pronounced, the stochastic factors introduce significant variability, indicating that these regions are also susceptible to extreme temperature events.

Global Patterns:

The overall pattern on the heatmap demonstrates a complex interplay between deterministic and stochastic factors. While the deterministic baseline provides a foundational trend, the stochastic elements introduce realistic variability, resulting in a heterogeneous pattern of temperature increases.

4. Discussion

This study presents a unique approach to modeling regional temperature increases due to global warming by employing a stochastic partial differential equation (SPDE) framework. This methodology allows us to incorporate various stochastic processes that reflect real-world uncertainties, providing a more comprehensive and realistic representation of potential climate change impacts. Our model includes factors such as solar explosions, economic upheavals, rising emissions, and irreversible changes, which are integrated into a base temperature model influenced by latitude.

The primary strength of our approach lies in its ability to capture the inherent uncertainties and random events that can significantly impact climate dynamics. Traditional deterministic models often fail to account for these stochastic elements, leading to potentially oversimplified or overly optimistic projections (Hasselmann, 1993). By incorporating stochastic processes, our model provides a more nuanced view of how different regions might experience temperature increases, considering the complex interplay of various factors.

4.1. Stochastic Modeling of Uncertainties:

Our SPDE model includes several stochastic elements:

(1): Solar Explosions: Modeled as a Poisson process, this reflects the random nature of solar events that can affect global climate patterns (Lockwood & Fröhlich, 2007).
(2): Economic Upheavals: Represented by a normal distribution, this accounts for the unpredictable nature of economic activities and their impact on greenhouse gas emissions (Stern, 2007).
(3): Rising Emissions: Also modeled by a normal distribution with a positive mean, this captures the uncertainty in future emission trajectories (IPCC, 2021).
(4): Irreversibility: Incorporated as a constant factor, this acknowledges the permanent changes in the climate system that cannot be reversed (Lenton et al., 2008).

4.2. Integration of Deterministic and Stochastic Components:

The base temperature model, influenced by latitude, provides a foundational understanding of how global warming affects different regions. The addition of stochastic processes to this model results in a more realistic simulation of temperature increases, offering a detailed heatmap that visualizes the severity of impacts across the globe.

4.3. Policy and Research Implications:

Our model can serve as a valuable tool for policymakers and researchers. By highlighting regions that are likely to suffer the most from temperature increases, it can guide the development of targeted mitigation and adaptation strategies (Oppenheimer et al., 2014). This approach also offers a framework for incorporating additional stochastic elements, making it adaptable to various climate scenarios and future research needs.

4.4. Potential Pitfalls

Despite its strengths, our approach has several potential pitfalls that must be acknowledged:

1. Simplified Stochastic Processes:

While our model includes stochastic elements, the processes are represented in a simplified manner. For instance, economic upheavals and rising emissions are modeled using normal distributions, which may not fully capture the complexities and interdependencies of real-world economic systems. Additionally, the Poisson process used for solar explosions assumes a constant rate, which might not reflect the true variability of solar activities (Solomon et al., 2007).

2.Parameter Uncertainty:

The parameters used in the stochastic processes (e.g., λ for solar explosions, μ_R and σ_R for rising emissions) are based on assumptions and available data, which might not be accurate or comprehensive. This parameter uncertainty can influence the model's outputs and lead to potential biases in the results (Berliner, 2003).

3. Spatial Resolution:

The model uses a 1-degree resolution grid, which may be too coarse to capture local variations in climate impacts. Finer resolution models would require significantly more computational resources but could provide more detailed and accurate projections (Diffenbaugh & Field, 2013).

4. Lack of Temporal Dynamics:

Our model focuses on the spatial distribution of temperature increases but does not explicitly account for temporal dynamics. Climate change impacts evolve over time, and a more comprehensive model would include time-dependent factors to simulate these changes accurately (Houghton, 2004).

5. Limited Scope of Stochastic Factors:

While we include several stochastic factors, there are other significant elements that could influence climate dynamics, such as volcanic eruptions, land-use changes, and technological advancements in emission reductions. Expanding the model to incorporate these factors would enhance its comprehensiveness (Lenton et al., 2008).

5. Conclusions

The SPDE approach presented in this study offers a novel and valuable perspective on regional temperature increases under global warming. By integrating stochastic processes, the model provides a more realistic representation of potential climate impacts, which is crucial for effective policy and research efforts. However, the simplifications and assumptions inherent in the model highlight the need for ongoing refinement and expansion to address its potential pitfalls. Future work should focus on improving the accuracy and resolution of stochastic elements, incorporating temporal dynamics, and expanding the scope of factors considered to ensure robust and reliable climate projections.

6. Attachment:

Python Code:

import numpy as np

import matplotlib.pyplot as plt

# Define the grid

x = np.linspace(-180, 180, 360)

y = np.linspace(-90, 90, 180)

X, Y = np.meshgrid(x, y)

# Adjusted base temperature model

def adjusted_base_temperature_severity(lat):

return 1.5 + 0.3 * np.cos(np.deg2rad(lat))

# Stochastic factors

np.random.seed(42) # For reproducibility

solar_explosions = np.random.poisson(lam=0.1, size=X.shape) # Poisson process for solar explosions

economic_upheavals = np.random.normal(loc=0.0, scale=0.2, size=X.shape) # Normal distribution for economic impacts

rising_emissions = np.random.normal(loc=0.5, scale=0.1, size=X.shape) # Normal distribution for rising emissions

irreversibility = 0.2 # Constant factor for irreversible changes

# Combined temperature severity model

Z = (adjusted_base_temperature_severity(Y) +

0.1 * solar_explosions +

economic_upheavals +

rising_emissions +

irreversibility)

# Plot the results

plt.figure(figsize=(12, 6))

plt.contourf(X, Y, Z, levels=20, cmap='hot')

plt.colorbar(label='Temperature Increase Severity (°C)')

plt.title('Adjusted Conceptual Heatmap of Climate Change Impact Severity')

plt.xlabel('Longitude')

plt.ylabel('Latitude')

plt.show()

References

Berliner, L. M. (2003). Uncertainty and climate change. Statistical Science, 18(4), 430-435.
Diffenbaugh, N. S., & Field, C. B. (2013). Changes in ecologically critical terrestrial climate conditions. Science, 341(6145), 486-492. [CrossRef]
Hasselmann, K. (1993). Optimal fingerprints for the detection of time-dependent climate change. Journal of Climate, 6(10), 1957-1971. [CrossRef]
Houghton, J. (2004). Global Warming: The Complete Briefing. Cambridge University Press. [CrossRef]
IPCC. (2021). Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change.
Lenton, T. M., Held, H., Kriegler, E., Hall, J. W., Lucht, W., Rahmstorf, S., & Schellnhuber, H. J. (2008). Tipping elements in the Earth's climate system. Proceedings of the National Academy of Sciences, 105(6), 1786-1793.
Lockwood, M., & Fröhlich, C. (2007). Recent oppositely directed trends in solar climate forcings and the global mean surface air temperature. III. Discussion of contributions to variability of surface air temperature. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 463(2086), 2447-2460. [CrossRef]
Oppenheimer, M., Campos, M., Warren, R., Birkmann, J., Luber, G., O’Neill, B., & Takahashi, K. (2014). Emergent risks and key vulnerabilities. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press.
Solomon, S., Qin, D., Manning, M., Averyt, K., Marquis, M., & Miller, H. L. (2007). Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press.
Stern, N. (2007). The Economics of Climate Change: The Stern Review. Cambridge University Press.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Stochastic Modeling of Climate Change Impact: Assessing Regional Temperature Increases Under Global Warming

Abstract

1. Introduction

2. Methodology

2.1. Mean Temperature Rise and Time Frame

2.2. Grid Definition

2.3. Base Temperature Model

2.4. Stochastic Processes

3. Results

3.1. Interpretation of the Heatmap

4. Discussion

4.1. Stochastic Modeling of Uncertainties:

4.2. Integration of Deterministic and Stochastic Components:

4.3. Policy and Research Implications:

4.4. Potential Pitfalls

5. Conclusions

6. Attachment:

References

MDPI Initiatives

Important Links

Subscribe