Prerpints.org logo
Preprint
Article

A Novel First-Principles Molecular Dynamics Approach for Testing the Attraction Forces in Hydrogen Storage on a 2D Material at Different Temperatures

Altmetrics

Downloads

86

Views

31

Comments

0

Submitted:

01 June 2024

Posted:

03 June 2024

You are already at the latest version

Alerts
Abstract
Our study utilized density functional theory (DFT) to explore a 2D MoP2 surface for hydrogen storage. Optimization determined a gravimetric capacity for pristine MoP2 of 5.72%, with an adsorption energy of ‒ 0.13 eV/molecule. For this surface with 12.5% Mo vacancies, we achieved 6.02% and ‒ 0.14 eV/molecule. We then introduced a novel criterion to test the attraction forces in hydrogen storage at a given temperature. This involved a first-principles molecular dynamics approach at various temperatures. To determine the number of molecules adsorbed on the surface at temperature T1, we conducted an FPMD calculation at T1, using the optimization as the initial system configuration. Subsequently, we performed a second FPMD calculation at a temperature T2 (with T2 ‹‹ T1), using the stable configuration of the first FPMD calculation as the initial configuration. If there were attraction forces on the molecules, they would move towards the surface. We identified as adsorbed molecules at temperature T1, only those that moved back toward the surface at temperature T2. The defective surface gave the best gravimetric capacity, ranging from 5.27% at 300 K to 6.02% at 77 K. The latter met the requirement from the US-DOE, indicating the potential practical application of our research in hydrogen storage.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Scientific interest in finding alternatives to the worldwide problems stemming from population growth and limited fossil fuel resources has increased in recent years. The focus has been on producing green energy and using materials to store it. Hydrogen storage is a desirable option for this purpose.
The development of materials for hydrogen storage remains a significant challenge. The US Department of Energy (US-DOE) highlights the importance of finding a material that can store hydrogen with high gravimetric and volumetric density while being environmentally friendly [1]. To achieve optimal adsorption and desorption, the adsorption energies for storing H2 molecules should fall within the range of 0.1 eV to 0.2 eV [2,3]. Various methods exist to generate renewable energy sources for hydrogen production. Electrolytic hydrogen production offers an alternative to hydrogen production for internal combustion engines and fuel cells [4]. The hydrogen evolution reaction (HER) is a critical electrocatalytic reaction, with hydrogen adsorption on the electrode playing a crucial role. In the past, Pt-based materials were considered the best HER catalysts. However, it is essential to find cheaper and more abundant alternatives to Pt materials [5]. Molybdenum sulfide was the first reported alternative to Pt-based materials for catalyzing the HER in acidic aqueous solutions [6]. Since then, Mo-based materials, including molybdenum phosphides and transition metal phosphides (TMPs), have gained prominence as low-cost HER electrocatalysis materials [7,8,9].
We investigated the direct interaction between a MoP2 surface and H2 molecules for hydrogen storage using DFT calculations. Additionally, we explored the influence of Mo vacancies on the gravimetric capacity of hydrogen adsorption on a MoP2 surface. Our study involved FPMD calculations at 300 K, 77 K, 4 K, and 3 K to assess the system's stability under varying conditions.

2. Materials and Methods

We performed ab initio DFT calculations to study hydrogen storage on the 2D material MoP2. We considered the pristine material and the same material with 12.5% Mo vacancies. We employed the generalized gradient approximation (GGA) with the exchange-correlation energy given by Perdew-Burke-Ernzerhof double-zeta polarized basis sets and norm-conserving pseudopotentials [10,11]. Our calculations used the SIESTA code [12] and the spin-polarized density functional formalism. We followed the Monkhorst–Pack scheme [13] and considered a Brillouin zone sampling of 24x24x1 k-points. We took an energy cutoff of 180 Ry for numerical integrations. The geometries of the studied systems converged until forces between atoms were smaller than 0.01 eV/Å. To consider dispersion forces, we included the Van der Waals interactions using Grimme's semiempirical approach [14].
We carried out our simulations of these systems with a supercell 2x2, with a separation between layers of 30 Å. In the case of the pristine 2DMoP2 system, the supercell consists of four molybdenum (Mo) atoms and eight phosphorus (P) atoms (Figure 1a). In comparison, the 2D MoP2 with a Mo vacancy has three molybdenum (Mo) particles and eight phosphorus (P) atoms (Figure 1b). In this manner, the Mo vacancy in the cell of twelve atoms corresponds to 12.5% of vacancies. In the system's initial configuration (pristine or with 12.5% of vacancies), we added hydrogen molecules one by one above a Mo or P atom to optimize the system, and the original distance of the hydrogen molecules from the surface was 3 Å.
Every structure was relaxed to determine the most stable configuration before the saturation of H2 molecules.
We calculated the adsorption energy using equation (1).
E ads = E final   configuration   – n E H + E surface
Where Eads is the adsorption energy, n is the number of hydrogen molecules we considered, EH is the total energy of one free H2 molecule, and Esurface is the total energy of the surface unit cell. We obtained by optimization an average adsorption energy of ‒ 0.13 eV per molecule.
We calculated the gravimetric capacity Wt% using equation (2).
Wt % = 100   n W H / n W E H + W surface
WH is the molecular hydrogen mass, n is the same as before, and Wsuface is the mass in the unit cell surface.
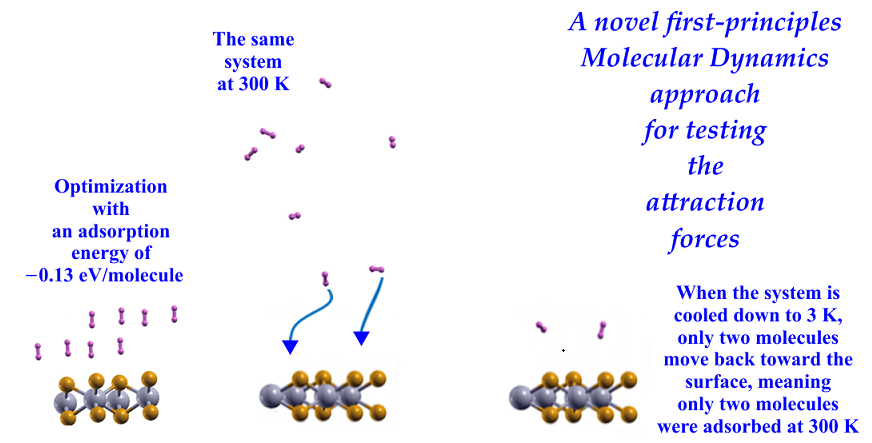
We established a new criterion to test the attraction forces in hydrogen storage at a given temperature. Thus, we took a first-principles molecular dynamics approach at different temperatures. So, if we want to know how many molecules remained attached to the surface at temperature T1, we proceed as follows. We performed an FPMD calculation at temperature T1, taking the optimization as the initial system configuration. Then, we perform a second FPMD calculation at a temperature T2 ( with T2 ‹‹ T1), bringing the stable configuration of the first FPMD calculation as the initial configuration. We identified as adsorbed H2 molecules at temperature T1, only those that moved back toward the surface at temperature T2.
With the optimization of the system and the adsorbed hydrogen molecules as the starting point, we used the Quantum Espresso Code [15] to perform the first-principles molecular dynamics calculations at several temperatures. We employed XCrysden [16] to visualize the system’s configurations.

3. Results

3.1. Hydrogen Storage on Pristine 2D MoP2

3.1.1. Optimization

The pristine monolayer can adsorb up to 16 H2 molecules—eight molecules per side, as shown in Fig. 2, which presents the final configurations for one side. We calculated the adsorption energy using equation (1).
E ads = E final   configuration   – n E H + E surface
Where Eads is the adsorption energy, n is the number of hydrogen molecules we considered, EH is the total energy of one free H2 molecule, and Esurface is the total energy of the surface unit cell. We obtained by optimization an average adsorption energy of ‒ 0.13 eV per molecule.
We calculated the gravimetric capacity Wt% using equation (2).
Wt % = 100   n W H / n W E H + W surface
WH is the molecular hydrogen mass, n is the same as before, and Wsuface is the mass in the unit cell surface.
We obtained a gravimetric capacity for hydrogen storage of 5.72%, and the average adsorption energy is ‒ 0.13 eV/molecule.

3.1.2. First-Principles Molecular Dynamics Calculations

We followed the criterion described in the Materials and Methods section to calculate the gravimetric capacity, determining how many molecules adsorbed the surface at a given temperature. Using the optimization of the system and the adsorbed hydrogen molecules as the starting point, we performed the first-principles molecular dynamics calculations at 300K.
We found that at 300 K, all the adsorbed H2 molecules in the initial optimization moved away from the surface, as Figure 3 shows.
We then reduced the temperature to 3 K and performed a second FPMD calculation to determine how many remained bound to the surface. Thus, we considered the stable configuration obtained at 300 K as the initial state for the second FPMD calculation, as shown in Figure 4. We identified as adsorbed H2 molecules only those that moved back to the surface. In this way, we obtained that at 300 K, the pristine surface retained only two H2 molecules per side, which implies 1.28% of gravimetric storage capacity.
Again, at 77 K, we considered the optimization configuration the initial state and performed an FPMD calculation, as shown in Figure 5, and used the same criterion. Afterward, we reduced the temperature to 3 K and performed another FPMD calculation to determine how many remained bound to the surface (see Figure 6). Thus, we identified as adsorbed H2 molecules only those that moved back to the surface. There were only three H2 molecules per side of the surface, with a gravimetric capacity for molecular hydrogen storage of 1.92%.
In the case of 4 K, Figure 7 shows the FPMD calculation where the optimization is the initial configuration. Notice that all the molecules remained close to the surface.
In the following FPMD calculation at 3 K, all the hydrogen molecules moved back to the surface, indicating that they adsorbed on the pristine 2D MoP2 surface, as Figure 8 shows. The gravimetric capacity for molecular hydrogen storage is 5.1% for 16 adsorbed hydrogen molecules (eight per side).
In summary, in the optimization, the pristine 2D MoP2 surface adsorbed up to 16 hydrogen molecules (8 per side), with a gravimetric molecular hydrogen storage capacity of 5.1% and an average adsorption energy of ‒ 0.13 eV/molecule. However, we performed an FPMD calculation at 300 K and applied our already mentioned criterion to determine how many molecules adsorbed the surface at a given temperature. At that temperature, we found that only two (per side) hydrogen molecules adsorbed on the pristine 2D MoP2 surface, with a gravimetric capacity of 1.28%. When we considered a temperature of 77 K and applied the same criterion, we found a gravimetric capacity for molecular hydrogen storage of 1.92%. For 4 K, the gravimetric capacity increases to 5.1%.

3.2. Hydrogen Storage on 2DMoP2 with Mo Vacancies

3.2.1. Optimization

To simulate the adsorption of H2 molecules on the surface of 2DMoP2 with vacancies, we considered a supercell 2x2x1, as Fig. 1 (b) shows. In this manner, we made a Mo vacancy in the cell of twelve atoms, corresponding to 12.5% of vacancies. Again, in the system's initial configuration, we added hydrogen molecules one by one above a Mo or P atom to optimize the system, and the original distance of the hydrogen molecules from the surface was 3 Å. We obtained that 2D MoP2 with Mo vacancies can adsorb up to 16 H2 molecules (eight molecules per side), as Figure 9 shows, and a gravimetric capacity of 6.0%. We calculated average adsorption energy of around ‒ 0.14 eV/molecule.

3.2.2. First-Principles Molecular Dynamics Calculations

We followed the procedure in Section 2.1 to calculate the gravimetric capacity at 300 k. Figure 10 shows the FPMD calculation at that temperature. As expected, all the molecules displaced away from the surface.
Figure 11 shows the subsequent FPMD calculation at 3 K, starting with the stable configuration at 300 K. Notice that seven hydrogen molecules (per side) moved towards the surface when the temperature decreased. Thus, the gravimetric capacity for hydrogen storage on the surface is 5.27%.
In the case of 77 K, we again considered the optimization configuration as the initial state and performed an FPMD calculation at that temperature, as Figure 12 shows. Again, all the molecules moved away from the surface.
In Figure 13, we present the subsequent FPMD calculation at 3 K, starting with the stable configuration at 77 K. Notice that all the eight hydrogen molecules (per side) moved towards the surface when the temperature decreased, showing a gravimetric capacity of 6.02%.
Figure 14 shows the FPMD calculation at 4 K, taking the optimization as the initial configuration. Again, we can notice that all the hydrogen molecules moved away from the surface. The elapsed time was two picoseconds.
In Figure 15, we present the subsequent FPMD calculation at 3 K, starting with the stable configuration at 4 K. Notice that all eight hydrogen molecules (per side) moved towards the surface when the temperature decreased, showing a gravimetric capacity of 6.02%.
In summary, when we considered the 2D MoP2 with 12.5% Mo vacancies and optimized the system, the surface adsorbed up to 16 hydrogen molecules (8 per side). This corresponds to a gravimetric molecular hydrogen storage capacity of 6.02%, and the average adsorption energy is ‒ 0.14 eV/molecule. However, when we applied our already described approach to determine how many molecules adsorbed the surface at a given temperature and performed an FPMD calculation at 300 K, we found that only seven (per side) hydrogen molecules adsorbed on the surface. The gravimetric capacity is 5.27%. Using the same methodology at 77 K, we found a gravimetric capacity for molecular hydrogen storage of 6.02%. As we expected, for 4 K, the gravimetric capacity is 6.02%, too.

4. Discussion

We performed ab initio DFT calculations to study hydrogen storage on the 2D material MoP2. We considered the pristine material and with Mo vacancies.
We found by optimization of the system that the pristine 2D MoP2 surface adsorbed a maximum of 16 hydrogen molecules (8 per side), with an average adsorption energy of ‒ 0.13 eV/molecule. Furthermore, we considered the same surface with 12.5% Mo vacancies and obtained by optimization a gravimetric capacity of 6.02% and an average adsorption energy of ‒ 0.14 eV/molecule. We had to consider dispersion forces. Thus, we included the Van der Waals interactions using Grimme's semiempirical approach [14].
We established a new criterion to test the attraction forces in hydrogen storage at a given temperature described in Section 2. Thus, we took a first-principles molecular dynamics approach at different temperatures. So, if we want to know how many molecules remained attached to the surface at temperature T1, we proceed as follows. We performed an FPMD calculation at temperature T1, taking the optimization as the initial system configuration. Then, we perform a second FPMD calculation at a temperature T2 ( with T2 ‹‹ T1), bringing the stable configuration of the first FPMD calculation as the initial configuration. We identified as adsorbed H2 molecules at temperature T1, only those that moved back toward the surface at temperature T2.
We followed the new criterion described above to calculate the gravimetric storage capacity for molecular hydrogen storage and report the results described in Section 3 for 300K, 77 K, and 4 K.
Our results suggest that using only optimization may lead to unreliable predictions for hydrogen storage. Applying our proposed criterion, we conclude that the 2D MoP2 surface with Mo vacancies was adequate for the same purpose. At 300 K, the defective 2D MoP2 with 12.5% Mo vacancies had a 5.27% gravimetric capacity (the US-DOE target is 5.5% for automotive-grade molecular hydrogen storage). At 77 K and below this temperature, this system reached a gravimetric capacity of 6.02%, above the US-DOE target. Here, the disadvantage is maintaining the material at that temperature during the application for hydrogen storage in automotive-grade molecular hydrogen storage. However, our results indicate that further investigation of this class of 2D materials is needed to achieve successful molecular hydrogen storage at room temperature.

Author Contributions

Conceptualization, LFM; Data curation, ALM, OST, and LFM; Formal analysis ALM, and LFM; Funding acquisition, LFM; Investigation, ALM, OST, and LFM; Methodology, ALM, OST, and LFM; Project administration, LFM; Resources, LFM; Validation, ALM, OST, and LFM; Writing—original draft, ALM and LFM; Writing—review & editing LFM All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Dirección General de Asuntos del Personal Académico de la Universidad Nacional Autónoma de México, grant number IN102323.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

We thank Dirección General de Asuntos del Personal Académico de la Universidad Nacional Autónoma de México for their partial financial support through Grant IN102323. We also thank UNAM-Miztli-Super-Computing Center for its technical assistance through the project LANCAD-UNAM-DGTIC-030.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Office of energy efficiency & renewable energy. DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles. Available online: https://www.energy.gov/eere/fuelcells/doetechnical-targets-onboard-hydrogen-storage-light-duty vehicles.
  2. Jena, P. Materials for Hydrogen Storage: Past, Present, and Future. J. Phys. Chem. Lett. 2011, 2, 206. [Google Scholar] [CrossRef]
  3. Zhou, J.; Wang, Q.; Sun, Q. Electric field enhanced hydrogen storage on polarizable materials substrates. Proc. Natl. Acad. Sci. USA 2010, 107, 2801. [Google Scholar] [CrossRef] [PubMed]
  4. Lasia, A. Mechanism and kinetics of the hydrogen evolution reaction. Int. J. of Hydrogen Energy 2019, 44, 19484. [Google Scholar] [CrossRef]
  5. Gao, Y.; Zhang, M.; Ding, J.; Hong, S.; Masa, J.; Liu, S.; Sun, Z. Simple synthesis of two-dimensional MoP2 nanosheets for efficient electrocatalytic hydrogen evolution. Elec. Comm. 2018, 97, 27. [Google Scholar]
  6. Yan, Y.; Xia, B.; Xu, Z.; Wang, X. Recent Development of Molybdenum Sulfides as Advanced Electrocatalysts for Hydrogen Evolution Reaction. ACS Catal 2014, 4, 1693–1705. [Google Scholar] [CrossRef]
  7. Kibsgaard, J.; Tsai, C.; Chan, K.; Benck, J.D.; Nørskov, J.K.; Abild-Pedersen, F.; Jaramillo, T.F. Designing an improved transition metal phosphide catalyst for hydrogen evolution using experimental and theoretical trends. Energy Environ. Sci 2015 , 8, 3022. [Google Scholar] [CrossRef]
  8. McEnaney, J.M.; Chance Crompton, J.; Callejas, J.F.; Popczun, E.J.; Biacchi, A.J.; Lewis, N.S.; Schaak, R.E. Amorphous molybdenum phosphide nanoparticles for electrocatalytic hydrogen evolution. Chem. Mater 2014, 26, 4826–4831. [Google Scholar] [CrossRef]
  9. Wei, C.; Qian, L.; Xing, Z.; Asiri, A.M.; Alamri, K.A.; Sun, X. MoP nanosheets supported on biomass-derived carbon flake: One-step facile preparation and application as a novel high-active electrocatalyst toward hydrogen evolution reaction. Applied Catalysis B: Environmental 2015, 164, 144–150. [Google Scholar]
  10. Troullier, N.; Martins, J.L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef] [PubMed]
  11. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  12. Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation Phys. Condens. Matter 2002, 14, 2745. [Google Scholar]
  13. Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  14. Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787. [Google Scholar] [CrossRef] [PubMed]
  15. Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
  16. Kokalj, A. XCrySDen—A New Program for Displaying Crystalline Structures and Electron Densities. J. Mol. Graph. Model. 1999, 17, 176–179. [Google Scholar] [CrossRef] [PubMed]
Preprints 108131 g001
Figure 1. The unit cell of the optimized configurations of 2DMoP2 pristine surface (a) and the unit cell with a Mo vacancy (b).
Figure 1. The unit cell of the optimized configurations of 2DMoP2 pristine surface (a) and the unit cell with a Mo vacancy (b).
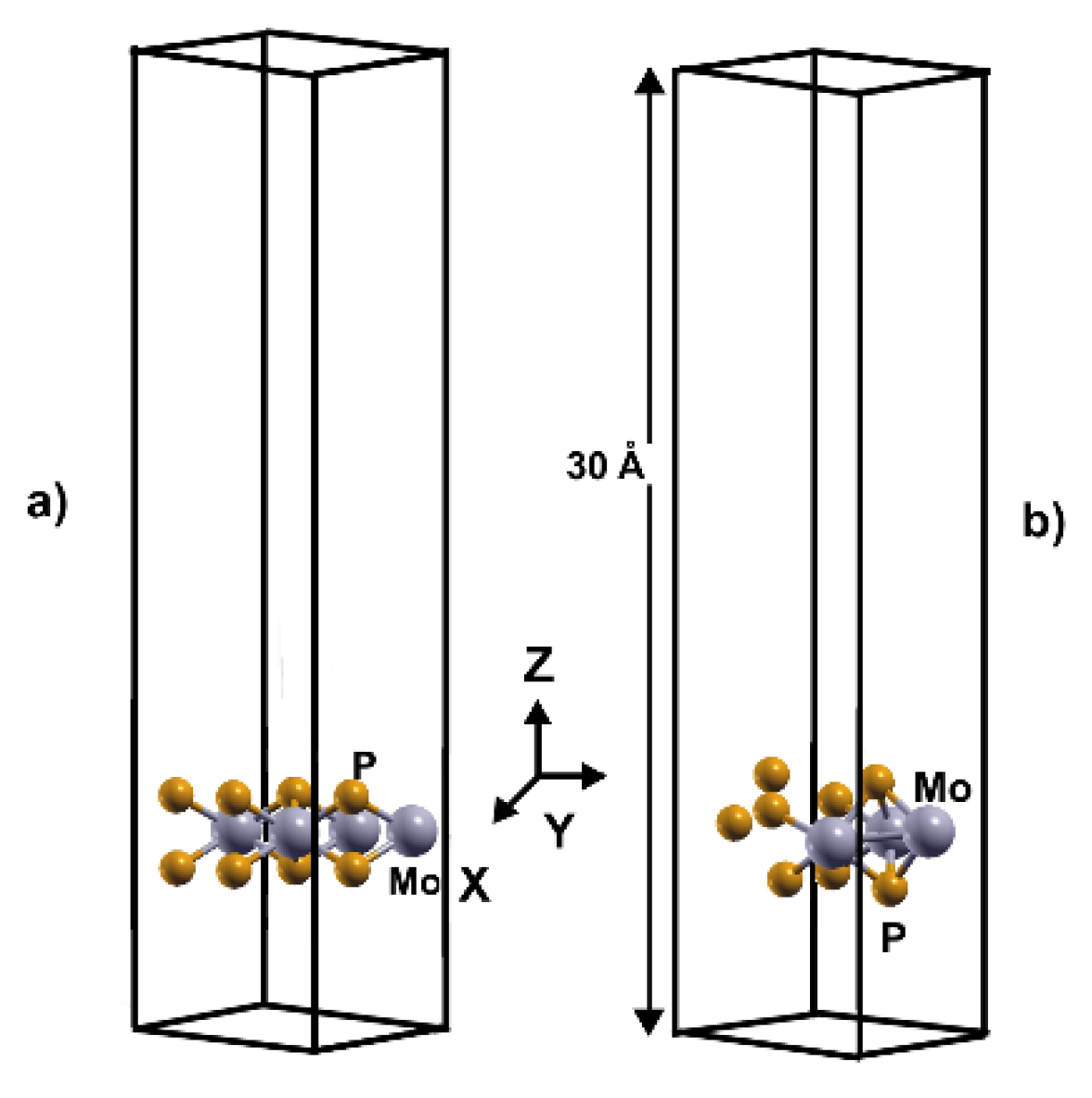
Preprints 108131 g001
Preprints 108131 g002
Figure 2. The optimized configuration of the 2DMoP2 pristine surface with eight adsorbed hydrogen molecules. This adsorption occurs on each side of the surface for 16 adsorbed molecules.
Figure 2. The optimized configuration of the 2DMoP2 pristine surface with eight adsorbed hydrogen molecules. This adsorption occurs on each side of the surface for 16 adsorbed molecules.
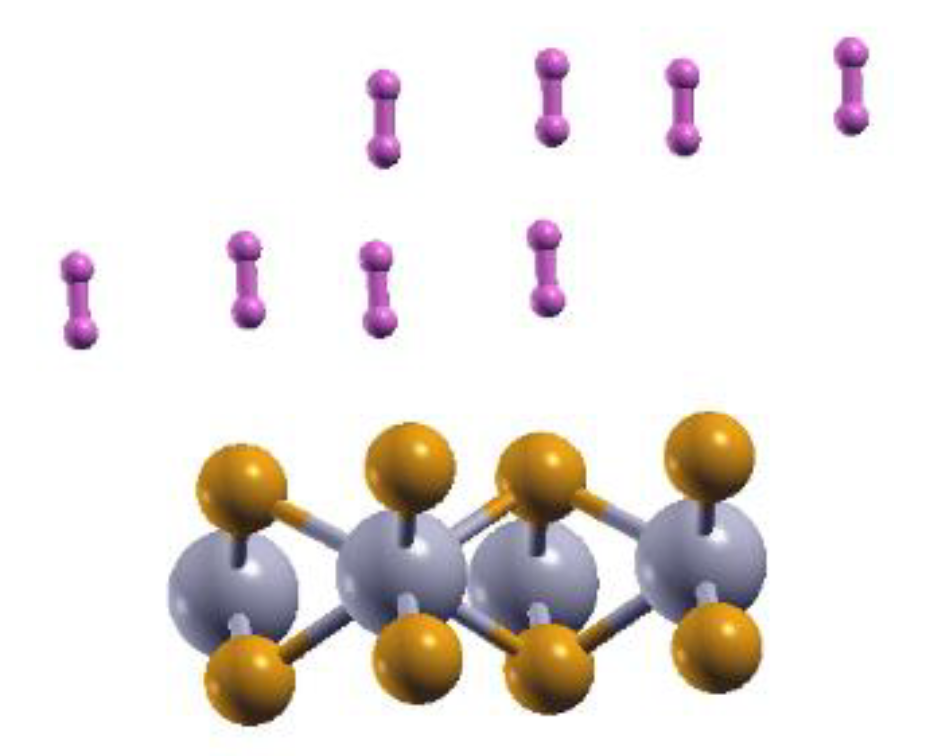
Preprints 108131 g002
Preprints 108131 g003
Figure 3. The FPMD calculation is at 300 K. The initial configuration is the optimization of the pristine 2D MoP2. The H2 molecules moved away from the surface, with one picosecond elapsed.
Figure 3. The FPMD calculation is at 300 K. The initial configuration is the optimization of the pristine 2D MoP2. The H2 molecules moved away from the surface, with one picosecond elapsed.
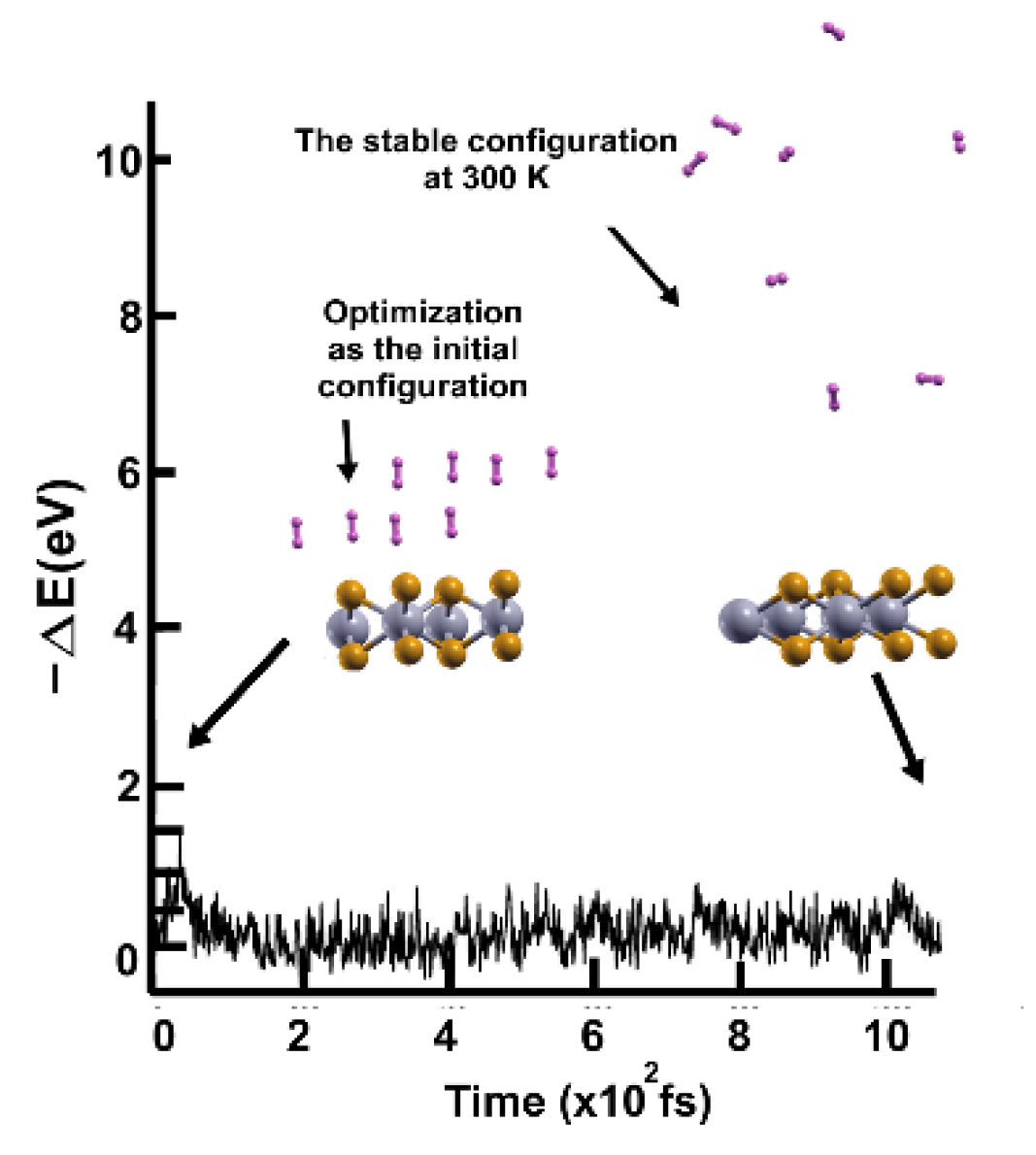
Preprints 108131 g003
Preprints 108131 g004
Figure 4. We performed the FPMD calculation at 3K, taking the initial configuration of the stable system as obtained at 300 K. Only two hydrogen molecules moved back to the surface, indicating that only those two remained adsorbed on the pristine 2D MoP2 surface at 300 K. The gravimetric capacity is 1.28% in this case.
Figure 4. We performed the FPMD calculation at 3K, taking the initial configuration of the stable system as obtained at 300 K. Only two hydrogen molecules moved back to the surface, indicating that only those two remained adsorbed on the pristine 2D MoP2 surface at 300 K. The gravimetric capacity is 1.28% in this case.
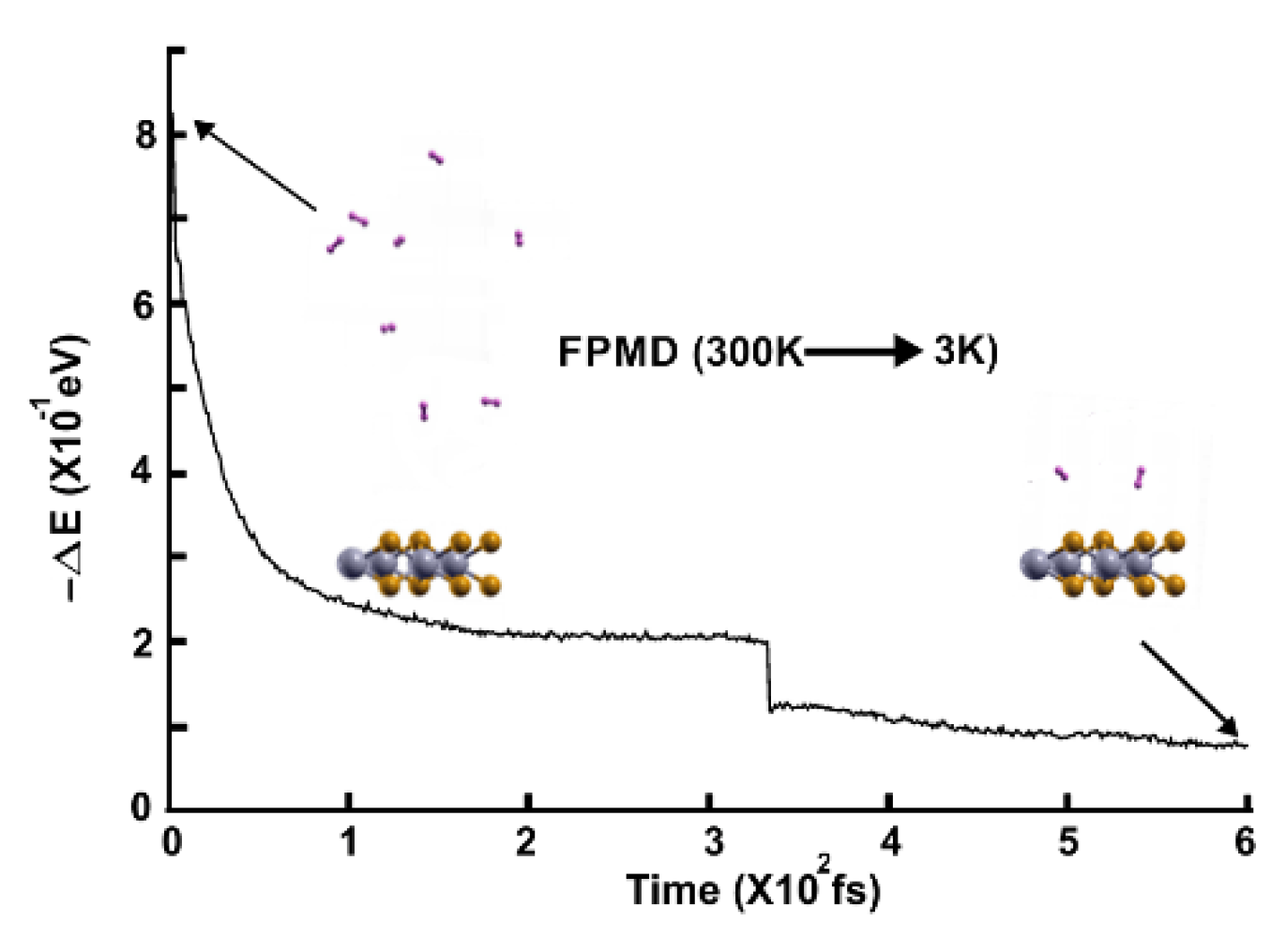
Preprints 108131 g004
Preprints 108131 g005
Figure 5. The FPMD calculation is at 77K, with the optimization as the initial configuration. All the molecules are displaced away from the surface.
Figure 5. The FPMD calculation is at 77K, with the optimization as the initial configuration. All the molecules are displaced away from the surface.
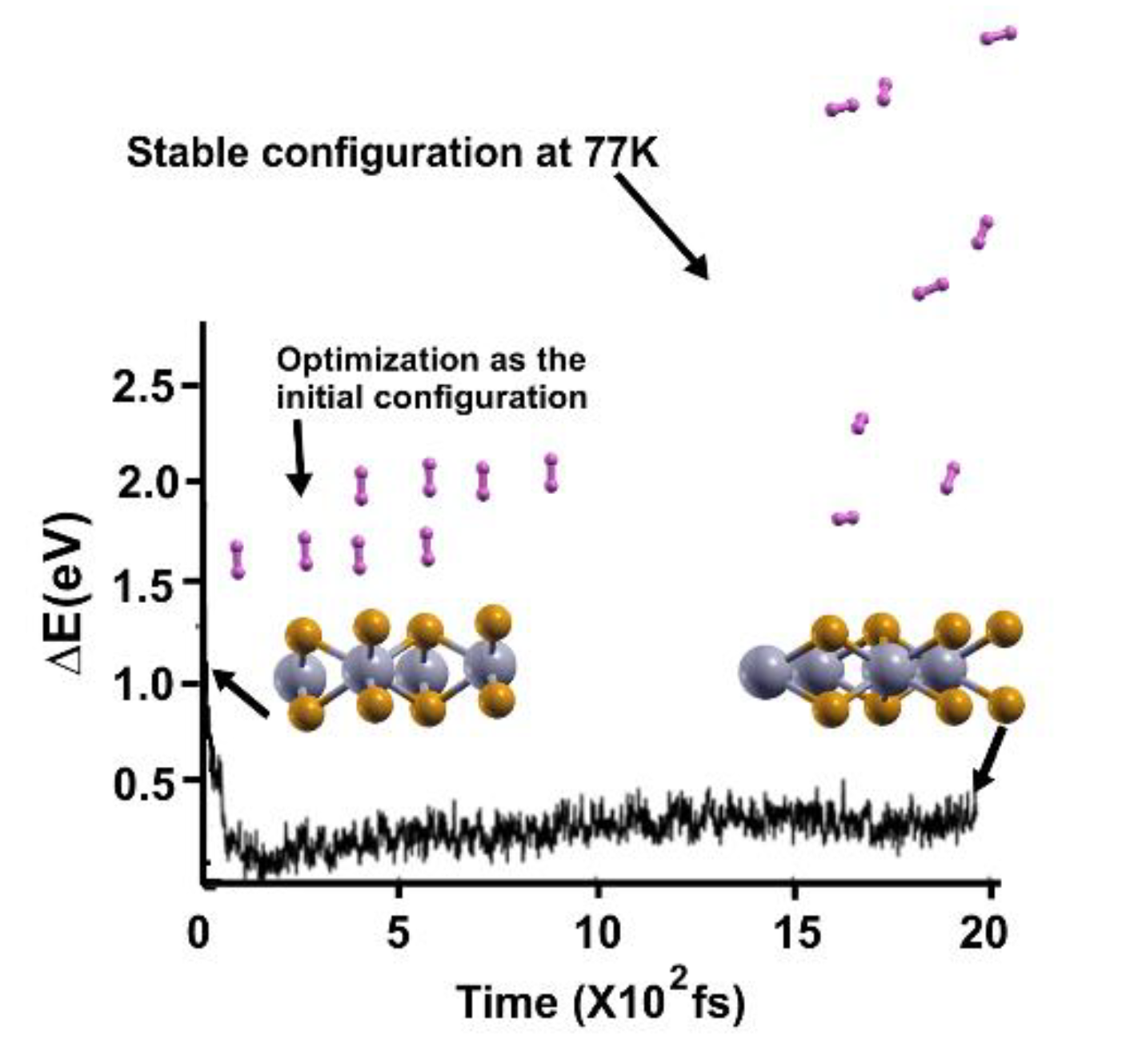
Preprints 108131 g005
Preprints 108131 g006
Figure 6. The FPMD calculation is at 3K, taking the initial configuration of the stable system as obtained at 77 K. Only three hydrogen molecules (per side) moved back to the surface, indicating that only those six remained adsorbed on the pristine 2D MoP2 surface at 77 K. The gravimetric capacity is 1.92%.
Figure 6. The FPMD calculation is at 3K, taking the initial configuration of the stable system as obtained at 77 K. Only three hydrogen molecules (per side) moved back to the surface, indicating that only those six remained adsorbed on the pristine 2D MoP2 surface at 77 K. The gravimetric capacity is 1.92%.
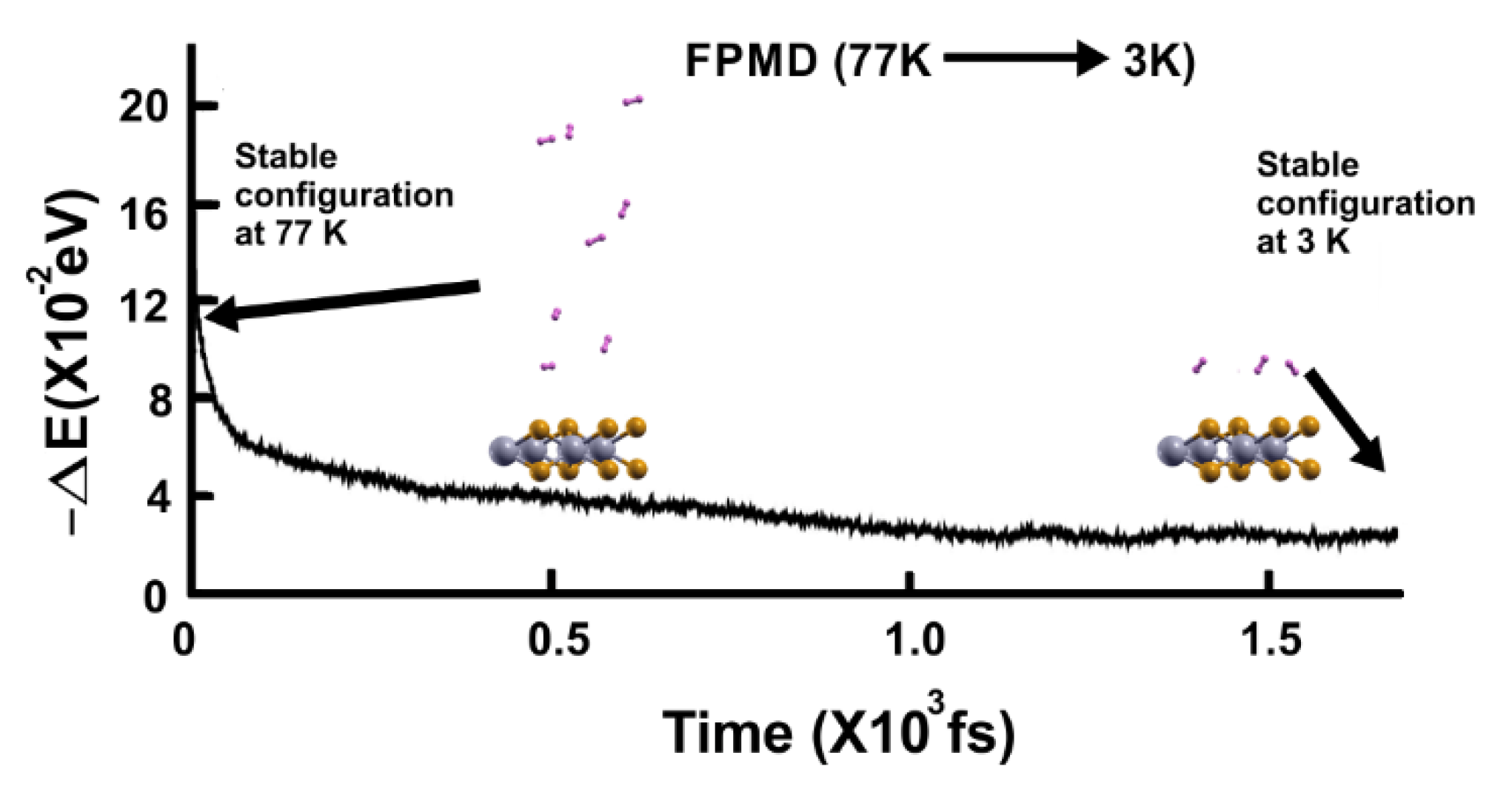
Preprints 108131 g006
Preprints 108131 g007
Figure 7. The FPMD calculation is at 4K, with the optimization as the initial configuration. All hydrogen molecules remained close to the surface.
Figure 7. The FPMD calculation is at 4K, with the optimization as the initial configuration. All hydrogen molecules remained close to the surface.
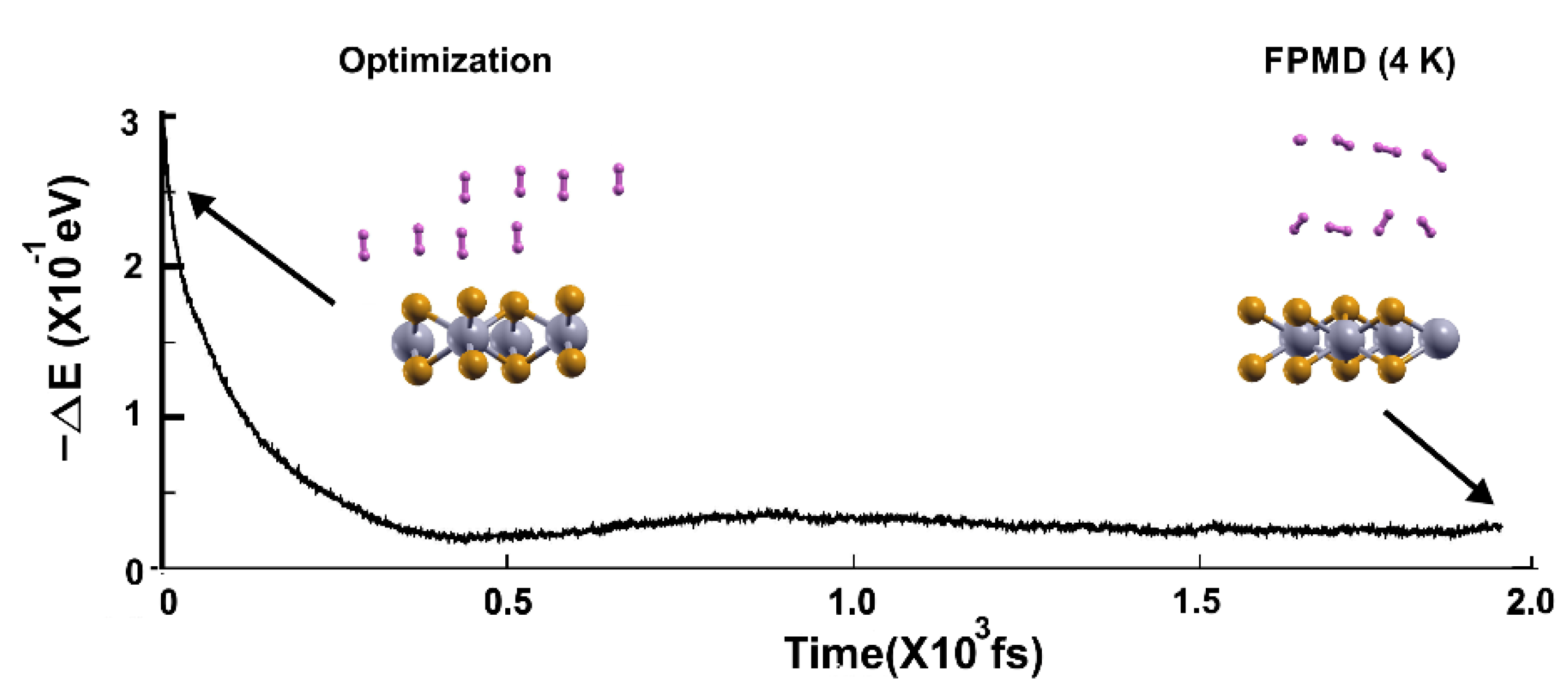
Preprints 108131 g007
Preprints 108131 g008
Figure 8. We performed the FPMD calculation at 3K, taking the initial configuration of the stable system as obtained at 4 K. All the hydrogen molecules moved back to the surface, indicating that they adsorbed on the pristine 2D MoP2 surface. The gravimetric capacity for molecular hydrogen storage is for 16 hydrogen molecules, 5.1%.
Figure 8. We performed the FPMD calculation at 3K, taking the initial configuration of the stable system as obtained at 4 K. All the hydrogen molecules moved back to the surface, indicating that they adsorbed on the pristine 2D MoP2 surface. The gravimetric capacity for molecular hydrogen storage is for 16 hydrogen molecules, 5.1%.
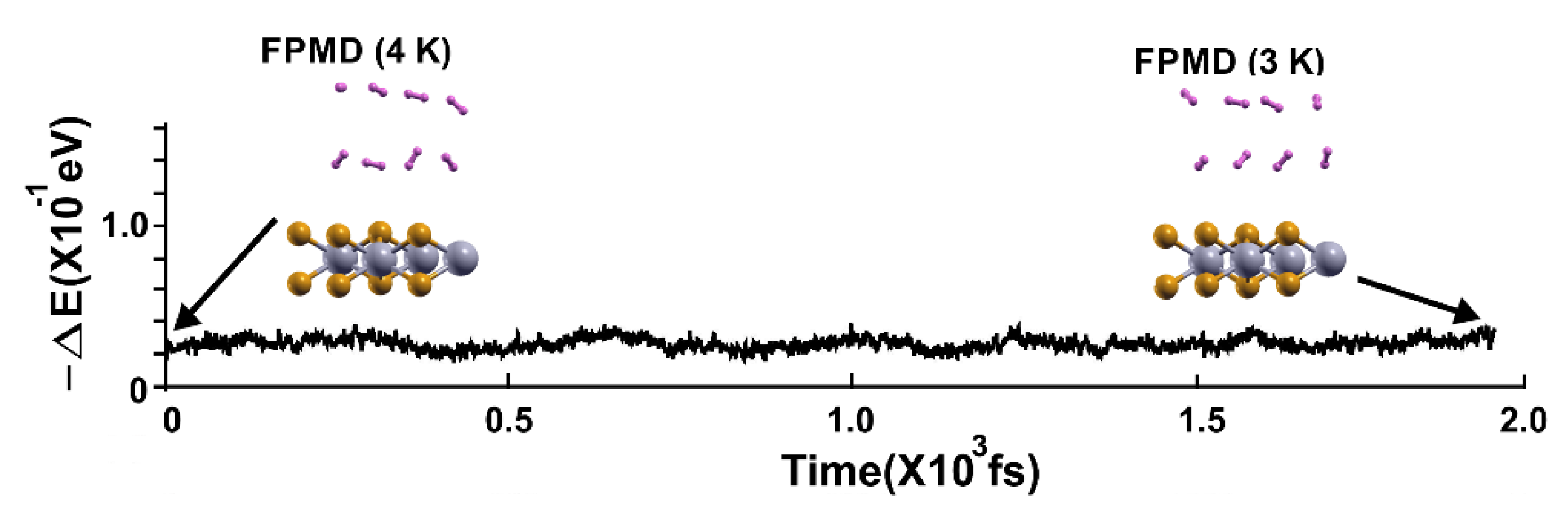
Preprints 108131 g008
Preprints 108131 g009
Figure 9. The optimized configuration is 2DMoP2 with 12.5% Mo vacancies and eight adsorbed hydrogen molecules. The adsorption occurs on each side of the surface for 16 adsorbed molecules. The average adsorption energy is ‒ 0.14 eV/molecule.
Figure 9. The optimized configuration is 2DMoP2 with 12.5% Mo vacancies and eight adsorbed hydrogen molecules. The adsorption occurs on each side of the surface for 16 adsorbed molecules. The average adsorption energy is ‒ 0.14 eV/molecule.
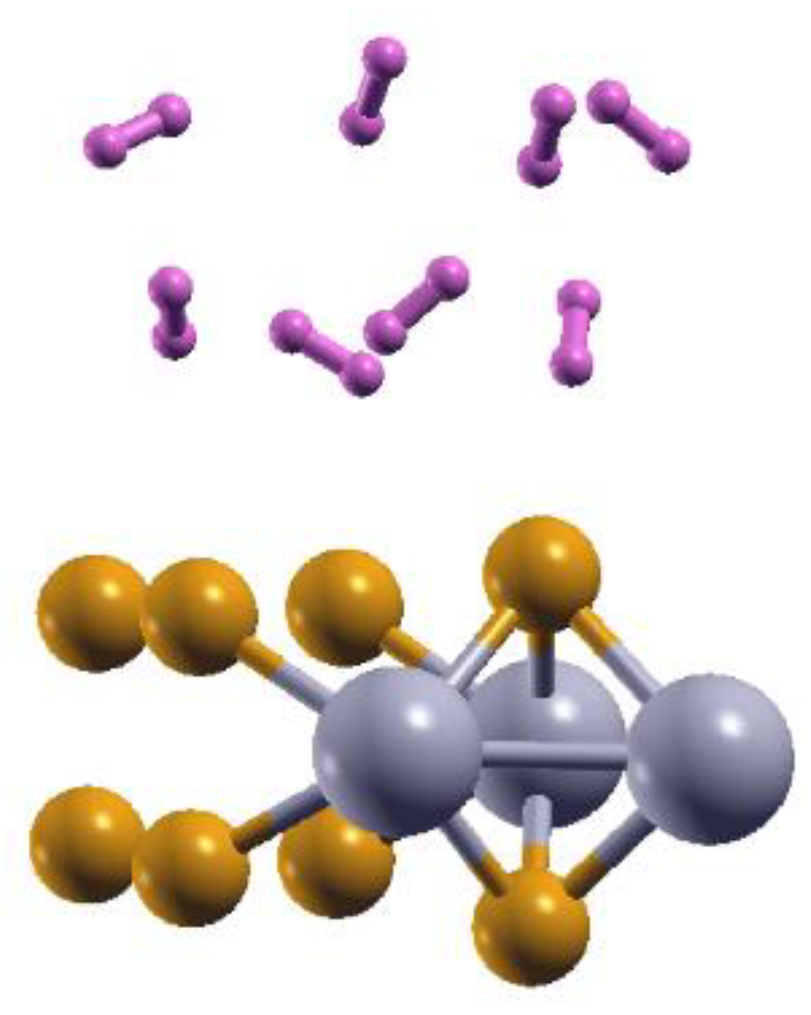
Preprints 108131 g009
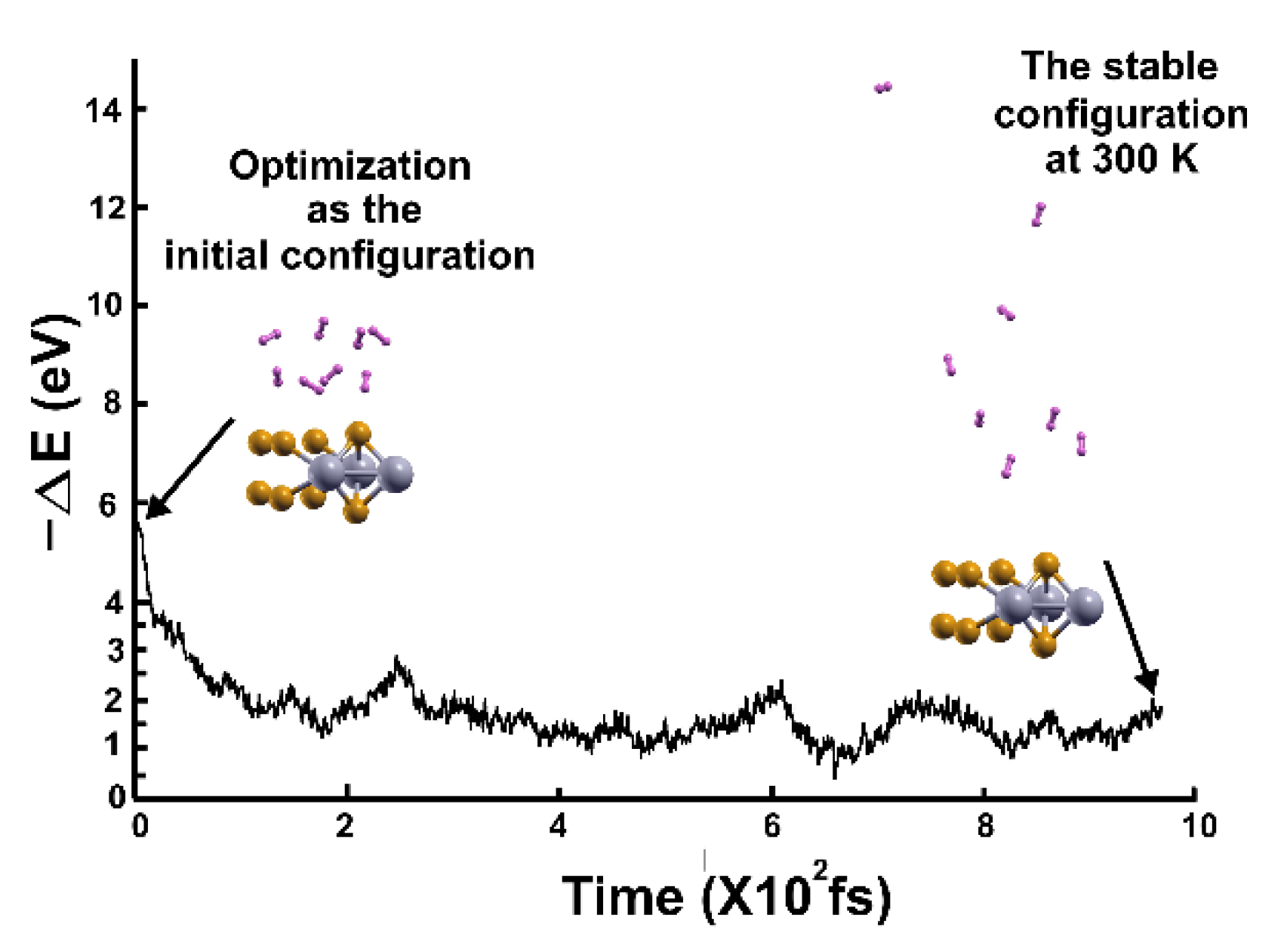
Preprints 108131 g010
Figure 10. FPMD calculation at 300 K, where the initial state is the optimization of the 2D MoP2 with 12.5% Mo vacancies. The hydrogen molecules moved away from the surface. The elapsed time was one picosecond.
Figure 10. FPMD calculation at 300 K, where the initial state is the optimization of the 2D MoP2 with 12.5% Mo vacancies. The hydrogen molecules moved away from the surface. The elapsed time was one picosecond.
Preprints 108131 g010
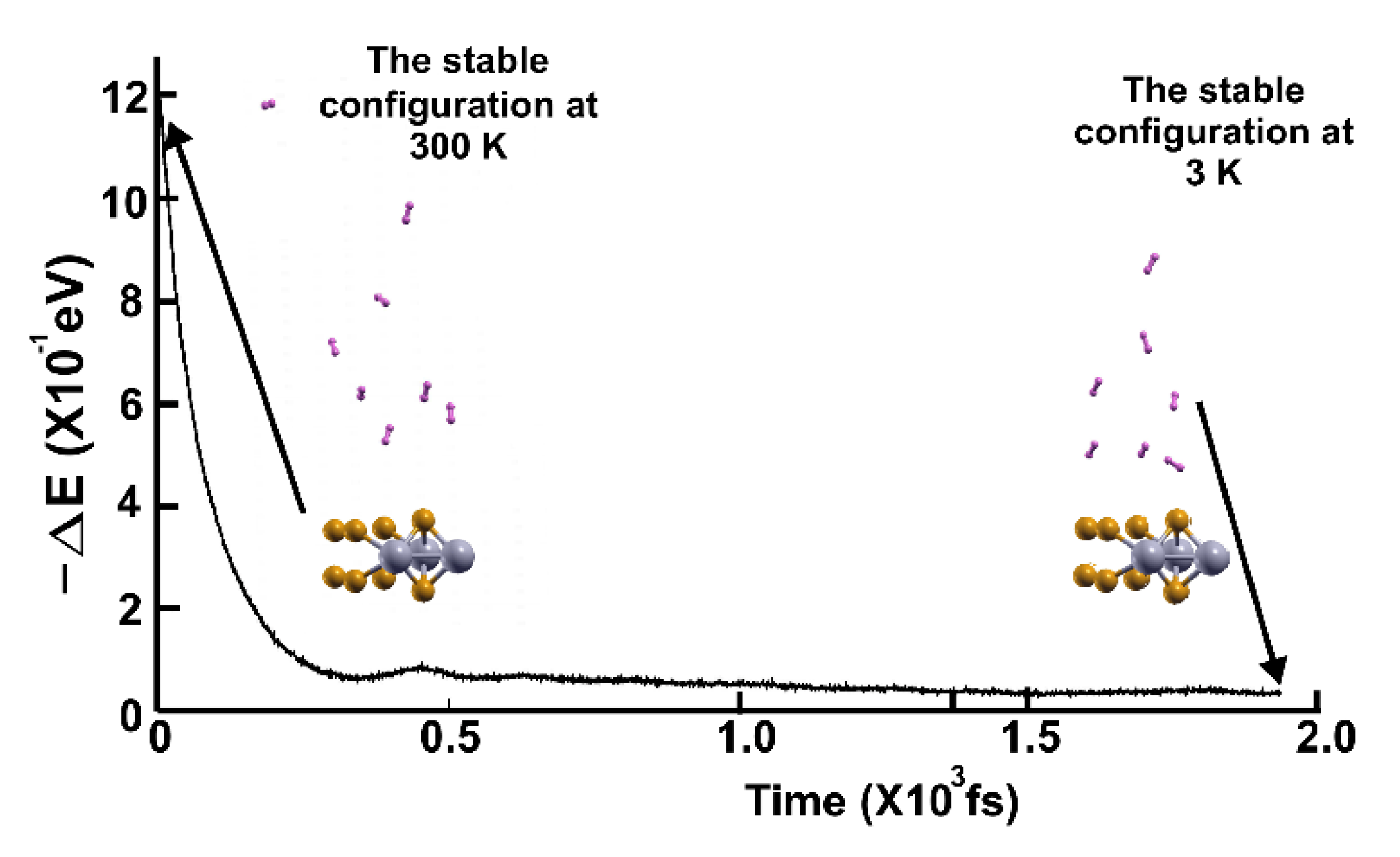
Preprints 108131 g011
Figure 11. FPMD calculation at 3 K, where the initial state is the stable configuration at 300 K of the 2D MoP2 with 12.5% Mo vacancies. Only seven hydrogen molecules remained attached to the surface; this corresponds to a gravimetric capacity for molecular hydrogen storage of 5.27%. The elapsed time was two picoseconds.
Figure 11. FPMD calculation at 3 K, where the initial state is the stable configuration at 300 K of the 2D MoP2 with 12.5% Mo vacancies. Only seven hydrogen molecules remained attached to the surface; this corresponds to a gravimetric capacity for molecular hydrogen storage of 5.27%. The elapsed time was two picoseconds.
Preprints 108131 g011
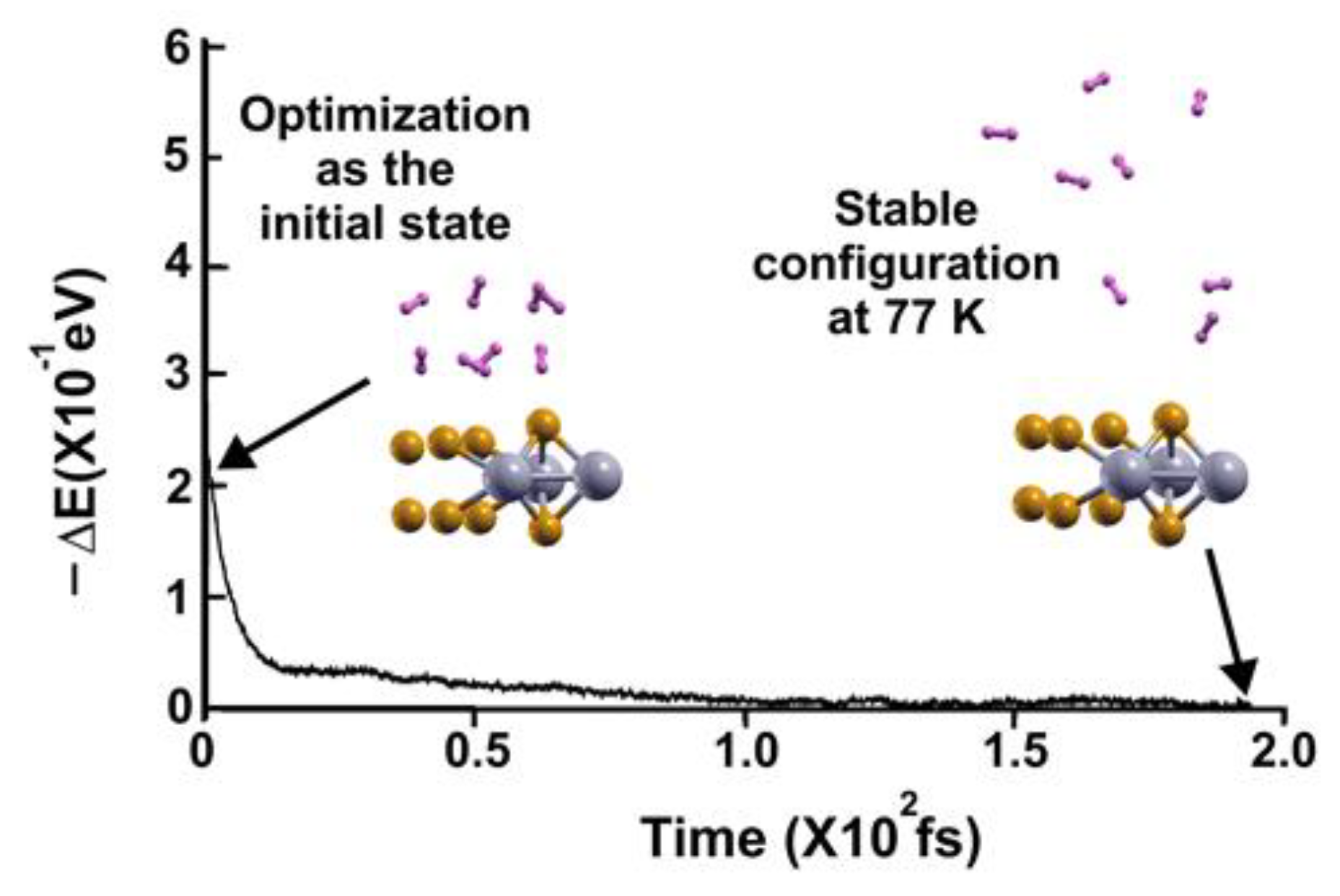
Preprints 108131 g012
Figure 12. FPMD calculation at 77 K, where the initial state is the optimization. All the molecules moved away from the surface. The elapsed time was two picoseconds.
Figure 12. FPMD calculation at 77 K, where the initial state is the optimization. All the molecules moved away from the surface. The elapsed time was two picoseconds.
Preprints 108131 g012
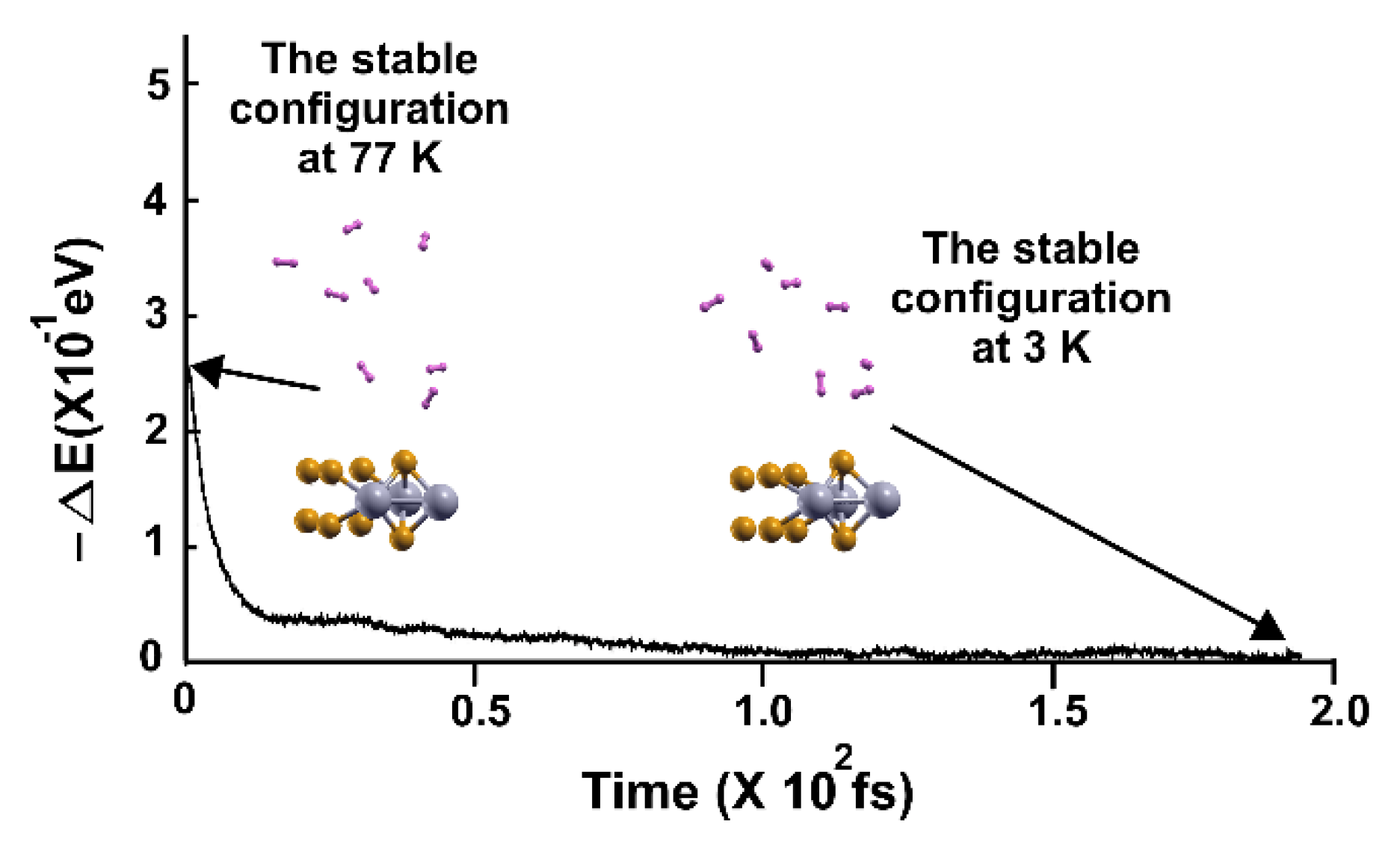
Preprints 108131 g013
Figure 13. FPMD calculation at 3 K, where the initial state is the stable configuration at 77 K of the 2D MoP2 with 12.5% Mo vacancies. All the hydrogen molecules remained attached to the surface; this corresponds to a gravimetric capacity for molecular hydrogen storage of 6.02%. The elapsed time was two picoseconds.
Figure 13. FPMD calculation at 3 K, where the initial state is the stable configuration at 77 K of the 2D MoP2 with 12.5% Mo vacancies. All the hydrogen molecules remained attached to the surface; this corresponds to a gravimetric capacity for molecular hydrogen storage of 6.02%. The elapsed time was two picoseconds.
Preprints 108131 g013
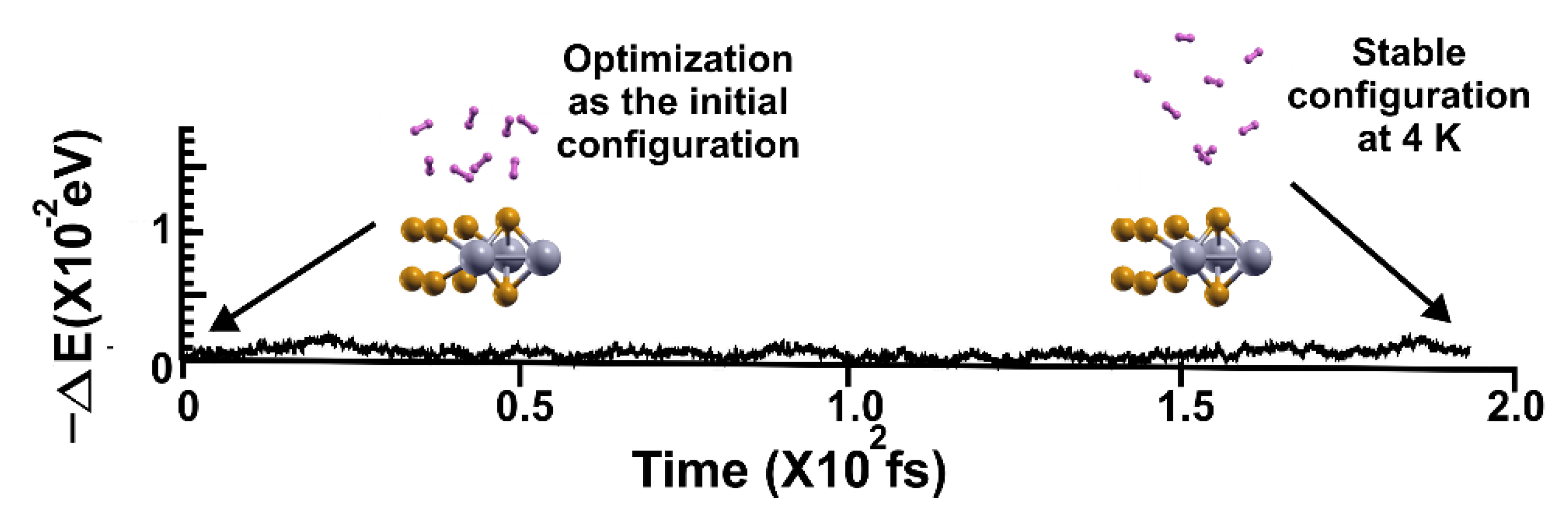
Preprints 108131 g014
Figure 14. FPMD calculation at 4 K, where the initial state is the optimization. All the molecules moved away from the surface. The elapsed time was two picoseconds.
Figure 14. FPMD calculation at 4 K, where the initial state is the optimization. All the molecules moved away from the surface. The elapsed time was two picoseconds.
Preprints 108131 g014
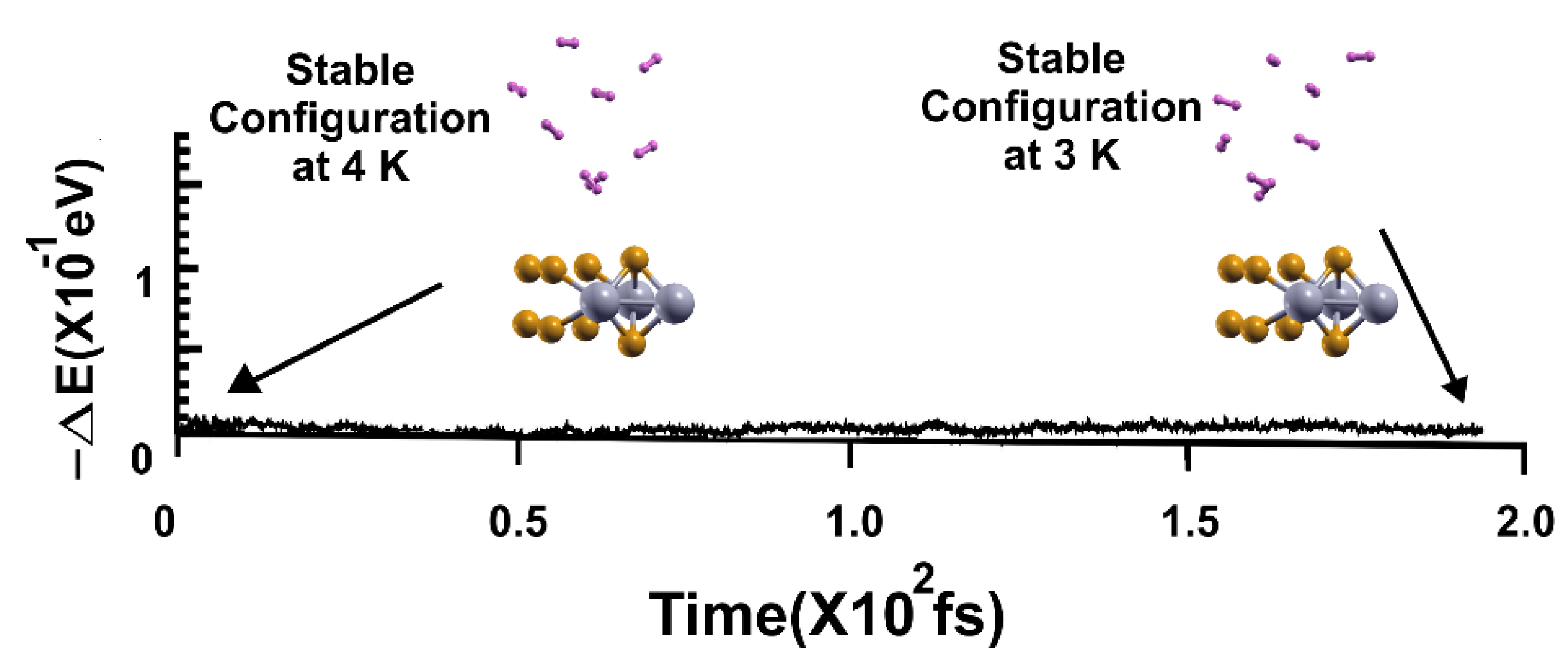
Preprints 108131 g015
Figure 15. FPMD calculation at 3 K, where the initial state is the stable configuration at 4 K of the 2D MoP2 with 12.5% Mo vacancies. As expected, the eight hydrogen molecules (per side) remained attached to the surface; the gravimetric capacity is 6.02%. The elapsed time was around two picoseconds.
Figure 15. FPMD calculation at 3 K, where the initial state is the stable configuration at 4 K of the 2D MoP2 with 12.5% Mo vacancies. As expected, the eight hydrogen molecules (per side) remained attached to the surface; the gravimetric capacity is 6.02%. The elapsed time was around two picoseconds.
Preprints 108131 g015
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated