Prerpints.org logo
Preprint
Article

Study on Key Properties and Model Establishment of Innovative Recycled Aggregate Pervious Concrete

Altmetrics

Downloads

65

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 June 2024

Posted:

04 June 2024

You are already at the latest version

Alerts
Abstract
Traditional concrete pavements have poor water permeability, while the strength of pervious concrete pavements is low. To solve these problems, this study designed Innovative recycled aggregate pervious concrete (I-RAPC) with controllable water permeability and high strength by using response surface methodology, and investigated the effects of different pore parameters (number, diameter, material, distribution form, etc.) on the performance of I-RAPC. And the strength discount factor method was proposed to construct the theoretical calculation model of compressive strength and pipe pore parameters, and the calculation model of water permeability coefficient was established at the same time. The results show that the fewer the number of holes and the smaller the pipe diameter of I-RAPC, the higher its compressive strength and the smaller the water permeability coefficient. The theoretical model of compressive strength can accurately evaluate the discounting effect of the pore parameters on the compressive strength of I-RAPC, and the maximum relative error is only 7.52%, and the maximum relative error of the calculation model of water permeability coefficient is only 4.42%. I-RAPC has the advantages of high strength and permeability with controllable performance, which overcomes the problems of random distribution of pore space, uncertainty of water permeability, and strength of ordinary pervious concrete.
Keywords: 
Subject: Engineering  -   Architecture, Building and Construction

1. Introduction

Since the 21st century, human beings have been faced with the problems of a lack of natural resources and environmental deterioration, such as urban flooding, water pollution, and other phenomena that occur frequently all over the world [1]. At the same time, with the rapid development of urban construction, there was also a large production of construction waste. According to statistics, the United States, China, and India are the three main producers of construction waste, and their total annual output has been close to 8 billion tons [2]. The traditional method of construction waste disposal generally chooses landfilling or stacking, which wastes limited land resources and has a great impact on the environment [3]. The resource utilization of construction waste is one of the goals pursued by the world environmental protection and sustainable development strategies.
Pervious concrete has an interconnected pore structure, which can make rainfall infiltrate rapidly. The compressive strength and the permeability coefficient of pervious concrete are 5.5~40 MPa and 0.3~14 mm/s, respectively. Because of its good permeability, it has been applied to the construction of low-impact development [4,5]. The combination of construction waste and pervious concrete to prepare recycled aggregate pervious concrete (RAPC) can not only effectively alleviate urban flooding and the urban heat island phenomenon but also reduce the adverse impact of construction waste on the environment. After the continuous research of many scholars in recent years, the related technologies of recycled aggregate and recycled aggregate pervious concrete are becoming more and more perfect, but the problems existing in the practical application of RAPC are also gradually emerging. First, there is a negative correlation between the strength and porosity of RAPC, which makes it difficult to have high strength and permeability at the same time, which limits the application range of RAPC [6]. On the other hand, the traditional pervious concrete pavement also has some problems, such as pore blockage, reduced durability, difficult maintenance, and so on [7,8]. Therefore, based on traditional permeable concrete, it is particularly important to explore a new type of pervious concrete with high strength and high permeability at the same time to solve the problems existing in RAPC [9,10,11].
Up till the present moment, there is little research on this new type of pervious concrete. For example, Niu et al. [12] prepared pervious concrete by artificially creating regular pipes connected penetrably in the concrete instead of the previous uniformly distributed pore structure. It is applied to different heavy rainfall levels, and the relationship between porosity and heavy rainfall level is established with the help of the water permeability coefficient, which provides a basis for the surface design of a new type of pervious concrete pavement. Zhu et al. [13] used the same method to make a new high-strength straight-hole recycled pervious concrete (HSRPC) for secondary highway pavement and used surface water depth and drainage time to describe the flooding resistance of HSRPC. Li et al. [14] manufactured high-strength pervious concrete (HSPC) pavement, which showed a compressive strength as high as 61.37 MPa within 7 days and the corresponding permeability coefficient of 13.02 mm/s. A drainage system was designed to remove the blocked dust in the pores of HSPC pavement. Therefore, compared with traditional pervious concrete, this innovative high-strength pervious concrete has more extensive application potential. However, their current research is still focused on the relationship between porosity, strength, and water permeability of concrete. And the strength and permeability of this type of pervious concrete are determined by the pore characteristic parameters (e.g., quantity, diameter, material, and location) of the pipeline, and there is also a certain relationship between each factor. How to quantify the correlation between the characteristic parameters of the new pervious concrete pipe and its performance to provide prediction guidance for practical engineering applications is a missing part of the current research. Therefore, in this paper, tubular products of different materials are embedded in the upper and lower connected pipes to make innovative pervious recycled aggregate concrete (I-RAPC), to analyze the influence of several characteristic parameters on the performance of I-RAPC.
Response surface methodology (RSM) can directly obtain the influence of multi-factor interaction on the performance of concrete through the response surface model and effectively predict the response results, which has the advantages of less test times, a short period, high precision, and a wide application range [15,16,17,18]. RSM tests on the representative local test sites and obtains the data, and the functional relationship between the factors and the result in the whole range is obtained by regression fitting [19]. Finally, the optimal level value of each factor for the response result can be obtained through optimization [20,21].
The above research and application show that I-RAPC has the advantages of high strength and high permeability compared with RAPC. However, at present, there is not enough research to explain the influence of different pipeline characteristic parameters on the performance of I-RAPC. Therefore, this paper focuses on the relationship between I-RAPC strength, permeability, and pipe characteristics and analyzes the relationship between each influencing factor and performance by the RSM to construct the prediction model of the I-RAPC performance index. At the same time, the theoretical calculation formula of the I-RAPC permeability coefficient is deduced, and the formula is verified by experiments. The research results can provide a theoretical basis for the popularization and application of I-RAPC and help to promote the resource utilization of construction solid waste.

2. Materials and Methods

2.1. Main Raw Materials and Mix Design

The recycled coarse aggregates (RCA) were obtained by crushing sieving waste concrete. Due to the diameter of the prepared I-RAPC pipe being 5-10mm, to reduce the negative impact of large particle size aggregates on the side wall of the concrete pipe (such as roughness and compactness), recycled coarse aggregates with particle sizes of 4.75-9.5mm were selected, and its basic physical performance indicators are listed in Table 1, Satisfying the requirements of the specification (JGJ/T 240-2011. 2011) [22]. The fine aggregates were continuous grade natural river sand, fineness modulus Mx=2.9, belongs to middle sand. The cement were P·O 42.5 ordinary Portland cement. Mixing water is tap water. The pipes included acrylic pipes (produced in Henan Weidu Glass product Co., Ltd.) and bamboo pipes (produced in Anji County Zhuyuan Bamboo Products Factory). The pipes that were not embedded in any pipe materials were defined as the concrete pipe hole. The elastic modulus of acrylic, bamboo and concrete pipe were 2.33GPa, 1GPa and 3GPa,respectively [24].
According to the Chinese national standard DL/T 5330-2015 [23], with reference to the design strength of C30 ordinary concrete, the water cement ratio of I-RAPC is determined to be 0.49 and the sand ratio to be 0.345. The mix design is shown in Table 2.

2.2. Experimental Design

In this study, the size of the I-RAPC specimen was 150mm×150mm×150mm. The reference group did not set pipes, while other concrete specimens are set with 1, 4, 5, and 9 pipes, respectively. The distribution forms include center (C), middle edge (EM), and corner of edge (EC) distribution forms. The specific distribution forms of pipes were shown in Figure 1. In addition, pipes could lead to differences in compressive strength between different compression surfaces. During the test, the positive and lateral compressive strengths were measured separately, where the positive and lateral compressive strengths refer to the strengths measured perpendicular and parallel to the axis of the pipe.

2.2.1. Design Plan of I-RAPC Response Surface Test

The I-RAPC response surface test design took the number, size (diameter), and material (elastic modulus, roughness) of the pipes as response factors, and designed a three factor and three level test, with the positive and lateral compressive strength and permeability coefficient as response values. Selected the I-RAPC style for the number and distribution of pipes numbered 1C, 4EM+1C, and 4EC+4EM+1C in Figure 1. Use Box Behnken Design (BBD) in Design Expert 10.0.3 software to perform response surface design analysis on it. The response surface methodology experimental design scheme is shown in Table 3.

2.2.2. I-RAPC Theoretical Model Construction Test Scheme

The I-RAPC compressive theoretical model construction test scheme is determined based on the I-RAPC strength of single pipes of different materials (concrete, acrylic), distinct diameters (5mm, 10mm), and different distribution forms (C, EM, MC, etc.). See Table 4 for the specific test plan.

2.3. Test Methods

2.3.1. Preparation Process

The test used the pre-wet aggregate method to mix concrete [25]. Based on the above mix ratio, the recycled coarse aggregate is first mixed with 1/2 water by a mixer to prevent the recycled coarse aggregate from absorbing mixed water in the subsequent mixing and hydration hardening process; then cement and sand are added, 1min is stirred, and the remaining water is poured into the remaining water to be mixed evenly and then loaded into a special mold test. Wet towels are covered after manual insertion and mechanical vibration. after indoor maintenance for 24h, the mold is removed and placed in the standard maintenance room to the specified age. The specific process is shown in Figure 2.
As shown in Figure 2, the pipes in I-RAPC were made by a special mold, and the internal diameters of the selected bamboo pipes and acrylic pipes were the same as those of the iron column arranged in the mold, ensuring that the internal diameters of the pipes in I-RAPC were consistent for each material.
The test indexes included I-RAPC strength performance (positive and lateral compressive strength) and permeability performance (water permeability coefficient). The specimen was 150×150×150mm standard cube, The average of the measured values of three specimens is used as the test results for the compressive strength and permeability coefficient of each group of specimens. When the difference between one measured value and the intermediate value exceeds 15% of the intermediate value, the intermediate value is taken as the experimental result. When the difference between two measured values and the median exceeds 15% of the median, the experimental data is invalid and needs to be retested to ensure the accuracy of the experimental data.

2.3.2. Compressive Strength Test

Taking the Positive and lateral of the test block as the pressure surface (When the concrete is tested under frontal pressure, the concrete surface is smoothed using a smoothing machine), it was completed on the DY-3008DX electro-hydraulic servo microcomputer-controlled pressure tester. According to the Standard for test method of mechanical properties on ordinary concrete (GB/T 50081-2002. 2002) [26], the loading speed was set at 0.5MPa/s. After the test, I-RAPC compressive strength was calculated according to Eq(1):
f c u = F m a x A
Where, f c u is cube compressive strength of the test block, MPa; F m a x is maximum load, N; A is stress area of test block, mm2, takes 22500mm2(150mm×150mm), the effect of pipe on the bearing surface area is not considered.

2.3.3. Permeability Test

The permeability coefficient is an intuitive indicator to represent the permeability performance of I-RAPC. This test is based on Darcy’s law constant head method and adopts a self-made permeable device (as shown in Figure 3), in which the head difference H is 200mm (ASTM C496 / C496M. 2011) [27]. To prevent the leakage of the non-test surface of the test piece from affecting the test data, the gap between the test piece and the permeable device is filled with plasticine. Before the test, adjust the water flow rate to make the water flow stably overflow from the top surface of the device and keep it stable for 60s. The test time of each test block shall be controlled within 25s. Calculate the permeability coefficient of I-RAPC according to Eq(2):
k = V L A H t
Where, k is permeability coefficient, mm/s; t is the measurement time, s; V is the volume of water in the beaker at time t , mm³; L is the height of the specimen, mm, takes 150mm; H is the head difference, mm.

2.3.4. Roughness Coefficient Test

Coefficient of roughness is a dimensionless comprehensive coefficient that measures the influence of boundary shape and roughness on water flow resistance. The magnitude of pipeline coefficient of roughness is mainly related to the surface roughness of the pipe material. Therefore, the engineering community generally infers the coefficient of roughness through a large amount of measured data. In this experiment, the coefficient of roughness values of different pipes was obtained through repeated experiments using the permeable device in Figure 3 and the Chézy-Manning formula, which is:
n = R 2 3 J 1 2 V p
Where, n is the roughness coefficient; R is the hydraulic radius, m; J is the hydraulic slope; V p is the average flow velocity of the pipeline cross-section, m/s.

3. Results and Discussion

3.1. Response Surface Methodology Analysis

3.1.1. Response Surface Model Construction and Analysis

According to the Weierstress polynomial optimal approximation theorem, most functions can be approximated by polynomials, and the polynomial approximation model can deal with a wide range of nonlinear problems. Therefore, in practical application, regardless of the relationship between independent variables and dependent variables, the polynomial approximation model can be used for analysis [28,29,30].
Multiple regression fitting analysis was carried out for positive and lateral compressive strength and permeability coefficient, respectively, and multiple regression equations of actual values were obtained as shown in Eq (4) ~ (6):
f c u − f r o n t = 61.30565 − 3.42578 x − 1.98603 d − 11.8321 E + 0.4375 x E + 0.70417 d E + 0.1283 x 2 + 1.46802 E 2
f c u − s i d e = 44.31826 − 1.78045 x + 0.09 d − 10.12039 E − 0.102 x d + 2.63789 x E − 0.79244 x E 2 + 3.25463 E 2
k a c t u r a l = − 39.36292 − 1.86225 x + 10.99522 d + 3951.26057 n + 0.4346 x d + 184.89167 x n − 1195.04989 d n − 0.69725 d 2 + 32227.75322 n 2 − 14356.66667 x n 2 + 75.94873 d 2 n
Where, f c u − f r o n t is the actual value of I-RAPC Positive compressive strength, MPa; f c u − s i d e is the actual value of I-RAPC lateral compressive strength, MPa; k a c t u r a l is the actual value of I-RAPC permeability coefficient, mm/s; x is the number of pipes; E is the elastic modulus of the pipe, GPa; n is the roughness coefficient of the pipe.
Analysis of variance and significance test were conducted for the regression equations above, as listed in Table 5. The values of p in the model are all less than 0.05, so the model is significant and can be used in subsequent optimization design; The lack of fit items the degree of fitting between the model and the test, i.e., the degree of difference between them. The values of p of the lack of fit items in the model were all greater than 0.05, indicating that there was no significant discrepancy between the model and the test, that is, the degree of non-correlation between the test data and the model was not obvious, and the model was credible.
Table 6 shows the statistical analysis results of the regression equation error of I-RAPC positive and lateral compressive strength and permeability coefficient. The model determination coefficients R2 is 0.9524, 0.9573, and 0.9993 respectively, indicating that the predicted value of the model was in good agreement with the actual value; the model correction determination coefficients Adj R2 is 0.9153, 0.9240 , and 0.9983, i.e., the model regression equation can simulate 91.53%, 92.40%, and 99.83% changes of response values, and the absolute values of the difference between the model correction determination coefficient Adj R2 and the model prediction determination coefficient Pred R2 are 0.1388, 0.1795, and 0.0408, which are less than 0.2, which proves that the regression model can fully explain the process problems. Adeq precision is 16.57, 22.923, and 113.46, which is reasonable if greater than 4. In addition, the coefficient of variation C.V. of the model is 3.79%, 2.55%, and 3.27%, less than 10%, which indicates that the test has high accuracy and reliability. Therefore, the regression equation of the model can replace the actual value of the test and analyze the test results. Figure 4 indicates the distribution of actual and predicted values of the response model. The corresponding point between the actual and predicted values is near the line y=x, i.e., the predicted value of the compressive strength response model is close to the actual value and has good agreement.
The experimental results and RSM model show that I-RAPC with bamboo pipe is lower than I-RAPC with the other two pipes (concrete, acrylic). The reason for this may be that bamboo pipes have a low elastic modulus and high coefficient of roughness, but the compressive strength of I-RAPC is proportional to elastic modulus within a certain range, and the permeability coefficient is inversely proportional to pipe coefficient of roughness. Therefore, only the I-RAPC performance test results of concrete pipes and acrylic pipes are compared and analyzed with the optimization prediction results of response surface model.

3.1.2. Response Surface and Contour Map

The three-dimensional response surface and contour map established by RSM can directly reflect the interaction between test factors, that is, when one factor is a certain value, the interaction between the other two factors affects the response value. The shape of the contour line can reflect the strength of the interaction effect. Ellipse indicates that the interaction between the two factors is significant, while the circle is opposite. Among the three influence factors, the number and diameter of pipes have the greatest influence on I-RAPC strength and permeability coefficient. Therefore, the interaction of the number and diameter of pipes on I-RAPC strength and permeability coefficient will be discussed in this part, and its response surface and contour diagram are illustrated in Figure 5 ~ Figure 7.
Figure 5 shows the interactive effect of the number and diameter of pipes on the front compressive strength of I-RAPC. From the response surface, the positive compressive strength of I-RAPC decreases with the increase of the number and diameter of pipes, and the effect of the number of pipes on the positive compressive strength is greater than the diameter of pipes. At the same time, by observing the mapping distribution of the response surface, it is found that the contour curvature in this range is relatively small and the degree of bending is low. Therefore, the interaction between the number and diameter of pipes on the positive compressive strength of I-RAPC is small [14]. At the same time, it is found that the positive compressive strength of the I-RAPC without the acrylic tube is slightly higher than that of the I-RAPC when the acrylic tube is embedded.
Figure 6 shows the interactive effect of the number and diameter of pipes on the lateral compressive strength of I-RAPC. From the response surface, the lateral compressive strength of I-RAPC decreases with the increase of the number and diameter of pipes, which is similar to that of the front compressive strength. At the same time, by observing the distribution of the response surface on the coordinate axis, it is found that the contour lines obviously bend when the acrylic tube is embedded, and the influence of the number and diameter of pipes on the lateral compressive strength of I-RAPC is interactive. At the same time, compared with the side compressive strength response surface of I-RAPC without embedded pipe, it is found that when the number of pipes is large, the embedded acrylic tube can slightly improve the lateral compressive strength of I-RAPC.
Figure 7 shows the interactive effect of the number and diameter of pipes on the permeability coefficient of I-RAPC. Through the distribution of the response surface, it can be seen that both the number and diameter of pipes have a great influence on the permeability coefficient, and the contour curvature is larger, indicating that the interaction of the two factors on I-RAPC is significant, and the higher the permeability coefficient is with the increase of the number and diameter of pipes. At the same time, it is found that the embedded acrylic tube can significantly increase the permeability coefficient of I-RAPC. When the number of pipes reaches 9 and the diameter of pipes reaches 10mm, the permeability coefficient can reach 27.144mm/s.

3.1.3. The Optimized Prediction Results Compared with the Actual Results

The optimization option in Design-Expert 10.0.3 software was utilized to set the input conditions (number of pipes, diameter, elastic modulus of material/coefficient of roughness) for solving, and the target response result and its suitability were obtained.
The absolute error ranges between the optimized prediction results and the actual results are 0.03~6.61MPa and 0.004~0.310mm/s, and the corresponding relative error ranges are 0.10%~27.30% and 0.33%~9.48%. The experimental results are similar to the model optimization prediction results, and the relative errors of most indexes are within 15%, which that the design experiment based on response surface analysis method has practical significance and has the advantage of fewer data required, but there are a few cases where the predicted values of the model differ greatly from the actual values. This is due to the response surface design which reduces the amount of experimentation that results in a loss of accuracy. Therefore, the response surface method can first implement a simple test design and law summary for the uncertain tests, and then further implement fine test to explore its essential law, which has a certain guiding significance for test and law exploration.

3.2. Compression Strength and Failure of Morphology

3.2.1. The Optimized Prediction Results Compared with the Actual Results

From the failure of morphology (Figure 8), when I-RAPC is under positive pressure, with the increase of load, the surface cracks first appear, and then develop from the middle to the pipes at the upper and lower ends, and finally forms an octagonal destruction pattern with positive and reverse connections. The surface concrete peels off continuously when the lateral is under pressure, vertical penetration cracks appear between the upper and lower pipes, and the pipes are damaged after deformation. As it can be seen, the existence of pipes changes the internal structure of concrete, and the failure mode is different from that of ordinary concrete, so I-RAPC is not easy to be damaged.
The I-RAPC compressive strength test results are illustrated in Figure 9, where C5, C10, A5, and A10 represent 5 mm and 10 mm concrete and acrylic pipe pores, respectively. The figure illustrates that I-RAPC compressive strength decreases as the number of pipe pores and diameter of pipe pores increase, which is consistent with the trend that the strength of ordinary recycled pervious concrete decreases as porosity increases, The main reason for the analysis is that the existence of the form of pipes destroys the pressure-bearing structure of the original dense concrete and forms a weak surface inside the concrete, so the more the number of pipes is, the more disadvantageous it is to the bearing pressure of concrete. Even so, the measured compressive strength is still much higher than that of RAPC [30]. The position of pipes will affect the Positive compressive strength 1EM>1EC>1C and the lateral compressive strength 1EM-T>1EC>1EM-S>1C for I-RAPC with the same number of pipes. In the case of multi-pipes, there are also 4EM>4EC and 5EM>5EC characteristics. That is to say, the lower the compressive strength of I-RAPC is when the position of the pipe is closer to the center of the concrete relative to the bearing surface. When a single pipe (such as the position of the EM-T) was filled with acrylic pipe (5 mm in diameter), the I-RAPC lateral compressive strength of the concrete pipe increased by 1.03MPa. Acrylic pipes can significantly enhance I-RAPC, and the maximum compressive strength can be increased by 5.45MPa.
In addition, different hole locations with the same number of holes also have certain effects on I-RAPC. For example, the distribution of EM pipes is better than that of EC, and its improvement on the compressive strength of I-RAPC is shown in Figure 10. When compared to the distribution pattern of EC holes, the distribution pattern of EM holes can improve compressive strength by 0.03~4.29MPa, or approximately 0.08~13.18 percent. As a result, the design of the I-RAPC suggests using the EM pipe pore distribution form to achieve greater strength.
There is a basic inverse relationship between porosity and strength of most solid materials [31,32], as shown in Eq (7):
S = S 0 e − k p
Where, S is the compressive strength of the material when porosity is p, MPa; S 0 is the intrinsic strength when porosity is zero, MPa; k is a constant; p is the porosity, %.
The fitting results of I-RAPC compressive strength and number of holes were obtained by the orthogonal distance regression method, as illustrated in Figure 11.
According to Eq (7), the general expression of the relationship between the I-RAPC strength of different pipe diameters and materials and the number of pipes is shown in Eq (8) and (9).
Concrete pipe I-RAPC:
S = S 0 e − k x
Acrylic pipe I-RAPC:
S = S 0 − 2 e − k x
Where, S is the compressive strength of the material when the number of pipes is x, MPa; S 0 is the intrinsic strength when the number of pipes is zero, MPa, takes 43.5MPa in this study; k is a constant, which is related to the hole material, diameter and I-RAPC strength type, specific k values are shown in Figure 11.

3.2.2. Theoretical Analysis

According to the test results, the more holes the I-RAPC has, the larger the pore diameter, the lower the compressive strength. Therefore, the strength reduction coefficient method is proposed, and the theoretical calculation model of I-RAPC compressive strength and pipe parameters is constructed.
The corresponding strength reduction factor c was defined as the ratio of I-RAPC strength of concrete single pipes at different positions to the strength of the reference group, as shown in Eq (10). The strength characteristics of I-RAPC were changed when the acrylic pipe was inserted into the pipe, so the reduction degree was calculated using the corresponding strength of the concrete pipe, as shown in Eq (11). The strength reduction coefficients of concrete pipes at various positions are calculated using the Eq (10) ,and the results of the calculations are shown in Table 7.
c = P c / P
a = P a / P c
Where, c is the strength reduction factor of the concrete single pipe; P c is the I-RAPC strength of concrete single pipes in different positions, MPa; P is the average strength of the reference group, MPa, takes 43.5MPa in this study; a is the strength reduction factor of the acrylic single pipe; P a is the I-RAPC strength of acrylic pipe in different positions, MPa.
The theoretical calculation model of I-RAPC compressive strength with different pipe parameters is established as follows:
f c u c = P · c 1 w · c 2 s x · c 2 c y · c 3 z
f c u a = f c u c · a 1 w · a 2 s x · a 2 c y · a 3 z
Where, f c u c and f c u a are the theoretical values of I-RAPC compressive strength with concrete and acrylic pipe, respectively, MPa; P is The strength of reference group, MPa; c1, a1 are the strength reduction coefficients of concrete and acrylic middle pipes, respectively; c2, a2 are the strength reduction coefficients of the middle pipes in the concrete and acrylic laterals, respectively; c2s, a2s are the located in the middle (top) part of the edge, respectively; c2c, a2c are the located in the middle (side) part, respectively; c3,a3 are the strength reduction coefficients of corner pipes of concrete and acrylic pipe, respectively; w, x, y, z are the number of different types of pipes, respectively.
The error between the calculated and actual values of I-RAPC compressive strength is illustrated in Figure 12. The absolute error range of I-RAPC compressive strength is 0.13~2.45MPa, and the relative error range is 0.43~7.52%, as illustrated in the figure. As a result, the theoretical I-RAPC compressive strength calculation model proposed in this paper can accurately quantify and predict the reduction effect of hole number, hole diameter, and hole distribution on I-RAPC compressive strength.

3.2.3. Permeability Coefficient

The permeability coefficient of I-RAPC is mainly determined by the number, diameter, and material (coefficient of roughness) of pipes. With the increase of the number and diameter of pipes, the coefficient of roughness decreases, and the permeability coefficient increases. Due to the unique characteristics of the upper and lower connecting pipes, the theoretical value of I-RAPC’s permeability coefficient can be obtained by combining the free outflow method of simple short pipe constant flow in hydraulics with Darcy’s law. The calculation process is as follows in Figure 13.
In the calculation, the viscous dissipation of the water body is ignored, and only the influence of external boundary conditions is considered. That is, in the experiment, there are water head loss along the way and local head loss, so the flow Q of the free outlet pipe can be calculated using the following Eq (14)~(15):
Q = μ c A 2 g H
μ c = 1 1 + λ · L / d + ∑ ζ
Where, Q is the flow, m3/s; μ c is the flow coefficient of pipe; A is the cross-sectional area of pipe, m2; g is the gravity acceleration, m/s2; H is the head difference, m; λ is the head loss coefficient along the course; L is the length of the pipe; d is the diameter of the pipe; ζ is the localized head loss coefficient.
In the Equation above, the determination of and values are the key, which can be obtained from the hydraulic Equation. The calculation and values can be seen in Table 8 and Table 9.
Local   head   loss   coefficient   ζ According to Darcy’s law, the theoretical value of the I-RAPC permeability coefficient can be calculated as follows:
k = μ c 2 g / H · L x A t / A s
Where, x is the number of pipes; A t is the water flow area of a single pipe, m2; A s is the top area of the I-RAPC, m2.
From Eq (16), the permeability coefficient is positively correlated with the flow coefficient and diameter of the pipe. When the roughness of the pipe is small, the flow coefficient of the pipe will increase. Therefore, embedding acrylic pipes will moderately increase the permeability coefficient of I-RAPC. At the same time, the influence of the pipe diameter on the permeability coefficient is more obvious. When the pipe diameter increases from 5mm to 10mm, the permeability coefficient can increase by more than four times. Comparing the theoretical value calculated with the actual value, the results are shown in Table 10. The absolute error range between the permeability coefficient of different pipe materials and diameters and the absolute error is 0.008 ~ 0.036mm/s, and the relative error range is 0.265 ~ 4.420%. It can be seen that the theoretical calculation formula of the I-RAPC permeability coefficient deduced in this paper has high accuracy.

4. Conclusions

The strength and permeability of Innovative Recycled Aggregate Pervious Concrete are investigated in this paper under various pipe parameters, and a theoretical calculation model is developed. It provides the foundation for its future development and application. The following are the primary conclusions:
(1) Based on the RSM, an optimization model of the I-RAPC was established, with the positive and lateral compressive strength and permeability coefficient as response values, and the number of pipes, diameter, and material as response factors. Utilizing multiple regression approximation equation fitting, variance analysis, and error statistical analysis, it is explored that the predicted value of the model is in good agreement with the actual value; The model regression equation can simulate more than 90% of the response value changed respectively, indicating high accuracy and reliability of the test, so the model regression equation can replace the real test value and analyze the test results.
(2) Compared with RAPC, I-RAPC has significant advantages in terms of strength and permeability. Among them, all I-RAPC test groups in this article have compressive strength between 20MPa and 45MPa, and the compressive strength and permeability coefficient are related to parameters such as pipe type, number, diameter, and position. Specifically, the more pipes there are, the larger the diameter of the pipe, the lower the strength, and the strength performance of a single pipe in the middle position is better than that in the corner position, The variation pattern of permeability coefficient is opposite to that of compressive strength. When the number of pipes reaches 9 and the diameter of the pipe is 10mm, the permeability coefficient can exceed 27mm/s. Moreover, when embedding acrylic pipes, the permeability coefficient of I-RAPC can be appropriately improved.
(3) A new compressive strength calculation model of recycled aggregate pervious concrete based on the strength reduction coefficient method is proposed. The model can accurately determine the reduction effect of hole number, hole diameter, and hole distribution on I-RAPC compressive strength. The maximum relative error between the calculated value and the actual value is only 7.52%, which can be used to predict the strength index of innovative recycled aggregate pervious concrete.
(4) The calculation formula of the single pipe permeability coefficient of the innovative recycled aggregate pervious concrete is deduced by the employment of the hydraulic method and Darcy’s law. The maximum relative error between the calculated value and the actual value is only 4.42%, which can be used to determine the permeability of innovative recycled aggregate pervious concrete.

Author Contributions

Conceptualization, P.Z.; methodology, Z.Z.; software, Z.Z.; validation, J.Z., P.Z. and S.C.; formal analysis, J.Z.; investigation, J.Z.; resources, S.C.; data curation, J.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, J.Z.; visualization, S.C.; supervision, P.Z.; project administration, P.Z.; funding acquisition, S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by two National Natural Science Foundation of China and Henan Provincial Science and Technology Research Project, grant number 52109154, 51979169 and 222102320439, respectively.

Data Availability Statement

Data will be made available on request.

Acknowledgments

This work was supported by the North China University of Water Resources and Electric Power. The authors also would like to acknowledge the support of National Natural Science Foundation of China (52109154, 51979169) and Henan Provincial Science and Technology Research Project (222102320439).

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Xu, J.; Dai, J.; Wu, X.; Wu, S.; Zhang, Y.; Wang, F.; Gao, A.; Tan, Y. Urban rainwater utilization: A review of management modes and harvesting systems. Front. Environ. Sci. 2023, 11, 118. [Google Scholar] [CrossRef]
  2. Huang, B.; Wang, X.; Kua, H.; Geng, Y.; Bleischwitz, R.; Ren, J. Construction and demolition waste management in China through the 3R principle. Resour. Conserv. Recycl. 2018, 129, 36–44. [Google Scholar] [CrossRef]
  3. Liu, Z.; Cai, C.; Peng, H.; Fan, F. Experimental study of the geopolymeric recycled aggregate concrete. J. Mater. Civil Eng. 2016, 28, 04016077. [Google Scholar] [CrossRef]
  4. Ohemeng, E.A.; Ekolu, S.O. Comparative analysis on costs and benefits of producing natural and recycled concrete aggregates: a south african case study. Case Stud. Constr. Mater. 2020, 13, e00450. [Google Scholar] [CrossRef]
  5. Chen, S.; Zhao, Y.; Bie, Y. The prediction analysis of properties of recycled aggregate permeable concrete based on back-propagation neural network. J. Clean. Prod. 2020, 276, 124187. [Google Scholar] [CrossRef]
  6. Cui, X.; Zhang, J.; Huang, D. Experimental study on the relationship between permeability and strength of pervious concrete. J. Mater. Civil Eng. 2017, 29, 04017217. [Google Scholar] [CrossRef]
  7. Ho, H.-L.; Huang, R.; Hwang, L.-C.; Lin, W.-T.; Hsu, H.-M. Waste-Based Pervious Concrete for Climate-Resilient Pavements. Materials 2018, 11, 900. [Google Scholar] [CrossRef]
  8. Chen, J.; Lee, C.T.; Lin, Y. Influence of engineering properties of porous asphalt concrete on long-term performance. J. Mater. Civil Eng. 2017, 29, 04016246–1. [Google Scholar] [CrossRef]
  9. Chen, S.; Zhou, J.; Liu, J.; Bie, Y.; Hu, Q. Sustainable ecological pervious concrete (SEPC) based on modified corn-cob coarse aggregate: Crushing morphology, strength, pore properties, and durability. Constr. Build. Mater. 2024, 426, 136194. [Google Scholar] [CrossRef]
  10. Bhutta, M.; Hasanah, N.; Farhayu, N.; Hussin, M. W.; Tahir, M.; Mirza, J. Properties of porous concrete from waste crushed concrete (recycled aggregate). Constr. Build. Mater. 2013, 47, 1243–1248. [Google Scholar] [CrossRef]
  11. Sahdeo, S.K.; Ransinchung, G.; Rahul, K.L.; Debbarma, S. Reclaimed Asphalt Pavement as a Substitution to Natural Coarse Aggregate for the Production of Sustainable Pervious Concrete Pavement Mixes. J. Mater. Civil Eng. 2021, 33, 04020469. [Google Scholar] [CrossRef]
  12. Shi, Z.; Zhu, P.; Yan, X.; Yang, L. Qiao, S.; Li, H. The rainstorm waterlogging resistance of a novel fiber-reinforced self-compacting recycled pervious concrete after freeze-thaw cycles. J. Build. Eng. 2024, 86, 108820. [Google Scholar] [CrossRef]
  13. Zhu, P.; Fan, H.; Yan, X.; Liu, H.; Wang, X.; Chen, C. Effect of Fatigue Loading on the Mechanical Properties and Resistance of High-strength Straight-hole Recycled Pervious Concrete to Rainstorm-based Waterlogging. J. Wuhan Univ. Technol.-Mater. Sci. Edit. 2023, 38, 141–148. [Google Scholar] [CrossRef]
  14. Li, J.; Zhang, Y.; Liu, G.; Peng, X. Preparation and performance evaluation of an innovative pervious concrete pavement. Constr. Build. Mater. 2017, 138, 479–485. [Google Scholar] [CrossRef]
  15. Zhang, D.; Tang, S.; Che, J. Concurrent subspace design optimization and analysis of hypersonic vehicles based on response surface models. Aerosp. Sci. Technol. 2015, 42, 39–49. [Google Scholar] [CrossRef]
  16. Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef] [PubMed]
  17. Ba, D.; Boyac, S.H. Modeling and optimization i: usability of response surface methodology. J. Food Eng. 2007, 78, 836–845. [Google Scholar]
  18. Güneyisi, E.; Gesoğlu, M.; Algın, Z.; Mermerdaş, K. Optimization of concrete mixture with hybrid blends of metakaolin and fly ash using response surface method. Compos. Pt. B-Eng. 2014, 60, 707–715. [Google Scholar]
  19. Bowerman, B.L. Statistical Design and Analysis of Experiments With Applications to Engineering and Science. Technometrics 1991, 33, 105–106. [Google Scholar] [CrossRef]
  20. Tunc, E.T.; Alyamac, K.E. Determination of the relationship between the los angeles abrasion values of aggregates and concrete strength using the response surface methodology. Constr. Build. Mater. 2020, 260, 119850. [Google Scholar] [CrossRef]
  21. Zhang, P.; Cheng, Y.; Tao, J.; Jiao, Y. Molding process design for asphalt mixture based on response surface methodology. J. Mater. Civil Eng. 2016, 28, 04016120. [Google Scholar] [CrossRef]
  22. Academy of Building Research. Technical specification for application of recycled aggregate. JGJ/T 240-2011, China, 2011.
  23. Academy of Building Research. Code for mix design of hydraulic concrete. DL/T 5330-2015, China, 2015.
  24. Nie, G.; Bao, Y.; Wan, D.; Yuan, T. Methods for evaluating mechanical properties of cement-based tubes. Mater. Rep. 2018, 32, 2072–2077. [Google Scholar]
  25. Li, H.; Huang, F.; Yi, Z.; Wang, Z.; Zhang, Y.; Yang, Z. Investigations of Mixing Technique on the Rheological Properties of Self-Compacting Concrete. Appl. Sci. 2020, 10, 5189. [Google Scholar] [CrossRef]
  26. Academy of Building Research. Standard for test method of mechanical properties on ordinary concrete. GB/T 50081-2002, China, 2002.
  27. American Society for Testing and Materials. Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. ASTM C496 / C496M, America, 2011.
  28. Li, Z.; Lu, D.; Gao, X. Optimization of mixture proportions by statistical experimental design using response surface method - A review. J. Build. Eng. 2021, 36, 102101. [Google Scholar] [CrossRef]
  29. Kalita, K.; Dey, P.; Haldar, S. Search for accurate RSM metamodels for structural engineering. J. Reinf. Plast. Compos. 2019, 38, 995–1013. [Google Scholar] [CrossRef]
  30. Ren, W.; Chen, H. Finite element model updating in structural dynamics by using the response surface method. Eng. Struct. 2010, 32, 2455–2465. [Google Scholar] [CrossRef]
  31. Zhang, Q.; Feng, X.; Chen, X.; Lu, K. Mix design for recycled aggregate pervious concrete based on response surface methodology. Constr. Build. Mater. 2020, 259, 119776. [Google Scholar] [CrossRef]
  32. Guo, Z.; Xu, L.; Lu, S.; Yan, L.; Zhu, Z.; Wang, Y. Study on the Effect of PVAc and Styrene on the Properties and Microstructure of MMA-Based Repair Material for Concrete. Materials 2023, 16, 3984. [Google Scholar] [CrossRef]
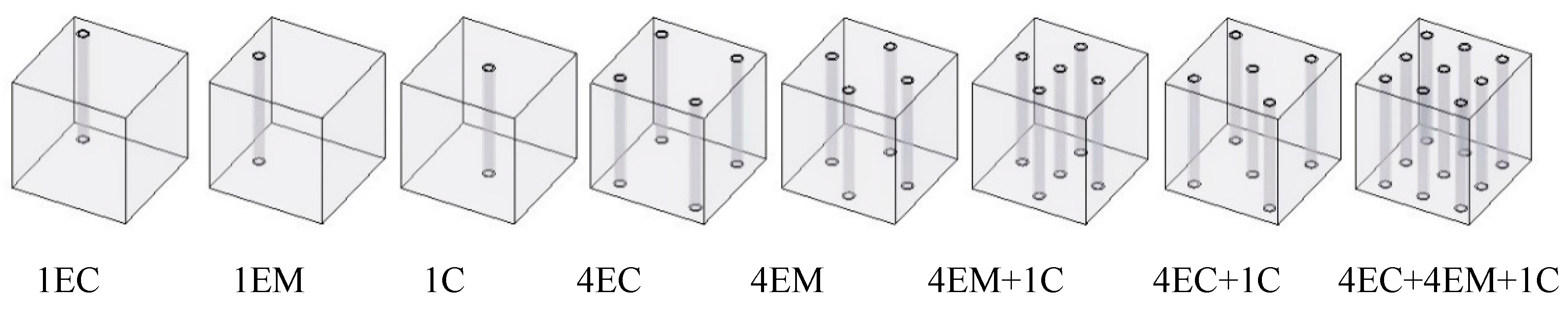
Preprints 108305 g001
Figure 1. Pipe distribution pattern of I-RAPC.
Figure 1. Pipe distribution pattern of I-RAPC.
Preprints 108305 g001
Preprints 108305 g002
Figure 2. The preparation process of I-RAPC.
Figure 2. The preparation process of I-RAPC.
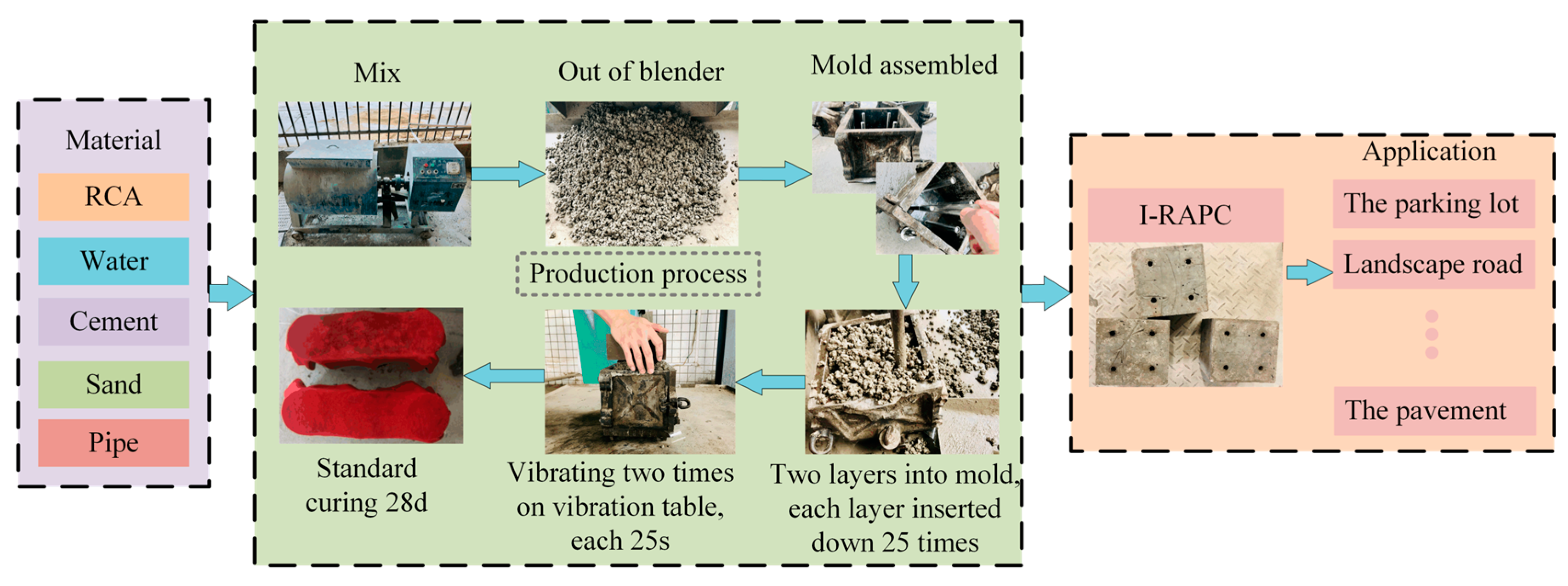
Preprints 108305 g002
Preprints 108305 g003
Figure 3. Measuring device for water permeability coefficient.
Figure 3. Measuring device for water permeability coefficient.
Preprints 108305 g003
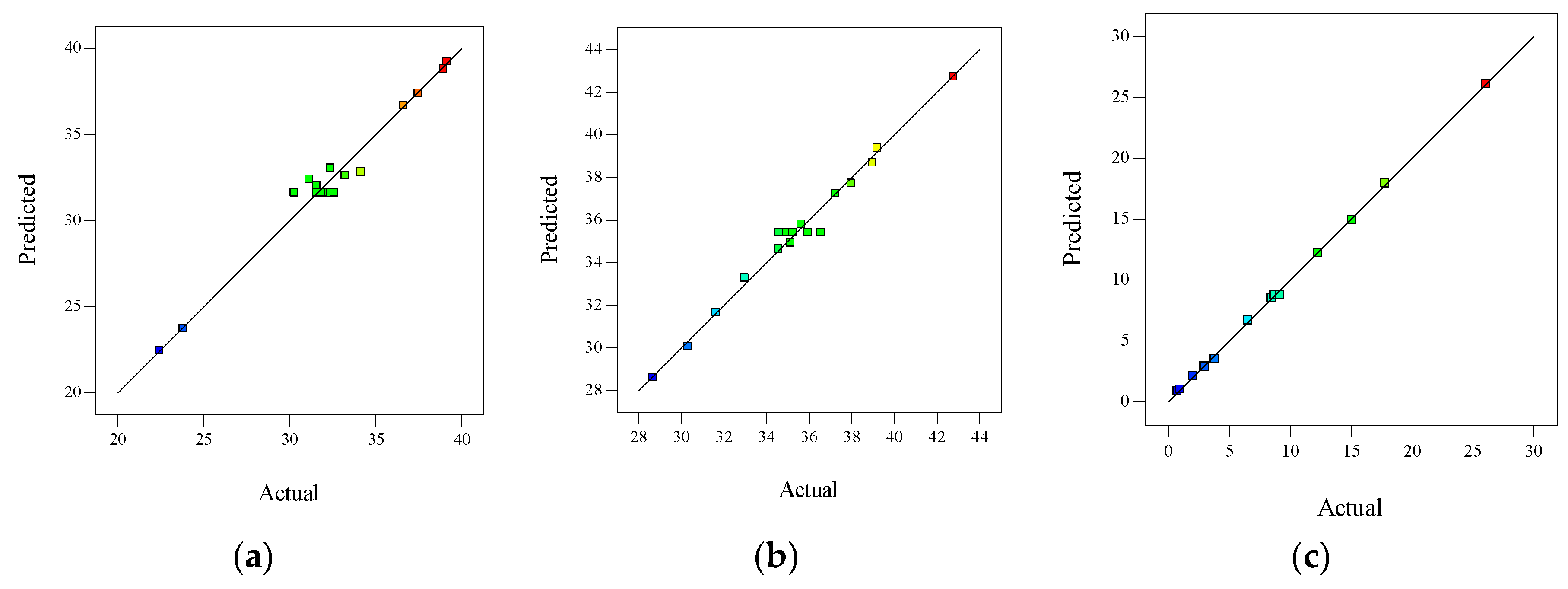
Preprints 108305 g004
Figure 4. Distribution diagram of model actual value and predicted value (a) Positive compressive strength; (b) Lateral compressive strength; (c) Permeability coefficient.
Figure 4. Distribution diagram of model actual value and predicted value (a) Positive compressive strength; (b) Lateral compressive strength; (c) Permeability coefficient.
Preprints 108305 g004
Preprints 108305 g005
Figure 5. The interaction of the number and diameter of the pipe on the positive compressive strength of I-RAPC. (a) The response surface (E =3GPa); (b) The contour (E =3GPa); (c) The response surface (E =2.33GPa); (d) The contour (E =2.33GPa).
Figure 5. The interaction of the number and diameter of the pipe on the positive compressive strength of I-RAPC. (a) The response surface (E =3GPa); (b) The contour (E =3GPa); (c) The response surface (E =2.33GPa); (d) The contour (E =2.33GPa).
Preprints 108305 g005
Preprints 108305 g006
Figure 6. The interaction of the number and diameter of pipe on the lateral compressive strength of I-RAPC. (a) The response surface (E =3GPa); (b) The contour (E =3GPa); (c) The response surface (E =2.33GPa); (d) The contour (E =2.33GPa).
Figure 6. The interaction of the number and diameter of pipe on the lateral compressive strength of I-RAPC. (a) The response surface (E =3GPa); (b) The contour (E =3GPa); (c) The response surface (E =2.33GPa); (d) The contour (E =2.33GPa).
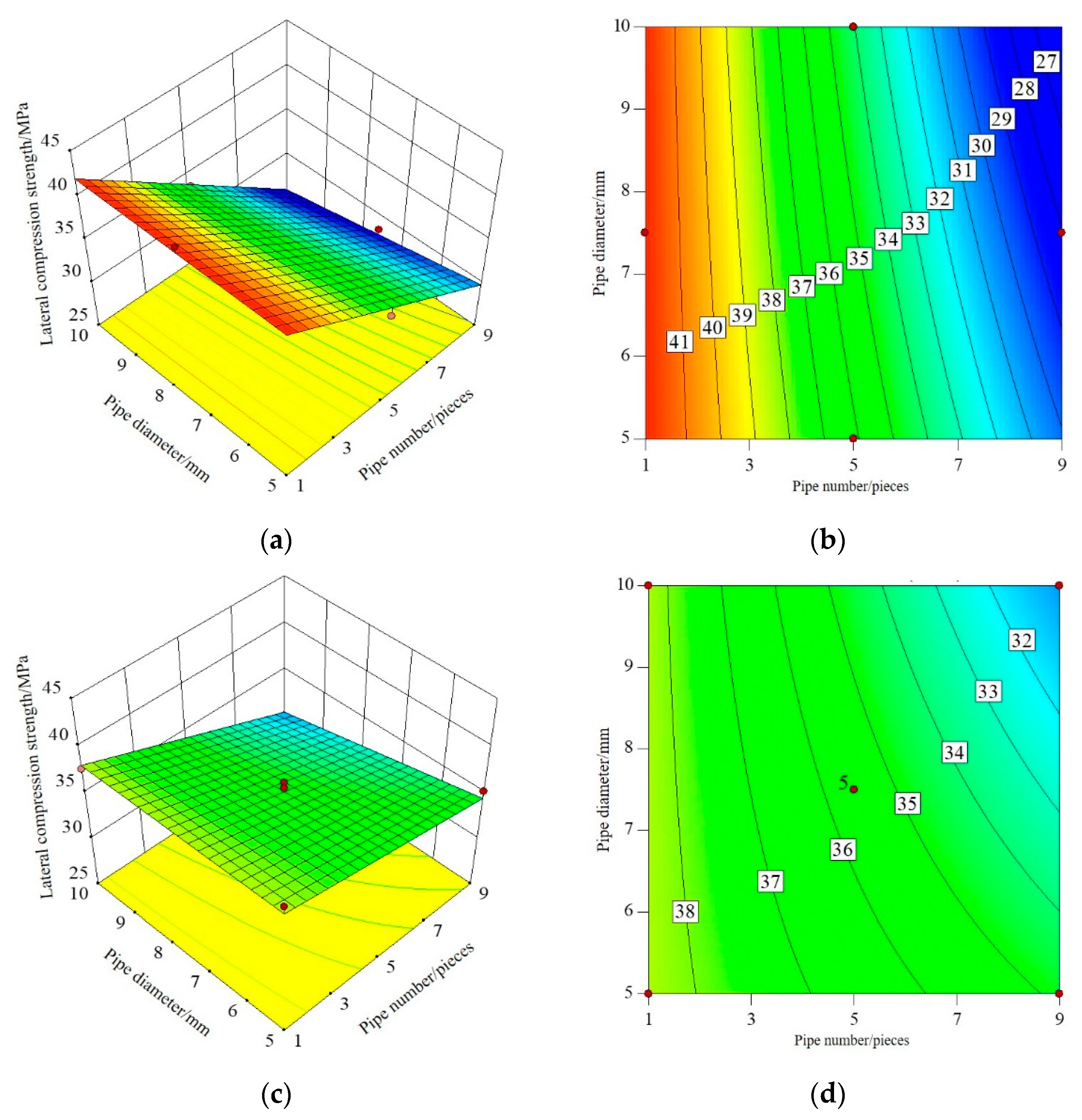
Preprints 108305 g006
Preprints 108305 g007
Figure 7. The interaction of the number and diameter of the pipe on the water permeability coefficient of I-RAPC. (a) The response surface (n =0.01); (b) The contour (n =0.01); (c) The response surface (n =0.0075); (d) The contour (n =0.0075).
Figure 7. The interaction of the number and diameter of the pipe on the water permeability coefficient of I-RAPC. (a) The response surface (n =0.01); (b) The contour (n =0.01); (c) The response surface (n =0.0075); (d) The contour (n =0.0075).
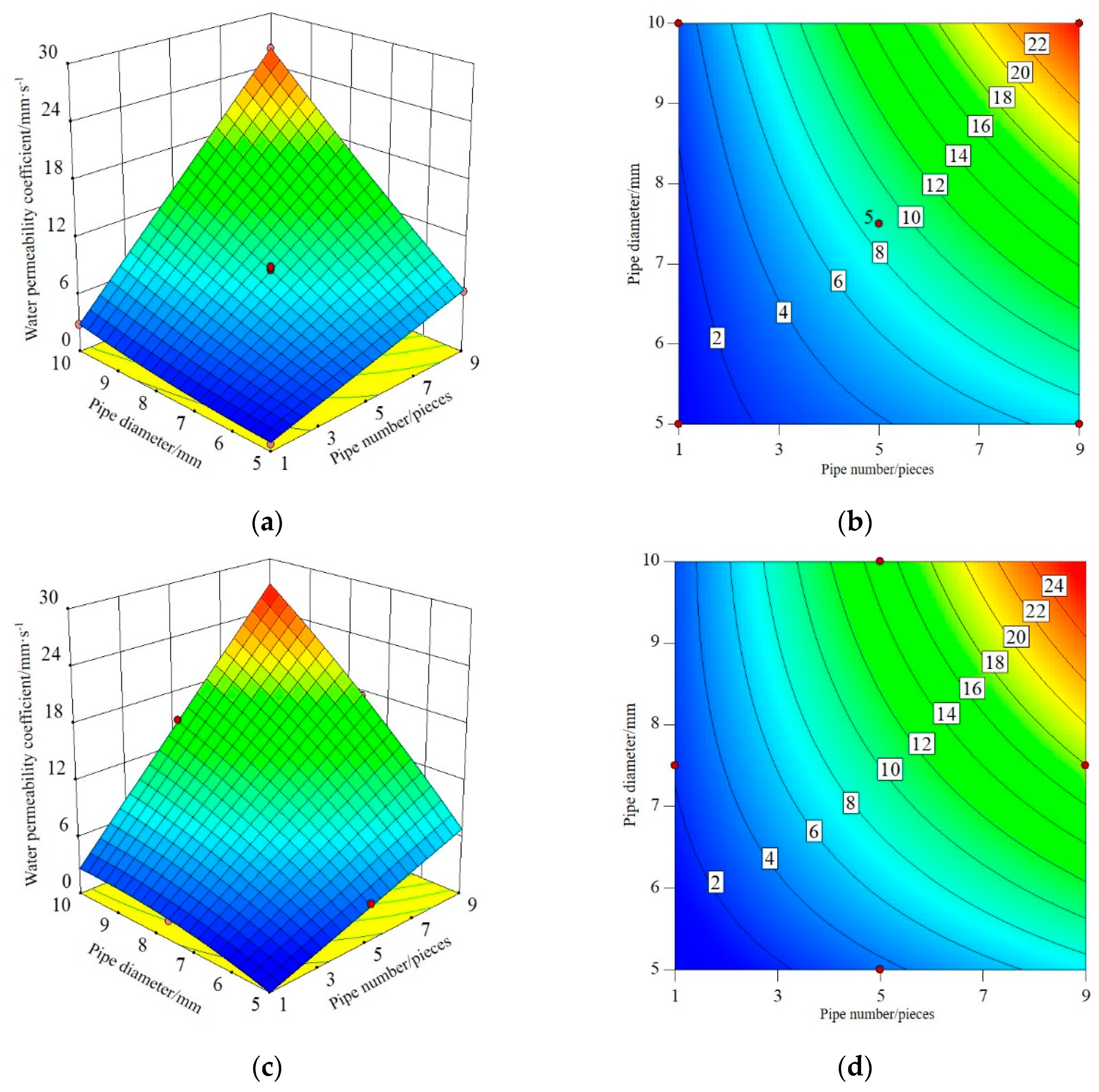
Preprints 108305 g007
Preprints 108305 g008
Figure 8. The failure of morphology of I-RAPC. (a) Positive compressive strength; (b) Lateral compressive strength.
Figure 8. The failure of morphology of I-RAPC. (a) Positive compressive strength; (b) Lateral compressive strength.
Preprints 108305 g008
Preprints 108305 g009
Figure 9. Effect of pipe on compressive strength of I-RAPC. (a) Positive compressive strength; (b) Lateral compressive strength.
Figure 9. Effect of pipe on compressive strength of I-RAPC. (a) Positive compressive strength; (b) Lateral compressive strength.
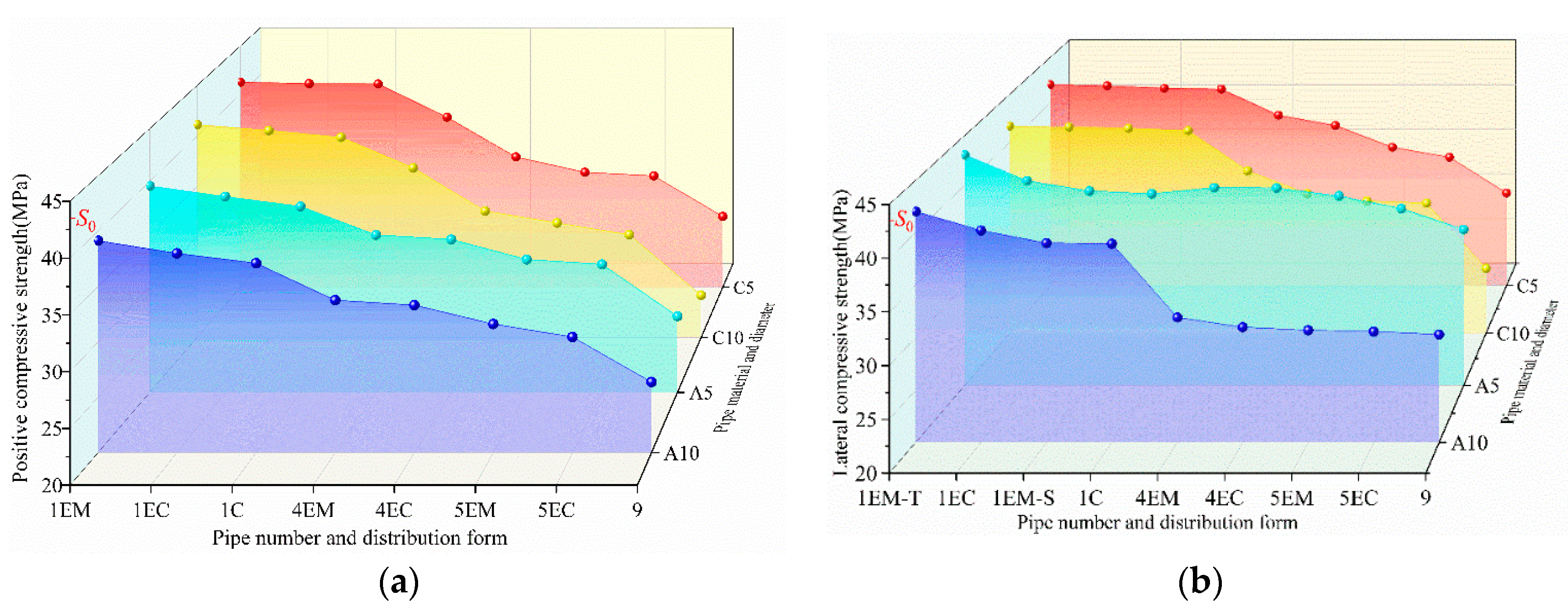
Preprints 108305 g009
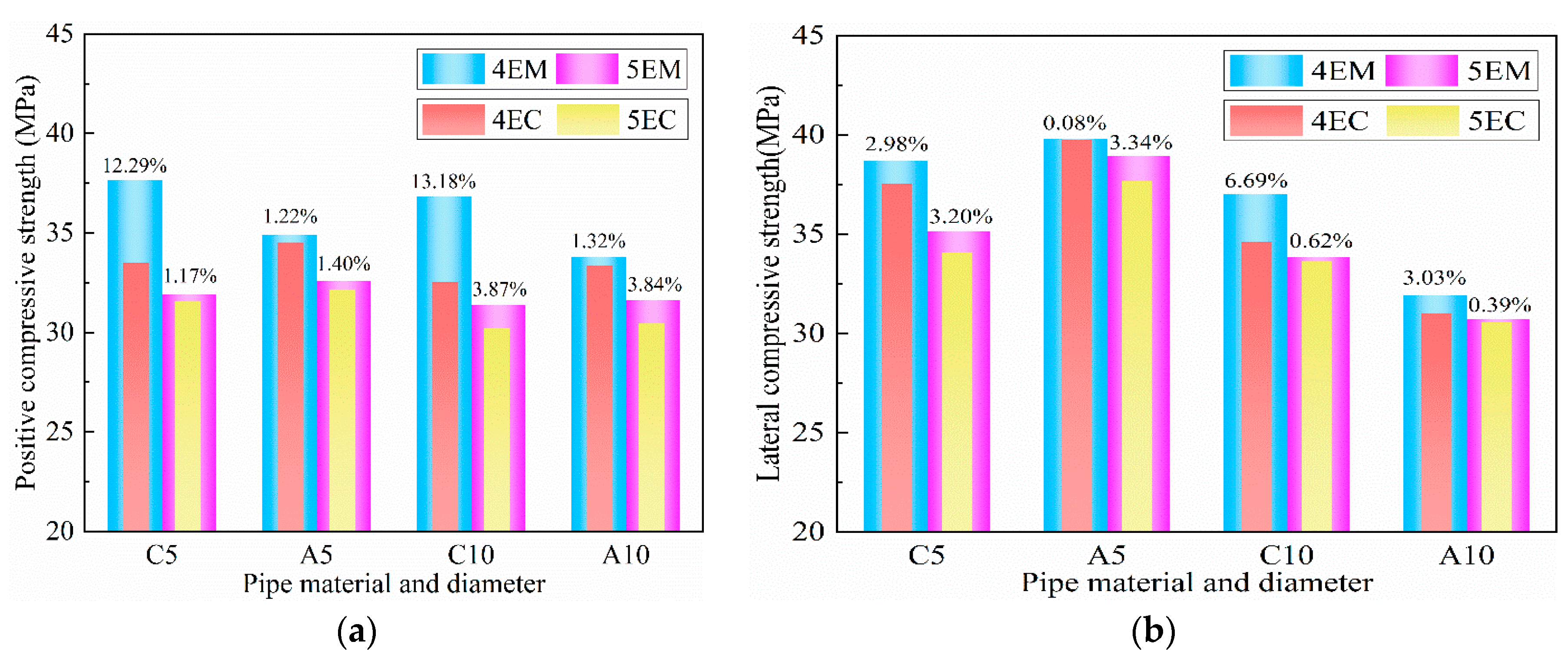
Preprints 108305 g010
Figure 10. Improvement degree of EM pipe distribution on I-RAPC compressive strength. (a) Positive compressive strength; (b) Lateral compressive strength.
Figure 10. Improvement degree of EM pipe distribution on I-RAPC compressive strength. (a) Positive compressive strength; (b) Lateral compressive strength.
Preprints 108305 g010
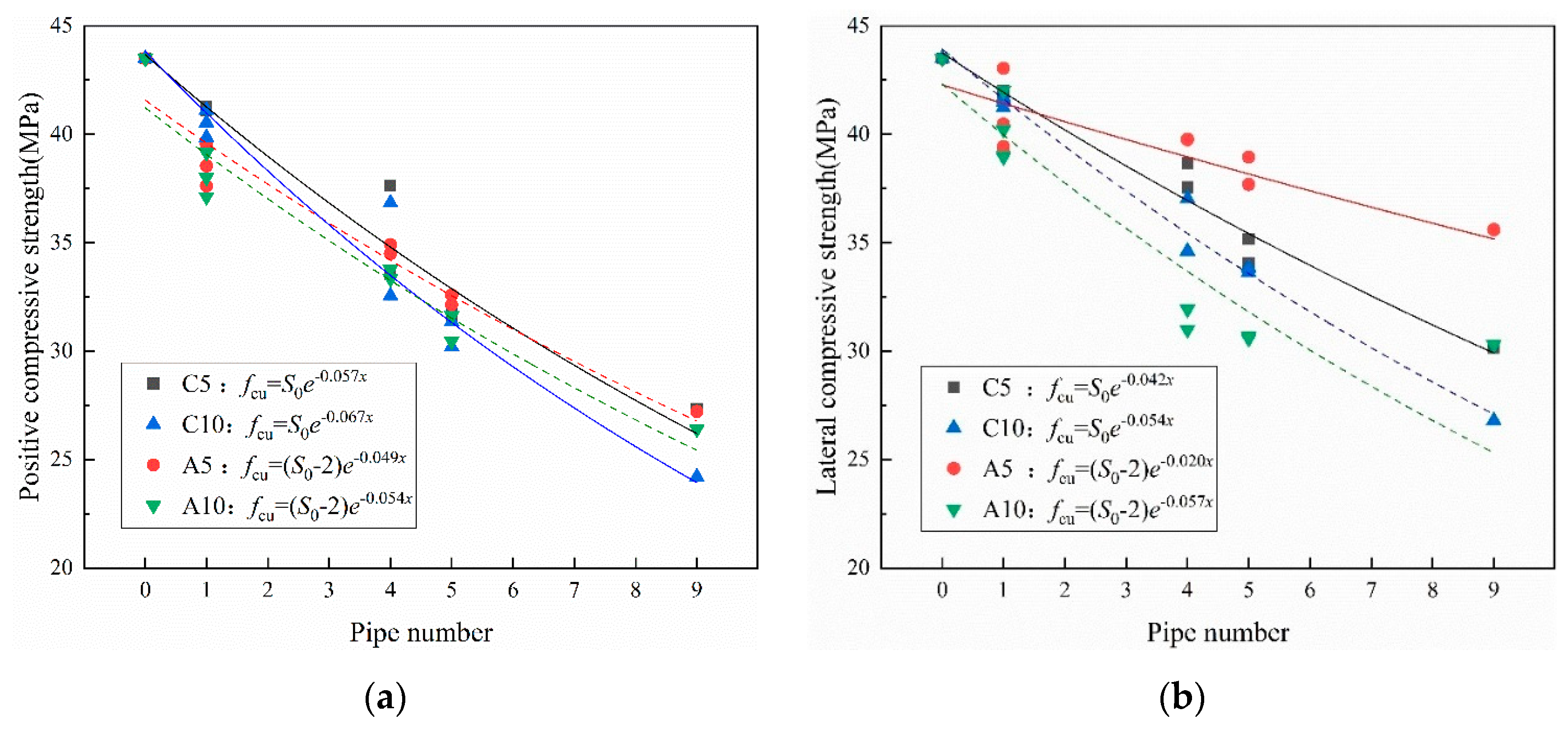
Preprints 108305 g011
Figure 11. Fitting results of I-RAPC compressive strength and pipe number. (a) Positive compressive strength; (b) Lateral compressive strength.
Figure 11. Fitting results of I-RAPC compressive strength and pipe number. (a) Positive compressive strength; (b) Lateral compressive strength.
Preprints 108305 g011
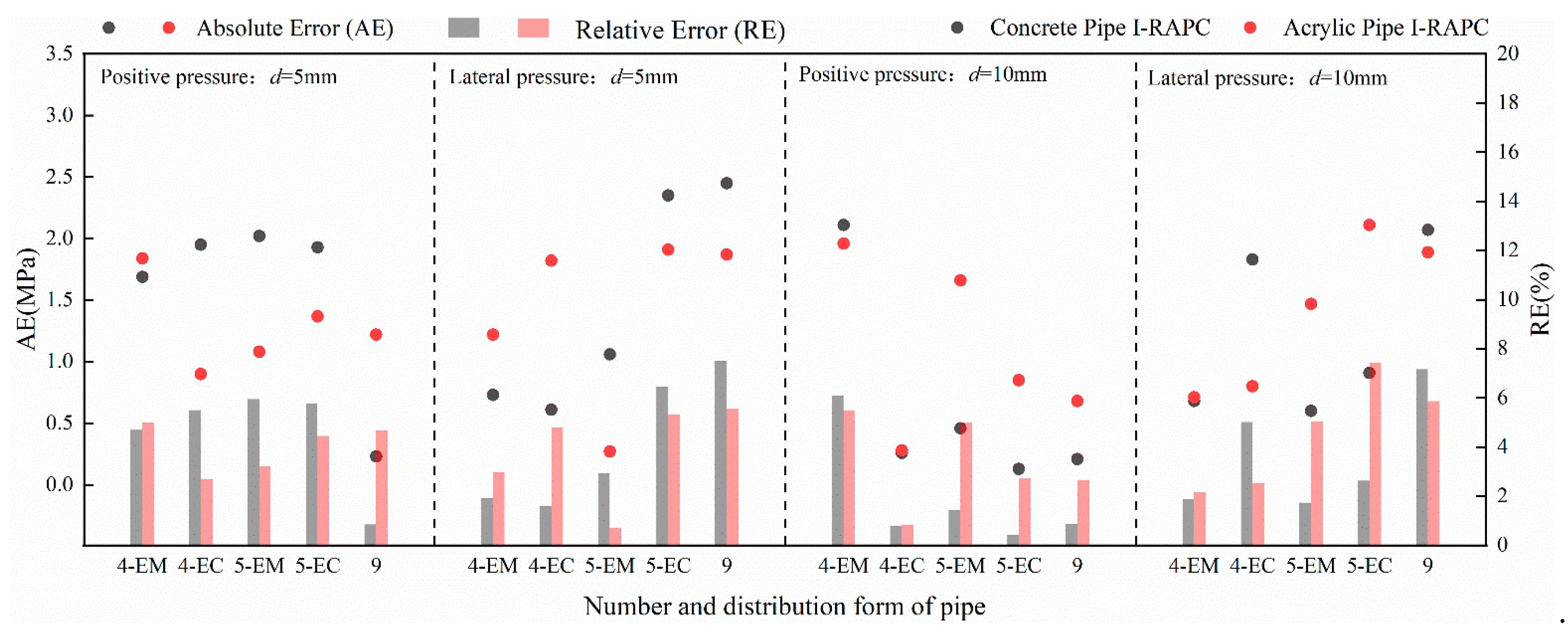
Preprints 108305 g012
Figure 12. The error diagram between the calculated value and actual value of I-RAPC compressive strength.
Figure 12. The error diagram between the calculated value and actual value of I-RAPC compressive strength.
Preprints 108305 g012
Preprints 108305 g013
Figure 13. Calculation diagram of water permeability coefficient (Unit: mm). (a) The water permeability device; (b) The size of section 1-1, 2-2.
Figure 13. Calculation diagram of water permeability coefficient (Unit: mm). (a) The water permeability device; (b) The size of section 1-1, 2-2.
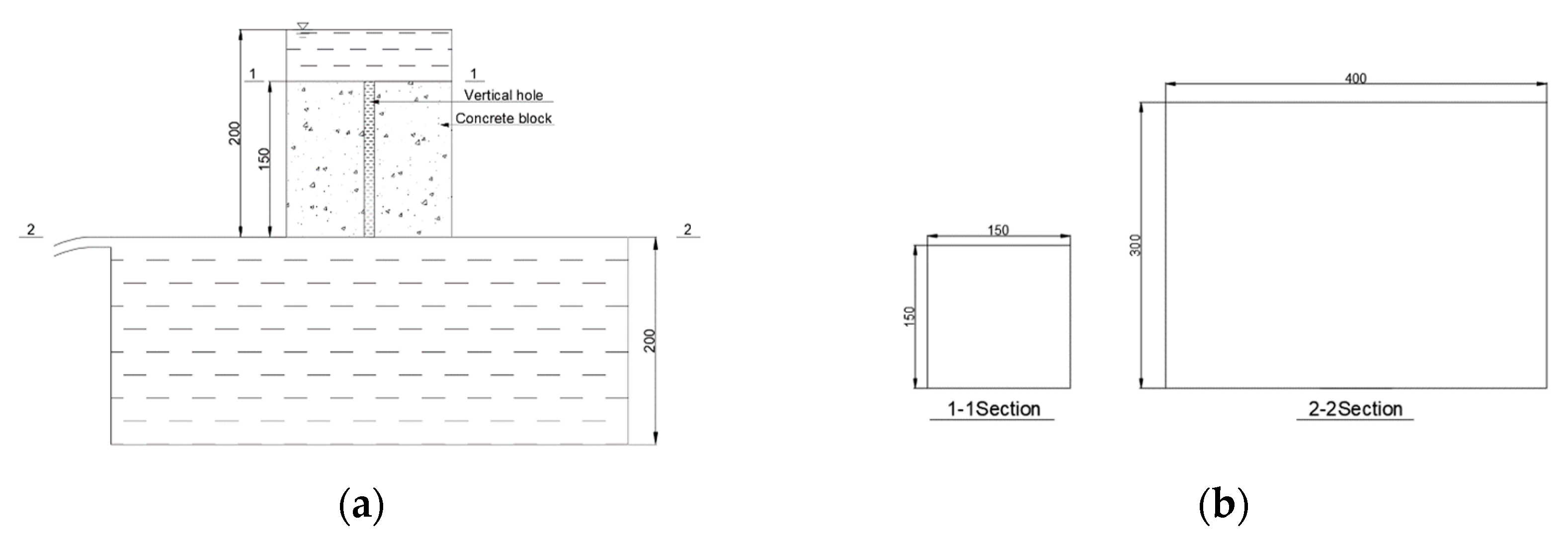
Preprints 108305 g013
Table 1. Index of recycled coarse aggregate.
Table 1. Index of recycled coarse aggregate.
Aggregate type Particle size/mm Apparent density/(kg·m-3) Bulk density/(kg·m-3) Sediment percentage/% Water content/% 15min water absorption/% Crushing index/%
Recycled coarse aggregate 4.75~9.5 2595 1245 0.25 2.80 4.70 15.54
Table 2. Mix design of I-RAPC.
Table 2. Mix design of I-RAPC.
Water cement ratio Material consumption per unit volume /(kg·m-3)
Cement RCA(4.75~9.5mm) Fine aggregate Water
0.49 418 1164 613 205
Table 3. Design of I-RAPC response surface test.
Table 3. Design of I-RAPC response surface test.
Experimental levers x: Number d: Diameter E: Elastic modulus n: Coefficient of roughness
(mm) (GPa)
Low 1 5.0 1.00(B) 0.0075(A)
Medium 5 7.5 2.33(A) 0.0100(C)
High 9 10 3.00(C) 0.0150(B)
Experimental data points 1 2 3 4 5 6 7 8 9 10 11 12 13~17
x 1 9 1 9 1 9 1 9 5 5 5 5 5
fcu d 5 5 10 10 7.5 7.5 7.5 7.5 5 10 5 10 7.5
E 2.33 2.33 2.33 2.33 1 1 3 3 1 1 3 3 2.33
x 1 9 1 9 1 9 1 9 5 5 5 5 5
k d 5 5 10 10 7.5 7.5 7.5 7.5 5 10 5 10 7.5
n 0.01 0.01 0.01 0.01 0.0075 0.0075 0.015 0.015 0.0075 0.0075 0.015 0.015 0.01
Notes: A: Acrylic pipe; B: Bamboo pipe; C: Concrete pipe; fcu: Compressive strength; k: Permeability coefficient; E: The elastic modulus of pipes; n: The coefficient of roughness.
Table 4. The plan of I-RAPC compressive strength theoretical model construction.
Table 4. The plan of I-RAPC compressive strength theoretical model construction.
Material Diameter Number Distribution form
Concrete(C)
Acrylic(A)		 5mm
10mm		 1 C/EM/EC
4,5 EM/EC
9 C, EM, EC
Table 5. Results of response model variance analysis.
Table 5. Results of response model variance analysis.
Category Sum of squares Degrees of freedom Mean square error F p value
Pr>F
Positive compressive strength Model 259.24 7 37.03 25.71 <0.0001 Significant
Lack of fit 9.97 5 1.99 2.67 0.1815 Insignificant
Lateral compressive strength Model 162.27 7 23.18 28.79 < 0.0001 Significant
Lack of fit 4.67 5 0.93 1.45 0.3698 Insignificant
Permeable coefficient Model 701.35 10 70.14 916.98 < 0.0001 Significant
Lack of fit 0.29 2 0.14 3.38 0.1385 Insignificant
Table 6. Regression equation error statistical analysis results.
Table 6. Regression equation error statistical analysis results.
Statistics project Positive / Lateral compressive strength / Permeability coefficient Statistics project Positive / Lateral compressive strength / Permeability coefficient
Std. Dev. 1.20/0.90/0.28 R-Squared 0.9524/0.9573/0.9993
Mean 31.46/35.24/8.47 Adj R-Squared 0.9153/0.9240/0.9983
C.V. % 3.79/2.55/3.27 Pred R-Squared 0.7765/0.7445/0.9575
PRESS 60.82/43.32/29.86 Adeq Precision 16.57/22.923/113.46
Table 7. Reduction coefficient of I-RAPC compressive strength.
Table 7. Reduction coefficient of I-RAPC compressive strength.
Coefficient category pipe material Diameter/mm pipe position
Center (C) c1 Edge middle (EM) c2 Edge corner (EC) c3
Edge middle top (EM-T) c2T Edge middle side (EM-S) c2s
Reduction coefficient of positive compressive strength Concrete 5 0.9444 0.9485 0.9453
10 0.9163 0.9453 0.9320
Acrylic 5 0.9158 0.9558 0.9375
10 0.9313 0.9521 0.9376
Reduction coefficient of lateral compressive strength Concrete 5 0.9545 0.9660 0.9568 0.9628
10 0.9478 0.9589 0.9553 0.9568
Acrylic 5 0.9434 1.0245 0.9476 0.9663
10 0.9447 1.0074 0.9407 0.9664
Notes: According to the characteristics of I-RAPC compression surface, When Positive pressure, the distribution forms of single pipes are C, EC, and EM (only one form); When the lateral pressure, the distribution forms of single pipes are C, EC, and EM respectively, and EM includes EM-T and EM-S.
Table 8. Calculation table of frictional head loss coefficient λ.
Table 8. Calculation table of frictional head loss coefficient λ.
pipe material Coefficient of roughness Diameter/mm Hydraulic radius/m Chezy’s coefficient C Head loss coefficient along the way λ
Concrete 0.01 5 0.00125 32.82 0.07285
10 0.0025 36.84 0.05782
Acrylic 0.0075 5 0.00125 43.76 0.04098
10 0.0025 49.12 0.03253
Table 9. Calculation table of local head loss coefficient ζ .
Table 9. Calculation table of local head loss coefficient ζ .
Section number Section form pipe diameter / mm Section area before change/mm2 Section area after change/mm2 Local   head   loss   coefficient   ζ
1-1 Suddenly shrink 5 22500 19.625 0.4996
10 22500 78.500 0.4983
2-2 Sudden expansion 5 19.625 120000 0.9997
10 78.500 120000 0.9987
Table 10. Theoretical and actual values of I-RAPC water permeability coefficient of a single pipe.
Table 10. Theoretical and actual values of I-RAPC water permeability coefficient of a single pipe.
pipe material pipe diameter/ mm Flow coefficient μc Flow Q(cm3/s) Permeability coefficient k(mm/s) Error
Calculated value Actual value Absolute error (mm/s) Relative error (%)
Concrete 5 0.5276 20.773 0.692 0.724 0.032 4.420
10 0.5452 85.832 2.861 2.897 0.036 1.243
Acrylic 5 0.5668 22.312 0.744 0.754 0.010 1.326
10 0.5763 90.726 3.024 3.016 0.008 0.265
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated