Prerpints.org logo
Preprint
Article

Dynamical Behaviors of a Stochastic SITRS Cholera Model With Ornstein-Uhlenbeck Process

Altmetrics

Downloads

145

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 June 2024

Posted:

05 June 2024

You are already at the latest version

Alerts
Abstract
In this study, a cholera infection model with the bilinear infection rate is developed by considering the perturbation of the infection rate by the mean-reverting process. First of all, we give the existence of a globally unique positive solution for a stochastic system at arbitrary initial value. On this basis, the sufficient condition for the model to have an ergodic stationary distribution is given by constructing proper Lyapunov functions and tight sets. This indicates in a biological sense the long-term persistence of cholera infection. Furthermore, after transforming the stochastic model to an relevant linearised system, an accurate expression for the probability density function of the stochastic model around a quasi-endemic equilibrium is derived. Subsequently, the sufficient condition to make the disease extinct is also derived. Eventually, the theoretical findings are shown by numerical simulations. Numerical simulations show that the impact of regression speed and fluctuation intensity on stochastic systems.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematical and Computational Biology

1. Introduction

Infectious diseases have always been an important issue in the field of global public health, with far-reaching impacts on the health of human societies, social order and economic stability. WHO has been actively promoting in-depth research on infectious diseases, with the aim of understanding the mechanisms of their occurrence, transmission and control, so as to provide a scientific basis for global health security [1,2,3]. Infectious diseases are diseases caused by pathogens that spread among populations, including viruses, bacteria, parasites, fungi, or other pathogens. These pathogens can be transmitted through different routes, such as airborne droplets, bloodborne, food and waterborne, making the control and prevention of infectious diseases extremely complex. One of the typical diseases transmitted from water sources is cholera [4].
Cholera is an infectious disease brought on by infection with the bacterium Vibrio cholerae [5]. Typical symptoms of Vibrio cholerae infection: after infection, it usually leads to the damage of autoimmune cells, which may cause the patient to have moderate or high fever, and if it is more serious, it may lead to coma or shock. Cholera can be transmitted by a variety of means, including waterborne, foodborne, contact and mosquito transmission [6]. Moreover, cholera patients and carriers are usually the major transmission source. This article combines the randomness of infectious diseases and focuses on the study of human to human contact transmission.
The spread of infectious diseases is a complex process that is influenced by various factors, such as population density, population mobility, pathogen characteristics, etc. Mathematical models can take these factors into account and describe the dynamics of infectious disease transmission by establishing a series of equations [7]. By solving and simulating these equations, scientists can better understand the laws of infectious disease transmission and develop more effective prevention and control strategies[8,9,10,11,12,13]. For instance, Wang et al.[14] proposed a model for spreading cholera epidemics with chronological age and infection age structures. Jiang et al.[15] constructed a diffusion cholera model with non-flux boundary conditions for seasonally forced endowment latency and bacterial hyperinfectivity.
In [16], Tilahun et al. researched a deterministic SITRS mathematical model for cholera by considering the direct contact transmission route as follows:
d S d t = A + p R − ξ S − β I S , d I d t = β I S − ( ξ + d + σ ) I , d T d t = σ I − ( ξ + γ + g ) T , d R d t = γ T − ( ξ + p ) R .
where S , I , T and R stand for susceptible, infected, treated and recovered populations, respectively. A is susceptible to this recruitment rate, β is the rate of contact between vulnerable and infected persons, p is the rate of immune loss among recovered individuals, ξ is the natural lethality rate, d is the disease lethality among infected persons, σ is the treatment rate among infected individuals, γ is the rate of recovery among treated individuals, and g is the disease lethality among treated individuals.
There are several conclusions for model (1) as follows:
(1) The number of basic regeneration is R 0 = β A ξ ( ξ + d + σ ) .
(2) The disease-free equilibrium point E 0 = ( S 0 , I 0 , T 0 , R 0 ) = ( A ξ , 0 , 0 , 0 ) of the system is global asymptotically stable for R 0 < 1 . The endemic equilibrium point E * = ( S * , I * , T * , R * ) of the system is local asymptotically stable for R 0 > 1 , where
S * = ξ + d + σ β , I * = ξ + γ + g σ T * , R * = γ ξ + p T * ,
T * = σ ( ξ + p ) ( β A − ξ ( ξ + d + σ ) ) β ( ξ + p ) ( ξ + γ + g ) ( ξ + d + σ ) − β σ p γ .
Additionally, the presence of random noise in ecosystems can also have an impact on population systems. Therefore random infectious models with environmental noise can more accurately reflect actual phenomena compared with traditional deterministic infectious disease models [17,18,19,20,21]. To simulate the influence of random noise on contact rate β , two techniques have been described by Zhang et al. [22]. One way is to use Gaussian white noise to interfere with parameter β . Another approach is to use the Ornstein-Uhlenbeck process of mean-reverting process to interfere with parameter β .
(1) In the first case,
β ( t ) = β + θ d B ( t ) .
B ( t ) is denoted as standard Brownian movement, θ is the intensity of white noise. Integrating the above equation and dividing by t which gives
1 t ∫ 0 t β ( s ) d s = β + θ B ( t ) t ∼ N ( β , θ 2 t )
This indicates that when t approaches 0, V a r [ β ( t ) ] will reach infinity, meaning that β fluctuates greatly. This has resulted in very unreasonable results. In [23], Allen’s research shows that compared to linear functions with white Gaussian noise, the mean-reverting process is better able to demonstrate environmental diversity.
In the second case,
d β ( t ) = k ( β − β ( t ) ) d t + θ d B ( t ) ,
which k , θ is normal number. k is the regression speed, θ is the fluctuation intensity. For the above equation, let m ( t ) = β ( t ) − β to get
d m ( t ) = − k m ( t ) d t + θ d B ( t ) .
By calculation, it is possible to obtain E [ m ( t ) ] = m 0 e − k t , V a r [ m ( t ) ] = θ 2 2 k ( 1 − e − 2 k t ) where m 0 : = m ( 0 ) . Unlike white noise, as t → 0 , V a r [ β ( t ) ] tends towards 0. However, it is easy to get that m ( t ) being ergodic, weakly converges to an invariant density
ζ ( x ) = k π θ e − k x 2 θ 2 , ( x ∈ R ) .
Using the ergodic theorem in [24], we get
lim t → ∞ 1 t ∫ 0 t | m ( δ ) | d δ = ∫ − ∞ + ∞ | x | ζ ( x ) d x = θ π k .
(2) For sufficiently short time periods, the correlation coefficient of the mean-reverting process is ρ ( Y ( t ) , Y ( t + Δ t ) ) = 1 − o ( Δ t ) , the correlation coefficient of white Gaussian noise is ρ ( Y ( t ) , Y ( t + Δ t ) ) = 0 .
(3) Also, since there are many interacting variables in the environment that affect the infectious disease system, and these variables are continuously changing. The fact that the Ornstein-Uhlenbeck process is continuous, as opposed to white Gaussian noise, makes the model more realistic and interpretable, and more reflective of the continuum of infectious diseases.
Prior to this, some scholars have used a mean-reverting process to study the kinetic behaviour of some infectious diseases [25,26,27,28]. For example, Liu[29] developed and analysed a stochastic model with two types of competitive prey and a mean-reverting process to better understand population dynamics. Zhang et al.[30] investigated a reaction-diffusion model of hepatitis B virus (HBV) infection incorporating a mean-reverting process.
Combining with the (1) and (2), the stochastic model is shown below:
d S d t = A + p R − ξ S − ( β + m ) I S , d I d t = ( β + m ) I S − ( ξ + d + σ ) I , d T d t = σ I − ( ξ + γ + g ) T , d R d t = γ T − ( ξ + p ) R , d m = − k m d t + θ d B ( t ) .
Throughout this paper, we set ( Ω , { F t } t ≥ 0 , P ) to be a complete probability space whose filtration { F t } t ≥ 0 fulfils the usual conditions ( it is right-continuous and F 0 includes all P -null sets).
The rest of the paper is organised as described below. Section 2 gives the uniqueness and the existence of the global positive solution for the system (4). The sufficient condition for the existence of an ergodic stationary distribution for the system (4) when the disease persists is given in Section 3. With the help of resolving the associated five-dimensional Fokker-Planck equation, Section 4 derives an explicit expression for the density function of the stationary distribution. Section 5 derives the sufficient condition for disease extinction. Section 6 illustrates our theoretical results by means of several numerical simulations and investigates the effects of the regression speed and the strength of the fluctuation on the system (4).

2. Existence and Uniqueness of the Global Solution

To analyse the dynamical behaviour of the infectious disease system, it is necessary to determine whether the solution is global.
Theorem 1. 
For any initial value ( S ( 0 ) , I ( 0 ) , T ( 0 ) , R ( 0 ) , m ( 0 ) ) ∈ R + 4 × R , on t ≥ 0 , there does exist a unique solution ( S ( t ) , I ( t ) , T ( t ) , R ( t ) , m ( t ) ) to system (4) which stays with probability 1 in R + 4 × R .
Proof of Theorem 1. 
It follows from the local Lipschitz continuity of the coefficients of model (4) that there has a unique local solution ( S ( t ) , I ( t ) , T ( t ) , R ( t ) , m ( t ) ) ∈ R + 4 × R on t ∈ [ 0 , τ b ) , where τ b represents the explosion time[31].
In the following we prove that the solution is global with the help of τ b = ∞ a . s . . In order to ensure that S ( 0 ) , I ( 0 ) , T ( 0 ) , R ( 0 ) and e m ( 0 ) are all within [ 1 a 0 , a 0 ] , we make a 0 > 0 sufficiently large. For each integer a > a 0 , defining the stopping time by
τ a = inf { t ∈ [ 0 , τ b ) : min { S ( t ) , I ( t ) , T ( t ) , R ( t ) , e m ( t ) } ≤ 1 a or max { S ( t ) , I ( t ) , T ( t ) , R ( t ) , e m ( t ) } ≥ a }
Here ∅ is the empty set and we define inf ∅ = ∞ . τ a is monotonically increasing as a → ∞ . Here we assume τ ∞ , which satisfies τ ∞ = lim a → ∞ τ a as well as τ ∞ ≤ τ b a . s . . On t ≥ 0 , τ b = ∞ a . s . and ( S ( t ) , I ( t ) , T ( t ) , R ( t ) , m ( t ) ) ∈ R + 4 × R a . s . hold because the condition τ ∞ = ∞ a . s . satisfies.
On the contrary, there are constants h > 0 and δ ∈ ( 0 , 1 ) that make P { τ ∞ ≤ h } > δ a . s . hold. Therefore, suppose that an integer a 1 ≥ a 0 makes P { τ a ≤ h } ≥ δ a . s . , ∀ a ≥ a 1 . Construct the following function:
H 1 ( S , I , T , R , m ) = ( S − 1 − ln S ) + ( I − 1 − ln I ) + ( T − 1 − ln T ) + ( R − 1 − ln R ) + m 4 4 .
Clearly, this function is non negative. For ∀ a ≥ a 0 and ∀ h > 0 , let H 1 use It o ^ ’s formula, which yields
d H 1 ( S , I , T , R , m ) = L H 1 d t + m 3 θ d B ( t ) .
From equations 1 to 4 of the system (4), we get
d ( S + I + T + R ) = [ A − ξ ( S + I + T + R ) − d T − g T ] d t ≤ [ A − ξ ( S + I + T + R ) ] d t ,
so
S ( t ) + I ( t ) + T ( t ) + R ( t ) ≤ A ξ .
Next, using the It o ^ ’s formula, the following conclusions can be drawn
L H 1 = ( 1 − 1 S ) [ A + p R − ξ S − ( β + m ) I S ] + ( 1 − 1 I ) [ ( β + m ) I S − ( ξ + d + σ ) I ] + ( 1 − 1 T ) [ σ I − ( ξ + γ + g ) T ] + ( 1 − 1 R ) [ γ T − ( ξ + p ) R ] − k m 4 + 3 2 θ 2 m 2 − k m 4 + 3 2 θ 2 m 2 − p R S + ξ + ( β + m ) I − ( β + m ) S + ( ξ + d + σ ) − σ I T + ( ξ + γ + g ) − γ T R + ( ξ + p ) ≤ A + 4 ξ + d + σ + γ + g + p + ( β + m ) I − m S − k m 4 + 3 2 θ 2 m 2 ≤ A + β A ξ + 4 ξ + d + σ + γ + g + p + sup m ∈ R ( − k m 4 + 3 2 θ 2 m 2 + 2 | m | A ξ ) ≤ c 1 .
Here c 1 is a normal number. Replacing the above inequality with (5) and performing the calculation, we get
d H 1 ( S , I , T , R , m ) ≤ c 1 d t + m 3 θ d B ( t ) .
The expectation while integrating from 0 to τ a ∧ h yields
E [ H 1 ( S ( τ a ∧ h ) , I ( τ a ∧ h ) , T ( τ a ∧ h ) , R ( τ a ∧ h ) , m ( τ a ∧ h ) ) ]
≤ H 1 ( ( S ( 0 ) , I ( 0 ) , T ( 0 ) , R ( 0 ) , m ( 0 ) ) + c 1 E [ ( τ a ∧ h ) ] ≤ H 1 ( ( S ( 0 ) , I ( 0 ) , T ( 0 ) , R ( 0 ) , m ( 0 ) ) + c 1 h .
Let Ω a = { τ a ≤ h } for a ≥ a 1 , then we get P ( Ω a ) ≥ δ , δ ∈ ( 0 , 1 ) . For every r ∈ Ω a , S ( τ a , r ) , I ( τ a , r ) , T ( τ a , r ) , R ( τ a , r ) and e m ( τ a , r ) are either equal to a or 1 a . Therefore,
H 1 ( ( S ( 0 ) , I ( 0 ) , T ( 0 ) , R ( 0 ) , m ( 0 ) ) + c 1 h
≥ E [ 1 Ω a H 1 ( S ( τ a ∧ h ) , I ( τ a ∧ h ) , T ( τ a ∧ h ) , R ( τ a ∧ h ) , m ( τ a ∧ h ) ) ] ≥ δ [ ( a − 1 − ln a ) ∧ ( 1 a − 1 − ln a ) ∧ 1 4 ( ln a ) 4 ] ,
where 1 Ω a ( r ) is the indicator function of Ω a . As a → ∞ , the above equation fulfils
∞ > H 1 ( S ( 0 ) , I ( 0 ) , T ( 0 ) , R ( 0 ) , m ( 0 ) ) + c 1 h = ∞ ,
which creates a conflict. This finishes the proof. □
Remark 1. 
It follows from Theorem 1 that there exists a unique global solution ( S ( t ) , I ( t ) , T ( t ) , R ( t ) , m ( t ) ) ∈ R + 4 × R . Consequently
d ( S + I + T + R ) ≤ [ A − ξ ( S + I + T + R ) ] d t
and
S ( t ) + I ( t ) + T ( t ) + R ( t ) ≤ A ξ + e − ξ t ( S ( 0 ) + I ( 0 ) + T ( 0 ) + R ( 0 ) − A ξ ) .
If S ( 0 ) + I ( 0 ) + T ( 0 ) + R ( 0 ) ≤ A ξ , then S ( t ) + I ( t ) + T ( t ) + R ( t ) ≤ A ξ a . s . . As a result, we always assume that Γ = { ( S , I , T , R , m ) ∈ R + 4 × R : 0 ≤ S + I + T + R ≤ A ξ } is the invariant set.

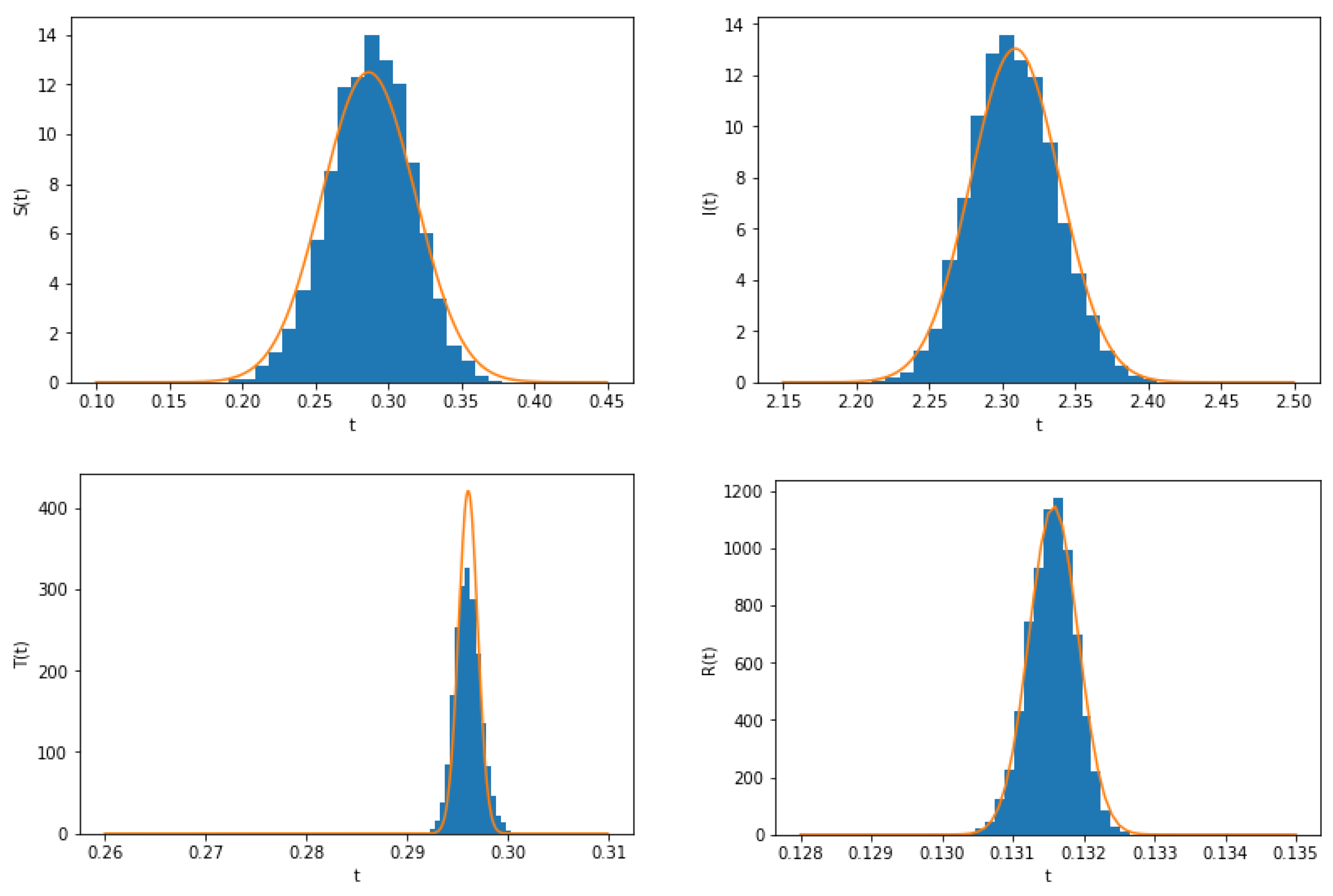
3. Stationary Distribution

When studying stochastic models, the stationary distribution is an essential instrument for studying disease persistence. This section derives the sufficient condition for the existence of a stationary distribution. Next, we give a related lemma.
Lemma 1. 
[32] In R d , define a temporally homogeneous Markov process F ( t ) whose characteristics satisfy a stochastic differential equation:
d F ( t ) = ψ ( F ( t ) ) d t + ∑ n = 1 k ϕ n ( F ( t ) ) d B n ( t ) .
Assume that ψ ( F ) , ϕ 1 ( F ) , ⋯ , ϕ n ( F ) ( t ≥ t 0 , F ∈ R d ) are continuous.
(1) The presence of an r > 0 results in
| ψ ( F 1 ) − ψ ( F 2 ) | + ∑ n = 1 k | ϕ n ( F 1 ) − ϕ n ( F 2 ) | ≤ r | F 1 − F 2 | , | ψ ( F ) | + ∑ n = 1 k | ϕ n ( F ) | ≤ r ( 1 + | F | ) .
(2) In R d ,a non-negative C 2 -function H ( x ) fulfills that L H ( F ) ≤ − 1 outside some compact set. F ( t ) is a stationary Markov process when conditions (1) and (2) are satisfied.
Theorem 2. 
If R 0 S = R 0 − A θ π k ξ ( ξ + d + σ ) > 1 holds, system (4) exists a stationary distribution π ( · ) .
Proof of Theorem 2. 
Define the following function:
H 2 = ln I + β ξ ( S + I ) + p β ξ ( ξ + p ) R + β p γ ξ ( ξ + p ) ( ξ + γ + g ) T .
Applying It o ^ ’s formula to the above equation, it can be concluded that
L ( − H 2 ) ≤ A ξ | m | + ( ξ + d + σ ) − A β ξ − β ξ [ p γ σ ξ ( ξ + p ) ( ξ + γ + g ) − ( ξ + d + σ ) ] I = A θ π k ξ + ( ξ + d + σ ) − A β ξ + A ξ ( | m | − θ π k ) + β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] I = − ( ξ + d + σ ) ( R 0 S − 1 ) + A ξ ( | m | − θ π k ) + β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] I ,
L ( − ln S ) = − A S − p R S + ξ + β I + m I ≤ − A S + β I + ξ + | m | A ξ ,
L ( − ln T ) = − σ I T + ( ξ + γ + g ) ,
L ( − ln R ) = − γ T R + ( ξ + p ) ,
L [ − ln ( A ξ − S − I − T − R ) ] = A − ξ ( S + I + T + R ) − d I − g T A ξ − S − I − T − R ≤ ξ − d I A ξ − S − I − T − R .
Denote
H ¯ ( S , I , T , R , m ) = − Z H 2 − ln S − ln T − ln R − ln ( A ξ − S − I − T − R ) + m 2 2 ,
and
B = 4 ξ + γ + g + p + A 2 2 ξ 2 k + θ 2 2 ,
where Z is a constant greater than 0 and sufficiently large and satisfies the following inequality:
− Z ( ξ + d + σ ) ( R 0 S − 1 ) + B ≤ − 2
H ¯ ( S , I , T , R , m ) has the least value H ¯ ( S 0 , I 0 , T 0 , R 0 , m 0 ) because H ¯ ( S , I , T , R , m ) → + ∞ with ( S , I , T , R , m ) close to the boundary of Γ . From this, assume the following non-negative function:
H ( S , I , T , R , m ) = H ¯ ( S , I , T , R , m ) − H ¯ ( S 0 , I 0 , T 0 , R 0 , m 0 ) .
Applying It o ^ ’s formula, one obtains
L H ≤ − Z ( ξ + d + σ ) ( R 0 S − 1 ) + Z A ξ ( | m | − θ π k ) + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] I − A S + β I + ξ + A ξ | m | − σ I T + ( ξ + γ + g ) − γ T R + ( ξ + p ) + ξ − d I A ξ − S − I − T − R − k m 2 + θ 2 2 ≤ − Z ( ξ + d + σ ) ( R 0 S − 1 ) + 4 ξ + γ + g + ε + A 2 2 ξ 2 k + θ 2 2 + β I − A S − σ I T − γ T R − d I A ξ − S − I − T − R + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] I − k m 2 2 + Z A ξ ( | m | − θ π k ) = Q ( S , I , T , R , m ) + Z A ξ ( | m | − θ π k ) ,
where
Q ( S , I , T , R , m ) = − Z ( ξ + d + σ ) ( R 0 S − 1 ) + 4 ξ + γ + g + ε + A 2 2 ξ 2 k + θ 2 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] I + β I − A S − σ I T − γ T R − d I A ξ − S − I − T − R − k m 2 2
The closed subset of U α is then defined as follows:
U α = { ( S , I , T , R , m ) ∈ Γ | S ≥ α , I ≥ α , T ≥ α 2 , R ≥ α 3 , S + I + T + R ≤ A ξ − α 2 , | m | ≤ 1 α } .
In order for the following inequality to hold, make α sufficiently small.
− 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] α + β α ≤ − 1 ,
− 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − A α ≤ − 1 ,
− 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − σ α ≤ − 1 ,
− 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − γ α ≤ − 1 ,
− 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − d α ≤ − 1 ,
− 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − k 2 α 2 ≤ − 1 .
Partition the complement of U α into the following 6 subsets:
U α , 1 c = { ( S , I , T , R , m ) ∈ Γ | I < α } ,
U α , 2 c = { ( S , I , T , R , m ) ∈ Γ | S < α } ,
U α , 3 c = { ( S , I , T , R , m ) ∈ Γ | I ≥ α , T < α 2 } ,
U α , 4 c = { ( S , I , T , R , m ) ∈ Γ | T ≥ α 2 , R < α 3 } ,
U α , 5 c = { ( S , I , T , R , m ) ∈ Γ | I ≥ α , S + I + T + R > A ξ − α 2 } ,
U α , 6 c = { ( S , I , T , R , m ) ∈ Γ | I ≥ α , | m | > 1 α } .
From this we arrive at the following results.
Case 1. ( S , I , T , R , m ) ∈ U 1 , α c , then
Q ( S , I , T , R , m ) ≤ − 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] α + β α ≤ − 1 .
Case 2. ( S , I , T , R , m ) ∈ U 2 , α c , then
Q ( S , I , T , R , m ) ≤ − 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − A α ≤ − 1 .
Case 3. ( S , I , T , R , m ) ∈ U 3 , α c , then
Q ( S , I , T , R , m ) ≤ − 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − σ α ≤ − 1 .
Case 4. ( S , I , T , R , m ) ∈ U 4 , α c , then
Q ( S , I , T , R , m ) ≤ − 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − γ α ≤ − 1 .
Case 5. ( S , I , T , R , m ) ∈ U 5 , α c , then
Q ( S , I , T , R , m ) ≤ − 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − d α ≤ − 1 .
Case 6. ( S , I , T , R , m ) ∈ U 6 , α c , then
Q ( S , I , T , R , m ) ≤ − 2 + Z β ξ [ ( ξ + d + σ ) − p γ σ ξ ( ξ + p ) ( ξ + γ + g ) ] A ξ + β A ξ − k 2 α 2 ≤ − 1 .
Based on the six cases shown above, there is
Q ( S , I , T , R , m ) ≤ − 1 , ∀ ( S , I , T , R , m ) ∈ Γ ∖ U α .
Furthermore, assuming c 2 > 0 , then
Q ( S , I , T , R , m ) ≤ c 2 < + ∞ , ∀ ( S , I , T , R , m ) ∈ Γ .
For the sake of writing, we denote J ( t ) = ( S ( t ) , I ( t ) , T ( t ) , R ( t ) , m ( t ) ) . For the arbitrary initial value J ( 0 ) ∈ Γ , we can have
0 ≤ E [ H ( J ( t ) ) ] t = E [ H ( J ( 0 ) ] t + 1 t ∫ 0 t E [ L H ( J ( δ ) ) ] d δ ≤ E [ H ( J ( 0 ) ) ] t + 1 t ∫ 0 t E [ Q ( J ( δ ) ) ] d δ + Z A ξ t ∫ 0 t E [ | m ( δ ) | − θ π k ] d δ .
Combining (3) with the infimum bound of the above inequality gives
0 ≤ lim t → ∞ inf 1 t ∫ 0 t E [ Q ( J ( δ ) ) ] d δ = lim t → ∞ inf 1 t ∫ 0 t E [ Q ( J ( δ ) ) 1 { J ( δ ) ∈ U α } ] d δ + lim t → ∞ inf 1 t ∫ 0 t E [ Q ( J ( δ ) ) 1 { J ( δ ) ∈ Γ ∖ U α } ] d δ ≤ c 2 lim t → ∞ inf 1 t ∫ 0 t P { J ( δ ) ∈ U α } d δ − lim t → ∞ inf 1 t ∫ 0 t P { J ( δ ) ∈ Γ ∖ U α } d δ ≤ − 1 + ( c 2 + 1 ) lim t → ∞ inf 1 t ∫ 0 t P { J ( δ ) ∈ U α } d δ ,
where 1 { J ( δ ) ∈ U α } and 1 { J ( δ ) ∈ Γ ∖ U α } are the indicator functions of the set { J ( δ ) ∈ U α } and { J ( δ ) ∈ Γ ∖ U α } . This suggests that
lim t → ∞ inf 1 t ∫ 0 t P { J ( δ ) ∈ U α } d δ ≥ 1 c 2 + 1 > 0 .
Therefore,
lim t → ∞ inf 1 t ∫ 0 t P { δ , J ( 0 ) , U α } d δ ≥ 1 c 2 + 1 , ∀ J ( 0 ) ∈ Γ .
Based on the above inequality and the invariant set Γ , the existence of an invariant probability measure on Γ can be proved using the result in [33]. This suggests that when the illness persists the system (4) has a stationary distribution on Γ . □

4. Density Function

This section presents an explicit representation of the density function of a stationary distribution. If R 0 S > 1 holds, there lies a quasi-endemic equilibrium E ¯ * = ( S * , I * , T * , R * , m * ) satisfying the following equations:
A + ε R * − ξ S * − β I * S * − m I * S * = 0 , β I * S * + m I * S * − ( ξ + d + σ ) I * = 0 , σ I * − ( ξ + γ + g ) T * = 0 , γ T * − ( ξ + p ) R * = 0 , − k m * = 0 .
Let x 1 = S − S * , x 2 = I − I * , x 3 = T − T * , x 4 = R − R * , x 5 = m − m * to obtain the linearized system
d x 1 = ( − a 11 x 1 − a 12 x 2 + a 14 x 4 − a 15 x 5 ) d t , d x 2 = ( a 21 x 1 + a 15 x 5 ) d t , d x 3 = ( a 32 x 2 − a 33 x 3 ) d t , d x 4 = ( a 43 x 3 − a 44 x 4 ) d t , d x 5 = − a 55 x 5 d t + θ d B ( t ) .
where
a 11 = β I * + ξ , a 12 = β S * , a 14 = p , a 15 = I * S * , a 21 = β I * , a 32 = σ , a 33 = ξ + γ + g ,
a 43 = γ , a 44 = ξ + p , a 55 = k .
Theorem 3. 
If R 0 S > 1 , the solution ( x 1 , x 2 , x 3 , x 4 , x 5 ) of the system (8) satisfies the normal probability density function Φ ( x 1 , x 2 , x 3 , x 4 , x 5 ) , which has the following form:
Φ ( x 1 , x 2 , x 3 , x 4 , x 5 ) = ( 2 π ) − 5 2 | Σ | − 1 2 e − 1 2 ( x 1 , x 2 , x 3 , x 4 , x 5 ) Σ − 1 ( x 1 , x 2 , x 3 , x 4 , x 5 ) T ,
where
Σ = ( a 15 a 32 q 1 ω 2 ) 2 θ 2 ( Y J 4 J 3 J 2 J 1 ) − 1 Σ 1 [ ( Y J 4 J 3 J 2 J 1 ) − 1 ] T ,
and
J 1 = 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 , J 2 = 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 ,
J 3 = 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 a 32 ω 1 1 0 0 0 0 0 1 , J 4 = 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 a 43 ω 2 1 ,
where
ω 1 = − a 11 + a 12 + a 21 , ω 2 = − a 11 + a 21 + a 33 ,
Y = − a 15 a 32 q 1 ω 2 − b 1 a 32 q 1 ω 2 h 3 h 4 h 5 0 a 32 q 1 ω 2 a 32 q 1 ω 2 ω 1 ( q 2 + q 3 − a 12 ) h 1 h 2 0 0 a 32 q 1 ω 2 ω 1 q 1 ( q 2 + q 3 ) a 14 a 32 q 1 ω 1 + q 2 2 0 0 0 q 1 q 2 0 0 0 0 1 ,
where
q 1 = a 43 ( − a 14 a 32 a 43 + ω 1 ω 2 ( − a 33 + a 44 + ω 2 ) ) ω 1 ω 2 2 , q 2 = − a 44 ω 1 ω 2 − a 14 a 32 a 43 ω 1 ω 2 ,
q 3 = − a 33 ω 1 ω 2 + a 14 a 32 a 43 ω 1 ω 2 ,
h 1 = q 1 q 3 ( q 2 + q 3 ) + q 1 q 2 2 + q 1 2 a 14 a 32 ω 1 − q 1 a 14 a 32 a 43 ω 1 , h 2 = q 2 3 + a 14 a 32 q 1 ω 2 ω 1 + a 14 a 32 q 1 ω 1 ( 2 q 2 + q 3 ) ,
h 3 = − a 12 a 32 q 1 ω 2 − a 12 a 32 q 1 ω 2 ω 1 ( q 2 + q 3 − a 12 ) + a 32 ω 2 ω 1 h 1 ,
h 4 = − a 14 a 32 a 43 q 1 − a 14 a 32 a 43 q 1 ω 1 ( q 2 + q 3 − a 12 ) + q 3 h 1 + q 1 h 2 ,
h 5 = a 14 a 32 q 1 ω 2 + a 14 a 32 q 1 ω 2 ω 1 ( q 2 + q 3 − a 12 ) + a 14 a 32 ω 1 h 1 + q 2 h 2 ,
Σ 1 = j 11 0 j 13 0 j 15 0 − j 13 0 − j 15 0 j 13 0 j 15 0 j 35 0 − j 15 0 − j 35 0 j 15 0 j 35 0 j 55 ,
where
j ^ = k 3 ( k 1 k 2 − k 3 ) − k 1 ( k 1 k 4 − k 5 ) , j ˜ = ( k 1 k 2 − k 3 ) ( k 3 k 4 − k 2 k 5 ) − ( k 1 k 4 − k 5 ) 2 ,
j 11 = k 2 ( k 3 k 4 − k 2 k 5 ) − k 4 ( k 1 k 4 − k 5 ) 2 j ˜ , j 13 = − k 3 k 4 − k 2 k 5 2 j ˜ , j 15 = k 1 k 4 − k 5 2 j ˜ ,
j 35 = − k 1 k 2 − k 3 2 j ˜ , j 55 = j ^ 2 k 5 j ˜ ,
b 1 = a 11 + a 33 + a 44 , b 2 = a 12 a 21 + a 33 a 44 + a 11 ( a 33 + a 44 ) , b 3 = a 11 a 33 a 44 + a 12 a 21 ( a 33 + a 44 ) ,
b 4 = a 12 a 21 a 33 a 44 − a 14 a 21 a 32 a 43 , k 1 = a 55 + b 1 , k 2 = a 55 b 1 + b 2 , k 3 = a 55 b 2 + b 3 ,
k 4 = a 55 b 3 + b 4 , k 5 = a 55 b 4 .
Proof of Theorem 3. 
Firstly, by setting d x = A x d t + G d B ( t ) , the system (8) is rewritten as:
d x = − a 11 − a 12 0 a 14 − a 15 a 21 0 0 0 a 15 0 a 32 − a 33 0 0 0 0 a 43 − a 44 0 0 0 0 0 − a 55 x d t + 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 θ d B ( t ) .
By calculating the characteristic polynomial of matrix A, we have
φ A ( λ ) = ( λ + a 55 ) ( λ 4 + b 1 λ 3 + b 2 λ 2 + b 3 λ + b 4 ) ,
where b 1 = a 11 + a 33 + a 44 , b 2 = a 12 a 21 + a 33 a 44 + a 11 ( a 33 + a 44 ) , b 3 = a 11 a 33 a 44 + a 12 a 21 ( a 33 + a 44 ) , b 4 = a 12 a 21 a 33 a 44 − a 14 a 21 a 32 a 43 . Clearly, A is a Hurwitz matrix because all of its eigenvalues have negative real parts, and one of the eigenvalues is λ 1 = − a 55 < 0 . According to [34], the density function Φ ( x 1 , x 2 , x 3 , x 4 , x 5 ) of model (8) can be substituted by the following Fokker-Planck equation:
− θ 2 2 ∂ 2 ∂ x 5 2 Φ + ∂ ∂ x 5 [ ( − a 55 x 5 ) Φ ] + ∂ ∂ x 1 [ ( − a 11 x 1 − a 12 x 2 + a 14 x 4 − a 15 x 5 ) Φ ]
+ ∂ ∂ x 2 [ ( a 12 x 1 + a 15 x 5 ) Φ ] + ∂ ∂ x 3 [ ( a 32 x 2 − a 33 x 3 ) Φ ] + ∂ ∂ x 4 [ ( a 43 x 3 − a 44 x 4 ) Φ ] = 0 ,
which can be approximated as the following Gaussian distribution:
Φ ( x ) = c exp { − 1 2 x D x T } .
Here D is satisfied with D G 2 D + A T D + D A = 0 . Assuming it is positive definite and D − 1 = Σ , we can obtain
G 2 + A Σ + Σ A T = 0 .
Next, we prove that Σ is positive definite matrix. Let
J 1 = 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 , J 2 = 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 ,
then
A 1 = ( J 2 J 1 ) A ( J 2 J 1 ) T = − a 55 0 0 0 0 − a 15 − a 11 + a 12 − a 12 0 a 14 0 − a 11 + a 12 + a 21 − a 12 0 a 14 0 − a 32 a 32 − a 33 0 0 0 0 a 43 − a 44 .
Next, let
J 3 = 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 a 32 ω 1 1 0 0 0 0 0 1 ,
where ω 1 = − a 11 + a 12 + a 21 , we have
A 2 = J 3 A 1 J 3 T = − a 55 0 0 0 0 − a 15 − a 11 + a 12 − a 12 0 a 14 0 ω 1 − a 12 0 a 14 0 0 a 32 ω 2 ω 1 − a 33 a 14 a 32 ω 1 0 0 − a 32 a 43 ω 1 a 43 − a 44 .
Then
J 4 = 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 a 43 ω 2 1 ,
where ω 2 = − a 11 + a 21 + a 33 , we get
A 3 = J 4 A 2 J 4 T = − a 55 0 0 0 0 − a 15 − a 11 + a 12 − a 12 − a 14 a 43 ω 2 a 14 0 ω 1 − a 12 − a 14 a 43 ω 2 a 14 0 0 a 32 ω 2 ω 1 q 3 a 14 a 32 ω 1 0 0 0 q 1 q 2 ,
where q 1 = a 43 ( − a 14 a 32 a 43 + ω 1 ω 2 ( − a 33 + a 44 + ω 2 ) ) ω 1 ω 2 2 , q 2 = − a 44 ω 1 ω 2 − a 14 a 32 a 43 ω 1 ω 2 , q 3 = − a 33 ω 1 ω 2 + a 14 a 32 a 43 ω 1 ω 2 . By following the steps in [34], the standard R 1 transformation matrix Y of A 3 can be obtained,
Y = − a 15 a 32 q 1 ω 2 − b 1 a 32 q 1 ω 2 h 3 h 4 h 5 0 a 32 q 1 ω 2 a 32 q 1 ω 2 ω 1 ( q 2 + q 3 − a 12 ) h 1 h 2 0 0 a 32 q 1 ω 2 ω 1 q 1 ( q 2 + q 3 ) a 14 a 32 q 1 ω 1 + q 2 2 0 0 0 q 1 q 2 0 0 0 0 1 ,
where
h 1 = q 1 q 3 ( q 2 + q 3 ) + q 1 q 2 2 + q 1 2 a 14 a 32 ω 1 − q 1 a 14 a 32 a 43 ω 1 , h 2 = q 2 3 + a 14 a 32 q 1 ω 2 ω 1 + a 14 a 32 q 1 ω 1 ( 2 q 2 + q 3 ) ,
h 3 = − a 12 a 32 q 1 ω 2 − a 12 a 32 q 1 ω 2 ω 1 ( q 2 + q 3 − a 12 ) + a 32 ω 2 ω 1 h 1 ,
h 4 = − a 14 a 32 a 43 q 1 − a 14 a 32 a 43 q 1 ω 1 ( q 2 + q 3 − a 12 ) + q 3 h 1 + q 1 h 2 ,
h 5 = a 14 a 32 q 1 ω 2 + a 14 a 32 q 1 ω 2 ω 1 ( q 2 + q 3 − a 12 ) + a 14 a 32 ω 1 h 1 + q 2 h 2 .
Then, using the standard R 1 transformation matrix for calculation, it can be obtained that
B = Y A 3 Y − 1 = − k 1 − k 2 − k 3 − k 4 − k 5 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 ,
where k 1 = a 55 + b 1 , k 2 = a 55 b 1 + b 2 , k 3 = a 55 b 2 + b 3 , k 4 = a 55 b 3 + b 4 , k 5 = a 55 b 4 . Then (9) can be written in this form below:
( Y J 4 J 3 J 2 J 1 ) G 2 ( Y J 4 J 3 J 2 J 1 ) T + ( Y J 4 J 3 J 2 J 1 ) A ( Y J 4 J 3 J 2 J 1 ) − 1 ( Y J 4 J 3 J 2 J 1 ) Σ ( Y J 4 J 3 J 2 J 1 ) T
+ ( Y J 4 J 3 J 2 J 1 ) Σ ( Y J 4 J 3 J 2 J 1 ) T [ ( Y J 4 J 3 J 2 J 1 ) A ( Y J 4 J 3 J 2 J 1 ) − 1 ] T = 0 ,
which can be expressed as
G 0 2 + B Σ 1 + Σ 1 B T = 0 ,
where Σ 1 = 1 ( a 15 a 32 q 1 ω 2 ) 2 θ 2 ( Y J 4 J 3 J 2 J 1 ) Σ ( Y J 4 J 3 J 2 J 1 ) T . Using the Lemma 3 in [35], Σ 1 may be stated as below:
Σ 1 = j 11 0 j 13 0 j 15 0 − j 13 0 − j 15 0 j 13 0 j 15 0 j 35 0 − j 15 0 − j 35 0 j 15 0 j 35 0 j 55 ,
where
j ^ = k 3 ( k 1 k 2 − k 3 ) − k 1 ( k 1 k 4 − k 5 ) , j ˜ = ( k 1 k 2 − k 3 ) ( k 3 k 4 − k 2 k 5 ) − ( k 1 k 4 − k 5 ) 2 ,
j 11 = k 2 ( k 3 k 4 − k 2 k 5 ) − k 4 ( k 1 k 4 − k 5 ) 2 j ˜ , j 13 = − k 3 k 4 − k 2 k 5 2 j ˜ , j 15 = k 1 k 4 − k 5 2 j ˜ ,
j 35 = − k 1 k 2 − k 3 2 j ˜ , j 55 = j ^ 2 k 5 j ˜ .
Using [35], the matrix Σ 1 is positive definite. It is possible to determine the precise expression of Σ , which is the positive definite matrix Σ = ( a 15 a 32 q 1 ω 2 ) 2 θ 2 ( Y J 4 J 3 J 2 J 1 ) − 1 Σ 1 [ ( Y J 4 J 3 J 2 J 1 ) − 1 ] T . This finishes the proof. □
Remark 2. 
According to Theorem 3, the solution ( S ( t ) , I ( t ) , T ( t ) , R ( t ) ) of the system (4) is known to obey the normal density function Φ ( S , I , T , R ) ∼ N ( ( S * , I * , T * , R * ) T , Σ ( 4 ) ) . Here, we define Σ ( 4 ) as the forth-order principal subform of Σ. As a result, S ( t ) , I ( t ) , T ( t ) and R ( t ) will have their respective convergence to the marginal density function:
Φ S ( s ) = 1 2 π φ 1 e − ( S − S * ) 2 2 φ 1 2 , Φ I ( i ) = 1 2 π φ 2 e − ( I − I * ) 2 2 φ 2 2 ,
Φ T ( t ) = 1 2 π φ 3 e − ( T − T * ) 2 2 φ 3 2 , Φ R ( r ) = 1 2 π φ 4 e − ( R − R * ) 2 2 φ 4 2 ,
where φ i 2 is the element in row i, column i on Σ. Namely, S ( t ) , I ( t ) , T ( t ) and R ( t ) will be convergent to the marginal distributions N ( S * , φ 1 2 ) , N ( I * , φ 2 2 ) , N ( T * , φ 3 2 ) and N ( R * , φ 4 2 ) , respectively.

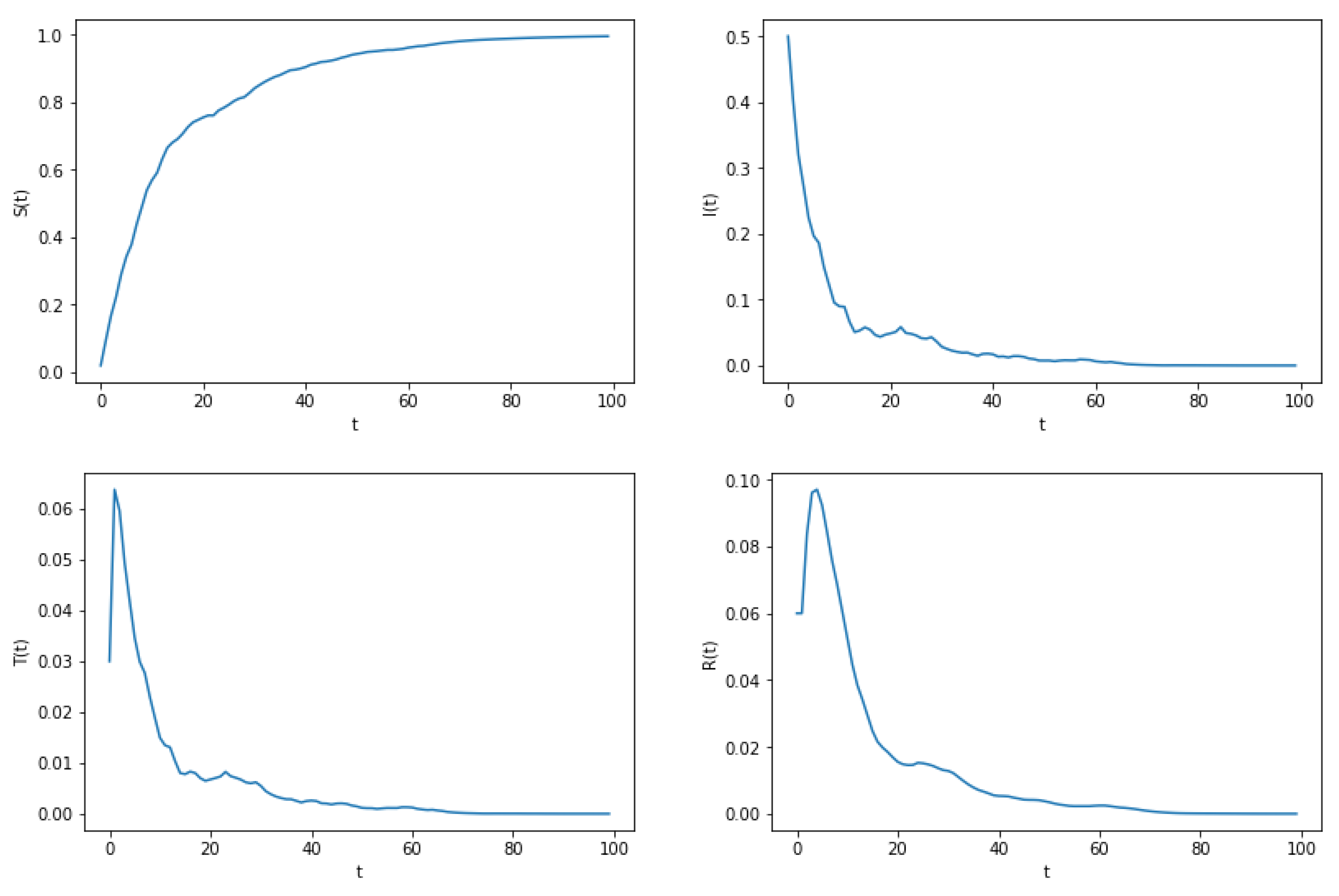
5. Extinction

This section provides the sufficient condition for cholera extinction.
Theorem 4. 
If R 0 E = R 0 + A θ π k ξ ( ξ + d + σ ) < 1 holds, then
lim t → ∞ sup ln I ( t ) t ≤ ( ξ + d + σ ) ( R 0 E − 1 ) < 0 a . s . .
That means that the contagiousness of the disease will vanish. Moreover,
lim t → ∞ S ( t ) = A ξ = S 0 , lim t → ∞ V ( t ) = 0 = V 0 , lim t → ∞ R ( t ) = 0 = R 0 .
Proof of Theorem 4. 
By making use of It o ^ ’s formula, we can calculate that
L H 2 = m S − ( ξ + d + σ ) + A β ξ + β ξ [ p γ σ ( ξ + p ) ( ξ + γ + g ) − ( ξ + d + σ ) ] I ≤ | m | A ξ − ( ξ + d + σ ) + A β ξ = | m | A ξ + ( ξ + d + σ ) ( R 0 − 1 ) .
Integrate the two sides of (10) separately, then divide by t to generate:
H 2 ( t ) t − H 2 ( 0 ) t ≤ ( ξ + d + σ ) ( R 0 − 1 ) + 1 t ∫ 0 t A ξ | m ( δ ) | d δ .
Then, using (3) and taking the limit, the following result can be obtained:
lim t → ∞ sup ln I ( t ) t ≤ lim t → ∞ sup ( H 2 ( t ) t − H 2 ( 0 ) t ) ≤ ( ξ + d + σ ) ( R 0 − 1 ) + lim t → ∞ 1 t ∫ 0 t A ξ | m ( δ ) | d δ = ( ξ + d + σ ) ( R 0 + A θ π k ξ ( ξ + d + σ ) − 1 ) < 0 ,
which indicates
lim t → ∞ I ( t ) = 0 a . s . .
Using (12),
d T = [ − ( ξ + γ + g ) T ] d t ,
can be determined from the third equation of the system (4), so that
lim t → ∞ T ( t ) = 0 , a . s . .
The same reasoning leads to
lim t → ∞ R ( t ) = 0 , lim t → ∞ S ( t ) = A ξ , a . s .
The argument for this theory is done. □
Remark 3. 
Observing that the expression for R 0 E can be easily extrapolated from R 0 E < 1 to R 0 < 1 , which means that the condition that makes the disease extinct in both deterministic and stochastic systems can be uniformly expressed as R 0 E < 1 . Similarly, the fact that it can be inferred from R 0 S > 1 to R 0 > 1 implies that R 0 S > 1 can be thought of as a uniform threshold which allows the disease to be prevalent in both deterministic and stochastic systems.

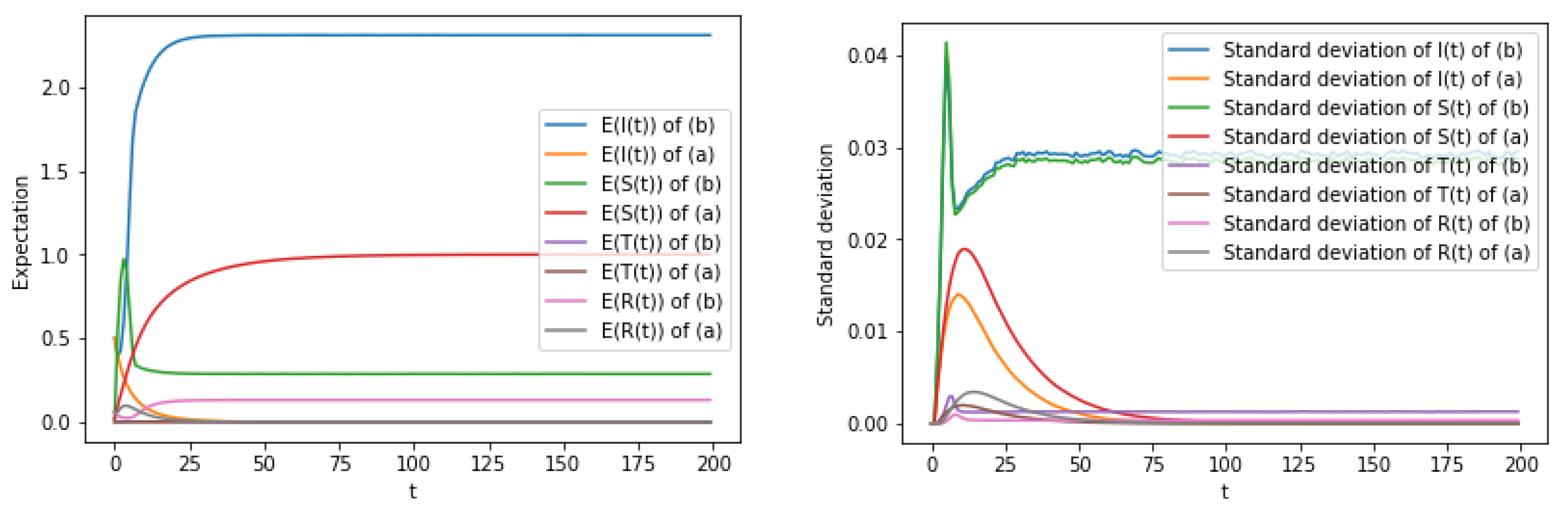
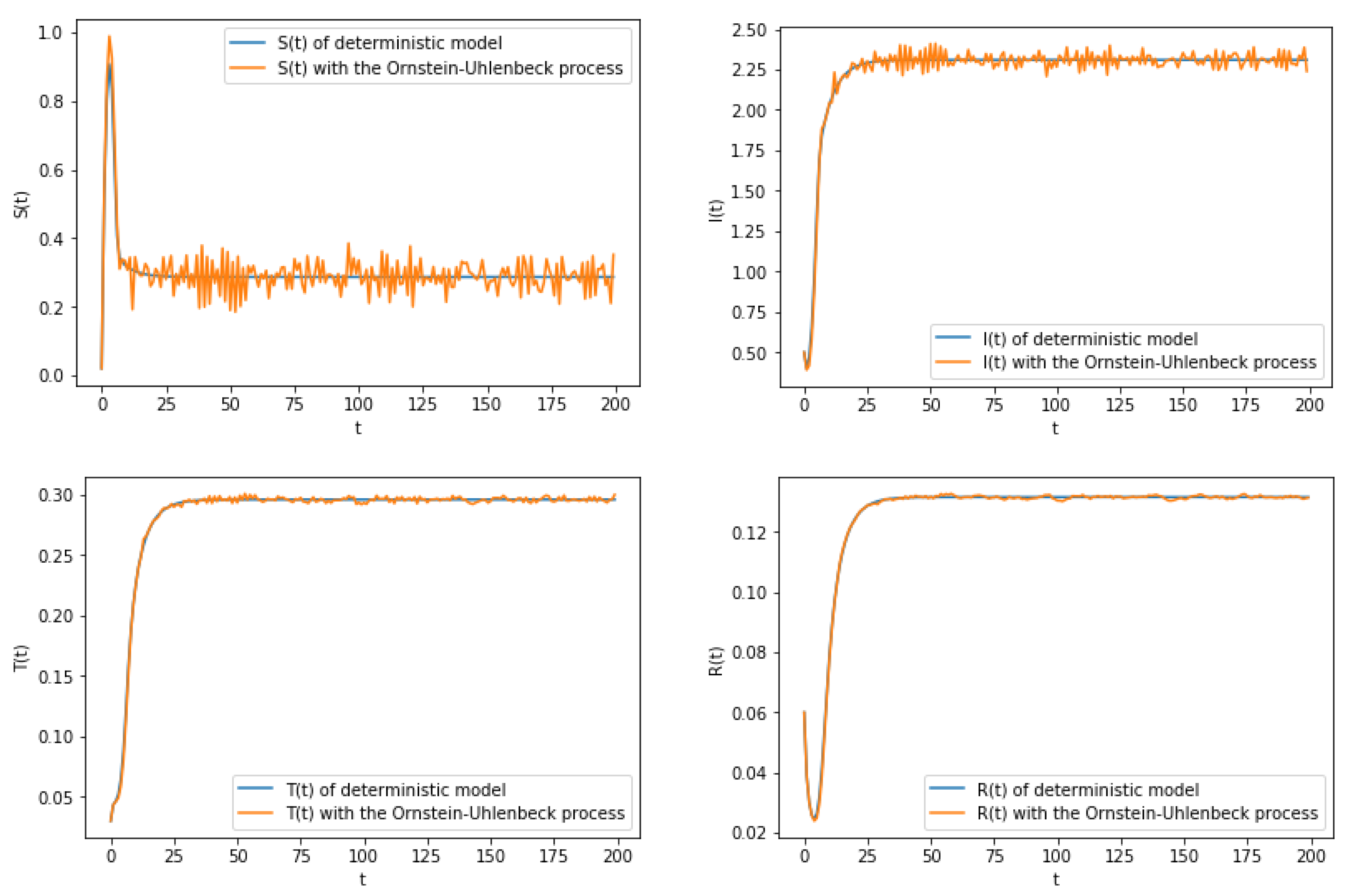
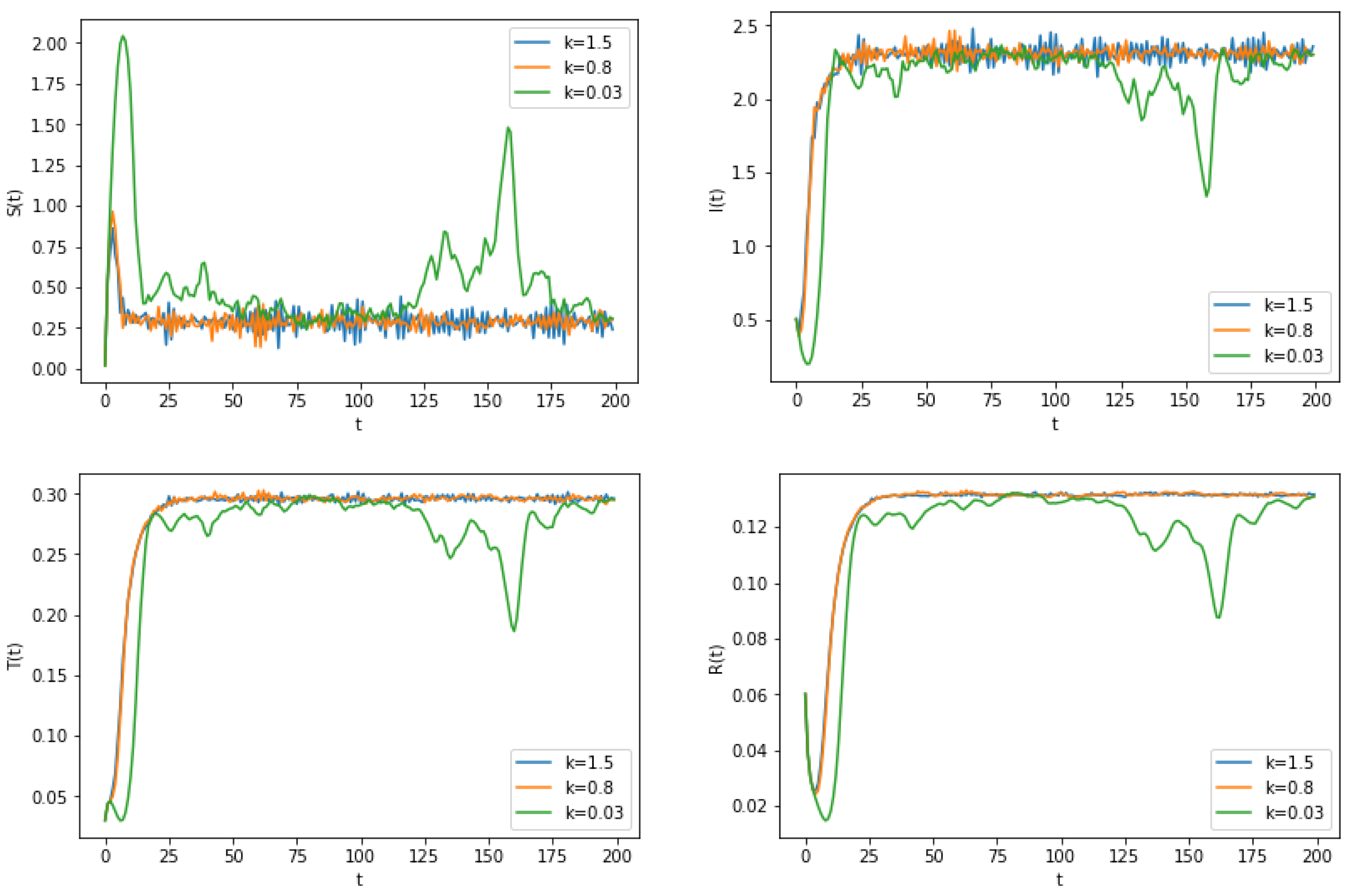
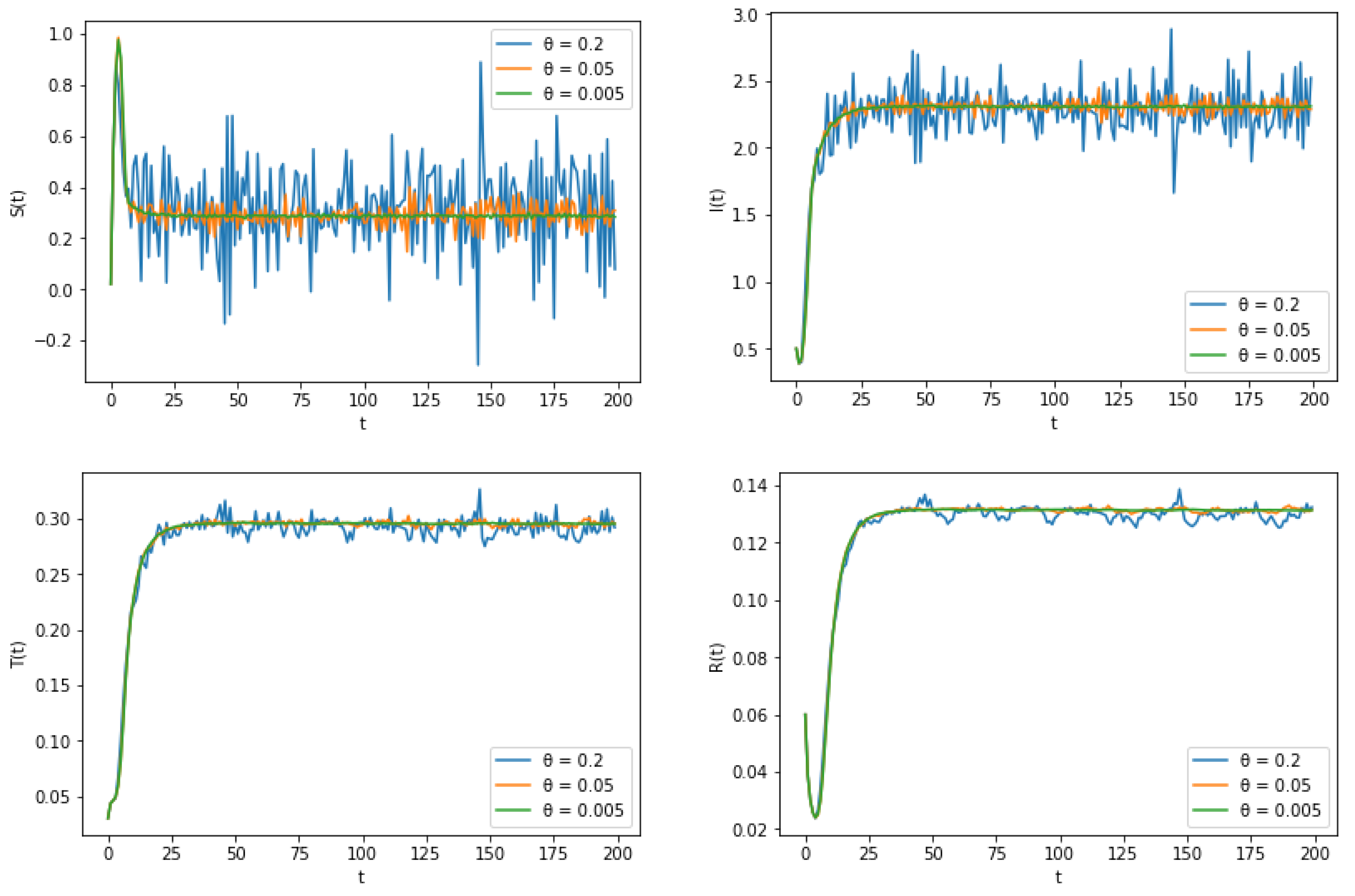
6. Numerical Simulation

In order to verify the correctness of the above proof, numerical simulation results are provided in this section. To begin with, we chose to simulate the model numerically using the Milstein method. Some of these parameter values are selected from [8,9,10,11,12,13]. We then discretize the model (5) to obtain the following corresponding discretized model:
S i + 1 = S i + [ A − ( β + m i ) S i I i − ξ S i + p R i ] Δ t , I i + 1 = I i + [ ( β + m i ) S i I i − ( ξ + d + σ ) I i ] Δ t , T i + 1 = T i + [ σ I i − ( ξ + γ + g ) T i ] Δ t , R i + 1 = R i + [ γ T i − ( ξ + p ) R i ] Δ t , m i + 1 = m i − k m i Δ t + θ h i Δ t + θ 2 2 ( h i 2 − 1 ) Δ t .
Example 6.1 Assume the parameters A = 0.5 , β = 0.75 , ξ = 0.15 , p = 0.3 , d = 0.015 , σ = 0.05 , γ = 0.2 , g = 0.04 , k = 0.8 , θ = 0.05 and the starting points in the below examples are all ( S ( 0 ) , I ( 0 ) , T ( 0 ) , R ( 0 ) , m ( 0 ) ) = ( 0.02 , 0.5 , 0.03 , 0.06 , − 0.9 ) . Note that R 0 S ≈ 11.1389 > 1 satisfies the requirement of Theorem 3.1. Intuitively, it can be seen that the values of the histogram revolve around P * = ( S * , I * , T * , R * ) ≈ ( 0.286667 , 2.309177 , 0.296048 , 0.131577 ) of the deterministic model. The solution ( S ( t ) , I ( t ) , T ( t ) , R ( t ) , m ( t ) ) of system (4) obeys the normal density function Φ ( S , I , T , R , m ) ∼ N ( ( 0.28667 , 2.30918 , 0.29605 , 0.13158 , 0 ) T , Σ ) . The matrix Σ is represented as:
Σ = 1 × 10 − 4 10.197829 − 9.762230 − 0.177322 − 0.082040 − 39.042279 − 9.762230 9.360669 0.160540 0.076008 37.471400 − 0.177322 0.160540 0.009003 0.002716 0.589101 − 0.082040 0.076008 0.002716 0.001207 0.317093 − 39.042279 37.471400 0.589101 0.317093 156.363696 .
From this, the following four marginal density functions are derived
Φ S ( s ) = 1 2 π φ 1 e − ( S − S * ) 2 2 φ 1 2 = 12.492697 e − 490.300445 ( S − 0.286667 ) 2 ,
Φ I ( i ) = 1 2 π φ 2 e − ( I − I * ) 2 2 φ 2 2 = 13.039370 e − 534.149840 ( I − 2.309177 ) 2 ,
Φ T ( t ) = 1 2 π φ 3 e − ( T − T * ) 2 2 φ 3 2 = 420.457136 e − 555383.953048 ( T − 0.296048 ) 2 ,
Φ R ( r ) = 1 2 π φ 4 e − ( R − R * ) 2 2 φ 4 2 = 1148.231844 e − 4141990.007581 ( R − 0.131577 ) 2 .
Preprints 108337 g001
Figure 1. The histogram and marginal density function of model (4). Parameter values: ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.8 , 0.05 ) .
Figure 1. The histogram and marginal density function of model (4). Parameter values: ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.8 , 0.05 ) .
Preprints 108337 g001
Example 6.2 Assume the parameters A = 0.05 , β = 0.09 , ξ = 0.05 , p = 0.3 , d = 0.015 , σ = 0.115 , γ = 0.7 , g = 0.04 , k = 0.8 , θ = 0.14 . At this point, R 0 E ≈ 0.9906 < 1 makes Theorem 4 hold. We have shown in Figure 2 that I ( t ) converges to 0 in an exponential manner with probability 1.
Example 6.3 Assume that the parameter values in group (a) are the values taken in Example 6.2, and the parameter values in group (b) are the values taken in Example 6.1. Through 10000 random simulations, Figure 3 shows the expectations and standard deviations of S ( t ) , I ( t ) T ( t ) and R ( t ) . This indicates that the disease will gradually disappear in situation (a), while in situation (b), the disease has grown into an epidemic.
Example 6.4 Consider the corresponding discretized deterministic SITRS model
S i + 1 = S i + [ A − β S i I i − ξ S i + p R i ] Δ t , I i + 1 = I i + [ β S i I i − ( ξ + d + σ ) I i ] Δ t , T i + 1 = T i + [ σ I i − ( ξ + γ + g ) T i ] Δ t , R i + 1 = R i + [ γ T i − ( ξ + p ) R i ] Δ t .
Assuming these parameters use the same values as in Example 6.1. Substitute the mean-reverting process to the model (1) and transform it to the stochastic SITRS model. Figure 4 shows that the model incorporating the mean-reverting process fluctuates around the deterministic model.
Example 6.5 To study the impact of regression rate k on disease progression, maintain the other parameter values selected from Example 6.1 and select different regression rates k. Figure 5 illustrates that as the regression speed k increases, the fluctuation of the disease decreases.
Example 6.6 With the aim of exploring the role of fluctuation intensity θ in disease progression, maintain the other parameter values selected from Example 6.1 and select different regression rates θ . Figure 6 reveals that the disease fluctuates more with an increasing intensity of fluctuation θ .

7. Conclusion

Cholera outbreaks have been frequent in recent years and the situation is critical. This shows that our knowledge of cholera is still inadequate, that the means of prevention and control are not perfect, and that the dynamics of the spread of the epidemic are very complex. In this work, we highlight the stochastic SITRS cholera epidemic model with an Ornstein-Uhlenbeck process. In general, existing literature always uses white noise to model fluctuations in the environment. However, on this basis, we adopt a new way of introducing random disturbances in the system, namely the Ornstein-Uhlenbeck process. To assure that the system (4) is mathematically and biologically justifiable, we prove that the system has a global solution. We then delve into the dynamics of the system (4). More specifically, the results of the analyses in this paper are shown below:
(1) In the presence of disease persistence, it is shown that the system (4) has an ergodic stationary distribution when R 0 S = R 0 − A θ π k ξ ( ξ + d + σ ) > 1 .
(2) Using the help of solving the relevant five-dimensional Fokker-Planck equation, we develop an exact expression for the probability density function of the model (4) near the quasi-local equilibrium.
(3) When R 0 E = R 0 + A θ π k ξ ( ξ + d + σ ) < 1 , the disease tends exponentially to extinction.
(4) Numerically, we also find a meaningful conclusion: smaller regression rates or larger fluctuation intensities make the stochastic system more volatile.
However, there are still many important topics that deserve further research. Firstly, due to the limitations of existing methods, the thresholds for disease extinction and prevalence have not been harmonised. Therefore, the identification of uniform thresholds for disease extinction and prevalence deserves further exploration. Secondly, in this paper we have only analysed the kinetic behaviour of stochastic SITRS models with treatment compartments. One could build more realistic and important models, for example, studying cholera infectious disease models with more compartments and the effect of a mean-reverting process perturbing other parameters on the dynamics of cholera epidemics transmission.

Author Contributions

Writing—review and editing, S. L.; writing—original draft and funding acquisition W. L. All authors read and agreed to the published version of the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China Tianyuan Mathematical Foundation (No. 12126312, No. 12126328). The authors gratefully acknowledge the Natural Science Foundation of Heilongjiang Province (No. LH2022E023), Heilongjiang Provincial Postdoctoral Science Foundation (LBH-Z23259) and the Northeast Petroleum University Special Research Team Project (No. 2022TSTD-05) for the support in publishing this paper.

Data Availability Statement

Some of these parameter values are selected from [8,9,10,11,12,13].

Acknowledgments

Thanks to the reviewers for their helpful comments and suggestions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ma, Z.; Zhou, Y.; Wu, J. Modeling and Dynamics of Infectious Diseases.; 1st ed.; Higher Education Press: Beijing, 2009; pp. 1–35. [Google Scholar]
  2. Cai, Y.; Kang, Y.; Banerjee, M.; Wang, W. A stochastic epidemic model incorporating media coverage. Commun. Math. Sci. 2016, 14, 893–910. [Google Scholar] [CrossRef]
  3. World Health Organization (WHO), Cholera-Global situation. Available online: https://www.who.int/emergencies/disease-outbreak-news/item/2023-DON437 (accessed on 11 February 2023).
  4. Beryl, M. O.; George, L. O.; Fredrick, N. O. Mathematical analysis of a cholera transmission model incorporating media coverage. Int. J. Pure. Appl. Math. 2016, 111, 219–231. [Google Scholar] [CrossRef]
  5. Fatima, S.; Krishnarajah, I.; Jaffar, M. Z. A. M.; Adam, M. B. A mathematical model for the control of cholera in Nigeria. Res. J. Environ. Earth Sci. 2014, 6, 321–325. [Google Scholar] [CrossRef]
  6. Nelson, E. J.; Harris, J. B.; Glenn M., J.; Galderwood, S. B.; Camilli, A. Cholera transmission: the host, pathogen and bacteriophage dynamic. Nat. Rev. Microbiol. 2009, 7, 693–702. [Google Scholar] [CrossRef] [PubMed]
  7. Su, T.; Zhang, X. Stationary distribution and extinction of a stochastic generalized SEI epidemic model with Ornstein-Uhlenbeck process. Appl. Math. Lett. 2023, 143, 108690. [Google Scholar] [CrossRef]
  8. He, J.; Bai, Z. Global hopf bifurcation of a cholera model with media coverage. Math. Biosci. Eng. 2023, 20, 18468–18490. [Google Scholar] [CrossRef]
  9. Lemos-Paiao, A. P.; Silva, C. J.; Torres, D. F. M. A cholera mathematical model with vaccination and the biggest outbreak of world’s history. AIMS Mathematics 2018, 3, 448–463. [Google Scholar] [CrossRef]
  10. Zhou, X.; Shi, X.; Wei, M. Dynamical behavior and optimal control of a stochastic mathematical model for cholera. Chaos Solitons Fractals 2022, 156, 111854. [Google Scholar] [CrossRef]
  11. Hartley, D. M.; Jr, J. G. M.; Smith, D. L. Hyperinfectivity: A critical element in the ability of V. cholerae to cause epidemics? PLoS Med. 2005, 3, e7. [Google Scholar] [CrossRef]
  12. Lemos-Paiao, A. P.; silva, C. J.; Torres D. F., M. An epidemic model for cholera with optimal control treatment. J. Comput. Appl. Math. 2017, 318, 168–180. [Google Scholar] [CrossRef]
  13. Mwasa, A.; Tchuenche, J. M. Mathematical analysis of a cholera model with public health interventions. Biosystems 2011, 105, 190–200. [Google Scholar] [CrossRef] [PubMed]
  14. Wang, X.; Yang, J.; Han, Y. Threshold dynamics of a chronological age and infection age structured cholera model with Neumann boundary condition. Z. Angew. Math. Phys. 2023, 74, 170. [Google Scholar] [CrossRef]
  15. Jiang, T.; Wang, J. Modeling and analysis of a diffusive cholera model with seasonally forced intrinsic incubation period and bacterial hyperinfectivity. J. Math. Anal. Appl. 2023, 527, 127414. [Google Scholar] [CrossRef]
  16. Tilahun, G. T.; Woldegerima, W. A. Wondifraw, A. Stochastic and deterministic mathematical model of cholera disease dynamics with direct transmission. Adv. Differ. Equ. 2020, 2020, 670. [Google Scholar] [CrossRef]
  17. Zhou, Y.; Jiang, D. Dynamical behavior of a stochastic SIQR epidemic model with Ornstein-Uhlenbeck process and standard incidence rate after dimensionality reduction. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106878. [Google Scholar] [CrossRef]
  18. Zhang, X.; Zhang, X. Threshold behaviors and density function of a stochastic parasite-host epidemic model with Ornstein–Uhlenbeck process. Appl. Math. Lett. 2024, 153, 109079. [Google Scholar] [CrossRef]
  19. Bao, K.; Rong, L.; Zhang, Q. Analysis of a stochastic SIRS model with interval parameters. Discrete Contin. Dyn. Syst. Ser. B 2019, 24, 4827–4849. [Google Scholar] [CrossRef]
  20. Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A. Dynamical behavior of a stochastic epidemic model for cholera. J. Franklin Inst. 2019, 356, 7486–7514. [Google Scholar] [CrossRef]
  21. Zaho, Y.; Lin, Y.; Jiang, D.; Mao, X.; Li, Y. Stationary distribution of stochastic SIRS epidemic model with standard incidence. Discrete Contin. Dyn. Syst. Ser. B 2016, 21, 2363–2378. [Google Scholar] [CrossRef]
  22. Zhang, X.; Yuan, R. A stochastic chemostat model with mean-reverting Ornstein-Uhlenbeck process and Monod-Haldane response function. Appl. Math. Comput. 2021, 394, 125833. [Google Scholar] [CrossRef]
  23. Allen, E. ; Environmental variability and mean-reverting processes. Discrete Contin. Dyn. Syst. Ser. B 2016, 21, 2073–2089. [Google Scholar] [CrossRef]
  24. Zhou, B.; Zhang, X.; Jiang, D.; Dai, Y. Dynamics and density function analysis of a stochastic SVI epidemic model with half saturated incidence rate. Chaos Solitons Fractals 2020, 137, 109865. [Google Scholar] [CrossRef]
  25. Alshammari, F. S.; Akyildiz, F. T. Epidemic waves in a stochastic SIRVI epidemic model incorporating the Ornstein-Uhlenbeck process. Mathematics 2023, 11, 3876. [Google Scholar] [CrossRef]
  26. Zhou, B.; Jiang, D.; Hayat, T. Analysis of a stochastic population model with mean-reverting Ornstein-Uhlenbeck process and Allee effects. Commun. Nonlinear Sci. Numer. Simul. 2022, 111, 106450. [Google Scholar] [CrossRef]
  27. Wu, S.; Yuan, S.; Lan, G.; Zhang, T. Understanding the dynamics of hepatitis B transmission: A stochastic model with vaccination and Ornstein-Uhlenbeck process. Appl. Math. Comput. 2024, 476, 128766. [Google Scholar] [CrossRef]
  28. Zhou, B.; Jiang, D.; Han, B.; Hayat, T. Threshold dynamics and density function of a stochastic epidemic model with media coverage and mean-reverting Ornstein–Uhlenbeck process. Math. Comput. Simul. 2022, 196, 15–44. [Google Scholar] [CrossRef]
  29. Liu, Q. ; A stochastic predator-prey model with two competitive preys and Ornstein-Uhlenbeck process. J. Biol. Dyn. 2023, 17, 2193211. [Google Scholar] [CrossRef] [PubMed]
  30. Zhang, Z.; Liang, G.; Chang, K. Stationary distribution of a reaction-diffusion hepatitis B virus infection model driven by the Ornstein-Uhlenbeck process. PLoS One 2023, 18, e0292073. [Google Scholar] [CrossRef] [PubMed]
  31. Mao, X. Stochastic Differential Equations and Applications 2nd ed.; Horwood, Chichester, UK, 2008; pp. 149-155.
  32. Khasminskii, R. Stochastic Stability of Differential Equations 2nd ed.; Springer-Verlag, Berlin Heidelberg, 2012; pp. 59-93.
  33. Meyn, S. P.; Tweedie, R. L. Stability of Markovian processes III: Foster-Lyapunov criteria for continuous-time processes. Adv. Appl. Probab. 1993, 25, 518–548. [Google Scholar] [CrossRef]
  34. Roozen, H. An asymptotic solution to a two-dimensional exit problem arising in population dynamics. SIAM J. Appl. Math. 1989, 49, 1793–1810. [Google Scholar] [CrossRef]
  35. Zhang, X.; Su, T. Jiang, D. Dynamics of a stochastic SVEIR epidemic model incorporating general incidence rate and Ornstein-Uhlenbeck process. J. Nonlinear Sci. 2023, 33, 76. [Google Scholar] [CrossRef]
Preprints 108337 g002
Figure 2. The trajectory of S ( t ) , I ( t ) , T ( t ) and R ( t ) in model (4) during disease extinction. Parameter values: ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.05 , 0.09 , 0.05 , 0.3 , 0.015 , 0.115 , 0.7 , 0.04 , 0.8 , 0.14 ) .
Figure 2. The trajectory of S ( t ) , I ( t ) , T ( t ) and R ( t ) in model (4) during disease extinction. Parameter values: ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.05 , 0.09 , 0.05 , 0.3 , 0.015 , 0.115 , 0.7 , 0.04 , 0.8 , 0.14 ) .
Preprints 108337 g002
Preprints 108337 g003
Figure 3. Computer simulations for expectation and standard deviation of the model (4). Parameter values: ( a ) : ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.05 , 0.09 , 0.05 , 0.3 , 0.015 , 0.115 , 0.7 , 0.04 , 0.8 , 0.14 ) , ( b ) : ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.8 , 0.05 ) .
Figure 3. Computer simulations for expectation and standard deviation of the model (4). Parameter values: ( a ) : ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.05 , 0.09 , 0.05 , 0.3 , 0.015 , 0.115 , 0.7 , 0.04 , 0.8 , 0.14 ) , ( b ) : ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.8 , 0.05 ) .
Preprints 108337 g003
Preprints 108337 g004
Figure 4. The trajectory of S ( t ) , I ( t ) , T ( t ) and R ( t ) of the stochastic model (4) with the mean-reverting process and deterministic model (1). Parameter values: ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.8 , 0.05 ) .
Figure 4. The trajectory of S ( t ) , I ( t ) , T ( t ) and R ( t ) of the stochastic model (4) with the mean-reverting process and deterministic model (1). Parameter values: ( A , β , ξ , p , d , σ , γ , g , k , θ ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.8 , 0.05 ) .
Preprints 108337 g004
Preprints 108337 g005
Figure 5. The trajectory of S ( t ) , I ( t ) , T ( t ) , R ( t ) for models (4) with different regression rates k. Parameter Values: ( A , β , ξ , p , d , σ , γ , g , θ ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.05 ) .
Figure 5. The trajectory of S ( t ) , I ( t ) , T ( t ) , R ( t ) for models (4) with different regression rates k. Parameter Values: ( A , β , ξ , p , d , σ , γ , g , θ ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.05 ) .
Preprints 108337 g005
Preprints 108337 g006
Figure 6. The trajectory of S ( t ) , I ( t ) , T ( t ) , R ( t ) for models (4) with different regression rates θ . Parameter Values: ( A , β , ξ , p , d , σ , γ , g , k ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.8 ) .
Figure 6. The trajectory of S ( t ) , I ( t ) , T ( t ) , R ( t ) for models (4) with different regression rates θ . Parameter Values: ( A , β , ξ , p , d , σ , γ , g , k ) = ( 0.5 , 0.75 , 0.15 , 0.3 , 0.015 , 0.05 , 0.2 , 0.04 , 0.8 ) .
Preprints 108337 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated