Prerpints.org logo
Preprint
Article

God’s Certainty-Uncertainty Principle versus Heisenberg’s Uncertainty Principle: A Possible Path to Unification of Gravity and Quantum Mechanics

Altmetrics

Downloads

227

Views

165

Comments

0

This version is not peer-reviewed

Submitted:

18 September 2024

Posted:

19 September 2024

You are already at the latest version

Alerts
Abstract
Einstein was skeptical of part of quantum mechanics, and he believed that Heisenberg’s uncertainty principle did not reflected the full depth of reality. He famously stated, ”God does not play dice with the universe.” However, since quantum mechanics has passed so many experimental tests, most physicists today assume that Einstein was wrong. Nevertheless, we will demonstrate that Heisenberg’s uncertainty principle must be modified to unify gravity with quantum mechanics. This modification leads to the Certainty-Uncertainty principle where the certainty part is strongly linked to gravity. This means Einstein likely was right in his intuition also on this point. The key is to understand that the de Broglie wavelength is not the actual wavelength of matter but merely a derivative of the true matter wavelength, namely the Compton wavelength. Furthermore, one must understand that the gravitational constant, first introduced in 1873, is simply a composite constant needed to rectify the incomplete definition of kilogram mass introduced into Newtonian gravity in 1873.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Two Steps in the Wrong Direction Seems to Be the Reason Gravity and Quantum Mechanics Not Was Unified Until Now

Einstein [1] already in 1916 in one of his most famous general relativity papers suggested that the next step in gravity would be quantum gravity or in his own words:
Because of the intra-atomic movement of electrons, the atom must radiate not only electromagnetic but also gravitational energy, if only in minute amounts. Since, in reality, this cannot be the case in nature, then it appears that the quantum theory must modify not only Maxwell’s electrodynamics but also the new theory of gravitation. —A. Einstein
It is important to remember that when Einstein discussed how a quantum theory must lead to a new quantum gravity theory, it was years before the development of key concepts in today’s quantum mechanics, such as Heisenberg’s uncertainty principle. It is often forgotten that Einstein was one of the first to be part of developing quantum theory. Einstein in 1905 proposed that light is also propagated and absorbed in quanta, today called photons. These photons came with energy according to the Planck–Einstein relation:  E = h f = h c λ . This was experimentally confirmed already in 1912 by Richardson and Compton [2] (the brother of Arthur Compton that we soon will come to).
Einstein was actually very skeptical of certain aspects of the developments in quantum mechanics that occurred in the 1920s. Therefore, unifying gravity with quantum mechanics could clearly involve modifying quantum mechanics. Einstein spent much of his remaining life trying to develop a new theory of gravity that could unify it with quantum theory, but he had very limited success. Many of the most brilliant physicists and mathematicians have been working on this unification for over a century with little success. If developing a unified theory of quantum gravity and quantum mechanics were simply a matter of solving or formulating some very complex equations, it likely would have already been accomplished and borne fruit.
Indeed, there have been multiple interesting ideas and models, such as Superstring Theory [3] and Loop Quantum Gravity (LQG) [4]. However, after they have been explored for many years they do not seem very promising; some even consider them failed theories, while others continue to work on them, hoping they will ultimately provide the answer, see [5,6,7].
Given the extensive efforts by numerous brilliant minds to unify gravity with quantum mechanics and other aspects of physics, it’s worth considering the possibility that the scientific community may have taken the wrong path at certain junctures in the history of physics. A thorough examination of the history of physics reveals several instances where crucial decisions led to the exploration of one path while leaving others unexplored or underexplored. We believe we have identified two such points where the physics community veered off course, resulting in unnecessary complexity and hindering efforts to unify gravity with quantum mechanics. By revisiting these junctures and exploring the alternative paths, along with deriving further insights from them, we are led to a remarkably simple and overlooked approach to unify gravity with quantum mechanics.
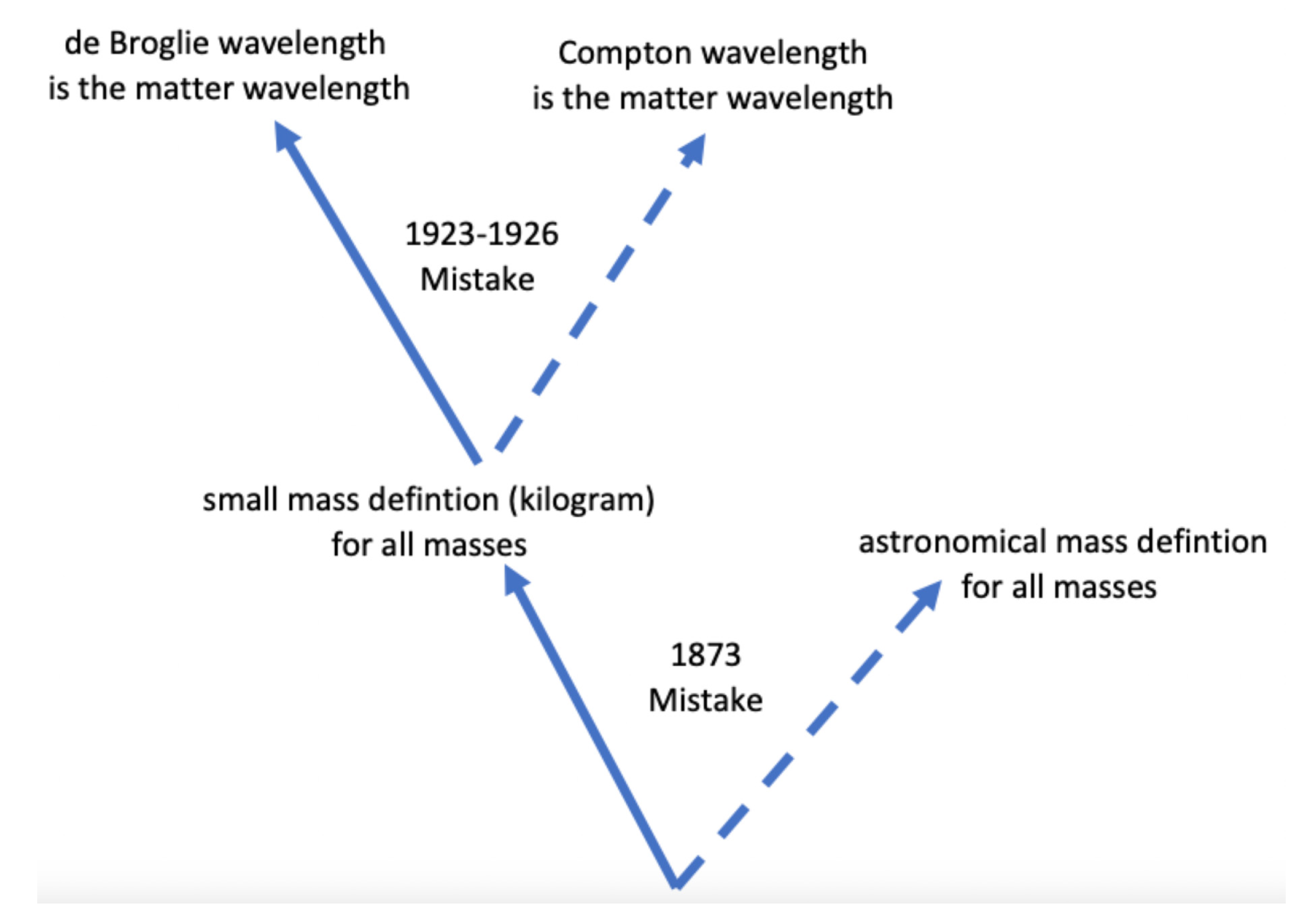
The first step in the wrong direction occurred in 1873 when the gravitational constant was introduced essentially ad hoc to make Newton’s formula work when the kilogram mass was used in gravitational equations. We will discuss this further in Section 5. In short, Newton had never introduced nor attempted to introduce what is known today as Newton’s gravitational constant. His formula was F = M n m n r 2 , which worked just as well as the modern formula F = G M m r 2 . The key question is: what does the gravitational constant then truly represent?
The second step in the wrong direction happened around 1923 to 1924 when it was assumed that the de Broglie wavelength was the matter wavelength, instead of the Compton wavelength. This topic will be explored in the next section. Figure 1 illustrates these two missteps, which have made it almost impossible to unify gravity with quantum mechanics. Understanding that the Compton wavelength is the true matter wavelength, and comprehending why the gravitational constant was needed and what it truly represents, are crucial steps forward.

2. Short Bacground on Some of the Challanges in Quantum Gravity Theory

Kiefer [7] has written an interesting paper titled "Quantum Gravity – An Unfinished Revolution," where he discusses some of the main unsolved problems in quantum gravity theory. First, he mentions that quantum gravity is not used in a concise way. We believe the reason for this is that little progress has been made in quantum gravity theory and that there are considerably different opinions on how to approach solving it. Kiefer then attempts to define it as: "We call quantum gravity any theory (or approach) in which the superposition principle is applied to the gravitational field." He and others take quantum mechanics as a given and mainly assume that gravity has to be modified to fit quantum mechanics.
Our view is different; we argue that gravity is related to the Planck scale and that uncertainty breaks down at this scale. There is no superposition at the Planck scale, so quantum gravity, in our view, is not about applying the superposition principle to the gravitational field, but rather understanding that the superposition principle and several other quantum interpretations break down at the Planck scale. The Planck mass particle is only in one state when observed, and we only observe it indirectly as gravity. However, we can also observe the Planck mass (gravity particle) indirectly in a way we will describe later in this paper.
Kiefer also points out that "Einstein’s theory, by itself, is incomplete" due to singularities. One can prove singularity theorems, which state that, given some assumptions, there are regions in spacetime where the theory breaks down. In particular, time zero, or the beginning of the universe, and the center of a black hole are such singularities where general relativity gives singularities. Yet another problem that Kiefer points out is "that quantum field theories are plagued by divergences which arise from probing spacetime at arbitrarily small scales," something that is typically handled by regularization and renormalization. Feynman called this:
The shell game that we play to find n and j is technically called renormalization. But no matter how clever the word, it is what I would call a dippy process!
We will argue that it is possible to build a quantum gravity theory that does not require incorporating superposition and entanglement, as these concepts break down and become irrelevant at the Planck scale. Furthermore, we propose that gravity is directly linked to what happens at the Planck scale. We will also explore how to avoid singularities in our new quantum gravity theory and how we can prevent infinite energies when probing spacetime at small scales. This is because the scale is limited to the Planck scale, which is again linked to gravity and a modification of Heisenberg’s uncertainty principle.
Related issues include whether our new quantum gravity theory can be described by Hilbert space, or if this is even necessary, a topic we will also discuss.
Einstein’s insight was to recognize that gravity can be represented by the geometry of space and time as unified into a four-dimensional entity called spacetime.
Our method to quantize gravity can be applied to a series of gravity theories: Newton’s theory, general relativity, relativistic modified Newtonian theory, and a new theory called collision spacetime. It seems we may need to move to a six-dimensional spacetime theory to fully eliminate singularities in gravity and transition from the non-conservation of spacetime to the conservation of spacetime. We will argue that this transition is necessary to be consistent with the conservation of energy. This paper is meant more as a way to open up new discussions around these suggested ideas than to provide definitive conclusions.

3. De Broglie Wavelength versus Compton Wavelength

Modern physics and quantum mechanics assume the de Broglie wavelength is the real matter wavelength. It was already known that light had particle-wave duality, so de Broglie [8] in his 1924 breakthrough PhD thesis suggested that matter also had to have wave properties in addition to particle properties. In addition, de Broglie in the same thesis presents the following formula for this matter wavelength, which today is known as the de Broglie wavelength:
λ b = h m v
The formula above is actually a good approximation when v ≪ c . Broglie [9] extended it also for relativistic effects and gave the formula
λ b = h m v γ
Davisson and Germer [10], in 1927, published their paper on Diffraction of Electrons, which experimentally strongly supported the idea that matter also had wave properties. The de Broglie hypothesis was therefore quickly accepted and praised after this experiment. However, one had not measured the de Broglie wavelength as predicted by the formulas above, just that the matter had wavelike properties. We will not question that matter has wavelike properties in addition to particle properties as this is fully in line also with out view. What we will question is if the mathematical de Broglie wavelength is the real matter wavelength. From the de Broglie matter wavelength formulas, we can clearly see that the formula cannot be valid for v = 0 , as this means division by zero, which is not allowed in mathematics. Further, even when v is just very close to zero, then the de Broglie wavelength for even an electron can become longer than the radius of the Hubble sphere. In our view, this is simply absurd. Proponents and specialists in quantum mechanics will defend that the de Broglie wavelength formula is not valid for v = 0 with the claim that the Heisenberg [11] uncertainty principle forbids particles to be fully at rest, so then the case of v = 0 is not relevant. They will even claim that the de Broglie wavelength going beyond the Hubble radius is avoided in this way as one has not been able to measure velocities as low as one needs to get this to happen.
However, we will claim that it is the Compton wavelength that is the real matter wavelength. Compton [12] in 1924 was describing what today is known as Compton scattering and based on this predicted what today is known as the Compton wavelength, given by:
λ c = h m c
Even if his theory was relativistic in the sense that he took into account that light moves at a speed of c when colliding with the electron, Compton still assumed that the electron when hit was standing still. So the Compton wavelength of the electron is related to the rest of the electron. The Compton wavelength has not only been discussed in relation to the electron, but the Compton wavelength of the proton has also been discussed, for example by Levitt [13] in 1958, who claimed the Compton wavelength of the proton was essential to understand the proton. In recent years, Bohr and Trinhammer [14] have indirectly pointed out that the current best estimates of the classical proton radius are exactly equal to four times the reduced Compton wavelength of the proton, R P = 4 λ ¯ c , P . We doubt this is a pure coincidence, even if that cannot be fully excluded.
Haug has shown in a series of publications that the Compton wavelength can be found for basically any mass without any knowledge of the Planck constant. The Compton wavelength for a mass larger than the Planck mass is shorter than the Planck length, so such a Compton wavelength can likely not exist physically. However, masses larger than the Planck mass, and many masses also smaller than the Planck mass, such as the Proton, are composite masses. The Compton wavelength of these masses is simply the aggregate of the Compton wavelength of their individual elementary particles, including photon-like elements as the photon wavelength of a rest mass particle is identical to the Compton wavelength. We have that the Compton wavelength of a composite mass must be given by:
m = ∑ i n m i ± ∑ j N E j c 2 h λ c 1 c = ∑ i = 1 n h λ c , i 1 c ± ∑ j = 1 N h c λ c , i c 2 λ c = 1 ∑ i = 1 n 1 λ c , i ± ∑ j = 1 N 1 λ c , j .
The reason for the plus-minus sign in front of energies is that the mass of composite particles can be both smaller than the mass of their composites due to binding energy released when the masses are bound. This formula holds for any composite mass as well as for any composite structure of photons, see also [15,16].
Unlike the de Broglie wavelength, the Compton wavelength is always valid, even when the particle is at rest. The Compton wavelength also does not become macroscopically large even if the velocity of the particle is small or at any velocity of the particle. The Compton wavelength always has a length we would associate with what simple logic would tell us about the lengths of the atomic and subatomic quantum world, that such a length simply has to be incredibly small. This again is in strong contrast to the de Broglie wavelength that, if we take the predictions from the de Broglie formula as given, can spread out on a macroscopic scale even for a single electron. Again, we will claim the latter is absurd.
As pointed out earlier, Compton derived his formula based on the assumption that the mass is at rest. Haug [17] has recently extended the work on Compton to derive a full relativistic Compton wavelength, also taking into account that the mass is initially moving. This simply leads to:
λ c = h m c γ
where γ = 1 / 1 − v 2 / c 2 . This means the de Broglie wavelength is always equal to the Compton wavelength times c v . However, again, we see the de Broglie wavelength is not defined for v = 0 while the Compton wavelength is.
We will conjecture that the de Broglie wavelength is not a real matter wavelength but, in reality, a pure mathematical derivative of the Compton wavelength. Further, we can summarize this section from a pure logical common-sense perspective that the Compton wavelength seems to make more sense than the de Broglie wavelength. Still, some will protest here as they will think this could not be the case, as the de Broglie wavelength and Compton wavelength have been studied so well that there cannot suddenly be a new and very different interpretation of the de Broglie wavelength. However, we will soon see that general relativity theory can easily be quantized if we rely on the Compton wavelength and not when relying on the de Broglie wavelength. Further, we will see how quantum mechanics needs to be reformulated or extended to achieve a nice and simple unification of gravity and quantum mechanics.

4. Domain Validity of Matter Wavelengths

Even if there is some repetition in this section from the previous section, we feel it is necessary to point out and precisely define the domain range of the de Broglie wavelength versus the Compton wavelength.
The de Broglie wavelength formula is not valid for v = 0 , and we have defined its valid domain for v below:
λ b = h m v γ = h p   when   0 < v < c
where p is the relativistic momentum p = m v γ that was first introduced by Max Planck [18] in 1906. And also, from λ b = λ c c v , we can see the de Broglie wavelength is not valid for v = 0 . This is very important, as a model that assumes the de Broglie wavelength is the real matter wavelength will not be able to model rest mass properly. Again, most physicists will think this is not needed due to the Heisenberg uncertainty principle that we will soon get back to. This means the valid domain for the de Broglie wavelength is 0 < v < c .
On the other hand, the Compton wavelength for a particle at rest is:
λ c = h m c   when   v = 0
and in the more general formula also taking into account v > 0 , we have:
λ c = h m c γ when 0 ≤ v < c
That is, the valid domain for the Compton wavelength is 0 ≤ v < c .
The relation between the de Broglie wavelength and the Compton wavelength is only valid where the domains of the two overlap. So we have:
λ b = λ c c v when 0 < v < c
and
λ c = λ b v c when 0 < v < c
In this latter equation, we do not encounter the problem of setting v = 0 directly. However, since the de Broglie wavelength is not valid for v = 0 , the domain for this equation is indeed 0 < v < c .
We can conclude that the Compton wavelength is valid in the full domain as the de Broglie wavelength and can likely be used to model all that the de Broglie wavelength can model related to what can be checked with real observations. However, the de Broglie wavelength cannot be used to model all that the Compton wavelength can predict, simply because the de Broglie wavelength cannot account for rest. As we will soon see, rest seems to play a central role in quantum gravity. Switching from the de Broglie wavelength as the matter wavelength to the Compton wavelength as the true matter wavelength can be mathematically seen as a form of domain stretching of existing concepts in quantum mechanics. As we will soon discuss, this likely has major implications and even seems to lead to the unification of gravity and quantum mechanics.

5. Quantization of Gravity and How It Is Linked to the Reduced Compton Frequency

Before delving into Heisenberg’s uncertainty principle and quantum mechanics, it’s worth noting a relatively new approach to quantize both Newton’s gravitational theory and Einstein’s general relativity, as well as other gravity theories. We’ll discover that gravity, when understood at a deeper level, is rooted in the reduced Compton frequency over the Planck time. This leads to the quantization of gravity and establishes a connection to the Planck scale, essentially forming a quantum gravity theory. We’ll also explore how this theory can be seamlessly unified with quantum mechanics. However, before that, we need to make slight modifications to quantum mechanics.
Newton introduced his gravity theory in 1686 [19]. It’s essential to recognize that his original gravitational force formula was:
F = M n m n r 2
Newton only expressed his formulas in words, but this was clearly the formula he stated. We use the symbols for mass M n and m n because Newton had a quite different view on mass compared to modern gravitational physics. Newton said mass was the quantity of matter and mentioned that matter consisted of indivisible particles. Newton also referred to indivisible time interval (see [20]).
Newton’s original gravity formula and its derivations were successfully used to predict phenomena such as the orbital velocity of moons and planets, and the relative size of planets, for several hundred years and still hold to this day [21,22]. In 1784, Michell [23] used Newton’s theory to calculate the radius of a gravitational object with a field so strong that not even light could escape. This radius was identical to today’s Schwarzschild radius. Again, Michell stated his calculations in words, but they led to a radius of r = 2 M n c 2 , which in modern notation would be r = 2 G M c 2 , indeed identical to the Schwarzschild radius [24].
Michell was the first to design an apparatus that could measure the gravitational field from a small macroscopic object on Earth. However, Michell died before he could build and use it. Cavendish [25] accomplished this task and published his work in 1798, where he measured the density of the Earth relative to a macroscopic object on Earth with known density. A series of books and papers incorrectly claim that Cavendish measured Newton’s gravitational constant. This is not true. Cavendish did not know about any gravitational constant nor tried to measure it, as pointed out by multiple researchers that carefully have studied this in detail: [26,27].
Maxwell [28] used the original Newton formula as late as early 1873. For example, he described gravitational acceleration as simply M n r 2 , and it was not because he had set any gravitational constant to one; rather, the mass definition itself, as he explained, was very different than the kilogram mass. At that time, there were two different mass standards. For small, manageable masses, one used kilograms in France and pounds in Great Britain. For astronomical masses, one used the Newtonian mass, which had dimensions of length cubed divided by time squared: [ L 3 · T − 2 ] . For a considerable time, researchers had wished to unify the mass units used for astronomical masses and small masses. They ended up choosing the kilogram. When switching to the kilogram, Newton’s original gravitational force formula and formulas derived from it would no longer work. To fix this, a constant had to be introduced.
So first, in 1873, Cornu and Baille [29] changed Newton’s gravitational force formula to F = f M m r 2 , where M and m were now masses in kilograms, and the gravity constant was f. In 1894, Boys [30] changed the symbol of the gravity constant to G. Einstein, however, used the symbol k. Naturally, the symbol used for the constant is purely cosmetic. What is important to understand is that the gravity constant was introduced to make Newton’s formula work after the mass definition was changed. The kilogram mass, as well as the pound mass, are arbitrary, human-selected clumps of matter. Gravity does not care if humans declare a certain amount of matter as a kilogram or a pound.
There is nothing wrong with the modern 1873 version of the Newton’s gravity force formula: F = G M m r 2 . It is simplly that it when written on this form and when one do not deeply understand what G stands for and that the mass needed to do gravitational prediction is in reality G M , which is the original Newton mass.
Thüring [31], as late as 1961, pointed out that the gravity constant had been somehow ad hoc inserted. Further, he pointed out that the gravity constant could not be associated with a unique physical property of nature. Despite the gravity constant being ad hoc inserted to make Newton’s gravity formula work after the mass dimensions and units were changed, it was brought over into general relativity theory without question. It is important to note that changing from the Newton mass to the kilogram mass was more than just changing units. To change the mass unit from, for example, kilograms to pounds or from pounds to kilograms is a trivial switch between units; it is a matter of choice. On the other hand, changing from the Newton mass to kilograms means going from just length and time units in the mass to something more diffuse, namely kilograms. This means even the dimensions have changed.
To make a long story short, the gravitational constant that Newton never invented, sought to invent, or tried to find was carried over into general relativity theory and plays an important role in a series of gravity theories. As long as one uses kilograms for mass, one indeed needs to use the gravitational constant. A gravitational constant would also be needed if we switched the mass definition to pounds. However, the gravitational constant would not be needed if one used the original Newtonian mass definition, where mass has units [ L 3 · T − 2 ] . The main point to understand here is that there is no deep theory behind the gravitational constant; it was basically ad hoc inserted to make Newton’s formula still work when switching to kilograms. Clearly, kilograms did not contain enough information about the mass in relation to gravity to be used on their own; they had to be multiplied by a constant that could be found by calibration.
Further, it is important to be aware that the gravitational force itself has never been measured directly, only indirectly through how it affects objects in the gravitational field, such as: light, clocks and satellites. The gravitational force formula is used to derive observable gravitational formulas. In all these observable gravitational phenomena, one has G M and not G M m in the prediction formulas. That is, the kilogram mass must always be corrected by multiplying it by the gravitational constant to make the formula work. If the small mass m is large enough to have a significant contribution to the observed gravitational phenomena, a real two-body problem, the gravitational parameter is μ = G M + G m and never G M m . Actually, in modern notation, Newton’s original gravitational force formula corresponds to:
M n m n r 2 = G M G m r 2
However the formula F = G M G m r 2 can only be used if one in derivations assume the small mass also is corrected by G. For example if we are going to derive the escape velocity we now have
1 2 G m v 2 − G M G m r = 0
which solved for v gives the standard formula:
v = 2 G M r
We could naturally also have this directly from Newtons original formula, as we then have
1 2 m n v 2 − M n m n r = 0
which solved for v gives the standard formula:
v = 2 M n r
and since M n = G M , it gives the same formula as in modern notation. The modern notation involving a gravitational constant G is, however, in reality, confusing. Most physicists will likely think that including G is not confusing and is how it must be, but that is almost certainly because they are used to always including a gravitational constant. The important point to understand at this point is that we can make all the predictions with Newton’s original formula just as we can with the 1873 version of the formula that is used today. Further, G was needed to put back into the mass something that was removed when switching from the Newtonian mass to the kilogram mass. Still, what exactly is G and the mass M from a deeper perspective?
Max Planck [32,33], only a few years after the gravitational constant was introduced, assumed there were three important universal constants: the gravitational constant G, the Planck constant ℏ, and the speed of light c. Combining this with dimensional analysis, he derived what he called natural units: a unique length l p = G ℏ c 3 , time t p = G ℏ c 5 , mass m p = ℏ c G , and temperature T p = 1 k B ℏ c 5 G , today known as the Planck units.
Eddington in 1918 [34] pointed out that a future quantum gravity theory would likely need to be linked to the Planck length. As we know, Newton never introduced the gravitational constant; it was first introduced ad hoc in 1873. It is worth asking if the gravitational constant could have a deeper meaning and even be derived from more fundamental entities. Cahill [35,36] in 1984 suggested that the Planck units were more central than the gravitational constant and that one could simply express the gravitational constant by solving the Planck mass formula for G, which gives G = ℏ c m p 2 . However, Cohen [37] in 1987 pointed out that expressing the gravitational constant in terms of Planck units and claiming the Planck units were more essential would lead to a circular problem, as no one knew how to find the Planck units without first finding G. This has changed in recent years, as it has been clearly demonstrated how to find the Planck length independently of any knowledge of G[15,38,39]. This means that we indeed can write G in terms of Planck units. We can solve the Planck length formula for G, which gives:
G = l p 2 c 3 ℏ
In addition, we can solve the Compton wavelength formula λ c = h M c for M, which gives:
M = h λ c 1 c = ℏ λ ¯ c 1 c
Since in all formulas used to predict observable gravitational phenomena we have either G M or G M + G m and never G M m , this means we always have:
G M = l p 2 c 3 ℏ ℏ λ ¯ c 1 c = c 2 l p l p λ ¯ c
That is, the Planck constant always cancels out. The term l p λ ¯ c is the reduced Compton frequency per Planck time.
This also means Einstein’s field equation can be rewritten as [40,41,42]:
R μ ν − 1 2 R g μ ν = 8 π G c 4 T μ ν R μ ν − 1 2 R g μ ν = 8 π l p 2 c ℏ T μ ν
The reason the Planck constant is there is to be canceled with the Planck constant in the energy tensor.
However, Einstein’s field equation itself says little; it needs to be solved for chosen boundary conditions. If we, for example, look at the Schwarzschild metric, we have:
d s 2 = − 1 − 2 G M c 2 r c 2 d t 2 + 1 − 2 G M r c 2 − 1 d r 2 − r 2 d Ω 2 d s 2 = − 1 − 2 l p r l p λ ¯ c , M c 2 d t 2 + 1 − 2 l p r l p λ ¯ c , M − 1 d r 2 − r 2 d Ω 2
That is, again, the Schwarzschild metric at a deeper level contains the term l p λ ¯ c , M , which is the reduced Compton frequency per Planck time. The Planck constant is nowhere to be seen. Importantly, the de Broglie wavelength is also nowhere to be seen. It is the reduced Compton wavelength, together with the Planck length and the speed of light (gravity), that are the keys to gravity at the deeper level. In this way, one introduces both quantization by the reduced Compton frequency per Planck time and also links to the Planck scale through the Planck length.
The reduced Compton wavelength in the Schwarzschild metric is the rest-mass wavelength. This cannot be accomplished by the de Broglie wavelength. Even if the Compton wavelength is equal to the de Broglie wavelength multiplied by v c , it is not valid for v = 0 as the de Broglie wavelength is not defined for v = 0 .
In addition, we have recently proposed unifying a series of solutions from Einstein’s field equations into one solution. The extremal solution of the Reissner-Nordström [43,44] metric as well as the minimal solution of the Haug-Spavieri [45] metric is given by:
d s 2 = − 1 − 2 G M c 2 r + G 2 M 2 c 4 r 2 c 2 d t 2 + 1 − 2 G M c 2 r + G 2 M 2 c 4 r 2 − 1 d r 2 + r 2 Ω 2 d s 2 = − 1 − 2 l p 2 c 3 ℏ ℏ λ ¯ c , M 1 c c 2 r + l p 4 c 6 ℏ 2 ℏ 2 λ ¯ c , M 2 1 c 2 c 4 r 2 c 2 d t 2 + 1 − 2 l p 2 c 3 ℏ ℏ λ ¯ c , M 1 c c 2 r + l p 4 c 6 ℏ 2 ℏ 2 λ ¯ c , M 2 1 c 2 c 4 r 2 − 1 d r 2 + r 2 Ω 2 d s 2 = − 1 − 2 l p r l p λ ¯ c , M + l p 2 r 2 l p 2 λ ¯ c , M 2 c 2 d t 2 + 1 − 2 l p r l p λ ¯ c , M + l p 2 r 2 l p 2 λ ¯ c , M 2 − 1 d r 2 + r 2 Ω 2 .
That is, now gravity is quantized. The reduced Compton frequency per Planck time, c λ ¯ t p = l p λ ¯ , is the number of Planck mass events per Planck time in the mass M. The rest mass Compton wavelength plays a central role here. If the reduced Compton wavelength is the true matter wavelength, then gravity is linked to rest mass. Rest mass, from mathematics, is strictly related to when a mass is at rest relative to the laboratory frame (the frame one observes from).
This extremal metric above be rewritten in multiple different forms that are the same, for example:
d s 2 = − 1 − 2 G n p m p c 2 r + k e n p q p n p q p r 2 G c 4 c 2 d t 2 + 1 − 2 G n p m p c 2 r + k e n p q p n p q p r 2 G c 4 − 1 d r 2 + r 2 Ω 2 .
We now see the last term k e n p q p n p q p r 2 G c 4 is quantized charge, where the quanta comes in Planck charge. The G c 4 is just a conversion factor needed to get the Joule energy into collision-length energy [46,47]. As we have F c F = k e q p q p r 2 m p m p r 2 = 1 , the metric above can again be rewritten as:
d s 2 = − 1 − 2 G n p m p c 2 r + k e n p q p n p q p r 2 G c 4 c 2 d t 2 + 1 − 2 G n p m p c 2 r + k e n p q p n p q p r 2 G c 4 − 1 d r 2 + r 2 Ω 2 .
That is, again, all gravity is now quantized. However, the deepest level is when we write it in the Compton wavelength form further up: Eq. (22). Also, the Schwarzschild metric is now the weak field solution of this metric. The Schwarzschild metric is normally considered to be valid also in strong gravitational fields, but it is unexplained why it gives the same radius of a black hole as plain Newton gives for a dark star r s = 2 G M c 2 and the same escape velocity formula v e = 2 G M r . We will claim Newton in reality is a weak field approximation. This happens as one calibrates the Schwarzschild solution to Newton before one gets out a practically useful metric. In the extremal solution above, we get an escape velocity of v e = 2 G M c 2 − G 2 M 2 c 4 r 2 , where the Schwarzschild escape velocity is the weak field approximation when ignoring the higher-order term needed to properly work in strong gravitational fields. This is not the main topic of this paper, but we mention it.
The most important takeaway from this section is that we can indeed quantize general relativity and other gravity theories in a very simple form by understanding that G is needed to fix an incomplete kilogram mass. Additionally, the gravitational constant, from a deeper perspective, can be represented by G = l p 2 c 3 ℏ . Furthermore, any kilogram mass can be expressed as M = ℏ λ ¯ c , M 1 c , and in all predictive gravity phenomena (involving one body), we have G M = l p 2 c 3 ℏ ℏ λ ¯ c , M 1 c = c 2 l p l p λ ¯ c , M , meaning the Planck constant cancels out and is not needed in quantum gravity, and further we incorporate the reduced Compton frequency per Planck time l p λ ¯ c , M and thereby get quantum gravity.
Gravity can be seen as Planck mass particles that fit the mathematics of micro black holes, emerging and vanishing at the reduced Compton frequency. These particles endure only for the Planck time and possess a radius equal to the Planck length. How does this tie into quantum mechanics? We’ll delve into that in the following section.

6. A New Defined Planck Mass Particle with Very Unique Properties

Einstein suggested quantized gravitational radiation as early as 1916. The term ’graviton’ was coined in 1934 by Soviet physicist Dmitry Blokhintsev. We conjecture that there is a particle related to gravity, which we refer to as the Planck mass particle. We are not the first one to suggest there is a Planck mass particle see also Motz [48,49]. However our approach differs considerably in that we will assume this particle only last the Planck time and is mathematically described by the Reissner-Nordstrom extremal black hole solution that we soon will get back to.
We propose that the Planck mass particle is the result of a photon-photon collision, creating a mass with the Planck mass. It is not controversial to predict that photon-photon collisions create mass, this is even assumed in standard theory, see [50]. The Planck mass is much larger than any known elementary particle and even larger than any known atom. However, we suggest that the Planck mass particle has a lifetime of only the Planck time, something we soon will demonstrate can be tested easily experimentally. This implies that this photon-photon collision particle could actually be the building block of even particles such as the electron. We assume the Planck mass particle comes in and out of existence at the reduced Compton frequency of matter. That is, at each reduced Compton time interval, there is a photon-photon collision that lasts for the Planck time. The mass of the electron is then given by:
m e = m p t p f = m p t p c λ ¯ e ≈ 9.13 × 10 − 31 kg
This approach also works for protons and, in fact, for any mass.
Einstein together with Rosen in 1935 attempted to determine whether general relativity alone could explain some gravity particle [51], they wrote
“These solutions involve the mathematical representation of physical space by a space of two identical sheets, a particle being represented by a ’bridge’ connecting these sheets.....It is the representation of an elementary electrical particle without mass."
This solution is no longer used as an attempt to describe particles as they indeed led to particles without mass, but is what today is know as wormholes or Einstein-Rosen bridge. Here, we will take a new approach also rooted in general relativity theory by examining the extremal solution of the Reissner-Nordström metric. In the extremal solution of the Reissner-Nordström metric, the electrostatic and gravitational forces perfectly counterbalance each other, as noted by multiple researchers, see for example Zee [52]. This is of great importance because it means that an extremal black hole should not collapse into a central singularity.
When it comes to a Planck mass Schwarzschild black hole, it has very high Hawking radiation, as the Hawking radiation is given by:
T H w = ℏ c 3 k b 8 π G M = ℏ c k b 4 π r s
So if the smallest mass that can create a black hole is the Planck mass then we see this gives maximum Hawking radiation. The evaporation time for a Planck mass particle is: t e v = 5120 π G m p 3 ℏ c 4 ≈ 8.68 × 10 − 40 which is not that far from the Planck time ≈ 10 − 44 s . The evaporation time of a Planck mass Schwarzschild black hole is therefore slightly above the Planck time.
On the other hand, the equivalent to Hawking radiation for a Reissner-Nordstrom black hole is given by (see Sorkin and Piran [53] and also [54]):
T R N = ℏ c r h 2 − r Q k b 2 π r h 2
where r h = G M c 2 + G 2 M 2 c 4 − r Q 2 . In the special case of no charge, r Q = 0 , and we are back to the Hawking radiation for a Schwarzschild black hole. On the other hand, for an extremal black hole, r Q = r h = G M c 2 and then the black hole radiation is zero. Sorkin and Piran conclude:
“We find that the evaporation proceeds to a stable endpoint corresponding to the extremal, charged black hole.”
Edery and Constantineau [55] have in recent years also demonstrated that extremal black holes have zero entropy and are time-independent throughout spacetime and correspond to a single classical microstate. Normally, it is assumed that quantum mechanics is superior to general relativity when it comes to the atomic and subatomic scale, and in that case, one could easily try to claim general relativity cannot be used all the way down to the Planck scale as one would then need to take into account quantum mechanics (quantum fluctuations) and therefore would need a quantum gravity theory before one can look at gravity effects at the subatomic scale and particularly all the way down to the Planck scale. We will, however, contest that view here and ask the reader for a moment to trust general relativity theory. The extremal solution of the Reissner-Nordstrom metric here tells us something important, and we suggest it could be that quantum mechanics instead needs to be modified to be consistent with general relativity theory.
The event horizon of an extremal black hole is r h = G M c 2 , which is half the Schwarzschild radius. The Planck mass particle is a Planck mass extremal Reissner-Nordström black hole with a radius equal to r h = G m p c 2 = l p . The electromagnetic force and the gravitational force are in perfect equilibrium, so it neither radiates nor collapses into a singularity. It still has a pure mathematical singularity at r = 0 , but since the gravity force is perfectly counterbalanced by the electrostatic force there is no reason to think the mass end up in the center r = 0 as seems to be the case in Schwarzschild as well as also non-extremal Reissner-Nordstrom, Kerr and Kerr-Newman black holes. The extremal black hole has very unique properties that prevent matter from collapsing into the sigularity, so there is logical as well as mathematical reasons to argue that the center singularity is not relevant for them.
Matter cannot be stored into a zero space volume at the center singularity and the extremal solution tells us exactly this, as the gravity force is perfectly balanced out by the electrostatic force. It has zero entropy since it is an extremal black hole and is time-independent throughout spacetime. However, we will claim it is time-independent throughout spacetime only for its lifetime, which we assume is the Planck time. We suggest that the Planck mass particle is a photon-photon collision lasting the Planck time. It is well known even in standard theory that photon-photon collisions are supposed to create mass (see [50]). Even if a photon moves at the speed of light, at the very collision point, it cannot move, and we will claim it must stand absolutely still. At first, this seems absurd. But if the radius of this particle (the collision between the building blocks of two photons) is just the Planck length and the lifetime is just the Planck time, then such a particle can only be observed from itself, that is, only from its rest frame. Assume we are two Planck lengths away from its center; the Planck mass particle has now dissolved before we have a chance to observe it, as it would take the Planck time for the information to reach us at the speed of light, and in that time, it has dissolved back into energy (photons).
Assume only the Planck mass particle micro black hole in physical reality creates an extremal black hole. Then the extremal solution of the Reissner-Nordström metric is only practically valid for such particles, and the space-time is then limited to the lifetime of the particle and its spatial extension. By it being a photon-photon collision standing still for the Planck time before dissolving into photons moving at the speed of light again, it seems to fit this solution and be able to logically explain why we can have the very strange property of time-independence throughout spacetime. It is simply because the space-time is not changing for the Planck time, and the extremal solution is only valid for the Planck mass particle lasting the Planck time and has an extension on the order of the Planck length.
The escape velocity of the extremal solution is given by [56]:
v e = 2 G M r − G 2 M 2 c 2 r 2
which for a Planck mass particle is
v e = 2 G m p l p − G 2 m p 2 c 2 l p 2 = c
This means only a photon can escape the Planck mass particle and nothing with rest-mass. In the Schwarzschild solution, the escape velocity v e = 2 G M r exceeds c as soon as one goes inside the black hole, pointing toward nothing can escape the black hole (when we disregard Hawking radiation). In the extremal black hole, the escape velocity always stays equal to c inside the black hole.
If this Planck mass particle is linked to gravity, that means quantum gravity is linked to absolute rest, as the particle only exists as a collision that can only be directly observed from itself. If we have many such particles, they can, however, be indirectly observed as gravity, something that might even help us indirectly detect the Planck mass particle, as demonstrated in Section 10.
There is one more important point here supporting that the Planck mass particle is at rest and that gravity is linked to rest and photon-photon collisions (internally in matter). The wavelength of a photon is equal to the Compton wavelength of the rest-mass energy. We will assume there is a minimum length for a relativistic length-contracted length. This means we must have:
λ ¯ 1 − v 2 c 2 ≥ l p
If we solve this for v, we get (see [59]):
v ≤ c 1 − l p 2 λ ¯ 2
For any observed elementary particle such as the electron, this speed limit will be very close to the speed of light and much higher than what has been achieved at the Large Hadron Collider for any particle, so it is not inconsistent with observations. Only when we have particles with mass close to the Planck mass particle, and in particular for the Planck mass particle, does something very interesting happen. For the Planck mass particle, the reduced Compton wavelength is equal to the Planck length λ ¯ = ℏ m p c = l p , so this means its speed is
v ≤ c 1 − l p 2 l p 2 ≤ 0
And since negative speeds are naturally meaningless, this implies that the speed of a Planck mass particle is always zero. It is always at rest during its lifetime. This may seem absurd until one understands that the Planck mass particle is likely a photon-photon collision, or more accurately. Even though a photon normally moves at the speed of light, at the exact moment it collides with another photon, it cannot be in motion. One might argue that it must be moving relative to some reference frame. However, if the photon-photon collision only lasts for the Planck time and has a radius equal to the Planck length, then the Planck mass particle can only be directly observed by being part of it.
As mentioned before, it can only be directly observed by being part of it, as it has a radius equal to the Planck length and a lifetime equal to the Planck time. So, all of this is actually consistent: it is at absolute rest, has zero entropy, and is time-independent throughout spacetime during its lifetime. It is crucial to emphasize ’during its lifetime,’ as the Planck mass particle’s lifetime is only the Planck time. This means that this particle does not exhibit wave-particle duality, has no spin, and there is no uncertainty associated with it. It is indeed time-independent throughout spacetime, but only during its lifetime, which is the Planck time.
This implies that gravity is very, very special. In our view, gravity is related to the Planck mass particle, which in turn is connected to absolute rest and absolute time. Absolute time enters general relativity through the extremal solution of the Reissner-Nordström metric and the Planck mass particle. Again, it can only be observed directly from its own frame. However, we can indirectly test this by detecting the Planck mass particle through a very simple method in weak fields that we will discuss in Section 10.
Table 1. This table summarize our findings about the Planck mass particle, which we describe using the Reissner-Nordstrom extremal solution from general relativity theory.
Table 1. This table summarize our findings about the Planck mass particle, which we describe using the Reissner-Nordstrom extremal solution from general relativity theory.
Property: Formula: Comments
Mass m p = ℏ c G = ℏ l p 1 c
Rest mass energy m p c 2 = ℏ c 5 G
Radius r H = G m p c 2 = G ℏ c 3 = l p Half of the Schwarzschild radius r s = 2 G M c 2 .
Volume V p = 4 3 π l p 3
Energ density = Planck density m p c 2 4 3 π l p 3
Surface acceleration a p = G m p l p 2 From zero to c in the Planck time.
Charge = Planck charge q p = e α = ℏ c α 10 7
Life time t p = G ℏ c 5
“Hawking" radiation in its life time T R N = ℏ c r h 2 − r Q k b 2 π r h 2 = 0 see Sorkin and Piran [53].
Maximum velocity in its life time v m a x = c 1 − l p 2 l p 2 = 0 Can only be observed
directly from its own frame
Escape velocity v e = 2 G m p l p − G 2 m p 2 c 2 l p 2 = c
Entropy in its life time 0 see Edery and Constantineau [55].
Radiation at end of life time E p = m p c 2 = ℏ c l p = ℏ f p
Singularity? Electromagnetism perfect
counterbalance gravity force

7. A Simple Solution to the Center Singularity

Stoica [60] mentions: "There are two outstanding problems in General Relativity (GR): the problem of singularities and the problem of quantizing gravity."
For example, the singularity at the Schwarzschild radius in the Schwarzschild metric can be removed by switching to Lemaître coordinates and is therefore known as an apparent singularity, which is not real. However, the central singularity remains a real physical singularity even under a coordinate change .
Central singularities became an even bigger problem when Hawking demonstrated mathematically that black holes can evaporate, potentially leaving a naked singularity. In this case, initial information seems to be partially lost at the singularity. However, extremal Reissner-Nordström Planck mass micro black holes do not evaporate within their lifetime, which is only the Planck time. At the very end of their lifetime, all information is evaporated, but by then it is no longer a black hole. Under this model, nothing can enter the central singularity, as the electrostatic and gravitational forces perfectly balance each other in the extremal Reissner-Nordström micro black hole, during the whole life time of the black hole.
In the view presented above, we must work with the extremal solution of the Reissner-Nordström metric when approaching lengths close to the Planck length. The Planck mass particle, as described in this paper, represents a perfect equilibrium between gravitational and electrostatic forces. This implies that the Planck mass particle, with its radius equal to the Planck length, does not collapse into a central singularity. This also means that the minimum meaningful radius in this solution to Einstein’s field equations is the Planck length. In this way, one avoids the central singularity while also achieving the quantization of space and time. The Reissner-Nordström metric is simply not valid for r = 0 , as it is meaningless to consider a radius smaller than the Planck length; no matter can be compressed into zero volume, and it is unnecessary, as the electrostatic force perfectly counterbalances the gravitational force.
What then about the Big Bang? The Big Bang also has a similar central singularity. However, if matter ultimately consists of Planck mass particles that fit the extremal solution of the Reissner-Nordström metric, then matter in Planck mass chunks cannot be compressed any further, in this way one avoid a center singularity. However still the Planck mass is so extremely dense that if one took all the mass and energy in the universe (for example the critical Friedmann universe) one could still compress it into about the size of a proton, see [61]. This would mean the universe started in a proton size mass with Planck mass density (sphere packed Planck mass particles), instead of a center singularity, if the Λ -CDM model can be made consistent with such a view should naturally be investigated further before any conclusion is made.
Even if we achieve quantization in general relativity and a metric solution to solve the central singularity (the extremal solution), we must also address how this can be made compatible with quantum mechanics. As we will demonstrate and discuss in the following sections, this necessitates a modified form of quantum mechanics.

8. From Heisenberg’s Uncertainty Principle to the Certainty-Uncertainty Principle

In 1927, Heisenberg [11] published his uncertainty principle1. He also wrote extensively about it in his book The Physical Principles of Quantum Theory," published in 1930 [58]. Here he states, Defining momentum as p x = m v x (where m = mass of electron, v x = x component of velocity), this uncertainty in velocity causes an uncertainty in p x of an amount Δ p x ; from which simple laws of optics, together with the empirically established law λ = h p , it can readily be shown that
Δ x Δ p x ≥ h .
This is naturally correct under Heisenberg’s assumptions, but again he based the uncertainty principle on the matter wavelength being the de Broglie wavelength: λ = h p . We will here explore the uncertainty principle more in depth if we relate it to the Compton wavelength instead of the de Broglie wavelength. We will first write:
x p t ≥ h
where x is the area in which the particle element of an elementary particle can be, and p t is what we will call the total Compton momentum, p t = m c γ . That is, we have replaced the standard momentum that is linked to the de Broglie wavelength with a momentum linked to the Compton wavelength, what we before have coined the Compton momentum [46].
Next, we replace x with the Compton wavelength, then we get:
λ c p t ≥ h λ c m c γ ≥ h λ c m c 1 − v 2 + ( Δ v ) 2 c 2 ≥ h
This we will call the Certainty-Uncertainty principle. That is, it takes into account both the uncertainty in where the particle can be observed but has a special case for a special particle, namely the Planck mass particle, that gives certainty in position. This will first become clear as we dive deeper into the equation above.
Further, if we solve the Compton wavelength formula λ = h m c with respect to the mass m, we can express the kilogram mass as m = h λ 1 c . Replacing this back into our Certainty-Uncertainty principle (see also [16]), we get:
λ c h λ 1 c c γ ≥ h γ ≥ 1 1 1 − v 2 + ( Δ v ) 2 ) c 2 ≥ 1
That is, as long as there is uncertainty in v, the left-hand side is greater than 1 and uncertain. However, as we have stated in the previous sections, the Planck mass particle is unique. It is a photon-photon collision that gives rise to mass lasting the Planck time. The maximum velocity of any particle with mass is v ≥ c 1 − l p 2 λ ¯ 2 . The maximum velocity formula for any elementary particle with mass we get from simply assuming the reduced Compton wavelength is the matter wavelength and that relativistic length contraction of this length is limited by the Planck length is the shortest possible even contracted length, this gives:
l p ≥ λ ¯ 1 − v 2 c 2 v ≤ c 1 − l p 2 l p 2 .
The reduced Compton wavelength of the Planck mass particle is the Planck length: λ ¯ c = ℏ m p c = l p , so the maximum velocity for the Planck mass particle is remarkably always v ≥ c 1 − l p 2 l p 2 = 0 , see [59]. Again, this sounds absurd, but only until one realizes this particle lasts only the Planck time and has a radius equal to the Planck length. To observe the Planck mass particle directly, one must therefore be part of the particle itself. In other words, one must be part of the same reference frame where all is at rest relative to one, but since the reference frame only lasts the Planck time, this causes no problems. It is impossible to observe a particle with a radius of the Planck length that lasts the Planck time if one, for example, is one Planck length away from it. This as even light would then need a Planck time to travel that distance, and in the Planck time the Planck mass particle dissolve into pure energy again, photons.
Next, let’s try to do similarly, but now with the de Broglie wavelength. We then get:
λ b p ≥ h λ b m v γ ≥ h
Next, as the rest mass m can only be expressed from the Compton wavelength formula and not from the de Broglie wavelength formula, we replace m with m = h λ c 1 c . This gives:
λ b h λ c 1 c v γ ≥ h λ b λ c v c γ ≥ 1
As the de Broglie wavelength is not defined when v = 0 , this will not allow us to have a particle at absolute rest. Going through the de Broglie wavelength instead of the Compton wavelength therefore does not allow for v = 0 . The uncertainty in Heisenberg’s uncertainty principle indeed comes from uncertainty in v as Heisenberg himself stated, but Heisenberg’s uncertainty principle does not allow for v = 0 . This is even obvious from Heisenberg’s uncertainty principle itself. If v = 0 and also the uncertainty in Δ v = 0 (for the Planck time) then the momentum p = m v γ = 0 and also the uncertainty in the momentum is then zero, so it will not be correct that Δ x Δ p ≥ h , then one will have 0 ≥ h which is not correct. So yes indeed Heisenberg’s uncertainty principle does not allow for v = 0 (which also means Δ v = 0 as is the case for the Planck mass particle and the Heisenberg uncertainty principle without modifications is therefore not compatible with the simple way to get quantum gravity as described above.
There are many possible implications from this. For example, the current interpretation of entanglement could even be wrong. We are fully aware that entanglement has been experimentally tested; however, the interpretation is based on certain assumptions. Einstein, Podolsky, and Rosen [62] suggested hidden variables could be the explanation behind it. Bell [63] disproved that Einstein, Podolsky, and Rosen could be right, and this led to rejection of hidden variables as an explanatory hypothesis. However, Bell’s theorem is based on the assumption that Heisenberg’s uncertainty principle always holds, see Clover [64,65]. If we switch to the view that the Compton wavelength is the true matter wavelength and that the de Broglie wavelength is only derivative, then we can transition from Heisenberg’s uncertainty principle to a certainty-Uncertainty principle. Bell’s theorem may no longer hold necessarily, and even the interpretation of entanglement can the possibly be rooted in some type of hidden variable hypothesis. At least, this should be investigated, as we now have a simple way to unify gravity and quantum mechanics that involves replacing the uncertainty principle with a certainty-uncertainty principle.

9. Hilbert Space and Unification with Gravity and Quantum Mechanics

Hilbert space plays a central role in quantum mechanics and is considered a requirement in standard quantum mechanics. However, Hilbert space is generally considered incompatible with general relativity. Therefore, a natural question arises: Is our new approach, which we claim to be a promising path toward the unification of gravity with a modified quantum mechanics, compatible with Hilbert space? While we will not reach firm conclusions in this section, we will discuss some issues related to Hilbert space in the context of our new perspective on quantum gravity theory.
General relativity and most gravity theories are consistent with local Lorentz symmetry, but break it globally due to the curvature of space-time. Consequently, Hilbert space is typically not achieved globally in the presence of gravity. That said, multiple authors have quantized certain metric spaces from general relativity to establish a Hilbert space for these cases. For example, Paulo et al. [66] applied a quantization procedure to Schwarzschild space-time and obtained a fractional differential equation. They used equations arising from the quantization of the FRW and Reissner–Nordström metrics to construct the respective Hilbert spaces (see also [67]).
Macías and Camacho [68] review the incompatibility between quantum theory and general relativity, focusing primarily on time. They point out—and even claim to prove—that the absolute nature of Newtonian time is present in quantum mechanics, despite the Schrödinger equation involving a time operator. They state: "Time in quantum mechanics is a Newtonian time, i.e., an absolute global time." They further explain that "quantization methods rely on the Newtonian global and absolute time... Since time is absolute, it can be factored out, reducing the quantization problem to constructing a Hilbert space for stationary states." Moreover, they argue that "the transition to (special) relativistic quantum field theories can be realized by replacing the unique absolute Newtonian external time with a set of timelike parameters associated with the naturally distinguished family of relativistic inertial frames."
However, in general relativity, time is considered dynamic and local, not an absolute external time—or at least, this is the current interpretation. We will challenge that view here. Let’s examine the Schwarzschild metric in our quantized form again. It is...
d s 2 = − 1 − 2 l p r l p λ ¯ c , M c 2 d t 2 + 1 − 2 l p r l p λ ¯ c , M − 1 d r 2 − r 2 d Ω 2
and in the extremal Reissner-Nordstrom metric it is
d s 2 = − 1 − 2 l p r l p λ ¯ c , M + l p 2 r 2 l p 2 λ ¯ c , M 2 c 2 d t 2 + 1 − 2 l p r l p λ ¯ c , M + l p 2 r 2 l p 2 λ ¯ c , M 2 − 1 d r 2 + r 2 Ω 2 .
Again, l p λ ¯ c , M = c λ ¯ c , M t p represents the reduced Compton frequency per Planck time. Thus, the Planck time is always present; it is the absolute time hidden within general relativity. This indicates that both quantization and absolute time are concealed in general relativity, which becomes apparent when G and M are rewritten in the manner discussed above. Whether incorporating absolute time into general relativity in this way can lead to consistency with Hilbert space requires considerably more investigation and discussion. Even if gravity seems inconsistent with global Lorentz symmetry, if gravity is linked to the Planck scale and the Planck mass particle described in Section 6, then only local Lorentz symmetry seems to be necessary, as is the case in general relativity theory.
Most researchers working on quantum gravity assume that quantum mechanics is fundamentally correct, and that it is primarily gravity that needs to be modified to become compatible with existing quantum mechanics, including Hilbert space. Our approach is fundamentally different. We assume that general relativity is essentially correct when viewed from a deeper perspective at the Planck scale. We conjecture that the only relevant particle for gravity is the Planck mass particle. The Planck particle, as an extremal Reissner-Nordström micro black hole, is fully stable and remains unchanged in space-time throughout its lifetime, which is the Planck time. Therefore, the relevant space-time for gravity is only the Planck space-time; in other words, only local Lorentz symmetry seems to be relevant, even if this should be discussed over time by multiple researchers. It can be seen as a hypothesis we here suggest.
We incorporate our quantized version off general relativity theory into quantum mechanics by modifying the Heisenberg uncertainty principle. For all particles except the Planck mass particle, the global space-time is relevant, and the Heisenberg uncertainty principle in its original form applies. However, for gravity, only the Planck scale and the Planck particle are relevant, so here the Heisenberg uncertainty principle is modified to a certainty principle consistent with the findings of Edery and Constantineau [55], with no changes in space-time. But again, the space-time is only linked to a time interval of the Planck time and a length interval of the Planck length. Particle-wave duality, as well as phenomena such as entanglement, play no role here in relation to gravity.
Regarding the assumption that gravity breaks global Lorentzian symmetry, we will look at this in a new way in our model. In our model, gravity is linked to photon-photon collisions that create an extremal Reissner-Nordström micro black hole particle with a radius of r h = G m p c 2 = l p , lasting only for the Planck time. This means that this particle can only be observed directly from its own reference frame. If one tries to observe it from even two Planck lengths away, it would have dissolved before it could be observed. This implies that gravity is related to absolute rest and absolute time and can only be observed directly from its own reference frame, the rest-frame. Still we can detect it indirectly as gravity as described in Section 10.
In this new perspective, gravity does not break Lorentz symmetry; instead, gravity corresponds to observing the unique rest frame related to gravity and the Planck mass particle. Detecting gravity, in our view, is detecting a unique rest frame that consists of photon-photon collisions. This naturally suggests minimal modifications to special relativity, as it implies that the maximum velocity is related to v m a x = c 1 − l p 2 λ ¯ 2 , which, in practice, is generally indistinguishable from v ≤ c for any practical purposes, but with significant consequences for the Planck mass particle, as discussed in Section 6. The maximum velocity for the graviton is zero, as it represents a collision between two photons that can only be directly observed from the photon-photon collision itself, and thus can only be observed directly from the absolute rest frame. Between graviton creations, the building blocks of the gravitons move at the speed of light, so it remains consistent with the idea that gravity propagates at the speed of light. Any detection of gravity, then, is the indirect observation of this rest frame.
There may be aspects we have overlooked in relation to Hilbert space, but we believe this is an interesting hypothesis that deserves discussion and wider availability.

10. How to Detect the Planck Mass Particle: The Graviton

In standard theory it is assumed almost impossible to detect the Planck scale even if many attempts have been made.In our theory the understanding of the quantum world and quantum gravity is considerably different than other approaches suggested before. In our theory to detect gravity is indirectly to detect the Planck scale and therefore the Planck mass particle. We will in this section show how we remarkably can detect the Planck scale from a simple Cavendish apparatus and even detect indirectly the collision time between photons and the radius of the Planck mass particle.
According to our quantum gravity theory, we propose that the particle responsible for gravity is a photon-photon collision lasting for the Planck time. During its incredibly short lifetime, it exhibits mathematical properties similar to those of an extremal Reissner-Nordström black hole, but then it dissolves back into pure energy (photons). In this work, we will demonstrate, based on our new understanding of the quantization of matter, that matter itself consists of photon-photon collisions occurring at the reduced Compton frequency and lasting for an unknown time t = x c where x is the radius of the extremal Planck mass micro black hole particle which is the Planck mass particle, or this is what we want to find out experimentally.
We will show that this time can be determined using a Cavendish apparatus setup, based on simply Newton gravitational theory from a deeper perspective as Newton theory is the weak field approximation for our metric.
We have the well-known relation:
κ θ = L F
where θ is the deflection angle, κ is the torsion coefficient of the suspending wire, and L is the distance between the small balls in a Cavendish apparatus. The natural resonant oscillation period of a torsion balance is given by:
T = 2 π I κ
where I is the moment of inertia:
I = m L 2 2 + m L 2 2 = m L 2 2
Substituting this back into (43), we get
T = 2 π m L 2 2 κ
We next solve this with respect to κ and get
κ = 2 π 2 m L 2 T 2
Now, substituting this back into Equation (42), we have
2 π 2 m L 2 T 2 θ = L F
For the force F, we can use Newton’s gravitational force:
2 π 2 m L 2 T 2 θ = L G M m r 2 2 π 2 L r 2 T 2 θ = G M
Now we are left with G M on one side and observables from the Cavendish apparatus measurements on the other side. However, as pointed out earlier, Newton never introduced or used a gravitational constant G, nor did Cavendish. The Newtonian mass M n is, however, equal to G M , but at a deeper level, we have:
G M = M n = c 3 M ¯ = c 3 l p c l p λ ¯ M = x c x λ ¯ M
where M ¯ is a new mass definition we in multiple papers have called collision-time mass. This means the collision-time mass consists of a photon-photon collision lasting the unknown collision-time x c that occurs at the reduced Compton frequency f = c λ ¯ M x c = x λ ¯ M over the collision-time. Since x at this stage is assumed to be completely unknown, so is the collision-time t = x c . However, we can easily determine these from the Cavendish apparatus measurements as we must have:
2 π 2 L r 2 T 2 θ = G M = c 3 t f = c 3 x c x λ ¯ M x = π r T c 2 L λ ¯ M θ
As T is simply the measured oscillation period in the Cavendish apparatus, L is the distance between the small balls in the apparatus, and r is the distance from the center of the small ball to the large ball in the apparatus, θ is the measured angle of the arm. These are all directly observable. The speed of light c can be easily measured without any knowledge of gravity or the gravitational constant G. The reduced Compton wavelength can also be easily determined without knowing G or ℏ, see . This means we can now find x and, naturally, x c , which, when performing a Cavendish experiment, will correspond to the Planck length and Planck time. Thus, the graviton, which is a photon-photon collision, can indirectly be detected when gravity is understood from this new quantized perspective.
This is not the same as finding G and then extracting the Planck length or Planck time from G. To do that, one would additionally need to know the kilogram mass of the large ball in the Cavendish apparatus. While it is possible to use the Cavendish apparatus to find G, this requires the definition of an arbitrary mass standard. The key insight here is that matter ’ticks’ at the reduced Compton frequency, and at the end of each reduced Compton time interval, we have a particle event that lasts an unknown time t = x c . By solving for x using measurable values from a Cavendish apparatus, along with knowledge of the reduced Compton wavelength, this can be determined.

11. Conclusions

We’ve demonstrated in a series of papers that it’s possible to quantize general relativity and other gravity theories in a straightforward manner while incorporating the Planck scale. This quantization arises from the reduced Compton frequency per Planck time, which can only be observed in integers, representing the number of Planck mass events. These events correspond to the number of Planck mass particles per Planck time in the gravitational mass of interest. However, aligning it with quantum mechanics requires modifications. For example, principles like Heisenberg’s uncertainty principle, initially derived under the assumption that matter wavelength was the de Broglie wavelength, need to be adjusted to a Certainty-Uncertainty principle rooted in the Compton wavelength as the true matter wavelength.
This suggests that Einstein’s skepticism towards quantum mechanics as a complete theory was justified. Even his assertion that there must be some underlying certainty in the system, famously expressed as "God does not play dice with the universe," seems to hold weight.

References

  1. A. Einstein. Näherungsweise integration der feldgleichungen der gravitation. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin, 1916.
  2. O. W. Richardson and C. T. Compton. The photoelectric effect. Science, 35:907, 1912. URL https://doi.org/10.1126/science.35.907.783. [CrossRef]
  3. S. Mukhi. String theory: A perspective over the last 25 years. Classical and Quantum Gravityu, 28:153001, 2011. [CrossRef]
  4. A. Ashtekar and E Bianchi. A short review of loop quantum gravity. Rep. Prog. Phys., 84:042001, 2021. [CrossRef]
  5. K. Krasnova and R. Percacci. Gravity and unification: A review. Classical and Quantum Gravity, 35:143001, 2018. [CrossRef]
  6. R. Howl, R. Penrose, and I. Fuentes. Exploring the unification of quantum theory and general relativity with a Bose–Einstein condensate. New Journal of Physics, 21:043047, 2019. [CrossRef]
  7. C. Kiefer. Quantum gravity – a unfinished revoluition. Invited contribution for EPS Grand Challenges: Physics for Society at the Horizon 2050 arXiv, 2023. URL https://arxiv.org/pdf/2302.13047.pdf.
  8. de. L. Broglie. Recherches sur la théorie des quanta. PhD Thesis (Paris), 1924.
  9. de. L. Broglie. An introduction to the Study of Wave Mechanics. Metheum & Co., Essex, 1930.
  10. C. Davisson and L. H. Germer. Diffraction of electrons by a crystal of nickel. Physical Review, 30(705):705, 1927. [CrossRef]
  11. W. Heisenberg. Über den anschaulichen inhalt der quantentheoretischen kinematik und mechanik. Zeitschrift für Physik, (43):172–198, 1927. [CrossRef]
  12. A. H. Compton. A quantum theory of the scattering of x-rays by light elements. Physical Review, 21(5):483, 1923. [CrossRef]
  13. L.S. Levitt. The proton Compton wavelength as the `quantum’ of length. Experientia, 14:233, 1958. [CrossRef]
  14. O. L. Trinhammer and H. G. Bohr. On proton charge radius definition. EPL, 128:21001, 2019. [CrossRef]
  15. E. G. Haug. Finding the Planck length multiplied by the speed of light without any knowledge of G, c, or h, using a newton force spring. Journal Physics Communication, 4:075001, 2020. [CrossRef]
  16. E. G. Haug. The Compton wavelength is the true matter wavelength, linked to the photon wavelength, while the de Broglie wavelength is simply a mathematical derivative, understanding this leads to unification of gravity and new quantum mechanics. Qeios, 2023. [CrossRef]
  17. E. G. Haug. Derivation of a relativistic Compton wave. European Journal of Applied Physics, 4:24, 2022. [CrossRef]
  18. M. Planck. Das prinzip der relativität und die grundgleichungen der mechanik. Verhandlungen Deutsche Physikalische Gesellschaft, 4, 1906.
  19. I Newton. Philosophiae Naturalis Principia Mathematica. London, UK, Jussu Societatis Regiae ac Typis Josephi Streater, 1686.
  20. E. G. Haug. God time = Planck time. Open Journal of Microphysics, 14:40, 2024. [CrossRef]
  21. I. B. Cohen. Newton’s determination of the masses and densities of the sun, jupiter, saturn, and the earth. Archive for History of Exact Sciences, 53(1):83, 1998. [CrossRef]
  22. E. G. Haug. Newton did not invent or use the so-called Newton’s gravitational constant; G, it has mainly caused confusion. Journal of Modern Physics, 13:179, 2022. [CrossRef]
  23. J. Michell. On the means of discovering the distance, magnitude &c.of the fixed stars, in consequence of the diminution of the velocity of their light, in case such a diminution should be found to take place in any of them, and such other data should be procured from observations. Philosophical Transactions of the Royal Society, 74, 1784. [CrossRef]
  24. K. Schwarzschild. über das gravitationsfeld einer kugel aus inkompressibler flussigkeit nach der einsteinschen theorie. Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik, page 424, 1916.
  25. H. Cavendish. Experiments to determine the density of the earth. Philosophical Transactions of the Royal Society of London, (part II), 88:469, 1798.
  26. B. E. Clotfelter. The Cavendish experiment as cavendish knew it. American Journal of Physics, 55:210, 1987. [CrossRef]
  27. L. Sean. Henry Cavendish and the density of the earth. The Physics Teacher, 37:34, 1999. [CrossRef]
  28. C. Maxwell. A Treatise on Electricity and Magnetism. Macmillan and Co., Oxford, UK, 1873.
  29. A. Cornu and J. B. Baille. Détermination nouvelle de la constante de l’attraction et de la densité moyenne de la terre. C. R. Acad. Sci. Paris, 76, 1873.
  30. C. V. Boys. On the Newtonian constant of gravitation. Nature, 5:330, 1894. [CrossRef]
  31. B. Thüring. The gravitational constant. Ann. Acad. Sci. Fennicae A, page 269, 1961.
  32. M. Planck. Natuerliche Masseinheiten. Der Königlich Preussischen Akademie Der Wissenschaften: Berlin, Germany, 1899. URL https://www.biodiversitylibrary.org/item/93034#page/7/mode/1up.
  33. M. Planck. Vorlesungen über die Theorie der Wärmestrahlung. Leipzig: J.A. Barth, p. 163, see also the English translation “The Theory of Radiation" (1959) Dover, 1906b.
  34. A. S. Eddington. Report On The Relativity Theory Of Gravitation. The Physical Society Of London, Fleetway Press, London, 1918.
  35. K. Cahill. The gravitational constant. Lettere al Nuovo Cimento, 39:181, 1984. [CrossRef]
  36. K. Cahill. Tetrads, broken symmetries, and the gravitational constant. Zeitschrift Für Physik C Particles and Fields, 23:353, 1984. [CrossRef]
  37. E. R. Cohen. Fundamental Physical Constants, in the book Gravitational Measurements, Fundamental Metrology and Constants. Edited by Sabbata, and Melniko, V. N., Netherland, Amsterdam, Kluwer Academic Publishers, p 59, 1987.
  38. E. G. Haug. Extraction of the speed of gravity (light) from gravity observations only. International Journal of Astronomy and Astrophysics, 9(2):97, 2019. [CrossRef]
  39. E. G. Haug. Planck units measured totally independently of big G. Open Journal of Microphysics, 12:55, 2022. [CrossRef]
  40. E. G. Haug. Planck quantization of Newton and Einstein gravitation. International Journal of Astronomy and Astrophysics, 6(2):206, 2016. [CrossRef]
  41. E. G. Haug. Different mass definitions and their pluses and minuses related to gravity. Foundations, 3:199–219., 2023. [CrossRef]
  42. E. G. Haug. CMB, Hawking, Planck, and Hubble scale relations consistent with recent quantization of general relativity theory. International Journal of Theoretical Physics, 63(57), 2024. [CrossRef]
  43. H. Reissner. Über die eigengravitation des elektrischen feldes nach der Einsteinschen theorie. Annalen der Physics, 355:106, 1916. [CrossRef]
  44. G. Nordström. On the energy of the gravitation field in Einstein’s theory. Koninklijke Nederlandsche Akademie van Wetenschappen Proceedings, 20:1238, 1918.
  45. E. G. Haug and G. Spavieri. Mass-Charge Metric in Curved Spacetime. International Journal of Theoretical Physics, 4(2):62, 2023. [CrossRef]
  46. E. G. Haug. Collision space-time: Unified quantum gravity. Physics Essays, 33(1):46, 2020b. [CrossRef]
  47. E. G. Haug. Unified quantum gravity field equation describing the universe from the smallest to the cosmological scales. Physics Essays, 35:61, 2022. [CrossRef]
  48. L. Motz. Gauge invariance and the quantization of mass (of gravitational charge). Nuov Cim B 12, 12:239, 1972. [CrossRef]
  49. L. Motz and J. Epstein. The gravitational charge 1/2ℏc as a unifying principle in physics. Il Nuovo Cimento, 51(1), 1979. [CrossRef]
  50. O. J. Pike, F. Mackenroth, E. G. Hill, and Rose S. J. A photon–photon collider in a vacuum hohlraum. Nature Photonics, 8, 2014. [CrossRef]
  51. A. Einstein and N. Rosen. The particle problem in the general theory of relativity. Phys. Rev., (48), 1935. URL https://journals.aps.org/pr/pdf/10.1103/PhysRev.48.73.
  52. A. Zee. Einstein gravity in a nutshell. Princeton University Press, Princeton, NJ, 2013.
  53. E. Sorkin and T. Piran. Formation and evaporation of charged black holes. Physical Review D, 63:124024, 2001. [CrossRef]
  54. E. G. Haug and G. Spavieri. The micro black hole cellular battery: The ultimate limits of battery energy density. Journal of High Energy Density Physics, 51:1, 2024. [CrossRef]
  55. A. Edery and B. Constantineau. Extremal black holes, gravitational entropy and nonstationary metric fields. Classical and Quantum Gravity, Volume 28, Number 4, 28:045003, 2011. [CrossRef]
  56. E. G. Haug. The extremal universe exact solution from einstein’s field equation gives the cosmological constant directly. Journal of High Energy Physics, Gravitation and Cosmology, 10:386, 2024. [CrossRef]
  57. E. H.. Kennard. Zur quantenmechanik einfacher bewegungstypen.
  58. W. Heisenberg. The Physical Principles of Quantum Theory. Translated by Carl Eckart and F. C. Hoyt, Dover Publications, University of Chicago, 1930.
  59. E. G. Haug. The ultimate limits of the relativistic rocket equation. The Planck photon rocket. Acta Astronautica, 136, 2017. [CrossRef]
  60. O. C. Stoica. The geometry of singularities and the black hole information paradox. Journal of Physics: Conference Series, 626:012028, 2015. [CrossRef]
  61. E. G. Haug and G. Spavieri. The Planck mass density radius of the universe. European Journal of Applied Physics, 4(2):40, 2022. [CrossRef]
  62. A. Einstein, B. Podolsky, and N. Rosen. Can quantum mechanical description of physical reality be considered complete? Phys. Rev., (47):777–780, 1935. [CrossRef]
  63. J. S. Bell. On the Einstein Podolsky Rosen paradox. Physics, 1, 1964. [CrossRef]
  64. M. Clover. Bell’s theorem: a new derivation that preserves Heisenberg and locality. arXiv:quant-ph/0409058, 2005.
  65. M. Clover. Bell’s theorem: A critique. arXiv, 2005. [CrossRef]
  66. E.S. Paulo, R.G.G. Amorim, and S.C. Ulho. On the hilbert space in quantum gravity. Universe, 8:413,2022. [CrossRef]
  67. S. C. Ulho. On the quantization of the charge–mass ratio. General Relativity and Gravitation, 49:3, 2016. [CrossRef]
  68. A. Macías and A. Camacho. On the incompatibility between quantum theory and general relativity. General Relativity and Gravitation, 663:15, 2008. [CrossRef]
1
See also Kennard [57].
Preprints 118495 g001
Figure 1. 
Figure 1. 
Preprints 118495 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated