Preprint
Article
Use of Digital Technology in Integrated Mathematics Education
This version is not peer-reviewed.
Submitted:
04 June 2024
Posted:
06 June 2024
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
The use of didactic and interactive materials is essential in generating interest among students and teachers in utilizing mathematical models and digital technologies for the educational process. These materials create a dynamic and engaging learning environment that promotes a deeper understanding of complex concepts and fosters a passion for learning. Additionally, integrating interactive materials into pilot courses can assist teachers in better assessing student learning and adjusting the teaching strategies accordingly and the teachers can receive valuable insights into students' strengths and weaknesses, allowing them to provide targeted support and intervention when needed. In this context, the purpose of this paper is to introduce an approach for solving mathematics problems embedded in technical scenarios within the defense and security fields with the aid of digital technology. In this way, students can visualize abstract concepts, experiment with different scenarios, and receive instant feedback on their understanding. This paper helps to reinforce key concepts and enhance problem-solving skills, sparking curiosity, creativity, and encouraging active participation and collaboration. Throughout the development of this proposal, good practices are adopted, and advice for improvement is collected while having a wide range of users, giving feedback, discussions, and testing (pilot) short-term learning/teaching/training activities.
Keywords:
student/teacher aid tools; digital technology; predictive and learning analytics; digital mathematics
Subject:
Computer Science and Mathematics - Applied Mathematics1. Introduction
Due to advancements in technology and teaching methods, education has become more diverse, accessible, and personalized. The emergence of online learning platforms, interactive tools, and virtual classrooms has revolutionized how students can engage with and absorb information. There is also a greater emphasis on holistic education, including social-emotional learning, critical thinking skills, and cultural competency. Nevertheless, besides memorizing facts and figures, education now aims to equip students with the necessary skills to succeed in a fast-changing world.
In light of the events of recent years, online teaching and learning have become a new reality [1]. The circumstances created by the COVID-19 pandemic have forced schools to adapt and find alternatives to the usual face-to-face teaching. Thus, most classes were conducted online [2], and the Internet and online platforms facilitated new learning experiences across various fields of study [3]. On the one hand, digital readiness has rapidly become a unique opportunity for students with fewer possibilities to participate in the learning process and expands their chances of success in the labor market. On the other hand, teachers in certain disciplines face challenges when using digital technologies.
While the teaching community has demonstrated a remarkable ability to innovate and embrace new approaches, many challenges, such as insufficient connectivity and digital infrastructure, have also become evident [4].
Although technology continues to be an unknown for many, the consensus among teachers is that it has proven to be an invaluable and indispensable tool, providing essential support in the educational process. Through collaborative efforts, students and teachers showed the efficacy of technology in conjunction with the sciences while also showing how passion and a desire for growth can make a significant impact.
In higher education, the process of adapting courses to the digital environment has presented specific challenges that may impede the effectiveness of the didactic act. However, universities have demonstrated their ability to overcome these obstacles and successfully adapt their courses to the online environment [5].
Progress has been made in online teaching and learning due to the availability of online tools and the determination of teachers and students. As a result, students are encouraged to learn and work independently, which is particularly beneficial during difficult and tense times [6]. This behavior supports the continuation of online learning and meets the real needs of students.
An essential component in the transfer of knowledge and competencies within higher education, whether in military academies or civilian universities, is Mathematics. During practical experience, a gap has been identified between teaching and learning mathematics [7]. Various courses such as Algebra, Calculus, or Special Mathematics are based on mathematical models. However, in many mathematics-related courses, a lack of connection between the required knowledge and its application has been identified [8].
Mathematics, a critical field in technical sciences, presents particular difficulties. It is often too abstract and theoretical. Moreover, presenting real-world applications or use cases to students can sometimes be an issue if the teachers have no practical expertise in that specific field. By using a dedicated digital solution and having the appropriate skills, teachers and specialists can better explain how mathematical models, theorems, and other concepts apply to real-world phenomena. This approach strengthens the connection between mathematics and its practical applications in the related fields.
Teaching mathematics in a contemporary digital environment seems to be inadequate among young audiences [9]. The traditional method of teaching mathematics involves presenting problems and formulas on a whiteboard using an ink marker, which is familiar and intuitive to teachers [10]. However, this approach is not easily replicable in an online teaching environment. Furthermore, the lack of skills in writing mathematical formulas presents a significant challenge. To provide adequate and engaging examples, careful consideration and selection of the best software for teaching and learning is crucial.
Since there are challenges in presenting equations, theorems, and concepts, the scope of this paper is to enhance interest in studying mathematics, to make mathematics problems and applications more understandable and accessible via the power of digital tools, and to develop students’ problem-solving skills by leveraging specialized digital solutions.
The paper begins with an analysis of a series of surveys of best practices among partner institutions and stakeholders [11]. These surveys provide a list of directions in defense and security education. Further, the paper introduces a scenario-based methodology for teaching mathematics on specific scenarios within the defense and security fields and it explores how various digital environments can be combined. In this context, a mixed approach between the traditional method of teaching mathematics and the alternative method based on digital technology appears to be the optimal solution. The expected outcomes of the mixed approach include improved performance in math-related tasks, better problem-solving skills, and enhanced analytical thinking among students. As a result, there is a need for teaching competencies in digital applied mathematics and for students to be able to work on problems within a digital environment. There are also limited opportunities for students and teachers from different disciplines to communicate using a common language, which could be digital (software) mathematics.
2. Theoretical Framework
The use of digital technology can enhance integrated mathematics education by providing interactive and engaging tools for learning and practice. Below are several ways in which digital technology can be integrated into mathematics education:
- -
- Online resources: Students can access a variety of online resources, such as video tutorials, interactive simulations, and practice exercises, to supplement their classroom learning.
- -
- Educational apps: There are numerous applications available that allow students to gain mathematics skills in a fun and engaging way [12]. These apps offer instant feedback and help students monitor their progress.
A series of surveys were conducted to analyze students’ digital competencies in mathematics learning for technical systems within the defense and security fields before and during the COVID-19 pandemic. The research was carried out on the territory of the European Union in several research centers and universities. The survey involved 1.047 students in the security and defense fields, subdivided by age and gender, as presented in Figure 1. Most of the students had different countries of residence than the countries of study. Additionally, a few students were from France, Greece, Hungary, Lithuania, Portugal, and Slovakia as countries of residence and study. Furthermore, some students were originally from countries outside the European Union, such as Afghanistan, Saudi Arabia, Burkina Faso, Cameroon, Mali, Moldova, Montenegro, and Senegal.
The majority of the students studied in the institutions taking part in the DIGICODE project [11] but with some exceptions and variability, especially for Romanian students. While most students were pursuing military and/or engineering studies, others were enrolled in diverse fields such as economics, information technology, health, humanities, languages, law, or social sciences. Their distribution concerning the course year shows that many students attended from the third year of their bachelor’s, thus ensuring the capability to confront the pre-pandemic situation with those during and after COVID-19 for most of the sample. The ratio between military students (cadets) and civilian students was about 4:1 (Figure 2).
According to the analyzed surveys, the majority of students had a positive perception of their digital skills. Only a small percentage (5.6%) rated their skills as “low” or “very low,” while a moderate portion (22%) expressed caution (Figure 3). Further, the technology and software used for learning resulted in a balanced distribution of satisfaction levels: 27.3% of students reported strong satisfaction, while 28.9% expressed being essentially unsatisfied. In education, technology serves as the means and not the end goal (which is learning), making methodology even more important. Therefore, proper attention must be given to technological aspects, such as the software used.
Most students also recognized the importance of technology in learning during pandemic times, with only 14.2% of them deeming it only “slightly” important or even “not at all” important. They are generally aware of the pivotal role it played during COVID-19, which is also possessed in remote learning apart from that emergency.
Students privileged “independence and self-direction” on the one hand and “collaboration and teamwork” on the other, putting a bit more aside “critical thinking and problem-solving skills” and “creativity and innovation,” probably because they perceive the two as less relevant to their learning (Figure 3).
3. Methods
Education in defense and security fields is crucial for preparing individuals to address evolving challenges in the public sector, private sector, or non-governmental organizations. By equipping learners with practical skills and knowledge, this type of education helps strengthen our collective ability to protect against threats and safeguard the well-being of communities and nations.
It is important to ensure a balance between different learning methods, with an emphasis on understanding the content, critical selection, focused attention, organizing concepts logically, and training and practicing skills with broad applicability.
Consequently, this paper proposes a methodology for teaching specific scenarios or use cases belonging to a technical discipline with the aid of digital technology. The proposed methodology for solving a scenario with a mixed approach is organized into three parts. The first part offers a background description of the analyzed scenario, the subsequent part provides the mathematical modeling of the scenario, and the final part involves a software implementation of the scenario in a virtual environment (Figure 4).
By using the software implementation part, the proposed methodology can offer graphical capabilities, allowing students to visualize mathematical concepts more intuitively and offering them a deeper understanding of abstract mathematical ideas. Since the computer algebra system can perform calculations much faster than traditional pen-and-paper methods, the students can spend less time on routine calculations and more time understanding and analyzing mathematical concepts. Another argument for using a software implementation is that it can help reduce calculation errors by providing step-by-step solutions and allowing students to check their work more efficiently, which can also build confidence in students’ mathematical abilities. Finally, a software implementation can handle mathematical problems that may need to be more complex and time-consuming to solve by hand. This allows students to tackle more challenging problems and develop problem-solving skills. In conclusion, a digital tool is valuable because it can enhance mathematics learning by increasing efficiency, providing visual representations, reducing errors, enabling exploration and experimentation, and facilitating complex problem-solving.
With regards to the engineering side of mathematics, a series of areas of interest (Figure 5) have been identified, in which scenario-based teaching can be a great tool for learning mathematics as it provides real-world context to mathematical concepts. By incorporating scenarios into learning, the trainees can understand how mathematical concepts are applied in practical situations, making mathematics more engaging and relevant, as they can see the value and purpose of their acquired skills, which also fosters a sense of accomplishment, creating a positive learning environment. In addition, scenario-based learning can also be an effective way to develop critical thinking and problem-solving skills. By working through scenarios and making decisions, the trainees must analyze information, evaluate options, and consider the potential consequences of their choices, which can lead to a deeper understanding of the subject matter and enhance retention.
Moreover, scenario-based learning can also be a valuable tool for professors looking to create engaging and effective learning experiences for their students. By presenting students with realistic scenarios that require them to apply their knowledge and skills, this approach can enhance learning outcomes and prepare students for real-world challenges.
Regarding a mathematical scenario, one way to handle and learn from it is to analyze the problem and understand the concepts involved carefully. This may require breaking down the problem into smaller parts, identifying essential information, and applying appropriate mathematical principles to solve it. Practicing problem-solving techniques, such as working through similar scenarios, seeking help or guidance from teachers or peers, and persisting even when faced with challenges, is also essential and helpful. Additionally, reflecting on the solution and considering different approaches or strategies can reinforce learning and enhance understanding of the mathematical concepts involved in the scenario.
Going further, a series of mathematical-based scenarios specific to defense and security fields are presented and solved through the mixed approach, composed of 2 methods: the clean mathematical method and the software-based implementation method.
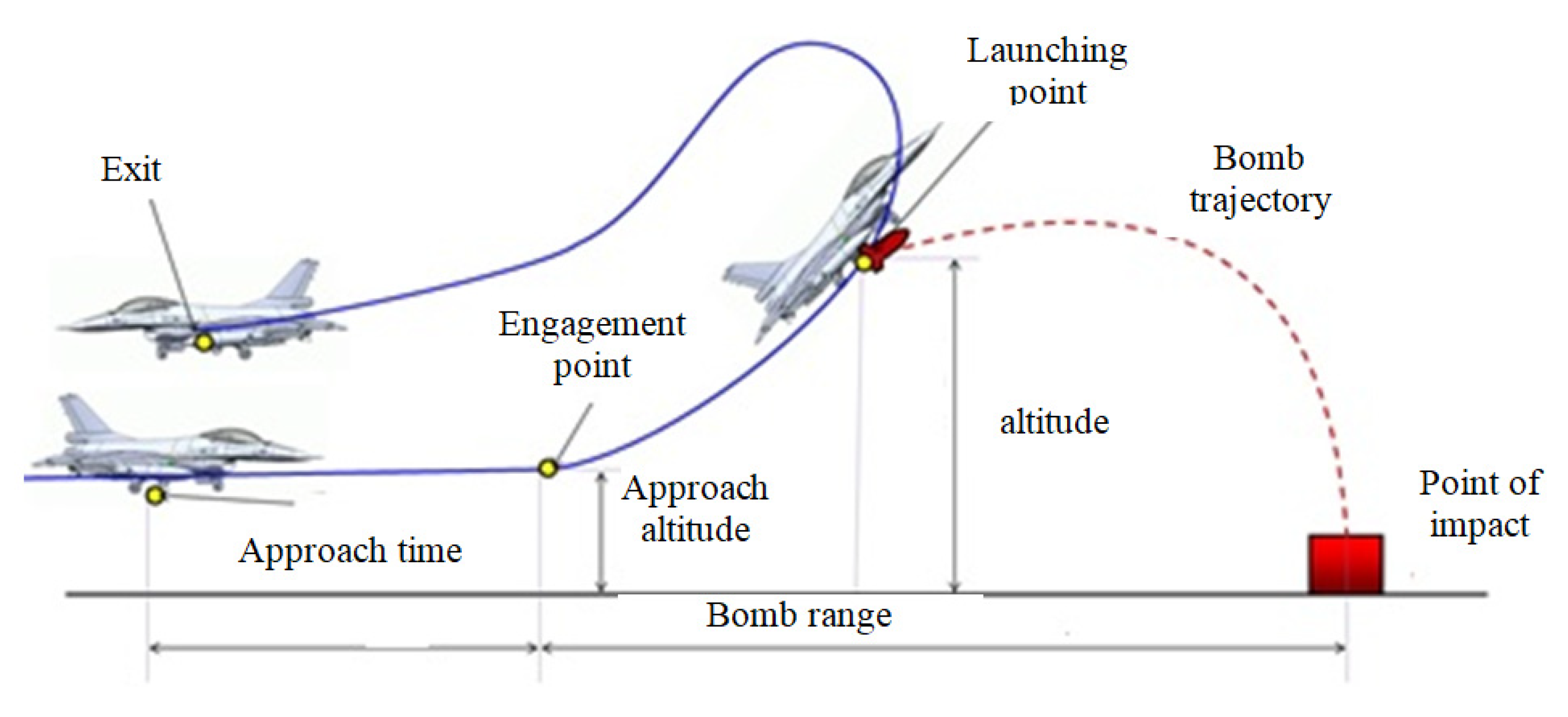
Scenario 1 - Automatic analysis of the motion of an aerospace vehicle
The flight of an aerospace vehicle (projectile, bomb, and missile) is a process based on a mathematical model with a high complexity [13]. A series of very important but, at the same time, very complex problems are represented by the determination of the behavior of the aerospace vehicle during the flight, the determination of the flight performances, and the determination of its general motion, considering the whole system of forces and moments acting on it. In the scenario of general motion in actual flight conditions, a series of difficulties appear, making it difficult to draw up the differential equations of motion in a form that is as complete as possible.
Figure 6.
Delivery of the aviation bombs.
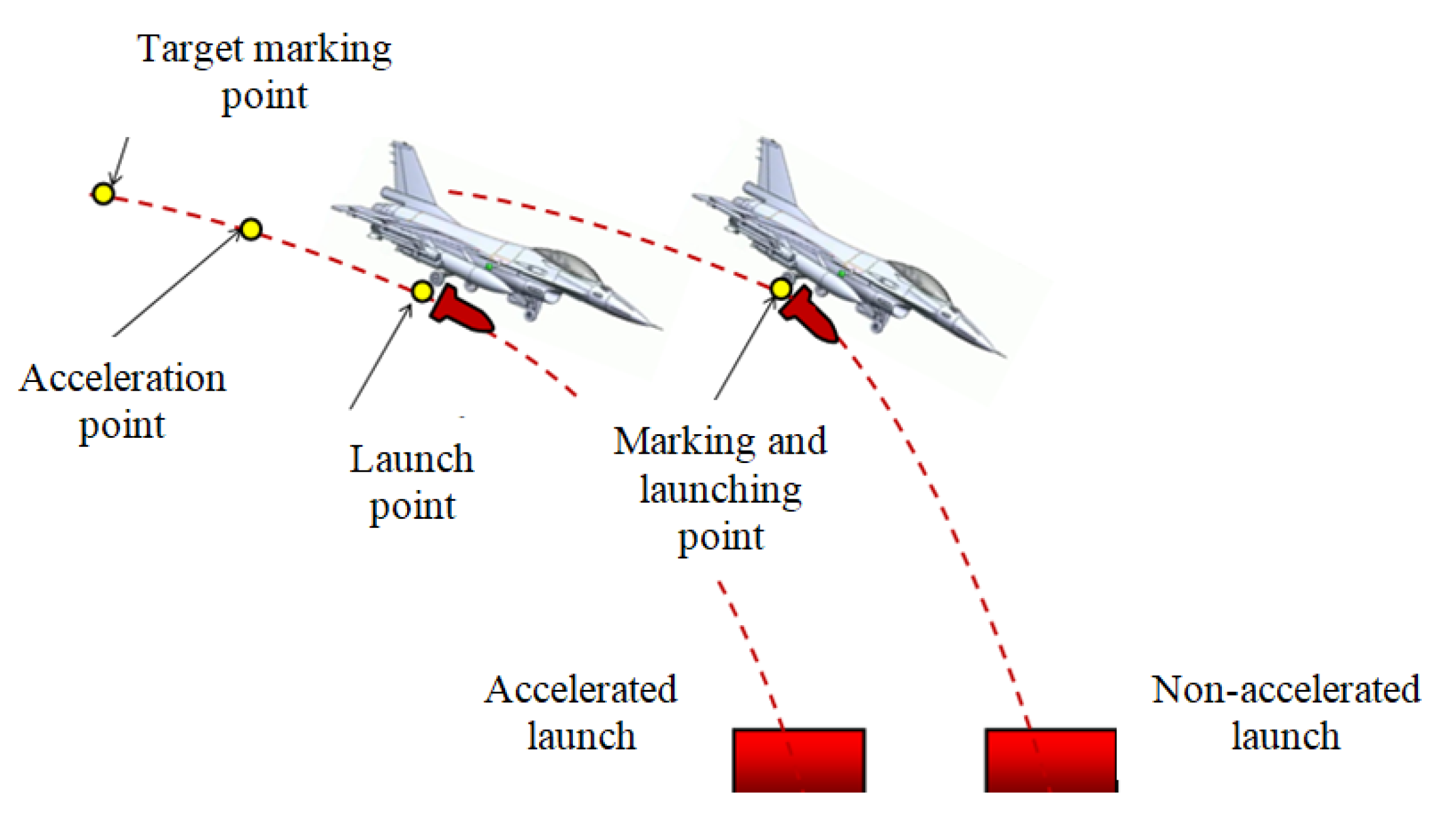
Therefore, the analysis of the motion of an aerospace vehicle is done by adopting a series of hypotheses designed to simplify the physical model of the phenomenon according to the purpose and reduce the complexity of the equations that describe the phenomenon. Thus, in the case of small incidences, the hypothesis of the independence between the longitudinal motion (and the motion from the launching plane) and the lateral motion is admitted.
Figure 7.
Launching lift aviation bombs.
Mathematical solution for Scenario 1
Trajectory calculation can be a difficult task, depending on the level of knowledge of the firing context and the level of detail implemented in the mathematical model of the trajectory. As in any modeling process of a physical phenomenon, in the case of trajectories, there will also be a compromise between the complexity of the model and the ease of obtaining results, as well as in terms of the agreement of numerical results with experimental ones. Reasonable results can be obtained with the help of simple trajectory models, especially to illustrate the application of the principles of the weapons use planning process. Subsequently, the model must be completed and developed to obtain accurate results that are as close as possible to reality.
Figure 8.
Launch of lateral impulse aviation bombs.
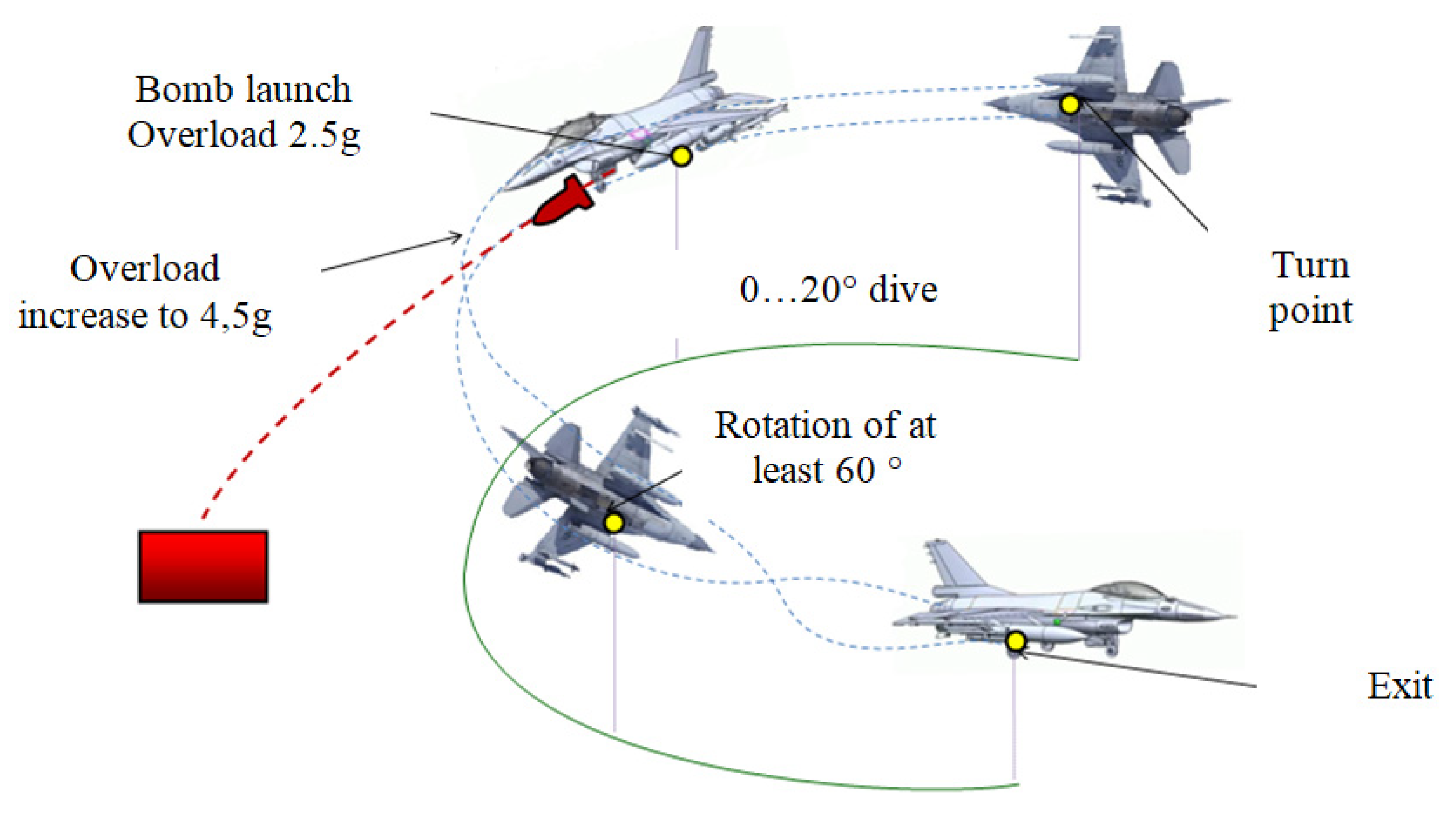
In the trajectory models presented below, the equations describing the motion of the projectile/bomb are developed based on the hypothesis that the motions in the vertical and horizontal planes are independent. Also, the components of the initial velocity in the two directions are considered to be known.
The coordinate axis systems, as well as the variables that define the position of the aerospace vehicle and its state of motion, are chosen to not limit the generality of the studied problem and lead to equations that, after appropriate transformations and simplifications, can be integrated by known methods [13].
The general laws of mechanics will be used to establish the general dynamic equations that express the motion of an aerospace vehicle’s center of mass and its motion around the center of mass. Also, the aerospace vehicle is considered to be a body with six degrees of freedom and absolute rigidity, thus excluding the influence of the structure’s elasticity.
Defining the and vectors through the components on the axes of the mobile system connected to the body of the aerospace vehicle, the vector equation of motion of the center of mass of the aerospace vehicle will be [14]:
where represent the mass of the aerospace vehicle, is the local (relative) derivative of velocity, and is the result of external forces acting on the aerospace vehicle.
Projecting the vector Equation (1) on the axes of the velocity-related system , the scalar equations of motion of the center of mass are obtained [15]. These equations are:
Considering the aerospace vehicle to be a symmetrical body of revolution (geometrically and in terms of mass distribution) [16] about the longitudinal axis , it turns out that the axes , and are the main axes of inertia, and the kinetic moment of the vehicle concerning the center of mass, , will be written:
where are the unit vectors of the axes , and .
The vector equation of motion of the aerospace vehicle around the center of mass will be written as below:
where is the local (relative) derivative of the kinetic moment?
Due to the longitudinal symmetry of the aerospace vehicle [17], the moments of inertia relative to the transverse axes will be equal, .
Projecting the vector Equation (6) on the axes of the system, the scalar equations of motion of the aerospace vehicle around the centre of mass are obtained:
Based on the above, considering an aerospace vehicle with its own fast rotational motion having the center of pressure in front of the center of mass and using the following notations for simplification of writing [18]:
The following forces and moment indices are taken into account [19]:
- -
- Force of gravity:
- -
- Thrust:
- -
- Drag force:
- -
- Lift force:
- -
- Lateral force:
- -
- Additional lift due to the pitching motion:
- -
- Additional lateral force due to yawing motion:
- -
- Main aerodynamic moment (pitching moment):
- -
- Yawing aerodynamic moment:
- -
- Axial moment:
- -
- Additional axial moment due to rolling motion:
- -
- Damping moment due to gas jet:
Using the forces and moments presented above, the following equations are obtained that describe the motion of the aerospace vehicle:
To complete the system of Equations (28)–(33) a series of kinematic ratios are introduced:
The Equations (28)–(29) form a system of 12 nonlinear first-order differential equations, representing the complete system of equations of general motion of the aerospace vehicle, which provides by integration time variation of parameters (unknown functions) , , , , , , , , , , and which determines both the motion of the center of mass and the motion around the center of mass of the studied aerospace vehicle [20].
The digital solution for Scenario 1
The spatial motion around the center of gravity is currently analyzed on short trajectory arcs, without taking into account the overall variation of the center of gravity velocity vector. The calculation of the trajectory is made considering the corresponding variations of the incidence angle and the drift angle, obtained by the separate study of the longitudinal motion and of the lateral motion; most of the time, however, to determine the trajectory, the well-known hypothesis of ballistic motion is admitted, without incidence, thus disregarding the effect of lift, the variation of which is conditioned, through incidence, by the motion around the center of gravity. To determine the trajectory a solution is to use Matlab [21] for modeling the equations of the trajectory [22].
Figure 9.
Matlab computing software for determining the trajectory.
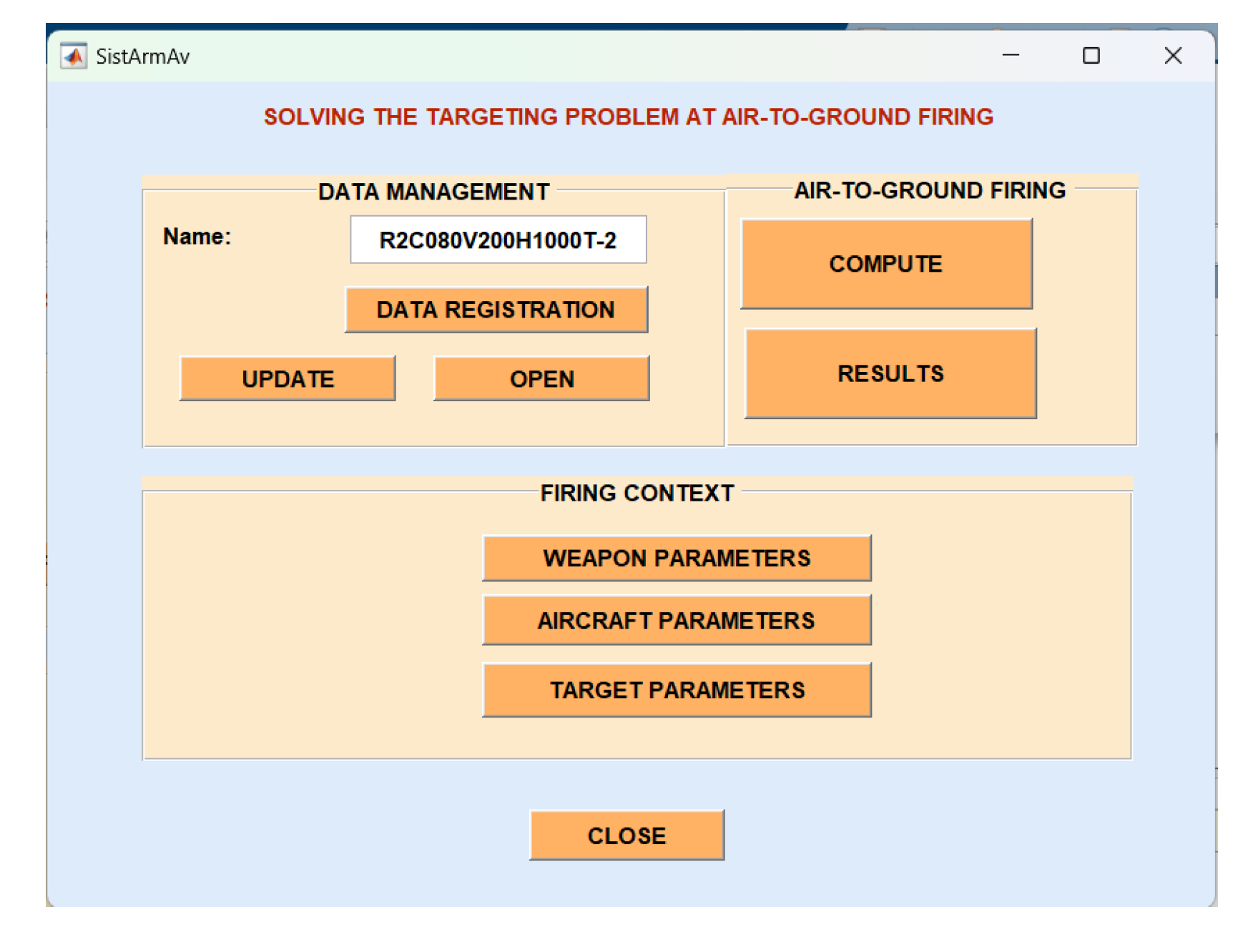
The interface developed in Matlab [23] offers the possibility of choosing different characteristics of the projectiles and the possibility of defining the parameters of aircraft. These parameters can be defined in terms of their physical characteristics, performance capabilities, and operating limitations (Figure 10). Establishing these parameters is important for ensuring safe and efficient operations, as well as for regulatory compliance and maintenance planning (Figure 11).
Figure 12, Figure 13 and Figure 14 present the evolution of the main parameters that describe the motion during the trajectory.
In 40 seconds, the aerospace vehicle travels a horizontal distance of about 9 km. During this period, the speed first increases (corresponding to the active period when the rocket engine is running). This period is followed by the active period, where, up to 25 s, the speed decreases due to the effect of the drag force, after which it shows a slight increase as an effect of the gravitational acceleration. The angle of incidence (as the difference between and ) has an oscillating damped evolution. The damping of the oscillation takes place in about 1 s (Figure 15). The pitch angular speed has an evolution similar to that of the angle of incidence.
Scenario 2 - Determine the velocity of a projectile using a ballistic pendulum
A ballistic pendulum is a device used to measure the speed of a projectile by capturing it in a pendulum and measuring the height to which the pendulum swings. It is often used in physics labs to demonstrate the principles of conservation of momentum and energy. The ballistic pendulum works by allowing a projectile to strike and become embedded in a large block of wood or other material attached to a pendulum. The change in momentum of the projectile can then be used to calculate its initial velocity.
Mathematical solution for Scenario 2
The bullet is fired into the pendulum, which then moves upwards a certain distance and at an angle that will be measured. From the height reached by the pendulum, its potential energy can be calculated. This potential energy is equal to the kinetic energy of the pendulum at the bottom of the swing immediately after the collision with the bullet. The bullet is fired into the pendulum, which then moves upwards a certain distance and at an angle that will be measured.
The approximate method assumes that the pendulum and the ball act together as a point mass. This method does not take into account the rotational inertia. It is slightly faster and easier than the second method but not as precise.
The potential energy of the pendulum at the final position can be calculated as bellow:
where M is the combined mass of the pendulum and the ball, g is the gravitational acceleration, and ∆h represents the change in height. Further, height is computed:
The momentum of the pendulum after the collision is:
Which is substituted into the previous equation to obtain:
Solving this equation for the momentum of the pendulum, we get:
This momentum is equal to the momentum of the ball before the collision:
Equating these two equations and replacing KE with the known potential energy, is obtained as it follows:
The digital solution for Scenario 2
To validate the result obtained through the analytical method, Simulink and SolidWorks environments were used to simulate the behavior of the ballistic pendulum.
SolidWorks allows students to design and create 3D models for their projects and assignments. The Student Edition of SolidWorks is a valuable tool for students studying engineering, design, and other related fields, allowing them to gain hands-on experience with a leading CAD software program. Using SolidWorks, students can design and analyze complex mechanical systems, structures, and components. They can learn how to apply engineering principles to solve real-world problems and optimize designs (Figure 16).
Using SolidWorks for teaching students can enhance their technical skills, creativity, problem-solving abilities, and collaboration skills, preparing them for careers in engineering, design, and other related fields.
The weight of the bullet and the weight of the projectile resulted from the calculation automatically performed by the Solidworks program (Figure 17).
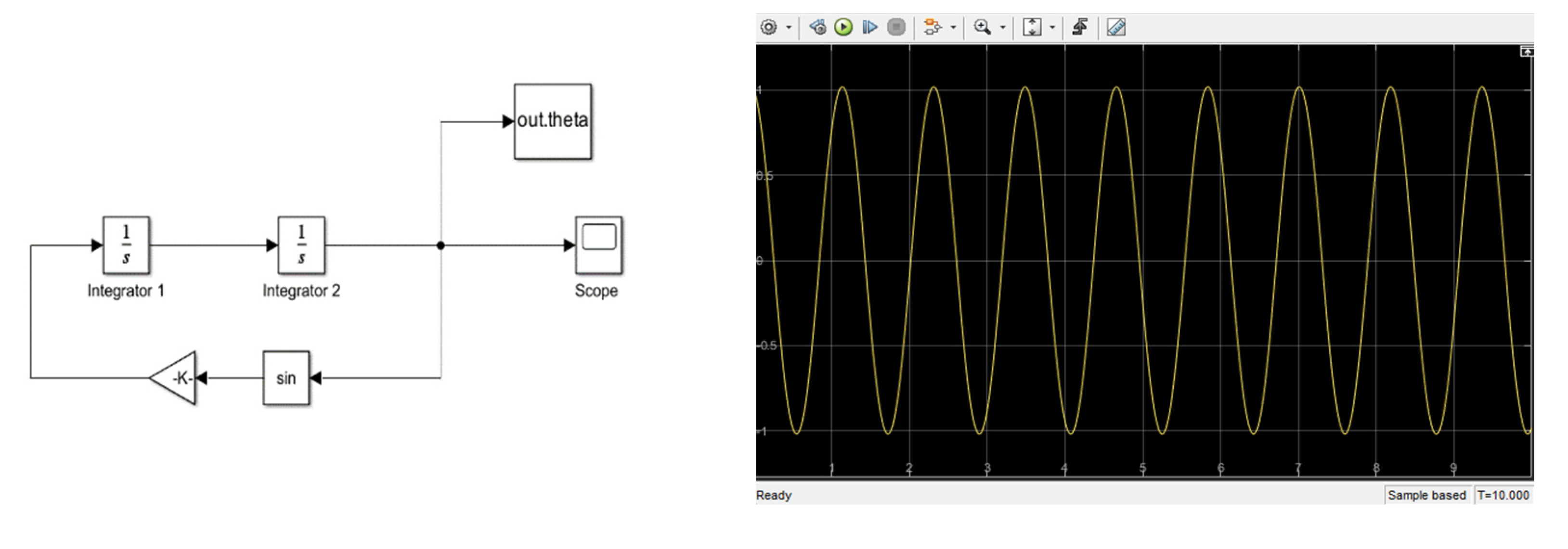
As an optional extension of the MATLAB software package, SIMULINK provides a graphical user interface for modeling and simulating dynamic systems. It provides access to various block diagrams, which allows quick and straightforward system modeling, simulating, and deployment without the need to write any simulation code.
Simulink’s interface is easy to use and understand, making it a great tool for students new to the field. It also provides access to a wide range of built-in blocks and libraries for students to create complex models without writing code from scratch. Additionally, Simulink has built-in support for real-time simulation and hardware-in-the-loop testing, allowing students to interface their models with physical systems for hands-on learning experiences (Figure 18). Overall, Simulink is a valuable tool for students looking to gain practical experience in the field of engineering and learn through hands-on experimentation.
Scenario 3 - Automatic people detection within an established perimeter
The proposed scenario for detecting people is integrated into a video surveillance system that performs real-time perimeter monitoring around a firing range and generates an alarm when people are detected inside this monitored area. Thus, the role of this system is to trigger the alarm to notify the human decision-maker responsible for the monitored area. When the alarm is triggered, the system presents the scene where a person was detected.
Mathematical solution for Scenario 3
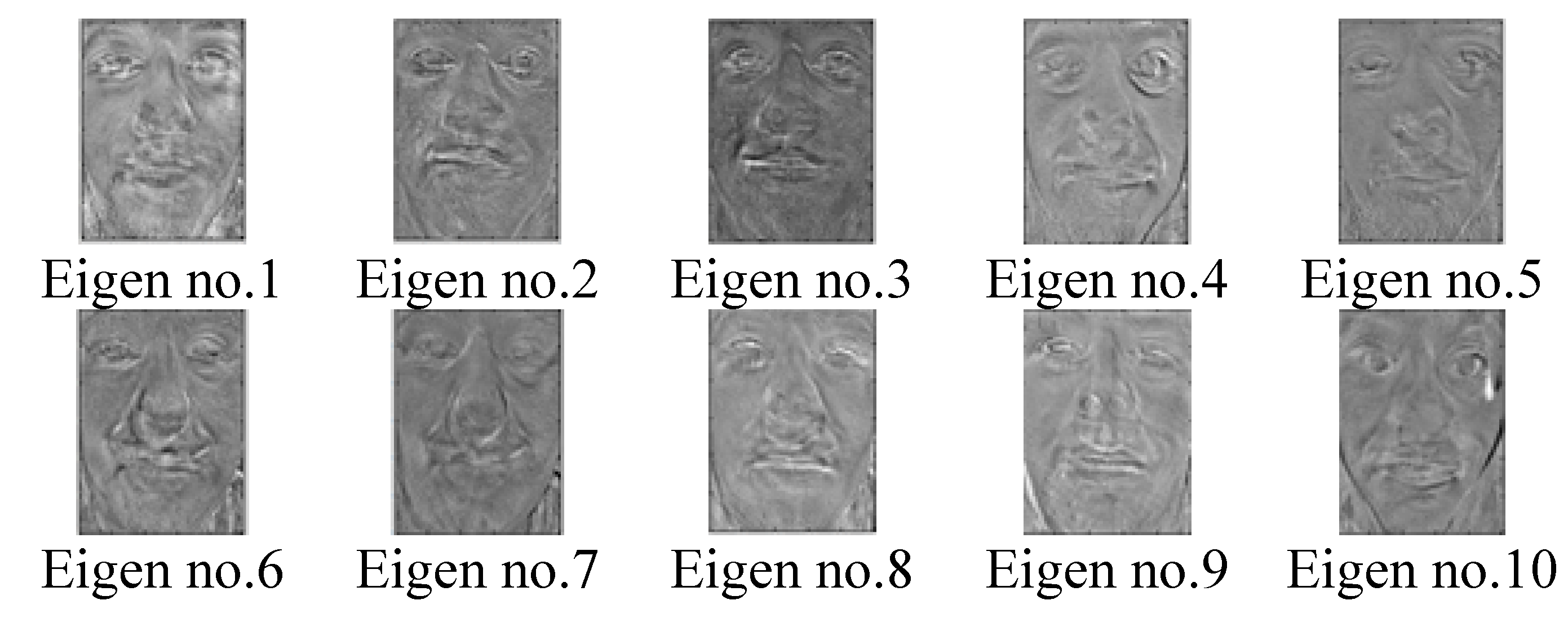
The people detection will be done through facial recognition, using Principal Component Analysis (PCA) [24], by reducing the number of variables for representing a face, a technique used in computer vision and pattern recognition. PCA is a method that reduces the dimensionality of data while retaining most of the variation in the data set.
In facial recognition, PCA is used to extract the most important features from a facial image [25]. These features are then compared to a database of known faces to determine a match. The process involves capturing an image of a person’s face, identifying key facial features such as eyes, nose, and mouth, and then using PCA to extract the most relevant information from these characteristics. Through this method, the system can accurately detect and identify individuals in real-time, making it a valuable tool for security and surveillance applications. Additionally, PCA can also help improve the speed and accuracy of facial recognition systems, making them more reliable and efficient in various environments [26].
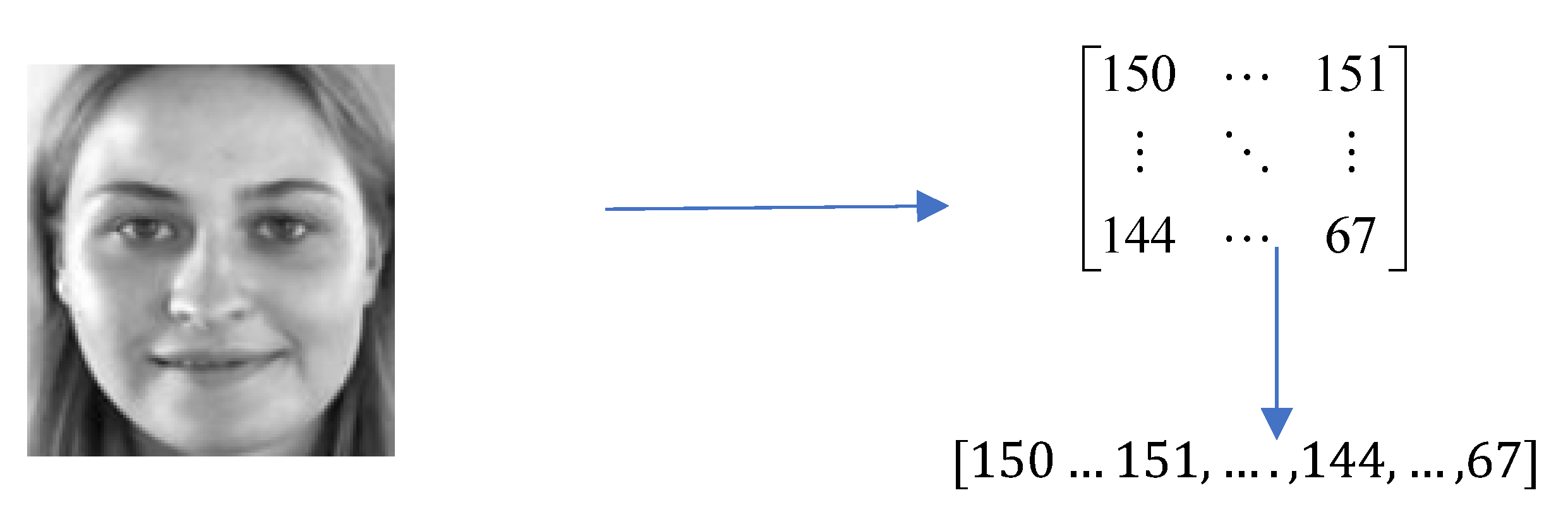
We will consider that we have several images of the same size available for several people in a database, and we can have one or more poses for the same person. We will consider that the person’s face is centered in any facial image. Thus, each pixel of an image can be considered a variable, and a face is thus represented as a vector of P variables (where P represents the number of pixels). Given the considerable number of variables involved, we can reduce the complexity of comparing two faces by approximating a face through a smaller number of variables. An image of n pixels can thus be considered a point in image space (n-dimensional space).
The image matrix turns into a line vector such that the line vector where , … represents the grey level of pixels. The vector is formed by transforming the image into a line vector; thus, for a 128x128 image, we will have the size n = 16384 (16K):
Figure 19.
Steps of image transformation [27].
Figure 19.
Steps of image transformation [27].
Given N images, each of n pixels, the entire set of images can be represented as a matrix D, where each image represents a line:
The first step of the PCA method is to move the origin of the data to the middle of the n variables, an operation that is equivalent to subtracting the average value of the variables in each image. In our case, the average image (average face) is calculated by averaging over all the columns of the matrix D. This average face is to be extracted from each image of the data set D. The obtained difference matrix is denoted by U. In the considered example, the average is:
The first step in determining the principal components of the D matrix is to calculate the covariance matrix of the U matrix. It can be easily seen that, due to the extraction of the average value from each column of the D matrix, the covariance matrix C can be expressed as:
The rank of the matrix U is max N, so there are max N nonzero eigenvalues for then it can be calculated the eigenvectors of the transposed matrix. Thus, if ϕ is an eigenvector of the transposed matrix, then is an eigenvector of the initial matrix The eigenvalues are the same as for the transposed matrix. Following the normalization of the eigenvectors, their set forms a basis in the space:
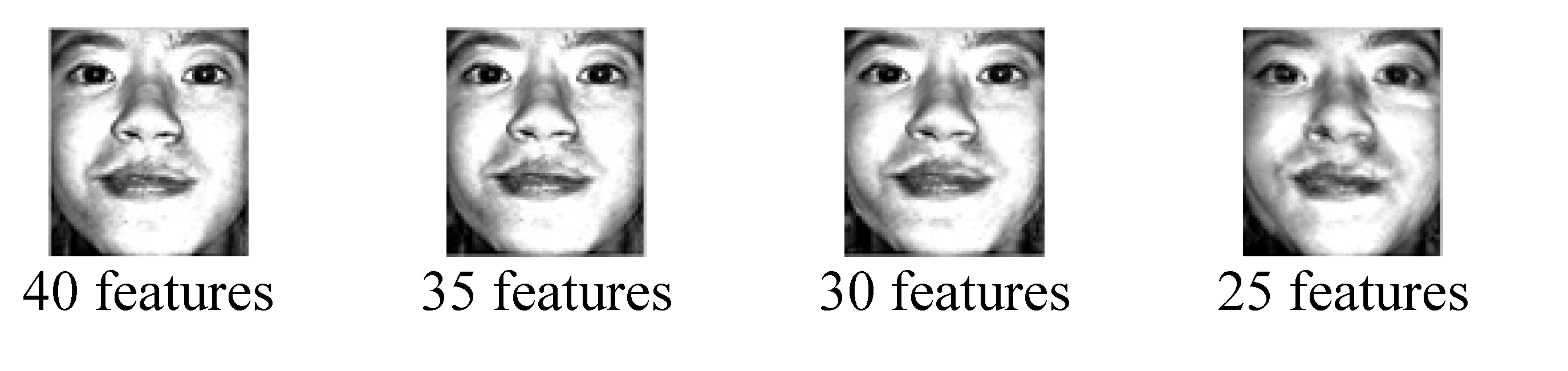
We will now express all the lines of the U matrix (the former faces from which the average face was subtracted) in the base formed by the eigenvectors. Each eigenvector corresponds to an eigenvalue that represents the variation of the U matrix data along the corresponding eigenvector. Therefore, instead of using all N eigenvectors, we will only use M representatives that correspond to the largest M eigenvalues. Typically, for the facial recognition problem, the value of M is quite small (between 20 and 50). Thus, we will express the lines of the matrix U in the M-dimensional basis formed by the M vectors chosen:
Each line will have M coefficients that are obtained by projecting that line (scalar product) onto each of the chosen vectors. Thus, an image is expressed in the new space of the chosen vectors (the space of the principal components) as follows:
We thus managed to reduce the image representation from an n-dimensional space (n=128x128) to an M-dimensional space. The original image can also be roughly reconstructed from the M vectors by applying the inverse transformation:
It can be shown that by choosing the M eigenvectors corresponding to the largest M eigenvalues, the squared error of the reconstruction of the matrix D is minimized (any other vectors lead to a larger error). The choice of M, however, depends on the data set D; for this, an M value can be chosen that allows a reconstruction superior to a given Peak signal-to-noise ratio (PSNR), or the following method can be adopted. Given that the sum of the eigenvalues is equal to the sum of the variations in the N directions given by the eigenvectors, one can calculate the percentage of “variation” preserved by choosing K principal vectors as follows:
K is chosen so that the percentage is at least equal to a given threshold (e.g., 95%).
Given a test image , the average image will be subtracted from it and then it will be expressed (projected) into the M-dimensional basis of the chosen eigenvectors, resulting in a set of coefficients . The closest image to the test image will be determined by evaluating a distance (e.g., Euclidean [28] or Mahalanobis [29]) between the W vector and the W’ vectors calculated for the other images of the database.
Euclidean distance between and is
Mahalanobis distance between and is
where represents the variation along the component with index i, and in the present case, it is equal to the eigenvalue corresponding to the eigenvector .
In a real system, an acceptance threshold T is chosen for the minimum distance between the test image and the database image. If the calculated distance is lower than T, then the person is recognized, and otherwise not. For this purpose, two types of errors are defined as follows:
- False positives (false alarms): a person in the database is not recognized.
- False negatives (missed alarms): an external person is recognized by the system.
The digital solution for Scenario 3
Python is a great programming language for education because it can be used for a wide range of applications, including web development, data analysis, artificial intelligence, and more. This makes it a versatile language that can be applied to many different fields. Programming in Python encourages students to think logically and analytically to solve problems. This can help develop critical thinking skills that are valuable in many different fields. Python is also widely used in the tech industry, meaning that students who learn Python in an educational setting will have valuable skills that can help them in their future careers.
Overall, Python is a great language for education because of its simplicity, versatility, and the skills it helps students develop. That is why Python was the digital environment in which face recognition was implemented. The digital solution was developed and tested on The Olivetti faces dataset.
The algorithm assumed the following steps:
- ✓
- Database initialization: Each entry in the dataset is composed of a person’s image, a vector of labels (a number is associated with each person), and a vector of strings (the name of the person appearing in the image).
- ✓
- Split into a training and a test set by keeping 25% of the data for testing.
- ✓
- Compute a PCA (eigenfaces) on the face dataset (treated as an unlabeled dataset): unsupervised feature extraction/dimensionality reduction.
- ✓
- ✓
- ✓
- The reduced vectors are introduced into a machine learning algorithm (support vector machines or logistic regression).
- ✓
- Quantitative evaluation of the model quality on the test set.
The first classification algorithm tried is SVM. At the end, the classification report is displayed as a report of some performance parameters that are automatically computed for a predictive analysis.
Figure 21.
Results obtained with SVM.

Repeat the previous experiment for the logistic regression algorithm.
Figure 22.
Results obtained with logistic regression.

4. Discussion
Digital technology offers students access to virtual manipulatives such as geometric shapes, number lines, and graphs, allowing them to explore mathematical concepts interactively and practically. When instructing mathematics to students within the defense and security education system, it is essential to utilize real-world applications and practical examples. This article proposes first to ensure that students have a strong foundation in fundamental mathematics topics such as algebra, calculus, and trigonometry, then connect these topics with engineering subjects relevant to their field. This approach aims to demonstrate the practical relevance of mathematics, fostering critical thinking and analytical skills in students when addressing mathematical challenges.
The future of education methodology is expected to be more personalized, flexible, and technology-driven, with a greater emphasis on skill development and lifelong learning. In this direction, virtual reality and augmented reality can create immersive learning experiences, enabling students to engage and interact with concepts more effectively [30]. In this sense, Augmented Reality (AR) holds the potential to transform the way mathematics is taught and learned by offering an interactive and engaging platform for students to explore mathematical concepts in a more immersive way. By combining virtual elements with the real world, augmented reality can enrich the learning experience and assist students in comprehending and visualizing abstract mathematical equations and theories. One approach to integrating augmented reality into mathematics education is through interactive apps and tools that allow students to manipulate virtual objects and visualize mathematical concepts in 3D [31]. For instance, students can use AR apps to graph equations, explore geometric shapes, or visualize vectors and matrices in a more tangible manner. This hands-on approach can aid students in gaining a better understanding of complex mathematical concepts by providing a more intuitive and interactive learning experience [32].
Artificial Intelligence (AI) learning tools are also a promising direction as they can provide personalized feedback and support to students, enabling them to progress at their own pace and identify areas where they may require additional assistance. Some of the key benefits of using AI learning tools include personalized learning [33], accessibility, immediate feedback, data-driven insights, and engaging [34] and interactive learning experiences [35]. Moreover, AI-driven learning tools have the potential to revolutionize education by providing personalized, accessible, and efficacious learning experiences that can assist students to attain their academic objectives and thrive in the rapidly evolving digital landscape.
Further, using game elements in education can also increase student engagement and motivation, making learning more enjoyable and effective [36]. Numerous educational games and applications can help students practice their math skills in a fun and interactive way. These resources serve as a valuable supplement to traditional classroom instruction, reinforcing fundamental concepts and affording students additional practice opportunities [37]. By framing mathematical lessons as quests or adventures, students can perceive themselves as embarking on a mission to conquer problems and attain specific objectives. This approach can make learning more exciting and immersive as students confront and surmount challenges and obstacles in their quest to enhance their mathematical abilities. Students are also encouraged to work collectively to solve problems and engage in friendly competition through mathematical games, which can foster a sense of camaraderie and teamwork while motivating students to strive for improvement [38].
Blockchain technology also has the potential to establish secure and transparent credentialing systems, such as digital diplomas and certificates, streamlining the process of verifying academic achievements. Additionally, it can securely store and track students’ progress and achievements in math concepts and exercises [39], enabling educators to assess individual performance and provide targeted support. Furthermore, this technology can facilitate peer-to-peer learning by allowing students to share and verify math solutions with each other, promoting collaboration and the exchange of ideas within the classroom [40].
Personalized learning platforms are also a valuable option because they use adaptive technology to track students’ progress and provide recommendations for additional resources based on their performance [41]. They can also utilize personalized learning algorithms to propose courses aligned with students’ interests and objectives [42].
Internet of Things devices can be used to create smart classrooms that are equipped with sensors and connected devices, allowing for more efficient and interactive learning environments [43].
3D printing technology offers the capability to create physical models and prototypes of concepts, allowing students to visualize and understand complex ideas tangibly. Visualization of geometric shapes such as cubes, spheres, and pyramids enhances students’ understanding of their properties and interrelations [44]. Creating manipulatives for hands-on learning, such as fraction bars, number lines, and base ten blocks, can help students better understand mathematical concepts. Furthermore, exploring complex equations and functions allows students to visually explore how changing variables affect the shape of the graph [45]. Customizing learning materials can be used to create custom learning materials tailored to individual students’ needs. For example, teachers can create tactile graphics for visually impaired students or custom puzzles for students who learn best through hands-on activities [46]. In this way, 3D printing technology also holds the potential to revolutionize mathematics education by making abstract concepts more concrete and compelling for students.
Overall, digital technology advancements are anticipated to revolutionize mathematics education by making it more personalized, interactive, collaborative, and data-driven. These transformations have the potential to improve student engagement, comprehension, and performance, ultimately leading to enhanced outcomes for students in mathematics education.
5. Conclusions
Analyzing the curricula of certain partner institutions [11], students in defense and security fields can greatly benefit from an innovative, practical-oriented approach to learning math. This teaching methodology can be beneficial for students in 1st and 2nd grade. Furthermore, educators in the defense and security sector can enhance their skills and competencies through this innovative approach to teaching applied math.
The use of digital tools for learning mathematics can be applied algorithmically, provided that it is not considered contradictory, as algorithmization should not be opposed to heuristic learning. Therefore, it is important to develop an algorithm, namely a unique sequence of operations, starting from a heuristic search process for solutions, so that heuristic and algorithmic approaches are not in opposition but in a dynamic and continuous relationship.
The general aim of the applied research described in this paper is to achieve the optimization of teaching and learning mathematics in higher education within the defense and security fields through the predominant use of problematization both as the main didactic method and as a teaching procedure within other teaching methods.
Author Contributions
A-L.C. conceived the paper, studied the scenarios for learning, and edited the paper C-E.M. studied the scenarios for learning, selected the references, and approved the final version. All authors have read and agreed to the published version of the manuscript.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
The results presented in this article were obtained with the support of the European Commission in the framework of the Erasmus+ Programme, KA220-HED - Cooperation partnerships in higher education, Contract no. 2023-1-BG01-KA220-HED-000156664.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zied Bahroun, Chiraz Anane , Vian Ahmed and Andrew Zacca, “Transforming Education: A Comprehensive Review of Generative Artificial Intelligence in Educational Settings through Bibliometric and Content Analysis,” Sustainability, vol. 15, no. 17, 2023.
- M. S. Alabdulaziz, “COVID-19 and the use of digital technology in mathematics,” Education and Information Technologies, vol. 26, p. 7609–7633, 2021.
- Alice Barana , Marina Marchisio and Matteo Sacchet , “Interactive Feedback for Learning Mathematics in a Digital Learning Environment,” Education Sciences, vol. 11, no. 6, 2021.
- Alison Clark-Wilson, Ornella Robutti and Mike Thomas, “Teaching with digital technology,” ZDM Mathematics Education, vol. 52, p. 1223–1242, 2020.
- Emad Mushtaha, Saleh Abu Dabous, Imad Alsyouf, Amr Ahmed and Naglaa Raafat Abdraboh, “The challenges and opportunities of online learning and teaching at engineering and theoretical colleges during the pandemic,” Ain Shams Engineering Journal, vol. 13, no. 6.
- Manuel Caeiro-Rodríguez, Mario Manso-Vázquez, Fernando A. Mikic-Fonte, Martín Llamas-Nistal, Manuel J. Fernández-Iglesias, Hariklia Tsalapatas, Olivier Heidmann, Carlos Vaz de Carvalho, Triinu Jesmin, Jaanus Terasmaa and Lene Tolstrup Sørensen, “Teaching Soft Skills in Engineering Education: An European Perspective,” IEEE Access, vol. 9, pp. 29222-29242, 2021.
- Mamurova Feruza Islomovna, Ruzieva Dilnoza Isomjonovna, Mamurov Islom, Khodjaeva Nodira Sharifovn and Mamurova Dilfuza Islomovna, “Designing the methodical system of the teaching process of computer graphics for the specialty of engineer-builder,” The journal of contemporary issues in business and government, vol. 27, no. 4, pp. 165-169, 2021.
- B. Kaur, “Mathematics Classroom Studies: Multiple Lenses and Perspectives,” in Proceedings of the 13th International Congress on Mathematical Education, 2017.
- Kai Wang , Guo-Yuan Sang , Lan-Zi Huang, Shi-Hua Li and Jian-Wen Guo , “The Effectiveness of Educational Robots in Improving Learning Outcomes: A Meta-Analysis,” Sustainability, vol. 15, no. 4637, 2023.
- Arturo Fuentes-Cabrera, María Elena Parra-González, Jesús López-Belmonte and Adrián Segura-Robles, “Learning Mathematics with Emerging Methodologies—The Escape Room as a Case Study,” Mathematics, vol. 8, no. 1586, 2020.
- [Online]. Available: https://digicodeproject.eu/.
- [Online]. Available: https://www.mathlearningcenter.org/apps.
- M. R. Driels, Weaponeering. Conventional Weapon System Effectiveness, AIAA Education Series, 2004.
- Nezar Sahbon and Michał Welcer, “Comparison of Two Aerodynamic Models for Projectile Trajectory Simulation,” Aerospace, vol. 11, no. 189, 2024.
- Scott M. Murman and Michael J. Aftosmis, “Cartesian-Grid Simulations of a Canard-Controlled Missile with a Spinning Tail,” AIAA-2003-3670, 21st AIAA Applied Aerodynamics Conference.
- Simon Box, Christopher M. Bishop and H.E.M. Hunt, “A Stochastic Six-Degree-of-Freedom Flight Simulator for Passively Controlled High Power Rockets,” Journal of Aerospace Engineering, vol. 24, no. 1.
- D F Lawden, “Calculations of Singular Extremal Rocket Trajectories,” Journal of Guidance, Control, and Dynamics, vol. 15, pp. 1361-1365, 1992.
- Moldoveanu C.E., Șomoiag P., Buono S. and Ben-Lisa A., “Researches concerning the aerodynamic and ballistic performances of an unguided missile,” in Proceedings of the 2nd Edition of The New Challenges in Aerospace Sciences International Conference, NCAS 2015,, Bucharest.
- Moldoveanu Cristian-Emil , Maximilien DU Parc and Somoiag Pamfil , “Aspects Regarding the Unguided Rocket Effectiveness,” Brasov, 2017.
- Wickramasinghe N.K., A. Harada and Y. Miyazawa, “Flight trajectory optimization for an efficient air transportation system,” in The 28th International Congress of the Aeronautical Sciences, Brisbane, Australia, 2012.
- Won Y. Yang, Young K. Choi, Jaekwon Kim, Man Cheol Kim, H. Jin Kim and Taeho Im, Engineering Mathematics with MATLAB, CRC Press, 2008.
- Dahalan, Md Nizam, Su Vin Cent and Mohd Shariff Ammoo, “Development of a computer program for rocket aerodynmic coefficients estimation,” Jurnal Mekanikal, vol. 28, pp. 28-43, 2009.
- D. K. Chaturvedi, Modeling and Simulation of Systems Using MATLAB and Simulink, CRC Press, 2010.
- Jolliffe, Ian T. and Cadima, Jorge, “Principal component analysis: a review and recent developments,” Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 374, no. 2065, 2016.
- Olufisayo S. Ekundayo and Serestina Viriri, “Facial Expression Recognition: A Review of Trends and Techniques,” Ieee Access , vol. 9, pp. 136944-136973, 2021.
- I. Michael Revina and W.R. Sam Emmanuel, “A Survey on Human Face Expression Recognition Techniques,” Journal of King Saud University - Computer and Information Sciences, vol. 33, no. 6, pp. 619-628, 2021.
- [Online]. Available: https://www.bioid.com/face-database/.
- K. J. Smith, Precalculus: A Functional Approach to Graphing and Problem Solving, Jones & Bartlett Publishers, 2013.
- P. Chandra, “On the generalised distance in statistics,” Proceedings of the National Institute of Sciences of India, vol. 2, no. 1, pp. 49-55, 1936.
- Timur Koparan, Hakan Dinar, Ezgi Taylan Koparan and Zeliha Sema Haldan , “Integrating augmented reality into mathematics teaching and learning and examining its effectiveness,” Thinking Skills and Creativity, no. 101245, 2023.
- Joel Weijia Lai and Kang Hao Cheong, “Adoption of Virtual and Augmented Reality for Mathematics Education: A Scoping Review,” IEEE Access , vol. 10, pp. 13693-13703, 2022.
- Awais Khan Jumani, Waqas Ahmed Siddique, Asif Ali Laghari, Ahad Abro and Abdullah Ayub Khan, “Virtual Reality and Augmented Reality for Education,” in Multimedia Computing Systems and Virtual Reality, CRC Press, 2022.
- Tira Nur Fitria, “Artificial Intelligence (AI) in education: Using AI Tools for teaching and learning process,” in Prosiding Seminar Nasional & Call for Paper STIE AAS, 2021.
- Sayed Fayaz Ahmad, Mohd. Khairil Rahmat, Muhammad Shujaat Mubarik, Muhammad Mansoor Alam and Syed Irfan Hyder, “Artificial Intelligence and Its Role in Education,” Sustainability, vol. 13, no. 22, 2021.
- Yousef Wardat, Mohammad A. Tashtoush, Rommel AlAli and Adeeb M. Jarrah, “ChatGPT: A revolutionary tool for teaching and learning mathematics,” Eurasia Journal of Mathematics, Science and Technology Education, vol. 19, no. 7, 2023.
- Noor Amalina Nisa Ariffin, Nik Muhammad Farhan Hakim Nik Badrul Alam, Azimah Suparlan, Nazirah Ramli and Yusharina Yusof, “Effectiveness of gamification in teaching and learning mathematics,” Journal on Mathematics Education, vol. 13, no. 1, pp. 173-190, 2022.
- Dorit Alt, “Assessing the benefits of gamification in mathematics for student gameful experience and gaming motivation,” Computers & Education, vol. 200, no. 104806, 2023.
- Hamidah Lukman, Nur Agustiani and Ana Setiani, “Gamification of Mathematics Teaching Materials: Its Validity, Practicality and Effectiveness,” International Journal of Emerging Technologies in Learning (iJET), vol. 18, no. 20, pp. 4-22, 2023.
- Patrick Ocheja, Brendan Flanagan, Hiroaki Ogata and Solomon Sunday Oyelere, “Visualization of education blockchain data: trends and challenges,” Interactive Learning Environments, vol. 31, no. 9, pp. 5970-5994, 2023.
- Goran Bjelobaba, Ana Savić, Teodora Tošić , Ivana Stefanović and Bojan Kocić, “Collaborative Learning Supported by Blockchain Technology as a Model for Improving the Educational Process,” Sustainability, vol. 15, no. 4780, 2023.
- Elena V. Soboleva , Khurshidzhon K. Zhumakulov, Kayumzhon P. Umurkulov, Gasanguseyn I. Ibragimov , Lyubov V. Kochneva and Maria O. Timofeeva, “Developing a Personalised Learning Model Based on Interactive Novels to Improve the Quality of Mathematics Education,” Eurasia Journal of Mathematics, Science and Technology Education, vol. 18, no. 2, 2022.
- Khanh-Phuong Thai, Hee Jin Bang and Linlin Li, “Accelerating Early Math Learning with Research-Based Personalized Learning Games: A Cluster Randomized Controlled Trial,” Journal of Research on Educational Effectiveness, vol. 15, no. 1, pp. 28-51, 2022.
- Khaula Zeeshan, Timo Hämäläinen and Pekka Neittaanmäki, “Internet of Things for Sustainable Smart Education: An Overview,” Sustainability, vol. 14, no. 7, 2022.
- Heather Ann Pearson and Adam Kenneth Dubé, “3D printing as an educational technology: theoretical perspectives, learning outcomes, and recommendations for practice,” Education and Information Technologies, pp. 1-28, 2022.
- Davy Tsz Kit Ng, Ming Fung Tsui and Manwai Yuen, “Exploring the use of 3D printing in mathematics education: A scoping review,” Asian Journal for Mathematics Education, vol. 1, no. 3, 2022.
- Kuen-Yi Lina, Shao-Chuan Lub, Hsien-Hsien Hsiao, Chia-Pin Kaod and P. John Williamse , “Developing student imagination and career interest through a STEM project using 3D printing with repetitive modeling,” Interactive Learning Environments, vol. 31, no. 5, pp. 2884-2898, 2023.
- Emad Mushtaha, Saleh Abu Dabous, Imad Alsyouf, Amr Ahmed and Naglaa Raafat Abdraboh, The challenges and opportunities of online learning and teaching at engineering and theoretical colleges during the pandemic, 101770 ed., vol. 13, Ain Shams Engineering Journal, 2022.
- Stella Timotheou, Ourania Miliou, Yiannis Dimitriadis, Sara Villagrá Sobrino, Nikoleta Giannoutsou, Romina Cachia, Alejandra Martínez Monés and Andri Ioannou, “Impacts of digital technologies on education and factors infuencing schools’ digital capacity and transformation: A literature review,” Education and Information Technologies, vol. 28, p. 6695–6726, 2023.
Figure 1.
Distribution of students over age, gender, and country of residence and study [11].
Figure 1.
Distribution of students over age, gender, and country of residence and study [11].
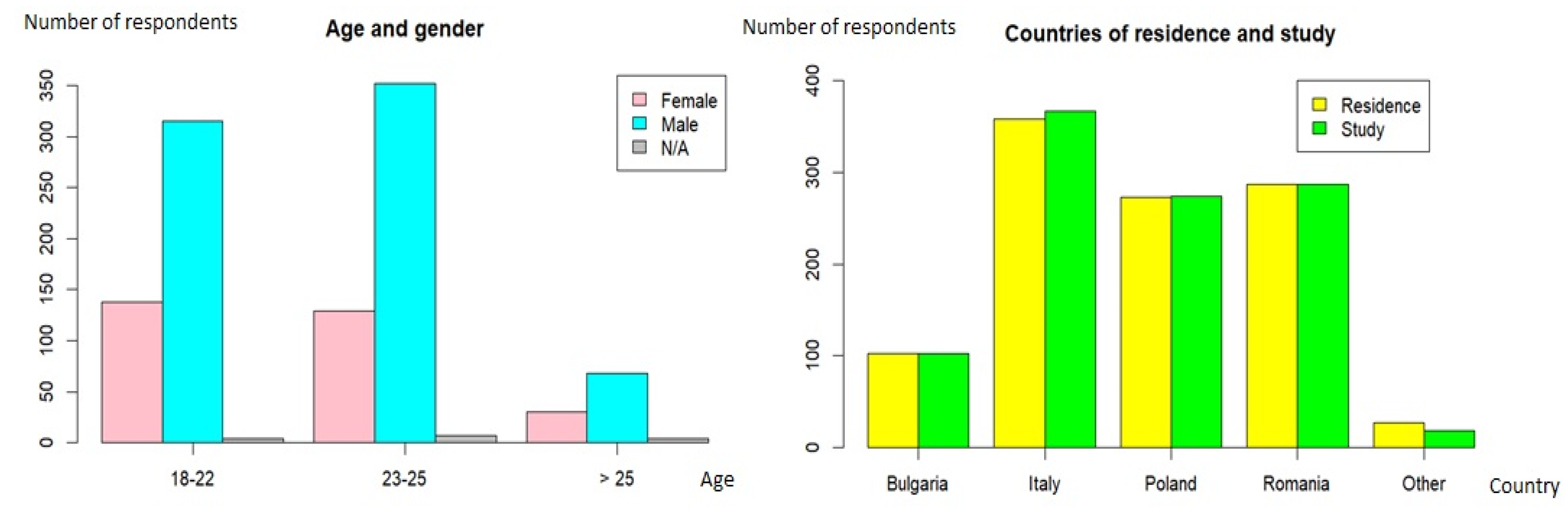
Figure 2.
Various distributions of students [11].
Figure 2.
Various distributions of students [11].
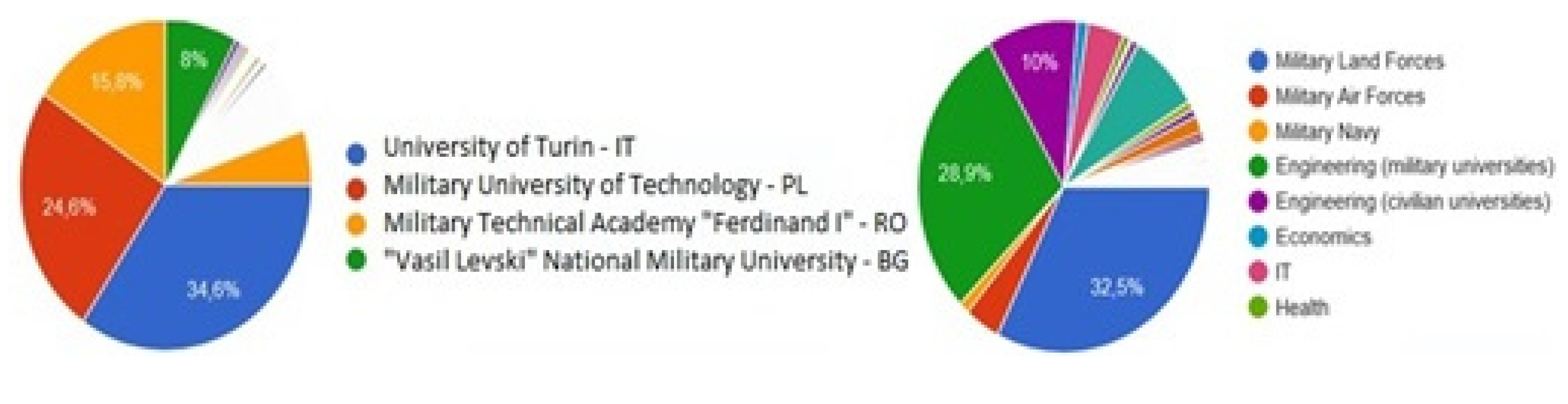
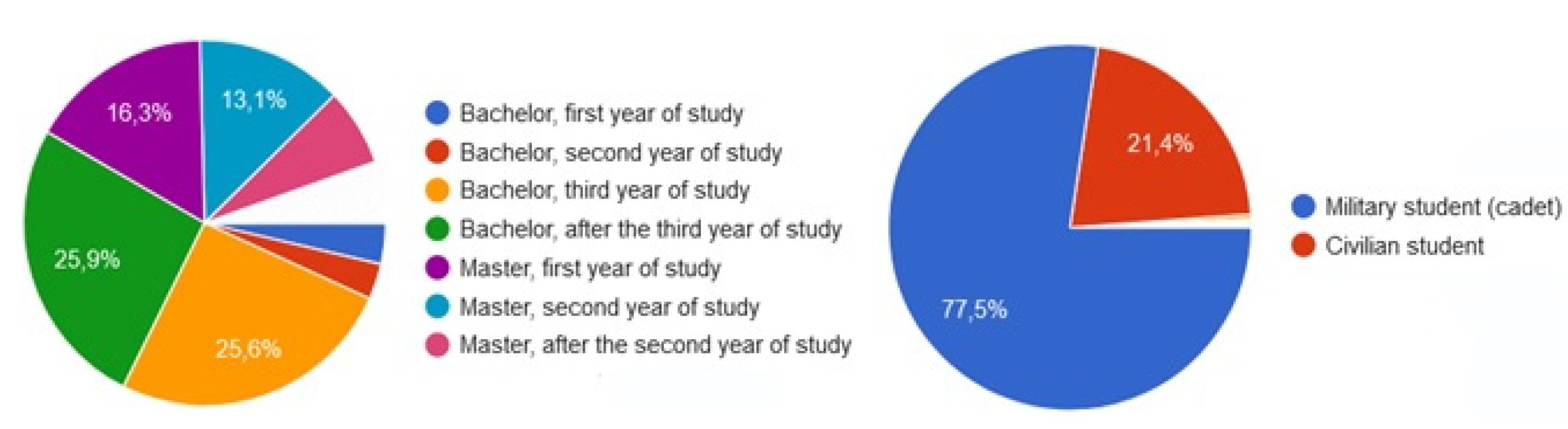
Figure 3.
Various answers report [11].
Figure 3.
Various answers report [11].
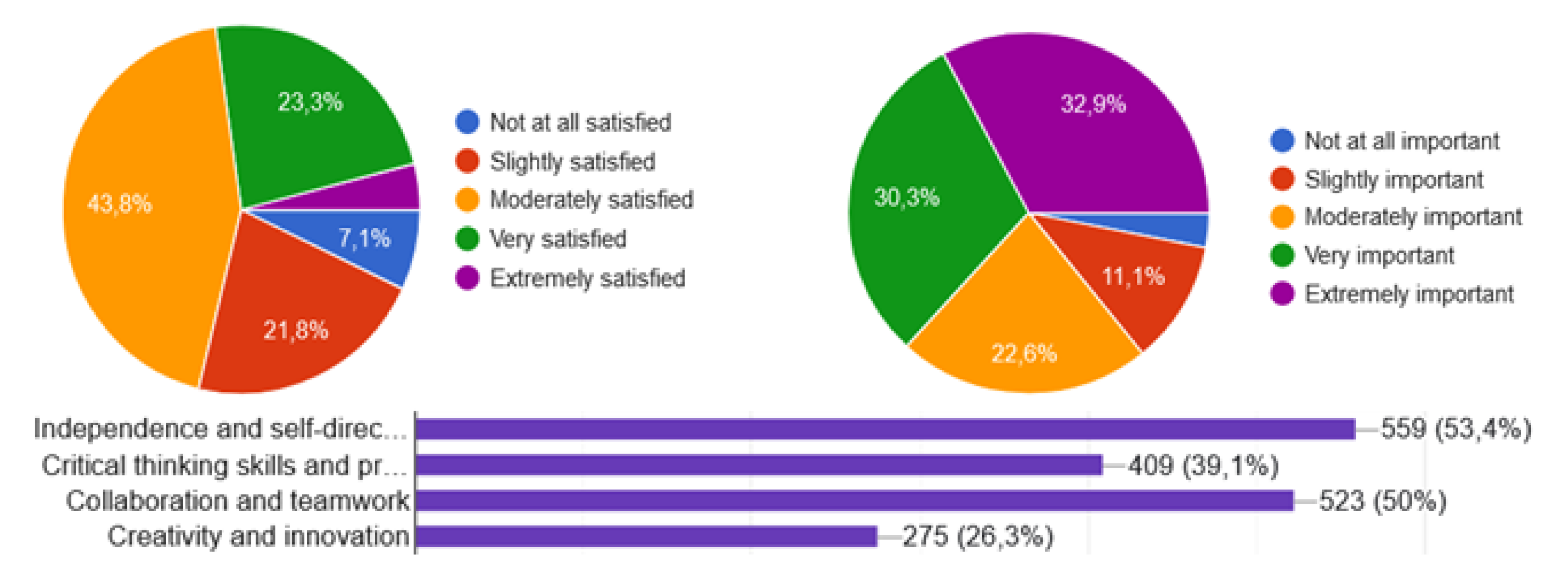
Figure 4.
The basic structure of the proposed methodology.
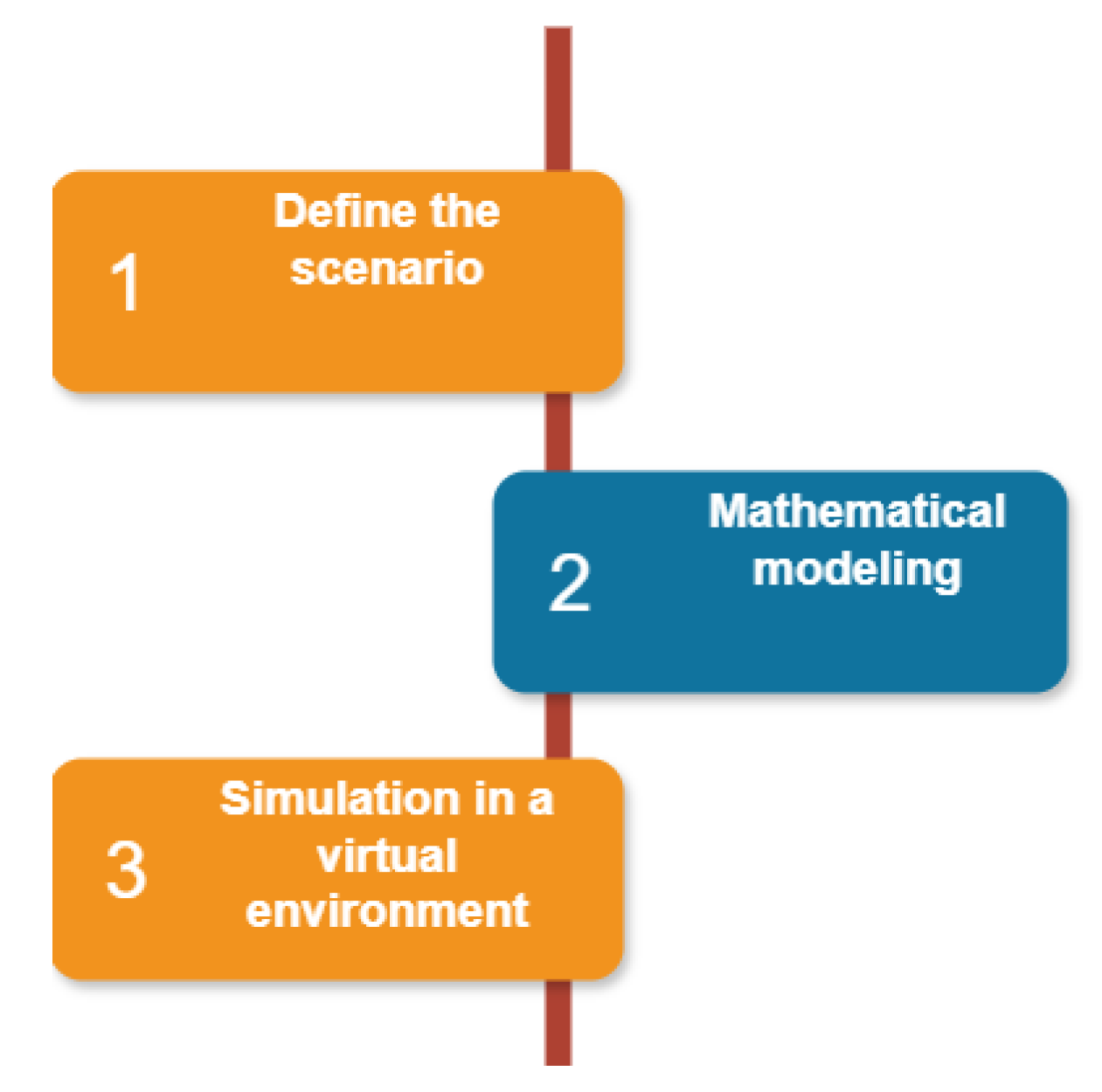
Figure 5.
Lists of mathematics topics.
Figure 10.
a) Matlab computing software for determining the trajectory; b) Matlab software menu for defining the parameters of the firing aircraft and the target on which the firing is performed.
Figure 10.
a) Matlab computing software for determining the trajectory; b) Matlab software menu for defining the parameters of the firing aircraft and the target on which the firing is performed.
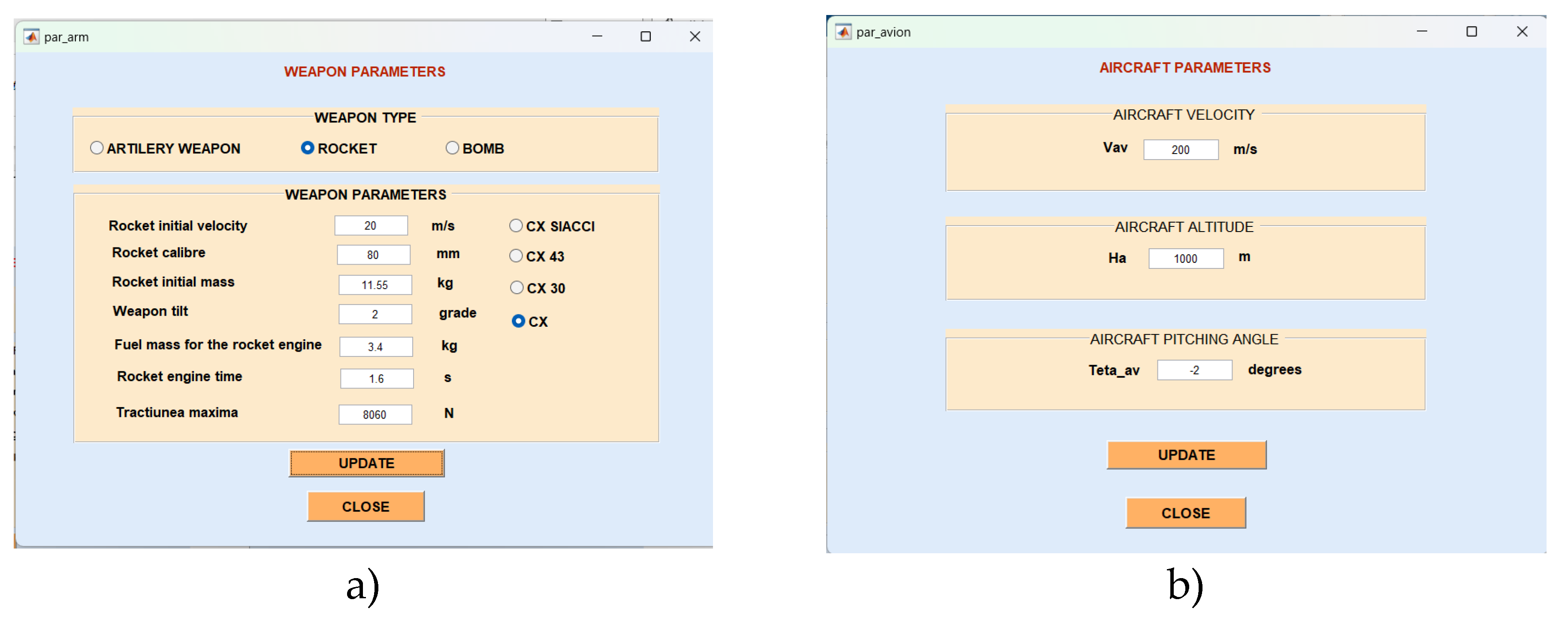
Figure 11.
Matlab software menu for defining the parameters of the firing aircraft and the target on which the firing is performed.
Figure 11.
Matlab software menu for defining the parameters of the firing aircraft and the target on which the firing is performed.
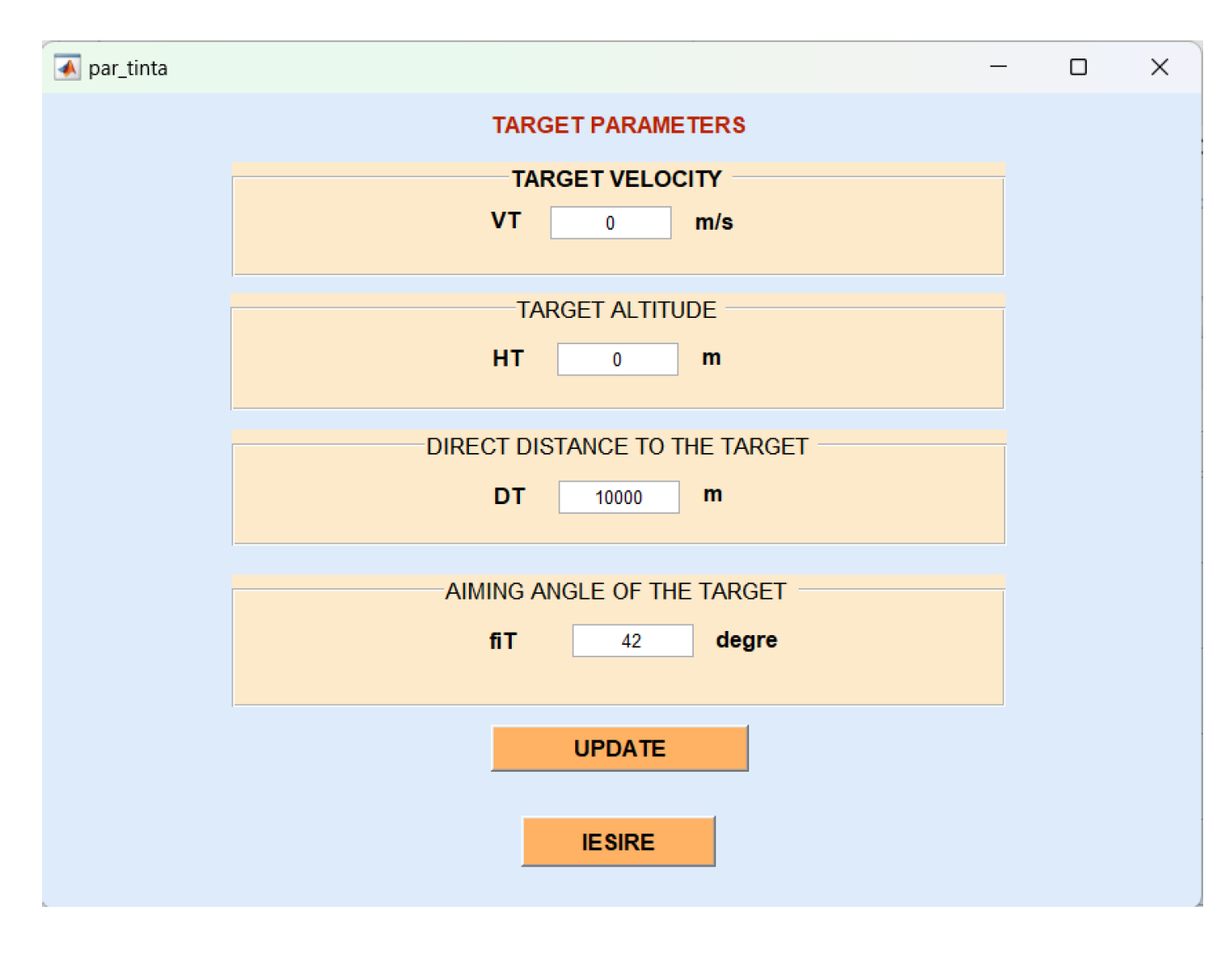
Figure 12.
Longitudinal trajectory of an aerospace vehicle.
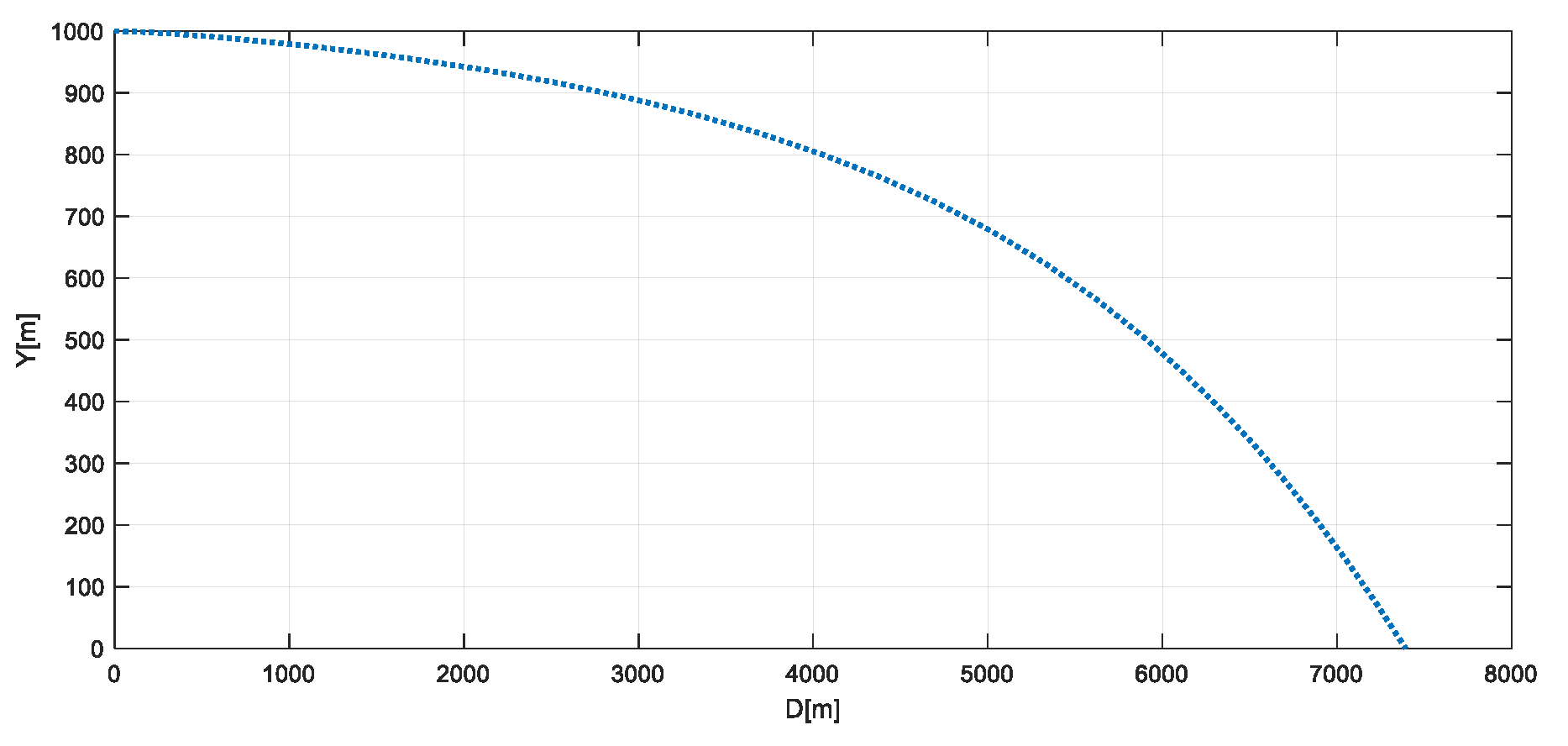
Figure 13.
The ammunition velocity during the trajectory.
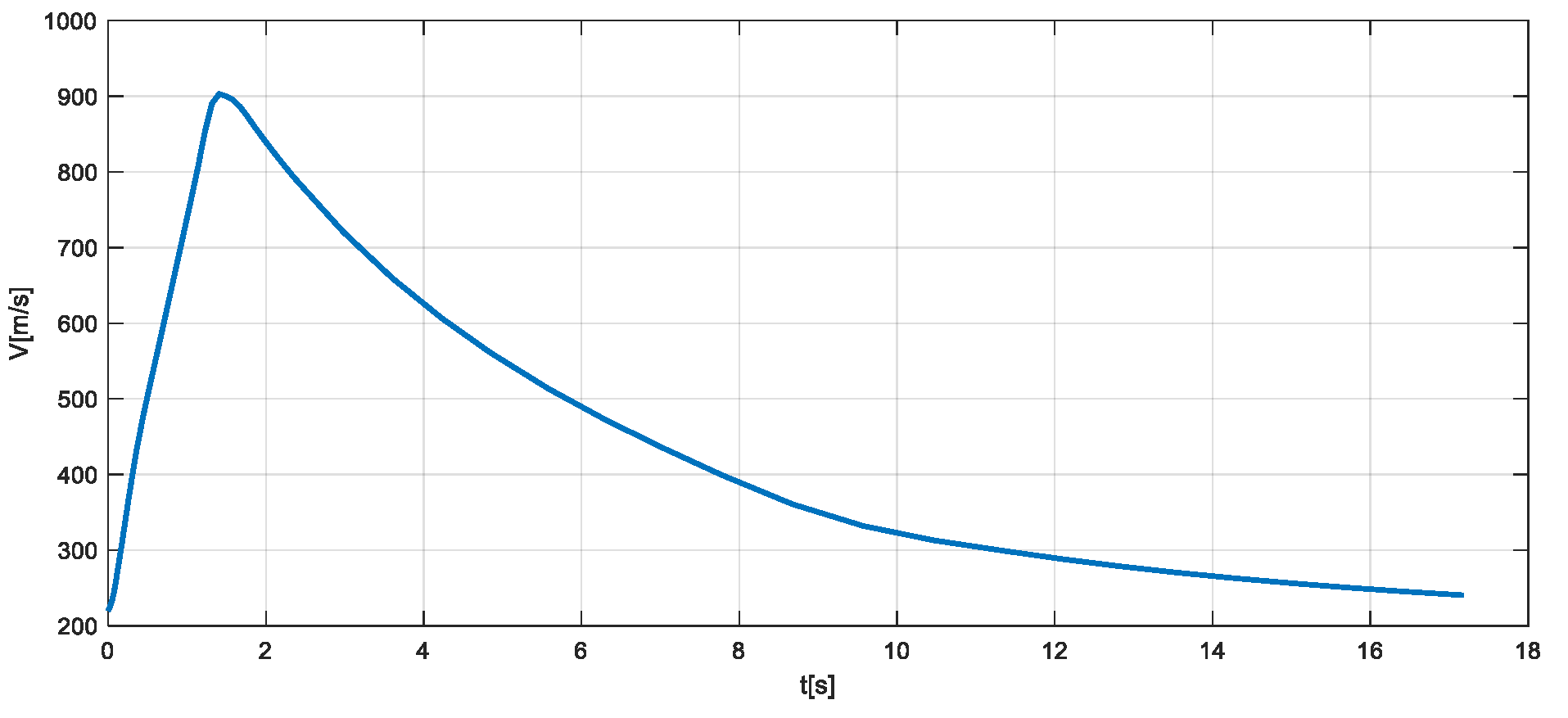
Figure 14.
Pith motion during the trajectory.
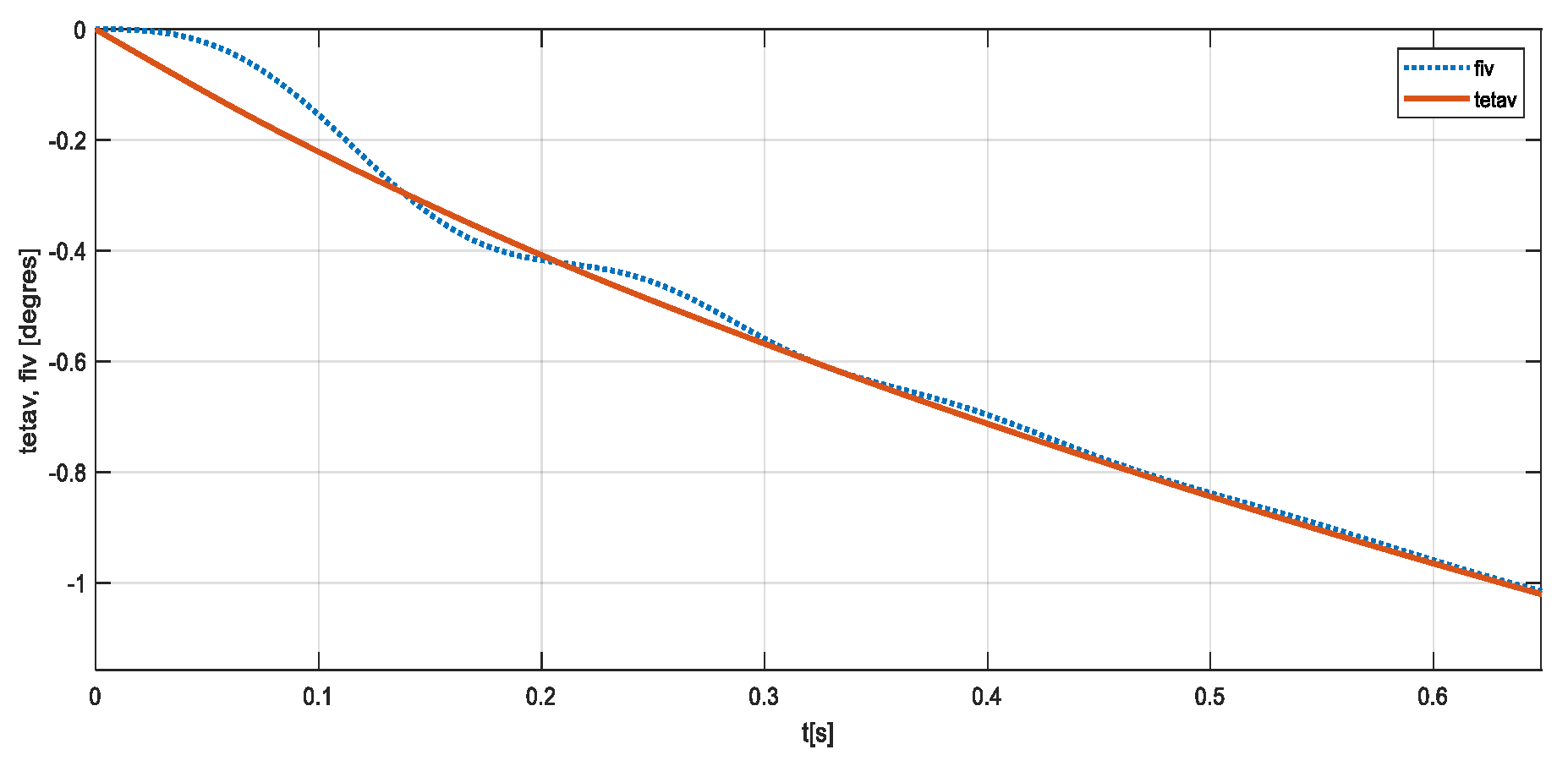
Figure 15.
The angular speed of the pitch rotation during the trajectory.
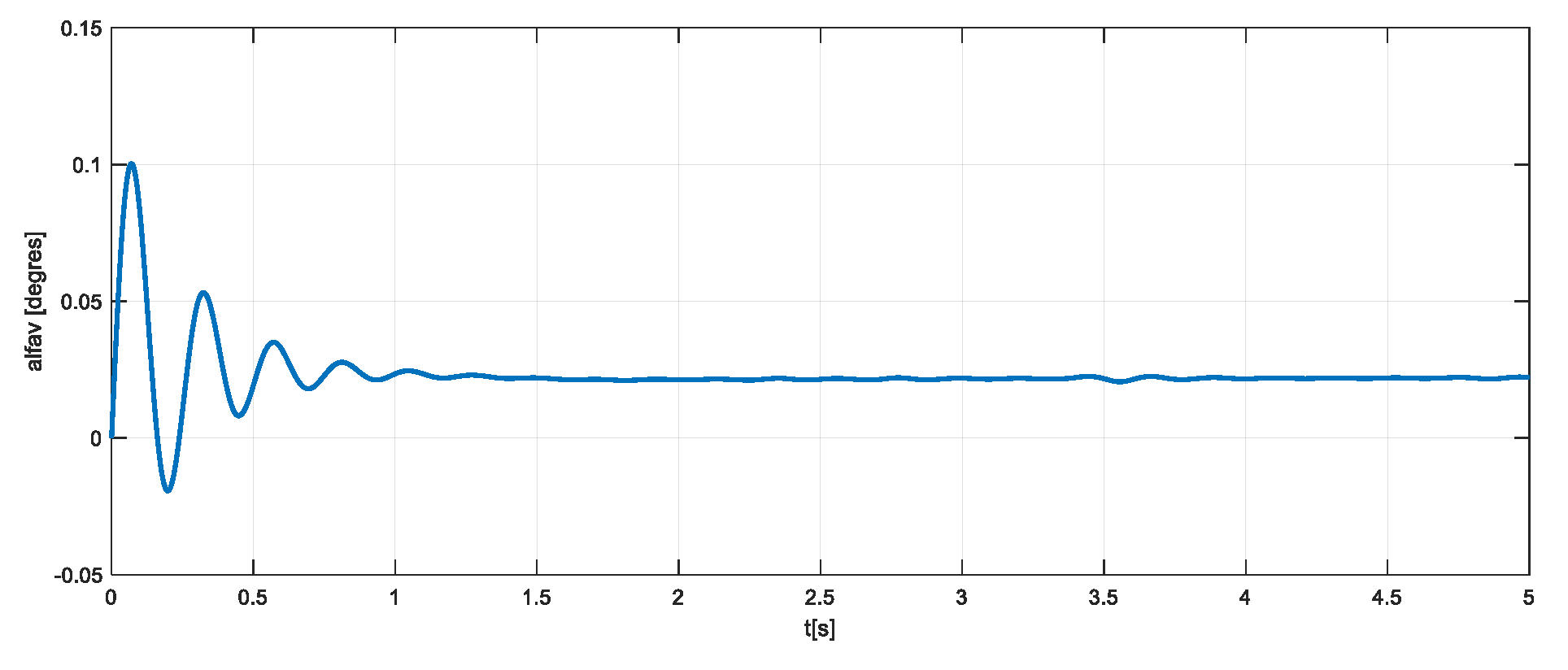
Figure 16.
Ballistic pendulum and its components.

Figure 17.
Bullet mass (left), pendulum mass (right).
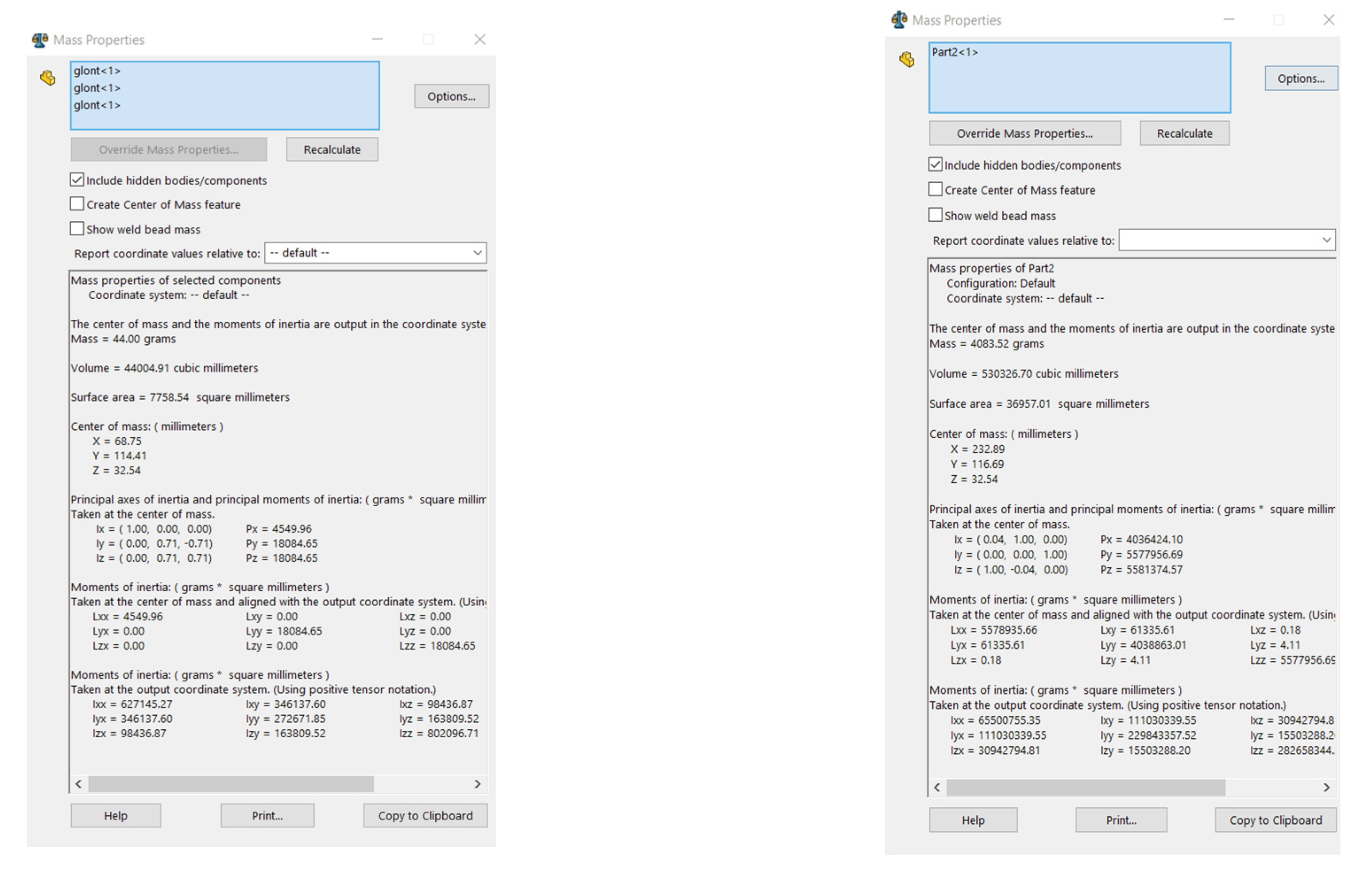
Figure 18.
Simulation schema of the pendulum in Simulink.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Downloads
130
Views
121
Comments
0
Subscription
Notify me about updates to this article or when a peer-reviewed version is published.
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated