Prerpints.org logo
Preprint
Article

An Integrated Route and Path Planning Strategy for Skid-Steer Mobile Robots in Assisted Harvesting Tasks with Terrain Traversability Constraints

This version is not peer-reviewed.

Submitted:

04 June 2024

Posted:

05 June 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
This article presents a combined route and path planning strategy to guide Skid-Steer Mobile Robots (SSMRs) in scheduled harvest tasks within expansive crop rows with complex terrain conditions. The proposed strategy integrates: i) a global planning algorithm based on the Traveling Salesman Problem under the Capacitated Vehicle Routing approach and Optimization Routing (OR-tools from Google) to prioritize harvesting positions by minimum path length, unexplored harvest points, and vehicle payload capacity, and ii) a local planning strategy using Informed Rapidly-exploring Random Tree (IRRT*) to coordinate scheduled harvesting points while avoiding low-traction terrain obstacles. The global approach generates an ordered queue of harvesting locations, maximizing the crop yield in a workspace map. In the second stage, the IRRT* planner avoids potential obstacles, including farm layout and slippery terrain. The path planning scheme incorporates a traversability model and a motion model of SSMRs to meet kinematic constraints. Experimental results in a generic fruit orchard demonstrated the effectiveness of the proposed strategy. In particular, the IRRT* algorithm outperformed RRT and RRT* with 96.1% and 97.6% smoother paths, respectively. The IRRT* also showed improved navigation efficiency, avoiding obstacles and slippage zones, making it suitable for precision agriculture.
Keywords: 
Subject: 
Computer Science and Mathematics  -   Robotics

1. Introduction

The Food and Agriculture Organization (FAO) forecasts that by 2030, a 70% increase in agricultural productivity will be necessary to sustain the growing global population of nearly 9 billion people [1]. To meet these new demands while adhering to stringent quality standards in the global markets, digital farming has become the prevailing path for future agricultural development. Thus, increasing agricultural productivity through the adoption of technological advances such as Artificial Intelligence and Robotics is currently contributing to the fulfillment of such goals [2,3]. For instance, agricultural processes will require autonomous mobility to assist primary tasks such as tillage, watering, sowing, fertilizing, and spraying, as well as central tasks such as supervising, hauling, and harvesting, among others. All of these tasks will require agricultural ground vehicles capable of autonomously planning their tasks and routes.
The process of manual harvesting in farmlands has typically relied on human labor and traditional farm equipment. Workers generally operate machines or tools to guide the harvesting of crops, such as fruits, vegetables, or grains, and then gather them for further processing. These processes are labor-intensive, time-consuming, and physically demanding [4]. Moreover, they rely on the expertise of farm workers to determine the optimal picking and collection times, preferred harvesting locations, quantity and quality of collected products. This challenging process, though operationally straightforward, encompasses several concerns [5]. The first shortcoming is that crop production can vary significantly between rows due to varied soil quality, sunlight exposure, and other environmental aspects. This makes it difficult to plan the assignment of workers to the highest-yield harvest areas. Similarly, harvesting perishable and fragile products that are subject to unpredictable weather and environmental conditions, such as fruits or vegetables, could jeopardize both the quantity and quality of the harvested product, entailing timely collection of products. Hence, it is appealing to conceive routing and path planning techniques for autonomous ground vehicles that prioritize harvesting locations based on closeness to harvesting points of maximum crop yield [6,7].
One of the key aspects to enhance the product collection process is the execution of planning strategies that consider the optimal sequence of multiple harvesting locations and navigation points [8]. Furthermore, optimizing product harvest in agriculture entails the efficient implementation of path-planning strategies that set appropriate sequences for coordinating harvest locations, where either manual or autonomous vehicles attend to the crop harvest by quickly positioning themselves near these harvest points. For instance, global planners focused on solving the Traveling Salesman Problem (TSP) enable the computation of combination sequences ordered for the shortest route according to specific navigation objectives [9,10]. However, a combined local path planning is usually required to guide the autonomous vehicle between global harvesting points, as proposed in this work. Beyond TSP, various methods such as those based on the Vehicle Routing Problem (VRP) [11,12], ant colony optimization [13,14], genetic algorithms [15], and others using heuristics [16] have also been aimed at exploring ordered routes of minimum traveling distance and reduced time (see [17,18] [and references therein]). In practice, TSP-based methods [19], addressing further than route travel optimization, are able to impact on vehicle resource utilization, load motion capacity, and energy efficiency when integrated into local planners, as proposed here in this study.
The efficient planning of feasible and adaptable paths is crucial for navigating around environments with static and dynamic obstacles. Existing local path planning methods primarily target the avoidance of predicted obstacles or adhere to structural characteristics outlined in workspace maps [20,21,22,23]. However, there remains a lack of practical approaches to integrate the need for priority waypoints within harvesting maps, all while taking into account the presence of obstacles and terrain traversability criteria. This gap highlights a critical issue in the existing classical methods, as exemplified in sampled-based approaches such as Dijkstra, A*, or Probabilistic Road Mapping (PRM) [24], to name a few. Although these methods aim to find the shortest path length toward reachable goals, they often neglect practical aspects such as motion dynamics feasibility, crop workspace layout, and terra-mechanical constraints proper of the inherent complexity of the environment. Therefore, these methods do not assure generating kinematically compatible paths with the robot’s motion dynamics. To address such limitations, probabilistic techniques focused on Rapidly-exploring Random Trees (RRT) [25,26,27,28] are often used for path planning applications subject to robot’s kinematic constraints. These RRT-based techniques offer a potential solution to the challenge of exploring feasible paths adapted to complex search workspaces [29]. However, only a few of its variants have demonstrated capabilities to integrate global path planners and generate feasible paths that consider uncertain motion dynamics and terrain traversability exploration criteria. This advantage of (RRT) comprises the main reason for using probabilistic approaches in this study.
The main contribution of this study is an integrated path-planning method composed of a global and a local planning strategy for assisted harvesting tasks in agricultural scenarios. The proposed global route planning approach is based on the TSP strategy for scheduling harvested locations, underlying insights of the CVRP approach to account for navigation objectives and constraints, whereas the local path planning uses a designed Informed Rapidly-exploring Random Tree star ( IRRT * ) approach. The proposed path planning strategy is able to generate kinematically feasible paths for Skid-Steer Mobile Robot (SSMR) dynamics that further account for the vehicle payload capacity and terrain traversability criteria. The key aspects of this research are as follows:
  • A global path planning strategy that integrates the Traveling Salesman Problem (TSP) and the Capacitated Vehicle Routing Problem (CVRP) methodologies, prioritizing the harvest points based on vehicle payload capacity constraints while considering closeness between crop harvest locations.
  • A local path planning coordinated with a global one that explores scheduled harvesting points based on IRRT * to achieve feasible and kinematically compatible paths with SSMR dynamics, accounting for obstacle avoidance and terrain traversability posed by low-traction surfaces.
  • The proposed strategy can generate paths that avoid difficult-to-crossing regions typical of agricultural farms, intending to reduce robot resources and prevent situations where robots get stuck.
  • The proposed planner can be used as a reference for motion controllers, enabling efficient driving over shortened and qualified paths, potentially reducing exposure times of products to the environment and thus the mistreatment of the agricultural harvest.
Beyond other planners that only consider the minimization of path length and disregard the agricultural production process, the proposed work also considered predicted crop yield maps with multiple harvesting locations between farm aisles to determine priority between navigation points until reaching storage terminals, sorting areas, or packing zones. The proposed strategy is capable of planning and re-planning paths as full-load or unforeseen obstacles are detected around the SSMR to avoid the harvest exposition to the environment, which is expected to improve product quality. The proposed strategy considers a map rendered as an RGB image, and then such an image is processed to provide a deployed representation proper for designing the planner. Then, taking specific exploration areas in the map, information about the current harvest positions and product quantity to be harvested for each crop row is used in the TSP-CVRP strategy to schedule the navigation path. The path contains a queue list of prioritized harvest points by maximizing load capacity. The resulting ordered list of harvesting points is used as input information for the local path planner ( IRRT * ). The local path planning strategy is then used as a reference path for a motion controller of autonomous agricultural vehicles. A comparative analysis is conducted to assess performance of the proposed strategy using metrics of path length, travel time, smoothness, proximity to obstacles, whereas metrics of cumulative tracking errors, controller effort, and total cumulative costs for the test controller.
This paper is organized as follows. The analysis of works related to this paper is presented in Section 2. Section 3 details the terra-mechanical models used in the path planning design, including those of the SSMR dynamics and the interaction with low-frictional terrains. Section 4 details the work methodology, incorporating the processing of the harvest map and the proposed integral path planning strategy. In Section 5, it is discussed several experimental results. Finally, conclusions of the work are given in Section 6. Nomenclature of variables used throughout this paper is summarized in Table 1.

2. Related Work

Beyond generating a navigation path either for manual or assisted guidance tasks [17], a path planning strategy requires a sequence of waypoints arranged to form a traversable route. In agriculture, such order is primarily driven by the need to prioritize navigation points, generally considering operative aspects such as closeness between harvesting locations, harvest product capacity, distribution of workers across rows, and product collection time [30]. For instance, in [29], traveling routes were obtained by optimizing travel costs through the solution of a Traveling Salesman Problem (TSP) to guarantee the vehicle’s return upon task completion in orchard fields. While this method aimed to minimize path length and execution times by spatially separating multiple regions, it targeted specific tasks for vehicles within predefined working schedules, rather than considering all potential workspaces and locations. Adapting path-planning strategies to the complexities of agricultural environments requires to incorporate capabilities from additional path-planning techniques. The path planning problem can also be formulated as a variant of the TSP [9,13,17], where travel costs between individual targets could be set. However, this approach does not account for scenarios where the vehicle has limited payload and has to transport products to different locations. To address this limitation, the Capacitated Vehicle Routing Problem (CVRP), as a variant of the TSP, has been developed involving vehicles with limited payload capacity [31]. In particular, the CVRP aims to find an optimal set of routes that minimizes the total travel cost in terms of path length and travel time, while ensuring that capacity constraints are met and all locations are visited [32,33]. Whereas global path-planning approaches are effective in many scenarios, they may be inadequate in environments where robots must navigate around obstacles [34]. Consequently, more adaptable path planners are required to devise trajectories that avoid them while accounting for other navigation characteristics such as robot’s dynamics and terra-mechanical constraints. For instance, sampling-based path planners based on Rapidly-exploring Random Trees [25] and their variants are commonly used for local path planning with obstacles, as proposed in unstructured layouts of orchard environments [35]. In that work, kinematic constraints were met and obstacles were avoided fusing RRT with artificial potential field techniques. Similarly, current works on sampled-based techniques and global planning methods integrate maneuverability criteria to optimize paths subject to speed constraints [36]. Considering terra-mechanical models of Hunt-Crossley in the design of path planners also allowed autonomous ground vehicles to adapt the maneuverability control to different uneven and flexible navigation surfaces [37]. Several agricultural applications using hybrid techniques based on RRT can be found in spraying, planting, and harvesting tasks [38,39,40,41,42]. However, to the best of the authors’ knowledge, there is a lack of integrated path-planning approaches that simultaneously consider sorted harvesting points according to the robot payload capacity and account for wheel-terrain interactions. Most path planning works consider static and dynamic obstacles surrounding the vehicle but few have taken into account the navigation terrain in assisted harvesting tasks, which could be considered as the primary terra-mechanical constraint that affects the navigation performance through a reduced tractive force exertion and wheel slippage [43]. Therefore, path planners that involves terrain traversability criteria to overcome terrain obstacles are more than welcome.
In contrast to the previous routing approaches, typical path planning methods for solving the shortest path problem encompass a variety of methodologies, where each of them arises strengths and limitations. For example, grid-based algorithms as Dijkstra’s and A* [44], offer resolution completeness but could become computationally burdensome for high-dimensional and complex problems. Conversely, sampling-based approaches such as RRT[45], Probabilistic Roadmaps (PRM) [46] and their variants [47] demonstrate asymptotically optimality and efficiency in irregular environments, particularly in navigating high-dimensional spaces. They ensure probabilistic completeness by guaranteeing a feasible solution when one exists. Improving the speed of path calculations in RRT is also a key concern, influenced by factors such as start and end point locations, search space size, sampling efficiency, and unexpected obstacles. To address those aspects, the work in [24] proposed fusing PRM and RRT, splitting the planning area in regions, and taking advantage of PRM. However, the integration disregards the robot kinematics, potentially affecting the path execution.
Efficient environment exploration poses a challenge for RRT-based path construction, as highlighted in [48]. In [49], it was introduced a hybrid RRT approach to improve workspace exploration by incorporating probabilistic learning techniques. The proposed method concurrently generates growing trees to explore probable boundary samples that could reach the destination point increasingly faster. An extended work is proposed in [50], where the selection of samples is made by filtering waypoints through clustering methods. On the other hand, evolutionary algorithms such as genetic approaches and optimization-based methods [51] offer additional advantages for efficiently solving high-dimensional problems. Nevertheless, they may encounter challenges such as being trapped in local optima. Additionally, incorporating the robot dynamics into path planning could be achieved by formulating an optimal control problem [52]. Nevertheless, this approach may face similar challenges as grid-based methods when dealing with high-dimensional spaces. For this reason, a variant of RRT * based on heuristics is used as a complementary tool for path planning integration.

3. Motion Models for Assisted Harvesting Tasks

Previous to the path-planning design, it is required to introduce a motion model of the test robot and terrain traversability according to the proposed methodology depicted in Figure 1.

3.1. Model of the Skid-Steer Mobile Robot

The motion model used in this work is an adapted version of a unicycle-type vehicle model for Skid-Steer Mobile Robots (SSMR), encompassing both lateral and longitudinal dynamics [2]. The SSMR model is used because the harvest payload can be maintained for a certain speed profile and uniformly distributed along its structure, as typically required in turns of farm headlines. This model integrates nonholonomic constraints, speeds, and control actions that allow kinematically compatible paths with the robot dynamics. The driveline model of the robot configures a four-wheel-drive scheme, with traction forces regulated by traction and turning torques. The forward dynamics of the robot model is as follows:
x ˙ y ˙ θ ˙ v ˙ x v ˙ y ω ˙ z = v x cos θ − a ω z sin θ v x sin θ + a ω z cos θ ω z p 0 ω z 2 + p 1 v x p 3 ω z v x + p 4 ω z p 6 ω z v x + p 7 ω z + 0 0 0 0 0 0 p 2 0 0 p 5 0 p 8 τ v τ ω
subject to nonholonomic constraints:
− x ˙ sin θ + y ˙ cos θ − v y + ( l ) ω z − b ω z = 0 v y − a ω z = 0
where ( x , y , θ ) denotes the robot pose; v x , v y , and ω z are the longitudinal, lateral, and angular speeds, respectively. The parameters l and a are length and width of the SSMR, respectively. The vector of model parameters p = [ p 1 , . . . , p 8 ] is obtained according to robot responses against torque inputs, and they are previously estimated in [53]. For more comprehensive information regarding the model, readers are referred to [43].

3.2. Model of the Terrain Traversability

The Coulomb friction model for the wheel-terrain interactions, as outlined in [54], defines the frictional force F f between the wheel and the navigation terrain, such that:
F f = μ · F N
where μ denotes the coefficient of static friction, and F N refers to the normal force, associated here with the full weight of the harvesting vehicle. In particular, normal reaction forces represent the vertical projection of the vehicle’s weight onto the surface normal, subject to variations due to changes in terrain conditions or weight on the harvest vehicle. The wheel-terrain interaction model assumes that static and kinetic friction forces are equivalent until the applied force exceeds the friction force μ · F N , potentially leading to slippage conditions or even wheel entrapment. For accurate path planning, representations of wheel-terrain interactions for each wheel of the vehicle are necessary. Consequently, the so-called MF-wheel model, based on Pacejka’s insights [55], is employed to characterize tangential forces for each wheel, capturing the complex wheel-terrain behavior:
F i j x = μ x ( σ s i j ) F N , i j z , F i j y = μ y ( α i j ) F N , i j z μ x ( σ s i j ) = D x sin C x arctan B x σ s i j μ y ( α i j ) = D y sin C y arctan B y α i j μ s = ( μ x , μ y )
where [ B · C · D · ] T represent parameters of the wheel model obtained from [56]; μ x , μ y , and μ s are coefficients of longitudinal, lateral and resultant friction, respectively. The wheel slip ratio σ s ∈ [ − 1 , 1 ] and sideslip angle α ∈ [ − π , π ] / 2 represent wheel speeds varying with respect to the robot chassis. The slip ratio σ s for each wheel is:
σ s i j = s i j ω i j r w , if ω i j r w > v i j x , ω i j r w ≠ 0 , while moving , s i j v i j x , if ω i j r w < v i j x , v i j x ≠ 0 , while braking , with s i j = ω i j r w − v i j x ,
where s i j represents the difference between the linear speed ω i j r w and longitudinal speed v i j x along the robot’s axis. To implement this model, both the coefficient of friction μ and normal force F N are required, which are assumed given in this work since the robot’s payload and terrain type are known a priori. It is worth noting that changes in surface characteristics are assumed to be minimal for the same testing area.

4. Integration of Route and Path Planning

The proposed path planning methodology was developed along three stages: i) processing of the navigation map, ii) planning of the global path based on the TSP-CVRP approach, and iii) planning of the local path with Informed RRT * a.k.a. IRRT * , as illustrated in Figure 1. The following Sections detail each of these scenarios.

4.1. Processing of the Navigation Map

A navigation map is assumed to acquire a top-view image of the harvesting area in the field, and then it is processed according to steps depicted in Figure 2. In the initial step, an RGB vision sensor captures an image I from the robot workspace (see Figure 2a). Subsequently, the background is removed from I to isolate structural features irrelevant to the navigation map [57], obtaining I n . From I n , a new image I b is binarized to simplify the map representation and reduce noise (see Figure 2b). Then, a non-linear median blur filter is applied to I b for noise reduction and smoothing while preserving the contour edges and boundaries between obstacles and free space. After I b is excluded from spurious readings, the navigation map is available for complementing with new information regarding the navigation terrain.
The structural map is augmented with information on geo-localized areas exposed to the potential slip phenomena, arising from previous navigation scenarios. Such information comprises friction coefficients computed with the wheel slip ratio and sideslip angles, being assigned to each map location in I b . Due to existing heterogeneous slipping areas, the associated slip region outlines are detected and enclosed in re-sizable rectangles (see Figure 2c. Then, adaptive thresholds are used to expand the blurred image I b with a contour area b s so that internal regions of structural obstacles could be filled to avoid unnecessary path searching (see Figure 2d).
By detecting contours and using artificial areas in the adaptive thresholding process, the method accurately identifies structural obstacles as shown in image I b c of Figure 2e. In particular, rectangular contours of the farm isles are also detected and filled to enclose and highlight structural obstacle regions in the occupancy grid. The crop rows detection effectively contributes to delineating the navigation space and further reducing noise. The bounding rectangles of the retained contours are then used to modify the occupancy grid O g , setting the corresponding regions to be free or occupied. Finally, the structural and slippage maps are joined in a single navigation map, as shown in Figure 2f.
Map representation of the navigation environment, where each cell (or pixel) corresponds to a relatively small region in the physical world. By classifying these cells as occupied or free, the proposed strategy can identify efficient navigation paths through complex scenarios involving structural obstacles, non-structural obstacles, and slippery zones. Specifically, the occupancy grid is defined as a 2D binary matrix O g , where each element O g ( i , j ) indicates whether the corresponding cell at row and column is free (0) or occupied (1). Thus, each element in O g directly maps to a corresponding element in the image representation O g .

4.2. Global Path Planning

This section presents the design of the global path-planning approach for assisted harvesting tasks. The path planning method aims to find an optimal route connecting harvesting points, visiting the same location only once, prioritizing the maximum harvest for each row, ensuring vehicle payload capacity, and maximizing closeness between harvesting locations. Hence, to determine a path that fulfills the former objectives, the TSP-CVRP algorithm is selected. This choice is made due to its ability to schedule coordinated points while meeting connection constraints.
The TSP-CVRP approach considers a graph G = ( P , E ) to represent potential connections between harvesting points. Such connection comprises P as the set of ordered harvesting locations H p = { h 0 , h 1 , . . . , h p } with h 0 denoting the initial crop depot and h p as the crop end-point. Similarly, E is the set of effective connections that pair harvesting points, and each edge e { i , j } ∈ E is associated with a non-negative cost C i j , computed as follows:
C i j = D i j × f w w j
where D i j is the Euclidean distance to quantify closeness between two any harvesting points; f w is a factor prioritizing reduced-distance connections, and w j is the weight for scheduling the order of travel points according to a distance D i j between harvesting locations in H p . For each harvesting point H p , it is assigned a specific demand q j and a single harvest depot denoted by q 0 . The accumulated harvest product obtained until weight w i j in the arrival position in j along the route search is limited to not overload the maximum load capacity Q of the SSMR. Thus, as it is required to find a route connecting ordered harvesting points with minimal total distance and payload constraints, the proposed optimization problem is:
Minimize : ∑ i = 1 n ∑ j = 1 n C i j δ i j Subject to :
∑ i , j = 1 n δ i j = 1 , ∀ i , j = 1 , 2 , … , n
δ i j = 0 , ∀ i , j ∉ F c
∑ i = 1 n w j δ i j ≤ q j , ∀ j = 1 , 2 , … , n
∑ j = 1 q j ≤ Q , ∀ j = 1 , 2 , … , n
u i − u j + n δ i j ≤ n − 1 , ∀ i ≠ j , 2 ≤ i , j ≤ n
where δ i j ∈ 0 , 1 is a binary constraint function, taking δ i j = 1 if there is a possible route of connection from node i to j and δ i j = 0 otherwise; w j denotes the product demand in weight assigned to a particular arriving node j; Q is the vehicle capacity for the maximum payload to haul along the overall planned route; F c is the set of unfeasible connections due to inaccessible workspace from opposite sides of the same harvesting row; n is the total number of nodes. The auxiliary variables u i , j are introduced to prevent the route from excluding the initial and endpoint harvest position, ensuring that the linkage of two consecutive points is met and the planned points do not generate isolated route loops. The objective function minimizes the overall travel cost through the computations of individual costs C i j for all connections between nodes i , j . The constraints ensure that each node is visited exactly once, whereas the total weight on any traversed route does not exceed the maximum payload limit Q (see Eq. 10)
In Algorithm 1, the TSP-CVRP method begins by building a map M p containing coordinates ( x i , y i ) without any specified order of the harvesting points H p (see line 1). Such harvest map is augmented with a separate map M w , which incorporates geo-localized weights associated with each point in H p (see code line 2). A list of unfeasible connections F c are previously identified with the binary constraint function and incorporated to M w . Before the execution of the TSP-CVRP algorithm, it is also specified the maximum payload Q under which the robot is capable of hauling throughout the navigation route (see code line 4).
Algorithm 1 Improved TSP-CVRP
Require: 
 
1:
H p ← Set harvesting points to visit  
2:
M w ← Build map of geo-localized weights for each H p  
3:
F c ← Set unfeasible node connections  
4:
Q ← Set maximum vehicle payload capacity  
Ensure: 
L ord  
5:
Initialize M c i j ← calculate _ calculate ( H p , M w )  
6:
Initialize empty route: L ord ← ∅  
7:
while unvisited _ nodes ( M c i j , L ord ) do  
8:
     C i j ← node _ min _ cost ( M c i j , F c ) with Eq. 6  
9:
    if  meet _ constraints ( L ord ∪ { C i j } , Q , F c ) with Eqs. 8-10. then  
10:
         L ord ← L ord ∪ { C i j }  
11:
    else 
12:
         L ord ← create _ new _ route ( C i j )  
13:
    end if 
14:
end while 
15:
return L o r d
The TSP-CVRP algorithm calculates the distances between all pairs of harvesting points { h i , h j } and arbitrary points on the map M w , represented as a cost matrix M c i j (line 5). For each iteration of the while-do loop in code lines 7-14, the next node C i j to visit is selected by finding the one with the minimum incremental cost detailed in Eq. 6, subject to constraints imposed by F c (line 3). This process continues until all locations are visited, as determined by the unvisited_nodes function (code line 7). The selected node C i j is added to the planned route L o r d if appending it to the current route meets constraints specified by Eqs. 8-10, as verified in the meet_constraints function of line 9. These constraints involve the vehicle payload capacity Q and the unfeasible connections F c . If these constraints are violated, the algorithm re-orders the route by removing the last node added and creating a new route with the current node C i j . In particular, as shown in code line 12, if all constraints are not achieved, a new possible route is generated with a selected node C i j , using the create_new_route function. The route planning algorithm returns the harvest points in L ord (see code code line 15).

4.3. Local Path Planning

Once the ordered sequence of harvesting points L o r d is generated to guide the harvest task, it is required to generate the navigation path to connect such points while avoiding obstacles and potential slippage areas. To do so, the RRT * [58] algorithm is selected to be adapted, incorporating feasibility conditions to navigate in low friction terrain under dynamics constraints and enhancing adaptability in the path search progress. Specifically, the proposed local planner combines principles of RRT * informed with probabilistic sampling for learning the efficient exploration of the environment with paths kinematically compatible with the robot dynamics [59]. Furthermore, it integrates the dynamical model of the SSMR and the traversability terrain model to ensure that the generated paths are capable of avoiding slip situations.
The proposed IRRT * algorithm is designed in six steps, considering a couple of given nodes assigned as start and goal points within the workspace. The steps for the path planning process are depicted in Figure 3, whereas lines of pseudo-code are presented in Algorithm 2. In the first step, the proposed algorithm generates a random sample within a bounded region, describing an adaptable area that guides the path search. Then, a second step involves extending the path on a tree towards the nearest node that could connect to the next sample node. Before linking the previous nodes, connection feasibility is checked in step three to ensure that the next node meets kinematic ans slip constraints. Subsequently, a set of neighbour nodes around the potential new node is identified within a radius changing according to the nodes in the tree. Then, it is selected the neighbour node (i.e., parent) from such set so that minimizes the path distance to each neighbour. Once the best node (i.e., node for minimum-cost) is selected, the new node is connected to the best parent and added to the tree, as illustrated in the parent node of step five (see Figure 3). A tree rewire process is finally carried out with the nearest neighbours to achieve the lowest path cost, and path smoothing is carried out between nodes of the resulting tree.
The previous planning process is detailed in Algorithm 2, and explained as follows. Briefly, the proposed algorithm required to initialize parameters, the environment map and a tree structure T (see code lines 1-9). Then, it is set the ordered harvest waypoints L ord from the TSP-CVRP path planning in code line 1 but only consecutive pairs are used for searching local paths (see code lines 7-8). The planner parameters were obtained in practice by guaranteeing reachability and path completeness according to the methodology suggested by [58]. Also, such parameters were tuned based on balancing path planning accuracy and computational efficiency, thus maintaining the overall path planning performance. The path search process is performed through the while-loop in code lines 10-28. A start and goal node are assigned from the harvest points. Thus, for each iteration, a new node z new is obtained by expanding the tree T from a random sample z rand towards the nearest node z nearest (see lines 11-13). Here, the robot stearability is checked between the past and new nodes before expanding, according to the maximum turning ratio and holonomic speed constraints of the skid-steer model in Eq 2. According to code line 14, it is verified with the feasibilty_check function if the link segment between the new and nearest node does not intersect any obstacles in the map O g , including structural obstacles and terrain traversability conditions on potential slip zones. In particular, the feasibility check function examines possible collisions across a navigation area rather than single points in a path, considering a circular region of radius r f and center z new , as follows:
∀ z ∈ | | z nearest − z new | | ≤ r f 2 : O g ( z ) ≠ 0
Navigation feasibility is analogously verified in this same feasibility_check function, considering the terrain traversability by comparing traction forces T f , i j exerted by wheels and soil resistance forces F f , i j offered by the navigation surface. Such forces are obtained based on the slip ratios of the MF-wheel model in Eqs. 3 and 4 (see Algorithm 3). Once the connection is feasible, the best node among a neighbour set and radius r is found according to the minimum distance criterion included in the select_best_parent function. If the best node again meets feasible constraints and it is added to T (code line 19), the algorithm performs a rewiring process to connect all new nodes in line 20. The resulting tree may feature potentially unfeasible sharp turns and jagged edges, paricularly when changing new exploration nodes extracted from the harvest points of the global path planning strategy. Therefore, to address such concern, a piecewise polynomial interpolation strategy was applied for path smoothing in code line 21. Indeed, it involved fitting a cubic polynomial approximation between each pair of consecutive nodes, resulting in a smoothed tree. As a result, if the tree reaches the goal node in line 24, the local path is set and the overall path p is connected in line 25 with all local paths after running the algorithm for all harvest points L ord .
Algorithm 2 Informed RRT * ( IRRT * )
Require: 
 
1:
L ord ← Set a list of ordered H p  
2:
O g ← Get a navigation map  
3:
N ← Number of probable samples  
4:
γ ← Sample rate  
5:
N s ← Neighbour size  
Ensure: 
p a t h : p  
6:
foriin L o r d do    
7:
     z start ← L o r d [ i ]    
8:
     z goal ← L ord [ i + 1 ]    
9:
     T ← initialize_tree ( ∅ , z start , T ) ;  
10:
    while  j ≤ N  do  
11:
         z rand ← sample_node( z start , γ )  
12:
         z nearest ← nearest _ node ( T , z rand )  
13:
         z new ← expand ( z nearest , z rand )  
14:
        if  feasibility _ check ( z nearest , z new , O g )  then  
15:
            r ← compute _ extended _ radius ( N s )  
16:
            N ( z new ) ← find _ neighbours ( T , z new , r )  
17:
            z best ← select _ best _ parent ( N ( z new ) , z new )  
18:
           if  feasibility _ check ( z best , z new , O g )  then  
19:
                T ← insert _ node ( T , z new , z best )  
20:
                T ← rewire _ tree ( T , z new , N ( z new ) )  
21:
                T ← smooth _ tree ( T , z new )  
22:
           end if 
23:
        end if 
24:
        if  path _ to _ goal ( T , z goal )  then  
25:
            p ← smooth_path( T );  
26:
           break  
27:
        end if 
28:
    end while 
29:
end for
Algorithm 3 Traversability Checking
Require: 
 
1:
σ s i j ← Slip ratios for i j -wheel  
2:
μ x ( σ s i j ) ← Coefficient of longitudinal static friction  
3:
μ y ( σ s i j ) ← Coefficient of lateral static friction  
4:
F N , i j ← Normal forces on each wheel surface  
5:
T f , i j ← Evenly allocated traction force on SSMR  
Ensure: 
Traversability of terrain  
6:
F f , i j ← μ s · F N , i j according to Eq. 3 and 4    
7:
return traversable ← T f , i j ≥ F f , i j  

4.4. Motion Controller for the Assessment of Path Planning

Following one of the hypotheses of this work, which suggests that the proposed path planning is able to improve maneuverability in environments with obstacles and terrain constraints, the performance of the planned path is assessed in a motion control strategy for completeness as part of the trails. To do so, the planned path that connects the navigation route was parameterized with a constant speed profile between each pair of consecutive sampling waypoints, considering a robot sampling time Δ t . Thus, the parameterized path is used as a reference for a motion control strategy, and the robot position obtained from a localization system is used as feedback (see the general scheme of the proposed path planning strategy of Figure 1). For simplicity in the implementation of the motion controller, a Proportional-Integral (PI) control technique based on algebraic approaches was used [30,60]; however, other motion control techniques could be used instead. The control parameters were previously tuned following guidelines in [61]. For more details regarding the tracking controller, the reader is encouraged to refer to [30].

5. Experiments Results and Analysis

This Section presents the results of the proposed learning-based routing scheme for path planning of SSMR in assisted harvesting tasks. The experiments were conducted in a multi-row crop environment designed to replicate those structured farm fields. The test map was acquired from a geo-localized environment of a generic fruit orchard similar to the one located at Lincoln Institute for Agri-Food Technology. Then, to test motion control, it was used the simulation software of Coppelia V-Rep [62]. The experiment involved building a 60×60 m map with eight harvest alleys, where each of them was distributed in 4m × 3m zones. In the environment, modifications were introduced to the navigation surface to change the conditions of the wheel-terrain interaction and intentionally produce the slip phenomena. To best explore a path required to transit waypoints between harvest alleys, a single waypoint was assigned to each allay under which the robot was tasked to navigate for crop harvesting.
The code used for implementing and testing the proposed solution will be available as a GitHub repository1. The route planning framework for the global path planning method used the Path Cheapest Arc strategy under the Search Heuristics scheme available in the OR-Tools of Google [63] to solve the optimization problem posed by the combinatorial search strategy of Eq. . The trials were performed on a Windows-based computer equipped with an Intel® Core™ i9-10870H CPU @2.2GHz (16CPUs) and 32GB of DDR4 RAM. This setup ensured all computations required to achieve the proposed path planning strategies. The performance metrics are presented in the following section.

5.1. Performance Metrics

Beyond the path length and travel time, for numerical analysis of the local path planning approaches, three performance metrics were introduced by following suggestions of previous works [53,64,65].

5.1.1. Obstacle Avoidance [65]

Path safety was assessed based on proximity of the path to obstacles. With prior knowledge about the set of obstacle locations O in the map, the minimum distance d between each point on the path and the nearest obstacle for each point is given by:
d = min o ∈ O ∥ p − o ∥ 2
where p = ( x p , i , y p , i ) , with i = 0 , . . . , N − 1 is a given point on the planned path; o is the position of the nearest obstacle to the path, and ∥ · ∥ denotes the Euclidean norm. Then, the assessment metrics for obstacle proximity are the average sum d ¯ o of all distance values for each sample point on the path, as well as the distance variability σ given by its standard deviation.

5.1.2. Path Smoothness [64]

This metric is aimed to measure path smoothness along the travel based on summing the acceleration components of the path such that:
S p a t h = 1 ( Δ t ) 2 ∑ t k = 0 t N − 1 Δ 2 ( x ( t k ) ) , Δ 2 ( y ( t k ) ) 2
where t k is the time step of the parameterized path, N is the total number of points comprising the planned path, and Δ t is the time interval between steps. The path smoothness S path essentially quantifies the rate of curvature changes along the path, with relatively small values of S p a t h indicating smooth paths.

5.1.3. Controller Effort [53]

The total motion controller effort can be computed as the contribution of the accumulative path tracking cost C x , y and control input C u , as follows:
C x , y = ∑ t k = 0 t N − 1 k x ( x ref ( t k ) − x ( t k ) ) 2 + k y ( y ref ( t k ) − y ( t k ) ) 2 C u = ∑ t k = 0 t N − 1 k v T v 2 ( t k ) + k ω T ω 2 ( t k ) C T o t = C x , y + C u
where k x , k y , k v , k w are positive constants that provide a consistent sum between costs along the path.

5.2. Global Path Planning Evaluation

Several trials were carried out to evaluate the TSP-CVRP planner under varying vehicle load capacities and different route waypoints. Assessment criteria included route efficiency, resource utilization, and overall optimization of the harvesting process. Figure 4 presents a set of six trials of route planning, depicting routes that connect locations prioritized to be visited according to the maximum weight of the harvested product with respect to the robot payload capacity and minimum travel costs represented by the interconnected-point distances. In particular, the experiments are performed initializing different start/end points and several SSMR payload capacities to evaluate the total load harvested by the robot along the traveled route. For instance, in Figure 4a, for an SSMR payload capacity of 28 Kg, the planner bypasses two collection points (8 and 10 Kg) from the same allay, which could provide the shortest distance if harvesting 8 Kg of the second alley. However, in this case, the route planner prioritized the highest harvested weight by traveling to additional locations in the field. Such prioritization achieved the maximum harvest load of 28 Kg compared to the SSMR payload capacity. Furthermore, Figure 4b shows that increasing the SSMR payload capacity to 42 Kg, the planned route enables the robot to visit all harvest points, given a total product quantity of 41 Kg (97.6%) distributed in the three allays. In this case, it is prioritized intending to achieve the maximum payload capacity despite visiting all positions. Conversely, Figure 4c illustrates a scenario with a limited vehicle capacity of 13 Kg, where the planner visits the nearest points of 8 Kg and 5 Kg and archives the maximum payload capacity before returning to the product depot. Subsequently, in Figs. Figure 4d-f, three additional tests feature several start and end harvest positions not matching among them, as well as varying vehicle payload capacities. Here it is shown that the planned route did not necessarily have to start and end at the product depot to maximize the harvested product (71.4%, 70.2%, and 80%), which is critical if the SSMR would have to re-start the harvest process or if it would need to supply a harvest point that is not necessarily the final depot. Moreover, all trials also evidenced that a single harvest point was visited only once, but also avoided back-and-forth travels between harvest allays.

5.3. Local Path Planning Evaluation

This section presents the results of evaluating the local planner in a harvesting environment, where the planner is a variant of the IRRT * algorithm to incorporate SSMR dynamics and a terrain traversability model. To qualitatively assess performance, three local planners are tested, i.e., RRT, RRT * , and the proposed IRRT * . Table 2 shows the parameters used to test the path-planning approaches. Figure 5 illustrates three different trials conducted under equal execution parameters, including sample number, sampling rate, neighbour size, and start/end points. The three algorithms approached a planned path in such a way that completed the navigation task between two harvesting points and avoided the obstacles in the farm environment; however, they present different path-planning characteristics. The left plot depicts the path obtained with the RRT algorithm, wherein an uneven path is observed by simple inspection. The RRT path has abrupt turns and a wide distribution of sampled points across the navigation map. Conversely, when qualitatively assessing the performance of the RRT * algorithm in the middle plot of Figure 5, the planned path presented a slightly smoother path. However, it still exhibits abrupt turns, even when the sampling process nearly covers the entire navigation map.
As shown in the right of Figure 5, it is observed that the proposed algorithm IRRT * yielded a feasible solution for autonomous navigation, as well as a smoother path with respect to the other two path planners (i.e., RRT and RRT * ). The IRRT * outperforms the other two comparison path planners in terms of exploration since the proposed approach only searched for confined areas close to the endpoint (as shown in greenish-yellow lines of Figure 5). Furthermore, the IRRT * operates on a safety navigation area delineated by black dotted lines. This constraint area was effectively extended around the path solution to avoid uncertain obstacles that may appear in the environment. This feature provides a significant advantage over RRT and RRT * because it ensures robust performance of the path planner under the presence of uncertain obstacles in the environment, thereby offering further flexibility and path adaptability.
Figure 6 shows the results of the three different test approaches, aimed at illustrating the ability to avoid structural and randomly located box obstacles in a farm scenario. In this test, the visiting order of the harvest points was taken as a reference to connect different start and end points along a whole harvesting task. It can be observed that all three methods effectively avoided the structural and box obstacles, and the proposed IRRT * again generates smoother and safer paths with respect to the other two path planners (i.e., RRT and RRT * ). Furthermore, unlike RRT and RRT * , the proposed algorithm avoids returning along counter-directions to prevent kinematically incompatible turns that SSMR robots are unable to perform. Instead, the proposed algorithm maintains the same route or smoothly adjusts the path to continue navigating (see scenarios 2 and 3 for IRRT * in Figure 6).
Figure 7 shows the path planning results for each path planner in three different scenarios under structural obstacles and variable-traction terrain conditions. This test focused on evaluating the path planning ability to avoid areas prone to slip. Minimum and maximum friction coefficients were used to represent the widest range of slip conditions, indicating areas where a robot may experience low and high traction terrain. The three local path planners were capable of connecting all scheduled points given by the TSP-CVRP planner, and each waypoint was visited only once. In particular, RRT was not able to present adaptive capabilities to slip conditions in any of the three scenarios. It is shown that the RRT and RRT * methods effectively avoided structural obstacles along the planned route but failed to navigate on low traction terrain, although slip areas were also considered obstacles in the environment. Moreover, in most scenarios, both RRT and RRT * provide unfeasible paths for SSMRs that require them to meet kinematic constraints. On the other hand, it was observed that the proposed IRRT * effectively connects the prioritized route points along off-slip travels, generating paths kinematically compatible with the robot’s dynamics. Indeed, the IRRT * algorithm prioritizes navigating in high-traction regions while generating obstacle-free paths. Furthermore, a particular case was observed in IRRT * for scenes 1 and 3 as shown in Figure 7c-i, where the path had to visit the same harvest point twice. Such a particular result was reasonable since the prioritized harvesting point was enclosed by a low-traction terrain region, and no other feasible solution that maintained the shortest local path length was available.

5.4. Evaluation of Path Tracking Performance

To quantitatively assess performance, it was conducted 150 motion control trials using pre-planned paths (see Figure 9). An example of the results is presented in Figure 8 and summarized in Table 3. It was demonstrated that all trials across the three approaches consistently avoided structural obstacles in the farm environment; however, only IRRT * successfully avoided low-traction surfaces with potential slip risk. The obstacle proximity for each approach was consistent, maintaining a safe collision distance. However, the greatest obstacle clearance was achieved with IRRT * throughout the travel, demonstrating adaptability to environmental obstacles (see Figure 9a-b). The obstacle avoidance capability of IRRT * also facilitated suitable maneuverability on challenging terrain, although the total length of the reference path for IRRT * (64.4m) was longer than those obtained with RRT * (47.4m) and RRT (41.7m). Similarly, IRRT * required longer time to navigate the path compared to the other methods, which is reasonable since the proposed approach prioritized avoiding obstacles fully over taking the shortest path, thereby traveling around the harvesting row. In addition, IRRT * produced a kinetically compatible path with smoothness, being 97.63% smoother than RRT and 96.1% smoother than RRT * , as shown in Figure 9c.
In terms of controller effort, the performance metrics of the motion controller are presented in Table 4. With IRRT * , the cumulative path tracking errors along the trial barely increased with RRT * regarding RRT and RRT * , which is related to the capability of avoiding obstacles. However, the controller effort of IRRT * reduced by about 76.1% compared to RRT and 53.1% compared to RRT * , which was attributed to qualified paths with smoothness obtained in the previous path planning process.

6. Conclusions

This article presented an integrated route and path planning strategy for Skid-Steer Mobile Robots (SSMRs) in assisted harvesting tasks within complex agricultural environments. The proposed approach effectively combined a global planning algorithm based on the Traveling Salesman Problem (TSP) and the Capacitated Vehicle Routing Problem (CVRP) with a local path planner based on the Informed Rapidly-exploring Random Tree Star ( IRRT * ) algorithm. The global planning strategy prioritized harvesting locations according to criteria of minimum path length, unexplored harvest points, and vehicle payload capacity constraints. This approach aimed to generate an ordered sequence of harvesting locations that maximized the harvested product yield within the workspace. The local IRRT * planner coordinated the scheduled harvesting points and simultaneously avoided obstacles characterized by low-traction terrain regions. In particular, IRRT * generated smoother and safer routes, maintaining larger average distance to obstacles and reducing control effort compared to (RRT) and ( RRT * ).
The path planning scheme incorporated the SSMR’s motion dynamics and a traversability model to ensure kinematically compatible paths that meet terrain constraints. By incorporating terrain traversability and kinematic constraints, the proposed strategy mitigated the risk of robot entrapment and enabled efficient navigation over shortened and qualified smooth paths, potentially maintaining the quality of the harvested product. Experimental results demonstrated that the proposed IRRT * outperformed the classical RRT and RRT * by achieving 96.1% and 97.6% smoother paths under terrain constraints, respectively. The IRRT * approach also exhibited improved navigation efficiency, avoiding obstacles and potential slippage zones. Future work may explore the integration of additional slip sensing systems and dynamic obstacle detection to further enhance robustness and path adaptability in real-world agricultural settings.
For reproducibility of this work, the code of the proposed algorithm and trial data will be made publicly available.

Acknowledgments

This work has been supported by ANID (National Research and Development Agency of Chile) Fondecyt Iniciación en Investigación 2023 Grant 11230962 and Grant 11240105.

Abbreviations

The following abbreviations are used in this manuscript:
TSP Traveling Salesman Problem
IRRT Informed Rapidly-exploring Random Tree
CVRP Capacitated Vehicle Routing Problem
SSMR Skid-Steer Mobile Robot
FAO Food and Agriculture Organization
PRM Probabilistic Road Mapping
RGB Red-Green-Blue

References

  1. Friedrich, T. A new paradigm for feeding the world in 2050 the sustainable intensification of crop production. Resource Magazine 2015, 22, 18–18. [Google Scholar]
  2. Prado, A.J.; Auat Cheein, F.A.; Blazic, S.; Torres-Torriti, M. Probabilistic self-tuning approaches for enhancing performance of autonomous vehicles in changing terrains. Journal of Terramechanics 2018, 78, 39–51. [Google Scholar] [CrossRef]
  3. Dominguez, X.; Prado, A.; Arboleya, P.; Terzija, V. Evolution of knowledge mining from data in power systems: The Big Data Analytics breakthrough. Electric Power Systems Research 2023, 218, 109193. [Google Scholar] [CrossRef]
  4. Prado, J.; Yandun, F.; Torres Torriti, M.; Auat Cheein, F. Overcoming the Loss of Performance in Unmanned Ground Vehicles Due to the Terrain Variability. IEEE Access 2018, 6, 17391–17406. [Google Scholar] [CrossRef]
  5. Wang, M.; Niu, C.; Wang, Z.; Jiang, Y.; Jian, J.; Tang, X. Model and Parameter Adaptive MPC Path Tracking Control Study of Rear-Wheel-Steering Agricultural Machinery. Agriculture 2024, 14. [Google Scholar] [CrossRef]
  6. Pan, W.; Wang, J.; Yang, W. A Cooperative Scheduling Based on Deep Reinforcement Learning for Multi-Agricultural Machines in Emergencies. Agriculture 2024, 14. [Google Scholar] [CrossRef]
  7. Guevara, L.; Khalid, M.; Hanheide, M.; Parsons, S. Probabilistic model-checking of collaborative robots: A human injury assessment in agricultural applications. Computers and Electronics in Agriculture 2024, 222, 108987. [Google Scholar] [CrossRef]
  8. Sánchez-Ibáñez, J.R.; Pérez-del Pulgar, C.J.; García-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21. [Google Scholar] [CrossRef] [PubMed]
  9. Furchì, A.; Lippi, M.; Carpio, R.F.; Gasparri, A. Route Optimization in Precision Agriculture Settings: A Multi-Steiner TSP Formulation. IEEE Transactions on Automation Science and Engineering 2023, 20, 2551–2568. [Google Scholar] [CrossRef]
  10. Graf Plessen, M. Coupling of crop assignment and vehicle routing for harvest planning in agriculture. Artificial Intelligence in Agriculture 2019, 2, 99–109. [Google Scholar] [CrossRef]
  11. He, P.; Li, J. The two-echelon multi-trip vehicle routing problem with dynamic satellites for crop harvesting and transportation. Applied Soft Computing 2019, 77, 387–398. [Google Scholar] [CrossRef]
  12. Dhirendra Prajapati, Felix T. S. Chan, Y.D.; Pratap, S. Sustainable vehicle routing of agro-food grains in the e-commerce industry. International Journal of Production Research 2022, 60, 7319–7344. [Google Scholar] [CrossRef]
  13. Yang, S.; Jia, B.; Yu, T.; Yuan, J. Research on Multiobjective Optimization Algorithm for Cooperative Harvesting Trajectory Optimization of an Intelligent Multiarm Straw-Rotting Fungus Harvesting Robot. Agriculture 2022, 12. [Google Scholar] [CrossRef]
  14. Gangadharan, M.M.; Salgaonkar, A. Ant colony optimization and firefly algorithms for robotic motion planning in dynamic environments. Engineering Reports 2020, 2, e12132. [Google Scholar] [CrossRef]
  15. Jia, W.; Zhang, Y.; Lian, J.; Zheng, Y.; Zhao, D.; Li, C. Apple harvesting robot under information technology: A review. International Journal of Advanced Robotic Systems 2020, 17, 1729881420925310. [Google Scholar] [CrossRef]
  16. Liu, L.; Wang, X.; Liu, H.; Li, J.; Wang, P.; Yang, X. A Full-Coverage Path Planning Method for an Orchard Mower Based on the Dung Beetle Optimization Algorithm. Agriculture 2024, 14. [Google Scholar] [CrossRef]
  17. Janos, J.; Vonasek, V.; Penicka, R. Multi-Goal Path Planning Using Multiple Random Trees. IEEE Robotics and Automation Letters 2021, 6, 4201–4208. [Google Scholar] [CrossRef]
  18. Yahia, H.S.; Mohammed, A.S. Path planning optimization in unmanned aerial vehicles using meta-heuristic algorithms: a systematic review. Environmental Monitoring and Assessment 2023, 195. [Google Scholar] [CrossRef]
  19. Carpio, R.F.; Maiolini, J.; Potena, C.; Garone, E.; Ulivi, G.; Gasparn, A. MP-STSP: A Multi-Platform Steiner Traveling Salesman Problem Formulation for Precision Agriculture in Orchards. 2021 IEEE International Conference on Robotics and Automation (ICRA), 2021, pp. 2345–2351. [CrossRef]
  20. Pak, J.; Kim, J.; Park, Y.; Son, H.I. Field Evaluation of Path-Planning Algorithms for Autonomous Mobile Robot in Smart Farms. IEEE Access 2022, 10, 60253–60266. [Google Scholar] [CrossRef]
  21. Tagliavini, L.; Colucci, G.; Botta, A.; Cavallone, P.; Baglieri, L.; Quaglia, G. Wheeled Mobile Robots: State of the Art Overview and Kinematic Comparison Among Three Omnidirectional Locomotion Strategies. Journal of Intelligent and Robotic Systems: Theory and Applications 2022, 106. [Google Scholar] [CrossRef]
  22. Castro, G.G.R.d.; Berger, G.S.; Cantieri, A.; Teixeira, M.; Lima, J.; Pereira, A.I.; Pinto, M.F. Adaptive Path Planning for Fusing Rapidly Exploring Random Trees and Deep Reinforcement Learning in an Agriculture Dynamic Environment UAVs. Agriculture 2023, 13. [Google Scholar] [CrossRef]
  23. Claussmann, L.; Revilloud, M.; Gruyer, D.; Glaser, S. A Review of Motion Planning for Highway Autonomous Driving. IEEE Transactions on Intelligent Transportation Systems 2020, 21, 1826–1848. [Google Scholar] [CrossRef]
  24. Xu, J.; Tian, Z.; He, W.; Huang, Y. A Fast Path Planning Algorithm Fusing PRM and P-Bi-RRT. 2020 11th International Conference on Prognostics and System Health Management (PHM-2020 Jinan), 2020, pp. 503–508. [CrossRef]
  25. Mashayekhi, R.; Idris, M.Y.I.; Anisi, M.H.; Ahmedy, I.; Ali, I. Informed RRT*-Connect: An Asymptotically Optimal Single-Query Path Planning Method. IEEE Access 2020, 8, 19842–19852. [Google Scholar] [CrossRef]
  26. Kontoudis, G.P.; Vamvoudakis, K.G. Kinodynamic Motion Planning With Continuous-Time Q-Learning: An Online, Model-Free, and Safe Navigation Framework. IEEE Transactions on Neural Networks and Learning Systems 2019, 30, 3803–3817. [Google Scholar] [CrossRef] [PubMed]
  27. Zhang, C.; Zhou, L.; Liu, H. Lalo-Check: A path optimization framework for sampling-based motion planning with tree structure. IEEE Access 2019, 7, 100733–100746. [Google Scholar] [CrossRef]
  28. Zhang, D.; Xu, Y.; Yao, X. An Improved Path Planning Algorithm for Unmanned Aerial Vehicle Based on RRT-Connect. 2018 37th Chinese Control Conference (CCC), 2018, pp. 4854–4858. [CrossRef]
  29. Xie, J.; Carrillo, L.R.G.; Jin, L. Path planning for UAV to cover multiple separated convex polygonal regions. IEEE Access 2020, 8, 51770–51785. [Google Scholar] [CrossRef]
  30. Cheein, F.A.; Torres-Torriti, M.; Hopfenblatt, N.B.; Prado, A.J.; Calabi, D. Agricultural service unit motion planning under harvesting scheduling and terrain constraints. Journal of Field Robotics 2017, 34, 1531–1542. [Google Scholar] [CrossRef]
  31. Peng, K.; Du, J.; Lu, F.; Sun, Q.; Dong, Y.; Zhou, P.; Hu, M. A Hybrid Genetic Algorithm on Routing and Scheduling for Vehicle-Assisted Multi-Drone Parcel Delivery. IEEE Access 2019, 7, 49191–49200. [Google Scholar] [CrossRef]
  32. Praveen, V.; Keerthika, D.P.; Sivapriya, G.; Sarankumar, A.; Bhasker, B. Vehicle Routing Optimization Problem: A Study on Capacitated Vehicle Routing Problem. Materials Today: Proceedings 2022, 64, 670–674. [Google Scholar] [CrossRef]
  33. Khajepour, A.; Sheikhmohammady, M.; Nikbakhsh, E. Field path planning using capacitated arc routing problem. Computers and Electronics in Agriculture 2020, 173, 105401. [Google Scholar] [CrossRef]
  34. Patle, B.K.; L, G.B.; Pandey, A.; Parhi, D.R.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Defence Technology 2019, 15, 582–606. [Google Scholar] [CrossRef]
  35. Ye, L.; Wu, F.; Zou, X.; Li, J. Path planning for mobile robots in unstructured orchard environments: An improved kinematically constrained bi-directional RRT approach. Computers and Electronics in Agriculture 2023, 215, 108453. [Google Scholar] [CrossRef]
  36. Zhao, Y.; Zhu, Y.; Zhang, P.; Gao, Q.; Han, X. A Hybrid A* Path Planning Algorithm Based on Multi-objective Constraints. 2022 Asia Conference on Advanced Robotics, Automation, and Control Engineering (ARACE), 2022, pp. 1–6. [CrossRef]
  37. Wang, N.; Li, X.; Zhang, K.; Wang, J.; Xie, D. A Survey on Path Planning for Autonomous Ground Vehicles in Unstructured Environments. Machines 2024, 12. [Google Scholar] [CrossRef]
  38. Papadakis, P. Terrain traversability analysis methods for unmanned ground vehicles: A survey. Engineering Applications of Artificial Intelligence 2013, 26, 1373–1385. [Google Scholar] [CrossRef]
  39. Al-Milli, S.; Seneviratne, L.D.; Althoefer, K. Track terrain modelling and traversability prediction for tracked vehicles on soft terrain. Journal of Terramechanics 2010, 47, 151–160. [Google Scholar] [CrossRef]
  40. Fernandez, B.; Herrera, P.J.; Cerrada, J.A. A Simplified Optimal Path Following Controller for an Agricultural Skid-Steering Robot. IEEE Access 2019, 7, 95932–95940. [Google Scholar] [CrossRef]
  41. Pragr, M.; Bayer, J.; Faigl, J. Autonomous robotic exploration with simultaneous environment and traversability models learning. Frontiers in Robotics and AI 2022, 9. [Google Scholar] [CrossRef] [PubMed]
  42. Dereci, U.; Karabekmez, M.E. The applications of multiple route optimization heuristics and meta-heuristic algorithms to solid waste transportation: A case study in Turkey. Decision Analytics Journal 2022, 4. [Google Scholar] [CrossRef]
  43. Prado, A.J.; Torres-Torriti, M.; Cheein, F.A. Distributed Tube-Based Nonlinear MPC for Motion Control of Skid-Steer Robots With Terra-Mechanical Constraints. IEEE Robotics and Automation Letters 2021, 6, 8045–8052. [Google Scholar] [CrossRef]
  44. Jiang, J.; Han, Z.; Li, J.; Wang, Y.; Wang, J.; Xu, S. Global Path Planning of UGVs in Large-Scale Off-Road Environment Based on Improved A-star Algorithm and Quadratic Programming. 2023 IEEE Intelligent Vehicles Symposium (IV), 2023, pp. 1–7. [CrossRef]
  45. Huang, C.; Tang, B.; Guo, Z.; Su, Q.; Gai, J. Agile-RRT*: A Faster and More Robust Path Planner With Enhanced Initial Solution and Convergence Rate in Complex Environments. IEEE Access 2024, 12, 58703–58714. [Google Scholar] [CrossRef]
  46. Fuad, M.; Wahyuni, S. Path Planning and Smoothing in Maze Exploration Using Virtual Mobile Robot-Based Modified Probabilistic Road Map. 2022 IEEE 8th Information Technology International Seminar (ITIS), 2022, pp. 15–20. [CrossRef]
  47. Elbanhawi, M.; Simic, M. Sampling-Based Robot Motion Planning: A Review. IEEE Access 2014, 2, 56–77. [Google Scholar] [CrossRef]
  48. Wang, H.; Li, G.; Hou, J.; Chen, L.; Hu, N. A Path Planning Method for Underground Intelligent Vehicles Based on an Improved RRT* Algorithm. Electronics (Switzerland) 2022, 11. [Google Scholar] [CrossRef]
  49. Chen, X.; Ruan, X.; Zhu, X. Intelligent RRT Exploration Mapping Method Based on Evolutionary Cognition in Unknown Environment. 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), 2020, Vol. 9, pp. 1013–1017. [CrossRef]
  50. Dong, G.; Qin, R.; Han, L.; Chen, J.; Xu, K.; Ding, X. Ground Contact Parameter Estimation Guided Gait Planning for Hexapod Robots. 2022 IEEE International Conference on Robotics and Biomimetics (ROBIO), 2022, pp. 1–6. [CrossRef]
  51. Sender, T.; Brudnak, M.; Steiger, R.; Vasudevan, R.; Epureanu, B. A Regret-Informed Evolutionary Approach for Generating Adversarial Scenarios for Black-Box Off-Road Autonomy Systems. IEEE Robotics and Automation Letters 2024, 9, 5354–5361. [Google Scholar] [CrossRef]
  52. Höffmann, M.; Patel, S.; Büskens, C. Optimal Coverage Path Planning for Agricultural Vehicles with Curvature Constraints. Agriculture 2023, 13. [Google Scholar] [CrossRef]
  53. Álvaro Javier Prado. ; Torres-Torriti, M.; Yuz, J.; Cheein, F.A. Tube-based nonlinear model predictive control for autonomous skid-steer mobile robots with tire terrain interactions. Control Engineering Practice 2020, 101. [Google Scholar] [CrossRef]
  54. Popov, V.L. , Heidelberg, 2017; pp. 151–172. doi:10.1007/978-3-662-53081-8_10.Friction. In Contact Mechanics and Friction: Physical Principles and Applications; Springer Berlin Heidelberg: Berlin, Heidelberg, 2017; pp. 151–172. [Google Scholar] [CrossRef]
  55. Jazar, R.N.; Jazar, R.N. Road dynamics. Advanced Vehicle Dynamics.
  56. K. V. Narasimha Rao, R. Krishna Kumar, R.M.; Misra, V.K. A study of the relationship between Magic Formula coefficients and tyre design attributes through finite element analysis. Vehicle System Dynamics 2006, 44, 33–63. [Google Scholar] [CrossRef]
  57. Zhang, J.; Wang, X.; Xu, L.; Zhang, X. An Occupancy Information Grid Model for Path Planning of Intelligent Robots. ISPRS International Journal of Geo-Information 2022, 11. [Google Scholar] [CrossRef]
  58. Gammell, J.D.; Barfoot, T.D.; Srinivasa, S.S. Informed Sampling for Asymptotically Optimal Path Planning. IEEE Transactions on Robotics 2018, 34, 966–984. [Google Scholar] [CrossRef]
  59. Qi, J.; Yang, H.; Sun, H. MOD-RRT*: A Sampling-Based Algorithm for Robot Path Planning in Dynamic Environment. IEEE Transactions on Industrial Electronics 2021, 68, 7244–7251. [Google Scholar] [CrossRef]
  60. Auat Cheein, F.A.; Scaglia, G.; Torres-Torriti, M.; Guivant, J.; Prado, A.J.; Arnò, J.; Escolà, A.; Rosell-Polo, J.R. Algebraic path tracking to aid the manual harvesting of olives using an automated service unit. Biosystems Engineering 2016, 142, 117–132. [Google Scholar] [CrossRef]
  61. Álvaro Javier Prado. ; Michałek, M.M.; Cheein, F.A. Machine-learning based approaches for self-tuning trajectory tracking controllers under terrain changes in repetitive tasks. Engineering Applications of Artificial Intelligence 2018, 67, 63–80. [Google Scholar] [CrossRef]
  62. Shamshiri, R.; Hameed, I.; Pitonakova, L.; Weltzien, C.; Balasundram, S.; Yule, I.; Grift, T.; Chowdhary, G. Simulation software and virtual environments for acceleration of agricultural robotics: Features highlights and performance comparison. International Journal of Agricultural and Biological Engineering 2018, 11, 15–31. [Google Scholar] [CrossRef]
  63. Perron, L.; Didier, F.; Gay, S. The CP-SAT-LP Solver. 29th International Conference on Principles and Practice of Constraint Programming (CP 2023); Yap, R.H.C., Ed.; Schloss Dagstuhl – Leibniz-Zentrum für Informatik: Dagstuhl, Germany, 2023. [Google Scholar] [CrossRef]
  64. Sunil, K.; Afzal, S. A novel hybrid framework for single and multi-robot path planning in a complex industrial environment. Journal of Intelligent Manufacturing 2024, 35, 587–612. [Google Scholar] [CrossRef]
  65. Zhang, X.; Zhu, T.; Du, L.; Hu, Y.; Liu, H. Local Path Planning of Autonomous Vehicle Based on an Improved Heuristic Bi-RRT Algorithm in Dynamic Obstacle Avoidance Environment. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
1
https://github.com
Preprints 108405 g001
Figure 1. General scheme of the integrated global and local planning strategy for SSMRs under terrain constraints.
Figure 1. General scheme of the integrated global and local planning strategy for SSMRs under terrain constraints.
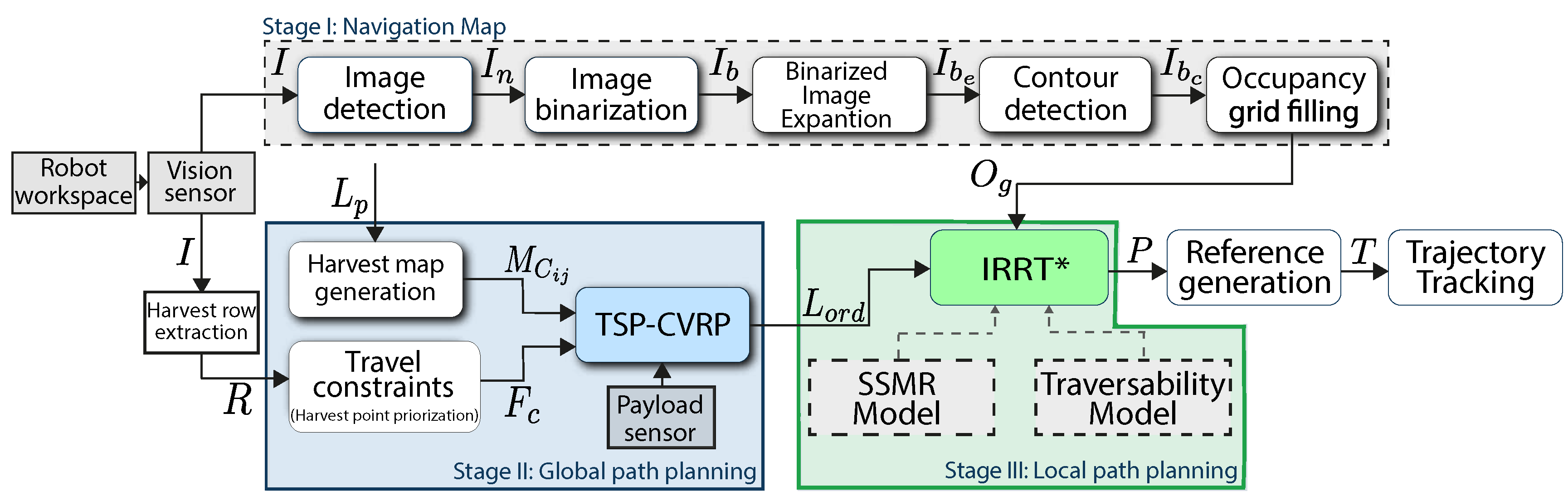
Preprints 108405 g001
Preprints 108405 g002
Figure 2. Illustration of the image processing to generate an occupancy grid map O g with safe navigation boundaries for path planning. The process involves capturing of image, background removal, median blur, traction terrain detection, adaptive thresholding, and contour detection. These process identifies obstacles and introduce safety margins around them, resulting in a environment map suitable for path planning.
Figure 2. Illustration of the image processing to generate an occupancy grid map O g with safe navigation boundaries for path planning. The process involves capturing of image, background removal, median blur, traction terrain detection, adaptive thresholding, and contour detection. These process identifies obstacles and introduce safety margins around them, resulting in a environment map suitable for path planning.
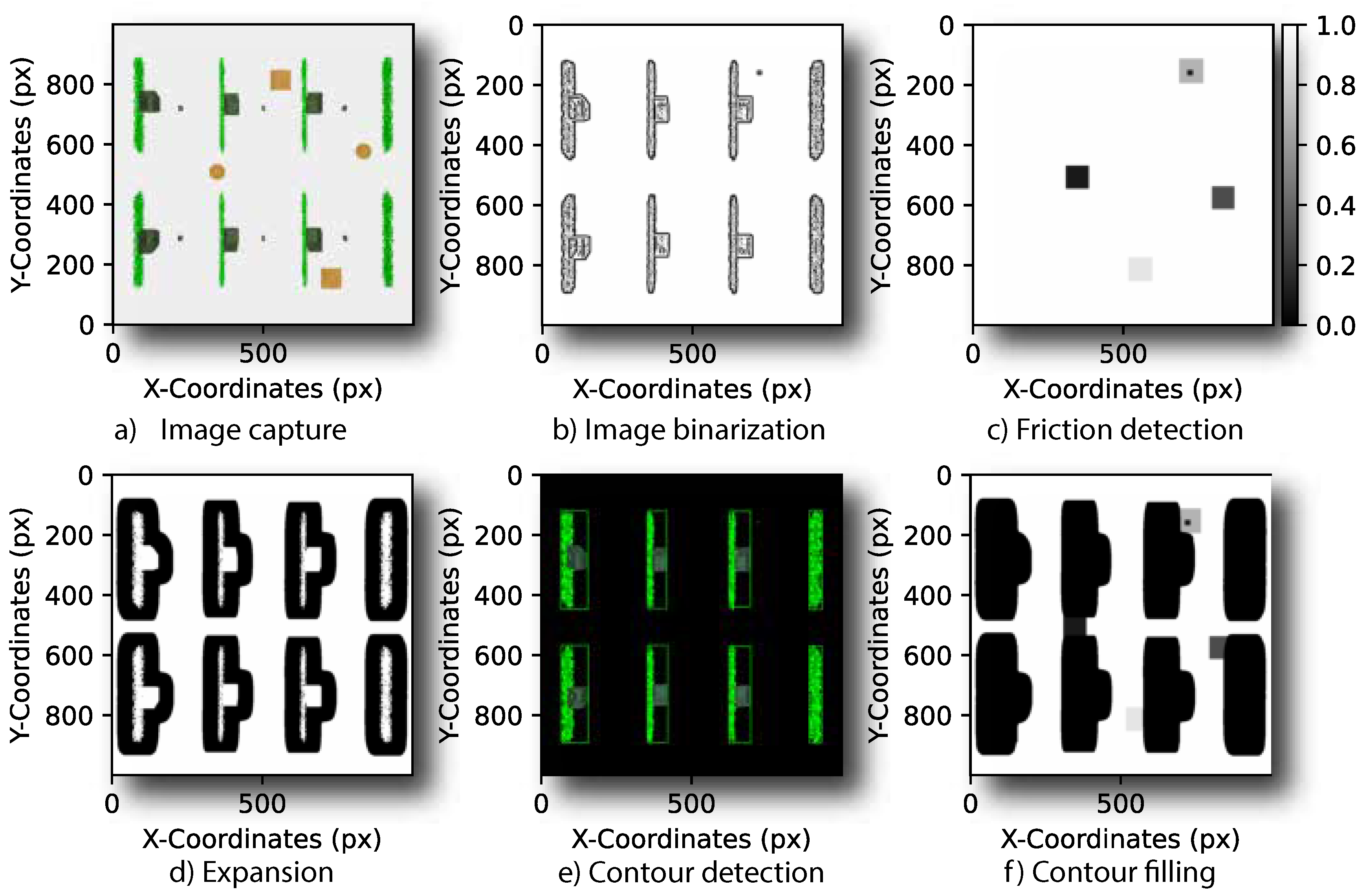
Preprints 108405 g002
Preprints 108405 g003
Figure 3. Illustration of the proposed IRRT * algorithm process, depicted in six steps. Step 1 involves generating a random informed sample within a safe area. Step 2 consists on extending a tree towards the sampled point. In Step 3, the feasibility of generated nodes is validated. Step 4 obtains neighbour nodes. Step 5 involves rewiring the tree with the nearest neighbours, considering the lowest path cost. Finally, Step 6 encompasses smoothing the resulting path.
Figure 3. Illustration of the proposed IRRT * algorithm process, depicted in six steps. Step 1 involves generating a random informed sample within a safe area. Step 2 consists on extending a tree towards the sampled point. In Step 3, the feasibility of generated nodes is validated. Step 4 obtains neighbour nodes. Step 5 involves rewiring the tree with the nearest neighbours, considering the lowest path cost. Finally, Step 6 encompasses smoothing the resulting path.
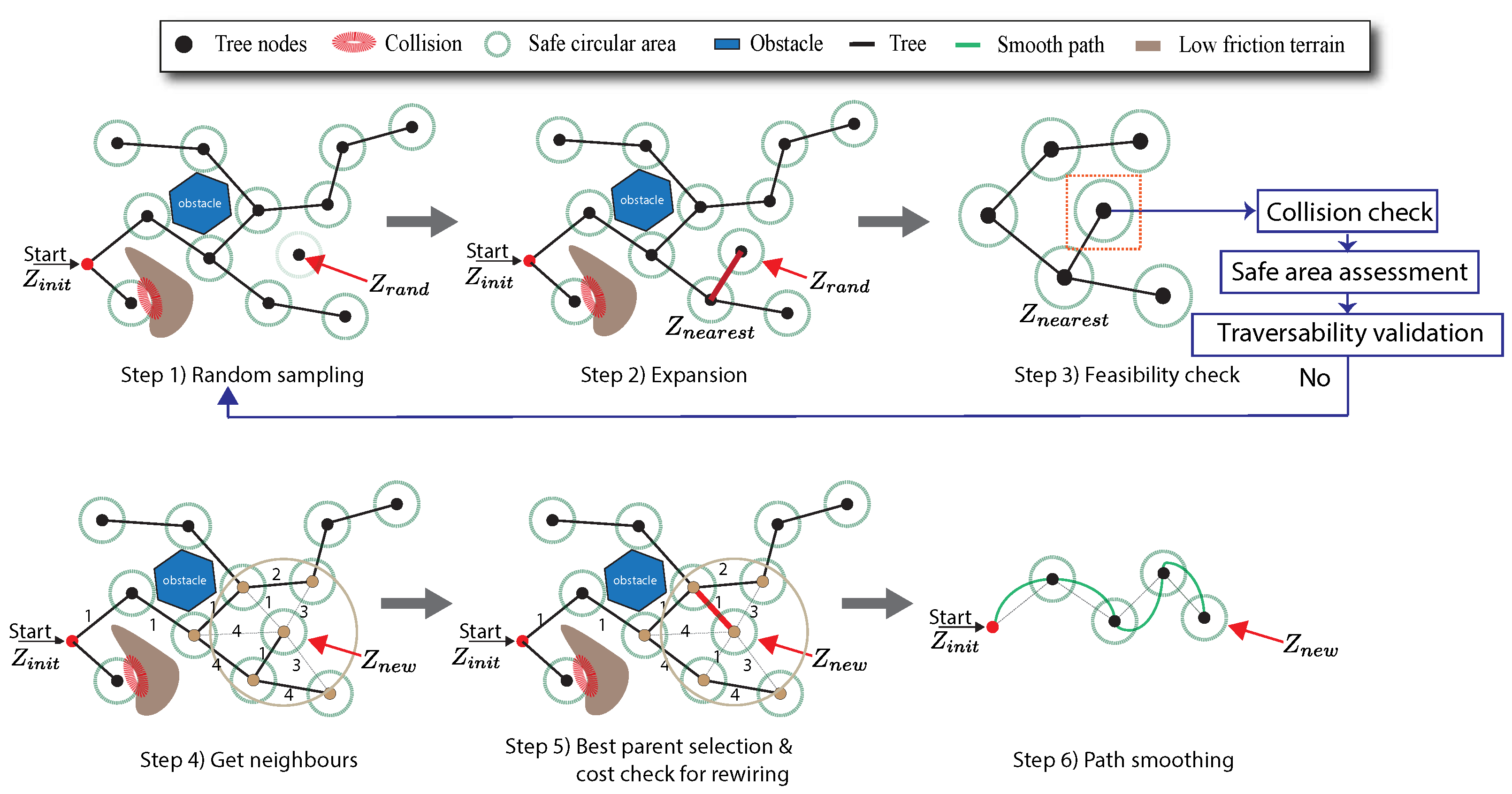
Preprints 108405 g003
Preprints 108405 g004
Figure 4. Results of the global planning approach. The first row depicts outcomes where the harvest depot corresponds to the start point, while the second row in scenarios where the start and end points do not necessarily match. If one compares the product harvest, travels were prioritized by minimizing the total travel cost and maximizing the harvested product with respect to the robot payload capacity. It is also shown that not only a harvest point is visited once, but also an alley, avoiding back-and-forth travels between crop rows.
Figure 4. Results of the global planning approach. The first row depicts outcomes where the harvest depot corresponds to the start point, while the second row in scenarios where the start and end points do not necessarily match. If one compares the product harvest, travels were prioritized by minimizing the total travel cost and maximizing the harvested product with respect to the robot payload capacity. It is also shown that not only a harvest point is visited once, but also an alley, avoiding back-and-forth travels between crop rows.
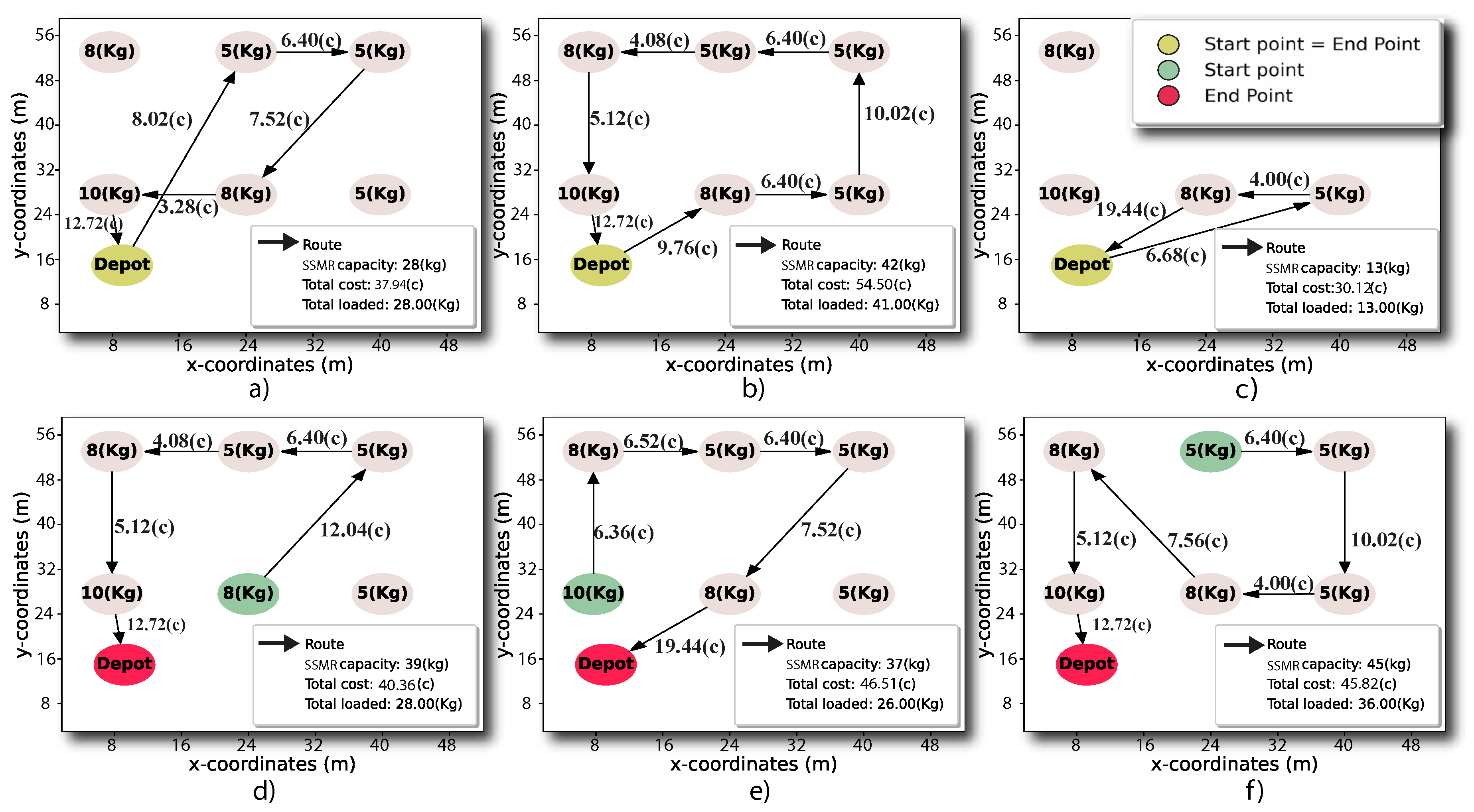
Preprints 108405 g004
Preprints 108405 g005
Figure 5. Results of local path planning strategies. Each column presents the path planning response with RRT, RRT * , and IRRT * , respectively. Examining among the three path planners, the RRT strategy yields non-smooth paths with wide sampling distribution (greenish-yellow lines), RRT * shows a smooth path with potential slip risk despite a full path search, and IRRT * generates a smooth path that avoids uncertain conditions of slip areas with localized exploration.
Figure 5. Results of local path planning strategies. Each column presents the path planning response with RRT, RRT * , and IRRT * , respectively. Examining among the three path planners, the RRT strategy yields non-smooth paths with wide sampling distribution (greenish-yellow lines), RRT * shows a smooth path with potential slip risk despite a full path search, and IRRT * generates a smooth path that avoids uncertain conditions of slip areas with localized exploration.
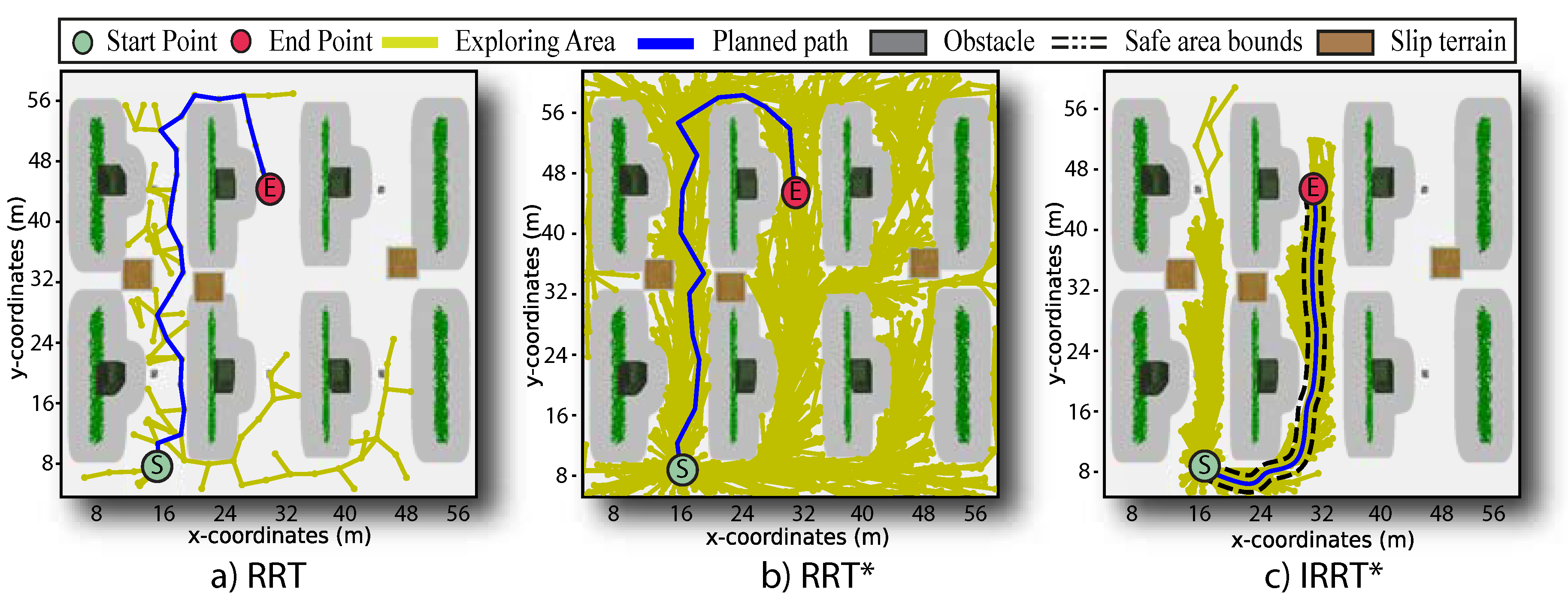
Preprints 108405 g005
Preprints 108405 g006
Figure 6. Results of the path planning algorithms when considering structural obstacles and variable obstacle positions in harvesting tasks. Each row shows the path planning results under three scenes where the obstacle distribution changed. On each column, it is depicted results of RRT, RRT * , and IRRT * , respectively. By examination, the proposed IRRT * method generates smoother and safer feasible paths compared to RRT and RRT * against changing obstacles in the navigation scene.
Figure 6. Results of the path planning algorithms when considering structural obstacles and variable obstacle positions in harvesting tasks. Each row shows the path planning results under three scenes where the obstacle distribution changed. On each column, it is depicted results of RRT, RRT * , and IRRT * , respectively. By examination, the proposed IRRT * method generates smoother and safer feasible paths compared to RRT and RRT * against changing obstacles in the navigation scene.
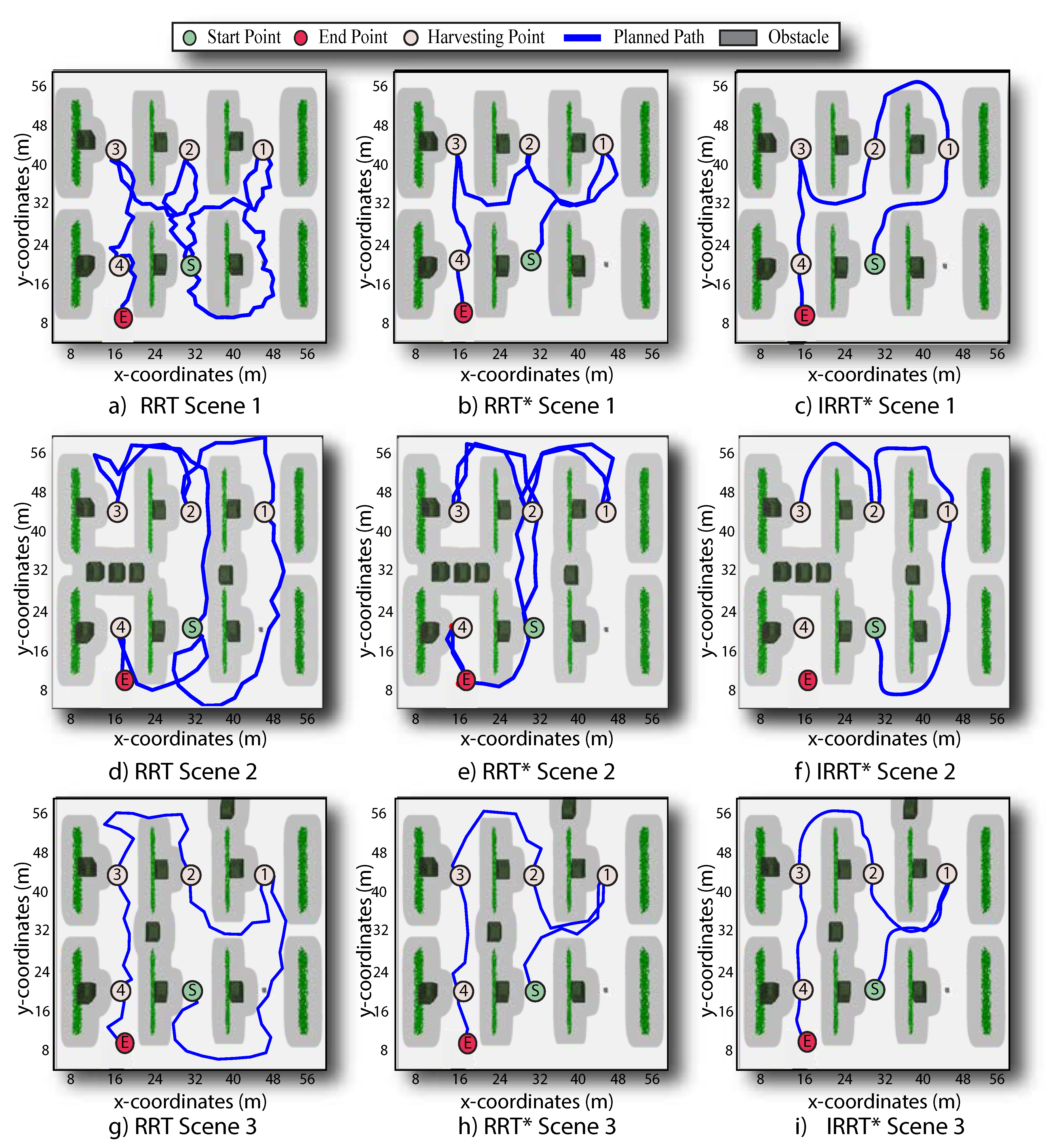
Preprints 108405 g006
Preprints 108405 g007
Figure 7. Results of the path planning algorithms when considering structural obstacles and terrain constraints by changing the wheel-terrain interaction in harvesting tasks. Paths on each column present the outcome for each path planning algorithm, whereas each row shows different scenes accounting for different slip areas. The RRT and RRT * algorithms effectively avoided obstacles but disregarded low-traction terrain regions; however, the proposed IRRT * generated feasible paths free from obstacles that connected route points while achieving terrain constraints.
Figure 7. Results of the path planning algorithms when considering structural obstacles and terrain constraints by changing the wheel-terrain interaction in harvesting tasks. Paths on each column present the outcome for each path planning algorithm, whereas each row shows different scenes accounting for different slip areas. The RRT and RRT * algorithms effectively avoided obstacles but disregarded low-traction terrain regions; however, the proposed IRRT * generated feasible paths free from obstacles that connected route points while achieving terrain constraints.
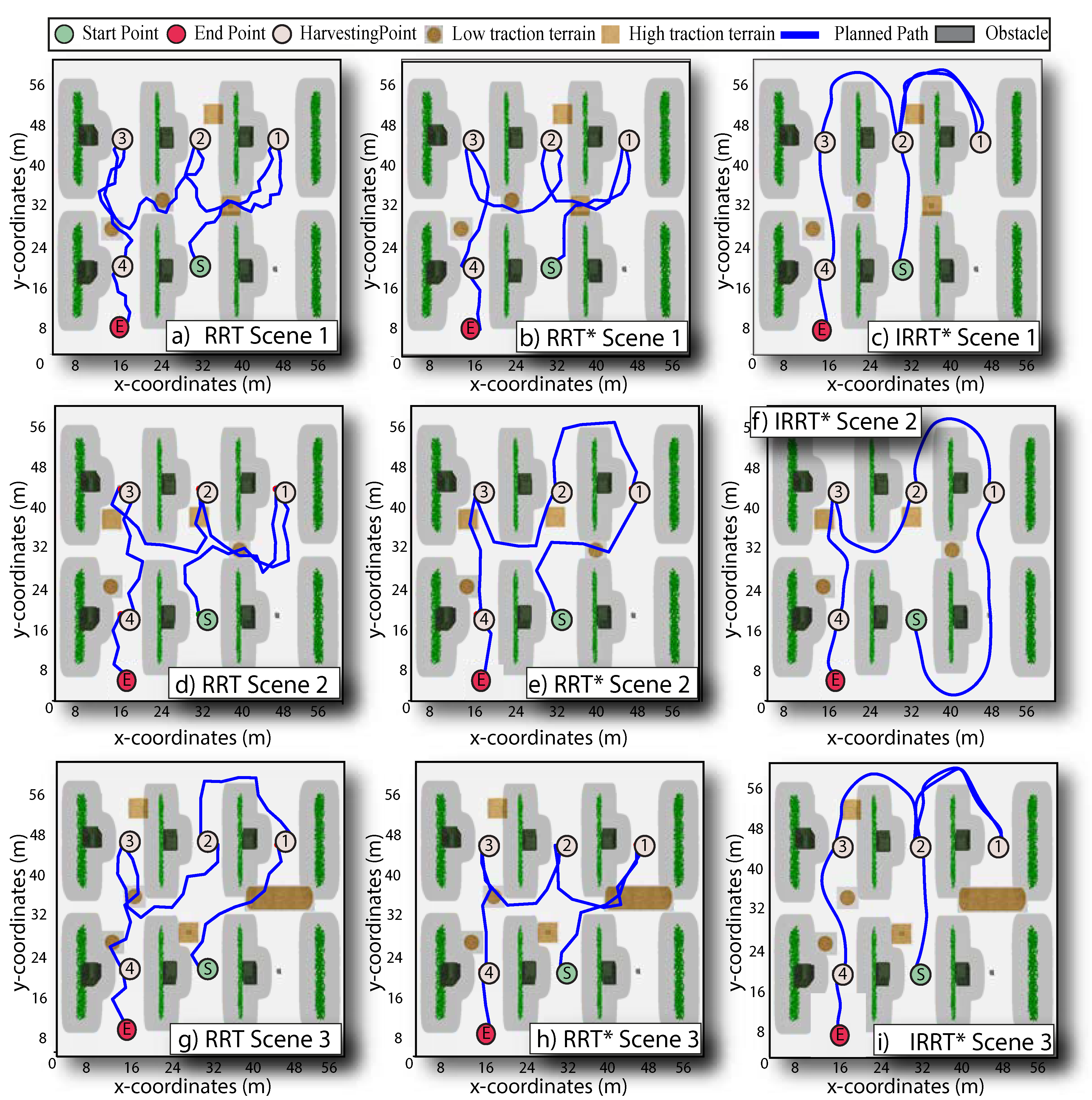
Preprints 108405 g007
Preprints 108405 g008
Figure 8. Results of trajectory tracking subject to structural obstacles and slip constraints, using the previously planned path as reference. Each trial shows that the motion controller was capable of tracking the parameterized path without colliding with structural obstacles. However, the motion controller using the IRRT * reference path outperforms RRT and RRT * regarding the adaptability to navigate on slippery terrain conditions along a favorable smooth path.
Figure 8. Results of trajectory tracking subject to structural obstacles and slip constraints, using the previously planned path as reference. Each trial shows that the motion controller was capable of tracking the parameterized path without colliding with structural obstacles. However, the motion controller using the IRRT * reference path outperforms RRT and RRT * regarding the adaptability to navigate on slippery terrain conditions along a favorable smooth path.
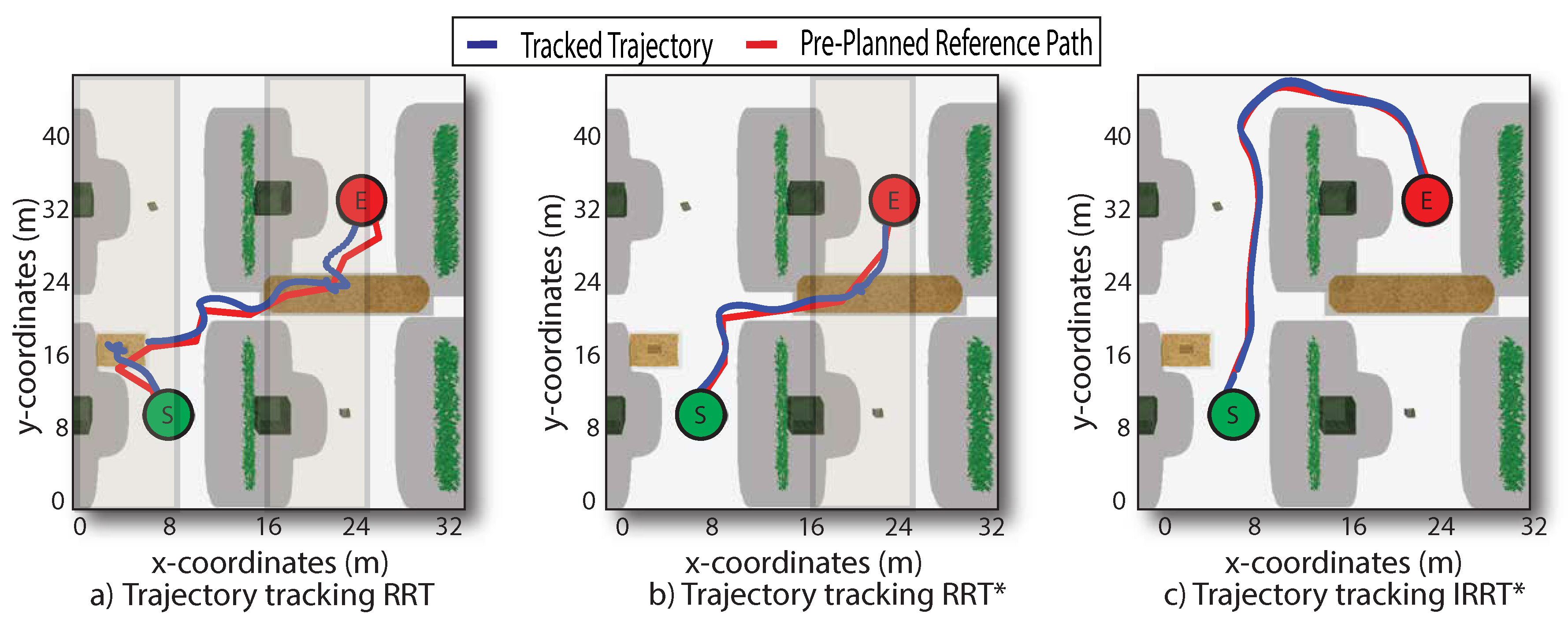
Preprints 108405 g008
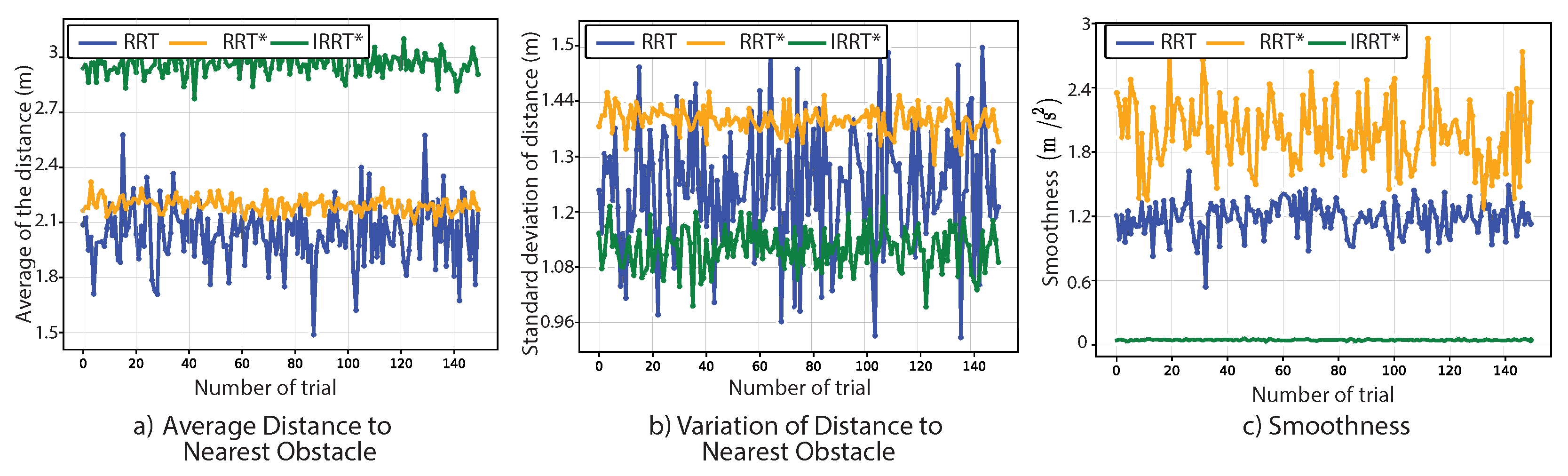
Preprints 108405 g009
Figure 9. Comparison of performance metrics obtained with the test path planning algorithms across 150 trials. a) illustrates the variation of the average distance from nodes to the nearest obstacles; b) presents the standard deviation of these distances for each method; and c) presents path smoothness. Upon inspection, the IRRT * approach indicates consistent smoother paths and longer distances to obstacles along the trails compared to IRRT * and IRRT * .
Figure 9. Comparison of performance metrics obtained with the test path planning algorithms across 150 trials. a) illustrates the variation of the average distance from nodes to the nearest obstacles; b) presents the standard deviation of these distances for each method; and c) presents path smoothness. Upon inspection, the IRRT * approach indicates consistent smoother paths and longer distances to obstacles along the trails compared to IRRT * and IRRT * .
Preprints 108405 g009
Table 1. A nomenclature summary of variables used in the proposed probabilistic path planning algorithms.
Table 1. A nomenclature summary of variables used in the proposed probabilistic path planning algorithms.
Traversability model
μ Coefficient of static friction
F N Normal force
F f Frictional force
Navigation map
I Image captured by a vision sensor
O g Occupancy grid representing the environment (pixels)
Global path planning
H p Harvest points
L p List of locations and weights of H p
R List of harvest rows for in each isle
Q Maximum payload capacity of the vehicle
w Harvest weight on each harvest point
q Harvest demand on each harvest point
L ord Route with ordered H p to be visited
Local path planning
z start Initial path planning state
T Tree
z rand New sample point in the O g
z best best node in terms of closeness to a neighbourhood
z nearest The nearest node from z r a n d
z new New node added to T
T f Traction force
N ( z new ) Neighbourhood of nodes around z new
Table 2. Parameters used in the path planning methods.
Table 2. Parameters used in the path planning methods.
Parameter RRT RRT * IRRT *
N Iterations 500 500 500
r f Safe navigation bounds 0.3m 0.3m 0.3m
N s Neighbour size 2.5m 2.5m 2.5m
r Extended ratio 1.2m 1.2m 1.2m
γ Sample rate 0.2 0.2 0.2
F N , i j Normal force per wheel - - 400N
Table 3. Performance metrics of the path planning approaches.
Table 3. Performance metrics of the path planning approaches.
Method Path planning Obstacle avoidance
Path
length [m]		 Travel
time [s]		 Smoothness
S p a t h [ m / s 2 ]		 Obstacle
proximity d ¯ o [m]		 Distance
variability σ [m]
RRT 47.4 1.8 1.97 2.0 ± 0.31
RRT * 41.7 41.6 1.18 2.2 ± 0.35
IRRT * 64.4 15.2 0.046 2.9 ± 0.28
Table 4. Performance metrics of motion control using the previously planned paths.
Table 4. Performance metrics of motion control using the previously planned paths.
Method C x
[m]		 C y
[m]		 C u
[ m 2 ]		 C T o t
RRT 178.96 132.06 93.4 311.02
RRT * 84.30 131.03 47.7 215.33
IRRT * 28.21 173.71 22.3 201.03
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated