Prerpints.org logo
Preprint
Article

Thermophysical Characterization of Materials for Energy-Efficient Double Diaphragm Preforming

Altmetrics

Downloads

96

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Applied Heat Transfer

Submitted:

06 June 2024

Posted:

07 June 2024

You are already at the latest version

Alerts
Abstract
The Double Diaphragm Forming (DDF) process uses vacuum pressure and heat to pre-shape composite reinforcements between flexible diaphragms. Accurate modelling of heat transfer within DDF requires knowledge of the thermophysical properties of the constituent materials. This study investigates the specific heat and thermal conductivity of silicone diaphragms, carbon fibers (chopped and powdered), thermoplastic veils, and their combinations. Experiments measured the specific heat of each material using differential scanning calorimetry and the thermal conductivity of silicone and carbon fabric preforms using the transient plane source method and modified transient plane source method respectively. The influence of reheating cycles on specific heat of carbon fiber-veil samples and the effect of compaction on thermal conductivity of silicone and carbon fabrics were explored. While silicone exhibited linear specific heat behavior, the thermoplastic veil showed non-linearity due to phase change. The combined carbon fiber-veil samples demonstrated slight non-linear specific heat variations depending on reheating cycles. Thermal conductivity of the fabric preforms decreased with the addition of thermoplastic veil and under vacuum-compaction conditions. The established temperature-dependent property relationships provide valuable data for optimizing DDF preforming parameters and enhancing energy efficiency in composite manufacturing.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The Double diaphragm forming (DDF) process offers a cost effective solution for shaping fabric plies in liquid composite molding (LCM) [1]. Unlike traditional autoclave molding, DDF allows for producing dry fabrics outside an autoclave environment, significantly reducing costs. The use of dry fabrics provides better handling, flexibility, and formability, enabling the production of complex shaped structural parts. This approach not only enhances production rates but also lowers overall energy consumption [2,3,4]. In the DDF process, silicone diaphragm membranes apply hydrostatic pressure to carbon fiber reinforcements, forming net-shaped 3D geometries from 2D layups. Heat is then applied to activate the binder material between the fabric layers, tacking them together and maintaining the desired shape after cooling. However, uneven binder heating during this stage can lead to defects like incompletely compacted preforms and irregular composite sheets [5,6]. These defects may arise from the shape of the formed product, uneven heating, or variations in preform thickness, which depends on process temperature, heating source type, and degree of compaction [7]. Furthermore, preform compaction behavior varies based on the binder system type, content, and preforming parameters. Higher binder content tends to increase thickness while decreasing elastic recovery and increasing permanent deformation. Managing these factors is crucial for improving the DDF process and producing high-quality dry preforms [8,9,10]. 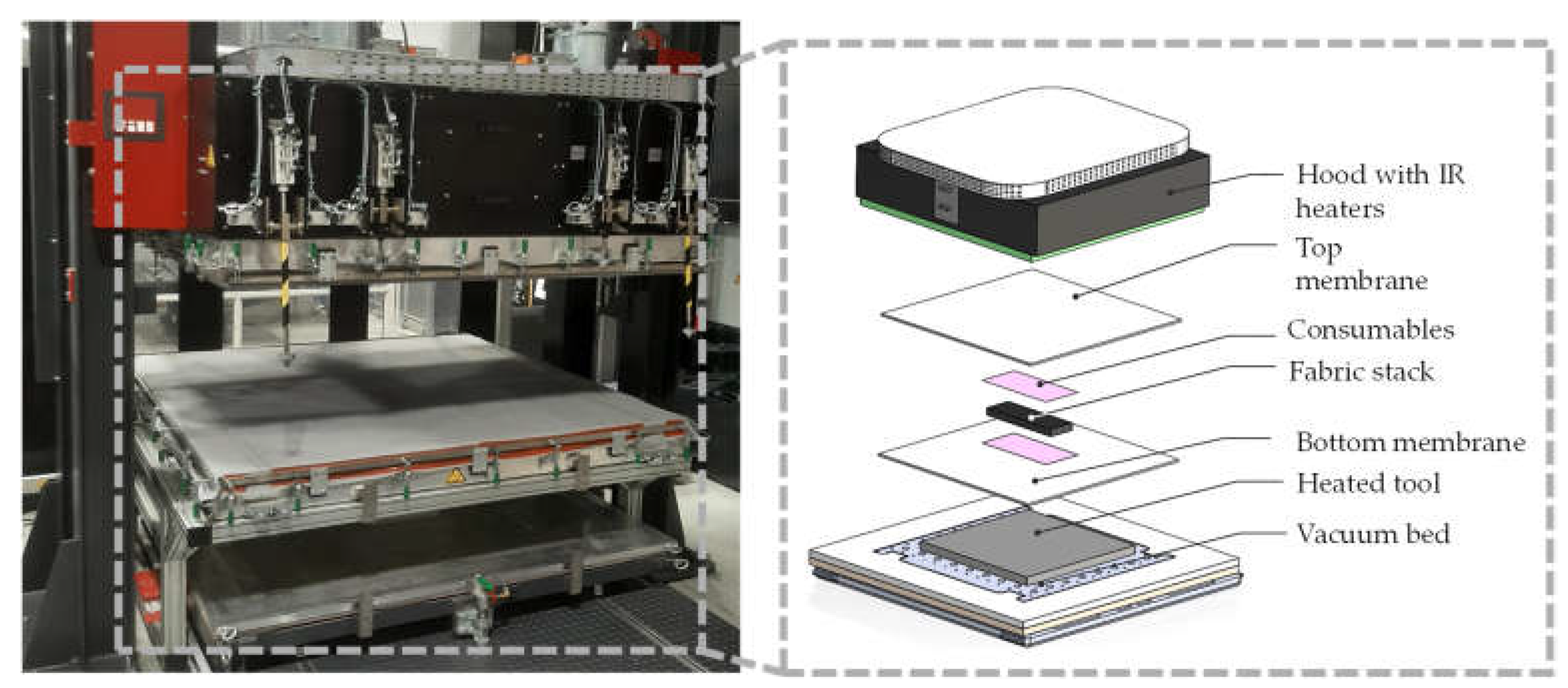Figure 1 illustrates the DDF process setup using the FILL DDF former, Austria. Multi-layer fabrics are assembled between two diaphragms and a vacuum is initially applied to compact them. A second vacuum molds the compacted stack with silicone onto the tool to achieve the required shape. The final stage involves applying heat via heated tools or infrared (IR) or a combination of both and cooling to retain the shape.
In DDF studies, researchers aim to understand how materials behave under varying temperature conditions. They heavily rely on finite element (FE) models, supported by experiments, to compare processing methods like thermoforming and isothermal approaches [11,12], and investigate temperature variation effects on final part quality and defects [13]. Advanced thermomechanical modelling techniques have been employed to better understand the influence of transient temperature on deformation behavior, considering phase transition effects [14]. Additionally, some approaches have focused on defining model-based material definitions (MBMD) that encompass chemistry, processing, and structure-property relationships at different scales, tailored to the location and orientation specifics of preforming [15,16,17]. While previous research has utilized numerical simulations to explore various DDF process aspects, a notable gap remains in understanding the heat transfer process involving woven dry carbon fiber reinforcements during preform heating [18]. Despite this, no numerical studies currently address this heat transfer process to accurately predict temperatures. Moreover, temperature dependent DDF studies have neglected crucial thermophysical properties like thermal conductivity and specific heat, focusing solely on mechanical properties. Considering these properties is vital for accurately modelling heat transfer during preforming under vacuum compaction conditions, alongside the binder material.
Under vacuum conditions for dry preforms, the primary heat transfer mode is conduction between woven carbon fiber tows, with minor contributions from gap radiation through pores [19]. Since the system operates under full vacuum, convection is negligible due to air absence. The anisotropic nature of fibers and woven structure imparts directional heat flow within the fabric. To measure this direction-dependent thermal conductivity, standard equipment like Hukseflux THISYS and THASYS devices are commonly used for fabrics and structural polymer composites [20,21]. However, the use of glycol can significantly affect measurements by influencing multilayer contact. To avoid this issue, infrared thermal mapping without binders is also employed to evaluate the heat transfer properties of woven and non-woven carbon fabrics [22]. Apart from carbon fabric studies, other material investigations include woven ceramic composites under compression (experimental and numerical) [23], aramid fabrics [24] , unit 3D textile structure [25], numerical particle embedded textile [26] and other numerical techniques [27,28,29,30].
For conductivity studies, laser flash analysis (LFA) has been used to determine conductivity in enhancing thermal conductivity of carbon fiber epoxy composites with embedded copper wire [31]. LFA has also determined through-thickness and in-plane conductivity of composites with orthogonal fibers [32] while an in-house device investigated high-temperature conductivity, specific heat, and thermal diffusivity of individual fibers [33]. However, this method is unsuitable for dry fabric testing due to fabric porosity and compaction load application limitations. Furthermore, LFA is primarily for isotropic homogeneous solids with diffusivity ranging from 0.1 to 1000 mm²/s and has limited applicability to porous anisotropic materials [34]. For dry fabric conductivity under preforming conditions, an MTPS sensor under vacuum replicated preforming compaction to study compaction load effects on thermal conductivity [35]. This study determined compaction load-dependent through-thickness thermal conductivity, showing fabric conductivity plateaued with increasing compaction load without binders. Existing studies have mainly focused on geometric heat transfer aspects in composites and dry textiles without considering preforming process conditions' impact, such as binder presence, on thermal conductivity. To bridge this gap, the present study aims to characterize heat transfer properties of woven carbon fiber fabrics with veil and silicone membrane, critical for heat energy transfer in the DDF material system.

2. Materials and Method

2.1. Materials

A 3k aerospace-grade 2/2 twill carbon fabric with an aerial weight of 204 g/m² (Style 452-5) from Engineered Cramer Composites (ECC), Germany (Figure 2a) were utilized. Additionally, portions of a silicone diaphragm membrane (Mosites #1453-D) from Mosites Rubber Company, USA, were used (Figure 2c). The binder material was Spunfab PA1203, a copolyimide adhesive web from Spunfab Ltd, Ohio, which has a melting range of 85 to 98 °C and medium viscosity (Figure 2b).
The carbon fabric thickness decreased to 0.204 mm from 0.38 mm due to vacuum compaction, while the silicone membrane maintained a consistent thickness of 1.52 mm, except in bridging regions. The experimental trials were conducted at an ambient temperature of 21 to 24 °C and a humidity level of 43%.

2.2. Through Thickness Thermal Conductivity of Carbon Fabrics with Veil

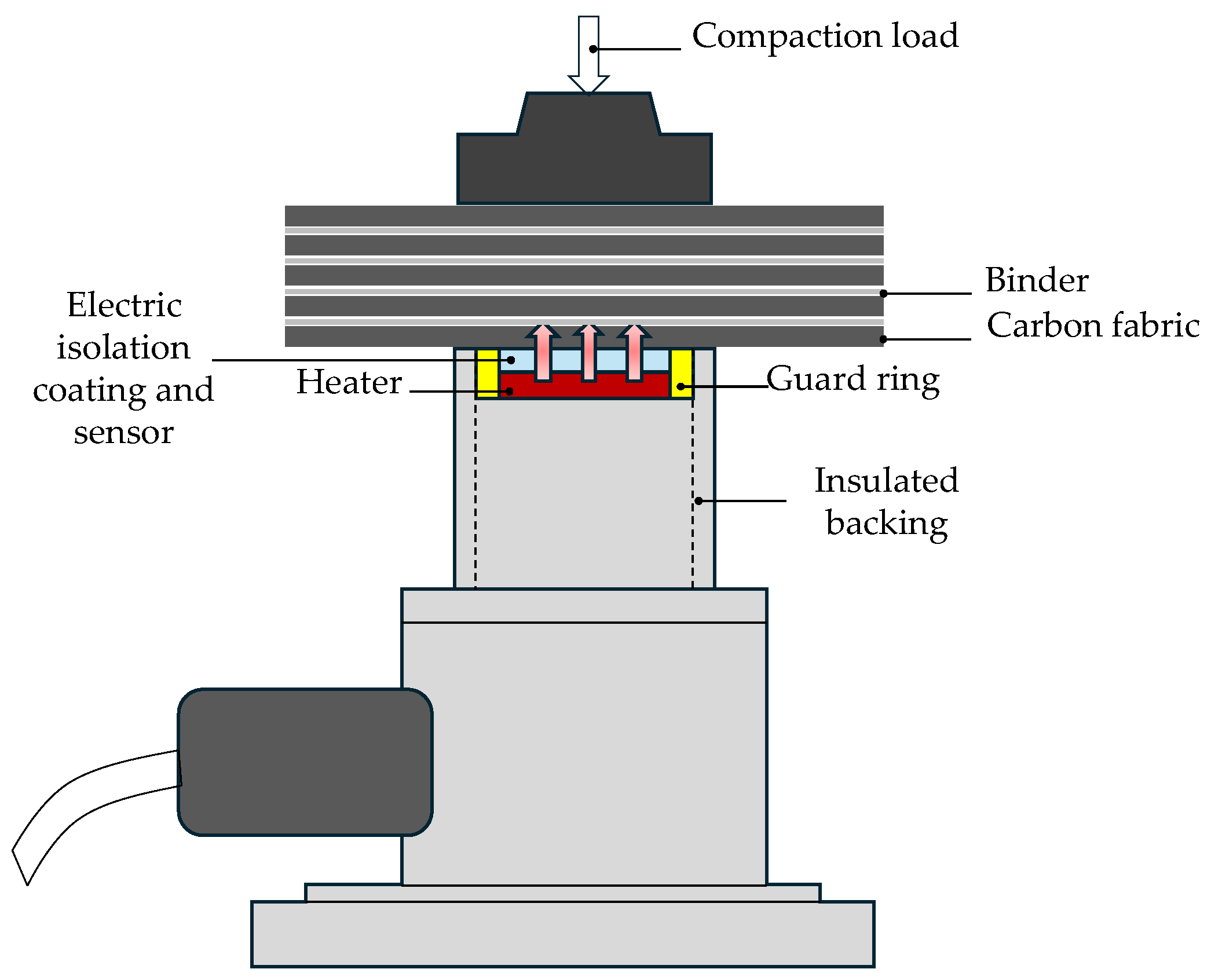
The thermal conductivity (TC) of the fabric (200 mm × 200 mm) with binder through its thickness was determined using the modified transient plane source (MTPS) method (Trident module, C-Therm Technologies Ltd., Canada), in accordance with ASTM D7984. This testing methodology was based on the experimental setup developed by Mojdeh et al., which was designed to measure the through-thickness TC of fabrics under preforming compaction conditions [35]. Given that the TC of fabrics plateaus after a 3000-gF compaction load, a compaction load of 3365 gf was chosen for testing the mixture of carbon fabrics with binder. In the present testing configuration (see Figure 3), ten layers of carbon fabrics were selected with nine layers of binder placed alternately between them, consistent with preforming process requirements. To ensure accurate temperature calibration and sensor stability, the MTPS textiles module was employed using a poly felt reference material at ambient conditions. The entire stack was placed on the MTPS sensor, where a one-sided interfacial heater/sensor within a guard ring applied a heat pulse. This setup measured the thermal effusivity of the stack over time to determine its TC. Two test cases were conducted to measure the TC of the fabrics with binder. In the first test case, the sample was tested under ambient conditions following ASTM D7984, with a 500-gF compaction load and no vacuum environment. In the second test case, the compaction load was increased to 3365 gF, and vacuum was applied within a vacuum chamber. Both tests were carried out in a 0/90 layup orientation.

2.3. Thermal Conductivity of Silicone Membrane

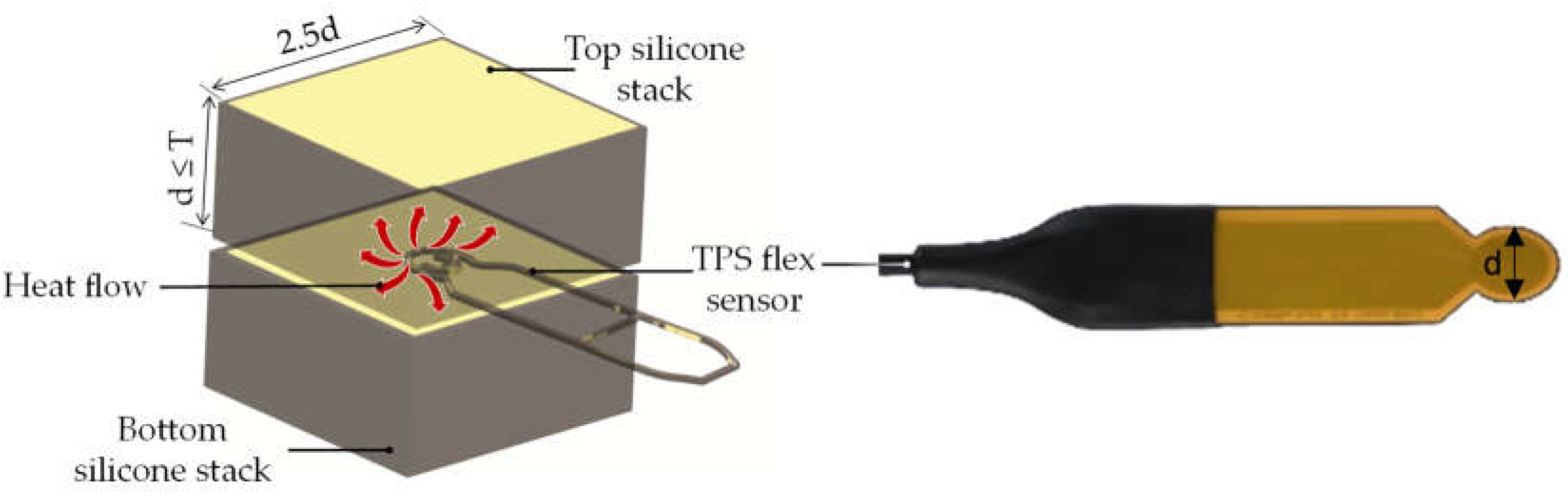
The thermal conductivity of the silicone membrane was measured using the transient plane source (TPS) technique with the C-Therm Thermal Conductivity Analyzer Flex Configuration. This method employs a double-sided sensor placed between two identical samples, utilizing an iterative process to determine the optimal testing parameters. The sensor features a bifilar nickel spiral that applies a consistent power pulse. The dynamic temperature response and changes in the temperature resistance of the sensor circuit are then analyzed using Equation ( 1 ) [36].
R t = R 0 1 + a ∆ T ¯ t
where R t is time-dependent resistance, R 0 is the initial resistance of TPS, a is the temperature coefficient of resistance (1/°C), and ∆ T ¯ ( t ) is the mean time-dependent temperature rise. The requirements for the testing sample, along with the operating principle and sensor diameters, are illustrated in Figure 4. As stated in the C-Therm manual, the required testing time is established using the initial default settings, and subsequent trials are executed using this specified time. The computation of this testing time was carried out using the formula outlined in (2).
t m a x = d 2 4 α
The initial step in this methodology involves conducting preliminary tests to identify the optimal testing conditions. These conditions include determining the testing time, the depth to which the heating signal penetrates the sample, and the linear variation of ΔT in relation to D(t), a shape function for the respective sensor. For this experiment, a sensor with a 6 mm diameter (serial F461, 8 rings) was used at a power level of 0.02 W. The parameters outlined in Table 1 were adjusted to optimize the conditions and ensure valid results. Validating the test results involved determining the appropriate testing time based on the initial valid test time and penetration depth requirements.
Optimization trials indicated that a testing time of 70 seconds was ideal, and this was repeated for five measurements to ensure accuracy and consistency.

2.4. Specific Heat Capacity of Materials

Differential Scanning Calorimetry (DSC) was conducted using a Netzsch GmbH 214 Polyma machine to characterize the specific heat capacity of the carbon fabric, silicone membrane, binder materials, following the ASTM E 1269 standard. This technique relies on three measurements for each trial: baseline, sapphire, and the sample material, all conducted with a closed lid configuration [38,39]. To provide an accurate characterization, three distinct sample types were selected: carbon fabric material, thermoplastic binder, and a representative mixture of veil (1.8 and 3.6 wt.%) and carbon fibers (CF) by weight, along with silicone. The weights of the samples, crucible, and sapphire standard, along with the number of samples tested, are presented in Table 2. Initially, the CF samples with chopped fibers were tested, followed by powdered CF samples (5 to 7 µm). This was then followed by binder material samples and a weight percentage mixture of powders and binder. Additionally, the effect of reheating on the CF and veil mixture samples was tested. The testing procedure involved equilibrating the specimens at 0°C for 35-45 minutes, followed by incrementally raising the temperature in a dynamic step to 220°C with a heating rate of 20 K/min. Another equilibration period of 35-45 minutes at 220°C followed. Heat flow data was collected during the dynamic step, and the analysis was conducted using NETZSCH Proteus analysis software to determine the specific heat capacity of the samples.

3. Results and Discussion

3.1. Through Thickness Thermal Conductivity of Fabircs with Veil

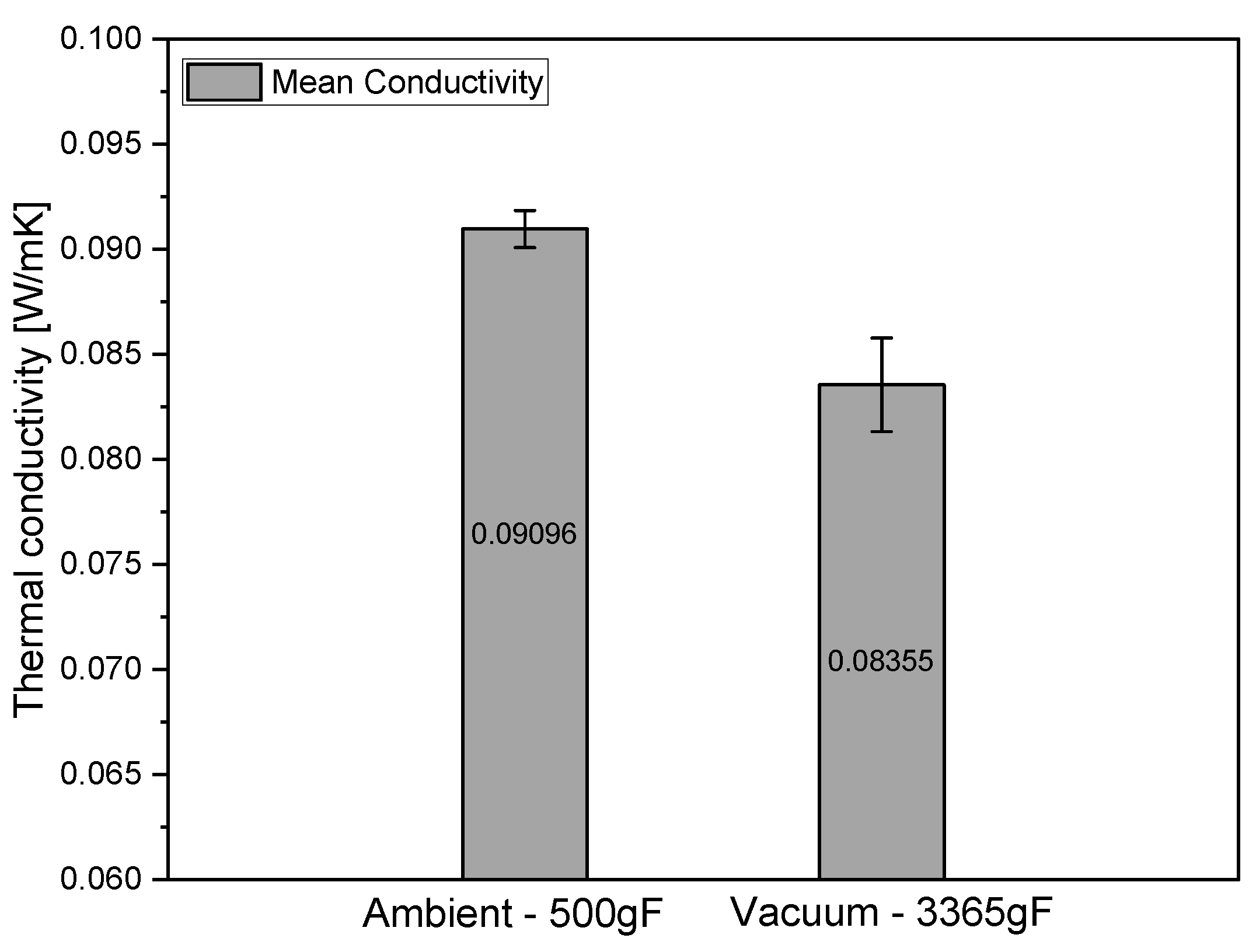
The results presented in Figure 5 provide valuable insights into the through-thickness thermal conductivity of carbon fabric and binder mixture samples, particularly under different test conditions in a 0/90 layup orientation. When tested without vacuum and under a 500gF load, the thermal conductivity was measured at 0.09096 W/m·K. Under full vacuum and a 3365gF load, the thermal conductivity notably decreased to 0.08355 W/m·K, indicating an 8% reduction in heat energy transfer.
For comparison, the thermal conductivity of carbon fabrics without binder under ambient conditions is reported at 0.127 W/m·K [35]. The addition of 3.6 wt.% binder under similar conditions resulted in a significant 28.3% decrease in thermal conductivity, affecting the energy transfer.
Under compaction load and vacuum, simulating preforming conditions, the thermal conductivity of the fabrics alone is reported to be 0.14 W/m·K [35]. However, with the inclusion of binder material, the thermal conductivity decreases by approximately 40%. This significant reduction in both scenarios is primarily due to altered contact interactions between fabric layers caused by the dry binder material, which creates more voids between adjacent layers.
The reduction in thermal conductivity under vacuum conditions becomes more pronounced after adding the binder. This occurs because the removal of air creates larger voids at the interface where the binders are present. In ambient conditions, air can aid in heat transfer, but its absence under vacuum leads to a more significant decrease in thermal conductivity. This underscores the critical role of air in thermal performance and the greater impact of binder addition when air is removed. These findings emphasize the substantial impact of both preforming conditions and binder addition on the thermal performance of dry carbon fabrics, highlighting the need to carefully consider these factors in the design and manufacturing processes.

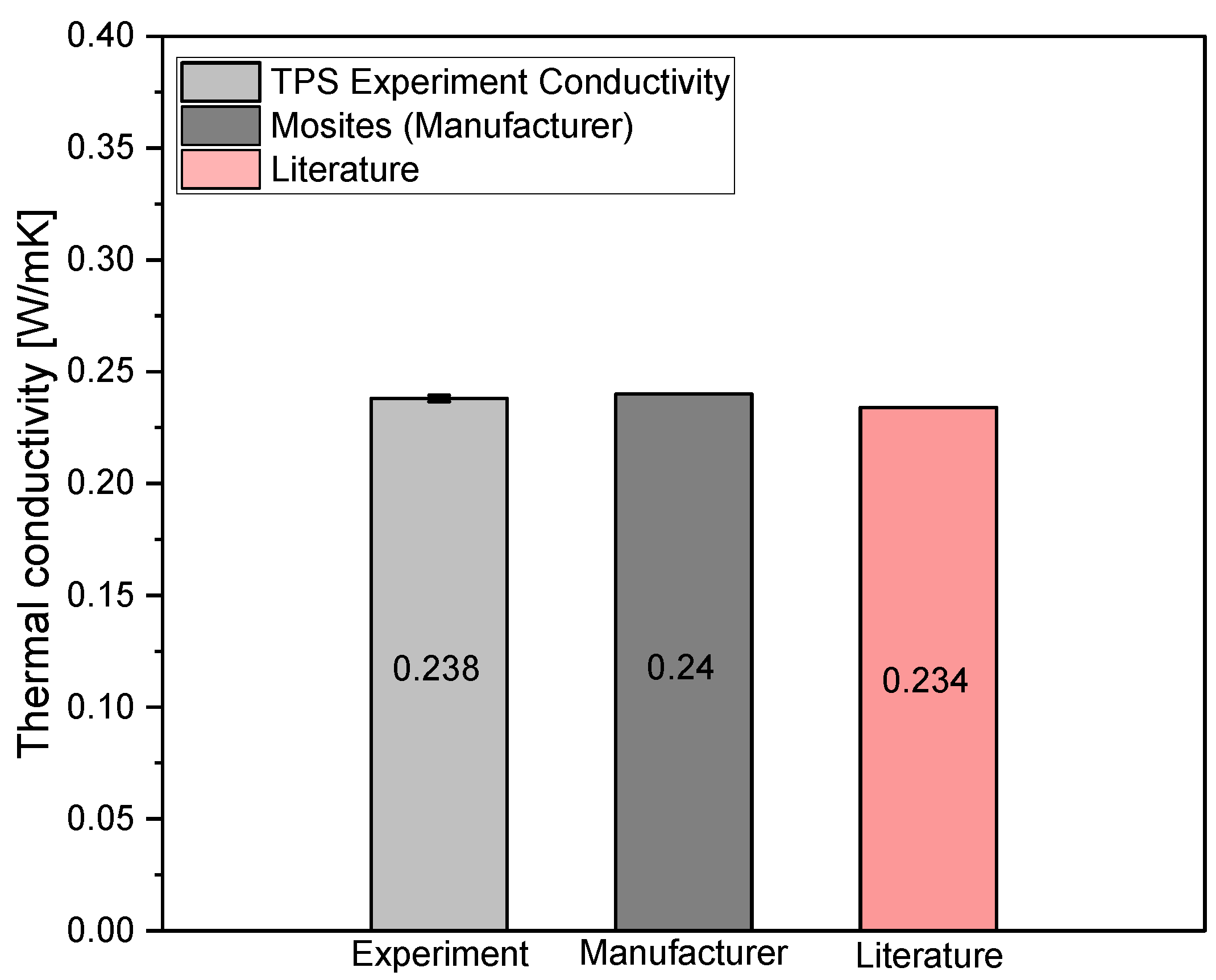
3.2. Thermal Conductivity of Silcione Membrane

Figure 6 presents the thermal conductivity measurements for the silicone membrane. The data indicates that silicone exhibits higher thermal conductivity compared to carbon fiber fabric. This disparity is primarily due to the porous nature of the fabric material, which reduces the frequency of fiber-to-fiber contacts necessary for efficient heat transfer. In contrast, the silicone membrane provides a more consistent and homogeneous solid medium, thereby enhancing heat transfer efficiency.
In fabric systems, thermal conductivity is highly dependent on fiber contacts to facilitate heat transfer. The silicone membrane, however, offers a uniform structure (isotropic) that supports more efficient thermal conductivity. These findings corroborate the accuracy and reliability of the measurements, aligning well with established information from the literature, and confirming the consistency of the experimental results.

3.3. Specific Heat Capacity of the Materials

The specific heat capacity of various materials was analyzed using Differential Scanning Calorimetry (DSC) with the Proteus analysis software. This process segmented the heat flow data into isothermal, dynamic, and subsequent isothermal steps. The data was then correlated against the measured sapphire standard data and the prerecorded sapphire data from the software. Calibration utilized the most repeatable baseline data obtained by comparing three baseline measurements of empty crucibles. The results for all measurements are presented below.

3.3.1. Chopped Carbon Fibers (CCF), Binder and CCF – Binder Mixture

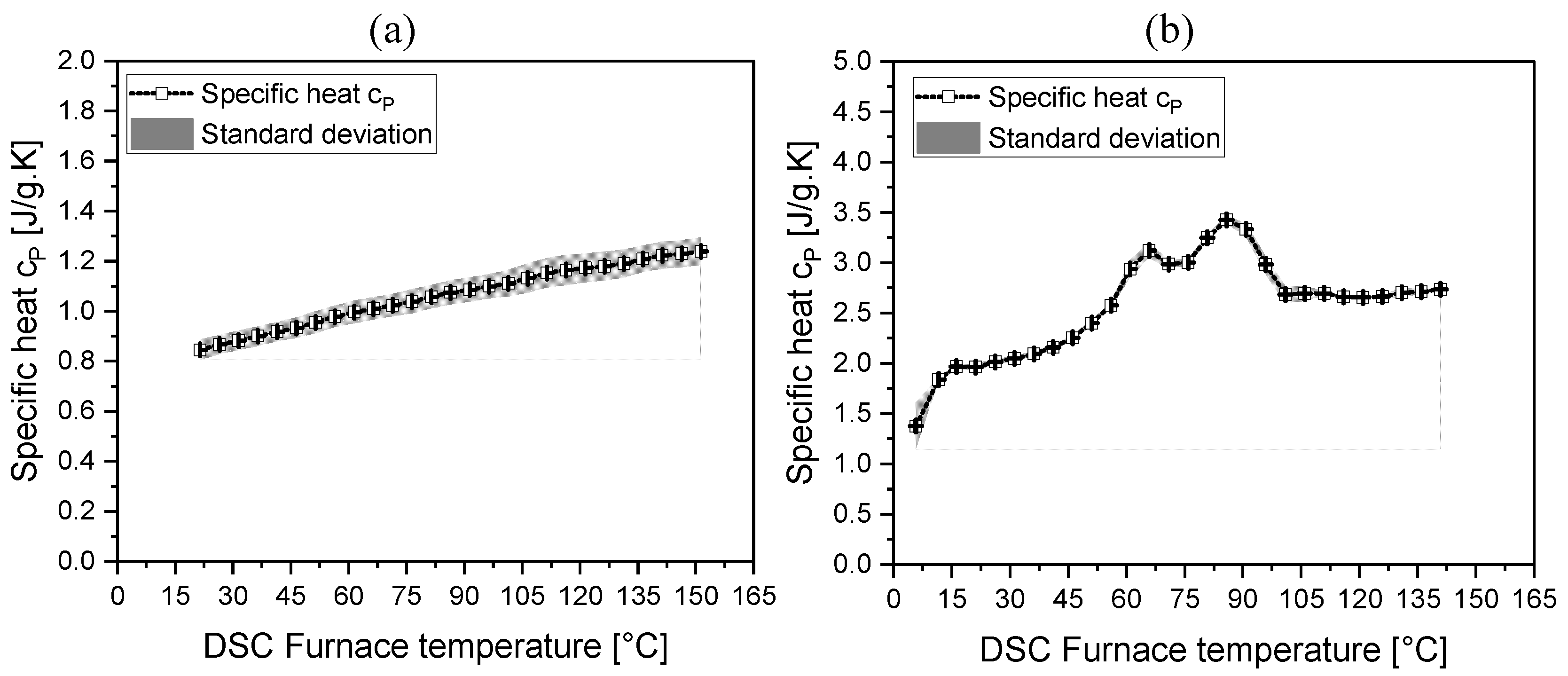
Figure 7 displays the specific heat capacity of chopped fibers and binder as a function of temperature. For chopped fibers, the specific heat capacity was measured as 0.84 J/g.K at 24°C and increased to 1.238 J/g.K at 150°C (see Figure 7a). For thermoplastic binders, the specific heat capacity was 1.96 J/g.K at 21°C and rose to 2.73 J/g.K at 140°C, with peaks observed at 65°C and 85°C due to phase changes in the binder (see Figure 7b). Both samples exhibited temperature-dependent behavior, with the binders showing Gaussian behavior around their peak points due to phase transitions.
The temperature-dependent specific heat capacity relations for chopped fibers (see equation 1) and binder are presented in Table 3. For binders, the non-linear behavior is divided into four segments based on temperature to accurately capture the specific heat capacity's temperature dependency. Equation (2) represents the temperature range from 20 °C to 65 °C, while Equation (3) covers the range from 65 °C to 75 °C, with R-squared values of 0.999. Equations (4) and (5) represent temperature ranges from 75 °C to 101 °C and 101 °C to 140 °C with R squared value of 0.999.
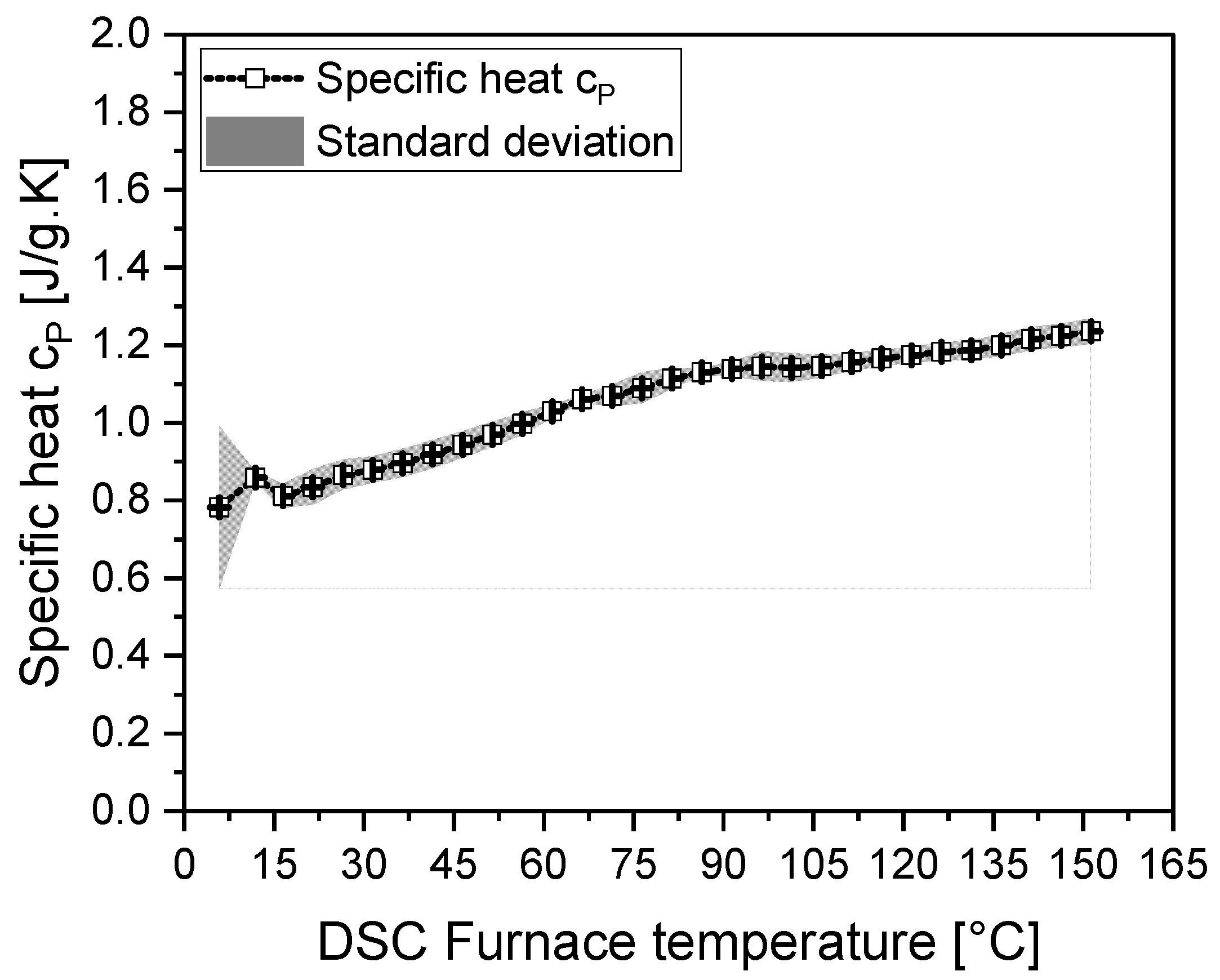
c P T = 0.75473 + 0.00428 T − 7.0744 E − 6 T 2 c P T = 1.9284 + 0.0124 e ( T 14.094 ) c P T = e ( 6.372 − 0.145 T + 9.958 E − 4 T 2 ) c P T = e ( − 7.407 + 0.199 T − 0.00116 T 2 ) c P T = 2.693 − 0.0028 T + 2.2058 E − 5 T 2 For the third case of CCF-binder mixture, the specific heat results are presented in Figure 8. The mixture of CCF and 1.8 Wt% binder also showed temperature-dependent behavior. The specific heat capacity at 21°C was 0.83 J/g.K and increased to 1.235 J/g.K at 150°C. However, there was a slight nonlinear behavior in the melting temperature range, with a 7% increase in specific heat at 80°C. The temperature-dependent relationship for the CCF-binder samples with 1.8% binder content is described by equations (6 and 7) for the temperature ranges of 15°C to 77°C and 77.86°C to 150°C, respectively. The curve fitting for these equations yields an R-squared value of 0.999.
c P T = 0.7161 + 0.0051 T
c P T = 1.1148 + 0.0014 ( T − 77.862 )
All samples exhibited slight standard deviations due to the packing of chopped fibers into the crucibles, which created uncontrolled contacts between the fibers. High standard deviations were also noted at the starting temperature regions due to the chosen ASTM standard ramp rate of 20 K/min.
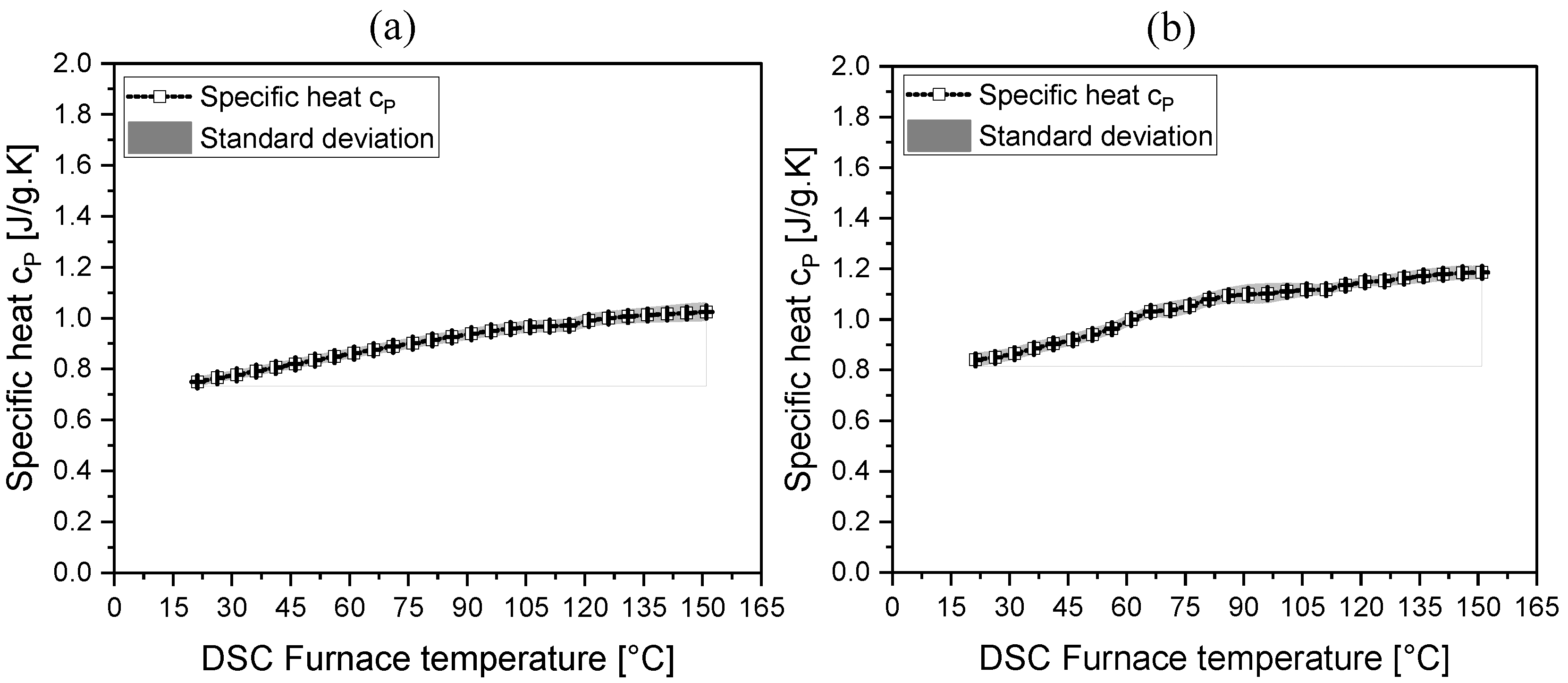
In the second testing configuration, powdered carbon fibers (5 to 7 µm) were tested along with a 3.5 Wt% mixture of binders. The results, shown in Figure 9, indicated that the specific heat capacity of PCF was 0.749 J/g.K at 21°C and 1.024 J/g.K at 150°C (see Figure 9a). Compared to chopped fibers, powdered fibers showed a 10% and 17% reduction in specific heat values at 21°C and 150°C, respectively. The standard deviation was slightly reduced, and the powdered fibers exhibited a more linear behavior over the tested temperature range. This can arise due to contamination of air and moisture in the samples with porous chopped fibers entrapping more in the sample when compared to the powdered samples. In addition to this possible experimental error resultant of weight measurements of chopped fibers can be possible as the sample masses have high standard deviation. The temperature-dependent relation for the specific heat of PCF samples, as represented by equation ( 8 ), is applicable within the temperature ranges of 15 to 150 °C. The curve fitting process yielded an R-squared value of 0.998, indicating a high degree of accuracy in modelling the specific heat behaviour over this temperature range.
c P T = 0.6724 + 0.0036 T − 8.5998 E − 6 T 2
For the PCF-binder mixture samples, the specific heat values were 0.84 J/g.K at 21°C and 1.18 J/g.K at 150°C. The additional 3.6 Wt% binder resulted in a 10.8% and 13.2% increase in specific heat at 21°C and 150°C, respectively, with a nonlinear variation of 14.6% in the melting region due to the binder's phase change. To further analyze the temperature-dependent specific heat, curve fitting was performed. Equation ( 9 ) applies for temperatures up to 85°C, while Equation ( 10 ) is suitable for temperatures ranging from 85°C to 150°C. The R-squared value for this fit is 0.994, indicating a strong correlation between the experimental data and the fitted model.
c P 1 T = 0.7564 + 0.0038 T
c P T = c P 1 T + 0.0016 T − 85

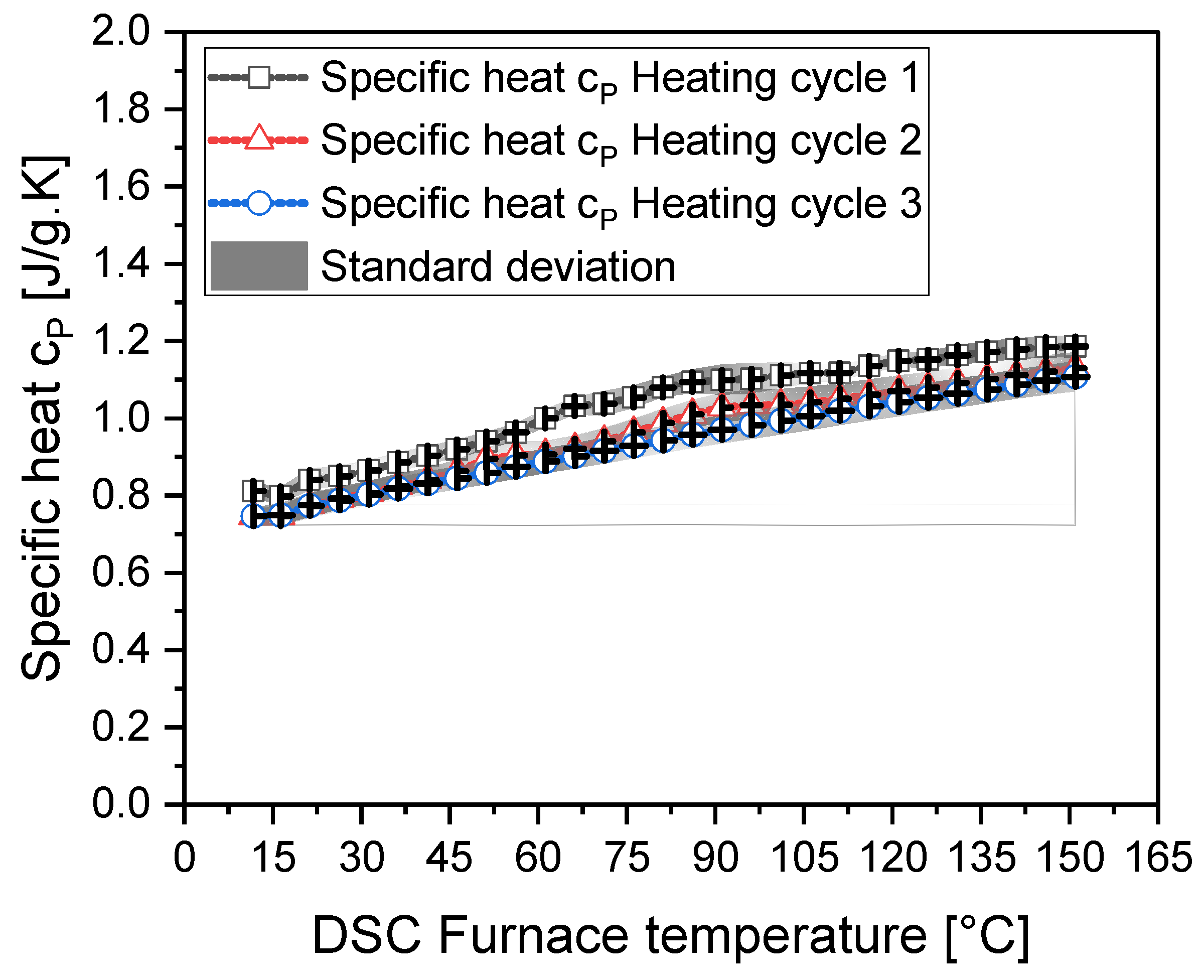
3.3.3. Effect of Reheating on Specific Heat for Powdered PCF - Binder Mixture

The effect of reheating on the specific heat capacity of the powdered CF and binder mixture was tested over three heating cycles, as some infusion processes occur at elevated temperatures. Figure 11 compares the specific heat across these cycles. In the first heating cycle, the specific heat was 8.8% higher at 21°C compared to subsequent cycles and showed a 1.12% variation at 150°C. The nonlinear behavior in the melting region became more linear in the second and third cycles, with a 9.2% reduction in the second cycle and a 12.93% reduction in the third cycle at 80°C. Comparing the second and third cycles, a 4.08% reduction at 80°C was observed, indicating a stabilization of specific heat behavior across cycles due to the binder's melting and flow into the powdered fibers, as well as the potential presence of moisture.

4. Conclusions

The study is aimed to investigate the thermal conductivity and specific heat capacity of materials used in the DDF process, including silicone diaphragms, carbon fibers (chopped and powdered), thermoplastic veils, and their combinations. The findings revealed that the thermal conductivity of carbon fabric samples with binder in a 0/90 layup orientation decreased under preforming conditions involving the application of full vacuum. The addition of 3.6 wt% binder significantly reduced thermal conductivity by decreasing fiber-to-fiber contact and creating more voids at the interface between two fabric layers. Silicone demonstrated higher thermal conductivity compared to carbon fiber fabric, attributed to its homogeneous solid medium facilitating efficient heat transfer.
Specific heat capacity measurements highlighted the temperature-dependent behavior of the materials. Chopped carbon fibers and thermoplastic binders exhibited increasing specific heat with temperature, with binders showing Gaussian behavior around phase change points. Mixed samples of chopped fibers and binder also displayed temperature-dependent specific heat with slight non-linear behavior in the melting range. Powdered carbon fibers showed a reduction in specific heat compared to chopped fibers, and the inclusion of binders increased specific heat, particularly in the melting region. Reheating cycles affected the specific heat of powdered carbon fiber and binder mixtures, with subsequent cycles leading to more linear behavior and reduced variations in specific heat.
These measurements provide essential data for accurate numerical modeling of heat transfer in the DDF process. The established temperature-dependent relationships for the specific heat of each material will aid in optimizing preforming parameters, enhancing the energy efficiency and overall effectiveness of composite manufacturing. The study underscores the importance of understanding the thermophysical properties of materials to improve the DDF process.

Author Contributions

Srikara Dandangi: Writing – original draft, Methodology, Investigation, Formal analysis, Data curation. Mohammad Ravandi: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Methodology, Investigation, Formal analysis, Conceptualization. Jamal Naser: Writing – review & editing, Methodology, Investigation, Formal analysis, Supervision. Adriano Di Pietro: Writing – review & editing, Supervision, Funding acquisition.

Funding

Please add: This research was funded by the Victorian Higher Education State Investment Fund (VHESIF) through the Aerostructures Innovation Research Hub (AIR Hub).

Data Availability Statement

Data will be made available on request.

Acknowledgments

The authors acknowledge the support of the Victorian government through the Victorian Higher Education State Investment Fund (VHE-SIF), as well as the Swinburne/CSIRO Industry 4.0 Test lab. Special thanks are extended to the digitalization team of the AIR Hub at Swinburne University of Technology for their invaluable support throughout the duration of this project.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. S. Luby and E. Bernardon, “Design of fabric preforms for double diaphragm forming,” undefined, 1992.
  2. S. Chen et al., “Double diaphragm forming simulation for complex composite structures,” Composites Part A: Applied Science and Manufacturing, vol. 95, pp. 346–358, 2017. [CrossRef]
  3. VERPOEST, “Composite Preforming Techniques,” Comprehensive Composite Materials, pp. 623–669, 2000. [CrossRef]
  4. S. V. Lomov and I. Verpoest, “Textile Composite Materials: Polymer Matrix Composites,” 2010. [CrossRef]
  5. N. Widmaier, R. Radjef, P. Middendorf, and B. Fox, “Double Diaphragm Forming of Bindered Unidirectional Dry-Fibre Tapes : Experimental Analysis of Forming Temperature,” Australian International Aerospace Congress, no. February, pp. 27–28, 2023.
  6. J. E. Cunningham, P. F. Monaghan, and M. T. Brogan, “Predictions of the temperature profile within composite sheets during pre-heating,” Composites Part A: Applied Science and Manufacturing, vol. 29, no. 1, pp. 51–61, Jan. 1998. [CrossRef]
  7. S. Aranda, F. Klunker, and G. Ziegmann, “COMPACTION RESPONSE OF FIBRE REINFORCEMENTS DEPENDING ON PROCESSING TEMPERATURE”.
  8. S. Aranda, F. Klunker, and G. Ziegmann, “Influence of the binding system on the compaction behaviour of NCF carbon fibre reinforcements,” ICCM International Conferences on Composite Materials, pp. 1–6, 2011.
  9. W. Wu, B. Jiang, L. Xie, F. Klunker, S. Aranda, and G. Ziegmann, “Effect of compaction and preforming parameters on the compaction behavior of bindered textile preforms for automated composite manufacturing,” Applied Composite Materials, vol. 20, no. 5, pp. 907–926, 2013. [CrossRef]
  10. K. Wei, D. Liang, M. Mei, D. Wang, X. Yang, and Z. Qu, “Preforming behaviors of carbon fiber fabrics with different contents of binder and under various process parameters,” Composites Part B: Engineering, vol. 166, pp. 221–232, Jun. 2019. [CrossRef]
  11. P. Bussetta and N. Correia, “Macroscale modelling approaches for,” Composites Part A: Applied Science and Manufacturing, vol. 113, pp. 12–31, Oct. 2018. [CrossRef]
  12. B. X. Chai et al., “Review of Approaches to Minimise the Cost of Simulation-Based Optimisation for Liquid Composite Moulding Processes,” Materials, vol. 16, no. 24, Art. no. 24, Jan. 2023. [CrossRef]
  13. P. Boisse, R. Akkerman, P. Carlone, L. Kärger, S. V. Lomov, and J. A. Sherwood, “Advances in composite forming through 25 years of ESAFORM,” Int J Mater Form, vol. 15, no. 3, p. 39, Apr. 2022. [CrossRef]
  14. N. Bigot, · Edouardo Guzman-Maldonado, · M’hamed Boutaous, · Shihe Xin, and N. Hamila, “A Coupled Thermo-mechanical Modelling Strategy Based on Alternating Direction Implicit Formulation for the Simulation of Multilayered CFRTP Thermo-stamping Process,” 123AD. [CrossRef]
  15. D. U. Furrer, D. M. Dimiduk, J. D. Cotton, and C. H. Ward, “Making the Case for a Model-Based Definition of Engineering Materials,” Integrating Materials and Manufacturing Innovation, vol. 6, no. 3, pp. 249–263, 2017. [CrossRef]
  16. Baran, K. Cinar, N. Ersoy, R. Akkerman, and J. H. Hattel, “A Review on the Mechanical Modeling of Composite Manufacturing Processes,” vol. 24, pp. 365–395, 2016. [CrossRef]
  17. R. Schnurr, F. Gabriel, J. Beuscher, and K. Dröder, “Model-based Heating and Handling Strategy for Pre-Assembled Hybrid Fibre-Reinforced Metal-Thermoplastic Preforms,” Procedia CIRP, vol. 85, pp. 177–182, Jan. 2019. [CrossRef]
  18. H. Borgwardt, “Continuous Preforming with Variable Web Height Adjustment,” pp. 317–324, 2013. [CrossRef]
  19. E. Codau, T.-C. Codau, I.-G. Lupu, A. Raru, and D. Farima, “Heat transfer simulation through textile porous media,” The Journal of The Textile Institute, vol. 114, no. 2, pp. 257–264, Feb. 2023. [CrossRef]
  20. Yue Yang, “THERMAL CONDUCTIVITY OF CARBON FIBRE FABRICS AND MULTI-SCALE COMPOSITES WITH HEAT,” Masters thesis report, no. August, 2013.
  21. S. Hind and F. Robitaille, “Measurement, modeling, and variability of thermal conductivity for structural polymer composites,” Polymer Composites, vol. 31, no. 5, pp. 847–857, 2010. [CrossRef]
  22. P. Kearney, C. Lekakou, and S. Belcher, “Measurement of the Heat Transfer Properties of Carbon Fabrics via Infrared Thermal Mapping,” Journal of Composites Science, vol. 6, no. 6, pp. 1–11, 2022. [CrossRef]
  23. R. Penide-Fernandez and F. Sansoz, “Anisotropic thermal conductivity under compression in two-dimensional woven ceramic fibers for flexible thermal protection systems,” International Journal of Heat and Mass Transfer, vol. 145, p. 118721, 2019. [CrossRef]
  24. X. Liu, T. Wang, M. Zhuang, B. Xin, and W. Liu, “Investigation of the Thermal Transfer Behavior of Single Layer Woven Fabrics at Different Temperatures,” vol. 11, [Online]. Available: http://www.jeffjournal.org.
  25. H. Shen, A. Yokoyama, and S. Sukigara, “Modeling of heterogeneous heat transfer in fabrics,” Textile Research Journal, vol. 88, no. 10, pp. 1164–1172, 2018. [CrossRef]
  26. H. Yu, D. Heider, and S. Advani, “Comparison of two finite element homogenization prediction approaches for through thickness thermal conductivity of particle embedded textile composites,” Composite Structures, vol. 133, pp. 719–726, 2015. [CrossRef]
  27. M. O. R. Siddiqui, D. Sun, and I. B. Butler, “Geometrical modelling and thermal analysis of nonwoven fabrics,” Journal of Industrial Textiles, vol. 48, no. 2, pp. 405–431, 2018. [CrossRef]
  28. Y. Yang, J. Qian, and Y. Chen, “Multi-scale modeling and thermal transfer properties of electric heating fabrics system,” International Journal of Clothing Science and Technology, vol. 31, no. 6, pp. 825–838, 2019. [CrossRef]
  29. T. Liu, M. Chen, J. Dong, R. Sun, and M. Yao, “Numerical simulation and experiment verified for heat transfer processes of high-property inorganic fiber woven fabrics,” Textile Research Journal, vol. 2022, pp. 13–14. [CrossRef]
  30. M. O. R. Siddiqui and D. Sun, “Thermal analysis of conventional and performance plain woven fabrics by finite element method,” Journal of Industrial Textiles, vol. 48, no. 4, pp. 685–712, 2018. [CrossRef]
  31. Y. Li, L. Li, Y. Li, H. Wang, P. Wang, and Y. Zhang, “The through-thickness thermal conductivity and heat transport mechanism of carbon fiber three-dimensional orthogonal woven fabric composite,” The Journal of The Textile Institute, vol. 115, no. 2, pp. 308–315, Feb. 2024. [CrossRef]
  32. J. D. Macías et al., “Thermal Characterization of Carbon Fiber-Reinforced Carbon Composites (C/C),” Applied Composite Materials, vol. 26, no. 1, pp. 321–337, Feb. 2019. [CrossRef]
  33. C. Pradere, J. C. Batsale, J. M. Goyhénèche, R. Pailler, and S. Dilhaire, “Thermal properties of carbon fibers at very high temperature,” Carbon, vol. 47, no. 3, pp. 737–743, Mar. 2009. [CrossRef]
  34. “Standard Test Method for Thermal Diffusivity by the Flash Method.” ASTM International, 2022. Accessed: May 30, 2024. [Online]. Available: https://compass.astm.org/document/?contentcode=ASTM%7CE1461-13R22%7Cen-US.
  35. M. Reghat, M. Ravandi, V. Zinnecker, and A. Di Pietro, “Through-thickness thermal conductivity characterisation of dry carbon fibre fabric,” Materials Letters, vol. 361, p. 136116, Apr. 2024. [CrossRef]
  36. 14:00-17:00, “ISO 22007-2:2022,” ISO. Accessed: May 31, 2024. [Online]. Available: https://www.iso.org/standard/81836.html.
  37. C.-T. T. Ltd, “Thermal Conductivity Instrument User Manual,” 2022, [Online]. Available: https://ctherm.com/thermal-conductivity-instruments/trident/.
  38. NETZSCH-Geraetebau GmbH, “DSC 214 Polyma,” no. 64777476. pp. 1–24, 2014. Accessed: Mar. 28, 2023. [Online]. Available: https://www.netzsch-thermal-analysis.com/ja/製品案内/示差走査熱量計-dsc-示差熱分析-dta/dsc-214-polyma/.
  39. “Standard Test Method for Determining Specific Heat Capacity by Differential Scanning Calorimetry.” ASTM International, 2018. Accessed: May 31, 2024. [Online]. Available: https://compass.astm.org/document/?contentCode=ASTM%7CE1269-11R18%7Cen-US.
  40. “Thermal Properties of Mosites #1453 Silicone | Silicone Rubber Data,” Mosites Rubber Company. Accessed: Feb. 22, 2024. [Online]. Available: https://www.mositesrubber.com/technical-resources/silicone-rubber-technical-info/thermal-properties-of-mosites-1453-silicone/.
Preprints 108539 g001
Figure 1. Schematic of double diaphragm forming process.
Figure 1. Schematic of double diaphragm forming process.
Preprints 108539 g001
Preprints 108539 g002
Figure 2. (a) Carbon fabric, (b) carbon fabric with binder, and (c) silicone membrane.
Figure 2. (a) Carbon fabric, (b) carbon fabric with binder, and (c) silicone membrane.
Preprints 108539 g002
Preprints 108539 g003
Figure 3. Schematic of the experimental setup using MTPS sensor.
Figure 3. Schematic of the experimental setup using MTPS sensor.
Preprints 108539 g003
Preprints 108539 g004
Figure 4. Operating principle and sample requirements for the TPS method [37].
Figure 4. Operating principle and sample requirements for the TPS method [37].
Preprints 108539 g004
Preprints 108539 g005
Figure 5. Through thickness thermal conductivity of CF fabrics with binder in no Vacuum, 500gF load, and Full vacuum, 3365gF compaction load.
Figure 5. Through thickness thermal conductivity of CF fabrics with binder in no Vacuum, 500gF load, and Full vacuum, 3365gF compaction load.
Preprints 108539 g005
Preprints 108539 g006
Figure 6. Thermal conductivity of silicone membrane and comparison with manufacturer (Mosites) [40] and literature values [38].
Figure 6. Thermal conductivity of silicone membrane and comparison with manufacturer (Mosites) [40] and literature values [38].
Preprints 108539 g006
Preprints 108539 g007
Figure 7. DSC results of specific heat capacity of (a) Chopped fibers and (b) Binder.
Figure 7. DSC results of specific heat capacity of (a) Chopped fibers and (b) Binder.
Preprints 108539 g007
Preprints 108539 g008
Figure 8. DSC Specific heat capacity of chopped fibers and binder.3.3.2. Powdered Carbon Fibers (PCF) and PCF – Binder Mixture.
Figure 8. DSC Specific heat capacity of chopped fibers and binder.3.3.2. Powdered Carbon Fibers (PCF) and PCF – Binder Mixture.
Preprints 108539 g008
Preprints 108539 g009
Figure 9. DSC specific heat capacity of (a) Powdered carbon fibers, (b) Powdered CF + Binder.
Figure 9. DSC specific heat capacity of (a) Powdered carbon fibers, (b) Powdered CF + Binder.
Preprints 108539 g009
Preprints 108539 g010
Figure 11. Influence of reheating on specific heat measurements of powdered CF and binder samples.
Figure 11. Influence of reheating on specific heat measurements of powdered CF and binder samples.
Preprints 108539 g010
Table 1. Trials carried out for parameter optimization for the TPS technique.
Table 1. Trials carried out for parameter optimization for the TPS technique.
Run Time [s] Probing depth [mm] Number of data points Δ T [°C] Power level [W]
1 3.50 1.150 207 10 0.36
2 5.07 1.177 298 10 0.30
3 4.02 1.140 236 8 0.30
4 20.00 4.905 1196 1 0.01
5 310.00 16.023 18596 2 0.20
6 90.00 6.390 5395 1.6 0.02
7 70.00 6.590 4270 1.6 0.02
Table 2. Samples and crucible masses used for DSC analysis.
Table 2. Samples and crucible masses used for DSC analysis.
Material Sample mass [mg] Crucible mass [mg] Number of samples tested Sapphire mass [mg]
CF chopped 6.895±0.281 51.372±0.345 5 37.7
CF powdered 22.36±0.248 51.573±0.21 7 37.7
Binder 8.99±0.0.259 51.50±0.206 5 37.7
CF chopped with Binder 7.599±0.6171 50.980±0.181 5 37.7
CF powder with Binder 17.394±0.035 50.986±0.211 5 37.7
Silicone 20.660 ± 0.231 51.20 ± 0.082 3 37.7
Table 3. Tempertaure dependent specific heat for CCP and Binder materials.
Table 3. Tempertaure dependent specific heat for CCP and Binder materials.
Material Temperature dependent Specific heat
CCF c P T = 0.75473 + 0.00428 T − 7.0744 E − 6 T 2 (1)
Binder c P T = 1.9284 + 0.0124 e ( T 14.094 )
c P T = e ( 6.372 − 0.145 T + 9.958 E − 4 T 2 )
c P T = e ( − 7.407 + 0.199 T − 0.00116 T 2 )
c P T = 2.693 − 0.0028 T + 2.2058 E − 5 T 2 		(2)
(3)
(4)
(5)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated