Entanglement and Generalized Berry Geometrical Phases in Quantum Gravity

Preprint

Article

Entanglement and Generalized Berry Geometrical Phases in Quantum Gravity

Altmetrics

Downloads

115

Views

Comments

A peer-reviewed article of this preprint also exists.

Diego J CIRILO-LOMBARDO

Norma G. SANCHEZ^*

Diego J CIRILO-LOMBARDO

Norma G. SANCHEZ^*

This version is not peer-reviewed

Submitted:

06 June 2024

Posted:

07 June 2024

You are already at the latest version

Alerts

Abstract

A new formalism is introduced that makes it possible to elucidate the physical and geometric content of quantum spacetime. It is based in the Minimum Group Representation Principle (MGRP). Within this framework new results for entanglement and geometrical/topological phases are found and implemented in cosmological and black hole space-times. Our main results here are: {\bf(i)} We find the Berry phases for inflation and for the cosmological perturbations and express them in terms of the observables, as the spectral scalar and tensor indices, $n_S$ an $n_T$, and the tensor to scalar ratio $r$. The Berry phase for de Sitter inflation is imaginary with the sign describing the exponential acceleration. {\bf(ii)} The pure entangled states in the minimum group (metaplectic) $Mp(n)$ representation for quantum de Sitter space-time and black holes are found. {\bf(iii)} For entanglement, the relation between the Schmidt type representation and the physical states of the $Mp(n)$ group is found: This is a {\it new non-diagonal} coherent state representation complementary to the known Sudarshan diagonal one. {\bf(iv)} Mean value generators of $Mp(2)$ are related to the adiabatic invariant and topological charge of the spacetime (matrix element of the transition $-\infty < t < \infty$). {\bf(v)} The basic {\it even} and {\it odd} $n$-sectors of the Hilbert space are intrinsic to the quantum spacetime and its discrete levels (in particular continuum for $n \rightarrow \infty$), they do not require any extrinsic generation process as the standard Schrodinger cat states, and are {\it entangled}. {\bf(vi)} The gravity or cosmological domains in one side and another of the Planck scale are {\it entangled}. Examples: The quantum primordial trans-Planckian de Sitter vacuum and the classical late de Sitter vacuum today; the central quantum gravity reqion and the external classical gravity region of black holes. The classical and quantum dual gravity regions of the space-time are entangled. {\bf(vii)} The general classical-quantum gravity duality is associated to the Metaplectic $Mp(n)$ group symmetry which provides the complete full covering of the phase space and of the quantum space-time mapped from it.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction and Results

In recent years a deep interest has been manifested not only in the search for a consistent theory of quantum gravity but also for a fundamental description of the dynamics in the quantum domain.

Recently, in Refs. [1,2] we have carried out a construction of the spacetime as a generalized coherent state of the

M p (n)

group (complying with the principle of the minimum group representation). We have implemented this framework both in black holes and de Sitter space-time, showing explicitly this quantum fundamental dynamics. This approach goes well in the direction of Refs [3,4] for quantum space-time and its discrete levels, explicit examples and fundamental quantum principles: the classical-quantum duality of Nature including gravity (classical-quantum gravity duality), Refs. [5,6,7].

Now, in this paper, let’s take another step in this novel and consistent conceptual description of the universe considering entanglement mechanisms and their relationship with geometrical and topological phases (namely, generalized Berry phases). The groups involved here are non compact.

Our formalism is fundamental to move towards a true information theory of quantum gravity given that the entire theory is self-consistent and has important points in favor: Such as that the basic states that respond to the principle of least group representation satisfy a new equation of positive energy conceptually similar to those proposed by Majorana [9,10] and Dirac [8] time ago and that were very recently discussed by Bogomolny in Ref. [11] related to the possible description of dark matter .

Taking advantage of our formalism, we find the Berry phases for inflation and for the cosmological perturbations and express them in terms of the observables, as the spectral scalar and tensor indices,

n_{S}

n_{T}

, and the tensor to scalar ratio r. The Berry phase for de Sitter inflation is imaginary with the sign describing the exponential acceleration. For entanglement, the pure entangled states for de Sitter space-time as well as for black holes are found.

The complete covering of the Hilbert space with the complete covering of the quantum space-time is realized by the Metaplectic group symmetry which equivalently provides the complete global CPT symmetric states .

The Classical-Quantum Duality of the space-time is also realized in the

M p (n)

symmetry, because the complete covering, the global complete space-time (and full phase space completion) is needed to make the classical-quantum space-time duality manifest (and the phase space mapped from it) .

It is worth to mention that similar discrete levels can be obtained from the global (complete) classical - quantum duality including gravity [3,5,6,7], namely classical-quantum gravity duality : The two even and odd (local) carts or sectors here and their global $(\pm)$ sum of states, reflect a relation between the $M p (n)$ symmetry and the classical-quantum gravity duality.
The two $\sqrt{(2 n + 1)}$ and $\sqrt{2 n}$ , even and odd sets separately are local coverings and they are entangled. The symmetric or antisymmetric sum of these states are global covering states, and they are necessary to cover completely the whole manifold.
Moreover, the corresponding $(\pm)$ global states are complete, CPT symmetric and unitary, the levels $n = 0, 1, 2, . . . .,$ cover the whole Hilbert space $H = H_{(+)} \oplus H_{(-)}$ and all the space-time regimes. In the Metaplectic group representation $M p (n)$ , this corresponds to the state sectors $H_{(1 / 4)}$ (even) and $H_{(3 / 4)}$ (odd), and as we find here these states are entangled.
The total n states range over all scales from the lowest excited levels to the highest excited ones covering the two dual branches $(+)$ and $(-)$ or Hilbert space sectors and corresponding space-time coverings. The two $(+)$ and $(-)$ dual sectors are entangled.

The consequences of these results are interesting because the classical-quantum gravity duality allows that signals or states in the quantum gravity (trans-Planckian) domaine, or semiquantum gravity (inflationary) domaine, do appear as low energy effects in the semiclassical/classical universe today.

From the results of this paper we see that the gravity domains from one side and the other of the Planck scale are entangled, for instance the black hole quantum interior and the classical exterior gravity domains. Similarly, for the cosmological domains: The quantum trans-Planckian primordial vacuum (constant curvature de Sitter phase, followed by a quasi-de Sitter (inflationary) phase), and the late classical dual de Sitter Universe today are entangled.

Other new entanglement results of this paper are:

The precise relation between the Schmidt type representation in the density matrix context and the physical state fulfilling the Minimal Group Representation Principle (MGRP), that is bilinear in the basic states of the $M p (n)$ group, is found.
The mapping for the physical state refers to a new non-diagonal coherent state representation complementary to that of the known Sudarshan diagonal representation.
The basic states in the Minimal Group Representation sense: $| 1 / 4 >$ and $| 3 / 4 >$ (belonging to the even and odd sectors of the Hilbert space respectively) are a intrinsic fundamental part of the very structure of the space-time itself and do not require an additional extrinsic generation process as in the standard Schrodinger cat states and their entanglement.

This paper is organized as follows:

In Section (II) we describe the Berry geometrical phases for non compact groups and the coherent state quantum evolution. In Section (III) we apply this framework to find the Berry phases for de Sitter inflation and the inflationary (tensor and scalar) perturbations. Section (IV) is devoted to Entanglement, its density matrix description and our generalized coherent states which allow to map the space-time metric into the Hilbert space. Section (V) deals with the

M p (n)

coherent states describing the quantum evolution of the spacetime, the associated adiabatic invariants and the topological structure. In Sections (VI) and (VII) we find the Entanglement with semi-coherent states and generalized Schrodinger cat states in the quantum space-time structure. In Section (VIII) we apply these results to find the Entanglement in de Sitter and black hole space-times. Section (IX) is devoted to Remarks and Conclusions.

2. Geometrical Phases and Noncompact Groups

2.1. SU(1,1) Coherent States and the Berry Phase

Our starting point is the coset coherent state definition according to Perelomov-Klauder [12,13,14] via the action of a displacement operator

D (ξ)

belonging to the coset and generally unitary, as follows:

|ψ〉 = U (ξ) |ψ_{0}〉 \to |k, ξ〉 = D (ξ) |k, 0〉

\begin{matrix} |k, ζ〉 & = exp (ξ K_{+} - ξ^{*} K_{-}) |k, 0〉 \\ = {(1 - {|ζ|}^{2})}^{k} exp (ζ K_{+}) |k, 0〉 \end{matrix}

where

ξ = - (χ / 2) e^{- i φ}, ζ = - tanh (χ / 2) e^{- i φ} = \frac{ξ}{|ξ|} tanh |ξ|

The parameter

ζ

is restricted by

|ζ| < 1 (d i s k)

, and the number k is known as the Bargmann index which separates different irreducible representations.

The state

|k, 0〉

meets the conditions:

K_{-} |k, 0〉 = 0

and

K_{0} |k, 0〉 = k |k, 0〉 .

If one assumes the diagonal operator

K_{0}

like the hamiltonian we have that

|k, ξ〉

is eigenstate of the following Hamiltonian:

\begin{matrix} \tilde{H} & = D (ξ) K_{0} D^{†} (ξ) \\ = K_{0} cosh χ + \frac{1}{2} (e^{- i φ} K_{+} + e^{i φ} K_{-}) sinh χ \end{matrix}

Taking into account

ζ

as a slowly varying function of the evolution parameter of the system (e.g. time) and

〈k, ζ |k, ζ〉 = 1

〈k, ζ| K_{+} |k, ζ〉 = \frac{2 k ζ^{*}}{(1 - {|ζ|}^{2})} = - k sinh χ e^{i φ}

then

〈k, ζ| \frac{d}{d t} |k, ζ〉 = k \frac{ζ^{*} \frac{d ζ}{d t} - ζ \frac{d ζ^{*}}{d t}}{(1 - {|ζ|}^{2})}

From the definitions for the Berry phase, with

R (t)

the set of parameters (generally of geometrical origin) we have:

\begin{matrix} γ (C) & = i \int_{0}^{T} d t 〈n, R| \frac{d}{d t} |n, R〉 \\ = i \int_{C} d R 〈n, R| \nabla_{R} |n, R〉 \end{matrix}

and the Berry phase expresses as

γ_{k} (C) = - i k \int_{C} \frac{ζ^{*} d ζ - ζ d ζ^{*}}{(1 - {|ζ|}^{2})}

Mp(2), SU(1,1) and Sp(2):

Let us to consider the brief description of the relevant symmetry group to perform the realization of the Hamiltonian operator of the problem. This group specifically is the Metaplectic

M p (2)

as well as the groups that are topologically covered by it. The generators of

M p (2)

are the following :

\begin{matrix} T_{1} & = \frac{1}{4} (q p + p q) = \frac{i}{4} (a^{+ 2} - a^{2}), \\ T_{2} & = \frac{1}{4} (p^{2} - q^{2}) = - \frac{1}{4} (a^{+ 2} + a^{2}), \\ T_{3} & = - \frac{1}{4} (p^{2} + q^{2}) = - \frac{1}{4} (a^{+} a + a a^{+}) \end{matrix}

(1)

with the commutation relations,

[T_{3}, T_{1}] = i T_{2}, [T_{3}, T_{2}] = - i T_{1}, [T_{1}, T_{2}] = - i T_{3}

being

q, p

(alternatively

a, a^{+})

the variables of the standard harmonic oscillator, as usual.

If we rewrite the commutation relations as:

[T_{3}, T_{1} \pm i T_{2}] = \pm (T_{1} \pm i T_{2}), [T_{1} + i T_{2}, T_{1} - i T_{2}] = - 2 T_{3}

we see that the states

|n〉

are eigenstates of

T_{3}

T_{3} |n〉 = - \frac{1}{2} (n + \frac{1}{2}) |n〉

and it is easy to see that:

T_{1} + i T_{2} = - \frac{i}{2} a^{2}, T_{1} - i T_{2} = \frac{i}{2} a^{+ 2} .

2.2. Quadratic Hamiltonians, the Parametric Oscillator and the Group Structure

The problem we are going to face: we know that the general parametric oscillator has a quadratic structure of the known form

\hat{H} = \frac{1}{2} [Z (t) {\hat{p}}^{2} + Y (t) (\hat{p} \hat{q} + \hat{q} \hat{p}) + X (t) {\hat{q}}^{2}]

(2)

therefore, using the group manifold precisely the

M p (2),

the association is direct

\hat{H} = - i [Z (t) {\hat{K}}_{+} + 2 Y (t) {\hat{K}}_{0} + X (t) {\hat{K}}_{-}]

(3)

since, for Eq. (1):

{\hat{K}}_{0} = i T_{1}, {\hat{K}}_{+} = - i (T_{2} + T_{3}), {\hat{K}}_{-} = i (T_{2} - T_{3}),

consequently:

[{\hat{K}}_{+}, {\hat{K}}_{-}] = - 2 {\hat{K}}_{0}, [{\hat{K}}_{0}, {\hat{K}}_{\pm}] = \pm {\hat{K}}_{\pm}

(4)

being then one of the possible representations, preserving the commutation relations at the algebra level, the following:

{\hat{K}}_{0} = (\begin{matrix} - 1 & 0 \\ 0 & 1 \end{matrix}), {\hat{K}}_{+} = (\begin{matrix} 0 & 0 \\ 1 & 0 \end{matrix}), {\hat{K}}_{-} = (\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix}) \to \hat{H} = - i (\begin{matrix} - Y (t) & X (t) \\ Z (t) & Y (t) \end{matrix}) .

(5)

Let us note that formally and for practical purposes we draw on a particular parameterization of

S O (1, 2)

, strictly according to the chain for any element

A_{α}

A_{α} : \in M p (2) \supset S p (2 R) \sim S U (1, 1) \supset S O (1, 2) \approx L (3)

(6)

This is for the obvious reason that

M p (2)

does not have finite realizations, being the double covering of

S U (1, 1)

S p (2 R)

, and the quadruple covering of

S O (1, 2)

, properties to take into account when signs, phases and connectivity become very important, as when determining the spectrum of physical states of a particular system.

Consequently, we remark here that the representation Eq.(5) is for practical purposes quite useful mainly at the level of making a more precise comparison at the time to pick a point of contact with other methods such as the one based on the Wei Norman theorem [22]. Strictly speaking (we will return to this point at the end of this paper) one must work independently of the representation as far as non-compact groups are concerned (e.g. infinite dimensional unitary representations).

2.3. Generalized Parametric Oscillator and the Berry Phase

H (t) = Z (t) \frac{p^{2}}{2 m} + \frac{ω_{0}}{2} Y (t) (p q + q p) + ϵ X (t) \frac{m {(ω_{0} q)}^{2}}{2}, (ϵ = \pm 1)

(7)

Introducing as usual, annihilation-creation operators in Eq.(7)

a = \frac{p - i m ω_{0} q}{\sqrt{2 m ω_{0} ℏ}}, a^{+} = \frac{p + i m ω_{0} q}{\sqrt{2 m ω_{0} ℏ}}

(8)

we obtain

H (t) = \frac{1}{2} [- (ϵ X (t) - Z (t)) (a^{+ 2} + a^{2}) + i Y (t) (a^{+ 2} - a^{2}) + (ϵ X (t) + Z (t)) (a a^{+} + a^{+} a)], (ϵ = \pm 1)

(9)

We note that using a Bogoliubov type transformation like

(\begin{matrix} b \\ b^{+} \end{matrix}) = (\begin{matrix} M_{+ -} & M_{- +} \\ M_{- -} & M_{+ +} \end{matrix}) (\begin{matrix} a \\ a^{+} \end{matrix})

(10)

where

M_{\pm \pm} = \frac{1}{2 \sqrt{κ Z}} [(Z \pm κ) \pm i Y]

(11)

and

κ = {(ϵ X Z - Y^{2})}^{1 / 2}

(12)

the Hamiltonian takes the form

H = ℏ \underset{κ (t) ω_{0}}{\underset{︸}{ω (t)}} (b^{+} b + \frac{1}{2})

(13)

due the canonical commutation relations are preserved, e.g.

[b, b^{+}] = [a, a^{+}] = 1 .

It is easy to see then, as proof, that

b^{+} b + b b^{+} = \frac{1}{4 κ} [2 (Z (t) - ϵ X (t)) (a^{+ 2} + a^{2}) + 2 (ϵ X (t) + Z (t)) (a a^{+} + a^{+} a) + 2 i Y (t) (a^{2} - a^{+ 2})]

(14)

The Heisenberg equation of motion of the system are

\begin{matrix} \frac{d b}{d t} & = - \frac{i}{ℏ} [b, H] + \frac{\partial b}{\partial t} \\ = - i ω b + \frac{i Z}{2 κ} [\frac{d}{d t} (\frac{Y}{Z} b - \frac{Y - i κ}{Z} b^{+})], \end{matrix}

\begin{matrix} \frac{d b^{+}}{d t} & = - \frac{i}{ℏ} [b^{+}, H] + \frac{\partial b^{+}}{\partial t} \\ = i ω b^{+} - \frac{i Z}{2 κ} [\frac{d}{d t} (\frac{Y}{Z} b^{+} + \frac{Y + i κ}{Z} b)], \end{matrix}

Note that for the purpose to find the Berry phase, the terms of interaction between the creation and annihilation operators can be distregarded due that are beyond the second order of adiabaticity. Consecuentlythe approximate solution

b (t) \to b (0) exp [- i \int [ω (t) - \frac{Z}{2 κ} \frac{d}{d t} (\frac{Y}{Z})] d t]

(15)

The second phase factor will be related with the Berry phase of the physical system: e.g.:

B_{p h} \to \int \frac{Z}{2 κ} \frac{d}{d t} (\frac{Y}{Z}) d t .

2.4. Coherent State Quantum Evolution

As we have seen so far, from the point of view of the dynamics the relevant symmetries are dominated by the metaplectic group and the groups covered by it, which define the symplectic and projective characteristics of the quantum phase space. Consequently, to illustrate the motion in the proyective Hilbert space it is appropiate to start the corresponding coherent state given by

|ξ〉 = e^{- {|ξ|}^{2}} \underset{n = 0}{\sum^{\infty}} |n〉 = e^{ξ b^{+ 2} - ξ^{*} b^{2}} |0〉

(16)

The Mp(2) Squeezed Vacuum and Physical States:

The displacement operator in the case of the vacuum squeezed is an element of Mp(2) written in the respective variables of the canonical annihilation and creation operators.

S (ξ) = exp \frac{1}{2} (ξ^{*} b^{2} - ξ b^{+ 2}) \in M p (2)

(17)

Seeing Eqs. (10)-( 18) the relationship is shown directly:

(\begin{matrix} b \\ b^{+} \end{matrix}) \to S (ξ) (\begin{matrix} a \\ a^{+} \end{matrix}) S^{- 1} (ξ) = (\begin{matrix} λ & μ \\ μ^{*} & λ^{*} \end{matrix}) (\begin{matrix} a \\ a^{+} \end{matrix})

(18)

From Eqs (17) (18), we see that the dynamics of these "square root" fields of

Φ_{γ}

, in the particular representation that we are interested in, is determined by considering these fields as coherent states in the sense that they are eigenstates of

a^{2}

via the action of the Mp

(2)

group that is of the type:

\begin{matrix} |Ψ_{1 / 4} (0, ξ, q)〉 & = \overset{+ \infty}{\sum_{k = 0}} f_{2 k} (0, ξ) \frac{{(a^{†})}^{2 k}}{\sqrt{(2 k)!}} |0〉 \end{matrix}

(19)

\begin{matrix} |Ψ_{3 / 4} (0, ξ, q)〉 & = \overset{+ \infty}{\sum_{k = 0}} f_{2 k + 1} (0, ξ) \frac{{(a^{†})}^{2 k + 1}}{\sqrt{(2 k + 1)!}} |0〉 \end{matrix}

(20)

For simplicity, we will take all normalization and fermionic dependence or possible fermionic realization, into the functions

f (ξ)

. Explicitly, at

t = 0

, the states are:

\begin{matrix} |Ψ_{1 / 4} (0, ξ, q)〉 = f (ξ) |α_{+}〉 \\ |Ψ_{3 / 4} (0, ξ, q)〉 = f (ξ) |α_{-}〉 \end{matrix}

(21)

where

|α_{\pm}〉

are the CS basic states in the subspaces

λ = \frac{1}{4}

and

λ = \frac{3}{4}

of the full Hilbert space. In other words, the action of an element of

M p (2)

keeps them invariant (coherent), ensuring the irreducibility of such subspace, e.g :

H \sim (\begin{matrix} H_{1 / 4} \\ H_{3 / 4} \end{matrix})

(22)

Consequently, the two symmetric and antisymmetric combinations

(\pm)

of the two sets of states

(1 / 4, 3 / 4)

will span all the Hilbert space:

H

|Ψ_{\pm}〉 = |Ψ_{1 / 4}〉 \pm |Ψ_{3 / 4}〉, |\pm〉 = |+〉 \pm |-〉

(23)

The time development is obtained by applying equation (15) to the combined state (sweeping the entire

H)

{|ξ〉}_{t} = e^{- i Γ (t, R)} |ξ e^{+ i Γ (t, R)}〉

or in the respective irreducible subspaces of

H

from the point of view of

M p (n)

\begin{matrix} {|Ψ_{1 / 4}〉}_{t} = e^{- i Γ (t, R)} |Ψ_{1 / 4} e^{+ i Γ (t, R)}〉 \\ {|Ψ_{3 / 4}〉}_{t} = e^{- i Γ (t, R)} |Ψ_{3 / 4} e^{+ i Γ (t, R)}〉 \end{matrix}

where the total phase (dynamical plus Berry phase) is

Γ (t, R (t)) = \underset{d y n . p h a s e}{\underset{︸}{\int ω (t) d t}} \underset{B e r r y p h a s e}{\underset{︸}{- \int \frac{Z}{2 κ} \frac{d}{d t} (\frac{Y}{Z}) d t}}

3. Relevant Applications in Cosmology

New illustrative applications of this formalism appear in the context of cosmology and black holes. These situations correspond to the cases

Z (t) = X (t) = 1

In general, the relevant term for the emergence of the Berry phase is the linear part in the temporal differential equation of the parametric oscillator, or the

(q p + p q)

term in the Hamiltonian Eq.(9) and thus the non vanishing coefficient

Y (t)

The diagonalization can be always performed through the Bogoliubov transformation Eq.(10) - Eq.(14) to the quadratic Hamiltonian. Therefore, for these cases we have:

H (t) = \frac{1}{2} [(1 - ϵ) (a^{+ 2} + a^{2}) + i Y (t) (a^{+ 2} - a^{2}) + (1 + ϵ) (a a^{+} + a^{+} a)]

(24)

M_{\pm \pm} = \frac{1}{2 \sqrt{κ}} [1 \pm κ \pm i Y] ϵ = \pm 1

(25)

(ϵ = - 1

corresponding to the inverted, eg with imaginary frequency, oscillator).

And the Hamiltonian becomes

H = ℏ ω (t) (b^{+} b + \frac{1}{2})

(26)

κ^{2} = (ϵ - Y^{2}), ℏ ω (t) = κ (t) ω_{0}

(27)

b^{+} b + b b^{+} = \frac{1}{2 κ} [(1 - ϵ) (a^{2} + a^{+ 2}) + i Y (t) (a^{2} - a^{+ 2}) + (1 + ϵ) + \frac{1}{2} (a a^{+} + a^{+} a)]

(28)

The Berry phase becoming

B_{p h a s e} = \int \frac{d t}{2 \sqrt{ϵ - Y^{2}}} \frac{d}{d t} Y

(29)

3.1. Berry Phase of de Sitter Inflation

Interestingly enough, de Sitter space-time can be described as an inverted harmonic oscillator, eg with imaginary frequency, both classically and at the quantum level, the Hamiltonian taking the same form of Eq. (26) with

{| κ |}^{2} = (1 + Y^{2}) .

The description of de Sitter inflation is preciselly that of a parametric oscillator with

Y (t) = H (t) = \sqrt{Λ (t) / 3},

the oscillator length being

l_{o s c} = 1 / H

. The Berry phase of de Sitter inflation is in fact imaginary, and with the sign describing the increasing exponential factor acceleration

B_{p h a s e} = - i \int_{t_{i n}}^{t_{e n d}} \frac{d t}{2 \sqrt{1 + H^{2}}} d_{t} H

(30)

This integral is explicitly solved as a function of H with limits

H (t_{e n d}) \equiv H_{e}

and

H (t_{i n}) \equiv H_{i}

B_{p h a s e} = i ln \sqrt{\frac{H_{i} + \sqrt{1 + H_{i}^{2}}}{H_{e} + \sqrt{1 + H_{e}^{2}}}}

the finite interval

[t_{i n}, t_{e n d}]

indicating the initial and the final time of inflation.

3.2. Berry Phase of the Inflationary Perturbations:

The linear quantum perturbations of Inflation, both the scalar

(S)

curvature fluctuations and the tensor

(T)

gravitational k - modes both satisfy a second order Schröedinger type equation in time:

Q^{″} {(η)}_{(S, T)} + [k^{2} - W^{2} {(η)}_{(S, T)}] Q {(η)}_{(S, T)} = 0

(31)

where

η

is the conformal time related to the cosmic time t by

d t = a (η) d η

, primes

(^{''})

denote the second derivative with respect to

η

, and the potential

W^{2} {(η)}_{(S, T)}

felt by the fluctuations is:

W^{2} {(η)}_{(S)} = a^{″} (η) / a (η)

(32)

W^{2} {(η)}_{(T)} = z^{″} (η) / z (η)

(33)

The variable z appropriately combines the inflaton field

ϕ (t)

and the accelerated expansion background described by the scale factor

a (t)

driven by

ϕ (t)

, the Hubble parameter being

H = a^{.} (t) / a (t)

z = a (t) \frac{ϕ^{.} (t)}{H}

(34)

\frac{d^{2} z}{d η^{2}} = a^{2} (z^{. .} + H z^{.})

(35)

Therefore, the scalar and tensor gravitational inflationary fluctuations both satisfy similar parametric harmonic oscillator equations with the Hamiltonian

H

H = \frac{1}{2} [P^{2} + Ω^{2} {(η)}_{(S, T)} Q^{2}]

(36)

Ω^{2} {(η)}_{(S, T)} \equiv k^{2} - W^{2} {(η)}_{(S, T)}

The two typical situations do appear:

Ω {(η)}_{(S, T)} Real : k^{2} > W^{2} {(η)}_{(S, T)}, (sub horizon k- modes)

Ω {(η)}_{(S, T)} Imaginary : k^{2} < W^{2} {(η)}_{(S, T)}, (super horizon k- modes)

H (P, Q)

correspond to the

(b, b^{+})

representation, and a canonical (Bogoliubov) transformation as Eq. (25):

(P, Q) \to (q, p)

, (equivalently

(b, b^{+}) \to (a, a^{+})

) yields

H

into the form:

H = \frac{1}{2} [p^{2} + Y {(η)}_{(S, T)} (p q + q p) + k^{2} q^{2}]

(37)

Y {(η)}_{(S)} = z^{'} / z, Y {(η)}_{(T)} = a^{'} / a

with

Ω^{2} {(η)}_{(S, T)} = (k^{2} - Y_{(S, T)}^{2}) - Y_{(S, T)}^{'} = ω^{2} - Y_{(S, T)}^{'}

(38)

Y_{(S, T)}^{'} = a " / a - Y^{2}

, and recall here that

η

is the conformal time,

(^{'}) \equiv d / d η

The Berry phase of the quantum inflationary fluctuations

(S, T)

is then:

B_{p h a s e, k} (S, T) = \int_{0}^{η_{e n d}} \frac{d η}{2 \sqrt{k^{2} - Y_{(S, T)}^{2}}} Y_{(S, T)}^{'}

(39)

The

η

interval in the integral depends on whether it refers to sub horizon or super horizons modes, eg on whether

k^{2} > Y^{2} {(η_{e n d})}_{(S, T)}

k^{2} < Y^{2} {(η_{e n d})}_{(S, T)}

respectively,

η_{e n d}

being then fixed by:

k^{2} = Y^{2} (η_{e n d}) .

Note that in the case of the cosmological perturbations the integral is explicitly solved as a function of

Y_{(S, T)} (η)

with limits

Y_{(S, T)} (0) \equiv Y_{0}

and

Y_{(S, T)} (η_{e n d}) \equiv Y_{e}

(i) subhorizon modes:

B_{p h a s e, k} (S, T) = \frac{1}{2} arctan [\frac{Y_{e} - Y_{0}}{\sqrt{(k^{2} - Y_{e}^{2}) (k^{2} - Y_{0}^{2})} + Y_{e} Y_{0}}]

(ii) superhorizon modes:

B_{p h a s e, k} (S, T) = i ln \sqrt{\frac{Y_{e} + \sqrt{Y_{e}^{2} - k^{2}}}{Y_{0} + \sqrt{Y_{0}^{2} - k^{2}}}}

We can also express the Berry phase in the inflationary slow roll regime which is well appropriated here because the Berry phase adiabaticity.

Y {(η)}_{(S, T)}

can be written in terms of the slow roll parameters

ϵ_{v}, η_{v}

, and therefore related to the cosmological observables: the scalar and tensor spectral indices

n_{S}

and

n_{T}

and the scalar to tensor ratio r:

W {(η)}_{(S, T)} = \frac{(ν_{(S, T)}^{2} - 1 / 4)}{η^{2}}

(40)

ν_{(S)} = 3 / 2 + 3 ϵ_{v} - η_{v} = 3 / 2 - (n_{s} - 1) / 2

ν_{(T)} = 3 / 2 + ϵ_{v} = 3 / 2 - n_{T} / 2

r = 16 ϵ_{v} = - n_{T} / 8

(41)

These expressions show the operational explicit applications of our framework. The analysis of these findings, their properties and the observable features in terms of real cosmological data exceeds the purpose of this paper and desserve future work.

4. Entanglement

4.1. Density Matrix Viewpoint

Let us consider the following state

|Φ〉 = |Φ_{A}〉 |Φ_{B}〉

subindex A and B indicate the corresponding subsystems. Usually one could even define (in the context of our previous works) the density matrix for an observable and an unobservable sector.

|Φ〉 = |Φ o〉 |Φ d〉

in such a way that the density matrix of the observable system is

ρ_{o} = T r_{d} |Φ〉 〈Φ|

and the corresponding entropy of the entanglement in this case

S_{E} = - T r_{o} ρ_{o} log ρ_{o}

Using the Schmidt decomposition, some pure state can be written as

|Φ〉 = \overset{n}{\sum_{i = 1} c_{i}} |v_{i A}〉 \otimes |u_{i B}〉

(42)

with

|v_{i A}〉, |u_{i B}〉

are orthonormal states in subsystem A and subsystem B respectively. If we see the structure of the Hilbert space(22) for a state

\in S U (1, 1)

the correspondence between (42) and the results of our previous papers is immediate as we will demonstrate below.

Not all states are separable states (and thus product states). Fix a basis for

H_{A}

and a basis for

H_{B}

subsystems.The most general state in

H_{A} \otimes H_{B}

is now of the form.

|Φ〉 = \sum_{i, j = 1} c_{i j} |v_{i A}〉 \otimes |u_{j B}〉

This state is separable if there exist vectors such that yielding

c_{i j} = c_{i A} c_{j B} / |Φ〉 = \sum_{i = 1} c_{i A} |v_{i A}〉 \otimes \sum_{j = 1} c_{j B} |u_{j B}〉

. And it is inseparable if for any vectors at least for one pair of coordinates

c_{i j} \neq c_{i A} c_{j B}

. If a state is inseparable, it is called an ’entangled state’. The typical case is one of the Bell states e.g.

\frac{|1_{A}〉 \otimes |0_{B}〉 - |0_{A}〉 \otimes |1_{B}〉}{\sqrt{2}}

of the four Bell states, which are (maximally) entangled pure states with the basis

\{|0_{A}〉, |1_{A}〉\} \in H_{A}

and

\{|0_{B}〉, |1_{B}〉\} \in H_{B}

. (These are pure states of the

H_{A} \otimes H_{B}

space, but which cannot be separated into pure states of each

H_{A}

and

H_{B}

space). If the composite system is in such state, it is impossible to attribute to either system A or system B a definite pure state.

Notice that while the von Neumann entropy of the whole entangled state is zero (as it is for any pure state), the entropy of the subsystems is greater than zero. In this sense, the systems are "entangled".

Recently, in previous recent works [1,2], we have seen that physical states are mappings of the group generators in a vector representation, and that these are expressed in the so called Sudarshan’s diagonal-representation and in a new non diagonal one that lead, as an important consequence, the physical states with spin content

λ = (1 / 2, 1, 3 / 2, 2)

Precisely, the generalized coherent states here generate a map that relates the metric

g_{a b}

, solution of the wave equation, to the specific subspace of the full Hilbert space where these coherent states live. Moreover, for operators

\in M p (2)

there exists an asymmetric - kernel leading for our case the following

λ = 1

state :

{g_{a b} (t, 1, α)|}_{H W} = 〈Ψ_{3 / 4} (t)| L_{a b} |Ψ_{1 / 4} (t)〉 = F {(\begin{matrix} α \\ α^{*} \end{matrix})}_{(1) a b}

(43)

where

F = e^{[- {(\frac{m}{\sqrt{2} |a|})}^{2} {[(α + α^{*}) - B]}^{2} + D]} e^{[ξ ϱ (α + α^{*})]} {|f (ξ)|}^{2}

where B and D are given by:

B = {(\frac{|a|}{m})}^{2} c_{1}, D = {(\frac{|a| c_{1}}{\sqrt{2} m})}^{2} + c_{2}

(44)

c_{1}

and

c_{2}

being constants characterizing the solution or its initial conditions;

ξ

is the fermionic super coordinate of the corresponding group manifold and

ϱ

is the fermionic part of the superfield solution.

This is so because the non-diagonal projector involved in the reconstruction formula of

L_{a b}

is formed with the

Ψ_{1 / 4}

and

Ψ_{3 / 4}

states which span completely the full Hilbert space. And this is precisely a particular case of the Schmidt decomposition of an SU(1,1) quantum state, namely

Φ_{a b} \equiv \underset{M p (2) r e p r e s e n t a t i o n}{\underset{︸}{〈Ψ_{3 / 4} (t)| L_{a b} |Ψ_{1 / 4} (t)〉}} \sim 〈Ψ_{3 / 4} (t)| {(\begin{matrix} a \\ a^{+} \end{matrix})}_{a b} |Ψ_{1 / 4} (t)〉 \to \underset{S c h m i d t - r e p r e s .}{\underset{︸}{Φ_{a b} = \overset{}{\sum_{n, m = 0} c_{a b}} v_{m 1 / 4} \otimes u_{n 3 / 4}^{*}}}

(45)

The above correspondence is fully consistent due to the fact that

|Ψ_{1 / 4} (t)〉, |Ψ_{3 / 4} (t)〉

are pure states (coherent) in each subspace

\in S U (1, 1)

and they are mutually orthogonal.

With more detaill we have in the

M p (n)

case from Eq. (45):

\begin{matrix} Φ_{a b} & = \sum_{n = 0, 1, 2 . .} \underset{u_{3 / 4}^{*}}{\underset{︸}{〈Ψ_{3 / 4} (t)| 2 n + 1〉}} \underset{c_{a b}}{\underset{︸}{〈2 n + 1| L_{a b} |2 n〉}} \underset{v_{1 / 4}}{\underset{︸}{〈2 n |Ψ_{1 / 4} (t)〉}} \\ = \sum_{n = 0, 1, 2 . .} (1 - {|ω|}^{2}) \frac{{(ω^{*} / 2)}^{2 n + 1}}{\sqrt{(2 n + 1)!}} {(\begin{matrix} 0 \\ \sqrt{2 n + 1} \end{matrix})}_{a b} \frac{{(ω / 2)}^{2 n}}{\sqrt{(2 n)!}} = \\ = \sum_{n = 0, 1, 2 . .} Ξ (n) {(\begin{matrix} 0 \\ \sqrt{2 n + 1} \end{matrix})}_{a b} ω^{*} \end{matrix}

(46)

Here we have used the discrete basis (series) in the disk of Mp(2) and its coverings.

Meanwhile the case

\begin{matrix} Ψ_{a b} & \equiv 〈Ψ_{1 / 4} (t)| L_{a b} |Ψ_{3 / 4} (t)〉 \neq 〈Ψ_{3 / 4} (t)| L_{a b} |Ψ_{1 / 4} (t)〉 \\ = \sum_{n = 0, 1, 2 . .} \underset{u_{3 / 4}^{*}}{\underset{︸}{〈Ψ_{1 / 4} (t)| 2 n〉}} \underset{c_{a b}}{\underset{︸}{〈2 n| L_{a b} |2 n + 1〉}} \underset{v_{1 / 4}}{\underset{︸}{〈2 n + 1 |Ψ_{3 / 4} (t)〉}} \\ = \sum_{n = 0, 1, 2 . .} Ξ (n) {(\begin{matrix} \sqrt{2 n} \\ 0 \end{matrix})}_{a b} ω \end{matrix}

(47)

with the definition

Ξ (n) = {(\frac{|ω|}{2})}^{2 n} \frac{(1 - {|ω|}^{2})}{2 \sqrt{(2 n)! (2 n + 1)!}}

We can see that the expressions Eq.(46) and Eq.(47) describe two definite chirality states showing the non compact analog to the SU(2) case with the respective spinors (discrete series inside the disc with characteristic complex variable

ω

It is also important to remark the following points:

(i) We have for Mp(2) a

\infty -

dimensional but unitary representation that maps it to the Lorentz group in 3-dimensional

L_{3}

(ii) We can see that :

〈Ψ_{3 / 4} (t)| L_{a b} |Ψ_{1 / 4} (t)〉 \neq 〈Ψ_{1 / 4} (t)| L_{a b} |Ψ_{3 / 4} (t)〉

This fact have also interesting implications, as for the realization of the CPT invariance and for the arrow of time. This is so because of the full covering of the Hilbert space by the

|1 / 4〉

and

|3 / 4〉

sets of states (even and odd sets) of the Metaplectic (Mp) group. In particular, the correspondence between the standard Schrodinger cat states and the basic states

|1 / 4〉

and

|3 / 4〉

of Mp(2) is discussed in Section VII.

(iii) From the point (ii) it can be seen that there would be a natural transition from the compact spinorial description of SU(2) for example, to the non-compact SU(1,1) description by taking as the basis of this transition the universal covering Mp(2).

Let us also notice that the bilinear state associated with spin 2 in this basis, similarly as in the expressions Eqs.(46-47), was associated with the spacetime metric, providing the space-time discretization condition for small n and the continuous spacetime for n

\to \infty

Consequently, and due to Eq. (43) the entanglement entropy is given by

S_{E} = - T r {|F α|}^{2} log {|F α|}^{2}

where

F

is due to expression Eq.(43).

5. Quantum Evolution, Adiabatic Invariants and Topological Structure

Now, we will provide the interpretation of the relation between the coherent states in the metaplectic representation and the quantum evolution of the spacetime. For this purpose we will need to start similarly to Eq. (18) with the association

(\begin{matrix} b \\ b^{+} \end{matrix}) \to (\begin{matrix} a_{(+)} \\ a_{(+)}^{+} \end{matrix}) \equiv L_{(+)}

and

(\begin{matrix} a \\ a^{+} \end{matrix}) \to (\begin{matrix} a_{(-)} \\ a_{(-)}^{+} \end{matrix}) \equiv L_{(-)}

where

a_{(\pm)}

correspond to operators

a (t)

for

t \to \pm \infty

(asymptotical values). Consecuently

a_{(-)}^{+} a_{(-)} |n (-)〉 = n |n (-)〉, a_{(+)}^{+} a_{(+)} |n (+)〉 = n |n (+)〉, e t c .

From Eq.(18) we have

\begin{matrix} L_{(+)} & = U L_{(-)} U^{- 1} = A L_{(-)}, \\ A & \in S U (1, 1), \end{matrix}

(48)

but now the element of the group is

U \in M p (2) / U = e^{- i γ T_{3 (-)}} e^{- i β T_{1 (-)}} e^{- i α T_{3 (-)}}

We can observe now that

M_{m n} = 〈m (+)| |n (-)〉

where as before

a_{(+)}^{+} a_{(+)} |m (+)〉 = m |m (+)〉

. We can see also that:

a_{(+)}^{+} a_{(+)} = U a_{(-)}^{+} a_{(-)} U^{- 1} .

From Eq. (48) :

|m (+)〉 = U |m (-)〉

then,

〈m (+)| |n (-)〉 = 〈m (-)| U^{- 1} |n (-)〉

with our matrix element

M_{m n} = 〈m| e^{i α T_{3 - i β T_{1}}} e^{i γ T_{3}} |n〉

where the index

(-)

was dropped for simplicity. Because

T_{3} |n〉 = - \frac{1}{2} (n + \frac{1}{2}) |n〉

M_{m n} = e^{- i α \frac{(2 m + 1)}{4}} e^{- i γ \frac{(2 n + 1)}{4}} 〈m| e^{i β T_{1}} |n〉

We can further consider the following quantity determines the transition probability of the oscillator from the state

|n (-)〉

to the state

|m (+)〉

W_{m n} = {|M_{m n}|}^{2} = {|〈m| e^{- \frac{β}{4} (a^{+ 2} - a^{2})} |n〉|}^{2}

In particular,

\begin{matrix} W_{n n} & = {|〈n| e^{- \frac{β}{4} (a^{+ 2} - a^{2})} |n〉|}^{2} \\ = {|〈n| 1 - \frac{β}{4} (a^{+ 2} - a^{2}) + {\frac{β}{32}}^{2} {(a^{+ 2} - a^{2})}^{2} - . . . . |n〉|}^{2} \\ = 1 - {\frac{β}{8}}^{2} {(n^{2} + n + 1)}^{2} + \cdot \cdot \cdot \end{matrix}

By taking

β < 1

β^{2}

, the above expression is the magnitude determining the accuracy of preservation of the adiabatic invariant of the classical oscillator, generally with time-dependent frequency, (parametric oscillator), as Eq.(3) related with the dynamical and geometrical phases.

Let us notice that in the transition probability

W_{m n}

the relevant generator of the tran- sition between the eigenstates of

T_{3}

of the respective system

| n ⟩

T_{1}

characteristic of the diabatic-adiabatic evolution of the physical system considered characteristic of the diabatic-adiabatic evolution of the physical system considered.

6. Entanglement with Semi-Coherent States

Let us briefly analyze in an algebraic description, the origin of the quantum relativistic effects as the prolongated highly oscillations effect or so called "Zitterbewegung".

There are two types of states in the "algebro-pseudo-differential" correspondence: the basic (non-observable) states and the observable physical states. In that case, the basic states are coherent states corresponding to the double covering of the

S L (2 C)

group, eg the Metaplectic group [1,2]: This is the responsible for projecting the symmetries of the 6 dimensional

M p (4)

group space to the 4 dimensional space-time by means of a bilinear combination of the

M p (4)

generators. The supermultiplet metric solution for the geometric Lagrangian is

g_{a b} (t, λ) = 〈ψ_{λ} (t)| L_{a b} |ψ_{λ} (t)〉

As we can see above, the physical state (which appears as a mapping of the non-compact generator of interest and its fundamental coverings) takes precisely the form of a Husimi quasi-probability usually represented as Q. Specifically,

g_{a b} (0, λ) = exp [A] exp [ξ ϱ (t)] χ_{f} 〈 ψ_{λ} (0) | L_{a b} | ψ_{λ} (0) 〉,

A (t) = - {(\frac{m}{|γ|})}^{2} t^{2} + c_{1} t + c_{2}, (c_{1}, c_{2}) \in C

(49)

where we have written the corresponding indices for the simplest supermetric state solution,

L_{a b}

are the corresponding generators

\in M p (n)

, and

χ_{f}

is coming from the odd generators of the big covering group of symmetries of the specific model.

Considering for simplicity the `square’ solution for the three compactified dimensions (spin

λ

fixed,

ξ \equiv - ({\bar{ξ}}^{\dot{α}} - ξ^{α})

), the exponential even fermionic part is given by:

\begin{matrix} ϱ (t) \equiv {\overset{\circ}{ϕ}}_{α} [(α e^{i ω t / 2} & + β e^{- i ω t / 2}) - {(σ^{0})}_{\dot{α}}^{α} (α e^{i ω t / 2} - β e^{- i ω t / 2})] \end{matrix}

(50)

\begin{matrix} + \frac{2 i}{ω} [{(σ^{0})}_{α}^{\dot{β}} {\bar{Z}}_{\dot{β}} + {(σ^{0})}_{\dot{α}}^{α} Z_{α}] \end{matrix}

(51)

{\overset{\circ}{ϕ}}_{α}, Z_{α}, {\bar{Z}}_{\dot{β}}

being constant spinors, and

α

and

β

are

C

-numbers (the constant

c_{1} \in C

in Eq. (49) due to the obvious physical reasons and the chirality restoration of the superfield solution).

By consistency, (and as in the string case), two geometric-physical options are related to the orientability of the superspace trajectory :

α = \pm β

. We take without loss of generality

α = + β

then, exactly, there are two possibilities:

(i) The compact case which is associated to the small mass limit (or

|γ| > > 1)

ϱ (t) = (\begin{matrix} {\overset{\circ}{ϕ}}_{α} cos (ω t / 2) + \frac{2}{ω} Z_{α} \\ - {\overset{\circ}{\bar{ϕ}}}_{\overset{\cdot}{α}} sin (ω t / 2) - \frac{2}{ω} {\bar{Z}}_{\dot{α}} \end{matrix})

(52)

(ii) The non-compact case, which can be associated to the imaginary frequency (

ω \to i ω

: generalized inverted oscillators) case:

ϱ (t) = (\begin{matrix} \overset{\circ}{ϕ} cosh (ω t / 2) + \frac{2}{ω} Z_{α} \\ - {\overset{\circ}{\bar{ϕ}}}_{\overset{\cdot}{α}} sinh (ω t / 2) - \frac{2}{ω} {\bar{Z}}_{\dot{α}} \end{matrix})

(53)

Obviously (in both cases), this solution represents a Majorana fermion where the

C

(or

h y p e r c o m p l e x

) symmetry (wherever the case) is inside the constant spinors.

The spinorial even part of the superfield solution in the exponent becomes:

ξ ϱ (t) = θ^{α} ({\overset{\circ}{ϕ}}_{α} cos (ω t / 2) + \frac{2}{ω} Z_{α}) - {\bar{θ}}^{\overset{\cdot}{α}} (- {\overset{\circ}{\bar{ϕ}}}_{\overset{\cdot}{α}} sin (ω t / 2) - \frac{2}{ω} {\bar{Z}}_{\dot{α}})

(54)

We easily see that in the above expression there appear a type of continuous oscillation between the chiral and antichiral part of the bispinor

ϱ (t)

, or Zitterbewegung as shown qualitatively in Figure 1 for suitable values of the group parameters.

6.1. Generation and Entanglement of Schrodinger Cat States

Let us remember that in general a "cat state" refers to a symmetric and antisymmetric combination of coherent Heisenberg-Weyl (HW) states with the property that they sweep even and odd states of the harmonic oscillations. The example of the definition in Ref [17] in terms of Heinserberg-Weyl displacement operators are

D_{\pm} (α) |0〉 \equiv |\pm α〉

\frac{1}{2} [D (α) \pm D (- α)] = D_{\pm} (α)

with the displacement operator standard definition

D (α) = e^{(α a^{+} - α^{*} a)}

We will now demonstrate, by comparing with the case of Ref. [18], that the theoretical construction and physical interpretation presented here and in our previous works [1,2,3,4,5,6,7] is relevant from the fundamental point of view as far as the very quantum structure of space-time is concerned.

The starting state in Ref. [18] is a cat coherent state as described above, but in our case here it is time dependent, the evolution operator being a Kerr type (non-linear) Hamiltonian described in the expression Eq. (56). To simplify the problem, the authors of Ref. [18] take a fixed interaction time

t = π / 2 Ω

where

Ω

is the coefficient of the anharmonic term:

|α, π / 2 Ω〉 = \frac{1}{\sqrt{2}} [e^{- i π / 4} |β〉 + e^{i π / 4} |- β〉]

with

β = α e^{i ω} .

Therefore, we observe that:

(i) The photoelectron or heterodyne number operator of Ref. [18] is simply

\hat{q} = \frac{1}{2} [cos (θ + ω t) (a + a^{+}) + i sin (θ + ω t) (a - a^{+})] + q_{0}

(55)

Let us compare with our operator in scalar form

\begin{matrix} ξ ϱ (t) & = ξ ϱ (t) + \bar{ξ} \bar{ϱ} (t) \\ = cos (ω t / 2) (θ^{α} {\overset{\circ}{ϕ}}_{α} + {\bar{θ}}_{\overset{\cdot}{α}} {\bar{ϕ}}^{\overset{\cdot}{α}}) + sin (ω t / 2) (θ^{α} {\overset{\circ}{ϕ}}_{α} - {\bar{θ}}_{\overset{\cdot}{α}} {\bar{ϕ}}^{\overset{\cdot}{α}}) + \frac{4}{ω} (θ^{α} Z_{α} - {\bar{θ}}_{\overset{\cdot}{α}} {\bar{Z}}^{\overset{\cdot}{α}}) \end{matrix}

Therefore, the identification is immediate between the solution field operators and the photonic creation and annihilation operators in the case of the cited Ref. [18].

(ii) The nonlinearity of the Kerr term (nonlinear optical medium) introduces the ingredient

S U (1, 1)

and the covering

M p (2)

in the simplest case, namely (remember that

Ω

is the oscillator non-linearity parameter and takes a specific form when the physical setting is defined)

H = ω \hat{n} + Ω {\hat{n}}^{2} = (ω + Ω) a^{+} a + Ω a^{+ 2} a^{2}

(56)

The evolution generator in our case contains all the elements of the group

O s p (n)

(or its covering

O M p (n)

), which is the largest symmetry harmonic oscillator as far as the a variables are concerned, with the odd part given by the generators:

F_{+} = \frac{1}{2} a^{+}

and

F_{-} = \frac{1}{2} a

6.2. Entanglement of coherent states and evolution of probability

We consider SU(1,1) states as an example, namely

\begin{matrix} |k, ζ〉 & = e^{(ξ K_{+} - ξ^{*} K_{-})} |k, 0〉 \\ = {(1 - {|ζ|}^{2})}^{k} e^{ζ K_{+}} |k, 0〉 \end{matrix}

Over the orthonormal basis

|k, m〉

we have

|k, ζ〉 = {(1 - {|ζ|}^{2})}^{k} \underset{m = 0}{\sum^{\infty}} [\frac{Γ (m + 2 k)}{m! Γ (2 k)}] ζ^{m} |k, m〉

where

ξ = - (χ / 2) e^{- i φ}, ζ = (ξ / |ξ|) t a n h |ξ| = - t a n h (χ / 2) e^{- φ}

Consequently, the parameter

ζ

is restricted to

|ζ| < 1

(disk) and

(χ, φ)

is coming from the parametrization of the quotient space is

S U (1, 1) / U (1)

(the upper sheet of the two-sheet hyperboloid), and the standard coherent state is specified by a unit pseudo Euclidean vector:

\hat{n} = (sinh χ cos φ, sinh χ sin φ, cosh χ)

The overlap

〈k, ζ_{a} |k, ζ_{b}〉 = {(1 - {|ζ_{a}|}^{2})}^{k} {(1 - {|ζ_{b}|}^{2})}^{k} {(1 - ζ_{a}^{*} ζ_{b})}^{- 2 k}

Then, an orthonormal state [15] to

|k, ζ_{b}〉

is:

|k, \tilde{ζ_{b}}〉 \equiv {(1 - {|ζ_{b}|}^{2})}^{k} \underset{m = 0}{\sum^{\infty}} [\frac{Γ (m + 2 k)}{m! Γ (2 k)}] [ζ_{b}^{m} + \frac{{(1 - {|ζ_{a}|}^{2})}^{k}}{{(1 - ζ_{a}^{*} ζ_{b})}^{2 k}} ζ_{a}^{m}] |k, m〉

where to simplify we denote as semi-coherent state the following:

|\tilde{α}〉 = \frac{|α〉 - |β〉 〈β |α〉}{\sqrt{1 - {|〈β |α〉|}^{2}}}

To make a construction like Bell’s for coherent states one orthonormalizes the SU(1,1) states for example to have a basis of the standard type

|1〉

and

|0〉

, namely

|α〉, |\tilde{α}〉

(with k fixed) consequently considering

|α〉

|\tilde{α}〉

, (

α

\tilde{α}

denoting the coherent state eigenvalues). They can be used for computing processes because they are orthonormal:

|ψ〉 = \frac{|α〉 \otimes |\tilde{α}〉 + e^{i φ} |\tilde{α}〉 \otimes |α〉}{\sqrt{2}}

(Let us notice from the expressions of the coherent state as a function of

|k, m〉

that the Bargmann index must be the same).

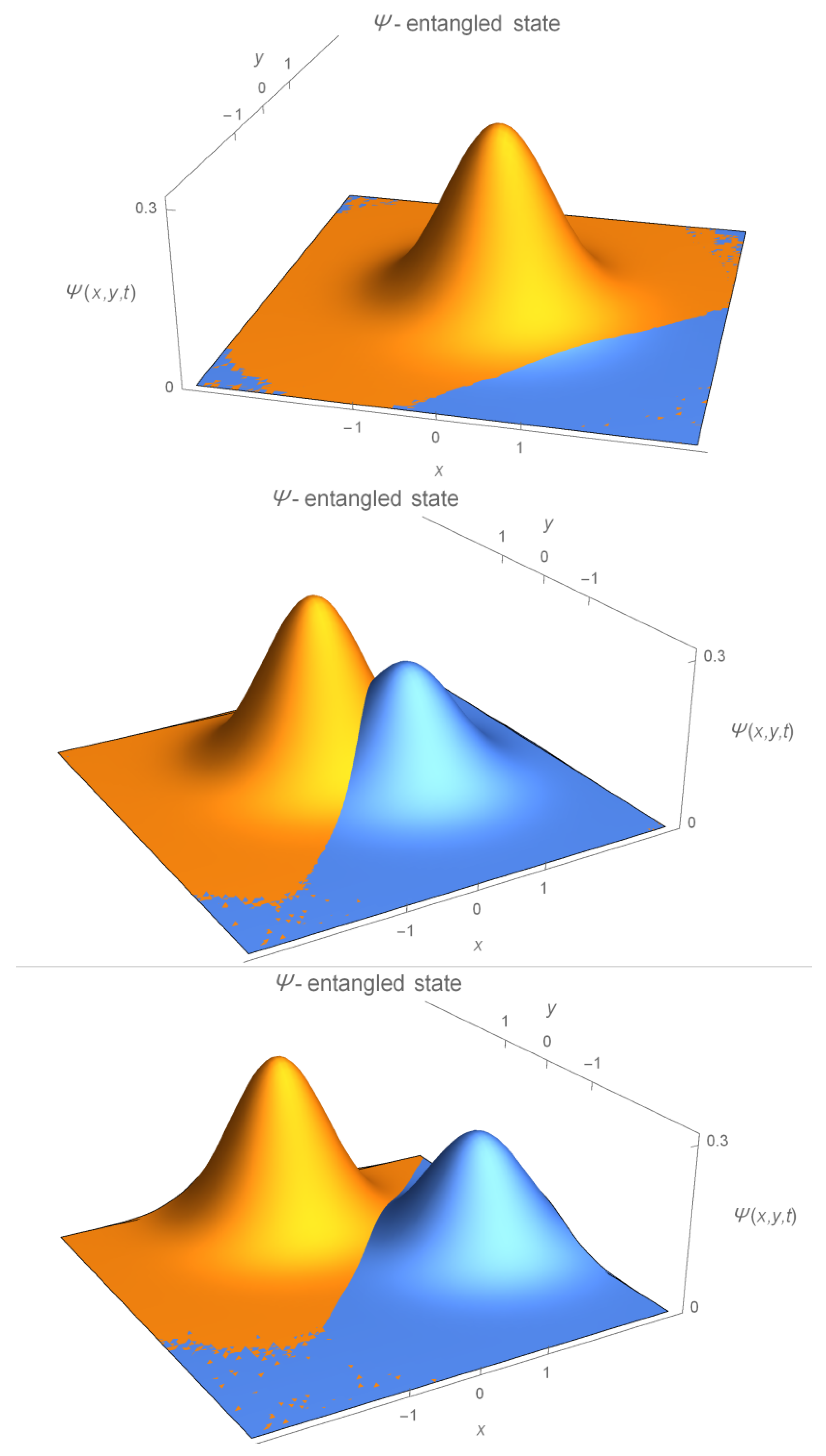
The Figure 3 below show the dynamics of the probability for

|\tilde{α}〉

which is a gaussian-type [16] entangled state where the degree of entanglement varies as a function of time.

By considering that the evolution equation is of Fokker-Planck type due to the fact that the Hamiltonian is of the type of Eq. (56), we have:

\frac{\partial P}{\partial t} = \frac{ϵ}{2} \sum_{i} [\frac{\partial (w_{i} P)}{\partial w_{i}} + \frac{1}{2} \frac{\partial^{2} (w_{i} P)}{\partial w_{i}^{2}}]

with

w_{i} = Re α, Im α, Re \tilde{α}, Im \tilde{α}, (i = 1 . . 4), \tilde{α} = \frac{α - β 〈β |α〉}{\sqrt{1 - {|〈β |α〉|}^{2}}},

and in standard form the probability:

P (α, α^{*}, \tilde{α}, {\tilde{α}}^{*}, t) = {|〈m, n |ψ, k〉|}^{2} .

7. Schrodinger Cat States and Mp(2): Even and Odd Sectors

From the point of view of the considered Hilbert space, divided into even and odd states we have the following apparent correspondence between standard cat states and the basic states of Mp(2), namely

|1 / 4〉

and

|3 / 4〉 :

where explicitly the standard cat Schrodinger states are

|α_{\pm}〉 = \frac{1}{\sqrt{2 \pm 2 e^{- 2 {|α|}^{2}}}} [|α〉 \pm |- α〉]

The situation from the point of view of the density matrices is clear in favor of the

M p (2)

states that follow the principle of minimum representation . In the case of the standard cat states, the density matrices for the even and odd sectors are the following

ρ_{\pm α} = \frac{1}{2 (1 \pm e^{- 2 {|α|}^{2}})} [|α〉 〈α| + |- α〉 〈- α| \pm (|- α〉 〈α| + |α〉 〈- α|)]

(58)

but in the fundamental case of the minimal group representation, we evidently have a diagonal representation (as described by Sudarshan) clearly differentiated into the corresponding even and odd subspaces.

ρ_{M p (2)} = \{\begin{matrix} |1 / 4〉 〈1 / 4| \to e v e n \\ |3 / 4〉 〈3 / 4| \to o d d \end{matrix}

(59)

Consequently, in the case of this last description Eq.(59) we see that the geometric substrate of spacetime is quantum in essence because we are in the minimal representation and it is diagonal (classical and quantum aspects are both represented), and where the power of coherent states in describing both continuum and discrete space-time is completely manifest. It must be also noticed:

(i) The states

|1 / 4〉, |3 / 4〉

are not the same standard cat states as from Ref. [18] but are a fundamental part of the very structure of the spacetime itself and do not require an extrinsic generation process.

(ii) The basic states could be forming a generalized state of the type

{|Ψ_{M p (2)}〉}_{g e n} = \frac{1}{\sqrt{{|A|}^{2} \pm {|B|}^{2}}} [A |1 / 4〉 \pm B |3 / 4〉]

(similar to the standard Schrodinger cat state

ρ_{\pm α}

) giving in this case the following density matrix:

ρ_{M p {(2)}_{g e n}} = \frac{1}{{|A|}^{2} \pm {|B|}^{2}} [{|A|}^{2} |1 / 4〉 〈1 / 4| + {|B|}^{2} |3 / 4〉 〈3 / 4| \pm (B^{*} A |3 / 4〉 〈1 / 4| + A^{*} B |1 / 4〉 〈3 / 4|)],

(60)

This expression is comparable in shape to the density matrix

ρ_{\pm α}

where the parameters A and B may be subject to extrinsic control conditions determined by Majorana Dirac type equations as we established in references [1,2].

8. Entanglement in Quantum de Sitter Space-Time and Black Hole Space-Times

In this Section we implement the entanglement results obtained in this paper in two important quantum gravitational examples: de Sitter and Black Hole quantum space-times. The basis of these quantum space-time descriptions can be found in Refs [3,4,5] [1,7]

The de Sitter space-time admits at both the classical and quantum levels a inverted, (ie with imaginary frequency) harmonic oscillator description, where the oscillator constant

κ_{o s c} = c / l_{o s c}

and oscillator length

l_{o s c}

are given by [3,7]:

l_{o s c d S}^{- 2} = {(\frac{m ω}{ℏ})}_{d S} = H^{2} = \frac{8 π G Λ}{3}

(61)

The oscillator length

l_{o s c}

is classically the Hubble radius, the Hubble constant

H = κ

being the surface gravity, as the black hole surface gravity is the inverse of (twice) the black hole radius.

For Anti-de Sitter space-time, the description is similar and, (because the AdS two sheet hyperbolid embedding in Minkowski space-time with respect to the deS one sheet hyperboloid), Anti-de Sitter is associated to the real frequency (non inverted) harmonic oscillator.

For the (Schwarzschild) black hole space-time description, the physical magnitudes as the oscillator constant and the oscillator length are related to the black hole mass M by:

l_{o s c B H}^{- 2} = {(\frac{m ω}{ℏ})}_{B H} = l_{P}^{- 2} {(\frac{m_{P}}{M})}^{2}

(62)

l_{P}

being the Planck length and

m_{P}

the Planck mass:

l_{P} = {(2 G ℏ / c^{3})}^{1 / 2}, h_{P} = c / l_{P}

The discrete states and their spectrum describe the quantum space-time levels.

Interestingly, the Metaplectic group states with its both sectors and discrete representations,

| 2 n 〉

and

| 2 n + 1 〉

, even and odd states, fully cover the complete Hilbert space

H

H = H_{(+)} \oplus H_{(-)}

(63)

The

(\pm)

symmetric and antisymmetric sum of the two kind (even and odd) states provides the complete covering of the Hilbert space and of the space-time mapped from it:

Ψ (n) = Ψ^{(+)} (2 n) + Ψ^{(-)} (2 n + 1)

(64)

The complete covering of the Hilbert space with the complete covering of the quantum space-time is realized by the Metaplectic group symmetry which equivalently provides the CPT symmetric states and unitarity states. For a different approach in the searching of these properties in black hole states see eg Refs [19,20].

The Classical-Quantum Duality of the space-time is also realized in the

M p (n)

symmetry, because the complete covering, the global complete space-time (and full phase space completion) is needed to make manifest the classical-quantum duality of the space-time (and its phase space mapped from it) .

It is worth to mention that similar discrete levels can be obtained from the global (complete) classical - quantum duality including gravity [3,5,6], namely classical-quantum gravity duality: The two even and odd (local) carts or sectors and their (global) $(\pm)$ sum of states, reflect a relation between the $M p (n)$ symmetry and the classical-quantum duality.
The two $\sqrt{(2 n + 1)}$ and $\sqrt{2 n}$ , even and odd sets are local coverings and they are entangled one to each other. The symmetric or antisymmetric sum of these sectors are global and they are required to cover the whole manifold.
Moreover, the corresponding $(\pm)$ global states are complete, CPT symmetric and unitary, the levels $n = 0, 1, 2, . . . .,$ cover the whole Hilbert space $H = H_{(+)} \oplus H_{(-)}$ and all the space-time regimes.
The total n states range over all scales from the lowest excited levels to the highest excited ones covering the two dual branches $(+)$ and $(-)$ or Hilbert space sectors and corresponding space-time coverings. The two $(+)$ and $(-)$ dual sectors are entangled.

This is interesting because the classical-quantum gravity duality allows that signals or states in the quantum gravity (trans-Planckian) domaine, or semiquantum gravity (inflationary) domaine, do appear as low energy effects in the semiclassical/classical universe today.

From the results of this paper, we have seen that such gravity or cosmological domains are entangled: The quantum trans-Planckian primordial phase is a quantum constant curvature de Sitter phase, followed by a quasi-de Sitter (inflationary) phase, and the late Universe today is a semiclassical and classical gravity de Sitter phase. The most quantum and primordial (trans-Planckian) period and its dual: the most classical and late (today) one are entangled.

9. Remarks and Conclusions

The results of this paper have both: fundamental and practical implications of quantum physics from a novel perspective:

(i) For the quantum space-time structure properties from one side, by studying in its description concepts as the Berry phase and more generally geometrical (Berry type) phases which untill now have been most purely studied in quantum systems but not in quantum gravity as we do here: This is in the quantum space-time context including its trans-Planckian domain and the role of the Metaplectic group which is non compact in this case.

(ii) Second, the new results on entanglement with the states of the Metaplectic group and its covering, which can be taken into account for the searching of new measurable signals: being them from black holes, the gravitational wave domaine and the high energy domain, or the de Sitter primordial phases (inflation and before inflation), and the late de Sitter cosmological vacuum (today dark energy).

(iii) Some points here considering the coherent state solutions and the entangled case are the following: As we have been pointed out in Ref [21], a remarkable property of the simple solution given by the physical state

g_{a b} (x)

is that it is localized in a particular position of the space–time. The supermetric coefficients a and

a *

play the important role of localize the fields in the bosonic part of the superspace, in a similar and suggestive form as the well-known “warp factors” of multidimensional gravity for a positive (or negative) tension brane.

But the essential difference here is due to the c-numbers a and

a *

coming from the

B_{0}

(even) fermionic part of the superspace under consideration. Therefore, not additional and/or topological structures that break the symmetries of the model (i.e., the reflection

Z_{2}

-symmetry) are required in our description: The natural structure of the superspace does produce this effect due to the symmetries of the Metaplectic group.

(iv) The Coherent (Gaussian type) solution is a very well-defined physical state in any Hilbert space from the mathematical point of view, contrarily to the case in the literature, e.g

u (y) = c exp (- H | y |)

[23] and references therein. In such a case, it was possible to find a manner to include it in any Hilbert space, but it was strongly needed to take special mathematical and physical particular assumptions whose meaning are not clear.

(v) In the entanglement case, as we can see in the Figures (Figure 2 and Figure 3), all the above properties are preserved. The locality is subject to the degree of entanglement and the limit when

a \to \infty

where the Gaussian condition (envelope) is lost. In such a limit, only the odd (fermionic) part of the super-manifold survives.

(vi) There exists a clear evidence of a time arrow coming from the physical states as a bilinear combination of the basic states of the Metaplectic

M p (n)

group. This appears in the appreciable asymmetry displayed by Figure 1 "Zitterbebegung" as in the fact (CPT) that:

〈Ψ_{3 / 4} (t)| L_{a b} |Ψ_{1 / 4} (t)〉 \neq 〈Ψ_{1 / 4} (t)| L_{a b} |Ψ_{3 / 4} (t)〉

(vii) The obtained Berry phase applied to the de Sitter inflation case is imaginary describing the inflationary exponential factor acceleration, as it must be. We also consider the case of cosmic perturbations in the slow roll regime and related the Berry phase to the cosmological observables: scalar and tensor spectral indices

n_{s}

and

n_{T}

and the ratio of tensor to scalar perturbations) .

(viii) From the density matrix viewpoint in the entanglement context, the precise relation between the Schmidt type representation and the physical state fulfilling the Minimal Group Representation Principle (MGRP), that is bilinear in the basic states of the

M p (n)

group, is found. The mapping for the physical state refers to a new non-diagonal coherent state representation complementary to that of the Sudarshan diagonal representation.

(ix) In the number basis

| n >

the physical state corresponding to

s = 2

(graviton, related to the space-time metric) provides the discretization of the space- time for small n, going to the continuum for

n \to \infty

(x) The basic states in the Minimal Group Representation sense:

| 1 / 4 >

and

| 3 / 4 >

(belonging to the even and odd sectors of the Hilbert space respectively) are a fundamental part of the very structure of the space-time itself and do not require an additional extrinsic generation process as in the standard Schrodinger cat states and their entanglement.

(xi) The entanglement results in quantum de Sitter space-time admit at both the classical and quantum levels an inverted, (ie. with imaginary frequency) harmonic oscillator description, (a real frequency (non inverted) harmonic oscillator in AdS).

(xii) In the entanglement results for the (Schwarzschild) black hole space-time, the physical magnitudes as the oscillator constant and the oscillator length are related to the black hole mass M and the Planck mass

m_{P}

l_{o s c B H}^{- 2} = {(m ω / ℏ)}_{B H} = l_{P}^{- 2} {(m_{P} / M)}^{2}

The external and internal regions of the black hole are classical-quantum duals of each other and are entangled. The entanglement occurs from the continuum external semiclassical/classical states and the discrete very quantum, Planckian and trans-Planckian states. Discrete states here describe the quantum space-time levels and their spectrum.

(xiii) Gravity or cosmological domains from one side and the other of the Planck scale are entangled: The quantum trans-Planckian primordial de Sitter phase (followed by a quasi-de Sitter (inflationary) phase), and the late Universe today semiclassical and classical gravity de Sitter phase are dual of each other and are entangled. This is interesting because the classical-quantum gravity duality allows that signals or states in the quantum gravity (trans-Planckian) primordial domaine do appear as low energy effects in the semiclassical/classical gravity universe today. Such effects desserve future investigations.

Acknowledgments

DJCL acknowledges the institutions CONICET and the Keldysh Institute of Applied Mathematics and the support of the Moscow Center of Fundamental and Applied Mathematics,Agreement with the Ministry of Science and Higher Education of the Russian Federation, No. 075-15-2022-283.

References

D. J. Cirilo-Lombardo, N. G. Sanchez, Phys. Rev. D108, 126001, (2023).
D. J. Cirilo-Lombardo, N. G. Sanchez, Universe, 10, 22 (2024). [CrossRef]
N. G. Sanchez, Phys. Rev. D 104, 123517 (2021).
N. G. Sanchez, Phys. Rev. D 107, 126018 (2023).
N. G. Sanchez, Int. J. Mod Phys D28, 1950055 (2019).
N. G. Sanchez, Int. J. Mod Phys A34, 1950155 (2019).
N. G. Sanchez, Gravit. Cosmol. 25, 91–102 (2019). [CrossRef]
Dirac, P.A.M. A positive energy relativistic wave equation. Proc. R. Soc. Lond. A, 322, 435 (1971).
Majorana, E. Teoria relativistica di particelle con momento intriciseco arbitrario, Nuovo Cimento 9, 335 (1932).
Fradkin, D.M. Comments on a paper by Majorana concerning elementary particles, EJTP 3, 305 (2006).
Bogomolny, E. Positive- Energy Dirac Particles and Dark Matter. Universe 2024, 10, 222. [Google Scholar] [CrossRef]
J.R. Klauder and B.-S. Skagerstam, Coherent States: Applications in Physics and Mathematical Physics, (World Scientific, Singapore, 1985).
John R. Klauder and E. C. G. Sudarshan, Fundamentals of Quantum Optics, Dover Publications (2006).
A. M. Perelomov, Generalized Coherent States and Their Applications, Springer Berlin, Heidelberg (1986).
Mathews, P. M. , Eswaran, K.: Semi-coherent states of the quantum harmonic oscillator. Il Nuovo Cimento B 17(2), 332 (1973).
van Enk, S.J.: Entanglement capabilities in infinite dimensions: multidimensional entangled coherent states. Phys. Rev. Lett. 91, 017902 (2003).
V.V. Dodonov, I. A. Malkin and V.I. Man'ko, Physica 72 (1974) 597-618.
B. Yurke and D Stoller, Physica B 151 (1988) 298-301.
G. ’t Hooft, Found. Phys. 46, no. 9, 1185 (2016); Found. Phys. 48, 1134 (2018).
G. ’t Hooft, Universe 2022, 8, 537. [CrossRef]
D. J. Cirilo-Lombardo, Physics Letters B661, 186–191 (2008).
J. Wei and E. Norman, Lie algebraic solution of linear differential equations. J. Math. Phys. 4, 575-581 (1963).
B. Bajc, G. Gabadadze, Phys. Lett. 2000.

Figure 1. Chiral-antichiral oscillation (zitterbebegung) giving the pattern of cat states from first principles. The asymmetry in the pattern can be seen, marking a preferential temporal evolution.

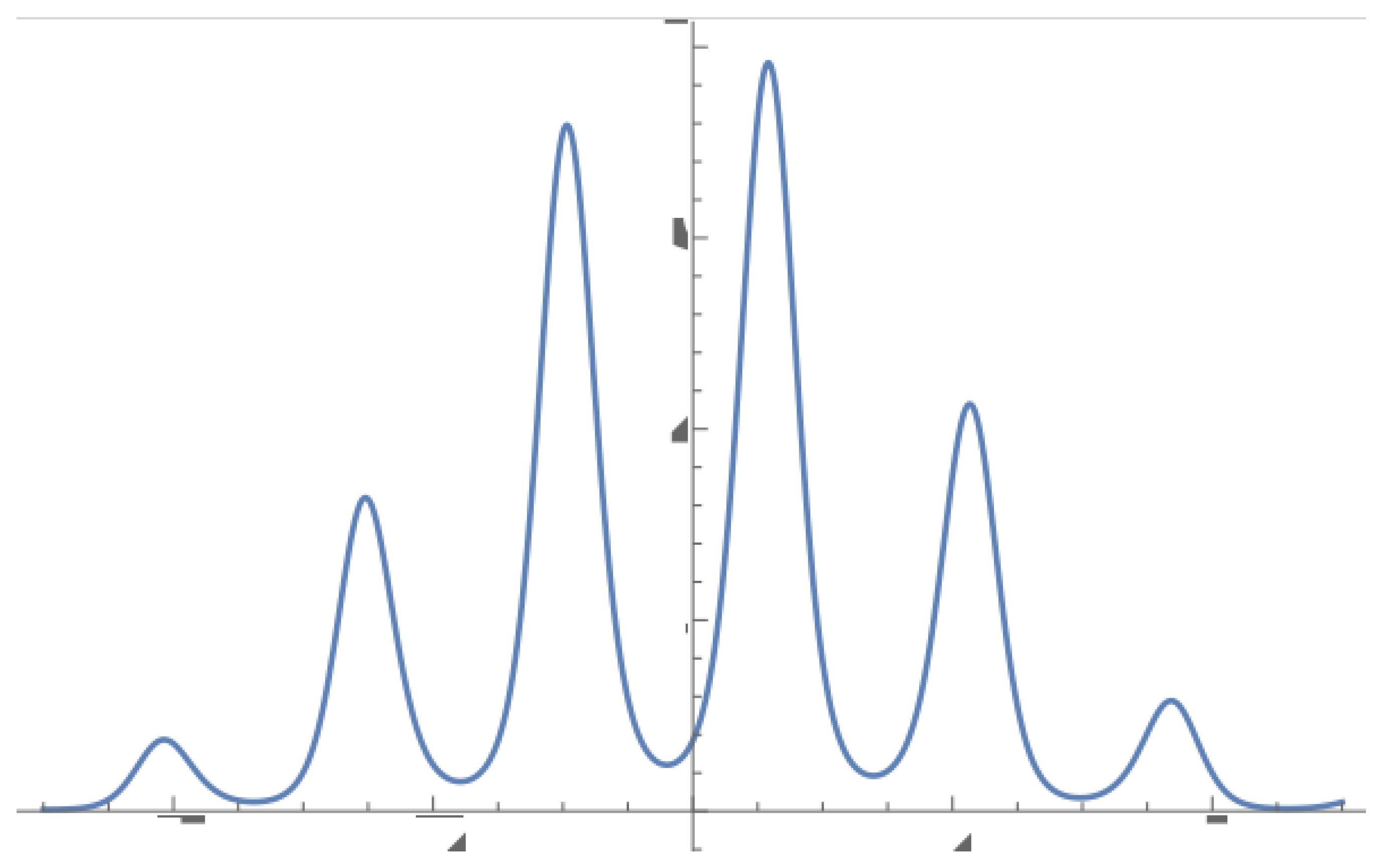
Figure 2. 3 D picture of the chiral-antichiral oscillation (cat states pattern).

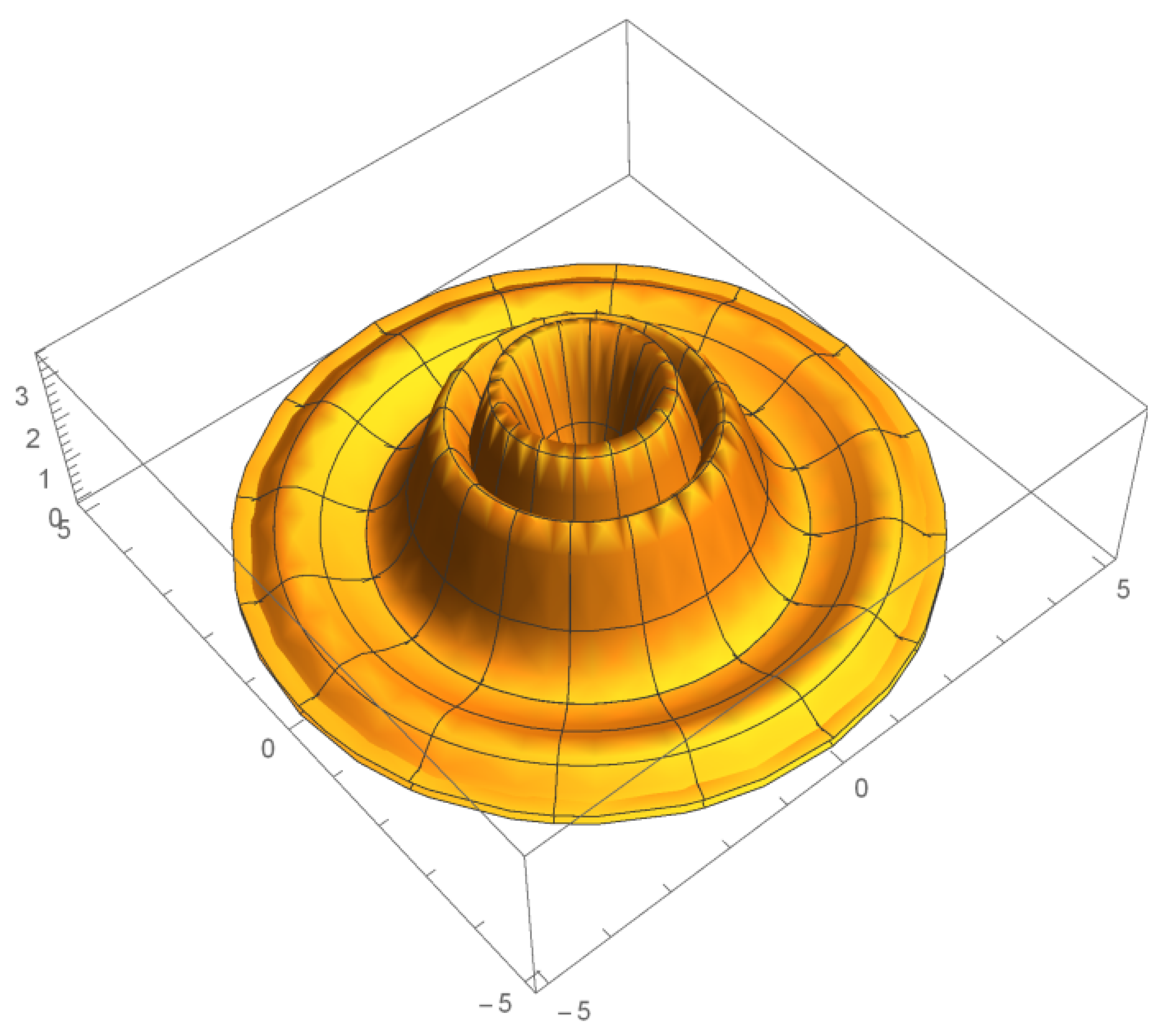
Figure 3. The three images show from top to down the entangled coherent state where the degree of entaglement varies as a function of time from the highest to the lowest degree controlled by the overlap

〈α | β〉

. Here

(x, y)

correspond to

Re \tilde{α}

and

Im \tilde{α}

〈α | β〉

. Here

(x, y)

correspond to

Re \tilde{α}

and

Im \tilde{α}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Entanglement and Generalized Berry Geometrical Phases in Quantum Gravity

Abstract

1. Introduction and Results

2. Geometrical Phases and Noncompact Groups

2.1. SU(1,1) Coherent States and the Berry Phase

2.2. Quadratic Hamiltonians, the Parametric Oscillator and the Group Structure

2.3. Generalized Parametric Oscillator and the Berry Phase

2.4. Coherent State Quantum Evolution

3. Relevant Applications in Cosmology

3.1. Berry Phase of de Sitter Inflation

3.2. Berry Phase of the Inflationary Perturbations:

4. Entanglement

4.1. Density Matrix Viewpoint

5. Quantum Evolution, Adiabatic Invariants and Topological Structure

6. Entanglement with Semi-Coherent States

6.1. Generation and Entanglement of Schrodinger Cat States

6.2. Entanglement of coherent states and evolution of probability

7. Schrodinger Cat States and Mp(2): Even and Odd Sectors

8. Entanglement in Quantum de Sitter Space-Time and Black Hole Space-Times

9. Remarks and Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe