Advances in Modeling Approaches for Oral Drug Delivery: Artificial Intelligence, Physiologically Based Pharmacokinetic, and First-Principle Models

Preprint

Review

Advances in Modeling Approaches for Oral Drug Delivery: Artificial Intelligence, Physiologically Based Pharmacokinetic, and First-Principle Models

Altmetrics

Downloads

353

Views

183

Comments

A peer-reviewed article of this preprint also exists.

Yehuda Arav^*

This version is not peer-reviewed

Submitted:

10 July 2024

Posted:

15 July 2024

You are already at the latest version

Alerts

Abstract

Oral drug absorption is the primary route for drug administration. However, this process hinges on multiple factors, including the drug’s physicochemical properties, formulation characteristics, and gastrointestinal physiology. Given its intricacy and the exorbitant costs associated with experimentation, the trial-and-error method proves prohibitively expensive. Theoretical models have emerged as a cost-effective alternative by assimilating data from diverse experiments and theoretical considerations. These models fall into three categories: data-driven models, encompassing classical pharmacokinetics, quantitative-structure models (QSAR), and machine/deep learning. Mechanism-based models include quasi-equilibrium, steady-state, and physiologically based pharmacokinetics, alongside first principles such as molecular dynamics and continuum models. This review provides an overview of recent modeling endeavors across these categories, evaluating their respective advantages and limitations. Additionally, a primer on partial differential equations and their numerical solutions is included in the supplementary materials, recognizing their utility in modeling physiological systems despite their mathematical complexity limiting their widespread application in this field.

Keywords:

Subject: Medicine and Pharmacology - Pharmacy

1. Introduction

Oral drug delivery is the most comfortable and commonly utilized route for administering drugs, with about

60 %

of all dosage forms in the worldwide market being oral [1,2]. It has attracted attention due to its unique advantages, including sustained and controllable delivery, ease of administration, feasibility for solid formulations, patient compliance, and an intensified immune response in the case of vaccines [3].

However, the extent and rate of drug absorption from the gastrointestinal (GI) tract into the bloodstream is a complex process that is influenced by various factors categorized into three main classes [4] (Figure 1). The first class encompasses the physicochemical and biological properties of the drug, including solubility, pKa, chemical and biological stability, and lipophilicity. The second class involves the physiological and anatomical properties of the GI tract, such as pH levels, gastric emptying rates, transit times through the small and large bowel, concentrations of micelles, active transport mechanisms, efflux processes, and gut wall metabolism. The third class comprises formulation factors, including dosage form, particle size distribution, and the properties of various delivery systems such as solutions, tablets, capsules, suspensions, emulsions, gels, and modified-release formulations.

Given this complexity, designing an oral formulation capable of achieving an appropriate pharmacokinetic profile for new drugs or optimizing existing drug formulations necessitates a methodology to estimate the extent and dynamics of absorption [5]. However, conducting extensive in vivo evaluations in preclinical species can be both costly and time-consuming, as it provides information specific to the conditions under which the experiments were conducted. Moreover, inter-species differences may result in unreliable predictions of oral bioavailability in humans when relying solely on in vivo animal data.

Mathematical models for oral drug absorption have increasingly influenced the development of oral drug delivery products over the past two decades, reducing the failure rate of new drugs due to poor drug-like properties from

30 - 40 %

during the 1990s to approximately

10 - 15 %

toady [6]. Over the years, various types of mathematical models have been developed, generally falling along a spectrum between data-driven, mechanism-based, and first-principles models. In its purest form, a data-driven model utilizes solely the observed data of the phenomena it represents. For example, characterizing the distribution and statistical properties of a measured variable is a data-driven model. Mechanism-based models describe the dynamics of the system by detailing the kinetics of the relevant processes after simplifications. For example, the Michaelis-Menten approximation [7] is often used to describe the metabolism rate of the hepatic enzyme CYP3A4, which is involved in the metabolism of many drugs, rather than detailing its full set of reactions [8]. Conversely, first-principles models rely solely on fundamental principles (such as thermodynamics, conservation of mass, energy and momentum) to describe system dynamics and estimate parameters. For instance, the Einstein-Stokes equation can be used to calculate the diffusion coefficient of a dye in still water [9]. Different model types have advantages and disadvantages regarding the questions at hand. This work aims to review the different types and provide insights into their strengths and weaknesses.

2. Overview of The Physiology and Mechanisms of Human Oral Drug Absorption

Oral drug delivery commences with the administration of a drug formulation to the buccal cavity (Figure 2). The buccal/sublingual is an attractive route of delivery for some highly water-soluble and absorbable drugs[10], due to its high compliance, avoiding the hepatic first-pass metabolism, and quick onset [11]. In the following, we will provide an overview of the absorption in the buccal/sublingual route, for further details see [12,13,14,15].

Following the disintegration of the buccal/sublingual formulation, the drug has to dissolve in the limited volume of human saliva (0.8 to 1.1mL, [11]) and permeate the epithelium. The buccal epithelium has a surface area of approximately

50 c m^{2}

[13], and it consists of 40 – 50 layers, only a few of which are shown in the schematics that describe the Buccal/sublingual absorption route in Figure 2.

The permeation of drugs across the epithelium and into the bloodstream occurs through various mechanisms, which involve either passive or active transport [16]. Passive transport is facilitated by the concentration gradient across the membrane and can occur through either the cell membrane (transcellular transport) or the paracellular pathway, where the drug traverses intercellular spaces. The paracellular route primarily facilitates the absorption of hydrophilic drugs, while transcellular transport is predominant for lipophilic compounds[15]. Additionally, active transport mechanisms, such as carrier-mediated transport, contribute to the transportation of certain drugs across the oral mucosa [13,17].

Several observations (See Vondracek et al. [18], and reference therein) support the presence of the cytochrome P450 (CYP) family in the buccal epithelium. The CYP family of enzymes is responsible for the oxidative metabolism of numerous endogenous and exogenous chemicals [18]. Consequently, some drugs that permeate the epithelium via the transcellular route may undergo metabolism, potentially reducing their bioavailability.

The buccal/sublingual route might be less preferable for poorly water-soluble drugs, which comprise approximately

40 %

of the drugs in the market. This is because the low solubility of the drugs, combined with the relatively small surface area, and short residence time, due to accidental swallowing and dilution with saliva[19], might limit their absorption. To increase the relevancy of this route, there is an effort to develop a novel delivery method that would increase drug solubility [11,20,21,22,23], or increase the residence time by developing formulations based on bioadhesive polymers[19].

Hence, the majority of the formulations are intended for absorption in the gastrointestinal tract (GIT), and reach the stomach after their ingestion (Figure 2). The stomach, resembling a bean-shaped muscular bag, serves as both a reservoir and a regulator for transfer to the small intestine (SI) via the pylorus sphincter [24]. Physiological conditions within the stomach vary depending on its contents [25]. In fasted state, the stomach typically maintains a pH of approximately 1-3 [3,25], possesses a surface area of roughly 3.5

m^{2}

[1], and contains 200-250mL of luminal fluids [25,26] containing specific enzymes crucial for food digestion [16]. Under these conditions, solid dosage forms such as tablets, capsules, and pellets may remain in the stomach for up to 2 hours [27], while the emptying rate of liquid solutions is proportional to the stomach content volume (e.g., first order), with a half-emptying time (

t_{1 / 2}

) typically ranging from 5 to 20 minutes [26,28].

After a meal, the pH of the stomach increases to between

1.88

and

4.98

, and its volume increases to

500 m L

or higher [25]. Under these conditions, the residence time of solid dosage can be 3-5 hours[27], while the emptying rate of fluids becomes constant (e.g. zero order), and may last approximately 120 minutes[26], depending on the caloric intake (low- and high-fat) of the meal[25,26]. For further information on the stomach anatomy and physiology in the presence or the absence of food see Cheng et al. [25]. The drug is emptied from the stomach to the small intestine (SI).

The SI is a lengthy (280cm) and narrow tube (

\approx 1 - 2 c m

diameter, [24]) that is primarily responsible for drug and nutrient absorption [24,29]. It connects to the stomach via the pylorus sphincter at one end and to the large intestine through the ileocecal sphincter at the other. Anatomically, the SI is segmented into three distinct regions: the Duodenum (20cm long), the Jejunum (104cm long), and the Ileum (156cm long) [24]. Surface area amplification within the intestinal fluid contact occurs through three structures: large folds, finger-like projections (villi), and smaller protrusions (microvilli) [24,29]. Large folds are typically located between the mid-duodenum and mid-ileum, with their size and density decreasing along the SI. Similarly, the amplification of villi and microvilli diminishes along the length of the SI [24,30]. This results in a surface area of approximately

250 - 300 m^{2}

[3,24]. The pH increases gradually along the SI from 5.5 in the Duodenum to 7-9 in the distal ileum [3,25]. The contents of the SI are propelled toward the ileocecal valve through the contraction of its walls. The transit time is 3-4 hours independent of the presence of food, and the form of the pharmaceutical formulation (tablets, pellets, and liquids) [27].

The large intestine (LI) resembles an imperfect cylinder, approximately 1.5 meters long, with a diameter ranging from 4 to 8 centimeters [3,31], and has a surface area of approximately

1.3 m^{2}

[1]. Its roles encompass the absorption of electrolytes and water, fermentation of unused energy substrates, immune system priming, production and absorption of vitamins and hormones, fecal transport to the rectum, and fecal storage until elimination [31]. Anatomically, the LI is segmented into four major parts: the ascending colon or cecum (20-25cm), the transverse colon (40-45cm), the descending colon (10-15cm), and the sigmoid colon (35-40cm) [31]. The pH within the colon varies slightly across different regions: 6.2-7.4 in the cecum, 5-8 in the transverse colon, 6-8 in the descending colon, and 7-8 in the sigmoid colon [31]. Undigested food is transferred from the small intestine to the cecum, resulting in initially liquid feces that gradually solidify as they traverse the LI [31]. Transit time through the LI is highly variable, influenced by factors such as diet, stress, mobility, medication, illness, and gender [32], estimated to range between 5 to 73 hours [33].

A solid formulation releases the drug as it progresses through the gastrointestinal tract (GIT). The rate of drug release from a formulation and its dissolution along the GIT depends on several factors, including the properties of the formulation itself, the physicochemical properties of the drug, and the composition of the GIT fluids. Formulations are frequently categorized according to the pattern of drug release from tablets, which commonly includes immediate-release, modified-release, and delayed-release formulations [34]. Immediate-release formulations rapidly release the drug after administration and represent the most prevalent type of tablet. Examples include disintegrating, chewable, effervescent, sublingual, and buccal tablets [34]. Modified-release formulations are designed to release the drug over time, and in delayed-release formulations the drug is liberated from the tablet sometime after administration, often to protect the drug from the gastric environment[34]. See Taylor and Aulton [34] and Alqahtani et al. [1] for an extensive review on oral drug formulations, and Homayun et al. [3] for a review on advances and upcoming technologies in oral administration.

When the drug that was released from the formulation is solid, it must dissolve in the GIT fluids before it can permeate the intestinal epithelium and reach the blood. The dissolution rate of the drug depends on the powder distribution size [30,35], the charge of the drug, and the pH of the environment in which it dissolves[5]. Following food intake, bile secretions from the gall bladder aid the dissolution and permeation of lipophilic compounds[36].

After dissolution, the drug becomes susceptible to chemical and biological degradation within the lumen of the GIT (Figure 2, Gastrointestinal route). Chemical degradation can occur under fasted conditions post-administration due to the harsh acidic environment within the stomach [3]. Biological degradation may occur in the stomach through gastric enzymes such as pepsin and gelatinase, as well as in the upper SI via digestive enzymes secreted by the pancreas, including lipases (fat degradation), amylase (starch degradation), peptidases (peptide disintegration), and trypsin (protein decomposition) [3]. Additionally, brush-border metabolism occurs on the surface of the SI by enzymes present within the brush-border membrane, such as Isomaltase, alkaline phosphatase, sucrose, and other peptidases [1]. Further degradation may arise from the intestinal flora of the colon, primarily located in the lower portion of the GI tract [1].

The permeation of free drugs through the gastrointestinal (GIT) epithelium occurs through mechanisms similar to those described for the buccal/sublingual absorption route. Specifically, drugs are absorbed either passively (via transcellular or paracellular routes) or through active transporters [3,4]. Unlike the buccal/sublingual epithelium, the GIT epithelium is arranged in a single-column layer (monolayer), primarily composed of enterocytes [1]. These cells express efflux transporters from the ATP-binding cassette (ABC) superfamily, along with cytochrome P450 (CYP) enzymes responsible for intracellular metabolism.

ABC transporters, including P-glycoprotein (P-gp, MDR1, ABCB1), multi-drug resistance-associated proteins (MRPs), and breast cancer resistance protein (BCRP, ABCG2), function to limit the intracellular accumulation of their substrates by facilitating efflux out of cells [37]. These efflux transporters, along with CYP enzymes, exhibit overlapping substrate specificity. Their combined action prolongs drug exposure to CYP enzymes while maintaining low concentrations, thereby preventing saturation [1,38]. This mechanism can limit the bioavailability of many drugs and may lead to drug-drug interactions, as some drugs can inhibit either P-gp or CYP enzymes [1]. See Murakami et al. [37] for an extensive review of efflux proteins in the intestine, and Alqahtani et al. [1] for further discussion on the metabolic barriers to absorption.

Following absorption in the GIT, the drug reaches the portal vein and passes through the liver before it reaches the systemic circulation [1,38,39,40,41]. As the drug passes through the liver, it might be metabolized by the hepatocytes of the liver that expresses the CYP, as well as other enzymes (first-pass metabolism). This first-pass metabolism represents a major metabolic barrier to drugs administrated through the gastrointestinal route [1].

3. Approaches for Mathematical Modeling

Mathematical modeling and computer simulations have become increasingly valuable in facilitating different aspects of the development of oral delivery of drugs. Due to the complexity of the oral absorption process, and its many aspects, different models were developed with various modeling techniques.

Generally, these models can be categorized into three different approaches: data-driven models, mechanism-based modeling, and first-principles modeling (see Figure 3).

Data-driven models are developed based on empirical data and do not rely on explicit theoretical principles. These models extract patterns and trends from observed data and are valuable for summarizing and presenting data concisely. Additionally, they can make predictions within the range of observed data, provided there is a sufficient amount of data available. Hence, the utility of these models is limited to scenarios where ample empirical data is available. For example, Fagerholm et al. integrated 14 different data-driven models to predict various pharmacokinetic parameters and used them to forecast the oral bioavailability of drugs [42].

First-principles models leverage fundamental physics principles, including the conservation of mass, momentum, and energy, as well as principles from thermodynamics, fluid dynamics, and other relevant disciplines. These models describe system dynamics by considering factors such as geometry, boundary conditions, and external forces. They provide detailed insights into phenomena and facilitate the investigation of dynamics across a wide range of parameter values. For example, Palmada et al. [43], used computational fluid dynamics (CFD) to investigate the effect of motility patterns on the flow field in the Duodenum. However, due to their inherent complexity, first-principles models require a wealth of detailed information, often limiting their applicability to relatively small physical domains.

Mechanism-based models integrate both approaches by representing system dynamics with simplified versions of first principles while incorporating data-driven models to address the complexities of the processes that were simplified. For instance, Physiologically Based Pharmacokinetic (PBPK) models describe the pharmacokinetics of drugs in the body by treating each organ as a well-mixed component. These models simplify Fick’s law of diffusion to account for drug uptake into organs, with the rate constants derived from experiments on drug biodistribution [44,45].

In the following section, we will examine the application of models employing various approaches for oral drug absorption.

4. Data-Driven Models

Data-driven models, also known as empirical models, are utilized to quantitatively describe empirical datasets and predict various properties. In the context of oral drug absorption, they can generally be categorized into three subcategories: Conventional Pharmacokinetic models, Conventional Quantitative Structure-Activity Relationship (QSAR) models, and Artificial Intelligence (AI) models that utilize Machine and Deep Learning models (ML and DL, respectively), and also referred to as deep QSAR [46], or non-linear QSAR[46].

In the following sections, we review the advancements made in each subcategory regarding oral drug absorption. For a comprehensive overview of classical Pharmacokinetic models, refer to [47]. To explore QSAR models in detail, see [48,49]. Additionally, for insights into the applications of AI in pharmacy, consult [50].

4.1. Conventional Pharmacokinetic

Conventional Pharmacokinetic models describe most commonly the kinetic of the drug in the plasma following oral absorption by fitting the plasma concentration profile in time to a two-exponent function [40,47], namely,

C_{p} = \frac{F \cdot k_{a} \cdot D}{V (k_{a} - \frac{C L}{V})} \cdot (e^{- \frac{C L}{V} \cdot t} - e^{- k_{a} \cdot t})

(1)

Where

C_{p}

is the concentration in plasma, F is the bioavailability,

k_{a}

is the absorption rate coefficient, D is the administrated dose, V is the volume of distribution of the drug in the body, and

C L

represents the clearance.

The parameters of Equation 1 usually cannot be estimated from the data of a single oral dose[40]. Hence, additional data is needed to estimate other parameters. The F,

C L

, and V are usually computed from plasma concentrations following intravenous (IV) administration. Estimation of F can also be achieved, under certain circumstances from urine data [40]. Due to the importance of these pharmacokinetic parameters, several studies presented methods for assessing them using QSAR, and ML and DL models will be reviewed in Section 4.2 and Section 4.3, respectively.

Equation 1 is derived by modeling the absorption from the gastrointestinal tract (GIT), as depicted in Figure 2 (Gastrointestinal absorption route), as a first-order process with a rate constant

k_{a}

. In this model, the body is treated as a well-mixed compartment, and elimination processes from the body are assumed to be first-order as well. Therefore, Equation 1 represents the solution of the ordinary differential equations (ODE) system [47],

\begin{matrix} \frac{d A_{1}}{d t} & = - k_{a} \cdot A_{1} \end{matrix}

(2)

\begin{matrix} V \frac{d C_{p}}{d t} & = \underset{A b s o r p t i o n r a t e}{\underset{︸}{k_{a} \cdot A_{1}}} - C L \cdot C_{p} \end{matrix}

(3)

\begin{matrix} A_{1} (0) = F \cdot D & ; C_{p} (0) = 0 \end{matrix}

(4)

Where

A_{1}

is the amount of drug in the GIT.

The value of

k_{a}

is determined through fitting empirical data. Consequently, Equation 1 allows for the quantitative comparison of two immediate-release formulations once the plasma concentration-time series is acquired. However, the assumption of first-order absorption usually implies that the rate-limiting process in absorption is the permeation through the intestinal epithelium and that the absorption mechanism is passive. Therefore, this model is limited in its applicability to soluble drugs administered in a fasted state within immediate-release formulations. Additionally, since

k_{a}

is derived from the plasma concentration-time series, estimating its value before experimentation data is available is challenging. To address these limitations, more sophisticated models are needed, which incorporate additional details of the absorption mechanisms. These advanced models will be discussed in Section 5.

4.2. Conventional Quantitative Structure-Activity Relationship (QSAR)

Conventional QSAR models establish a linear relationship, using multivariate statistics, between values of chemical descriptors computed from molecular structure and experimentally measured chemical properties, such as charge, solubility, and partition coefficient, as well as bioactivities, such as passive intestinal permeability and intrinsic hepatic clearance [48,51]. The assumption that underlies the conventional (linear) QSAR modeling is that similar compounds exhibit similar biological effects, and that gradual changes in compound structure are accompanied by gradual changes in potency, or the so-called similarity-property principle (SPP) [48]. See [46,48] for a reviews on QSAR modeling.

Estimating the absorption, distribution, metabolism, and elimination (ADME) of a new compound is an essential step in the screening process [16,49]. Over the past two decades, numerous QSAR models have been developed to predict these properties. For a comprehensive review of QSAR models for predicting ADME properties, refer to [49,52,53,54]. Here, we provide an short overview.

Estimating the oral absorption is a key step in screening new drug candidates. The drug solubility and permeability in the GIT, together with the hepatic first-pass are considered to be the leading factors that determine F[52]. Hence, QSAR models were developed to estimate to predict the permeability [52,55,56,57,58], solubility[42,55,59], intrinsic hepatic clearance[42], and predict F either directly from molecular descriptors [42,55,60,61,62,63,64] or by using the output of other QSAR models [65]. Since efflux transporters, such as P-gp, may play an important role in the absorption, QSAR models were developed to estimate the affinity of the drugs to P-gp [66]. However, training a QSAR model to predict F directly from the drug descriptors, without explicitly considering the properties of formulation (e.g particle size that disintegration and dissolution rates), might lead to inconsistencies. For example, the bioavailability of Griseofulvin is doubled following administration as a micronized formulation [30]. Hence, it is important to perform rigorous quality checks on the database being used and ensure that all the entries describe similar absorption conditions. QSAR models for estimating drug distribution include the prediction of V [67] and its protein binding[42,68,69,70]. QSAR models that estimating the first-pass metabolism and the elimination predict the intrinsic hepatic clearance [71,72,73], and the systemic clearance [72,73]. QSAR models were also developed to estimate the buccal permeability[74] and bioavailability[75].

QSAR modeling has been utilized in the design of formulations, as mixing the drug with various excipients to create a formulation can enhance its solubility, efficacy, and stability. Therefore, the selection of suitable excipients depends on both the physical and chemical properties of the drugs and the type of formulation [76]. Specifically, QSAR models were developed for the selection of excipients [77], Formulation Stability [78], and design controlled release formulations [79]. See Kulkarni et al. [80] and Aguillar et al. [81] for a review on QSAR modeling in formulation design.

QSAR models that predict a numerical property value based on the molecular characteristics of a drug are preferred as they allow for molecule selection based on arbitrary criteria. However, achieving an adequately accurate regression model can often prove challenging, and classification may come in handy. Classification models determine whether a molecule belongs to a specific property class (e.g., ’high’ or ’low’), sometimes providing the probability of class membership [60,82].

4.3. Artificial Intelligence (AI)

AI models leverage ML and DL algorithms to augment traditional QSAR models and perform large-scale dataset classification. These models are categorized into supervised and unsupervised learning based on their learning processes (Figure 4). Supervised learning employs established input-output relationships, where known features are utilized to predict output values, while unsupervised learning focuses on discovering hidden structures within data, aiming to group similar instances together based solely on their inherent characteristics [50,83].

Supervised learning algorithms enhance traditional QSAR models by establishing non-linear relationships between chemical descriptors, derived from molecular structures, and experimentally measured chemical and biological activity properties [48,50]. The transition from linear to non-linear relationships is pivotal, particularly as databases expand to include structurally diverse active compounds with few or no common scaffolds. In such cases, the departure from the SPP assumption becomes crucial. Structural differences among active compounds are often abrupt and non-gradual, necessitating the adoption of non-linear modeling approaches to satisfactorily capture Structure-Activity Relationships (SARs) [48]. See Muratov et al. [48] a review on different supervised learning algorithms used in QSAR modeling, and Sarkar et al. [83] for a review on AI algorithms.

In recent years, non-linear QSAR models, based on ML and DL techniques, have become the most popular strategy to develop QSAR models for the prediction of ADME properties of drug candidates[84], and formulation design[85]. Similarly to conventional QSAR, non-linear QSAR models were developed to estimate the permeability [49,82,86], physio-chemical properties [58,59], distribution [49,82], affinity to P-gp[87,88], hepatic clearance [49,82], metabolism by the CYP family[89,90,91,92], and F in fasted [59] and fed states [93]. For reviews on using AI for ADME properties, and other usage in the pharmaceutical industry see Refs. [46,49,50,53,94].

Unsupervised learning is a type of machine learning in which the algorithm is not provided with labeled data. Instead, it is tasked with identifying patterns and relationships within the data independently. Hence, unsupervised learning algorithms are used to develop clustering methods that would help identifying groups, and thus increase the screening efficiency. Butina et al. [95] developed an unsupervised clustering method for the generation of drug groups based on the standard daylight’s fingerprints and Tanimoto similarity. Korolev et al. [96] used unsupervised learning to assess the metabolism and toxicity of drugs using a a database of known human cytochrome P-450 substrates. Further applications of unsupervised models are dimensionality reduction of complex high-dimensionality datasets [50,97]

5. Mechanism-Based Models

Mechanism-based models combine physiological and physiochemical principles with a simplified representation of underlying mechanisms. Developing such models presents a challenge due to the system’s complexity, involving decisions about which mechanisms to include and determining the appropriate level of detail needed for their representation.

Building on the work of Yu et al. [98], we categorize Mechanism-based models into three subcategories: Quasi-equilibrium, Steady-state, and Dynamic or Physiologically based pharmacokinetic (PBPK) models. These distinctions are based on their treatment of spatial and temporal variables[4]. Specifically, Quasiequalibrium models are independent of spatial or temporal variables, Steady-state are independent of the temporal variables, but depend on the spatial variable, and dynamic models depend on spatial and temporal variables.

5.1. Quasiequalibrium

One of the earliest theories devised to elucidate the oral absorption process is the pH-partition hypothesis[98], rooted in the theoretical framework proposed by Jacobs [99], and extensive studies conducted during the 1950s and 1960s [100,101,102]. According to this hypothesis, only the non-ionic form of the drug can traverse the passive transcellular pathway.

The pH-partition hypothesis was subsequently incorporated into the Absorption Potential (AP) concept, introduced by Dressman et al. [103]. This concept correlates qualitatively the extent of drug absorption in the gastrointestinal tract (GIT) to physiological and physiochemical factors such as the administered dose, solubility, lipophilicity, and charge. Mathematically, the AP is defined as:

A P = log (\frac{P I_{u n}}{D_{0}})

(5)

Here,

A P

represents the absorption potential, P denotes the partition coefficient,

I_{u n}

indicates the fraction of the unionized form at pH 6.5, and

D_{0}

is the dose number, given by

D_{0} = \frac{D}{V_{S I} C_{s}}

(6)

In this expression, D signifies the dose,

C_{s}

denotes the drug solubility, and

V_{S I}

represents the volume in the intestine, typically assumed to be 250 mL [103].

Macheras and Symillides [104] used the AP to provide quantitative estimation of F for drugs that are not limited by the dissolution rate,

F = \frac{{(10^{A P})}^{2}}{{(10^{A P})}^{2} + I_{u n} (1 - I_{u n})}

(7)

With the constraints that

A P = 1000

when

A P > 1000

and that

D_{0} = 1

when

D_{0} > 1

[98].

At first glance, the AP absorption model presented in Equation 7 appears similar to a QSAR model, utilizing the drug’s physicochemical properties, including charge, lipophilicity, solubility, and administered dose, to predict oral absorption. However, it diverges from QSAR models by integrating a deeper understanding of the physiological and chemical aspects of the absorption process. The assumption that underlies the development of QSAR models is that these connections will emerge from the data, given a sufficient amount of it.

5.2. Steady-State

The Steady-state models were developed to enhance the outcomes of the Quasi-equilibrium models by adopting a more physiological approach and calculating F by considering both dissolution and permeation rates along the small intestine (SI) [98].

Several studies [105,106,107] have employed the macroscopic mass balance approach to calculate F [98]. In this approach, the SI is described as a cylindrical tube whose radius is

R_{S I}

, and its length is

L_{S I}

. The fraction that was absorbed is computed by assuming a steady state and integrating along the SI. This approach has been extended to account for the effect of the drug maximal solubility [106], and degradation along the SI[107].

The models developed using the macroscopic approach take into account the solubility limit of the drug, but not its dissolution rate [108]. Oh et al. [109] employed a microscopic approach to develop a model that takes into account the dissolution kinetics, albeit of monodisperse powder. This model also conceptualized the SI as a straight cylinder, but assumed that the contents of the SI are convected as a plug flow with a volume of 250 mL. That is, the model neglected the mixing along the SI. Using non-dimensional analysis, three dimensionless groups were defined: the dose number (

D_{0}

), the absorption number (

A n

), and the dissolution number (

D n

), expressed as follows:

\begin{matrix} A n & = P_{e f f} \cdot \frac{π R_{S I} L_{S I}}{Q_{S I}} \end{matrix}

(8)

\begin{matrix} D n & = \frac{D C_{s}}{ρ r_{0}^{2}} \cdot \frac{π R_{S I}^{2} L_{S I}}{Q_{S I}} \end{matrix}

(9)

Here,

P_{e f f}

is the effective permeability coefficient,

R_{S I}

and

L_{S I}

represent the radius and length of the SI, respectively,

Q_{S I}

denotes the flow in the SI,

ρ

is the drug density, and

r_{0}

stands for the initial particle radius. When

D_{0}

is very high the drug is not expected to have dissolution problems. High

A n

reflects a drug with high permeability and high Dn reflects a drug with a high dissolution rate.

These 3 dimensionless groups were the basis for the definition of the well-known Biopharmaceutics Classification System (BCS), using the An and Dn, as the

D_{0}

was recognized as a factor with lesser importance [28]. The drugs were divided into 4 classes: Class 1 with high An, and high Dn (high permeability/high dissolution); Class 2 with high An and low Dn, provided that

D_{0}

is not too large (high permeability/low dissolution); Class 3 with low An and high Dn (low permeability/high dissolution); Class 4 with low An and low Dn (low permeability/low dissolution). The BCS has further adapted to the Developability Classification System (DCS) and the refined Developability Classification System (rDCS), which are tools for assessing the developability of new drug candidates [110]. Wu and Bennet [111] extended the BCS to the Biopharmaceutics Drug Disposition Classification System (BDDCS), which also takes into account the drug disposition, including routes of drug elimination and the effects of efflux and absorptive transporters.

5.3. Dynamic Physiologically Based Pharmacokinetic (PBPK) Models

Dynamic Physiologically Based Pharmacokinetic (PBPK) models were developed to calculate the absorption rate by incorporating the kinetics of physiological processes in oral drug absorption. These models are often integrated with pharmacokinetic models to predict plasma concentration-time profiles.

Dynamic PBPK models for oral absorption consider both spatial and temporal variables. Generally, these models are classified into compartmental and dispersion models. Both types of models treat the temporal variable as continuous but differ in their treatment of the spatial variable. Compartmental models represent the spatial variable as a series of one or more well-mixed compartments, whereas dispersion models treat it as a continuous variable.

In the following section, we will review these two subtypes.

5.3.1. Compartmental Models

Compartmental models represent the GIT as a series of one or more well-mixed compartments, where each compartment maintains a uniform concentration. The transfer kinetics between these compartments are assumed to be linear. Representing the SI as a series of well-mixed components is a rough approximation of the spatial variable, that has no physical basis[108]. As such, the number of compartments varied between one and four compartments[26,112,113,114,115,116,117,118]. However, since the number of compartments affected the simulation results, Yu et al. [108] set the number of compartments to 7 by fitting the model prediction of the SI intestinal transit to the mean measured time[108]. The compartments were then correlated to the physiology based on transit times [98,108]. The first half of the first compartment represents the duodenum, the second half of the first compartment, along with the second and third compartments, does the jejunum, and the rest of the compartments do the ileum.

The 7-compartment intestinal transit model was later extended to account for the absorption of a passive fully dissolved drug, the compartmental absorption and transit (CAT) model [119]. That is, the intestinal transit and absorption are described with the following system of ODEs,

\frac{d Y_{n}}{d t} = K_{t} Y_{n - 1} - K_{t} Y_{n} - k_{a} Y_{n} n = 1 . . N

(10)

Where

N = 7

is the number of compartments,

Y_{n}

is the fraction amount of drug in compartment n,

K_{t}

is the transfer rate constant.

The Advanced CAT (ACAT) [41], and the advanced dissolution, absorption, and metabolism (ADAM) [120,121] extended the CAT model to include first-pass metabolism, absorption from the LI, dissolution and solubility, release kinetics, intestinal metabolism, active transport, and food effects. The two models differ in their modeling approach of the dissolution process. The ACAT model uses the Noyes-Whitney approach that utilizes the film model[122], while the ADAM model corrects for the spherical shape of the particle[123].

The commercially available version of the ACAT model, GastroPlus

^{T M}

, include several additional improvements that facilitated its usage. It has been used to justify a biowaiver for a selected BCS 2 compounds[124] and determine the impact of different formulation factors such as solubility, particle size, size distribution, and food on the absorption of drugs[125,126,127,128,129,130,131]. The ADAM model is also available commercially, Symcyp®, and is used to predict the effect of drug release rate on the absorption[120,132,133,134], to allow the optimization of paediatric drug[135,136], and to investigate drug-drug interactions [137]. Additional compartmental models are reviewed in Huang et al. [4].

Compartmental models gain much popularity in estimating oral drug absorption due to their mathematical simplicity, intuition, easy correlation with pharmacokinetic models, and the availability of commercial software.

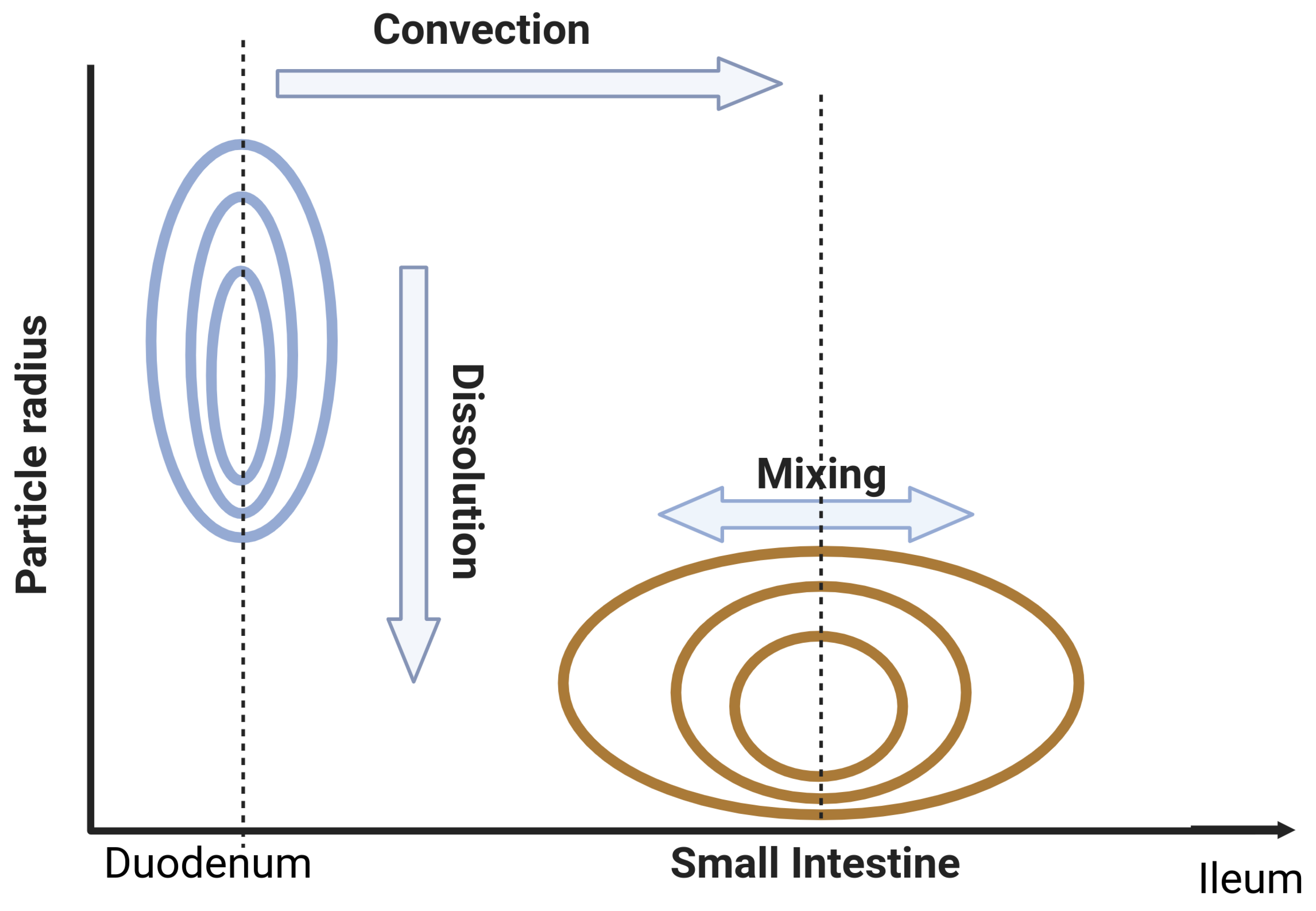
However, correlating a compartment with a physiological segment of the SI lacks a physical basis [108]. To delve deeper into this issue, we must consider that intestinal motility both propels and spreads intestinal content along the SI [108]. Consequently, as each compartment is well-mixed, the number of compartments N dictates the extent of ’spread’, while the kinetic transfer rate

K_{t}

governs the mean velocity (Figure 5a). Therefore, determining N based on the mean transit time of the SI, as done in the procedure with the CAT model [108], does not guarantee that the model accurately reflects the ’mixing’ rate observed in the SI, as it fails to account for this factor. As N approaches infinity, the model converges to the dispersion model with only the convection term, but without the ’mixing term’ (refer to Section 5.3.2 and Appendix A for further details).

Consequently, the determination of the volume available for drug dissolution lacks a robust physiological foundation, potentially leading to the underestimation or overestimation of the actual surface area available for absorption and the concentration of the drug. Moreover, this discrepancy may also result in the overestimation or underestimation of efflux transport and enzymatic metabolism, as these processes are contingent upon the drug’s concentration.

Another implication of using the compartmental approach pertains to the description of the dissolution rate. The dissolution rate of a drug from a powder particle (whether monodisperse or polydisperse) depends on both the amount of the drug and the particle radius [122,123]. However, the kinetics of the undissolved drug in compartmental models are simplified and track only a single variable. Consequently, to account for dissolution, the particle radius must remain fixed, as only the amount of undissolved drug is computed. This could potentially lead to an underestimation of the dissolution rate, as the dissolution rate increases with decreasing particle size due to the increase in surface area [30].

As a result of these simplifications, compartmental models might overestimate or underestimate absorption. Arav et al. [30] demonstrated that the non-commercial version of the ACAT model overestimated the absorption of griseofulvin in both micronized and non-micronized formulations. The continuous models that will be described next address some of these issues.

5.3.2. Continuous Models

The continuous model was first suggested by Ho et al. [138] and describes the SI as a straight tube whose length is

L_{S I}

and its radius is

R_{S I}

. The concentration in the tube,

C (x, t)

is assumed to be well mixed in the radial direction, and therefore the concentration depends only on the distance x from the pylorus, and time. Intestinal motility is described as a convection in uniform velocity and dispersion that accounts for the mixing (Figure 5b). The equation that describes the dynamics of intestinal motility, and the passive absorption of a completely dissolved drug is the partial differential equation (PDE),

\frac{\partial C}{\partial t} + \frac{\partial}{\partial x} \underset{SI motility}{\underset{︸}{[{\underset{︸}{u C}}_{Convection} - {\underset{︸}{D_{e f f} \frac{\partial}{\partial x} C}}_{Mixing}]}} = \underset{Absorption}{\underset{︸}{- \frac{2 \cdot S A_{S I} \cdot P_{i n t}}{R_{S I}} C}}

(11)

Where u is the axial velocity,

D_{e f f}

is the mixing rate (dispersion) coefficient,

R_{S I}

is the intestinal radius,

S A_{S I}

is the surface area amplification, and

P_{i n t}

is the intrinsic permeation coefficient of the drug[30,98]. The influx from the stomach and the outflux to the LI are given by the boundary conditions (See Appendix A for further details).

The continuous model provides a more physiologically accurate representation of the small intestine (SI) [98], but its mathematical complexity has hindered its widespread adoption. Since its introduction in 1983 by Ho et al. [138], only a few studies have employed it [24,30,139,140].

The mathematical complexity of Equation 11 entails two main challenges. Firstly, understanding the interpretation of the equation, and secondly, devising methods to solve it. We provide a detailed explanation of these two aspects in Appendix A, and here we will provide a brief overview.

The left-hand side (LHS) of Equation 11 delineates SI motility, while the right-hand side (RHS) denotes the alteration in concentration due to absorption. The crucial distinction lies in the fact that the LHS terms merely redistribute the drug along the SI, thereby maintaining the total amount constant, whereas the RHS describes a process that diminishes the total amount (e.g. a sink term). SI motility is described as a combination of two processes. The uniform movement along the SI is delineated by a convection term, while the mixing along the SI is described as a dispersion term, similar to the transfer of material by turbulence eddies in highly turbulent regimes [141]. The dispersion term describes mixing since it corresponds to a flux proportional to the concentration gradient, moving from a region of high concentration to a region of low concentration. It is worth noting that

u, D_{e f f}, S A_{S I}

and

P_{i n t}

can depend on the spatial or the temporal variable (or both).

Solving the model of Equation 11 can be achieved with an analytical solution for simplistic cases. Ho et al. [138] used it for the case of the stomach as an infinite reservoir and took into account the passive absorption of completely soluble drug. Wilmann et al. [24,139] extended this model to account for stomach emptying, and took into account the limited solubility of the drug, assuming a rapid dissolution rate.

However, for more detailed equations, the models have to be solved numerically. Arav et al. [30] extended the model to account for the dissolution rate of polydisperse powders in the stomach and the SI, and developed computer software to solve this non-linear set of PDEs. The model of Arav et al. [30] addresses two key limitations of the compartmental model: firstly, it provides a more physiologically accurate representation of mixing, and secondly, it considers changes in particle size distribution resulting from dissolution. The model was then used to find the optimal particle size distribution (mean and geometric standard deviation) that would ensure that dissolution is not the rate-limiting step in absorption. However, the mathematical aspects of this model are somewhat intricate and are further elucidated in Appendix B.

Recently, the dispersion model was further developed to elucidate the absorption kinetics of levodopa following controlled-release administration [140]. Their findings refute the previous hypothesis of an ’absorption window’ in the upper small intestine for levodopa [142], demonstrating instead that levodopa is uniformly absorbed along the entire small intestine. Subsequently, the model was leveraged to optimize the properties of the controlled-release formulation to prolong therapeutic efficacy.

6. First-Principles Models

First-principles models utilize fundamental physical and chemical principles to elucidate phenomena in great detail. Compared to Mechanism-based models, they provide a more intricate description of the system, enabling exploration of aspects where experimental data may be lacking or difficult to obtain. For instance, Lee et al. [143] investigated the impact of posture and gastroparesis on drug dissolution and distribution within the stomach using a biomimetic in silico simulator based on realistic stomach anatomy and morphology. However, owing to their heightened complexity, the application of these models is typically constrained to specific temporal and spatial domains, focusing solely on particular aspects of the overall oral drug absorption process.

In the context of oral drug absorption, we can distinguish between Molecular modeling that simulates biomolecular dynamics at an atomistic level, and continuum models that describe the movement and behavior of drug substances within the gastrointestinal (GI) tract as continuous entities, without considering individual particles or molecules.

6.1. Molecular Modeling

Molecular models simulate biomolecular dynamics at an atomistic level [144,145]. This field encompasses various applications, with molecular docking and Molecular dynamics (MD) simulation being widely utilized components within the pharmaceutical domain. These computational approaches play a crucial role in identifying potential leads for subsequent experimental testing, both in vitro and in vivo [146].

MD simulation predicts the dynamics of the atoms’ position at a molecular level. Similarly to docking simulations, MD simulation is also based on the structure of the biomolecules. In traditional "all-atom" MD simulations the model includes all the interacting atoms in the system, including the solutes. Due to its high level of detail, the simulations are limited both in length and time scale. Currently, simulations include

10^{8} - 10^{9}

atoms and run to a

μ s

scale[145]. In the context of oral drug absorption, MD is applied to estimate drug permeability and solubility. Unlike data-driven models, it provides some mechanistic understanding that can be used for optimization[147]. Other uses include optimization of nanoparticles design and function, as well as drug loading had release profile[147]. For recent reviews on the application of MD in drug discovery see [145,148,149,150,151,152,153,154]. Some recent reviews can be found on drug formulation and drug delivery aspects[147,155,156,157].

6.2. Continuum Models

Continuum models encompass various phenomena, such as mass transfer, fluid flow, and elastic deformations, as continuous fields. This implies that the model’s variables are typically functions of spatial and temporal variables, akin to the continuous models represented in Equation 11. The distinction between mechanism-based models and first-principle continuum models lies in the level of simplification employed. For instance, the mechanism-based dispersion model encapsulates fundamental mechanisms of intestinal motility, such as convection and longitudinal spreading, as uniform flow and longitudinal mixing, with parameters derived from experimentation [30]. In contrast, Fullard et al. [158] devised a first-principle continuum model that delineates intestinal motility by computing the elastic deformation of intestinal walls coupled with the incompressible Navier-Stokes equations to predict the flow patterns in a rabbit intestine as a result of the contractions.

Hence, continuum models prove to be particularly valuable in tackling problems for which acquiring adequate experimental data is challenging, but where a thorough comprehension of the physical system is available. Several studies have recently addressed gastric and intestinal motility [43,143,158], dissolution [159], drug permeation [160], and the design of controlled release formulations [161].

7. Discussion

Oral drug delivery is favored as a route for administering drugs due to its non-invasive nature, convenience, and high patient compliance[1,2]. However, the physiological, physical, and chemical intricacies of the oral route pose challenges in developing new formulations and ensuring the acceptable bioavailability of new drug candidates. Since the experimental trial-and-error approach is expensive, mathematical models were developed over the past few decades as valuable tools for integrating experimental data, thus reducing the number of required experiments [162].

A Mathematical model is designed to address a certain problem, by taking as input the data that the modeler deemed as relevant and producing the desired output. Over the years, different approaches were taken to develop model, namely data-driven, mechanism-based, and first-principles models (Table 1). Each approach address a different problem domain.

Data-driven models, including conventional PK, QSAR, ML, and DL models, are essentially ’black-box’ systems that correlate specific inputs to outputs. Consequently, these models require a substantial dataset, operating on the assumption that the information within the data is sufficient for classifying or predicting new data. Essentially, they interpolate data from the provided dataset, making them suitable for high-throughput screening. However, due to their ’black-box’ nature, understanding the reasons for mispredictions—and therefore finding ways to correct them—can be challenging.

Mechanism-based models, including quasi-equilibrium, steady-state, and PBPK models, incorporate physical and chemical principles while simplifying the dynamics of various physiological processes. Developing a mechanism-based model involves the modeler’s decision on the importance of different processes and their mathematical description, often relying on in vivo or in vitro experimental data, as well as other mathematical models. When model predictions deviate from experimental data, the modeler is prompted to explore new hypotheses or increase the detail in process descriptions, thus guiding the selection and conducting of new experiments. Consequently, the development process is iterative, as new processes are introduced into the model and hypotheses are examined. For example, Arav and Zohar [140] recently developed a PBPK dispersion model for the absorption of levodopa following its administration in a controlled release formulation. The presence of dissolved levodopa in the stomach induces a ’lag’ in gastric emptying. Incorporating this feature in the model was essential to obtain the erratic plasma concentrations reported during the first hours after administration. Moreover, using the model, it was possible to dispute the common hypothesis of an ’absorption window’ in the upper SI and to show that levodopa is equally absorbed along the entire SI. These results were then used to optimize the release rate of controlled release formulations. Thus, as models developed under this approach require more details, they are less suited for high-volume screening.

First-principles models, such as molecular dynamics and continuum models, offer highly detailed physicochemical representations that address processes governed by physical and chemical phenomena. These models are employed to tackle various challenges, such as comprehending the flow field induced by the contraction of the small intestine (SI) walls, or optimizing the structure of nanoparticles. Due to their high complexity, both mathematically and numerically, these models are typically constrained by spatial and temporal scales. Consequently, the primary distinction between Mechanism-based models and First-principles models lies in their focus: Mechanism-based models primarily operate on an organ scale or larger (e.g., multiple organs or the body scale), whereas First-principles models concentrate on an organ scale or smaller (e.g., flow in an organ, tissue, cellular, or atomic level).

8. Conclusions

In this review, we have examined the advancements in mathematical modeling of oral drug absorption. The allure of oral delivery systems, coupled with the challenges and high costs associated with developing new drugs and formulations, underscores the imperative for sophisticated mathematical models aimed at reducing both costs and development time.

Over the years, three primary approaches have emerged: data-driven models, mechanism-based models, and first-principles models. These approaches differ in the problem domains they address and the mathematical tools they employ, although some overlap may occur. Specifically, data-driven models are geared towards high-throughput screening and predicting scalar values, while mechanism-based models focus on physiological problems, concentrating on dynamics at an organ scale or larger (e.g., multiple organs or the entire body). First-principles models target physicochemical problems and zoom in on an organ scale or smaller (e.g., flow in an organ, tissue, cellular, or atomic level).

In conclusion, all three approaches play crucial roles in enhancing oral drug delivery. A promising course of action involves integrating these approaches to leverage their respective strengths and enhance overall effectiveness.

Funding

This research received no external funding.

Data Availability Statement

Not relevant.

Acknowledgments

ChatGPT, a language model developed by OpenAI [163], was used to identify and rectify grammatical errors, improve sentence construction, and enhance overall readability.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations and Symbols

The following abbreviations and symbols are used in this manuscript:

$A_{1}$	The amount of drug in the GIT
ACAT	Advanced CAT
ADAM	The advanced dissolution, absorption, and metabolism
ADME	Absorption, Distribution, Metabolism and Elimination
An	The absorption number
AP	Absorption Potential
BCS	Biopharmaceutics Classification System
BDDCS	Biopharmaceutics Drug Disposition Classification System
C	Concentration along the SI
CAT	The compartmental absorption and transit
$C L$	Clearance from the body
$C_{p}$	Plasma blood concentration
CYP	Cytochrome P450
D	The dose
$D n$	The Dissolution number
DL	Deep learning
$D_{0}$	Dose number
DCS	Developability Classification System
$D_{e f f}$	The along SI dispersion (mixing) coefficient
F	Oral Bioavailability (fraction absorbed)
GIT	Gastrointestinal tract
$I_{u n}$	The fraction of the unionized form at pH 6.5
IV	Intra-venous
$k_{a}$	Absorption coefficient
$K_{t}$	The rate transfer coefficient
LHS	Equation left hand side
LI	Large Intestine
$L_{S I}$	The length of the SI
MD	Molecular dynamics
ML	Machine learning
ODE	Ordinary differential equations
P	Partition coefficient
PBPK	Physiologically based pharmacokinetic
PDE	Partial differential equations
$P_{e f f}$	The effective drug permeability
$P_{i n t}$	The intrinsic permeability of the SI
PK	Pharmacokinetics
$Q_{S I}$	The flow flux in the SI
QSAR	Quantitative structure–activity relationship
rDCS	Refined Developability Classification System
$r_{0}$	Initial particle radius
RHS	Equation right hand side
$R_{S I}$	The radius of the SI
SAR	Structure-Activity Relationships
$S A_{S I}$	The surface area factor of the SI
S	Solubility
SI	Small Intestine
SPP	Similarity-property principle
u	The velocity along the SI
V	Volume of distribution
$V_{S I}$	Water content of the SI
$Y_{i}$	The fraction of the amount of the drug in compartment i
$ρ$	The drug density

Appendix A. Partial Differential Equations (PDE)

Appendix A.1. Interpratation

A partial differential equation (PDE) describes the dynamics of a variable that extends across multiple dimensions. This differs from an ordinary differential equation (ODE), which describes the dynamics of a variable dependent on only one dimension, typically the time in a pharmaceutical context. Hence, the equation describes the concomitant change of the variables in the different dimensions.

For example, consider a variable that describes the dynamics of the concentration in a tube that is well mixed in the radial direction. Hence, the concentration is a function of x, the distance from the beginning of the tube (a spatial variable), and time t (a temporal dimension). That is, the concentration can be described as

C (x, t)

We further assume that there is only a process that convects the contents of the tube at a uniform velocity u toward its end. The dynamics of the system are obtained by inspecting an arbitrary region along the tube between

x_{0}

and

x_{0} + d x

, and assuming that the concentration is constant in this section. That is

C (x_{0} + \frac{d x}{2}, t)

is the concentration between

x_{0}

and

x_{0} + d x

at time t. Consequently,

C (x_{0} + \frac{d x}{2}, t) d x

is the amount of material in time t. The amount of material at time

t + d t

is obtained by adding the flux into the region and subtracting the flux out of the region from the amount that is currently in the cell. Since the material is convected at velocity u, the amount of material that flows into the region during

d t

u C (x_{0}, t) d t

. Hence,

C (x_{0} + \frac{d x}{2}, t + d t) d x = C (x_{0} + \frac{d x}{2}, t) d x + u C (x_{0}, t) d t - u C (x_{0} + d x, t) d t

(A1)

Rearranging the terms in Equation A1, we obtain,

\frac{C (x_{0} + \frac{d x}{2}, t + d t) - C (x_{0} + \frac{d x}{2}, t)}{d t} = - \frac{u C (x_{0} + d x, t) - u C (x_{0}, t)}{d x}

(A2)

Taking

d x

and

d t

to be infinitesimal in Equation A2, we obtain,

\frac{\partial C}{\partial t} = - \frac{\partial}{\partial x} u C

(A3)

Where

\frac{\partial}{\partial t}

, and

\frac{\partial}{\partial x}

are the partial derivatives with respect to the temporal and spatial dimensions, respectively. As can be seen, Equation A3 is PDE as it involves derivatives in two different dimensions, in contrast to an ODE that involves a derivative only in one dimension. We note that Equation A3 is the convection process in the dispersion process (Equation 11).

To complete the description of Equation A3, it is necessary to state the initial conditions and the boundary conditions. The initial conditions state the value of the variable at the beginning of the simulation, that is,

C (x, t_{0}) = f (x)

(A4)

Where

f (x)

is some known function.

The boundary conditions state the value of the variable at the beginning and end of the tube over time. Generally, there are 3 different types of boundary conditions: Dirichlet, Neumann, and mixed (or Robin). The Dirichlet condition determines the value of the variable over time, the Neumann conditions determine the value of the derivative of the variable over time, and the mixed condition determines the mixture of the boundary conditions over time. The Neumann and mixed conditions are used to determine the flux out of the domain.

For example, a Dirichlet boundary condition at the beginning of the tube and Neumann boundary condition at its end (assuming that its length is L),

\begin{matrix} C (0, t) & = g (t) \end{matrix}

(A5)

\begin{matrix} {\frac{\partial C}{\partial x}|}_{x = L} & = h (t) \end{matrix}

(A6)

Determine that the concentration at the beginning of the tube is

g (t)

and that the flow out of the tube is

h (t)

. Using

h (t) = u C (L, t)

will denote an open-ended tube.

Selecting the type of boundary condition depends on the model. For further details on various boundary conditions see [164,165,166].

It is noteworthy that Equation A2 also describes the compartmental model without the absorption term (Equation 10). To illustrate this, we define

C_{i} (t) \equiv C (i \cdot d x + \frac{d x}{2}, t)

as the concentration in compartment i. Setting

K_{i} = \frac{u}{d x}

as the transfer rate, and

Y_{i} = \frac{C_{i} d x}{D}

as the dose fraction with D as the administrated dose, Equation A2 can be expressed by considering

d t

as infinitesimal,

\frac{d Y_{i}}{d t} = K_{t} Y_{i - 1} - K_{t} Y_{i}

(A7)

The derivation of Equation A7 shows that the compartmental model is equivalent to the coarse discretization of the constant convection velocity along the SI. Hence, the mixing along the SI is determined by the number of compartments, and not from physiological considerations.

Figure A1. Schematic representation of the flux into a cell in (a) 1D and (b) 2D

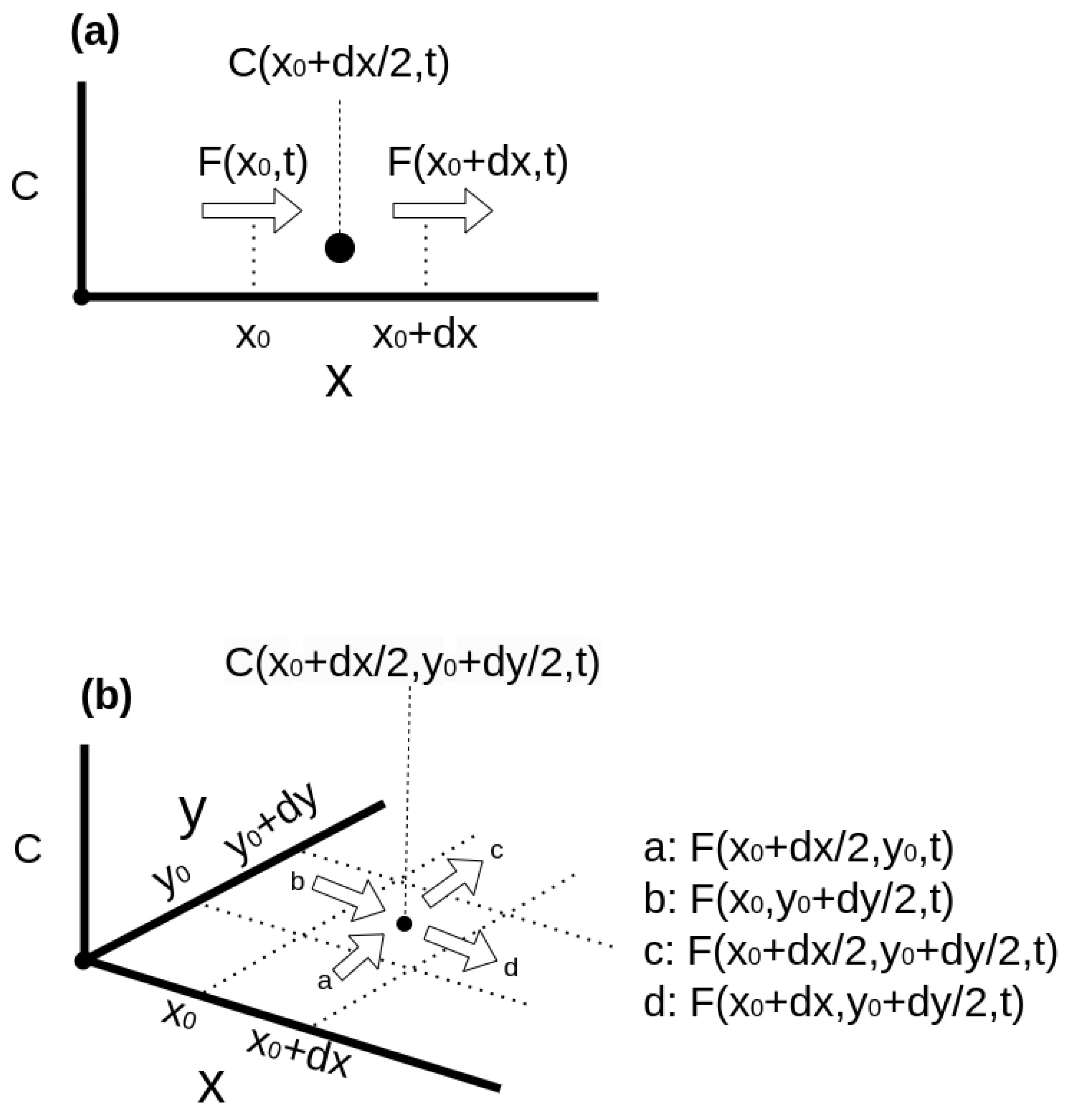
Equation A3 represents a specific case of a uniform flow along the tube. However, this presentation can be generalized by considering a flux function F into and out of each cell (Figure A1a). Then, Equation A1 can be written as,

C (x_{0} + \frac{d x}{2}, t + d t) d x = C (x_{0} + \frac{d x}{2}, t + d t) d x + F (x_{0}, t) d t - F (x_{0} + d x, t) d t

(A8)

Where F is the flux function. Rearranging the terms and taking

d x

and

d t

as infinitesimal values, we obtain,

\frac{\partial C}{\partial t} = - \frac{\partial}{\partial x} F

(A9)

Armed with this understanding, we can now interpret the SI motility term in the dispersion model (Equation 11),

F = u C - D_{e f f} \frac{\partial C}{\partial x}

(A10)

The flux is governed by the constant convection term, while the spread is characterized by a ’Fick’-like diffusion term. This diffusion term represents a flux from areas of high to low concentrations, proportional to the concentration gradient. Consequently, in well-mixed regions, where the concentration remains constant, the flux equals zero.

The right-hand side (RHS) of Equation A9 illustrates the redistribution of concentration along the tube while maintaining a constant total material quantity. Terms that either increase or decrease the variable’s value are referred to as sink and source terms, respectively. Incorporating the sink/source term

s s (x, t)

into Equation A9 yields:

\frac{\partial C}{\partial t} = - \frac{\partial}{\partial x} F + s s

(A11)

Here,

s s

is greater than 0 for source terms and less than 0 for sink terms. It’s worth noting that

s s

can be time-dependent and can be greater than 0 for certain x values and less than or equal to 0 for others at a certain time.

To complete the description, we will now describe the PDE that describes the dynamics of the concentration in a 2D domain (Figure A1b). The derivation of the equation is similar to the 1D case, and we obtain,

\frac{\partial C}{\partial t} = - \frac{\partial}{\partial x} F - \frac{\partial}{\partial y} F = - \nabla \cdot F

(A12)

Appendix A.2. Solving PDE

PDEs typically cannot be solved analytically, except for very simple cases. However, physiological modeling often yields systems of equations, which may be nonlinear, necessitating a numerical solution. Methods and techniques for numerically solving PDEs are discussed in detail in [164,165,166]. Here, we provide a brief overview.

Numerical solutions of PDEs involve discretizing both spatial and temporal dimensions. For simplicity, we consider a 1D case, where the spatial and temporal dimensions are discretized into uniform intervals of

Δ t

and

Δ x

, respectively.

Let,

C_{j}^{i}

denotes the i-th time step in the j-th position in space, that is,

C_{j}^{i} = C (j \cdot Δ x, i \cdot Δ t)

(A13)

Hence, the solution in time step i is the vector,

{\vec{C}}^{i} = (\begin{matrix} C_{0}^{i} \\ C_{1}^{i} \\ \cdot \\ \cdot \\ \cdot \\ C_{N}^{i} \end{matrix})

(A14)

Where N is the number of points in the spatial dimension.

Discretizing Equation A12 yields the system,

M^{i} {\vec{C}}^{i + 1} = S^{i} {\vec{C}}^{i} + {\vec{F}}^{i}

(A15)

Where

M^{i}

and

S^{i}

are the matrices for time step i and

{\vec{F}}^{i}

is the forces vector in time i. Hence, computing the next time step is obtained by solving the linear

The value of the components of

M^{i}, S^{i}

, and

{\vec{F}}^{i}

are determined by the spatial and temporal discretization scheme that was used. The most common temporal schemes include the explicit and implicit Euler, and Crank-Nicolson methods [165]. The spatial terms are discretized according to the finite-difference, finite-element, finite-volume, or spectral methods[164,165,166]. The finite differences method is usually easier to implement and used for problems with simpler geometry. The finite element and finite volume methods are used for more complex problems, with the finite element methods employed more often to solve elliptic and parabolic PDEs (e.g. where information is transmitted instantaneously, or by gradual diffusion over time), and finite volume employed for problems where the information evolves at a finite-speed wave-like propagation[164,165,166]. In spectral methods, the system is represented in a different base (such as Fourier or wavelet bases). The advantage of spectral methods is that they require a smaller number of grid points. However, they are usually limited to rectangular domains, and treating non-cyclic boundaries may require special treatment [167].

A software that assembles matrices

M^{i}, S^{i}

, and

{\vec{F}}^{i}

and solves Equation A15 varies between a complete off-the-shelf solution to a low-level solution. An off-the-shelf solution like Comsol[168], or Fluent[169] includes software for meshing (constructing the geometric model), setting up boundary conditions, solving the model, and analyzing the results. Off-the-shelf solutions are used in engineering and therefore can be utilized to solve first-principles models. However, these solutions are usually expensive and limited to a certain set of equations.

Solving an arbitrary set of equations typically requires specialized software and often involves coding the model equations. Given the CPU-intensive nature of numerical computations, it is imperative to develop optimized code to ensure the model is solved within a reasonable timeframe. However, developing such optimized code demands high expertise and is time-consuming. Consequently, third-party numerical software libraries are frequently utilized for various components. Linear equation solvers such as PETSc [170], Hypre [171], and Trilinos [172] are commonly used to solve Equation A15 after assembling the matrices

M^{i}

S^{i}

, and

{\vec{F}}^{i}

. Assembling the matrices involves implementing discretization schemes to describe different operators and boundary conditions while considering the geometry.

OpenFOAM [173] is an open-source library that extends C++ by incorporating tensor algebra. It employs the finite volume method for discretizing and solving the governing equations, using a math-like flavor of C++. OpenFOAM also includes tools for mesh creation, solution, and analysis. Utilizing third-party libraries enables programmers to employ higher-level programming languages like Java and Python, further accelerating the development process.

Appendix B. Dispersion Model with Dissolution

Arav et al. [30] introduced the extension of the continuous dispersion model to include the dissolution dynamics. However, it was explained there very briefly, and as such it was difficult to comprehend it. Here we reiterate the essentials of the model and provide a more detailed explanation.

We describe first the dissolution kinetics of a single powder particle, and then extend it to the dissolution of polydisperse in the GIT.

The mass of a powder particle with a radius r is given by,

m (t) = \frac{4 π}{3} \cdot ρ \cdot r^{3} (t)

(A16)

Where

ρ

is the drug density and

r (t)

is the radius of the particle at time t. Hence, the dissolution rate of the particle can be written as,

\frac{d m}{d t} = 4 π r^{2} (t) \cdot ρ \cdot \frac{d r (t)}{d t}

(A17)

The dissolution flux is computed from

\frac{d r (t)}{d t}

, the change rate of particle radius[174],

ρ \cdot \frac{d r (t)}{d t} = - J

(A18)

Where J is the dissolution rate. Hence, the rate of mass loss of a single particle due to dissolution (Equation A17) is its surface area multiplied by the dissolution flux.

The dissolution rate J is described by the Noyes-Whitney equation [123]:

J = \frac{D_{w} (C_{s} - C)}{ζ (r)}

(A19)

where

D_{w}

represents the molecular diffusion coefficient,

C_{s}

denotes the saturation concentration in water, and

ζ

stands for the thickness of the hydrodynamic diffusion layer [30]. In Arav et al. [30],

ζ (r)

is defined as r for particles smaller than

30 μ m

and

30 μ m

otherwise.

Pharmaceutical powder is typically polydisperse [115], and thus the collective dissolution rate of all particles depends on their distribution. If we denote the number of particles with radius r at time t as

n (r, t) d r

, then its change over time due to dissolution is given by:

n (r, t + d t) d r = n (r, t) d r + κ \cdot n (r, t) d t - κ \cdot n (r + d r, t) d t

(A20)

where

κ = \frac{d r (t)}{d t} = - \frac{J}{ρ}

represents the rate at which the powder particle radius changes.

Reordering the terms we obtain the PDE equation for the dissolution of a polydisperse powder,

\frac{\partial n}{\partial t} + \frac{\partial κ n}{\partial r} = 0

(A21)

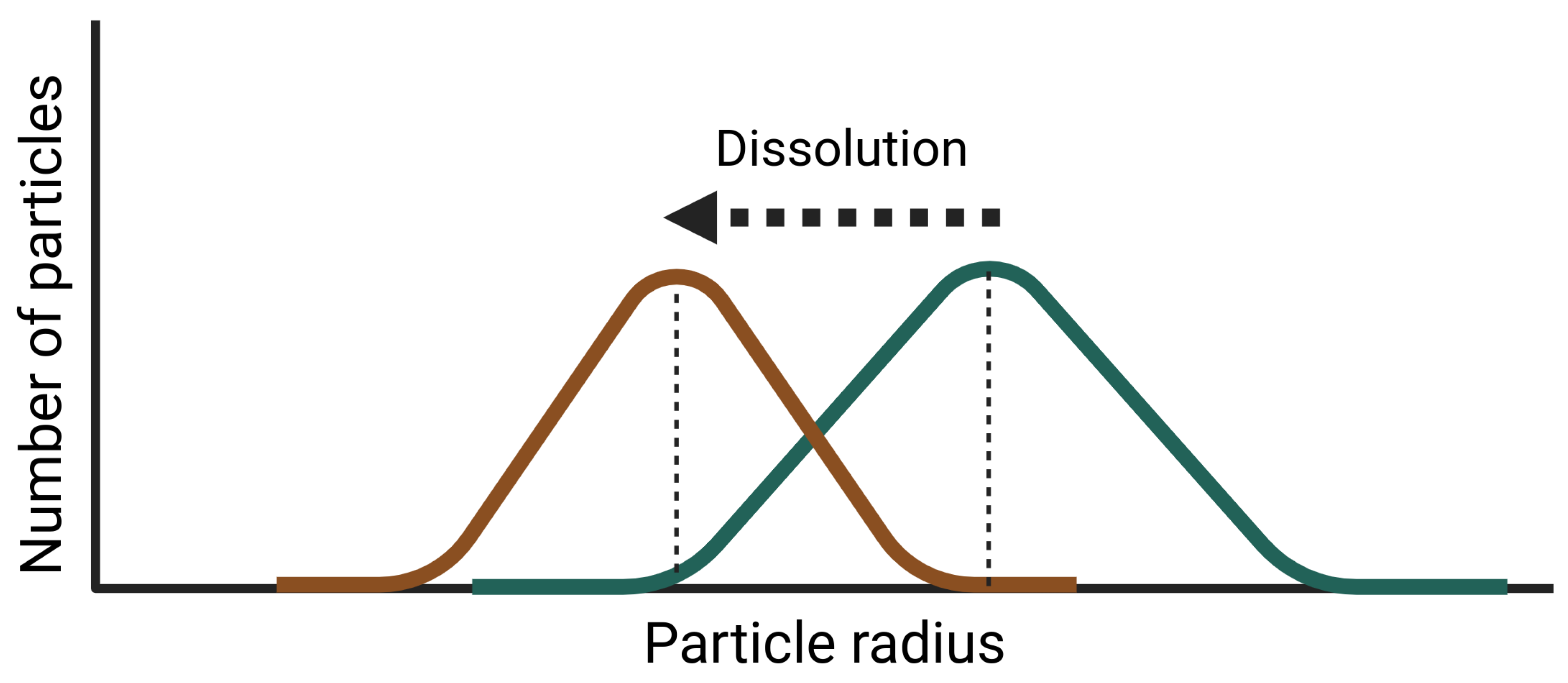
Hence, the dissolution process ’shifts’ the particle size distribution to the left (Figure A2).

Figure A2. The change in the particle distribution due to dissolution. The Green line is

t_{0}

and the brown line is

t_{1} > t_{0}

Figure A2. The change in the particle distribution due to dissolution. The Green line is

t_{0}

and the brown line is

t_{1} > t_{0}

The total amount that dissolved is computed by integrating the mass loss rate of all the powder particles. Hence, we obtain the integrodifferential equation,

\frac{d A}{d t} = \int 4 π r^{2} \cdot ρ \cdot κ (r) \cdot n d r

(A22)

Where A is the total amount that dissolved.

In the dispersion model, the powder is dispersed and mixed along the SI and dissolves simultaneously. Hence,

n_{S I} (x, r, t) d x d r

is the number of powder particles between x and

x + d x

with a radius between r and

d + d r

. The convection, mixing, and dissolution along the SI are described with the PDE (Figure A3),

\frac{\partial n_{S I}}{\partial t} + \frac{\partial}{\partial x} \underset{SI motility}{\underset{︸}{[{\underset{︸}{u \cdot n_{S I}}}_{Convection} - {\underset{︸}{D_{e f f} \frac{\partial}{\partial x} n_{S I}}}_{Mixing}]}} + \underset{Dissolution}{\underset{︸}{\frac{\partial κ \cdot n_{S I}}{\partial r}}} = 0

(A23)

Differing from compartmental models, Equation A23 utilizes experimental data to determine the mixing rate along the SI, while also considering variations in dissolution rate due to changes in particle size distribution. The equation for the dissolved drug along the SI is given in Arav et al. [30].

Figure A3. The change in the particle distribution due to intestinal convection and dissolution. The Green line is

t_{0}

and the brown line is

t_{1} > t_{0}

Figure A3. The change in the particle distribution due to intestinal convection and dissolution. The Green line is

t_{0}

and the brown line is

t_{1} > t_{0}

References

Alqahtani, M.S.; Kazi, M.; Alsenaidy, M.A.; Ahmad, M.Z. Advances in Oral Drug Delivery. Frontiers in Pharmacology 2021, 12. [CrossRef]
Schneckener, S.; Grimbs, S.; Hey, J.; Menz, S.; Osmers, M.; Schaper, S.; Hillisch, A.; Göller, A.H. Prediction of Oral Bioavailability in Rats: Transferring Insights from in Vitro Correlations to (Deep) Machine Learning Models Using in Silico Model Outputs and Chemical Structure Parameters. Journal of Chemical Information and Modeling 2019, 59, 4893–4905. [CrossRef]
Homayun, B.; Lin, X.; Choi, H.J. Challenges and recent progress in oral drug delivery systems for biopharmaceuticals. Pharmaceutics 2019, 11. [CrossRef]
Huang, W.; Lee, S.L.; Yu, L.X. Mechanistic approaches to predicting oral drug absorption. AAPS Journal 2009, 11, 217–224. [CrossRef]
Lin, L.; Wong, H. Predicting oral drug absorption: Mini review on physiologically-based pharmacokinetic models. Pharmaceutics 2017, 9. [CrossRef]
Sun, D.; Gao, W.; Hu, H.; Zhou, S. Why 90Acta Pharmaceutica Sinica B 2022, 12, 3049–3062.
Wienkers, L.C.; Heath, T.G. Predicting in vivo drug interactions from in vitro drug discovery data. Nature Reviews Drug Discovery 2005, 4, 825–833. [CrossRef]
Guengerich, F.P.; Isin, E.M. Mechanisms of Cytochrome P450 Reactions. Acta Chim. Slov 2008, 55, 7–19.
Mehrer, H.; Stolwijk, N.A. Heroes and Highlights in the History of Diffusion The Open-Access Journal for the Basic Principles of Diffusion Theory, Experiment and Application 2009. 11, 1–32.
Benedetti, M.S.; Whomsley, R.; Poggesi, I.; Cawello, W.; Mathy, F.X.; Delporte, M.L.; Papeleu, P.; Watelet, J.B. Drug metabolism and pharmacokinetics. Drug Metabolism Reviews 2009, 41, 344–390.
He, S.; Mu, H. Microenvironmental pH Modification in Buccal/Sublingual Dosage Forms for Systemic Drug Delivery. Pharmaceutics 2023, 15. [CrossRef]
Kanade, T.; Gupta, A.; Mahajan, S.; Darwhekar, G. Review on Sublingual Tablets – A Promising Formulation for Instant Action. Int. J. in Pharm. Sci 2023, 1, 250–260. [CrossRef]
Pather, I.; Rathbone, M.J.; Sevda, .; Enel, S. Current status and the future of buccal drug delivery systems. Expert Opin. Drug Deliv 2008, 5, 531–542. [CrossRef]
Pinto, S.; Pintado, M.E.; Sarmento, B. In vivo, ex vivo and in vitro assessment of buccal permeation of drugs from delivery systems. Expert Opinion on Drug Delivery 2020, 17, 33–48. [CrossRef]
Wanasathop, A.; Patel, P.B.; Choi, H.A.; Li, S.K. Permeability of buccal mucosa. Pharmaceutics 2021, 13. [CrossRef]
Fedi, A.; Vitale, C.; Ponschin, G.; Ayehunie, S.; Fato, M.; Scaglione, S. In vitro models replicating the human intestinal epithelium for absorption and metabolism studies: A systematic review. Journal of Controlled Release 2021, 335, 247–268. [CrossRef]
Naoki, U.; Yoshiteru, W.; Takahisa, S.; Junko, M.; Yoshiaki, M.; Mitsuo, M. Carrier-Mediated Transport of Monocarboxylic Acids in Primary Cultured Epithelial Cells from Rabbit Oral Mucosa. Pharmaceutical Research 1997, 14.
Vondracek, M.; Xi, Z.; Larsson, P.; Baker, V.; Mace, K.; Pfeifer, A.; Tjälve, H.; Donato, M.; Gomez-Lechon, M. Cytochrome P450 expression and related metabolism in human buccal mucosa , to significant xenobiotic metabolism in human buccal epithelium. Notably, metabolic activation of AFB 1 was not activity in SVpgC2a under both monolayer and organotypic. Carcinogenesis 2001, 22, 481–488.
Fonseca-Santos, B.; Chorilli, M. An overview of polymeric dosage forms in buccal drug delivery: State of art, design of formulations and their in vivo performance evaluation. Materials Science and Engineering C 2018, 86, 129–143. [CrossRef]
Badawy, S.I.F.; Hussain, M.A. Microenvironmental pH modulation in solid dosage forms. Journal of Pharmaceutical Sciences 2007, 96, 948–959. [CrossRef]
Doherty, C.; York, P. Microenvironmental pH control of drug dissolution. International Journal of Pharmaceutics 1989, 50, 223–232.
Taniguchi, C.; Kawabata, Y.; Wada, K.; Yamada, S.; Onoue, S. Microenvironmental pH-modification to improve dissolution behavior and oral absorption for drugs with pH-dependent solubility. Expert Opinion on Drug Delivery 2014, 11, 505–516. [CrossRef]
Yang, M.; He, S.; Fan, Y.; Wang, Y.; Ge, Z.; Shan, L.; Gong, W.; Huang, X.; Tong, Y.; Gao, C. Microenvironmental pH-modified solid dispersions to enhance the dissolution and bioavailability of poorly water-soluble weakly basic GT0918, a developing anti-prostate cancer drug: Preparation, characterization and evaluation in vivo. International Journal of Pharmaceutics 2014, 475, 97–109. [CrossRef]
Willmann, S.; Schmitt, W.; Keldenich, J.; Lippert, J.; Dressman, J.B. A physiological model for the estimation of the fraction dose absorbed in humans. Journal of Medicinal Chemistry 2004, 47, 4022–4031. [CrossRef]
Cheng, L.; Wong, H. Food effects on oral drug absorption: Application of physiologically-based pharmacokinetic modeling as a predictive tool. Pharmaceutics 2020, 12, 1–18. [CrossRef]
Oberle, R.L.; Amidon, G.L. The Influence of Variable Gastric Emptying and Intestinal Transit Rates on the Plasma Level Curve of Cimetidine; An Explanation for the Double Peak Phenomenon. Journal of Pharmacokinetics and Biopharmaceutics 1987, 15.
Davis, S.S.; Hardy, J.G.; Fara, J.W. The transit of dosage forms through the small intestine. Gut 1986, 27, 886–892. [CrossRef]
L., A.G.; Hans, L.; P., S.V.; R., C.J. A Theoretical Basis for a Biopharmaceutic Drug Classification: The Correlation of in Vitro Drug Product Dissolution and in Vivo Bioavailability. Pharmaceutical Research 1995, 12, 413–420.
DeSesso, J.M.; Jacobson, C.F. Anatomical and physiological parameters affecting gastrointestinal absorption in humans and rats. Food and Chemical Toxicology 2001, 39, 209–228. [CrossRef]
Arav, Y.; Bercovier, M.; Parnas, H. Selecting the particle size distribution for drugs with low water solubility mathematical model. Drug Development and Industrial Pharmacy 2012, 38, 940–951.
Schütt, M. A DIGITAL TWIN OF THE HUMAN COLON FOR THE DESIGN AND OPTIMISATION OF COLON-TARGETED DRUG DELIVERY SYSTEMS 2022.
den Mooter, G.V. Colon drug delivery. Expert opinion on drug delivery 2006, 3, 111–125.
Wilson, C.G. The transit of dosage forms through the colon. International Journal of Pharmaceutics 2010, 395, 17–25. [CrossRef]
G., T.K.M.; E., A.M. Aulton’s Pharmaceutics - The Design and Manufacture of Medicines, elvesier ed.; 2022.
ATK, L.; ME, F.; KC, J. Dissolution modeling: factors affecting the dissolution rates of polydisperse powders. Pharmaceutical research 1993, 10, 1308–1314.
Glomme, A.; März, J.; Dressman, J., Predicting the intestinal solubility of poorly soluble drugs.; Wiley-VCH: Weinheim, Germany, 2006; pp. 259–280.
Murakami, T.; Takano, M. Intestinal effl ux transporters and drug absorption. Expert Opin. Drug Metab. Toxicol 2008, 4, 923–939. [CrossRef]
Watkins, P.B. The barrier function of CYP3A4 and P-glycoprotein in the small bowel. Advanced Drug Delivery Reviews 1997, 27, 161–170.
SD, H.; KE, T.; PB, W.; KS, L.; LZ, B.; MF, P.; RR, M.; DK, T.; DG, B.; RJ, F.; SA., W. Molecular and physical mechanisms of first-pass extraction. Drug Metab Dispos. 1999, 27, 161–166.
Rowland, M.; Tozer, T.N.; Derendorf, H.; Hochhaus, G. Clinical Pharmacokinetics and Pharmacodynamics; 2011.
Agoram, B.; Woltosz, W.S.; Bolger, M.B. Predicting the impact of physiological and biochemical processes on oral drug bioavailability a a a. Advanced Drug Delivery Reviews 2001, 50, 41–67.
Fagerholm, U.; Hellberg, S.; Spjuth, O. Article advances in predictions of oral bioavailability of candidate drugs in man with new machine learning methodology. Molecules 2021, 26. [CrossRef]
Nadun, P.; E, C.J.; K, C.L.; Vinod, S. Modelling Flow and Mixing in the Proximal Small Intestine. 2020.
Sager, J.E.; Yu, J.; Ragueneau-Majlessi, I.; Isoherranen, N. Physiologically Based Pharmacokinetic (PBPK) Modeling and Simulation Approaches: A Systematic Review of Published Models, Applications, and Model Verification. Drug Metabolism and Disposition 2015, 43.
Lin, W.; Chen, Y.; Unadkat, J.D.; Zhang, X.; Wu, D.; Heimbach, T. Applications, Challenges, and Outlook for PBPK Modeling and Simulation: A Regulatory, Industrial and Academic Perspective. Pharmaceutical Research 2022, 39, 1701–1731. [CrossRef]
Tropsha, A.; Isayev, O.; Varnek, A.; Schneider, G.; Cherkasov, A. Integrating QSAR modelling and deep learning in drug discovery: the emergence of deep QSAR. Nature Reviews Drug Discovery 2024, 23, 141–155. [CrossRef]
Zou, H.; Banerjee, P.; Leung, S.S.Y.; Yan, X. Application of Pharmacokinetic-Pharmacodynamic Modeling in Drug Delivery: Development and Challenges. Frontiers in Pharmacology 2020, 11. [CrossRef]
Muratov, E.N.; Bajorath, J.; Sheridan, R.P.; Tetko, I.V.; Filimonov, D.; Poroikov, V.; Oprea, T.I.; Baskin, I.I.; Varnek, A.; Roitberg, A.; Isayev, O.; Curtalolo, S.; Fourches, D.; Cohen, Y.; Aspuru-Guzik, A.; Winkler, D.A.; Agrafiotis, D.; Cherkasov, A.; Tropsha, A. QSAR without borders. Chemical Society Reviews 2020, 49, 3525–3564. [CrossRef]
Komura, H.; Watanabe, R.; Mizuguchi, K. The Trends and Future Prospective of In Silico Models from the Viewpoint of ADME Evaluation in Drug Discovery. Pharmaceutics 2023, 15.
Vora, L.K.; Gholap, A.D.; Jetha, K.; Thakur, R.R.S.; Solanki, H.K.; Chavda, V.P. Artificial Intelligence in Pharmaceutical Technology and Drug Delivery Design. Pharmaceutics 2023, 15.
De, P.; Kar, S.; Ambure, P.; Roy, K. Prediction reliability of QSAR models: an overview of various validation tools. Archives of Toxicology 2022, 96, 1279–1295. [CrossRef]
Stenberg, P.; Bergström, C.A.S.; Luthman, K.; Artursson, P. Theoretical Predictions of Drug Absorption in Drug Discovery and Development. Clin Pharmacokinet 2002, 41.
Lombardo, F.; Gifford, E.; Shalaeva, M.Y. In Silico ADME Prediction: Data, Models, Facts and Myths. Mini Reviews in Medicinal Chemistry 2003, 3, 861–875.
Linnankoski, J. MATHEMATICAL MODELLING OF INTESTINAL DRUG ABSORPTION Dissertations in Health Sciences 2024.
Lawless, M.; Dibella, J.; Bolger, M.B.; Clark, R.D.; Huehn, E.; Waldman, M.; Zhang, J.; Lukacova, V. In silico PREDICTION OF ORAL BIOAVAILABILITY. 2016.
Williams, J.; Siramshetty, V.; Nguyen, D.T.; Padilha, E.C.; Kabir, M.; Yu, K.R.; Wang, A.Q.; Zhao, T.; Itkin, M.; Shinn, P.; Mathé, E.A.; Xu, X.; Shah, P. Using in vitro ADME data for lead compound selection: An emphasis on PAMPA pH 5 permeability and oral bioavailability. Bioorganic and Medicinal Chemistry 2022, 56. [CrossRef]
Linnankoski, J.; Ranta, V.P.; Yliperttula, M.; Urtti, A. Passive oral drug absorption can be predicted more reliably by experimental than computational models-Fact or myth. European Journal of Pharmaceutical Sciences 2008, 34, 129–139. [CrossRef]
de Waterbeemd, H.V.; Smith, D.A.; Beaumont, K.; Walker, D.K. Property-based design: Optimization of drug absorption and pharmacokinetics. Journal of Medicinal Chemistry 2001, 44, 1313–1333. [CrossRef]
Falcón-Cano, G.; Ángel Cabrera-Pérez, M.; Molina, C. ADME prediction with KNIME: In silico aqueous solubility consensus model based on supervised recursive random forest approaches. ADMET and DMPK 2020, 8, 251–273. [CrossRef]
Yoshida, F.; Topliss, J.G. QSAR model for drug human oral bioavailability. Journal of Medicinal Chemistry 2000, 43, 2575–2585. [CrossRef]
Zhao, Y.H.; Abraham, M.H.; Le, J.; Hersey, A.; Luscombe, C.N.; Beck, G.; Sherborne, B.; Cooper, I. Rate-Limited Steps of Human Oral Absorption and QSAR Studies. Pharmaceutical Research 2002, 19.
Moda, T.L.; Montanari, C.A.; Andricopulo, A.D. Hologram QSAR model for the prediction of human oral bioavailability. Bioorganic and Medicinal Chemistry 2007, 15, 7738–7745. [CrossRef]
Wei, M.; Zhang, X.; Pan, X.; Wang, B.; Ji, C.; Qi, Y.; Zhang, J.Z. HobPre: accurate prediction of human oral bioavailability for small molecules. Journal of Cheminformatics 2022, 14. [CrossRef]
Price, E.; Kalvass, J.C.; Degoey, D.; Hosmane, B.; Doktor, S.; Desino, K. Global Analysis of Models for Predicting Human Absorption: QSAR, in Vitro, and Preclinical Models. Journal of Medicinal Chemistry 2021, 64, 9389–9403. [CrossRef]
Donovan, D.H.O.; Fusco, C.D.; Kuhnke, L.; Reichel, A. Trends in Molecular Properties, Bioavailability, and Permeability across the Bayer Compound Collection. Journal of Medicinal Chemistry 2023, 66, 2347–2360. [CrossRef]
Desai, P.V.; Sawada, G.A.; Watson, I.A.; Raub, T.J. Integration of in silico and in vitro tools for scaffold optimization during drug discovery: Predicting P-glycoprotein efflux. Molecular Pharmaceutics 2013, 10, 1249–1261. [CrossRef]
Berellini, G.; Springer, C.; Waters, N.J.; Lombardo, F. In silico prediction of volume of distribution in human using linear and nonlinear models on a 669 compound data set. Journal of Medicinal Chemistry 2009, 52, 4488–4495. [CrossRef]
Zhu, X.W.; Sedykh, A.; Zhu, H.; Liu, S.S.; Tropsha, A. The use of pseudo-equilibrium constant affords improved QSAR models of human plasma protein binding. Pharmaceutical Research 2013, 30, 1790–1798. [CrossRef]
Votano, J.R.; Parham, M.; Hall, L.M.; Hall, L.H.; Kier, L.B.; Oloff, S.; Tropsha, A. QSAR modeling of human serum protein binding with several modeling techniques utilizing structure-information representation. Journal of Medicinal Chemistry 2006, 49, 7169–7181. [CrossRef]
Sun, L.; Yang, H.; Li, J.; Wang, T.; Li, W.; Liu, G.; Tang, Y. In Silico Prediction of Compounds Binding to Human Plasma Proteins by QSAR Models. ChemMedChem 2018, 13, 572–581. [CrossRef]
Pirovano, A.; Brandmaier, S.; Huijbregts, M.A.; Ragas, A.M.; Veltman, K.; Hendriks, A.J. QSARs for estimating intrinsic hepatic clearance of organic chemicals in humans. Environmental Toxicology and Pharmacology 2016, 42, 190–197. [CrossRef]
Gombar, V.K.; Hall, S.D. Quantitative structure-activity relationship models of clinical pharmacokinetics: Clearance and volume of distribution. Journal of Chemical Information and Modeling 2013, 53, 948–957. [CrossRef]
Simeon, S.; Montanari, D.; Gleeson, M.P. Investigation of Factors Affecting the Performance of in silico Volume Distribution QSAR Models for Human, Rat, Mouse, Dog & Monkey. Molecular Informatics 2019, 38. [CrossRef]
Kokate, A.; Li, X.; Williams, P.J.; Singh, P.; Jasti, B.R. In silico prediction of drug permeability across buccal mucosa. Pharmaceutical Research 2009, 26, 1130–1139. [CrossRef]
Scherrer, R.A. Multi-pH QSAR: II. Regression Analysis Sensitive Enough to Determine the Transition-State pKa of Human Buccal Absorption. Molecular Informatics 2011, 30, 251–255. [CrossRef]
Mehta, C.H.; Narayan, R.; Nayak, U.Y. Computational modeling for formulation design. Drug Discovery Today 2019, 24, 781–788. [CrossRef]
Gaikwad, V.L.; Bhatia, N.M.; Singhvi, I.; Mahadik, K.R.; Bhatia, M.S. Computational Modeling of Polymeric Physicochemical Properties for Formulation Development of a Drug Containing Basic Functionality. Journal of Pharmaceutical Sciences 2017, 106, 3337–3345. [CrossRef]
DeBoyace, K.; Wildfong, P.L. The Application of Modeling and Prediction to the Formation and Stability of Amorphous Solid Dispersions. Journal of Pharmaceutical Sciences 2018, 107, 57–74.
Landín, M.; Rowe, R.C.; York, P. Advantages of neurofuzzy logic against conventional experimental design and statistical analysis in studying and developing direct compression formulations. European Journal of Pharmaceutical Sciences 2009, 38, 325–331.
Kulkarni, A.S.; Kasabe, A.J.; Bhatia, M.S.; Bhatia, N.M.; Gaikwad, V.L. Quantitative Structure–Property Relationship Approach in Formulation Development: an Overview. AAPS PharmSciTech 2019, 20.
JE, A., Ed. Formulation tools for pharmaceutical development; Woodhead publishing, 2013.
Obrezanova, O.; Segall, M.D. Gaussian processes for classification: QSAR modeling of ADMET and target activity. Journal of Chemical Information and Modeling 2010, 50, 1053–1061. [CrossRef]
Sarker, S.; Jamal, L.; Ahmed, S.F.; Irtisam, N. Robotics and artificial intelligence in healthcare during COVID-19 pandemic: A systematic review. Robotics and Autonomous Systems 2021, 146. [CrossRef]
Fluetsch, A.; Lascio, E.D.; Gerebtzoff, G.; Rodríguez-Pérez, R. Adapting Deep Learning QSPR Models to Specific Drug Discovery Projects. Molecular Pharmaceutics 2024, 21, 1817–1826.
Yang, Y.; Ye, Z.; Su, Y.; Zhao, Q.; Li, X.; Ouyang, D. Deep learning for in vitro prediction of pharmaceutical formulations. Acta Pharmaceutica Sinica B 2019, 9, 177–185. [CrossRef]
Paixão, P.J.P.A. In Silico Prediction of Human Oral Bioavailability. Artificial Neural Networks and Physiologically Based Models 2010.
Kong, X.; Lin, K.; Wu, G.; Tao, X.; Zhai, X.; Lv, L.; Dong, D.; Zhu, Y.; Yang, S. Machine Learning Techniques Applied to the Study of Drug Transporters. Molecules 2023, 28. [CrossRef]
Kumar, S.; Deepika, D.; Kumar, V. Pharmacophore Modeling Using Machine Learning for Screening the Blood–Brain Barrier Permeation of Xenobiotics. International Journal of Environmental Research and Public Health 2022, 19. [CrossRef]
Plonka, W.; Stork, C.; Šícho, M.; Kirchmair, J. CYPlebrity: Machine learning models for the prediction of inhibitors of cytochrome P450 enzymes. Bioorganic and Medicinal Chemistry 2021, 46.
Sinha, K.; Ghosh, J.; Sil, P.C. Machine Learning in Drug Metabolism Study. Current Drug Metabolism 2022, 23.
Ai, D.; Cai, H.; Wei, J.; Zhao, D.; Chen, Y.; Wang, L. DEEPCYPs: A deep learning platform for enhanced cytochrome P450 activity prediction. Frontiers in Pharmacology 2023, 14. [CrossRef]
Holmer, M.; de Bruyn Kops, C.; Stork, C.; Kirchmair, J. Cypstrate: A set of machine learning models for the accurate classification of cytochrome p450 enzyme substratesand non-substrates. Molecules 2021, 26. [CrossRef]
Bennett-Lenane, H.; Griffin, B.T.; O’Shea, J.P. Machine learning methods for prediction of food effects on bioavailability: A comparison of support vector machines and artificial neural networks. European Journal of Pharmaceutical Sciences 2022, 168. [CrossRef]
Maltarollo, V.G.; Gertrudes, J.C.; Oliveira, P.R.; Honorio, K.M. Applying machine learning techniques for ADME-Tox prediction: A review. Expert Opinion on Drug Metabolism and Toxicology 2015, 11, 259–271. [CrossRef]
Butina, D. Unsupervised data base clustering based on daylight’s fingerprint and Tanimoto similarity: A fast and automated way to cluster small and large data sets. Journal of Chemical Information and Computer Sciences 1999, 39, 747–750. [CrossRef]
Korolev, D.; Balakin, K.V.; Nikolsky, Y.; Kirillov, E.; Ivanenkov, Y.A.; Savchuk, N.P.; Ivashchenko, A.A.; Nikolskaya, T. Modeling of human cytochrome P450-mediated drug metabolism using unsupervised machine learning approach. Journal of Medicinal Chemistry 2003, 46, 3631–3643. [CrossRef]
Vamathevan, J.; Clark, D.; Czodrowski, P.; Dunham, I.; Ferran, E.; Lee, G.; Li, B.; Madabhushi, A.; Shah, P.; Spitzer, M.; Zhao, S. Applications of machine learning in drug discovery and development. Nature Reviews Drug Discovery 2019, 18, 463–477. [CrossRef]
Yu, L.X.; Lipka, E.; Crison, J.R.; Amidon, G.L. Transport approaches to the biopharmaceutical design of oral drug delivery systems: Prediction of intestinal absorption. Advanced Drug Delivery Reviews 1996, 19, 359–376. [CrossRef]
Jacobs, M.H. SOME ASPECTS OF CELL PERMEABILITY TO WEAK ELECTROLYTES. Symp. Quant. Biol. 1940, 8, 30–39.
Schanker, L.S.; Shore, P.A.; Brodie, B.B.; Hogben, C.A.M. ABSORPTION OF DRUGS FROM THE STOMACH I. THE RAT. Journal of Pharmacology and Experimental Therapeutics 1957, 120.
Hogben, C.A.M.; Schanker, L.S.; Tocco, D.J.; Brodie, B.B. ABSORPTION OF DRUGS FROM THE STOMACH. II. THE HUMAN. Journal of Pharmacology and Experimental Therapeutics 1957, 120.
Schanker, L.S.; Tocco, D.J.; Brodie, B.B.; Hogben, C.A.M. ABSORPTION OF DRUGS FROM THE RAT SMALL INTESTINE. Journal of Pharmacology and Experimental Therapeutics 1958, 123.
Dressman, J.B.; Amidon, G.L.; Fleisher, D. Absorption potential: Estimating the fraction absorbed for orally administered compounds. Journal of Pharmaceutical Sciences 1985, 74, 588–589. [CrossRef]
Macheras, P.E.; Symillides, M.Y. Toward a quantitative approach for the prediction of the fraction of dose absorbed using the absorption potential concept. Biopharmaceutics & Drug Disposition 1989, 10, 43–53. [CrossRef]
Amidon, G.L.; Sinko, P.J.; Fleisher, D. Estimating Human Oral Fraction Dose Absorbed: A Correlation Using Rat Intestinal Membrane Permeability for Passive and Carrier-Mediated Compounds. Pharmaceutical Research 1988, 5.
Sinko, P.J.; Leesman, G.D.; Amidon, G.L. Predicting Fraction Dose Absorbed in Humans Using a Macroscopic Mass Balance Approach. Pharmaceutical Research: An Official Journal of the American Association of Pharmaceutical Scientists 1991, 8, 979–988. [CrossRef]
Sinko, P.J.; Leesman, G.D.; Amidon, G.L. Mass Balance Approaches for Estimating the Intestinal Absorption and Metabolism of Peptides and Analogues: Theoretical Development and Applications. Pharmaceutical Research: An Official Journal of the American Association of Pharmaceutical Scientists 1993, 10, 271–275. [CrossRef]
Yu, L.X.; Crison, J.R.; Amidon, G.L. Compartmental transit and dispersion model analysis of small intestinal transit flow in humans. International Journal of Pharmaceutics 1996, 140, 111–118.
Oh, D.M.; Curl, R.L.; Amidon, G.L. Estimating the Fraction Dose Absorbed from Suspensions of Poorly Soluble Compounds in Humans: A Mathematical Model. Pharmaceutical Research: An Official Journal of the American Association of Pharmaceutical Scientists 1993, 10, 264–270. [CrossRef]
Beran, K.; Hermans, E.; Holm, R.; Sepassi, K.; Dressman, J. Projection of Target Drug Particle Size in Oral Formulations Using the Refined Developability Classification System (rDCS). Pharmaceutics 2023, 15. [CrossRef]
Wu, C.Y.; Benet, L.Z. Predicting drug disposition via application of BCS: Transport/absorption/ elimination interplay and development of a biopharmaceutics drug disposition classification system. Pharmaceutical Research 2005, 22, 11–23. [CrossRef]
Goodacre, B.C.; Murray, P.J. A MATHEMATICAL MODEL OF DRUG ABSORPTION. Journal of Clinical Pharmacy and Therapeutics 1981, 6, 117–133. [CrossRef]
Pang, S.K.; Peng, H.B.; Noh, K. The segregated intestinal flow model (SFM) for drug absorption and drug metabolism: Implications on intestinal and liver metabolism and drug–drug interactions. Pharmaceutics 2020, 12. [CrossRef]
Dressman, J.B.; Fleisher, D. Mixing-Tank Model for Predicting Dissolution Rate Control of Oral Absorption. Journal of Pharmaceutical Sciences 1986, 75, 109–116. [CrossRef]
Hintz, R.J.; Johnson, K.C. The effect of particle size distribution on dissolution rate and oral absorption. International Journal of Pharmaceutics 1989, 51, 9–17. [CrossRef]
Dressman, J.B.; Fleisher, D.; Amidon, G.L. Physicochemical Model for Dose-Dependent DrugAbsorption. Journal of Pharmaceutical Sciences 1984, 73, 1274–1279. [CrossRef]
Luner, P.E.; Amidon, G.L. Description and simulation of a multiple mixing tank model to predict the effect of bile sequestrants on bile salt excretion. Journal of Pharmaceutical Sciences 1993, 82, 311–318. [CrossRef]
Grass, G.M. Simulation models to predict oral drug absorption from in vitro data. Advanced Drug Delivery Reviews 1997, 23, 199–219. [CrossRef]
Yu, L.X.; Amidon, G.L. A compartmental absorption and transit model for estimating oral drug absorption. International Journal of Pharmaceutics 1999, 186, 119–125.
Jamei, M.; Yang, J.; Turner, D.; Yeo, K.R.; Tucker, G.T.; Hodjegan, A.R.H. A Novel Physiologically A Novel Physiologically-Based Mechanistic Model for Predicting Oral Based Mechanistic Model for Predicting Oral Drug Absorption: The Advanced Dissolution, Absorption, and Drug Absorption: The Advanced Dissolution, Absorption, and Metabolism (ADAM) Model Metabolism (ADAM) Model Objectives Objectives The ADAM Model The ADAM Model A Case Study A Case Study. Clin Pharmacol Ther 1996, 60, 731–738.
Dokoumetzidis, A.; Kalantzi, L.; Fotaki, N. Predictive models for oral drug absorption: from in silico methods to integrated dynamical models. Expert opinion on drug metabolism & toxicology 2007, 3, 491–505. [CrossRef]
Hörter, D.; Dressman, J.B. Influence of physicochemical properties on dissolution of drugs in the gastrointestinal tract. Advanced Drug Delivery Reviews 2001, 46, 75–87. [CrossRef]
Wang, J.; Flanagan, D.R. General solution for diffusion-controlled dissolution of spherical particles. 1. Theory. Journal of Pharmaceutical Sciences 1999, 88, 731–738. [CrossRef]
Tubic-Grozdanis, M.; Bolger, M.B.; Langguth, P. Application of Gastrointestinal Simulation for Extensions for Biowaivers of Highly Permeable Compounds. AAPS J 2008, 10, 213–226. [CrossRef]
Zhang, T.; Wells, E. A Review of Current Methods for Food Effect Prediction During Drug Development. Current Pharmacology Reports 2020, 6, 267–279. [CrossRef]
Dannenfelser, R.M.; He, H.; Joshi, Y.; Bateman, S.; Serajuddin, A.T. Development of clinical dosage forms for a poorly water soluble drug I: Application of polyethylene glycol–polysorbate 80 solid dispersion carrier system. Journal of Pharmaceutical Sciences 2004, 93, 1165–1175. [CrossRef]
Kuentz, M.; Nick, S.; Parrott, N.; Röthlisberger, D. A strategy for preclinical formulation development using GastroPlus™ as pharmacokinetic simulation tool and a statistical screening design applied to a dog study. European Journal of Pharmaceutical Sciences 2006, 27, 91–99. [CrossRef]
Wei, H.; Dalton, C.; Maso, M.D.; Kanfer, I.; Löbenberg, R. Physicochemical characterization of five glyburide powders: a BCS based approach to predict oral absorption. European journal of pharmaceutics and biopharmaceutics : official journal of Arbeitsgemeinschaft fur Pharmazeutische Verfahrenstechnik e.V 2008, 69, 1046–1056. [CrossRef]
Arafat, M.; Sarfraz, M.; Aburuz, S. Development and In Vitro Evaluation of Controlled Release Viagra® Containing Poloxamer-188 Using Gastroplus™ PBPK Modeling Software for In Vivo Predictions and Pharmacokinetic Assessments. Pharmaceuticals 2021, Vol. 14, Page 479 2021, 14, 479. [CrossRef]
Dalia, S.H.; Basim Mohsin Mohamed, M. Formulation of metoclopramide HCl gastroretentive film and in vitro- in silico prediction using Gastroplus® PBPK software. Saudi Pharmaceutical Journal 2022, 30, 1816–1824. [CrossRef]
Gajewska, M.; Blumenstein, L.; Kourentas, A.; Mueller-Zsigmondy, M.; Lorenzo, S.; Sinn, A.; Velinova, M.; Heimbach, T. Physiologically Based Pharmacokinetic Modeling of Oral Absorption, pH, and Food Effect in Healthy Volunteers to Drive Alpelisib Formulation Selection. AAPS Journal 2020, 22, 1–13. [CrossRef]
Ghoneim, A.M.; Mansour, S.M. The effect of liver and kidney disease on the pharmacokinetics of clozapine and sildenafil: A physiologically based pharmacokinetic modeling. Drug Design, Development and Therapy 2020, 14, 1469–1479. [CrossRef]
Lewis, G.J.; Ahire, D.; Taskar, K.S. Physiologically-based pharmacokinetic modeling of prominent oral contraceptive agents and applications in drug–drug interactions. CPT: Pharmacometrics & Systems Pharmacology 2024, 13, 563–575. [CrossRef]
Chiney, M.S.; Ng, J.; Gibbs, J.P.; Shebley, M. Quantitative Assessment of Elagolix Enzyme-Transporter Interplay and Drug–Drug Interactions Using Physiologically Based Pharmacokinetic Modeling. Clinical Pharmacokinetics 2020, 59, 617–627. [CrossRef]
Shao, W.; Shen, C.; Wang, W.; Sun, H.; Wang, X.; Geng, K.; Wang, X.; Xie, H. Development and Validation of Physiologically Based Pharmacokinetic Model of Levetiracetam to Predict Exposure and Dose Optimization in Pediatrics. Journal of Pharmaceutical Sciences 2023, 112, 2667–2675. [CrossRef]
Correia, M.G.S. Developing in vitro and in silico approaches to predict clinical outcomes: focus on paediatrics 2021.
Cohen-Rabbie, S.; Zhou, L.; Vishwanathan, K.; Wild, M.; Xu, S.; Freshwater, T.; Jain, L.; Schalkwijk, S.; Tomkinson, H.; Zhou, D. Physiologically Based Pharmacokinetic Modeling for Selumetinib to Evaluate Drug-Drug Interactions and Pediatric Dose Regimens. The Journal of Clinical Pharmacology 2021, 61, 1493–1504. [CrossRef]
Ho, N.F.H.; Merkle, H.P.; Higuchi, I. QUANTITATIVE, MECHANISTIC AND PHYSIOLOGICALLY REALISTIC APPROACH TO THE BIOPHARMACEUTICAL DESIGN OF ORAL DRUG DELIVERY SYSTEMS. DRUG DEVELOPMENT AND INDUSTRIAL PHARMACY 1983, 9, 1111–1184.
Willmann, S.; Schmitt, W.; Keldenich, J.; Dressman, J.B. A Physiologic Model for Simulating Gastrointestinal Flow and Drug Absorption in Rats. Pharmaceutical Research 2003, 20, 1766–1771.
Arav, Y.; Zohar, A. Model-based optimization of controlled release formulation of levodopa for Parkinson’s disease. Scientific reports 2023, 13. [CrossRef]
Davies, J.T.J.T. Turbulence phenomena; an introduction to the eddy transfer of momentum, mass, and heat, particularly at interfaces; Academic Press, 1972; p. 412.
Urso, D.; Chaudhuri, K.R.; Qamar, M.A.; Jenner, P. Improving the Delivery of Levodopa in Parkinson’s Disease: A Review of Approved and Emerging Therapies. CNS Drugs 2020, 34, 1149–1163. [CrossRef]
Lee, J.H.; Kuhar, S.; Seo, J.H.; Pasricha, P.J.; Mittal, R. Computational modeling of drug dissolution in the human stomach: Effects of posture and gastroparesis on drug bioavailability. Physics of Fluids 2022, 34. [CrossRef]
Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nature Structural Biology 2002 9:9 2002, 9, 646–652. [CrossRef]
Salo-Ahen, O.M.; Alanko, I.; Bhadane, R.; Alexandre, A.M.; Honorato, R.V.; Hossain, S.; Juffer, A.H.; Kabedev, A.; Lahtela-Kakkonen, M.; Larsen, A.S.; Lescrinier, E.; Marimuthu, P.; Mirza, M.U.; Mustafa, G.; Nunes-Alves, A.; Pantsar, T.; Saadabadi, A.; Singaravelu, K.; Vanmeert, M. Molecular dynamics simulations in drug discovery and pharmaceutical development. Processes 2021, 9, 1–63. [CrossRef]
Adelusi, T.I.; Oyedele, A.Q.K.; Boyenle, I.D.; Ogunlana, A.T.; Adeyemi, R.O.; Ukachi, C.D.; Idris, M.O.; Olaoba, O.T.; Adedotun, I.O.; Kolawole, O.E.; Xiaoxing, Y.; Abdul-Hammed, M. Molecular modeling in drug discovery. Informatics in Medicine Unlocked 2022, 29. [CrossRef]
Bunker, A.; Róg, T. Mechanistic Understanding From Molecular Dynamics Simulation in Pharmaceutical Research 1: Drug Delivery. Frontiers in Molecular Biosciences 2020, 7. [CrossRef]
Vivo, M.D.; Masetti, M.; Bottegoni, G.; Cavalli, A. Role of Molecular Dynamics and Related Methods in Drug Discovery. Journal of Medicinal Chemistry 2016, 59, 4035–4061.
Hollingsworth, S.A.; Dror, R.O. Molecular Dynamics Simulation for All. Neuron 2018, 99, 1129–1143. [CrossRef]
Liu, X.; Shi, D.; Zhou, S.; Liu, H.; Liu, H.; Yao, X. Molecular dynamics simulations and novel drug discovery. Expert Opinion on Drug Discovery 2018, 13, 23–37. [CrossRef]
Bera, I.; Payghan, P.V. Use of Molecular Dynamics Simulations in Structure-Based Drug Discovery. Current Pharmaceutical Design 2019, 25, 3339–3349. [CrossRef]
Martinez-Rosell, G.; Giorgino, T.; Harvey, M.J.; de Fabritiis, G. Drug Discovery and Molecular Dynamics: Methods, Applications and Perspective Beyond the Second Timescale. Current Topics in Medicinal Chemistry 2017, 17. [CrossRef]
Ganesan, A.; Coote, M.L.; Barakat, K. Molecular dynamics-driven drug discovery: leaping forward with confidence. Drug Discovery Today 2017, 22, 249–269. [CrossRef]
Fox, S.J.; Li, J.; Tan, Y.S.; Nguyen, M.N.; Pal, A.; Ouaray, Z.; Yadahalli, S.; Kannan, S. The Multifaceted Roles of Molecular Dynamics Simulations in Drug Discovery. Current Pharmaceutical Design 2016, 23.
Lee, H. Molecular Simulations of PEGylated Biomolecules, Liposomes, and Nanoparticles for Drug Delivery Applications. Pharmaceutics 2020, 12, 1–23. [CrossRef]
Al-Qattan, M.N.; Deb, P.K.; Tekade, R.K. Molecular dynamics simulation strategies for designing carbon-nanotube-based targeted drug delivery. Drug Discovery Today 2018, 23, 235–250.
Rocco, P.; Cilurzo, F.; Minghetti, P.; Vistoli, G.; Pedretti, A. Molecular Dynamics as a tool for in silico screening of skin permeability. European journal of pharmaceutical sciences : official journal of the European Federation for Pharmaceutical Sciences 2017, 106, 328–335. [CrossRef]
Fullard, L.A.; Lammers, W.J.; Ferrua, M.J. Advective mixing due to longitudinal and segmental contractions in the ileum of the rabbit. Journal of Food Engineering 2015, 160, 1–10. [CrossRef]
Kubinski, A.M.; Shivkumar, G.; Georgi, R.A.; George, S.; Reynolds, J.; Sosa, R.D.; Ju, T.R. Predictive Drug Release Modeling Across Dissolution Apparatuses I and II using Computational Fluid Dynamics. Journal of pharmaceutical sciences 2023, 112, 808–819. [CrossRef]
Valibeknejad, M.; Abdoli, S.M.; Alizadeh, R.; Mihăilă, S.M.; Raoof, A. Insights into transport in mucus barrier: Exploring particle penetration through the intestinal mucus layer. Journal of Drug Delivery Science and Technology 2023, 86, 104752. [CrossRef]
Walsh, J.P.; Ghadiri, M.; Shirazian, S. CFD approach for simulation of API release from solid dosage formulations. Journal of Molecular Liquids 2020, 317. [CrossRef]
Wang, W.; Ye, Z.; Gao, H.; Ouyang, D. Computational pharmaceutics - A new paradigm of drug delivery. Journal of Controlled Release 2021, 338, 119–136. [CrossRef]
.
LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems (Cambridge Texts in Applied Mathematics); Cambridge University Press, 2002; p. 578.
Ames, W.F. Numerical methods for partial differential equations; Academic Press, 1977; p. 365.
Gockenbach, M.S. Partial Differential Equations 2011. [CrossRef]
Fu, H.; Liu, C. A BUFFERED FOURIER SPECTRAL METHOD FOR NON-PERIODIC PDE. Article in International Journal of Numerical Analysis and Modeling 2011, 9, 460–478.
Multiphysics, C. Introduction to COMSOL multiphysics®. COMSOL Multiphysics, Burlington, MA, accessed Feb 1998, 9, 2018.
Inc., A. ANSYS Fluent User’s Guide 2024. Accessed: 2024-05-26.
Balay, S.; Abhyankar, S.; Adams, M.F.; Brown, J.; Brune, P.; Buschelman, K.; Dalcin, L.; Dener, A.; Eijkhout, V.; Gropp, W.D.; Kaushik, D.; Knepley, M.G.; McInnes, L.C.; Mills, R.T.; Munson, T.; Rupp, K.; Sanan, P.; Smith, B.F.; Zampini, S.; Zhang, H.; Zhang, H. PETSc/TAO Users Manual 2024. ANL-21/39 - Revision 3.21.
Laboratory, L.L.N. HYPRE: High Performance Preconditioners 2024. Accessed: 2024-05-26.
Developers, T. Trilinos Project Website 2024. Accessed: 2024-05-26.
Foundation, O. OpenFOAM: The Open Source CFD Toolbox User Guide 2024. Accessed: 2024-05-26.
Ozturk, S.S.; Palsson, B.O.; Dressman, J.B. Dissolution of lonizable Drugs in Buffered and Unbuffered Solutions. Pharmaceutical Research: An Official Journal of the American Association of Pharmaceutical Scientists 1988, 5, 272–282. [CrossRef]

Figure 1. Factors influencing oral drug absorption. Created with BioRender.com

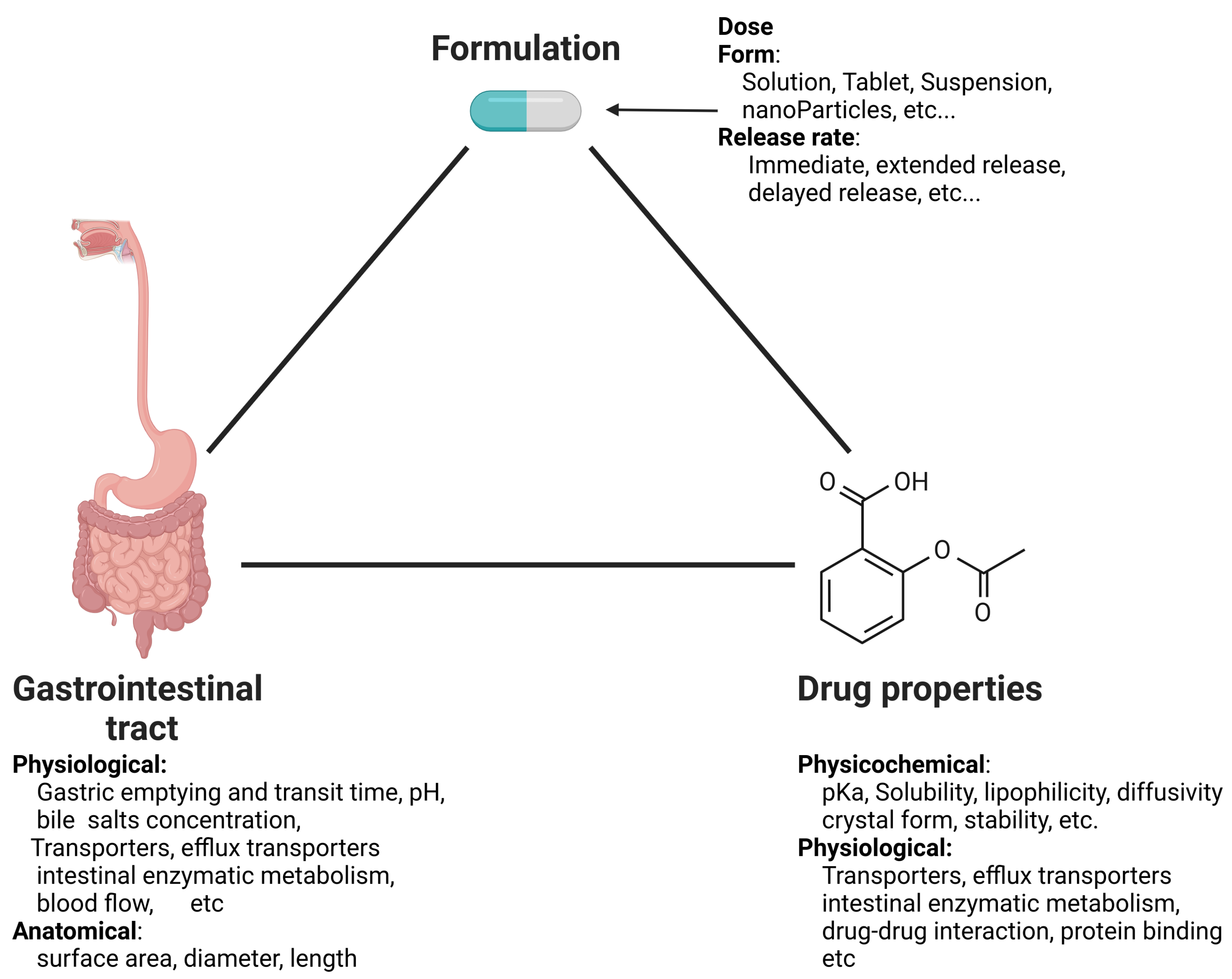
Figure 2. Schematic overview of oral drug absorption. Created with BioRender.com

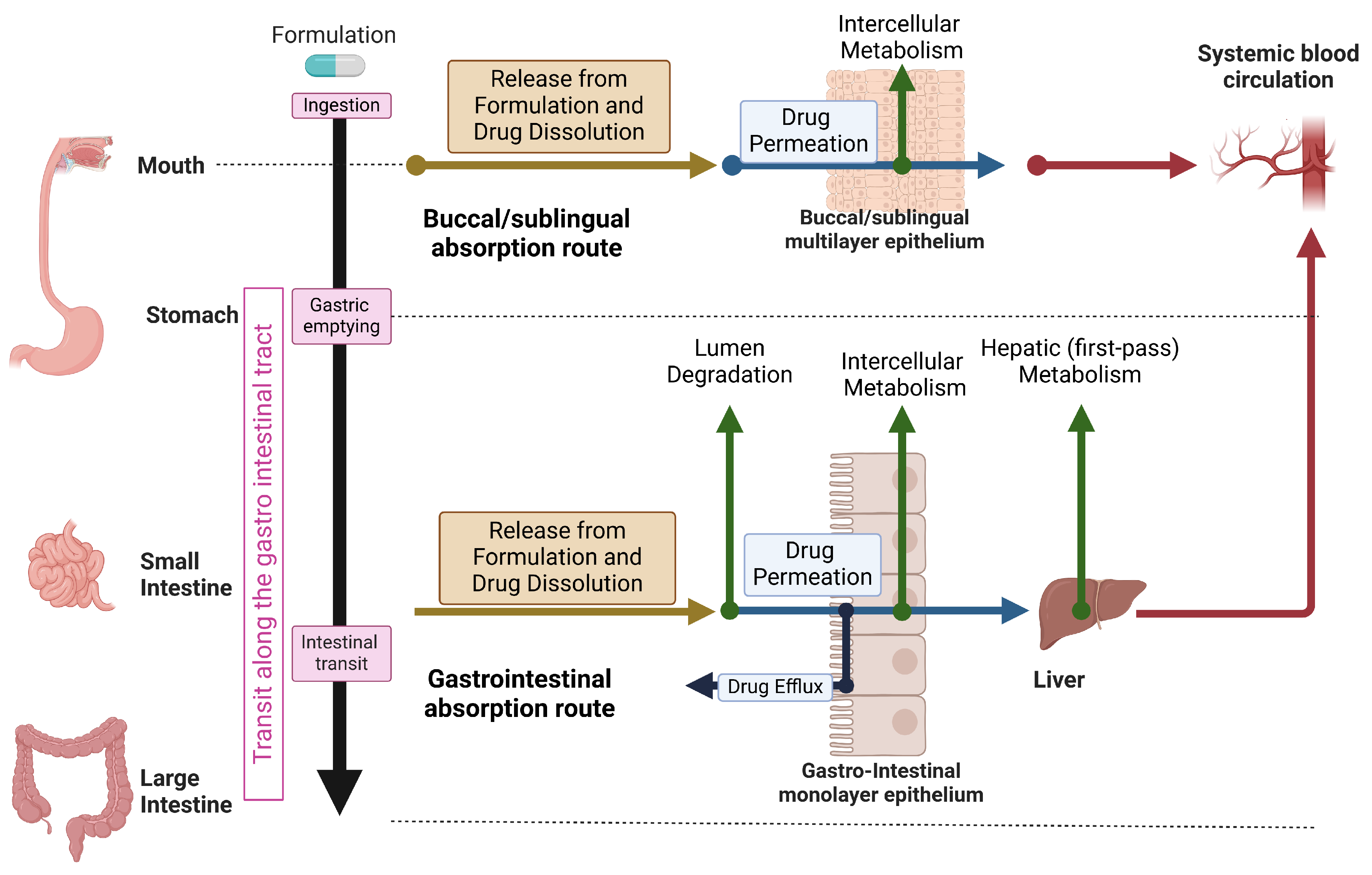
Figure 3. The types of models used to facilitate oral drug absorption.

Figure 4. Different supervised and unsupervised AI learning models/tools for pharmaceutical applications. Taken from Vora et al. [50].

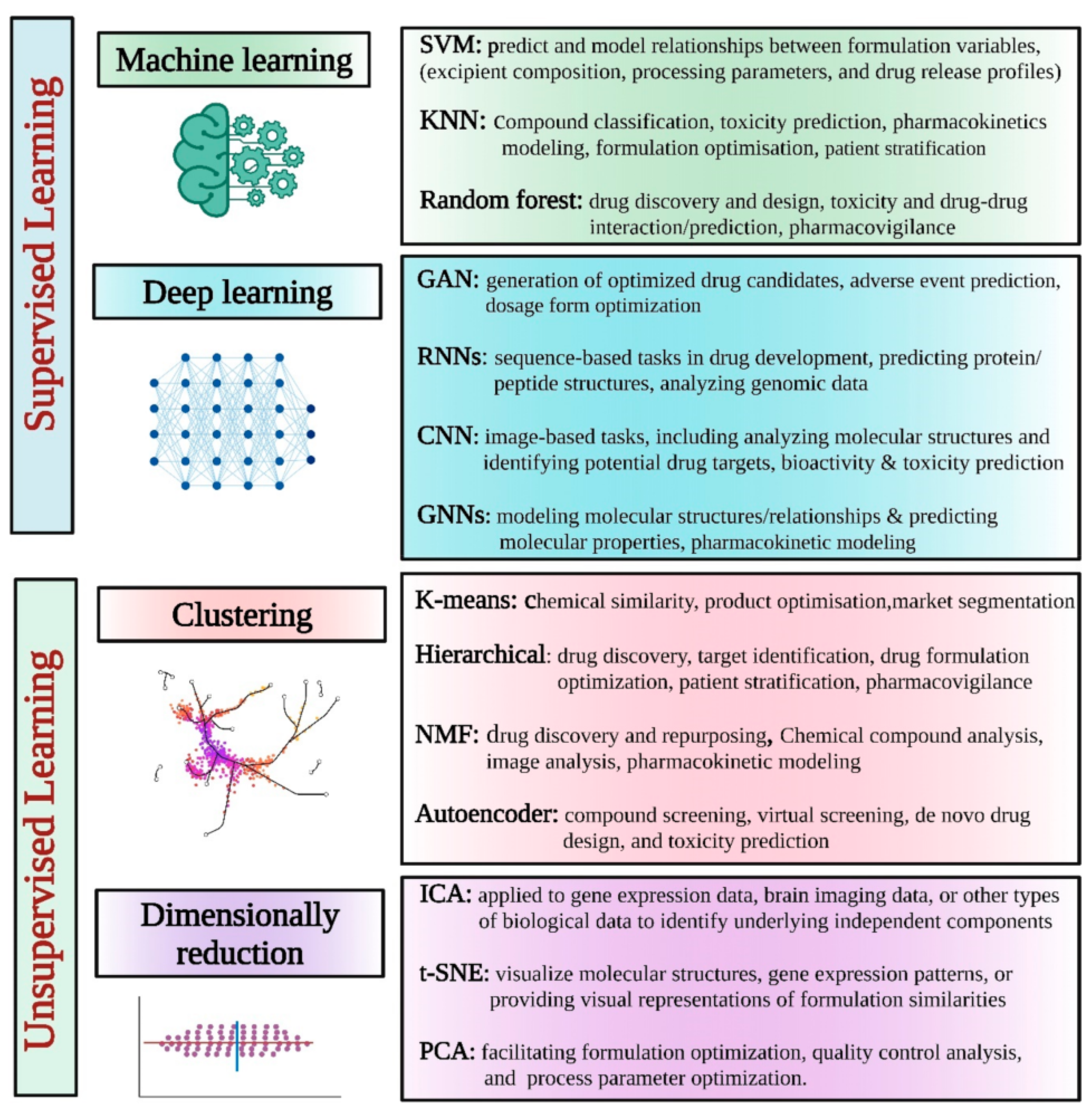
Figure 5. Schematic representation of the intestinal transit of dissolved drug in compartmental and continuous models. (a) Compartmental model: Mixing is implicitly determined by the number of compartments and their assigned volumes. (b) Continuous model: The mixing process is explicitly described by a ’mixing’ term with a coefficient obtained from experiments.

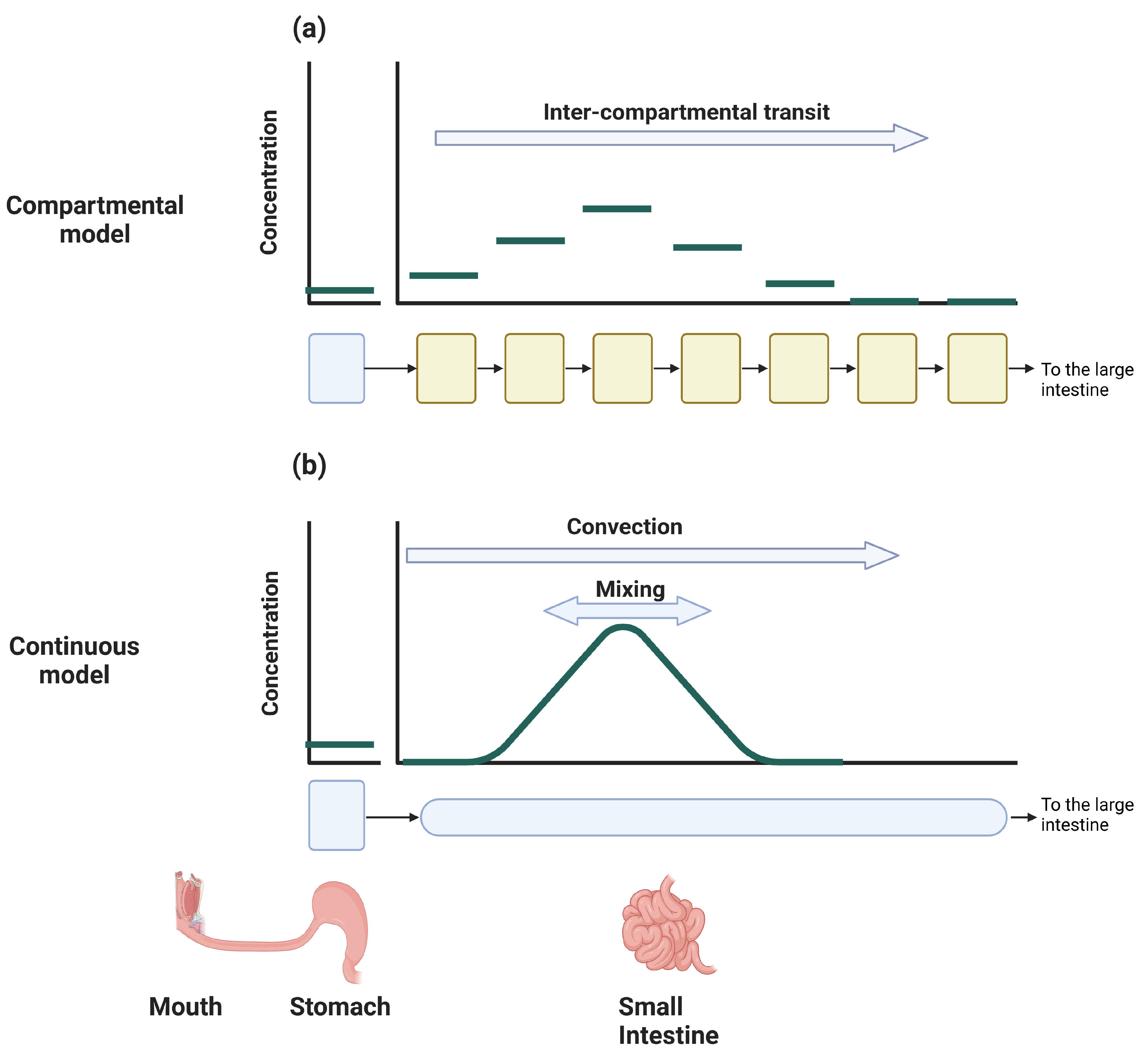
Table 1. The usage and limitations of the different modeling approach .

Modeling Approach	Usage/Properties	Limitations
Data-Driven	High throughput screening Extract patterns from large datasets	Requires large datasets Harder to provide a physical interpretation
Mechanism-based	Focuses on physiological processes Misprediction enhances comprehension.	Requires physiological understanding Results depend on the simplification methodology
First-Principles	Focuses on physical-chemical processes. Misprediction enhances comprehension	High complexity limits spatial and temporal scales Complex mathematics Intensive computational resources

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Advances in Modeling Approaches for Oral Drug Delivery: Artificial Intelligence, Physiologically Based Pharmacokinetic, and First-Principle Models

Abstract

1. Introduction

2. Overview of The Physiology and Mechanisms of Human Oral Drug Absorption

3. Approaches for Mathematical Modeling

4. Data-Driven Models

4.1. Conventional Pharmacokinetic

4.2. Conventional Quantitative Structure-Activity Relationship (QSAR)

4.3. Artificial Intelligence (AI)

5. Mechanism-Based Models

5.1. Quasiequalibrium

5.2. Steady-State

5.3. Dynamic Physiologically Based Pharmacokinetic (PBPK) Models

5.3.1. Compartmental Models

5.3.2. Continuous Models

6. First-Principles Models

6.1. Molecular Modeling

6.2. Continuum Models

7. Discussion

8. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations and Symbols

Appendix A. Partial Differential Equations (PDE)

Appendix A.1. Interpratation

Appendix A.2. Solving PDE

Appendix B. Dispersion Model with Dissolution

References

MDPI Initiatives

Important Links

Subscribe