Multi-Agent DRL-Based Dynamic Task Offloading in D2D-MEC Network to Minimize Average Task Delay with Deadline Constraints

Device to Device (D2D) is a pivotal technology in the next generation of communication, allowing for direct task offloading between mobile devices (MDs) to improve the efficient utilization of idle resources. This paper proposes a novel algorithm for dynamic task offloading between active MDs and idle MDs in the D2D-MEC (Mobile Edge Computing) system by deploying multi-agent deep reinforcement learning (DRL) to minimize the long-term average delay of delay-sensitive tasks under deadline constraints. Our core innovation is a dynamic partitioning scheme for idle and active devices in the D2D-MEC system, accounting for stochastic task arrivals and multi-time-slot task execution, which has been insufficiently addressed in existing literature. We adopt a queue-based system to formulate a dynamic task offloading optimization problem. To address the challenges of large action space and coupling of actions across time slots, we model the problem as a Markov Decision Process (MDP) and perform the multi-agent DRL through Multi-Agent Proximal Policy Optimization (MAPPO). We employ a centralized training with decentralized execution (CTDE) framework to enable each MD to make offloading decisions solely based on its local system state. Extensive simulations demonstrate the efficiency and fast convergence of our algorithm. In comparison with the existing sub-optimal results deploying single-agent DRL, our algorithm reduces the average task completion delay by 11.0% and the ratio of dropped tasks by 17.0%.

Keywords:

Subject: Computer Science and Mathematics - Computer Networks and Communications

1. Introduction

Recently , Mobile Edge Computing (MEC) has emerged as a promising computing paradigm that aims to reduce response time for computation tasks and enhance the Quality of Experience (QoE) of users by offloading tasks to edge servers [1]. However, the dynamic and random nature of task arrivals can lead to a significant increase in workload during certain periods. This surge in workload poses challenges for edge servers, making it difficult to meet the latency requirements of tasks like face recognition, virtual reality, augmented reality, online games, and more. D2D technology addresses this issue by enabling MDs to offload tasks directly to idle MDs, facilitating resource utilization and collaboration across the network. [2].

In D2D-MEC networks, MDs typically operate in two modes: requester MDs (active devices) and server MDs (idle devices) [2]. Requester MDs can offload tasks to server MDs or edge server, while server MDs not only handle their own tasks but also accept tasks from other requester MDs. This approach can effectively utilize idle resources within the network by enabling task offloading and collaboration among mobile devices. However, most existing research in this field primarily emphasizes static partitioning of MDs, where active devices and idle devices are pre-determined [3]. This restricts the flexibility of D2D communication in real-world scenarios. Additionally, the dynamic nature of task arrivals and the need for collaboration among active devices present considerable challenges for task offloading in D2D-MEC.

In order to ensure a high Quality of Experience (QoE) for users in Mobile Edge Computing (MEC) systems, it is crucial to process tasks within their deadlines, especially for delay-sensitive tasks. Zuo et al. [4] propose an alternating iterative algorithm, based on continuous relaxation and greedy rounding (CRGR), to achieve the Nash equilibrium. Abbas et al. [5] introduce an algorithm that maximizes the number of completed tasks through hierarchical and iterative allocation while minimizing energy consumption and monetary costs. Hamdi et al. [6] put forth a layered optimization method to maximize energy efficiency (EE) in D2D-MEC systems under delay constraints. However, none of the aforementioned studies considered stochastic task arrivals or dynamic partitioning of D2D devices.

The DRL algorithms have been successfully applied to the task offloading problem in MEC in various existing works [7,8,9,10,11]. [7,8] propose learning algorithms based on Q-learning or deep Q-learning network (DQN) for task offloading in MEC systems. Luo et al. [9] introduce a distributed learning algorithm based on the asynchronous advantage actor-critic (A3C) technique to optimize energy consumption and quality of experience in software-defined mobile edge networks. Li et al. [11], Qiao et al. [12] design a reinforcement learning framework for D2D edge computing and networks to address challenges related to the dynamic nature and uncertainty of the environment. However, most of the aforementioned studies predominantly utilize single-agent reinforcement learning algorithms or overlook the unknown load dynamics at each mobile device. Due to the dynamical and random nature of MEC systems, the decision space size increases exponentially with the number of mobile devices, which may bring the curse of dimensionality and struggle to converge for single-agent DRL algorithms.

In this paper, we investigate the dynamic task offloading problem in D2D-MEC system for delay-sensitive tasks under delay constraints. Our objective is to minimize the long-term average task delay under deadline constraints. To achieve this, we propose a dynamic D2D partitioning approach for MDs set based on queuing-based system, considering the dynamic load level of MDs and the presence of multiple time-slot tasks. To tackle the challenges posed by a huge decision space and coupling of actions across time slots, we formulate the problem as a cooperative Markov game and propose a multi-agent(MA) DRL-based algorithm based on MAPPO technique and implementation in CDTE manner. Our main contributions can be summarized as follows:

We introduce a novel dynamic D2D partitioning method based on queuing system for handling delay-sensitive tasks in D2D-MEC networks. Furthermore, we formulate the problem of minimizing the long-term average task delay under deadline constraints as a dynamic assignment problem, considering the random load level at MDs and multi-slot spanned tasks. Our proposed model surpasses existing approaches by providing a more precise characterization of task latency and improving the utilization of network computing resources. Additionally, it exhibits superior scalability and practicality.
We formulate the dynamic offloading problem as a cooperative Markov game and propose a multi-agent DRL-based algorithm utilizing the MAPPO technique to address the exponential growth of the decision space. Our proposed algorithm, based on the CDTE framework, enables online task decision-making in the dynamic and volatile network environment, relying solely on its local observations.
We conduct comprehensive experiments and the numerical results demonstrate the effectiveness and fast convergence of our proposed algorithm in a time-varying system environment. Compared to the sub-optimal outcomes obtained by deploying single-agent DRL, our algorithm, which enables distributed decision-making, achieves a significant reduction of 11.0% in average task completion delay and a 17.0% decrease in ratio of dropped tasks.

The rest of this paper is organized as follows. Section 2 presents a review of related works. In Section 3, we provide details of system model. In Section 4, we formulate the task offloading problem with delay constraint as a dynamic assignment problem. In Section 4, we propose a multi-agent DRL-based algorithm based on MAPPO technique. The experimental setup and numerical results are presented in Section 6.1. Finally, Section 7 concludes this paper.

2. Related Works

Studies on optimization to reduce the latency of delay-sensitive task in D2D-MEC network have been attract plenty of attentions. Yang et al. [13] propose a novel offloading framework for the multi-server MEC network to jointly optimize jobs offloading decision and computing resource allocation by using multi-task learning. Chai et al. [14] propose a heuristic algorithms based on Kuhn–Munkres algorithm and Lagrangian dual method for jointly computation offloading and resource allocation in a D2D-MEC systems. However, the above studies did not consider the cooperation among mobile devices. He et al. [15], He et al. [16] classify MDs into active and idle devices based on their ability to complete tasks on time through local computing or according to devices’ running states (including computing and transmitting states). Peng et al. [1] take into account the dynamic partitioning of devices, and proposed an online resource coordinating and allocating scheme based on Lyapunov optimization framework. But they assume that data computing and transmitting are implement in parallel without considering the waiting time in the queue.

Due to the ability to extract valuable knowledge from the environment and make adaptive decisions, DRL technology has received significant attention recently for edge computing task offloading [7,8,17,18]. Chen et al. [8] first propose a DQN-based algorithm to handle the huge state spaces and learn the optimal computation offloading policy. Wang et al. [19] propose a task offloading algorithm based on meta-reinforcement learning to enable the model to quickly adapt to different environments. However, the above research works are based on single-agent and make centralized decision, which maybe impractical in the real world as the number of MDs increasing due to exploration of the decision space in MEC system. Some works based on multi-agent RDL scheme are proposed for task offloading problems [20,21,22]. However, the majority of these approaches relied on the Multi-Agent Deep Deterministic Policy Gradient(MDDPG) framework, which may encounter training instability and necessitates training distinct policy networks and value networks for each individual agent. Consequently, this results in heightened computational complexity within large-scale multi-agent systems.

3. System Model

In this paper, we consider a heterogeneous MEC network system consisting of D mobile devices and an edge server with D2D communication support, which is denoted as

D = {0, 1, 2, \dots, D}

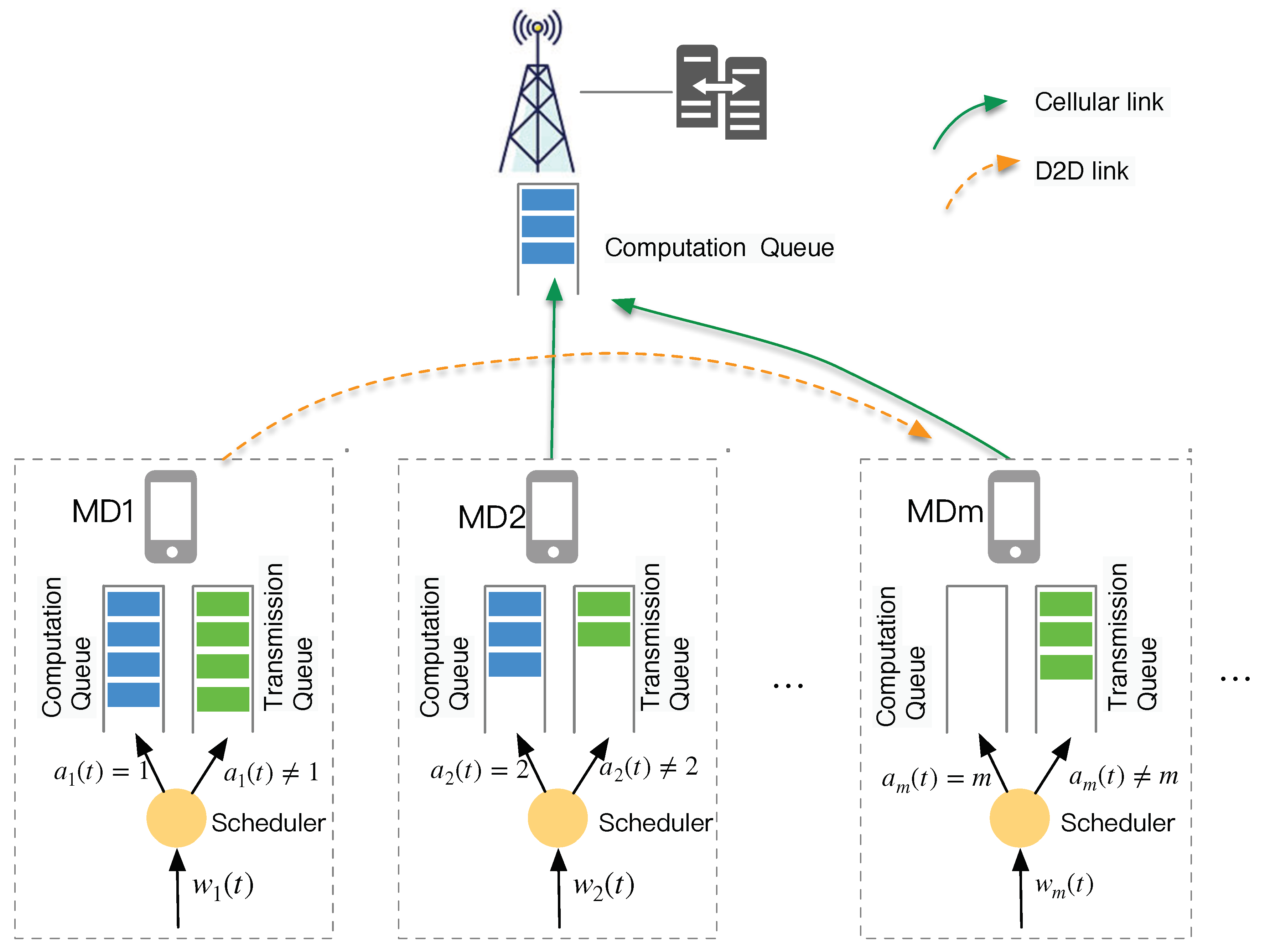
, where 0 represents the edge server. The system architecture is illustrated in Figure 1. We assume that the D2D-MEC system operates in discrete time slots represented by

T = {1, 2, \dots, T}

, where each time slot last for

Δ t

seconds. In each time slot, tasks are generated in each MD in a certain probability.

In the following subsections, we present the details of the device model, computation model, transmission model, energy model, and delay model employed in the system. The key notation used in this paper is summarized in Table 1.

To accurately mode the service time of computation task, we adopt queuing system to represent the task processing procedure. Each MD

d \in [1, D]

has two types of queues: computation queue

Q_{d}^{c o m p}

used for task execution and transmission queue

Q_{d}^{t r a n}

used to offload task to D2D devices or edge server. For the edge server, there only exists one computation queue, denoted as

Q_{0}^{c o m p}

Since the load of MDs are varying stochastic, we dynamically divide MDs set into idle devices (requester) and active devices (server) based on the backlog of their computation queues, which are defined as follows:

1) Idle device: In time slot t,

Q_{d}^{c o m p} (t) = \emptyset

. Idle devices can provide computing service for other MDs by D2D link.

2) Active device: In time slot t,

Q_{d}^{c o m p} (t) \neq \emptyset

. Active device only process task locally, or offload tasks to edge server or idle MDs, but cannot accept tasks from other MDs.

3.1. Task Model

We consider time-sensitive tasks, such as virtual reality (VR) or animation rendering, that can span over multiple time slots. At time t, each MD m stochastically generate a computation task, denoted as

w_{m} (t)

, specified by a three-tuple

< s_{m}^{t}, c_{m}^{t}, τ_{m}^{t} >

, where

s_{m}^{t}

represents the size of task w in 1-bit unit,

c_{m}^{t}

denotes the computation complexity of task w measured in the number of CPU cycles required for a 1-bit operation, and

τ_{m}^{t}

indicates the task deadline for completion (an integer multiple of the time slot). Each job should be processed within

τ_{m}^{t}

time slot to avoid incurring an expiration penalty.

We assume that each task is indivisible such that the system adopt a binary offloading mode, which allows tasks to be executed either locally or offloaded to edge server through cellular links, or transferred to idle devices via D2D links. Each MD employs with a scheduler that determines the target device for task execution. The active devices set at slot t is denoted as

AD (t) = {a d_{1}, a d_{2}, \dots, a d_{| AD (t) |}}

, and the idle devices at slot t is denoted as

ID (t) = {i d_{0}, i d_{1}, i d_{2}, \dots, i d_{| ID (t)} |}

, where

i d_{0}

represents the edge server which is always regarded as idle device due to its sufficient computing resource. Hence, we have

| AD (t) | + | ID (t) | = D

3.2. Computation Model

The computation queue follows the First-In-First-Out (FIFO) principle, where tasks in the queue buffer must wait for the completion of the preceding task before being scheduled. The computing delay of a task is composed of two parts: waiting time and execution time.

Let

\tilde{t}

denote the time slot of task

w_{m} (t)

placed in the queue

Q_{d}^{c o m p}

at device

d \in D

, and

l_{m, d}^{c o m p} (t)

denote the time slot of task

w_{m} (t)

to be completely processed or dropped in device d. Note that if task is computed locally, we have

\tilde{t} = t

and

l_{m, d}^{c o m p} (t)

can be written as

l_{m}^{c o m p} (t)

. Hence, the amount of time slots that task

w_{m} (t)

will wait for scheduling to execute in computation queue

Q_{d}^{c o m p}

can be expressed as follows :

ϕ_{m, d}^{c o m p} (t) = {[\max_{t^{'} \in \{0, 1, \dots, t - 1\}, d^{'} \in [1, D]} l_{d^{'}, d}^{c o m p} (t^{'}) - \tilde{t} + 1]}^{+}

(1)

where the operator

{[x]}^{+} = m a x \{0, x\}

, and we set

l_{d^{'}, d}^{c o m p} (0) = 0

for presentation simplicity. The term

\max_{t^{'} \in \{0, 1, \dots, t - 1\}, d^{'} \in [1, D]} l_{d^{'}, d}^{c o m p} (t^{'})

determines the time slot when all the task placed in the computation queue

Q_{d}^{c o m p}

before time slot

\tilde{t}

has either been processing or dropped. Hence,

ϕ_{m, d}^{c o m p} (t)

determines the number of waiting time slots in the computation queue.

For each task

w_{m} (t)

that arrives at the computation queue

Q_{d}^{c o m p}

at the beginning of time slot

\tilde{t}

, it will either be processed completely or dropped in slot

l_{m, d}^{c o m p} (t)

\begin{matrix} l_{m, d}^{c o m p} (t) = \min {\tilde{t} + ϕ_{m, d}^{c o m p} (t) + ⌈ \frac{s_{m}^{t} c_{m}^{t}}{f_{d} Δ t} ⌉ - 1, t + τ_{m}^{t} - 1} \end{matrix}

(2)

where

f_{d}

represents the process rate of device d. Specifically, the task

w_{m} (t)

will be scheduled to execute at the beginning of slot

\tilde{t} + ϕ_{m, d}^{c o m p} (t)

. is the ceiling function, which means devices only switch to execute next task at the beginning of a new time slot. The term

⌈\frac{s_{m}^{t} c_{m}^{t}}{f_{d} Δ t}⌉

represents the total time slots required to process task completely. Considering the deadline of task, here use min operator to determine the minor value of process completely and the drop time slot.

In the case when multiple offloaded tasks or a newly generated task arrive at device d simultaneously, they will enter queue

Q_{d}^{c o m p}

according to the following rules: (1) offloaded tasks have higher priority than locally generated tasks. (2) among the offloaded tasks, tasks with shorter deadlines will be placed ahead in the queue.

3.3. Task Offloading Model

We assumed that cellular links and D2D links operate on different frequency bands and adopt orthogonal frequency division multiple access (OFDMA) for access. Therefore, communication between any two devices does not interfere with the communication between other devices [23]. The transmission queue

Q_{d}^{t r a n}, d \in [1, D]

also follows FIFO principle. Similar to computation queue, let

l_{m}^{t r a n} (t)

denote the slot when

w_{m} (t)

is successfully transmitted to the target device or dropped since from it enters queue

Q_{d}^{t r a n}

, that we have the amount of time slots that

w_{m} (t)

will wait for transfer in

Q_{d}^{t r a n}

as follows:

ϕ_{m}^{t r a n} (t) = {[\max_{t^{'} \in \{0, 1, \dots, t - 1\}} l_{m}^{t r a n} (t^{'}) - t + 1]}^{+}

(3)

where

l_{m}^{t r a n} (t)

represents the time slot that task

w_{m} (t)

leaves the queue

Q_{d}^{t r a n}

, and we set

l_{m}^{t r a n} (0) = 0

for presentation simplicity. The term

\max_{t^{'} \in \{0, 1, \dots, t - 1\}} l_{m}^{t r a n} (t^{'})

determines the time slot when all the task placed in the transmission queue before time slot t has either been processing or dropped.

In mobile device

m \in [1, D]

, task

w_{m} (t)

placed in the transmission queue at the beginning of time slot t, then task

w_{m} (t)

will either be completely sent or dropped in time slot

l_{m}^{t r a n} (t)

\begin{matrix} l_{m}^{t r a n} (t) = \min \{t + ϕ_{m}^{t r a n} + \underset{θ}{argmin} \{s_{m}^{t} \leq \sum_{i = t}^{t + θ} r_{m} (i) Δ t\}, t + τ_{m}^{t} - 1\} \end{matrix}

(4)

where

r_{m} (t)

represents the transmission rate of MD m in t. Specifically, the task

w_{m} (t)

will start to transmit at the beginning of time slot

t + ϕ_{m}^{t r a n} (t)

. The term

\underset{θ}{argmin} \{s_{m}^{t} \leq \sum_{i = t}^{t + θ} r_{m} (i) Δ t\}

represents the total time slots required to transfer data successfully, where

r_{m} (i) Δ t

represents transfer data size in slot i. Hence,

l_{m}^{t r a n} (t)

decides the time slot when task will either be sent successfully or dropped.

The transmission rate

r_{m} (t)

of MD m at t can be calculated based on Shannon’s theorem:

r_{m} (t) = B_{m} (t) {log}_{2} (1 + \frac{p_{m} h_{m}^{d} (t)}{N_{0}})

(5)

where

B_{m} (t)

is the bandwidth allocated to MD m and

p_{m}

represents the transmission power of device m, which is a constant value.

h_{m}^{d} (t)

represents the channel gain between device m and target device d at time slot t, which keeps fix within a time slot and follows a Rayleigh distribution that varies over time.

N_{0}

represents the white noise during transmission. Here we adopt the average bandwidth allocation scheme, that the total bandwidth is allocated equally among each pair of communicating nodes.

Due to the negligible size of task results compared to the original task data, the transmission time for task result return is extremely short. Therefore, similar to [17], the transmission time for task result return is ignored.

3.4. Task Delay Model

Let

a_{m} (t) = m

denote the target device to execute task

w_{m} (t)

, we have

a_{m} (t) \in ID (t) ⋃ {m}

a_{m} (t) = m

, which means task

w_{m} (t)

will be processed locally, base on eq.(2) we have the total delay

L_{m} (t) = l_{m}^{c o m p} (t) - t + 1

, which can be written as

L_{m}^{l o c} (t) = \min \{ϕ_{m}^{c o m p} (t) + ⌈\frac{s_{m}^{t} c_{m}^{t}}{f_{m} Δ t}⌉, τ_{m}^{t}\}

(6)

a_{m} (t) \neq m

, then task

w_{m} (t)

will be offloaded to remote device d to process. Such that transmission delay is

L_{m}^{t r a n} (t) = l_{m}^{t r a n} (t) - t + 1

, processing delay is

L_{m}^{c o m p} (t) = ϕ_{m, d}^{c o m p} (t) + ⌈ \frac{s_{m}^{t} c_{m}^{t}}{f_{m} Δ T} ⌉

. Hence we have the total delay of remote execution task as :

L_{m}^{r e m} (t) = \min \{L_{m}^{t r a n} (t) + L_{m}^{c o m p} (t), τ_{m}^{t}\}

(7)

Therefore, the total delay of task

w_{m} (t)

can be derived as follows:

L (m, t) = 1_{(a_{m} (t) = m)} L_{m}^{l o c a l} (t) + 1_{(a_{m} (t) \neq m)} L_{m}^{r e m} (t)

(8)

where

1 (\cdot)

is an indicator function that outputs 1 when · is true and 0 otherwise.

4. Problem Formulation

In this paper, we aim to minimize the long-term average task delay under deadline constraints by making task offloading decisions

A (t) = {a_{1} (t), a_{2} (t), \dots, a_{d} (t)}

at each MD in each time slot t. The objective function at slot t is written as

\frac{1}{D} \sum_{d = 1}^{D} L (d, t)

. Therefore, the task offloading optimization can be formulated as:

P 1 :

\begin{matrix} (P 1) min_{A (t)} \frac{1}{T} \sum_{t = 1}^{T} \frac{1}{D} \sum_{d = 1}^{D} L (d, t) \\ s . t . \end{matrix}

(9a)

\begin{matrix} L (d, t) \leq τ_{d}^{t}, \forall d \in [1, D] \end{matrix}

(9b)

\begin{matrix} a_{d} (t) \in ID (t) ⋃ {d}, \forall d \in [1, D] \end{matrix}

(9c)

In problem

P 1

, constraint (9a) ensures tasks are completed or dropped upon reaching their deadlines, minimizing average task delay. Constraint (9b) specifies the target device for task execution, including both idle devices and the local device where the task is generated.

Problem

P 1

can be classified as a dynamic assignment problem, characterized by its complexity in high-dimensional space and being NP-hard. The time complexity of this problem increases exponentially with the cardinality of the sets of available devices

| AD (t) |

and idle devices

| ID (t) |

at each time slot t. Additionally, the strong coupling of action decisions across multiple time slots exacerbates the computational challenge.

Even the offline information of system is known advance, it is challenging to be solve by traditional technique due to the curse of dimensionality. Hence, we propose a novel algorithm with low complexity that operates online using a multi-agent DRL framework.

5. Algorithm Design

Proximal Policy Optimization (PPO) is a robust policy gradient algorithm within the actor-critic framework, demonstrating exceptional performance in diverse reinforcement learning tasks [24]. Its simplicity and effectiveness have made it a popular choice for numerous RL applications, addressing the stability and sample efficiency concerns of traditional policy gradient methods through careful policy network update clipping and the use of a surrogate objective function.

Moving beyond single-agent DRL methods, MAPPO extends the capabilities of PPO, particularly excelling in scenarios where multiple agents need to interact and make decisions independently. This extension offers a scalable and efficient solution for cooperative decision-making in complex environments, showcasing its significance in addressing challenges that go beyond the scope of single-agent approaches.

In this section, we present a novel framework for task offloading based on multi-agent DRL technique. Leveraging the MAPPO technique, our proposed algorithm, builds upon the cooperative decision-making abilities of MAPPO to effectively address the dynamic offloading challenges in MEC systems. By formulating the problem as a cooperative Markov game and employing the CTDE architecture, our algorithm provides a robust and efficient solution for dynamic offloading in MEC systems, effectively managing the heavy communication burden and offering scalability in decision-making processes.

Firstly, we formulate the problem of minimizing long-term average task delay as a cooperative Markov game.

5.1. MDP of P1

5.1.1. State

Our algorithm incorporates both local and global states. The local state includes the system information of each MD and is used to train the Actor network for individual decision-making. On the other hand, the global state comprises the entire system information at the current time slot and is utilized to train the Critic network.

At the beginning of slot t, each device

m \in [1, D]

observes its state information, which includes task properties such as task size, task complexity, and expiration time, as well as information about the computation queue, transmission queue, and channel state. Let

B_{m}^{c o m p} (t) = \max_{t^{'} \in 0, 1, \dots, t - 1, m^{'} \in [1, D]} l_{m^{'}, m}^{c o m p} (t^{'}) - t + 1

denote the backlog of computation queue at slot t, and

B_{m}^{t r a n} (t) = \max_{t^{'} \in 0, 1, \dots, t - 1} l_{m}^{t r a n} (t^{'}) - t + 1

denote the backlog of transmission queue MD, we obtain the local state vector as follows:

S_{m} (t) = (s_{m}^{t}, c_{m}^{t}, τ_{m}^{t}, B_{m}^{c o m p} (t), B_{m}^{t r a n} (t), h_{m} (t), \vec{i d (t)})

(10)

where

\vec{i d (t)}

is a two dimension vector, consists of the index and the backlog of computation queue of all idle devices. We assume that each idle MD will broadcast its state of computation queue at the end of each time slot. For device m at time slot t, if no task is generated,

s_{m}^{t}, c_{m}^{t}, τ_{m}^{t}

are both set to be 0.

The global state integrates the local state information from each MD and the queue information from the edge server, denoted as:

S (t) = (S_{1} (t), S_{2} (t), \dots, S_{D} (t))

(11)

5.1.2. Action

At the beginning of slot t, when MD m generates a task

w_{m} (t)

, the scheduler decides whether to execute the task locally or offload it to an idle device. Therefore, the action vector of each MD can be present as:

A (t) = (i d_{0}, i d_{1}, i d_{2}, \dots, i d_{ID}) \cup m

(12)

5.1.3. Reward

According to problem

P 1

, the optimization objective is the ratio of the total task delay to the task deadline. Therefore, the reward signal can be directly defined as:

r (t) = \frac{\sum_{m \in [1, D]} 1_{(a_{m}^{t} = m)} L_{m}^{l o c a l} (t) + 1_{(a_{m}^{t} \neq m)} L_{m}^{r e m} (t)}{\sum_{m \in [1, D]} 1 (s_{m}^{t}) \neq 0)}

(13)

where the item

\sum_{m \in [1, D]} 1 (s_{m}^{t}) \neq 0)

represents all tasks generated in time slot t.

5.2. Mutil-Agent DRL-Based Algorithm

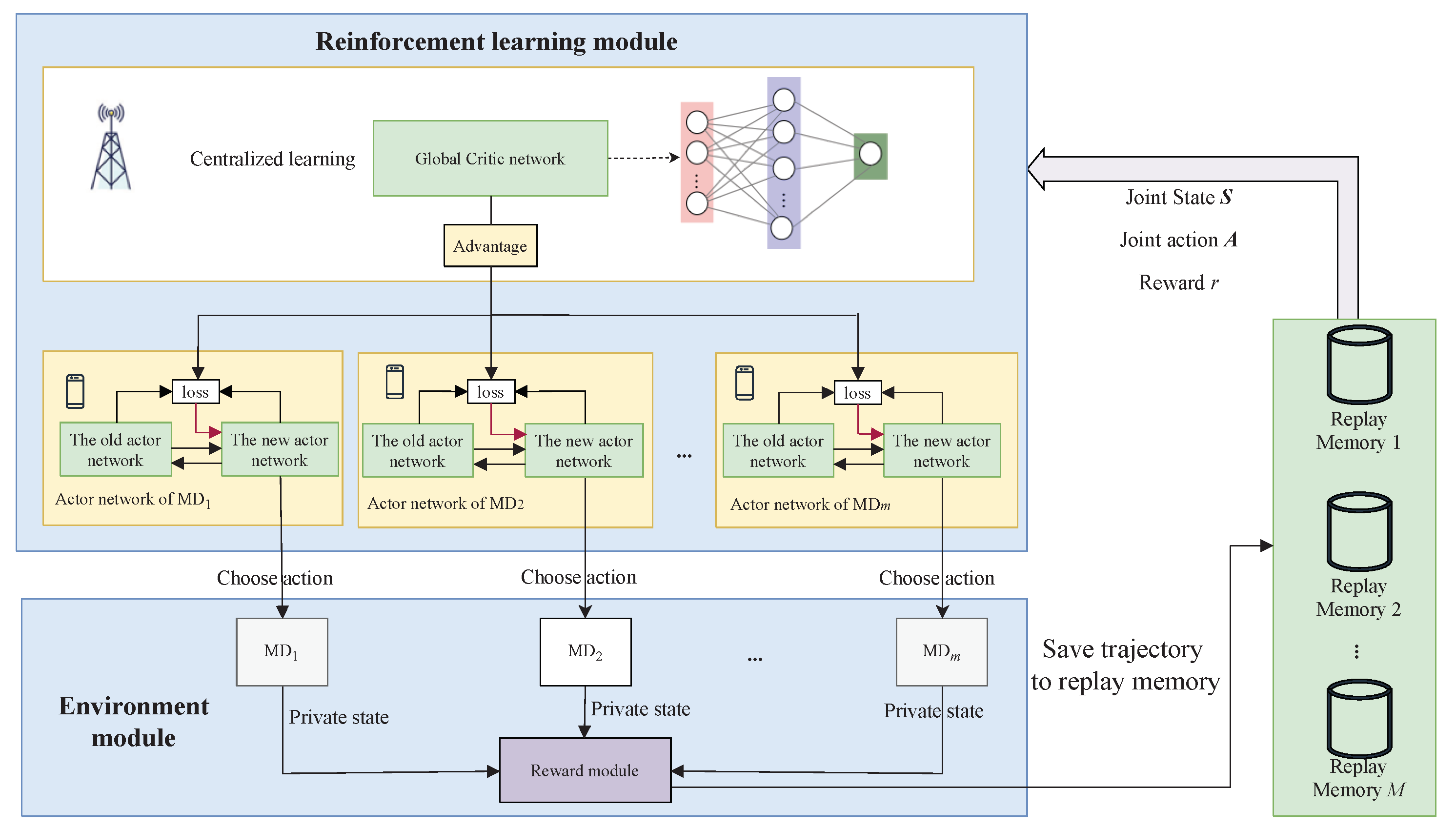
To reduce the exponential decision space of P1, we propose a multi-agent DRL-based algorithm that leverages the state-of-the-art multi-agent RL named MAPPO. MAPPO exhibit significantly higher algorithmic runtime efficiency and comparable data sample efficiency compared to off-policy algorithms under limited computing resources, which make it well-suited for MEC system. Here we adopt the popular CTDE architecture, which consists of two crucial components: one central Critic network and multi Actor networks. The architecture of the Multi-agent DRL algorithm is depicted as Figure 2. The process involves two phases, described below.

1) Centralized training

We utilize a global Critic network to obtain the accurate evaluations of the global system states to guide the training of Actor networks on each MD. Similar to PPO algorithm, these networks are trained as follows:

a) Firstly, each agent m interacts with environment by randomly sampling actions based on its observed system state

S_{m} (t)

and executing the selected action. Then agents observe the local state in the next time slot, obtain the reward

r_{m} (t + 1)

. The trajectory data

(S_{m} (t), a_{m} (t), r_{m} (t + 1), S_{m} (t + t))

is stored in the local experience replay pool.

Afterward, agent m sent its local state

S_{m} (t)

, the next time step state

S_{m} (t + 1)

, and local reward

r_{m} (t + 1)

to the central controller for further processing.

b) By aggregating the information from each agent, we acquire the global state

S (t)

S (t + 1)

and global reward

r (t)

. These values serve as inputs to the Critic network to for computing the state values

V (S)

and

V (S^{'})

. Here we employ a target network to compute the Temporal Difference (TD) target and TD error

δ_{t} = r (t) + γ V (S (t + 1)) - V (S (t)

, where

γ

is the discount factor.

In the training phase, the system samples a batch of trajectories from the replay memory in the central controller and performs updates on the Critic network. The update equation for the Critic network can be be expressed as follows:

\begin{matrix} L (ϕ_{c r i}) = E_{S (t), A (t)} [ & r (t) + γ V_{ϕ_{c r i}} (S (t + 1)) - V_{ϕ_{c r i}} {(S (t))]}^{2} \end{matrix}

(14)

where

V_{ϕ_{c r i}} (.)

is the value function of Critic network under parameter

ϕ_{c r i}

We employ Generalized Advantage Estimation (GAE) trick to compute the advantage function as follows,

{\hat{A}}_{t} = \sum_{l = 0}^{\infty} {(γ λ)}^{l} δ_{t + l}

(15)

where

γ

is used to determines the importance given to future rewards, while

λ

is a parameter similar to

T D (λ)

, with a trade-off between variance and bias.

δ_{t + l}^{V}

refers to the

l - s t e p

TD error, which is computed as

δ_{t + l} = r (t + l) + γ V (t + l + 1) - V (t + l)

The value of GAE will be broadcasted to each agent for training the actor network.

c) Upon receiving the advantage function

{\hat{A}}_{t}

, each agent conducts batch sampling from its own experience replay pool and calculates the surrogate value by considering the probability distribution of old and new actions along with the advantage function

{\hat{A}}_{t}

. This surrogate value is used to update the parameters of the actor network. The update equation for the Actor network at agent m is as follows:

\begin{matrix} L (θ_{m}^{a c t}) = E_{π_{θ_{m}}} [min (ψ_{t} (θ_{m}^{a c t}) {\hat{A}}_{t}, clip (ψ_{t} (θ_{m}^{a c t}), 1 - ϵ, 1 + ϵ) {\hat{A}}_{t})] \end{matrix}

(16)

where

ψ_{t} (θ_{m}^{a c t}) = \frac{π_{θ_{m}} (a_{m} (t) | S_{m} (t))}{π_{θ_{m}}^{o l d} (a_{d} (t) | S (t))}

represents the probability ratio,

ϵ

is a hyperparameter in PPO that limits the deviation between the new and old networks and

{\hat{A}}_{t}

is used to assess the quality of action

A (t)

in state

S (t)

2) Decentralized Execution

After completing centralized training, the Critic network becomes unnecessary. The Actor network is deployed to each individual MD and utilizes locally observed system states for decision-making. Communication is not required during the decision-making process. Decentralized decision-making is fast and can be performed in real-time.

The details of our MARL dynamic offloading algorithm are summarized in Algorithm 1.

Algorithm 1:Multi-agent DRL-Based Dynamic Offloading Algorithm

6. Simulation Result and Analyses

6.1. System Parameter Settings

To verify our algorithm, we conducted extensive simulations, demonstrating its convergence and performance superiority compared to baseline algorithms. Table 2 lists the basic system parameters.

The centralized Critic networks and the Actor network in each MD utilize a three-layer network structure with 64 nodes in the intermediate layer. During the neural network training process, a batch size of 64 is employed, the learning rate is set to 1e-3, and the number of MDs is fixed at 20. The task generation probability gradually increases from 0.1 to 0.5. Network parameters are updated using the Adam optimizer. To ensure high randomness and unpredictability in the experimental data generation, the relationship between random numbers and the task generation probability determines whether a task is generated. The channel gains between devices follow the Rayleigh distribution.

6.2. Algorithm Convergence Performance

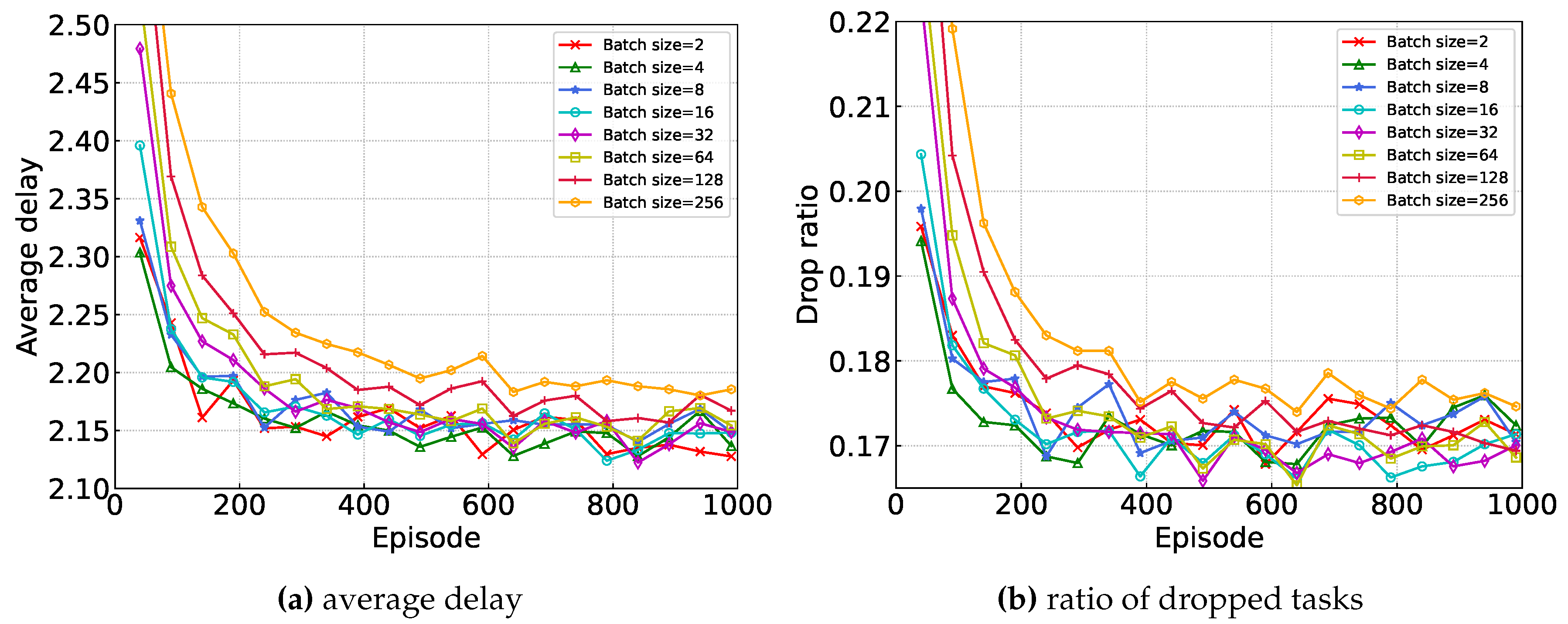
In this part, we mainly study the convergence performance of the proposed algorithm under different values of different hyper-parameters. We consider 1000 episodes and each episode has 100 time frames. The experimental results are shown in Figure 3, where the X-axis represents the episodes and the Y-axis represents the average completion delay of the task (the average time required by the task from creation to completion).

Figure 3 shows the convergence of the proposed algorithm under different batch sizes which means the number of training examples utilized in one iteration. Generally, as the batch size increases, the gradient estimation during each training step becomes more accurate, thereby reducing the variance of parameter updates. However, larger batch sizes may make the model more prone to getting stuck in local minima and lose some ability to escape from them. On the other hand, smaller batch sizes can provide more randomness, helping the model to jump out of local minima. As we can see from Figure 3, changing the parameter of batch size has only about a 1% impact on performance. Thus we choose appropriate batch size(e.g., 64) to speed up the convergence speed without reducing the performance significantly.

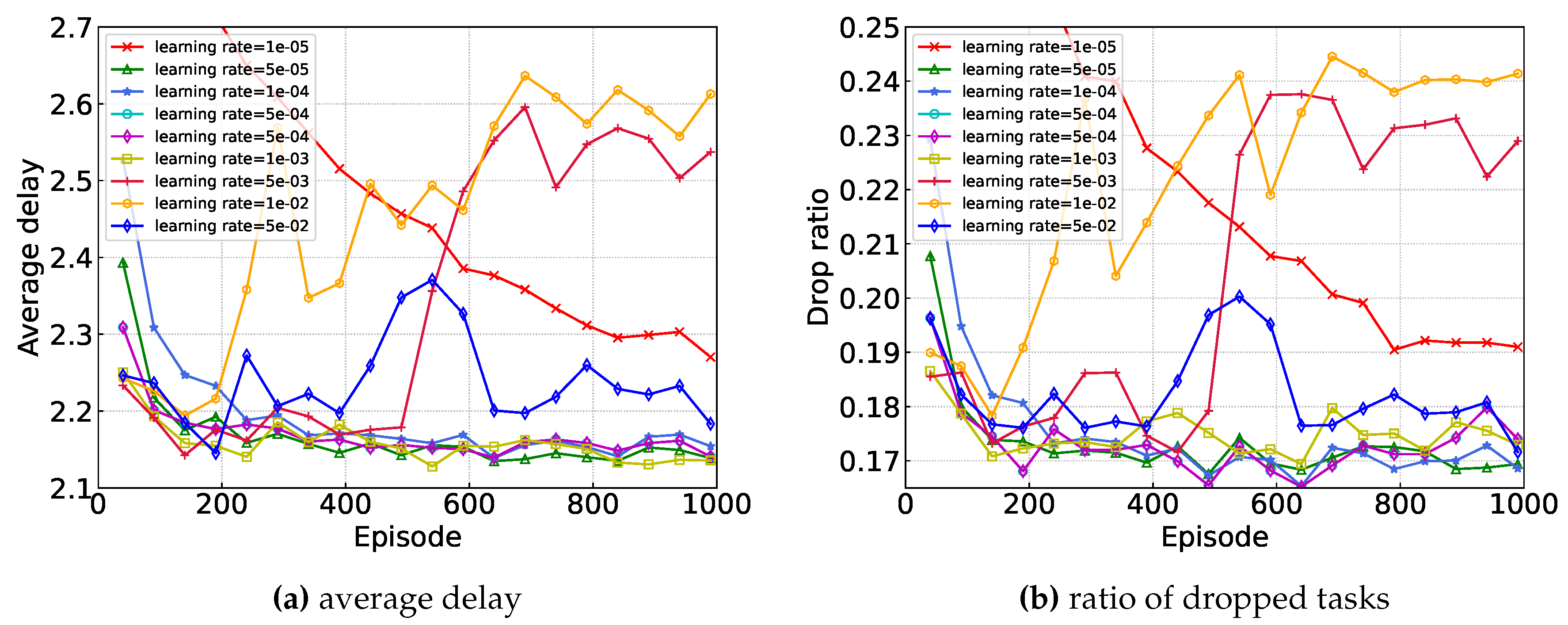
Figure 4 shows the convergence of the proposed algorithm under different learning rates which is a tuning parameter in an optimization algorithm that determines the step size at each iteration while moving toward the minimum of a loss function. In Figure 4, when learning rate is too small (e.g. 1e-5) ,it will lead to a relatively slow convergence and therefore require more computational resources. But if the learning rate is too large(e.g. 1e-2, 5e-2) , the neural network can’t converge to a good performance because of the great vibration of loss function.

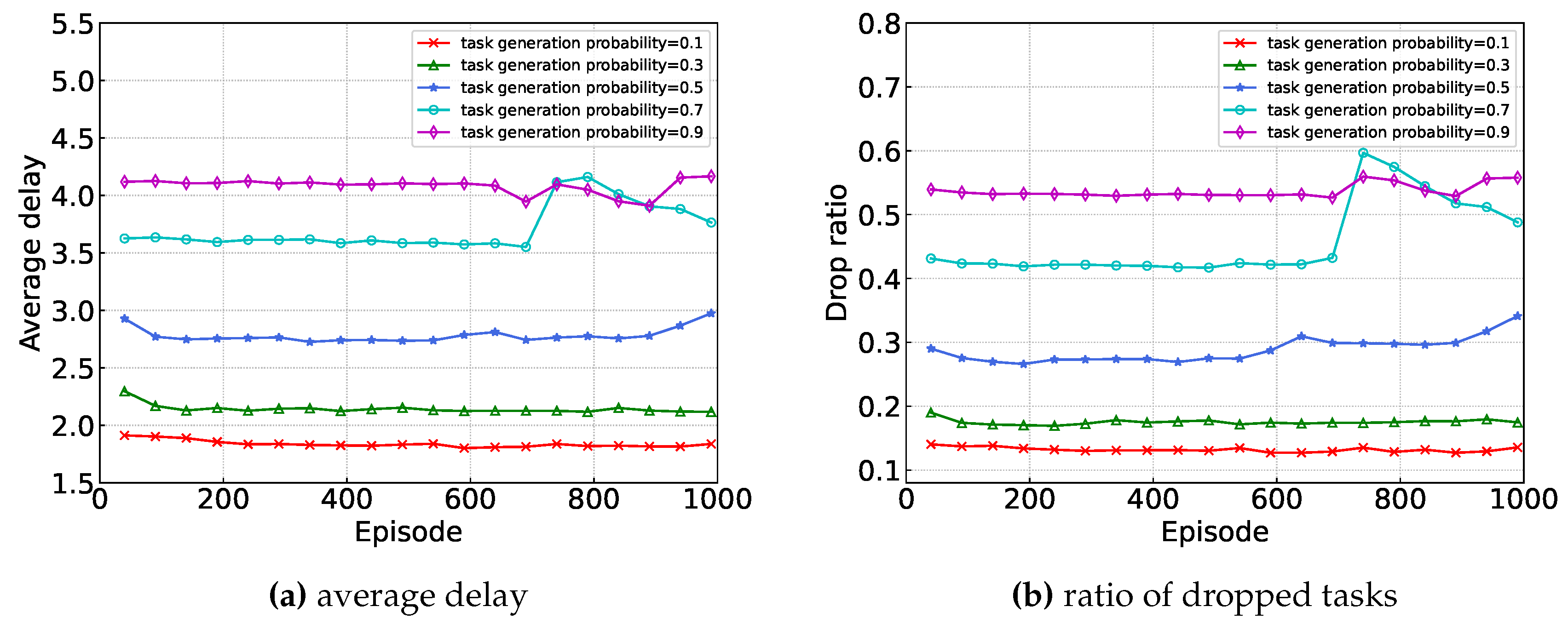
Figure 5 shows the convergence of the proposed algorithm under different task generation probabilities, where the task generation probability is the probability of each device producing a task in each time frames. As shown in Figure 5, there is an obvious correlation between task generation probability and algorithm performance: the larger the task generation probability, the larger the average delay. This is because with limited computing and communication resources, the higher the probability of task generation, the less resources are allocated on average, and the higher the delay of task completion.

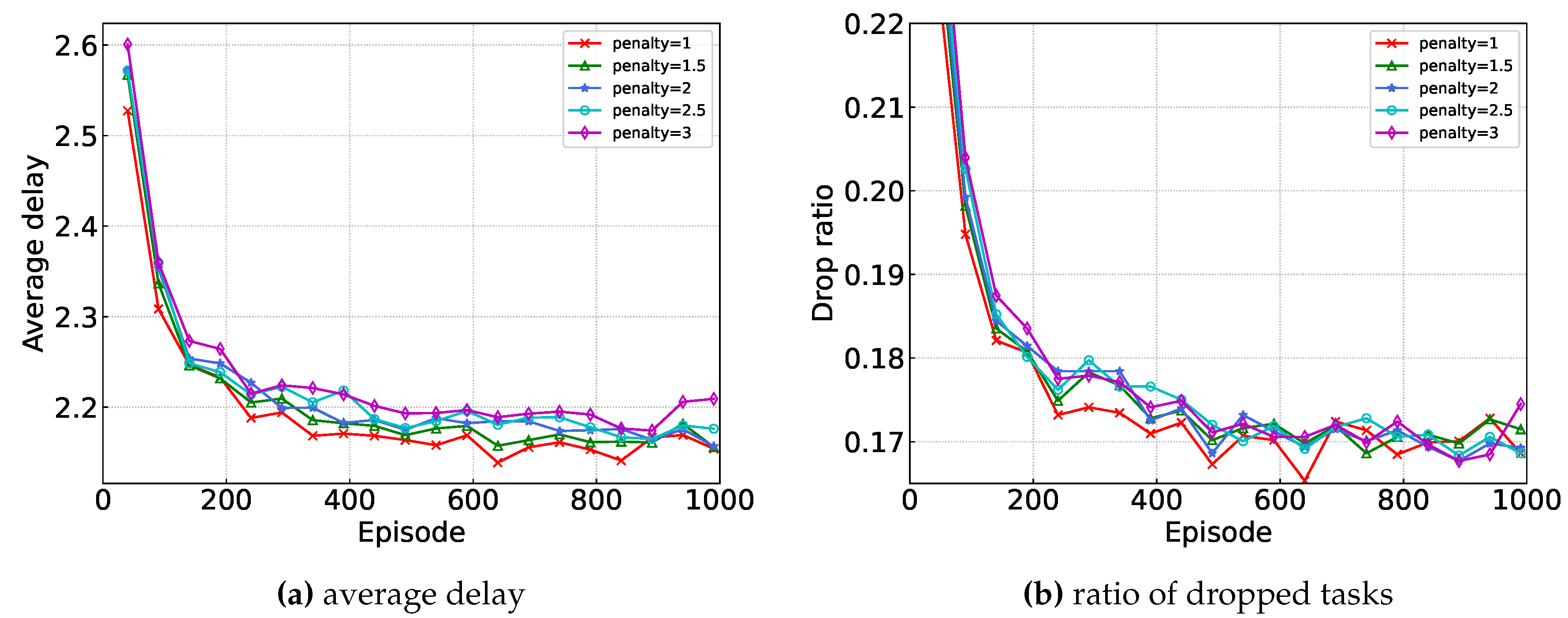
Figure 6 illustrates the performance of proposed algorithm under different drop penalty values, where the penalty value are represented as:

C (S (t), A (t)) = \{\begin{matrix} P e n a l t y V a l u e, & if task is dropped \\ \frac{1_{(a_{m} (t) = m)} L_{m}^{l o c a l} (t) + 1_{(a_{m} (t) \neq m)} L_{m}^{r e m} (t)}{τ_{m}^{t}}, & if task is not dropped \end{matrix}

(17)

Generally, as the penalty value increases, the model should prone to dropout and thus result in a decrease in the drop ratio. Interestingly, the experimental results show the opposite behavior. This may be due to the change from a continuous range of penalty values with an upper limit of 1 to discrete values. This change may make it difficult for the Critic network to converge, resulting in the observed results.

6.3. Performance Comparison Evaluation

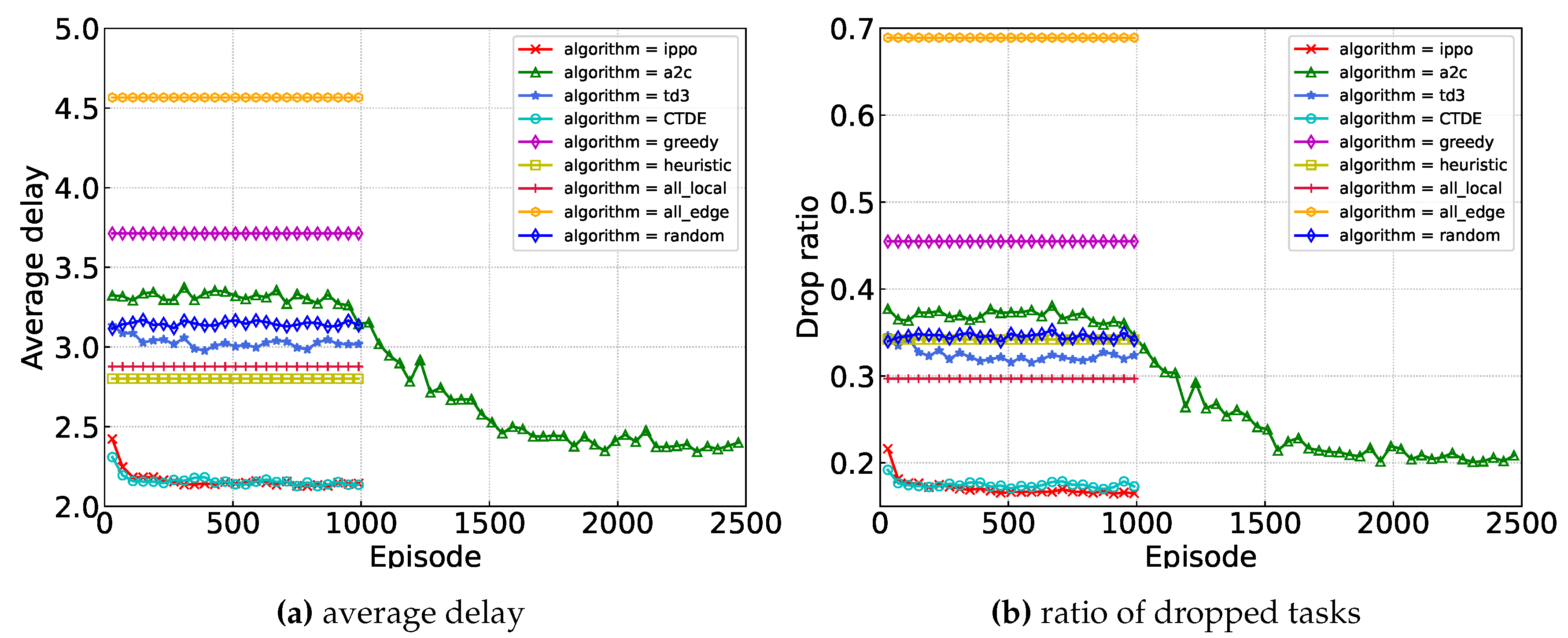
To valuate the performance of our algorithm, we consider the following benchmark algorithms:

1) IPPO: Each agent employs an independent PPO algorithm to select actions based on global state information;

2) A2C: A2C algorithm is used to sample from

{(1 + N)}^{N}

types of actions;

3) TD3:The multidimensional discrete action space is transformed into multiple continuous actions, and the selection of an action is based on the shortest Euclidean distance [2];

4) Heuristic: If a task can be completed within two time slots, it is computed locally; otherwise, it is offloaded to the edge server;

5) All_local: All tasks are executed locally;

6) All_edge: All tasks are offloaded to edge server;

7) Greedy: The action with the shortest expected time, considering the current queue situation and channel status, is selected;

8) Random: Actions for each task are randomly selected. Here we use two performance metrics: the average delay and the drop ratio(ratio of the number of timeout tasks to the total number of tasks).

Figure 7 illustrates the convergence of our proposed algorithm and baseline algorithms. It can be observed that our algorithm presents similar performance to the IPPO algorithm in terms of the delay metric. However, our algorithm only relies on local state information for decision-making, significantly reducing communication overhead. In comparison to the sub-optimal A2C algorithm, our approach achieves an 11.0% reduction for the delay metric and a 17.0% reduction for the drop ratio metric.

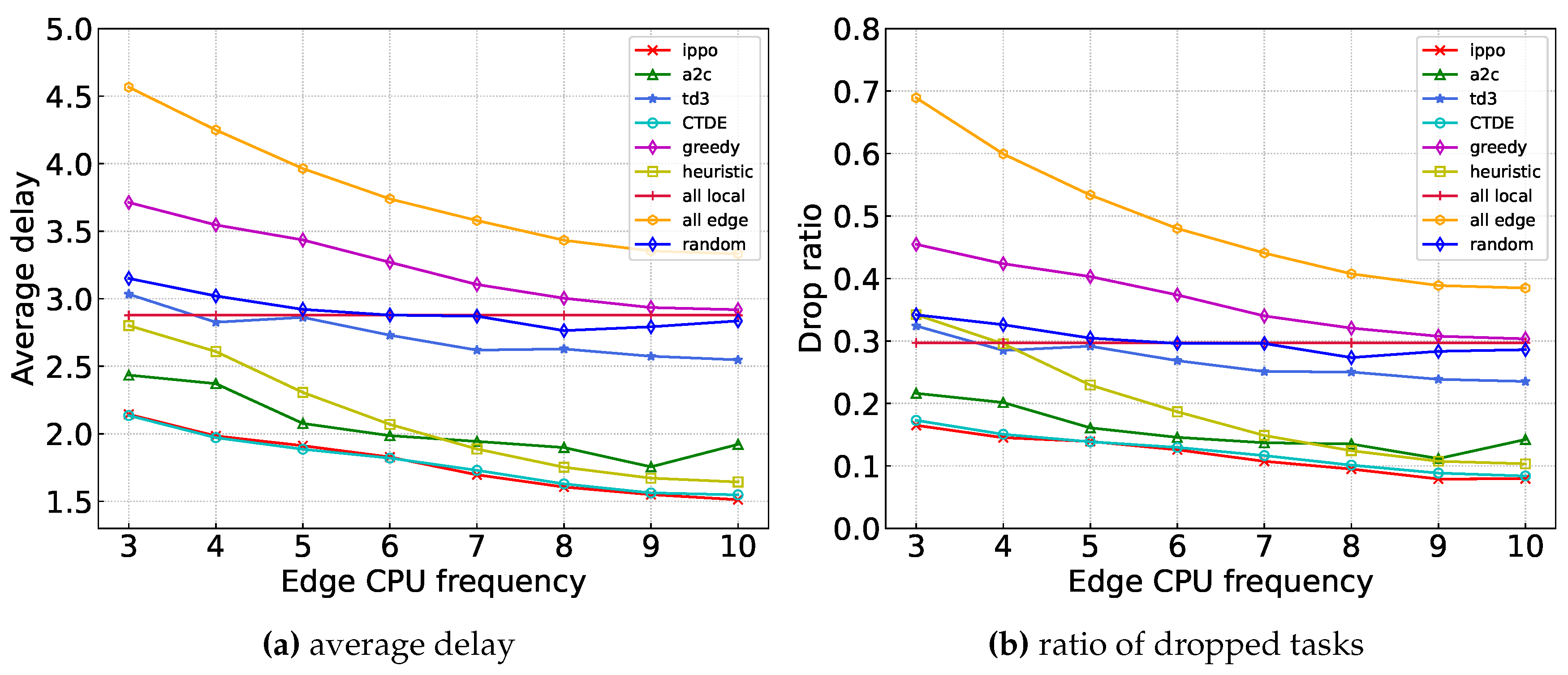
Figure 8 illustrates the comparison of the average delay and drop ratio between our proposed algorithm and the baseline algorithms under different edge server frequencies. As the computing power of the edge server increases, the overall system computing resources increase, resulting in decreased average delay and drop ratio. It is important to note that the all_local algorithm, which does not rely on edge servers, maintains a stable performance curve.

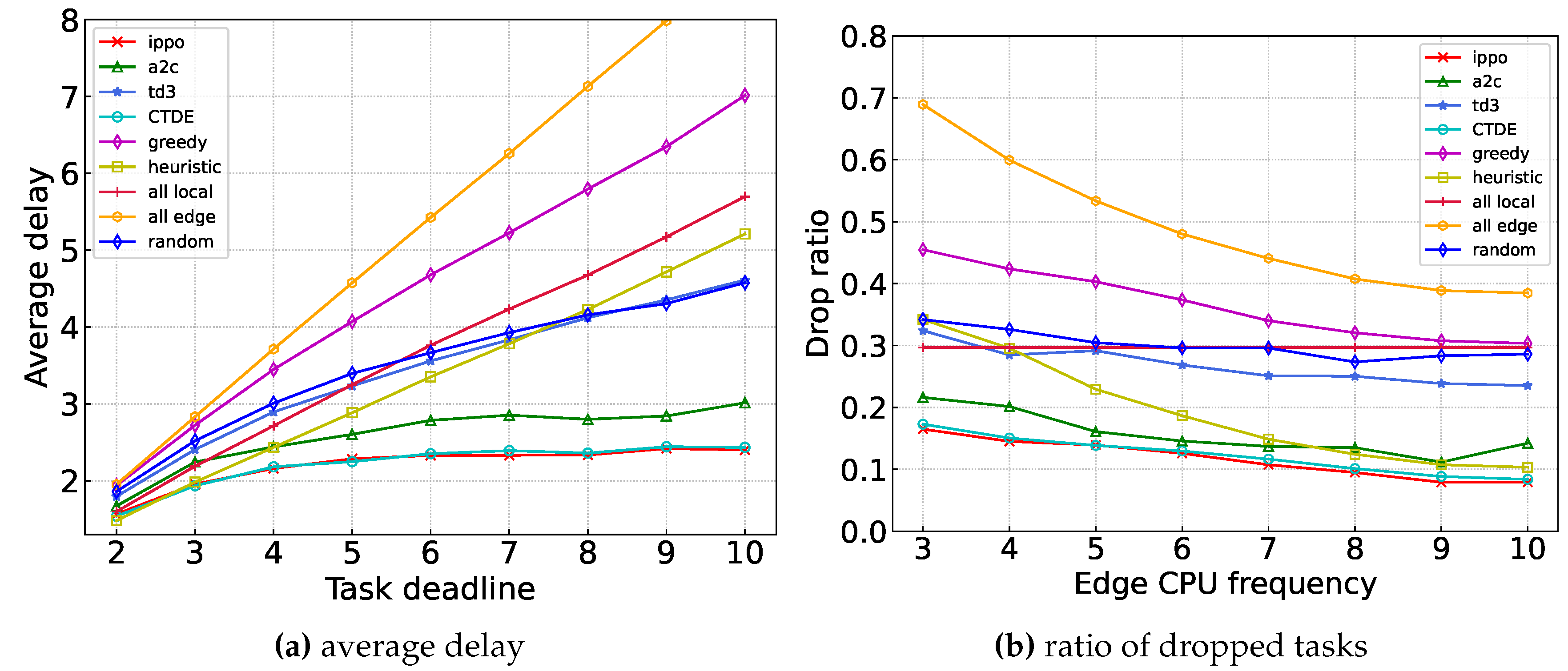
Figure 9 shows the comparison of the average delay and drop ratio between our proposed algorithm and the baseline algorithms under different task deadlines. From Fig. Figure 9, it is evident that several benchmark algorithms, such as all_local, all_edge, or greedy, face a limitation imposed by the deadline, causing the average delay to approach the upper limit, i.e., the deadline itself. Consequently, as the deadline increases, the average delay also grows, while the drop ratio decreases due to the slack in the deadline. In contrast, the CTDE, IPPO, and A2C algorithms exhibit superior performance. When the deadline is less than 5, their curves resemble those of other algorithms, although relatively flat. However, as the deadline continues to increase, these algorithms reach a stable curve, suggesting that the tasks have been fully processed.

7. Conclusion

In this paper, we investigate the dynamic task offloading problem in D2D-MEC systems for delay-sensitive tasks under delay constraints. We propose a dynamic partitioning approach for D2D MDs set based on queuing-based system. We formulate the minimization long-term average task delay with deadline constraints problem as a cooperative Markov game and propose a multi-agent DRL-based algorithm. Our proposed algorithm is implemented in a CTDE manner, which enables each MD to make offloading decisions solely based on its local system state. Extensive simulations show the efficiency of our algorithm. For the future work, we will consider bandwidth resource allocation strategy in the D2D-MEC network.

Author Contributions

Conceptualization, H.H. and X.M. ; methodology, X.Y. and H.H.; software, X.M.; validation, H.H. and X.L.; investigation, X.M.; resources, H.H.; writing—original draft preparation, X.M.; writing—review, H.H., X.Y., X. L. and H.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research is supported in part by the Science and Technology Foundation of Guangdong Province, China, No. 2021A0101180005. The corresponding author is Xuefeng Liao.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Available on request.

Acknowledgments

The authors would like to thank the editor and all reviewers for their valuable comments and efforts on this article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Peng, J.; Qiu, H.; Cai, J.; Xu, W.; Wang, J. D2d-assisted multi-user cooperative partial offloading, transmission scheduling and computation allocating for mec. IEEE Transactions on Wireless Communications 2021, 20, 4858–4873. [Google Scholar] [CrossRef]
Zhang, T.; Zhu, K.; Wang, J. Energy-efficient mode selection and resource allocation for d2d-enabled heterogeneous networks: A deep reinforcement learning approach. IEEE Transactions on Wireless Communications 2020, 20, 1175–1187. [Google Scholar] [CrossRef]
Fang, T.; Yuan, F.; Ao, L.; Chen, J. Joint task offloading, d2d pairing, and resource allocation in device-enhanced mec: A potential game approach. IEEE Internet of Things Journal 2021, 9, 3226–3237. [Google Scholar] [CrossRef]
Zuo, Y.; Jin, S.; Zhang, S.; Han, Y.; Wong, K.-K. Delay-limited computation offloading for mec-assisted mobile blockchain networks. IEEE Transactions on Communications 2021, 69, 8569–8584. [Google Scholar] [CrossRef]
Abbas, N.; Sharafeddine, S.; Mourad, A.; Abou-Rjeily, C.; Fawaz, W. Joint computing, communication and cost-aware task offloading in d2d-enabled het-mec. Computer Networks 2022, 209, 108900. [Google Scholar] [CrossRef]
Hamdi, M.; Hamed, A.B.; Yuan, D.; Zaied, M. Energy-efficient joint task assignment and power control in energy-harvesting d2d offloading communications. IEEE Internet of Things Journal 2021, 9, 6018–6031. [Google Scholar] [CrossRef]
Huang, L.; Bi, S.; Zhang, Y.-J.A. Deep reinforcement learning for online computation offloading in wireless powered mobile-edge computing networks. IEEE Transactions on Mobile Computing 2019, 19, 2581–2593. [Google Scholar] [CrossRef]
Chen, X.; Zhang, H.; Wu, C.; Mao, S.; Ji, Y.; Bennis, M. Optimized computation offloading performance in virtual edge computing systems via deep reinforcement learning. IEEE Internet of Things Journal 2018, 6, 4005–4018. [Google Scholar] [CrossRef]
Luo, J.; Yu, F.R.; Chen, Q.; Tang, L. Adaptive video streaming with edge caching and video transcoding over software-defined mobile networks: A deep reinforcement learning approach. IEEE Transactions on Wireless Communications 2019, 19, 1577–1592. [Google Scholar] [CrossRef]
Zhao, N.; Liang, Y.-C.; Niyato, D.; Pei, Y.; Wu, M.; Jiang, Y. Deep reinforcement learning for user association and resource allocation in heterogeneous cellular networks. IEEE Transactions on Wireless Communications 2019, 18, 5141–5152. [Google Scholar] [CrossRef]
Li, G.; Chen, M.; Wei, X.; Qi, T.; Zhuang, W. Computation offloading with reinforcement learning in d2d-mec network. In 2020 International Wireless Communications and Mobile Computing (IWCMC), pages 69–74. IEEE, 2020.
Qiao, G.; Leng, S.; Zhang, Y. . Online learning and optimization for computation offloading in d2d edge computing and networks. Mobile networks and applications 2019, 1–12. [Google Scholar] [CrossRef]
Yang, B.; Cao, X.; Bassey, J.; Li, X.; Qian, L. Computation offloading in multi-access edge computing: A multi-task learning approach. IEEE transactions on mobile computing 2020, 20, 2745–2762. [Google Scholar] [CrossRef]
Chai, R.; Lin, J.; Chen, M.; Chen, Q. . Task execution cost minimization-based joint computation offloading and resource allocation for cellular d2d mec systems. IEEE Systems Journal 2019, 13, 4110–4121. [Google Scholar] [CrossRef]
He, Y.; Ren, J.; Yu, G.; Cai, Y. . D2d communications meet mobile edge computing for enhanced computation capacity in cellular networks. IEEE Transactions on Wireless Communications 2019, 18, 1750–1763. [Google Scholar] [CrossRef]
He, Y.; Ren, J.; Yu, G.; Cai, Y. Joint computation offloading and resource allocation in d2d enabled mec networks. In <italic>ICC 2019-2019 IEEE International Conference on Communications (ICC)</italic>, pages 1–6. IEEE, 2019b.
Tang, M.; Wong, V.W.S. Deep reinforcement learning for task offloading in mobile edge computing systems. IEEE Transactions on Mobile Computing 2020. [Google Scholar] [CrossRef]
Bi, S.; Huang, L.; Wang, H.; Zhang, Y.-J.A. Lyapunov-guided deep reinforcement learning for stable online computation offloading in mobile-edge computing networks. IEEE Transactions on Wireless Communications 2021, 20, 7519–7537. [Google Scholar] [CrossRef]
Wang, J.; Hu, J.; Min, G.; Zomaya, A.Y.; Georgalas, N. . Fast adaptive task offloading in edge computing based on meta reinforcement learning. IEEE Transactions on Parallel and Distributed Systems 2020, 32, 242–253. [Google Scholar] [CrossRef]
Huang, X.; Leng, S.; Maharjan, S.; Zhang, Y. . Multi-agent deep reinforcement learning for computation offloading and interference coordination in small cell networks. IEEE Transactions on Vehicular Technology 2021, 70, 9282–9293. [Google Scholar] [CrossRef]
Sacco, A.; Esposito, F.; Marchetto, G.; Montuschi, P. . Sustainable task offloading in uav networks via multi-agent reinforcement learning. IEEE Transactions on Vehicular Technology 2021, 70, 5003–5015. [Google Scholar] [CrossRef]
Gao, H.; Wang, X.; Ma, X.; Wei, W.; Mumtaz, S. . Com-ddpg: A multiagent reinforcement learning-based offloading strategy for mobile edge computing. arXiv 2020, arXiv:2012.05105,. [Google Scholar]
Wang, H.; Lin, Z.; Lv, T. Energy and delay minimization of partial computing offloading for d2d-assisted mec systems. In 2021 IEEE Wireless Communications and Networking Conference (WCNC), pages 1–6. IEEE, 2021.
Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]

Figure 1. Architecture of D2D-MEC network.

Figure 2. Architecture of Multi-agent DRL algorithm

Figure 3. Performance evaluation under different batch sizes.

Figure 4. Performance evaluation under different batch sizes.

Figure 5. Performance evaluation under different task generation probabilities.

Figure 6. Performance evaluation under different penalties.

Figure 7. Performance of different algorithms.

Figure 8. Performance of different algorithms across different edge cpu frequency.

Figure 9. Performance of different algorithms across different task deadline.

Table 1. KEY NOTATIONS.

Symbol	Definition
$D$	The set of mobile deivces
$T$	The whole time slots
$Δ t$	The duration of time slot t
$w_{m} (t)$	The computation task generated on mobile device m at time slot t
$s_{m}^{t}$	The size of task $w_{m} (t)$
$c_{m}^{t}$	The computation complexity of task $w_{m} (t)$
$τ_{m}^{t}$	The deadline of task $w_{m} (t)$
$A (t)$	The task offloading decision for all MDs at time slot t
$a_{m}^{t} (t)$	The offloading decision of the mth active device at time slot t
$Q_{d}^{c o m p}$	The computing queue of mobile device d
$Q_{d}^{t r a n}$	The transmission queue of mobile device d
$l_{m, d}^{c o m p} (t)$	The time slot when task $w_{m} (t)$ is fully processed at mobile device d
$l_{m}^{t r a n} (t)$	The time slot when task $w (m, t)$ transmission is completed at device m
$ϕ_{m, d}^{c o m p} (t)$	The waiting time slots of task $w_{m} (t)$ in computation queue at mobile device d
$ϕ_{m}^{t r a n} (t)$	The waiting time slots of task $w_{m} (t)$ in transmission queue at mobile device m
$r_{m} (t)$	The transmission rate of mobile device m at time slot t
$p_{m}$	The transmission power at device m
$h_{m}^{d} (t)$	The channel gain between active device m and idle device d at slot t
$N_{0}$	The white noise
$B_{m} (t)$	The bandwidth of device m at time slot t
$L (m, t)$	The total duration of task $w (m, t)$ from generation to execution completion
$S_{m} (t)$	Local observation information of device m on time slot t
$S (t)$	Global state information on time slot t
$r (t)$	Reward in time slot t

Table 2. Simulation system parameters.

parameters	values
Mobile device number D	20
The CPU frequency of mobile device $f_{d}$	2 GHz
The CPU frequency of edge server $f_{0}$	3 GHz
Minimum task size $s_{m i n}$	3 Mbits
Maximum task size $s_{m a x}$	10 Mbits
Minimum task complexity $c_{m i n}$	0.5 gigacycles per Mbits
Maximum task complexity $c_{m a x}$	2 gigacycles per Mbits
Minimum task generation probability	0.1
Maximum task generation probability	0.5
Total bandwidth B	3 MHz
Device transmission power $p_{d}$	3 W
White noise $N_{0}$	-14 dbm\Hz

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Multi-Agent DRL-Based Dynamic Task Offloading in D2D-MEC Network to Minimize Average Task Delay with Deadline Constraints

Abstract

1. Introduction

2. Related Works

3. System Model

3.1. Task Model

3.2. Computation Model

3.3. Task Offloading Model

3.4. Task Delay Model

4. Problem Formulation

5. Algorithm Design

5.1. MDP of P1

5.1.1. State

5.1.2. Action

5.1.3. Reward

5.2. Mutil-Agent DRL-Based Algorithm

6. Simulation Result and Analyses

6.1. System Parameter Settings

6.2. Algorithm Convergence Performance

6.3. Performance Comparison Evaluation

7. Conclusion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe