Central Difference Variational Filtering Based on Conjugate Gradient Method for Distributed Imaging Application

Preprint

Article

Central Difference Variational Filtering Based on Conjugate Gradient Method for Distributed Imaging Application

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

06 June 2024

Posted:

07 June 2024

You are already at the latest version

Alerts

Abstract

Airborne distributed position and orientation system (ADPOS), which integrates multi-inertia measurement units(IMUs), data-processing computer and Global Navigation Satellite System (GNSS), serves as a key sensor in new higher-resolution airborne remote sensing, such as array SAR, multinode imaging loads and so on. ADPOS can provide multinode high accuracy spatio-temporal reference information to realize multinode motion compensation with the various state estimation methods such as Central Difference Kalman Filtering (CDKF), modifed CDKF. However, these methods focus on noise optimization based on known nonlinear models and its linear minimum variance estimation criterion, which cannot gain better estimation performance for high-dimensional nonlinear systems. For this reason, the variational optimization process based on conjugate gradient algorithm is proposed for the estimation of filtering update step, which is more efficient than linear minimum variance estimation criterion. Therefore, aiming at ADPOS with high-dimensional and nonlinearity, Central Difference Variational Filtering (CDVF) using variational optimization based on conjugate gradient algorithm for mean correction in the filtering update stage is devoted to advancing the estimation accuracy of multinode motion parameters. A real ADPOS flight test has been conducted, the experimental results show that the accuracy of the slave motion parameters has a distinct progress than the up to date CDKF, and the compensation performance is distinct.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

With the development of airborne remote sensing system, its higher imaging resolution and three-dimensional imaging is increasingly arousing more interest in new research field, such as interferometric SAR (InSAR) and array antenna SAR imaging, where both locate multiantenna on different positions [20].Correspondingly, the motion compensation equipment is developed from a single POS to multiple in different locations with the assistance of ADPOS [1,5,20].In terms of system architecture of ADPOS, a integrated system collecting a high precision inertial measurement unit (IMU) and GNSS [6] are viewed the master POS, which integrates strapdown inertial solution and state correction to fuse the information of inertial and satellite sensors based on the linear model, while several low cost slave systems rely on fusing the information of the master and itself to improve parameter accuracy using various state estimation algorithms, then the whole system provides multinode high-frequency and high-accuracy motion parameters to the multinode loads for higher-resolution three-dimension imaging [7].

In order to compensate motion errors for multinode loads, ADPOS has to address the deterministic errors by calibration and stochastic errors using recursive state estimation. Comparing with deterministic errors, stochastic errors are more difficult when the inertial sensors for ADPOS are determined, therefore filter estimation algorithms play a vital role in the transfer alignment of DPOS, which has an direct impact on the recursive state estimation performance. The transfer model of the ADPOS in nature is nonlinear.However, earlierly the most-used KF is subject to the divergence that results from approximations during any linearization process [8,9]. And then EKF becomes the more widely applied estimator for the nonlinear model using via a first-order linearization method based on a suboptimal recursive estimation framework. However, EKF has some fatal shortcomings, dramatically degrades the accuracy and cause divergence of the state estimation when the nonlinear characteristic is very strong [3].

In order to overcome the shortcomings of above state estimation methods, then a series of nonlinear filtering algorithms are deduced to proceed nonlinear state estimation in the past years on the basis of the tradional state estimation algorithm [9]. Above these algorithms, several nonlinear state estimation are generated from deterministic sampling methods or numerical methods and both the linear minimum variance criterion is applied to the filtering update process [10], such as the widely used unsecnted Kalman filter [11], central difference Kalman filter [12] and so on. In view of that the algorithm flow is obtained by using the linear minimum variance criterion approximately, which is not the real case, then more efficient filtering update methods integrates the Kalman filter frame work need to be considered. nonlinear state estimation algorithms based on deterministic sampling using a new probabilistic framework are developed such as unscented Kalman filter (UKF) and central difference Kalman filter (CDKF) , where both rely on approximating the probability density distribution of the nonlinear function using a series of deterministic samples according to certain principles [4]. For the advantages, these state estimation algorithm processes remain free of Jacobian matrix calculation and truncation error to deal with nonlinear estimation problems [20], then higher estimation accuracy is achieved. Also, compared with the UKF algorithm, the CDKF algorithm uses fewer parameters to generate sigma points to conduct nonlinear estimation but the same estimation accuracy, which is the most widely used in nonlinear estimation [25]. However, the transfer alignment model is more high dimentional, CDKF and modified CDKF cannot fill the estimation accuracy requirement. How to deal with CDKF to achive better performance is very important once the high-dimention model is given.

For the filtering update process, one can treat it as an unconstrained optimization problem to be solved. Among of these fields, the steepest descent algorithm (gradient descent algorithm), Newton method and related Quasi-Newton method, conjugate gradient algorithm are used widely [13,14]. Conjugate gradient algorithm lies between the steepest descent algorithm and Newton method, which only employs the first order derivative information and overcome the defect of slow convergence of steepest descent algorithm, also is immune to the calculation and storage of Hessian matrix. Because of simple structure, smaller storage capacity, high numerical efficiency, conjugate gradient method has been one of the most efficient methods to solve the nonlinear optimization problem and used in many fields. Developed from Hestenes and Stiefel in the 1950s, conjugate gradient methods has been studied by many researchers [15], there are many derivatives developed from the basic methods, such as Hestenes-Steifel (HS) method [16], Fletcher-Reeves (FR) method [17], Polak-Ribiére-Polyak (PRP) method [18], conjugate descent (CD) method [19], Liu- Storey (LS) method [21], Dai-Yuan (DY) method [22] and so on, which differs from others in the selection of step length factors. Specially, the FR, CD, DY method performs well in convergence performance, but poor in numerical performance; while the PRP, LS, HS methods can realize self-correcting when encounter small step size continuously, then show better numerical performance. Here we focus on the PRP method to conduct the conjugate gradient to achieve optimization.

Compared with general filtering estimation methods and its related derivatives which use linear minimum variance criterion to assume that the state estimation is a linear regression with the observation [23], variational optimization is an effective method to replace the Kalman linear regression by quadratic terms about observation to nonlinearities [24], such as combine the conjugate gradient method with variational optimization to state mean estimation, which can achieve higher state estimation accuracy. On the other hand, for error covariance matrix estimation, the original update by general nonlinear filtering is used to estimate the state estimation covariance matrix, which takes place in parallel with state update. Motivated by the above description, based on the superiority of variational optimization by conjugate gradient method and the central difference Kalman filter adopts fewer parameters to achieve estimation, a central difference based variational filtering algorithm (CDVF) is proposed to contribute to the information fusion process of the master and slave systems of ADPOS. The main contributions of this paper can be summarized as the following aspects.

1) For the filtering prediction stage, the CDVF algorithm uses the Central difference Kalman filtering interpolation method to substitute derivative computation to propagate the system characteristic;

2) For the filtering update stage, the CDVF algorithm uses variational optimization by conjugate gradient method to conduct the state update instead of the linear minimum variance estimation; Meanwhile, the state estimation covariance matrix update is to be in progress parallel with the state update by the original central difference Kalman filtering;

3) Real flight test is conducted to verify the proposed algorithm, detailed experiment results are presented and show superiority of the proposed algorithm.

The outline of the reminder of this work is arranged as follows: In Section 2, the background theories including linear minimum variance criterion, central difference Kalman filtering algorithm, conjugate gradient optimization method are listed successively; Compare with the linear minimum variance criterion based central difference Kalman filtering algorithm, combine the central difference interpolation method, variational optimization method by conjugate gradient method, the central difference variational filtering algorithm is proposed in Section 3; The detailed experiment validation process including experiment design, data processing, result analysis are located in Section 4; Finally, the conclusion and future work are displayed in the last section.

2. Related Theories

In this section, the related theories including linear minimum variance criterion for nonlinear systems and developed nonlinear central difference Kalman filtering, conjugate gradient method for variational optimization will be displayed successively to serve for the next section.

Given the nonlinear system with additive noise as

\{\begin{matrix} x_{k} = f (x_{k - 1}) + G_{k - 1} w_{k - 1} \\ y_{k} = H_{k} x_{k} + v_{k} \end{matrix}

(1)

where

k \in Z

x_{k} \in R^{n}

denotes the state vector at discrete-time k,

y_{k} \in R^{n_{y}}

denotes the measurement vector at time k,

f (\cdot) : R^{n} ⟶ R^{n}

is the nonlinear state transition function,

G_{k - 1} \in R^{n \times n_{w}}

is the process noise coefficient matrix,

H_{k} : R^{n} ⟶ R^{n_{y}}

is the measurement matrix,

w_{k - 1} \in R^{n_{w}}

v_{k} \in R^{n_{y}}

are mutually independent noise vectors, and

E [w_{k - 1} w_{k - 1}^{T}] = Q_{k - 1}

E [V_{k} V_{k}^{T}] = R_{k}

2.1. Linear Minimum Variance (LMV) Criterion for Nonlinear Systems [23]

Let

x

is the variable to be estimated,

y

is the observation of

x

, if the following equality holds for

{\hat{x}}_{L} (y) = A y + b

E [{(x - \hat{x})}^{T} (x - \hat{x})] |_{\hat{x} = {\hat{x}}_{L} (y)} = \min

(2)

then

{\hat{x}}_{L} (y)

is the linear minimum variance estimation of

x

y

, also can be denoted as

E^{*} [x / y]

. Also,

A

and

b

can be calculated as

A = C_{xy} C_{y}^{- 1}, b = E [x] - C_{xy} C_{y}^{- 1} E [y]

(3)

then the linear minimum variance estimation of

x

based on

y

is formulated as

{\hat{x}}_{L} (y) = E [x] + C_{xy} C_{y}^{- 1} (y - E [y])

(4)

and the estimation error covariance matrix is

P = C_{xx} - C_{xy} C_{y}^{- 1} C_{yx}

(5)

For nonlinear systems as (1), let

y_{1 : k} = [y_{1}, y_{2}, . . ., y_{k}]

, the linear minimum variance estimation of

x

based on

y_{1 : k}

can be displayed as

{\hat{x}}_{k} = E^{*} [x_{k} / y_{1 : k}] = E^{*} [x_{k} / y_{1 : k - 1}, y_{k}]

(6)

According to the linearity of linear minimum variance estimation, it has

\begin{matrix} {\hat{x}}_{k} & = E^{*} [x_{k} / y_{1 : k - 1}] + E^{*} [x_{k} / y_{k}] - E [x_{k}] \\ = {\hat{x}}_{k}^{-} + E^{*} [x_{k} / y_{k}] - E [x_{k}] \end{matrix}

(7)

On the basis of (3),

\begin{matrix} E^{*} [x_{k} / & y_{k}] = E [x_{k}] + C_{xy} C_{y}^{- 1} (y_{k} - E [y_{k}]) \\ = & E [x_{k}] + E [(x_{k} - E [x_{k}]) {(y_{k} - E [y_{k}])}^{T}] \\ \cdot & {E [(y_{k} - E [y_{k}]) {(y_{k} - E [y_{k}])}^{T}]}^{- 1} (y_{k} - E [y_{k}]) \end{matrix}

(8)

Let

\begin{matrix} P_{x y} & = E [(x_{k} - E [x_{k}]) {(y_{k} - E [y_{k}])}^{T}] \\ P_{y} & = E [(y_{k} - E [y_{k}]) {(y_{k} - E [y_{k}])}^{T}] \\ K_{k} & = P_{x y} P_{y}^{- 1} \end{matrix}

(9)

then

E^{*} [x_{k} / y_{k}] = E [x_{k}] + K_{k} (y_{k} - E [y_{k}])

(10)

Approximate

E [x_{k}]

{\hat{x}}_{k}^{-}

E [y_{k}]

{\hat{y}}_{k}^{-}

, then combine (7), one can check that

{\hat{x}}_{k} = {\hat{x}}_{k}^{-} + K_{k} (y_{k} - {\hat{y}}_{k}^{-})

(11)

and

\begin{matrix} P_{x y} & = E [(x_{k} - {\hat{x}}_{k}^{-}) {(y_{k} - {\hat{y}}_{k}^{-})}^{T}] \\ P_{y} & = E [(y_{k} - {\hat{y}}_{k}^{-}) {(y_{k} - {\hat{y}}_{k}^{-})}^{T}] \end{matrix}

(12)

Considering that

P_{y x} = P_{x y}^{T}

and

P_{y}

is symmetric, then formula (4) is realized as

P_{k} = P_{k}^{-} - P_{x y} P_{y}^{- 1} P_{x y}^{T} = P_{k}^{-} - K_{k} P_{y} K_{k}^{T}

(13)

By the above deduction, the linear minimum variance estimation for nonlinear systems is formulated, but only the approximate results are achieved because of the nonlinearity of the system, then the different nonlinear filtering or smoothing algorithms are devoted to using different numerical calculation methods to derive

{\hat{x}}_{k}^{-}

P_{x y}

and

P_{y}

2.2. Central Difference Kalman Filtering

For system (1), under the assumption of Gaussian distribution, apply the linear minimum variance criterion and the Gaussian weighted integrals to the nonlinear filtering equation, the Gaussian filtering is obtained [10]. Especially, Stirling’s interpolation approximation generates the central difference Kalman filtering and is used to solve the numerical integrals to complete the recursive estimation [12].

By the above description, the central difference Kalman filtering algorithm in each step for system (1) is listed as:

• At time

k - 1

, the Gaussian posterior density function is

p (x_{k - 1} | y_{1 : k - 1}) = N ({\hat{x}}_{k - 1}, P_{k - 1})

, where

{\hat{x}}_{k - 1} = E [x_{k - 1} | y_{1 : k - 1}]

and

P_{k - 1} = E [(x_{k - 1} - {\hat{x}}_{k - 1}) {(x_{k - 1} - {\hat{x}}_{k - 1})}^{T} | y_{1 : k - 1}]

• Determine the set of sigma points

χ_{i, k - 1}

according to

\begin{matrix} χ_{0, k - 1} = {\hat{x}}_{k - 1} \\ χ_{l, k - 1} = {\hat{x}}_{k - 1} + υ {(S_{k - 1})}_{l} \\ χ_{l + n, k - 1} = {\hat{x}}_{k - 1} - υ {(S_{k - 1})}_{l} \end{matrix}

(14)

where

P_{k - 1} = S_{k - 1} S_{k - 1}^{T}

i = 0, 1, . . ., 2 n, l = 1, 2, . . ., n

S_{k - 1} = chol (P_{k - 1})

υ = \sqrt{3}

• Propagate the set of sigma points in accordance with the system equation as

χ_{i, k}^{-} = f (χ_{i, k - 1})

and the predictive probability density function (pdf)

p (x_{k} | y_{1 : k - 1})

is approximated by the Gaussian pdf

N ({\hat{x}}_{k}^{-}, P_{k}^{-})

, where

{\hat{x}}_{k}^{-} = \sum_{i = 0}^{2 n} ω_{i}^{0} χ_{i, k}^{-}

(15)

\begin{matrix} P_{k}^{-} = \sum_{l = 1}^{n} [ω_{l}^{1} (χ_{l, k}^{-} - χ_{l + n, k}^{-}) {(χ_{l, k}^{-} - χ_{l + n, k}^{-})}^{T} + ω_{l}^{2} \\ \cdot (χ_{l, k}^{-} + χ_{l + n, k}^{-} - 2 χ_{0, k}^{-}) {(χ_{l, k}^{-} + χ_{l + n, k}^{-} - 2 χ_{0, k}^{-})}^{T}] \\ + G_{k - 1} Q_{k - 1} G_{k - 1}^{T} \end{matrix}

(16)

where

ω_{0}^{0} = \frac{υ^{2} - n}{υ^{2}}, ω_{l}^{0} = ω_{l + n}^{0} = \frac{1}{2 υ^{2}}, ω_{l}^{1} = \frac{1}{4 υ^{2}}, ω_{l}^{2} = \frac{υ^{2} - 1}{4 υ^{2}}

• Determine the set of predictive sigma points

ϑ_{i, k}

at time instant k according to

ϑ_{0, k} = {\hat{x}}_{k}^{-}, ϑ_{l, k} = {\hat{x}}_{k}^{-} + υ {(S_{k}^{-})}_{l}, ϑ_{l + n, k} = {\hat{x}}_{k}^{-} - υ {(S_{k}^{-})}_{l}

(17)

and

P_{k}^{-} = S_{k}^{-} {(S_{k}^{-})}^{T}

• Update the state estimation, compute the posterior pdf

p (x_{k} | y_{1 : k}) = N ({\hat{x}}_{k}, P_{k})

with the measurement

y_{k}

Ξ_{i, k} = H_{k} ϑ_{i, k}

(18)

{\hat{y}}_{k}^{-} = \sum_{i = 0}^{2 n} ω_{i}^{0} Ξ_{i, k}

(19)

\begin{matrix} P_{y} & = \sum_{l = 1}^{n} [ω_{l}^{1} (Ξ_{l, k} - Ξ_{l + n, k}) {(Ξ_{l, k} - Ξ_{l + n, k})}^{T} + ω_{l}^{2} (Ξ_{l, k} \\ + Ξ_{l + n, k} - 2 Ξ_{0, k}) {(Ξ_{l, k} + Ξ_{l + n, k} - 2 Ξ_{0, k})}^{T}] + R_{k} \end{matrix}

(20)

P_{x y} = \sum_{l = 1}^{n} \sqrt{ω_{l}^{1}} S_{k}^{-} {[Ξ_{l, k} - Ξ_{l + n, k}]}^{T}

(21)

K_{k} = P_{x y} P_{y}^{- 1}

(22)

{\hat{x}}_{k} = {\hat{x}}_{k}^{-} + K_{k} (y_{k} - {\hat{y}}_{k}^{-})

(23)

P_{k} = P_{k}^{-} - K_{k} P_{y} K_{k}^{T}

(24)

In consideration of that the measurement equation of (1) is linear, then the covariance matrix update of central difference Kalman filtering can be simplified as

\begin{matrix} P_{y} & = \sum_{l = 1}^{n} [ω_{l}^{1} (Ξ_{l, k} - Ξ_{l + n, k}) {(Ξ_{l, k} - Ξ_{l + n, k})}^{T} + ω_{l}^{2} (Ξ_{l, k} \\ + Ξ_{l + n, k} - 2 Ξ_{0, k}) {(Ξ_{l, k} + Ξ_{l + n, k} - 2 Ξ_{0, k})}^{T}] + R_{k} \\ = H_{k} P_{k}^{-} H_{k}^{T} + R_{k} \end{matrix}

(25)

P_{x y} = \sum_{l = 1}^{n} \sqrt{ω_{l}^{1}} S_{k}^{-} {[Ξ_{l, k} - Ξ_{l + n, k}]}^{T} = P_{k}^{-} H_{k}^{T}

(26)

K_{k} = P_{x y} P_{y}^{- 1} = P_{k}^{-} H_{k}^{T} {(H_{k} P_{k}^{-} H_{k}^{T} + R_{k})}^{- 1}

(27)

P_{k} = P_{k}^{-} - K_{k} P_{y} K_{k}^{T} = P_{k}^{-} - P_{k}^{-} H_{k}^{T} {(H_{k} P_{k}^{-} H_{k}^{T} + R_{k})}^{- 1} H_{k} P_{k}^{-}

(28)

By the above deduction, one can simply the filtering covariance matrix update, then it can be in progress in parallel with state update by using the one-step prediction

P_{k}^{-}

and measurement matrix

H_{k}

, measurement noise covariance

r_{k}

2.3. Conjugate Gradient Method for Unconstrained Optimization Problems

For the unconstrained optimization problems, different algorithms are available, such as the steepest descent method, Newton and quasi-Newton methods, conjugate gradient method, etc. Compared with the linear minimum variance criterion which uses the linear method to complete the filtering update, the conjugate gradient method can be used to improve the filtering update process of the filtering algorithms.

Conjugate gradient method is very efficient for solving large-scale unconstrained optimization problem, detailed description is presented as follows. For the unconstrained optimization problem (matrix

A

is positive definite)

F (x) = \frac{1}{2} x^{T} A x - x^{T} b

(29)

then

r (x) = \nabla F (x)

denotes the gradient of

F (x)

\nabla^{2} F (x) = A

. Here we will show the algorithm flow of conjugate gradient method. The most important point is to decide the step length factor

β

, popular algorithms such as FR, PRP, HS, DY and so on, the difference lies on the selection of

β

, here we list the algorithm flow of PRP conjugate gradient method as following [18].

Algorithm 1:Conjugate gradient method (PRP)

Initialization:

r_{1} = \nabla F (x_{1}) = A x_{1} - b

p_{1} = r_{1}

m = 1

α_{m} = \frac{- r_{m}^{T} p_{m}}{p_{m}^{T} A p_{m}}

x_{m + 1} = x_{m} + α_{m} p_{m}

r_{m + 1} = A x_{m + 1} - b

β_{m + 1} = \frac{r_{m + 1}^{T} (r_{m + 1} - r_{m})}{r_{m}^{T} r_{m}}

p_{m + 1} = - r_{m + 1} + β_{m + 1} p_{m}

3. Central Difference Variational Filtering Algorithm

On the basis of the above subsections, the central difference variational filtering algorithm is developed, where the central difference Kalman filtering algorithm to conduct the state prediction, covariance matrix prediction and update, and the conjugate gradient method to update the state instead the LMV criterion. Combine the algorithm flow of central difference Kalman filtering and conjugate gradient method, here we present the outline of central difference variational filtering algorithm as follows [24].

Step 1: Sigma points generation. At time instant

k - 1

, generate sigma points

χ_{i, k - 1}

as (14).

Step 2: Prediction. Conduct (15) and

\begin{matrix} {\tilde{S}}_{k}^{-} & = [\sqrt{ω_{1}^{1}} (χ_{1, k}^{-} - χ_{1 + n, k}^{-}) \sqrt{ω_{2}^{1}} (χ_{2, k}^{-} - χ_{2 + n, k}^{-}) \\ . . . \sqrt{ω_{n}^{1}} (χ_{n, k}^{-} - χ_{2 n, k}^{-}) \sqrt{ω_{1}^{2}} (χ_{1, k}^{-} + χ_{1 + n, k}^{-} - 2 χ_{0, k}^{-}) \\ \sqrt{ω_{2}^{2}} (χ_{2, k}^{-} + χ_{2 + n, k}^{-} - 2 χ_{0, k}^{-}) \\ . . . \sqrt{ω_{n}^{2}} (χ_{n, k}^{-} + χ_{2 n, k}^{-} - 2 χ_{0, k}^{-})]^{T} \end{matrix}

(30)

P_{k}^{-} = {\tilde{S}}_{k}^{-} {({\tilde{S}}_{k}^{-})}^{T} + G_{k - 1} Q_{k - 1} G_{k - 1}^{T}

(31)

Step 3: Update.

(1) State update.

Define the cost function

J (x)

\begin{matrix} J (x) & = \frac{1}{2} {(y_{k} - H_{k} x)}^{T} R_{k}^{- 1} (y_{k} - H_{k} x) \\ + \frac{1}{2} {(x - {\hat{x}}_{k}^{-})}^{T} {(P_{k}^{-})}^{- 1} (x - {\hat{x}}_{k}^{-}) \end{matrix}

(32)

then the object is to find

{\hat{x}}_{k} = arg min_{x} J (x)

and

\dot{J} (x) \geq 0

In order to use the conjugate gradient method, given the following transformation:

x_{k} - {\hat{x}}_{k}^{-} = M_{k} z_{k}

, where

M_{k}

is determined by the one-step prediction covariance matrix

P_{k}^{-}

M_{k} M_{k}^{T} = P_{k}^{-}

By the transformation, cost function can be revised as

\begin{matrix} J (z_{k}) & = \frac{1}{2} z_{k}^{T} z_{k} + \frac{1}{2} {(Y_{k} - H_{k} M_{k} z_{k})}^{T} R_{k}^{- 1} (Y_{k} - H_{k} M_{k} z_{k}) \end{matrix}

(33)

where

Y_{k} = y_{k} - H_{k} {\hat{x}}_{k}^{-}

, then it can be easily checked that

\begin{matrix} \nabla J (z_{k}) & = z_{k} - M_{k}^{T} H_{k}^{T} R_{k}^{- 1} (Y_{k} - H_{k} M_{k} z_{k}) \end{matrix}

(34)

and

\begin{matrix} \nabla^{2} J (z_{k}) & = I + M_{k}^{T} H_{k}^{T} R_{k}^{- 1} H_{k} M_{k} \end{matrix}

(35)

For the application of DPOS,

R_{k}

denotes the measurement noise covariance which is decided by sensors noise level and then

R_{k}

is a diagonal matrix with poitive elements, then the second order derivative

\nabla^{2} J (z_{k})

is positive definite. In addition,

x_{k}

can be obtained from the optimization process of

z_{k}

by conjugate gradient method and

x_{k} = {\hat{x}}_{k}^{-} + M_{k} z_{k}

The specific optimization process

z_{k}

is given as:

1) Initialize

r_{1} = \nabla J (z_{1})

P_{1} = r_{1}

z_{1} = 0

m = 1

;

2) Calculate

Γ_{m} = \nabla^{2} J (z_{m})

α_{m} = \frac{- r_{m}^{T} p_{m}}{p_{m}^{T} Γ_{m} p_{m}}

;

z_{m + 1} = z_{m} + α_{m} p_{m}

;

r_{m + 1} = \nabla J (z_{m + 1})

;

β_{m + 1} = \frac{r_{m + 1}^{T} (r_{m + 1} - r_{m})}{r_{m}^{T} r_{m}}

;

p_{m + 1} = - r_{m + 1} + β_{m + 1} p_{m}

;

Then by 1)-6), one can use the conjugate gradient method to obtain the estimation of

z_{k}

recursively, and then

x_{k}

can be calculated as the state estimation.

(2) Covariance matrix update.

One can use the measurement linearity and formula (28) to calculation the error covariance matrix update.

By the above descriptions, the proposed central difference variational filtering algorithm has been presented, the detailed algorithm flow can be showed in Algorithm 2.

Algorithm 2:Central difference variational filtering algorithm

Initialization:

{\hat{x}}_{0}, P_{0}

Prediction

For

k = 1

to N do

P_{k - 1} = S_{k - 1} S_{k - 1}^{T}

χ_{0, k - 1} = {\hat{x}}_{k - 1}, χ_{l, k - 1} = {\hat{x}}_{k - 1} + υ {(S_{k - 1})}_{l}, χ_{l + n, k - 1} = {\hat{x}}_{k - 1} - υ {(S_{k - 1})}_{l}

i = 0, 1, . . ., 2 n, l = 1, 2, . . ., n

υ = \sqrt{3}

χ_{i, k}^{-} = f (χ_{k - 1}^{i})

{\hat{x}}_{k}^{-} = \sum_{i = 0}^{2 n} ω_{i}^{0} χ_{i, k}^{-}

{\tilde{S}}_{k}^{-} = [\sqrt{ω_{1}^{1}} (χ_{1, k}^{-} - χ_{1 + n, k}^{-}) \sqrt{ω_{2}^{1}} (χ_{2, k}^{-} - χ_{2 + n, k}^{-}) . . . \sqrt{ω_{n}^{1}} (χ_{n, k}^{-} - χ_{2 n, k}^{-}) \sqrt{ω_{1}^{2}} (χ_{1, k}^{-} + χ_{1 + n, k}^{-} - 2 χ_{0, k}^{-}) \sqrt{ω_{2}^{2}} (χ_{2, k}^{-} +

χ_{2 + n, k}^{-} - 2 χ_{0, k}^{-}) . . . \sqrt{ω_{n}^{2}} (χ_{n, k}^{-} + χ_{2 n, k}^{-} - 2 χ_{0, k}^{-})]

P_{k}^{-} = {\tilde{S}}_{k}^{-} {({\tilde{S}}_{k}^{-})}^{T} + G_{k - 1} Q_{k - 1} G_{k - 1}^{T}

end

Update

Initialization:

r_{1} = \nabla J (z_{1})

p_{1} = r_{1}

z_{1} = 0

m = 1

For

m = 1, 2, . . ., M

α_{m} = \frac{- R_{m}^{T} p_{m}}{p_{m}^{T} A p_{m}}

Γ_{m} = \nabla^{2} J (z_{m})

α_{m} = \frac{- r_{m}^{T} p_{m}}{p_{m}^{T} Γ_{m} P_{m}}

z_{m + 1} = z_{m} + α_{m} p_{m}

10.

r_{m + 1} = \nabla J (z_{m + 1})

11.

β_{m + 1} = \frac{R_{m + 1}^{T} (R_{m + 1} - R_{m})}{R_{m}^{T} R_{m}}

11.

p_{m + 1} = - R_{m + 1} + β_{m + 1} p_{m}

12.

m = m + 1

13:

x_{k} = x_{k}^{-} + M_{k} z_{M}

14:

P_{k} = P_{k}^{-} - P_{k}^{-} H_{k}^{T} {(H_{k} P_{k}^{-} H_{k}^{T} + R_{k})}^{- 1} H_{k} P_{k}^{-}

end

Return

{\hat{x}}_{k}

P_{k}

4. Experiment Validation

This section we apply the proposed algorithm to the master and slave system information fusion of DPOS. Specially, use the master system motion parameters and lever arm compensation as the external measurement of slave system, then by the proposed algorithm to estimate errors and correct the strapdown solution of the slave system. Detailed slave system error model is depicted in this section firstly, and then flight test and experimental results compared with the existing central difference filtering algorithm are given.

4.1. State-Space Model

Generally, level east-north-up frame is selected as navigation frame (n frame),

i, p, b, e

denote the inertial frame, platform frame, slave system body frame, the earth-fixed frame, respectively. To present the state-space description of the slave system, we firstly list the error model of position, velocity, attitude and inertial sensors of system briefly [7], as shown below.

The fundamental inertial error model description is as follows.

\begin{matrix} {\dot{ϕ}}^{n} = (I - C_{n}^{p}) ω_{i n}^{n} + δ ω_{i n}^{n} - C_{b}^{n} ε^{b} - C_{b}^{n} w_{ε}^{b} \\ δ {\dot{V}}^{n} = (I - C_{p}^{n}) f^{n} - (2 δ ω_{i e}^{n} + δ ω_{e n}^{n}) \times V^{n} \\ - (2 ω_{i e}^{n} + ω_{e n}^{n}) \times δ V^{n} + C_{b}^{n} \nabla^{b} + C_{b}^{n} w_{\nabla}^{b} \\ δ \dot{L} = - \frac{V_{N} δ h}{{(R_{M} + h)}^{2}} + \frac{δ V_{N}}{R_{M} + h} \\ δ \dot{λ} = \frac{V_{E} sec L tan L δ L}{R_{N} + h} - \frac{V_{E} sec L δ h}{{(R_{N} + h)}^{2}} + \frac{sec L δ V_{E}}{R_{N} + h} \\ δ \dot{h} = δ V_{U} \\ {\dot{ε}}^{b} = 0 \\ {\dot{\nabla}}^{b} = 0 \end{matrix}

(36)

where

ϕ^{n} = {[ϕ_{E} ϕ_{N} ϕ_{U}]}^{T}

denotes the attitude angle error, the velocity error is

δ V^{n}

δ L

δ λ

and

δ h

are the errors of latitude, longitude and altitude, respectively.

ε^{b}

denotes the gyroscopes constant drift vector in b frame and

w_{ε}^{b}

is the gyroscopes random noises.

\nabla^{b}

is the accelerometers constant bias and

w_{\nabla}^{b}

is the random noises of accelerometers. The symbols

ω_{i n}^{n}

ω_{i e}^{n}

ω_{e n}^{n}

can be found in detail in related literatures, and

δ ω_{i n}^{n}

δ ω_{i e}^{n}

δ ω_{e n}^{n}

are the errors, respectively.

f^{n}

is the specific forces measured by the accelerometers.

C_{b}^{n}

and

C_{n}^{p}

are the direction cosine matrices between n frame and b frame, p frame and n frame, respectively.

Also, consider the misalignment angle between the master and slave system as constant, that is,

{\dot{μ}}_{x} = {\dot{μ}}_{y} = {\dot{μ}}_{z} = 0

, and the flexible lever arm effect can be described by the Markov model as follows.

\begin{matrix} {\ddot{ζ}}_{x} + 2 η_{x} {\dot{ζ}}_{x} + η_{x}^{2} ζ_{x} = ξ_{x} \\ {\ddot{ζ}}_{y} + 2 η_{y} {\dot{ζ}}_{y} + η_{y}^{2} ζ_{y} = ξ_{y} \\ {\ddot{ζ}}_{z} + 2 η_{z} {\dot{ζ}}_{z} + η_{z}^{2} ζ_{z} = ξ_{z} \end{matrix}

(37)

where

ζ_{i}, i = x, y, z

is the flexure angle,

η_{i} = 2.146 / τ_{i}

is the parameter,

τ_{i}

is the correlation,

ξ_{i}

is the noise vector.

Differences of velocity and attitude between the master and slave system are used as the measurement

y = {[δ ϕ δ θ δ γ δ V_{E}^{^{'}} δ V_{N}^{^{'}} δ V_{U}^{^{'}}]}^{T}

(38)

then state space model can be given as

\begin{matrix} \dot{x} = f (x) + G w \\ y = H x + V \end{matrix}

(39)

where

x = [ϕ_{E} ϕ_{N} ϕ_{U} δ V_{E} δ V_{N} δ V_{U} δ L δ λ δ h

ε_{x} ε_{y} ε_{z} \nabla_{x} \nabla_{y} \nabla_{z} μ_{x} μ_{y} μ_{z} ζ_{x} ζ_{y} ζ_{z} {\dot{ζ}}_{x}

{\dot{ζ}}_{y} {\dot{ζ}}_{z}]^{T}

and the nonlinear function

f

is decided by (36)-(37).

w

and

v

are the process noise vector with zero mean, variance

Q

and measurement noise with zero mean, variance

R

, respectively.

Matrices

G

and

H

are

\begin{matrix} G = [\begin{matrix} C_{b}^{n} & 0_{3 \times 3} \\ 0_{3 \times 3} & C_{b}^{n} \\ 0_{9 \times 3} & 0_{9 \times 3} \end{matrix}] \end{matrix}

(40)

\begin{matrix} H = [\begin{matrix} H_{1} & 0_{3 \times 3} & 0_{3 \times 9} & H_{2} & H_{3} & 0_{3 \times 3} \\ 0_{3 \times 3} & I_{3 \times 3} & 0_{3 \times 9} & 0_{3 \times 3} & 0_{3 \times 3} & 0_{3 \times 3} \end{matrix}] \end{matrix}

(41)

where the elements of

H

are dicided by the cosine direction matrix of the master system, and for brevity, omitted here.

4.2. Experiment Process and Result Analysis

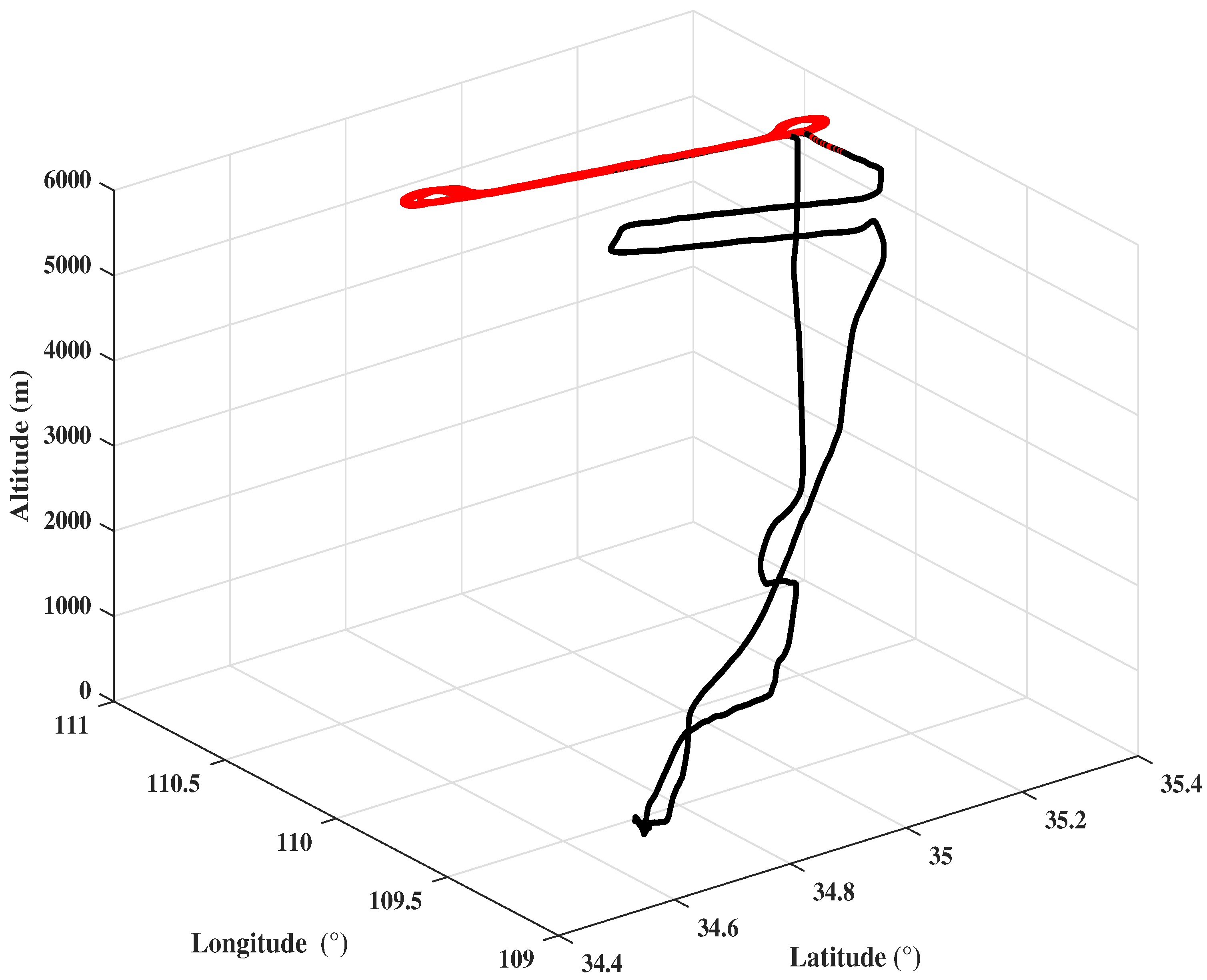
DPOS flight test is arranged for the algorithm validation, where the experiment equipment contains the flight plane, DPOS system, distributed SAR antenna for imaging, shown in Figure 1. In detail, the master system includes a high accuracy fiber gyroscope IMU and a GPS receiver, the slave system installs only same IMU, and the master and slave system locates near the SAR antenna, respectively. Distributed data processing computer is installed in the cabin to complete data processing and storage for the master and slave systems, then send motion parameters information to the imaging antenna. In addition, the rovering GPS antenna is fixed on the top of the plane, the GPS base station is in a clearing below the imaging area and data is collected for post-processing. The whole flight test lasts 4 hours, and the trajectory is shown in Figure 2, where the red line denotes the imaging area.

Figure 1. Flight airplane.

Figure 2. Flight experiment trajectory.

Table 1. Performance index of the experiment devices.

Items	Index
Gyrosocpe constant drift	0.01° /h
Accelerometer constant bias	20 $μ$ g

After the data acquisition, we firstly fuse the GPS information and the master system to obtain the external measurement of the slave system. Then we conduct noise adding on the slave system data to lower the inertial sensors accuracy to 0.1

^{\circ}

/h and 100

μ

g, respectively. And the noise adding is determined according to the real inertial sensors noise characteristic. Next establishing the Markov model on the calibrated initial lever arm between the master and slave system

r_{0} = [1.5214 3.4452 - 0.0851]

(m) to describe the flexure lever arm among the imaging area. Finally, after completing the above process, the proposed algorithm and existing Central Difference Kalman filtering algorithm in literature [20] are used to fuse the master and slave system information, motion parameters of slave system is obtained. The method in literature [20] is also concentrated on improvement of the filtering update process, which adopts the

H_{\infty}

filtering algorithm to suppress the disturbances on the filtering accuracy. Our proposed method is also served for this, which improves the filtering process by using the conjugate gradient method to substitute the linear minimum variance estimation. Next the comparison between these methods is showed in detail.

By processing the experiment data, the master system motion parameters information and lever arm transformation as the reference of slave system, the error curves of the slave system in dashed line are shown in Figure 3, Figure 4 and Figure 5, respectively. Since the DPOS is served for imaging task, then we only concentrate on the imaging area. Also, the imaging task is composed of several laps around imaging area, every lap lasts for about 600s, then 600s data result is presented to show the superiority of the proposed algorithm.

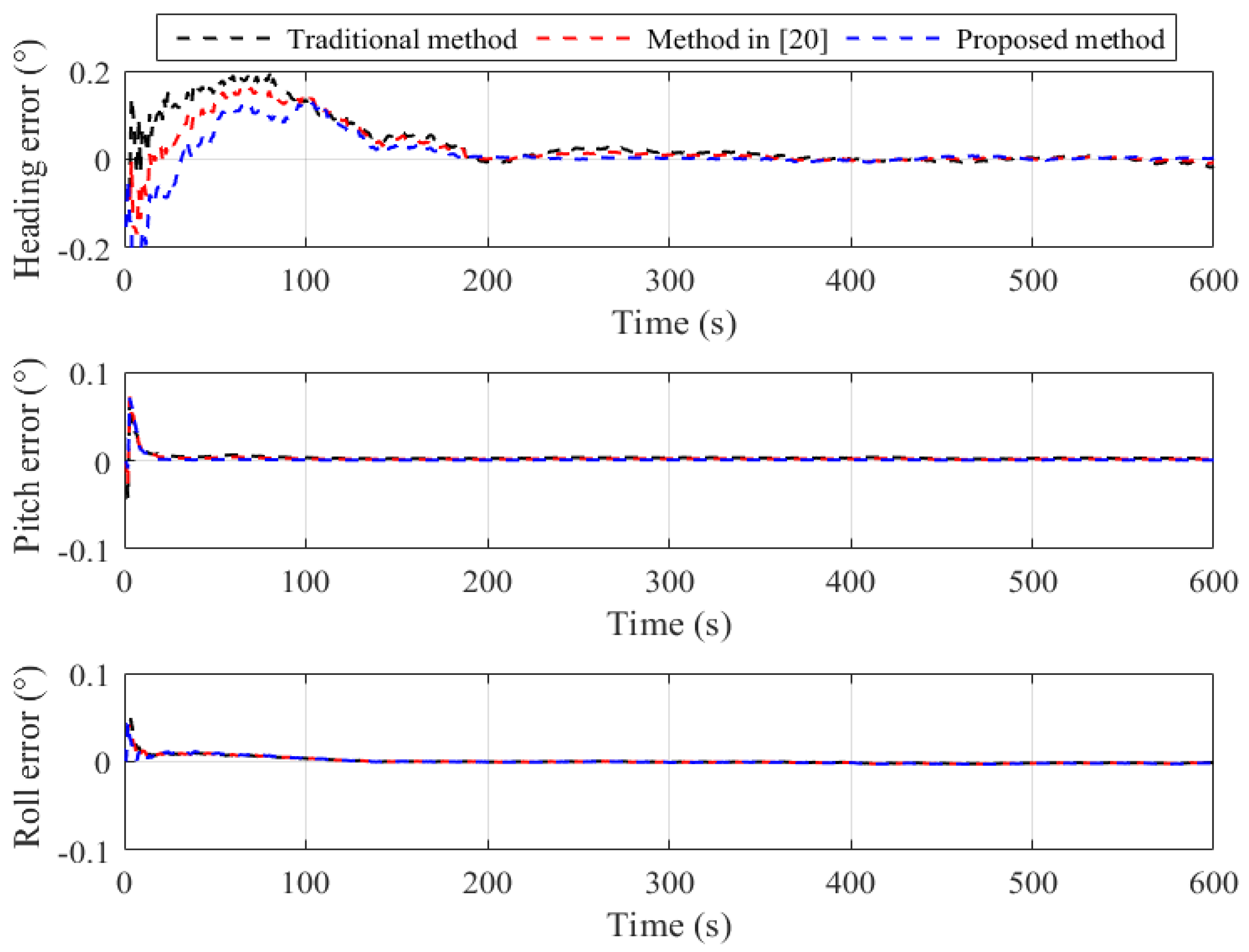
Figure 3 presents the attitude estimation comparison,including the heading error, pitch error and roll error comparison of the above three methods. In Figure 3, the proposed method seems easier to converge than the traditional method and the method in [20] from the curve. In the filtering prediction stage, compared with the traditional linear minimum variance estimation update and

H_{\infty}

filtering update in [20], the proposed method uses the central difference kalman filtering interpolation method and conjugate gradient iteration update to substitute derivative computation to propagate the system characteristic, to some extent, the CDVF can suffer adverse effects by big maneuvers like turns.

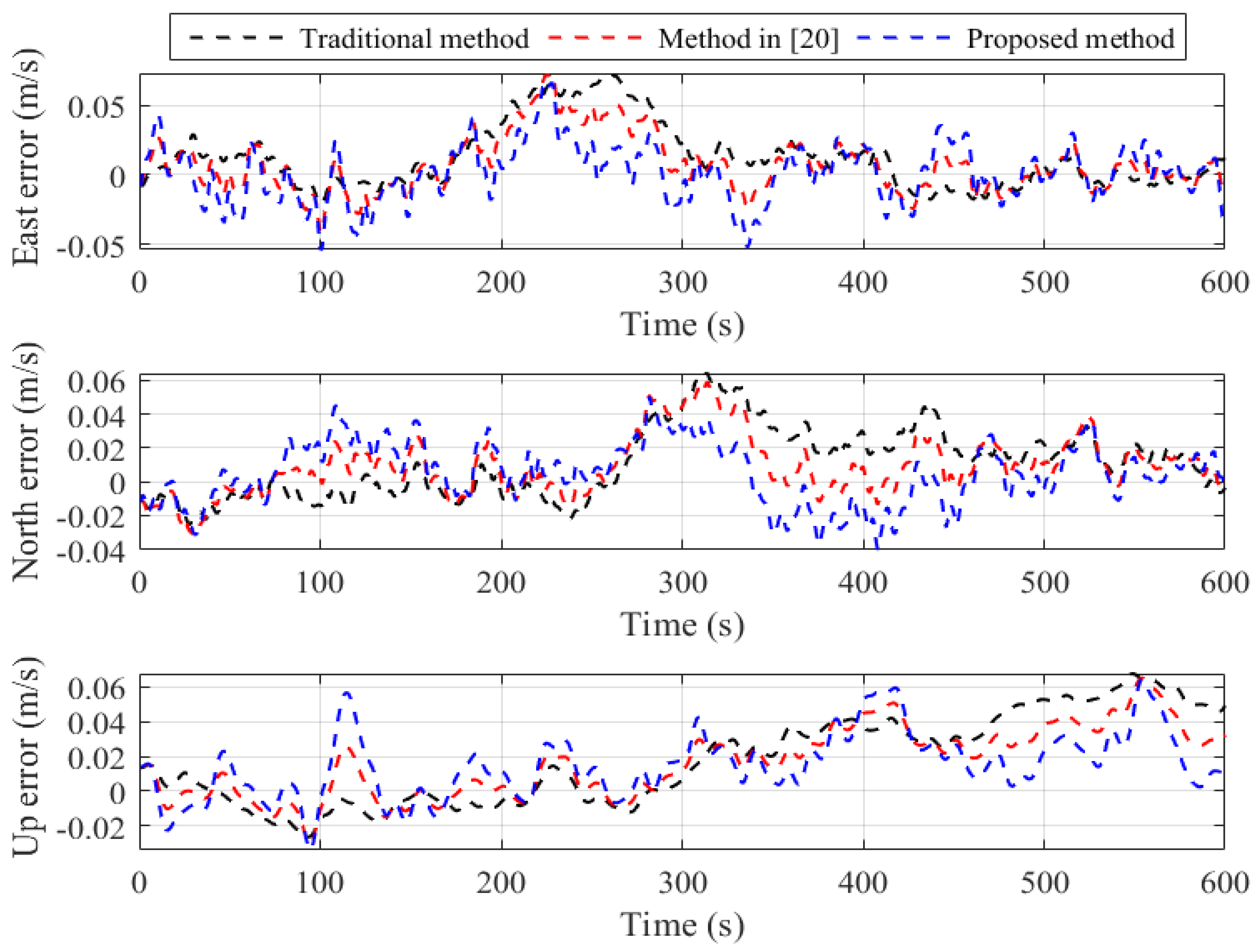
Figure 4 shows the accuracy of the proposed approach is higher and more stable than that of the traditional method in terms of the east velocity error, the north velocity error and up velocity error. The proposed method uses variational optimization by conjugate gradient method to conduct the state update instead of the linear minimum variance estimation; Meanwhile, the state estimation covariance matrix update is to be in progress parallel with the state update by the original central difference kalman filtering and it could in theory be more accurate since they capture more estimation than the linear minimum variance and

H_{\infty}

filtering update process in [20].

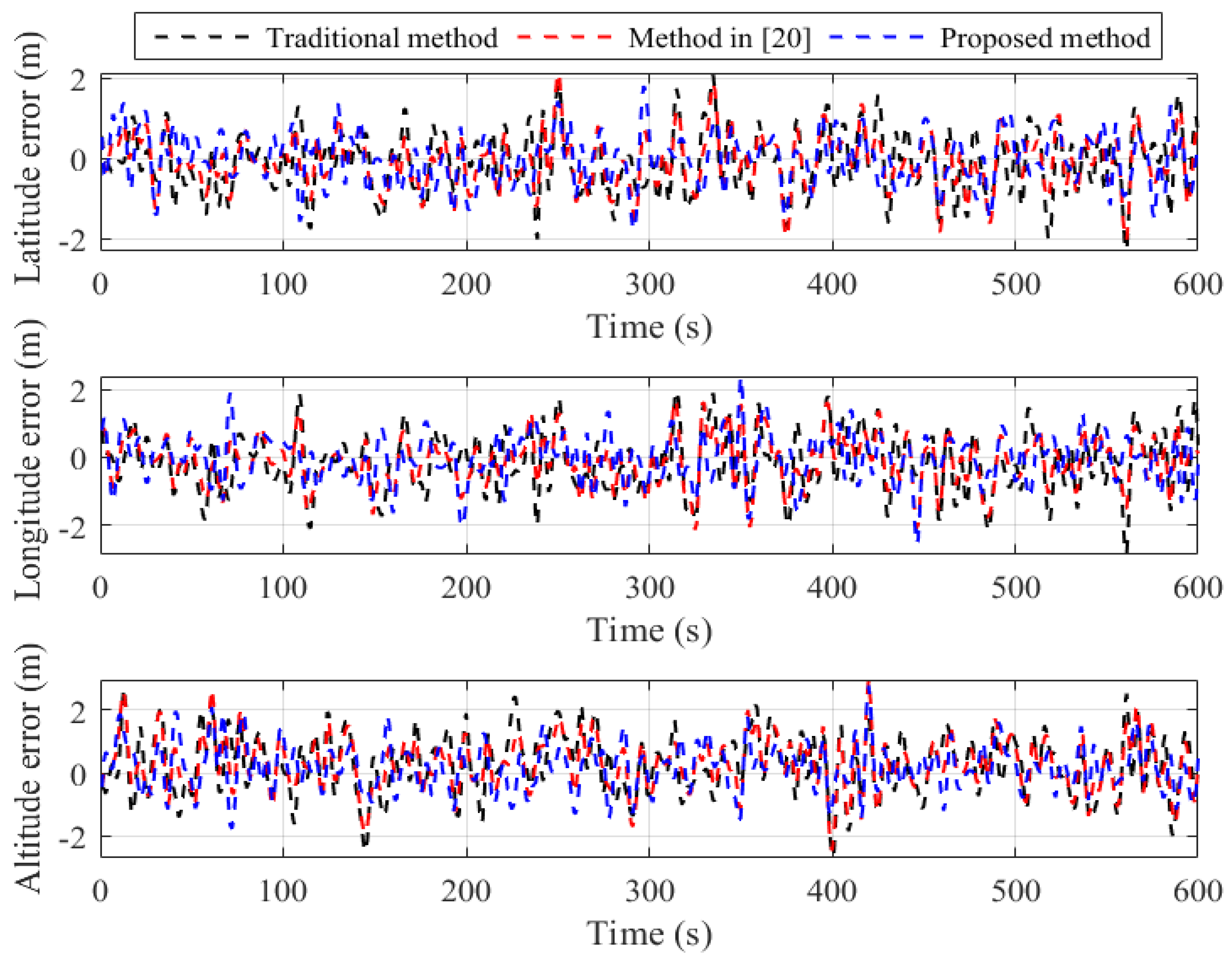
Figure 5 indicates the accuracy of the position is significantly improved via the proposed approach compared to the traditional method and

H_{\infty}

filtering update process in [20]. From the Figure 5, the stability of the proposed method is stronger than that of the existing two methods in terms of latitude, longitude and height. From Figure 4 and Figure 5, on one hand, the east velocity error is in accordance with the longitude error in Figure 5; on the other hand, the latitude error in Figure 5 varies as the north velocity error varies, which meets the error propagation law of inertial systems.

What’s more, a table of their accuracy statistics is presented in a detailed quantization form. From the table, the accuracy of the proposed approach is almost all higher than that of the traditional method and

H_{\infty}

filtering update process in [20], which is in accordance with Figure 2, Figure 3 and Figure 4 in above. In terms of the heading error, pitch error and roll error, their improvement is 22.2%,10.5% and 12.5%, respectively. The velocity errors of the two approaches about east velocity error, north velocity and up velocity are reduced by 19.2%, 18.1% and 22.5%, respectively. In addition, the latitude error, longtitude error and height error are reduced by 17.3%, 19.8% and 23.9%, respectively. In the terms of algorithm complexity, the proposed algorithm is slower than the other algorithms, but it is almost unaffected for the data processing computer. In a word, the estimation performance of the motion parameter is improved using CDVF based on conjugate gradient method.

In two-dimensional images, due to the presence of overlapping masking, multiple targets of different heights fall into the same distance and azimuth unit, making it difficult to achieve target reconstruction and recognition. As shown in Figure 6, overlapping phenomena have occurred between buildings and the ground, as well as between buildings, making it difficult to determine information such as the number, structure, size, and location of buildings.

The motion estimation of the proposed method is used to compensate array SAR with three-dimensional imaging capability, which can achieve three-dimensional imaging of complex targets such as buildings. Using ADPOS data for motion compensation of 2D imaging of multi-channel array SAR, achieving multi-channel consistency compensation through image registration and amplitude phase correction, then focusing in high dimensions, modeling buildings, and pasting scattering information on the model to obtain 3D imaging results, as shown in the Figure 7. It can be seen that the 3D imaging results clearly reflect the structural information of the building and the texture information of the side and roof, greatly reducing the difficulty of SAR image interpretation and verifying the effectiveness of the method proposed in this paper.

5. Conclusion and Future Work

In this work, a central difference variational filtering algorithm is developed to serve for the master and slave system information fusion of ADPOS. Compared with the general state estimation methods which is established on the LMV criterion approximately, this work takes full use of the advantages of variational optimization in the filtering update stage and then central difference variational filtering algorithm is proposed, applied to the ADPOS filght test, the experiment results show the proposed algorithm has a distinct improvement in the multinode motion parameters accuracy, which can be used in array imaging.

In the future, more efficient filtering algorithm will be considered and low cost slave systems will be used in the flight test, which optimize the filtering process by better optimization methods, also real-time performance will be considered to advance the development of areial distributed imaging application.

Author Contributions

Conceptualization, Wen Ye and Y.Y.; methodology, Hongmei Chen.; software,Wen Ye; validation, Fubo Chen; formal analysis, Wen Ye; investigation, Wen Ye; resources, Fubo Zhang; data curation,Wen Ye; writing—original draft preparation, Wen Ye; writing—review and editing, Wen Ye and Hongmei Chen; visualization, Wen Ye and Hongmei Chen; supervision, Hongmei Chen.; project administration, Wen Ye and Hongmei Chen; funding acquisition,Wen Ye and Hongmei Chen. All authors have read and agreed to the published version of the manuscript

Funding

This work was supported in part by the National Key RD Program of China under Grant 2023YFC2205603, the National Natural Science Foundation of China under Grant U1804161, Grant 61901431, the UK Engineering and Physical Sciences Research Council under Grants EPX0353521 and EPY0009861, the Basic Research of National Institute of Metrology under Grant AKYJJ1906, the Henan science and technology research under Grant 222102210269, the Haizhi project of Henan Association for science and technology under Grant HZ202201, the cultivation plan of young teachers of Henan University of Technology under Grant 21420169, the innovation fund of Henan University of Technology under Grant 2021zkcj07.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Acknowledgments

Conflicts of Interest

The authors declare no conflicts of interest.

References

Yihong Sun, Xiaolin Gong,Ling Yang, Dawei Wang, Fubo Zhang,“ A motion information acquisition algorithm of multiantenna SAR installed on flexible and discontinuous structure based on distributed POS," IEEE Transactions on Geoscience and Remote Sensing,vol.60,pp.1-12, 2022. [CrossRef]
Xiaolin Gong, Yihong Sun, “An innovative distributed filter for airborne distributed position and orientation system," Aerosp. Sci. Technol.,vol.119,Dec.2021.
Altan Aytac, Rifat Haciog,“Model predictive control of three-axis gimbal system mounted on UAV for real-time target tracking under external disturbances," Mechanical Systems and Signal Processing,vol.138, 2020.
Yag I, Altan A,“Artificial Intelligence-Based Robust Hybrid Algorithm Design and Implementation for Real-Time Detection of Plant Diseases in Agricultural Environments," Biology,vol.11, Nov.2022.
Z. Lu, J. Fang, H. Liu, X. Gong, and S. Wang, “Dual-filter transfer alignment for airborne distributed POS based on PVAM," Aerosp. Sci. Technol., vol. 71, pp. 136-146, Dec. 2017.
B. Wang, Y. Liu, and W. Ye, “Dual Adaptive Factors-Based Integrated Navigation Performance Improvement for Airborne POS," IEEE Sensors J., vol. 19, no. 20, pp. 9479-9485, Oct. 2019.
B. Wang, W. Ye, and Y. Liu, “Variational Bayesian Cubature RTS Smoothing for Transfer Alignment of DPOS," IEEE Sensors J., vol. 20, no. 6, pp. 3270 - 3279, Mar. 2020. [CrossRef]
R. E. Kalman, “A new approach to linear filtering and prediction problems," J. Basic Eng., vol. 81, no. 1, pp. 35-45, Mar. 1960.
K. Ito, K. Xiong, “Gaussian filters for nonlinear filtering problems," IEEE Trans.automat.control, vol. 45, no. 5, pp. 910-927, May 2000.
S. Srkk, Bayesian Filtering and Smoothing. Cambridge, U.K.: Cambridge University Press, 2013.
S. J. Julier, J. K. Uhlmann, and H. F. Durrant-Whyte, “A New Approach for Filtering Nonlinear Systems," American Contr. Conf., pp. 1628-1632, Jun. 1995.
M. M. Andreasen, “Non-linear DSGE models and the central difference Kalman filter," J. Appl. Econom., vol. 28, no. 6, pp. 929-955, Sep. 2013.
J. Nocedal, and S. J. Wright, Numerical optimization. New York, USA: Springer, 2006.
F. B. Joseph, C. G. Jean, L. Claude, A. S. Claudia, Numerical optimization: theoretical and practical aspects. New York, USA: Springer, 2006.
W. W. Hager, H. Zhang, “A survey of nonlinear conjugate gradient methods," Pacific J. Optimization, vol. 2, no. 1, pp. 35-58, Jan. 2006.
M. R. Hestenes, and E. L. Stiefel, “Methods of Conjugate Gradients for Solving Linear Systems," J. res. nat. bur. stand, vol. 49, no. 6, pp. 81-85, 1952.
R. Fletcher, C. M. Reeves, “Function minimization by conjugate gradients," Computer Journal, vol. 7, no. 2, pp. 149-154, Jan. 1964.
Z. J. Shi, J. Shen, “Convergence of the Polak-Ribiére-Polyak conjugate gradient method," Nonlinear Analysis: Theory Methods and Applications, vol. 66, no. 6, pp. 1428-1441, Mar. 2007. [CrossRef]
R. Fletcher. Practical methods of optimization, vol1: Unconstrained optimization. Chichester: John Wiley & Sons, 1980.
B. Wang, W. Ye and Y. Liu, “Enhanced Disturbance Suppression Method Based on Nonlinear H_∞ Filtering for Distributed POS in Aerial Earth Observation Imaging Application," IEEE Tran. Geosci. Remote Sens., vol. 60, pp. 1-9, 2022.
Y. Liu, C. Storey, “Efficient generalized conjugate gradient algorithms, part 1: Theory," J. Optimization Theory Applications, vol. 69, no. 1, pp. 129-137, 1991.
Y. H. Dai, Y. X. Yuan, “A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property," SIAM J. Optimization, vol. 19, no. 1, pp. 177-182, 1999.
D. Simon, “Optimal State Estimation: Kalman, H_∞, and Nonlinear Approaches," John Wiley & Sons, 2006.
M. Lei, Z. Jing, and S. Hu, “Scaled unscented transform-based variational optimality filter," IEEE Inter. Conf. Inf. Fusion, Singapore, Jul. 2012.
W. Ye, J. Li, J. Fang and X. Yuan, “EGP-CDKF for Performance Improvement of the SINS/GNSS Integrated System," IEEE Transactions on Industrial Electronics, vol. 65, no. 4, pp. 3601-3609,April 2018. [CrossRef]

Figure 3. Attitude estimation comparison.

Figure 4. Velocity estimation comparison.

Figure 5. Position estimation comparison.

Figure 6. 2D imaging

Figure 7. 3D imaging after compensation

Table 2. RMSE comparison between the algorithms.

	Items	Traditional	method in [20]	Proposed
Attitude ( $^{\circ}$ )	Heading	0.066	0.058	0.050
	Pitch	0.006	0.005	0.004
	Roll	0.005	0.004	0.003
Velocity (m/s)	East velocity	0.026	0.023	0.019
	North velocity	0.023	0.020	0.016
	Up velocity	0.031	0.026	0.022
Position (m)	Latitude	0.748	0.645	0.580
	Longitude	0.848	0.713	0.660
	Height	0.976	0.870	0.741

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Central Difference Variational Filtering Based on Conjugate Gradient Method for Distributed Imaging Application

Abstract

1. Introduction

2. Related Theories

2.1. Linear Minimum Variance (LMV) Criterion for Nonlinear Systems [23]

2.2. Central Difference Kalman Filtering

2.3. Conjugate Gradient Method for Unconstrained Optimization Problems

3. Central Difference Variational Filtering Algorithm

4. Experiment Validation

4.1. State-Space Model

4.2. Experiment Process and Result Analysis

5. Conclusion and Future Work

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe