Preprint

Article

Adjustment of the Nonlinear Schumacher and Hall Model in Mixed Form for Volume Estimation in Dense Ombrophilous Forest, Amazon, Brazil

Altmetrics

Downloads

119

Views

Comments

Jadson Coelho de Abreu^*,

Maricélia Moreira dos Santos,Wegliane Campelo Silva,Verena Holanda da Costa,Fernando Galvão Rabelo,Perseu da Silva Aparício

Jadson Coelho de Abreu^*,

Maricélia Moreira dos Santos,Wegliane Campelo Silva,Verena Holanda da Costa,Fernando Galvão Rabelo,Perseu da Silva Aparício

This version is not peer-reviewed

Submitted:

06 June 2024

Posted:

07 June 2024

You are already at the latest version

Alerts

Abstract

Volumetric models are a crucial tool for forest management. The study aimed to adjust the mixed model by Schumacher and Hall for estimating commercial volume in a dense ombrophilous forest situated in Ferreira Gomes, Amapá, Brazil. Cubage data from 100 sample trees of 5 species were used to adjust the Schumacher and Hall model in fixed and mixed non-linear forms with the diameter class as a random effect. In addition, the same model was also adjusted for each class to verify whether good equations will be generated by stratifying by diameter class. After analysis, it was found that most of the equations by diameter class do not present all significant parameters. On the other hand, the mixed models using class as a random effect showed good results. Finally, it can be seen that mixed models are a much better alternative than stratification by diameter class for volume estimation.

Keywords:

Subject: Biology and Life Sciences - Forestry

1. Introduction

The geometrically irregular shape of the tree trunk induces variability in estimates to calculate volume, some in a destructive way and others not. The volume of trees is the variable of greatest interest for commercial purposes.

To achieve parametric values with greater precision in the calculation of volume, the rigorous cubing technique is usually used (MACHADO; FIGUEIREDO FILHO, 2006; SOUZA et al., 2017), which consists of applying n sections on the stem to collect the diameter successively at fixed heights (CAMPOS, 2014).

Considering that rigorous cubing is an expensive activity, non-destructive methods (such as volume estimates) are applied, where conventionally form factor, form quotient, and volume equations are used. These are developed through a regression model, in which the diameter at 1.30 m of the soil (D) and commercial height of the trees are used as independent variables (hm) (MCTAGUE et al., 1989; MARTINS et al., 2016).

Due to the variability of the data, these equations may present a lower precision, if the data are not collected properly, decreasing the reliability to subsidize the economic analyzes. In general, regression models may present heterogeneity of variance, autocorrelation and absence of normality in residues for native forests. Therefore, the data collection step is essential to be able to generate equations with more reliability besides the models chosen for adjustment.

The use of volume equations stands out in the forestry sector because they have the advantage of calculating solid volume, tree by tree, through statistical models, which are tested to present the smallest possible errors. Among the various models in the literature to express the volume of wood as a function of diameter and height, the model proposed by Schumacher and Hall is one of the most used in forestry sector, which popularity is mainly attributed to its accuracy and ease of adjustment, resulting in estimates that are almost always unbiased (CAMPOS; LEITE, 2017).

The reliable estimates of the commercial volume equations enabled the determination, by Brazilian legislation (IBAMA, IN n° 030/2002) (from the second year of exploration), of the calculation of the geometric volume of standing trees. This calculation is conducted through tree volume equations developed specifically for the areas submitted to the Sustainable Forest Management Plan (BRASIL, 2003).

A volumetric equation is adjusted for a “mix” of tree species. However, the conformation of the trunk can vary among tropical species due to different plant responses to extreme edaphoclimatic factors. In this way, generating equations of populations can provide more accurate answers in volumetric estimates when compared with form factor or equation for the “mix” of species.

Besides the traditional volume equation approaches, volumetric modeling can be approached via mixed models. These models have been notable for their capacity to provide accurate estimates of the volume in native forests. The high heterogeneity of forests, characterized by various species, topography, density, site conditions, age, and other variables, is a challenge for traditional methods. The use of mixed models can offer a more comprehensive and detailed comprehension of forest structure, contributing significantly to the sustainable management of these ecosystems.

Given the legal requirement to develop equations for volume estimation in native forests, combined with the complexity of estimating dendrometric variables with high heterogeneity, this study hypothesizes that the Schumacher and Hall model will achieve greater accuracy with the inclusion of random effects. The objective of the study is to adjust the mixed model by Schumacher and Hall for estimating commercial volume in a dense ombrophilous forest situated in Ferreira Gomes, Amapá, Brazil.

2. Materials and Methods

Study Area

The study was developed in the Amapá National Forest, a Sustainable Use Conservation Unit created by the Brazilian Federal Decree nº 97,360 on April 10, 1989, located in the municipalities of Pracuúba, Ferreira Gomes and Amapá, Amapá, Brazil, with an area of 459,867.17 hectares, according to its Management Plan.

The Management Plan of the Amapá National Forest, approved by the Chico Mendes Institute for Biodiversity Conservation (ICMBio) Decree nº 1 on October 10, 2014, defined the zoning stage, highlighting the Sustainable Forest Management Zone which encompasses 268,549.59 hectares. In 2021, the company RRX Timber acquired two Forest Management Units within this zone through a bidding process organized by the Brazilian Forest Service (SFB), with areas of 39,073 and 112,994 hectares, respectively.

Sampling

The study was conducted in the area of effective management of the Production Unit I, operated by RRX Timber. The exploitation of commercial trees began in the dry season (July/2023). The trees explored were tonka beans (Dipteryx odorata (Aubl.) Forsyth f.), angelim vermelho (Dinizia excelsa Ducke), angelim pedra (Hymenolobium petraeum Ducke), ipê (Handroanthus albus (Cham.) Mattos) e maçaranduba (Manilkara elata (Allemão ex Miq.) Monach)

One hundred trees with diameters at 1.30 m above ground level (D) ≥ 50 cm were randomly selected for rigorous cubing across different diameter classes (Class 1: 50 < D < 60 cm; Class 2: 60 < D < 70 cm; Class 3: 70 < D < 80 cm; Class 4: 80 < D < 90 cm; Class 5: 90 < D < 100 cm; Class 6: 100 < D < 110 cm; Class 7: 110 < D < 120 cm; Class 8: 120 < D < 130 cm; and Class 9: D > 130 cm). The rigorous cubing process to obtain the commercial volume (vm) was performed according to the Smalian’s formula with logs L = 1 m.

Data Analysis

Using the data on commercial volume, diameters at 1.30 m above ground level, and commercial heights, it was initially adjusted the Schumacher and Hall (1933) fixed model in its nonlinear form. According to Abreu et al. (2023), this was the best model for the study area, given by:

v_{m i} = β_{0} D_{i}^{β_{1}} h_{m i}^{β_{2}} + ε_{i}

where: vmi = commercial volume in m³; Di = diameter at 1.30 m above ground level in m; hmi = commercial height in meters; β0 to β2 = model parameters; ε = random error.

The model adjustment was performed using the method of maximum likelihood through the R package glm2 (R DEVELOPMENT CORE TEAM, 2014).

Subsequently, the model by Schumacher and Hall (1933) was adjusted considering the structure of a nonlinear mixed model by including random intercepts and slope coefficients, considering the diameter classes and subsequently the species as random effects, resulting in the following models:

v_{m i} = (β_{0} + a_{0}) D_{i}^{{(β}_{1} + b_{1})} h_{m i}^{{(β}_{2} + b_{2})} + ε_{i}

where: β0, β1 and β2 = fixed model parameters;

a_{0}

= random intercept for the

i

-th diameter class or species;

b_{1 i}

b_{2 i}

= random slope coefficients for the

i

-th diameter class or species.

The mixed nonlinear model is mathematically represented (MELLO, 2014) as:

y_{i} = f (x_{i}, ϕ_{i}) + ε_{i},

ε_{i} N (0, R_{i})

, where:

y_{i}

is (

n_{i} x

1) vector of the dependent variable, f is the nonlinear function,

x_{i}

is (

n_{i} x

s_{1}

) matrix of known covariates,

ϕ_{i}

is (

s_{1} x

1) vector of parameters, consisting of only fixed-effect coefficients or the composition of fixed and random,

ε_{i}

is (

n_{i} x

1) vector of errors, 0 is a null vector,

R_{i}

is variance and positive covariance matrix for the errors.

The coefficients of the vector

ϕ_{i}

can be expressed as (LITTELL et al., 2006; PINHEIRO et al., 2021):

ϕ_{i} = A_{i} β + B_{i} b_{i}, b_{i} N (0, D)

, where:

A_{i}

B_{i}

are matrices for fixed and random effects, respectively;

β

is (

S_{1} x

1) vector of coefficients with fixed effects,

b_{i}

is (

S_{2} x

1) vector of random parameters, in which they assume a multivariate normal distribution, with mean vector zero and the variance and covariance matrix D.

The mixed model was adjusted using the method of maximum likelihood through the R package nlme (R DEVELOPMENT CORE TEAM, 2014). For the fixed and mixed form model, the Akaike Information Criterion (AIC), the correlation coefficient (

r_{y \hat{y}}

) between observed and estimated volume, the root mean square error (RMSE%), bias, and graphical analysis of residuals were employed (BINOTI et al., 2015).

The result of the inclusion of the random effect in the intercept and in the slopes was verified using the likelihood ratio test (RESENDE et al., 2014), where the significance of the difference (D) between the deviations [-2log(L)] for the models with and without the random effect was determined by comparing the calculated value with the tabulated value using the χ2 test at a 5% significance level.

For comparison purposes, the Schumacher and Hall model was also adjusted for each diameter class using the nonlinear least squares method, using the t-test on the parameters to verify whether it is possible to generate satisfactory volume equations with a smaller number of samples.

3. Results

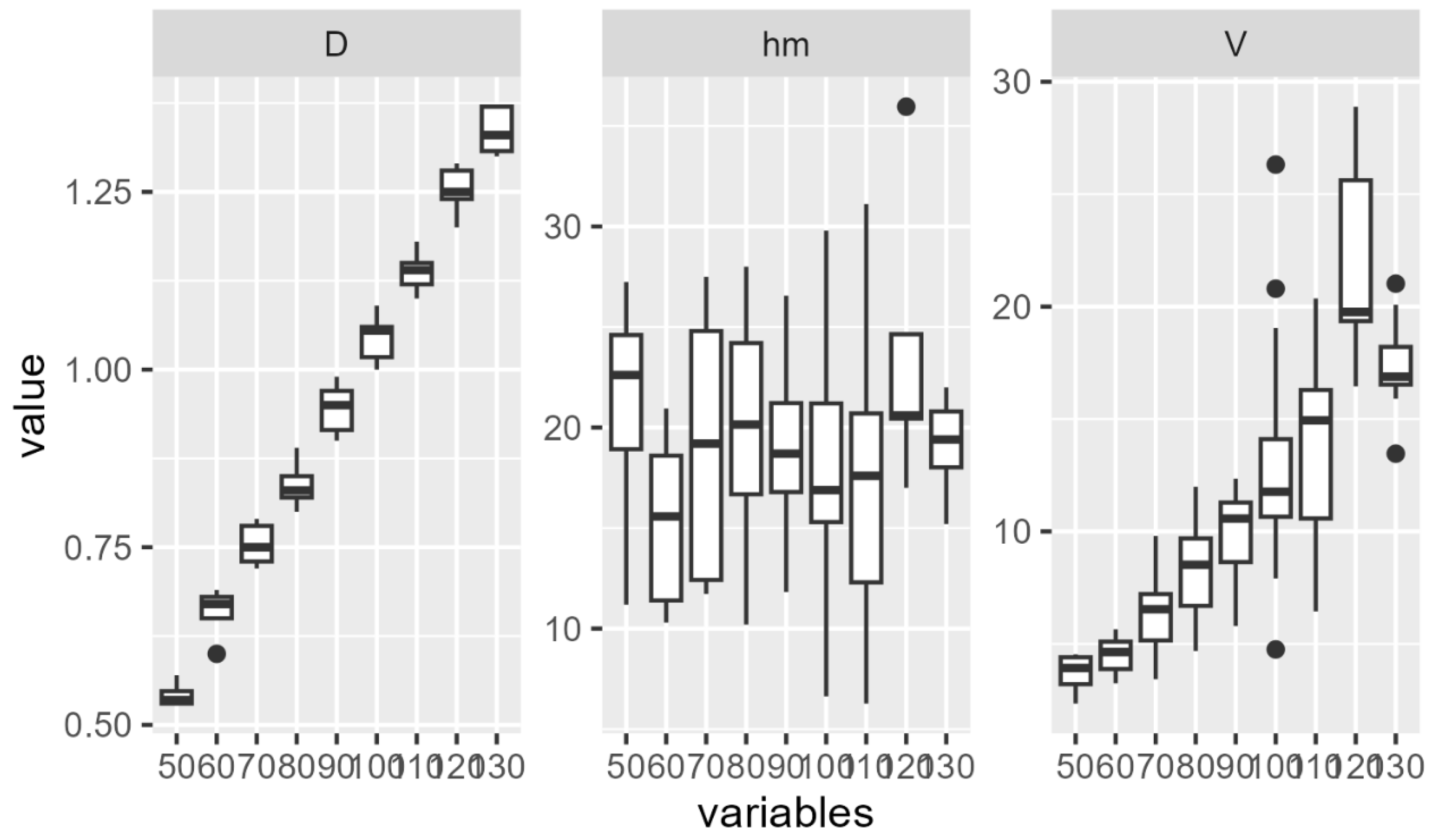
Considering the total number of sample trees used in the analyzes (100), the diameters at 1.30 m above ground level (D) ranged from 0.53 to 1.37 m and the commercial heights (h_m) from 6.27 to 35.96 m (Table 1). As for the volume (V_m), it ranged from 2.34 to 28.89 m³, with an average of 10.566 m³, respecting the maximum harvest limit of 30 m³/ha.

Dipteryx odorata has an average diameter of 0.70 m, an average height of 19.21 m, and an average volume of 5.97 m³. Dinizia excelsa has an average diameter of 1.01 m, an average height of 16.88 m, and an average volume of 11.36 m³. Handroanthus albus stands out with an average height of 25.58 m, making it the tallest among the species analyzed, and an average volume of 11.14 m³. Manilkara huberi has an average diameter of 0.81 m, an average height of 21.39 m, and an average volume of 8.39 m³. Hymenolobium petraeum has an average diameter of 0.82 m, an average height of 17.81 m, and an average volume of 7.97 m³.

These results provide a comprehensive view of the structural characteristics of the trees in the studied forest sample, allowing a better understanding of the diversity and distribution of the tree species.

These statistics can also be visualized in the box plot by diameter class (Figure 1), where the natural trend of growth in diameter and volume per class is observed. However, this same behavior is not evident in relation to height, considering that the commercial height (hm) may have different dimensions depending on the quality of the stem.

After adjusting the Schumacher and Hall model in the fixed form, it was found that it presented a good adjustment, with all parameters being significant and satisfactory test statistic (AIC=407.0609, RQME=1.77, r=94.54, bias=-0.03). Similar results were found by Chicorro et al. (2003), Scolforo et al. (2008), Rufini et al. (2010), Stolariková et al. (2014), Abreu et al. (2017) and Silva et al. (2024).

v_{m i} = 1.04941 D_{i}^{1.79458} h_{m i}^{0.80946}

In the mixed form, with the inclusion of the random effect, except for the bias, which indicates that the mixed model overestimates slightly more than the fixed model, it stood out as the best option, with all parameters significant (AIC= 400.4468, RQME= 1.49, r=96.19, bias=-0.04).

v_{m i} = 1.4505368 D_{i}^{2.0241437} h_{m i}^{0.7059324}

In the maximum likelihood ratio test, the random effect species was not significant, possibly due to the imbalance in the data, with a larger number of individuals of Dinizia excelsa (63) compared to only 4 of Hymenolobium petraeum. However, with the inclusion of the random effect of the diameter class, the maximum likelihood ratio test was highly significant (p<0.005).

The equations that take into account the random patterns of the forest, such as the diameter classes, were more accurate than a single fixed equation. These equations by class, after adding up the fixed parameters with the random effects in each class, are detailed in Table 2.

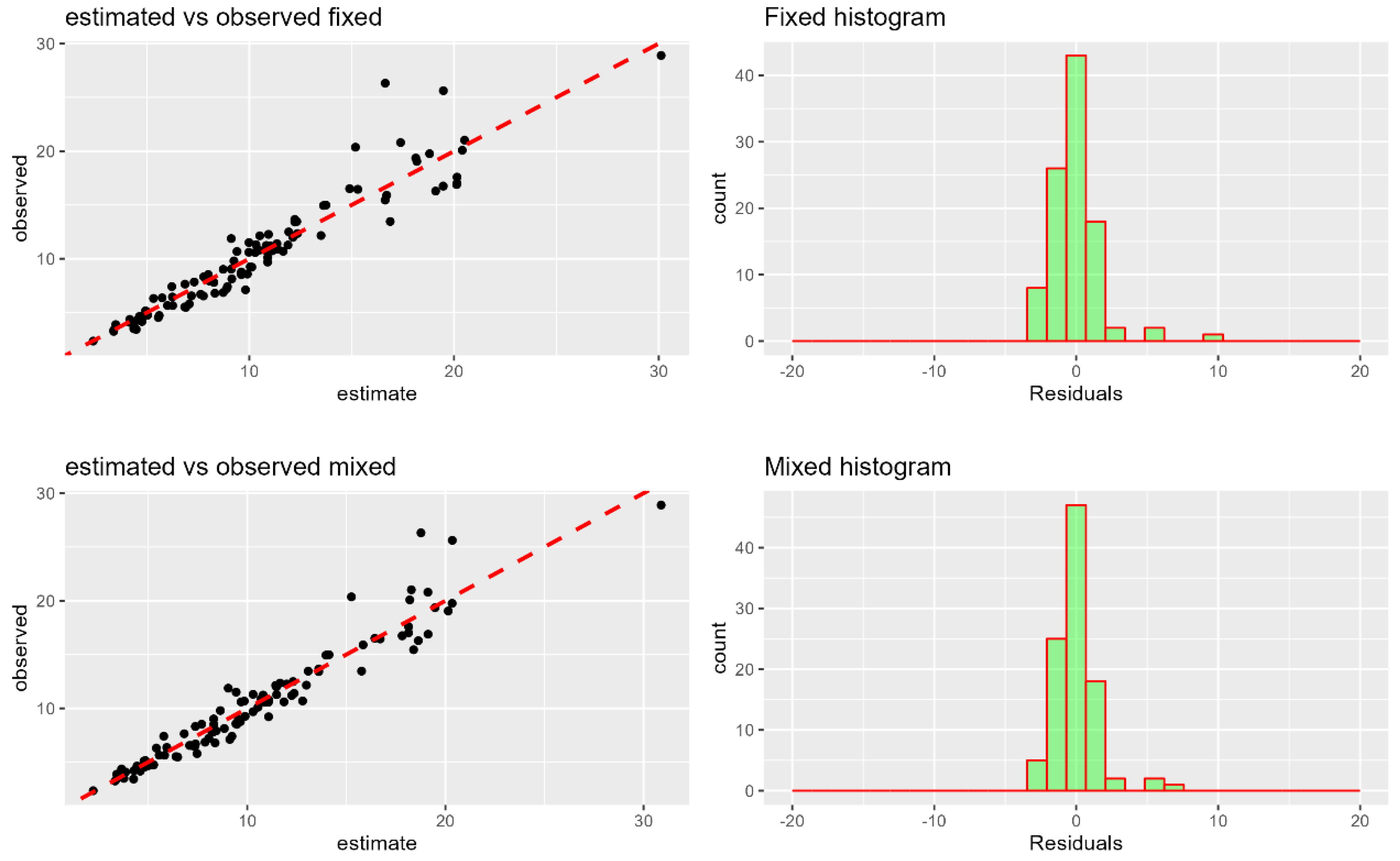
In Figure 2, it is observed that the mixed model exhibits a residual distribution slightly more centered around the x-axis on zero value compared to the fixed model, also observing a greater proximity of the points to the 90º line formed by the observed volumes and those estimated by the equations.

In Table 3, the equations adjusted by nonlinear ordinary least squares in each diameter class can be observed. It is possible to notice that, with the exception of the class 100 equation, none of the others all significant parameters.

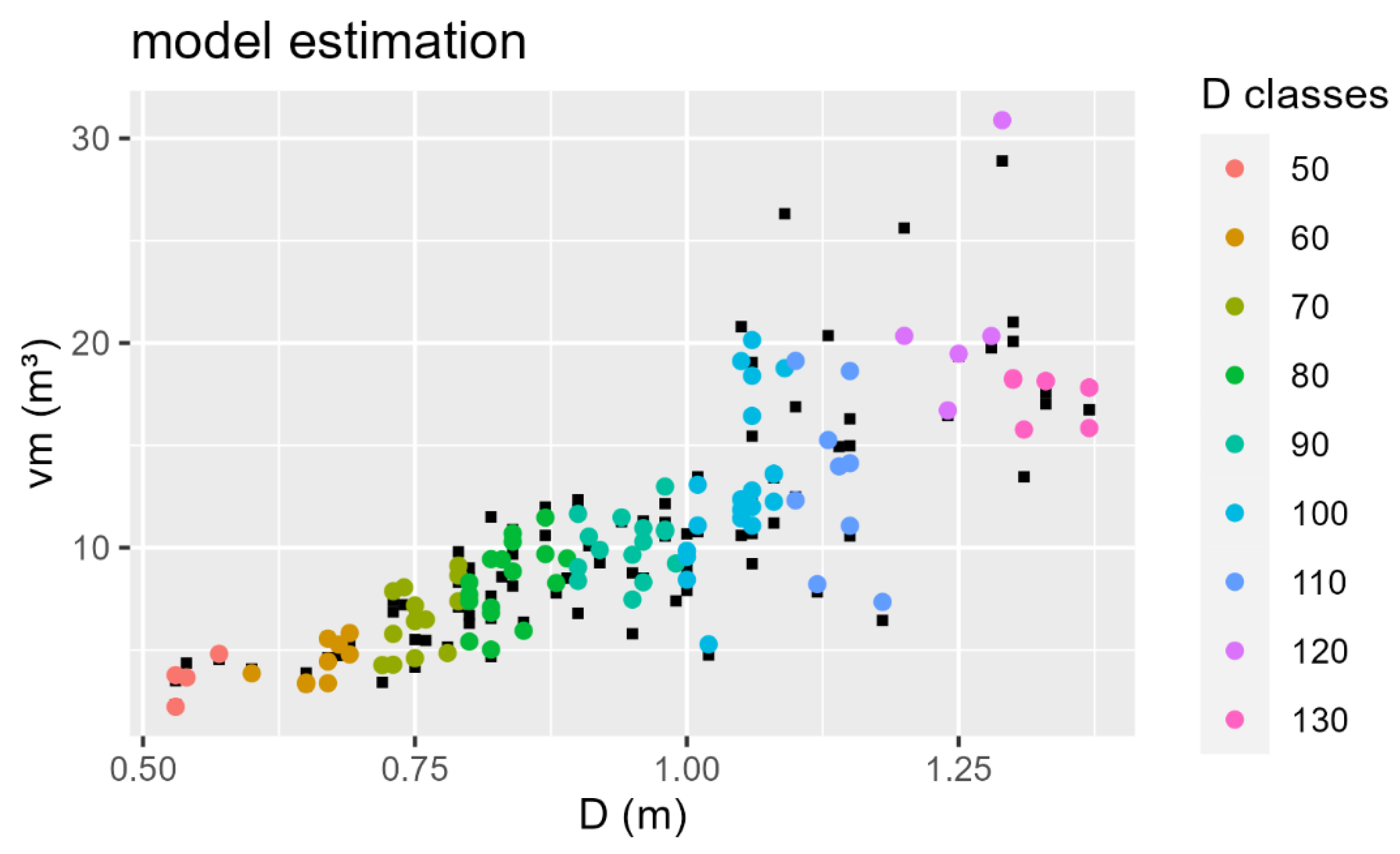
In Figure 3, the estimates of the Schumacher and Hall model in mixed form are presented. In general, the model was able to predict the volume in all diameter classes.

4. Discussion

Unbalanced data are a common challenge in forest studies, especially when using mixed models to analyze variables such as diameter at 1.30 m above ground level, commercial height (hm) and commercial volume (vm). The imbalance occurs when the number of observations is not uniform between the different levels of a categorical variable, such as species or sample plots (FITZMAURICE et al., 2011; GELMAN and HILL, 2006). In this study, a significant imbalance can be observed in the samples collected for different species, which may influence the accuracy of the parameters estimates and the statistical power of tests. This imbalance in studies of native forests is common, given that this is a highly heterogeneous environment.

Furthermore, according to Brasil (2003), in sustainable forest management, it is only allowed to cut down trees with a diameter above 50 cm and a maximum of 30 m³/ha for commercial forest management. Therefore, in some samples, not all species have individuals in these conditions, and it is not permitted to cut down more trees to equal the number of individuals per species in the sample.

Imbalance can lead to heterogeneity in variance between groups, making it difficult to estimate fixed and random effects parameters (WEST et al., 2014). To solve these effects, diameter class was used as a random effect, as this variable reduces the imbalance in the sample, as suggested by Monteiro et al. (2021).

The distribution and histogram of residuals (Figure 2) confirm the superiority of the equation generated from the Schumacher and Hall model in mixed form, with a higher concentration of errors close to error class 0 and a smaller amplitude on the x-axis. This behavior of the Schumacher and Hall model was also observed in studies conducted by Monteiro et al. (2021) to estimate volume in different forest typologies in the Amapá State Forest (FLOTA), using mixed models and diameter classes as random effects.

The histograms of the percentage residuals for the fixed and mixed models display an adequate distribution, remaining within a variation range of -10% to 10%. Although there are some outliers, as observed in the fixed model where the residuals reach the limit of 10%, these discrepancies can be considered insignificant. This is due to the fact that such outliers represent a small portion in relation to the data set used for the adjustment and do not exert a significant influence on the model estimates (Costa et al., 2012).

The dispersion and histogram of the residuals of the Schumacher and Hall model are more concentrated near the error class 0, which demonstrates a greater capacity for accuracy in volume estimation. This behavior was also observed in the results of the study conducted by Lima et al. (2020) for comparison and selection of a generic model for volume estimation for the Amapá State Forest.

It can be observed that the non-linear models adjusted by diameter class, by nonlinear ordinary least squares, do not present all parameters as significant. However, nonlinear models do not have the same interpretation as linear models; in nonlinear regression, in general, they are based on large sample theory (BATE and WATES, 1988; HUET et al., 2004).

This theory suggests that, when samples are large, least squares and maximum likelihood estimators in nonlinear regression models, with normal error terms, are almost normally distributed, are nearly unbiased, and have variance very close to the minimum (GUJARATI and PORTER, 2011). For example, class 50, which contains only 4 samples, is considerably far from providing a satisfactory equation. Therefore, the use of mixed models in native forests is ideal, since obtaining enough samples to represent the entire forest is an expensive task. In this way, mixed models can provide satisfactory equations with a smaller number of samples.

5. Conclusions

Mixed models using class as a random effect showed satisfactory results. Specifically, the Schumacher and Hall model in mixed form emerged as the most suitable choice for volume estimation in the Amapá National Forest. This is due to its ability to capture variability between diameter classes more efficiently, suggesting that the mixed approach is more robust and effective for volume estimation in forests with uneven age structure. This finding indicates that the use of mixed models has the potential to provide more accurate and reliable estimates, thus contributing to more effective management and conservation of forest resources

Author Contributions

Conceptualization, Jadson Abreu; Data curation, Verena Costa; Formal analysis, Jadson Abreu; Funding acquisition, Perseu Aparício; Methodology, Verena Costa; Project administration, Fernando Rabelo; Validation, Wegliane Silva; Visualization, Maricélia Santos; Writing – original draft, Jadson Abreu; Writing – review & editing, Maricélia Santos.

Acknowledgments

We would like to express our gratitude to RRX Timber for all the logistical support and funding that made this research project possible. Your contribution not only enables our investigation but also demonstrates a valuable commitment to forest management in the state of Amapá. We thank the Universidade do Estado do Amapá (UEAP), which, through the edict PROGRUPOS/PROPESP for supporting scientific research projects, made it possible to purchase permanent materials and consumables for field activities, demonstrating the University’s commitment to its researchers.

References

Abreu, J.C.; Soares, C.P.B.; Leite, H.G. Assessing alternatives to estimate the stem volume of a seasonal semi-. deciduous forest. Revista floresta, Curitiba 2017, 47, 375–382. [Google Scholar] [CrossRef]
Abreu, J.C.; Aparicio, P.S.; Silva, W.C.; Costa, V.H. Modelagem volumétrica na floresta nacional do Amapá. RGSA (ANPAD) 2023, 18, 1–9. [Google Scholar]
Bates, D.M.; Watts, D.G. Nonlinear Regression Analysis and Its Applications; Wiley, 1988; 365p. [Google Scholar]
Brasil, 2003. Instrução Normativa, nº05, de 11 de dezembro de 2006. Dispõe sobre procedimentos técnicos para elaboração, apresentação, execução e avaliação técnica de Planos de Manejo Florestal Sustentável-PMFSs nas florestas primitivas e suas formas de sucessão na Amazônia Legal, e dá outras providências. D.O.U., 13/12/2006, Seção 1.
Binoti, M.L.M.S.; Leite, H.G.; Binoti, D.H.B.; Gleriani, J.M. Prognose em nível de povoamento de clones de eucalipto empregando redes neurais artificiais. CERNE 2015, 21, 97–105. [Google Scholar] [CrossRef]
Campos, J.C.C.; Leite, H.G. Mensuração florestal: Perguntas e respostas, 5 ed.; Editora UFV: Viçosa, 2017. [Google Scholar]
Campos, O.J. Cubagem de árvores. 2014. 87 f. Dissertação. (Mestrado Profissional em Matemática), Universidade Federal de Santa Catarina, Florianópolis, SC, 2014.
Chicorro, J.F.; Resende, J.L.P.; Leite, H.G. Equações de volume e de taper para quantificar multiprodutos da madeira em floresta atlântica. Revista Árvore, Viçosa-MG 2003, 27, 799–809. [Google Scholar] [CrossRef]
Costa, T.R.; Campos, L.; Cysneiros, F.J.A.; Cunha Filho, M. Modelos lineares mistos: Uma aplicação na curva de lactação de vacas da raça Sindi. Revista Brasileira de Biometria, São Paulo 2012, 30, 23–49. [Google Scholar]
Gujarati, D.N.; Porter, D.C. Econometria básica, 5ed.; Bookman: São Paulo, 2011; 918p. [Google Scholar]
Fitzmaurice, G.M.; Laird, N.M.; Ware, J.H. Applied Longitudinal Analysis, 2ed.; John Wiley & Sons, 2011; 752p. [Google Scholar]
Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Cambridge University Press: Cambridge, 2006; 648p. [Google Scholar]
Huet, S.; Bouvier, A.; Poursat, M.-A.; Jolivet, E. Applied Nonlinear Regression, 2 ed.; Cambridge University Press: Cambridge, 2004; 242p. [Google Scholar]
Lima, R.B.; Rutishauser, E.; Silva, J.A.A.; Guedes, M.C.; Herault, B.; Oliveira, C.P.; Aparício, P.S.; Sotta, E.D.; Silva, D.A.S.; Ferreira, R.L.C. Accurate Estimation of Commercial Volume in Tropical Forests. Forest Science, [s. l] 2020, 67, 14–21. [Google Scholar] [CrossRef]
Littel, R.C.; Milliken, G.A.; Stroup, W.W.; Wolfinger, R.D.; Schabengerger, O. SAS system for mixed models, 2o ed.; SAS Institute: Cary, North Carolina, 2006; 814p. [Google Scholar]
Machado, S.A.; Figueiredo Filho, A. Dendrometria, 2ed.; Unicentro: Guarapuava, 2006; 316p. [Google Scholar]
Martins, A.P.M.; Carvalho, D.E.; Schmidt, L.N.; Gorenstein, M.R.; Cyrsneiros, V.C. Eficiência de métodos para estimativa do volume total de Corymbia citriodora. Sciencias Agrarias. Paraná 2016, 15, 178–184. [Google Scholar]
Mello, M.N. Modelo não linear misto aplicado a análise de dados longitudinais em um solo localizado em Paragominas, PA. Tese, Universidade de São Paulo, 2014. [Google Scholar]
Mctague, J.; Batista, J.L.F.; Stiner, L.H. Equações de volume total, volume comercial e forma do tronco para plantações de Eucalyptus nos estados de São Paulo e Rio de Janeiro. Instituto de Pesquisas e Estudos Florestais 1989, 56–63. [Google Scholar]
Monteiro, B.C.; Abreu, J.C.; Souza, R.L.F.; Santos, B.C.; Oliveira, I.R.; Lima, R.B. Uso de modelos mistos para estimativa de volume de árvores individuais em tipologias florestais no Estado do Amapá. Biota Amazonia, Macapá 2021, 11, 7–10. [Google Scholar]
R core team. R: A language and environment for statistical computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
Resende, M.D.V. de; Silva, F.F. e; Azevedo, C.F. Resende, M.D.V. de; Silva, F.F. e; Azevedo, C.F. Estatística matemática, biométrica e computacional: Modelos mistos, multivariados, categóricos e generalizados (REML/BLUP), inferência bayesiana, regressão aleatória, seleção genômica, QTL-GWAS, estatística espacial e temporal, competição, sobrevivência. Viçosa: Suprema gráfica e Editora Ltda, 2014. 882p.
Rufini, A.L.; Scolforo, J.R.S.; Oliveira, A.D.; Mello, J.M. Equações volumétricas para o cerrado sensu stricto, em Minas Gerais. Revista Cerne, Lavras 2010, 16, 1–11. [Google Scholar] [CrossRef]
Pinheiro, J.; Bates, D.; Debroy, S.; Sarkar, D.; Heisterkamp, S.; Van Willigen, B.; Maintainer, R. Package ‘nlme’. Linear and nonlinear mixed effects models, version, 3(1). 2021.
Souza, H.S.; Drescher, R.; Vendruscolo, D.G.S.; Moura, J.P.V.M.; Siqueira, T.A.S.; Mamoré, F.M.D. Comparação de métodos de cubagem para eucalipto. Revista Brasileira de Biometria, Lavras 2017, 35, 15–26. [Google Scholar]
Schalaegel, B.E. Testing, reporting, and using biomass estimation models. In: Southern forest biomass workshop. Proceedings, 1981; 95–112. [Google Scholar]
Schumacher, F.X.; Hall, F.D.S. Logarithmic expression of timber-tree volume. Journal of Agriculture Research 1933, 47, 719–734. [Google Scholar]
Scolforo, J.R.S.; Rufini, A.L.; Mello, J.M.; Oliveira, A.D.; Silva, C.P.C. Equações para estimar o volume de madeira das fisionomias, em Minas Gerais. ln: Scolforo, J.R. S.; Oliveira, A.D.; Acerbi Júnior, F.W. (Org.). Inventário Floresta de Minas Gerais. Belo horizonte, MG p: 67-114. 2008.
Silva, G.F.; Mendonça, A.R.; Dias, A.N.; Nogueira, G.S.; Silva, J.A.A.; Oliveira, M.L.R.; Ferreira, R.L.C. Padronização da Simbologia em Mensuração e Manejo Florestal; Edição dos Autores: Viçosa, 2022; 66p. [Google Scholar]
Silva, A.V.S.; Souza, R.G.T.; Souza, R.L.F.; Santos, R.M.; Lima, R.B.; Abreu, J.C. Use of machine learning, fixed and mixed models for volume estimation in floodplain forest in the Amazon estuary. FLORESTA, Curitiba, PR 2024, 54, e-83115. [Google Scholar]
Stolariková, R.; Šálek, L.; Zahradník, D.; Dragoun, L.; Jeřábková, L.; Marušák, R.; Merganič, J. Comparison of tree volume equations for small-leaved lime (Tilia cordata Mill.) in the Czech Republic. Scandinavian Journal of Forest Research 2014, 29, 757–763. [Google Scholar] [CrossRef]
Vibrans, A.C.; Moser, P.; Oliveira, L.Z.; Maçaneiro, J.P. Height-diameter models for three subtropical forest types in southern Brazil. Ciência e Agrotecnologia 2015, 39, 205–215. [Google Scholar] [CrossRef]
West, B.T.; Welch, K.B.; Galecki, A.T. Linear Mixed Models: A Practical Guide Using Statistical Software, 2 ed; CRC Press: New York, 2014; 440p. [Google Scholar]

Figure 1. Box plot for dendrometric variables in the Amapá National Forest.

Figure 2. Line at 90 degrees between observed and estimated volume and histogram of residuals for fixed and mixed models in the Amapá National Forest.

Figure 3. Observed and estimated values by the mixed model in the Amapá National Forest.

Table 1. Descriptive statistics of data for adjusting volume equations in the Amapá National Forest.

Total of samples
Variable	N	$\bar{x}$	s	Minimum	Q1	Median	Q3	Maximum
D (m)	100	0,944	0,209	0,53	0,79	0,95	1,08	1,37
Hm (m)	100	18,968	5,607	6,27	15,44	18,525	22,25	35,96
Vm (m³)	100	10,566	5,487	2,345	6,517	9,742	13,431	28,892
Dipteryx odorata
Variable	N	$\bar{x}$	s	Minimum	Q1	Median	Q3	Maximum
D (m)	5	0,700	0,137	0,530	0,590	0,670	0,825	0,900
Hm (m)	5	19,218	6,151	11,400	13,305	19,200	25,140	26,560
Vm (m³)	5	5,976	3,646	3,496	3,688	4,637	8,934	12,350
Dinizia excelsa
Variable	N	$\bar{x}$	s	Minimum	Q1	Median	Q3	Maximum
D (m)	63	1,014	0,194	0,530	0,890	1,050	1,130	1,370
Hm (m)	63	16,880	4,920	6,270	12,430	17,000	20,150	29,800
Vm (m³)	63	11,364	5,554	2,345	7,403	10,688	15,449	26,317
Handroanthus albus
Variable	N	$\bar{x}$	s	Minimum	Q1	Median	Q3	Maximum
D (m)	16	0,871	0,209	0,53	0,79	0,95	1,08	1,37
Hm (m)	16	25,588	5,607	6,27	15,44	18,525	22,25	35,96
Vm (m³)	16	11,140	5,487	2,345	6,517	9,742	13,431	28,892
Manilkara huberi
Variable	N	$\bar{x}$	s	Minimum	Q1	Median	Q3	Maximum
D (m)	12	0,814	0,091	0,690	0,743	0,795	0,900	0,960
Hm (m)	12	21,394	3,042	15,580	19,250	21,675	22,850	27,300
Vm (m³)	12	8,393	2,190	5,100	6,579	8,225	10,478	11,304
Hymenolobium petraeum
Variable	N	$\bar{x}$	s	Minimum	Q1	Median	Q3	Maximum
D (m)	4	0,828	0,171	0,600	0,655	0,850	0,978	1,010
Hm (m)	4	17,813	1,800	16,680	16,760	17,035	19,643	20,500
Vm (m³)	4	7,972	3,971	4,081	4,699	7,173	12,044	13,459

Table 2. Mixed models by random effect in the Amapá National Forest.

Class	Equation
50	$v_{m i} = 1.461701 D_{i}^{2.009546} h_{m i}^{0.7025686}$
60	$v_{m i} = 1.470927 D_{i}^{1.997483} h_{m i}^{0.6997888}$
70	$v_{m i} = 1.360165 D_{i}^{2.142372} h_{m i}^{0.7331614}$
80	$v_{m i} = 1.467769 D_{i}^{2.001569} h_{m i}^{0.7007405}$
90	$v_{m i} = 1.548898 D_{i}^{1.895547} h_{m i}^{0.6762939}$
100	$v_{m i} = 1.052051 D_{i}^{2.545103} h_{m i}^{0.8259994}$
110	$v_{m i} = 1.533423 D_{i}^{1.915822} h_{m i}^{0.6809594}$
120	$v_{m i} = 1.431008 D_{i}^{2.049691} h_{m i}^{0.7118185}$
130	$v_{m i} = 1.728889 D_{i}^{1.660159} h_{m i}^{0.6220612}$

Table 3. Parameters of the equations adjusted by diameter class in the Amapá National Forest.

D classes	n	β₀	β₁	β₂
50	4	1,773489353 ^n.s	1,602817916 ^n.s	0,565126596 ^n.s
60	9	1,534694699 ^n.s	1,519672922 ^n.s	0,61831325*
70	13	2,616639119 ^n.s	3,188227686 ^n.s	0,59672971*
80	17	1,135528111*	1,142376223 ^n.s	0,740011957*
90	15	0,976424564 ^n.s	1,103870316 ^n.s	0,810075526*
100	20	0,706766198*	4,308626104*	0,927571908*
110	9	1,933428887 ^n.s	1,71763492 ^n.s	0,612492127*
120	5	2,755973181 ^n.s	-2,326905219 ^n.s	0,823749367*
130	8	0,646560364 ^n.s	0,852725907 ^n.s	1,029523986*

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.