Preprint

Article

A study of Tennis Tournaments by Means of an Agent-Based Model Calibrated with a Genetic Algorithm

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Salvatore Prestipino,

Andrea Rapisarda^*

Salvatore Prestipino,

Andrea Rapisarda^*

This version is not peer-reviewed

Submitted:

04 June 2024

Posted:

10 June 2024

You are already at the latest version

Alerts

Abstract

Direct competitions involve competitors that mutually contend for the same resource or objective. A controlled, well-documented, and data-rich field involving direct competition is represented by sports. Usually the winner of sports competitions is believed to be the one with the greatest talent, however, there are other factors that contribute to the outcome of a competition, there are in fact random, unpredictable events that can change the outcome of a competition. For this reason, if one wants to understand the properties of a competition is necessary to have a method to evaluate the importance of the talent or aptitude of a competitor, as opposed to the importance of chance, in determining the outcome of the competition itself. In this work we study the sport of tennis using the data obtained from the Association of Tennis Professionals (ATP) tournaments. We construct an agent-based model that is able to produce data analogous to the real one; this model depends on three parameters, the talent, the action of chance, and the weight of talent. In particular, we don't fix the values of these parameters and we fit the model results using a genetic algorithm, in this way, we study all the possible combinations of parameters, in the parameter space, that are able to reproduce the real systems data. We show that the model fits well the real data only for limited regions of the parameter space. On these limited regions of the parameter space are possible further optimization of the model results, limiting the values of parameters. In this way, our agent-based model, by means of this genetic algorithm calibration, is able to provide us with useful information without any a priori constraints.

Keywords:

Subject: Computer Science and Mathematics - Other

1. Introduction

The study of competitions is an important topic concerning different scientific fields, physics [1,2], biology[3], economics [4], etc. This interest is justified by the fact that competition is a common phenomenon in nature and society, and so it is important to understand its mechanics. When we think about the outcome of competitions, we assume that they are determined almost exclusively by the talents, properties or inclinations of the competitors, but this is not the case as general studies have recently demonstrated [5,6]. A lot of other work has been done to understand the recipes for success [7,8,9,10], and it seems that the outcome of the competition depends on a series of factors, among which the action of chance, represented by all the events that cannot be predicted a priori, plays a major role.

In order to better understand competitions, we want to focus on sports, which gives us access to a large amount of data. For this type of competitions, previous studies, [11,12,13,14,15], although using different approaches, have again shown that the talent or preparation of the athletes is not the only factor determining the outcome of competitions and that the action of chance is an important component of competitions.

To study the phenomenon of competition, previous works [11,12,13] have developed multiparametric models capable of reproducing the data of real competitions, the calibration of these models has been obtained by fixing some parameters with reasonable values extrapolated be antecedent works, with these constraints, the models have been able to provide information regarding the role of chance in contraposition to that of talent in determining the outcome of competitions.

In this paper, as in other works cited above, we want to construct an agent-based model [16], a type of model used for the study of complex systems [17,18] in a wide range of scientific fields [19,20,21]; useful for reproducing relations between simulated agents and a virtual environment composed of a set of rules.

However, we want to avoid constraining the parameters of the model, in order to obtain information on all the parameters that are important for the competitions, according to the model, and so obtain also information that has been inferred in other works. In particular, we concentrate our study on the sport of tennis using the data from the Association of Tennis Professionals (ATP) tournaments [22,23,24].

Tennis is a sport in which two individuals compete against each other, it is an example of direct competition, where the two competitors are somehow linked to each other, in fact, in this type of competition an event that favors one competitor will at the same time disadvantage the opposing competitor.

For a direct competition of the 1 vs 1 type, based on the sport of tennis, in order to simulate the tennis matches and replicate the tournaments data. The model constructed in this way depends on a set of three parameters, the weight of talent, the standard deviation of the talent distribution, and the standard deviation of the chance distribution. Thus, we infer the shape of the talent and chance distributions, chosen to be Gaussian and symmetric with respect to zero. but we don’t set other constrain on the possible values of the parameters.

Having few assumptions about the values of the parameters, we use a genetic algorithm [25] and related computations to explore a large number of possible combinations for the parameters to calibrate the model on the basis of the real data. In order to better understand the results of our calibration, we therefore use the talent distribution used in previous work to reject some unrealistic results and thus obtain information about the role of chance and talent encoded in the values of the parameters used in our model.

2. Materials and Methods

2.1. Data Preparation

In order to construct a model of the direct competition for the sport of tennis, we need to prepare the data in a way that highlights the properties of the system. In particular, the data used in this paper consists of 108411 matches played in 2125 tournaments, these are men’s singles matches that belong to the ATP tournaments from 1991 to 2021 of the Grand Slams, Masters 1000, ATP 500, and ATP 250. Acquired using online resources [22,23,24].

We want to estimate the performance of the two competitors involved in a match, with this type of information it is then possible to aggregate all the performances of all the players involved in all the matches to construct a distribution of the performance that we can then try to reproduce with a model.

We decided to construct a numerical estimate of performance based on the simple match score. In fact, the score can be seen as the result of the total balance of "positive" and "negative" actions performed by the two competitors during the match.

To understand how this performance value is constructed in the case of tennis matches, it is necessary to briefly summarize how points are awarded in this sport [26,27].

In tennis, the winner of a match is the player who wins at least two of three sets in a three-set match, or wins at least three sets in a five-set match.

A set is conquered by winning at least six games and trailing the opponent by at least two points. If both players win at least six games ending in a tie, a tie-break is played, which consists of an extra game to decide the set winner.

A game is won by the first player to score 4 points, with an advantage of at least 2 points over his opponent; if this is not the case, the game continues until one player scores 2 points more than his opponent and wins the game.

What is used to calculate a numerical value for the performance is the total number of points scored during the sets by the two competitors involved in the match. So the number of sets and games won is not taken into account, only the cumulative score, with the additional information about the winner of the match, the data is split into the performance of the winner and the performance of the loser.

In order to calculate a performance value that takes into account the score and is expressed using a number between 0 and 1, it is natural to use the ratios between the scores of the two competitors and the total number of points scored by both during the match. By defining the performance in this way, the value obtained for the winner of the match is linked to the value obtained for the loser in a specular manner, so if the performance of one player is underwhelming, the performance of the other is enhanced, decoupling the two performances would be extremely difficult.

That’s why in the distribution of the score performance shown in Figure 1(a), are presented two histograms, one, representing the winning players and the other one representing the losing ones. The symmetry of these distributions with respect to 0.5 is significant, the distance and the intersection of the two distributions from each other are features that we aim to reproduce with the agent-based model.

Another feature of the data is highlighted when we study how the width of the score performance distribution changes over the different stages of the tournaments, the width of the distribution contains information concerning the difference between the score performance of the winners and that of the losers players. We can calculate the full width at half maximum (FWHM) considering the normalized histograms of the score performances of the winners and losers and performing a Gaussian fit on them.

The Figure 1(b) shows that from the first round, labeled with an

x = 6

, to the final labeled with

x = 0

, the FWHM of the score performance distribution tends to decrease with a certain slope, this is another feature that we want to reproduce with the agent-based model.

2.2. The Direct Competition Model Core

In order to develop an agent-based model for the sport of tennis, it is necessary to establish the mechanism that allows an agent-player to score a point. This mechanism must depend on the sportive performance of the agent-player in such a way to emulate a real situation. Previous work [9,11,12] have used an equation to obtain a numerical value of the sportive performance of an agent-player. We have adapted this equation to the case of a direct competition of two agent-player, and obtained a system of equations:

\begin{matrix} {\tilde{P}}_{1}^{[a, σ_{t}, σ_{c}]} (t) = \frac{1}{2} + \frac{d_{1, 2}^{[a, σ_{t}, σ_{c}]} (t)}{2} \\ {\tilde{P}}_{2}^{[a, σ_{t}, σ_{c}]} (t) = \frac{1}{2} - \frac{d_{1, 2}^{[a, σ_{t}, σ_{c}]} (t)}{2} \end{matrix}

(1)

with

\begin{matrix} d_{1, 2}^{[a, σ_{t}, σ_{c}]} (t) & = a (T_{1}^{[σ_{t}]} - T_{2}^{[σ_{t}]}) + (1 - a) [2 C {(t)}^{[σ_{c}]} - 1] \end{matrix}

(2)

where

d_{1, 2}^{[a, σ_{t}, σ_{c}]} (t)

is the distance in terms of performance between the two competitors: the agent with the label 1 against the one with the label 2. This quantity depends on the variable t, the iteration for which the quantity is calculated, and on a series of parameters:

The talent weight $a$ , defined with values between 0 and 1, determines the importance of talent over chance, for $a = 1$ performance is purely talent dependent, for $a = 0$ performance is purely chance dependent.
The standard deviation of the talent distribution $σ_{t}$ , of a normal distribution, centered at 0.5 and truncated between 0 and 1, from which the constant values $T_{1}$ and $T_{2}$ , the talents of the agents 1 and 2 involved in a match, are drawn.
The standard deviation of the chance distribution $σ_{c}$ , of a normal distribution, centered at 0.5 and truncated between 0 and 1, from which the chance value $C (t)$ , recalculated at each iteration, is drawn.

Using

d_{1, 2}^{[a, σ_{t}, σ_{c}]} (t)

is possible to obtain the values of

{\tilde{P}}_{1}^{[a, σ_{t}, σ_{c}]} (t)

and

{\tilde{P}}_{2}^{[a, σ_{t}, σ_{c}]} (t)

, that are the relative sportive performance of agents 1 and 2, respectively. The values of

{\tilde{P}}^{[a, σ_{t}, σ_{c}]} (t)

are between 0 and 1, and for the two agents involved in the match they assume specular values with respect to the value 0.5.

Using the equations 1 it is possible to assign points, at each iteration

t

, on the basis of the greater value of the performance between

{\tilde{P}}_{1}^{[a, σ_{t}, σ_{c}]} (t)

and

{\tilde{P}}_{2}^{[a, σ_{t}, σ_{c}]} (t)

. Having a way to assign the points in a simulated match, it is possible to replicate the structure of rules of a real Tennis match and obtain a winner agent and a loser agent.

It is also possible to reproduce the structure of a tournament, and thus obtain the ranking of the agents playing in the tournament and the relative number of scored points, so that we can obtain data comparable to the real ones. The simulated tournaments have been constructed with a total of 128 agents-players, a number close to the average number of players that participate in the ATP tournaments, each simulated tournament has new agents with a talent drawn from a predetermined talent distribution. The initial pairings between agents are random, and the subsequent ones are dictated by the winning agent-player, the simulated tournaments are composed of 7 rounds, the winner of the final simulated game is the tournament winner.

3. Results

3.1. The Agent-Based Model Simulation

The developed agent-based model in constructed using the equations 1, so it depends on the same three parameters, the talent weight

a

, the standard deviations of the distribution of talent

σ_{t}

and the standard deviations of the distribution of chance

σ_{c}

. Having chosen the values of the three parameters, the model runs a series of virtual tournaments, we collect the data obtained from the virtual tournaments to construct, as in the real case, a score performance distribution.

Figure 1(c) shows the distribution obtained considering 10000 simulated tournaments, each with 128 agents-players participating, with fixed parameters

a

= 0.3,

σ_{t}

= 0.2,

σ_{c}

= 0.2. The distribution obtained from the model has the same characteristics as that obtained from the real data, its shape depends on the three parameters of the model, so with the right combination of parameters it’s possible to obtain a distribution that fits the real distribution. An interesting feature observed in the simulations is that for a value of

a

equal to 1, so with pure talented based tournaments, the area of intersection between the losing and winning parts of the score distribution disappears, so the presence of this intersection is due to the action of chance.

With the same set of parameters used for the distribution in Figure 1(c), Figure 1(d) instead shows the variation of the FWHM at different stages of the tournaments. We can see that the model is able to reproduce the same kind of trend for the FWHM shown for the real data. This trend, which has also been shown in other works [11,12,13], is due to the fact that the most talented players are selected to participate in the later stages of the tournaments.

3.2. Calibration of the Agent-Based Model on the Real Data

To fit the simulated data of the agent-based model to the data obtained from the real tournaments, we use a genetic algorithm, this type of algorithm is often used in optimization problems [25], even with agent-based models [28]. In particular, the use of a genetic algorithm allows us to explore the entire 3D parameter space of the agent-based model in search of parameter values that make the simulated results adhere to the real data.

The genetic algorithm is an algorithm that attempts to simulate a natural selection process for the possible solutions of a model. In this specific case, what the genetic algorithm compares using the fitness function is the score performance distribution of the real data and the simulated data. A fitness function is therefore needed to quantify the ability of the model to fit the data when certain parameters are set. The fitness function chosen to be used for such comparisons is the reciprocal of a generalized Euclidean distance:

\begin{matrix} d (p, q) = \sqrt{{(p_{1} - q_{1})}^{2} + {(p_{2} - q_{2})}^{2} + . . . + {(p_{n} - q_{n})}^{2}} \\ f (p, q) = 1 / d (p, q) \end{matrix}

(3)

where

p_{1}, p_{2} . . . p_{n}

and

q_{1}, q_{2} . . . q_{n}

refer to the abscissae of the two normalized histograms representing the compared score performance distributions,

d (p, q)

is the generalized Euclidean distance and

f (p, q)

is the fitness function.

In this particular case, the genetic algorithm optimizes the value of three genes, which are the three parameters of the model. For all three genes, the range of possible values is between 0.01 and 1.00. These values can be varied with steps of at least 0.01, so the algorithm is computed on a 3D lattice of 0.01 steps; this implies 1000000 possible combinations of the parameters. The algorithm begins its optimization process with a population of initial individuals, 30 in this specific case, for which the values of the genes are taken randomly within the mentioned domain.

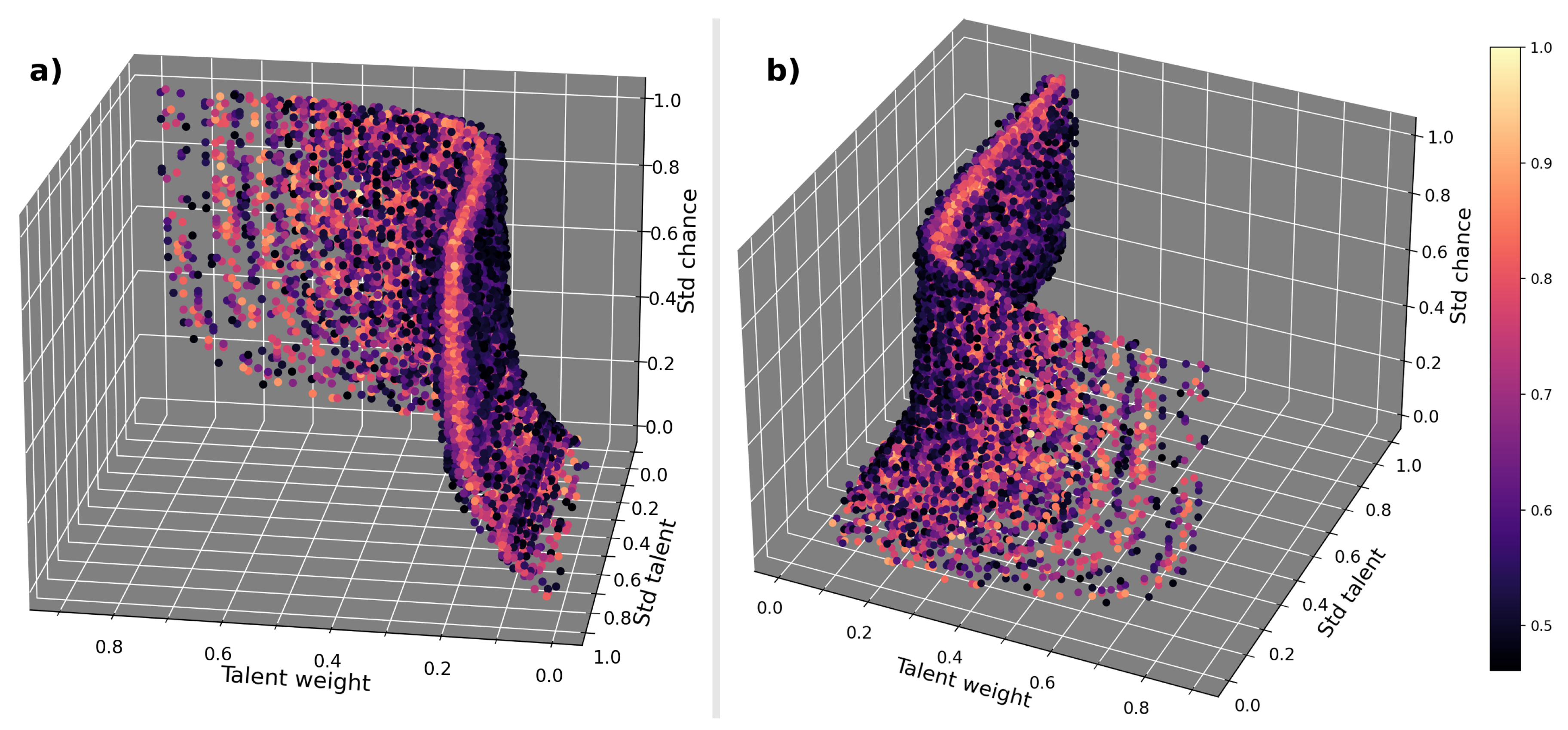
The Figure 2 shows that the points of the parameter space with higher fitness values are distributed on a thin surface, the layer with the lighter color, so the good parameters for the model are limited to the points on this surface. It is possible to further limit the number of good parameters for the model, in fact, it is possible to establish witch of the points on the surface found using the genetic algorithm are able to emulate even the behavior of the FWHM on the different stages of the tournaments of the real data.

Performing this additional confrontation for all the good points of the parameter space found, would be really onerous in terms of computational efficiency, so we take a fit of the surface with high fitness values and take a limited number of points appropriately distributed on this surface, in this way, we are able to make additional comparison and tuning between the real data, and the data produced by the agent-based model. For each of the selected 1450 points on the surface referred above, hereafter referred to as the surface of maximum fitness, it is possible to calculate the score performance distributions refereed to the different tournaments stages, we can then fit these distributions with a Gaussian curve and calculate the FWHM, so that for each point of the maximum fitness surface we obtain a curve similar to the one shown in Figure 1(d). The FWHM trend of the simulated data, obtained for each of the 1450 points of interest in the parameter space, is then compared with the FWHM trend of the real data, shown in the Figure 1(b), using the same

f (p, q)

shown in the equation 3. Thus, for each point, we obtain a sort of fitness value for the two FWHM trends, simulated and real. This quantity, which will be called "verisimilitude" from here on, so as not to confuse it with the fitness used in the context of the genetic algorithm, is greater when the two trends being compared are similar.

Figure 3 shows the result obtained by using the method described above, the color map used in the Figure 3, allows us to visually identify the areas with the highest verisimilitude. Not all areas are equally highlighted by the color map, two regions stand out among the points in the parameter space that seem to possess high values of verisimilitude. Table 1 shows the weighted mean values, in terms of verisimilitude, of the parameters in the two regions mentioned above, these values have been calculated taking into account only the parameters with normalized verisimilitude higher than 0.774. The values in green in the table correspond to an area with low values of

a

and

σ_{c}

, the values in red in the table correspond to the area with high values of

a

and

σ_{c}

, the

σ_{t}

values are less variable in the two areas, but the parameters in the green area generally have higher values than those in the red area, the red area in particular can have very low values.

These weighted mean values represent in a compact way the properties of the parameters with a high verisimilitude in the two regions. The differences in the values obtained for these two areas lead us to carry out further analysis.

3.3. Calibration on the Final Phases of the Tournaments

The agent-based model constructed is deliberately simple, built using a limited number of parameters, however, for the initial phases of real tournaments, there may be several discrepancies between the different tournaments, concerning, for example the fact that the different tournaments in reality have a different number of stages up to the final. There may also be differences in the way participants are selected. Thus, in the early stages, it is possible to have very different distributions of talents for the participating players in different tournaments.

The model does not predict these discrepancies; there may also be other factors, in addition to those given as examples, that are not taken into account and therefore not reproduced by the model. However, these discrepancies and differences from an ideal model tend to diminish in the more advanced stages of the tournaments, because, the tournament has a selection capacity that tends to mitigate any inhomogeneities in the talent distribution of the participants. It is therefore expected that in the final stages of the tournaments it will be easier to adapt the agent-based model to the real data.

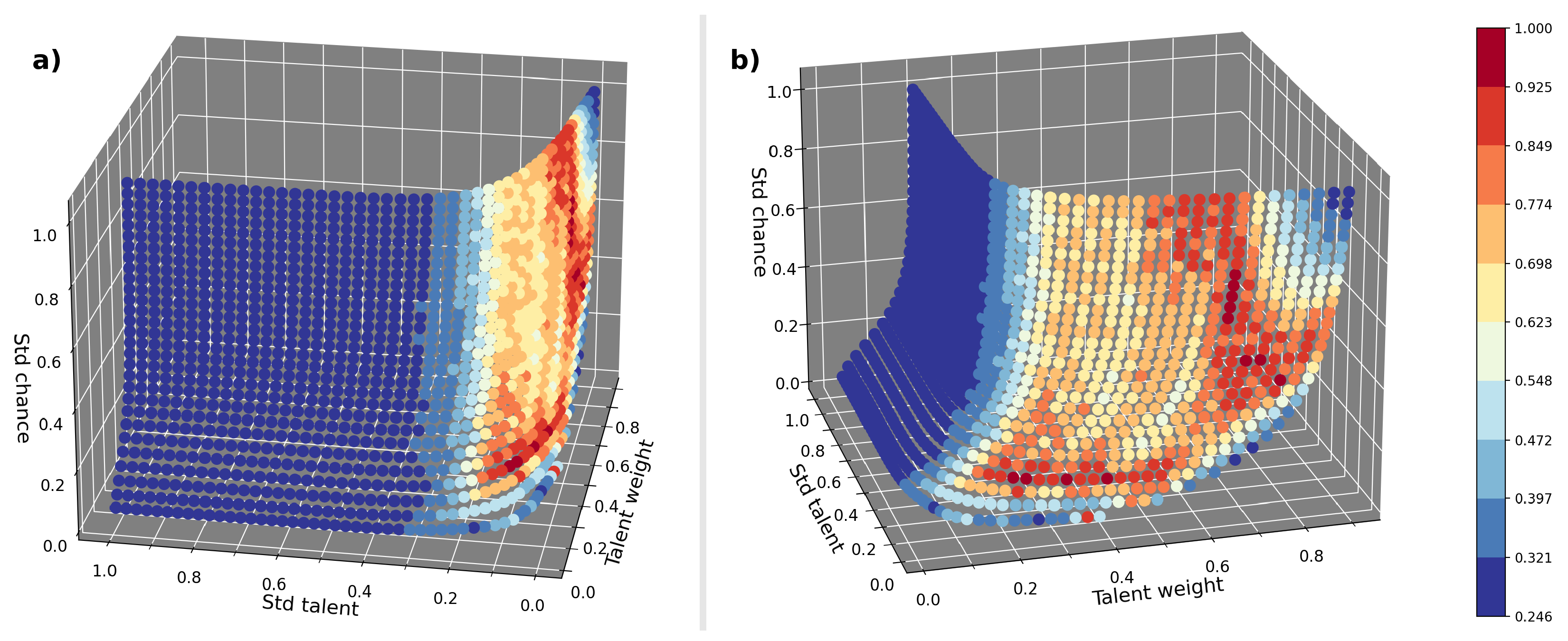
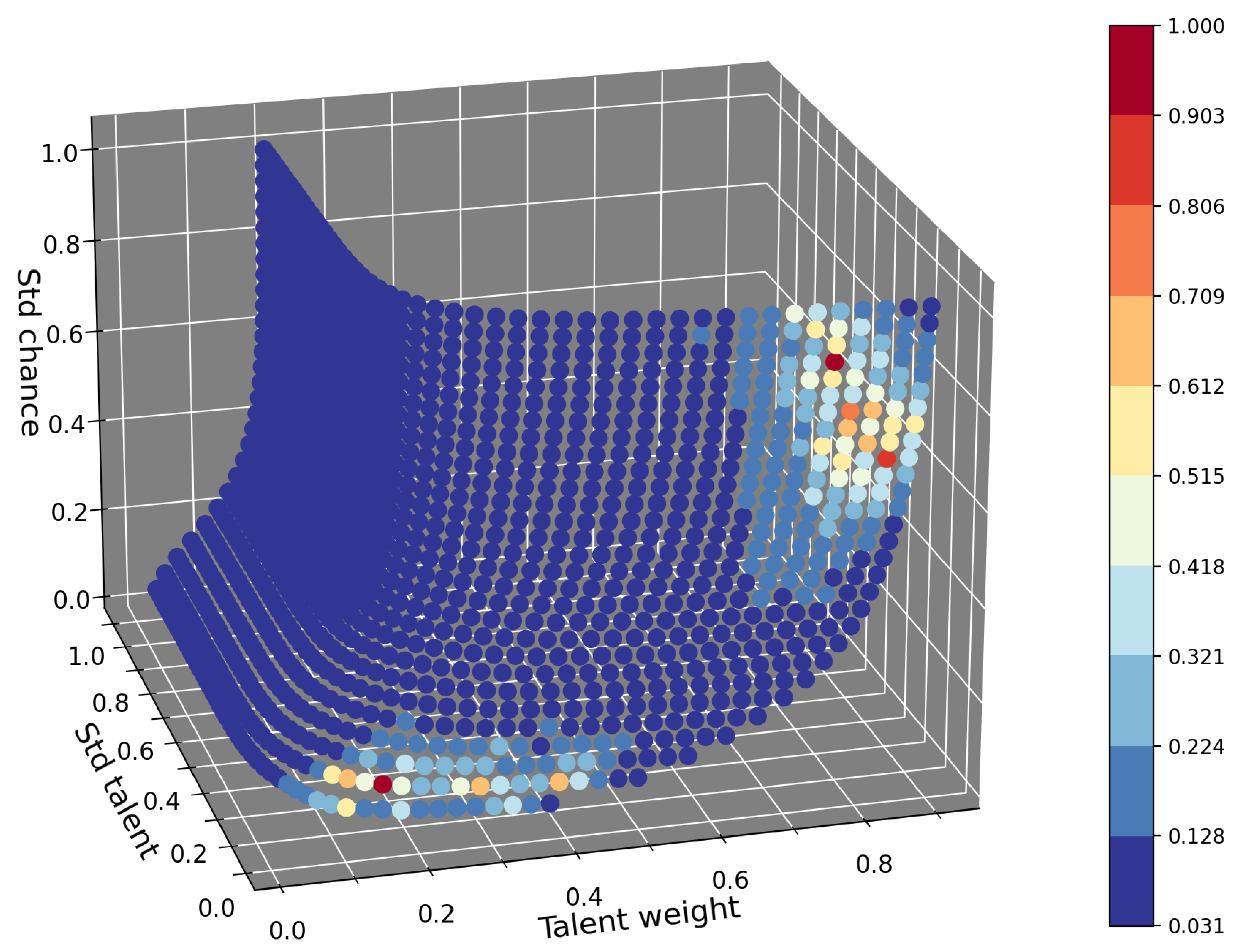
Comparing only the tournament phases from the round of 16 onwards, thus the last 4 tournament phases; we obtain what is shown in Figure 4.

It can be observed that there are only a limited number of points in the parameter space that occupy the parts in the high verisimilitude limit, so only a limited number of points can be identified that are closer to the real trend in the later stages of the tournaments.

The Table 2 shows us the weighted average of the parameters, and the parameters with the the highest verisimilitude for the two separate areas on the surface of maximum fitness observed in Figure 4. For the highest verisimilitude parameters highlighted in green, we have

σ_{c} = 0.08

σ_{t} = 0.09

and a talent weight

a = 0.17

, for this point, the model predicts that chance plays a role dictated by small fluctuations, given the limited amplitude of the distribution corresponding to the value of

σ_{c}

considered, but very relevant given the low value of the talent weight

a

, with players having a narrow talent distribution.

For the highest verisimilitude parameters highlighted in red we have

σ_{c} = 0.90

σ_{t} = 0.03

and

a = 0.78

. So lower values of

σ_{t}

characterize this point. The chance distribution is wider, meaning that random events that could change the fate of the matches are more frequent, but since the talent weight

a

is high, much higher than the point examined above, chance has less weight in determining the outcome of the matches.

3.4. Calibration by Parameter Constraint

The study of the real data with the agent-based model gives us two possible results, or rather two possible interpretations of the data, in fact we find two areas of interest on the surface of maximum fitness. We can compare our results with previous work to understand which of the two interpretations of the data is an artefact of the model and which reflects the real situation.

For both model calibrations carried out in the previous sections, the region on the surface of maximum fitness with low values of

σ_{c}

, have many parameters, (for example in Table 2 we get

σ_{t} = 0.09

for the parameter with maximum verisimilitude) that give a talent distribution with amplitude similar to that used in other works [11,12], a normal distribution with

σ_{t} = 0.1

and mean

μ = 0.6

, derived from the population IQ distribution and thus obtained from real data.

We can use this talent distribution in our model, and also fix

σ_{c}

, taking into account the green values in the Table 2,Table 1 and considering the average of the averages of the

σ_{c}

values, obtaining

σ_{c} = 0.12

as the best representative value, for the region of low values of

σ_{c}

, on the surface of maximum fitness.

By setting

σ_{t} = 0.1

with

μ = 0.6

and

σ_{c} = 0.12

in our agent-based model, it is possible to calibrate again the model minimizing the distance between the data reproduced by the model and the real one, using the same method as in the previous sections, with only

a

as a free parameter.

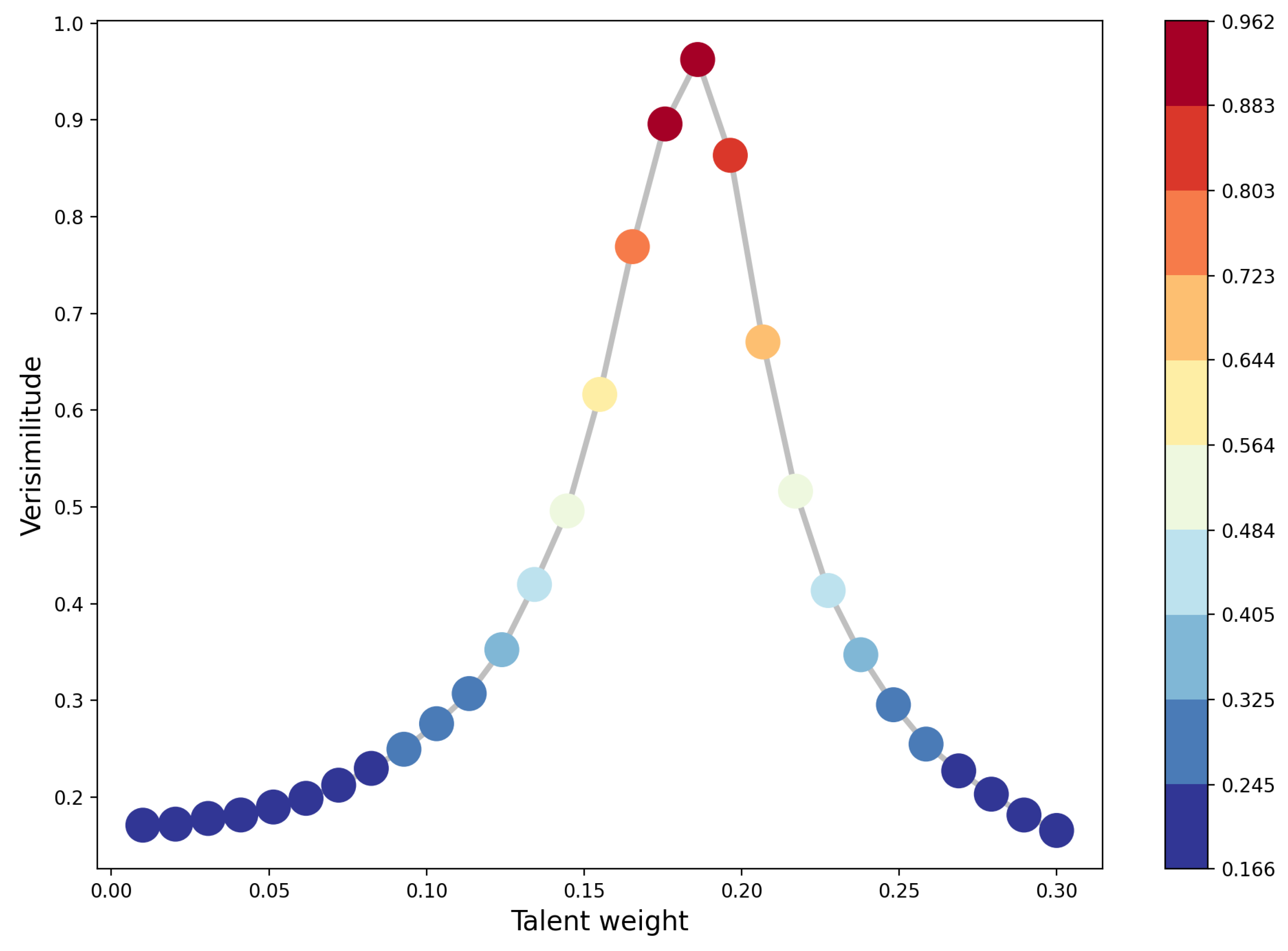
Figure 5 shows the result of the calibration. The normalized verisimilitude value shown, is obtained by simultaneously taking into account the score performance distribution and the trend of the FWHM, confronting them with the real data through

f (p, q)

shown in the equation 3, and then taking into account the normalized average value.

The values of the talent weight

a

with a normalized verisimilitude greater than

0.85

are three, as shown in the Figure 5. Thus, fixing the values of the other two parameters, with plausible values suggested by the free parameter model of the previous sections and the literature, the value of the talent weight

a

for tennis competitions on the ATP tour is between

0.18

and

0.20

. These values are in good agreement with other works on the subject [13].

4. Discussion

In this paper we have studied the impact of random events, the action of chance, as opposed to the role of talent in determining the outcome of a direct competition, in particular we have studied the tennis competitions, and the data obtained from the ATP tournaments.

The aim of this work was to obtain as much information as possible about this type of competition, with the fewest assumptions about the parameters of the model, in order to obtain the widest range of information. To do this, we have developed an agent-based model capable of reproducing the main features of the data, in particular the score performance distribution and the trends of the FWHM of these distributions over the different phases of the tournaments. The agent-based model developed depends on three parameters, the talent weight

a

, the standard deviation of the talent distribution

σ_{t}

and the standard deviation of the chance distribution

σ_{c}

, so we have made the assumption that talent and chance can be described by a normal distribution centered on 0.5. Then, we used a genetic algorithm to analyze the parameter space, and thus consider all the possible combinations of parameters of the model able to make the simulated score performance distribution similar to the real one. The use of a genetic algorithm allowed us to make very few assumptions about the values of the parameters and thus allowed us to find a surface, the surface of maximum fitness, in which the points, corresponding to the parameter triads, are able to reproduce score performance distributions very similar to the real ones.

Considering then only a limited set of 1450 points, uniformly distributed on this surface of maximum fitness, we made a further calibration of the agent-based model comparing another feature of the data, the trend of the FWHM for the different phases of the tournaments. This allowed us to further restrict the set of parameters that are able to reproduce the trend of the real data. We performed this further calibration by first considering all phases of the tournament, and then considering only the last 4 phases of the tournament, in an attempt to mitigate the effects of factors not considered by the agent-based model.

In both cases, we found a limited set of good points able to reproduce the real data, these points are distributed in two regions of the surface of maximum fitness, the regions with high values of

σ_{c}

, characterized by higher values of talent weight

a

and lower values of

σ_{t}

, and the regions with low values of

σ_{c}

, characterized by lower values of

a

and higher values of

σ_{t}

. The most interesting fact about these two regions is that they underline a sort of redundancy in the equations that govern the agent-based model. In fact, it seems that for the model

a

and

σ_{c}

are two parameters able to counterbalance their effects, at high value of talent weight

a

correspond low value of chance weight, so we have found a region with high values of chance weight but small amplitude of the chance distribution, and a region with low values of chance weight but large amplitude of the chance distribution.

The agent-based model and the genetic algorithm therefore give us two areas of interest on the surface of maximum fitness, but only one of the two regions contains parameters that correspond to the real situation, the other one is given by this sort of redundancy of the model. The two areas have talent distributions of different amplitude, this gives us the possibility to choose one of the two areas by selecting a specific talent distribution. So we choose the area on the surface of maximum fitness with parameters having low value of

σ_{c}

and slightly higher values

σ_{t}

than the other area of solutions. This choice was made by comparing our results with previous works [11,12,13]: the parameters on the low

σ_{c}

area have

σ_{t}

values similar to the talent distribution used in the cited works, extrapolated from the IQ distribution, thus obtained from the real data.

Using the IQ talent distribution and a

σ_{c} = 0.12

obtained considering the average of our solutions in the low

σ_{c}

area, we carried out a further calibration of the agent-based model and obtained a value talent weight between

a = [0.18, 0.20]

. This value is in good agreement with previous works on the subject [11,12,13]. This result gives us confidence on the fact that the solutions in the low

σ_{c}

region of the surface of maximum fitness are those to be considered. The solution given in the table with maximum verisimilitude in this region, obtained by our agent-based model trained with a genetic algorithm, has

a = 0.17

σ_{t} = 0.09

and

σ_{c} = 0.08

. These values seem reasonable, in fact, with

σ_{c}

in this range we expect that the random events that occur in the match to be mostly small, such as wind that can change the trajectory of the ball, uneven ground, etc., and the events that can change the outcome of the match to be rare, such as an injury. With

σ_{t}

in the predicted range, we expect the majority of players to have similar talents, with only a few individuals having talents that are greater or lesser than others. Last but not least, for the talent weight

a

in the predicted range, we expect the action of chance to play a large role in determining the outcome of a match. However, this doesn’t mean that talent doesn’t matter, as previous works have shown [5,9,12,13], but that in a match between two individuals of similar talent, chance plays a major role, confirming the so-called talent paradox [13] and we expect the outcome to be in favor of one rather than the other by sheer luck. Talent becomes more important as the difference in talent between the two competitors increases, but even when mitigated, chance cannot be ignored.

The model therefore predicts a scenario in which there are many random events, most of which are small, but which become important when the talents of the players are all comparable. Our agent-based model, trained with the help of a genetic algorithm, gives the range of values that the parameters

a

σ_{t}

and

σ_{c}

can take, based on real data, providing very useful information about this type of competition.

Our study is able to infer the values of quantities that are really important, but it has also allowed us to better understand the sensitivity of this type of models to the values of the parameters, we have highlighted the possibility of a kind of redundancy, and better understood the importance of choosing the right values for the parameters. The choice of the chance distribution with the right characteristics seems to be really important in this type of model, in fact the talent weight and the chance distribution seem to have a complementary role.

Another thing that could be considered is to use distributions with unfixed centers of symmetry for the talent and chance distributions, although this would make the model depend on 5 parameters instead of 3, making convergence to the real data more difficult.

Even without these modifications, we have established a useful method that is applicable to a wide range of competitions, involving individuals or entities competing against each other for extrapolating quantitative information regarding the role of chance and randomness in the final outcomes.

References

Nisperuza, J.; Rubio, J.P.; Avella, R. Density probabilities of a Bose-Fermi mixture in 1D double well potential. Journal of Physics Communications 2022, 6, 025004. [CrossRef]
Meerson, B.; Sasorov, P.V. Domain stability, competition, growth, and selection in globally constrained bistable systems. Phys. Rev. E 1996, 53, 3491–3494. [CrossRef]
Miao, R.; Chun, H.; Feng, X.; Gomes, A.C.; Choi, J.; Pereira, J.P. Competition between hematopoietic stem and progenitor cells controls hematopoietic stem cell compartment size. Nature Communications 2022. [CrossRef]
Metcalfe, J.; Ramlogan, R.; Uyarra, E. Economic Development and the Competitive Process. Centre on Regulation and Competition (CRC) Working papers 30612, University of Manchester, Institute for Development Policy and Management (IDPM), 2002.
Rapisarda, A.; Pluchino, A.; Biondo, A.E. Talent Versus Luck: The Role Of Randomness In Success And Failure. Advances in Complex Systems (ACS) 2018. [CrossRef]
Barabási, A.L. Untangling performance from success. EPJ Data Science 2016. [CrossRef]
Sinatra, R.; Wang, D.; Deville, P.; Song, C.; Barabási, A.L. Quantifying the evolution of individual scientific impact. Science 2016. [CrossRef]
Fraiberger, S.P.; Sinatra, R.; Resch, M.; Riedl, C.; Barabási, A.L. Quantifying reputation and success in art. Science 2018, 362, 825–829. [CrossRef]
Pluchino, A.; Burgio, G.; Rapisarda, A.; Biondo, A.E.; Pulvirenti, A.; Ferro, A.; Giorgino, T. Exploring the role of interdisciplinarity in physics: Success, talent and luck. PLoS ONE 2018. [CrossRef]
Roberta Sinatra Chiara Zappalà, Sandro Sousa, T.C.A.P.A.R. Early Career Wins and Tournament Prestige Characterize Tennis Players’ Trajectories. EPJ Data Science 2024. [CrossRef]
Rapisarda, A.; Sobkowicz, P.; Frank, R.H.; Biondo, A.E.; Pluchino, A. Inequalities, chance and success in sport competitions: Simulations vs empirical data. Elsevier B.V 2020. [CrossRef]
Zappalà, C.; Pluchino, A.; Rapisarda, A.; Biondo, A.E.; Sobkowicz, P. On the role of chance in fencing tournaments: An agent-based approach. PLoS ONE 2022. [CrossRef]
Zappalà, C.; Rapisarda, A.; Biondo, A.E.; Pluchino, A. The Paradox of Talent: how Chance affects Success in Tennis Tournaments, 2023. [CrossRef]
Fink, T.M.A.; Coe, J.B.; Ahnert, S.E. Single elimination competition. Europhysics Letters 2008, 83, 60010. [CrossRef]
Ben-Naim, E.; Hengartner, N.; Redner, S.; Vazquez, F. Randomness in Competitions. Journal of Statistical Physics 2013. [CrossRef]
Salgado, M.; Gilbert, N., Agent Based Modelling. In Handbook of Quantitative Methods for Educational Research; Teo, T., Ed.; SensePublishers: Rotterdam, 2013; pp. 247–265. [CrossRef]
Bak, P.; Paczuski, M. Why Nature is complex. Physics World 1993, 6, 39. [CrossRef]
Cenani, S. Emergence and complexity in agent-based modeling: Review of state-of-the-art research. Journal of Computational Design 2021. [CrossRef]
Hawick, K.A. An Agent Model Formulation of the Ising Model. Technical report, Information and Mathematical Sciences, Massey University, Albany, North Shore 102-904, Auckland, New Zealand, 2003.
Sznajd-Weron, K.; Jędrzejewski, A.; Kamińska, B. Toward Understanding of the Social Hysteresis: Insights From Agent-Based Modeling. Perspectives on Psychological Science 2023, 19. [CrossRef]
Levayer, R. Cell competition: Bridging the scales through cell-based modeling. Current Biology 2021, 31, R856–R858. [CrossRef]
ATP tour site, info and statistics about tennis. https://www.atptour.com/en/.
ATP tour site, for tennis data. https://datahub.io/sports-data/atp-world-tour-tennis-data.
JeffSackmann github repository of tennis data. https://github.com/JeffSackmann/tennis_atp.
Lingaraj, H. A Study on Genetic Algorithm and its Applications. International Journal of Computer Sciences and Engineering 2016, 4, 139–143.
tennis rules and info site. https://olympics.com/en/news/tennis-rules-regulations-how-to-play-basics.
tennis rules site. http://protennistips.net/tennis-rules/.
Joyce, K.E.; Hayaska, S.; Laurienti, P.J. A genetic algorithm for controlling an agent-based model of the functional human brain. Biomed Sci Instrum 2012.
Fernández, R.; Chalmandrier, L.; Brandl, R.; Pinkert, S.; Zeuss, D.; Hof, C. Trait overdispersion in dragonflies reveals the role and drivers of competition in community assembly across space and season. Ecography 2023, 2024, 1–14. [CrossRef]

Figure 1. In these figures we show the characteristics of the real and simulated data, highlighting the similarity of the data obtained. In (a) the histogram is constructed by taking into account the score performance values obtained from the 108411 matches played in the ATP tournaments from 1991 to 2021. The values for the winners are shown in blue, the values for the losers are shown in red, in the center is visible an intersection between the curve obtained for the winners and the curve obtained for the losers. In (b) the figure shows the trend of the FWHM of the score performance distributions with respect to the stages of the tournaments. A number is assigned to each stage, 0 is assigned to the final, 1 to the quarter-finals, etc. A linear fit is also shown to highlight the trend of the FWHMs. In (c) is shown the score performance distribution obtained using the agent-based model to simulate 10000 tournaments with 128 agents participating in each, with fixed parameters equal to

a

= 0.3,

σ_{t}

= 0.2,

σ_{c}

= 0.2. In (d) we show, for the same number of simulated tournaments and parameters, the trend of the FWHMs of the score performance distributions for the different stages of the tournaments. A number is assigned to each stage, with 0 being assigned to the final.

a

= 0.3,

σ_{t}

= 0.2,

σ_{c}

(a)	(b)

(c)	(d)

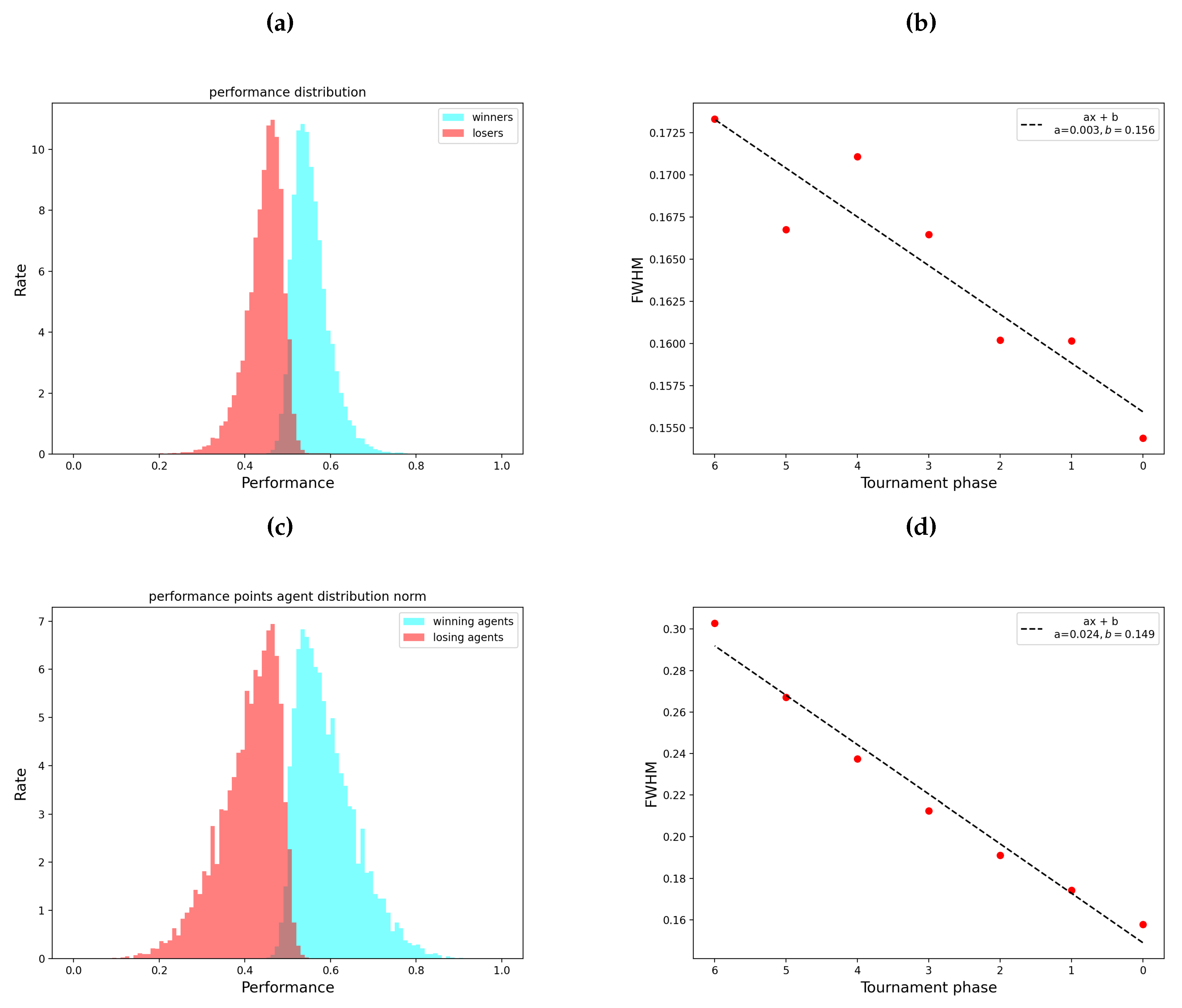
Figure 2. The figures show, from two different angles, the results of the genetic algorithm. In the graph, the points represent a triad of parameters, the talent weight

a

, the standard deviation of the talent distribution

σ_{t}

, the standard deviation of the chance distribution

σ_{c}

, while the colors represent the normalized fitness value relative to the points, only the points with a fitness greater than 0.46 are shown.

Figure 2. The figures show, from two different angles, the results of the genetic algorithm. In the graph, the points represent a triad of parameters, the talent weight

a

, the standard deviation of the talent distribution

σ_{t}

, the standard deviation of the chance distribution

σ_{c}

, while the colors represent the normalized fitness value relative to the points, only the points with a fitness greater than 0.46 are shown.

Figure 3. The images show, from two different perspectives, the result of the comparison between the real and simulated FWHM trends at the different stages of the tournaments for the points on the surface of maximum fitness. In particular, for each evenly distributed point on this surface, 7000 tournaments have been simulated for each set of parameters. The color map highlights the areas that better match the real data with higher values of normalized verisimilitude.

Figure 4. The image shows the result of the comparison between the real and simulated FWHM trends for the last four tournament phases, so from the round of 16 to the final. Again, 7000 tournaments were simulated for each point on the surface of maximum fitness, and the color map, of the normalized verisimilitude, highlights the areas that better match the real data.

Figure 5. The figure shows the values of the talent weight

a

in correspondence to a normalized verisimilitude value, which determines how much the value

a

is able to produce results that are similar to the real ones.

Figure 5. The figure shows the values of the talent weight

a

in correspondence to a normalized verisimilitude value, which determines how much the value

a

is able to produce results that are similar to the real ones.

Table 1. The table shows the weighted average, weighted by verisimilitude, of the parameters for the two regions with high verisimilitude values observed on the surface of maximum fitness in Figure 3. Only the points with a normalized verisimilitude greater than 0.774 are used to calculate the mean values of the parameters. The values in green are obtained for the regions with low values of

σ_{c}

, the values in red are obtained for the regions with high values of

σ_{c}

σ_{c}

, the values in red are obtained for the regions with high values of

σ_{c}

	$a$	$σ_{t}$	$σ_{c}$
w. mean	$0.34$	$0.07$	$0.16$
w. mean	$0.66$	$0.04$	$0.67$

Table 2. The table shows the parameter values of the two points with the highest verisimilitude, and the weighted average of the points with normalized verisimilitude greater than 0.321 for the two regions, on the surface of maximum fitness, highlighted in Figure 4 with high verisimilitude. The points in green, in the table, belong to the region with a low value of

σ_{c}

, the red ones belong to the region with a high value of

σ_{c}

σ_{c}

, the red ones belong to the region with a high value of

σ_{c}

	$a$	$σ_{t}$	$σ_{c}$
max ver.	$0.17$	$0.09$	$0.08$
w. mean	$0.23$	$0.07$	$0.07$
max ver.	$0.78$	$0.03$	$0.90$
w. mean	$0.80$	$0.02$	$0.79$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.