Prerpints.org logo
Preprint
Article

Josephson Diode Effect in Parallel-Coupled Double Quantum Dots Connected to Majorana Nanowires

Altmetrics

Downloads

153

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 June 2024

Posted:

10 June 2024

You are already at the latest version

Alerts
Abstract
We study theoretically the Josephson diode effect (JDE) realized in a system composed of parallel-coupled double quantum dots (DQDs) sandwiched between two semiconductor nanowires deposited on an s-wave superconductor surface. Due to the combined effects of the proximity-caused superconductivity, strong Rashba spin-orbit interaction and Zeeman splitting inside the nanowires, a pair of Majorana bound states (MBSs) may possibly emerge at opposite ends of each nanowire. Different phase factors arisen from the superconductor substrate can be generated in the coupling amplitudes between the DQDs and MBSs prepared at the left and right nanowires, and will result in the Josephson current. We find that the critical Josephson currents in positive and negative directions are different from each other in amplitude within an oscillation period with respective to the magnetic flux penetrating through the system, a phenomenon known as the JDE. It arises from the quantum interference effect in this double-path device, and can hardly occur in system of one QD coupled to MBSs. Our results also show that the diode efficiency can reach up to 50%, and depends on the overlap amplitude between the MBSs and the energy levels of the DQDs adjustable by gate voltages. The present model is realizable within current nanofabitication technologies and may find practical use in interdisciplinary field of Majorana and Josephson physics.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Diode is one of the basic devices in semiconductor technology, and is characterized by different amplitudes of currents flowing in opposite directions. It depends on the lack of an inversion symmetry center in a system and is one of the central building blocks required to build powerful instruments, such as a transistor. In many superconductors-based systems, a similar effect named as superconductor or Josephson diode effect (JDE) appears due to broken time-reversal and inversion symmetries [1,2,3,4,5,6]. The JDE can result in direction-dependent (nonreciprocal) critical currents driven by phase difference between superconductors and is fascinating in various applications due to its connection to fundamental properties of diverse superconducting systems [1,2,3,4,5,6,7,8]. Generally, time-reversal symmetry may be broken by an external magnetic field, which exerts impacts on specific term in the systems’ Hamiltonian related to inversion symmetry breaking [9], such as spin-orbit interaction (SOI). Therefore, the JDE can be used to detect SOI strength [10] or existence of a topological phase in nanowires in proximity-contacted with a superconductor [5,10,11]. The JDE is also promising in design of electronic devices including photodetectors, ac/dc converters, superconducting qubits [8], and racetrack memory devices [12] etc.
The JDE was demonstrated as early as 1970s in superconducting quantum interference devices (SQUIDs) based on superconductor bridges [13] and Josephson junctions [14]. It was also observed in non-centrosymmetric conventional superconductor thin films in the device geometry [15]. Since then, many experimental and theoretical platforms for the realization of JDE has been continuously proposed, such as non-centrosymmetric superconductors [14,15], stacks of different superconductors with broken inversion symmetries [16], Andreev molecules [17], artificial superlattices [2], topological semimetals and insulators [5], insulator heterostructure devices [18], nanowires [10], and disordered systems [19]. Another efficient platform proposed to achieve high diode efficiency relies on a Josephson current interferometer, in which conjunct Josephson junctions with nonsinusoidal current-phase relations form a SQUID. In such systems, the Josephson currents are contributed from higher harmonics other than the usual 2 π -periodic ones with a magnetic flux penetrating through the SQUID loop [6,8,14]. It has recently been demonstrated in two-dimensional electron and many three- and four-terminal setups in which the diode efficiencies at equilibrium can reach up to about 30% [20,21].
Conventional s-wave superconductors in proximity contacted with semiconductor nanowires, which have strong Rahsba spin-orbit interaction and are subjected to external magnetic fields, have been demonstrated for the realization of topological superconductivity [6,8,10,11], a topological state that hosts Majorana bound states (MBSs) [22,23]. The MBSs are charge-neutral topologically protected quasiparticles that are spatially separated, i.e., character of spatial nonlocality [24]. They offer an attractive way for constituting Majorana qubits [25,26] allowing to store information in a nonlocal manner and immune to decoherence by a local disturbance [27]. Along with the intensive investigations on preparation and detection of MBSs, exploiting their possible applications is also an active research subject in condensed matter physics. For example, in systems with MBSs side-coupled to quantum dots (QDs) which are connected to external leads, the sign of thermopower which measures the induced bias voltage in response to a temperature difference can be reversed by QDs-MBSs hybridization strength or MBS-MBS overlap amplitude [28,29]. Moreover, the magnitudes of both the thermopower and thermoelectric efficiency in such systems can be obviously enhanced [28,29,30]. Since the MBSs often emerge with the help of spin-orbit interaction, strong magnetic field or magnetic materials, they also play an important role in the research field of spintronics [31]. In recent years, some works have been devoted to the study of Josephson current through a QD connected to two semiconductor nanowires hosting MBSs (MNWs) [32,33,34,35,36], which are stimulated by the interesting results found in various system composed of QDs connected to superconductors with normal phase [37,38,39,40,41,42,43,44,45,46]. It was shown that the Josephson current driven by the topological phase difference is quite stronger than that by normal phase difference, and the bent angle formed by the two MNWs as well as the magnetic fields in the QD will significantly suppress the Josephson current [32,33].
Until now, there are two limitations in previous work on Josephson current through MNWs-QD-MNWs systems: one is that only the current’s magnitude and period were studied, whereas less attention has been paid on the control of its direction [32,33,34,35,36]; the other is that only single QD was proposed to be inserted between two MNWs, and the interesting quantum interference effect was left untouched [14,16,20,21,38,40,41,42,43,46,47]. In view of these, we propose a structure composed of parallel double QDs (DQDs) sandwiched between the left and right MNWs to achieve the JDE based on quantum interference effect arising from the two transport paths through the DQDs, as well as the magnetic flux penetrating through the loop, which is shown in Figure 1. We emphasize that the present device can be experimentally realized in terms of that reported in Ref. [48], in which DQDs connected to two normal leads couple to each other via both superconductor hosting MBSs and normal tunnel barrier. If the leads in Ref. [48] are replaced by the superconductor connecting the DQDs, their system is exactly the one studied here. In some previous work, DQDs has been proposed to be inserted between conventional superconductor leads to generate spin-correlated electron pairs, and to control the Josephson current and its critical one [40,41,43,44,49]. Our studies show that in this MNWs-DQDs-MNWs, the period, magnitude, and the directions of the Josephson current can be effectively adjusted with the help of dots’ energy levels, overlap amplitude between the MBSs, as well as the magnetic flux through the loop. Accordingly, tunable JDE with large value of diode efficiency emerges, and may find real use in design of superconductor-based instruments.

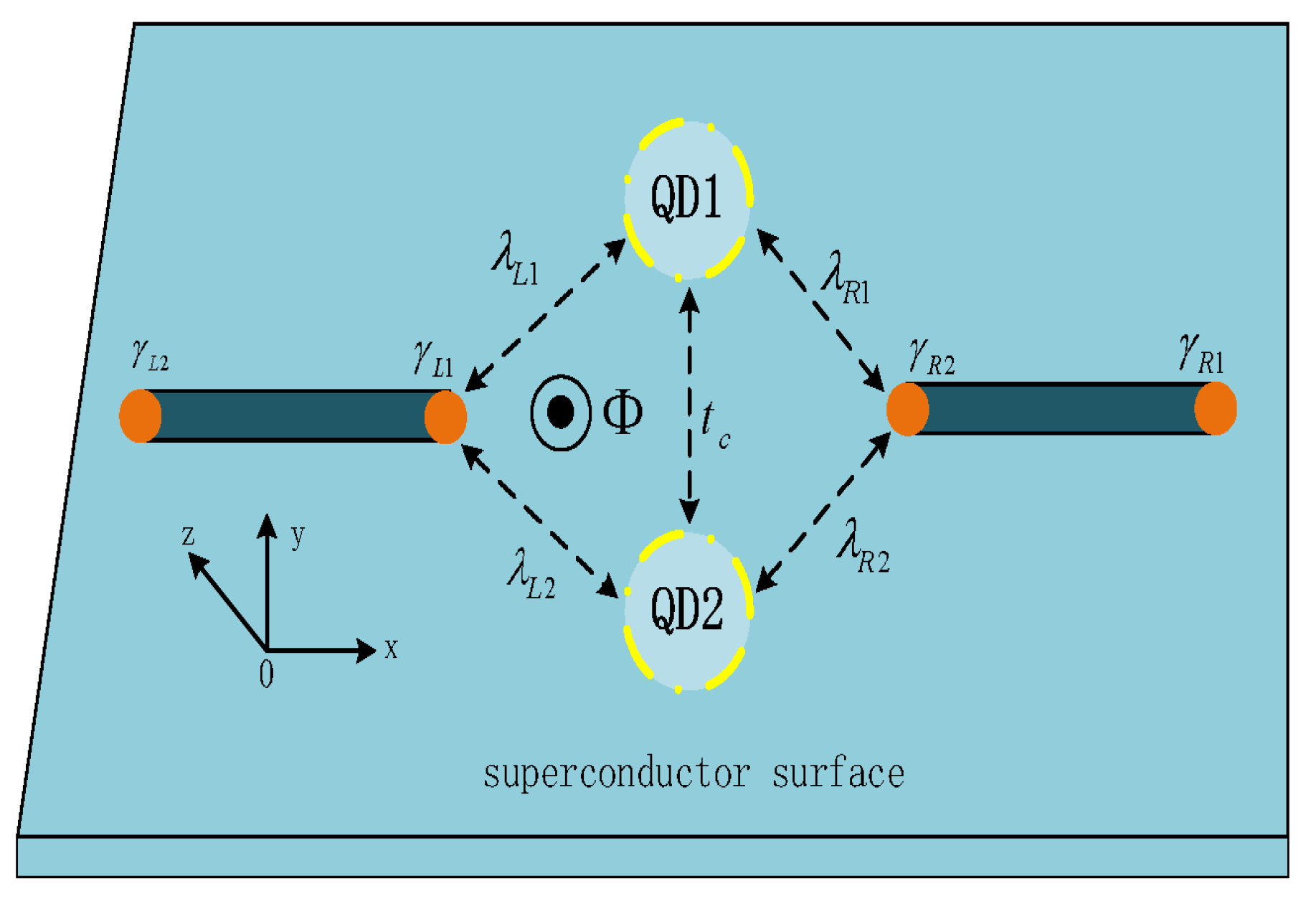
2. Model and Method

The Hamiltonian of the present structure is divided into three parts as H = H D Q D s + H M N W s + H T [32,33,39,40], in which the Hamiltonian of the DQDs and interaction between them is given by
H D Q D s = ∑ i ε i d i † d i + t c ( d 1 † d 2 + d 2 † d 1 ) ,
where the creation (annihilation) operator d i † ( d ı ) is for electrons in dot-i with spin-independent energy level ε i . In experiments, the dots’ level can be tuned via gate voltages V g , and is given by ε i = ε i 0 − e V g , where ε i 0 is the bare energy level in dot-i. The tunnel coupling strength between the DQDs is t c . The Hamiltonian H M M W s denotes the left and right MNWs connected to the DQDs, whose explicit expression is as follows [32,33,50],
H M N W s = i ∑ α = L , R ε α γ α 1 γ α 2 ,
where ε L / R is for direct hybridization strength between the MBSs prepared at the ends of the α -th nanowire. In what follows, we assume ε L = ε R = δ M . The creation and annihilation operators of the MBSs satisfies the relationship of γ α j = γ α j † ( j = 1 , 2 ) , and { γ α i , γ α ′ j } = 2 δ α , α ′ δ i , j [32,51] due to the unique self-conjugate character of the MBSs. Tunnel coupling between the DQDs and the MNWs is described by the Hamiltonian of H T = ∑ α = L , R H d α , in which [32,33]
H D L = ∑ i = 1 , 2 ( λ L i d i − λ L i * d i † ) γ L 1 ,
H D R = i ∑ i = 1 , 2 ( λ R d i − λ R * d i † ) γ R 2 ,
in which λ α i stands for coupling strength between QD-i and the MNW- α . Note that there is a phase factor φ α in λ α i , which arises from the proximity of the MNWs to the superconductor substrates and induces the Josephson current, with λ α i = | λ α i | exp ( i φ α / 2 ) . In the present paper, we set φ L = φ and φ R = 0 for the sake of clarity [32]. As usual, we make an unitary transformation to change the Majorana fermion representation to a conventional fermion representation one: [32,51] f L / R = ( γ L / R 1 + i γ L / R 2 ) / 2 and f L / R † = ( γ L / R 1 − i γ L / R 2 ) / 2 . Then we rewrite the total Hamiltonian in a matrix form to calculate the Green’s functions needed for the Josephson current. In the basis of Ψ † = ( d 1 † , d 1 , d 2 † , d 2 , f L † , f L , f R † , f R ) , the transformed Hamiltonian H ˜ = 1 2 Ψ † H Ψ is given by [32,33,34,35]:
H ˜ = H ˜ D Q D s H ˜ D L H ˜ D R H ˜ L D H ˜ L 0 H ˜ R D 0 H ˜ R ,
in which the 4 × 4 sub-matrix H ˜ D Q D s = diag ( ε 1 , − ε 1 , ε 2 , − ε 2 ) + t c σ x ⊗ σ z with σ x / z being the Pauli matrix of the x / z -component, and the symbol ⊗ denotes the matrix direct product. Similarly, the 2 × 2 sub-matrix H ˜ L = H ˜ R = δ M σ z , and the interaction between the DQDs and MBSs are
H ˜ L D = 1 2 − λ L 1 * e i ϕ / 4 λ L 1 e − i ϕ / 4 − λ L 2 * e − i ϕ / 4 λ L 2 e i ϕ / 4 − λ L 1 * e i ϕ / 4 λ L 1 e − i ϕ / 4 − λ L 2 * e − i ϕ / 4 λ L 2 e i ϕ / 4 ,
H ˜ R D = 1 2 λ R 1 e − i ϕ / 4 λ R 1 e i ϕ / 4 λ R 2 e i ϕ / 4 λ R 2 e − i ϕ / 4 − λ R 1 e − i ϕ / 4 − λ R 1 e i ϕ / 4 − λ R 2 e i ϕ / 4 − λ R 2 e − i ϕ / 4 .
The dc Josephson current J tunneling between the two MNWs via the DQDs is calculated in terms of the nonequilibrium Green’s function technique [32,37,38,39,40]
J = e h ∫ d ε Re Tr [ σ ˜ z ( Σ ˜ a G d a − Σ ˜ r G d r ) ] f ( ε ) ,
where σ ˜ z = 1 2 × 2 ⊗ σ z , and Σ ˜ r / a = Σ L r / a − Σ R r / a with the retarded/advanced self-energies due to the MNWs. The self-energies are calculated by Σ α r / a = H ˜ D α g α r / a H ˜ α D [19,26,29]. The free retarded/advanced Green’s function of the MNW is g α r / a = [ ε 1 2 × 2 − H ˜ α + ± i 0 + ] − 1 . The retarded/advanced Green’s function of the DQDs is then obtained with the help of Dyson’s equation as [32,37,38,39,40] G d r / a = [ ε 1 4 × 4 − H ˜ D Q D s − ( Σ L r / a + Σ R r / a ) ] − 1 [32,39]. In Equation (6), f ( ε ) = 1 / [ 1 + exp ( ε / k B T ) ] is the equilibrium Dirac-Fermi function, where T and k B denote the temperature and Boltzmann constant, respectively.

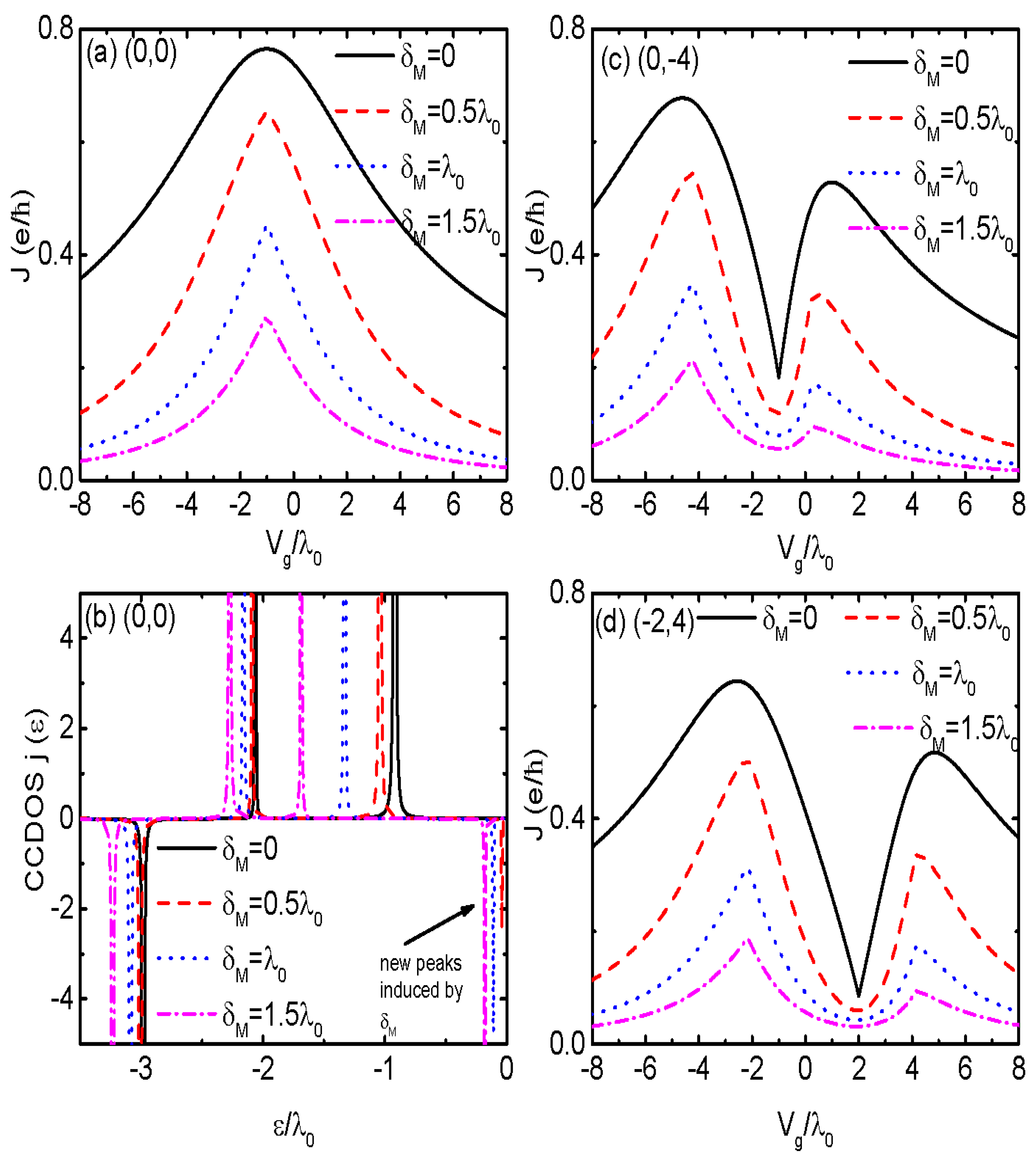
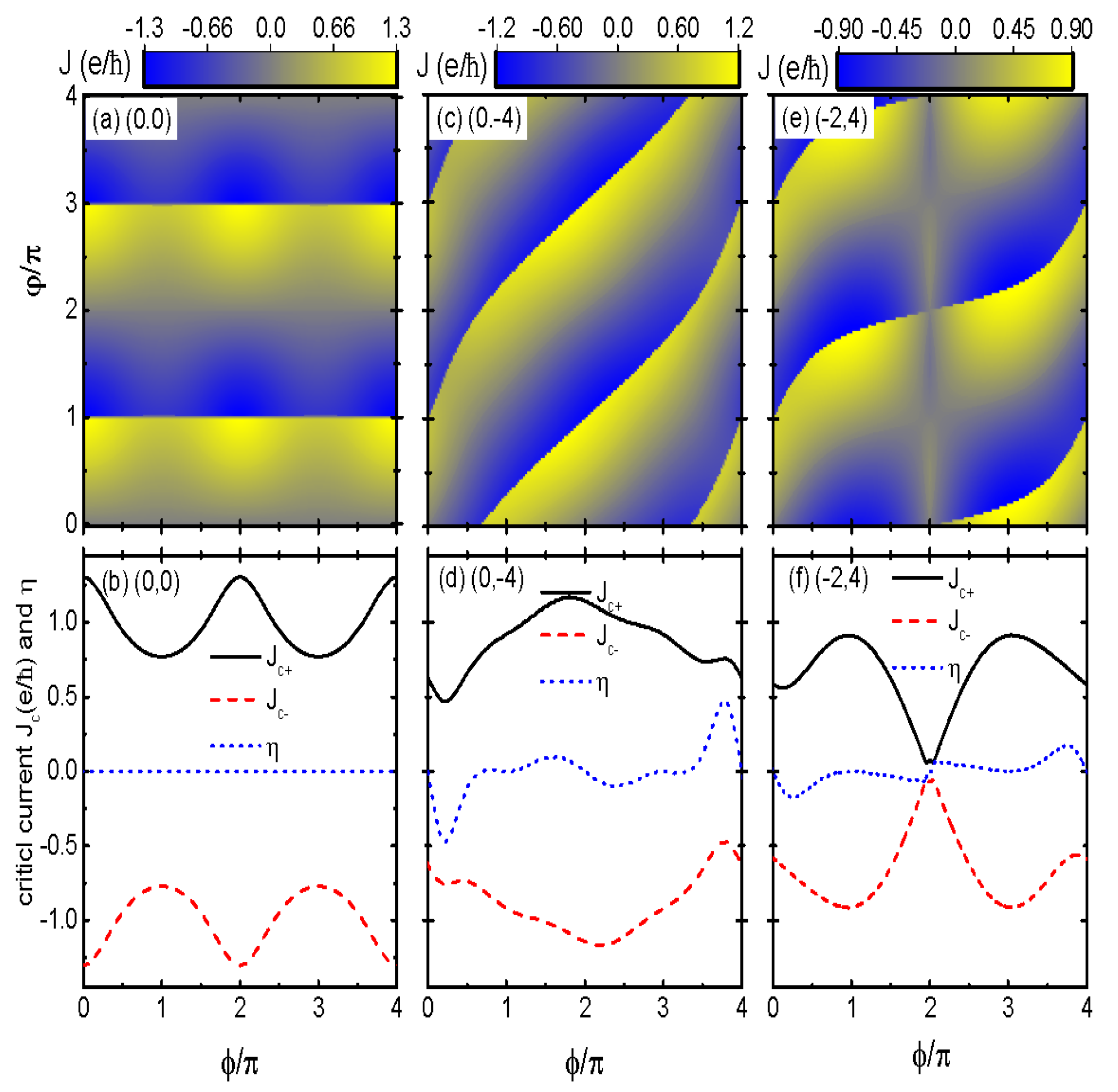
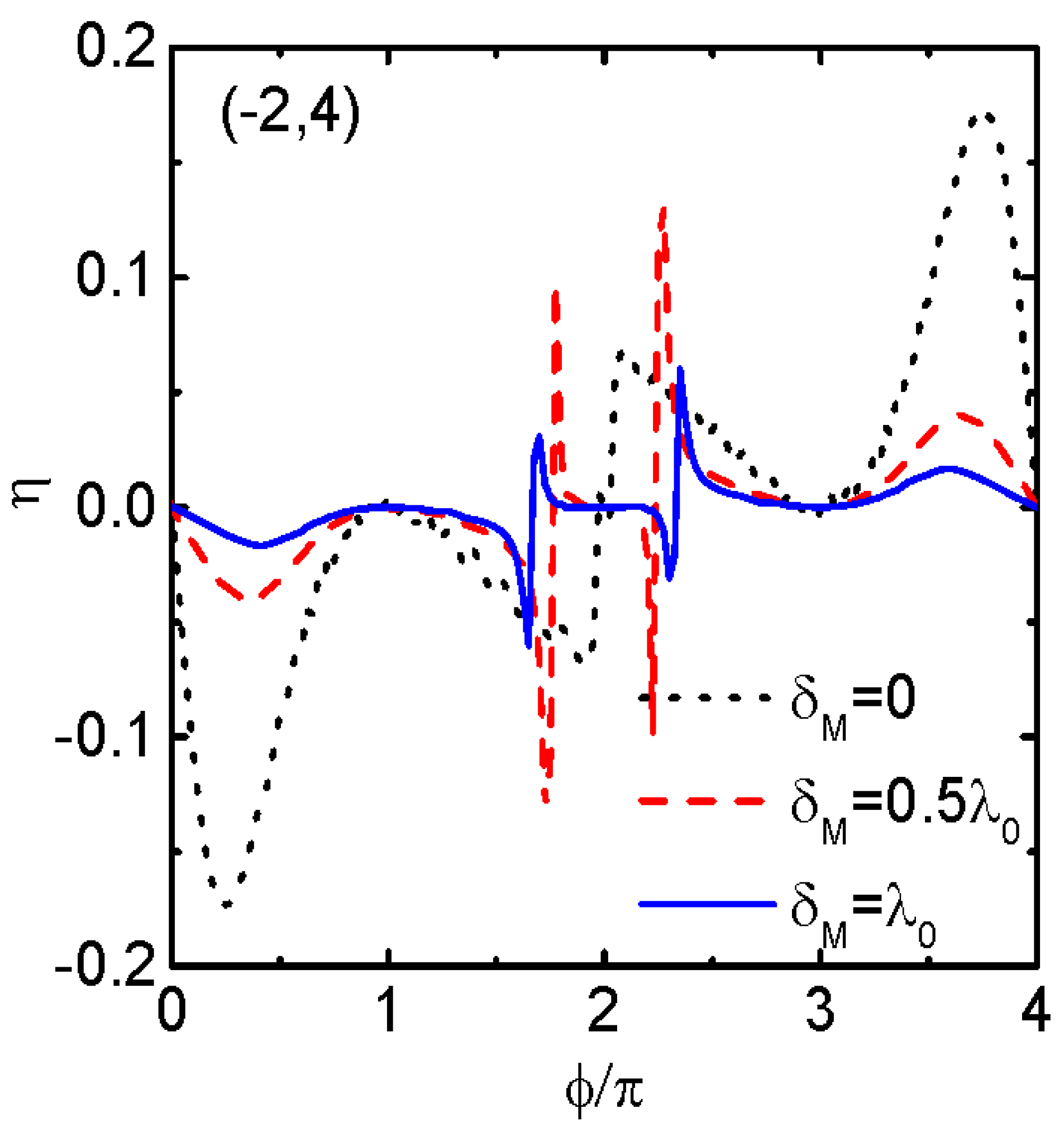
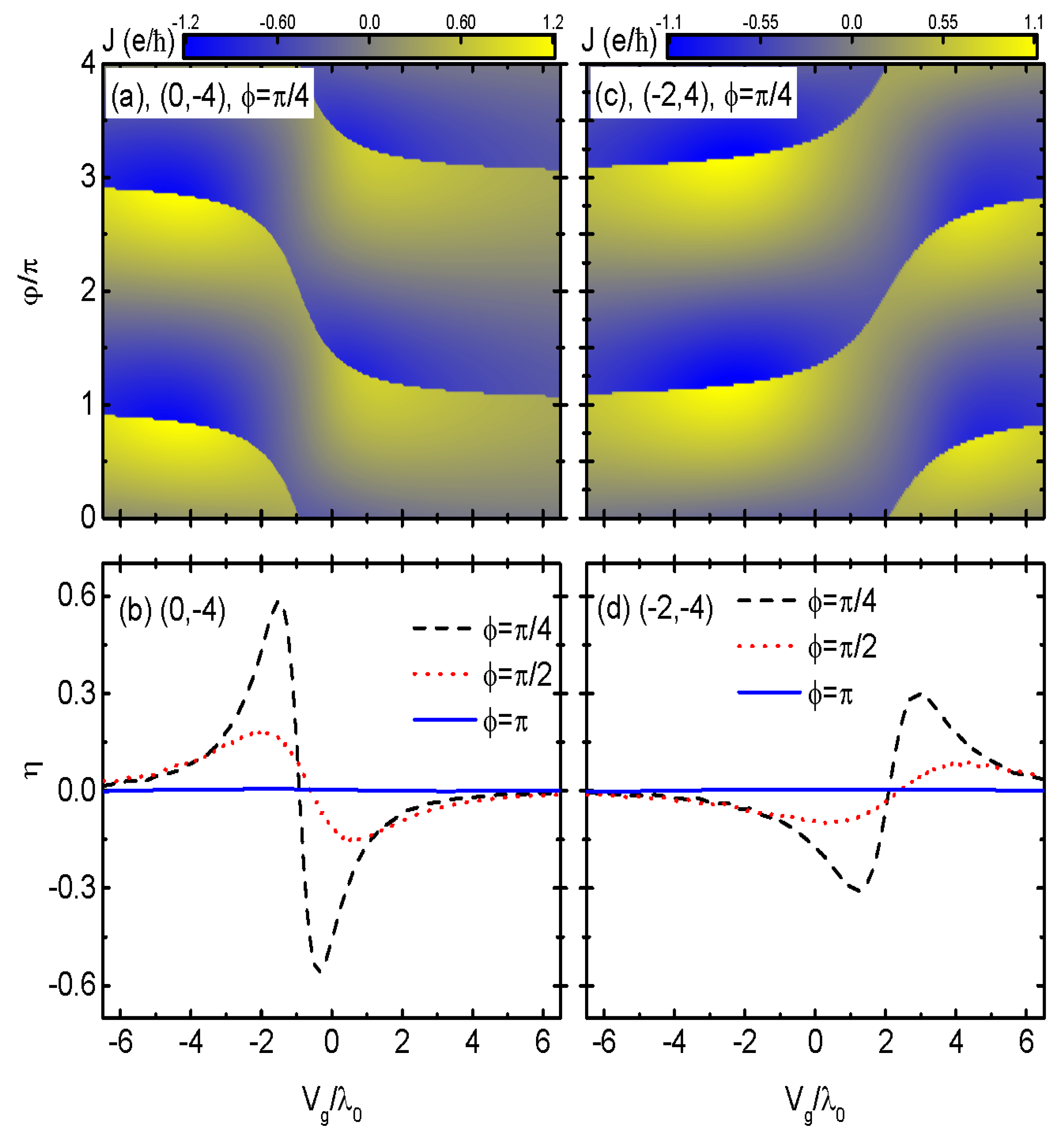
3. Numerical Results

In numerical calculations, we consider the case of the DQDs couple to the left and right MNWs with equal strengths λ α i = λ 0 ≡ 1 , which is set to be the energy unit. In Figure 2 we present the gate voltage V g dependence of the Josephson current J with different direct hybridization coupling strength between the MBSs δ M and energy levels ( ε 1 0 , ε 2 0 ) for fixed ϕ = π and φ = π / 2 . First, we diagonalize the Hamiltonian H D Q D s for the DQDs and transform the QDs’ discrete energy states into a pair of bonding and antibonding states,
H D Q D s = ε + c + † c + + ε − c − † c − ,
in which c − ( + ) is the annihilation operator for the bonding (antibonding) state of the DQDs with energy
ε ± = ε ¯ ± ( Δ ε 2 ) 2 + t c 2 ,
where ε ¯ = ( ε 1 + ε 2 ) / 2 and Δ ε = ε 1 − ε 2 .
For the case of QDs’ energy level configuration of ( 0 , 0 ) and δ M = 0 , there is only one current peak associated with the bonding state with energy ε − . Therefore, the peak position will shift towards lower (higher) energy regime with increasing (decreasing) t c . Note in this totally symmetrical structure, i.e., the energy levels of the DQDs are the same ( Δ ε = 0 ) and are coupled to the MNWs with equal strengths ( λ α i = λ 0 ) , the antibonding state ε + disappears and only the bonding state contributes to the Josephson current through the DQDs. When the MBSs at the opposite ends of the MNWs are hybridized to each other ( δ M ≠ 0 ) , the position of the Josephson current peak remains unchanged as shown in Figure 2a. With increasing δ M , the current’s amplitude is reduced which is in consistent with previous results [32,33]. Moreover, the width of the peak is narrowed by increasing δ M . To explain the dependence of the Josephson current on the direct hybridization of the MBSs δ M , we shows the current-carrying density of states (CCDOS) j ( ε ) = Re Tr [ σ ˜ z ( Σ ˜ a G d a − Σ ˜ r G d r ) ] f ( ε ) varying with respective to energy ε . Since at zero temperature, only the states located in negative energy regime contribute to the Josephson current, we only show the behaviors of j ( ε ) for the case of ε < 0 . When the MBSs at the MNWs are decoupled to each other ( δ M = 0 ) , there are three peaks in j ( ε ) , of which two positive and one negative as is indicated by the black solid line in Figure 2b. When δ M ≠ 0 , a negative peak is induced in j ( ε ) around the Fermi energy of the MNWs μ = 0 , and its height is increased by increasing δ M . As a result of it, the current’s amplitude is reduced. The additional current peak originates from the fact that the MBSs in the same MNWs are destroyed by their overlap.[50,51]
If the energy levels in the two QDs are different from each other ε 1 ≠ ε 2 , there are two current peaks corresponding to the two molecular states ε ± in the DQDs as shown in Figure 2c,d, in which ( ε 1 0 , ε 2 0 ) are set to be (0,-4) and (-2,4), respectively. The height of the current peak at bonding state ε − is lower than that at the antibonding state ε + . When the MBSs in the same MNWs are overlapped ( δ M ≠ 0 ), the current peaks in Figure 2c,d are lowered and narrowed as in the case of Figure 2a. Moreover, the positions of the peaks are slightly changed by δ M for the cases of ε 1 ≠ ε 2 , which is different from the case in ( 0 , 0 ) . It should be noted that the reduction of the Josephson current peaks in Figure 2c,d is mainly induced by charge flowing through the two molecular states ε ± . This is different from the case in Figure 2a, where the charge flows only through the bonding state ε 1 . It means that electrons will transport through the DQDs whenever their energy is in resonant with the bonding and antibonding states, even if ε 1 or ε 2 is away from the Fermi level.
We now study the influences of the magnetic flux ϕ and phase difference φ on J, critical Josephson currents J c ± , as well as the diode efficiency η = ( J c + − | J c − | ) / ( J c + + | J c − | ) [45] for different dots’ level configurations for fixed value of δ M = 0 . For the case of ( 0 , 0 ) , the oscillation period of both the Josephson current J and its critical counterpart J c ± is 2 π versus either ϕ or φ as shown in Figure 3a,b. The Josephson current J in Figure 3a has an abrupt jump from positive to negative value at φ = n π ( n = 0 , 1 , 2 , ⋯ ⋯ ) . This is identical to the case in systems of a single QD sandwiched between two MNWs.[32,33] The current J in Figure 3a also has a maximum value at ϕ = n π ( n = 0 , 1 , 2 , ⋯ ⋯ ) , and does not change its sign when ϕ is varied. This behavior is also identical to the structure in which the DQDs are connected to conventional non-topological superconductors (S-DQDs-S)[38,39]. The positive and negative critical currents as functions of ϕ in Figure 3b are antisymmetrical with respective to each other, i.e., J c + = − J c − , hence the diode efficiency η ≡ 0 as is indicated by the blue dotted line therein. For the cases of dots’ energy levels of ( 0 , − 4 ) and ( − 2 , 4 ) , the Josephson current J in Figure 3c,e are 4 π -period function of ϕ and φ , and its sign depends on the values of both ϕ and φ These results are similar to those found in S-DQDs-S [38,39]. It means that the normal 2 π -period Aharonov-Bohm oscillations such as for ( 0 , 0 ) is destroyed and complex periodic interference effects occurs by changing the dots’ levels [40]. Correspondingly, electron transport processes including current’s amplitude or directions are controllable by adjusting both the magnetic flux and the dots’ energy levels.
The period of the positive and negative critical currents J c ± in Figure 3d,f is the same as that of J, which individually corresponds to the cases of (0,-4) and (-2,4). Now J c + and J c − are not antisymmetrical to each other, i.e., J c + ≠ − J c − at most value of ϕ , and the phenomenon of JDE emerges accordingly. We find that the diode efficiency is anti-symmetrical with respective to ϕ = 2 n π and exhibits triple-peak configuration, of which two higher ones locate around ϕ = 4 n π ± π / 4 and two lower ones at the two sides of ϕ = 2 n π , respectively. It shows that η depends on the energy levels of the QDs and the magnetic flux. For example, the absolute maximum of η for ( 0 , − 4 ) in Figure 3d emerged at about 4 n π ± π / 4 can reach up to 0.5 . Whereas for the level configuration of ( − 2 , 4 ) , the absolute maximum of the diode efficiency is about 0.2 at about the same value of ϕ . The above results show that the JDE can be efficiently controlled by combined functions of the QDs’ energy levels and the magnetic flux which induces complex interference effects.
In Figure 4, we present the impacts of MBS-MBS overlap amplitude δ M on the diode efficiency η with fixed QDs’ energy levels configuration ( − 2 , 4 ) . From the figure one can see that the diode efficiency remains as a 4 π − periodic function of ϕ in the presence of finite δ M , and is anti-symmetrical with respective to ϕ = 2 n π . With increasing δ M , the peaks’ heights around ϕ = 4 n π ± π / 4 are lowered with almost unchanged locations. The double-peak configuration around ϕ = 2 n π in the case of δ M , however, evolves into a triple-peak one for δ M ≠ 0 as is indicated by the red dashed and blue dotted lines. Moreover, the two pairs of peaks, which are shifted individually to magnetic flux values of greater and smaller than ϕ = 2 n π , keep as the same shape as those of δ M = 0 , i.e., one positive and one negative. The heights of the two pairs of the peaks change nonlinearly with respective to δ M . For the chosen values of δ M , the maximum of η first increases (by comparing the black dotted line for δ M = 0 with the red dashed line for δ M = 0.5 λ 0 ), and then decreases (the blue solid line for δ M = λ 0 ). The results displayed in Figure 4 indicate that by properly adjusting the value of δ M , one can change either the amplitude or the sign of the diode efficiency. In experiments, δ M depends on the lengths of the MNWs and superconductor coherence [24], which can all be used for change the JDE.
Dependence of the Josephsonc current on the gate voltage V g and phase difference φ for fixed magnetic flux ϕ = π / 4 and different values of bare dots’ energy levels are displayed in Figure 5a for ( 0 , − 4 ) and 5(c) for ( − 2 , 4 ), respectively. In both of the cases of ( 0 , − 4 ) and ( − 2 , 4 ), the Josephson current varying a function of V g is a 4 π − periodic function of φ , and jumps from positive to negative or vice versa at a particular φ . The value of the particular φ depends on both the dots’ energy levels through the gate voltage V g and the magnetic flux, whereas the amplitude of J has no obvious change. This result is quite different from that in S-DQDs-S, in which the current is significantly reduced as the dots’ energy levels are tuned away from the Fermi level[40,41]. As for the diode efficiency η , it is zero in the case of ϕ = π regardless of the value of dots’ energy levels ε i 0 as is shown by the blue solid lines in Figure 5b,d. The diode efficiency η develops two peaks with opposite signs for the cases of ϕ = π / 4 and π / 2 , and their locations and heights are varied when the value of magnetic flux is changed. Here only the results of δ M are displayed, we have examined that for finite MBS-MBS overlap amplitude δ M ≠ 0 , the behaviors of the diode efficiency are similar to those in Figure 4 and we do not list them here.

4. Summary

In summary, we have investigated the JDE in a MNW/DQDs/MNW Josephson junction. It is found that when the energy levels of the DQDs are aligned with the Fermi levels in the MNWs, the Josephson current is a 2 π − period function with respective to both the phase difference arisen from the substrate superconductors and the magnetic flux penetrating through the system. Now the positive and negative critical Josephson currents are the same, and the JDE can not emerge. When the DQDs’ energy levels are tuned away from the Fermi energies in the MNWs, the oscillation period of the Josephson current becomes to be 4 π with respective to the magnetic flux as well as phase difference. Moreover, the positive and negative critical Josephson currents are different from each other and induce the JDE accordingly. Our results show that both the magnitude and the sign of the diode efficiency can be adjusted with the help of the DQDs’ energy levels and the overlap amplitude between the MBSs, as well as the value of the magnetic flux. The present results are beyond the reach of MNW/singl-QD/MNW junction, and can be realized with the help of current nanotechnology.

Author Contributions

Writing—original draft preparation, Y.M. Gao, F. Chi; writing review and editing, M. H. Jiang, Z.C. Yi, L.M. Liu and F. Chi. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Education Science Planning Project of the Department of Education in Guang-dong Province (no. 2023GXJK542), the Educational Quality Project of the Department of Education in Guang-dong Province of China (no. SJD202302), the Graduate Joint Training Base (Zhongshan) Special Project in Guang-dong Province of China (no. 4YYJS04), the Private University Scientific Research Project of Guangdong Private Education Association of China (no. GMG2024041), Project of Guangdong University Teaching Management Institute of China (no. GDZLGL2325) the Educational Quality Project of Zhongshan Institute of University of Electronic Science and Technology of China (no. SFTD2022232023XYWLSZ10), the Engineering Technology Center of Regular Universities in Guangdong Province (no. 2021GCZX005), and the Key Laboratory of Regular Universities in Guangdong Province (no. 2023KSYS011)

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data included in this study are available upon request by contact with the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hu, J.P.; Wu, C.J.; Dai, X. Proposed Design of a Josephson Diode. Phys. Rev. Lett. 2007, 99, 067004. [Google Scholar] [CrossRef] [PubMed]
  2. Ando, F.; Miyasaka, Y.; Li, T. et al. Observation of superconducting diode effect. Nature 2020, 584, 373. [Google Scholar] [CrossRef] [PubMed]
  3. Ideue, T.; Iwasa, Y. One-way supercurrent achieved in an electrically polar film. Nature 2020, 584, 349. [Google Scholar] [CrossRef]
  4. Jiang, K.; Hu, J. Superconducting diode effects. Nat. Phys. 2022, 18, 1145. [Google Scholar] [CrossRef]
  5. Pal, B.; Chakraborty, A.; Sivakumar, P.K. et al. Josephson diode effect from Cooper pair momentum in a topological semimetal. Nat. Phys. 2022, 18, 1228. [Google Scholar] [CrossRef] [PubMed]
  6. Nadeem, M.; Fuhrer, M.S.; Wang, X. The superconducting diode effect. Nat. Rev. Phys. 2023, 5, 558. [Google Scholar] [CrossRef]
  7. Linder, J.; Robinson, J.W. Superconducting spintronics. Nat. Phys. 2015, 11, 307. [Google Scholar] [CrossRef]
  8. Braginski, A.I. Superconductor electronics: status and outlook. J. Supercond. Nov. Magn. 2019, 32, 23. [Google Scholar] [CrossRef]
  9. Yuan, N.F.Q.; Fu, L. Supercurrent diode effect and finite-momentum superconductors. Proc. Natl. Acad. Sci. 2022, 119, e2119548119. [Google Scholar] [CrossRef]
  10. Legg, H.F.; Loss, D.; Klinovaja, J. Superconducting diode effect due to magnetochiral anisotropy in topological insulators and Rashba nanowires. Phys. Rev. B 2022, 106, 104501. [Google Scholar] [CrossRef]
  11. Lotfizadeh, N.; Schiela, W.F.; Pekerten, B. et al. Superconducting diode effect sign change in epitaxial Al-InAs Josephson junctions. Commun. Phys. 2024, 120. [Google Scholar] [CrossRef]
  12. Hess, R.; Legg, Henry, F.; Loss, D.; Klinovaja, J.Josephson transistor from the superconducting diode effect in domain wall and skyrmion magnetic racetracks. Phys. Rev. B 2023, 108, 174516, https://journals.aps.org/prb/abstract/10.1103/PhysRevB.108.174516. [CrossRef]
  13. Fulton, T.A.; Dynes, R.C. Current-Phase Relations in Superconducting Bridges. Phys. Rev. Lett. 1970, 25, 794, https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.25.794. [Google Scholar] [CrossRef]
  14. Fulton, T.A.; Dunkleberger, L.N.; Dynes, R.C. Quantum Interference Properties of Double Josephson Junctions. Phys. Rev. B 1972, 6, 855, https://journals.aps.org/prb/abstract/10.1103/PhysRevB.6.855. [Google Scholar] [CrossRef]
  15. Sivakov, A.G.; Turutanov, O.G.; Kolinko, A.E.; Kolinko, A.S. Pokhila. Spatial characterization of the edge barrier in wide superconducting films. Low. Temp. Phys. 2018, 44, 226, https://pubs.aip.org/aip/ltp/article/44/3/226/252269/Spatial-characterization-of-the-edge-barrier-in. [Google Scholar] [CrossRef]
  16. Tsang, W.T.; Van Duzer, T. dc analysis of parallel arrays of two and three Josephson junctions. J. Appl. Phys. 1975, 46, 4573, https://pubs.aip.org/aip/jap/article/46/10/4573/7643/dc-analysis-of-parallel-arrays-oftwo-and-three. [Google Scholar] [CrossRef]
  17. Pillet, V.; Benzoni, J.D.; Griesmar, J. et al. Nonlocal Josephson effect in Andreev molecules. Nano Letters 2019, 19, 7138. [Google Scholar] [CrossRef]
  18. Maiani, A.; Flensberg, K.; Leijnse, M. et al. Nonsinusoidal current-phase relations in semiconductor-superconductor-ferromagnetic insulator devices. Phys. Rev. B 2023 107, 245415. [CrossRef]
  19. Ilic, S.; Bergeret, F. S. Theory of the supercurrent diode effect in rashba superconductors with arbitrary disorder. Phys. Rev. Lett. 2022, 128, 177001. [Google Scholar] [CrossRef]
  20. Gupta, M.; Graziano, G.V.; Pendharkar, M. et al. Gate-tunable superconducting diode effect in a three-terminal Josephson device. Nat. Commun. 2023, 14, 3078. [Google Scholar] [CrossRef] [PubMed]
  21. Coraiola, M.; Svetogorov, A.E.; Haxell, D.Z. Flux-Tunable Josephson Diode Effect in a Hybrid Four-Terminal Josephson Junction. ACS Nano 2024, 18, 9221. [Google Scholar] [CrossRef] [PubMed]
  22. Lutchyn, R.M.; Bakkers, E.P.; Kouwenhoven, L.P. Majorana zero modes in superconductor-semiconductor heterostructures. Nat. Rev. Mater. 2018, 3, 52. [Google Scholar] [CrossRef]
  23. Flensberg, K.; von Oppen, F.; Stern, A. Engineered platforms for topological superconductivity and Majorana zero modes. Nat. Rev. Mater. 2021, 6, 944. [Google Scholar] [CrossRef]
  24. Prada, E.; Aguado, R.; San-Jose, P. Measuring Majorana nonlocality and spin structure with a quantum dot. Phys. Rev. B 2017, 96, 085418. [Google Scholar] [CrossRef]
  25. Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
  26. Alicea, J.; Oreg, Y.; Refael, G. Non-abelian statistics and topological quantum information processing in 1d wire networks. Nat. Phys. 2011, 7, 412. [Google Scholar] [CrossRef]
  27. Lian, B.; Sun, X.Q.; Vaezi, A.; Zhang, S.C. Topological quantum computation based on chiral Majorana fermions. Proc. Natl. Acad. Sci. 2018, 115, 10938. [Google Scholar] [CrossRef] [PubMed]
  28. Lopez, R.; Lee, M.; Serra, L.; Lim, J. Thermoelectrical detection of majorana states. Phys. Rev. B 2014, 89, 205418. [Google Scholar] [CrossRef]
  29. Chi, F.; Fu, Z.G.; Liu, J.; Li, K.; Wang, Z.; Zhang, P. Thermoelectric effect in a quantum dot side-coupled to majorana bound states. Nanoscale Res. Lett. 2020, 15, 79. [Google Scholar] [CrossRef] [PubMed]
  30. Hong, L.; Chi, F.; Fu, Z.G.; Hou, Y.F.; Wang, Z. Large enhancement of thermoelectric effect by majorana bound states coupled to a quantum dot. J. Appl. Phys. 2020, 127, 124302. [Google Scholar] [CrossRef]
  31. Liu, X.; Li, X.; Deng, D.L.; Liu, X.J.; Das, S.D. Majorana spintronics. Phys. Rev. B 2016, 94, 014511. [Google Scholar] [CrossRef]
  32. Xu, L.T.; Li, X.Q.; Sun, Q.F. Majorana dc Josephson current mediated by a quantum dot. J. Phys. Condens. Matter 2017, 29, 195301. [Google Scholar] [CrossRef]
  33. Stefanski, P. Properties of the Majorana-state tunneling Josephson junction mediated by an interacting quantum dot. J. Phys. Condens. Matter 2019, 31, 185301. [Google Scholar] [CrossRef]
  34. Chi, F.; Jia, Q.S.; Liu, J.; Gao, Q.G.; Yi, Z.C.; Liu, L.M. Enhancement of the Josephson Current in a Quantum Dot Connected to Majorana Nanowires. Nanomaterials 2023, 13, 1482. [Google Scholar] [CrossRef]
  35. Zhang, H.R.; Sun, L.L.; Liu, J. Josephson dc Current through T-Shaped Double-Quantum-Dots Hybridized to Majorana Nanowires. Coatings 2023, 13, 523. [Google Scholar] [CrossRef]
  36. Gao, Y.; Zhang, X. Tunable Josephson Current through a Semiconductor Quantum Dot Hybridized to Majorana Trijunction. Coatings 2023, 13, 1627. [Google Scholar] [CrossRef]
  37. Sun, Q.F.; Wang, J.; Lin, T.H. Photon-assisted andreev tunneling through a mesoscopic hybrid system. Phys. Rev. B 1999, 59, 13126. [Google Scholar] [CrossRef]
  38. Sun, Q.F.; Wang, J.; Lin, T.H. Control of the supercurrent in a mesoscopic four-terminal Josephson junction. Phys. Rev. B 2000, 62, 648. [Google Scholar] [CrossRef]
  39. Zhu, Y.; Sun, Q.F.; Lin, T.H. Andreev bound states and the π-junction transition in a superconductor/quantum-dot/superconductor system. J. Phys. Condens. Matter 2001, 13, 8783. [Google Scholar] [CrossRef]
  40. Pan, H.; Lin, T.H. Control of the supercurrent through a parallel-coupled double quantum dot system. Phys. Rev. B 2006, 74, 235312. [Google Scholar] [CrossRef]
  41. Cheng, S.G.; Sun, Q.F. Josephson current transport through T-shaped double quantum dots. J. Phys. Condens. Matter 2008, 20, 505202. [Google Scholar] [CrossRef]
  42. Hofstetter, L.; Csonka, S.; Nygard, J. et al. Cooper pair splitter realized in a two-quantum-dot Y-junction. Nature 2009, 461, 960. [Google Scholar] [CrossRef]
  43. Deacon, R.; Oiwa, A.; Sailer, J. et al. Cooper pair splitting in parallel quantum dot Josephson junctions. Nat. Commun. 2015, 6, 7446. [Google Scholar] [CrossRef]
  44. Debbarma, R.; Aspegren, M.; Bostrom, F.V. et al. Josephson Current via Spin and Orbital States of a Tunable Double Quantum Dot, Phys. Rev. B 2022, 106, L180507. https://journals.aps.org/prb/pdf/10.1103/PhysRevB.106.L180507.
  45. Sun, Y.F.; Mao, Y.; Sun, Q.F. Design of Josephson diode based on magnetic impurity. Phys. Rev. B 2023, 108, 214519. [Google Scholar] [CrossRef]
  46. Giazotto, F.; Martinez-Perez, M. The Josephson heat interferometer. Nature 2012, 492, 401. [Google Scholar] [CrossRef]
  47. Souto, R.S.; Leijnse, M.; Schrade, C. Josephson Diode Effect in Supercurrent Interferometers. Phys. Rev. Lett. 2022, 129, 267702. [Google Scholar] [CrossRef]
  48. Dvir, T.; Wang, G.; van Loo, N. et al. Realization of a minimal Kitaev chain in coupled quantum dots. Nature, 2023, 614, 445. [Google Scholar] [CrossRef]
  49. Debbarma, R.; Tsintzis, A.; Aspegren, M. et al. Josephson Junction π-0 Transition Induced by Orbital Hybridization in a Double Quantum Dot. Phys. Rev. Lett. 2023, 131, 256001. [Google Scholar] [CrossRef]
  50. Flensberg, K. Tunneling characteristics of a chain of Majorana bound states. Phys. Rev. B 2010, 82, 180516(R). [Google Scholar] [CrossRef]
  51. Liu, D.E.; Baranger, H.U. Detecting a majorana-fermion zero mode using a quantum dot. Phys. Rev. B 2011, 84, 201308R. [Google Scholar] [CrossRef]
Preprints 108668 g001
Figure 1. (a) Schematic diagram for the studied system which is composed of parallel double quantum dots (DQDs) coupled to the left and right nanowires hosting Majorana bound states (MBSs) at their ends. The MBSs are denoted by γ α i with α = L , R and i = 1 , 2 , and interact to the QDs with strengths of λ α i . The DQDs are coupled to each other via tunnel barrier of amplitude t c . In the presence of a magnetic flux Φ threading through the system, an additional phase factor ϕ is added to λ α i .
Figure 1. (a) Schematic diagram for the studied system which is composed of parallel double quantum dots (DQDs) coupled to the left and right nanowires hosting Majorana bound states (MBSs) at their ends. The MBSs are denoted by γ α i with α = L , R and i = 1 , 2 , and interact to the QDs with strengths of λ α i . The DQDs are coupled to each other via tunnel barrier of amplitude t c . In the presence of a magnetic flux Φ threading through the system, an additional phase factor ϕ is added to λ α i .
Preprints 108668 g001
Preprints 108668 g002
Figure 2. (Color online) Josephson current and CCDOS individually in (a) and (b) for the case of dot levels ε 1 0 = ε 2 0 = 0 , i.e., configuration of (0,0). (c) and (d) are for the Josephson current in the configurations of (0,-4) and (-2,4), respectively. The tunnel-coupling strength between the dots are fixed at t c = λ 0 , ϕ = π , and φ = π / 2 .
Figure 2. (Color online) Josephson current and CCDOS individually in (a) and (b) for the case of dot levels ε 1 0 = ε 2 0 = 0 , i.e., configuration of (0,0). (c) and (d) are for the Josephson current in the configurations of (0,-4) and (-2,4), respectively. The tunnel-coupling strength between the dots are fixed at t c = λ 0 , ϕ = π , and φ = π / 2 .
Preprints 108668 g002
Preprints 108668 g003
Figure 3. Josephson current J as a function of ϕ and φ , and positive (negative) critical current J c + ( − ) , diode efficiency η as functions of ϕ for the configurations of (0,0) in (a) and (b), (0,-4) in (c) and (d), and (-2,4) in (e) and (f), respectively. Other parameters are t c = λ 0 and V g = δ M = 0 .
Figure 3. Josephson current J as a function of ϕ and φ , and positive (negative) critical current J c + ( − ) , diode efficiency η as functions of ϕ for the configurations of (0,0) in (a) and (b), (0,-4) in (c) and (d), and (-2,4) in (e) and (f), respectively. Other parameters are t c = λ 0 and V g = δ M = 0 .
Preprints 108668 g003
Preprints 108668 g004
Figure 4. Diode efficiency η as a function of ϕ for dots’ level configuration ( − 2 , 4 ) and different values of MBS-MBS overlap amplitude δ M . Other parameters are as in Figure 3.
Figure 4. Diode efficiency η as a function of ϕ for dots’ level configuration ( − 2 , 4 ) and different values of MBS-MBS overlap amplitude δ M . Other parameters are as in Figure 3.
Preprints 108668 g004
Preprints 108668 g005
Figure 5. Josephson current J as a function of φ and V g for ϕ = π / 4 , and diode efficiency η as a function of V g for different values of ϕ . The dots’ level configurations are ( 0 , − 4 ) in (a) and (b), and (-2,4) in (c) and (d) at δ M = 0 . Other parameters are as in Figure 3.
Figure 5. Josephson current J as a function of φ and V g for ϕ = π / 4 , and diode efficiency η as a function of V g for different values of ϕ . The dots’ level configurations are ( 0 , − 4 ) in (a) and (b), and (-2,4) in (c) and (d) at δ M = 0 . Other parameters are as in Figure 3.
Preprints 108668 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated