Prerpints.org logo
Preprint
Article

Global Sensitivity Analysis of Structural Reliability Using Cliff Delta

Altmetrics

Downloads

91

Views

63

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 June 2024

Posted:

11 June 2024

You are already at the latest version

Alerts
Abstract
This paper introduces innovative sensitivity indices based on Cliff's Delta for global sensitivity analysis of structural reliability. These indices build on Sobol's method, using binary outcomes (success or failure), but avoid the need to calculate failure probability Pf and the associated distributional assumptions of resistance R and load F. Cliff's Delta, originally for ordinal data, evaluates the dominance of resistance over load without specific assumptions. The mathematical formulations for computing Cliff's Delta between R and F quantify structural reliability by assessing the random realizations of R > F using a double-nested-loop approach. The derived sensitivity indices, based on the squared value of Cliff's Delta​, exhibit properties analogous to those in Sobol's sensitivity analysis, including first-order, second-order, and higher-order indices. This provides a comprehensive framework for evaluating the contributions of input variables and their interactions on structural reliability. This method is particularly significant for FEM applications, where repeated simulations of R or F are computationally intensive. The double-nested-loop algorithm of Cliff's Delta maximizes the extraction of information about structural reliability from these simulations. However, the high computational demand of Cliff's Delta is a disadvantage. Future research should optimize computational demands, especially for small Pf​, where the inner loop may often be unnecessary.
Keywords: 
Subject: Engineering  -   Civil Engineering

MSC:  65C50; 60H99

1. Introduction

Global sensitivity analysis (GSA) focuses on attributing the uncertainties of model outputs, or related performance indicators, to their inputs, thereby assessing the impact of input uncertainties on outputs or performance indicators [1,2]. Various GSA methods have been developed for this purpose [3,4]. These methods include the screening method [5,6], variance-based methods [7,8], moment-independent methods [9,10], and derivative-based methods [11,12]. Among these, variance-based sensitivity indices, also known as Sobol’ indices [7,8], are particularly notable for their mathematical elegance in measuring the individual, interaction, and total contributions of each input to the model output uncertainty, see, e.g. [13,14].
In the limit state method, probabilistic reliability analysis is based on the estimation of the failure probability [15]. Sobol' indices have been widely used in structural reliability analysis to pinpoint variables that significantly influence failure probability [16,17]. These sensitivity indices, which focus on failure probability Pf, are derived from the variance decomposition of a binary function representing failure and success [16,17]. Fort et al. [18] expanded on Sobol's sensitivity indices by introducing a contrast function in place of variance, allowing the indices to be oriented towards variance, probability, and quantile. This approach maintains the non-negative property of the indices and ensures that their sum equals one, as in traditional Sobol sensitivity analysis. Extending GSA to Pf and design quantile represented a significant advancement in civil engineering, as these quantities are crucial in structural reliability assessments [19,20].
The development of GSA methods focused on reliability demands precise estimation of Pf [21]. However, the complexity of mathematical models and the difficulty of uncertainty propagation using sampling-based methods such as Monte Carlo (MC) simulations, due to the large number of runs required, present significant challenges [22]. Nonlinear finite element models are particularly demanding on CPU time [23], which further complicates the process of structural reliability estimation, see, e.g., [24,25]. To ensure the most accurate estimate of Pf​, it is essential to develop methods that provide precise Pf ​estimates while minimizing the computational costs associated with repeated calls to the computational model [26,27].
The computational burden can be reduced by using metamodels, also known as surrogate models, which approximate the behavior of complex models with simpler ones [28,29]. Methods such as polynomial response surface [30,31], response surface based multi-fidelity model [32], polynomial chaos expansion (PCE) [33,34], Gaussian process [35,36], Kriging [37,38], and neural network [39,40,41] are used to the creation of such metamodels. While the use of metamodels significantly reduces computational burden by approximating complex models with simpler ones, there are some critical drawbacks to this approach [42,43,44]. Despite the efficiency of new meta-models in sampling [45,46], traditional (quasi-) Monte Carlo methods remain the primary choice for practical sensitivity analysis [3,4].
Existing research frequently explores the rate of advancements across various Monte Carlo based reliability applications [47,48], but there is a notable lack of studies focusing on the implications of these advancements for enhancing the efficiency of reliability-oriented global sensitivity analyses (GSAs). Ensuring the accurate estimation of failure probability Pf with the available number of simulations is critical because it directly influences reliability assessments and decision-making processes. More accurate Pf estimation is advantageous when using both the original model and the metamodel, depending on the available computational resources.
The solution proposed in this article involves adopting an alternative measure of structural reliability based on Cliff's Delta [48], which can be calculated using double-nested-loop simulations. This approach enhances the precision of Pf estimation without requiring additional computational effort, offering a robust alternative to traditional metamodel-based GSA. By maximizing the utility of existing simulations, this method ensures that reliability analyses are both more accurate and computationally efficient.

2. Cliff Delta

Cliff delta, denoted as δC​, was initially devised by Norman Cliff, primarily for handling ordinal data [49]. It serves as a metric to assess the frequency with which values from one distribution exceed those in another distribution. A key feature of δC is that it does not necessitate any specific assumptions regarding the distributions’ form or variability.
The formula for computing the sample estimate of δC is expressed as:
δ C = ∑ i = 1 m ∑ j = 1 n [ y i > y j ] − [ y i < y j ] m ⋅ n , where δ C ∈ [ – 1 , 1 ]
In this equation, the two distributions are characterized by sizes n and m, with respective elements yi and yj​. Here, the notation [⋅][⋅] refers to the Iverson bracket notation, resulting 1 if the condition within the brackets holds true, and 0 otherwise. This statistical approach allows for an intuitive comparison of two distributions by quantifying the dominance of one distribution over the other.
Building upon the foundational description of δC​, this measure is specifically applied to assess the relationship between resistance R and load force F within a framework of structural reliability. In the limit state, a structure is reliable if R ≥ F, otherwise failure occurs [19]. Let the difference between R and F be denoted as
Z = R – F,
where R and F are statistically independent random variables. In the Monte Carlo simulations, these variables are represented as arrays R and F, corresponding to resistance and force, respectively. Cliff's delta, δC​, is utilized to quantitatively evaluate the extent to which values of resistance exceed or fall below those of force, thereby providing fundamental insights into system reliability.
Assuming arrays R and F are of equal size, with n entries each, the formula for calculating δC is simplified to:
δ C = ∑ i = 1 n ∑ j = 1 n [ R i > F j ] − [ R i < F j ] n 2 , where δ C ∈ [ – 1 , 1 ]
In this expression, Ri and Fj represent the i-th and j-th entries in the R and F arrays, respectively, denoting random realizations of resistance and force. The Iverson brackets, [⋅][⋅], return 1 when the enclosed condition is true and 0 otherwise. This formulation facilitates a direct comparison between resistance and force across all sampled scenarios.
The estimation of δC between the measurements of resistance and force provides a metric quantifying the frequency with which resistance values surpass those of force. Employed as a statistical tool, this measure assesses how frequently resistance can withstand or exceed applied forces.

3. Sensitivity Measures of Cliff's Delta

Although Cliff's delta has been applied in numerous studies, see e.g. [50,51,52,53,54], its utilization in global sensitivity analysis of reliability is absent. This chapter demonstrates that the sensitivity measures based on the squared value of Cliff's delta, δ C 2 ​, exhibit properties similar to variance in Sobol's sensitivity analysis [7,8], oriented to reliability [16,17].

3.1. Approximation of Failure Probability with Cliff's Delta in Sensitivity Analysis

In the limit state, a structure is considered reliable if R ≥ F; otherwise, failure occurs. The probability of failure Pf can be defined as the overload probability that F > R (i.e., Z < 0). The failure probability can be expressed as the mean value of the binary reliability function of the Bernoulli distribution, where 1 occurs if Z < 0, and 0 otherwise:
P f = P ( Z < 0 ) = E ( 1 Z < 0 ) ,
where:
1 Z < 0 = | Z | − Z 2 | Z | .
The conventional measure of reliability is 1−Pf​. The variance of the Bernoulli distribution of the random variable 1Z < 0 can be written as:
V ( 1 Z < 0 ) = P f ( 1 − P f ) .
The second moment is a function of Pf, which is useful for the formulation of Sobol sensitivity indices, computable through the estimation of the conditional realizations of Pf [21]. If the variance V(1Z<0) is used in the decomposition within Sobol sensitivity analysis, the first-order sensitivity index of the variance function 1Z<0 can be expressed as:
S i = V ( E ( 1 Z < 0 | X i )   ) V ( 1 Z < 0 ) = V ( 1 Z < 0 ) − E ( V ( 1 Z < 0 | X i )   ) V ( 1 Z < 0 ) = P f ( 1 − P f ) − E ( P f | X i ( 1 − P f | X i ) ) P f ( 1 − P f ) .
The concept of sensitivity analysis based on Cliff's Delta is predicated on the assumption that Cliff's Delta can be expressed as
δ C = P ( Z > 0 ) − P ( Z < 0 ) = ( 1 − P f ) − P f = 1 − 2 P f .
The failure probability Pf can be calculated using Cliff's Delta as follows:
P f = 1 − δ C 2 .
Similarly, the second moment can be approximated and written as a function of Cliff's Delta as:
V ( 1 Z < 0 ) = P f ( 1 − P f ) = ( 1 − δ C 2 ) ( 1 − 1 − δ C 2 ) = 1 − δ C 2 4 .
Substituting this into the Equation (7), the Sobol sensitivity index can be expressed using δC as:
S i = 1 − δ C 2 4 − E ( 1 − δ C 2 | X i 4 ) 1 − δ C 2 4 = E ( δ C 2 | X i ) − δ C 2 1 − δ C 2 .
This formulation provides an alternative method for calculating the sensitivity index, which carries all the advantages and disadvantages associated with the estimation of Cliff's Delta compared to failure probability.

3.2. Sensitivity Indices Based on Cliff Delta

In the development of sensitivity indices for the evaluation of structural reliability, the use of the squared measure of Cliff's delta, δ C 2 ​, has been proposed. This chapter delineates the formal definitions of these indices, categorized from first to higher orders. The sensitivity indices are computed as ratios of differences normalized by a constant, 1-C, where C0 is defined as square of Cliff's delta, δ C 2 ​.
C 0 = δ C 2 ,
where δ C 2 represents the measure calculated when all input random variables, X1, X2,..XM, of R and F are random.
The first-order sensitivity index, Si​, is defined to quantify the effect of a single variable Xi on the change observed in the squared Cliff's delta, δ C 2 ​. It is calculated as follows:
S i = E ( δ C 2 | X i ) − C 0 1 − C 0 .
In Equation (13), having frozen one potential source of variation (Xi​), the resulting E ( δ C 2 | X i ) will be higher than the corresponding total or unconditional Cliff's delta, where C0= δ C 2 ​​. For example, if Xi were the sole source of change in the distance between R and F, fixing it to x i * would result in ( δ C 2 | X i = x i * ) =1.
The second-order sensitivity index, Sij​, extends the analysis to pairs of variables, evaluating the joint effect of Xi and Xj on the change of δ C 2 ​. This index is expressed as:
S i j = E ( δ C 2 | X i , X j ) − C 0 1 − C 0 − S i − S j .
Similarly, the third-order index, Sijk​, considers the combined influence of three variables Xi​, Xj​, and Xk​. It is calculated by:
S i j k = E ( δ C 2 | X i , X j , X k ) − C 0 1 − C 0 − S i − S j − S k − S i j − S i k − S j k .
Other Cliff's sensitivity indices, which quantify higher-order interaction effects, are defined analogously. The sensitivity index of the last order can be expressed as follows:
S 1 , 2 , ... , M = E ( δ C 2 | X 1 , X 2 , ... , X M ) − C 0 1 − C 0 − ∑ p = 1 M − 1 ∑ 1 ≤ i 1 < ... < i p ≤ M S i 1 , i 2 , ... , i p = 1 − ∑ p = 1 M − 1 ∑ 1 ≤ i 1 < ... < i p ≤ M S i 1 , i 2 , ... , i p ,
where E( δ C 2 |X1, X2,…,XM)=1 is ensured due to the nature of Cliff's delta, which assumes a value of either 1 or -1 when all input random variables are fixed. Consequently, each element in the array R adopts a consistent identical value denoted as v1, and similarly, every element in the array F maintains another consistent identical value, denoted as v2. It should be noted that these constants v1 and v2 are generally different.
The sum of all indices equals one. This characteristic is guaranteed by the computation of the last order sensitivity index, as shown in Equation (16), which is derived from the difference between 1 and the sum of all lower order sensitivity indices.
∑ i S i + ∑ i ∑ j > i S i j + ∑ i ∑ j > i ∑ k > j S i j k + ... + S 123... M = 1 .
The non-negativity of sensitivity indices is proven due to their association with variance, see Equation (10), and the Sobol decomposition of variance. The fixing multiple input variables typically leads to a higher value of δ C 2 (with a limit of one in the last order sensitivity index) compared to a constant C0. The properties of sensitivity indices based on Cliff's delta and their comparison with classical Sobol sensitivity analysis will be further explored in later chapters.

3.3. Sensitivity Indices Based on Failure Probability

The impact of input variables on the failure probability Pf can be analyzed using sensitivity analysis based on contrast functions [18]. Unlike Sobol's sensitivity analysis, contrast-oriented sensitivity analysis employs a contrast function, whose minimizer is of primary interest [55,56]. Fort [18] demonstrates that employing the quadratic contrast function, which calculates the mean of the squared deviations from the average, results in the well-known Sobol sensitivity indices [7,8]. In reliability-oriented sensitivity analysis, the mean value is considered as the failure probability Pf as the first moment of the binary reliability function Pf = E(1Z<0), while the variance, upon which Sobol's sensitivity analysis is based, is considered as the second moment of the binary reliability function V(1Z<0) = Pf (1- Pf).
The first-order sensitivity index, Ci​, quantifies the main effect of a single variable Xi on the variance of the binary reliability function:
C i = V ( E ( 1 Z < 0 | X i )   ) V ( 1 Z < 0 ) = P f ( 1 − P f ) − E ( P f | X i ( 1 − P f | X i ) ) P f ( 1 − P f ) .
In this equation, the freezing of the source of variation Xi affects Pf​. The sensitivity index Ci indicates by how much one could reduce, on average, the output variance of the binary function 1Z<0 if Xi could be fixed. Hence, it is a measure of the main effect.
The second-order sensitivity index, Cij​, measure the pair effects of Xi and Xj on the variance of binary function 1Z<0 ​. This index can be write as:
C i j = V ( E ( 1 Z < 0 | X i , X j )   ) V ( 1 Z < 0 ) − S i − S j .
Similarly, the third-order index, Cijk​, considers the combined influence of three variables Xi​, Xj​, and Xk​, calculated by:
C i j = V ( E ( 1 Z < 0 | X i , X j , X k )   ) V ( 1 Z < 0 ) − S i − S j − S k − S i j − S i k − S j k .
Higher-order contrast sensitivity indices, which quantify higher-order interaction effects, are defined analogously. The sum of all sensitivity indices equals one.
∑ i C i + ∑ i ∑ j > i C i j + ∑ i ∑ j > i ∑ k > j C i j k + ... + C 123... M = 1 .
The non-negativity of sensitivity indices is guaranteed by their derivation from Sobol's sensitivity analysis [6,7,8], see also [19,21].

4. The case study

In the case study, the new sensitivity indices are compared with the results of Sobol sensitivity analysis using a simple example. In Equation (2), the resistance can be considered as:
R =  X1·X2+X2·X3+K,
where K is constant. The load force is considered as
F = X4·X5.
All input random variables, X1, X2,…,X5​, follow a Gaussian probability density function with a mean value of zero and a standard deviation of one.
Table 1 presents the estimated values of C0 = δ C 2 ​, where δ C is obtained using n = 12,000 runs of the Latin Hypercube Sampling (LHS) method [57,58]. The conditional values of δ C are estimated using double-nested-loop computation of LHS method. When a single input variable, Xi​, is fixed, it is sampled using n=12,000 runs, and for each realization, δ C is calculated again using n=12,000 runs of the LHS method. This numerical procedure is analogous to Sobol [7,8], but the sensitivity measurement is not based on variance but on Cliff's delta. In computing of Si, the computational complexity of E( δ C 2 |Xi) is n2=144,000,000.
In the Table 1, the data in the last column represent a set of values that are highly consistent, with low variance. Most values range between 0.924 and 0.940, with a last exceptions approaching 1.000. In Table 1, the value 1 is always present on the last row, ensuring that the sum of all indices equals one.
The column with K=0 exhibits values close to zero, indicating the absence of dominance of R over F in the observations of δ C 2 ​​. Conversely, values far from zero suggest a dominance of R over F in the observation of δ C 2 ​​.
In general, the strong influence of an input variable or variables occurs when the mean value of the fixed realizations of δ C 2 ​​ is significantly different from C0​, see Equations (13), (14), and (15). It can be noted that the accuracy of estimation of sensitivity indices is lowest for K=4, where the conditioned realizations of δ C 2 ​ in the last column of Table 1 are very consistent, with low variance, and are minimally different from C0.
The influences of input variables and their groups, as expressed by sensitivity indices, are displayed in Figure 1, Figure 2 and Figure 3.
In the Figure 1, all first-order sensitivity indices are zero. The second-order sensitivity indices S12=0.18 and S23​=0.18 have the same value, which is due to the nature of Equation 10 and the same characteristics of the input random variables. The dominant influence is the interaction effect of variables X4 and X5, as indicated by the value S45=0.26.
Increasing the value of the constant K distances the random realizations of resistance R from load action F and enhances the value of Cliff's Delta. The interaction effects indicated by sensitivity indices S12​, S23​, and S45 decrease with increasing K, while the proportion of third, fourth, and fifth-order sensitivity indices increases, see Figure 2 and Figure 3.
In sensitivity analysis based on Cliff's Delta, the impact of input variables on the observed changes in δ C 2 is quantified using sensitivity indices of the first order and higher orders. To derive meaningful conclusions and categorize input variables into influential, less influential, and non-influential groups, it is essential to assign the effects of each input variable without the complexity of interpreting numerous sensitivity indices.
To achieve this, the concept of the total effect index is employed. This index captures the comprehensive contribution of a factor, Xi​, to the changes observed in δ C 2 ​. Specifically, it encompasses both the first-order effects and all higher-order effects resulting from interactions. The total effect index provides a robust measure of the impact that each input variable has on the δ C 2 ​, accounting for all potential interactions.
For instance, in a five-factor model, the total effect of the factor X1 is calculated by summing all terms in Equation (17) where the factor X1 is included.
S T 1 = S 1 + S 12 + S 13 + S 14 + S 15 + S 123 + S 124 + S 125 + S 134 + S 135 + S 145 + S 1234 + S 1235 + S 1245 + S 1345 + S 12345   .
This sum accounts for X1 ​direct influence on δ C 2 as well as its synergistic effects with other factors. The total effect measure provides the educated answer to the question, Which factor can be fixed anywhere over its range of variability without affecting the δ C 2 . The total effect index reflects both the main and the interaction influences of X1 on the outcome, providing a comprehensive view of its relative importance in the system's reliability, measured by the distance from F to R. Total effects for the case study are displayed in Figure 4.
The sensitivity analysis results show the Total Sensitivity Indices for each input variable (X1, X2, X3, X4, X5) across five distinct constant values (K=0, 1, 2, 3, 4), using Cliff's delta as the sensitivity measure.
As K increases from 0 to 4, a general trend of increasing total sensitivity indices is observed for X1, X2, as depicted in Figure 4. For X3, the total sensitivity indices exhibit a slightly convex pattern. An increasing trend for X3 is observed from K=1 to K=4. This suggests that these variables become more influential with higher values of K, as measured by Cliff's delta. Conversely, the sensitivity indices for X4 and X5 decrease with increasing K.
The variable X2 consistently exhibits the highest total sensitivity index across all tested values of K, indicating its dominant influence on Cliff's delta. This effect is attributable to X2's involvement in both additive terms of the resistance function, as shown in Equation (22). The variables X1 and X3 also demonstrate an increasing influence, although they remain slightly less dominant than X2 but are notably more influential than X4 and X5 as K increases. The influence of X4 and X5, which are involved in the load force equation, decreases especially as K surpasses 1, highlighting their reduced significance in affecting Cliff's delta.
The sensitivity analysis outcomes reflect a decreasing probability P(R<F), which diminishes as K increases. The Cliff delta-based sensitivity analysis exhibits characteristics of reliability-oriented sensitivity analysis [19], describing the change in the influence of each variable on Cliff's delta due to K. The influence of the results of the sensitivity indices by the value of the deterministic quantity K is the main difference compared to Sobol sensitivity analysis.
The results of the classical Sobol sensitivity analysis can be calculated analytically. Non-zero values of Sobol's sensitivity indices were obtained only for second-order sensitivity indices S 12 S o b ​=1/3​, S 23 S o b ​=1/3​, S 45 S o b ​=1/3 , other Sobol indices are zero. The total effect Sobol sensitivity indices are S T 1 S o b ​=1/3​, S T 2 S o b ​=2/3​, S T 3 S o b ​=1/3​, S T 4 S o b ​=1/3​, S T 5 S o b ​=1/3. The dominant influence of the input variable X2 confirms the most important conclusions of the newly introduced sensitivity analysis based on Cliff's Delta, however, there are differences. The results of Sobol's sensitivity analysis are independent of the value of the constant K, because Sobol's indices are based on the decomposition of variance, which the deterministic variable K does not affect.
Although classic Sobol's sensitivity analysis of model output is empathetic to the results of reliability-oriented types of sensitivity analyses, it is not directly oriented towards reliability, as Sobol sensitivity indices do not reflect changes in Pf [19].
The sensitivity indices results based on Cliff's Delta closely resemble those obtained from the sensitivity analysis based on Pf ​. The pie chart on the left side of Figure 4 is practically identical to the chart in Figure 1. Moreover, the pie chart on the right side of Figure 4 is very similar to the chart on the right side of Figure 5. The results of the sensitivity analysis are the same, but the sensitivity scale is different. Overall, this demonstrates a high degree of similarity between Cliff's Delta and Pf, from which useful conclusions can be drawn.
The sensitivity indices based on Cliff's Delta are derived from the calculation of Pf using Cliff's Delta. While it may seem that estimating Cliff's Delta is more demanding compared to Pf​, using double-loop simulations to estimate Cliff's Delta leads to a more accurate numerical estimate of Pf and extracts more information from the available simulations. It can be noted that a similar double-loop simulation is used for estimating Pf based on the numerical integration of the distributions of the random variables R and F , see e.g. [59].
The advantage of estimating Cliff's Delta is that it does not require knowledge of the distributions or approximation approaches of the random variables R and F. This flexibility allows for a more robust analysis in practical scenarios where precise distribution functions may not be available or easily determined.

5. Comparative Analysis of Pf Estimations Using Cliff's Delta and Basic Definition

It can be showed that the estimation of Pf according to Equation (9) is more accurate compared to the basic definition in Equation (4) when Cliff's delta is calculated using a double nested-loop simulation according to Equation (3).
Let Pf ​denote the failure probability estimated from a binomial distribution, and let n represent the number of simulations or experiments.
P f = 1 n ∑ i = 1 n 1 Z < 0 .
The standard error SE for the failure probability estimation is provided by the binomial distribution
S E 1 ( P f ) = P f ( 1 − P f ) n .
The estimate of the failure probability Pf using Cliff’s Delta in Equation (9) is more accurate because it utilizes an increased number of simulations through a double-nested-loop process. However, the standard error SE2(Pf) for this estimate cannot be straightforwardly determined using an analytical formula similar to SE1(Pf). Instead, empirical observations indicate that the standard error for Pf estimated with Cliff’s Delta is smaller. This improved accuracy is attributed to the increased statistical information gained from the double-nested-loop simulations. The accuracy of both estimates can be demonstrated in the following case study using the Monte Carlo method.
The limit state of a rod made of elastic material, subjected to axial tension, is being studied. Let resistance R have a Gaussian probability density function with a mean value μR=9 kN and standard deviation σR​=0.9 kN, and let F have a Gaussian probability density function with a mean value μF​=4 kN and standard deviation σF=1.218887 kN. Under these assumptions, Z is a random variable with a Gaussian probability density function with a mean value μZ=9−4=5 kN and standard deviation σZ =(0.92+1.2188872)0.5=1.515 kN. ​The failure probability Pf ​=0.000483477 is evaluated by numerical integration of the Gaussian probability density function of Z from negative infinity to zero. According to EN1990 [15], a structure designed with this failure probability is classified in reliability class RC1 for reference periods of 1 and 50 years.
The aim of the case study is to compare the accuracy of Pf estimation according to the basic definition in Equation (4) and the alternative formula in Equation (9). The procedure is as follows: In the first step, the random variables R and F are simulated for 10,000 runs using the Monte Carlo (MC) method. The estimation of Pf from Equation (4) is plotted in Figure 6 as the first blue point from the left. The estimation of Pf from Equation (9) is plotted in Figure 7 as the first blue point from the left. Next, another 10,000 runs of MC are generated, and the procedure is repeated. In total, 100 estimates of Pf according to Equation (4) are plotted in the left quarter of Figure 6, and 100 estimates of Pf according to Equation (9) are plotted in the left quarter of Figure 7. This procedure is further repeated for 100,000, 1 million, and 10 million runs of the Monte Carlo (MC) method, as shown in the subsequent quarters in Figure 6 and Figure 7.
The numerical study revealed that the failure probability Pf estimation using Cliff's Delta δC, see Equation (9), is more accurate compared to the basic definition, see Equation (4). As illustrated in Figure 6 and Figure 7, the alternative method resulted in noticeably lower standard deviations σPf (approximately three times smaller) across varying Monte Carlo run counts, indicating improved consistency and precision. In contrast, the basic definition exhibited higher variability, especially with fewer Monte Carlo runs. These findings underscore the efficacy of the alternative formula for more reliable Pf estimation in structural reliability assessments.

6. Discussion

In civil engineering, estimating the resistance R using nonlinear FEM calculations is very time-consuming, and studies are limited by the number of computationally expensive Monte Carlo or LHS method runs required to accurately simulate real structural behavior, see e.g., [60,61,62,63]. In recent years, the role of mathematical models that offer quick analytical solutions has become increasingly significant due to their efficiency in providing rapid responses [64,65]. For each model, it is useful to utilize all realized simulations to estimate failure probability as efficiently as possible.
Equation (9) offers an efficient alternative for estimating Pf with high utilization of information from the realized runs of the computational model. Although estimating Cliff's Delta is more numerically demand than direct estimation of failure probability using Equation (4), the same number of model runs (the same number of random realizations of R and F) ensures a more accurate estimation of failure probability Pf, see Figure 6 compared to Figure 7. These advantages highlight the utility of Cliff's Delta in both reliability and sensitivity analysis, making it an innovative tool for engineers and researchers to gain deeper insights into the reliability and performance of structural systems.
The computational complexity of estimating Cliff's Delta can be effectively reduced by optimizing computer algorithms. The following function formulates the algorithm for calculating Cliff's Delta using ten thousand random realizations of R and F in arrays AR and AF. In the Delphi programming language, the function to calculate Cliff's Delta can be written as follows:
`pascal
const max=10000;
var
 AR,AF: array[1..max] of Single;
 AB : array[1..max] of Boolean;
Function Cliffd:extended;
var i1,i2 :integer;
  Dominant, Dominated : Int64;
begin
 Dominant:=0;
 Dominated:=0;
 for i1:=1 to max do
 begin
 if AB[i1] then Dominant:=Dominant+max
    else
 for i2:=1 to max do
 begin
  if (AR[i2]>AF[i1]) then Inc(Dominant) else
  if (AR[i2]<AF[i1]) then Inc(Dominated);
  end;
 end;
 Cliffd:=(Dominant-Dominated)/(max*max);
end;
`
Before calling the function, the array AB is populated with random realizations for which the inner loop runs are unnecessary.
`pascal
for i1 := 1 to max do if AF[i1] < 5.49836 then AB[i1] := true else AB[i1] := false;
`
The constant 5.49836 is the smallest value of the random variable R generated by the Monte Carlo method. If a random realization of F is less than 5.49836, then all random realizations of R are less than 5.49836, and the inner loop does not need to be executed; it is sufficient to assign Dominant:=Dominant+max. In the case study, using max=10000, the estimation of Cliff's Delta was accelerated by approximately two times.
The algorithm efficiently reduces the double-loop computational burden especially for Cliff's Delta estimates close to one (very small Pf values), where the vast majority of random realizations of R are much higher than F. According to the EN1990 [15] standard, common building structures are designed with a Pf around 7.2 ·10-5. For estimating the standard error of the Pf ​using Equation (25), one needs to perform 1,388,889 Monte Carlo simulation runs to achieve a coefficient of variation of 0.1. This results in a standard error of SE1=7.2⋅10−6. In practice, this requires conducting Monte Carlo runs until 100 failure events are observed, i.e., 100 runs where Z < 0. Subsequently, using Equation (9) instead of Equation (4) will improve the accuracy of the Pf estimate.
Conducting sensitivity analysis based on Cliff's Delta offers functionalities that are identical to sensitivity analysis based on failure probability focused on reliability. Cliff's Delta provides a robust measure for evaluating the extent to which one distribution dominates another without making specific assumptions about the distributions' form or variability. This flexibility is particularly valuable in reliability studies where input variables may not follow normal distributions or exhibit significant variability. By focusing on the frequency with which resistance values exceed load values, Cliff's Delta directly aligns with the fundamental concepts of reliability engineering. The ability to estimate failure probabilities using Cliff's Delta enhances the robustness of reliability and sensitivity analysis, especially in cases where performing additional resistance or load simulations is numerically difficult or impossible.

7. Conclusions

In this article, an alternative measure of structural reliability based on Cliff's Delta has been adopted to ensure more accurate estimation of failure probability Pf with the available number of simulations. Using Cliff's Delta increases the accuracy of the Pf estimate by making better use of the statistical information from the data. This approach replaces the traditional failure probability calculations and provides enhanced flexibility and robustness in applications of structural reliability.
The adaptation of Cliff's Delta, initially developed for ordinal data, has been successfully applied to evaluate the sensitivity of structural reliability. This adaptation allows for the evaluation of the dominance of resistance over load without specific distributional assumptions, making it particularly suitable for structural reliability analysis. The mathematical formulations for computing Cliff's Delta between resistance R and load action F have been presented. This formulation effectively quantifies the reliability of a structure by evaluating the probability that resistance exceeds load.
Sensitivity indices based on the squared value of Cliff's Delta δ C 2 have been derived, demonstrating properties analogous to those used in Sobol's sensitivity analysis. This includes first-order, second-order, and higher-order sensitivity indices, which offer a comprehensive framework for evaluating the contributions of individual variables and their interactions to the overall reliability of the system. These indices provide a nuanced understanding of the factors influencing structural reliability.
The application of Cliff's Delta in reliability-oriented sensitivity analysis allows for a more computationally efficient evaluation of structural reliability. This is particularly beneficial in engineering applications where finite element method (FEM) calculations and repeated simulations of R or F are computationally expensive.
While the current study provides a foundation, future work could focus on optimizing the computational algorithms for estimating Cliff's Delta, particularly for global sensitivity analysis of reliability.

Funding

The work has been supported and prepared within the project “Metamodel-assisted probabilistic assessment in bridge structural engineering (MAPAB)” of The Czech Science Foundation (GACR, https://gacr.cz/) no. 22-00774S, Czechia.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

Not applicable

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Wei, P.; Lu, Z.; Song, J. Variable importance analysis: a comprehensive review. Reliab. Eng. Syst. Saf. 2015, 142, 399–432. [Google Scholar] [CrossRef]
  2. Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
  3. Liu, X.; Wei, P.; Rashki, M.; Fu, J. A probabilistic simulation method for sensitivity analysis of input epistemic uncertainties on failure probability. Struct Multidiscipl Optim 2024, 67, 3. [Google Scholar] [CrossRef]
  4. Liu, J.; Liu, H.; Zhang, C.; Cao, J.; Xu, A.; Hu, J. Derivative-variance hybrid global sensitivity measure with optimal sampling method selection. Mathematics 2024, 12, 396. [Google Scholar] [CrossRef]
  5. Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
  6. Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: West Sussex, UK, 2008. [Google Scholar]
  7. Sobol, I.M. Sensitivity estimates for non-linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
  8. Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
  9. Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
  10. Xu, J.; Hao, L.; Mao, J.-F.; Yu, Z.-W. Simultaneous reliability and reliability-sensitivity analyses based on the information-reuse of sparse grid numerical integration. Struct Multidiscipl Optim 2023, 66, 7. [Google Scholar] [CrossRef]
  11. Zhao, Y.; Li, X.; Cogan, S.; Zhao, J.; Yang, J.; Yang, D.; Shang, J.; Sun, B.; Yang, L. Interval parameter sensitivity analysis based on interval perturbation propagation and interval similarity operator. Struct Multidiscipl Optim 2023, 66, 179. [Google Scholar] [CrossRef]
  12. Li, H.; Chen, H.; Zhang, J.; Chen, G.; Yang, D. Direct probability integral method for reliability sensitivity analysis and optimal design of structures. Struct Multidiscipl Optim 2023, 66, 200. [Google Scholar] [CrossRef]
  13. Parreira, T.G.; Rodrigues, D.C.; Oliveira, M.C.; Sakharova, N.A.; Prates, P.A.; Pereira, A.F.G. Sensitivity analysis of the square cup forming process using PAWN and Sobol indices. Metals 2024, 14, 432. [Google Scholar] [CrossRef]
  14. Wang, H.; Zhao, Y.; Fu, W. Utilizing the Sobol’ sensitivity analysis method to address the multi-objective operation model of reservoirs. Water 2023, 15, 3795. [Google Scholar] [CrossRef]
  15. European Committee for Standardization. EN 1990:2002: Eurocode—Basis of Structural Design; European Committee for Standardization: Brussels, Belgium, 2002. [Google Scholar]
  16. Li, L.Y.; Lu, Z.Z.; Feng, J.; Wang, B.T. Moment-independent importance measure of basic variable and its state dependent parameter solution. Struct. Saf. 2012, 38, 40–47. [Google Scholar] [CrossRef]
  17. Wei, P.; Lu, Z.; Hao, W.; Feng, J.; Wang, B. Efficient sampling methods for global reliability sensitivity analysis. Comput. Phys. Commun. 2012, 183, 1728–1743. [Google Scholar] [CrossRef]
  18. Fort, J.C.; Klein, T.; Rachdi, N. New sensitivity analysis subordinated to a contrast. Commun. Stat. Theory Methods 2016, 45, 4349–4364. [Google Scholar] [CrossRef]
  19. Kala, Z. Sensitivity analysis in probabilistic structural design: A comparison of selected techniques. Sustainability 2020, 12, 4788. [Google Scholar] [CrossRef]
  20. Kala, Z. Global sensitivity analysis of quantiles: New importance measure based on superquantiles and subquantiles. Symmetry 2021, 13, 263. [Google Scholar] [CrossRef]
  21. Kala, Z. New importance measures based on failure probability in global sensitivity analysis of reliability. Mathematics 2021, 9, 2425. [Google Scholar] [CrossRef]
  22. Zhang, J. Modern Monte Carlo methods for efficient uncertainty quantification and propagation: A survey. Wiley Interdiscip Rev Comput Stat 2021, 13, e1539. [Google Scholar] [CrossRef]
  23. Kaveh, A. Computational Structural Analysis and Finite Element Methods; Springer International Publishing: Cham, 2014. [Google Scholar]
  24. Kala, Z.; Valeš, J. Sensitivity assessment and lateral-torsional buckling design of I-beams using solid finite elements. J. Constr. Steel. Res. 2017, 139, 110–122. [Google Scholar] [CrossRef]
  25. Jindra, D.; Kala, Z.; Kala, J. Probabilistically modelled geometrical imperfections for reliability analysis of vertically loaded steel frames. J. Constr. Steel. Res. 2024, 217, 108627. [Google Scholar] [CrossRef]
  26. Thaler, D.; Elezaj, L.; Bamer, F.; Markert, B. Training data selection for machine learning-enhanced Monte Carlo simulations in structural dynamics. Appl. Sci. 2022, 12, 581. [Google Scholar] [CrossRef]
  27. Zhang, J.; Wang, B.; Ma, H.; Li, Y.; Yang, M.; Wang, H.; Ma, F. A Fast reliability evaluation strategy for power systems under high proportional renewable energy—A hybrid data-driven method. Processes 2024, 12, 608. [Google Scholar] [CrossRef]
  28. Zhang, P.; Zhang, S.; Liu, X.; Qiu, L.; Yi, G. A Least squares ensemble model based on regularization and augmentation strategy. Appl. Sci. 2019, 9, 1845. [Google Scholar] [CrossRef]
  29. Dadras Eslamlou, A.; Huang, S. Artificial-neural-network-based surrogate models for structural health monitoring of civil structures: A literature review. Buildings 2022, 12, 2067. [Google Scholar] [CrossRef]
  30. Ren, W.X.; Chen, H.B. Finite element model updating in structural dynamics by using the response surface method. Eng. Struct. 2010, 32, 2455–2465. [Google Scholar] [CrossRef]
  31. Nima, P.; Tang, X.W.; Yang, Q. Energy evaluation of triggering soil liquefaction based on the response surface method. Appl. Sci. 2019, 9, 694. [Google Scholar] [CrossRef]
  32. Aruna, A.; Ganguli, R. Multi-fidelity response surfaces for uncertainty quantification in beams using coarse and fine finite element discretizations. International Journal for Computational Methods in Engineering Science and Mechanics 2020, 22, 103–122. [Google Scholar] [CrossRef]
  33. Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
  34. Novák, L.; Zhang, S.; Liu, X. Physics-informed polynomial chaos expansions. J. Comput. Phys. 2024, 506, 112926. [Google Scholar] [CrossRef]
  35. Marrel, A.; Iooss, B. Probabilistic surrogate modeling by Gaussian process: A review on recent insights in estimation and validation. Reliab. Eng. Syst. Saf. 2024, 247, 110094. [Google Scholar] [CrossRef]
  36. Cong, H.; Wang, B.; Wang, Z. A novel Gaussian process surrogate model with expected prediction error for optimization under constraints. Mathematics 2024, 12, 1115. [Google Scholar] [CrossRef]
  37. Song, Z.; Liu, Z.; Zhang, H.; Zhu, P. An improved sufficient dimension reduction-based Kriging modeling method for high-dimensional evaluation-expensive problems. Comput Methods Appl Mech Eng 2024, 418, 116544. [Google Scholar] [CrossRef]
  38. E, S.; Wang, Y.; Xie, B.; Lu, F. An adaptive Kriging-based fourth-moment reliability analysis method for engineering structures. Appl. Sci. 2024, 14, 3247. [Google Scholar] [CrossRef]
  39. Sun, G.; Kang, J.; Shi, J. Application of machine learning models and GSA method for designing stud connectors. J. Civ. Eng. Manag. 2024, 30, 373–390. [Google Scholar] [CrossRef]
  40. Pan, L.; Novák, L.; Lehký, D.; Novák, D.; Cao, M. Neural network ensemble-based sensitivity analysis in structural engineering: Comparison of selected methods and the influence of statistical correlation. Comput Struct 2021, 242, 106376. [Google Scholar] [CrossRef]
  41. Hein, H.; Jaanuska, L. Stiffness parameter prediction for elastic supports of non-uniform rods. Acta Comment. Univ. Tartu. Math. 2024, 28, 119–130. [Google Scholar]
  42. Yeh, I.C.; Cheng, W.-L. First and second order sensitivity analysis of MLP. Neurocomputing 2010, 73, 2225–2233. [Google Scholar] [CrossRef]
  43. Tsokanas, N.; Pastorino, R.; Stojadinović, B. A Comparison of surrogate modeling techniques for global sensitivity analysis in hybrid simulation. Mach. Learn. Knowl. Extr. 2022, 4, 1–21. [Google Scholar] [CrossRef]
  44. Lucay, F.A. Accelerating global sensitivity analysis via supervised machine learning tools: Case studies for mineral processing models. Minerals 2022, 12, 750. [Google Scholar] [CrossRef]
  45. Dubourg, V.; Sudret, B. Meta-model-based importance sampling for reliability sensitivity analysis. Struct. Saf. 2014, 49, 27–36. [Google Scholar] [CrossRef]
  46. Sudret, B.; Mai, C.V. Computing the derivative-based global sensitivity measures using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2015, 134, 241–250. [Google Scholar] [CrossRef]
  47. Robens-Radermacher, A.; Unger, J.F. Efficient structural reliability analysis by using a PGD model in an adaptive importance sampling schema. Adv. Model. Simul. Eng. Sci. 2020, 7, 29. [Google Scholar] [CrossRef]
  48. Li, M.; Feng, Y.; Wang, G. Estimating failure probability with neural operator hybrid approach. Mathematics 2023, 11, 2762. [Google Scholar] [CrossRef]
  49. Cliff, N. Dominance statistics: Ordinal analyses to answer ordinal questions. Psychological Bulletin 1993, 114, 494–509. [Google Scholar] [CrossRef]
  50. Ajibode, A.; Shu, T.; Gulsher, L.; Ding, Z. Effectively combining risk evaluation metrics for precise fault localization. Mathematics 2022, 10, 3924. [Google Scholar] [CrossRef]
  51. Ge, X.; Fang, C.; Bai, T.; Liu, J.; Zhao, Z. An empirical study of class rebalancing methods for actionable warning identification. IEEE Transactions on Reliability 2023, 72, 1648–1662. [Google Scholar] [CrossRef]
  52. Pushkar, S. Strategies for LEED-NC-certified projects in Germany and results of their life cycle assessment. Buildings 2023, 13, 1970. [Google Scholar] [CrossRef]
  53. Samal, S.; Zhang, Y.-D.; Gadekallu, T.R.; Nayak, R.; Balabantaray, B.K. SBMYv3: Improved MobYOLOv3 a BAM attention-based approach for obscene image and video detection. Expert Systems 2023, 40, e13230. [Google Scholar] [CrossRef]
  54. Tak, A.Y.; Ercan, I. Ensemble of effect size methods based on meta fuzzy functions. Eng Appl Artif Intell 2023, 119, 105804. [Google Scholar] [CrossRef]
  55. Kala, Z. Estimating probability of fatigue failure of steel structures. Acta Comment. Univ. Tartu. Math. 2019, 23, 245–254. [Google Scholar] [CrossRef]
  56. Kala, Z. Global sensitivity analysis of reliability of structural bridge system. Eng. Struct. 2019, 194, 36–45. [Google Scholar] [CrossRef]
  57. McKey, M.D.; Beckman, R.J.; Conover, W.J. A comparison of the three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
  58. Iman, R.C.; Conover, W.J. Small sample sensitivity analysis techniques for computer models with an application to risk assessment. Commun. Stat. Theory Methods 1980, 9, 1749–1842. [Google Scholar] [CrossRef]
  59. Kala, Z. From probabilistic to quantile-oriented sensitivity analysis: New indices of design quantiles. Symmetry 2020, 12, 1720. [Google Scholar] [CrossRef]
  60. Arrayago, I.; Rasmussen, K.J.R. Reliability of stainless steel frames designed using the Direct Design Method in serviceability limit states. J. Constr. Steel. Res. 2022, 196, 107425. [Google Scholar] [CrossRef]
  61. Liu, W.; Rasmussen, K.J.R.; Zhang, H.; Xie, Y.; Liu, Q.; Dai, L. Probabilistic study and numerical modelling of initial geometric imperfections for 3D steel frames in advanced structural analysis. Structures 2023, 57, 105190. [Google Scholar] [CrossRef]
  62. Gocál, J.; Vičan, J.; Odrobiňák, J.; Hlinka, R.; Bahleda, F.; Wdowiak-Postulak, A. Experimental and numerical analyses of timber–steel footbridges. Appl. Sci. 2024, 14, 3070. [Google Scholar] [CrossRef]
  63. Ferreira Filho, J.O.; da Silva, L.S.; Tankova, T.; Carvalho, H. Influence of geometrical imperfections and residual stresses on the reliability of high strength steel welded I-section columns using Monte Carlo simulation. J. Constr. Steel. Res. 2024, 215, 108548. [Google Scholar] [CrossRef]
  64. Botean, A.I. The use of trigonometric series for the study of isotropic beam deflection. Mathematics 2023, 11, 1426. [Google Scholar] [CrossRef]
  65. Mürk, A.; Lellep, J. Asymmetric dynamic plastic response of stepped plates. Acta Comment. Univ. Tartu. Math. 2024, 28, 19–28. [Google Scholar] [CrossRef]
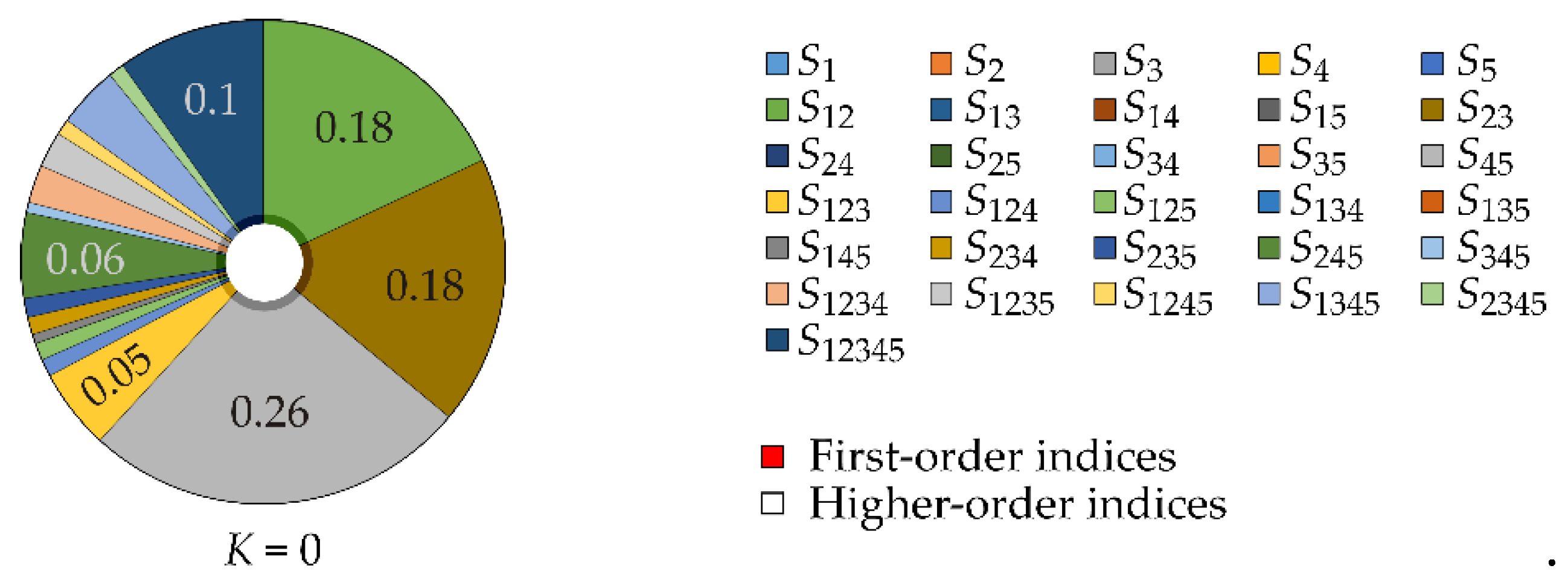
Preprints 108817 g001
Figure 1. Cliff's Delta sensitivity indices for K=0.
Figure 1. Cliff's Delta sensitivity indices for K=0.
Preprints 108817 g001
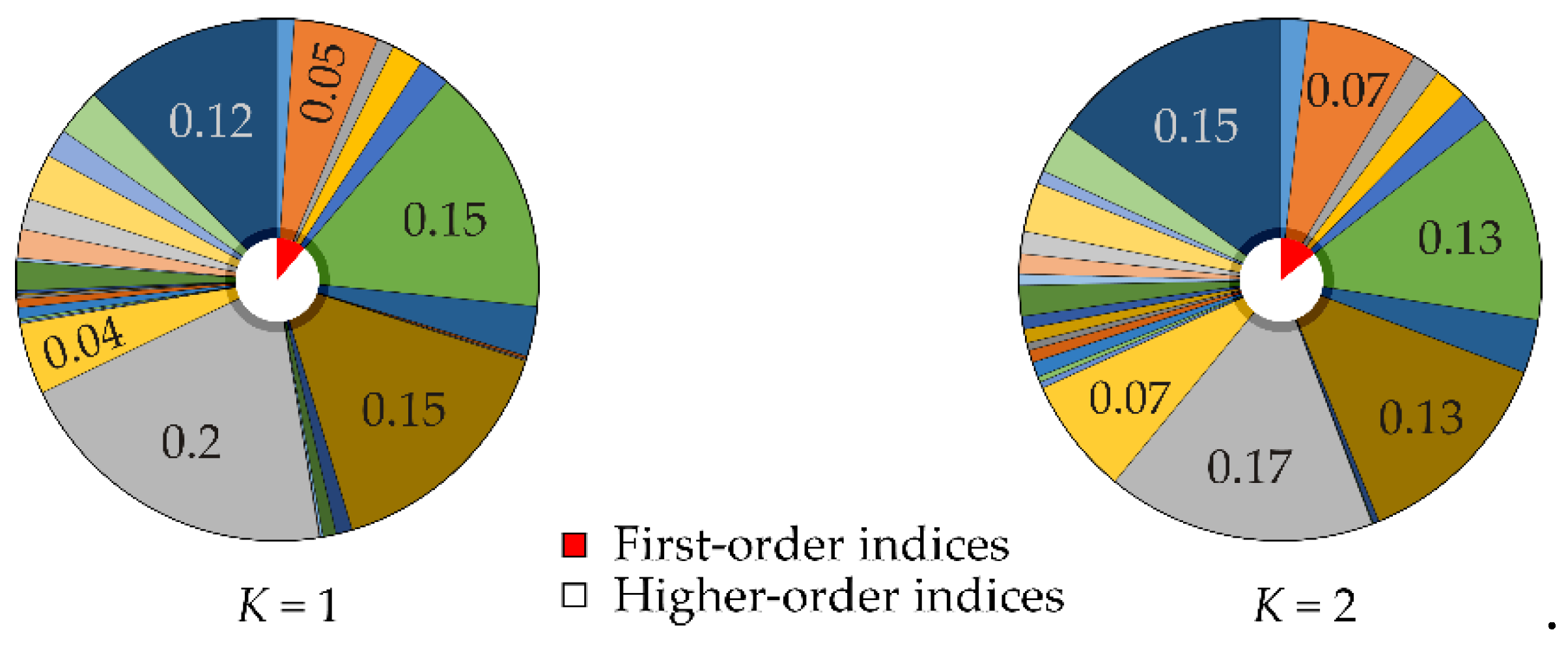
Preprints 108817 g002
Figure 2. Cliff's Delta sensitivity indices for K=0 and K=0.
Figure 2. Cliff's Delta sensitivity indices for K=0 and K=0.
Preprints 108817 g002
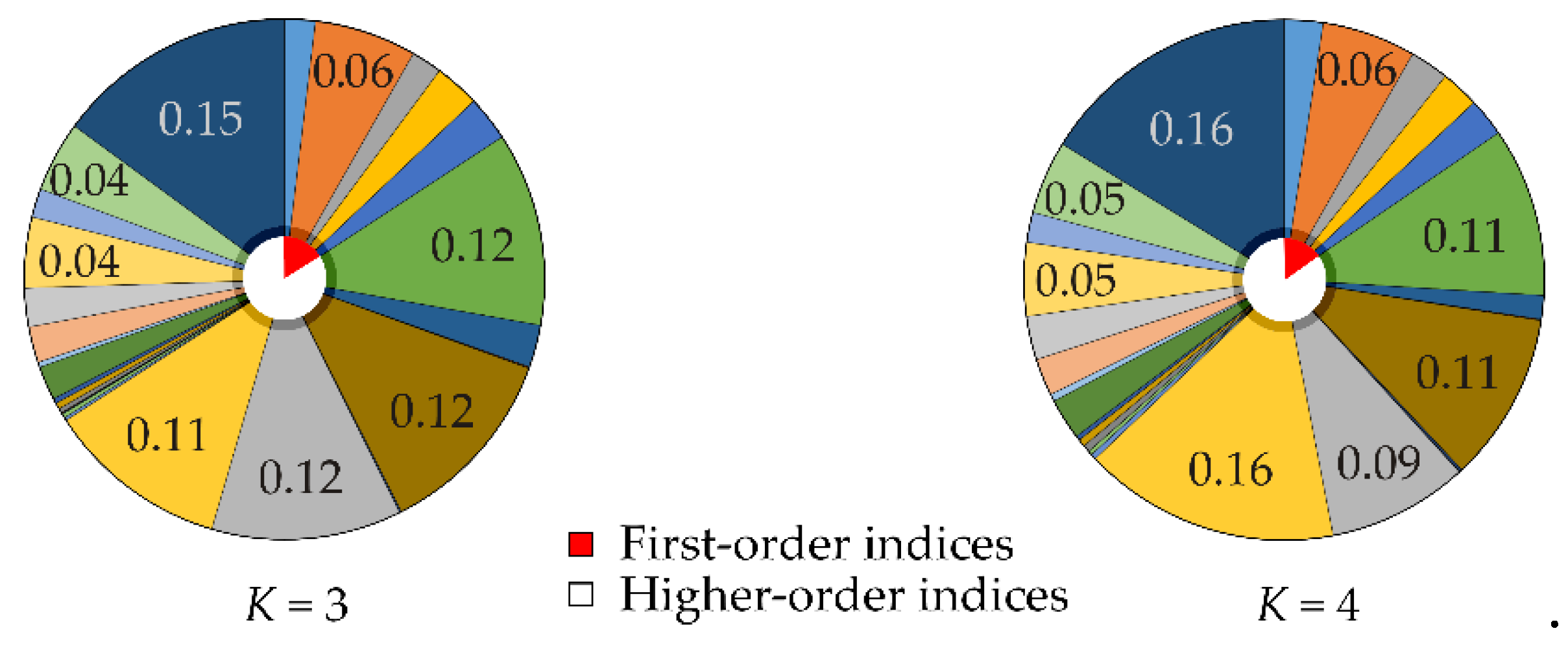
Preprints 108817 g003
Figure 3. Cliff's Delta sensitivity indices for K=3 and K=4.
Figure 3. Cliff's Delta sensitivity indices for K=3 and K=4.
Preprints 108817 g003
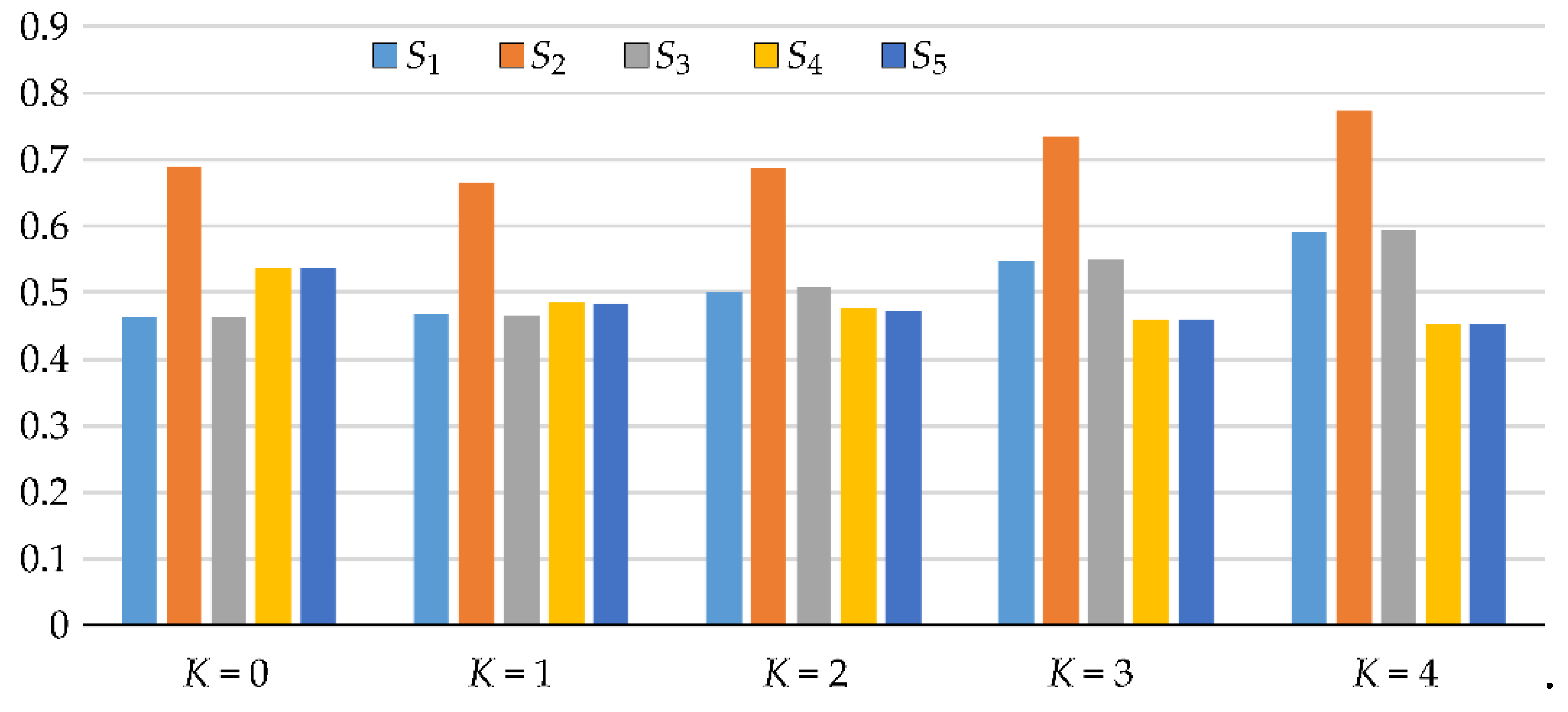
Preprints 108817 g004
Figure 4. Cliff's Delta total sensitivity indices for all K.
Figure 4. Cliff's Delta total sensitivity indices for all K.
Preprints 108817 g004
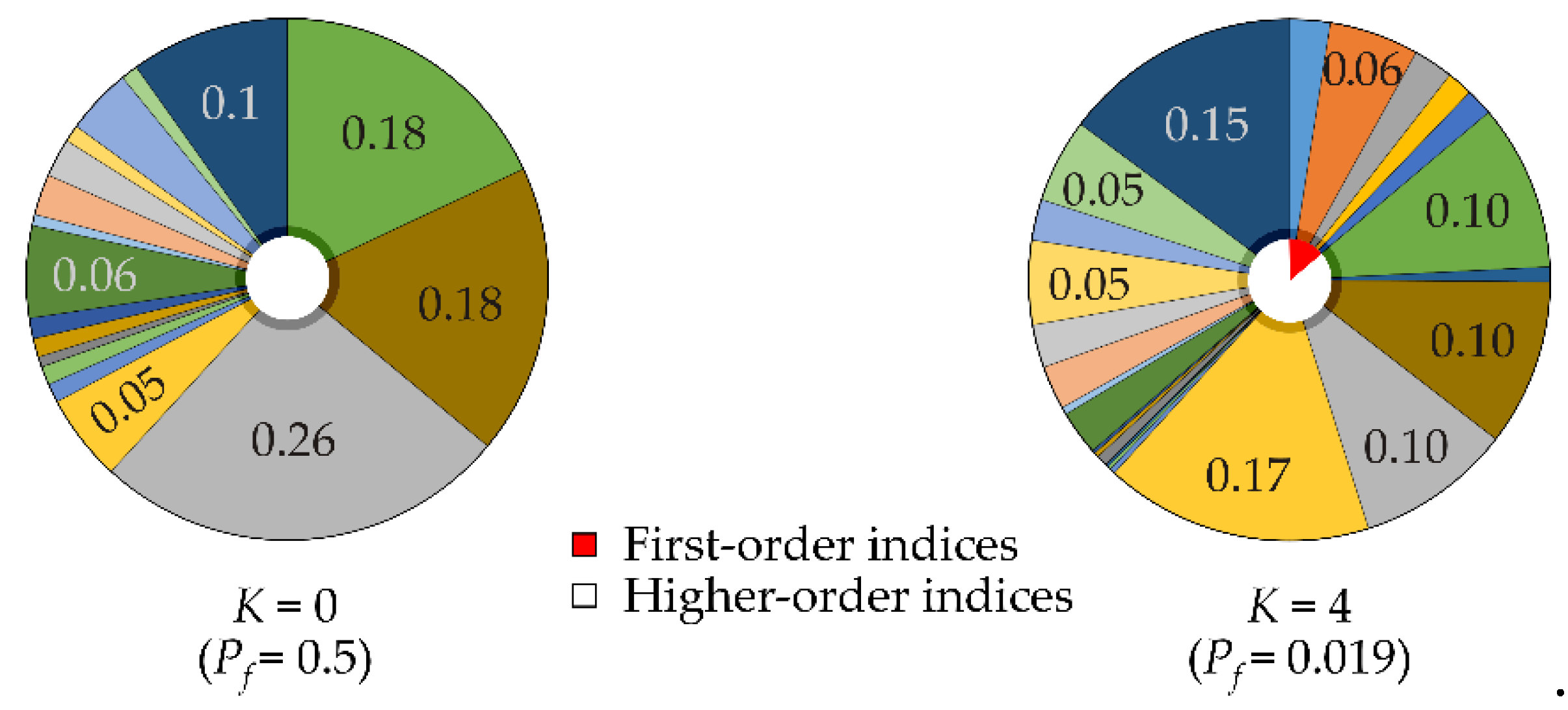
Preprints 108817 g005
Figure 5. The results of sensitivity analysis based on failure probability from Equation (21).
Figure 5. The results of sensitivity analysis based on failure probability from Equation (21).
Preprints 108817 g005
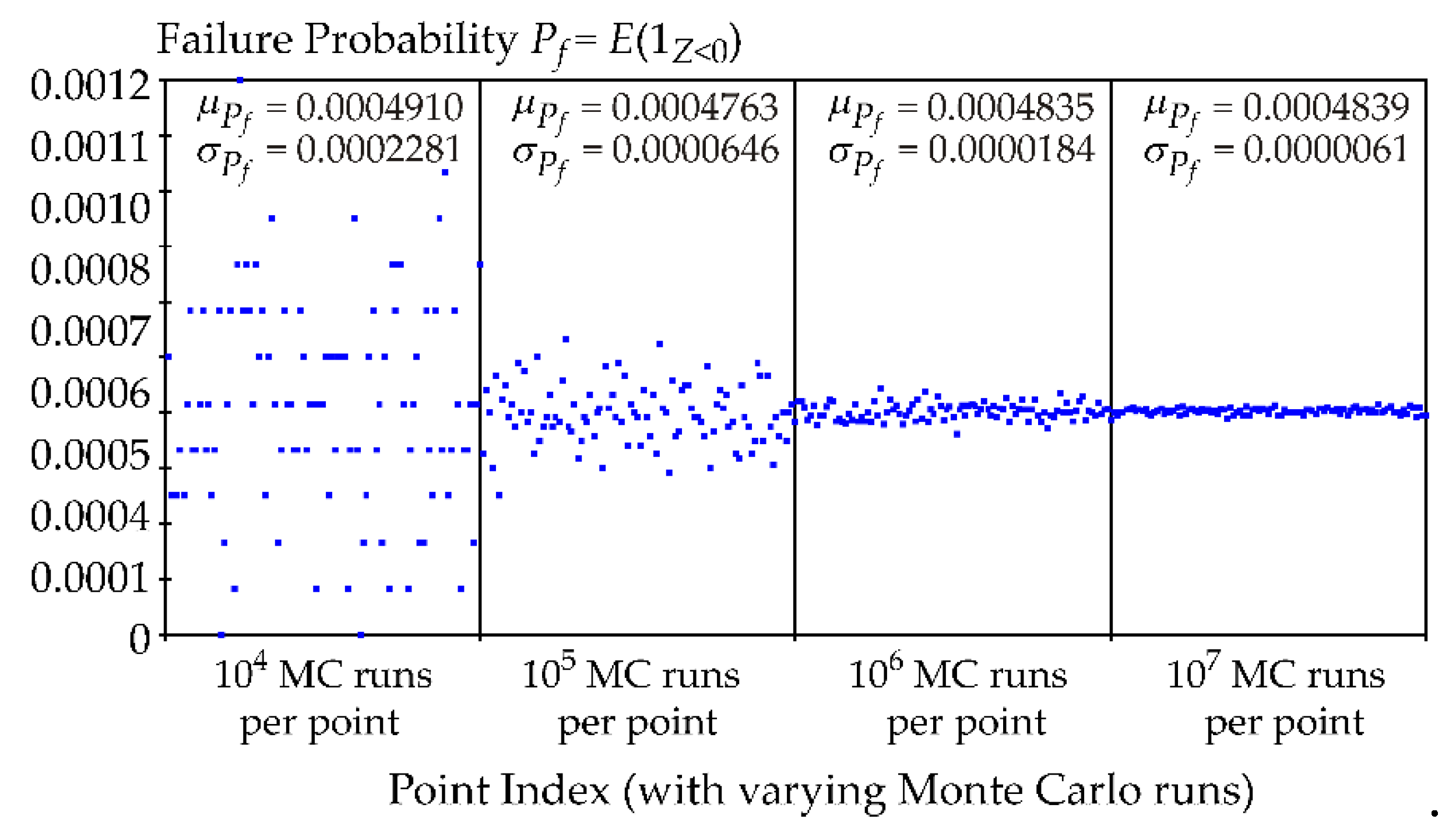
Preprints 108817 g006
Figure 6. Convergence of Pf estimation using basic definition with varying MC run counts.
Figure 6. Convergence of Pf estimation using basic definition with varying MC run counts.
Preprints 108817 g006
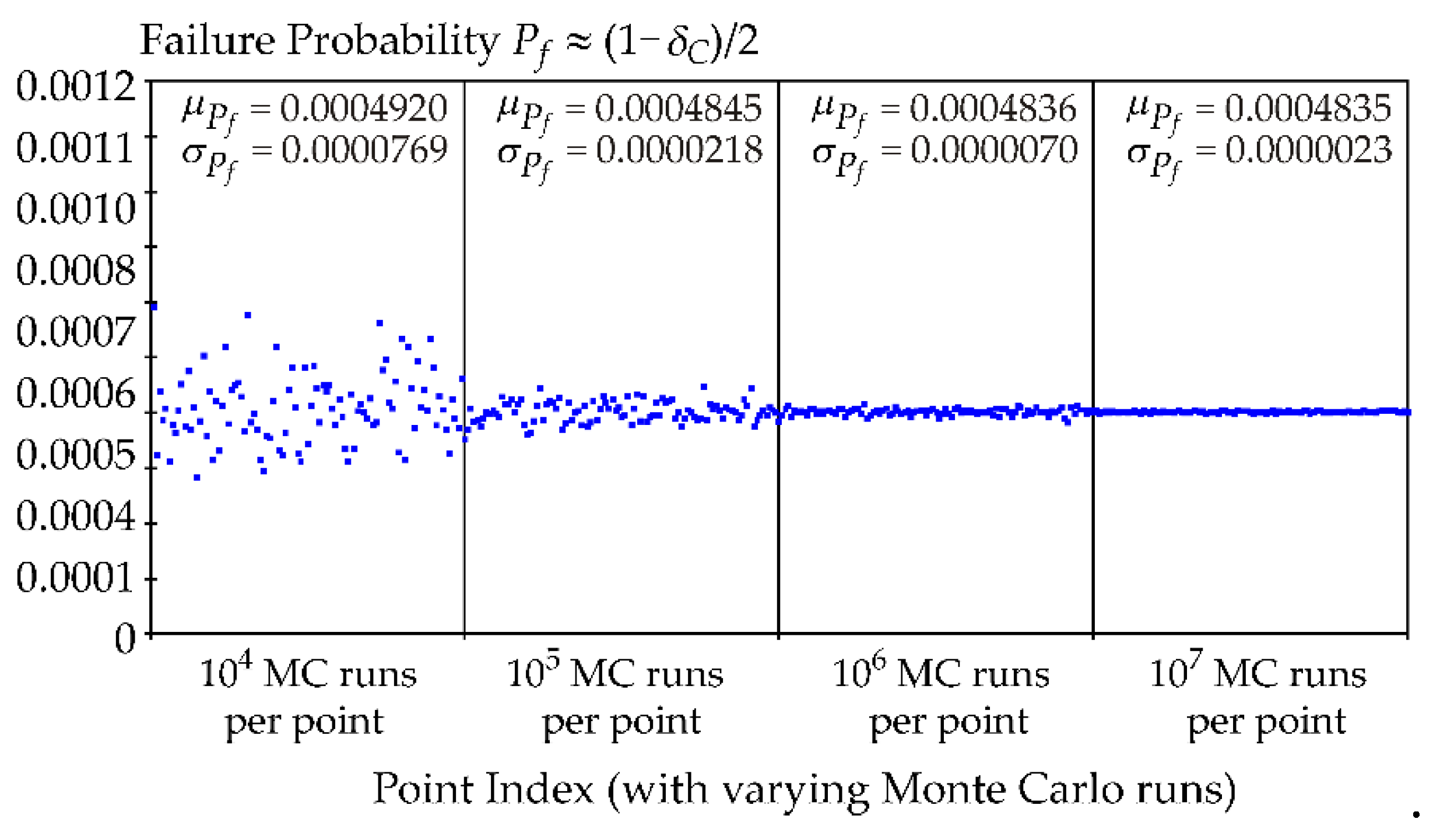
Preprints 108817 g007
Figure 7. Convergence of Pf estimation using Cliff's Delta with varying MC run counts.
Figure 7. Convergence of Pf estimation using Cliff's Delta with varying MC run counts.
Preprints 108817 g007
Table 1. Average values of δ C 2 for sequentially fixed input variables.
Table 1. Average values of δ C 2 for sequentially fixed input variables.
Conditional   Mean   of   δ C 2 K=0 K=1 K=2 K=3 K=4
C = δ C 2 0 0.3150 0.6504 0.8323 0.9221
E ( δ C 2 |X1) 0 0.3223 0.6556 0.8355 0.9240
E ( δ C 2 |X2) 0 0.3508 0.6745 0.8430 0.9266
E ( δ C 2 |X3) 0 0.3223 0.6556 0.8355 0.9240
E ( δ C 2 |X4) 0 0.3284 0.6576 0.8371 0.9239
E ( δ C 2 |X5) 0 0.3284 0.6576 0.8371 0.9239
E ( δ C 2 |X1, X2) 0.1803 0.4633 0.7270 0.8664 0.9367
E ( δ C 2 |X1, X3) 0 0.3509 0.6746 0.8432 0.9267
E ( δ C 2 |X1, X4) 0 0.3362 0.6628 0.8413 0.9265
E ( δ C 2 |X1, X5) 0 0.3362 0.6628 0.8413 0.9265
E ( δ C 2 |X2, X3) 0.1803 0.4633 0.7270 0.8664 0.9367
E ( δ C 2 |X2, X4) 0 0.3704 0.6825 0.8478 0.9286
E ( δ C 2 |X2, X5) 0 0.3704 0.6825 0.8478 0.9286
E ( δ C 2 |X3, X4) 0 0.3370 0.6628 0.8392 0.9252
E ( δ C 2 |X3, X5) 0 0.3370 0.6628 0.8392 0.9252
E ( δ C 2 |X4, X5) 0.2581 0.4820 0.7238 0.8616 0.9326
E ( δ C 2 |X1, X2, X3) 0.4145 0.6274 0.8169 0.9133 0.9604
E ( δ C 2 |X1, X2, X4) 0.1918 0.4852 0.7357 0.8713 0.9385
E ( δ C 2 |X1, X2, X5) 0.1918 0.4852 0.7357 0.8713 0.9385
E ( δ C 2 |X1, X3, X4) 0 0.3702 0.6827 0.8481 0.9287
E ( δ C 2 |X1, X3, X5) 0 0.3702 0.6827 0.8481 0.9287
E ( δ C 2 |X1, X4, X5) 0.2644 0.4923 0.7303 0.8664 0.9356
E ( δ C 2 |X2, X3, X4) 0.1925 0.4844 0.7363 0.8722 0.9395
E ( δ C 2 |X2, X3, X5) 0.1925 0.4844 0.7363 0.8722 0.9395
E ( δ C 2 |X2, X4, X5) 0.3151 0.5425 0.7561 0.8760 0.9393
E ( δ C 2 |X3, X4, X5) 0.2649 0.4928 0.7298 0.8644 0.9343
E ( δ C 2 |X1, X2, X3, X4) 0.4630 0.6677 0.8346 0.9231 0.9648
E ( δ C 2 |X1, X2, X3, X5) 0.4630 0.6677 0.8346 0.9231 0.9648
E ( δ C 2 |X1, X2, X4, X5) 0.5361 0.6802 0.8236 0.9083 0.9539
E ( δ C 2 |X1, X3, X4, X5) 0.3123 0.5449 0.7569 0.8768 0.9397
E ( δ C 2 |X2, X3, X4, X5) 0.5361 0.6802 0.8236 0.9083 0.9539
E ( δ C 2 | X1, X2, X3, X4, X5) 1 1 1 1 1
1 Table 1 presents the average values of δ C 2 for various fixed input variables, computed using the LHS method with n=12,000 runs. The conditional values of δ C 2 are estimated using a double-nested-loop computation.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated