2.1. Application of the Developed Tool to Design a Reference Propulsion System
In order to focus on the tool’s functionality, the RPS contains a common rotor-stator stage. However, the functionality of the design of various sub-components like the composite-blades, the disk, the adjustable nozzle, or the -printed standard inlet should be verified within the RPS to enable their similar application within the future innovative propulsion system (IPS), having a contra-rotating stage. Besides, this reduces the complexity of the validation process of this initial step as the total pressure distribution has to be measured and compared at a single engine stage only compared to the two positions after each rotors of the IPS later.
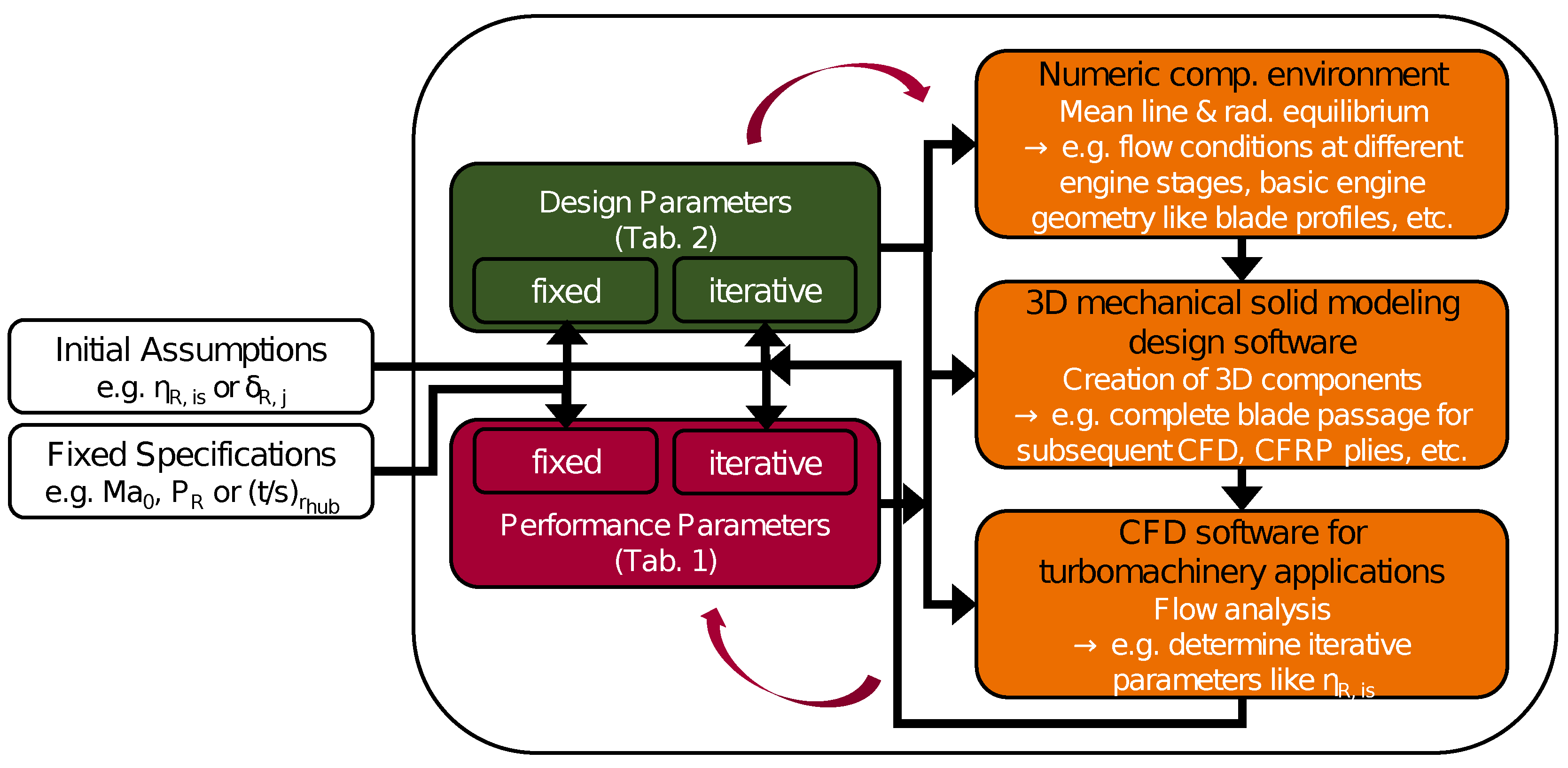
In principle, the automated tool chain, shown in
Figure 1, is based on an iterative,
CFD-based calculation of initially unknown parameters like the rotor’s isentropic compressor efficiency or total pressure losses over inlet, stator and nozzle.
The inputs into the tool can be split up into the two categories
performance and
design parameters. Due to the tool’s iterative character both categories contain not only fixed parameters but also values that require initial assumptions at the beginning, replaced by
CFD results for later iterations. The main entries of the first category and their chosen values for the
RPS design are summarized in
Table 1 and discussed in the following.
The actual calculation part of the tool chain mainly consists of three parts, indicated by the individual orange boxes on the right hand side of
Figure 1. Within a numeric computing environment the first step is to determine the general design of the various components like the blades, standard inlet, casing, or nozzle. By a mean line approach the values of (total) pressure
and (total) temperature
are calculated from the
performance parameters, among others from the total pressure ratios
. They relate the total pressure conditions before and after a certain component. For instance, the fixed total pressure ratio over the rotor
specifies the ratio of the total pressure
at the rotor’s outlet to its value at the inlet, indicated by the subscripts
and
, respectively, as follows:
The total pressure losses over inlet, stator and nozzle, given by the respective total pressure ratios
,
and
and defined similar to that of the rotor, enable the determination of the total pressure at all engine stages. However, as indicated in
Table 1 they have to be determined iteratively by the
CFD later in contrast to the fixed value of
. The flight Mach number,
, results from the planned tool validation by a static engine operation within the test bed set up at the institute. Together with an altitude specification, the inlet total pressure
and temperature
as well as the static outlet pressure
are set, based on the
International Standard Atmosphere [
23]. By the assumption of an adiabatic inlet, stator and nozzle and by incorporating the isentropic efficiency
the total temperature at all stages can be determined, too. The difference in total temperature over the rotor is used, in terms, to determine the required specific work for the specified total pressure ratio. Together with the available motor’s shaft power
and further specifications like axial flow Mach numbers at different stages or hub radii this allows the calculation of the engine’s mass flow and general radii. Afterwards,
Euler’s turbine equation is utilized to calculate the required flow deflection from the determined specific work and rotation speed input
. Finally, a radial equilibrium is implemented to calculate the flow angles not only at the mean line radius but also at all other radial positions.
The value of chosen for the total pressure ratio facilitates a comparability to current developments of electric, ducted propulsion systems. In contrast to fans of state-of-the-art aircraft engines, reaching values up to , it appears to be relatively low. However, this enables, in terms, relatively low rotation speeds without avoiding undercutting recommendations like a DeHaller number across the entire span. Subsequently, the strength requirements regarding the blades are relatively low in the first place for the RPS to gain experience for scaling it later within the IPS. The stage inflow Mach number at the engine’s mean line had to be found as a trade off between the mutually from this Mach number dependent number and radial blade length. The minimal number of occurs at the hub, increasing to at the mean line and at the shroud, based on the mentioned radial equilibrium approach and the chosen free vortex design principle. Due to the low Mach numbers set inside the engine and the low total pressure ratio a high isentropic efficiency and small total pressure losses within inlet, stator and nozzle could be found iteratively. The range of the motor’s shaft power was chosen with regard to the maximum output power of the installed power supply within the test bed of . Besides, it includes margins for testing at speeds larger than design point speed and the estimated losses within the motor and its electronic speed controller (ESC).
Whereas the
performance parameters rather describe the actual engine cycle, based on the flight mission and deployment scenario, the group of
design parameters contains specifications that finalize the engine’s design within the first part of the design tool, affecting the engines performance. The most important parameters of this category are summarized in
Table 2.
In contrast to the iterative
performance parameters, representing global specifications, the iterative
design parameter deviation angle
must be specified for the three radial positions
j meanline (
), hub and shroud. All radial positions in between are linearly interpolated to find
. Their values must be iteratively adjusted so that the initially specified, global performance parameter total pressure ratio
and its corresponding total pressure increase
over the rotor are achieved within the subsequent
CFD simulation. The actual metal angles
of the blade’s
NACA 65 profile [
24] are increased from the original calculation, based on
Euler’s turbine equation and the
radial equilibrium, by the found angles
. The fixed parameters of this group are, apart from the tip clearance TC, based on findings of other, similar research activities. For instance, the number of the rotor blades
and the respective inverse of the solidity,
, the axial spacing between the rotor and stator
and the maximum relative blade thickness
were chosen following the results of systematic experimental and numerical variations in [
25,
26,
27]. Though all those investigations were made on contra-rotating stages the findings were nevertheless adopted here to test all the designed engine components by a geometry close to that of the future
IPS. To account for the varying deflection over the span the solidity is adjusted by
towards hub and shroud to increase efficiency. Besides, the relative thickness is increased from shroud to hub to account for the increasing load. Since the manufacturing quality and, subsequently, the operational behavior of the blades was not known yet during input parameter specification, the tip clearance
was chosen relatively large to
. For optimal results, all fixed values of both
performance and
design parameters would have to be varied, too, to find an optimal design. However, as for the
RPS design the validation of the tool is of utmost importance and not the optimization of the engine’s performance itself, the parameters were not optimized at this point.
The general geometry, calculated within the actual iteration’s first step from the input parameters, is subsequently utilized in a 3D mechanical solid modeling design software to generate the actual 3D components. This includes not only the actual blades of the rotor but also casing components like the nozzle or the standard inlet in accordance with
VDI ISO 5167 [
28], taken over into the
CFD analysis afterwards. For a more detailed description of the geometry calculation refer to the previous publication in [
14].
Within the third step, the engine’s performance is investigated by a steady-state CFD simulation, focusing on the iterative parameters. In order to reduce the calculation effort, a single blade passage, created as negative from the CAD components, is modeled by allying rotational periodicity at the domain boundaries in circumferential directions. Four stationary domains for inlet, stator, nozzle, and outlet as well as one rotating domain for the rotor are set up. The inlet includes an additional volume ahead of the actual beginning of the standard inlet, having an axial length and diameter of two and four times of the rotor’s outer diameter, respectively. Similar, the outlet enlarges the blade passage by the simulation of the free flow after the nozzle where this volume has an axial length and diameter of three and four times the rotor’s outer diameter.
Besides, the nozzle’s outer flow is included by enlarging this outlet domain upstream from the actual nozzle’s outlet plane. At the interfaces between the domains itself, the
mixing plane approach is used by defining the corresponding pitch angles in dependency of the number of rotor and stator blades. Within the rotating rotor domain, the shroud’s wall is set up as
contra-rotating as it does not rotate with the rotor. In contrast, the hub is included as rotating wall. To account for friction effects, the
no slip wall approach is utilized for all wall boundaries. Besides, all walls are set to be adiabatic. The application of inflation layers on all surfaces including the in- and outlet ensures a normalized wall distance
to include boundary layer effects. In addition, the mesh is refined at all of these surfaces and turbulence is included by the
Shear Stress Transport (SST) approach. All outer boundaries are specified by the
entrainment and
opening pressure and temperature option to define them either as total or static values, depending on weather the surface is flowed through into or out of the domain. Finally, the engine speed is set by the angular velocity of the rotor domain. During the actual iterative design process of the
RPS, the compressible
Reynolds-averaged Navier Stokes Equations, implemented in
Ansys CFX, are solved for a steady-state solution and the different variables like total pressure ratios or efficiencies are determined mass flow averaged in accordance with the implemented calculations used for the design tool. Returning to the iterative adjustment of the design parameters discussed above, the upper part of
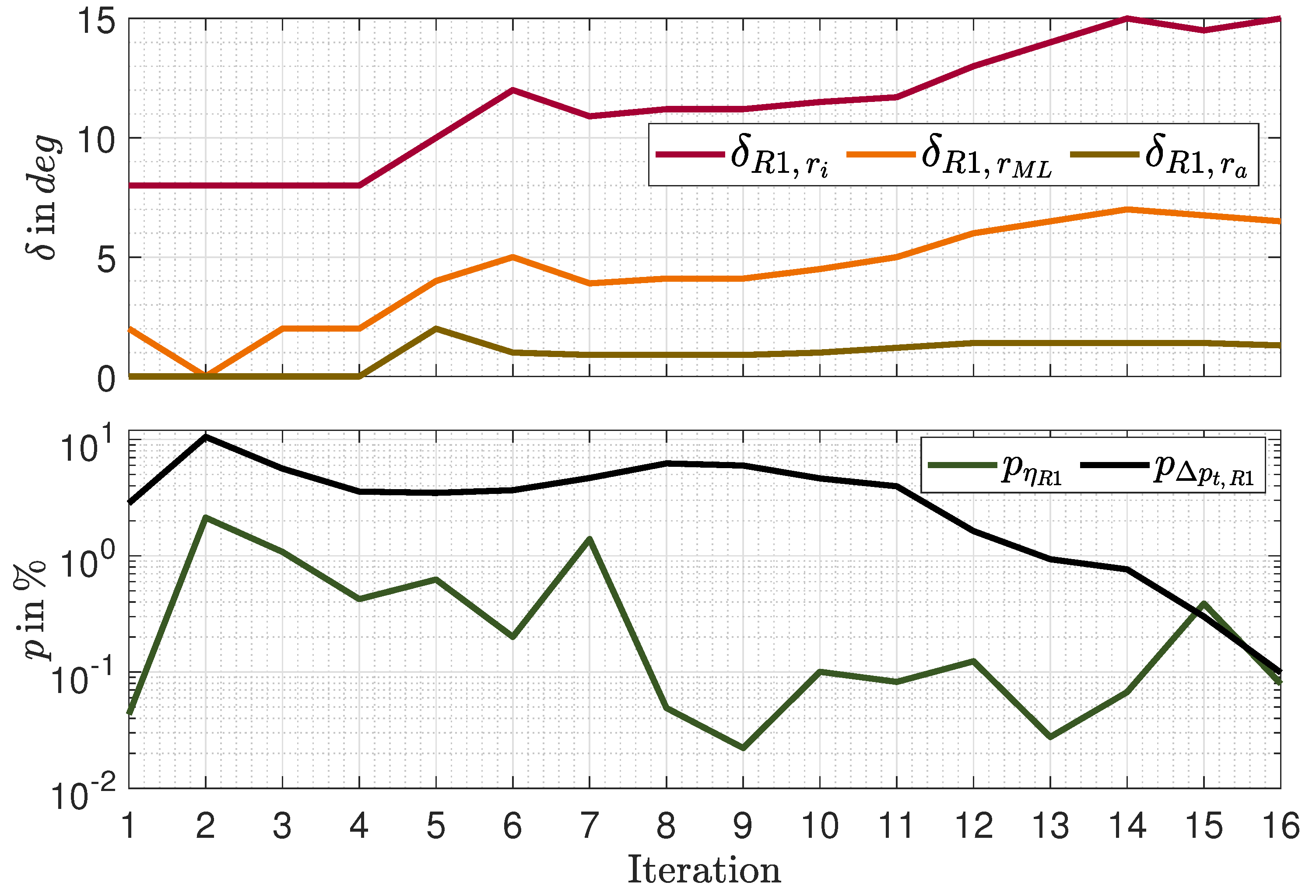
Figure 2 visualizes the iterative adjustment of the deviation angle. Since the rotor was designed in accordance with the
free vortex design principle to receive a constant increase in enthalpy over the span, the required fluid deflection at the hub is much larger than that at the shroud to balance out the lower circumferential speed of the blade at lower radial positions. Therefore, significant deviations between the desired and within
simulated flow angles can be detected, especially close to the hub, resulting in a reduced increase in total pressure calculated by the
CFD. As discussed above, in common design tools the attempt to avoid this is the application of empiric correlations to determine the required corrections of the blade’s trailing edge angle. In contrast, within the design tool approach discussed here the three local deviation angles are adjusted from iteration step to step as plotted in the upper part of
Figure 2 in accordance with the results shown in
Figure 2. Initial values were taken from the
IPS design presented in [
14]; due to design differences like other solidities the final values differ. The minimization of the local deviations results in decreased deviation of the global specifications of the total pressure increase
as shown in the lower part of
Figure 2 by the black curve. The deviations
p of the other iterative, global performance parameters are calculated between the result of the actual and the previous iteration step, representing a rate of change. Similar to the resulting green curve of the deviation of the isentropic efficiency plotted within the lower part of
Figure 2, these rates decline with increasing iteration step. After the
iteration all deviations of the global performance parameters undercut the chosen abortion criterion of
. The final
RPS geometry of this iteration is shown as
CAD rendering in
Figure 3.
Typically, the results of a
simulation depend on the quality of the applied mesh. Based on the previously mentioned requirement to undercut an
value of 4 on all surfaces, the first layer thickness of all inflation layers was set to
. In order to find suitable values for the general and the refinement element size, a systematic mesh convergence study was carried out, based on the
Richardson Extrapolation [
29]. The described blade passage was simulated by three different meshes at design speed; the results are summarized in
Table 3.
All meshes are geometrically similar as the refinements and inflation layers were placed in all cases on all surfaces. As prescribed in [
29], an averaged volume element edge length
h is calculated from the element number and total volume of the blade passage, used to ensure the meshes are refined by at least a factor of
. For the convergence study the simulated values of total pressure increase
, mass flow
and isentropic rotor efficiency
were considered. In contrast to the iterative design process, focusing on achieving the specified total pressure increase over the rotor
, the experimental setup allows the measurement of the total pressure increase from ambient to the rotor’s outlet plane only. Though this is explained in detail below in the context of the test bed description, this enlarged value is taken into account here already, indicated by the subindex 0. In the order mentioned above, the apparent orders
p of
,
and
result for the considered outputs. Due to the small relative errors
and
of the second simulated mesh, related to the finest mesh 3 and the extrapolated results, respectively, a further reduction of the element size did not seem to be meaningful. Besides, not only steady-state simulations of the blade passage in design point operation are carried out as for the iterative design process. Instead, the performance map of the engine is calculated by transient simulations to consider unsteady behavior, especially during throttling. These transient simulations require the simulation of two adjacent blade passages of all domains except for the stator. Since the number of rotor blades is nearly twice the number of stator blades, this ensures the required pitch ratio close to unity at all domain interfaces. Therefore, the number of elements for those transient simulations is approximately twice the number stated in
Table 3. To find a trade-off between solution accuracy and computing effort, the second mesh was chosen for the later performance map simulations, resulting in slightly increased errors but halved element number compared to the finest mesh.
However, not only the local discretization but also the discretization in time has to be reviewed for transient simulations. It is specified by the simulated number of time steps per passing period which, in terms, describes the duration of a rotor blade passing the following stator blade. Apart from the doubled blade passages for the majority of domains, the interfaces between the domains are changed to
transient rotor stator for these simulations. Besides, the steady-state simulations are aborted if all root-mean-square residuals undercut a value of
. For the transient calculations, the following two criterions have to be reached instead in accordance with typical recommendations for transient simulations. First, the arithmetic averages of the calculated mass flow and total pressure ratio over two intervals, one equaling a total, the other one a half revolution of the rotor, are within a relative tolerance. Second, the coefficients of variation of the same two outputs, calculated from the standard deviation divided by the mean, both considered over a whole revolution, have to be within a certain relative tolerance, too. Adjusted for the case considered here, the solutions can be considered converged if a tolerance of
is undercut by both criterions where the final outputs were calculated as mean of the entire last revolution. Finally, for the selection of a suitable number of time steps per period not only the result accuracy was reviewed but also weather nearly all time steps of the final revolution undercut the same residual target of
like the steady state solutions. Three different numbers of time steps per period were considered as summarized in
Table 4.
Similar to the discussion of the local discretization above, relative errors of the same three outputs, referred to the finest simulation of the third case, were calculated. Since unsteady behavior is of relevance when simulating throttled behavior, not only simulations with the design nozzle but with a reduced outlet area to were considered here, too. Again, a trade-off was found in the second option of five time steps per period as the deviations to the third case are small compared to the doubled computing effort.
Overall, it could be demonstrated that, as expected, the deviations between initial specification and CFD recalculations significantly decreased by directly incorporating CFD instead of relying on empirical formulations, while the effort increased due to the iterative nature. However, a final evaluation of the entire tool chain will only be possible during the experimental validation phase below, incorporating the influence of the composite manufacturing. To reduce the number of iterations, simple correlations could be implemented to obtain better initial values. Additionally, while reaching the global convergence limit is possible, adjusting only three radial positions seems insufficient to achieve the desired pressure rise across the entire span range. Especially for the design of the future contra-rotating propulsor, local flow distortions would be critical, as they could lead to local flow separations at the subsequent second rotor. Therefore, the number of radial adjustment points should be increased. Based on the discussion of the discretization in time a simulation option was found that seems to be suitable to calculate the entire performance map of the engine. Since the deviations between the steady-state and transient results account to , and regarding the result of total pressure increase, mass flow and efficiency, the transient simulation seems to confirm the steady-state results. As, in addition, the computing effort is similar, a transient simulation could be used for future iterative-design processes already.
2.2. Carbon Composite Blades
The final blade and overall engine geometry of the
iteration were afterwards transferred into a manufacturable design maintaining the aerodynamic surfaces and geometries. Apart from the composite blades, discussed in the following, the design of further components is summarized later. The most significant advantage of using composite structures lies in the substantial reduction of weight, up to
, compared to traditional metallic blades. This reduction enables highly dynamic behavior and enhances the engine’s gravimetric power density. Additionally, there is an increase in the blade’s safety factor and a potential decrease of up to
in the maximum relative profile thickness, leading to aerodynamic advantages [
30,
31]. However, despite these advantages, the widespread adoption of composite blades faces certain challenges. Issues related to repairability and recycling remain open questions. Furthermore, the manufacturing process for composite blades is more complex and labor-intensive compared to traditional milling methods, relying heavily on manual craftsmanship. Consequently, the application of composite blades is currently limited and predominantly reserved for a few large-scale projects.
While research projects of a similar scale to the
ELAPSED project are scarce, one noteworthy example is the
counter-rotating integrated shrouded propfan (CRISP) project conducted by
DLR [
32]. This project utilizes a standard structure of the individual composite plies for the two rotors, which deliver a pressure ratio of
at mass flow rate of
. This employed structure adheres to a typical symmetrical layup of composite plies, allowing for quasi-isotropic properties. It consists of a symmetrical arrangement of 128 plies, following the
orientation, forming an organo sheet. This sheet is subsequently subjected to hot forming and machined to achieve the desired contour. The primary load considerations for these blades, however, are radial and torsional stresses. Therefore, within the
CRISP project, various approaches to numerically optimize the layup configuration are being explored, enabling a reduction of the maximum displacement by up to
[
33].
For the ELAPSED project, however, two approaches have been developed to enable the adoption of this technology in smaller research endeavors. Firstly, the development of a new design tool, as previously explained, has streamlined the direct and automated integration of both composite layers and moulding creation. This represents a significant departure from the previously intricate and time-consuming process of generating these layers and mouldings for existing designs created in different programs. In this context, where the contour or outer geometry of the blade is precisely known in the form of a point cloud and does not need to be separately imported or recreated, the design tool allows for the flexible calculation of the maximum local ply count based on the to be specified ply thickness and maximum relative blade thickness, both being input parameters for the design tool. Additionally, a fundamental layup configuration is embedded within the code. Since a common configuration of individual blades mounted on an inner disk was chosen, the blade consists not only of the actual blade, its upper part, but it includes a blade root as well. This lower part has a front and rear nose that is used to mount the blades into the disk’s lugs.
Exemplarily, the resulting ply structure of the blade’s tip is shown in the left-hand part of
Figure 4. It consists not only of the two outer plies, predefined by the aerodynamic surface, but also out of two inner layers on both suction and pressure side, resulting in a total of six layers in its center. Since the blade’s maximum thickness increases towards the hub, the number of plies in the transition from the actual blade to the root accounts to 12. As shown in the center of
Figure 4, all layers do not end at the transition to the root but are wrapped around a carbon fleece utilized in the root. The layers are finally unwrapped within the CAD software to receive the individual
ply shown on the right-hand side of
Figure 4. All these steps described so far are included in the design tool described above and are processed automatically.
The second approach developed in this context involves the utilization of cutting-edge
stereolithography (SLA) printing technology. Due to the intricate blade geometry, conventional composite manufacturing methods such as autoclave production were not feasible options. Instead, the design tool automatically generates five moulding parts. Apart from the two main parts for both pressure and suction side, based on the blade geometry similar to the creation of the individual plies, three further parts are used for the blade’s root. To replace the costly and time-intensive milling procedures in the production of these mouldings, several
printing options were explored. However, due to the requirement for a smooth surface finish,
fused deposition modeling (FDM) printers did not meet the criteria. Instead,
SLA printers were employed, reducing the labor involved in moulding production significantly as no further manual post-processing is required. The mouldings for the reference propulsion system blades were still produced using glass reinforced resins. This material meets the strength requirements for moulding pressing but exhibited high brittleness. Consequently, the mouldings could only be used 2-3 times, and occasional chipping from the mouldings resulted in rejected blades. However, through systematic variation of post-curing duration and temperature on newer and even more cost-effective resins, followed by tensile and notch impact tests, the ductility and maximal elongation could be increased significantly by factor five, even offering a smoother surface finish. The initial version with mouldings printed by an
FDM printer, resulting in the uneven surface discussed above, compared to the final version of an
RPS blade with a smooth surface, is presented in
Figure 5. Since both blades are not used within the rotor their small flaws on the surface are not post-treated by filling them with a mixture of resign and ground carbon fiber.
Several tested
prepreg materials did not yield satisfactory results because of the small radii within the transition zone. Instead, traditional dry
twill fabric is employed. It is impregnated with the infusion resin
MGS RIMR426, cut to match the
plies discussed earlier, and positioned into the mouldings via hand-laminating. To accommodate torsion, the outermost plies are oriented at
, while all inner plies are oriented at
relative to the radial direction. Subsequently, the five-part moulding is pressed together, and the blade cures initially at room temperature before being relieved out of the mouldings and tempered by
for another hour. Due to the anisotropic material behavior and the consequent need to model the individual plies and their interaction in an
FEM analysis, such structural analysis regarding elongation and strength is considerably more complex compared to metallic materials, for example. Consequently, for the
RPS, which experiences relatively low loads, this analysis was omitted and the already discussed ply orientation was chosen based on the findings in [
33]. Instead, the tensile tests discussed below are intended to be used in the future for validating such a detailed
FEM model. This validated model will then be employed to calculate the significantly more heavily loaded blades of the
IPS prior to their production. However, different post-curing conditions of the blades were tested, resulting in the optimal tempering discussed above.
Apart from the eleven blades produced for the actual rotor, eighteen further blades were manufactured. Those were used, on the one hand, for initial tests regarding the printer selection, based on the achievable surface smoothness. On the other hand, they were used for the following tensile and bending tests, including a variation of the blade’s curing conditions. Since the overall production time could be reduced to 2 hours per blade, this process seems to be an applicable option within the university’s context. However, the rotor should be used to validate the design tool. Consequently, any geometric deviations from the CAD could prove critical, potentially leading to discrepancies in behavior compared to the CFD calculations. Compared to the target maximum thickness of at the blades’ tip, the respective mean value measured accounts to having a standard deviation of . Besides, the chord is measured to at the blade’s tip with a standard deviation of whereas the target was . This will be revisited during the tool validation later. To compensate for inequalities in the radial length of the blades the entire rotor with the finally assembled blades was machined down to the desired outer radius in one step, with the radius determined based on the tensile tests and commissioning tests discussed in detail below. In addition to ensuring geometric reproducibility, which could thus be guaranteed, reproducibility of blade mass for balancing is crucial for rotor operation. Therefore, at least a static balancing could be carried out successfully ensuring that the rotor’s center of gravity lies within the engine axis. A balancing mass was applied under the base of all blades scheduled for the rotor operation after curing. This mass consists of the same resin material already used for the actual plies but was reinforced here with ground carbon fiber. Subsequently, material was removed from the balancing mass again using a precision scale having an accuracy of , resulting in an average blade mass of with a very low standard deviation of .
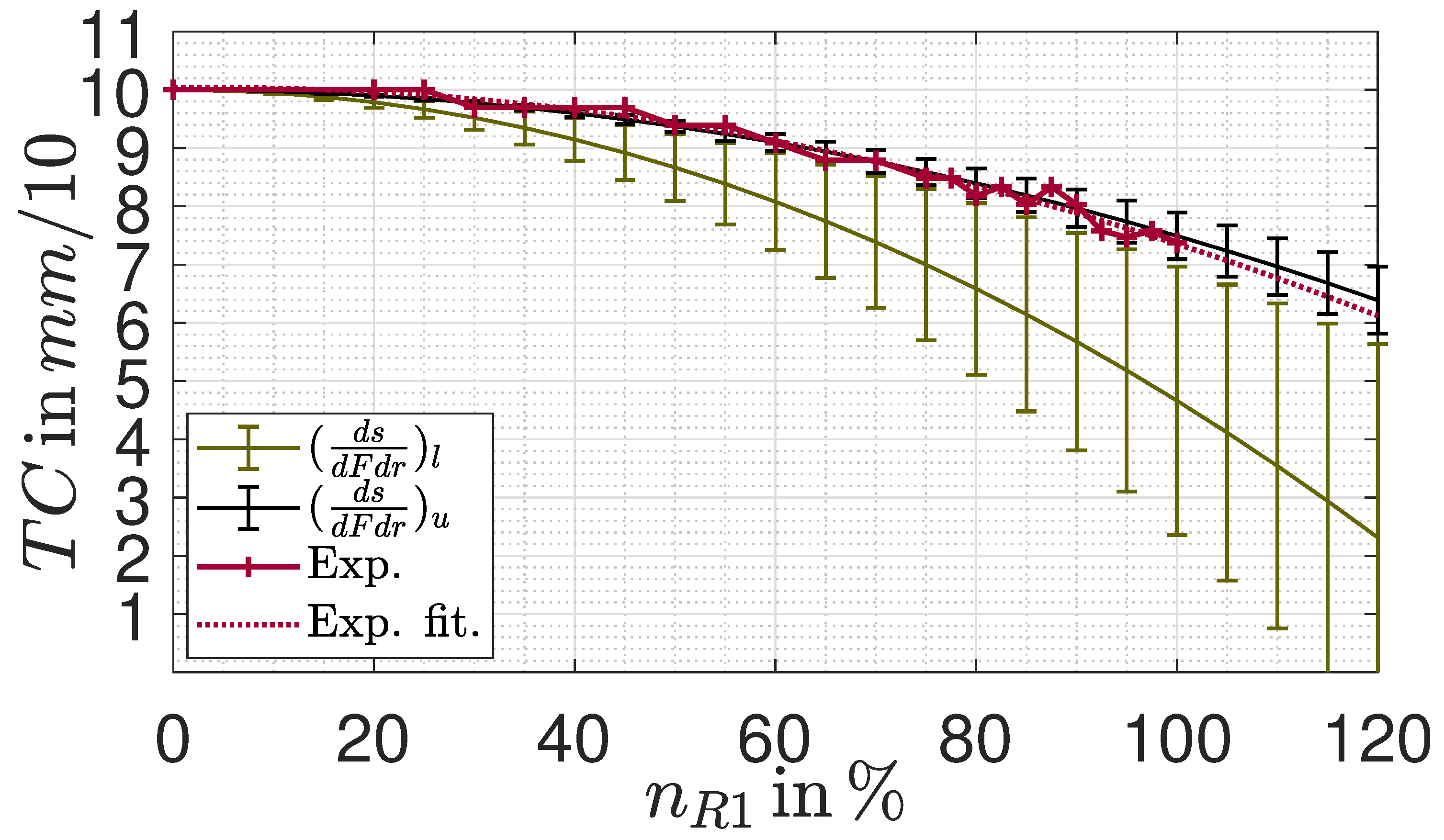
As previously mentioned, the tip clearance between the blade and casing at design point speed is one of the input parameters for the design tool. While a smaller value enhances the blade’s performance by reducing reverse flow and swirl effects, a certain margin must be maintained to prevent grinding of the blades at the casing, for instance during maneuvers resulting in unexpected blade elongation effects. Given the anticipated relatively high E-modulus for composite blades, a moderate of has been selected. However, due to the radial loads caused by rotation, blade tip grinding is necessary to establish a specific at , which then reduces to the chosen with increasing engine speed. The blade elongation causing the reduction in tip clearance depends mainly on the material’s Young’s modulus E. Since composite belongs to the category of anisotropic materials, its Young’s modulus in a particular considered direction, in this case the radial direction, is heavily influenced by the layer sequence and structure. Unlike isotropic materials, performing an FEM calculation to determine the anticipated elongation is projected to be quite resource intensive. Furthermore, since this approach necessitates subsequent validation owing to the multitude of boundary conditions that need to be set, this step is omitted. Instead, the blade’s performance is experimentally validated both by tensile and operational tests, discussed in the following, and the findings are leveraged to determine an expected blade elongation and a suitable .
As a basis for defining an appropriate testing procedure, a calculation of the expected blade loading is carried out. The blades are exposed to the centrifugal and aerodynamic forces. While the latter load is indicated by the subindex
, a subindex for indicating centrifugal forces is omitted in the following for the sake of improved readability. First, the centrifugal force
F caused by the actual blade is calculated, excluding the root since it is clamped into the disk. At any radial position
between hub and shroud,
and
, respectively, the effective force can be determined by integration as follows:
The blade’s cross section
varies across the radius and is therefore set by the
CAD data. Besides, a constant density
across the entire blade is assumed, calculated from the measured mass and the
model volume. According to this approach, the maximum centrifugal force occurs at the transition into the foot:
where the angular velocity
corresponds to the design point speed of
. With increasing radius it diminishes, reaching zero at the blade’s tip. Though, in contrast, the aerodynamic axial force of
at design point, determined from the
CFD simulation, is much smaller, the blade behavior under this load is experimentally tested, too.
Since the samples are not standardized, the testing procedure for the tensile test must be conducted in accordance with
DIN EN ISO 527-5 [
34]. To facilitate the experiments in academic research, this test setup was chosen as it is designed for a universal testing machine capable of operating in both tension and compression directions. The model used here for both tests is the
inspekt table 50 kN by
Hegewald & Peschke. It features wedge-screw grips on both the lower fixed and the upper movable traverse. The lower clamping of the blade is achieved by using a two-part holder, similar to the engine’s disk, which is bolted to the lower traverse. An adapter for the upper traverse is utilized to avoid torsional moments on the blade caused by its twisted geometry. To clamp the curved and twisted tip surface using the jaws of the clamping tool, flat outer surfaces of the elements used to apply the forces are required. To mill the negative profiles of the blade’s pressure and suction side, the manufacturing of these elements as depicted in
DIN EN ISO 527-5 is only partially feasible. Instead, their thickness had to be increased and the use of cross-laminated
glass-fiber reinforced plastics (GFRP) fabrics is unsuitable due to the cutting of a significant portion of the fibers during the manufacturing process, leading to the loss of required properties. Given that
DIN EN ISO 527-5 mandates that the strength values and coefficient of variation must be at least equivalent to those of
GFRP, the commonly used aviation-grade aluminum 7075 is employed. The stipulated radial extension of those profiles,
, is reduced to
to cover as little of the blade as possible while avoiding slipping. To enhance the coefficient of friction at the contact interface, the elements are subjected to
SiC sandblasting. There is no adhesive bonding between the blades and the described elements. It is worth mentioning that the pressure side element is additionally employed in the bending test to achieve a uniform load distribution on the blade tip.
This approach ensures that all carbon fibers are effectively stressed, thus closely simulating engine operational conditions.
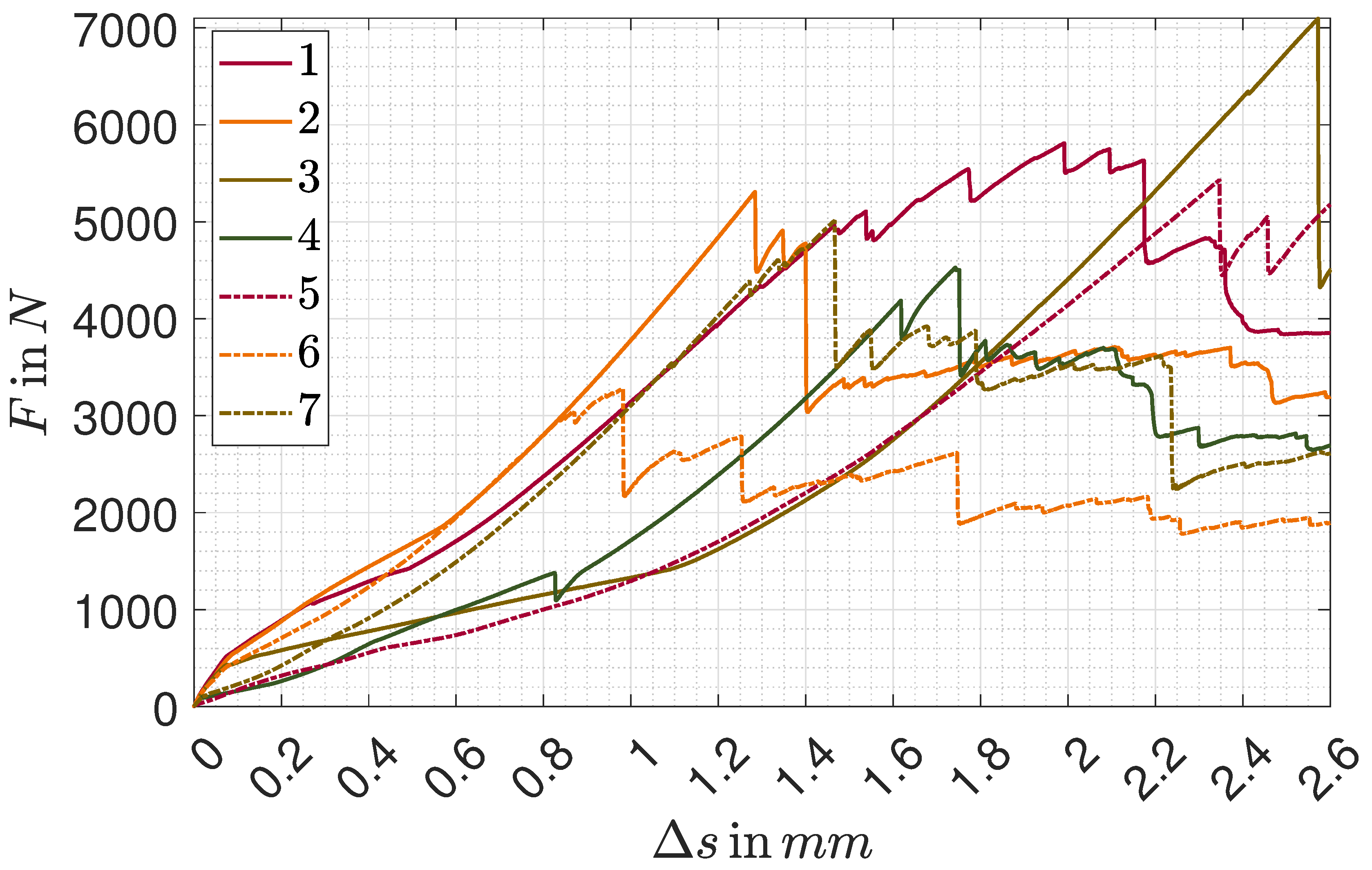
The subsequently discussed test series was conducted on blades of identical design and curing conditions mentioned above and like the ones actually installed on the engine. In
Figure 6, the measured absolute elongation
is plotted in dependency of the blade
i and the applied force
F. Upon examining this diagram, two distinct gradient regions become evident. While the slope is relatively shallow and intermittently wavering for forces
, a linear, steeper increase is observed above this threshold. The lower slope likely results from preload compensation. Reviewing the videos and photos taken during the experiments indicate additional slipping effects of the blade within its clamping, causing sudden, minor decreases of the applied load.
In general, all blades withstood the expected maximum operational load at design point speed, given above in equation
3. In all cases that a damage pattern became visible, causing the final, massive load decrease, it could be classified as delamination at the transition from blade to blade root at the trailing edge (see
Figure 7).
Therefore, the safety factors
S summarized in the first line of
Table 5 are calculated from the maximum measured load, in dependency of the lowest and highest strength blade as well as averaged over all blades, and the estimated operational load at the transition between blade and root, determined above in equation
3.
Noteworthy is the case of blade number 6, considered the most critical scenario due to its notable deviation from the other samples, achieving a maximum of only. Nonetheless, it maintains a safety factor of , allowing it to withstand. If the rotational speed is increased to , the increased load estimation of decreases this safety factor to only, allowing it to withstand, albeit with a marginal reserve. However, a safety factor of could be determined within the bending test, derived from the most conservative force calculation at the design point.
Returning to the tensile testing, a specific
Young’s modulus cannot be calculated since the blade’s cross-section varies across its radial extension whereas the elongation
was measured over the entire blade only. However, averaged slopes
can be determined from the measured elongation and load as well as the radial extension of the blade
where
represents the radius of the outer clamping. These slopes are separated into two cases as discussed above. On the one hand, the lower gradient
represents the initial, shallow slope measured during tensile tests. On the other hand, the upper, steeper slope is described by
, based on the assumption that the clamping effects do not occur during operation. Both cases are evaluated, summarized in the lower part of
Table 5, and utilized to calculate the expectable blade elongation
as follows:
assuming that the considered
is the same for all radial positions and applying equation
2 to calculate the individual elongations of each increment
at radius
r. The resulting tip clearances in dependency of the relative engine speed with regard to the design point speed are plotted in
Figure 9, evaluated for an initial
of
at installation condition. The error bars are formed by the results of the lowest and highest strength blade, respectively. It can be inferred that at
an elongation between
and
is present on average, considering the lower and upper slope.
These results pave the way for engine testing in terms of a tip clearance measurement. The utilized high-speed camera
FASTCAM Mini AX200 was positioned in front of the engine. For these tests, the engine was not equipped with its standard inlet but with a similar one having a smaller axial length. This enabled to capture the tip clearance within the red square in dependency of the engine speed as shown in the upper part of
Figure 9. A frame rate of
, a zoom lens and an additional lighting source behind the engine facilitated analyzable shots. From the videos of the individual speeds those photos were selected where the individual blades are at the same circumferential position to ensure comparability. The actual tip clearance was determined from the calibrated length between two reference positions at the casing and at the blade’s tip, exemplary shown in the bottom part of
Figure 8.
Figure 8.
Tip clearance quantification by a high-speed camera.
Figure 8.
Tip clearance quantification by a high-speed camera.
Figure 9.
Experimentally measured tip clearance in dependency of the actual engine speed
n, compared to the expected results from the tensile tests based on
Table 5.
Figure 9.
Experimentally measured tip clearance in dependency of the actual engine speed
n, compared to the expected results from the tensile tests based on
Table 5.
Besides, the captured videos were evaluated for critical flutter effects, differing elongations of the individual blades or misbalancing not detectible within the former static balancing. However, all these tests were negative.
In order to definitely avoid contact to the casing, a conservative grinding of the blades’ tips was conducted to achieve a tip clearance at installation condition of .
The actual measured tip clearance and a resulting, exponential fitted curve are included in
Figure 9 as solid and dotted red line. On the one hand, there is a good agreement between the measured elongation and the calculated values based on the upper, larger gradient measured by the tensile tests though the calculations seem to underestimate the actual elongation slightly. Three possible assumptions could be considered for this deviation. First, it appears reasonable that the the density within the actual blade area is higher than that of the root due to the fleece used within it. Second, the blades are slightly thicker than initially designed as discussed previously. Both would result in higher centrifugal forces and therefore larger elongations when assuming that the deviating thickness results from additional resin which only increases mass but does not bear significant loads. In addition, the calculated slopes are averaged over both the actual blade and the transition zone. Due to the strong curvature of the transition in comparison with the plane structure of the actual blade it can be expected that their slopes vary widely. On the other hand, the resulting tip clearance at design point, approximately
, is larger than the initially specified value of
and further discussed below within the context of the CFD-validation.
Nevertheless, the test procedure seems to be a suitable indicator to predict the actual operational behavior. Even if the potential range of expectable tip clearances appears to be large and requires careful commissioning tests of the engine including a tip clearance measurement, the calculations could be used to determine more appropriate values for
than set here. To improve the calculation accuracy further, the elongations of the different zones should be measured individually due to their substantial difference in ply structure, for instance by optical measurement systems. Besides, elongations of the inner disk were excluded and may account for deviations between tensile test and experimental results, too. Addressing the second research question raised above, it can be summarized that the design, manufacturing and commissioning of composite-blades became feasable. Key factors are the direct integration of the manufacturing procedure into the design tool itself and the utilization of innovative approaches like the
printed mouldings, reducing the manufacturing effort massively. Besides, the safety factors calculated above indicate a safe operation over a wide range of engine speeds and the test procedure could be verified. However, the higher total pressure ratio of the future contra-rotating propulsor requires larger engine speeds. To account for the subsequent higher loads, the blade design, especially the layer structure, should be optimized. To improve the design procedure, the test results could be utilized to set up a detailed
FEM model that takes the individual ply orientation and anisotropic material characteristics of a composite structure into account. Besides, further comparisons of different blade curings or the selection of other materials of both resin and actual fabric seem to be beneficial. However, a composite rotor could be successfully manufactured, compared to the initial
rendering in
Figure 10. Within the following it will now be examined whether this composite rotor does not compromises the design tool validation.
2.3. Experimental Setup
Apart from the rotor being the engine’s main component, the nozzle and the test bed are discussed briefly in the following as they are the key-elements enabling the actual design tool validation. In addition to the actual design point calculation, considered by the tool as discussed at the beginning, the operating behavior at off-design points is of particular relevance. For axial compressors and fans, the operating point of highest efficiency is typically close to the surge limit. However, typically less efficient operating points are chosen that have a larger margin to this limit [
35]. As the later contra-rotating engine aims to enlarge the operating range towards more efficient operating points through targeted adjustment of operating parameters, especially the speed ratio, it is essential that not only the design point but also the off-design points are accurately represented using the
CFD utilized for the design tool. Consequently, this will be revisited in the following experimental tool validation, too. Therefore, an adjustable nozzle was constructed. It has 16 segments which can be moved via a servo to adjust the nozzle’s outer geometry and the size of the nozzle’s outlet cross section
. Furthermore, each of the segments is slightly curved, so that the outlet cross sectional area is always in a near circle shape, which reduces losses. Because of the relatively low static pressure and low temperature it was possible to produce most parts of the nozzle at the institute. The segments of the nozzle were
-printed out of
polylactide (PLA), which has reduced the costs as well as shortened the production time. To validate that the size of
stayed consistent during operation and testing, pictures were taken and superimposed by a high-speed camera both in and out of operation. Since the variable nozzle’s outlet widened at higher engine speeds, fully
-printed outer nozzles with different sizes that fulfill the requirement of a constant outlet cross section were printed, utilized and successfully tested instead whereas the adjustable nozzle’s design will be improved. Those differently sized nozzles were also taken over into the
to simulate the engine behavior at throttled and unthrottled conditions, too.
The test bed built at the institute serves for both static engine testing and experimental measurements in a wind tunnel, particularly in conjunction with the
particle image velocimetry (PIV) system. Besides, it is designed not only for the current single-engine reference propulsion system but is also preconfigured for a future, dual-engine contra-rotating configuration. Its data acquisition system, based on
National Instruments (NI) soft- and hardware, includes various modules for data collection. This includes an ambient temperature measurement using
PT100 sensors, a six-component strain gauge for force and momentum measurement along the engine’s axes, and a digital pressure sensing system with a focus on absolute and differential pressure measurements. Having a rated accuracy of
full scale, the strain gauge can measure up to
and the engine and the gauge are horizontally orientated before testing. All pressure sensors are rated with an accuracy of
of their full scale, having an effective resolution of
. Whereas the absolute pressure can be obtained by a 0 to
absolute sensor with a resulting maximum error of
, the differential sensor can measure up to
, resulting in a maximum deviation of
with a resolution of
. The offset of all pressure sensors is regularly taken and compensated. Additionally, the absolute mechanical engine speed
n is captured using a laser-based light barrier system, consisting of a hole within the spinner cone and an edge counting within a digital input module. Data are read from the
NI DAQ system by a connected measurement and control PC running
LabVIEW-based data acquisition and control software. All parameters are collected with an adjustable frequency; for the following
were chosen as steady state operation should be measured only. Due to the static operation outside the wind tunnel for the following tool validation, the obtained static inlet conditions of temperature and pressure equal their total values
and
, respectively. According to the
Mach number similarity, they are used to calculate the corrected engine speed
as follows [
35]:
These calculations are performed using a reference temperature
and pressure
derived from the
ISA standard atmosphere[
23] at an altitude of
, which equals the institute’s altitude. Since those reference conditions were already set within the design tool as inputs as well as in the following
CFD as boundary conditions on inlet and outlet surfaces, the mechanical design speed of
equals the corrected design speed, stored within the control software. To enable operation at higher temperatures, resulting in higher mechanical speeds, a slightly oversized water cooled brushless motor was selected and installed. It is powered by a water-cooled
electronic speed controller (ESC), which is, in turn, supplied by a
power source capable of providing up to
. To accommodate future operation with two electric motors having a combined power of up to
, a second identical power supply unit is already integrated into the test bed. The
ESC generates the required sinusoidal signal by selectively applying voltage to the motor’s three phases, with the duty cycle of this signal determining the time-averaged voltage. The actual motor speed then results in accordance with the motor-specific
rating. However, the actual speed is governed by further factors such as motor heating or the internal resistance of cables and the motor. The
ESC is controlled via a
PWM signal from the
DAQ system, with the duty cycle regulated by the measurement and control system to maintain a constant corrected speed set by the user.
To protect the various sensor cables from the strong magnetic field of the motor supply, shielded cables are exclusively used. Mass flow rate is calculated from the differential pressure, measured between the engine’s inlet and the ambient, and the cross sections inlet and is corrected similar to the engine speed as shown above [
35]:
Additionally, the total pressure difference to ambient can be measured within the engine using a radial traversing unit, enabling the calculation of area averaged values. This unit is equipped with a calibrated, miniature five-hole probe from Vectoflow. This probe features five pressure ports in its head, allowing the determination of both total pressure and flow angles.