Prerpints.org logo
Preprint
Article

Ensemble Machine Learning on Fusion of Sentinel Time Series Imagery with High-Resolution Orthoimagery for Improved Land Use Land Cover Mapping

This version is not peer-reviewed.

Submitted:

09 June 2024

Posted:

11 June 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
In the United States, several land use and land cover (LULC) data sets are available based on Landsat. These data sets often fail to accurately represent the features on the ground despite having several advantages over other data. Detailed mapping of complex heterogeneous landscapes for informed decision-making is possible using high spatial resolution orthoimagery from the National Agricultural Imagery Program (NAIP). However, large-area mapping at this resolution remains challenging due to radiometric differences between scenes, low spectral depth of imagery, landscape heterogeneity, and computational limitations. Machine learning (ML) techniques have shown promise in improving LULC maps. The primary purposes of this study are to examine and evaluate bagging (Random Forest; RF), Boosting (Gradient Boosting Machines [GBM] and Extreme Gradient Boosting [XGB]), and stacking ensemble models on sentinel 2A fusion data on NAIP imagery. We also compared the accuracy based on random cross-validation (80% / 20% split) without accounting for spatial autocorrelation and target-oriented validation (10 clusters) accounting for spatial structures of the training data set. To make the LULC map of a portion of Tom Green and Irion counties in central Texas, we used a time series of sentinel data and NAIP orthoimagery. We created several spectral indices, structural variables, and geometry-based variables, reducing the dimensionality of features generated on Sentinel and NAIP data. The random and target-oriented validation results show that autocorrelation in the training data offers over-optimistic results. In our case, the overestimation ranged from 2 % to 3.5 %. The XGB-boosted stacking ensemble on-base learners (RF, XGB, and GBM) improved model performance over individual base-learner. The main contribution of this research is that meta-learners are just as sensitive to overfitting as base models, as these algorithms are not designed to account for spatial information. Finally, we show that the fusion of Sentinel 2A data with NAIP data improves land use land cover classification using Geographic Object-Based Image Analysis (GEOBIA).
Keywords: 
Subject: 
Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Accurate extraction of information from remote seeing data for environmental monitoring, land use planning, and management of natural resources is of utmost importance. Unlike field-based data, remote sensing offers cost-effective, time-efficient and frequent data delivery over a broad geographical extent. Land Use Land Cover (LULC) maps derived from satellite imagery are available at different scales (subnational, national, continental, or global). In the recent past, high-resolution map production was hindered by the geographical coverage of an area by satellite sensors and the cost of commercial data such as RapidEye [1,2]. In the last two decades, several mapping efforts have been accomplished in the United States especially using Landsat data [3,4]. Landsat satellite images are still the dominant data in land cover mapping sources; however, these maps are regional with a relatively low spatial resolution (30 m) and often do not capture small-scale resources present on the grounds, their distribution, and appropriate fragmentation quantification.
The National Agricultural Imagery Program (NAIP) started a pilot project in 2000 to acquire high-resolution digital aerial imagery of the conterminous United States. With the launch of Landsat in 1972, pixel-based classification soon became the dominant paradigm [5]. However, with the advent of high-resolution satellite sensing, another paradigm criticized the pixel-based approach, which focuses on grouping high-resolution pixels into one based on some criteria, called Geographic Object-Based Image Analysis (GEOBIA). Several studies have employed pixel-based [6,7,8] or object-based [9] approaches to NAIP data. Comparative studies have shown that GEOBIA yields higher accuracy than traditional pixel-based classification [10]. Although NAIP data are acquired chiefly for agricultural purposes, they have been used in relatively large (county to state)-scale LULC classification.
In the recent decade, remote sensing data analysis has benefited from exploiting the power of learning (ML) algorithms in LULC classification, such as support vector machines (SVM) [11,12], Decision Trees (DT) [13], Random Forest (RF) [9,14,15], Nearest Neighbor [16,17], Deep Learning (DL) [18]. More recently, ensemble ML and DL have gained much attention in various fields, especially in applied remote sensing work, because they can handle high-resolution images to capture fine structural information. This study focused on the examination of the stacking ensemble in classification problems.
Although building an appropriate stacking ensemble model to improve model accuracy and reduce biases is possible, current state-of-the-art practices involve model evaluation using holdout data (a random subset of training data). The data collection process is not usually random; therefore, a random selection of observations to create the testing data set does not guarantee independence from training observations when a spatial dependency is inherent in the data. Spatial dependency in the sampling data arises from spatial sampling biases, as observers tend to collect data from a clustered hotspot of their activity. This phenomenon of spatial dependency [19] is called spatial autocorrelation (SAC) [20]. When spatial data are autocorrelated, the considered model fails to account for a critical determinant that is spatially structured and thus causes spatial structure in the response. Another SAC issue in the input data set can result in unreliable results through validation approaches because an observation point cannot act as spatially independent validation of proximity data points [21,22]. Using such cross-validation approaches without accounting for spatial structures of a input data provides overoptimistic results, making accuracy assessment unreliable[9].
We used target-oriented validation strategies to reduce spatial bias in training data in LULC classification problems, which groups similar observations into cluster. The resultant clusters are treated as folds in Machine Learning (ML). Of the total identified clusters, all except one are used in model training, and the remaining cluster is used for model testing. Model training stops when all clusters are used in testing models. Comparing the performance of LULC classification based on random-k-fold and target-oriented cross-validation, we demonstrated a reduction in overinflation of overall accuracy. This study uses sentinel 2A and NAIP data to evaluate bagging, boosting, and stacking on sentinel-fused NAIP data using the GEOBIA approach.

2. Materials and Methods

2.1. Study Area

The study area (Figure 1, 5381.73 km2) covers a heterogeneous landscape in central Texas Irion and Tom Green County. The mean annual precipitation is 508 mm, and the minimum and maximum temperatures range from 0° C to 35° C. Most of the study area is situated on the Semiarid Edwards Plateau with scattered woody vegetation [23]. The current cropland area in the area was converted from the Red Prairie area [23]. The study area covers the forests of live oak (Quercus fusiformis), Texas oak (Q. buckleyi), Ashe juniper (Juniperus ashei), and mixed grass prairie with scatted honey mesquite (Prosopis glandulosa) [23].

2.2. Imagery Data Set

2.2.1. NAIP Orthoimagery

The national agriculture imagery program acquires digital orthophoto quarter-quads (DOQQ) every 2-3 years. NAIP images DOQQS used in this study were acquired in 2020 between August 23 and October 18 through ten flight missions. Each DOQQ contains four working bands, including red (465 – 676 nm), green (604 – 664 nm), blue (533 – 587 nm), and near infrared (NIR) (420 – 492 nm). The spatial resolution of the entire data set is 0.6 m, and the radiometric resolution is 8-bit [digital number values range: 0 to 255].

2.2.2. Sentinel Multi-Spectral Imagery

The sentinel-2 multispectral instrument was developed by the European Space Agency (ESA), which consists of a constellation of two polar-orbiting satellites in the same Sun-synchronous orbit covering areas from 56° to 84° latitude [24,25]. Sentinel-2 has 13 spectral bands between visible and short-wave infrared, with three bands at 60, six at 20 m, and four at 10 m spatial resolution. The radiometric resolution of 13 bands is 12-bit [digital number values range 0-4095]. The temporal resolution of Sentinel 2B is five days, while Sentinel 2A has a slightly coarser temporal resolution of ten days.
This study uses 11 Sentinel 2A images from 2020, one image per month except for February. The criterion for image selection was that the images must have little or no contamination from clouds or haze. All Sentinel 2A scenes were downloaded in level-1C processing format from the Copernicus Open Access Hub (https://scihub.copernicus.eu/) on June 07, 2021. This study only used four bands (red, green, blue and Near infrared) available at 10 m spatial resolution.

2.3. Layer Generation and Dicing

We first calculated the soil-adjusted vegetation index (SAVI) on each image using several sentinel imagery. Then we extracted all near-infrared bands and produced principal component axes (PCA) [9,26,27]. Next, we also run PCA on SAVI layers. Finally, we calculated textures on the first PCA axis on SAVI layers [28,29].
To harness the high spatial resolution of NAIP imagery and the radiometric and temporal resolution of Sentinel imagery, we used former data sources for image segmentation for quality objects using eCognition software [30]. Due to the large extent of the study area, all necessary images were first generated, and then all layers were diced (clipped) into manageable sizes. Next, we generated several features based on NAIP and Sentinel images on each object/polygon in situ in eCognition. Finally, all objects with generated features were exported to merge into the final dataset.

2.4. Selection of Features

Combining geometry, spectral bands, spectral indices, principal component axes on NAIP data, spectral indices, and PCAs on near infrared and spectral indices resulted in several variables or features. However, since these features were produced on the original NAIP and Sentinel bands, the information held by these features became redundant. Therefore, we performed recursive feature elimination (RFE) in the scikit-learn package in Python [31] to retain the most critical features. An RFE relies on variable importance scores calculated using training data [32].

2.5. Machine Learning Algorithms: Level 0

2.5.1. Random Forest

Random Forest (RF) is an ensemble learning technique proposed by Breiman [33]. An RF uses several classification and regression trees to make a prediction. Initial data are split into in-bag (about 2/3rd of the data) and the remaining one-third into out-of-bag (OOB) samples. Trees are created using in-bag samples, whereas OOB samples are used to estimate the OOB error [33]. The central idea of RF is that several bootstrap aggregated classifiers perform better than a single classifier [33]. Each tree is created by bootstrapping of in-bag samples. The resulting classification is based on the majority votes of all trees for the most frequent input feature x , C ^ r f B = m a j o r i t y v o t e C ^ B x 1 B , where C ^ B x is the class predictin of the bth random forest tree. Each decision tree is independently produced, and each node is split using a randomly selected defined number of features (mtry). RF has been widely applied in the classification of LULC using multispectral [9,34,35].

2.5.2. Gradient Boosting

Gradient Boosting Machines (GBM) [36] tries to build the boosting procedure as an optimization task over a differential loss function in an iterative fashion. A classical GBM paradigm trains a series of base learners that minimizes some loss function iteratively in a sequence [37]. In classification problems, GBM uses multi-class logistic likelihood algorithms for fitting criteria. Extreme gradient boosting (XGB) implements a traditional GBM that builds additive models while optimizing the loss function [38].

2.6. Stacking Ensemble Machine Learning

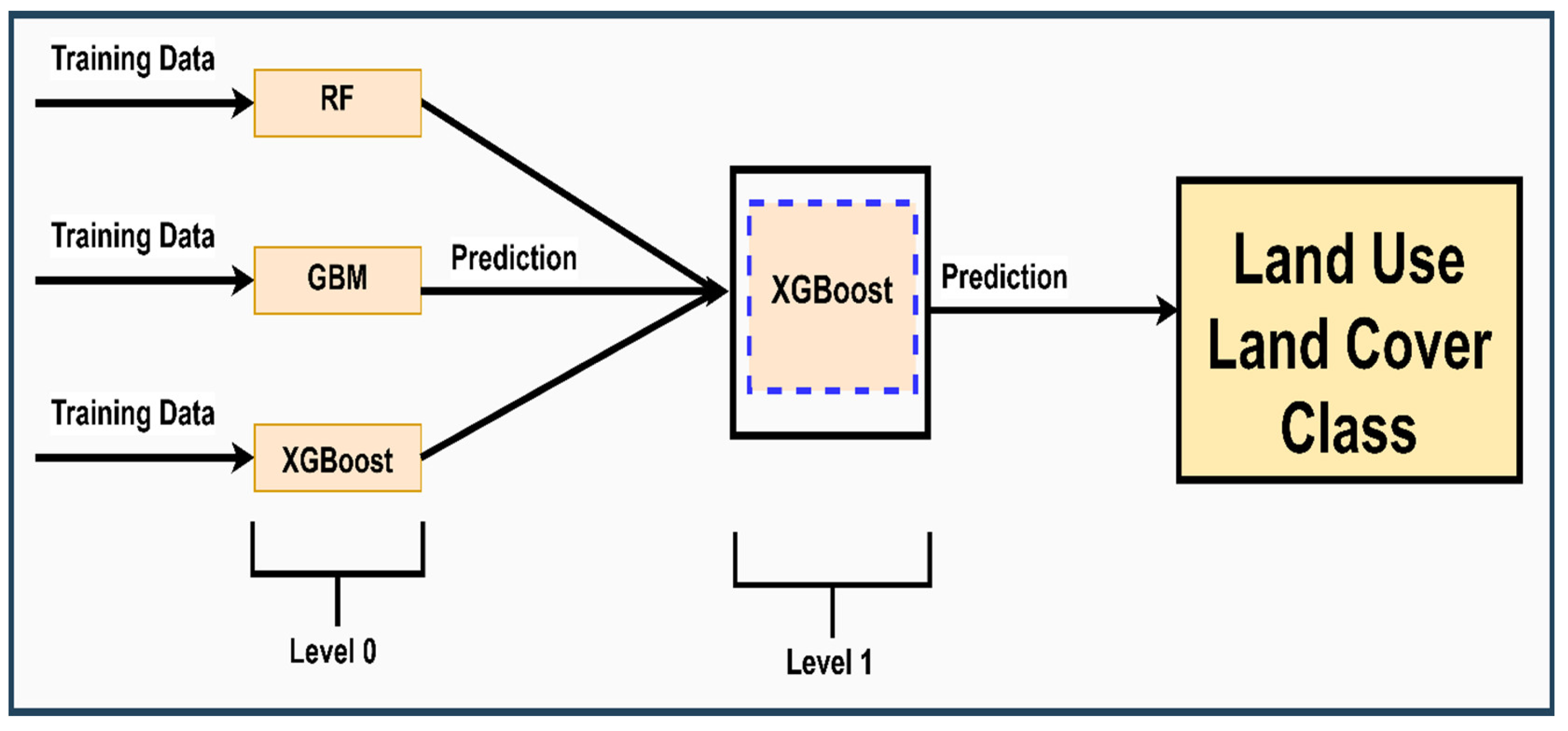
Before stacking models, all base learning algorithms (level 0) were first developed. Stacking, also called stack generalization (level 1), uses meta-learning to integrate different algorithms. Stacking ensemble machine learning algorithms (in this case, classification trees and boosted trees) estimate base learner generalization biases and minimize these biases while stacking [39]. The essence of stacking is to use the level-1 model to learn from the predictions of the base models (level-0). Generally, a stacked generalization framework improves prediction performance compared to the best level-0 model. We tested RF, GBM, XGB, and logistic regression and selected the model that produced better results than the base learner. Figure 2 shows the basic workflow of the stack generalization used in this study.

2.7. Accuracy Assessment

The performance of the base and stack models was measured using holdout (20%) of the total data in the event of random cross-validation. In the target-oriented validation, the holdout data varied at each iteration (Appendix A). Five performance criteria derived from the confusion matrix were evaluated to evaluate the model. These criteria were: a) overall accuracy, b) Precision (User’s Accuracy), c) Recall (Producer’s accuracy), d) Kappa [40], and e) Mathews correlation coefficient [41]- MCC is robust to data imbalances. In general, the higher the values of these performance metrics, the better the performance of the classifiers in discriminating land use land cover classes.

3. Results

3.1. Level 0 and Level 1 Classification Comparison

Overall accuracy (OA), Kappa and MCC of three base learners were relatively close to one another (Table 2) when random cross-validation was used on holdout (20%) data. All metrics were derived based on the confusion matrix (Figure 2: Appendix). XGB produced the highest OA (0.942), followed by GBM and Random Forest. Kappa and MCC followed the same pattern: XGB produced the highest Kappa and MCC statistic. GBM, followed by XGB, yielded the highest producer’s accuracy on cropland.
Table 1. Performance metrics produced by base-learners and meta-learners using random cross-validation. These statistics were calculated based on a confusion matrix produced in the holdout data set (Figure 3).
Table 1. Performance metrics produced by base-learners and meta-learners using random cross-validation. These statistics were calculated based on a confusion matrix produced in the holdout data set (Figure 3).
Model Accuracy
statistic		 Land Use Land Cover Class
Cropland Grassland Shrubland Built ups Water Shadow
Random Forest Precision 0.9804 0.8977 0.9669 0.9015 0.9737 1
Recall 0.9259 0.965 0.9733 0.9632 0.74 0.75
F1-Statistic 0.9524 0.9301 0.9701 0.9313 0.8409 0.8571
Overall accuracy [ 0.9326], Kappa [ 0.9141], MCC [ 0.9149]
GBM Precision 0.9813 0.9363 0.9605 0.9086 0.9762 0.9
Recall 0.9722 0.955 0.9733 0.9421 0.82 0.8182
F1-Statistic 0.9767 0.9455 0.9669 0.9251 0.8913 0.8571
Overall accuracy [ 0.9407], Kappa [ 0.9248], MCC [ 0.925]
XGB Precision 0.9811 0.9234 0.973 0.9278 0.9545 0.878
Recall 0.963 0.965 0.96 0.9474 0.84 0.8182
F1-Statistic 0.972 0.9438 0.9664 0.9375 0.8936 0.8471
Overall accuracy [ 0.942], Kappa [ 0.9265], MCC [ 0.9267]
Stacking Precision 0.972 0.9363 0.9613 0.9424 0.9545 0.9024
Recall 0.963 0.955 0.9933 0.9474 0.84 0.8409
F1-Statistic 0.9674 0.9455 0.977 0.9449 0.8936 0.8706
Overall accuracy [ 0.9474], Kappa [ 0.9334], MCC [ 0.9335]
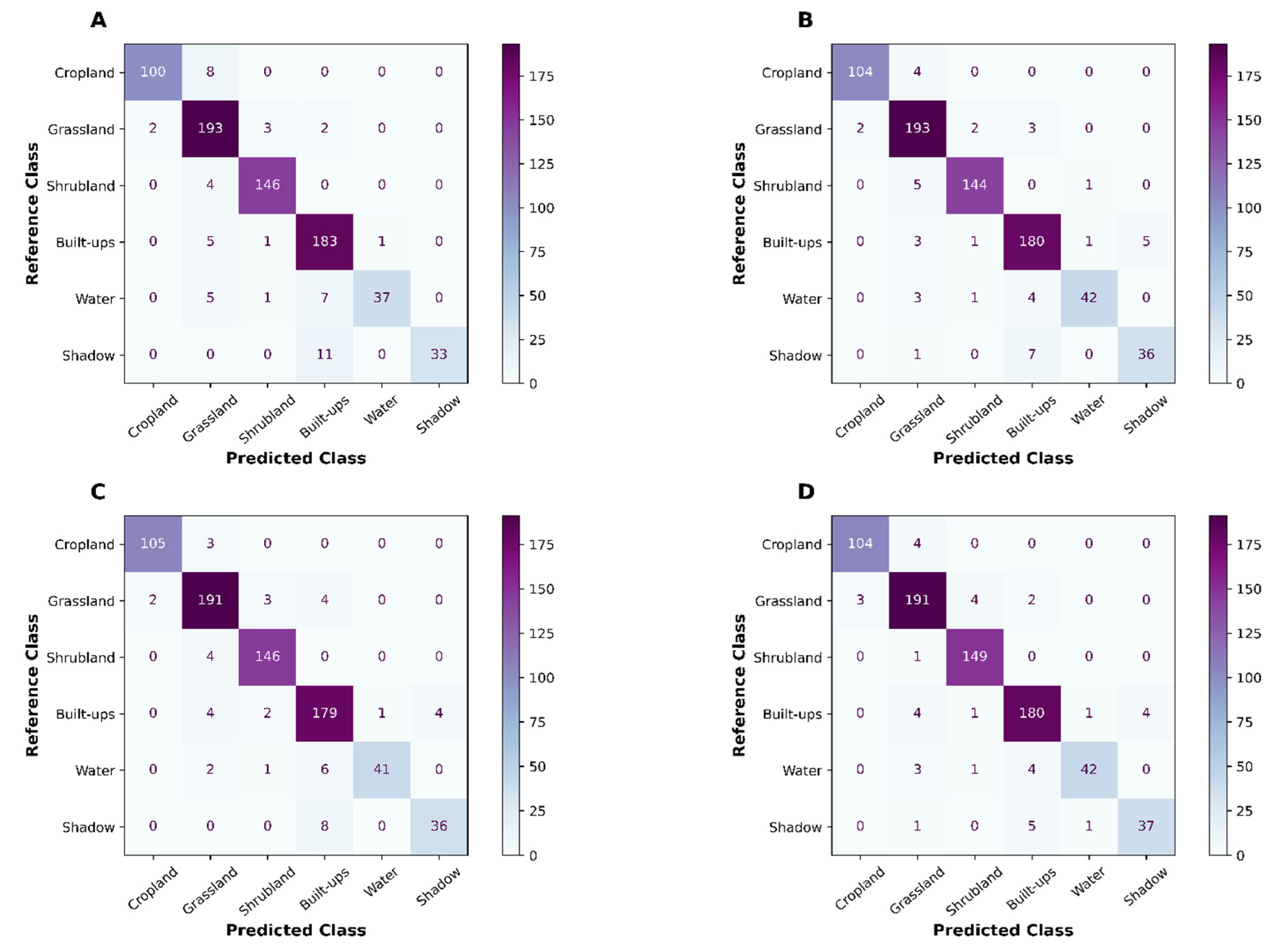
The stacking model (Level 1) produced the highest OA, Kappa, and MCC statistics. At the class level, the stacking model did not produce the best results; however, it was consistent with other competitive models. Across the classes, the stacking model produced the best accuracy in the Water, Shrubland, and Shadow classes.
Preprints 108839 g003
Figure 3. Confusion Matrices produced on holdout (20%) of the total training data using RF (A), GBM (B), XGB (C) and stacking (XGB, D) classifiers.
Figure 3. Confusion Matrices produced on holdout (20%) of the total training data using RF (A), GBM (B), XGB (C) and stacking (XGB, D) classifiers.
Preprints 108839 g003

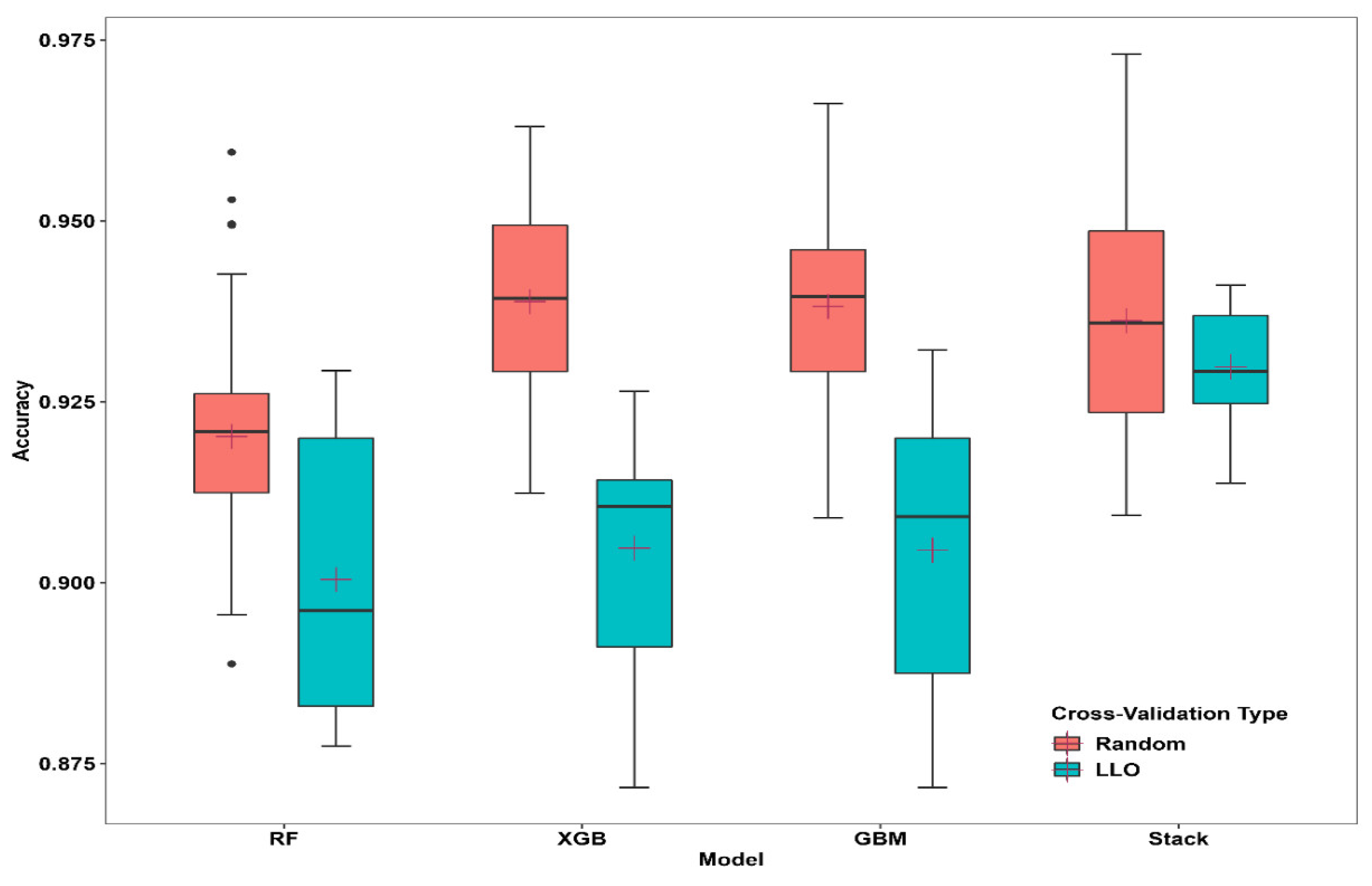
4.2. Identifying and Reducing Overfitting

Both cross-validation approaches produced competitive overall accuracy statistics. Selected base learners and stack models produced higher accuracy statistics when repeated random cross-validation (10 folds, five repetitions). However, the overall accuracy values were reduced when predicted at unknown locations, hinting at spatial overfitting of the models.
Preprints 108839 g004
Figure 4. Box plot of overall accuracy across folds in the base-learner model and meta-learner model using random CV and target-oriented CV. The horizontal black lines in the boxplot indicate the median, and the crosshairs indicate the mean.
Figure 4. Box plot of overall accuracy across folds in the base-learner model and meta-learner model using random CV and target-oriented CV. The horizontal black lines in the boxplot indicate the median, and the crosshairs indicate the mean.
Preprints 108839 g004
A random validation data set that was not part of the training or testing data set showed slightly different statistics on the performance matrices (Table 2). In general, LLO-CV resulted in similar statistics and three accuracy metrics those lower than were produced on holdout data. This indicates that the random CVs in these models could predict better when the testing dataset was closer to the training dataset. On the other hand, LLO-CV showed stable results from the training data set. The Mathews correlation coefficient suggested that all base models and stack models were consistent and produced better spatial prediction abilities (Random-CV [MCC]< LLO-CV [MCC]). The class-level prediction ability of these models varied significantly in both cross-validation strategies (Appendix B).

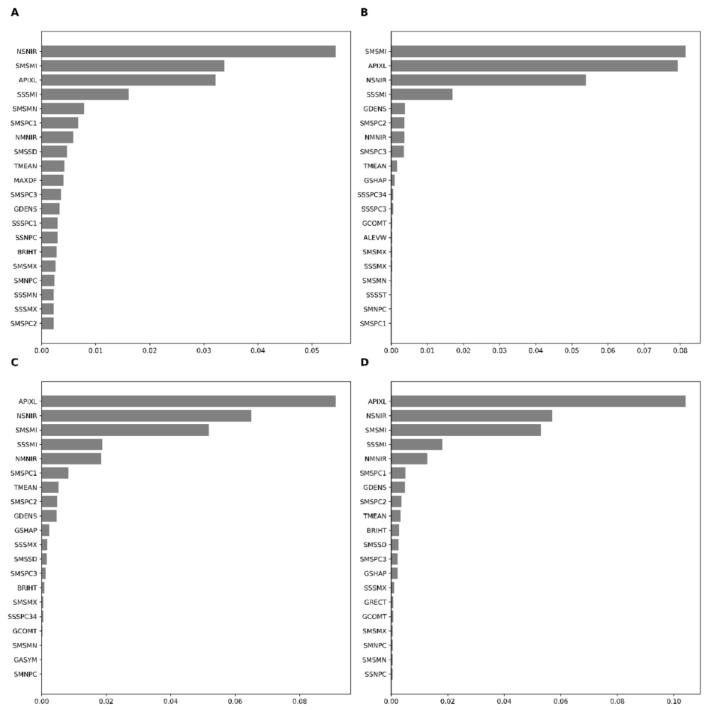
4.3. Contribution of Features

The 20 highest contributing features across base learners (RF, XGB, and GBM), and meta-learner, indicate that SAVI (minimum: SMSMI), SAVI standard deviation (SSSMI), the density of an object (GDENS), NAIP’s near-infrared band standard deviation (NSNIR) and area of the object (AIPXL) were among the essential features. Permutation-based variable importance demonstrated similar features as important features of boosting (GBM and XGB) except few exceptions in the top ten features. For example, the mean GLCM of PCA1 on SAVI was indicated as one of the important features in GBM but not in XGB. The stacking algorithm (meta-learner) found the area of objects (AIPXL) as the most important feature, followed by SMSMI, NSNIR, and SMSSD.
In general, the area of objects, density mean, and standard deviation of SAVI in the time-series sentinel band and the standard deviation on the near-infrared band of NAIP data were among the most significant. On the contrary, the standard deviation from the PCA bands extracted in time-series SAVI layers of the sentinel images was not so crucial in the LLO cross-validations (Figure 5). Random CV demonstrated patterns somewhat similar to those of LLO-CV. The XGB and stacking algorithms precisely identified the same variables as the most critical features in Random-CV (Appendix C). The final map based on stacking and LLO-CV is presented in Figure 6.

4. Discussion

An accurate LULC mapping plays a critical role in land use planning. Accurate LULC mapping using high-resolution imagery is time-relevant despite several land use land cover maps at the national level. Machine learning on remotely sensed data has become widespread and promises to improve classification results over traditional supervised methods [42]. Our study employs object-based implementation of bagging (Random Forest), Boosting (GBM and XGB), and stacking ensemble machine learning in land use land cover mapping. This study showed that super-learners machine learning enables users to enhance the discrimination ability of base learners in multi-class classification problems. The improvement was apparent in the target-oriented cross-validation approach with consistency and reduced overfitting problems in contrast to base learners and meta-learners in random cross-validation approaches. Our results suggest that meta-learners outperform base learners by training weak-performing learners into super-learners. Although the meta-learner showed improved accuracy over base learners, our validation results do not warrant that meta-learner ML models consistently improve discrimination ability among classes. The LLO validation approach demonstrated that the meta-learner was weak in discriminating between grassland, shrubland, and Built-ups. Usually, a variety of ensemble models are subjectively selected to decrease variance (bagging), reduce bias (boosting), and improve the predictive power of the classifier (Stacking). In our case, we used two boosting models based on our initial classification results with different hyperparameters. We did not find significant performance metrics in one of the widely used ensembles of machine learning models, such as SVM. However, studies have shown the improved performance of SVM when used as meta-learners. In stacking ensemble models, each base learner should be carefully selected as a candidate base learner.
Our evaluation showed that the random cross-validation method introduces spatial overfitting when the spatial structure of the data is not considered. All models performed better, producing better evaluation metrics but resulting in smaller accuracy metrics when used with target-oriented validation. This highlights that the discrimination ability of the models increased when the training and testing samples were in proximity. However, when tested with the independent validation dataset, the accuracy metrics performed poorer than usual training/testing data splitting. Unlike random cross-validation, the consistent performance of learners in target-oriented validation methods showed that avoidance of spatial structure in the data could overcome spatial overfitting issues [22,43]. Despite the advocation to account for spatial structure in remote sensing data [44] and its implications of failing to do so, the debate is ongoing on whether spatial validation approaches should be used to improve the model performance [22,45,46]. Such debates usually involve when response variables are on an interval-or-ratio scale because testing assumptions of parametric analysis are straightforward.
However, our approach indicates that spatial structures in the data can still inflate overall model performances if the training data are spatially structured. Mannel et al. [47] reported that the random cross-validation of training data resulted in 5-8% inflation of overall accuracy when training data were autocorrelated. In our case, the overall accuracy overestimation based on random cross-validation ranged from 2 % to 3.4%. Moreover, our approach showed that the spatial structure in the data still exists even after feature selection. A possible limitation of variable selection is based on the fact that different algorithms calculate the importance of the variable differently. For example, RFE depends on the importance of initial model training. RFE removes the least important features until the best subset is determined [32]; however, the algorithm ranks the features without considering their importance and prediction ability in spatial space [43].
Our evaluation of random and target-oriented validation in sentinel time series and NAIP fusion showed that spatial resolution of NAIP, variation in the near-infrared band of NAIP, variations of SAVI, and size of objects were among the most important factors for the assessment of land use land cover in a heterogeneous landscape of Texas. Using time-series sentinel data was to help discriminate vegetation from other classes. However, NAIP DOQQS were captured in the fall, which hindered the generation of meaningful high-resolution information from NAIP data. Moreover, the noise in the data may have cumulative effects due to the use of multi-temporal sentinel data by increasing dimensionality and redundancy. As described above, RFE failed to remove such variables effectively. Feature selection combined with a target-oriented validation approach reduces the overestimation of accuracy.

5. Conclusions

High-resolution Land Use Land Cover (LULC) maps are essential for land use planning, habitat fragmentation, and yield estimation. Therefore, it is axiomatic that more accurate and reliable high-resolution maps can provide a critical decision base for land managers, researchers, and wildlife biologists. However, accurate high-resolution LULC map generation is prohibited by the cost associated with high-resolution remotely sensed data. The National Agricultural Imagery Program (NAIP) in the United States captures high spatial resolution (0.6 m) data every 2-3 years. However, effective use of these data is marred by heterogeneity in sensors, multiple acquisitions, higher volume, and low radiometric resolution. On the other hand, Sentinel spectral bands are slightly coarse (10 to 20 m) but have high temporal, spectral, and radiometric resolutions; they can provide more detailed information over the years.
This study demonstrated the efficacy of sentinel data fusion in NAIP data and the effect of a target-oriented validation approach in reducing spatial overfitting. In multi-class LULC mapping, we demonstrated a 2- 3.5% accuracy inflation using random k-fold cross-validation. Furthermore, independent validation data sets suggested that target-oriented CV produces consistent accuracy metrics, which is consistent with the fact that target-oriented validation avoids overinflation of accuracy metrics.
This study applied widely used bagging algorithms (Random Forest) and Boosting (GBM and XGB) in remote sensing. In addition, we stacked these models to improve the final classification. The main contribution of this research is that meta-learners are just as sensitive to overfitting as base models that are not designed to consider spatial autocorrelation. Therefore, we hypothesized that classification performance could be improved by harvesting spatial resolution from NAIP and time-series information from Sentinel data. Furthermore, the boost algorithms were proficient in discriminating classes compared to bagging. The LULC map generated from stacking dissimilar machine learning models on sentinel fusion in NAIP data coupled with feature selection and target-oriented validation can be pragmatic for improved land use management and assist decision-makers in a cost-effective way of accurate quantification of resources on the ground. Testing different base learners with target-oriented validations in different landscapes on a relatively large scale would offer insight into improving land use land cover data over the existing national dataset.

Author Contributions

Conceptualization, M.S..; methodology, M.S..; software, M.S.; validation, M.S., C.P.Q, R.D.C., N.E.M, S.S.K and G.P.; formal analysis, M.S.; writing—original draft preparation, M.S.; writing—review and editing, M.S., C.P.Q, R.D.C., N.E.M, S.S.K, G.P., X.S; visualization, M.S.; funding acquisition, C.P.Q, S.D.K, N.E.M, S.S.K, and G.P.

Funding

This research was funded by the Texas Comptroller’s Office.

Data Availability Statement

Data sets used in this study are available in registries that are freely accessible to the public. National Agricultural Imagery Program (NAIP) acquired Digital Ortho Quadrangle Quads (DOQQS) data are accessible through EarthExplorer (https://earthexplorer.usgs.gov/) and Sentinel data collected by European Space Agency can be accessed through (https://dataspace.copernicus.eu/, previously https://scihub.copernicus.eu/dhus/#/home ).

Acknowledgments

We thank the Texas Comptroller’s Office for financial assistance with this study. In addition, we extend our thanks to Urbanovsky Foundation for the Research Assistantship to the first author. Finally, thanks are due to the National Agricultural Imagery Program (NAIP) for Digital Ortho Quadrangle Quads (DOQQS) data and European Space Agency for Sentinel data.

Conflicts of Interest

The authors declare no conflicts of interest.

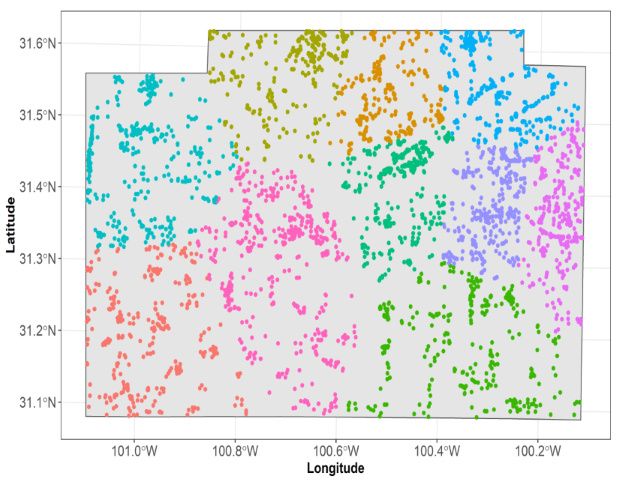
Appendix A

Clustering of training data points. Each color represents the fold in machine learning. We use clustering of k-means on spatial coordinates of training data points to group these data points.
Preprints 108839 i001

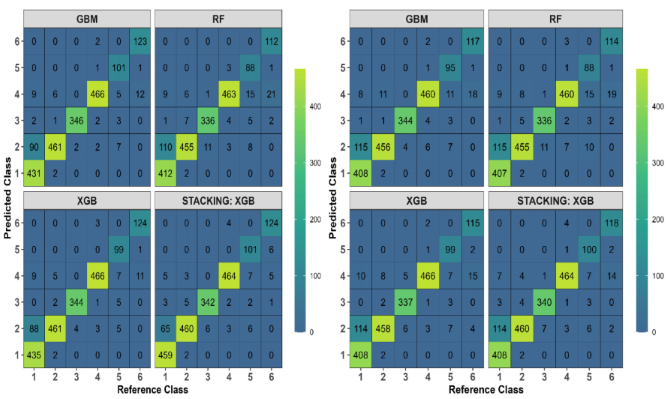
Appendix B: Confusion Matrices produced on Independent Validation Data Points, Left (Random Cross-Validation), Right (Target-Oriented Cross-Validation).. Validation Data Points Were Generated Using Random Sampling, and Labeling Was Performed Using Google Earth Pro.

Preprints 108839 i002

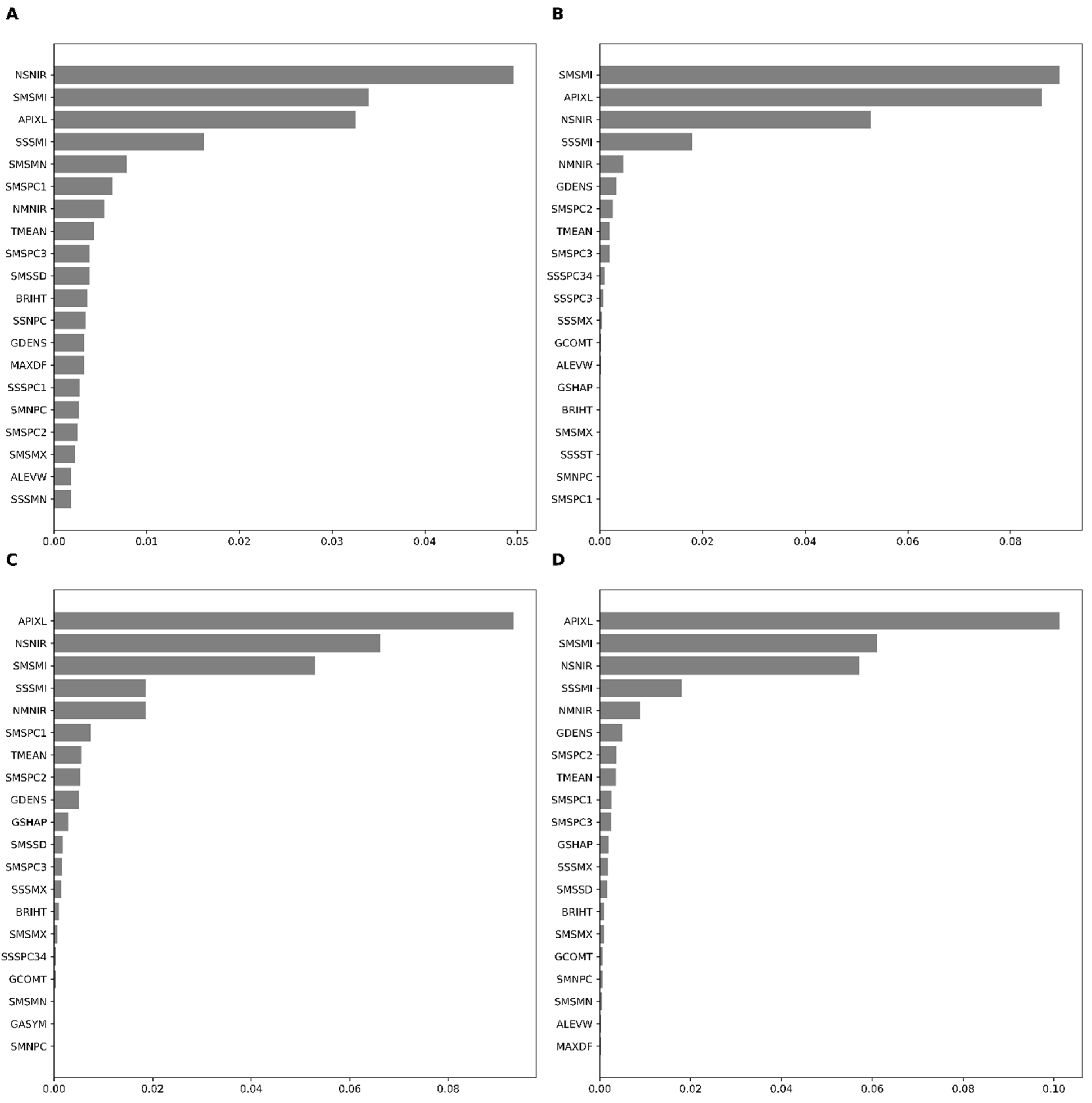
Appendix 3: Permutation-Based Variable Importance of Base Learners (RF (A), GBM (B), XGB (C)) and Stack Learner (Stack-XGB) in Random Cross Validation Approach.

Preprints 108839 i003

Appendix D: Comparisons of Base-Learner and Stacking Ensemble Performance Using Target-Oriented Validation.

Preprints 108839 i004

References

  1. Hirayama, H.; Sharma, R. C.; Tomita, M.; Hara, K. Evaluating Multiple Classifier System for the Reduction of Salt-and-Pepper Noise in the Classification of Very-High-Resolution Satellite Images. Int. J. Remote Sens. 2019, 40, 2542–2557. [Google Scholar] [CrossRef]
  2. Maxwell, A. E.; Strager, M. P.; Warner, T. A.; Zégre, N. P.; Yuill, C. B. Comparison of NAIP Orthophotography and Rapideye Satellite Imagery for Mapping of Mining and Mine Reclamation. GIScience Remote Sens. 2014, 51, 301–320. [Google Scholar] [CrossRef]
  3. Homer, C. G. C.; Dewitz, J. A. J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N. D. N.; Wickham, J. D. J.; Megown, K. Completion of the 2011 National Land Cover Database for the Conterminous United States-Representing a Decade of Land Cover Change Information; 2015; Vol. 81. [CrossRef]
  4. Fry, J. A.; Xian, G.; Jin, S.; Dewitz, J. A.; Homer, C. G.; Yang, L.; Barnes, C. A.; Herold, N. D.; Wickham, J. D. Completion of the 2006 National Land Cover Database for the Conterminous United States. Photogramm. Eng. Remote Sensing 2011, 77, 858–864. [Google Scholar]
  5. Castilla, G.; Hay, G. J. Image Objects and Geographic Objects BT - Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G. J., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2008; pp. 91–110. [Google Scholar] [CrossRef]
  6. Hayes, M. M.; Miller, S. N.; Murphy, M. A. High-Resolution Landcover Classification Using Random Forest. Remote Sens. Lett. 2014, 5, 112–121. [Google Scholar] [CrossRef]
  7. Knight, J. F.; Tolcser, B. P.; Corcoran, J. M.; Rampi, L. P. The Effects of Data Selection and Thematic Detail on the Accuracy of High Spatial Resolution Wetland Classifications. Photogramm. Eng. Remote Sensing 2013, 79, 613–623. [Google Scholar] [CrossRef]
  8. Zurqani, H. A.; Post, C. J.; Mikhailova, E. A.; Cope, M. P.; Allen, J. S.; Lytle, B. A. Evaluating the Integrity of Forested Riparian Buffers over a Large Area Using LiDAR Data and Google Earth Engine. Sci. Rep. 2020, 1–16. [Google Scholar] [CrossRef] [PubMed]
  9. Subedi, M. R.; Portillo-Quintero, C.; Kahl, S. S.; McIntyre, N. E.; Cox, R. D.; Perry, G. Leveraging NAIP Imagery for Accurate Large-Area Land Use/Land Cover Mapping: A Case Study in Central Texas. Photogramm. Eng. Remote Sens. 2023, 89, 547–560. [Google Scholar] [CrossRef]
  10. Li, X.; Shao, G. Object-Based Land-Cover Mapping with High Resolution Aerial Photography at a County Scale in Midwestern USA. Remote Sens. 2014, 6, 11372–11390. [Google Scholar] [CrossRef]
  11. Zylshal; Sulma, S. ; Yulianto, F.; Nugroho, J. T.; Sofan, P. A Support Vector Machine Object Based Image Analysis Approach on Urban Green Space Extraction Using Pleiades-1A Imagery. Model. Earth Syst. Environ. 2016, 2, 54. [Google Scholar] [CrossRef]
  12. Tzotsos, A.; Argialas, D. Support Vector Machine Classification for Object-Based Image Analysis. In Object-Based Image Analysis; Springer, 2008; pp 663–677.
  13. Ruiz, L. Á.; Recio, J. A.; Crespo-Peremarch, P.; Sapena, M. An Object-Based Approach for Mapping Forest Structural Types Based on Low-Density LiDAR and Multispectral Imagery. Geocarto Int. 2018, 33, 443–457. [Google Scholar] [CrossRef]
  14. Amini, S.; Homayouni, S.; Safari, A.; Darvishsefat, A. A. Object-Based Classification of Hyperspectral Data Using Random Forest Algorithm. Geo-Spatial Inf. Sci. 2018, 21, 127–138. [Google Scholar] [CrossRef]
  15. van Leeuwen, B.; Tobak, Z.; Kovács, F. Machine Learning Techniques for Land Use/Land Cover Classification of Medium Resolution Optical Satellite Imagery Focusing on Temporary Inundated Areas. J. Environ. Geogr. 2020, 13, (1–2). [Google Scholar] [CrossRef]
  16. Myint, S. W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-Pixel vs. Object-Based Classification of Urban Land Cover Extraction Using High Spatial Resolution Imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
  17. Yu, Q.; Gong, P.; Clinton, N.; Biging, G.; Kelly, M.; Schirokauer, D. Object-Based Detailed Vegetation Classification with Airborne High Spatial Resolution Remote Sensing Imagery. Photogramm. Eng. Remote Sensing 2006, 72, 799–811. [Google Scholar] [CrossRef]
  18. Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; Gao, J.; Zhang, L. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
  19. Legendre, P.; Dale, M. R. T.; Fortin, M. J.; Gurevitch, J.; Hohn, M.; Myers, D. The Consequences of Spatial Structure for the Design and Analysis of Ecological Field Surveys. Ecography (Cop.). 2002, 25, 601–615. [Google Scholar] [CrossRef]
  20. Getis, A. A History of the Concept of Spatial Autocorrelation: A Geographer’s Perspective. Geogr. Anal. 2008. [Google Scholar] [CrossRef]
  21. Stehman, S. V.; Foody, G. M. Key Issues in Rigorous Accuracy Assessment of Land Cover Products. Remote Sens. Environ. 2019, 231, 111199. [Google Scholar] [CrossRef]
  22. Roberts, D. R.; Bahn, V.; Ciuti, S.; Boyce, M. S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J. J.; Schröder, B.; Thuiller, W.; Warton, D. I.; Wintle, B. A.; Hartig, F.; Dormann, C. F. Cross-Validation Strategies for Data with Temporal, Spatial, Hierarchical, or Phylogenetic Structure. Ecography (Cop.). 2017, 40, 913–929. [Google Scholar] [CrossRef]
  23. Griffith, G. E.; Bryce, S.; Omernik, J.; Rogers, A. Ecoregions of Texas; 2007.
  24. Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; Meygret, A.; Spoto, F.; Sy, O.; Marchese, F.; Bargellini, P. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
  25. Hagolle, O.; Sylvander, S.; Huc, M.; Claverie, M.; Clesse, D.; Dechoz, C.; Lonjou, V.; Poulain, V. SPOT-4 (Take 5): Simulation of Sentinel-2 Time Series on 45 Large Sites. Remote Sens. 2015, 7, 12242–12264. [Google Scholar] [CrossRef]
  26. Legendre, P.; Legendre, L. Numerical Ecology, Third.; Elsevier, 2012.
  27. Good, E. J.; Kong, X.; Embury, O.; Merchant, C. J.; Remedios, J. J. An Infrared Desert Dust Index for the Along-Track Scanning Radiometers. Remote Sens. Environ. 2012, 116, 159–176. [Google Scholar] [CrossRef]
  28. Franklin, S. E.; Wulder, M. A.; Gerylo, G. R. Texture Analysis of IKONOS Panchromatic Data for Douglas-Fir Forest Age Class Separability in British Columbia. Int. J. Remote Sens. 2001, 22, 2627–2632. [Google Scholar] [CrossRef]
  29. Haralick, R. M.; Dinstein, I.; Shanmugam, K. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973; SMC-3, 610–621. [Google Scholar] [CrossRef]
  30. Trimble. ECognition Developer 9;Sunnyvale, CA, USA. Sunnyvale, CA, USA 2020.
  31. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; Perrot, M.; Duchesnay, E. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  32. Kuhn, M.; Johnson, K. Classification Trees and Rule-Based Models BT - Applied Predictive Modeling; Kuhn, M., Johnson, K., Eds.; Springer New York: New York, NY, 2013; pp. 369–413. [Google Scholar] [CrossRef]
  33. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  34. Silveyra Gonzalez, R.; Latifi, H.; Weinacker, H.; Dees, M.; Koch, B.; Heurich, M. Integrating LiDAR and High-Resolution Imagery for Object-Based Mapping of Forest Habitats in a Heterogeneous Temperate Forest Landscape. Int. J. Remote Sens. 2018, 39, 8859–8884. [Google Scholar] [CrossRef]
  35. Guo, L.; Chehata, N.; Mallet, C.; Boukir, S. Relevance of Airborne Lidar and Multispectral Image Data for Urban Scene Classification Using Random Forests. ISPRS J. Photogramm. Remote Sens. 2011, 66, 56–66. [Google Scholar] [CrossRef]
  36. Friedman, J. Greedy Function Approximation : A Gradient Boosting Machine Author ( s ): Jerome H. Friedman Source : The Annals of Statistics, Vol. 29, No. 5 ( Oct., 2001 ), Pp. 1189-1232 Published by : Institute of Mathematical Statistics Stable URL : Http://Www. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar]
  37. Feng, J.; Xu, Y.-X.; Jiang, Y.; Zhou, Z.-H. Soft Gradient Boosting Machine. 2020, 1–16.
  38. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, California,, USA: ACM; 2016; pp. 785–794. [Google Scholar]
  39. Wolpert, D. Stacked Generalization. Neural Networks 1992, 5, 241–259. [Google Scholar] [CrossRef]
  40. Congalton, R. G. A Review of Assessing the Accuracy of Classifications of Remotely Sensed Data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
  41. Matthews, B. W. Comparison of the Predicted and Observed Secondary Structure of T4 Phage Lysozyme. Biochim. Biophys. Acta - Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef] [PubMed]
  42. Dou, J.; Yunus, A. P.; Bui, D. T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C. W.; Han, Z.; Pham, B. T. Improved Landslide Assessment Using Support Vector Machine with Bagging, Boosting, and Stacking Ensemble Machine Learning Framework in a Mountainous Watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
  43. Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving Performance of Spatio-Temporal Machine Learning Models Using Forward Feature Selection and Target-Oriented Validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
  44. Congalton, R. G. A Comparison of Sampling Schemes Used in Generating Error Matrices for Assessing the Accuracy of Maps Generated from Remotely Sensed Data. Photogramm. Eng. Remote Sens. 1998, 54, 593–600. [Google Scholar]
  45. Wadoux, A. M. J. C.; Heuvelink, G. B. M.; de Bruin, S.; Brus, D. J. Spatial Cross-Validation Is Not the Right Way to Evaluate Map Accuracy. Ecol. Modell. 2021, 457, 109692. [Google Scholar] [CrossRef]
  46. Karasiak, N.; Dejoux, J. F.; Monteil, C.; Sheeren, D. Spatial Dependence between Training and Test Sets: Another Pitfall of Classification Accuracy Assessment in Remote Sensing. Mach. Learn. 2021. No. 0123456789. [Google Scholar] [CrossRef]
  47. Mannel, S.; Price, M.; Hua, D. Impact of Reference Datasets and Autocorrelation on Classification Accuracy. Int. J. Remote Sens. 2011, 32, 5321–5330. [Google Scholar] [CrossRef]
Preprints 108839 g001
Figure 1. Study Area, within a red rectangle, with a red, green, and blue combination of the Sentinel 2A image of June 2018. The black line indicates the administrative boundary of Irion and Tom Green counties. Overview of the study area within the context of Texas.
Figure 1. Study Area, within a red rectangle, with a red, green, and blue combination of the Sentinel 2A image of June 2018. The black line indicates the administrative boundary of Irion and Tom Green counties. Overview of the study area within the context of Texas.
Preprints 108839 g001
Preprints 108839 g002
Figure 2. A schematic overview of stacking ensemble machine learning using bagging and boosting algorithms.
Figure 2. A schematic overview of stacking ensemble machine learning using bagging and boosting algorithms.
Preprints 108839 g002
Preprints 108839 g005
Figure 5. Permutation-based feature importance of RF (A), GBM (B), XGB (C), and stack (D) models in target-oriented validation.
Figure 5. Permutation-based feature importance of RF (A), GBM (B), XGB (C), and stack (D) models in target-oriented validation.
Preprints 108839 g005
Preprints 108839 g006
Figure 6. Classified map of the study area based on the stacking model (meta-learner) using target-oriented cross-validation. Several subsets in the study area using Level 0 and Level 1 are presented in Appendix D.
Figure 6. Classified map of the study area based on the stacking model (meta-learner) using target-oriented cross-validation. Several subsets in the study area using Level 0 and Level 1 are presented in Appendix D.
Preprints 108839 g006
Table 2. Accuracy metrics produced in the independent validation dataset. These metrics were produced on the confusion matrix.
Table 2. Accuracy metrics produced in the independent validation dataset. These metrics were produced on the confusion matrix.
Cross-Validation Classifier Accuracy Metrics (%)
Overall Accuracy Kappa MCC
Random-CV RF 89.64 86.94 87.45
GBM 90.6 88.17 88.54
XGB 90.75 88.35 88.75
LLO-CV STACK 91.08 88.79 89.15
RF 89.93 87.31 87.77
GBM 92.92 91.09 91.26
XGB 92.96 91.15 91.33
STACK 93.98 92.43 92.57
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated