The Impact of Pause and Filler Words Encoding on Dementia Detection with Contrastive Learning

Dementia, primarily caused by neurodegenerative diseases like Alzheimer’s disease (AD), affects millions worldwide, making detection and monitoring crucial. To enable these tasks, we propose encoding in-text pauses and filler words (i.e., “uh” and “um”) in text-based language models, and thoroughly evaluate their effect in performance. Additionally, we suggest using contrastive learning to improve performance in a multi-task framework. Our results demonstrated the effectiveness of our approaches in enhancing the model’s performance, achieving 87% accuracy and an 86% F1-score. Compared to the state-of-the-art, our approach has similar performance despite having significantly fewer parameters. This highlights the importance of pause and filler word encoding on the detection of dementia.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Dementia is a progressive cognitive disorder caused by neurodegenerative diseases, with Alzheimer’s disease (AD) being the most prevalent form [1]. AD accounts for a significant majority of dementia cases, affecting millions worldwide. Given the extensive impact of AD and the current lack of a cure, early detection of dementia is crucial. Detecting the disease in its early stages can allow for timely intervention, which can slow the progression of symptoms and provide better management options. Early diagnosis can greatly improve the quality of life for individuals living with dementia, enabling them and their families to plan and access support sooner [2].

In recent years, Deep Neural Networks (DNNs) have shown considerable promise in this area. By utilizing DNNs, models can be enhanced with data features that facilitate the early detection of dementia. Researchers have employed audio recordings, textual data, and biomedical imaging to detect dementia. In this paper, we focus specifically on textual data to leverage large language models (LLMs). LLMs are pre-trained models trained on vast corpora of data from various topics. Some well-known LLMs include BERT and its variants [3,4], GPT-3 [5], and others. These models contain contextual information within the text, enabling the extraction of syntactic and semantic information. Due to this contextualized training, they excel in downstream tasks such as semantic analysis, question answering, and named entity recognition [6,7,8].

In the literature, researchers employ various approaches for classification based on textual data. In early attempts, researchers fed the textual data to models after applying specific data-cleaning techniques [9,10]. Some studies suggest using transfer learning through LLMs to leverage their enriched features [11,12]. Other researchers have introduced innovative methods, such as contrastive learning (CL), which involves learning from the data itself to separate the feature space for each class [13,14]. Due to the limited data available in this field, several authors have proposed various augmentation techniques to mitigate this issue [15,16,17]. These augmentation methods aim to increase the dataset size, enhancing the model’s ability to generalize and perform better.

In [11,18], the authors proposed a technique where pause information is encoded within the text, a feature typically used in speech-based analysis. Pauses are introduced using special characters, enabling the language model to recognize these features, which has been shown to enhance model performance. In [11], for their experiments, the authors utilized the ADReSS dataset [19] and employed temporal word alignment to implement their methodology. Building on this idea, we apply a similar concept to the Pitt Corpus Cookie Theft dataset [20]. However, we take a different approach in our modeling that does not involve temporal word alignment, which follows the directions in [18]. Instead, we explore alternative methods to encode pauses and language information directly within the textual data. This approach allows us to investigate the impact of pause information on model performance, potentially offering new insights into dementia detection through textual analysis.

Another approach of interest in this paper is contrastive learning (CL). Researchers have adopted contrastive methods to perform dementia detection, relying on the data itself to improve the representation space to enhance model performance. In this paper, we employ a technique called dual contrastive learning (DualCL) [21], which has demonstrated strong performance with general textual data. In Section 3.3, we provide a detailed explanation of this methodology.

The main objective of this paper is to enhance model accuracy through the exploration of in-text encoding and contrastive learning, which can be considered a multi-task learning scheme. As shown in [22,23,24], multi-task learning can be beneficial in improving model performance. To achieve this, we will utilize LLMs (transfer learning). Our findings suggest that these approaches are effective in improving model performance. Below, we summarized our contributions:

Proposing in-text pause and other language features (uh/um) encoding.
Thoroughly evaluating different pauses to provide insight on how they affect model performance.
Proposing the use a contrastive learning to improve performance.
Combining in-text pause encoding and DualCL in a multitask manner.

To the best of the authors’ knowledge, the proposed approaches as stated above and in subsequent sections have not been explored by other authors in the literature. Our work extends our previous research presented in [18], where we initially introduced in-text encoding. The differences between our new work and the previous one are summarized in our contributions.

Our paper is organized as follows: in Section 2, the dataset preparation, in-text pause encoding, and contrastive learning scheme are explained in details. In Section 3, The results for all the experiments are presented. In Section 4, our results are discussed in a broad sense in the field. In Section 5, The paper is concluded.

2. Materials and Methods

In this section, we outline the data preparation and modeling steps necessary. First, in the data preparation step, the data is cleaned and standardized. In the second step, in-text encoding schemes are introduced. Finally, the models are presented.

2.1. Dataset Preparation

In this study, the Pitt Corpus Cookie Theft dataset [20] from DementiaBank is used. These transcripts are rich in detail, including the patients’ demographic information like gender and age, as well as clinical data such as dementia severity. Additionally, they contain syntactic details to ensure language consistency, timestamps, and dialogues between researchers and participants. This dataset contains 243 and 305 recordings and CHAT style transcriptions for control and dementia groups, respectively. Throughout our experiments, we use the transcriptions for our training and evaluation. For our analysis, we specifically exclude certain special characters found in the conversations, such as "[//]", "&-uh", "&=laughs", among others. Each of these symbols has its meaning, which can be found in the DementiaBank documentation [20].

2.2. In-Text Pause Encoding

In this section, an in-text pause encoding scheme is explained. In this methodology, a relationship between pauses and dementia diagnosis within the textual information is explored. Lately, this topic has been of interest in the literature [11,18] in which the classification is done based on the frequency and duration of pauses within the speech.

An important reason to use textual information over audio recordings is that while audio recordings are very rich in information, they are very complex and require significant computational resources to properly be utilized. Additionally, transcripts from standard tests provide an additional layer of privacy. The transcripts of the audio can be obtained once and they can be used for training and evaluation. The transcription can be done by very powerful tools such as Whisper [25] and Wave2vec [26] models.

As mentioned in Section 2.1, for our experiments the Cookie Theft dataset is used in our study. We follow the same methodology as was introduced in [18] to construct the in-text pause encodings. In the dataset, some special characters indicate different pause lengths. To be specific, the symbols “(.)”, “(..)”, and “(...)” represent short, medium, and long pauses, respectively. These pauses are measured in seconds or a fraction of a second, depending on the type of the pause. For short, medium, and long pause the pause lengths are under 0.5 sec, 0.5-2 sec, and over 2 sec, respectively [11]. We replace these symbols with “Sh”, “Me”, and “Lo” to be inserted within the text. Also, a vector that contains the frequency of each pause is used in our analysis.

Given a sample text of the form

“ seg 1 (. . .) seg 2 (.) seg 3 (. .) . . .^{''},

we introduce the following encodings: In-place (I), End-Sequence (S), Frequency (F), and Vector (V). Each of these combinations can be present or absent in the encoding, which results in 16 different combinations in total. The base text takes the form

“ seg 1 seg 2 seg 3 . . . “ .

The baseline where no encoding and vector information is included is represented by

B_{0}

. The experiments showed that models performed better when they were provided with a secondary numerical vector input corresponding to the frequencies of the pauses in the form

[# Sh, # Me, # Lo],

where #Sh, #Me and #Lo represent the number of short, medium, and long pauses, respectively. It should be mentioned that all the combinations include the secondary vector input, which has its secondary model.

For example, if a text only contains the in-place encoding, it is represented as

E_{I_{1}, S_{0}, F_{0}, V_{0}}

. In this case, our samples text takes the form

“ seg 1 \begin{matrix} Lo \end{matrix} seg 2 \begin{matrix} So \end{matrix} seg 3 \begin{matrix} Me \end{matrix} . . . “

The end-sequence encoding, attaches all the pauses in the order that they are happening in the text to the end of the text as follows:

“ seg 1 seg 2 seg 3 . . . \begin{matrix} Lo \end{matrix} \begin{matrix} Sh \end{matrix} \begin{matrix} Me \end{matrix} . . . “ .

The third encoding, frequency encoding, creates a text with the count of each pause type attached to each pause type (e.g. “Sh”) and is attached to the end of the text as follows:

“ seg 1 seg 2 seg 3 . . . \begin{matrix} # Sh \end{matrix} \begin{matrix} Sh \end{matrix} \begin{matrix} # Me \end{matrix} \begin{matrix} Me \end{matrix} \begin{matrix} # Lo \end{matrix} \begin{matrix} Lo \end{matrix} “,

Lastly, the vector encoding is similar to the frequency encoding, but the pause type is not included in the encoding. It can be shown as follows:

“ seg 1 seg 2 seg 3 . . . \begin{matrix} # Sh \end{matrix} \begin{matrix} # Me \end{matrix} \begin{matrix} # Lo \end{matrix} “ .

As an example, the model with input that include frequency and vector encoding is represented as

E_{I_{0}, S_{0}, F_{1}, V_{1}}

. All 16 different combinations can be seen in Table 1. All combinations are explored in Section 3.

It should be mentioned that later in our experiments, specific symbol that have been discarded from the text, "uh" and "um", will be added to the text to add more language features to the pipeline and study their effects.

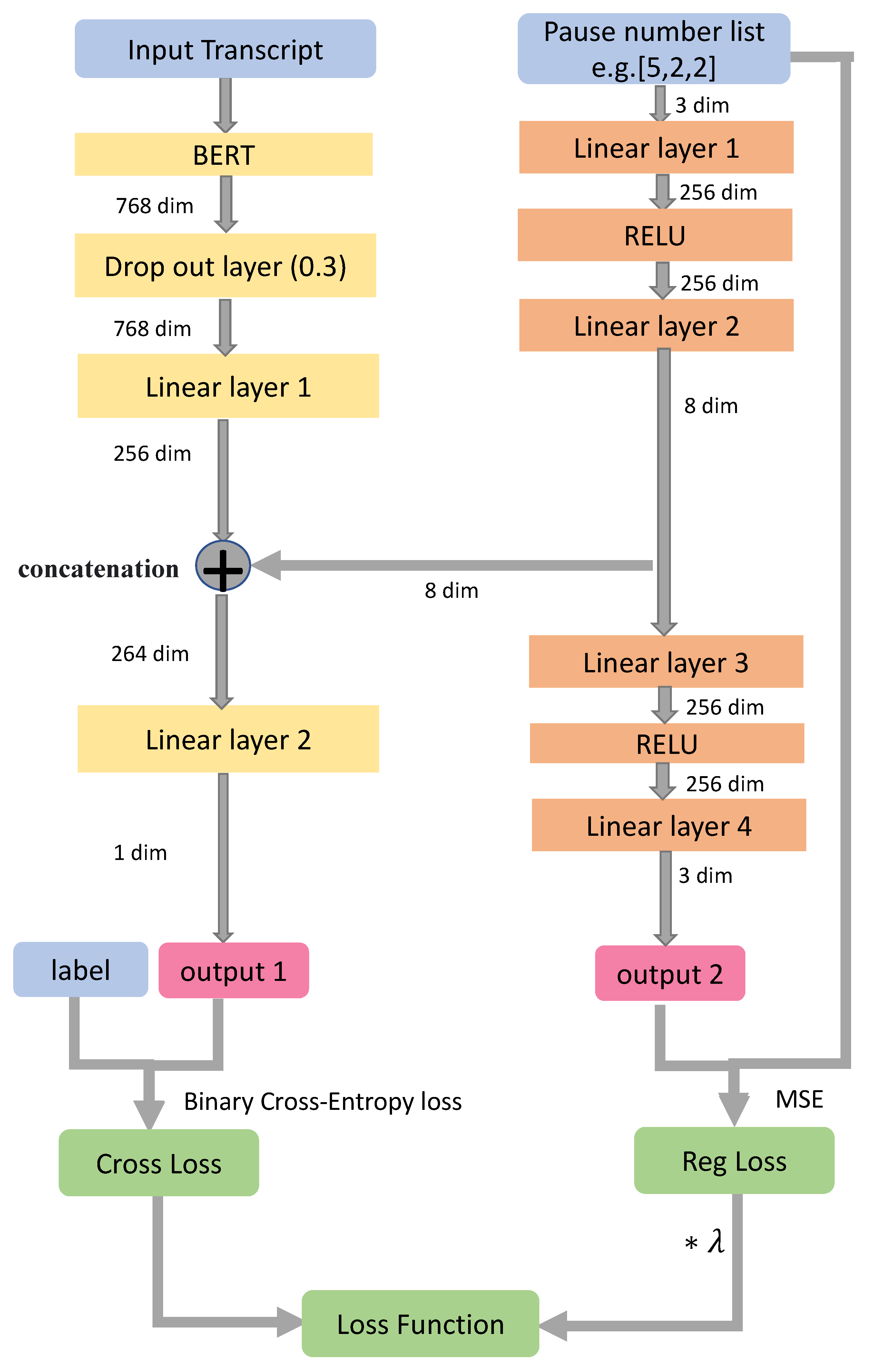
2.3. Modeling

In this section, we present the modeling for our two different approaches. In the first case, a classifier based on cross-entropy is introduced. In the second case, a constrative learning approach is utilized. Both models are formulated within a multi-task setup.

2.3.1. Model for In-Text Encoding Scheme

In this section, the model for training and inference using in-text encoding is described. In order to leverage the pre-trained LLMs, the BERT-base-uncased model [27] is serving as our base model to extract features for the classification layers. These layers consist of a dropout layer and two linear layers. Additionally, a secondary network that processes frequency vectors is laid out. This network consists of linear layers in an auto-encoder format. This network will serve as a regularizer for the main network. The model is depicted in the Figure 1. The primary network makes use of a classification loss, and the secondary network incorporates a regularization loss. As shown in [28], several architectures were considered to get the best fit for our this task.

For the classification loss, cross-entropy is used as follows

L_{C l a s s i f i c a t i o n} = \sum_{i = 1}^{N} C E (y_{i}, {\hat{y}}_{i}),

where

C E, y_{i}, {\hat{y}}_{i}

, and N are the cross-entropy loss, ground-truth label, predicted label, and number of samples, respectively. For the regularization loss, the mean square error (MSE) loss is used as follows

L_{R e g u l a r i z a t i o n} = M S E (V_{F}, {\hat{V}}_{F}),

where

V_{F}

and

{\hat{V}}_{F}

are true frequency input and its reconstruction, respectively. So, the total optimization cost becomes

L = L_{C l a s s i f i c a t i o n} + λ L_{R e g u l a r i z a t i o n},

where

λ

is a hyper-parameter to be optimized.

It should be noted that the secondary network is present for all the experiments, except for the baseline

B_{0}

2.3.2. Contrastive Learning

In this section, we propose using CL for classification. CL is a well-established approach that employs pairs of positive and negative examples to guide the deep learning model. Over time, CL has gained significant traction, surpassing earlier benchmarks and enhancing performance in fully supervised, semi-supervised, and self-supervised learning environments.

The core of CL is the creation of meaningful representations through the comparison of positive and negative instance pairings. The essential principle is that in an embedded space, similar examples should be close together, while distinct instances should be farther apart. CL helps models find relevant features and similarities in the dataset by approaching learning as a differentiation process.

In this paper, we will be using an approach that authors in [21] proposed. The authors proposed the Dual Contrastive Learning (DualCL) framework that is a method that concurrently trains on the features of input samples and the parameters of classifiers. Essentially, DualCL treats the classifier parameters as extended samples linked to various labels. It then leverages CL to draw comparisons between these input samples and the extended, or augmented, samples. This approach allows for a more integrated and holistic learning process, where both the sample features and classifier parameters are understood and developed in relation to each other.

In this section, we go over the modeling portion of the experiments. We borrow the notations from [21]. The focus is on a text classification task encompassing K different classes. The dataset under consideration, denoted as

{\{x_{i}, y_{i}\}}_{i = 1}^{N}

, comprises N individual training instances. Each instance consists of an input sentence

x_{i} \in R^{L}

, comprising L words, alongside its corresponding label

y_{i}

. For clarity, the study uses

I = {1, 2, \dots, N}

to represent the index set of the training samples and

K = {1, 2, \dots, K}

to denote the index set of the labels.

We explore the self-supervised contrastive learning. This technique involves a dataset of N training samples, each accompanied by at least one augmented version within the set. If

j (i)

represents the index of the augmented sample originating from the i-th sample, the standard formula for contrastive loss is as follows:

L_{self} = \frac{1}{N} \sum_{i \in I} - log \frac{exp (z_{i} \cdot z_{j (i)} / τ)}{\sum_{a \in A_{i}} exp (z_{i} \cdot z_{a} / τ)}

where

z_{i}

signifies the normalized form of

x_{i}

. The set

A_{i} : = I ∖ {i}

is the contrastive samples’ set. The dot product is represented by the symbol ·, and

τ > 0

acts as the temperature factor. In this context, the i-th sample is labeled as the anchor, the

j (i)

-th sample is considered a positive sample, and the rest of the samples, totaling

N - 2

, are deemed negative in relation to the i-th sample.

In the context of feature representation

z_{i}

and classifier

θ_{i}

for a given input example

x_{i}

, the goal is to align the softmax transformation of

θ_{i} \cdot z_{i}

with the actual label of

x_{i}

. The column of

θ_{i}

that corresponds to the true label of

x_{i}

is represented as

θ_{i}^{*}

. The objective is to maximize the dot product

θ_{i}^{*} \cdot z_{i}

, thereby enhancing the representation of both

θ_{i}

and

z_{i}

with supervised learning.

To achieve this, the dual contrastive loss is introduced. This loss function aims to maximize the dot product

θ_{i}^{*} \cdot z_{j}

when

x_{j}

shares the same label as

x_{i}

, and minimize it when

x_{j}

has a different label. This approach is designed to leverage the relationships between various training samples, effectively distinguishing between those with similar and dissimilar labels.

For a given anchor

z_{i}

, derived from the input

x_{i}

, we categorize

{\{θ_{j}^{*}\}}_{j \in P_{i}}

as positive samples and

{\{θ_{j}^{*}\}}_{j \in A_{i} ∖ P_{i}}

as negative samples. The contrastive loss is then defined as:

L_{z} = \frac{1}{N} \sum_{i \in I} \frac{1}{|P_{i}|} \sum_{p \in P_{i}} - log \frac{exp (θ_{p}^{*} \cdot z_{i} / τ)}{\sum_{a \in A_{i}} exp (θ_{a}^{*} \cdot z_{i} / τ)}

In this formula,

τ

is a positive real number that serves as the temperature factor. The set

A_{i} : = I ∖ {i}

includes the indices of all contrastive samples, while

P_{i} : = \{p \in A_{i}

y_{p} = y_{i}\}

denotes the set of positive sample indices. The term

|P_{i}|

represents the size or cardinality.

To continue, with

θ_{i}^{*}

as the anchor,

{\{z_{j}\}}_{j \in P_{i}}

are considered positive samples, and

{\{z_{j}\}}_{j \in A_{i} ∖ P_{i}}

are negative samples. This forms the basis for another type of contrastive loss, defined as:

L_{θ} = \frac{1}{N} \sum_{i \in I} \frac{1}{|P_{i}|} \sum_{p \in P_{i}} - log \frac{exp (θ_{i}^{*} \cdot z_{p} / τ)}{\sum_{a \in A_{i}} exp (θ_{i}^{*} \cdot z_{a} / τ)}

The dual contrastive loss then combines these two contrastive loss terms:

L_{Dual} = L_{z} + L_{θ}

In the joint training and prediction phase, the goal is to ensure that

θ_{i}

is an effective classifier for

z_{i}

. This is achieved using a modified cross-entropy loss, designed to maximize

θ_{i}^{*} \cdot z_{i}

for each input

x_{i}

L_{CE} = \frac{1}{N} \sum_{i \in I} - log \frac{exp (θ_{i}^{*} \cdot z_{i})}{\sum_{k \in K} exp (θ_{i}^{k} \cdot z_{i})},

where

θ_{i}^{k}

is the k-th column of

θ_{i}

To train the encoder f effectively, both training objectives are minimized simultaneously, enhancing the quality of the feature representations and the classifiers. The overall loss function is given as:

L_{overall} = (1 - α) L_{CE} + α L_{Dual}

Here,

α

is a hyperparameter that modulates the impact of the dual contrastive loss in the overall training process. Later on in our experiments,

L_{R e g u l a r i z a t i o n}

will be added to the

L_{overall}

as follows

L_{overall} = (1 - α) L_{CE} + α L_{Dual} + λ L_{R e g u l a r i z a t i o n},

where

λ

is a hyperparameter to be optimized. This formulation will benefit from the secondary network shown in Figure 1. It represents a clear multi-task learning paradigm, from which the training can greatly benefit. Our experiments in Section 3.3 demonstrated that this is indeed the case.

3. Results

In this section, we go over the impact of in-text encoding of pauses (Section 3.1) and filler words (Section 3.2). In Section 3.3, we study the effects of CL on the model performance.

3.1. In-Text Pause Encoding Results

We study the effect of in-text encoding on model performance. The results are summarized in Table 2. The row for

B_{0}

corresponds to the base model without any in-text encoding information available. All 16 combinations mentioned in the Table 1 have been explored. In all experiments, we used 20-fold cross-validation to evaluate the results. We used Adam optimizer [29] with default parameters. For

λ

, we chose 0.75. For each fold, all models are trained for 20 epochs and best performance are reported.

As can be seen, for the

E_{I_{0}, S_{0}, F_{0}, V_{0}}

model, performance is around 0.58 and 0.56 for accuracy and f1-score, respectively. In this case, no in-text encoding is applied. For

E_{I_{1}, S_{0}, F_{0}, V_{0}}

, where in-text encoding is applied, we observe a drop in performance but still within the standard deviation of the model with no in-text encoding. This indicates that in-place encoding is not helpful on its own. For all other encodings, we observe a significant performance boost compared to the first two encodings. In particular, Encoding

E_{I_{1}, S_{0}, F_{1}, V_{0}}

, where in-place pauses and their corresponding frequencies are combined achieved the highest accuracy and f1-score, 0.84 and 0.85, respectively. In all experiments in Table 2, all artifacts and symbols are removed from the text, including “uh” and “um” filler words.

We also explored the effect of introducing single pauses (short, medium, or long), or a pair of them but did not observe a clear pattern that lead us to believe that one combination is better than the others. Appendix A provides the details of this analysis.

3.2. Filler Word Encoding Results

We expand our previous analysis by considering the filler words “uh” and “um”. It’s been shown that filler word count plays a role in differentiating the dementia group from the control group [30,31,32]. Our results are presented in three phases as shown in Table 3. We either fix the encoding for filler words and vary the encoding for the pauses, or vice versa. For phase 1, we fix the encoding for the filler words to use

F i l l e r (E_{I_{0}, S_{0}, F_{0}, V_{0}})

, i.e., we only include the vector of counts, and vary the encoding for the pauses. For phase 2, we fix the encoding of the pauses to use

P a u s e (E_{I_{1}, S_{1}, F_{1}, V_{1}})

, i.e., the pause in which all pause encoding are present, and vary the filler word encoding. Finally, for phase 3, we fix the encoding of the filler words to

F i l l e r (E_{I_{1}, S_{1}, F_{0}, V_{1}})

and vary the encoding for the pauses. The motivation of this analysis is to measure the impact of different choices of pause and filler word encoding.

In phase 1,

F i l l e r (E_{I_{0}, S_{0}, F_{0}, V_{0}})

has been used where only the filler words (i.e., uh/um) are added to the text. Compared to the best results in Table 2, a 1% performance enhancement can be seen in terms of f1-score over multiple encodings. Although the average performance is the same as in Table 2, individual encodings showed better performance in most cases. This fact motivated phase 2 experiments.

Given the improvements by adding uh/um to the text, we started to encode them as we did for pause information. In phase 2, a new I, S, F, V is introduced for the uh/um encoding. To find which of these combinations result in the best performance, we first fixed a pause encoding,

P a u s e (E_{I_{1}, S_{1}, F_{1}, V_{1}})

, to perform this experiment. It can be observed that the

F i l l e r (E_{I_{1}, S_{1}, F_{0}, V_{1}})

and

F i l l e r (E_{I_{0}, S_{1}, F_{0}, V_{0}})

resulted in the best performance. Out of convenience, we chose

F i l l e r (E_{I_{1}, S_{1}, F_{0}, V_{1}})

moving forward. In phase 3, the filler word encoding is fixed to repeat the experiments for all 16 pause encoding experiments.

The main difference, in terms of performance, between phase 1 and 2 can be seen in for encodings

E_{I_{0}, S_{0}, F_{0}, V_{0}}

and

E_{I_{1}, S_{0}, F_{0}, V_{0}}

(first two rows). There is roughly 30% improvement across both metrics, which shows the effectiveness of the filler encoding. Also, due to these improvements, the average performance over all the encodings have improved by 4% and 5% for accuracy and f1-score, respectively. The results in phase 3 are similar to phase 2, but

P a u s e (E_{I_{1}, S_{0}, F_{1}, V_{1}})

achieved 85% and 86% in accuracy and f1-score, respectively, which is the best performance over all the phases.

In this section, we extended our work in [18] by exploring different aspect of the in-text pause encoding. Also, we incorporated filler words to text and found the optimal setup for this approach, which resulted in significant performance improvement in some pause encodings and also improved model performance overall.

3.3. Contrastive Learning

In this section, we go over the results of using CL to perform the classification. To do so, we used the DualCL framework as presented in Section 2.3.2. For more clarity, the samples in the same class are considered positive, while if they belong to different classes, they are considered negative samples. We used 20-fold cross-validation with 20 epochs for the evaluation of the model performance. We used the Adam optimizer [29] with default parameters. For hyperparameters

λ

and

α

, we chose 0.75 and 0.5 after doing a grid search between [0-1].

The first two rows in Table 4 show the impact of CL on the base model

B_{0}

. Compared to the baseline,

B_{0}

, CL model achieved roughly 30% improvement across both metrics, which shows the effectiveness of the CL approach. Keeping the filler words (third row) also improves accuracy, and F1 scores an additional 1%. Compared to previous results, we achieved a new best accuracy of 86%, which is an improvement by 1%.

Since the dataset for training is small, we explored the augmentation techniques to improve model performance. We used similar augmentation techniques for previous sections, but it did not improve model’s performance. So, we did not report them in this paper. In Table 4 (rows 4 and 5), a contextualized embedding augmentation [33] is used to generate more samples. In particular, we used the BERT model for this contextualized augmentation. The choice of augmentation is very important, given the fact that too many changes can affect performance negatively due to the nature of the dataset and task. We generated three augmented samples per each ground-truth samples for training. In this case, when uh/um is not included, the model have a better performance in accuracy, better than all the results before. This might be due to the fact that augmentation imposes some changes, which in combination with uh/um impact the classification negatively. Compared to the results where no augmentation is utilized, the accuracy has improved by 1 % and the f1-score stayed the same.

Previously, we observed that combining pause and filler word encoding improved performance. It is only natural to combine these results with CL. For doing so, we chose the best result from Table 3 phase 3, namely

E_{I_{1}, S_{0}, F_{1}, V_{1}}

(

P a u s e (E_{I_{1}, S_{0}, F_{1}, V_{1}})

and

F i l l e r (E_{I_{1}, S_{1}, F_{0}, V_{1}})

), to apply CL. Table 4 (last two rows) shows the results for this encoding. We observe a 2% increase in accuracy for this model.

In Table 5, we take a closer look at the impact of CL on pause encoding by repeating the experiments for Table 2 with CL present. An immediate conclusion that can be drawn from this table compared to Table 2 is that average accuracy has increased by 3%, which shows improvement in performance over all the encodings. In terms of f1-score, the average stayed the same, which is due to some improvements but also some drops in performance. We also note that the variances in Table 2 are lower than the variance in Table 5. This is an indication that adding CL decreases the stability of the model.

4. Discussion

In this work, we proposed to use in-text encoding to improve the model’s performance. We studied the effect of different types of pauses in Table A2 but did not see a significant difference on their performance. This may be due to not picking a relevant separation for the scale of pauses. Since filler words have proven to be an important indicator for dementia detection, in Table 3, we investigated this fact and observed that for some pause encodings the performance improved. It should be mentioned that the average performance over all the pause encoding was the same as the average in Table 2. In the next step, we introduced the filler words encoding in Table 3. The average accuracy and f1-score improved by 4% and 5%, respectively.

In the second portion of our modeling, we introduced DualCL to train the model. Table 4 shows the results for the cases where the filler words are absent or present. In the case where they are present, we can observe a 1% performance boost compared to the best prior results. Also, in Table 4, we used a contextualize augmentation to further improve the results. In the case where the filler words are not used, the model’s accuracy increased by 1% compared to the best accuracy in Table 4 with no augmentation. It should be mentioned that, we performed augmentation for all prior experiments, but the results were not satisfactory to report.

Lastly, we combined in-text encoding with the CL method. Table 5 shows that the average accuracy over all the pause encoding have improved by 3%, which this combination is very effective. It should be mentioned that, the combination resulted in higher standard deviation compared to other experiments. the Last row in Table 3, shows the results for pause and filler encoding with CL approach. This combination resulted in the best overall performance over both accuracy and f1-score.

In Table 6, we compared our results with some models in the literature that used the Pitt corpus dataset for classification. To the best of our knowledge, results in [34] are state-of-the-art results. They thoroughly examined different choices for the input types (whole text or sentences), augmentation, pre-trained LLMs, and classifiers. After the investigations, they proposed to use sentence-based rather than text-based pre-trained language models. The best model (S-BERT) uses sentences as input to the BERT-large model, with linear regression as the classifier. S-BERT achieved 0.88 and 0.87 in accuracy and f1-score, respectively. Our model is short 1% in performance in both metrics. In our modeling we use the BERT-base model, which has much fewer parameters compared to BERT-large. Also, we used the whole text, not the sentences in each text, for classification. Authors in [34] also reported results for the text-based approach (T-BERT). Compared to that results, our model have 2% improvement in both metrics. This shows our model is more efficient in processing whole text than the model proposed in [34].

5. Conclusions

In this paper, we proposed an in-text encoding methodology and the integration of contrastive learning (CL) in our modeling scheme. We demonstrated that incorporating pauses and other language features (such as "uh" and "um" filler words) within the text model can considerably enhance performance. Additionally, we showed that combining the CL approach with in-text encoding can further improve the model’s performance. Overall, our modeling proved to be effective in distinguishing between the dementia and control groups.

The main limitation of our approach is related to automatic transcription. Accurate transcription with relatively precise timestamps is essential for the successful application of our method. For future work, we plan to incorporate other language features such as elongated words (e.g. "uhhh", "perrfect", etc.) within the text to study their effects which the current language model may not properly encode them for analysis. We also plan to incorporate adaptive pause threshold within the models, and explore a combination of well-chosen augmentation techniques and sentence-based pre-trained large language models.

Author Contributions

Conceptualization, R.S.; methodology, R.S.; validation, R.S., and S.G.; formal analysis, R.S., S.G., and E.L.; investigation, R.S., S.G.; resources, R.S., S.G.; data curation, R.S., and S.G.; writing—original draft preparation, R.S., S.G., and E.L.; writing—review and editing, R.S., E.L., S.G., K.H., and A.J.; supervision, E.L., K.H., and A.J.; project administration, R.S., S.G., E.L., K.H., and A.J.; funding acquisition, E.L., K.H., and A.J. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Science Foundation (NSF) under awards IIS-1915599 and IIS-2037328.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A. Effects of Pause Subsets

In Table A1 and Table A2, the effect of each pause type is explored. To study how each type of pause affects the model performance, first, we removed each pause individually, and then we just kept one pause at a time. To understand the effect of each pause on the model performance, we compare the best performance for each case to the average performance in Table 2. It should be mentioned that in the secondary network, the corresponding number associated with the removed pause frequency is set to zero.

If the short pauses are removed (the other two types are still present), the average accuracy and f1-score are decreased by 1% and 2%, respectively. This shows that short pauses are important in dementia detection. In the case where the medium pauses are removed, the average accuracy is the same, but the average f1-score dropped by 1%. Compared, to the short pause case, the effect is less severe. When the long pauses are removed, results are similar to the medium case. To study the effect of each pause on performance individually, we go over the case where only one pause is present in our analysis. First, If only short pauses are present, the model’s performance drops by 1% and 2% for accuracy and f1-score respectively. In case of medium pauses, the model performance is preserved, which shows the significance of this type of pause. For Long pauses, the accuracy is preserved, but there is a 1% decrease in f1-score.

Table A1. Effects of Pause Removal on Average Performance

Pauses Included	acc	$Δ$ acc	F1	$Δ$ F1
All Pauses	0.79	-	0.80	-
Short Removed	0.78	-0.01	0.78	-0.02
Medium Removed	0.79	-	0.79	-0.01
Long Removed	0.79	-	0.79	-0.01
Short Only	0.78	-0.01	0.78	-0.02
Medium Only	0.79	-	0.80	-
Long Only	0.79	-	0.78	-0.02

Table A2. Studying the effect of each pause and their combinations on the model’s performance.

	Short Removed		Medium Removed		Long Removed		Short Only		Medium Only		Long Only
Input Type	acc	F1	acc	F1	acc	F1	acc	F1	acc	F1	acc	F1
$E_{I_{0}, S_{0}, F_{0}, V_{0}}$	0.53± 0.09	0.39± 0.30	0.53± 0.08	0.40± 0.28	0.53± 0.07	0.40± 0.30	0.51± 0.09	0.32± 0.35	0.58± 0.08	0.56± 0.26	0.52± 0.07	0.39± 0.33
$E_{I_{1}, S_{0}, F_{0}, V_{0}}$	0.50± 0.06	0.36± 0.31	0.53± 0.08	0.43± 0.20	0.55± 0.09	0.43± 0.27	0.51± 0.06	0.39± 0.30	0.52± 0.09	0.35± 0.34	0.52± 0.08	0.31± 0.31
$E_{I_{0}, S_{1}, F_{0}, V_{0}}$	0.84± 0.07	0.86± 0.06	0.83± 0.06	0.84± 0.06	0.83± 0.07	0.85± 0.06	0.82± 0.07	0.84± 0.07	0.83± 0.06	0.85± 0.05	0.83± 0.06	0.85± 0.06
$E_{I_{0}, S_{0}, F_{1}, V_{0}}$	0.82± 0.07	0.84± 0.06	0.84± 0.06	0.86± 0.05	0.81± 0.05	0.83± 0.05	0.83± 0.06	0.85± 0.05	0.82± 0.06	0.84± 0.05	0.83± 0.07	0.85± 0.06
$E_{I_{0}, S_{0}, F_{0}, V_{1}}$	0.83± 0.07	0.85± 0.06	0.83± 0.05	0.84± 0.05	0.83± 0.07	0.85± 0.06	0.81± 0.08	0.84± 0.06	0.84± 0.06	0.85± 0.06	0.82± 0.06	0.84± 0.05
$E_{I_{1}, S_{1}, F_{0}, V_{0}}$	0.81± 0.07	0.83± 0.06	0.83± 0.06	0.85± 0.06	0.83± 0.06	0.85± 0.05	0.84± 0.07	0.85± 0.07	0.83± 0.07	0.85± 0.06	0.81± 0.08	0.84± 0.07
$E_{I_{1}, S_{0}, F_{1}, V_{0}}$	0.81± 0.05	0.83± 0.04	0.84± 0.06	0.85± 0.06	0.81± 0.08	0.84± 0.06	0.82± 0.06	0.85± 0.06	0.82± 0.07	0.84± 0.07	0.83± 0.08	0.85± 0.07
$E_{I_{1}, S_{0}, F_{0}, V_{1}}$	0.81± 0.06	0.83± 0.05	0.82± 0.05	0.84± 0.04	0.83± 0.06	0.8± 0.05	0.83± 0.06	0.85± 0.06	0.82± 0.06	0.85± 0.05	0.82± 0.06	0.84± 0.06
$E_{I_{0}, S_{1}, F_{1}, V_{0}}$	0.81± 0.07	0.84± 0.06	0.83± 0.06	0.85± 0.05	0.83± 0.07	0.85± 0.06	0.82± 0.08	0.84± 0.07	0.81± 0.06	0.84± 0.04	0.82± 0.08	0.84± 0.07
$E_{I_{0}, S_{1}, F_{0}, V_{1}}$	0.84± 0.06	0.85± 0.06	0.82± 0.07	0.84± 0.06	0.82± 0.07	0.85± 0.06	0.82± 0.06	0.83± 0.05	0.83± 0.06	0.85± 0.06	0.83± 0.08	0.86± 0.07
$E_{I_{0}, S_{0}, F_{1}, V_{1}}$	0.82± 0.07	0.84± 0.06	0.83± 0.06	0.84± 0.06	0.83± 0.07	0.85± 0.06	0.81± 0.08	0.83± 0.07	0.83± 0.06	0.85± 0.05	0.82± 0.06	0.84± 0.05
$E_{I_{1}, S_{1}, F_{1}, V_{0}}$	0.82± 0.08	0.84± 0.07	0.83± 0.06	0.85± 0.05	0.83± 0.06	0.84± 0.06	0.82± 0.06	0.84± 0.05	0.82± 0.06	0.84± 0.05	0.83± 0.06	0.85± 0.06
$E_{I_{1}, S_{1}, F_{0}, V_{1}}$	0.83± 0.07	0.85± 0.06	0.81± 0.05	0.83± 0.05	0.83± 0.06	0.84± 0.06	0.82± 0.06	0.84± 0.05	0.82± 0.07	0.84± 0.06	0.82± 0.08	0.85± 0.06
$E_{I_{1}, S_{0}, F_{1}, V_{1}}$	0.83± 0.08	0.85± 0.06	0.83± 0.06	0.84± 0.05	0.81± 0.06	0.83± 0.05	0.81± 0.07	0.84± 0.05	0.82± 0.07	0.85± 0.06	0.83± 0.06	0.85± 0.05
$E_{I_{0}, S_{1}, F_{1}, V_{1}}$	0.82± 0.07	0.85± 0.06	0.82± 0.07	0.84± 0.06	0.83± 0.07	0.85± 0.07	0.83± 0.06	0.84± 0.05	0.84± 0.06	0.85± 0.06	0.82± 0.08	0.84± 0.06
$E_{I_{1}, S_{1}, F_{1}, V_{1}}$	0.82± 0.07	0.85± 0.06	0.82± 0.07	0.85± 0.06	0.81± 0.08	0.85± 0.07	0.83± 0.06	0.85± 0.05	0.84± 0.06	0.86± 0.06	0.83± 0.06	0.84± 0.06
$E_{A v e r a g e}$	0.78	0.78	0.79	0.79	0.79	0.79	0.78	0.78	0.79	0.80	0.79	0.78

References

A.D. International. Dementia statistics. Available online: https://www.alz.co.uk/research/statistics (accessed on 27 May 2024).
Yiannopoulou, K.G.; Papageorgiou, S.G. Current and future treatments in Alzheimer disease: an update. Journal of central nervous system disease 2020, 12, 1179573520907397. [Google Scholar] [CrossRef] [PubMed]
Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2019, arXiv:1810.04805. [Google Scholar]
Liu, Y.; Ott, M.; Goyal, N.; Du, J.; Joshi, M.; Chen, D.; Levy, O.; Lewis, M.; Zettlemoyer, L.; Stoyanov, V. RoBERTa: A Robustly Optimized BERT Pretraining Approach. arXiv 2019, arXiv:1907.11692. [Google Scholar]
Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. arXiv 2020, arXiv:2005.14165. [Google Scholar]
Chandra, R.; Kulkarni, V. Semantic and sentiment analysis of selected Bhagavad Gita translations using BERT-based language framework. IEEE Access 2022, 10, 21291–21315. [Google Scholar] [CrossRef]
Qu, C.; Yang, L.; Qiu, M.; Croft, W.B.; Zhang, Y.; Iyyer, M. BERT with history answer embedding for conversational question answering. In Proceedings of the 42nd international ACM SIGIR conference on research and development in information retrieval; 2019; pp. 1133–1136. [Google Scholar]
Hakala, K.; Pyysalo, S. Biomedical named entity recognition with multilingual BERT. In Proceedings of the 5th workshop on BioNLP open shared tasks; 2019; pp. 56–61. [Google Scholar]
Ahmed, M.R.; Zhang, Y.; Feng, Z.; Lo, B.; Inan, O.T.; Liao, H. Neuroimaging and machine learning for dementia diagnosis: recent advancements and future prospects. IEEE reviews in biomedical engineering 2018, 12, 19–33. [Google Scholar] [CrossRef]
Javeed, A.; Dallora, A.L.; Berglund, J.S.; Ali, A.; Ali, L.; Anderberg, P. Machine learning for dementia prediction: a systematic review and future research directions. Journal of medical systems 2023, 47, 17. [Google Scholar] [CrossRef] [PubMed]
Yuan, J.; Bian, Y.; Cai, X.; Huang, J.; Ye, Z.; Church, K. Disfluencies and Fine-Tuning Pre-Trained Language Models for Detection of Alzheimer’s Disease. In Proceedings of the Interspeech; 2020; Vol. 2020, pp. 2162–6. [Google Scholar]
Valsaraj, A.; Madala, I.; Garg, N.; Baths, V. Alzheimer’s dementia detection using acoustic & linguistic features and pre-trained BERT. In Proceedings of the 2021 8th International Conference on Soft Computing & Machine Intelligence (ISCMI); IEEE, 2021; pp. 171–175. [Google Scholar]
Cai, H.; Huang, X.; Liu, Z.; Liao, W.; Dai, H.; Wu, Z.; Zhu, D.; Ren, H.; Li, Q.; Liu, T.; et al. Multimodal Approaches for Alzheimer’s Detection Using Patients’ Speech and Transcript. In Proceedings of the International Conference on Brain Informatics; Springer, 2023; pp. 395–406. [Google Scholar]
Guo, Z.; Liu, Z.; Ling, Z.; Wang, S.; Jin, L.; Li, Y. Text classification by contrastive learning and cross-lingual data augmentation for alzheimer’s disease detection. In Proceedings of the 28th international conference on computational linguistics; 2020; pp. 6161–6171. [Google Scholar]
Afzal, S.; Maqsood, M.; Nazir, F.; Khan, U.; Aadil, F.; Awan, K.M.; Mehmood, I.; Song, O.Y. A data augmentation-based framework to handle class imbalance problem for Alzheimer’s stage detection. IEEE access 2019, 7, 115528–115539. [Google Scholar] [CrossRef]
Mirheidari, B.; Blackburn, D.; O’Malley, R.; Venneri, A.; Walker, T.; Reuber, M.; Christensen, H. Improving Cognitive Impairment Classification by Generative Neural Network-Based Feature Augmentation. In Proceedings of the INTERSPEECH; 2020; pp. 2527–2531. [Google Scholar]
Jain, V.; Nankar, O.; Jerrish, D.J.; Gite, S.; Patil, S.; Kotecha, K. A novel AI-based system for detection and severity prediction of dementia using MRI. IEEE Access 2021, 9, 154324–154346. [Google Scholar] [CrossRef]
Soleimani, R.; Gou, S.; Haley, K.L.; Jacks, A.; Lobaton, E. Dementia Detection by In-Text Pause Encoding. Submitted for publication In EMBC 2024.
Luz, S.; Haider, F.; de la Fuente, S.; Fromm, D.; MacWhinney, B. Alzheimer’s Dementia Recognition through Spontaneous Speech: The ADReSS Challenge. Proceedings of the INTERSPEECH 2020, China, 2020. [Google Scholar]
Becker, J.T.; Boiler, F.; Lopez, O.L.; Saxton, J.; McGonigle, K.L. The Natural History of Alzheimer’s Disease: Description of Study Cohort and Accuracy of Diagnosis. Archives of Neurology 1994, 51, 585–594. [Google Scholar] [CrossRef] [PubMed]
Chen, Q.; Zhang, R.; Zheng, Y.; Mao, Y. Dual Contrastive Learning: Text Classification via Label-Aware Data Augmentation. arXiv 2022, arXiv:/2201.08702. [Google Scholar]
Zhou, X.; Koltun, V.; Krähenbühl, P. Tracking objects as points. In Proceedings of the European conference on computer vision; Springer, 2020; pp. 474–490. [Google Scholar]
Harutyunyan, H.; Khachatrian, H.; Kale, D.C.; Ver Steeg, G.; Galstyan, A. Multitask learning and benchmarking with clinical time series data. Scientific data 2019, 6, 96. [Google Scholar] [CrossRef]
Cramér, H.; Wold, H. Some theorems on distribution functions. Journal of the London Mathematical Society 1936, 1, 290–294. [Google Scholar] [CrossRef]
Radford, A.; Kim, J.W.; Xu, T.; Brockman, G.; McLeavey, C.; Sutskever, I. Robust Speech Recognition via Large-Scale Weak Supervision. arXiv 2022, arXiv:2212.04356. [Google Scholar]
Baevski, A.; Zhou, H.; Mohamed, A.; Auli, M. wav2vec 2.0: A Framework for Self-Supervised Learning of Speech Representations. arXiv 2020, arXiv:2006.11477. [Google Scholar]
Hugging Face. Available online: https://huggingface.co/google-bert/bert-base-uncased (accessed on 16 May 2024).
Guo, S. Enhancing Dementia Detection in Text Data through NLP by Encoding Silent Pauses. 2024.
Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
Karlekar, S.; Niu, T.; Bansal, M. Detecting linguistic characteristics of Alzheimer’s dementia by interpreting neural models. arXiv preprint arXiv:1804.06440, arXiv:1804.06440 2018.
Wieling, M.; Grieve, J.; Bouma, G.; Fruehwald, J.; Coleman, J.; Liberman, M. Variation and change in the use of hesitation markers in Germanic languages. Language Dynamics and Change 2016, 6, 199–234. [Google Scholar] [CrossRef]
Tottie, G. Uh and um as sociolinguistic markers in British English. International Journal of Corpus Linguistics 2011, 16, 173–197. [Google Scholar] [CrossRef]
Kobayashi, S. Contextual Augmentation: Data Augmentation by Words with Paradigmatic Relations. arXiv 2018, arXiv:1805.06201. [Google Scholar]
Roshanzamir, A.; Aghajan, H.; Soleymani Baghshah, M. Transformer-based deep neural network language models for Alzheimer’s disease risk assessment from targeted speech. BMC Medical Informatics and Decision Making 2021, 21, 1–14. [Google Scholar] [CrossRef] [PubMed]
Pan, Y.; Mirheidari, B.; Reuber, M.; Venneri, A.; Blackburn, D.; Christensen, H. Automatic hierarchical attention neural network for detecting AD. In Proceedings of the Interspeech 2019.International Speech Communication Association (ISCA); 2019; pp. 4105–4109. [Google Scholar]
Saltz, P.; Lin, S.Y.; Cheng, S.C.; Si, D. Dementia Detection using Transformer-Based Deep Learning and Natural Language Processing Models. In Proceedings of the 2021 IEEE 9th International Conference on Healthcare Informatics (ICHI); 2021; pp. 509–510. [Google Scholar] [CrossRef]
Nambiar, A.S.; Likhita, K.; Pujya, K.V.S.S.; Gupta, D.; Vekkot, S.; Lalitha, S. Comparative study of Deep Classifiers for Early Dementia Detection using Speech Transcripts. In Proceedings of the 2022 IEEE 19th India Council International Conference (INDICON); 2022; pp. 1–6. [Google Scholar] [CrossRef]

Figure 1. Model Architecture for in-text encoding scheme.

Table 1. Different In-Text Encoding Schemes.

Input Type	Example
Original	“sen1 (...) sen2 (.),sen3 , (..) …”
$E_{I_{0}, S_{0}, F_{0}, V_{0}}$	“sen1 sen2 sen3 ...“
$E_{I_{1}, S_{0}, F_{0}, V_{0}}$	“sen1 Lo sen2 Sh sen3 Me ...”
$E_{I_{0}, S_{1}, F_{0}, V_{0}}$	“sen1 sen2 sen3 ... Lo Sh Me ...”
$E_{I_{0}, S_{0}, F_{1}, V_{0}}$	“sen1, sen2, sen3 ..., #ShSh#MeMe#LoLo“
$E_{I_{0}, S_{0}, F_{0}, V_{1}}$	“sen1, sen2, sen3 ...,#Sh#Me#Lo”
$E_{I_{1}, S_{1}, F_{0}, V_{0}}$	“sen1 Lo sen2 Sh sen3 Me ..., Lo Sh Me ...”
$E_{I_{1}, S_{0}, F_{1}, V_{0}}$	“sen1 Lo sen2 Sh sen3 Me ..., #ShSh#MeMe#LoLo ...”
$E_{I_{1}, S_{0}, F_{0}, V_{1}}$	“sen1 Lo sen2 Sh sen3 Me ..., #Sh#Me#Lo”
$E_{I_{0}, S_{1}, F_{1}, V_{0}}$	“sen1, sen2, sen3 ..., Lo Sh Me ..., #ShSh#MeMe#LoLo ...”
$E_{I_{0}, S_{1}, F_{0}, V_{1}}$	“sen1, sen2, sen3 ..., Lo Sh Me ..., #Sh#Me#Lo”
$E_{I_{0}, S_{0}, F_{1}, V_{1}}$	“sen1, sen2, sen3 , ..., #ShSh#MeMe#LoLo ..., #Sh#Me#Lo”
$E_{I_{1}, S_{1}, F_{1}, V_{0}}$	“sen1 Lo sen2 Sh sen3 Me ..., Lo Sh Me ..., #ShSh#MeMe#LoLo...”
$E_{I_{1}, S_{1}, F_{0}, V_{1}}$	“sen1 Lo sen2 Sh sen3 Me ..., Lo Sh Me ..., #Sh#Me#Lo”
$E_{I_{1}, S_{0}, F_{1}, V_{1}}$	“sen1 Lo sen2 Sh sen3 Me ..., #ShSh#MeMe#LoLo ..., #Sh#Me#Lo”
$E_{I_{0}, S_{1}, F_{1}, V_{1}}$	“sen1, sen2, sen3 ..., Lo Sh Me ..., #ShSh#MeMe#LoLo ..., #Sh#Me#Lo”
$E_{I_{1}, S_{1}, F_{1}, V_{1}}$	“sen1 Lo sen2 Sh sen3 Me ..., Lo Sh Me ..., #ShSh#MeMe#LoLo ...,#Sh#Me#Lo”

Table 2. In-text Pause Encoding Results for 16 Different Combinations.

Input Type	Acc.	F1
$E_{I_{0}, S_{0}, F_{0}, V_{0}}$	0.58±0.11	0.56±0.24
$E_{I_{1}, S_{0}, F_{0}, V_{0}}$	0.50±0.07	0.46±0.25
$E_{I_{0}, S_{1}, F_{0}, V_{0}}$	0.83±0.06	0.85±0.05
$E_{I_{0}, S_{0}, F_{1}, V_{0}}$	0.83±0.06	0.84±0.06
$E_{I_{0}, S_{0}, F_{0}, V_{1}}$	0.81±0.08	0.84±0.06
$E_{I_{1}, S_{1}, F_{0}, V_{0}}$	0.83±0.07	0.84±0.07
$E_{I_{1}, S_{0}, F_{1}, V_{0}}$	0.84±0.06	0.85±0.06
$E_{I_{1}, S_{0}, F_{0}, V_{1}}$	0.82±0.06	0.83±0.06
$E_{I_{0}, S_{1}, F_{1}, V_{0}}$	0.83±0.06	0.84±0.05
$E_{I_{0}, S_{1}, F_{0}, V_{1}}$	0.82±0.06	0.84±0.05
$E_{I_{0}, S_{0}, F_{1}, V_{1}}$	0.82±0.06	0.84±0.06
$E_{I_{1}, S_{1}, F_{1}, V_{0}}$	0.83±0.07	0.85±0.06
$E_{I_{1}, S_{1}, F_{0}, V_{1}}$	0.83±0.06	0.85±0.05
$E_{I_{1}, S_{0}, F_{1}, V_{1}}$	0.83±0.05	0.85±0.04
$E_{I_{0}, S_{1}, F_{1}, V_{1}}$	0.82±0.07	0.84±0.06
$E_{I_{1}, S_{1}, F_{1}, V_{1}}$	0.83±0.08	0.85±0.07
$E_{A v e r a g e}$	0.79	0.80
$B_{0}$	0.56±0.11	0.42±0.27

Table 3. In-text Filler Word Encoding Results.

	Phase 1		Phase 2		Phase 3
Input Type	Acc.	F1	Acc.	F1	Acc.	F1
$E_{I_{0}, S_{0}, F_{0}, V_{0}}$	0.53	0.41	0.83	0.85	0.84	0.85
$E_{I_{1}, S_{0}, F_{0}, V_{0}}$	0.57	0.46	0.83	0.85	0.84	0.86
$E_{I_{0}, S_{1}, F_{0}, V_{0}}$	0.82	0.85	0.84	0.86	0.83	0.85
$E_{I_{0}, S_{0}, F_{1}, V_{0}}$	0.82	0.84	0.83	0.85	0.83	0.86
$E_{I_{0}, S_{0}, F_{0}, V_{1}}$	0.84	0.86	0.84	0.85	0.82	0.84
$E_{I_{1}, S_{1}, F_{0}, V_{0}}$	0.84	0.86	0.84	0.85	0.84	0.86
$E_{I_{1}, S_{0}, F_{1}, V_{0}}$	0.84	0.86	0.84	0.85	0.83	0.84
$E_{I_{1}, S_{0}, F_{0}, V_{1}}$	0.84	0.86	0.84	0.85	0.83	0.85
$E_{I_{0}, S_{1}, F_{1}, V_{0}}$	0.83	0.85	0.81	0.84	0.82	0.84
$E_{I_{0}, S_{1}, F_{0}, V_{1}}$	0.83	0.85	0.83	0.85	0.83	0.85
$E_{I_{0}, S_{0}, F_{1}, V_{1}}$	0.82	0.84	0.83	0.85	0.83	0.85
$E_{I_{1}, S_{1}, F_{1}, V_{0}}$	0.82	0.84	0.82	0.84	0.84	0.85
$E_{I_{1}, S_{1}, F_{0}, V_{1}}$	0.83	0.85	0.84	0.86	0.82	0.84
$E_{I_{1}, S_{0}, F_{1}, V_{1}}$	0.82	0.84	0.82	0.84	0.85	0.86
$E_{I_{0}, S_{1}, F_{1}, V_{1}}$	0.84	0.85	0.81	0.84	0.82	0.84
$E_{I_{1}, S_{1}, F_{1}, V_{1}}$	0.83	0.86	0.84	0.85	0.83	0.84
$E_{A v e r a g e}$	0.79	0.80	0.83	0.85	0.83	0.85

Table 4. Results showing impact of Contrastive Learning (CL) and Data Augmentation (Aug) on Different Models.

Input Type	Acc.	F1
$B_{0}$	0.56 ± 0.11	0.42 ± 0.27
$B_{0}$ + CL	0.85 ± 0.04	0.84 ± 0.04
$B_{0}$ with Fillers + CL	0.86 ± 0.04	0.85 ± 0.04
$B_{0}$ + CL + Aug	0.87 ± 0.05	0.85 ± 0.05
$B_{0}$ with Fillers + CL + Aug	0.85 ± 0.05	0.84 ± 0.05
$P a u s e (E_{I_{1}, S_{0}, F_{1}, V_{1}}), F i l l e r (E_{I_{1}, S_{1}, F_{0}, V_{1}})$	0.85 ± 0.06	0.86 ± 0.06
$P a u s e (E_{I_{1}, S_{0}, F_{1}, V_{1}}), F i l l e r (E_{I_{1}, S_{0}, F_{1}, V_{1}})$ + CL	0.87 ± 0.08	0.86 ± 0.09

Table 5. CL Results for 16 Combinations of Pause Encodings with no Filler Words.

Input Type	Acc.	F1
$E_{I_{0}, S_{0}, F_{0}, V_{0}}$	0.83 ± 0.08	0.82 ± 0.09
$E_{I_{1}, S_{0}, F_{0}, V_{0}}$	0.85 ± 0.08	0.84 ± 0.10
$E_{I_{0}, S_{1}, F_{0}, V_{0}}$	0.84 ± 0.08	0.81 ± 0.11
$E_{I_{0}, S_{0}, F_{1}, V_{0}}$	0.82 ± 0.08	0.80 ± 0.07
$E_{I_{0}, S_{0}, F_{0}, V_{1}}$	0.85 ± 0.08	0.83 ± 0.11
$E_{I_{1}, S_{1}, F_{0}, V_{0}}$	0.84 ± 0.09	0.82 ± 0.11
$E_{I_{1}, S_{0}, F_{1}, V_{0}}$	0.80 ± 0.10	0.78 ± 0.11
$E_{I_{1}, S_{0}, F_{0}, V_{1}}$	0.81 ± 0.09	0.79 ± 0.11
$E_{I_{0}, S_{1}, F_{1}, V_{0}}$	0.78 ± 0.08	0.79 ± 0.09
$E_{I_{0}, S_{1}, F_{0}, V_{1}}$	0.84 ± 0.09	0.82 ± 0.10
$E_{I_{0}, S_{0}, F_{1}, V_{1}}$	0.82 ± 0.08	0.80 ± 0.10
$E_{I_{1}, S_{1}, F_{1}, V_{0}}$	0.79 ± 0.08	0.77 ± 0.13
$E_{I_{1}, S_{1}, F_{0}, V_{1}}$	0.77 ± 0.09	0.72 ± 0.15
$E_{I_{1}, S_{0}, F_{1}, V_{1}}$	0.79 ± 0.09	0.77 ± 0.12
$E_{I_{0}, S_{1}, F_{1}, V_{1}}$	0.80 ± 0.09	0.79 ± 0.14
$E_{I_{1}, S_{1}, F_{1}, V_{1}}$	0.83 ± 0.07	0.81 ± 0.09
$E_{A v e r a g e}$	0.82	0.80

Table 6. Comparison of different methods using Pitt corpus dataset

Input Type	Acc.	F1	No. params
S-BERT [34]	0.88	0.87	340M
T-BERT [34]	0.85	0.84	340M
Y. Pan et al. [35]	–	0.84	–
P. Saltz et al. [36]	0.76	0.76	110M
ALBERT+BiLSTM[37]	0.79	0.81	11M
Ours	0.87	0.86	110M

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Impact of Pause and Filler Words Encoding on Dementia Detection with Contrastive Learning

Abstract

1. Introduction

2. Materials and Methods

2.1. Dataset Preparation

2.2. In-Text Pause Encoding

2.3. Modeling

2.3.1. Model for In-Text Encoding Scheme

2.3.2. Contrastive Learning

3. Results

3.1. In-Text Pause Encoding Results

3.2. Filler Word Encoding Results

3.3. Contrastive Learning

4. Discussion

5. Conclusions

Author Contributions

Funding

Conflicts of Interest

Appendix A. Effects of Pause Subsets

References

MDPI Initiatives

Important Links

Subscribe