Prerpints.org logo
Preprint
Article

Characterization of Overtopping Volumes from Focused Wave Groups over Smooth Dikes with Emerged Toe: Insights from Physical Model Tests

Altmetrics

Downloads

91

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 June 2024

Posted:

11 June 2024

You are already at the latest version

Alerts
Abstract
This research examines the overtopping volumes associated with focused wave groups on smooth dikes with an emerged toe. Focused wave groups are employed to represent the highest waves of random sea states in a compact form, obviating the need to model the entire irregular wave train. The study investigates how overtopping volumes are affected by focus location and phase. Results from 418 experimental tests have been gathered and analyzed. The experiments employed first-order wave generation theory to analyse structural response. Subsequent studies will address the errors induced by this approximation and compare it with second-order wave generation. The experiments simulated extreme wave impacts on an idealised coastal layout, comprising a 1:6.3 foreshore slope and three different dike slopes, including vertical structures, with the initial still water level set below the dike toe. The study employed NewWave theory for generating focused wave groups, aiming to extend recent research on wave overtopping under varied conditions. The results, analysed in both dimensional and non-dimensional forms, indicate that overtopping volumes are significantly influenced by the focus phase. Critical focus locations were identified at a distance of one-third of the deep-water wavelength from the toe.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Wave overtopping is considered a key aspect of coastal structural design. The primary challenge in evaluating the resilience of urban areas to wave overtopping and associated flooding lies in the accurate estimation of overtopping: this encompasses not only the determination of mean discharge values but also the assessment of the volumes associated with individual overtopping events caused by large waves within a sea state. All this is exacerbated by the changing climate [1]: climate change scenarios, in fact, including sea level rise and increases storminess, raise the critical question of how to protect coastal urban areas from flood risks and sea level rise. Recent events such as storms Gloria in January 2020 [2] and Ciarán in early November 2023 have highlighted the vulnerability of coastal urban areas. This increased risk implies significant changes in coastal conditions, with an expected increase in average water levels and wave variables such as wave height and period, having important implications for wave-driven coastal processes, according to the study by Morim et al. [3].
The design of coastal structures to minimize or prevent wave overtopping is more and more necessary to ensure coastal safety. Traditionally, the mean flow rate has been used as a design criterion, but there is still uncertainty as to whether it adequately represents the real hazard. The EurOtop manual [4] establishes criteria based on the average discharges, while recognizing the difficulties of establishing precise limits for all conditions. Studies, such as those by Endoh and Takahashi [5] and Sandoval and Bruce [5], highlight the limitation of a single average flow value or maximum overtopping volume. Recently, there has been a shift towards re-evaluating the risks associated to wave overtopping. Rather than relying on mean discharges, new criteria are being established based on the specific properties of each overtopping flow [6]. This is supported by various studies ([5,7,8,9,10]). Improving the understanding of individual overtopping flows is crucial to guide the design of coastal structures. This has been emphasized by [7,8,9]. It is crucial to assess the distinct risks associated with distinct overtopping events, such as the potential to sweep pedestrians off their feet or require evacuation measures. Accurately predicting and characterizing significant overtopping events is crucial in certain scenarios. As highlighted by Hughes and Thornton [7] and Whittaker et al. [10], the accurate structural design of coastal defenses must consider individual wave properties.
In order to characterize individual overtopping volumes on sea dikes with emerged toe and associated to maximum wave heights in a random sea state, the present study has employed focused wave groups rather than simulating whole irregular sea states. Generation of focused wave groups offers several advantages, including improved repeatability, the ability to evaluate model and scale effects, the potential for improved measurement, and improved model resolution for large wave interactions ([10]).
In the field of offshore engineering, the so-called NewWave theory was introduced by [11] as a compact and focused wave group specifically designed for engineering purposes. NewWave offers an alternative to study wave-structure interaction (WSI) of extreme events, since it models the statistically most probable surface elevation shape associated with the maximum waves of with waves characterized by a specified exceedance probability within a random sea state ([12]). More and more applications in the field of coastal engineering have used NewWave and focused wave groups. In fact, focused wave groups can help understand the connection between wave properties and structural responses, either centered on coastal defenses (e.g. [13,14,15]) or applied to floating structures and wave energy converters (e.g. [16,17,18]).
Whittaker et al. [19] validated the use of focused wave groups for WSI problems in the coastal zone, suggesting that a single incident wave group could replicate extreme coastal responses within a specific sea state. In [10], the authors studied the impact of focused wave groups on an inclined seawall, analyzing overtopping volumes and horizontal forces through physical laboratory experiments and numerical simulations. The research found that total overtopping volumes strongly depend on focus location, phase angle at focus, and linear wave amplitude. Changing the phase of the group at focus could significantly increase the total overtopped volume. Craciunescu and Christou [20] developed a model for wave breaking energy dissipation using focused wave groups. Xiao et al. [21] conducted an experimental and numerical investigation of focused wave groups across a typical fringing reef profile, examining their impact on a vertical wall attached to the reef flat. They suggested that extreme coastal responses within a specific sea state can be replicated using only a single incident wave group. Recently, Mortimer et al. [22] explored run-up on vertical walls in shallow and intermediate water, focusing on the effects of second-order correction for generating focused wave groups. Additionally, Altomare et al. [23] employed focused wave groups to investigate the structural response and failure mechanism of a pier under severe wave breaking conditions.
The present article employs similar methodology as in [10] but extends the analysis further to different hydrodynamic conditions, foreshore and dike slopes. While in [10] the authors use NewWave to analyze the overtopping of gentle dikes with a 1:2 slope on a 1:20 planar beach and submerged toes, in this study, we examine a varying foreshore slope with dikes that have an emerged toe (i.e. still water level below the toe level) and different slopes, namely 1:2, 1:0.5 and vertical. The influence of water level is examined, whereas in [10] only one water level was studied. The importance of the water level lies in the induced wave breaking and its location. Differences in wave overtopping results for different water levels are caused by the breaking, which eventually affects energy dissipation and structural responses. Focused wave groups have been generated by means of first-order wave generation theory for the present work. A first analysis based on first-order approximation is acceptable at a preliminary stage, although this limits the applicability of the present study and requires future analysis implemented second-order wave generation theory ([24,25]). In fact, linear or first-order theory might induce the generation of spurious free waves, especially in extremely shallow water conditions. Limitations of the results will be discussed further in the next sections.
The document is organized into separate sections, each dedicated to different facets of the study. Section 2 elucidates the experimental setup. Section 3 establishes the scaling of overtopping volume and defines the parameter space for volume dependence. Section 4 presents results, detailing the reliance of both dimensional and non-dimensional overtopping volumes on focused wave parameters, geometrical configurations, and hydrodynamic conditions. Lastly, Section 5 engages in a discussion of the discoveries and derives conclusions from the investigation.

2. Experimental Model

2.1. Model Setup

The experimental investigation was carried out in the CIEMito small-scale wave and current flume at the Maritime Engineering Laboratory of Universitat Politècnica de Catalunya – BarcelonaTech (LIM/UPC). This flume setup is depicted in Figure 1. Model scale was 1:50, based on Froude similarity. The model, constructed from plywood, features a dike at the end of a sloping emerged foreshore designed to induce wave breaking before reaching the toe of the structure. Various dike slopes with the same structural height were examined, including a vertical wall and two sloping dikes (specifically 1:2 and 1:0.5, being H:V). The foreshore consisted of three modular plywood elements, each measuring 1 meter in length. The last element, including the emerged part of the beach, had a slope of 1:6.3, which was employed to induce plunging wave breaking for the selected wave conditions, while the slope of the stretch before it has a slope of 1:11. For each dike slope, the structural height was maintained equal to 0.04 m. Positioned at a distance of 10.22 m from the wavemaker at its rest position, the dike toe was situated at z=0.32 m, where z=0 m represents the vertical coordinate of the flume bottom at the wavemaker location.
Resistive wave gauges (WG) and one acoustic wave gauge (AWG0) distributed along the flume were employed to measure water surface elevation, and an overtopping tank, equipped with an ultrasonic proximity sensor (AWG1), was utilized to quantify the volume of overtopping. The specific locations of the wave gauges are indicated in Table 1.
Scale effects on wave overtopping volumes at the employed 1:50 model scale have been assessed. It is worth mentioning that Heller [26] outlined criteria for flow-structure interaction, suggesting investigation scales that balance model size and scale effects. Besides, large-scale tests for vertical structures, as indicated by [4], validate the scalability of formulas derived from small-scale studies ([27]). Notwithstanding it, further examination is needed to fully exclude scale effects. The analysis concentrates on viscous forces and surface tension, aligning with [4]. Reynolds and Weber numbers for wave overtopping (Req and Weq) are computed and compared to critical limits (Req > 10^3 and Weq > 10) defined by [28]. The calculation of Req and Weq involves assessing the run-up of focused wave groups, overtopping flow velocity, and depth. To perform the calculation of Req, wave run-up estimation, detailed by [29], is utilized. Deep-water wave characteristics have been used for the scope, i.e. measured at WG0 location. For Weq, overtopping flow velocity and depth are determined from [4]. The calculated Req and Weq for the cases presented in this study surpass 103 and 10, respectively, indicating the absence of scale effects.

2.2. Hydrodynamic Conditions: Focused Wave Groups

The time series for each wave group was generated using the NewWave theory. NewWave was originally designed for generation and propagation of a compact wave train on a horizontal bottom. The selected focal point regulates the dispersion of the wave group during shoaling and breaking while propagating. A NewWave-type focused wave group comprising N infinitesimal wave components is given by:
η x , t = A σ 2 ∑ i = 1 N S η η ω i cos ⁡ k i x - x f - ω i t - t f + ϕ Δ ω
where Sηη is the power spectral density, t is time, and x is the horizontal distance from generation, ω is the angular frequency, σ is the standard deviation of the sea state (being σ 2 = ∑ S η η ω i Δ ω ); ki is the wavenumber of the i-th wave component with angular frequency ωi and related to it by the familiar linear dispersion relation ω 2 = g k * t a n h ( k h ) ,where g is the acceleration due to gravity and h is the water depth ([10]). All wave components come into phase at the focus location xf and focus time tf to form a large wave with a linear focus amplitude equal to A, calculated to represent “the amplitude of the largest wave in a sea surface time series of N waves in a narrow-banded linear random sea” ([24]). If a Rayleigh distribution of the wave height is assumed, then A can be defined as:
A = 2 σ 2 ln ⁡ N
Once the target significant wave height, Hm0, is defined, being Hm0=4σ, the target value of A is calculated from the standard deviation, σ. Table 2 lists the range of parameters examined in the present study. Wave conditions are expressed in model scale. Values of significant wave height and spectral period reported in the table correspond to the ones measured at WG0 location, rather than the target or theoretical ones. This choice is justified by the fact that overtopping volumes will be scaled by measured deep-water wave height and wavelength (see Section 3), which are employed in lieu of local wave conditions at the toe of the structure. This is due to the difficulty in accurately estimating the wave conditions at the toe in the event of wave breaking and very or extremely shallow water conditions. Further application, in fact, would necessitate sophisticated numerical modelling and/or ad-hoc experimental campaigns ([30]).
All data with overtopping volume lower than 600 l/m (value expressed in prototype conditions) have been excluded from the analysis, concentrating on extreme wave conditions and overtopping events only. It is worthy to remember that 600 l/m is the threshold of tolerable overtopping for pedestrians indicated in [4]. In total 418 tests have been gathered and analyzed.
Whittaker et al. [19] confirmed the continued applicability of the NewWave theory in relatively shallow waters (kh<0.5), indicating that linear frequency dispersion remains the primary mechanism despite the increasing influence of nonlinear effects due to changes in bathymetry. It is important to highlight that the minimum value of kh at the focus location for the tests conducted in the current study is 0.10. This value is calculated considering the local water depth of the nearest point to the dike and the wavelength in deep waters. This location corresponds to extremely shallow foreshore conditions, as per the classification proposed by [31], with a ratio of local water depth to deep-water significant wave height, ht/Hm0,o, equal to 0.78. In most cases, waves break before reaching this location. Consequently, all assumptions based on the propagation of a compact wave train and linear theory become invalid. Despite this, it was considered worthwhile to investigate the response when focusing was theoretically induced after the waves had broken.

3. Parameter Definition and Scaling Laws in Wave Overtopping

The problem being studied is defined by eight variables. The first one, object of the study, is the overtopping volume associated to maximum wave height in a random sea state, here computed as the total volume caused by the focused wave group. Other two variables are the focus wave location (xf) and the phase at focus (ϕ). The remaining five variables are related to the hydrodynamic conditions and the geometrical layout. These variables include deep-water significant wave height (Hm0,o), spectral period (Tm-1,0,o), water depth (either in deep-water, h, or at the toe, ht), dike slope (cotα), and foreshore slope (cotθ). In order to compare results for different wave conditions and dike slopes, and due to the wide range of hydrodynamic deep-water conditions, dimensionless variables have been employed instead of dimensional ones. At first, the total overtopping volume per meter width associated to the focused wave group, Vmax, has been scaled on the instantaneous volume flux over the half wave period, defined by [32], as:
V 0 = H m 0 , o L m − 1,0 , o 2 π
where Lm-1,0,o denotes the deep-water wavelength calculated from the spectral period Tm-1,0,o. The method for achieving a dimensionless overtopping volume (Vmax/V0) has been described and analyzed by Ibrahim and Baldock [33], hereafter referred to as IB2020. This method has also been used in [34] for predicting mean overtopping discharge on promenades and further developed in [35] for overtopping on fringing reefs. In a physical sense, rationalizing the scaling of the volume flux involves equating it to the volume of fluid displaced by a wavemaker that finally reaches and overtops a structure, which presents a deficit in the freeboard with respect to the expected wave run-up. The volume flux V0 will be used later on to compare the dependence of overtopping volume for each dike slope and each initial water depth. IB2020 finally proposed empirical model for overtopping on truncated beaches, where the volume depends on the offshore wave conditions and the foreshore slope angle. The proposed scaling factor is defined as:
V * = c o n s t * V 0 tan n ⁡ θ f R c R u
Where n is either 0.5 or 1, Rc is the crest freeboard and Ru the run-up height. It is important to note that the slope angle of the foreshore remains constant throughout our analysis. However, as explained hereafter, we will also consider the combined effect of the foreshore and dike slopes. We will define an equivalent foreshore slope that will no longer be constant and will be employed for the definition of V* based on eq (4).
To consider the different dike slopes combined with the foreshore slope (where actually the waves are breaking before reaching the dike), the equivalent slope is proposed for the definition of the breaker parameter. The definition of the equivalent slopes resembles the one proposed in [36] but with an important difference. Wave run-up must be assessed as indicated in [36], employing the wave characteristics at the dike toe. However, this calculation is not performed to finally define the equivalent slope, because of the large uncertainty to apply the proposed semi-empirical formula for the wave run-up estimation for the studied layout (for instance, dike with emerged toe, from gentle to vertical and steep foreshore). Hence, rather than employing an iterative approach to estimate the equivalent slope, the first estimate based on the crest freeboard and the deep-water significant wave height is used:
cot ⁡ δ = R c + h t cot ⁡ α + ( H m 0 , o − h t o e ) cot ⁡ θ ( H m 0 , o + R c )
For scaling the volume, based on Equations (4) and (5) the following will be used:
V * = V 0 tan ⁡ δ
Besides, in order to study the variability of overtopping volumes in a non-dimensional form, three other dimensionless variables are defined. The first two of them are characteristic variable describing the wave overtopping based on deep-water wave conditions and local water depth ([30]): the non-dimensional freeboard, Rc/Hm0,o and the shallowness (see [31]), ht/Hm0,o. The ratio between water depth and wave height was previously employed by [37], but the local significant wave height at the toe of the structure was employed. Finally, a non-dimensional focused location is defined as:
X = x t − x f L m − 1,0 , o
Where xt is the location of the dike toe and xt – xf therefore expresses the distance between dike and focus location, which is then scaled by the deep-water wavelength. Either the V0 or V* are employed as scaling factors for wave overtopping (i.e. factors employed to define a non-dimensional individual overtopping volume), not necessarily they consider explicitly the influence of the water depth. By employing V0 this aspect is not considered, while in V* the local water depth is considered only to calculate the equivalent slope. Hence, we refer to the overtopping formula proposed by [30] for average overtopping discharge. The formula is represented in Equations (8)–(15) and can be expanded further in Equations (16)–(17) to obtain the overtopping volume V’=qTm-1,0,o. Actually this is consistent with the scale parameter of the Weibull distribution usually employed to analyse individual overtopping volumes associated to a specific exceedance probability in a random sea state (see, for example: [4,38,39]): the individual overtopping volume is scaled by the mean value of the Weibull distribution, which can be expressed as the product of the mean discharge by the mean wave period, divided by the probability of overtopping waves in a whole random sea storm. Therefore, referring to [30], for vertical dikes with ht/Hm0,o≤ 0.1, mean overtopping discharge can be expressed as follows:
q g · H m 0 , o 3 = a · exp ⁡ − b · R c H m 0 , o + c · h t H m 0 , o  
where
a = 0.09 · tan ⁡ θ 1.75 s m − 1,0 , o 0.90   ;
b = 6.05 · s m − 1,0 , o 0.35 tan ⁡ θ 0.50   ;
and
c = 1.45 · s m − 1,0 , o 3.25 tan ⁡ θ 3.45   .
While for sloping dikes with with ht/Hm0,o≤ 0.1, the formula is:
q g · H m 0 , o 3 = d · exp ⁡ − e · R c H m 0 , o + f · h t H m 0 , o  
where
d = 1.35 · tan ⁡ θ 0.35 · s m − 1,0 , o 0.85
e = 3.75 · s m − 1,0 , o 0.70 tan ⁡ θ 0.70 · tan ⁡ α 0.60  
and
f = 0.35 · s m − 1,0 , o 0.35 tan ⁡ θ 1.30  
The coefficients a, b, c, d, e and f are therefore function of the seabed slope, the dike slope and the deep-water wave steepness, defined as s m − 1,0 , o = H m 0 , o / L m − 1,0 , o . The scaling volume based on by [30], hereafter indicated as VL21, can be expressed for vertical and sloping structures respectively as
V L 21 = T m − 1,0 , o g · H m 0 , o 3 a · exp ⁡ − b · R c H m 0 , o + c · h t H m 0 , o  
V L 21 = T m − 1,0 , o g · H m 0 , o 3 d · exp ⁡ − e · R c H m 0 , o + f · h t H m 0 , o  

4. Results

The results of the experimental campaign are hereafter shown both in dimensional and dimensionless form. For the former, although all quantities have been already defined in model scale, it is more practical and of immediate understanding to express the measured overtopping volumes upscaled to prototype conditions. Figure 2 shows the free-surface elevation at each wave gauge position of a focused wave group producing a total volume over the 1:2 dike that resulted larger than 2000 l/m (this value expressed in prototype). The focus phase is equal to 0° (crest-focused) in the shown example and focused location is at WG7 position. Wave transformation is clear between WG7 and AWG0, where wave shoaling and breaking take place. Snapshots of focused wave group overtopping the three sea dikes are reported in Figure 3 for the same test case and water depth, namely h=0.30 m, Hm0,o≈0.065m and Tm-1,0,o≈1.75s, ϕ=270°, xf=9.58 (AWG0 location). The process becomes more violent and turbulent as the dike slope increases. While for the 1:2 dike (Figure 3a) wave overtops the slope smoothly (almost no splashes), typical of the so-called “green” overtopping flows, for the 1:0.5 (Figure 3b) and vertical slopes (Figure 3c) the process becomes more and more turbulent, due to the higher exerted wave reflection and the consequent inversion of the wave momentum flux.

4.1. Focused Wave Parameter Space

Variation in overtopping volume based on focused wave location and phase was assessed for each dike slope and initial water level. The investigation included four different water levels for the 1:2 and vertical slopes, namely 0.31m, 0.30m, 0.29m, and 0.28m. For the 1:0.5 slope, only three water levels were tested, namely 0.31m, 0.30m, and 0.28m. It is important to note that the toe is located at z=0.32 m, resulting in an emergent toe for all water levels. The parameter space investigated with focused wave groups has been already described and is reported in Table 2. The coordinates of xf are expressed with respect to the position of the wavemaker at rest (x=0 m). Remind that the toe of the dike is located at x=10.22 m. All aforementioned dimensional quantities are expressed in model scale. Four focused locations and four different phase angles with increments of 90° have been considered. The focal points were chosen to vary from the horizontal bottom, 0.68 m from the beach toe to 0.64 m from the toe of the dike, covering a length of approximately 3 m along the wave flume, corresponding each focal position to the wave gauges WG5, WG6, WG7 and AWG0, respectively.
The variation of total volumes as function of focus phase and location for different dike slopes and water depths are shown in Figure 4, Figure 5 and Figure 6. The volumes are scaled up to prototype conditions. In order to facilitate visualization of the results, the volumes are expressed in logarithmic scale. It should be noted that colorbars have different scales for each water depth. Using the same scale for all water depths would prevent the appreciation of the small variations in volume due to the different order of magnitude of volumes with low water depths and large water depths. Experimental contours have been smoothed by interpolating the results onto a finer grid (Δxf =0.15m, Δϕ=15°). The analysis for extreme events does not include the combination of wave conditions and water level that resulted in overtopping volumes smaller than 600 l/m in prototype. The blank areas in the figures indicate where this data has been removed.
Overall, the results indicate that varying the location and phases of focused waves can optimize total volume for different water levels. Despite the different experimental setup, the bands of maximum and minimum volumes look similar to those presented in [10,15], where wave run-up and overtopping of focused wave group was studied for mild foreshore slopes and 1:2 dikes. Yet, the results are more scattered for the 1:0.5 slope and for the vertical dike. Actually, the laboratory measurements of the total overtopping volume present two difficulties for correct interpretation. First, as shown, they are quite sparse in xf, which created some issues when using a standard contour plot, see also [15] to this respect. Secondly, although gathered for different water depths, they include data from all different wave conditions, namely wave height and wave period. About the latter, [21] noticed the influence of wave period on the wave-structure interaction induced by focused wave group, fact that has not been explicitly treated in other works.
There is, therefore, a clear need to present the data in a uniform and scaled manner to enable proper comparison. The volumes are scaled initially by the volume flux V0 (see Equation (3)). The variation of dimensionless volumes as function of focus phase and location for different dike slopes and water depths are shown in Figure 7, Figure 8 and Figure 9. Besides, the position of the focused is expressed in dimensionless form (see Equation (7)) for a better understanding of the dependence of the phenomenon on the wave period.
For a 1:2 slope, the overtopping volume decreases as the freeboard height increases and the toe becomes more exposed. This is not so evident for the steep slope (1:0.5) and the vertical wall. A possible explanation lies in the same nature and magnitude of the overtopping phenomenon (see Figure 3): whereas for the smooth slope a clear green water overtopping can be observed, where a continuous sheet of water passes over the crest, for the other two structures the group of waves hits them, creating a vertical jet or plume that falls over the crest of the structure. In addition to the variation in water level, a variation in the breaking depth determines the propagation of the broken wave and its consequent interaction with the structure.
Clear vertical bands, hence proportional to the wavelength, can be identified in the Figure 7, Figure 8 and Figure 9. For all structures, we can find specific dimensionless focus location that maximize of the volume: for water levels 0.31 m and 0.30 m, at a distance from the dike toe equal to approximately the 0.30 and 0.52 of the wavelengths a peak in the measure volume is noticed. A third peak is noticed at about 0.75Lm-10,o although sometimes less in magnitude. For an initial water depth of 0.28 m, there are very few overtopping cases, making it difficult to interpret the results. The 1:2 dike exhibits large volumes for phases of 0° and 90°, for h=0.31 m and 0.29 m. A peak at xf=0.75Lm-10,o and ϕ=270° is also noticeable for h=0.30 m. In the case of the 1:0.5 dike slope, volumes seem maximize for asymmetric wave forms in the groups (i.e. phases of 90° and 270°). The vertical slope shows similar behavior for h=0.31 m, while for h=0.29 m a wider band between X=0.5 and X=0.75 is observed. For h=0.29 m, instead, large volumes are observed for the crest-focused wave groups only (i.e. ϕ=0°).
It is evident that when the overtopping volume is scaled by the volume flux and considering non-dimensional distances from the dike toe, similar patterns for the three different dike slopes are recognized, particularly for the two highest water levels. [10] observed that large overtopping volumes increased monotonically with focus wave amplitude, and clear bands dependent on focus location and phase could be identified. However, the authors attributed the different behavior of small overtopping volumes to wave-wave interaction within the focus group. If the first wave in the group is reflected instead of overtopping the structure, it may cause the second wave to break prematurely and lose most of its energy. This can happen more frequently and with larger waves on steep slopes, which reflect more and cause greater energy loss. The interaction between waves and steep structures, which is here dominated by heavy wave breaking, reflection, and changes in wave momentum resulting even in high uprush and splashes, makes it more challenging to generalize the results.

4.2. Dependence on Scaled Parameters

To enhance comprehension of the relationship between total overtopping volumes and scaled parameters, this section presents a detailed analysis of the impact of the equivalent slope (as defined in Equation (5)), dimensionless freeboard, and shallowness. The variation of Vmax/V0 on the relative freeboard and the equivalent slope is depicted in Figure 10; the results are gathered per focused location. It is evident that larger values of the equivalent slope, expressed as the cotangent of the angle with respect to the horizontal, result in larger overtopping volumes. As the foreshore is not varied in the present analysis, larger values of cotδ actually correspond to larger values of cotα. Hence, the mildest equivalent dike slope exhibits largest overtopping, fact that was already evident from Figure 3, Figure 4, Figure 5 and Figure 6. This fact confirms the results from IB2020 where the was demonstrated for a truncated beach the dependence of the volume on the offshore wave conditions and the slope angle. Here the only difference with IB2020 is that the foreshore slope is replaced by an equivalent slope. Looking at the focused location, we can conclude from Figure 10 that xf closer to the dike toe exhibits similar overtopping than focus location far from the toe but with corresponding smaller freeboard: a focus location closer to the dike triggers large event also for large freeboards.
Based on the results previously shown, Figure 11 shows the dependence of the dimensionless volume Vmax/V* on the relative freeboard and shallowness. To use the V* (Equation (6)) rather than V0 (Equation (3)) is meant to include the influence of the slope (both foreshore and dike) in the analysis. Reduction in the local water level to which corresponds an increase in the effective freeboard leads to small overtopping volumes. Nevertheless, especially for high values of the shallowness, the lower freeboard does not determine necessarily the largest overtopping. Although the focus is often on the location closer to the dike to maximize overtopping volumes, it is important to note that in almost all cases, waves have already broken before reaching that location. Therefore, the target focus wave amplitude is not actually achieved, and the celerity of each wave component is dominated by the local water depth rather than the period.
Finally, an attempt is made to collect all data, including different slopes, wave conditions, and water depths, in a dimensionless form to achieve a general pattern for maximizing overtopping volume as a function of focus phase and location. First of all, considering that the local water depth is considered in the definition of the equivalent slope, the results in terms of Vmax/V* are plotted in Figure 12. Clusters can be clearly identified: the dimensionless volume is maximized for specific bands in X and for phases between 0° and 90° mostly, confirming the results showed above. Peaks are still noticeable around ϕ equal to 180° but lower in magnitude. To confirm these results, in term of general interpretation of the data, including the effect of local water depth and dike slope, the same volumes have been scaled on VL21 (see, Equations (16) and (17)), which also explicitly consider the effect of the relative freeboard. Results are depicted in Figure 13. The analysis reveals that the largest overtopping volumes, adjusted in accordance with specified parameters, manifest notably at X=0.32 with ϕ ranging between 0° and 90°. A secondary band exhibiting maximal volumes becomes apparent at X=0.76. Additionally, discernible peaks are observed at focus phases of 180° and 270° for X=0.70 and X=1.1, respectively. The results overall underscore the differential impact of the sequence of individual waves within the wave group, as well as their propagation, transformation, and breaking dynamics, contingent upon the specific location of the focus.

5. Discussion and Conclusions

In this study, we investigated wave overtopping volumes using focused wave groups on smooth dikes with emerged toe. Main objective is to study how the volumes associated to maximum wave height values in a random sea state depend on the range of focus location and phases. Providing precise guidance on how to maximize wave overtopping for a given sea state and structural layout would be beneficial in experimental practices where focused wave groups can be used instead of long time series of irregular waves. In fact, the use of focused wave groups offers several advantages, including increased repeatability, improved measurement capabilities, and better resolution of models used to investigate significant wave interactions.
Our findings reveal that the location of the focus point and the phase angle at focus are critical factors affecting wave energy concentration and subsequent overtopping volumes. Optimizing the focus location near the seawall enhances wave energy concentration towards the structure, leading to increased overtopping rates. Additionally, variations in the phase angle result in changes in wave characteristics, directly impacting overtopping volumes. By manipulating these parameters through small-scale physical model tests, we were able to observe their direct impact on overtopping responses.
Yet, the focus location and phase exhibit distinct influences on wave structure interaction. The phase angle at the point of focus assumes paramount importance in configuring the wave's characteristics, such as asymmetry, and the spatial distribution of constituent waves within the group. Although frequently disregarded in empirical forecasts of cumulative overtopping volumes during random sea states, phase data assumes significance in optimizing responses for singular extreme events ([15,42]).
The focal point assumes a pivotal role in delineating the dispersion patterns of focused wave groups as they approach and undergo breaking along the shoreline. Alignment of the focus location proximate to the dike tends to accentuate the concentration of wave energy, thereby engendering notable effects of wave overtopping. Contrariwise, if the focus location lies offshore from the dike, it facilitates dispersion prior to reaching its location, thereby mitigating potential overtopping effects. It is crucial to emphasize that in the present study, it is possible for waves to break before reaching the target focused location. Consequently, the wave groupness may be affected, as the assumption that all wave components come into phase at the target focused location may not be met. Nevertheless, it has been deemed highly interesting to explore the response of coastal structures in extremely shallow water conditions, which are quite common worldwide. This is despite the fact that a linear approximation of the focused wave group generation and propagation is employed.
To study the dependence of overtopping volumes on focus location and phase, for different hydrodynamic conditions, water levels and dike slopes, different scaling for the maximum volumes have been analyzed and compared. Starting from the volume flux defined by IB2020, this research reveals that more complex scaling, including the influence of both the foreshore and local water depth, help to comprehend the complex wave structure interaction, despite the wide variation of data in the parameter space. Considering three dike slopes (1:2, 1:0.5 and vertical), in combination with a rather steep foreshore (1:6.3) and seawall emergent toe, the study reveals that dimensionless volumes are in general maximized for focus phases of 0° and 90° if the focus location is placed at about one-third of the offshore wavelength from the dike toe. Phase angles of 180° and 270° lead the smallest volumes, in general. These findings confirmed that wave phasing, often disregarded in assessment of coastal risk associated to overtopping events, plays a fundamental role and can lead to important differences in maximum volumes, even for the same deep-water wave conditions.
To summarize the main findings of the presented research for the design of experimental campaigns, it can be concluded that wave overtopping is maximized for focus locations at the dike toe or equal to one third of the deep-water wavelength, combined with focus location phases between 0° and 90°. This eases the definition of wave conditions to test in experimental or numerical flumes. According to [43], the design wave height for wave-structure interaction, equal to 1.8-2 the significant wave height, should be assessed at the dike toe or at a distance from it equal to five times the significant wave height. Based on this in combination with the outcomes of the present research, it can be inferred that the maximum wave height used for wave overtopping assessment of extreme individual overtopping events should be defined between the dike toe and 1/3Lm-1,0,o, as the wave components are focused and the wave shape is maximized at these locations.
In conclusion, the experimental study on wave overtopping volumes using focused wave groups has provided valuable insights into the complex interplay between wave characteristics and coastal structure responses. The findings highlight the significance of focus location and phase angle in influencing overtopping behavior and demonstrate the advantages of using focused wave groups for studying coastal engineering phenomena.
It is essential to consider the study's limitations, such as investigating only one foreshore slope, analyzing dikes with emerged toes only, and utilizing first-order generation of focused wave groups. Future research will involve a more in-depth analysis of the influence of water levels by implementing corrected second-order generation for bound-long waves and examining the effects of wave setup on wave overtopping prediction ([44,45]). Additionally, further analysis will be carried out to explore the combined effects of multiple factors, including wave height, period, water depths, and foreshore slope, in order to derive a semi-empirical expression for wave overtopping volumes.

Author Contributions

Conceptualization, C.A. and X.G.; methodology, C.A.; formal analysis, C.A.; investigation, C.A. and X.G; resources, C.A.; data curation, C.A.; writing—original draft preparation, C.A.; writing—review and editing, C.A. and X.G; supervision, X.G.; project administration, C.A.; funding acquisition, C.A. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the project GLORIA PID2020-115030RJ-I00 financed by MCIN/AEI/ 10.13039/501100011033 "Adquirir conocimientos sobre el riesgo de rebase para las zonas costeras urbanizadas". Besides, Dr. Corrado Altomare acknowledges funding from Spanish government and the European Social Found (ESF) under the programme ‘Ramón y Cajal 2020’ (RYC2020-030197-I / AEI / 10.13039/501100011033).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

The authors would like to express their gratitude to Joaquim Sospedra and Dr. Andrea Marzeddu for their invaluable assistance during the experimental campaign, as well as to Maria Garcia Sanmartí for her contributions in data gathering and preliminary data screening.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Intergovernmental Panel On Climate Change (Ipcc), The Ocean and Cryosphere in a Changing Climate: Special Report of the Intergovernmental Panel on Climate Change, 1st ed. Cambridge University Press, 2022. [CrossRef]
  2. Amores, M. Marcos, D. S. Carrió, and L. Gómez-Pujol, ‘Coastal impacts of Storm Gloria (January 2020) over the north-western Mediterranean’ Nat. Hazards Earth Syst. Sci., vol. 20, no. 7, pp. 1955–1968, Jul. 2020. [CrossRef]
  3. J. Morim et al., ‘Robustness and uncertainties in global multivariate wind-wave climate projections’, Nat. Clim. Chang., vol. 9, no. 9, pp. 711–718, Sep. 2019. [CrossRef]
  4. EurOtop, Manual on wave overtopping of sea defences and related structures. An overtopping manual largely based on European research, but for worldwide application. Van der Meer, J.W., Allsop, N.W.H., Bruce, T., De Rouck, J., Kortenhaus, A., Pullen, T., Schüttrumpf, 2018. [Online]. Available: www.overtopping-manual.com.
  5. Sandoval and, T. Bruce, ‘Wave overtopping hazard to pedestrians: Video evidence from real accidents’, in Coasts, Marine Structures and Breakwaters 2017, Liverpool, UK: ICE Publishing, Jan. 2018, pp. 501–512. [CrossRef]
  6. A. Koosheh, A. Koosheh, A. Etemad-Shahidi, N. Cartwright, R. Tomlinson, and M. R. A. Van Gent, ‘Individual wave overtopping at coastal structures: A critical review and the existing challenges’, Applied Ocean Research, vol. 106, p. 102476, Jan. 2021. [CrossRef]
  7. S. A. Hughes and C. I. Thornton, ‘Estimation of time-varying discharge and cumulative volume in individual overtopping waves’, Coastal Engineering, vol. 117, pp. 191–204, Nov. 2016. [CrossRef]
  8. Formentin, Gaeta, Palma, Zanuttigh, and Guerrero, ‘Flow Depths and Velocities across a Smooth Dike Crest’, Water, vol. 11, no. 10, p. 2197, Oct. 2019. [CrossRef]
  9. S. M. Formentin and B. Zanuttigh, ‘Semi-automatic detection of the overtopping waves and reconstruction of the overtopping flow characteristics at coastal structures’, Coastal Engineering, vol. 152, p. 103533, Oct. 2019. [CrossRef]
  10. N. Whittaker, C. J. Fitzgerald, A. C. Raby, P. H. Taylor, and A. G. L. Borthwick, ‘Extreme coastal responses using focused wave groups: Overtopping and horizontal forces exerted on an inclined seawall’, Coastal Engineering, vol. 140, pp. 292–305, Oct. 2018. [CrossRef]
  11. P. Tromans, A. R. Anaturk, and P. Hagemeijer, ‘A new model for the kinematics of large ocean waves-application as a design wave’, Proc. ISOPE-91, vol. 3, Jan. 1991.
  12. M. Hann, D. Greaves, A. Raby, and B. Howey, ‘Use of constrained focused waves to measure extreme loading of a taut moored floating wave energy converter’, Ocean Engineering, vol. 148, pp. 33–42, Jan. 2018. [CrossRef]
  13. A. C. Hunt-Raby, A. G. L. Borthwick, P. K. Stansby, and P. H. Taylor, ‘Experimental measurement of focused wave group and solitary wave overtopping’, Journal of Hydraulic Research, vol. 49, no. 4, pp. 450–464, Aug. 2011. [CrossRef]
  14. B. Hofland, I. Wenneker, and P. Van Steeg, ‘Short test durations for wave overtopping experiments’, Sep. 2014.
  15. C. N. Whittaker, C. J. Fitzgerald, A. C. Raby, P. H. Taylor, J. Orszaghova, and A. G. L. Borthwick, ‘Optimisation of focused wave group runup on a plane beach’, Coastal Engineering, vol. 121, pp. 44–55, Mar. 2017. [CrossRef]
  16. P. Ropero-Giralda et al., ‘Efficiency and survivability analysis of a point-absorber wave energy converter using DualSPHysics’, Renewable Energy, vol. 162, 2020. [CrossRef]
  17. B. Tagliafierro et al., ‘Numerical validations and investigation of a semi-submersible floating offshore wind turbine platform interacting with ocean waves using an SPH framework’, Applied Ocean Research, vol. 141, p. 103757, Dec. 2023. [CrossRef]
  18. G. Zhu, Z. Shahroozi, S. Zheng, M. Göteman, J. Engström, and D. Greaves, ‘Experimental study of interactions between focused waves and a point absorber wave energy converter’, Ocean Engineering, vol. 287, p. 115815, Nov. 2023. [CrossRef]
  19. N. Whittaker, A. C. Raby, C. J. Fitzgerald, and P. H. Taylor, ‘The average shape of large waves in the coastal zone’, Coastal Engineering, vol. 114, pp. 253–264, 2016. [CrossRef]
  20. C. C. Craciunescu and M. Christou, ‘Wave breaking energy dissipation in long-crested focused wave groups based on JONSWAP spectra’, Applied Ocean Research, vol. 99, p. 102144, Jun. 2020. [CrossRef]
  21. L. Xiao, K. Fang, M. Huang, D. Wang, and Z. Liu, ‘Focused wave group propagation over fringing reef and its impact on the vertical wall mounted on a reef flat: Experiment and RANS modeling’, Ocean Engineering, vol. 289, p. 116150, Dec. 2023. [CrossRef]
  22. W. Mortimer, R. Calvert, A. Antonini, D. Greaves, A. Raby, and T. S. Van Den Bremer, ‘Implications of second-order wave generation for physical modelling of force and run-up on a vertical wall using wave groups’, Coastal Engineering, vol. 180, p. 104259, Mar. 2023. [CrossRef]
  23. C. Altomare, X. Gironella, A. Marzeddu, M. Viñes Recasens, C. Mösso, and J. Sospedra, ‘Impact of focused wave groups on pier structures: A case study of severe breaking waves at Pont del Petroli during storm Gloria’ Front. Built Environ., vol. 10, p. 1372906, May 2024. [CrossRef]
  24. J. Orszaghova, P. H. Taylor, A. G. L. Borthwick, and A. C. Raby, ‘Importance of second-order wave generation for focused wave group run-up and overtopping’, Coastal Engineering, vol. 94, pp. 63–79, 2014. [CrossRef]
  25. W. Mortimer, A. Raby, A. Antonini, D. Greaves, and T. S. Van Den Bremer, ‘Correct generation of the bound set-down for surface gravity wave groups in laboratory experiments of intermediate to shallow depth’, Coastal Engineering, vol. 174, p. 104121, Jun. 2022. [CrossRef]
  26. V. Heller, ‘Scale effects in physical hydraulic engineering models’, Journal of Hydraulic Research, vol. 49, no. 3, pp. 293–306, 2011. [CrossRef]
  27. J. Pearson, T. Bruce, N. W. H. Allsop, and V. Gironella, ‘Violent wave overtopping - measurements at large and small scale’, in Proceedings of 28th International Conference of Coastal Engineering (ASCE), 2002, p. 12.
  28. H. Schüttrumpf and H. Oumeraci, ‘Layer thicknesses and velocities of wave overtopping flow at seadikes’, Coastal Engineering, vol. 52, no. 6, pp. 473–495, Jun. 2005. [CrossRef]
  29. M. Yuhi, H. Mase, S. Kim, S. Umeda, and C. Altomare, ‘Refinement of integrated formula of wave overtopping and runup modeling’, Ocean Engineering, vol. 220, p. 108350, Jan. 2021. [CrossRef]
  30. C. H. Lashley, J. C. H. Lashley, J. Van Der Meer, J. D. Bricker, C. Altomare, T. Suzuki, and K. Hirayama, ‘Formulating Wave Overtopping at Vertical and Sloping Structures with Shallow Foreshores Using Deep-Water Wave Characteristics’, J. Waterway, Port, Coastal, Ocean Eng., vol. 147, no. 6, p. 04021036, Nov. 2021. [CrossRef]
  31. B. Hofland, X. Chen, C. Altomare, and P. Oosterlo, ‘Prediction formula for the spectral wave period T m-1,0 on mildly sloping shallow foreshores’, Coastal Engineering, vol. 123, pp. 21–28, 17. 20 May. [CrossRef]
  32. A. Svendsen, ‘Mass flux and undertow in a surf zone’, Coastal Engineering, vol. 8, no. 4, pp. 347–365, Nov. 1984. [CrossRef]
  33. M. S. I. Ibrahim and T. E. Baldock, ‘Swash overtopping on plane beaches – Reconciling empirical and theoretical scaling laws using the volume flux’, Coastal Engineering, vol. 157, p. 103668, 2020. [CrossRef]
  34. C. Altomare, D. B. Laucelli, H. Mase, and X. Gironella, ‘Determination of Semi-Empirical Models for Mean Wave Overtopping Using an Evolutionary Polynomial Paradigm’, JMSE, vol. 8, no. 8, p. 570, Jul. 2020. [CrossRef]
  35. A. Astorga-Moar and T. E. Baldock, ‘Assessment of wave overtopping models for fringing reef fronted beaches.’, Coastal Engineering, vol. 186, p. 104395, Dec. 2023. [CrossRef]
  36. B. Altomare, T. Suzuki, X. Chen, T. Verwaest, and A. Kortenhaus, ‘Wave overtopping of sea dikes with very shallow foreshores’, Coastal Engineering, vol. 116, pp. 236–257, Oct. 2016. [CrossRef]
  37. Y. Goda, ‘Derivation of unified wave overtopping formulas for seawalls with smooth, impermeable surfaces based on selected CLASH datasets’, Coastal Engineering, vol. 56, no. 4, pp. 385–399, Apr. 2009. [CrossRef]
  38. C. Franco and L. Franco, ‘Overtopping Formulas for Caisson Breakwaters with Nonbreaking 3D Waves’, J. Waterway, Port, Coastal, Ocean Eng., vol. 125, no. 2, pp. 98–108, Mar. 1999. [CrossRef]
  39. P. Besley, Overtopping of seawalls: Design and assessment manual. Almondsbury, Bristol, Swindon, Wilts: Environment Agency ; WRc [distributor], 1999.
  40. T. Lykke Andersen, H. F. Burcharth, and F. X. Gironella, ‘Single wave overtopping volumes and their travel distance for rubble mound breakwaters’, in Coastal Structures 2007, Venice, Italy: World Scientific Publishing Company, Jun. 2009, pp. 1241–1252. [CrossRef]
  41. P. Mares-Nasarre, J. Molines, M. E. Gómez-Martín, and J. R. Medina, ‘Individual wave overtopping volumes on mound breakwaters in breaking wave conditions and gentle sea bottoms’, Coastal Engineering, vol. 159, p. 103703, Aug. 2020. [CrossRef]
  42. A. Romano, G. Bellotti, R. Briganti, and L. Franco, ‘Uncertainties in the physical modelling of the wave overtopping over a rubble mound breakwater: The role of the seeding number and of the test duration’, Coastal Engineering, vol. 103, pp. 15–21, Sep. 2015. [CrossRef]
  43. Y. Goda, Random Seas and Design of Maritime Structures, 2nd ed., vol. 15. in Advanced Series on Ocean Engineering, vol. 15. WORLD SCIENTIFIC, 2000. [CrossRef]
  44. M. Buccino, A. Di Leo, S. Tuozzo, L. F. Còrdova Lopez, M. Calabrese, and F. Dentale, ‘Wave overtopping of a vertical seawall in a surf zone: A joint analysis of numerical and laboratory data’, Ocean Engineering, vol. 288, p. 116144, Nov. 2023. [CrossRef]
  45. S. Tuozzo, M. Calabrese, and M. Buccino, ‘An overtopping formula for shallow water vertical seawalls by SWASH’, Applied Ocean Research, vol. 148, p. 104009, Jul. 2024. [CrossRef]
Preprints 108876 g001
Figure 1. Experimental model setup in the CIEMito flume: cotα= [0, 0.5, 2].
Figure 1. Experimental model setup in the CIEMito flume: cotα= [0, 0.5, 2].
Preprints 108876 g001
Preprints 108876 g002
Figure 2. Example of free-surface elevations at nine wave gauges (results in model scale).
Figure 2. Example of free-surface elevations at nine wave gauges (results in model scale).
Preprints 108876 g002
Preprints 108876 g003
Figure 3. Snapshot of wave overtopping of the three different dike slopes: example of large individual overtopping.
Figure 3. Snapshot of wave overtopping of the three different dike slopes: example of large individual overtopping.
Preprints 108876 g003
Preprints 108876 g004
Figure 4. Variation in total overtopping volume (upscaled to prototype and expressed and in logarithmic scale) over the range of focus locations, xf, phases (at focus) and water level tested for the 1:2 dike slope.
Figure 4. Variation in total overtopping volume (upscaled to prototype and expressed and in logarithmic scale) over the range of focus locations, xf, phases (at focus) and water level tested for the 1:2 dike slope.
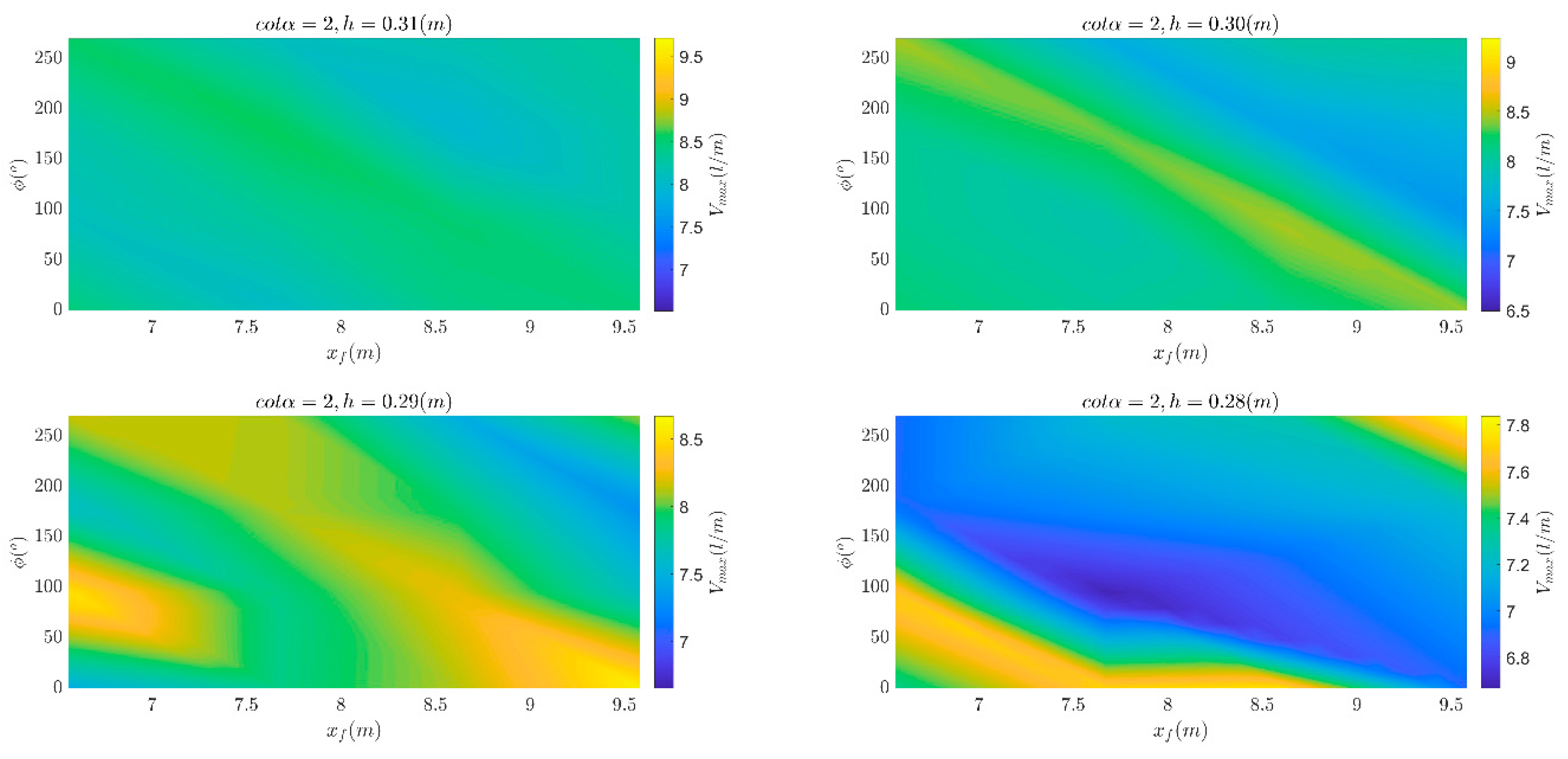
Preprints 108876 g004
Preprints 108876 g005
Figure 5. Variation in total overtopping volume (upscaled to prototype and expressed and in logarithmic scale) over the range of focus locations, xf, phases (at focus) and water level tested for the 1:0.5 dike slope.
Figure 5. Variation in total overtopping volume (upscaled to prototype and expressed and in logarithmic scale) over the range of focus locations, xf, phases (at focus) and water level tested for the 1:0.5 dike slope.
Preprints 108876 g005
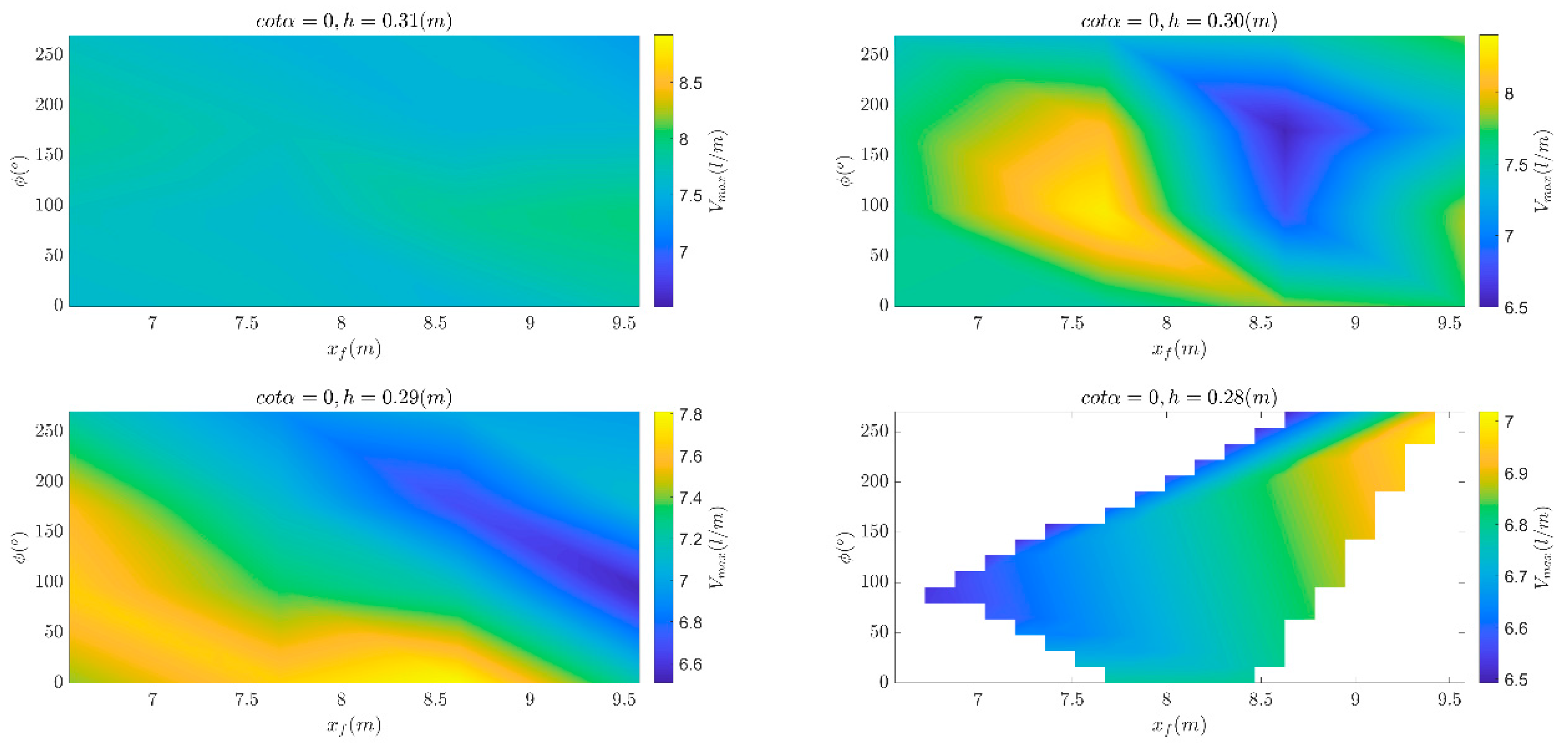
Preprints 108876 g006
Figure 6. Variation in total overtopping volume (upscaled to prototype and expressed and in logarithmic scale) over the range of focus locations, xf, phases (at focus) and water level tested for the vertical dike.
Figure 6. Variation in total overtopping volume (upscaled to prototype and expressed and in logarithmic scale) over the range of focus locations, xf, phases (at focus) and water level tested for the vertical dike.
Preprints 108876 g006
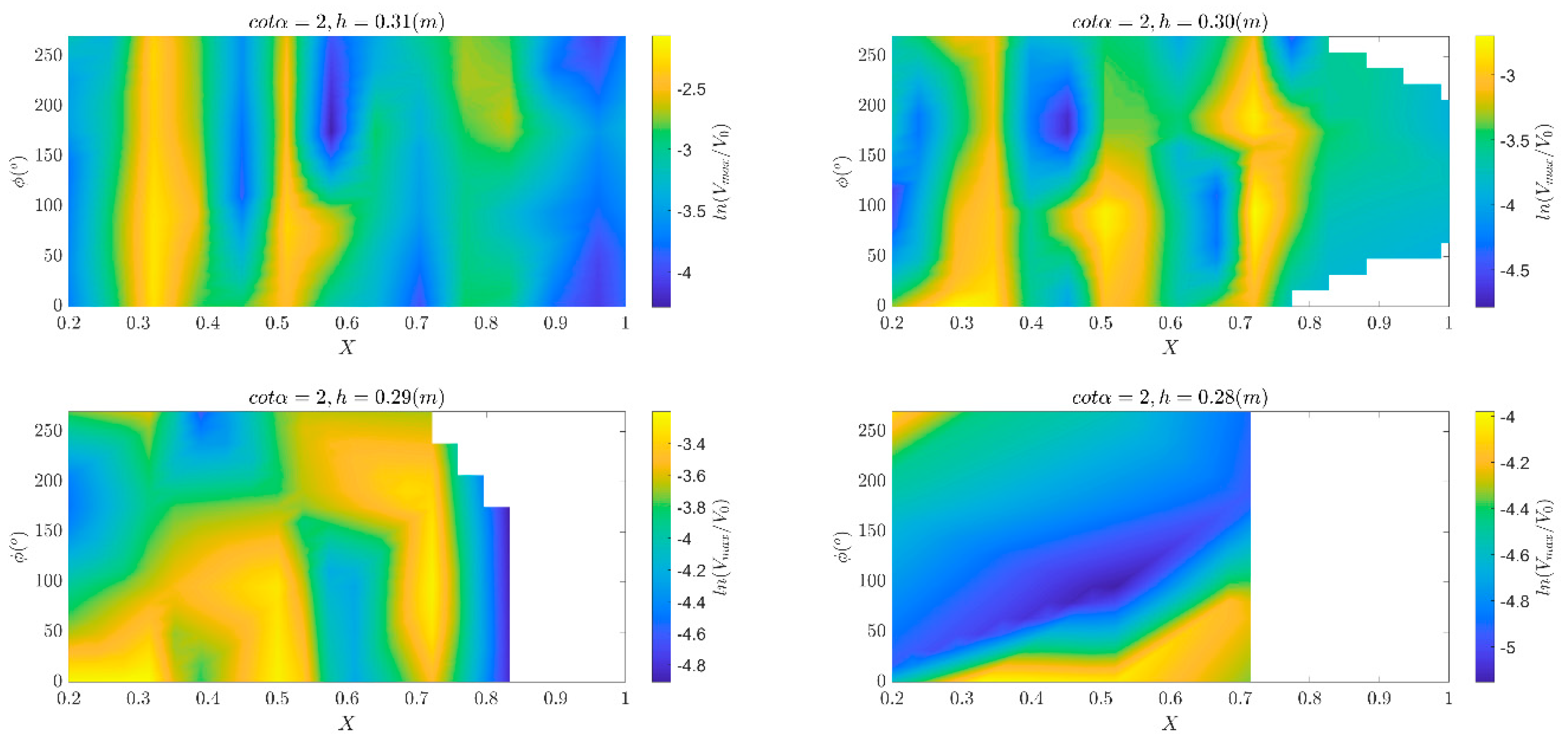
Preprints 108876 g007
Figure 7. Variation in non-dimensional total overtopping volume (Vmax/V0) over the range of non-dimensional focus locations, X, phases (at focus) and water level tested for the 1:2 dike slope.
Figure 7. Variation in non-dimensional total overtopping volume (Vmax/V0) over the range of non-dimensional focus locations, X, phases (at focus) and water level tested for the 1:2 dike slope.
Preprints 108876 g007
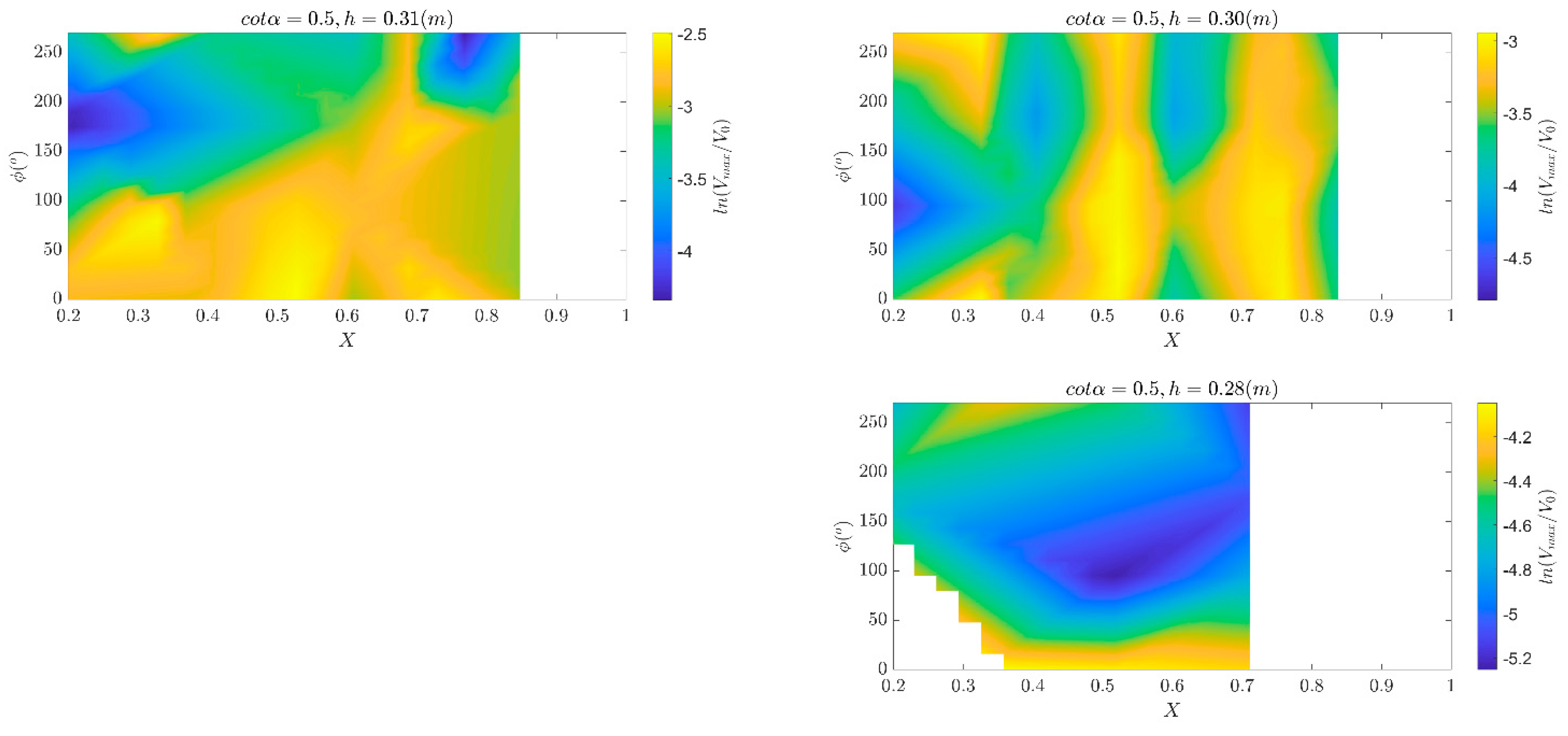
Preprints 108876 g008
Figure 8. Variation in non-dimensional total overtopping volume (Vmax/V0) over the range of non-dimensional focus locations, X, phases (at focus) and water level tested for the 2:1 dike slope.
Figure 8. Variation in non-dimensional total overtopping volume (Vmax/V0) over the range of non-dimensional focus locations, X, phases (at focus) and water level tested for the 2:1 dike slope.
Preprints 108876 g008
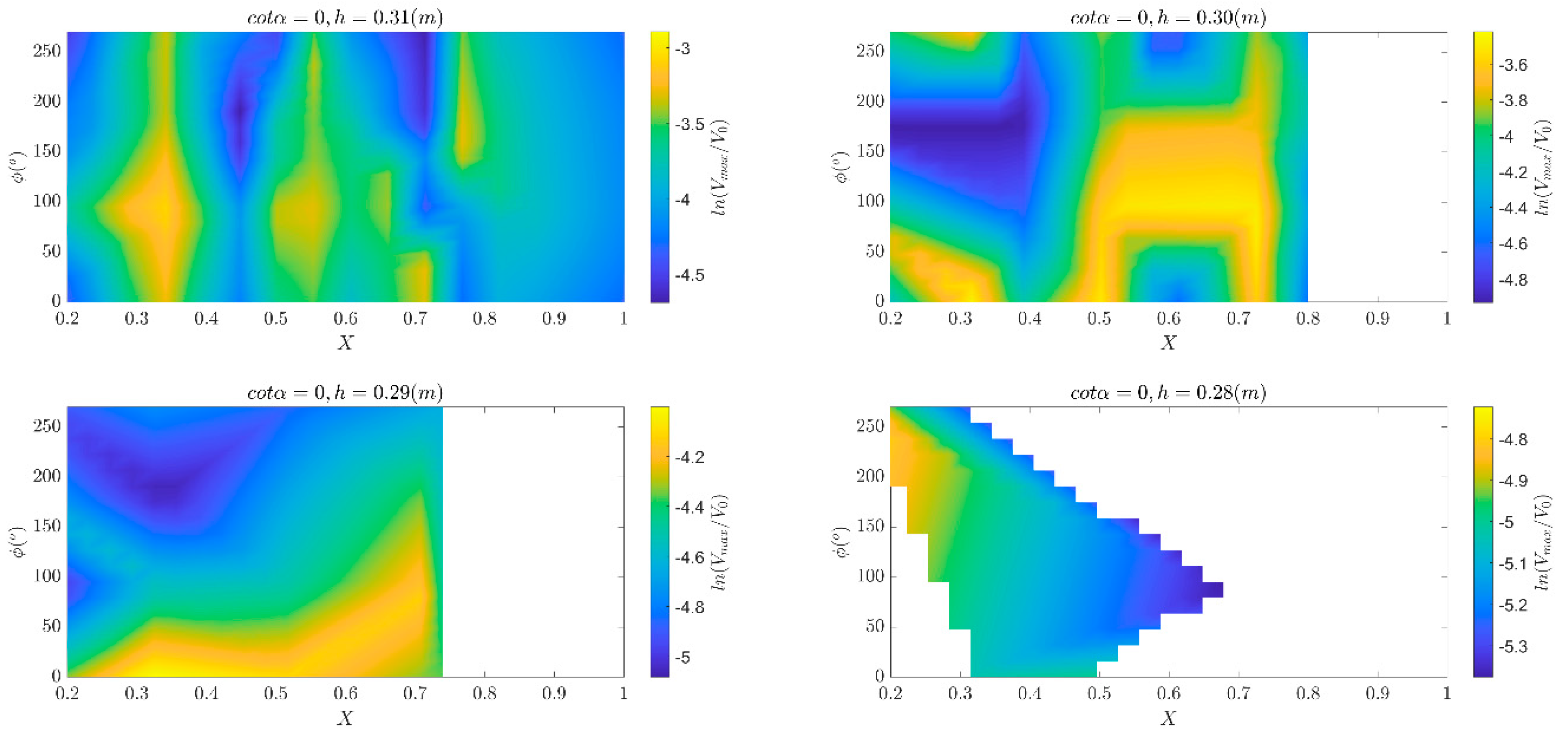
Preprints 108876 g009
Figure 9. Variation in non-dimensional total overtopping volume (Vmax/V0) over the range of non-dimensional focus locations, X, phases (at focus) and water level tested for the vertical dike.
Figure 9. Variation in non-dimensional total overtopping volume (Vmax/V0) over the range of non-dimensional focus locations, X, phases (at focus) and water level tested for the vertical dike.
Preprints 108876 g009
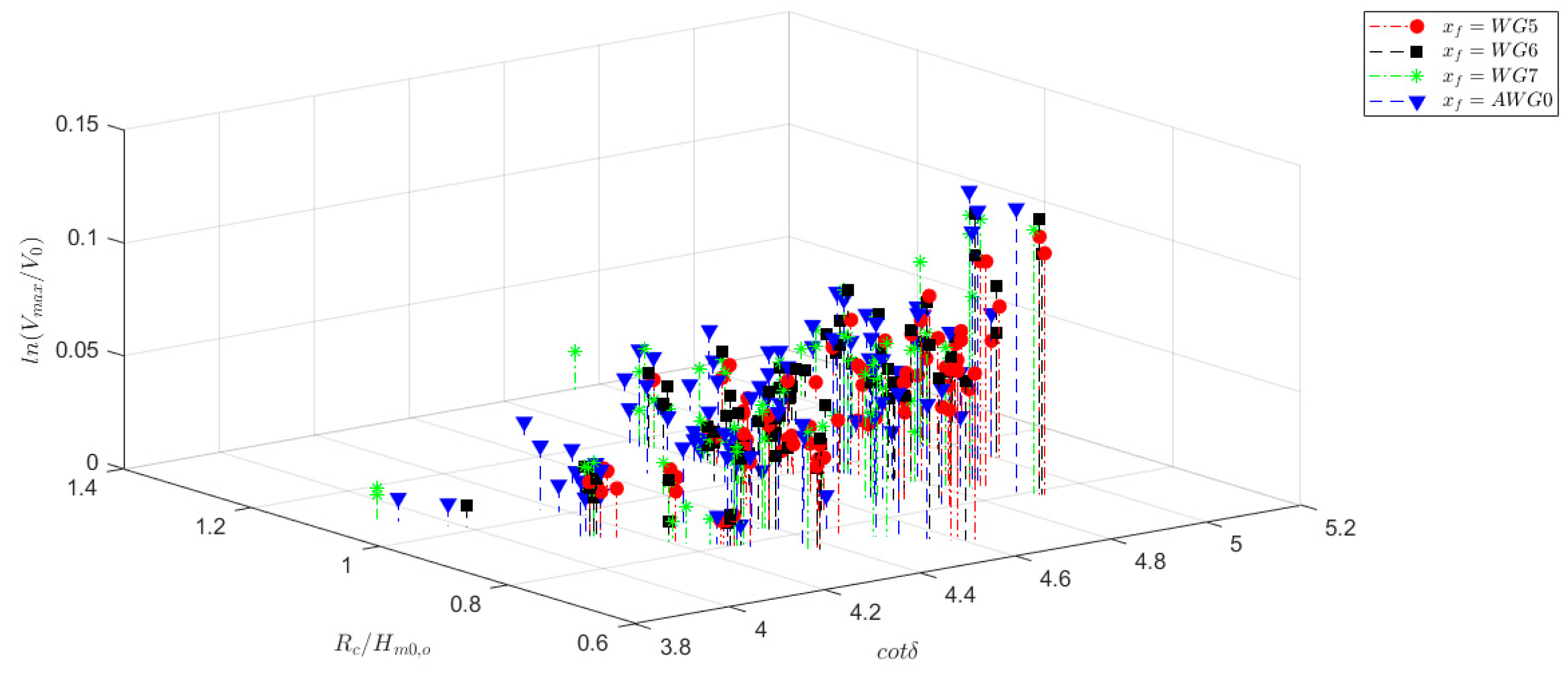
Preprints 108876 g010
Figure 10. Variation of the dimensionless volume Vmax/V0 on the relative freeboard and equivalent slope. Results are gathered per focus location.
Figure 10. Variation of the dimensionless volume Vmax/V0 on the relative freeboard and equivalent slope. Results are gathered per focus location.
Preprints 108876 g010
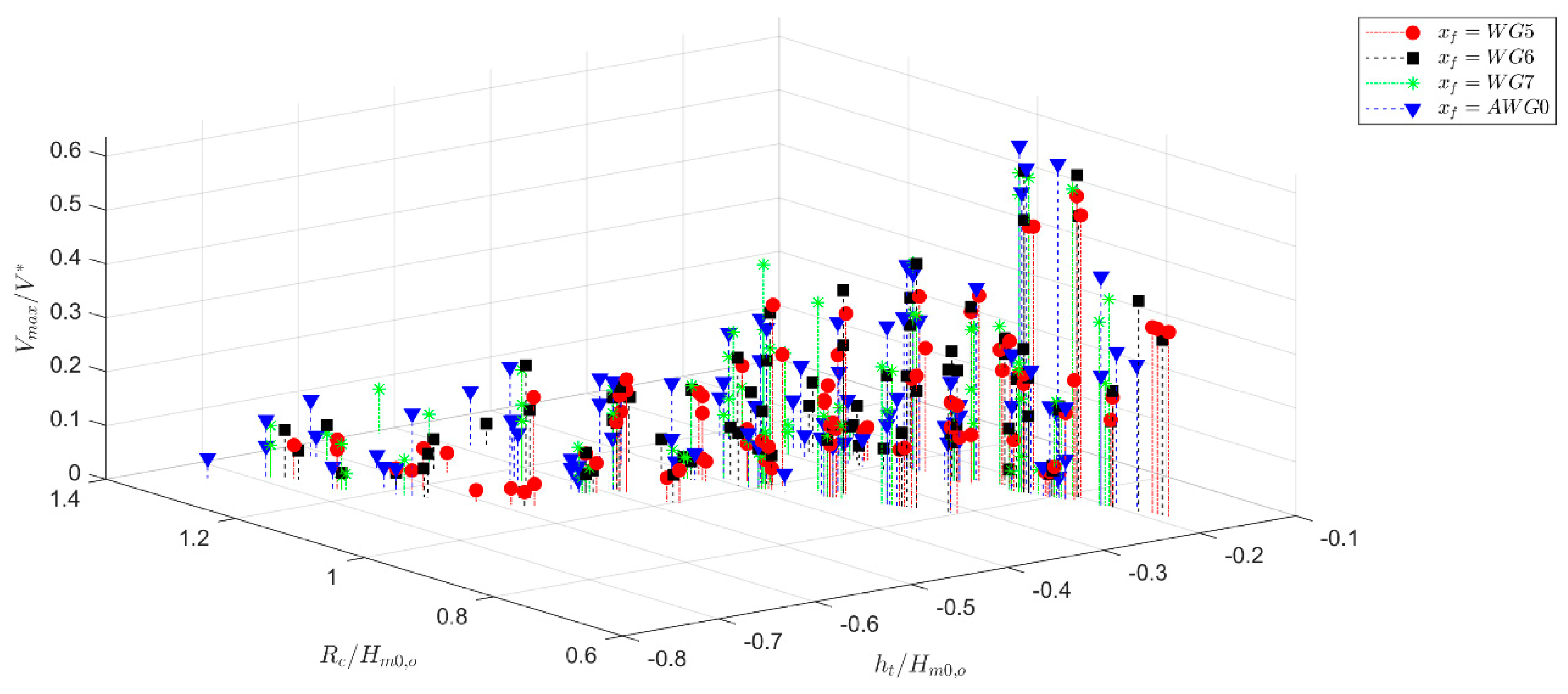
Preprints 108876 g011
Figure 11. Variation of the dimensionless volume Vmax/V* on the relative freeboard and shallowness. Results are gathered per focus location.
Figure 11. Variation of the dimensionless volume Vmax/V* on the relative freeboard and shallowness. Results are gathered per focus location.
Preprints 108876 g011
Preprints 108876 g012
Figure 12. Variation in non-dimensional total overtopping volume (Vmax/V*) over the range of non-dimensional focus locations, X, phases (at focus) and water level testes for all tests.
Figure 12. Variation in non-dimensional total overtopping volume (Vmax/V*) over the range of non-dimensional focus locations, X, phases (at focus) and water level testes for all tests.
Preprints 108876 g012
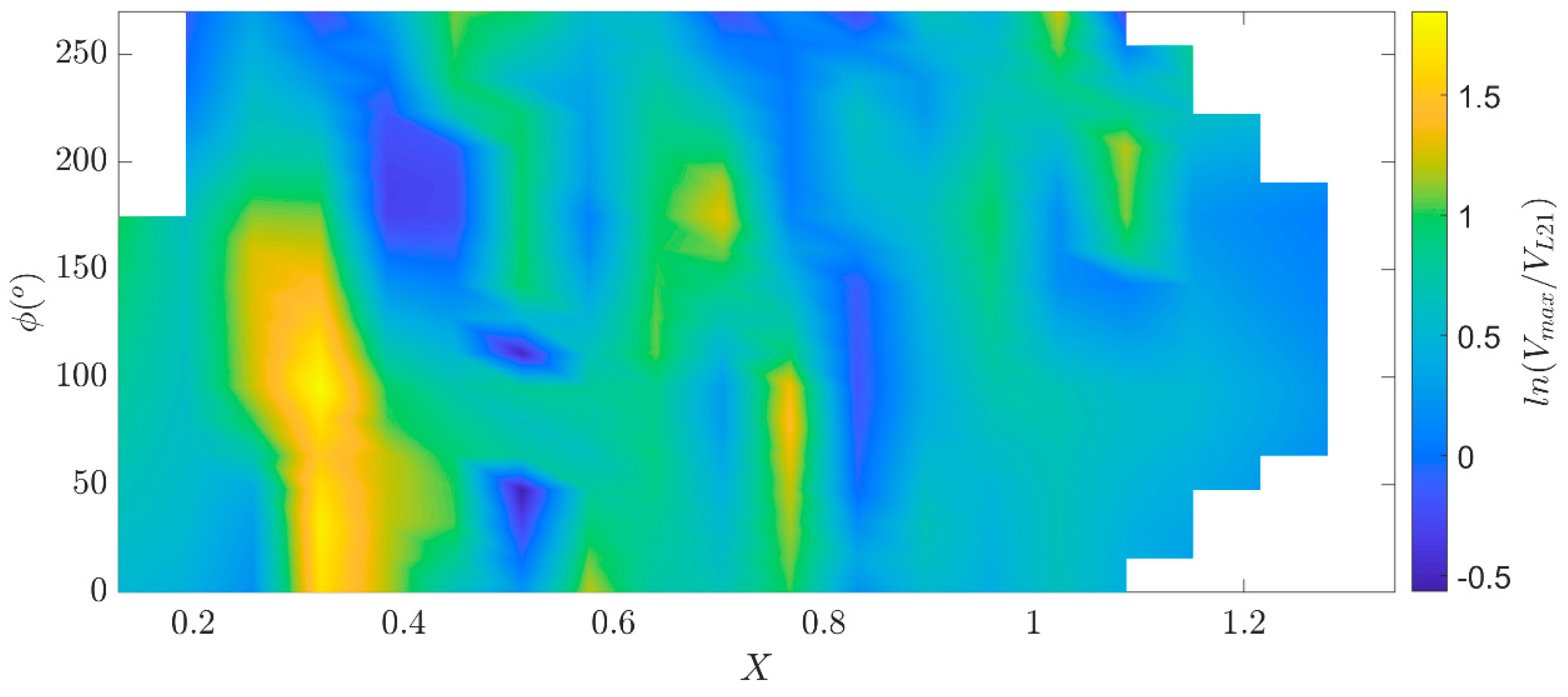
Preprints 108876 g013
Figure 13. Variation in non-dimensional total overtopping volume (Vmax/VL21) over the range of non-dimensional focus locations, X, phases (at focus) and water level testes for all tests.
Figure 13. Variation in non-dimensional total overtopping volume (Vmax/VL21) over the range of non-dimensional focus locations, X, phases (at focus) and water level testes for all tests.
Preprints 108876 g013
Table 1. Wave gauge location for surface elevation measurement along the CIEMito flume.
Table 1. Wave gauge location for surface elevation measurement along the CIEMito flume.
Wave gauge WG0 WG1 WG2 WG3 WG4 WG5* WG6* WG7* AWG0*
Distance from the wave maker (m) 4.00 4.15 4.36 4.65 5.23 6.56 7.67 8.64 9.58
*wave gauges where focal location has been established.
Table 2. Hydrodynamic laboratory conditions, focus locations and phases at focus, and water depths considered for the overtopping physical model tests for each dike slope.
Table 2. Hydrodynamic laboratory conditions, focus locations and phases at focus, and water depths considered for the overtopping physical model tests for each dike slope.
Parameter Dike 1:2 Dike 1:0.5 Vertical dike
Hm0 (m) 0.0456- 0.0712 0.0498- 0.0760 0.0468- 0.0726
Tm-1,0 (s) 1.32-1.82 1.48-1.82 1.42-1.82
xf (m) (relative to the wavemaker) 6.56, 7.66, 8.64, 9.58
xf (m) (relative to the dike toe) 0.64, 1.58, 2.55, 3.66
φ (°) 0, 90, 180, 270
h (m) (at the wavemaker) 0.28, 0.29, 0.30, 0.31 0.28, 0.30, 0.31 0.28, 0.29, 0.30, 0.31
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated