Preprint
Article
Thermodynamic Energy Analysis of a Superconducting Shielding Magnetic Field Model
Altmetrics
Downloads
79
Views
17
Comments
0
This version is not peer-reviewed
Submitted:
09 June 2024
Posted:
12 June 2024
You are already at the latest version
Alerts
Abstract
The Meissner effect is a special property of superconductors. In this paper, based on the characteristics of the Meissner effect, a superconducting phase transition model of a superconductor under a changing magnetic field is proposed. A thermodynamic analysis was performed on the model to calculate both the changes in the thermodynamic parameters of the superconductor during the phase transition and the changes in the overall work and energy of the model. For Model 1 in the present study, the thermodynamic energy of the superconductor was not conserved due to the phase change of the superconductor under a changing magnetic field.

Keywords:
Subject: Physical Sciences - Condensed Matter Physics
I. Background
In thermodynamic superconductivity analysis, two-fluid theory is used to analyze the phase transition of superconductors from a macroscopic perspective of an object in accordance with the first law of thermodynamics. The analysis mainly elucidates changes in physical quantities such as temperature, volume, pressure, electromagnetic energy, work, free energy, and heat. The thermodynamic parameters of a phase change can be divided into two categories. One category is related to the total amount of substance in the physical system, including volume V, energy E, internal energy U, total magnetization M of the object, and entropy S. The other category involves quantitative strength, such as pressure P, temperature T, and magnetic field strength H [1]. Thermodynamic analysis is based on the first law of thermodynamics, that is, the conservation of energy. The calculations, based on theoretical formulas, are validated by a considerable amount of experimental data, which in turn validates the law of energy conservation.
1. To conveniently describe the thermodynamic analysis of the superconducting shielding model below, it is necessary to introduce the basic thermodynamic formulas of the two-fluid model [2]:
According to two-fluid theory, when the strength of a magnetic field in a magnetic medium is H and the magnetic moment of a superconductor is M, . Here, μ0 is the vacuum magnetic permeability, and the magnetic field is assumed to be a static magnetic field generated by the permanent magnet. Therefore, the excitation magnetic field is not considered, and the work done by the magnetic field is μ0HdM.
The Gibbs free energy with an applied magnetic field is defined as follows:
When the physical quantities change slightly, the free energy is differentiated as:
If the external magnetic fields H and M are changed and the temperature and pressure remain unchanged (i.e., =0), then we have the following:
According to the first law of thermodynamics, when T and p are constant, the internal energy of a magnetized object changes as follows:
The first term in the above formula is the heat change in the magnetized object, and the latter two terms are the work done on the object. Therefore, substituting (4) into (3) gives the following:
Then, the object is magnetized by a magnetic field with strength H. When the magnetic moment is M, the free energy of the object changes as follows:
A magnetic field that is applied to a superconductor generates negative magnetization. When completely magnetized, H = -M, and the change in the free energy per unit volume of the superconducting phase transition is as follows:
When the magnetization of the superconductor reaches the critical value of -M=Hc, ; then,
Assuming that the pressure p and the field strength H remain constant and the temperature T changes, and based on Formula (1) and Formula (4) of the first law of thermodynamics, S = −() p, H. If the magnetic field is completely suppressed during superconductivity, then according to Formula (8), the entropy difference per unit volume between the two phases is as follows:
From this, the latent heat of the phase change of volume V at temperature T is as follows:
When the temperature T decreases, Hc increases. Therefore, Q>0, indicating that the phase transition of the superconductor from a normal state to a superconducting state releases heat and vice versa.
Formula (9) shows that for a type I superconductor, there is an abrupt change in H at the critical temperature, and thus, there is latent heat from the phase change. For a type II superconductor, there is no abrupt change in Hc1 and Hc2 at the phase change, and therefore, there is no latent heat. Different superconductors undergo phase changes at different temperatures and have different latent heats of phase change. For example, when Sn is at 1.8 K, the latent heat of phase change is the greatest at approximately 2.5 mJ/g∙K, and that of Hg is the greatest at 2.4 K at 3.7 mJ/g∙K.
The above analysis assumes that the V and p of the superconducting phase transition are unchanged. However, the actual V and p slightly change. According to the thermodynamic volume change formula,
Based on the experimental data,/ ≈ -10-7 T·cm2/N, and / ≈ -5-6 K·cm2/N. Substituting these data into Formula (11) indicates that at lower temperatures, [2], suggesting that the changes in V and p of the superconductor phase transition are several orders of magnitude smaller than those of other physical quantities and thus can be completely ignored in the calculation. Therefore, in the following analysis, V and p are assumed to remain unchanged, and their influence is not considered.
According to the above formulas, the superconductor phase change is reversible during the superconductor phase change transformation process, and the total energy is conserved in the whole process. According to the relevant literature, for a superconductor in the Meissner state in a changing magnetic field, the transformations among the electromagnetic energy flowing into the superconductor, the internal magnetic field energy, the electric field energy, and the kinetic energy of the superconducting electrons are completely reversible; that is, there are no losses in the superconductor [3].
2. Since the analysis model in this paper involves the magnetic field shielding function of superconductors in the superconducting state, the current technological status of superconductor magnetic field shielding must be introduced before analysis.
The magnetic field shielding function of superconductors is generated by the characteristics of the Meissner effect . When a superconductor is in a superconducting state, it generates an anti-magnetic field to an external magnetic field, which suppresses the magnetic flux (magnetic field lines). Thus, the magnetic field cannot reach the other side of the superconductor. As shown in Figure 1, the permanent magnet is placed inside a cylindrical superconductor (the superconductor in the superconducting shielding test generally has a cylindrical structure); therefore, when the magnetic field is shielded, it cannot reach outside of the cylindrical superconductor. The generated anti-magnetic field forms a very thin layer on the outer surface of the superconductor, with a thickness ranging from 10-2 to 10-1 μm [4,5]. Due to the very thin infiltration layer, a superconducting film of approximately 0.1 mm is commonly used in practice to conduct experiments. The superconducting current and anti-magnetic field are generated on the surface of the superconductor, the internal magnetic flux is zero, the magnetic field cannot pass through the superconductor, the magnetic field is shielded, and the strength of the other side of the superconductor (the side facing away from the magnetic field) significantly decreases. The magnetic field shielding effect is usually expressed in decibels (dB) of shielding effectiveness. The experimental data show that the yttrium barium copper oxide (YBCO) superconductor can easily achieve a shielding effectiveness of 20~60 dB. The shielding effectiveness of a three-layer cylindrical shield combined with copper, iron and a superconductor can reach 90 dB [4,5]. According to the shielding effectiveness formula, the shielding effect can reach more than 99%. In terms of the ability of superconductors to shield magnetic fields, a large amount of data has shown that some superconductors can shield magnetic fields in the range of 2~20 T, and superconductors with high critical temperatures (Tc) have good magnetic shielding effects [4].
For Type I superconductors, the magnetic field shielding process is simple, and the effect is obvious, but the critical magnetic field is little. For Type II high-temperature superconductors that undergo a superconducting phase change in a magnetic field, a flux pinning effect occurs that affects the shielding effect. However, this will not eliminate the basic shielding function of the superconductor, much less affect the qualitative analysis of thermodynamics in this paper. Additionally, the shielding effect can be improved by changing the superconducting material, ambient temperature, magnetic field strength and other factors; therefore, the pinning flux and hysteresis effect are not considered in this analysis.
Once the above two points are explained, the thermodynamic formula for superconductivity and the shielding characteristic of the superconducting phase change can be used to perform a thermodynamic analysis of the following models.
II. Thermodynamic Analysis of a Superconducting Shielded Magnetic Field
The thermodynamic analysis model of the superconducting shielding analyzed in this paper (hereafter referred to as Model 1) is shown in Figure 2. Specifically, on two sides of a disc-shaped superconductor (for convenience of illustration, the superconductor in the following view is simplified to a circular structure), there is a fixed permanent magnet (hereafter referred to as the fixed magnet) and a movable permanent magnet (hereafter referred to as the moving magnet).
Model 1 exhibits a dynamic model of the moving magnet undergoing repeated motion. The specific movement process is described as follows: the superconductor is initially in a normal state, and the moving magnet is close to the superconductor. The superconductor phase changes to a superconducting state when the temperature drops. At this time, the superconductor shields the fixed magnetic field, and the moving magnet moves away from the superconductor. The superconductor returns to the normal state when the temperature rises. At this moment, the moving magnet is brought close to the superconductor to complete one cycle.
During this process, the thermodynamic changes in the model system are analyzed, with a focus on the changes in thermodynamic quantities caused by the action of the two permanent magnets on the superconductor. The effects of work and energy between the two permanent magnets are analyzed, and the variations in the thermodynamic parameters of the entire model are analyzed.
Symbols in the diagrams: s represents the superconducting state, n represents the normal state, and the arrow represents the displacement direction.
Because of the interaction and energy between fixed and moving magnets in the analysis of Model 1, before the analysis, two formulas [6] need to be introduced. The first is the field strength formula of the permanent magnet. As shown in Figure 3, the field strength of a cylindrical permanent magnet with a height of L at its pole center a is ; then, the magnetic field at distance b from the central axis of the magnet can be simplified as follows:
The second formula describes the work of the static magnetic field [7]. As shown in Figure 4, assuming that the field strength of the left permanent magnet 1 at b is and that the field strength of the right permanent magnet 2 at b is , the formula for the work done by permanent magnet 1 by moving permanent magnet 2 to point b can be simplified as follows:
Since the effect of the two permanent magnets on the superconductor in Model 1 is influenced by the magnetic field, according to the principle of magnetic field superposition, the effect of the magnetic field of each permanent magnet on the superconductor is analyzed separately. In addition, the comprehensive influence of the two permanent magnets on the superconductor is evaluated. The two magnets are completely equivalent; similarly, the effect between the magnetic fields of two permanent magnets can also be analyzed separately. Thus, we analyzed three small systems: the fixed magnet and the superconductor, the moving magnet and the superconductor, and the fixed magnet and the moving magnet. The thermodynamic analysis of Model 1 has been completed, so it is easy to clearly express.
To provide the thermodynamic process in Model 1 in detail, the following calculations are carried out in four steps according to the cyclic form shown in Figure 5:
In Figure 5, assume that the field strength at the fixed magnet pole (a) is H1a. The field strengths at b and c are H 1b and H1c, respectively; the field strength at the moving magnet pole (b) is H2b, and the field strength at d is H2d. Point o represents a point sufficiently far away; μ3 represents the magnetic permeability of the superconductor. W1 and W2 represent the work done on the superconductor by the fixed magnet and the moving magnet, respectively; W represents the work done by the fixed magnet on the moving magnet when the moving magnet moves to point b; F represents the magnetic field force between the fixed magnet and the moving magnet (m1 and m2 are the magnetic moments; L is the distance from the field source, and this formula represents only the presence of a magnetic field and is not used for work calculations in the analysis). S represents the displacement of the moving magnet; Q1 and Q2 are the heat released by the influence of the fixed and moving magnets on the superconductor during its phase transition, respectively; and (1→2) represents the effect of fixed magnet 1 on moving magnet 2.
In Step ①, the superconductor is initially assumed to be a paramagnetic medium in a normal state. In this case, the surrounding magnetic field has no effect, and the moving magnet is located close to the superconductor. If the moving magnet itself is magnetically saturated, then it will not be affected by external influences. A magnetic field will generate an induction magnetic field [8,9] but will be subjected to a magnetic field force F of a constant magnetic field. Since the moving magnet is not displaced, it is not subjected to the magnetic field force.
In Step ②, the superconductor is converted from the normal state to the superconducting state, and the magnetic field of the fixed magnet is shielded. The magnetic field of the fixed magnet cannot influence the moving magnet. Since the moving magnet has no induced magnetic field due to the fixed magnet, after the fixed magnetic field is removed, the moving magnet will be displaced. The thermodynamic strength is unaffected, but at this moment, the fixed magnet no longer generates a magnetic field force on the moving magnet.
After the superconductor phase changes to a superconducting state, it is subjected to the superposition of the magnetic fields of the fixed magnet and the moving magnet. Suppose the field strength of the magnet at the superconductor is H1c, the field strength of the moving magnet at the superconductor is H2d, and the magnetization of the superconductor is M; then, the induction anti-magnetic field of the superconductor is as follows: , , and the integral is At this moment, the free energy of the superconductor increases, and heat is released: .
In Step ③, the moving magnet moves from the superconductor. During this process, it is subjected to the repulsive force of the superconductor’s anti-magnetic field. The anti-magnetic field strength away from the surface is given by becoming, and the magnetic field of the moving magnet does negative work on the system:, that is, the work done by the repulsion force of the anti-magnetic field of the superconductor. At this time, the free energy of the superconductor decreases, and at the same time, it absorbs some of the heat: . When the moving magnet is far away, the magnetic field of the fixed magnet is shielded by the superconductor and does not affect the moving magnet.
In step ④, the phase of the superconductor changes to the normal state, the superconductor returns to the paramagnetic state, the strength of the magnetic field changes from M=-H1c to M=0, and the constant magnetic field negatively affects the superconductor:. The free energy of the superconductor decreases again while absorbing heat:.
After the superconductor phase changes to the normal state, it returns to the paramagnetic state and no longer shields the magnetic field. The magnetic field of the fixed magnet passes through the superconductor and generates a magnetic field force on the moving magnet. At this moment, the moving magnet is brought close to the superconductor, and the moving magnet performs positive work by the magnetic field force of the fixed magnet’s magnetic field during its approach. The moving magnet moves from point o, which is far enough away from point b, and the work done by fixed magnet on the moving magnet is . After approaching the superconductor, the internal magnetic field strength of the superconductor is the result of the superposition of magnetic fields H1c and H2d of the moving magnet. Since the superconductor is paramagnetic with a permeability of μ3 = 1 at this time, the work performed by the moving magnet on the superconductor during the approaching process is 0. Model 1 recycles to the Step 1 state.
Via the above four steps, the summary calculation of the thermodynamic quantities of one complete cycle of Model 1 shows that the work of the two permanent magnets W1 and W2 on the superconductor cancel. Furthermore, the heat absorption and release of superconductors Q1 and Q2 are canceled. The final residual thermodynamic quantity is the work performed by the magnetic field of the fixed magnet on the moving magnet: .
According to the thermodynamic analysis results of Model 1, the energy of the total model system is not conserved during a complete phase change transformation cycle.
In fact, the moving magnet of Model 1 can also be replaced by a ferromagnet, as shown in Figure 6. The ferromagnet does not have a magnetic field and theoretically has no thermodynamic effect on the superconductor; therefore, the thermodynamic analysis of the model is simpler. Only the mutual influence between the fixed magnet and superconductor, as well as between the fixed magnet and ferromagnet, needs to be considered. The overall analysis of the fixed magnet and superconductor clearly shows energy conservation. However, the motion process of the fixed magnet and ferromagnet shows that due to the artificial interruption of the magnetic field of the fixed magnet, in a cyclic process, there is residual work on the ferromagnet. Based on the above analyses, the overall model system energy is not conserved.
III. Temperature and Caloric Control of the Model System during the Superconducting Phase Transition
In terms of the temperature and heat control of the system during the superconducting phase transition, although it has been theoretically proven that the latent heat of the superconducting phase transition is reversible, in practice, it may be considered that the heat is constantly dissipated and consumed, and the temperature control of the superconducting process may also constantly consume heat. It may be difficult to verify the heat balance of the system in the experiment. Therefore, an adiabatic box filled with an ideal gas is often used for illustration (Figure 6). The superconductor is cylindrical, and the fixed magnet is placed inside the cylindrical superconductor. The temperature of the gas in the box is heated or cooled by compressing or releasing the pressure on the piston to control the variation in the temperature in the box so that a superconducting phase change can occur. The piston does positive work or negative work, which raises or cools the temperature inside the box. During one complete cycle, the heat in the box is not dissipated; therefore, the heat is conserved. This method can also be used as an experimental method to validate the model in practice.
IV. Quantitative Analysis
Based on Formula (7) and the magnetic field strengths of several groups of fixed magnets and moving magnets listed in Table 1, the variation in the free energy in Model 1 is calculated.
Figure 7 shows the sizes of the fixed magnet and the moving magnet as well as the indicated distances from the superconductor. First, The magnetic field strengths of the two permanent magnets at four points are calculated. Then, the work W1 and W2 performed by the two permanent magnets on the superconductor and the work W performed by the fixed magnet on the moving magnet are calculated based on the thermodynamic formula of superconducting and the static magnetic field formula.
According to Figure 7, the magnetic field intensity data of several groups of magnetic poles for fixed magnets and moving magnets are given (a Class II superconductor is used when Hc is higher and the temperature control range is enlarged, but the analysis method is also applicable). According to the state change process of Model 1, the calculations are performed. The work performed by the fixed magnet on the moving magnet and the work performed by the two permanent magnets on the superconductor are calculated. Table 1 lists the calculation results.
Table 1 lists the work W1 and W2 performed by the two permanent magnets and the work W performed by the fixed magnet on the moving magnet during the phase transformation process of the superconductor. In the process of one complete cycle, the two permanent magnets perform work W1 and W2 on the superconductor and then perform negative work -W1 and -W2 on the superconductor successively, contributing 0 to the system energy. Although the term can ultimately be cancelled out, it has a significant impact on the energy during the phase change process. In addition, for comparison with W, calculations are carried out. W is the residual work of Model 1 after one cycle.
V. Conclusion
Citing the mature superconducting shielding theory, in this paper, a superconducting shielding physical model is proposed, and the derivation is completely based on existing mature superconducting thermodynamic formulas. The derivation process does not propose new assumptions. Therefore, the derivation and demonstration processes are sufficient and reliable. However, the thermodynamic analysis results of Model 1 reveal that in the process of a complete superconducting phase change conversion cycle, the energy of the total model system is not conserved. This may seem implausible and even impossible. However, using the superconducting thermodynamic analysis formula based on the first law of thermodynamics to analyze the superconducting shielding model, the derivation result negates the first law. Therefore, there are occasions where the first law of thermodynamics is not absolutely applicable.
References
- Yu, L. Phase transitions and critical phenomena (I). Physics,1980.9(4),1-2.
- Zhang, Y. Superconducting Physics. Hefei, University of Science and Technology of China Press,2009.31-36,42-43.
- Zhao S, Wang H, Yang X, Wang Q. Changes of the electromagnetic field and energy in a superconductor at the Meissner state under the action of an alternating external magnetic field.. Chinese Journal of Low Temperature Physics,2015.37(1),66-69.
- Hu X. Simulation study of magnetic shielding characteristics of multilayer shield containing superconductivity. Master's thesis. Changsha: Hunan University,2015.1-66].
- Zhang W, Zhang J, Si L, Liu D, Hu X, et al. Simulation study of magnetic shielding characteristics of multilayer shield containing superconductivity.Chinese Journal of Low Temperature Physics,2017.39(2),16-21.
- Hu Y, Chen H. Electromagnetism and electrodynamics [Volume 2]. Beijing, Science Press,2014.87-88.
- Guo S. Electrodynamics.Beijing, Higher Education Press,2008.78.
- Yan M, Peng X. Fundamentals of Magnetism and Magnetic Materials. Hangzhou, Zhejiang University Press,2019.248-251.
- Dai D, Qian K. Ferromagnetics.Beijing, Science Press,2017.112-113.
Figure 1.
Field distribution generated by a real magnetic field around the superconductor.
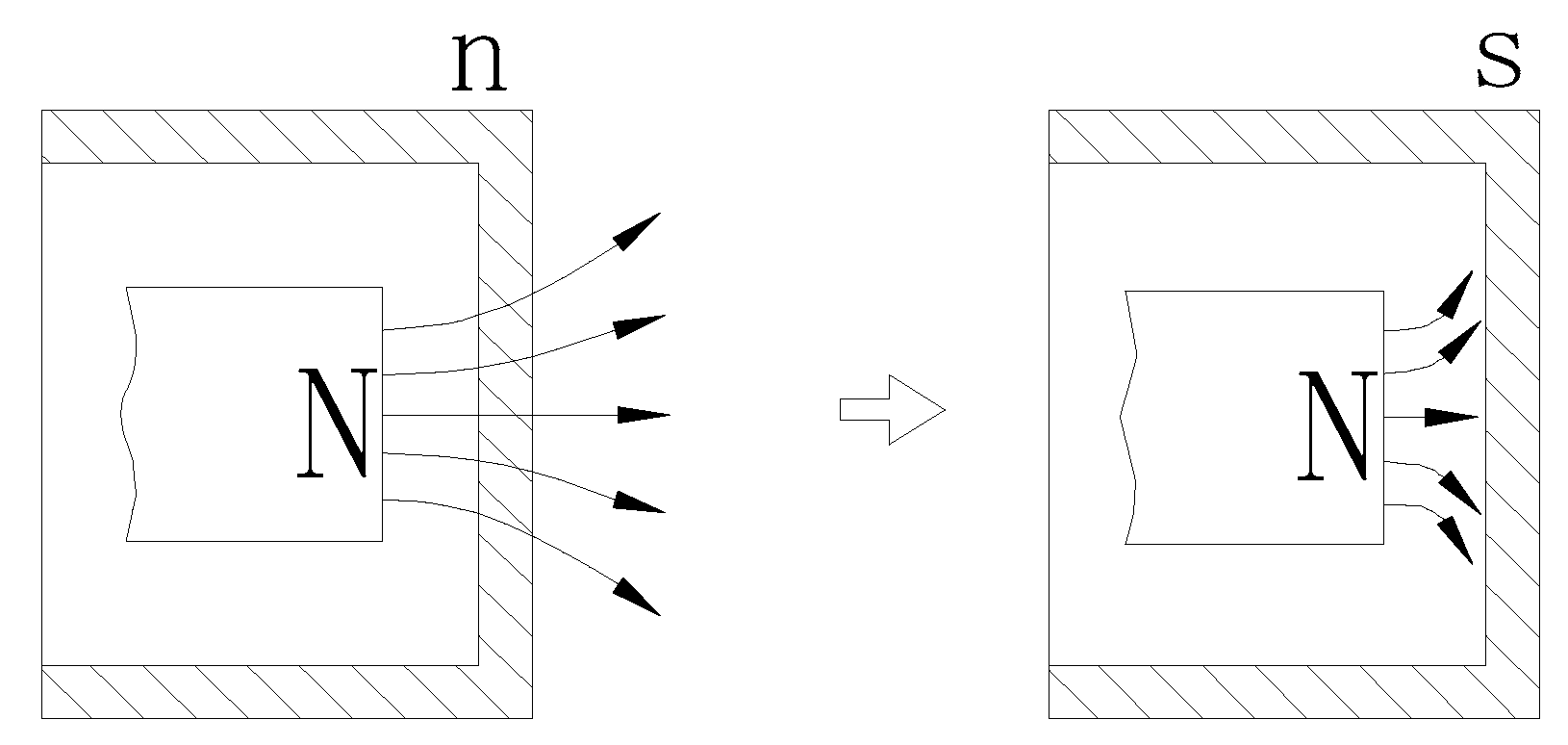
Figure 2.
Superconducting phase transition model with the addition of a moving magnet.
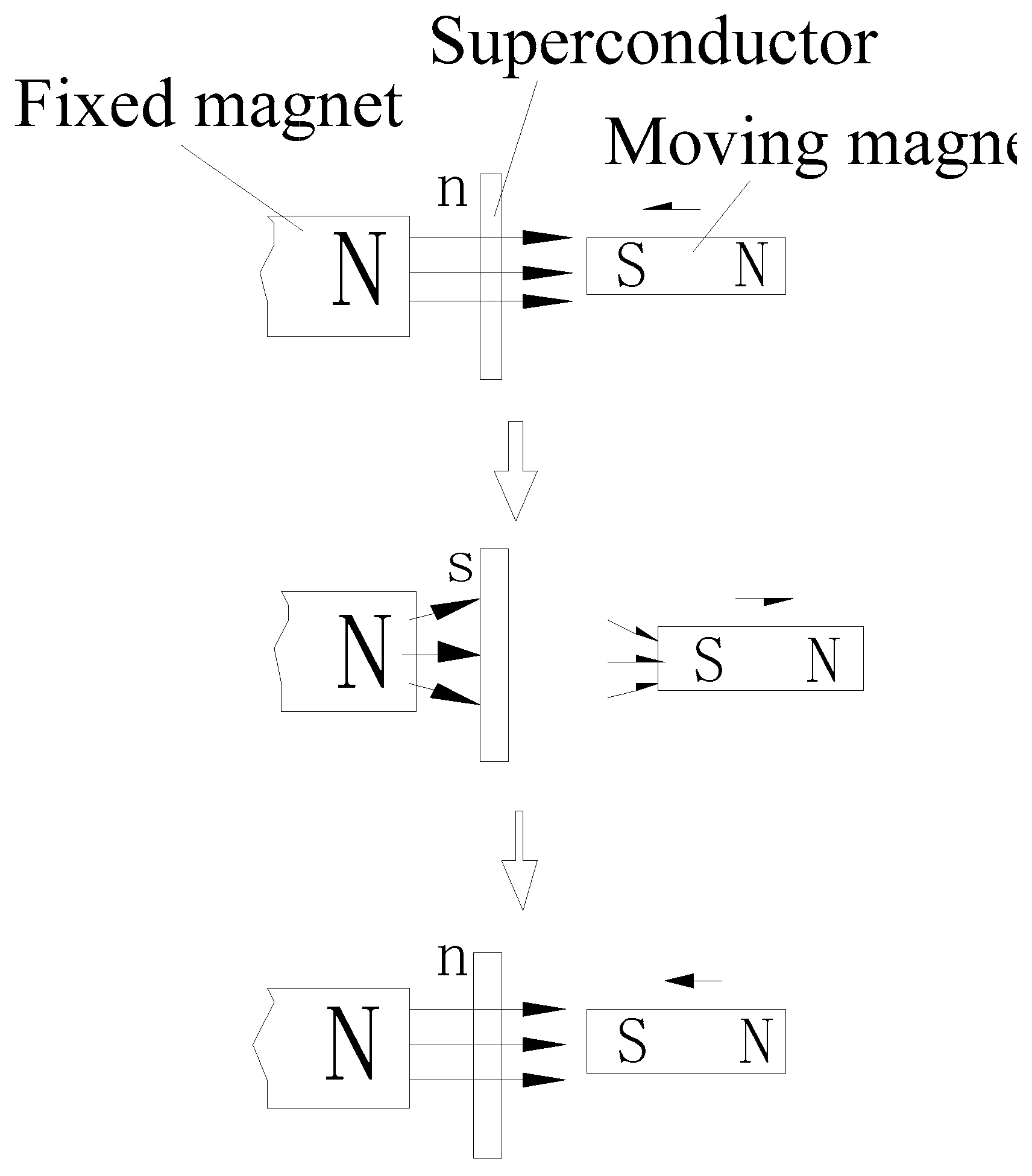
Figure 3.
Diagram for calculating the magnetic field strength of the permanent magnet.
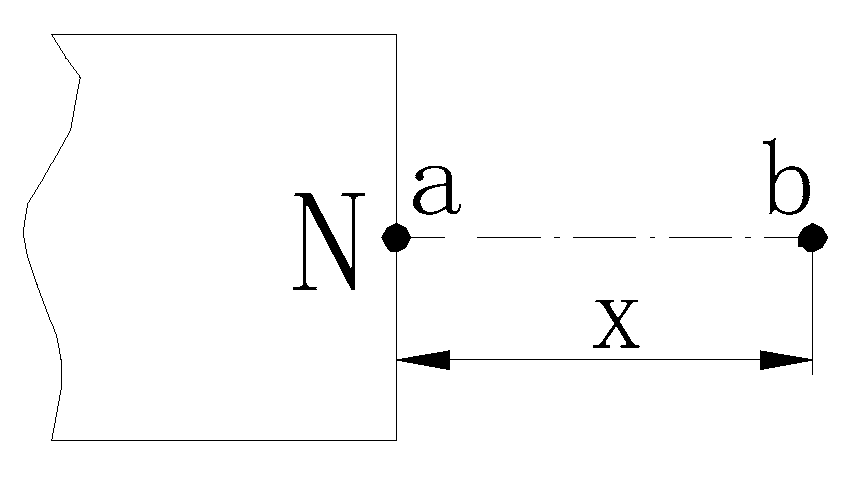
Figure 4.
Diagram for calculating the work done on the permanent magnet by a static magnetic field.
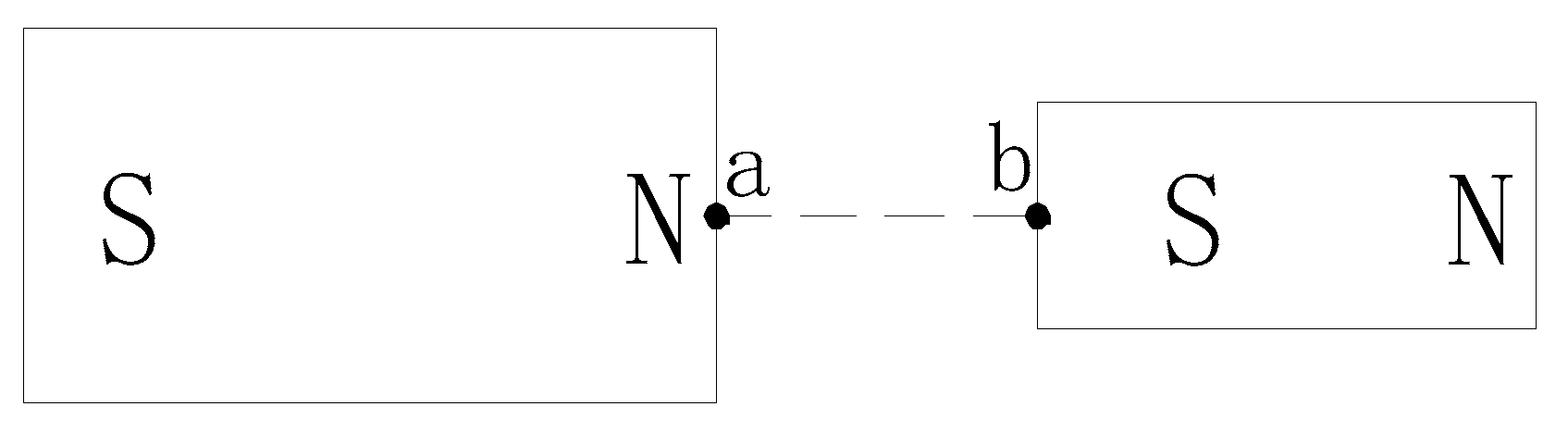
Figure 5.
Thermodynamic analysis steps for Model 1.

Figure 6.
Schematic diagram of the superconducting phase transition at the controlled temperature of the adiabatic box.
Figure 6.
Schematic diagram of the superconducting phase transition at the controlled temperature of the adiabatic box.
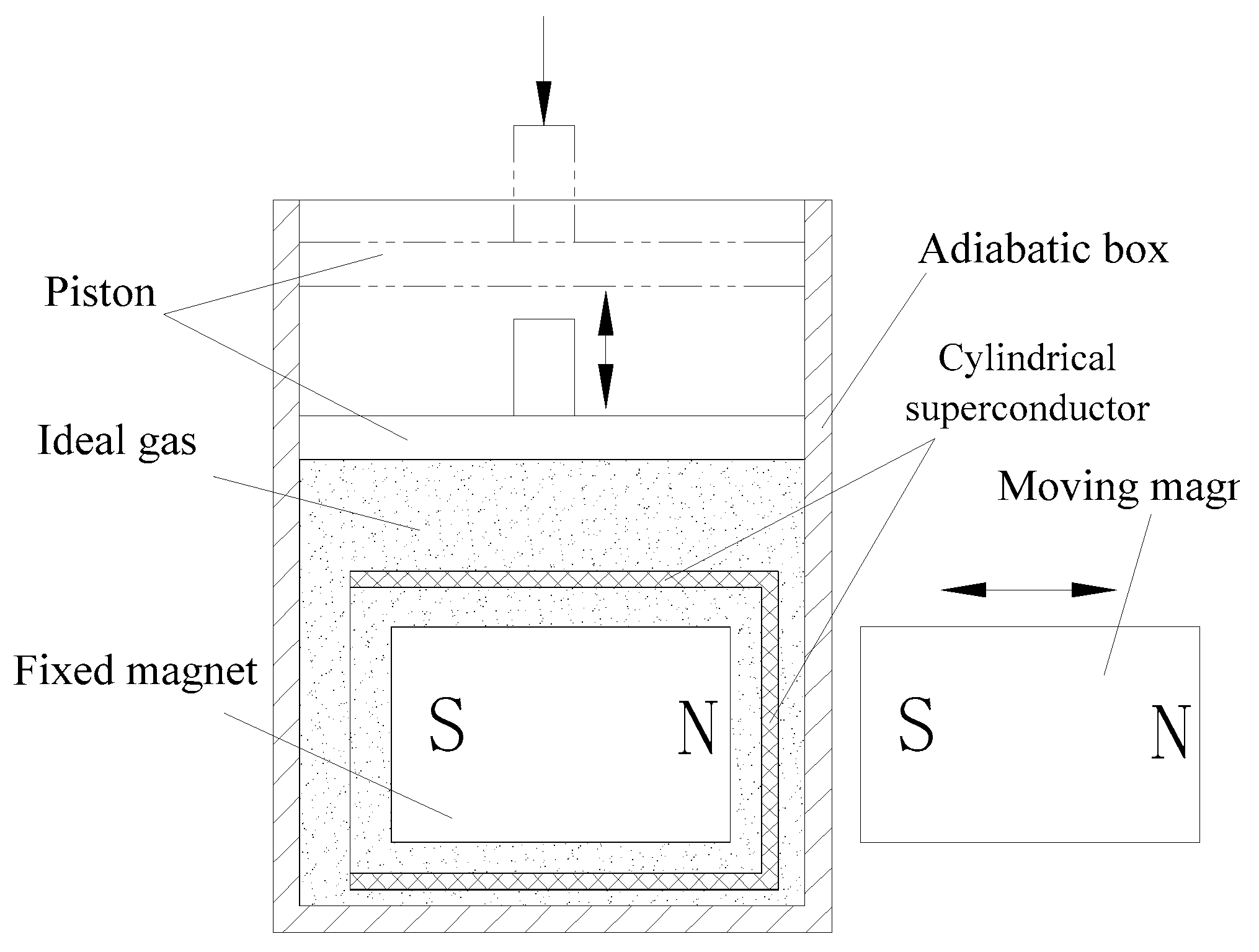
Figure 7.
Schematic diagram of the energy change of Model 1 used for the calculation.
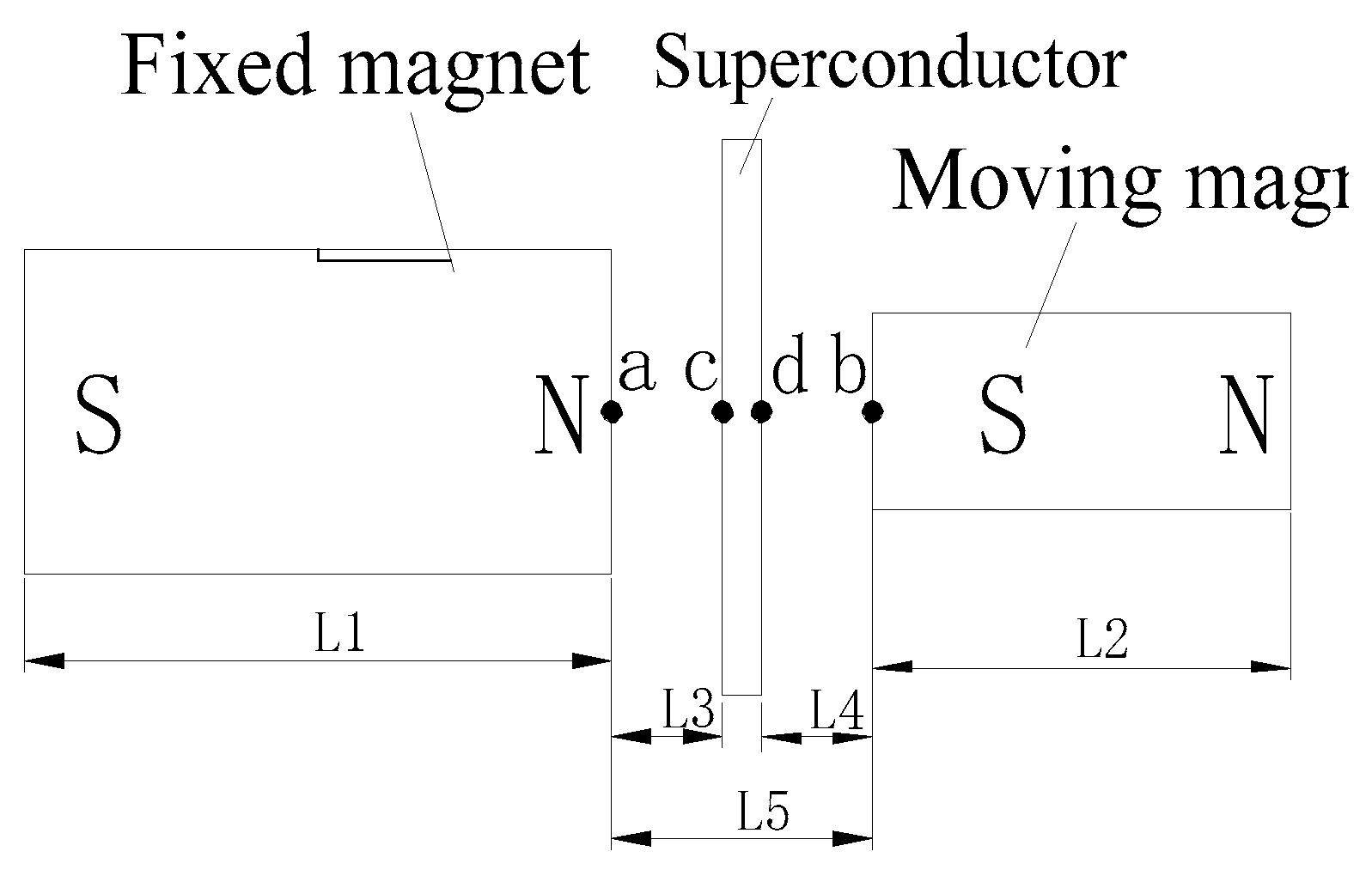
Table 1.
Specific value of each parameter under different initial parameters.
| H1a (mT) | H2b | L1 (mm) | L2 | L3 | L4 | L5 | H1b | H1c | H2d | W1 | W2 | W (µJ) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 10 | 50 | 50 | 0.5 | 0.5 | 6 | 1.3 | 1.9 | 0.2 | 1.8 | 0.0 | 6.5 |
| 100 | 20 | 50 | 50 | 0.5 | 0.5 | 6 | 1.3 | 1.9 | 0.4 | 1.8 | 0.1 | 13.0 |
| 100 | 50 | 50 | 50 | 0.5 | 0.5 | 6 | 1.3 | 1.9 | 1.0 | 1.8 | 0.5 | 32.5 |
| 100 | 80 | 50 | 50 | 0.5 | 0.5 | 6 | 1.3 | 1.9 | 1.5 | 1.8 | 1.2 | 52.0 |
| 100 | 100 | 50 | 50 | 0.5 | 0.5 | 6 | 1.3 | 1.9 | 1.9 | 1.8 | 1.8 | 65.0 |
| 80 | 100 | 50 | 50 | 0.5 | 0.5 | 6 | 1.0 | 1.5 | 1.9 | 1.2 | 1.8 | 52.0 |
| 50 | 100 | 50 | 50 | 0.5 | 0.5 | 6 | 0.7 | 1.0 | 1.9 | 0.5 | 1.8 | 32.5 |
| 20 | 100 | 50 | 50 | 0.5 | 0.5 | 6 | 0.3 | 0.4 | 1.9 | 0.1 | 1.8 | 13.0 |
| 10 | 100 | 50 | 50 | 0.5 | 0.5 | 6 | 0.1 | 0.2 | 1.9 | 0.0 | 1.8 | 6.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





