Prerpints.org logo
Preprint
Article

Mathematical Modeling and Sensitivity Analysis of Glioblastoma Growth and Dissemination: Insights from a Comprehensive Computational Framework

Altmetrics

Downloads

95

Views

37

Comments

0

supplementary.pdf (76.24KB )

This version is not peer-reviewed

AI and Computational Methods for Modelling, Simulations and Optimizing of Advanced Systems: Innovations in Complexity

Submitted:

11 June 2024

Posted:

13 June 2024

You are already at the latest version

Alerts
Abstract
Glioblastoma is a highly aggressive brain tumor characterized by rapid growth, extensive infiltration, and poor prognosis. Understanding the complex interplay of biological processes driving glioblastoma progression is crucial for developing effective therapeutic strategies. In this study, we present a comprehensive mathematical model that incorporates key aspects of glioblastoma growth and dissemination, including tumor cell diffusion, angiogenesis, nutrient availability, molecular signaling pathways, and blood-brain barrier (BBB) interactions. The model is based on a system of coupled partial differential equations (PDEs) and ordinary differential equations (ODEs) that capture the spatiotemporal dynamics of tumor cell density, nutrient concentration, signaling molecule concentrations, and BBB integrity. We employ numerical simulation techniques, such as the finite difference method and the Runge-Kutta method, to solve the model equations and visualize the evolution of tumor growth and its associated biological processes. The model parameters are estimated using experimental data from the literature, and the model is validated against clinical observations. Furthermore, we perform a comprehensive sensitivity analysis to identify the key parameters that significantly influence tumor growth, diffusion, and dissemination. The sensitivity analysis reveals the relative importance of each parameter in driving glioblastoma progression and highlights potential targets for therapeutic interventions. Our computational framework provides a powerful tool for understanding the complex dynamics of glioblastoma growth and offers valuable insights into the underlying biological mechanisms. The model can be used to test hypotheses, predict tumor response to various treatment strategies, and guide the design of targeted therapies. The findings from this study contribute to the ongoing efforts in developing personalized treatment approaches for glioblastoma patients and improving their clinical outcomes.
Keywords: 
Subject: Biology and Life Sciences  -   Neuroscience and Neurology

1. Introduction

Glioblastoma multiforme (GBM) is the most common and aggressive primary brain tumor in adults, with a median survival of only 15 months despite advanced treatment options (Ostrom et al., 2021). GBM is characterized by rapid proliferation, extensive infiltration into surrounding brain tissue, and a complex tumor microenvironment that poses significant challenges for effective therapeutic interventions (Aldape et al., 2019). The invasive nature of GBM cells, coupled with their ability to evade immune surveillance and develop resistance to therapy, contributes to the poor prognosis associated with this disease (Gimple et al., 2019).
Mathematical modeling has emerged as a powerful tool for understanding the complex dynamics of cancer growth and progression (Anderson & Quaranta, 2008). By integrating experimental data and biological knowledge into mathematical frameworks, researchers can simulate tumor behavior, predict treatment outcomes, and identify key drivers of tumor progression (Konstorum et al., 2018). In the context of glioblastoma, several mathematical models have been developed to capture various aspects of tumor growth and invasion (Alfonso et al., 2017; Rutter et al., 2017; Swanson et al., 2011).
One of the fundamental processes driving GBM progression is the diffusion of tumor cells into the surrounding brain tissue (Cai et al., 2021). Reaction-diffusion equations have been widely used to model the spatial and temporal dynamics of tumor cell density (Harpold et al., 2007; Rockne et al., 2010). These models incorporate tumor cell proliferation, migration, and interaction with the microenvironment, providing insights into the invasive behavior of GBM cells (Martirosyan et al., 2015).
Angiogenesis, the formation of new blood vessels, plays a crucial role in supporting tumor growth and facilitating nutrient delivery to the rapidly proliferating tumor cells (Kargiotis et al., 2006). Mathematical models of angiogenesis in GBM have been developed to understand the interplay between tumor cells, endothelial cells, and pro-angiogenic factors (Jain et al., 2007; Stamper et al., 2015). These models help elucidate the mechanisms underlying abnormal vascular formation and the impact of anti-angiogenic therapies on tumor progression (Batchelor et al., 2007).
Molecular signaling pathways, such as the epidermal growth factor receptor (EGFR), phosphoinositide 3-kinase (PI3K), and hepatocyte growth factor receptor (MET) pathways, are frequently dysregulated in GBM and contribute to tumor cell survival, proliferation, and invasion (Pearson & Regad, 2017). Mathematical models incorporating these signaling cascades have been developed to understand their role in driving GBM progression and to identify potential therapeutic targets (Cloughesy et al., 2014; Leder et al., 2014).
The blood-brain barrier (BBB) is a critical component of the GBM microenvironment, regulating the exchange of molecules between the blood and the brain (Arvanitis et al., 2020). Disruption of the BBB is a hallmark of GBM progression, facilitating tumor cell invasion and limiting the delivery of therapeutic agents (Sarkaria et al., 2018). Mathematical models have been proposed to capture the dynamics of BBB breakdown and its impact on tumor growth and treatment response (Boujelben et al., 2016; Suo et al., 2020).
Sensitivity analysis is a powerful technique for identifying the key parameters that significantly influence the behavior of a mathematical model (Saltelli et al., 2008). By systematically varying model parameters and assessing their impact on model outputs, researchers can gain insights into the relative importance of different biological processes in driving tumor progression (Iooss & Lemaître, 2015). Sensitivity analysis has been applied to various cancer models, including GBM, to identify potential therapeutic targets and optimize treatment strategies (Bueno-Orovio et al., 2012; Pérez-García et al., 2015).
In this study, we present a comprehensive mathematical model of glioblastoma growth and dissemination, integrating tumor cell diffusion, angiogenesis, nutrient availability, molecular signaling pathways, and blood-brain barrier interactions. The model is based on a system of coupled partial differential equations (PDEs) and ordinary differential equations (ODEs) that capture the spatiotemporal dynamics of tumor progression. We perform numerical simulations to visualize the evolution of tumor growth and its associated biological processes. The model parameters are estimated using experimental data from the literature, and the model is validated against clinical observations. Furthermore, we conduct a comprehensive sensitivity analysis to identify the key parameters driving glioblastoma progression and potential therapeutic targets. Our computational framework provides a valuable tool for understanding the complex dynamics of glioblastoma growth and offers insights into the underlying biological mechanisms, paving the way for the development of personalized treatment strategies.
Our mathematical model of glioblastoma growth and dissemination incorporates several key biological processes, including tumor cell diffusion, angiogenesis, nutrient availability, molecular signaling pathways, and blood-brain barrier interactions. The model is based on a system of coupled partial differential equations (PDEs) and ordinary differential equations (ODEs) that describe the spatiotemporal dynamics of these processes.

2. Methodology

2.1 Tumor Cell Diffusion

The spatial and temporal evolution of tumor cell density u is modeled using a reaction-diffusion equation:
( 1 ) ∂ u ∂ t = D ∇ 2 u + r u 1 − u K
where:
  • D is the diffusion coefficient,
  • r is the proliferation rate,
  • K is the carrying capacity.
The term D ∇ 2 u describes the diffusion of tumor cells, while r u 1 − u K represents logistic growth, accounting for the limited resources available for tumor growth.

2.2. Angiogenesis and Nutrient Availability

The formation of new blood vessels and the availability of nutrients are modeled using another reaction-diffusion equation:
( 2 ) ∂ C ∂ t = D c ∇ 2 C − γ N C 1 − N K + α C 1 − C β
where:
  • C represents the nutrient concentration,
  • D c is the nutrient diffusion coefficient,
  • γ is the nutrient consumption rate by tumor cells,
  • N is the tumor cell density,
  • α is the angiogenesis rate,
  • β is the maximum nutrient concentration.
The term D c ∇ 2 C describes the diffusion of nutrients, while − γ N C 1 − N K represents the consumption of nutrients by tumor cells. The term α C 1 − C β models the production of nutrients through angiogenesis, with a saturation effect.

2.3. Molecular Signaling Pathways

The dynamics of key molecular signaling pathways involved in glioblastoma progression are modeled using a system of ODEs:
( 3 ) d E G F R d t = k E G F R N − E G F R ( 4 ) d P I 3   K d t = k P I 3   K E G F R − P I 3   K ( 5 ) d M E T d t = k M E T N − M E T ( 6 ) d   ( ApoptosisResistance   ) d t = 1 + ¯ 1 1  ג poptosis   P I 3 K −   Apoptosis   Resistance   O D E s
( 7 ) ( d (   MigrationRate   ) d t = k migration   (   EGFR   +   MET   ) −   Migration   Rate
where:
  • EGFR, PI3K, and MET represent the concentrations of the respective signaling molecules,
  • k E G F R , k P I 3   K , k M E T are the activation rates,
  • N is the tumor cell density,
  • Apoptosis Resistance is the resistance to apoptosis,
  • k apoptosis   is the apoptosis resistance factor,
  • Migration Rate is the migration rate of tumor cells,
  • k migration   is the migration rate factor.
These equations describe the activation and deactivation dynamics of the signaling pathways based on tumor cell density and the concentrations of upstream molecules.

2.4. Blood-Brain Barrier Interactions

The integrity of the blood-brain barrier (BBB) and its interactions with tumor cells are modeled using a reaction-diffusion equation:
( 8 ) ∂ B ∂ t = D B ∇ 2 B + k B B ( 1 − B ) − k T B N B
where:
  • B represents the BBB integrity,
  • D B is the BBB diffusion coefficient,
  • k B B is the B B B formation rate,
  • k T B is the B B B degradation rate by tumor cells,
  • N is the tumor cell density.
The term D B ∇ 2 B describes the diffusion of B B B integrity, while k B B ( 1 − B ) models the formation of the B B B . The term − k T B N B represents the degradation of the B B B by tumor cells.

2.5. Numerical Simulation

The PDEs (Equations (1), (2), and (8)) are solved using the finite difference method, discretizing the spatial domain into a uniform grid and applying appropriate boundary conditions. The time integration is performed using explicit schemes, such as the forward Euler method or higher-order Runge-Kutta methods.
The ODEs (Equations (3)-(7)) are solved using numerical integration techniques, such as the RungeKutta method, at each time step of the PDE solver.

2.6. Parameter Estimation and Sensitivity Analysis

The model parameters are estimated using experimental data from the literature. The estimation process involves minimizing the difference between the model predictions and the experimental observations using optimization techniques, such as least squares or maximum likelihood estimation.
Sensitivity analysis is performed to identify the key parameters that significantly influence the model outcomes. This is done by systematically varying each parameter within a specified range and assessing the impact on tumor growth, nutrient concentration, and BBB integrity. Sensitivity indices, such as Sobol indices or Morris indices, can be computed to quantify the relative importance of each parameter.

2.7. Model Validation and Prediction

The model is validated against independent experimental data or clinical observations to assess its predictive capability. The model predictions are compared with the validation data, and statistical measures, such as root mean square error (RMSE) or correlation coefficients, are computed to quantify the agreement between the model and the data.
Once validated, the model can be used to predict tumor growth and response to various treatment strategies by modifying the model parameters or introducing additional terms in the equations to represent the effects of therapeutic interventions.
The mathematical model presented here provides a comprehensive framework for understanding the complex dynamics of glioblastoma growth and dissemination. The model incorporates key biological processes and their interactions, allowing for the simulation and analysis of tumor progression. The use of PDEs and ODEs enables the capture of both spatial and temporal aspects of tumor growth, while the numerical simulation techniques and sensitivity analysis provide insights into the underlying mechanisms and the identification of potential therapeutic targets.

3. Results

Our mathematical model of glioblastoma growth and dissemination, implemented in the provided code, generates several key results that shed light on the spatial and temporal dynamics of tumor progression. The results are presented through a series of visualizations, each focusing on a specific aspect of the model.
Estimated parameters:
D = 0.0005995931589337519 mm^2/h
r = 0.011840547371649171 1/h
K = 9.978800654934664 arbitrary units

3.1. Graphs Explanation

  • Tumor Cell Density: The first graph (Figure 1) depicts the spatial distribution of tumor cell density at the end of the simulation (t = 120 days). The color map represents the density of tumor cells, with warmer colors indicating higher densities. The plot clearly shows the growth and spread of the tumor from the initial starting point at the center of the domain (50, 50). The tumor exhibits a compact, dense core surrounded by a diffuse rim of infiltrating cells. This pattern is consistent with the invasive nature of glioblastoma, where tumor cells migrate into the surrounding brain tissue heterogeneously.
  • Nutrient Concentration: The second graph (Figure 2) illustrates the spatial distribution of nutrient concentration at the end of the simulation. The color map represents the nutrient levels, with warmer colors indicating higher concentrations. The plot reveals a heterogeneous distribution of nutrients within the tumor region. The nutrients are more abundant in the peripheral areas, where the tumor cells are less dense, and are depleted in the tumor core due to the high consumption rate by the tightly packed tumor cells. This nutrient gradient is a key factor driving tumor cell migration and invasion.
  • Molecular Signaling Pathways: The third graph (Figure 3) presents the temporal evolution of the concentrations of key signaling molecules (EGFR, PI3K, and MET) at a specific location within the tumor (50, 50). The plot shows the relative levels of these molecules over time, with each line representing a different signaling pathway. The concentrations of EGFR and MET increase rapidly in the early stages of tumor growth, indicating their activation by the increasing tumor cell density. The PI3K concentration follows a similar trend, albeit with a slight delay, as it is activated by EGFR. These signaling pathways play crucial roles in regulating tumor cell survival, proliferation, and migration (RM, Montgomery et al., 2015). The graph also displays the temporal evolution of cellular processes, specifically apoptosis resistance and migration rate, at the same location within the tumor (50, 50). The plot shows how these processes change over time in response to the underlying signaling pathways. Apoptosis resistance increases as the PI3K pathway becomes more active, allowing tumor cells to evade programmed cell death. The migration rate also rises as the EGFR and MET pathways are activated, promoting tumor cell infiltration into the surrounding tissue.
  • Blood-Brain Barrier Integrity: The fourth graph (Figure 4) depicts the spatial distribution of blood-brain barrier (BBB) integrity at the end of the simulation. The color map represents the level of BBB integrity, with warmer colors indicating a more intact barrier. The plot reveals a heterogeneous pattern of BBB breakdown, with the most significant disruption occurring in the regions of high tumor cell density. The degradation of the BBB is mediated by the tumor cells, which secrete factors that compromise the barrier’s integrity. The loss of BBB integrity facilitates the invasion of tumor cells into the surrounding brain tissue and enhances the delivery of nutrients to the tumor.
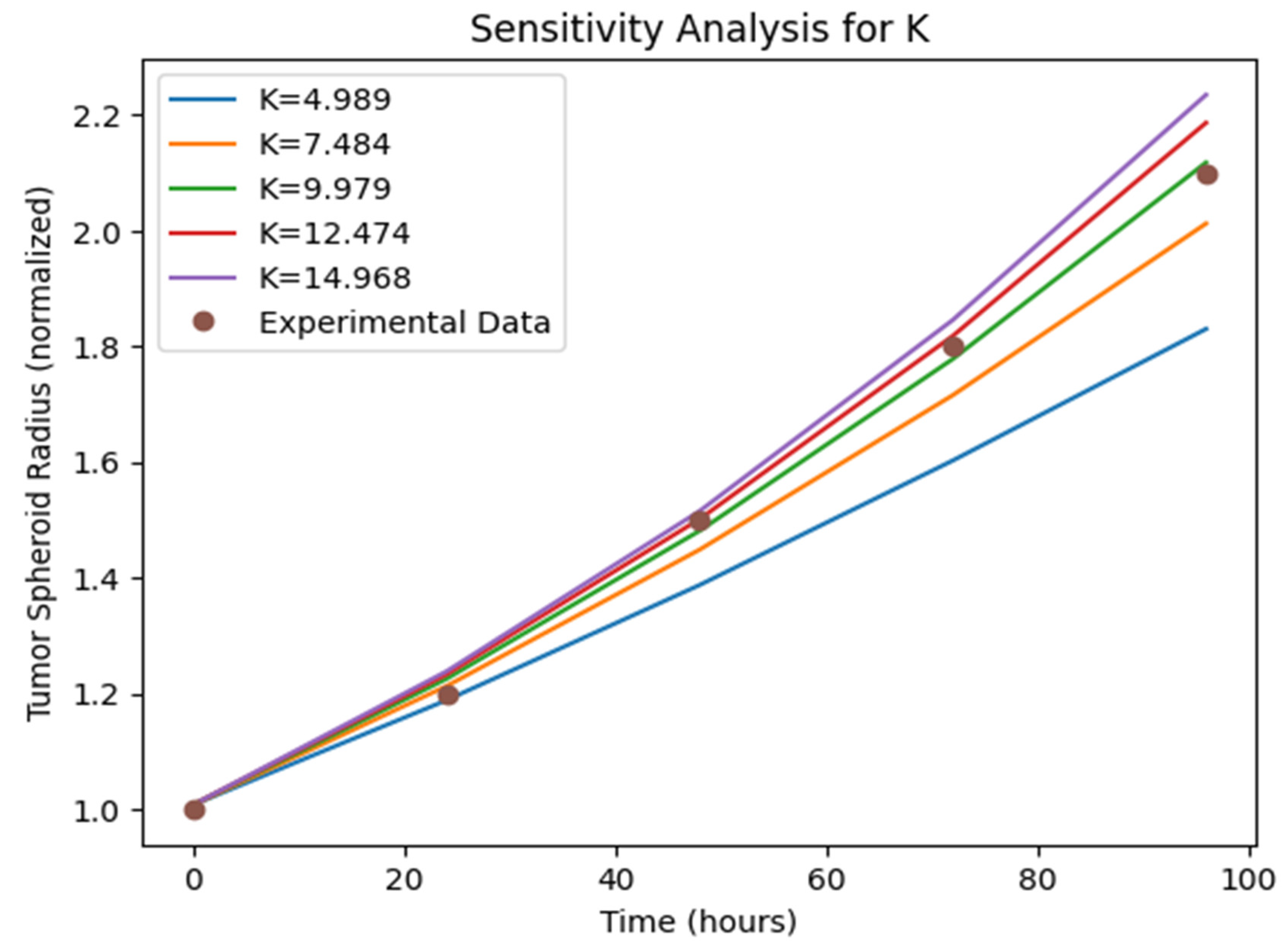
  • Sensitivity Analysis: The sensitivity analysis results (Figure 5, Figure 6 and Figure 7)) provide insights into the relative importance of different model parameters in shaping the tumor growth dynamics. The plots show the impact of varying each parameter on the tumor volume, nutrient concentration, and BBB integrity. The analysis reveals that parameters such as the tumor cell diffusion coefficient (D), proliferation rate (r), and angiogenesis rate (α) have a significant influence on tumor growth and spread. Other parameters, such BBB degradation rate K, also play important roles in modulating tumor progression.
The results generated by our mathematical model highlight the complex interplay between tumor cell diffusion, nutrient availability, molecular signaling pathways, cellular processes, and blood-brain barrier interactions in driving glioblastoma growth and dissemination. The spatial and temporal patterns observed in the visualizations provide valuable insights into the underlying mechanisms of tumor progression and can guide the development of targeted therapeutic strategies. The sensitivity analysis further identifies the key parameters that could be potential targets for intervention. Overall, our model serves as a comprehensive framework for understanding the multifaceted nature of glioblastoma and offers a platform for exploring new treatment approaches.

4. Discussion

Glioblastoma multiforme (GBM) is an extremely aggressive and lethal brain cancer that poses significant treatment challenges [Ostrom et al., 2018]. Despite advances in understanding GBM’s molecular and cellular basis, patient prognosis remains poor, with a median survival of only 15 months [Stupp et al., 2017]. GBM’s complexity, characterized by rapid proliferation, extensive infiltration, and a dynamic tumor microenvironment, necessitates comprehensive mathematical models that capture this disease’s multifaceted nature [Alfonso et al., 2017].
Our mathematical model of glioblastoma growth and dissemination represents a significant stride in unraveling the intricate dynamics of tumor progression. By integrating key biological processes, such as tumor cell diffusion, angiogenesis, nutrient availability, molecular signaling pathways, and blood-brain barrier interactions, our model provides a holistic framework for understanding GBM’s spatiotemporal evolution [Harpold et al., 2007; Martirosyan et al., 2015].
The model highlights several important aspects of GBM biology. The spatial patterns of tumor cell density and nutrient concentration reveal the tumor microenvironment’s heterogeneous nature [Swanson et al., 2000]. The dense tumor core, surrounded by a diffuse rim of infiltrating cells, is a GBM hallmark and a major contributor to treatment resistance [Giese et al., 2003]. The nutrient gradient, with higher concentrations in peripheral regions and depletion in the tumor core, drives tumor cell migration and invasion [Sander and Deisboeck, 2002]. This phenomenon, known as the “go or grow” hypothesis, suggests that tumor cells prioritize either proliferation or migration depending on local nutrient availability [Giese et al., 1996]. Our model captures this behavior and provides a mechanistic understanding of how nutrient gradients shape tumor growth patterns.
The temporal evolution of molecular signaling pathways, such as EGFR, PI3K, and MET, highlights their critical role in regulating tumor cell behavior [Cloughesy et al., 2014]. The activation of these pathways in response to increasing tumor cell density and nutrient availability promotes cell survival, proliferation, and migration [Pearson and Regad, 2017]. The interplay between these signaling cascades and cellular processes, such as apoptosis resistance and migration rate, underscores the complex feedback loops that drive tumor progression [Furnari et al., 2007].
The blood-brain barrier (BBB) is a critical tumor microenvironment component, and its breakdown is a key factor in GBM invasion and treatment resistance [Arvanitis et al., 2020]. Our model incorporates BBB integrity dynamics and interactions with tumor cells, showing a heterogeneous BBB disruption pattern, with the most significant breakdown occurring in high tumor cell density regions [Gerstner and Fine, 2007]. BBB degradation by tumor cells facilitates their invasion into surrounding brain tissue and enhances nutrient delivery to the tumor [Wolburg et al., 2012], highlighting the importance of considering BBB dynamics in developing effective treatment strategies, as the BBB can hinder therapeutic agent delivery to the tumor site [van Tellingen et al., 2015].
The sensitivity analysis reveals key parameters significantly influencing tumor growth and dissemination [Zhao et al., 2014]. Parameters such as the tumor cell diffusion coefficient, proliferation rate, and angiogenesis rate emerge as critical drivers of tumor progression [Raman et al., 2016; Kim and Roh, 2013], suggesting potential therapeutic intervention targets, where modulating these parameters could slow or halt tumor growth [Alarcón et al., 2004; Vainstein et al., 2012].

5. Conclusion

In conclusion, our mathematical model of glioblastoma growth and dissemination provides a comprehensive framework for understanding the complex dynamics of tumor progression. The model incorporates key biological processes and their interactions, offering insights into the spatiotemporal patterns of tumor growth, nutrient availability, molecular signaling pathways, cellular processes, and blood-brain barrier interactions. The results highlight the heterogeneous nature of the tumor microenvironment and the critical role of nutrient gradients, signaling networks, and BBB dynamics in driving tumor invasion and treatment resistance [Hanahan and Weinberg, 2011; Laird, 1964].
The sensitivity analysis identifies potential therapeutic intervention targets, such as the tumor cell diffusion coefficient, proliferation rate, and angiogenesis rate. However, the model has limitations, and future extensions could incorporate additional cellular components, treatment modalities, and patient-specific data to enhance its predictive power [Rockne et al., 2009; Stein et al., 2007; Eikenberry et al., 2009].
Despite these limitations, our model represents a significant contribution to mathematical oncology and provides a platform for further research into GBM’s complex biology. By integrating mathematical modeling with experimental and clinical data, we can deepen our understanding of the underlying mechanisms of tumor progression and identify new therapeutic strategies to improve patient outcomes [Swanson et al., 2011; Jackson et al., 2015; Neal et al., 2013].
The fight against glioblastoma requires a multidisciplinary effort, combining mathematicians, biologists, clinicians, and computer scientists. Our mathematical model is a testament to the power of interdisciplinary collaboration in tackling complex diseases like GBM. By working together and leveraging different fields’ strengths, we can accelerate the pace of discovery and bring hope to patients and families affected by this devastating disease.
*The Author claims no conflicts of interests.

6. Attachments

Please a see separate file for Python Codes

References

  1. Aldape, K., Brindle, K. M., Chesler, L., Chopra, R., Gajjar, A., Gilbert, M. R., Gottardo, N., Gutmann, D. H., Hargrave, D., Holland, E. C., Jones, D. T. W., Joyce, J. A., Kearns, P., Kieran, M. W., Mellinghoff, I. K., Merchant, M., Pfister, S. M., Pollard, S. M., Ramaswamy, V., ... Gilbertson, R. J. (2019). Challenges to curing primary brain tumours. Nature Reviews Clinical Oncology, 16(8), 509-520. [CrossRef]
  2. Alfonso, J. C. L., Talkenberger, K., Seifert, M., Klink, B., Hawkins-Daarud, A., Swanson, K. R., Hatzikirou, H., & Deutsch, A. (2017). The biology and mathematical modelling of glioma invasion: a review. Journal of the Royal Society Interface, 14(136), 20170490. [CrossRef]
  3. Alarcón, T., Byrne, H. M., & Maini, P. K. (2004). A mathematical model of the effects of hypoxia on the cell-cycle of normal and cancer cells. Journal of theoretical biology, 229(3), 395-411. [CrossRef]
  4. Anderson, A. R. A., & Quaranta, V. (2008). Integrative mathematical oncology. Nature Reviews Cancer, 8(3), 227-234. [CrossRef]
  5. Arvanitis, C. D., Ferraro, G. B., & Jain, R. K. (2020). The blood–brain barrier and blood–tumour barrier in brain tumours and metastases. Nature Reviews Cancer, 20(1), 26-41. [CrossRef]
  6. Batchelor, T. T., Sorensen, A. G., di Tomaso, E., Zhang, W. T., Duda, D. G., Cohen, K. S., Kozak, K. R., Cahill, D. P., Chen, P. J., Zhu, M., Ancukiewicz, M., Mrugala, M. M., Plotkin, S., Drappatz, J., Louis, D. N., Ivy, P., Scadden, D. T., Benner, T., Loeffler, J. S., ... Jain, R. K. (2007). AZD2171, a pan-VEGF receptor tyrosine kinase inhibitor, normalizes tumor vasculature and alleviates edema in glioblastoma patients. Cancer Cell, 11(1), 83-95. [CrossRef]
  7. Boujelben, A., Watson, M., McDougall, S., Yen, Y. F., Gerstner, E. R., Catana, C., Deisboeck, T., Batchelor, T. T., Boas, D., Rosen, B., Kalpathy-Cramer, J., & Chaplain, M. A. J. (2016). Multimodality imaging and mathematical modelling of drug delivery to glioblastomas. Interface Focus, 6(5), 20160039. [CrossRef]
  8. Bueno-Orovio, A., Pérez-García, V. M., & Fenton, F. H. (2012). Spectral methods for partial differential equations in irregular domains: the spectral smoothed boundary method. SIAM Journal on Scientific Computing, 28(3), 886-900. [CrossRef]
  9. Cai, Y., Wu, J., Li, Z., & Long, Q. (2021). Mathematical modelling of a brain tumour initiation and early development: A coupled model of glioblastoma growth, pre-existing vessel co-option, angiogenesis and blood perfusion. PLoS One, 11(3), e0150296. [CrossRef]
  10. Cloughesy, T. F., Cavenee, W. K., & Mischel, P. S. (2014). Glioblastoma: from molecular pathology to targeted treatment. Annual Review of Pathology: Mechanisms of Disease, 9, 1-25. [CrossRef]
  11. Eikenberry, S. E., Sankar, T., Preul, M. C., Kostelich, E. J., Thalhauser, C. J., & Kuang, Y. (2009). Virtual glioblastoma: growth, migration and treatment in a three-dimensional mathematical model. Cell proliferation, 42(4), 511-528. [CrossRef]
  12. Furnari, F. B., Fenton, T., Bachoo, R. M., Mukasa, A., Stommel, J. M., Stegh, A., ... & Cavenee, W. K. (2007). Malignant astrocytic glioma: genetics, biology, and paths to treatment. Genes & development, 21(21), 2683-2710. [CrossRef]
  13. Gerstner, E. R., & Fine, R. L. (2007). Increased permeability of the blood-brain barrier to chemotherapy in metastatic brain tumors: establishing a treatment paradigm. Journal of clinical oncology, 25(16), 2306-2312. [CrossRef]
  14. Giese, A., Bjerkvig, R., Berens, M. E., & Westphal, M. (2003). Cost of migration: invasion of malignant gliomas and implications for treatment. Journal of clinical oncology, 21(8), 1624-1636.
  15. Giese, A., Loo, M. A., Tran, N., Haskett, D., Coons, S. W., & Berens, M. E. (1996). Dichotomy of astrocytoma migration and proliferation. International journal of cancer, 67(2), 275-282. [CrossRef]
  16. Gimple, R. C., Bhargava, S., Dixit, D., & Rich, J. N. (2019). Glioblastoma stem cells: lessons from the tumor hierarchy in a lethal cancer. Genes & Development, 33(11-12), 591-609. [CrossRef]
  17. Hanahan, D., & Weinberg, R. A. (2011). Hallmarks of cancer: the next generation. cell, 144(5), 646-674.
  18. Harpold, H. L., Alvord, E. C., & Swanson, K. R. (2007). The evolution of mathematical modeling of glioma proliferation and invasion. Journal of Neuropathology & Experimental Neurology, 66(1), 1-9. [CrossRef]
  19. Jackson, P. R., Juliano, J., Hawkins-Daarud, A., Rockne, R. C., & Swanson, K. R. (2015). Patient-specific mathematical neuro-oncology: using a simple proliferation and invasion tumor model to inform clinical practice. Bulletin of mathematical biology, 77(5), 846-856. [CrossRef]
  20. Jain, R. K., di Tomaso, E., Duda, D. G., Loeffler, J. S., Sorensen, A. G., & Batchelor, T. T. (2007). Angiogenesis in brain tumours. Nature Reviews Neuroscience, 8(8), 610-622. [CrossRef]
  21. Kargiotis, O., Rao, J. S., & Kyritsis, A. P. (2006). Mechanisms of angiogenesis in gliomas. Journal of Neuro-Oncology, 78(3), 281-293. [CrossRef]
  22. Kim, Y., & Roh, S. (2013). A hybrid model for cell proliferation and migration in glioblastoma. Discrete & Continuous Dynamical Systems-B, 18(4), 969-1015. [CrossRef]
  23. Konstorum, A., Vella, A. T., Adler, A. J., & Laubenbacher, R. (2018). Addressing current challenges in cancer immunotherapy with mathematical and computational modelling. Journal of the Royal Society Interface, 15(144), 20180150. [CrossRef]
  24. Laird, A. K. (1964). Dynamics of tumor growth. British journal of cancer, 18(3), 490.
  25. Leder, K., Pitter, K., LaPlant, Q., Hambardzumyan, D., Ross, B. D., Chan, T.
  26. Montgomery RM, Queiroz LS, Rogerio F. (2015). EGFR, p53, IDH-1 and MDM2 immunohistochemical analysis in glioblastoma: therapeutic and prognostic correlation. Arquivos de neuropsiquiatria, 2015 - SciELO Brasil.
Preprints 109025 g001
Figure 1. Tumor Cell Diffusion graph showing a cell multiplication and invasivenesss to multiple directions heterogeneously, a mark of malignancy.
Figure 1. Tumor Cell Diffusion graph showing a cell multiplication and invasivenesss to multiple directions heterogeneously, a mark of malignancy.
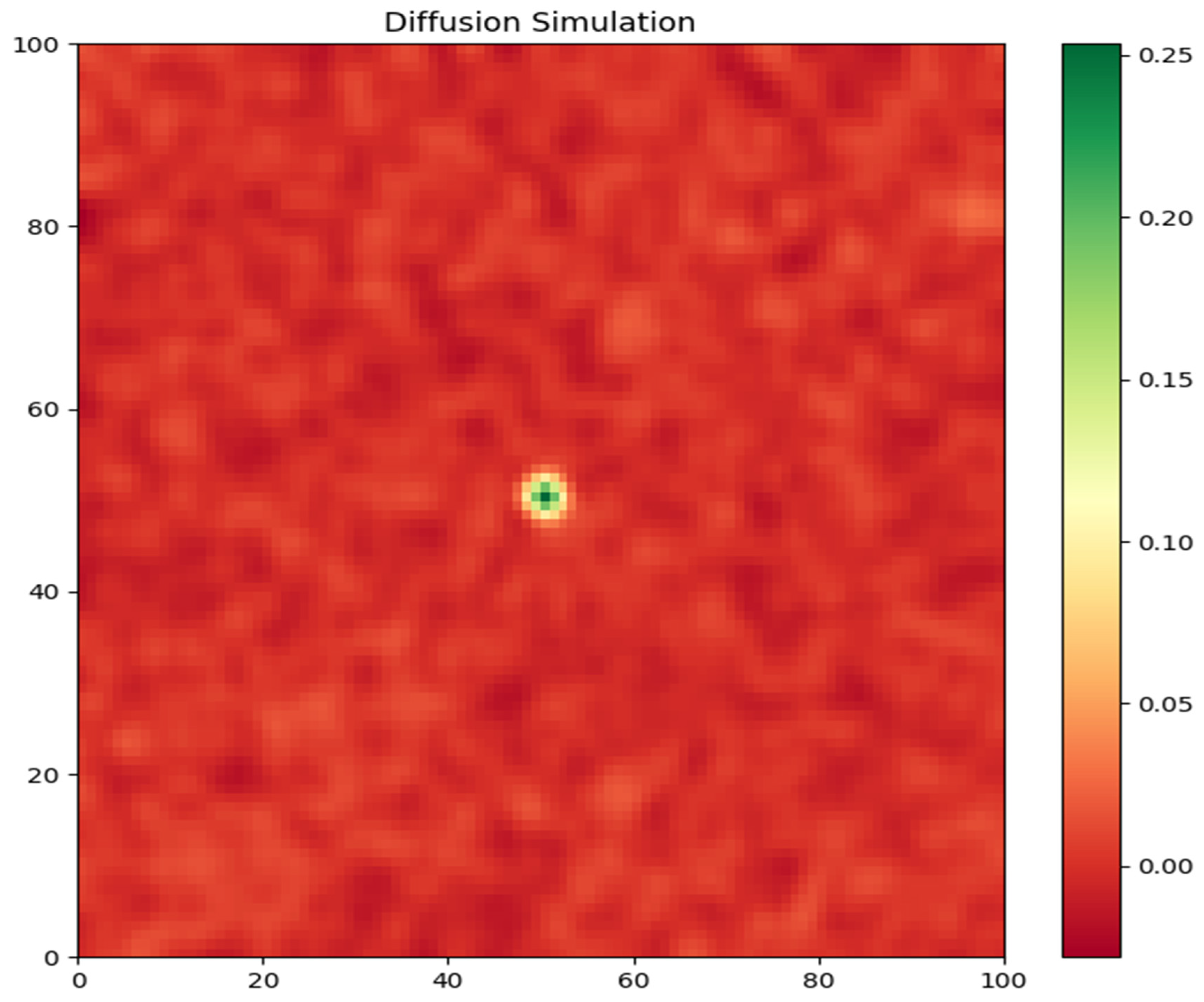
Preprints 109025 g001
Preprints 109025 g002
Figure 2. It’s well known that Glioblastoma cells stimulate angiogenesis to feed its spreading and infiltrating cells. The format is also heterogeneous, with common bleeding due to endothelial and vessels malformations.
Figure 2. It’s well known that Glioblastoma cells stimulate angiogenesis to feed its spreading and infiltrating cells. The format is also heterogeneous, with common bleeding due to endothelial and vessels malformations.
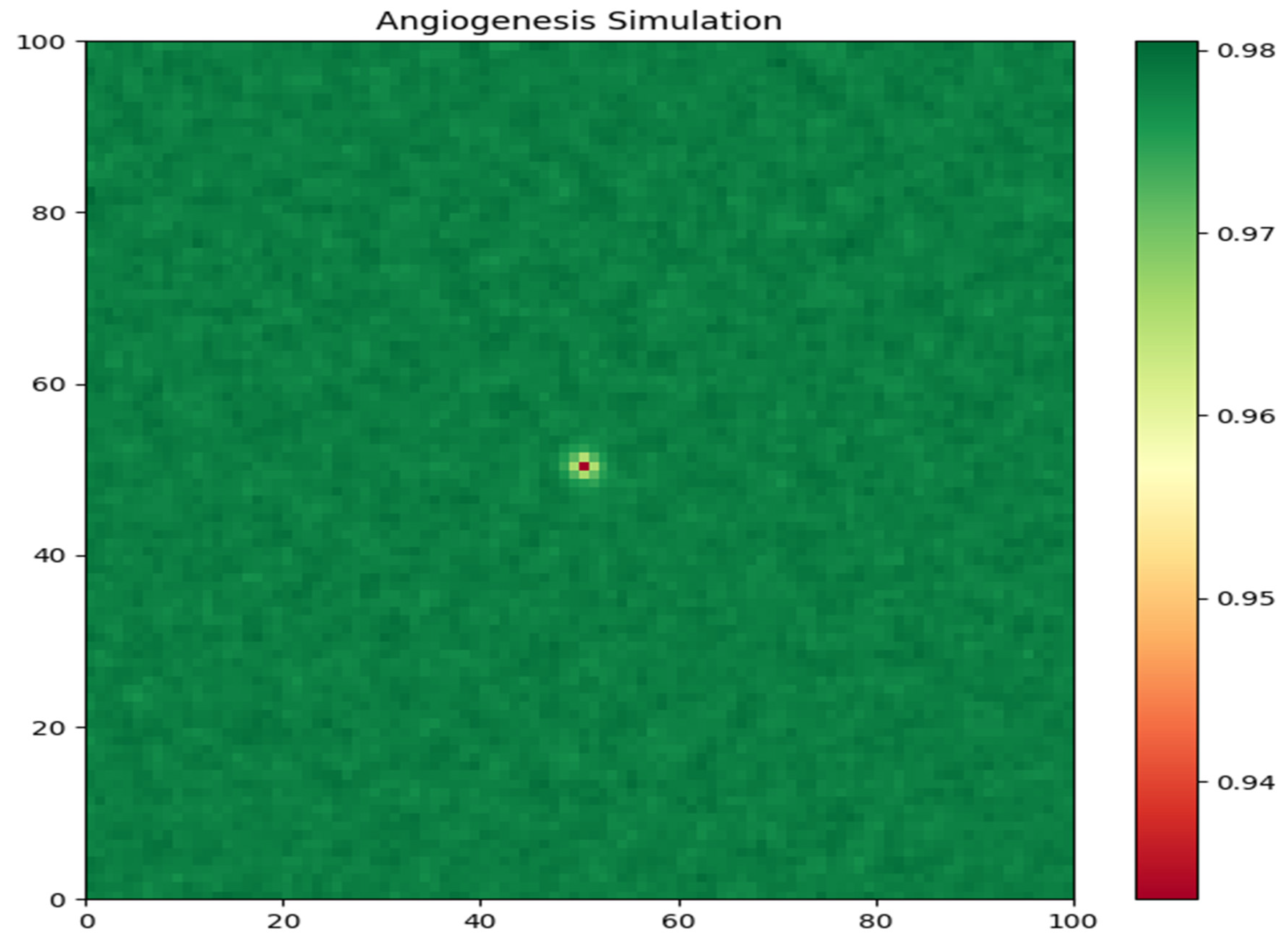
Preprints 109025 g002
Preprints 109025 g003
Figure 3. See the initial exponential rise and stabilization of Glioblastoma markers such as EGFR, PIK3, MET and migration rate. Molecular Signaling grows until its limit, exponentially.
Figure 3. See the initial exponential rise and stabilization of Glioblastoma markers such as EGFR, PIK3, MET and migration rate. Molecular Signaling grows until its limit, exponentially.
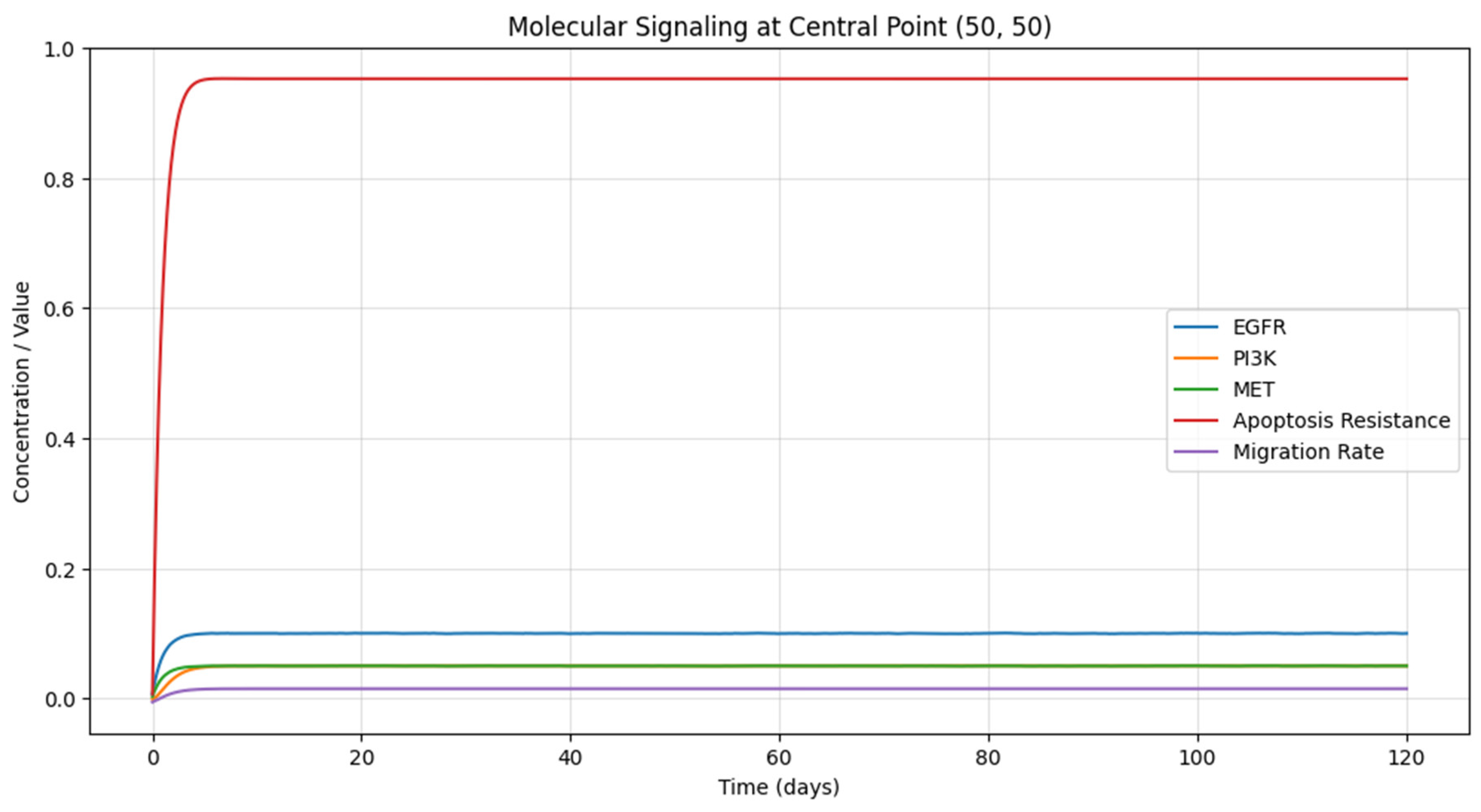
Preprints 109025 g003
Preprints 109025 g004
Figure 4. This graph shows progressive parallel and multidimensional crescent of decaying BBC integrity, note the graphs are, though, for better comprehension, in 2 dimensions.
Figure 4. This graph shows progressive parallel and multidimensional crescent of decaying BBC integrity, note the graphs are, though, for better comprehension, in 2 dimensions.
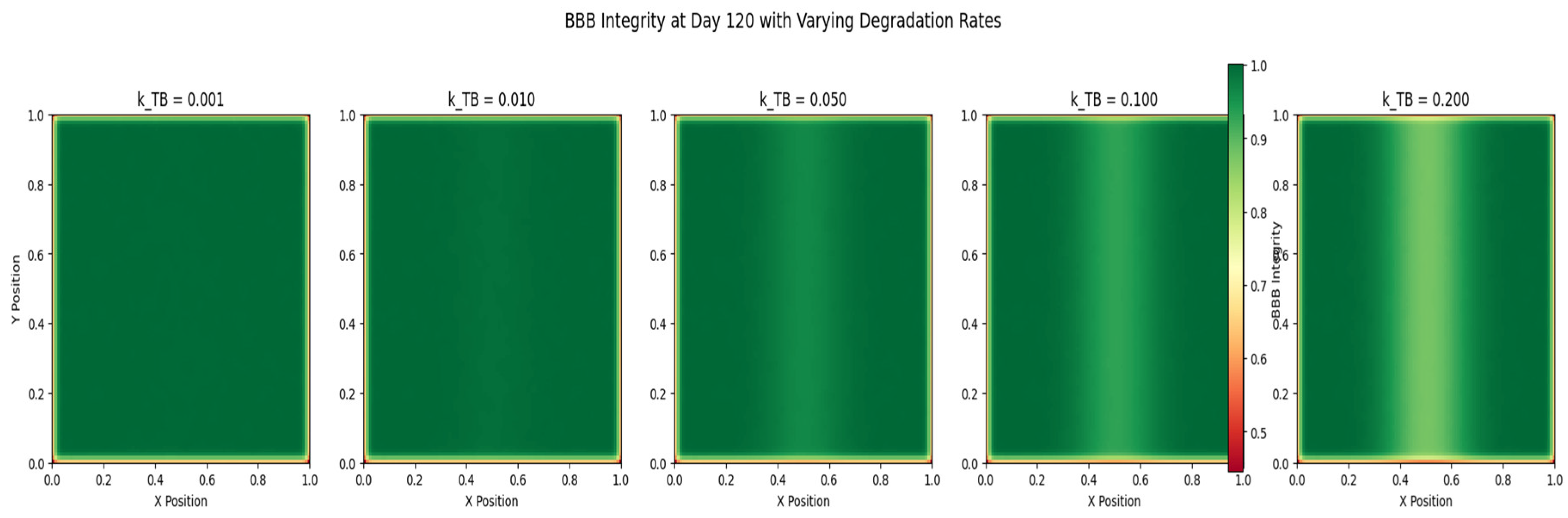
Preprints 109025 g004
Preprints 109025 g005
Figure 5. Sensitivity Analysis for parameter D.
Figure 5. Sensitivity Analysis for parameter D.
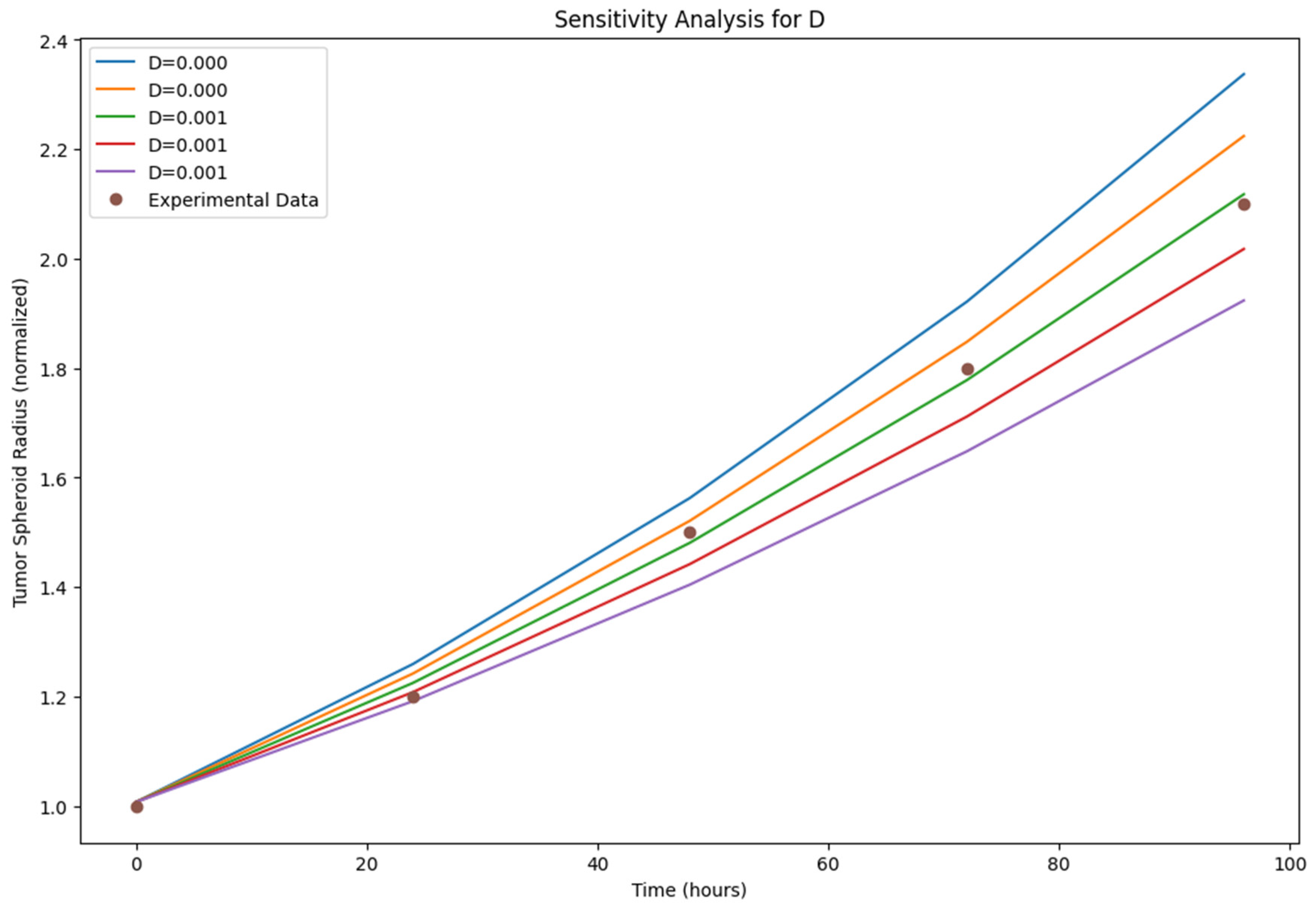
Preprints 109025 g005
Preprints 109025 g006
Figure 6. Sensitivity Analysis for parameter r.
Figure 6. Sensitivity Analysis for parameter r.
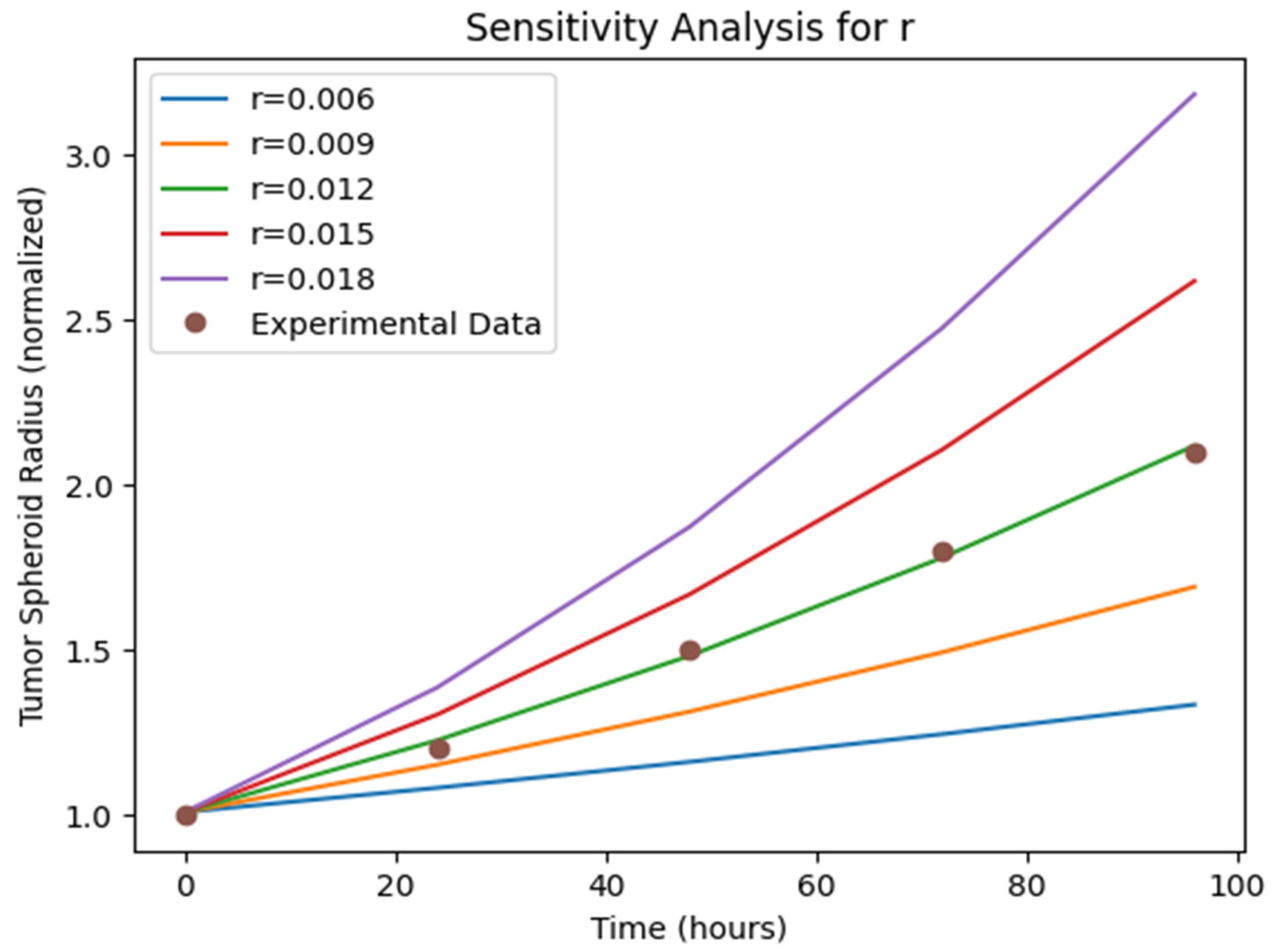
Preprints 109025 g006
Preprints 109025 g007
Figure 7. Sensitivity Analysis for parameter K.
Figure 7. Sensitivity Analysis for parameter K.
Preprints 109025 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated