Preprint
Article
Fractional Order, Interval Parameter, State Space Model of the One-Dimensional Heat Transfer Process
Altmetrics
Downloads
69
Views
16
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
11 June 2024
Posted:
12 June 2024
You are already at the latest version
Alerts
Abstract
In the paper the new, fractional order, state space model of a heat transfer in a one- 1
dimensional metallic rod is addressed. The fractional orders of derivative along space and time 2
are not exactly known and they are described by intervals. The proposed model is the interval 3
expanding of the state space fractional model of the one dimensional heat transfer. It is expected to 4
better describe the reality because interval order of each real process is hard to estimate. Elementary 5
properties of the proposed model are analysed. Theoretical results are experimentally validated using 6
data from real experimental laboratory system.
Keywords:
Subject: Engineering - Control and Systems Engineering
1. Introduction
The modeling of processes and plants hard to describe using another mathematical tools is one of the main areas of application of the Fractional Order (FO) calculus.
Fractional order models of various physical phenomena have been presented by many Authors for years. Fundamental results are presented e.g. by [1,2] (the heating of an one dimensional beam), [3] (FO models of chaotic systems and Ionic Polymer Metal Composites), [4]. FO models of diffusion processes are considered u.a. by [5] [6], and [7]. A collection of results using new Atangana-Baleanu operator can be found in [8]. This book presents i.e. the FO blood alcohol model, the Christov diffusion equation and fractional advection-dispersion equation for groundwater transport processes.
Recently FO models are used u.a. to describe a spread of diseases. As examples can be given the modeling of the dynamics of COVID using Caputo-Fabrizio operator presented by [9] or the model of transmission of Zika virus using Atangana-Baleanu operator is proposed by [10].
Models of temperature fields are considered by many Authors, e.g. [11,12]. Analytical solution of the two-dimensional, IO heat transfer equation is presented in the paper [13]. Numerical methods of solution of PDE-s can be found, e.g., in [14]. Fractional Fourier integral operators are analyzed u.a. by [15]. It is important to note that a significant part of known investigations deals only with a steady-state temperature fields with omitting their dynamics.
The state space FO models of the one dimensional heat transfer have been proposed in many previous papers of author from years [16,17,18,19,20,21,22,23]. These models used different FO operators: Grünwald-Letnikov, Caputo, Caputo-Fabrizio and Atangana-Baleanu as well as discrete operators CFE and FOBD. Each proposed model has been thoroughly theoretically and experimentally verified. In addition, each of them assures better accuracy in the sense of square cost function than its IO analogue.
The sensitivity of the FO model to uncertainty of coefficients describing the heat conduction and heat exchange was analysed in the paper [24]. In this paper the uncertainty of fractional orders has not been considered. Such an analysis is given in this paper.
The papers [25] and [26] present the generalization of FO models mentioned above to the two dimensional case.
This article presents the generalization of the model given by [20] to the case when both fractional orders are described by intervals. Such an approach should better describe reality, because really the fractional orders are hard to estimate in contrast to parameters describing the heat transfer and heat conduction. From knowledge of author it turns out that such a model has not been proposed yet. The interval fractional order system was considered e.g. by [27], but this paper deals with the interval state operator and known interval order of derivative along the time.
The paper is organized as follows. Preliminaries recall some basic ideas from fractional calculus, necessary to present results. Next the experimental system and its FO model with interval orders is presented and analyzed. Finally theoretical results are validated using experiments.
2. Preliminaries
At the beginning the non integer order, integro-differential operator is presented (see e.g. [1,4,28,29]).
Definition 1.
(The elementary non integer order operator) The non integer order integro-differential operator is defined as follows:
where a and t denote time limits for operator calculation, denotes the non integer order of the operation.
Next an idea of complete Gamma Euler function is recalled (see for example [29]):
Definition 2.
(The complete Gamma function)
An idea of Mittag-Leffler function needs to be given next. It is a non integer order generalization of exponential function and it plays crucial role in the solution of a FO state equation. The two parameter Mittag-Leffler function is defined as follows:
Definition 3.
(The two parameter Mittag-Leffler function)
For we obtain the one parameter Mittag-Leffler function:
Definition 4.
(The one parameter Mittag-Leffler function)
The fractional order, integro-differential operator (1) can be expressed by three fundamental definitions, given by Grünwald and Letnikov (GL definition), Riemann and Liouville (RL definition) and Caputo (C definition). Relations between Caputo and Riemann-Liouville, between Riemann-Liouville and Grünwald-Letnikov operators are given e.g. in [4,30]. Discrete versions of these operators are deeply analysed by [31]. The C definition has a simple interpretation of an initial condition (it is analogical as in integer order case) and intuitive Laplace transform. Additionally its value from a constant equals to zero, in contrast to e.g. RL definition. That’s why in the further consideration the C definition will be applied. It is recalled beneath.
Definition 5.
(The Caputo definition of the FO operator)
In (5) V is a limiter of the non integer order: . If then consequently is considered and the definition (5) takes the form:
Finally a fractional linear state equation using Caputo definition needs to be recalled. It takes the following form:
where is the fractional order of the state equation, , , are the state, control and output vectors respectively, are the state, control, and output matrices.
3. The Experimental System and Its Model with Fractional, Interval Orders
The experimental heat plant is shown in Figure 1. It has the form of a thin copper rod long. To simplify assume that its length equals to 1.0. This allows to express the localization and length of heater and RTD sensors with respect to 1.0. The rod is heated by the electric heater long located at the end of the rod. An output temperature is measured with the use of miniature RTD sensors (Pt100) long attached in points: 0.29, 0.50 and 0.73 of rod length. The input signal of the system is the standard current from range . It is amplified to the range and it is the input signal for the heater. Signals from the RTD-s are read directly by analog input module in the PLC. Data from PLC are collected by SCADA application. The whole system is connected via PROFINET. The temeprature distribution with respect to time and length is shown in the Figure 2.
The fundamental, time continuous model describing the heat conduction and dissipation in the rod is the partial differential equation of the parabolic type with the homogeneous Neumann boundary conditions at the ends, the homogeneous initial condition, the heat exchange along the length of rod and distributed control and observation. This equation with integer orders of both differentiations has been discussed in many papers, for example in [32,33,34].
The FO expanding of this model is presented with details in the papers [16,17]. In this paper its version with interval fractional order along the length is proposed. It takes the following form:
In (8) , are known coefficients of heat conduction and heat exchange, is a steady-state gain.
The non integer orders and are not exactly known and they are described by the following intervals:
where:
where . This deviation can be also expressed in percents:
where:
where or equivalently .
The intervals and build the vector of uncertain orders q:
All the vectors q build the space of uncertain orders Q:
The set Q can be interpreted as the rectangle in the plane stretched on the following vertices:
The center of the rectangle Q is defined by the nominal values of orders:
The interval form of orders and expands the heat transfer equation (8) to the infinite set of equations, limited by vertices (15).
The differential equation (8) can be expressed as beneath:
where:
In (18) denotes the field of the state operator A, , denotes the first and second derivative along the length, is the standard scalar product.
The basis of the state space is spanned by eigenvectors of the state operator A:
3.1. The Decomposition of the Spectrum
The eigenvalues of the state operator A depend only on interval order :
and consequently for the interval each eigenvalue expands to the interval too:
Consequently the diagonal state operator has interval, diagonal form:
The spectrum of the state operator A is a set of all its eigenvalues:
For exactly known the spectrum contains negative, real, single, separated eigenvalues ordered by indices n: . The most poorly damped eigenvalue is called the dominant (leading) eigenvalue. This property allows to easily decompose a system into single, scalar subsystems associated to particular eigenvalues. This is presented with details by [16,17].
However for interval situation gets more complicated due to particular eigenvalues expand to intervals. This implies that eigenvalues associated to different modes can partially overlap. In such a situation the spectrum decomposition is impossible because there exist two or more different, indistinguishable eigenvalues. This situation is illustrated by the Figure 3.
The above situation can occur if the interval is too wide. Simultaneously, narrow range of uncertainty guarantees the distinguishability of the spectrum. The maximum values of and assuring the distinguishability are described by the following Propositions.
Proposition 1.
(The maximum size of assuring the distinguishability of any two eigenvalues) Consider the interval spectrum (23) of the system (17). Assume that the relative uncertainty of the order β is equal Δ.
The size assuring the distinguishability of two eigenvalues and is expressed by the following inequality:
where:
Proposition 2.
(The maximum size of assuring the distinguishability of two adjacent eigenvalues)
Consider the interval spectrum (23) of the system (17). Assume that the relative uncertainty of the order β is equal Δ.
The size assuring the distinguishability of the two adjacent eigenvalues n and is expressed by the following inequality:
where:
The proof of both propositions is given beneath.
Proof.
Consider two different interval eigenvalues and denote they by and . Assume that they are partially overlapped. This is expressed as follows:
Using logarithm function we obtain:
After some elementary transformations we obtain (24) and the proof is completed. Assuming and gives directly condition (26). □
It is important to note that the maximum uncertainty permitted from point of view of spectrum decomposition does not depend on the value of and it is determined only by location of eigenvalues, described by their indices.
Using the condition (24) the maximum order N assuring the distinguishability of all eigenvalues for given uncertainty can be given too. It is described by the following proposition.
Proposition 3.
(The maximum dimension of the model N guaranteeing the distinguishability of the spectrum )
Consider the interval spectrum (23) of the system (17). Assume that the relative uncertainty of the order β is equal Δ.
The maximum size N of the model assuring the distinguishability of all eigenvalues meets the following inequality:
where:
Proof.
The dependence (30) gives the implicit condition to estimate N. However it can be easily applied numerically. This will be shown in the section “Simulations”.
3.2. The Input and Output Operators
Next recall the form of input and output operators, presented e.g. in [35]. They do not depend on interval orders of the system.
The input operator B describes the location and construction of heater. It is as follows:
where , is the shaping function of the heater:
According to (19) and (34) each element takes the following form:
The output operator C describes the location and size of RTD-s. It is as beneath:
In (36) , is the output sensor function:
Using (19) and (37) yields:
It is important to note that the operators B and C do not depend on the uncertain orders and .
The shaping function and sensor function are piecevise constant functions.
3.3. The Step and Impulse Responses of the System with Interval Orders
If the control is the Heaviside function: then the analytical formula of step response is as beneath:
where is the one parameter Mittag-Leffler function, , and are expressed by (20), (35) and (38) respectively. Analogically we can compute the impulse response:
In (40) is two parameter Mittag-Leffler function.
The non integer order model described by (17) - (40) is infinite dimensional. It is obvious that its practical use requires its reduction to finite dimensional form. This can be done by truncating further modes in state equation (17) and computing solution (39) or (40) as a finite sum. Consequently operators A, B and C reduce to matrices as well as the both time responses take the form of finite sums:
In (41) and (42) N is the order of finite approximation. Its value determines the accuracy of the model. It can be estimated using numerical or analytical methods (see [17]).
The time responses (41) and (42) are functions of interval orders collected in the vectors (13): , . This expands they to sectors limited by the borders of intervals and :
In (43) and (44) are defined by (15). Analogically the nominal time responses are expressed as follows:
where is the vector of nominal parameters (16).
The most obvious way to describe the sensitivity of the step response to uncertainty of the orders is to propose the sensitivity functions in the form and . However such explicit functions are hard to compute.
The sensitivity can be also tested using the following relative dynamic deviations :
where and:
3.4. The Steady-State Response
The steady-state response of the system is as follows:
where are expressed as follows:
in (50) and are described by (35) and (38) respectively.
The responses do not depend on the order , but they are affected by the interval order only. From the point of view of the geometric interpretation the rectangle (14), (15) reduces to the section limited by the limits of the order . This is expressed as beneath:
where nominal and limit values re described a s follows:
and consequently the whole response (49) takes the form of the following interval:
The relative deviation of the steady-state response from its nominal value is the limit value of deviation expressed by (47):
4. Experiments and Simulations
The experiments were done using the system presented in the section I. The experimental step response was realized by change of input signal from to of its maximum range. The time-spatial temperature distribution is shown in the Figure 2. During experiments the sample time was equal: , the number of samples was equal: and the final time was equal: . The size and location of heater and sensors are given in the Table 1.
The analysis of sensitivity was done using parameters of the model estimated numerically via minimization of the MSE cost function for all sensors together (see [17]- caption of the Fig. 6). These parameters are recalled in the Table 2. The values of and are set as the nominal values and .
The impact of uncertainties and to model was examined numerically. Results are presented in the next subsections.
4.1. The Analysis of the Spectrum Decomposition
At the beginning the impact of the uncertainty to spectrum decomposition was tested using conditions (24), (26) and (30).
The general condition (24) was examined for indices and describing rather distant eigenvalues. Results are completed in the Table 3.
Next the distinguishability of adjacent eigenvalues was tested using condition (26). Results are illustrated by the Figure 4.
The Table 3 and Figure 4 show that the distinguishability is harder to keep for “further” eigenvalues with higher indices n.
Finally the maximum order N assuring the distinguishability of the whole spectrum was computed using condition (30). To make it easier denote the left and right side of inequality (30) by and :
Using this notation the condition (30) turns to the following form:
The condition (57) was tested numerically for and . Numerical solution of the inequality (57) is shown in the Figure 5.
The diagrams in the Figure 5 show that for the maximum size of model is equal 13 and for this maximum size is equal 23. In general, the increasing of the uncertainty causes the decreasing of the order of the model N assuring the distinguishability of the spectrum.
4.2. The Sensitivity of the Dynamics
The sensitivity of the step response to uncertainties of both orders was tested using dynamic relative deviations (47) computed using data from the Table 2. Both uncertainties was set to: and . All vertex step responses for all outputs are compared to nominal one and experimental in the Figure 6. Time trends of all deviations for all outputs of the system are shown in the Figure 7.
4.3. The Sensitivity of the Steady-State Response
The relative steady-state error (55) was examined for small uncertainty included in the range and big uncertainty from range separately. Results are illustrated by Figure 8 and Figure 9.
- The sensitivity of the steady-state response to uncertainty strongly depends on the localisation of the RTD. Its is highest for the most distant sensor 3 and smaller for sensors 1 and 2.
- For small uncertainty the deviation is approximately a linear function of and both deviations are approximately the same.
- For bigger uncertainty the deviation is a nonlinear function of and nonlinearity is variuos for different outputs. Additionally, the upper deviation is much bigger than lower .
5. Final Conclusions
The results presented in the paper can be summarized that the uncertainty of both fractional orders impacts to crucial properties of the model: the distinguishability of the spectrum, the step and steady-state responses. The disturbation of order affects only to dynamics, but the disturbation of the order expressed by disturbs all considered properties of the model.
Next, the impact of the disturbation is determined by its size and the place of measurement. Small disturbation (circa 1%) strongly disturbs the output 3 furthest from the heater and slightly interferes with the measurement at output 2, placed halfway along the length of the rod. In turn, a large disturbance (greater than 50%) disturbs output 1 the least.
Further research of the presented issues will include among others theoretical justification of numerical results and investigation of discrete, approximated models using CFE and FOBD approximations.
Acknowledgment
This paper was supported by the AGH project no 16.16.120.773.
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, 1999. [Google Scholar]
- Dzieliński, A.; Sierociuk, D.; Sarwas, G. Some applications of fractional order calculus. Bulletin of the Polish Academy of Sciences, Technical Sciences 2010, 58, 583–592. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Petras, I. Fractional Order Systems: Modeling and Control Applications. In World Scientific Series on Nonlinear Science; Chua, L.O., Ed.; University of California: Berkeley, 2010; pp. 1–178. [Google Scholar]
- Das, S. Functional Fractional Calculus for System Identification and Controls; Springer: Berlin, 2010. [Google Scholar]
- Gal, C.; Warma, M. Elliptic and parabolic equations with fractional diffusion and dynamic boundary conditions. Evolution Equations and Control Theory 2016, 5, 61–103. [Google Scholar]
- Popescu, E. On the fractional Cauchy problem associated with a Feller semigroup. Mathematical Reports 2010, 12, 181–188. [Google Scholar]
- Sierociuk, D.; Skovranek, T.; Macias, M.; Podlubny, I.; Petras, I.; Dzielinski, A.; Ziubinski, P. Diffusion process modeling by using fractional-order models. Applied Mathematics and Computation 2015, 257, 2–11. [Google Scholar] [CrossRef]
- Gómez, J.F.; Torres, L.; (Eds), R.E. Fractional Derivatives with Mittag-Leffler Kernel. Trends and Applications in Science and Engineering. In Studies in Systems, Decision and Control, vol. 194; Kacprzyk, J., Ed.; Springer: Switzerland, 2019; pp. 1–339. [Google Scholar]
- A., B.; hadj Moussa Y., E.; Hammouch.; S., U. A fractional-order model describing the dynamics of the novel coronavirus (COVID-19) with nonsingular kernel. Chaos, Solitons and Fractals 2021, 146, 1–11.
- M., F.; A., A.; S., A.; T., B.; A., A.; H., A. Modeling and analysis of fractional order Zika model. AIMS Mathematics 2022, 7, 3912–3938. [CrossRef]
- Dlugosz, M.; Skruch, P. The application of fractional-order models for thermal process modelling inside buildings. Journal of Building Physics 2015, 1, 1–13. [Google Scholar] [CrossRef]
- Ryms, M.; Tesch, K.; Lewandowski, W. The use of thermal imaging camera to estimate velocity profiles based on temperature distribution in a free convection boundary layer. International Journal of Heat and Mass Transfer 2021, 165, 120686. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method. Entropy 2019, 21, 597–618. [Google Scholar] [CrossRef]
- Olsen-Kettle, L. Numerical solution of partial differential equations; The University of Queensland: Queensland, Australia, 2011. [Google Scholar]
- Al-Omari, S.K. A fractional Fourier integral operator and its extension to classes of function spaces. Advances in Difference Equations 2018, 1, 1–9. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Gawin, E.; Mitkowski, W. Modeling heat distribution with the use of a non-integer order, state space model. International Journal of Applied Mathematics and Computer Science 2016, 26, 749–756. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Gawin, E.; Mitkowski, W. Parameter identification for non integer order, state space models of heat plant. In Proceedings of the MMAR 2016 : 21th international conference on Methods and Models in Automation and Robotics : 29 August–01 September 2016, Międzyzdroje, Poland; 2016; pp. 184–188. [Google Scholar]
- Oprzedkiewicz, K.; Stanislawski, R.; Gawin, E.; Mitkowski, W. A new algorithm for a CFE approximated solution of a discrete-time non integer-order state equation. Bulletin of the Polish Academy of Sciences. Technical Sciences 2017, 65, 429–437. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Mitkowski, W.; Gawin, E. An accuracy estimation for a non integer order, discrete, state space model of heat transfer process. In Proceedings of the Automation 2017 : innovations in automation, robotics and measurment techniques : 15-17 March, Warsaw, Poland; 2017; pp. 86–98. [Google Scholar]
- Oprzędkiewicz, K.; Mitkowski, W.; Gawin, E.; Dziedzic, K. The Caputo vs. Caputo-Fabrizio operators in modeling of heat transfer process. Bulletin of the Polish Academy of Sciences. Technical Sciences 2018, 66, 501–507. [Google Scholar]
- Oprzędkiewicz, K.; Gawin, E. The practical stability of the discrete, fractional order, state space model of the heat transfer process. Archives of Control Sciences 2018, 28, 463–482. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Mitkowski, W. A memory efficient non integer order discrete time state space model of a heat transfer process. International Journal of Applied Mathematics and Computer Science 2018, 28, 649–659. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K. Non integer order, state space model of heat transfer process using Atangana-Baleanu operator. Bulletin of the Polish Academy of Sciences. Technical Sciences 2020, 68, 43–50. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K. Fractional order, discrete model of heat transfer process using time and spatial Grünwald-Letnikov operator. Bulletin of the Polish Academy of Sciences. Technical Sciences 2021, 69, 1–10. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Mitkowski, W.; Rosol, M. Fractional order model of the two dimensional heat transfer process. Energies 2021, 14, 1–17. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Mitkowski, W.; Rosol, M. Fractional order, state space model of the temperature field in the PCB plate. Acta Mechanica et Automatica 2023, 17, 180–187. [Google Scholar] [CrossRef]
- Kaczorek, T. Stability of interval positive fractional discrete-time systems. International Journal of Applied Mathematics and Computer Science 2018, 28, 451–456. [Google Scholar] [CrossRef]
- Kaczorek, T. Singular fractional linear systems and electrical circuits. International Journal of Applied Mathematics and Computer Science 2011, 21, 379–384. [Google Scholar] [CrossRef]
- Kaczorek, T.; Rogowski, K. Fractional Linear Systems and Electrical Circuits; Bialystok University of Technology: Bialystok, 2014. [Google Scholar]
- Bandyopadhyay, B.; Kamal, S. Solution, Stability and Realization of Fractional Order Differential Equation. In Stabilization and Control of Fractional Order Systems: A Sliding Mode Approach, Lecture Notes in Electrical Engineering 317; Springer: Switzerland, 2015; pp. 55–90. [Google Scholar]
- D., M.; E., G.; M., W. Comparison of h-difference fractional operators. In Advances in the Theory and Applications of Non-integer Order Systems; et al, W.M., Ed.; Springer: Switzerland, 2013; pp. 1–178.
- Oprzędkiewicz, K. The interval parabolic system. Archives of Control Sciences 2003, 13, 415–430. [Google Scholar]
- Oprzędkiewicz, K. A controllability problem for a class of uncertain parameters linear dynamic systems. Archives of Control Sciences 2004, 14, 85–100. [Google Scholar]
- Oprzędkiewicz, K. An observability problem for a class of uncertain-parameter linear dynamic systems. International Journal of Applied Mathematics and Computer Science 2005, 15, 331–338. [Google Scholar]
- Oprzędkiewicz, K. Positivity problem for the one dimensional heat transfer process. ISA Transactions 2021, 112, 281–291. [Google Scholar] [CrossRef]
Figure 1.
The experimental system
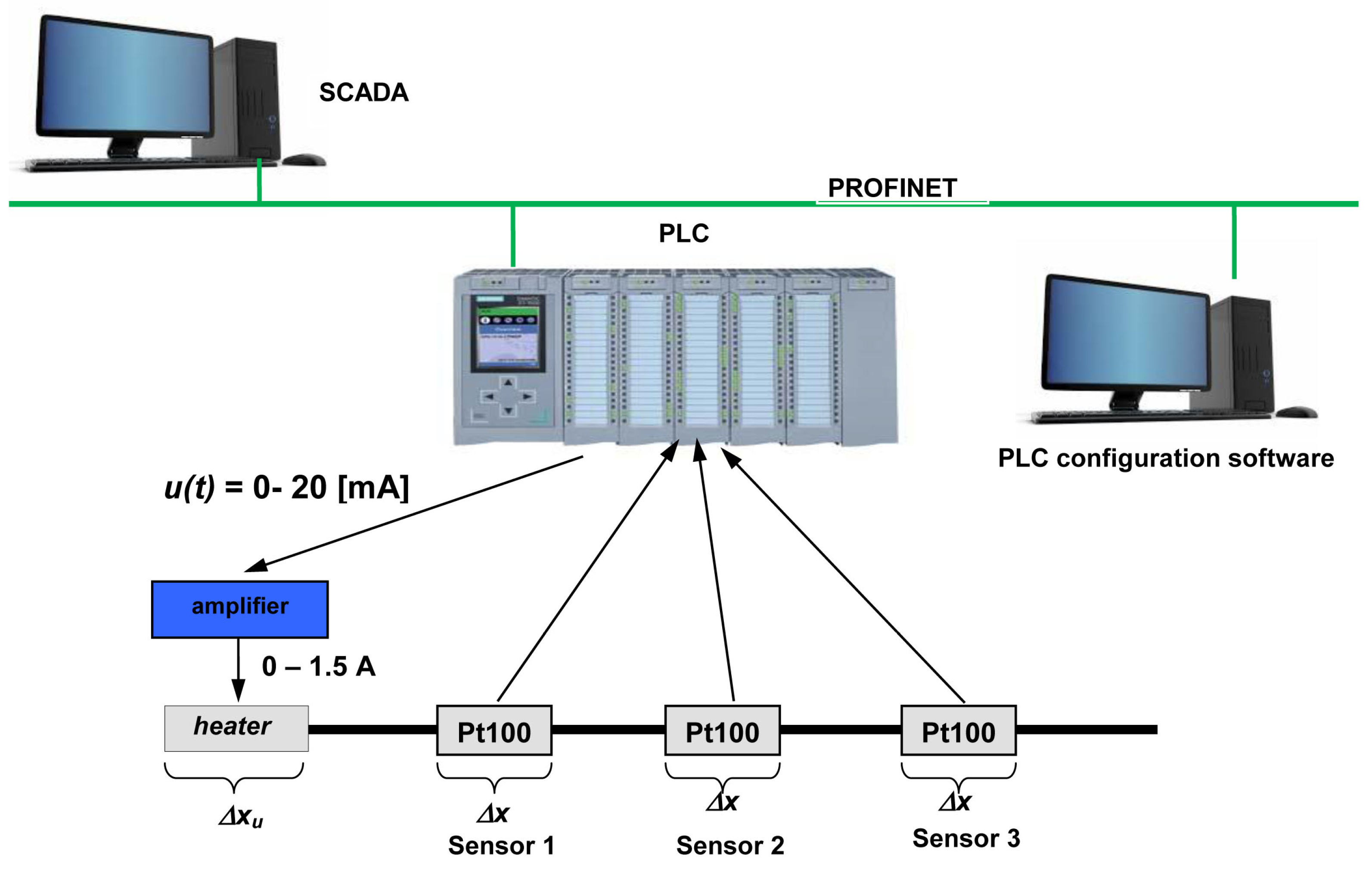
Figure 2.
The spatial-time temperature distribution in the plant
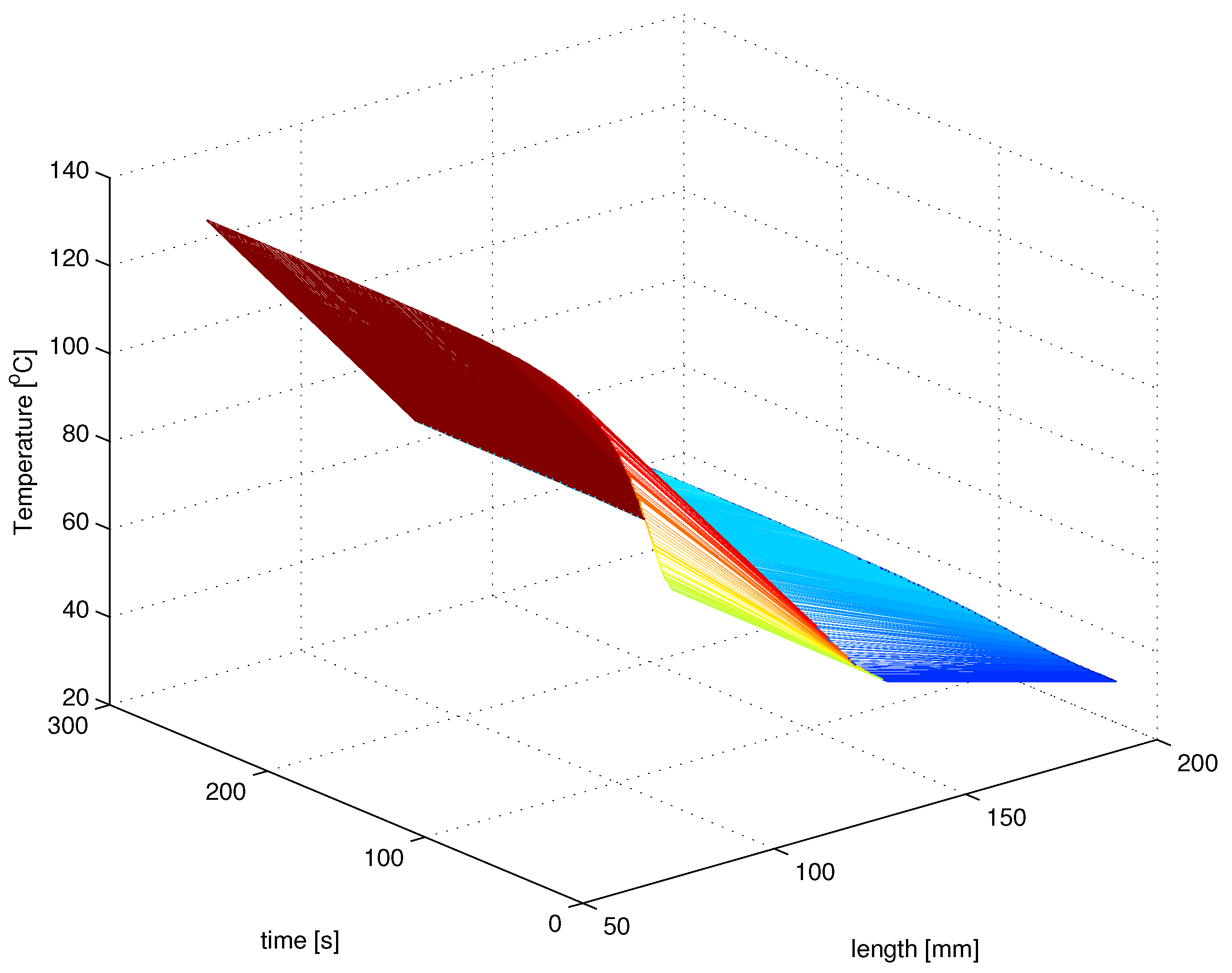
Figure 3.
The part of specrum with eigenvalues and : overlapped in the top and non overlapped in the bottom.
Figure 3.
The part of specrum with eigenvalues and : overlapped in the top and non overlapped in the bottom.

Figure 4.
The maximum uncertainty assuring the distinguishability of two adjacent eigenvalues.
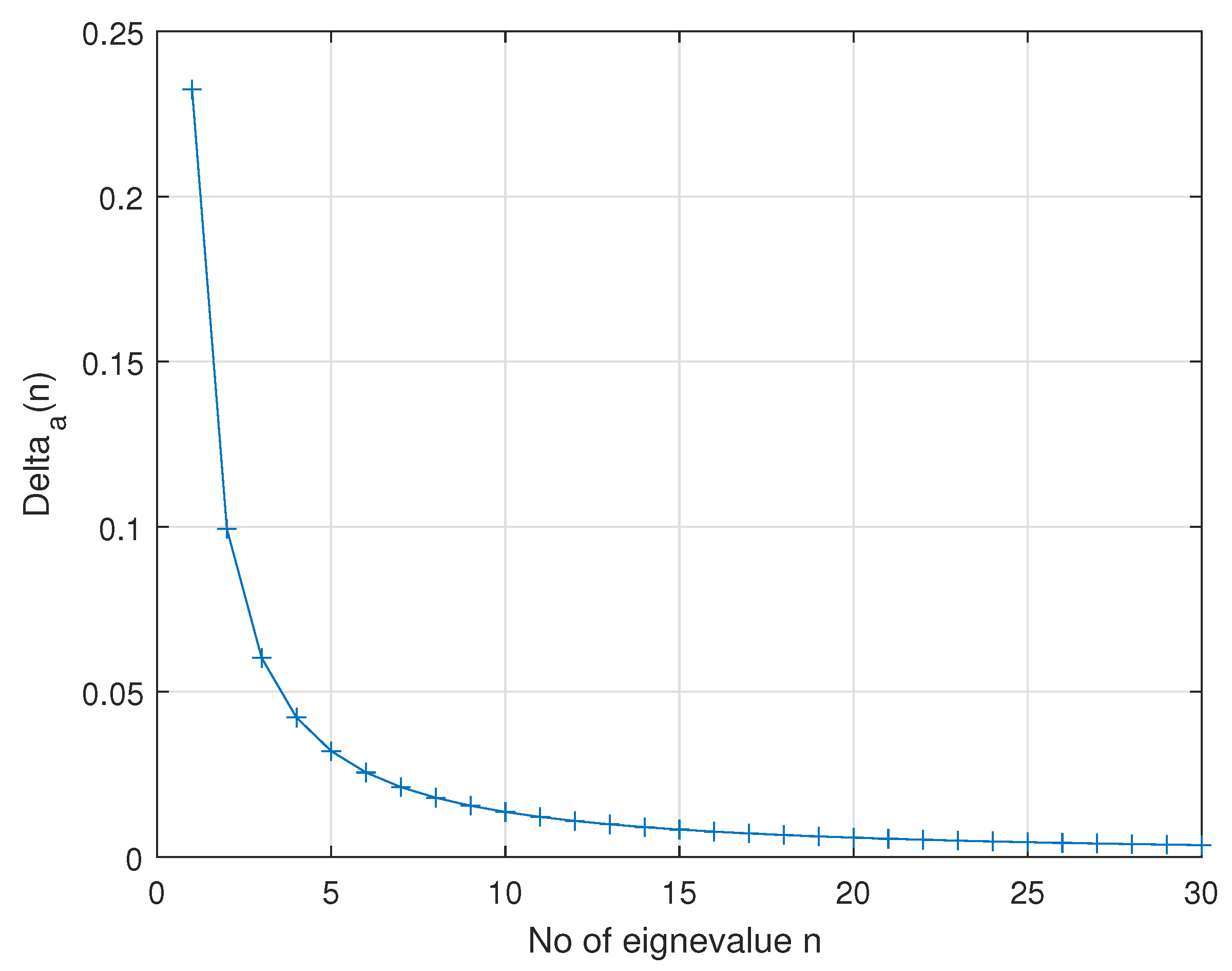
Figure 5.
The maximum N assuring the distinguishability of all eigenvalues for (left) and (right).
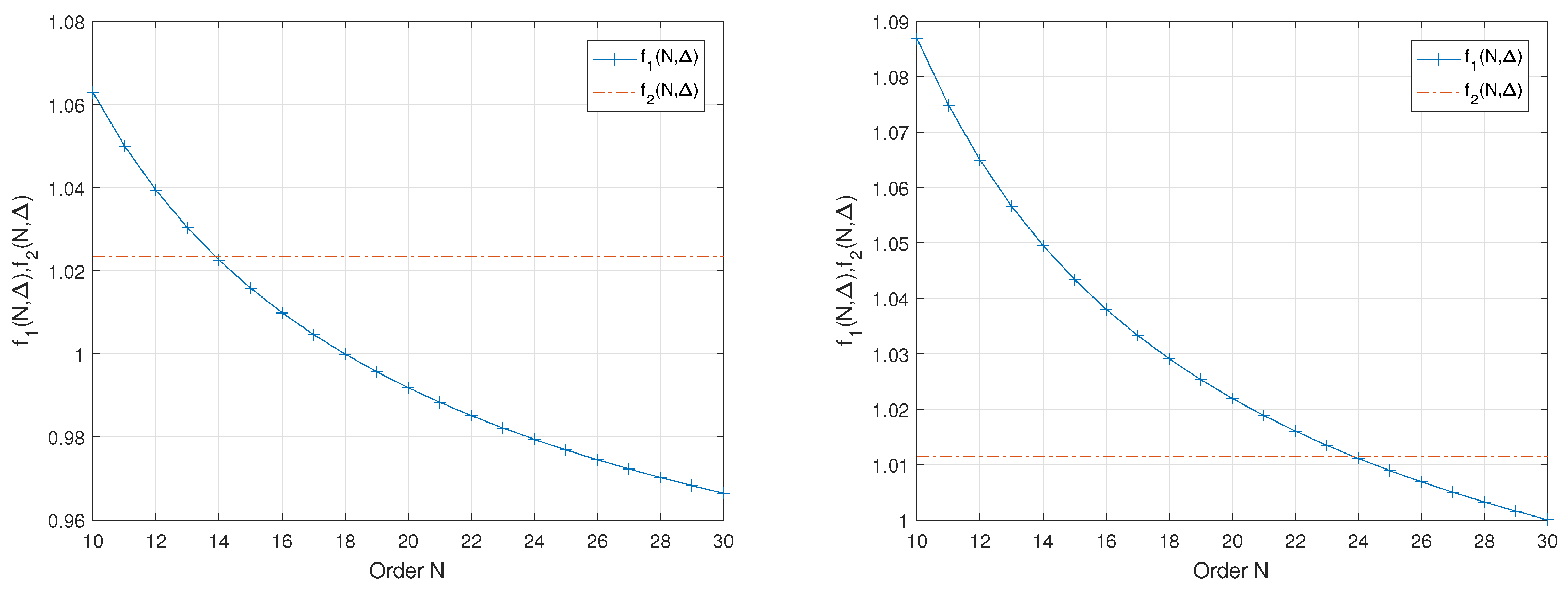
Figure 6.
The vertex step responses (43) of the model for and for outputs 1-3 (1-top, 3-bottom)
Figure 6.
The vertex step responses (43) of the model for and for outputs 1-3 (1-top, 3-bottom)
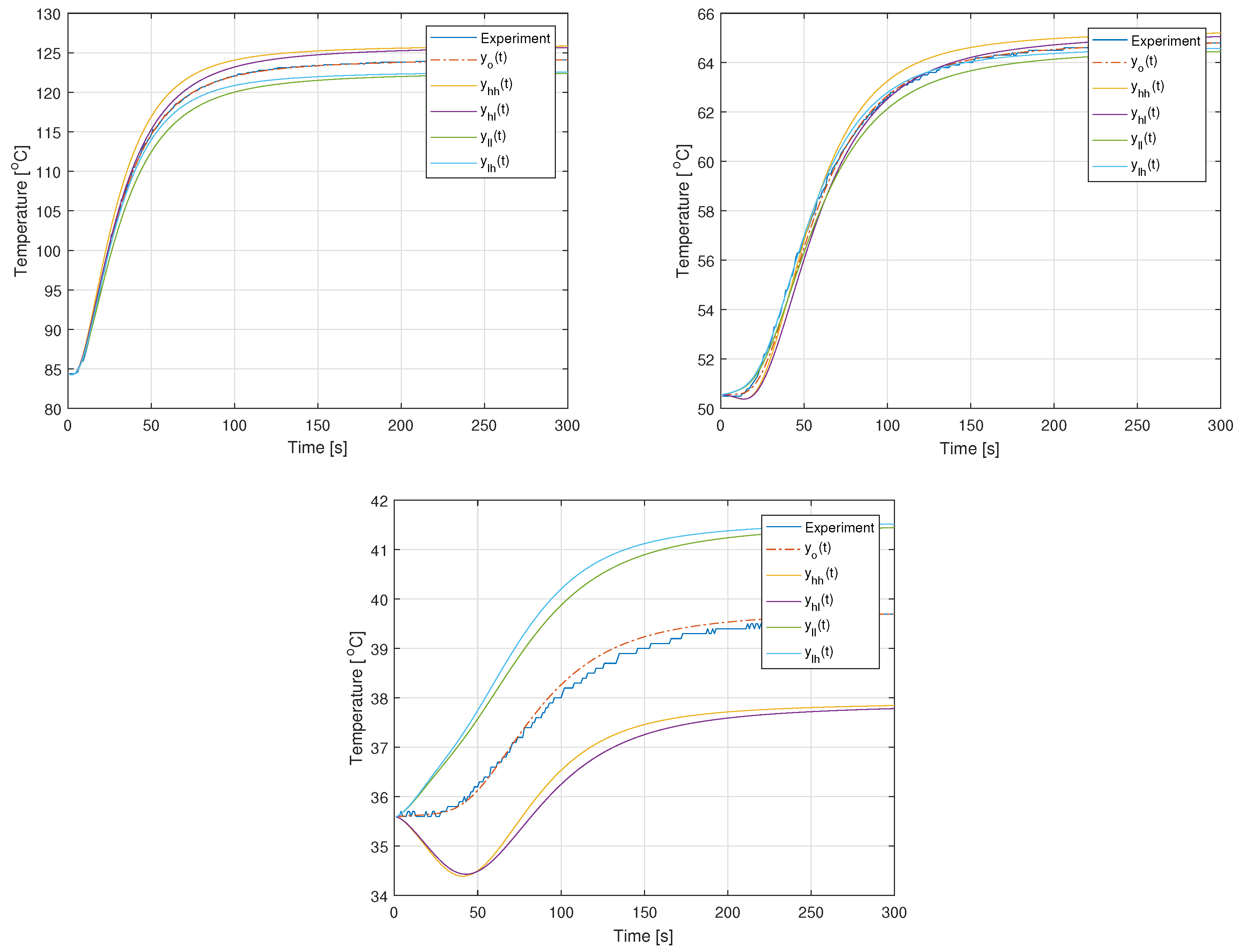
Figure 7.
The relative deviations (47) for and for outputs 1-3 (1-top, 3-bottom).
Figure 7.
The relative deviations (47) for and for outputs 1-3 (1-top, 3-bottom).
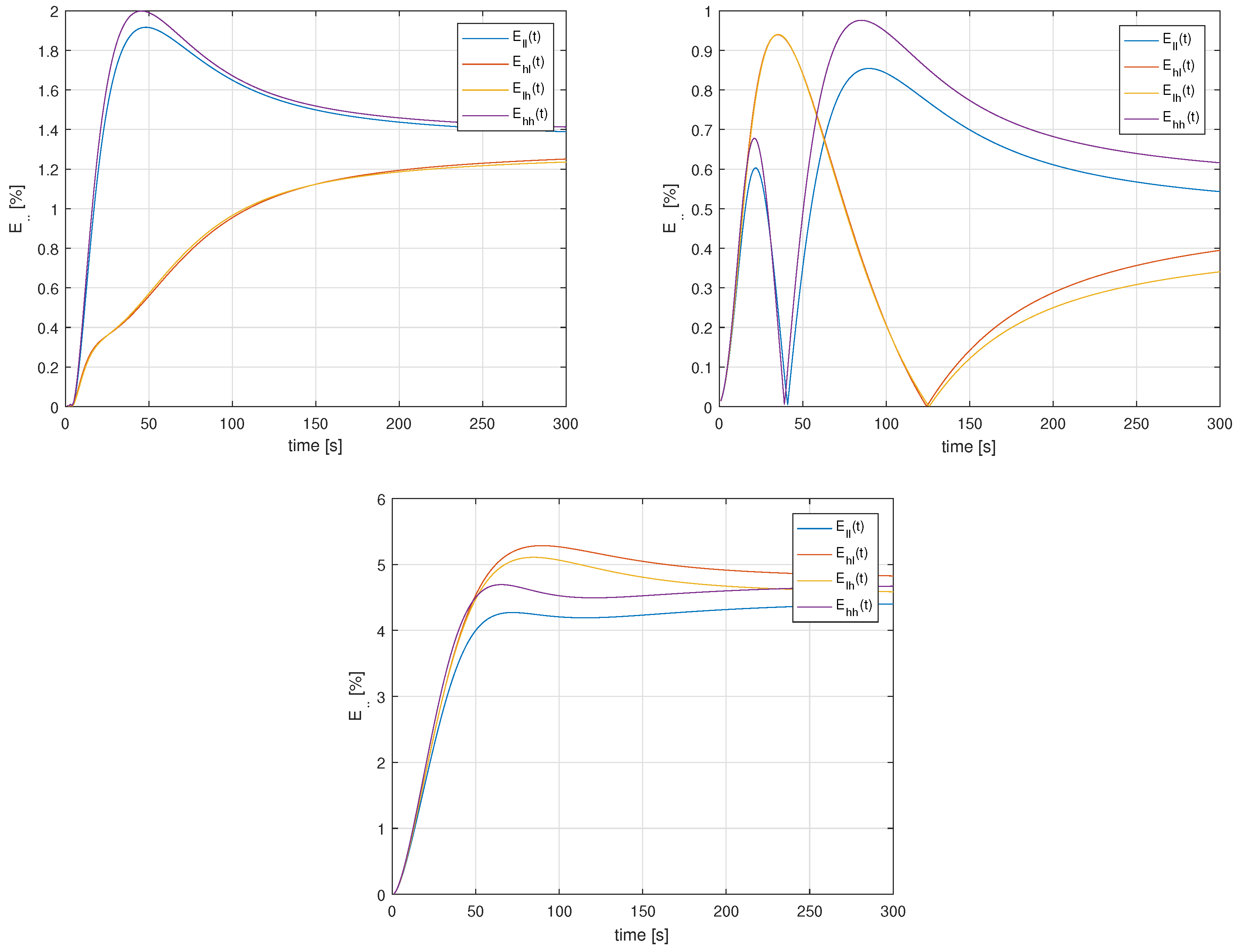
Figure 8.
The relative steady-state deviation (55) as a function of the small uncertainty for all outputs of the plant.
Figure 8.
The relative steady-state deviation (55) as a function of the small uncertainty for all outputs of the plant.
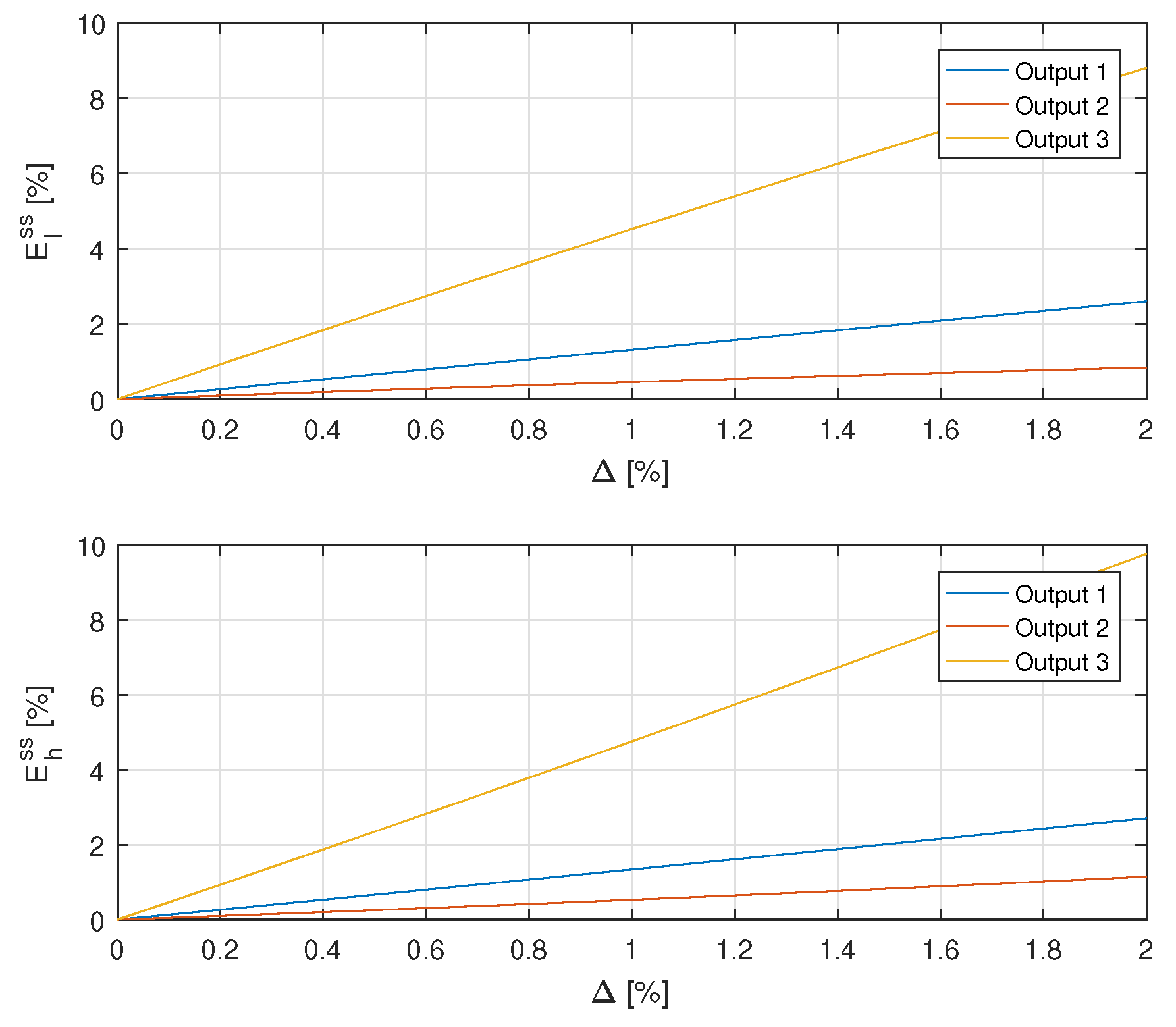
Figure 9.
The relative steady-state deviation (55) as a function of the big uncertainty for all outputs of the plant.
Figure 9.
The relative steady-state deviation (55) as a function of the big uncertainty for all outputs of the plant.
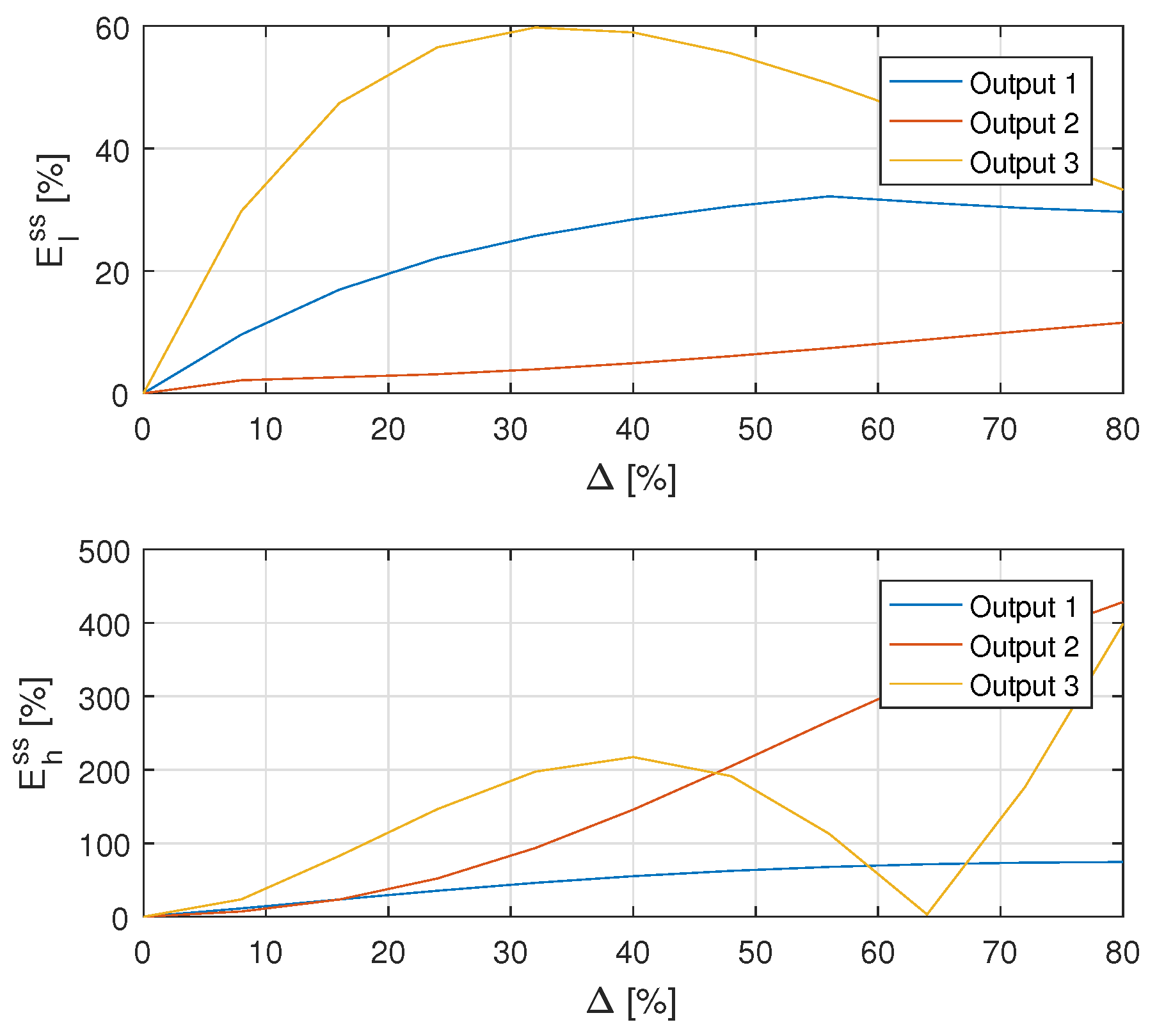
Table 1.
The size and the location of the heater and the sensors
| 0.14 | 0.06 | 0.26 | 0.47 | 0.70 |
Table 2.
The parameters of the model
| N | ||||
|---|---|---|---|---|
| 0.930289 | 1.998808 | 0.000410 | 0.0677066 | 22 |
Table 3.
The maximum size allowing to distinguish two different eigenvalues
| 2 | 10 | 0.3045 |
| 2 | 30 | 0.4242 |
| 5 | 20 | 0.2011 |
| 10 | 25 | 0.1173 |
| 15 | 25 | 0.0622 |
| 20 | 25 | 0.0262 |
| 25 | 30 | 0.0205 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






