Prerpints.org logo
Preprint
Article

Comparative Studies on the Radiative Heat Transfer in Arc Plasma and Its Impact in a Model of a Free-Burning Arc

Altmetrics

Downloads

127

Views

63

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 June 2024

Posted:

12 June 2024

You are already at the latest version

Alerts
Abstract
The radiative heat transfer in arc plasma models is considered from the point of view of its description in terms of a net emission coefficient, the method of spherical harmonics in its lowest order, and the discrete ordinate method. Net emission coefficients are computed applying approximate and numerical approaches, the multi-band representation of the spectral absorption coefficient with three kinds of its averaging and two datasets. The self-consistent access to the radiative heat transfer is applied to a two-dimensional axisymmetric model of free-burning arc in argon at atmospheric pressure. The results obtained from the models employing the net emission coefficient, the method of spherical harmonics, and the discrete ordinate method are compared.
Keywords: 
Subject: Physical Sciences  -   Fluids and Plasmas Physics

1. Introduction

Electric arcs find a wide range of applications. They appear in gases and vapours at low, atmospheric and high pressure. Being characterized by low voltage, emission of high-intensity light, and production of heat, electric arcs are utilized in material processing (welding, cutting, furnaces), lamps, switching devices, etc. Industrial applications require a high degree of automation, accuracy, reliability, and stability of the arc plasma diagnostics (see [1] and the references therein). Electrical measurements (voltage and current) provide a method for the control of the arc stability. Fluctuations of the arc attachment on the electrode lead to changes in the arc length and in turn in the arc voltage [2]. Optical imaging allows for a three-dimensional analysis of the plasma structure [3]. Optical emission spectroscopy as a non-intrusive method and in combination with advanced cameras and detectors enables the measurement of the plasma temperature in the arc core, which is assumed close to the state of local thermodynamic equilibrium (LTE) [4]. Laser scattering methods that in general avoid the assumption of LTE have been applied to obtain the electron temperature and density [5]. Nevertheless, it is difficult or even hardly possible to determine experimentally the complex conditions inside the arc plasma. Modelling and simulation of arc plasma for various applications have been, therefore, intensively developed over the years (see e.g. [6,7,8,9,10] among others). An electric arc implies a multiphysics problem since the arc generation is generally accompanied by interrelated electromagnetics, fluid flow and heat transfer. State-of-the-art models of arc plasma have been developed that focus in particular on the effects of turbulence [11], non-equilibrium [12,13], arc-electrode interaction [14,15,16] as more details can be found in the review works [1,16] and the references therein.
Due to the high temperatures in the arc plasmas, the treatment of the plasma radiation is an important issue in their modelling [17,18]. The divergence of the radiative heat flux appears as a sink term in the equation of energy conservation in magneto-hydrodynamic (MHD) models of LTE arc plasma. It represents the interaction between the radiation and the plasma matter and is related to the radiative intensity. Arc plasmas are heated up to temperatures of tens of thousands of kelvins that implies irradiation by neutral and charged particles that covers the spectral region (1012-1016) Hz, where tens of thousands of spectral lines exist. The change of the spectral radiative intensity along a line of sight due to emission and absorption is governed by the equation of radiative transfer (RTE) with account for the spatial distributions of temperature and pressure, and the equilibrium plasma composition. The computation of the radiative heat flux for every frequency and direction in space within the arc model becomes hardly affordable. In order to overcome the computational overhead and keep the arc model feasible and though capable of predicting the arc behaviour, simplifications are usually introduced. An overview and analysis of methods is given in [17]. A common approach used in many arc models makes use of introducing a net emission coefficient (NEC) [19] obtained for an isothermal cylinder of a given radius. This approach is often reduced to the computation of the radiative heat losses in the arc as a function of the local values of temperature and pressure although NEC is strongly speaking determined by the entire temperature profile in the arc [19]. Although this approach can provide reasonable results for the plasma temperature for a well-chosen value of the radius, for which the NEC is computed, there remains inconsistency regarding situations with deviations from a cylindrical shape of the arc. Other approaches for solving the RTE with account for emission and absorption of radiation as well as effects on the plasma boundaries are the method of spherical harmonics (P1 as the lowest order) and the discrete ordinate method (DOM) [20]. The application of the DOM to models of gas circuit breakers has been considered in [21].
In the present work, we revisit the physical background of the radiative heat transfer, we give an overview of approximate methods for its computation, and we follow a self-consistent access in the treatment of the radiative heat transfer in models of LTE arc plasma that account for the arc-electrode interaction [22,23]. The derivation of governing relations used in the methods under consideration is given as supplementary material. NEC, P1 and DOM are implemented into a 2D model of a free-burning arc. The multiband approximation of the absorption coefficient is applied to obtain the NECs and in the P1 and DOM approaches for two datasets regarding the spectral absorption coefficient. The plasma temperature and the radiative losses predicted by the NEC, P1 and DOM approaches are compared. The impact of using different datasets for the spectral absorption coefficient is studied. These detailed studies and the self-consistent account for the radiative heat transfer in state-of-the-art LTE arc plasma models instead of pre-imposed profiles of the plasma temperature [20,21] constitutes the originality of the work.

2. Physical Background

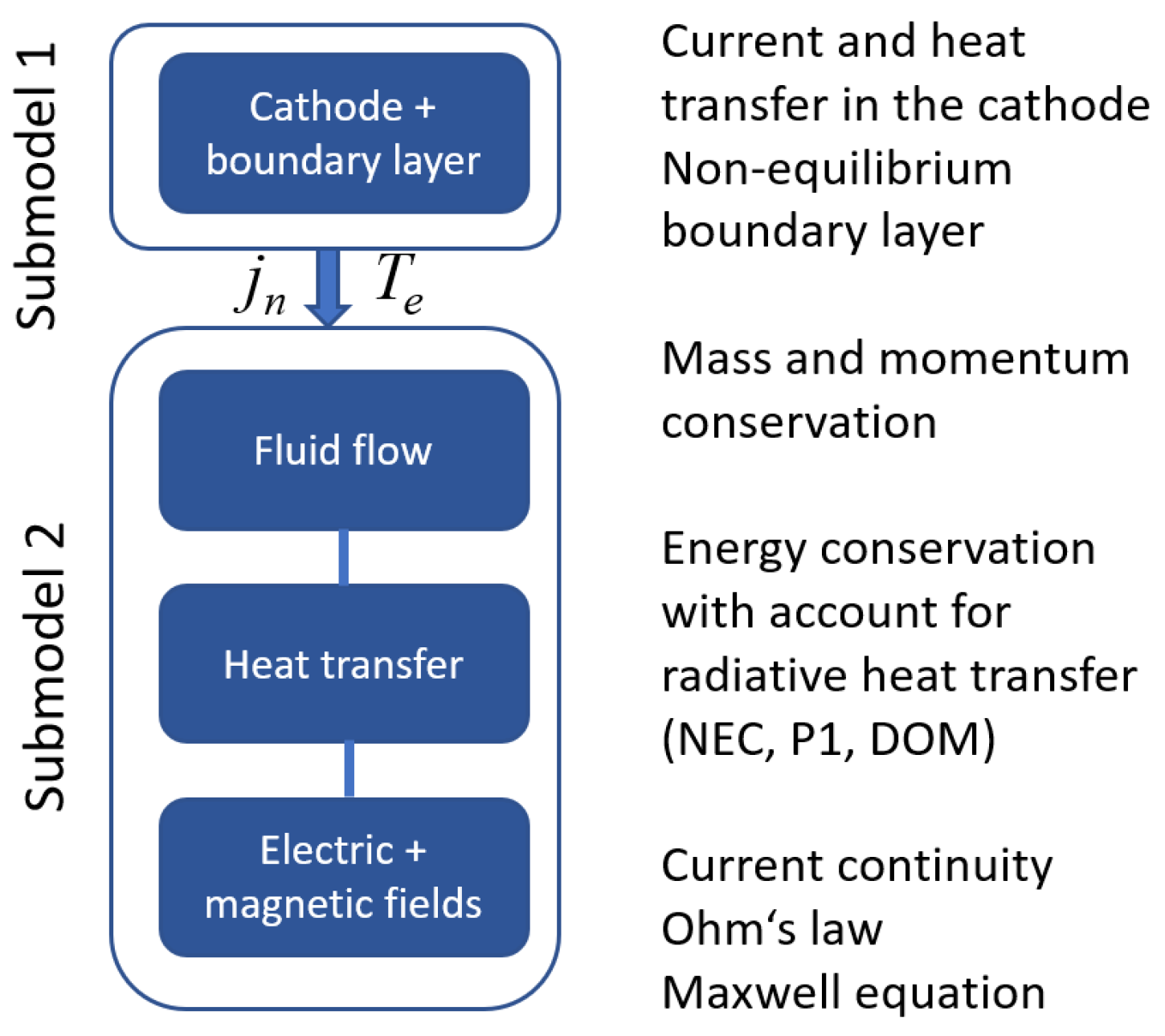
An almost complete description of the basic LTE arc model employed in this work can be found in the previously published works [22,23]. Here, its main features are briefly summarized. A model of a thermionic cathode made of doped tungsten and its non-equilibrium boundary layer (submodel 1 in Figure 1) and a MHD model of the LTE arc plasma in argon at atmospheric pressure and the anode (submodel 2 in Figure 1) are coupled through a dimensionless interface along the edge between the cathode and the plasma. For a given total current, the first submodel solves for the current and the heat transfer within the cathode applying as boundary conditions pre-computed transfer functions for the normal current density and heat flux as functions of the surface temperature of the cathode and the voltage drop in the boundary layer. These transfer functions are obtained by solving the energy balance of the non-equilibrium boundary layer [24]. Among the results, the distribution of the normal current density (jn) and the electron temperature (Te) along the plasma edge are computed. These quantities serve as boundary conditions of the second submodel. Notice that in the LTE arc plasma, electrons and heavy particles are characterized by a common temperature (Te=T). The second submodel solves the equations for conservation of mass, momentum, and energy, the equations describing the current continuity, the Ohm’s law, and the Maxwell equation [23]. The thermodynamic and transport properties of the argon plasma are from [25,26] while those of the solid materials are from [27,28]. In what follows, the attention is focused on the energy conservation equation, in which the radiative heat transfer is taken into account.
The energy conservation equation for a stationary LTE arc plasma is written as
ϱ C p u · ∇ T + ∇ · q + q r = α p T u · ∇ p + τ : ∇ u + Q .
In Eq. (1), ρ denotes the mass density, C p is the specific heat capacity at constant pressure, T is the plasma temperature, u is the velocity vector, q is the conductive heat flux, qr is the radiative heat flux, α p = − 1 ϱ ∂ ϱ ∂ T is the coefficient of thermal expansion, p is the pressure, τ is the viscous stress tensor for a Newtonian fluid, and Q contains other heat sources such as the Joule heating and the transport of electron enthalpy.
The divergence of the radiative heat flux ∇ · q r is of greatest interest in this work since it represents the interaction between radiation and matter. For an absorbing-emitting medium, the radiative intensity I ν ( r , s ) is defined as the radiative energy per unit time and unit area normal to the rays per unit solid angle and frequency (Figure 2) [19,29]. Here, r is a position vector fixing the location of a point in space, and s is a unit direction vector.
The change of the spectral radiative intensity along a line of sight into direction s is given by the radiative transfer equation (RTE) [Modest], which in the case of no scattering reads:
s . ∇ I ν = d I ν d s = κ ν B ν − κ ν I ν .
In Eq. (2), κ ν denotes the spectral absorption coefficient, the Plank intensity B ν = 2 h c 2 ν 3 e h ν / k B T − 1 is introduced with h and k B   being respectively the Plank and the Boltzmann constants, and c is the speed of light. This equation shows how the intensity is amplified by emission and decreased by absorption. The integration of the RTE equation over the solid angle gives the divergence of the spectral radiative heat flux
∇ · q r ν = ∫ Ω = 0 4 π s . ∇ I ν d Ω = ∫ Ω = 0 4 π κ ν B ν d Ω − ∫ Ω = 0 4 π κ ν I ν d Ω .
Integrated over the spectrum, the divergence of the radiative heat is now being
∇ · q r = 4 π ∫ 0 ∞ κ ν B ν d ν − ∫ 0 ∞ ∫ Ω = 0 4 π κ ν I ν d Ω d ν
or
∇ · q r = 4 π ∫ 0 ∞ κ ν B ν d ν − ∫ 0 ∞ κ ν G ν d ν
as the incident radiation G ν = ∫ Ω = 0 4 π I ν d Ω is introduced. Eq. (5) shows that ∇ · q r is obtained through integration over the directional coordinates and the spectrum and therefore, it depends on the distribution of the plasma temperature in the medium. This refers to the quantity net emission coefficient [18] introduced as
ε N = 1 4 π ∇ · q r .
At the arc edge, absorption of radiation originating from the arc center can lead to negative values of the NEC ε N [18]. Since an exact evaluation of ∇ · q r is usually not feasible, approximations can be invoked [19,29].

3. Overview of Approximate Methods Used in the Present Work

The approximate methods considered in the present work involve simplifications with respect to the spectral properties of the arc plasma, and the treatment of the directional integration, i.e., the solution of the RTE (2). These methods are briefly summarized below.

3.1. Multi-Band Approximation for the Spectral Absorption Coefficient

In this approximation, the spectral properties of the plasma (the spectral absorption coefficient κ ν ) are assumed to be uniform over a set of frequency intervals [19]. In the case only one interval is used, the approximation reduces to the grey model. The increase of the number of spectral bands improves the accuracy and increases the computational effort. The number of spectral bands and their boundaries are chosen considering the behaviour of the absorption coefficient (see below for the computation of the absorption coefficient). Five intervals with boundaries 0.003, 1.0, 2.8, 3.8, 6.67, and 10.0 in units of 1015 Hz as reported in [30] are used in the present work. The evaluation of the spectral absorption coefficient κ ν in each interval of frequencies [ ν i ,   ν i + 1 ] can be performed applying Plank ( κ P ) or Rosseland ( κ R ) averaging [19] or a combination of both ( κ h ) leads to a hybrid mean value [31]. The idea behind the hybrid mean absorption coefficient is to weight the overestimate and the underestimate expected by respectively the Plank and Rosseland mean absorption coefficients [32]. The corresponding equations read
κ P = ∫ ν i ν i + 1 κ ν B ν d ν / ∫ ν i ν i + 1 B ν d ν   ,
κ R − 1 = ∫ ν i ν i + 1 κ ν − 1 d B ν d T d ν / ∫ ν i ν i + 1 d B ν d T d ν
κ h = γ κ R + 1 − γ κ P , γ = ( κ P − κ R ) / κ P .
According to Eq. (9), κ h could become negative if κ R / κ P > 2 (not the case in argon).
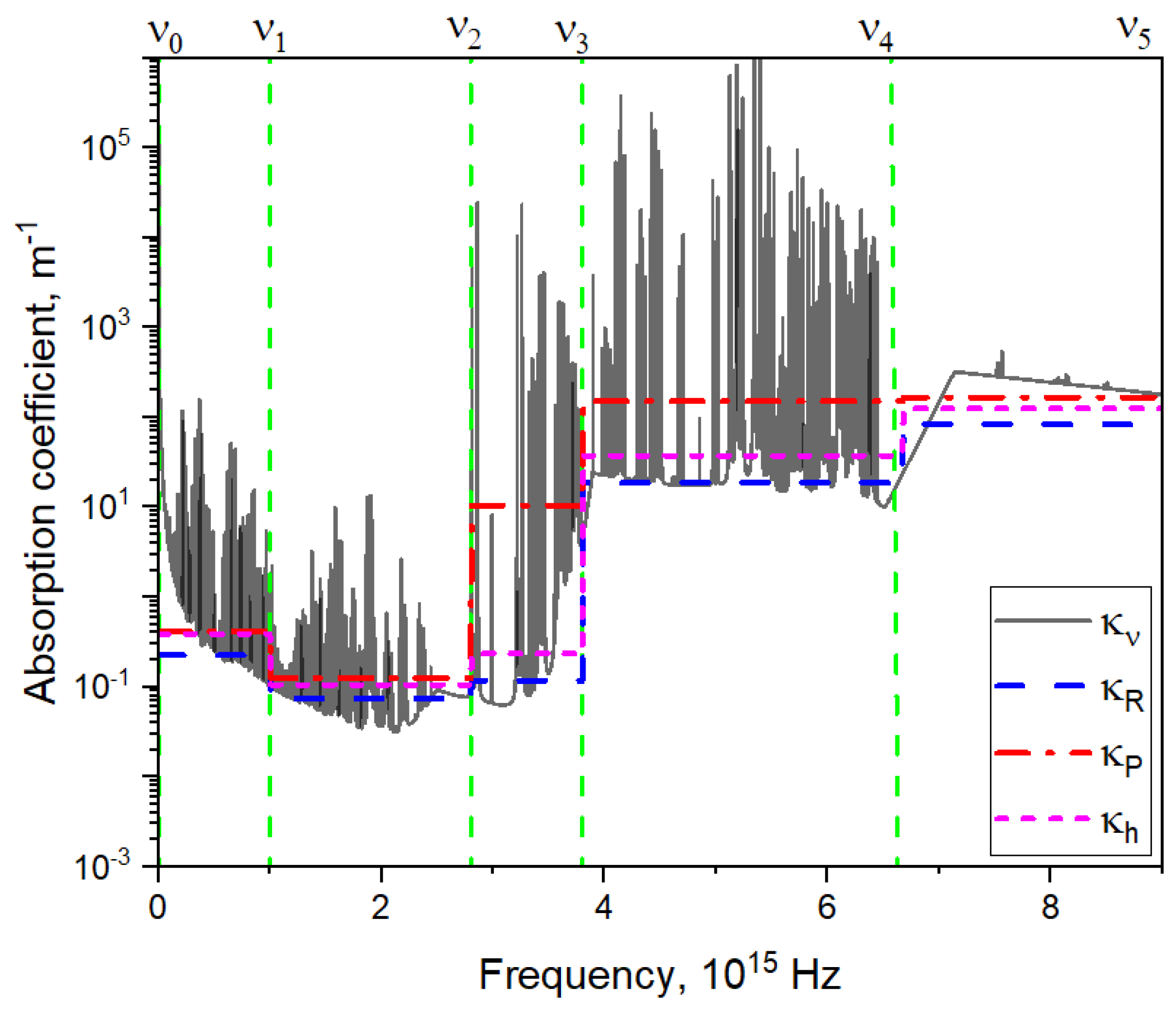
As an example, the spectral absorption coefficient ( κ ν ) of Ar plasma at a pressure of 1 bar and a temperature of 20000 K is shown in Figure 3 along with the mean absorption coefficients κ R , κ P , and κ h . In some spectral intervals, the difference between κ P and κ R becomes quite large.

3.2. The P1 Method of Spherical Harmonics

In the method of spherical harmonics, the RTE (2) is transformed into a set of partial differential equations [19]. The governing equations of the approximation of lowest order known as the P1-approximation are written as follows
∇ · q r r = κ 4 π B − G r ,
q r r = − 1 3 κ ∇ G r .
The derivation of Eq. (11) is provided in the Appendix A. Notice that the index “ν” denoting the corresponding spectral quantity is dropped. A second-order partial differential equation for G r is derived from Eqs. (10) and (11)
∇ · − D P 1 ∇ G r = κ 4 π B − G r ,
where D P 1 = 1 3 κ . The boundary condition at opaque walls (Marshak boundary condition [19]) reads
n · − D P 1 ∇ G r = q r , n e t ,
with q r , n e t being the net radiative flux absorbed by the boundary and n is the surface normal. Depending on the surface emissivity ϵ ∈ ( 0,1 ) , the boundary surface is treated as gray with
q r , n e t = ϵ 2 2 − ϵ 4 π B η − G
or black ϵ = 1 . The quantity η ∈ ( 0,1 ) accounts for the fractional emissive power in a given spectral interval. The net radiative flux at flow inlets and outlets is computed in the same manner as at walls assuming emissivity of one.

3.3. The Discrete Ordinate Method

The DOM solves the RTE (2) by means of a discretization of the angular space, i.e., the integral over all directions is replaced by numerical quadratures of discrete directions j
∫ Ω = 0 4 π I d Ω = ∑ j ​ ω j I j .
The number of directions gives the number of the dependent variables to be solved for.
With intensities have been obtained, the radiative heat flux, the incident radiation, and the divergence of the radiative heat flux can be determined (see Eqs. (3) and (5)).
The boundary condition at opaque walls reads
I j , b n d = ϵ B η + 1 − ϵ π q r , o u t
for all directions s j such that n · s j < 0 .

3.4. Approximate Net Emission Coefficient

Eq. (6) relates the net emission coefficient and the divergence of the radiative heat flux ∇ · q r . Approximate net emission coefficient can be obtained by solving the RTE (2) for cylindrical isothermal plasmas of various temperatures and radii [18]. Approximate analytical expressions for the net emission coefficient at the center of homogeneous plasma were presented in [18,33] as
ε A = ∫ 0 ∞ B ν κ ν exp ⁡ − κ ν R d ν ,
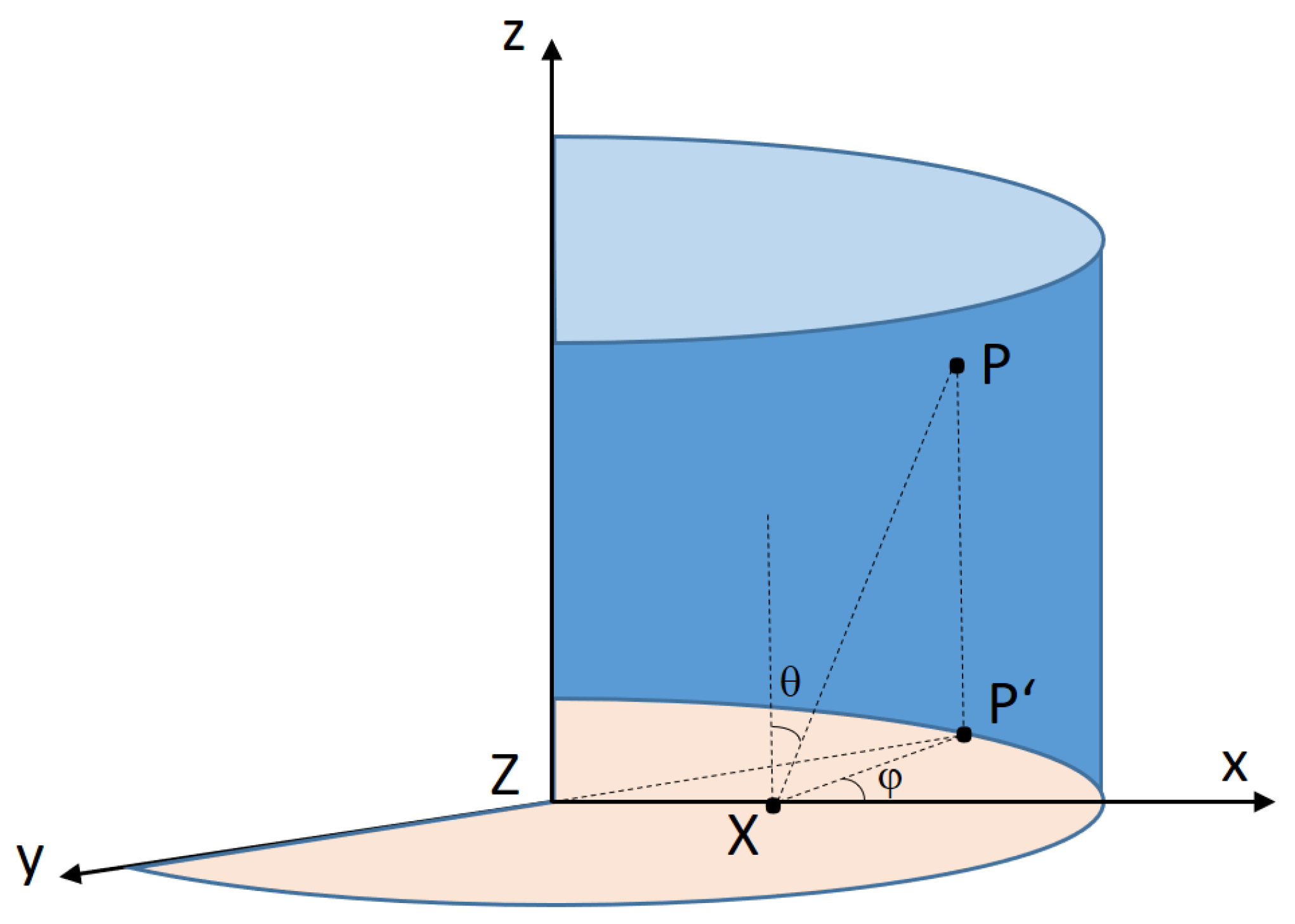
where R denotes the radius of the cylinder. The derivation of Eq. (17) is provided in Appendix B. The directional vector is defined by the spherical coordinates θ and φ (see Figure 4). Point X is located insight the plasma (taken for convenience on the x-axis). The integration along the line XP ( θ ≠ 0 ) can be transformed into integration along the line Z P ′, which is perpendicular to the z axis of the cylindrical plasma.
The evaluation of the value of ε A according to Eq. (17) for a given value of the radius R can be done by applying the multi-band approach [34] and employing the Planck, Rosseland and the hybrid mean absorption coefficients considered in the subsection 3.1.
Alternatively, numerical solutions by means of the P1 and DOM methods in a combination with the multi-band approximation of the spectral absorption coefficient are considered in the present work, and the NEC is obtained from the evaluated divergence of the radiative heat flux according to Eq. (6). Solutions of the RTE are obtained in a three-dimensional geometry and the approximate NECs are evaluated for several values of the radius R and the length L (R << L) of the cylinder.

4. Computation of the Absorption Coefficient

The spectral absorption coefficient plays a crucial role in the propagation of radiation in participating media as it is indicated by Eq. (2) and the subsequent relations. The accurate knowledge of this quantity is thus a necessity for any calculations involving a radiative transfer. The accurate determination poses a big challenge as every process resulting in a loss of radiation have to be included in the evaluation process.
The number of processes is significantly reduced in the case of argon as working gas. Since argon is a noble gas, the gas under LTE conditions is composed mainly of atomic species alleviating the need for evaluation of radiation–molecular interaction processes. Furthermore, the LTE assumption enables the evaluation of the emission coefficient instead of direct absorption coefficient evaluations, as these coefficients are related to each other by the Kirchhoffs law:
ε ν = κ ν B ν T ,
where ε ν denotes the spectral emission coefficient, and κ ν , B ν have been already defined in section 2. The evaluation of the emission coefficient instead of that of the direct absorption coefficient is preferable in certain cases.
Three kinds of transition processes have to be taken into account, when evaluating the absorption coefficient in an atomic gas. These are bound-bound, bound-free and free-free transitions. The naming convention is derived from an electron state in the vicinity of an atom or an ion before and after the absorption of radiation in the form of a photon.
The bound-bound transition, often called photo-absorption or line radiation, is associated with the absorption of a photon by electron found in the bound state of the argon atom or ion. The absorbed energy excites the electron to the higher, but still bound energy state. The resulting contribution to the absorption coefficient can be expressed as
κ ν = I p , T P ν 1 − exp − h ν / k T
where I p , T = π r 0 c f i k N i is the total line intensity, P ν is the line profile, generally calculated as an approximation to the Voigt profile, and 1 − exp − h ν / k T is a correction factor accounting for induced emission. In the above expressions the r 0 is the classical electron radius, f i k is the oscillator strength of line, c is the speed of light constant and
N i = g i N Q int T e − E i k T
is the population density of the lower level with statistical weight g i and energy E i , and Q int denotes the internal partition function. The line profile P ν expresses an averaging of the absorption of many absorbing atoms each in slightly different conditions stemming either from a thermal motion (Doppler broadening), a close proximity to charged particle (Stark broadening), a close proximity to particle with dipole momentum (van der Waals broadening) or a close proximity to a particle with a similar structure of electron levels (Resonance broadening). Details of each broadening mechanism falls out of the scope of this work and can be found in relevant textbooks such as [35].
Bound-free transition, also called photo-absorption or radiative recombination, represents another important process in the evaluation of the absorption coefficient. The process is associated with the formation of a positive ion and a free electron due to absorption of radiation. The transition is characterized by a continuous absorption coefficient, with sharp drops at certain frequency known as absorption edges. The frequency of these edges is governed by the energy structure of the involved atoms and corresponds to the energy difference between the bound states and the ionization level. Some approximations to the evaluation of bound-free absorption coefficient are provided e.g., in [36,37].
Finally, the free-free transition, known as the inverse Bremsstrahlung or simply the Bremsstrahlung from the emission point of view, represents the absorption of radiation by a free electron in the electric field produced by a neutral particle with a dipole momentum or an ion. The contribution of this process to the total absorption coefficient is generally small with exception of the low frequency limit. The calculation procedure depends on whether the process is calculated in the vicinity of a neutral atom or an ion. This topic is considered in detail e.g., in [38].
The absorption coefficient is evaluated using the Kirchhoffs law. Two separate datasets were considered in the present work, each one obtained in a slightly different way as follows.
  • Dataset I
The plasma composition for the given pressure of 1 bar and temperature values from 300 K up to 30000 K is obtained using the mass action law, the energy levels of the species (ArI-IV), and their internal partition functions [37]. The spectral absorption coefficient is then deduced from these population densities as the sum of several radiative contributions for wavelengths between 30 nm and 4500 nm: the atomic continuum comprising the Bremsstrahlung in electron-ion collisions, Bremsstrahlung in electron-atom collisions, radiative recombination and attachment, and atomic and ionic spectral lines. An almost complete description and the data used is given in [37]. Compared to [37], the number of atomic energy levels was extended according the NIST data [39] to include 427 energy levels for ArI, 417 for ArII, 125 for ArIII, and 58 for ArIV. In particular, attention was paid to the description of the atomic lines. Instead using an escape factor as in [37], the line-by-line method was employed that takes into account a fine treatment of the profiles of the atomic lines and their broadening due to Doppler effect, Van der Waals interaction, and Stark effect. This treatment is a complex and long task since these effects modify the shape of the line profiles depending on the pressure and the temperature. For the 9551 lines of argon species (2758 for ArI, 5804 for ArII, 843 for ArIII and 146 for ArIV), the wavelength-grid involves 9267017 points at 300 K, and 1256961 points at 30000 K.
  • Dataset II
The same plasma composition utilized in Dataset I is used to calculate the radiation properties for Dataset II, thus keeping the plasma composition of both data sets equal. The spectral absorption coefficients are calculated with consideration of radiation processes including bound-bound (atomic and ionic lines), bound-free (photoionization continuum) and free-free (Bremsstrahlung) processes. Data for known atomic lines were taken from the NIST database. In total, 804 atomic and ionic lines of argon were considered (412 for ArI, 300 for ArII, 68 for ArIII and 24 for ArIV). Several broadening mechanisms for each line were considered, including Doppler, Stark, Van der Waals and resonance broadening. The final line profile was calculated using Whiting approximation to the Voigt line profile [40]. Two data sources were utilized for evaluation the photoionization process on the absorption properties of argon. Primary source were cross sections published by Opacity Project supplemented by hydrogenic approximation according to [36] in case of missing cross sections. In total, 1203 energy levels of argon atoms and ions were considered (176 cross sections and 27 hydrogenic for ArI, 238 cross sections and 23 hydrogenic for ArII, 225 cross sections and 231 hydrogenic for ArIII and 338 cross sections and 52 hydrogenic for ArIV). The Bremstrahlung contribution was calculated for both neutral argon and argon ions. The radiation contribution was calculated in the range from 1·1011 Hz (3 mm) to 1.2·1016 Hz (25 nm) with fixed frequency step of 1010 Hz resulting in the total number of 1199991 frequency-grid points.

5. Results and Discussion

The main objective of the present work is the self-consistent access to the radiative heat transfer in models of LTE arc plasma. For that purpose, the NEC, P1 and DOM methods are implemented into a 2D axisymmetric model of a free-burning arc and the computed plasma parameters are compared. Each method requires the knowledge of the radiative properties of the plasma. In the framework of the arc model employing the NEC, the values of the NEC have to be computed prior to the simulation and provided as a function of the temperature. The arc models employing the P1 and the DOM methos make use of a mean absorption coefficient (Planck, Rosseland, hybrid) obtained as a function of the temperature for a number of frequency bands. In order to provide a consistent data for comparison, the NECs for isothermal cylindrical plasma in argon at atmospheric pressure are presented first. Then, the results from the model of the free-burning arc are presented and discussed.

5.1. Isothermal Cylindrical Plasma

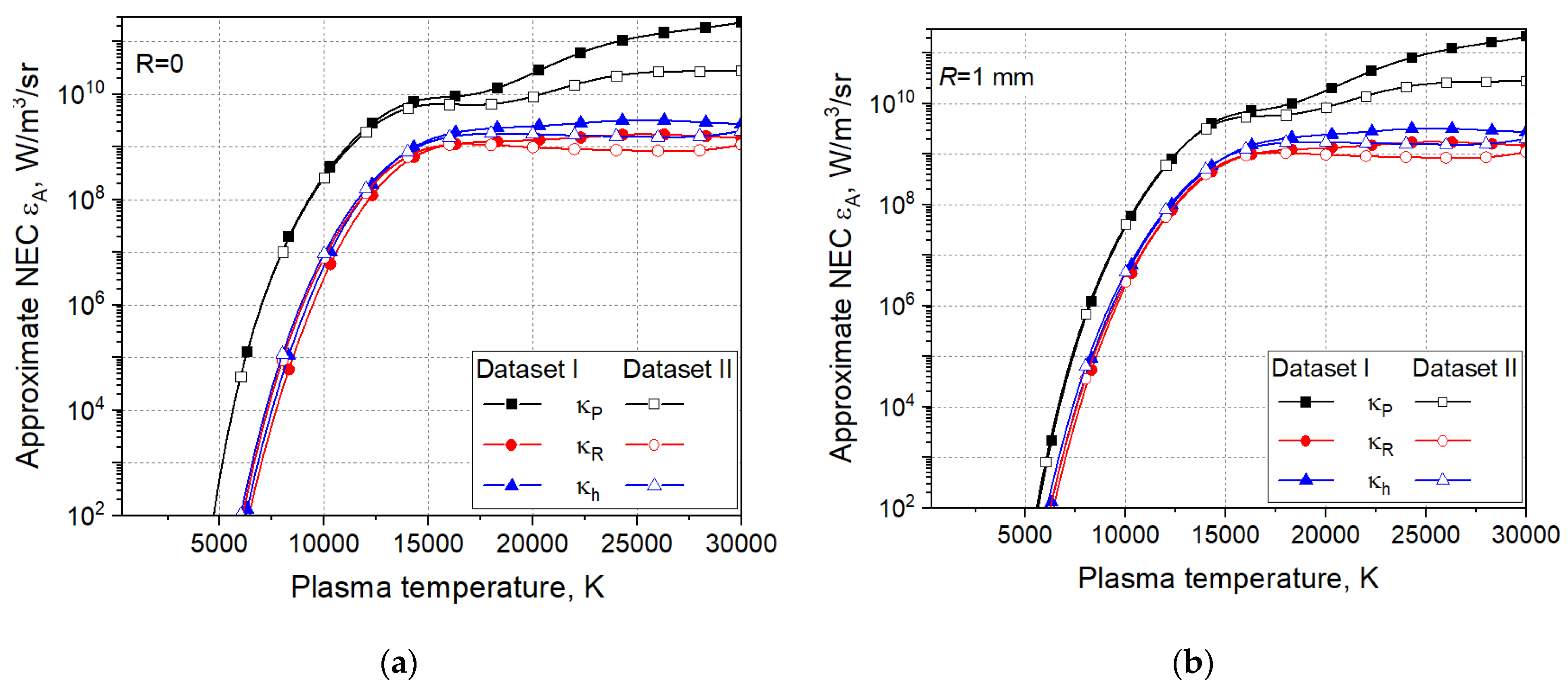
The net emission coefficient as considered above represents the radiative power per unit volume and unit solid angle that is irradiated from a cylindrical isothermal plasma of radius R into the surrounding. Approximate NECs ε A are obtained using Eq. (17) for plasma temperatures up to 30000 K. The results are shown in Figure 5 for various plasma radii R, mean absorption coefficients ( κ P , κ R , κ h ) and datasets (I, II). For the sake of a convenient reading, curves with solid symbols are assigned to Dataset I, while open symbols are assigned to Dataset II. NECs obtained with the Planck mean absorption coefficient κ P are presented by rectangles, while circles correspond to the Rosseland mean absorption coefficient κ R , and triangles denote NECs obtained with the hybrid mean absorption coefficient κ h .
The dependence of the approximate NECs ε A on the radius R is related to the exponential term in Eq. (17). For a given temperature, the spectral absorption coefficient is constant and the product κ ν R (the optical thickness) increases with the increase of R, which leads to the decrease of ε A . The NECs obtained applying the Planck mean absorption coefficient κ P are larger than those applying the Rosseland mean value κ R since κ P > κ R (see Figure 3). The employment of the hybrid mean absorption coefficient κ h leads to values of ε A between those applying κ P and κ R . Although the general course of the NECs obtained with datasets I and II is similar, a more pronounced difference appears for temperatures beyond 15000 K.
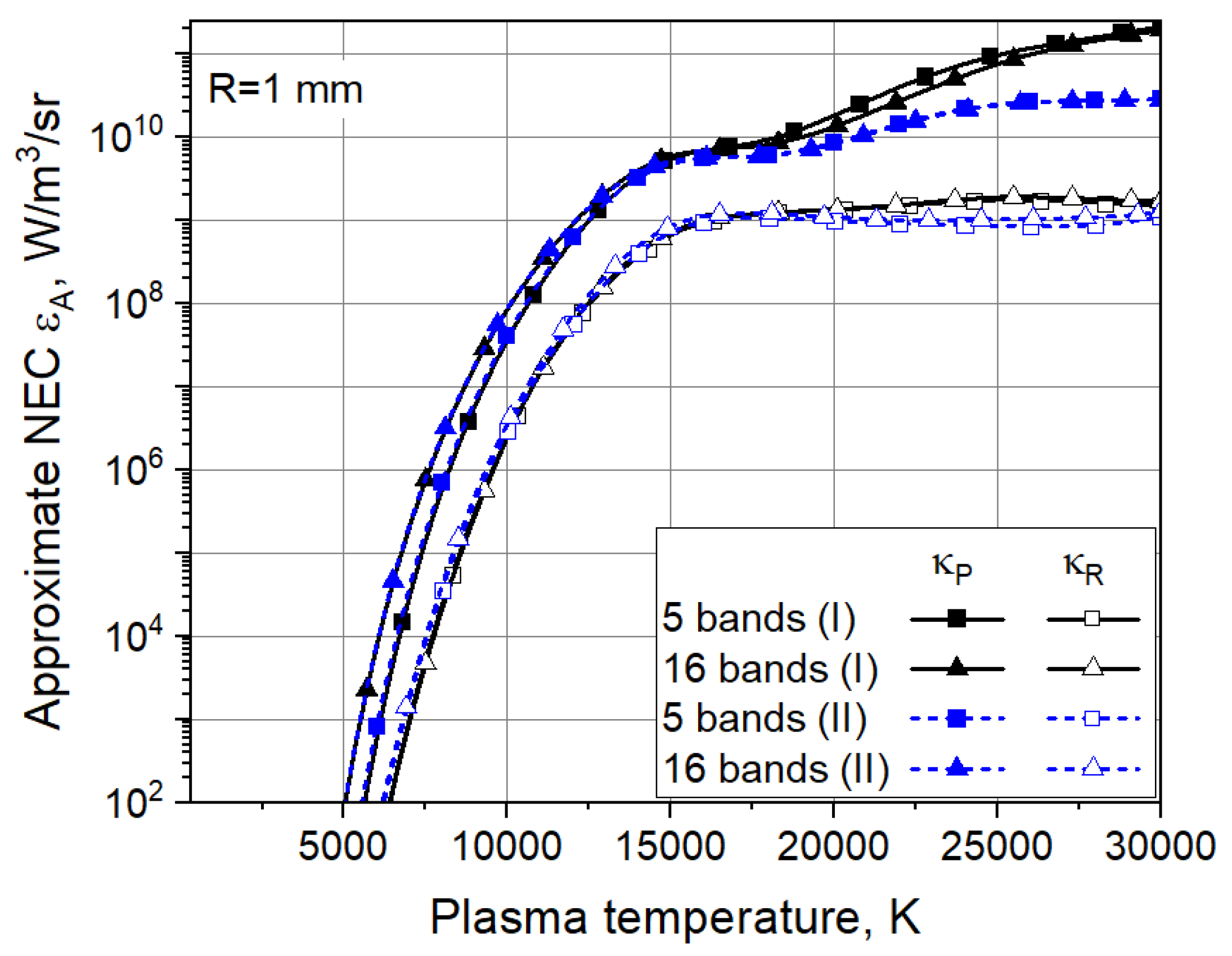
Figure 6 shows the influence of the number of spectral bands on the values of approximate NECs ε A obtained for a radius of the plasma R=1 mm, applying the mean absorption coefficients κ P and κ R , and datasets I and II. Here, approximate NECs are calculated applying a division of the frequency region (0.003-10). 1015 Hz into 5 and 16 spectral intervals [34]. The results for 5 and 16 spectral bands agree well that justifies the usage of the 5-band approximation in the further studies.
for a plasma radius R=1 mm. The results are obtained for mean absorption coefficients κ P and κ R , datasets I and II, and 5 or 16 spectral bands.
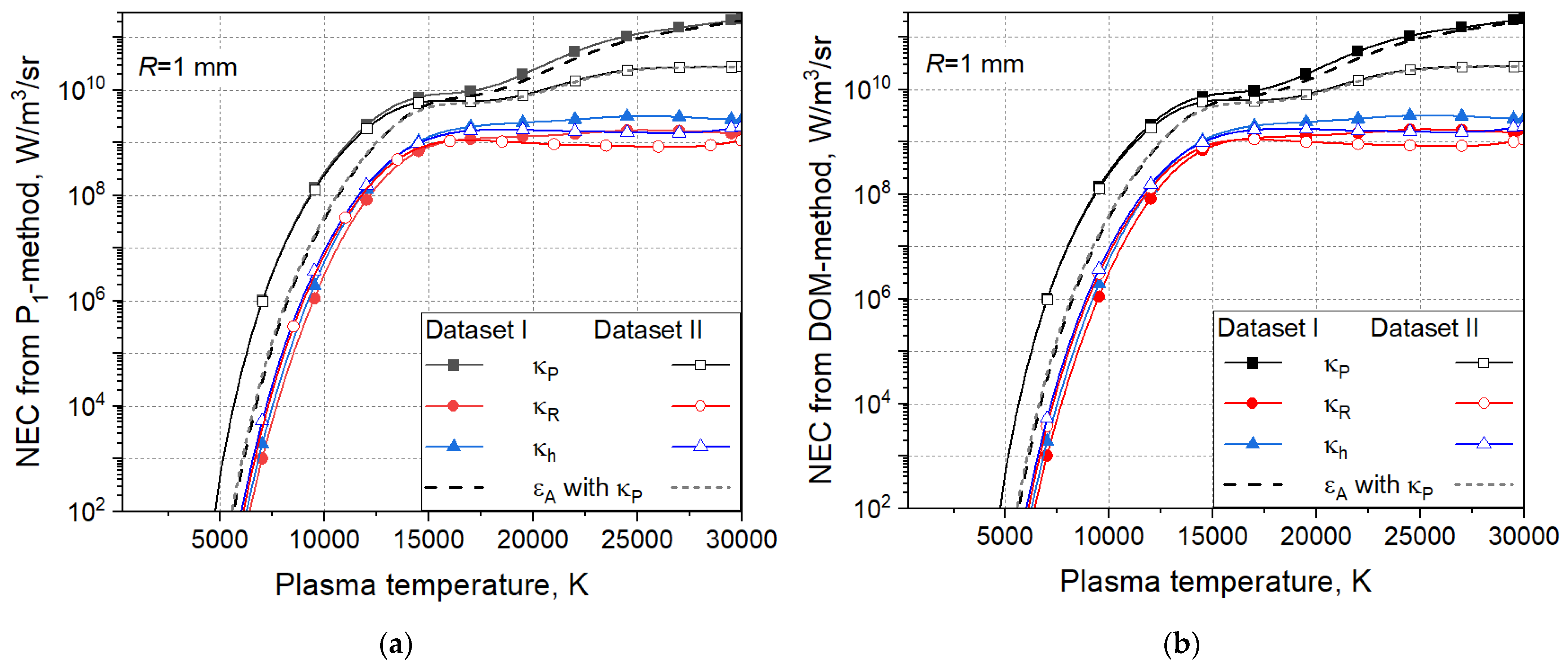
Figure 7 shows the NECs ε N obtained from the evaluated divergence of the radiative heat flux according to Eq. (6) in a 3D geometry of the isothermal cylindrical plasma (Figure 4). The ambient temperature is set at 300 K and the plasma temperatures is varied from 300 K up to 30000 K. As for the study cases in Figure 6, mean absorption coefficients ( κ P , κ R , κ h ) and datasets (I, II) are varied. The absorption coefficients employ the 5-band approximation. The cylindrical plasma has a radius R=1 mm and a length L=20 mm. The computational domain is resolved by means of about 20000 elements. Twelve directions are used in the DOM to discretize the angular space. The results of the P1 method practically coincide with those of the DOM method (see also Figure 8). They indicate the same behavior with respect to the variation of the mean absorption coefficient and the dataset like the results for the approximate NECs ε A in Figure 5b. Nevertheless, the values of ε N are somewhat higher than those of ε A for both datasets as indicated by the dash lines representing ε A computed with the Planck mean value κ P of the absorption coefficient. Furthermore, a control sample at a plasma temperature of 15000 K shows that ε N ~ (0.9-1.3).109 W/m3/sr (in cases κ R , κ h ) and ε N ~ (6.2-8.1) .109 W/m3/sr (in case κ P ), while ε A ~ (0.7-0.9).109 W/m3/sr (in cases κ R , κ h ) and ε A ~ (4.8-5.5) .109 W/m3/sr (in case κ P ).
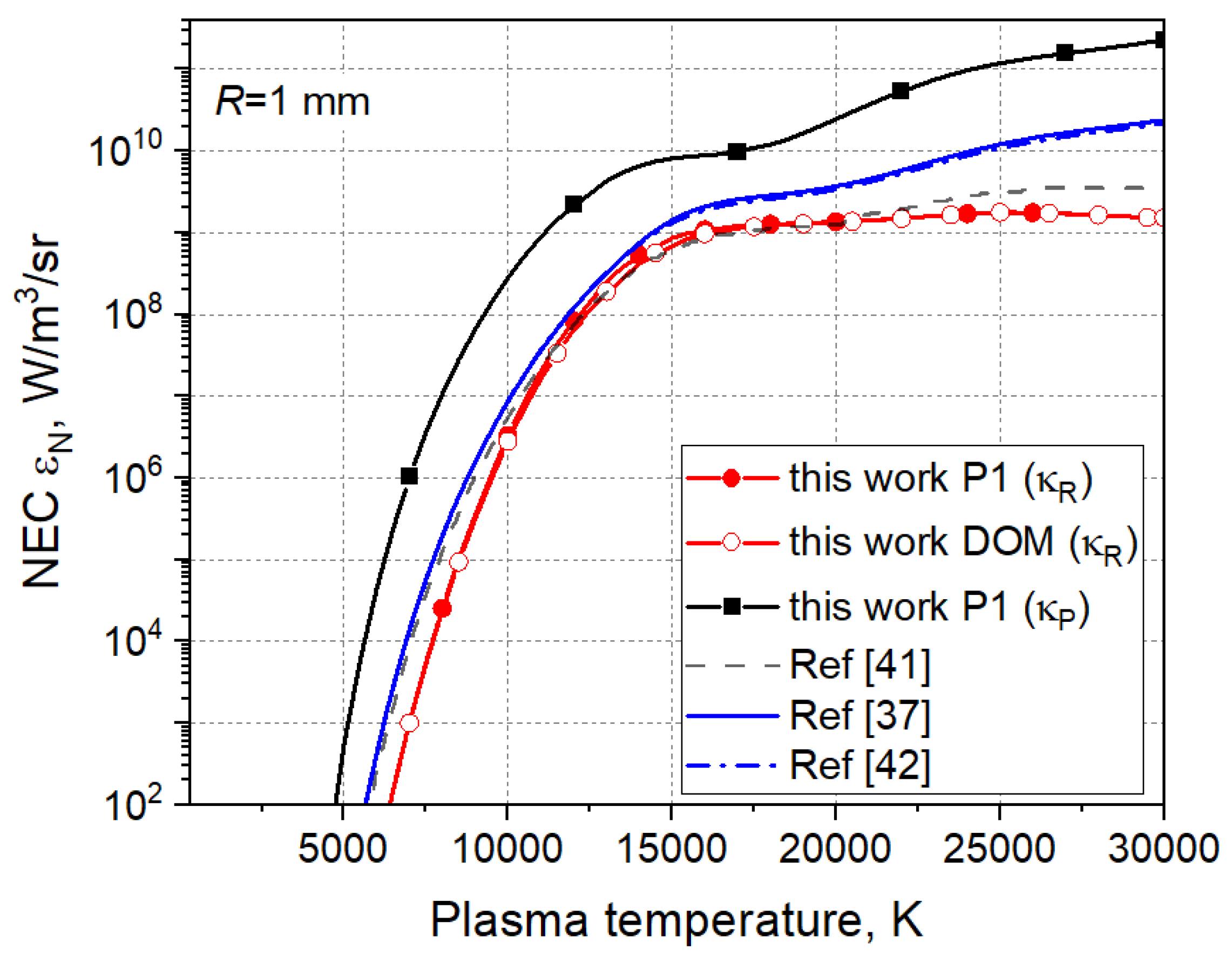
Figure 8 shows a comparison of NECs ε N with some published data. The ε N -values obtained with the P1 and DOM methods and mean absorption coefficients κ R ,   κ P based dataset I are shown since they enclose the largest and the lowest predicted NECs. Notice that the NECs presented in references [37,41,42] apply in general parent data to dataset I. The P1 and DOM results with κ R coincide and are in a good agreement with those in the work [41]. Furthermore, they agree well with the NECs obtained in [37,42] for plasma temperatures between 10000 K and 15000 K, but deviate stronger for temperature beyond 20000 K. The P1 and DOM results with κ P exceed the NECs in the works [37,41,42] over the whole temperature range. The introduction of the hybrid mean absorption coefficient κ h will reduce in a certain degree the deviation between the present and previously published data (see Figure 8) and can be therefore seen as a good candidate for applications in arc plasma models.
The evaluation of the NECs ε N in this work provides consistent datasets for the comparison of the results of arc models, in which the radiative heat transfer is considered in terms of NEC, the P1, and the DOM approaches.

5.2. The Free-Burning Arc

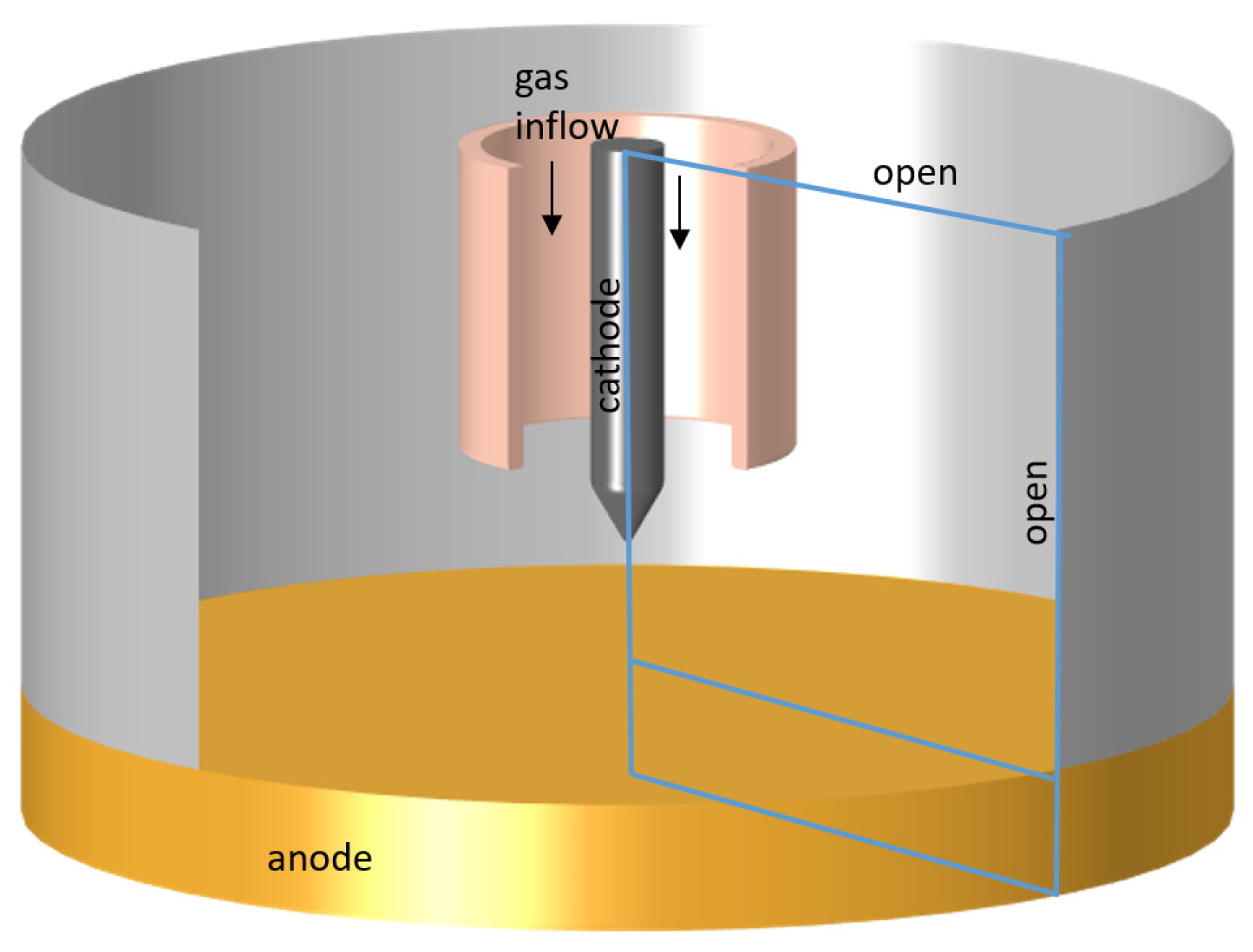
The model of the free-burning arc in this work employs a tungsten-inert gas arrangement and the 2D axisymmetric computational domain are presented in Figure 9. It includes a La-W cathode with a length of 20 mm, a radius of 2 mm, and a truncated 60° conical tip (a plateau radius of 0.2 mm). The anode is a water-cooled cooper plate with a radius of 33 mm and a thickness of 7 mm. The distance between the cathode tip and the anode is 8 mm. The arc is burning in atmospheric pressure argon at direct current of 100 A. The gas is fed with a flow rate of 12 slm through a nozzle with an inner radius of 8 mm.
Simulations are performed applying the NECs ε N (with R=1 mm) the P1, and the DOM methods. The data for the implementation of the radiative heat transfer (see Eq. (1)) are based on 5-bands hybrid mean absorption coefficients κ h and datasets I and II. The boundary conditions for the RTE (2) are set according to respectively Eq. (14) for the P1 method and Eq. (16) for the DOM method. Temperature-dependent values for the emissivity of tungsten [43] and copper [44] are considered. The open boundaries are considered with emissivity of one (see subsections 3.2 and 3.3).
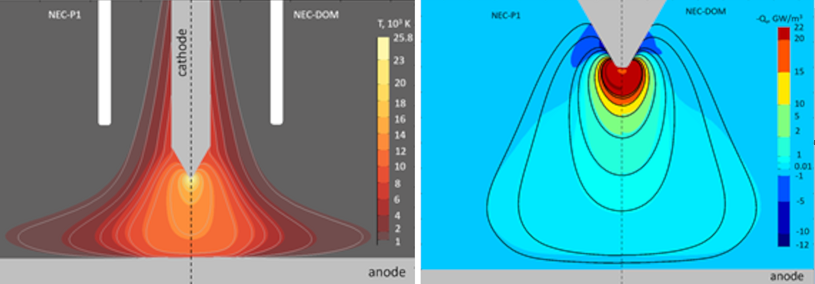
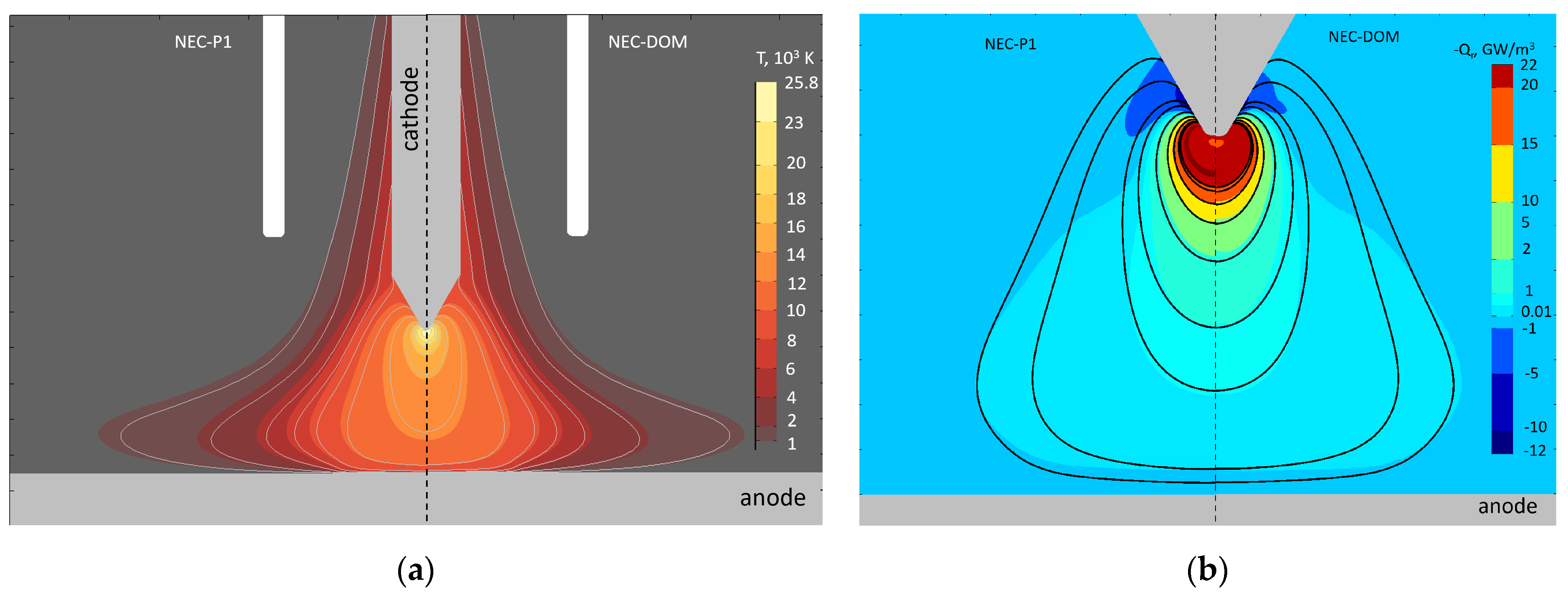
Figure 10 presents the distribution of the plasma temperature T (a) and the radiative term -Qr (b) obtained applying the NEC ε N , the P1 method and the DOM with the hybrid absorption coefficient based on dataset I. The results from the model with the NEC are given shown with the uniformly coloured contour lines on both the left- and right-hand side of each graph. The results from the models applying the P1 method and the DOM are shown as filled contours in a colour map to be are compared side by side with each other and with the NEC-results. The contour lines overlap with the edge between the filled contours when the results are in agreement. The NEC contours are taken at the same levels as the filled ones for the plasma temperature and the positive range of the -Qr-values in Figure 10b. Both the P1 method and the DOM predict negative -Qr-values in the region surrounding the cathode tip and close to the anode. This means that the radiation is absorbed there in contrast to the predictions of the models applying the NECs. Note that the results from the P1 and the DOM only slightly differ from each other. In general, the contours of equal temperature predicted by the models with the NECs agree well in the hot arc core with those from the P1 method and the DOM and deviations are observed in the arc periphery. The filled contours of equal temperature from the model with the P1 method are slightly broadener than those with the DOM. The difference in the filled contours representing the -Qr-values from the models with the P1 method and the DOM is well pronounced near the cathode tip as shown in Figure 10b.
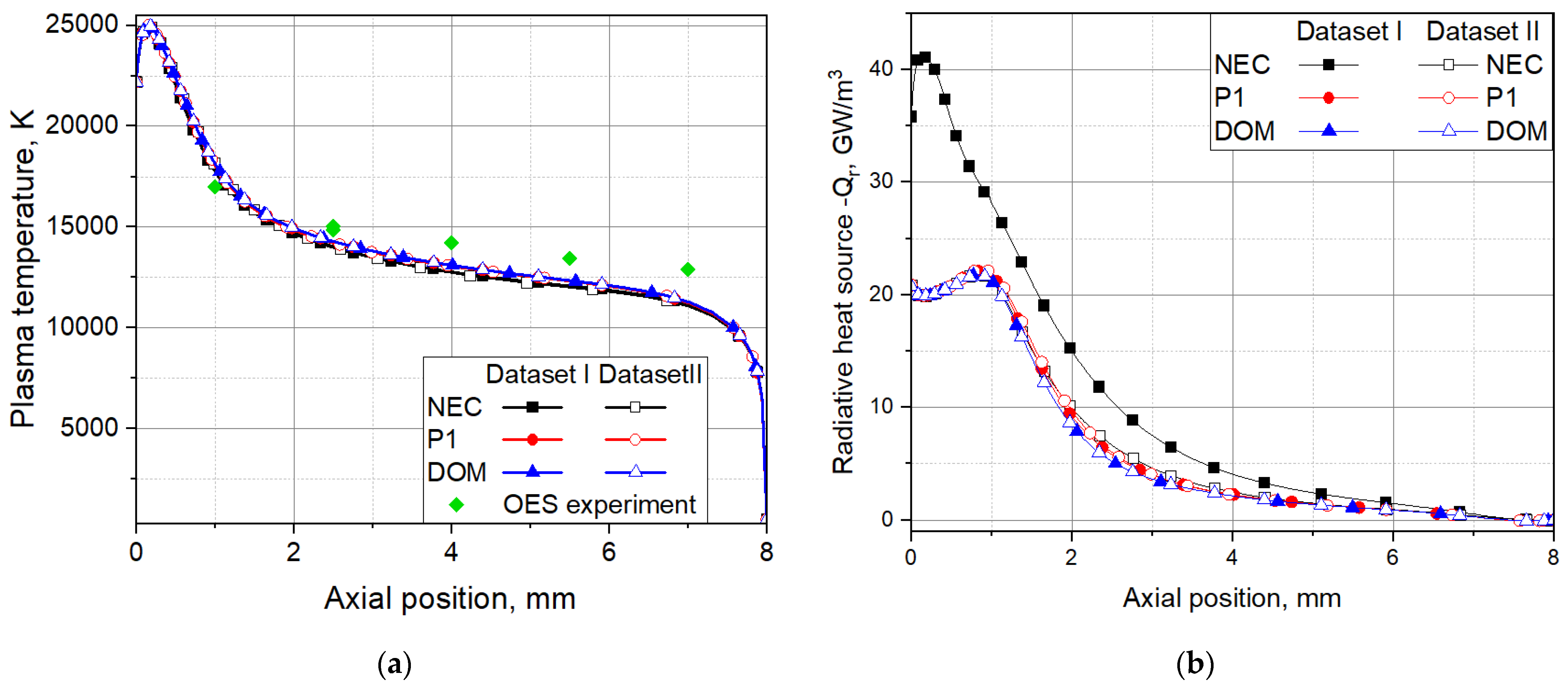
The distributions of the predicted plasma temperature and the radiative heat source along the arc axis obtained with the models applying NEC, P1 and DOM as well as different data sets for the absorption coefficient are shown in Figure 11. Note that the axial position of the end of the cathode tip is zero, while that of the anode surface is at 8 mm. Experimental values from optical emission spectroscopy (OES) [45] are shown as well in Figure 11a. Note that the values of the plasma temperature on the arc axis obtained with the various models and data sets are very close to each other. They fairly agree with the experimental values. The distribution of the -Qr-values on the arc axis in Figure 11b shows that the values from the model with the NEC based on dataset 1 are higher than the other results by a factor of up to two. This effect results from the higher NEC ε N for database I (see Figure 7a,b). Negative values of -Qr are obtained close to the anode surface.
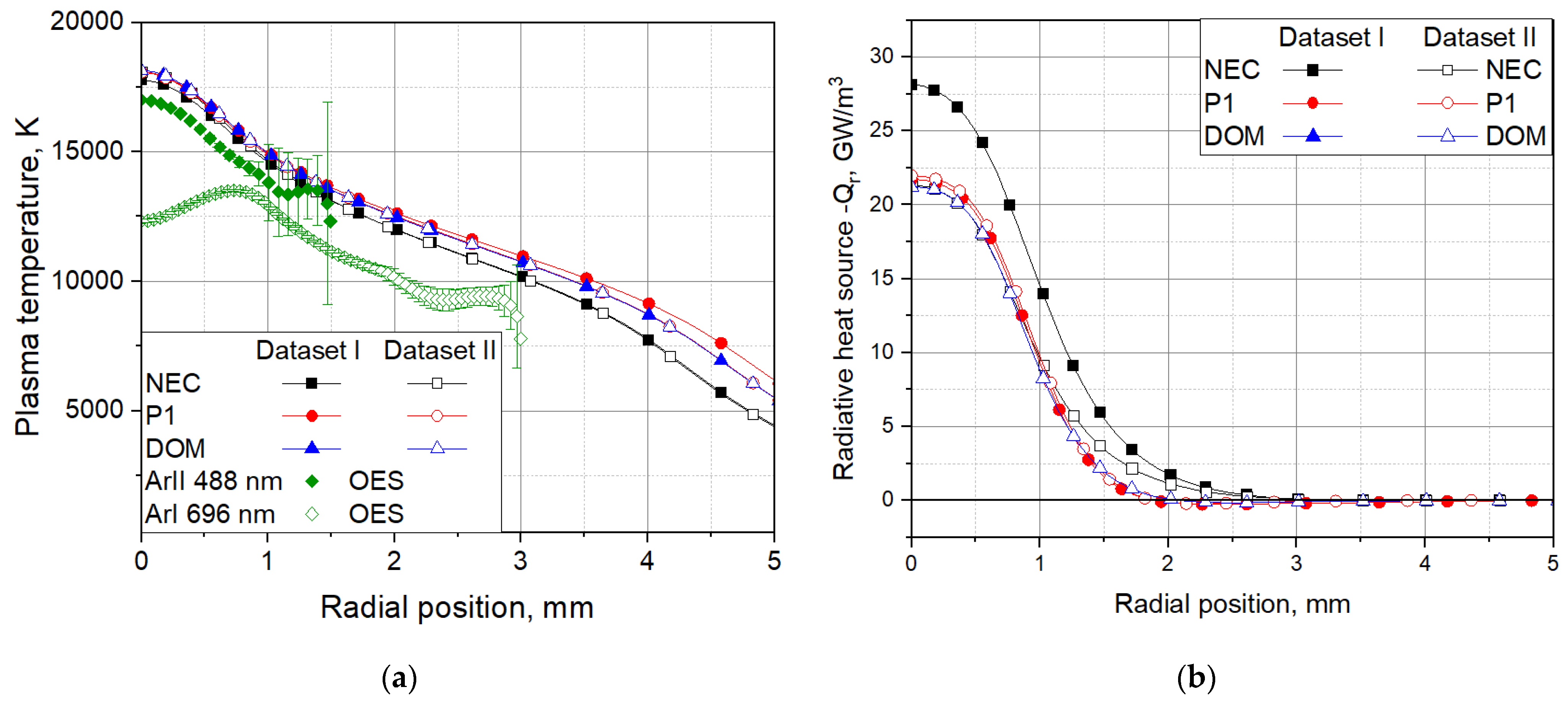
The distributions of the plasma temperature and the radiative heat source along a lineout that is perpendicular to the arc axis and is drawn in a distance of 1 mm from the cathode tip are shown in Figure 12. Similarly to Figure 11, the results are obtained with the models applying NEC, P1 and DOM as well as different data sets for the absorption coefficient. Experimental data for the plasma temperature are shown in Figure 12a. Note that the OES data for two spectral lines (Ar I at 696 nm and Ar II at 488 nm) are shown in order to show temperatures above 15000 K close the arc axis (radial position zero). The results show that for radial positions close to the zero, the temperatures obtained by the models with NEC, P1 and DOM are very similar. Deviations are obtained toward the arc periphery as the model with the P1 method predicts the highest values. Note that the accuracy of the experimental values in the arc periphery is comparable with the deviations resulting from the applied methods of computation of the radiative heat transfer. The radial distribution of the -Qr-values (Figure 12b) shows again the higher values from the model with NEC based on dataset I and similar result for the P1 and DOM. Note that the model with NEC and dataset II shows a well pronounced deviation from the P1- and DOM-results for radial positions beyond 1 mm.
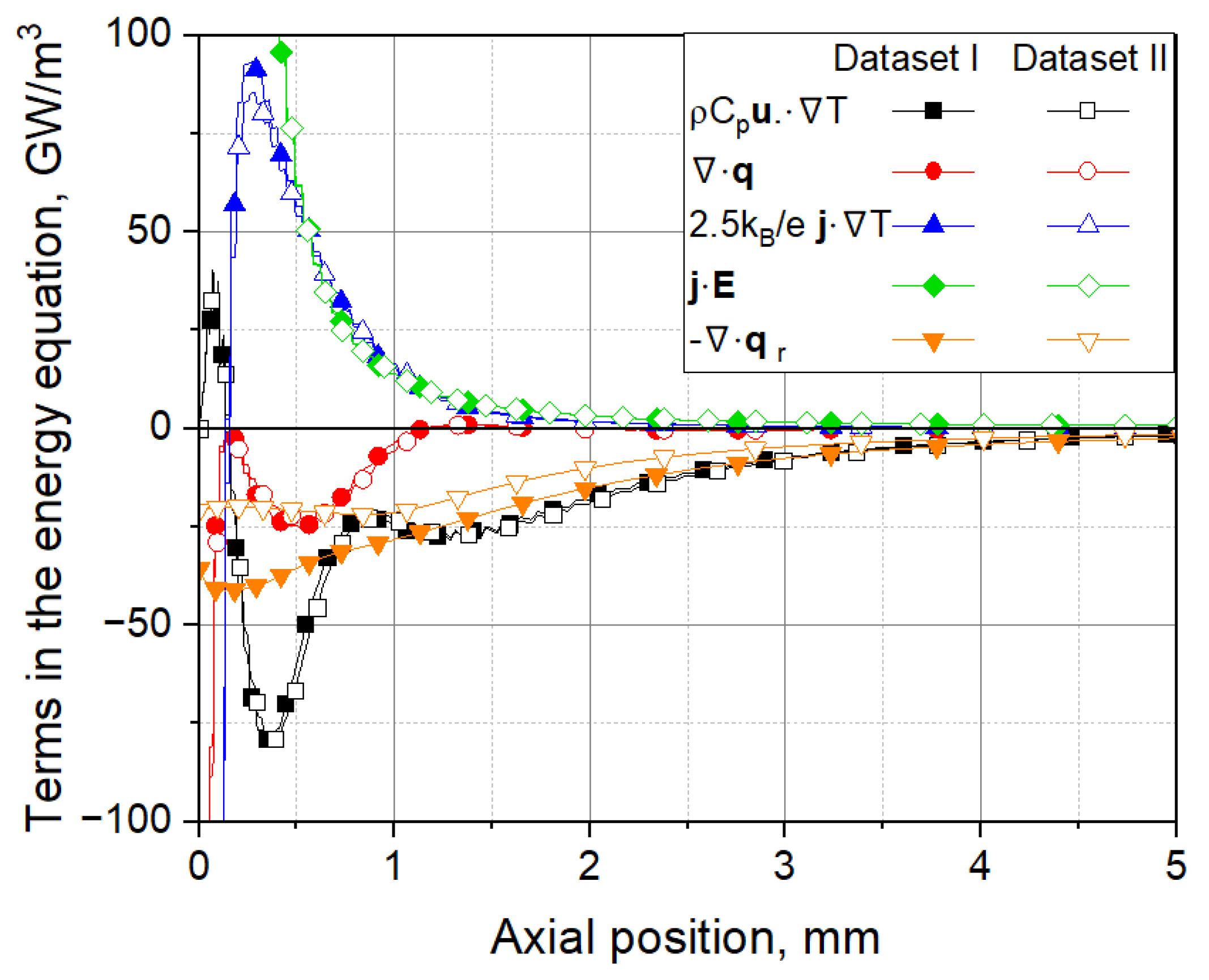
In order to explore the impact of the description of the radiative heat transfer on other terms in the equation of energy conservation Eq. (1) than Qr, Figure 13 presents their axial distribution for the models with NECs and datasets I and II. The results show that the deviations in the terms other than Qr are small. It seems that the difference in the Qr-terms is distributed in smaller parts among the other terms in Eq. (1) so that its effect on the plasma temperature is of minor importance. The Joule heating ( j · E ) and the transport of electron enthalpy ( 2.5   k B j · ∇ T ) are combined in the term Q on the right-hand-side of Eq. (1). The Joule heating is the dominant term for axial positions below 0.5 mm from the cathode tip. The transport of electron enthalpy and the convective term ( ϱ C p u · ∇ T ) as well as the divergence of the conductive heat flux ∇ · q reach their maxima in the vicinity of the cathode. The radiative term Q r = − ∇ · q r and the convective term are dominating for distances from the cathode tip beyond 1 mm. The impact of the datasets is weaker in this region. Note that the terms accounting for viscous dissipation and pressure work in Eq. (1) are of minor importance and are not shown in Figure 13.

6. Conclusions

The present work is focused on the account of the radiative heat transfer in arc plasma models. State-of-the-art LTE models of a free-burning arc applying NECs, the P1-method, and the DOM are employed to study the effects resulting from the various methods and absorption data. NECs are computed using analytical approximations and a three-dimensional solution of the equation of radiative transfer from an isothermal cylinder in the framework of the multi-band approximation for various definitions of the mean absorption coefficient (Planck, Rosseland, hybrid) with the P1 and the DOM. A self-consistent access to the radiative heat transfer is realized in the model of free-burning arc. The main results are summarized in what follows.
  • The approximate ( ε A ) and the numerically obtained ( ε N ) NECs depend on the datasets for the spectral absorption coefficient in particular for plasma temperatures beyond about 15000 K. The approximate NEC ε A is lower than ε N independent of the datasets that have been used.
  • The NECs obtained with a division of the spectrum into 5 and 16 spectral bands are very close to each other. The P1 method and the DOM for solving the equation of radiative transfer provide practically the same numerical NECs ε N .
  • The NECs depend on the way of averaging the spectral absorption coefficient within the spectral bands. NECs that are obtained applying the Planck mean values are larger than those applying the Rosseland mean values. A hybrid definition of the mean absorption coefficient provides intermediate values.
  • The implementation of the NEC for a plasma radius of 1 mm, the P1 method and the DOM with five spectral bands and a hybrid mean value of the spectral absorption coefficient into the model of the free-burning arc shows very similar values of the plasma temperature in the hot arc core and deviations in the range of 1000 K in the arc periphery. Such deviations can hardly be approved in experiments with optical emission spectroscopy.
  • The arc models with the P1 method and the DOM indicate negative radiative losses (absorption of radiation) near the electrodes in contrast to the models with NEC.
  • The predicted plasma temperature in the models with NECs is practically the same despite the discrepancy in the radiative loss term Qr for the two datasets for the spectral absorption coefficient, which are considered in the present study.

Author Contributions

Conceptualization M.B.; methodology, M.B., Y.C. and P.K.; software, M.B., Y.C. and P.K.; investigation, M.B.; resources, M.B., Y.C. and P.K.; writing—original draft preparation, M.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data supporting the results of this study are openly available on https://www.inptdat.de/node/671, reference [46].

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

In the P1-approximation, the radiation intensity is expressed in terms of a scalar function a ( r ) and a vector function b ( r ) [19]
I r , s = a r + b ( r ) · s ,
Notice that the index “ν” denoting the spectral quantities is dropped for the sake of shortness. The four unknowns are related to physical quantities. For example, the incident radiation
G r = ∫ Ω = 0 4 π I r , s d Ω = ∫ Ω = 0 4 π a r + b ( r ) · s d Ω = 4 π a r ,
since ∫ Ω = 0 4 π s d Ω = ∫ 0 2 π ∫ 0 π sin ⁡ θ cos ⁡ φ sin ⁡ θ sin ⁡ φ cos ⁡ θ sin ⁡ θ d θ d φ = ( 0,0 , 0 ) .
q r r = ∫ Ω = 0 4 π I r , s s d Ω = ∫ Ω = 0 4 π a r s d Ω + b ( r ) · ∫ Ω = 0 4 π s s d Ω = 4 π 3 b ( r ) ,
since ∫ Ω = 0 4 π s s d Ω = 4 π 3 δ ^ with δ ^ being the unit tensor. Hence,
I r , s = 1 4 π G r + 3 4 π q r r · s
and s . ∇ I r , s is computed as
s . ∇ I r , s = ∇ · s I r , s = ∇ · s 1 4 π G r + 3 4 π q r r · s = ∇ · s 1 4 π G r + 3 q r r · s
Applying the RTE (2), one gets
∇ · s 1 4 π G r + 3 q r r · s = κ B − I r , s = κ B − 1 4 π G r − 3 4 π q r r · s
and the integration over all solid angles yields
∫ Ω = 0 4 π ∇ · s 1 4 π G r + 3 q r r · s d Ω = ∫ Ω = 0 4 π κ B − 1 4 π G r − 3 4 π q r r · s d Ω
∇ · 1 4 π G r ∫ Ω = 0 4 π s d Ω + ∇ · 3 4 π q r r ∫ Ω = 0 4 π s s d Ω = ∫ Ω = 0 4 π κ B − 1 4 π G r d Ω − ∫ Ω = 0 4 π κ 3 4 π q r r · s d Ω
In which the first term on the left-hand-side and the second term on the right-hand-side are zero. Therefore, Eq. (A8) becomes
∇ · q r r = κ 4 π B − G r
A multiplying the RTE by components of the directional vector s and integrating over all directions Ω yields for the left-hand-side
1 4 π ∇ · G r ∫ 4 π ​ s s d Ω + 3 q r r · ∫ 4 π ​ s s s d Ω = 1 4 π ∇ · G r 4 π 3 δ ^ = 1 3 ∇ G r
and for the right-hand-side
κ B ∫ 4 π ​ s d Ω − 1 4 π G r ∫ 4 π ​ s d Ω − 3 4 π q r r · ∫ 4 π ​ s s d Ω = − κ 3 4 π q r r · 4 π 3 δ ^ = − κ q r r
and finally, from Eq. (A10) and (A11) one gets
q r r = − 1 3 κ ∇ G r
Equations (A9) and (A12) provide the governing set of one scalar and one vector equations for the quantities G r and q r r in the P1-approximation.

Appendix B

Lowke [18] computed approximate net emission coefficients at the center of cylindrical isothermal plasma of various temperatures and radii R as
ε A ν = κ ν B ν − J ν = κ ν B ν G 1 κ ν R ,
where J ν represents the average radiative intensity, i.e.,
J ν = 1 4 π ∫ 4 π ​ I ν d Ω ,
and G 1 x = ∫ 0 π / 2 sin ⁡ θ e − x / sin ⁡ θ d θ with θ is being the polar angle and x = κ ν r . The incident radiation is
G ν = ∫ 4 π ​ I ν d Ω = 4 π J ν = 4 π B ν 1 − G 1 κ ν R .
The derivation is given for the sake of completeness in the Appendix A.
In order to evaluate the net emission coefficient, G 1 x must be obtained.
One considers the distance s along the line of sight XP. Point X corresponds to s=0 and point P corresponds to s=L. Multiplying the RTE Eq. (2) by an integrating factor e − ∫ s L κ η d η , where L is the plasma boundary, one gets
d I ν d s e − ∫ s L κ η d η = κ ν B ν e − ∫ s L κ η d η − κ ν I ν e − ∫ s L κ η d η
d I ν d s e − ∫ s L κ η d η = κ ν B ν e − ∫ s L κ η d η − d d s I ν e − ∫ s L κ η d η + d I ν d s e − ∫ s L κ η d η .
Here, the relation
d d s e − ∫ s L κ η d η = d d s − ∫ s L κ η d η e − ∫ s L κ η d η = κ η e − ∫ s L κ η d η
is used. Then,
d d s I ν e − ∫ s L κ η d η = κ ν B ν e − ∫ s L κ η d η
If, the point, where the radiation intensity is sought, is placed in the coordinate origin, then replacing ρ =L-s applies to the intensity in point Z in direction – Ω
I ν 0 , − Ω = ∫ 0 L κ ν ( ρ ) B ν ( ρ ) e − ∫ 0 ρ κ ρ ' d ρ ' d ρ
Therefore, the average radiation intensity can be expressed as
J ν = 1 4 π ∫ 4 π ​ I ν d Ω
and
J ν = 1 2 π ∫ ρ ' = 0 ρ ∫ θ = 0 π / 2 ∫ φ = 0 2 π κ ν ( ρ ' ) B ν ( ρ ' ) e − ∫ 0 ρ ' κ ρ ' ' d ρ ' ' sin ⁡ θ d φ d θ d ρ '
The integration is taken along straight lines from the center of the arc ( ρ ' = 0 ) to the edge of the arc ( ρ ' = ρ ), and the direction of the lines is given by the spherical coordinates θ , φ . The integration along lines for θ ≠ π / 2 can be transformed to integration along lines perpendicular to the arc axis by using d ρ = d r / sin ⁡ θ .
J ν = ∫ r ' = 0 R κ ν B ν d r ' ∫ θ = 0 π / 2 e − ∫ 0 r ' κ / sin ⁡ θ d r ' ' d θ .
Let us consider the integral ∫ θ = 0 π / 2 e − ∫ 0 r ' κ / sin ⁡ θ d r ' ' d θ . Then,
∫ θ = 0 π / 2 e − ∫ 0 r ' κ d r ' ' / sin ⁡ θ d θ = ∫ θ = 0 π / 2 e − x / sin ⁡ θ d θ
where x = ∫ 0 r ' κ d r ' ' . This integral can be expressed through the recurrence relation
G n = ∫ θ = 0 π / 2 sin n ⁡ θ e − x / sin ⁡ θ d θ
as G 0 . Notice that
G 1 = ∫ θ = 0 π / 2 sin ⁡ θ e − x / sin ⁡ θ d θ
and
∫ 0 x G 0 x ' d x ' = − ∫ θ = 0 π / 2 d θ ∫ 0 x sin ⁡ θ e − x ' / s i n θ d − x ' s i n θ = − ∫ θ = 0 π / 2 d θ ∫ 0 − x / s i n θ sin ⁡ θ d e − x ' / s i n θ = − ∫ θ = 0 π 2 d θ e − x ' s i n θ sin ⁡ θ 0 − x s i n θ = − ∫ θ = 0 π 2 d θ sin ⁡ θ e − x s i n θ − 1 = ∫ θ = 0 π 2 sin ⁡ θ d θ − ∫ θ = 0 π 2 sin ⁡ θ e − x s i n θ d θ = − cos ⁡ θ 0 π 2 − G 1 x = 1 − G 1 x
Hence,
J ν = ∫ x ' = 0 κ ν R B ν d x ' ∫ θ = 0 π / 2 e − ∫ 0 r ' κ / sin ⁡ θ d r ' ' d θ = B ν 1 − G 1 κ ν R
The approximate net emission coefficient is finally expressed as
ε A ν = κ ν B ν − J ν = κ ν B ν G 1 κ ν R

References

  1. Murphy, A.B.; Uhrlandt, D. Foundation of high-pressure thermal plasmas, Plasma Sources Sci. Technol. 2018 27, 063001. [CrossRef]
  2. Fauchais, P.; Coudert, J.F.; Vardelle, M., Eds. Diagnostics in thermal plasma Plasma Diagnostics, Academic, Boston, 1989.
  3. Colombo, V.; Concetti, A.; Ghedini, E.; Dallavalle, S.; Vancini, M. High-speed imaging in plasma arc cutting: a review and new developments, Plasma Sources Sci. Technol. 2009 18, 023001. [CrossRef]
  4. Bachmann, B.; Kozakov, R.; Gött, G.; Ekkert, K.; Bachmann, J.P.; Marques, J.L.; Schöpp, H.; Uhrlandt, D.; Schein, J. High-speed three-dimensional plasma temperature determination of axially symmetric free-burning arcs, J. Phys. D: Appl. Phys. 2013 46, 125203. [CrossRef]
  5. Murphy, A.B.; D Farmer, A.J.; Haidar, J. Laser-scattering measurement of temperature profiles of a free-burning arc. Appl. Phys. Lett., 1992 60, pp. 1304-1306. [CrossRef]
  6. [Hsu1984] Hsu, K.C.; Pfender, E. Modeling of a free-burning, high-intensity arc at elevated pressures. Plasma Chem. Plasma Process., 1984, 4, pp. 219-234. [CrossRef]
  7. [Simonin1992] Simonin, O.; Delalondre, C.; Violett, P.-L. Modelling in thermal plasma and electric arc column, Pure & Appl. Chem., 1992, 64, pp. 623-628. [CrossRef]
  8. [Wendelstorf1996] Wendelstorf, J.; Decker, I.; Wohlfart, H.; Simon, G. TIG and plasma arc modelling: a survey, In Mathematical Modelling of Weld Phenomena, Ed. Cerjak, H., Book- Institute of Materials, 650, London, 1997, pp.848-897.
  9. Gleizes, A.; Gonzalez, J.- J.; Freton, P. Thermal plasma modelling, 2005 J. Phys. D: Appl. Phys., 38, pp. R153–83. [CrossRef]
  10. Trelles, J.P.; Heberlein, J.V.R. Simulation results of arc behavior in different plasma spray torches, J. Therm. Spray Tech., 2006, 15, pp. 563–569. [CrossRef]
  11. Shigeta, M. Turbulence modelling of thermal plasma flows, J. Phys. D: Appl. Phys., 2016, 49, 493001. [CrossRef]
  12. Trelles, J.P.; Heberlein, J.V.R.; Pfender, E. Non-equilibrium modelling of arc plasma torches, J. Phys. D: Appl. Phys. 2007, 40, pp. 5937–5952. [CrossRef]
  13. Baeva, M.; Kozakov, R.; Gorchakov, S.; Uhrlandt, D. Two-temperature chemically non-equilibrium modelling of transferred arcs, Plasma Sources Sci. Technol. 2012, 21, 055027. [CrossRef]
  14. Baeva, M.; Benilov, M.S.; Almeida, N.A.; Uhrlandt, D. Novel non-ewuilibrium modelling of a DC electric arc in argon, J. Phys. D: Appl. Phys. 2016, 49, 245205. [CrossRef]
  15. Choquet, I. Gas tungsten arc models including the physics of the cathode layer: remaining issues, Welding in the World, 2018, 62, pp. 177-196. [CrossRef]
  16. Benilov, M.S. Modeling the physics of interaction of high-pressure arcs with their electrodes: advances and challenges, J. Phys. D: Appl. Phys. 2020, 53, 013002. [CrossRef]
  17. Nordborg, H.; Iordanis, A.A. Self-consistent radiation based modelling of electric arcs: I. Efficient radiation approximations, J. Phys. D: Appl. Phys. 2008, 41, 135205. [CrossRef]
  18. Tanaka, Y.; Fujino, T.; Iwao, T. Review of thermal plasma simulation technique, IEEJ Trans., 2019, 14, pp. 1582-1594. [CrossRef]
  19. Lowke, J.J. Predictions of arc temperature profiles using approximate emission coefficients for radiation losses, JQSRT, 1974, 14, pp.111-122. [CrossRef]
  20. Modest, M. F. Radiative Heat Transfer 3rd edn, Elsevier inc., Amsterdam, 2013.
  21. Iordanis, A.A,; Franck, C.M. Self-consistent radiation based modelling of electric arcs: II. Application to gas circuit breakrs, J. Phys. D: Appl. Phys., 2008, 41, 135206. [CrossRef]
  22. Mohsni, C.; Baeva, M.; Franke, St.; Gortschakow, S.; Araoud, Z.; Charrada, K. Effect of a bidirectional coupling of a LTE arc column to a refractory cathode in atmospheric pressure argon, Phys. Plasmas, 2020, 27, 073514. [CrossRef]
  23. Baeva, M.; Zhu, T.; Kewitz, T.; Testrich, H.; Foest, R. Self-consistent cathode-plasma coupling and role of the fluid flow approach in torch modelling, J. Therm. Spray. Technol., 2021, 30, pp. 1737–1750. [CrossRef]
  24. Benilov, M.S. Theory and Modelling of Arc Cathodes. Plasma Sources Sci. Technol., 2002, 11, pp. A49-A54. [CrossRef]
  25. Pateyron, B.; Delluc, G.; Calve, N. T&T Winner-Software for Thermo-Chemistry, Univ. Limoges, 2015, 87051 Limoges Cedes, France.
  26. Murphy, A.B,; Arundel, C.J. Transport Coefficients of Argon, Nitrogen, Oxygen, Argon-Nitrogen, and Argon-Oxygen Plasmas, Plasma Chem. Plasma Process., 1994, 14(4), pp. 451-490. [CrossRef]
  27. Smith, D.; Altovsky, I.V.; Barabash, V.R.; Beeston, J. 1991 ITER Blanker, Shield and Material Database, ITER Documentation Series (IAEA, Vienna), Vol. 29.
  28. Touloukian, Y.S. 1970 Thermal Conductivity: Metallic Elements and Alloys (IFI/Plenum).
  29. Tencer, J.; Howell, J.R. Coupling radiative heat transfer in participating media with other heat transfer modes. J Braz. Soc. Mech. Sci. Eng., 2016, 38, pp. 1473–1487. [CrossRef]
  30. Bartlova, M; Bogatyreva, N.; Aubrecht, V. Radiation heat transfer in thermal argon plasma with iron vapours, Plasma Phys. Technol., 2014, 1, pp. 8-10.
  31. Kloc, P.; Aubrecht, V.; Bartlova, M. and Fuchs, R. Comparison of mean absorption methods for radiation transfer models in air plasma at various pressures, Plasma Chem Plasma Process, 2023, 43, pp. 429-447. [CrossRef]
  32. Kozu, S.; Fujino, T.; Yoshino, T.; Mori, T. Radiative transfer calculation of CO2 thermal plasma using a hybrid Plack-Rosseland mean absorption coefficient, In Proceedings of the 22nd Int. Conf. Gas Discharges and Their Applications, Novi Sad, Serbia, pp. 127-130, 2-7 September 2018.
  33. Church, C.H.; Schlecht, R.G.; Liberman, I.; Swanson, B.W. Studies of highly radiative plasmas using the wall-stabilized pulsed arc discharge, AIAA, 1966, 4, pp. 1947-1953. [CrossRef]
  34. Bogatyreva, N.; Bartlova, M.; Aubrecht, V. Absorption properties of argon arc plasma, In Proceedings of the 43rd EPS Conference on Plasma Physics, pp. 481-484, Leuven, Belgum, 4-8 July 2016.
  35. Griem, H. R. Plasma Spectroscopy, Mc.Graw-Hill, 1964.
  36. Liebermann R.W.; Lowke, J.J. Radiation emission coefficients for sulfur hexafluoride arc plasmas, JQSRT, 1976, 16, pp. 253–64. [CrossRef]
  37. Cressault ,Y.; Gleizes, A. Thermal plasma properties for Ar–Al, Ar–Fe and Ar–Cu mixtures used in welding plasmas processes: I. Net emission coefficients at atmospheric pressure, J. Phys. D: Appl. Phys., 2013, 46, 415206. [CrossRef]
  38. Cabannes, F. and Chapelle, J. Spectroscopic plasma diagnostic reactions under plasma conditions, vol 1. Wiley-Interscience, New York, 1971.
  39. Kramida, A; Ralchenko, Yu; Reader, J and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.10), [Online]. Available: https://physics.nist.gov/asd [2022, November 15]. National Institute of Standards and Technology, Gaithersburg, MD. [CrossRef]
  40. Whitting, E.E. An empirical approximation to the Voigt profile, JQSRT, 1968, 8, pp. 1379–84. [CrossRef]
  41. Essoltani, A.; Proulx, P.; Boulos, M.I.; Gleizes, A. Volumetric emission of argon plasmas in the presence of vapors of Fe, Si, and AI, Plasma Chem. Plasma Process., 1994, 14, pp. 437-450. [CrossRef]
  42. Cressault, Y. A recent computation according to [37] with updated line data.
  43. Lassner, E.; Schubert, W.D. Tungsten: Properties, Chemistry, Technology of the Element. Alloys, and Chemical Compounds, Springer, New York, 1999. [CrossRef]
  44. Incorpera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A. S. Fundamentals of Heat and Mass Transfer, 6th edn, John Wiley, New York, 2006.
  45. Baeva, M.; Gorchakov, S.; Kozakov, R.; Uhrlandt, D.; Schoenemann, T. Non-equilibrium modelling of the electrical characteristics of a free-burning arc, High Voltage Engineering, 2013, 39, pp. 2159-2165.
  46. Baeva, M.; Cressault, Y.; Kloc, P. Comparative studies on the radiative heat transfer in a self-consistent model of a free-burning arc in argon —Dataset.
Preprints 109063 g001
Figure 1. Schematics of the arc plasma model.
Figure 1. Schematics of the arc plasma model.
Preprints 109063 g001
Preprints 109063 g002
Figure 2. Graphical representation of the directional irradiation.
Figure 2. Graphical representation of the directional irradiation.
Preprints 109063 g002
Preprints 109063 g003
Figure 3. Spectral absorption coefficient ( κ ν ) of Ar plasma at a pressure of 1 bar and a temperature of 20000 K and the mean absorption coefficients κ R , κ P , and κ h .
Figure 3. Spectral absorption coefficient ( κ ν ) of Ar plasma at a pressure of 1 bar and a temperature of 20000 K and the mean absorption coefficients κ R , κ P , and κ h .
Preprints 109063 g003
Preprints 109063 g004
Figure 4. The geometry of a cylindrical arc plasma.
Figure 4. The geometry of a cylindrical arc plasma.
Preprints 109063 g004
Preprints 109063 g005
Figure 5. Approximate net emission coefficient ε A obtained for mean absorption coefficients κ P , κ R , κ h ; datasets I and II, and for plasma radii: (a) R=0; (b) R=1 mm.
Figure 5. Approximate net emission coefficient ε A obtained for mean absorption coefficients κ P , κ R , κ h ; datasets I and II, and for plasma radii: (a) R=0; (b) R=1 mm.
Preprints 109063 g005
Preprints 109063 g006
Figure 6. Approximate net emission coefficient ε A
Figure 6. Approximate net emission coefficient ε A
Preprints 109063 g006
Preprints 109063 g007
Figure 7. Net emission coefficient ε N obtained by (a) the P1 and (b) DOM methods with a 5-band spectral absorption coefficient for a radius of 1 mm, mean absorption coefficients, and datasets.
Figure 7. Net emission coefficient ε N obtained by (a) the P1 and (b) DOM methods with a 5-band spectral absorption coefficient for a radius of 1 mm, mean absorption coefficients, and datasets.
Preprints 109063 g007
Preprints 109063 g008
Figure 8. NECs obtained in the present work by means of the P1 and the DOM methods for a plasma radius R=1 mm in comparison with published data.
Figure 8. NECs obtained in the present work by means of the P1 and the DOM methods for a plasma radius R=1 mm in comparison with published data.
Preprints 109063 g008
Preprints 109063 g009
Figure 9. The arrangement of the free-burning arc with the 2D computational domain.
Figure 9. The arrangement of the free-burning arc with the 2D computational domain.
Preprints 109063 g009
Preprints 109063 g010
Figure 10. Contours of equal plasma temperature T (a) and the radiative source -Qr (b) from the models of the free-burning arc with the NEC ε N and the P1 method (a) and the NEC ε N and the DOM method. The hybrid absorption coefficient is based on dataset I.
Figure 10. Contours of equal plasma temperature T (a) and the radiative source -Qr (b) from the models of the free-burning arc with the NEC ε N and the P1 method (a) and the NEC ε N and the DOM method. The hybrid absorption coefficient is based on dataset I.
Preprints 109063 g010
Preprints 109063 g011
Figure 11. The plasma temperature T (a) and the radiative source -Qr (b) along the axis from the models of the free-burning arc with the NEC ε N (squares), the P1 method (circles), and the DOM (triangles). The hybrid absorption coefficient is based on datasets I (solid symbols) and II (open symbols). Experimental data from OES of the spectral line ArII (solid diamonds) are presented as well.
Figure 11. The plasma temperature T (a) and the radiative source -Qr (b) along the axis from the models of the free-burning arc with the NEC ε N (squares), the P1 method (circles), and the DOM (triangles). The hybrid absorption coefficient is based on datasets I (solid symbols) and II (open symbols). Experimental data from OES of the spectral line ArII (solid diamonds) are presented as well.
Preprints 109063 g011
Preprints 109063 g012
Figure 12. The plasma temperature T (a) and the radiative source -Qr (b) along a lineout in a distance of 1 mm from the cathode tip and perpendicular to the axis. The results are from the models of the free-burning arc with the NEC ε N (squares), the P1 method (circles), and the DOM (triangles). The hybrid absorption coefficient is based on datasets I (solid symbols) and II (open symbols). Experimental data from OES of spectral lines Ar I (open diamonds) and Ar II (solid diamonds) are presented as well.
Figure 12. The plasma temperature T (a) and the radiative source -Qr (b) along a lineout in a distance of 1 mm from the cathode tip and perpendicular to the axis. The results are from the models of the free-burning arc with the NEC ε N (squares), the P1 method (circles), and the DOM (triangles). The hybrid absorption coefficient is based on datasets I (solid symbols) and II (open symbols). Experimental data from OES of spectral lines Ar I (open diamonds) and Ar II (solid diamonds) are presented as well.
Preprints 109063 g012
Preprints 109063 g013
Figure 13. Axial distribution of terms in the equation of energy conservation from simulations with NEC ε N and Datasets I and II.
Figure 13. Axial distribution of terms in the equation of energy conservation from simulations with NEC ε N and Datasets I and II.
Preprints 109063 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated