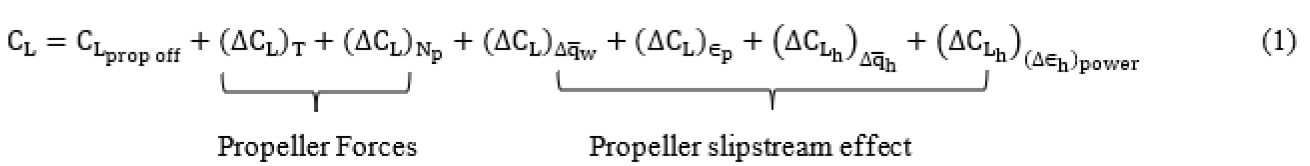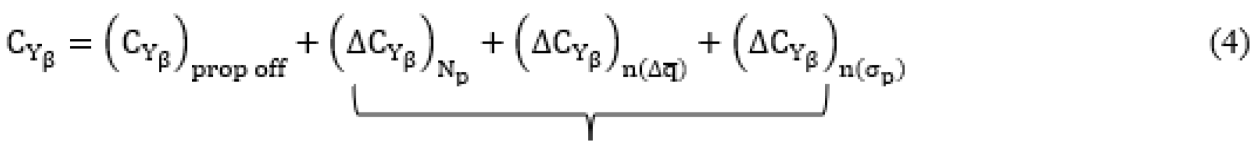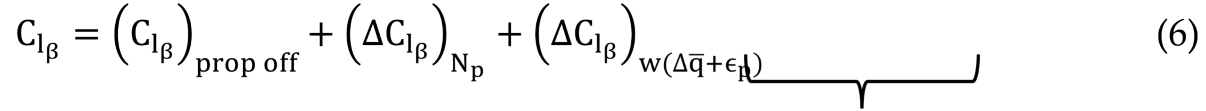Propeller Effects and Elasticity in Aerodynamic Analysis of Small Propeller-Driven Aircraft

Preprint

Article

Propeller Effects and Elasticity in Aerodynamic Analysis of Small Propeller-Driven Aircraft

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Mohsen Rostami^*

This version is not peer-reviewed

Submitted:

11 June 2024

Posted:

12 June 2024

You are already at the latest version

Alerts

Abstract

The impact of propeller effects and power contribution on the aerodynamics of small aircraft is indispensable. The aerodynamic analysis of wings in flight varies from rigid wing analysis due to wing deflection caused by transferred aerodynamic loads. This paper investigates the intertwined influence of propeller effects and elasticity on the aerodynamics of small propeller-driven aircraft. Through a detailed methodology, a twin-engine propeller-driven aircraft is analyzed as a case study, providing insights into the proposed approach. Two critical analyses are presented: an examination of propeller effects in rigid aircraft and the incorporation of elastic wing properties. The former establishes a foundational understanding of aerodynamic behaviour, while the latter explores the impact of wing elasticity on performance. Validation is achieved through comparative analysis with wind tunnel test results from a similar rigid structure aircraft. Utilizing NASTRAN software, aerodynamic analysis of the elastic aircraft is conducted, complemented by semi-empirical insights. The results highlight the importance of these factors across different angles of attack. Furthermore, deviations from the rigid aircraft configuration emphasize the considerable influence of static aeroelasticity analysis, notably increasing longitudinal characteristics by approximately 20%, while showing a lower impact of 5% in lateral-directional characteristics. This study contributes to enhanced design and operational considerations for small propeller-driven aircraft, with implications for future research and innovation, particularly for the purpose of efficient concepts in advanced air mobility.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Currently, there is an increasing interest in daily passenger and cargo transport by small aircraft over distances that have been traditionally served by ground transportation vehicles. Although the idea of using small aircraft for transportation is not novel, over recent years there have been significant enhancements in technologies and societal variations that may make these operations become a practical part of our daily life. The convergence of advanced technologies, such as electric propulsion and autonomy, along with new business models, such as mobile application-based ride sharing and network-enabled on-demand services, bring new general aviation markets [1,2,3]. Advanced air mobility (AAM) is the general term defined by NASA for these new small aircraft. AAM services fall into two categories of urban air mobility (UAM) and regional air mobility (RAM) [4,5]. UAM is the transport system that transfers people or goods by air within cities. RAM will be responsible for the transportation of goods and people to rural and remote communities [6]. AAM has the potential to enhance our daily transportation by reducing the travel time, avoiding traffics on the ground and within the cities, smooth the travel between different parts of a city, and advance regional mobility, particularly in areas underserved by the modern air transportation [7].

The propeller effects and the power contribution to the aerodynamics of a small aircraft are essential. From the beginning of the airplane introduction, this has always been important to realize the propeller behavior due to the generation of substantial lateral forces in the presence of side wind [8,9]. Recently, much research has enhanced semi-empirical procedures to study the aerodynamics of sophisticated propeller aircraft and the propeller effects on the stability and handling quality [10,11,12,13]. These research presented an augmented and combined analytical procedures and design data compendia to account for the restrictions of the earlier approaches [8]. Among those, the semi-empirical multidisciplinary analysis program, MAPLA has been developed for the optimization of small conventional and eVTOL aircraft. MAPLA consists of five primary disciplines of weight and balance, aerodynamics, propulsion, stability, and control as well as performance. In a series of previous studies, MAPLA was demonstrated to be able to model the characteristics of small conventional and eVTOL aircraft with an acceptable precision [10,14,15,16].

In the design process of new airplanes, the performance of wing is dominated by the aero-structural-coupled system [17]. Due to the deflection of wings in flight which results from aerodynamic loads that are transferred to the wing structure, the aerodynamic analysis of the wing in flight is different than the rigid wing analysis [18,19]. In order to simulate this behavior, the general approach is to couple the aerodynamic solver and the structural computations. This coupling would need an iteration loop to find the equilibrium solution [20,21,22].

Among aero-structural coupling analysis tools, NASTRAN is a finite element analysis program that was originally developed for NASA [23]. In aero-structural coupling problems, structural and aerodynamic grids are connected by interpolation [24]. This approach enables the independent selection of grid points for both the structural model and the aerodynamic elements of lifting surfaces or bodies. The structural model for a wing may encompass a one-, two-, or three-dimensional array of grid points, while the aerodynamic theory may employ lifting surface theory or strip theory. A versatile interpolation method is available to connect various combinations seamlessly. Any aerodynamic panel or body can be subdivided into subregions for interpolation, utilizing separate functions for each. This interpolation method, known as splining, involves mathematical analysis of beams and plates, including linear splines that generalize infinite beams to accommodate torsional and bending degrees of freedom, surface splines that address solutions for infinite uniform plates, and explicit user-defined interpolation methods [25,26].

Static (or quasi-steady) aeroelasticity investigation is an interdisciplinary field that combines knowledge of aerodynamics, elasticity, and inertial forces [27,28,29]. By understanding and addressing static aeroelastic effects, engineers can ensure the stability and structural integrity of aircraft under various operating conditions, contributing to safer and more reliable flight operations [30]. Structural analysts are primarily concerned with the aerodynamic load redistribution and the resulting internal structural load and stress redistributions [31,32]. They also consider the possibility of static aeroelastic instability, such as divergence. Aerodynamicists and control systems analysts are interested in aerodynamic load redistribution and its effects on aerodynamic stability and control derivatives. The static aeroelastic capability in Nastran addresses these needs by computing aircraft trim conditions, followed by the recovery of structural responses, aeroelastic stability derivatives, and static aeroelastic divergence dynamic pressures [25,33].

The primary objective of this paper is to investigate the significance of propeller effects and elasticity in the aerodynamic analysis of small propeller-driven airplanes. Subsequently, the methodology section elaborates on the proposed procedure in detail, offering a comprehensive insight into the analytical approach. The results pertaining to a twin-engine propeller-driven aircraft are presented meticulously, serving as a case study to illustrate the application of the proposed methodology.

2. Materials and Methods

The methodology section delineates two key analyses: firstly, an examination of propeller effects in rigid aircraft, followed by the integration of elastic wing properties to explore alterations in aerodynamic characteristics. The analysis of propeller effects in rigid aircraft serves as the foundational step, providing insights into the aerodynamic behavior under normal operating conditions. Subsequently, the incorporation of elastic wing properties enriches our understanding by exploring how these variables influence aerodynamic performance. Validation of the studied aircraft is accomplished through a comparative analysis with wind tunnel test results obtained from a similar twin-engine propeller-driven aircraft with a rigid structure. Furthermore, the aerodynamic analysis of the elastic aircraft is conducted utilizing NASTRAN software, complemented by semi-empirical findings derived from the rigid aircraft analysis.

2.1. Rigid Aircraft Aerodynamic Analysis with Propeller Effects

The semi-empirical analysis program MAPLA, initially designed for optimizing small, general aviation aircraft, underwent enhancements for increased efficacy. Its original implementation encompasses five crucial disciplines: aerodynamics, propulsion, performance, weight and balance, as well as stability and control, amalgamating cutting-edge analytical procedures and design data collections into a fully automated method. For this investigation, the propulsion module specifically computes the propeller and power effects on longitudinal and lateral-directional aerodynamic coefficients and stability derivatives of rigid aircraft. Within each subprogram, power-on static stability and control derivatives were initially estimated across various aircraft components, including the wing, fuselage, nacelle, horizontal tail, vertical tail, and high-lift surfaces. The total power-on static stability and control derivatives were subsequently derived by amalgamating these individual contributions. Following this, the dynamic characteristics of the aircraft were estimated using static derivatives. The propulsion module's development was rooted in NASA's work, with enhancements tailored to generalize its application, particularly for small aircraft design and development purposes. In a series of previous investigations, this tool demonstrated its capability to model small aircraft characteristics with commendable precision [8,12,14,15,16,34].

The propeller effects on the lift forces could be divided into two groups such as those created from propeller forces and those created from the propeller slipstream. Hence the aircraft lift could be presented by [34,35]

where propeller forces components are from propeller thrust vector,

{(∆ C_{L})}_{T}

and propeller normal force,

{(∆ C_{L})}_{N_{p}}

. And propeller slipstream effects contain the lift due to the power-induced change in dynamic pressure,

{(∆ C_{L_{h}})}_{∆ {\bar{q}}_{h}}

and lift change because of the propeller downwash for wing,

{(∆ C_{L})}_{∆ {\bar{q}}_{w}} + {(∆ C_{L})}_{\in_{p}}

and horizontal tail,

{(∆ C_{L_{h}})}_{{(∆ \in_{h})}_{p o w e r}}

The same could be done to present the pitching moment coefficient of the aircraft in the presence of propeller effects [34,35]

Where similar to the lift equation, propeller forces components are from propeller thrust vector,

{(∆ C_{m})}_{T}

and propeller normal force,

{(∆ C_{m})}_{N_{p}}

. And propeller slipstream effects contain the contribution of the power-induced change in dynamic pressure,

{(∆ C_{m_{0}})}_{∆ {\bar{q}}_{w}}

and propeller slipstream-induced dynamic-pressure and angle of attack changes on the wing,

{{(∆ C_{m})}_{w_{L}} = (∆ C_{m})}_{∆ {\bar{q}}_{w}} + {(∆ C_{m})}_{\in_{p}}

, propeller slipstream on nacelle free moments,

{(∆ C_{m})}_{n_{p}}

, and propeller slipstream on dynamic-pressure and downwash on the horizontal tail,

{(∆ C_{m})}_{h}

The following components are necessary for the aircraft drag change due to the propeller effects. Firstly, the propeller thrust components parallel to the X-stability axis. Secondly, the change in slipstream stream dynamic pressure. Thirdly, the change in induced drag due to the lift component of the direct propeller forces. And finally, the change in cooling drag. These components are summarized as [34,35]

where

- n (T_{c}^{'} / prop) \cos α_{T}

is the component of total thrust parallel to the velocity vector,

∆ C_{D_{0}}

is the change in profile drag coefficient due to power,

∆ C_{D_{i}}

is the induced drag coefficient due to power and

{(∆ C_{D})}_{c o o l i n g d r a g}

is the change in the cooling system drag coefficient due to power.

The power effects on the side force derivative include the propeller normal force contribution,

{(∆ C_{Y_{β}})}_{N_{p}}

, propeller-induced increase in dynamic pressure,

{(∆ C_{Y_{β}})}_{n (∆ \bar{q})}

and power-induced sidewash,

{(∆ C_{Y_{β}})}_{n (σ_{p})}

[34,35]

The propeller and power effects on the weathercock stability also include the propeller normal force contribution,

{(∆ C_{n_{β}})}_{N_{p}}

, propeller-induced increase in dynamic pressure,

{(∆ C_{n_{β}})}_{n (∆ \bar{q})}

and power-induced sidewash,

{(∆ C_{n_{β}})}_{n (σ_{p})}

[34,36].

Finally, the propeller and power effects on the dihedral derivative include the propeller side force contribution,

{(∆ C_{l_{β}})}_{N_{p}}

and the propeller-induced increase in dynamic pressure and downwash,

{(∆ C_{l_{β}})}_{w (∆ \bar{q} + ϵ_{p})}

[36].

Change in dihedral derivative due to propeller effects and power on Propeller forces

2.1.1. Rigid Aircraft Analysis Validation

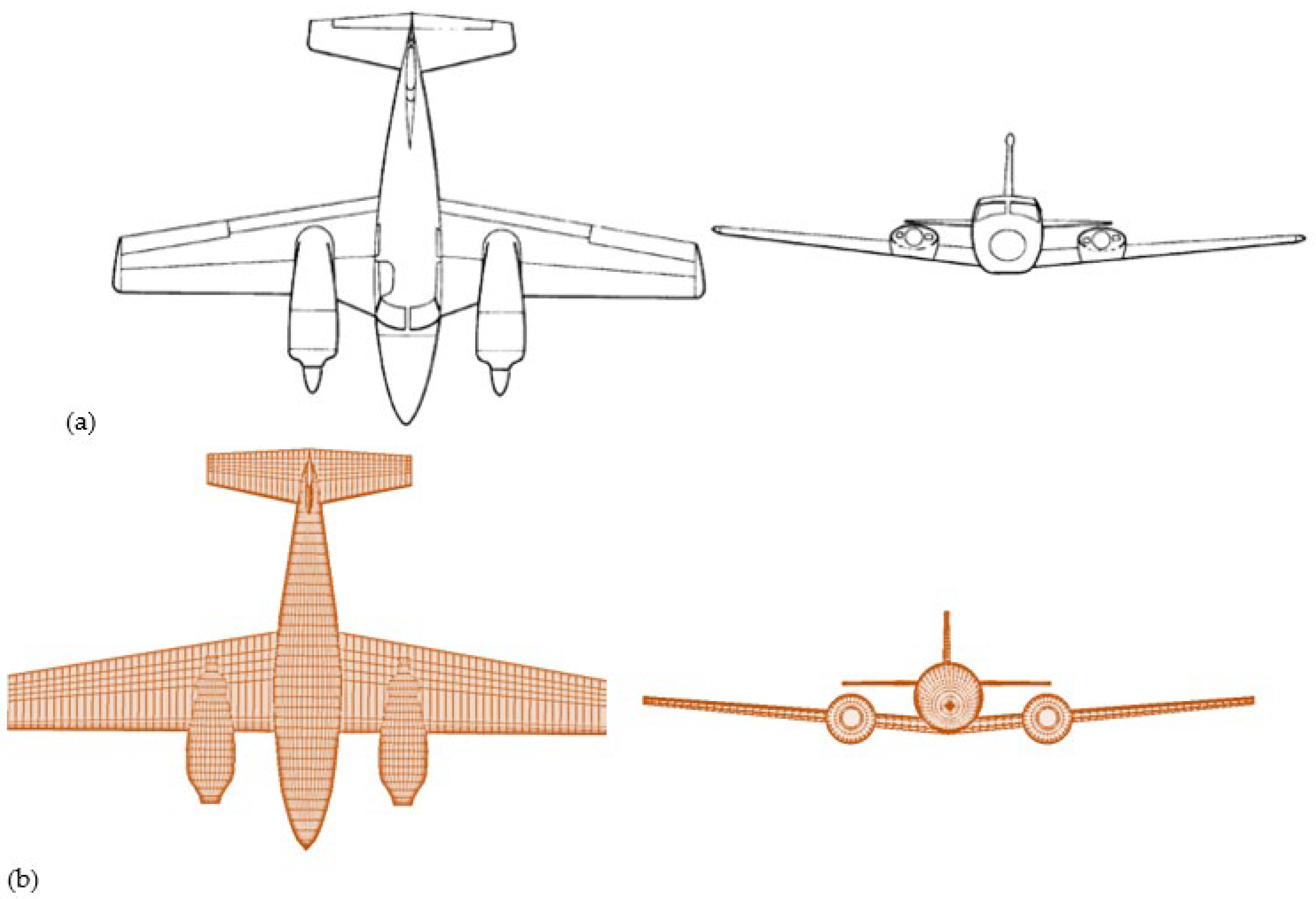
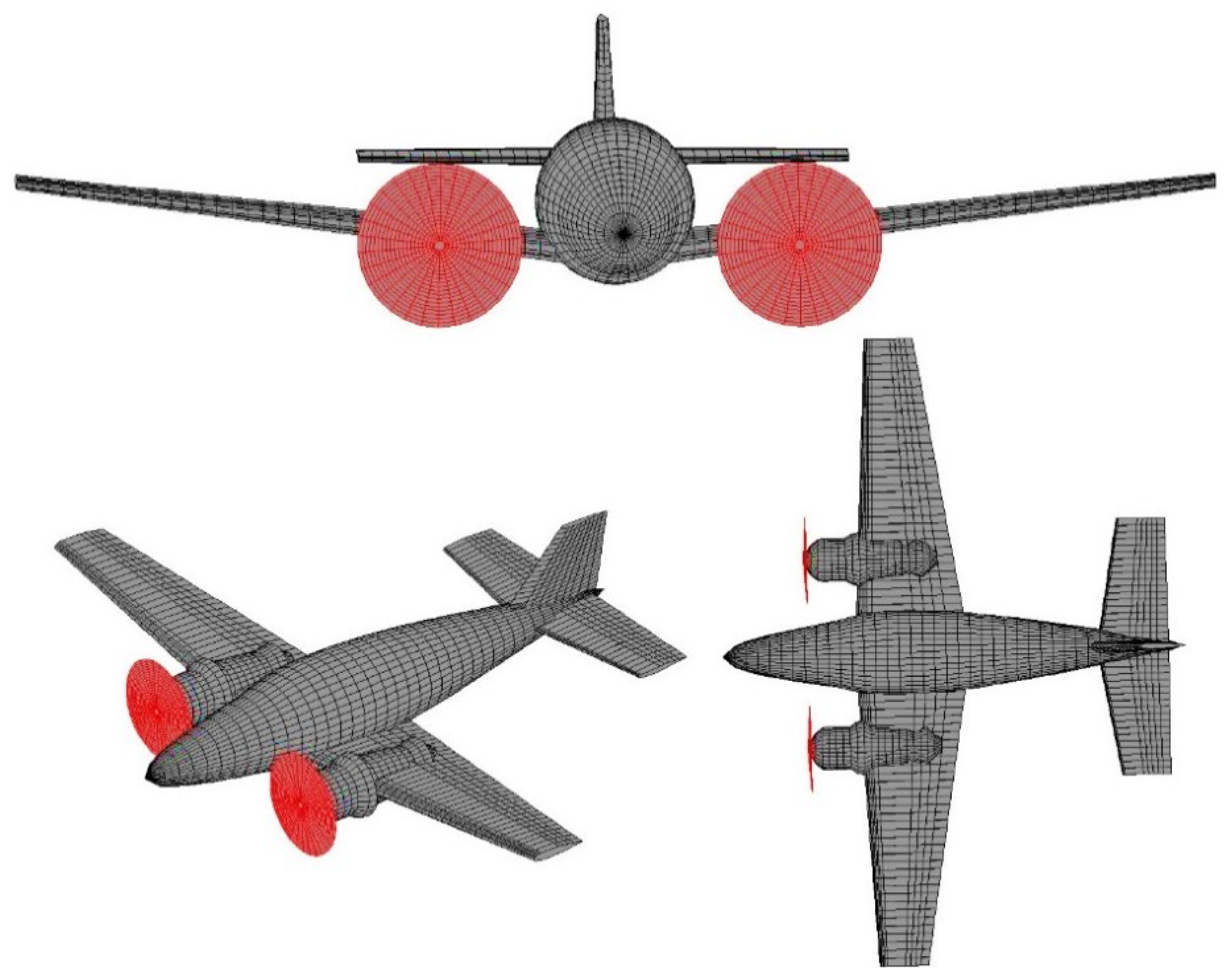
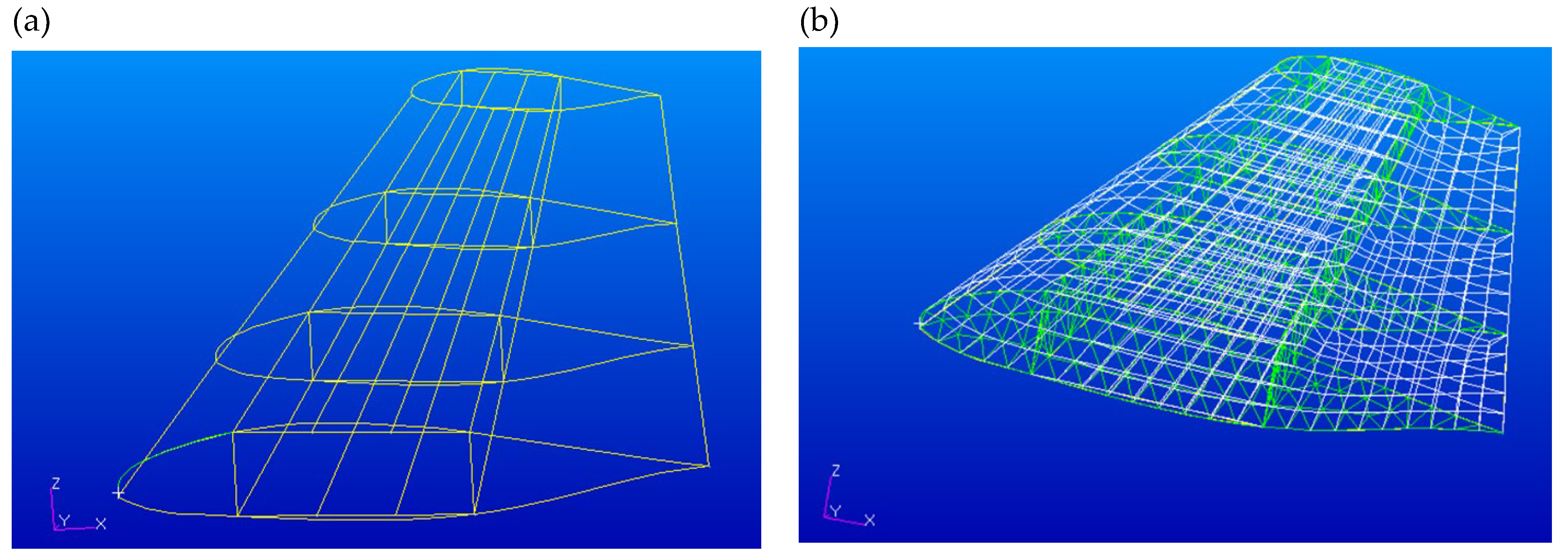
To validate the calculated results, the aerodynamics module outcomes were compared with wind tunnel test data of a twin-engine propeller-driven small aircraft [35,36]. Figure 1a and Figure 1b depict the geometry of the original aircraft model and the modelled aircraft using MAPLA, respectively. Additionally, Table 1 outlines the general characteristics of the small twin-engine propeller airplane and properties of the investigated flight condition.

Figure 1. The twin-engine propeller-driven small airplane under investigation is referenced from NASA’s report [35,36], denoted as a. for the reported aircraft and b. for the modeled aircraft utilizing MAPLA.

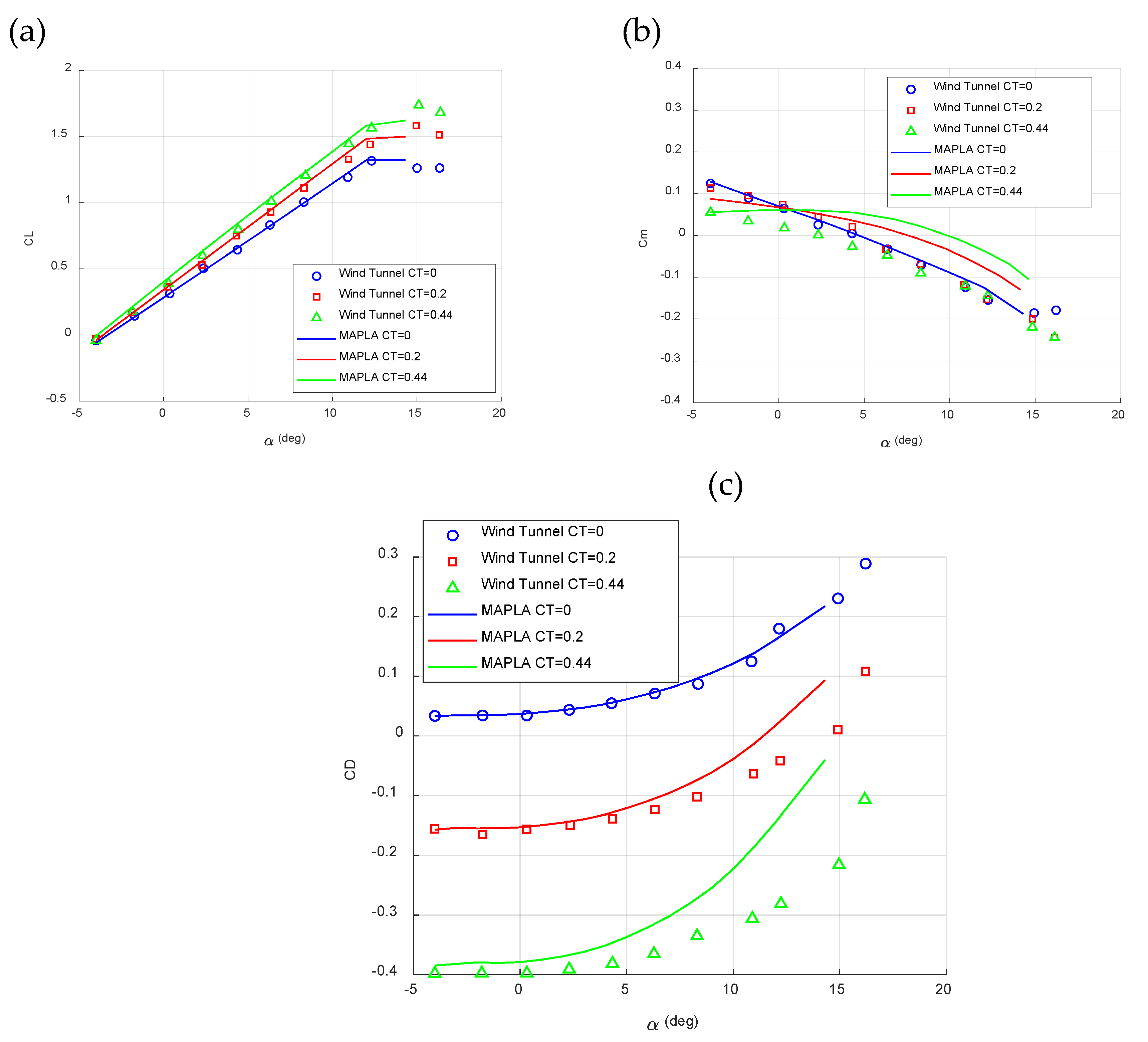
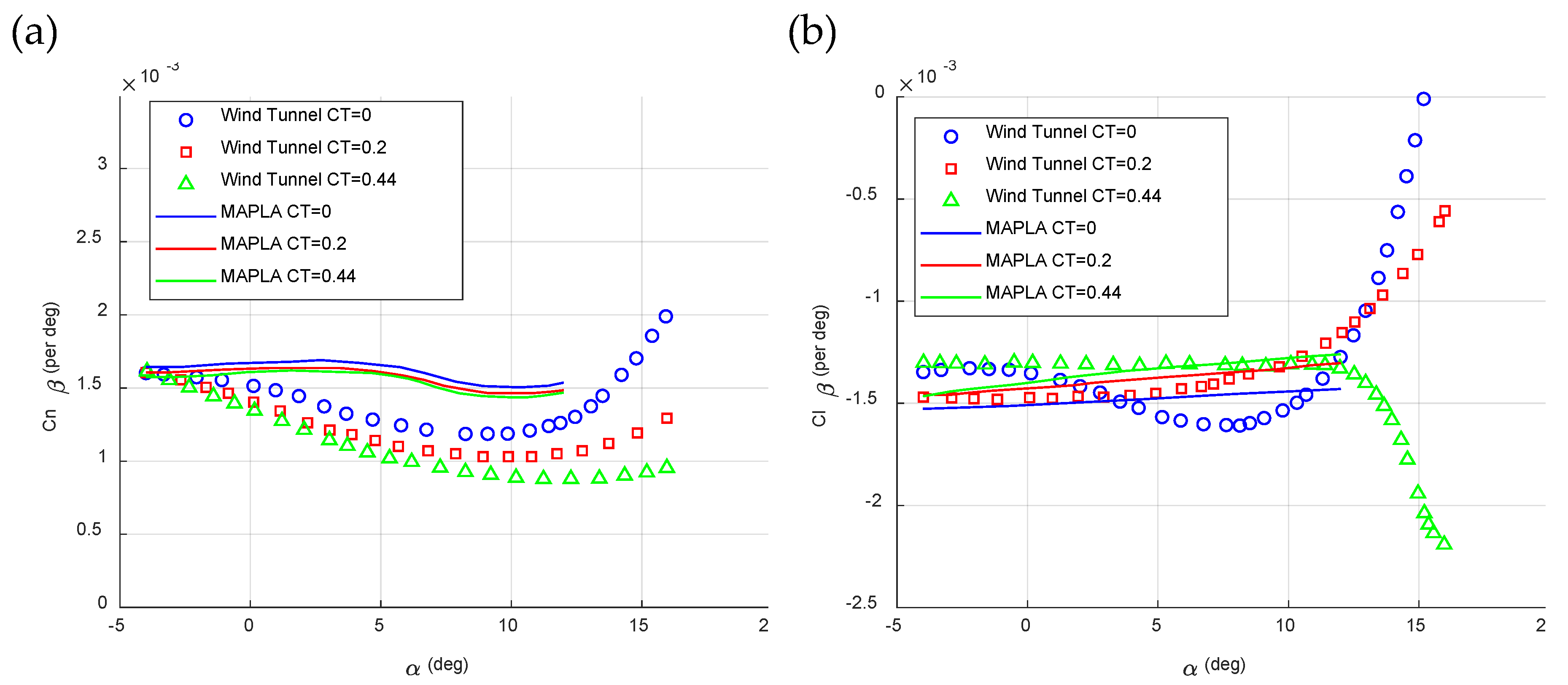
In the subsequent sections, Figure 2a to Figure 2c delineate the longitudinal aerodynamic characteristics of the investigated aircraft across various flight conditions. Additionally, Figure 3a and Figure 3b compare the lateral-directional aerodynamic characteristics of the twin-engine propeller-driven small aircraft using MAPLA with the corresponding data obtained from available wind tunnel tests [35,36]. All results are presented from the power-off conditions where the trust coefficient of the propellers, CT is equal to zero up to CT=0.2 and CT=0.44. The trust coefficient parameter that is counting for propeller effects could be defined using:

C T = \frac{T h r u s t}{{\bar{q}}_{\infty} S_{w}}

(7)

Where

{\bar{q}}_{\infty}

is the dynamic pressure ratio in newton per square meter and

S_{w}

is the surface area of the wing in suare meter.

The deviation results of MAPLA from wind tunnel test results are presented in Table 2. With respect to the deviation results presented in Table 1, MAPLA’s results present an accuracy of 5% for lift coefficient values from power-off conditions to the case of CT=0.2 and even higher CT values of 0.44. The same could be seen for the power off conditions for drag coefficient results. However, as power increases the results’ deviation also increases up to 15% for CT=0.2 and 35% for CT=0.44. For the case of pitching moment coefficient results, MAPLA presented higher deviation from the wind tunnel test results starting from 10% for the power-off condition and increasing up to 20% and 50% for CT=0.2 and CT=0.44, respectively. On the other side, for lateral-directional characteristics, MAPLA reported higher deviation from wind tunnel test results where for the weather-cock stability analysis, the reported value for power-off conditions showed a deviation of 35% and this value increased for the higher power conditions up to 40% for CT=0.2 and up to 45% for CT=0.44.This is while, the dihedral effect characteristic showed a better accuracy by 25% deviation from wind-tunnel test results in CT=0, 15% in CT=0.2 and 10% in CT=0.44. Overall, MAPLA showed a better accuracy for longitudinal aerodynamic characteristics compared to the lateral-directional characteristics. The results indicated that MAPLA’s aerodynamics module is able to determine the aerodynamic characteristics of the small aircraft to acceptable accuracy for low fidelity analysis where conceptual and preliminary studies are of interest. However, compared to the other methods such as DATCOM [34], MAPLA’s results are closer to the wind tunnel test data in almost all studied conditions for linear angles of attacks.

2.2. Elastic Wing Integration

In this study, the aeroelastic analysis are based on the NASTRAN approach for static aeroelastic problems and deals with the interaction of aerodynamic and structural forces on a flexible vehicle that results in a redistribution of the aerodynamic loading as a function of airspeed [25]. The static aeroelastic study here addresses the static aeroelastic problem in aircraft trim condition.

Three matrix equations summarize the relationships required to define a set of aerodynamic influence coefficients [25,37]. These are the basic relationships between the lifting pressure and the dimensionless vertical or normal velocity induced by the inclination of the surface to the airstream; i.e., the downwash (or normalwash),

\{w_{j}\} = [A_{j j}] {f_{j} / q}

(8)

the substantial differentiation matrix of the deflections to obtain downwash,

\{w_{j}\} = [D_{j k}^{1} + i k D_{j k}^{2}] \{u_{k}\} + \{w_{j}^{g}\}

(9)

and the integration of the pressure to obtain forces and moments,

\{P_{k}\} = [S_{k j}] {f_{j}}

(10)

where

w_{j}

denotes the downwash,

w_{j}^{g}

is the static aerodynamic downwash and includes the static incidence distribution that may arise from an initial angle of attack, camber, or twist.

f_{j}

is the pressure on lifting element j and q is the dynamic pressure.

k

is the reduced frequency and equal to

ω b_{s} / V

where

ω

is the angular frequency,

b_{s}

is the reference semichord and

V

is the free-streem velocity.

A_{j j}

is the aerodynamic influence coefficient matrix, a function of Mach number and reduced frequency.

u_{k}

and

P_{k}

are displacements and forces at aerodynamic grid points, respectively.

D_{j k}^{1}

and

D_{j k}^{2}

real and imaginary parts of substantial differentiation matrix, respectively. And

S_{k j}

is the integration matrix.

The three matrices presented as equations 8 through 10 can also be combined to give an aerodynamic influence coefficient matrix [25]:

[Q_{k k}] = [S_{k j}] {[A_{j j}]}^{- 1} [D_{j k}^{1} + i k D_{j k}^{2}]

(11)

Structural and aerodynamic grids are connected by interpolation. This allows the independent selection of grid points of the structure and aerodynamic elements of the lifting surfaces/bodies in a manner best suited to the particular theory. The interpolation method is called splining. The structural degrees of freedom are chosen as the independent degrees of freedom and the aerodynamic degrees of freedom are dependent. The splining methods lead to an interpolation matrix,

[G_{k g}]

hat relates the components of structural grid point deflections

{u_{g}}

to the deflections of the aerodynamic grid points

{u_{k}}

\{u_{k}\} = [G_{k g}] \{u_{g}\}

(12)

In the case of static aeroelasticity, the downwash relation presented as Equation 8 becomes:

\{w_{j}\} = [D_{j k}] \{u_{k}\} + [D_{j x}] \{u_{x}\} + \{w_{j}^{g}\}

(13)

where

\{w_{j}\}

is the vector of aerodynamic degrees of freedom, also called angle of attack,

\{u_{k}\}

is the vector of aerodynamic displacements or deformations,

\{u_{x}\}

is the vector of “extra aerodynamic points” used to describe control surface deflections and overall rigid body motions.

\{w_{j}^{g}\}

is an initial static aerodynamic downwash that includes the static incidence distribution that may arise from an initial angle of attack, camber, or washout (twist).

[D_{j k}]

denotes the substantial derivative matrix for the aerodynamic displacements. This is basically the

D_{j k}^{1}

term in Equation 11 where the

D_{j k}^{2}

term is not used for the extra aerodynamic points [25].

The theoretical aerodynamic pressures could be derived from:

\{f_{j}\} = \bar{q} {[A_{j j}]}^{- 1} {w_{j}}

(14)

where

\{f_{j}\}

is the vector of pressure on lifting elements. And finally the aerodynamic forces could be presented by

\{P_{k}\} = \bar{q} [W_{k k}] [S_{k j}] {[A_{j j}]}^{- 1} \{w_{j}\} + q [S_{k j}] \{\frac{f_{j}^{e}}{\bar{q}}\}

(15)

where

[W_{k k}]

is a matrix of empirical correction factors to adjust each theoretical aerodynamic box lift and moment to agree with experimental data for incidence changes [25,38].

\{\frac{f_{j}^{e}}{\bar{q}}\}

is the vector of experimental pressure coefficients at some reference incidence (e.g., zero angle of attack) for each aerodynamic element.

3. Results

In this section, the results of the rigid airplane will be initially presented, followed by the elastic wing analysis. These analyses will then be integrated to provide comprehensive aerodynamic characteristics of the full aircraft.

3.1. Rigid Aircraft Aerodynamic Analysis

The aerodynamic characteristics of the twin-engine small aircraft, utilizing the geometry outlined in Figure 4 (generated by MAPLA’s geometry module) and detailed in Table 3, have been examined across various flight conditions. This comprehensive analysis aims to better understand the behavior of the investigated airplane, particularly in relation to propeller effects.

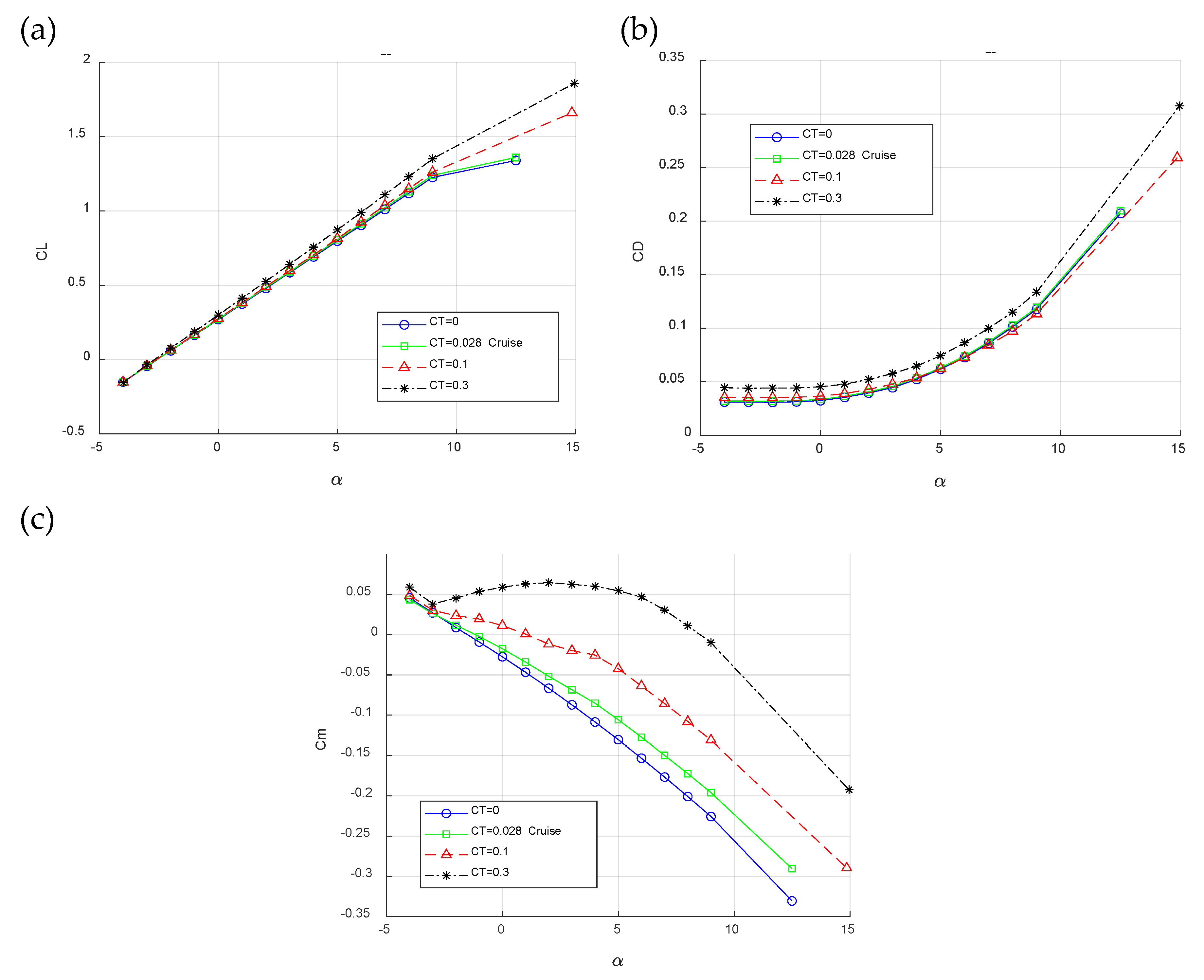
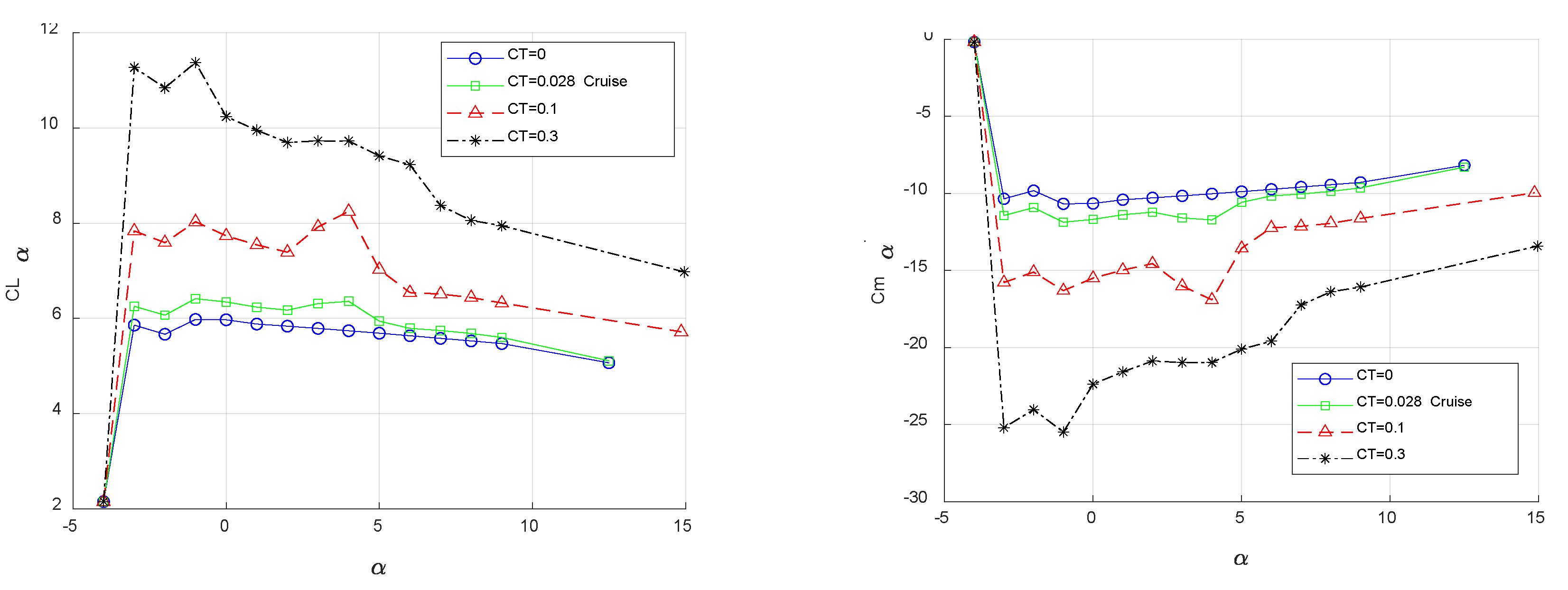
The longitudinal aerodynamic characteristics of the twin-engine propeller-driven aircraft, utilizing the geometry outlined in Table 3, are analyzed in Figure 5 across various flight conditions, including power-off, cruise, and different thrust coefficients such as medium (0.1) and higher (0.3) values typical of take-off conditions. The results highlight significant changes attributed to propeller effects in all longitudinal aerodynamic characteristics compared to the power-off condition. Notably, while lift and drag characteristics exhibit relatively minor alterations with increased values, the pitching moment coefficient demonstrates substantial variations due to heightened propeller effects, as indicated by the thrust coefficient.

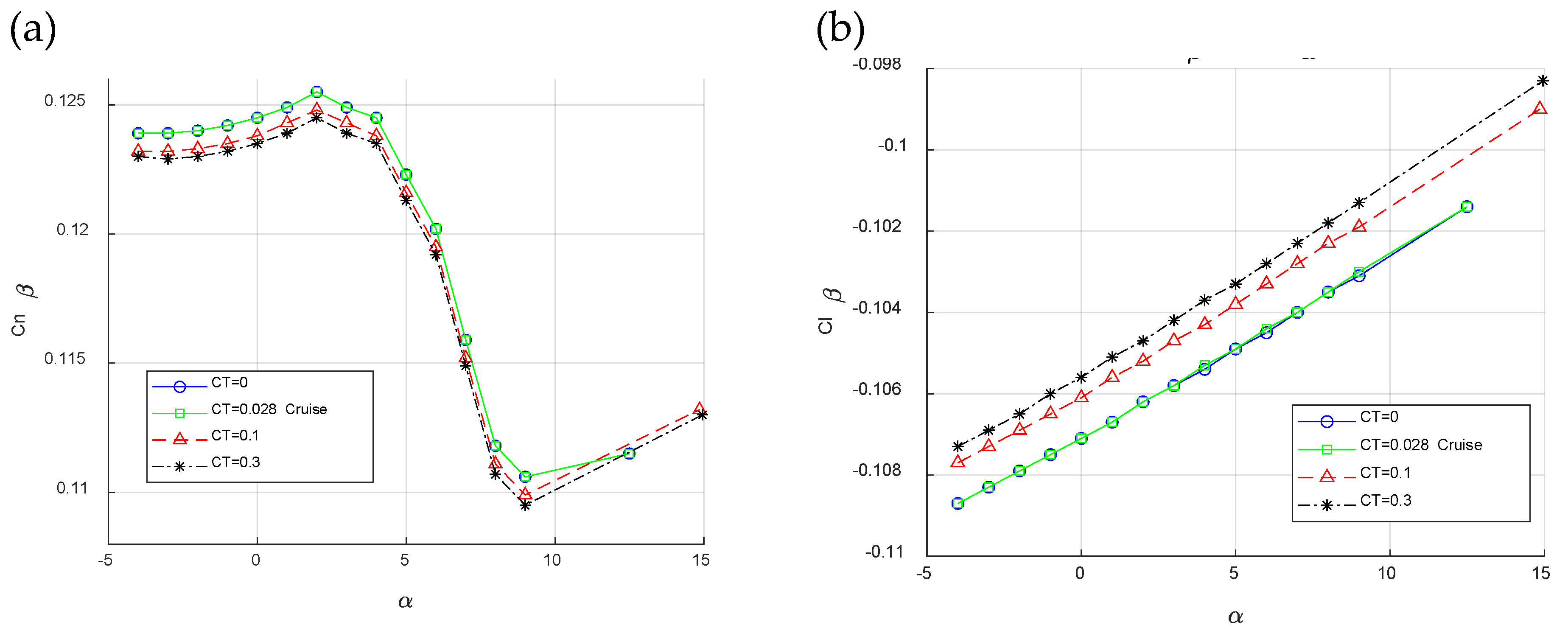
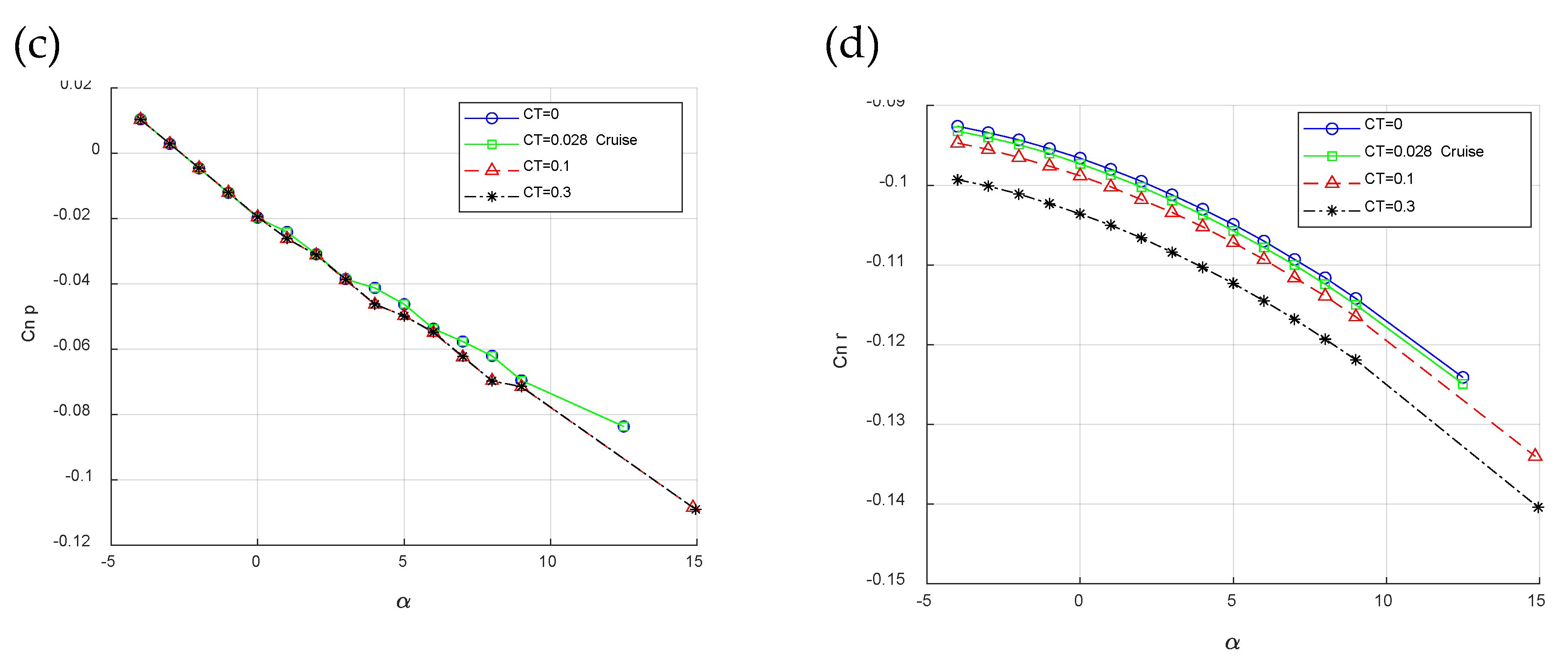
Figure 6 illustrates the lateral-directional static results of the twin-engine propeller-driven small aircraft in different flight conditions. It is evident that, similar to the longitudinal characteristics, propeller effects intensify the values across all angles of attack.

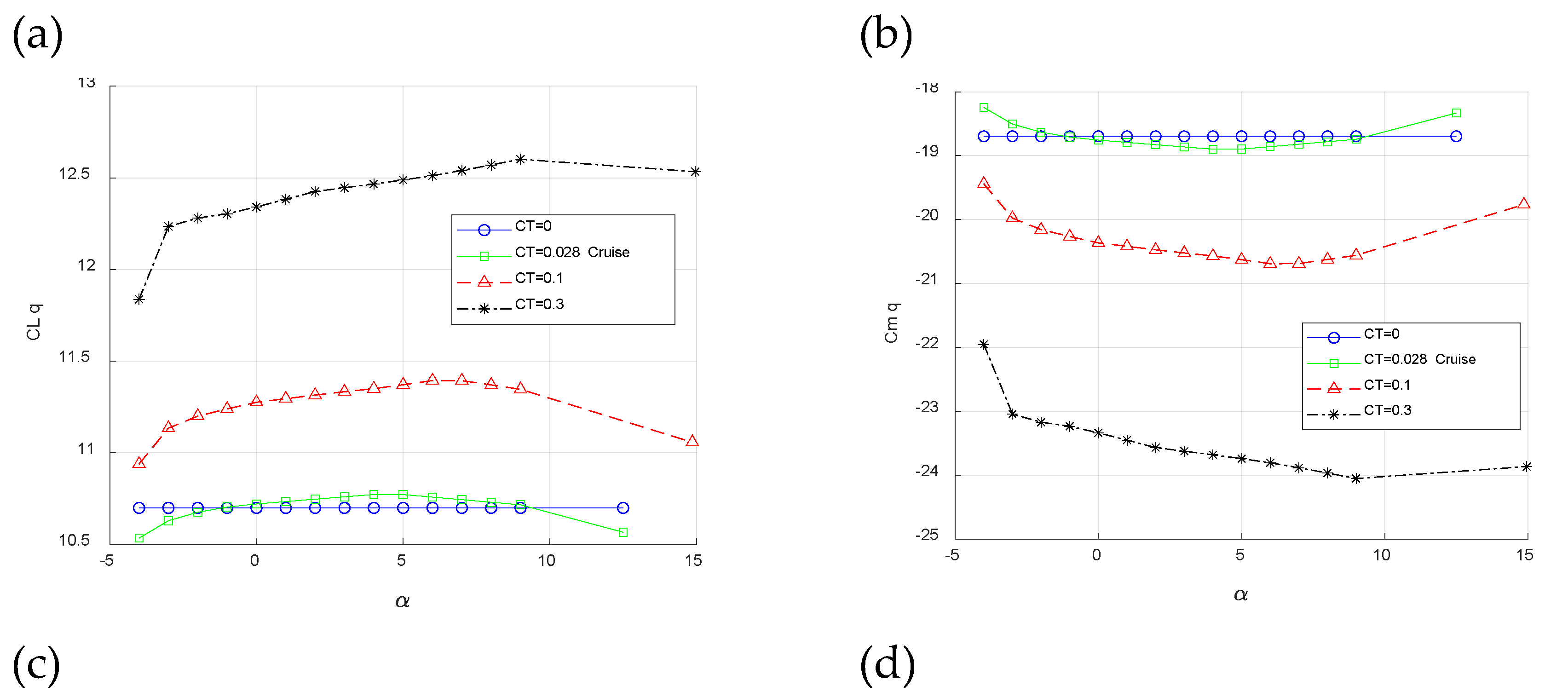
Figure 7 shows the longitudinal dynamic characteristics results of the twin-engine propeller-driven small aircraft. It is notable that, similar to the trends observed in the static characteristics, the influence of propeller effects amplifies the values across all angles of attack for the longitudinal dynamic characteristics. This indicates a consistent pattern where the propulsion system significantly impacts the aircraft's dynamic behavior, underscoring the importance of considering propeller effects in aerodynamic analyses for accurate performance predictions.

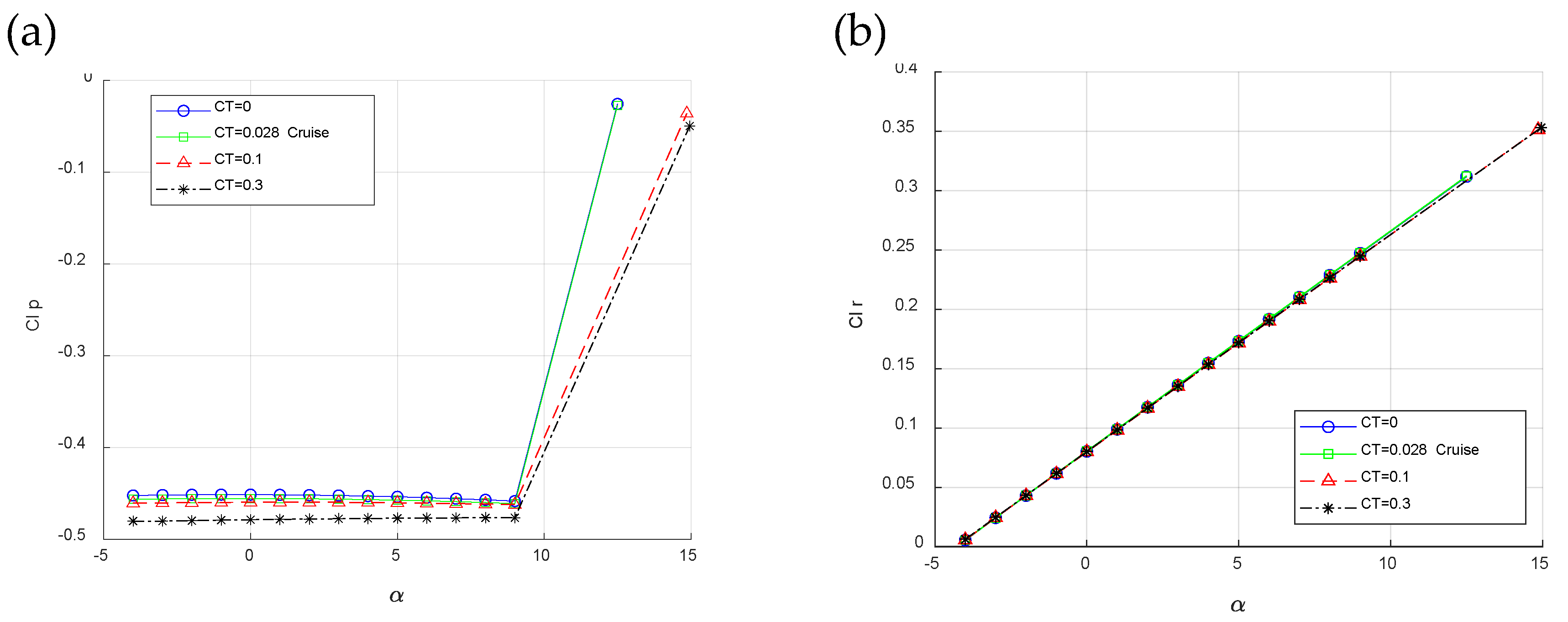
Finally, Figure 8 shows the lateral-directional dynamic characteristics of the of the twin-engine propeller-driven small aircraft. Remarkably, akin to the observations made in the static characteristics, the influence of propeller effects is discernible, intensifying the values across all angles of attack. However, it is noteworthy that the results for Cl_p and Cn_r were more significantly impacted by the propeller effects compared to those of Cl_r and Cn_p. This consistency highlights the significant impact of propeller dynamics on the aircraft's lateral-directional behavior, underscoring the need to account for such effects for comprehensive aerodynamic analysis and design optimization.

3.2. Aircraft Aerodynamic Analysis with Elastic Wing Integration

As previously mentioned, the aeroelastic analysis presented here adopts the NASTRAN approach, primarily focusing on static aeroelastic problems. This approach delves into the intricate interaction between aerodynamic and structural forces acting upon a flexible vehicle, leading to the redistribution of aerodynamic loading relative to airspeed. Specifically, the static aeroelastic study addresses the static aeroelastic problem under aircraft trim conditions [25]. The wing modeling process was conducted using PATRAN, adhering to the methodology proposed by [39]. Figure 9 illustrates the resulting geometry of the wing considered for analysis in the subsequent steps.

In the subsequent phase, the Aero-Structure Coupling module of NASTRAN is employed to generate the coupled aerodynamic and structural models for aeroelastic analysis. The resultant Aero-Structural Coupling model is depicted in Figure 10. Following the creation of the Aero-Structural Coupling model, the Aeroelastic Analysis module is utilized, with the solution type set to Static Aeroelasticity. Specifically, the Flexible Trim method from NASTRAN is employed for this analysis.

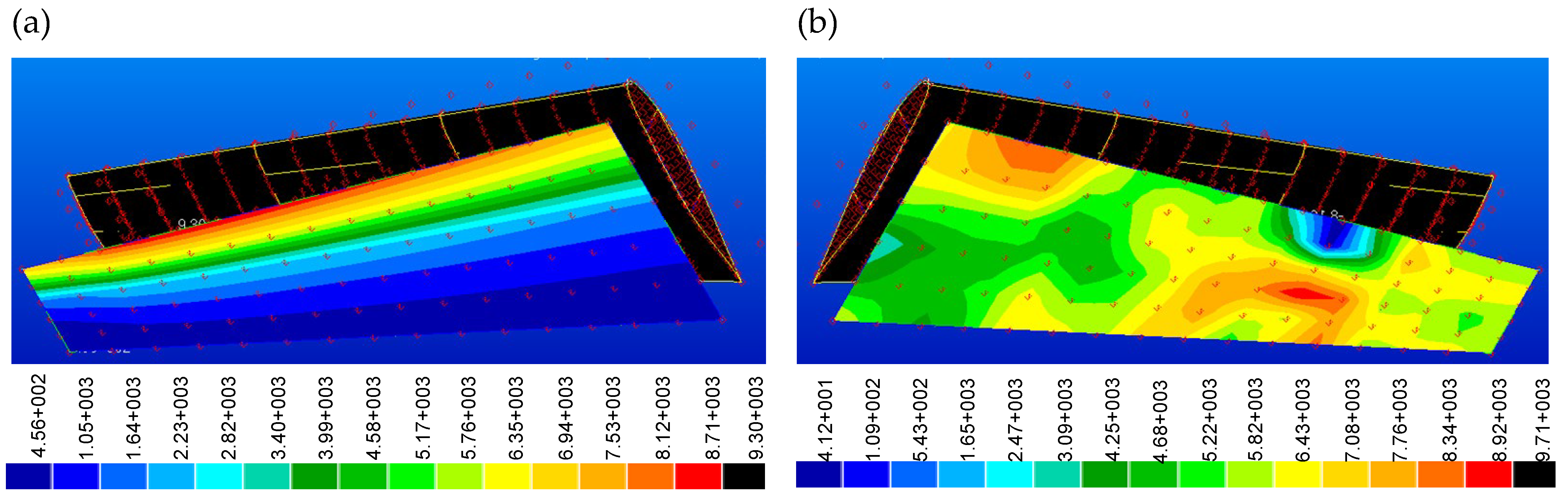
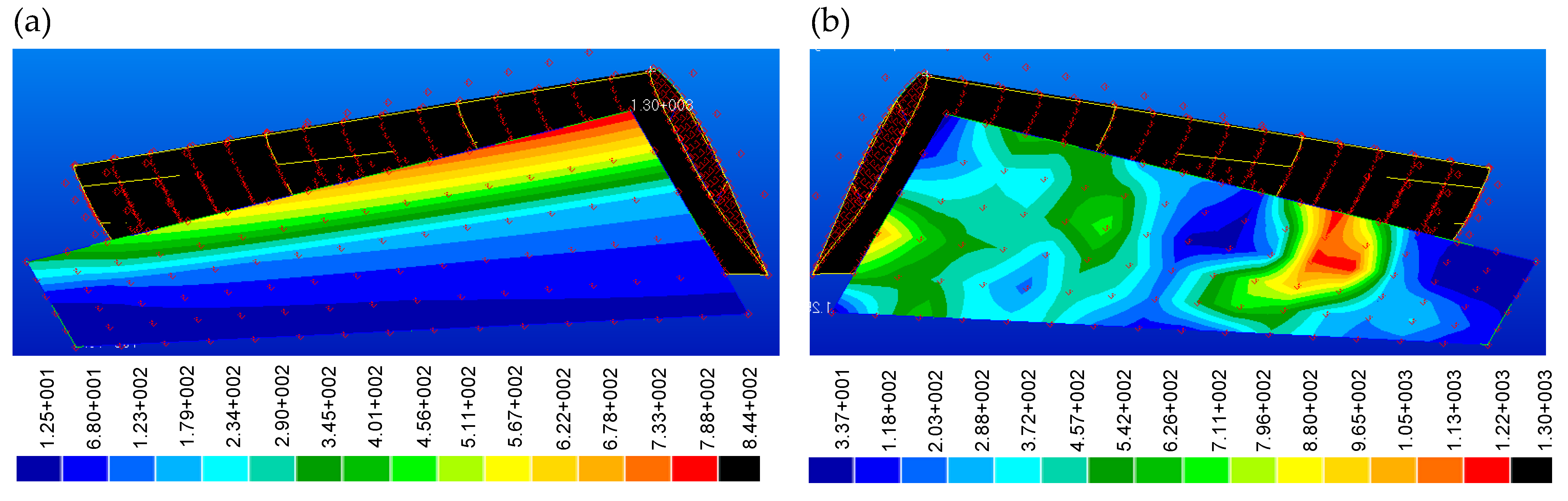
Figure 11a presents the pressure distribution across the wing surface in Newton per square meter, emphasizing aerodynamic behavior while assuming rigid components within the wing model considering cruise flight condition at a speed of 90 m/s. Notably, a linear distribution of pressure along the wingspan is evident, accompanied by chordwise nonlinear behavior. Higher pressure values are observed on the front side, contrasting with lower values on the aft side of the wing model. This depiction provides valuable insights into the interaction between aerodynamic forces and the wing structure under conditions of rigidity. In contrast, Figure 11b explores the same analysis while accounting for the presence of elastic components within the wing model. As illustrated, the pressure distribution is influenced by the behavior of elasticity. This representation offers a nuanced understanding of how aerodynamic forces are impacted by the incorporation of elasticity into the wing structure. By comparing these two scenarios, we gain valuable insights into the effects of structural flexibility on aerodynamic behavior and its consequential implications for overall aircraft performance. The resulting aerodynamic characteristics for both rigid and elastic configurations of the total aircraft are consolidated in Table 1, covering the linear range of angle of attack.

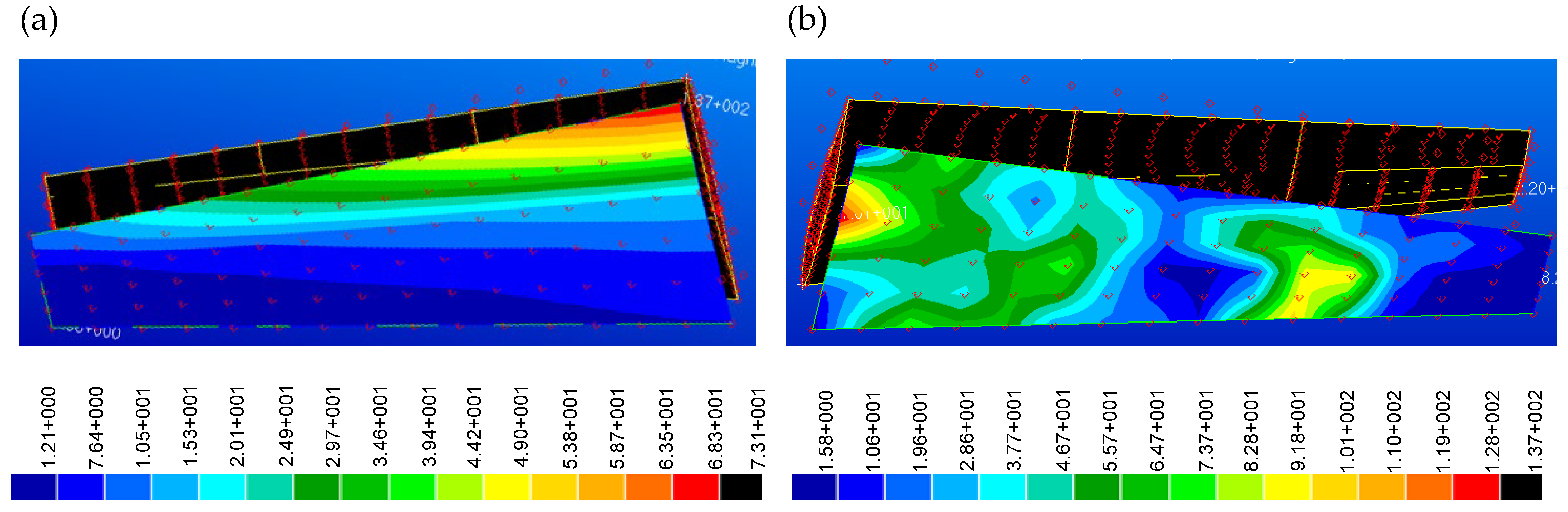
Figure 12a illustrates the moment distribution across the wing surface in Newton per meter, assuming rigid components within the wing model considering cruise flight condition at a speed of 90 m/s. Notably, it reveals a linear distribution of moment along the wingspan, accompanied by chordwise nonlinear behavior. Higher moment values are concentrated on the front side, contrasting with lower values on the aft side of the wing model. This depiction provides valuable insights into the interaction between moment changes and the wing structure under conditions of rigidity. In contrast, Figure 12b delves into the same analysis, this time considering the moment distribution of elastic components within the wing model. As depicted, the moment distribution is notably influenced by the behavior of elasticity. By comparing these two scenarios, we gain valuable insights into the effects of structural flexibility on moment behavior and its consequential implications for overall aircraft performance.

Finally, Figure 13a illustrates the force distribution across the wing surface in Newton, emphasizing aerodynamic behavior under the assumption of rigid components within the wing model at a speed of 90 m/s. As with the previous characteristics, a linear distribution of force along the wingspan is evident, accompanied by chordwise nonlinear behavior. Higher force values are concentrated on the front side, while lower values are observed on the aft side of the wing model. This representation offers valuable insights into the interaction between aerodynamic forces and the wing structure under conditions of rigidity. In contrast, Figure 13b delves into the same analysis, this time considering the force distribution of elastic components within the wing model. As depicted, the force distribution is notably influenced by the behavior of elasticity. This representation offers a nuanced understanding of how aerodynamic forces are impacted by the incorporation of elasticity into the wing structure. By comparing these two scenarios, we gain valuable insights into the effects of structural flexibility on force behavior throughout the wing model surface and its consequential implications for overall aircraft performance. The resulting aerodynamic characteristics for both rigid and elastic configurations of the total aircraft are consolidated in Table 1, encompassing the linear range of angle of attack.

In the subsequent step, leveraging MAPLA’s modular capability, the aerodynamic analysis for the wing component was updated using the attained aerodynamic results from NASTRAN. Subsequently, the remaining analysis was conducted by running MAPLA based on the new results for the wing, while considering propeller effects and power contributions. The summary of the results for both rigid and elastic aircraft configurations in different power settings is presented in Table 4, focusing on the linear angles of attack. Furthermore, the presentation of the average deviation from the rigid aircraft configuration offers a more comprehensive understanding, enabling a clearer distinction of the contribution and significance of aeroelasticity in the analysis. Regarding these deviations, it is evident that the aircraft would be notably influenced by elasticity, particularly for longitudinal characteristics, with an increase of nearly 20%. Conversely, for lateral-directional characteristics, this effect appears to be relatively lower, with an estimated impact of approximately 4%. The results achieved in this study are also consistent with the other studies involved with the aeroelasticity aircraft analysis [40].

5. Conclusions

In conclusion, this paper explored the critical influence of propeller effects, power contribution, and elasticity on small propeller-driven aircraft aerodynamics. Through meticulous analysis, a twin-engine propeller-driven aircraft was examined, shedding light on their combined impact. Validation through comparative analysis and NASTRAN software utilization reinforced our findings. Leveraging MAPLA’s capability, the aerodynamic analysis was updated for the wing component, considering propeller effects and power contributions. Results underscore the significance of these factors at various angles of attack. Additionally, deviations from the rigid aircraft configuration highlighted a substantial impact of aeroelasticity, particularly in longitudinal characteristics, with approximately 20% increase, and a lower impact of less than 5% in lateral-directional characteristics. This study advances small propeller-driven aircraft design considerations, offering insights for future research in UAM. By deepening the understanding of aerodynamic complexities, future works can contribute to more efficient and optimized aircraft designs in the evolving aviation landscape.

Author Contributions

Conceptualization, M.R.; Methodology, M.R.; Software, M.R.; Formal analysis, M.R...; Writing—original draft, M.R; Preparation, M.R.; Data curation, M.R.; Writing—review and editing, M.R. All authors have read and agreed to the published version of the manuscript.

Funding

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

L.A. Garrow, B. German, N.T. Schwab, M.D. Patterson, N. Mendonca, Y.O. Gawdiak, J.R. Murphy, A Proposed Taxonomy for Advanced Air Mobility, (2022) 1–25. [CrossRef]
S. Du, Y. Zha, Q. Zhao, Research on Aerodynamic Test Validation and the Vector Force Control Method for an E-STOL Fan Wing Unmanned Aerial Vehicle, Aerospace. 11 (2024). [CrossRef]
J. Wen, Y. Song, H. Wang, D. Han, C. Yang, Training Sample Pattern Optimization Based on a Swarm Intelligence Algorithm for Tiltrotor Flight Dynamics Model Approximation, Aerospace. 10 (2023). [CrossRef]
NASA website, Advanced Air Mobility Mission Overview, Available: https://www.nasa.gov/aam [Accessed February 2024].
Transport Canada, Advanced Air Mobility, Available: https://tc.canada.ca/en/aviation/advanced-air-mobility [Accessed February 2024].
FAA website, Section 6. Advanced Air Mobility, Available: https://www.faa.gov/air_traffic/publications/atpubs/aim_html/chap11_section_6.html [Accessed February 2024].
L. Kiesewetter, K.H. Shakib, P. Singh, M. Rahman, B. Khandelwal, S. Kumar, K. Shah, A holistic review of the current state of research on aircraft design concepts and consideration for advanced air mobility applications, Prog. Aerosp. Sci. 142 (2023) 100949. [CrossRef]
M. Rostami, J. Chung, D. Neufeld, Vertical tail sizing of propeller-driven aircraft considering the asymmetric blade effect, Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. (2021) 1–12. [CrossRef]
M. Benedict, T. Jarugumilli, I. Chopra, Effect of rotor geometry and blade kinematics on cycloidal rotor hover performance, J. Aircr. 50 (2013) 1340–1352. [CrossRef]
M. Rostami, S.A. Bagherzadeh, Development and validation of an enhanced semi-empirical method for estimation of aerodynamic characteristics of light, propeller-driven airplanes, Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 232 (2018) 638–648. [CrossRef]
J.A. Cole, M.D. Maughmer, M. Kinzel, G. Bramesfeld, Higher-order free-wake method for propeller-wing systems, J. Aircr. 56 (2019) 150–165. [CrossRef]
M. Rostami, J. Chung, H.U. Park, Design optimization of multi-objective proportional–integral–derivative controllers for enhanced handling quality of a twin-engine, propeller-driven airplane, Adv. Mech. Eng. 12 (2020). [CrossRef]
M.A. Clarke, R.M. Erhard, J.J. Alonso, Aerodynamic Optimization of Wing-Mounted Propeller Configurations for Distributed Electric Propulsion Architectures, AIAA Aviat. Aeronaut. Forum Expo. AIAA Aviat. Forum 2021. (2021) 1–19. [CrossRef]
M. Rostami, J. Chung, Multidisciplinary Analysis Program For Light Aircraft (Mapla), (2021). [CrossRef]
M. Rostami, J. Bardin, D. Neufeld, J. Chung, EVTOL Tilt-Wing Aircraft Design under Uncertainty Using a Multidisciplinary Possibilistic Approach, Aerospace. 10 (2023). [CrossRef]
M. Rostami, J. Bardin, D. Neufeld, J. Chung, A Multidisciplinary Possibilistic Approach to Size the Empennage of Multi-Engine Propeller-Driven Light Aircraft, Aerospace. 9 (2022). [CrossRef]
G.K.W. Kenway, J.R.R.A. Martins, Multipoint high-fidelity aerostructural optimization of a transport aircraft configuration, J. Aircr. 51 (2014) 144–160. [CrossRef]
G.R. Andersen, D.L. Cowan, D.J. Piatak, Aeroelastic modeling, analysis and testing of a morphing wing structure, Collect. Tech. Pap. - AIAA/ASME/ASCE/AHS/ASC Struct. Struct. Dyn. Mater. Conf. 1 (2007) 359–373. [CrossRef]
S. Tiomkin, D.E. Raveh, A review of membrane-wing aeroelasticity, Prog. Aerosp. Sci. 126 (2021) 100738. [CrossRef]
P. Geuzaine, G. Brown, C. Harris, C. Farhat, Aeroelastic dynamic analysis of a full F-16 configuration for various flight conditions, AIAA J. 41 (2003) 363–371. [CrossRef]
N. V. Taylor, C.B. Allen, A. Gaitonde, D.P. Jones, A structure-coupled CFD method for time-marching flutter analysis, Aeronaut. J. 108 (2004) 389–401. [CrossRef]
M.A. Woodgate, K.J. Badcock, A.M. Rampurawala, B.E. Richards, D. Nardini, M.J. DeC Henshaw, Aeroelastic calculations for the hawk aircraft using the euler equations, J. Aircr. 42 (2005) 1005–1012. [CrossRef]
NASA STRuctrual ANalysis (NASTRAN), Available: https://software.nasa.gov/software/LAR-16804-GS#:~:text=NASTRAN%20is%20a%20finite%20element,for%20insight%20into%20structural%20behavior [Accessed February 2024].
S. Kilimtzidis, V. Kostopoulos, Static Aeroelastic Optimization of High-Aspect-Ratio Composite Aircraft Wings via Surrogate Modeling, Aerospace. 10 (2023). [CrossRef]
MSC Nastran 2017 - Aeroelastic Analysis User’s Guide, (2017).
D. Solano, D. Sarojini, J. Corman, D. Mavris, Structural sizing of unconventional aircraft under static and dynamic aeroelastic loading, AIAA Scitech 2020 Forum. 1 PartF (2020). [CrossRef]
H. Guo, Y. Yan, H. Xia, L. Yu, B. Lv, The Prediction and Correction Method of Aircraft Static Aeroelastic Effects: A Review of Recent Progress, Actuators. 11 (2022). [CrossRef]
J.E. Guerrero, M. Sanguineti, K. Wittkowski, Variable cant angle winglets for improvement of aircraft flight performance, Springer Netherlands, 2020. [CrossRef]
N.T.B. Hoang, Computational investigation of variation in wing aerodynamic load under effect of aeroelastic deformations, J. Mech. Sci. Technol. 32 (2018) 4665–4673. [CrossRef]
W. Scholten, D. Hartl, Uncoupled method for static aeroelastic analysis, J. Fluids Struct. 101 (2021) 103221. [CrossRef]
S. Guo, Aeroelastic optimization of an aerobatic aircraft wing structure, Aerosp. Sci. Technol. 11 (2007) 396–404. [CrossRef]
M.R. Amoozgar, S.A. Fazelzadeh, H. Haddad Khodaparast, M.I. Friswell, J.E. Cooper, Aeroelastic stability analysis of aircraft wings with initial curvature, Aerosp. Sci. Technol. 107 (2020) 106241. [CrossRef]
A. Crovato, H.S. Almeida, G. Vio, G.H. Silva, A.P. Prado, C. Breviglieri, H. Guner, P.H. Cabral, R. Boman, V.E. Terrapon, G. Dimitriadis, Effect of levels of fidelity on steady aerodynamic and static aeroelastic computations, Aerospace. 7 (2020) 1–22. [CrossRef]
M. Rostami, S.A. Bagherzadeh, Development and validation of an enhanced semi-empirical method for estimation of aerodynamic characteristics of light, propeller-driven airplanes, Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 232 (2018) 638–648. [CrossRef]
H. Wolowicz., R. B. Yancey, “Longitudinal Aerodynamic Characteristics of Light, Twin-Engine Propeller-Driven Airplanes,” Nasa Technical Note, (1972).
H. Wolowicz., R. B. Yancey, “Lateral Directional Aerodynamic Characteristics of Light, Twin-Engine Propeller-Driven Airplanes,” Nasa Technical Note, pp. 17-56, (1972).
W. P. Rodden, and J. D. Revell, Errata:” The Status of Unsteady Aerodynamic Influence Coefficients”. AIAA Journal, 1(3), 724-725, (1963).
J.P. Giesing, T.P. Kalman, W.P. Rodden, Correction Factor Techniques for Improving Aerodynamic Prediction Methods, NASA Rep. (1976).
J. Morlier, “Wing Creation using PCL/PATRAN”, DMSM/ISAE, SUPAERO, (2011), Available: https://docplayer.net/12545262-Wing-creation-using-pcl-patran.html.
W. P. Rodden, C. T. Wilson, D. N. Herting, E. D. Bellinger, and R. H. MacNeal, “Static Aeroelastic Addition to MSC/NASTRAN”, The MacNeal-Schwendler Corporation, Los Angeles, California.

Figure 2. Comparison of longitudinal aerodynamic characteristics between the twin-engine small airplane using MAPLA and wind tunnel test results [35,36], considering: a. Lift coefficient, b. Drag coefficient, and c. Pitching moment coefficient across various flight conditions, with an empty weight at CG=10%.

Figure 3. Comparison of lateral-directional aerodynamic characteristics between the investigated twin-engine small airplane using MAPLA and wind tunnel test results [35,36], focusing on: a. Weathercock stability, and b. Effective dihedral coefficient across various flight conditions, with an empty weight at CG=10%.

Figure 4. The investigated twin-engine propeller-driven small airplane

Figure 5. Results of investigated twin-engine propeller-driven small aircraft model in various flight conditions where CT=0, CT=0.028, CT=0.1 and CT=0.3 versus angle of attack for: a. Lift coefficient. b. Drag coefficient results. c. Pitching moment coefficient.

Figure 6. Results of investigated twin-engine propeller-driven small aircraft model in 1/rad in various flight conditions where CT=0, CT=0.028, CT=0.1 and CT=0.3 versus angle of attack for: a. Side-force derivatives. b. Effective dihedral coefficient. c. Weathercock stability coefficient.

Figure 7. Results of investigated twin-engine propeller-driven small aircraft model in 1/rad various flight conditions where CT=0, CT=0.028, CT=0.1 and CT=0.3 versus angle of attack for: a. Lift coefficient due to pitch rate. b. Lift coefficient due to vertical acceleration. c. Pitching moment coefficient due to pitch rate. d. Pitching moment coefficient due to vertical acceleration.

Figure 8. Results of investigated twin-engine propeller-driven small aircraft model in 1/rad in various flight conditions where CT=0, CT=0.028, CT=0.1 and CT=0.3 versus angle of attack for: a. Lift coefficient due to pitch rate. b. Lift coefficient due to vertical acceleration. c. Pitching moment coefficient due to pitch rate. d. Pitching moment coefficient due to vertical acceleration.

Figure 9. a. Schematic of the modelled wing in Patran considering four airfoil sections and the connection boxes b. Schematic of the mesh model in Patran.

Figure 10. The coupled aerodynamic model and structural model (Aero-Structural Coupling model) for aeroelastic analysis in Nastran

Figure 11. The pressure distribution on the wing in Newton per square meter (a). considering rigid components on the model; (b) considering elastic components on the model.

Figure 12. The moment distribution on the wing in Newton-meters (a). considering rigid components on the model; (b) considering elastic components on the model.

Figure 13. The force distribution on the wing in Newton (a). considering rigid components on the model; (b) considering elastic components on the model.

Table 1. The general characteristics of the aircraft employed in the validation process for MAPLA [35,36]

Parameter	Description	Value
$b_{w}$	Wingspan, m	10.97
MAC	Mean aerodynamic chord, m	1.51
$S_{w}$	Wing Surface Area, m2	16
AR	Aspect Ratio	7.52
M	Mach number	0.25
$W_{T O_{m a x}}$	Max take-off weight, Kg	980
CG	Center of mass, %	10
h	Altitude, m	0

Table 2. Deviation of the aerodynamic characteristics for the investigated twin-engine aircraft.

Aerodynamic characteristics	Deviation from wind tunnel tests (linear angles)
Aerodynamic characteristics	CT=0	CT=0.2	CT=0.44
$C L$	$5 %$	$5 %$	$5 %$
$C D$	$5 %$	$15 %$	$35 %$
$C m$	$10 %$	$20 %$	$50 %$
${C n}_{β}$	$35 %$	$40 %$	$45 %$
${C l}_{β}$	$25 %$	$15 %$	$10 %$

Table 3. Geometry parameters and the descriptions for the small twin-engine propeller-driven aircraft

Component	Parameter	Description	Value
Fuselage	$l_{f}$	Fuselage length, m	8.6
	$S_{f}$	Planform area of fuselage, sq m	8.0
	$w_{f}$	Maximum width of the fuselage, m	1.545
Horizontal Tail	$i_{h}$	Horizontal tail incidence angle, deg	1.92
	bh	Horizontal tail span, m	4.95
	$c_{r_{h}}$	Horizontal tail root chord, m	1.29
	$c_{t_{h}}$	Horizontal tail tip chord, m	0.82
	${Λ_{L E}}_{h}$	Leading edge sweep angle of horizontal tail, deg	12.2
	lh	Distance, parallel to X-body axis, from the nose of fuselage to the horizontal tail mean aerodynamic chord, m	8.32
Vertical Tail	bv	Vertical tail span, m	1.847
	$c_{r_{v}}$	Vertical tail root chord, m	1.955
	$c_{t_{v}}$	Vertical tail tip chord, m	0.874
	$ϕ_{T E}$	Trailing edge sweep angle of vertical tail, deg	17.15
	lv	Distance along X-body axis from the nose of fuselage to leading edge of tip chord of vertical tail, m	9.08
Wing	$i_{w}$	Wing incidence angle, deg	2.74
	$α_{t w i s t}$	Wing incidence angle	-3.15
	bw	Wing span, m	11.95
	$c_{r_{w}}$	Wing root chord, m	2.143
	$c_{t_{w}}$	Wing tip chord, m	0.9
	${Λ_{L E}}_{w}$	Wing leading edge sweep angle, deg	3.2
	${Λ_{T E}}_{w}$	Wing trailing edge sweep angle, deg	-9.5
	lw	Distance, parallel to X-body axis, from the nose of fuselage to the leading edge of wing mean aerodynamic chord, m	2.76
	$Γ$	Wing dihedral angle, deg	7.5
Engine and Propeller	$η_{p}$	Propeller efficiency, %	80
	$\overset{´}{β}$	Propeller blade angle at 0.75 Rp, deg	20
	$n_{b}$	Number of blades	3
	$b_{p_{0.3}}$	Width of propeller blade at 30%, m	0.144
	$b_{p_{0.6}}$	Width of propeller blade at 60%, m	0.16
	$b_{p_{0.9}}$	Width of propeller blade at 90%, m	0.118
	$R_{p}$	Propeller Radius, m	0.993
	$P_{m a x}$	Maximum power per engine, hp	300
	$n_{e}$	Number of engines	2
Weight and Balance	CG	Center of mass, %	20
Weight and Balance	$W_{T O_{m a x}}$	Max take-off weight, Kg	2500

Table 4. The rigid and elastic aircraft aerodynamic characteristics and the deviation from rigid aircraft for different flight conditions and power settings

Aerodynamic Characteristics	Rigid Airplane (MAPLA)				Elastic Airplane (MAPLA + NASTRAN)				Average Deviation
Aerodynamic Characteristics	CT=0	CT=0.028	CT=0.1	CT=0.3	CT=0	CT=0.028	CT=0.1	CT=0.3
$C D_{α}$ (rad^-1)	0.315	0.314	0.311	0.318	0.39	0.39	0.39	0.39	% 22.5
$C L_{α}$ (rad^-1)	6.05	6.11	6.19	6.57	6.98	7.04	7.13	7.58	% 15.3
$C l_{\dot{α}}$ (rad^-1)	5.49	5.81	7.00	9.23	6.44	6.81	8.21	10.83	% 17.3
$C l_{q}$ (rad^-1)	10.70	10.71	11.28	12.37	12.42	12.43	13.09	14.36	% 16.0
$C m_{α}$ (rad^-1)	-1.17	-1.01	-0.68	-0.10	-1.40	-1.21	-0.81	-0.12	% 19.7
$C m_{\dot{α}}$ (rad^-1)	-9.32	-10.20	-13.47	-19.61	-11.4	-12.43	-16.41	-23.89	% 21.8
$C m_{q}$ (rad^-1)	-18.70	-18.74	-20.37	-23.42	-22.2	-22.25	-24.19	-27.81	% 18.8
$C n_{β}$ (rad^-1)	0.12	0.12	0.12	0.12	0.13	0.13	0.13	0.13	% 4.2
$C l_{β}$ (rad^-1)	-0.11	-0.11	-0.11	-0.10	-0.13	-0.13	-0.13	-0.13	% 20.6
$C l_{p}$ (rad^-1)	-0.45	-0.46	-0.46	-0.48	-0.59	-0.60	-0.60	-0.62	% 30.4

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Propeller Effects and Elasticity in Aerodynamic Analysis of Small Propeller-Driven Aircraft

Abstract

1. Introduction

2. Materials and Methods

2.1. Rigid Aircraft Aerodynamic Analysis with Propeller Effects

2.1.1. Rigid Aircraft Analysis Validation

2.2. Elastic Wing Integration

3. Results

3.1. Rigid Aircraft Aerodynamic Analysis

3.2. Aircraft Aerodynamic Analysis with Elastic Wing Integration

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe